| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
В хорошем соответствии с результатами измерений уравнение Ван-дер-Ваальса показывает сближение точек 2 и 5 по мере повышения температуры, что позволяет получить из этого уравнения
параметры критического состояния  ), при котором удельные объемы (плотности) кипящей жидкости и насыщенного пара совпадают. Действительно, уравнение Ван-дер-Ваальса йвляется относительно объема алгебраическим уравнением третьей степени, йоэтому при фиксированном давлении и температуре имеет три корня:
), при котором удельные объемы (плотности) кипящей жидкости и насыщенного пара совпадают. Действительно, уравнение Ван-дер-Ваальса йвляется относительно объема алгебраическим уравнением третьей степени, йоэтому при фиксированном давлении и температуре имеет три корня:

или

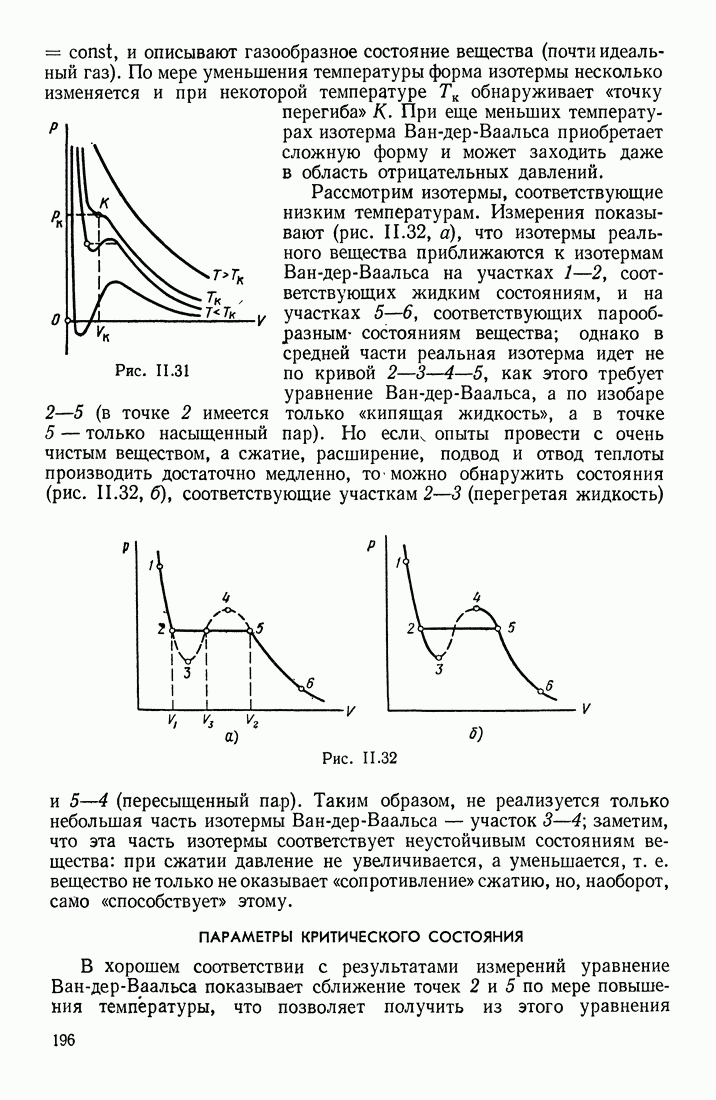
При температурах выше критических это уравнение имеет один действительный и два мнимых корня, т. е. каждому значению давления и температуры соотвеютвует только одно действительное значение объема вещества. При температурах ниже критической это уравнение имеет три действительных корня; один корень дает удельный объем кипящей жидкости (точка 2 на рис. 11.32); второй корень есть объем насыщенного цара (точка 5), третий корень соответствует неустойчивому состоянию вещества. В критическом состоянии все три корня совпадают:  Решая уравнение Ван-дер-Ваальса для критического состояния
Решая уравнение Ван-дер-Ваальса для критического состояния  получаем:
получаем:

Пользуясь этими соотношениями, можно по известным  вычислить критические параметры вещества и, наоборот, по критическим параметрам найти постоянные уравнения Ван-дер-Ваальса. Так как величина
вычислить критические параметры вещества и, наоборот, по критическим параметрам найти постоянные уравнения Ван-дер-Ваальса. Так как величина  равна учетверенному собственному объему самих молекул вещества, то критический объем в 12 раз больше этого объема. Зная
равна учетверенному собственному объему самих молекул вещества, то критический объем в 12 раз больше этого объема. Зная  или
или  и представляя молекулы в виде шариков, можно приблизительно оценить объем и диаметр молекул.
и представляя молекулы в виде шариков, можно приблизительно оценить объем и диаметр молекул.
Уравнение Ван-дер-Ваальса не является точным уравнением состояния реальных веществ. Если величины  считать постоянными, то обнаруживаются расхождения между измеренными и рассчитанными значениями параметров
считать постоянными, то обнаруживаются расхождения между измеренными и рассчитанными значениями параметров  и
и  в частности, реальные изотермы не совпадают с изотермами Ван-дер-Ваальса. Для того чтобы получить хорошее совпадение, приходится для различных областей давления или температуры придавать величинам
в частности, реальные изотермы не совпадают с изотермами Ван-дер-Ваальса. Для того чтобы получить хорошее совпадение, приходится для различных областей давления или температуры придавать величинам  различные значения. Поэтому уравнение Ван-дер-Ваальса используется не столько для точных расчетов, сколько для выяснения связей между величинами, характеризующими свойства вещества. Примером могут служить полученные из этого уравнения формулы (3.7), в которых обнаружилась связь между критическими параметрами вещества и постоянными
различные значения. Поэтому уравнение Ван-дер-Ваальса используется не столько для точных расчетов, сколько для выяснения связей между величинами, характеризующими свойства вещества. Примером могут служить полученные из этого уравнения формулы (3.7), в которых обнаружилась связь между критическими параметрами вещества и постоянными  к
к 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть I. МЕХАНИКА
- § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ
- ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ
- § 2. ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ
- СИЛА. ДЕФОРМАЦИЯ. МАССА
- ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ
- ИМПУЛЬС. РАБОТА. МОЩНОСТЬ
- ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА
- ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ
- § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ
- § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
- ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ
- § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ
- Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ
- § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ
- § 13. СТОЛКНОВЕНИЕ ШАРОВ
- § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ
- Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
- § 15. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- § 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
- § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
- § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ
- § 21. АВТОКОЛЕБАНИЯ
- Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ
- § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
- § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
- ВОЛНА В УПРУГОЙ СРЕДЕ
- § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ
- § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ
- § 26. СТОЯЧИЕ ВОЛНЫ
- § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ЭФФЕКТ ДОПЛЕРА
- ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ
- § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ
- Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
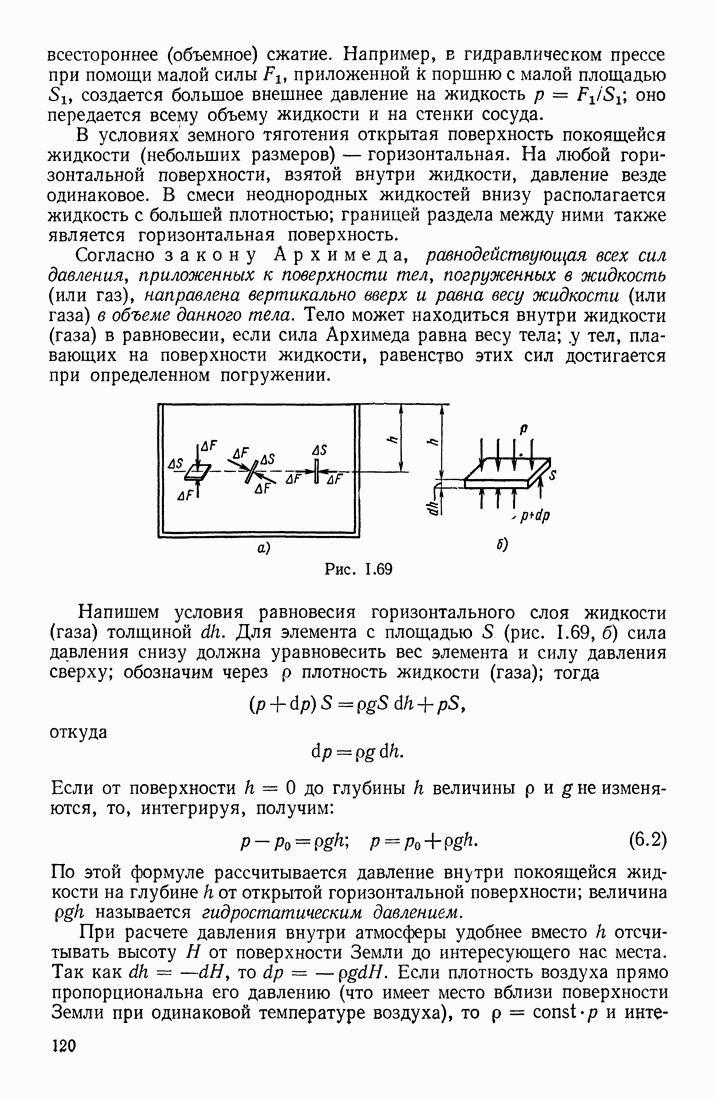
- § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
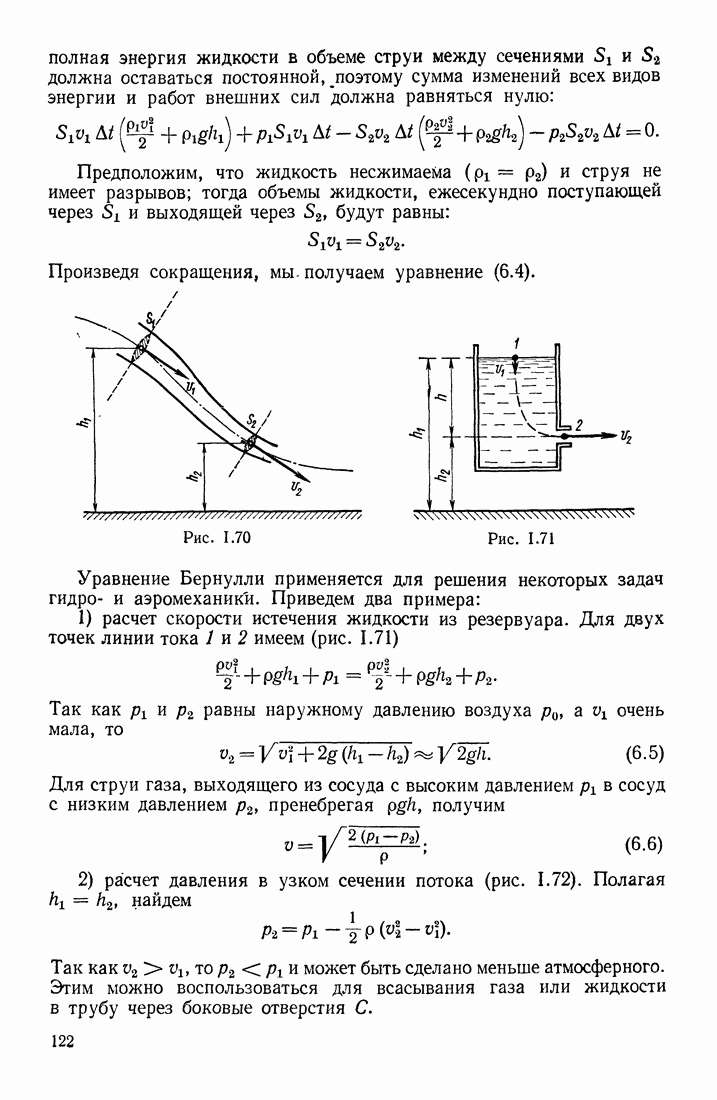
- § 30. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ
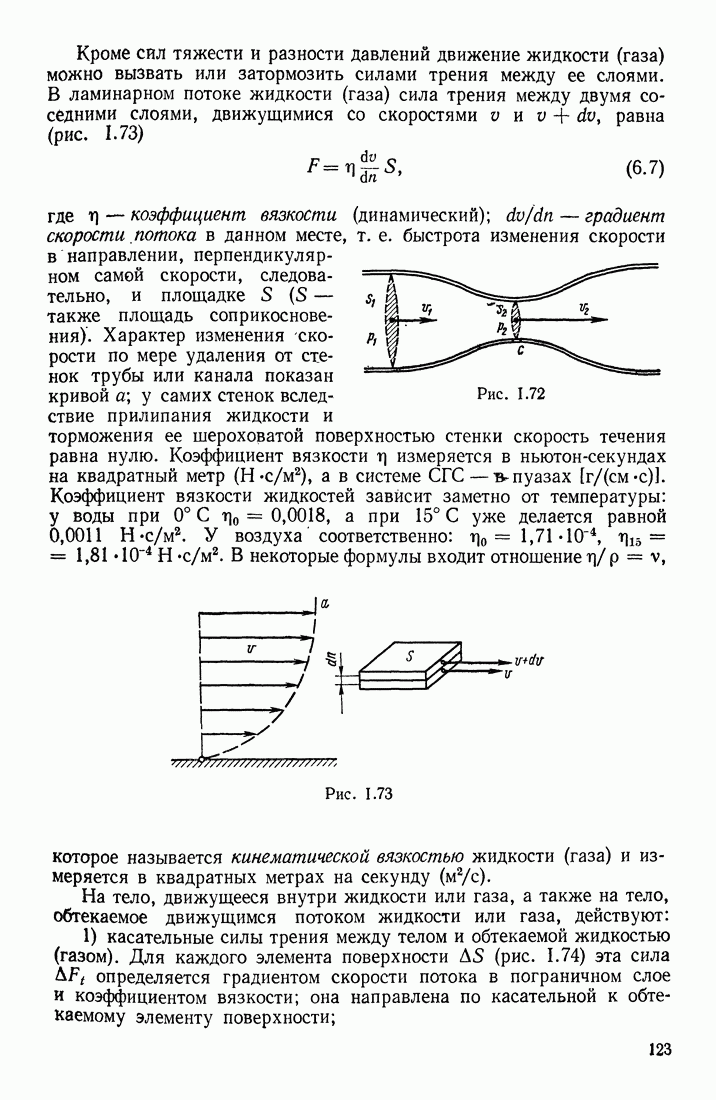
- СЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ
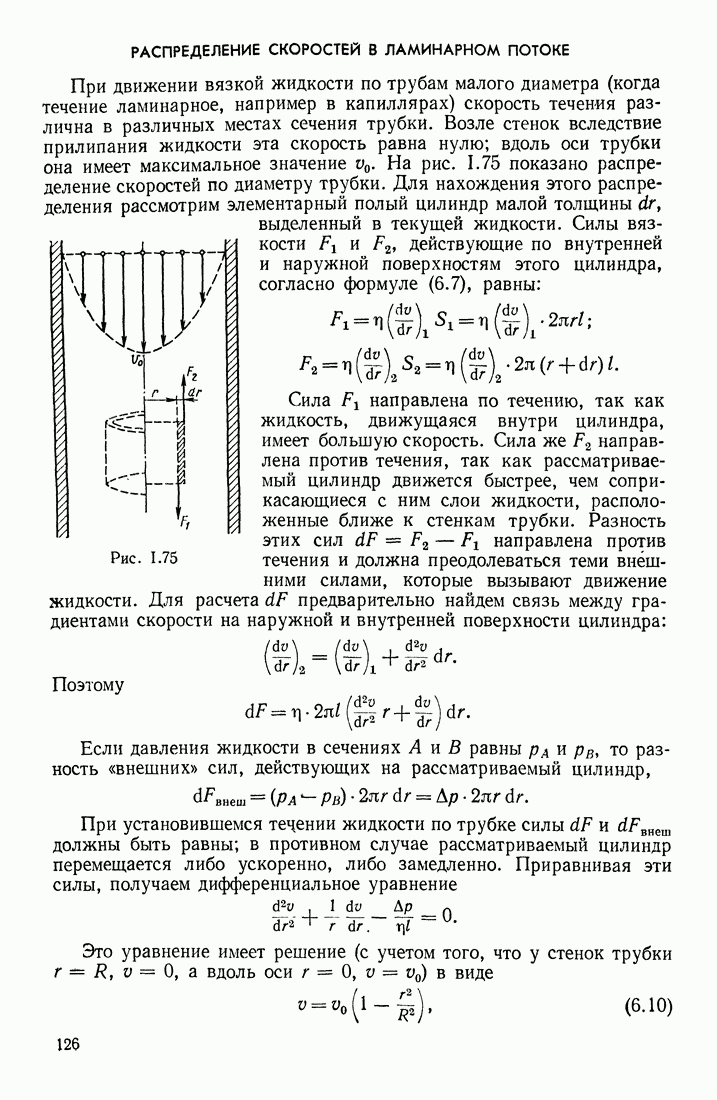
- РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ
- Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ
- § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ
- § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ
- СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
- ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
- § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ
- § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ
- КРУГОВЫЕ ПРОЦЕССЫ
- § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ
- ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
- ЭНТРОПИЯ И ВЕРОЯТНОСТЬ
- Глава 2. ИДЕАЛЬНЫЙ ГАЗ
- § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ
- § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- ЦИКЛ КАРНО
- ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ
- ПАРАДОКС ГИББСА
- § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА
- § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ
- ПАР
- ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ
- § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
- ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- СВОЙСТВА ЖИДКОСТЕЙ
- МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ
- § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ
- ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- КИПЕНИЕ
- УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ
- § 18. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ
- КРИСТАЛЛИЗАЦИЯ
- ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
- ТРОЙНАЯ ТОЧКА
- § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- ТЕПЛОЕМКОСТЬ КРИСТАЛЛА
- ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ
- УПРУГОСТЬ И ПЛАСТИЧНОСТЬ
- ЖИДКИЕ КРИСТАЛЛЫ
- Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА
- § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА
- ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА
- ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ
- § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ
- § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- ЭЛЕКТРОСТРИКЦИЯ
- ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- СЕГНЕТОЭЛЕКТРИКИ
- ЭЛЕКТРЕТЫ
- § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
- Глава 2. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА
- § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ
- § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ
- § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА
- ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА
- ПРАВИЛА КИРХГОФА
- ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА
- § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
- ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ
- ЭФФЕКТ ПЕЛЬТЬЕ
- § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА
- § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ
- ДВИЖЕНИЕ ИОНОВ В ГАЗЕ
- ВИДЫ РАЗРЯДОВ В ГАЗАХ
- ПЛАЗМА
- § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ
- § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ
- ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
- ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ
- ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ
- Глава 3. ЭЛЕКТРОМАГНЕТИЗМ
- § 17. МАГНИТНОЕ ПОЛЕ
- § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
- § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ
- § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
- ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- ЭФФЕКТ ХОЛЛА
- § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
- § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ
- РАМКА В МАГНИТНОМ ПОЛЕ
- ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА
- § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ
- ИНДУКТИВНОСТЬ СОЛЕНОИДА
- РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ
- ВЗАИМНАЯ ИНДУКЦИЯ
- ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
- ТОКИ ФУКО
- § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА
- § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА
- НАМАГНИЧЕННОСТЬ
- МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ
- ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
- ФЕРРОМАГНЕТИКИ
- ПАРАМАГНИТНЫЙ РЕЗОНАНС
- § 26. МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ
- Глава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
- § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ
- ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ
- Часть IV. ОПТИКА И ФИЗИКА АТОМА
- § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА
- СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ
- ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
- ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ
- § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА
- § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА
- СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД
- СВЕТ И ЦВЕТ
- ДИСПЕРСИЯ СВЕТА
- РАССЕЯНИЕ СВЕТА
- § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ
- § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ
- ДИФРАКЦИОННАЯ РЕШЕТКА
- § 6. РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
- ПОЛЯРИЗОВАННЫЙ СВЕТ
- СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ
- ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ
- § 8. ПОНЯТИЕ О ГОЛОГРАФИИ
- Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
- § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА
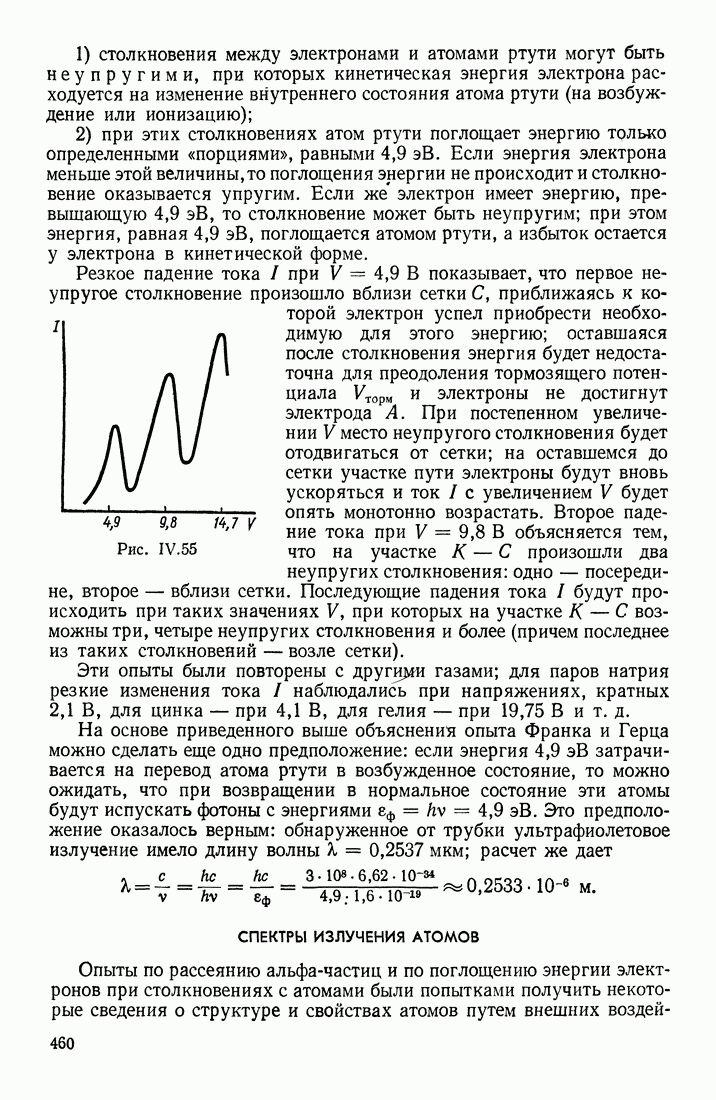
- ОПЫТ ФРАНКА И ГЕРЦА
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- ТЕОРИЯ АТОМА ВОДОРОДА
- § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- ЭФФЕКТ КОМПТОНА
- ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- ФОРМУЛА ДЕ БРОЙЛЯ
- ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
- УРАВНЕНИЕ ШРЕДИНГЕРА
- РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА
- СВОБОДНЫЙ ЭЛЕКТРОН
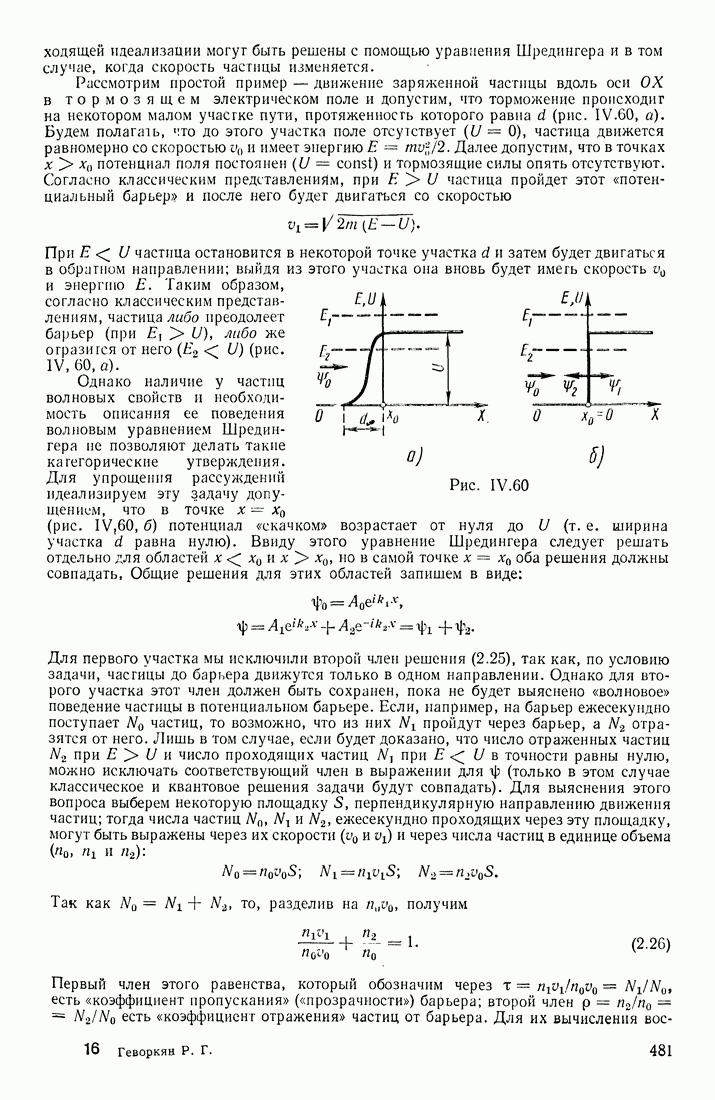
- ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
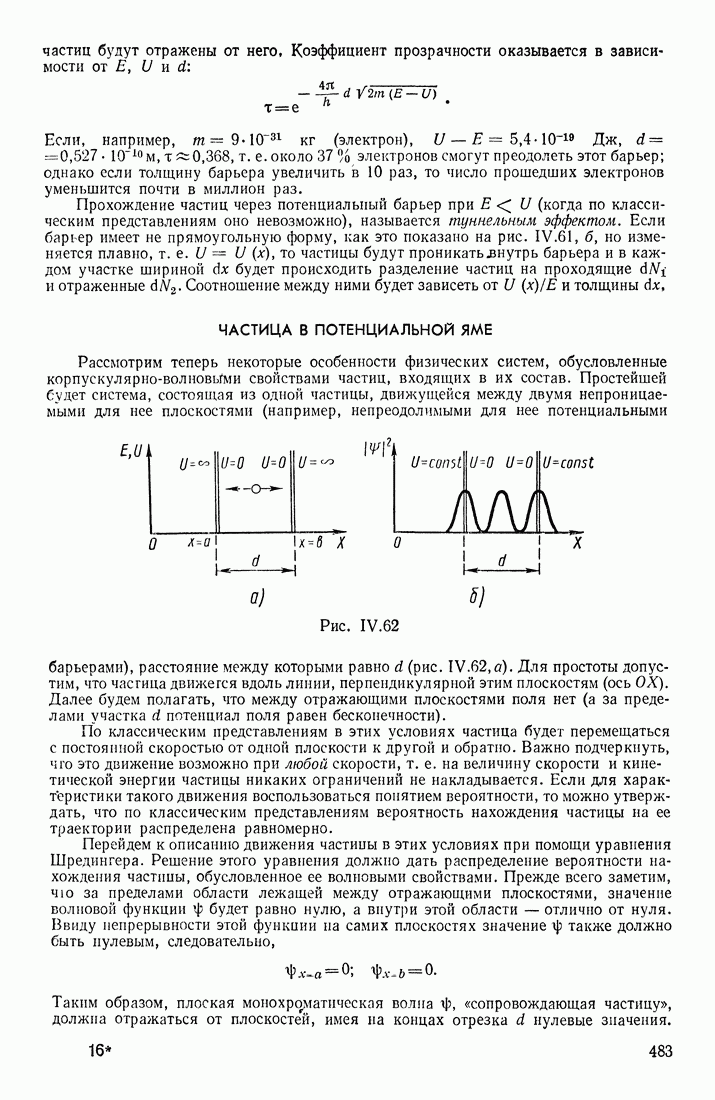
- ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
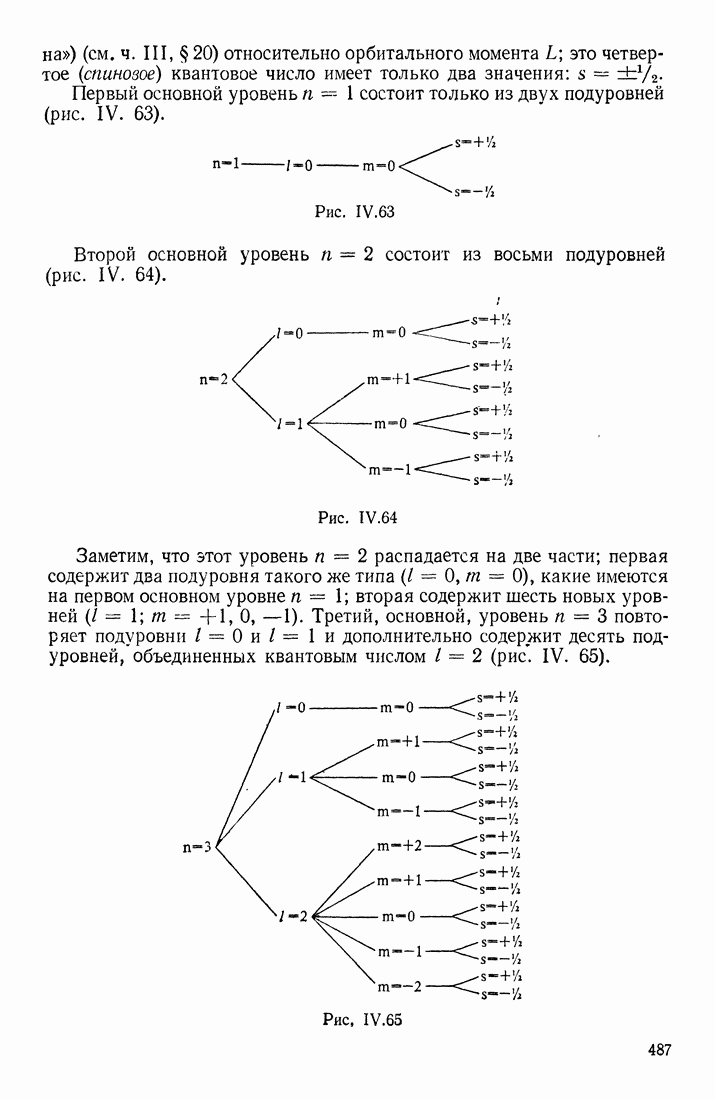
- АТОМ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА
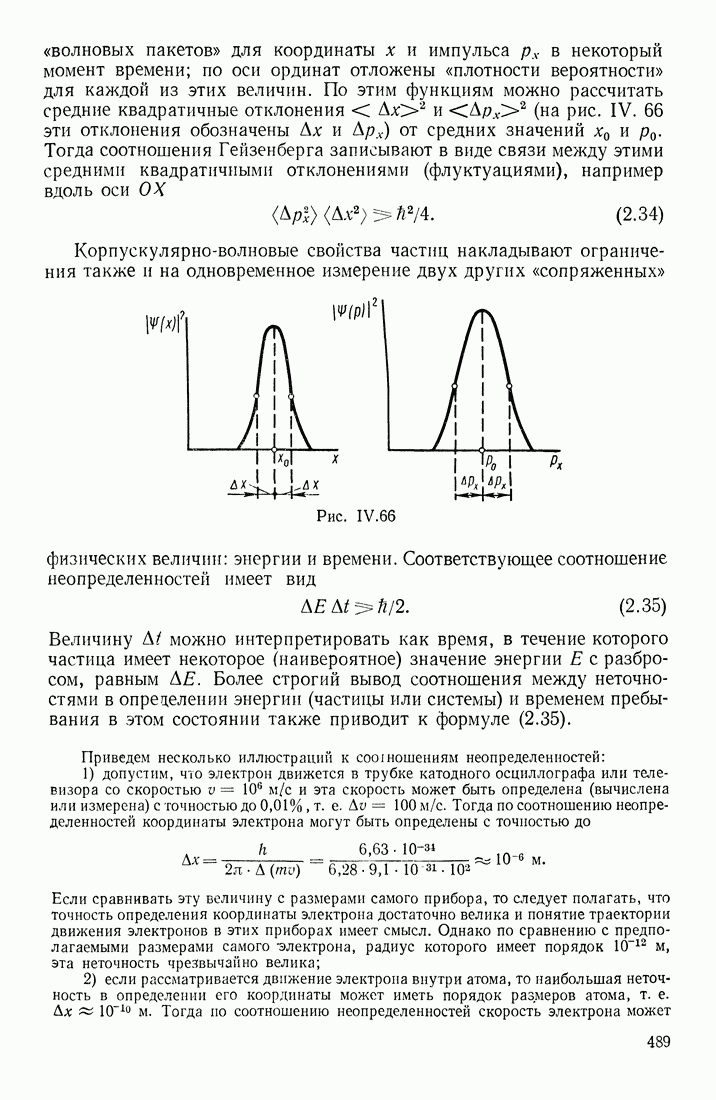
- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
- РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ
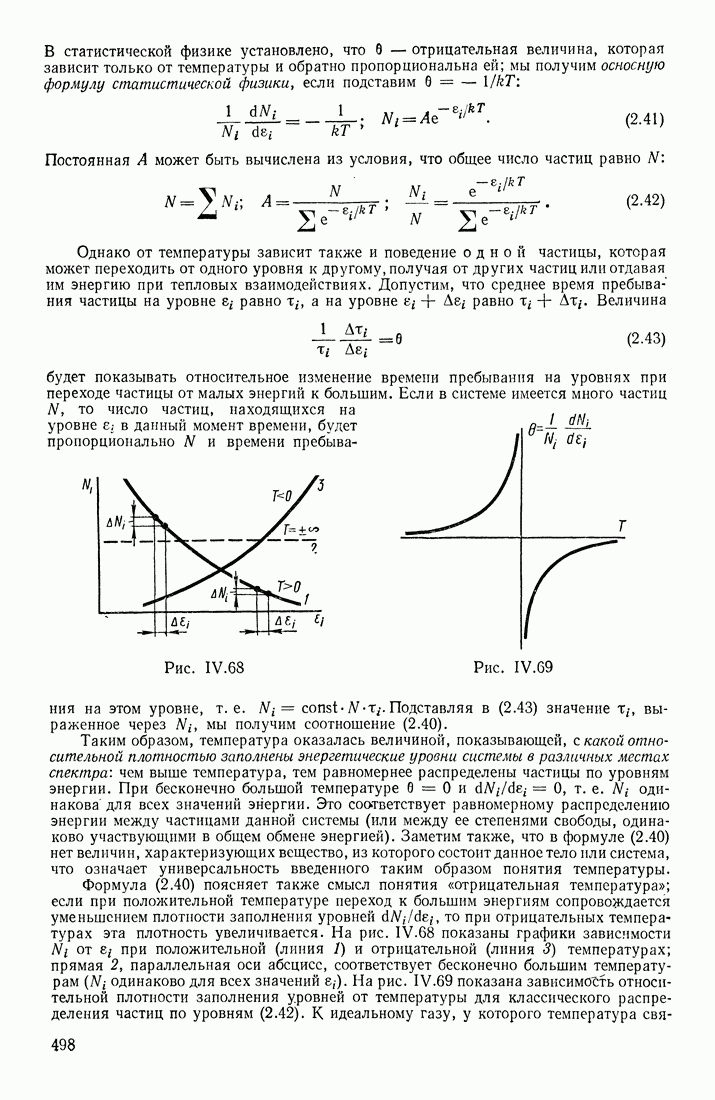
- ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ
- ТЕМПЕРАТУРА
- ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ
- РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
- § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ
- ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ
- ИОННАЯ СВЯЗЬ
- РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ
- Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ
- § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ
- СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ
- КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
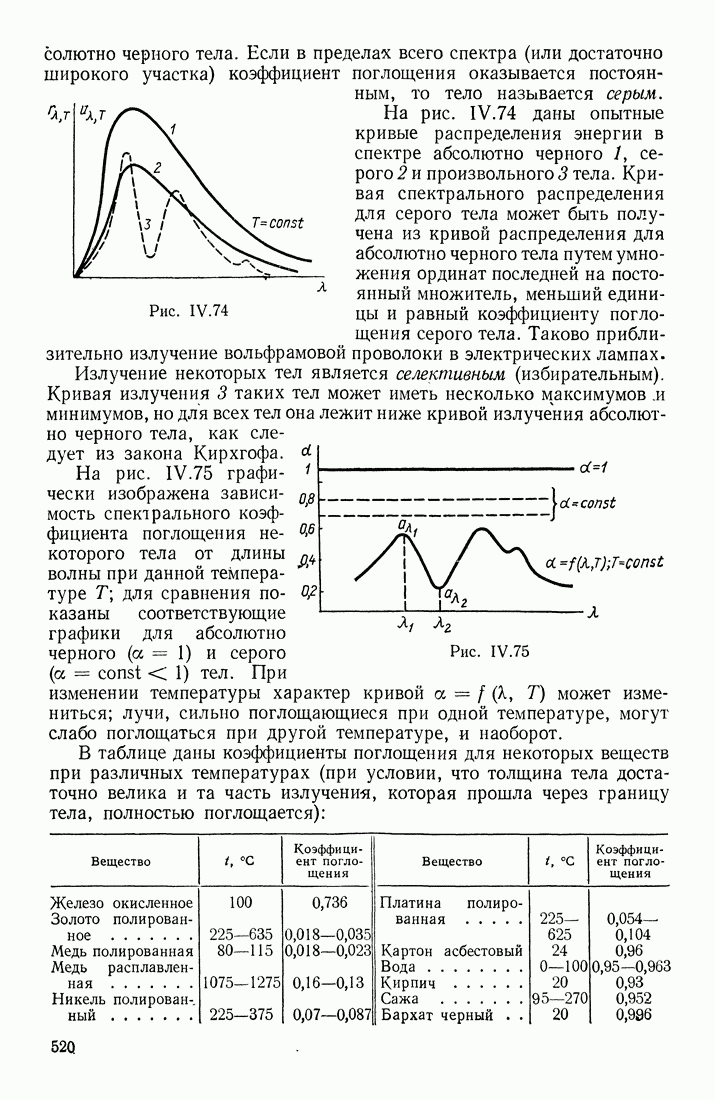
- § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
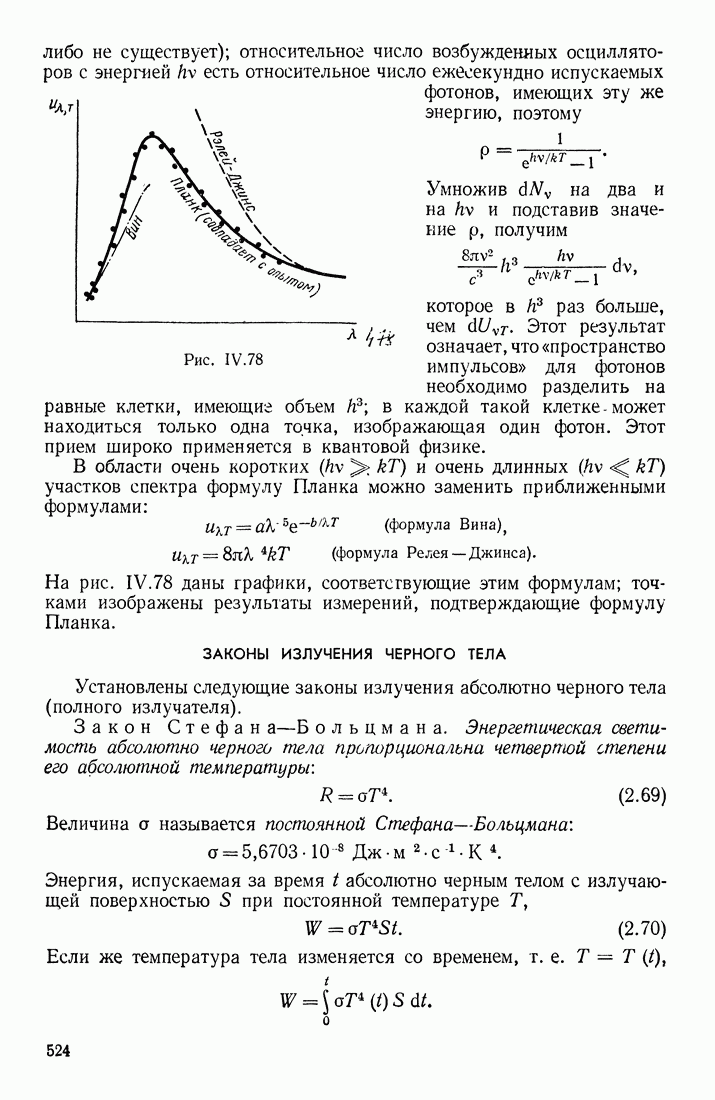
- ФОРМУЛА ПЛАНКА
- ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА
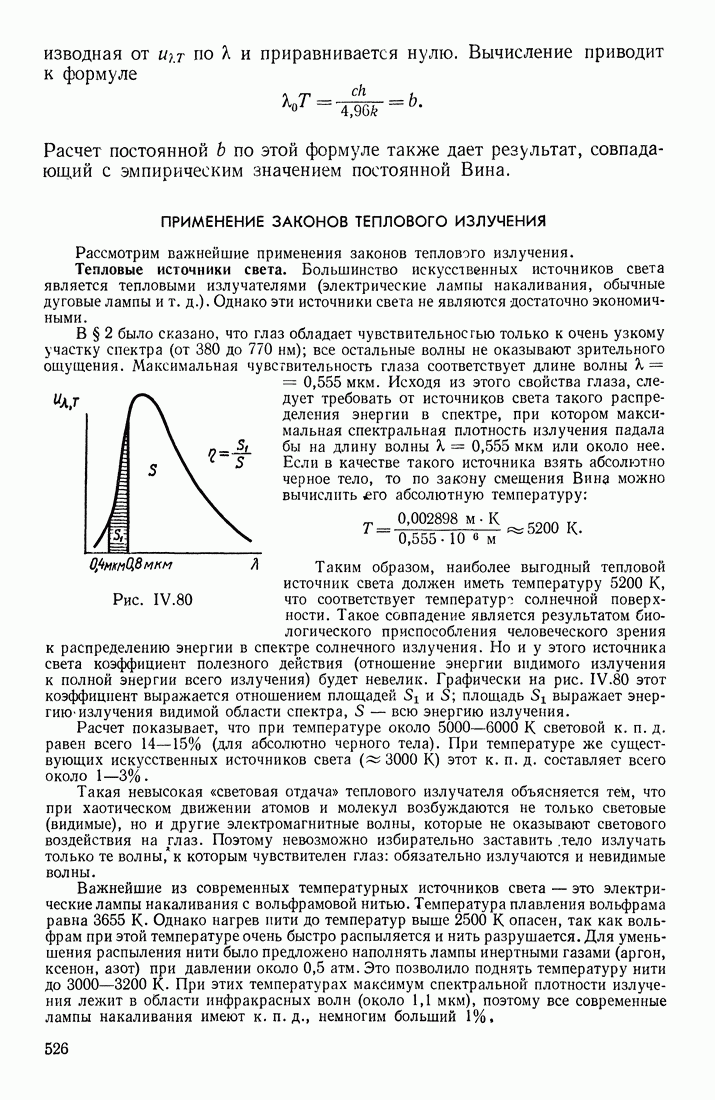
- ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ
- ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР
- ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
- ДОЗИМЕТРИЯ
- § 17. ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ
- ПРИРОДА ЛЮМИНЕСЦЕНЦИИ
- ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ
- ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ
- ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ
- § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ
- ЛАЗЕРЫ
- ПРЕИМУЩЕСТВА ЛАЗЕРОВ
- ПРИМЕНЕНИЕ ЛАЗЕРОВ
- Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР
- РАДИОАКТИВНОСТЬ
- ВНУТРИЯДЕРНЫЕ СИЛЫ
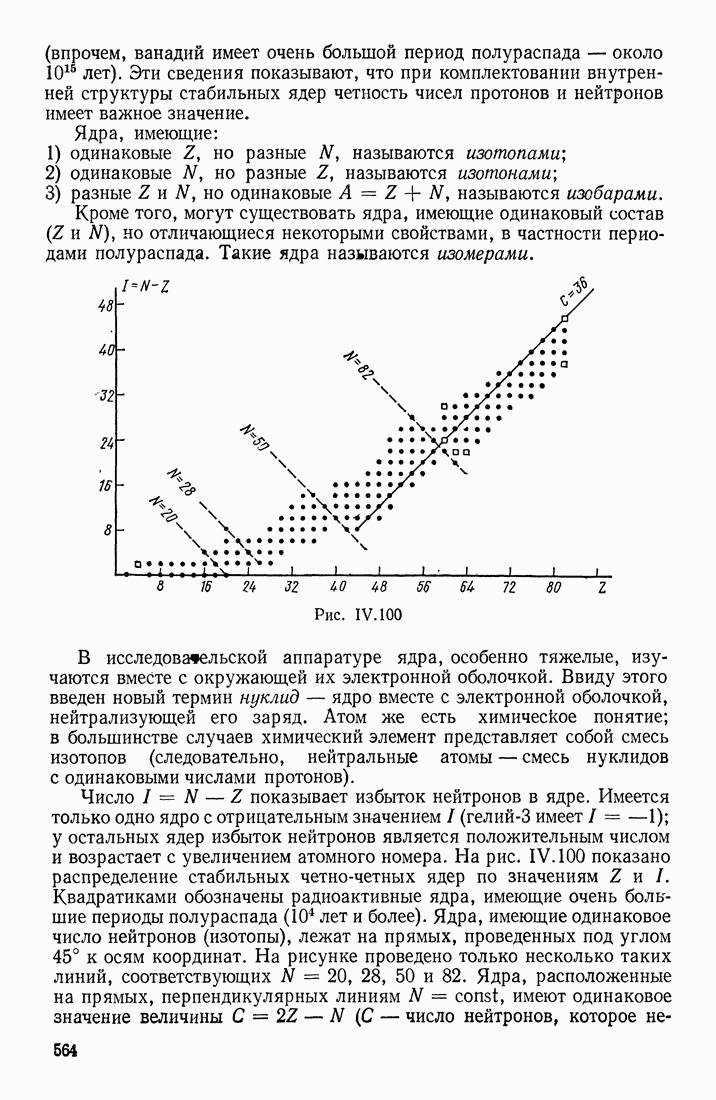
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
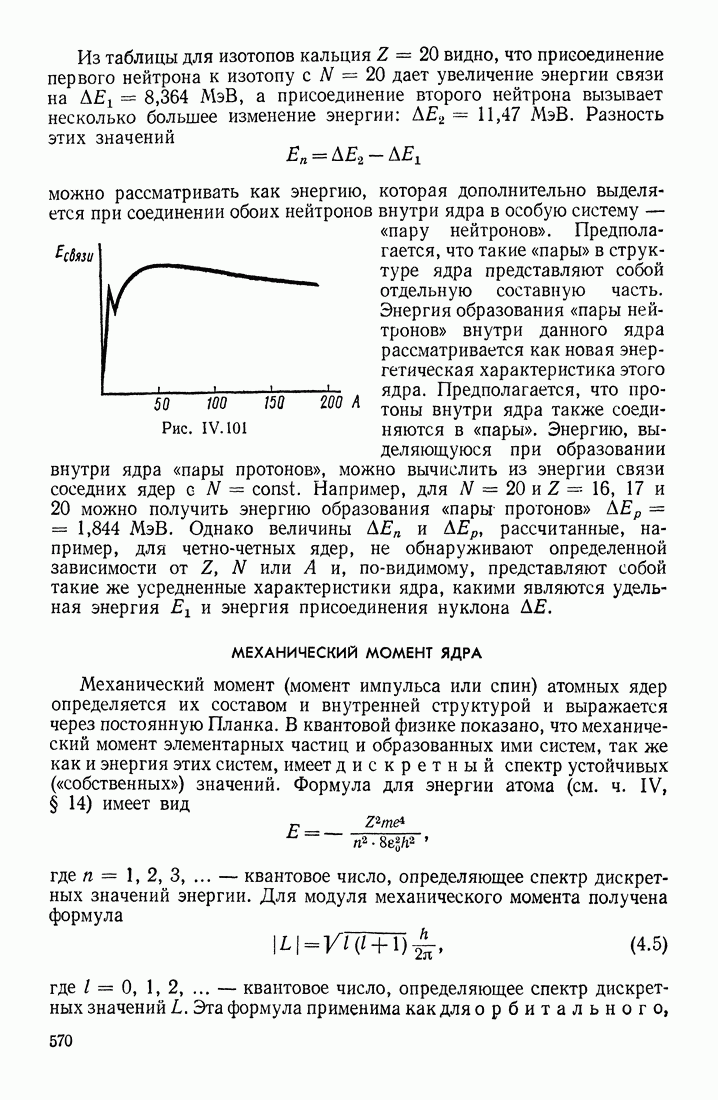
- МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА
- МАГНИТНЫЕ МОМЕНТЫ ЯДЕР
- ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР
- СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ
- § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР
- КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА
- ОБОЛОЧЕЧНАЯ МОДЕЛЬ
- ОБОБЩЕННАЯ МОДЕЛЬ
- ОПТИЧЕСКАЯ МОДЕЛЬ
- УСЛОВИЕ СТАБИЛЬНОСТИ
- § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ
- СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
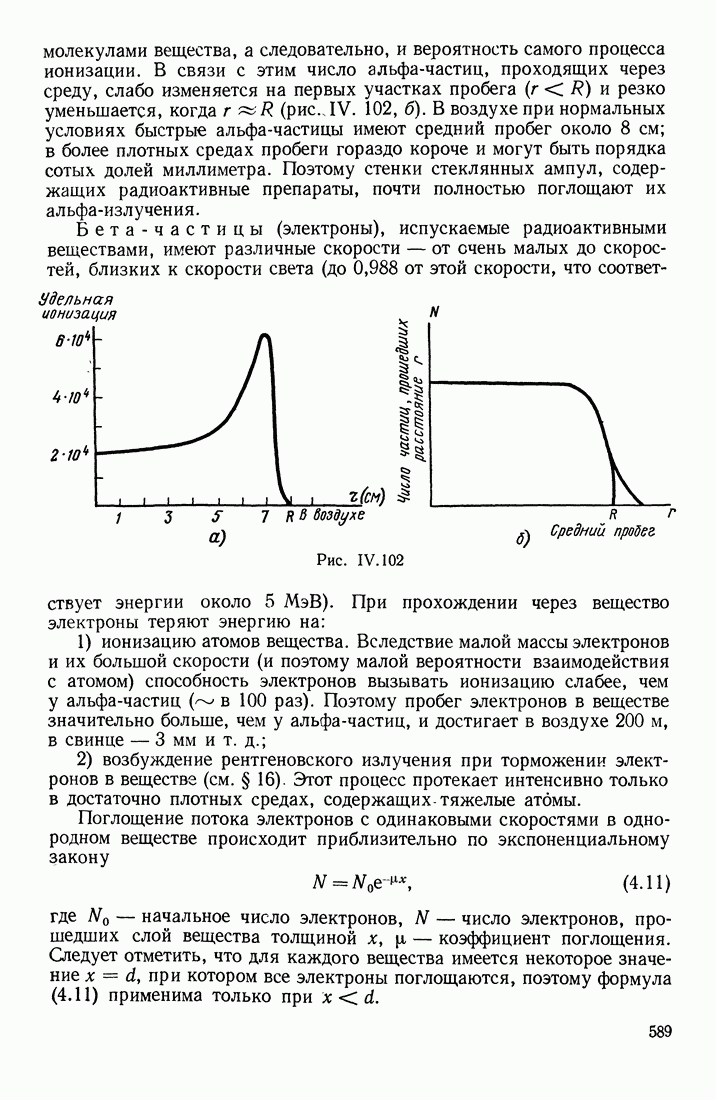
- ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
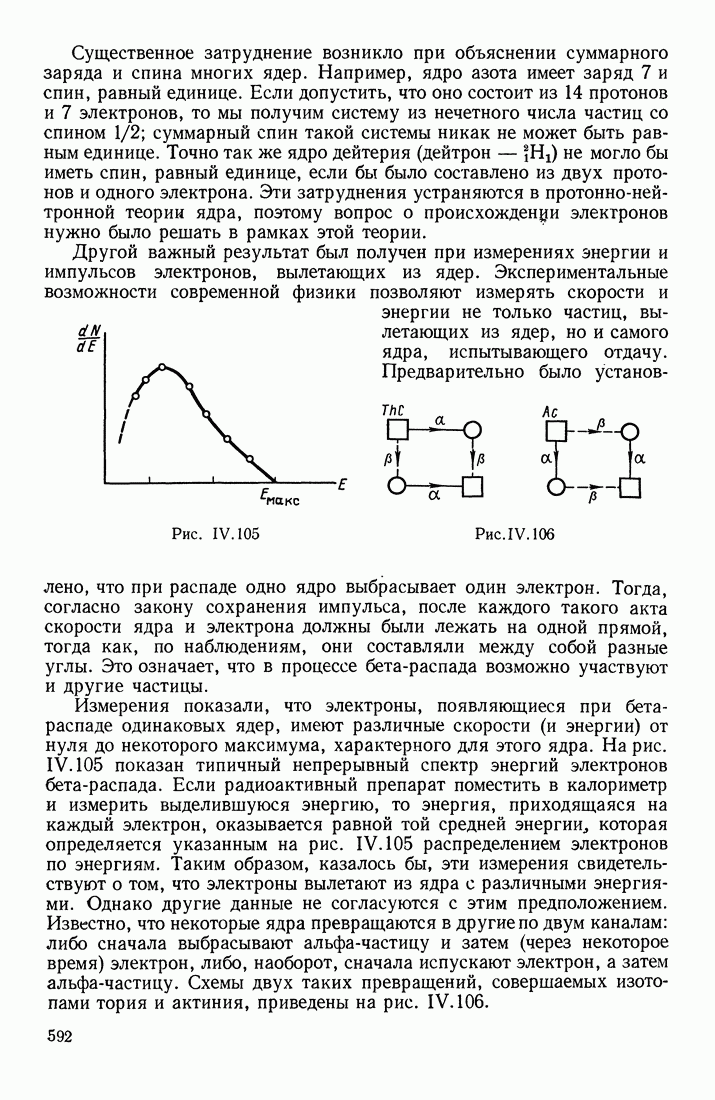
- БЕТА-РАСПАД ЯДЕР
- ЭНЕРГИЯ СВЯЗИ ЯДЕР
- ИЗОМЕРЫ
- § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ
- ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ
- ЯДЕРНЫЕ РЕАКТОРЫ
- ЯДЕРНЫЙ СИНТЕЗ
- § 23. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- РАСПАДЫ ЧАСТИЦ
- ВИДЫ ВЗАИМОДЕЙСТВИЯ
- ЗАКЛЮЧЕНИЕ
- § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ
- § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ
- § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ
- § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ
- § 6. О ДУАЛИЗМЕ В ФИЗИКЕ