| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
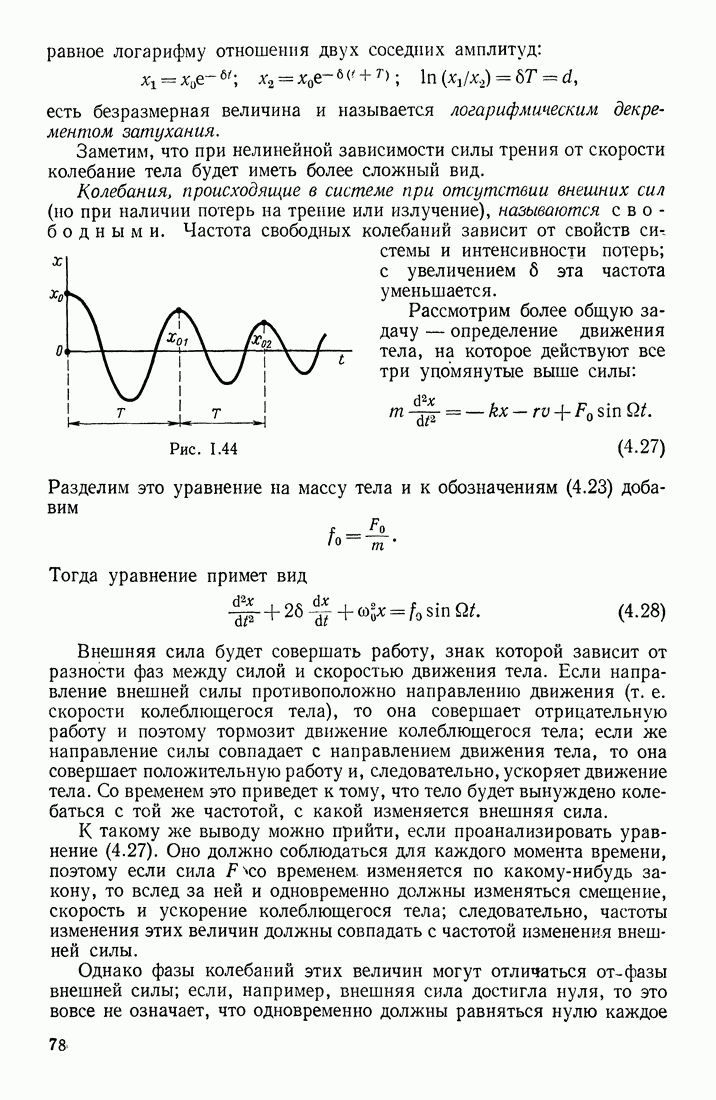
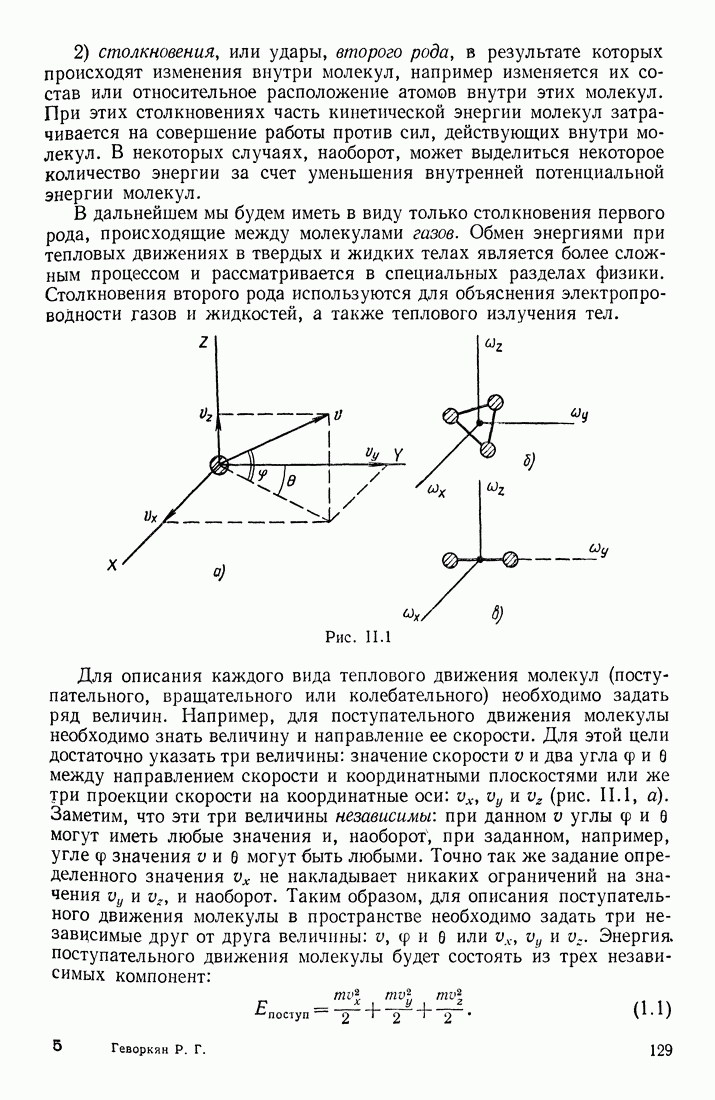
§ 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
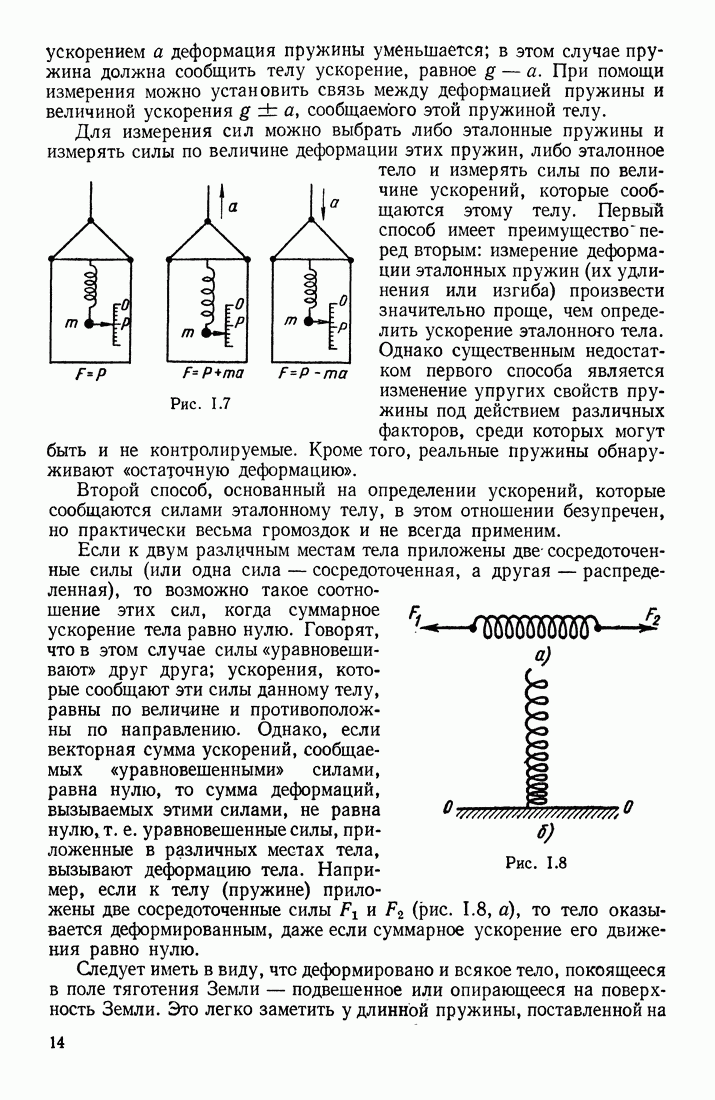
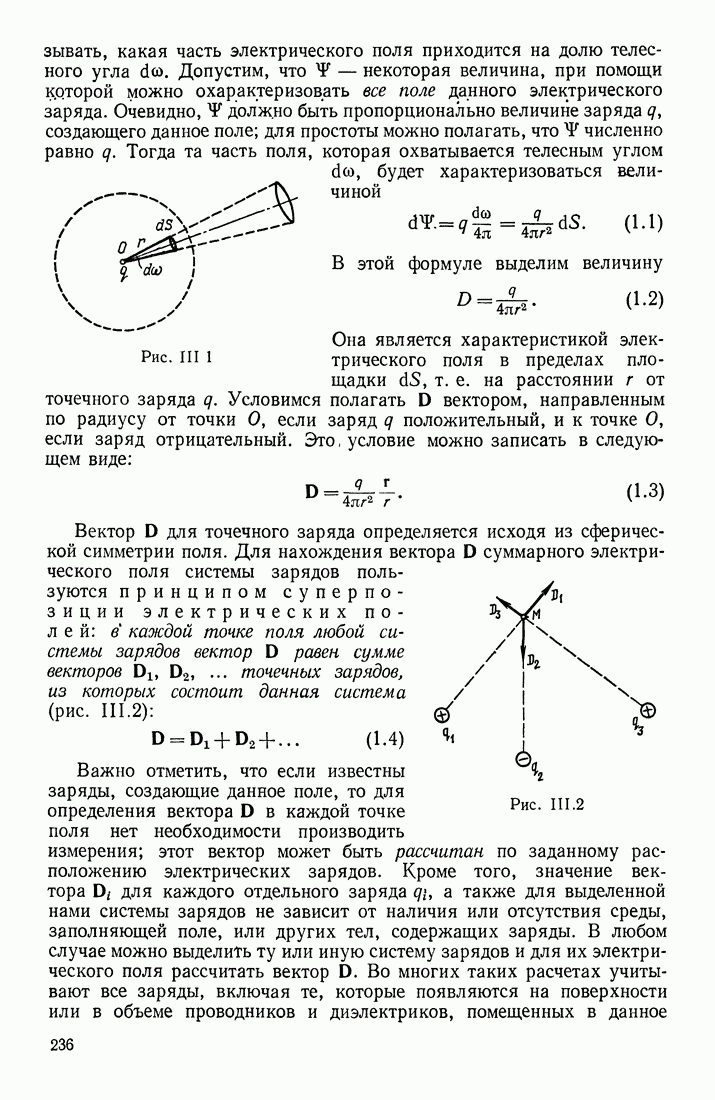
Допустим, что по прямолинейному бесконечно длинному проводнику очень малого сечения течет ток  Магнитное поле вокруг проводника можно полагать прямо пропорциональным току
Магнитное поле вокруг проводника можно полагать прямо пропорциональным току  Проведем через проводник две бесконечные плоскости I и II, составляющие между собой угол
Проведем через проводник две бесконечные плоскости I и II, составляющие между собой угол  а в плоскости, перпендикулярной проводнику, проведем окружность некоторого радиуса
а в плоскости, перпендикулярной проводнику, проведем окружность некоторого радиуса  (рис. III. 49), так что
(рис. III. 49), так что  Так как магнитное поле вокруг проводника имеет цилиндрическую симметрию, то величина
Так как магнитное поле вокруг проводника имеет цилиндрическую симметрию, то величина  будет показывать, какая часть всего магнитного поля заключена между плоскостями
будет показывать, какая часть всего магнитного поля заключена между плоскостями  Обратим внимание на величину
Обратим внимание на величину

Очевидно, что ее можно рассматривать как некоторую характеристику магнитного поля  расстоянии
расстоянии  от бесконечно длинного прямолинейного проводника с током
от бесконечно длинного прямолинейного проводника с током  Будем полагать ее аектором, направленным по касательной к окружности (в соответствии с правилом правого винта, ввинчиваемого по направлению тока в проводнике; рис. III. 49). Однако в общем случае проводник может иметь любую форму; поэтому для расчета вектора
Будем полагать ее аектором, направленным по касательной к окружности (в соответствии с правилом правого винта, ввинчиваемого по направлению тока в проводнике; рис. III. 49). Однако в общем случае проводник может иметь любую форму; поэтому для расчета вектора  в каждой точке магнитного поля вокруг проводника произвольной формы необходимо найти некоторый общий метод. Таким методом может быть следующий. Будем полагать,
в каждой точке магнитного поля вокруг проводника произвольной формы необходимо найти некоторый общий метод. Таким методом может быть следующий. Будем полагать,
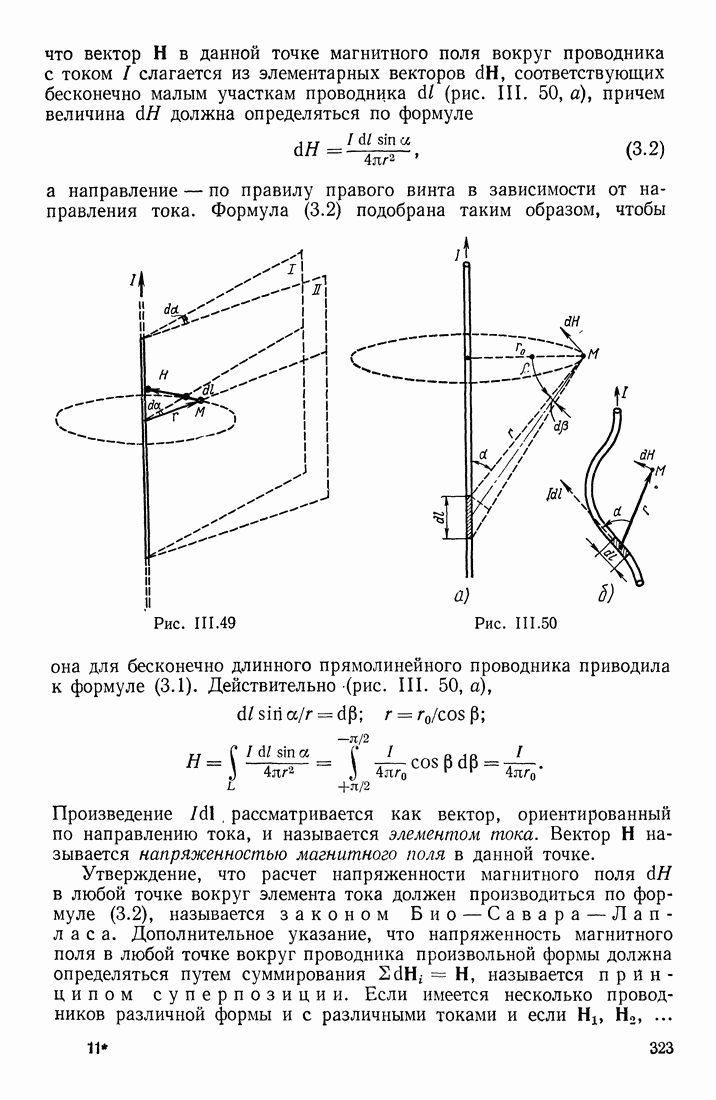
что вектор  в данной точке магнитного поля вокруг проводника с током
в данной точке магнитного поля вокруг проводника с током  слагается из элементарных векторов
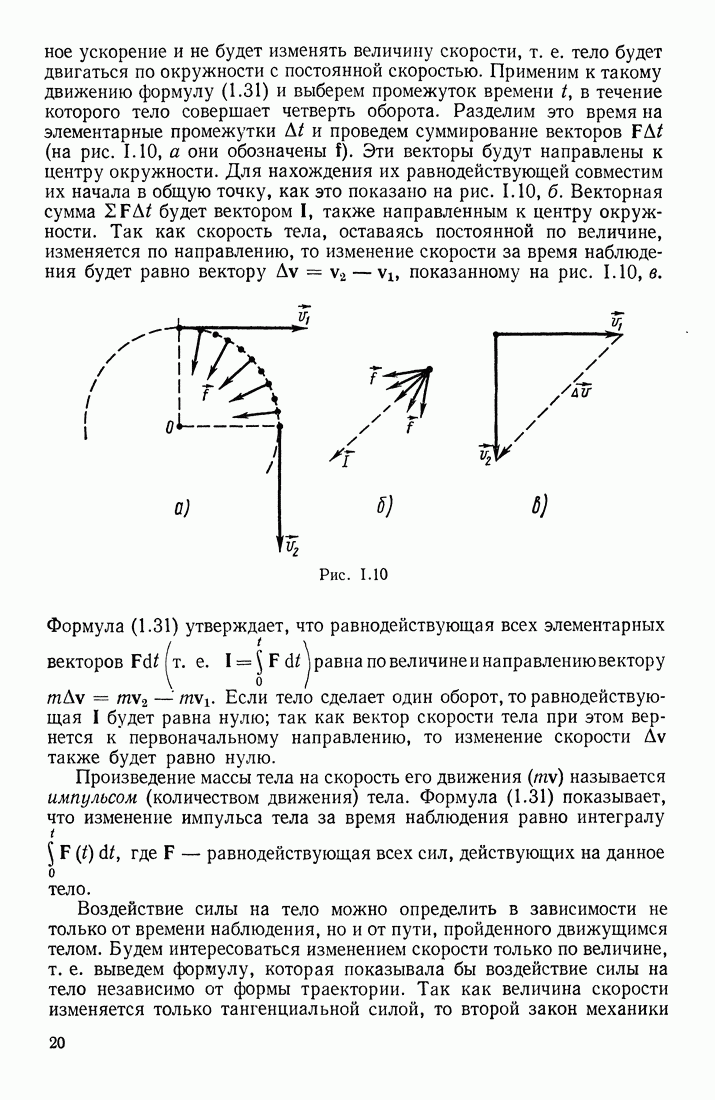
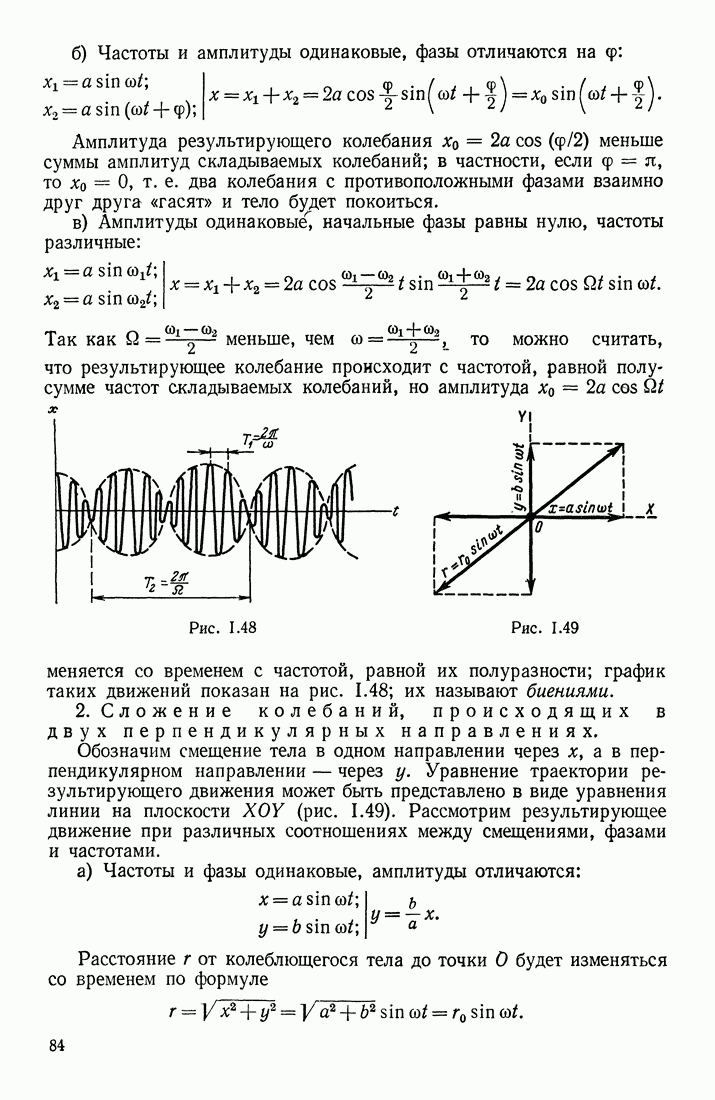
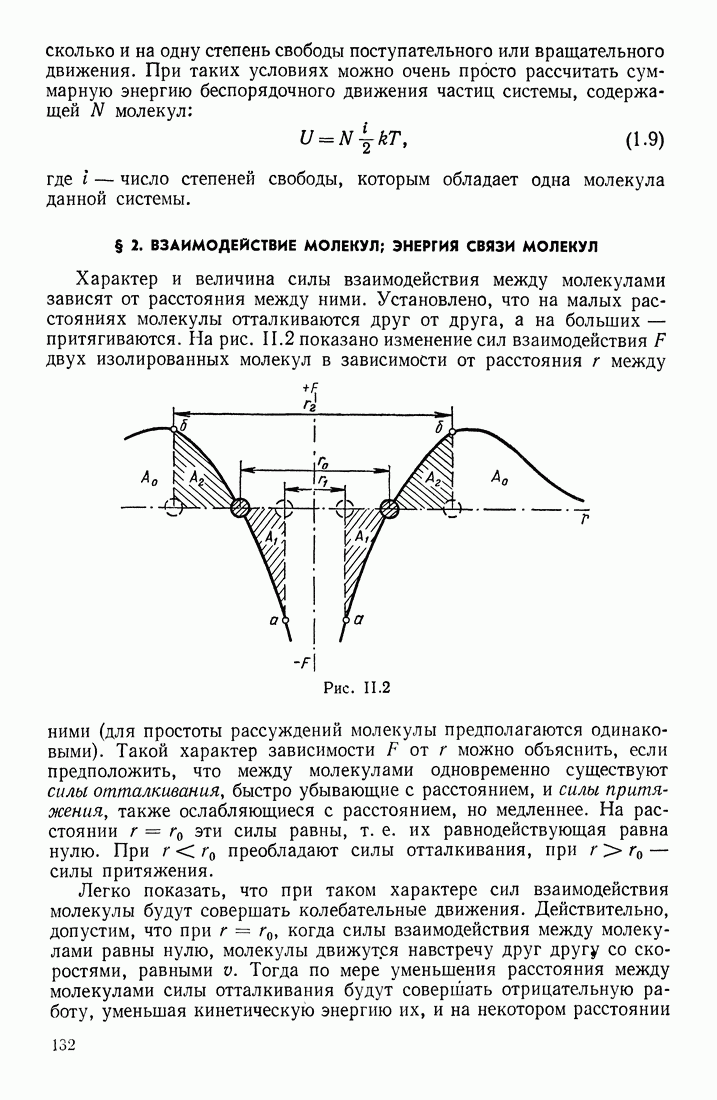
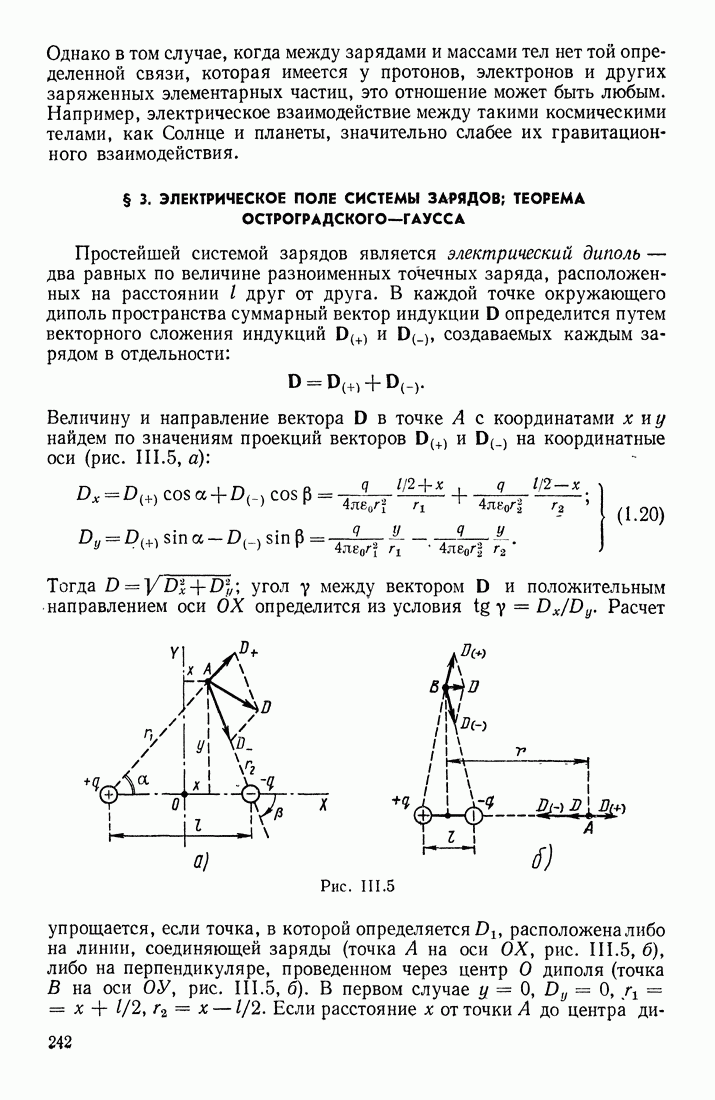
слагается из элементарных векторов  соответствующих бесконечно малым участкам проводника d (рис. III. 50, а), причем величина
соответствующих бесконечно малым участкам проводника d (рис. III. 50, а), причем величина  должна определяться по формуле
должна определяться по формуле

а направление — по правилу правого винта в зависимости от направления тока.

Рис. III.49

Рис. III.50
Формула (3.2) подобрана таким образом, чтобы она для бесконечно длинного прямолинейного проводника приводила к формуле (3.1). Действительно (рис. III. 50, а),

Произведение  рассматривается как вектор, ориентированный по направлению тока, и называется элементом тока. Вектор
рассматривается как вектор, ориентированный по направлению тока, и называется элементом тока. Вектор  называется напряженностью магнитного поля в данной точке.
называется напряженностью магнитного поля в данной точке.
Утверждение, что расчет напряженности магнитного поля  в любой точке вокруг элемента тока должен производиться по формуле (3.2), называется законом Био - Савара — Лапласа. Дополнительное указание, что напряженность магнитного поля в любой точке вокруг проводника произвольной формы должна определяться путем суммирования
в любой точке вокруг элемента тока должен производиться по формуле (3.2), называется законом Био - Савара — Лапласа. Дополнительное указание, что напряженность магнитного поля в любой точке вокруг проводника произвольной формы должна определяться путем суммирования  называется принципом суперпозиции. Если имеется несколько проводников различной формы и с различными токами и если
называется принципом суперпозиции. Если имеется несколько проводников различной формы и с различными токами и если 
есть напряженности поля в данной точке, создаваемые каждым из этих проводников в отдельности (при отсутствии других), то, согласно принципу суперпозиции, суммарная напряженность поля в этой точке равна

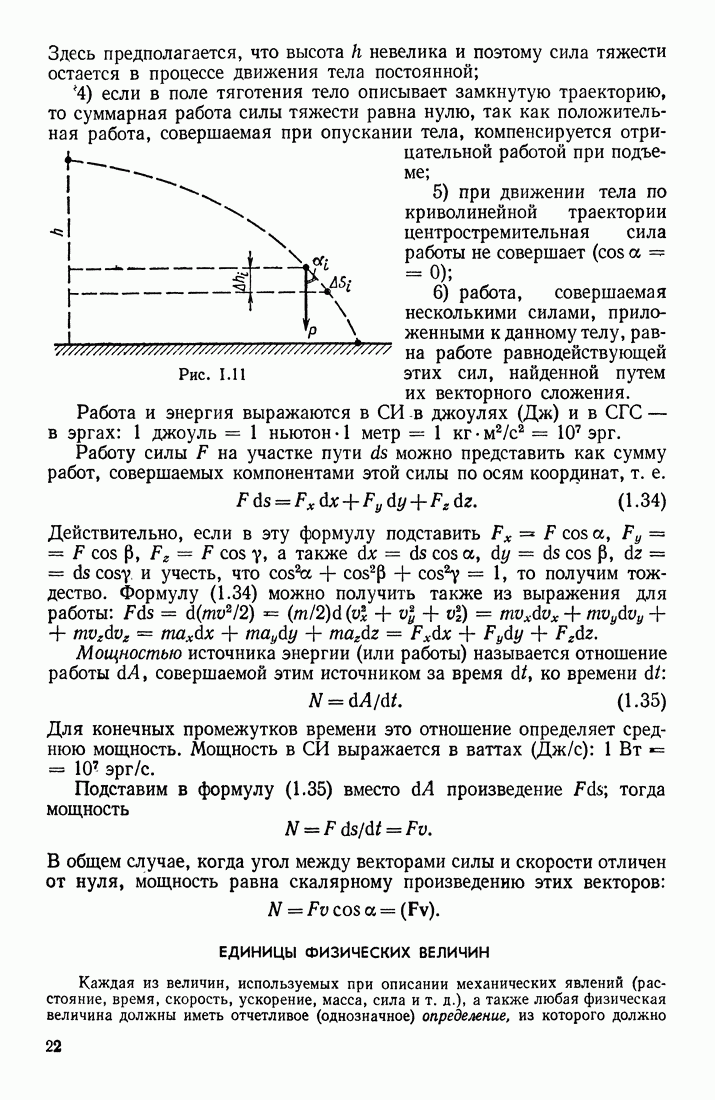
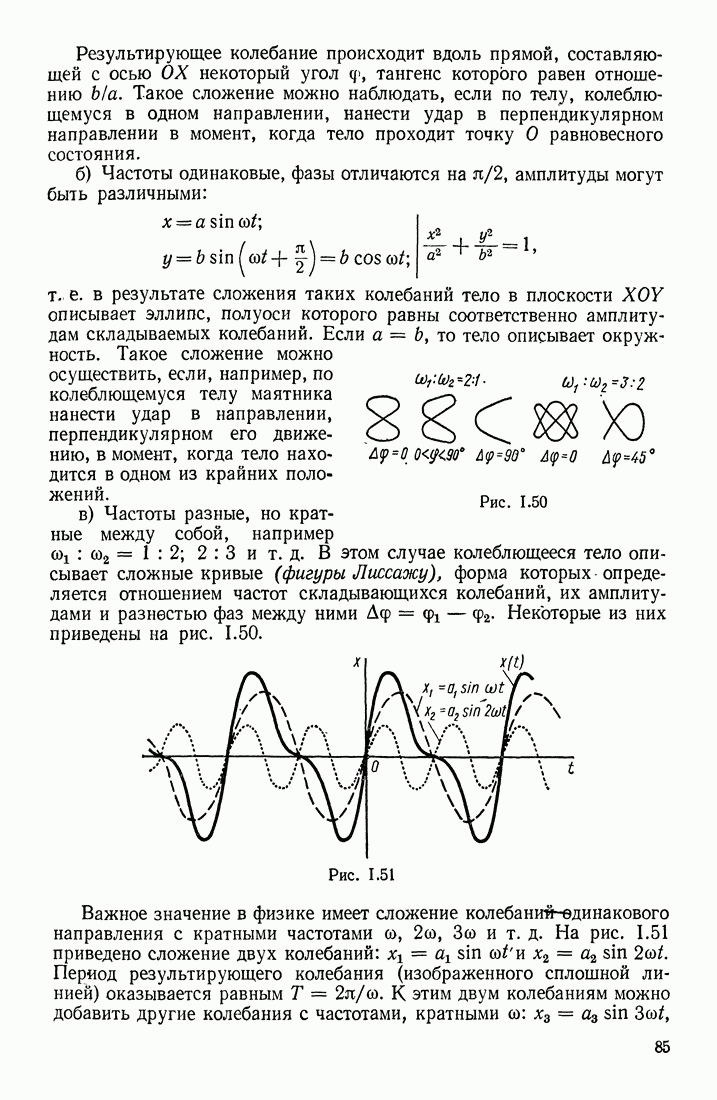
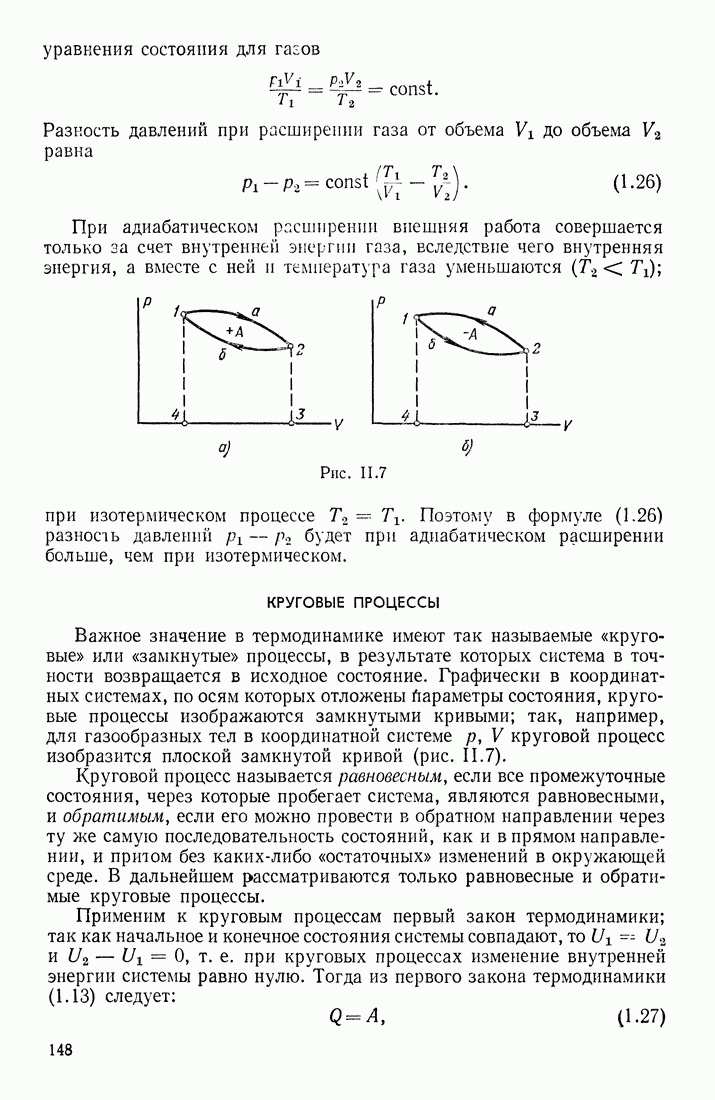
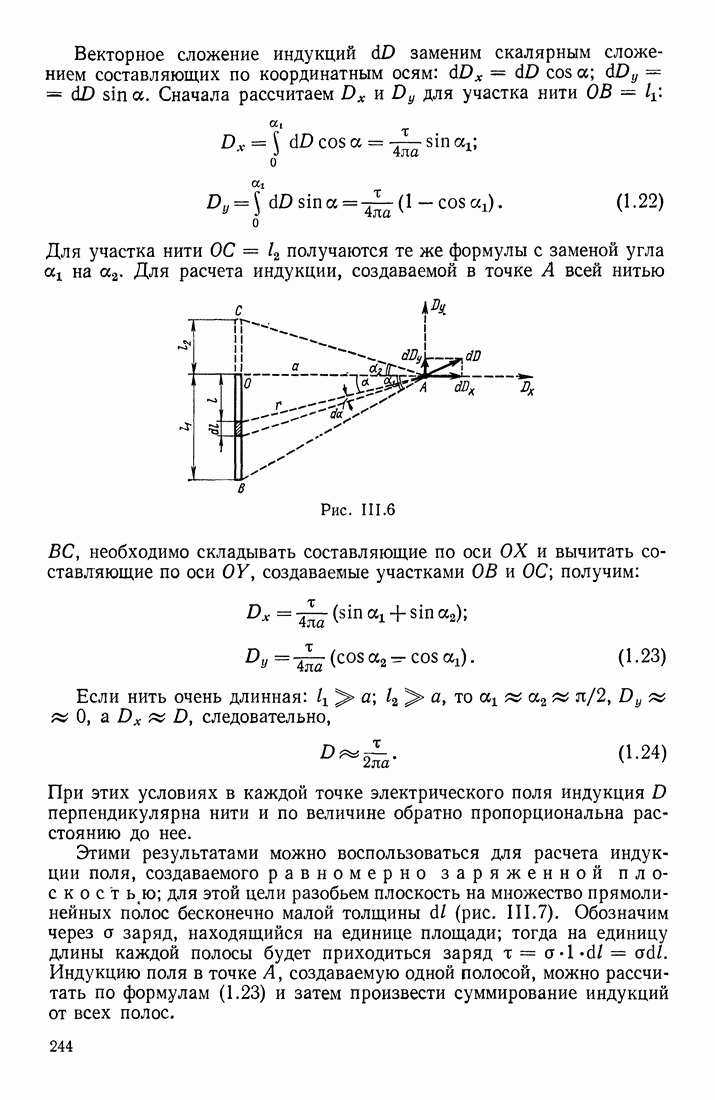
Укажем на одно важное следствие из закона Био-Савара-Лапласа, которое облегчает расчеты магнитных полей. Допустим, что по проводнику произвольной формы (рис. III. 51) течет ток  По закону Био-Савара-Лапласа, напряженность магнитного поля
По закону Био-Савара-Лапласа, напряженность магнитного поля  создаваемого этим током в точке
создаваемого этим током в точке  можно рассчитать, вычислив интеграл по замкнутому контуру тока:
можно рассчитать, вычислив интеграл по замкнутому контуру тока:


Рис. III.51
Проведем теперь в магнитном поле некоторую воображаемую замкнутую линию  (любой формы и размеров) и разделим ее на элементарные участки
(любой формы и размеров) и разделим ее на элементарные участки  Для каждого участка составим произведение
Для каждого участка составим произведение  угол между направлением
угол между направлением  и касательной
и касательной  к линии) и найдем их сумму вдоль всей, линии
к линии) и найдем их сумму вдоль всей, линии  т. е. вычислим интеграл
т. е. вычислим интеграл  Расчет, который мы не приводим ввиду его сложности, дает весьма простой результат — для линии обхода любой формы и размеров:
Расчет, который мы не приводим ввиду его сложности, дает весьма простой результат — для линии обхода любой формы и размеров:

Если изменить направление тока в проводнике, то в каждой точке поля вектор  изменит свое направление на обратное, косинусы углов
изменит свое направление на обратное, косинусы углов  будут иметь противоположный знак и интеграл сделается отрицательным. Знак этого интеграла, изменится также и при перемене направления обхода по линии
будут иметь противоположный знак и интеграл сделается отрицательным. Знак этого интеграла, изменится также и при перемене направления обхода по линии  вследствие чего изменятся направления касательных
вследствие чего изменятся направления касательных  Ввиду этого направление обхода и направление тока должны быть связаны между собой правилом знаков, а именно, если вращатьправый винт по выбранному нами направлению обхода линии
Ввиду этого направление обхода и направление тока должны быть связаны между собой правилом знаков, а именно, если вращатьправый винт по выбранному нами направлению обхода линии  то его перемещение должно соответствовать положительному направлению тока
то его перемещение должно соответствовать положительному направлению тока 
Полученный результат (3.5) не зависит ни от формы контура с током, ни от формы замкнутой линии  Если линия
Если линия  охватывает несколько проводников с токами
охватывает несколько проводников с токами  то, согласно принципу суперпозиции, интеграл (3.5) будет равен алгебраической сумме этих токов. Если линия
то, согласно принципу суперпозиции, интеграл (3.5) будет равен алгебраической сумме этих токов. Если линия  охватывает один и тот же ток
охватывает один и тот же ток  раз, то интеграл (3.5) равен
раз, то интеграл (3.5) равен  наконец, если
наконец, если  не охватывает тока, то интеграл (3.5) оказывается равным нулю, т. е. токи, протекающие за пределами контура
не охватывает тока, то интеграл (3.5) оказывается равным нулю, т. е. токи, протекающие за пределами контура  в правую часть формулы (3.5) не входят.
в правую часть формулы (3.5) не входят.
Интеграл  называется циркуляцией вектора напряженности вдоль данной замкнутой линии обхода, Утверждение,
называется циркуляцией вектора напряженности вдоль данной замкнутой линии обхода, Утверждение,
что эта циркуляция равна алгебраической сумме сил токов, охватываемых линией обхода,

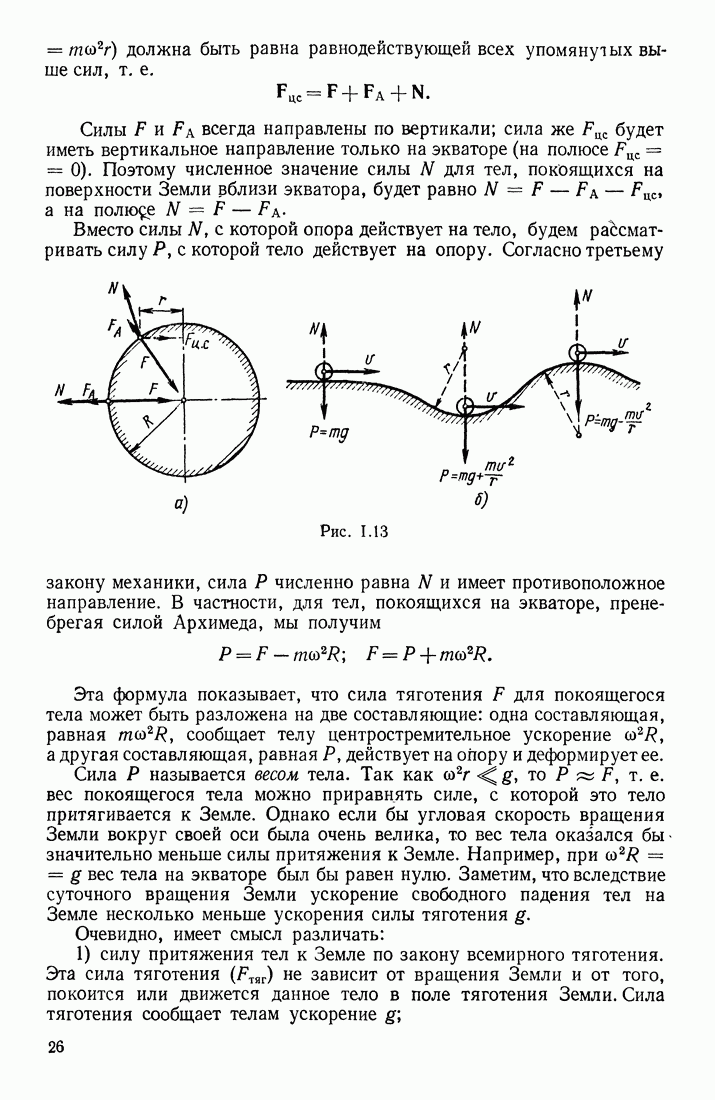
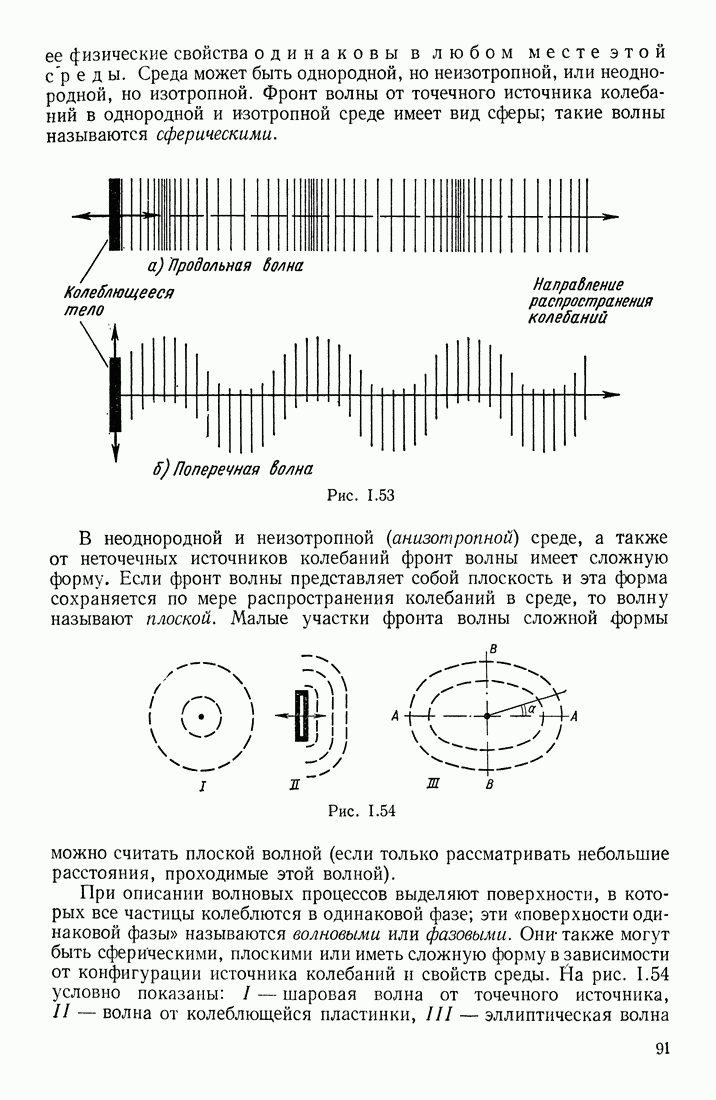
называется теоремой о циркуляции напряженности магнитного поля или законом полного тока. Этим законом можно воспользоваться для расчета напряженности магнитного поля, причем выбирается удобный контур обхода; в частности, удобно производить обход вдоль такой линии, в каждой точке которой  Такие линии называются силовыми линиями магнитного поля.
Такие линии называются силовыми линиями магнитного поля.

Рис. III.52
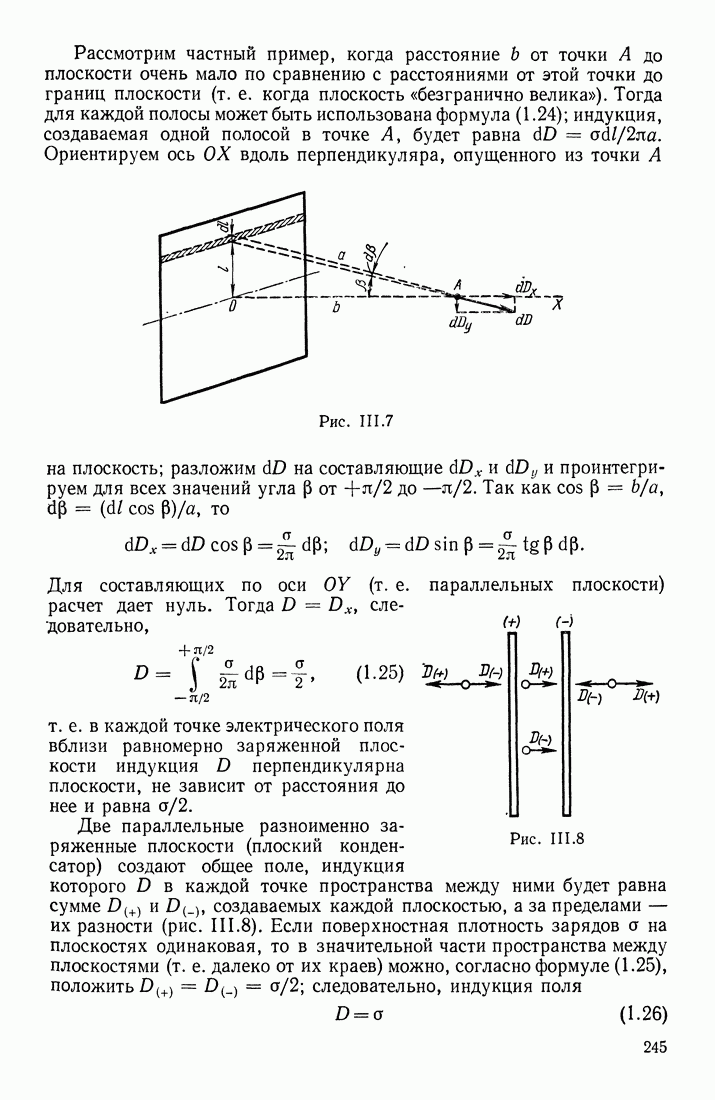
Магнитное поле называется однородным, если во всех точках поля напряженность одинакова и по величине и по направлению; поэтому поле вокруг прямолинейного проводника с током является неоднородным. При графическом изображении геометрических характеристик магнитного поля пользуются силовыми линиями, вдоль которых напряженность поля ориентирована по касательным. Силовые линии вокруг бесконечно длинного прямолинейного проводника с током имеют вид концентрических окружностей (рис. III. 52). Силовым линиям придается направление, соответствующее направлению напряженности поля; очевидно, что в однородном магнитном поле силовые линии будут параллельными прямыми. Условились, что число силовых линий, проводимых через единицу площади (перпендикулярной этим линиям), должно быть численно равно величине напряженности поля  в этом месте. Если в магнитном поле выбрана площадка
в этом месте. Если в магнитном поле выбрана площадка  а а есть угол между нормалью к этой площадке и вектором
а а есть угол между нормалью к этой площадке и вектором  то произведение
то произведение

будет «числом» силовых линий, проведенных через эту площадку (это число называют также потоком вектора напряженности через данную площадку).
Приведем некоторые расчеты магнитных полей:
1) магнитное поле движущегося заряда. Полагая, что в элементе тока  содержится
содержится  электронов, имеющих скорости упорядоченного движения о, найдем напряженность поля
электронов, имеющих скорости упорядоченного движения о, найдем напряженность поля  создаваемую в данной точке одним движущимся электроном. Так как сила тока
создаваемую в данной точке одним движущимся электроном. Так как сила тока  заряд электрона),
заряд электрона),  то
то

2) напряженность магнитного поля в центре плоского кругового тока. В формуле (3.4)  будет одинаково для всех элементов
будет одинаково для всех элементов
тока, расположенных по окружности (рис. III.53),  , а все векторы
, а все векторы  направлены в одну сторону, поэтому вместо
направлены в одну сторону, поэтому вместо  векторного сложения можно произвести интегрирование:
векторного сложения можно произвести интегрирование:

Для «плоской катушки», имеющей  витков одинакового радиуса,
витков одинакового радиуса,

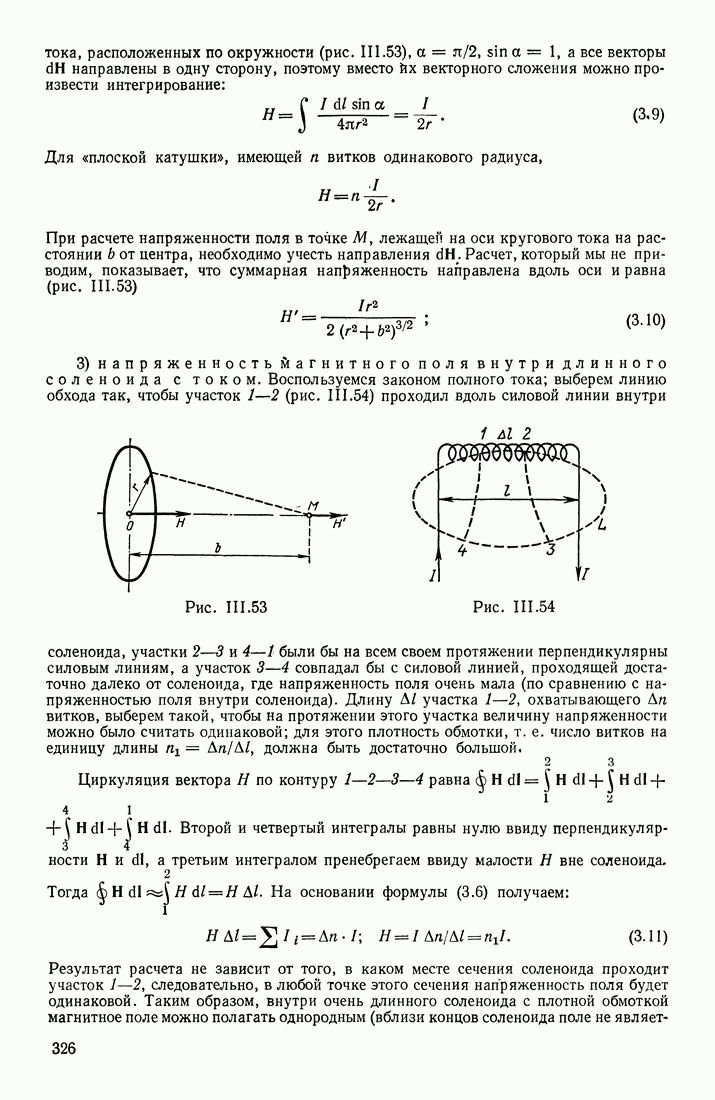
При расчете напряженности поля в точке  лежащей на оси кругового тока на расстоянии
лежащей на оси кругового тока на расстоянии  от центра, необходимо учесть направления
от центра, необходимо учесть направления  Расчет, который мы не приводим, показывает, что суммарная напряженность направлена вдоль оси и равна (рис. II 1.53)
Расчет, который мы не приводим, показывает, что суммарная напряженность направлена вдоль оси и равна (рис. II 1.53)

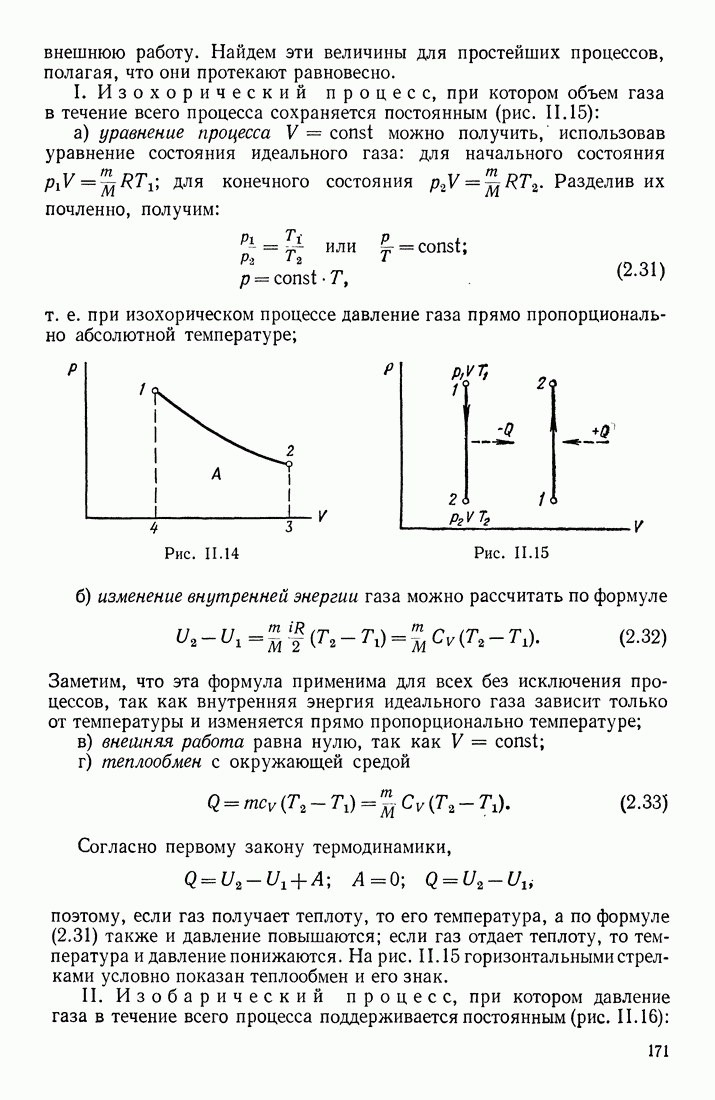
3) напряженность Магнитного поля внутри длинного соленоида с током. Воспользуемся законом полного тока; выберем линию обхода так, чтобы участок 1—2 (рис. II 1.54) проходил вдоль силовой линии внутри соленоида, участки 2—3 и 4—1 были бы на всем своем протяжении перпендикулярны силовым линиям, а участок 3—4 совпадал бы с силовой линией, проходящей достаточно далеко от соленоида, где напряженность поля очень мала (по сравнению с напряженностью поля внутри соленоида).

Рис. III.53

Рис. III.54
Длину  участка 1—2, охватывающего
участка 1—2, охватывающего  витков, выберем такой, чтобы на протяжении этого участка величину напряженности можно было считать одинаковой; для этого плотность обмотки, т. е. число витков на единицу длины
витков, выберем такой, чтобы на протяжении этого участка величину напряженности можно было считать одинаковой; для этого плотность обмотки, т. е. число витков на единицу длины  должна быть достаточно большой,
должна быть достаточно большой,
Циркуляция вектора  по контуру 1—2—3—4 равна
по контуру 1—2—3—4 равна  Второй и четвертый интегралы равны нулю ввиду перпендикулярности
Второй и четвертый интегралы равны нулю ввиду перпендикулярности  а третьим интегралом пренебрегаем ввиду малости
а третьим интегралом пренебрегаем ввиду малости  вне соленоида, Тогда
вне соленоида, Тогда  На основании формулы (3.6) получаем:
На основании формулы (3.6) получаем:

Результат расчета не зависит от того, в каком месте сечения соленоида проходит участок 1—2, следовательно, в любой точке этого сечения напряженность поля будет одинаковой. Таким образом, внутри очень длинного соленоида с плотной обмоткой магнитное поле можно полагать однородным (вблизи концов соленоида поле не является
однородным). Иногда в качестве линии обхода берут всю силовую линию соленоида и тогда формула

(где I — длина соленоида;  полное число витков) даст среднюю напряженность магнитного поля внутри соленоида;
полное число витков) даст среднюю напряженность магнитного поля внутри соленоида;
4) напряженность магнитного поля внутри толстых проводников с током. Для расчета напряженности на расстоянии  от оси проводника выберем линию обхода в виде окружности радиуса
от оси проводника выберем линию обхода в виде окружности радиуса  (рис. III.55) с центром на оси проводника. Если проводник прямолинейный и бесконечно длинный, то вдоль эгой линии обхода напряженность магнитного поля будет везде одинакова и в каждой точке направлена по касательной
(рис. III.55) с центром на оси проводника. Если проводник прямолинейный и бесконечно длинный, то вдоль эгой линии обхода напряженность магнитного поля будет везде одинакова и в каждой точке направлена по касательной  Тогда
Тогда  Эта линия охватывает площадь
Эта линия охватывает площадь  Если плотность тока в различных местах сечения проводника одинакова и равна
Если плотность тока в различных местах сечения проводника одинакова и равна  то суммарный ток, проходящий через
то суммарный ток, проходящий через  следовательно, охватываемый линией обхода, равен
следовательно, охватываемый линией обхода, равен  Тогда на основании формулы (3.6)
Тогда на основании формулы (3.6)

Так как  то
то

Таким образом, на оси проводника  напряженность поля
напряженность поля  а по мере удаления от оси растет прямо пропорционально расстоянию вплоть до боковой поверхности проводника. В точках, лежащих за пределами объема проводника, применение соотношения (3.6) приводит к формуле (3,1), согласно которой напряженность магнитного поля обратно пропорциональна расстоянию от оси проводника.
а по мере удаления от оси растет прямо пропорционально расстоянию вплоть до боковой поверхности проводника. В точках, лежащих за пределами объема проводника, применение соотношения (3.6) приводит к формуле (3,1), согласно которой напряженность магнитного поля обратно пропорциональна расстоянию от оси проводника.

Рис. III.55
Выше рассматривались магнитные поля вокруг потоков электрических зарядов — внутри проводников или в вакууме; пользуясь законом Био-Савара-Лапласа, можно рассчитать напряженность в любой точке их полей, т. е. найти функции  Однако магнитные поля создаются также и связанными зарядами (электронами и ионами), движущимися в атомах и молекулах вещества. Если электрон описывает замкнутую траекторию, то он создает вокруг себя магнитное поле, которое аналогично магнитному полю проводника такой же формы и размеров, как и траектория, с силой тока в нем
Однако магнитные поля создаются также и связанными зарядами (электронами и ионами), движущимися в атомах и молекулах вещества. Если электрон описывает замкнутую траекторию, то он создает вокруг себя магнитное поле, которое аналогично магнитному полю проводника такой же формы и размеров, как и траектория, с силой тока в нем  где
где  число оборотов в секунду по этой орбите
число оборотов в секунду по этой орбите  показывает, сколько раз в секунду электрон проходит через одну и ту же точку орбиты, поэтому не есть количество электричества, проходящее через эту точку в секунду, т. е. сила тока).
показывает, сколько раз в секунду электрон проходит через одну и ту же точку орбиты, поэтому не есть количество электричества, проходящее через эту точку в секунду, т. е. сила тока).
Токи, вызванные движением зарядов в атомах и молекулах вещества, называются молекулярными. Так как напряженности полей складываются векторно, то при беспорядочной ориентации молекулярных токов какого-нибудь тела общее поле вокруг этого тела будет практически отсутствовать. В телах, имеющих вокруг себя магнитное поле (постоянные магниты, электромагниты), молекулярные токи имеют некоторую упорядоченность; однако расчет общего магнитного поля этих токов затруднен, так как неизвестны ни силы этих токов, ни их расположение и ориентации в объеме тел; кроме
того, форма и размеры намагниченных тел могут быть различными.
Поэтому при изучении магнитного поля вокруг намагниченных тел прибегают к некоторым упрощенным приемам (см. § 25, 26).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть I. МЕХАНИКА
- § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ
- ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ
- § 2. ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ
- СИЛА. ДЕФОРМАЦИЯ. МАССА
- ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ
- ИМПУЛЬС. РАБОТА. МОЩНОСТЬ
- ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА
- ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ
- § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ
- § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
- ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ
- § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
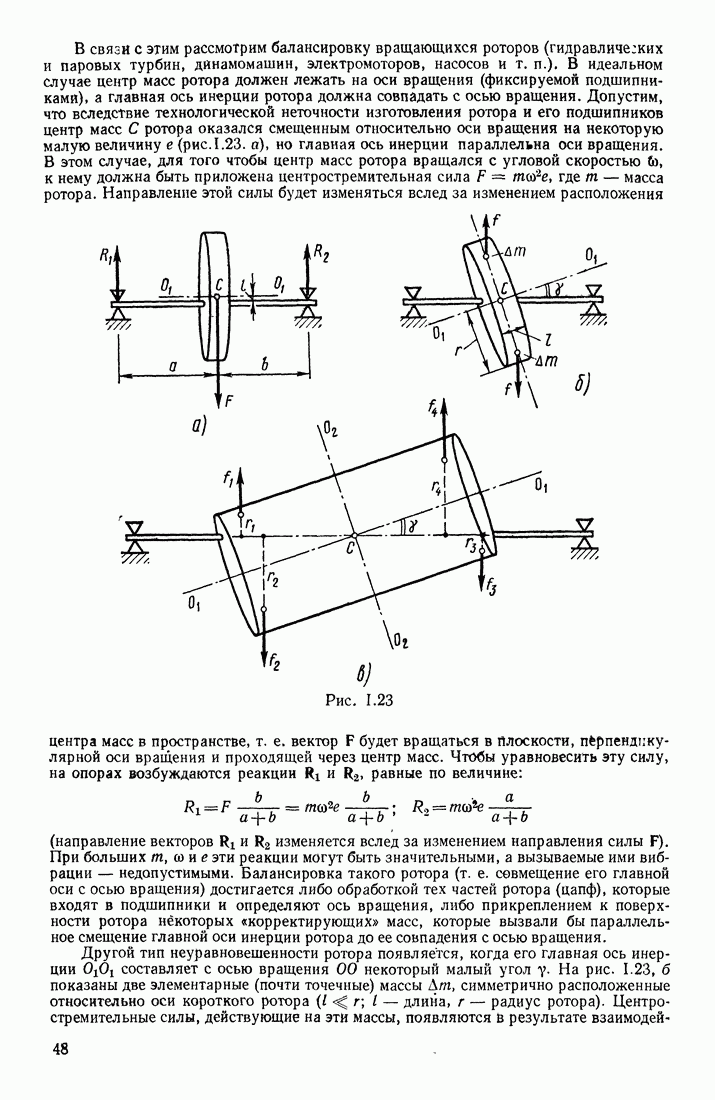
- § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ
- Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ
- § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
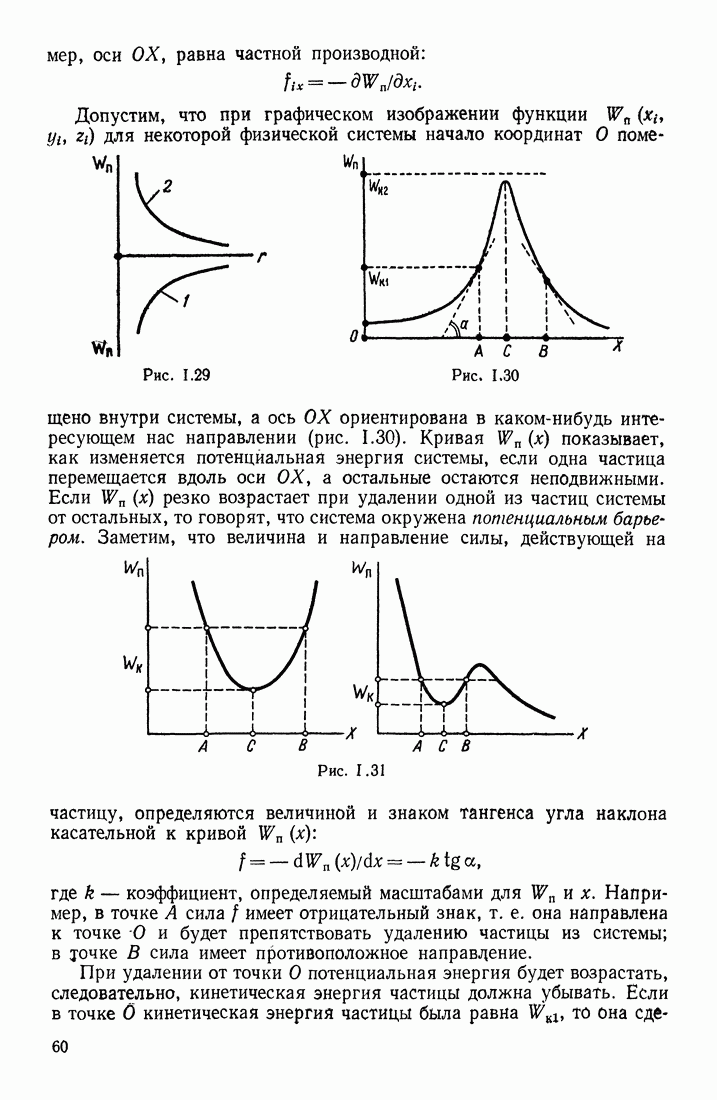
- § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ
- § 13. СТОЛКНОВЕНИЕ ШАРОВ
- § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ
- Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
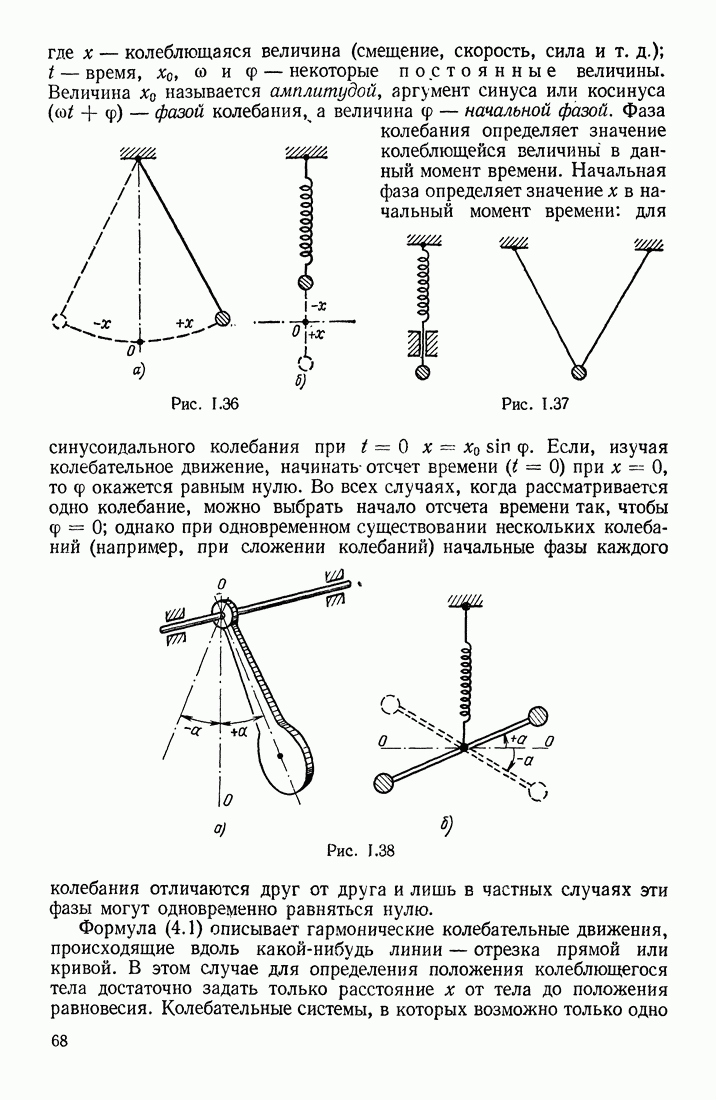
- § 15. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
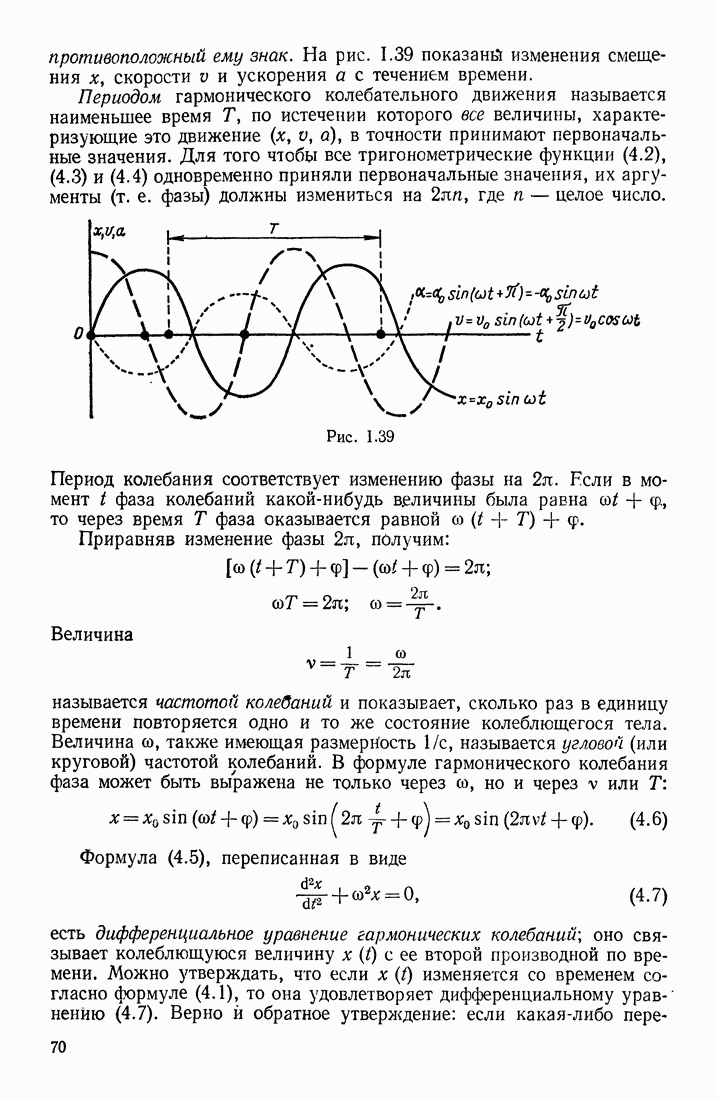
- § 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
- § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
- § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ
- § 21. АВТОКОЛЕБАНИЯ
- Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ
- § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
- § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
- ВОЛНА В УПРУГОЙ СРЕДЕ
- § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ
- § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ
- § 26. СТОЯЧИЕ ВОЛНЫ
- § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ЭФФЕКТ ДОПЛЕРА
- ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ
- § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ
- Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
- § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
- § 30. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ
- СЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ
- РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ
- Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ
- § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ
- § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ
- СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
- ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
- § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ
- § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ
- КРУГОВЫЕ ПРОЦЕССЫ
- § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ
- ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
- ЭНТРОПИЯ И ВЕРОЯТНОСТЬ
- Глава 2. ИДЕАЛЬНЫЙ ГАЗ
- § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ
- § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- ЦИКЛ КАРНО
- ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ
- ПАРАДОКС ГИББСА
- § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА
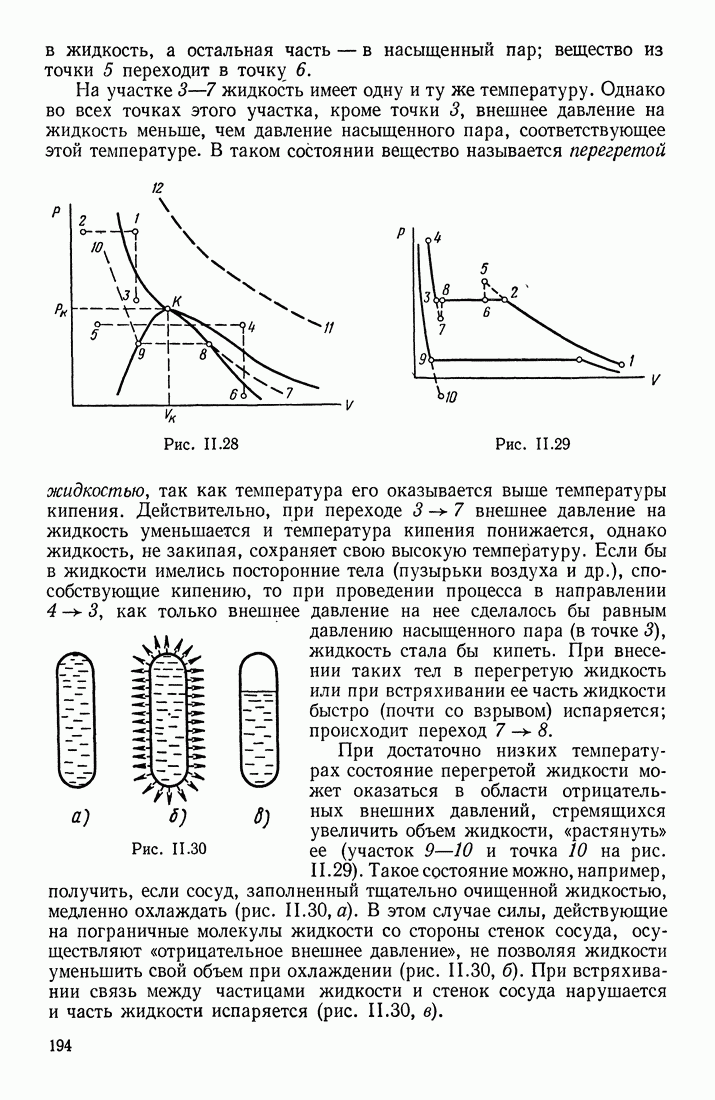
- § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ
- ПАР
- ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ
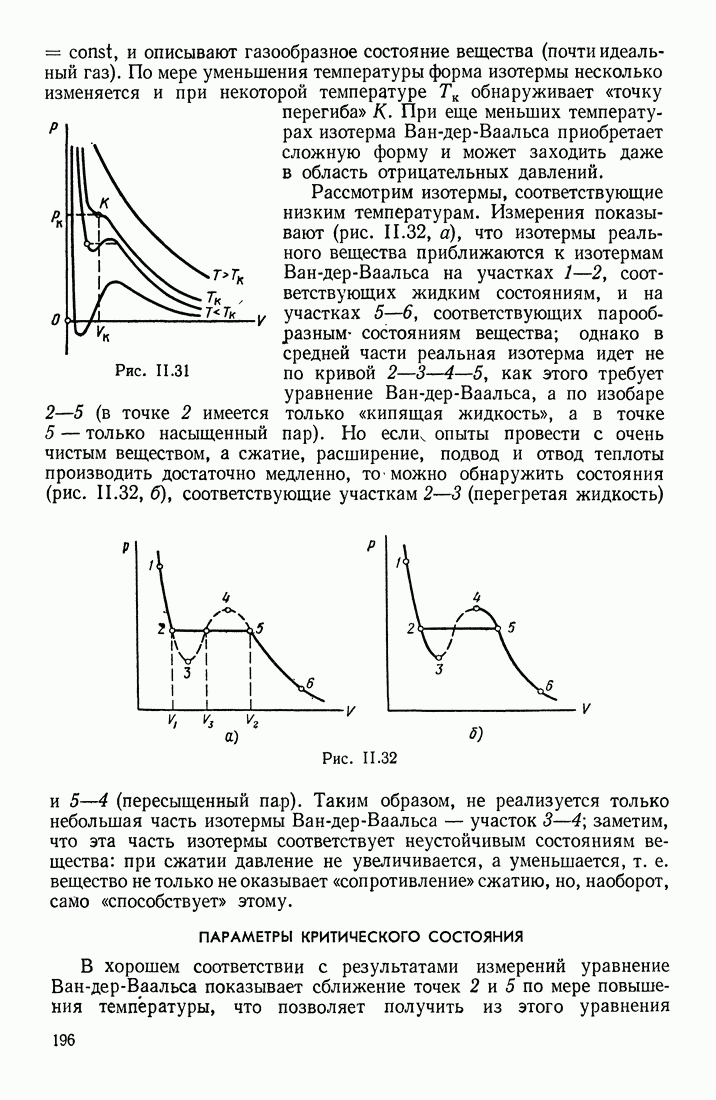
- § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
- ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- СВОЙСТВА ЖИДКОСТЕЙ
- МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ
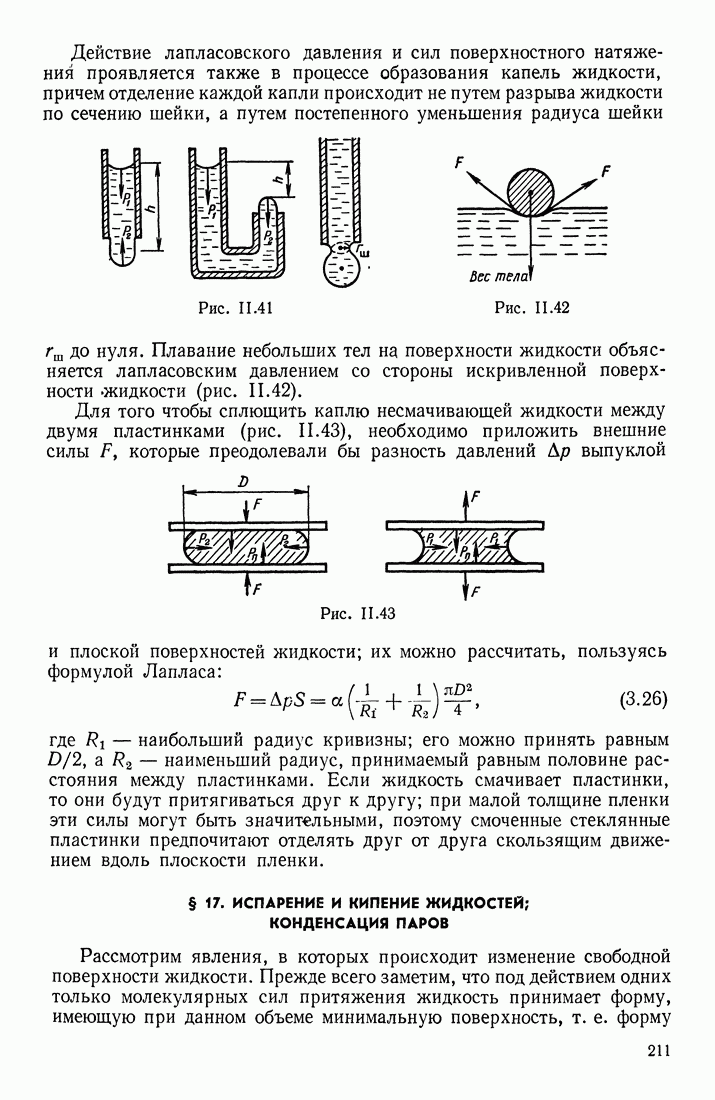
- § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ
- ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- КИПЕНИЕ
- УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ
- § 18. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ
- КРИСТАЛЛИЗАЦИЯ
- ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
- ТРОЙНАЯ ТОЧКА
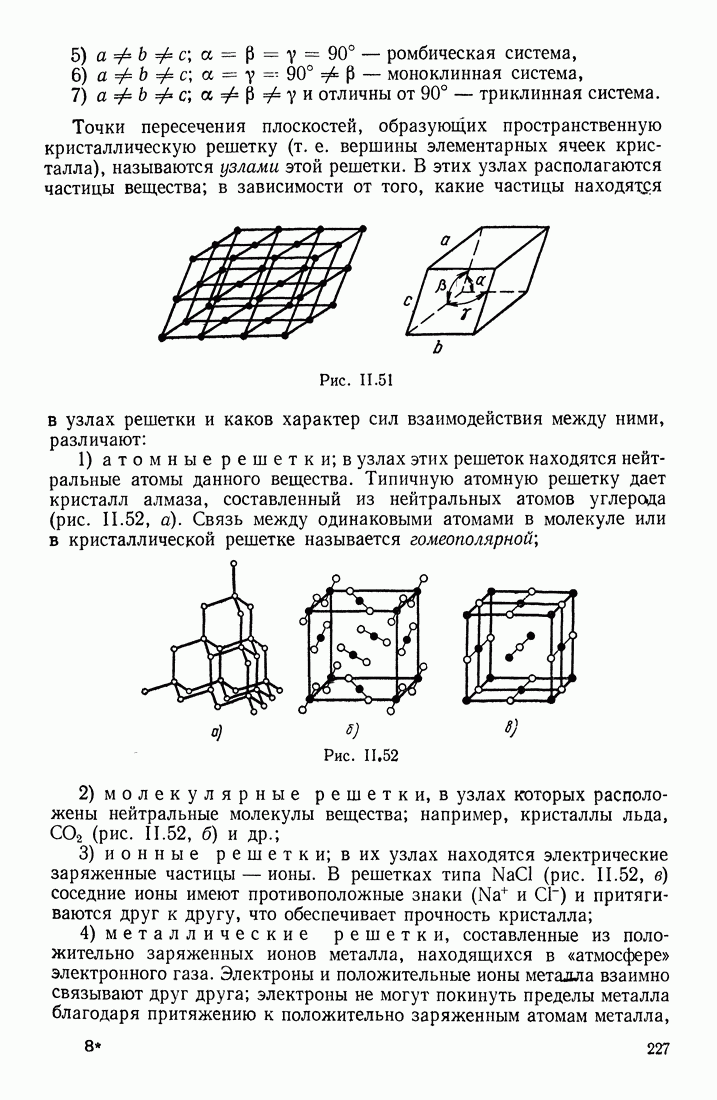
- § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- ТЕПЛОЕМКОСТЬ КРИСТАЛЛА
- ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ
- УПРУГОСТЬ И ПЛАСТИЧНОСТЬ
- ЖИДКИЕ КРИСТАЛЛЫ
- Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА
- § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА
- ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА
- ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ
- § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ
- § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- ЭЛЕКТРОСТРИКЦИЯ
- ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- СЕГНЕТОЭЛЕКТРИКИ
- ЭЛЕКТРЕТЫ
- § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
- Глава 2. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА
- § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ
- § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ
- § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА
- ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА
- ПРАВИЛА КИРХГОФА
- ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА
- § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
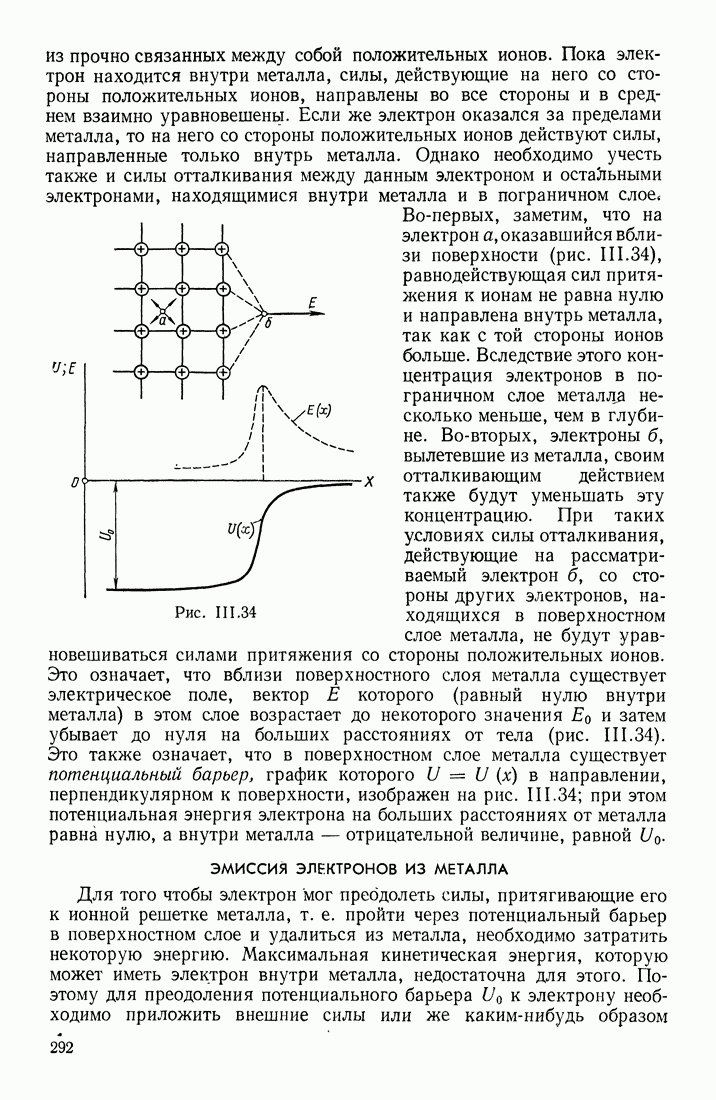
- ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ
- ЭФФЕКТ ПЕЛЬТЬЕ
- § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА
- § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ
- ДВИЖЕНИЕ ИОНОВ В ГАЗЕ
- ВИДЫ РАЗРЯДОВ В ГАЗАХ
- ПЛАЗМА
- § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ
- § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ
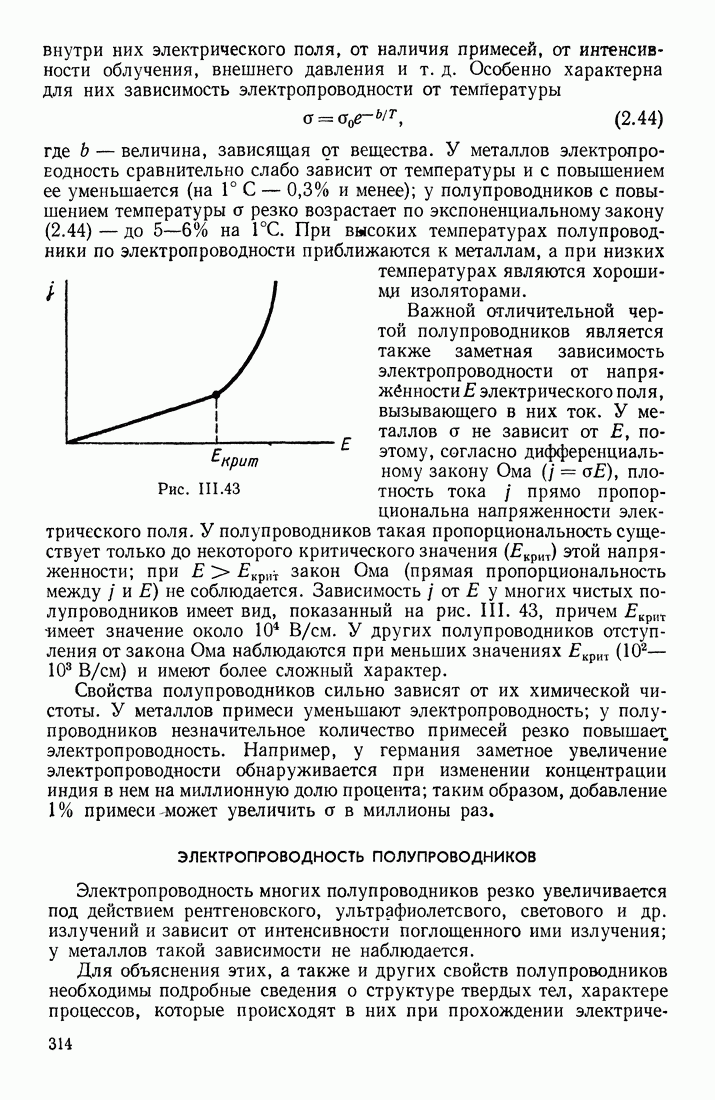
- ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
- ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ
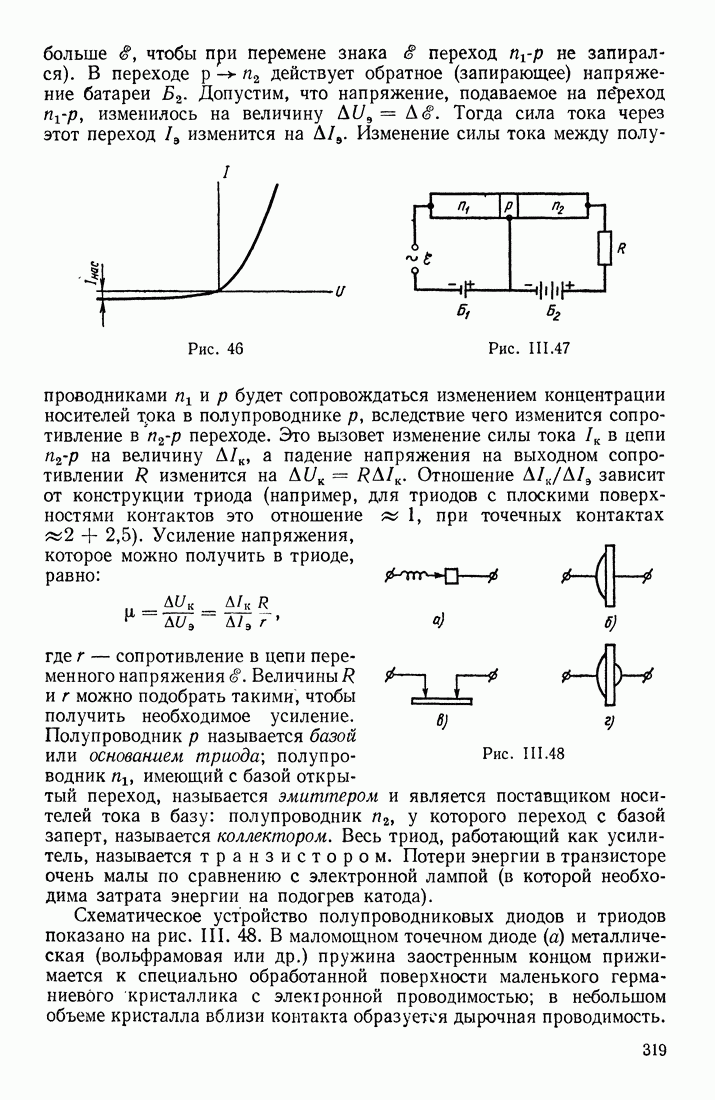
- ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ
- Глава 3. ЭЛЕКТРОМАГНЕТИЗМ
- § 17. МАГНИТНОЕ ПОЛЕ
- § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
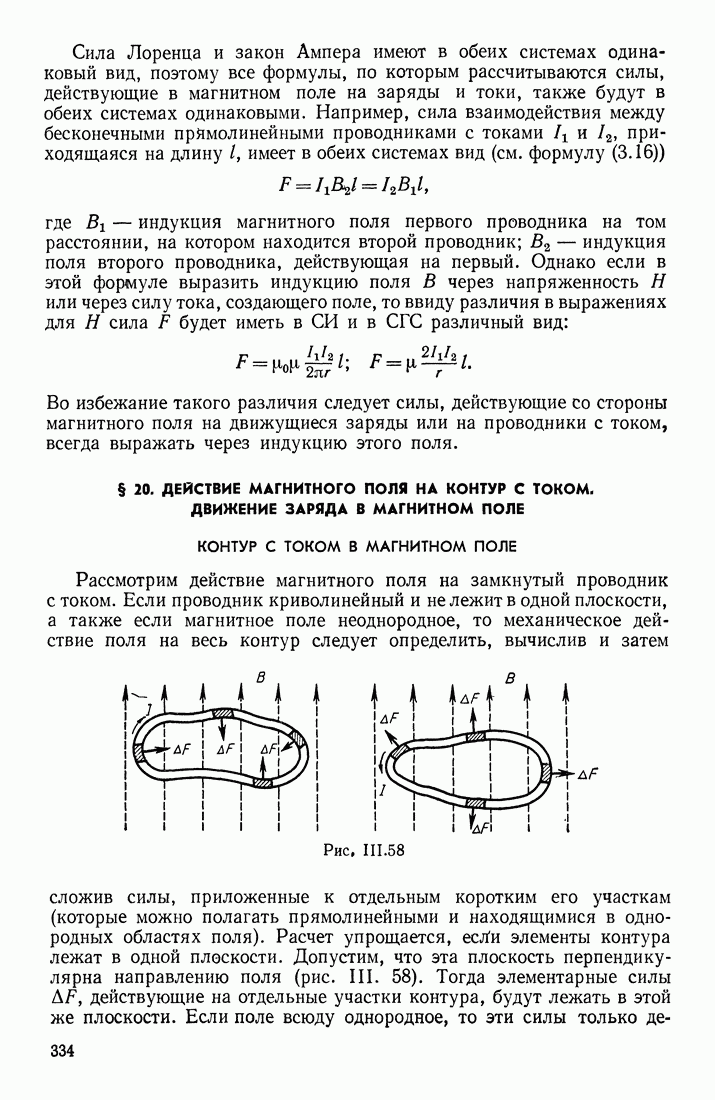
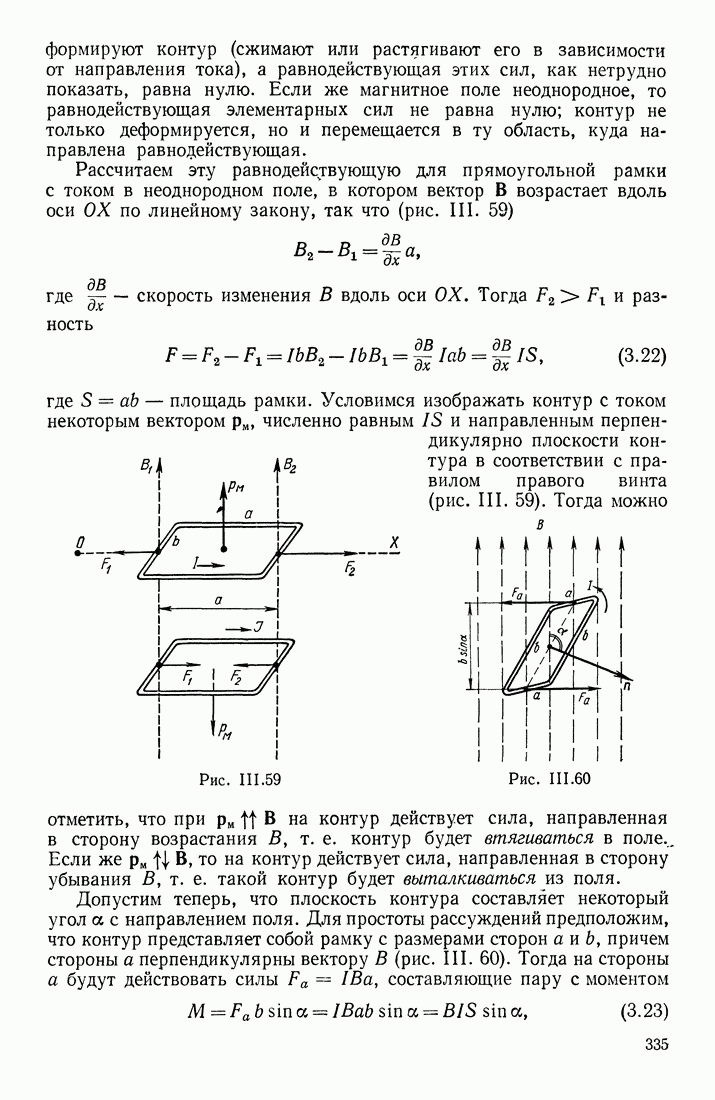
- § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ
- § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
- ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- ЭФФЕКТ ХОЛЛА
- § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
- § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ
- РАМКА В МАГНИТНОМ ПОЛЕ
- ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА
- § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ
- ИНДУКТИВНОСТЬ СОЛЕНОИДА
- РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ
- ВЗАИМНАЯ ИНДУКЦИЯ
- ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
- ТОКИ ФУКО
- § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА
- § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА
- НАМАГНИЧЕННОСТЬ
- МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ
- ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
- ФЕРРОМАГНЕТИКИ
- ПАРАМАГНИТНЫЙ РЕЗОНАНС
- § 26. МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ
- Глава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
- § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ
- ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ
- Часть IV. ОПТИКА И ФИЗИКА АТОМА
- § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА
- СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ
- ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
- ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ
- § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА
- § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА
- СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД
- СВЕТ И ЦВЕТ
- ДИСПЕРСИЯ СВЕТА
- РАССЕЯНИЕ СВЕТА
- § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ
- § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ
- ДИФРАКЦИОННАЯ РЕШЕТКА
- § 6. РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
- ПОЛЯРИЗОВАННЫЙ СВЕТ
- СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ
- ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ
- § 8. ПОНЯТИЕ О ГОЛОГРАФИИ
- Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
- § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА
- ОПЫТ ФРАНКА И ГЕРЦА
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- ТЕОРИЯ АТОМА ВОДОРОДА
- § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- ЭФФЕКТ КОМПТОНА
- ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- ФОРМУЛА ДЕ БРОЙЛЯ
- ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
- УРАВНЕНИЕ ШРЕДИНГЕРА
- РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА
- СВОБОДНЫЙ ЭЛЕКТРОН
- ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
- ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
- АТОМ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА
- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
- РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ
- ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ
- ТЕМПЕРАТУРА
- ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ
- РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
- § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ
- ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ
- ИОННАЯ СВЯЗЬ
- РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ
- Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ
- § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ
- СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ
- КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
- ФОРМУЛА ПЛАНКА
- ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА
- ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ
- ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР
- ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
- ДОЗИМЕТРИЯ
- § 17. ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ
- ПРИРОДА ЛЮМИНЕСЦЕНЦИИ
- ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ
- ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ
- ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ
- § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ
- ЛАЗЕРЫ
- ПРЕИМУЩЕСТВА ЛАЗЕРОВ
- ПРИМЕНЕНИЕ ЛАЗЕРОВ
- Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР
- РАДИОАКТИВНОСТЬ
- ВНУТРИЯДЕРНЫЕ СИЛЫ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
- МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА
- МАГНИТНЫЕ МОМЕНТЫ ЯДЕР
- ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР
- СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ
- § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР
- КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА
- ОБОЛОЧЕЧНАЯ МОДЕЛЬ
- ОБОБЩЕННАЯ МОДЕЛЬ
- ОПТИЧЕСКАЯ МОДЕЛЬ
- УСЛОВИЕ СТАБИЛЬНОСТИ
- § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ
- СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
- БЕТА-РАСПАД ЯДЕР
- ЭНЕРГИЯ СВЯЗИ ЯДЕР
- ИЗОМЕРЫ
- § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ
- ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ
- ЯДЕРНЫЕ РЕАКТОРЫ
- ЯДЕРНЫЙ СИНТЕЗ
- § 23. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- РАСПАДЫ ЧАСТИЦ
- ВИДЫ ВЗАИМОДЕЙСТВИЯ
- ЗАКЛЮЧЕНИЕ
- § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ
- § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ
- § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ
- § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ
- § 6. О ДУАЛИЗМЕ В ФИЗИКЕ