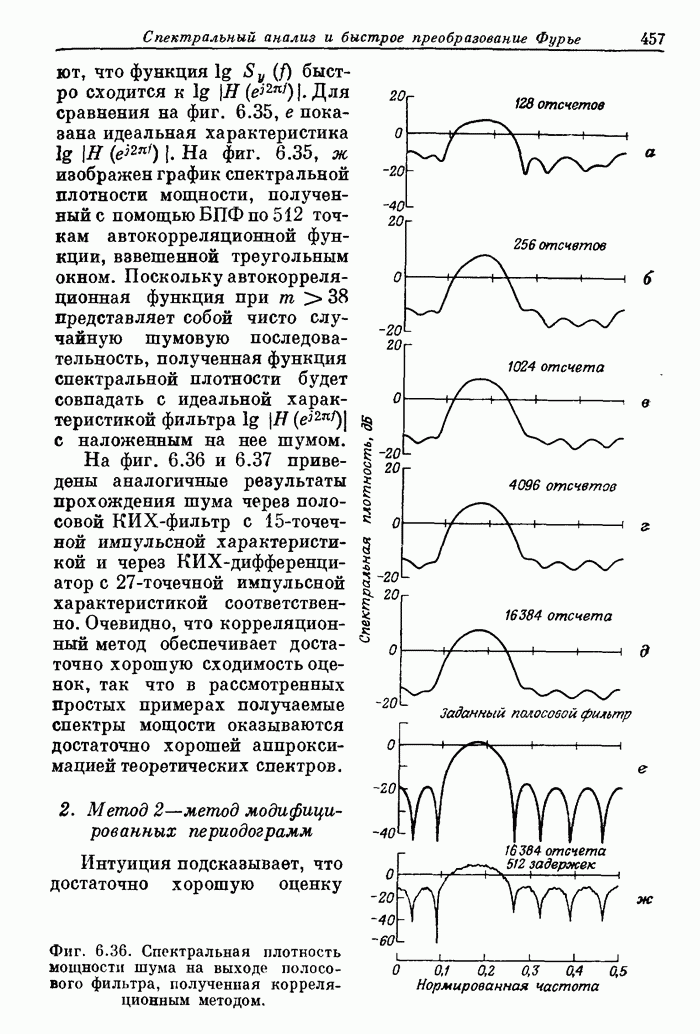
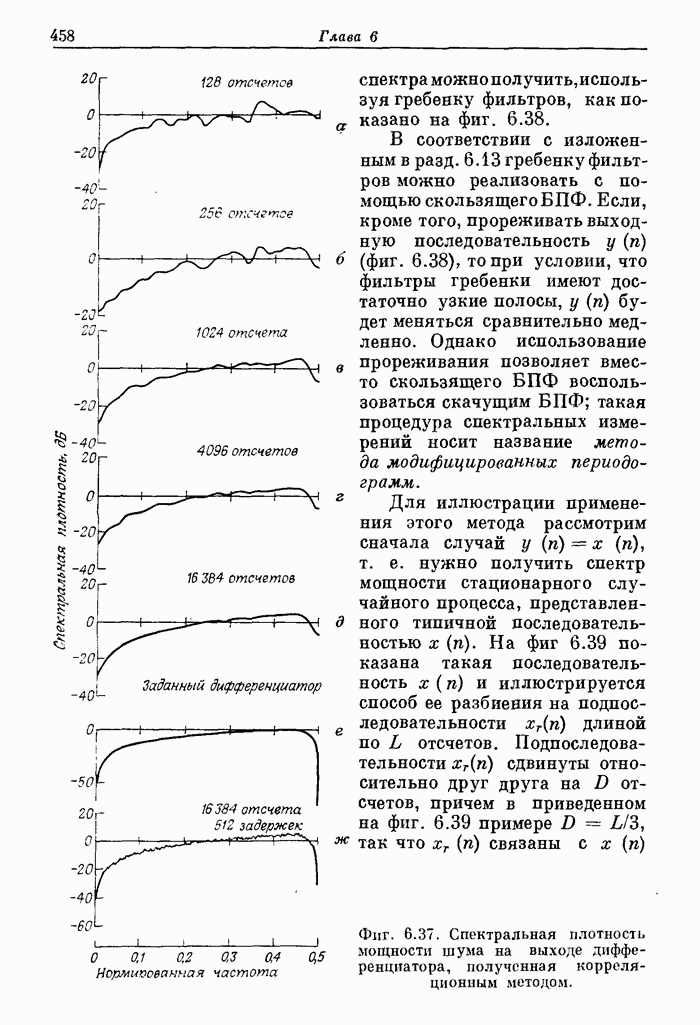
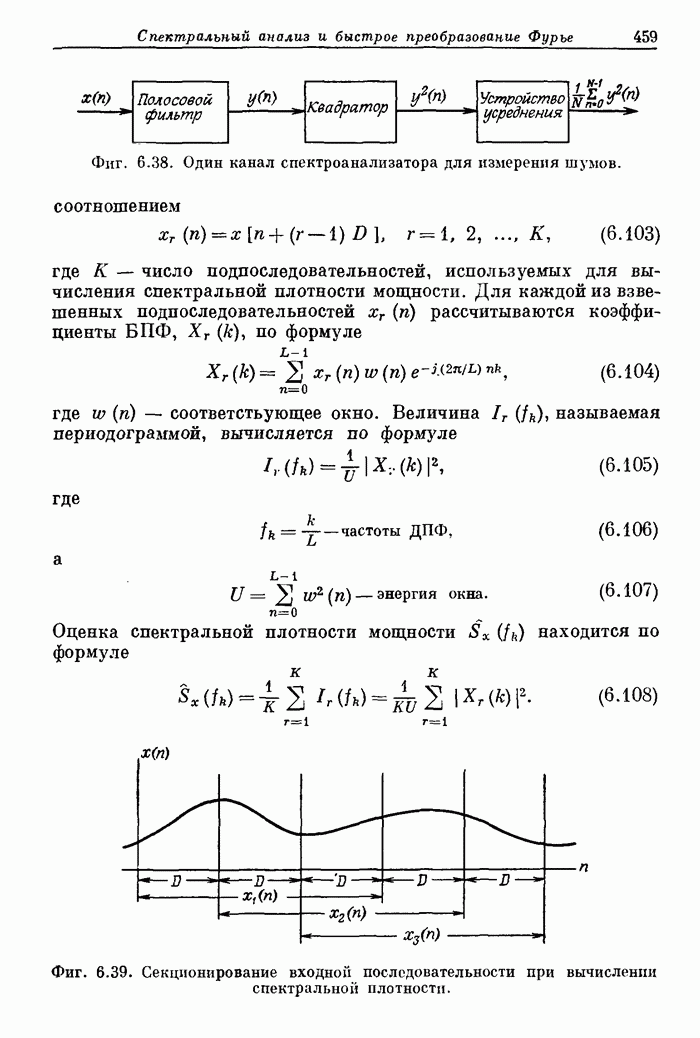
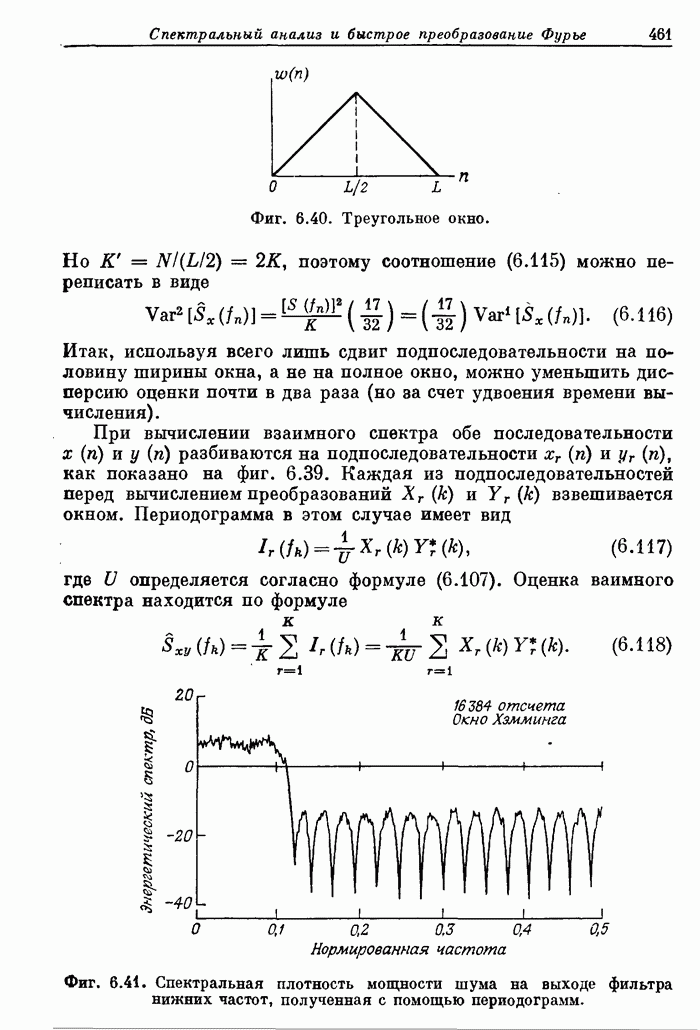
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.7. Делители и устройства с плавающей запятой
В системах цифровой обработки сигналов, как и в других вычислительных системах, основной упор делается на достижение быстродействия одних и тех же узлов. Самыми важными из них, несомненно, являются сумматоры и умножители, рассмотренные в предыдущих разделах. Перейдем теперь к изложению методов построения быстродействующих делителей, а также сумматоров с плавающей запятой. Дело в том, что алгоритмы цифровой фильтрации и БПФ используются в задачах все большей сложности, поэтому возникает необходимость представлять себе, как производятся операции, отличные от сложения и умножения. Оказывается, что для построения всех устройств, рассматриваемых в настоящем разделе, можно с успехом использовать идею нетактируемых матриц, достигая при этом большого быстродействия при умеренных размерах устройства. Можно ожидать, что уже в ближайшем будущем прогресс технологии производства интегральных схем лишь подтвердит справедливость этих утверждений.
1. Четырехквадрантный матричный делитель
Рассмотрим четырехквадрантный делитель, составленный из комбинационной матрицы суммирующих и вычитающих логических элементов. Будем считать, что на вход схемы поступают 24-разрядное делимое (числитель) и 12-разрядный делитель (знаменатель), оба в дополнительном коде, а на выходе образуются 12-разрядные частное и остаток. Можно рассматривать случаи, когда делитель и делимое являются произвольными целыми или дробными числами или константами. Будем считать, что входные числа — правильные дроби с запятой, расположенной непосредственно правее знакового разряда; это будет учтено при построении логики индикации переполнения.
В основу работы матричной схемы положен метод деления без восстановления остатка. С целью упрощения описания этого метода примем сначала, что делимое и делитель — положительные правильные дроби, причем делитель больше делимого или равен ему. При этих условиях частное также будет, очевидно, положительной правильной дробью. Для получения первого значащего разряда частного вычисляется частичное делимое как разность между делимым и пробным делителем, равным половине фактического. Если частичное делимое положительно, то в качестве разряда частного принимается единица. Если же оно отрицательно, т. е. если пробный делитель «не умещается» в делимом, то искомый разряд равен нулю. При обычном делении (с восстановлением остатка) в этом случае нужно сложить пробный делитель с частичным делимым для восстановления исходного делимого и попытаться вычесть новый пробный делитель. При делении без восстановления остатка используется тот факт, что каждый последующий пробный делитель в два раза меньше предыдущего. Поэтому сложение пробного делителя (т. е. операция восстановления) с последующим вычитанием его половины всегда будет совпадать с простым добавлением половины пробного делителя. Таким образом, если первый значащий разряд частного равен 1, то предыдущее значение пробного делителя делится пополам и затем вычитается из частичного делимого для получения следующего разряда частного. Если же первый разряд частного равен нулю, то пробный делитель делится пополам и затем добавляется к частичному делимому для получения следующего разряда частного. Эта процедура продолжается до тех пор, пока не будет получено требуемое количество разрядов частного. Преимущества этого алгоритма отчетливо выявляются при реализации его в виде нетактируемой матрицы. В нем нет обратных связей и шагов «назад», процесс протекает без всяких условий от начала и до конца.
Практическая реализация этого алгоритма для четырехквадрантного случая (когда приходится учитывать все возможные комбинации знаков делителя и делимого) требует некоторых дополнительных манипуляций. Основой матричного деления является последовательность этапов сложения и вычитания. На каждом этапе в зависимости от знаков частичного делимого и самого делителя производится либо сложение, либо вычитание соответствующего делителя из соответствующего частичного делимого. На матрицу может поступать любая комбинация знаков делителя и делимого, но в конце при определенных комбинациях необходима коррекция разрядов частного.
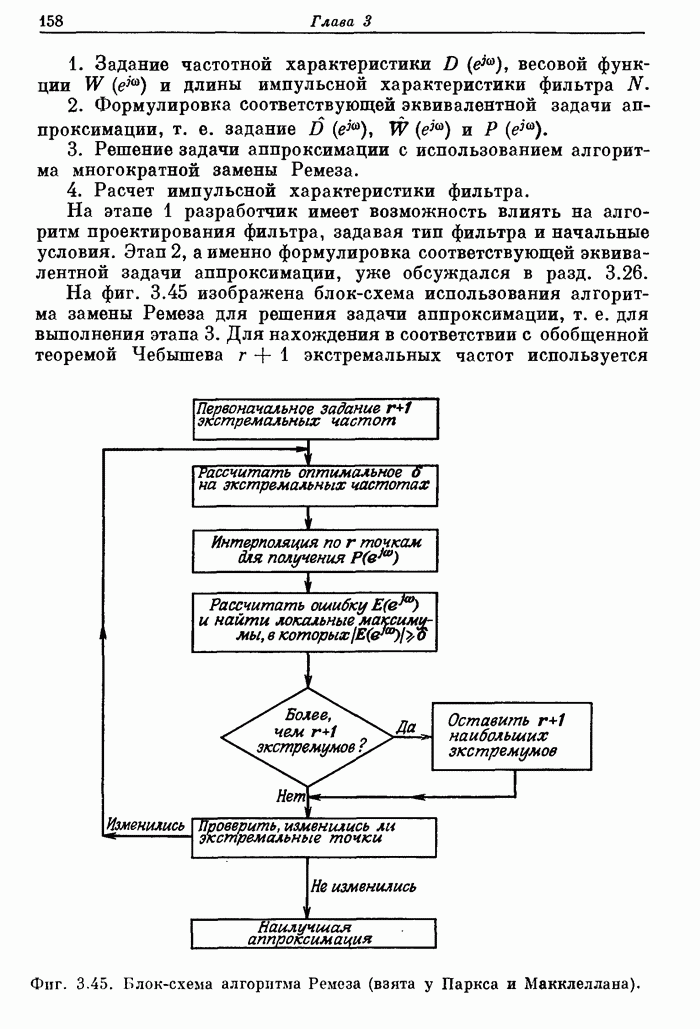
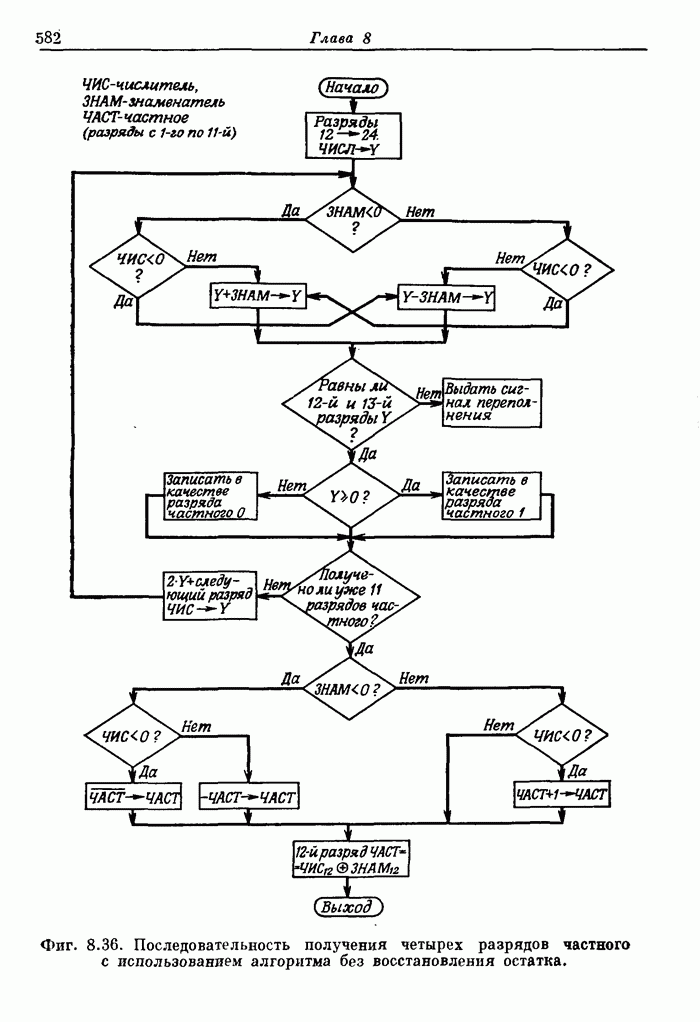
На верхней большей части блок-схемы рассматриваемого алгоритма (фиг. 8.36) представлена процедура получения разрядов частного, а на нижней части показан процесс заключительной коррекции. Вычисление разрядов частного на каждом этапе производится но следующим правилам:
1. Если текущее частичное делимое положительно, в соответствующий разряд частного записывается 1. В противном случае записывается 0.
2.
Если делитель ![]() текущее
частичное делимое имеют одинаковые знаки, следующий пробный делитель нужно
вычесть.
текущее
частичное делимое имеют одинаковые знаки, следующий пробный делитель нужно
вычесть.
3. Если делитель и текущее частичное делимое имеют разные знаки, следующий пробный делитель следует добавить.

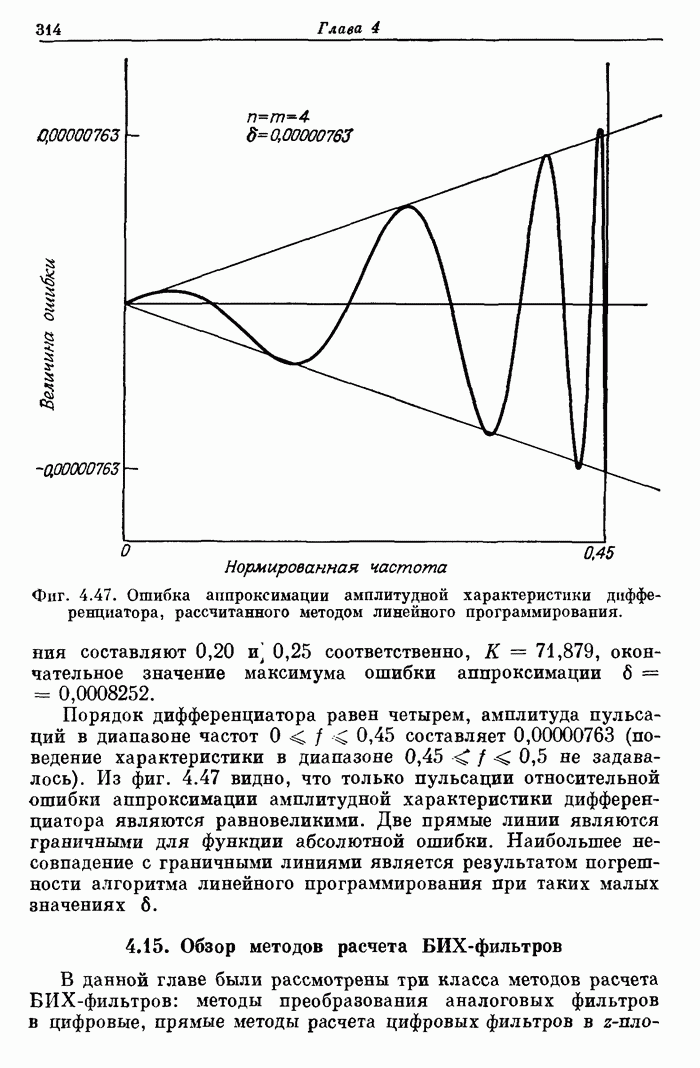
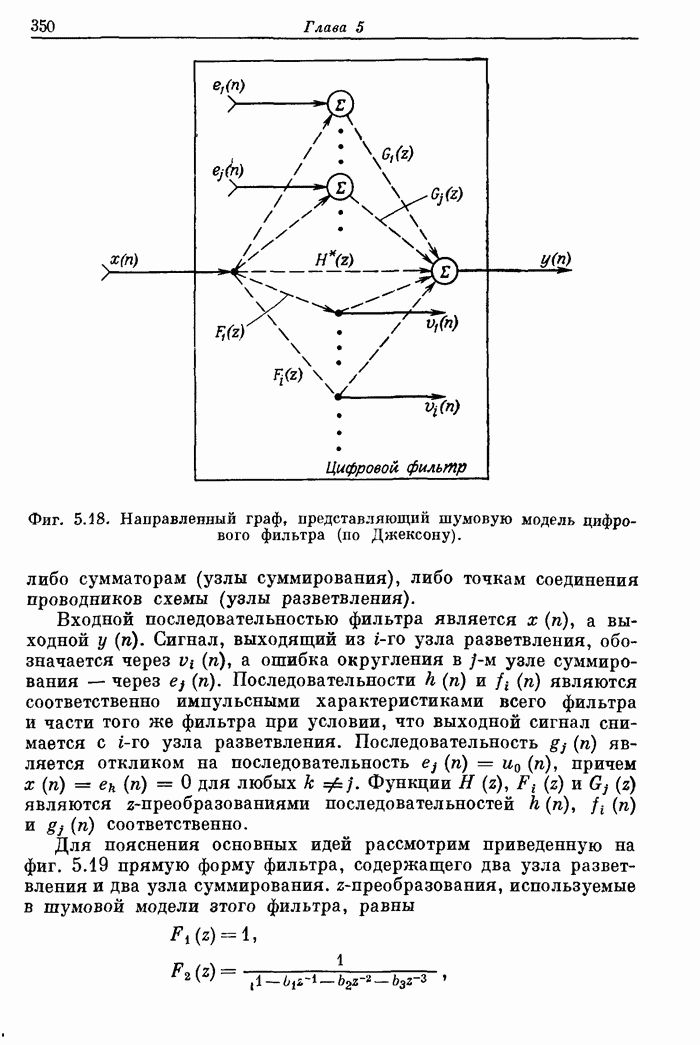
Фиг. 8.36. Последовательность получения четырех разрядов частного с использованием алгоритма без восстановления остатка.
Из приведенных выше правил вытекают два интересных следствия. Во-первых, если делимое положительно, то независимо от знака делителя частное будет правильным. Во-вторых, если делимое отрицательно, то независимо от знака делителя будет получен обратный код частного. Правильное значение частного в дополнительном коде получается после дополнительной коррекции, основанной на учете знаков операндов. Предположим, например, что делитель положительный, а делимое отрицательное. В этом случае отрицательное частное будет получено в обратном коде. Поэтому для перехода к дополнительному коду к результату необходимо добавить 1. Предположим теперь, что и делитель и делимое отрицательны. Ясно, что частное должно быть положительным. Но ответ будет получен в обратном коде, поэтому необходима простая инверсия разрядов частного. Во всех случаях коррекцию результата можно производить с помощью дополнительного этапа сложения (вычитания) на выходе матрицы. Лишь в одном случае коррекция не нужна — когда и делитель и делимое положительные. Коррекция осуществляется по следующим правилам.
1. Если и делитель и делимое положительные, присвоить знаковому разряду частного значение 0 и ничего не делать со значащими разрядами.
2. Если и делитель и делимое отрицательные, присвоить знаковому разряду частного значение 0 и проинвертировать значащие разряды.
3. Если делитель положительный, а делимое отрицательное, присвоить знаковому разряду значение 1 и добавить 1 в младший разряд частного.
4. Если делитель отрицательный, а делимое положительное, присвоить знаковому разряду значение 1, проинвертировать значащие разряды частного и добавить к нему 1.
В
принципе при ![]() -разрядном
делителе (включая знаковый разряд) для представления всех сумм и разностей в
матричной схеме достаточно
-разрядном
делителе (включая знаковый разряд) для представления всех сумм и разностей в
матричной схеме достаточно ![]() разрядов. Разность (или сумма) между
любым частичным делимым и его пробным делителем также может быть представлена
не более чем
разрядов. Разность (или сумма) между
любым частичным делимым и его пробным делителем также может быть представлена
не более чем ![]() разрядами (включая знак). Таким
образом, для рассматриваемого случая (фиг. 8.36) оба разряда, 12-й и
13-й, отведенные во всех частичных делимых под знаковые, обязательно будут
одинаковыми. В противном случае выдается сигнал переполнения. С точки зрения
дробных операндов этот сигнал означает, что делимое по величине больше
делителя. Такой режим запрещен, так как в этом случае частное превысит 1 и его,
следовательно, нельзя представить правильной дробью, у которой все значащие
разряды находятся справа от запятой. Это обстоятельство и фиксируется сигналом
переполнения.
разрядами (включая знак). Таким
образом, для рассматриваемого случая (фиг. 8.36) оба разряда, 12-й и
13-й, отведенные во всех частичных делимых под знаковые, обязательно будут
одинаковыми. В противном случае выдается сигнал переполнения. С точки зрения
дробных операндов этот сигнал означает, что делимое по величине больше
делителя. Такой режим запрещен, так как в этом случае частное превысит 1 и его,
следовательно, нельзя представить правильной дробью, у которой все значащие
разряды находятся справа от запятой. Это обстоятельство и фиксируется сигналом
переполнения.

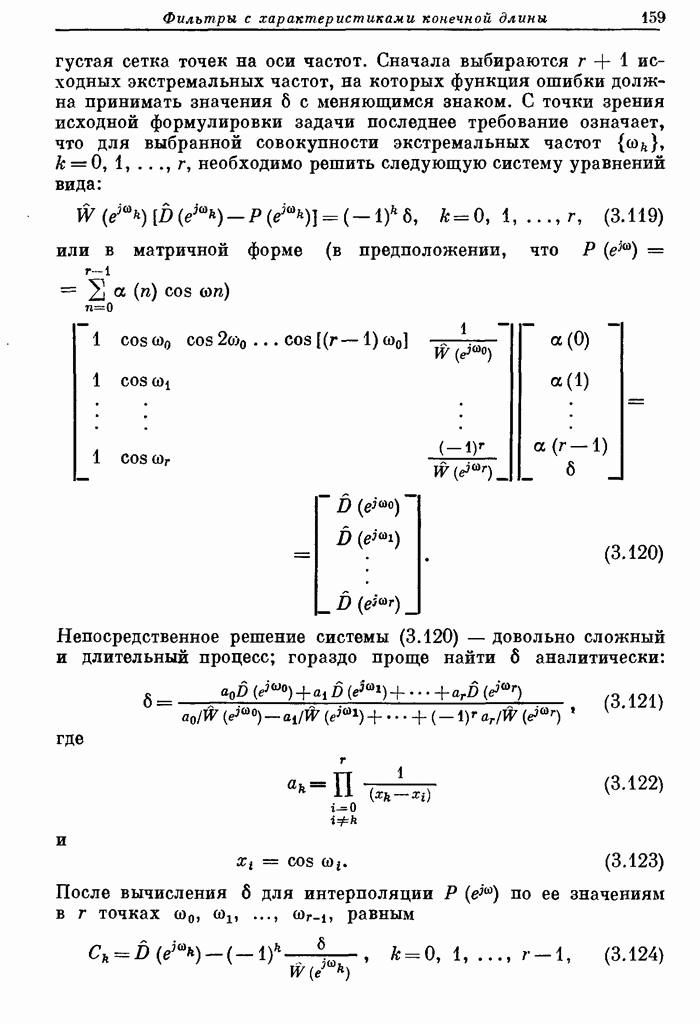
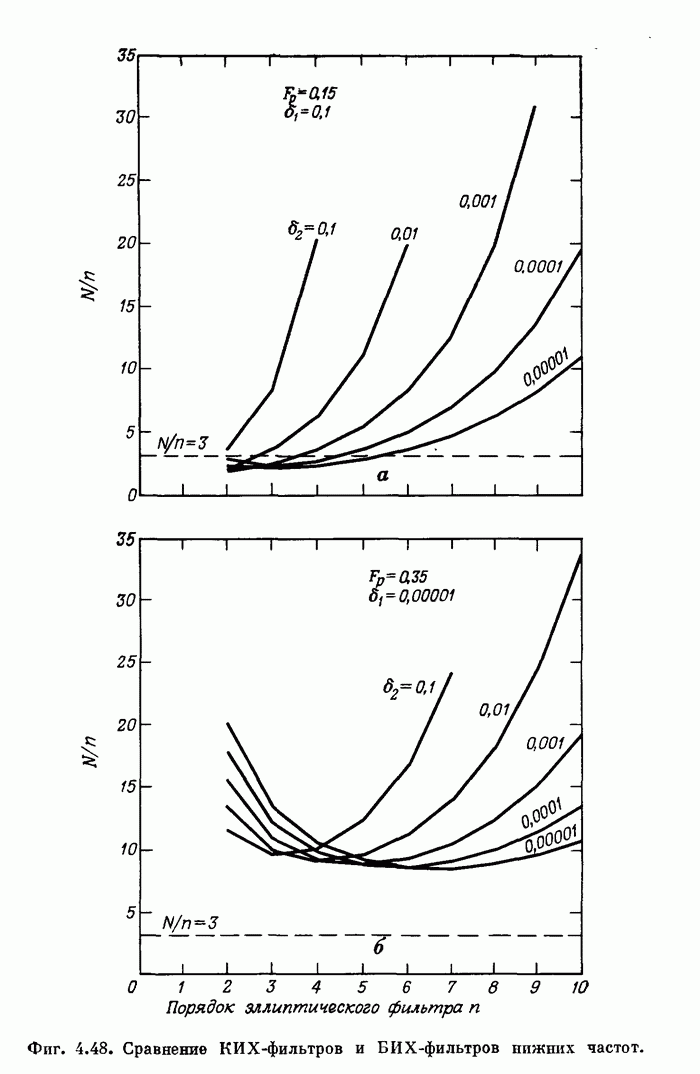
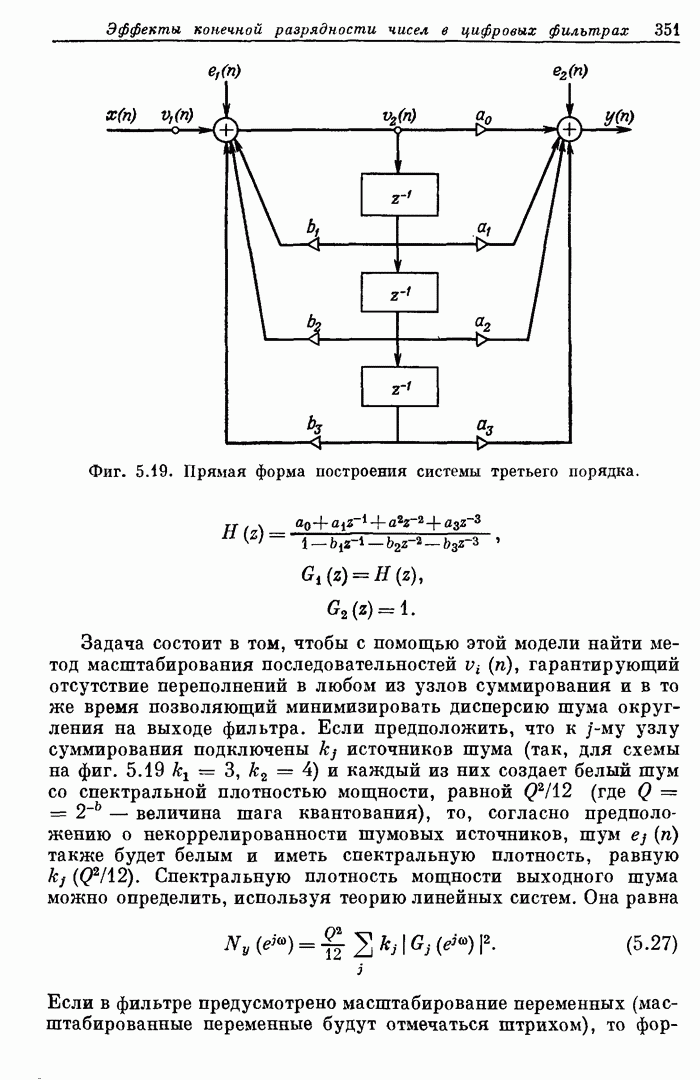
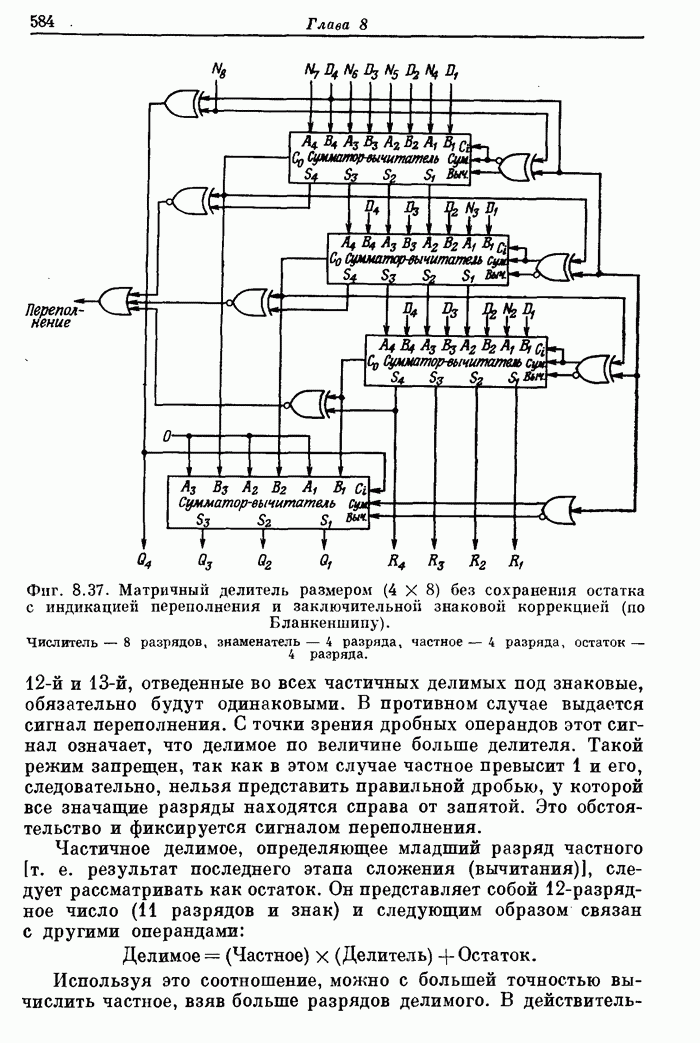
Фиг. 8.37. Матричный делитель размером (4х8) без сохранения остатка с индикацией переполнения и заключительной знаковой коррекцией (по Бланкеншипу). Числитель — 8 разрядов, знаменатель — 4 разряда, частное — 4 разряда, остаток — 4 разряда.
Частичное делимое, определяющее младший разряд частного [т. е. результат последнего этапа сложения (вычитания)], следует рассматривать как остаток. Он представляет собой 12-разрядное число (11 разрядов и знак) и следующим образом связан с другими операндами:
Делимое = (Частное) х (Делитель) + Остаток.
Используя это соотношение, можно с большей точностью вычислить частное, взяв больше разрядов делимого. В действительности получение уточненного частного — довольно сложная операция, для выполнения которой необходимо знание величины остатка и его знака.
На фиг. 8.37 показан пример построения
устройства для деления восьмиразрядного делимого на четырехразрядный делитель
с четырехразрядными частным и остатком на выходе. Простым наращиванием его
можно довести до 24/12 разрядов. Представленные на схеме сумматоры-вычитатели
могут быть построены на основе двухнаносекундной четырехразрядной ИС ЭСЛ типа МС10181
(арифметико-логическое устройство). Эта ИС в зависимости от управляющего
сигнала может быть запрограммирована или на сложение, или на вычитание.
Вычитание осуществляется путем изменения знака числа на входе В с
последующим суммированием. Фактически для выполнения этой операции требуется
проинвертировать разряды ![]() и добавить единицу. Инверсия
внутри ИС предусмотрена, но для добавления единицы необходимо во время вычитания
подать сигнал на вход
и добавить единицу. Инверсия
внутри ИС предусмотрена, но для добавления единицы необходимо во время вычитания
подать сигнал на вход ![]() (вход переноса в младший разряд).
(вход переноса в младший разряд).
В соответствии со сделанными ранее
выводами следует ожидать, что для выполнения всех сложений (вычитаний)
потребуется пять разрядов, так как делитель имеет четыре разряда. Однако можно
показать, что ![]() -й
разряд легко получить, используя выход переноса
-й
разряд легко получить, используя выход переноса ![]() -го разряда и немного изменив правила.
Сформулируем коротко эти упрощенные правила:
-го разряда и немного изменив правила.
Сформулируем коротко эти упрощенные правила:
1. Первый этап. Если знаки делителя и делимого не совпадают, следует производить сложение, если совпадают — вычитание.
2.
Все последующие этапы. Если выходной сигнал переноса (![]() )
) ![]() -го разряда предыдущего
сумматора-вычитателя равен 1, нужно записать 1 в разряд частного. Кроме того,
если выходной сигнал переноса отличается от знакового разряда делителя, то на
данном этапе следует произвести вычитание, а в противном случае — сложение.
-го разряда предыдущего
сумматора-вычитателя равен 1, нужно записать 1 в разряд частного. Кроме того,
если выходной сигнал переноса отличается от знакового разряда делителя, то на
данном этапе следует произвести вычитание, а в противном случае — сложение.
3.
Переполнение. Если на любом этапе выходной сигнал переноса ![]() -го разряда совпадает с
выходным сигналом суммы этого же
-го разряда совпадает с
выходным сигналом суммы этого же ![]() -го разряда, сформировать сигнал
переполнения.
-го разряда, сформировать сигнал
переполнения.
4. Заключительная коррекция. Это правило удобнее всего сформулировать в виде следующей таблицы:
|
Знак Делителя ( |
Знак Делимого ( |
Коррекция частного |
Знак частности ( |
Сложение |
Вычитание |
Вход Перехода ( |
|
+ |
+ |
Отсутствует |
+ |
V |
|
|
|
+ |
- |
|
- |
V |
|
V |
|
- |
+ |
|
- |
|
V |
V |
|
- |
- |
|
+ |
|
V |
|
Логические уравнения имеют вид

В
соответствии с этими уравнениями в рассматриваемой схеме осуществляется
управление на этапе заключительной коррекции. Отметим, что входное число ![]() в схеме
коррекции всегда равно нулю.
в схеме
коррекции всегда равно нулю.
Схема 24/12-разрядного делителя состоит из 12 12-разрядных каскадов. На первых 11 формируются разряды частного, на последнем выполняется коррекция. Каждый каскад состоит из трех ИС МС10181, включенных по схеме образования ускоренного переноса на 9 разрядов. Таким образом, всего требуется 36 корпусов МС10181. На каждом каскаде все небходимые разряды частичного делимого образуются за 13 нс, поэтому вся операция деления занимает 12x13 = 156 нс. Количество корпусов, необходимых для управления и индикации переполнения, а также для распределения данных, незначительно. Следовательно, этот делитель требует меньшего количества корпусов, чем умножитель двенадцатиразрядных чисел, построенный на той же логической серии.
2. Цифровые устройства с плавающей запятой
Весьма часто динамический диапазон разрабатываемых систем имеет важное значение. Его можно значительно расширить, используя представление чисел с плавающей запятой. Это представление обычно применяется в задачах обработки больших числовых массивов, например при обращении матриц большого размера и при решении задач линейного программирования, т. е. когда значения чисел, получающихся в процессе вычислений, могут меняться в широких пределах.
Есть все основания для того, чтобы
использовать представление чисел с плавающей запятой при создании цифровых
фильтров и блоков БПФ. Рекурсивные цифровые фильтры с полюсами, расположенными
вблизи единичной окружности, обладают большим усилением на частотах вблизи
полюсов, поэтому уровень выходного сигнала может сильно меняться в зависимости
от входной частоты. На каждом этапе БПФ уровень сигнала может увеличиться
вдвое, поэтому при ![]() -точечном БПФ возможно усиление в
-точечном БПФ возможно усиление в ![]() раз.
раз.
Использование плавающей запятой при фильтрации и БПФ, по-видимому, не создает дополнительных трудностей, связанных с округлением, но часто улучшает работу устройств. Однако при этом приходится использовать больший объем оборудования во многих универсальных ЦВМ операции с плавающей запятой реализуются не аппаратурными, а программными средствами, что приводит к удлинению программ и увеличению времени их выполнения. Алгоритмы работы устройств умножения и сложения с плавающей запятой сложнее, чем аналогичные алгоритмы с фиксированной запятой.
При умножении с плавающей запятой производится суммирование порядков сомножителей и умножение с фиксированной занятой их мантисс. Поскольку величина мантиссы (в десятичной системе) больше или равна 0,5, но меньше 1, то произведение двух мантисс заключено между 0,25 и 1. Это означает, что произведение будет либо выровнено по левому разряду), либо смещено на один разряд. В качестве упражнения составьте схему четырехразрядного устройства сложения порядков для умножителя с плавающей запятой.
При сложении с плавающей запятой необходимо выполнить следующие операции:
1. Определить, какой из двух порядков больше.
2. Из большего порядка вычесть меньший.
3. Полученную разность использовать для сдвига вправо мантиссы с меньшим порядком.
4. Сложить обе мантиссы.
5. Определить количество старших разрядов суммы, состоящих из одних нулей (или единиц).
6. Произвести выравнивание суммы по левому разряду и вычесть из большего порядка найденное количество одинаковых старших разрядов.
Очевидно, что устройство, выполняющее перечисленные операции, значительно сложнее сумматора с фиксированной запятой. Кроме того, данный алгоритм является довольно медленным, поскольку приходится выполнять последовательность операций, требующих принятия решения. По этой причине, несмотря на преимущества вычислений с плавающей запятой по сравнению с вычислениями с фиксированной запятой, выбор между ними часто неочевиден.
Основным
узлом сумматора, в котором выполняются операции 3 и 6, является устройство
сдвига на произвольное число разрядов. Проще всего эти операции выполнить с
помощью последовательного регистра сдвига и счетчика числа сдвигов, однако
затрачиваемое при этом время довольно значительно. Другой метод состоит в
разработке логической матрицы, в которой предусмотрены все сдвиги. Он
позволяет достичь большого быстродействия, но требует большего объема
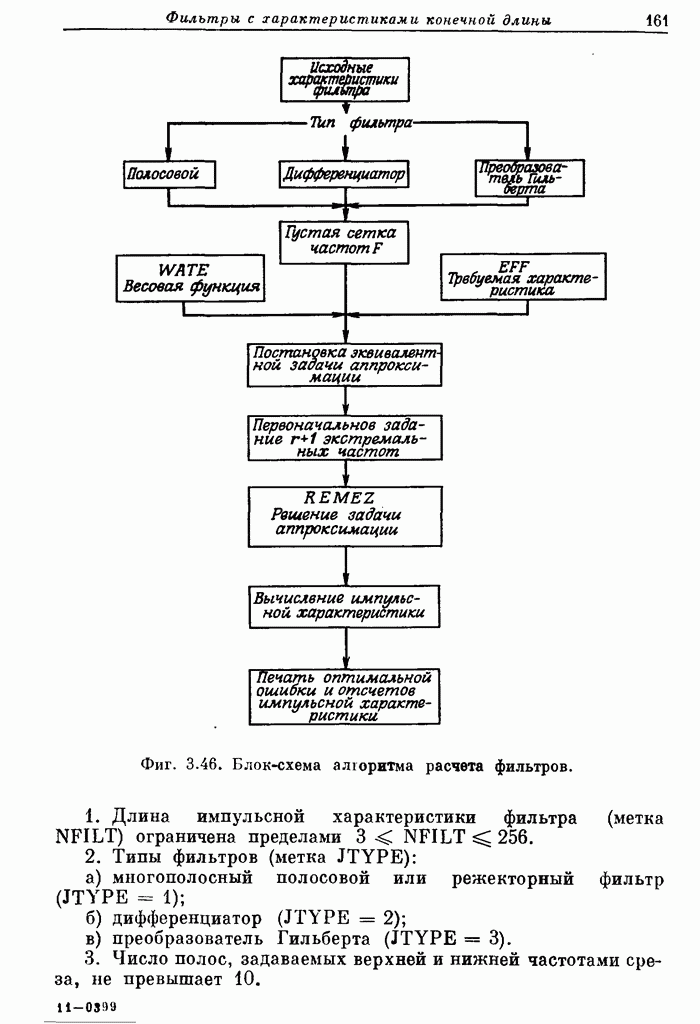
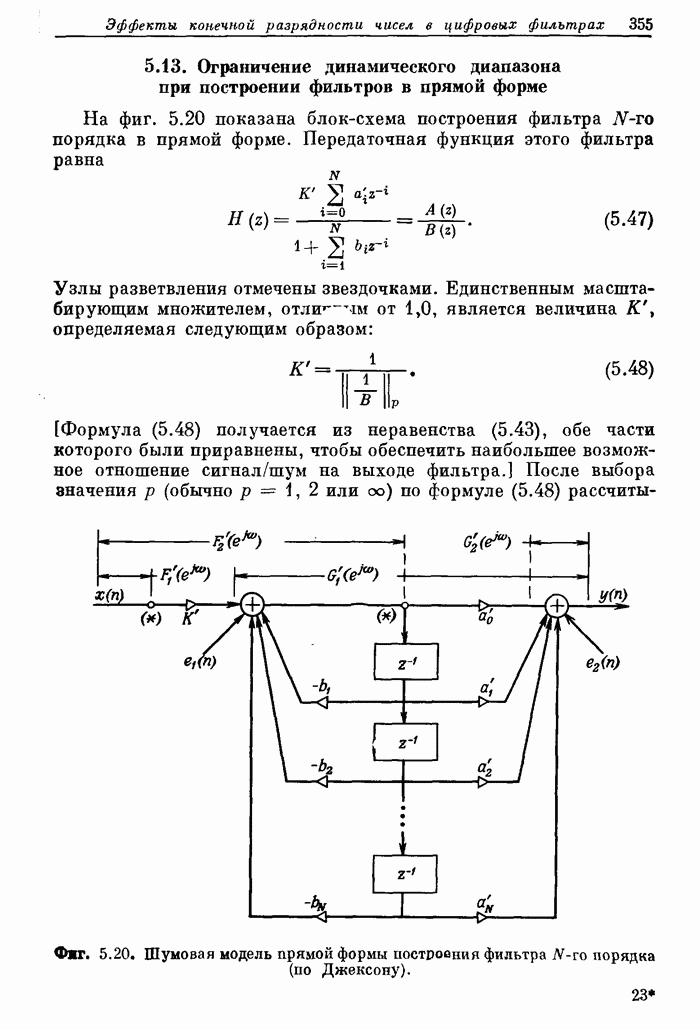
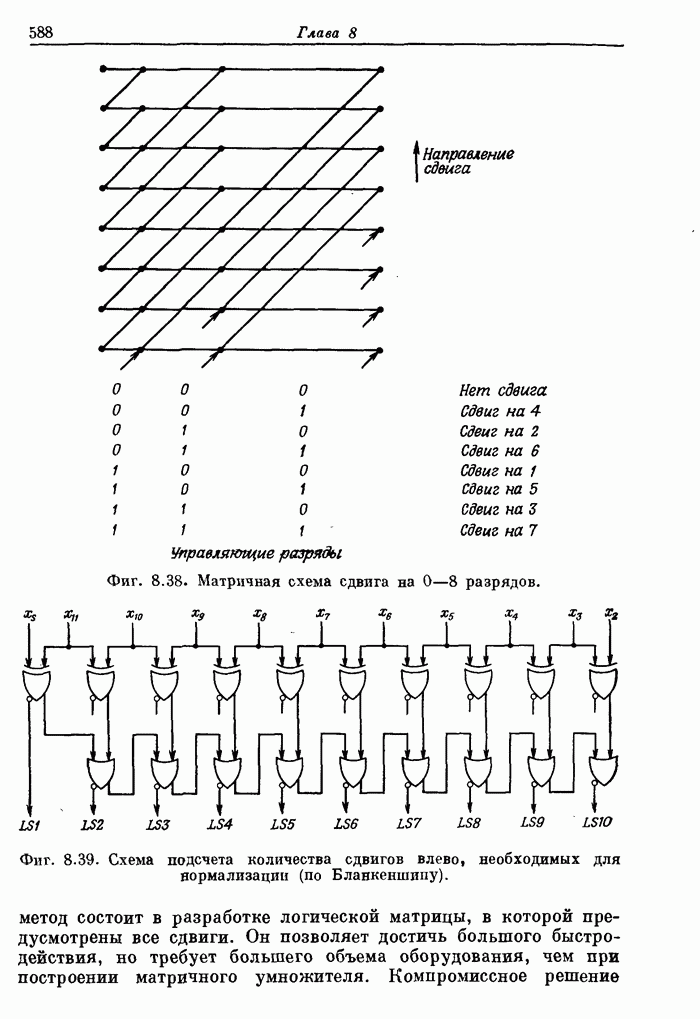
оборудования, чем при построении матричного умножителя. Компромиссное решение показано на фиг.
8.38. Каждая точка представляет собой управляемый переключатель, с помощью
которого входная линия подключается к одной из двух выходных линий. В данной
схеме восемь различных сдвигов обеспечиваются тремя уровнями переключателей; в
общем случае для ![]() -разрядной
сдвигающей цепи необходимо обеспечить
-разрядной
сдвигающей цепи необходимо обеспечить ![]() уровней переключения.
уровней переключения.

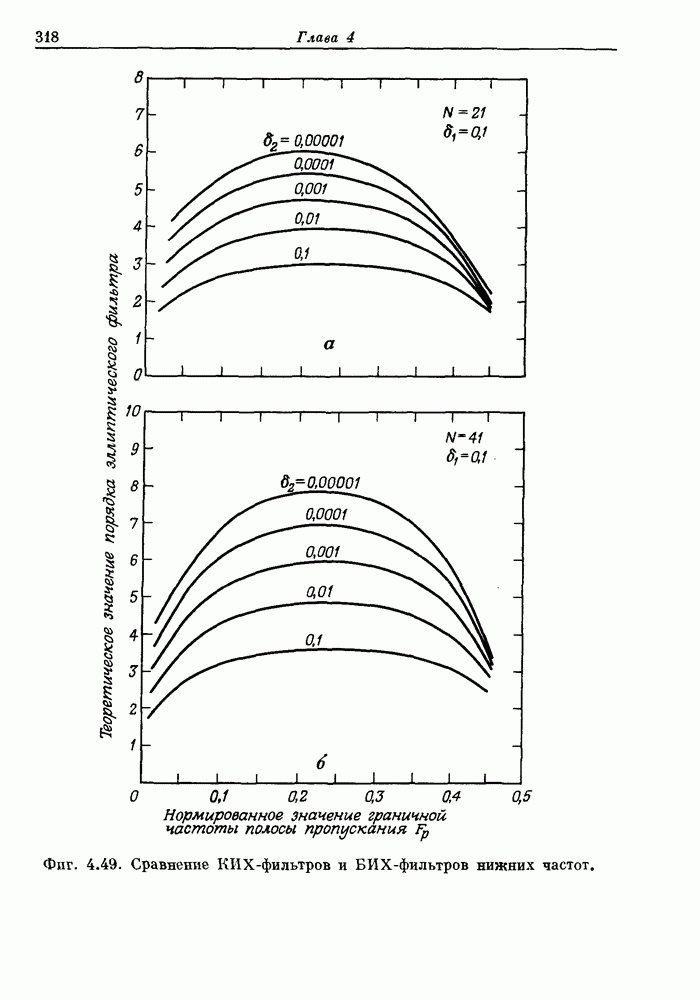
Фиг. 8.38. Матричная схема сдвига на 0—8 разрядов.

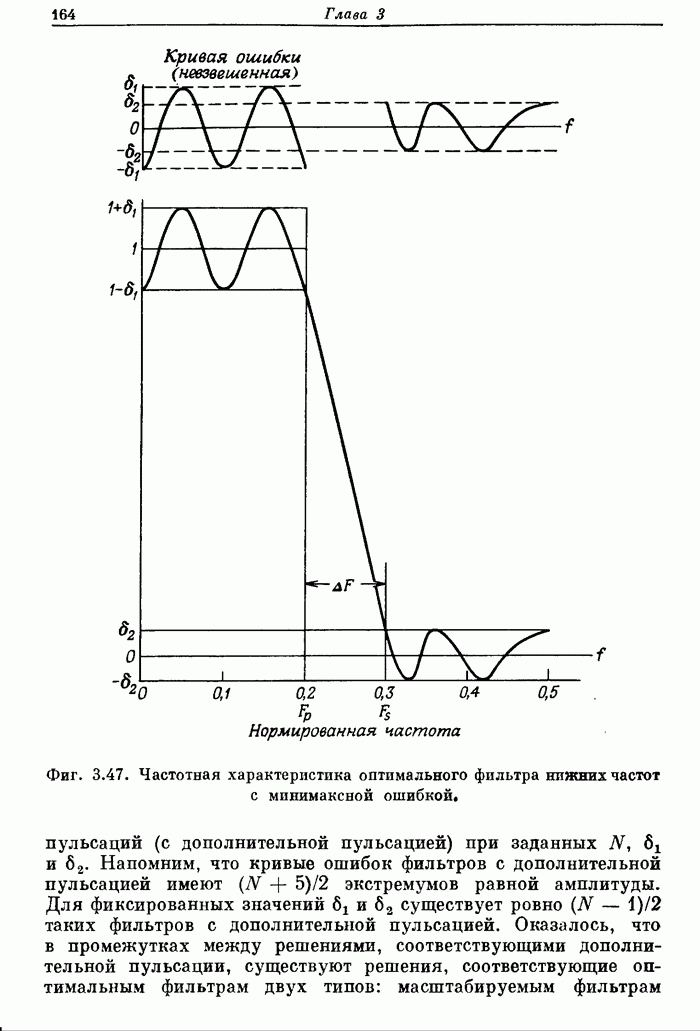
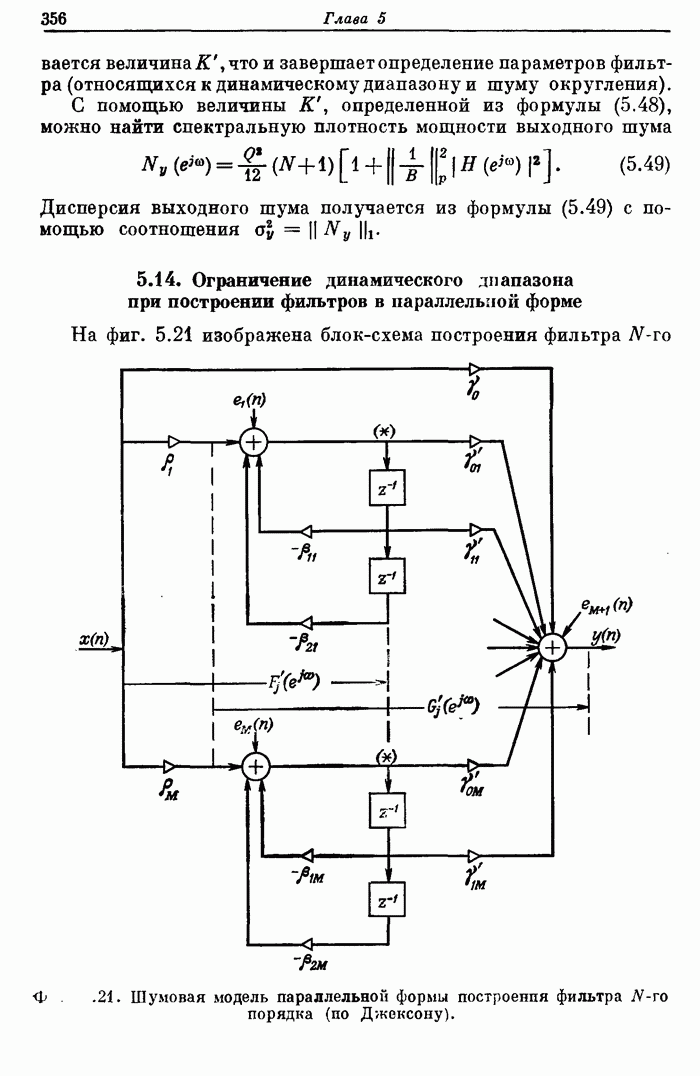
Фиг. 8.39. Схема подсчета количества сдвигов влево, необходимых для нормализации (по Бланкеншипу).

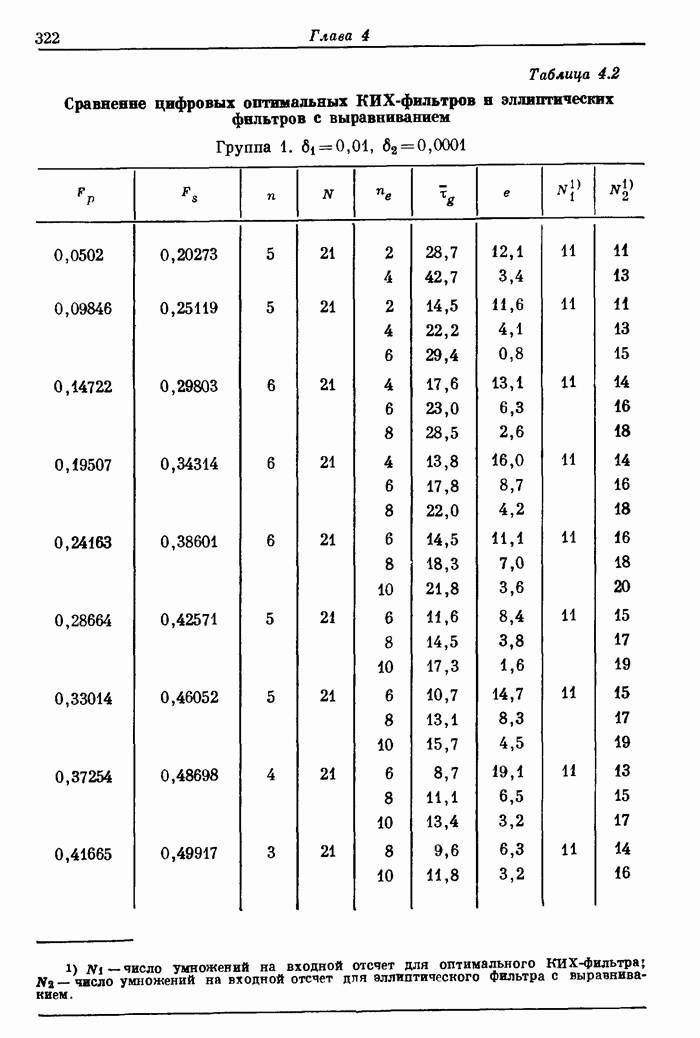
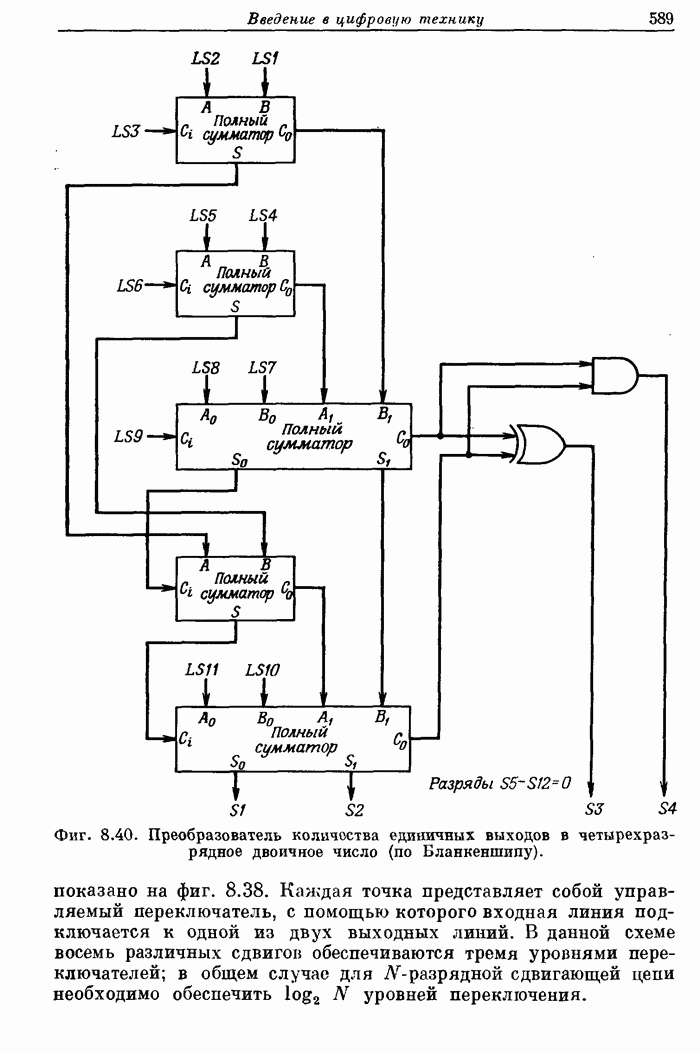
Фиг. 8.40. Преобразователь количества единичных выходов в четырехразрядное двоичное число (по Бланкеншипу).
Для выполнения пятой операции при сложении с плавающей запятой необходимо иметь логическую схему подсчета количества одинаковых старших разрядов. На фиг. 8.39 и 8.40 показаны схемы, предназначенные для решения этой задачи для случая 12-разрядного числа. Первая схема (фиг. 8.39) преобразует 11 входных разрядов в 10 выходных. Количество единичных выходов определяется количеством сдвигов влево, необходимых для нормализации входного числа. Вторая схема (фиг. 8.40) составлена из полных сумматоров и выполняет операцию подсчета количества единичных выходов первой схемы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
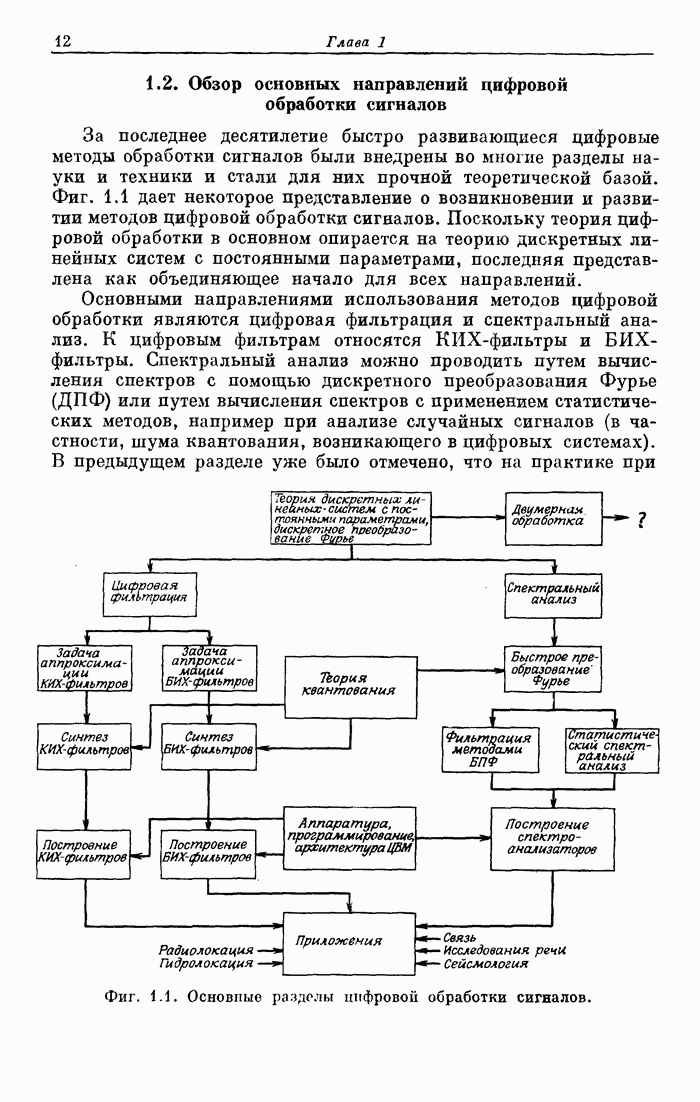
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
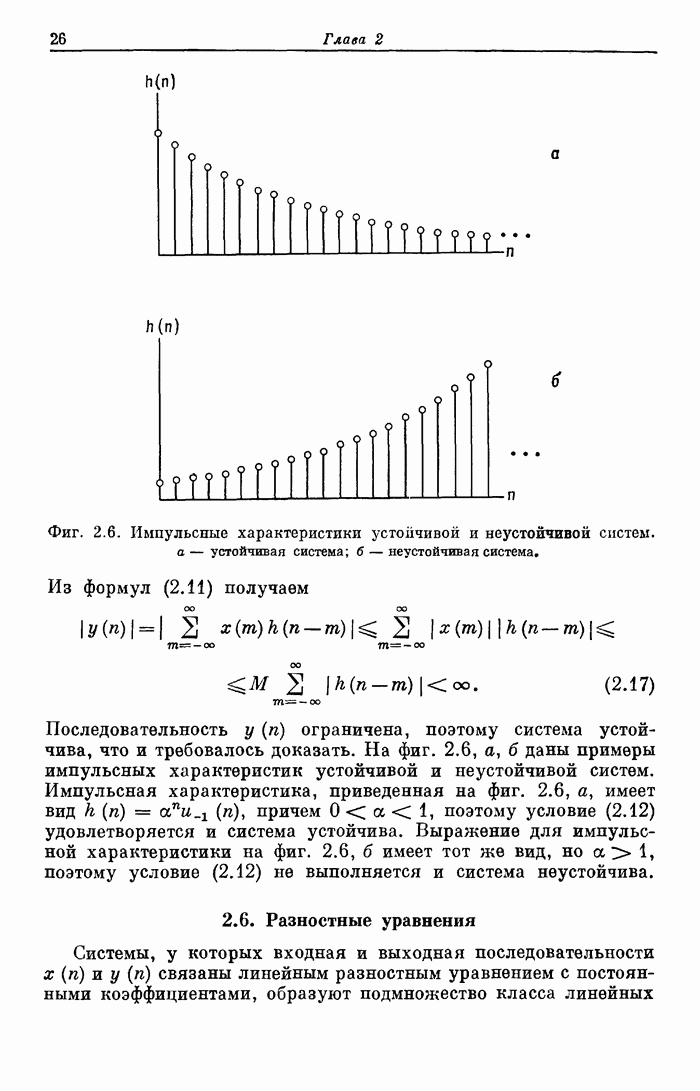
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
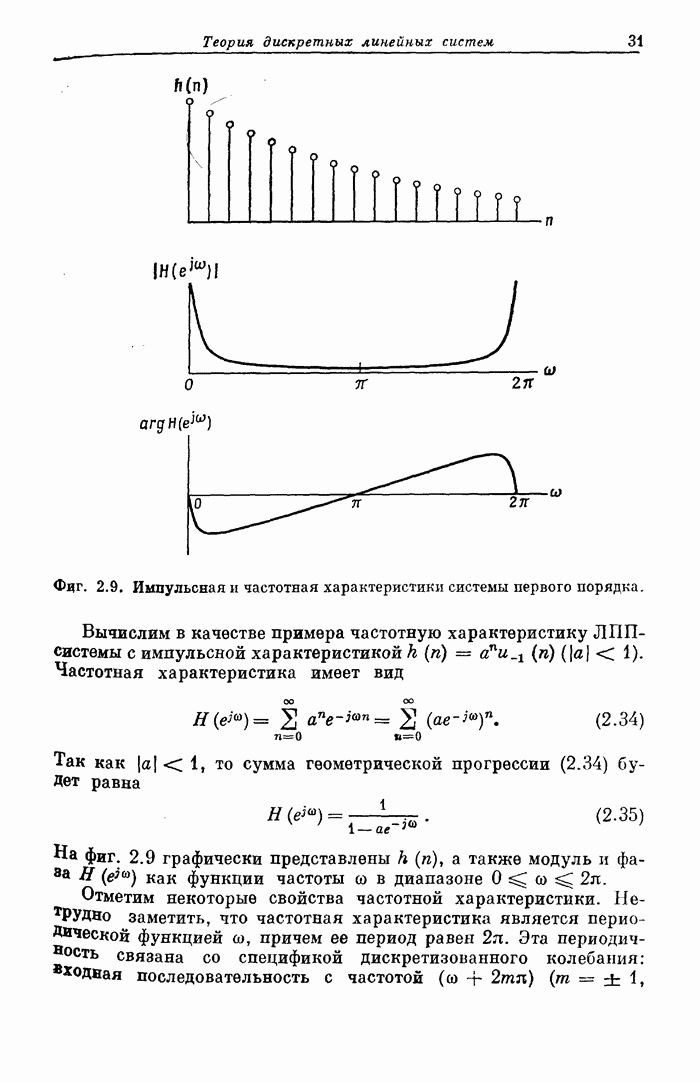
- 2.7. Частотная характеристика
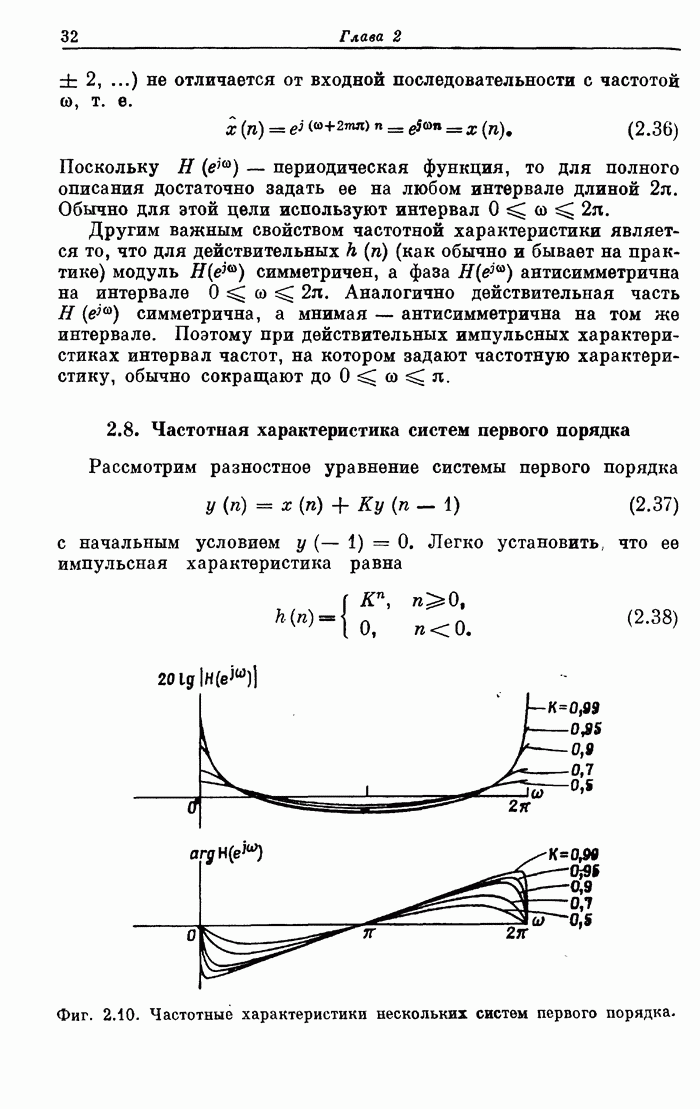
- 2.8. Частотная характеристика систем первого порядка
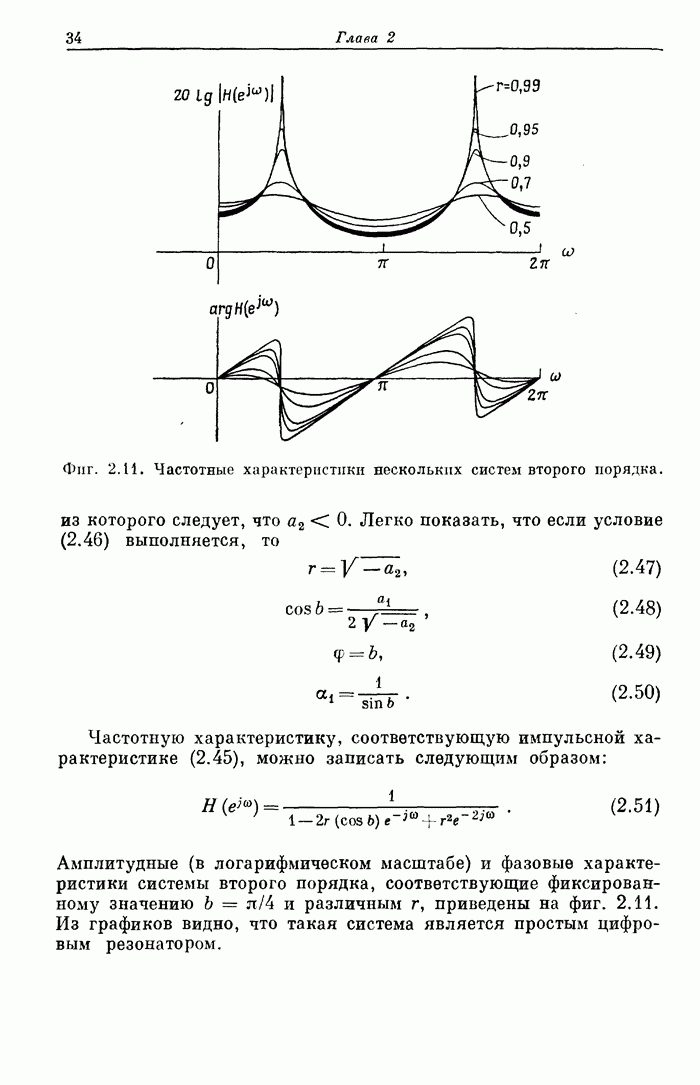
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
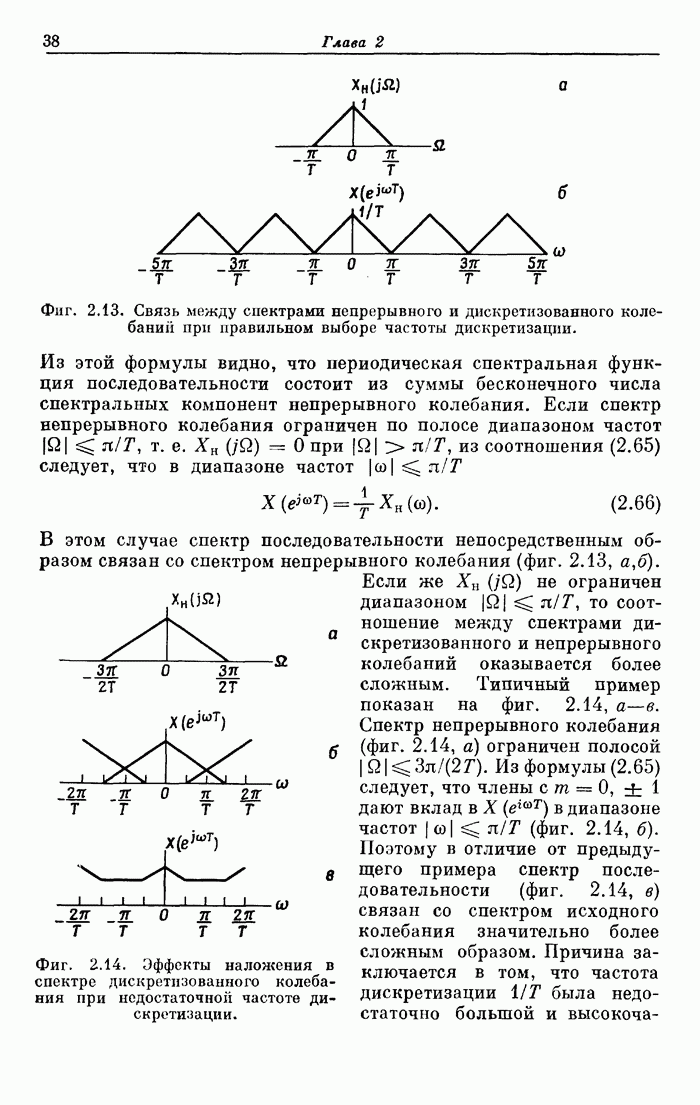
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
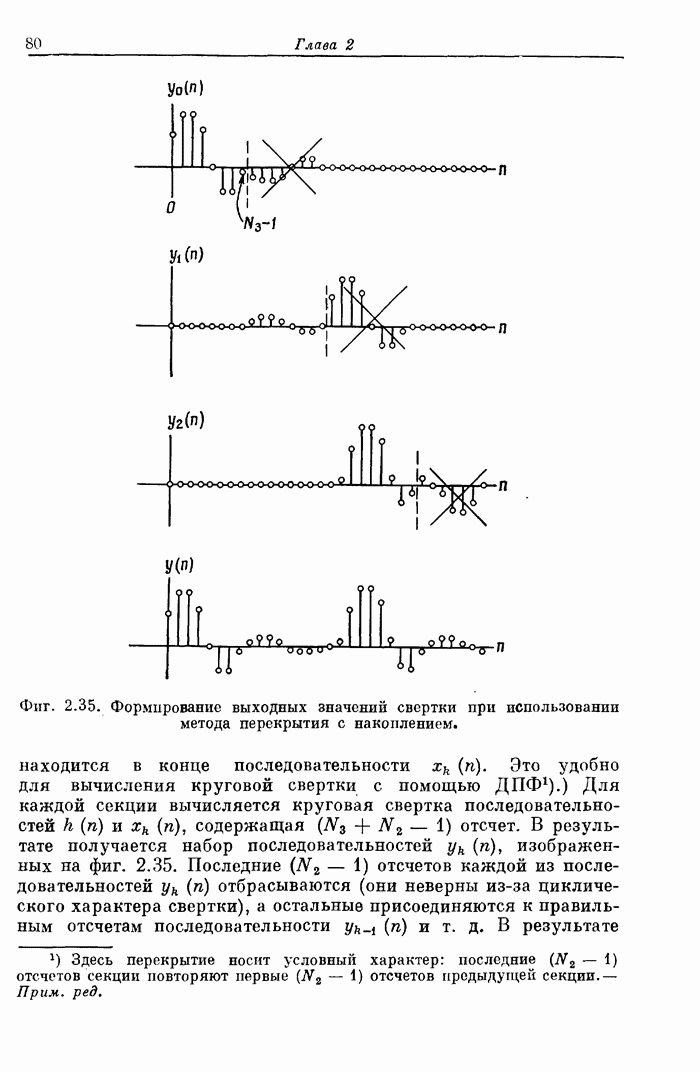
- 2.25. Секционированные свертки
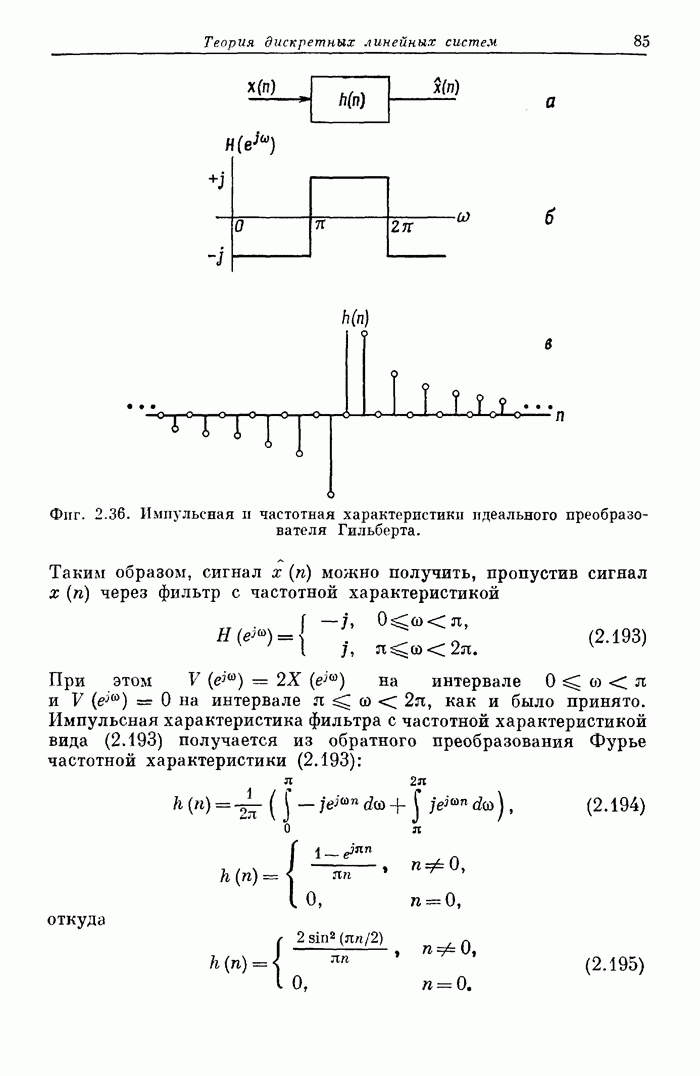
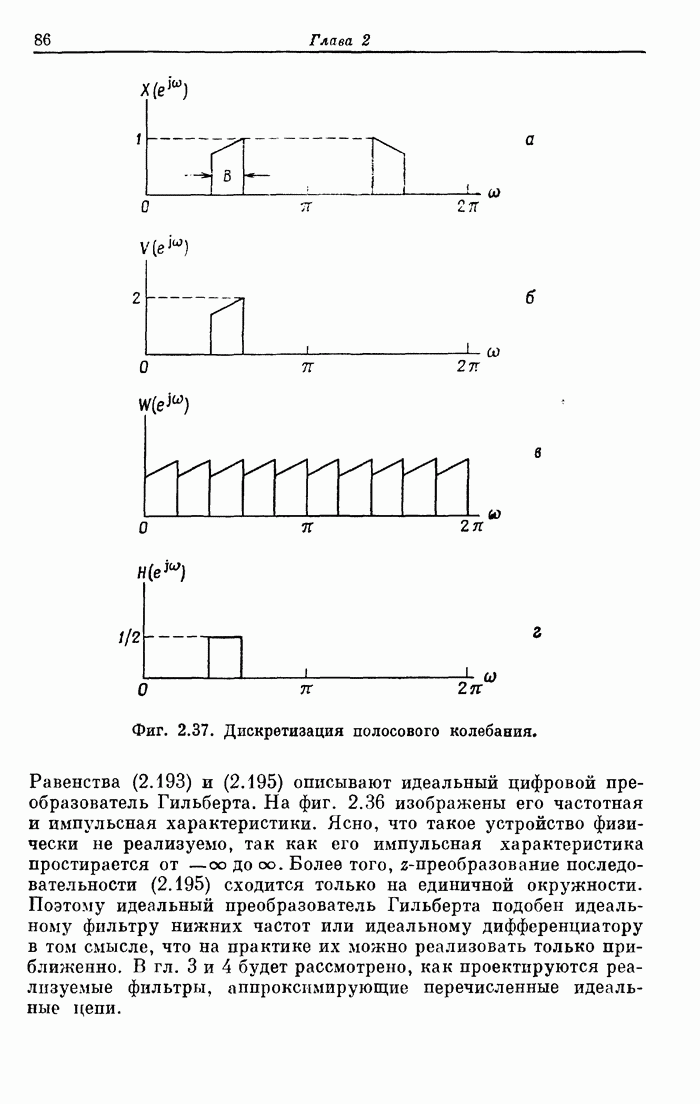
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
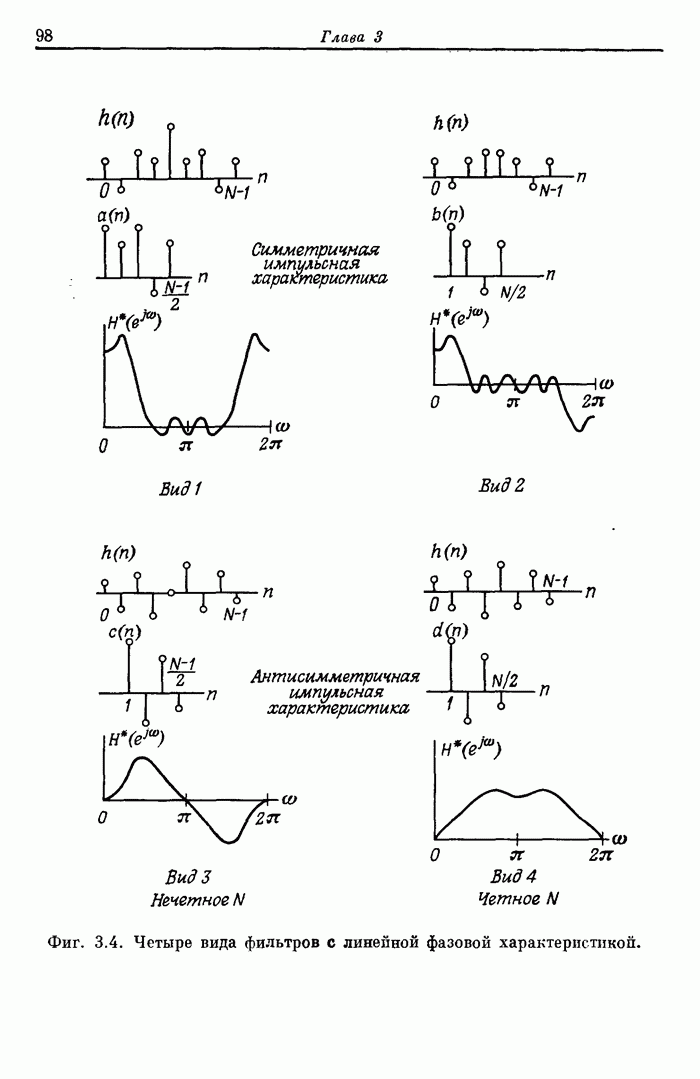
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
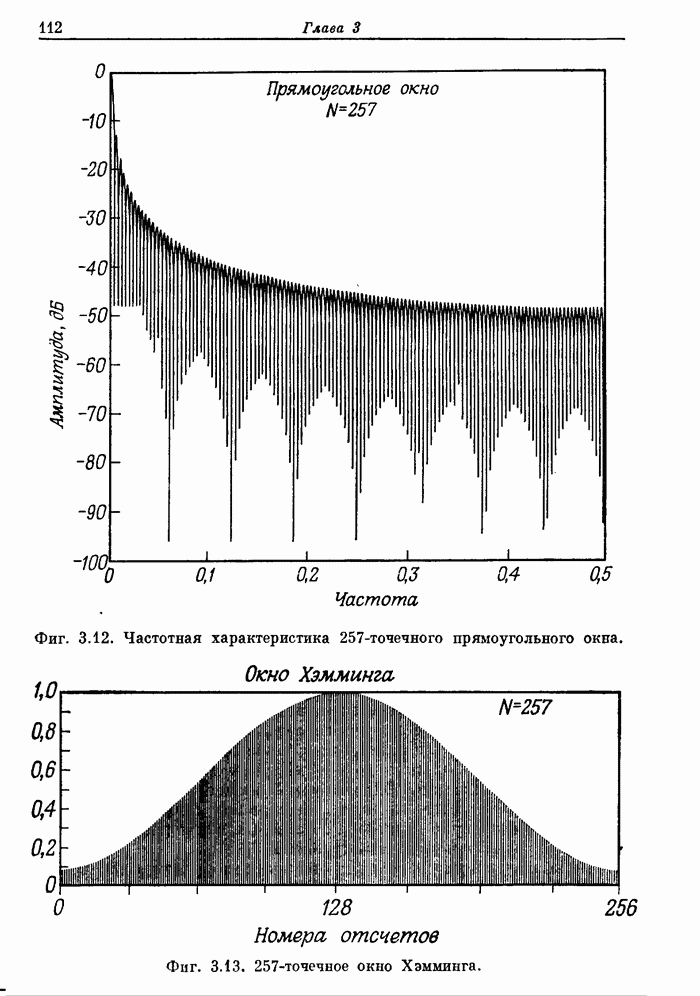
- 3.9. Прямоугольное окно
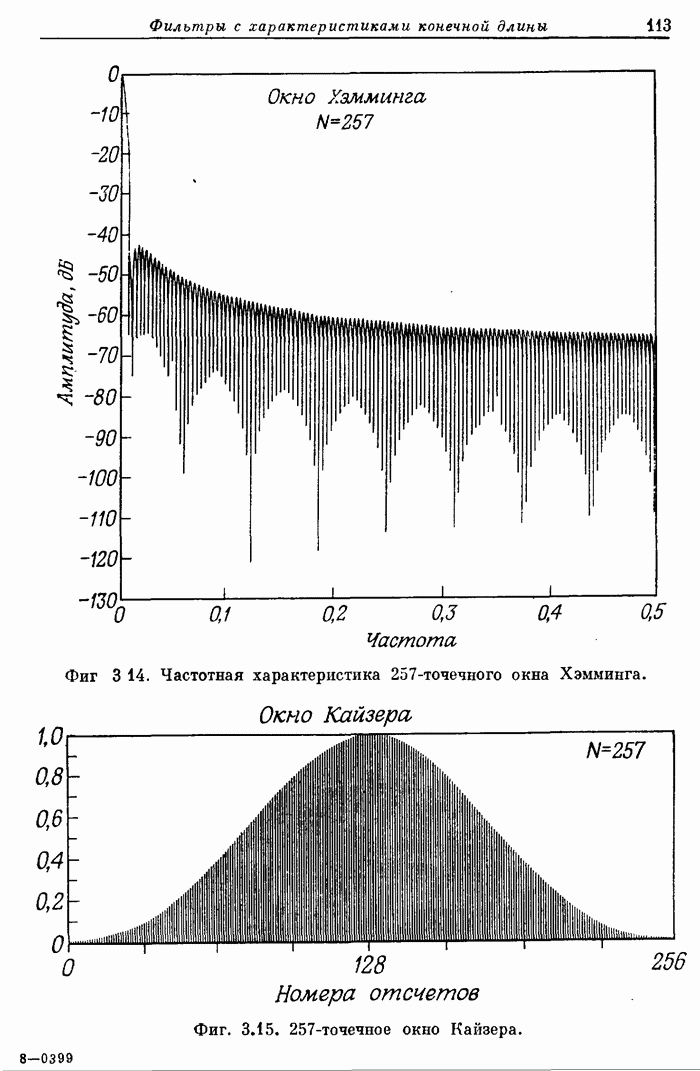
- 3.10. «Обобщенное» окно Хэмминга
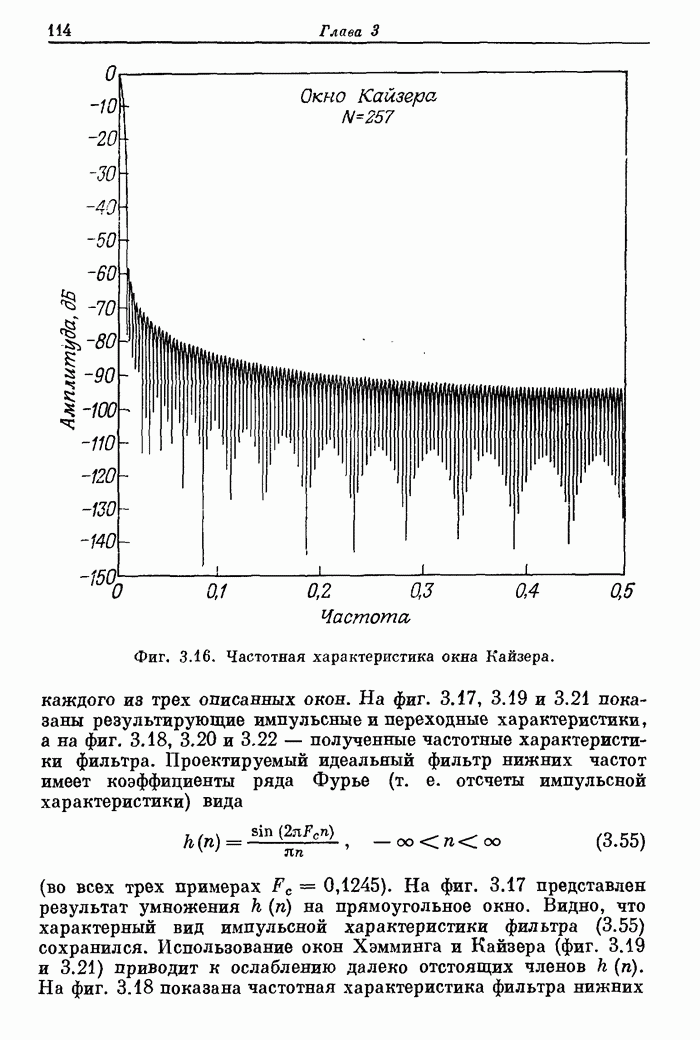
- 3.11. Окно Кайзера
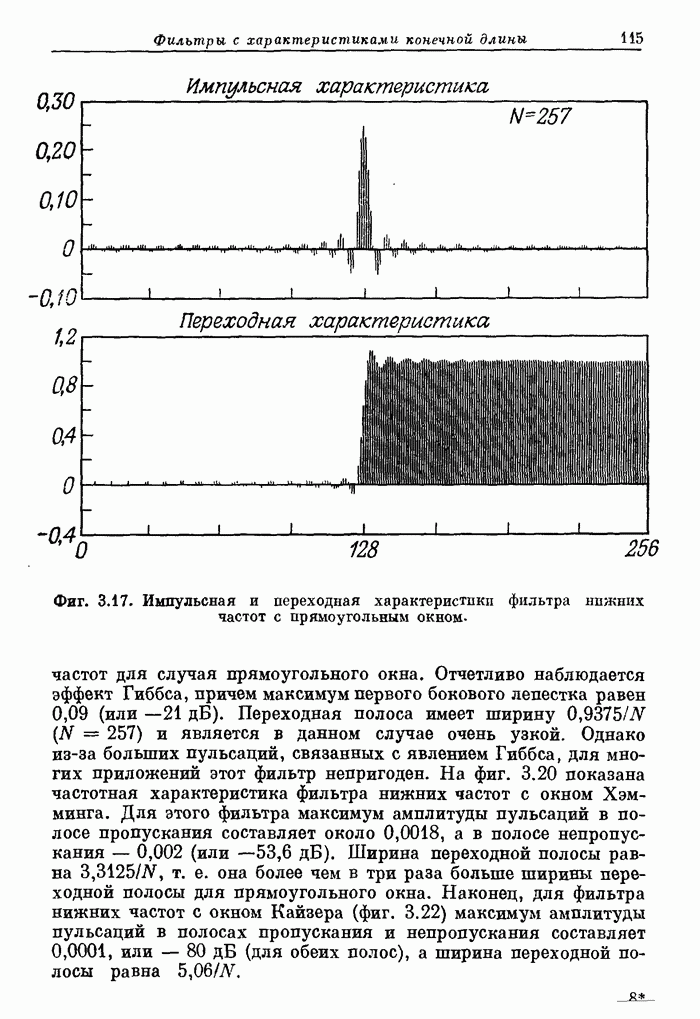
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
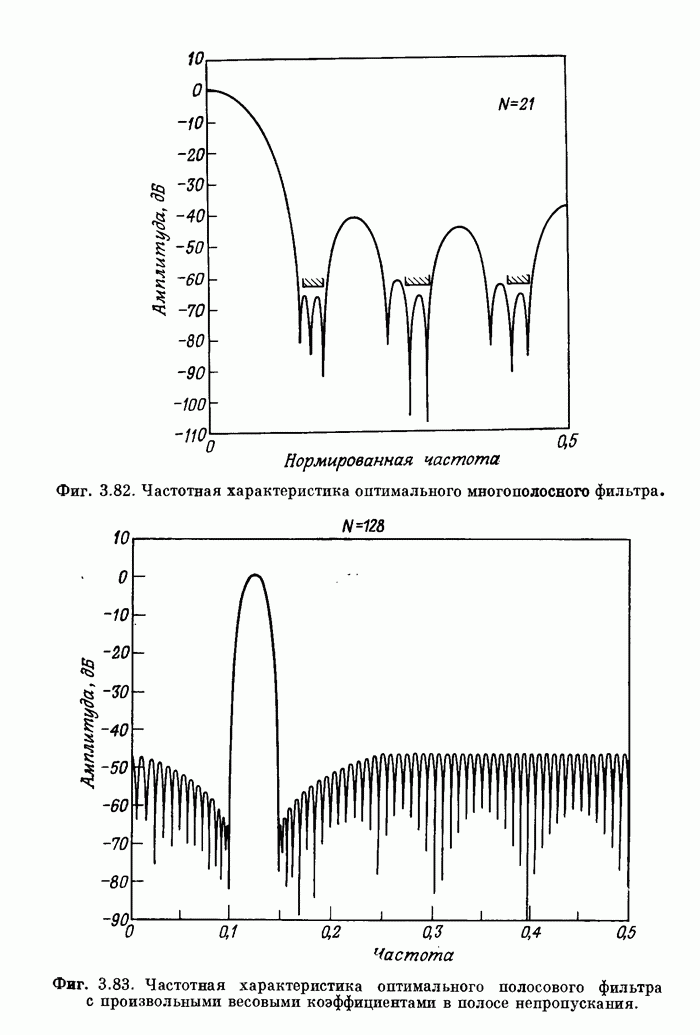
- 3.38. Многополосные оптимальные КИХ-фильтры
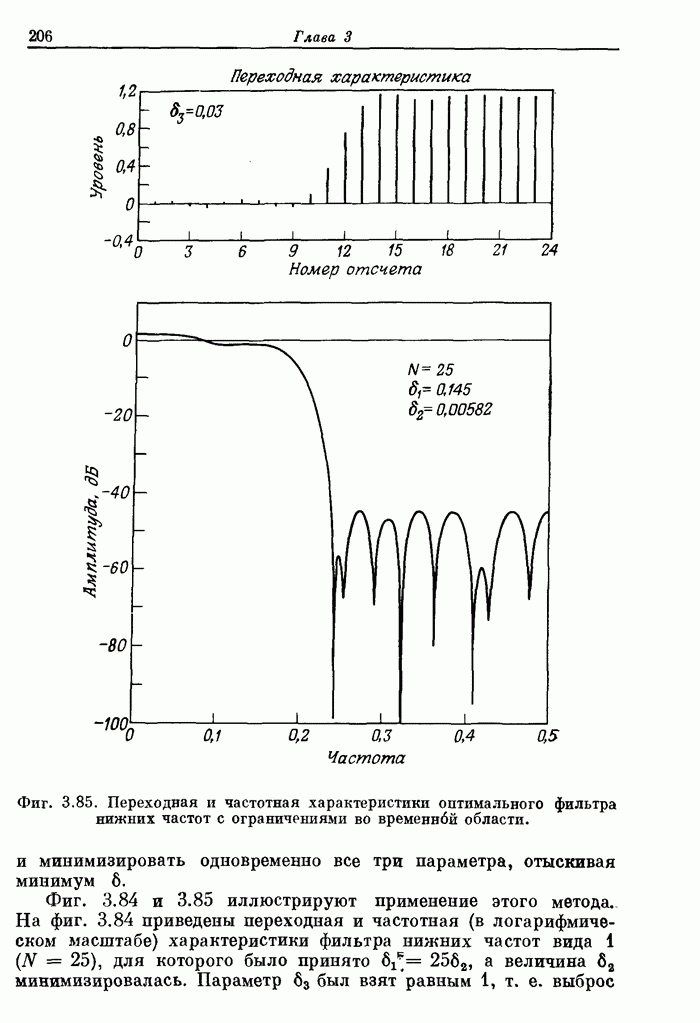
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
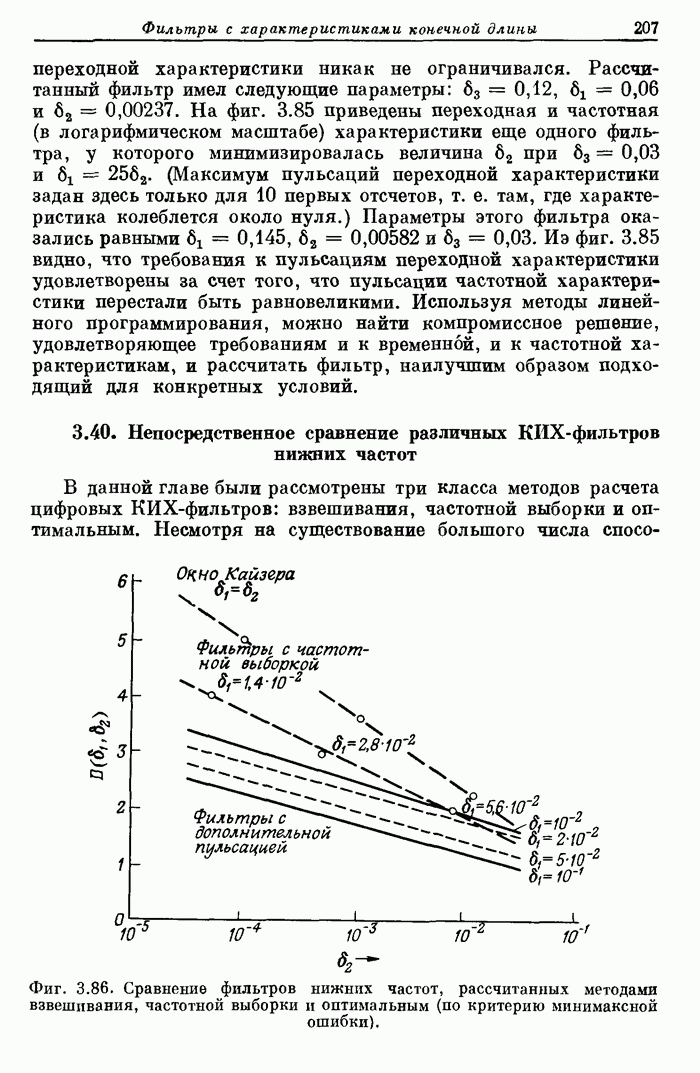
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
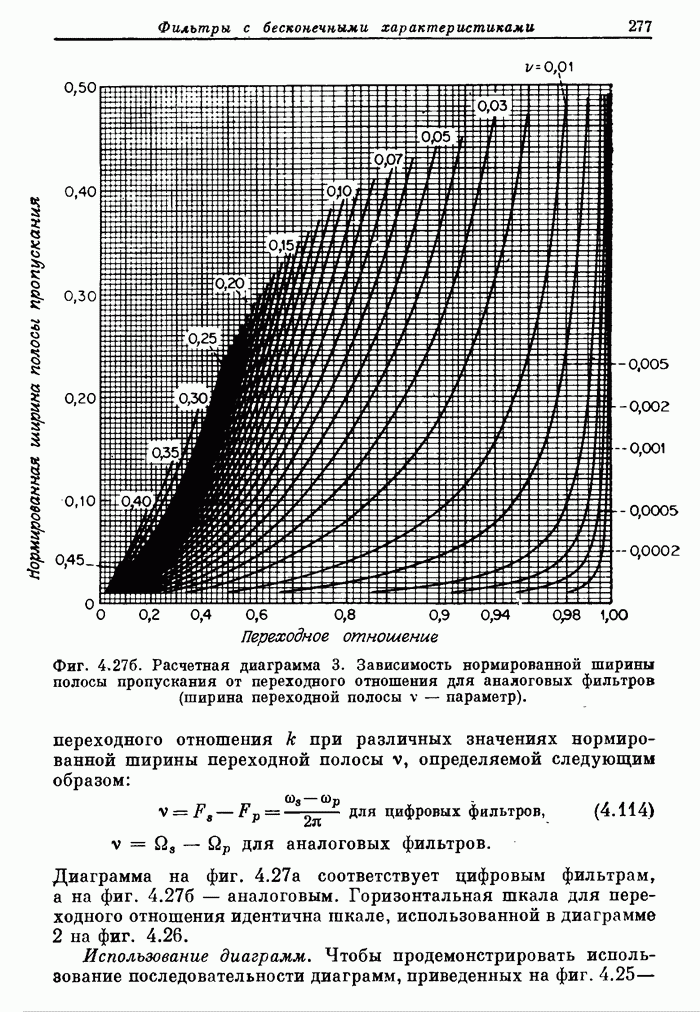
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
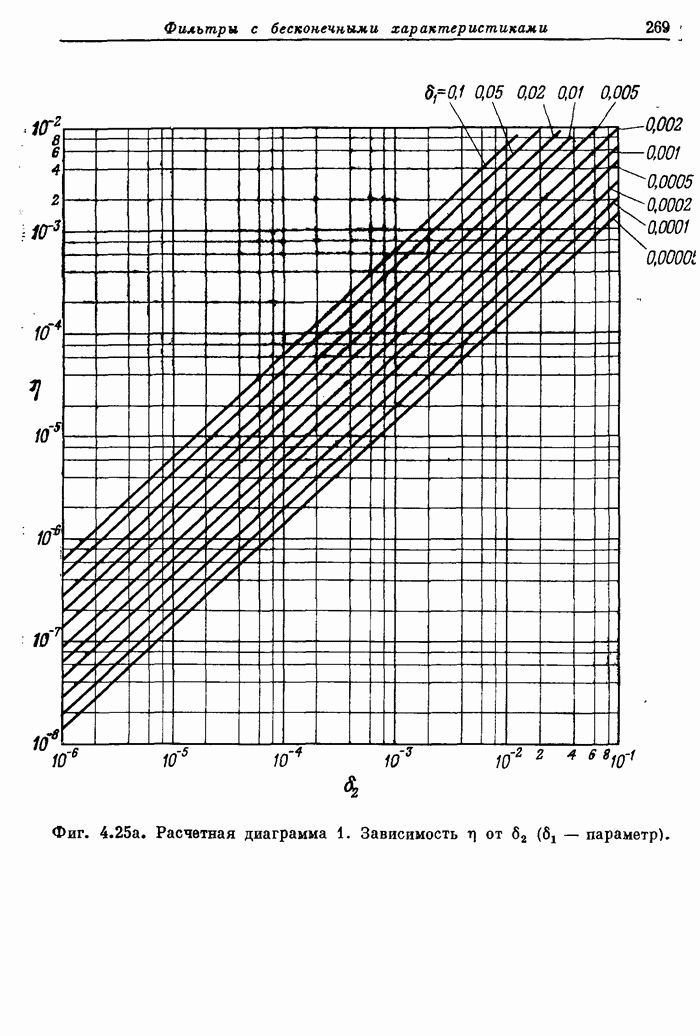
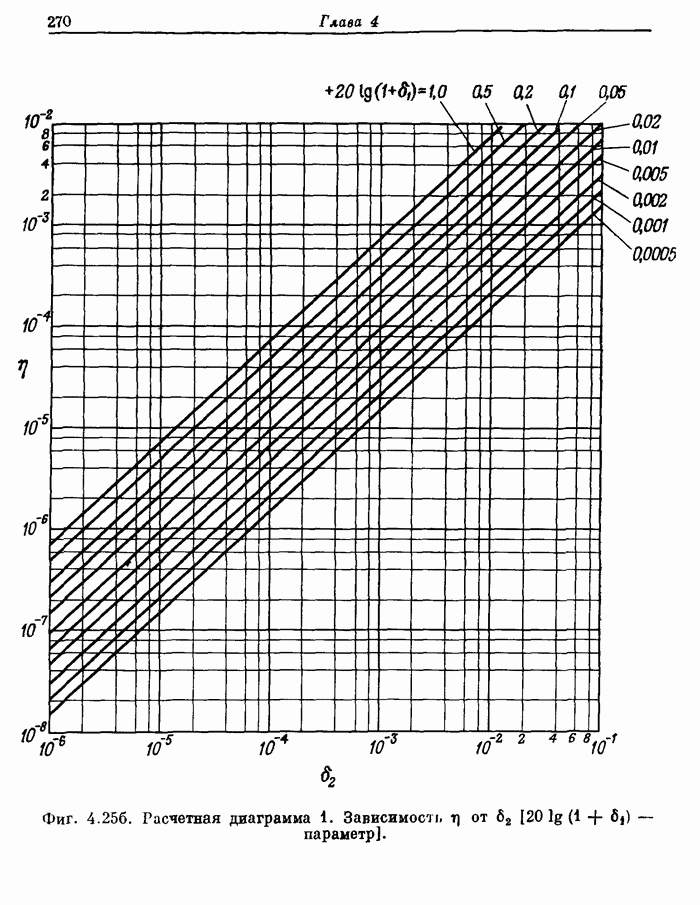
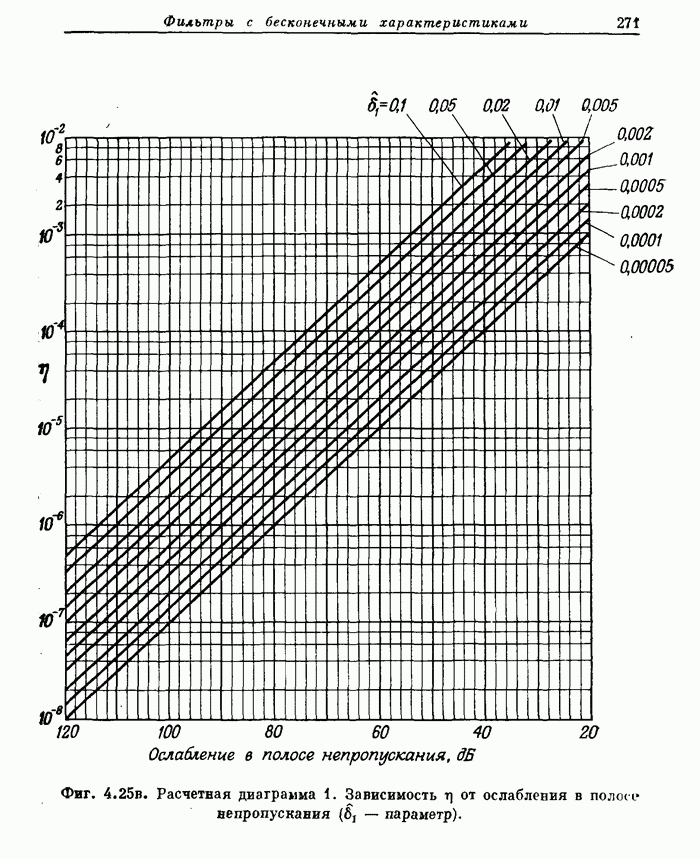
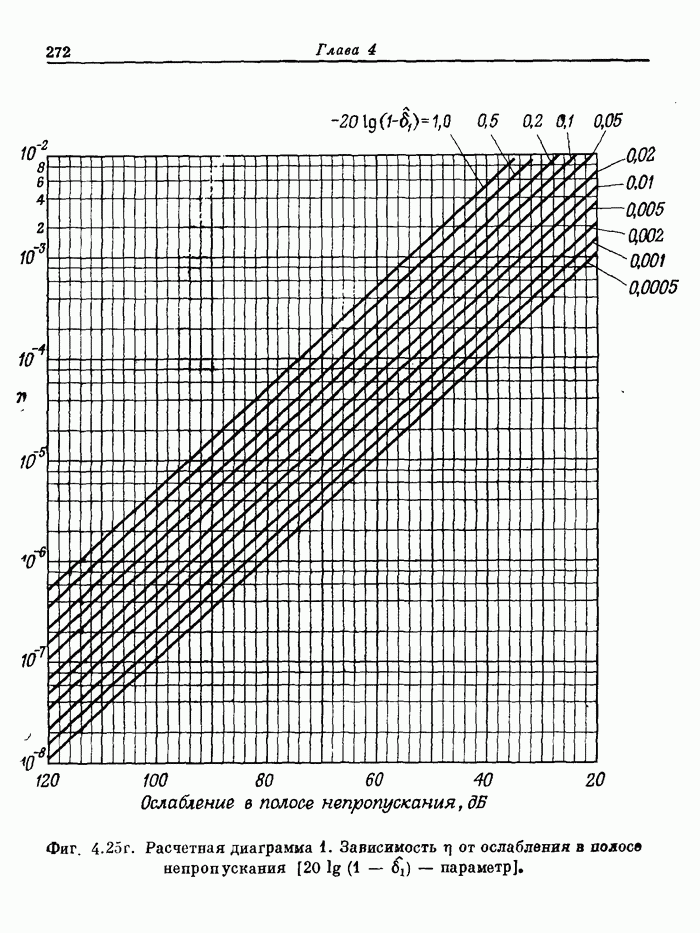
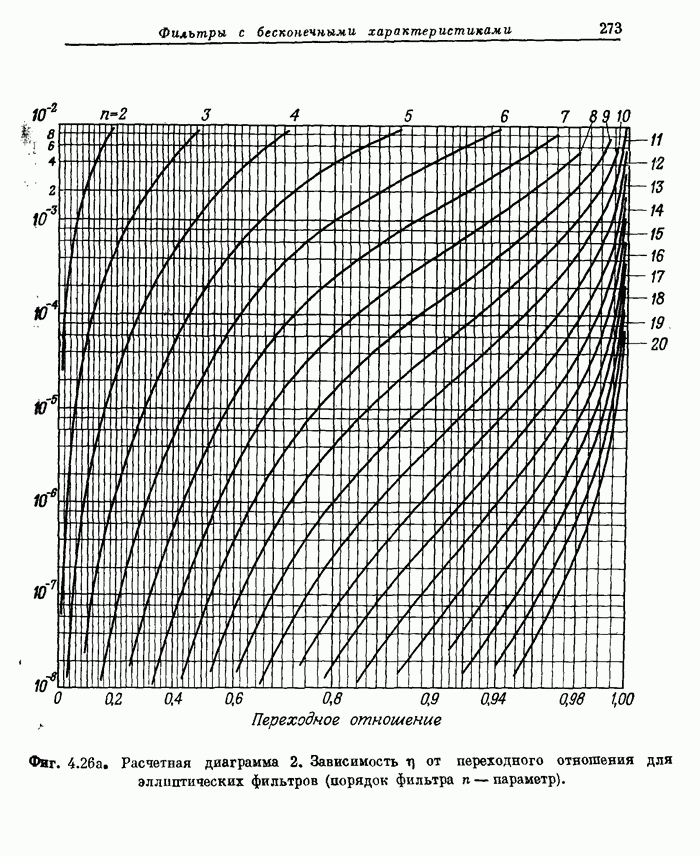
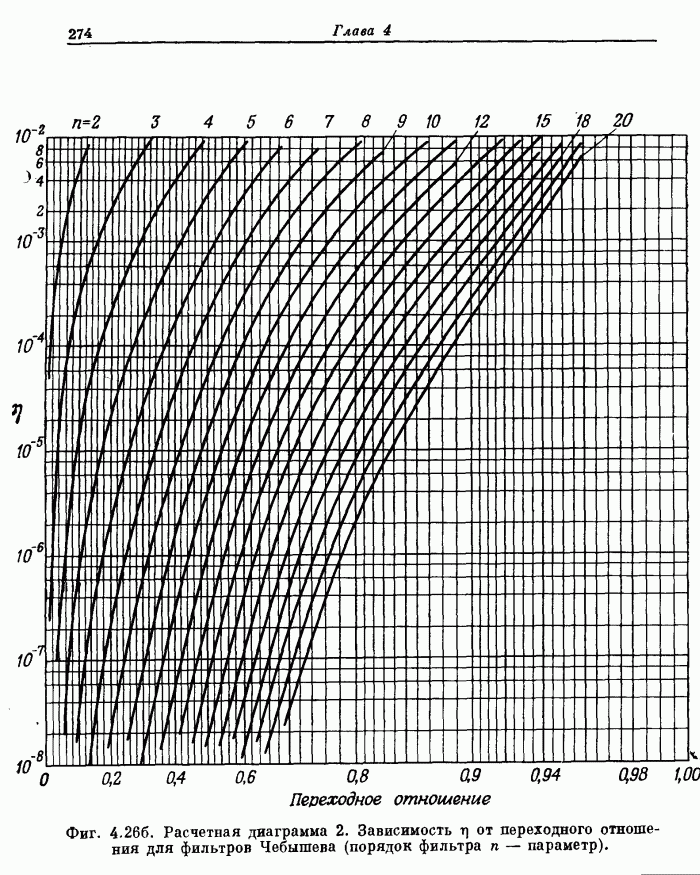
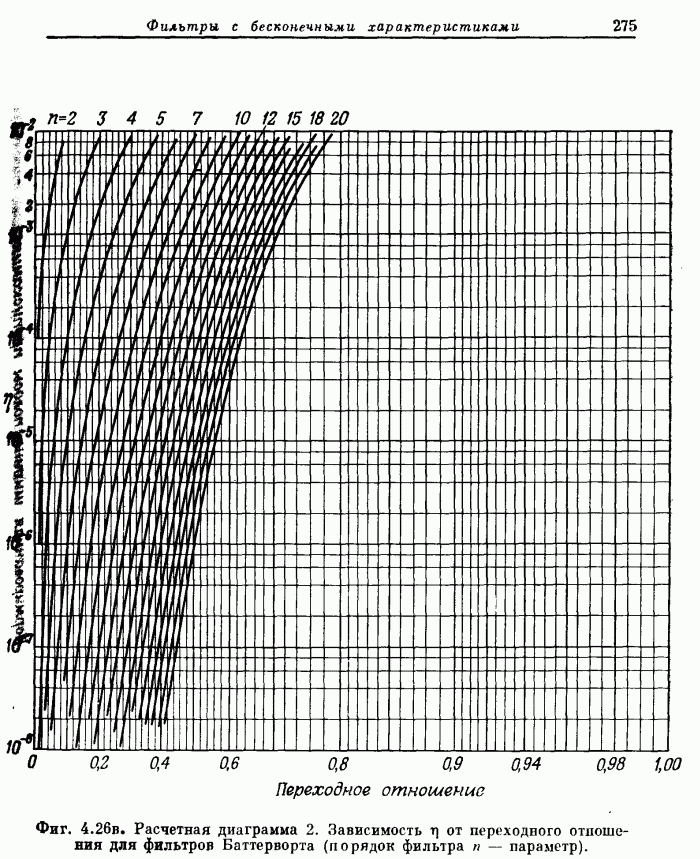
- 4.10. Расчетные диаграммы фильтров нижних частот
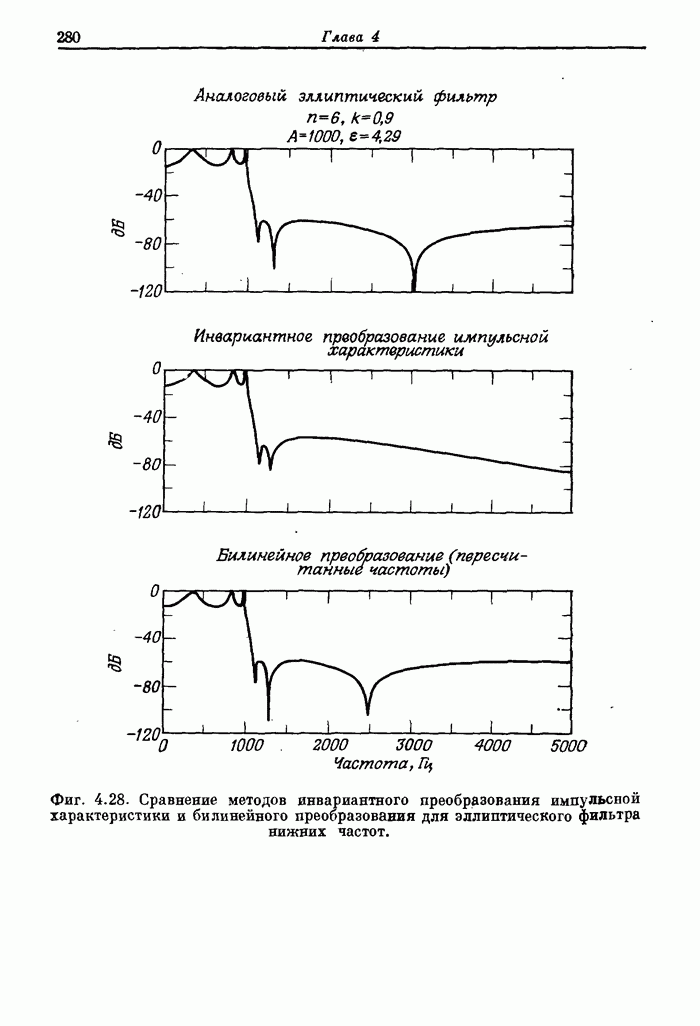
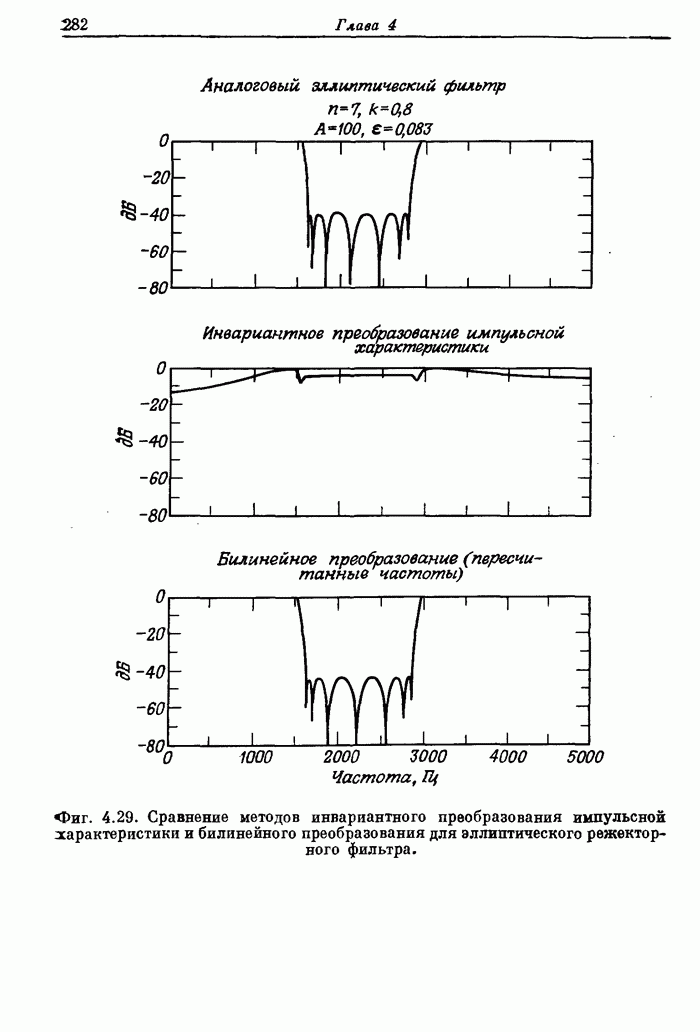
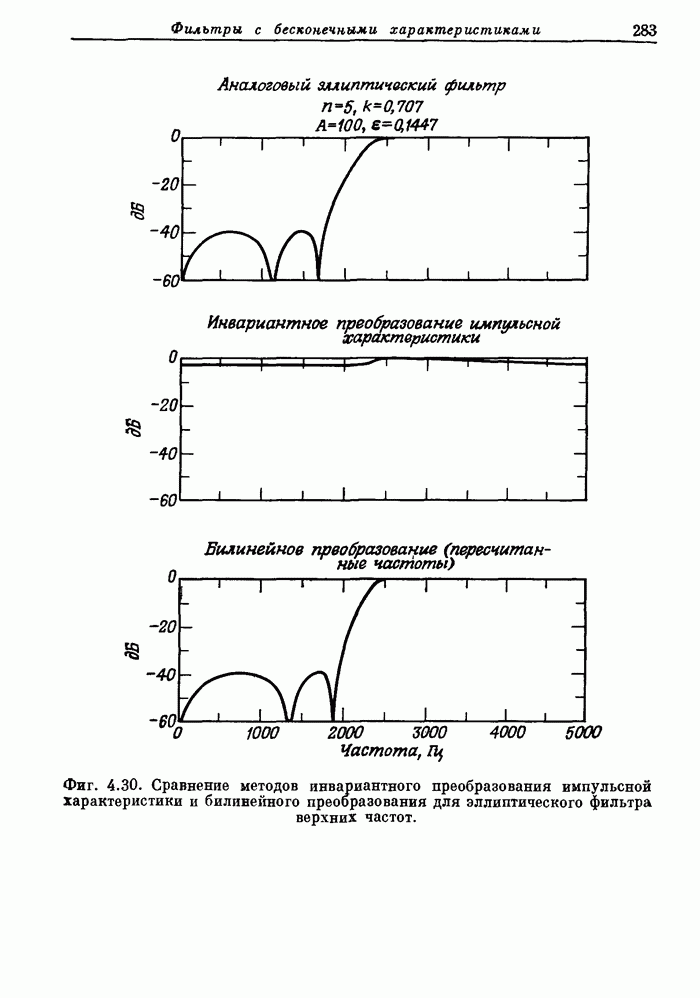
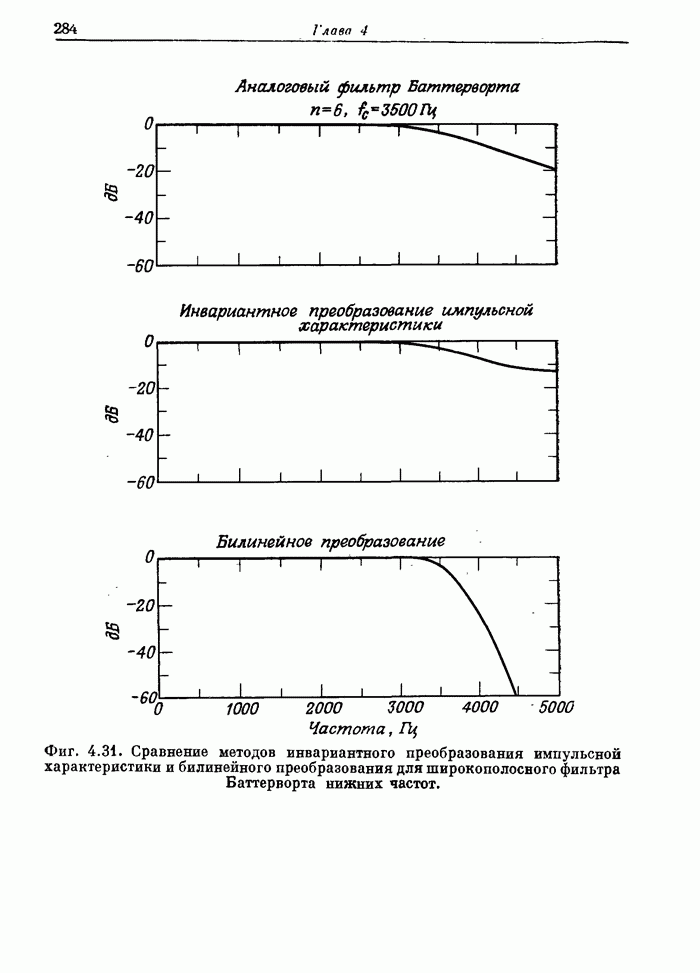
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
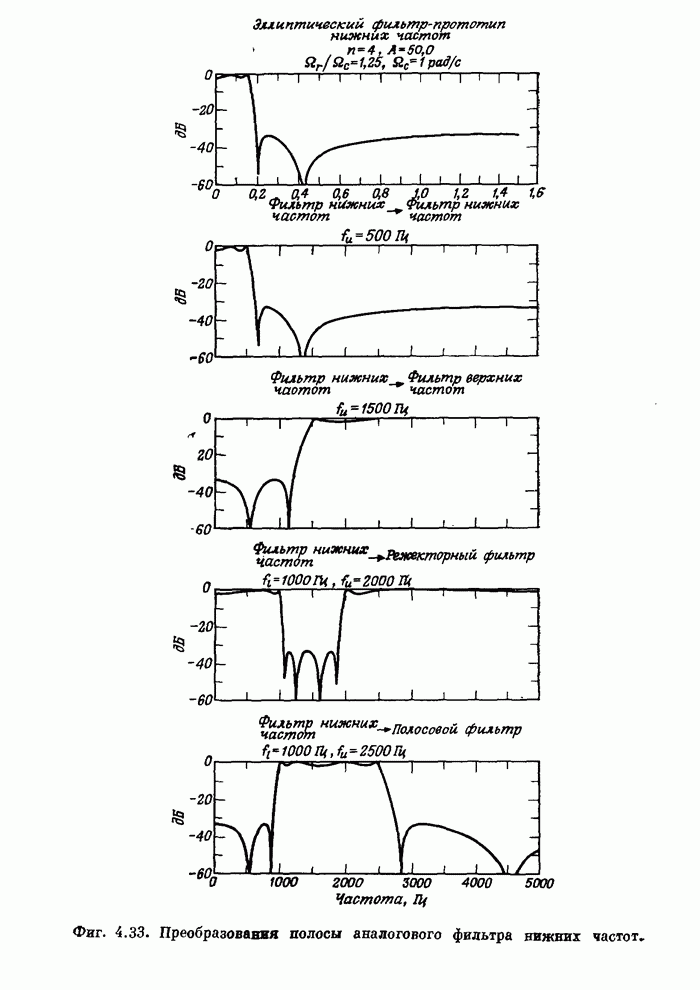
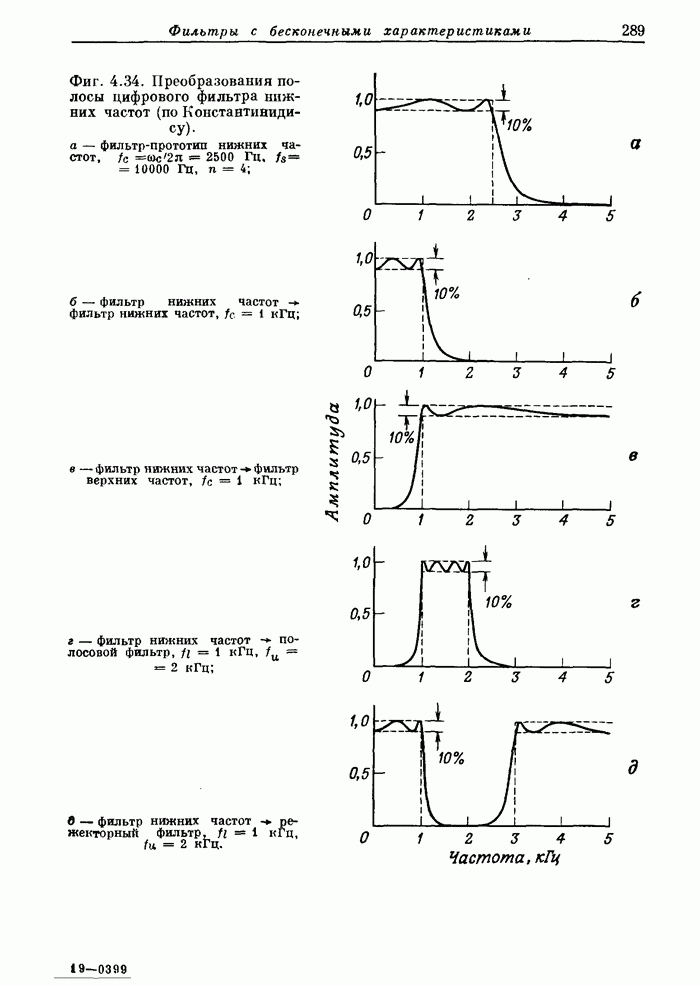
- 4.12. Частотные преобразования
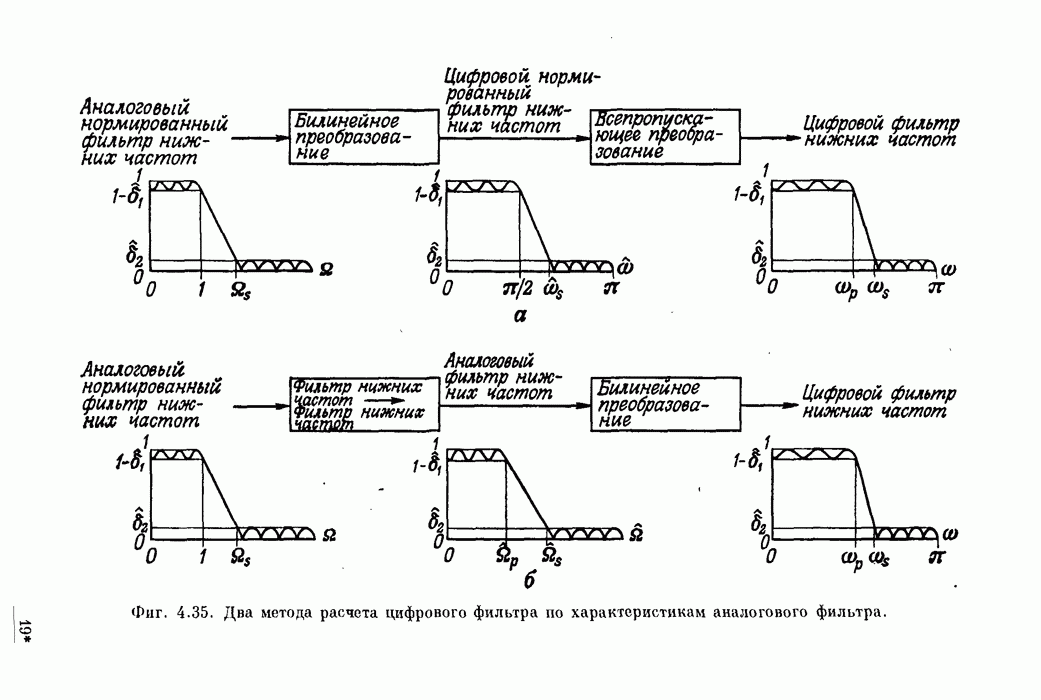
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
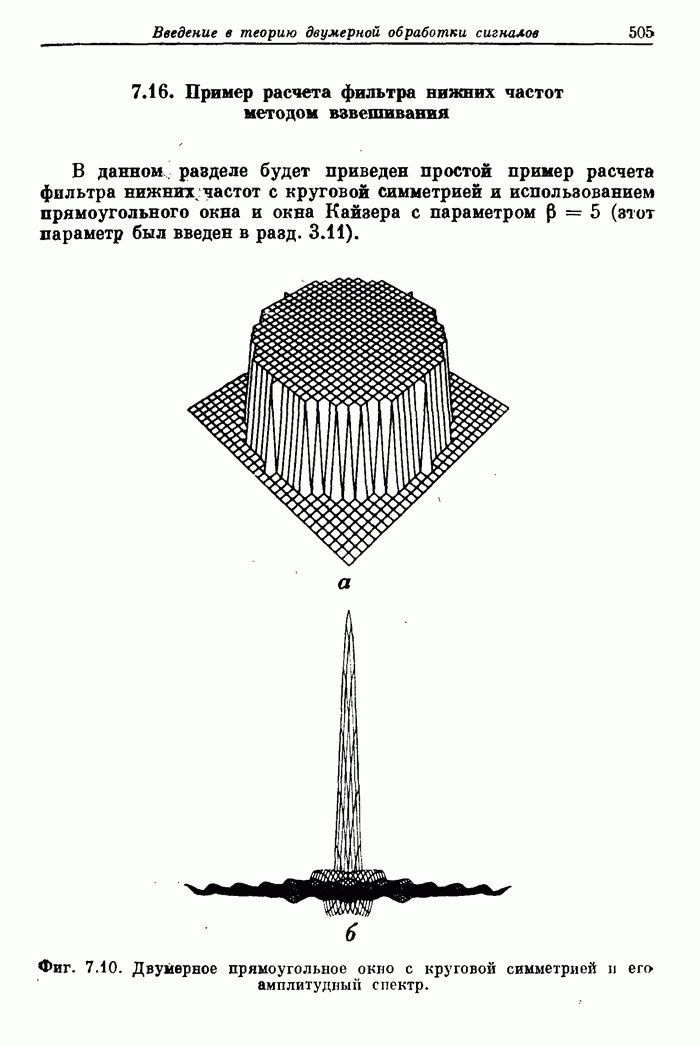
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
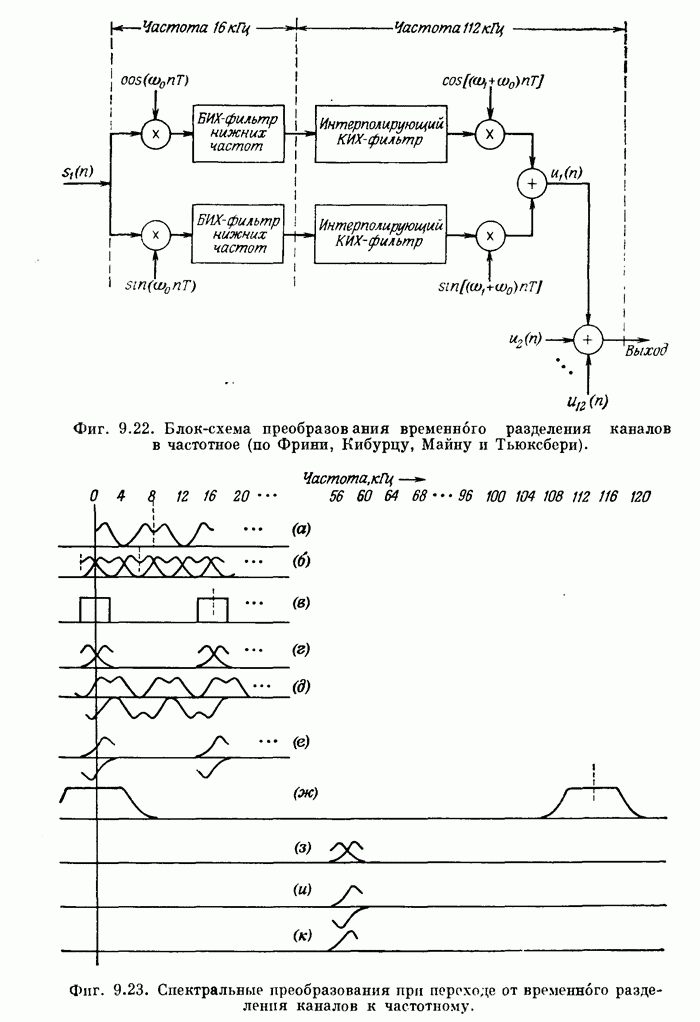
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
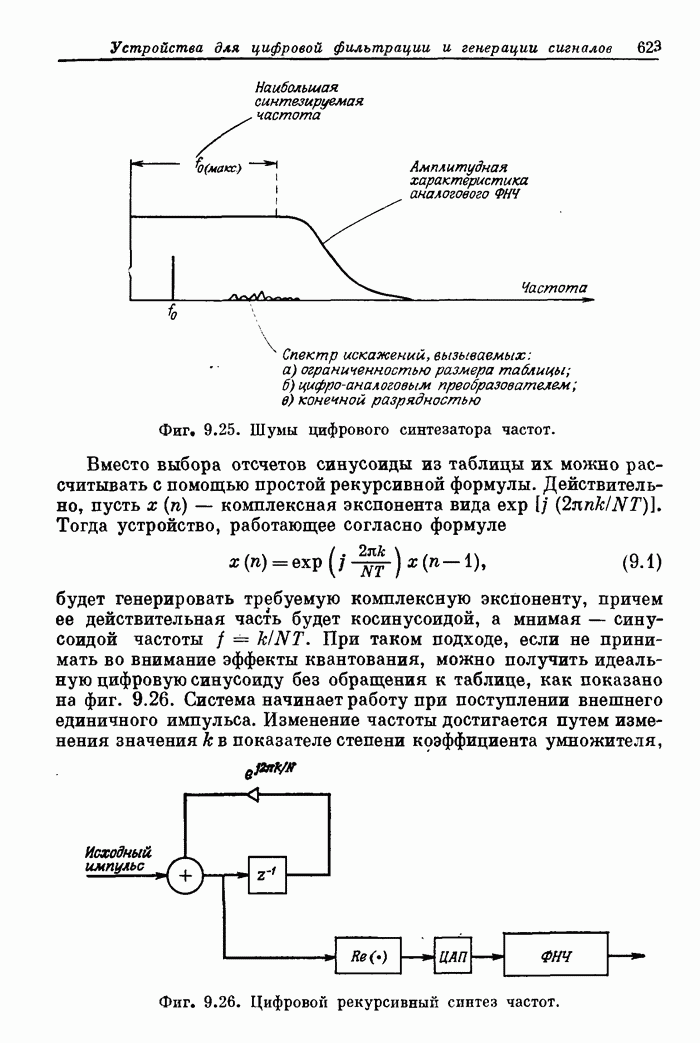
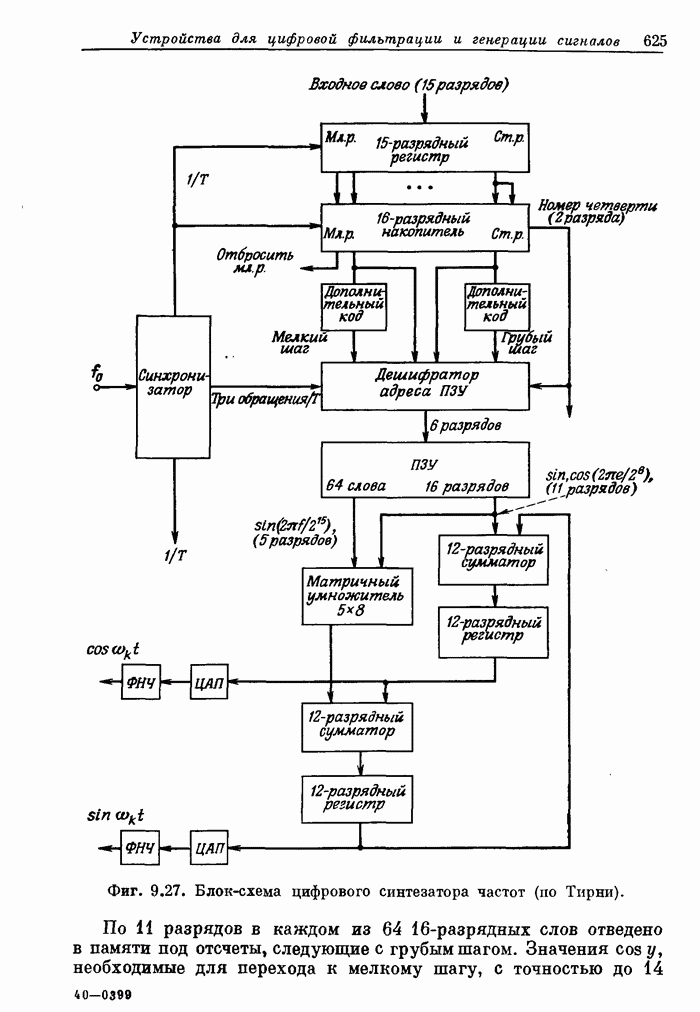
- 9.12. Специализированный цифровой синтезатор частот
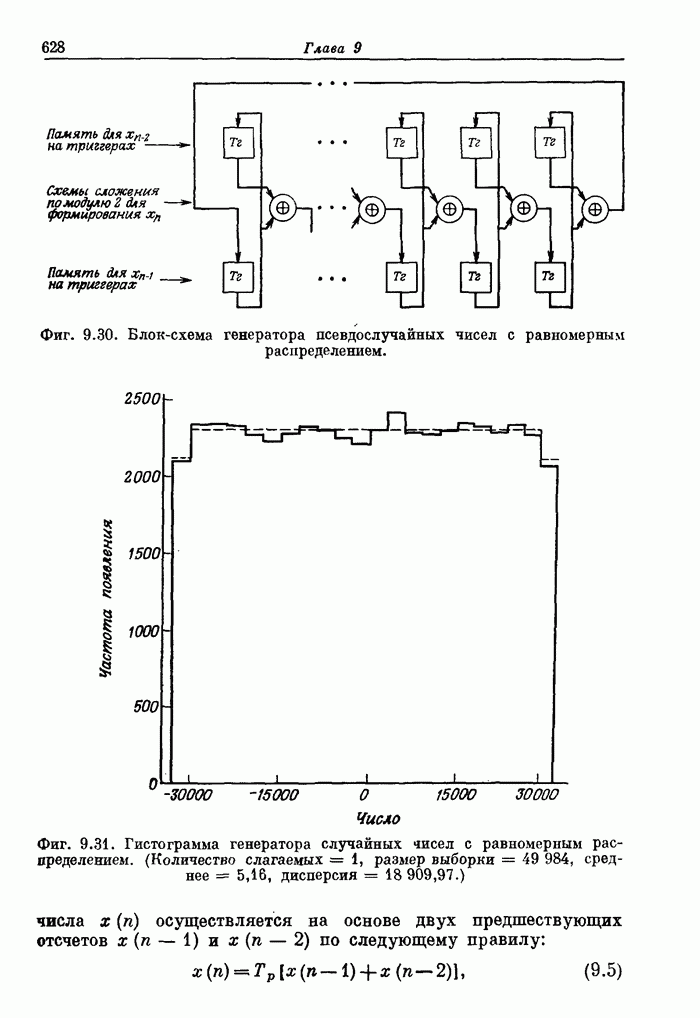
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
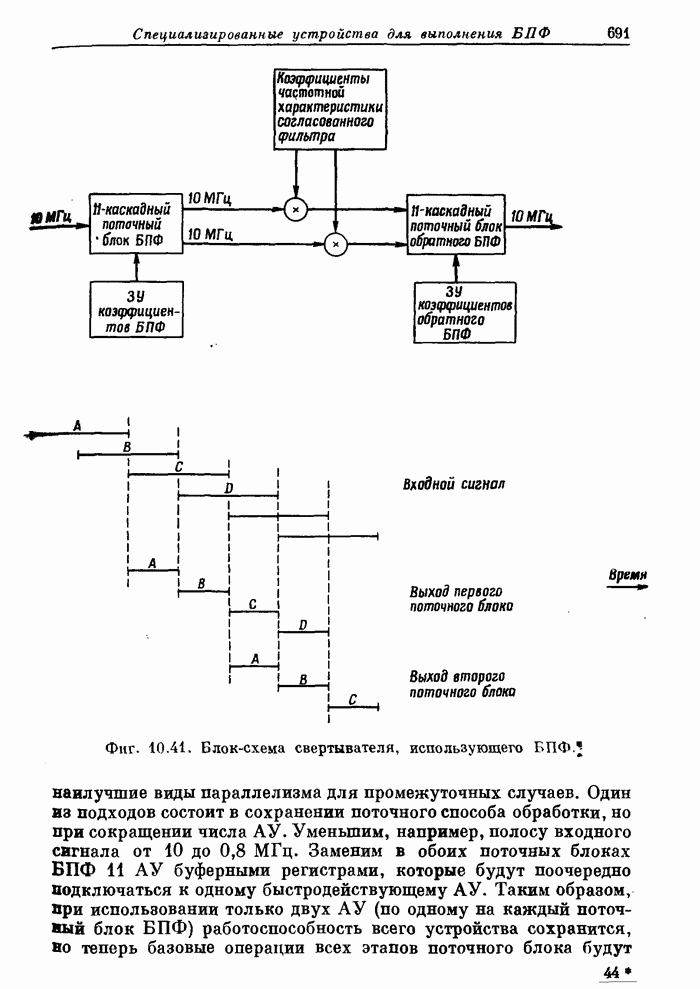
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
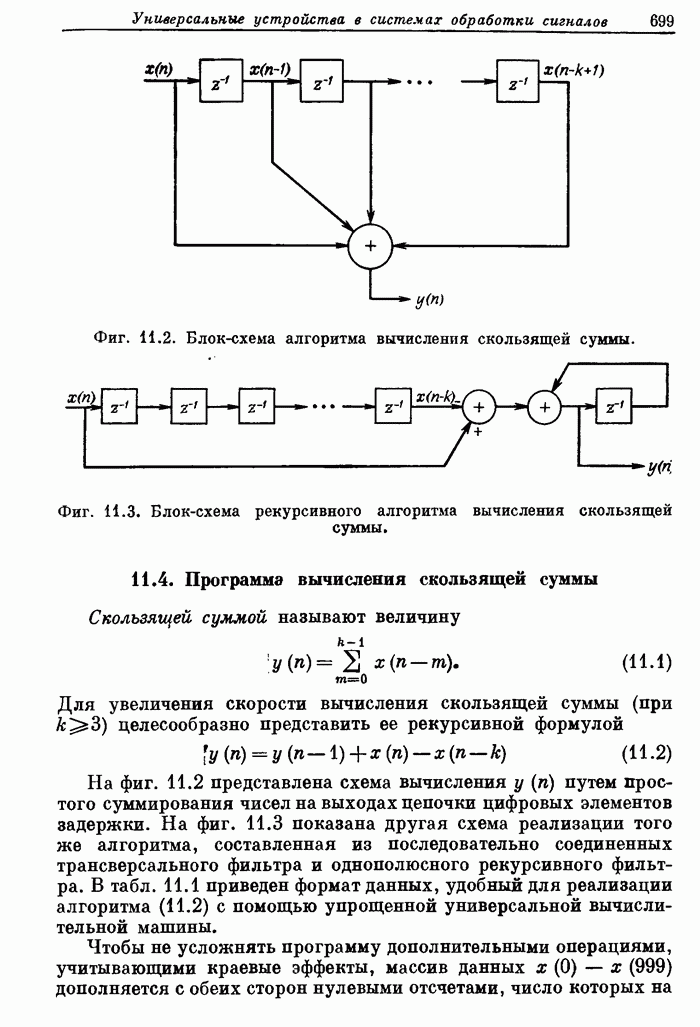
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
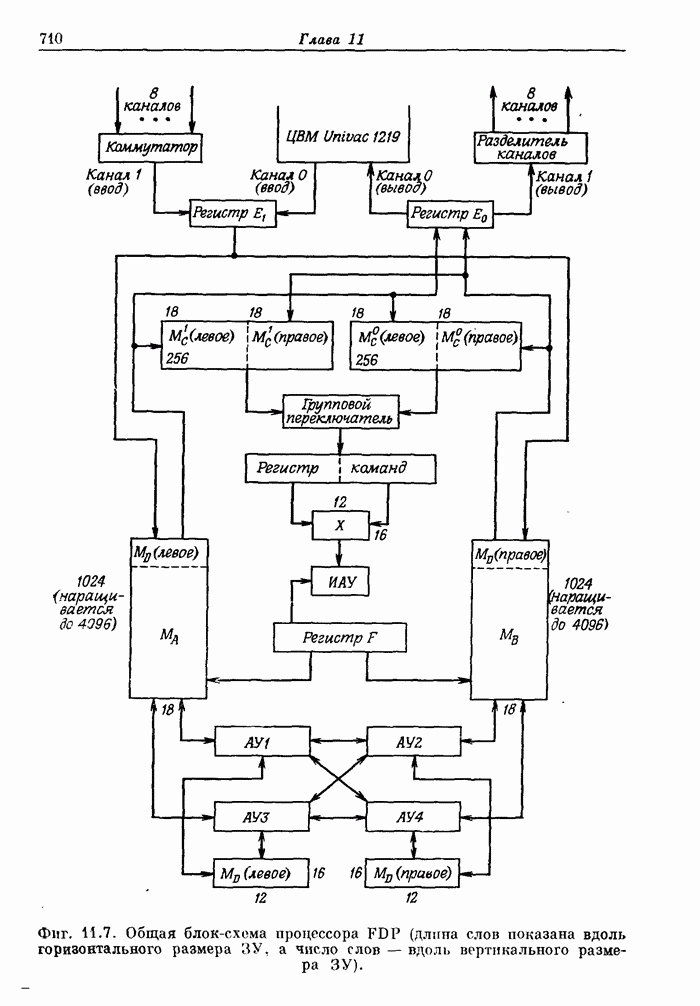
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
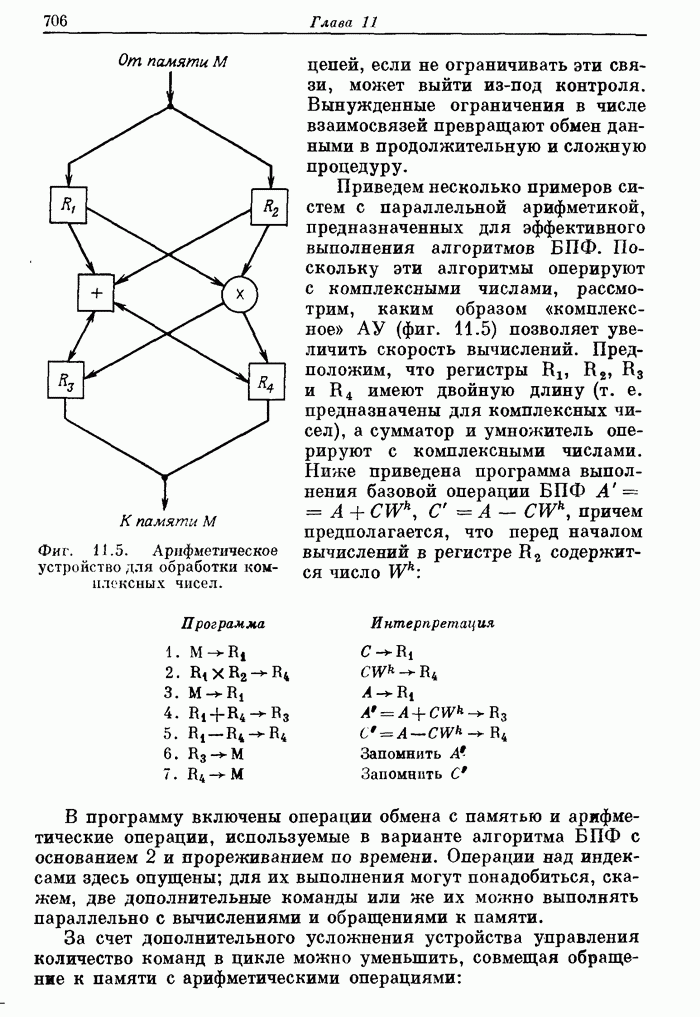
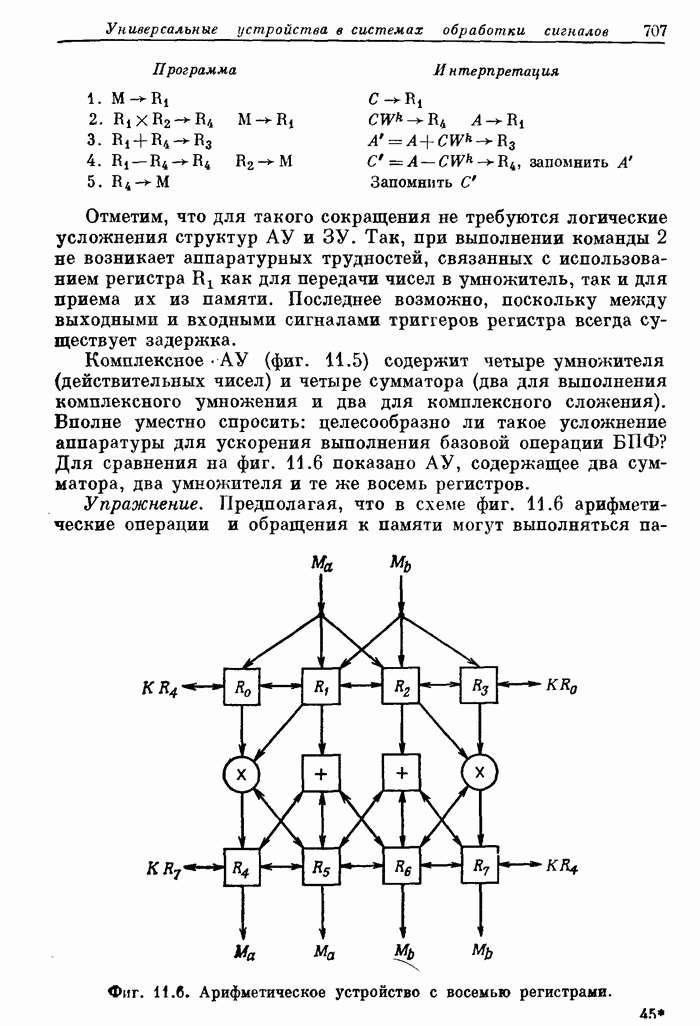
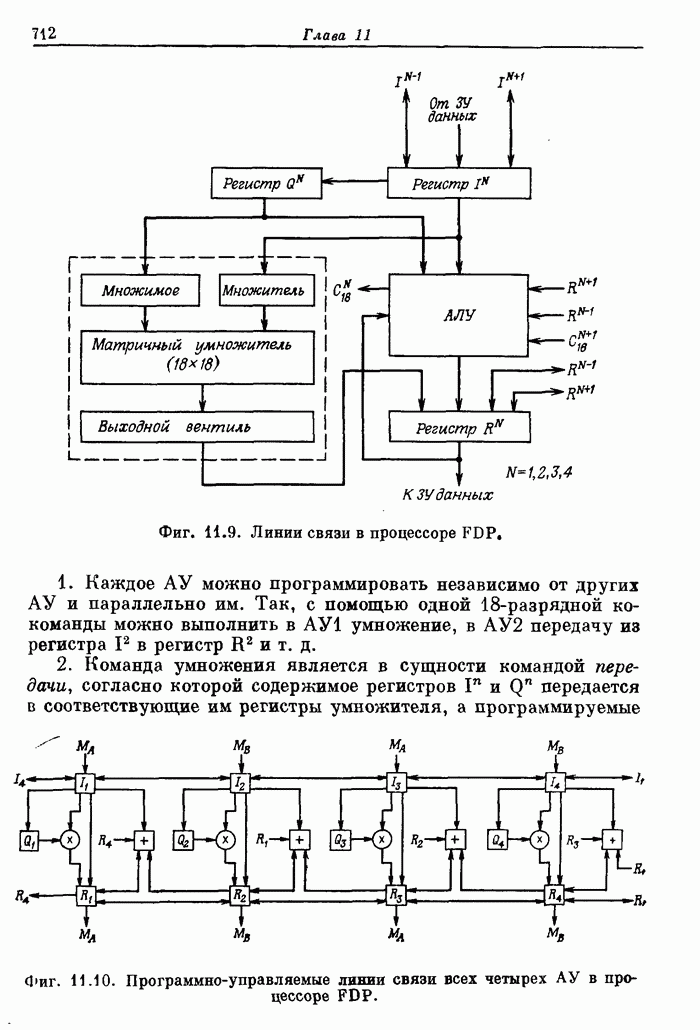
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
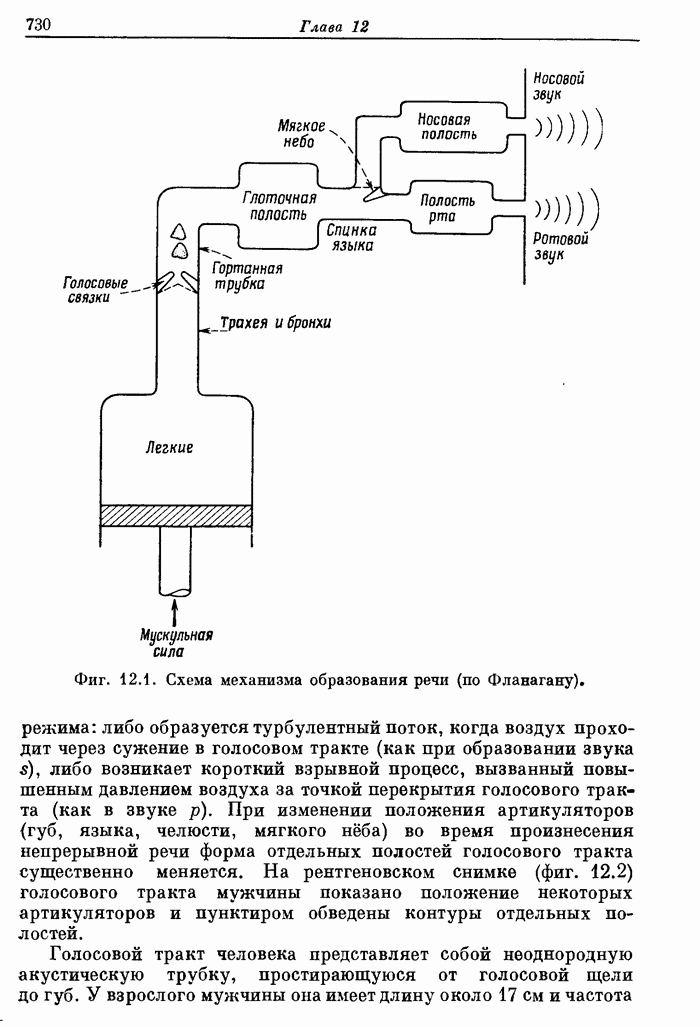
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
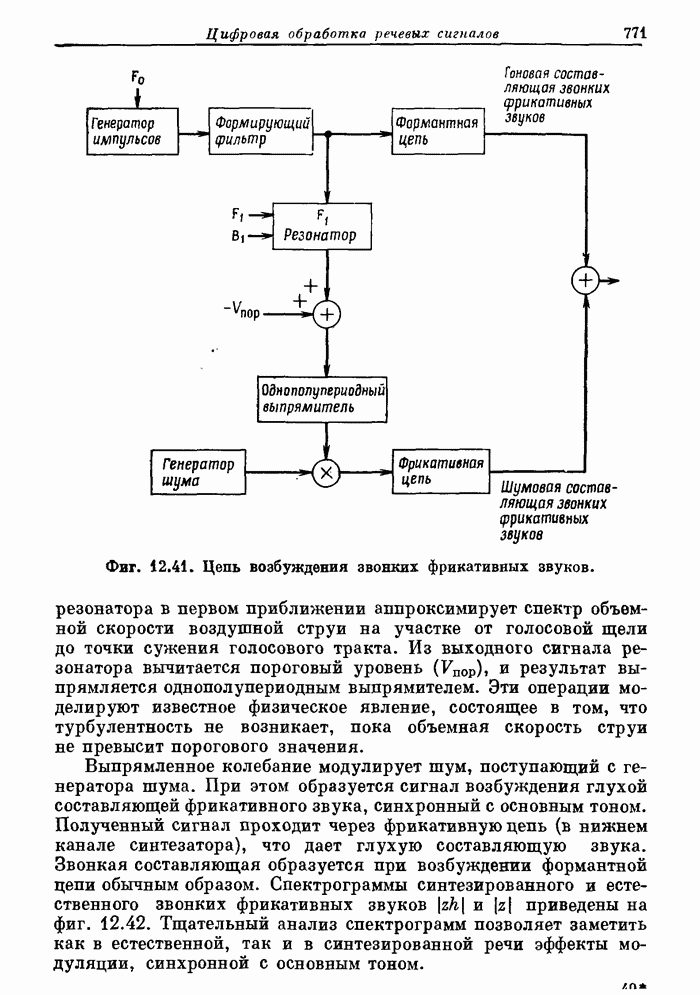
- 12.16. Цепь возбуждения звонких фрикативных звуков
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
- 12.19. Линейное прогнозирование речи
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
- 13.3. Выбор сигналов и функция неопределенности
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение