| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.14. Применение методов оптимизации для расчета БИХ-фильтров
Перейдем к описанию последнего класса методов расчета БИХ-фильтров, называемых методами оптимизации. Отличительная черта этих методов заключается в том, что система уравнений, составленная относительно коэффициентов фильтра, не может быть решена в явной форме.
Поэтому для нахождения коэффициентов приходится использовать расчетные формулы математических методов оптимизации, минимизирущих, согласно выбранному критерию, некоторую ошибку. С помощью последовательных приближений можно в конечном счете свести ошибку к минимуму; можно также задать определенное число выполняемых итераций и после выполнения их считать расчет законченным. В данном разделе будет описано применение нескольких методов оптимизации для расчета фильтров.
1. Минимизация среднеквадратической ошибки
Пусть  -преобразование импульсной характеристики БИХ) фильтра имеет вид
-преобразование импульсной характеристики БИХ) фильтра имеет вид

т. е. фильтр строится из последовательно соединенных блоков второго порядка. Обозначим заданную амплитудную характеристику фильтра через  . Пусть
. Пусть  , где
, где  , — дискретный ряд необязательно равномерно расположенных частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра. Тогда, согласно Штейглицу, квадрат суммарной ошибки на всех частотах, рассматриваемый в функции параметров фильтра, можно представить следующим образом:
, — дискретный ряд необязательно равномерно расположенных частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра. Тогда, согласно Штейглицу, квадрат суммарной ошибки на всех частотах, рассматриваемый в функции параметров фильтра, можно представить следующим образом:
 (4.143)
(4.143)
где  -мерный вектор искомых коэффициентов
-мерный вектор искомых коэффициентов
 (4.144)
(4.144)
Минимизация квадрата ошибки (4.143) сводится к нахождению оптимального значения вектора  (обозначим его через
(обозначим его через  ), для которого
), для которого
 (4.145)
(4.145)
Задачу минимизации можно решить, применив методы нелинейной оптимизации, скажем алгоритм Флетчера — Пауэла, при использовании которого предполагается, что градиент минимизируемой функции известен. Прежде чем перейти к рассмотрению способа расчета градиента, целесообразно исключить из вычислений коэффициент усиления А фильтра, поскольку он может быть рассчитан аналитически. Введя
 (4.146)
(4.146)
и
 (4.147)
(4.147)
получим
 (4.148)
(4.148)
Оптимальное значение А (равное А*) можно найти, продифференцировав правую часть (4.148) по А и приравняв производную к нулю, что дает
 (4.149)
(4.149)
Теперь задача сводится к минимизации функции ошибки
 (4.150)
(4.150)
Градиент функции  по
по  равен
равен
 (4.151)
(4.151)
Второй член в правой части (4.151) равен нулю, так как значение А минимизирует Q. Итак, формулу (4.151) можно записать следующим образом:

Так как
 (4.153)
(4.153)
то
 (4.154)
(4.154)
Формулу (4.154) можно использовать для вычислений. Итак, все вычисления, необходимые для расчета фильтров с использованием алгоритмов оптимизации типа алгоритма Флетчера—Пауэла, оказываются вполне выполнимыми.
При использовании методов оптимизации учитывается поведение только амплитудной характеристики, поэтому некоторые нолюсы или нули после завершения итераций могут оказаться за пределами единичного круга. В этом случае можно прежде всего заменить полюс с полярными координатами  , оказавшийся вне единичного круга, на полюс с координатами
, оказавшийся вне единичного круга, на полюс с координатами  находящийся внутри единичного круга.
находящийся внутри единичного круга.
Амплитудная характеристика фильтра при такой замене остается неизменной, так как полюс заменяется на его зеркальное отображение. Однако после того, как все полюсы оказываются внутри единичного круга, появляется возможность с помощью дополнительного анализа еще больше оптимизировать квадрат ошибки. Такая ситуация возникает достаточно часто, и в этих случаях оптимизация должна производиться двумя этапами:
1. Использование программы оптимизации для минимизации ошибки  без каких-либо ограничений на расположение нулей и полюсов.
без каких-либо ограничений на расположение нулей и полюсов.
2. После завершения итераций инвертирование всех полюсов и нулей, оказавшихся вне единичного круга. После этого продолжение программы оптимизации для нахождения нового минимума ошибки.
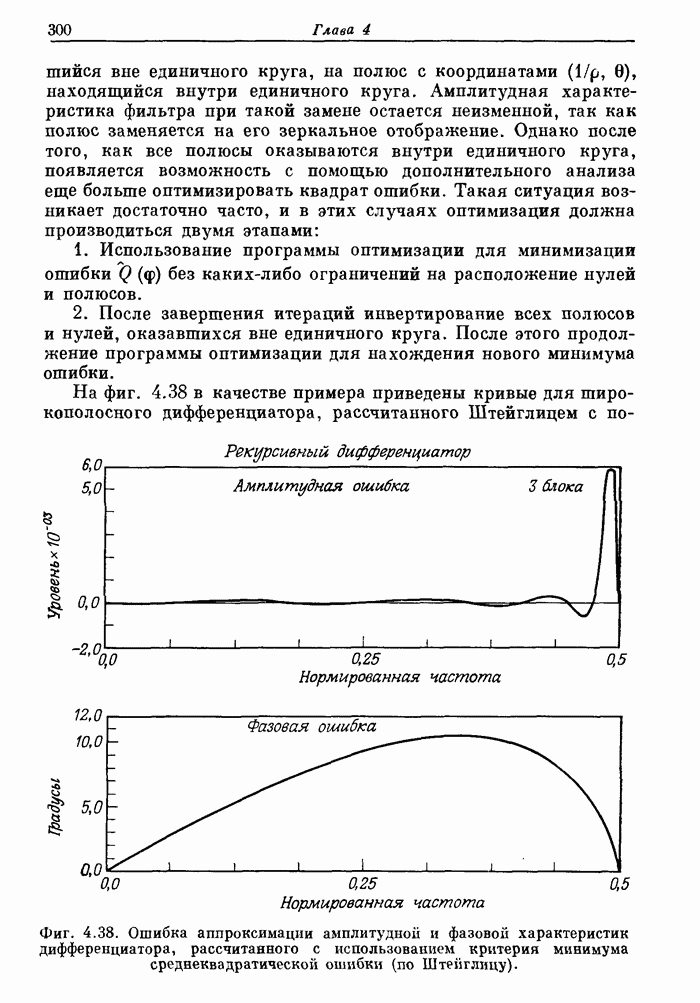
На фиг. 4.38 в качестве примера приведены кривые для широкополосного дифференциатора, рассчитанного Штейглицем с помощью описанного метода.

Фиг. 4.38. Ошибка аппроксимации амплитудной и фазовой характеристик дифференциатора, рассчитанного с использованием критерия минимума среднеквадратической ошибки (по Штейглицу).
При расчете использовалось 

На фиг. 4.38 приведены кривые ошибок аппроксимации амплитудной и фазовой характеристик дифференциатора.
2. Минимизация Lp-ошибки
Дечки показал, что от рассмотренного выше критерия минимума среднеквадратической ошибки можно перейти к критериям ошибки более высокого порядка. Более того, ошибку аппроксимации для характеристики групповой задержки фильтра можно определить так же, как для амплитудной характеристики.
Выразим z-преобразование импульсной характеристики фильтра через z-преобразования К последовательно включенных блоков 2-го порядка, представив полюсы и нули в полярных координатах:
 (4.155)
(4.155)
Искомый вектор неизвестных параметров определим следующим образом:
 (4.156)
(4.156)
Амплитудная характеристика фильтра будет равна
 (4.157)
(4.157)
а характеристика групповой задержки этого же фильтра будет описываться формулой

Задачу расчета БИХ-фильтра по заданной амплитудной характеристике  или характеристике групповой задержки
или характеристике групповой задержки  можно рассматривать как задачу минимизации ошибок
можно рассматривать как задачу минимизации ошибок  -аппроксимации, определяемых следующими формулами:
-аппроксимации, определяемых следующими формулами:
 (4.159)
(4.159)
 (4.160)
(4.160)
Эти формулы представляют ошибки аппроксимации амплитудной характеристики и характеристики групповой задержки соответственно в функции вектора параметров  . При
. При  и
и  (для всех
(для всех  ) минимизация Lp-ошибки будет идентична минимизации по критерию минимума среднеквадратической ошибки, рассмотренной в предыдущем разделе. Можно показать, что случай
) минимизация Lp-ошибки будет идентична минимизации по критерию минимума среднеквадратической ошибки, рассмотренной в предыдущем разделе. Можно показать, что случай  будет соответствовать критерию Чебышева (т. е. минимаксному критерию).
будет соответствовать критерию Чебышева (т. е. минимаксному критерию).

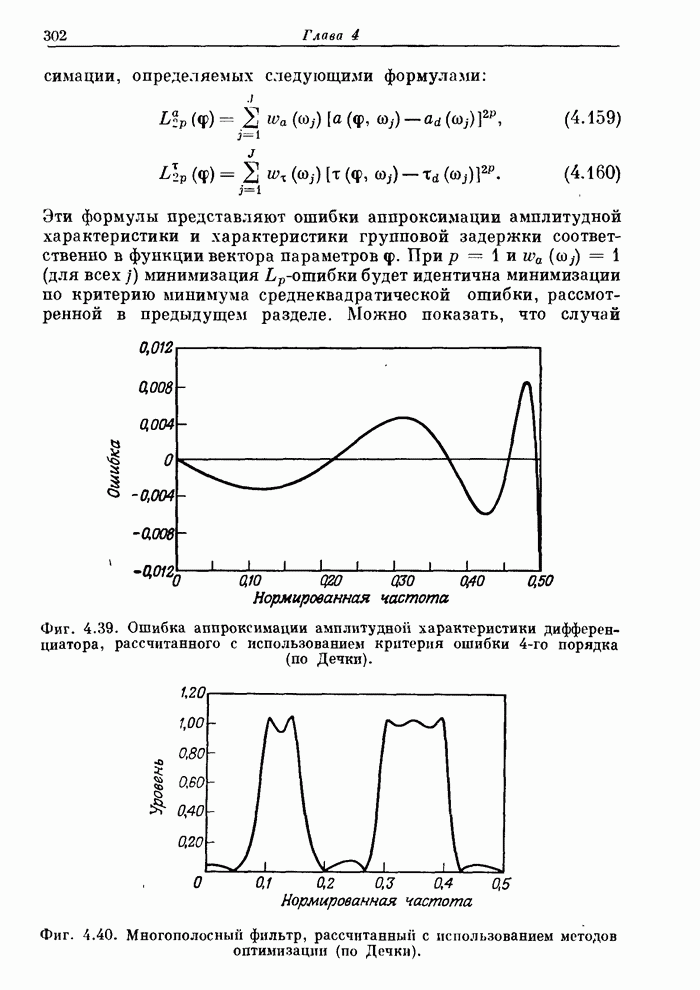
Фиг. 4.39. Ошибка аппроксимации амплитудной характеристики дифференциатора, рассчитанного с использованием критерия ошибки 4-го порядка (по Дечки).

Фиг. 4.40. Многополосный фильтр, рассчитанный с использованием методов оптимизации (по Дечки).

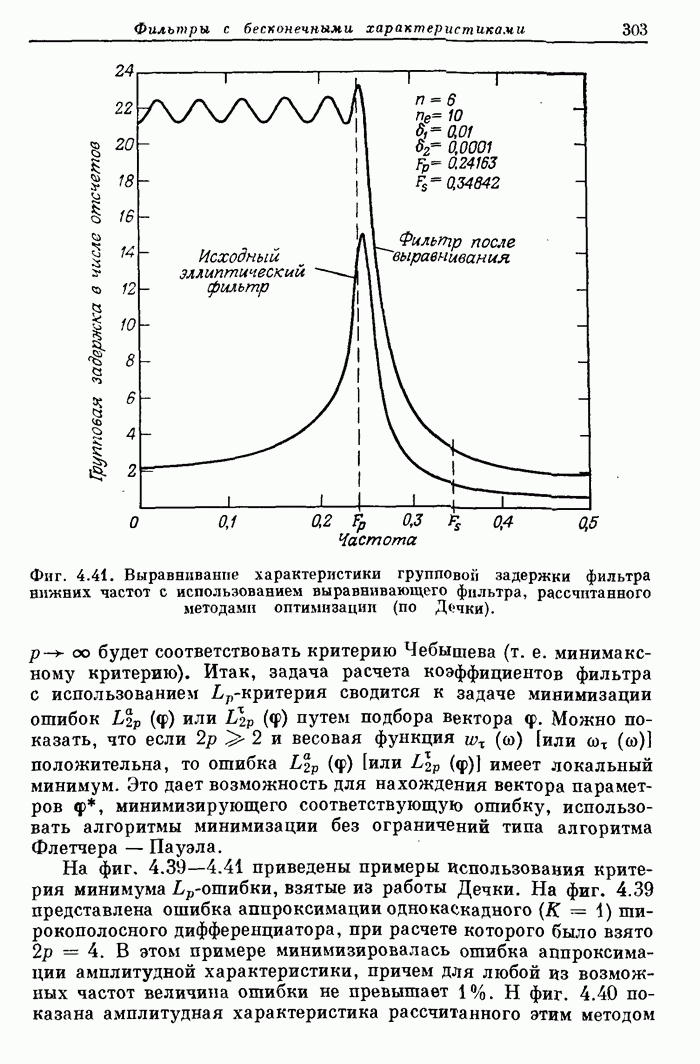
Фиг. 4.41. Выравнивание характеристики групповой задержки фильтра нижних частот с использованием выравнивающего фильтра, рассчитанного методами оптимизации (по Дечки).
Итак, задача расчета коэффициентов фильтра с использованием Lp-критерия сводится к задаче минимизации ошибок  или
или  путем подбора вектора
путем подбора вектора  . Можно показать, что если
. Можно показать, что если  и весовая функция
и весовая функция  положительна, то ошибка
положительна, то ошибка  имеет локальный минимум. Это дает возможность для нахождения вектора параметров
имеет локальный минимум. Это дает возможность для нахождения вектора параметров  , минимизирующего соответствующую ошибку, использовать алгоритмы минимизации без ограничений типа алгоритма Флетчера — Пауэла.
, минимизирующего соответствующую ошибку, использовать алгоритмы минимизации без ограничений типа алгоритма Флетчера — Пауэла.
На фиг. 4.39-4.41 приведены примеры использования критерия минимума Lp-ошибки, взятые из работы Дечки. На фиг. 4.39 представлена ошибка аппроксимации одно каскадного  широкополосного дифференциатора, при расчете которого было взято
широкополосного дифференциатора, при расчете которого было взято  . В этом примере минимизировалась ошибка аппроксимации амплитудной характеристики, причем для любой из возможных частот величина ошибки не превышает 1%. На фиг. 4.40 показана амплитудная характеристика рассчитанного этим методом фильтра, который был получен из фильтра 10-го порядка с двумя полосами пропускания и тремя полосами непропускания (К = 5).
. В этом примере минимизировалась ошибка аппроксимации амплитудной характеристики, причем для любой из возможных частот величина ошибки не превышает 1%. На фиг. 4.40 показана амплитудная характеристика рассчитанного этим методом фильтра, который был получен из фильтра 10-го порядка с двумя полосами пропускания и тремя полосами непропускания (К = 5).
В полосе ненропускания величина ошибки составляет приблизительно 0,1 (что обеспечивает ослабление на 20 дБ). Последний пример приведен на фиг. 4.41, где представлены характеристики групповой задержки исходного эллиптического фильтра и эллиптического фильтра, полученного после выравнивания его групповой задержки. Выравнивающая цепь состояла из включенных последовательно с исходным эллиптическим фильтром всепропускающих цепей, не оказывающих влияния на амплитудную характеристику фильтра. Порядок выравнивающей всепропускающей цепи был равен  , индекс ошибки
, индекс ошибки  . Как видно из фиг. 4.41, после выравнивания пульсации групповой задержки фильтра стали равновеликими.
. Как видно из фиг. 4.41, после выравнивания пульсации групповой задержки фильтра стали равновеликими.
3. Оптимизация в w-плоскости с использованием всепропускающих цепей
Весьма простая методика оптимизации, предложенная Дечки, может быть использована в случае, когда рассчитываемый БИХ-фильтр имеет равновеликие пульсации в полосе пропускания и обеспечивает аппроксимацию с равновеликими пульсациями произвольной характеристики в полосе непропускания или в полосе пропускания. Рассмотрим эту методику. Для этого запишем квадрат амплитудной характеристики фильтра в виде
 (4.161)
(4.161)
где  — рациональная передаточная функция, подобная, но не идентичная рациональной функции Чебышева, использовавшейся при расчете эллиптических фильтров. Вместо того чтобы сразу найти функцию
— рациональная передаточная функция, подобная, но не идентичная рациональной функции Чебышева, использовавшейся при расчете эллиптических фильтров. Вместо того чтобы сразу найти функцию  , целесообразно сначала перенести решение задачи аппроксимации из z-плоскости в некоторую новую плоскость (назовем ее w-плоскостью), такую, чтобы полоса пропускания (или непропускания) фильтра отображалась на всю мнимую ось в w-плоскости. В этом случае оказывается возможным достаточно просто записывать передаточные функции всепропускающих цепей в
, целесообразно сначала перенести решение задачи аппроксимации из z-плоскости в некоторую новую плоскость (назовем ее w-плоскостью), такую, чтобы полоса пропускания (или непропускания) фильтра отображалась на всю мнимую ось в w-плоскости. В этом случае оказывается возможным достаточно просто записывать передаточные функции всепропускающих цепей в  -плоскости; используя эти всепропускающие функции, можно получить такую функцию
-плоскости; используя эти всепропускающие функции, можно получить такую функцию  которая будет осциллировать между 0 и 1 при изменении w вдоль мнимой оси от 0 до
которая будет осциллировать между 0 и 1 при изменении w вдоль мнимой оси от 0 до  Таким образом, функция
Таким образом, функция  будет иметь в w-плоскости равновеликие пульсации. В зависимости от характера отображения эти равновеликие пульсации
будет иметь в w-плоскости равновеликие пульсации. В зависимости от характера отображения эти равновеликие пульсации  можно отобразить либо в полосу пропускания фильтра в z-плоскости, либо в полосу непропускания. При этом поведение характеристики фильтра в другой полосе будет полностью определяться еще не найденными значениями коэффициентов всепропускающего фильтра.
можно отобразить либо в полосу пропускания фильтра в z-плоскости, либо в полосу непропускания. При этом поведение характеристики фильтра в другой полосе будет полностью определяться еще не найденными значениями коэффициентов всепропускающего фильтра.
Для расчета коэффициентов всепропускающего фильтра, которые обеспечили бы аппроксимацию с равновеликими пульсациями любой характеристики в полосе, где она не была задана, можно использовать методы последовательного приближения. Рассмотрим сначала методику получения функции  .
.
Чтобы определить передаточную функцию, модуль которой постоянен вдоль всей мнимой оси, рассмотрим всепропускающую функцию вида

где  либо действительные, либо образуют комплексно сопряженные пары. Так как
либо действительные, либо образуют комплексно сопряженные пары. Так как  , то
, то  можно записать в виде
можно записать в виде
 (4.163)
(4.163)
где
 (4.164)
(4.164)
причем 
Введем действительную функцию  следующим образом:
следующим образом:
 (4.166)
(4.166)
Аналитически продолжая (4.166), получим
 (4.167)
(4.167)
Таким образом, найдена искомая функция  имеющая в
имеющая в  -плоскости равновеликие пульсации модуля вдоль оси
-плоскости равновеликие пульсации модуля вдоль оси  независимо от значений коэффициентов
независимо от значений коэффициентов  всепропускающего фильтра. Рассмотрим теперь случай отображения из z-плоскости в плоскость, соответствующий равновеликим пульсациям в полосе пропускания при произвольной характеристике в полосе непропускания. Аналогично можно было бы рассмотреть и другой случай отображения, соответствующий равновеликим пульсациям в полосе непропускания при произвольной характеристике в полосе пропускания, но так как этот случай обычно представляет меньший интерес, то ниже он не рассматривается.
всепропускающего фильтра. Рассмотрим теперь случай отображения из z-плоскости в плоскость, соответствующий равновеликим пульсациям в полосе пропускания при произвольной характеристике в полосе непропускания. Аналогично можно было бы рассмотреть и другой случай отображения, соответствующий равновеликим пульсациям в полосе непропускания при произвольной характеристике в полосе пропускания, но так как этот случай обычно представляет меньший интерес, то ниже он не рассматривается.
Для отображения полосы пропускания фильтра из z-плоскости на всю мнимую ось в w-плоскости воспользуемся следующим преобразованием:

Обратное преобразование из w-плоскости в z-плоскость можно найти, решив (4.168) относительно z:
 (4.169)
(4.169)
где

С помощью преобразования (4.168) дуга единичной окружности из z-плоскости, соответствующая частотам  (т. е. полосе пропускания фильтра), отображается на всю мнимую ось в w-плоскости (предполагается, что фильтр имеет единственную полосу пропускания и две или более полосы непропускания). Полосы пропускания фильтра из z-плоскости отображаются следующим образом:
(т. е. полосе пропускания фильтра), отображается на всю мнимую ось в w-плоскости (предполагается, что фильтр имеет единственную полосу пропускания и две или более полосы непропускания). Полосы пропускания фильтра из z-плоскости отображаются следующим образом:
 (4.171)
(4.171)
Здесь  — действительная часть w. Для фильтра нижних частот во всех приведенных выше формулах
— действительная часть w. Для фильтра нижних частот во всех приведенных выше формулах 
Преобразование z-плоскости в w-плоскость иллюстрируется на фиг. 4.42, где в каждой из плоскостей изображены область пропускания (с равновеликими пульсациями  и области непропускания.
и области непропускания.
Теперь остается лишь привести методику расчета коэффициентов  входящих в формулу (4.167), которые дали бы возможность аппроксимировать произвольную амплитудную характеристику в полосе непропускания, а также методику получения передаточной функции
входящих в формулу (4.167), которые дали бы возможность аппроксимировать произвольную амплитудную характеристику в полосе непропускания, а также методику получения передаточной функции  , или, что то же самое, функции
, или, что то же самое, функции  , по функции
, по функции  Рассмотрим сначала вторую из этих двух задач как более простую.
Рассмотрим сначала вторую из этих двух задач как более простую.
Если нули функции  расположены на единичной окружности (как это обычно имеет место при аппроксимации с равновеликими пульсациями), то корни в w-плоскости будут действительными и иметь четную кратность, так как в этом случае оба комплексно сопряженных нуля будут отображаться в одну и ту же точку на действительной оси в w-плоскости.
расположены на единичной окружности (как это обычно имеет место при аппроксимации с равновеликими пульсациями), то корни в w-плоскости будут действительными и иметь четную кратность, так как в этом случае оба комплексно сопряженных нуля будут отображаться в одну и ту же точку на действительной оси в w-плоскости.

Фиг. 4.42. Отображение из z-плоскости в w-плоскость (по Дечки).
Поэтому выражение (4.167) можно представить следующим образом:

где  — преобразованные нули фильтра. Введя вспомогательные многочлены
— преобразованные нули фильтра. Введя вспомогательные многочлены  и
и  , равные
, равные

и
 (4.174)
(4.174)
запишем формулу (4.161) в виде

из которой после разложения на множители получим
 (4.176)
(4.176)
Корни функции  располагаются в правой полуплоскости w, что гарантирует устойчивость искомого фильтра с передаточной функцией Н (z). [Кроме того, при расчетах удобнее находить корни функции
располагаются в правой полуплоскости w, что гарантирует устойчивость искомого фильтра с передаточной функцией Н (z). [Кроме того, при расчетах удобнее находить корни функции  в
в  -плоскости и преобразовывать их затем обратно в z-плоскость, так как в w-плоскости они обычно легче разделяются, чем корни Н(z) в z-плоскости.]
-плоскости и преобразовывать их затем обратно в z-плоскость, так как в w-плоскости они обычно легче разделяются, чем корни Н(z) в z-плоскости.]
Наконец приведем алгоритм расчета коэффициентов  , обеспечивающих заданную форму амплитудной характеристики в полосе непропускания. Простой способ аппроксимации получается при использовании для описания амплитудной характеристики в полосе непропускания функции ее логарифма:
, обеспечивающих заданную форму амплитудной характеристики в полосе непропускания. Простой способ аппроксимации получается при использовании для описания амплитудной характеристики в полосе непропускания функции ее логарифма:

откуда

При этом для расчета значений  , таких, чтобы величина ошибки аппроксимации функции а, задаваемой формулой (4.178), была минимаксной для всей полосы непропускания, можно использовать достаточно простые методы (например, алгоритм Ремеза).
, таких, чтобы величина ошибки аппроксимации функции а, задаваемой формулой (4.178), была минимаксной для всей полосы непропускания, можно использовать достаточно простые методы (например, алгоритм Ремеза).
Таким образом, выше было показано, что БИХ-фильтры с равновеликими пульсациями в полосе пропускания (или в полосе непропускания) и произвольной характеристикой в полосах непропускания (или в полосах пропускания) можно рассчитывать путем перенесения решения задачи аппроксимации из z-плоскости в ( -плоскость, такую, чтобы полоса пропускания фильтра в z-плоскости отображалась на всю мнимую ось в w-плоскости. В этой новой w-плоскости синтезируется всепропускающая функция, модуль которой постоянен на всей мнимой оси. Затем из этой всепропус-кающей функции с помощью простой подстановки формируется передаточная функция, модуль которой имеет вдоль мнимой оси в w-плоскости равновеликие пульсации независимо от значений коэффициентов всепропускающей функции. Наконец, с помощью простой методики рассчитываются оптимальные значения коэффициентов всепропускающего фильтра, которые используются для аппроксимации в z-плоскости требуемой частотной характеристики в полосе непропускания. Проиллюстрируем применение этого метода на двух примерах, взятых из работы Дечки.
-плоскость, такую, чтобы полоса пропускания фильтра в z-плоскости отображалась на всю мнимую ось в w-плоскости. В этой новой w-плоскости синтезируется всепропускающая функция, модуль которой постоянен на всей мнимой оси. Затем из этой всепропус-кающей функции с помощью простой подстановки формируется передаточная функция, модуль которой имеет вдоль мнимой оси в w-плоскости равновеликие пульсации независимо от значений коэффициентов всепропускающей функции. Наконец, с помощью простой методики рассчитываются оптимальные значения коэффициентов всепропускающего фильтра, которые используются для аппроксимации в z-плоскости требуемой частотной характеристики в полосе непропускания. Проиллюстрируем применение этого метода на двух примерах, взятых из работы Дечки.

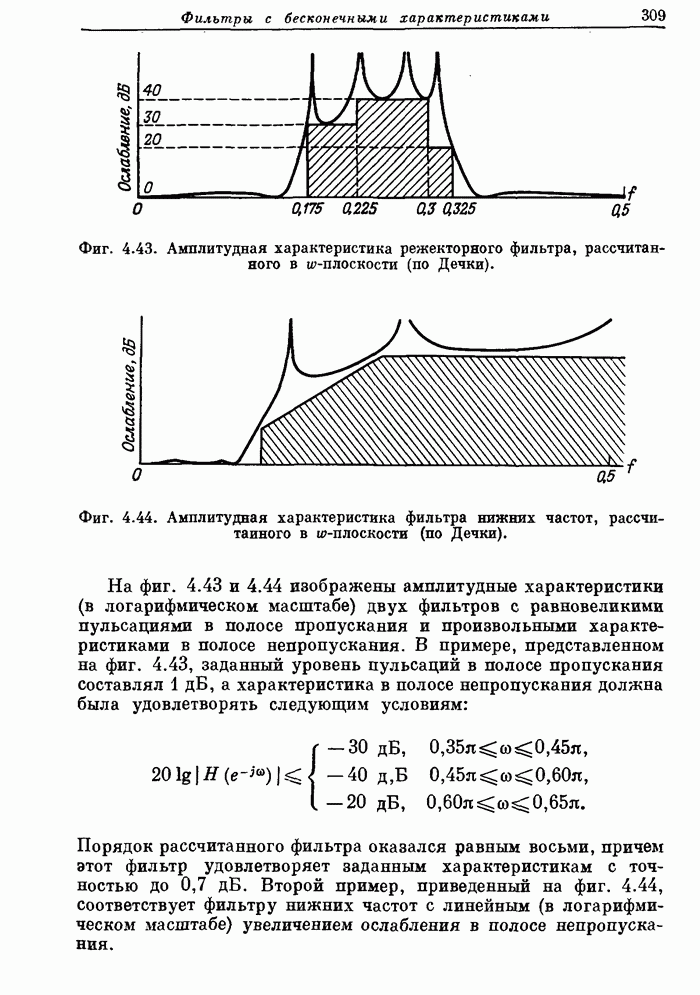
Фиг. 4.43. Амплитудная характеристика режекторного фильтра, рассчитанного в w-плоскости (по Дечки).

Фиг. 4.44. Амплитудная характеристика фильтра нижних частот, рассчитанного в w-плоскости (по Дечки).
На фиг. 4.43 и 4.44 изображены амплитудные характеристики (в логарифмическом масштабе) двух фильтров с равновеликими пульсациями в полосе пропускания и произвольными характеристиками в полосе непропускания. В примере, представленном на фиг. 4.43, заданный уровень пульсаций в полосе пропускания составлял 1 дБ, а характеристика в полосе непропускания должна была удовлетворять следующим условиям:

Порядок рассчитанного фильтра оказался равным восьми, причем этот фильтр удовлетворяет заданным характеристикам с точностью до 0,7 дБ. Второй пример, приведенный на фиг. 4.44, соответствует фильтру нижних частот с линейным (в логарифмическом масштабе) увеличением ослабления в полосе непропускания.
4. Расчет БИХ-фильтров методами линейного программирования
Методы линейного программирования могут быть использованы для расчета БИХ-фильтров, обеспечивающих аппроксимацию с равновеликими пульсациями заданной амплитудной характеристики. Если передаточная функция цифрового фильтра равна

то  можно представить в виде
можно представить в виде
 (4.180)
(4.180)
где
 (4.1816)
(4.1816)
Поэтому квадрат амплитудной характеристики фильтра [т. е. значения (4.180) на единичной окружности] равен отношению тригонометрических полиномов:
 (4.182)
(4.182)
Обе функции  линейно зависят от коэффициентов
линейно зависят от коэффициентов  Рассмотрим, каким образом можно использовать методы линейного программирования для нахождения таких значений коэффициентов
Рассмотрим, каким образом можно использовать методы линейного программирования для нахождения таких значений коэффициентов  которые обеспечили бы аппроксимацию заданного квадрата амплитудной характеристики
которые обеспечили бы аппроксимацию заданного квадрата амплитудной характеристики  функцией
функцией  причем максимум ошибки аппроксимации был бы минимизирован (т. е. чтобы аппроксимация имела равновеликие пульсации).
причем максимум ошибки аппроксимации был бы минимизирован (т. е. чтобы аппроксимация имела равновеликие пульсации).
Итак, задача аппроксимации заданной функции квадрата амплитудной характеристики  сводится к нахождению таких коэффициентов фильтра, при которых
сводится к нахождению таких коэффициентов фильтра, при которых
 (4.183)
(4.183)
Здесь  — функция допуска для ошибки аппроксимации, позволяющая учитывать неодинаковый вес ошибок аппроксимации на различных частотах. Функции
— функция допуска для ошибки аппроксимации, позволяющая учитывать неодинаковый вес ошибок аппроксимации на различных частотах. Функции  обычно известны (или, как будет показано в приведенном ниже примере, зависят от некоторого параметра), поэтому неравенство (4.183) можно представить с помощью следующей системы неравенств, линейных относительно неизвестных
обычно известны (или, как будет показано в приведенном ниже примере, зависят от некоторого параметра), поэтому неравенство (4.183) можно представить с помощью следующей системы неравенств, линейных относительно неизвестных 

или
 (4.185)
(4.185)
Эти, а также следующие дополнительные линейные неравенства:
 (4.186)
(4.186)
 (4.187)
(4.187)
полностью определяют задачу аппроксимации. Для решения системы линейных неравенств (4.185)-(4.187) из левой части каждого из них вычитается вспомогательная переменная w, которая затем минимизируется. Если значение w оказывается равным нулю, то это означает, что решение задачи аппроксимации существует, причем значения коэффициентов можно получить обычным методом линейного программирования. Если же оказывается, что w О, то это означает, что решения задачи аппроксимации не существует, поэтому для ее решения нужно изменить либо  либо
либо  .
.
Рассмотрим в качестве примера расчет фильтра нижних частот с равновеликими пульсациями и коэффициентом передачи, равным 1 в полосе пропускания и 0 в полосе непропускания. Допустим, что максимальная ошибка аппроксимации равна  в полосе непропускания и
в полосе непропускания и  (величина постоянной К выбирается разработчиком) в полосе пропускания. Заданная амплитудная характеристика такого фильтра нижних частот изображена на фиг. 4.45, а. Величина
(величина постоянной К выбирается разработчиком) в полосе пропускания. Заданная амплитудная характеристика такого фильтра нижних частот изображена на фиг. 4.45, а. Величина  неизвестна, причем в процессе расчета она должна быть минимизирована (результирующий фильтр в данном случае будет, очевидно, эллиптическим, но здесь он используется только для иллюстрации метода). Заданная функция квадрата амплитудной характеристики фильтра, равная квадрату функции, изображенной на фиг. 4.45, а, приведена на фиг. 4.45, б.
неизвестна, причем в процессе расчета она должна быть минимизирована (результирующий фильтр в данном случае будет, очевидно, эллиптическим, но здесь он используется только для иллюстрации метода). Заданная функция квадрата амплитудной характеристики фильтра, равная квадрату функции, изображенной на фиг. 4.45, а, приведена на фиг. 4.45, б.

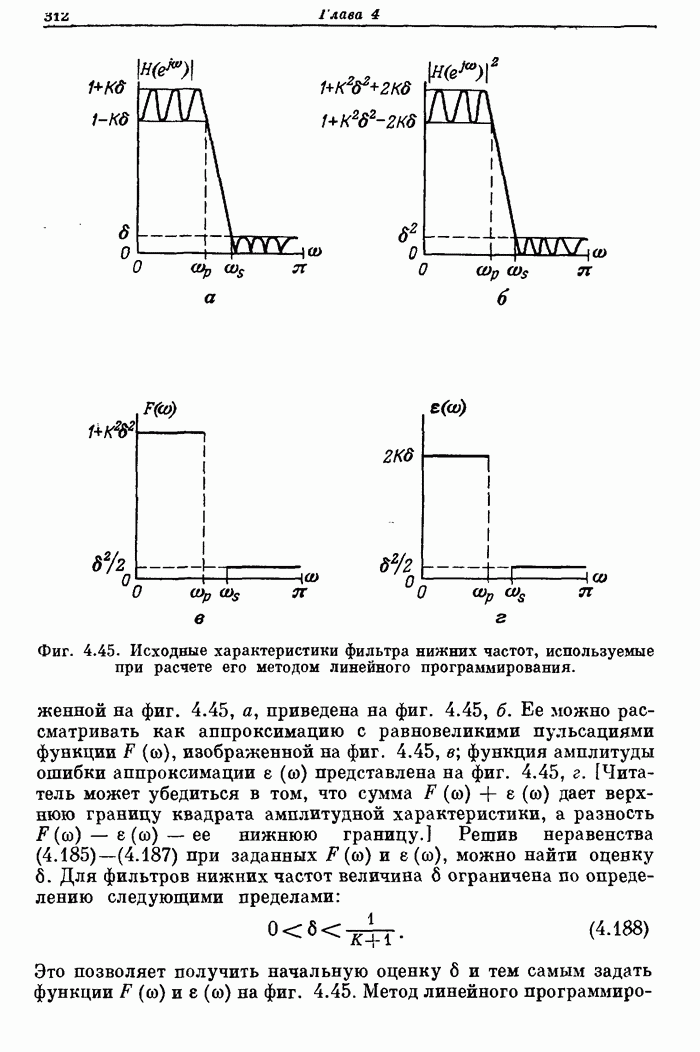
Фиг. 4.45. Исходные характеристики фильтра нижних частот, используемые при расчете его методом линейного программирования.
Ее можно рассматривать как аппроксимацию с равновеликими пульсациями функции  , изображенной на фиг. 4.45, в; функция амплитуды ошибки аппроксимации
, изображенной на фиг. 4.45, в; функция амплитуды ошибки аппроксимации  представлена на фиг. 4.45, г. [Читатель может убедиться в том, что сумма
представлена на фиг. 4.45, г. [Читатель может убедиться в том, что сумма  дает верхнюю границу квадрата амплитудной характеристики, а разность
дает верхнюю границу квадрата амплитудной характеристики, а разность  — ее нижнюю границу.] Решив неравенства (4.185)-(4.187) при заданных
— ее нижнюю границу.] Решив неравенства (4.185)-(4.187) при заданных  и
и  , можно найти оценку
, можно найти оценку  . Для фильтров нижних частот величина
. Для фильтров нижних частот величина  ограничена по определению следующими пределами:
ограничена по определению следующими пределами:

Это позволяет получить начальную оценку  и тем самым задать функции
и тем самым задать функции  на фиг. 4.45. Метод линейного программирования дает возможность для выбранного значения
на фиг. 4.45. Метод линейного программирования дает возможность для выбранного значения  определить, имеет ли заданная система неравенств какое-либо решение.
определить, имеет ли заданная система неравенств какое-либо решение.

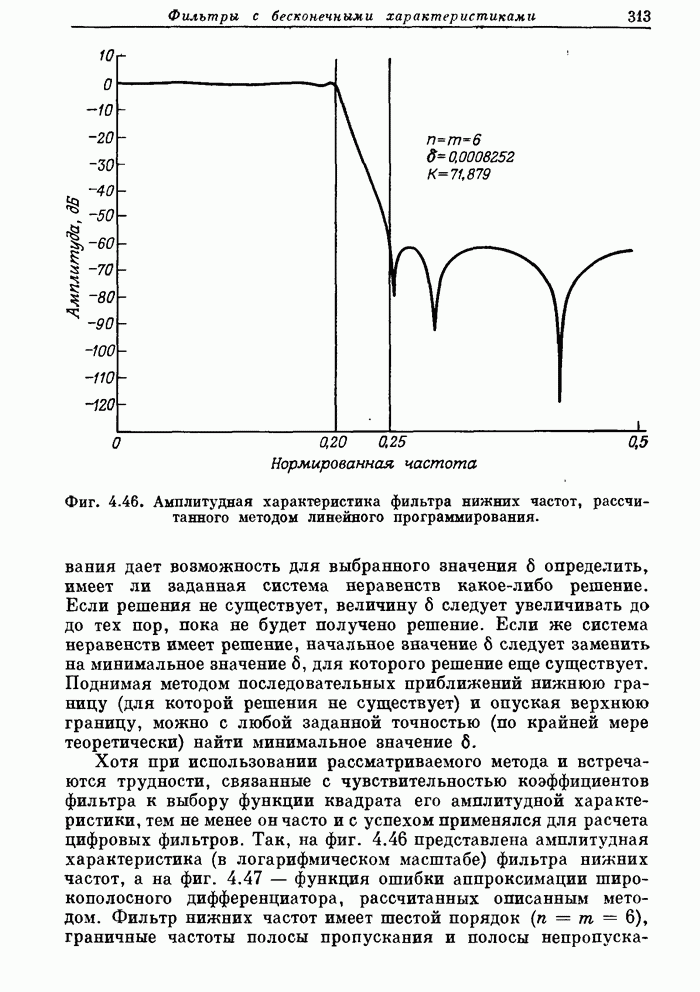
Фиг. 4.46. Амплитудная характеристика фильтра нижних частот, рассчитанного методом линейного программирования.
Если решения не существует, величину  следует увеличивать до до тех пор, пока не будет получено решение. Если же система неравенств имеет решение, начальное значение
следует увеличивать до до тех пор, пока не будет получено решение. Если же система неравенств имеет решение, начальное значение  следует заменить на минимальное значение
следует заменить на минимальное значение  , для которого решение еще существует. Поднимая методом последовательных приближений нижнюю границу (для которой решения не существует) и опуская верхнюю границу, можно с любой заданной точностью (по крайней мере теоретически) найти минимальное значение
, для которого решение еще существует. Поднимая методом последовательных приближений нижнюю границу (для которой решения не существует) и опуская верхнюю границу, можно с любой заданной точностью (по крайней мере теоретически) найти минимальное значение  .
.
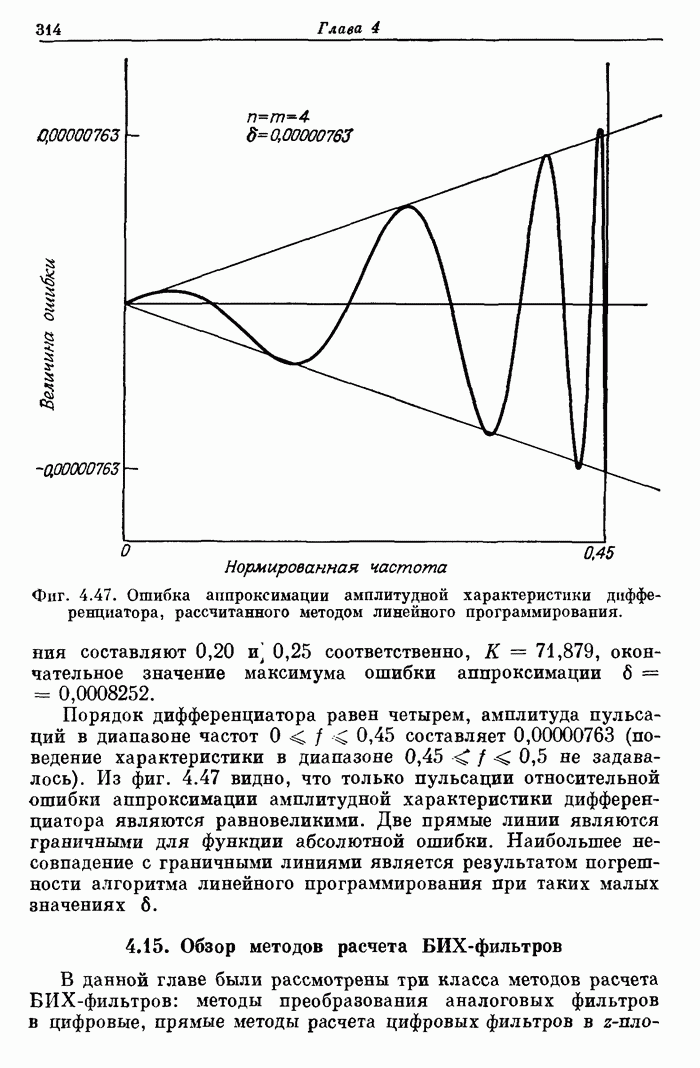
Хотя при использовании рассматриваемого метода и встречаются трудности, связанные с чувствительностью коэффициентов фильтра к выбору функции квадрата его амплитудной характеристики, тем не менее он часто и с успехом применялся для расчета цифровых фильтров. Так, на фиг. 4.46 представлена амплитудная характеристика (в логарифмическом масштабе) фильтра нижних частот, а на фиг. 4.47 — функция ошибки аппроксимации широкополосного дифференциатора, рассчитанных описанным методом.

Фиг. 4.47. Ошибка аппроксимации амплитудной характеристики дифференциатора, рассчитанного методом линейного программирования.
Фильтр нижних частот имеет шестой порядок  граничные частоты полосы пропускания и полосы непропускания составляют 0,20 и, 0,25 соответственно,
граничные частоты полосы пропускания и полосы непропускания составляют 0,20 и, 0,25 соответственно,  , окончательное значение максимума ошибки аппроксимации
, окончательное значение максимума ошибки аппроксимации  .
.
Порядок дифференциатора равен четырем, амплитуда пульсаций в диапазоне частот  составляет 0,00000763 (поведение характеристики в диапазоне
составляет 0,00000763 (поведение характеристики в диапазоне  не задавалось). Из фиг. 4.47 видно, что только пульсации относительной ошибки аппроксимации амплитудной характеристики дифференциатора являются равновеликими. Две прямые линии являются граничными для функции абсолютной ошибки. Наибольшее несовпадение с граничными линиями является результатом погрешности алгоритма линейного программирования при таких малых значениях
не задавалось). Из фиг. 4.47 видно, что только пульсации относительной ошибки аппроксимации амплитудной характеристики дифференциатора являются равновеликими. Две прямые линии являются граничными для функции абсолютной ошибки. Наибольшее несовпадение с граничными линиями является результатом погрешности алгоритма линейного программирования при таких малых значениях  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
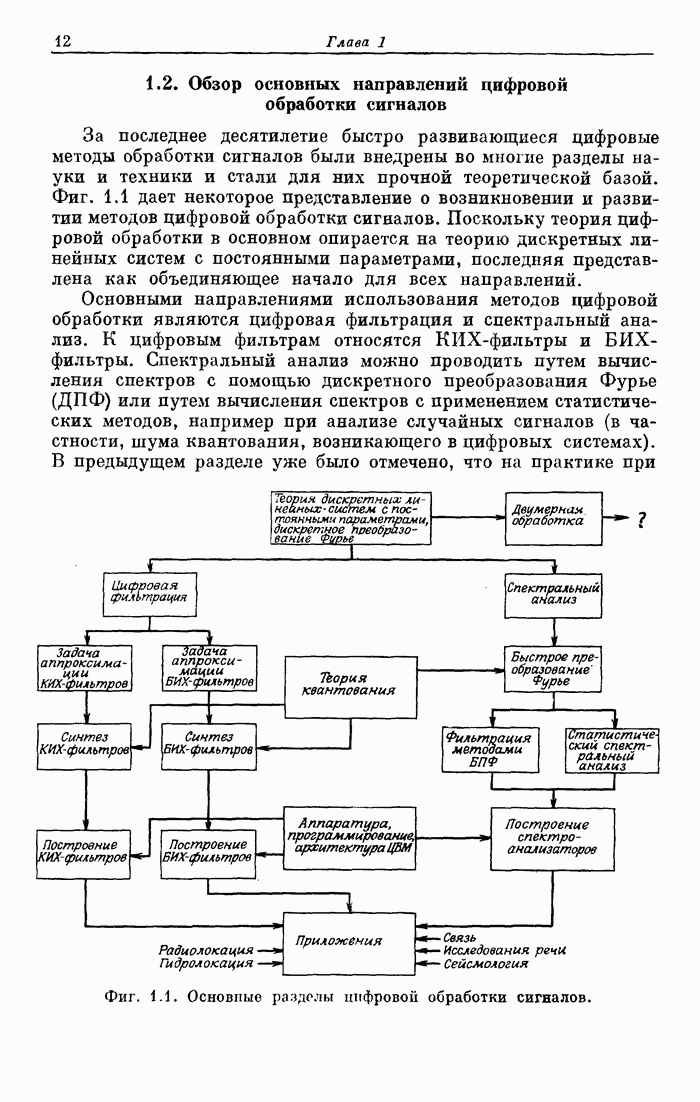
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
- 2.5. Физическая реализуемость. Устойчивость
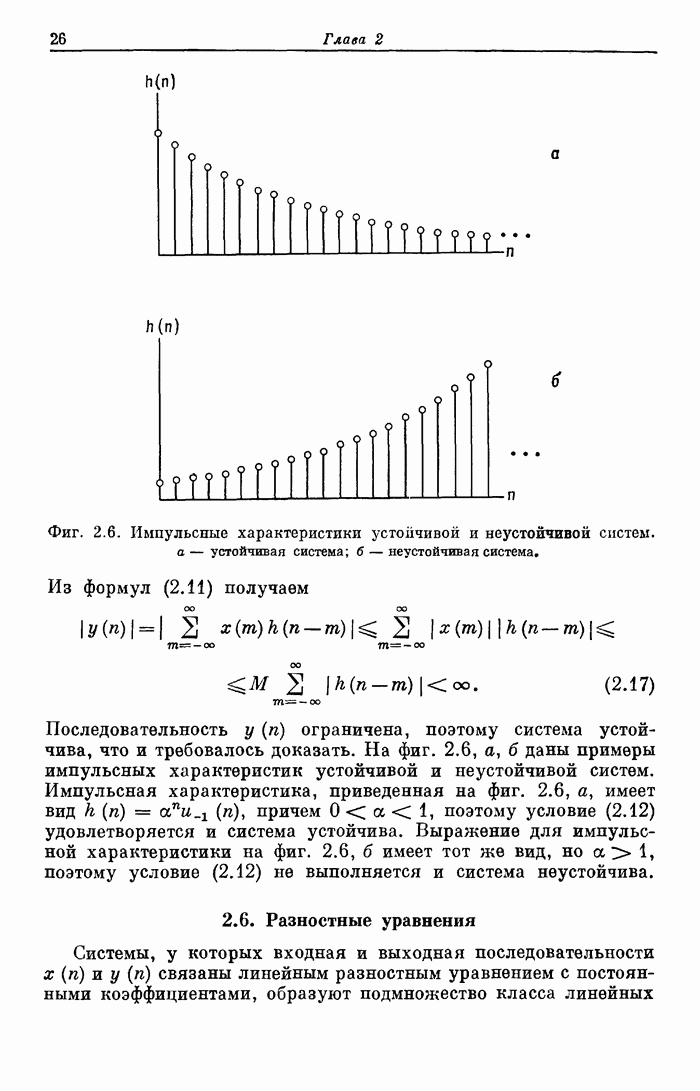
- 2.6. Разностные уравнения
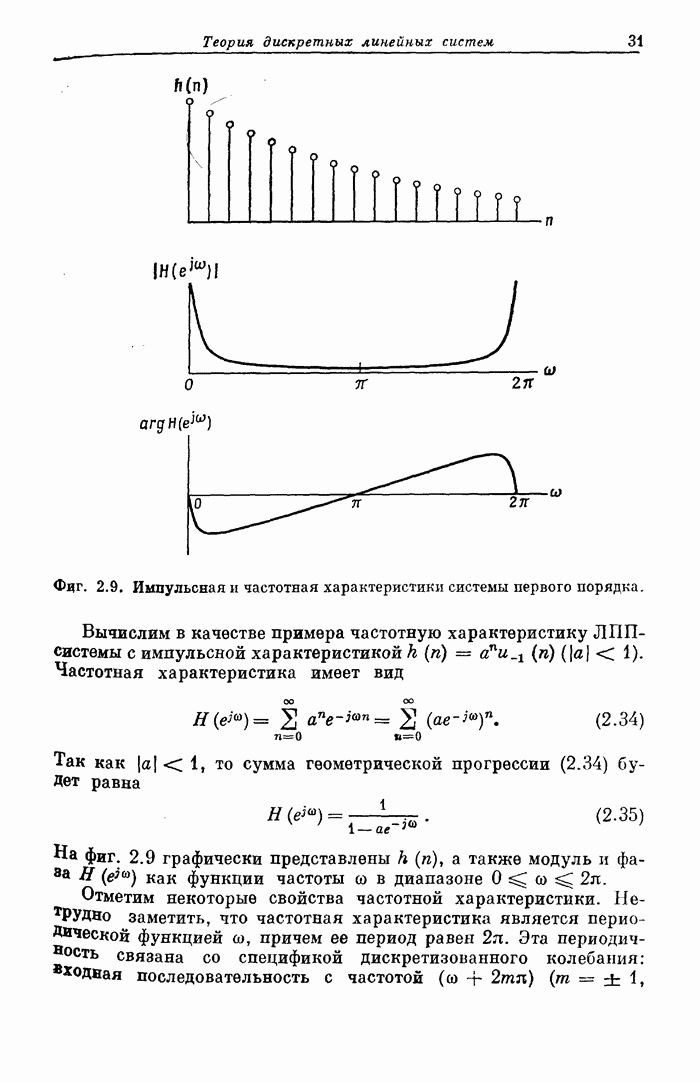
- 2.7. Частотная характеристика
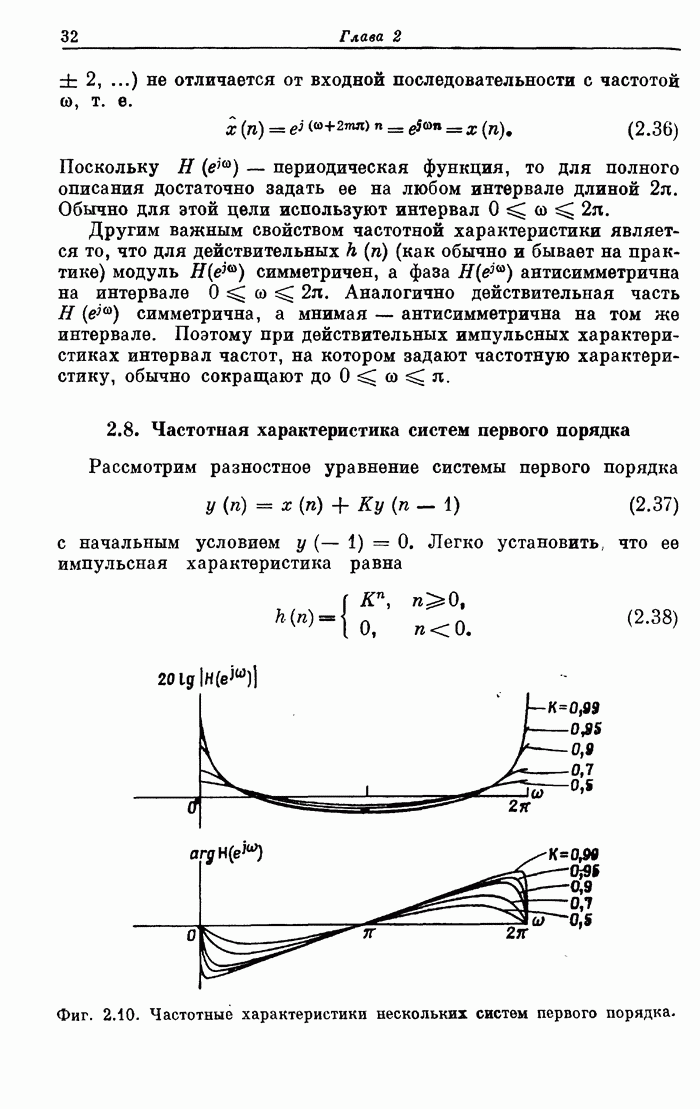
- 2.8. Частотная характеристика систем первого порядка
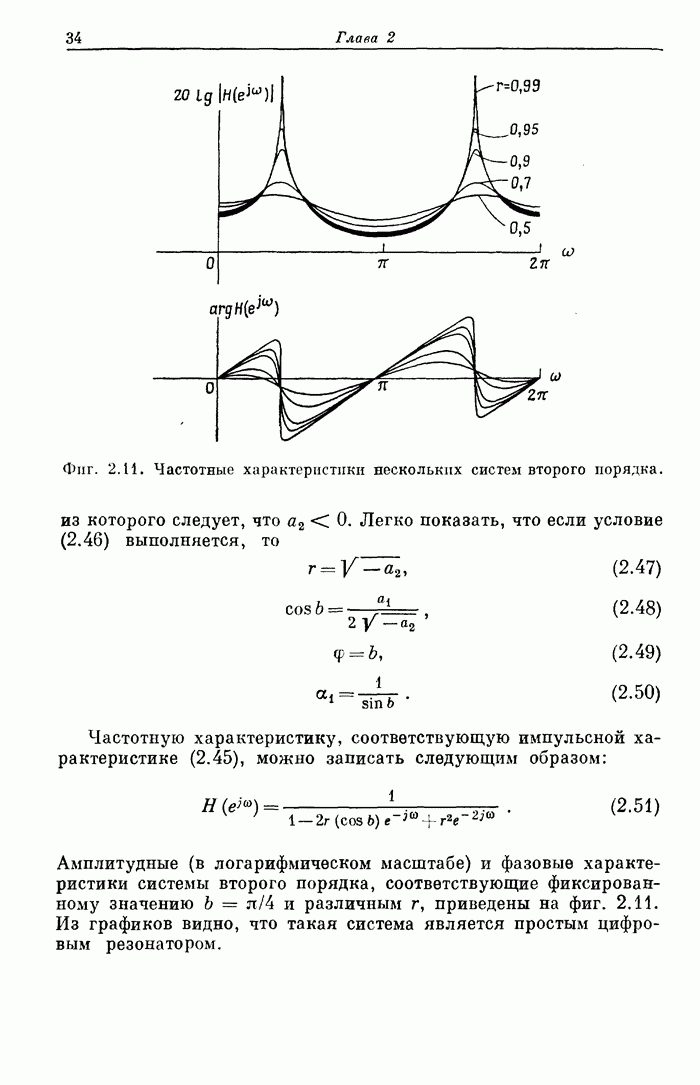
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
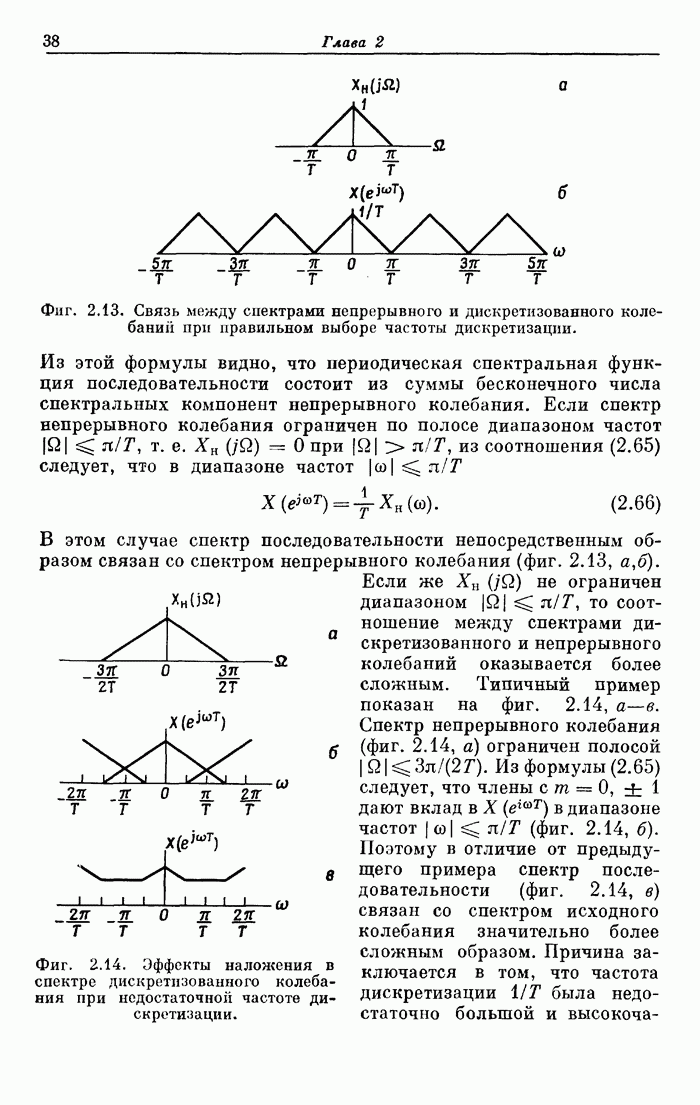
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
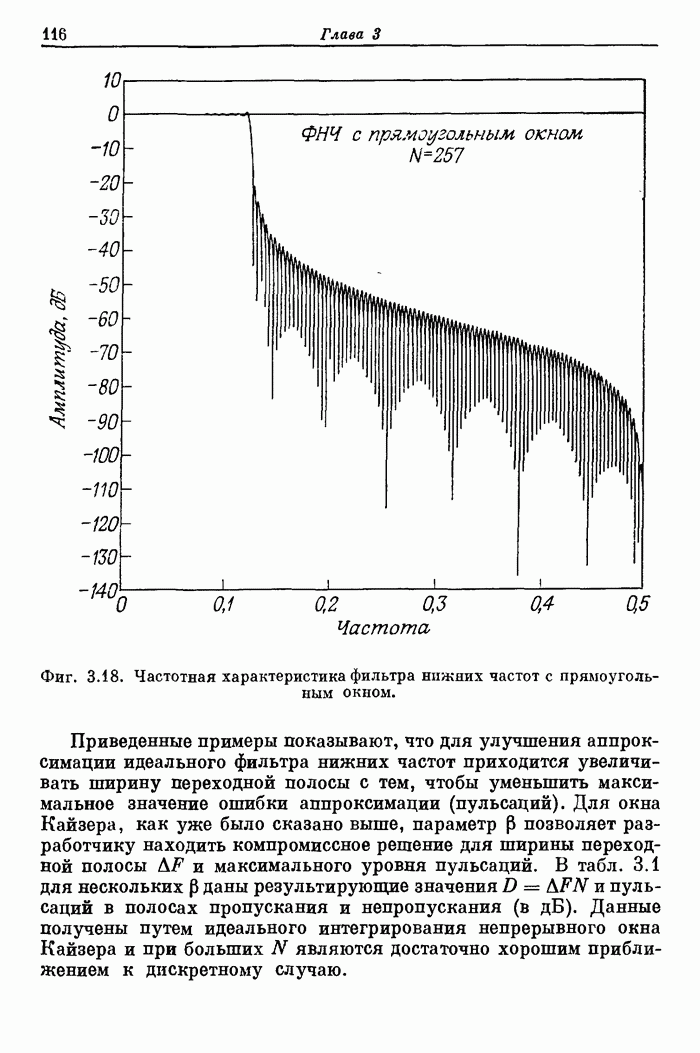
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
- 3.38. Многополосные оптимальные КИХ-фильтры
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
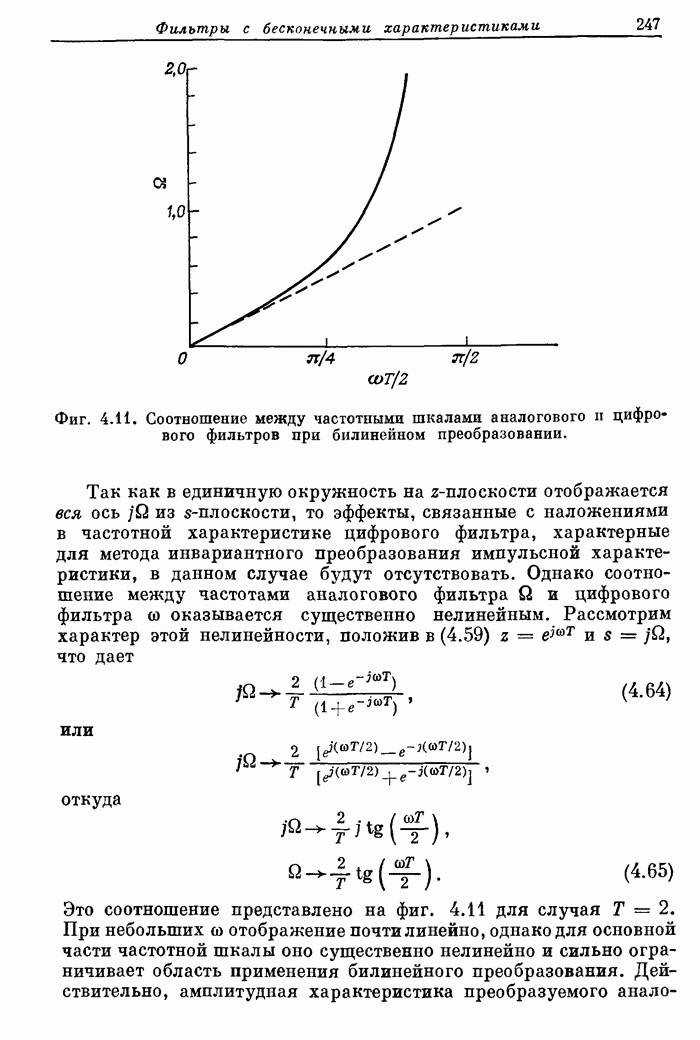
- 4.7. Билинейное z-преобразование
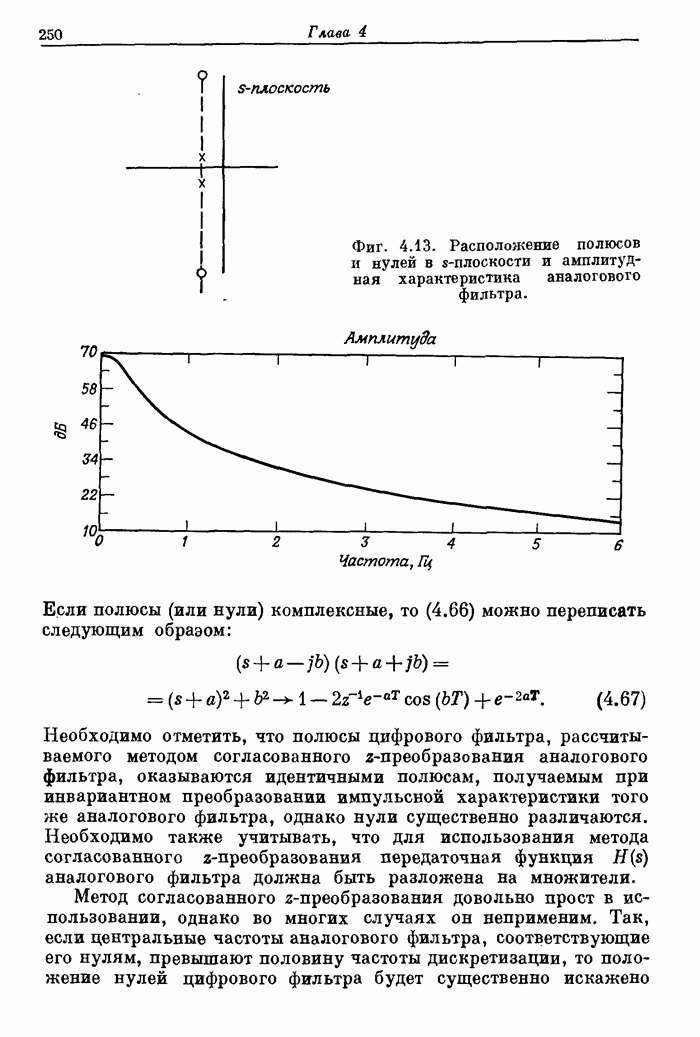
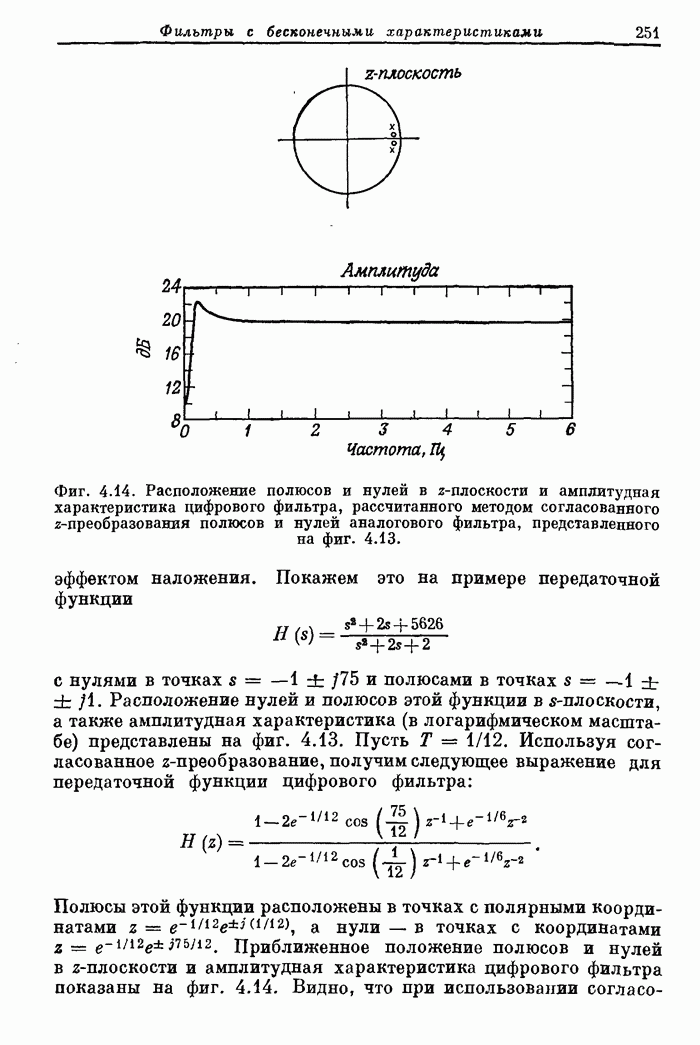
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
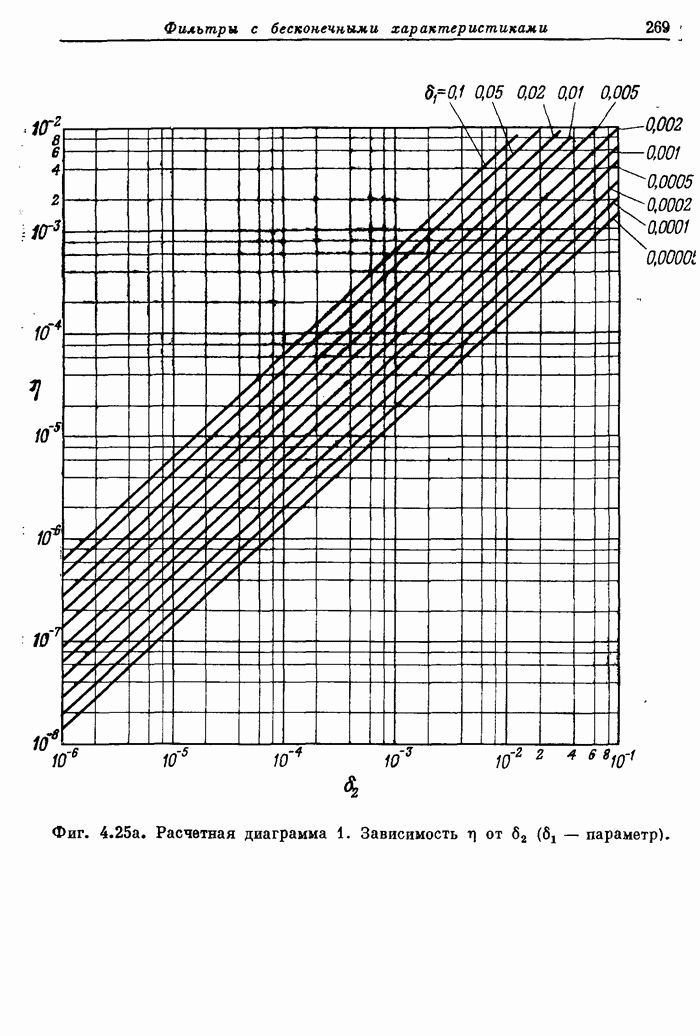
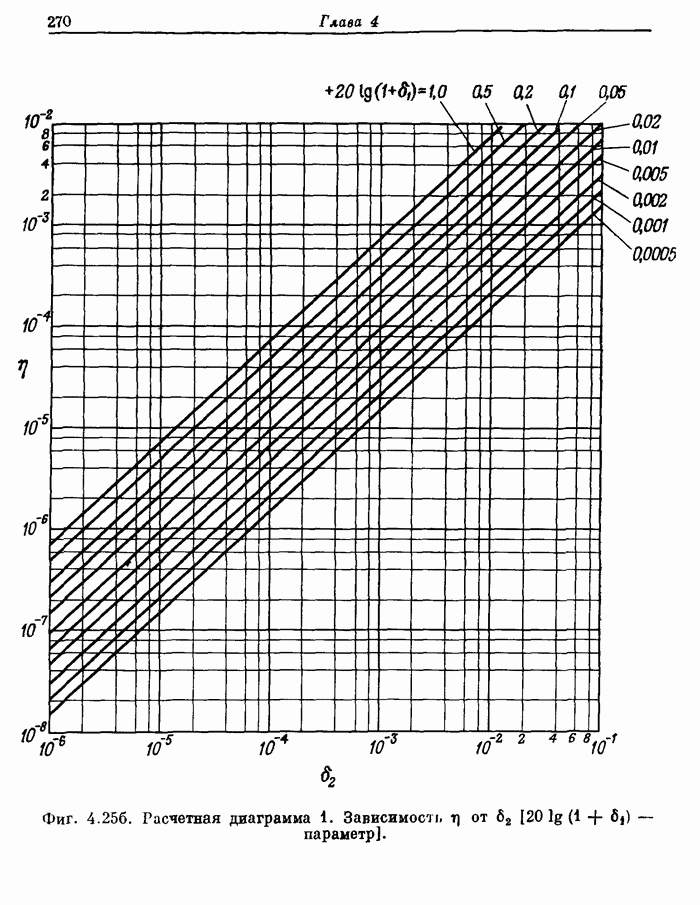
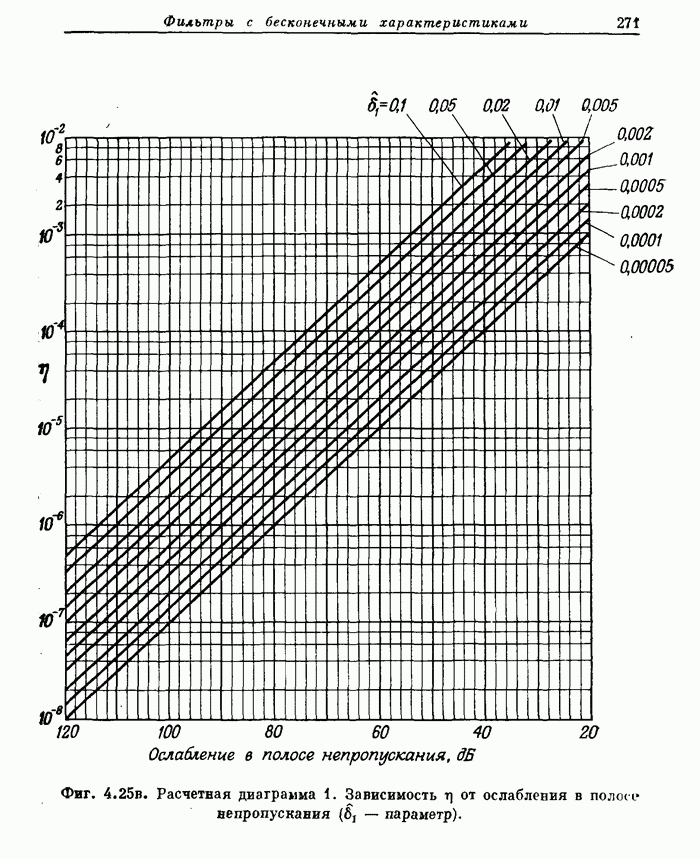
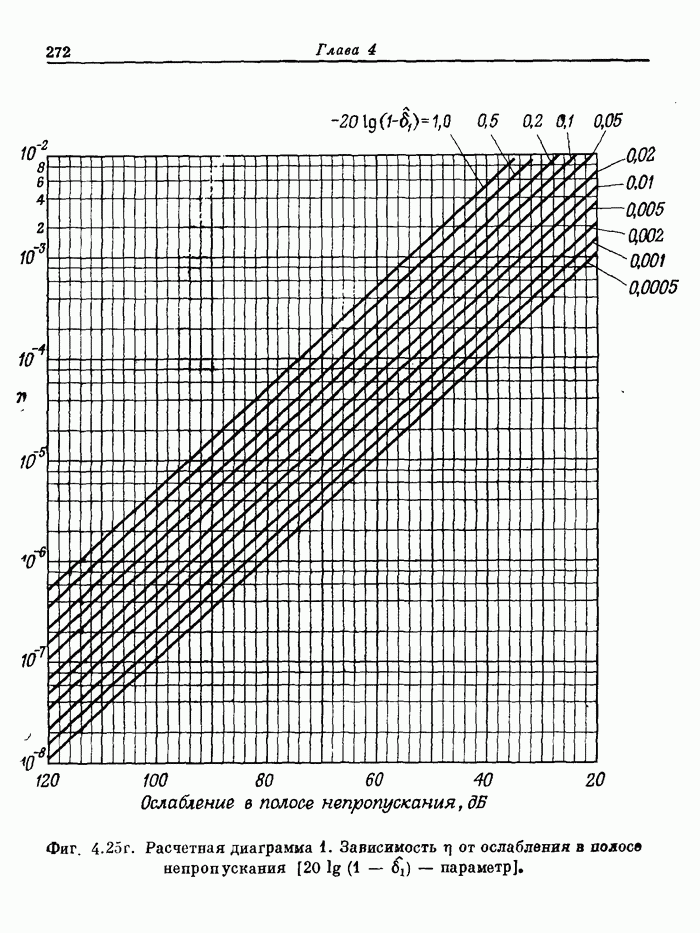
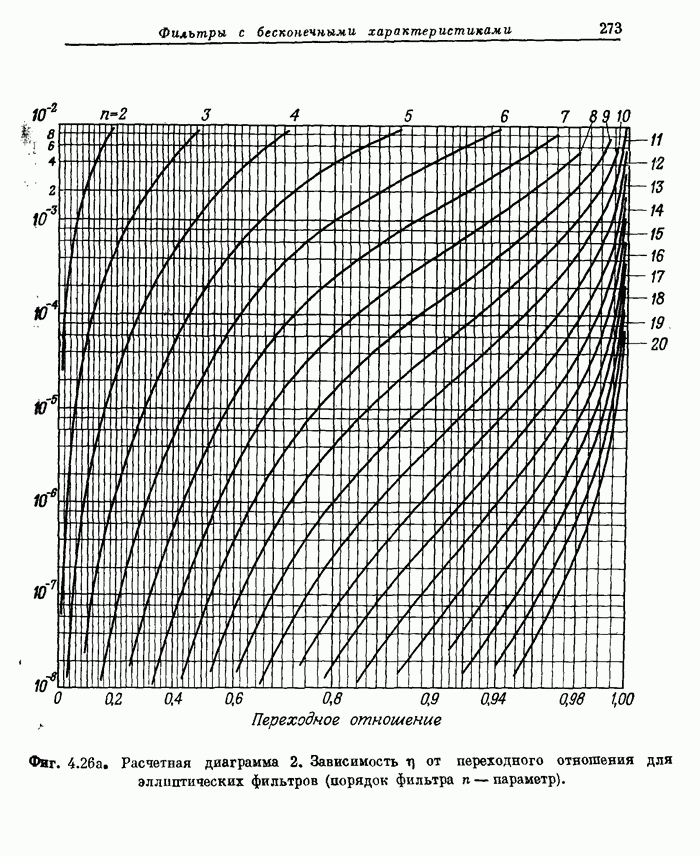
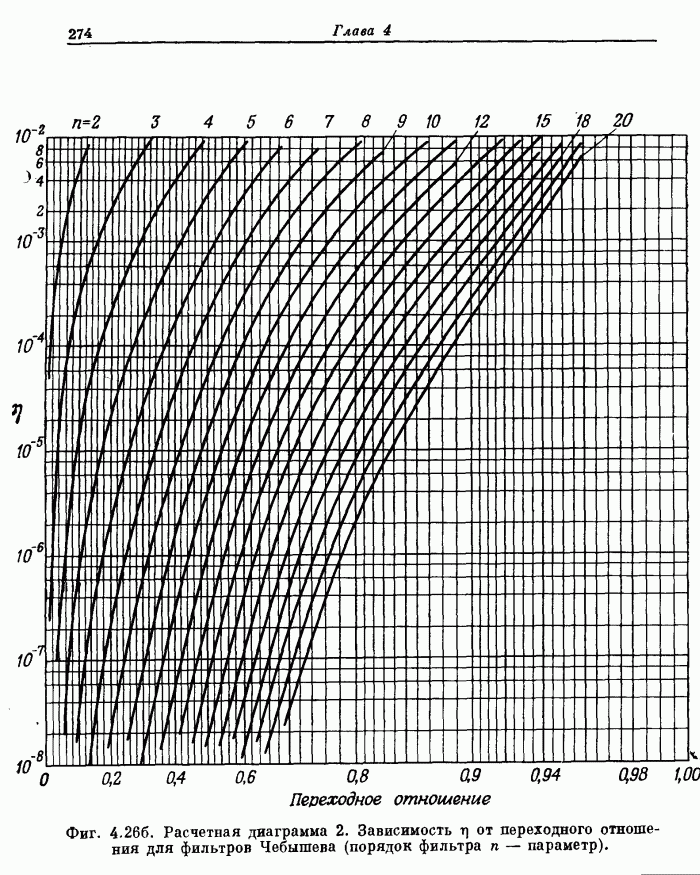
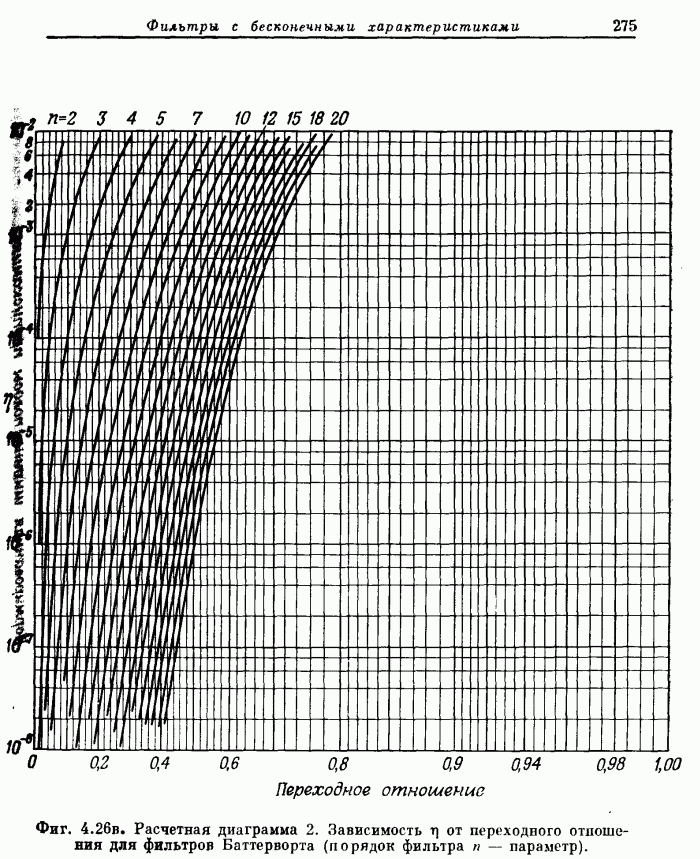
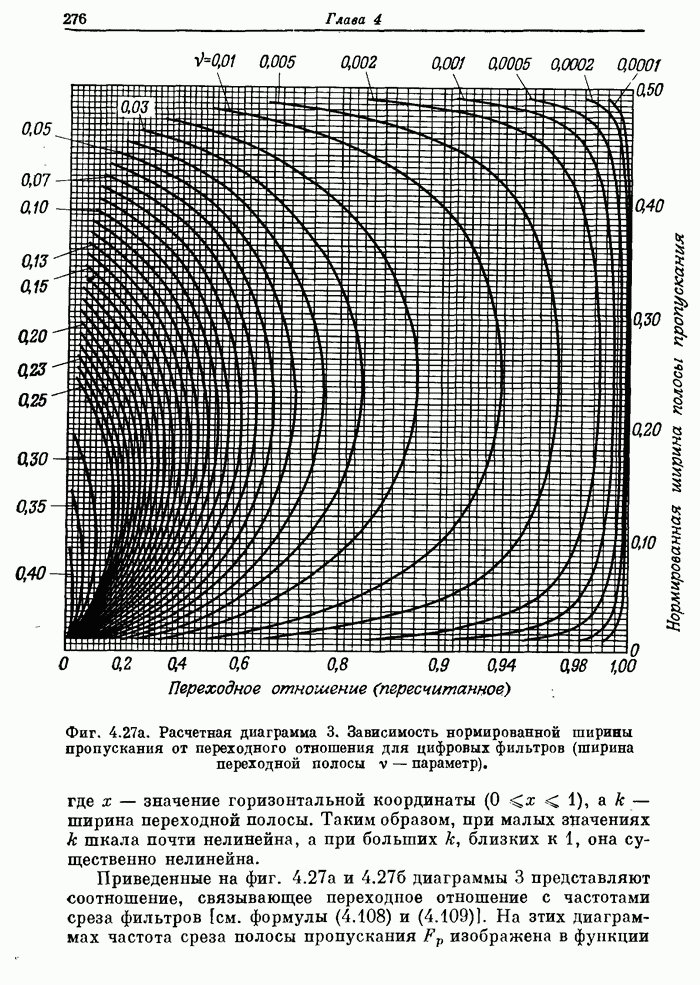
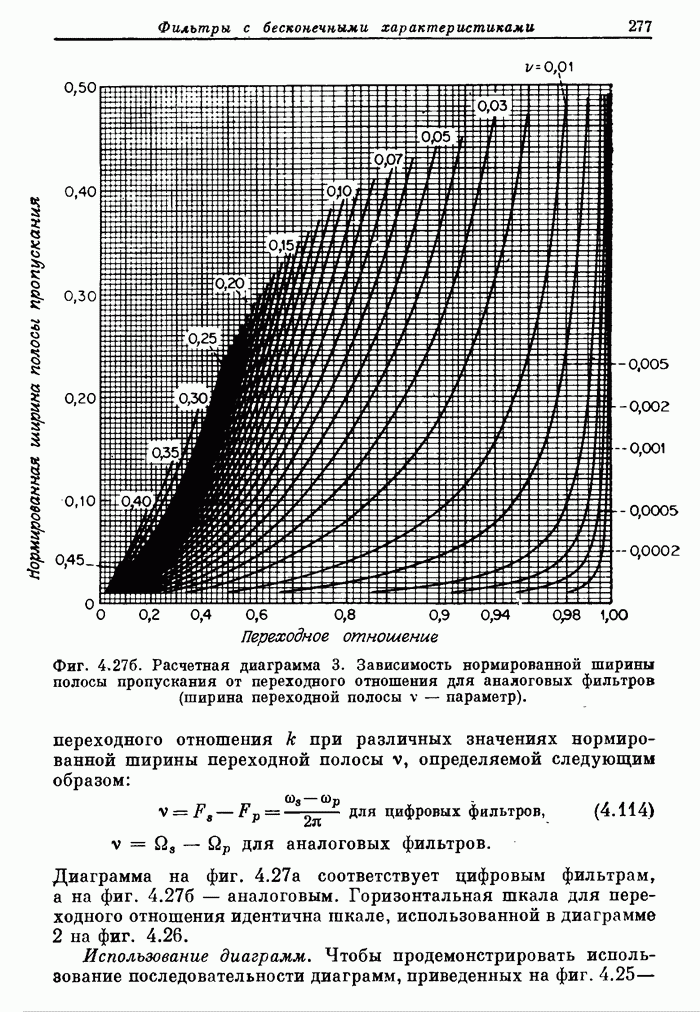
- 4.10. Расчетные диаграммы фильтров нижних частот
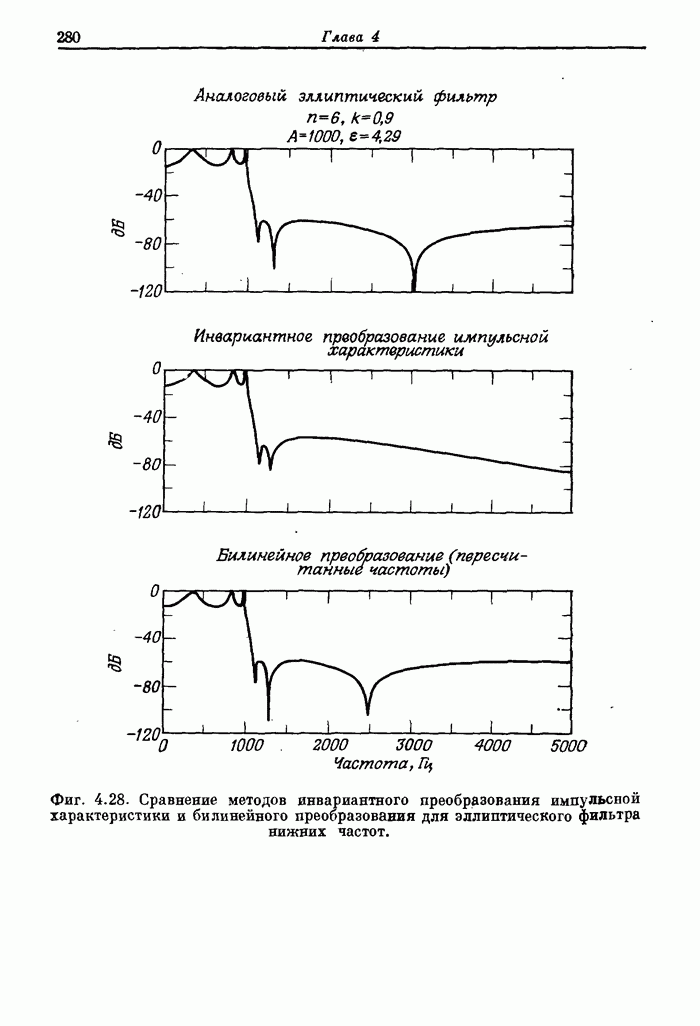
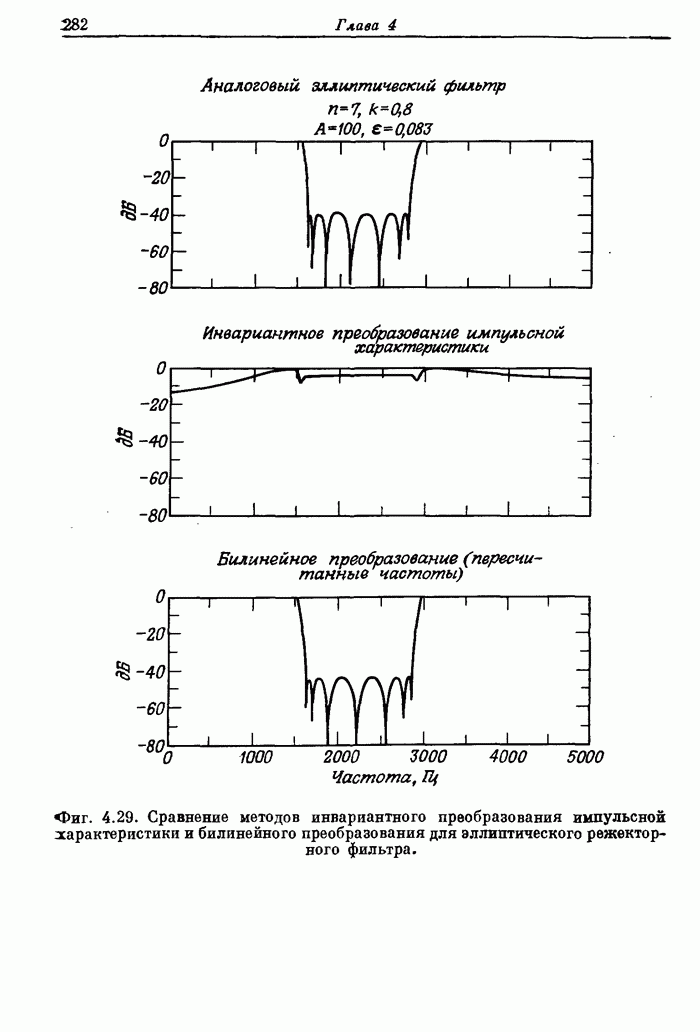
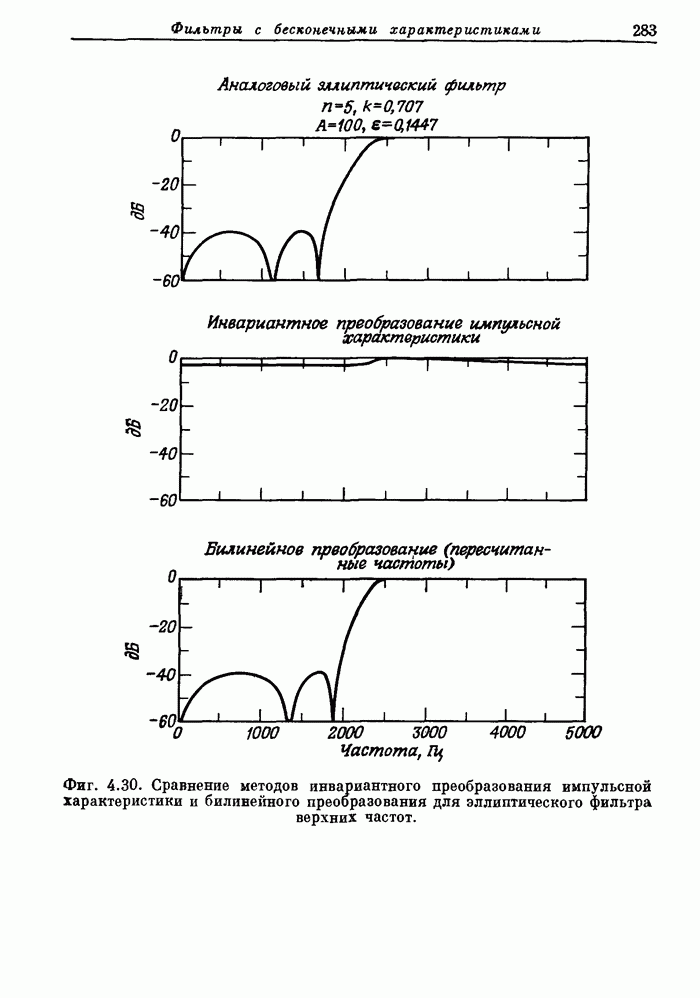
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
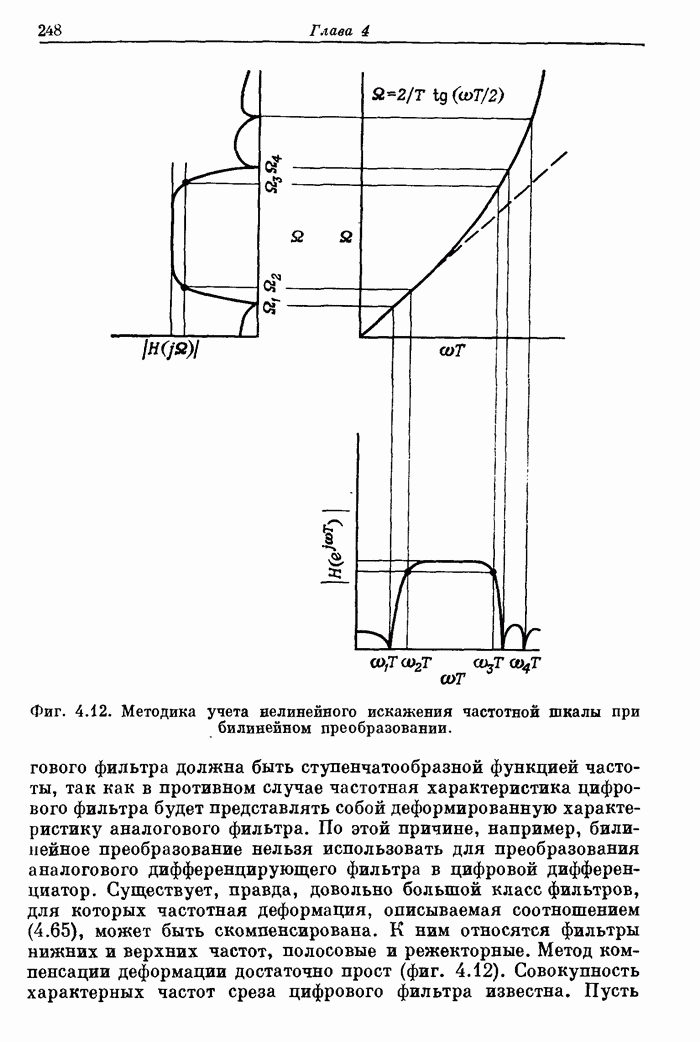
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
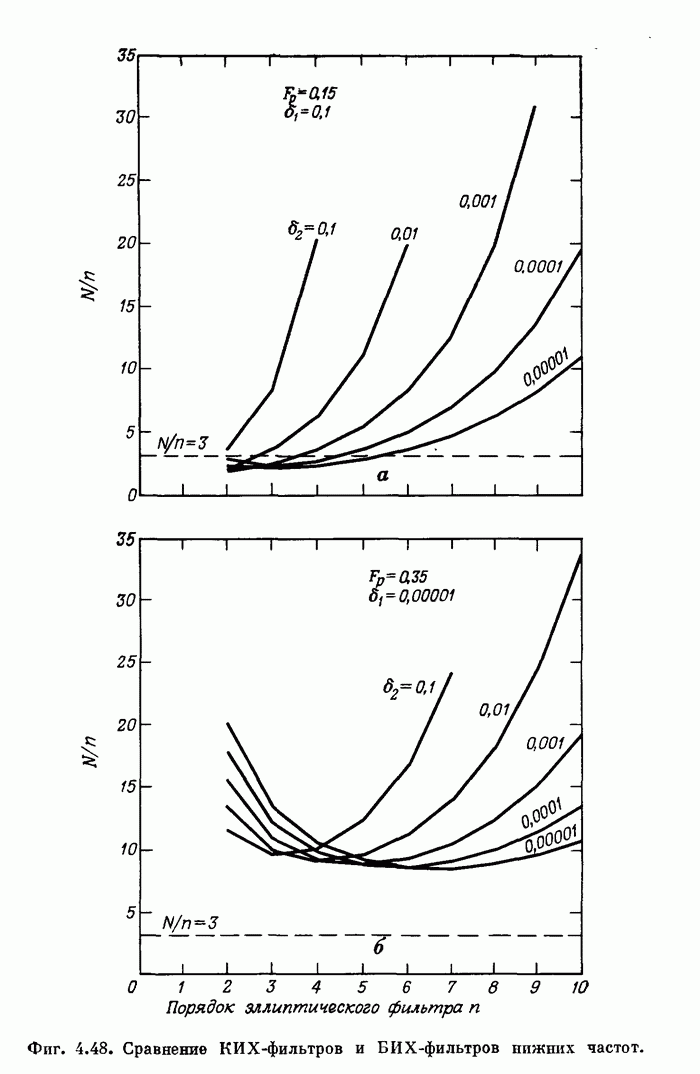
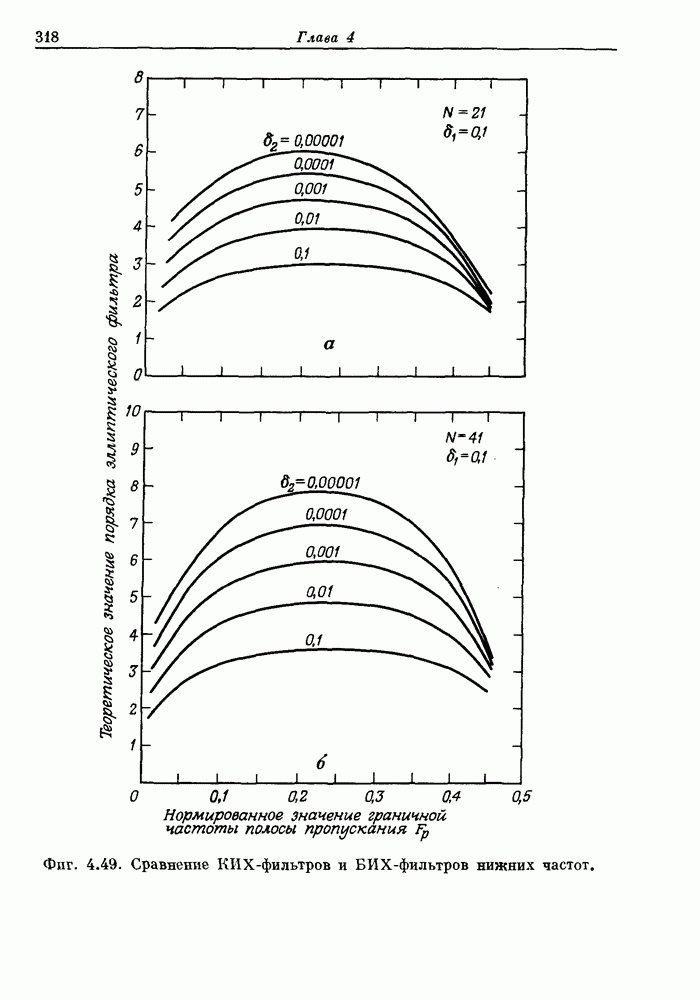
- 4.16. Сравнение КИХ- и БИХ-фильтров
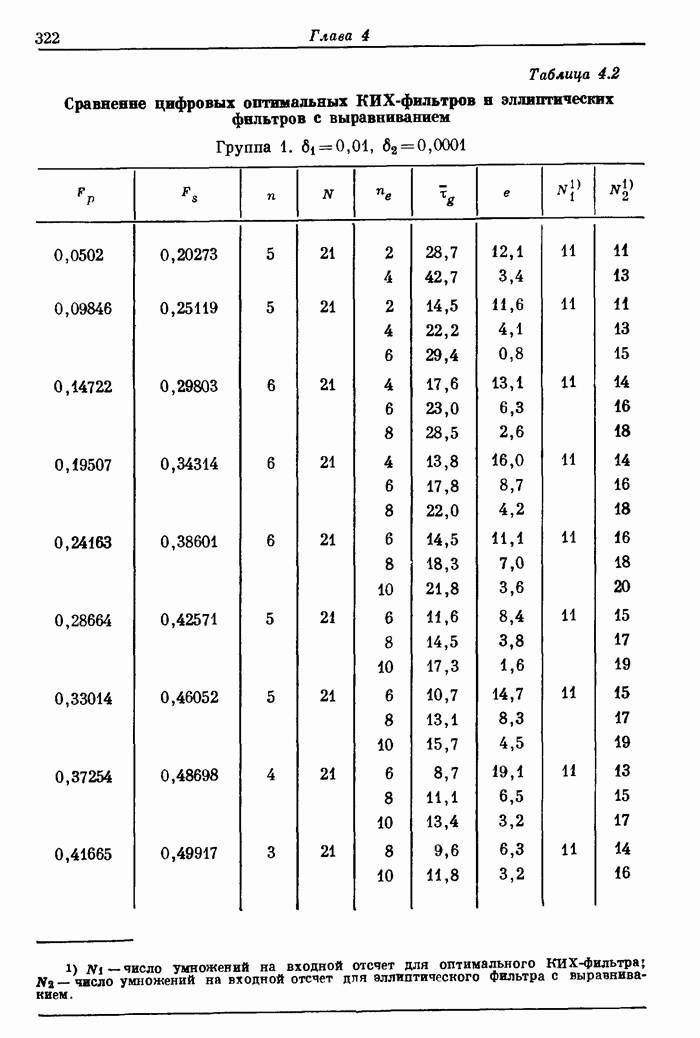
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
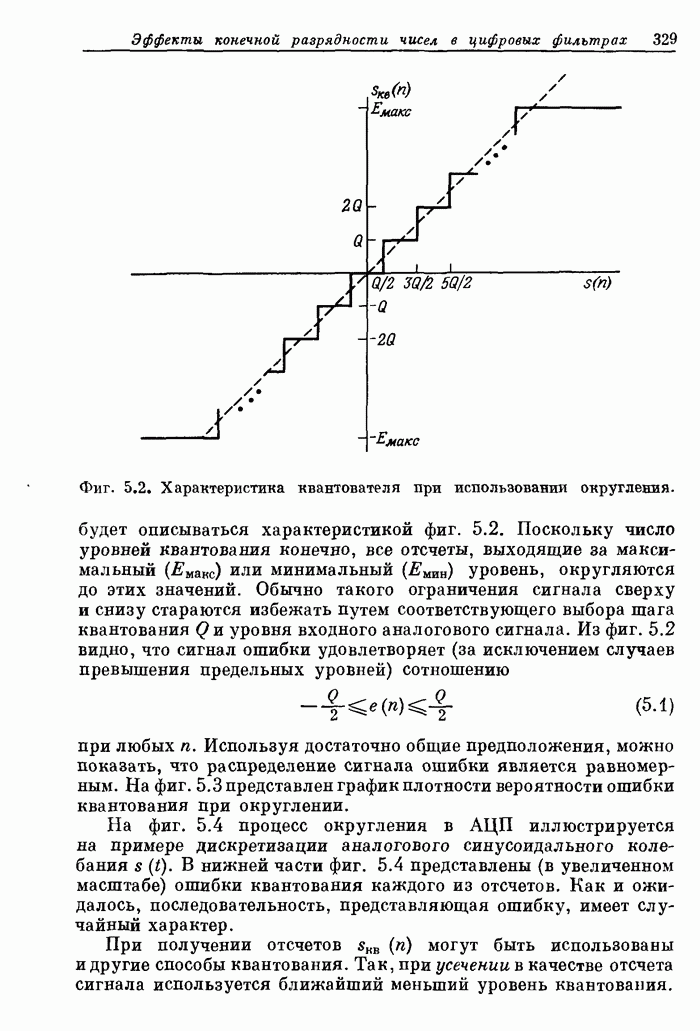
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
- 9.12. Специализированный цифровой синтезатор частот
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
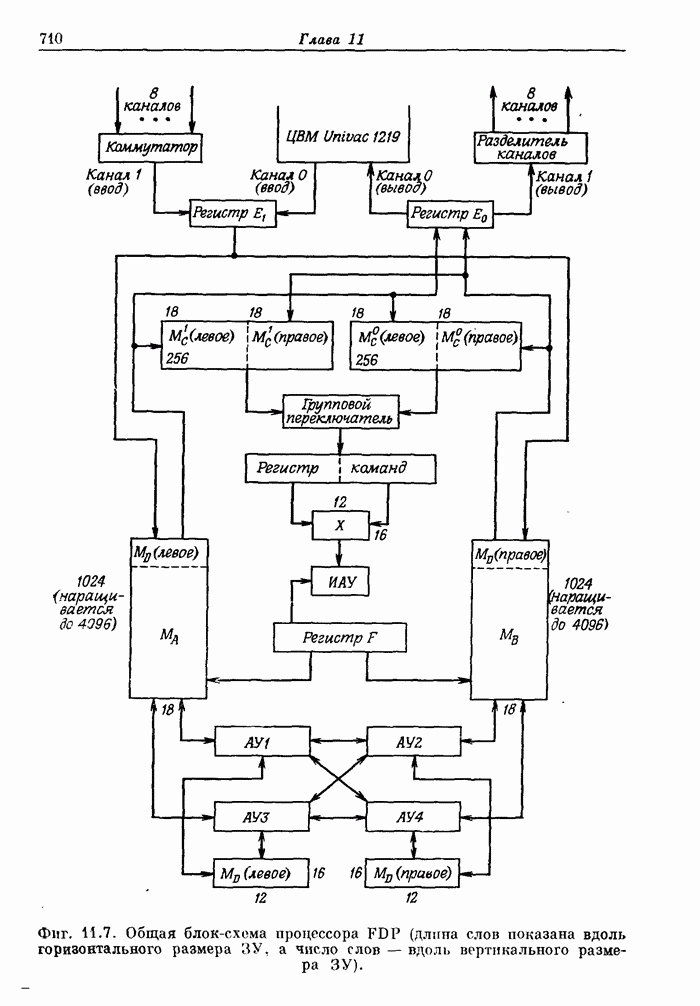
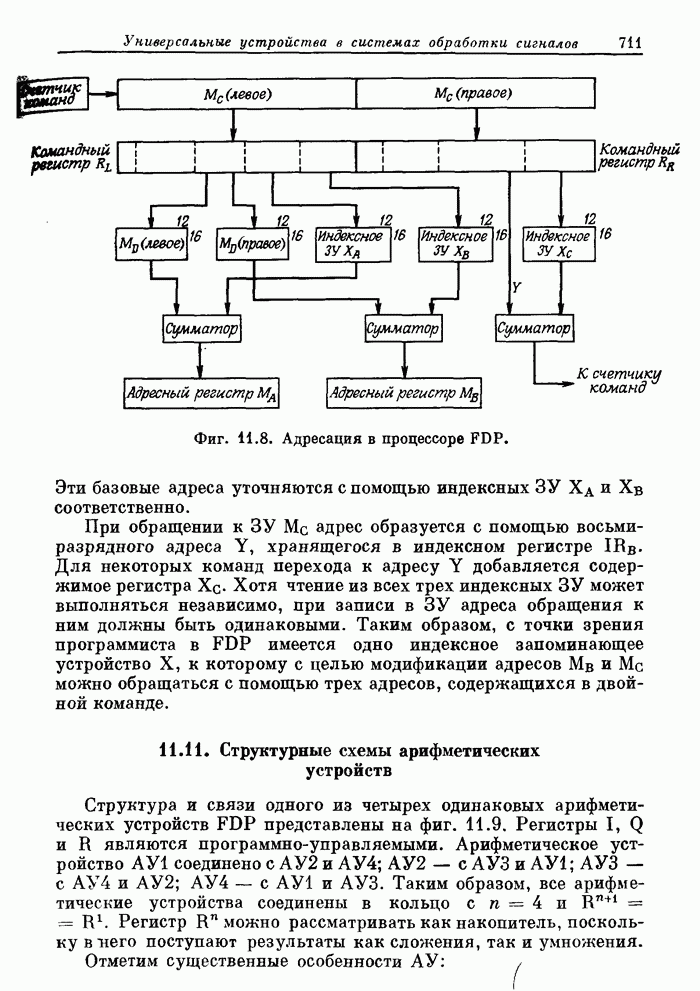
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
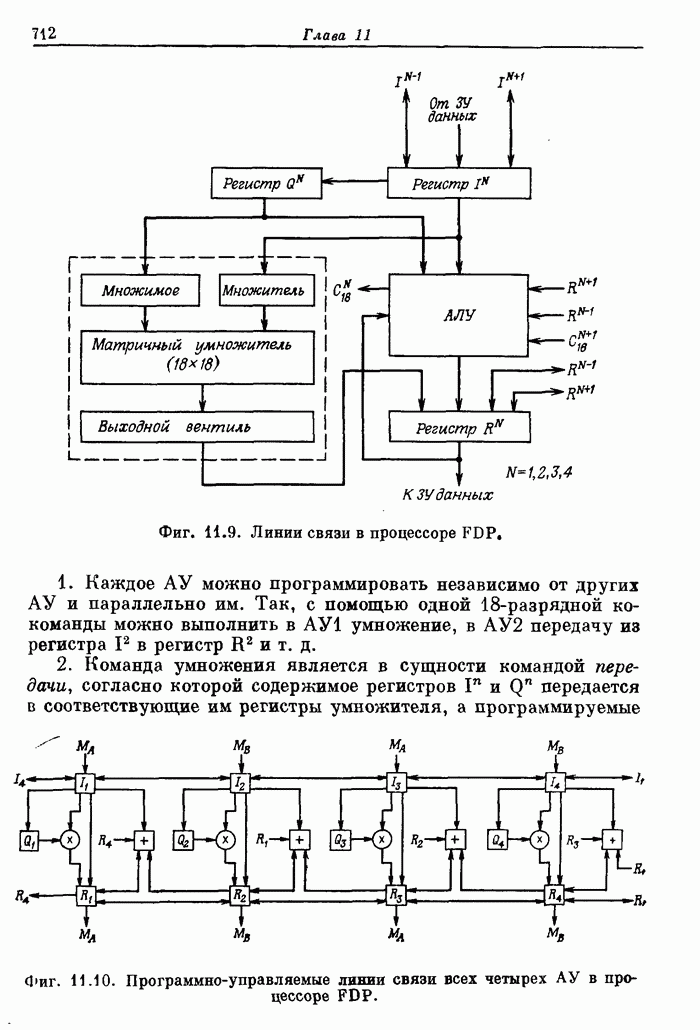
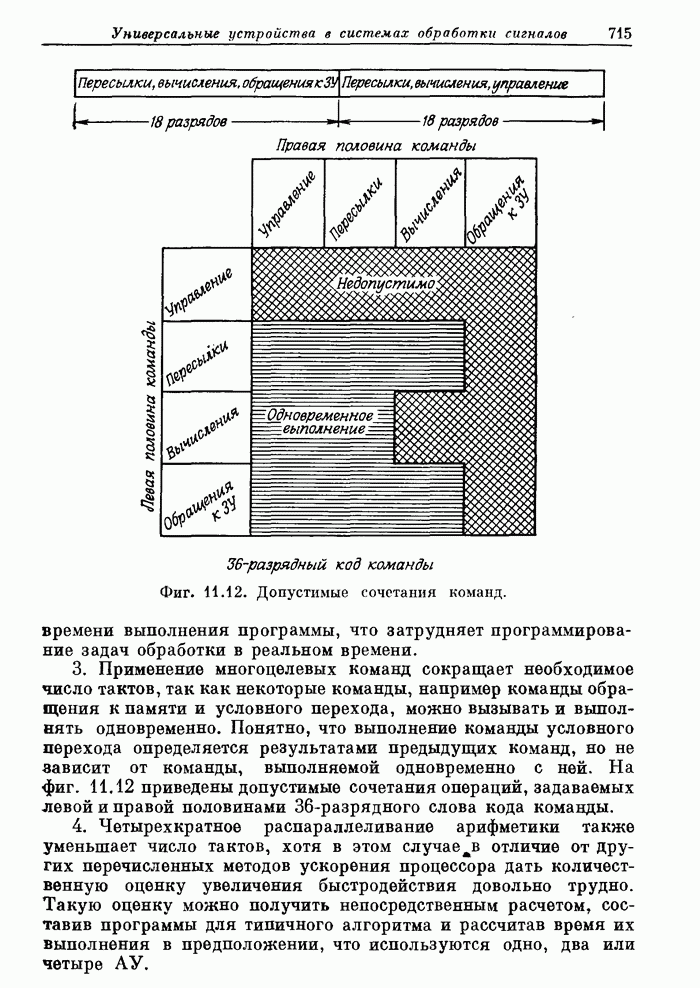
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
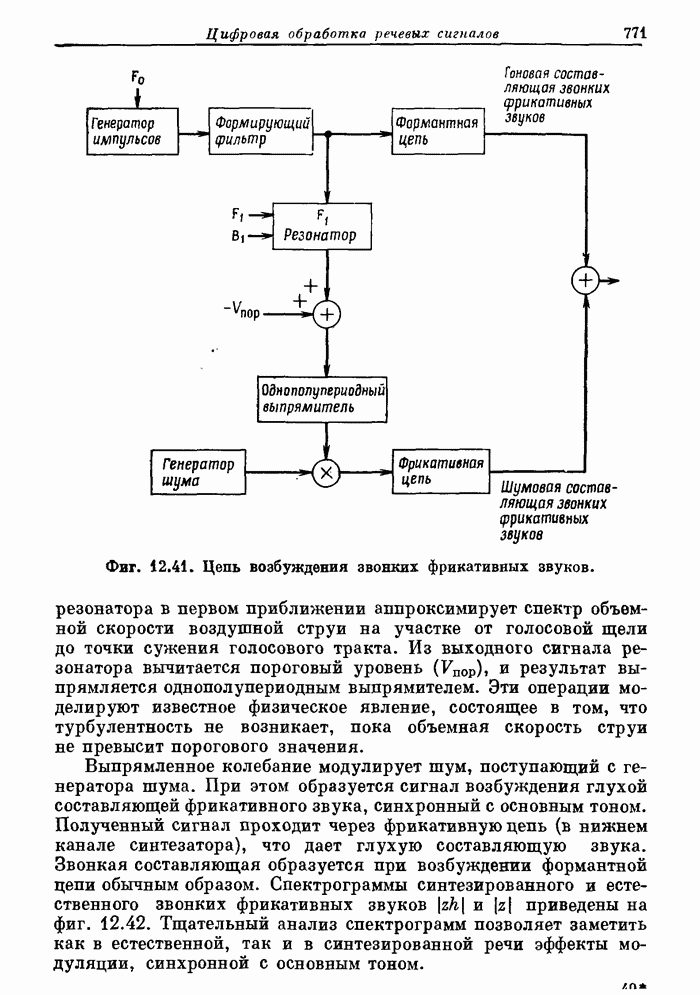
- 12.16. Цепь возбуждения звонких фрикативных звуков
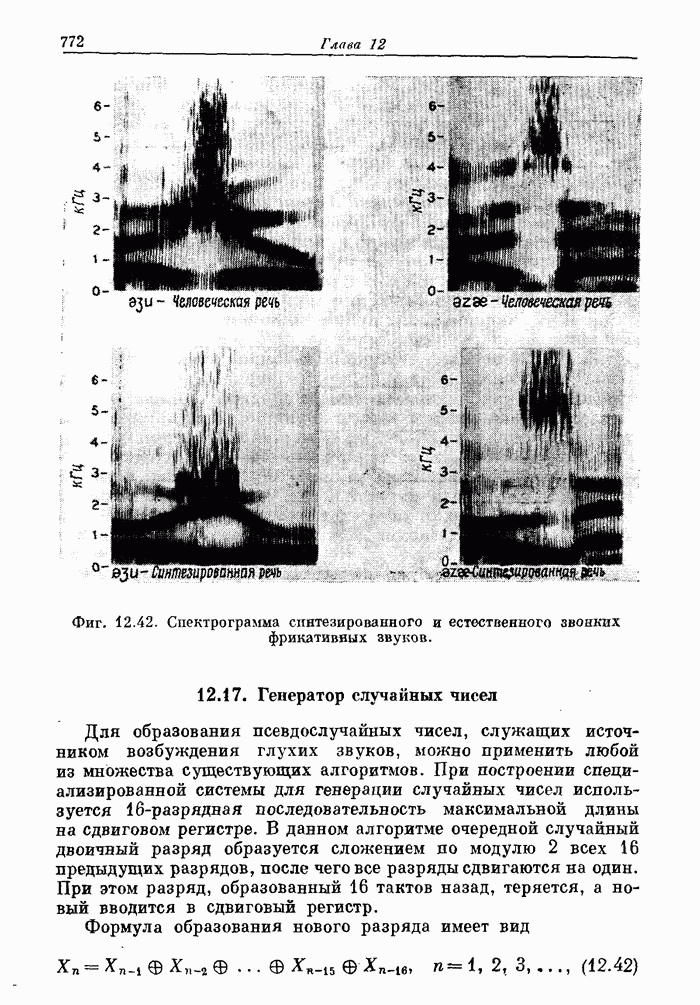
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
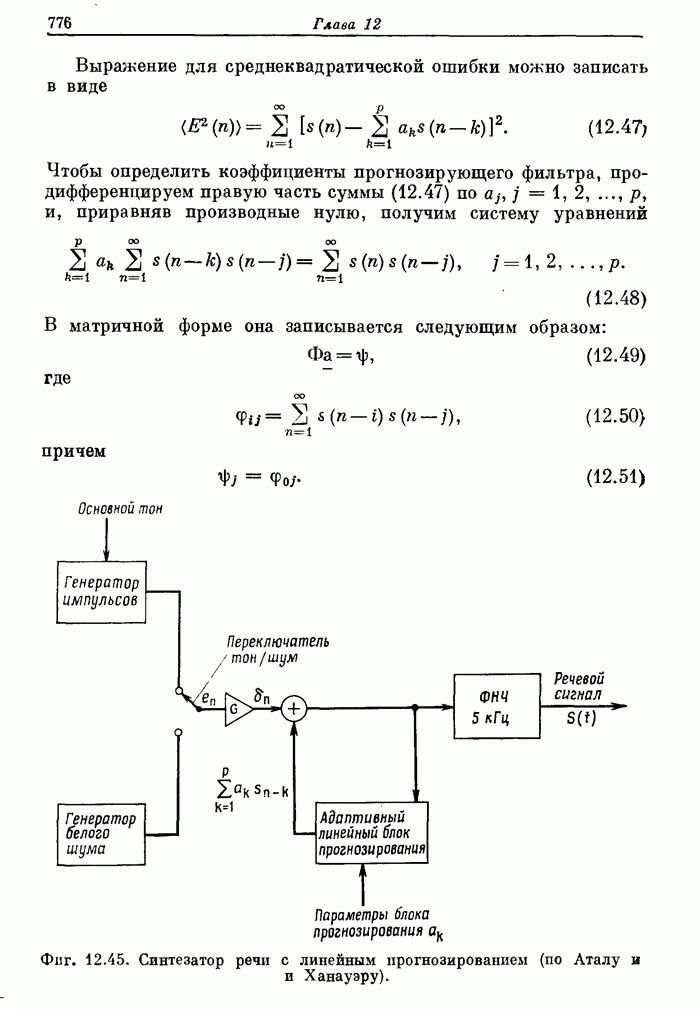
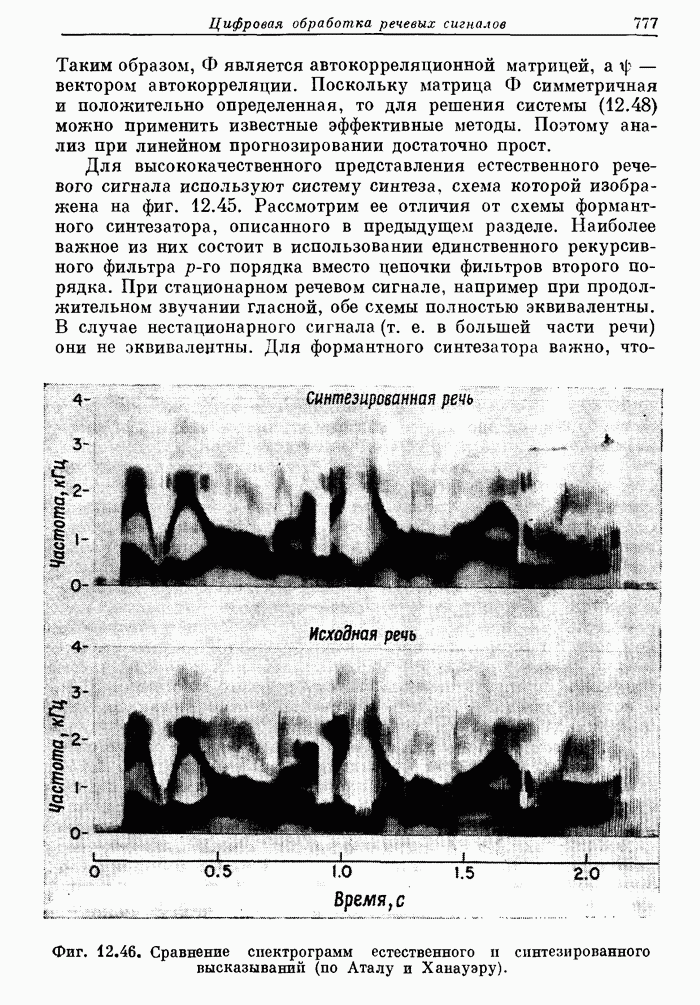
- 12.19. Линейное прогнозирование речи
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
- 13.3. Выбор сигналов и функция неопределенности
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение