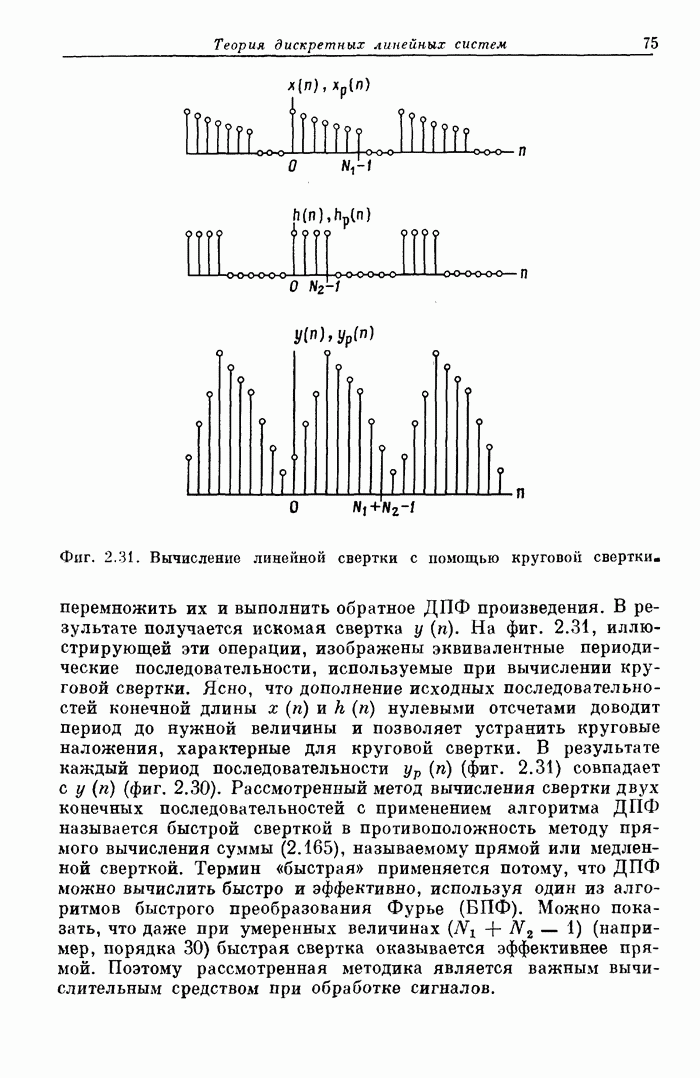
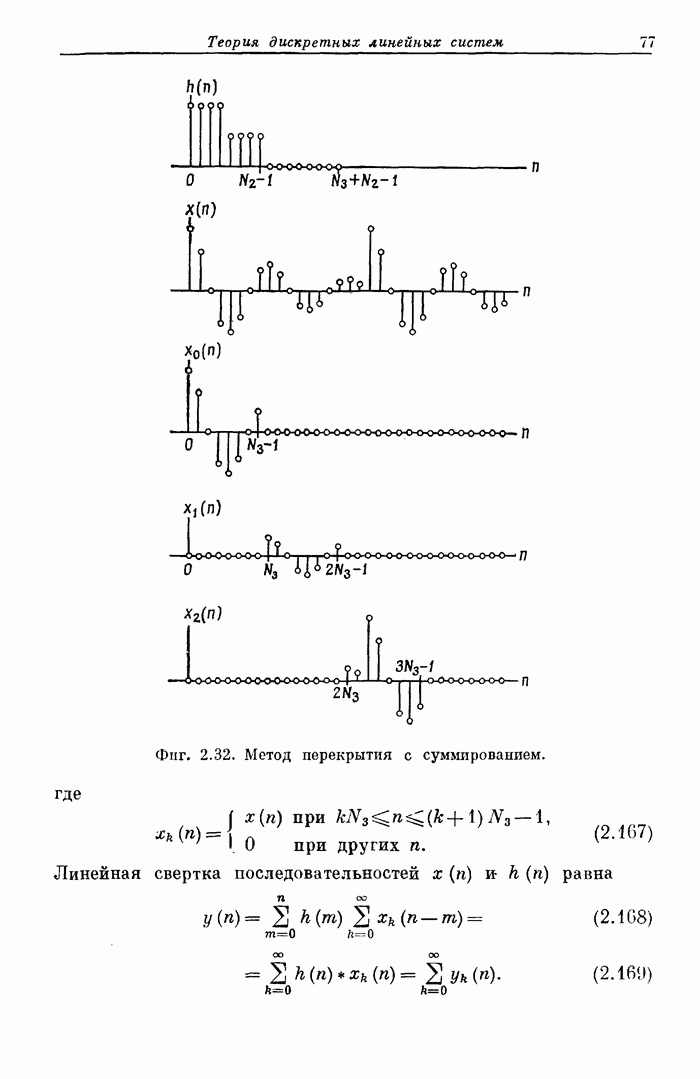
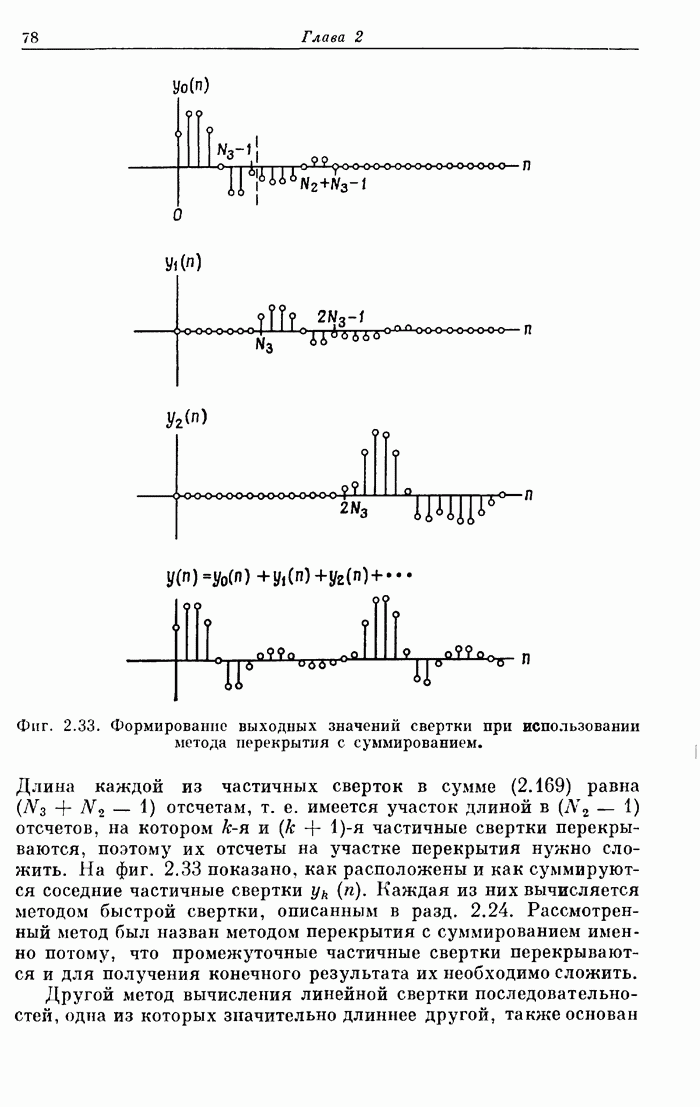
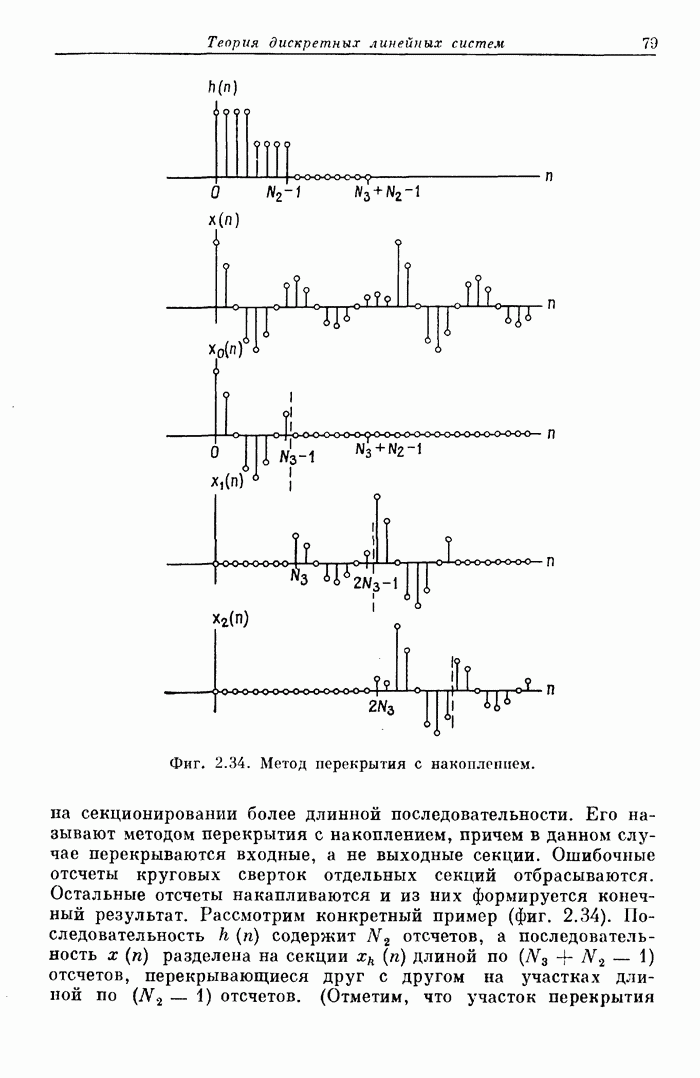
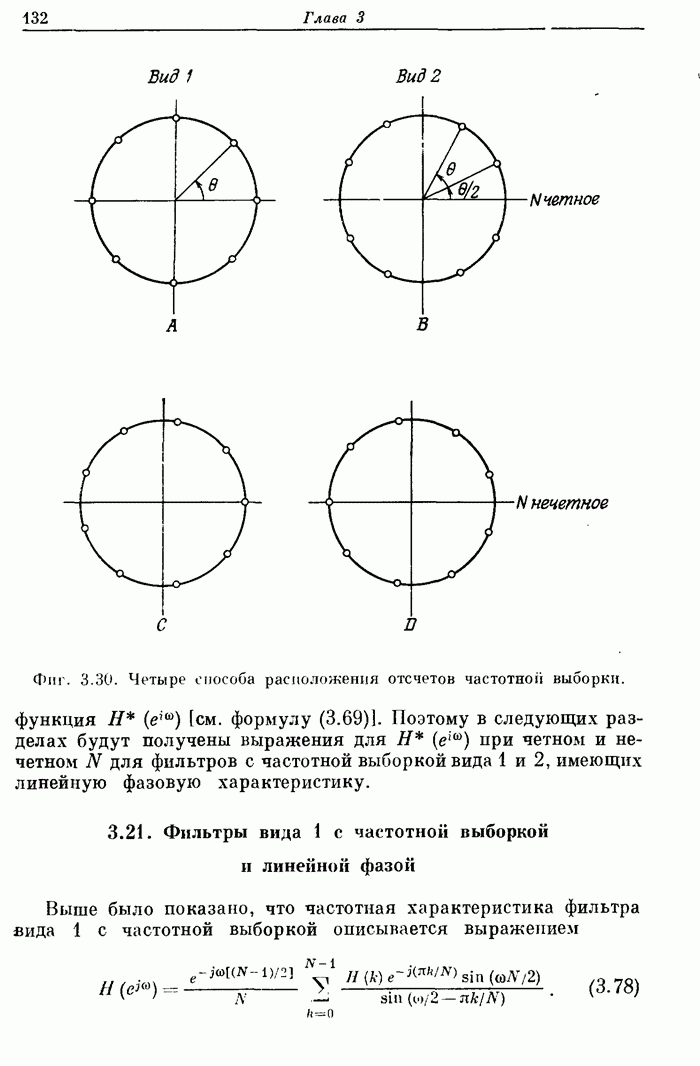
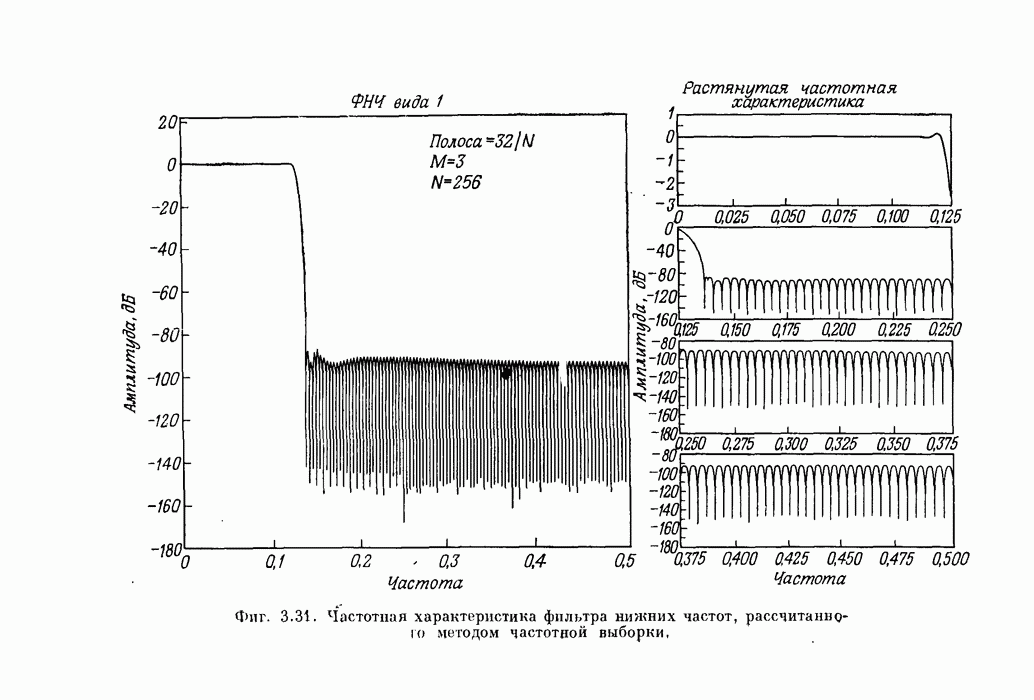
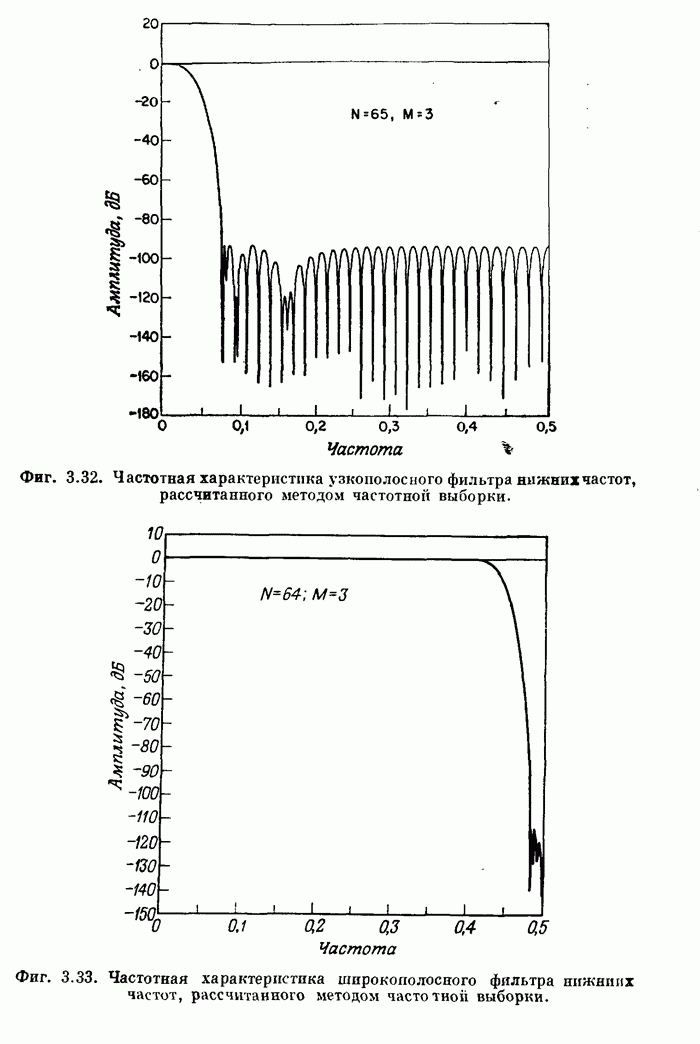
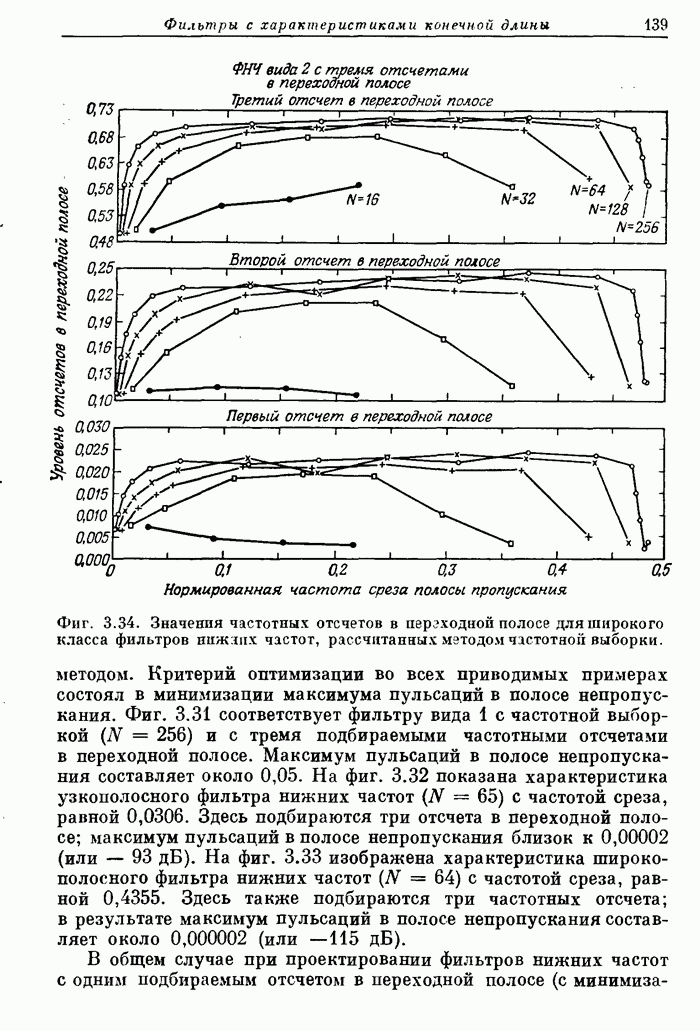
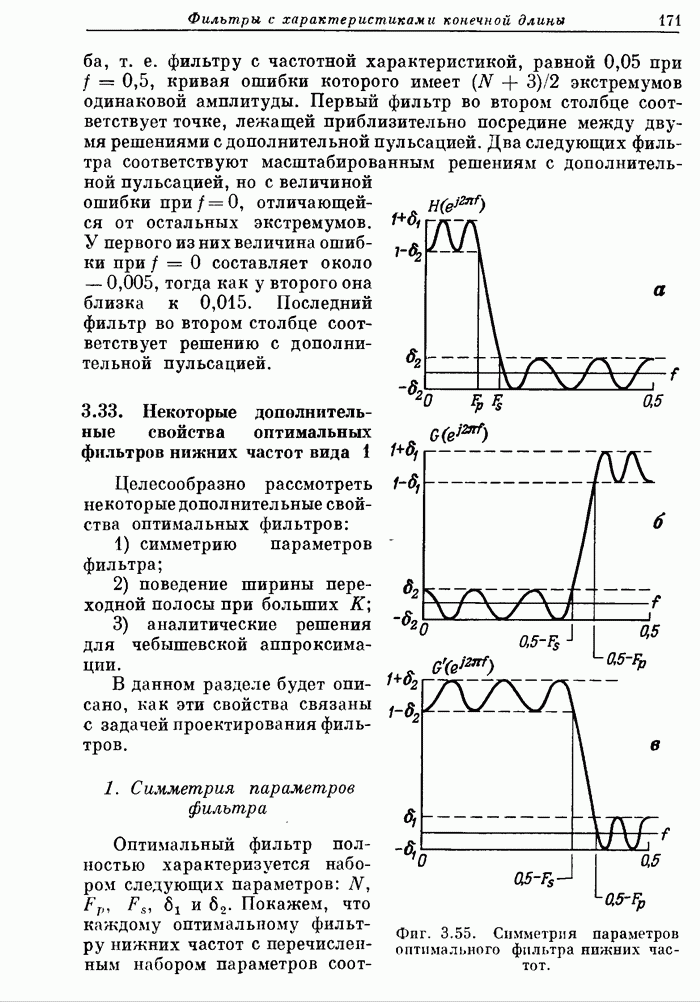
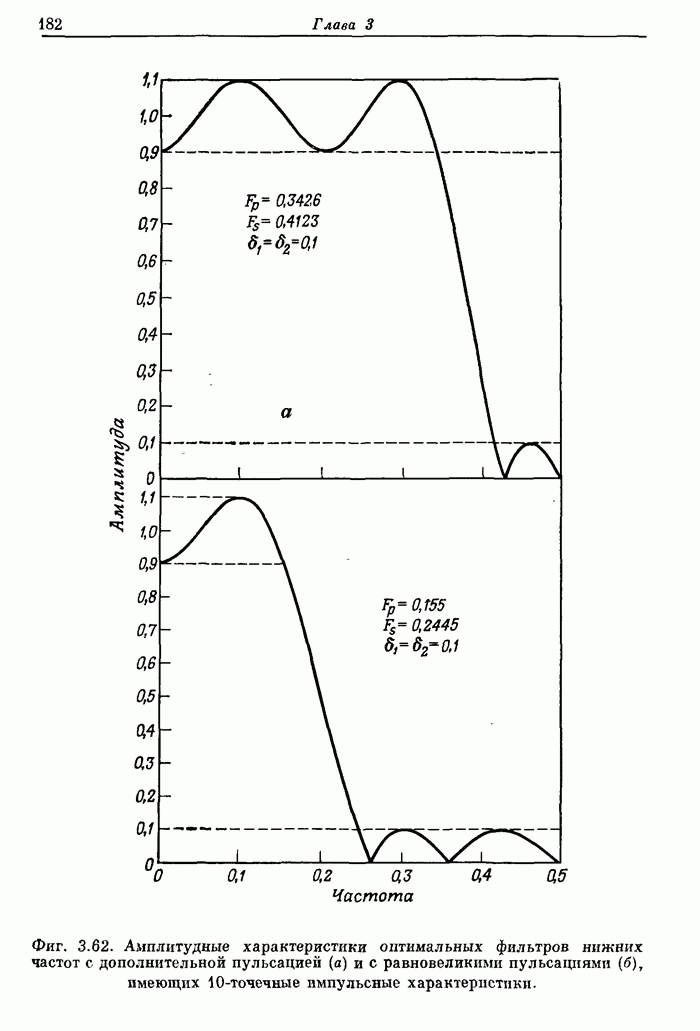
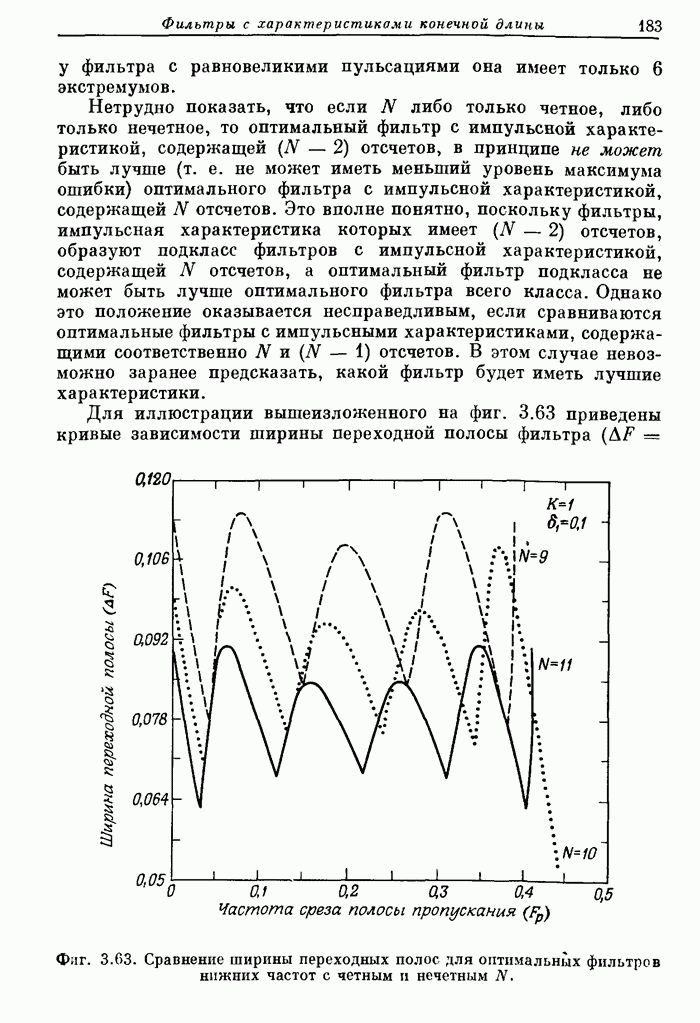
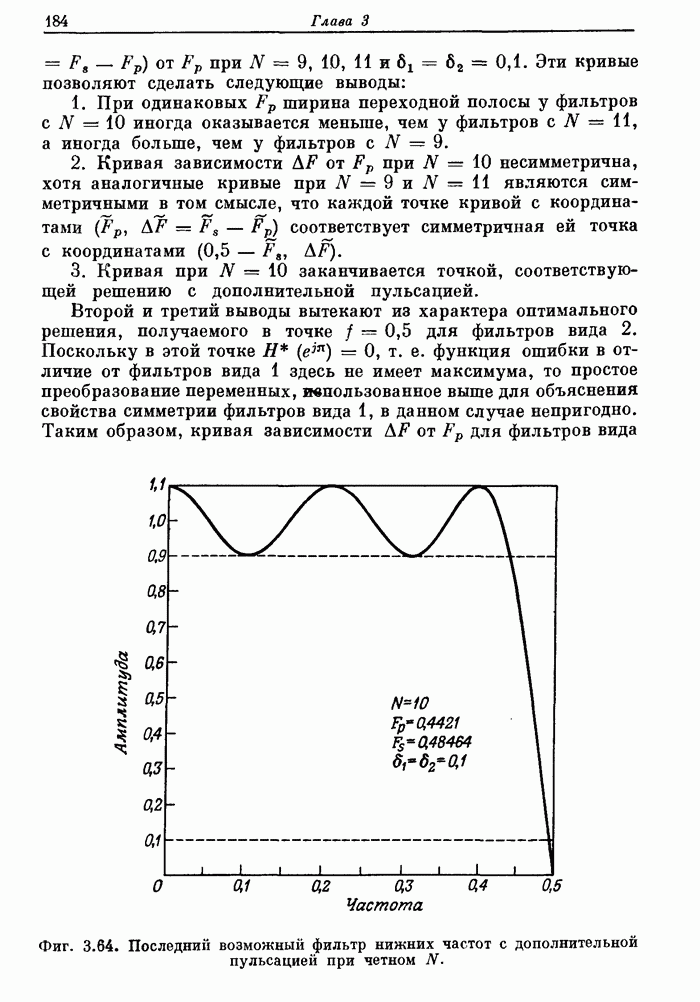
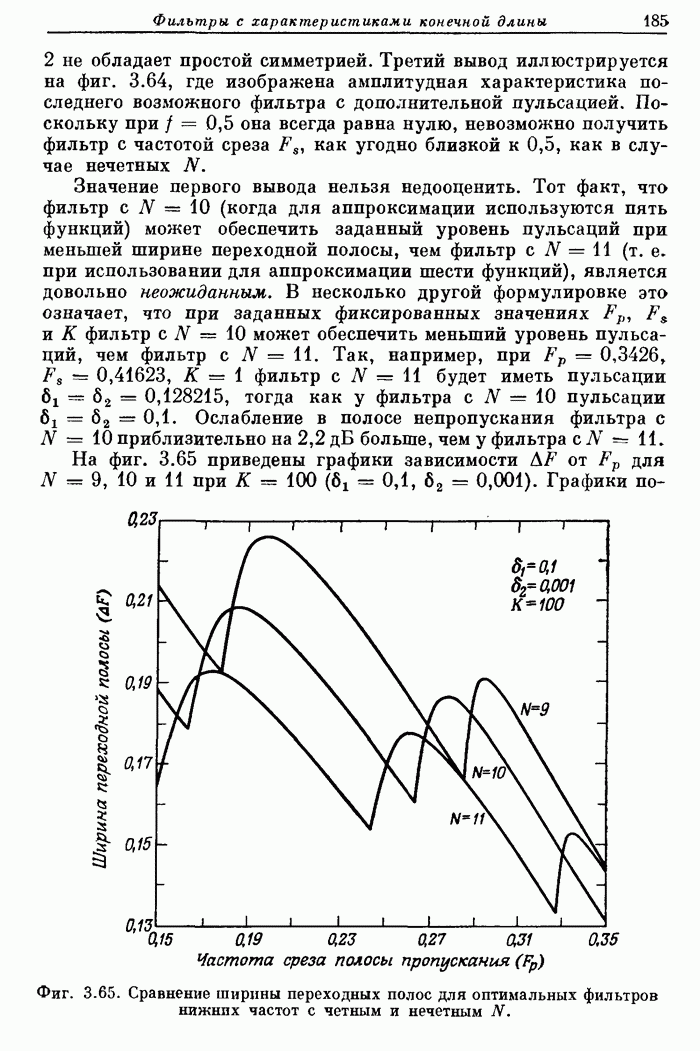
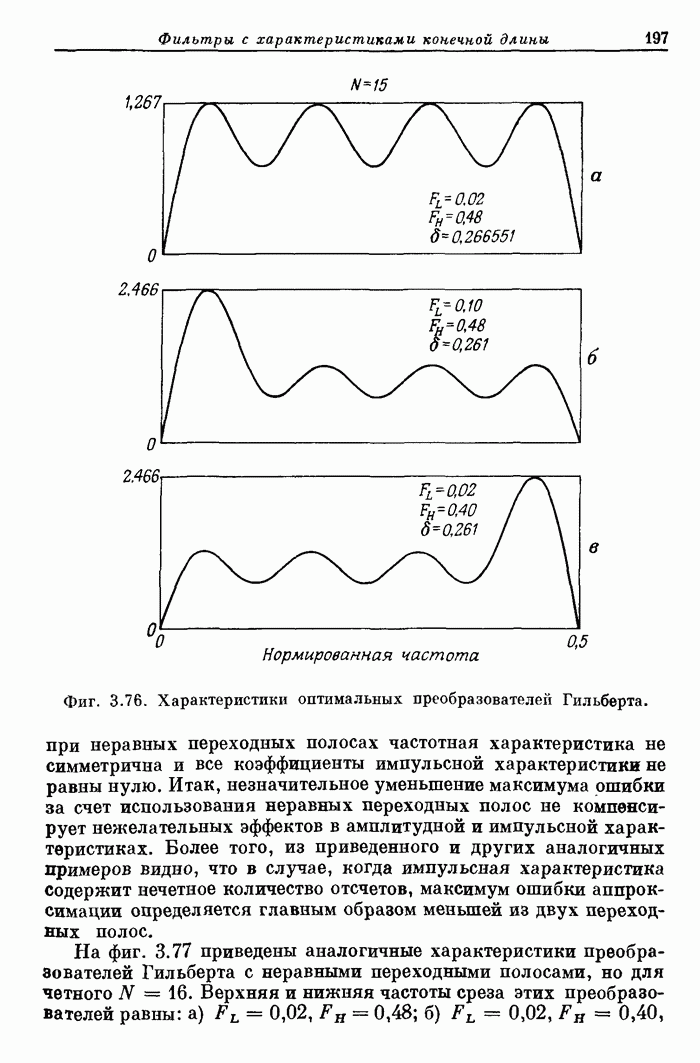
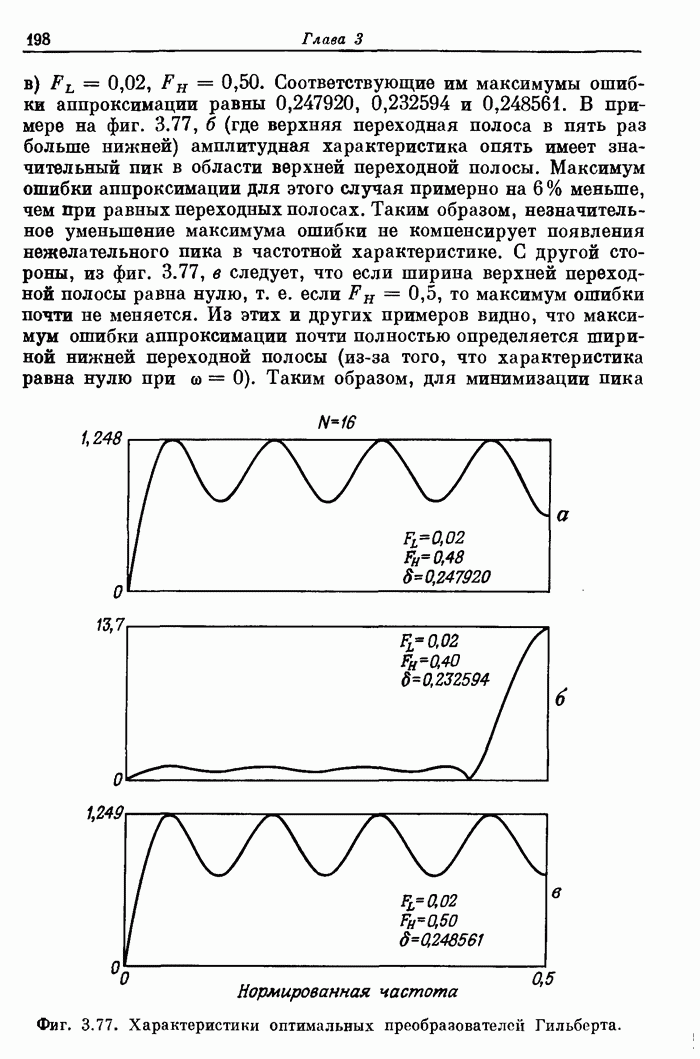
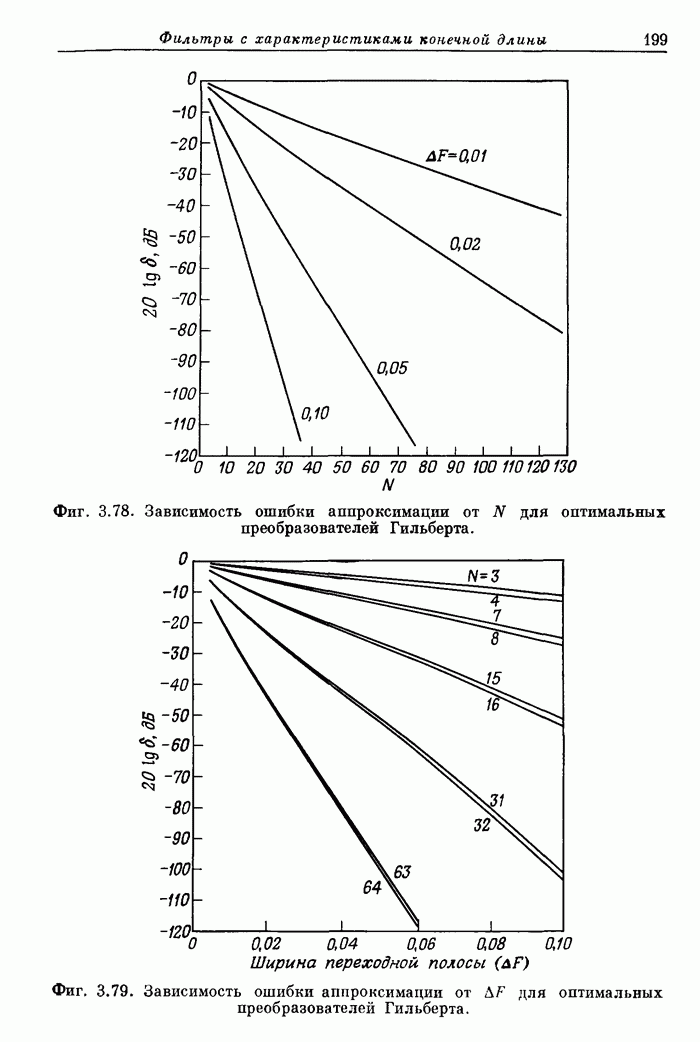
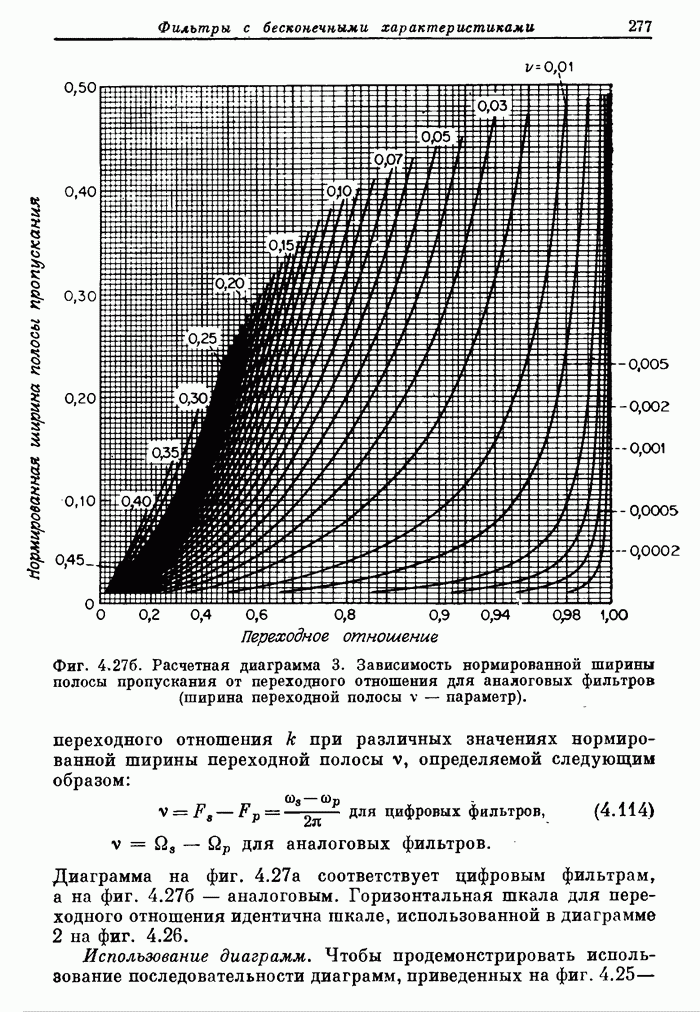
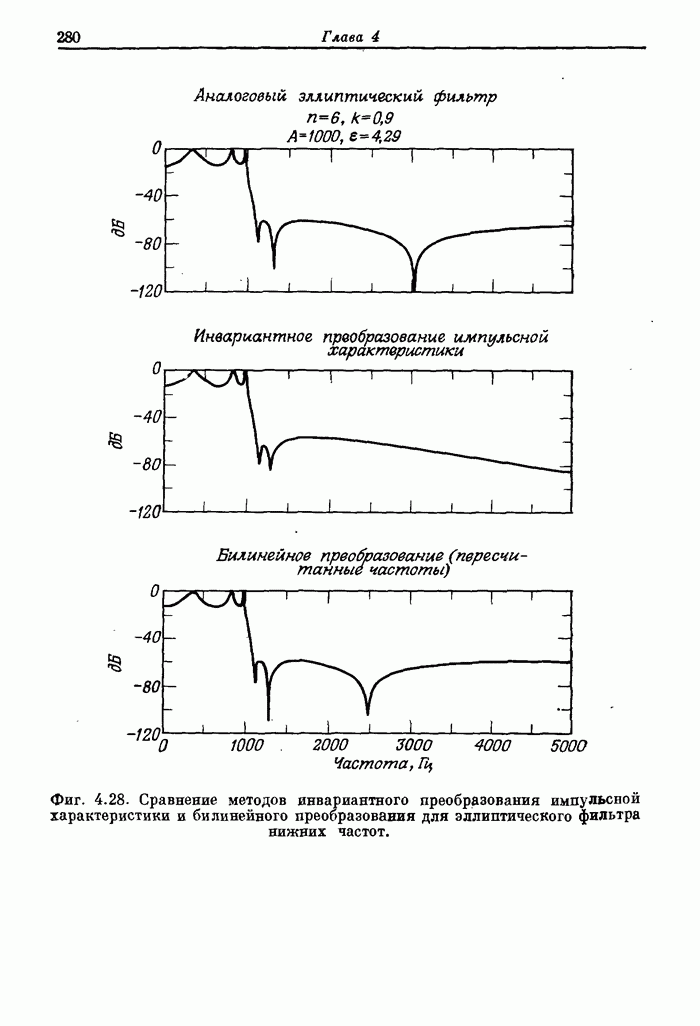
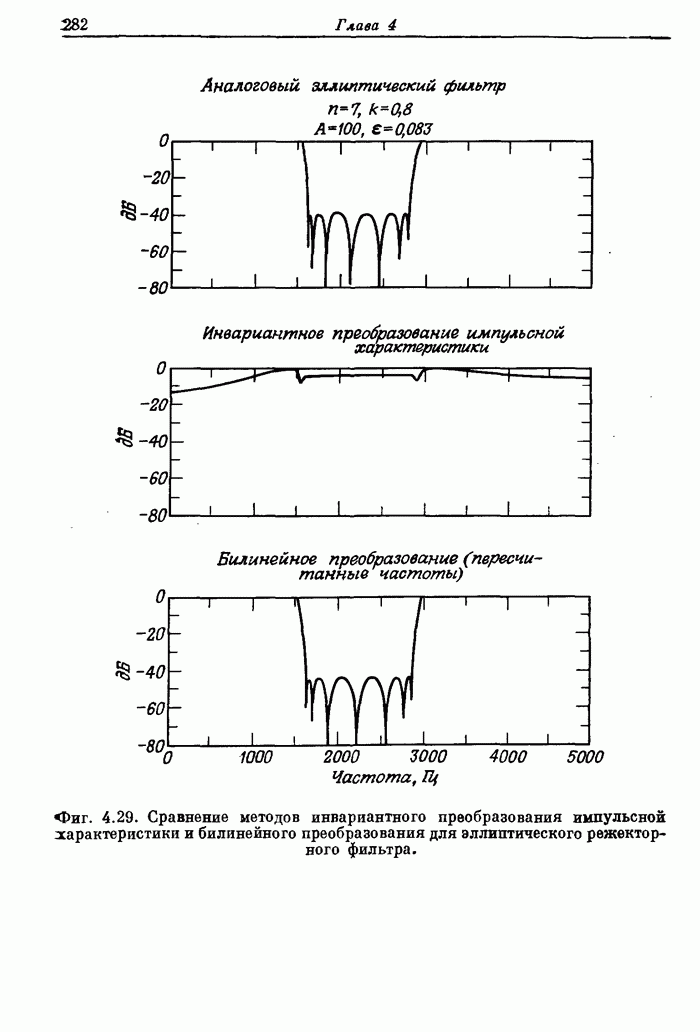
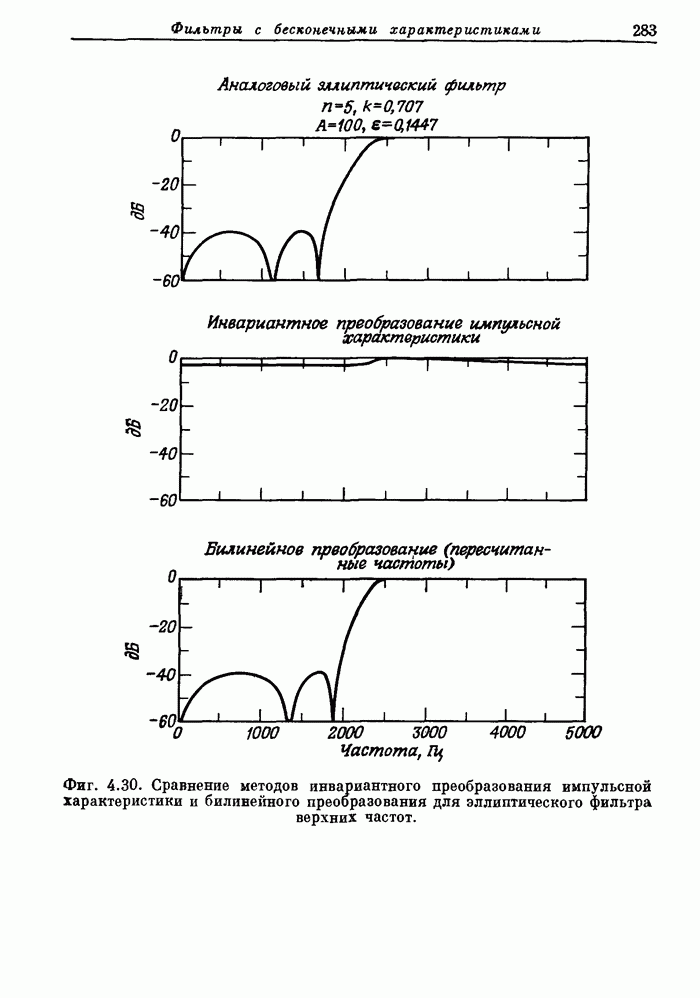
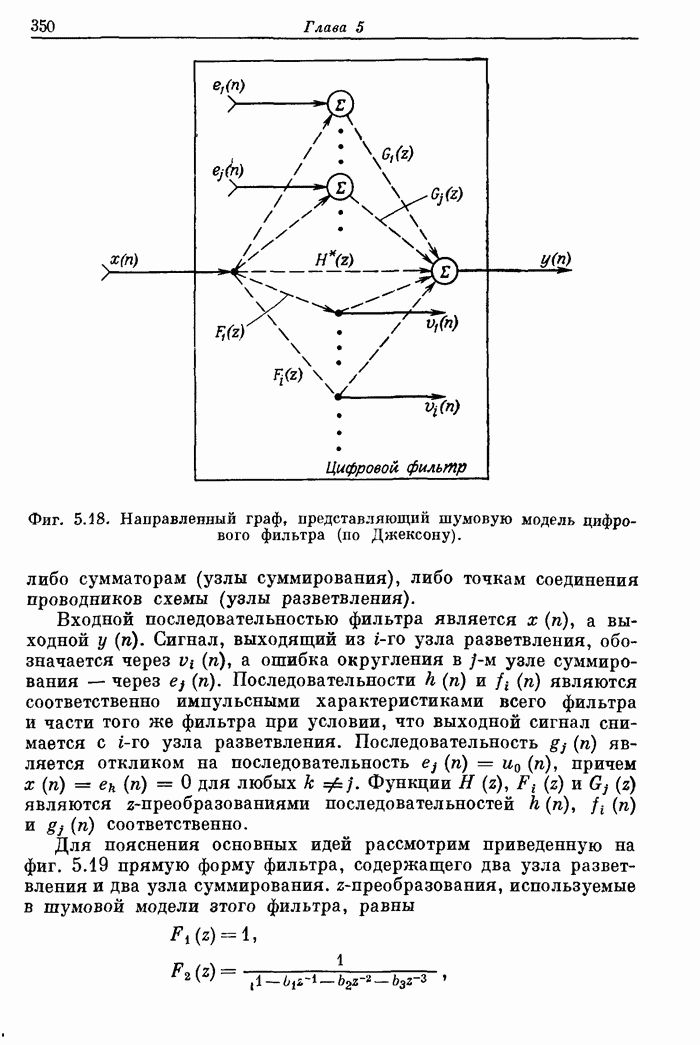
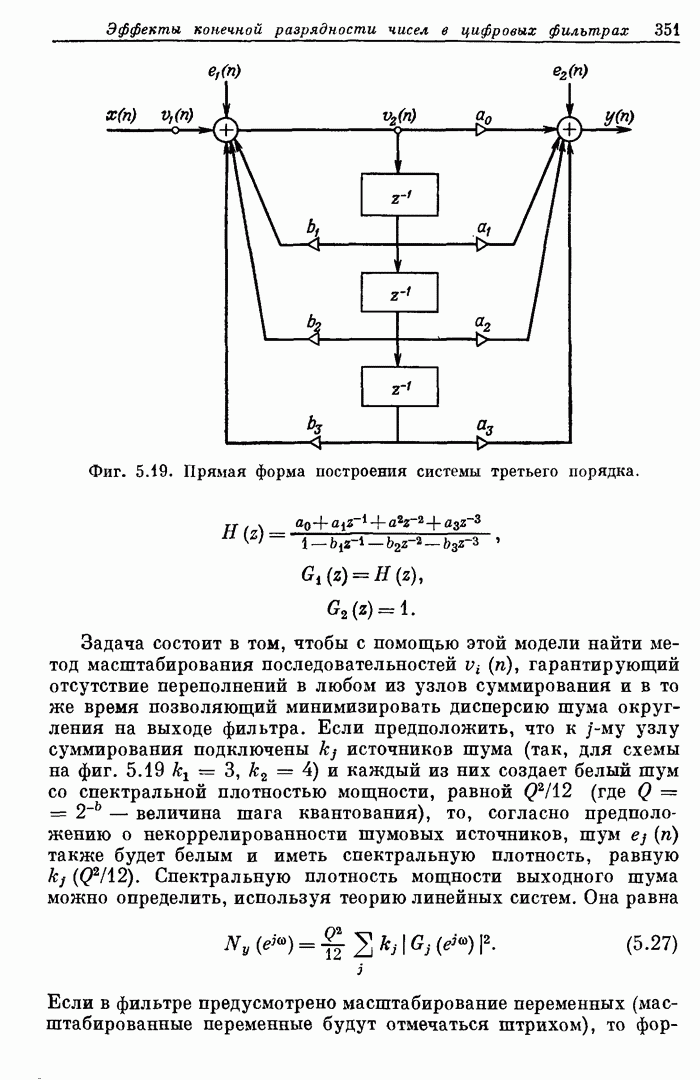
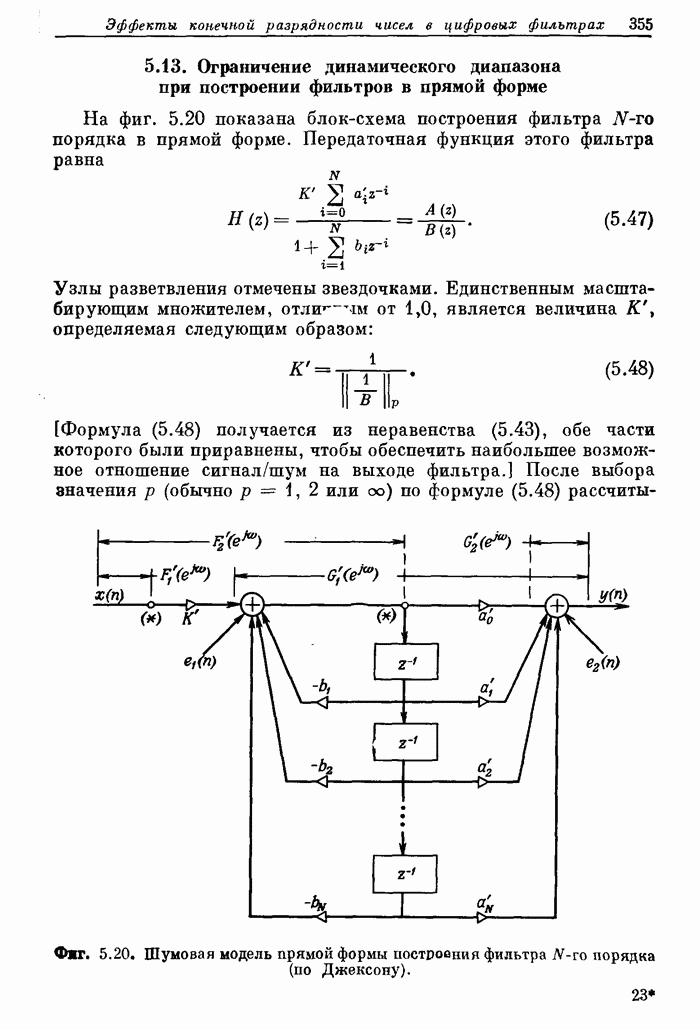
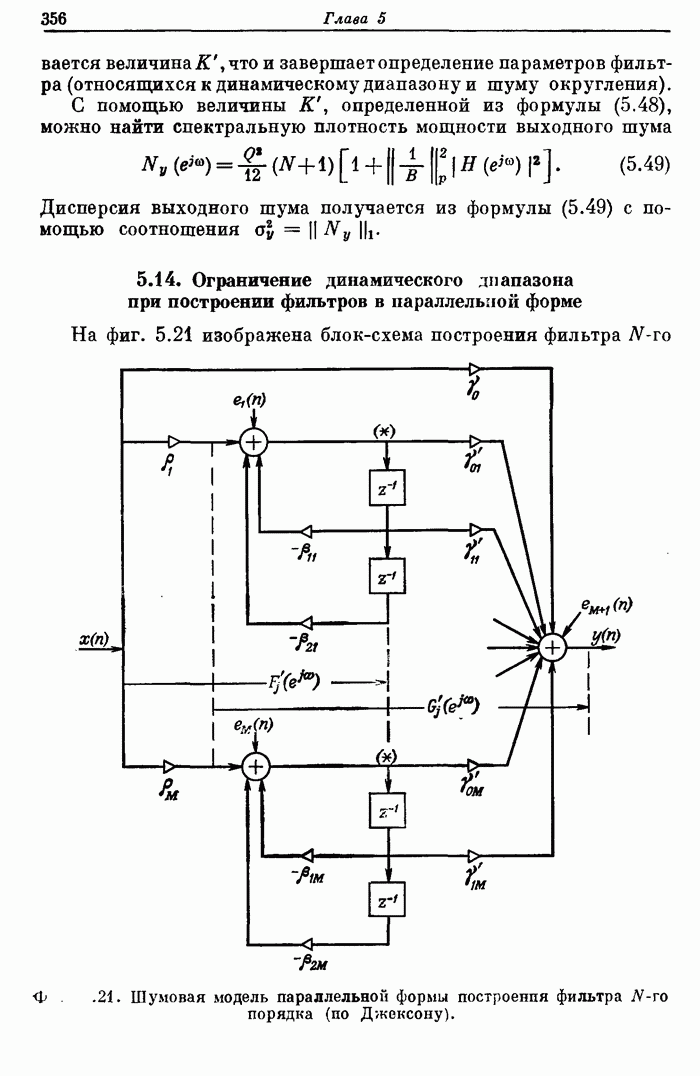
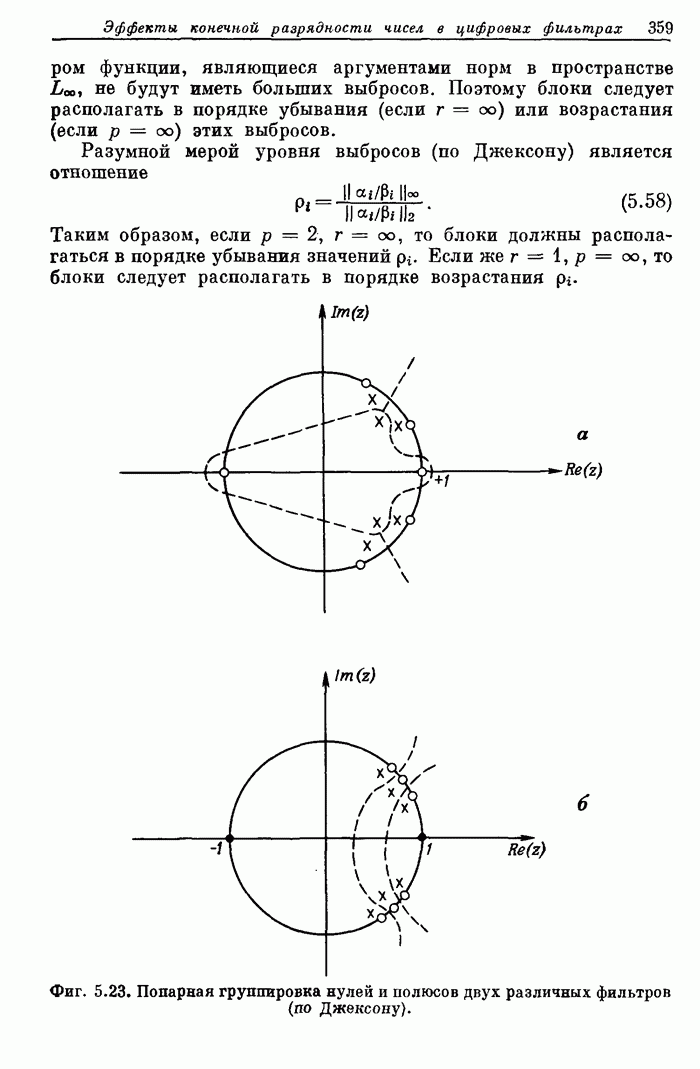
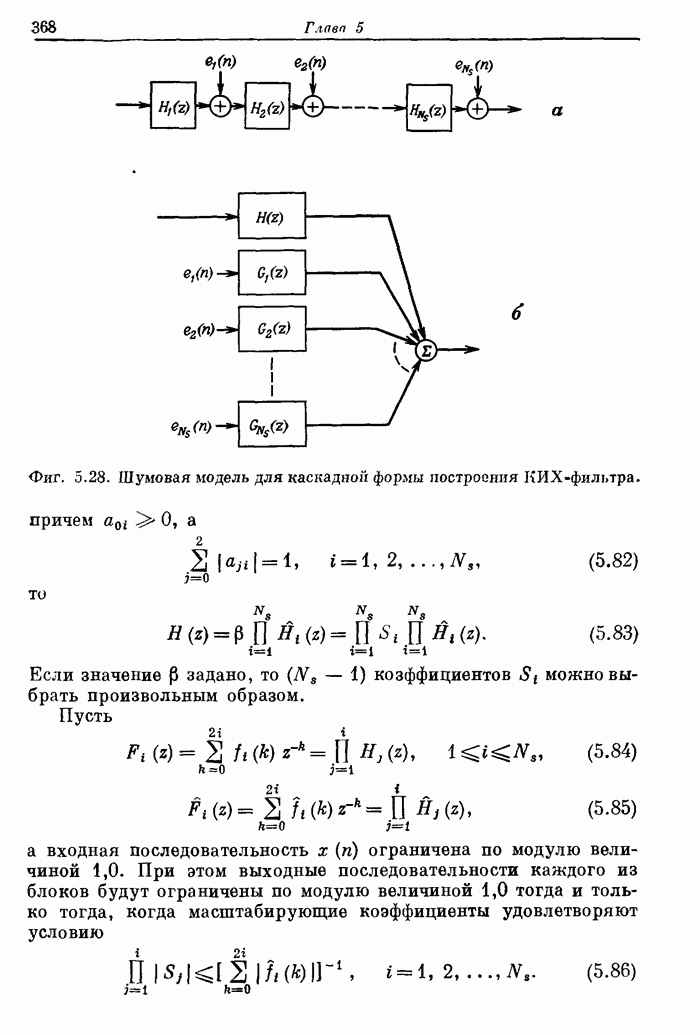
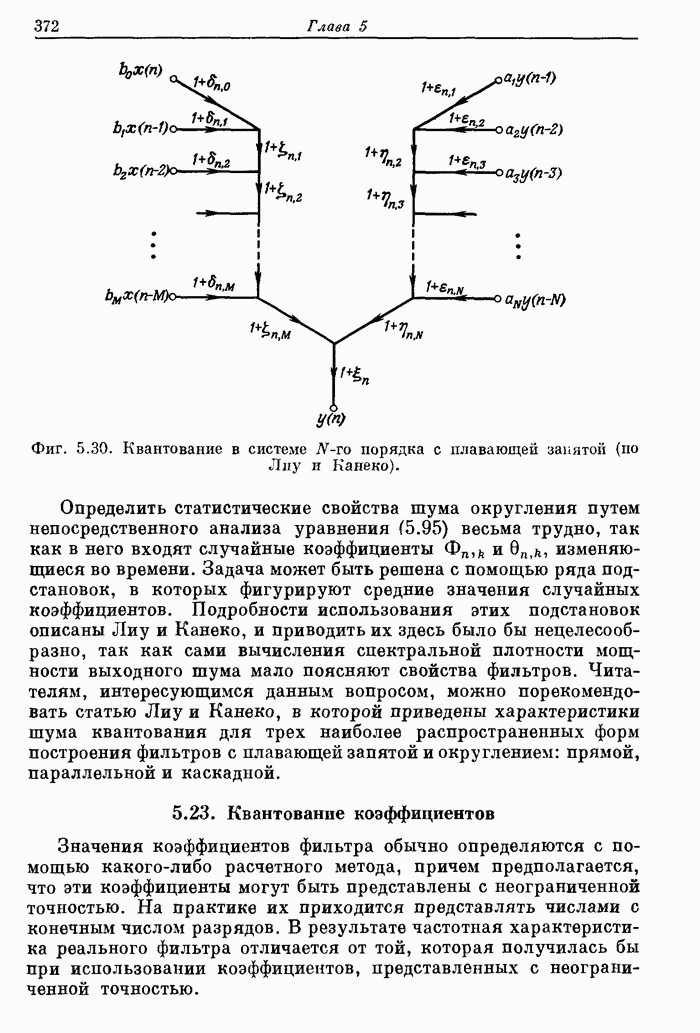
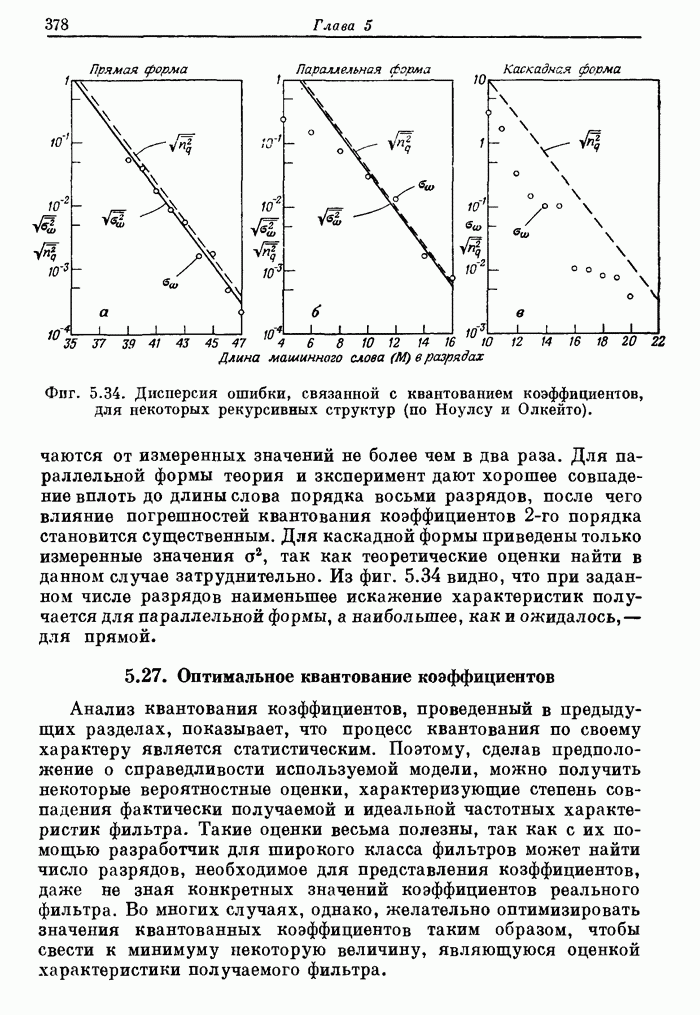
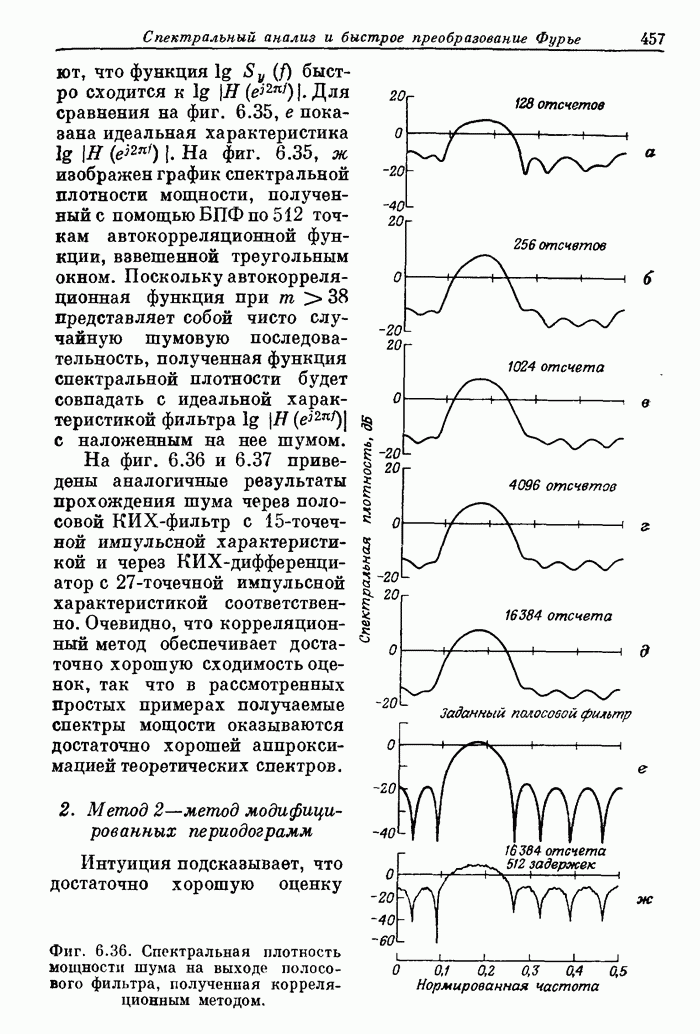
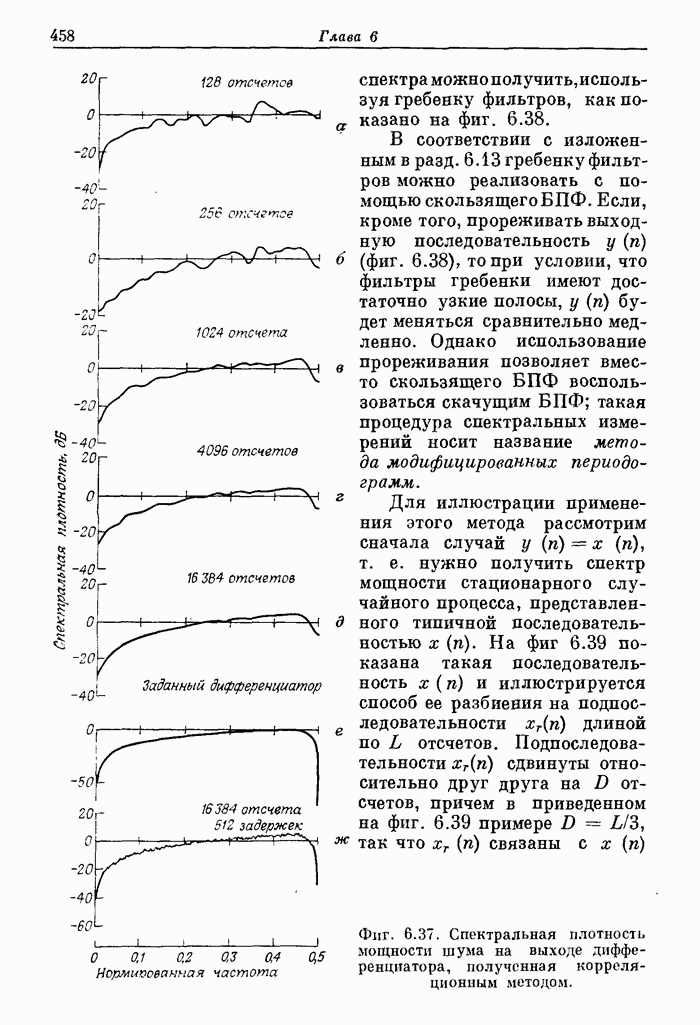
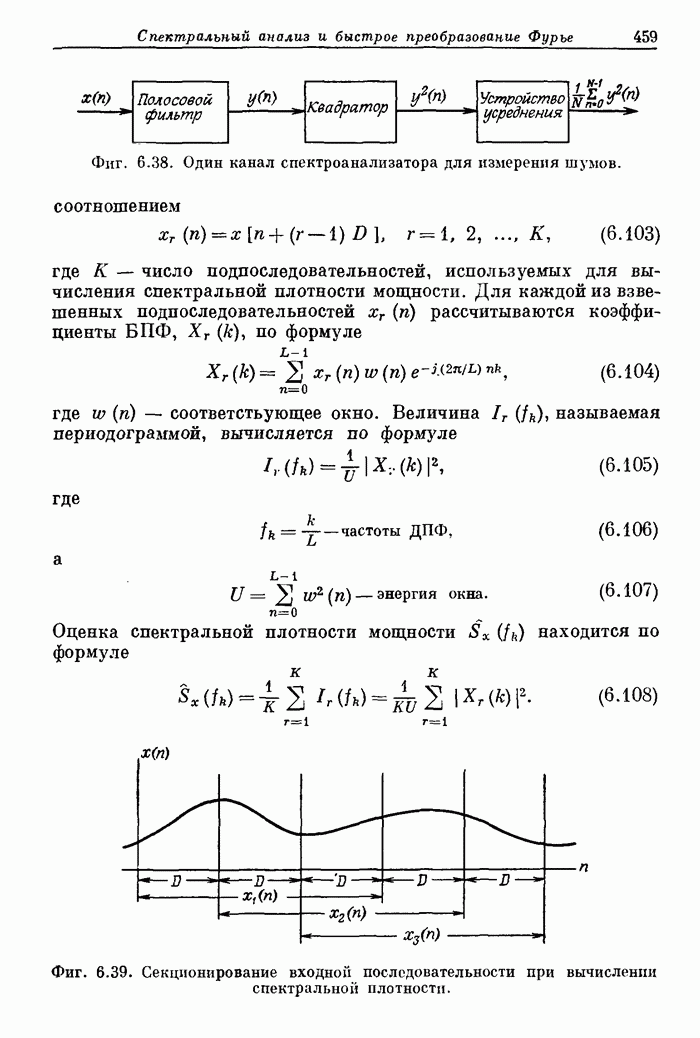
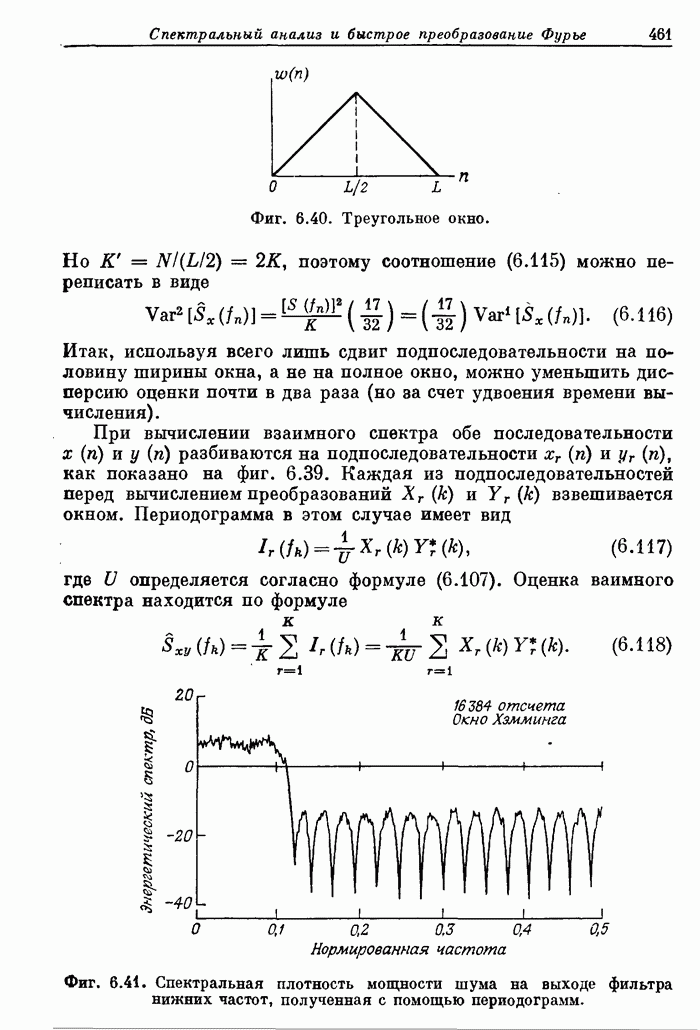
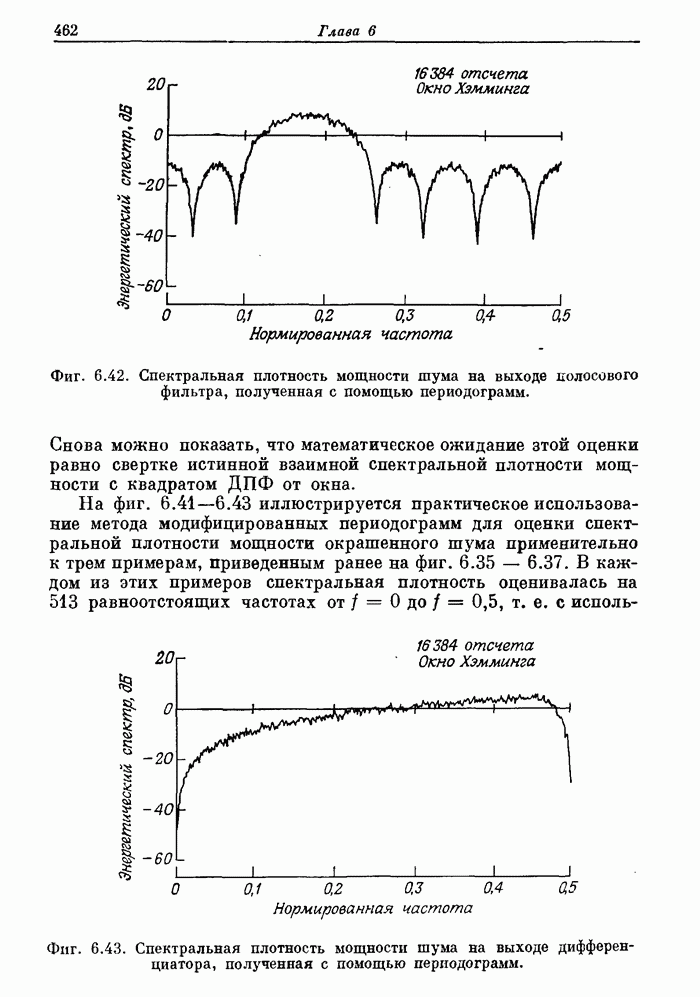
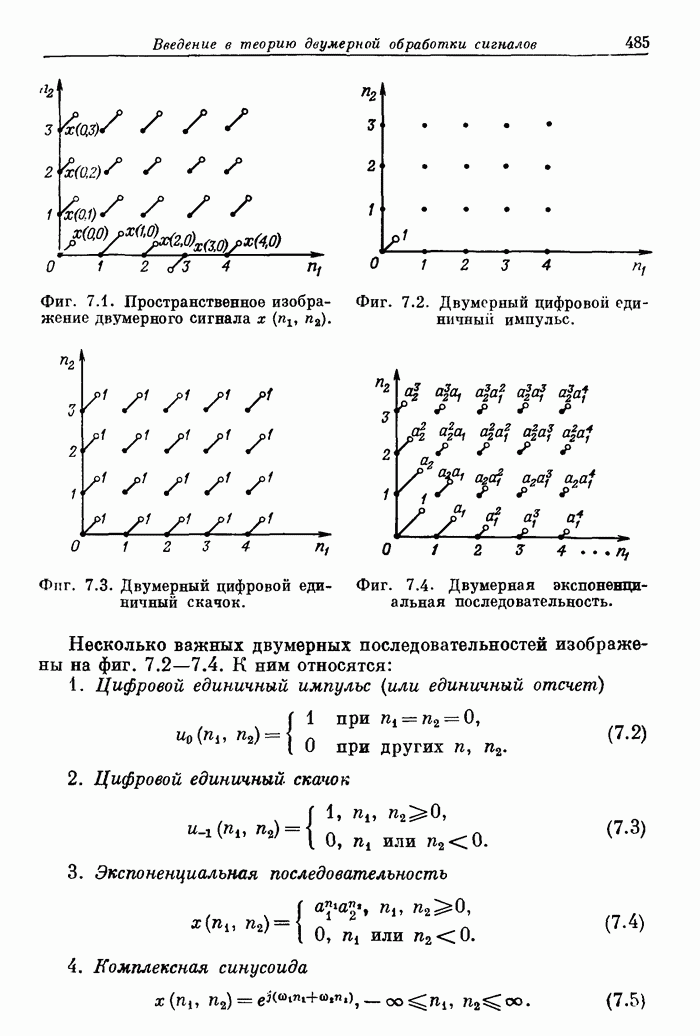
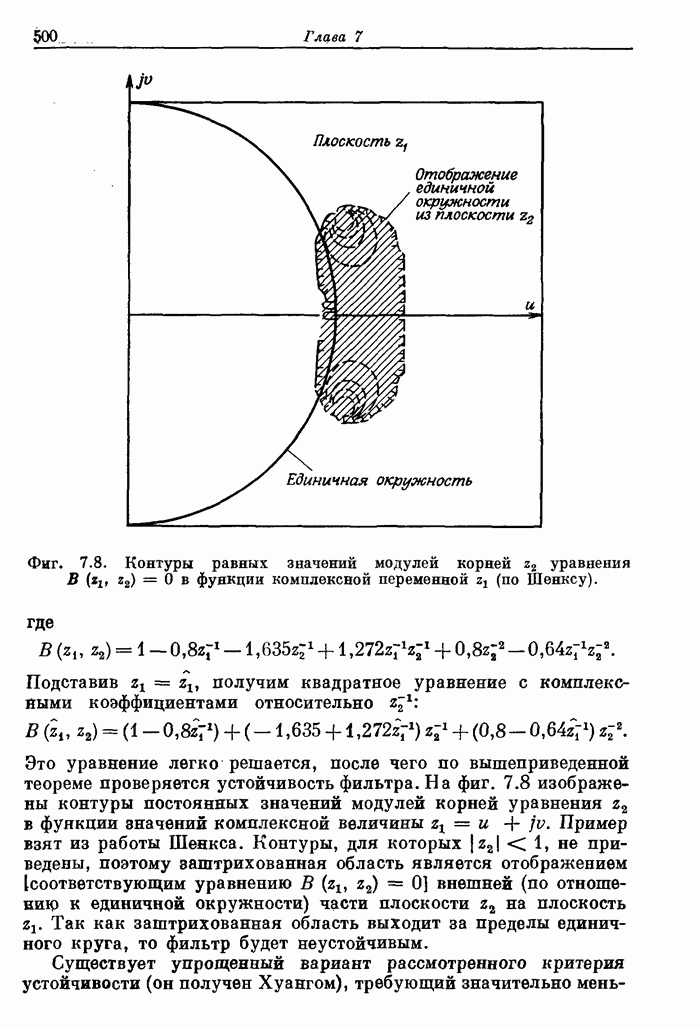
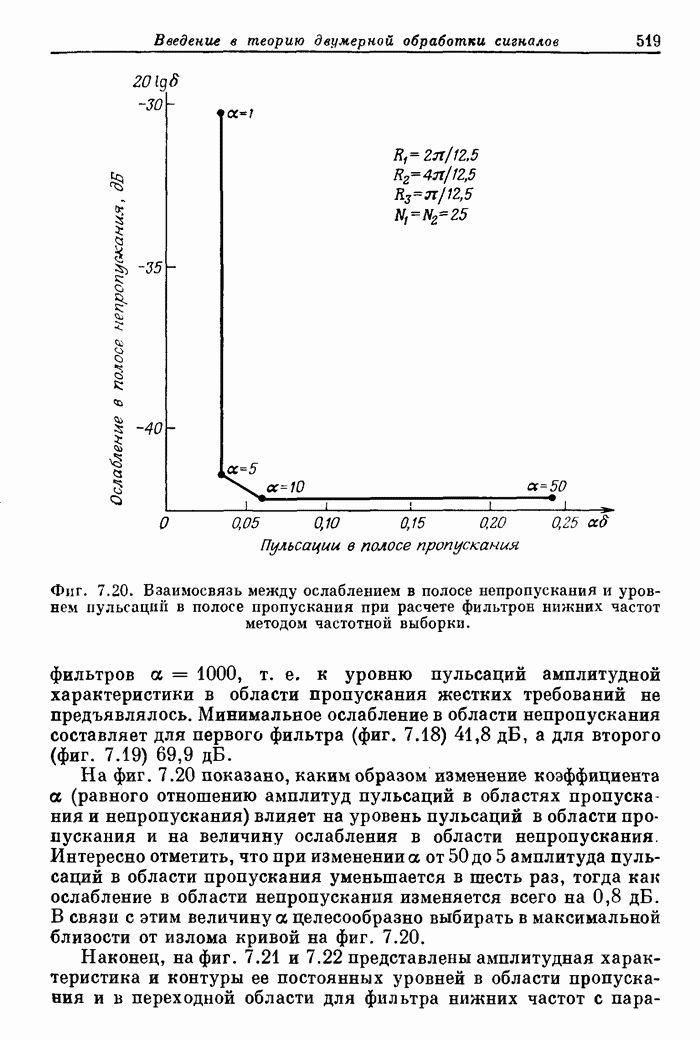
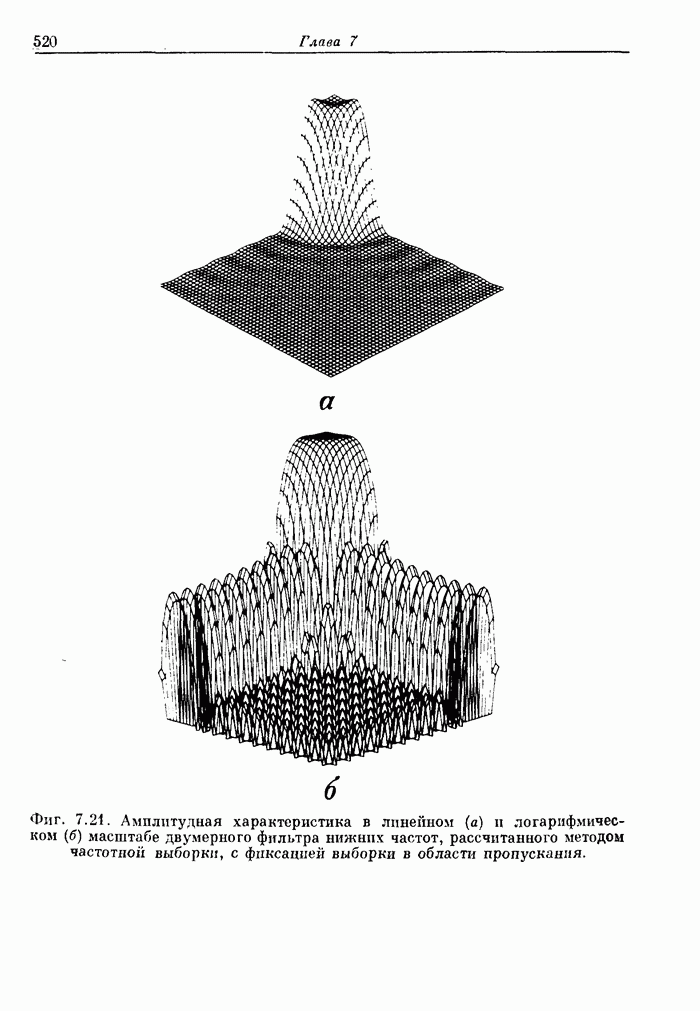
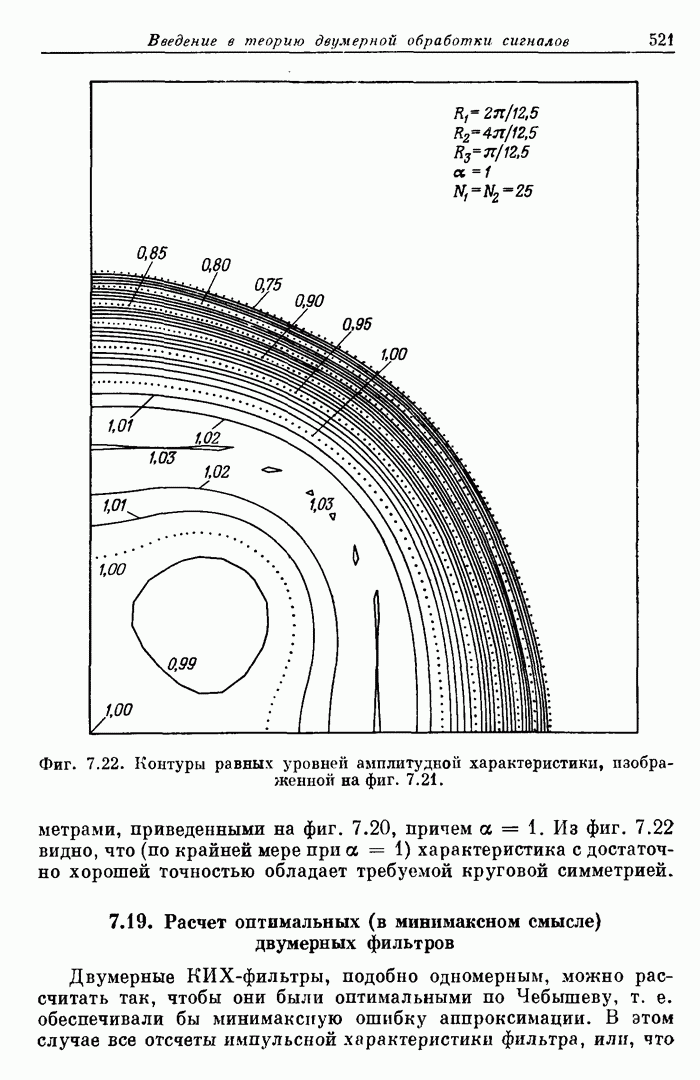
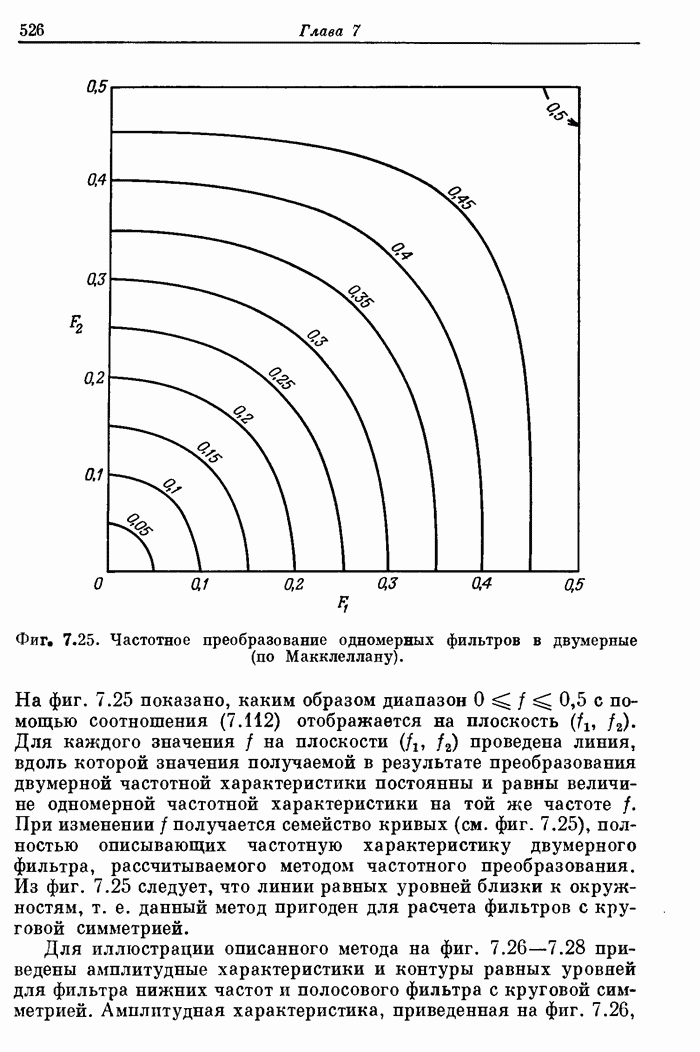
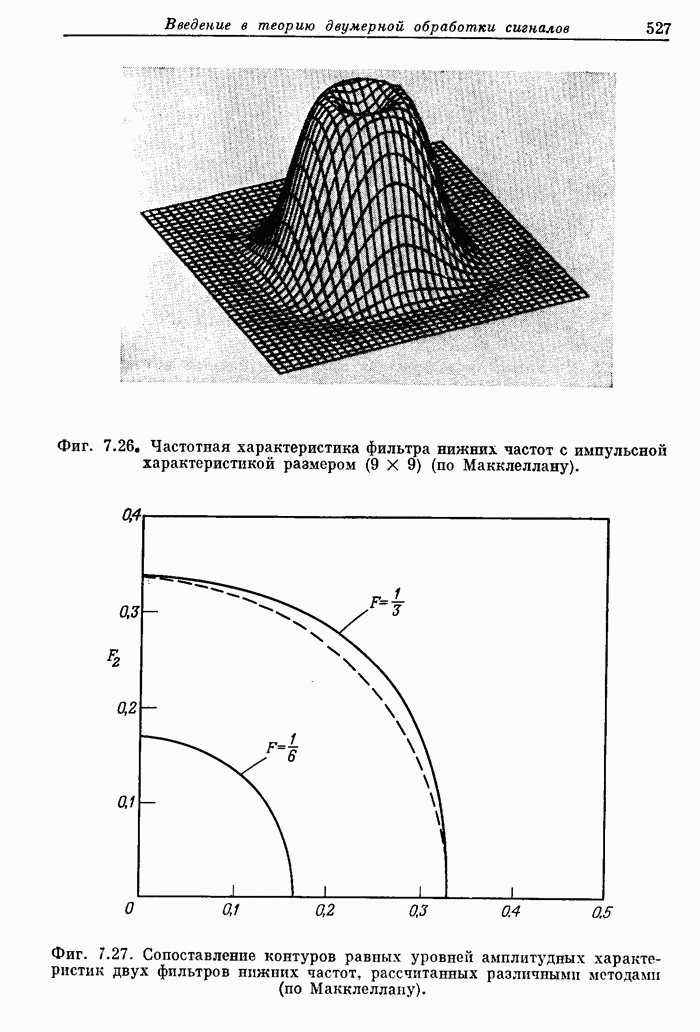
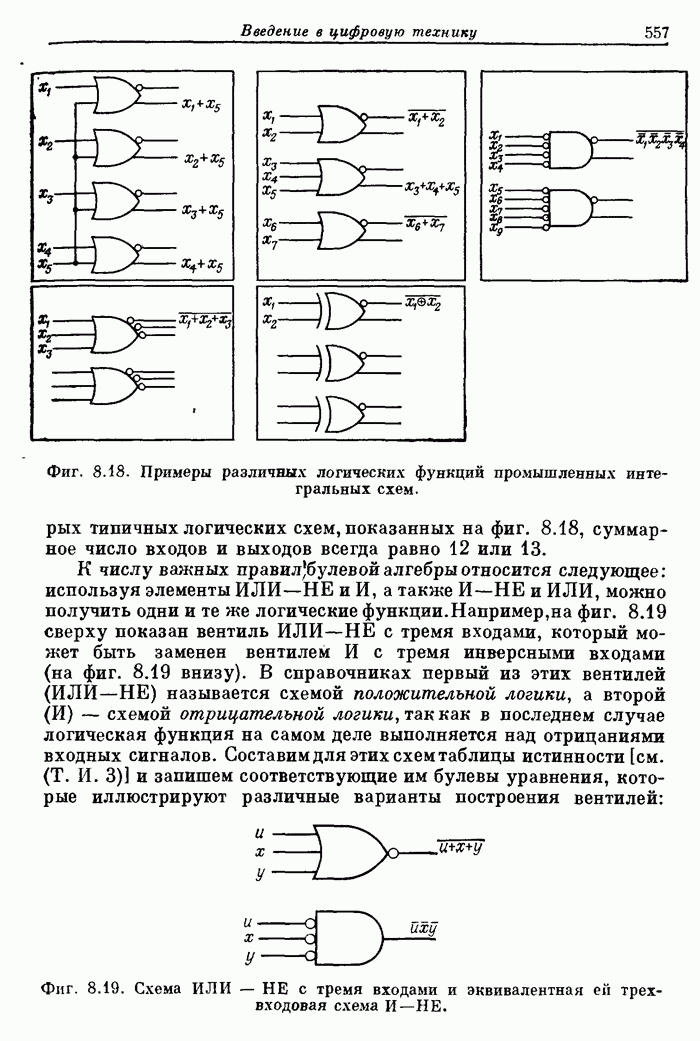
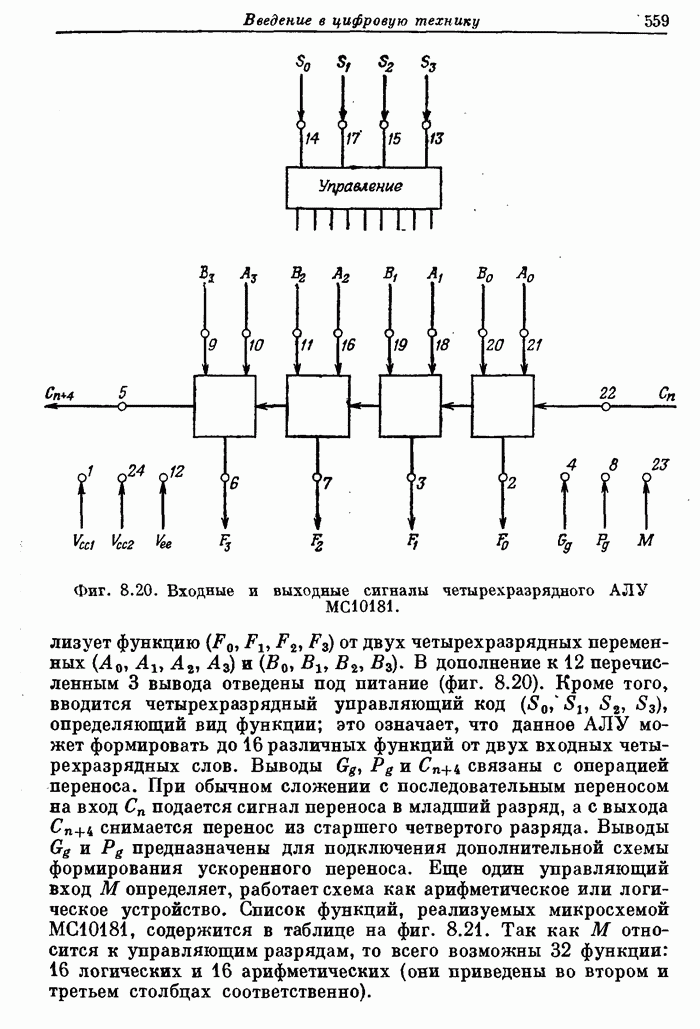
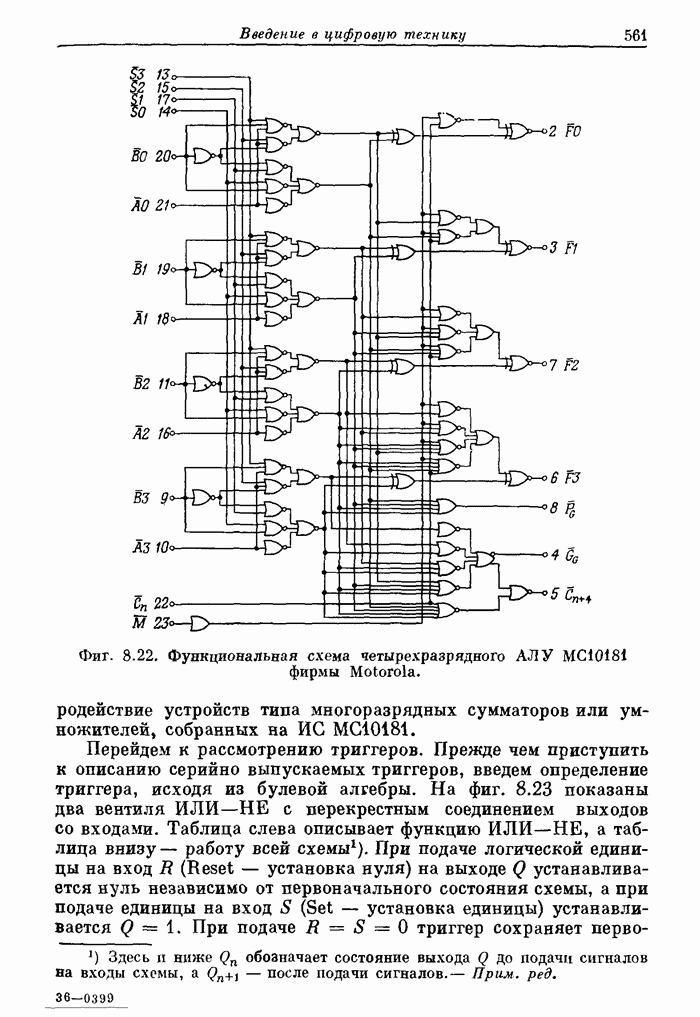
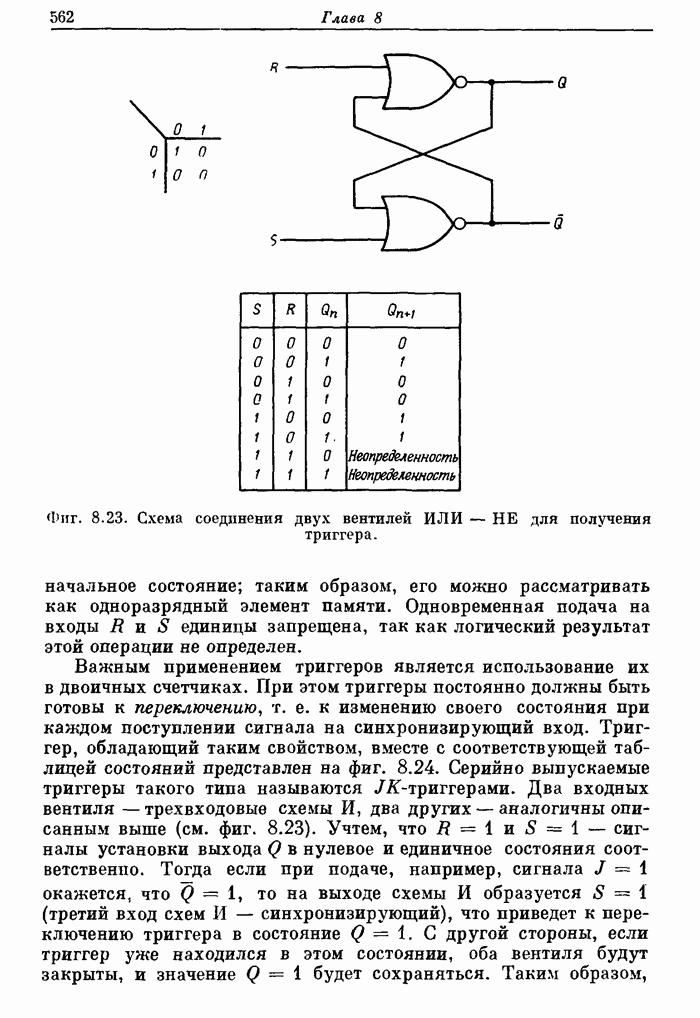
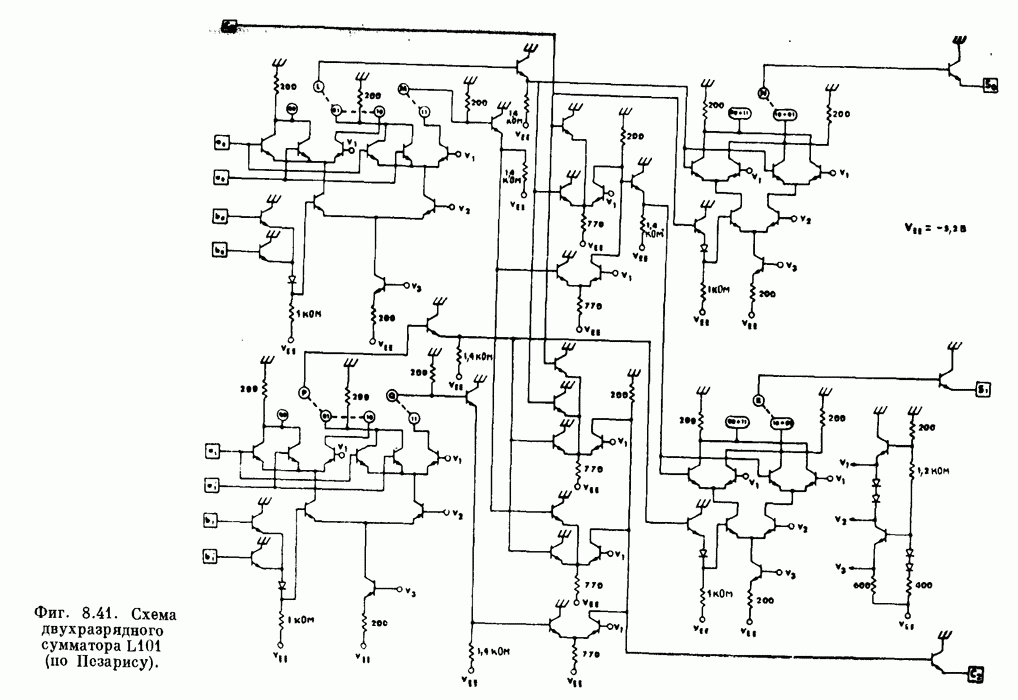
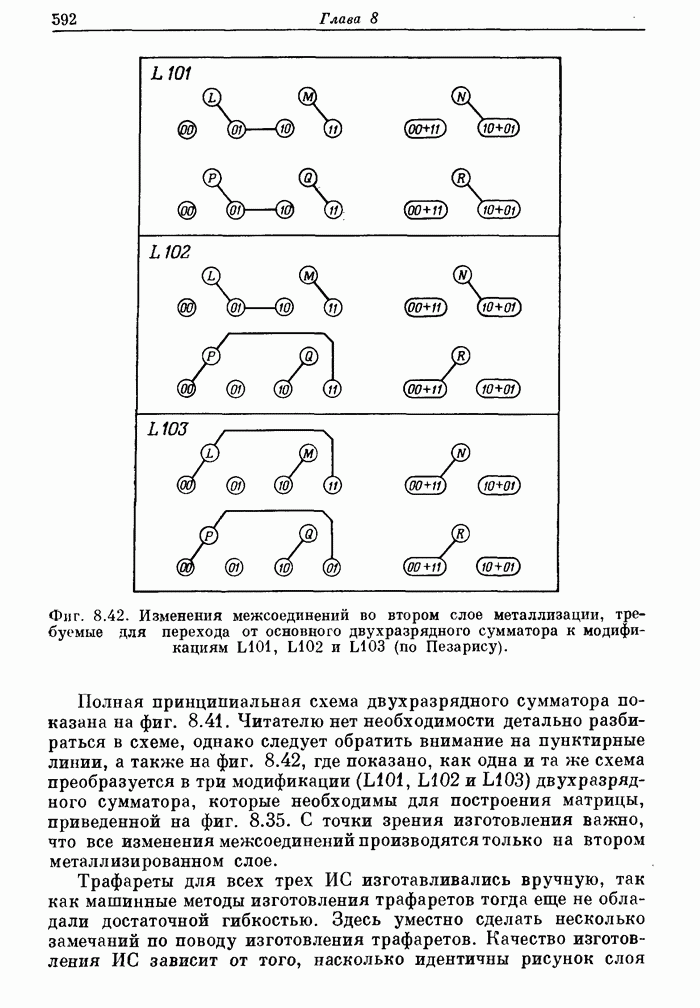
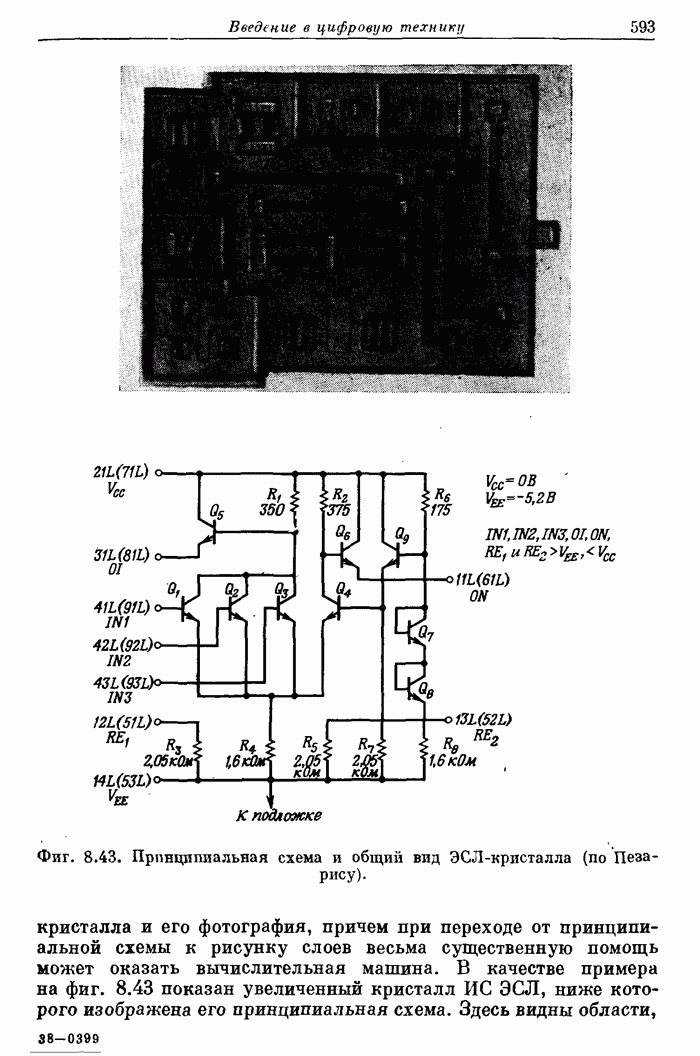
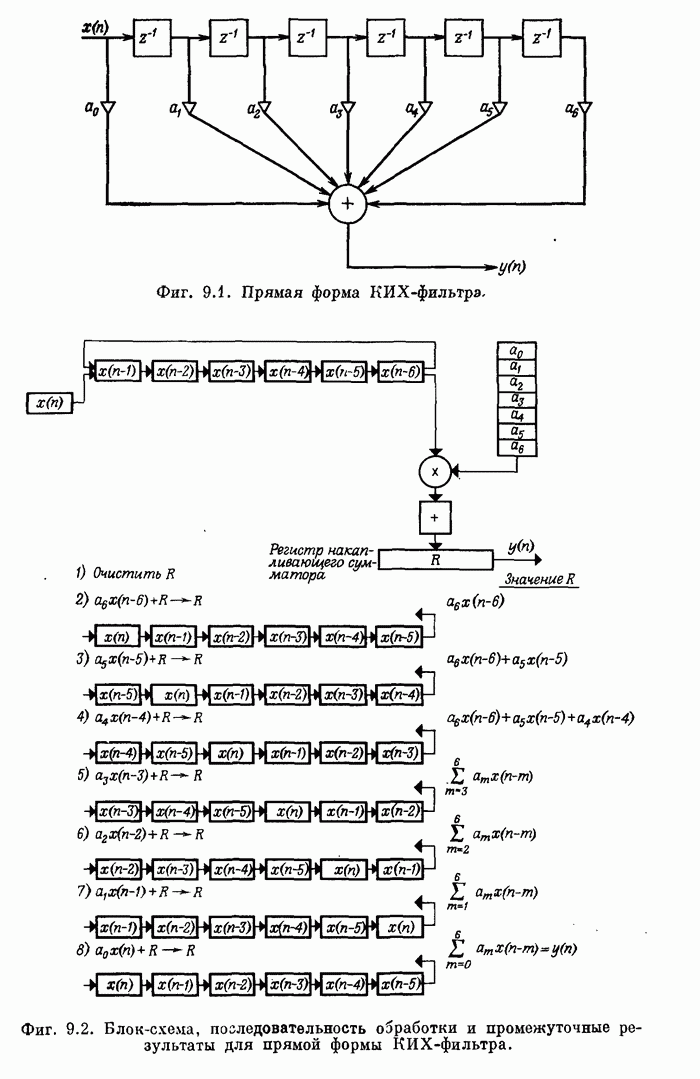
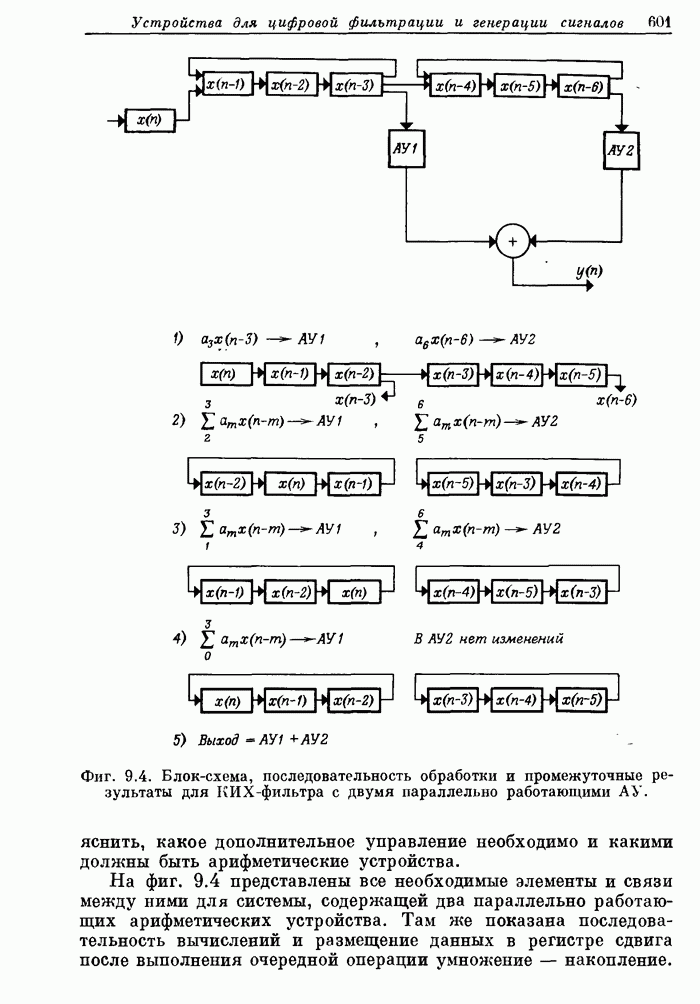
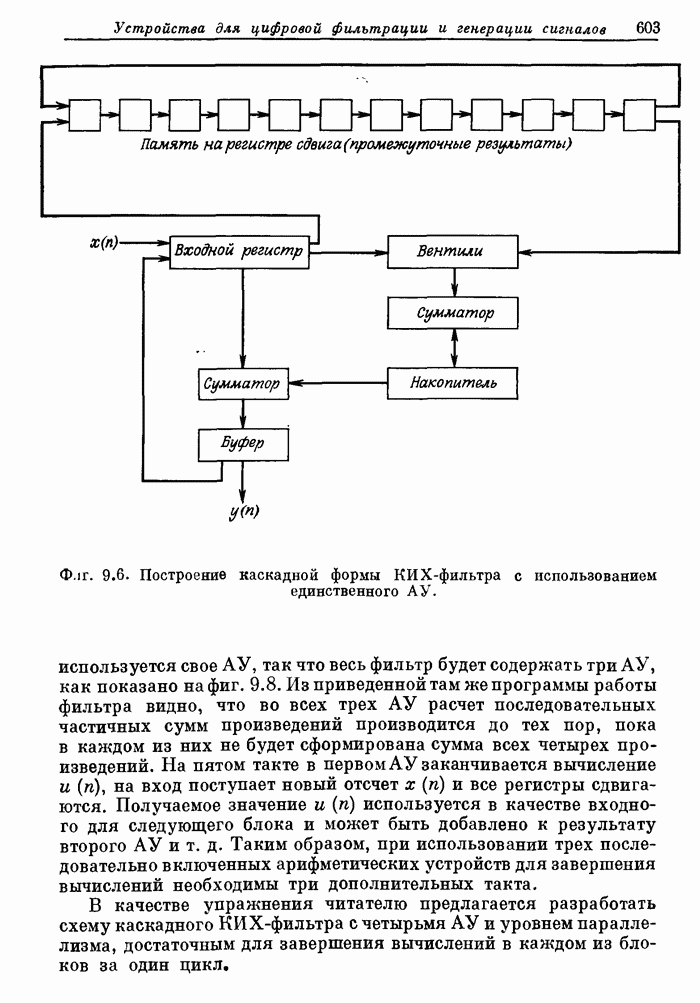
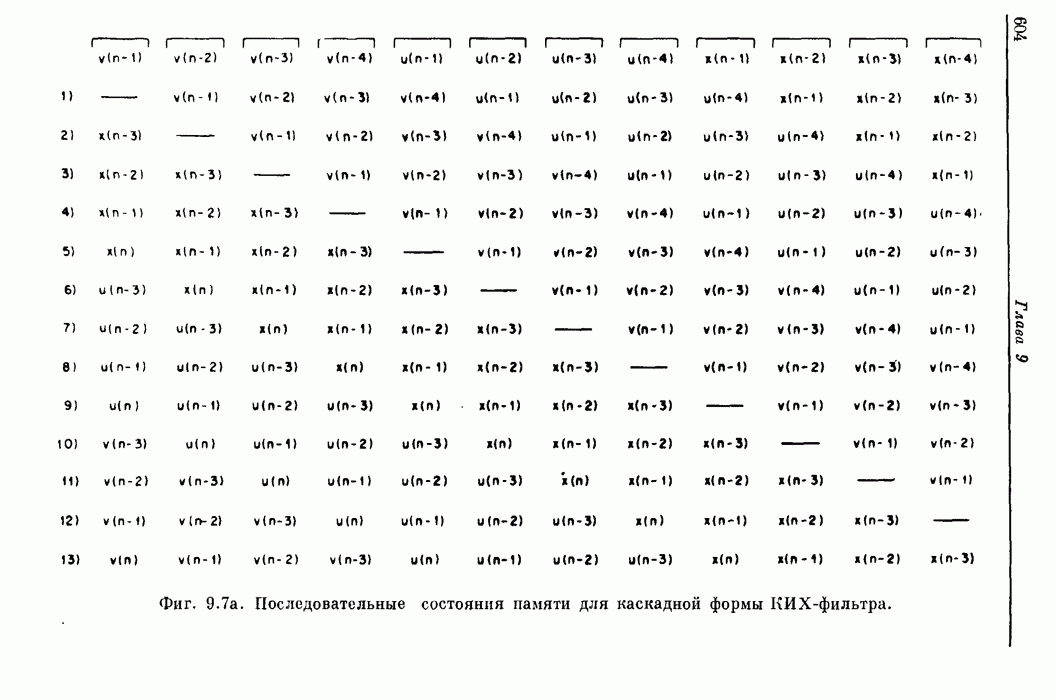
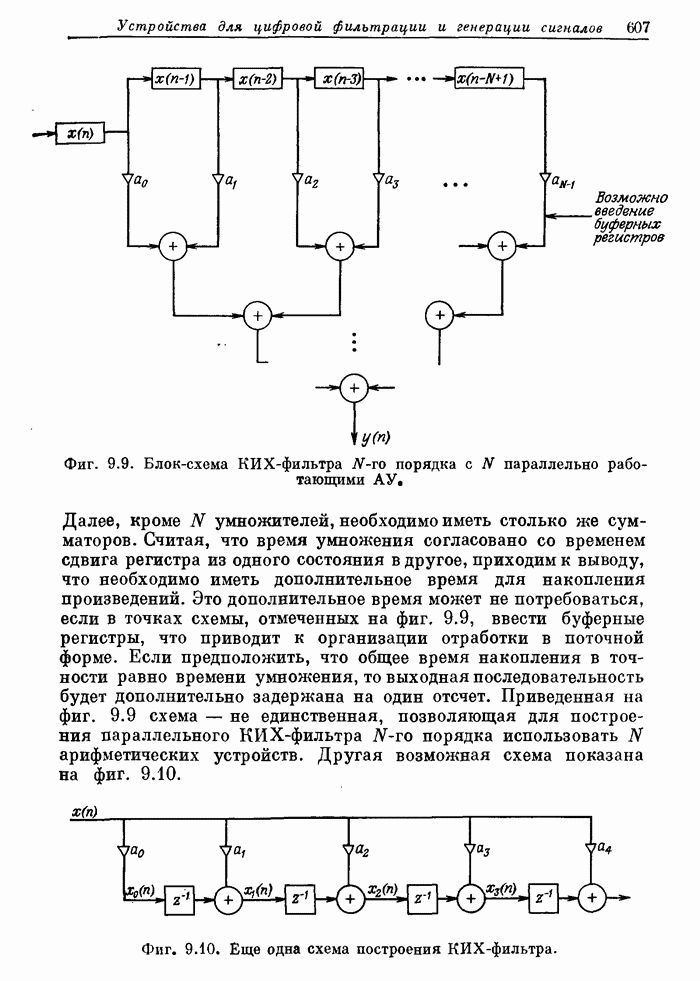
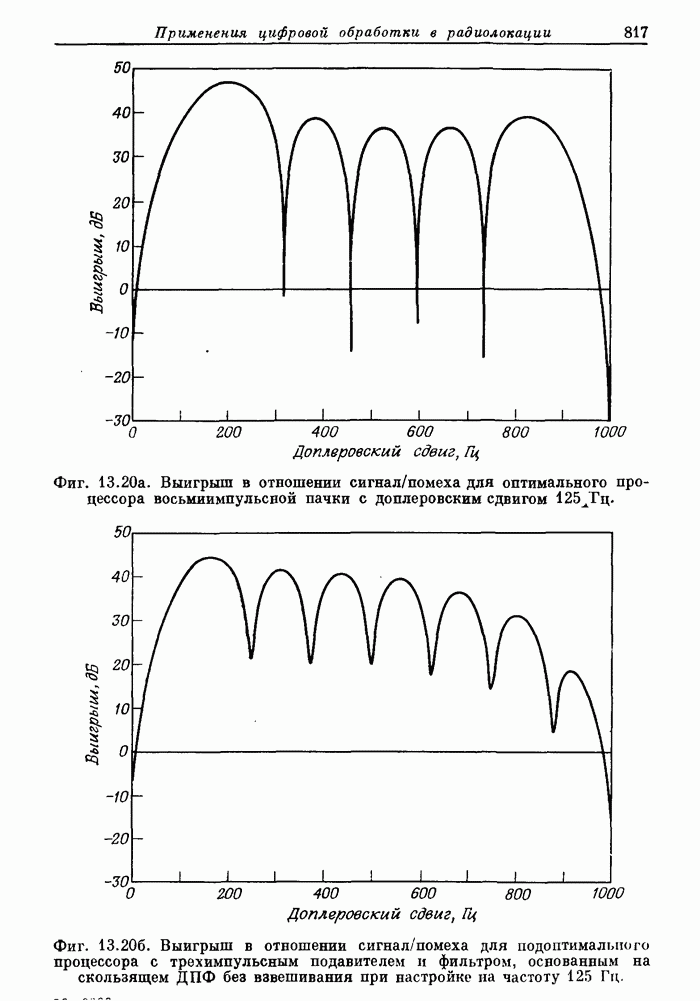
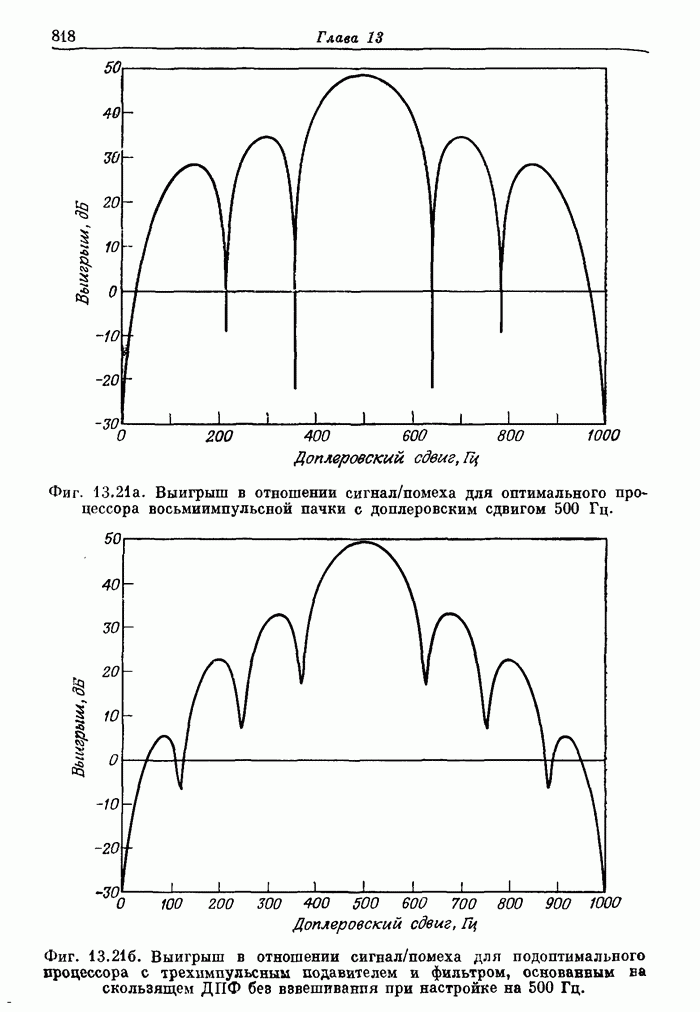
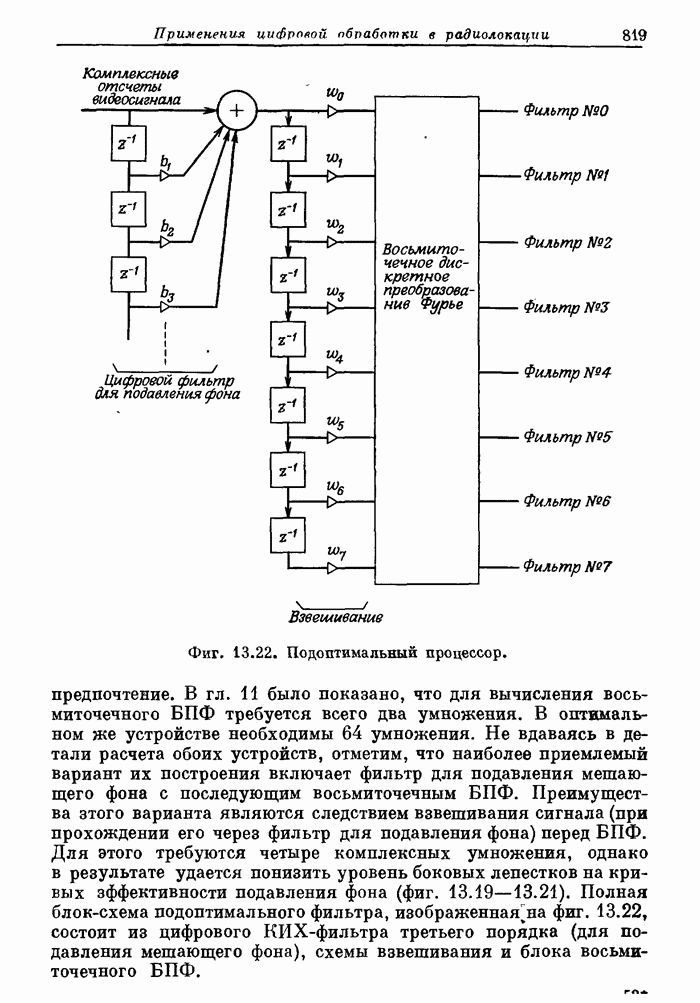
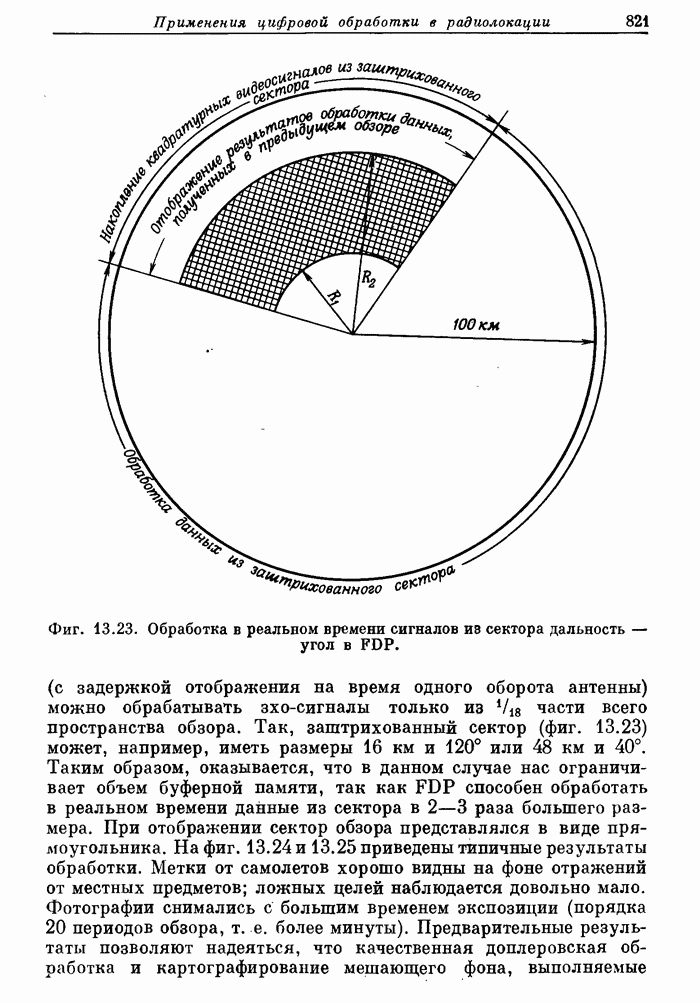
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
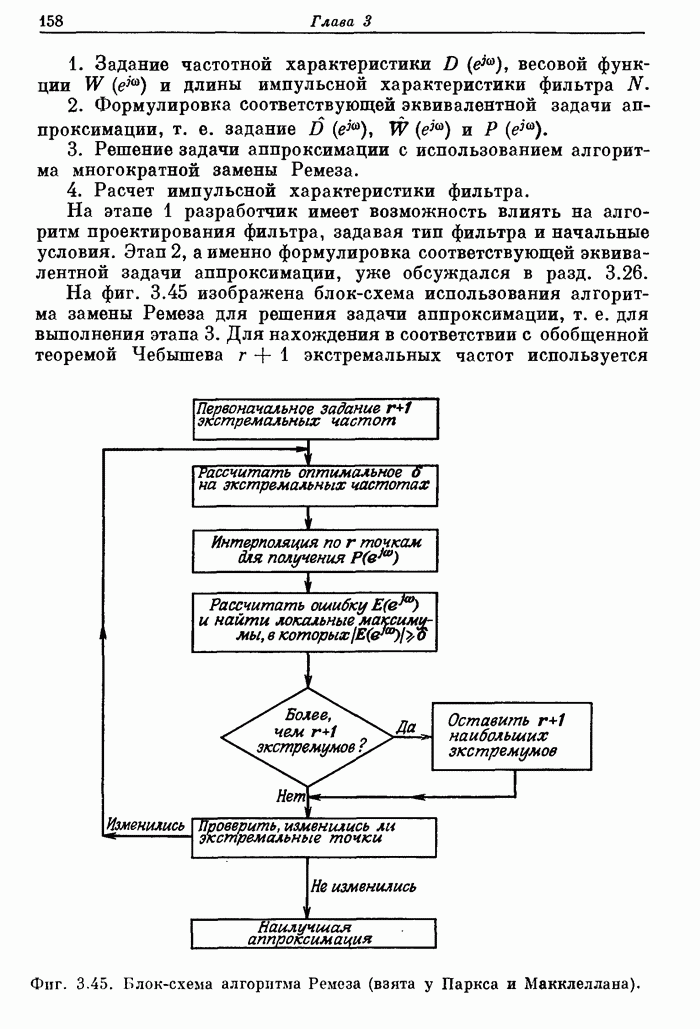
Приложение
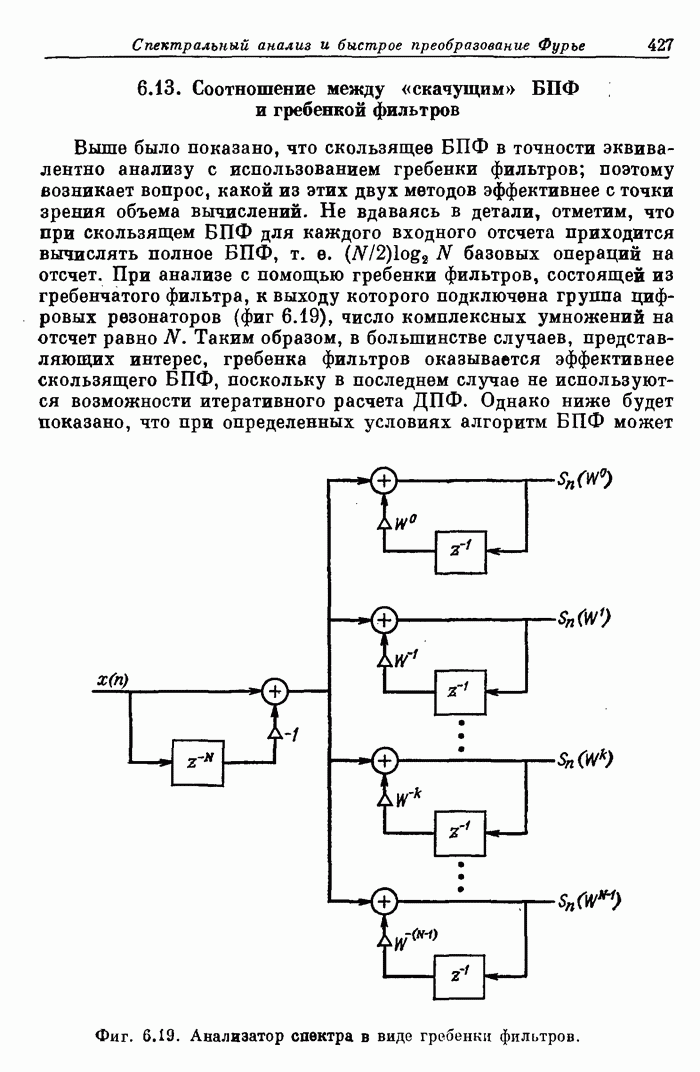
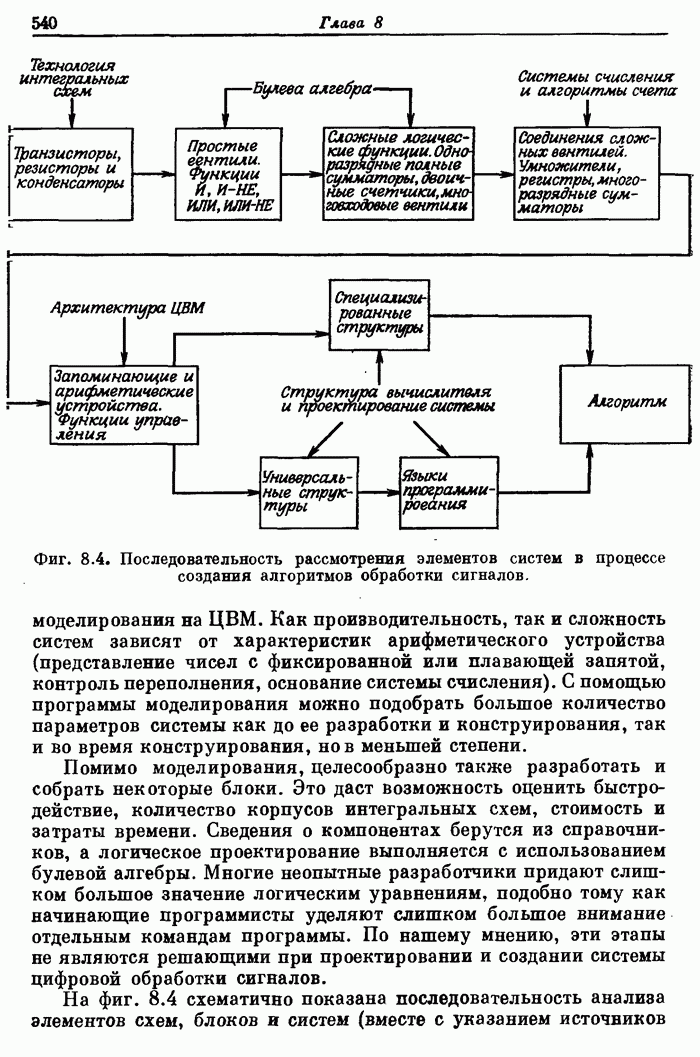
В приложении приведена написанная на ФОРТРАНе программа расчета разнообразных оптимальных (минимаксных) КИХ- фильтров, в том числе фильтров нижних и верхних частот, полосовых, режекторных, а также дифференциаторов и преобразователей Гильберта.
Для иллюстрации применения этой программы даны четыре примера. Текст программы приводится сразу за примерами.
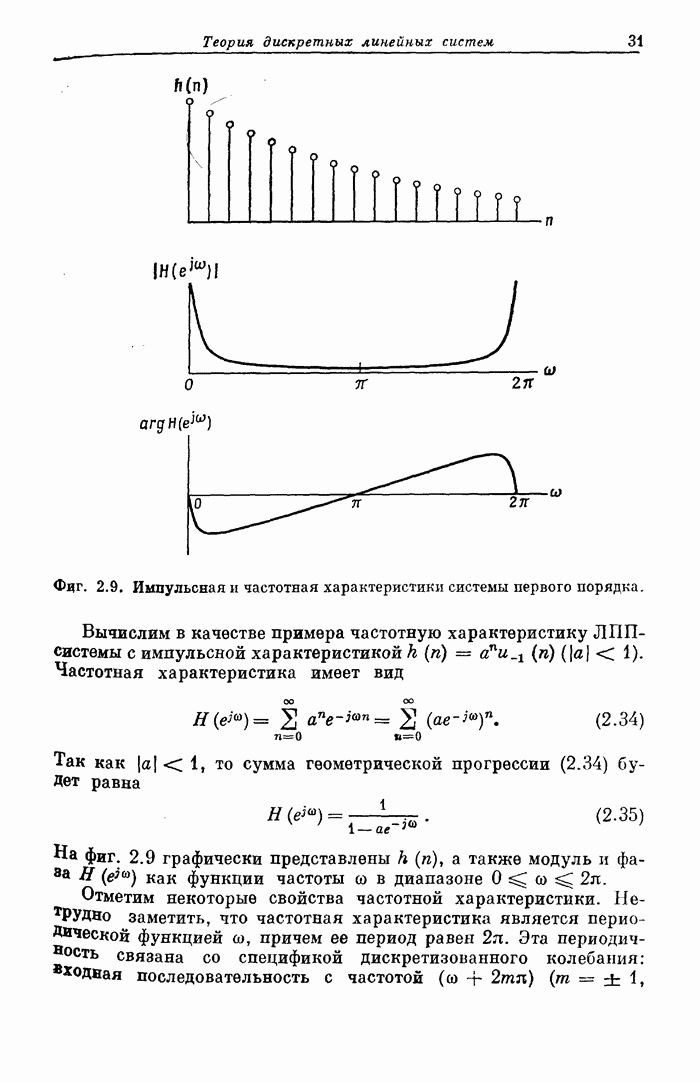
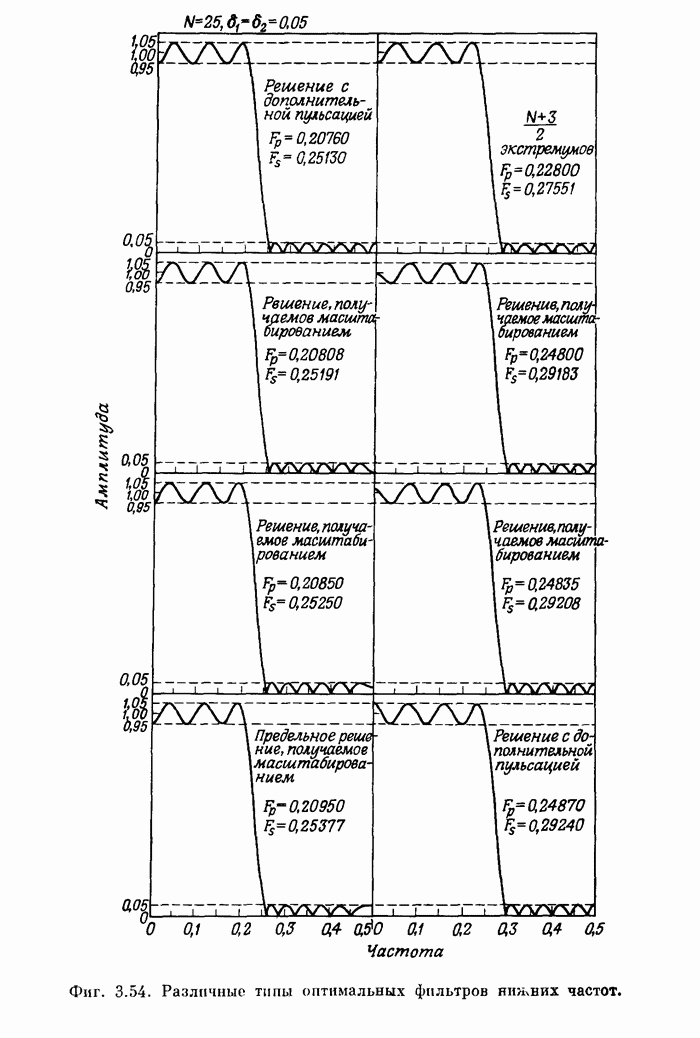
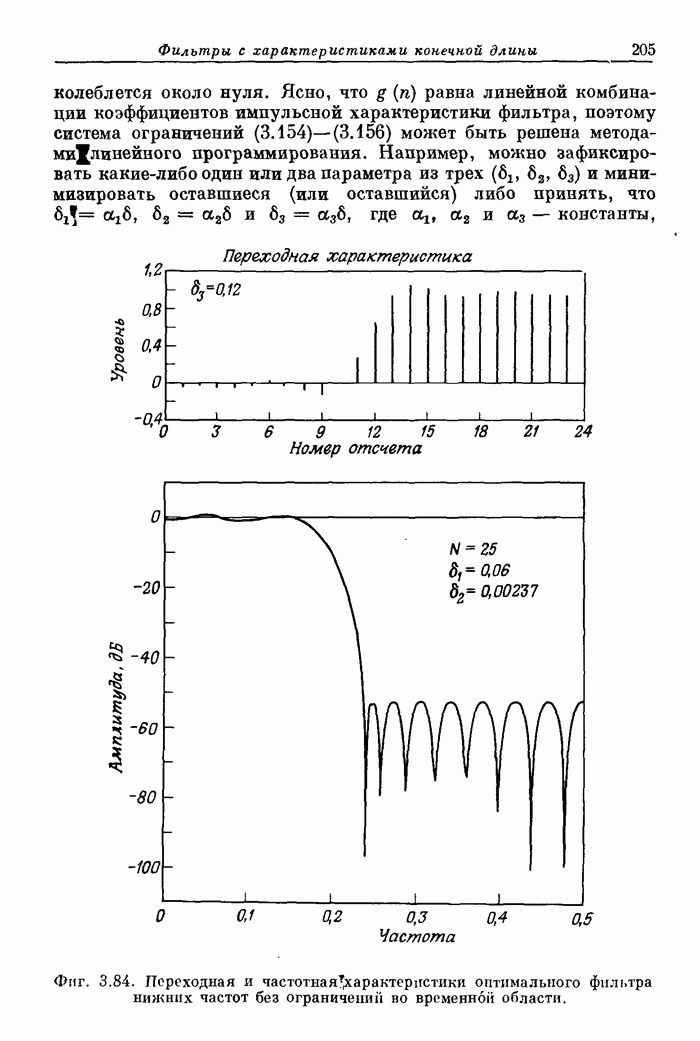
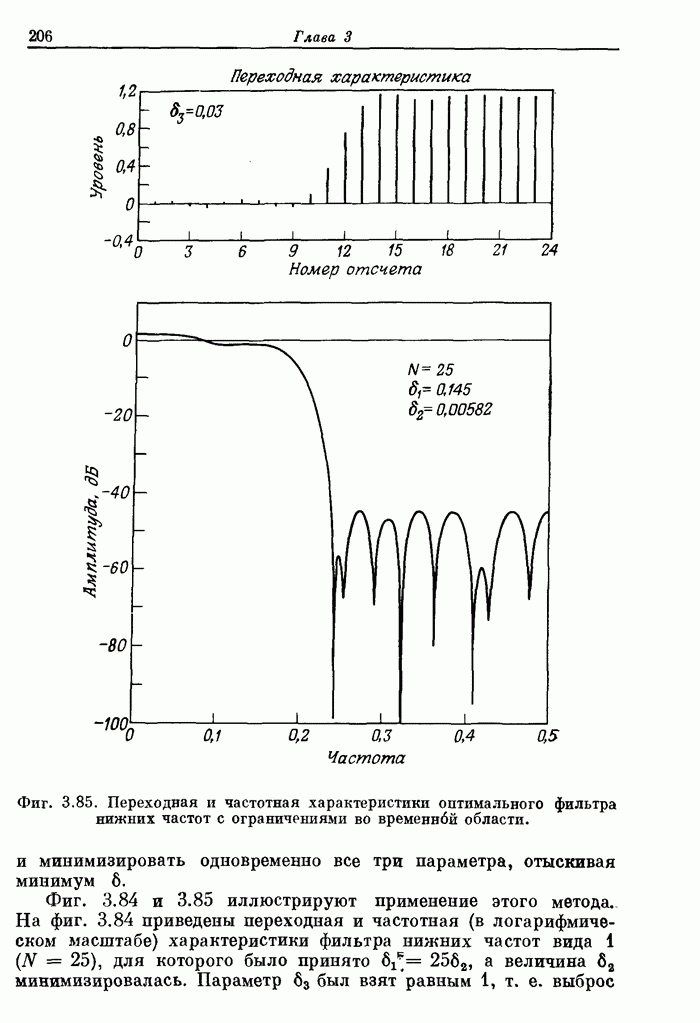
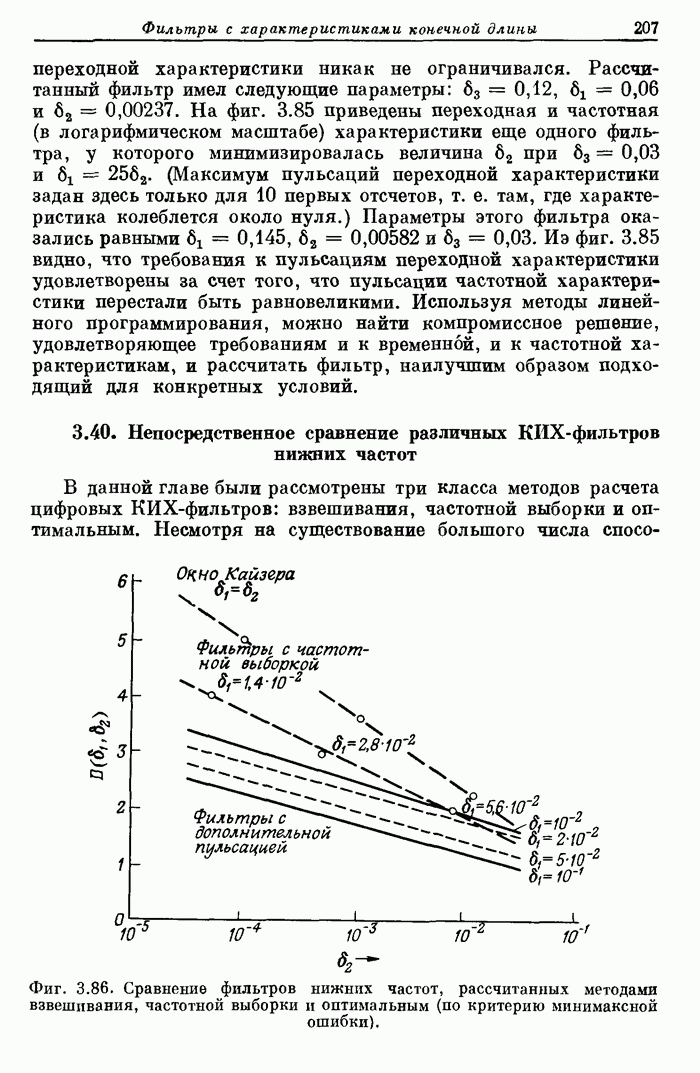
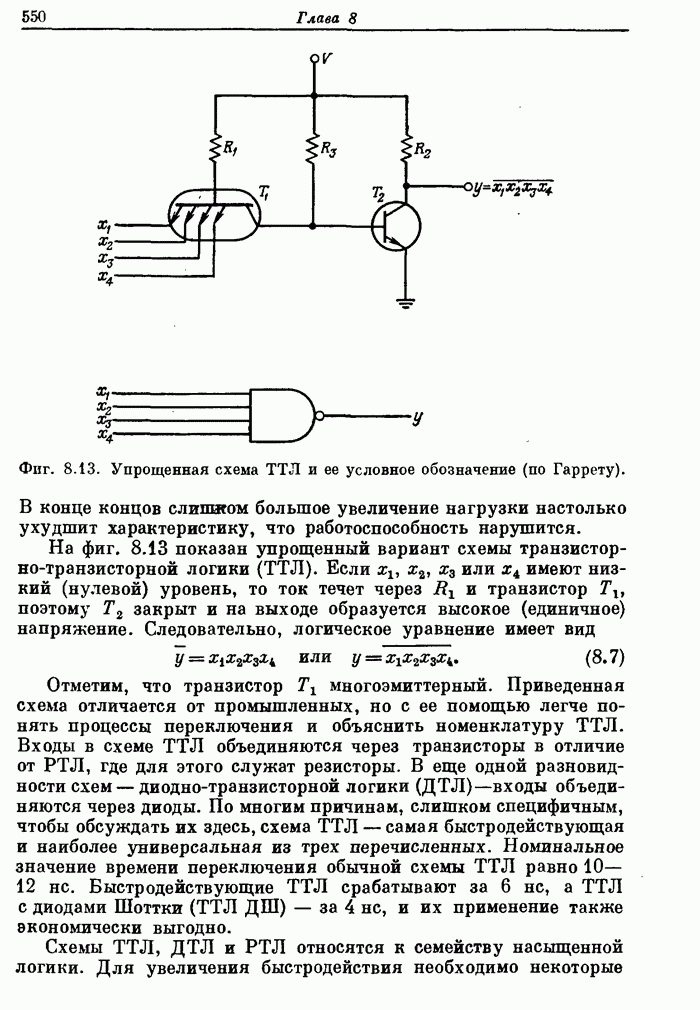
Пример 1. Рассчитать 24-точечный фильтр нижних частот с частотой среза полосы пропускания 0,08, частотой среза полосы непропускания 0,16 и отношением максимумов пульсаций 1,0.
Входные
параметры в этом примере равны: ![]() ,
, ![]() ,
, ![]() и
и ![]() . Следовательно,
перфокарты с заданными характеристиками имеют вид
. Следовательно,
перфокарты с заданными характеристиками имеют вид

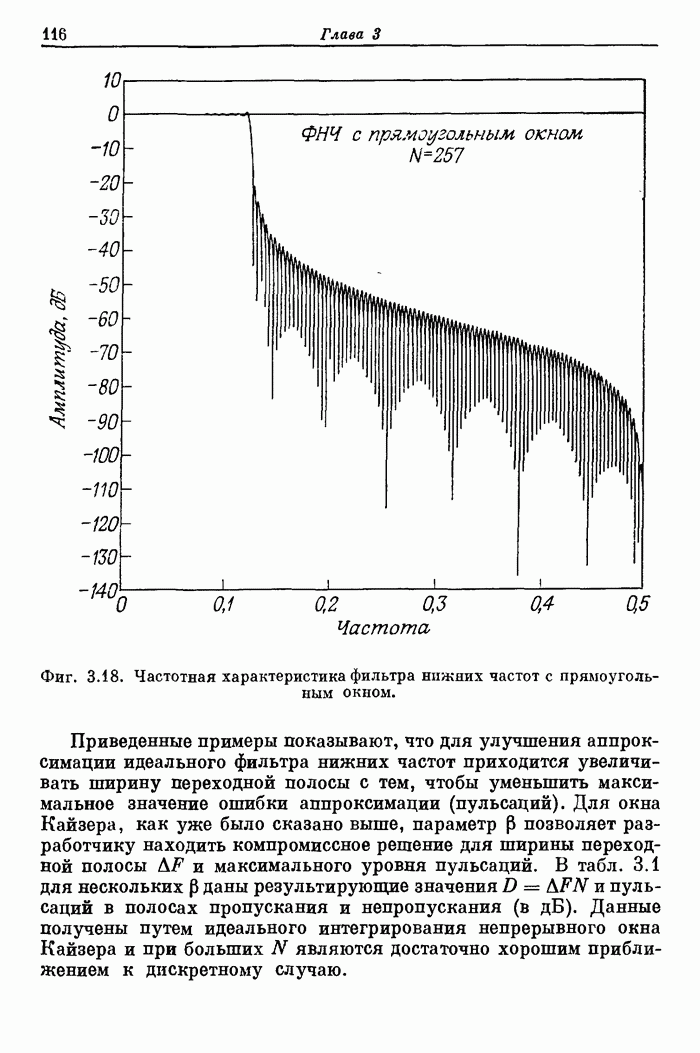
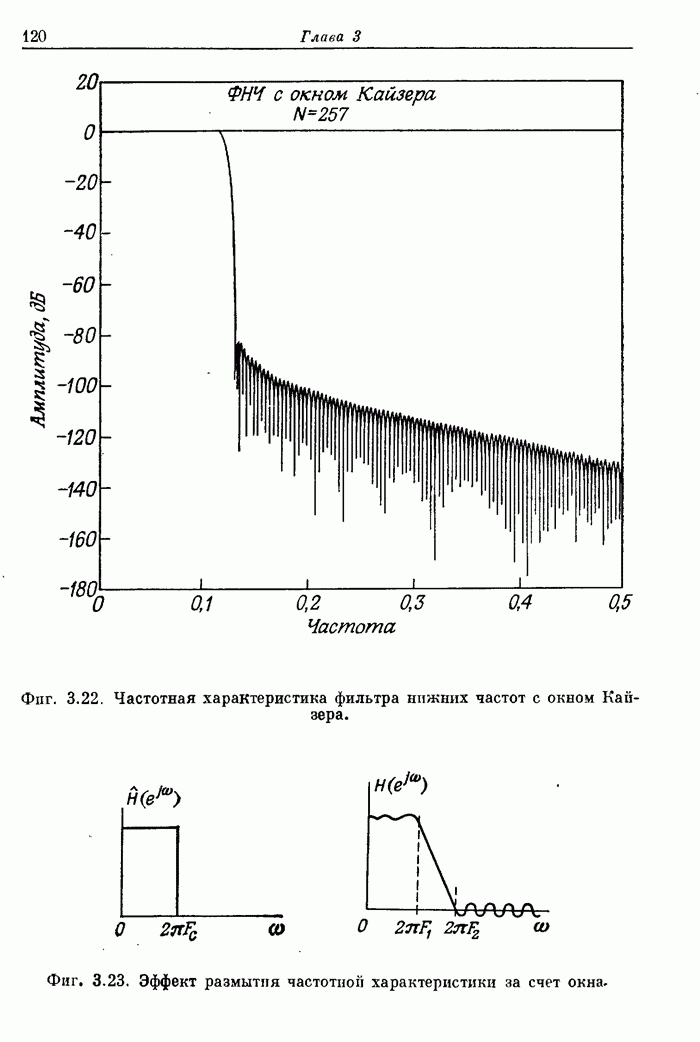
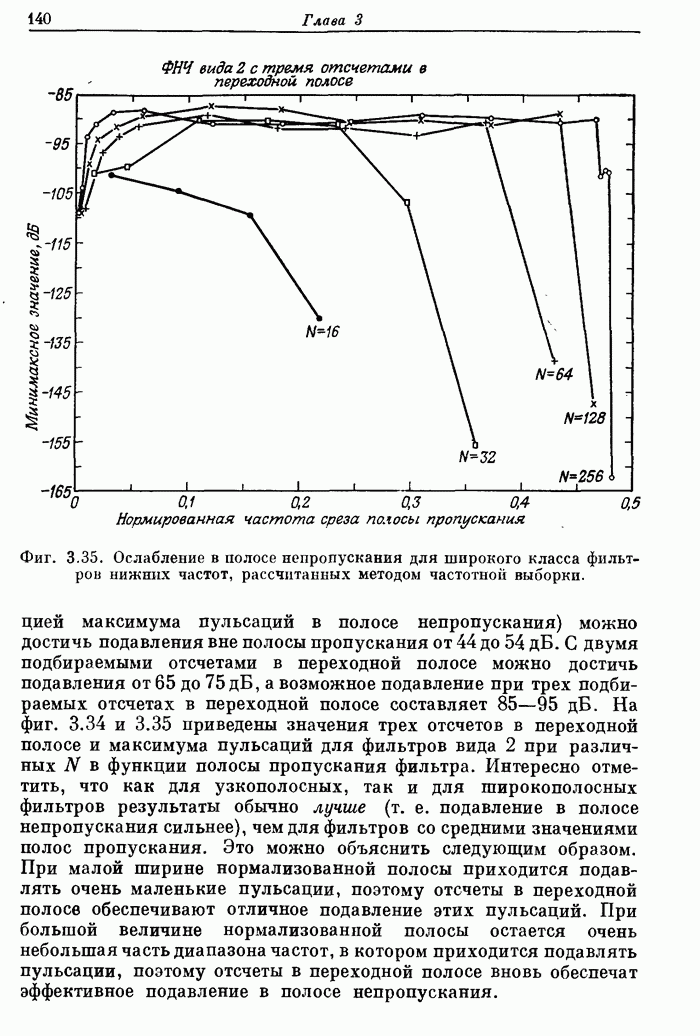
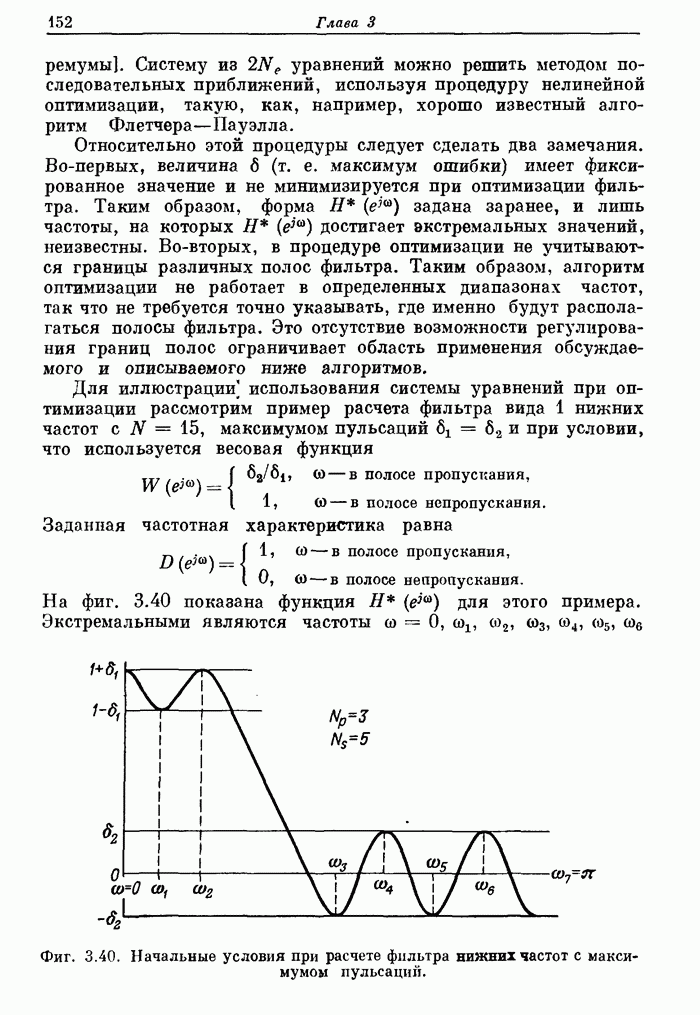
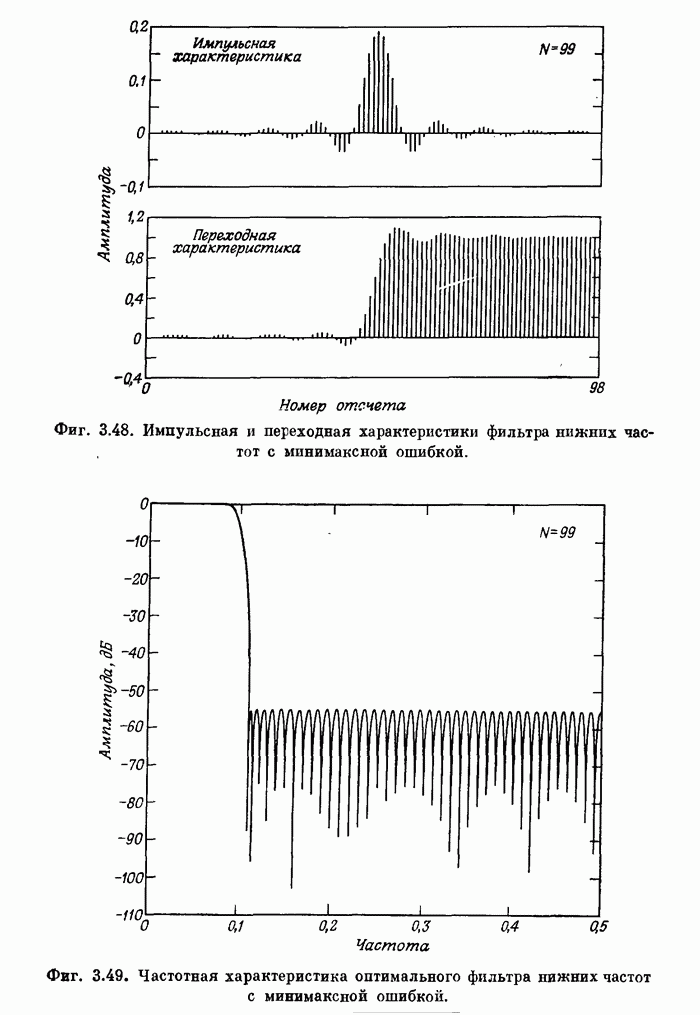
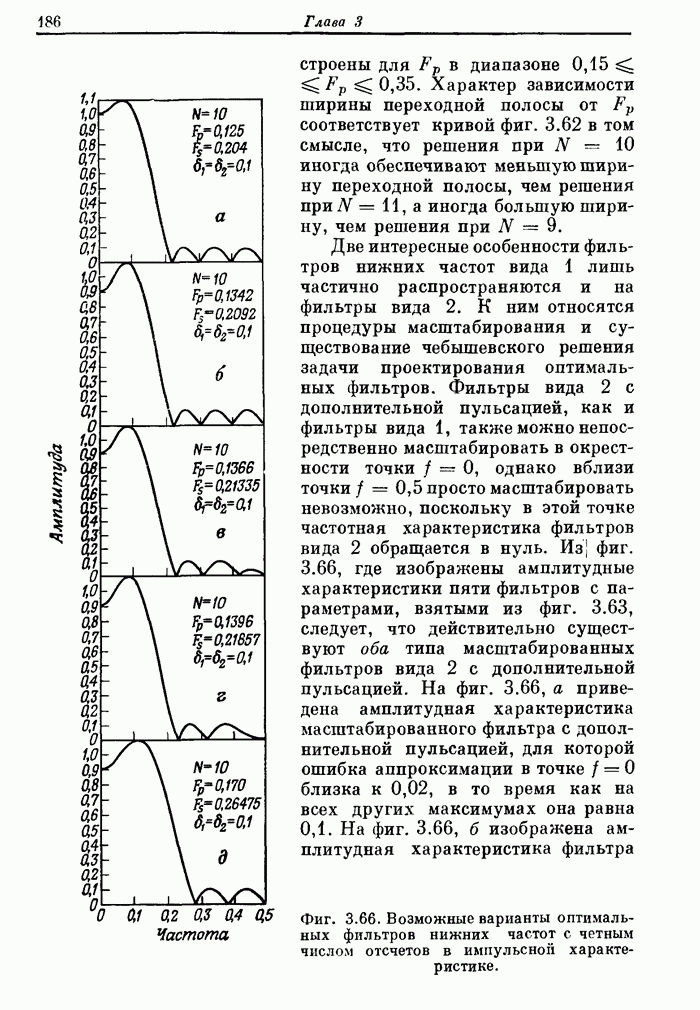
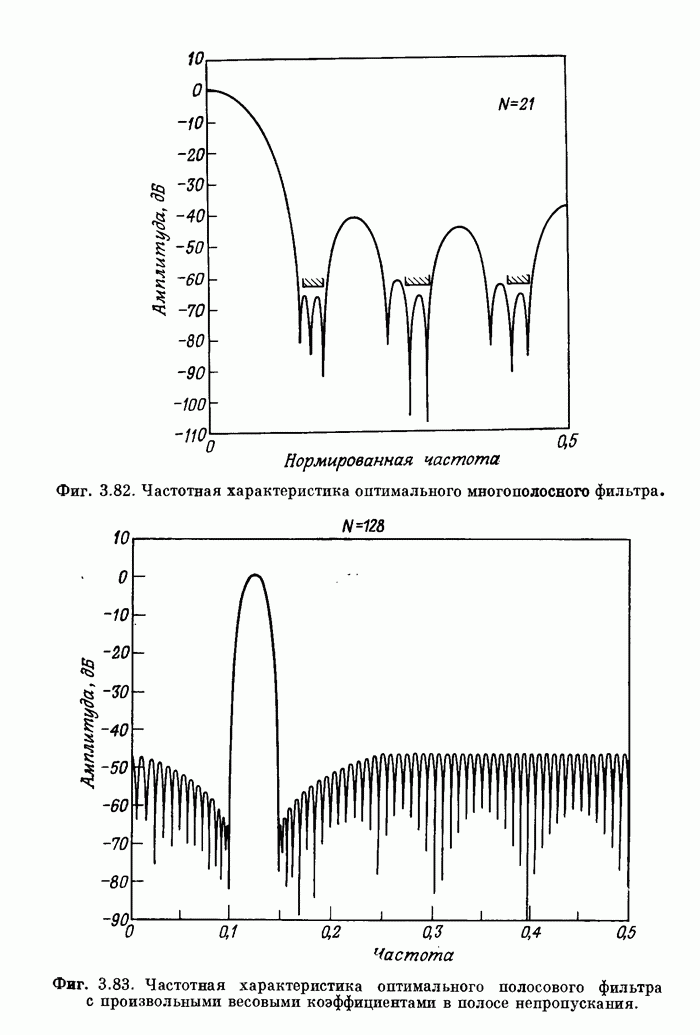
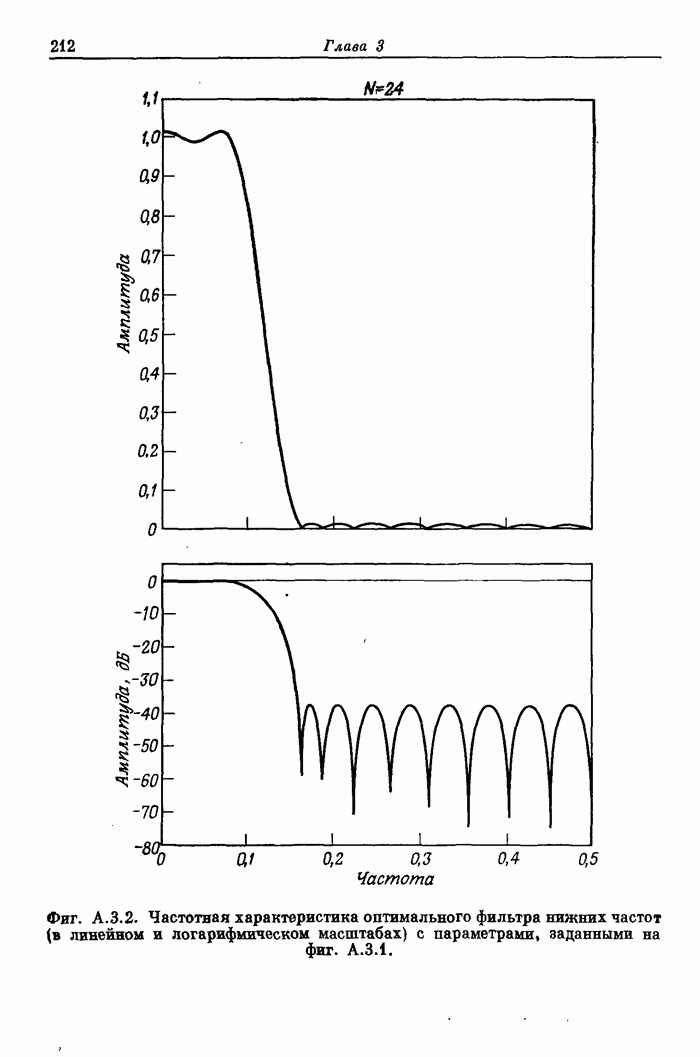
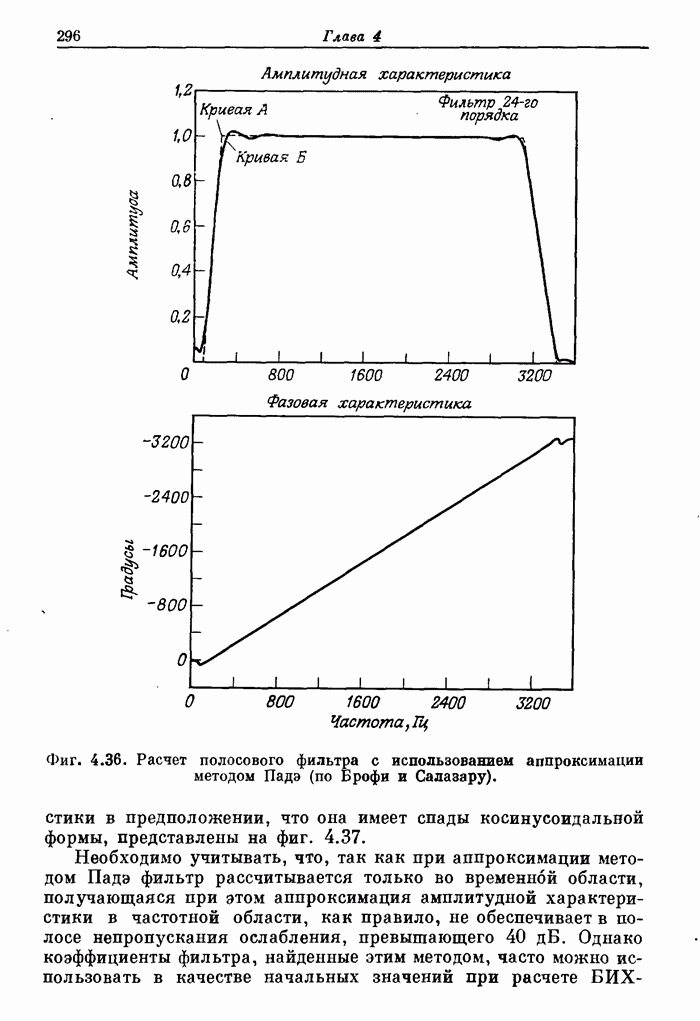
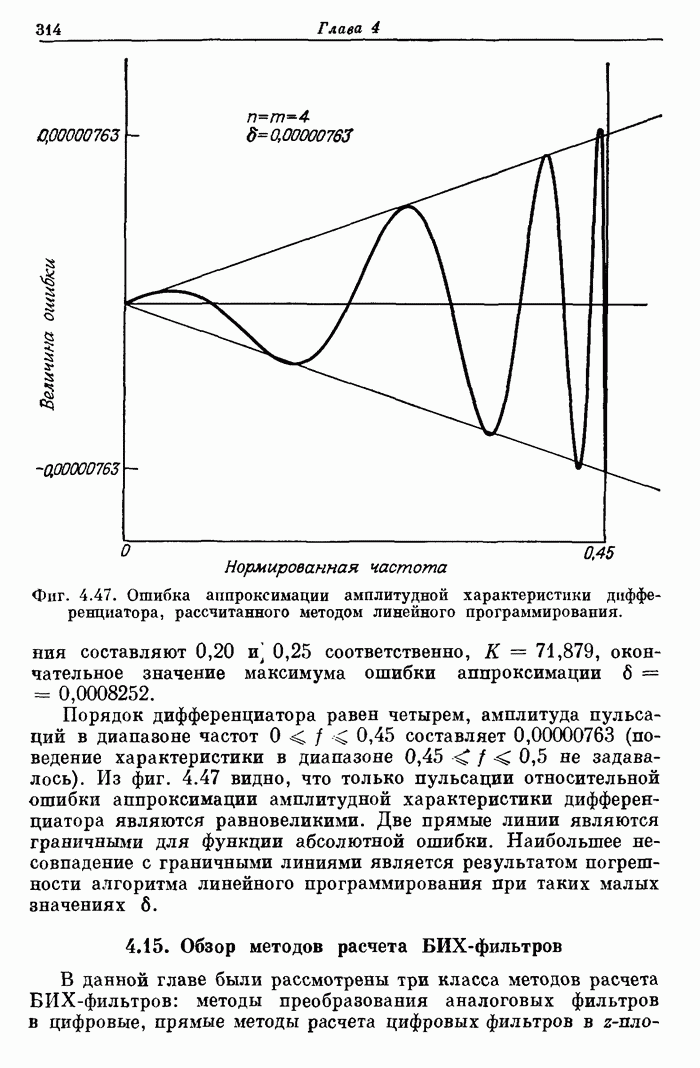
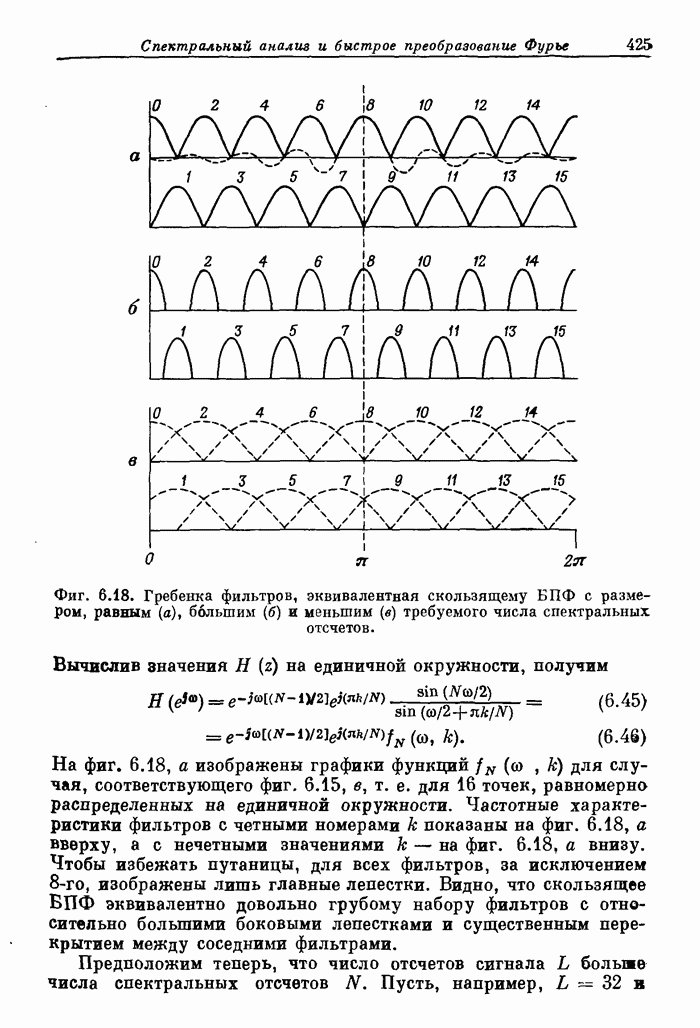
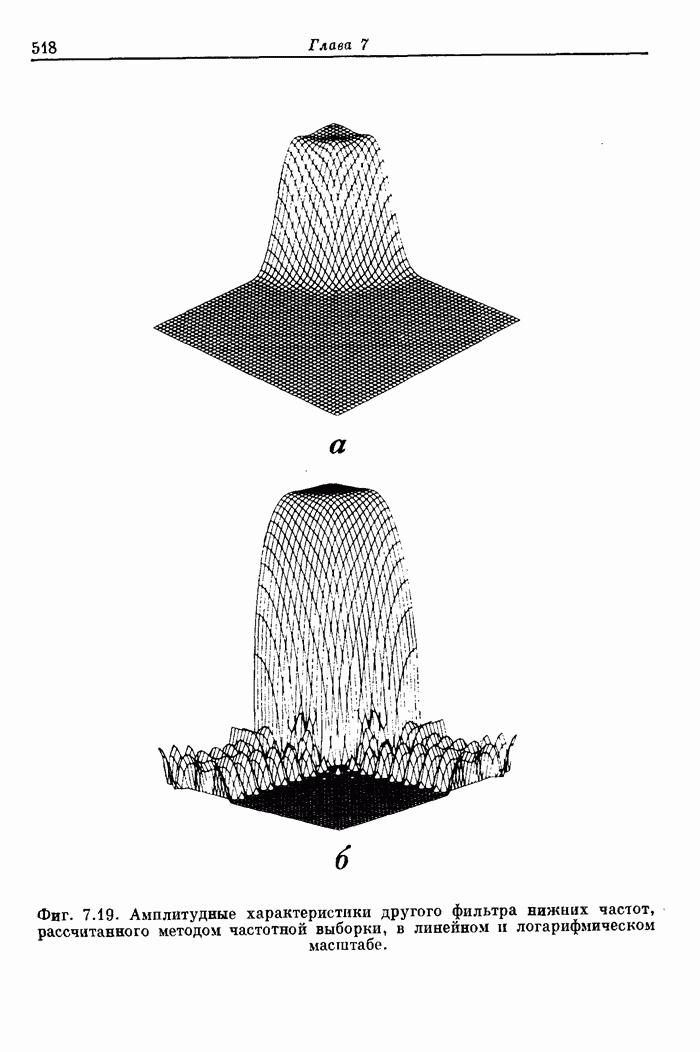
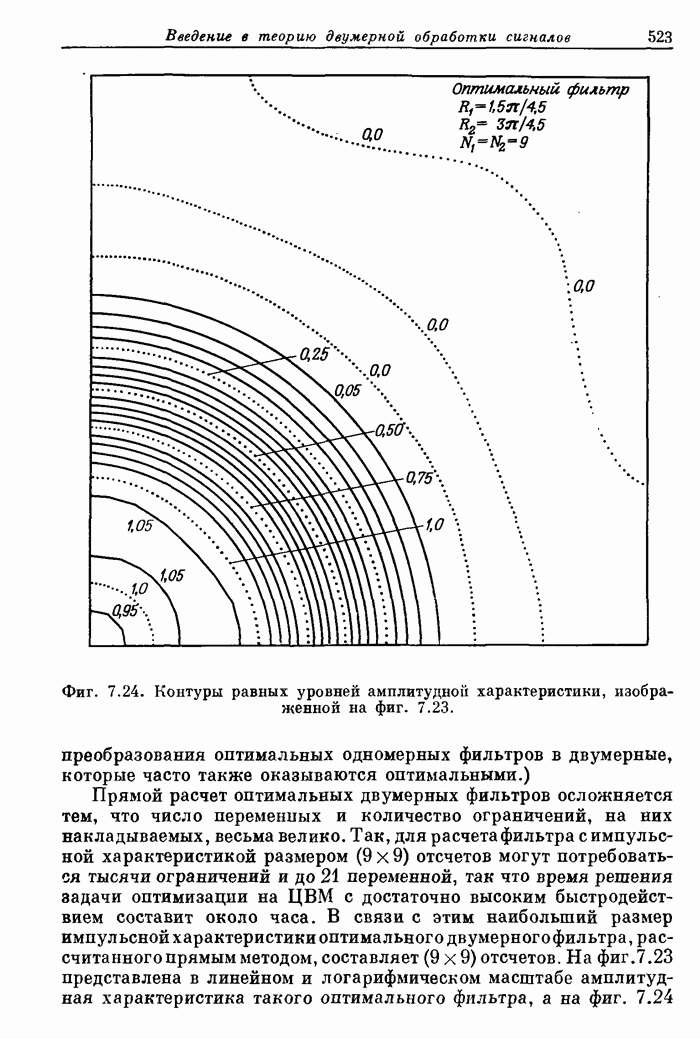
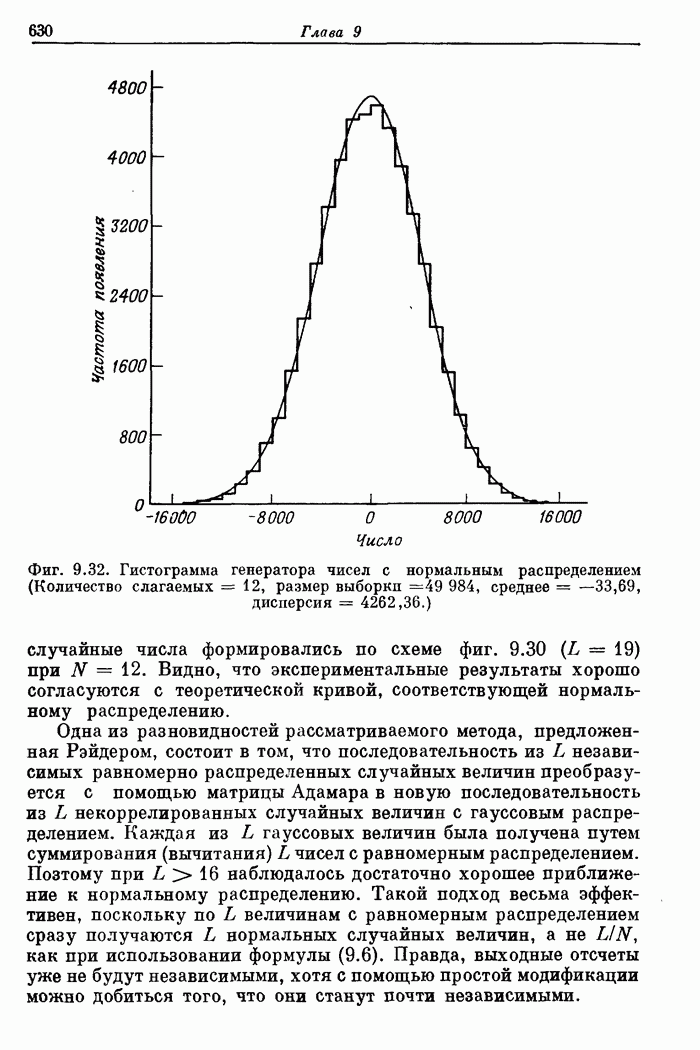
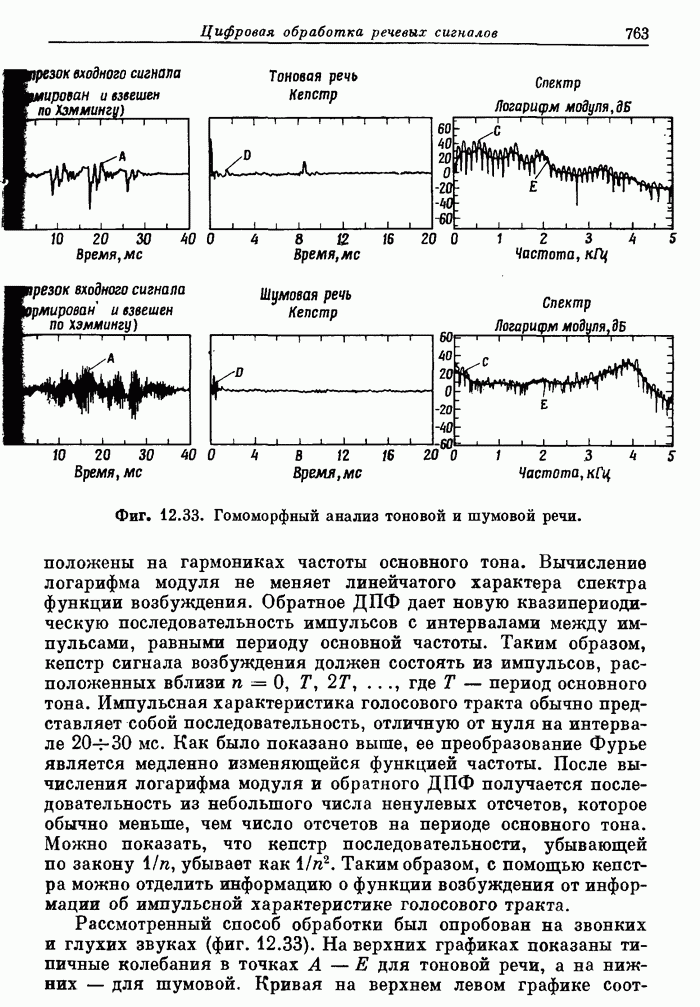
Фиг. A.3.1. Распечатка результатов расчета 24-точечного оптимального
фильтра нижних частот.
Карта 1. 24, 1, 2, 0, 16
Карта 2. 0, 0.08, 0.16, 0.5
Карта 3. 1, 0
Карта 4. 1, 1
В
карте 1 заданы (но порядку) ![]() , вид
фильтра, число полос, признак перфорации и сетка для интерполяции; в карте 2
заданы границы каждой полосы; карта 3 содержит заданные значения характеристики
в каждой полосе; карта 4 определяет заданные веса для пульсаций в каждой
полосе. На фиг. А.3.1 приведена распечатка результатов расчета (включая время
счета на ЦВМ Honeywell 6000), а на
фиг. А.3.2 изображена частотная характеристика рассчитанного фильтра нижних
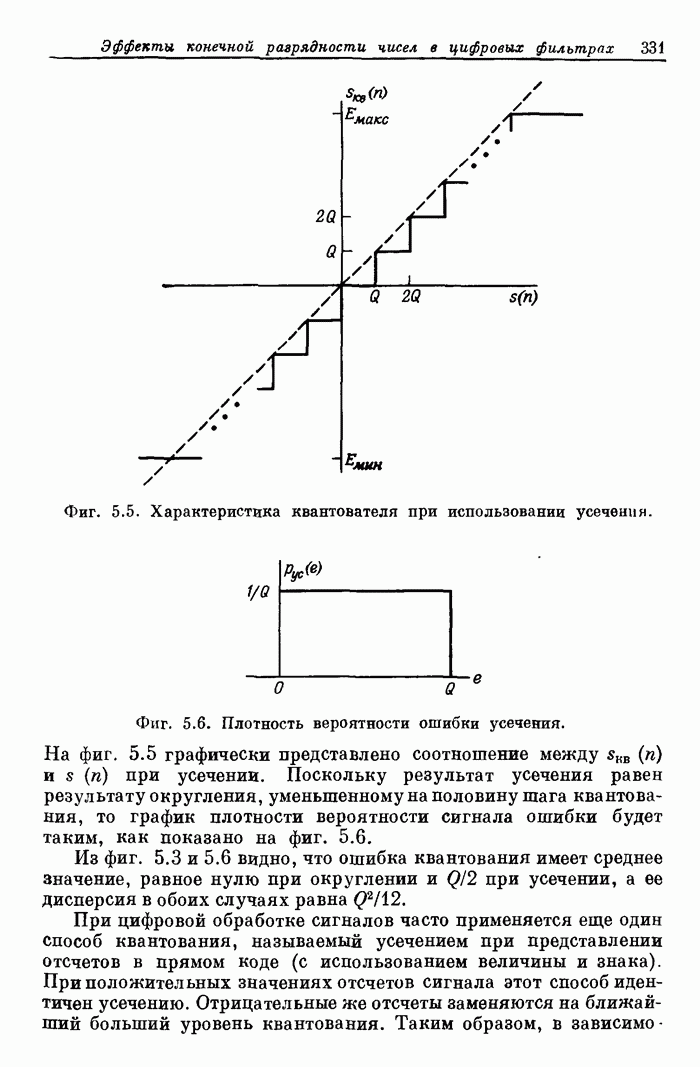
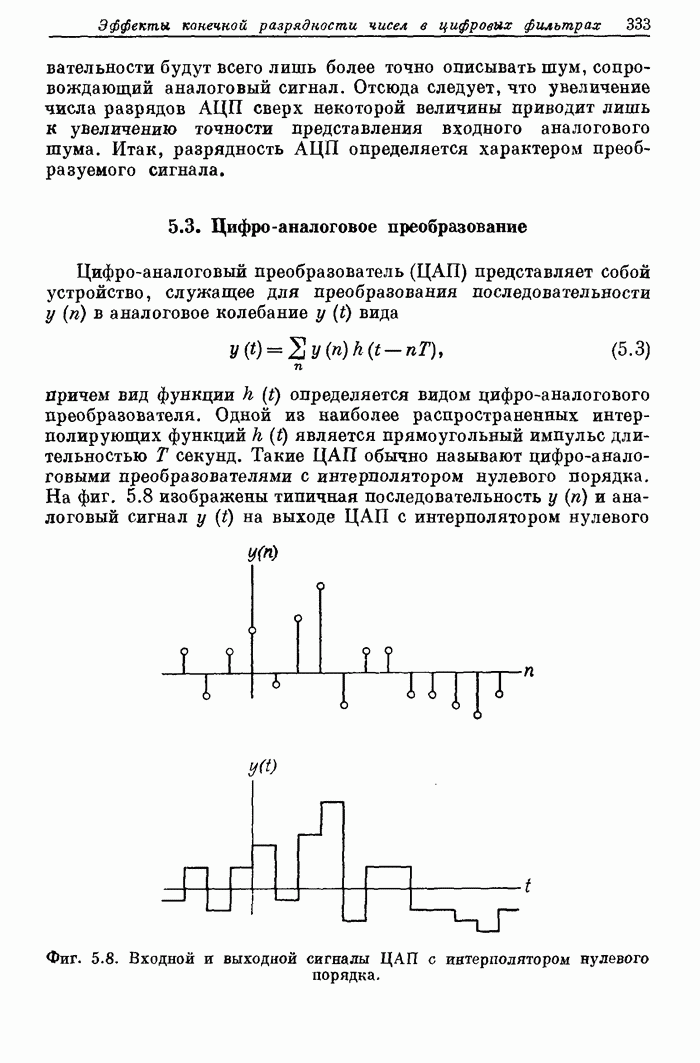
частот. Из распечатки на фиг. А.3.1 видно, что полученные значения пиков
пульсаций равны
, вид
фильтра, число полос, признак перфорации и сетка для интерполяции; в карте 2
заданы границы каждой полосы; карта 3 содержит заданные значения характеристики
в каждой полосе; карта 4 определяет заданные веса для пульсаций в каждой
полосе. На фиг. А.3.1 приведена распечатка результатов расчета (включая время
счета на ЦВМ Honeywell 6000), а на
фиг. А.3.2 изображена частотная характеристика рассчитанного фильтра нижних
частот. Из распечатки на фиг. А.3.1 видно, что полученные значения пиков
пульсаций равны ![]() (-56,4
дБ).
(-56,4
дБ).

Фиг. А.3.2. Частотная характеристика оптимального фильтра нижних частот (в линейном и логарифмическом масштабах) с параметрами, заданными на фиг. А.3.1.
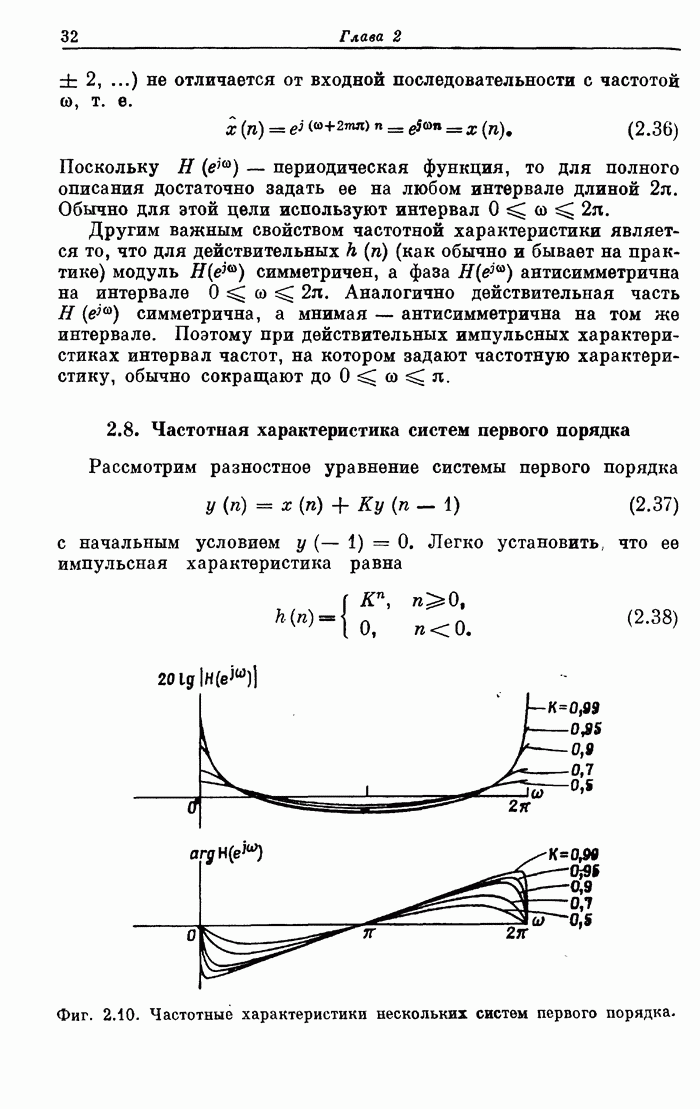
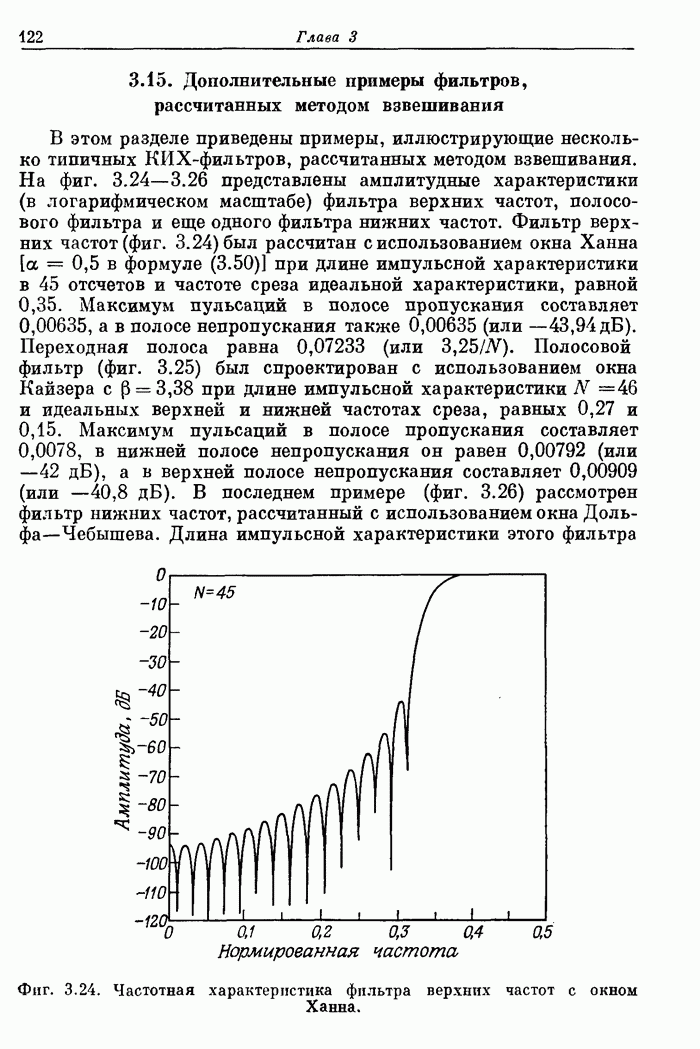
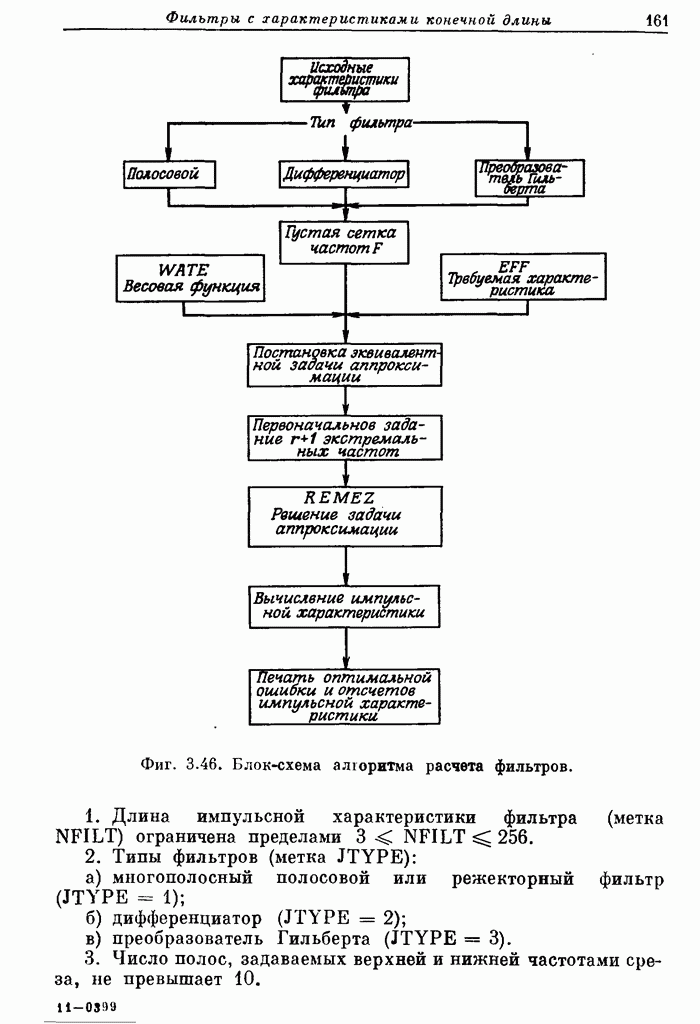
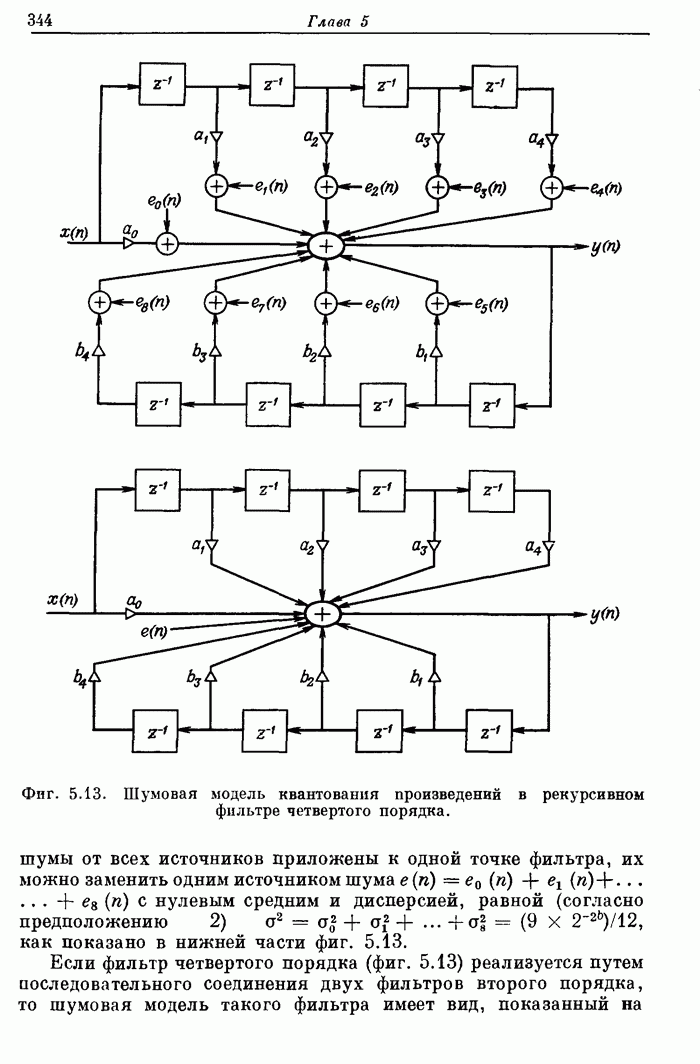
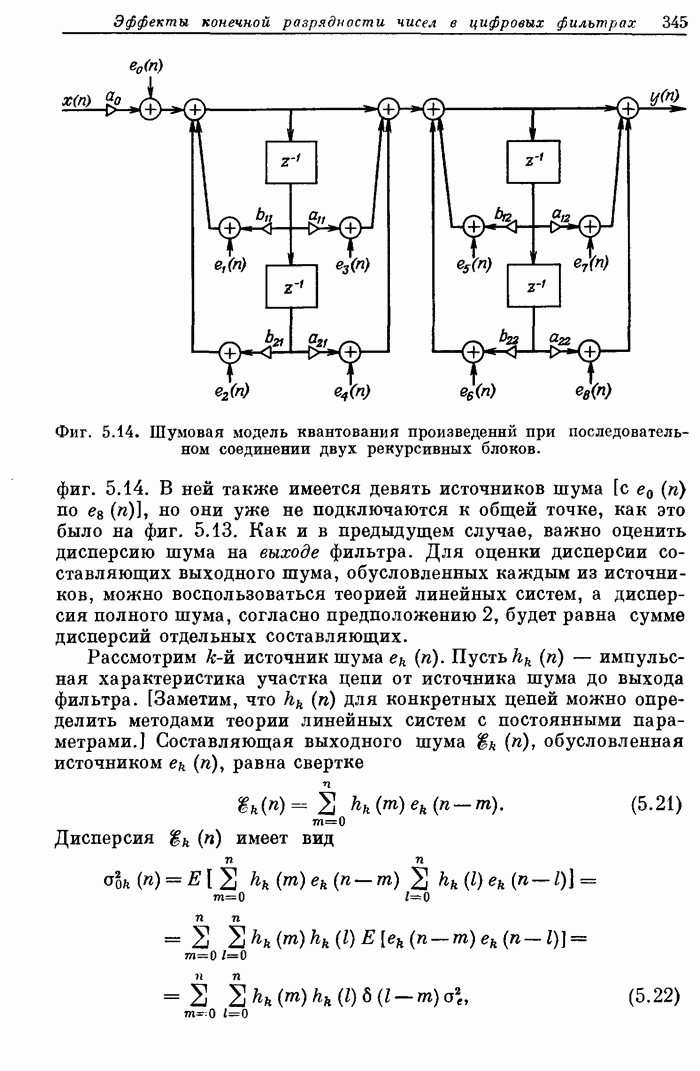
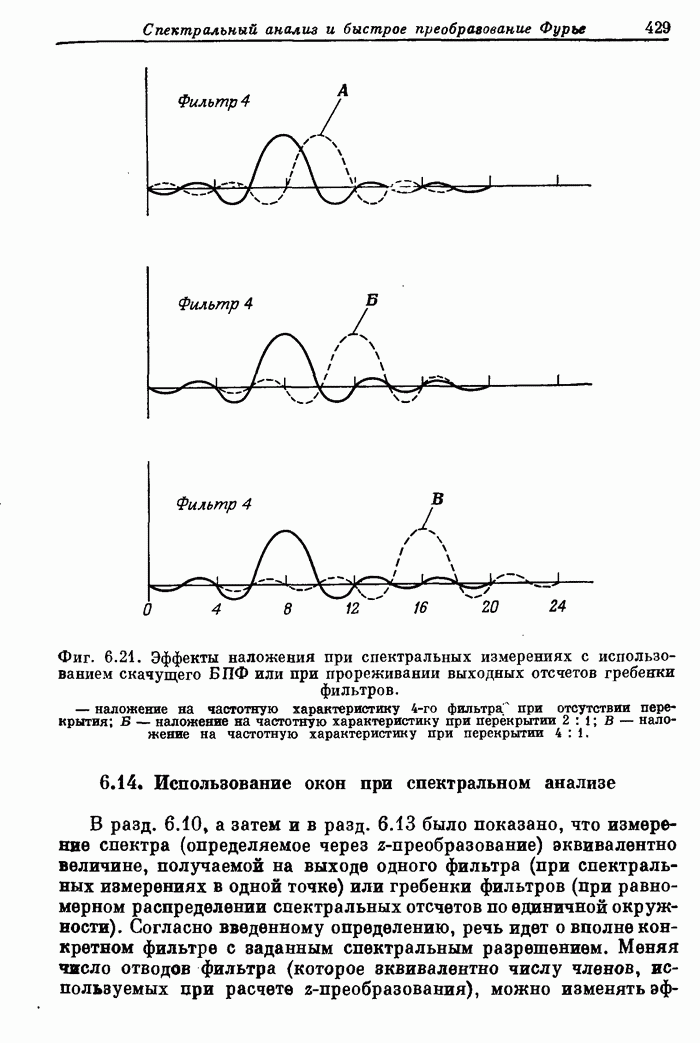
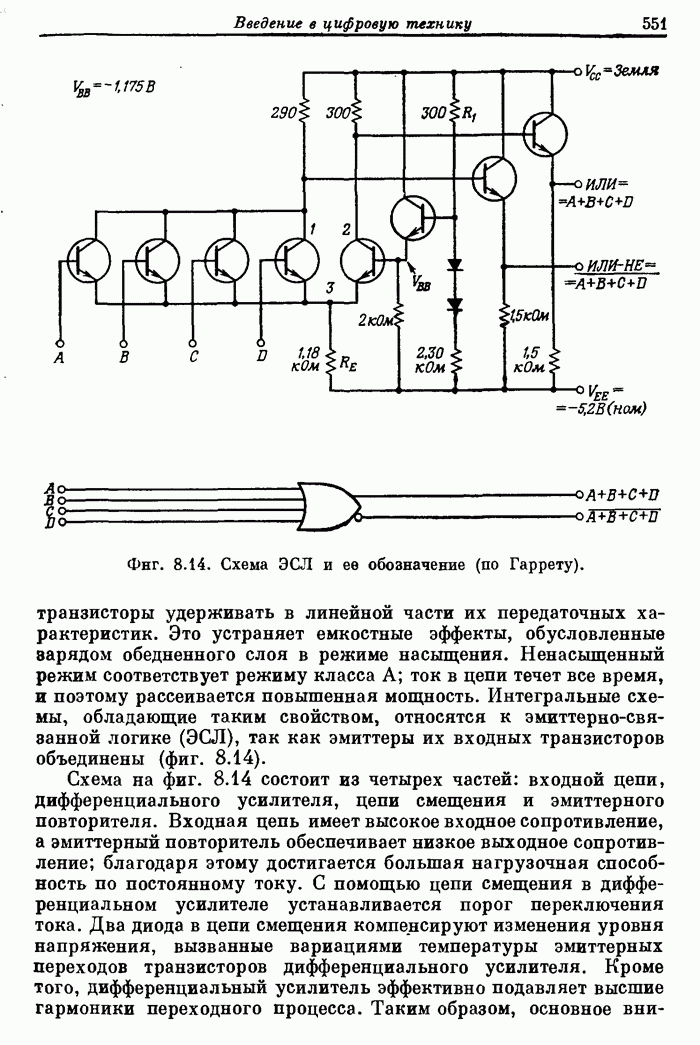
Пример 2. Рассчитать 32-точечный полосовой фильтр с частотами среза полосы непропускания 0,1 и 0,425, частотами среза полосы пропускания 0,2 и 0,35 и весовыми коэффициентами пульсаций, равными 10 и 1 в полосах непропускания и пропускания соответственно.
В этом случае перфокарты с заданными характеристиками имеют вид
Карта 1. 32, 1, 3, 0, 16
Карта 2. 0, 0.1, 0.2, 0.35, 0.425, 0.5
Карта 3. 0, 1, 0
Карта 4. 10, 1, 10
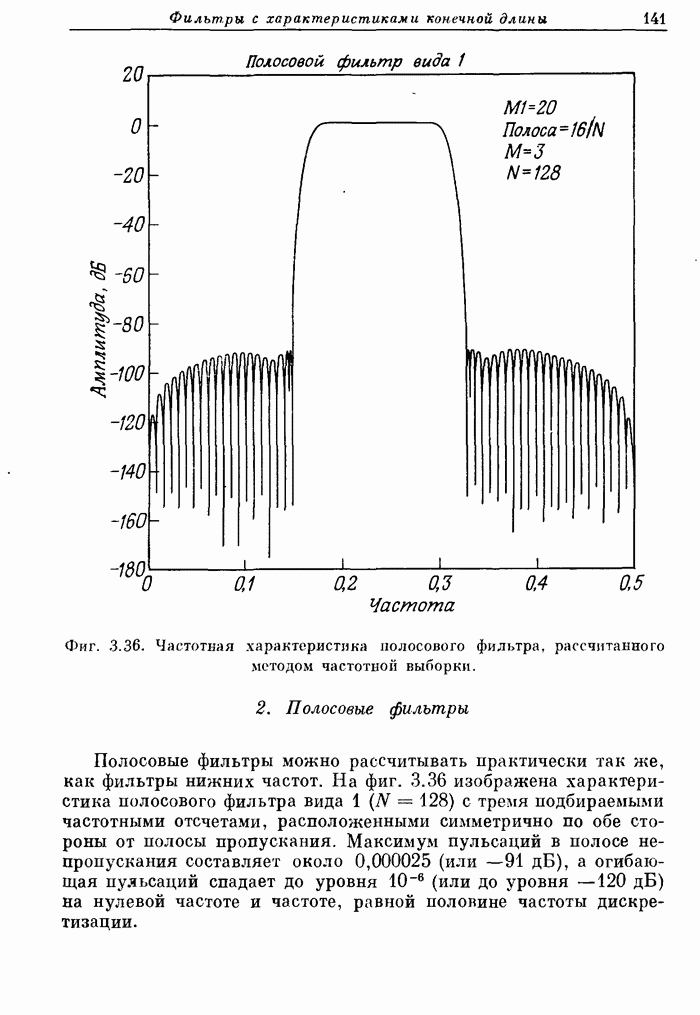
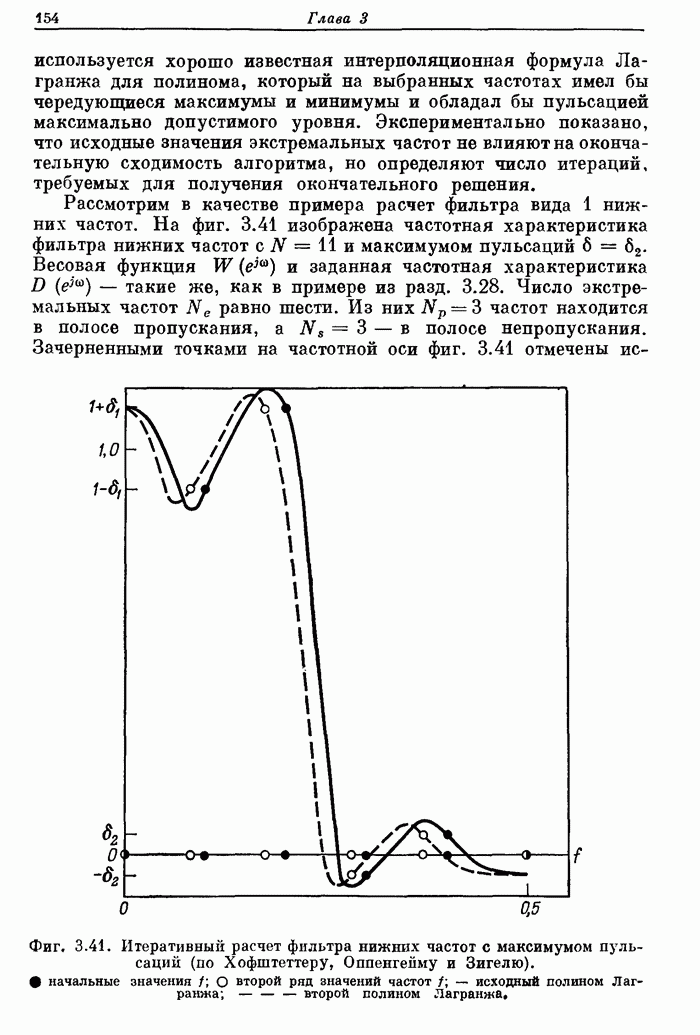
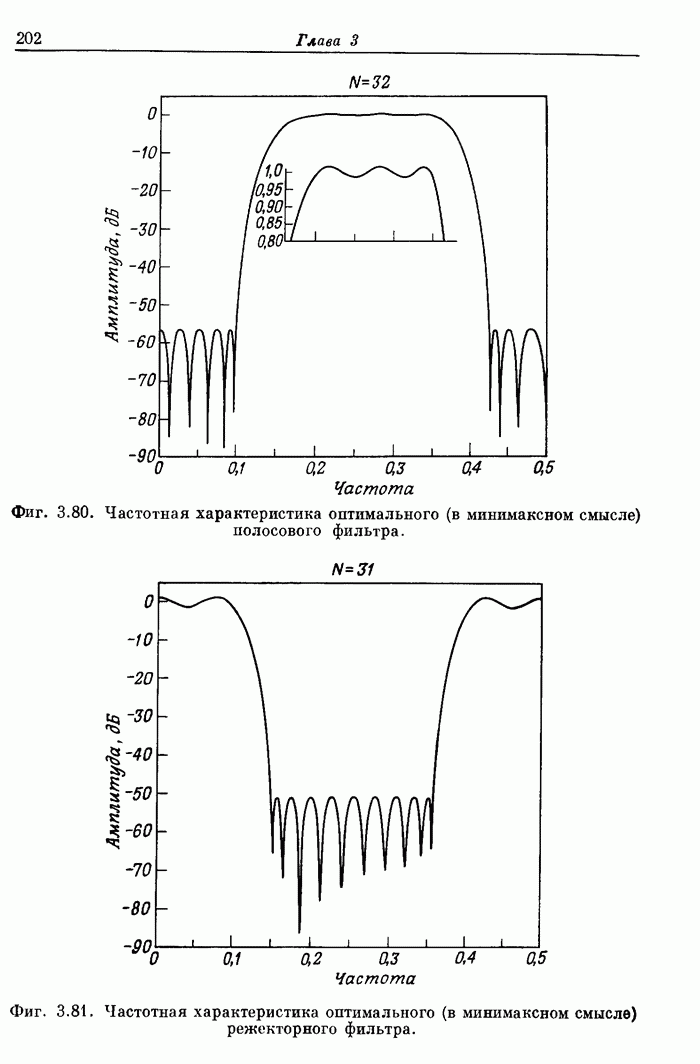
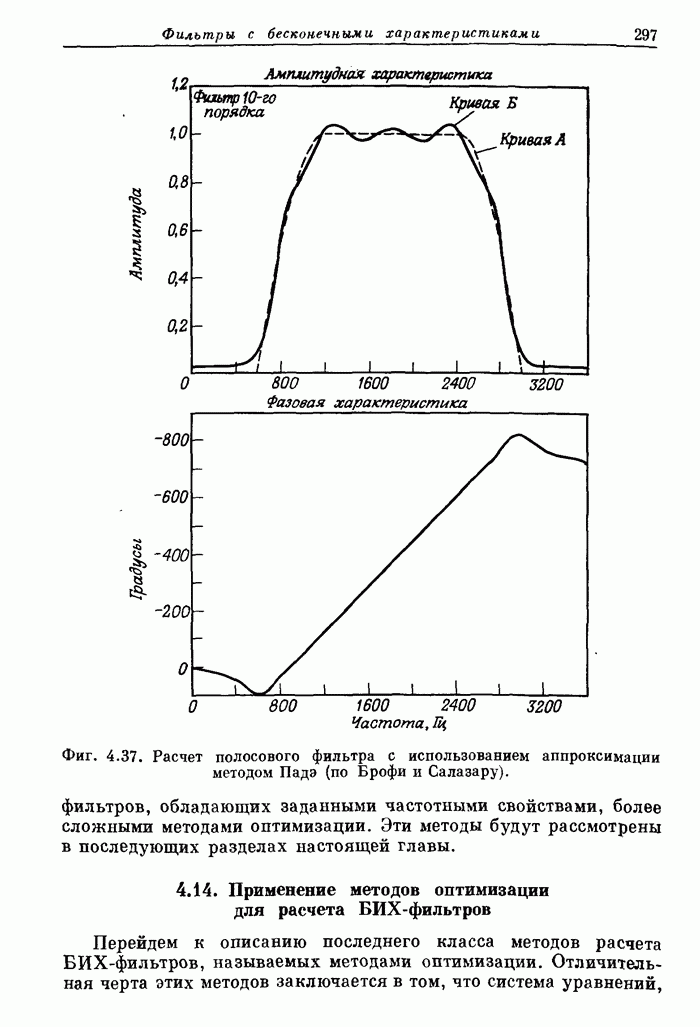
На фиг. А.3.3 приведена распечатка результатов расчета этого фильтра; частотная характеристика рассчитанного фильтра показана на фиг. 3.80.

Фиг. A.3.3. Распечатка результатов расчета 32-точечного оптимального
полосового фильтра.
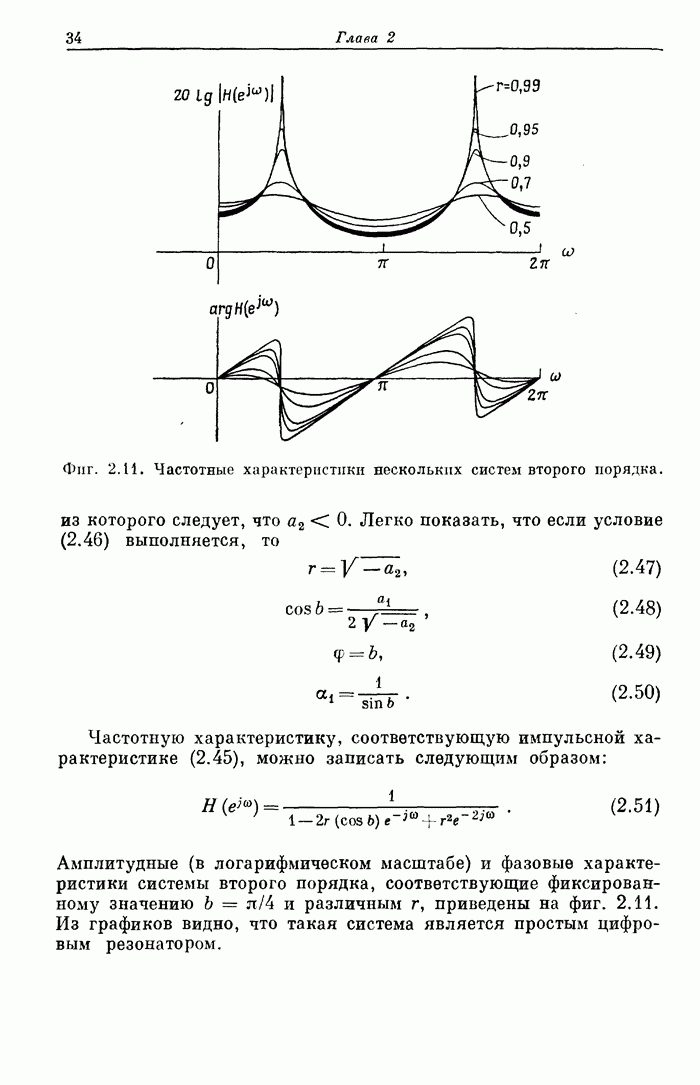
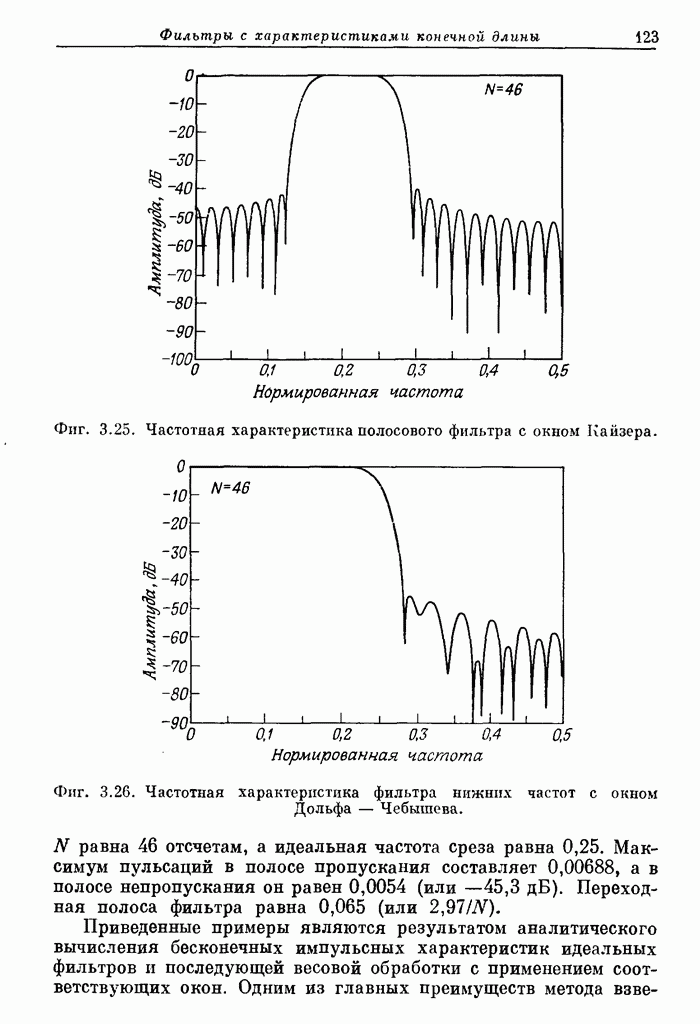
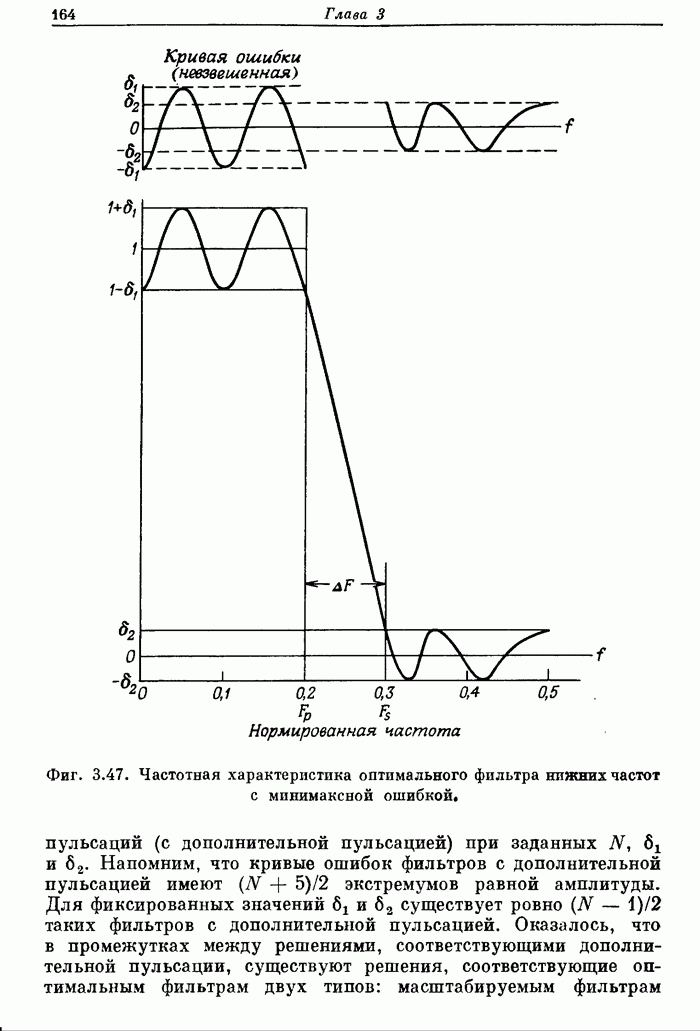
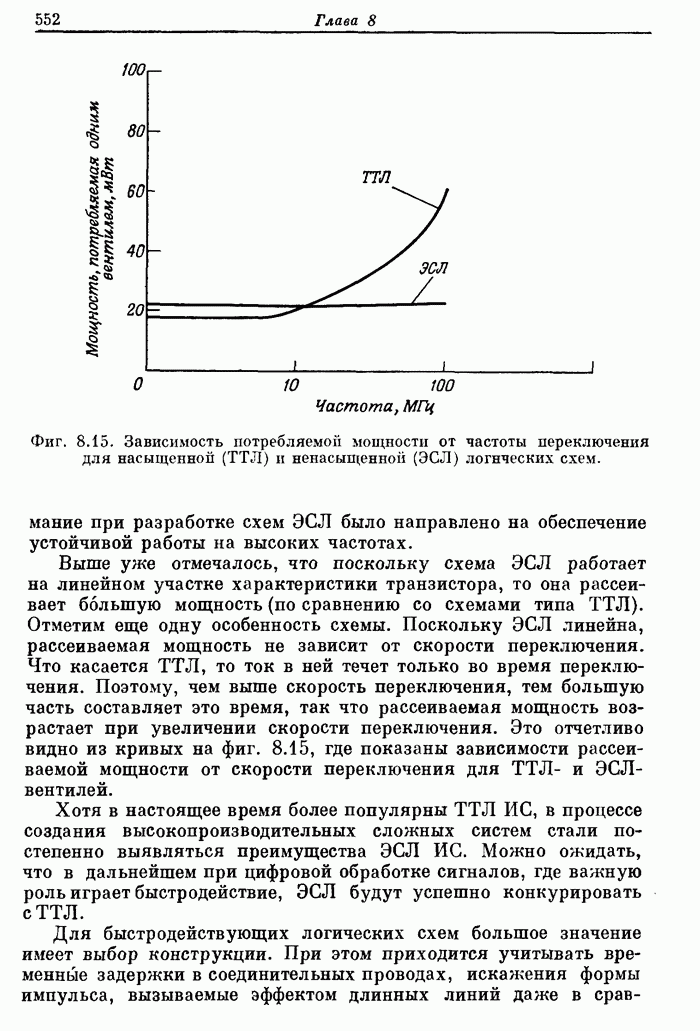
Пример 3. Рассчитать 32-точечный дифференциатор с частотой среза 0,5.
Перфокарты с заданными характеристиками в этом случае имеют вид
Карта 1. 32, 2, 1, 0, 16
Карта 2. 0, 0.5
Карта 3. 1
Карта 4. 1
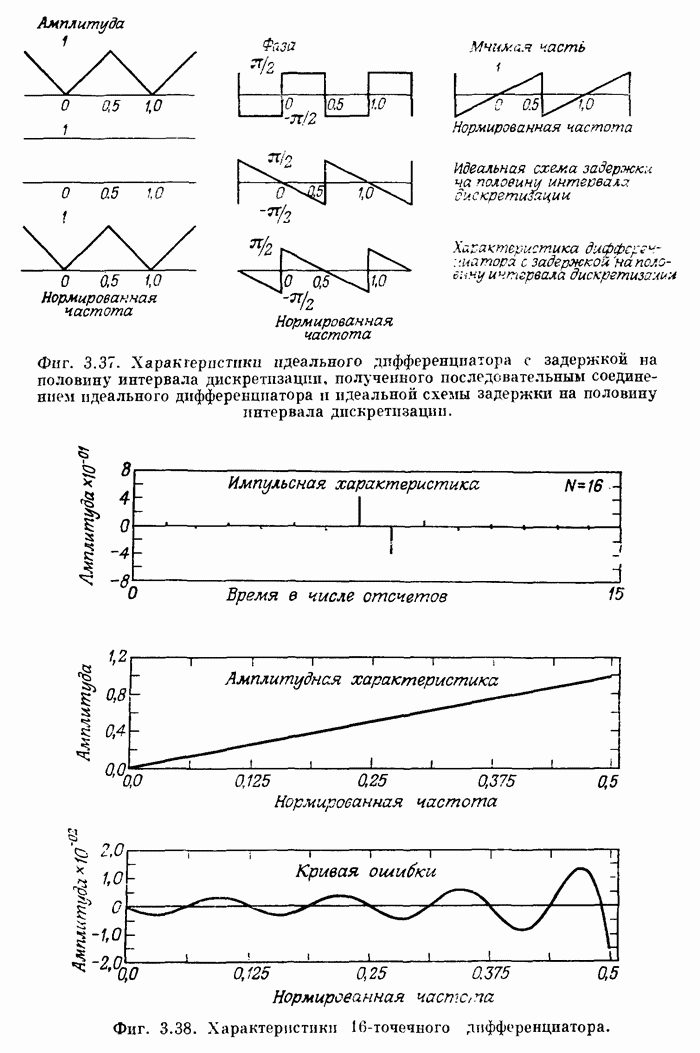
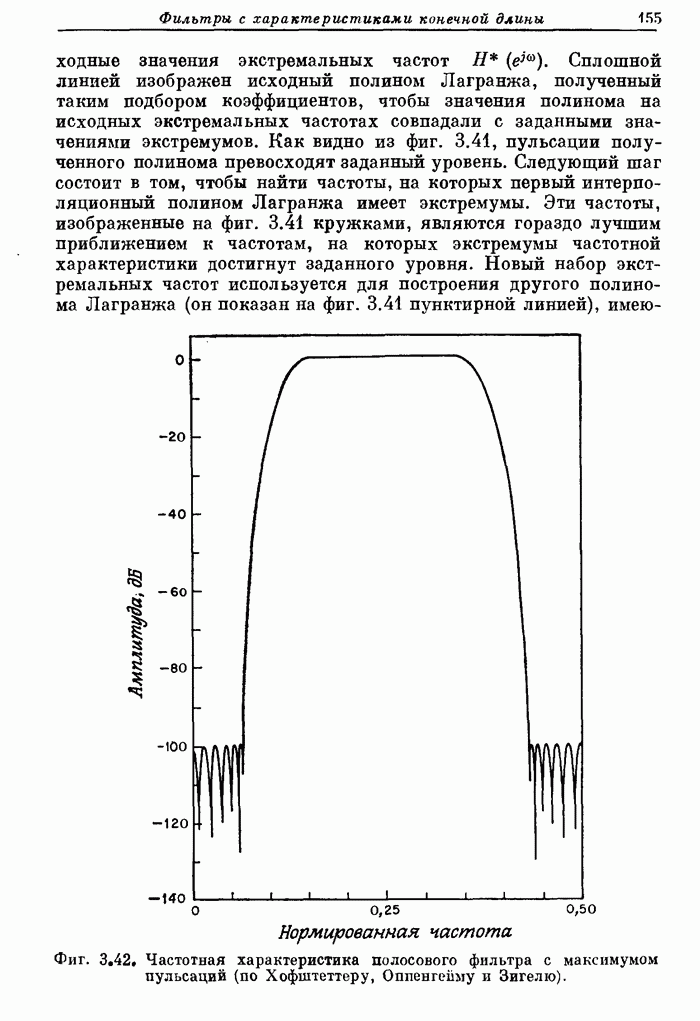
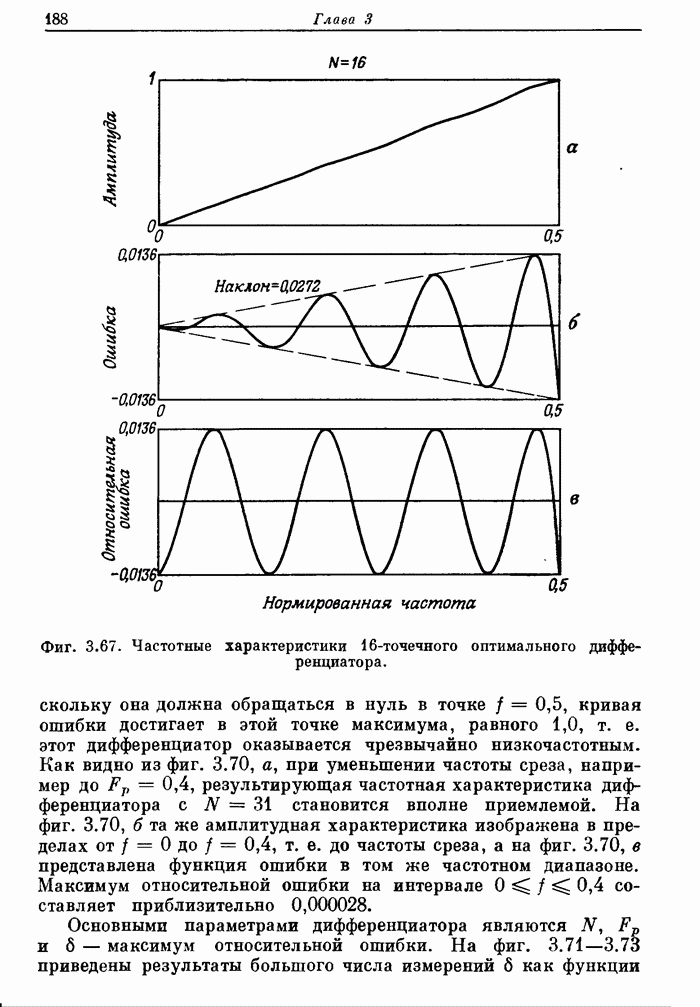
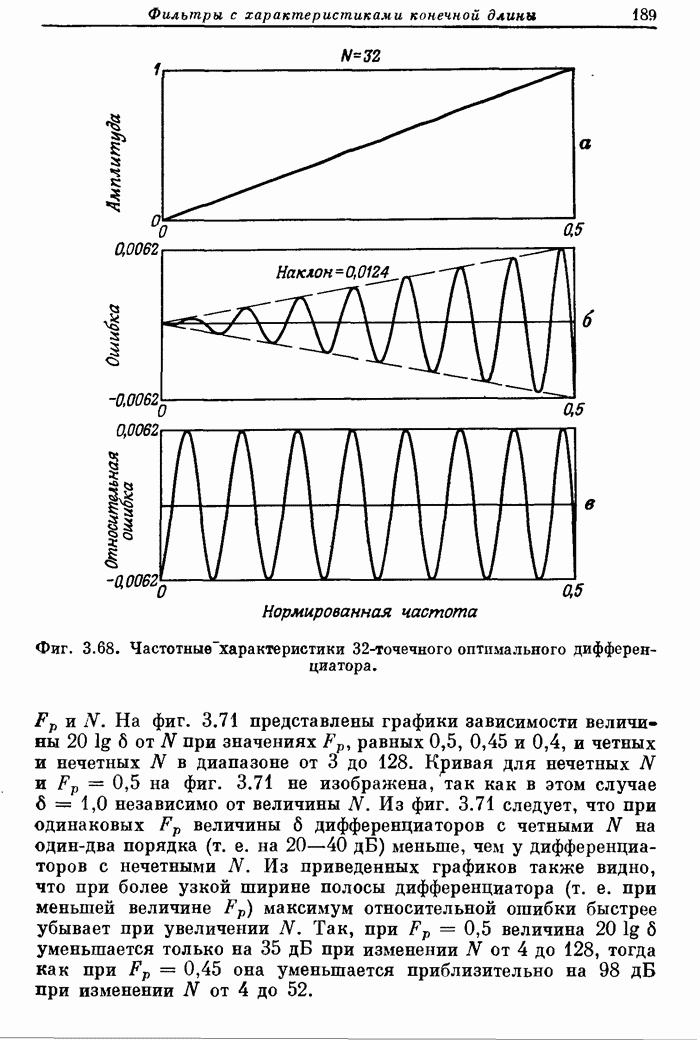
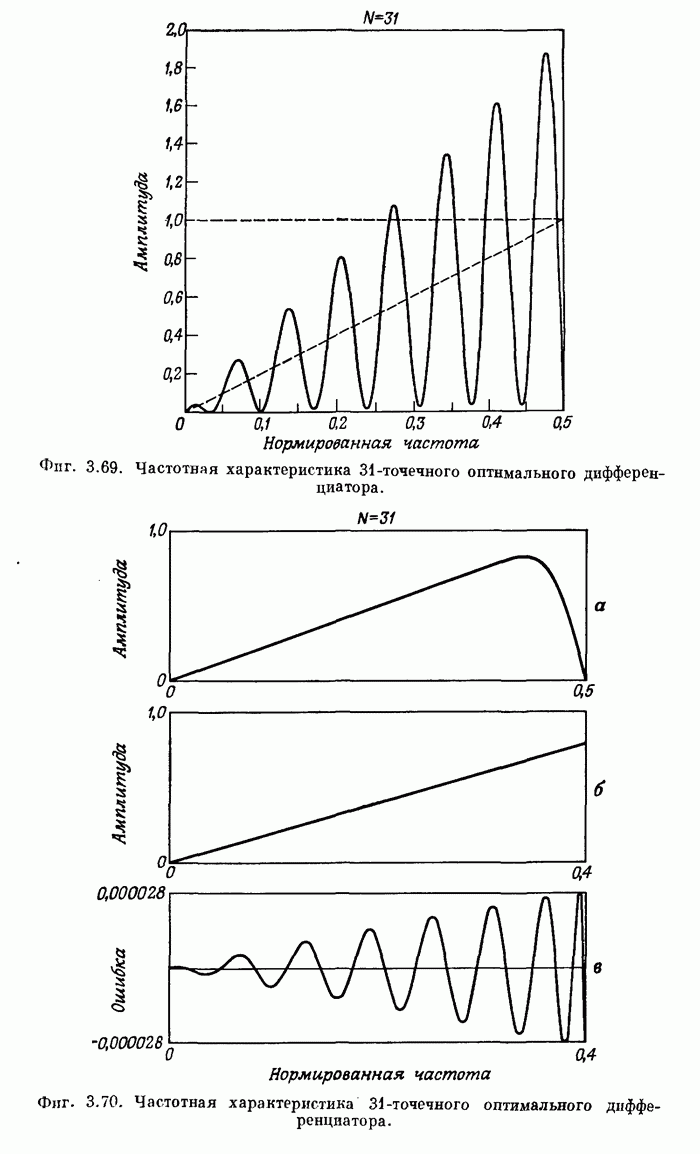
На фиг. А.3.4 приведена распечатка результатов расчета на ЦВМ этого дифференциатора, а его частотная характеристика показана на фиг. 3.68.

Фиг. A.3.4. Распечатка результатов расчета 32-точечного оптимального дифференциатора.
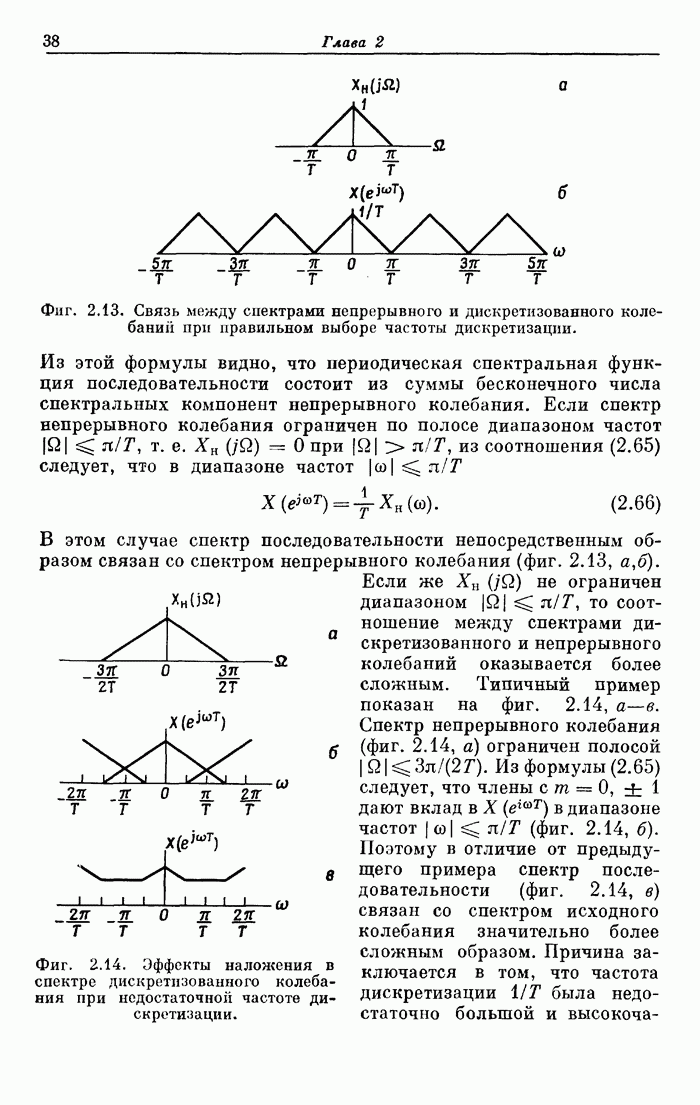
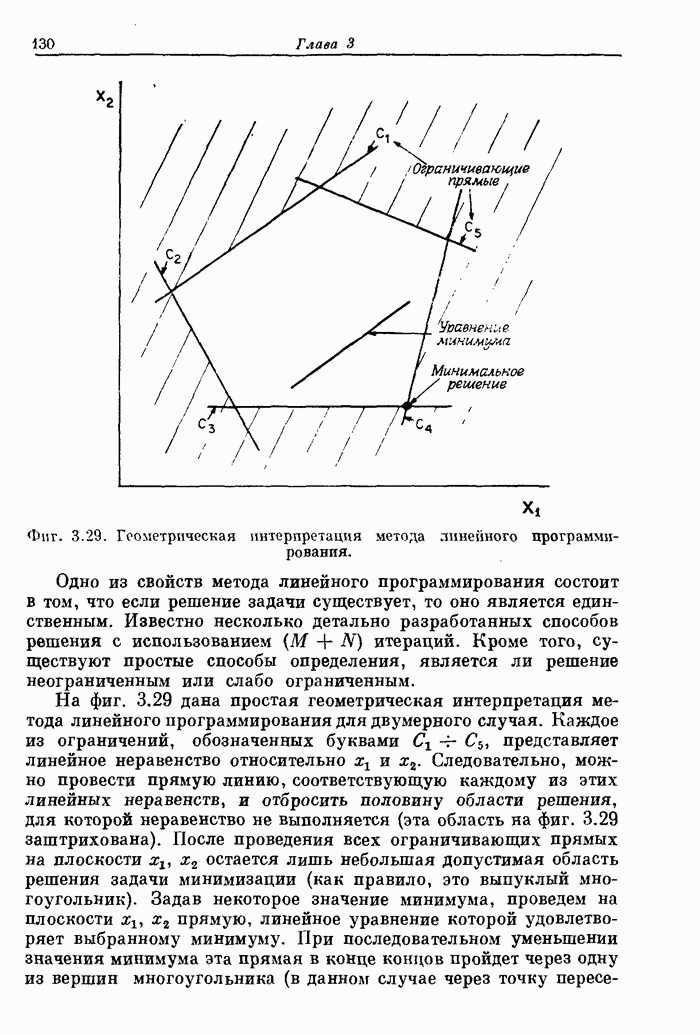
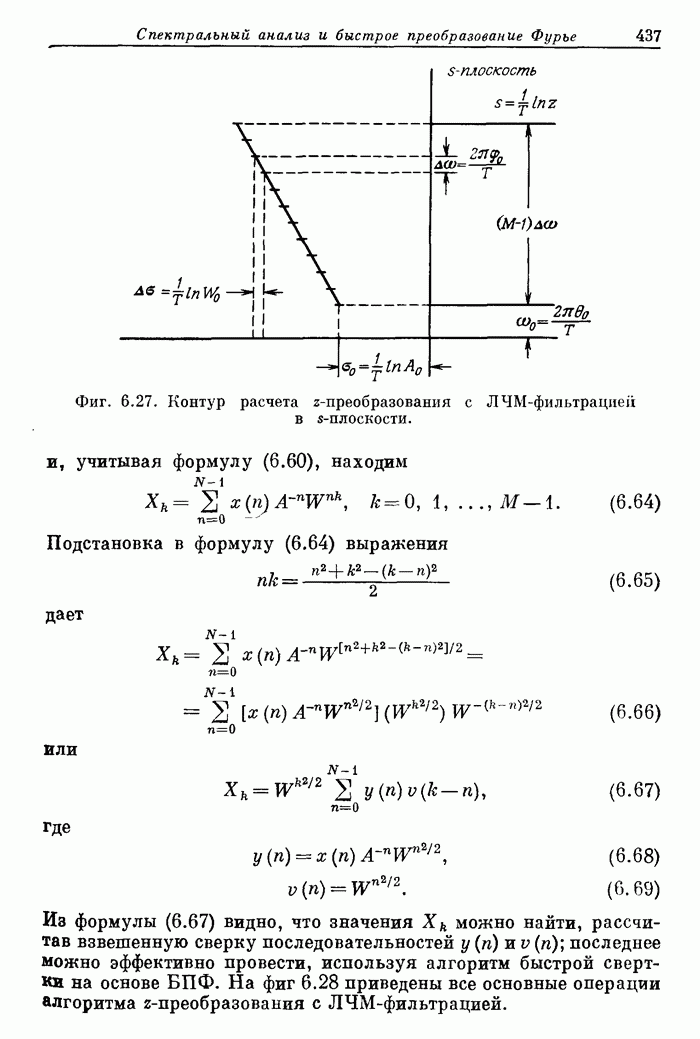
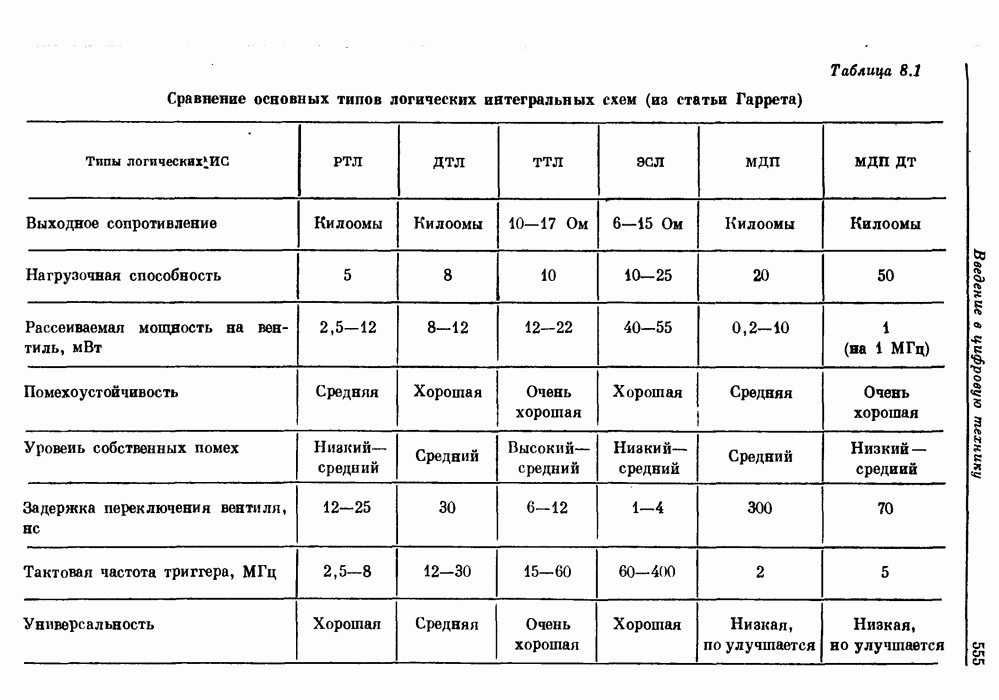
Пример 4. Рассчитать 20-точечный преобразователь Гильберта с граничными частотами 0,05 и 0,5.
Входные перфокарты в этом примере имеют вид
Карта 1. 20, 3, 1, 0, 16
Карта 2. 0.05, 0.5
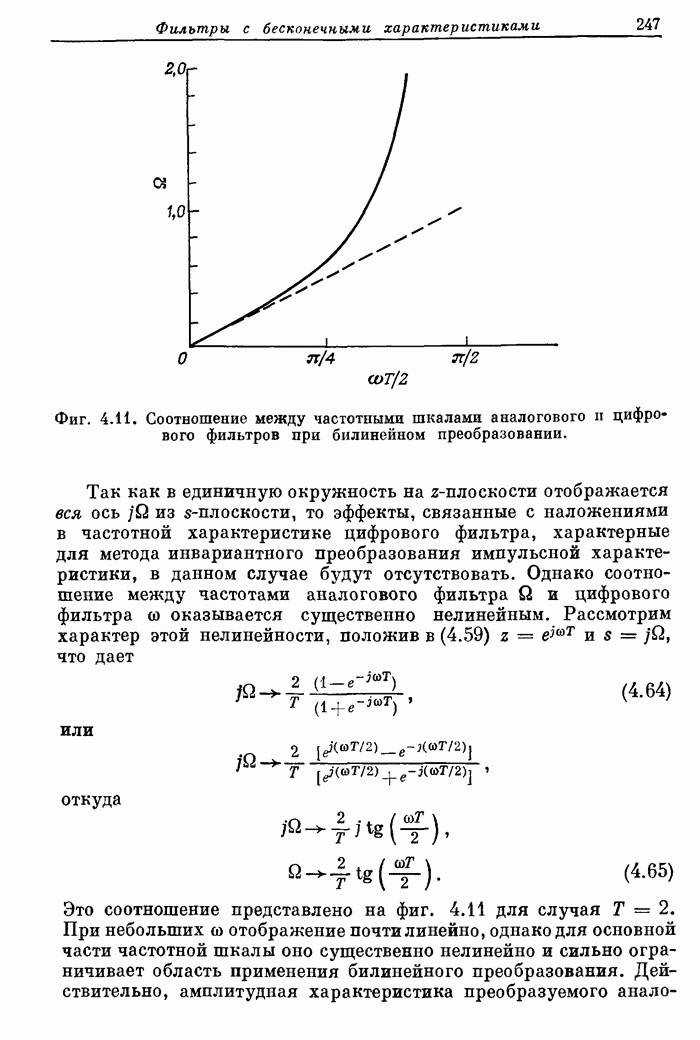
Карта 3. 1
Карта 4. 1

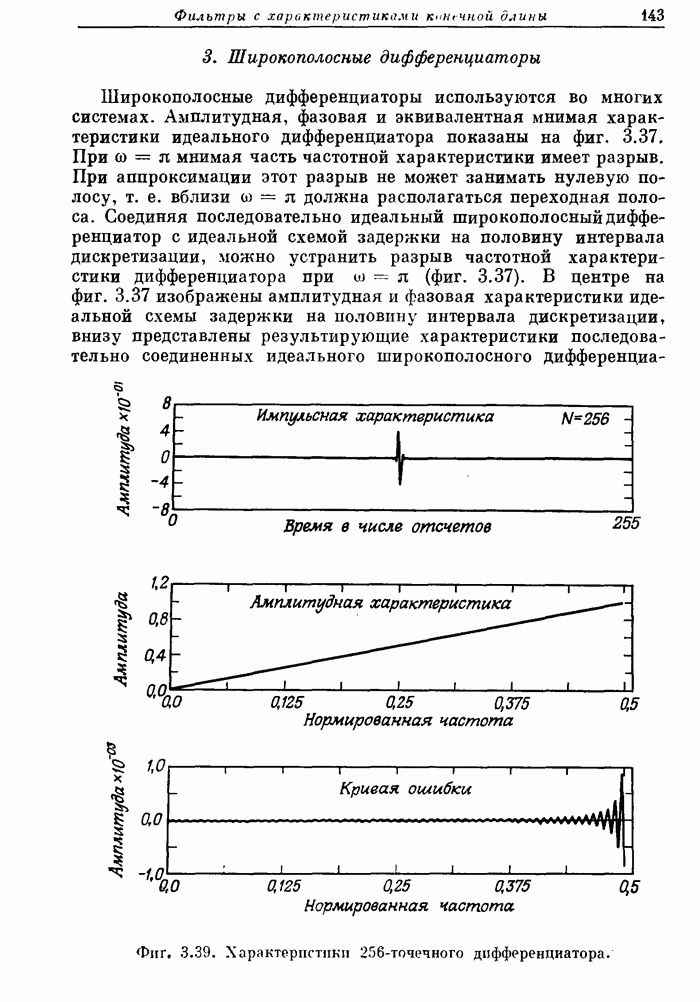
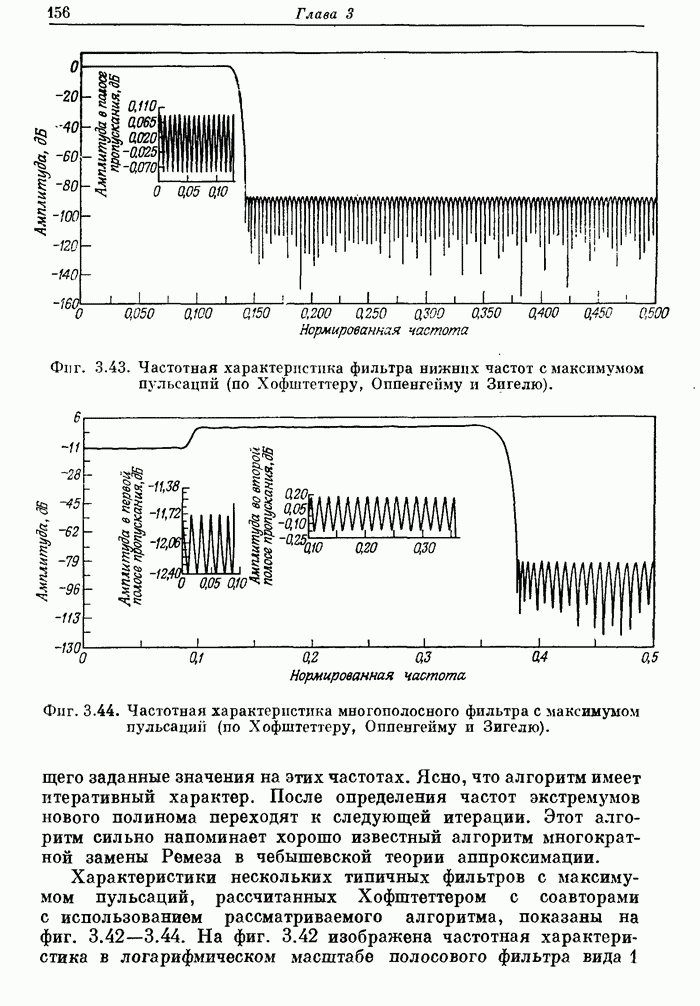
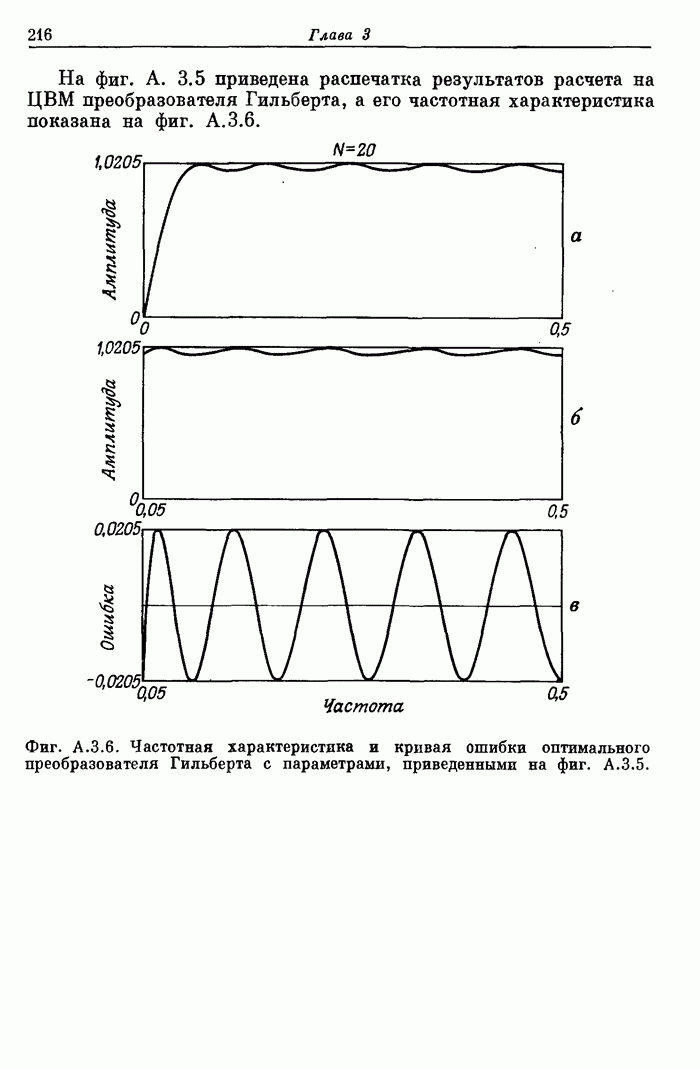
Фиг. A.3.5. Распечатка результатов расчета 20-точечного оптимального
преобразователя Гильберта.
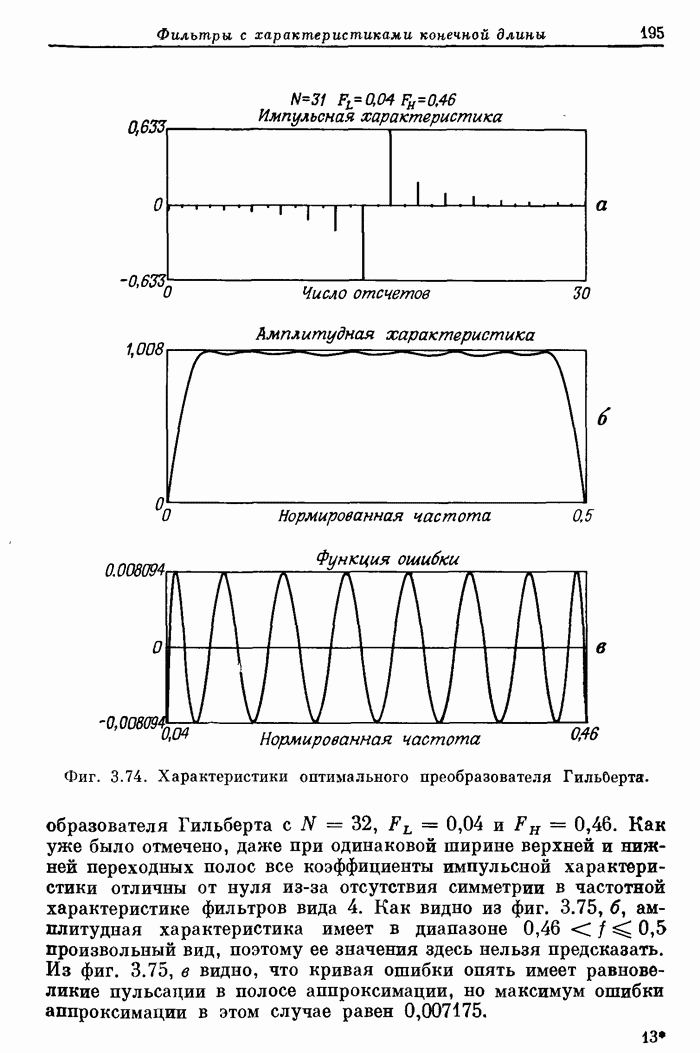
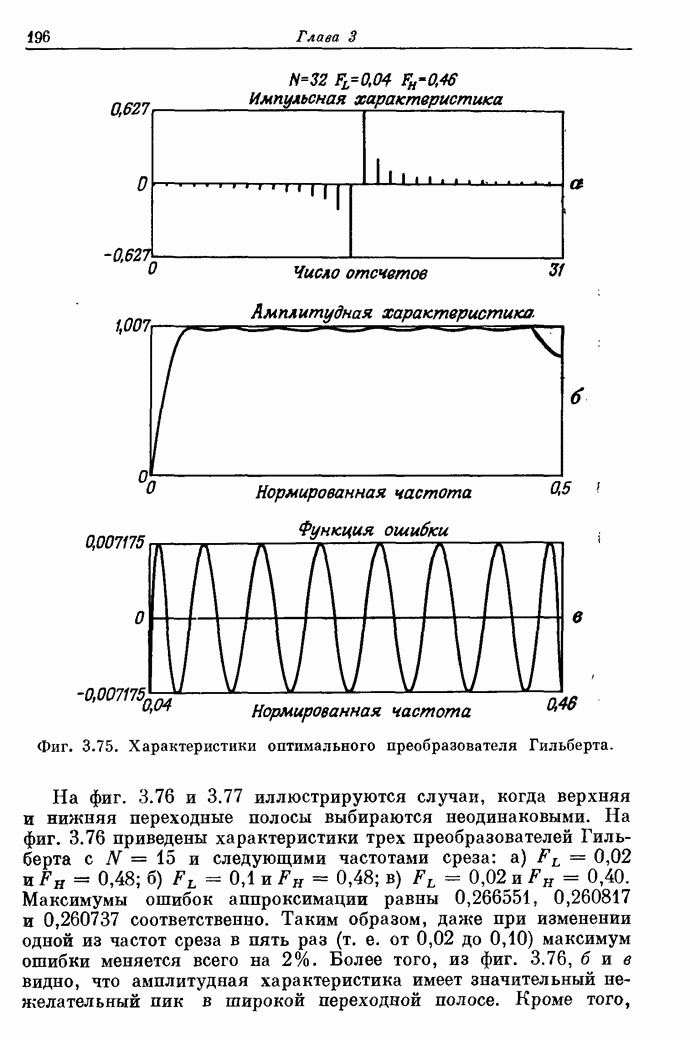
На фиг. А. 3.5 приведена распечатка результатов расчета на ЦВМ преобразователя Гильберта, а его частотная характеристика показана на фиг. А.3.6.

Фиг. A.3.6.Чатотная характеристика и кривая ошибки оптимального преобразователя Гильберта с параметрами, приведенными на фиг. А.3.5.
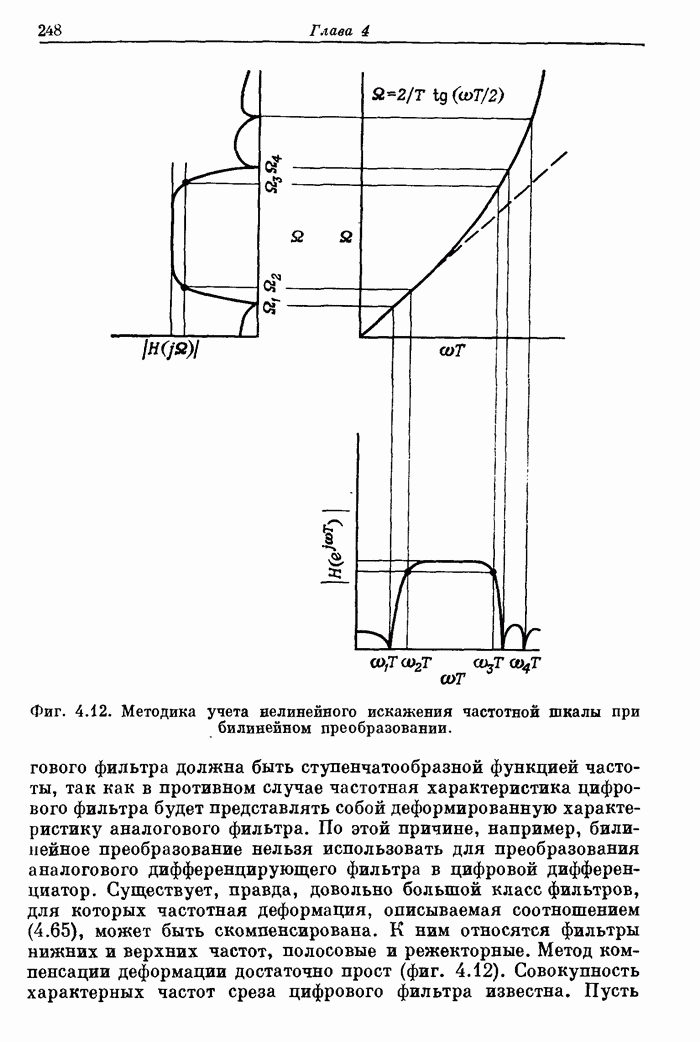
Программа расчета КИХ-фильтров
С PROGRAM FOP. THE DESIGN OF LINEAR PHASE FINITE IMPULSE
С RESPONSE (FIR) FILTERS USING THE REMEZ EXCHANGE ALGORITHM
С JIM MCCLELLAN, RICE UNIVERSITY, APRIL 13, 1973
C THREE TYPES OF FILTERS ARE INCLUDED—BANDPASS FILTFRS
C DIFFERENTIATORS, AND HILBERT TRANSFORM FILTERS C
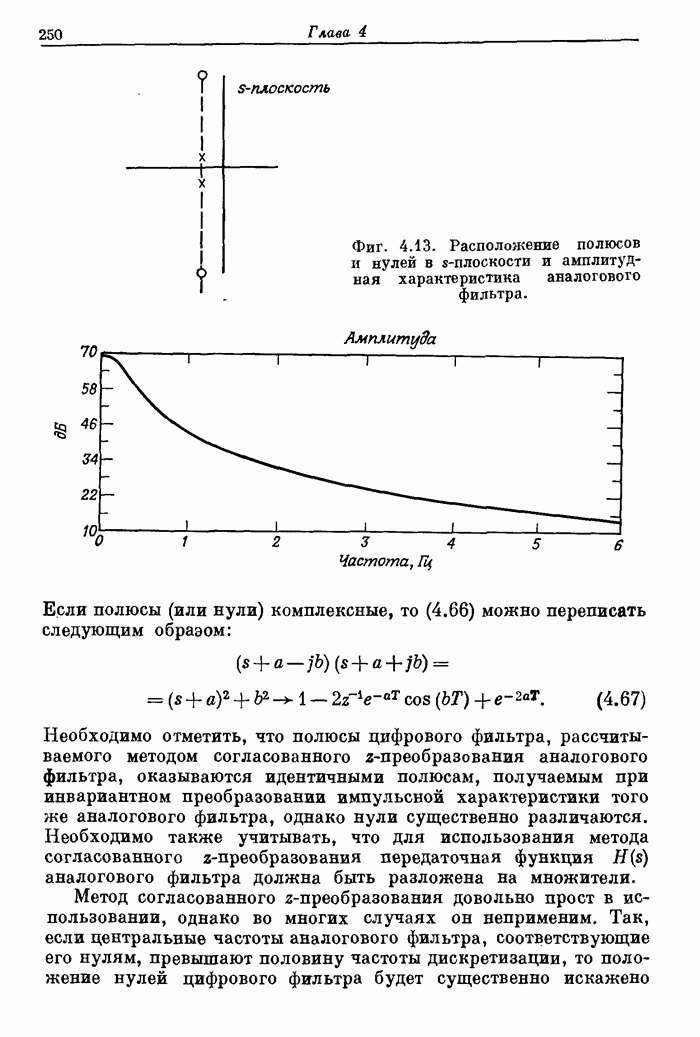
C THE INPUT DATA CONSISTS OF 5 CARDS C
C CARD 1—FILTER LENGTH, TYPE OF FILTER. 1-NULTIPLE
C PASSBAND/STOPBAND, 2-DIFFERENTIATOR, 3-HILBERT TRANSFORM
C FILTER. NUMBER OF BANDS, CARD PUNCH DESIRED, AND GRID
C DENSITY.
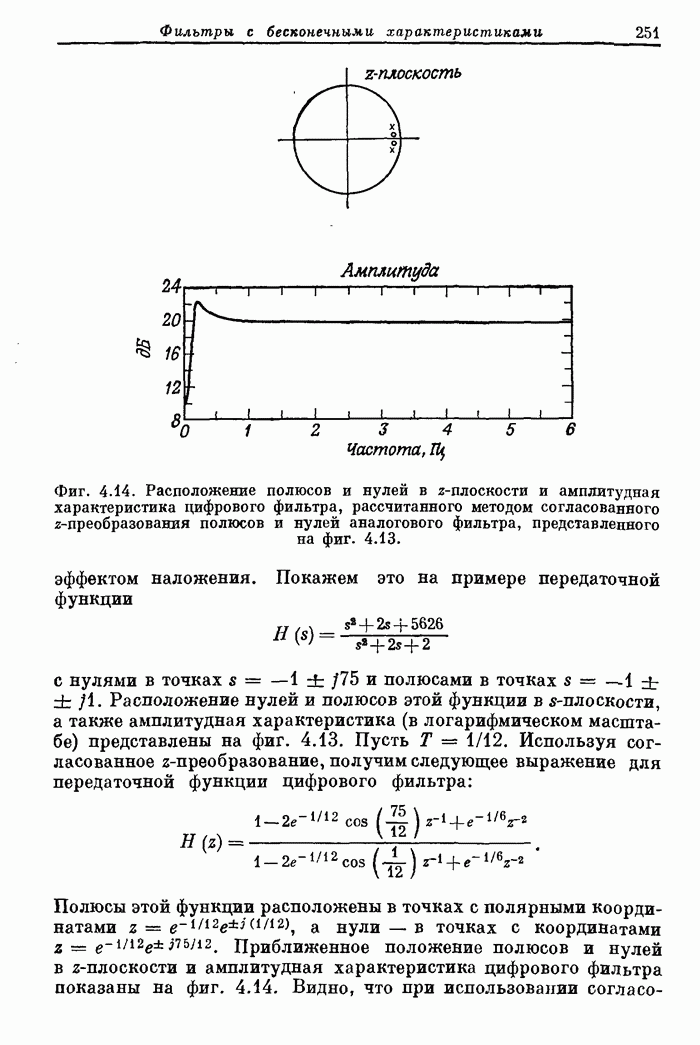
C
C CARD 2—BANDEDGES, LOWER AND UPPER EDGES FOR EACH BAND
C WITH A MAXIMUM OF 10 BANDS. С
C CARD 3—DESIRED FUNCTION (OR DESIRED SLOPE IF A
С DIFFERENTIATOR) FOR EACH BAND.
C
C CARD 4—WEIGHT FUNCTION IN EACH BAND. FOR A
C DIFFERENTIATOR, THE WEIGHT FUNCTION IS INVERSELY
C PROPORTIONAL TO F.
C
C THE FOLLOWING INPUT DATA SPECIFIES A LENGTH 32 BANDPASS
C FILTER WITH STOPBANDS 0 TO 0.1 AND 0.425 TO 0.5, AND
C PASSBAND FROM 0.2 TO 0.35 WITH WEIGHTING OF 10 IN THE
C STOPBANDS AND 1 IN THE PASSBAND. THE IMPULSE RESPONSE
C WILL BE PUNCHED AND THE GRID DENSITY IS 32. C
С SAMPLE INPUT DATA SETUP
C 32,1,3,1,32
C 0,0.1,0.2,0.35,0.425,0.5
С 0,1,0
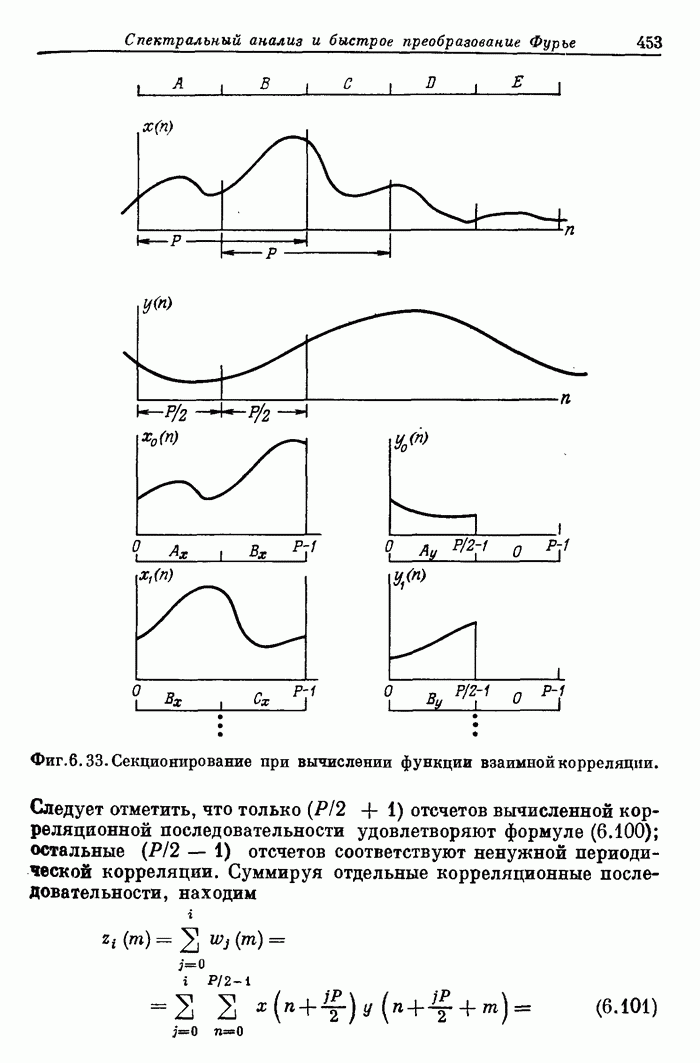
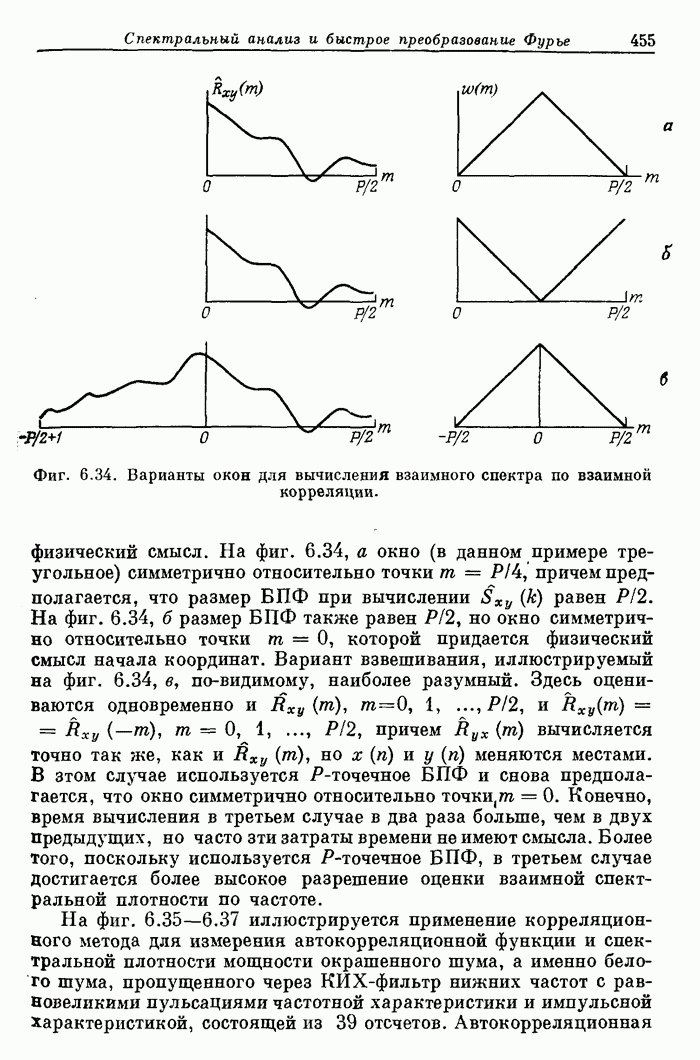
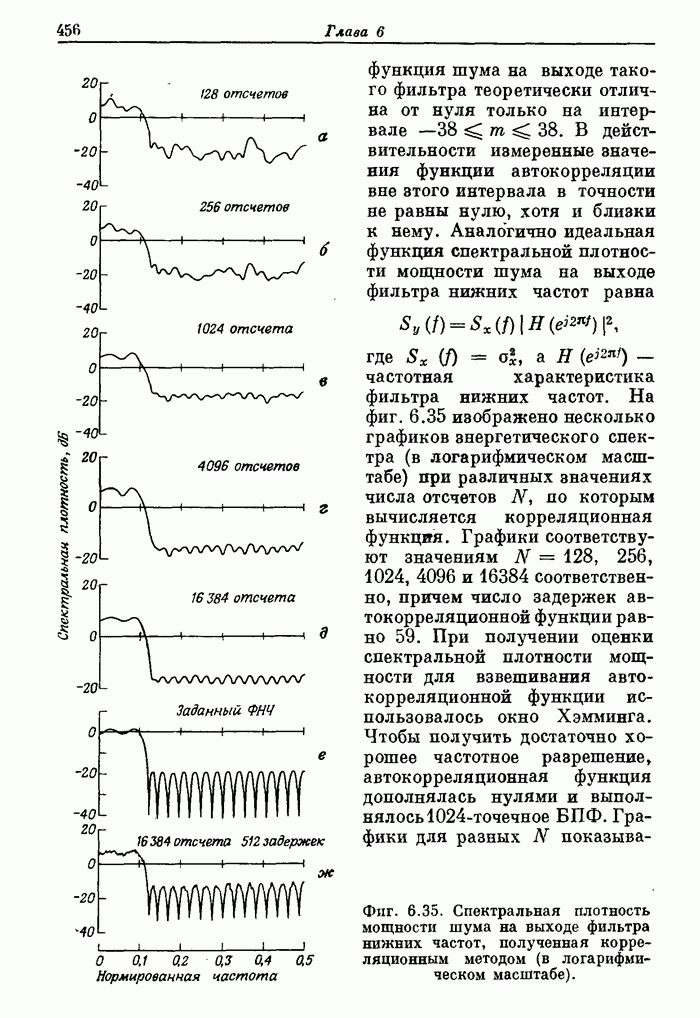
С 10,1,10 С
С THE FOLLOWING INPUT DATA SPECIFIES A LENGTH 32 WIDEBAND
С DIFFERENTIATOR WITH SLOPE 1 AND WEIGHTING OF 1/F. THE
С IMPULSE RESPONSE WILL NOT BE PUNCHED AND THE GPID
С DENSITY IS ASSUMED TO BE 16.
С
С 32,2,1,0,0
С 0,0.5
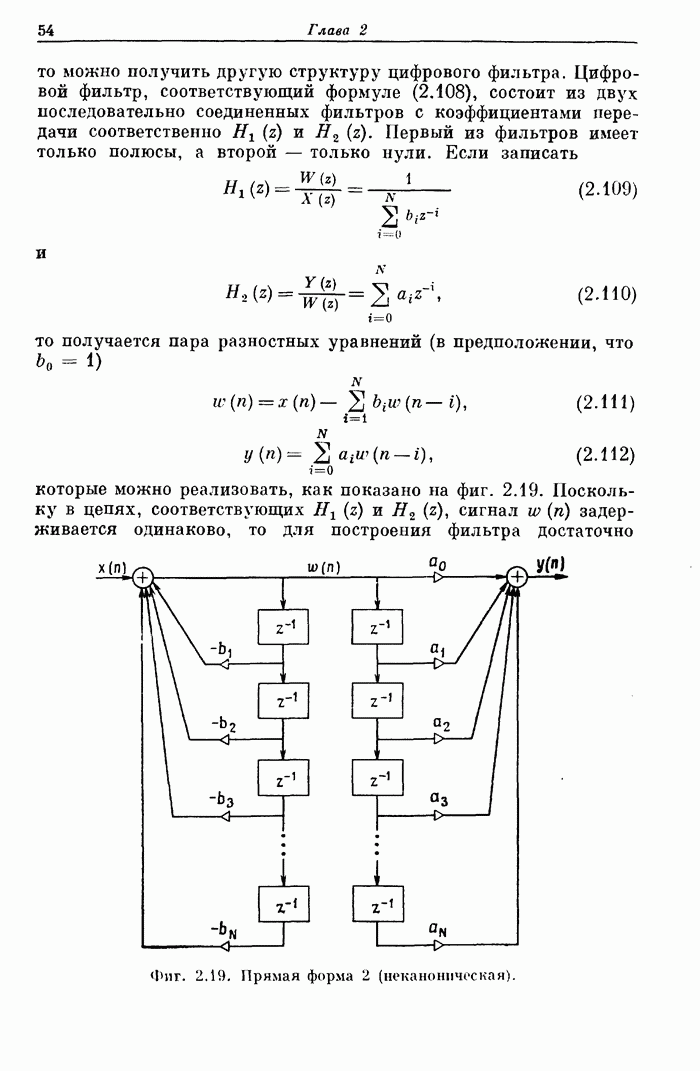
С 1.0
С 1.0 С С
COMMO NPI2,AD,DEV,X,Y,GRID,DES,WT,ALPHA,IEXT,NFCNS,NGRID
DIMENSION I EXT (66) , AD (66) , ALPHA (66) ,X(66) ,Y(66) DIMENSION H(66)
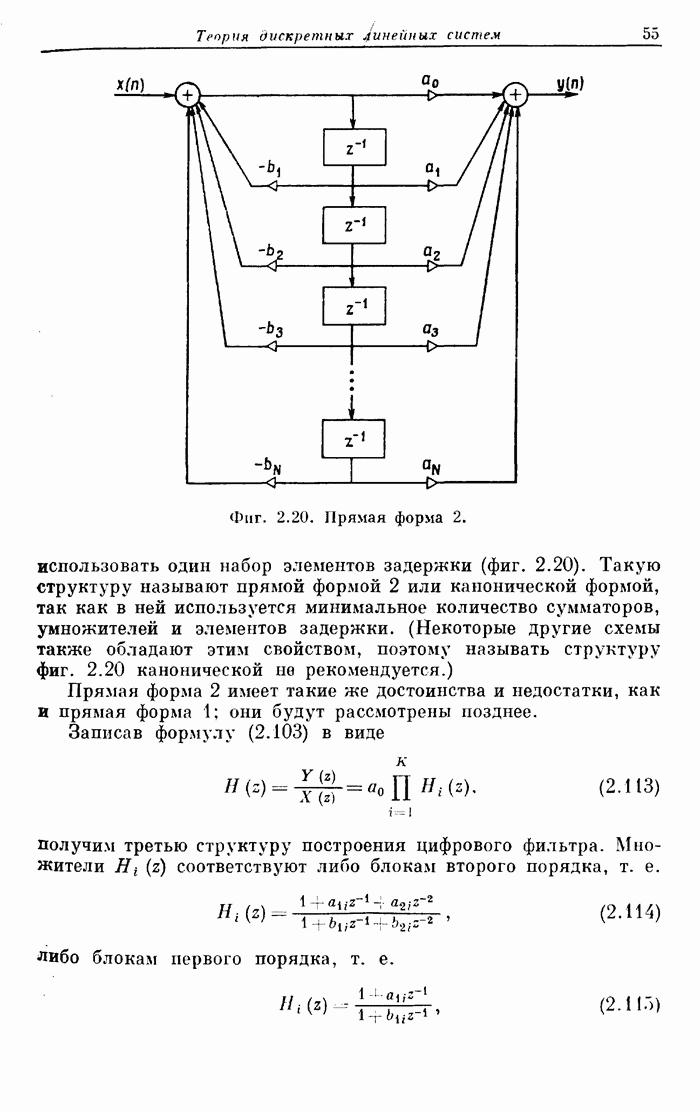
DIMENSION DES(1045),GRID(1045),WT(1045)
DIMENSION EDGE(20),FX(10),WTX(10),DEVIAT(10)
DOUBLE PRECISION PI2,PI
DOUBLE PRECISION AD,DEV,X,Y
PI2=6.2831853 07179586
PI=3.141592653589793
С
С THE PROGRAM IS SET UP FOR A MAXIMUM LENGTH OF 128, BUT
С THIS UPPER LIMIT CAN BE CHANGED BY REDIMENSIONING THE
С ARRAYS I EXT, AD, ALPHA, X, Y, H TO BE NFMAX/2 ♦ 2.
С THE ARRAYS DES, GRID, AND WT MUST DIMENSIONED
С 16(NFMAX/2 ♦ 2) .
С
NFMAX=128
100 CONTINUE
JTYPE=0
С
С PROGRAM INPUT SECTION
С
READ *,NFILT,JTYPE,NBANDS,JPUNCH,LGRID IF(NFILT.GT.NFMAX.OR,NFILT.LT.3) CALL ERROR
IF(NBANDS.LE.0) NBANDS=1
С
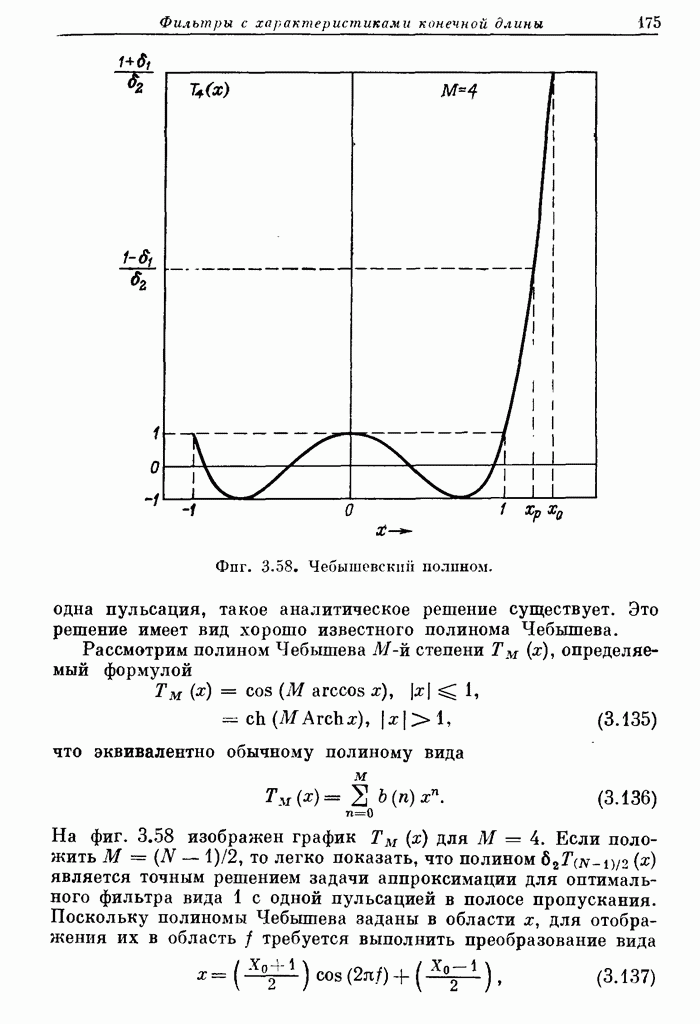
С GRID DENSITY IS ASSUMED TO BE 16 UNLESS SPECIFIED
С OTHERWISE
С
IF(LGRID.LE.O) LGRID=16
JB=2*NBANDS
READ », (EDGE(J) ,J=1,JB)
READ »,(FX(J) ,J = 1, NBANDS)
READ ♦ , (WTX(J),J=1,NBANDS)
IF(JTYPE.EQ.0) CALL ERROR
NEG= 1
IF(JTYPE.EQ.1) NEG=0
NODD=NFILT/2 NODD=NFILT-2»
NODD NFCNS=NFILT/2
IF(NODD.EQ.1.AND.NEG.EQ. 0)
NFCNS=NFCNS+1
С
С SET UP THE DENSE GRID. THE NUMBER OF POINTS IN THE GRID
С IS (FILTER LENGTH ♦ 1)♦GRID DENSITY/2
С
GRID (1) =EDGE (1)
DELF=LGRID* NFCNS
DELF=0.5/DELF
IF(NEG.EQ.O) GO TO 135
IF(EDGE(1).LT.DELF) GRID(1)= DELF 135
135 CONTINUE
J=1
L= 1
LBAND=1 14 0
140 FUP=EDGE(L*1) 145
145 TEMP=GRID(J)
С
С CALCULATE THE DESIRED MAGNITUDE RESPONSE AND THE WEIGHT
С FUNCTION ON THE GRID
С
DES(J) =EFF(TEMP,FX,WTX,LBAND,JTYPE) WT(J)=WATE(TEMP,FX,WTX,LBAND,JTYPE)
GRID(J)=TEMP*DELF
IF (GRID (J) .GT.FUP)
GO TO 145
150 GRID (J-1)=FUP
DES(J-1)=EFF(FUP,FX,WTX,LBAND,JTYPE)
WT(J-1)=WATE(FUP,FX,WTX,LBAND,JTYPE) LBAND=LBAND+1
L=L+ 2
IF(LBAND.GT.NBANDS) GO TO 160
GRID(J) =EDGE(L)
GO TO 140 160
160 NGRID=J-1
IF(NEG.NE.NODD) GO TO 165
I F (GRID (NGRID) .GT. (0.5-DELF) ) NGRI D=NGRID-1
С
С SET UP A NEW APPROXIMATION PROBLEM WHICH IS EQUIVALENT
С TO THE ORIGINAL PROBLEM
С
IF(NEG) 170,170,180
170 IF(NODD.EQ.1)
GOTO 200
DO 175 J=1,NGRID
CHANGE=DCOS(PI*GRID(J))
DES (J) =DES (J) /CHANGE
175 WT(J)=WT(J) «CHANGE
GO TO 200
180 IF(NODD.EQ.1) GO TO 190
DO 185 J*1,NGRID
CHANGE=DSIN(PI»GRID(J)) DES (J) *DES (J) /CHANGE
185 WT (J) =WT (J) «CHANGE
GO TO 200
190 DO 195 J*1,NGRID
CHANGE=DSIN(PI2«GRID(J))
DES (J) =DES (J) /CHANGE
195 WT(J)=WT(J)«CHANGE
С
С INITIAL GUESS FOR THE EXTREMAL FREQUENCIES—EQUALLY
С SPACED ALONG THE GRID
С
200 TEMP=FLOAT(NGRID-1)/FLOAT(NFCNS)
DO 210 J=1,NFCNS
210 IEXT(J) = (J-1) «TEMP*1
IEXT(NFCNS*1)=NGRID
NM1=NFCNS-1
NZ-NFCNS*1
С
С CALL THE REMEZ EXCHANGE ALGORITHM TO DO THE APPROXIMATION
С PROBLEM
С
C ALL REMEZ(EDGE,NBANDS)
С
С CALCULATE THE IMPULSE RESPONSE.
С
IF(NEG) 300,300,320
300 IF(NODD.EQ.O) GO TO 310
DO 305 J=1,NM1
305 H (J) =0.5*ALPHA(NZ-J)
H(NFCNS)-ALPHA(1) GO TO 350
310 H(1)=0.25*ALPHA (NFCNS)
DO 315 J=2,NM1
315 H(J)=0.25*(ALPHA(NZ-J)♦ALPHA(NFCNS*2-J))
H(NFCNS) =0.5«ALPHA(1) ♦0.25»ALPHA(2)
GO TO 350
320 IF(NODD.EQ.0) GO TO 330
H(1)~Q.25»ALPHA(NFCNS)
H(2)=0.2S«ALPHA (NM1)
DO 325 J=3,NM1
325 H(J)=0.25«(ALPHA(NZ-J) -ALPHA(NFCNS*3-J)) H(NFCNS)=0.5«ALPHA(1)-0.25«ALPHA(3)
H (NZ) =0.0
GO TO 350
330 H(1)=0.25«ALPHA(NFCNS)
DO 335 J=2,NM1
335 Н(J)=0.25*(ALPHA(NZ-J)-ALPHA(NFCNS+2-J))
H(NFCNS)=0.5*ALPHA(1)-0.25*ALPHA(2)
С
С PROGRAM OUTPUT SECTION.
С
350 PRINT 360
360 FORMAT(1H1, 7 0(1H*)//25X,'FINITE IMPULSE RESPONSE (FIR)' 125X,"LINEAR PHASE DIGITAL FILTER DESIGN*/
225X,'REMEZ EXCHANGE ALGORITHM'/) IF(JTYPE.EQ.1) PRINT 365
365 FORMAT(25X,'BANDPASS FILTER'/)
IF(JTYPE.EQ.2) PRINT 370
370 FORMAT(25X,'DIFFERENTIATOR'/)
IF (JTYPE.EQ.3) PRINT 375
375 FORMAT(25X,'HILEERT TRANSFORMER'/)
PRINT 378 ,NFILT
378 FORMAT(15X,*FILTER LENGTH = ',13/)
PRINT 350
380 FORMAT(15X,* ***** IMPULSE RESPONSE **••*')
DO 381 J=1,NFCNS
K=NFILT+1-J
IF(NEG.EQ.O) PRINT 382,J,H(J),K
IF(NEG.EQ.I) PRINT 383,J,H(J),K
385 CONTINUE
382 FORMAT(20X,'H(',13,*) = '.E15.8,* = H(*,I4,*)*)
383 FORMAT (20X,'H(*,I3,*) = *,E15.8," = -H(*,I4,')*) IF(NEG.EQ.1.AND.NODD.EQ.1) PRINT 384,NZ
384 FORMAT(20X,'H(*,13,') = 0.0') DO 450 K=1,NBANDS,4
KUP=K+3
IF(KUP.GT.NBANDS) KUP=NBANDS PRINT 385,(J,J=K,KUP)
385 FORMAT(/24X,4('BAND*,I 3,8X) )
PRINT 390, (EDGE (2*J-1) ,J=K,KUP)
390 FORMAT(2X,'LOWER BAND EDGE',5F15.9)
PRINT 395,(EDGE(2*J),J=K,KUP)
395 FORMAT(2X,'UPPER BAND EDGE',5F15.9)
IF(JTYPE.NE.2) PRINT
400, (FX (J) , J=K, KUP)
FORMAT(2X,'DESIRED VALUE*,2X,5F15.9)
IF(JTYPE.EQ.2) PRINT 405,(FX(J),J=K,KUP)
405 FORMAT(2X,*DESIRED SLOPE',2X,5F15.9)
410, (WTX(J) , J=K,KUP)
410 FORMAT(2X,* WEIGHTING*,6X,5F15.9)
DO 420 J=K,KUP
420 DEVIAT (J) =DEV/WTX (J)
PRINT 425,(DEVIAT(J),J=K,KUP)
425 FORMAT(2X,'DEVIATION',6X,5F15.9)
IF(JTYPE.NE.1)
GO TO 450 DO
430 J=K,KUP 430 DEVIAT(J)=20.0*ALOG10(DEVIAT(J) )
PRINT 435, (DEVIAT(J),J=K, KUP)
435 FORMAT(2X,'DEVIATION IN DB',5F15.9)
450 CONTINUE
PRINT 455,(GRID (IEXT(J)),J=1,NZ)
455 FORMAT(/2X,'EXTREMAL FREQUENCIES'/(2X,5F12.7))
PRINT 460
460 FORMAT(/1X,70 (1H*)/1 Hi)
IF (JPUNCH. NE. 0) PUNCH * , (H (J) , J= 1,NFCNS)
IF(NFILT.NE.O) GO TO 100
RETURN
END
FUNCTION EFF(TEMP,FX,WTX,LBAND,JTYPE)
С
С FUNCTION TO CALCULATE THE DESIRED MAGNITUDE RESPONSE
С AS A FUNCTION OF FREQUENCY.
С
DIMENSION FX(5),WTX(5)
IF(JTYPE.EQ.2) GO TO
EFF=FX (LBAND)
RETURN 1 EFF=FX (LBAND) «TEMP
RETURN
END
FUNCTION WATE (TEMP,FX,WTX,LbAND,JTYPE)
С
С FUNCTION TO CALCULATE THE WEIGHT FUNCTION AS A FUNCTION
С OF FREQUENCY.
С
DIMENSION FX(5),WTX(5)
IF(JTYPE.EQ.2) GO TO 1
WATE=WTX (LBAND)
RETURN
IF(FX(LBAND).LT.0.0001) GO TO 2
WATE=WTX (LBAND) /TEMP
RETURN
WATE=WTX(LBAND)
RETURN
END
SUBROUTINE ERROR PRINT 1
1 FORMAT(' ************ ERROR IN INPUT DATA **********')
STOP
END
SUBROUTINE REMEZ(EDGE,NBANDS)
С
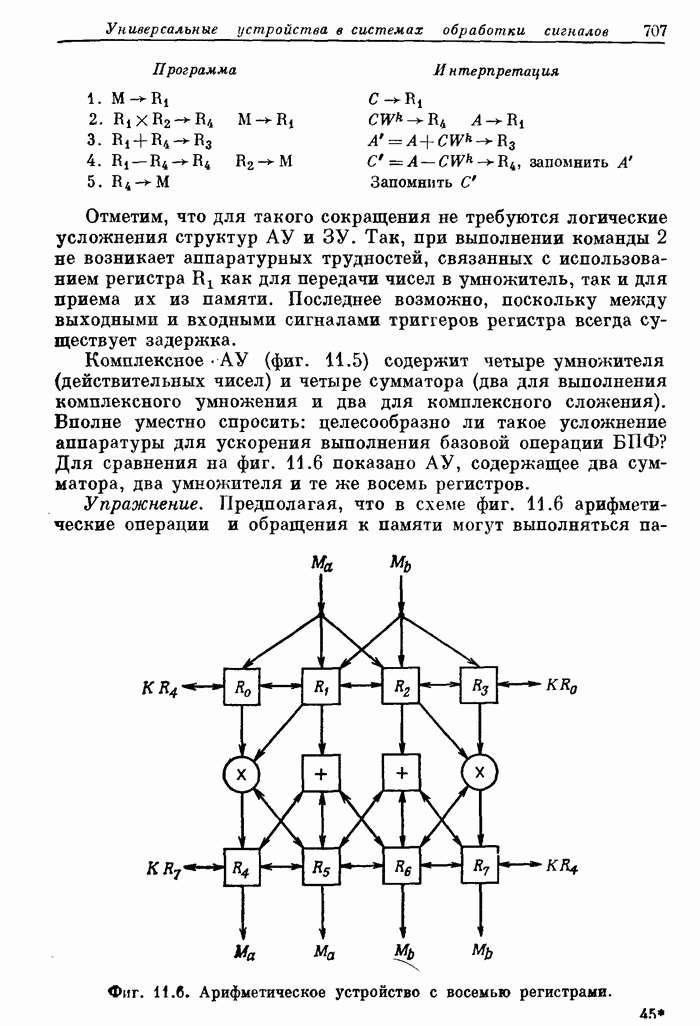
С THIS SUBROUTINE IMPLEMENTS THE REMEZ EXCHANGE ALGORITHM С FOR THE WEIGHTED CHEBYCHEV APPROXIMATION OF A CONTINUOUS
С FUNCTION WITH A SUM OF COSINES. INPUTS TO THE SUBROUTINE
С ARE A DENSE GRID WHICH REPLACES THE FREQUENCY AXIS, THE
С DESIRED FUNCTION ON THIS GRID, THE WEIGHT FUNCTION ON THE
С GRID, THE NUMBER OF COSINES, AND AN INITIAL GUESS OF THE
С EXTREMAL FREQUENCIES. THE PROGRAM MINIMIZES THE CHEBYCHEV
С ERROR BY DETERMINING THE BEST LOCATION OF THE EXTREMAL
С FREQUENCIES (POINTS OF MAXIMUM ERROR) AND THEN CALCULATES С THE COEFFICIENTS OF THE EEST APPROXIMATION.
COMMON PI2,AD,DEV,X,Y,GRID,DES,WT,ALPHA,IEXT,NFCNS,NGRID DIMENSION EDGE(20)
DIMENSION IEXT(66),AD(66),ALPHA(66),X(66),Y(66)
DIMENSION DES (1045) ,GRID(1045) ,WT(1045)
DIMENSION A (66) ,P(65) ,Q(65)
DOUBLE PRECISION P12,DNUM,DDEN,DTEMP , A , P , Q
DOUBLE PRECISION AD,DEVrX,Y
С
С THE PROGRAM ALLOWS A MAXIMUM NUMBER OF ITERATIONS OF 25
С
ITRMAX=25
DEVL=-1.0
NZ=NFCNS*1
NZZ=NFCNS*2
NITER=0
100 CONTINUE
lEXT(NZZ) =NGRID»1
NITER=NITER*1
IF(NITER.GT.ITRMAX) GO TO 400
DO 110 J=1,NZ DTEMP=GRID(IEXT(J))
DTEMP= DCOS (DTEMP*PI 2)
110 X (J) =DTEMP
JET=(NFCNS-1)/15*1
DO 120 J=1,NZ
120 AD(J)=D(J,NZ» JET)
DNUM=0.0
DDEN=0.0 K=1
DO 130 J=1,NZ L=IEXT(J)
DTEMP=AD (J) *DES (L)
DNUM=DNUM*DTEMP DTEMP=K*AD (J) /WT (L)
DDEN= DDEN♦DTEMP
130 K=-K
DEV=DNUM/DDEN NU=1
IF(DEV.GT.O.O) Nl)=-1
DEV=-NU*DEV
K=NU
DO 140 J=1,NZ L=IEXT(J)
DTEMP=K*DEV/WT(L) Y (J) =DES (L) ♦DTEMP
140 K=-K
IF(DEV.GE,DEVI) GO TO 150
CALL OUCH GO TO 400
150 DEVL=DEV
JCHNGE=0
K1=IEXT(1)
KNZ=IEXT(NZ)
KLOW=0
NUT=-NU J=1
С
С SEARCH FOR THE EXTREMAL FREQUENCIES OF THE BEST
С APPROXIMATION
С
200 IF(J.EQ.NZZ) YNZ=COMP
IF(J.GE.NZZ) GO TO 300
KUP'IEXT (J+l)
L-IEXT (J) ♦ 1
NUT=-NUT
IF (J. EQ. 2) Y 1=C0MP C
OMP=DEV
IF(L.GE.KUP) GO TO 220
ERR=GEE(L,NZ)
ERR=(ERR-DES(L))*WT(L)
DTEMP=NUT* ERR-COMP
IF(DTEMP.LE.0.0) GO TO 220 COM P= NUT* ERR
210 L=L*1
IF(L.GE.KUP) GO TO 215
ERR=GEE (L, NZ)
ERR=(ERR-DES(L))*WT(L)
DTEMP=NUT*ERR-COMP
IF(DTEMP.LE.0.0) GO TO 215
COMP=NUT*ERR GO TO 210
215 IEXT(J)=L-1 J=J*1
KLOW=L-1
JCHNGE=JCHNGE*1 GO TO 200
220 L=L-1
225 L=L-1
IF(L.LE.KLOW) GO TO 250
ERR=GEE(L,NZ)
ERR=(ERR-DES(L))*WT(L)
DTEMP= NUT* ERR-COMP
IF(DTEMP.GT.0.0) GO TO 230
IF(JCHNGE.LE.0) GO TO 225
GO TO 2 60 230
COMP=NUT*ERR
235 L=L-1
IF(L.LE.KLOW) GO TO 240
ERR=GEE(L,NZ)
ERR=(ERR-DES(L))*WT(L)
DTEMP= NUT* ERR-COMP
IF(DTEMP.LE.0.0) GO TO 240
COMP=NUT*ERR GO TO 235
240 KLOW=IEXT (J)
IEXT (J) =L*1
J=J*1
JCHNGE=JCHNGE*1 GO TO 200
250 L=IEXT(J)♦1
IF(JCHNGE.GT.0) GO TO 215
255 L=L*1
IF (L.GE. KUP) GO TO 260
ERR=GEE(L,NZ)
ERR= (ERR-DES (L) ) *WT(L)
DTEMP-NUT*EPR-COMP
IF(DTEMP.LE.0.0) GO TO 255
COMP=NUT*ERR GO TO 210
260 KLOW=IEXT(J) J=J*1 GO TO 200
300 IF(J.GT.NZZ) GO TO 320
IF (K1. GT. IEXT (1) )
K1=IEXT(1)
IF (KNZ . LT. IEXT (N2) )
KNZ= IEXT (NZ»
NUT1=NUT
NUT=-NU
L=0
KUP=K1
COMP=YNZ* (1.00001)
LUCK=1
310 L=L*1
IF(L.GE.KUP) GO TO 315
ERR=GEE(L,NZ)
ERR=(ERR-DES(L))*WT(L)
DTEMP=NUT*ERR-COMP
IF(DTEMP.LE.0.0) GO TO 310
COMP=NUT*ERR J=NZZ GO TO 210
315 LUCK=6
GO TO 325 320
IF(LUCK.GT.9) GO TO 350
IF(COMP.GT.Y1)
Y1=COMP
K1 = IEXT (NZZ)
325 L=NGRID*1 KLOW-KNZ
NUT=-NUT1 COMP-Y1*(1.00001)
330 L=L-1
IF(L.LE.KLOW) GO TO 340
ERR=GEE(L,NZ)
ERR= (ERR-DES (L) ) *WT (L)
DTEMP=NUT*ERR-COMP
IF (DTEMP.LF.0.0) GO TO 330
J=NZZ
COMP=NUT* ERR
LUCK=LUCK*10 GO TO 235
340 IF(LUCK.EQ.6) GO TO 370
DO 345 J=1,NFCNS
345 I EXT (NZZ-J) = I EXT (NZ-J)
IEXT( 1) =K1 GO TO 100
350 KN=IEXT(NZZ)
DO 360 J=1,NFCNS
360 IEXT(J)=IEXT(J*1)
IEXT(NZ) =KN GO TO 100
370 IF (JCHNGE.GT.0) GO TO 100
С CALCULATION OF THE COEFFICIENTS OF THE BEST APPROXIMATION
С USING THE INVERSE DISCRETE FOURIER TRANSFORM
С
400 CONTINUE
NM1=NFCNS-1
FSH=1.0E-06
GTEMP=GRID(1)
X (NZZ)=-2.0
CN=2*NFCNS-1
DELF=1.0/CN
L= 1
KKK=0
IF(EDGE(1).EQ.0.0.AND.EDGE(2*NBANDS).EQ.0.5) KKK=1
IF(NFCNS.LE.3) ККК=1
IF(ККК.EQ.1) QO ТО 405
DTEMP=DCOS(PI2«GFID(1))
DNUM=DCOS(PI2«GRID(NGRID))
AA=2.0/(DTEMP-DNOM)
BB=-(DTEMP*DNUM)/(DTEMP-DNUM)
405 CONTINUE
DO 430 Js 1,NFCNS
FT=(J-1)«DELE
XT=DCOS(PI2 «FT)
IF(KKK.EQ.1) GO TO 410
XT= (XT-PB)/АА
FT=ARCOS(XT)/PI 2
410 XE=X(L)
IF(XT.GT.XE) GO TO 420
IF( (XE-XT) .LT.FSH) GO TO 415
L=L* 1 GO TO 410
415 A (J) =Y (L)
GO TO 425
4 20 IF ((XT-XE) .LT.FSH) GO TO 415
GRID(1) =FT A (J) =GEF (1,N2)
425 CONTINUE
IF(L.GT.1) L=L-1
430 CONTINUE
GRID(1)=GTEMP
DDEN=PI2/CN
DO 510 J*1,NFCNS
DTEMP=0.0
DNUM=(J-1)«DDEN
IF(NM1.LT.1) GO TO 505
DO 500 K=1,NM1
500 DTEMP=DTEMP*A(K*1)«DCOS(DNUM«K)
505 DTEMP=2.0«DTEMP*A(1)
510 ALPHA(J)sDTEMP
DO 550 J»2,NFCNS
550 ALPHA(J)=2«ALPHA(J)/CN
ALPHA(1)=ALPHA(1)/CN IF(KKK.EQ.1) GO TO 545 P(1)=2.0«ALPHA(NFCNS)«BB*ALPHA(NM1)
P(2)=2.0«AA«ALPHA(NFCNS)
Q(1)=ALPHA(NFCNS-2)-ALPHA(NFCNS)
DO 540 J=2,NM1
IF(J.LT.NMI) GO TO 515
AA=0.5«AA BB=0.5«BB
515 CONTINUE
P (J*1)=0.0
DO 520 K=1,
J A(K)=P(K) 520
P(K) =2.0«BB»A(K)
P (2) =P (2) *A(1) »2.0«AA JM1=J-1
DO 525 K=1,JM1
525 P(K)=P(K) *Q(K) *AA»A(K*1)
JP1=J*1
DO 530 K=3,JP1
530 P(K)=P(K) *AA«A (K-1)
IF(J.EQ.NMI) GO TO 540
DO 535 K=1,J
535 Q(K)=-A(K)
Q(1)=Q(1) *ALPhA (NFCNS-1-J)
540 CONTINUE
DO 543 J=1,NFCNS
543 ALPHA(J)=P(J)
545 CONTINUE
IF(NFCNS.GT.3) RETURN
ALPHA(NFCNS*1)=0.0
ALPHA(NFCNS*2)=0.0
RETURN
END
DOUBLE PRECISION FUNCTION D(K,N,M)
С
С FUNCTION TO CALCULATE THE LAGRANGE INTERPOIATION
С COEFFICIENTS FOR USE IN THE FUNCTION GEE.
С
COMMON PI2,AD,DEV,X,Y,GRID,DES,WT,ALPHA,IEXT,NFCNS,NGRID
DIMENSION IEXT(66),AD(66),ALPHA(66),X(66),Y(66)
DIMENSION DES(1045),GRID(1045),WT(1045)
DOUBLE PRECISION AD,DEV,X,Y
DOUBLE PRECISION Q
DOUBLE PRECISION PI2
D=1.0
Q=X(K)
DO 3 L=1,M
DO 2 J=L,N,M
IF(J-K) 1,2, 1
1) D=2.0»D*(Q-X(J))
2) CONTINUE
3) CONTINUE D=1.0/D
RETURN
END
DOUBLE PRECISION FUNCTION GEE(K,N)
С
С FUNCTION TO EVALUATE THE FREQUENCY RESPONSE USING THE
С LAGRANGE INTERPOIATION FORMULA IN THE BARYCENTRIC FORM
С
COMMON PI2,AD,DEV,X,Y,GRID,DES,WT,ALPHA,IEXT,NFCNS,NGRID DIMENSION IEXT(66),AD(66),ALPHA(66),X(66),Y (66)
DIMENSION DES(1045),GRID(1045),WT(1045)
DOUBLE PRECISION P,C,D,XF
DOUBLE PRECISION PI2
DOUBLE PRECISION AD,DEV,X,Y
P=0.0
XF=GRID(K)
XF=DCOS (PI2*XF)
D=0.0
DO 1 J=1,
N C=XF-X
(J) C=AD(J)/C
D=D*C
P=P*C»Y(J)
GEE=P/D RETURN
END
SUBROUTINE OUCH PRINT 1
1 FORMAT('**************FAILURE TO CONVERGE*************/
OPROBABLE CAUSE IS MACHINE ROUNDING ERROR*/
2'0THE IMPULSE RESPONSE MAY BE CORRECT"/
3'OCHECK WITH A FREQUENCY RESPONSE*)
RETURN
END
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
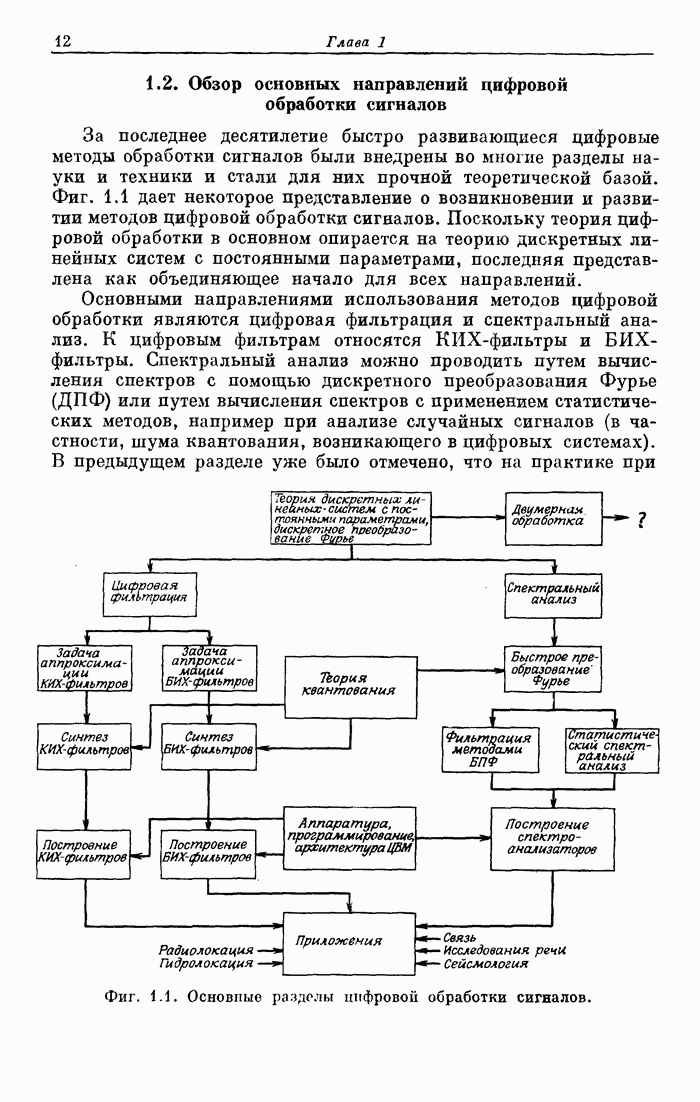
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
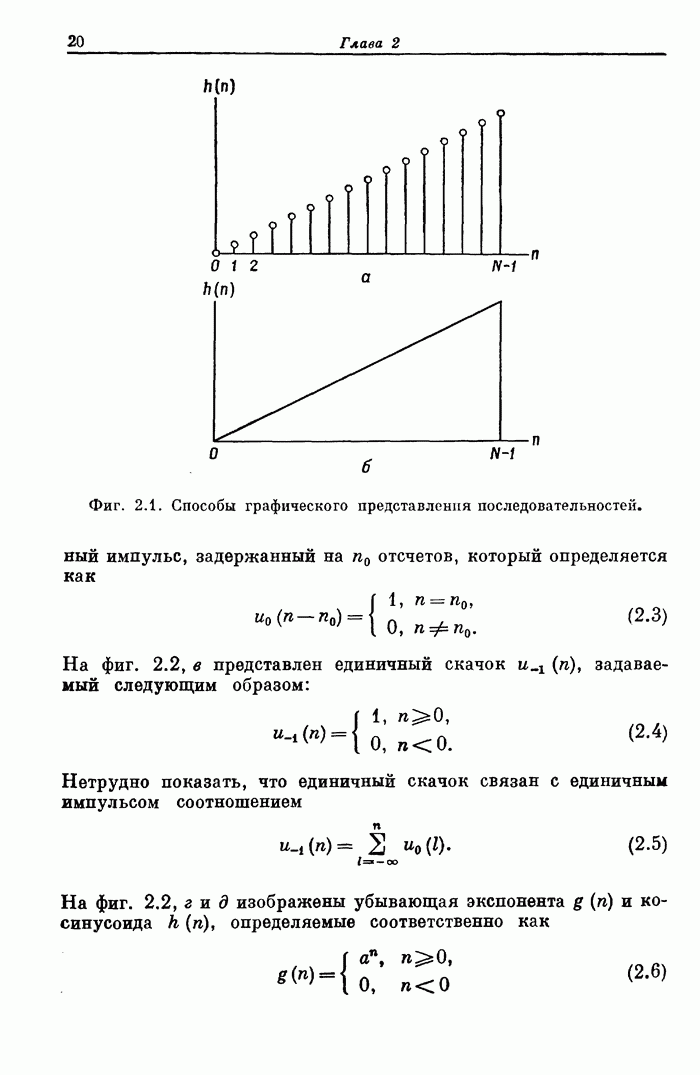
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
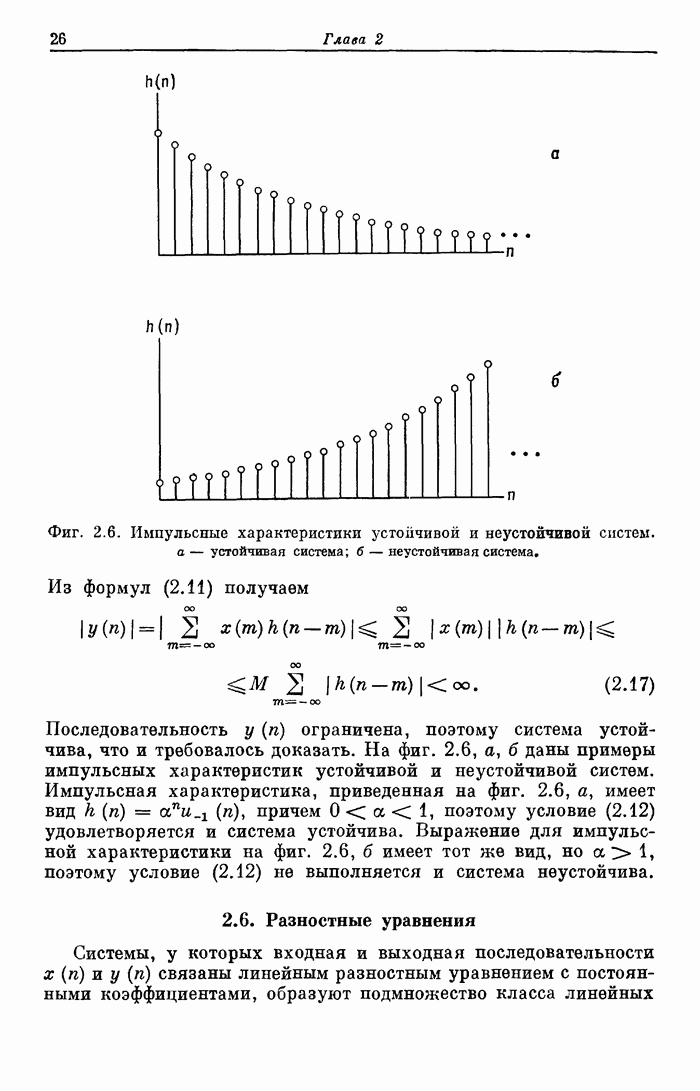
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
- 2.7. Частотная характеристика
- 2.8. Частотная характеристика систем первого порядка
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
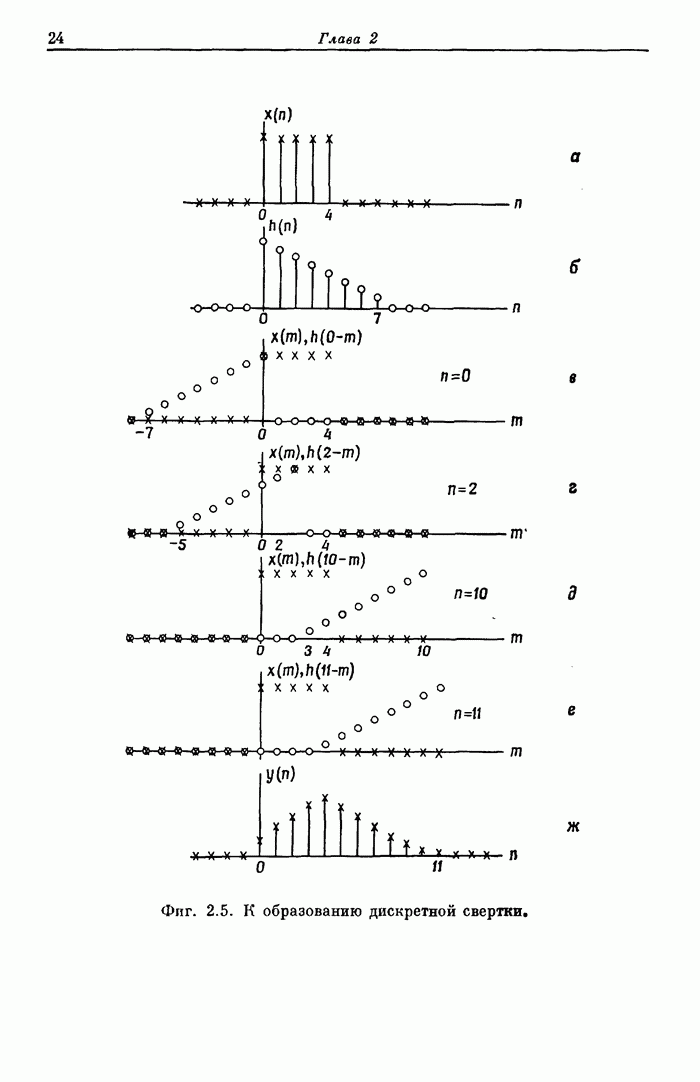
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
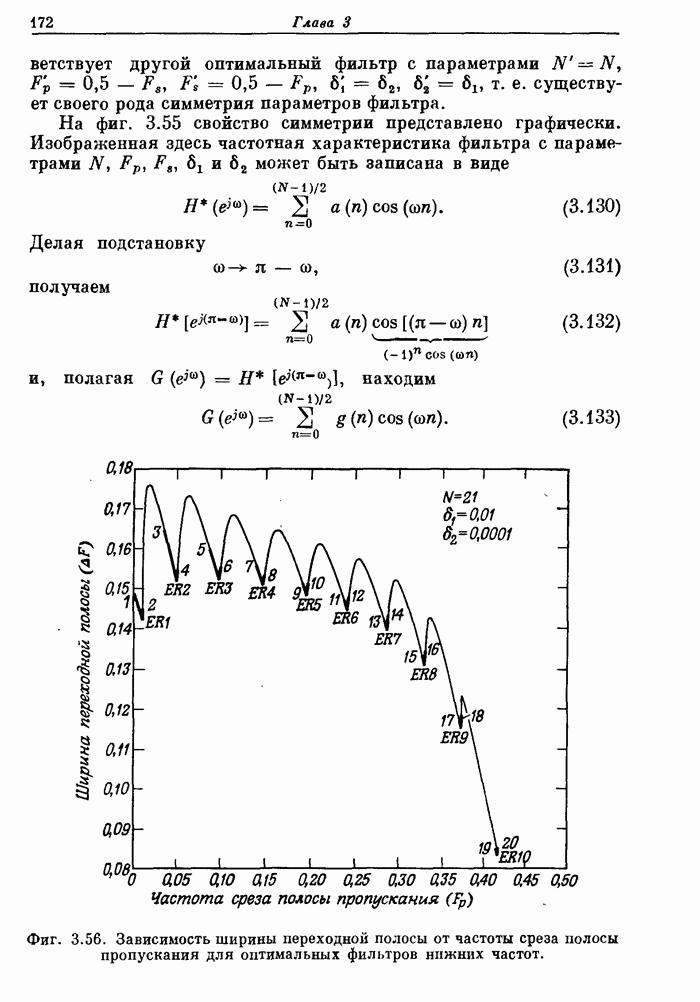
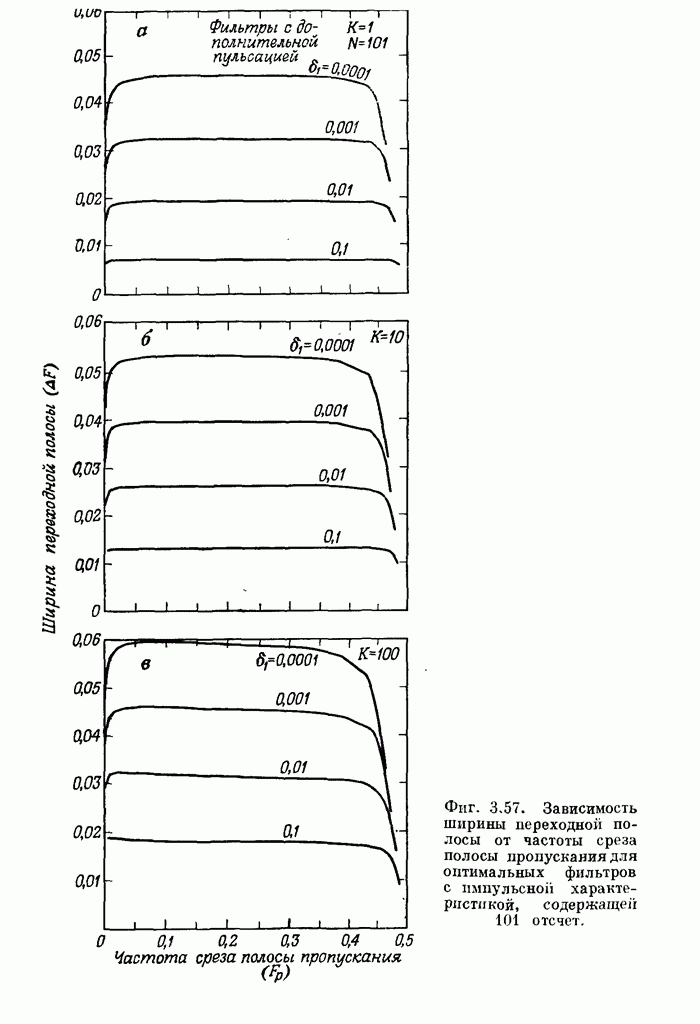
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
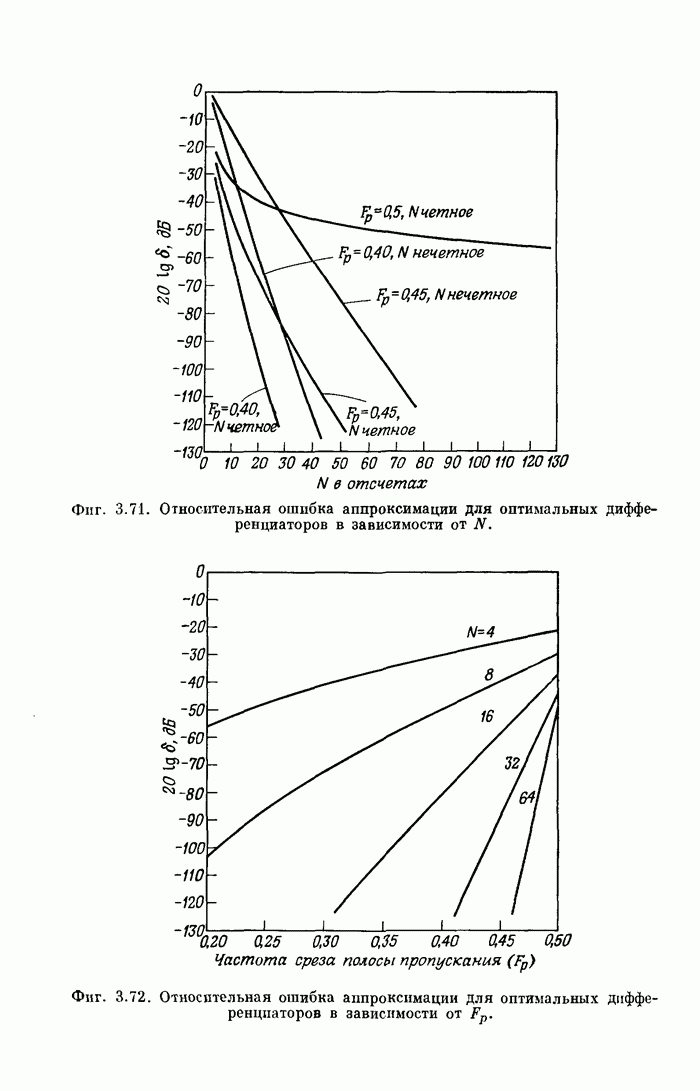
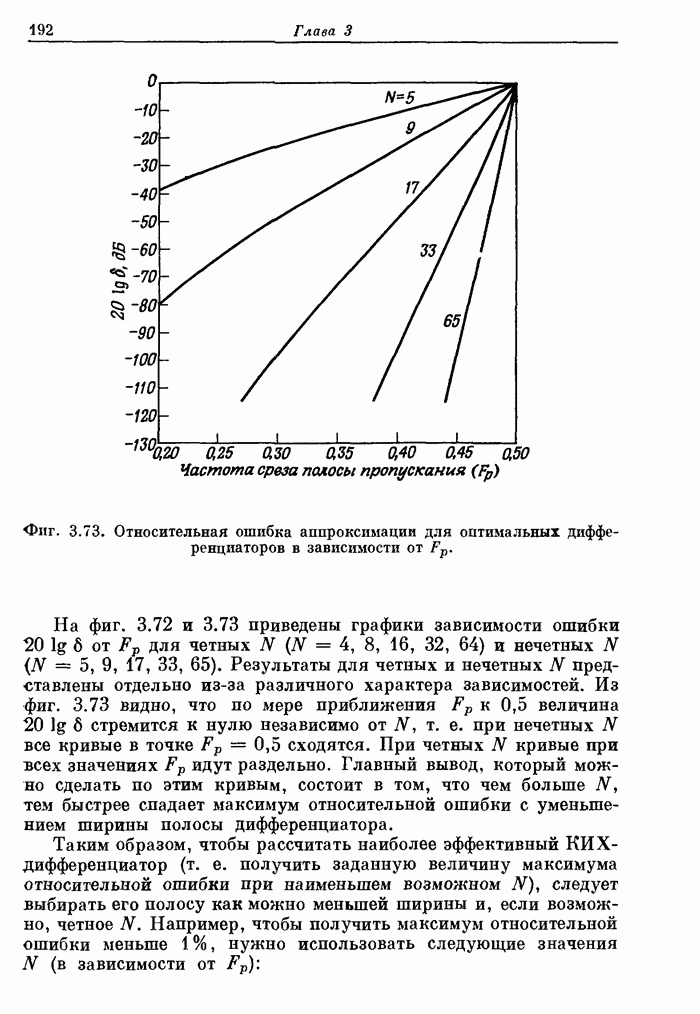
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
- 3.38. Многополосные оптимальные КИХ-фильтры
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
- 4.10. Расчетные диаграммы фильтров нижних частот
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
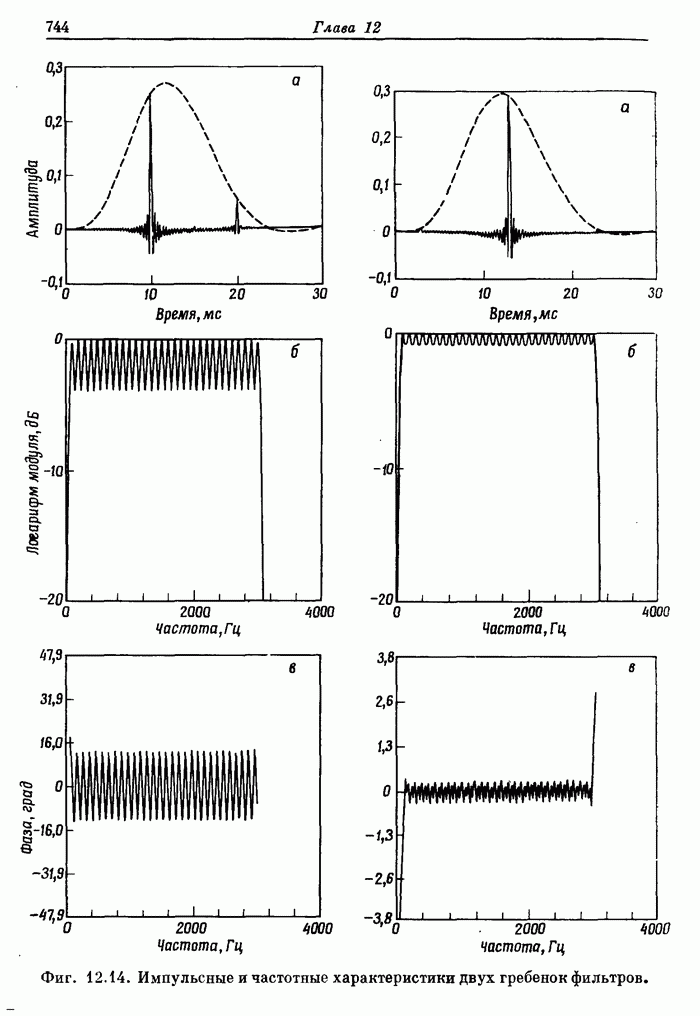
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
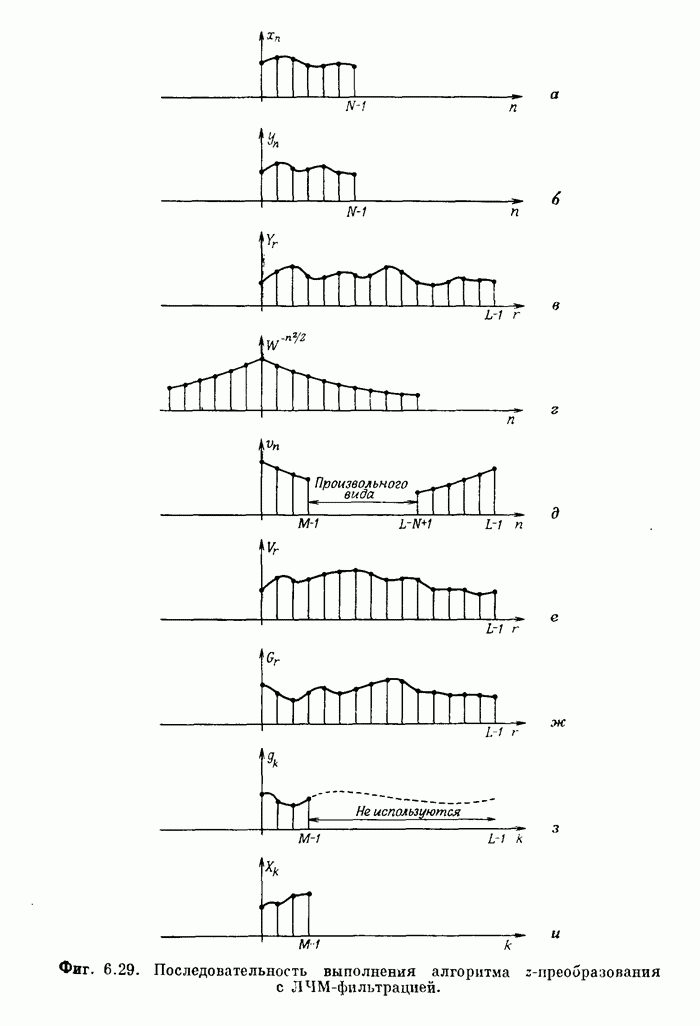
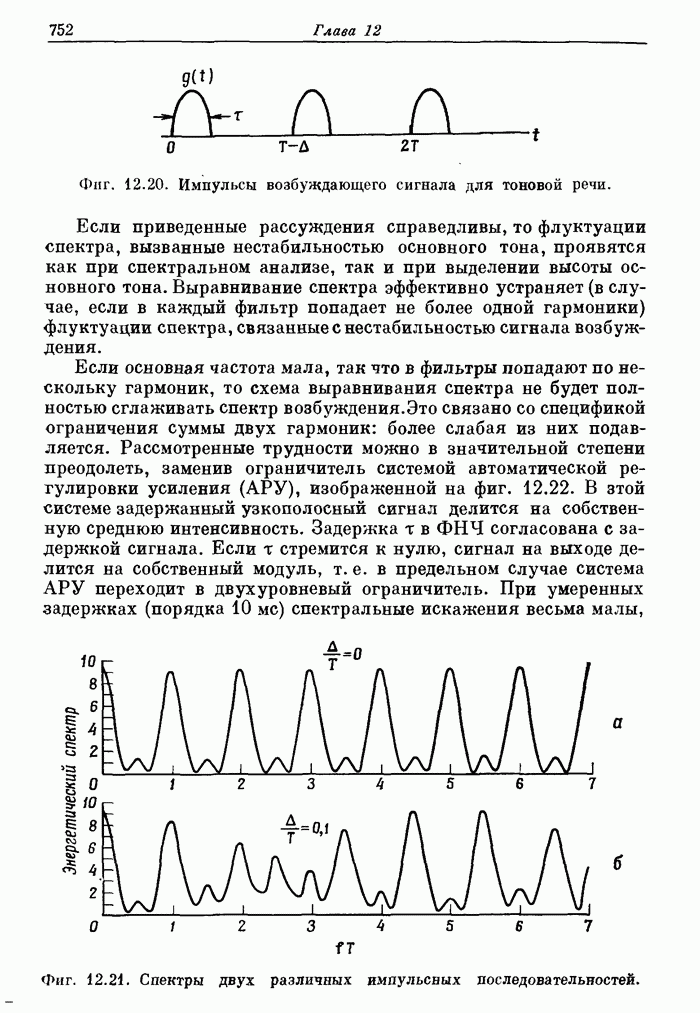
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
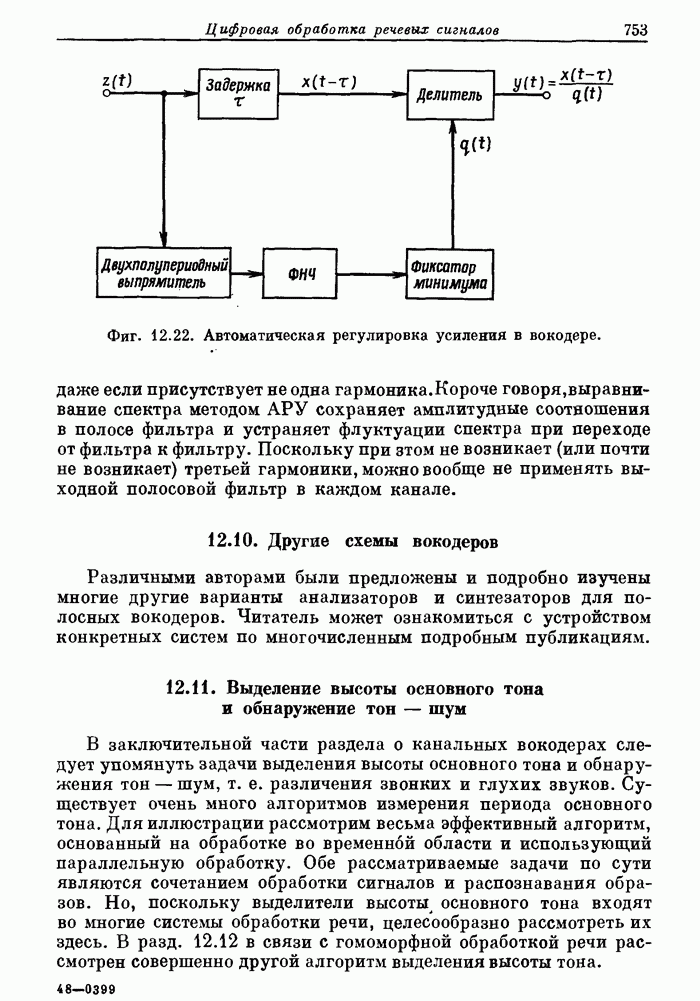
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
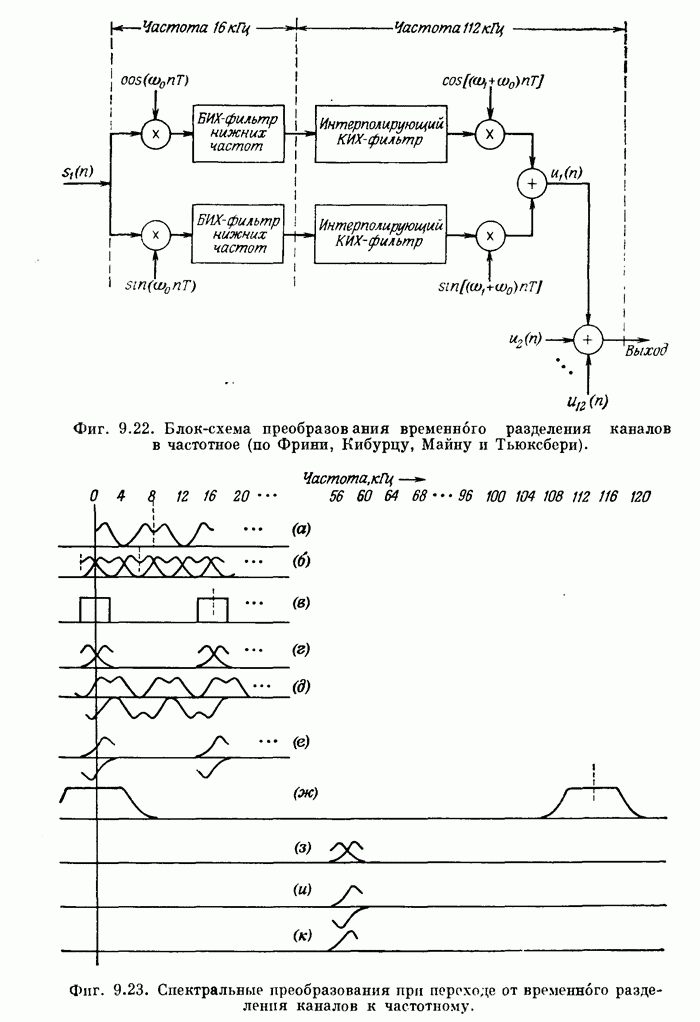
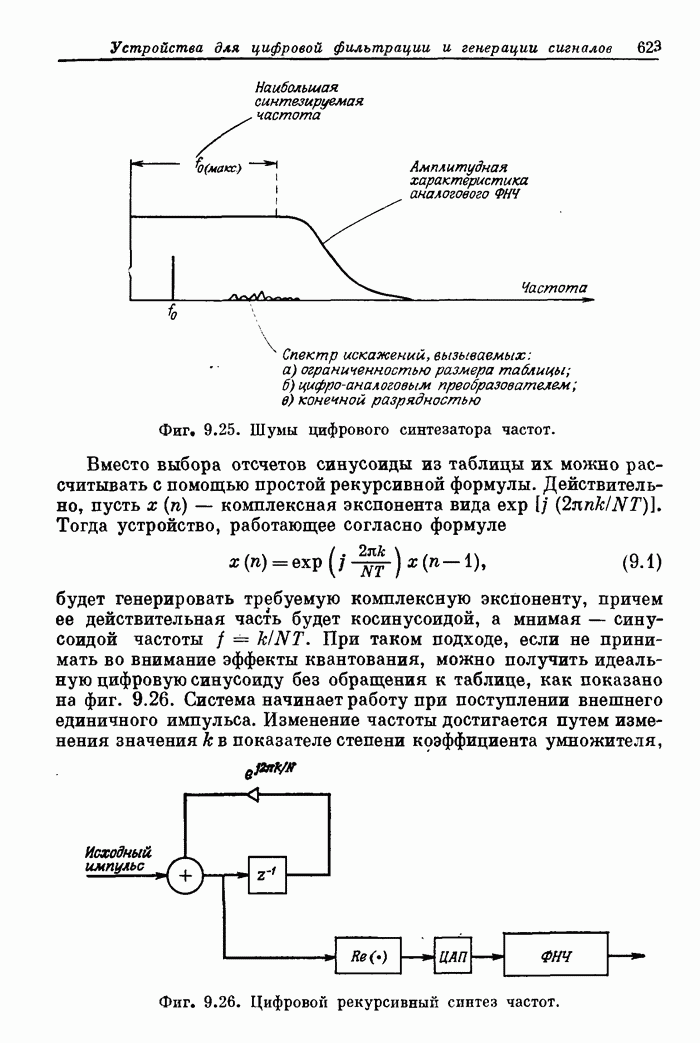
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
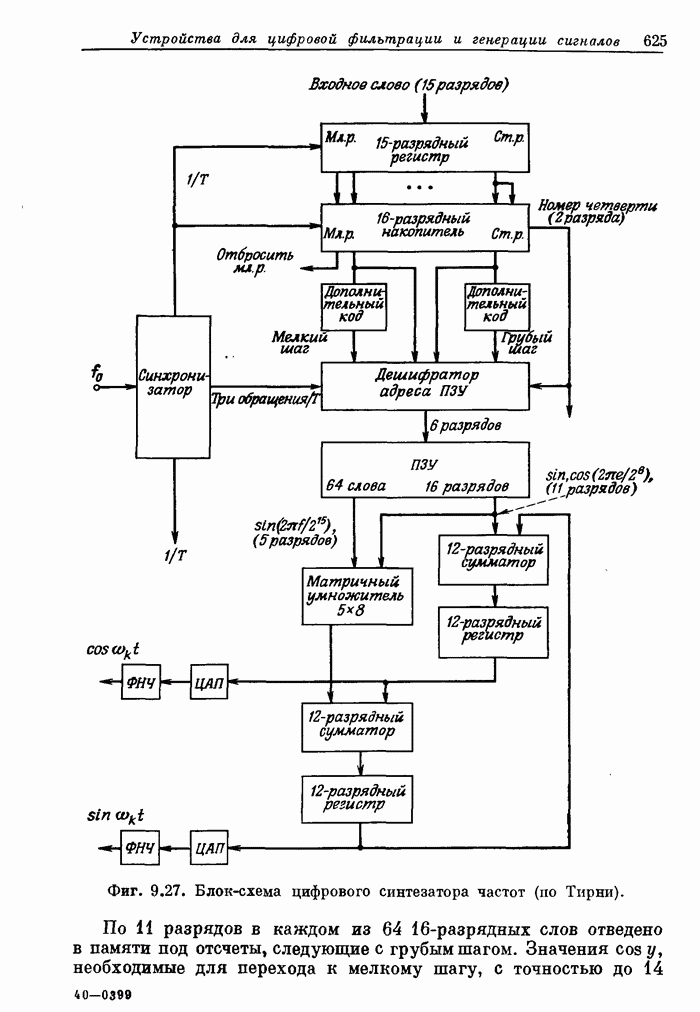
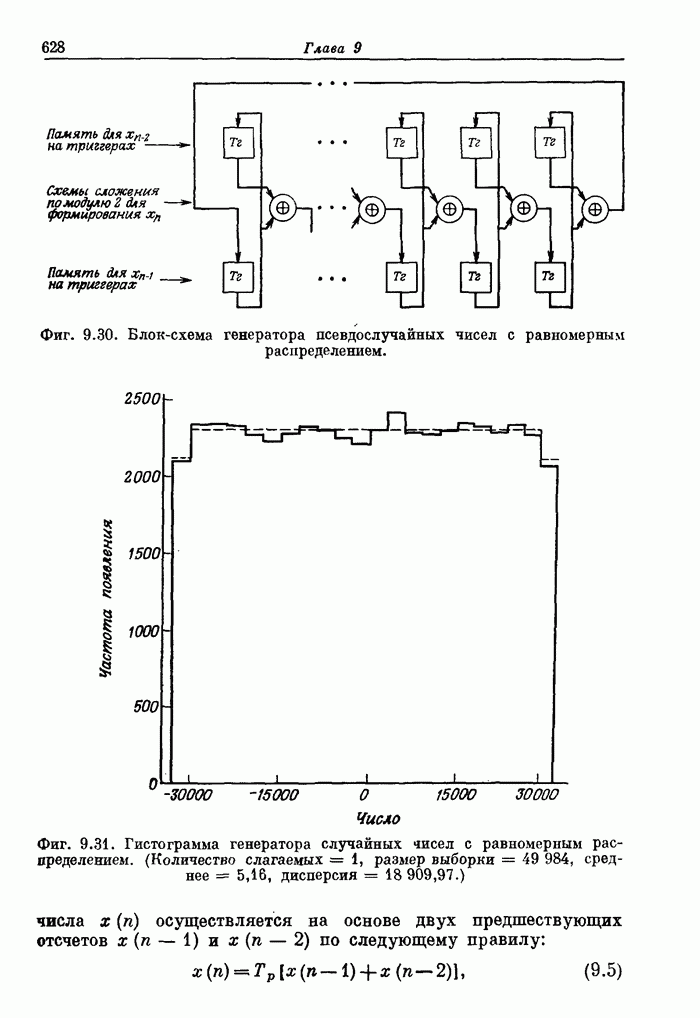
- 9.12. Специализированный цифровой синтезатор частот
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
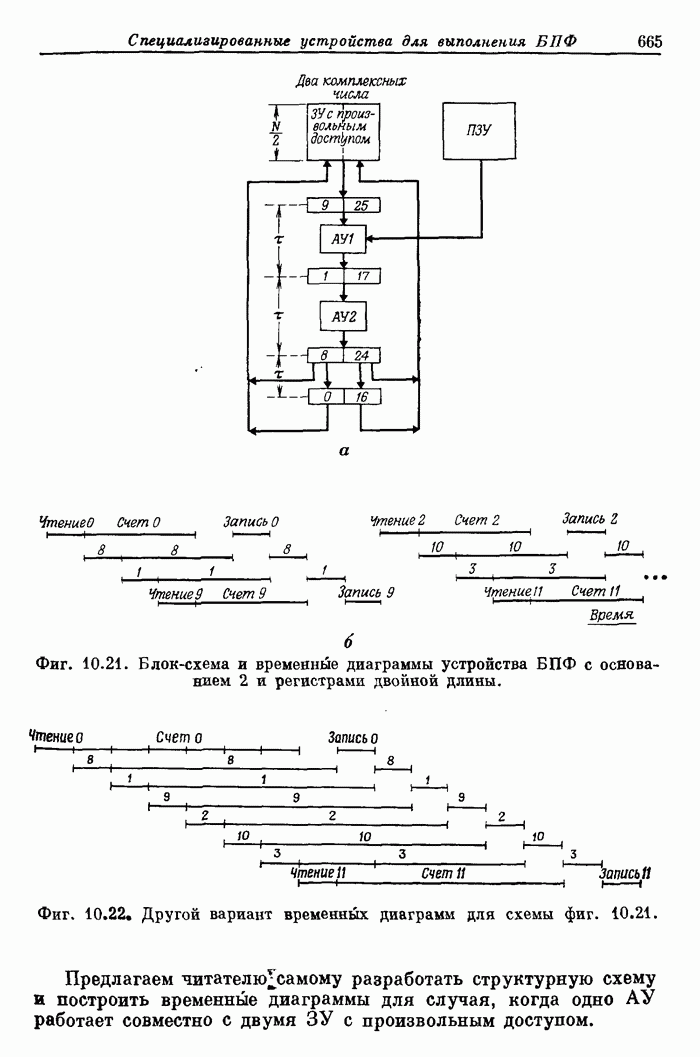
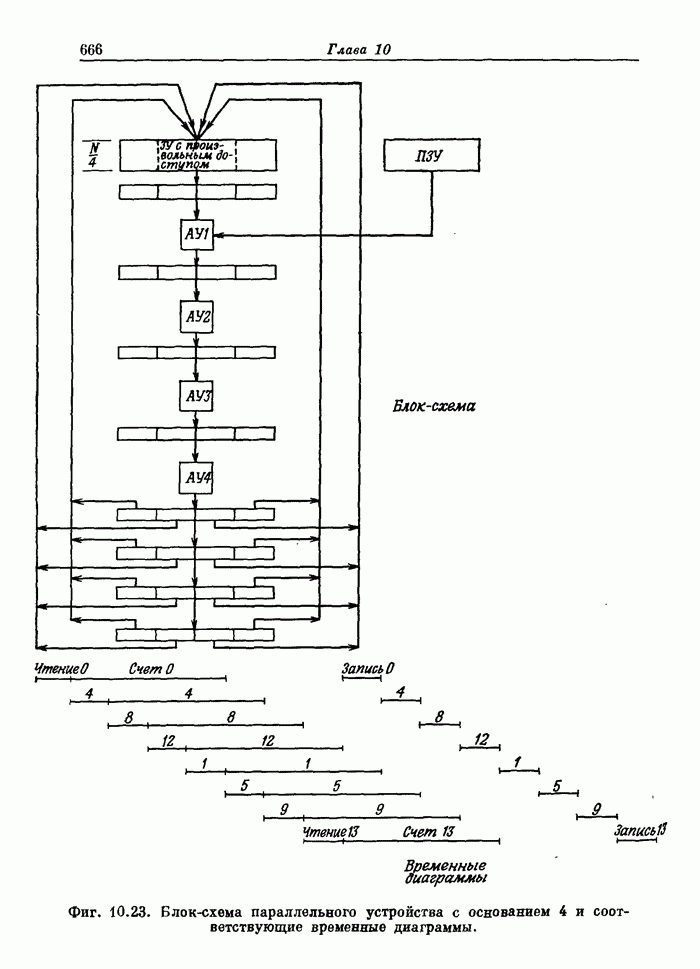
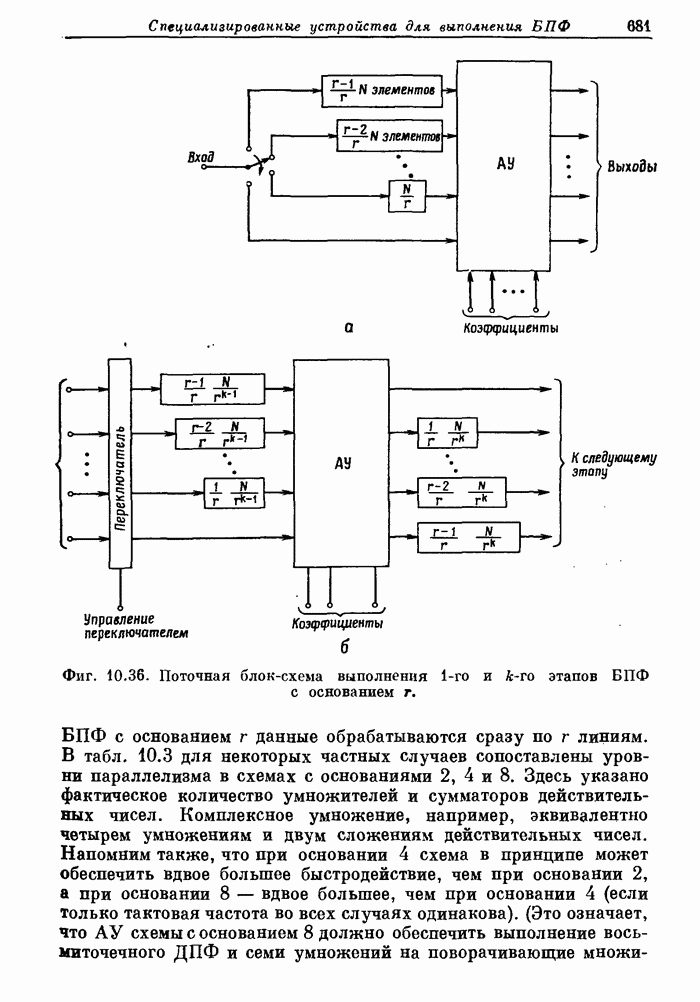
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
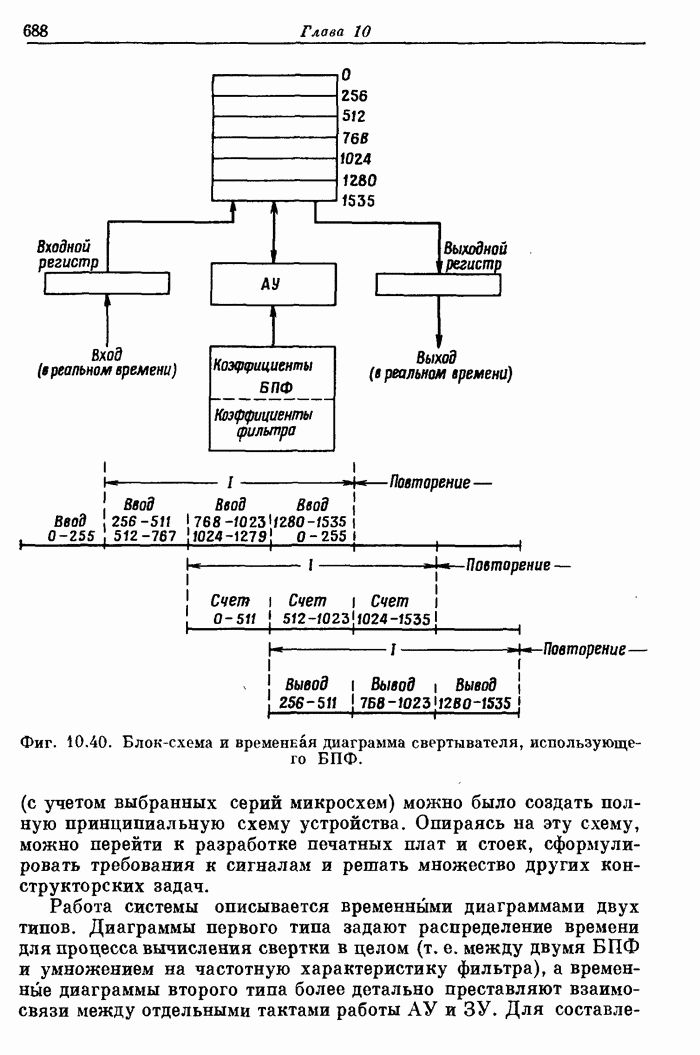
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
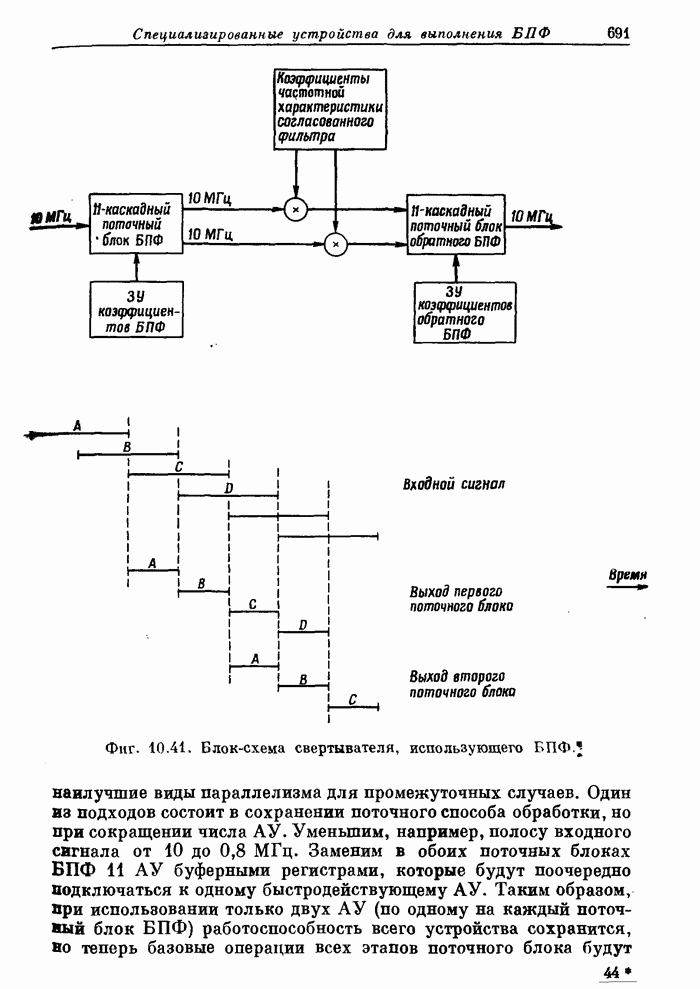
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
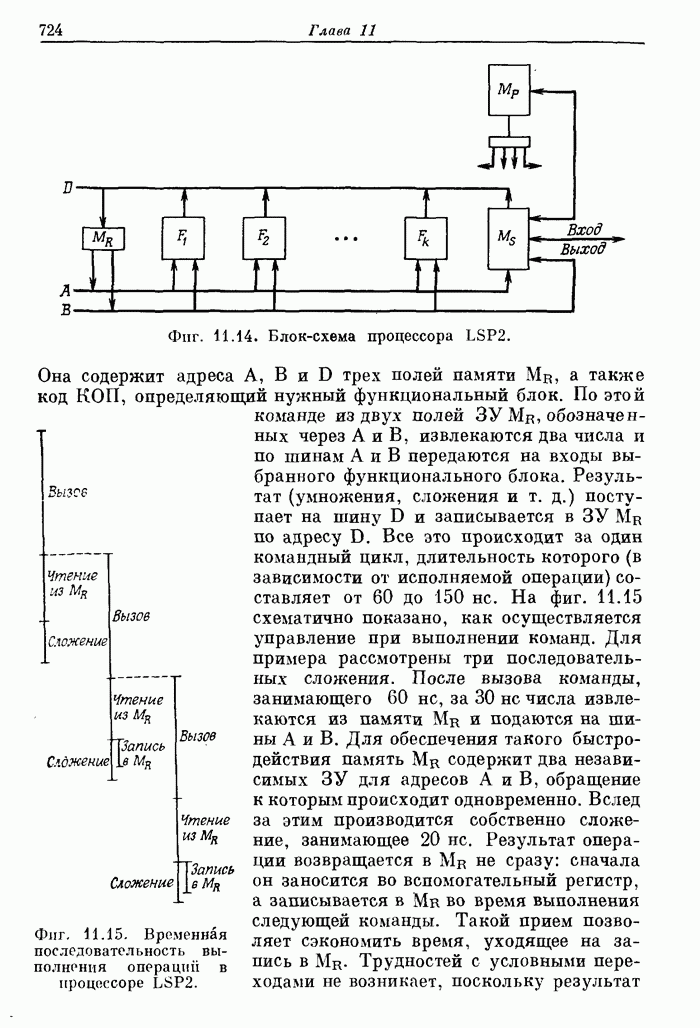
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
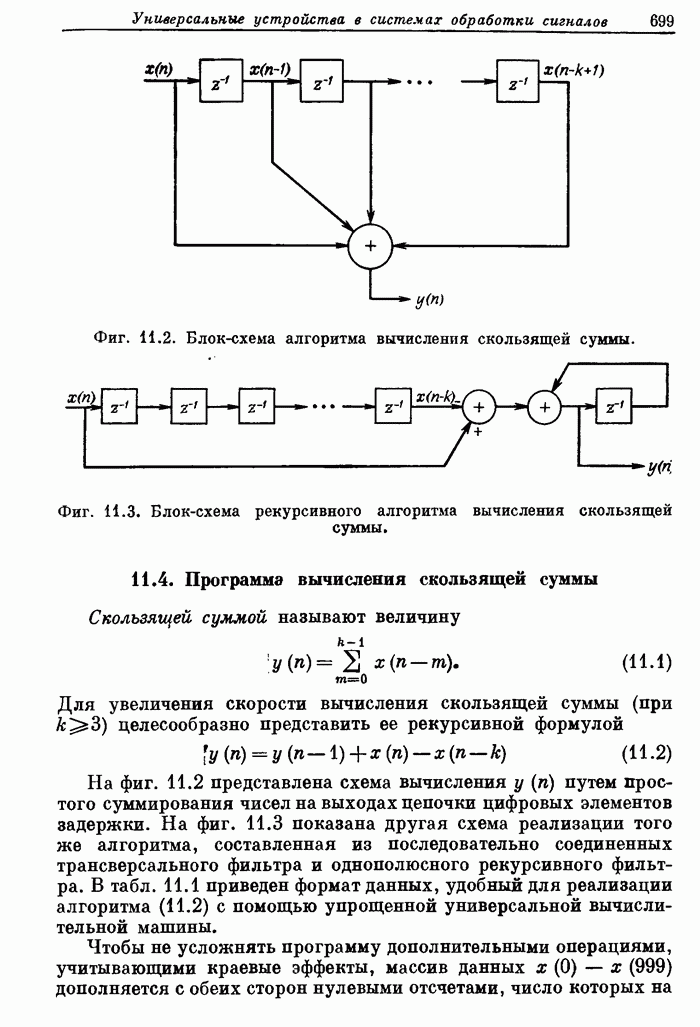
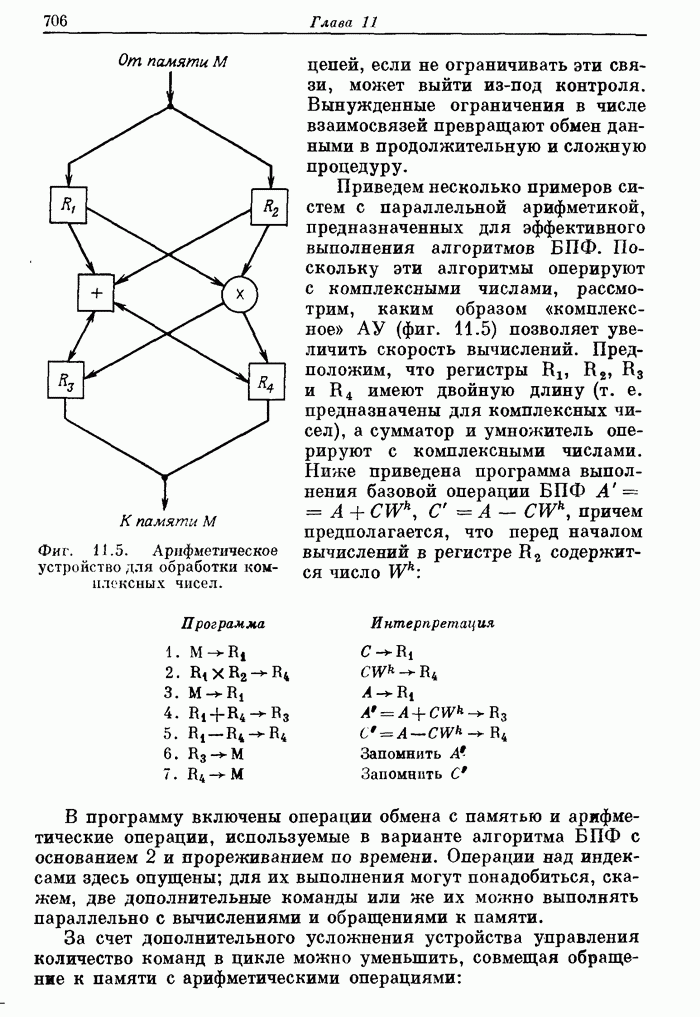
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
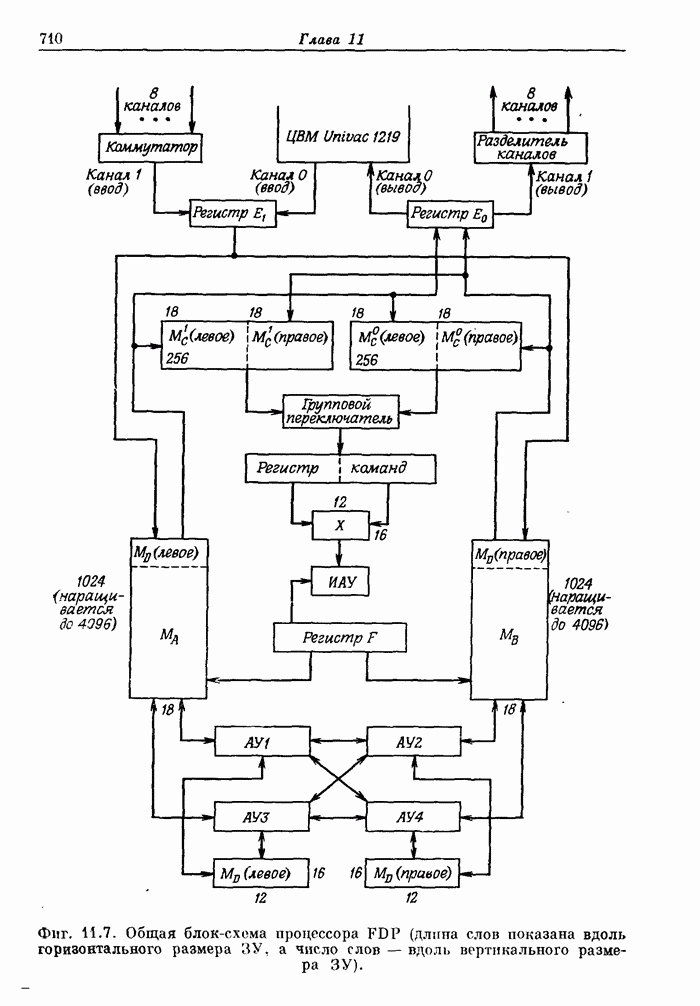
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
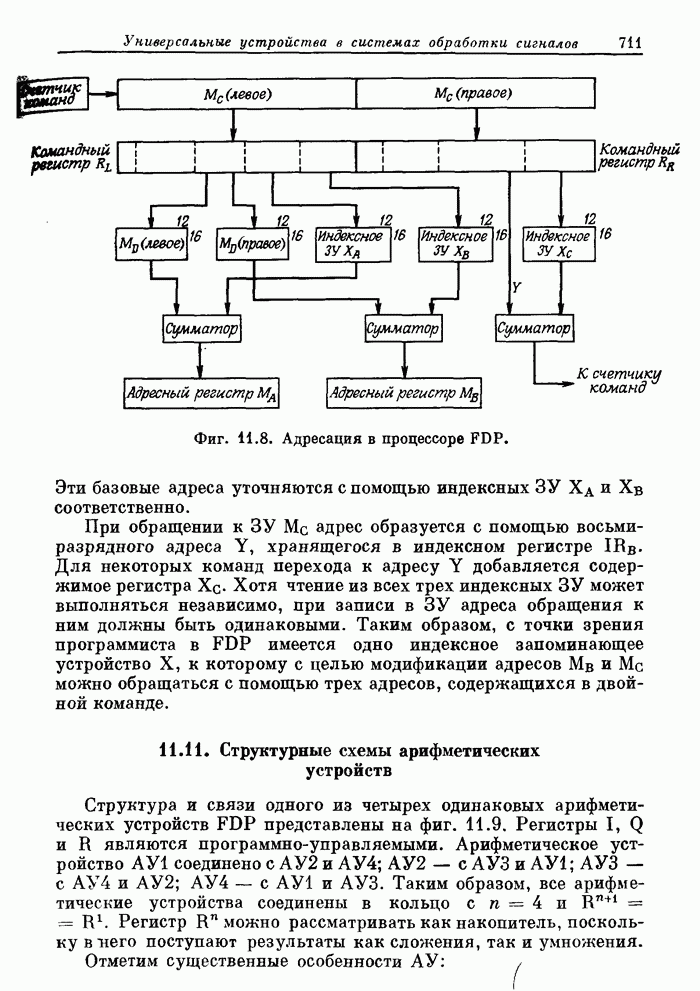
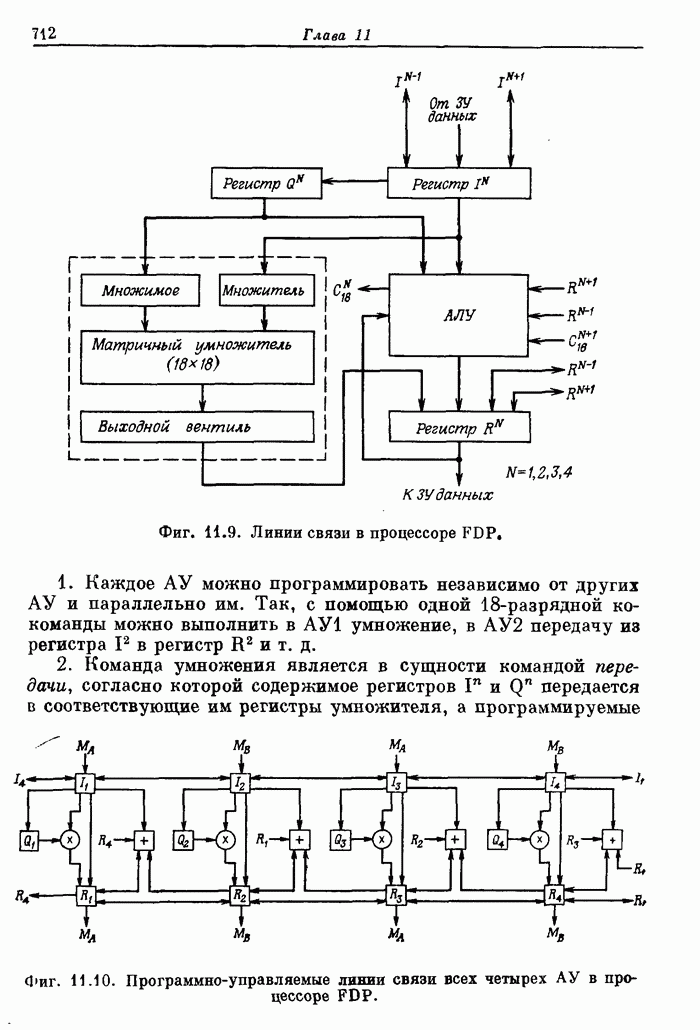
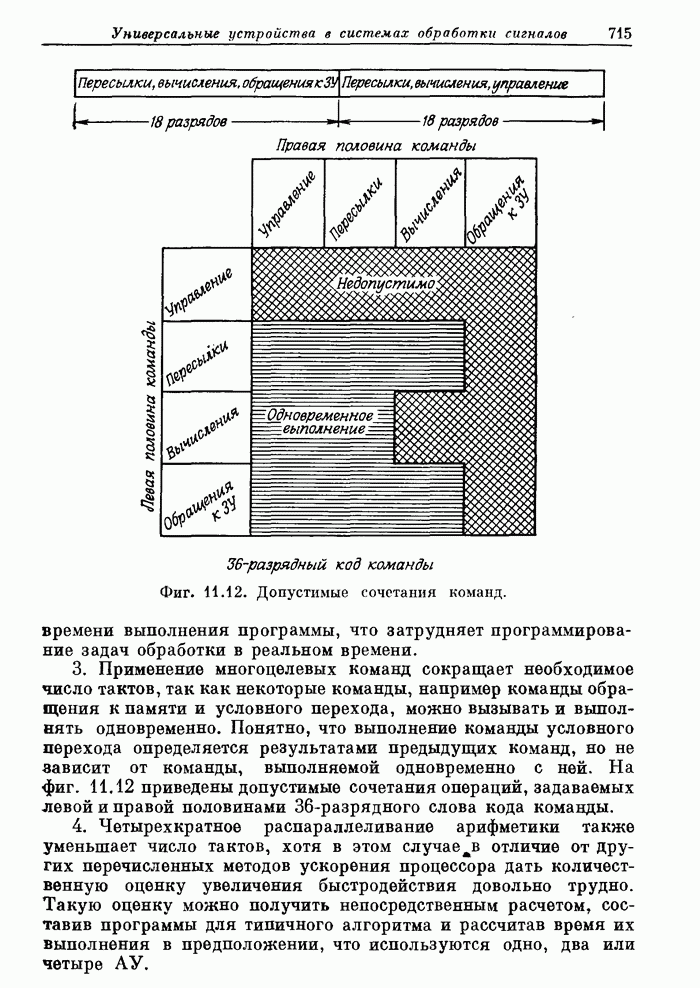
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
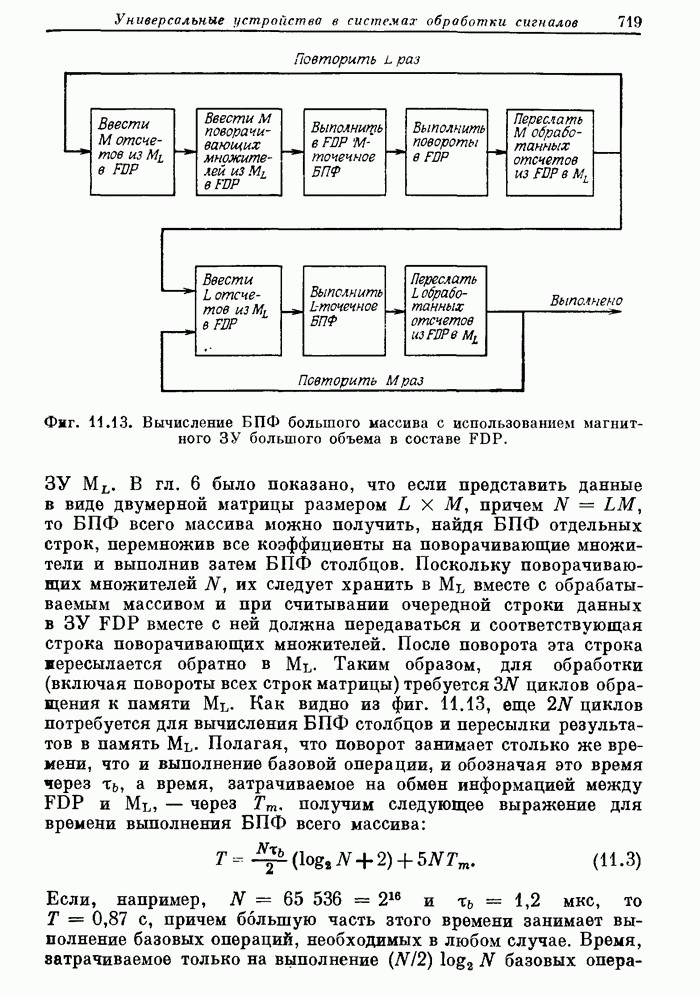
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
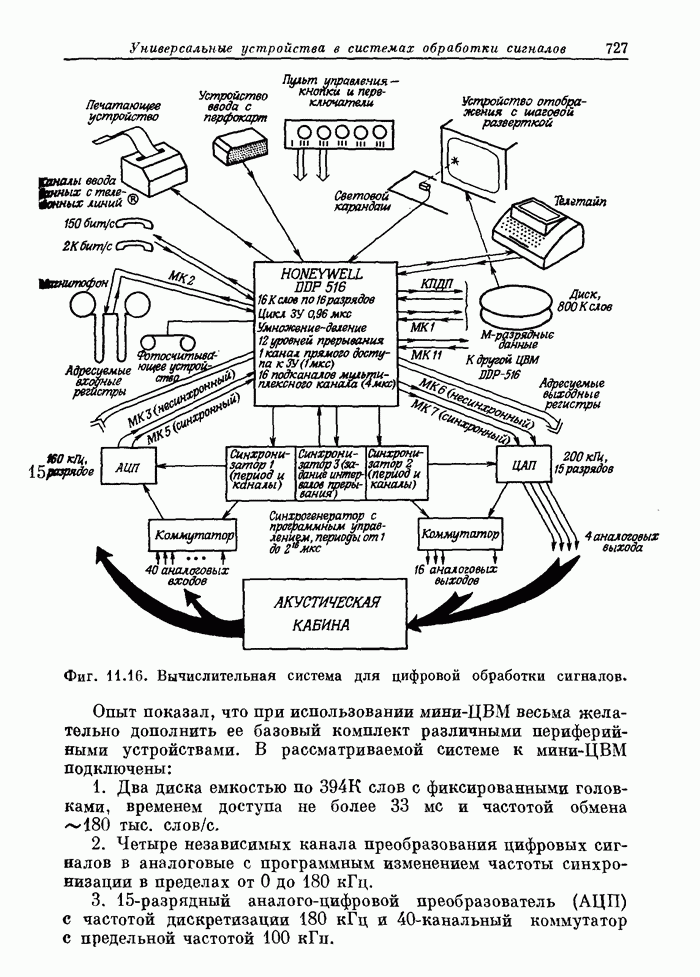
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
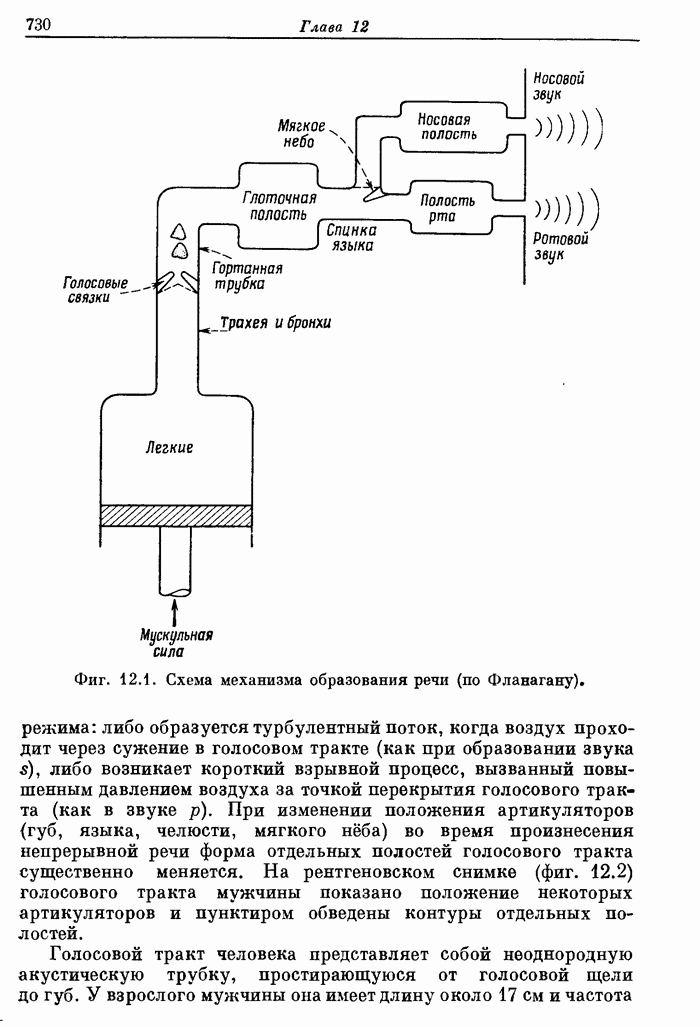
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
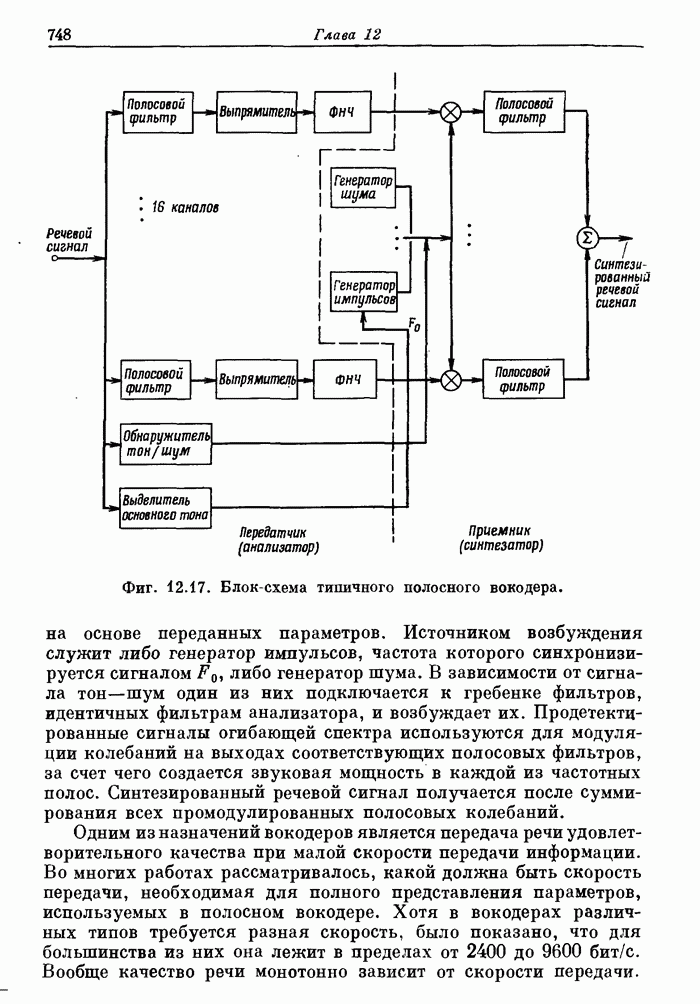
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
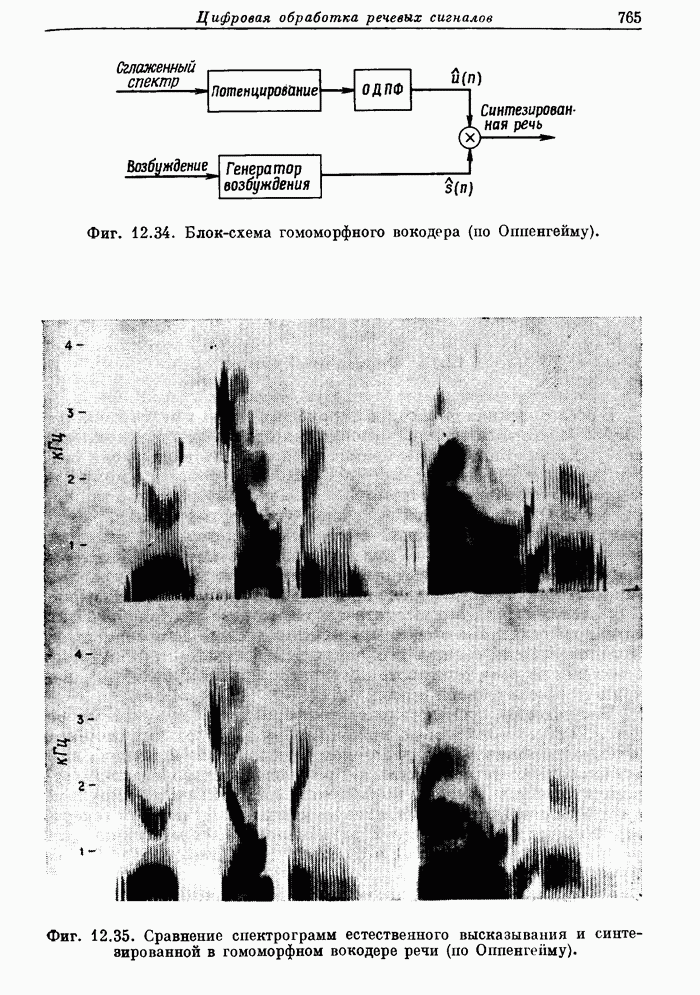
- 12.14. Гомоморфный вокодер
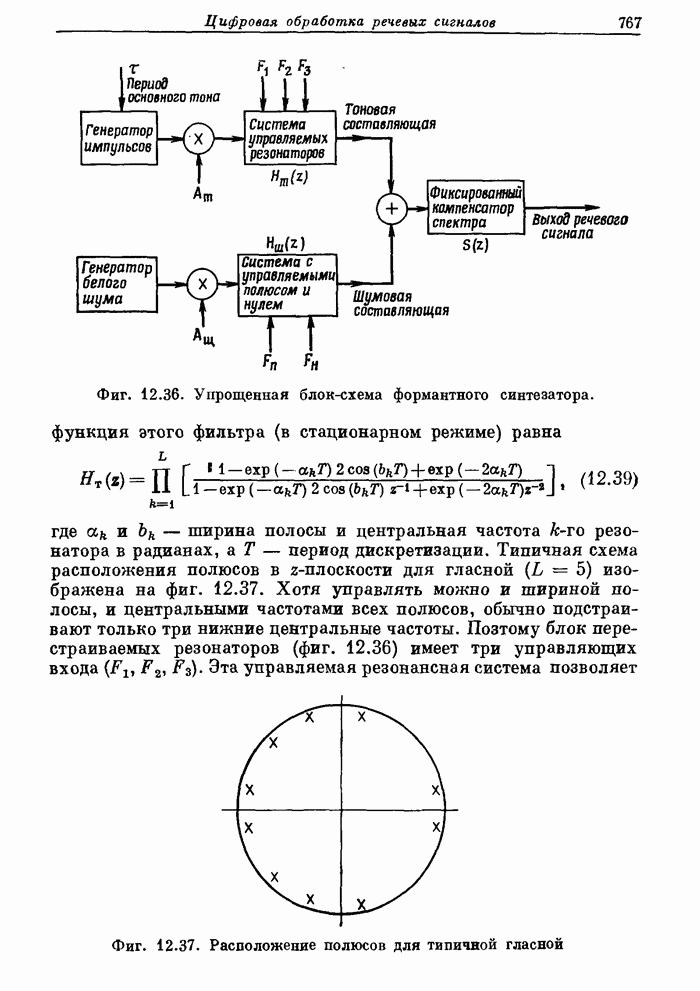
- 12.15. Формантный синтез
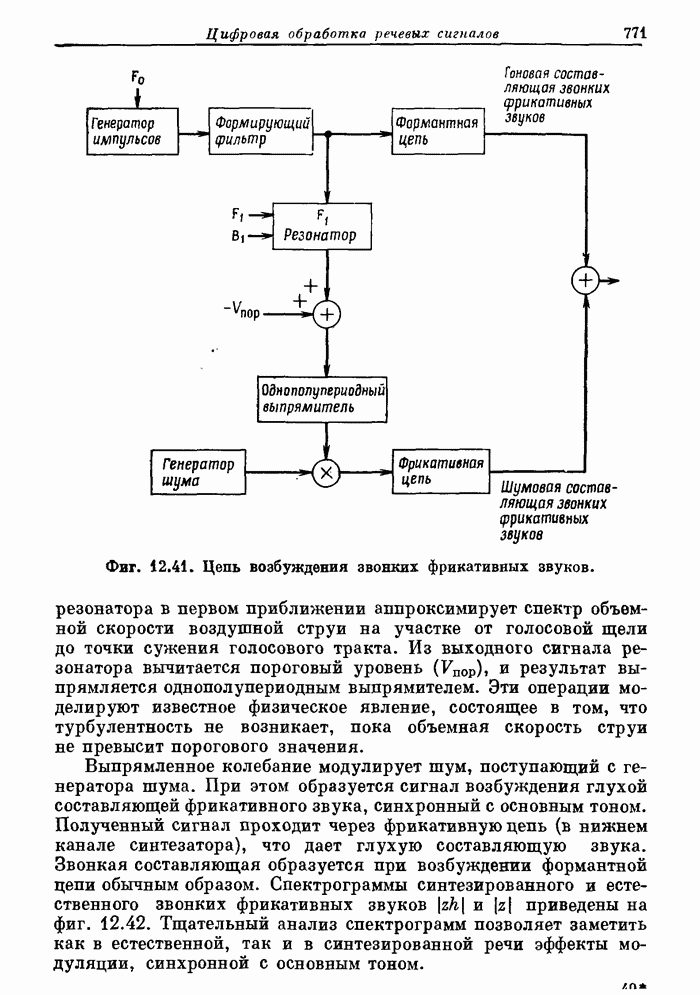
- 12.16. Цепь возбуждения звонких фрикативных звуков
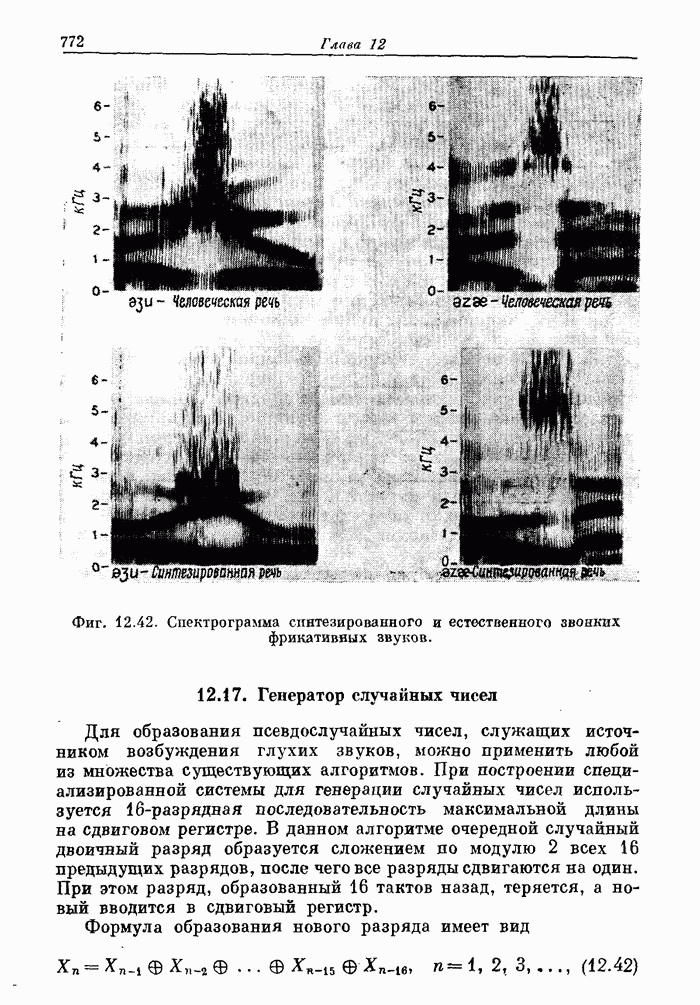
- 12.17. Генератор случайных чисел
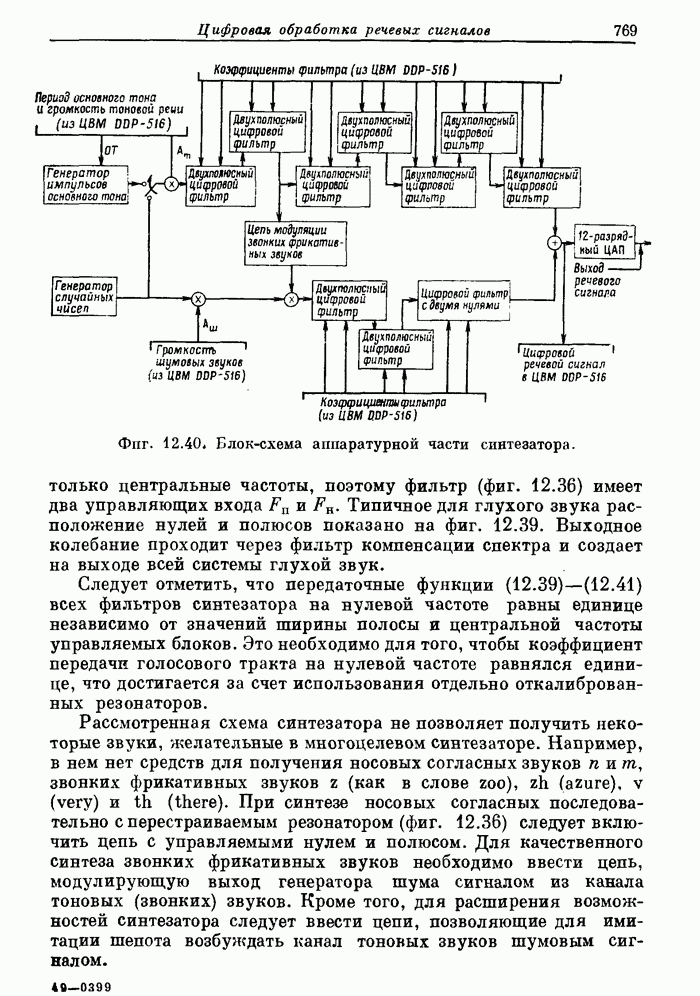
- 12.18. Цифровая обработка в формантном синтезаторе
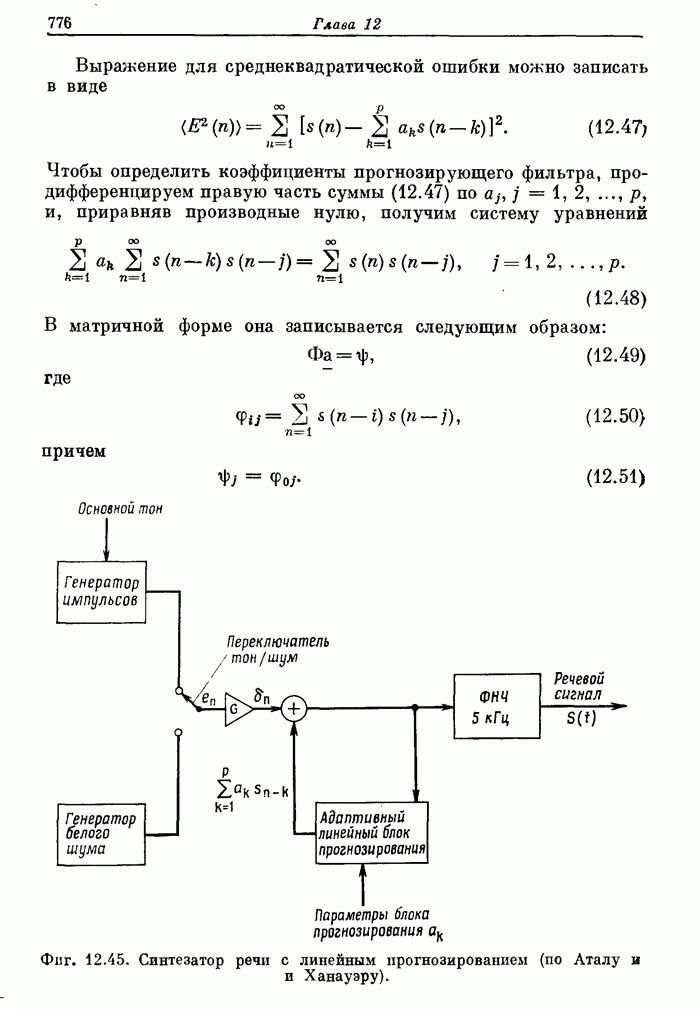
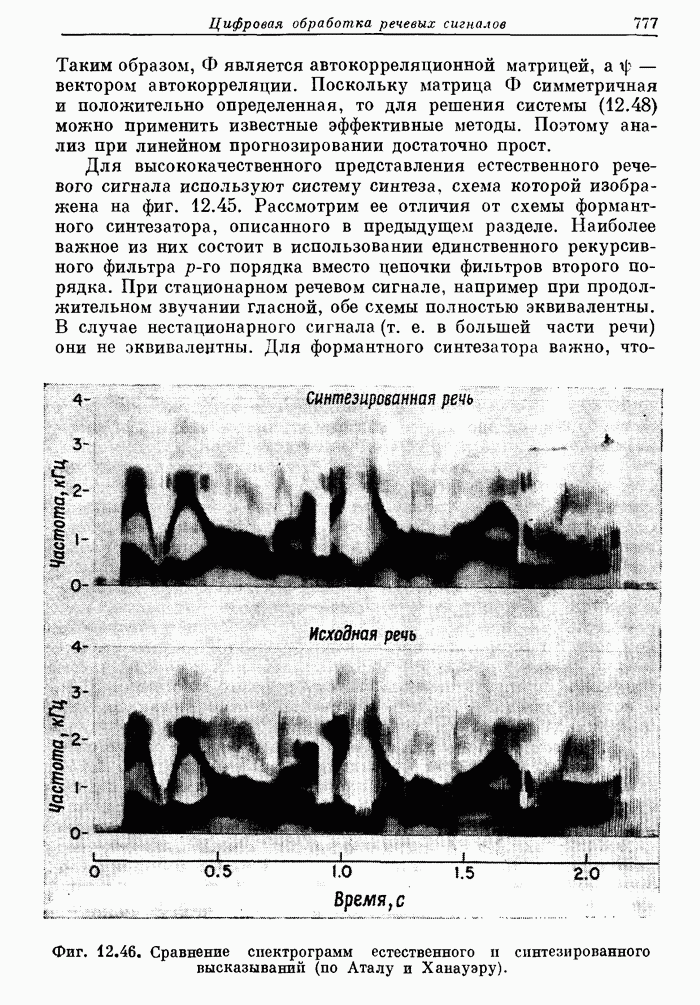
- 12.19. Линейное прогнозирование речи
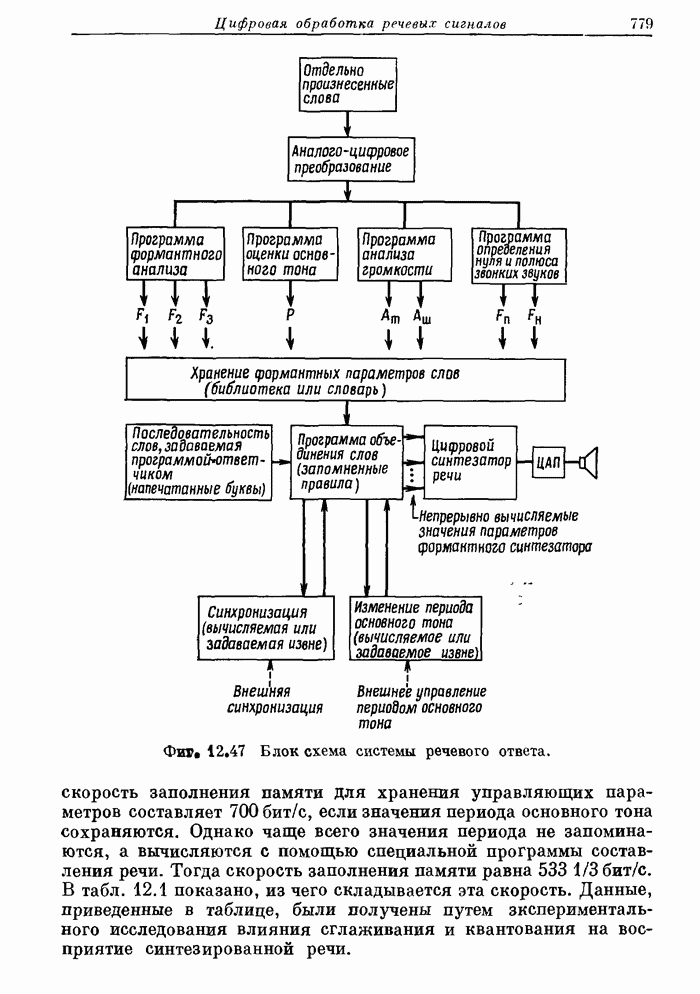
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
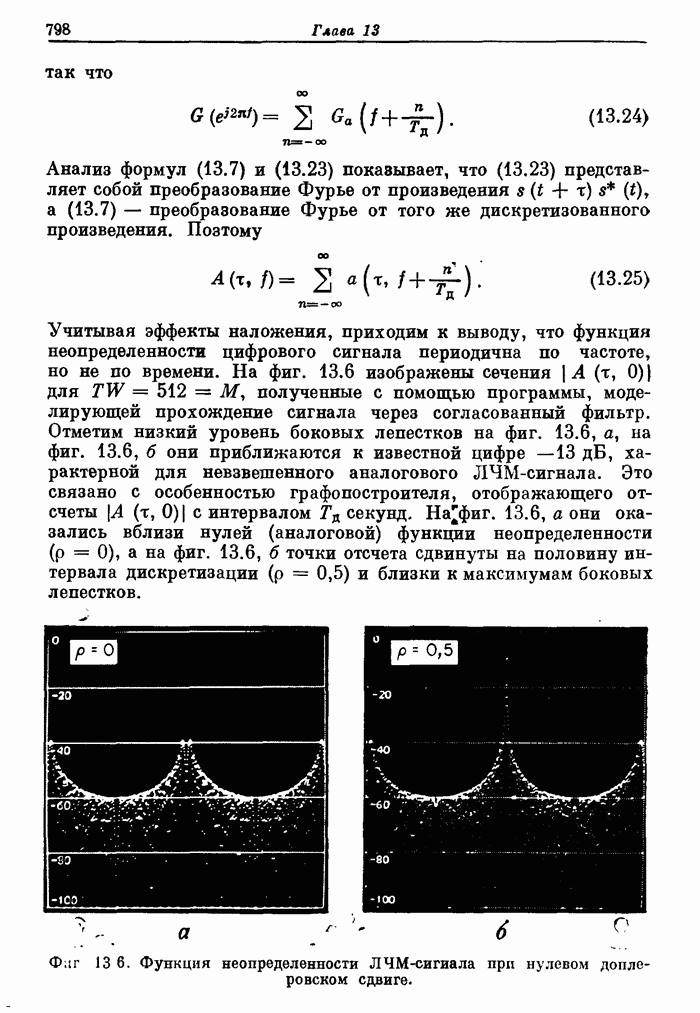
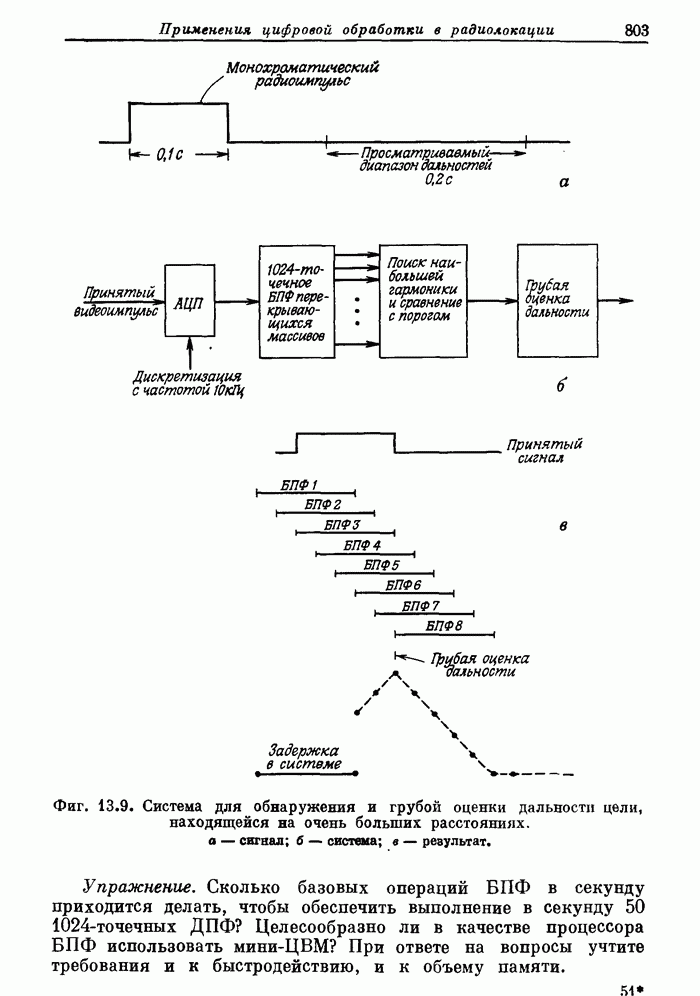
- 13.3. Выбор сигналов и функция неопределенности
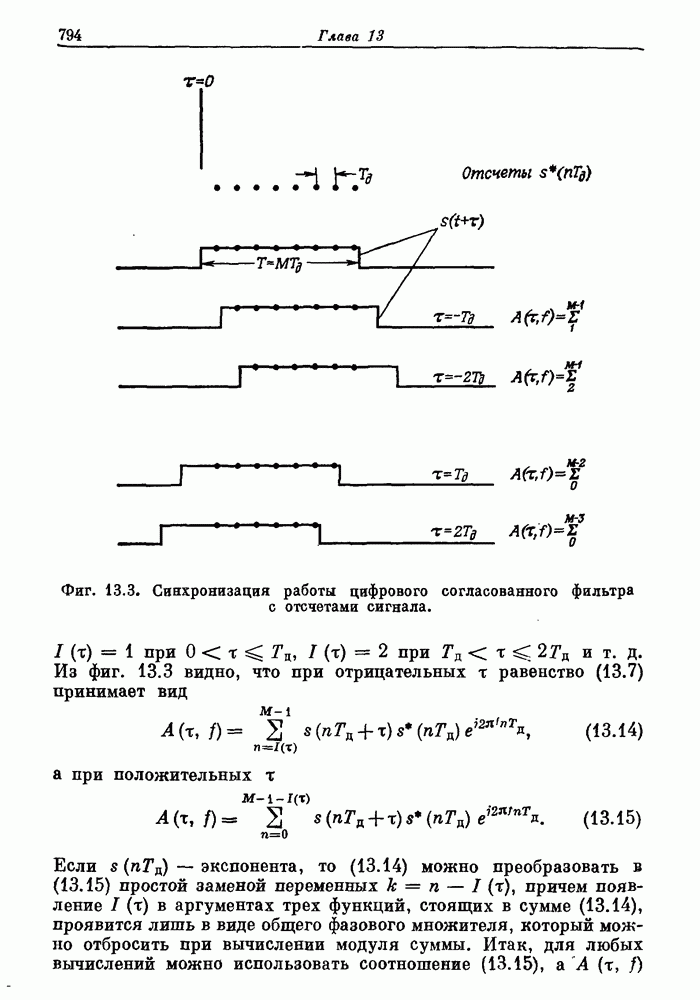
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение