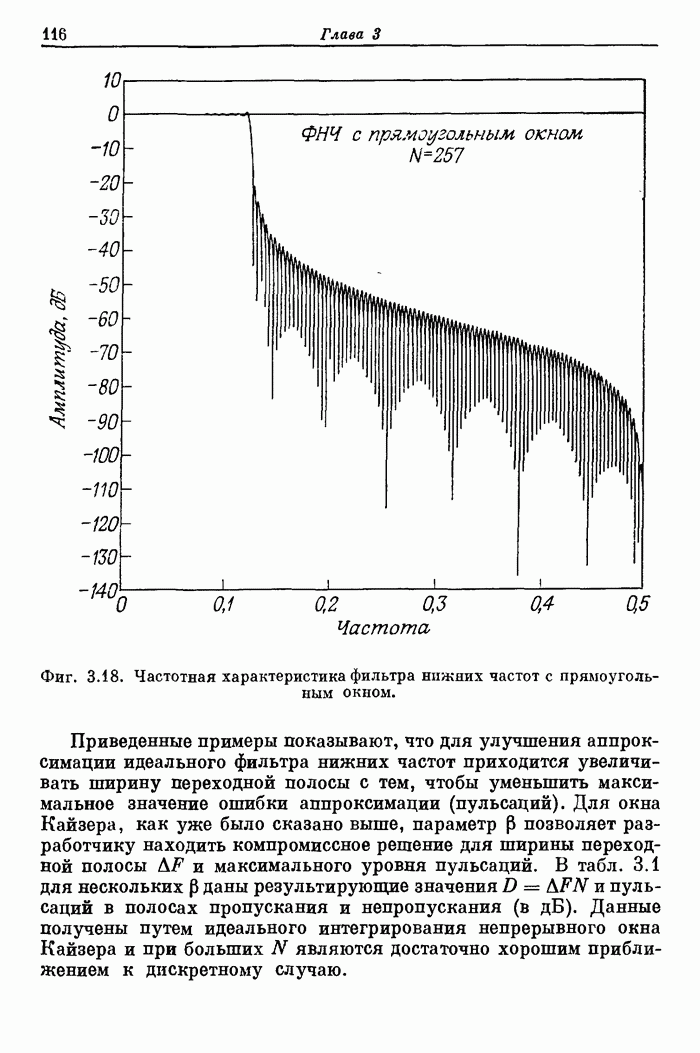
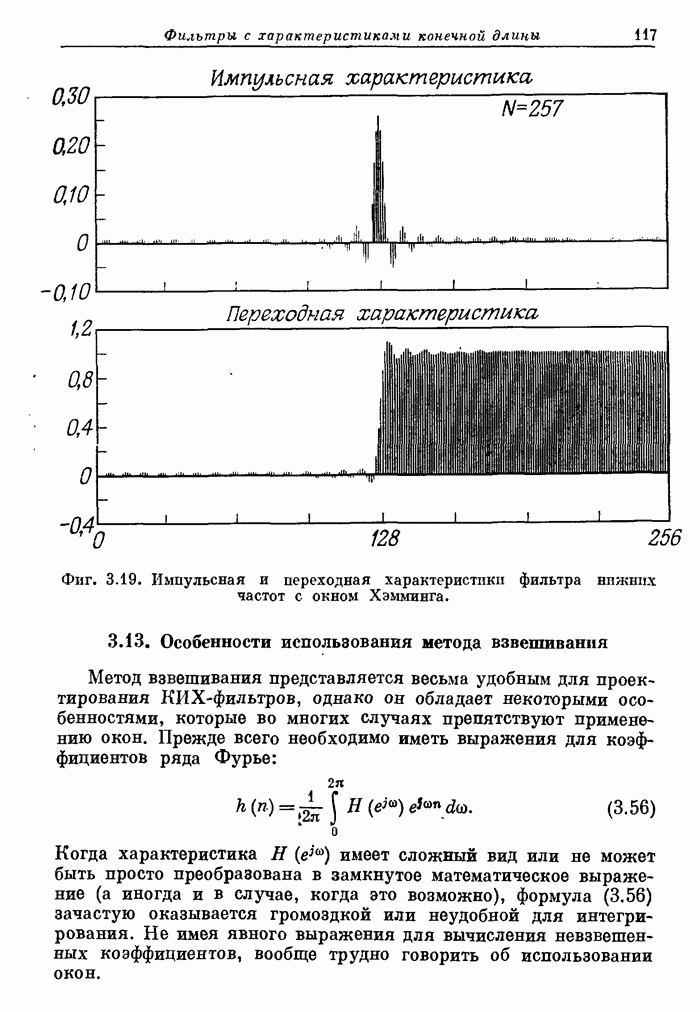
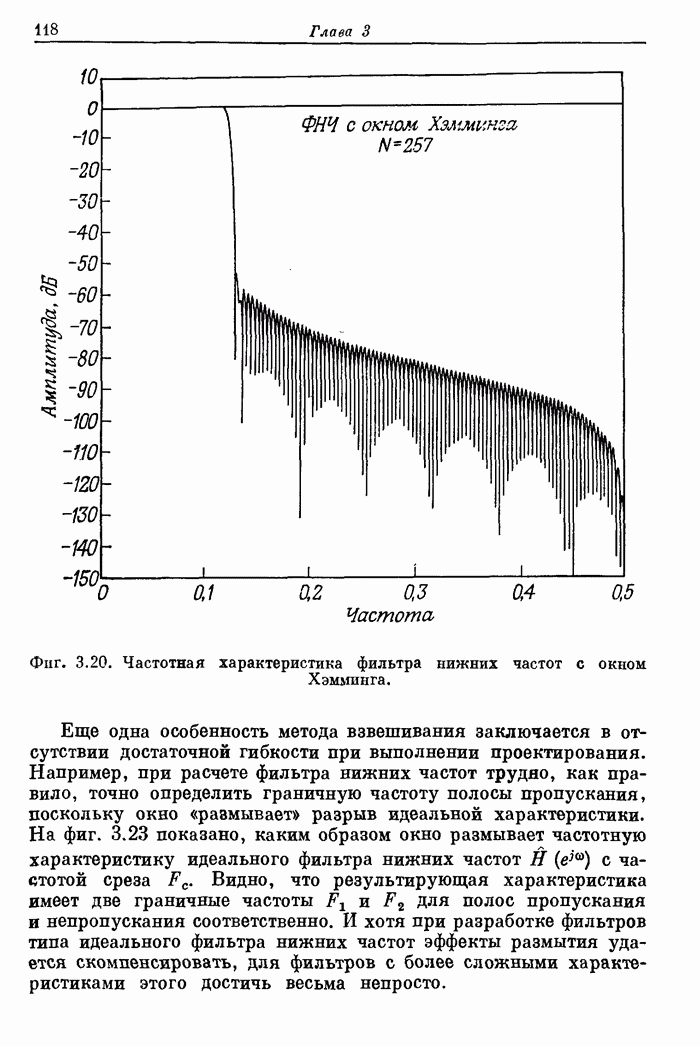
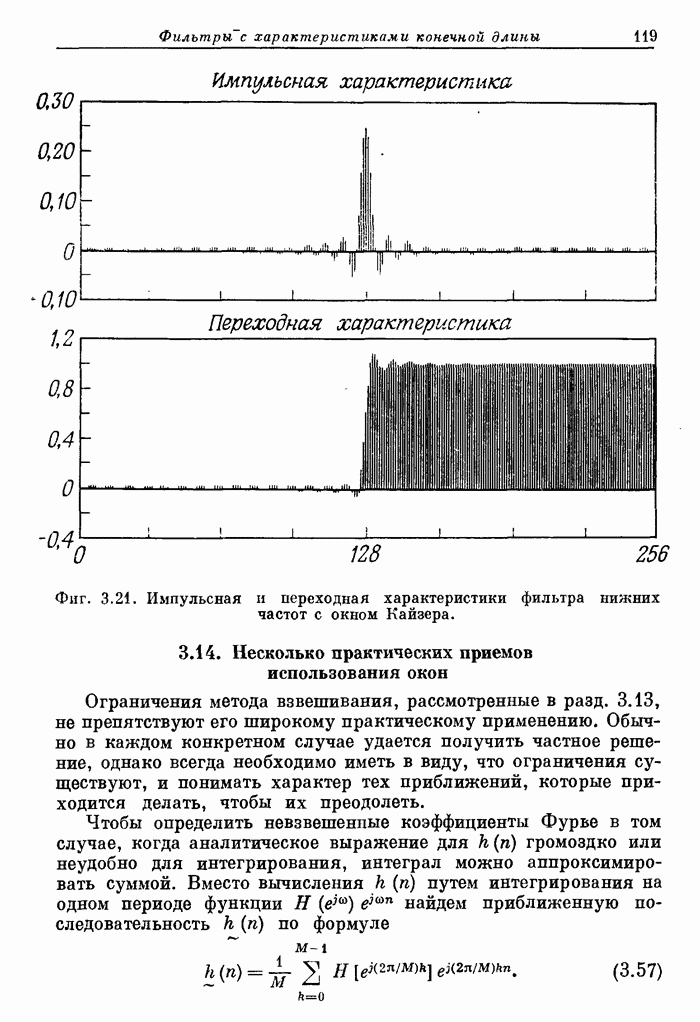
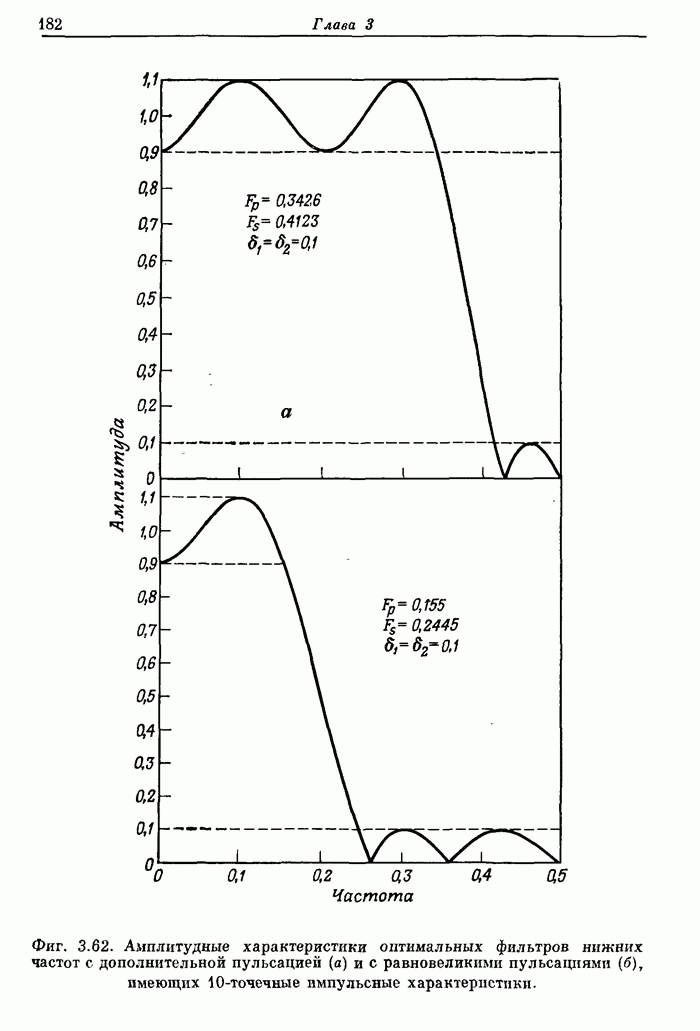
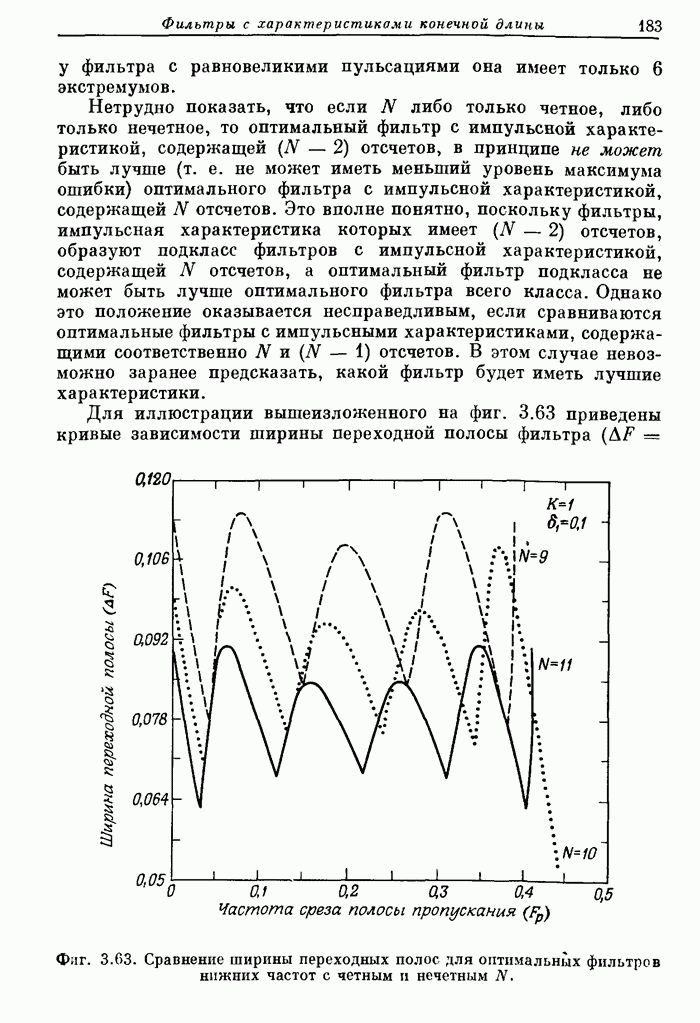
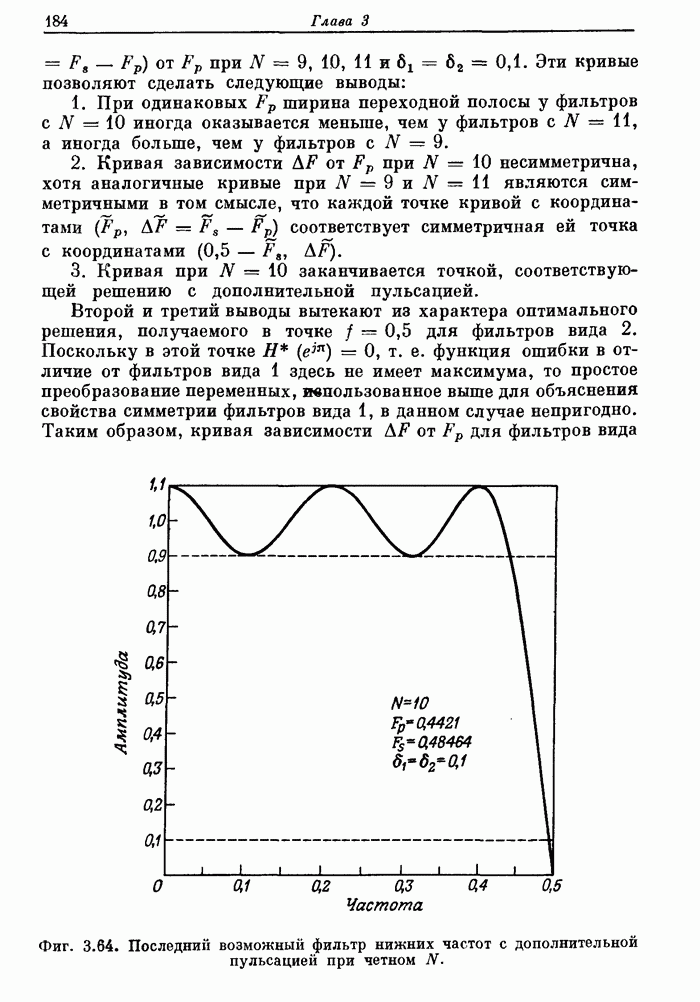
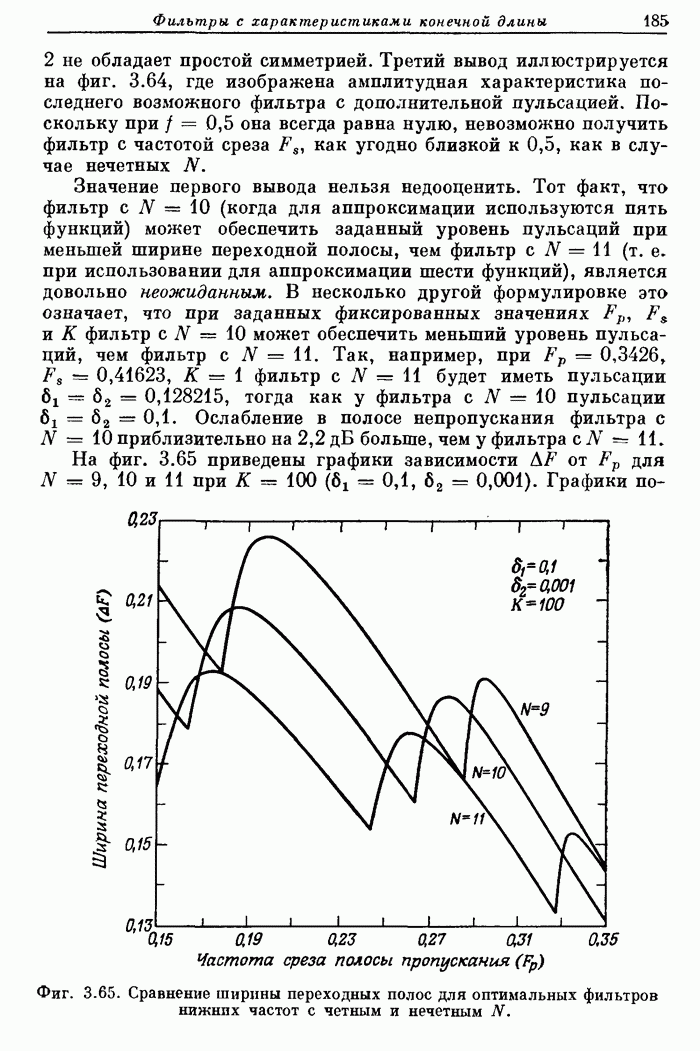
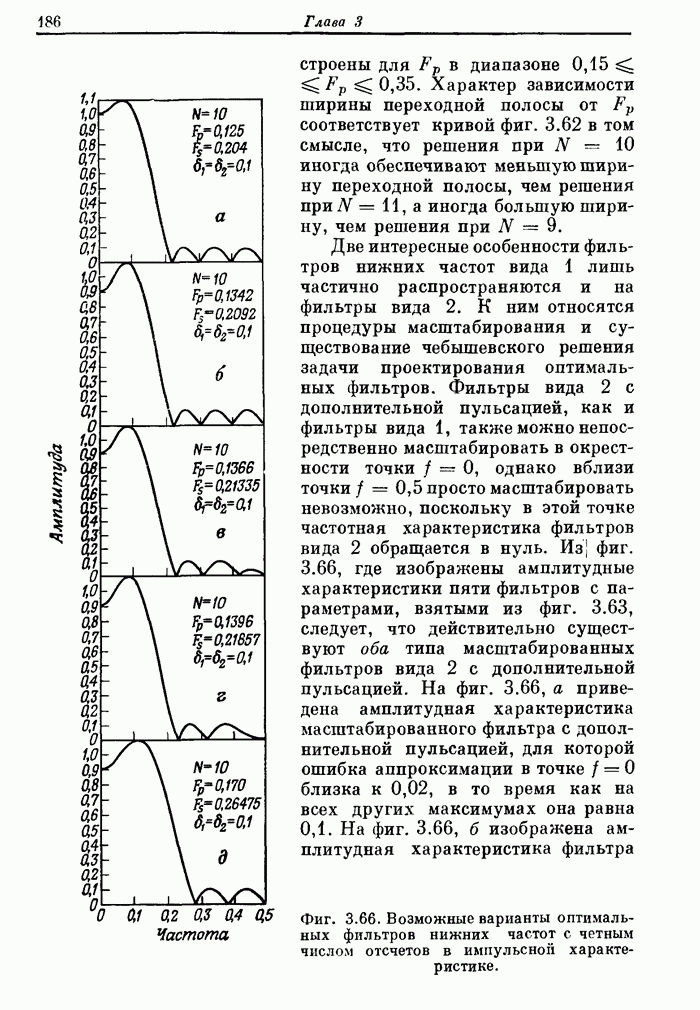
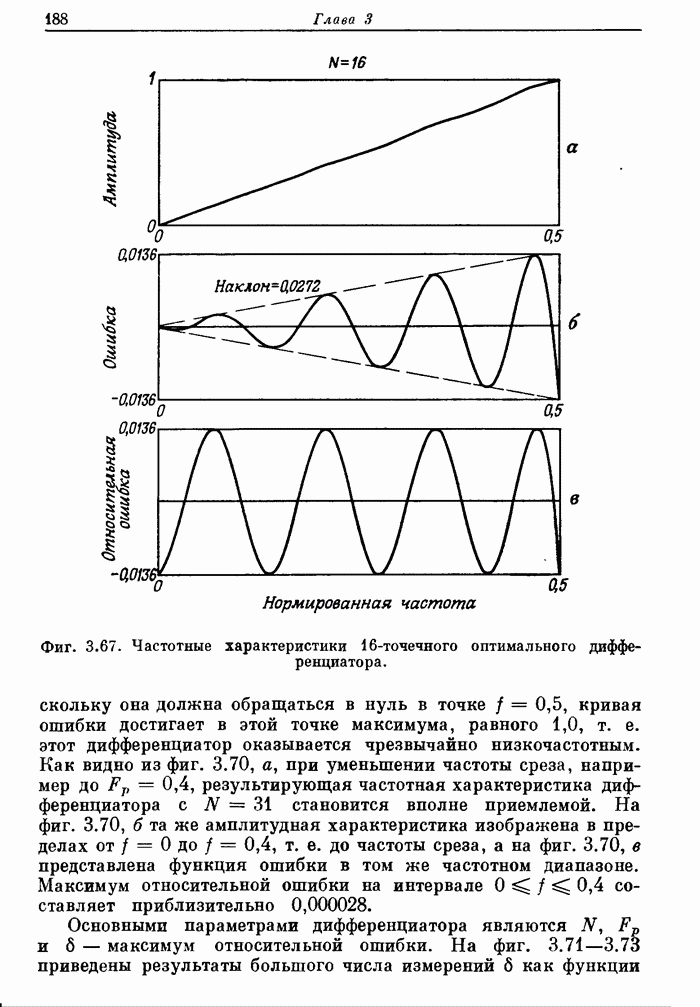
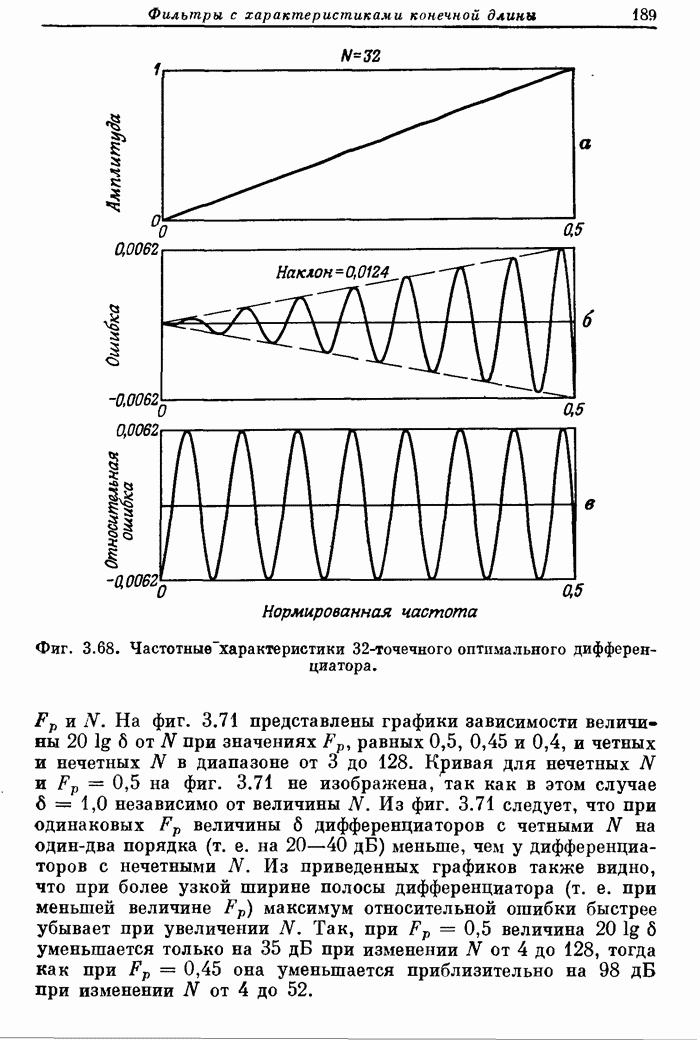
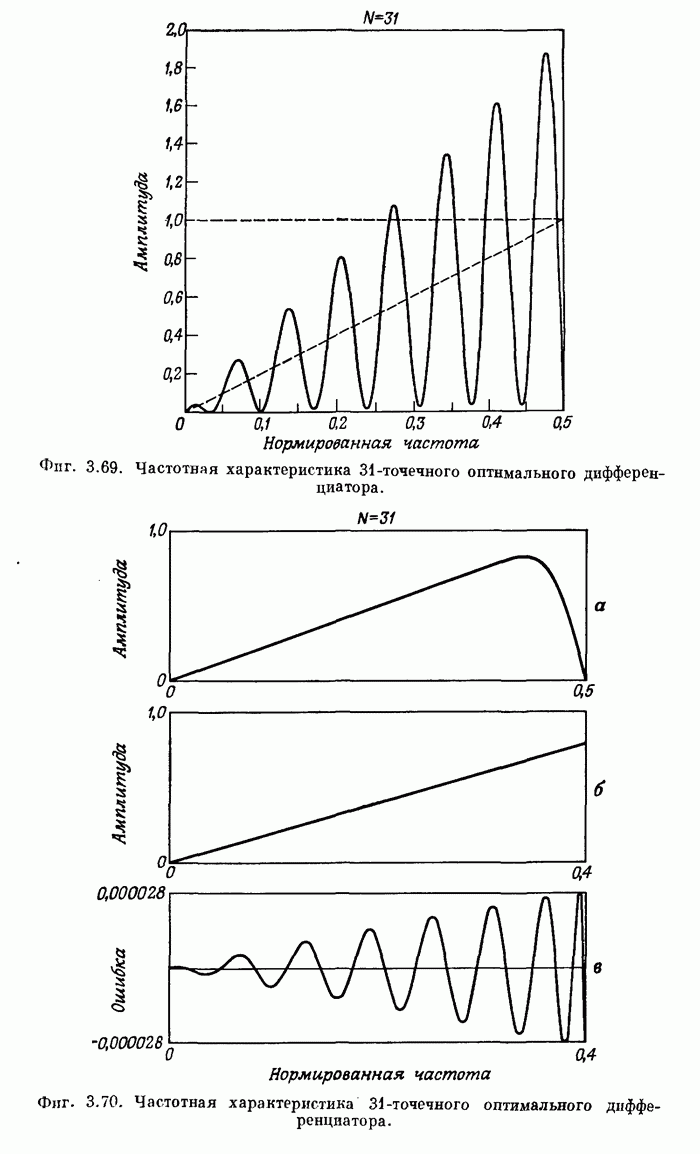
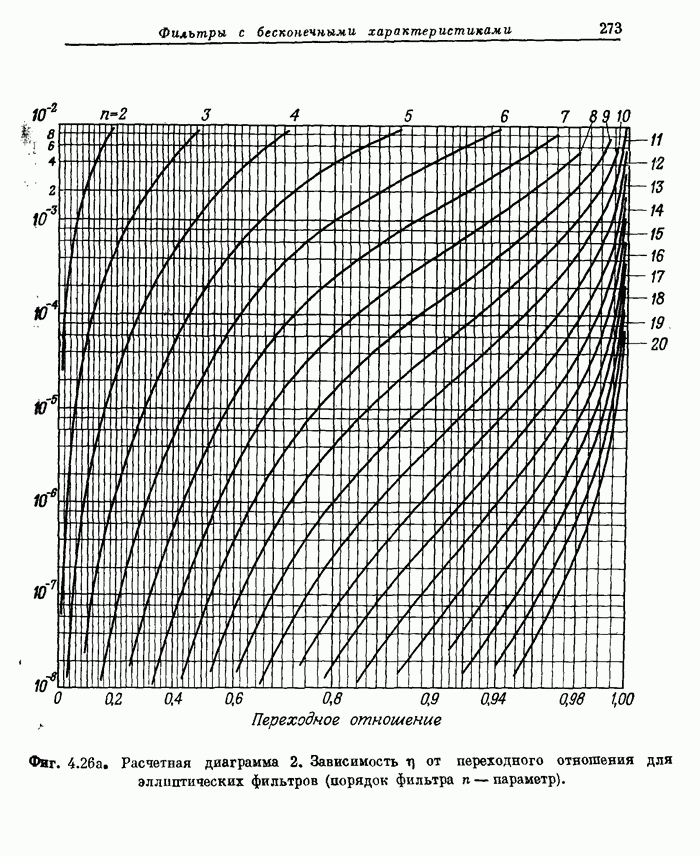
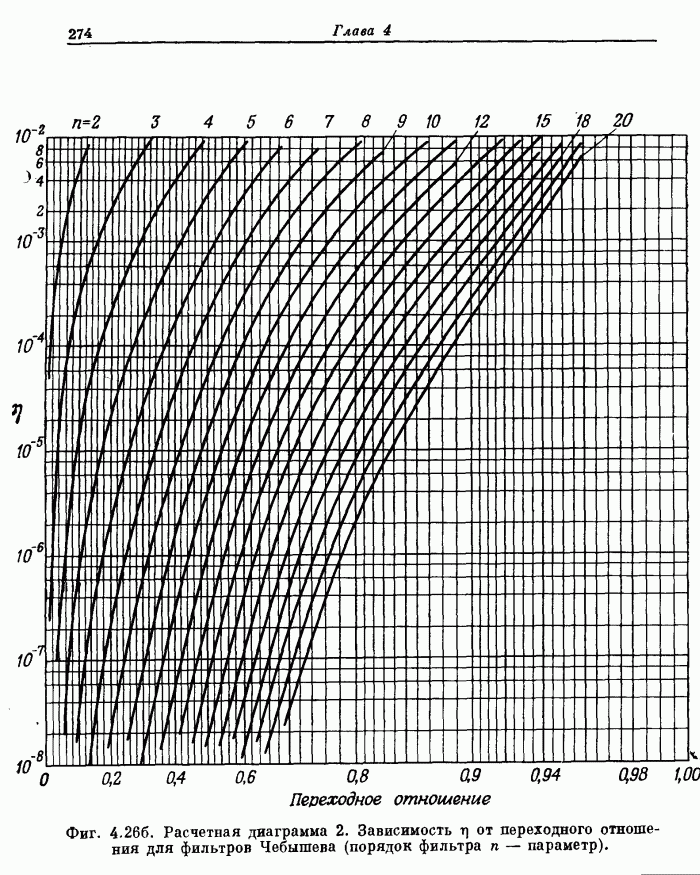
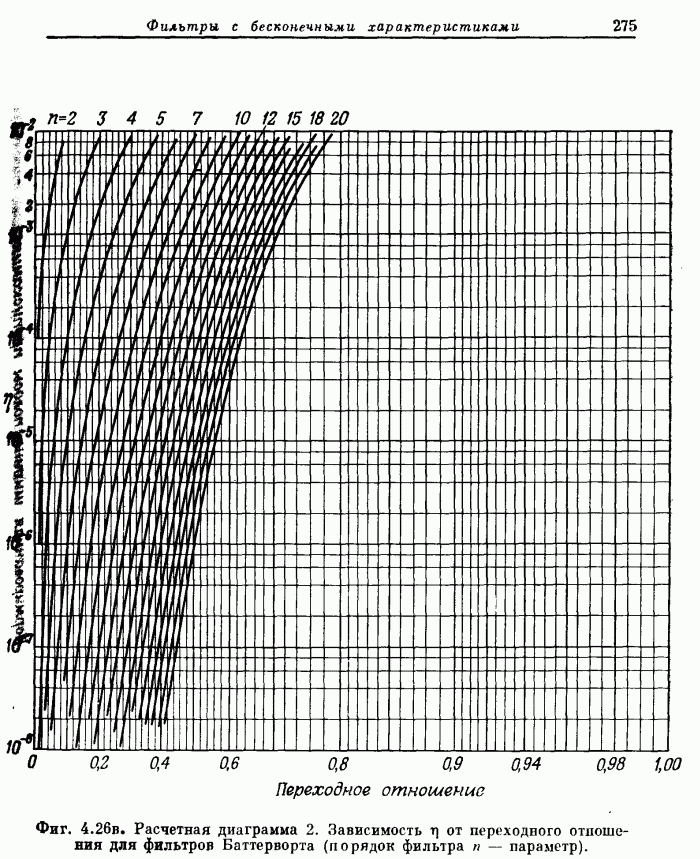
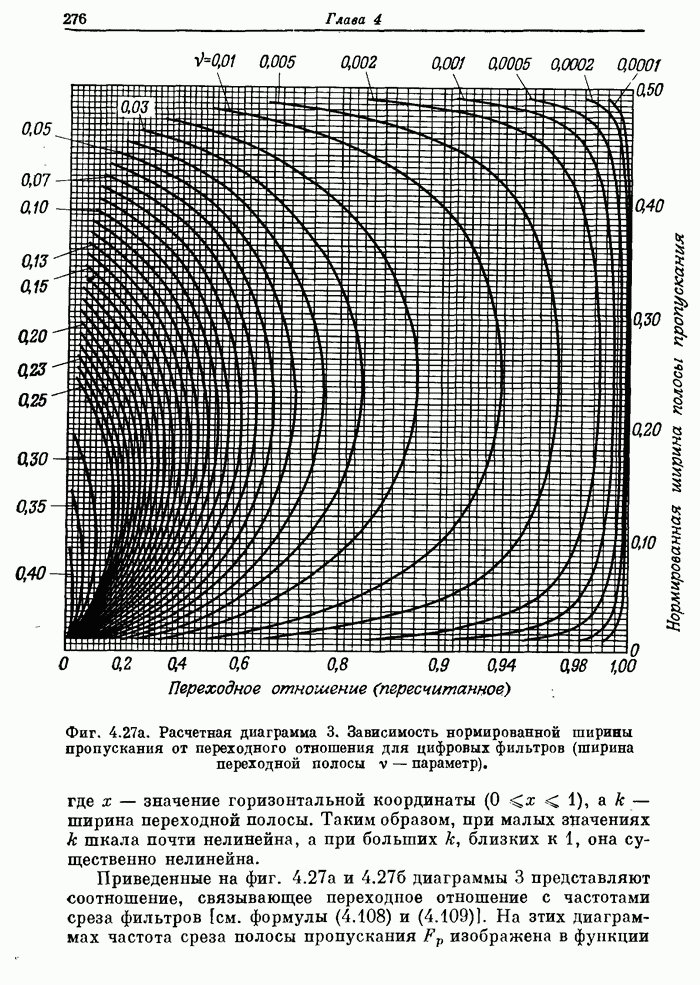
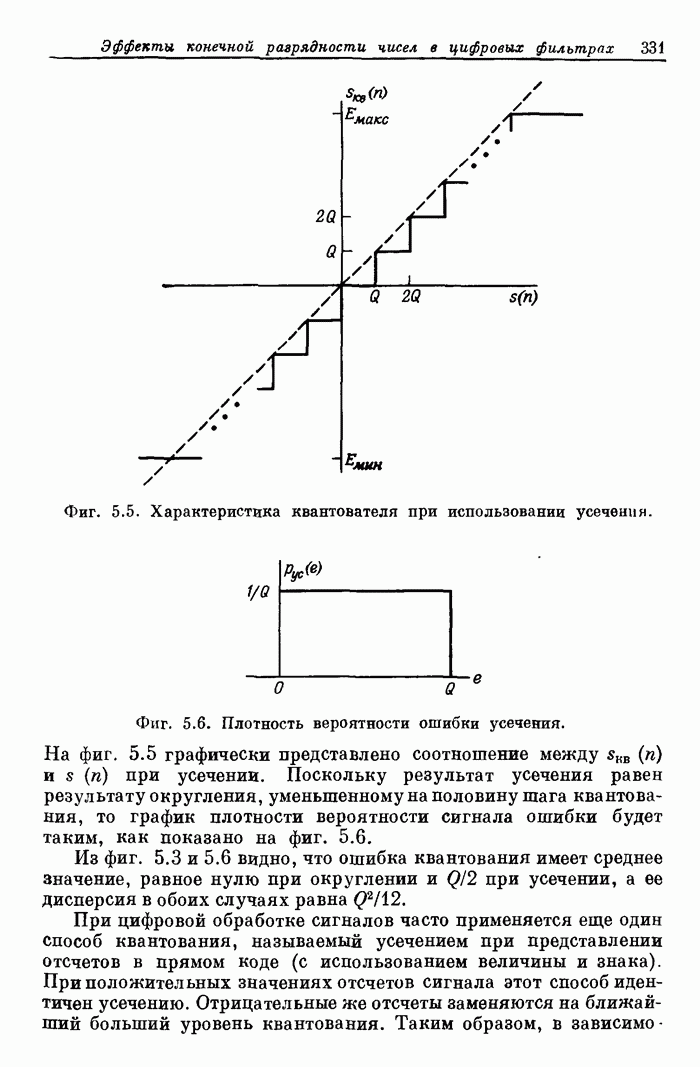
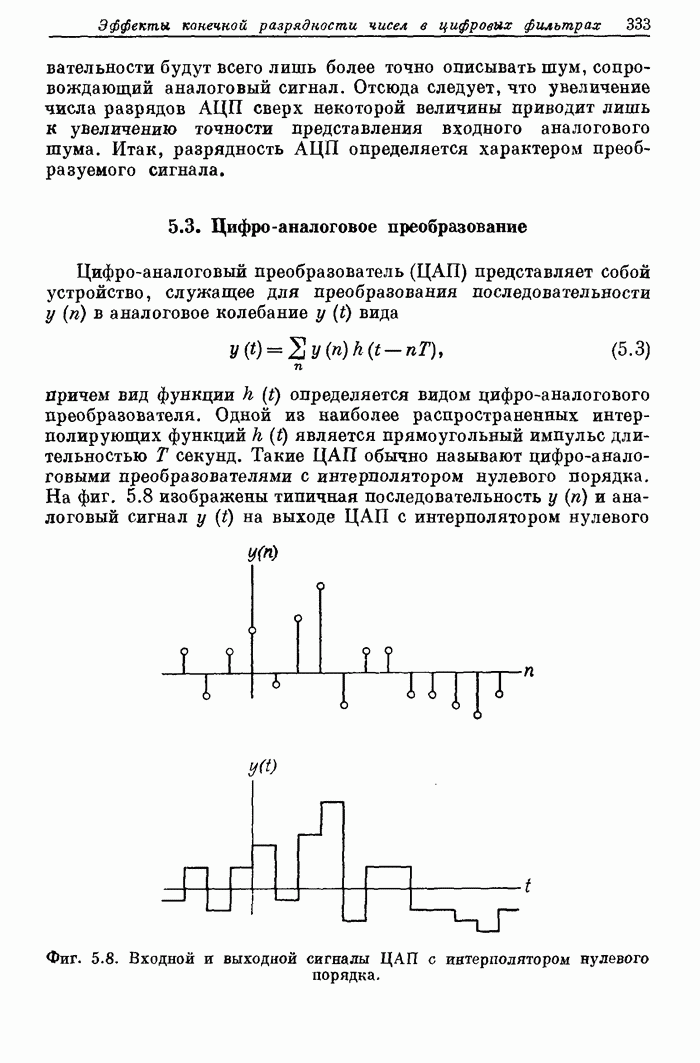
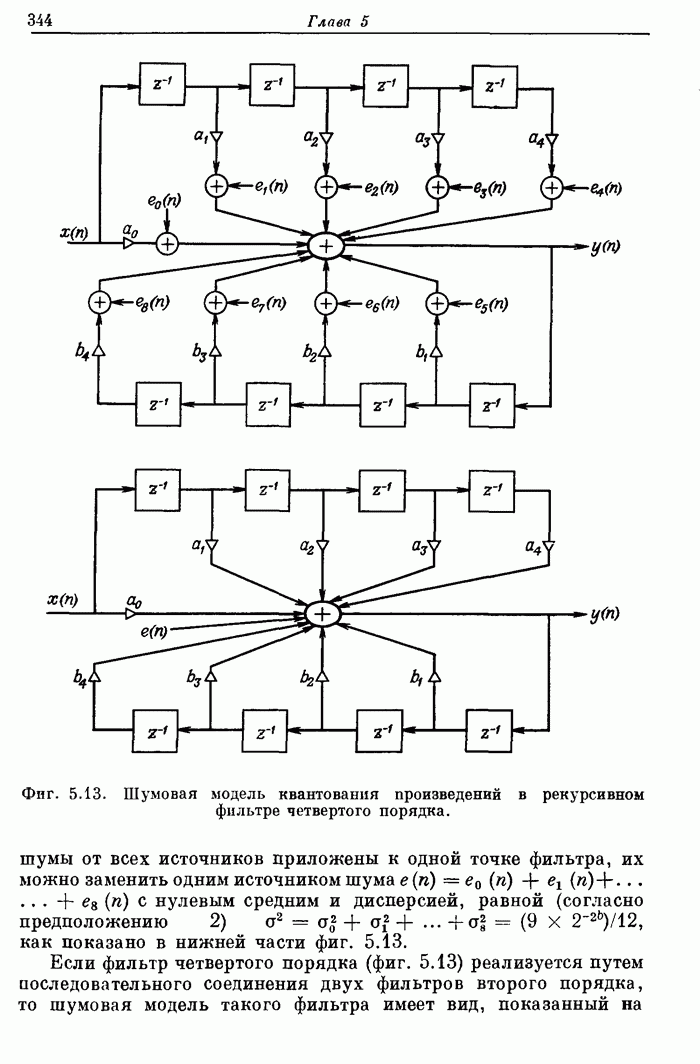
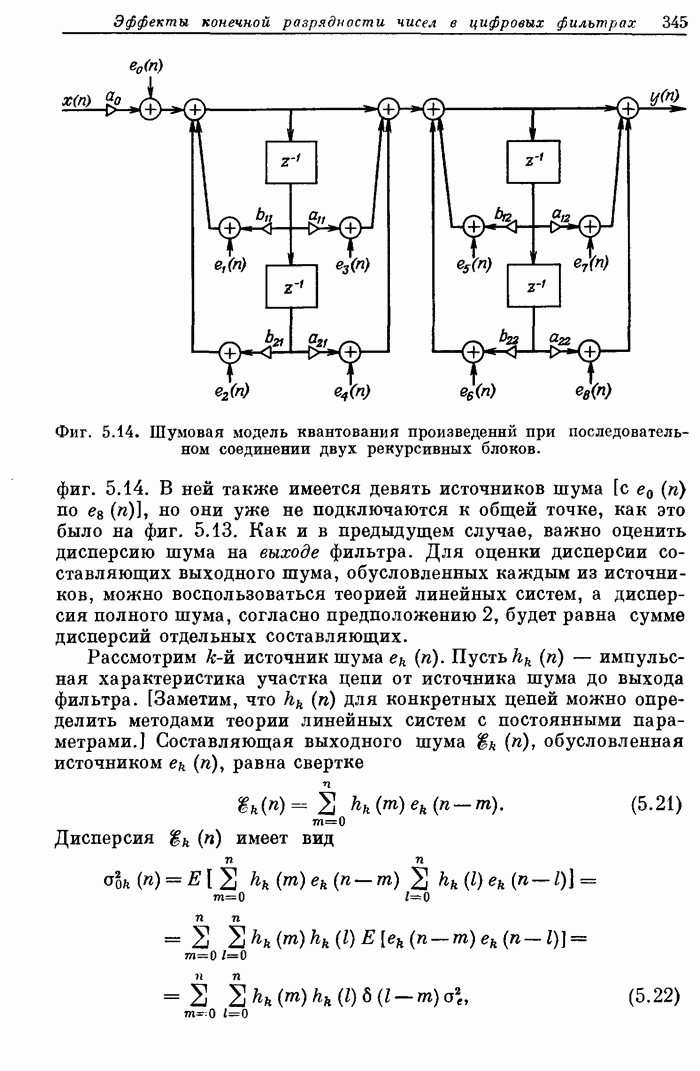
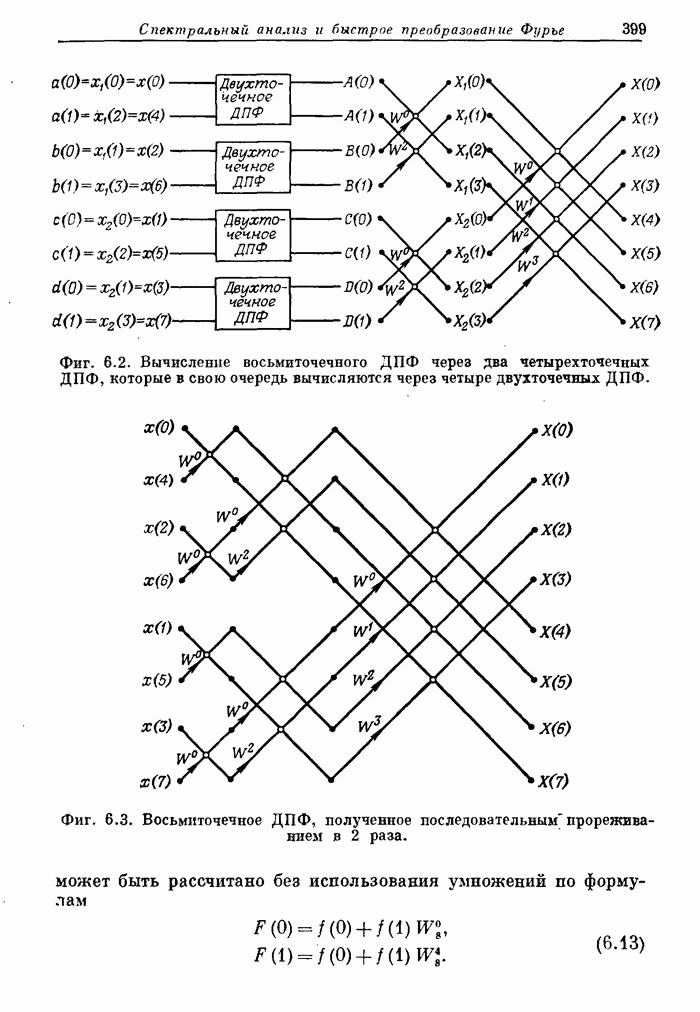
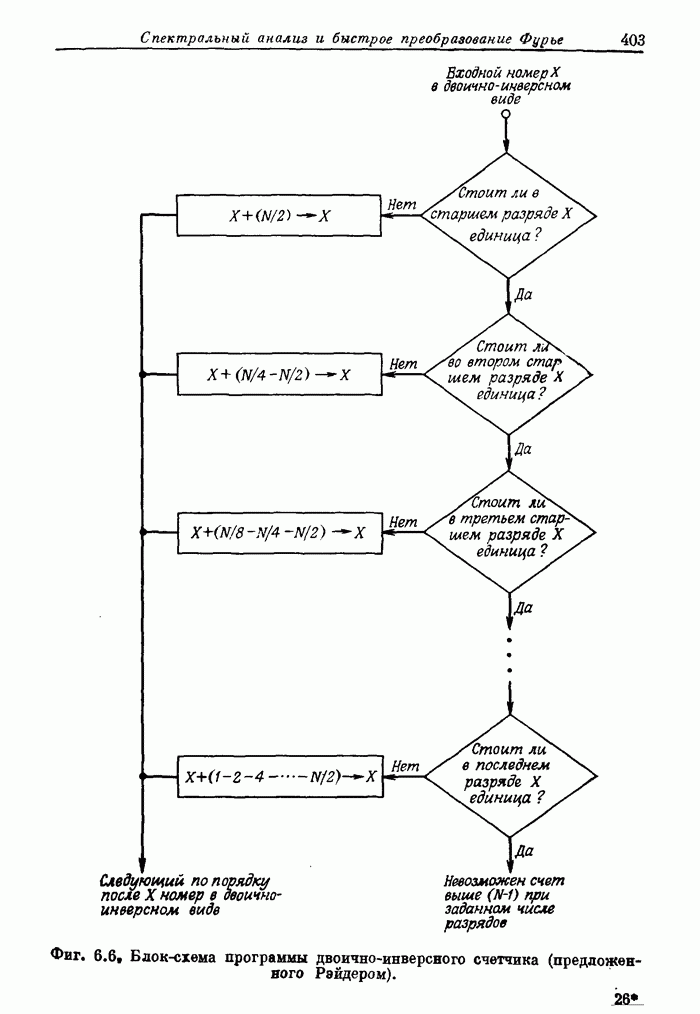
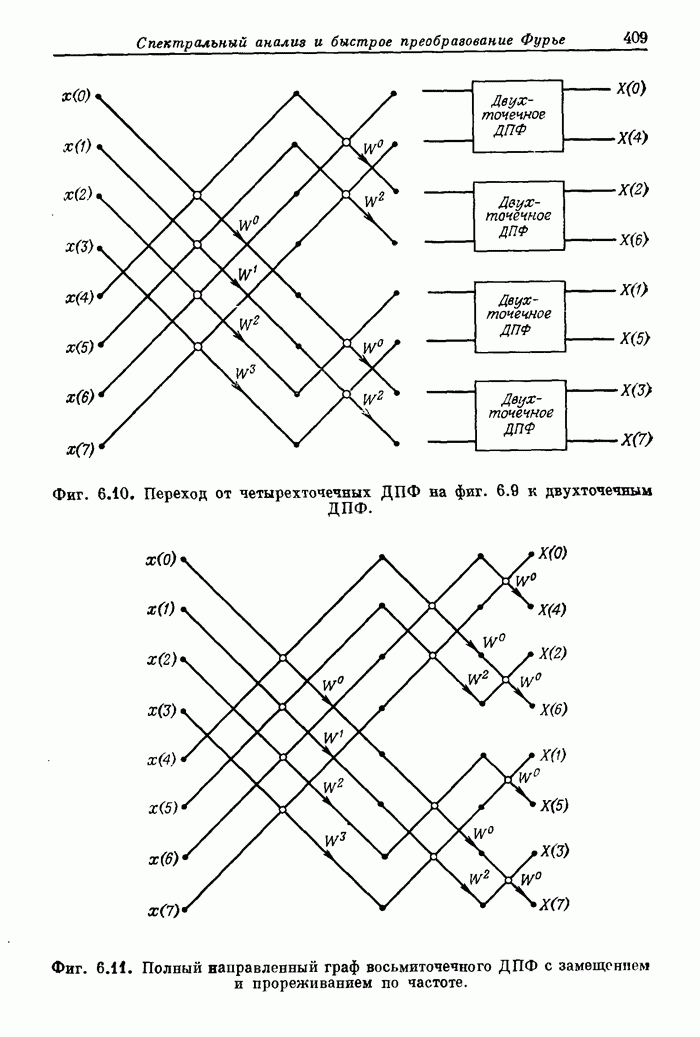
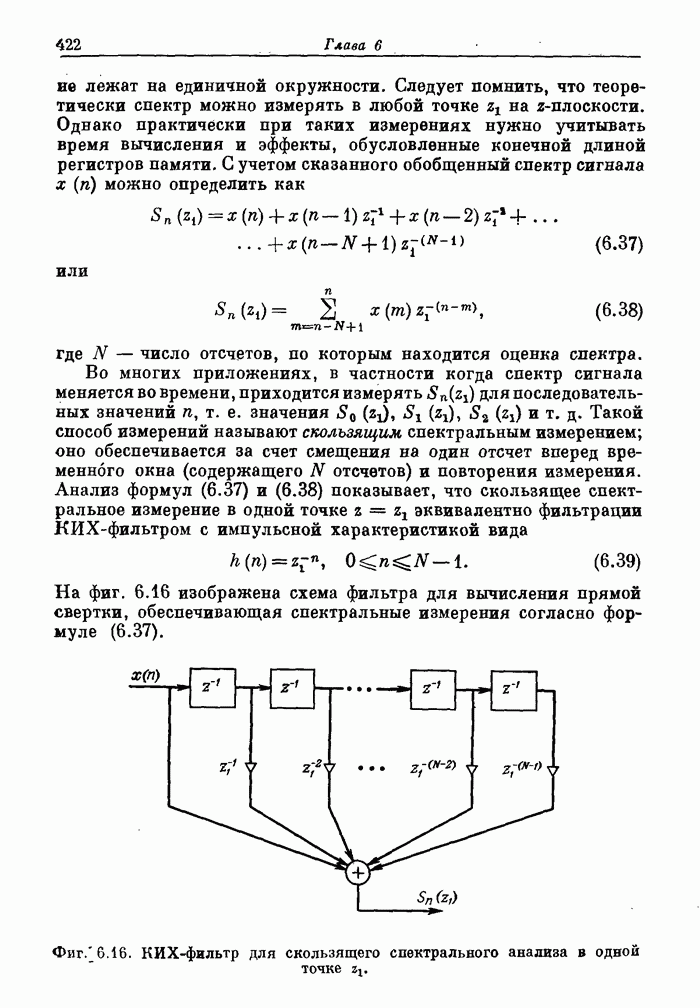
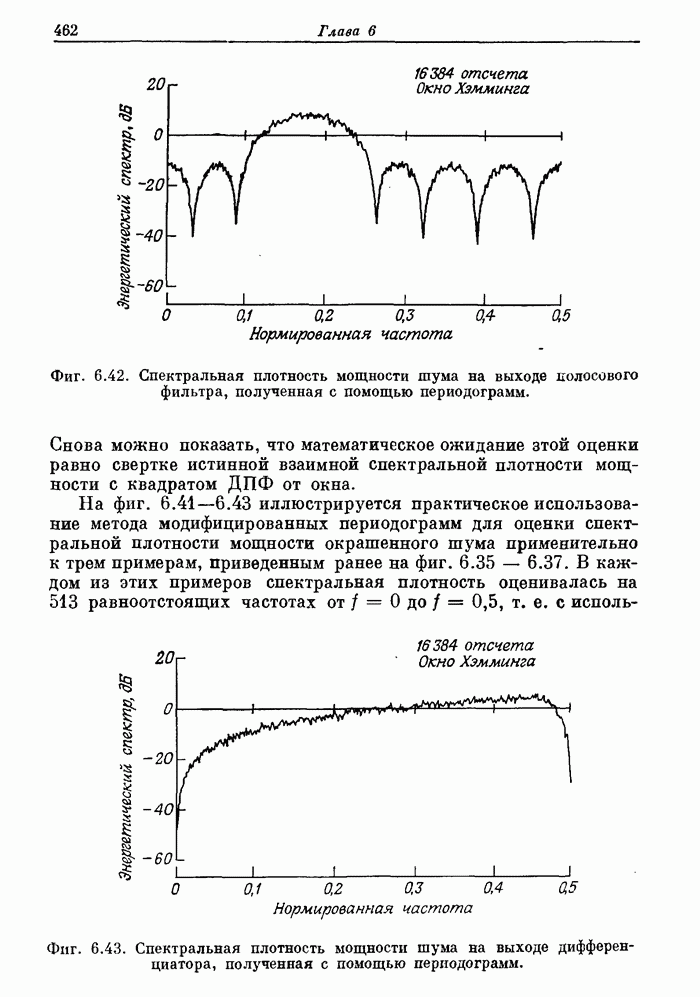
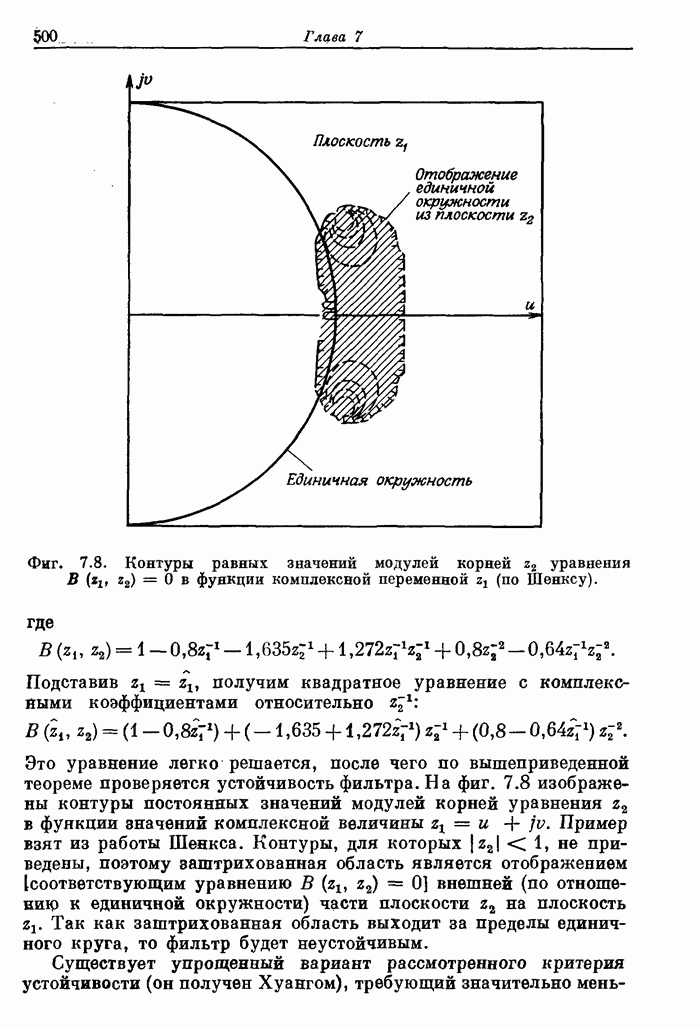
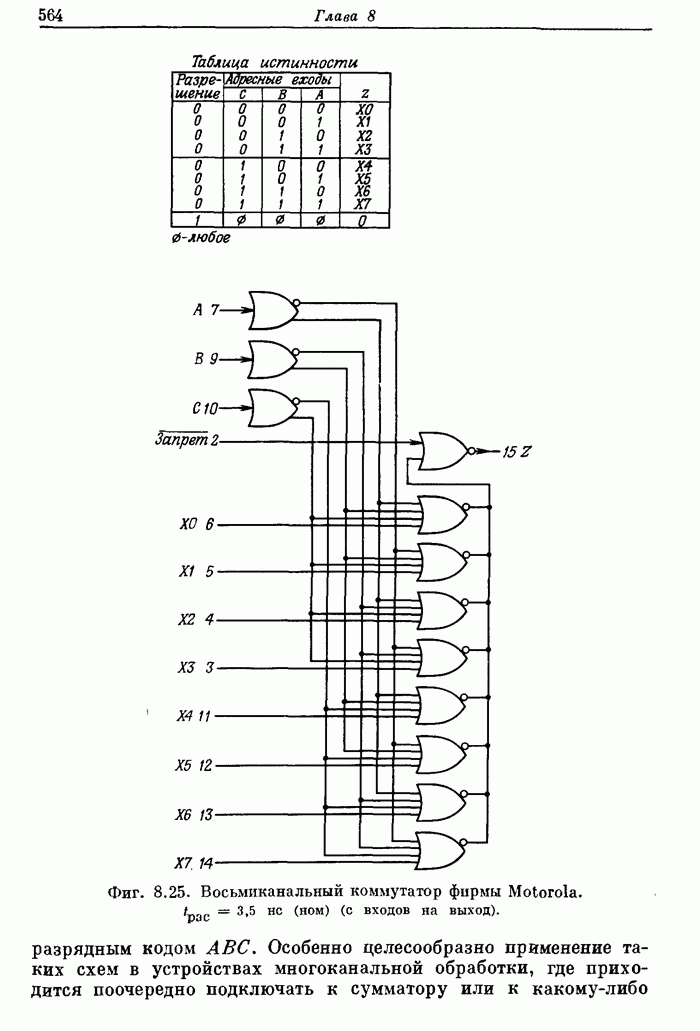
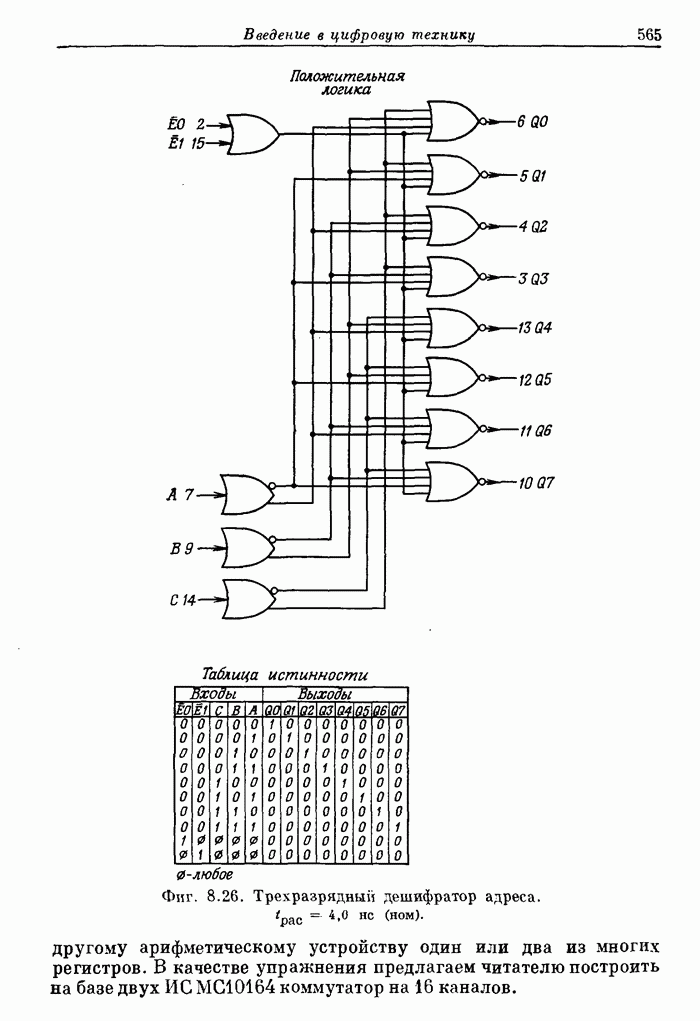
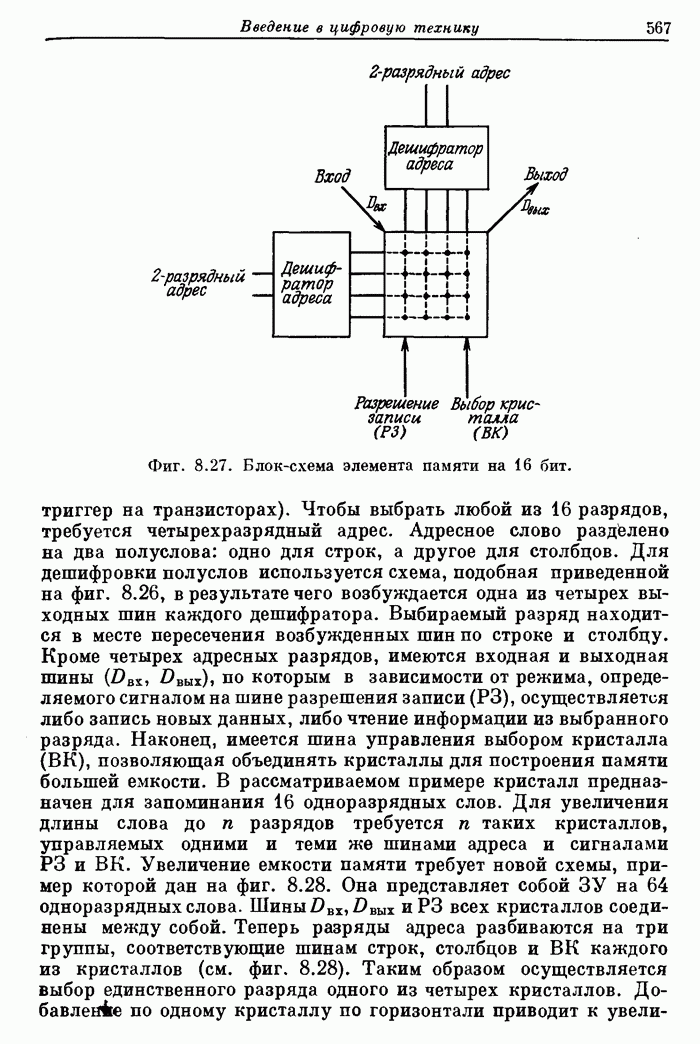
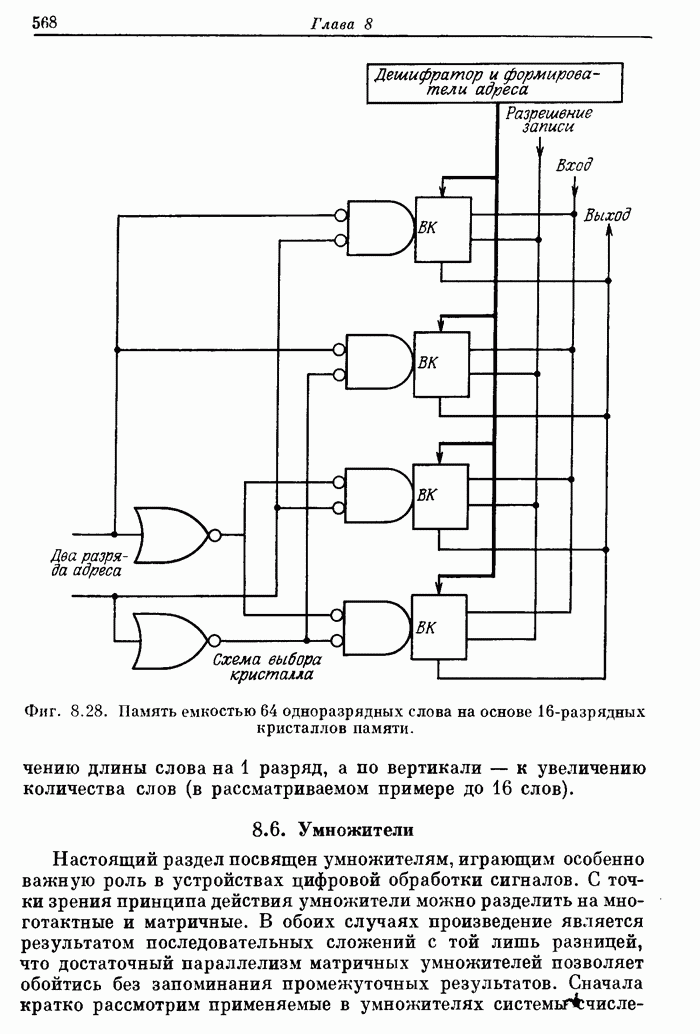
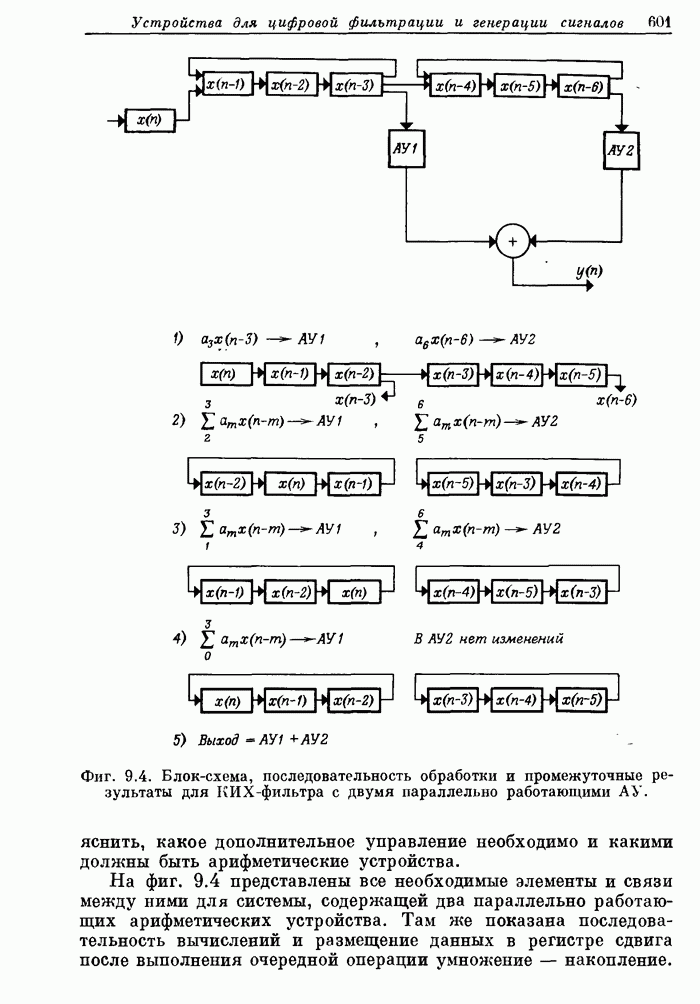
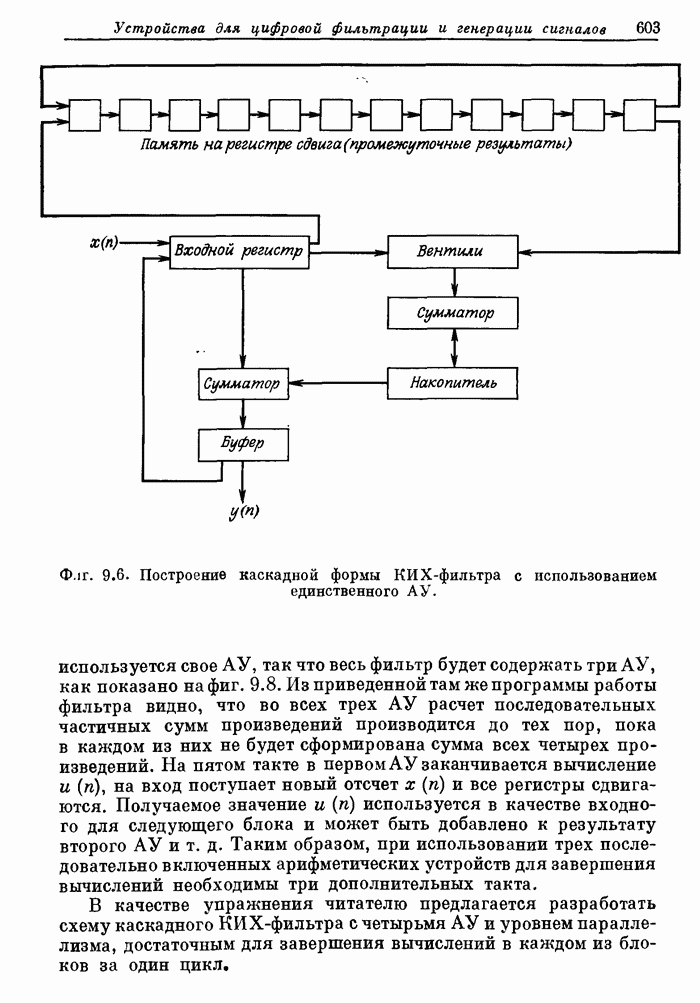
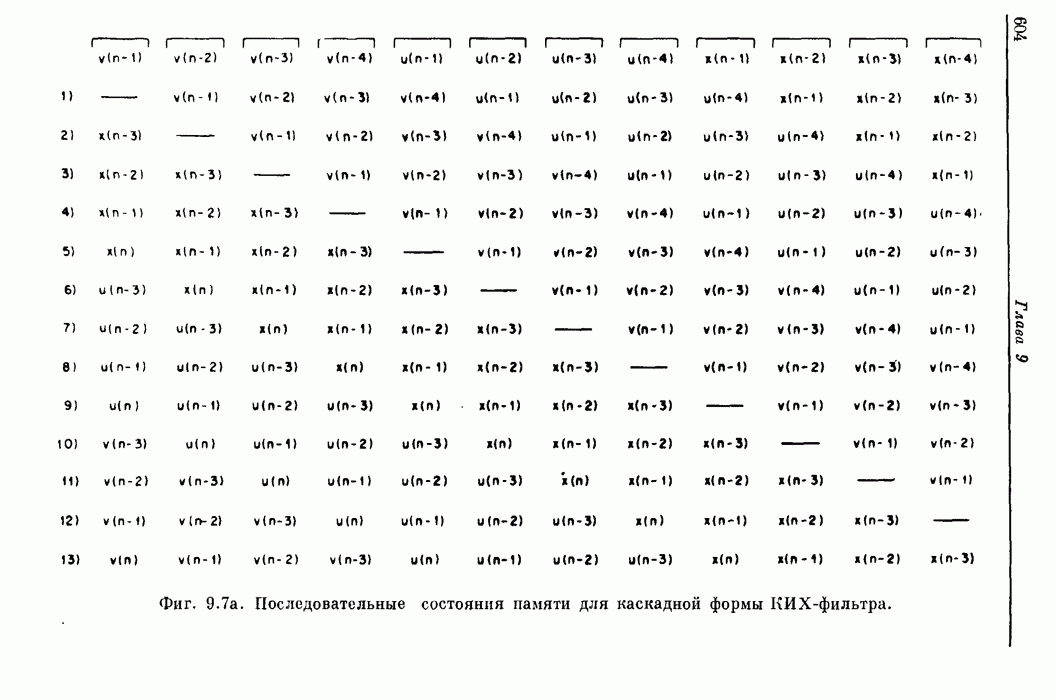
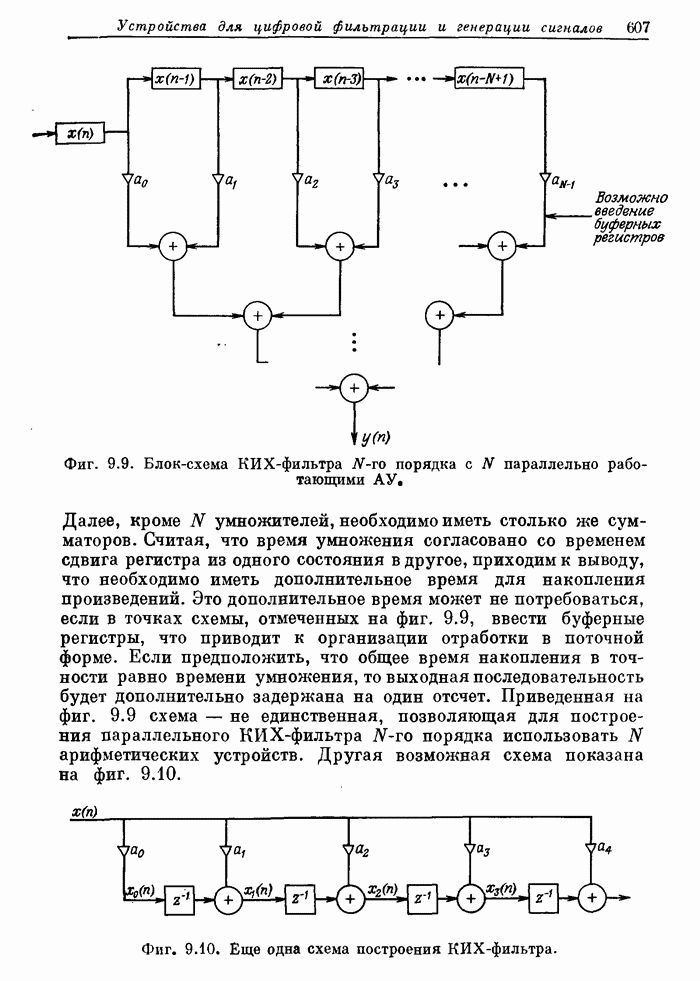
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
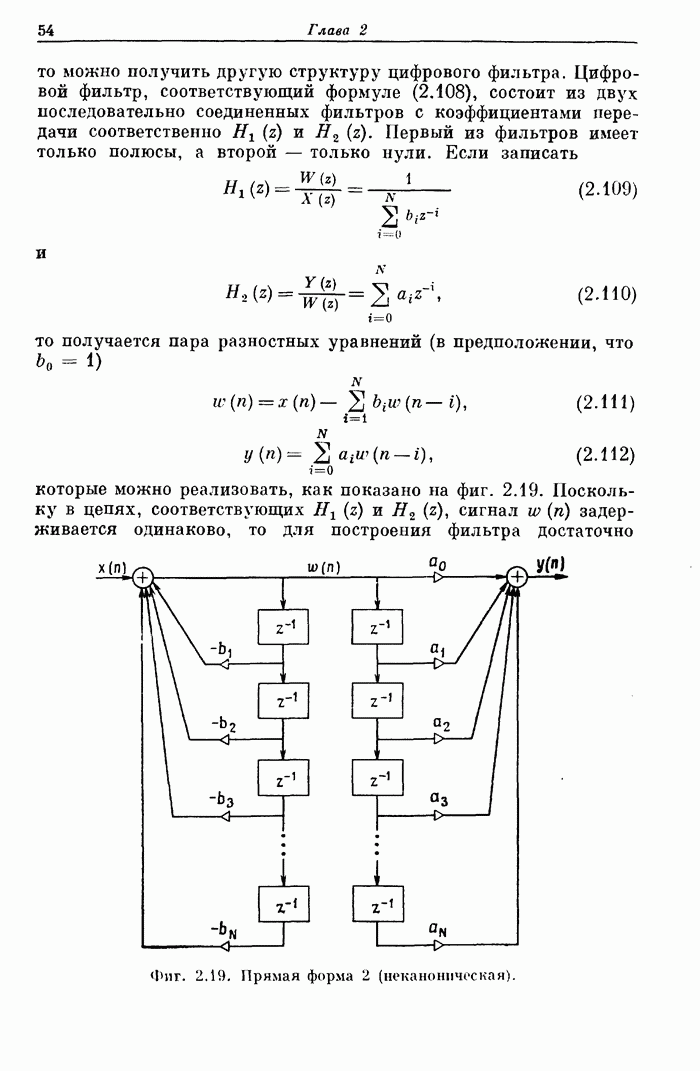
54
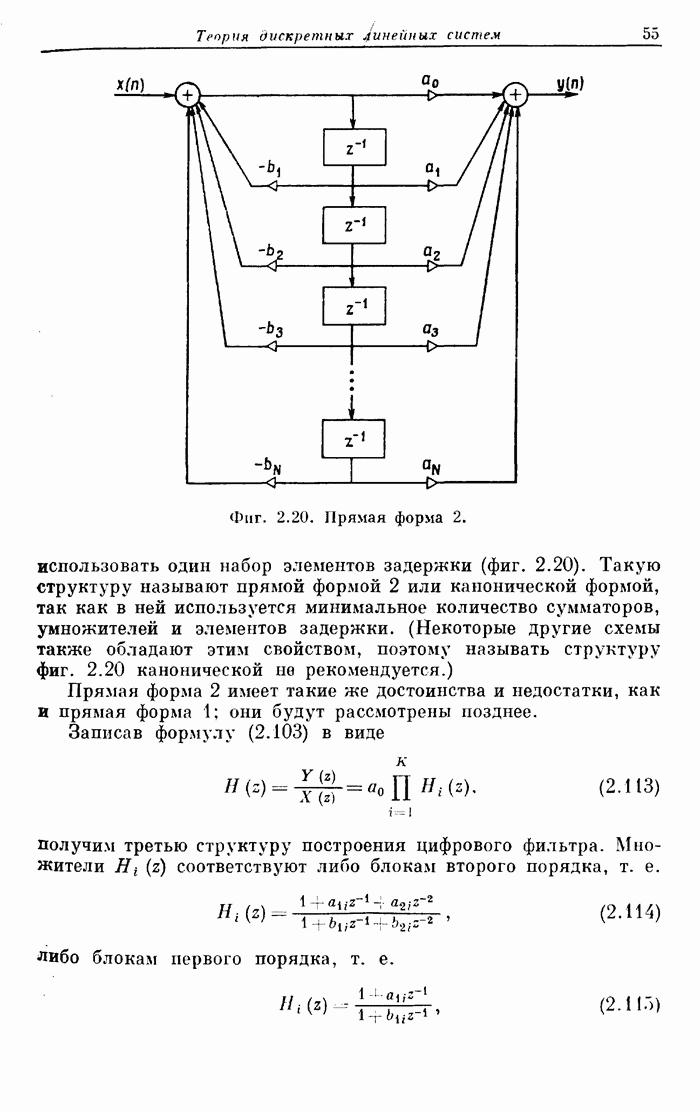
55
56
57
58
59
60
61
62
63
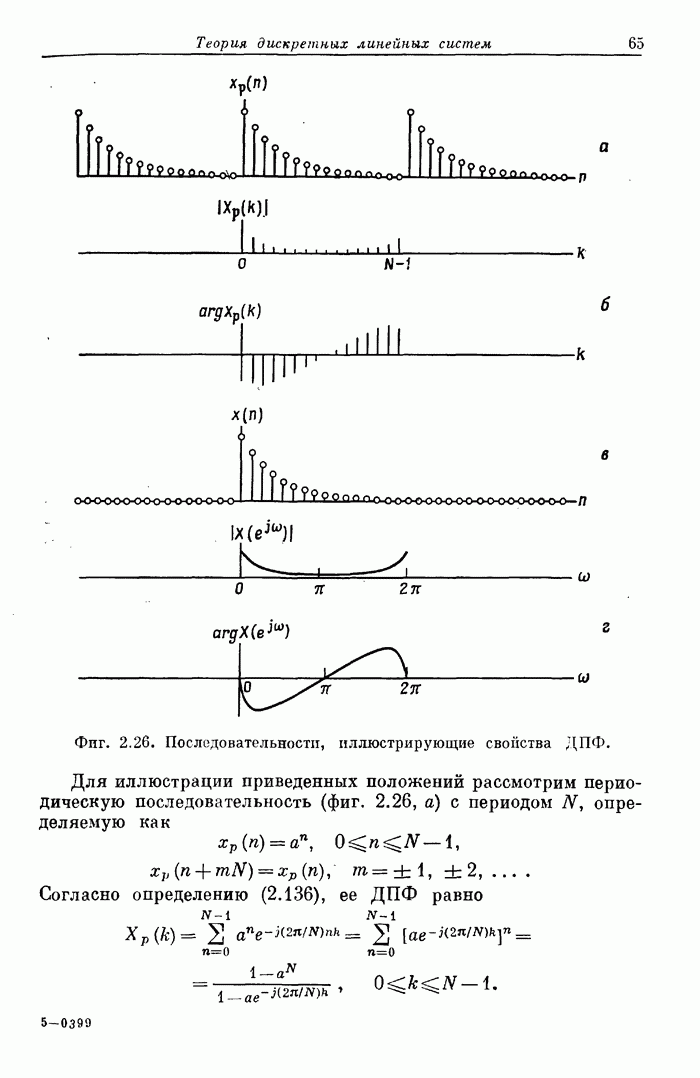
64
65
66
67
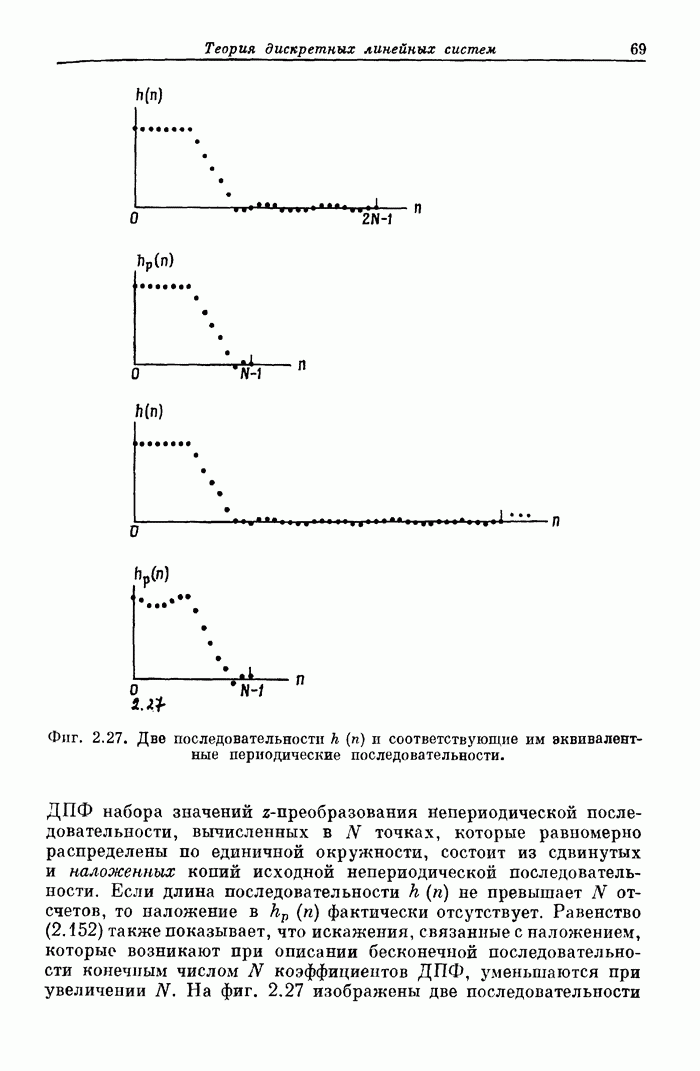
68
69
70
71
72
73
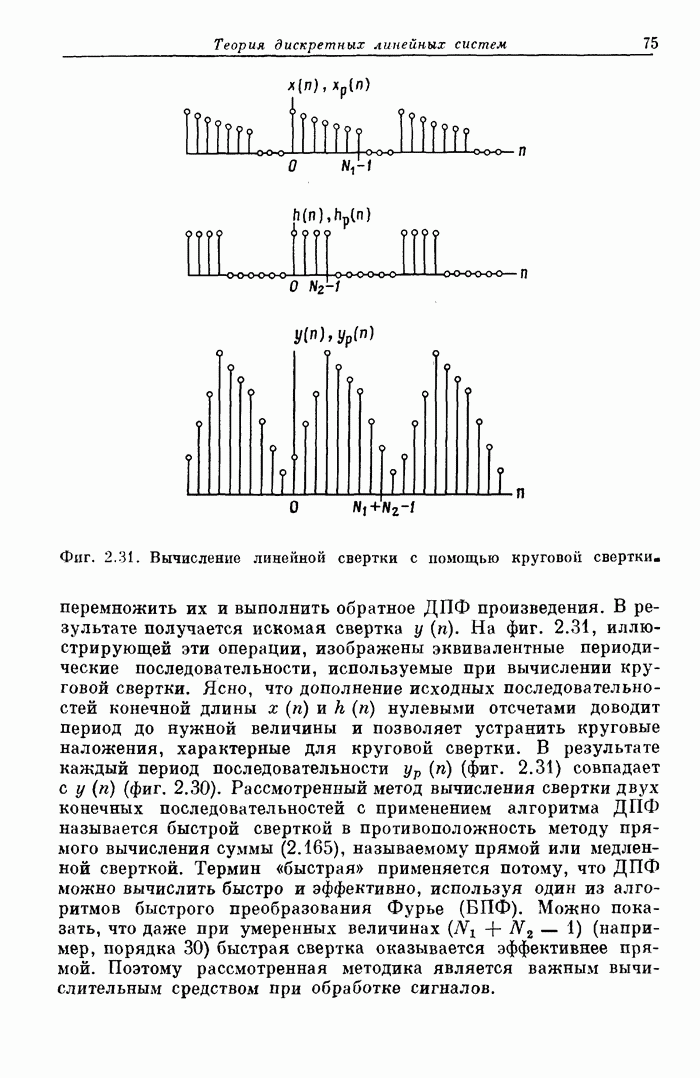
74
75
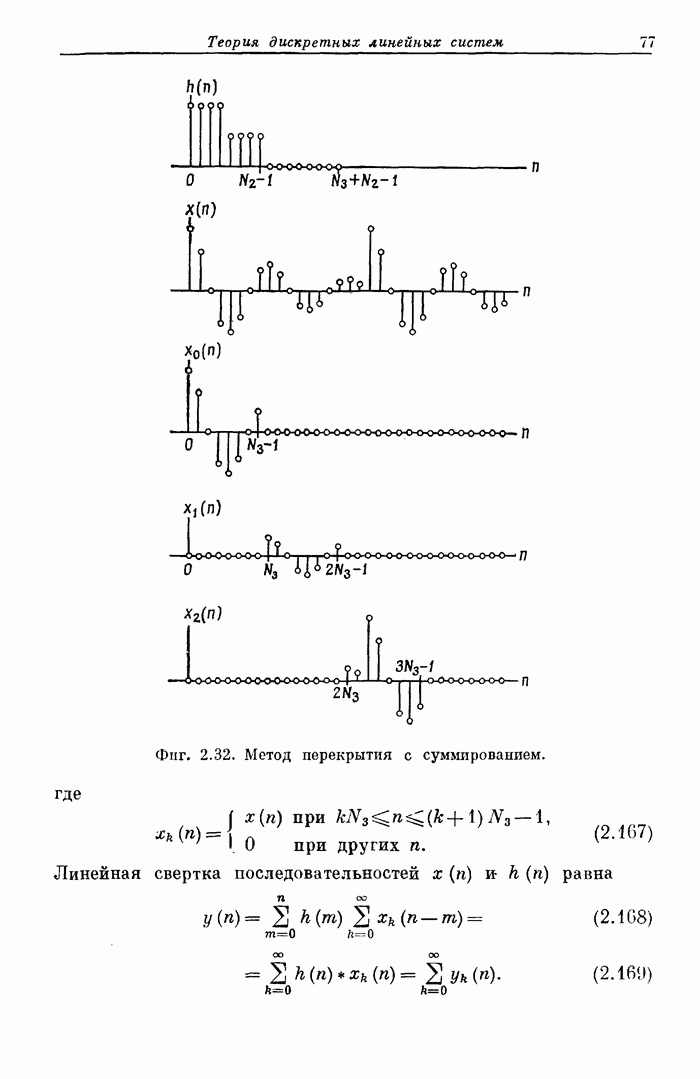
76
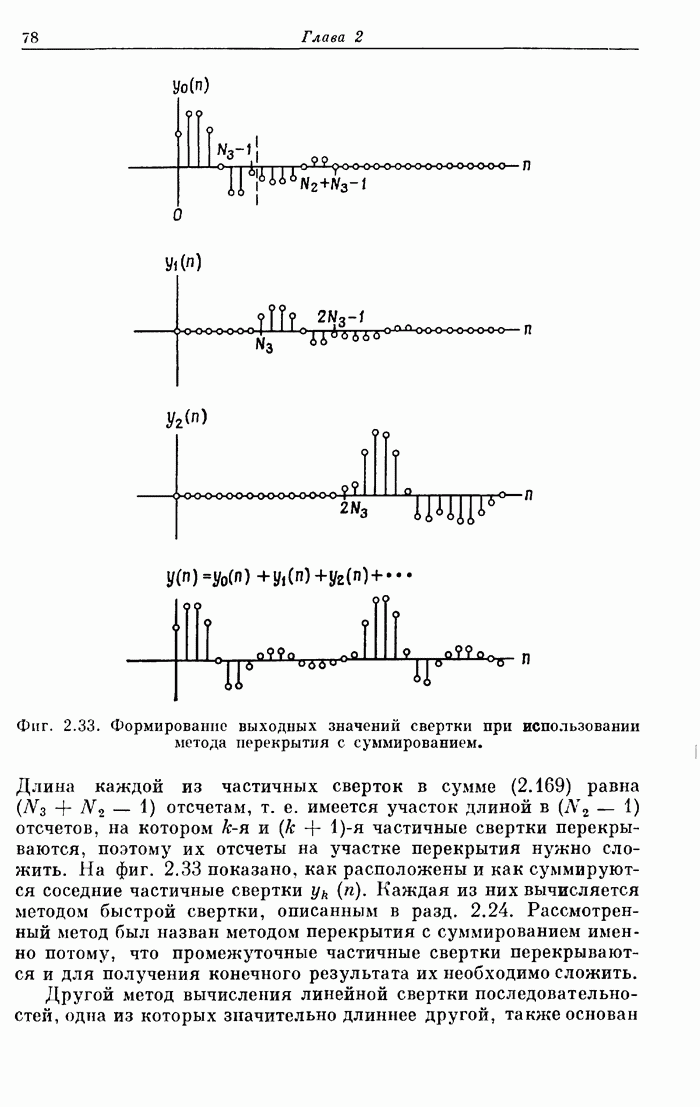
77
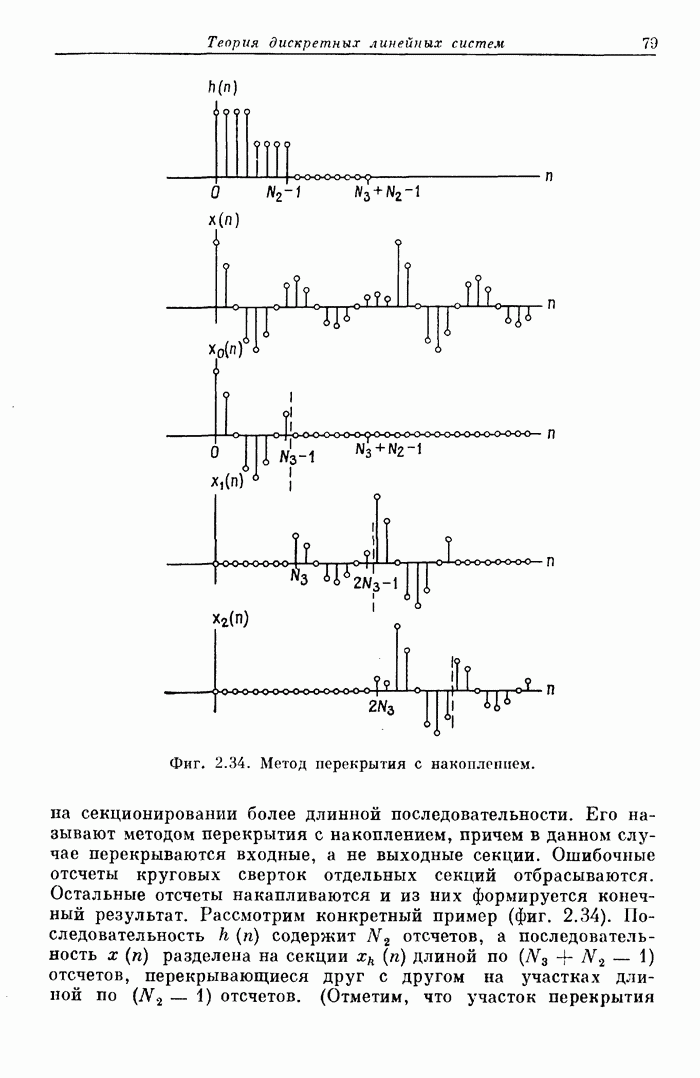
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
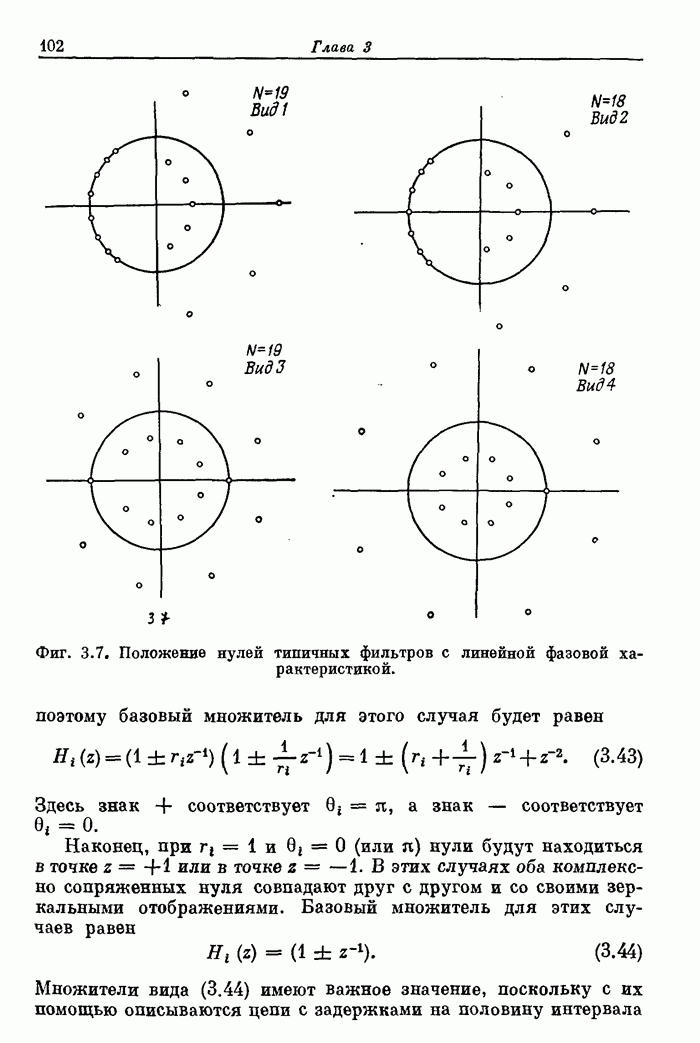
101
102
103
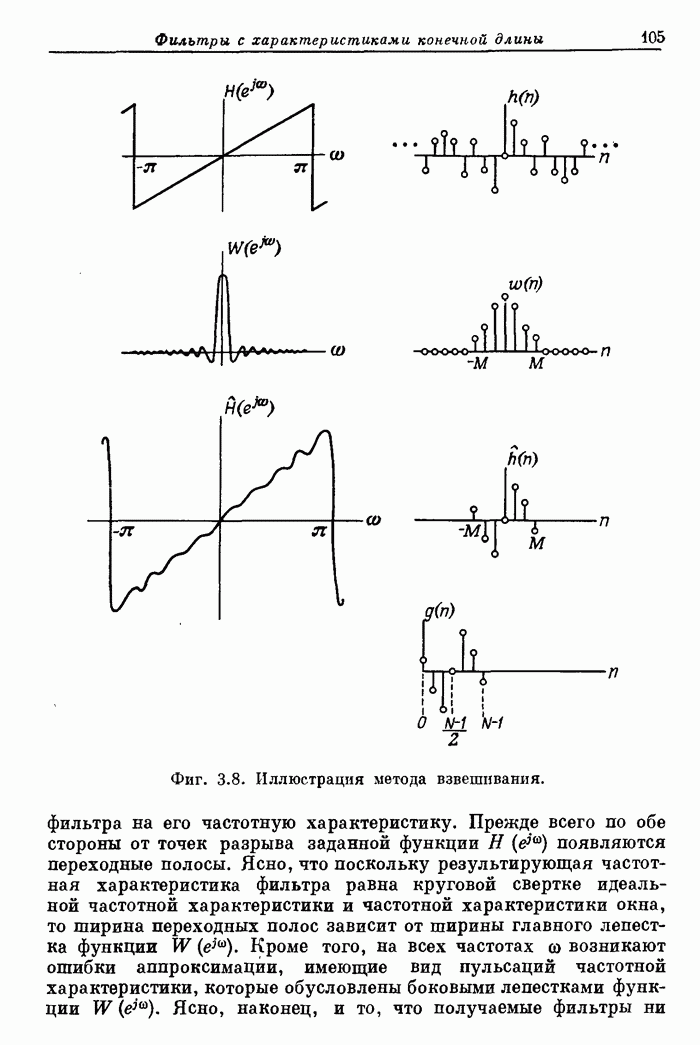
104
105
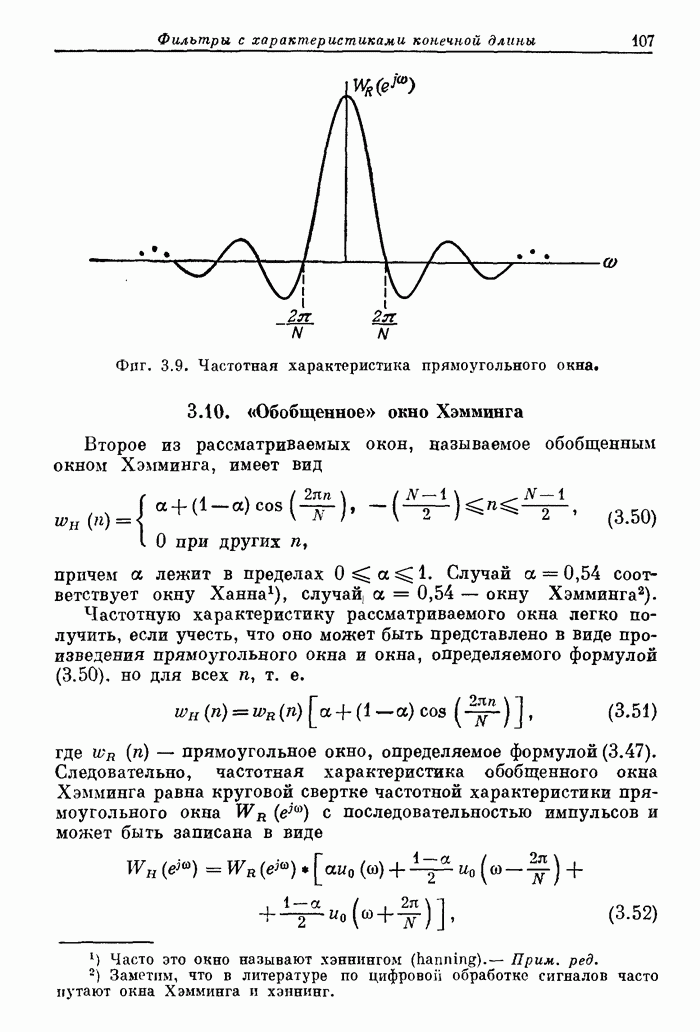
106
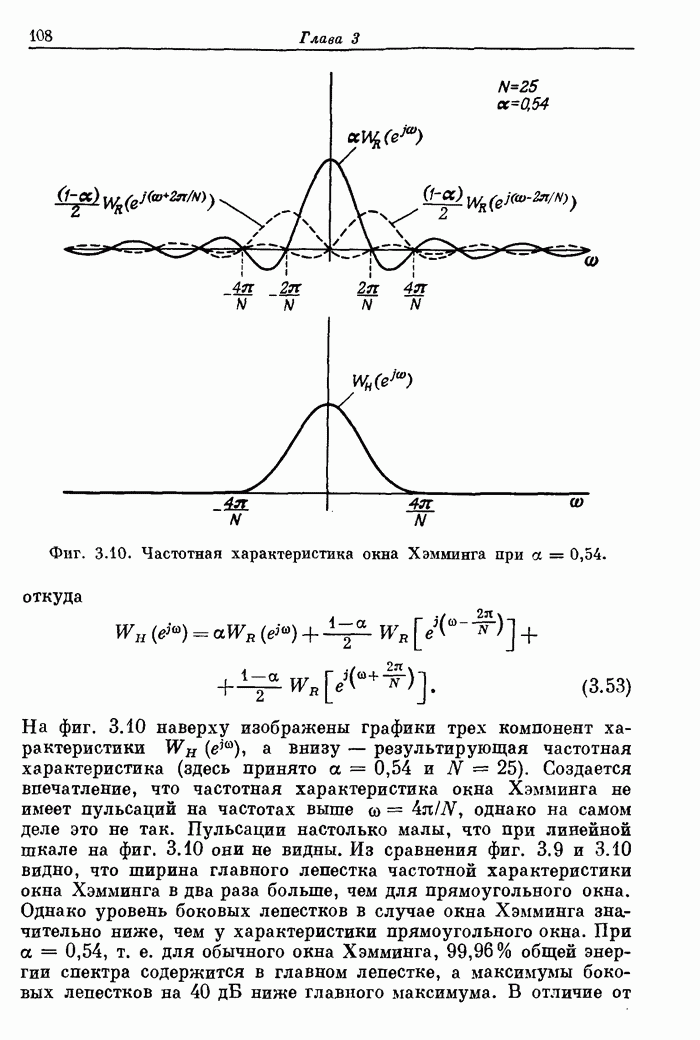
107
108
109
110
111
112
113
114
115
116
117
118
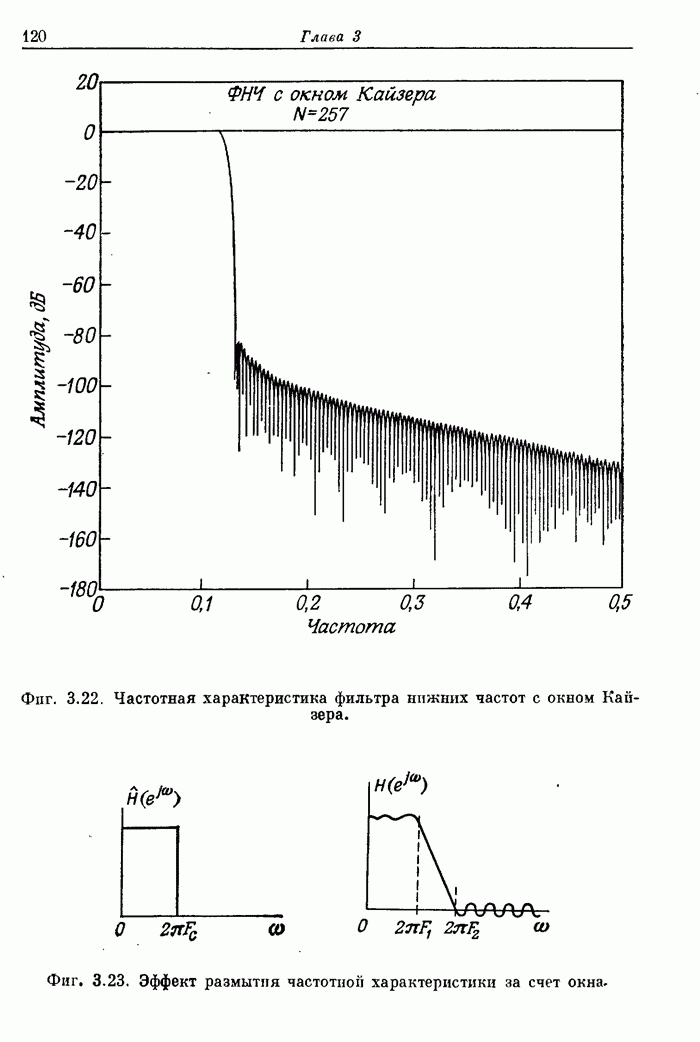
119
120
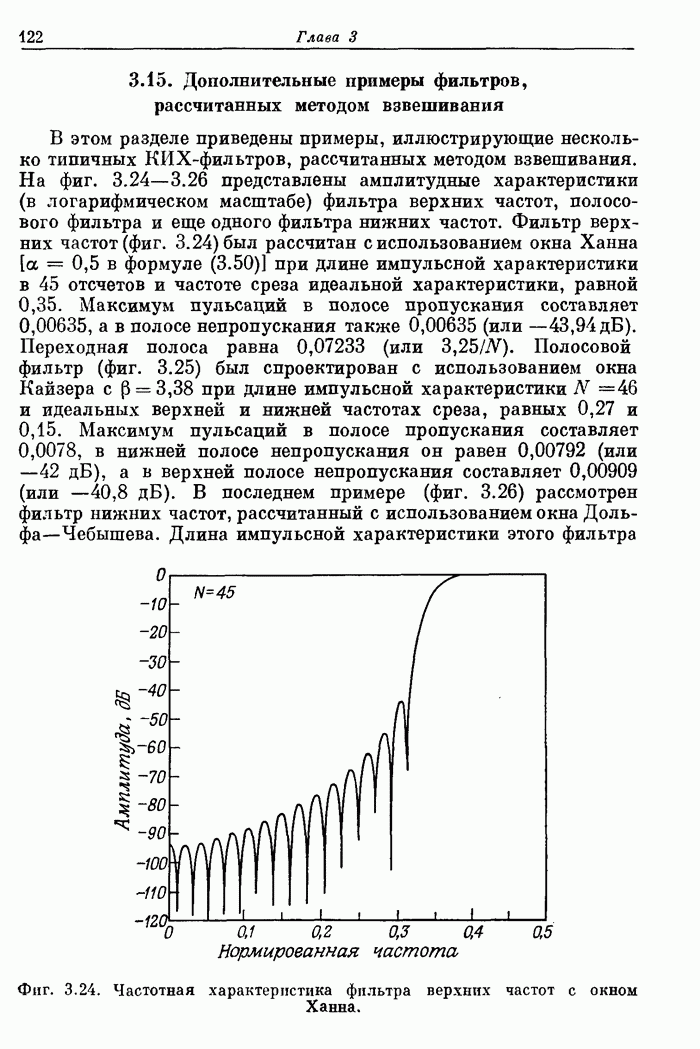
121
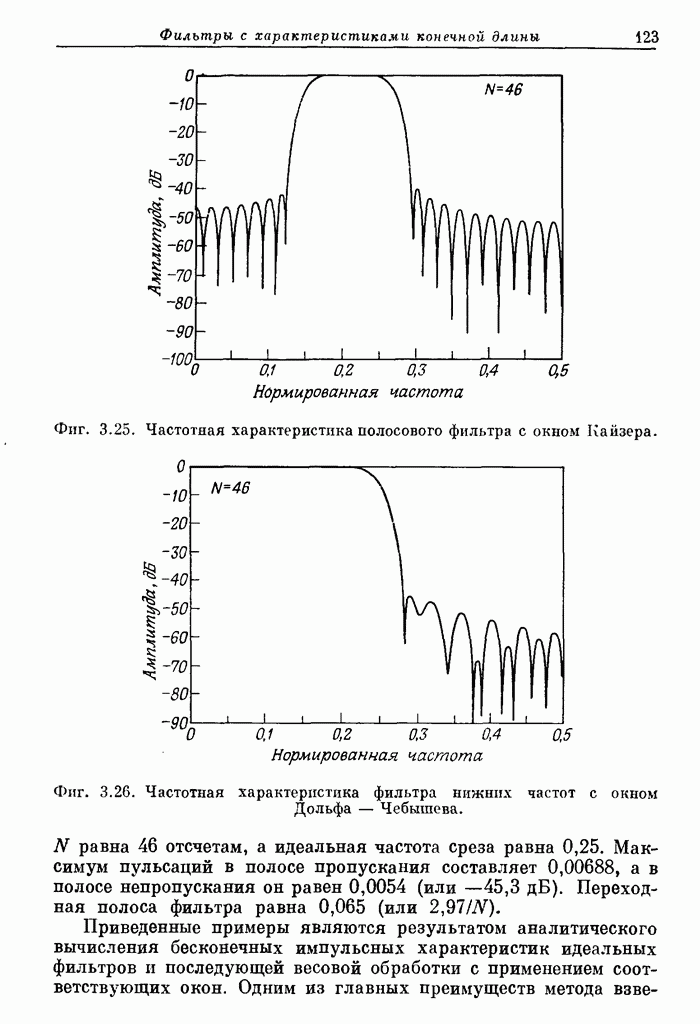
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
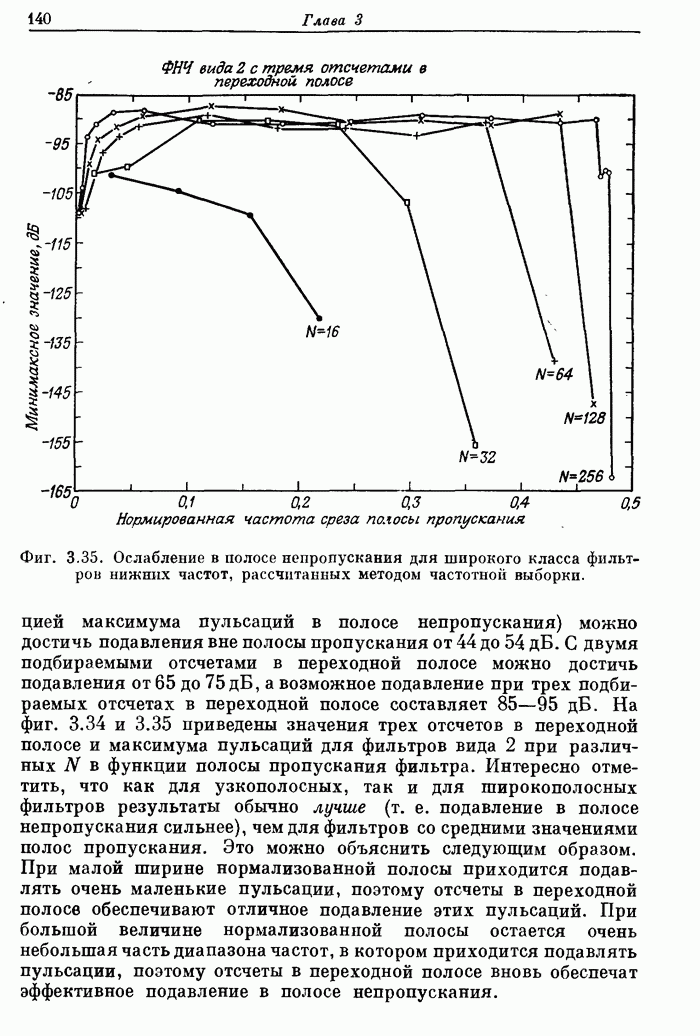
140
141
142
143
144
145
146
147
148
149
150
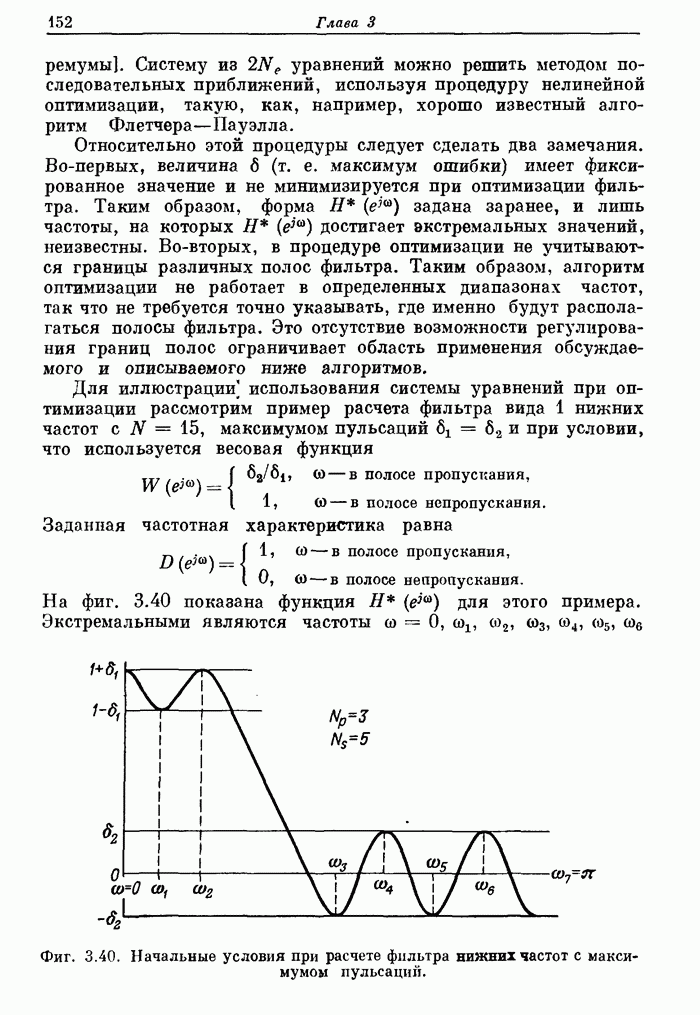
151
152
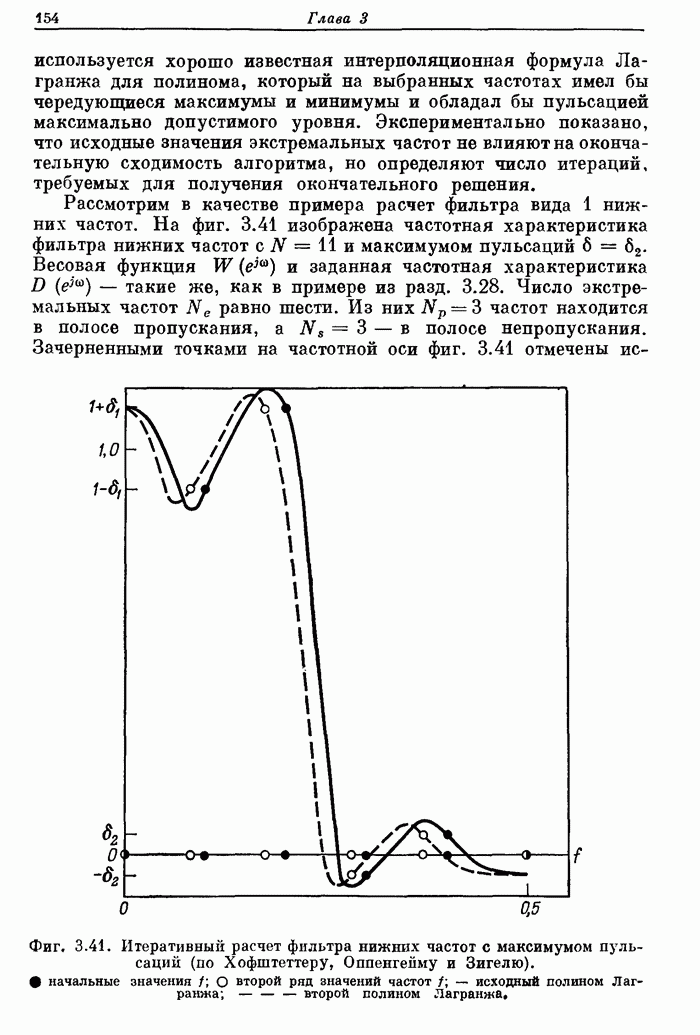
153
154
155
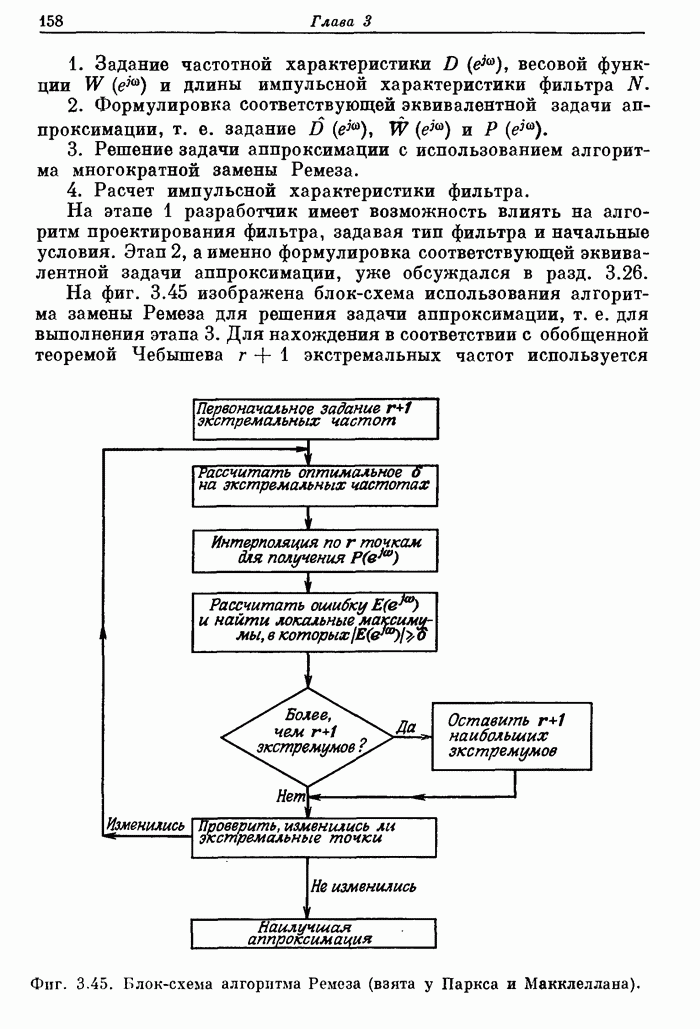
156
157
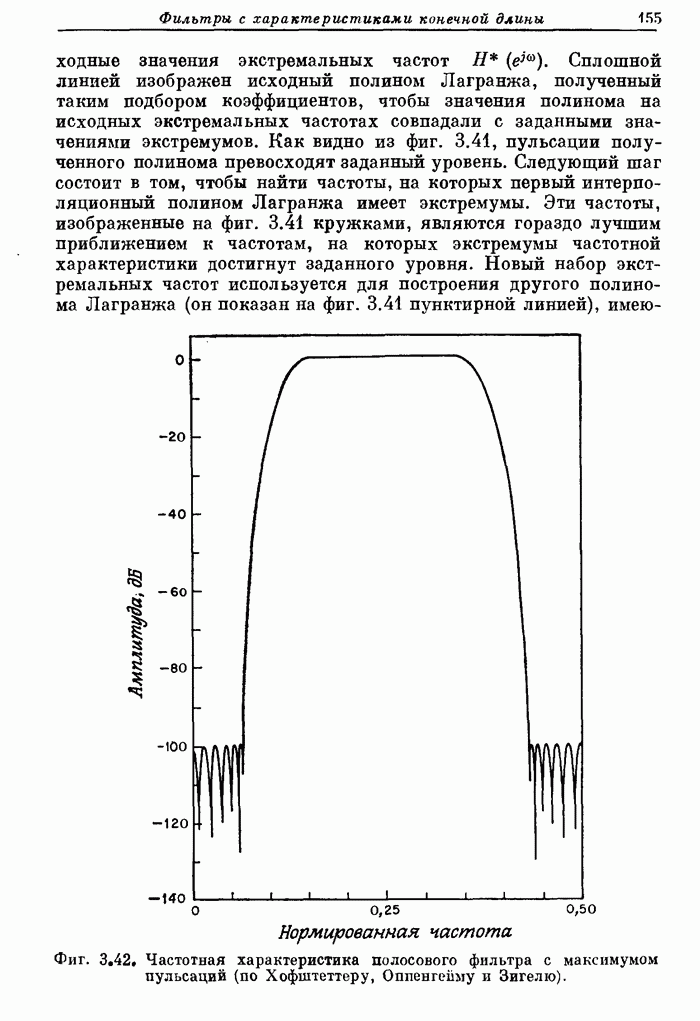
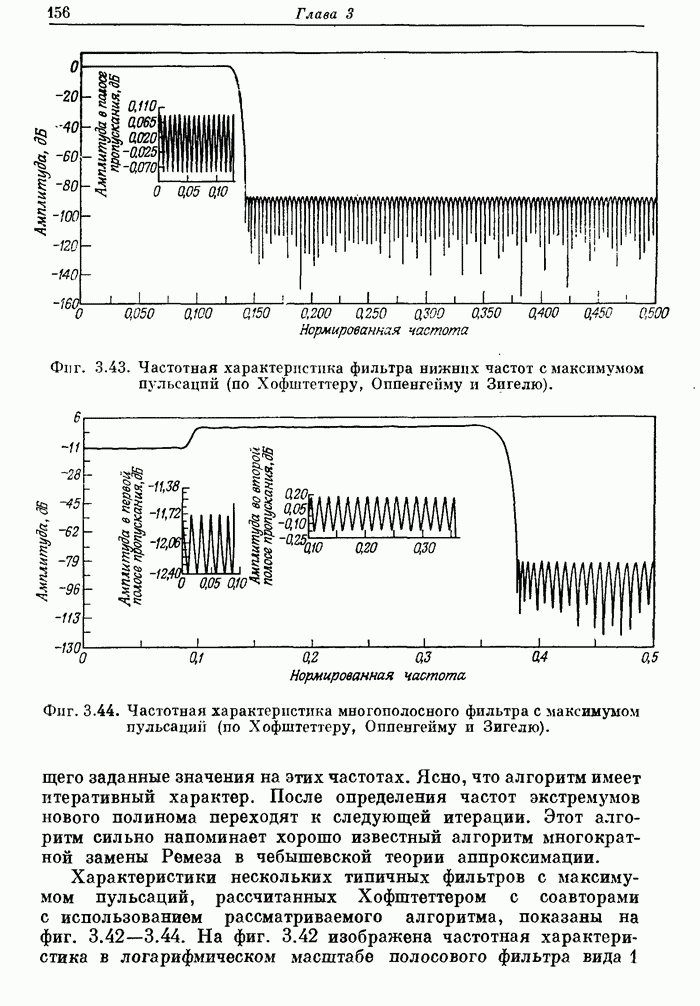
158
159
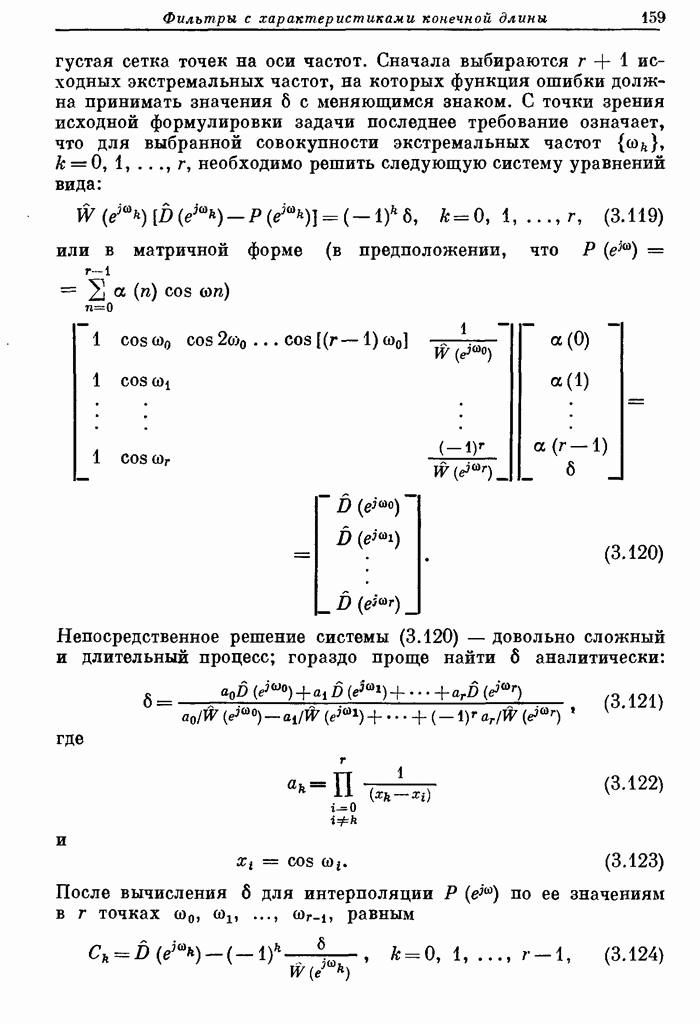
160
161
162
163
164
165
166
167
168
169
170
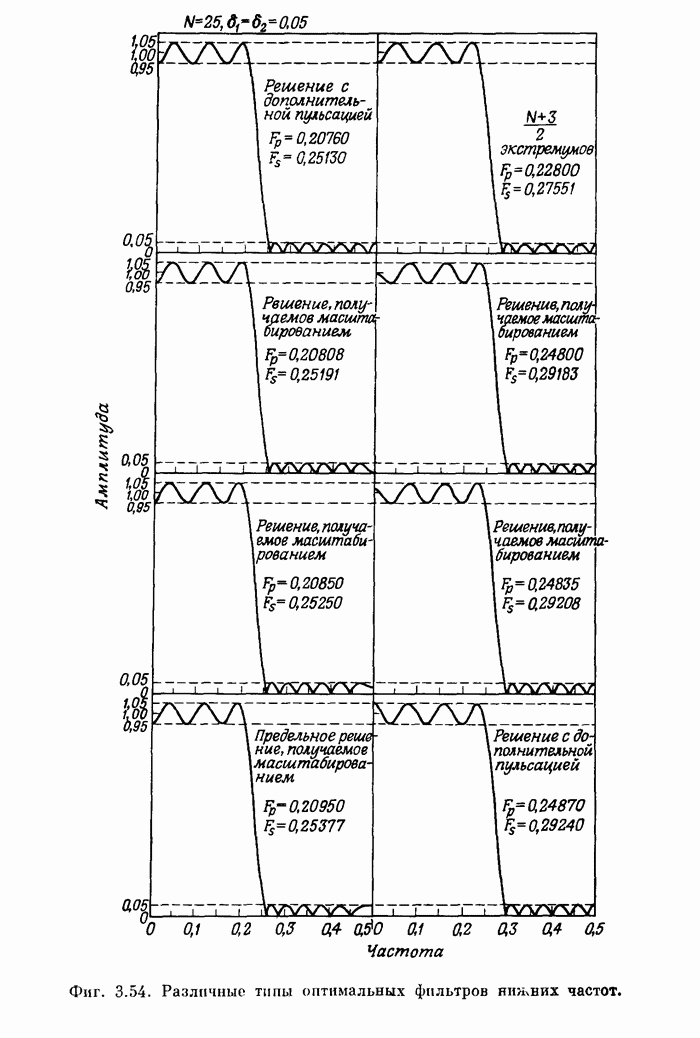
171
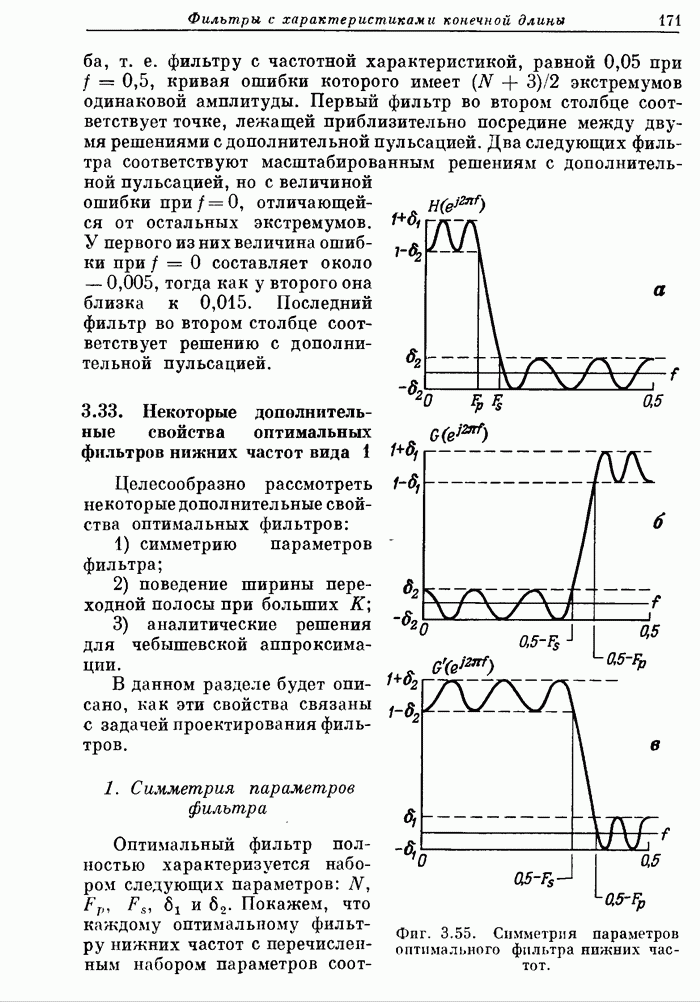
172
173
174
175
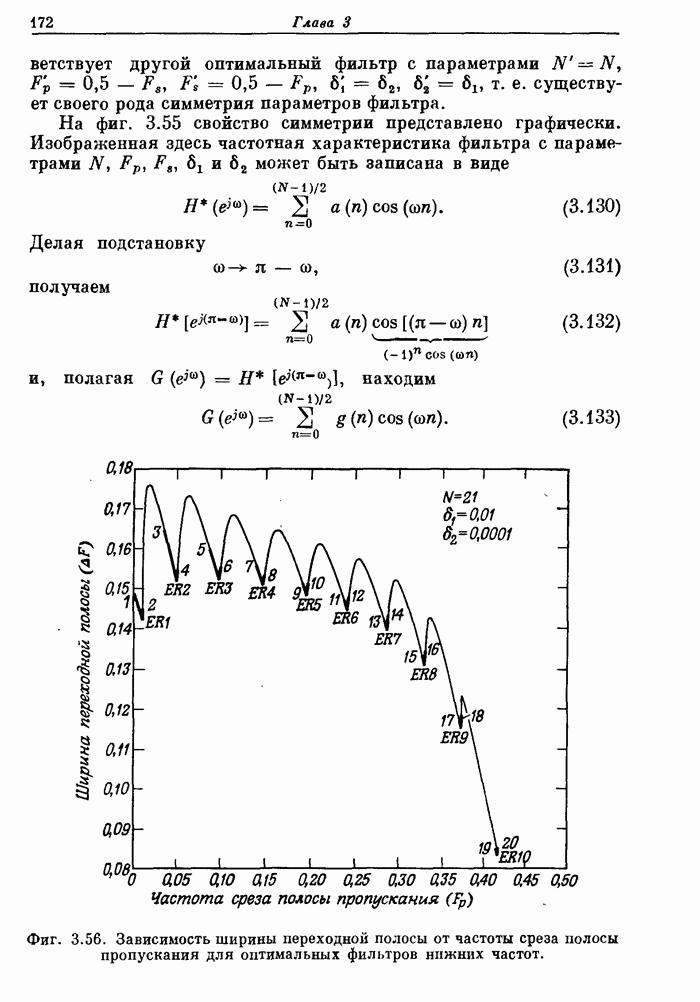
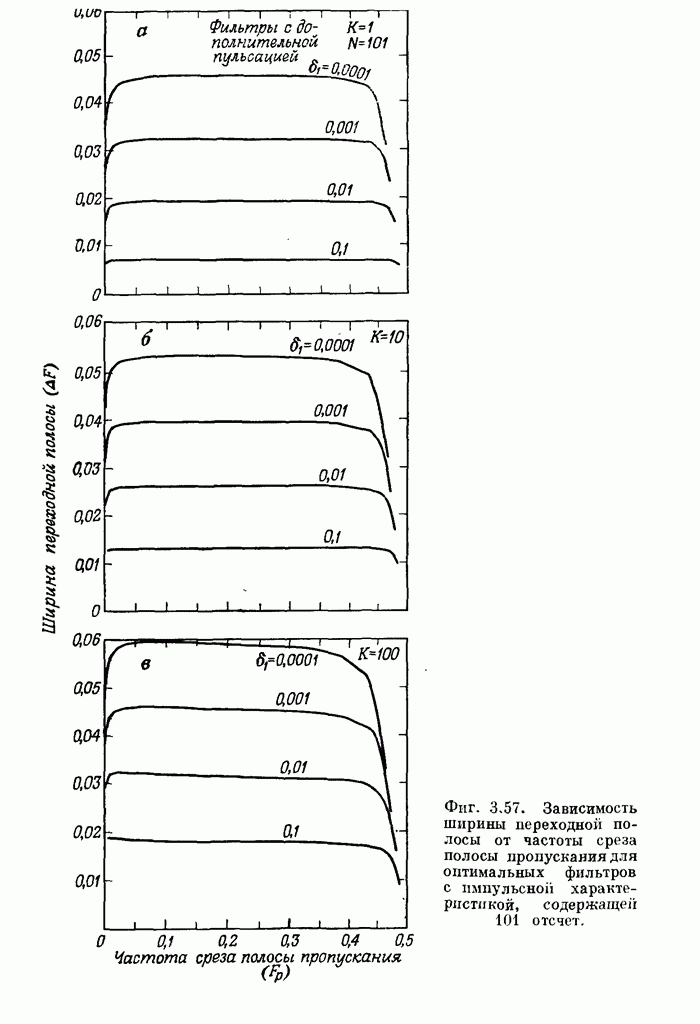
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
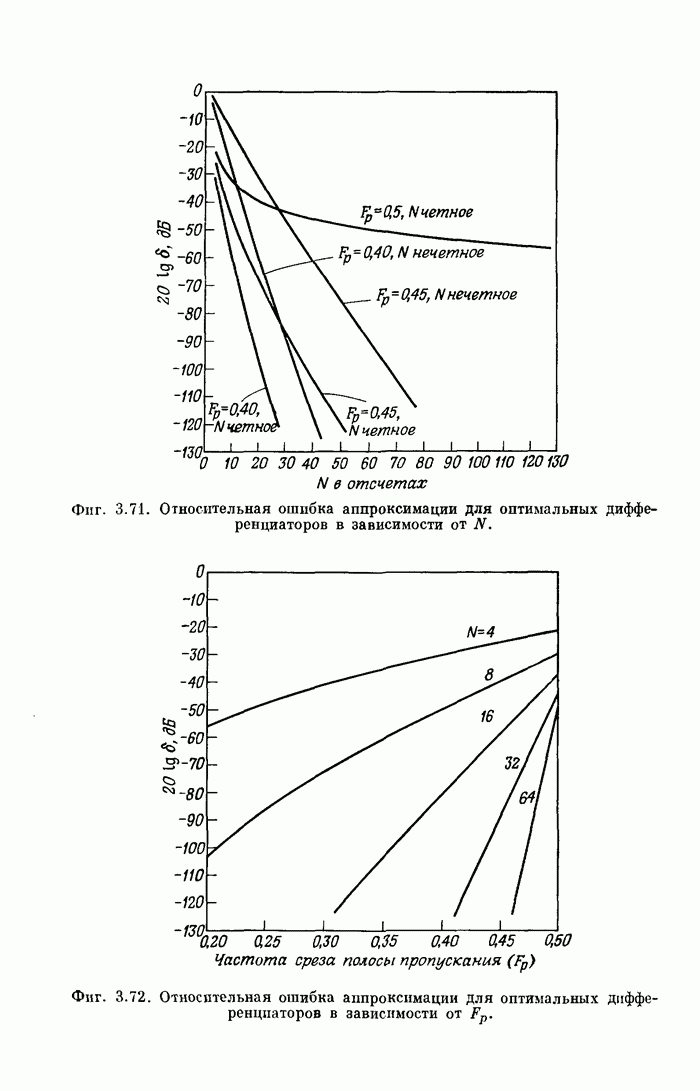
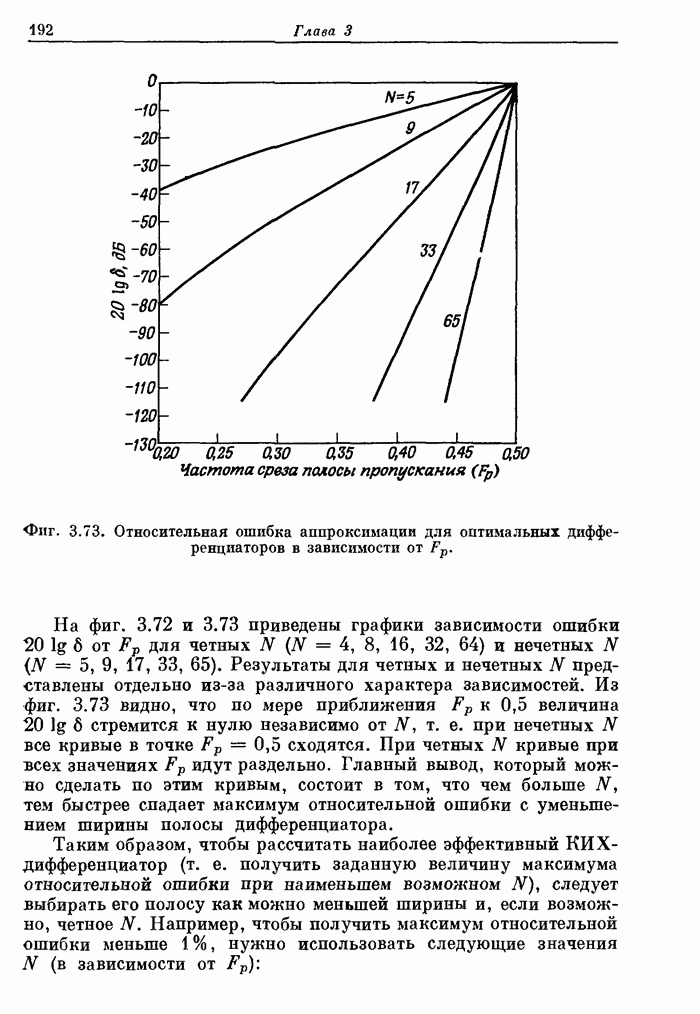
191
192
193
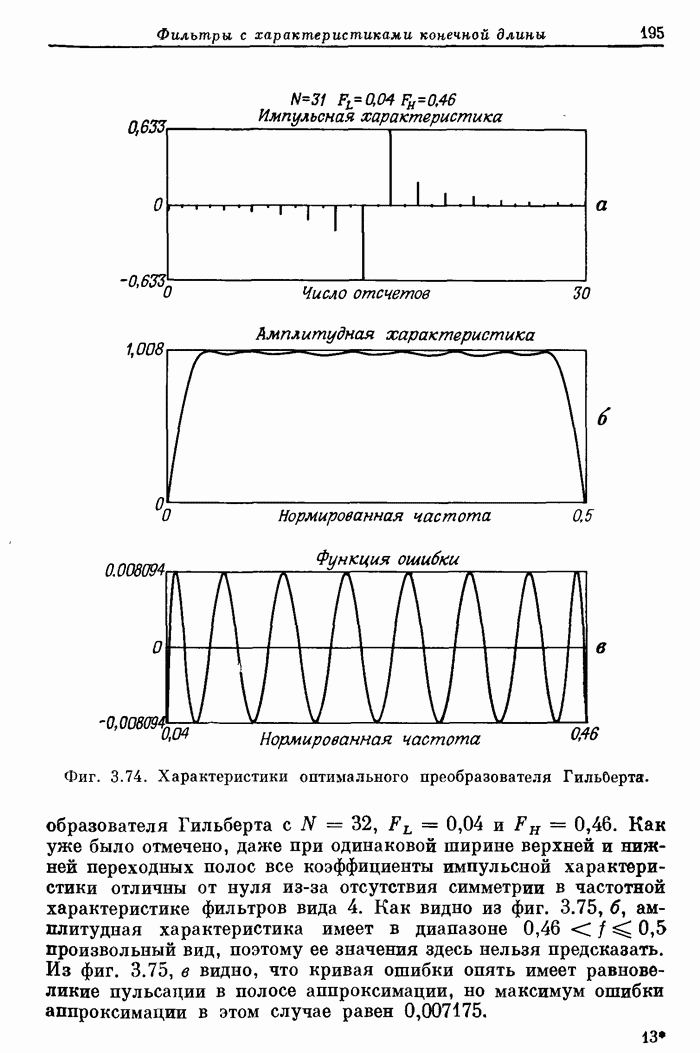
194
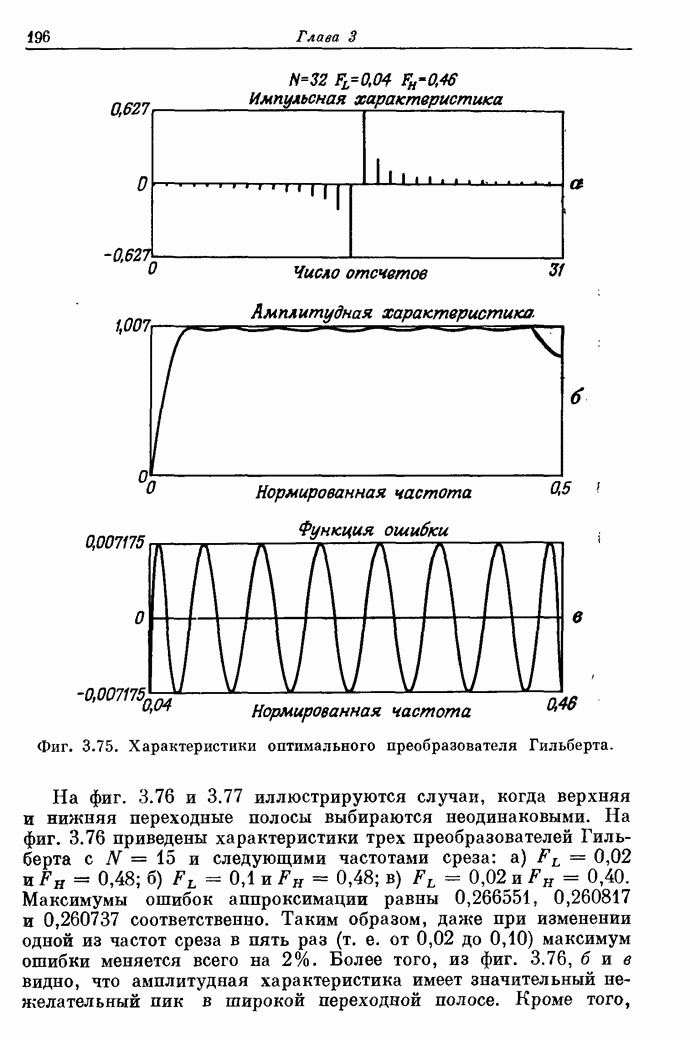
195
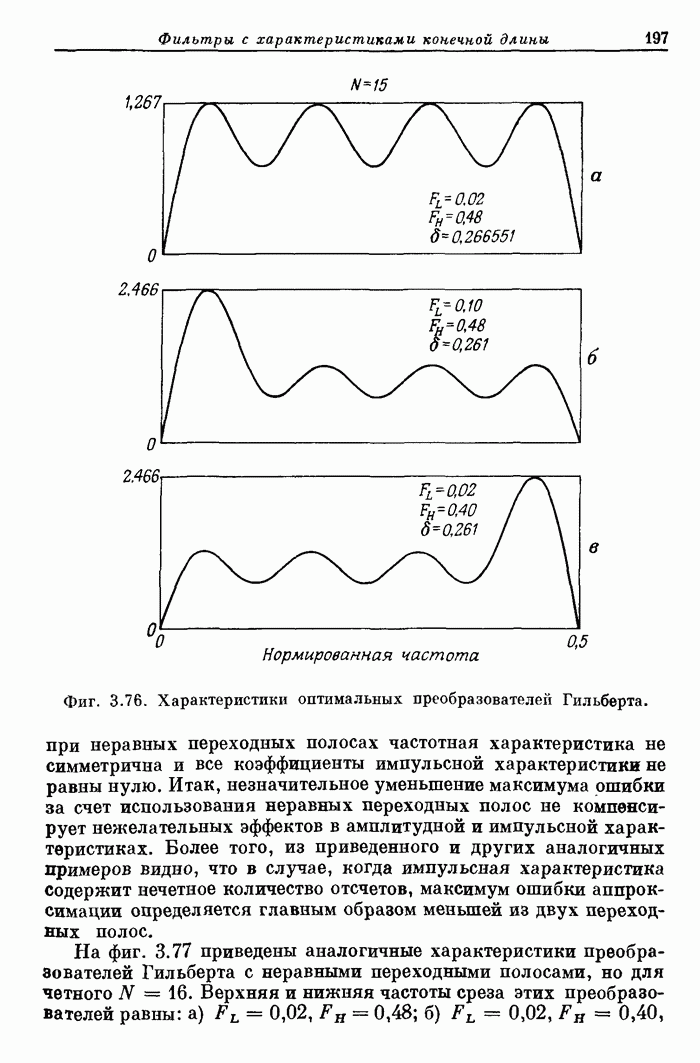
196
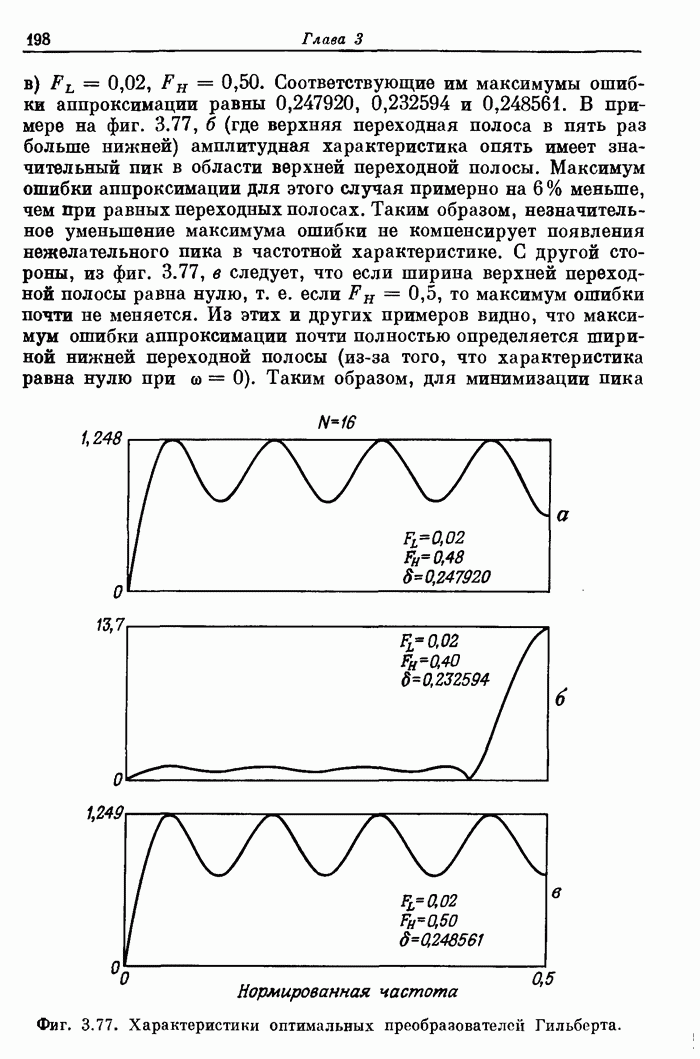
197
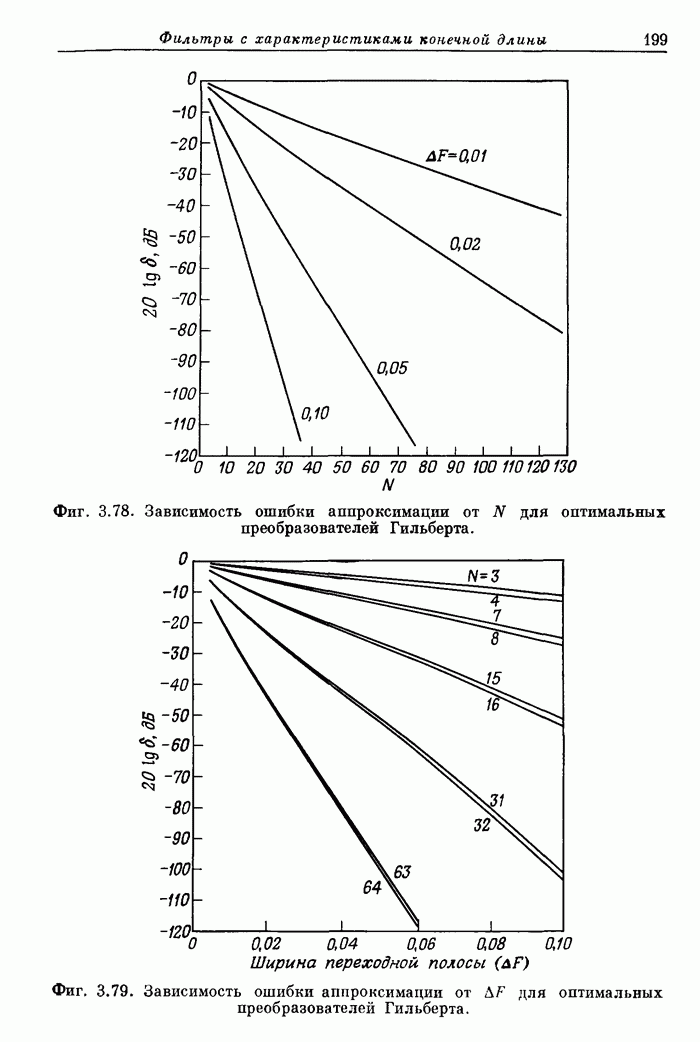
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
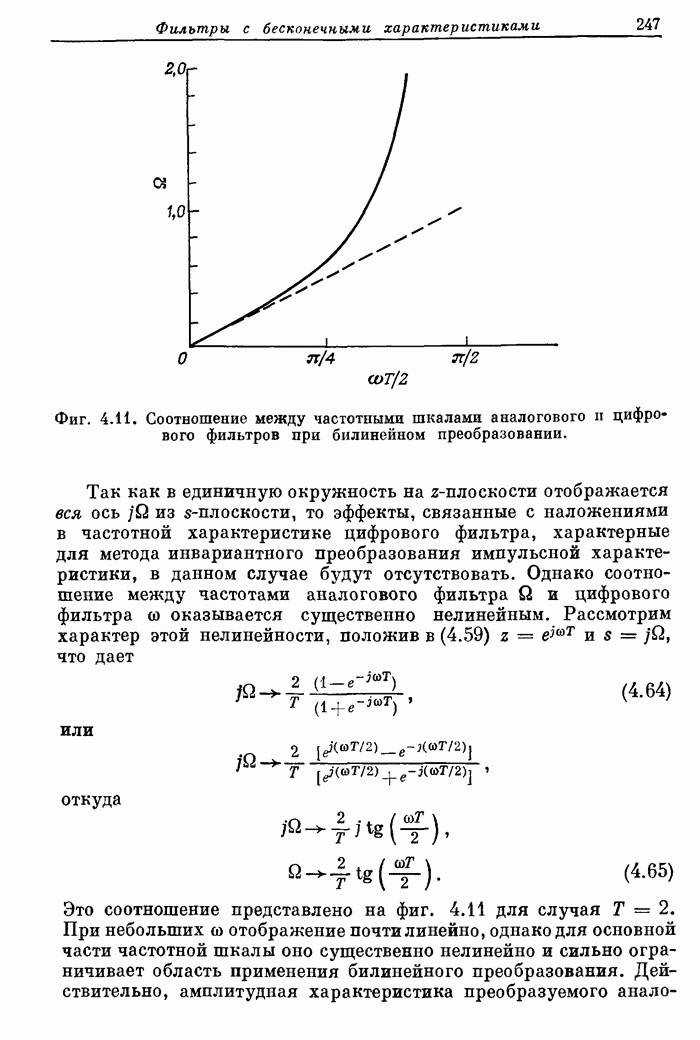
246
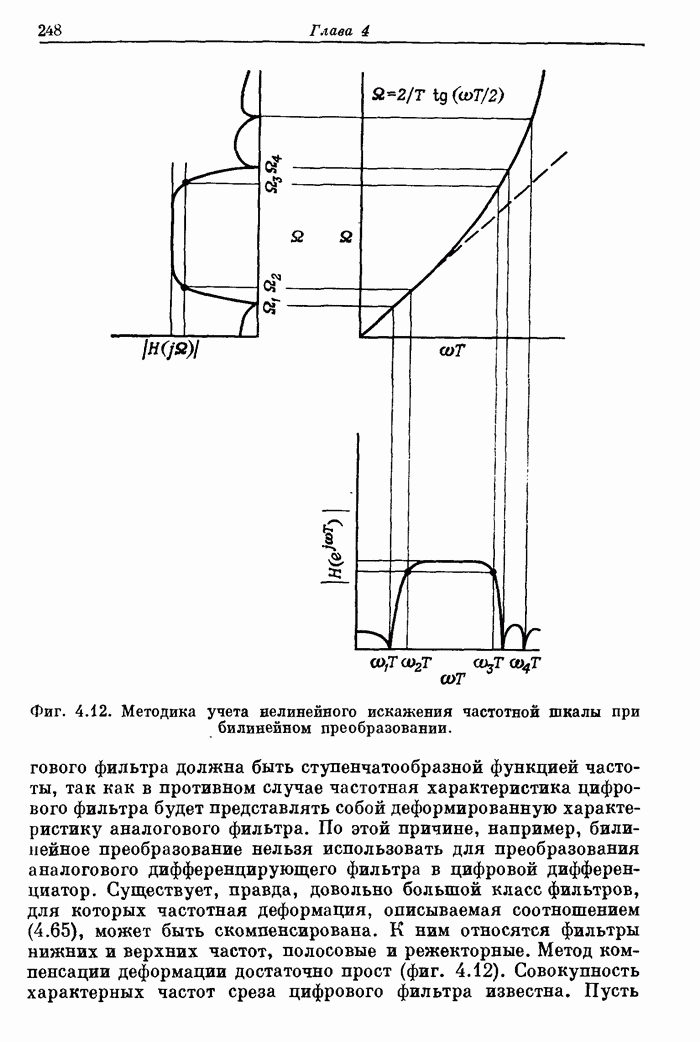
247
248
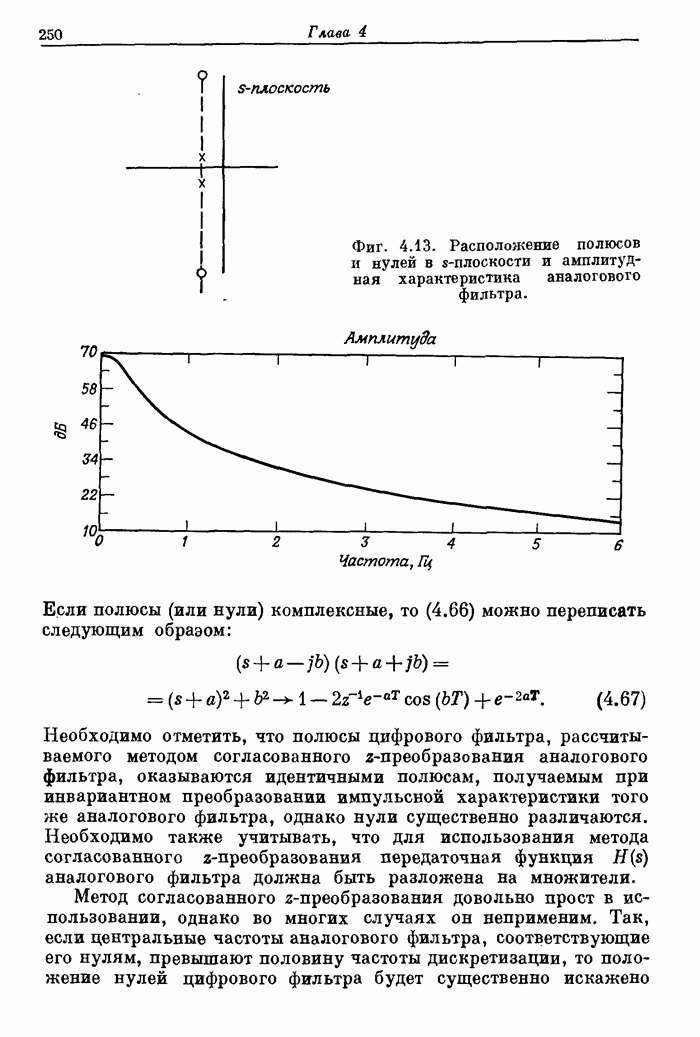
249
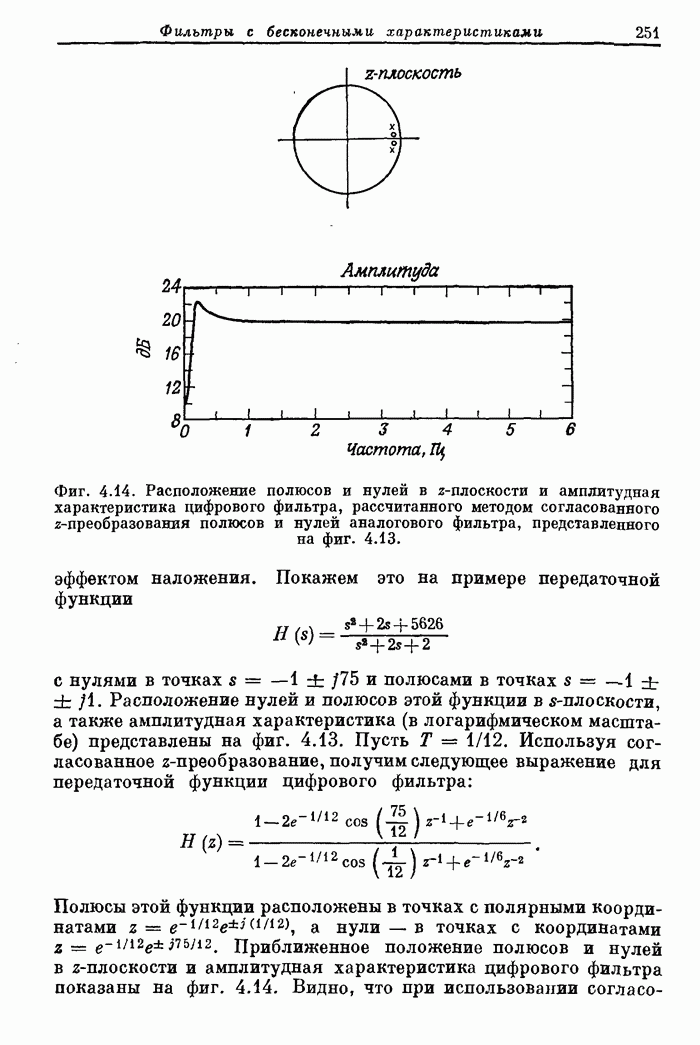
250
251
252
253
254
255
256
257
258
259
260
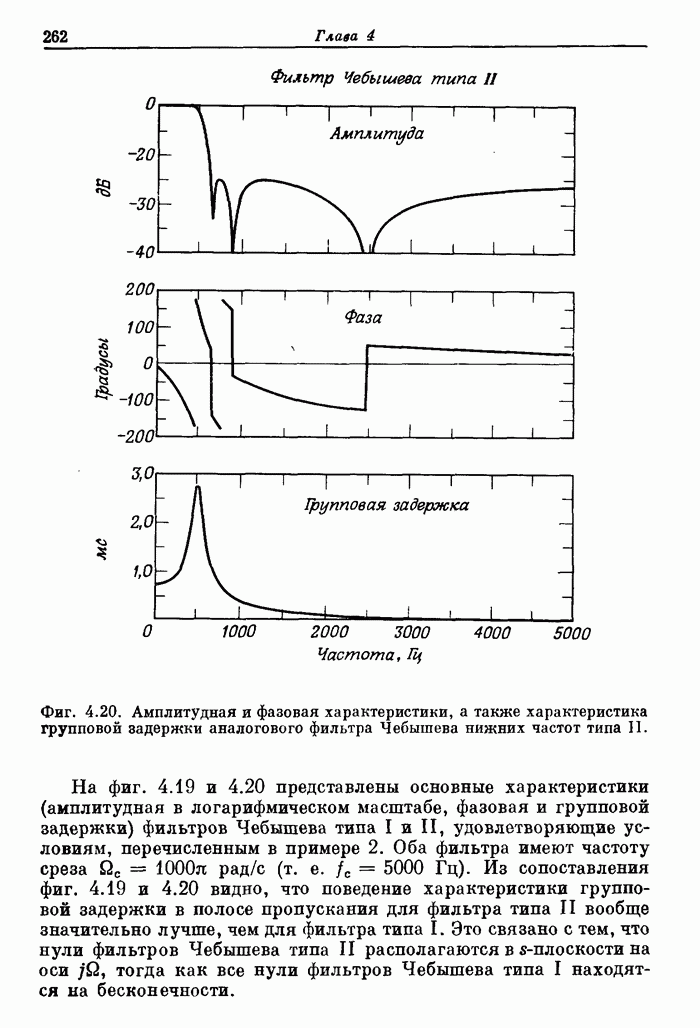
261
262
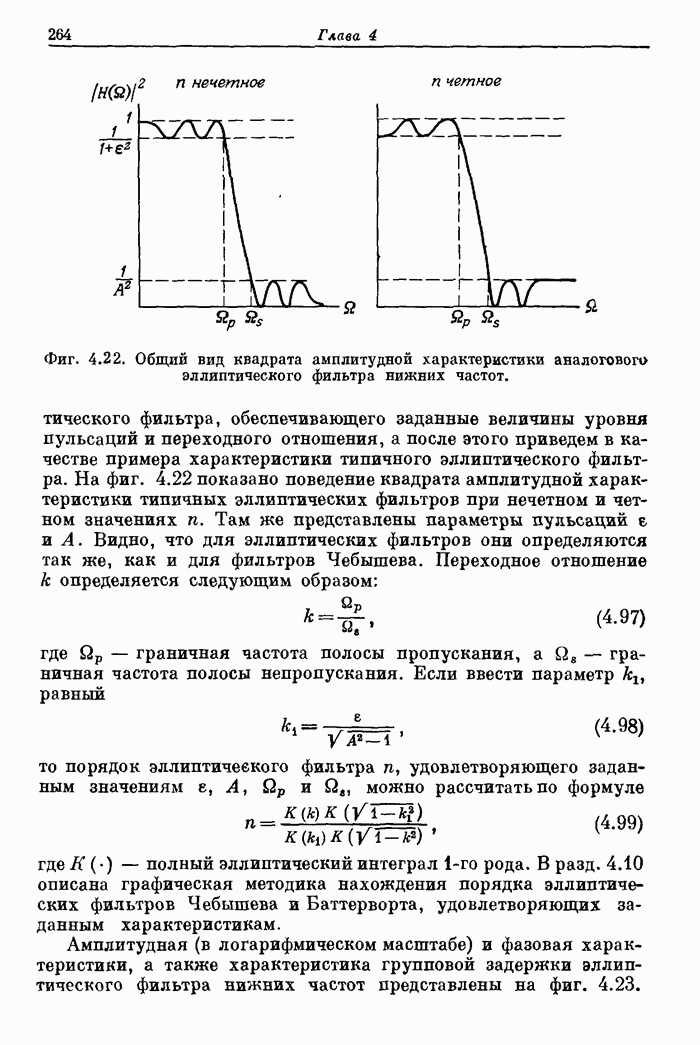
263
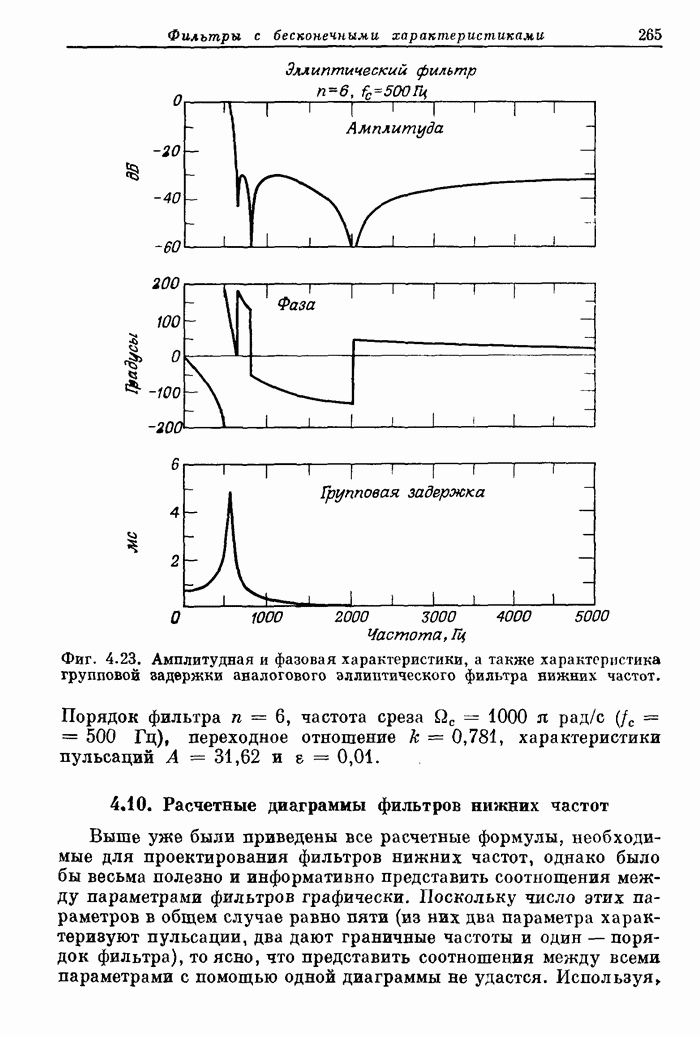
264
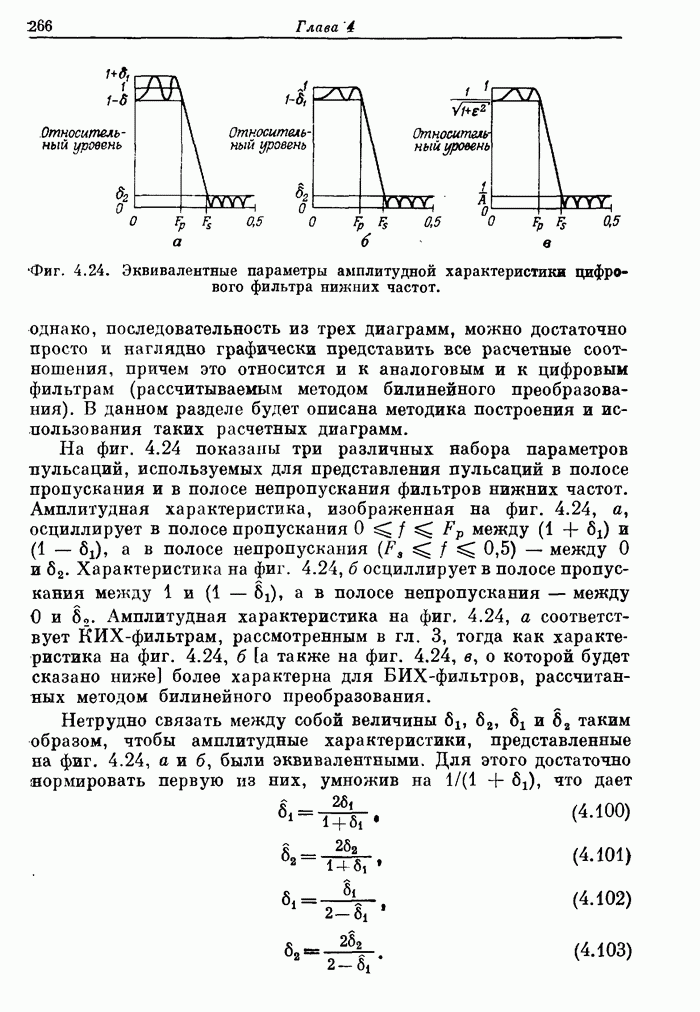
265
266
267
268
269
270
271
272
273
274
275
276
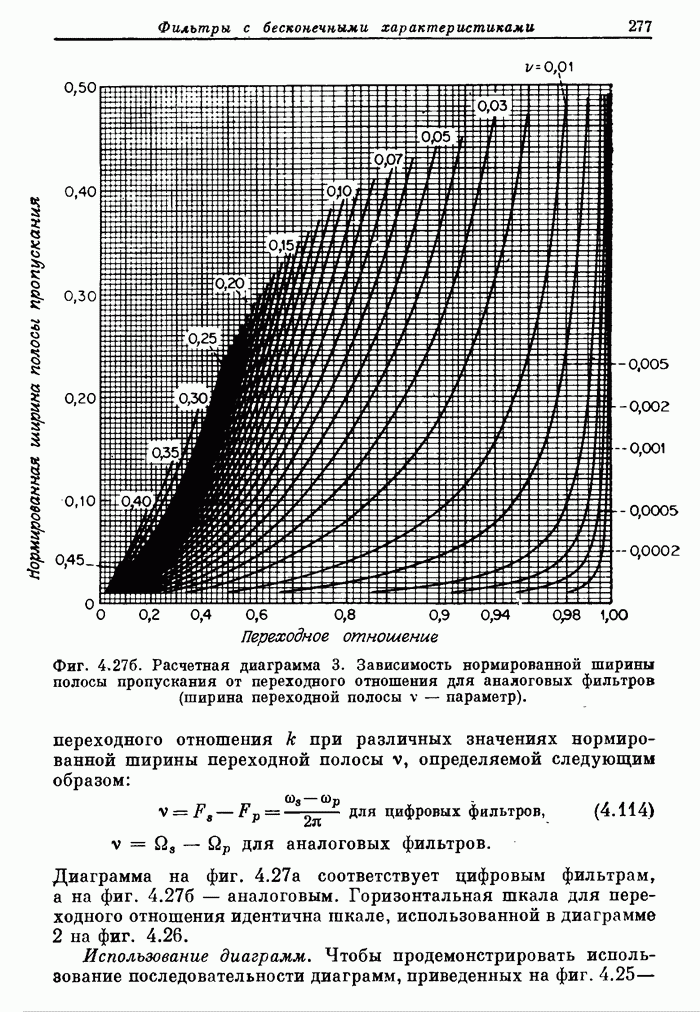
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
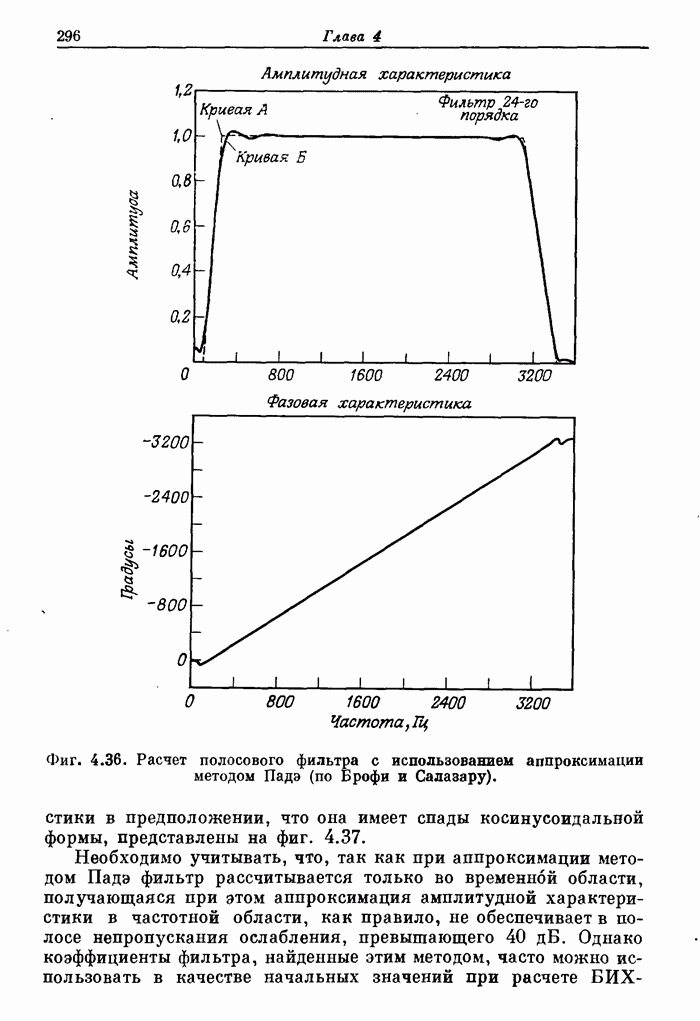
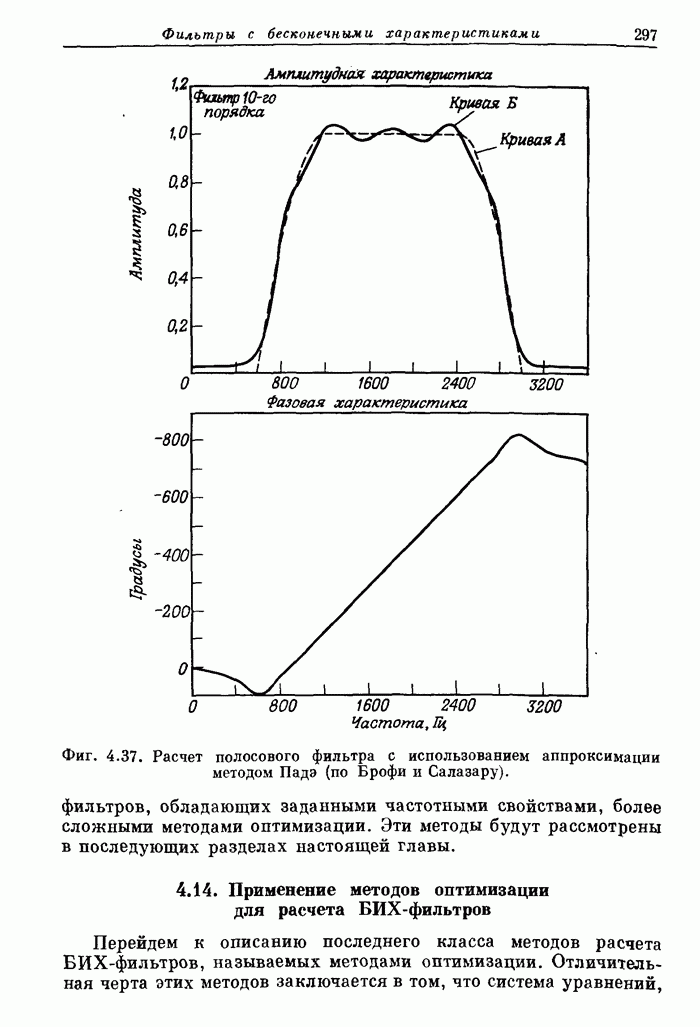
295
296
297
298
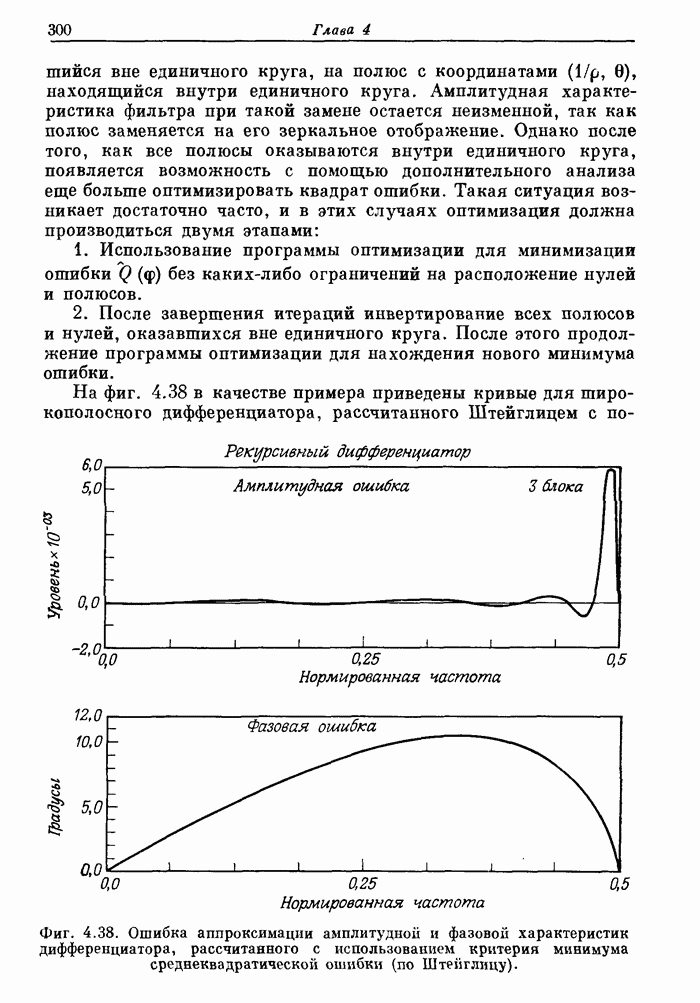
299
300
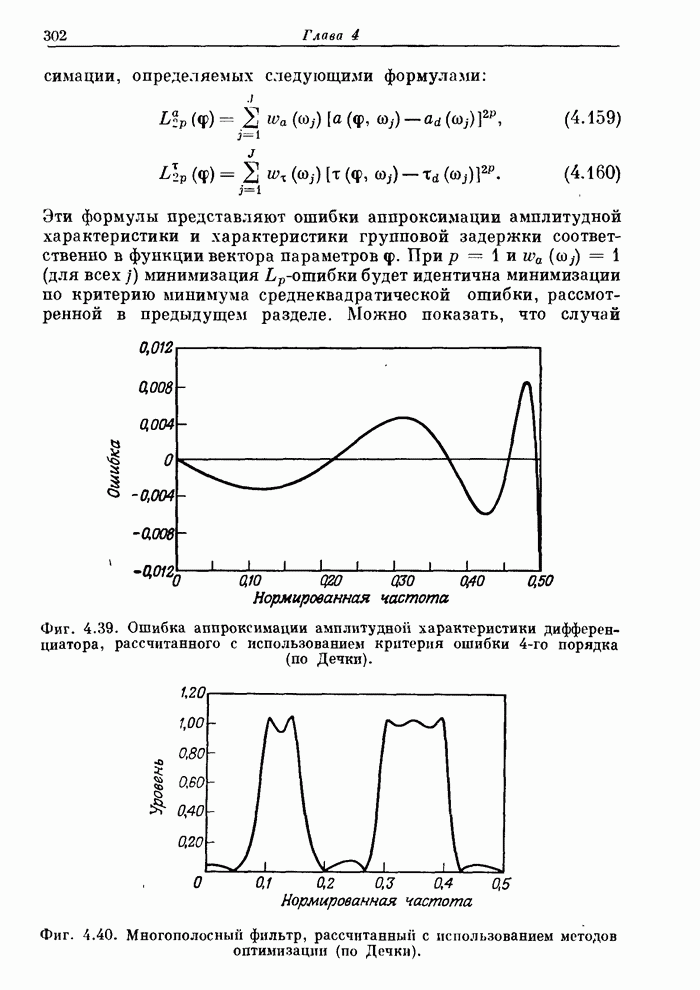
301
302
303
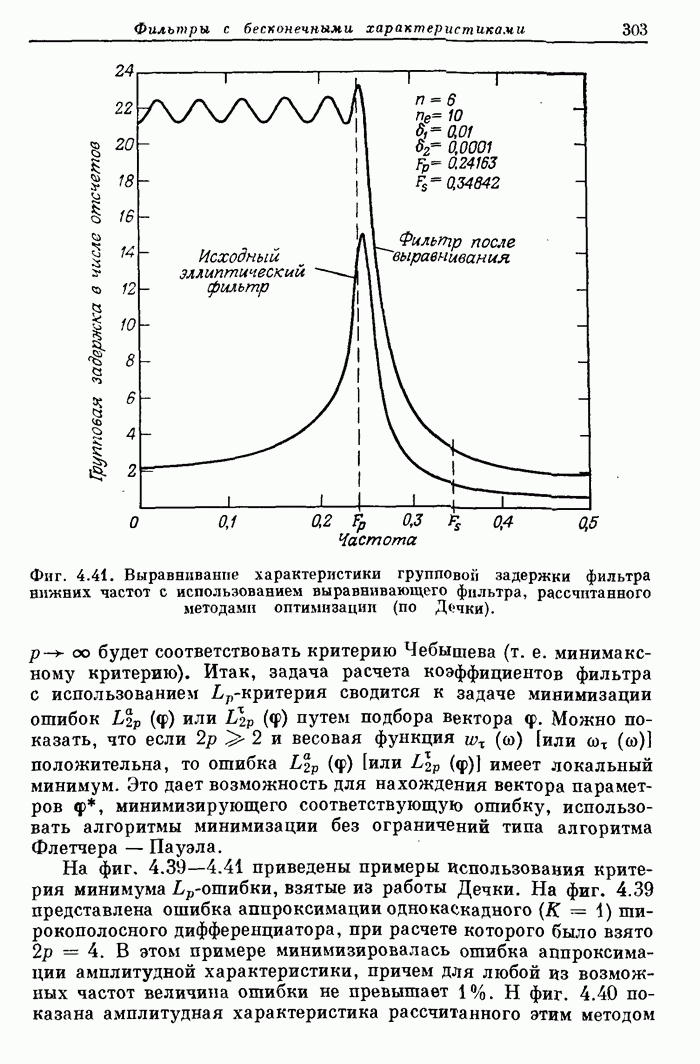
304
305
306
307
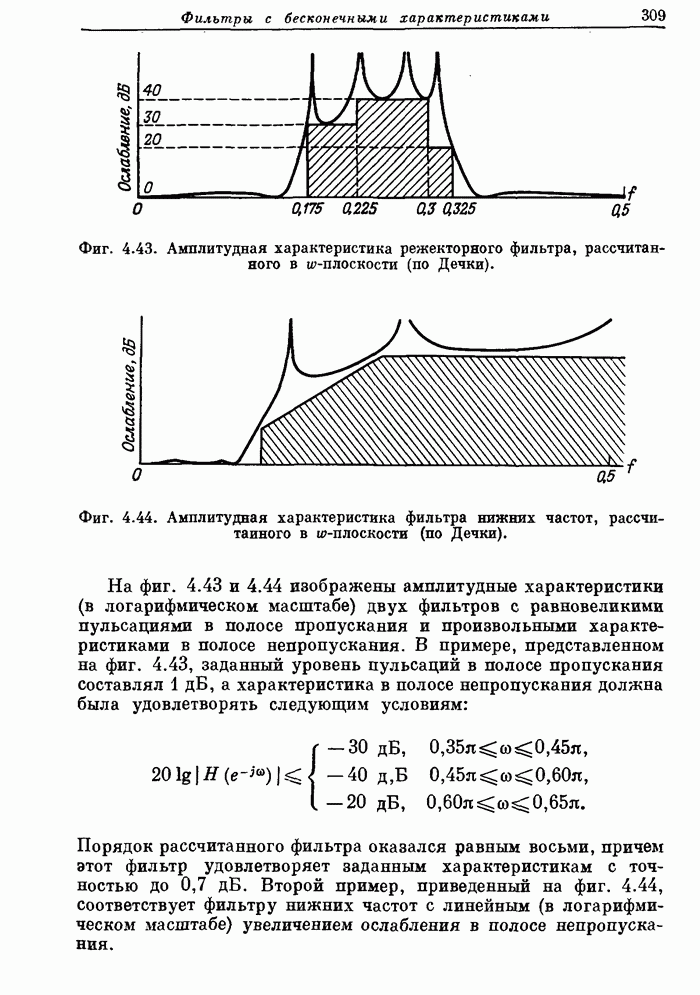
308
309
310
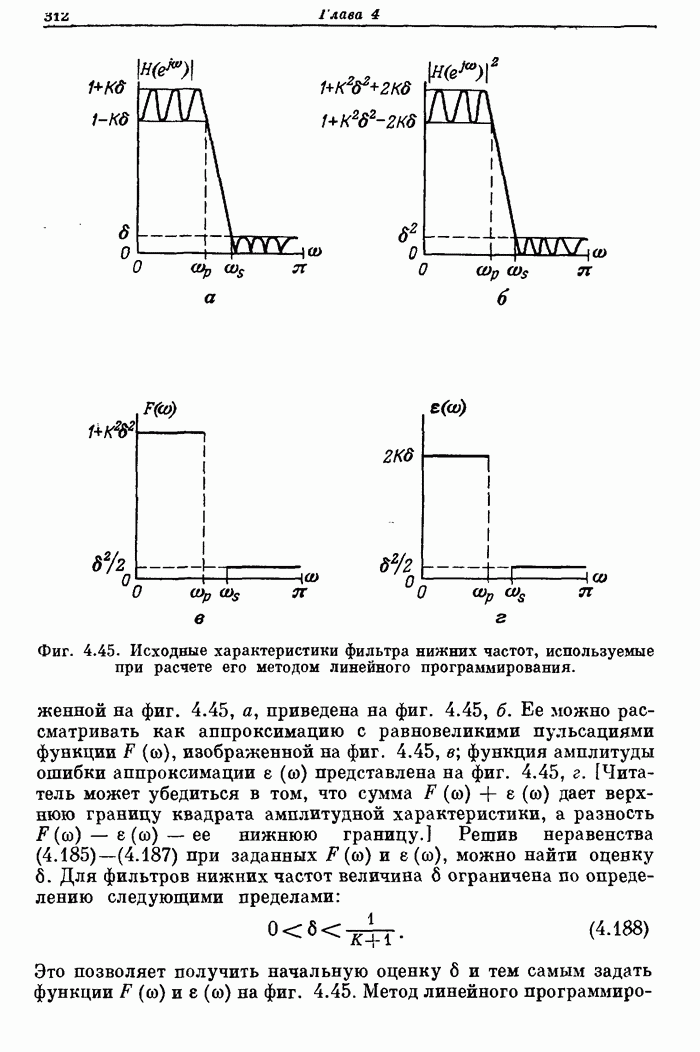
311
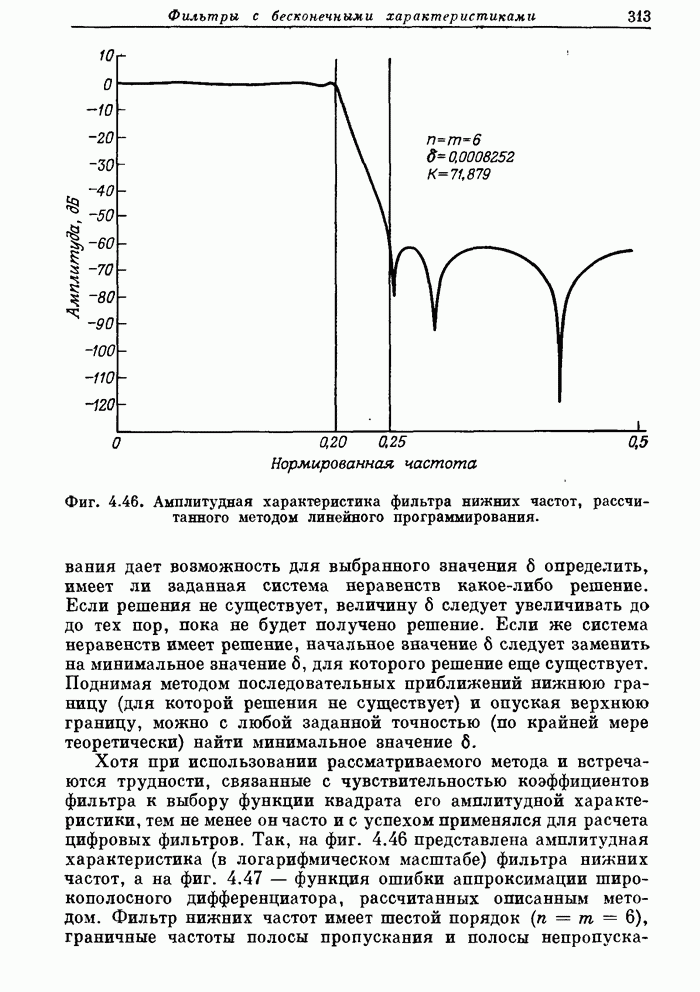
312
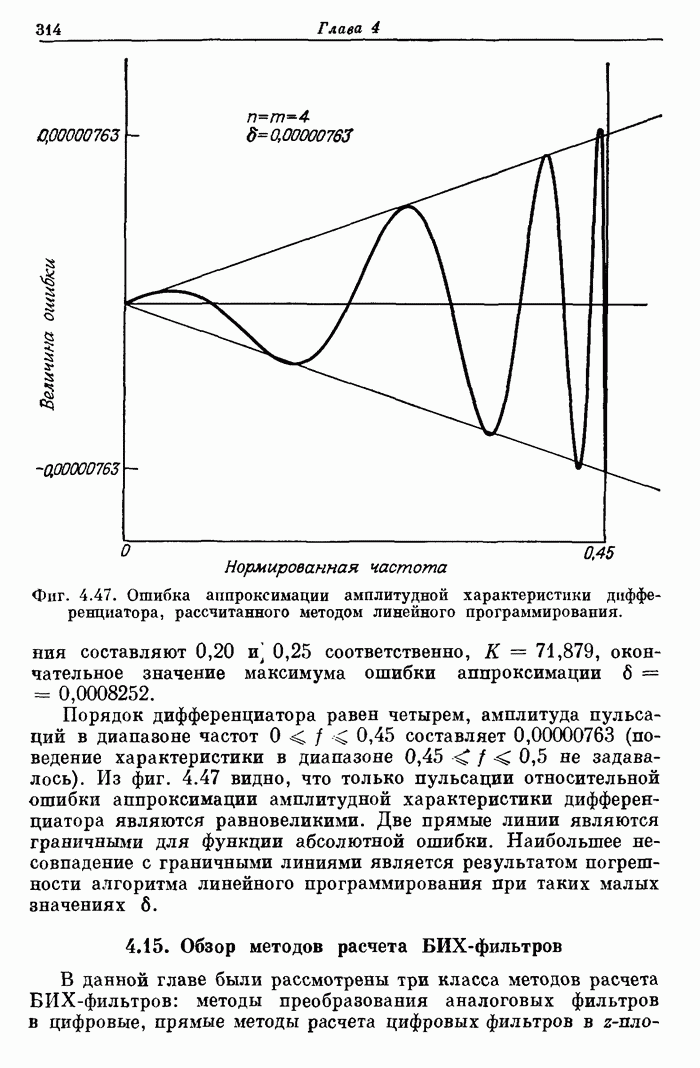
313
314
315
316
317
318
319
320
321
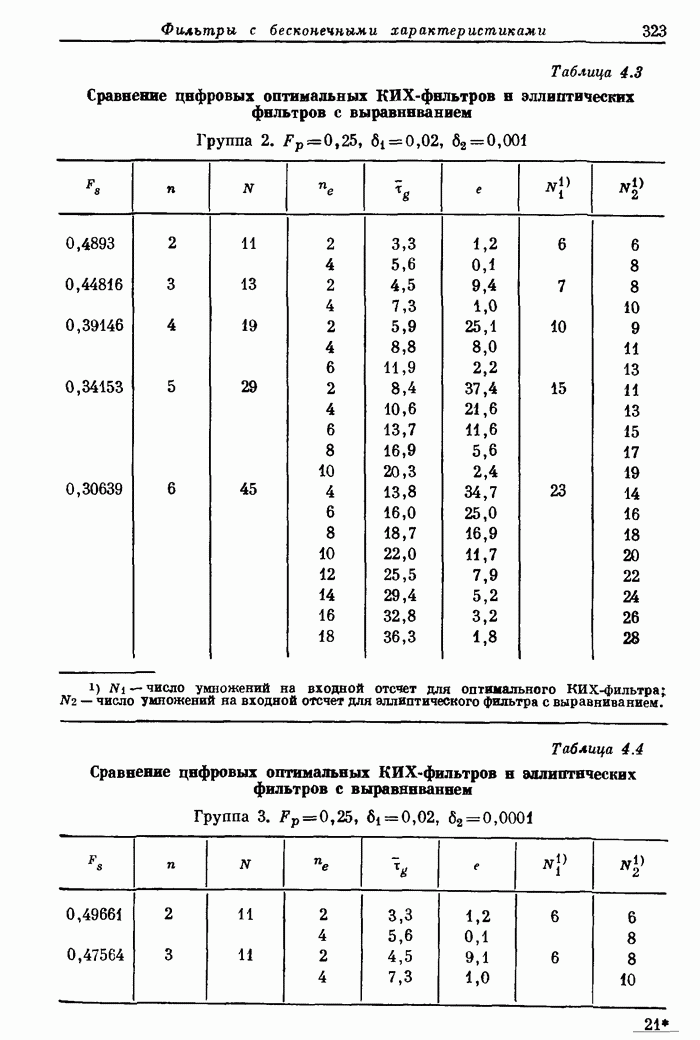
322
323
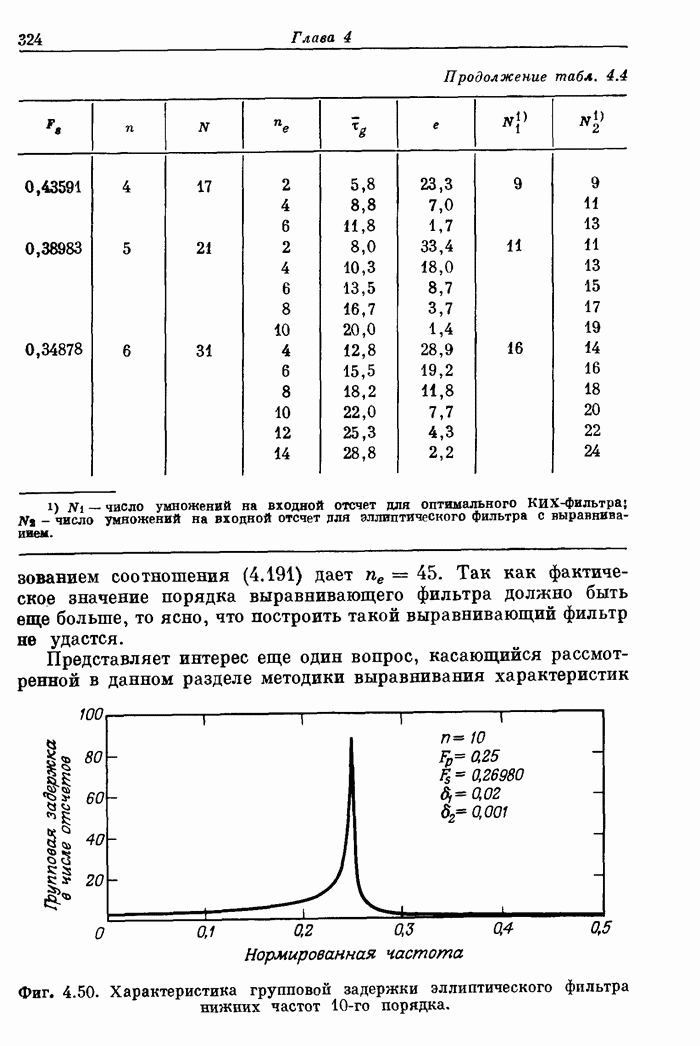
324
325
326
327
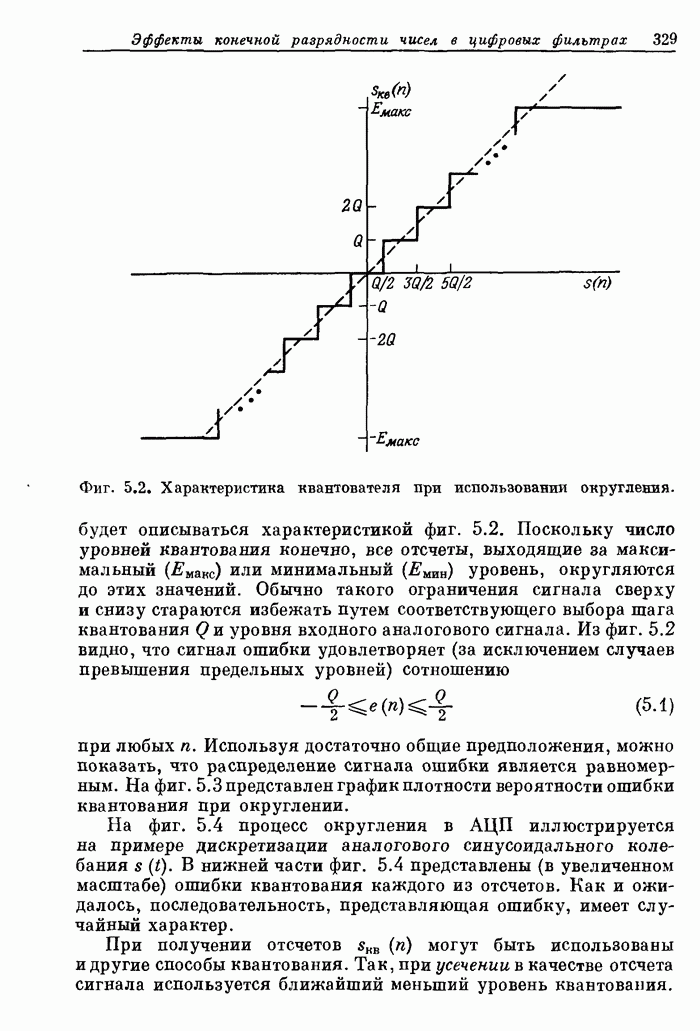
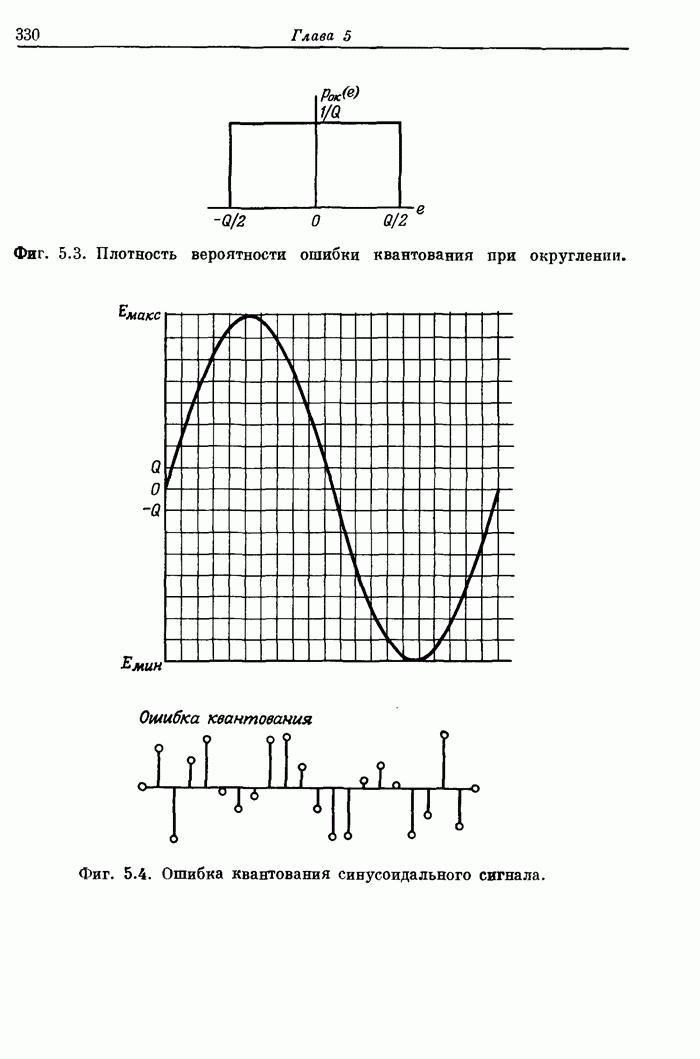
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
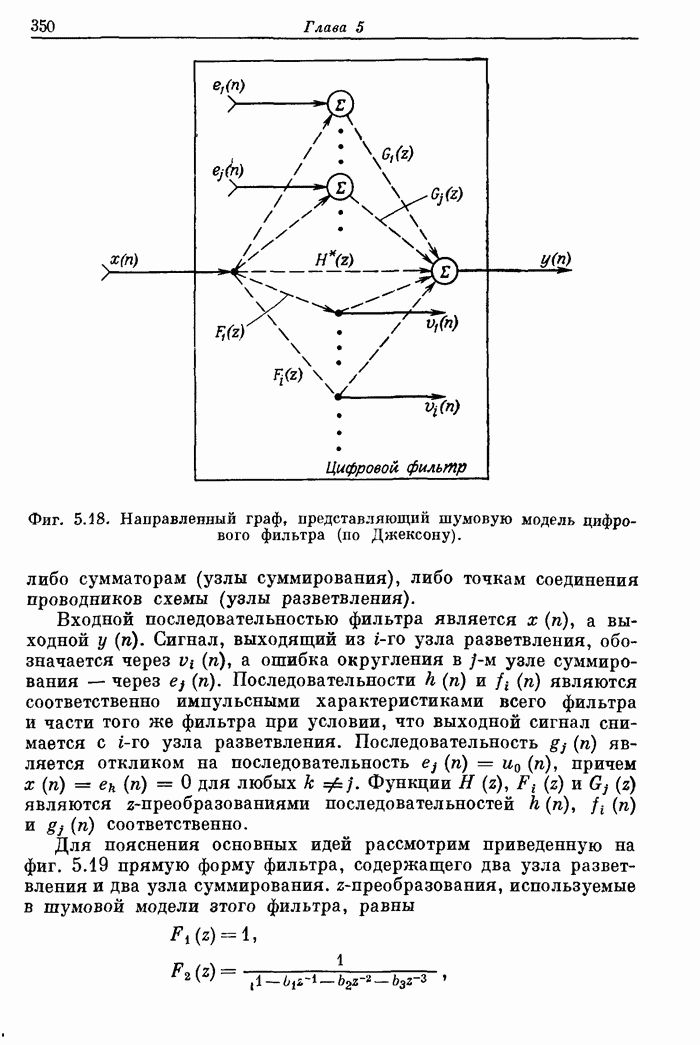
349
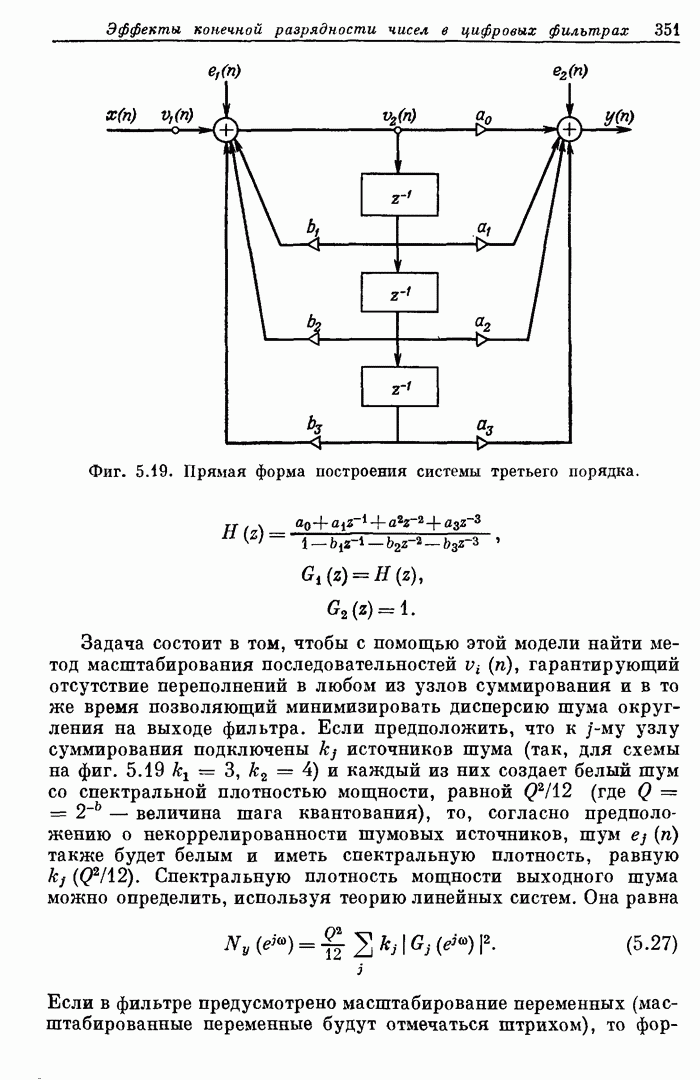
350
351
352
353
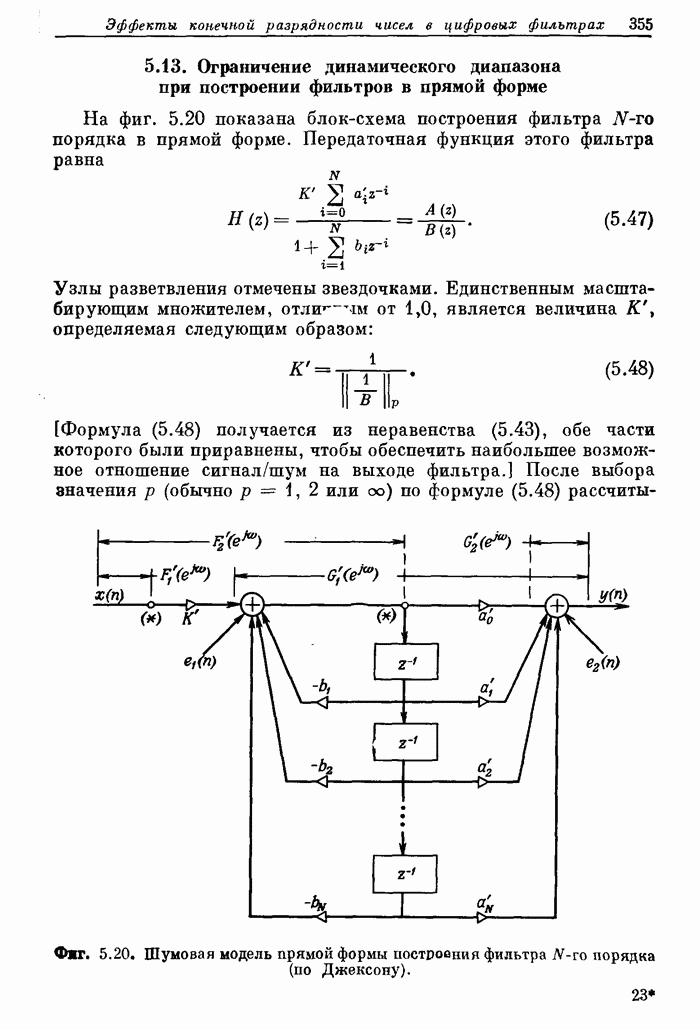
354
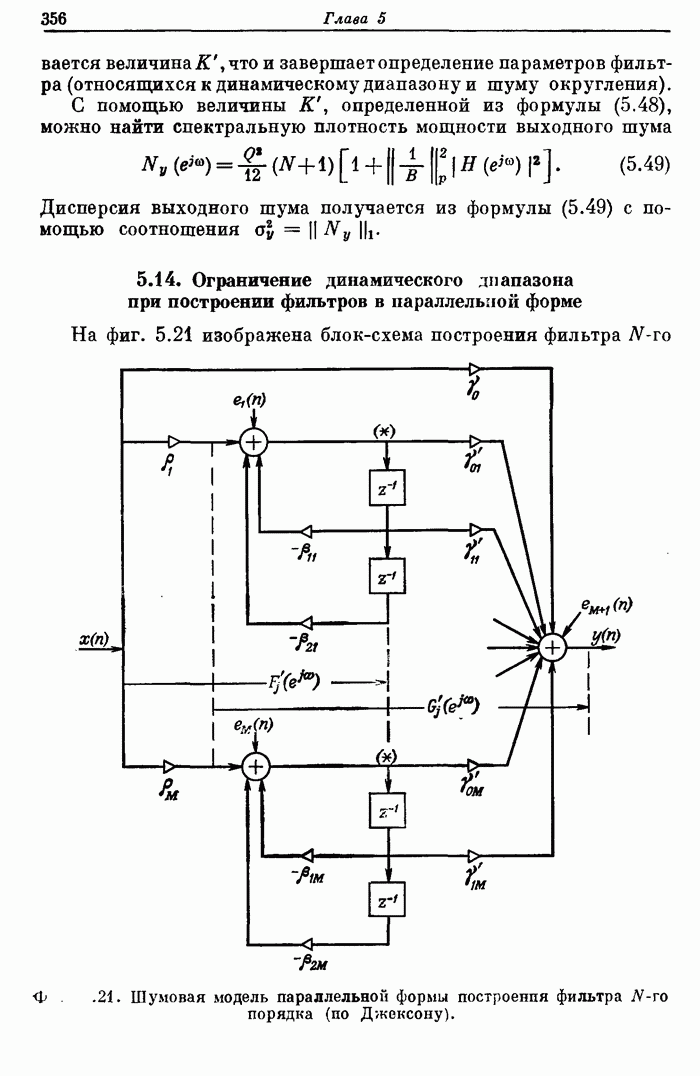
355
356
357
358
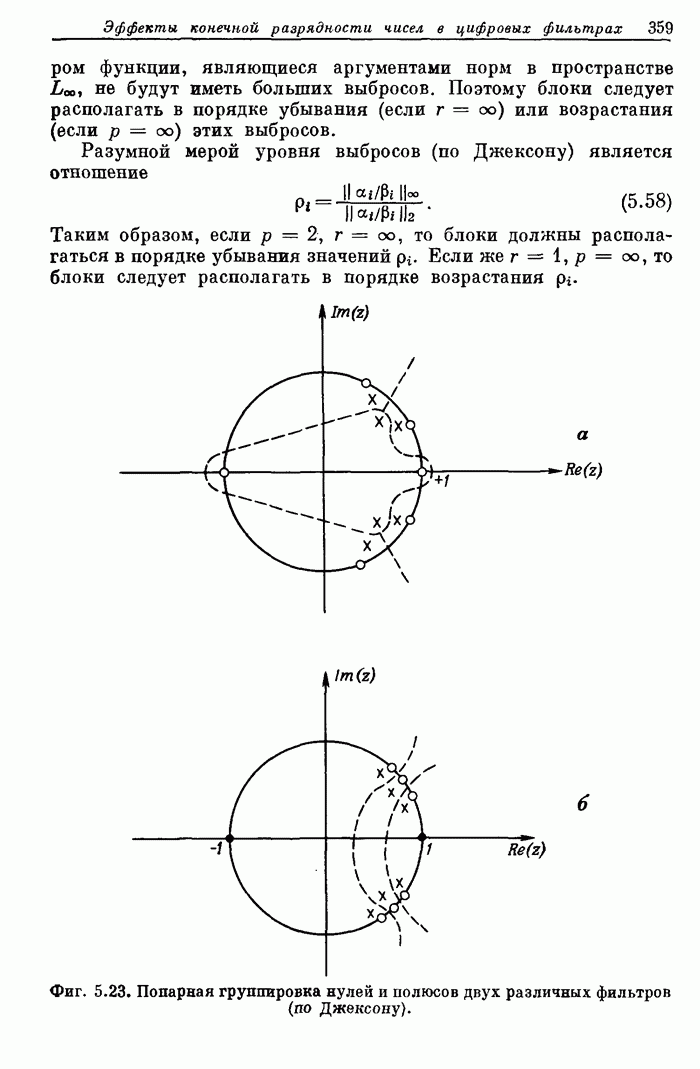
359
360
361
362
363
364
365
366
367
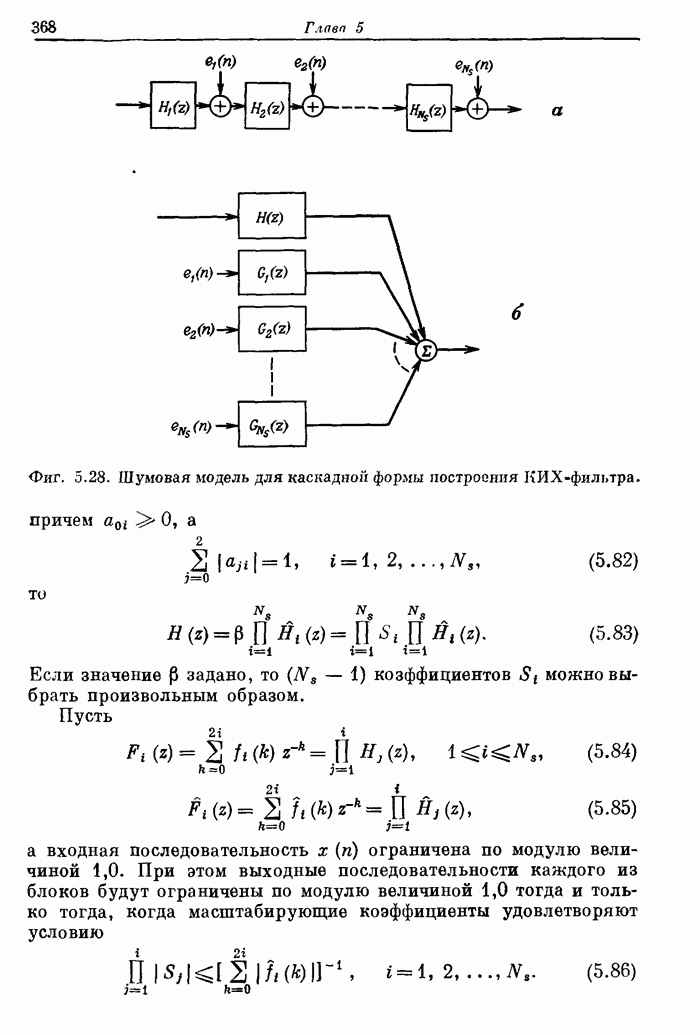
368
369
370
371
372
373
374
375
376
377
378
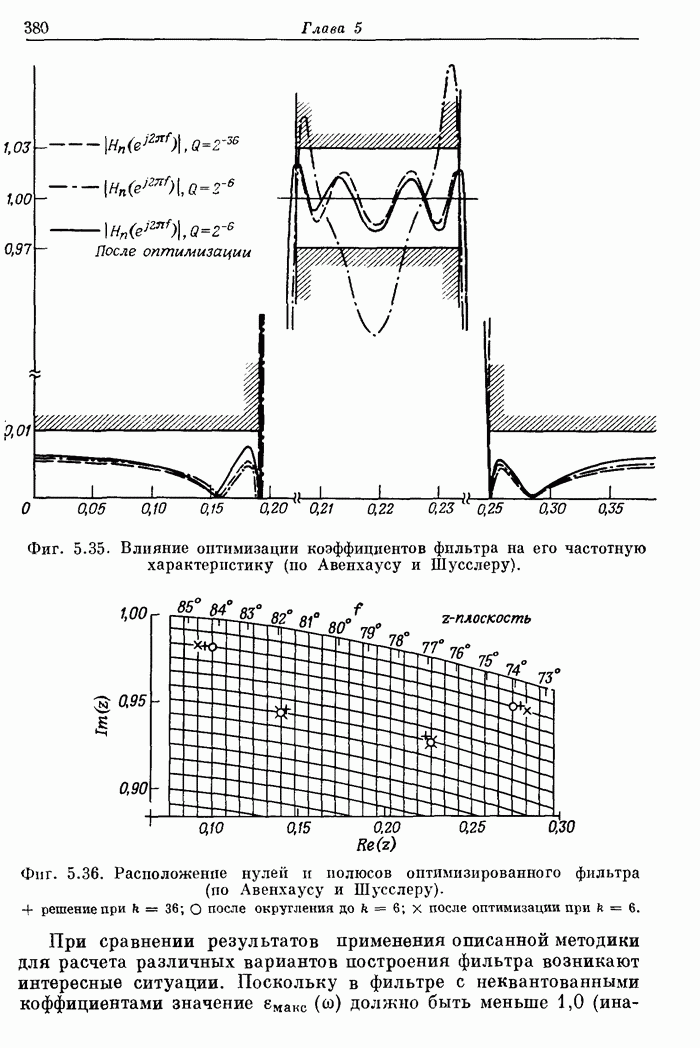
379
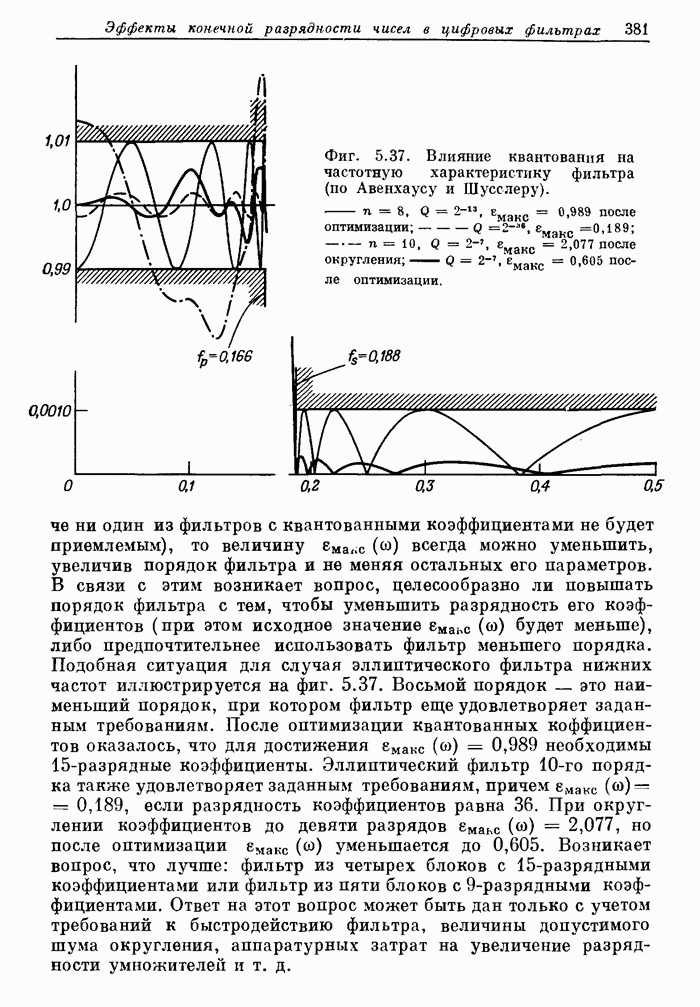
380
381
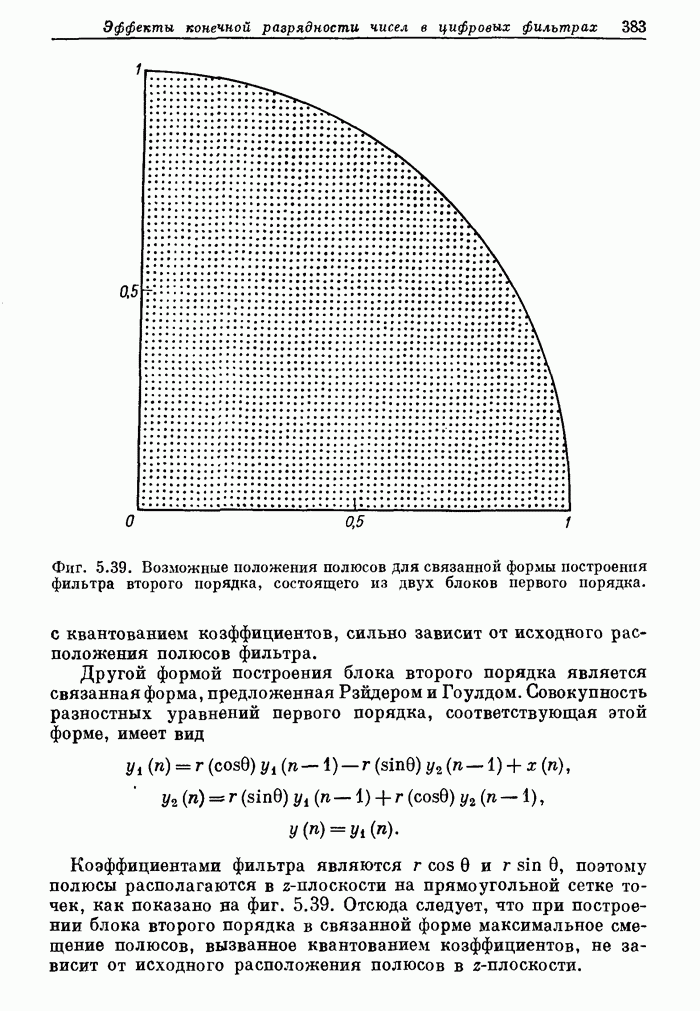
382
383
384
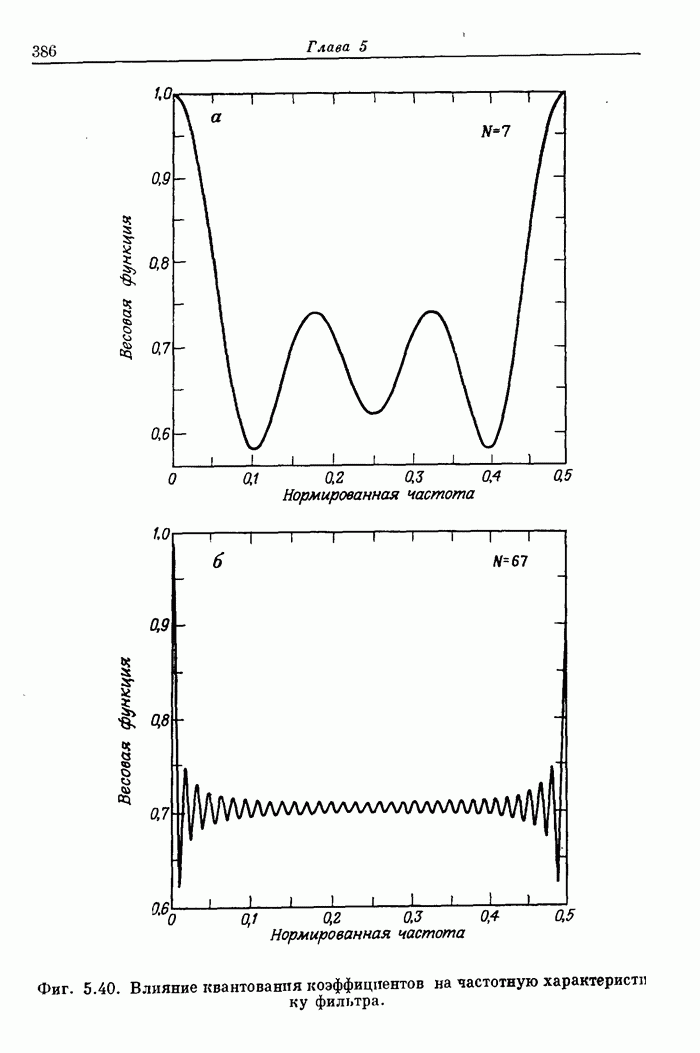
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
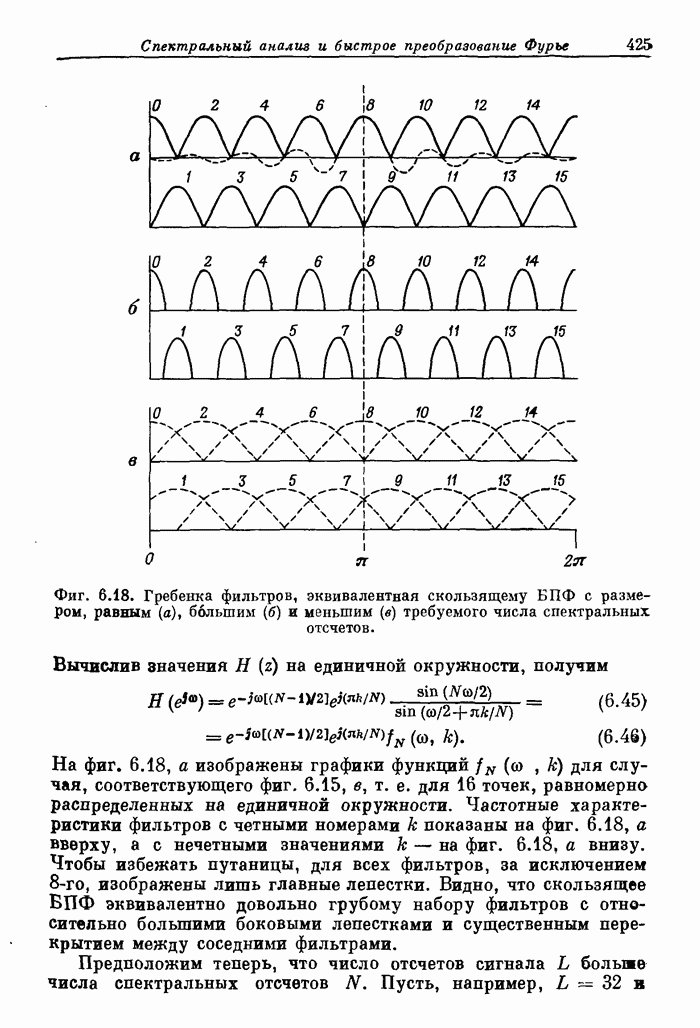
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
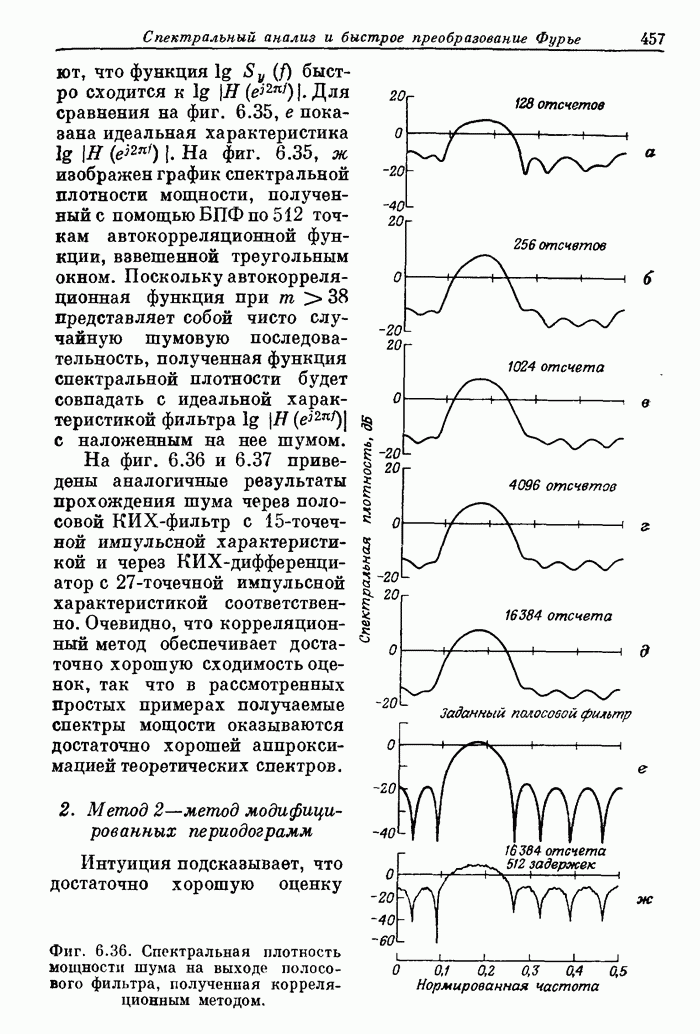
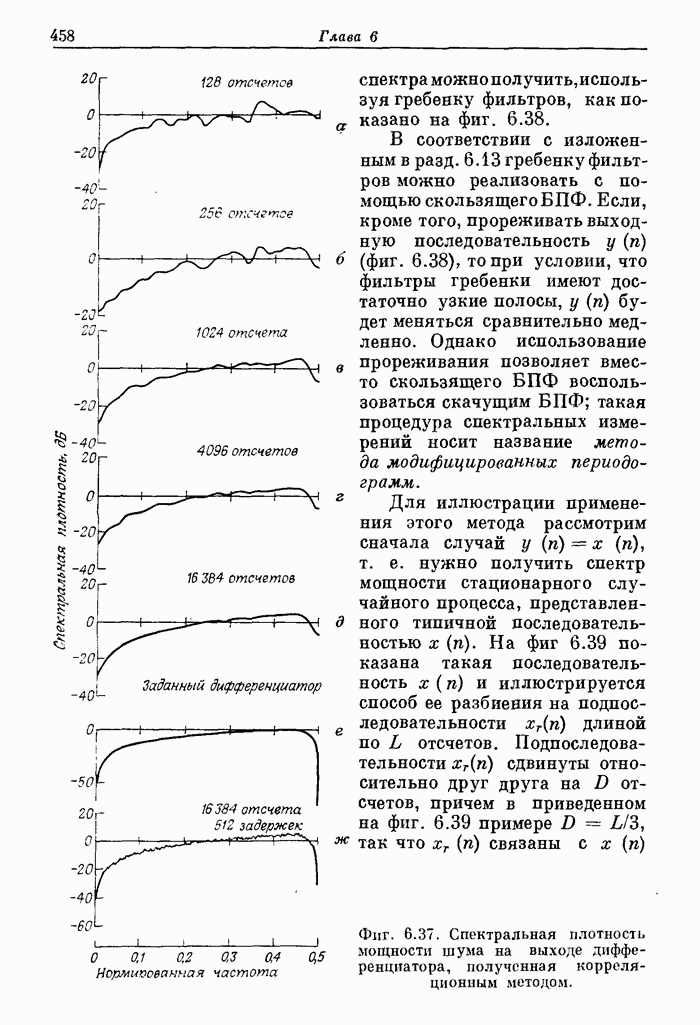
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
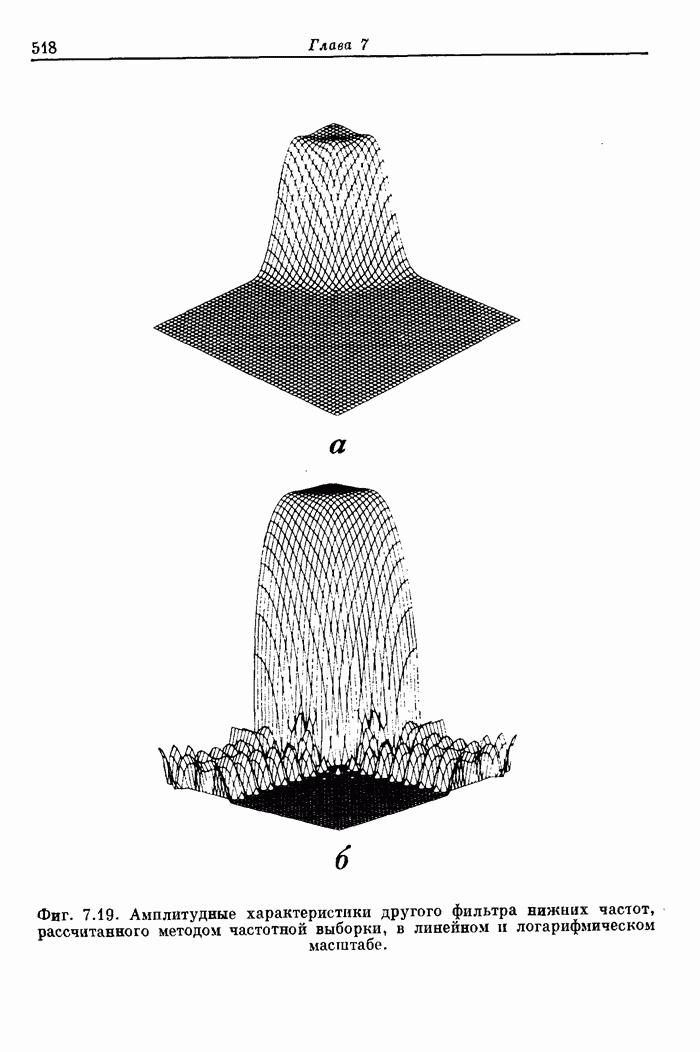
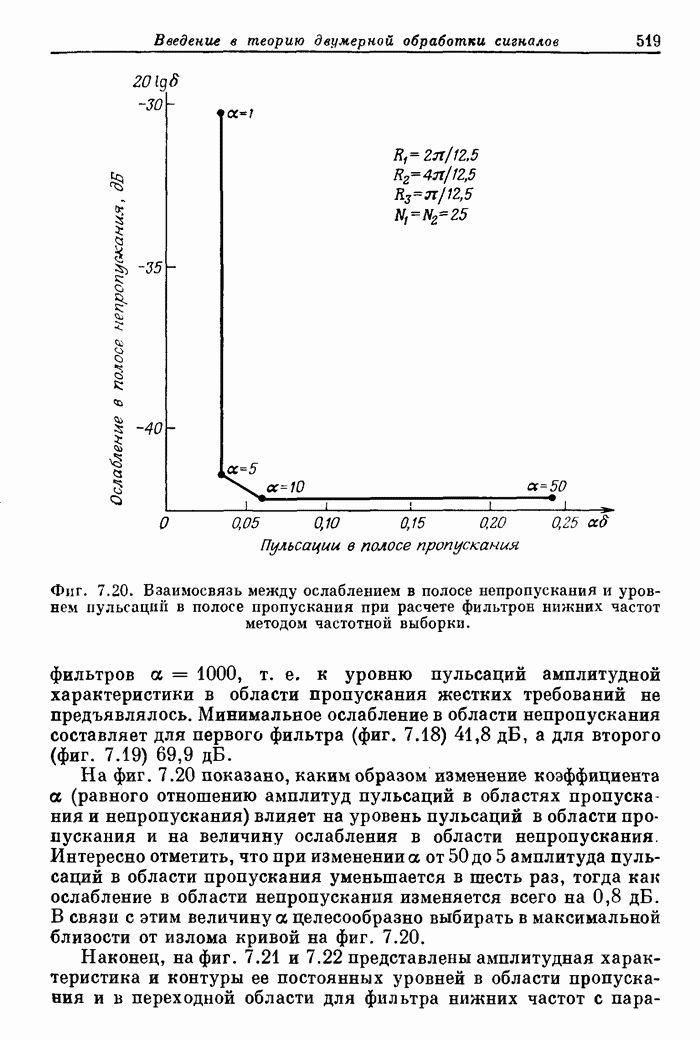
519
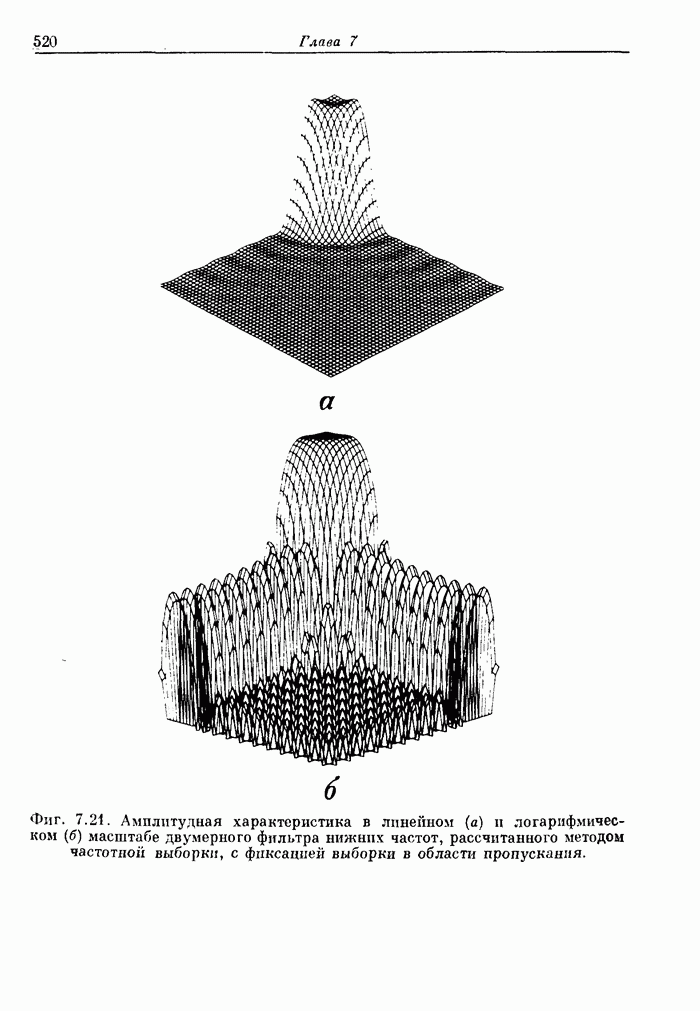
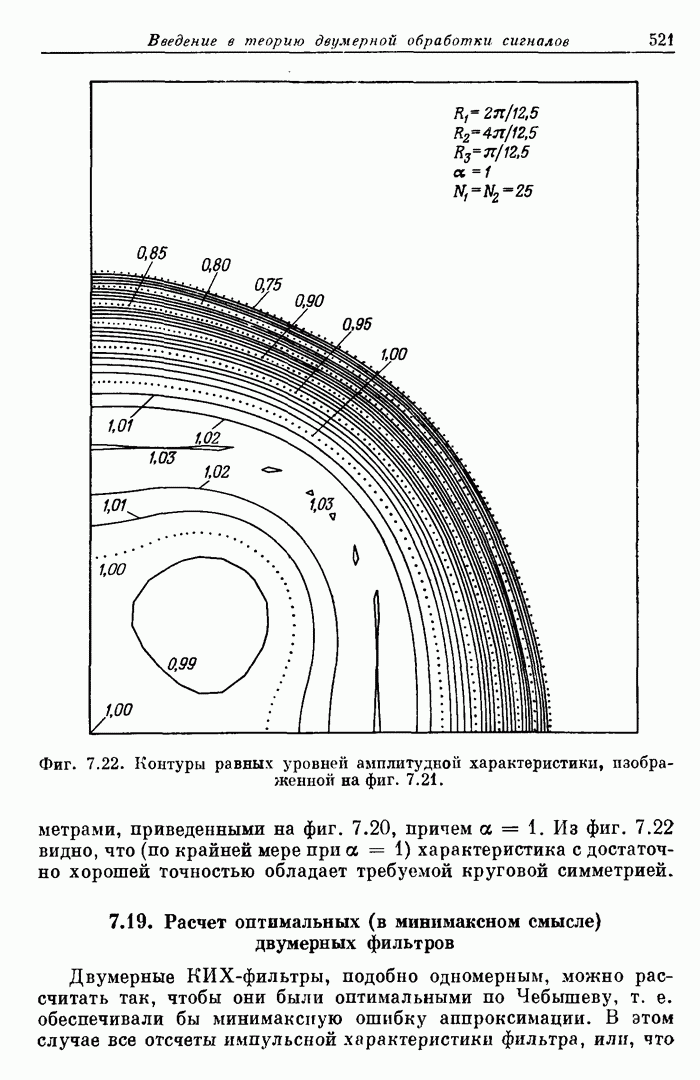
520
521
522
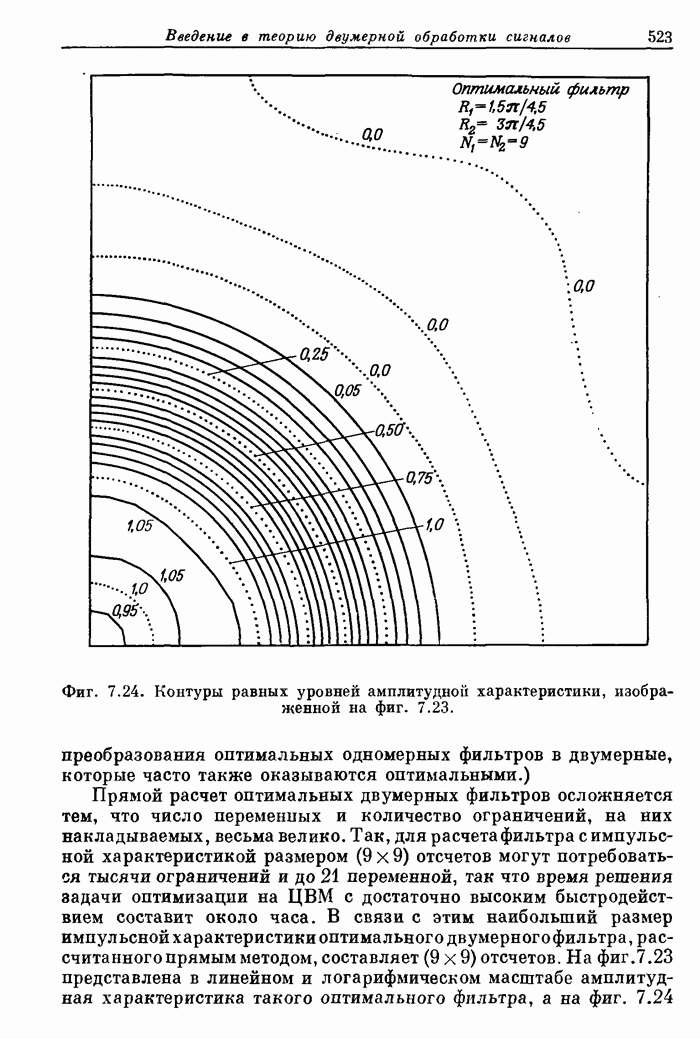
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
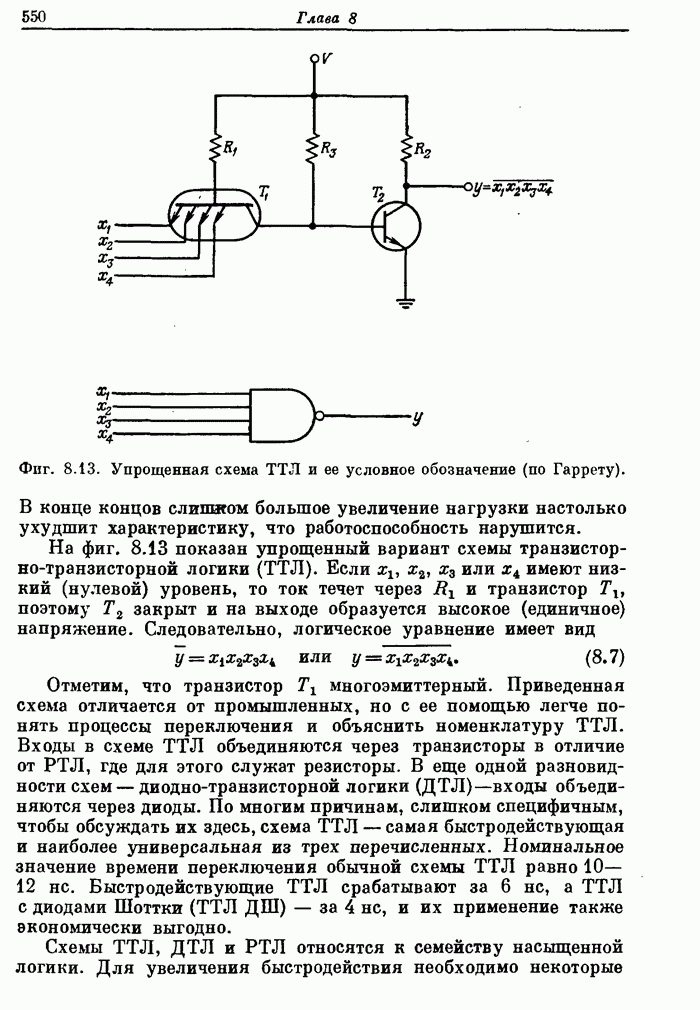
549
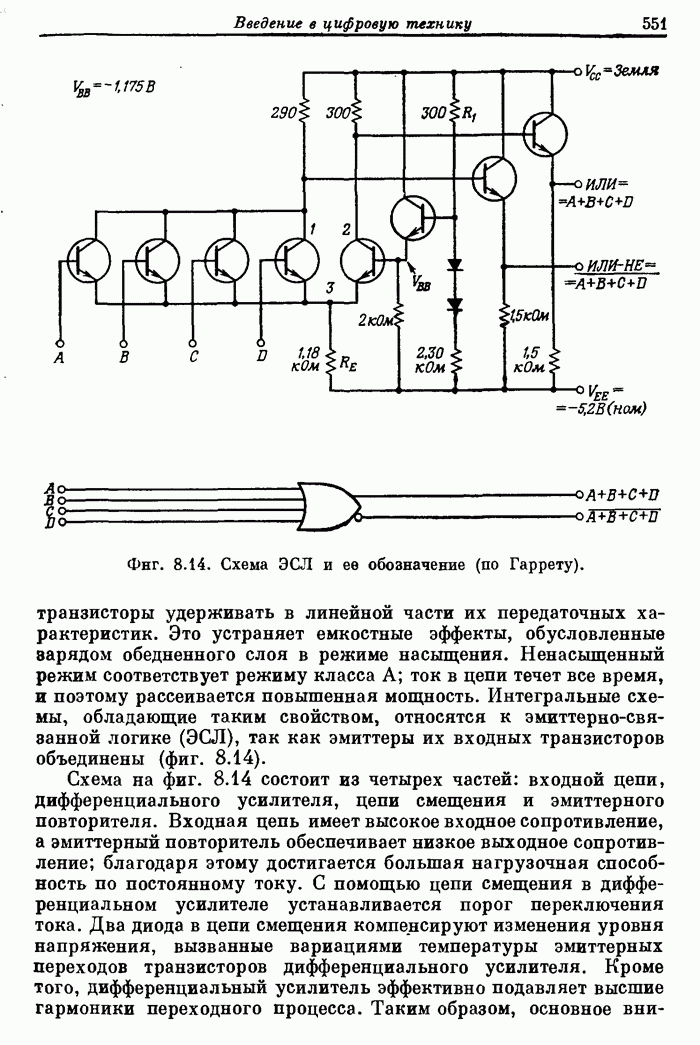
550
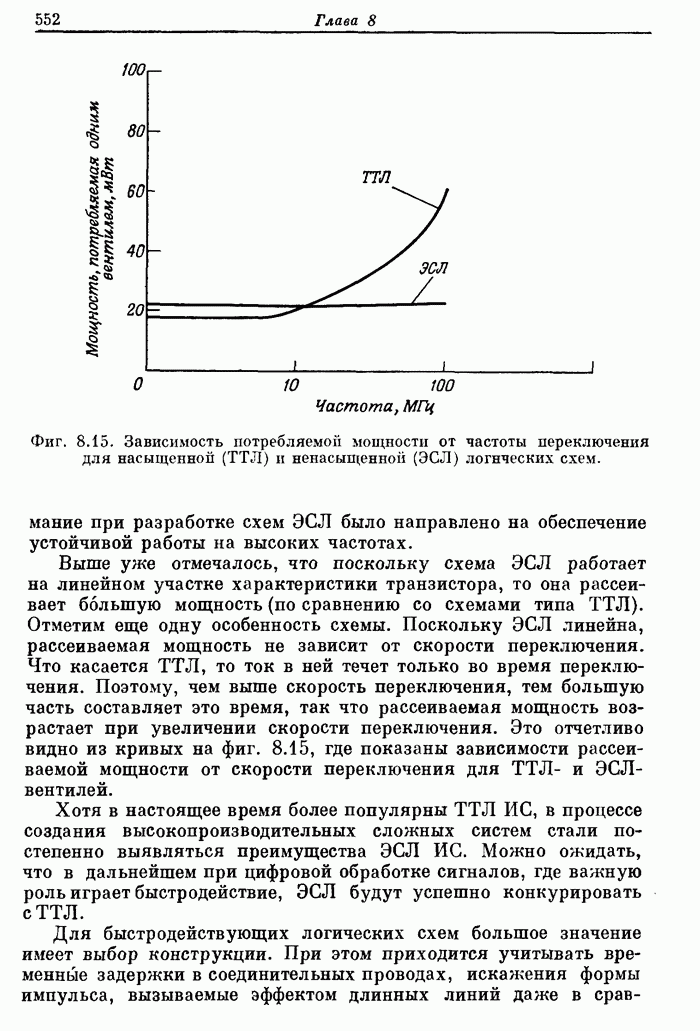
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
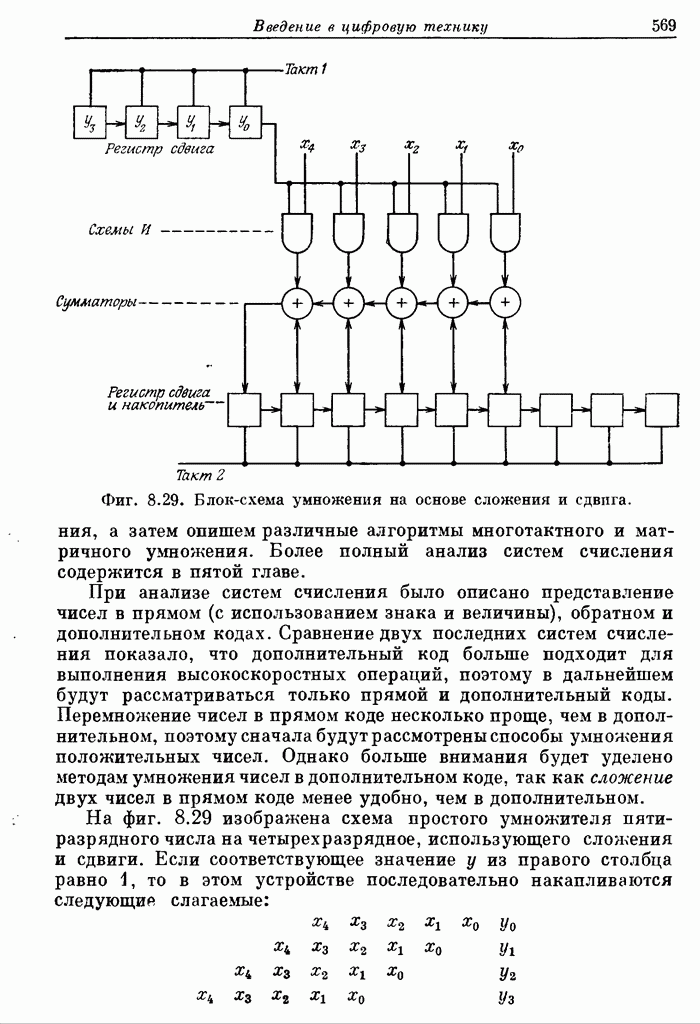
569
570
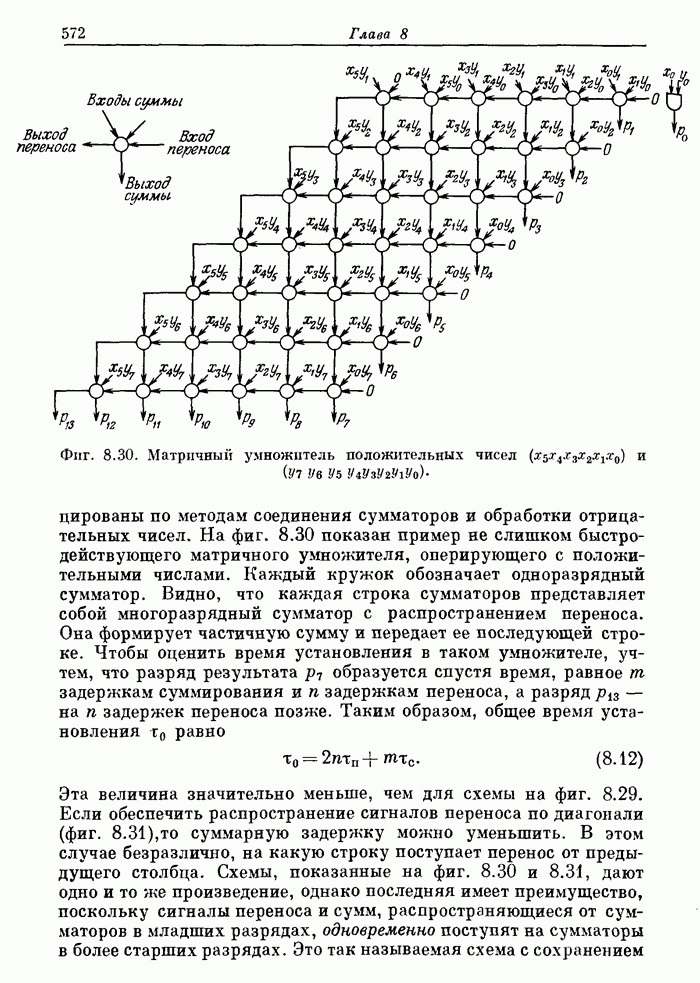
571
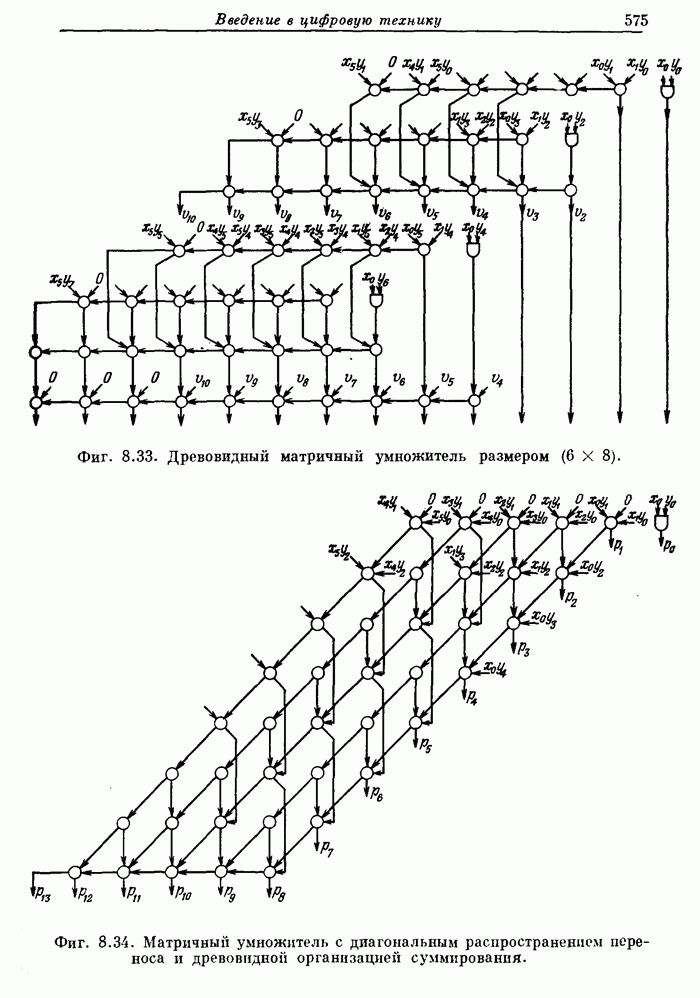
572
573
574
575
576
577
578
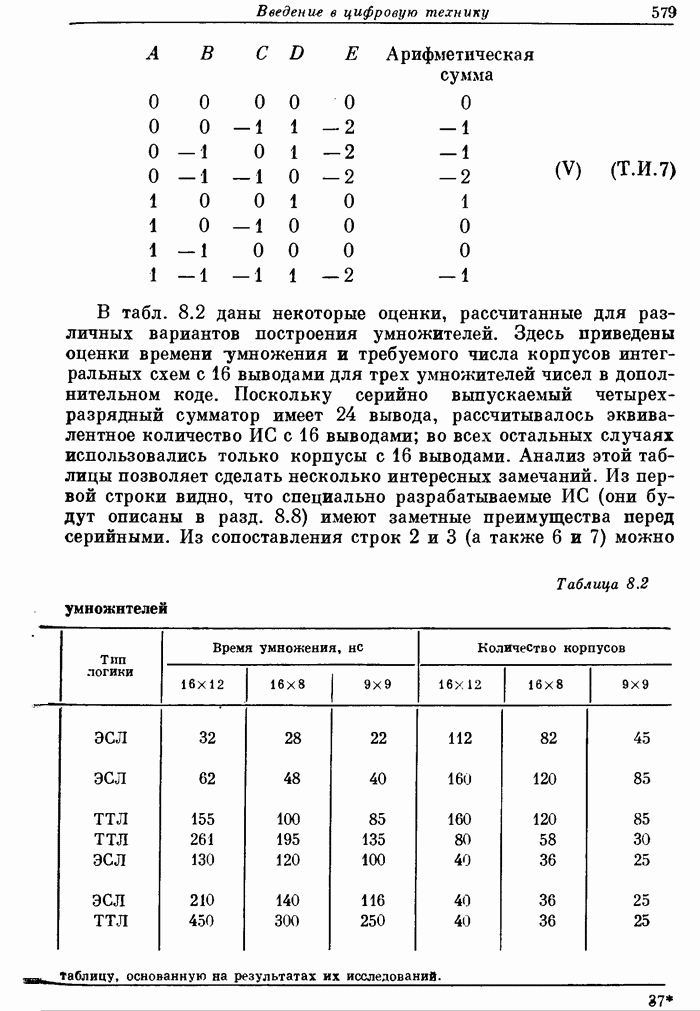
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
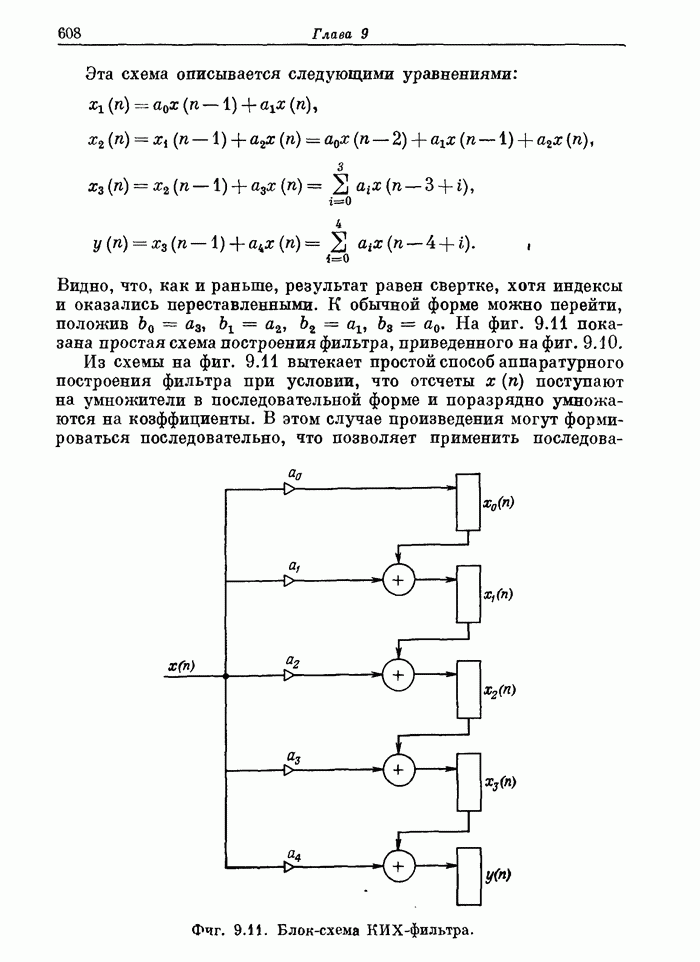
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
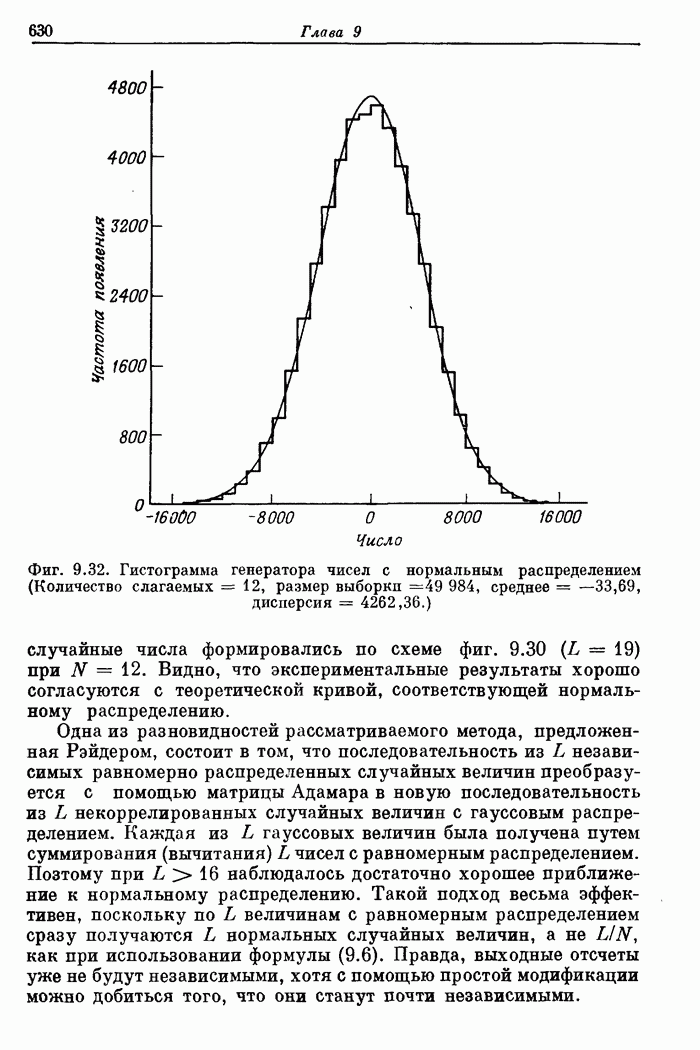
630
631
632
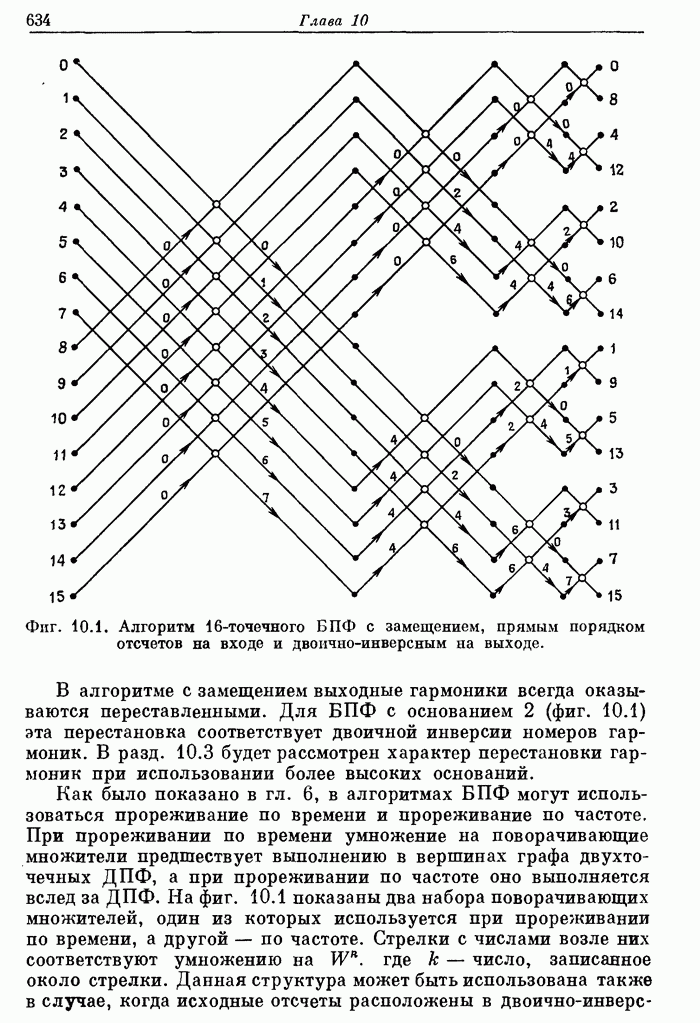
633
634
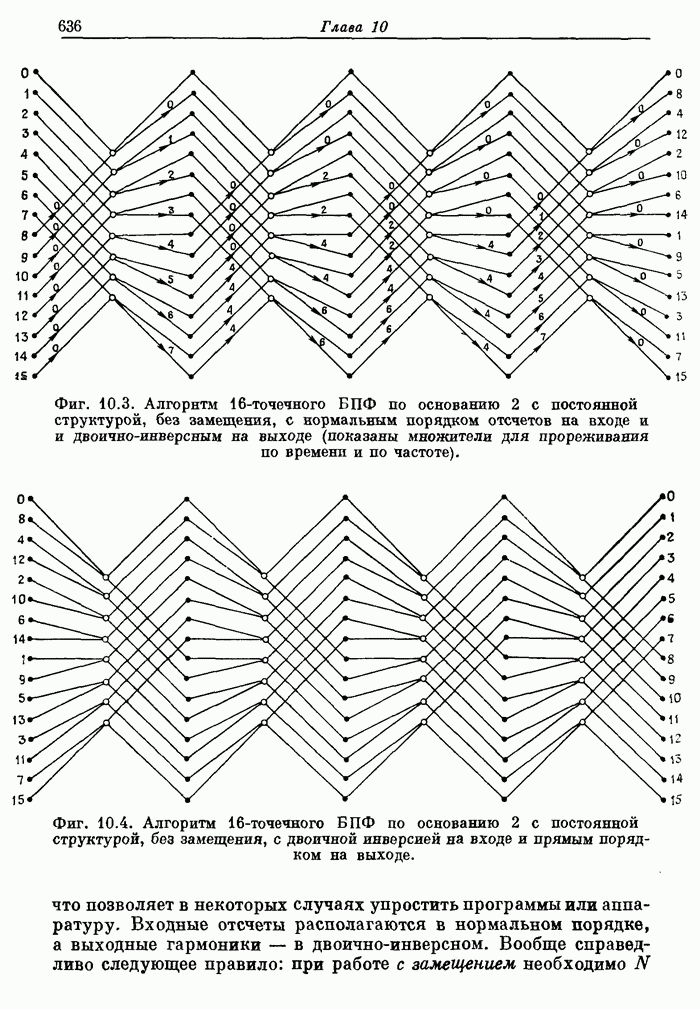
635
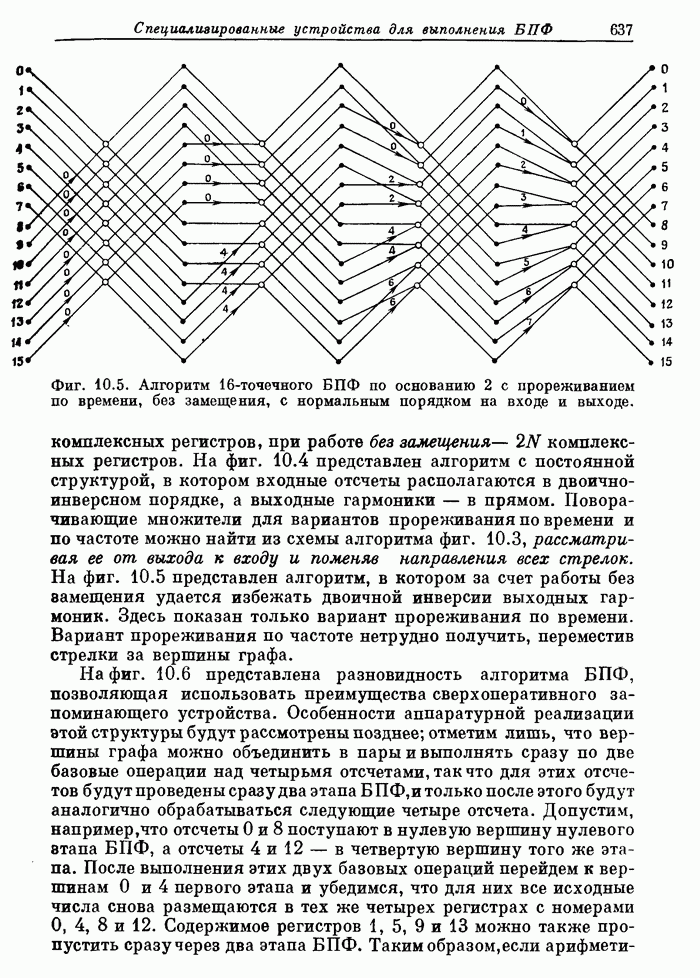
636
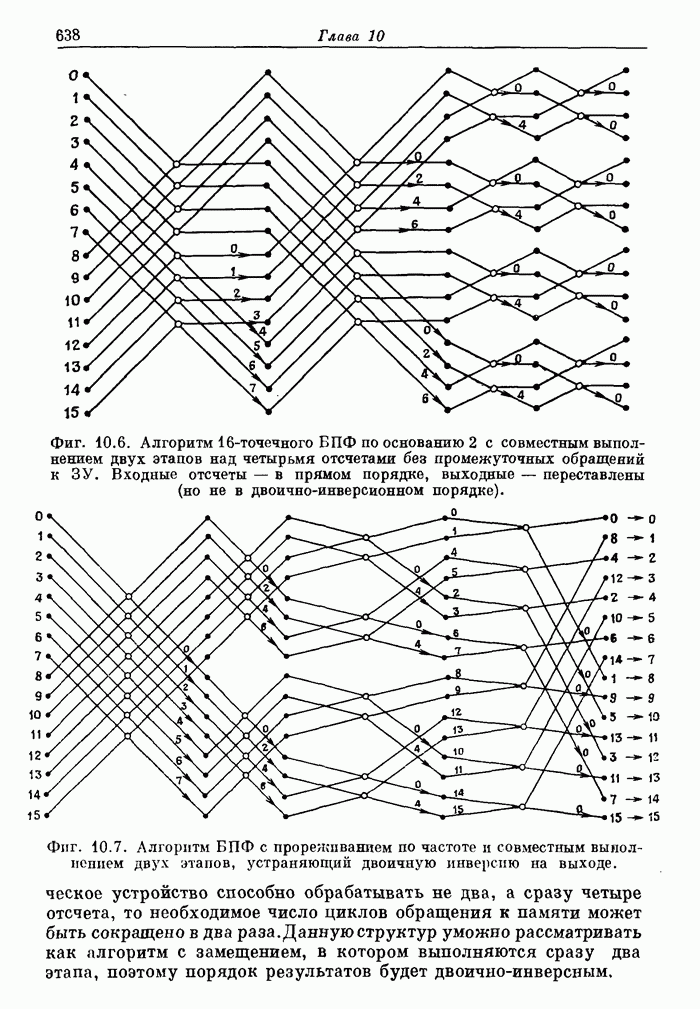
637
638
639
640
641
642
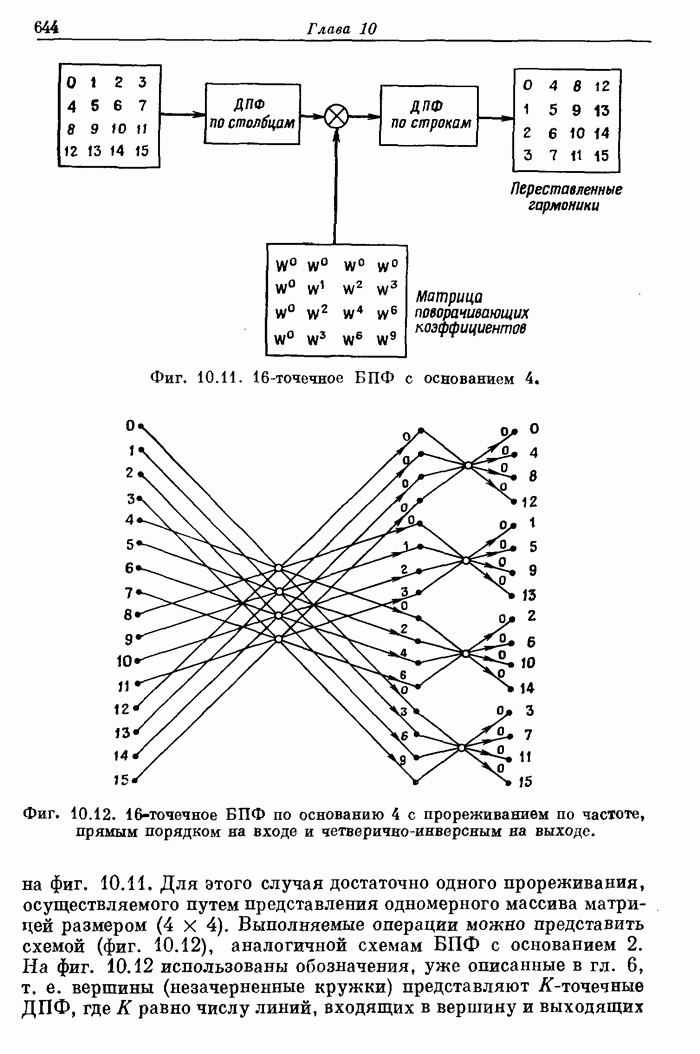
643
644
645
646
647
648
649
650
651
652
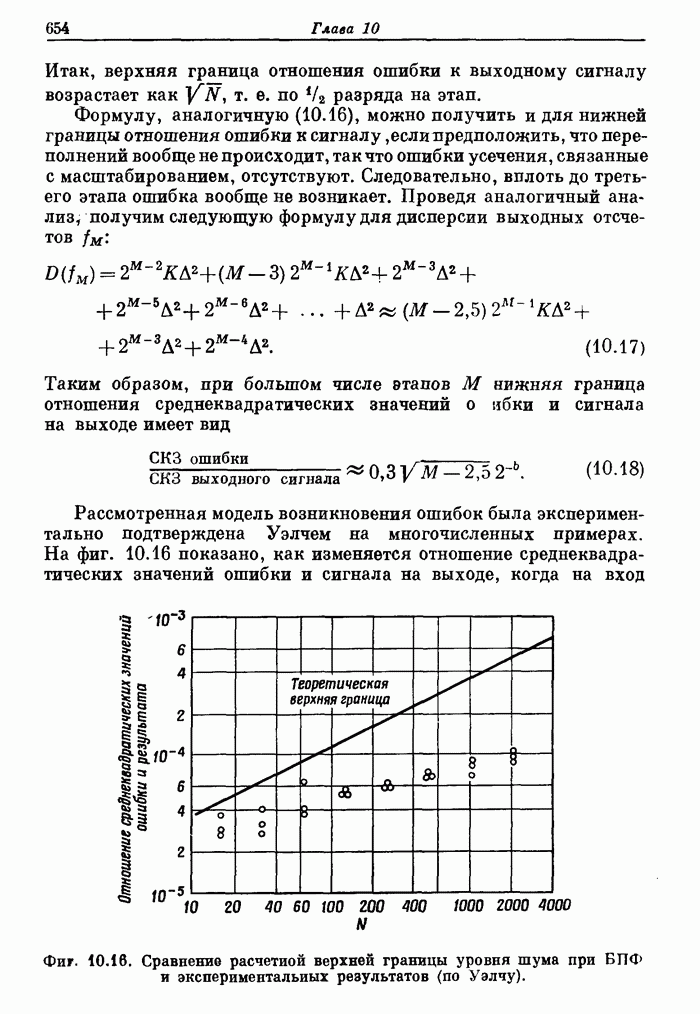
653
654
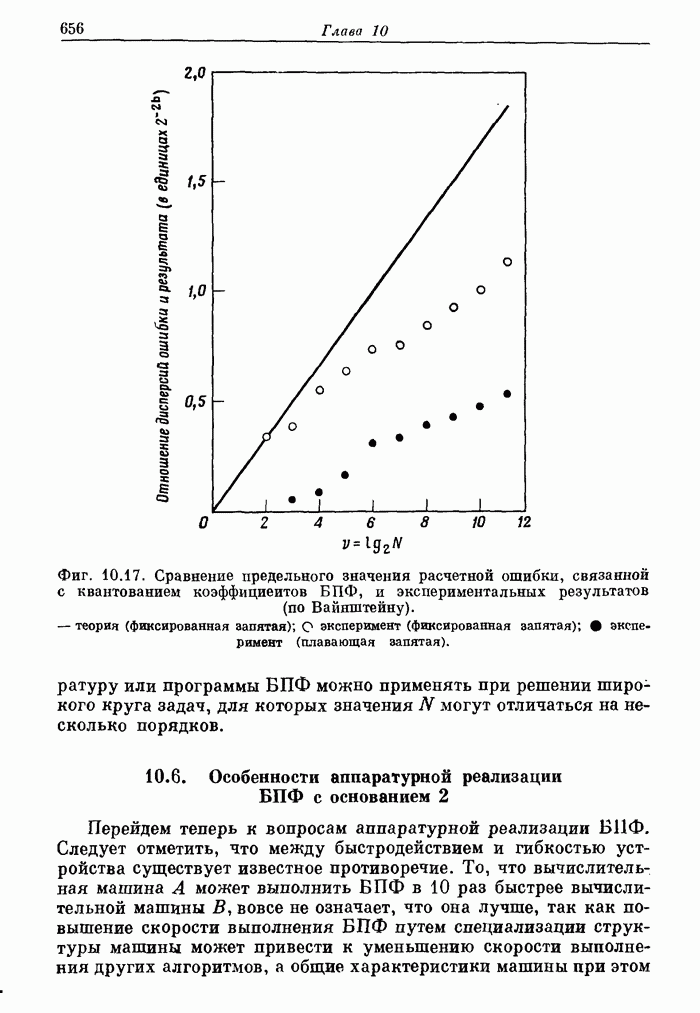
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
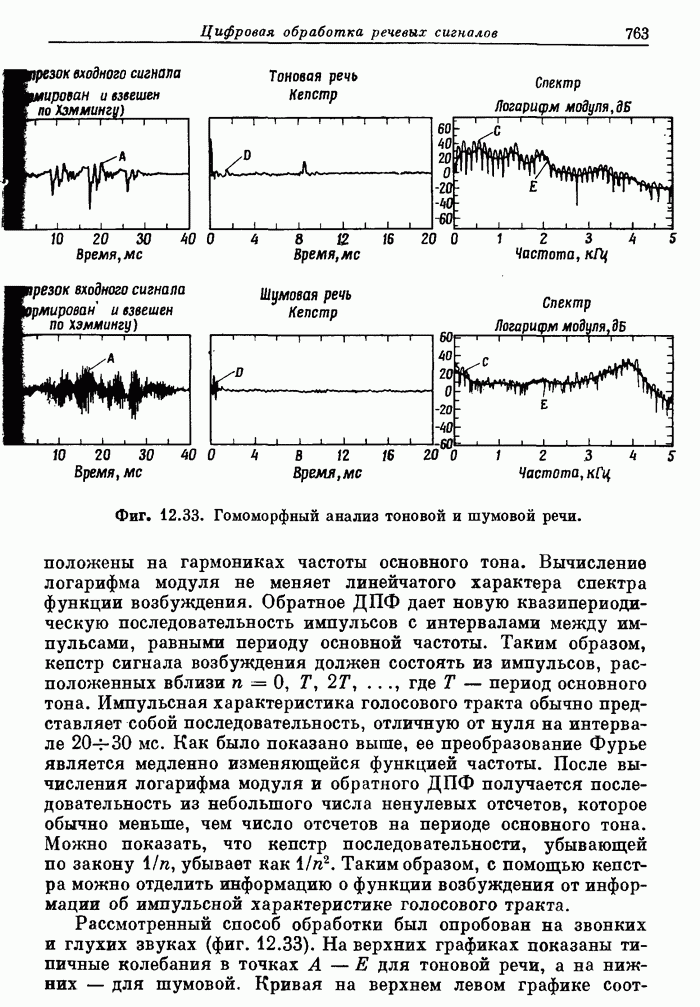
762
763
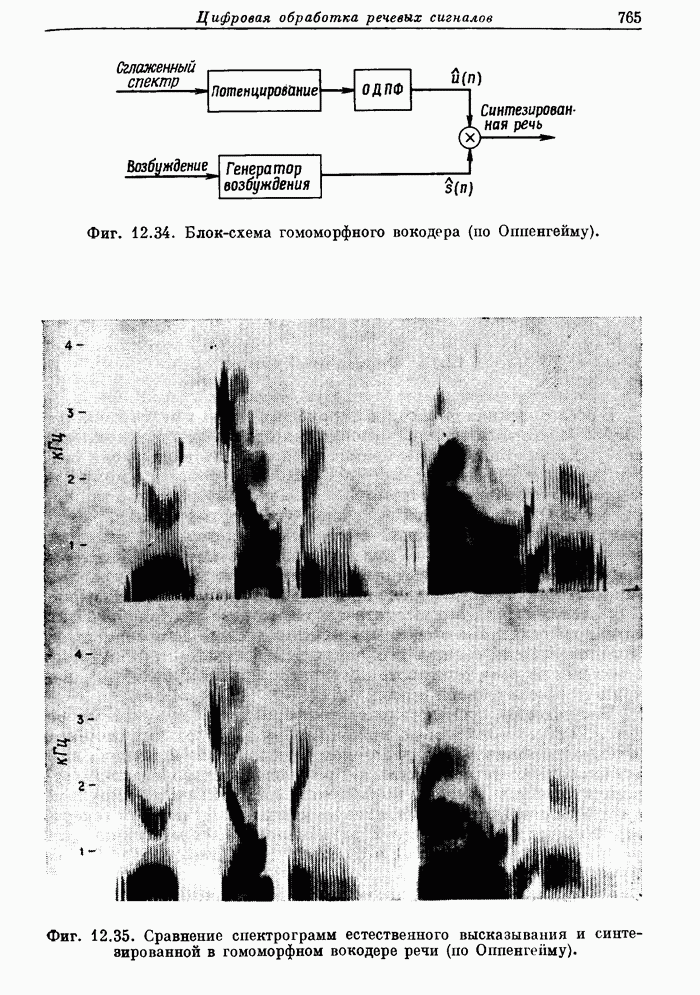
764
765
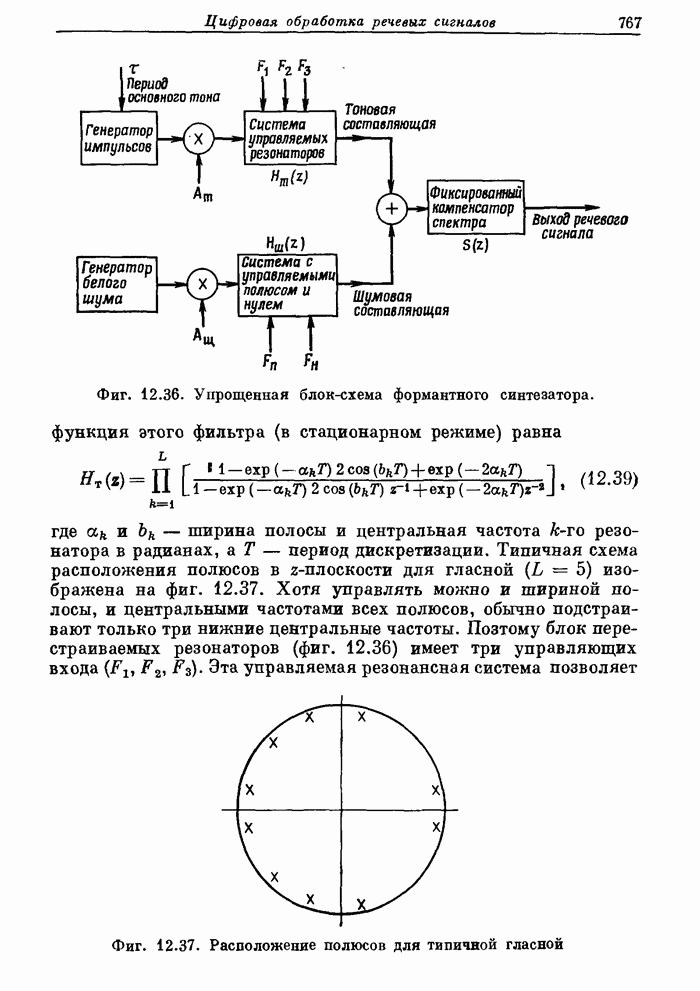
766
767
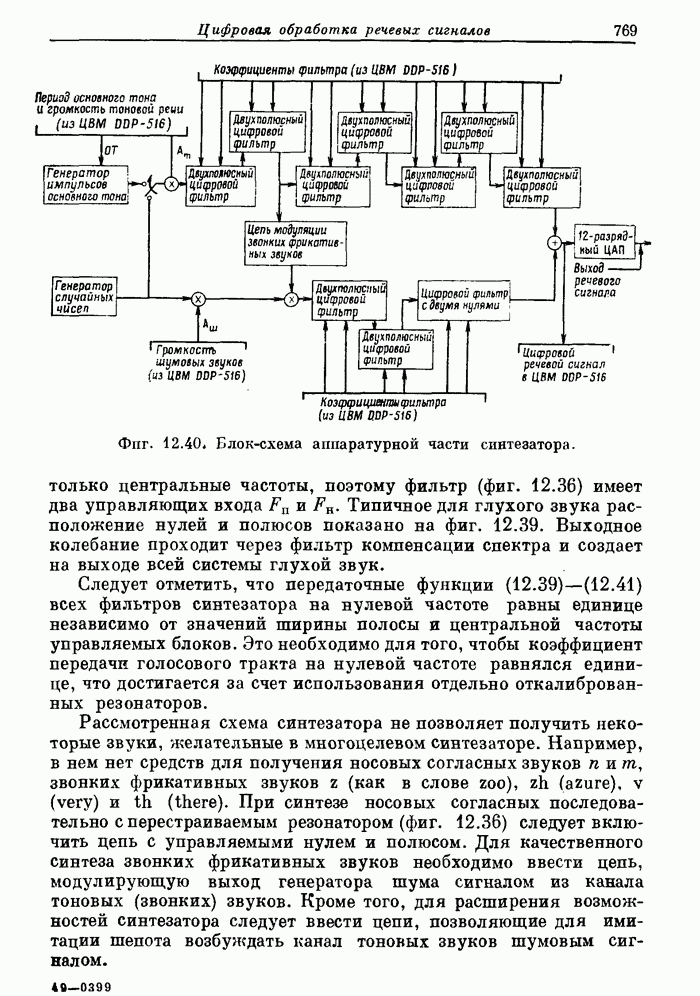
768
769
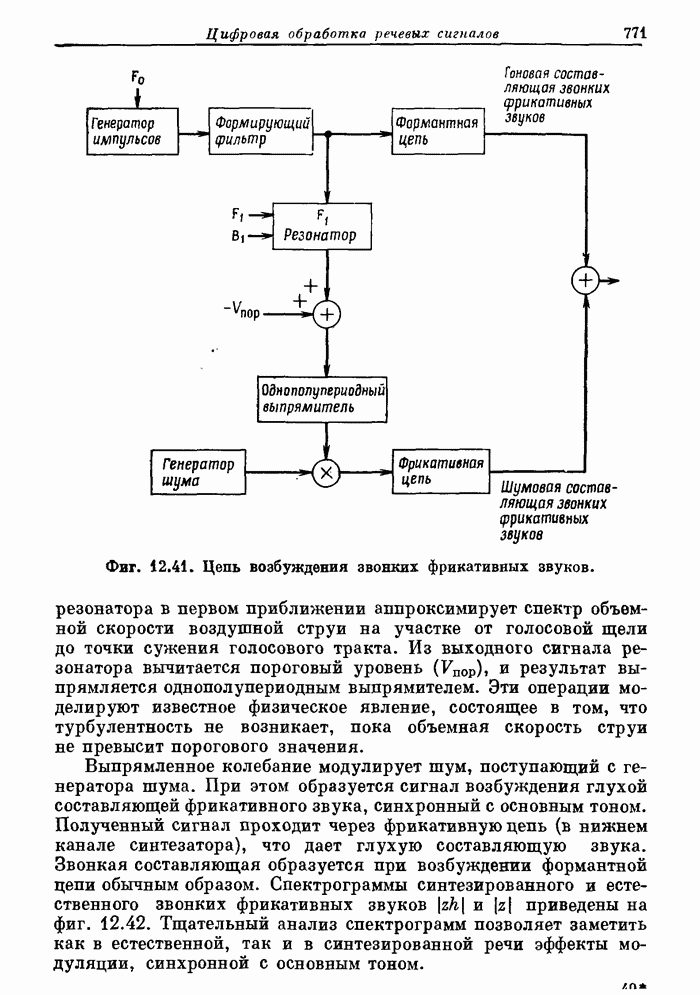
770
771
772
773
774
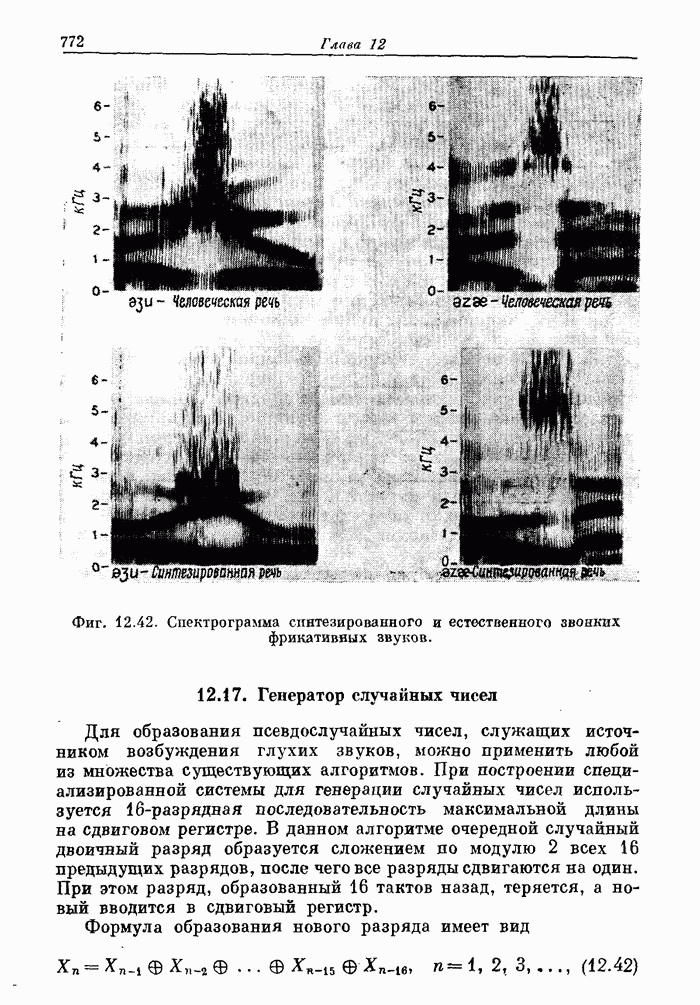
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
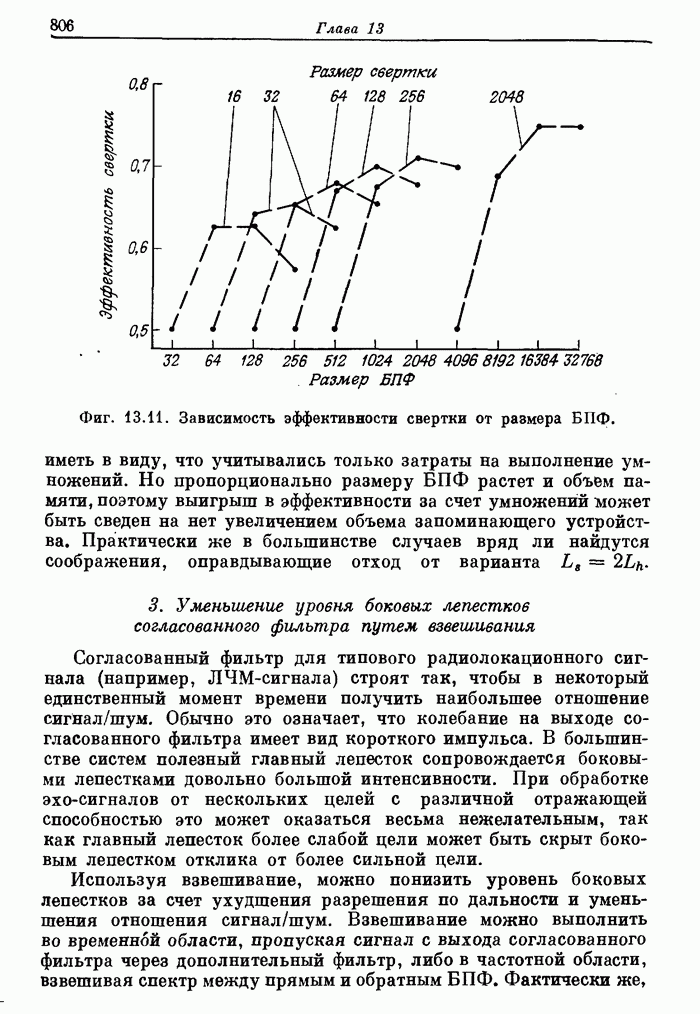
805
806
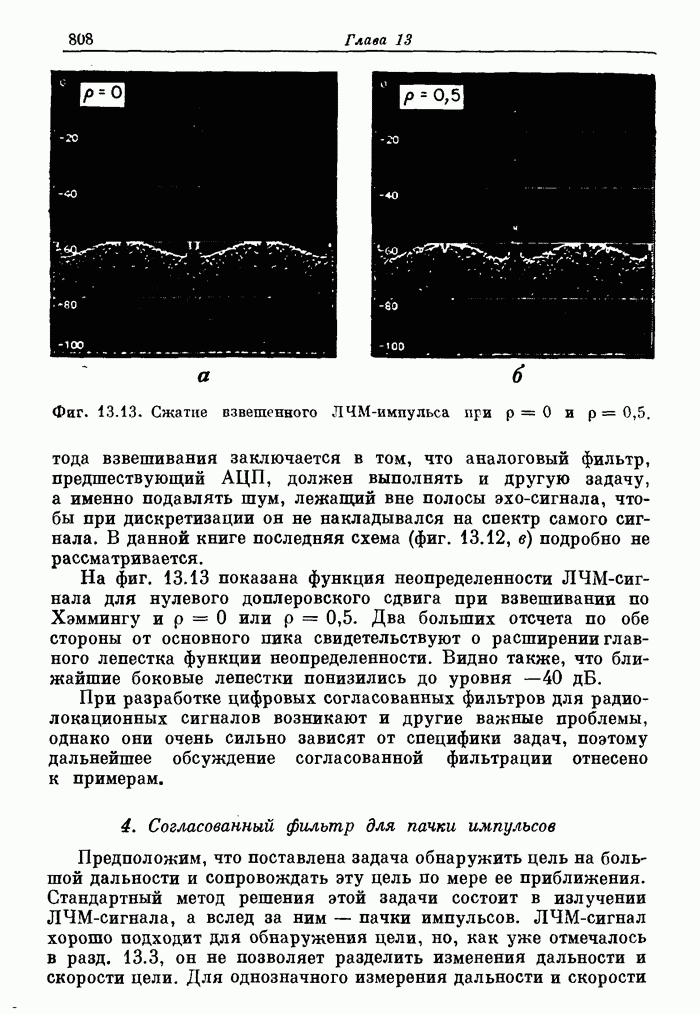
807
808
809
810
811
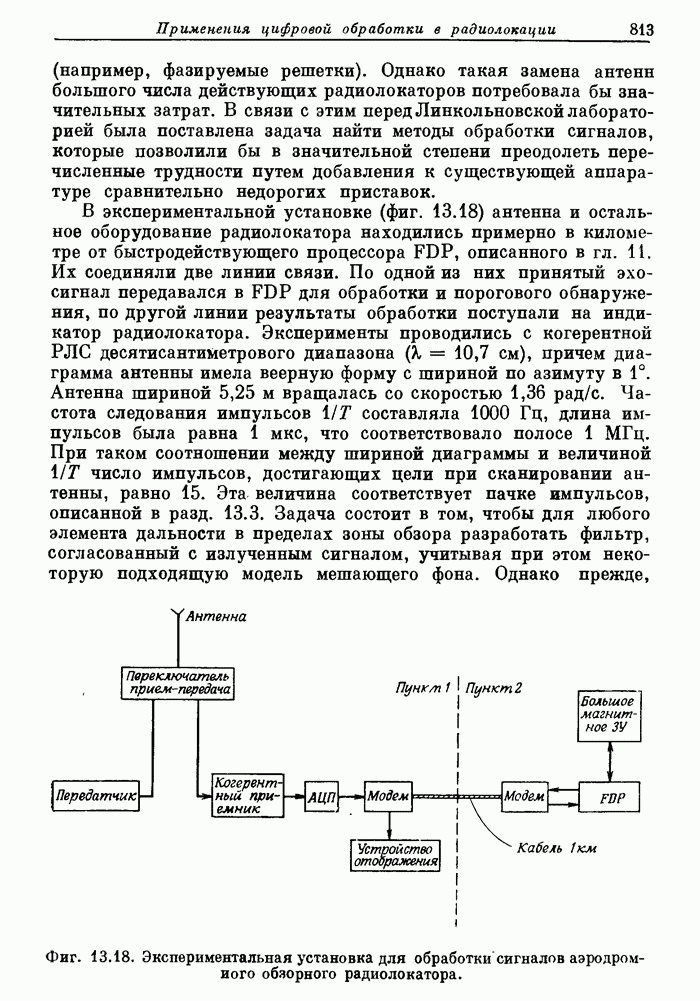
812
813
814
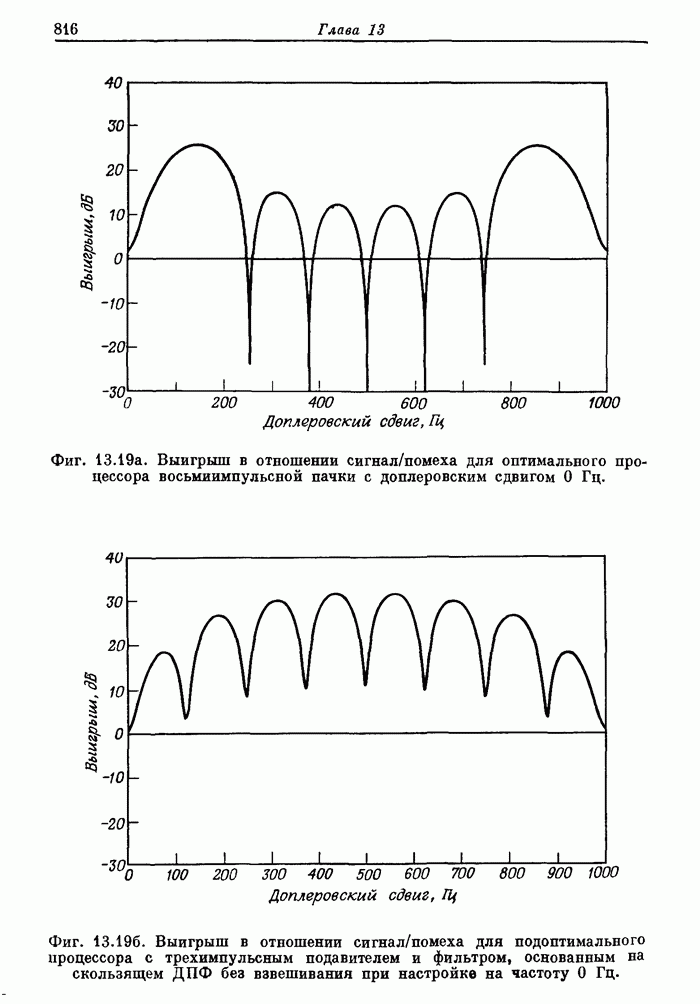
815
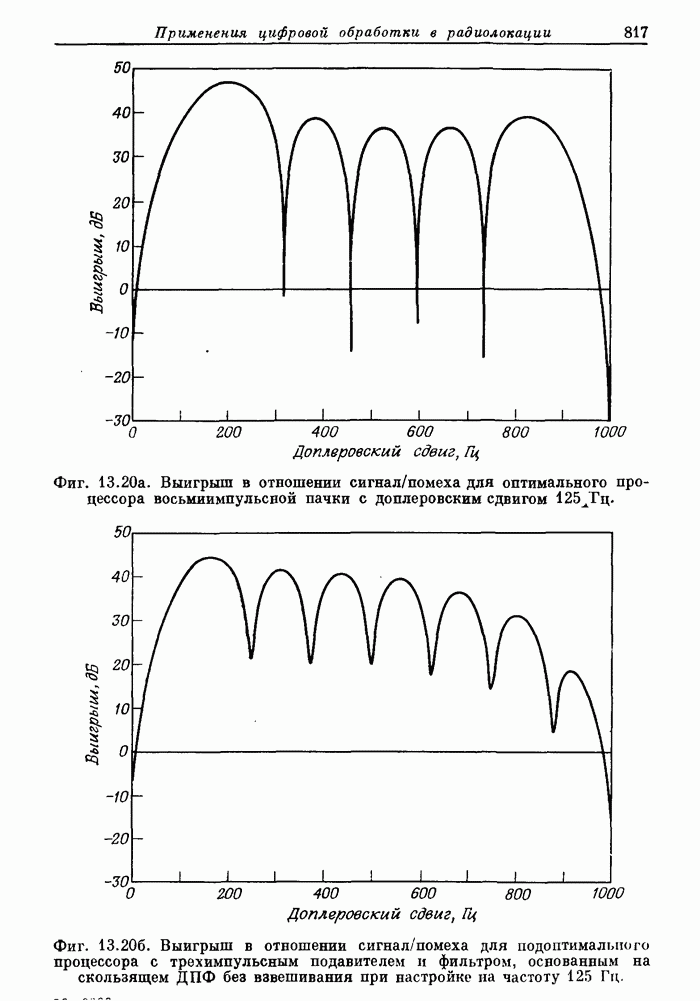
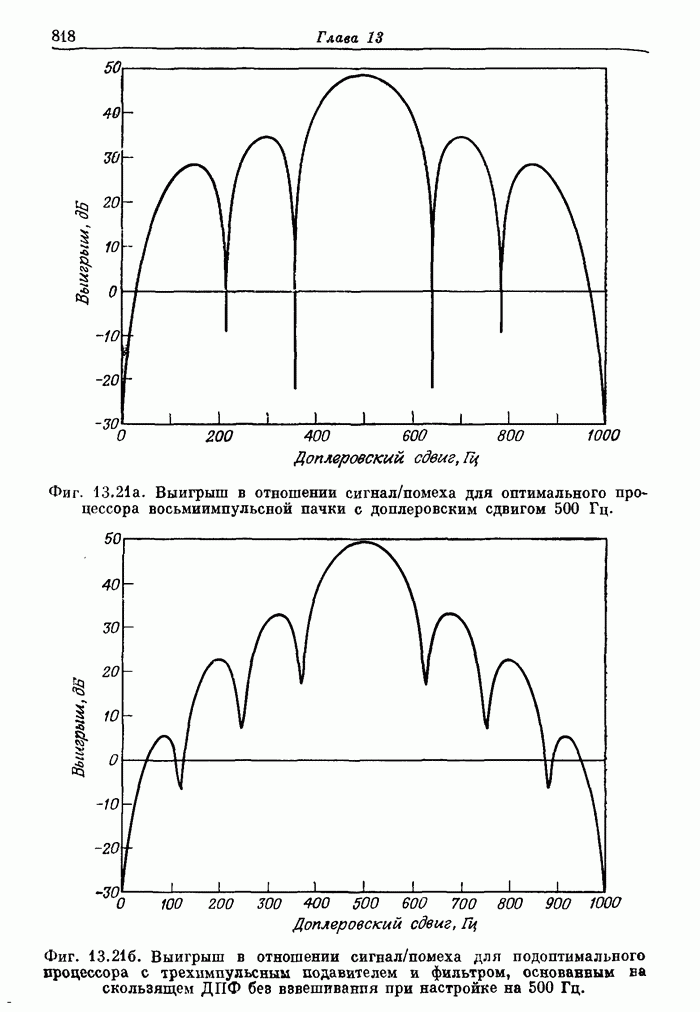
816
817
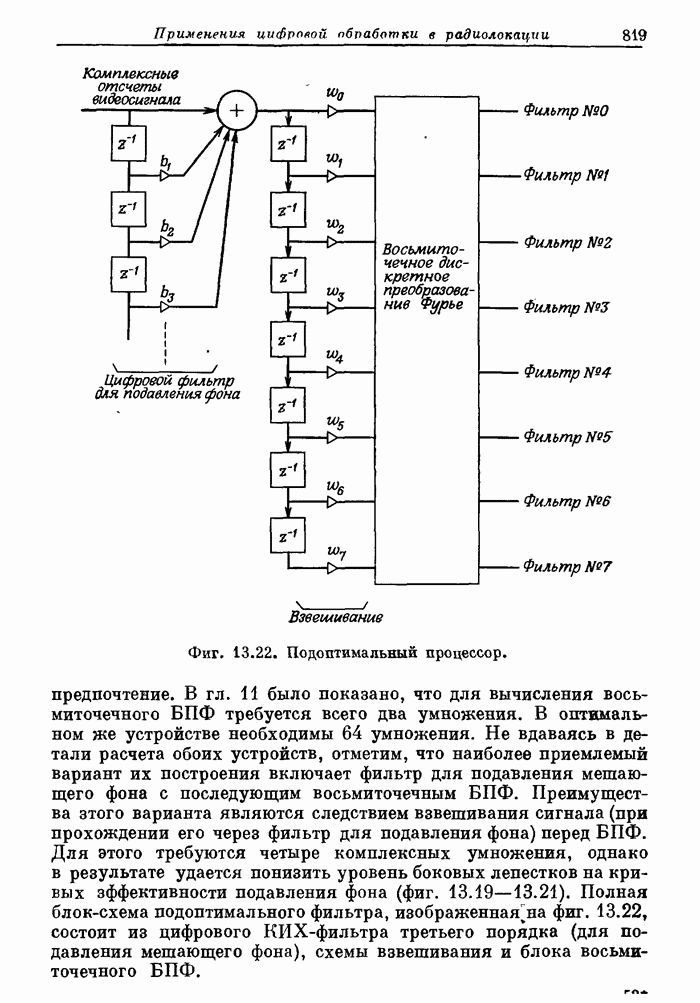
818
819
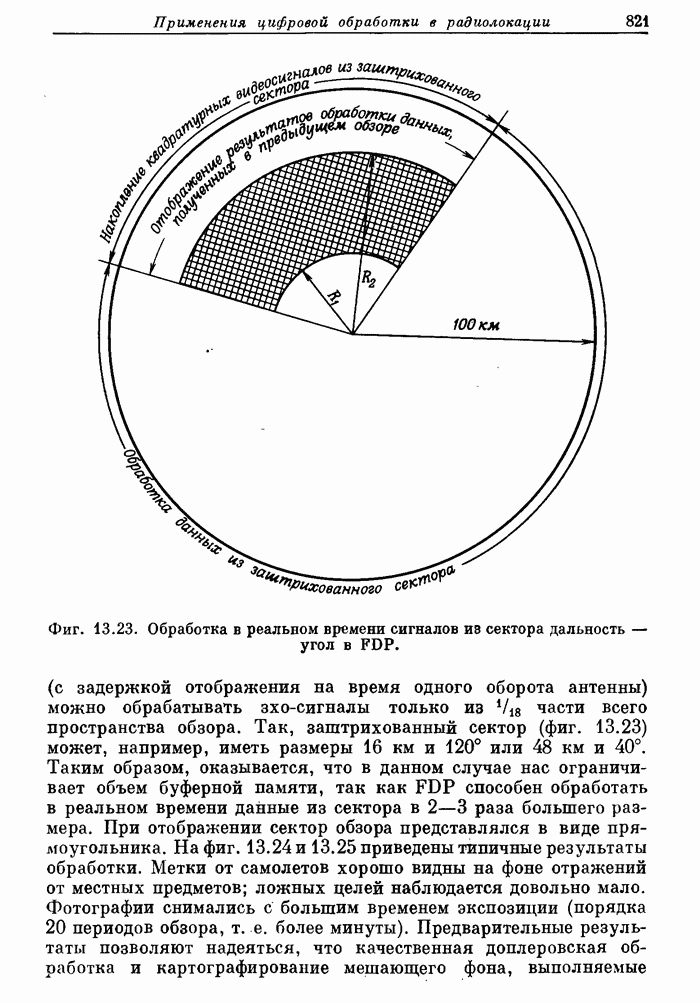
820
821
822
823
824
825
826
827
828
829
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
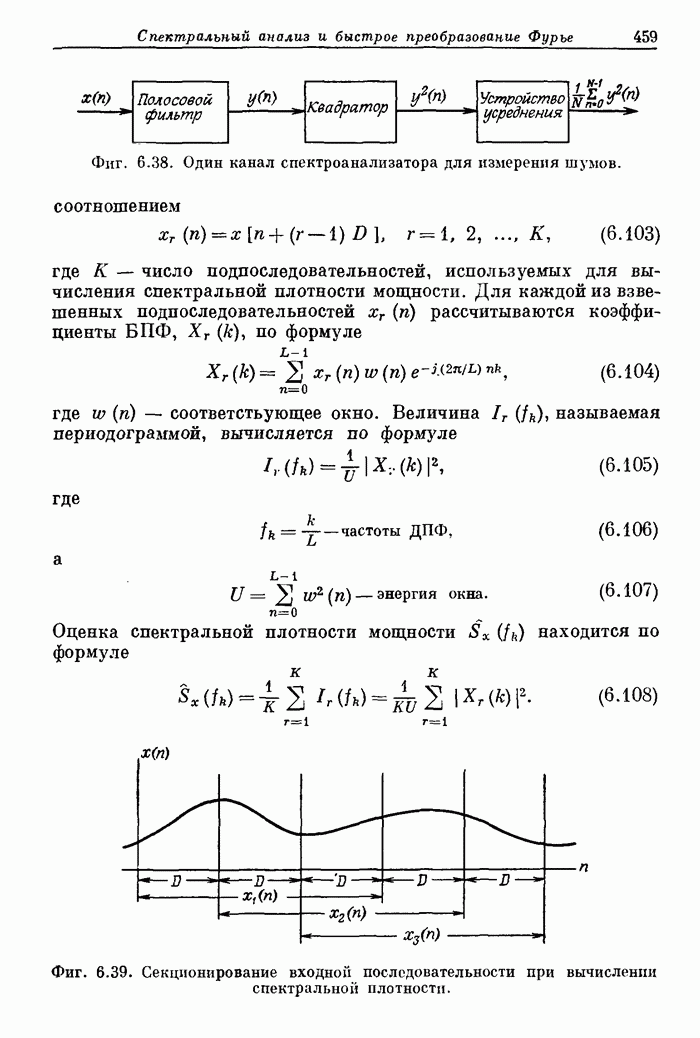
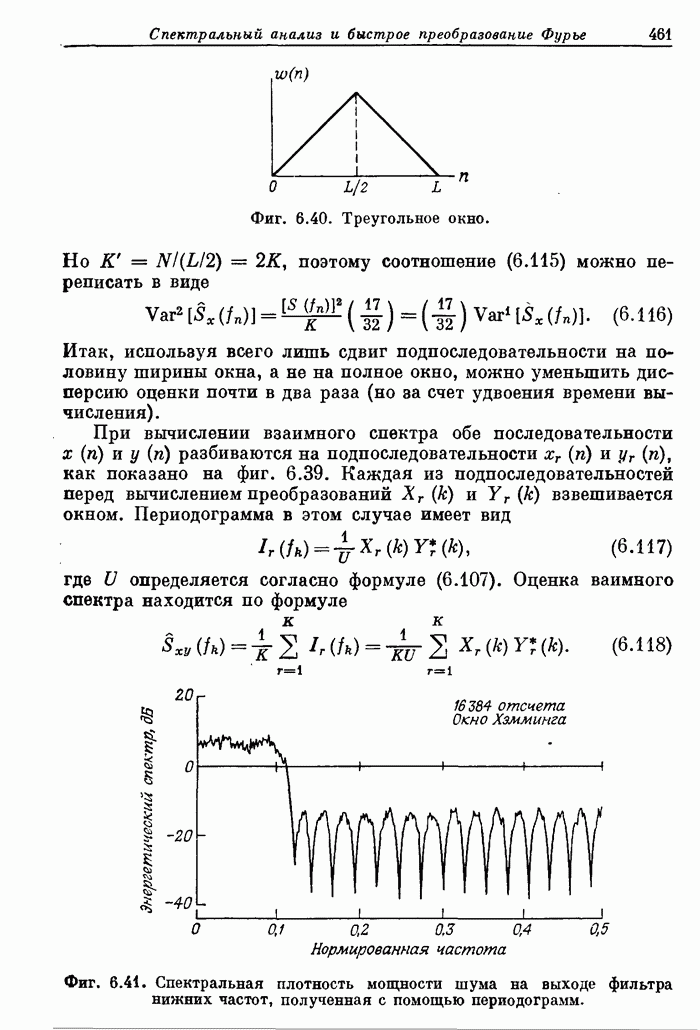
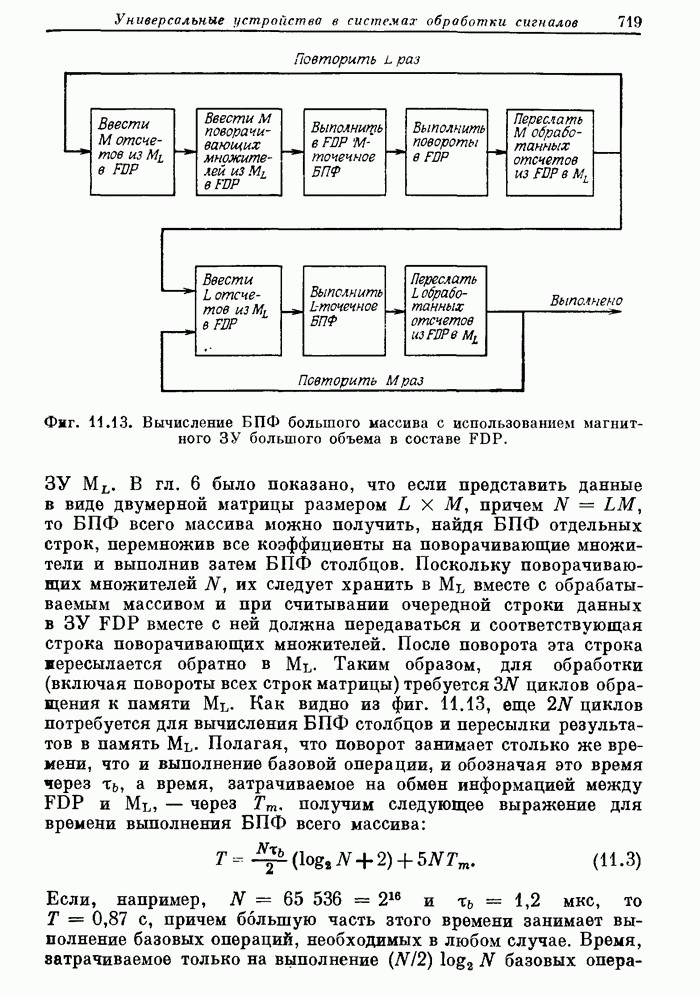
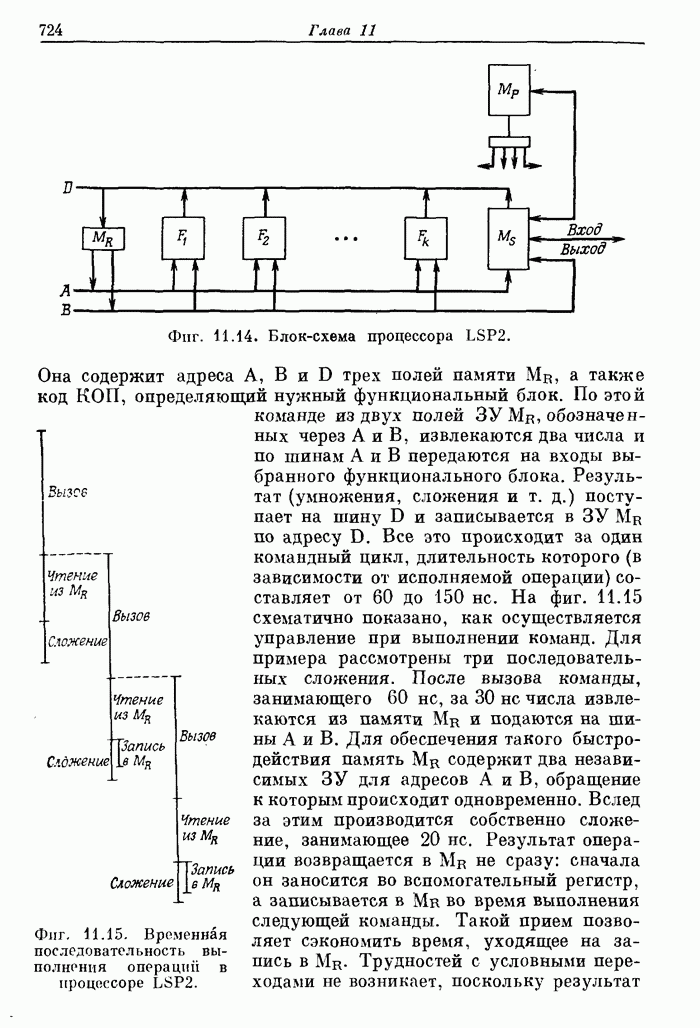
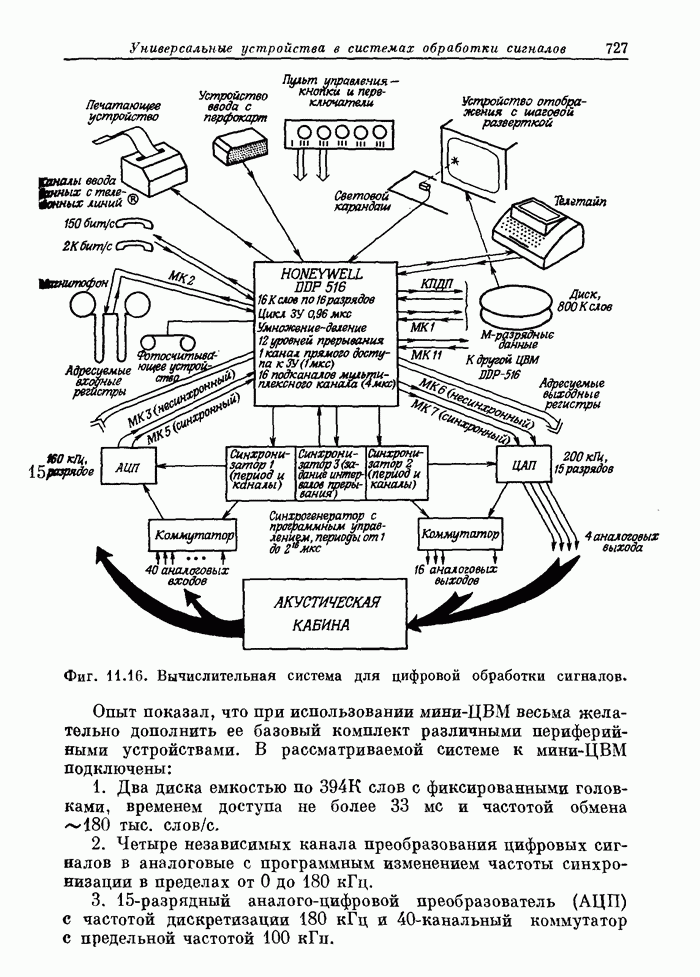
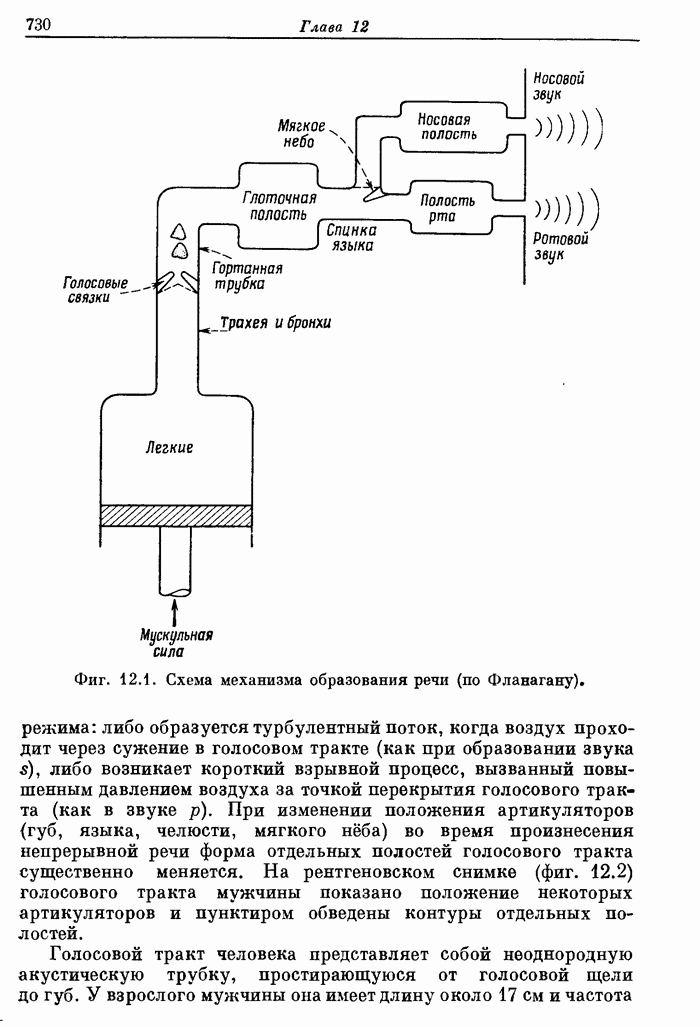
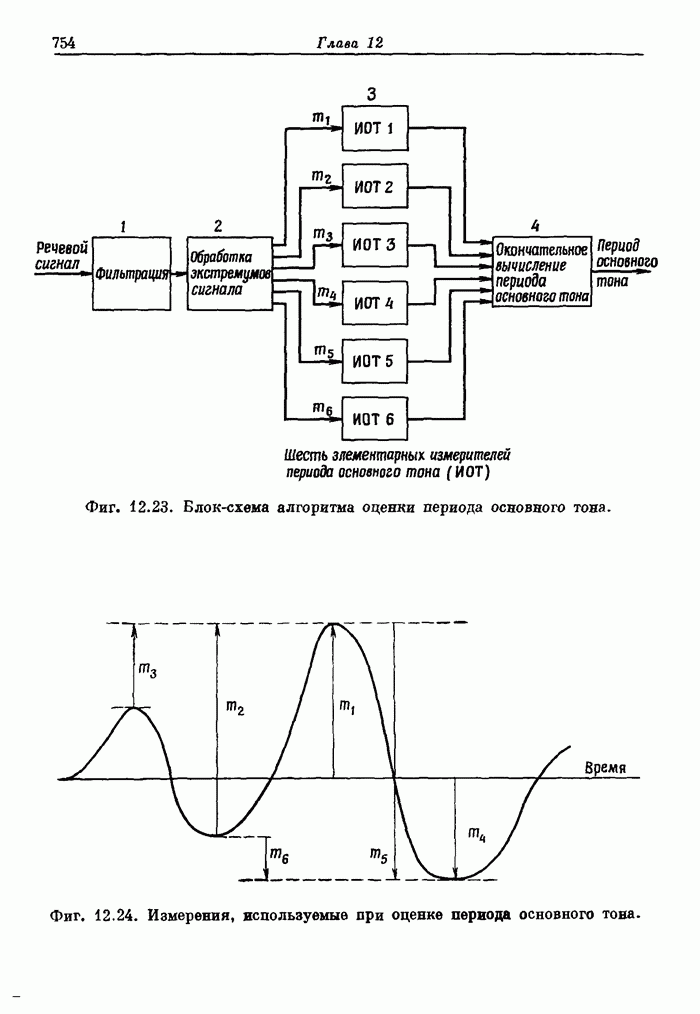
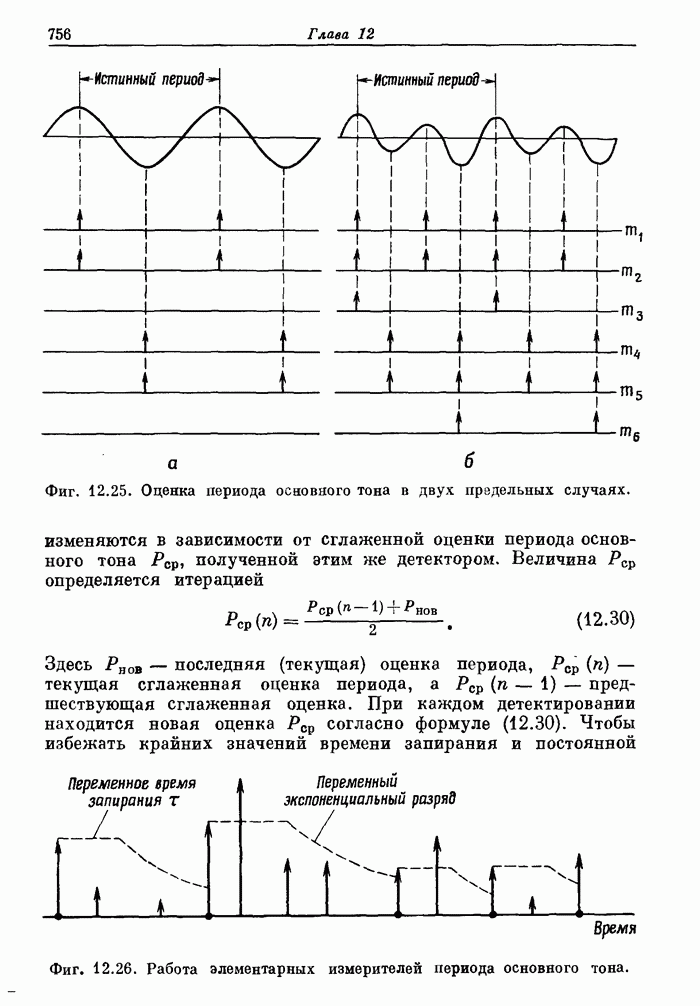
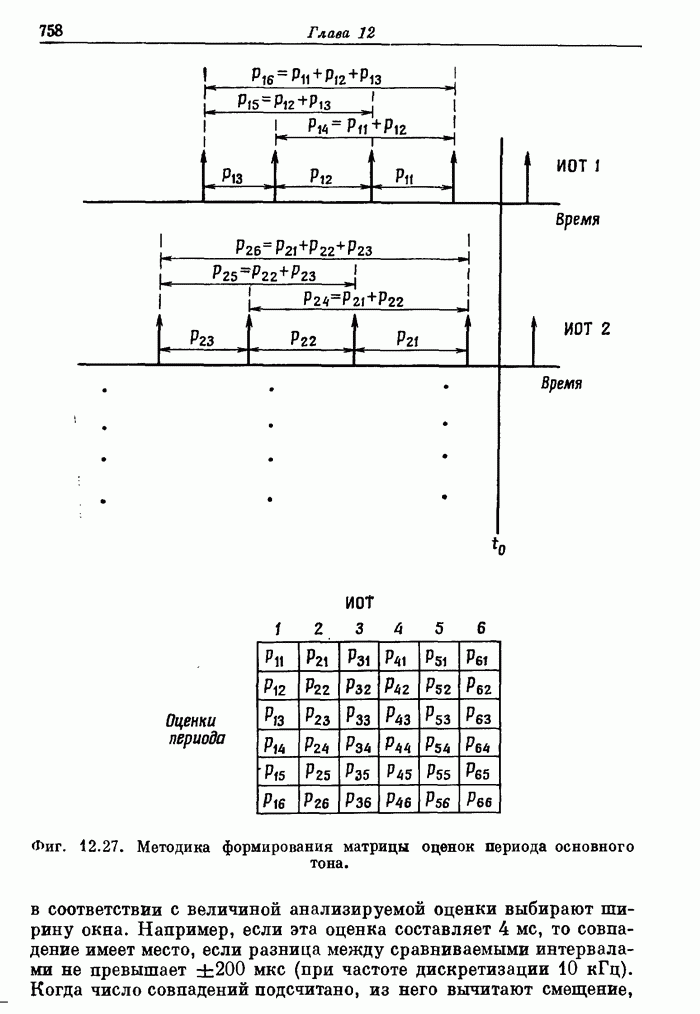
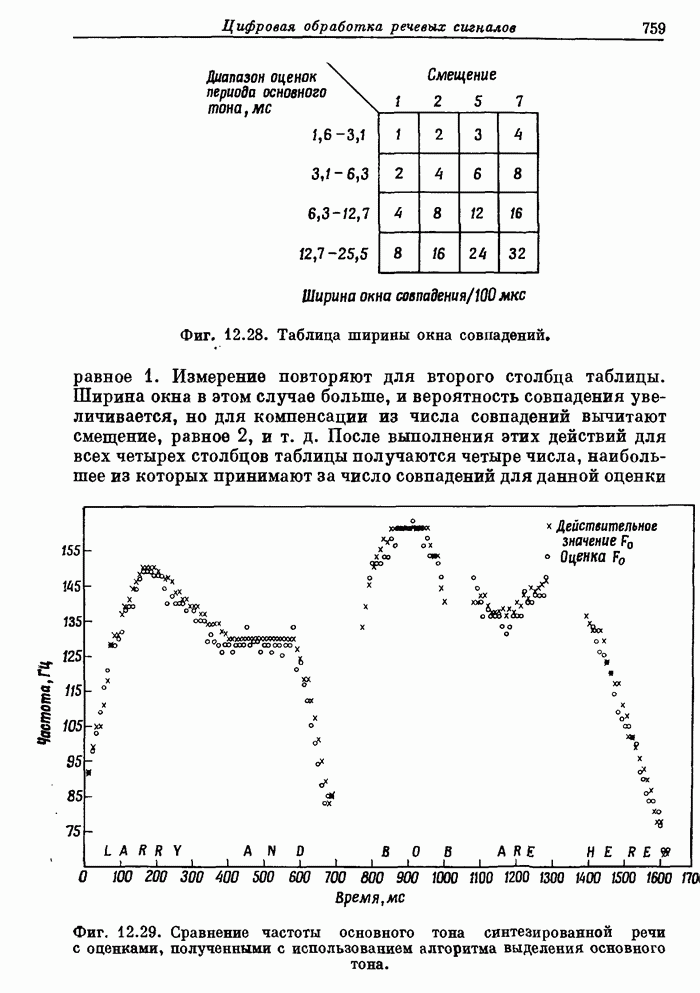
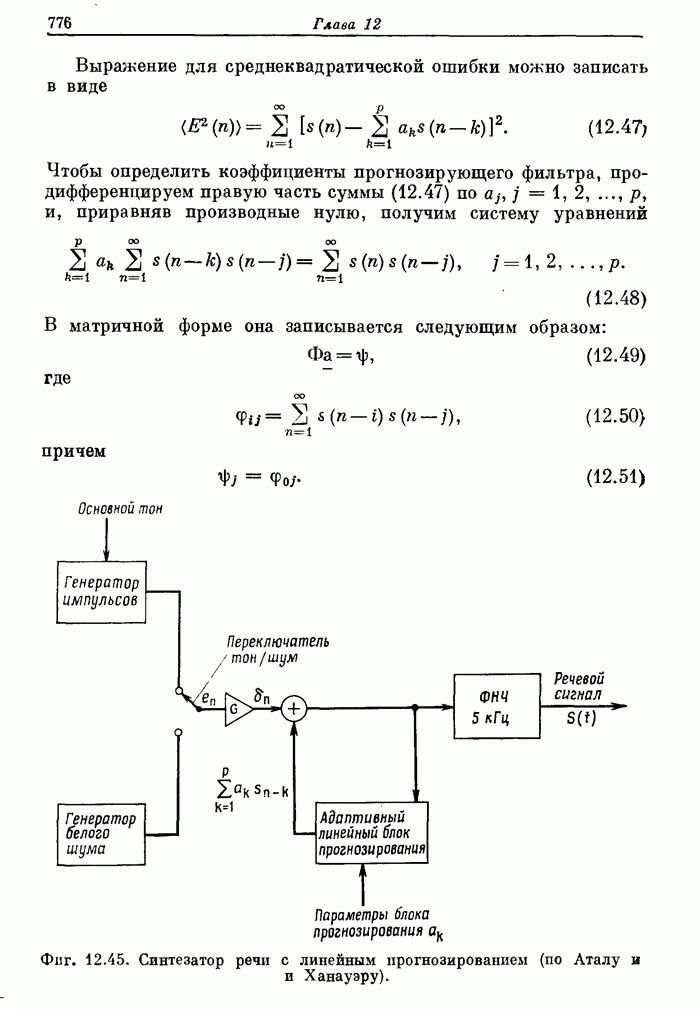
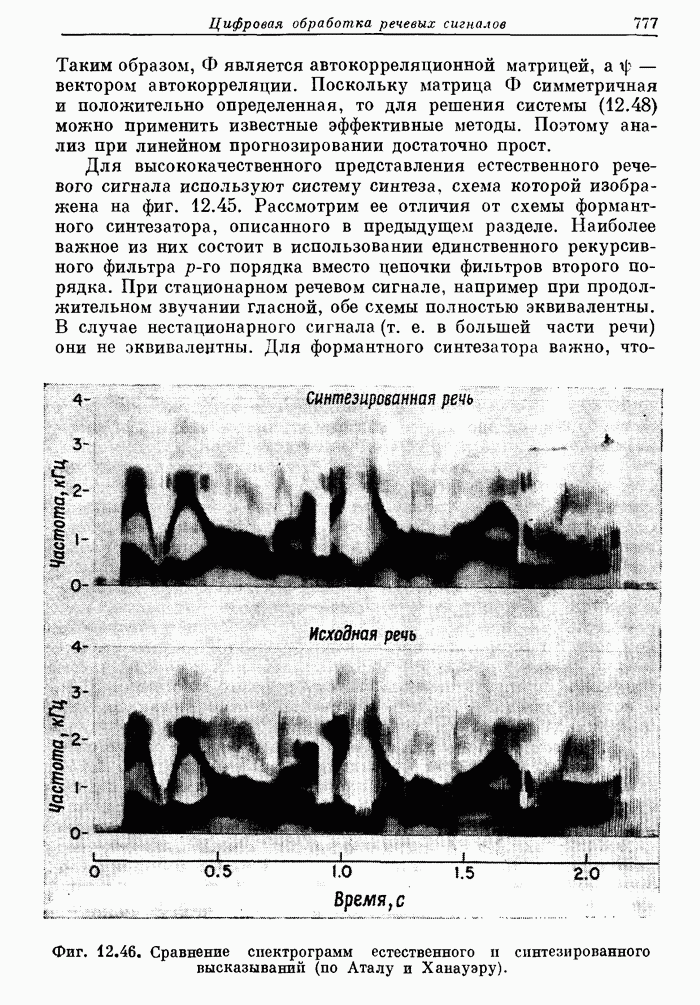
7.10. Двумерное ДПФ
Завершая общее описание двумерных сигналов и систем, рассмотрим коротко двумерное ДПФ и эффективный способ его вычисления с помощью одномерного БПФ.
Двумерный периодический сигнал удовлетворяет условию

где  — период по первой координате,
— период по первой координате,  — период по второй координате, а
— период по второй координате, а  — произвольные целые числа. Индекс
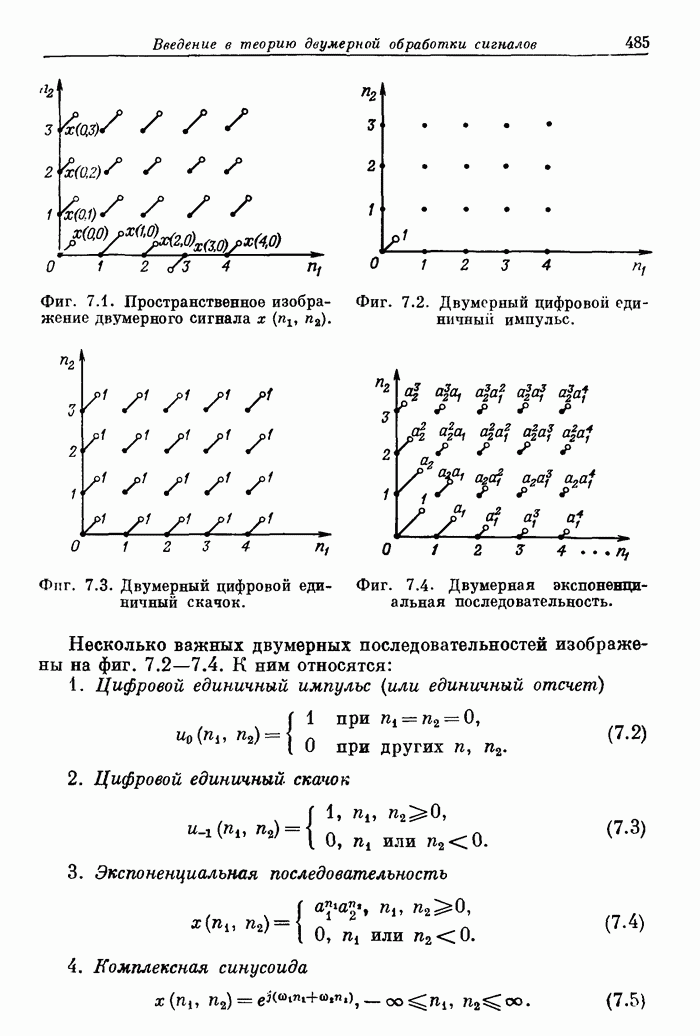
— произвольные целые числа. Индекс  в формуле (7.38) указывает, что сигнал периодичен. Как и в одномерном случае, двумерный периодический сигнал можно представить линейной комбинацией конечного числа комплексных экспонент, причем
в формуле (7.38) указывает, что сигнал периодичен. Как и в одномерном случае, двумерный периодический сигнал можно представить линейной комбинацией конечного числа комплексных экспонент, причем  кратны их периодам, т. е.
кратны их периодам, т. е.

Коэффициенты Фурье  представляют амплитуду составляющей
представляют амплитуду составляющей  при
при  . Значения коэффициентов
. Значения коэффициентов  легко найти, вычислив значения двумерного z-преобразования на одном периоде последовательности
легко найти, вычислив значения двумерного z-преобразования на одном периоде последовательности  на частотах
на частотах  , что дает
, что дает

Соотношение (7.39) называют двумерным обратным дискретным преобразованием Фурье, а (7.41) — двумерным дискретным преобразованием Фурье.
Рассмотрим некоторые свойства преобразований (7.39) и (7.41). Одно из важных свойств связано с возможностью вычисления двумерных преобразований (7.39) и (7.41) с помощью последовательности одномерных ДПФ, а другое — с обобщением преобразований (7.39) и (7.41) на сигналы конечной длины. Первое свойство можно показать, переписав преобразование (7.41) в виде

При изменении  от 0 до
от 0 до  суммы в квадратных скобках образуют
суммы в квадратных скобках образуют  одномерных ДПФ. Обозначив результат каждого из одномерных ДПФ через
одномерных ДПФ. Обозначив результат каждого из одномерных ДПФ через  , перепишем соотношение (7.41) в виде
, перепишем соотношение (7.41) в виде

Полученное соотношение снова представляет собой  одномерных ДПФ, соответствующих изменению
одномерных ДПФ, соответствующих изменению  от 0 до
от 0 до  . Вышеизложенное легко обобщить на случай обратного ДПФ.
. Вышеизложенное легко обобщить на случай обратного ДПФ.
Второе свойство, заключающееся в том, что ДПФ полностью представляет последовательность конечной длины  , легко проверить, если в формулах (7.39) и (7.41) положить значения
, легко проверить, если в формулах (7.39) и (7.41) положить значения  равными нулю вне области
равными нулю вне области  . Такие последовательности будем называть последовательностями конечной длины и обозначать через
. Такие последовательности будем называть последовательностями конечной длины и обозначать через  . Хотя последовательность
. Хотя последовательность  уже не является периодической, ее значения совпадают на одном периоде со значениями ее периодического эквивалента, так что ДПФ и обратное ДПФ дают возможность просто и точно найти коэффициенты Фурье последовательности конечной длины. Главное различие между
уже не является периодической, ее значения совпадают на одном периоде со значениями ее периодического эквивалента, так что ДПФ и обратное ДПФ дают возможность просто и точно найти коэффициенты Фурье последовательности конечной длины. Главное различие между  и периодической последовательностью
и периодической последовательностью  состоит в том, что преобразование Фурье от
состоит в том, что преобразование Фурье от  является непрерывной функцией частот
является непрерывной функцией частот  тогда как спектр периодической последовательности
тогда как спектр периодической последовательности  состоит из линий, расположенных на кратных частотах.
состоит из линий, расположенных на кратных частотах.
Выше рассматривалось применение прямого и обратного ДПФ для фильтрации одномерных сигналов. Они могут быть использованы и в двумерном случае. По-видимому, метод быстрой свертки, основанный на алгоритме БПФ, является наиболее важным средством выполнения двумерной фильтрации.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
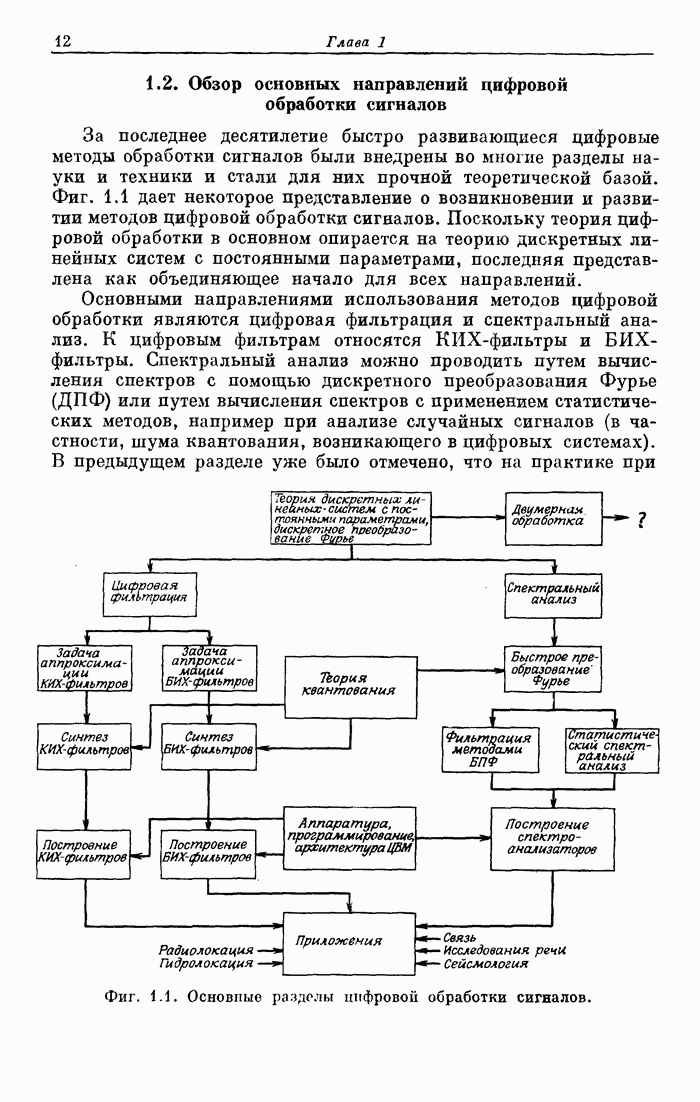
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
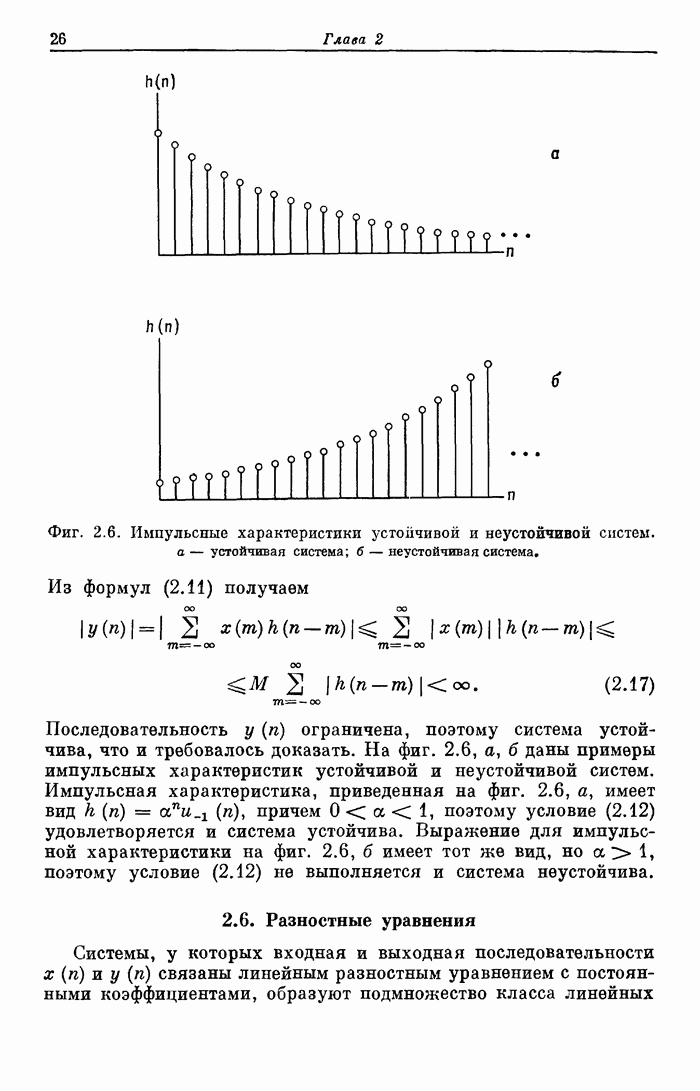
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
- 2.7. Частотная характеристика
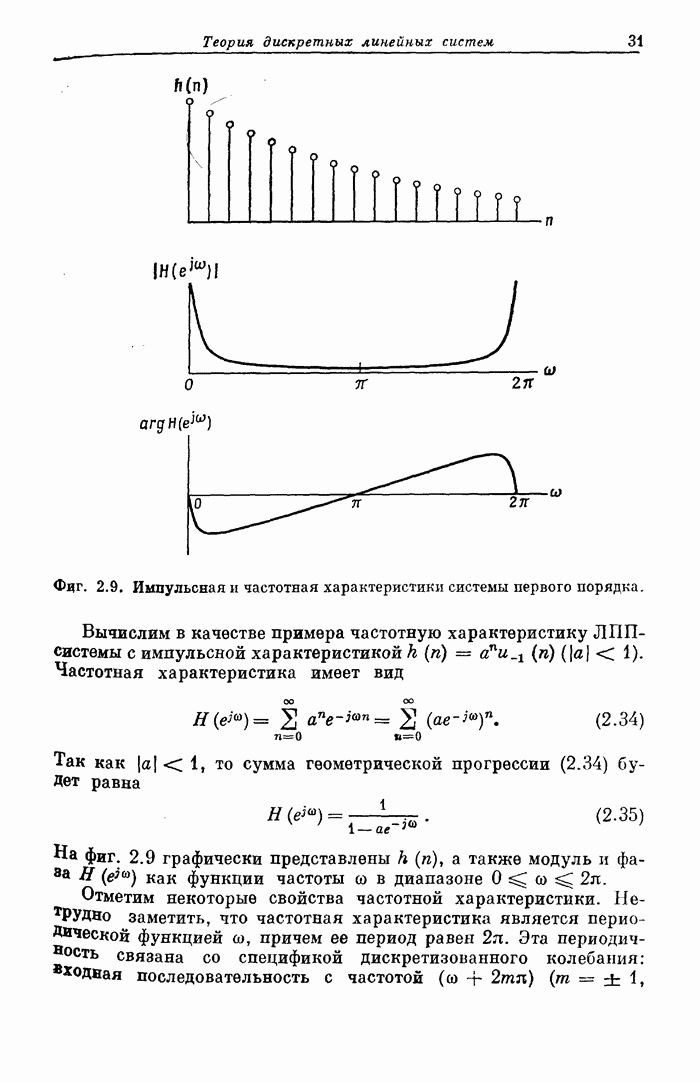
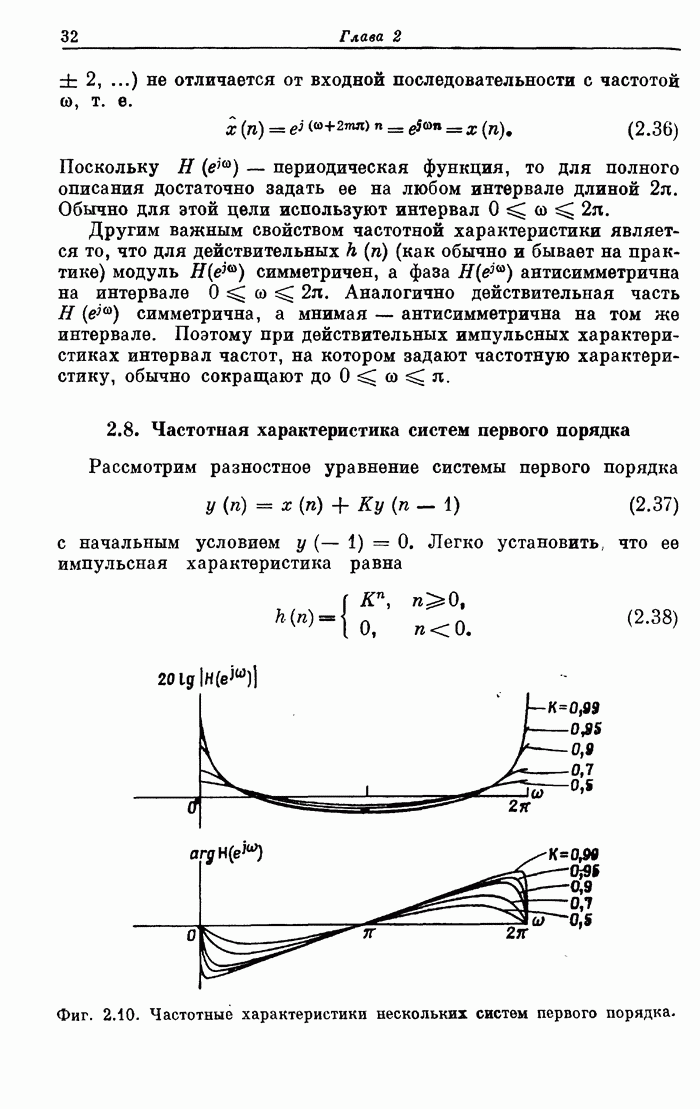
- 2.8. Частотная характеристика систем первого порядка
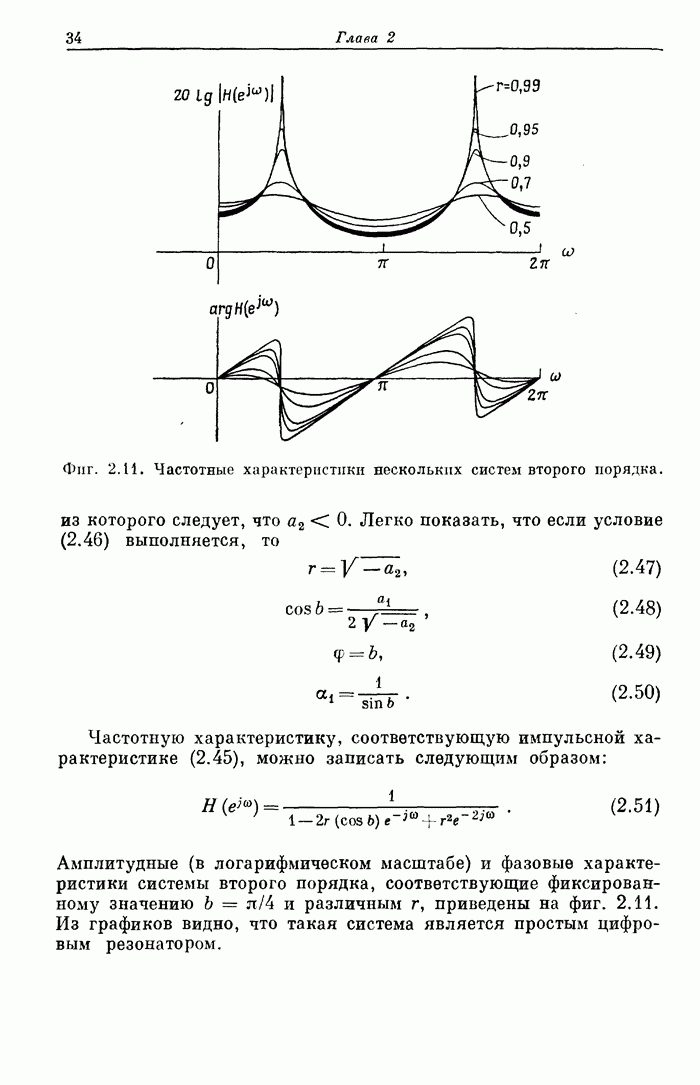
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
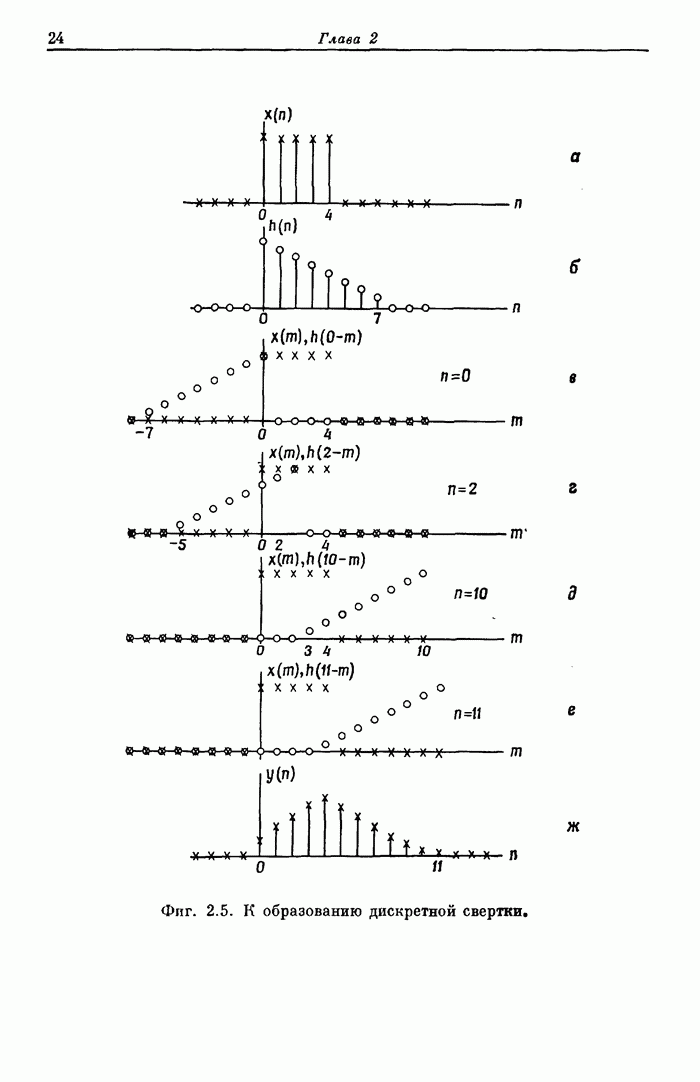
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
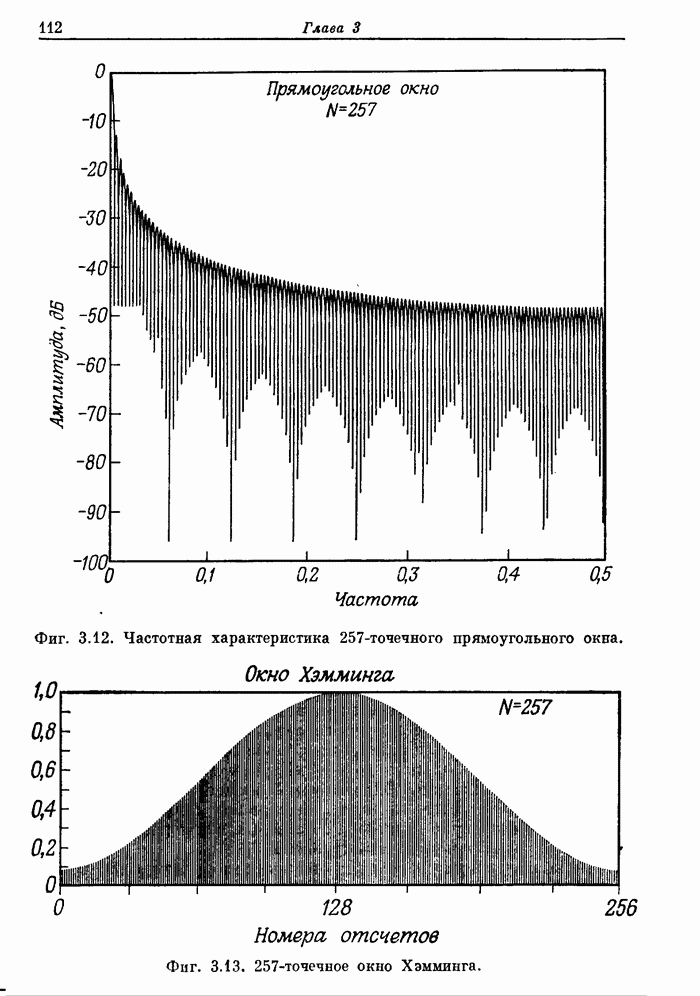
- 3.9. Прямоугольное окно
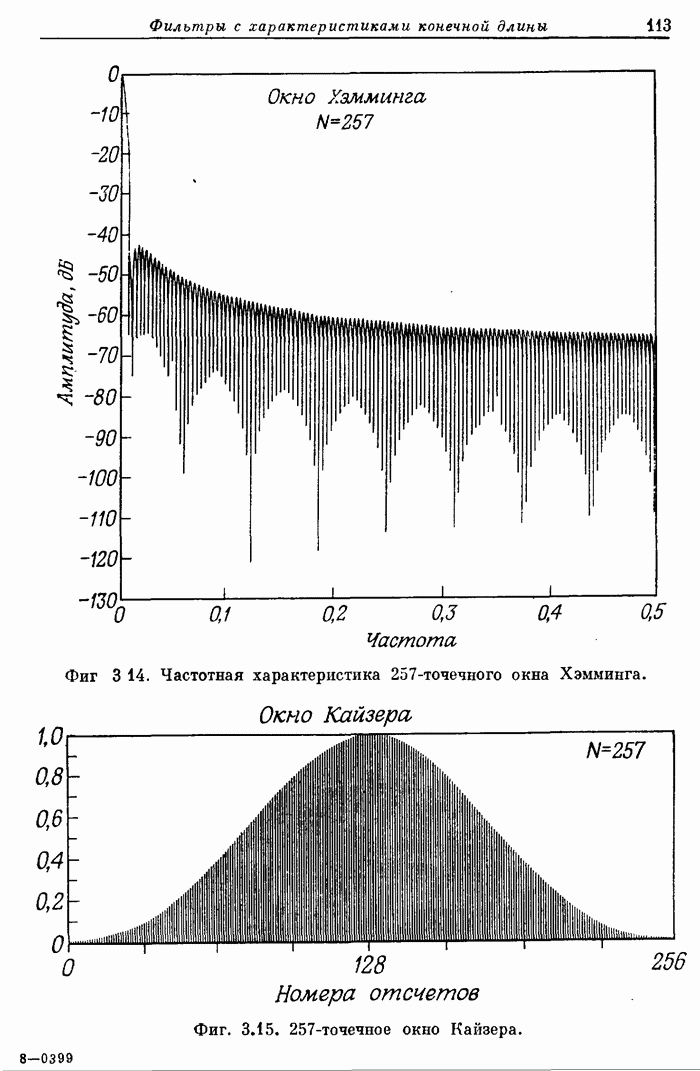
- 3.10. «Обобщенное» окно Хэмминга
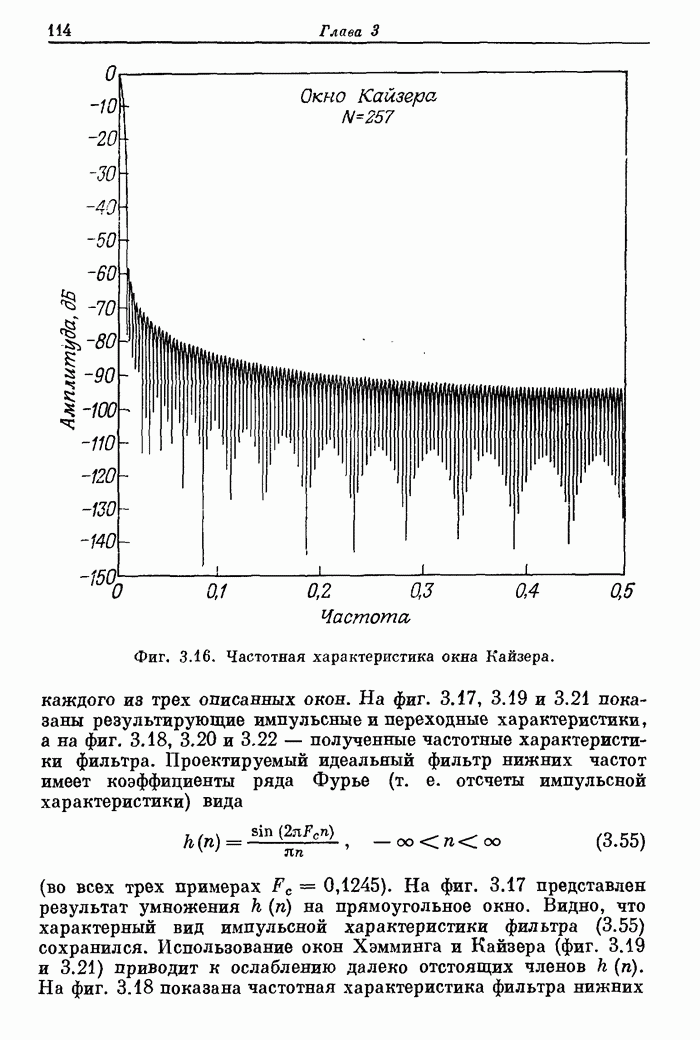
- 3.11. Окно Кайзера
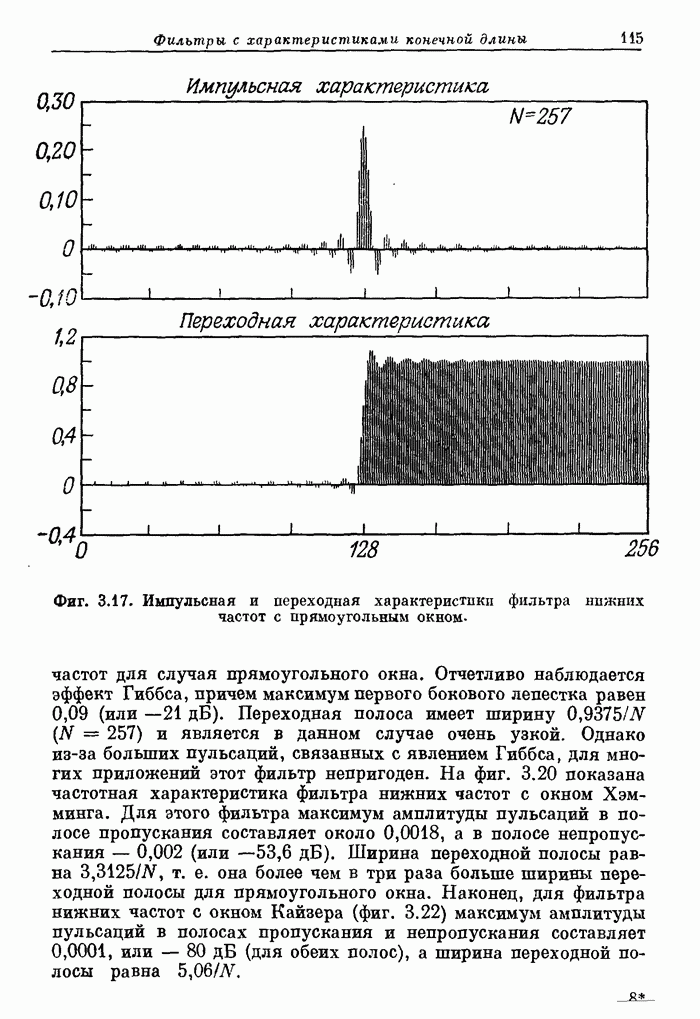
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
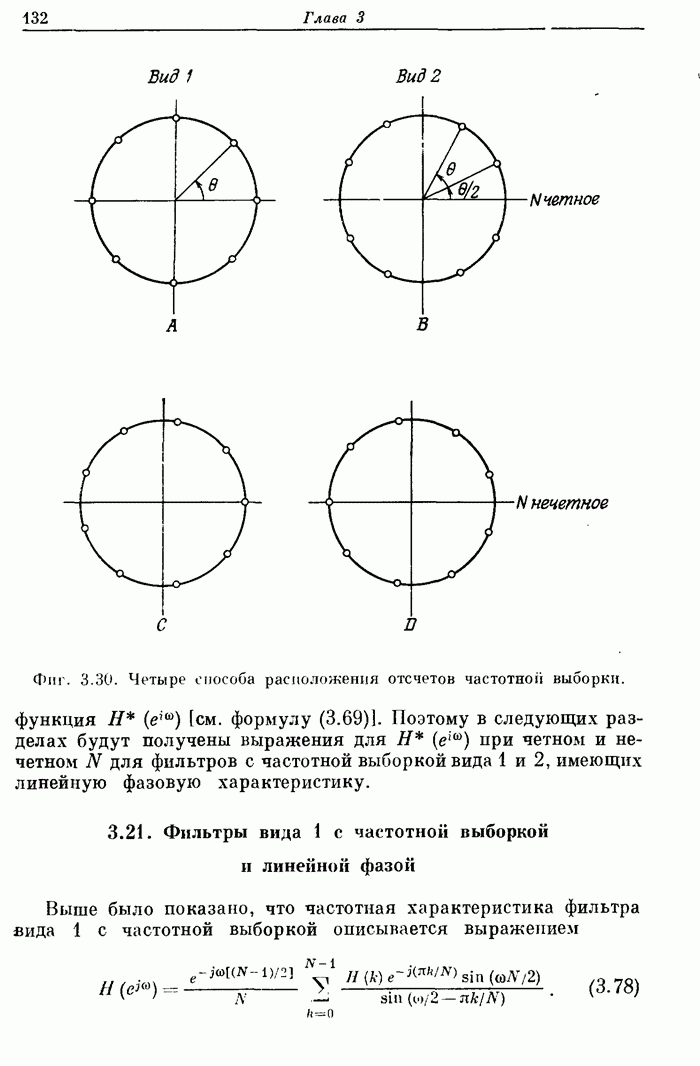
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
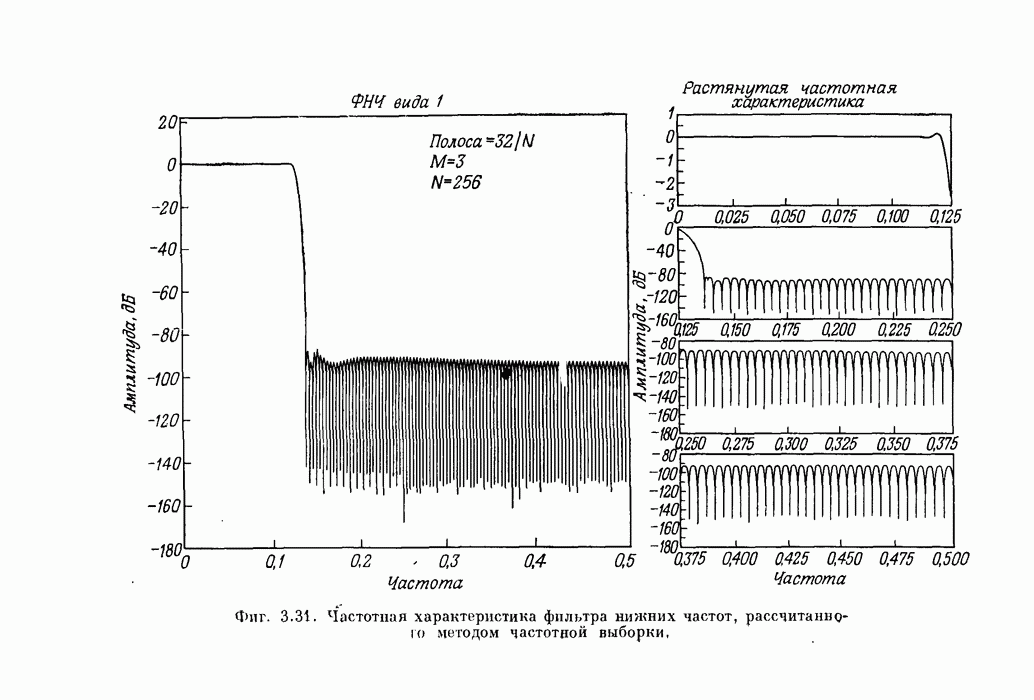
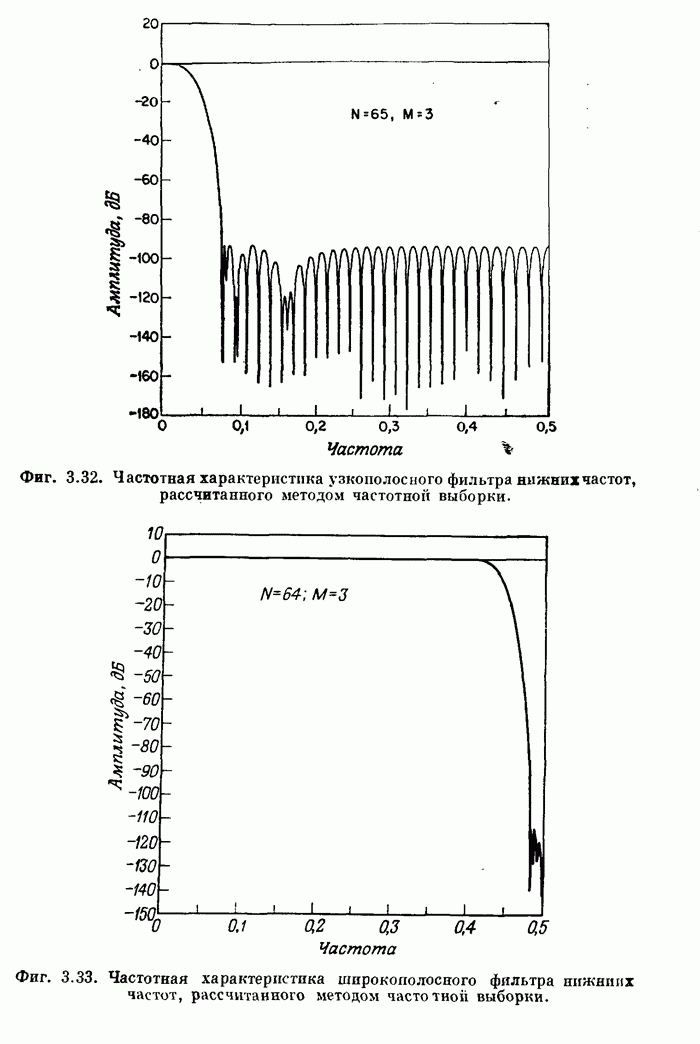
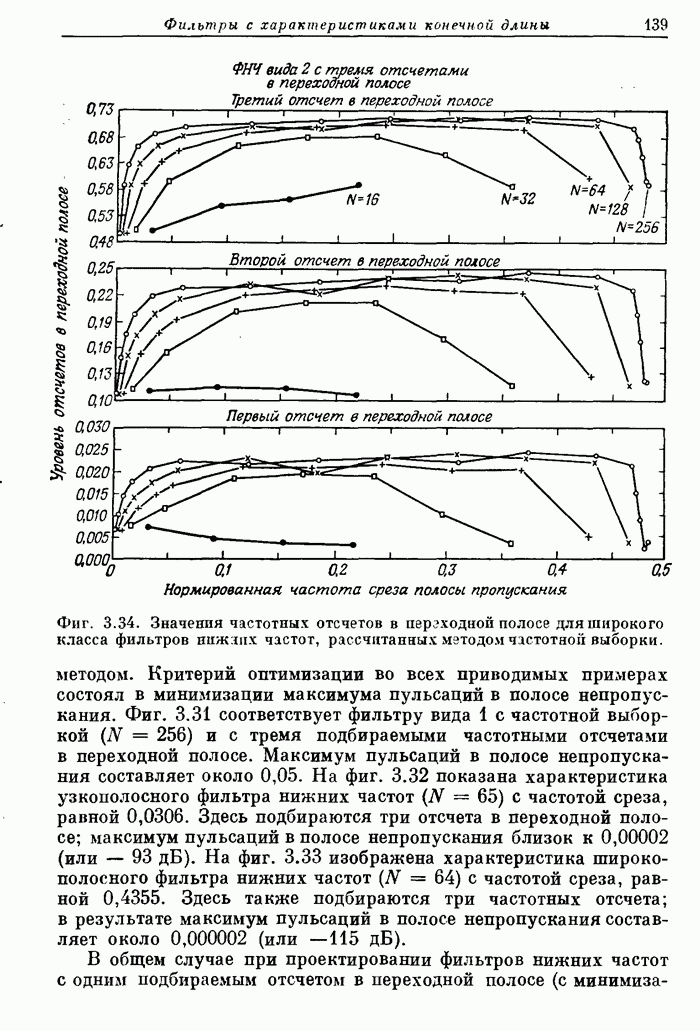
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
- 3.38. Многополосные оптимальные КИХ-фильтры
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
- 4.10. Расчетные диаграммы фильтров нижних частот
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
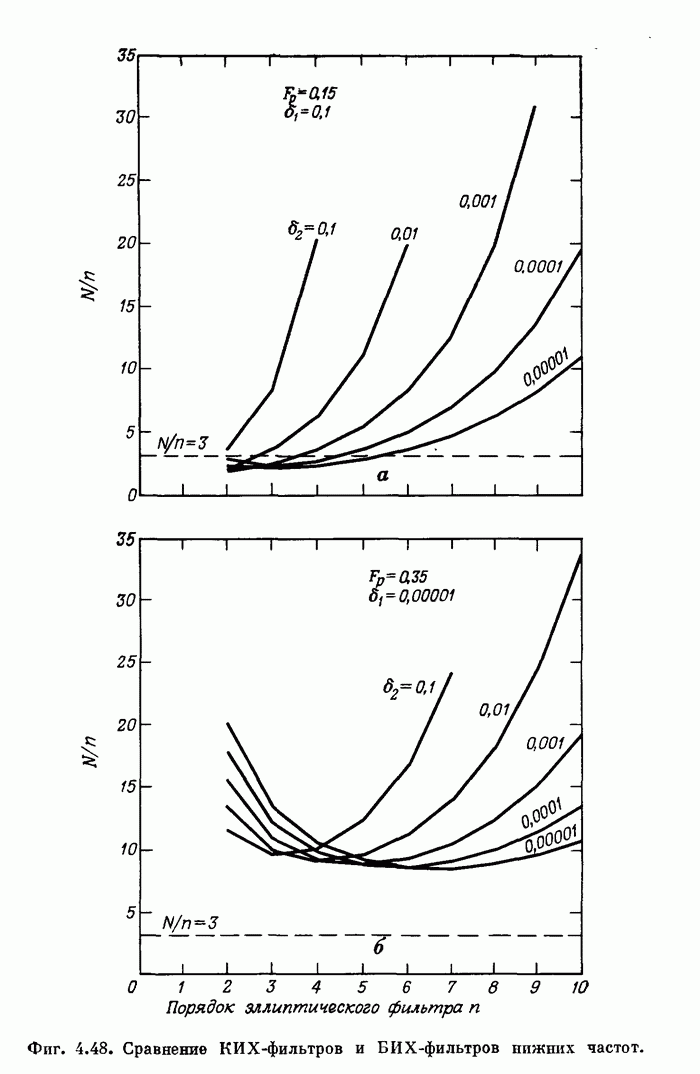
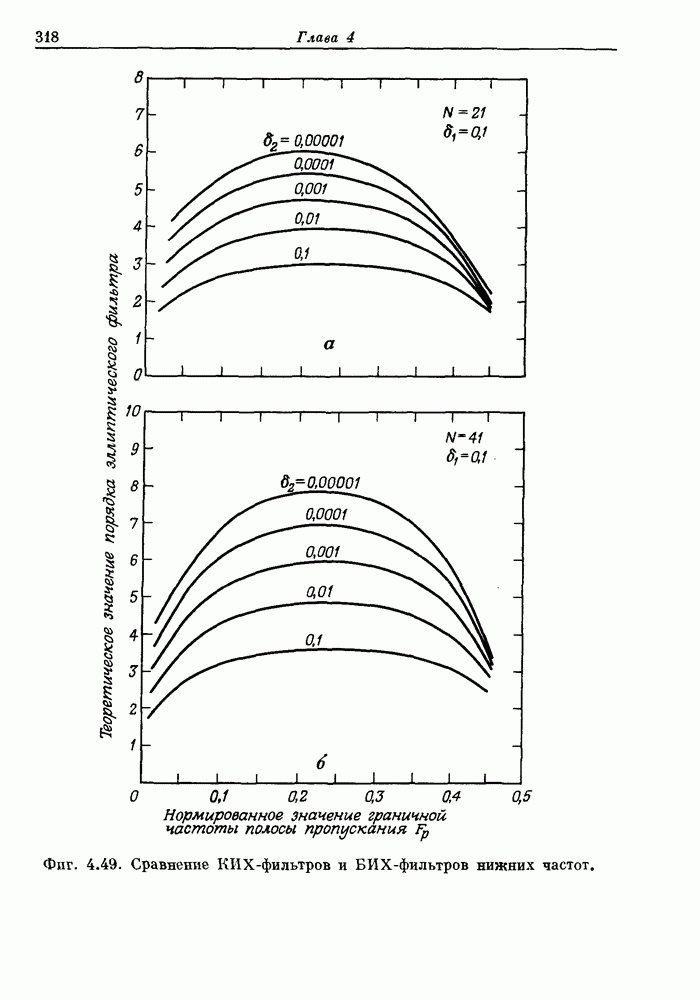
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
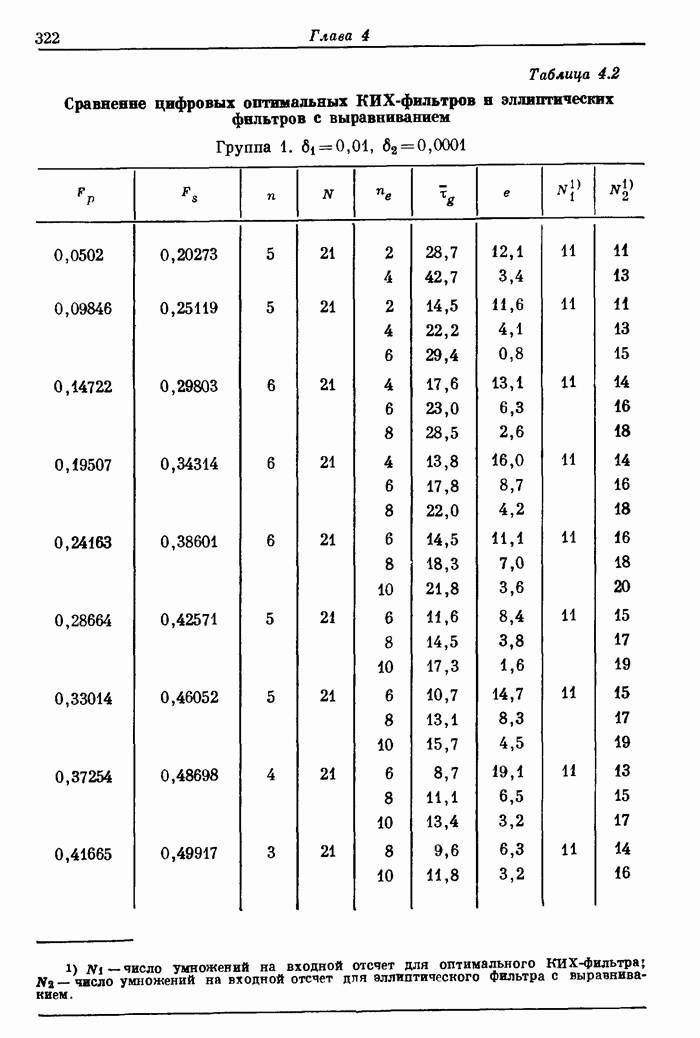
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
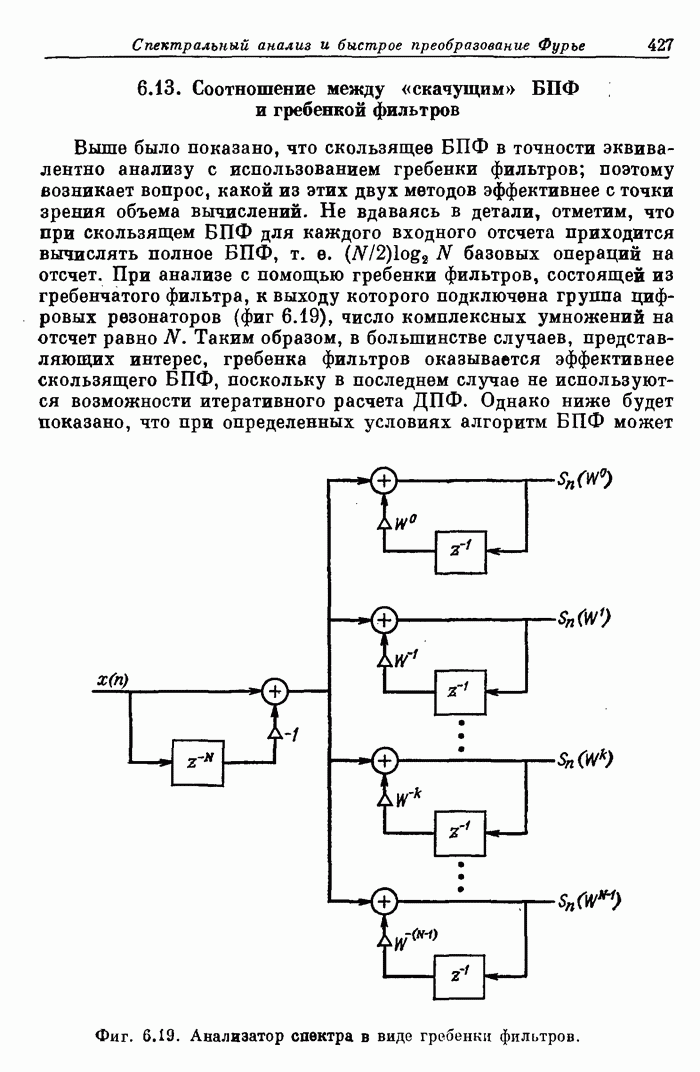
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
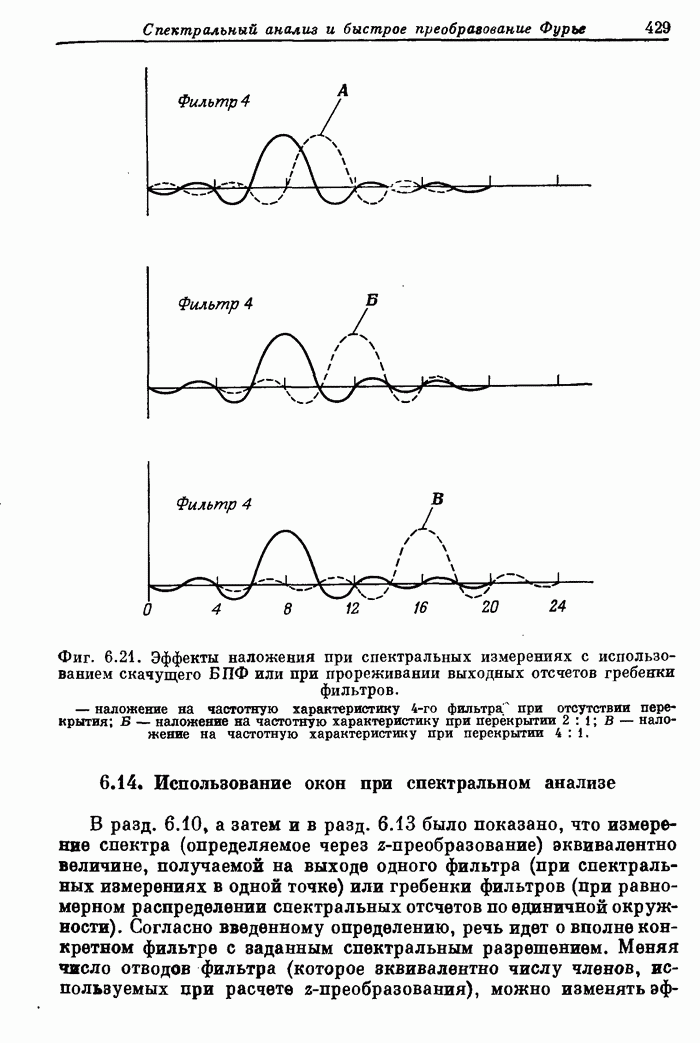
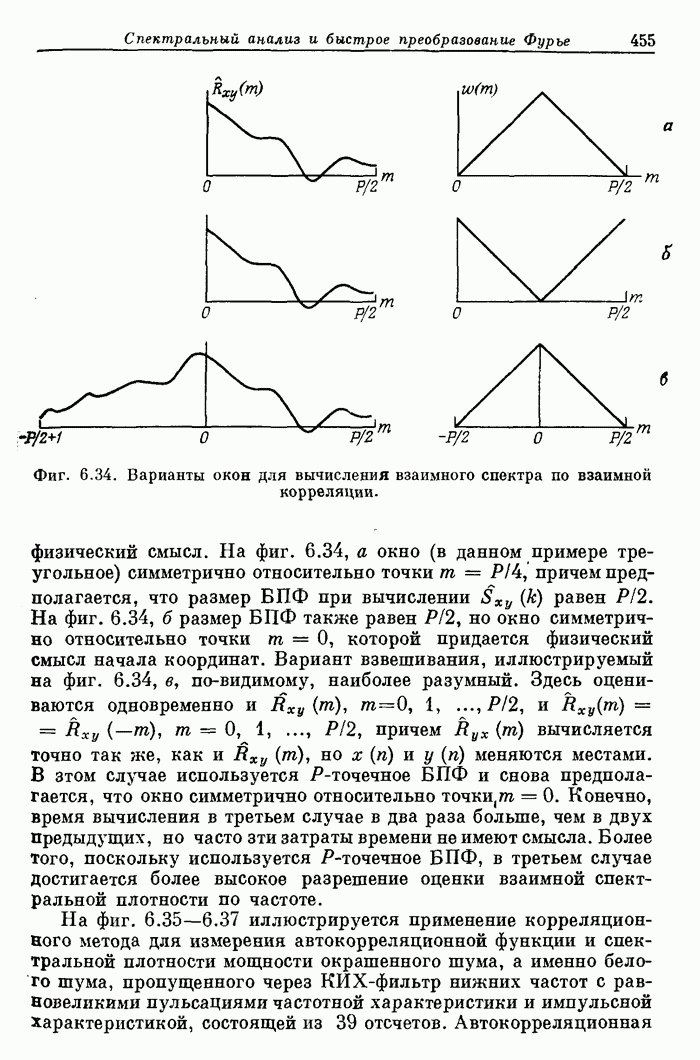
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
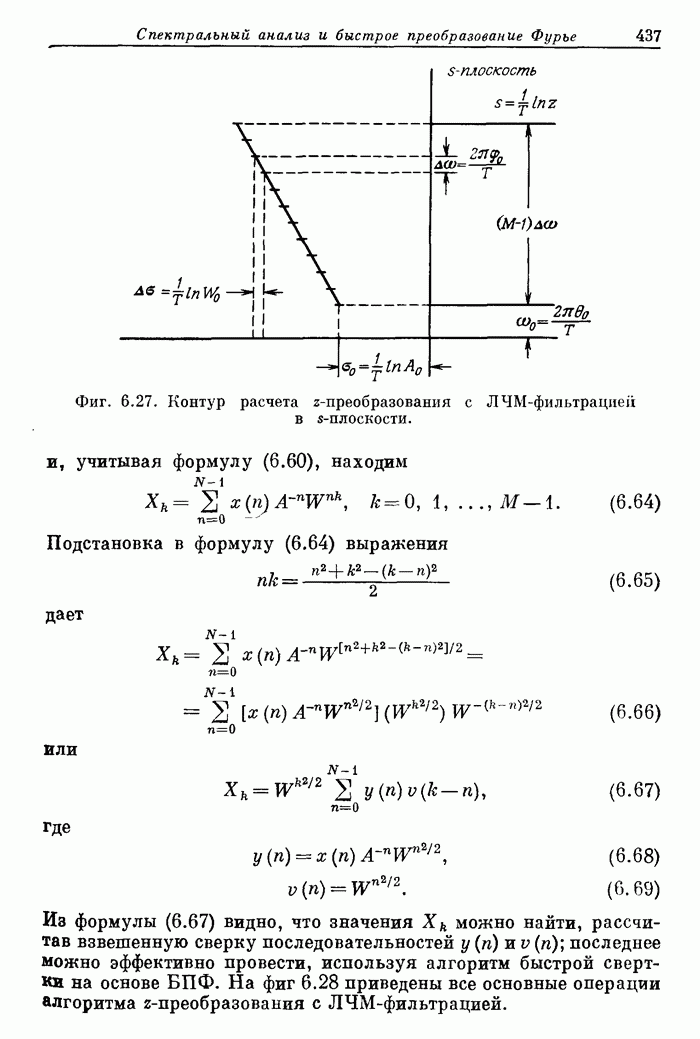
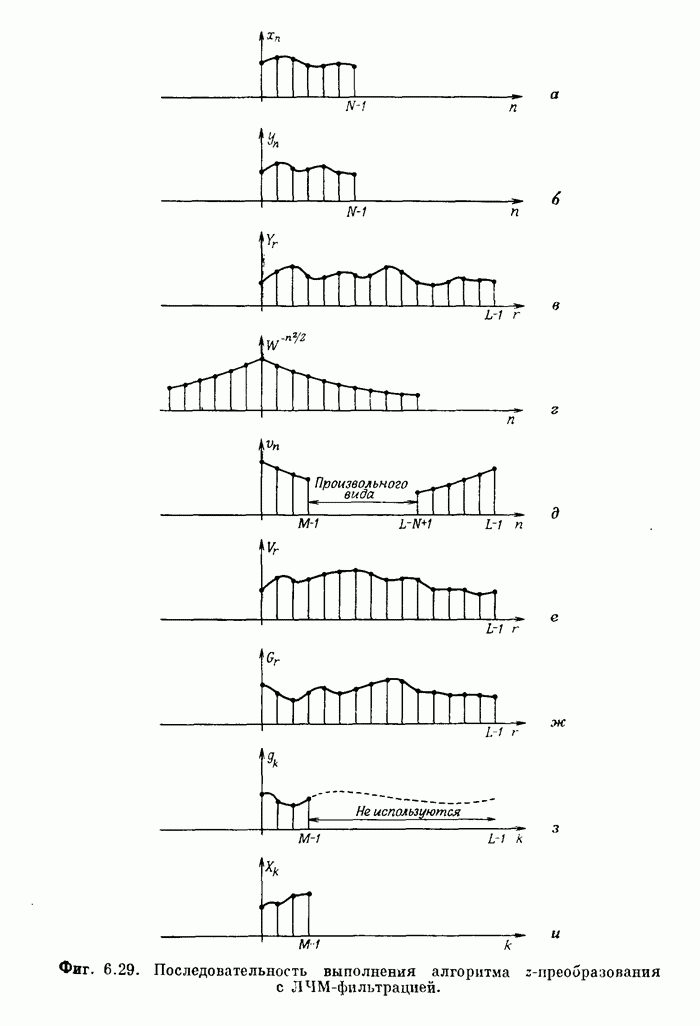
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
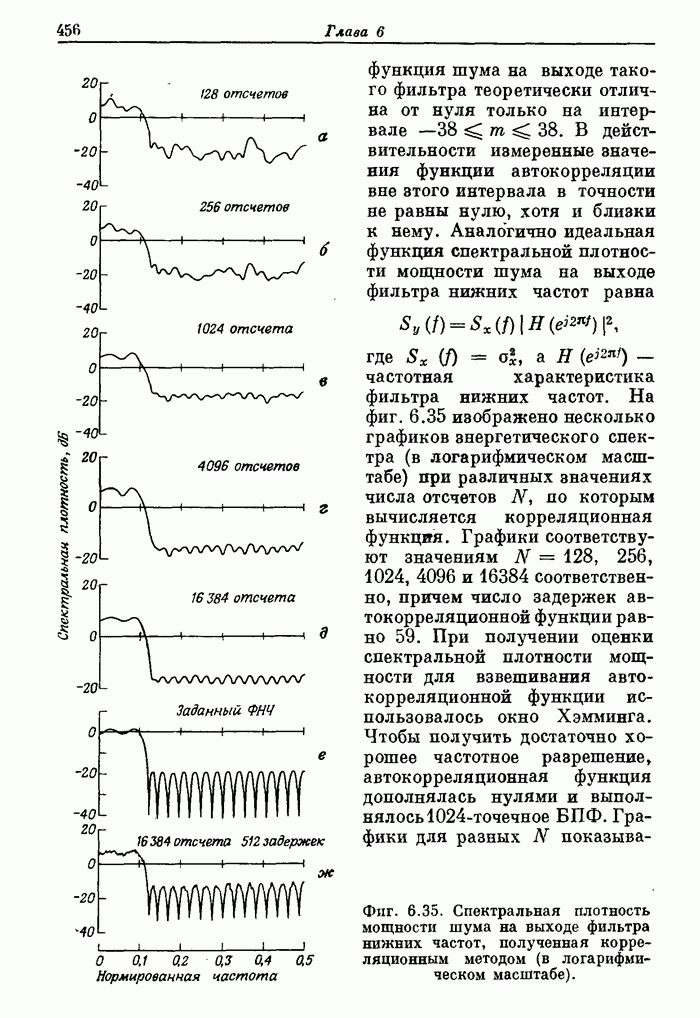
- 6.18. Энергетический спектр случайных сигналов
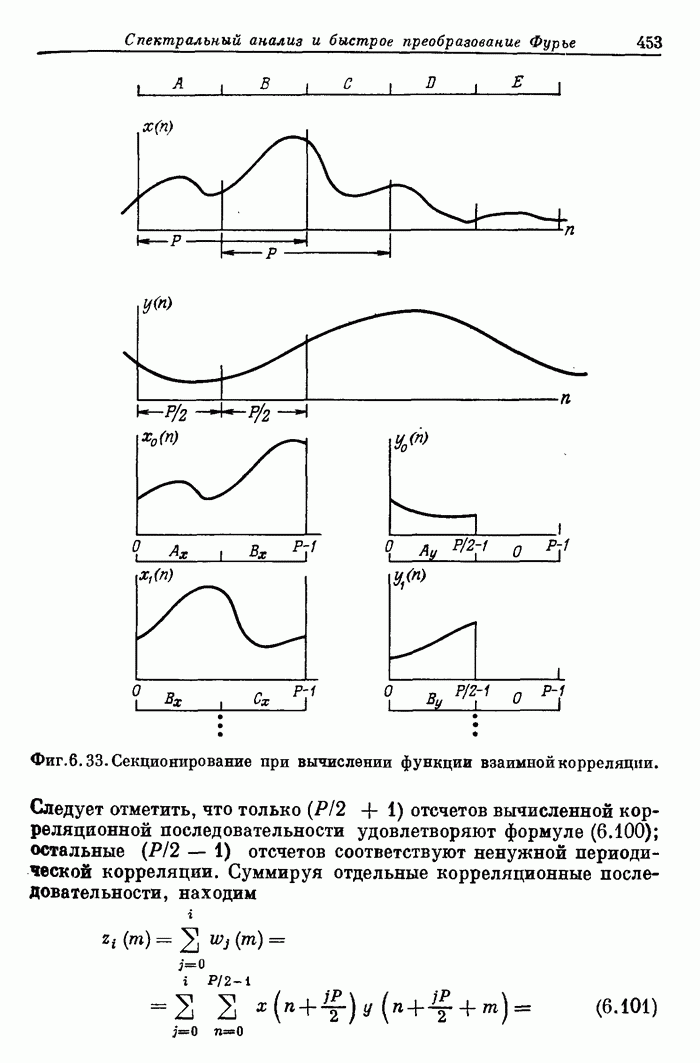
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
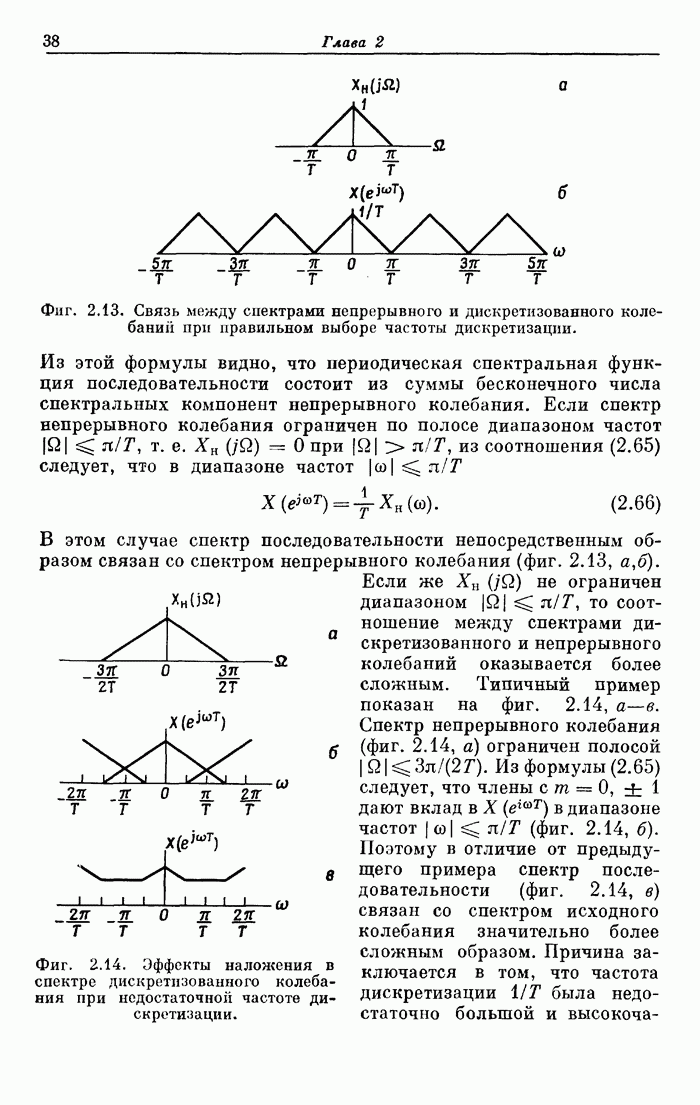
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
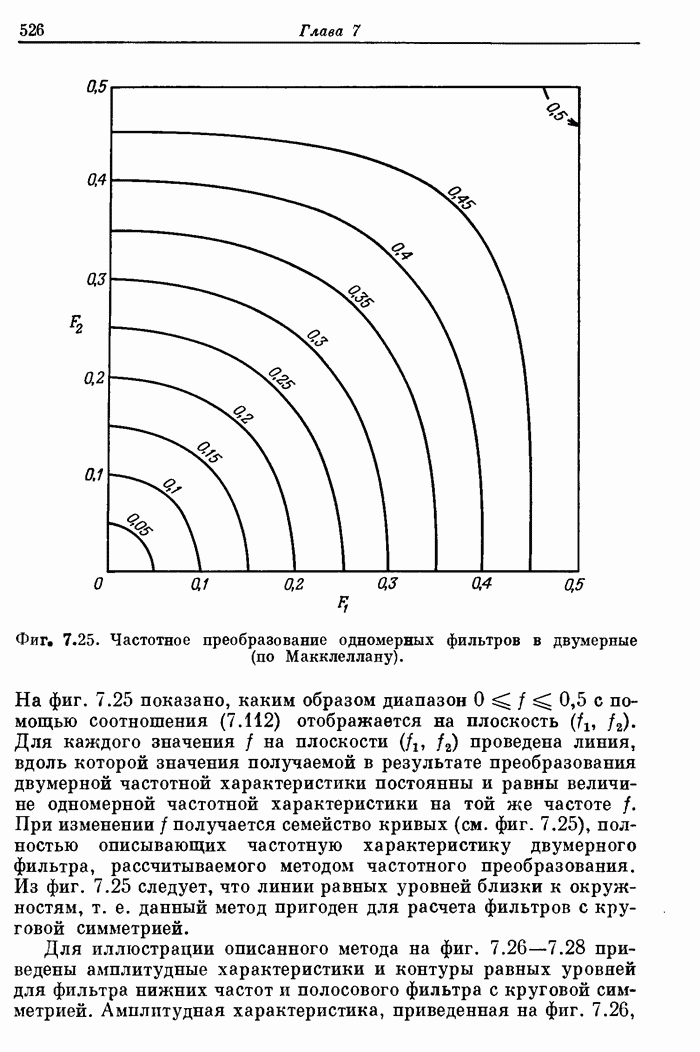
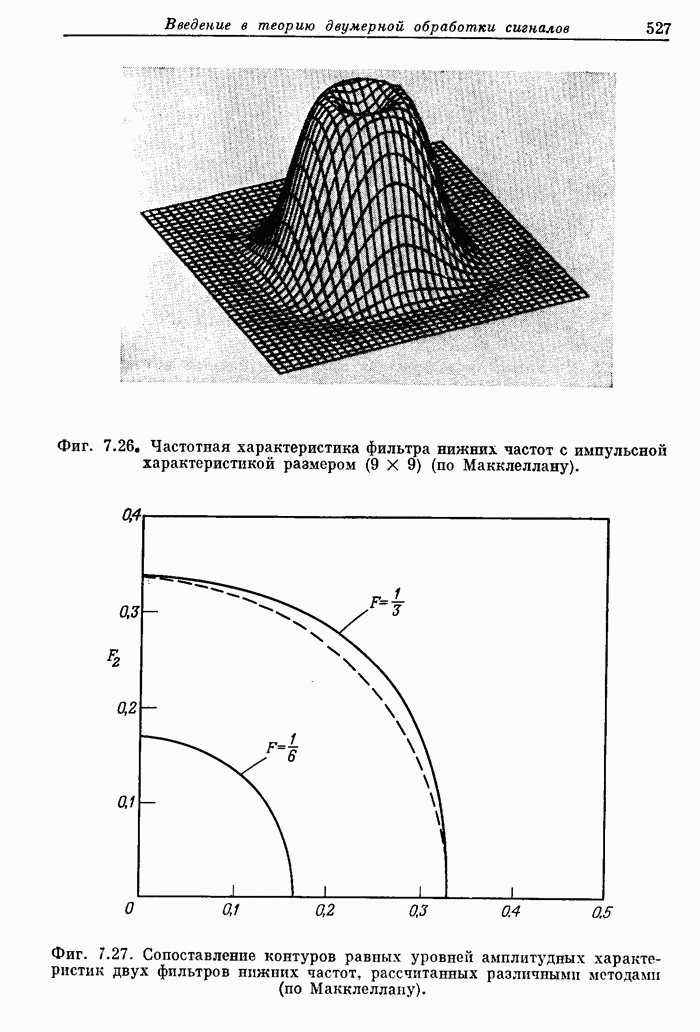
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
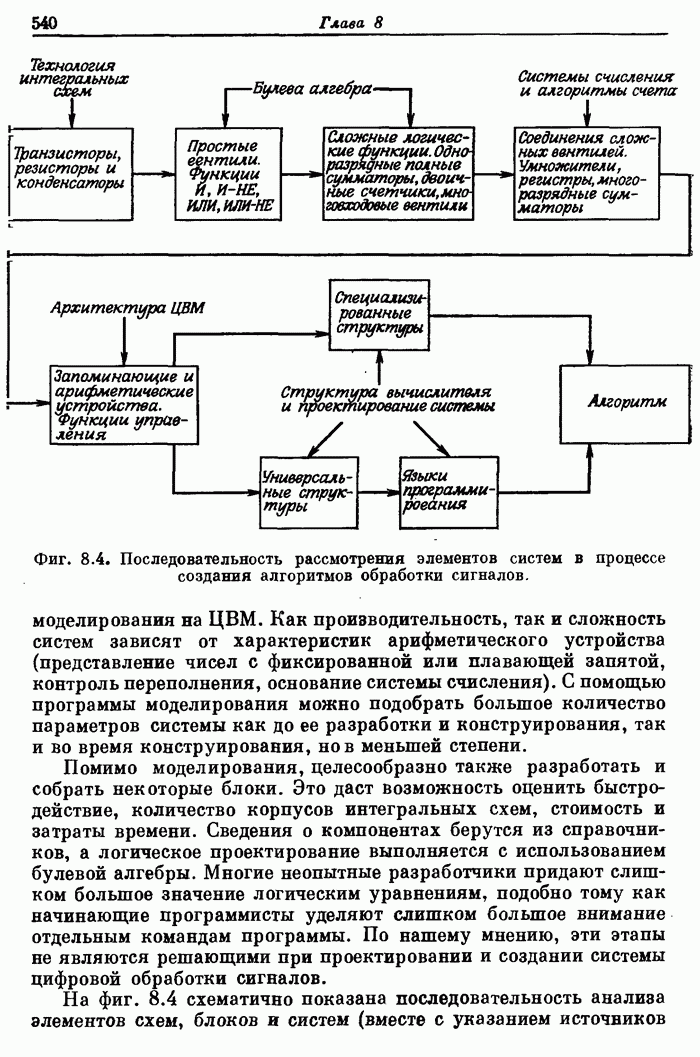
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
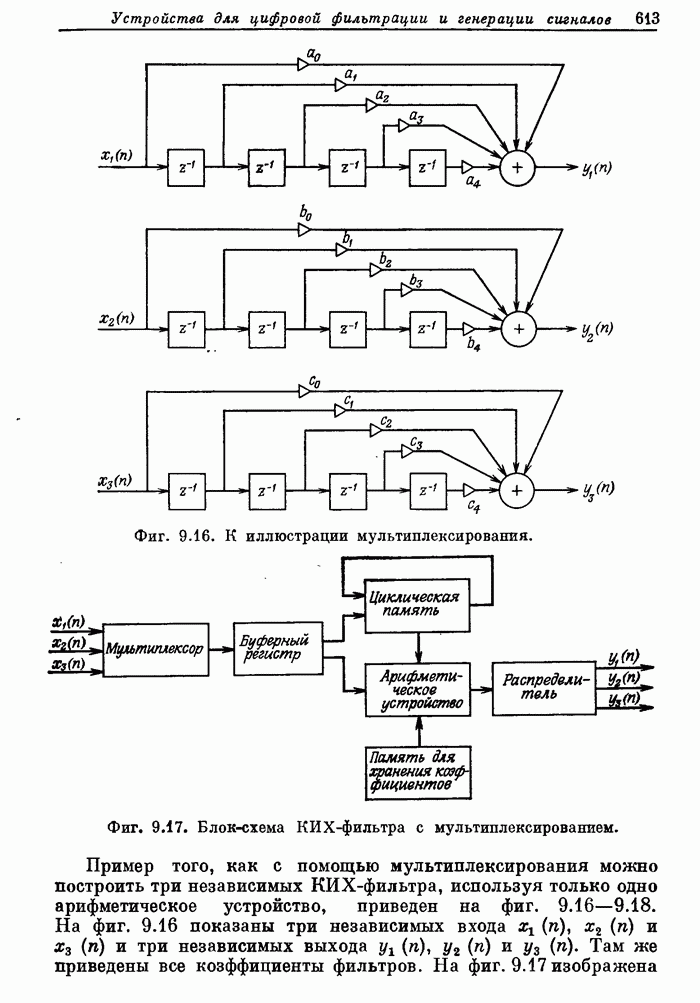
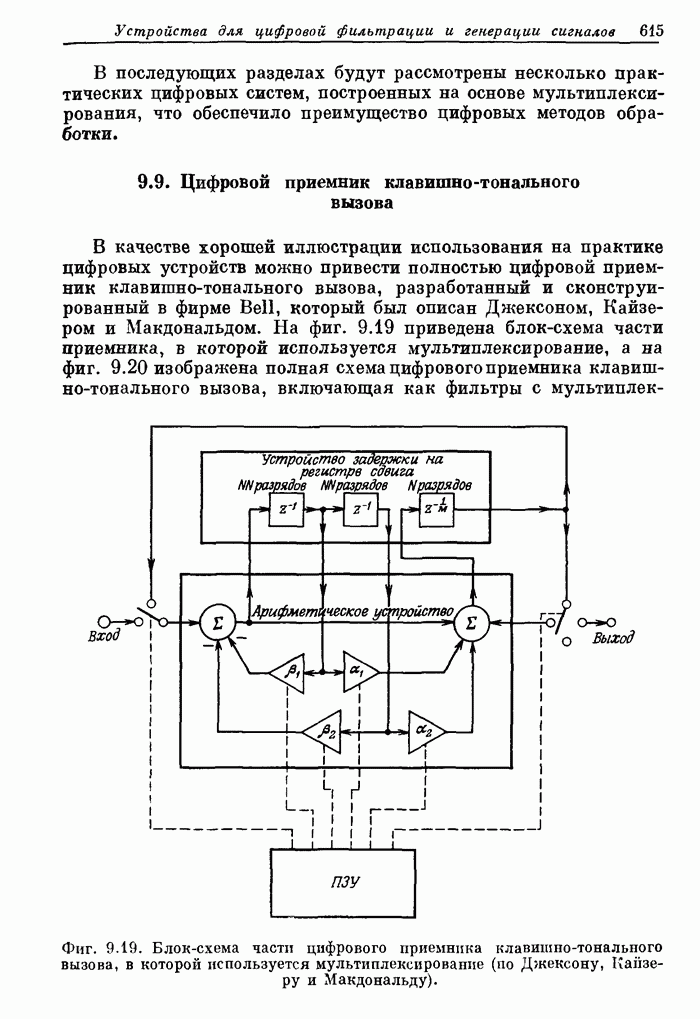
- 9.8. Мультиплексирование
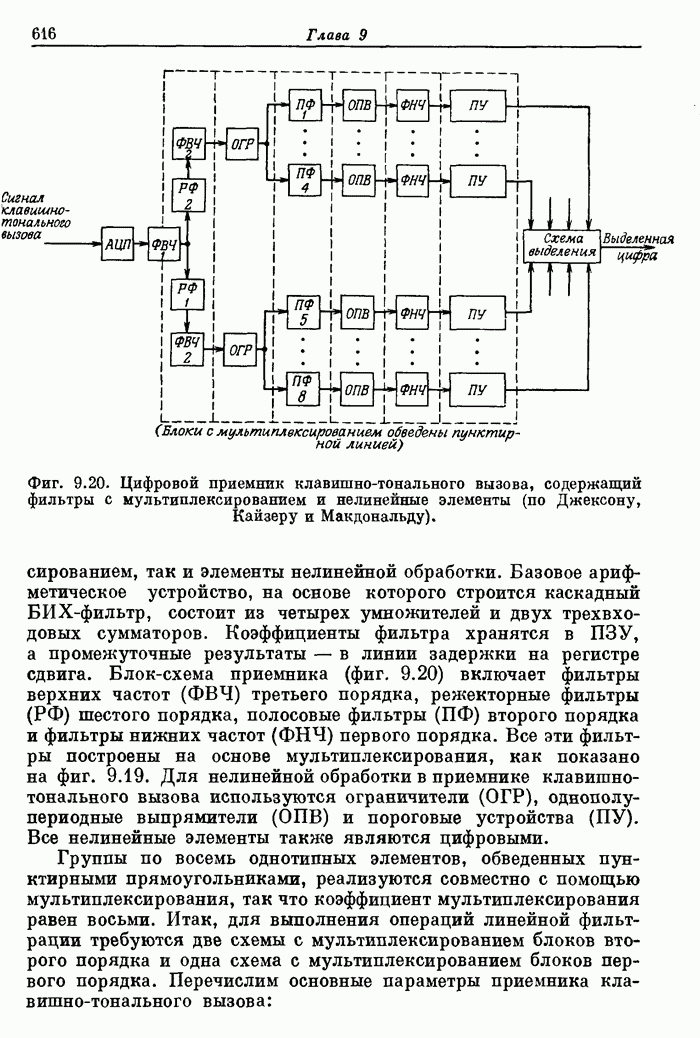
- 9.9. Цифровой приемник клавишно-тонального вызова
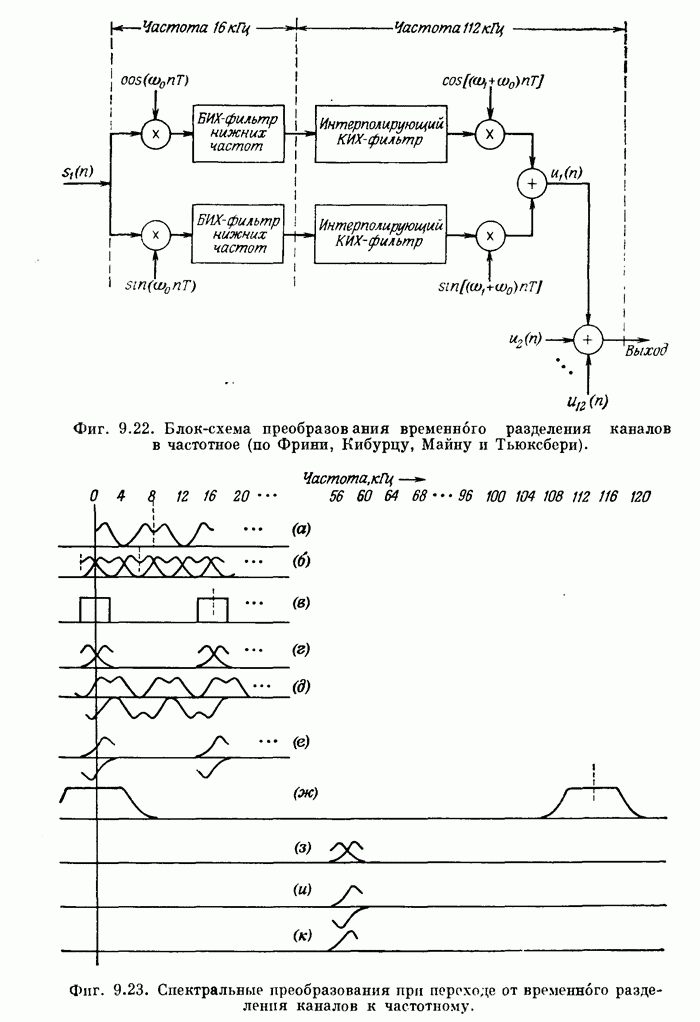
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
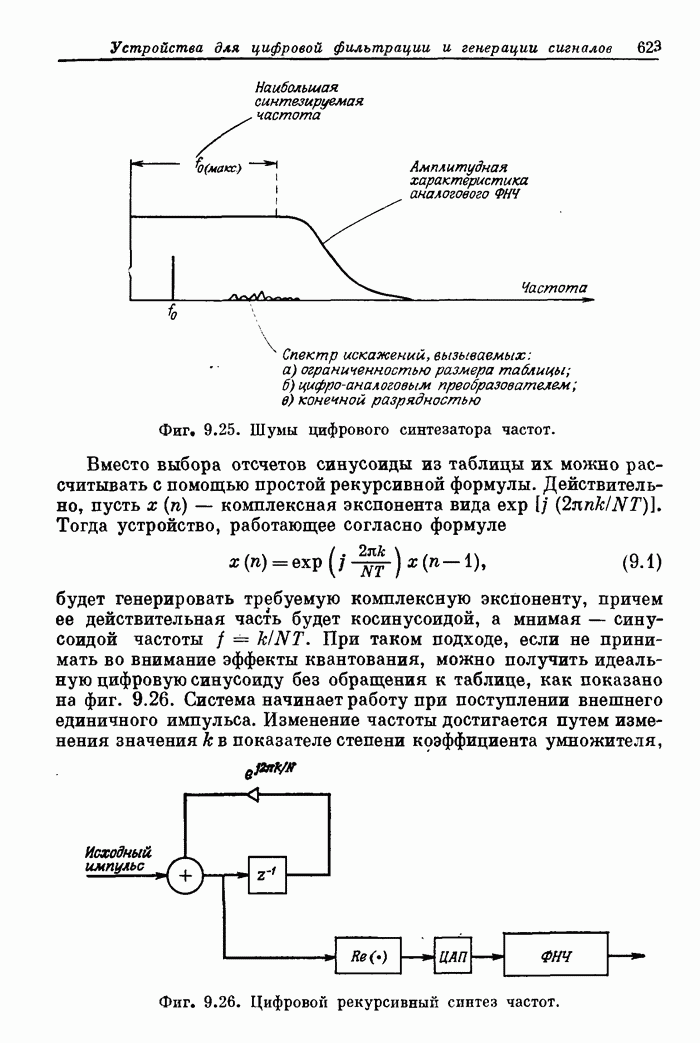
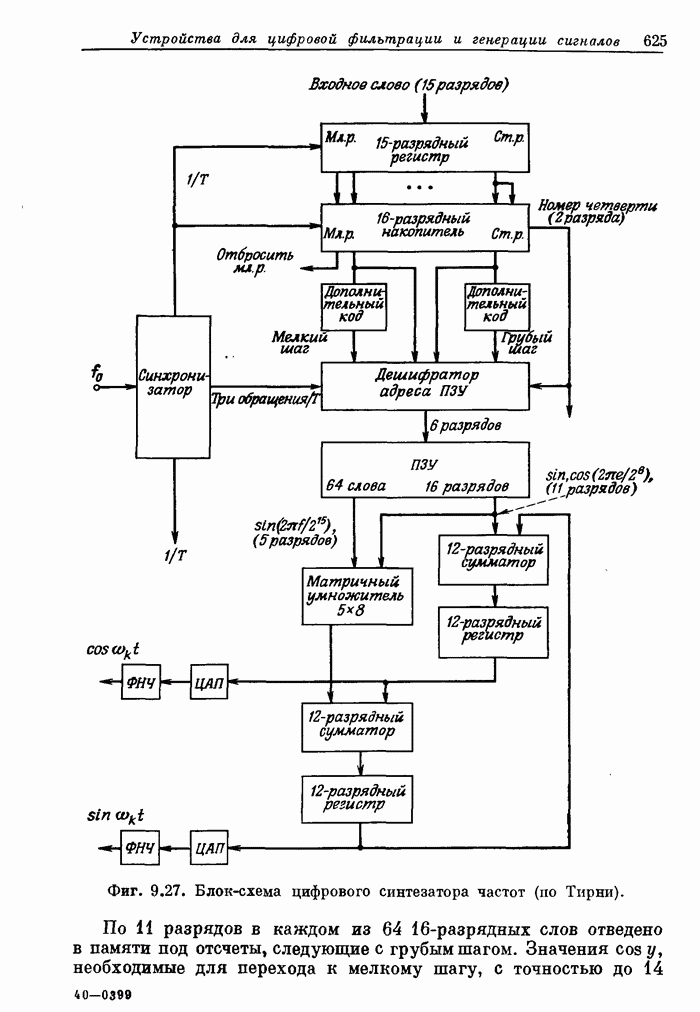
- 9.12. Специализированный цифровой синтезатор частот
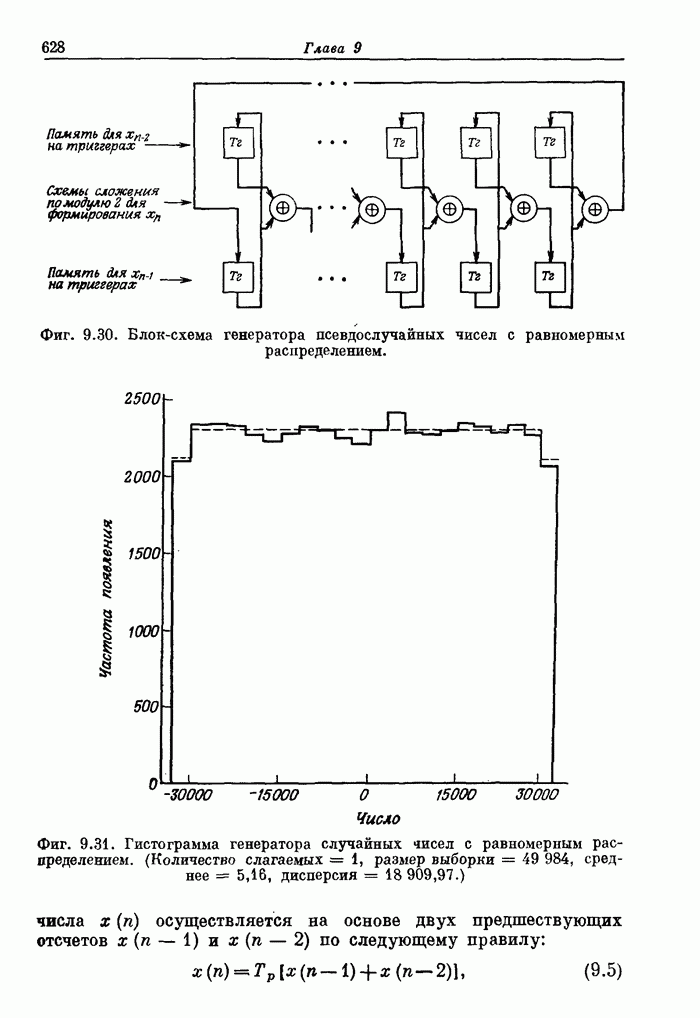
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
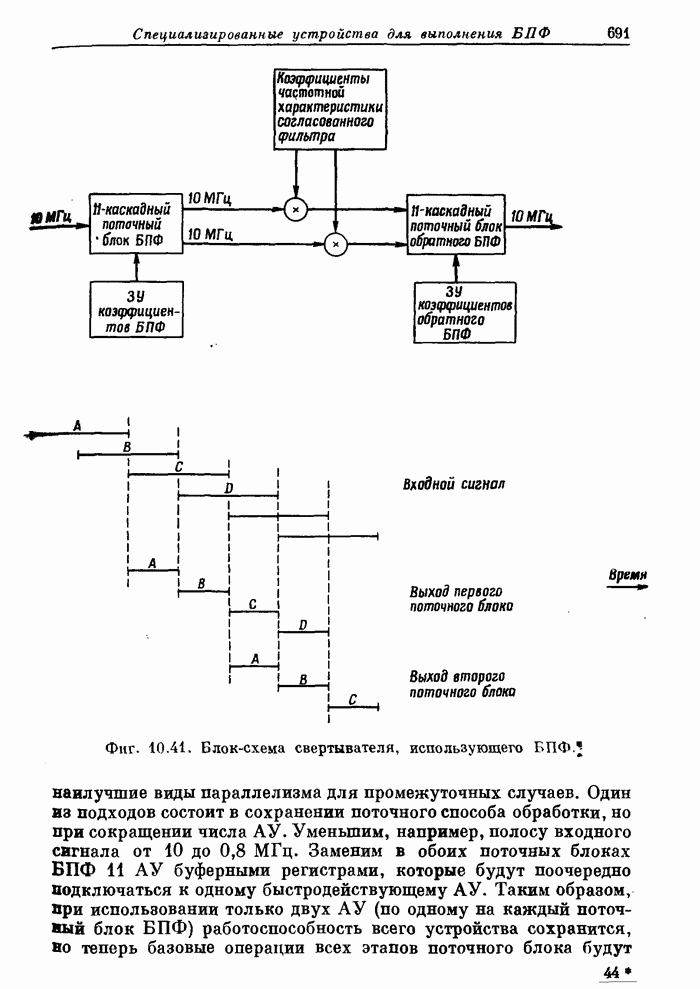
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
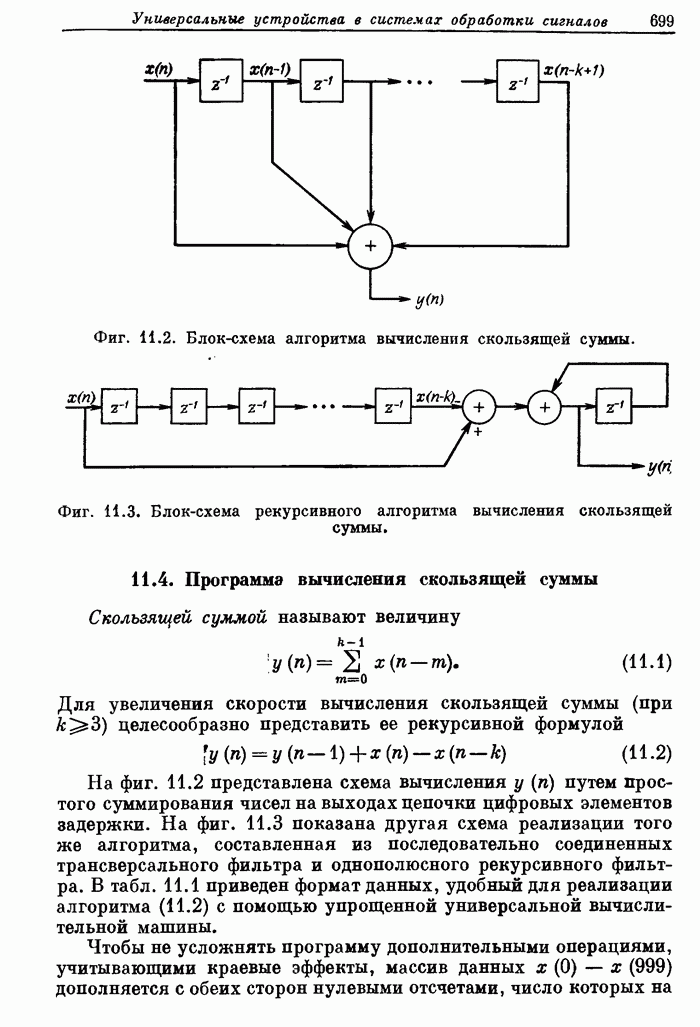
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
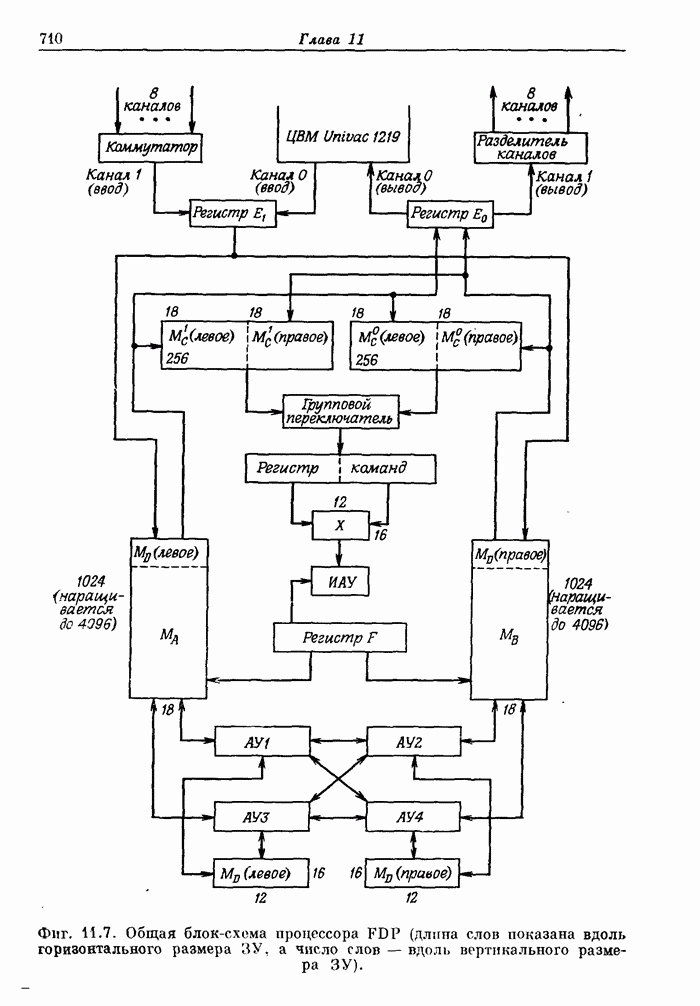
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
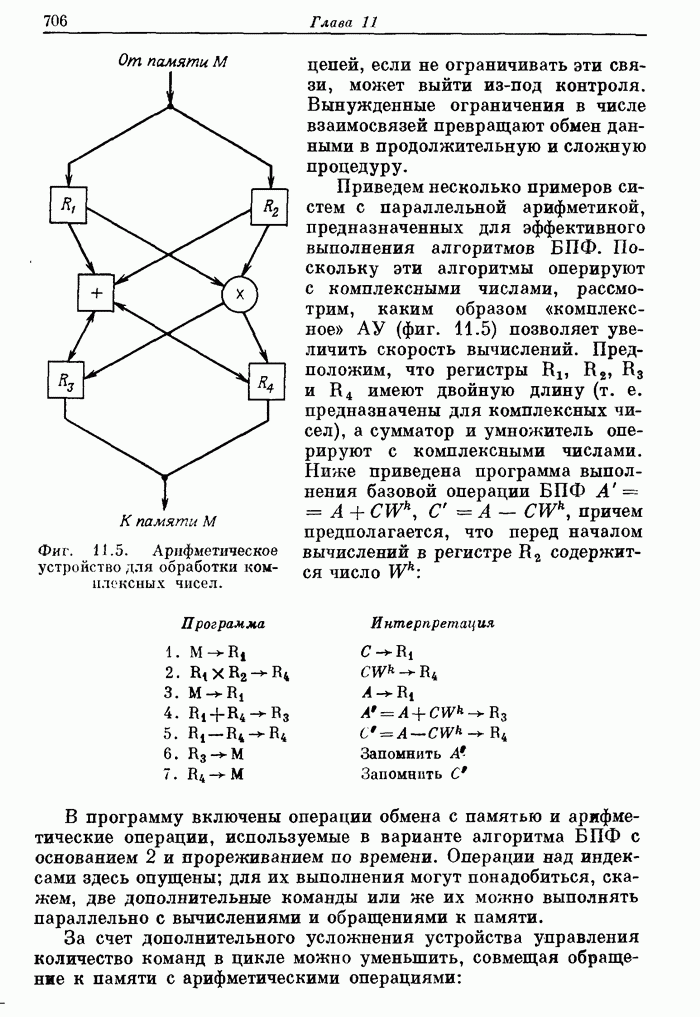
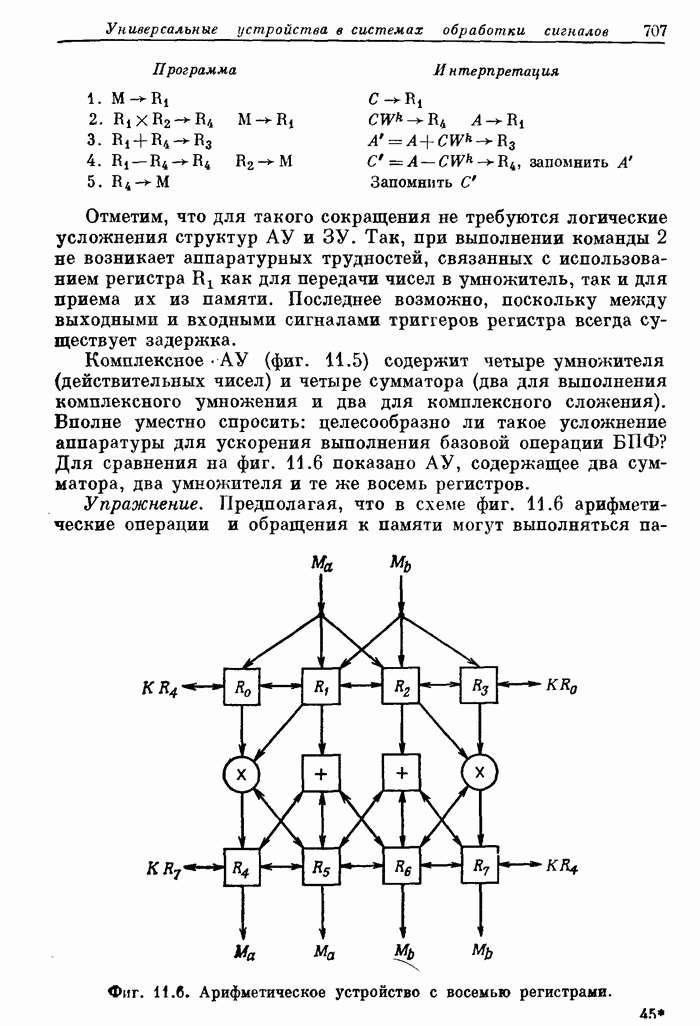
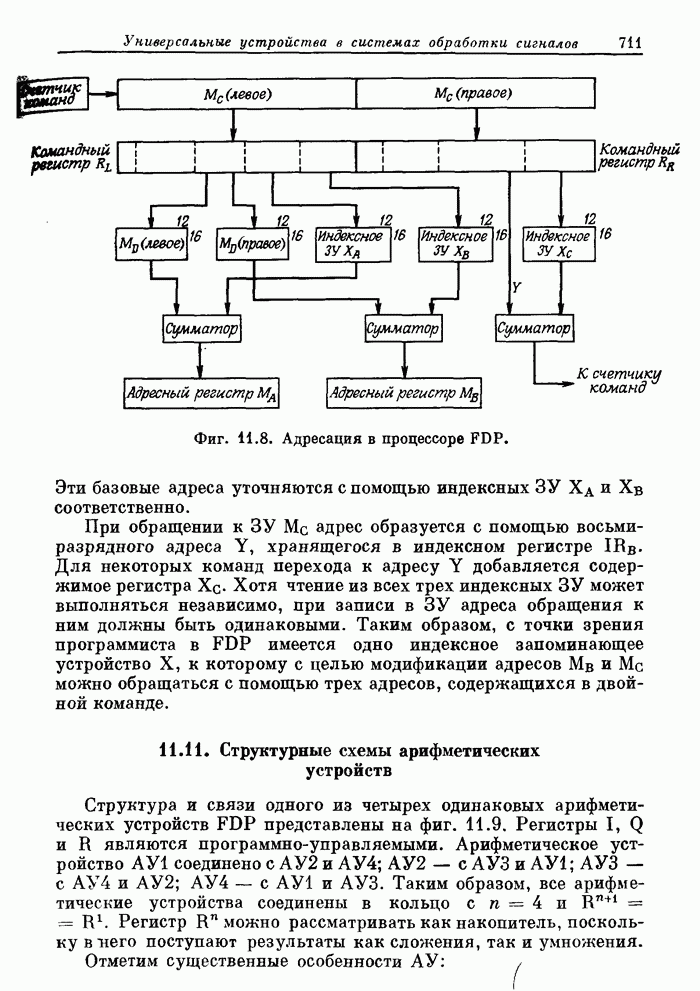
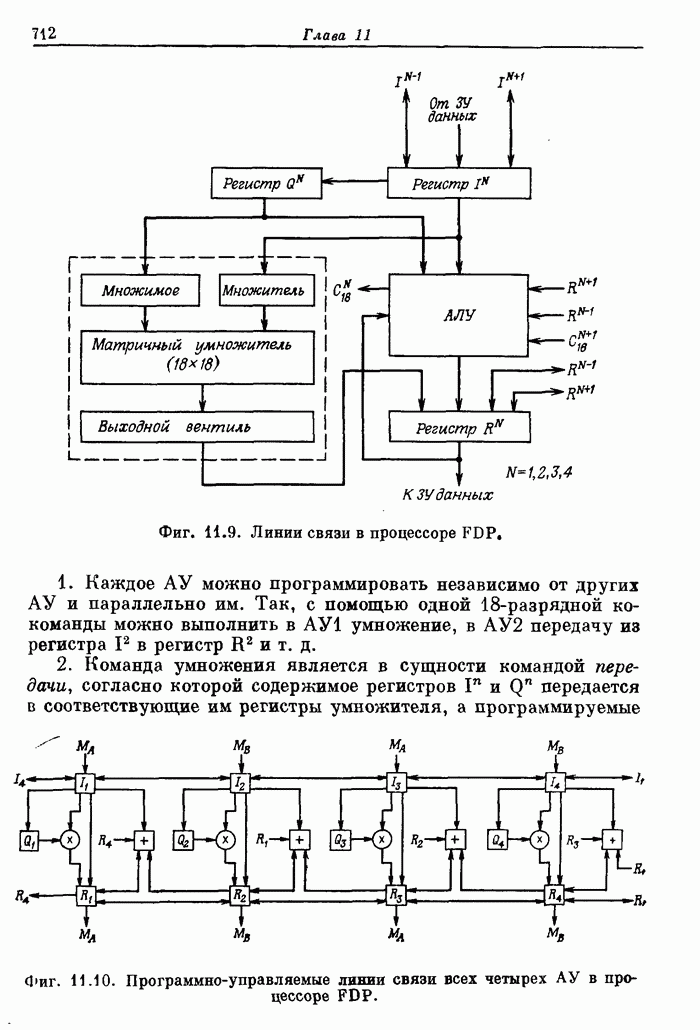
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
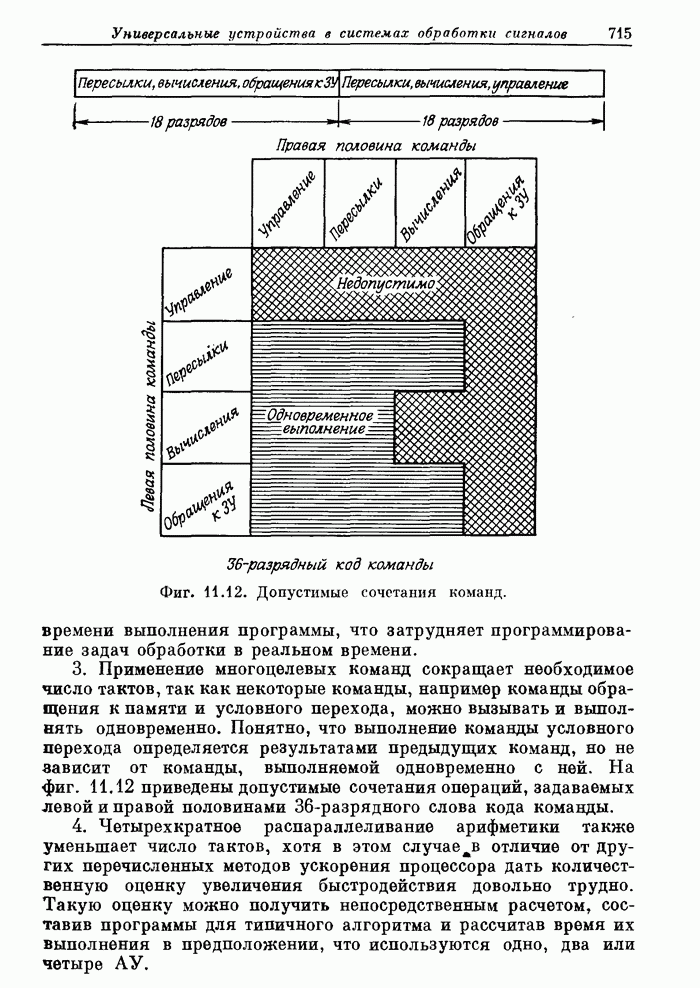
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
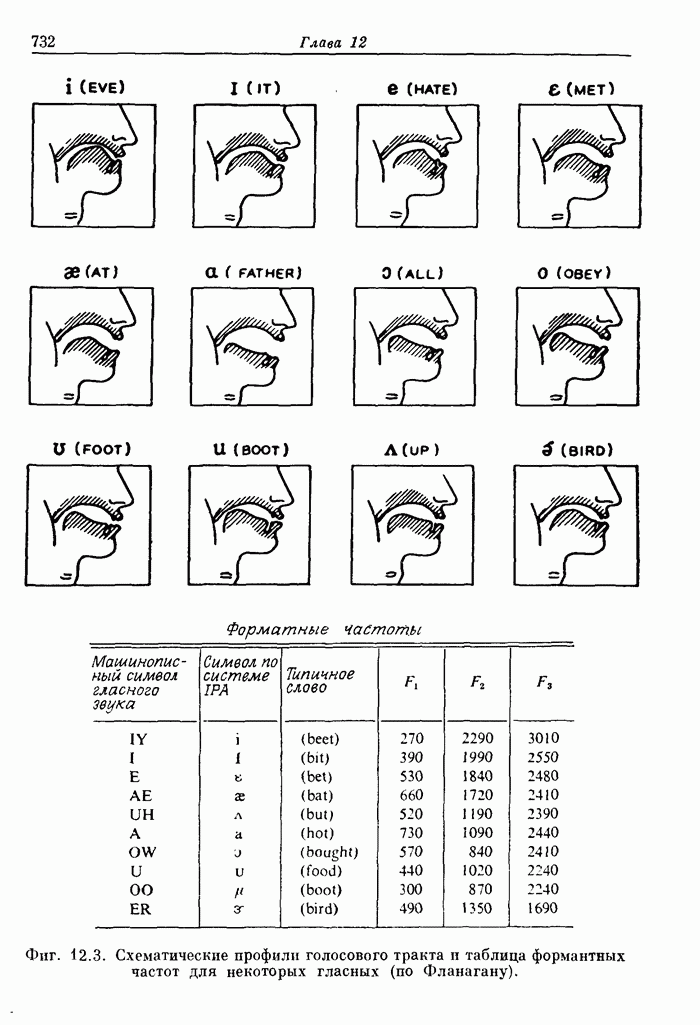
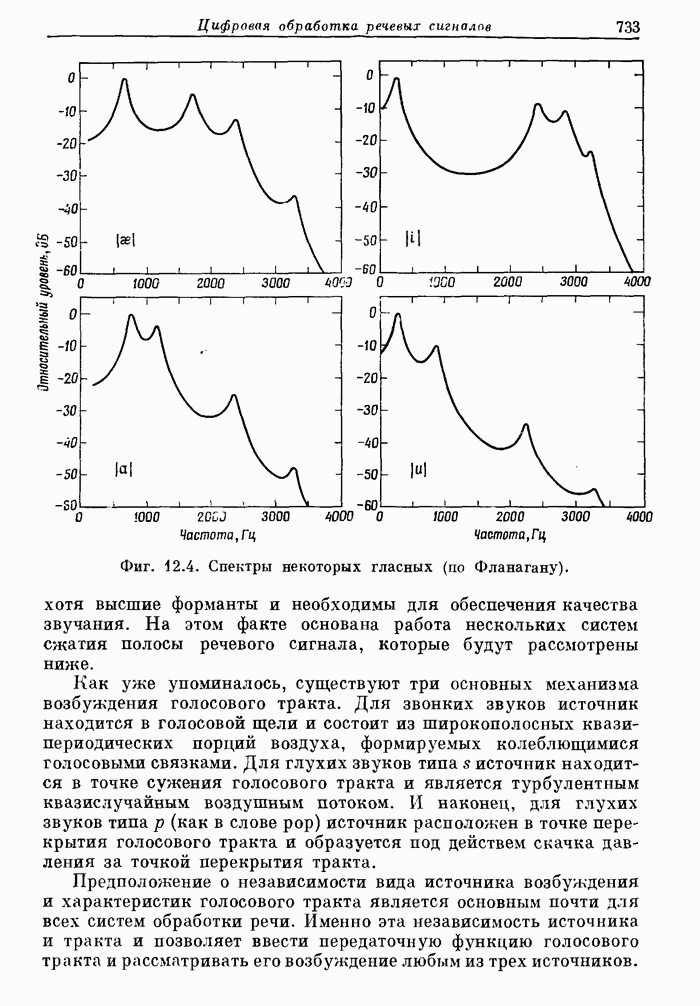
- 12.2. Модель образования речи
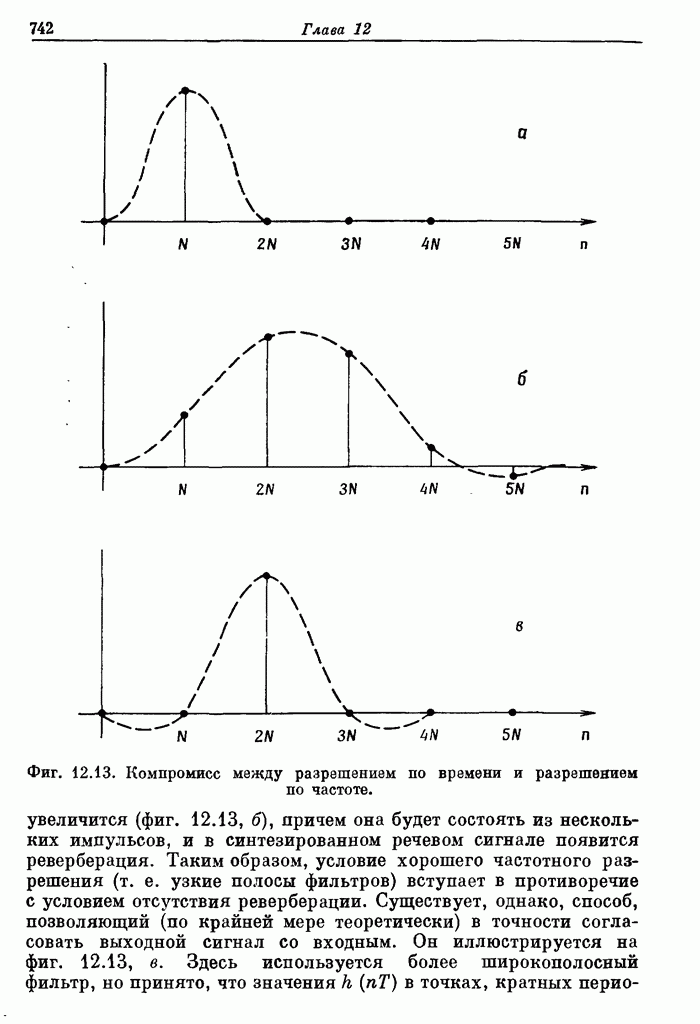
- 12.3. Кратковременный спектральный анализ
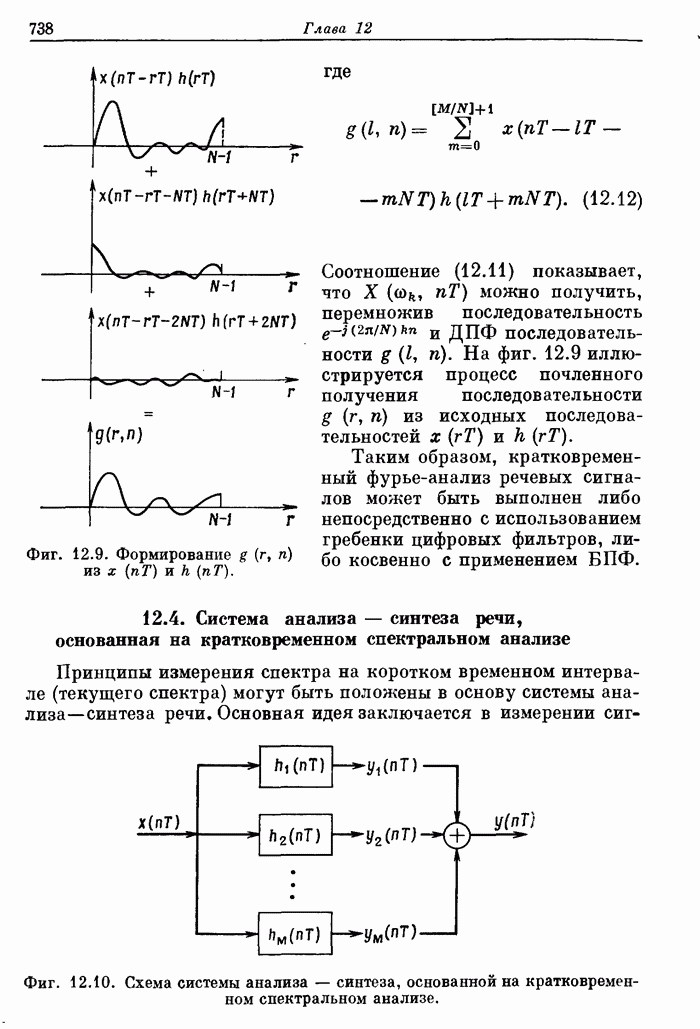
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
- 12.16. Цепь возбуждения звонких фрикативных звуков
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
- 12.19. Линейное прогнозирование речи
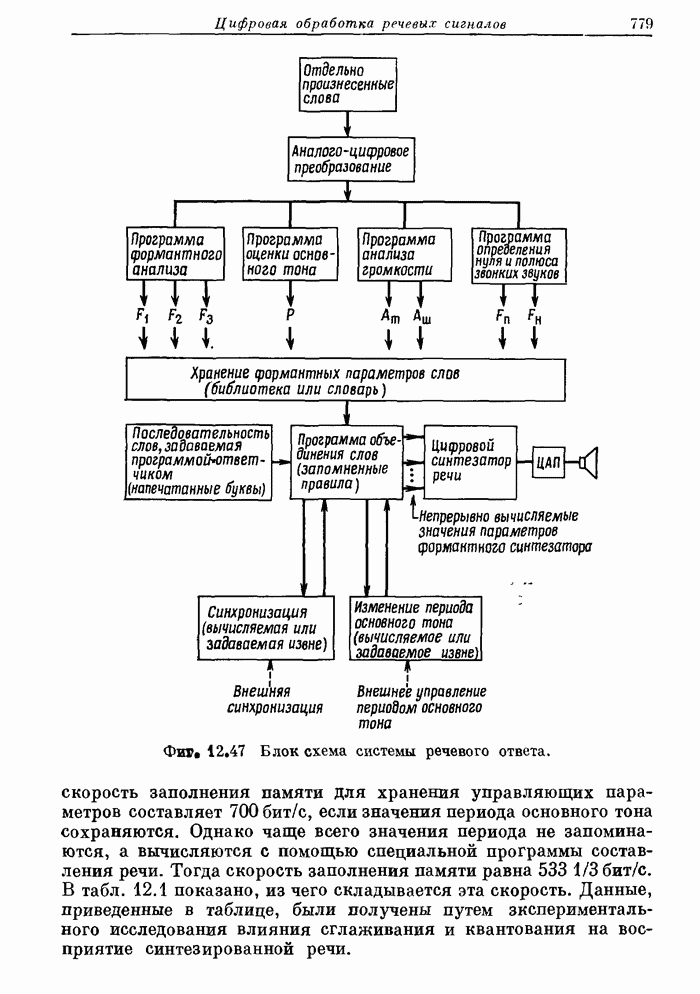
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
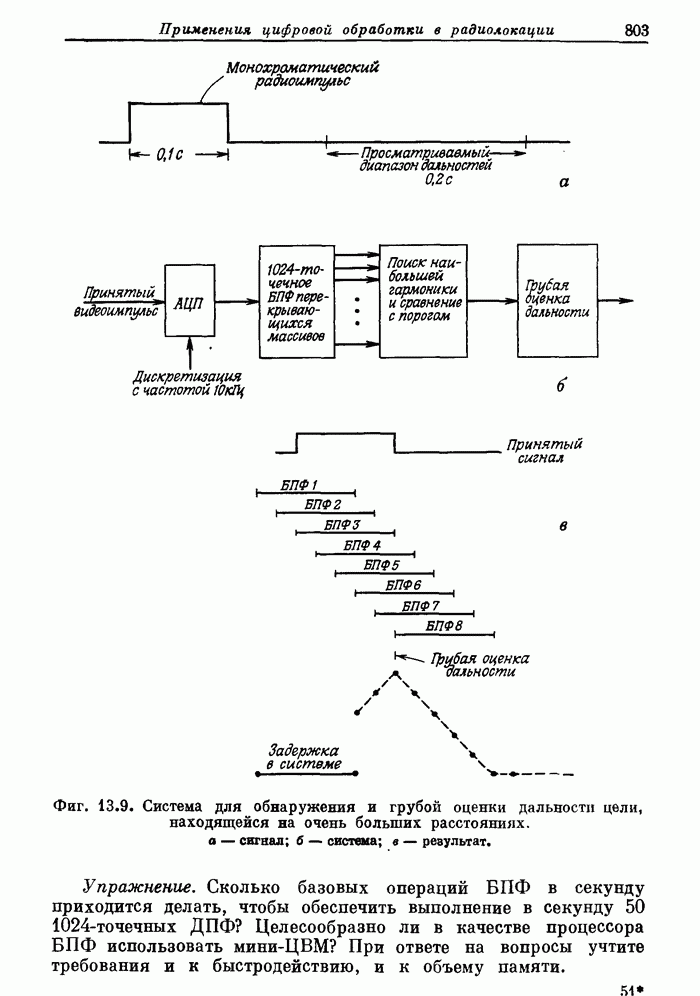
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
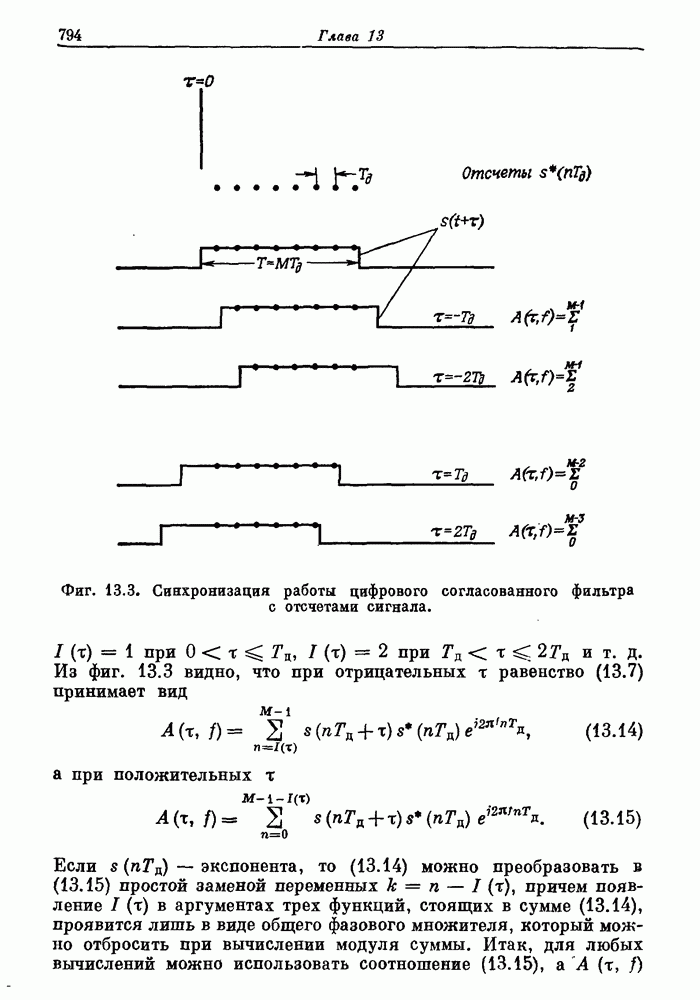
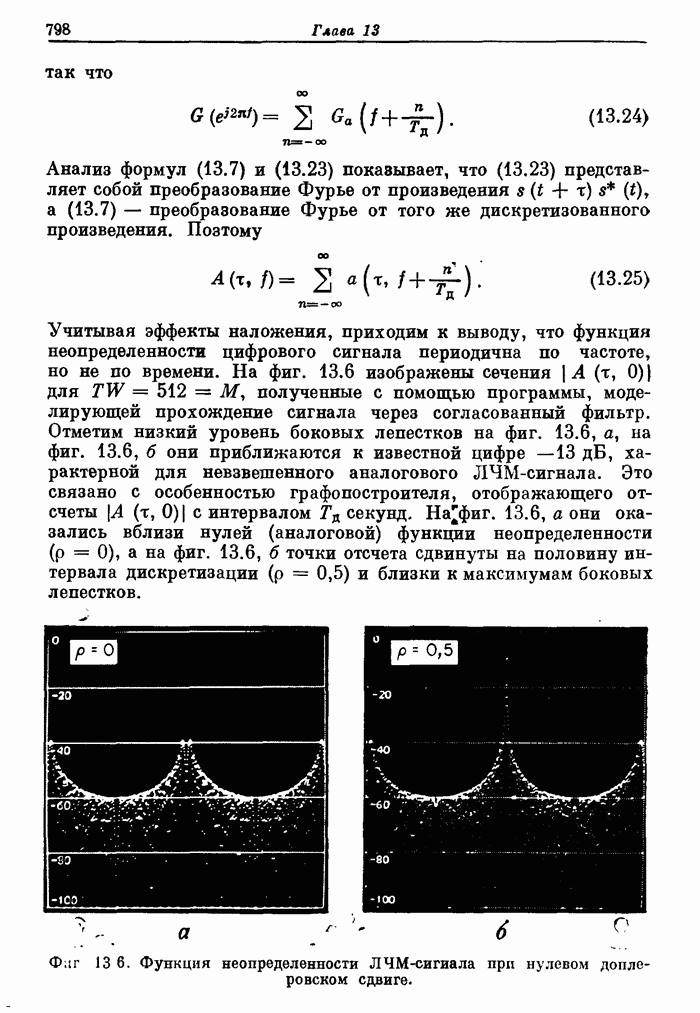
- 13.3. Выбор сигналов и функция неопределенности
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение