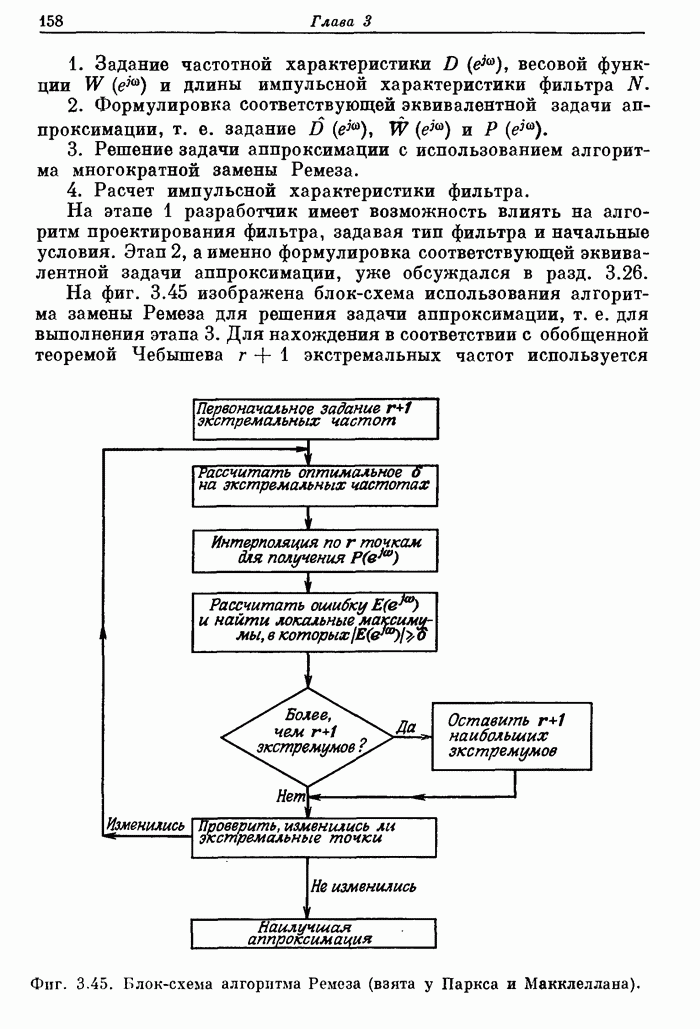
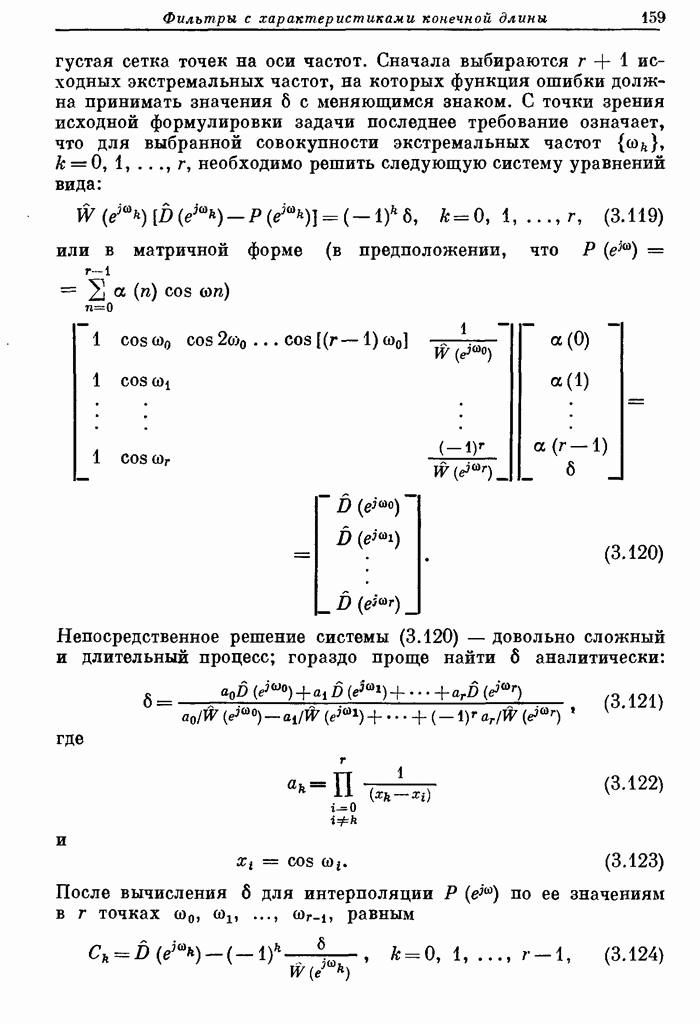
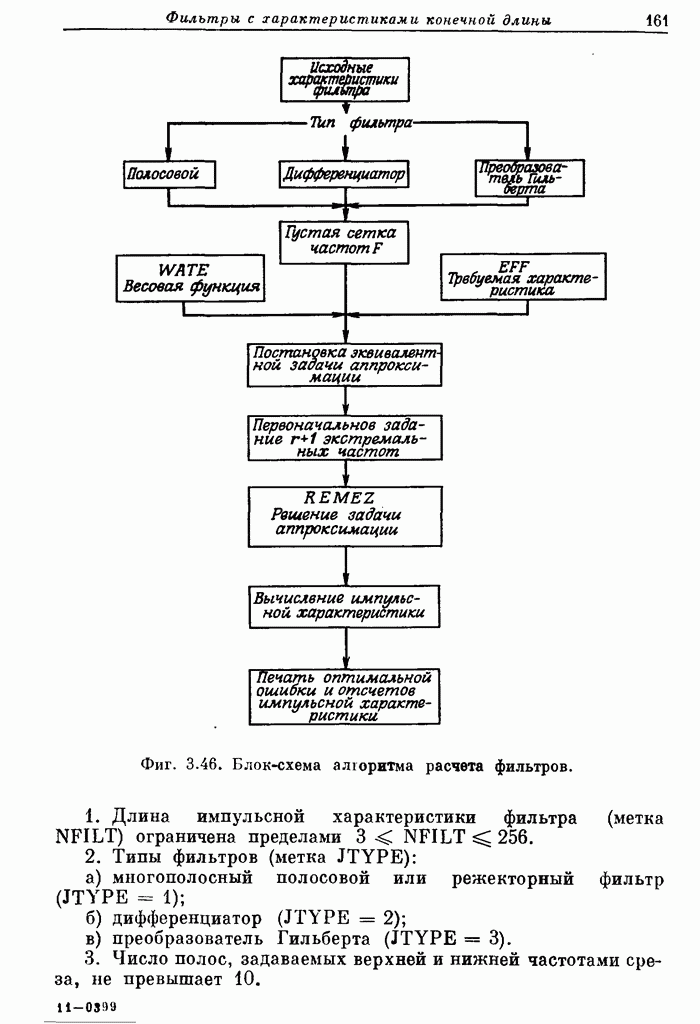
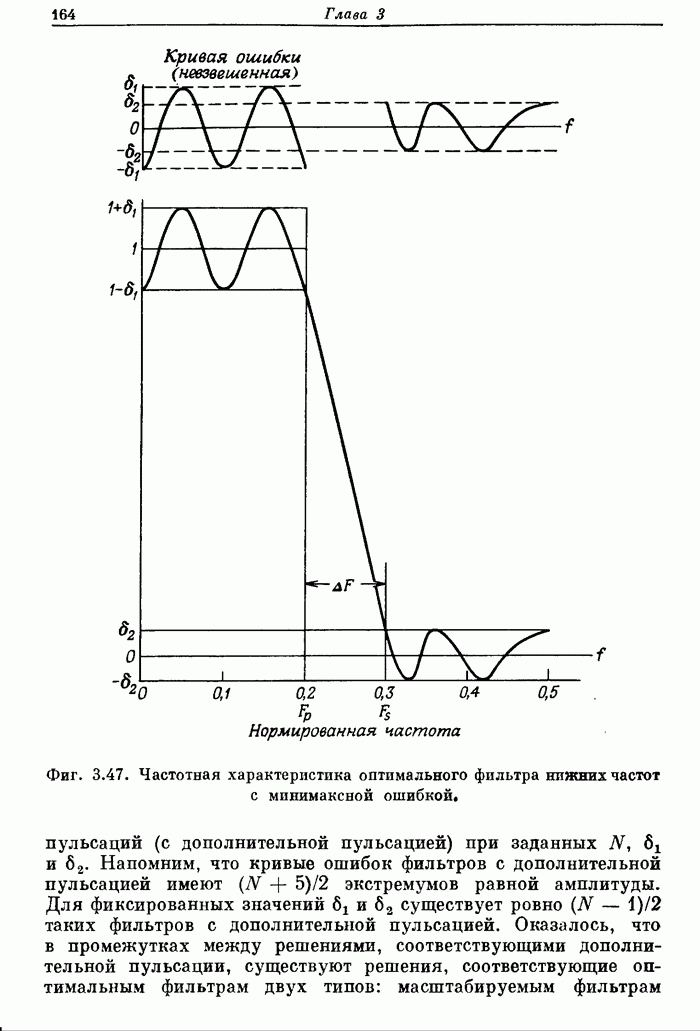
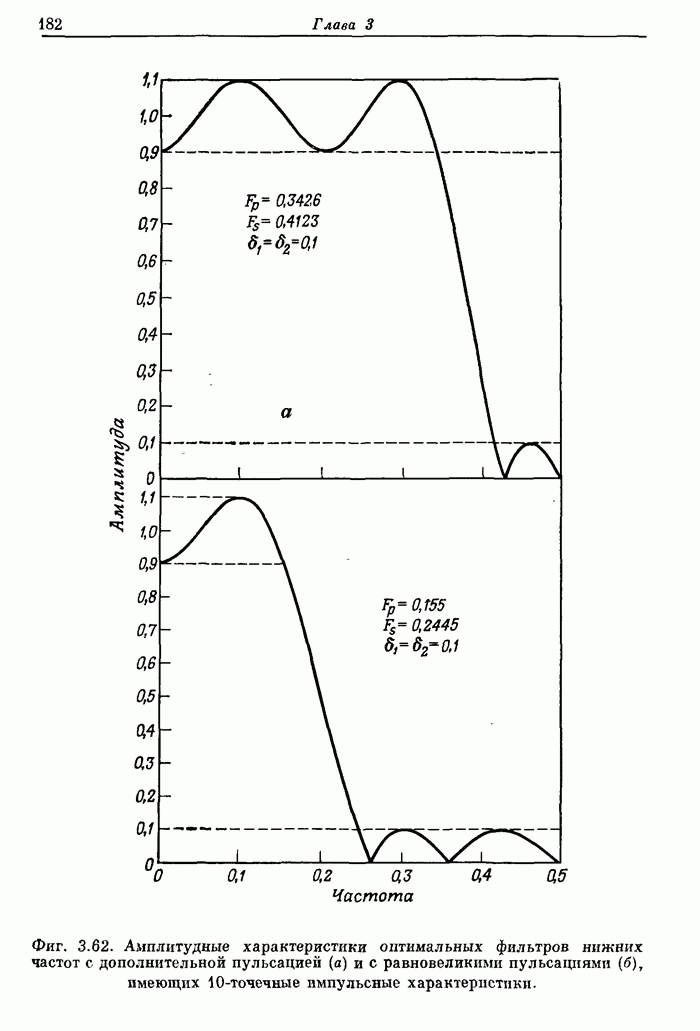
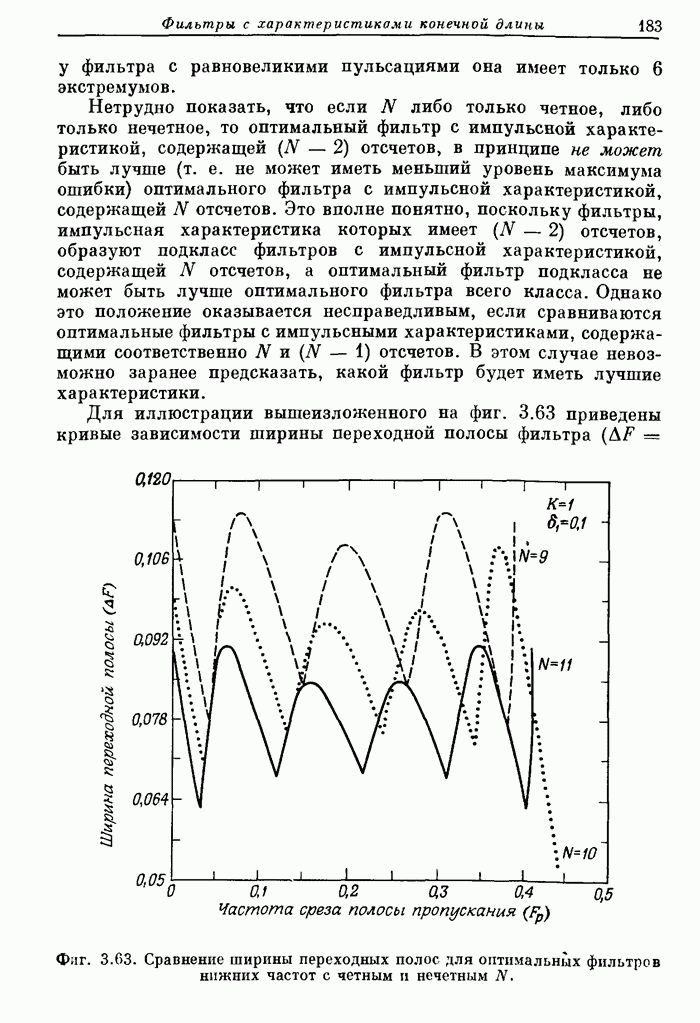
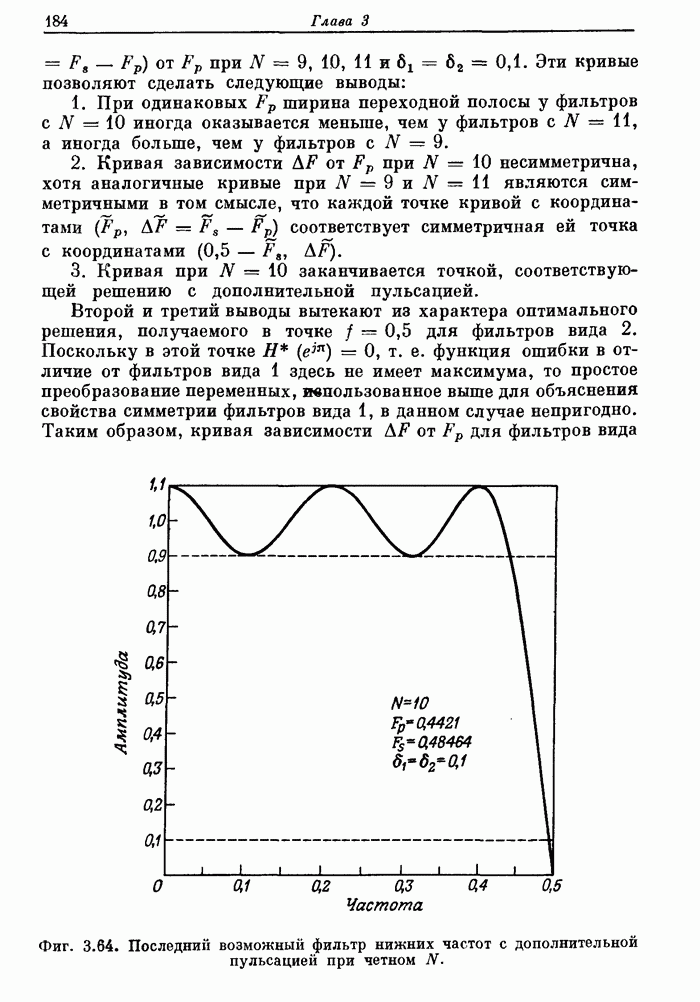
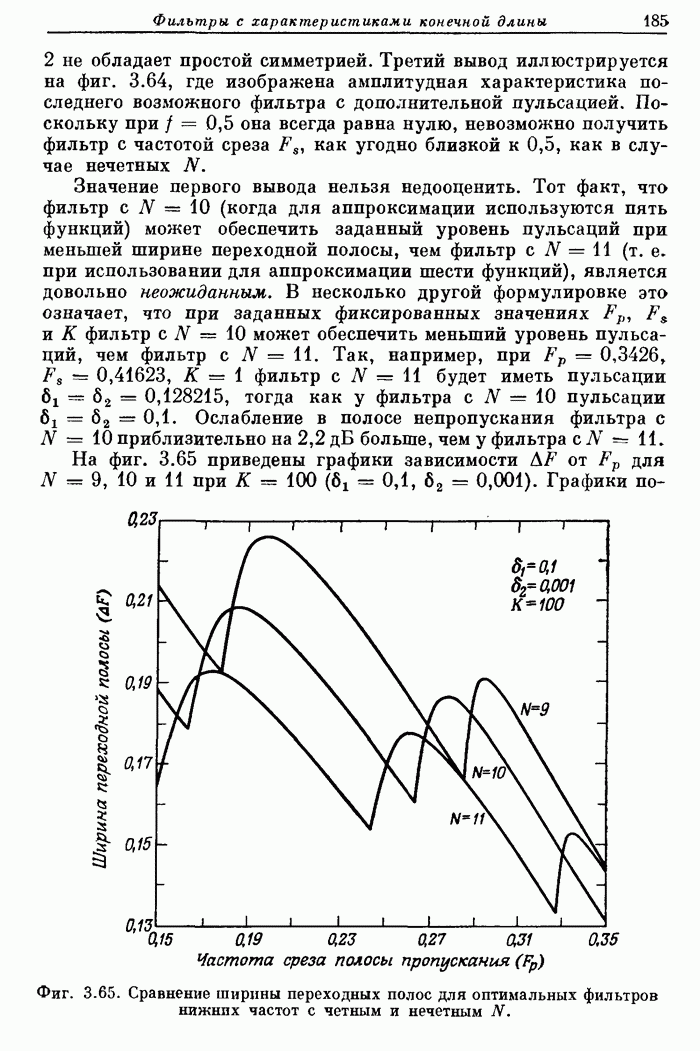
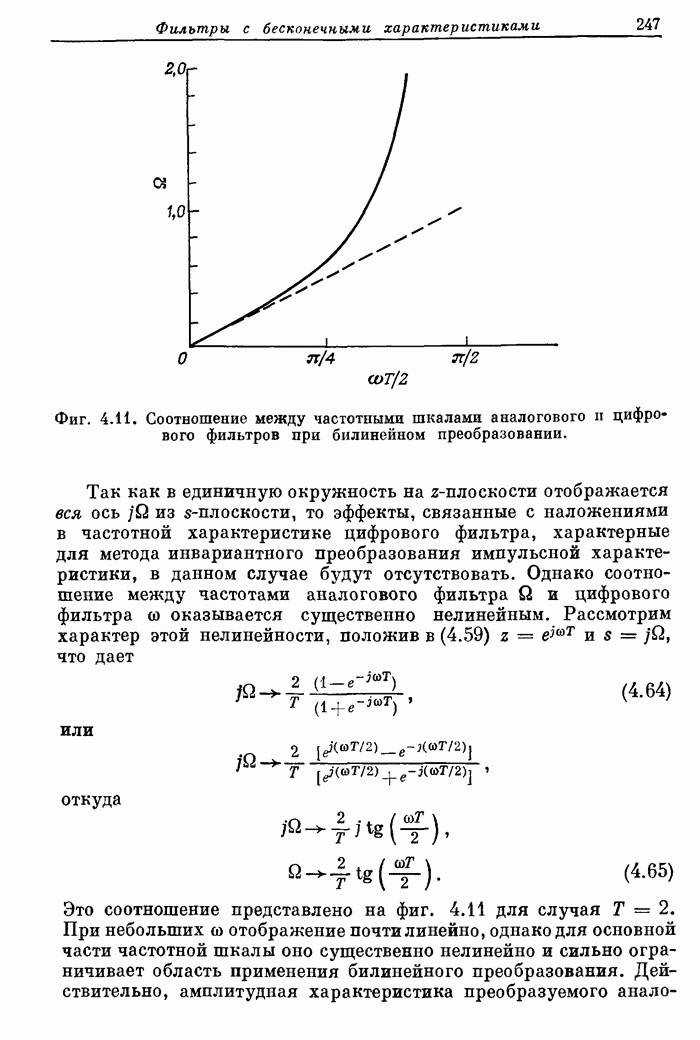
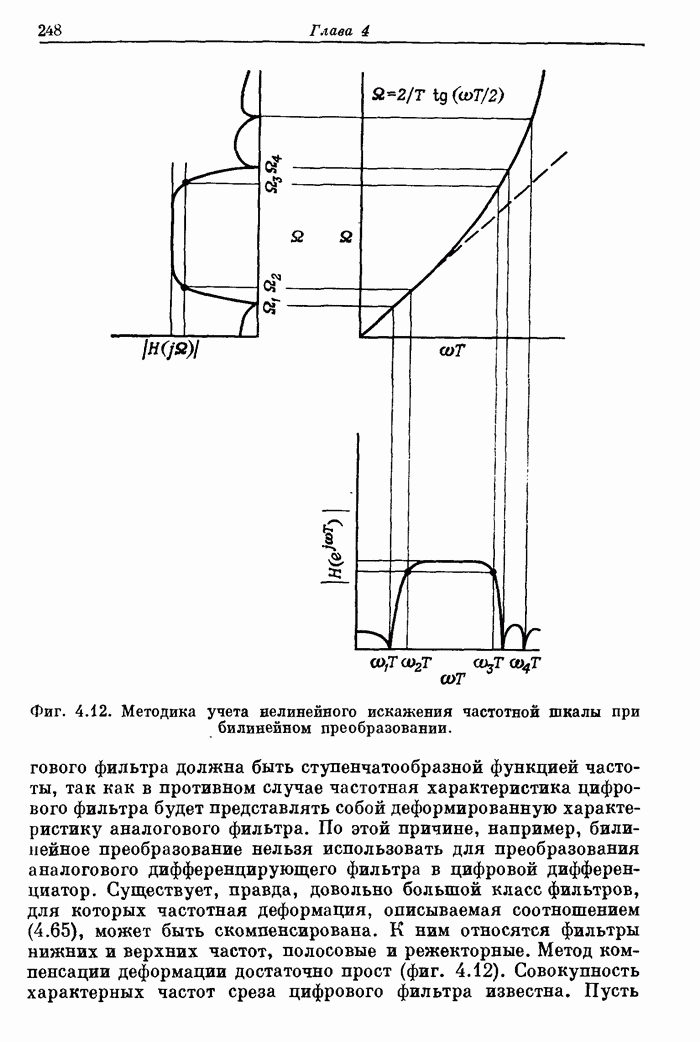
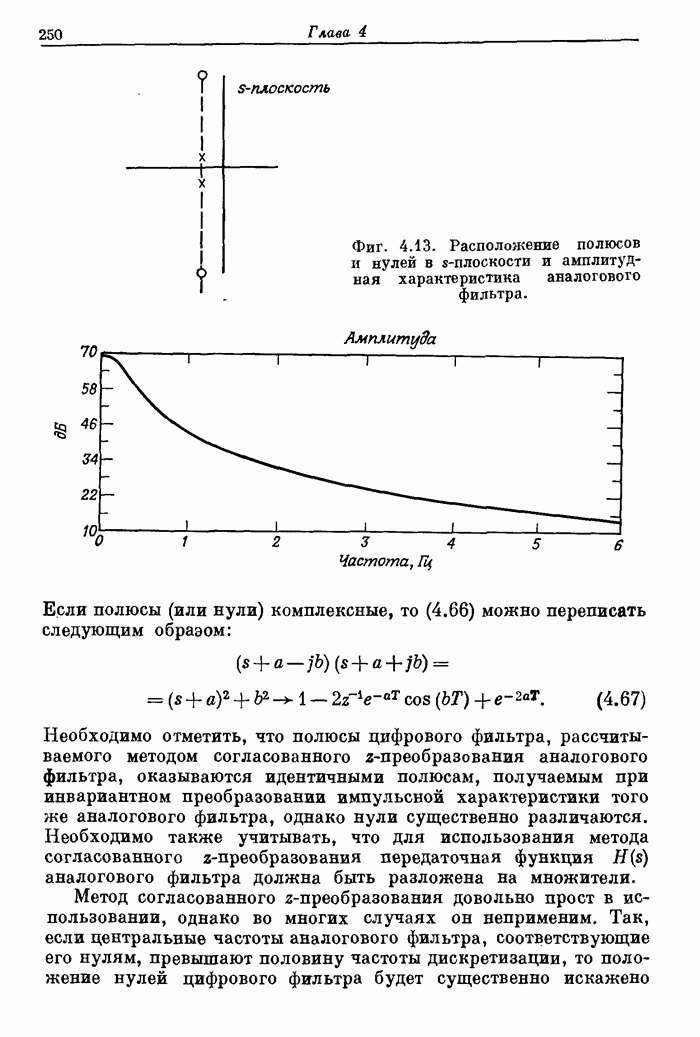
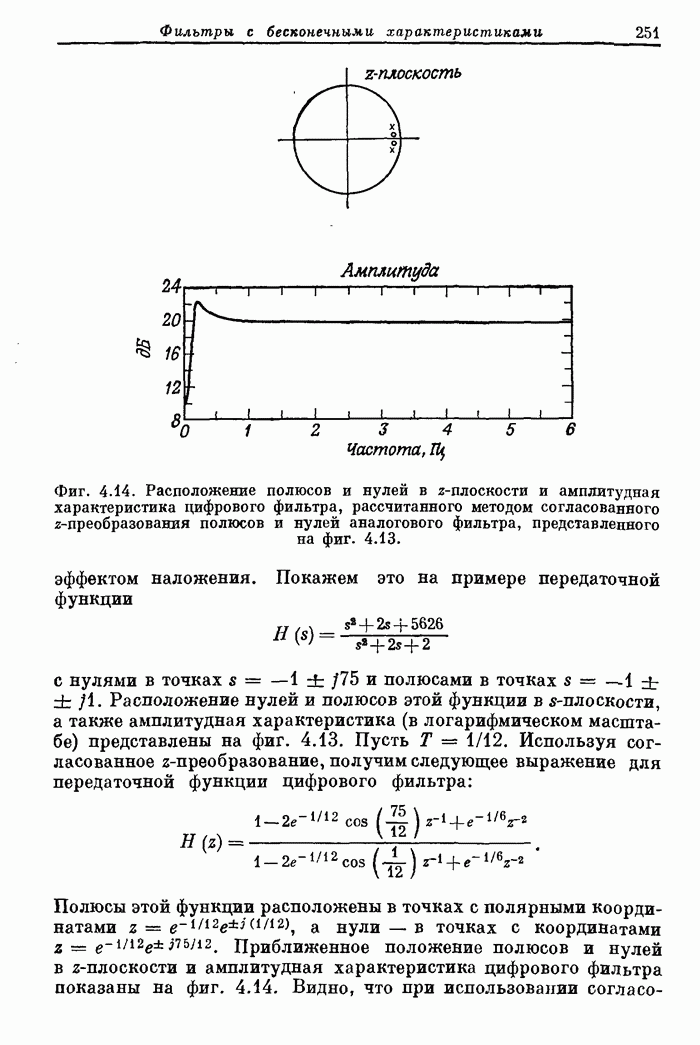
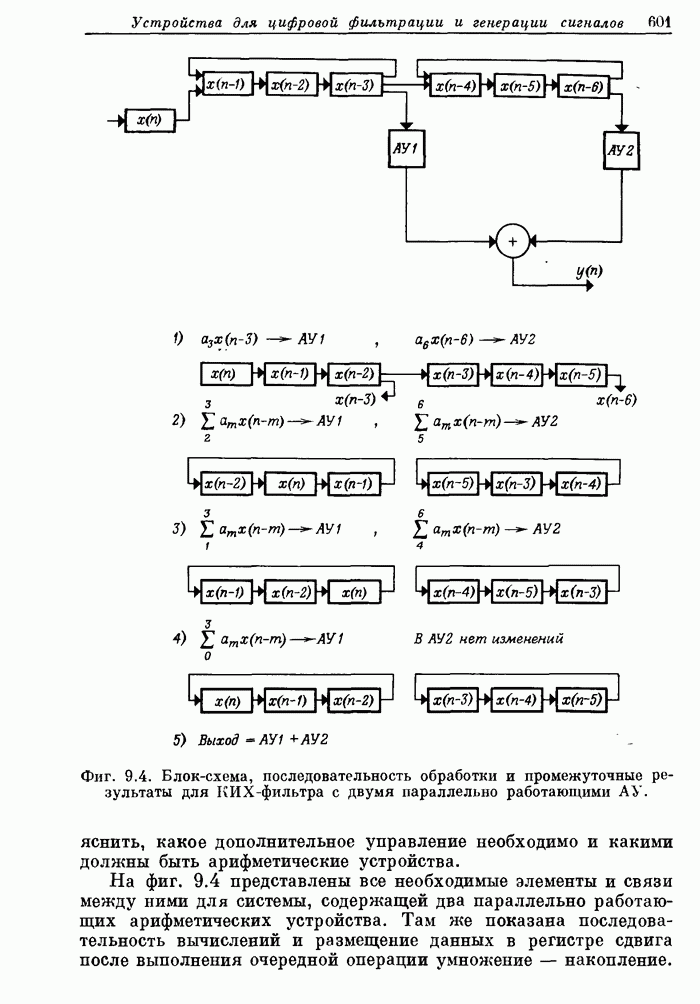
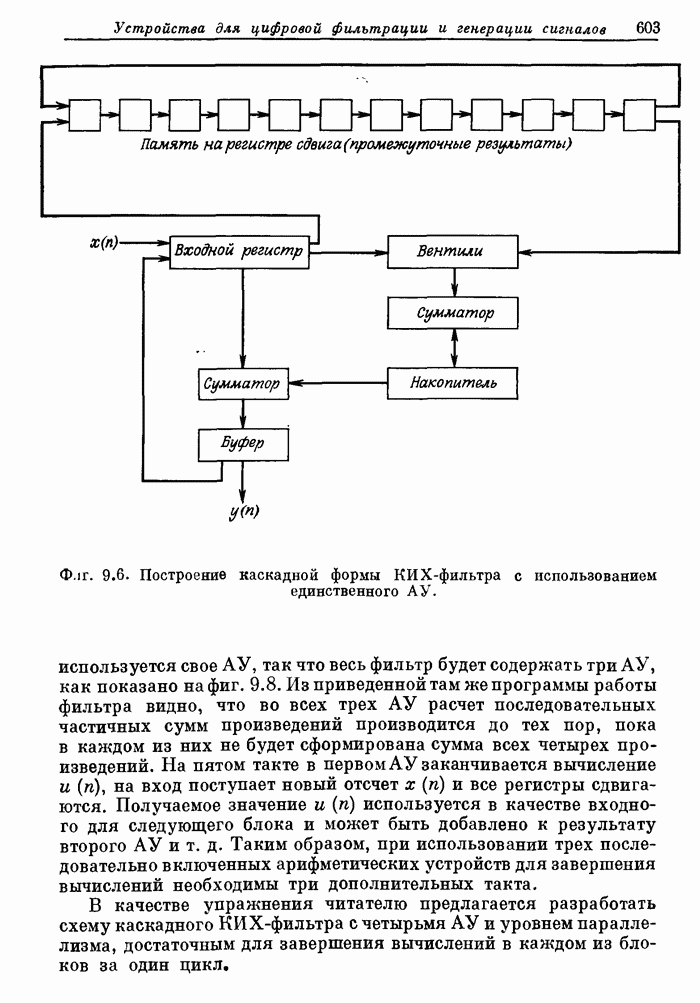
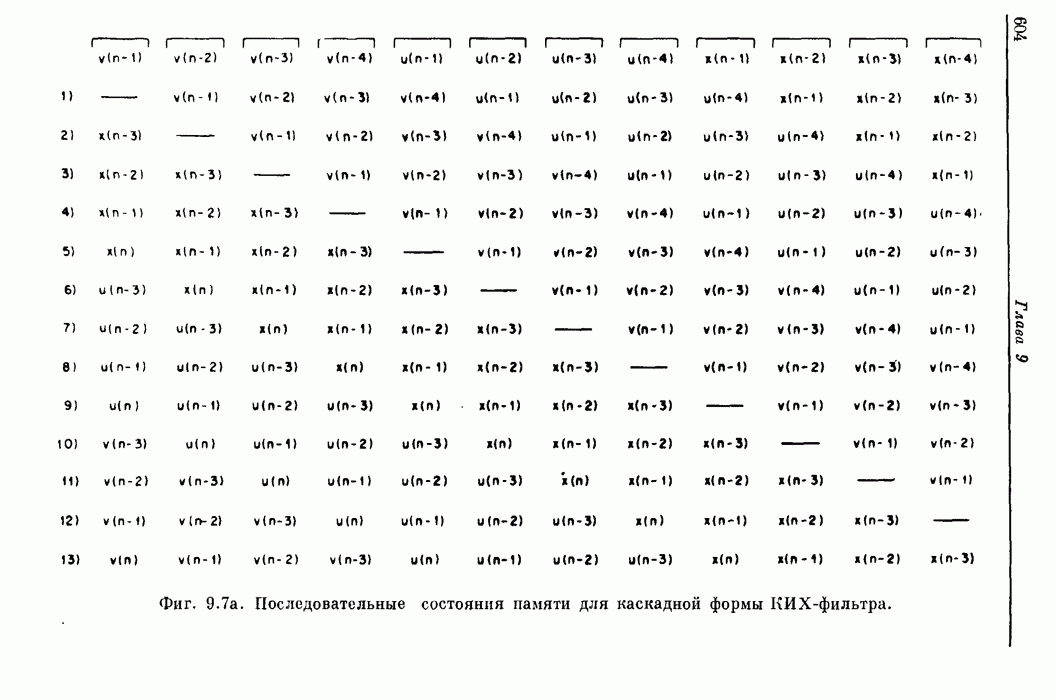
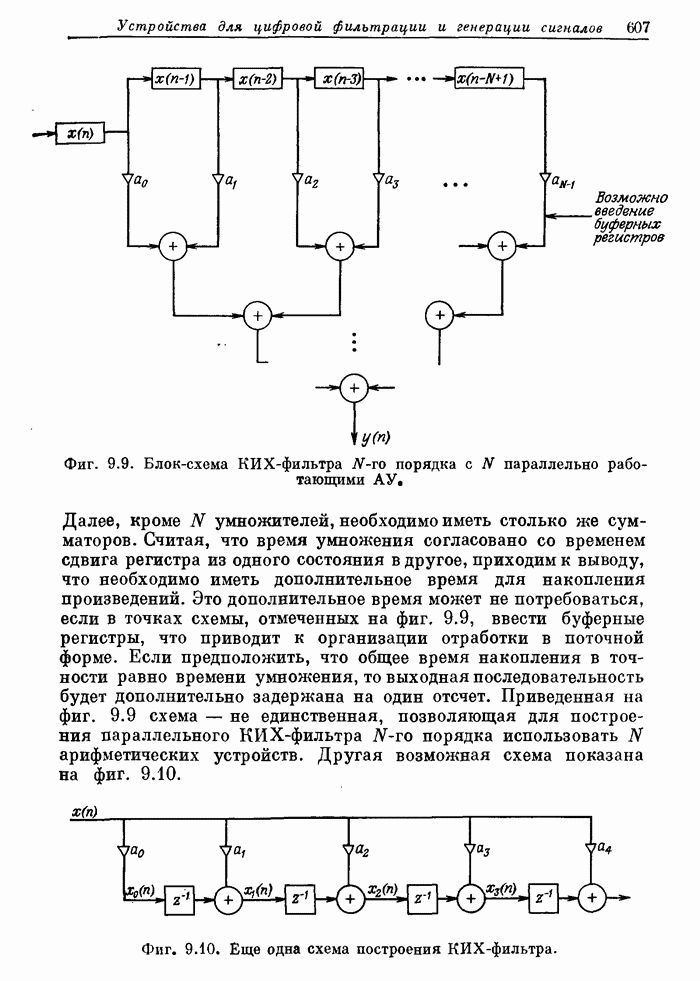
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
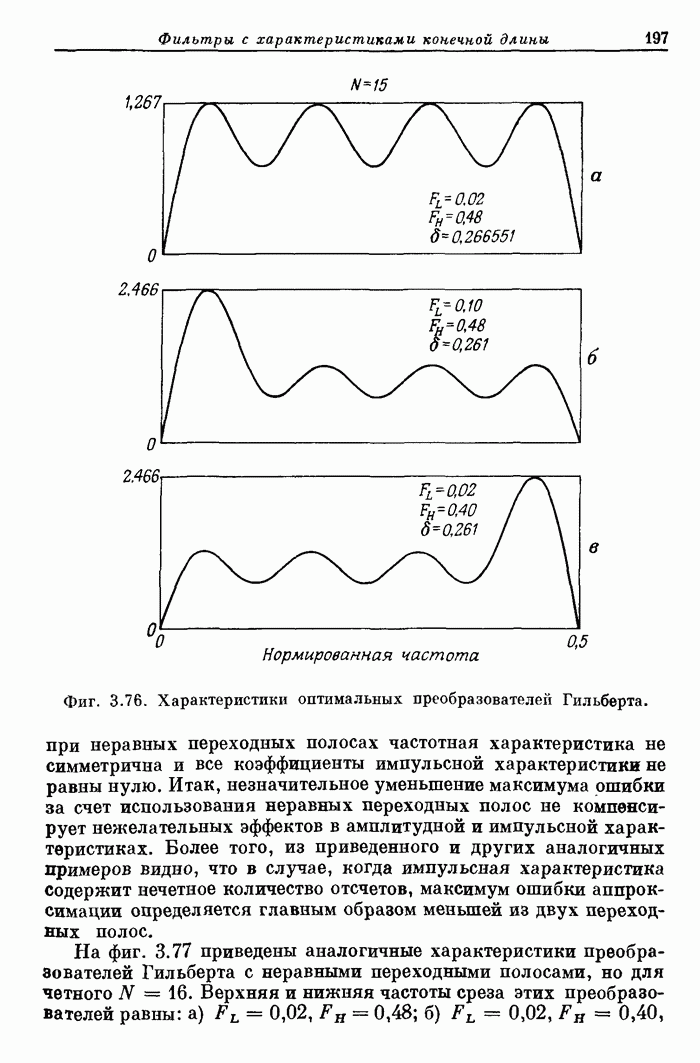
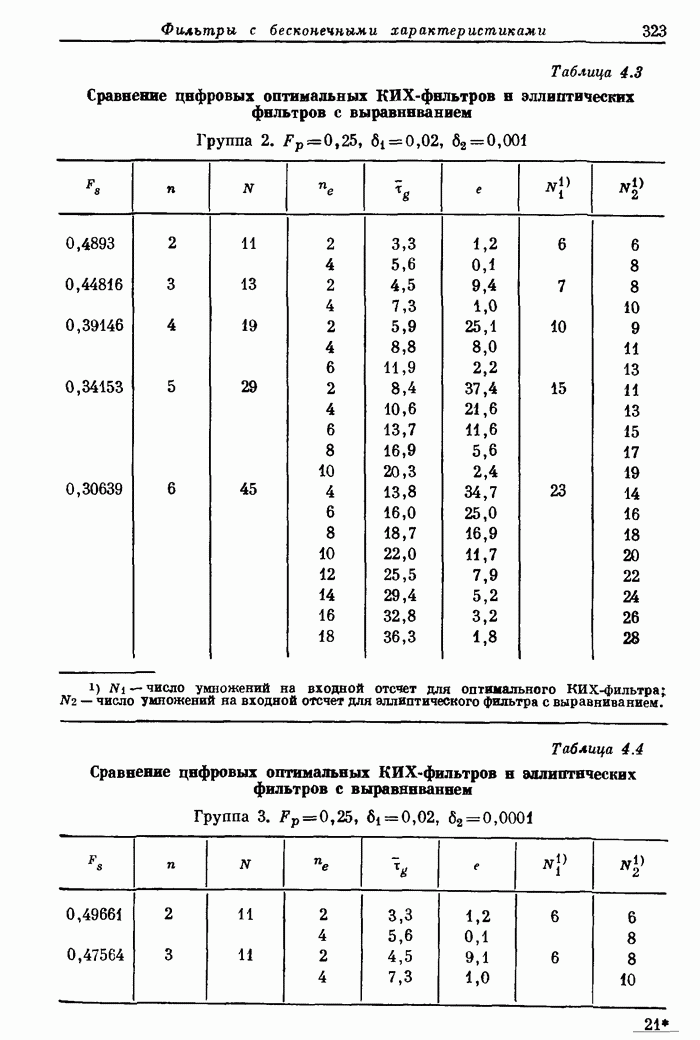
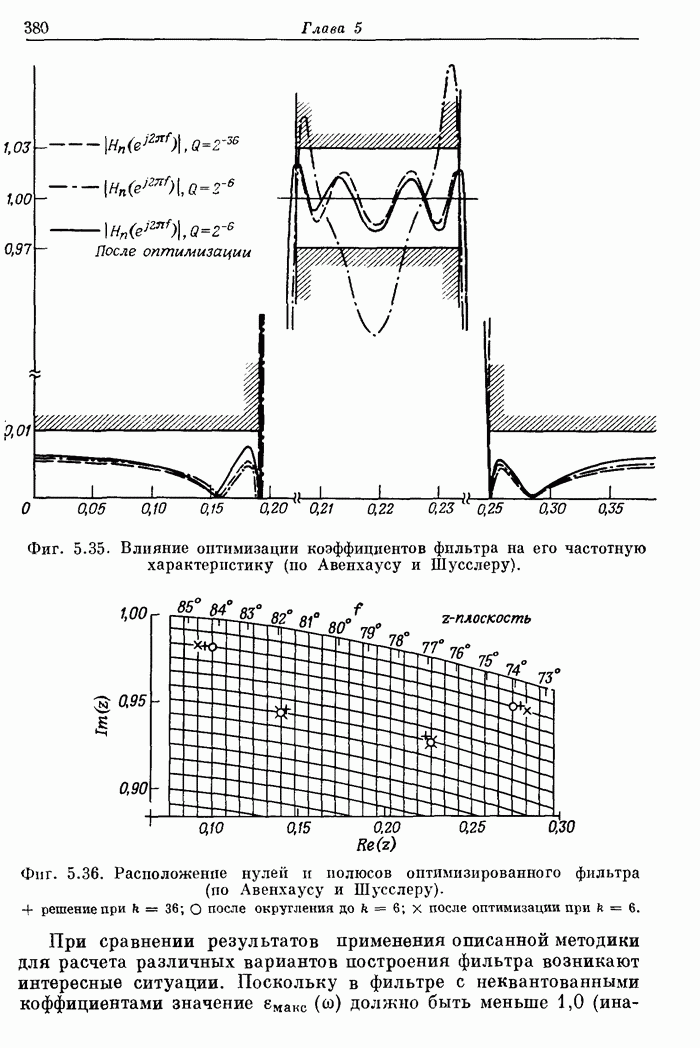
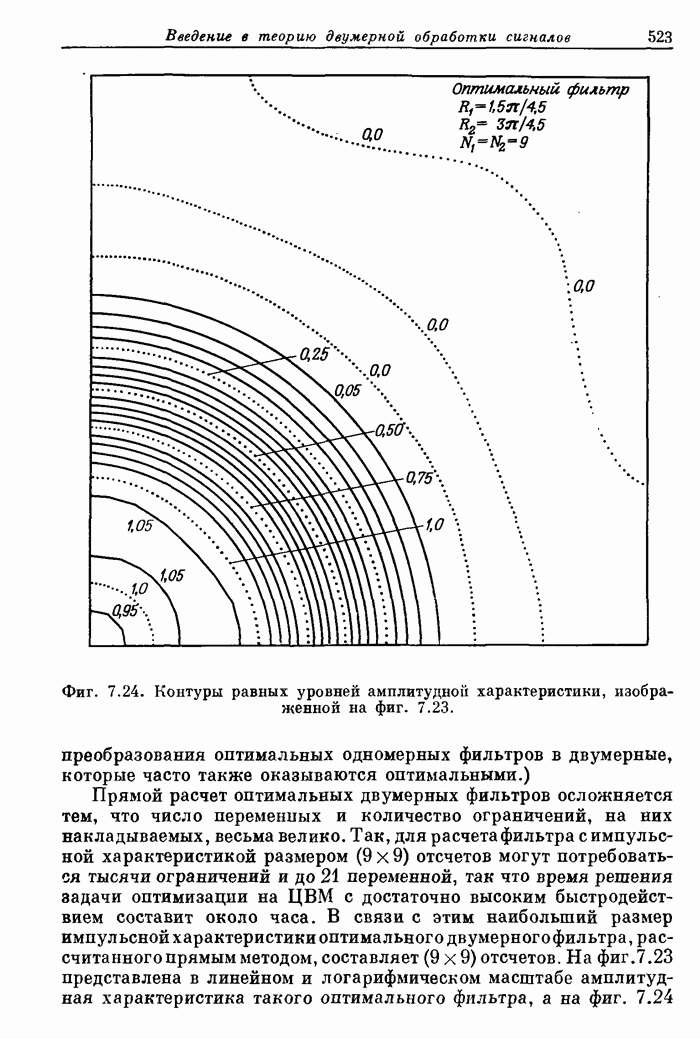
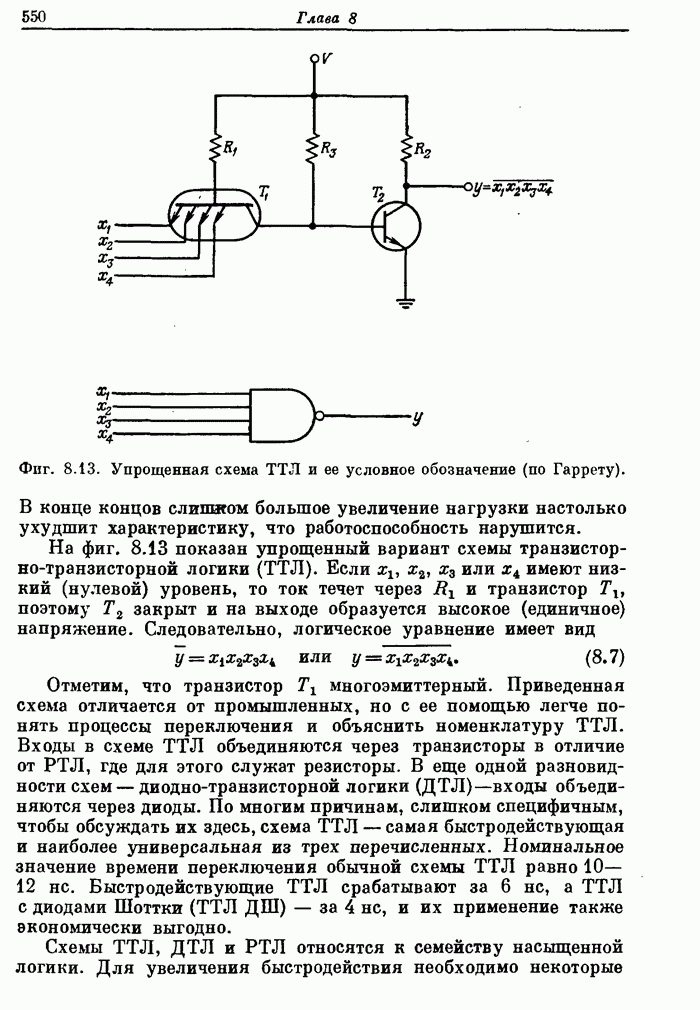
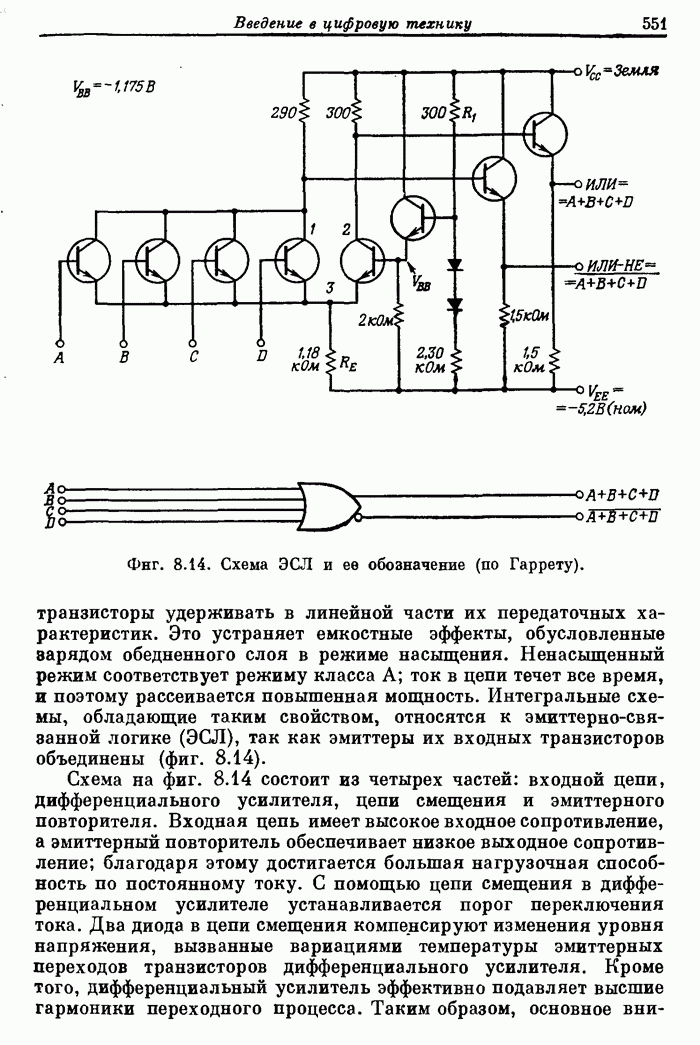
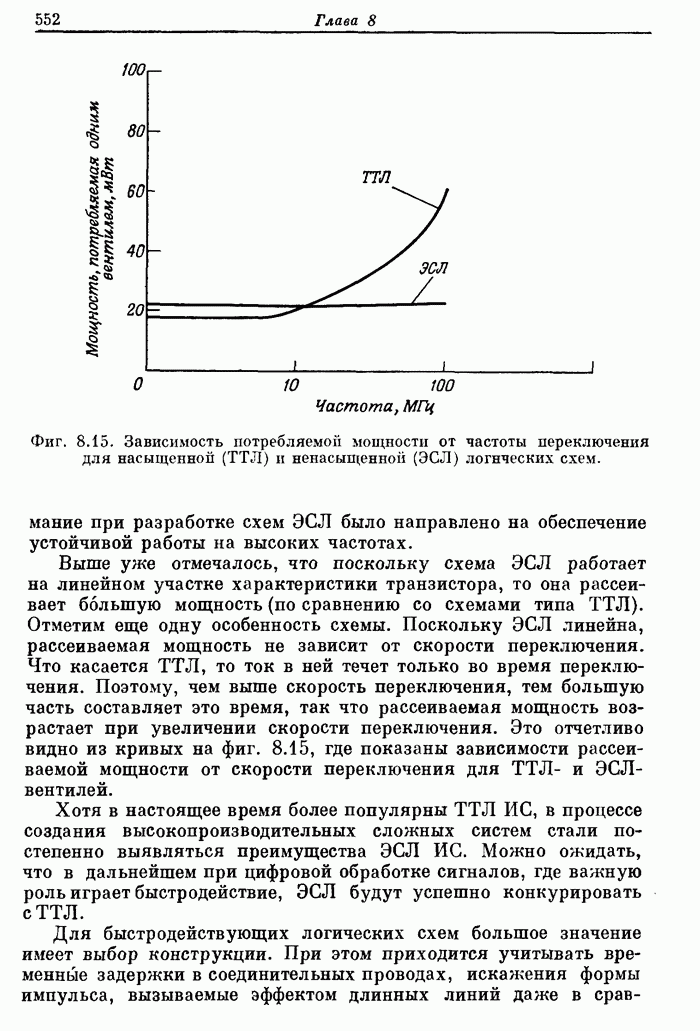
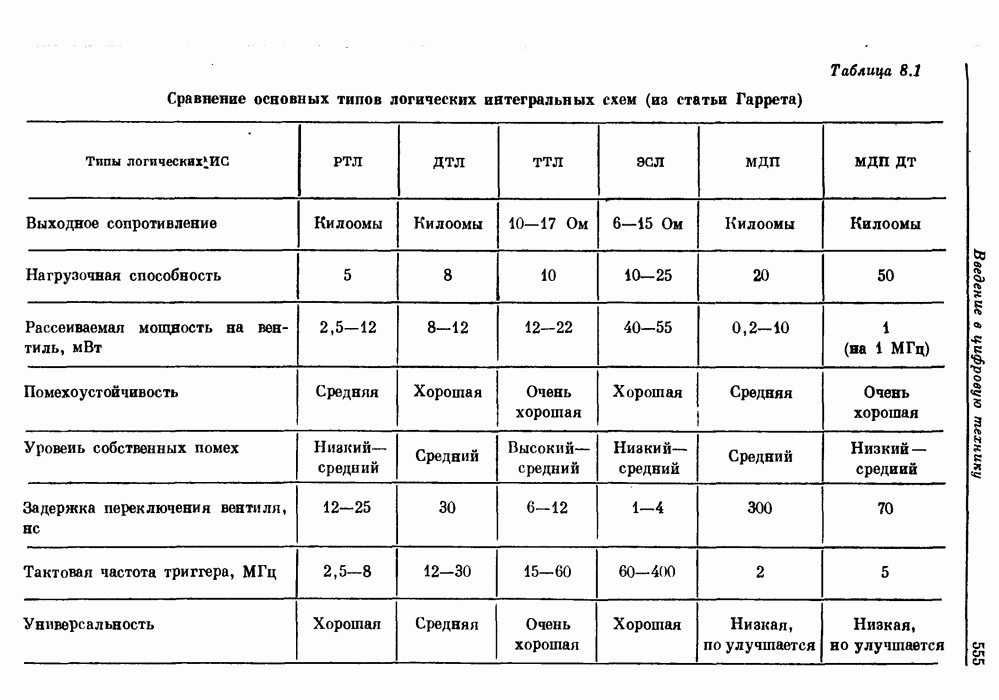
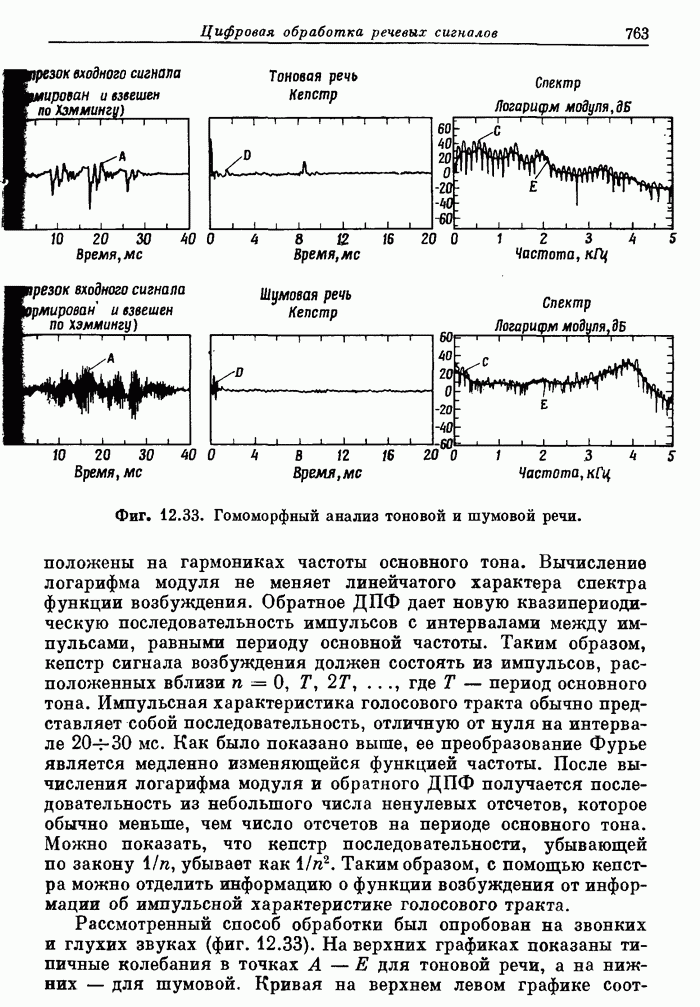
10.5. Эффекты квантования в алгоритмах БПФ
При
составлении программ (или при аппаратурной реализации БПФ) необходимо учитывать
эффекты, связанные с представлением обрабатываемых чисел и коэффициентов с
ограниченной точностью. К таким эффектам относятся шумы округления при усечении
результатов умножений, погрешности масштабирования промежуточных результатов с
целью устранения возможных переполнений, а также погрешности преобразования,
связанные с конечной точностью представления коэффициентов ![]() . Уэлч и ряд других авторов подробно проанализировали влияние
шума округления и масштабирования для алгоритмов БПФ по основанию 2 с
прореживанием по времени и по частоте при условии, что все арифметические
операции выполняются с фиксированной или плавающей запятой. Вопрос, связанный с
точностью представления коэффициентов, не рассматривался столь подробно,
поэтому ниже будут приведены лишь качественные результаты. Сначала будут
рассмотрены вопросы реализации алгоритмов БПФ с основанием 2 при выполнении
арифметических операций с фиксированной запятой.
. Уэлч и ряд других авторов подробно проанализировали влияние
шума округления и масштабирования для алгоритмов БПФ по основанию 2 с
прореживанием по времени и по частоте при условии, что все арифметические
операции выполняются с фиксированной или плавающей запятой. Вопрос, связанный с
точностью представления коэффициентов, не рассматривался столь подробно,
поэтому ниже будут приведены лишь качественные результаты. Сначала будут
рассмотрены вопросы реализации алгоритмов БПФ с основанием 2 при выполнении
арифметических операций с фиксированной запятой.
Если
последовательность ![]() из
из ![]() отсчетов имеет коэффициенты ДПФ
отсчетов имеет коэффициенты ДПФ ![]() , то, согласно
теореме Парсеваля,
, то, согласно
теореме Парсеваля,
![]() (10.3)
(10.3)
т.
е. средняя мощность выходных гармоник в ![]() раз превышает среднюю мощность
исходной последовательности. Следовательно, значения ДПФ последовательности
будут, вообще говоря, существенно превышать значения самой последовательности.
Поэтому при использовании арифметики с фиксированной запятой необходимо во
избежание переполнений ввести масштабирование. Чтобы показать, как могут
возникать переполнения, рассмотрим базовую операцию на
раз превышает среднюю мощность
исходной последовательности. Следовательно, значения ДПФ последовательности
будут, вообще говоря, существенно превышать значения самой последовательности.
Поэтому при использовании арифметики с фиксированной запятой необходимо во
избежание переполнений ввести масштабирование. Чтобы показать, как могут
возникать переполнения, рассмотрим базовую операцию на ![]() -м этапе БПФ с
прореживанием по времени. Пусть
-м этапе БПФ с
прореживанием по времени. Пусть ![]() и
и
![]() -
входные числа базовой операции, a,
-
входные числа базовой операции, a, ![]() и
и ![]() - выходные числа, причем
- выходные числа, причем ![]() -
поворачивающий
множитель. Тогда
-
поворачивающий
множитель. Тогда
 (10.4)
(10.4)
Из
формулы (10.4) видно, что при переходе от этапа к этапу модули чисел, вообще
говоря, увеличиваются, поэтому их нужно масштабировать сдвигом вправо. Нетрудно
показать, что от этапа к этапу максимальное значение модуля комплексных чисел
не убывает ![]() ,
как видно из соотношения (10.4), удовлетворяет неравенству.
,
как видно из соотношения (10.4), удовлетворяет неравенству.
![]() (10.5)
(10.5)
Следовательно, уровень сигнала на каждом этапе увеличивается не быстрее, чем на один двоичный разряд.
Учитывая вышеизложенное, можно предложить три метода масштабирования:
1.
Сдвиг вправо на один разряд на каждом этапе. Если ![]() для любых
для любых ![]() и числа сдвигаются
на разряд вправо после каждого этапа итерации (кроме последнего), то
переполнения не произойдет.
и числа сдвигаются
на разряд вправо после каждого этапа итерации (кроме последнего), то
переполнения не произойдет.
2.
Контроль последовательности, гарантирующий выполнение условия ![]() для всех
для всех ![]() . На
каждом этапе БПФ вычисляется массив
. На
каждом этапе БПФ вычисляется массив ![]() и если хотя бы один отсчет массива
превысит по модулю 1/2, весь массив масштабируется сдвигом вправо на разряд.
и если хотя бы один отсчет массива
превысит по модулю 1/2, весь массив масштабируется сдвигом вправо на разряд.
3.
Проверка на переполнение. При этом исходная последовательность масштабируется
так, чтобы ![]() и
и
![]() были
меньше единицы (а не
были
меньше единицы (а не ![]() , как в двух предыдущих методах). Если
в ходе базовой операции фиксируется переполнение, то все числа последовательности,
включая результаты уже выполненных на данном этапе (без переполнения) базовых
операций, сдвигаются на разряд вправо, после чего итерация продолжается с той
базовой операции, где произошло переполнение. На каждом этапе может произойти
более чем одно переполнение, но не больше двух.
, как в двух предыдущих методах). Если
в ходе базовой операции фиксируется переполнение, то все числа последовательности,
включая результаты уже выполненных на данном этапе (без переполнения) базовых
операций, сдвигаются на разряд вправо, после чего итерация продолжается с той
базовой операции, где произошло переполнение. На каждом этапе может произойти
более чем одно переполнение, но не больше двух.
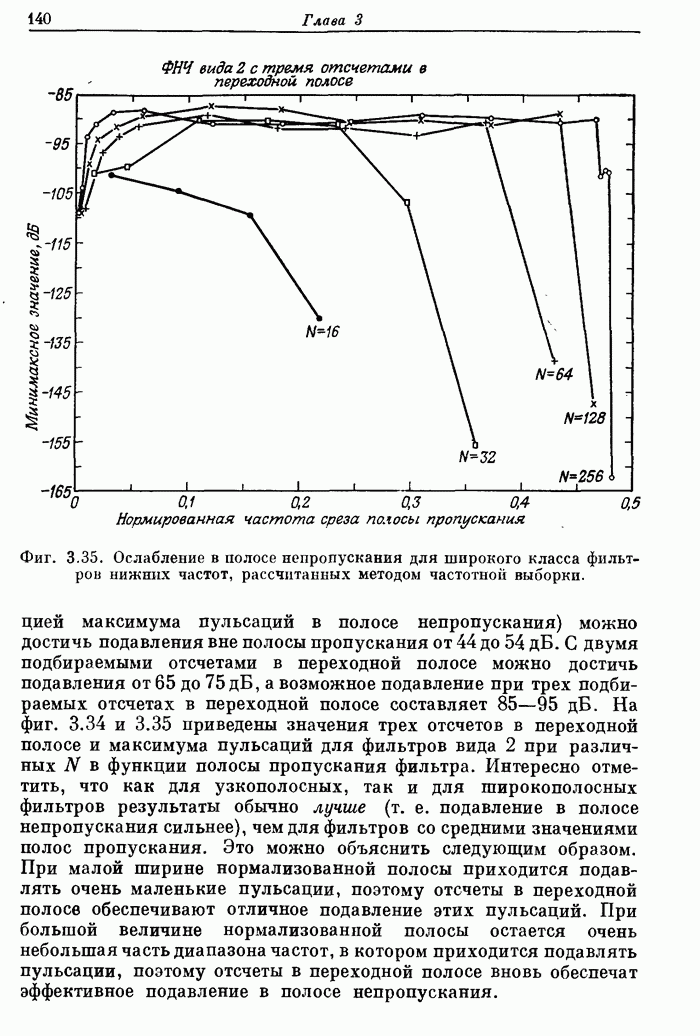
Первый метод связан с наименьшими затратами времени и наиболее прост для программирования. Однако он дает наименьшую точность, так как масштабирование на каждом этапе приводит к ненужному ухудшению точности в случаях, когда его можно было не производить. Второй метод требует больших затрат времени (поскольку на каждом этапе приходится вычислять модули всех чисел массива), и в то же время он не слишком точный, так как весь массив всегда масштабируется таким образом, чтобы модули всех его элементов не превышали 1/2, поэтому один разряд памяти данных не используется. Третий метод является самым точным, но здесь приходится повторно обрабатывать всю последовательность всякий раз, когда обнаруживается переполнение.
Уэлч разработал довольно простую методику расчета граничных значений уровня шума округления, возникающего при БПФ. Наличие шума округления обусловлено двумя факторами:
1.
Появлением погрешности при округлении произведения ![]() в формулах (10.4). Если
в формулах (10.4). Если ![]() и
и ![]() представлены
представлены ![]() -разрядными числами
(т. е. действительная и мнимая части
-разрядными числами
(т. е. действительная и мнимая части ![]() и
и ![]() содержат по
содержат по ![]() разрядов),
то после округления каждого из четырех действительных произведений, входящих в
разрядов),
то после округления каждого из четырех действительных произведений, входящих в ![]() , до
, до ![]() -разрядного числа
получается ошибка, равномерно распределенная на интервале
-разрядного числа
получается ошибка, равномерно распределенная на интервале ![]() и имеющая нулевое среднее и
дисперсию, равную
и имеющая нулевое среднее и
дисперсию, равную ![]() .
.
2.
Сдвигом Суммы на один разряд вправо, если при сложении происходит переполнение.
Если младший разряд, при сдвиге выходящий за пределы регистра, равен нулю, то
ошибки не будет. Если же он равен единице, то в зависимости от знака числа
возникает ошибка величиной ![]() . Дисперсия этой ошибки равна
. Дисперсия этой ошибки равна ![]() .
.
Верхнюю
границу отношения среднеквадратического значения шума округления к среднеквадратическому
значению выходных гармоник можно получить, предположив, что переполнение происходит
на каждом этапе, так что числа каждый раз приходится масштабировать. Если ![]() - отсчеты,
получаемые на
- отсчеты,
получаемые на ![]() -м
этапе, то
-м
этапе, то ![]() - их дисперсия,
определяемая как
- их дисперсия,
определяемая как
 , (10.6)
, (10.6)
причем
![]() .
(10.7)
.
(10.7)
где
![]() , так что
, так что
![]() .
Равенство (10.7) получается в предположении, что на первом же этапе может произойти
переполнение, поэтому в числах нулевого этапа (т. е. в исходных отсчетах)
один младший разряд отбрасывается. На первом этапе базовая операция содержит
умножения только на
.
Равенство (10.7) получается в предположении, что на первом же этапе может произойти
переполнение, поэтому в числах нулевого этапа (т. е. в исходных отсчетах)
один младший разряд отбрасывается. На первом этапе базовая операция содержит
умножения только на ![]() , поэтому шум округления произведений
отсутствует.
, поэтому шум округления произведений
отсутствует.
На
втором этапе, согласно предположению, также может произойти переполнение,
поэтому массив ![]() нужно предварительно промасштабировать.
Следовательно, дисперсия
нужно предварительно промасштабировать.
Следовательно, дисперсия ![]() будет равна
будет равна
![]() , (10.8)
, (10.8)
причем множитель 4 отражает тот факт, что ошибка при усечении выходных чисел на первом этапе будет вдвое больше ошибки, обусловленной усечением выходных чисел на нулевом этапе, поэтому дисперсия возрастает в четыре раза.
На втором этапе
алгоритма БПФ с прореживанием по времени выполняются умножения только на ![]() и
и ![]() поэтому ошибка,
связанная с округлением произведений, опять будет равна нулю. Итак, в
предположении, что числа
поэтому ошибка,
связанная с округлением произведений, опять будет равна нулю. Итак, в
предположении, что числа ![]() также масштабируются, получим
следующую формулу для дисперсии ошибки на втором этапе БПФ:
также масштабируются, получим
следующую формулу для дисперсии ошибки на втором этапе БПФ:
![]() (10.9)
(10.9)
причем множитель 42 указывает на удвоение ошибки усечения при переходе от первого этапа ко второму.
На
всех последующих этапах в большинстве базовых операций выполняются нетривиальные
умножения. Так, на третьем этапе половина базовых операций содержит такие
умножения, на четвертом этапе — три четверти и т. д. Согласно формулам (10.4),
общее выражение для действительной части результата базовой операции,
выполняемой на ![]() - м этапе, имеет
вид
- м этапе, имеет
вид
![]() (10.10)
(10.10)
Аналогичное
выражение можно записать и для мнимой части. Для тех базовых операций, где
умножение на ![]() не
является тривиальным, дисперсия результата
не
является тривиальным, дисперсия результата ![]() (включая шум округления всех
произведений и шум усечения при масштабировании) имеет вид
(включая шум округления всех
произведений и шум усечения при масштабировании) имеет вид
 (10.11)
(10.11)
где
слагаемое ![]() учитывает
дисперсию шума округления на
учитывает
дисперсию шума округления на ![]() -м
этапе, а член
-м
этапе, а член![]() -
дисперсию шума, связанную с масштабированием на этом же этапе. Как уже
отмечалось, оба эти члены равны
-
дисперсию шума, связанную с масштабированием на этом же этапе. Как уже
отмечалось, оба эти члены равны
 (10.12)
(10.12)
Третье
слагаемое суммы (10.11) содержит произведение квадрата модуля ![]() и
и ![]() . Поскольку
. Поскольку ![]() , это слагаемое
совпадает с первым членом суммы. Второе слагаемое равно произведению
, это слагаемое
совпадает с первым членом суммы. Второе слагаемое равно произведению ![]() на среднее
значение квадрата модуля переменных, преобразуемых на
на среднее
значение квадрата модуля переменных, преобразуемых на ![]() -м этапе. Дисперсия
-м этапе. Дисперсия ![]() равна
равна ![]() (поскольку
(поскольку
![]() представляется
представляется
![]() -разрядным
числом с погрешностью). Чтобы определить средний квадрат модуля переменных,
обрабатываемых на
-разрядным
числом с погрешностью). Чтобы определить средний квадрат модуля переменных,
обрабатываемых на ![]() -м
этапе, нужно знать величину
-м
этапе, нужно знать величину ![]() ,
представляющую собой средний квадрат модуля исходного массива чисел, равный
,
представляющую собой средний квадрат модуля исходного массива чисел, равный
 (10.13)
(10.13)
Учитывая,
что среднее значение квадрата модуля увеличивается от этапа к этапу вдвое,
получим, что на выходе ![]() -го этапа оно будет равно
-го этапа оно будет равно ![]() . Тогда дисперсия
. Тогда дисперсия ![]() становится равной
становится равной
![]() (10.14)
(10.14)
если
во всех базовых операциях ![]() -го этапа
выполняются нетривиальные умножения. Бели же ввести
-го этапа
выполняются нетривиальные умножения. Бели же ввести ![]() — долю базовых операций с
нетривиальными умножениями
— долю базовых операций с
нетривиальными умножениями ![]() , — то второе и третье слагаемые суммы
(10.14) следует умножить на
, — то второе и третье слагаемые суммы
(10.14) следует умножить на ![]() . Так, если
. Так, если ![]() (как это имеет
место на первом и втором этапах), то равенство (10.14) переходит в (10.8) (при
(как это имеет
место на первом и втором этапах), то равенство (10.14) переходит в (10.8) (при ![]() ) или в (10.9) (при
) или в (10.9) (при ![]() ). Бели принять,
что
). Бели принять,
что ![]() на
третьем этапе и
на
третьем этапе и ![]() на
всех последующих этапах, причем номер последнего этапа равен
на
всех последующих этапах, причем номер последнего этапа равен ![]() , то, согласно
формулам (10.7)-(10.14), получим
, то, согласно
формулам (10.7)-(10.14), получим
 (10.15)
(10.15)
Поскольку
среднее значение квадратов модулей элементов выходного массива ![]() равно
равно ![]() , то средний квадрат их
действительных (или мнимых) частей равен
, то средний квадрат их
действительных (или мнимых) частей равен ![]() .
Таким образом, оценкой отношения среднеквадратических значений (СКЗ) шума и
сигнала на выходе (в пределе при больших
.
Таким образом, оценкой отношения среднеквадратических значений (СКЗ) шума и
сигнала на выходе (в пределе при больших ![]() )
является величина
)
является величина
 (10.16)
(10.16)
Итак,
верхняя граница отношения ошибки к выходному сигналу возрастает как![]() , т. е. по
, т. е. по ![]() разряда
на этап.
разряда
на этап.
Формулу,
аналогичную (10.16), можно получить и для нижней границы отношения ошибки к
сигналу, если предположить, что переполнений вообще не происходит, так что
ошибки усечения, связанные с масштабированием, отсутствуют. Следовательно,
вплоть до третьего этапа ошибка вообще не возникает. Проведя аналогичный анализу
получим следующую формулу для дисперсии выходных отсчетов ![]() :
:
 (10.17)
(10.17)
Таким
образом, при большом числе этапов ![]() нижняя граница отношения среднеквадратических
значений ошибки и сигнала на выходе имеет вид
нижняя граница отношения среднеквадратических
значений ошибки и сигнала на выходе имеет вид
![]() (10.18)
(10.18)
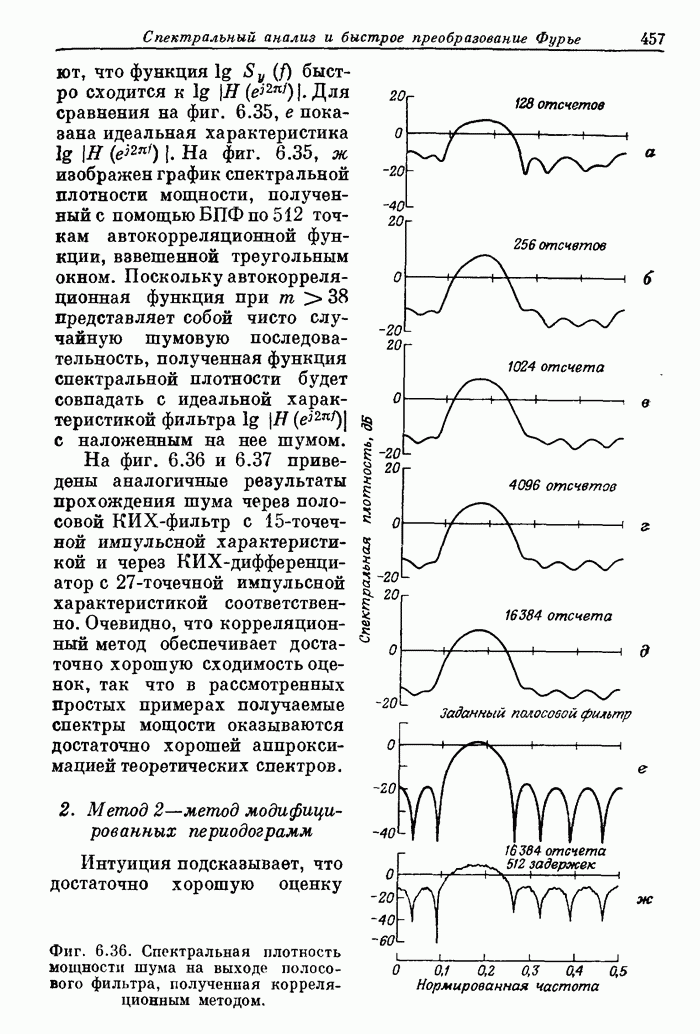
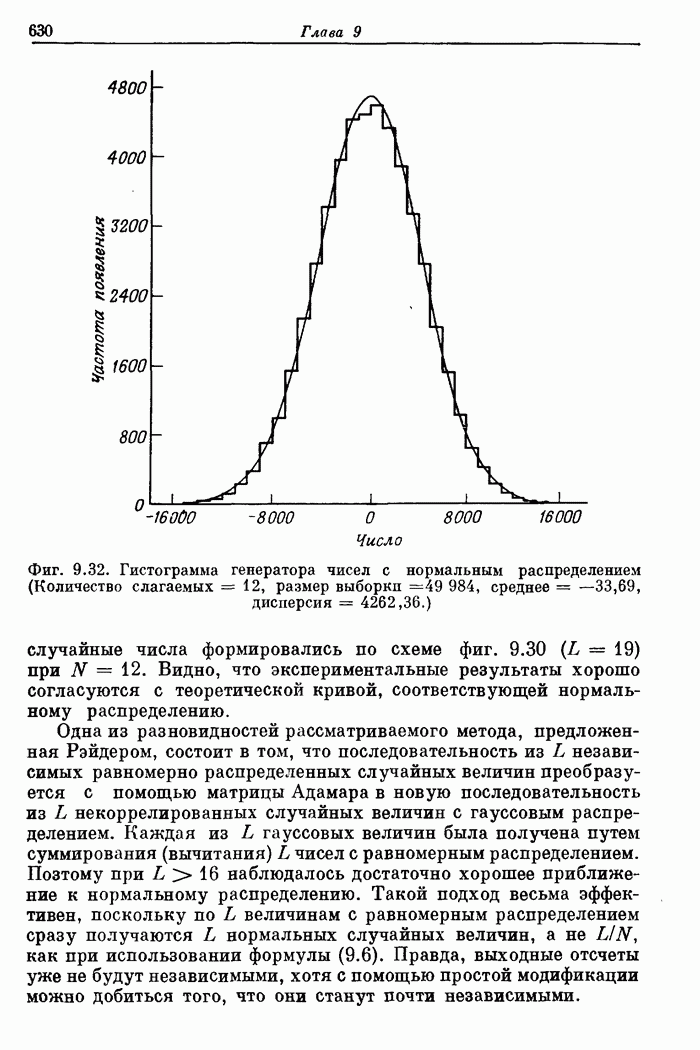
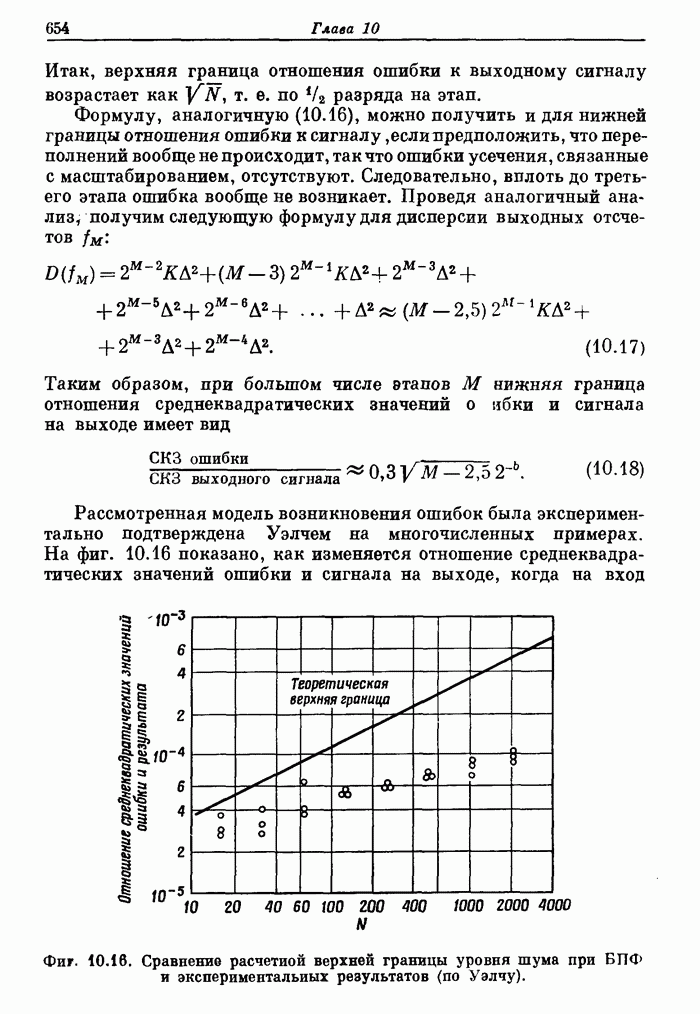
Рассмотренная
модель возникновения ошибок была экспериментально подтверждена Уэлчем на
многочисленных примерах. На фиг. 10.16 показано, как изменяется отношение
среднеквадратических значений ошибки и сигнала на выходе, когда на вход поступают
случайные числа с нулевым средним, равномерно распределенные на интервале (-1,
1), причем разрядность чисел равна 17. В этом случае ![]() .
Как видно из графика, теоретическая верхняя граница хорошо согласуется с
экспериментальными данными, хотя ее наклон несколько больше, чем в эксперименте.
Нижняя граница [см. формулу (10.18)] не приведена, так как она является слишком
оптимистичной и малопригодна для практики.
.
Как видно из графика, теоретическая верхняя граница хорошо согласуется с
экспериментальными данными, хотя ее наклон несколько больше, чем в эксперименте.
Нижняя граница [см. формулу (10.18)] не приведена, так как она является слишком
оптимистичной и малопригодна для практики.

Фиг. 10.16. Сравнение расчетной верхней границы уровня шума при БПФ и экспериментальных результатов (по Уэлчу).
Хотя
выше был рассмотрен вариант алгоритма БПФ с прореживанием по времени, переход
к другим вариантам несложен, и оценки верхней и нижней границ отношения
среднеквадратических значений ошибки и сигнала, описываемые формулами (10.16)
и (10.18), справедливы и для них. Таким образом, при разработке систем БПФ с
фиксированной запятой можно руководствоваться формулой (10.16). Зная Максимальный
размер преобразуемого массива ![]() и
требуемое отношение среднеквадратических значений ошибки и выходного сигнала,
можно выбрать длину слова
и
требуемое отношение среднеквадратических значений ошибки и выходного сигнала,
можно выбрать длину слова ![]() так, чтобы обеспечить требуемую
точность.
так, чтобы обеспечить требуемую
точность.
В
анализе, проведенном выше, рассматривались ошибки, связанные с округлением
произведений и масштабированием, которое используется, чтобы избежать
переполнений. При вычислении БПФ существует еще один источник погрешностей,
обусловленный неточным представлением значений поворачивающих множителей ![]() . Хотя полный
анализ этого эффекта еще не проводился, Вайнштейн, используя предположение о
случайном характере погрешностей представления коэффициентов, получил простое
выражение для отношения среднеквадратических значений ошибки и сигнала на выходе
. Хотя полный
анализ этого эффекта еще не проводился, Вайнштейн, используя предположение о
случайном характере погрешностей представления коэффициентов, получил простое
выражение для отношения среднеквадратических значений ошибки и сигнала на выходе
 (10.19)
(10.19)
Здесь
![]() — число
разрядов, используемых для представления коэффициентов. Из формулы
(10.19) видно, что дисперсия ошибки с ростом
— число
разрядов, используемых для представления коэффициентов. Из формулы
(10.19) видно, что дисперсия ошибки с ростом ![]() увеличивается
весьма медленно. И хотя эта формула весьма приближенная, экспериментальные
измерения подтверждают основной вывод о том, что дисперсия ошибки
действительно с ростом
увеличивается
весьма медленно. И хотя эта формула весьма приближенная, экспериментальные
измерения подтверждают основной вывод о том, что дисперсия ошибки
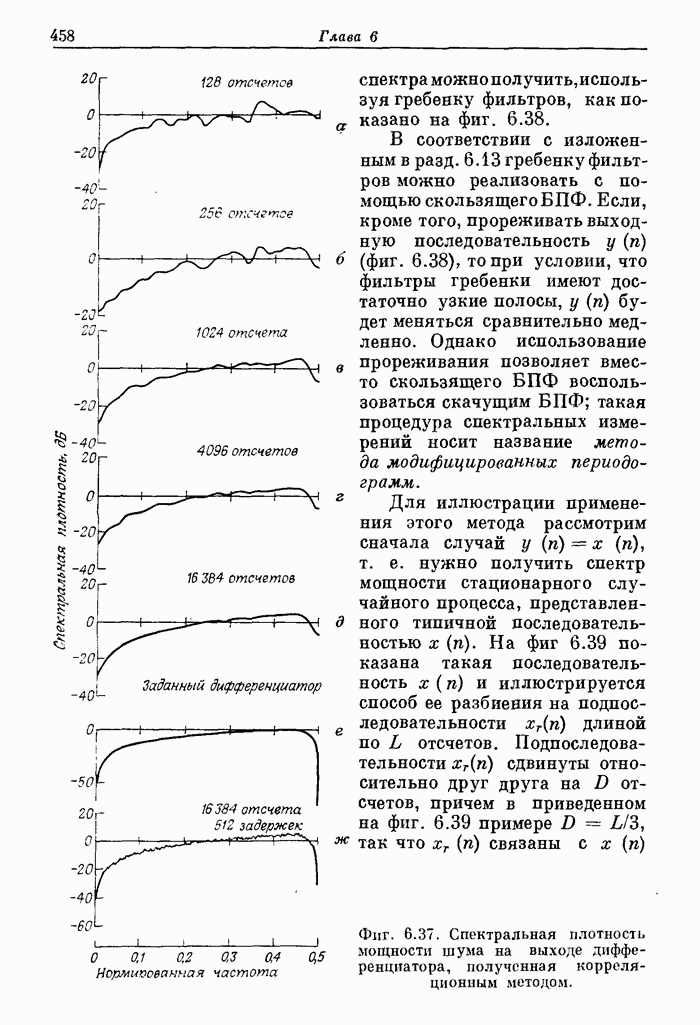
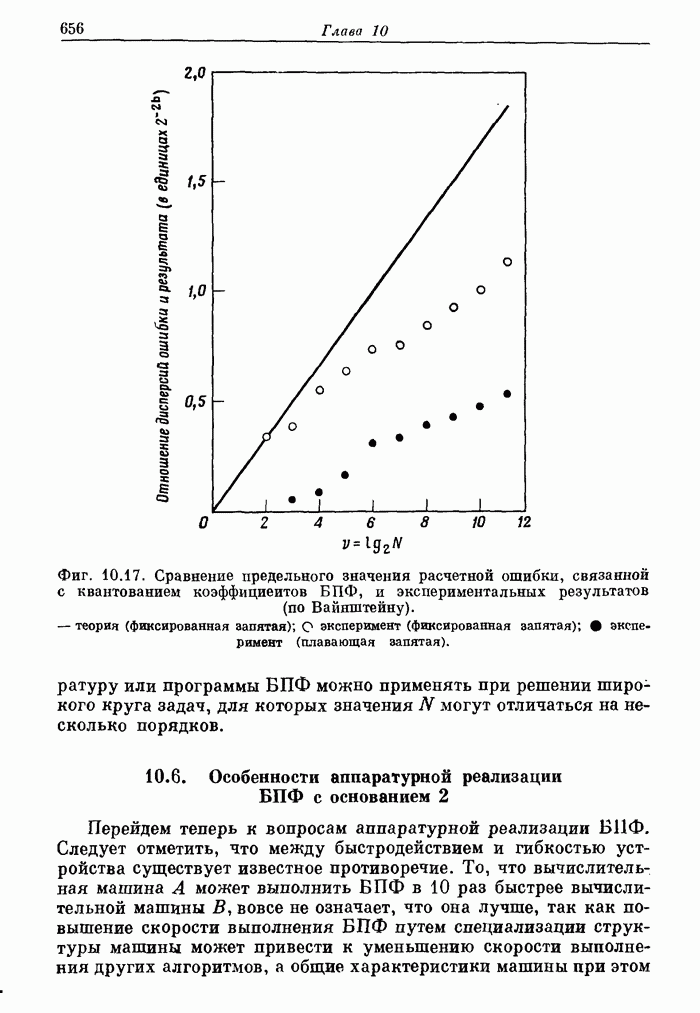
действительно с ростом ![]() увеличивается очень медленно. На фиг.
10.17 приведены результаты, полученные Вайнштейном для случаев выполнения
арифметических операций с фиксированной и плавающей запятой. Основное следствие
из приведенных результатов заключается в том, что фиксированная длина слова
(достаточно большая, чтобы обеспечить заданную точность представления
коэффициентов) может использоваться для широкого диапазона значений
увеличивается очень медленно. На фиг.
10.17 приведены результаты, полученные Вайнштейном для случаев выполнения
арифметических операций с фиксированной и плавающей запятой. Основное следствие
из приведенных результатов заключается в том, что фиксированная длина слова
(достаточно большая, чтобы обеспечить заданную точность представления
коэффициентов) может использоваться для широкого диапазона значений ![]() . Поэтому аппаратуру или
программы БПФ можно применять при решении широкого круга задач, для которых
значения
. Поэтому аппаратуру или
программы БПФ можно применять при решении широкого круга задач, для которых
значения ![]() могут отличаться на несколько
порядков.
могут отличаться на несколько
порядков.

Фиг. 10.17. Сравнение предельного значения расчетной
ошибки, связанной с квантованием коэффициентов БПФ, и экспериментальных
результатов (по Вайнштейну). - теория (фиксированная запятая); ![]() - эксперимент
(фиксированная запятая); • - эксперимент (плавающая запятая).
- эксперимент
(фиксированная запятая); • - эксперимент (плавающая запятая).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
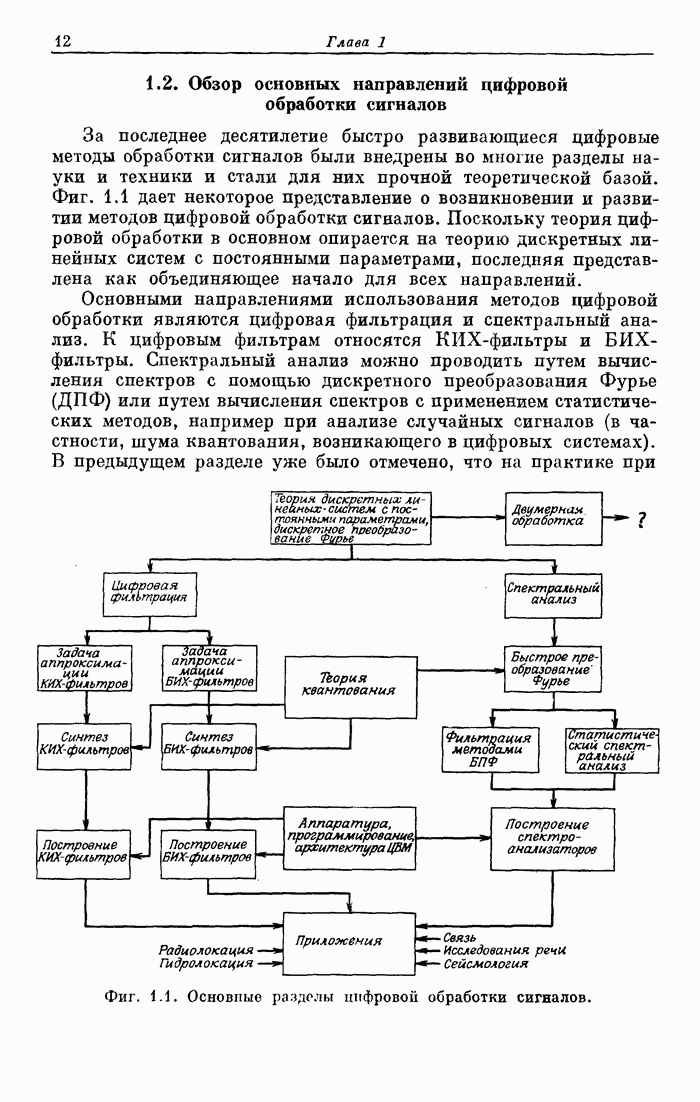
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
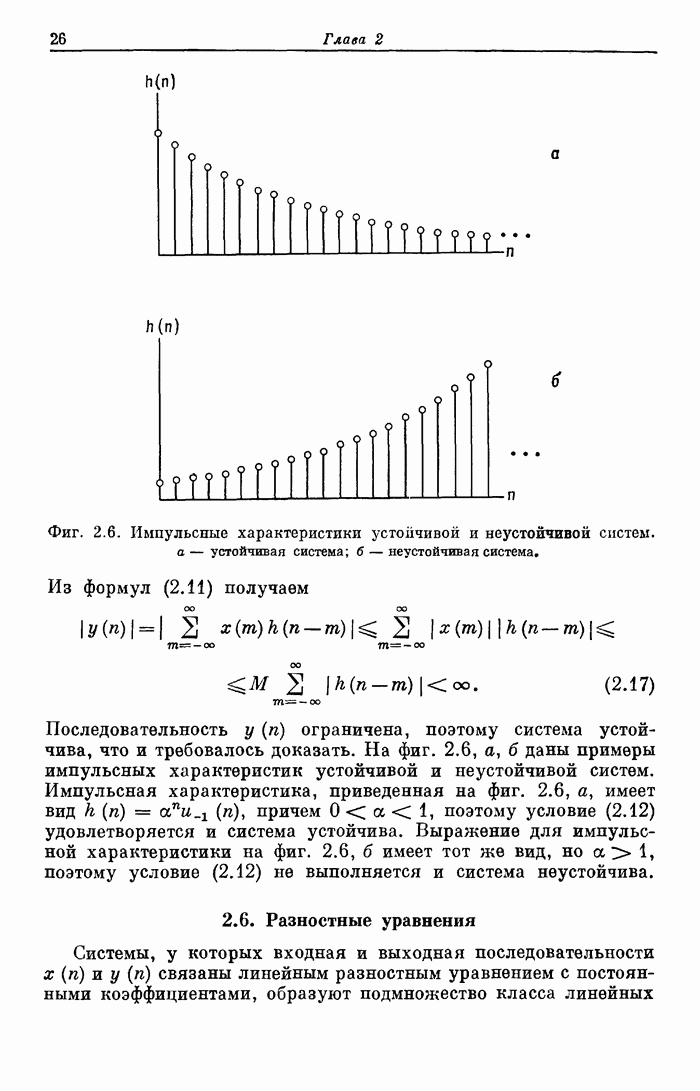
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
- 2.7. Частотная характеристика
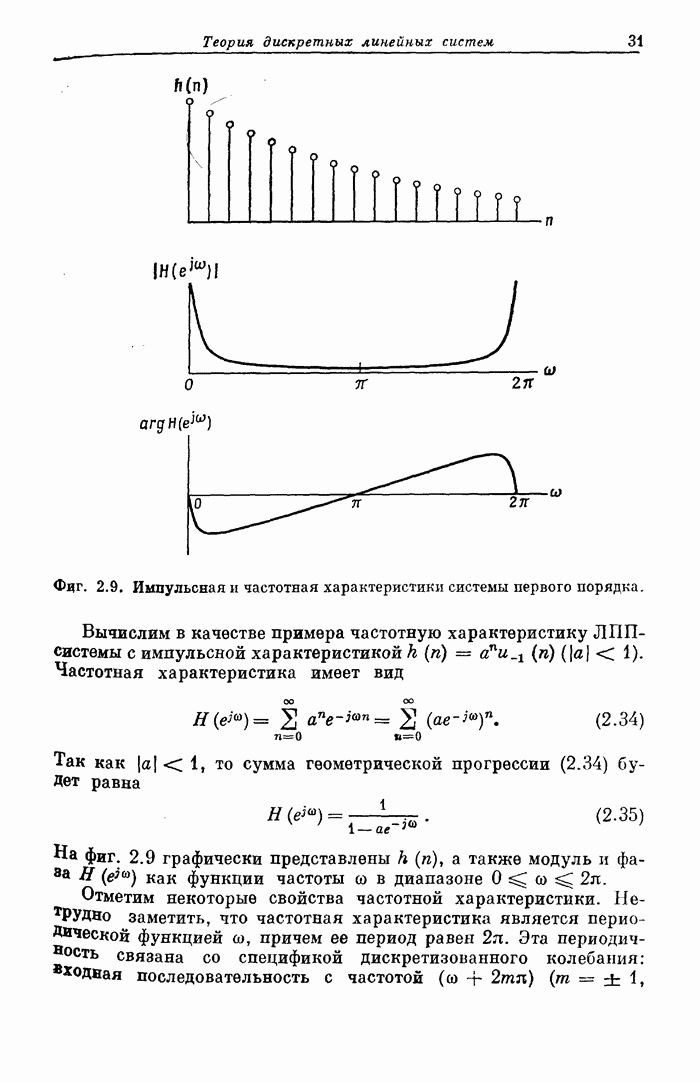
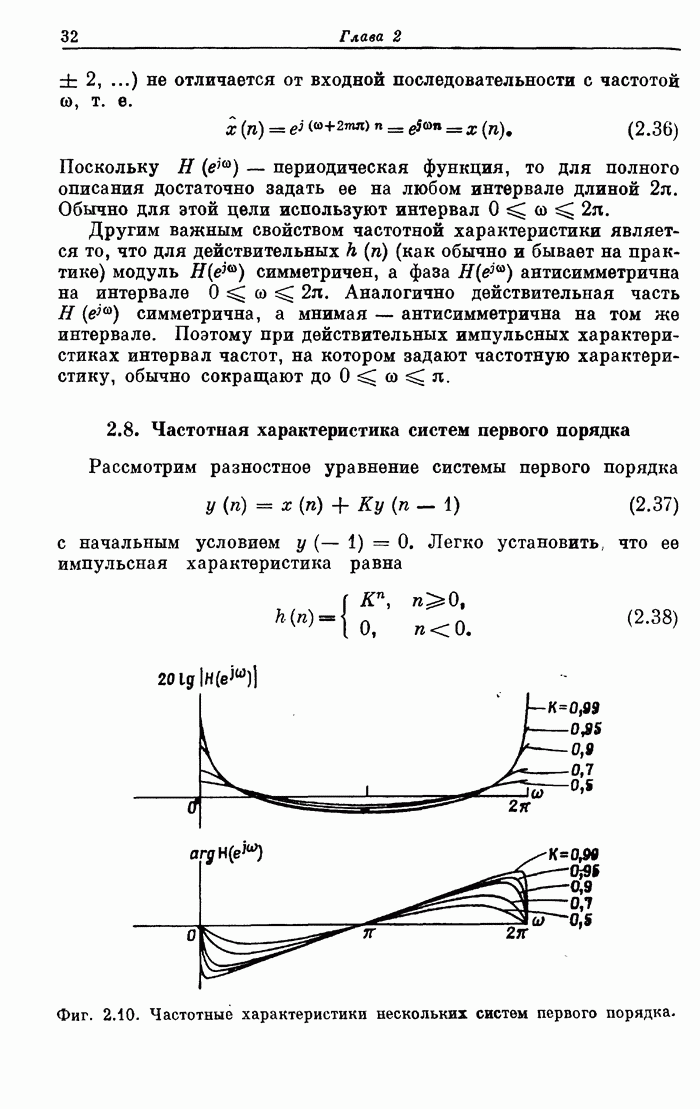
- 2.8. Частотная характеристика систем первого порядка
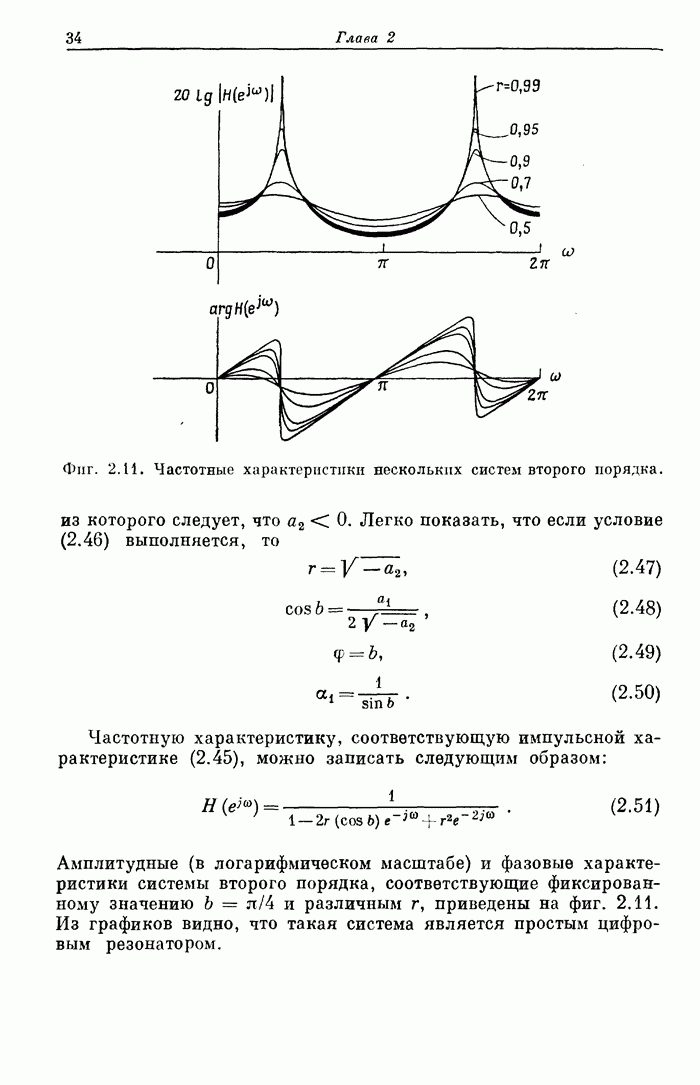
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
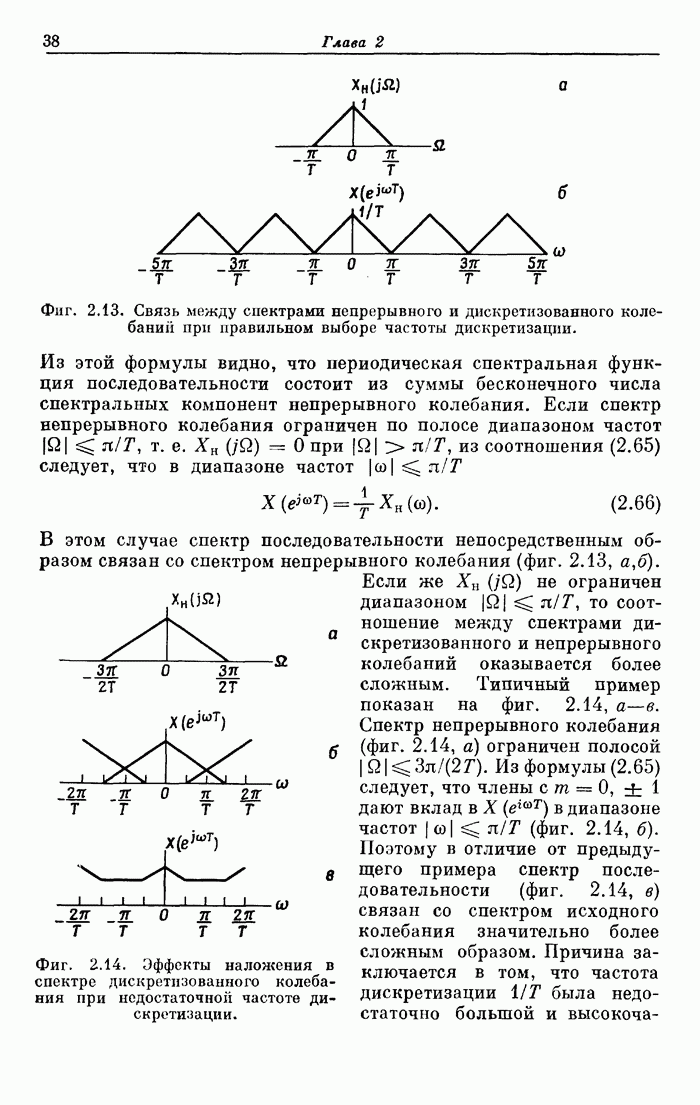
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
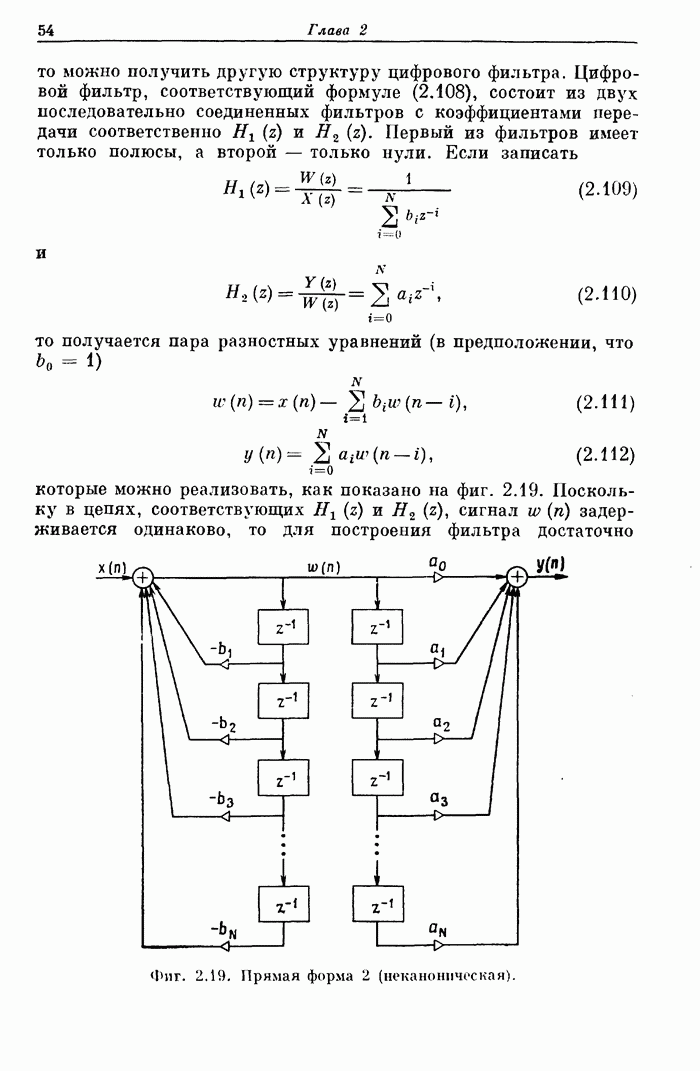
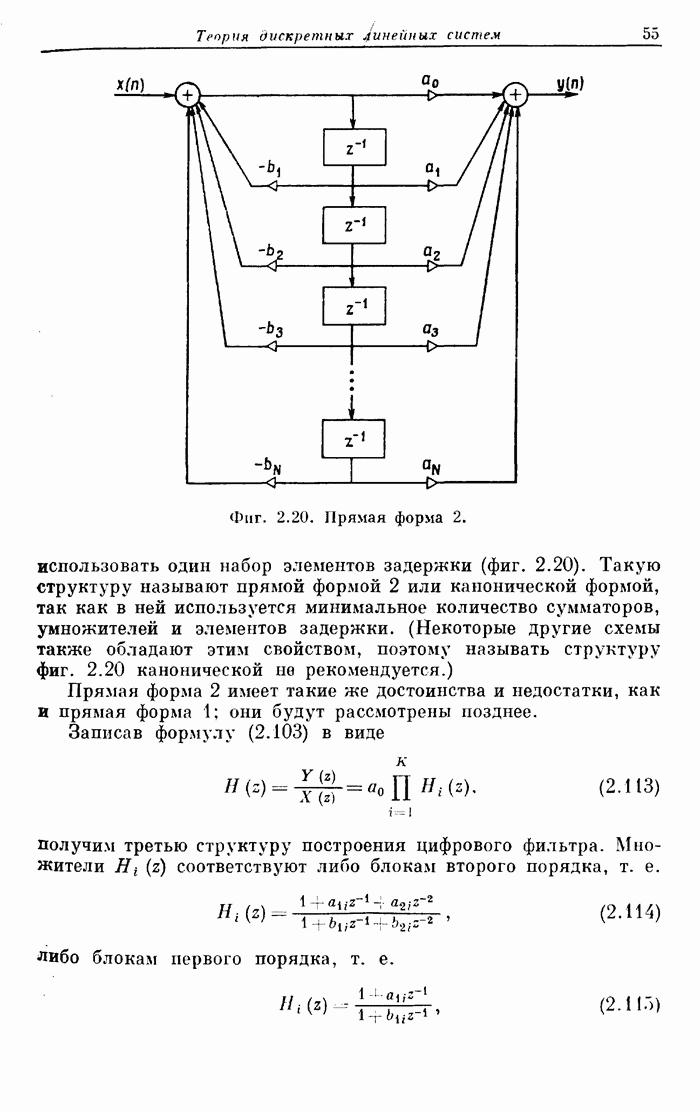
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
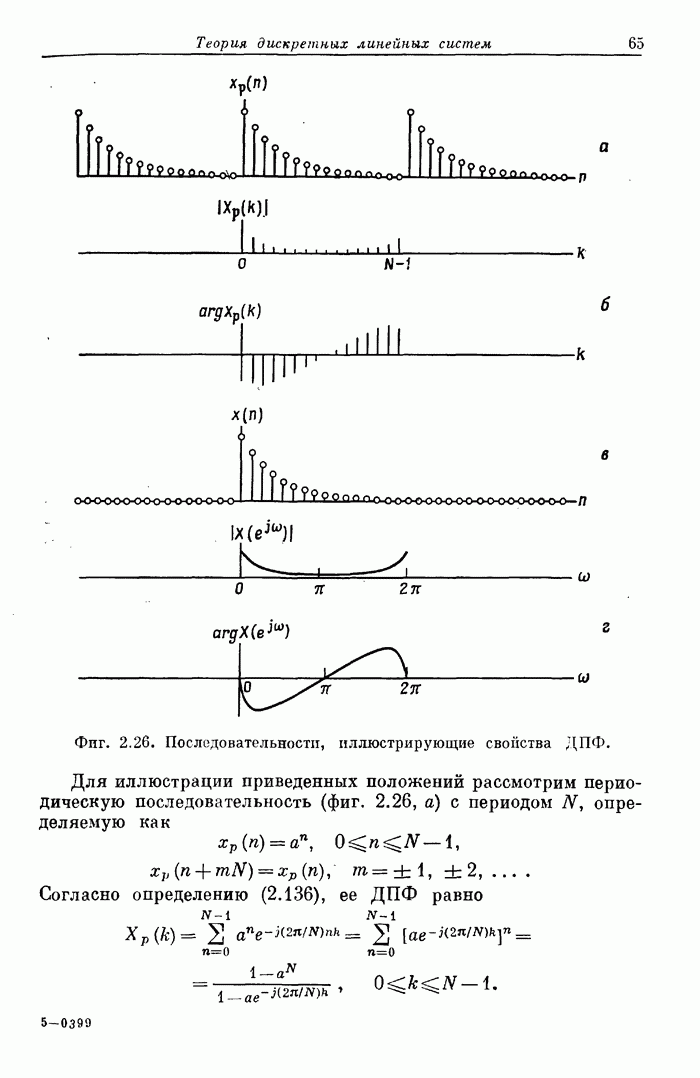
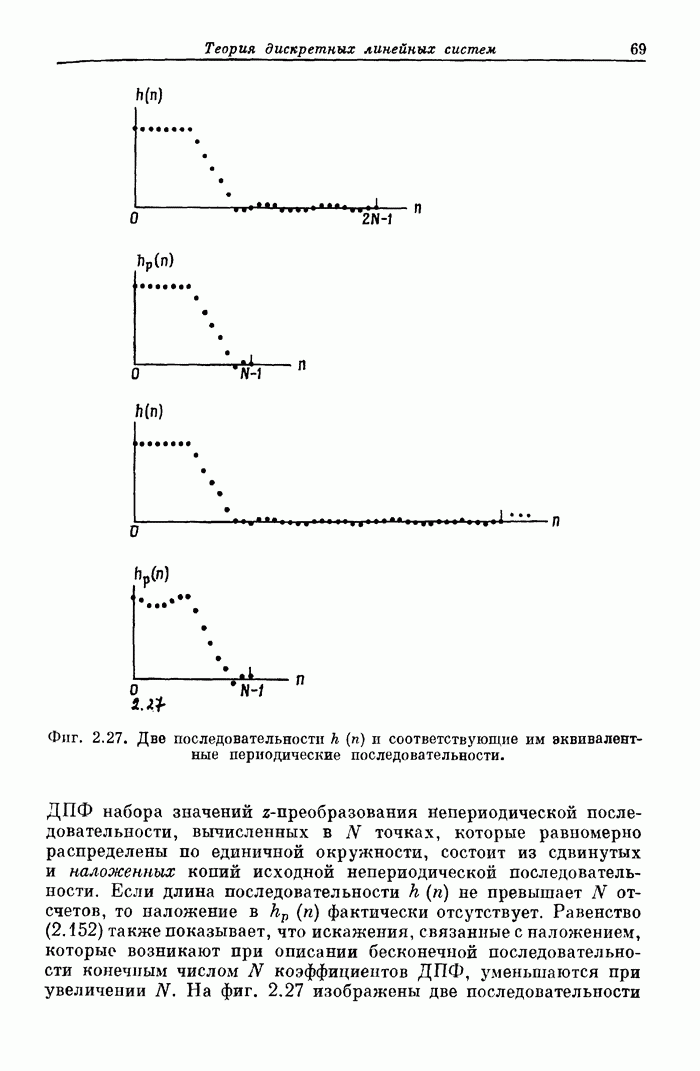
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
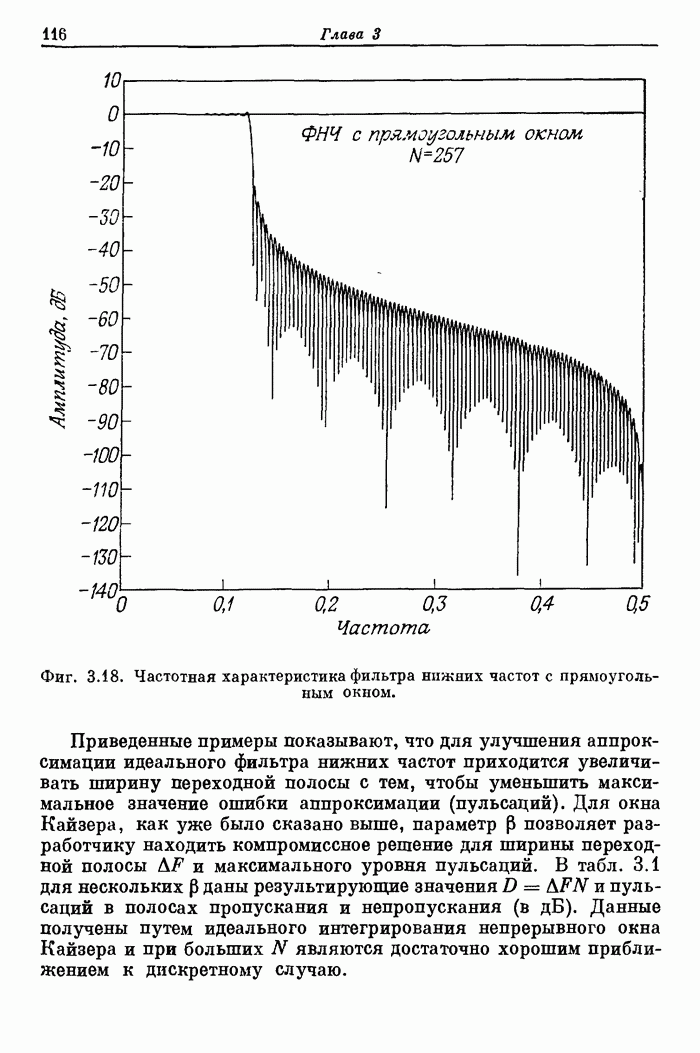
- 3.12. Примеры фильтров нижних частот с различными окнами
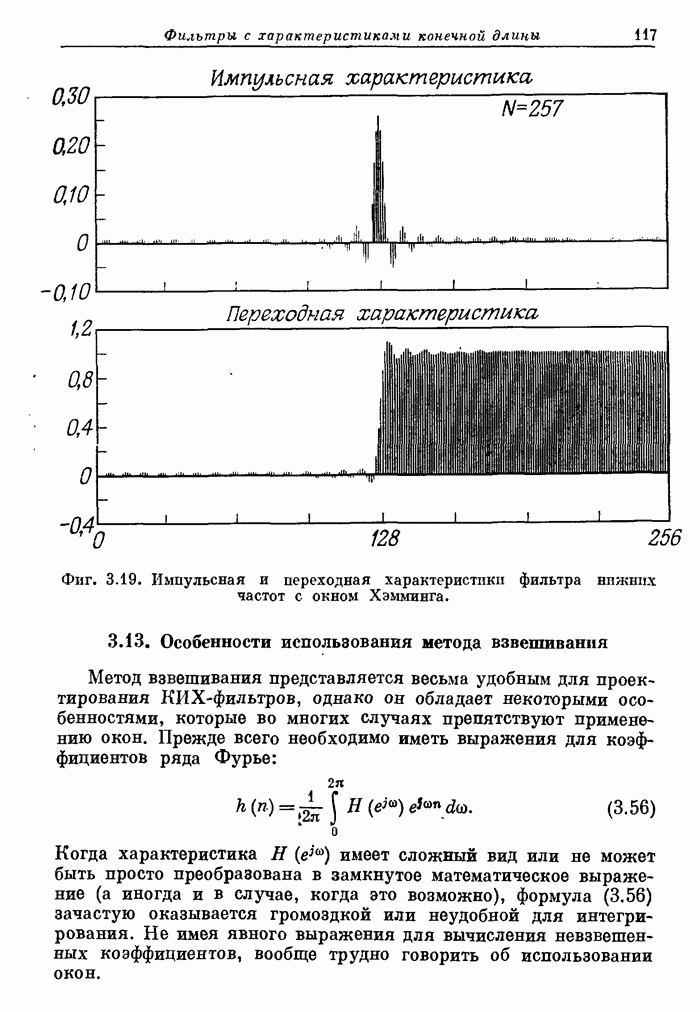
- 3.13. Особенности использования метода взвешивания
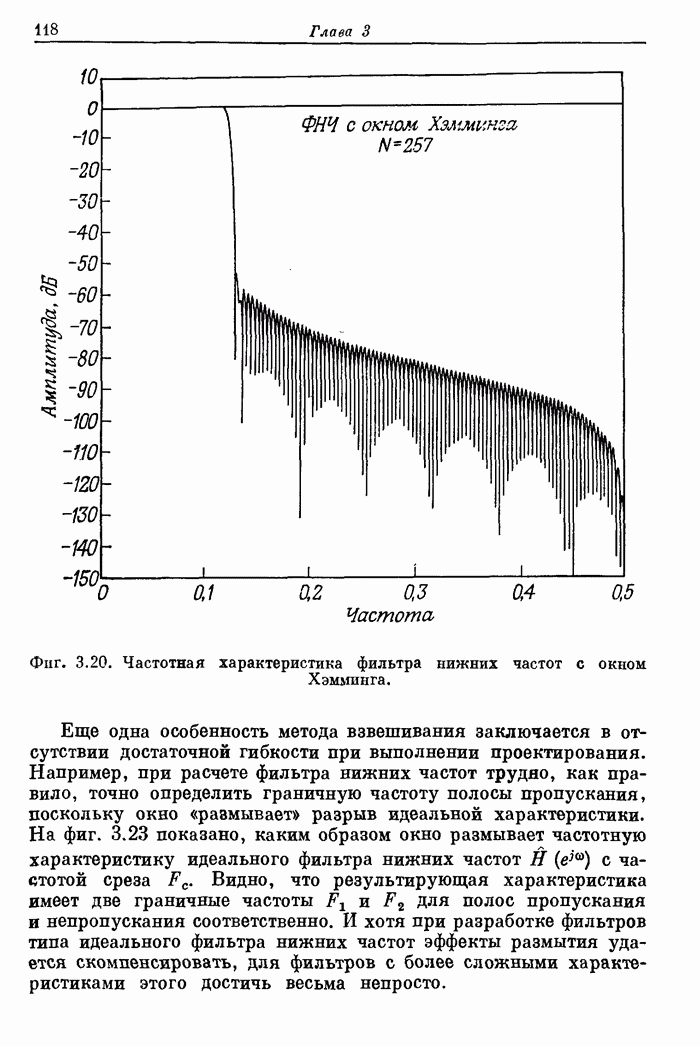
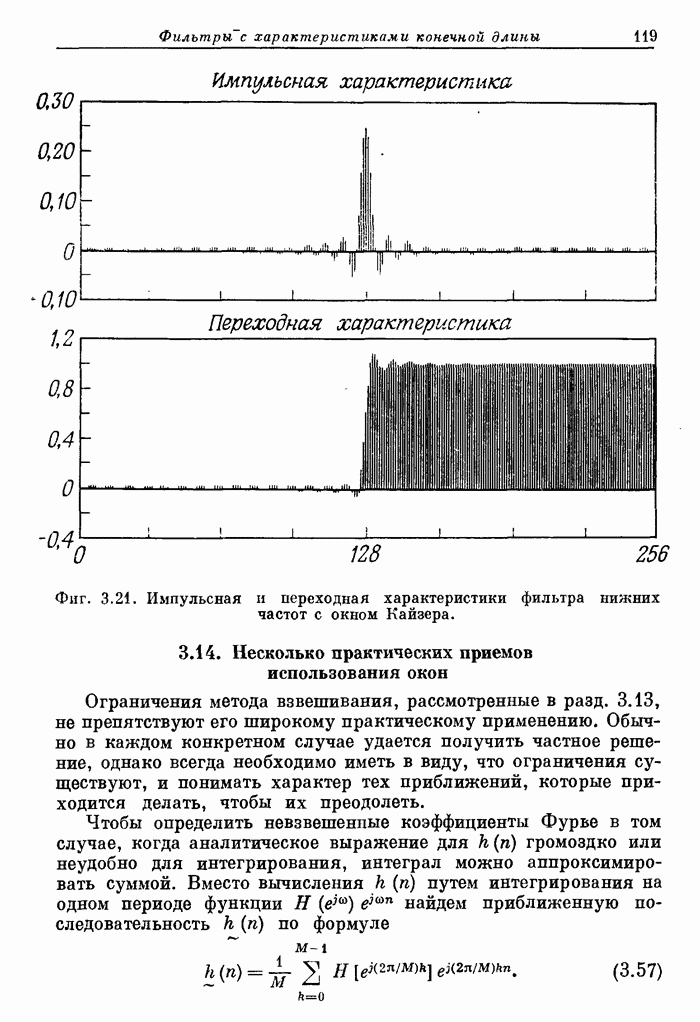
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
- 3.38. Многополосные оптимальные КИХ-фильтры
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
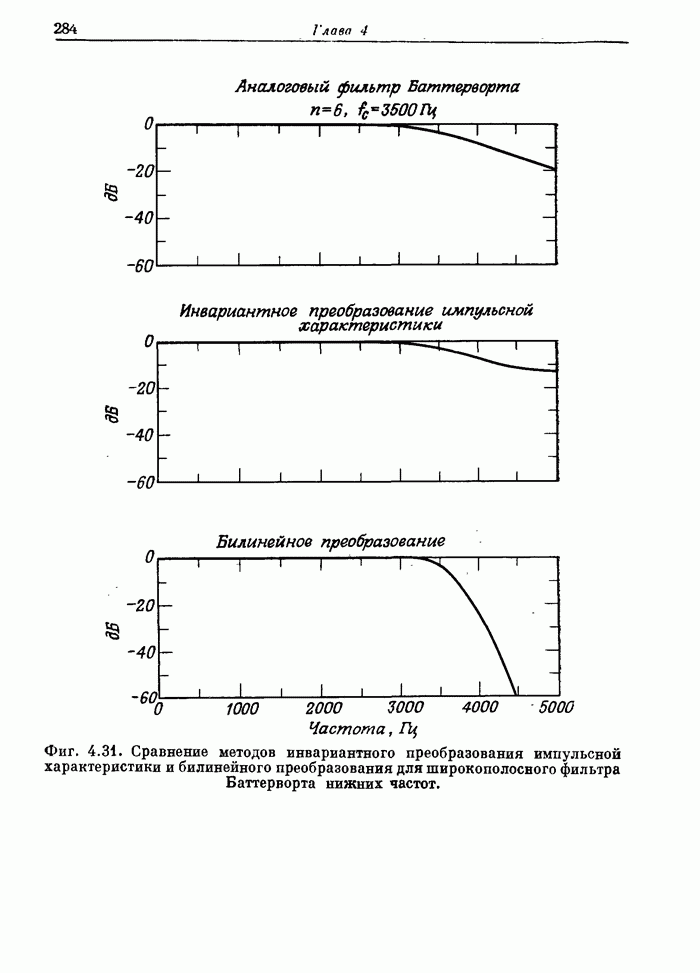
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
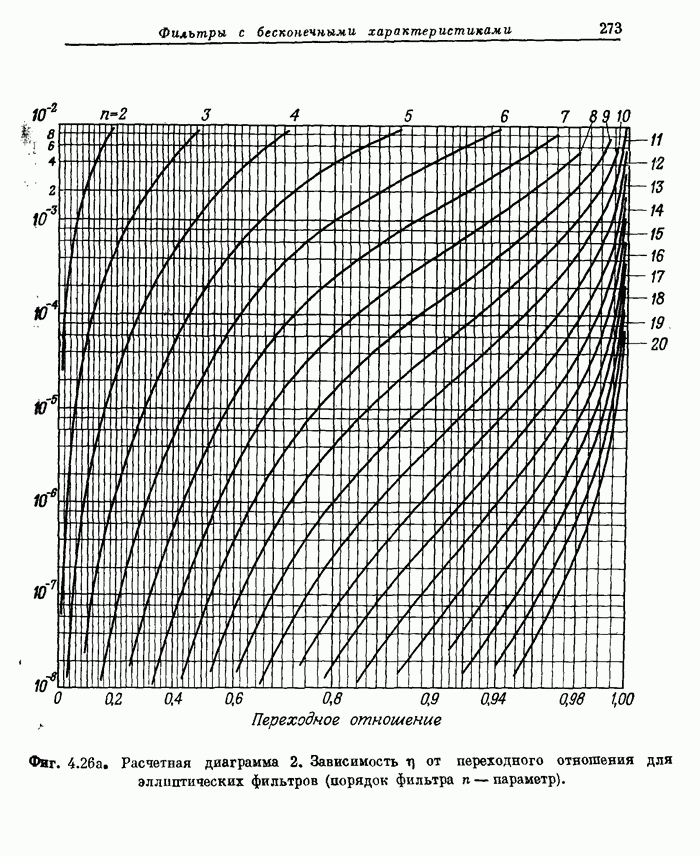
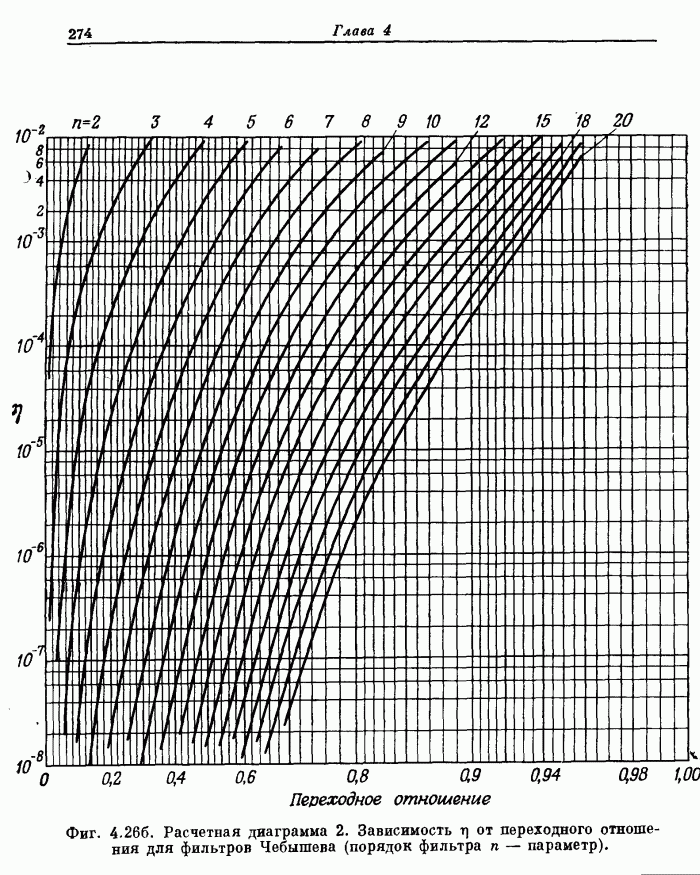
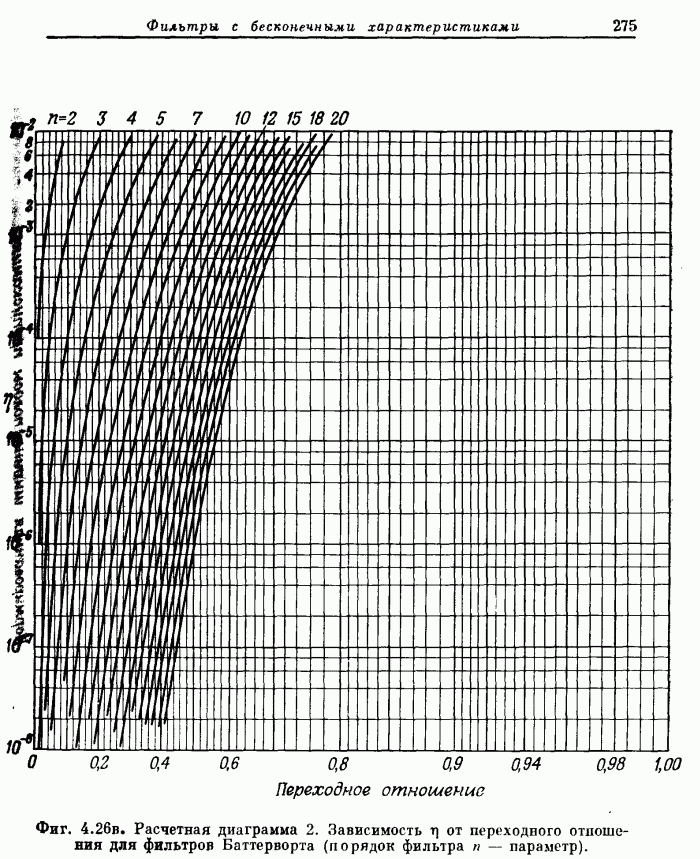
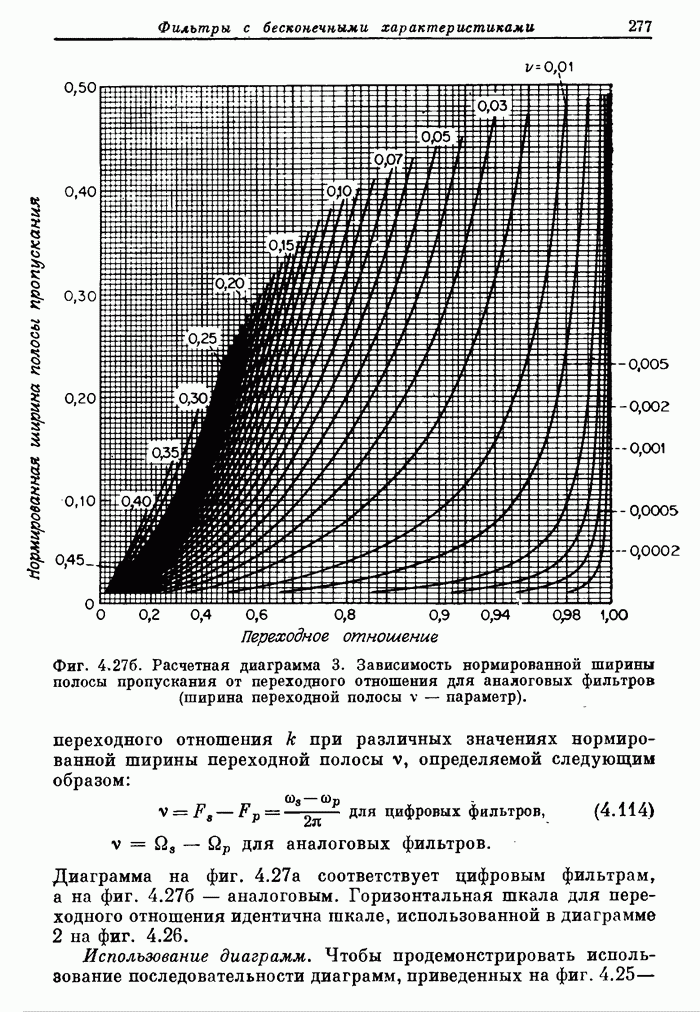
- 4.10. Расчетные диаграммы фильтров нижних частот
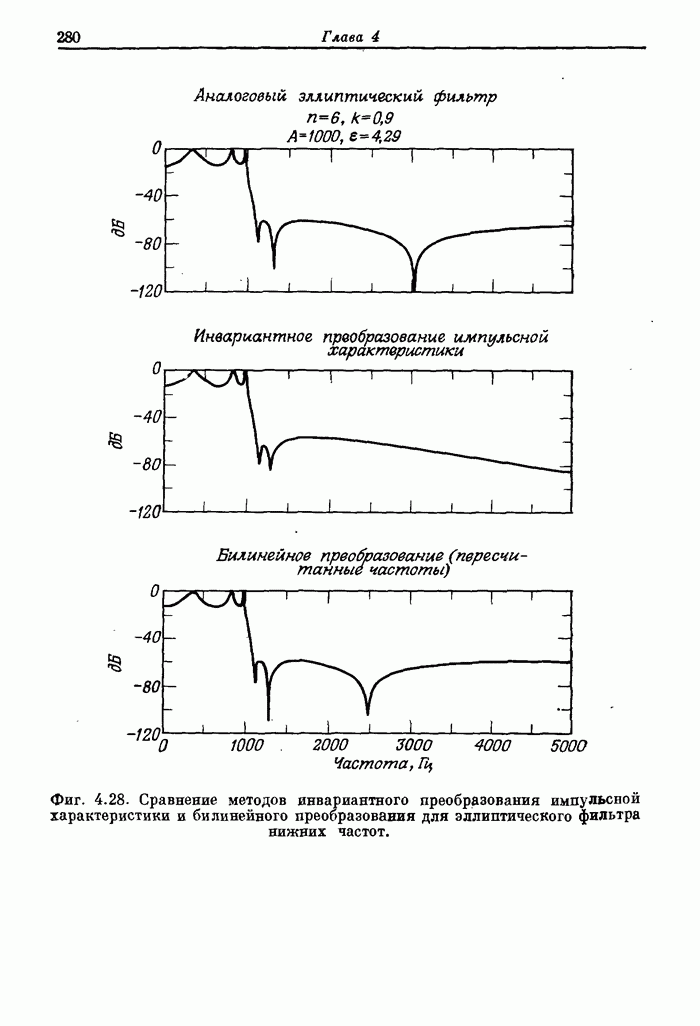
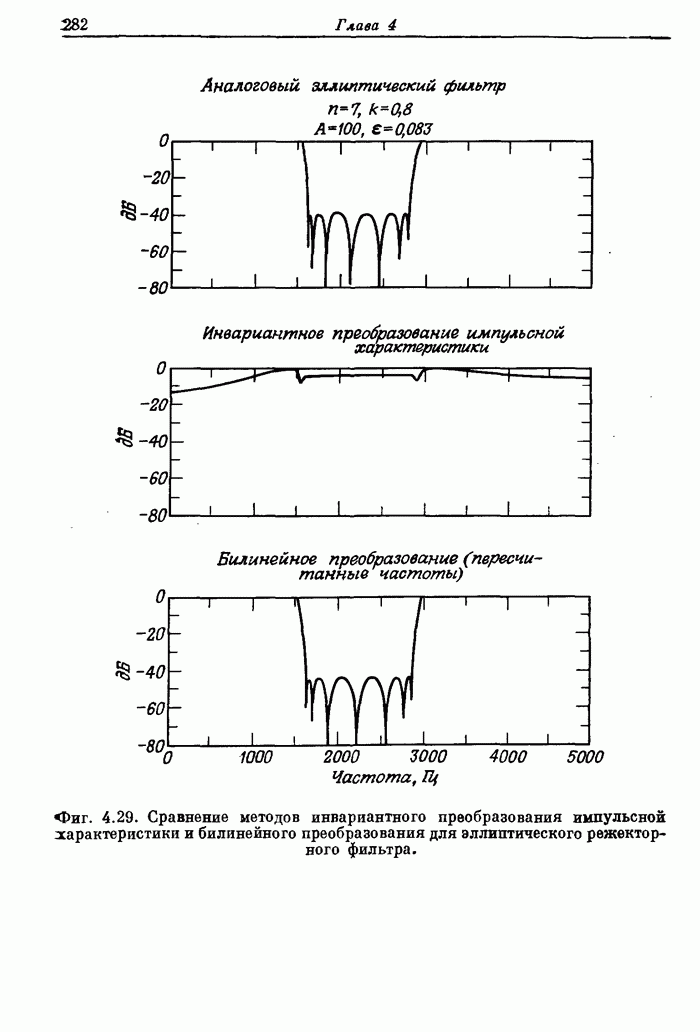
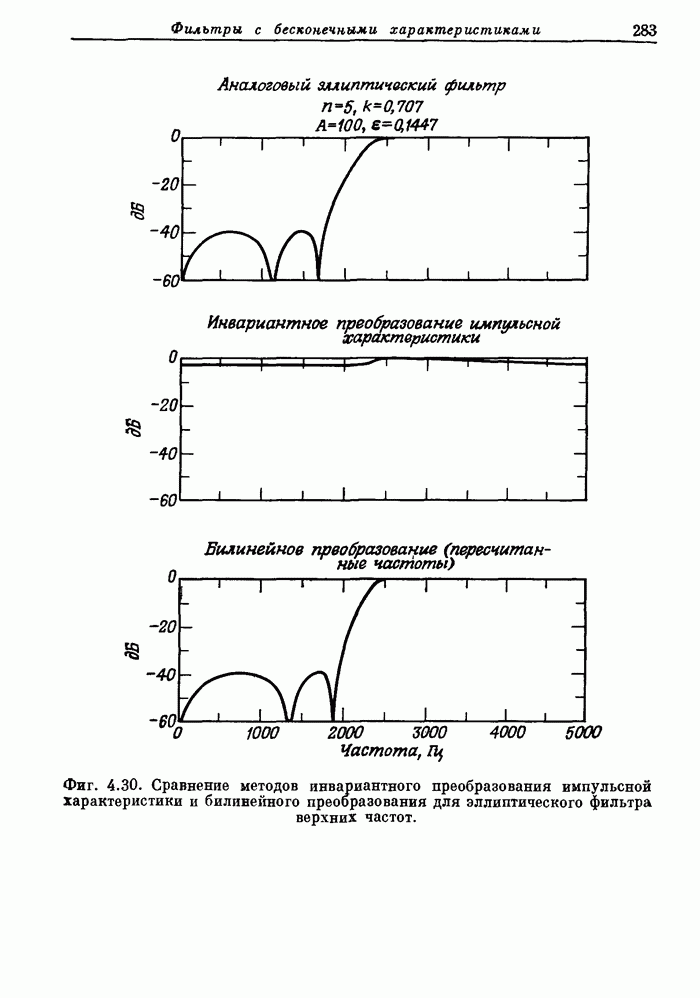
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
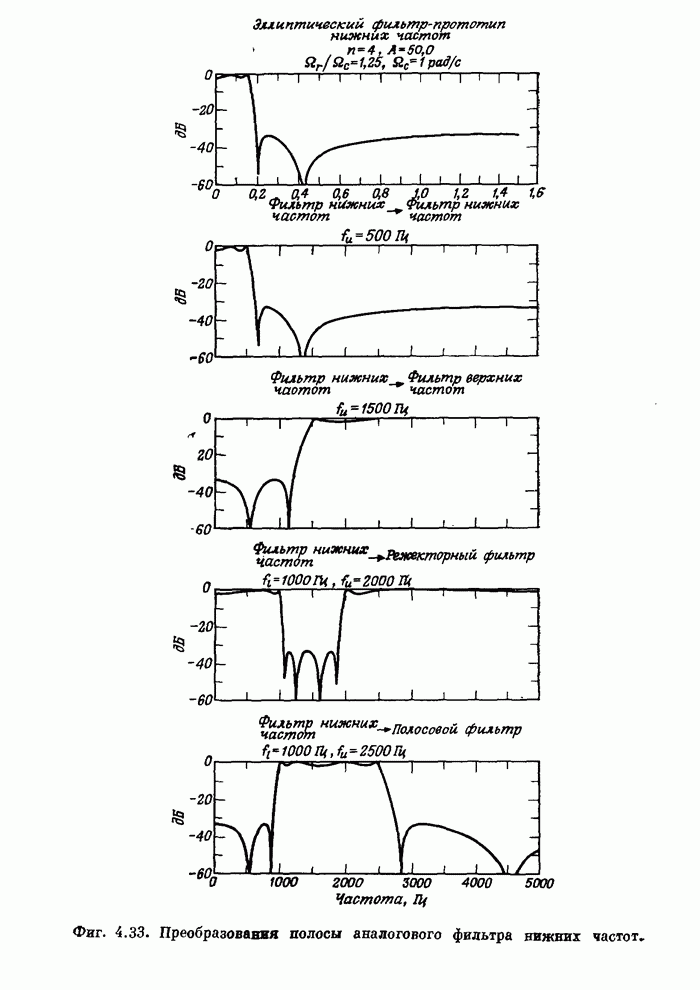
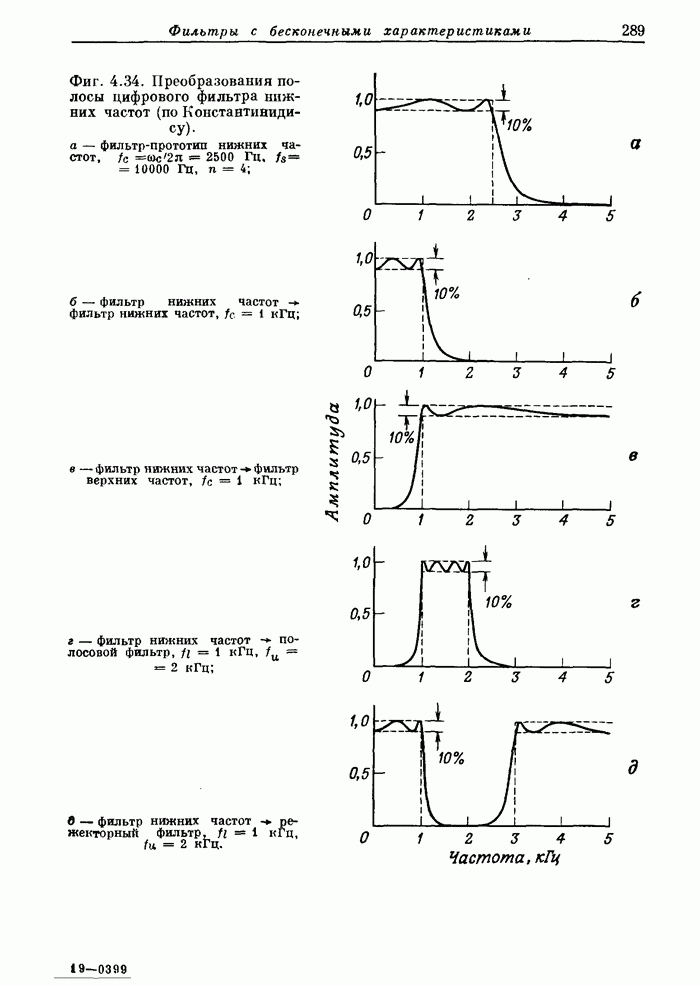
- 4.12. Частотные преобразования
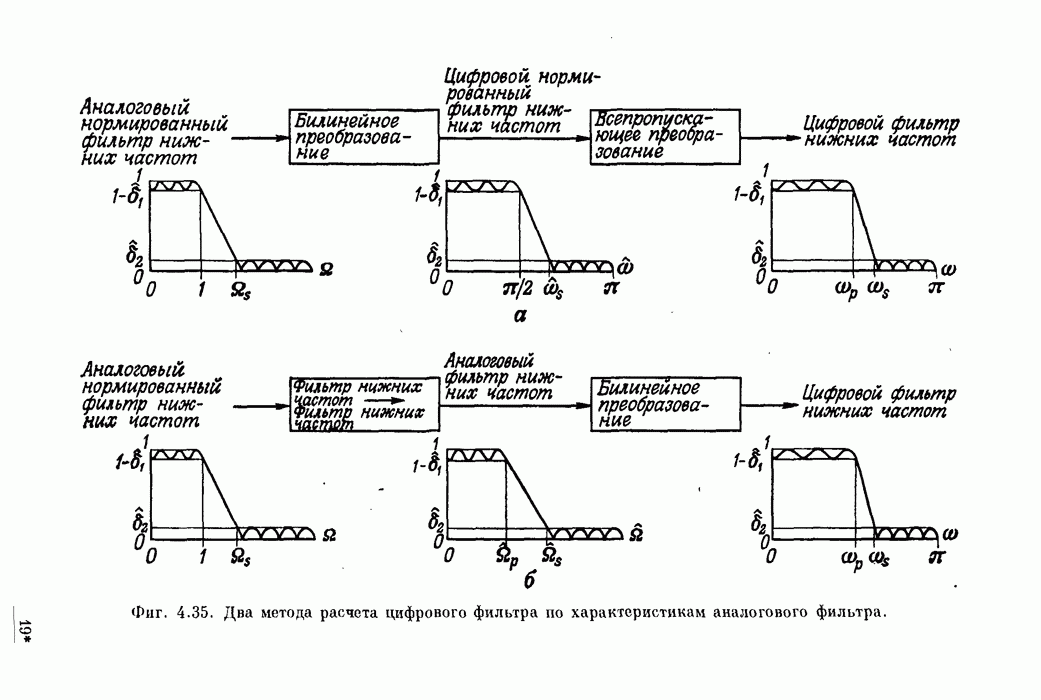
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
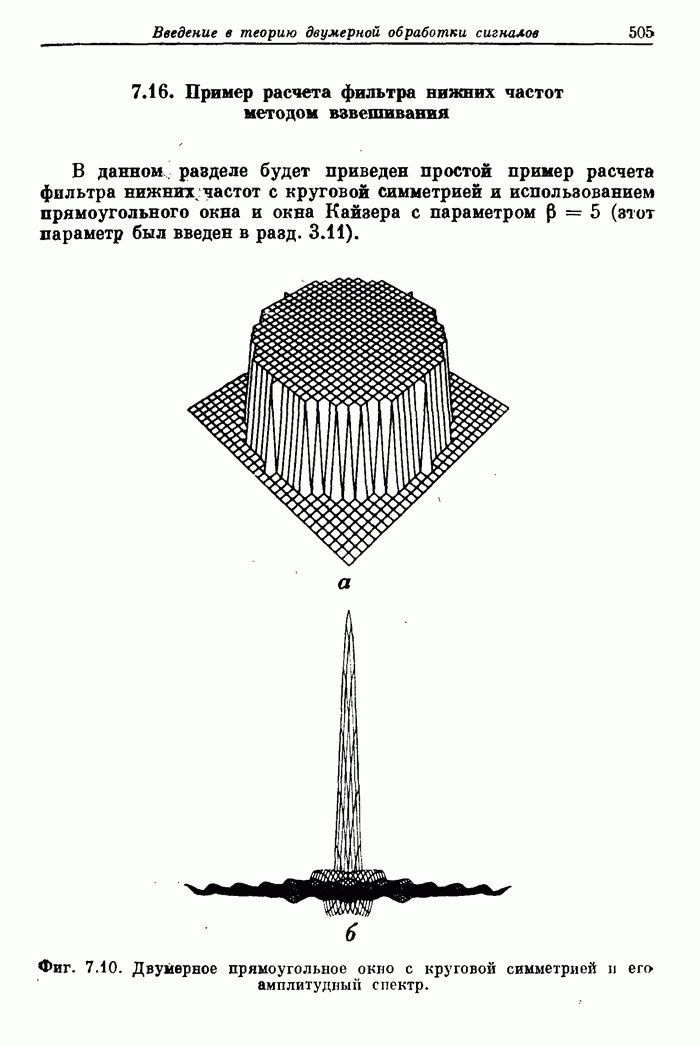
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
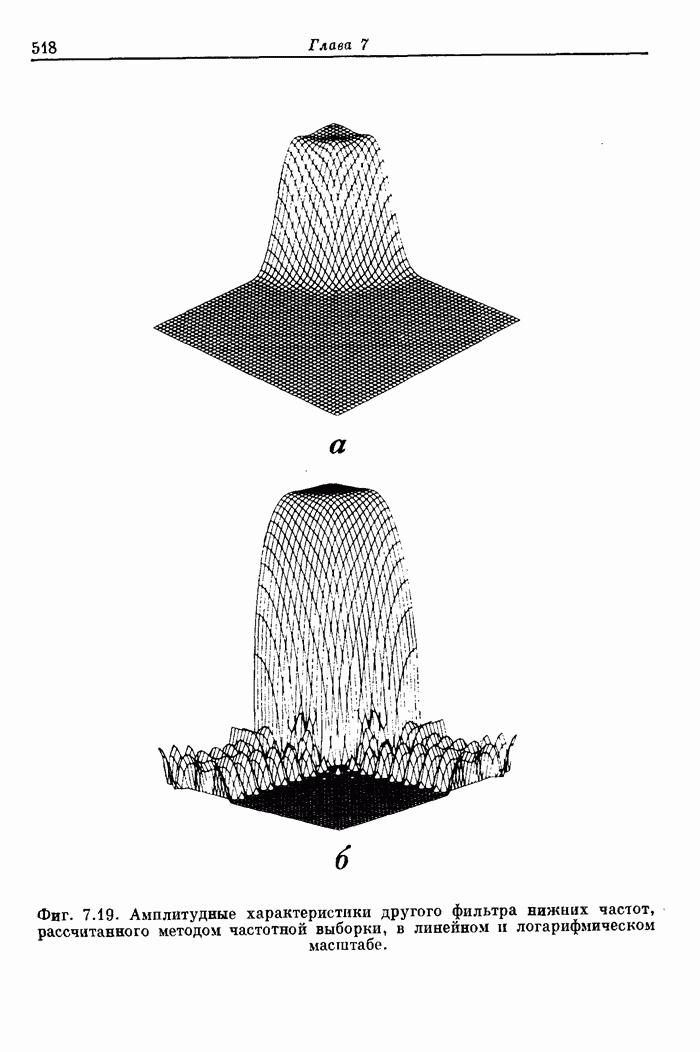
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
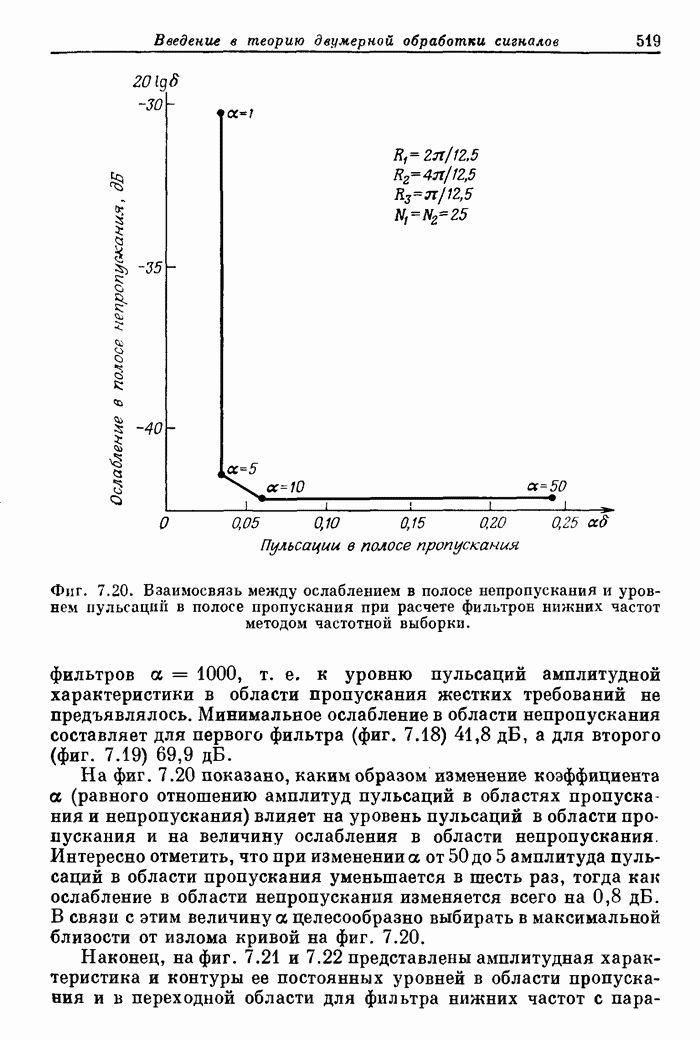
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
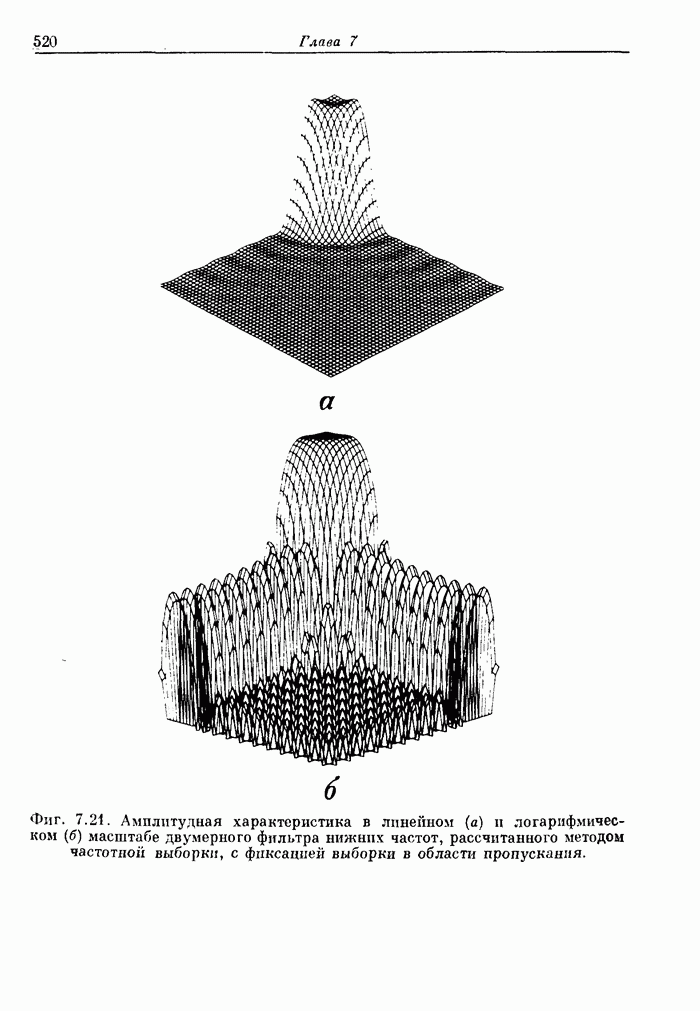
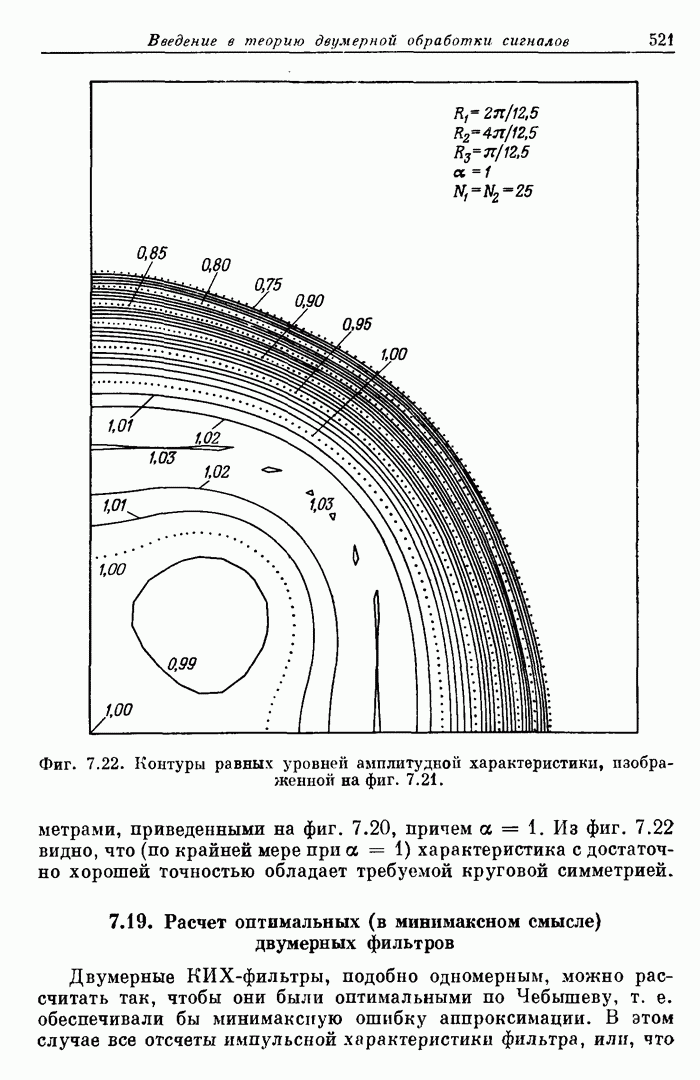
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
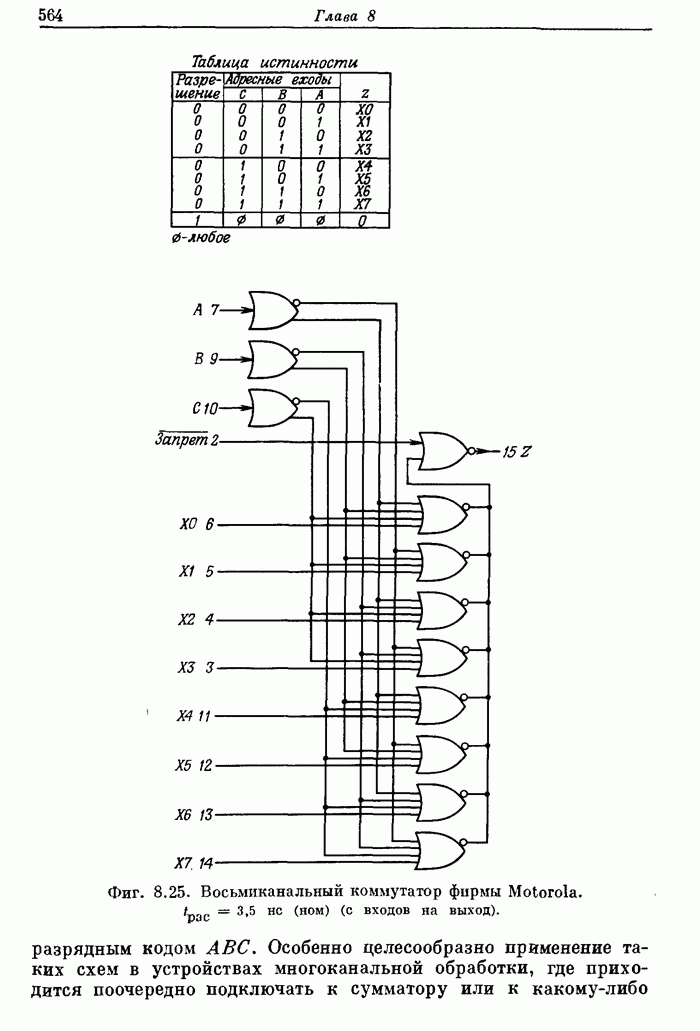
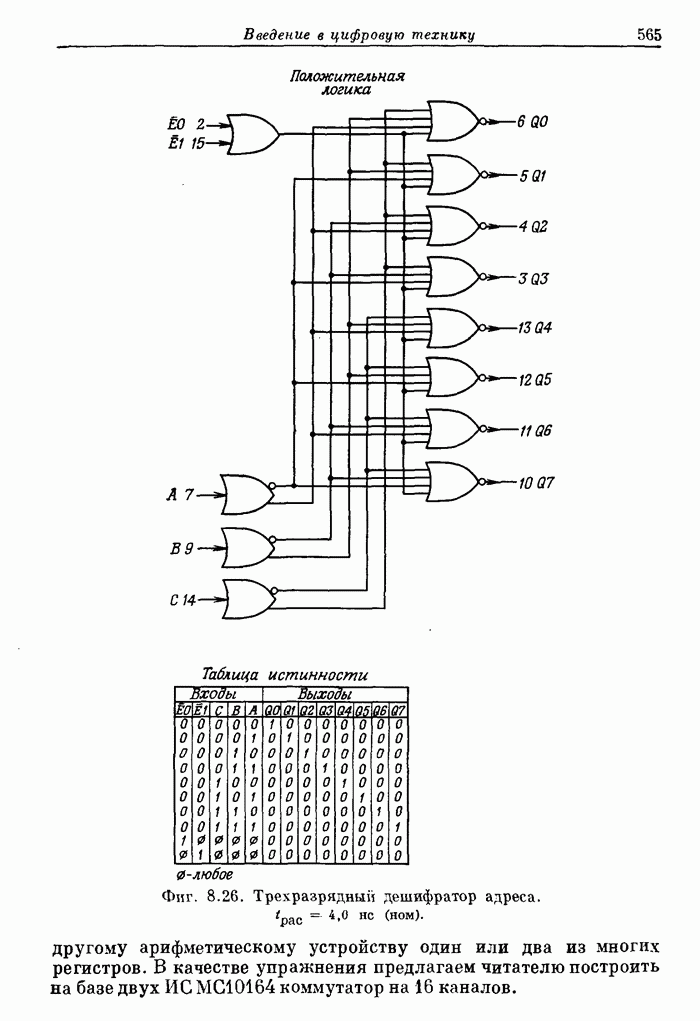
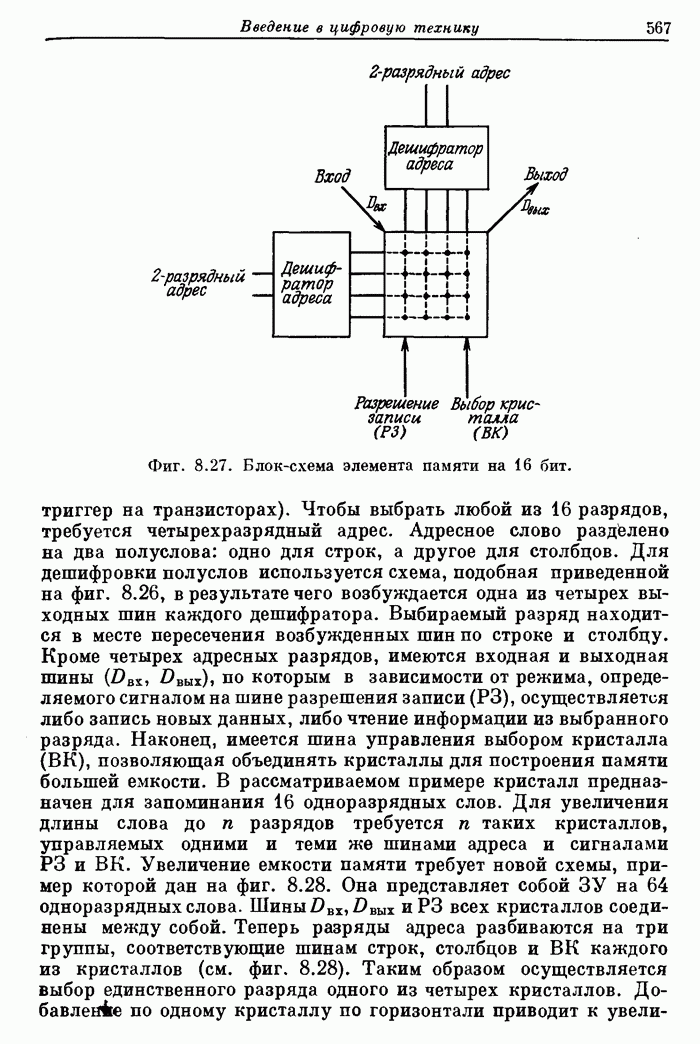
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
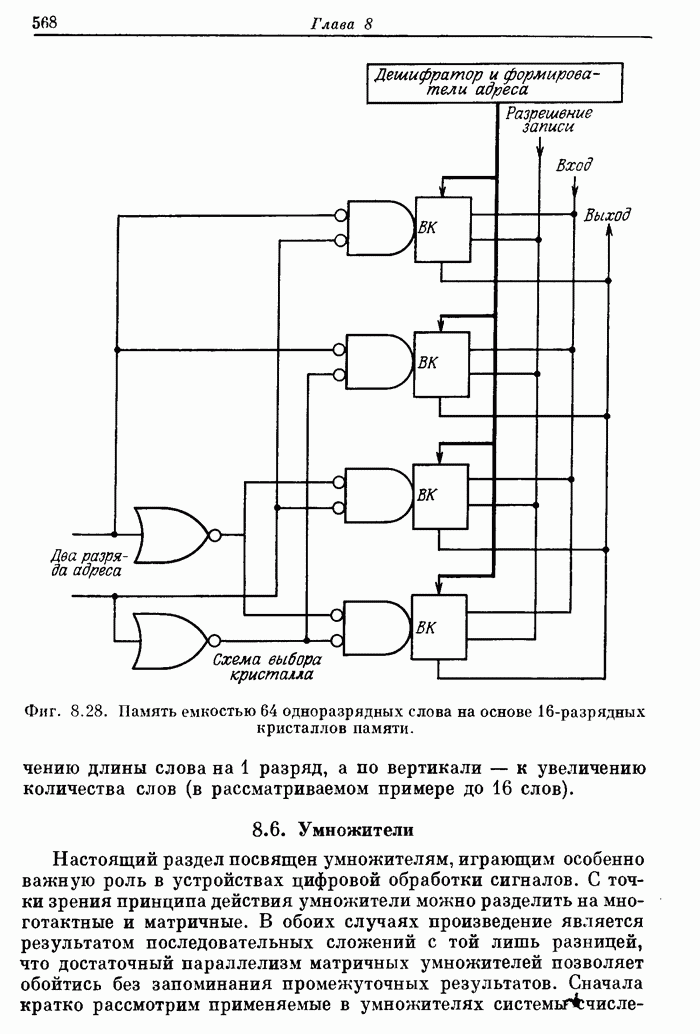
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
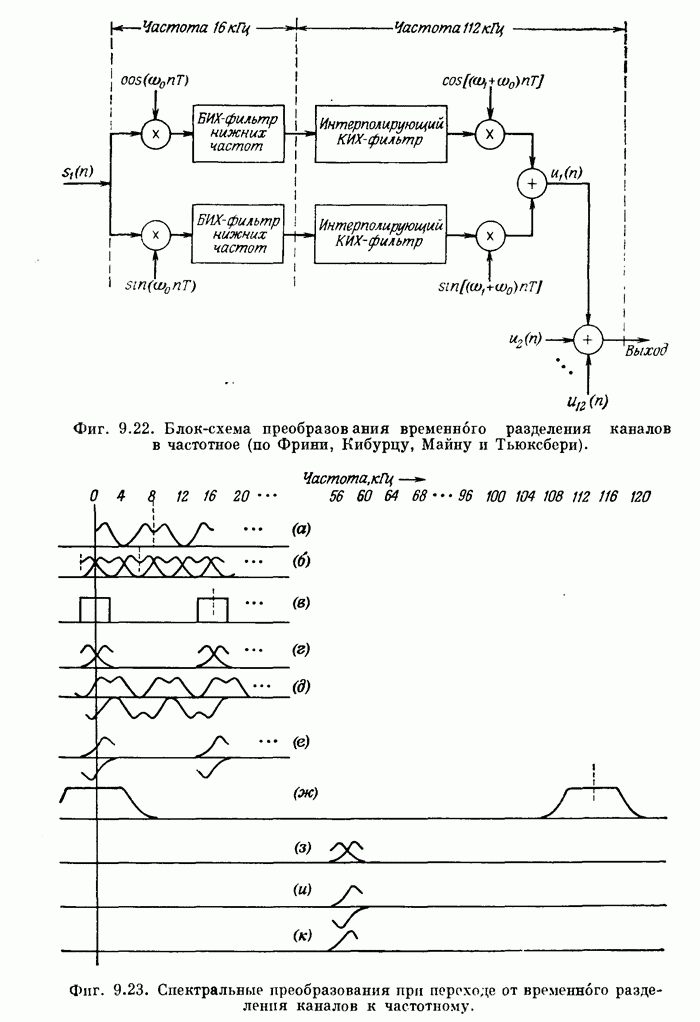
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
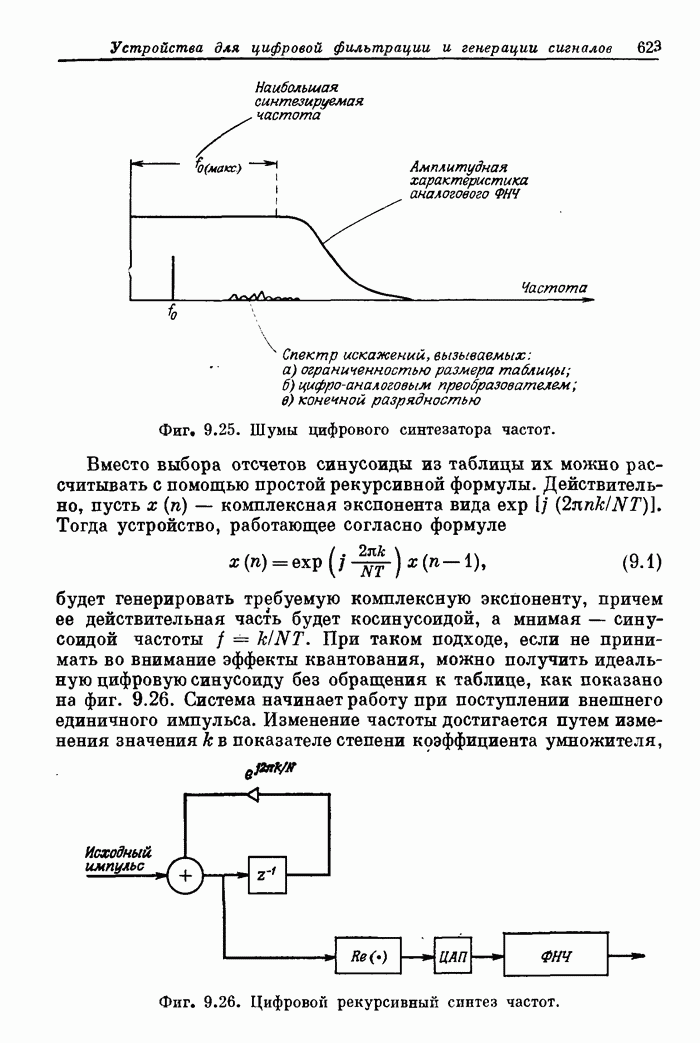
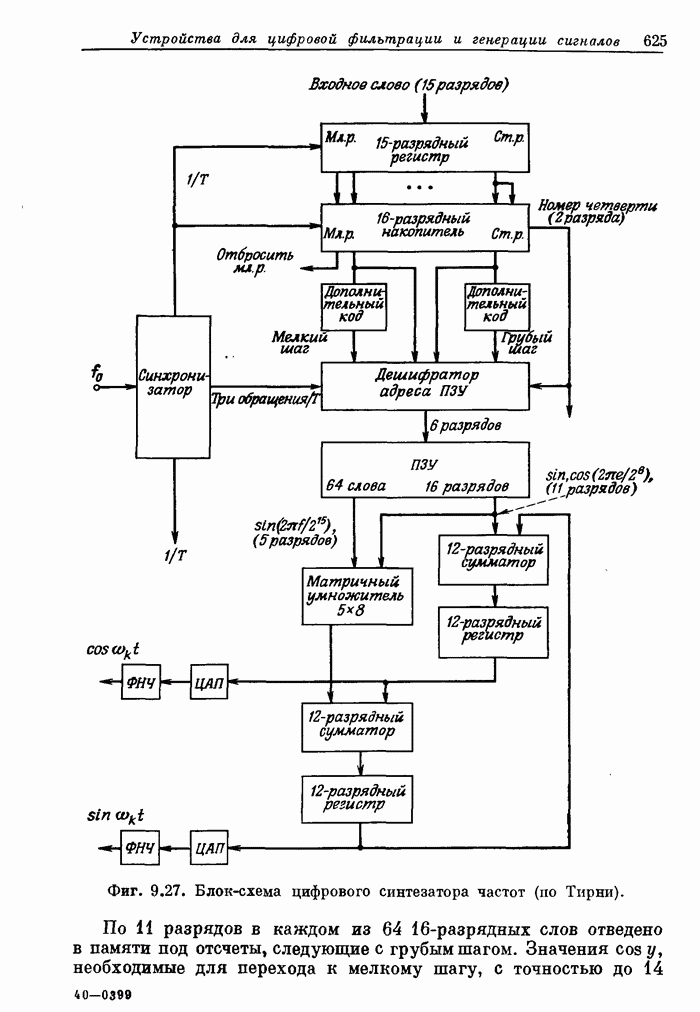
- 9.12. Специализированный цифровой синтезатор частот
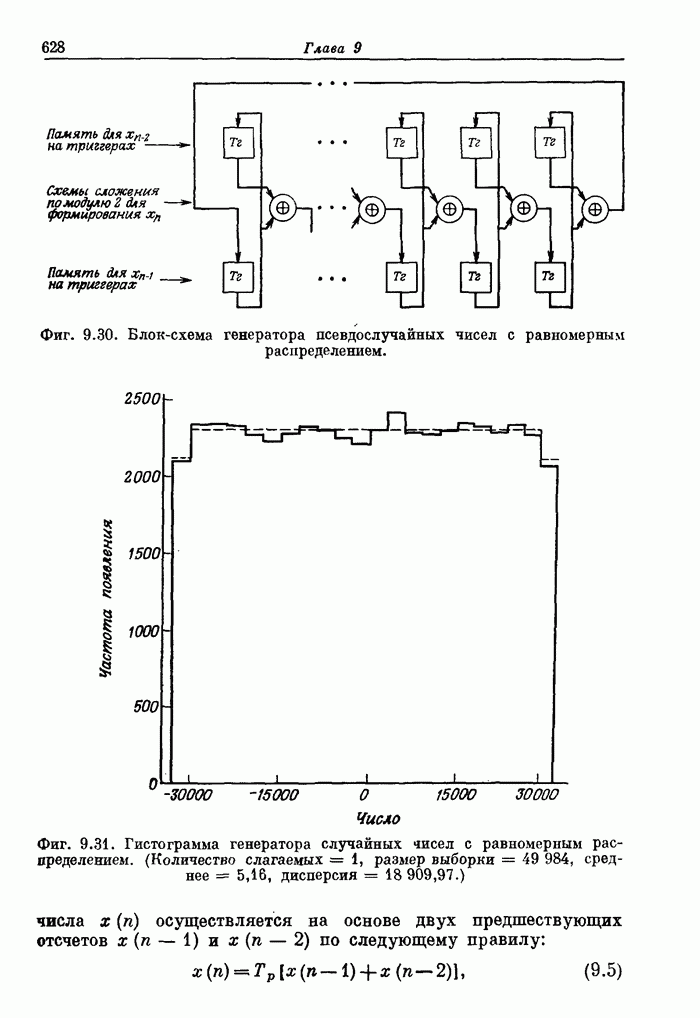
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
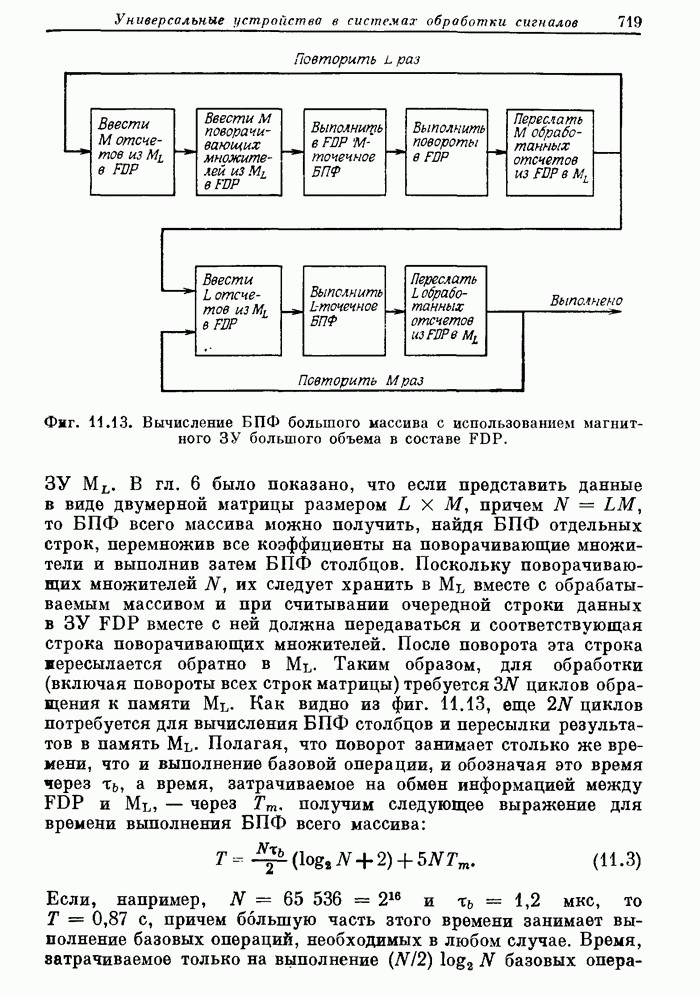
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
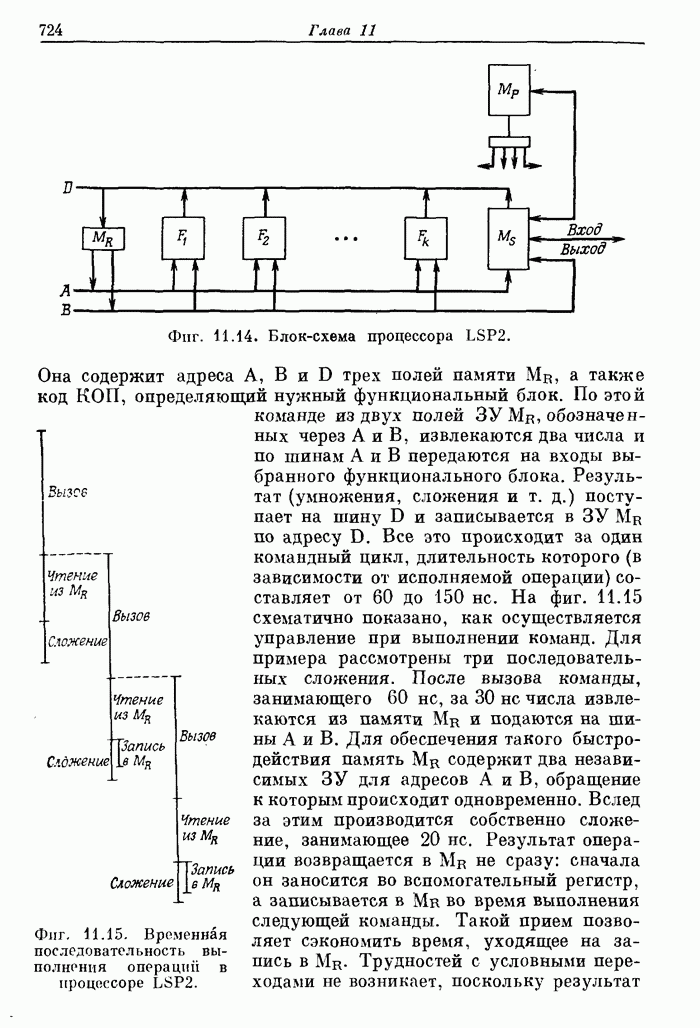
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
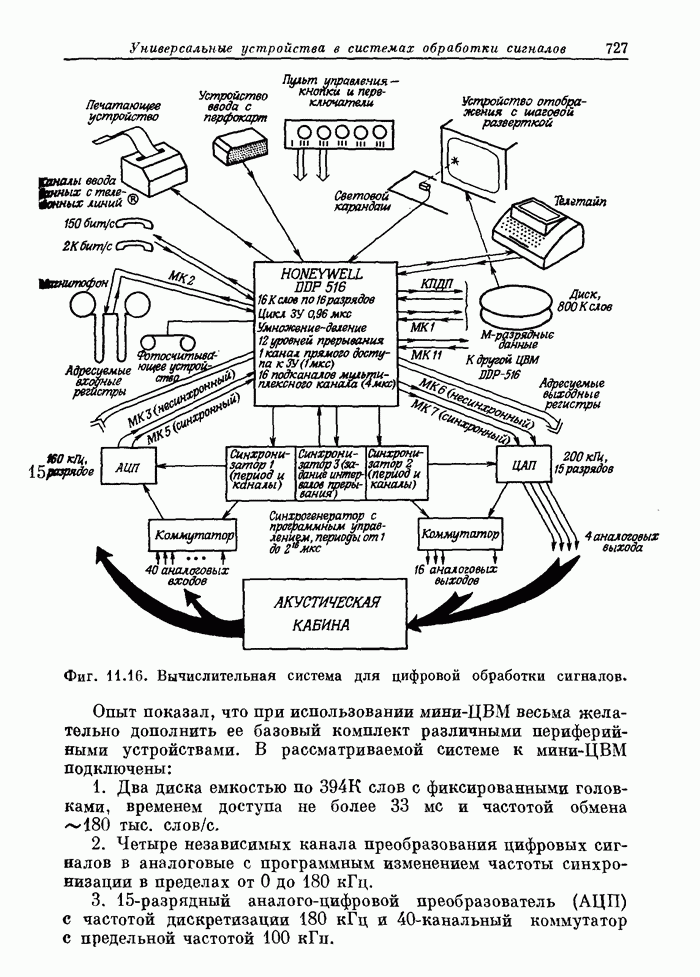
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
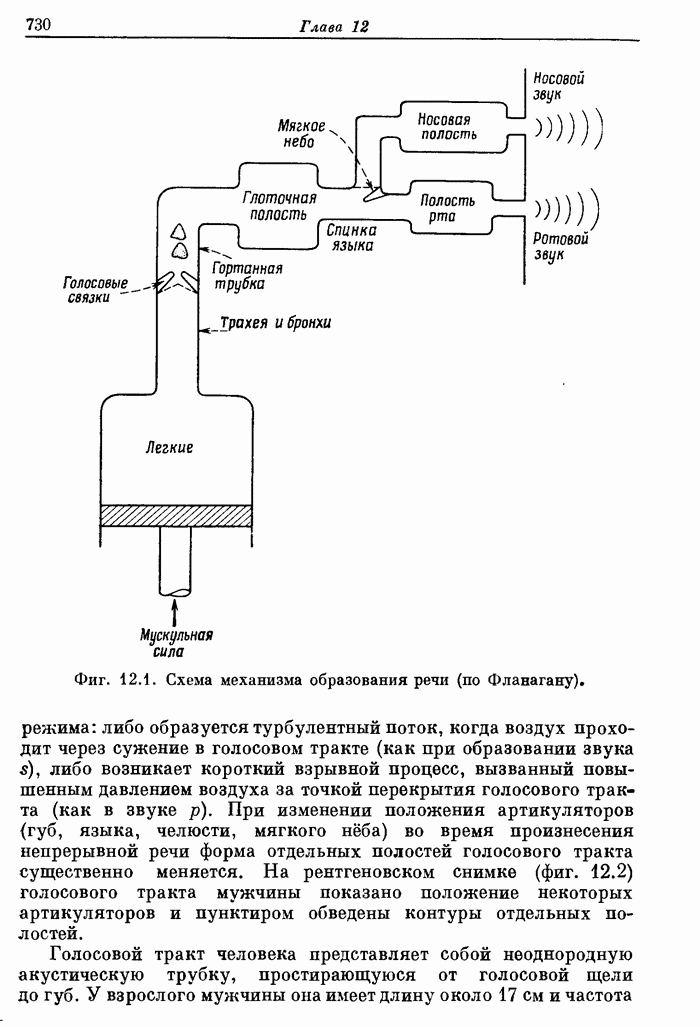
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
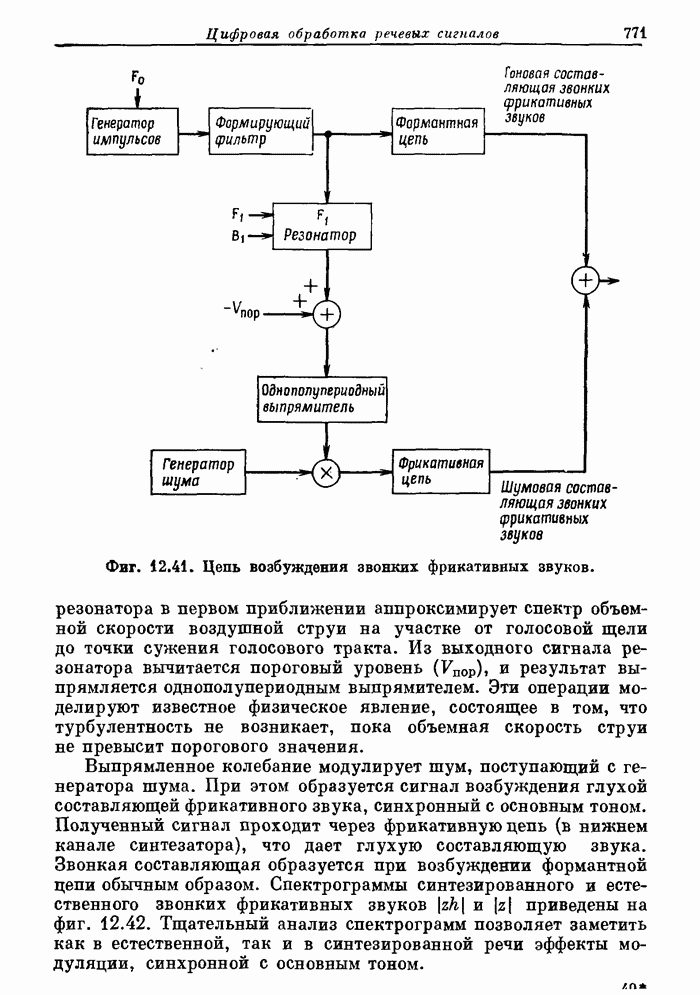
- 12.16. Цепь возбуждения звонких фрикативных звуков
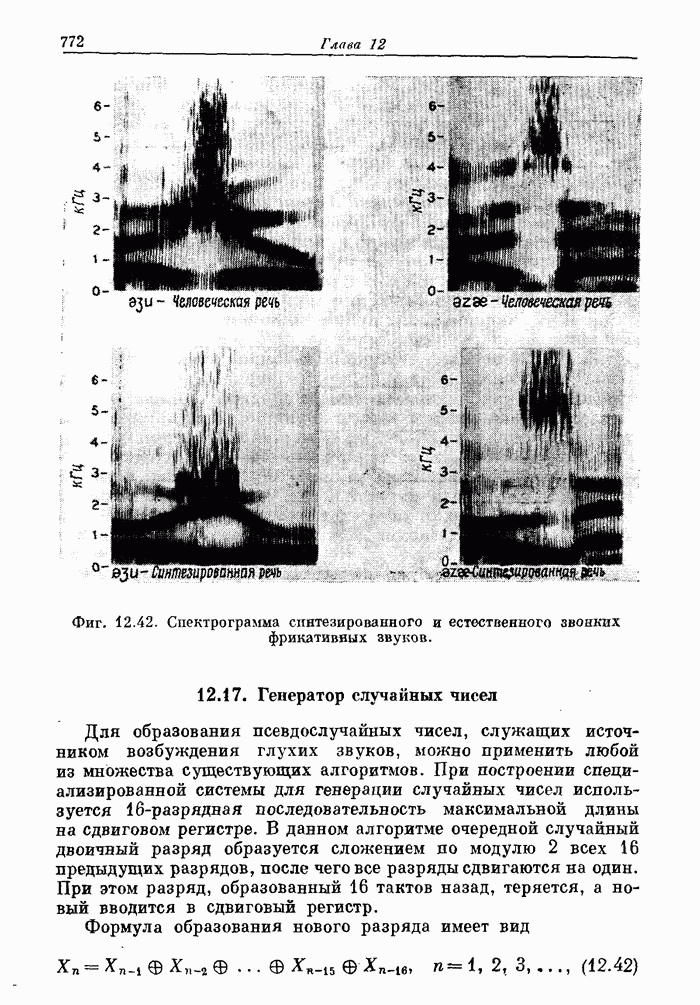
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
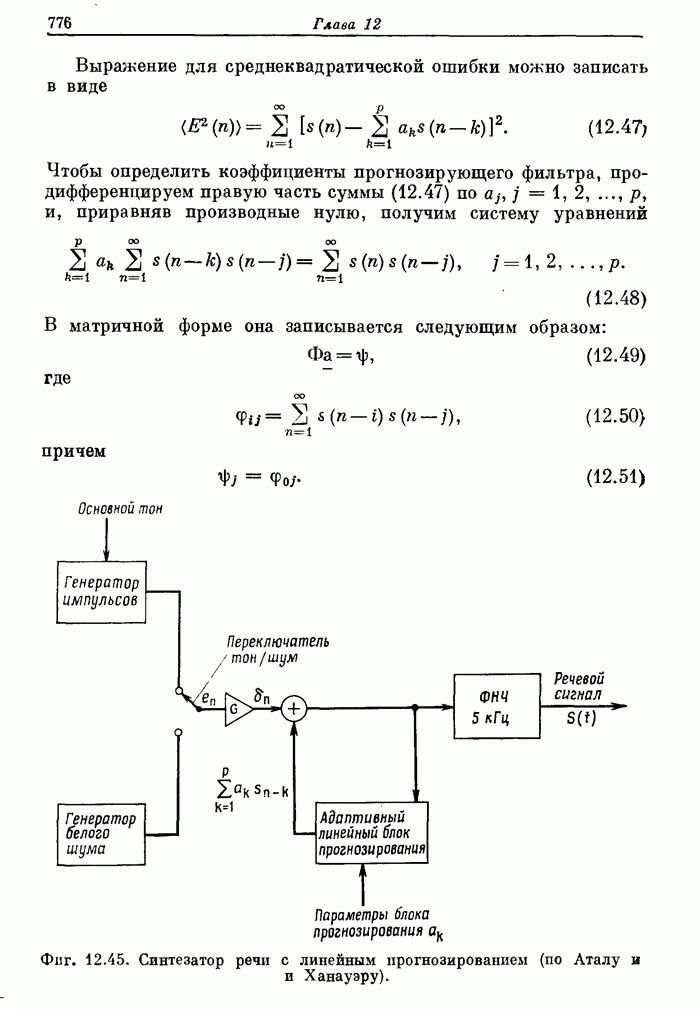
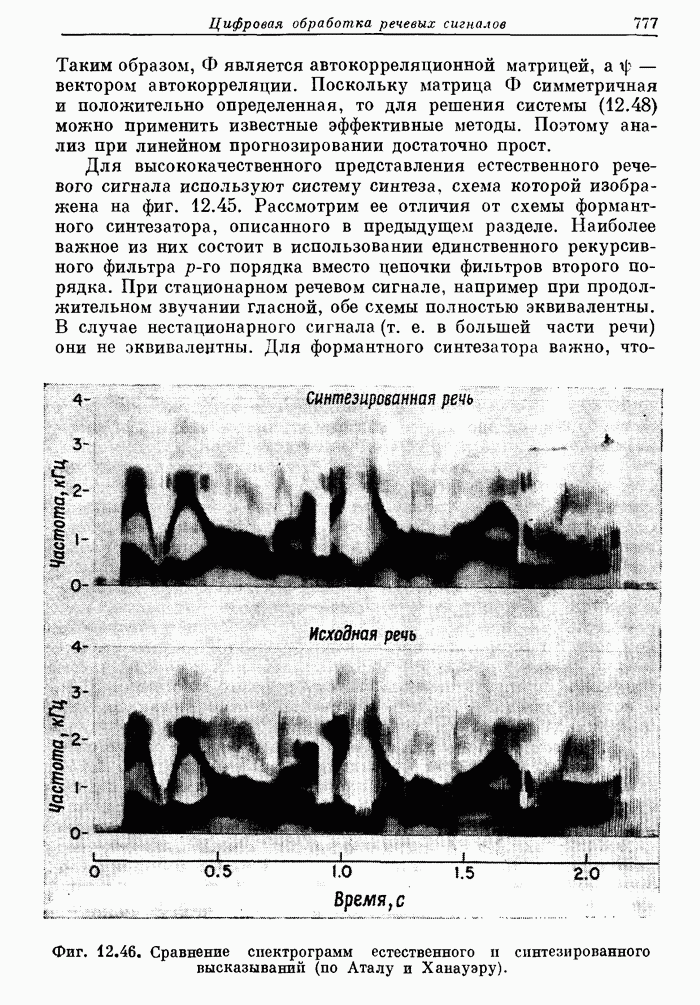
- 12.19. Линейное прогнозирование речи
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
- 13.3. Выбор сигналов и функция неопределенности
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение