| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.8. Единый подход к алгоритмам БПФ
Существует много различных алгоритмов БПФ, однако оказывается, что все они могут быть получены с помощью последовательного применения единственной операции, а именно представления одномерного массива чисел двумерным. Этот единый подход и будет описан в настоящем разделе, но сначала рассмотрим некоторые вопросы терминологического характера.
При вычислении  -точечного ДПФ
-точечного ДПФ  -точечной последовательности целое N может быть либо простым, либо составным числом (до сих пор считалось, что N состоит из большого числа сомножителей и равно степени 2). Если N простое, его нельзя разложить на произведение меньших целых чисел. В этом случае одномерный сигнал
-точечной последовательности целое N может быть либо простым, либо составным числом (до сих пор считалось, что N состоит из большого числа сомножителей и равно степени 2). Если N простое, его нельзя разложить на произведение меньших целых чисел. В этом случае одномерный сигнал  невозможно представить в виде двумерного массива, поэтому для такого сигнала не существует алгоритма БПФ. В большинстве практических задач вполне допустимо искусственное удлинение обрабатываемой последовательности путем добавления нулей, приводящее к тому, что результирующий спектр представляет собой некоторую интерполяцию спектра неудлиненной последовательности.
невозможно представить в виде двумерного массива, поэтому для такого сигнала не существует алгоритма БПФ. В большинстве практических задач вполне допустимо искусственное удлинение обрабатываемой последовательности путем добавления нулей, приводящее к тому, что результирующий спектр представляет собой некоторую интерполяцию спектра неудлиненной последовательности.
Пусть, например, N = 60. Это число можно представить как произведение меньших чисел различным образом:  и т. д. В зависимости от порядка следования сомножителей и их общего количества могут быть получены различные формы алгоритма БПФ. Для характеристики разложения обычно используется понятие «основание». Понятие «смешанное основание» означает, что не все сомножители N одинаковы. Для N = 60 все формы алгоритма БПФ имеют смешанные основания. Если N можно представить в виде произведения одинаковых сомножителей
и т. д. В зависимости от порядка следования сомножителей и их общего количества могут быть получены различные формы алгоритма БПФ. Для характеристики разложения обычно используется понятие «основание». Понятие «смешанное основание» означает, что не все сомножители N одинаковы. Для N = 60 все формы алгоритма БПФ имеют смешанные основания. Если N можно представить в виде произведения одинаковых сомножителей  , то соответствующий алгоритм называют алгоритмом БПФ с основанием
, то соответствующий алгоритм называют алгоритмом БПФ с основанием  . Например, если
. Например, если  то получаются рассмотренные в предыдущих разделах главы алгоритмы БПФ с основанием 2. Если же N записать как 64 = 8x8, то получится алгоритм БПФ с основанием 8.
то получаются рассмотренные в предыдущих разделах главы алгоритмы БПФ с основанием 2. Если же N записать как 64 = 8x8, то получится алгоритм БПФ с основанием 8.
Очень важно отметить, что разложение числа на множители можно выполнить различйыми способами. Так, N = 60 можно представить как 12 х 5, а затем 12 — как 4 х 3. С другой стороны, можно было бы записать  , далее
, далее  . Таким образом, для выявления общих закономерностей следует провести тщательный анализ свойств разложения очередного числа на два сомножителя. Возьмем в качестве примера снова N 60 и запишем одно из возможных разложений обрабатывавмого массива в виде матрицы из (5x12) номеров отсчетов сигнала:
. Таким образом, для выявления общих закономерностей следует провести тщательный анализ свойств разложения очередного числа на два сомножителя. Возьмем в качестве примера снова N 60 и запишем одно из возможных разложений обрабатывавмого массива в виде матрицы из (5x12) номеров отсчетов сигнала:

Далее, поскольку столбцы содержат по 5 (т. е. простое число) отсчетов, они больше не могут быть разложены. Однако строки, состоящие из 12 отсчетов, можно представить в виде матриц размером (3x4). Например, первая строка будет иметь вид

Остальные строки можно представить аналогично. Итак, теперь нужно установить, каким образом, оперируя с двумерным массивом, можно получить ДПФ исходного одномерного массива.
Для получения основного результата будем считать, что входные отсчеты пронумерованы по строкам и по столбцам, поэтому их номера могут быть представлены следующими парами чисел:

Далее, пусть текущий номер столбца равен  — текущий номер строки. Если исходный номер отсчета обозначить через
— текущий номер строки. Если исходный номер отсчета обозначить через  , то
, то

где М—число столбцов. L-число строк (в данном примере М = 12, L = 5).
Допустим, что мы можем найти ДПФ двумерного массива с двойными номерами, тогда результат должен иметь вид двумерного массива с двойными номерами. Пусть  — переменные исходного сигнала, а
— переменные исходного сигнала, а  — переменные двумерного ДПФ по столбцам и строкам, которые преобразуются в одну переменную следующим образом:
— переменные двумерного ДПФ по столбцам и строкам, которые преобразуются в одну переменную следующим образом:

Теперь коэффициенты одномерного ДПФ  можно выразить через преобразование массива
можно выразить через преобразование массива  , используя простую подстановку формул (6.28) и (6.29) в выражение для ДПФ (6.2), что дает
, используя простую подстановку формул (6.28) и (6.29) в выражение для ДПФ (6.2), что дает

Разлагая  с учетом того, что
с учетом того, что  и располагая соответствующие переменные под знаками суммирования, преобразуем формулу (6.30) к следующему виду:
и располагая соответствующие переменные под знаками суммирования, преобразуем формулу (6.30) к следующему виду:

Эта формула при правильной интерпретации содержит все необходимые сведения, позволяющие связать преобразование одномерного массива с преобразованием того же массива, представленного в виде двумерной матрицы. Заметим прежде всего, что внутренняя сумма представляет собой ДПФ  столбца исходного массива с ядром преобразования
столбца исходного массива с ядром преобразования  . Таким образом, можно сформулировать первый шаг последовательности расчета
. Таким образом, можно сформулировать первый шаг последовательности расчета  :
:
1. Вычислить  -точечные ДПФ всех столбцов. Результат является функцией s и
-точечные ДПФ всех столбцов. Результат является функцией s и  , причем
, причем  меняется от 0 до
меняется от 0 до  .
.
Обозначим его через  и перепишем формулу (6.31):
и перепишем формулу (6.31):

Отсюда следует, что второй шаг вычисления  сводится к следующему:
сводится к следующему:
2. Найти новый массив  , умножая каждый элемент
, умножая каждый элемент  на поворачивающий множитель
на поворачивающий множитель  .
.
Теперьформула (6.32) принимает вид

Она представляет М-точечные ДПФ каждой из строк с номерами s. Поэтому последний шаг алгоритма заключается в следующем:
3. Вычислить М-точечные ДПФ всех строк матрицы  с ядром преобразования
с ядром преобразования  .
.
Описанная методика напоминает вычисление двумерного ДПФ, когда сначала вычисляются ДПФ строк, а затем столбцов, но шаг 2 отсутствует. Разделимость ядра преобразования с более высокой размерностью и является причиной того, что при расчете ДПФ с более высокой размерностью требуется меньше операций, чем при расчете одномерного ДПФ при одинаковом общем числе отсчетов.
Здесь важно отметить, что после введения поворачивающих множителей, т. е. после второго шага описанной выше методики, способы расчета двумерного ДПФ и одномерного ДПФ массива, представленного в виде двумерной матрицы, становятся эквивалетными, причем при каждом таком представлении для выполнения шага 2 требуется дополнительно до N умножений. Более подробно вопрос о времени вычисления будет рассмотрен ниже в этом разделе.
Следует отметить, что изменение порядка суммирования в формуле (6.30) на обратный дает

так что порядок вычисления  становится следующим:
становится следующим:
1. Умножить отсчеты сигнала  на поворачивающие множители
на поворачивающие множители  .
.
2. Вычислить М-точечные ДПФ всех строк.
3. Вычислить L-точечные ДПФ всех столбцов.
В целом методика вычисления преобразования идентична рассмотренной ранее, но отдельные операции выполняются в другом порядке: умножения на поворачивающие множители здесь предшествуют вычислению ДПФ строк, тогда как раньше они выполнялись после вычисления ДПФ столбцов. Эти отличия не только напоминают, но и действительно связаны с обсуждавшимся выше различием между алгоритмами БПФ с основанием 2 при прореживании по времени и по частоте.
Отметим еще одно важное свойство методики преобразования, вытекающее из формулы (6.30), в которой переменные  являются номерами столбцов, а
являются номерами столбцов, а  — номерами строк. При увеличении
— номерами строк. При увеличении  на единицу номер отсчета исходного массива
на единицу номер отсчета исходного массива  также возрастает на 1, тогда как при увеличении на 1 номера столбца преобразованного массива
также возрастает на 1, тогда как при увеличении на 1 номера столбца преобразованного массива  аргумент
аргумент  возрастает на L. Это означает, что в результате преобразования номера строк и столбцов меняются местами. Последнее обстоятельство настолько важно, что для его иллюстрации приведем пример вычисления 15-точечного ДПФ с использованием разложения (3x5). Исходную матрицу сигнала можно записать следующим образом:
возрастает на L. Это означает, что в результате преобразования номера строк и столбцов меняются местами. Последнее обстоятельство настолько важно, что для его иллюстрации приведем пример вычисления 15-точечного ДПФ с использованием разложения (3x5). Исходную матрицу сигнала можно записать следующим образом:


Результирующая матрица гармоник ДПФ будет иметь вид
Таблица 6.1

Если N = 30 = 5x6 = 5x2x3, то основную теорему разложения можно использовать дважды, начав с разложения (5x6), а затем выполнить шеститочечные ДПФ, используя для этого разложение (2x3). Этот случай целесообразно рассмотреть на конкретном примере. Другие N читатель может проанализировать самостоятельно. Начнем с нумерации 30 отсчетов исходной матрицы сигнала:
Матрица 

Теперь рассчитаем шесть пятиточечных ДПФ всех столбцов; умножив элементы полученной матрицы на поворачивающие множители, получим новую матрицу  :
:

Далее, вместо того чтобы непосредственно вычислять пять шеститочечных ДПФ, представим каждую строку, содержащую шесть элементов, в виде матрицы размером  Так, первые две строки матрицы
Так, первые две строки матрицы  переписываются следующим образом: Строка 1
переписываются следующим образом: Строка 1

Строка 2

Таким образом, искомые шеститочечные ДПФ можно найти, вычисляя ДПФ столбцов, содержащих по два элемента, умножая результаты ДПФ на поворачивающие множители и затем рассчитывая ДПФ строк, содержащих по три элемента. Вычисление заканчивается, когда таким образом будут преобразованы все пять матриц размера (2x3).
Перечислим все операции, требуемые для выполнения 30-точечного ДПФ с использованием разложения (5x2x3):
1) 6 пятиточечных преобразований;
2) 30 умножений на поворачивающие множители;
3) 15 двухточечных преобразований;
4) 30 умножений на поворачивающие множители;
5) 10 трехточечных преобразований.
Используя этот пример, можно рассчитать, сколько операций необходимо для общего случая  :
:
1) LM -точечных преобразований;
2) LMP умножений на поворачивающие множители;
3) MP L-точечных преобразований;
4) LMP умножений на поворачивающие множители;
5) LP М-точечных преобразований.
Чтобы оценить уменьшение объема вычислений за счет использования алгоритма БПФ, рассмотрим несколько частных случаев. Прежде всего положим  где L и М — простые числа, большие 2. Из формулы (6.2) следует, что М-точечное ДПФ требует
где L и М — простые числа, большие 2. Из формулы (6.2) следует, что М-точечное ДПФ требует  «операций», состоящих из умножения и сложения в комплексной форме. Учитывая это, получим следующее общее число операций для разложения вида
«операций», состоящих из умножения и сложения в комплексной форме. Учитывая это, получим следующее общее число операций для разложения вида  :
:

Член LM учитывает количество умножений на поворачивающие множители, выполняемых между преобразованиями строк и столбцов (строго говоря, эти LM действий состоят только из комплексного умножения и поэтому требуют несколько меньше времени, чем вся «операция»). Ясно, что при выполнении  -точечного ДПФ самым громоздким прямым методом потребовалось бы
-точечного ДПФ самым громоздким прямым методом потребовалось бы  операций. Таким образом, с помощью формулы (6.34) можно оценить выигрыш во времени вычислений, характерный для преобразования с использованием разложения. Если, например,
операций. Таким образом, с помощью формулы (6.34) можно оценить выигрыш во времени вычислений, характерный для преобразования с использованием разложения. Если, например,  то
то  относится к числу операций при прямом расчете ДПФ как 17:55. Очевидно, что с ростом N выигрыш увеличивается. Например, если N = 15, L = 5, М = 3, то
относится к числу операций при прямом расчете ДПФ как 17:55. Очевидно, что с ростом N выигрыш увеличивается. Например, если N = 15, L = 5, М = 3, то  будет относиться к числу операций при прямом расчете ДПФ как 9:15.
будет относиться к числу операций при прямом расчете ДПФ как 9:15.
Рассмотрим теперь случай, когда N можно разложить на три простых целых сомножителя, т. е.  . Нетрудно показать, что в этом случае число операций равно
. Нетрудно показать, что в этом случае число операций равно

Например, при  относится к числу операций при прямом расчете ДПФ как
относится к числу операций при прямом расчете ДПФ как  , т. е. достигнуто уменьшение числа операций почти на порядок. Чтобы оценить выигрыш в общем случае, изменим обозначения и положим
, т. е. достигнуто уменьшение числа операций почти на порядок. Чтобы оценить выигрыш в общем случае, изменим обозначения и положим  . Тогда
. Тогда

С помощью полученных формул можно достаточно точно определить величину выигрыша при условии, что все числа  простые (и не равные 2), так как только в этом случае общее число операций при
простые (и не равные 2), так как только в этом случае общее число операций при  -точечном преобразовании равно N. Если же числа
-точечном преобразовании равно N. Если же числа  не являются простыми или
не являются простыми или  необходимо быть очень осторожными в оценках. Например, как было показано выше, при двухточечном ДПФ (т. е.
необходимо быть очень осторожными в оценках. Например, как было показано выше, при двухточечном ДПФ (т. е.  ) умножения вообще не используются. Это же справедливо и для
) умножения вообще не используются. Это же справедливо и для  . При
. При  число умножений существенно меньше 64. В связи с этим при разложении N на такие сомножители, как 2, 4 или 8, полученные выше формулы непригодны. Рассмотрим, например, N, равное степени 2, скажем
число умножений существенно меньше 64. В связи с этим при разложении N на такие сомножители, как 2, 4 или 8, полученные выше формулы непригодны. Рассмотрим, например, N, равное степени 2, скажем  . Тогда член формулы (6.36), учитывающий двухточечные ДПФ, включает только комплексные сложения и вычитания, тогда как член
. Тогда член формулы (6.36), учитывающий двухточечные ДПФ, включает только комплексные сложения и вычитания, тогда как член  учитывает умножения на поворачивающие множители. В зтом случае формула (6.36) становится весьма неудобной для оценок, поскольку приходится сопоставлять затраты времени на умножение и на сложение.
учитывает умножения на поворачивающие множители. В зтом случае формула (6.36) становится весьма неудобной для оценок, поскольку приходится сопоставлять затраты времени на умножение и на сложение.
Чтобы получить направленный граф (подобный графам на фиг. 6.3 и 6.11) для самого общего случая разложения, необходимо расширить круг обозначений, введенных на фиг. 6.3 и 6.11. Это сделано на фиг. 6.13, где 30-точечный массив представлен в виде двумерного массива, содержащего 5 строк и 6 столбцов, со следующими элементами (числа обозначают номера элементов исходного массива):

На первом этапе БПФ выполняются 6 пятиточечных ДПФ, так что незачерненные кружки на фиг. 6.13 обозначают полные ДПФ, размер которых равен числу линий, входящих в кружок и выходящих из него.

Фиг. 6.13. Направленный граф 30-точечного БПФ, основанного на последовательных прореживаниях за счет представления одномерных массивов двумерными.
Узлы направленного графа обозначают регистры, содержащие входные и выходные отсчеты ДПФ. Все выходные отсчеты ДПФ умножаются на поворачивающие множители; для обозначения этой операции введено 30 стрелок, около которых записаны значения коэффициентов W. Следующий зтап состоит в вычислении ДПФ всех строк. Поскольку строки содержат по 6 элементов, каждая из них может быть представлена в виде матрицы с 2 строками и 3 столбцами.
В примере, приведенном на фиг. 6.13, каждая шеститочечная строка преобразуется с помощью: 1) трех двухточечных ДПФ; 2) умножений на поворачивающие множители; 3) двух трехточечных ДПФ.
Отметим также следующую особенность обозначения. Строго говоря, каждая линия, выходящая из незачерненного кружка, должна иметь свою стрелку с коэффициентом W. Если, однако, учесть, что  , то такой поворачивающий множитель можно опустить. Во всех приводимых направленных графах (в том числе и на фиг. 6.3 и 6.11) авторы по своему усмотрению решали, ввести или опустить
, то такой поворачивающий множитель можно опустить. Во всех приводимых направленных графах (в том числе и на фиг. 6.3 и 6.11) авторы по своему усмотрению решали, ввести или опустить  . При нахождении поворачивающих множителей для второго этапа графа на фиг. 6.13 необходимо помнить, что для него коэффициент W равен TF, поэтому матрица поворачивающих множителей для каждой из прореживаемых строк исходной матрицы, содержащей 5 строк и 6 столбцов, имеет вид
. При нахождении поворачивающих множителей для второго этапа графа на фиг. 6.13 необходимо помнить, что для него коэффициент W равен TF, поэтому матрица поворачивающих множителей для каждой из прореживаемых строк исходной матрицы, содержащей 5 строк и 6 столбцов, имеет вид

В заключение осталось рассмотреть характер перестановки данных на фиг. 6.13. Если бы весь массив из 30 отсчетов был преобразован в матрицу размером (5x6) (и никак иначе), то строки и столбцы матрицы результатов оказались бы просто переставленными относительно исходной матрицы. Так как в действительности каждая строка также прореживалась, то это привело к дополнительной перестановке результатов. Окончательный порядок следования результатов ДПФ показан на фиг. 6.13.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
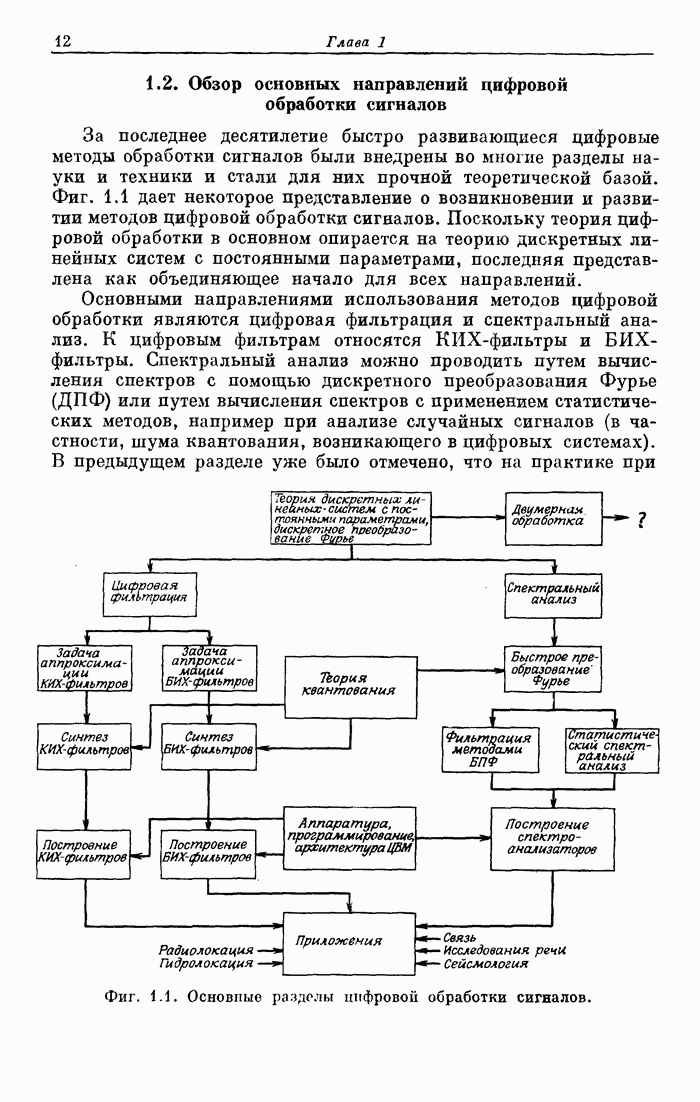
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
- 2.5. Физическая реализуемость. Устойчивость
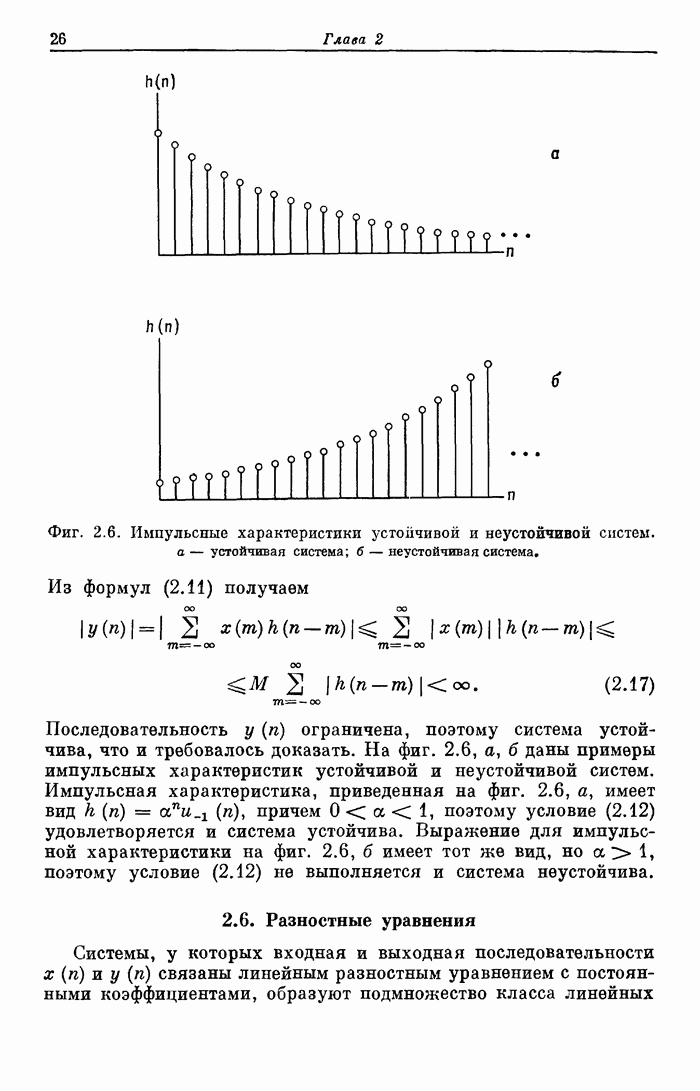
- 2.6. Разностные уравнения
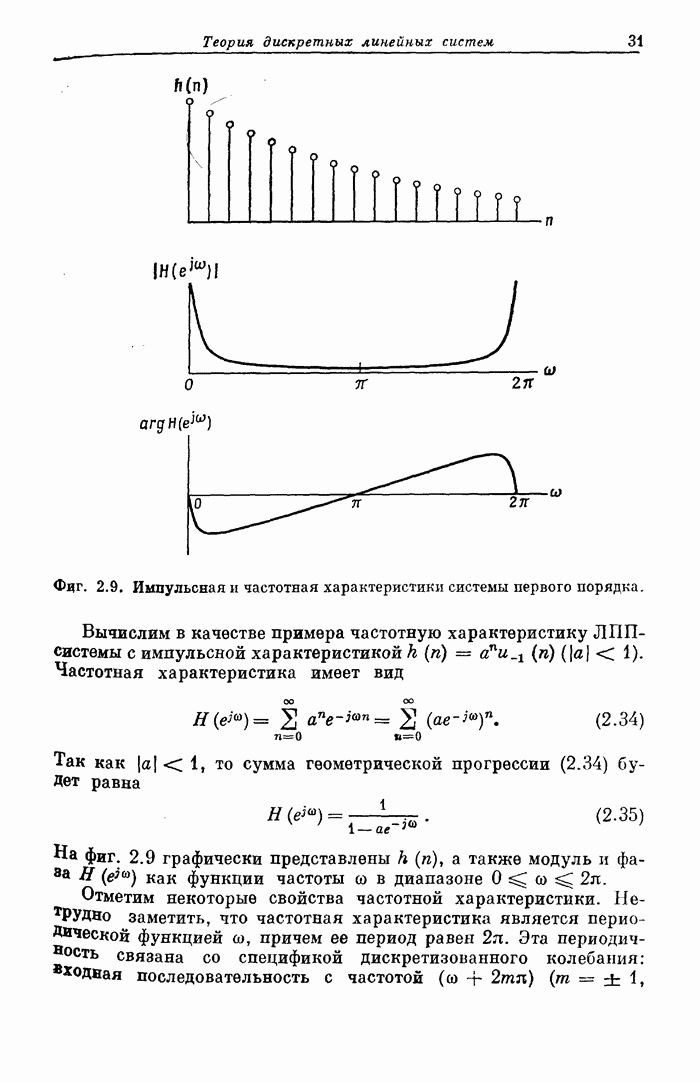
- 2.7. Частотная характеристика
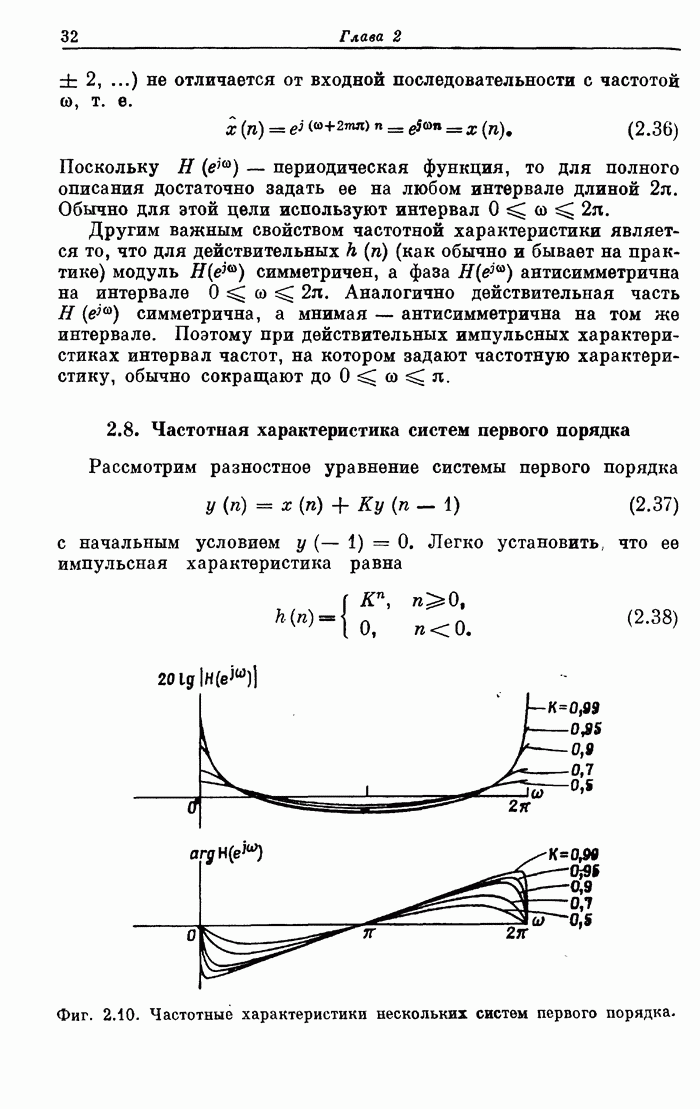
- 2.8. Частотная характеристика систем первого порядка
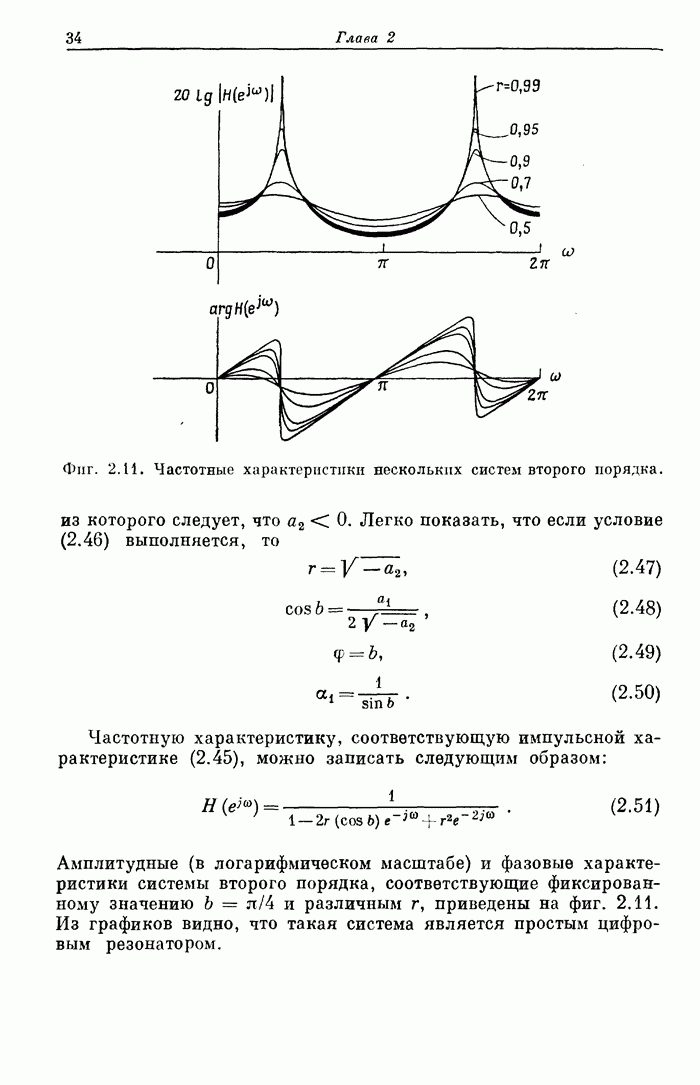
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
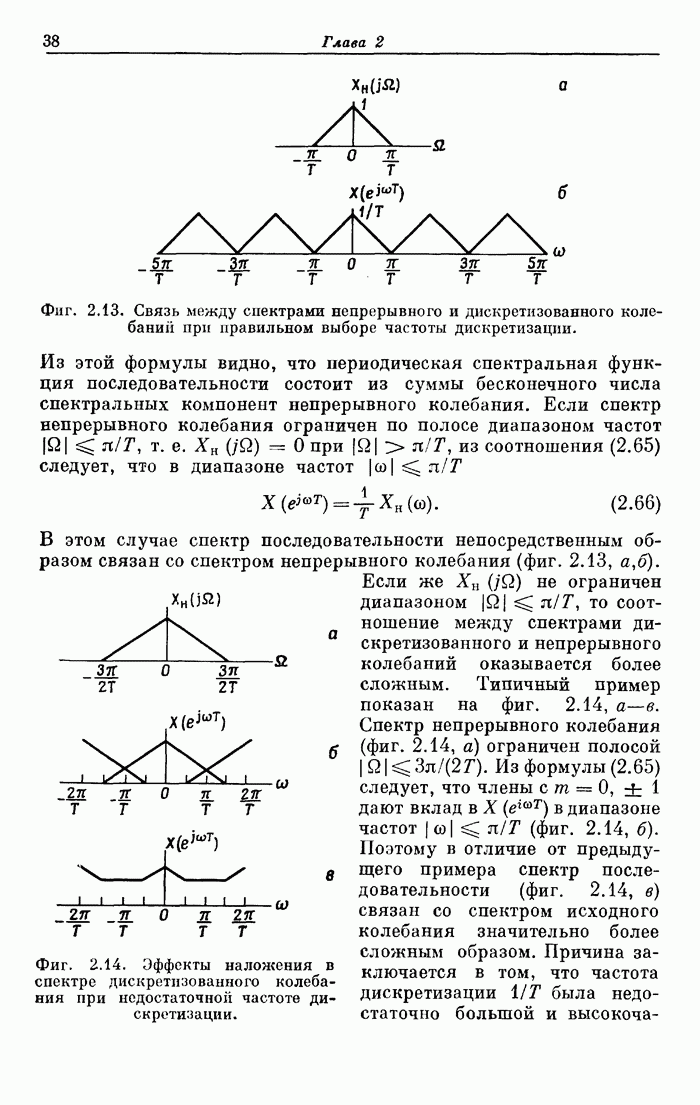
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
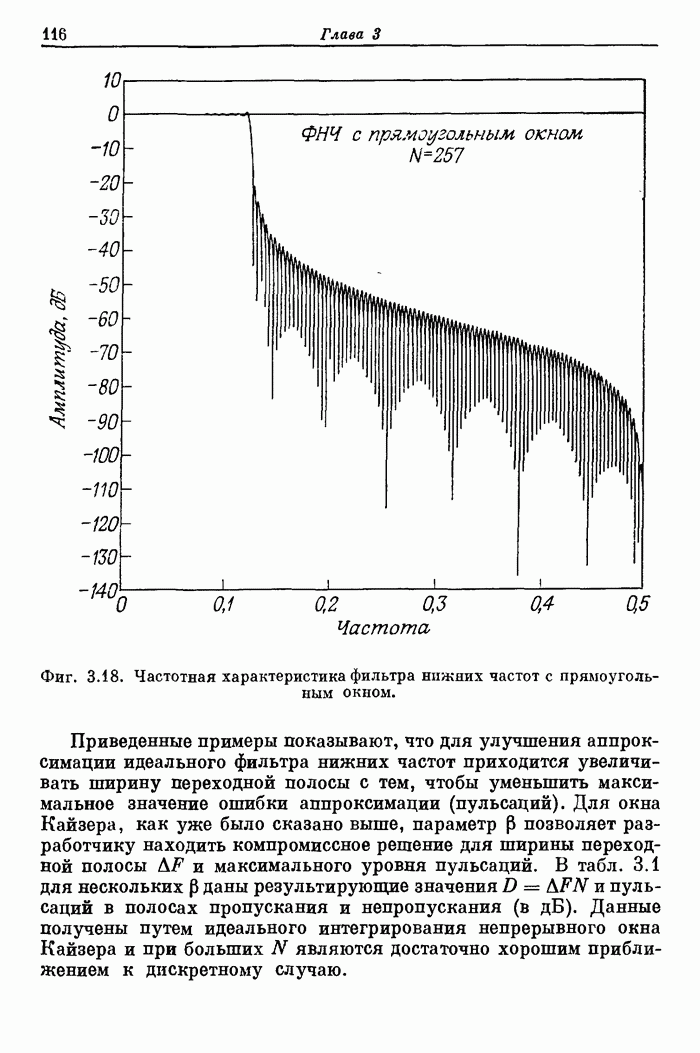
- 3.12. Примеры фильтров нижних частот с различными окнами
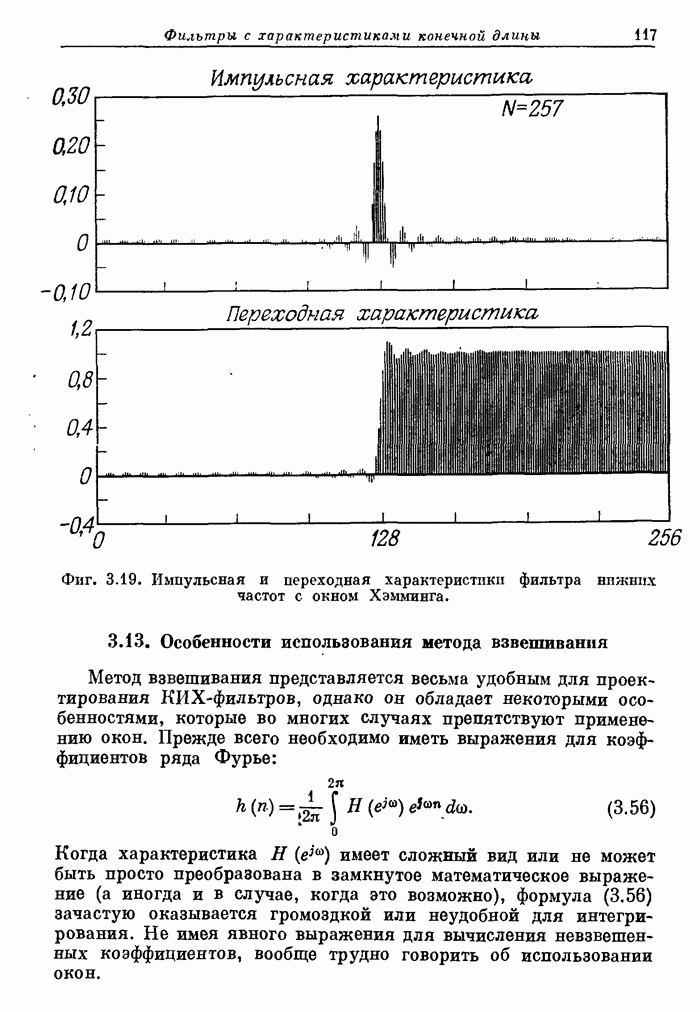
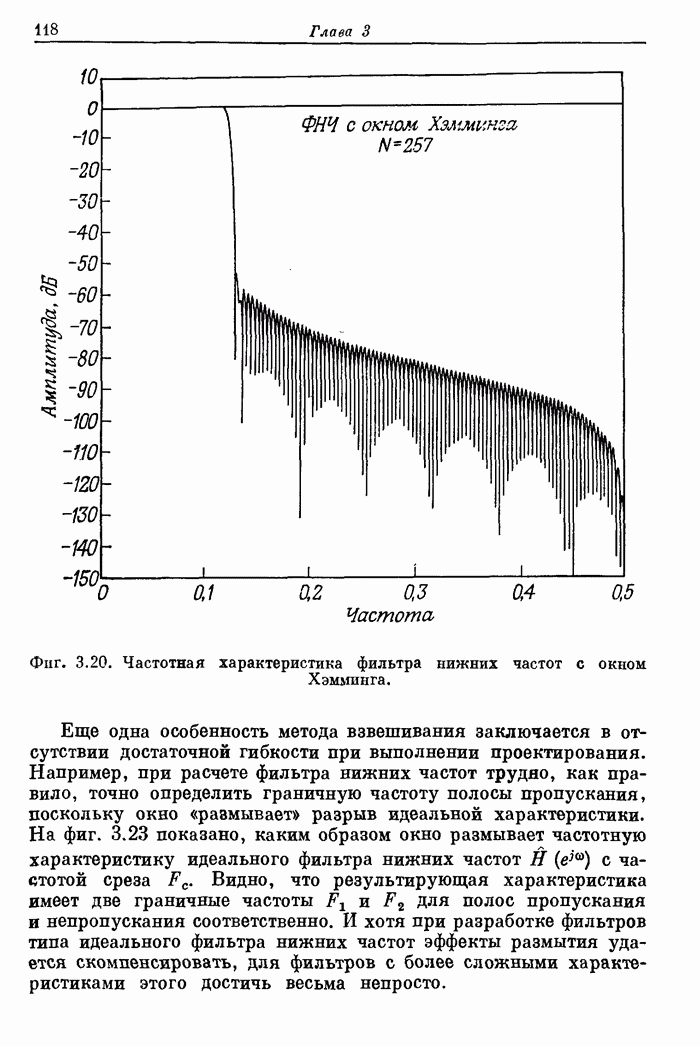
- 3.13. Особенности использования метода взвешивания
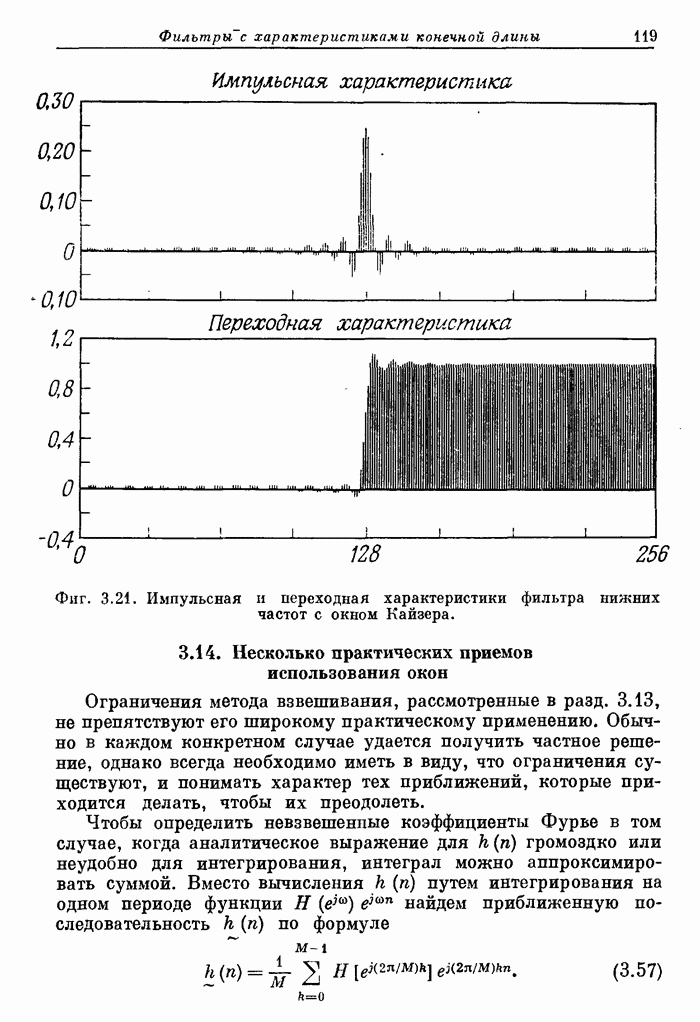
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
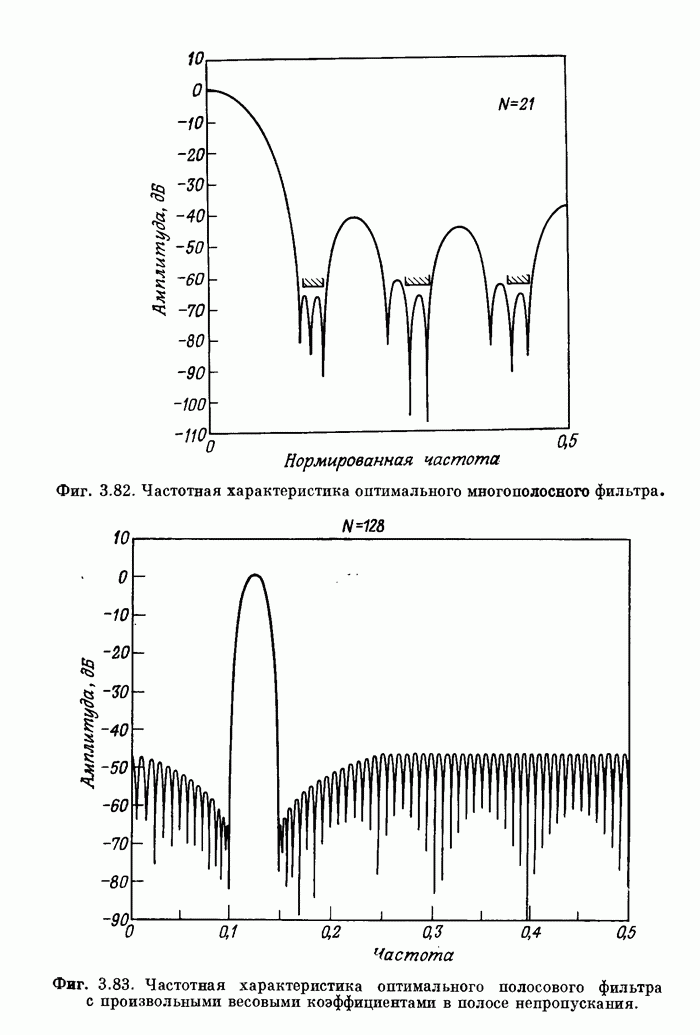
- 3.38. Многополосные оптимальные КИХ-фильтры
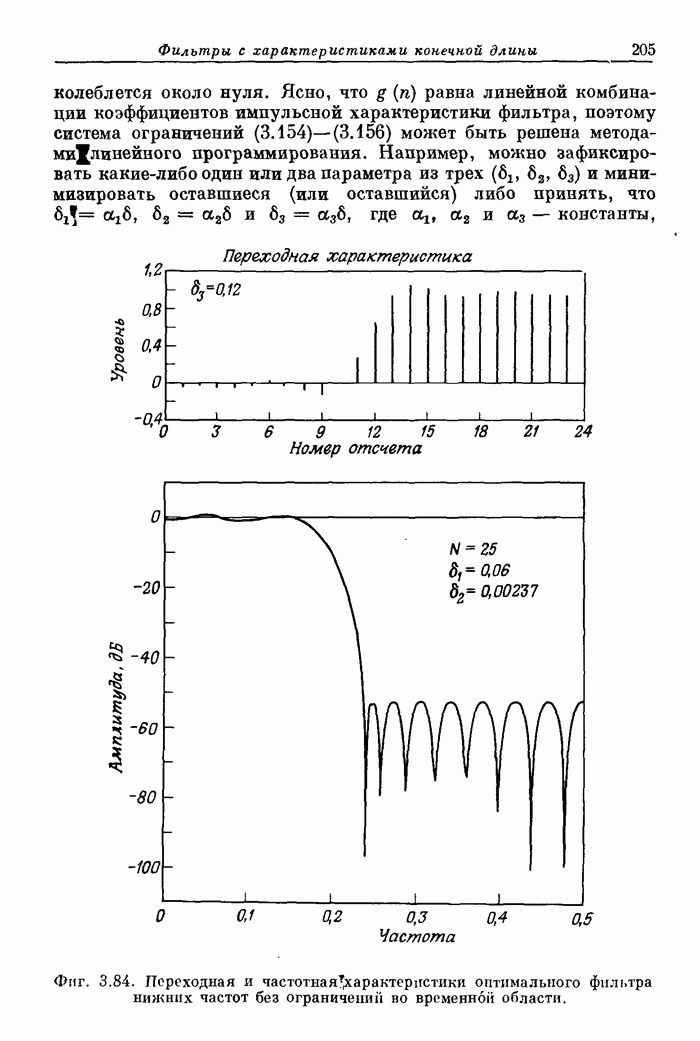
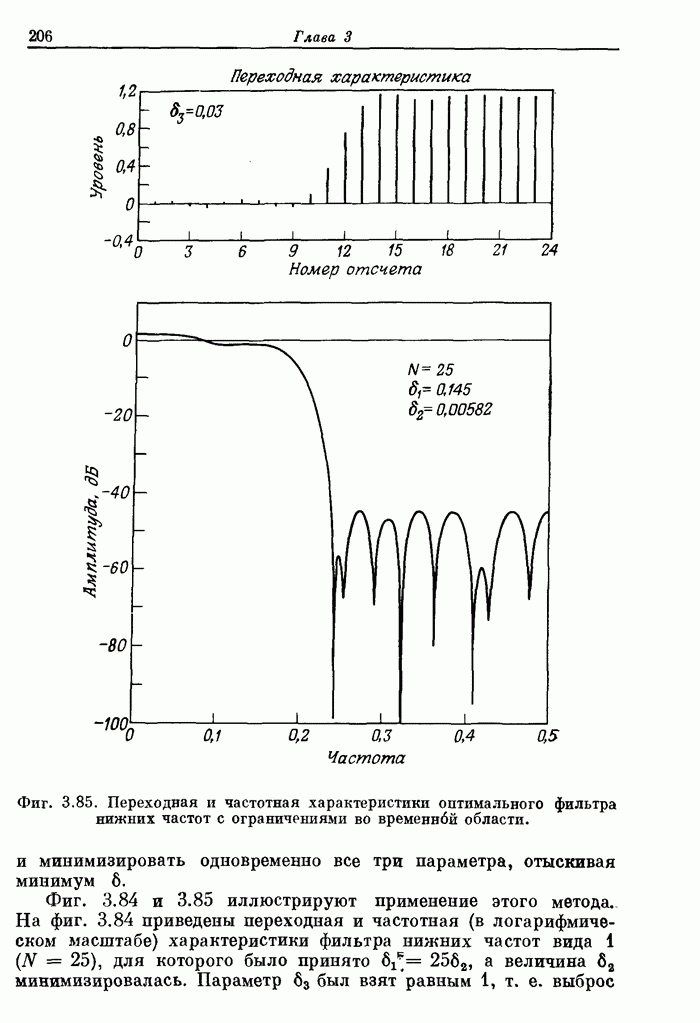
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
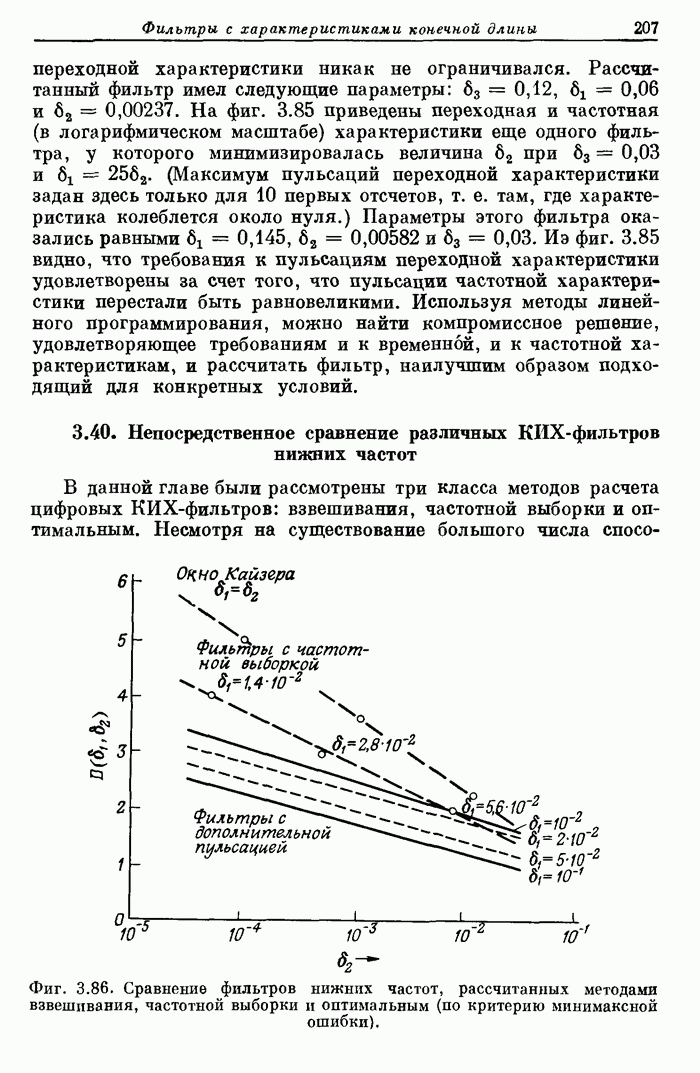
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
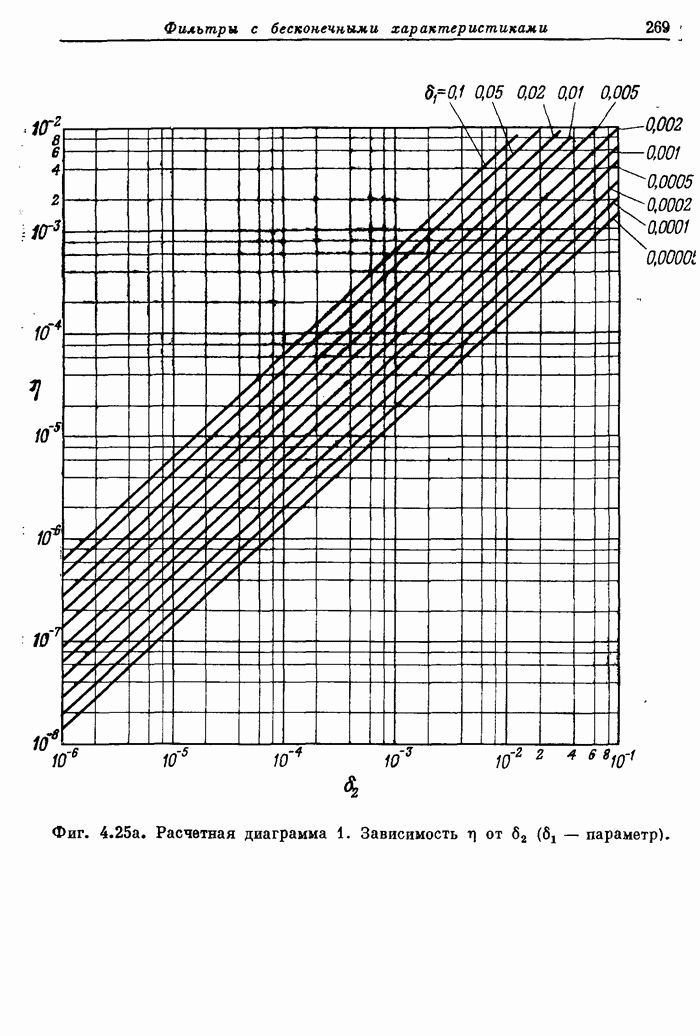
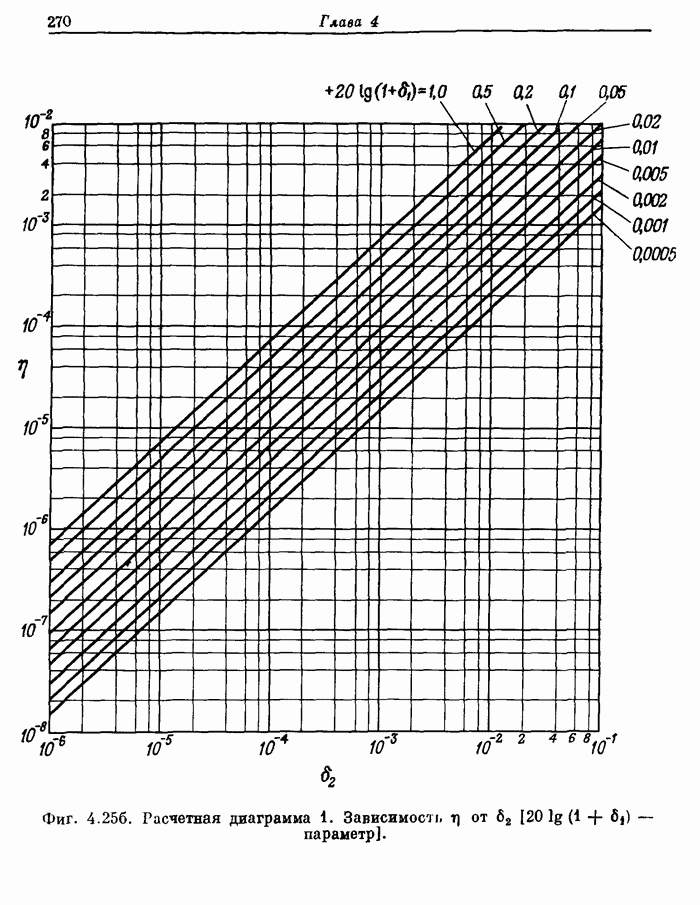
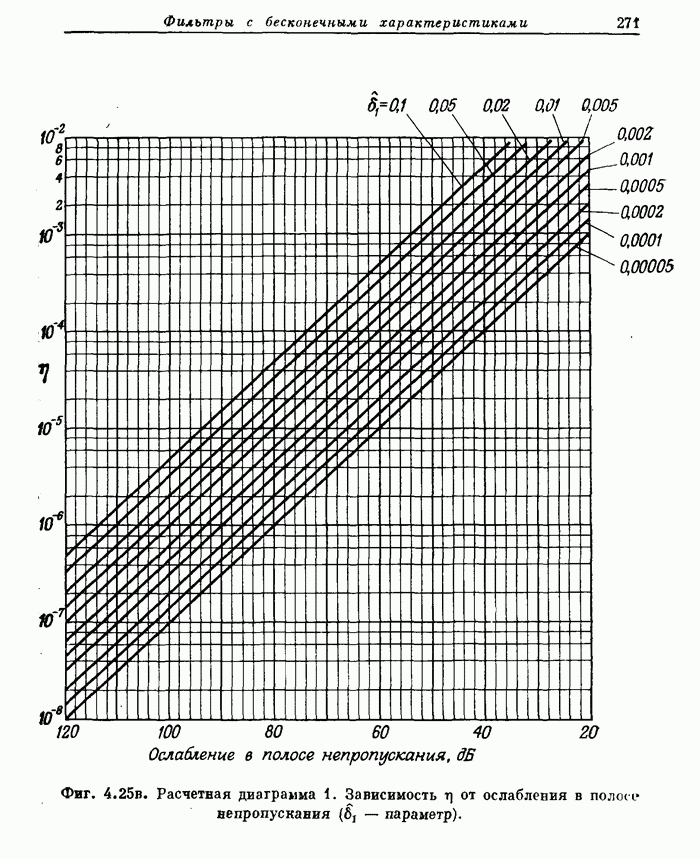
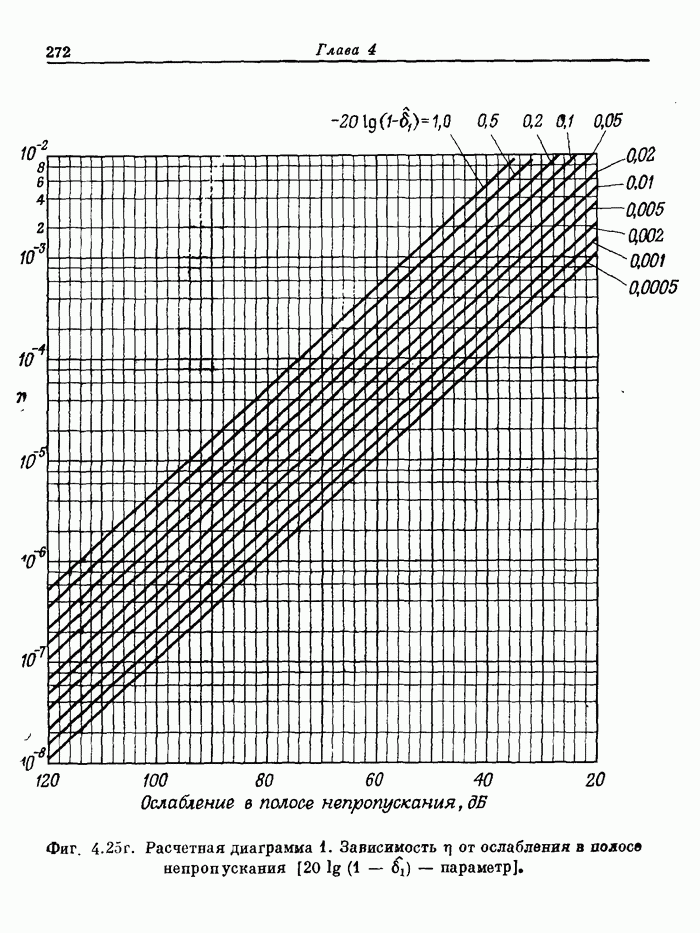
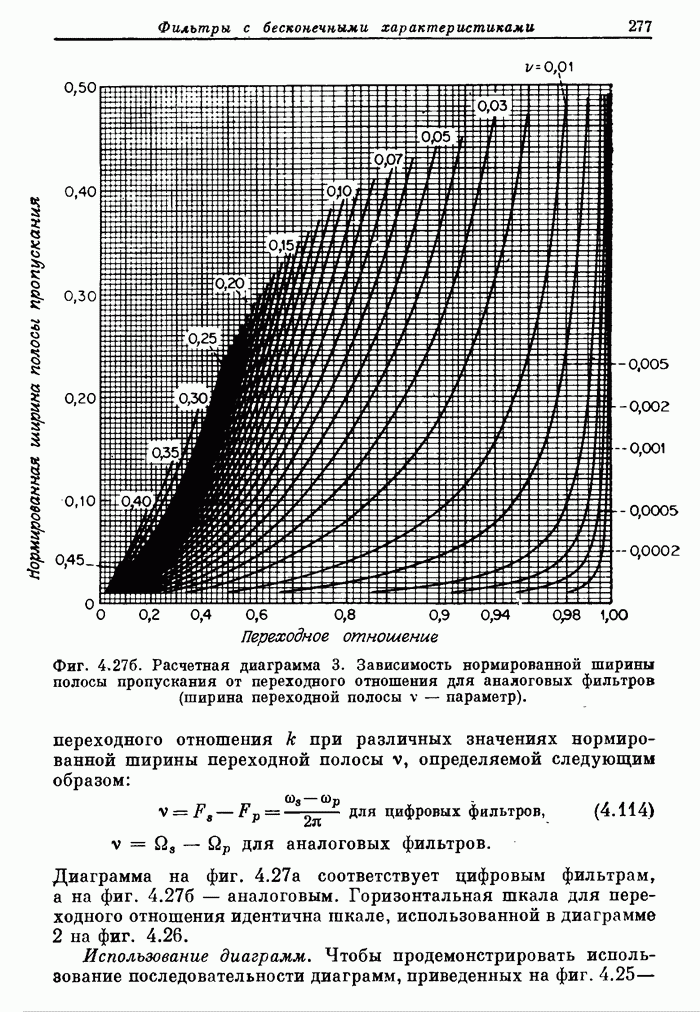
- 4.10. Расчетные диаграммы фильтров нижних частот
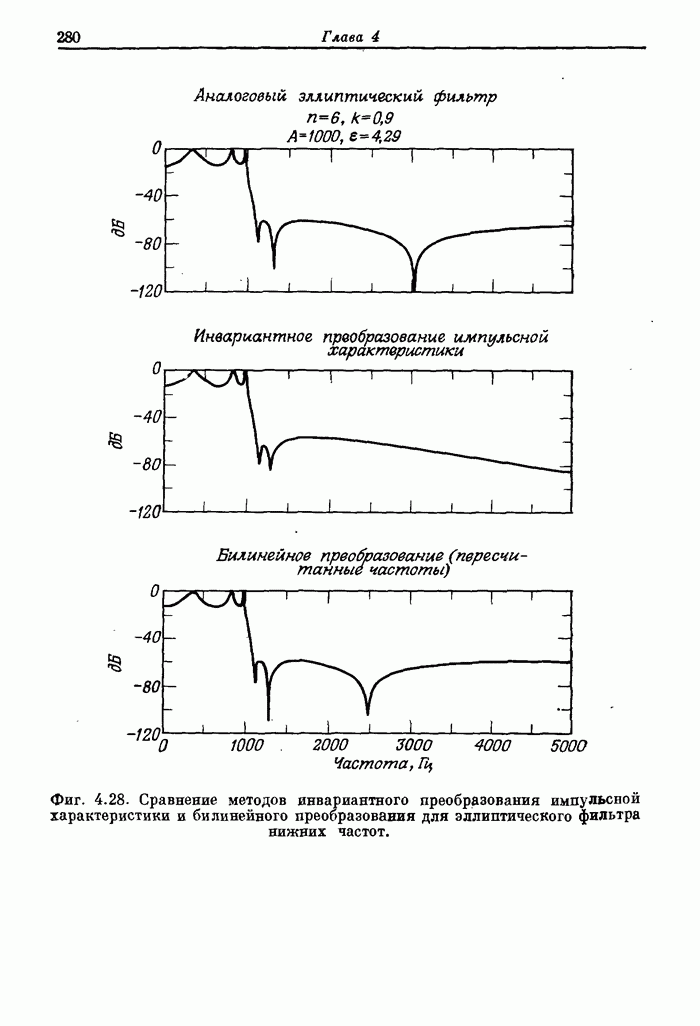
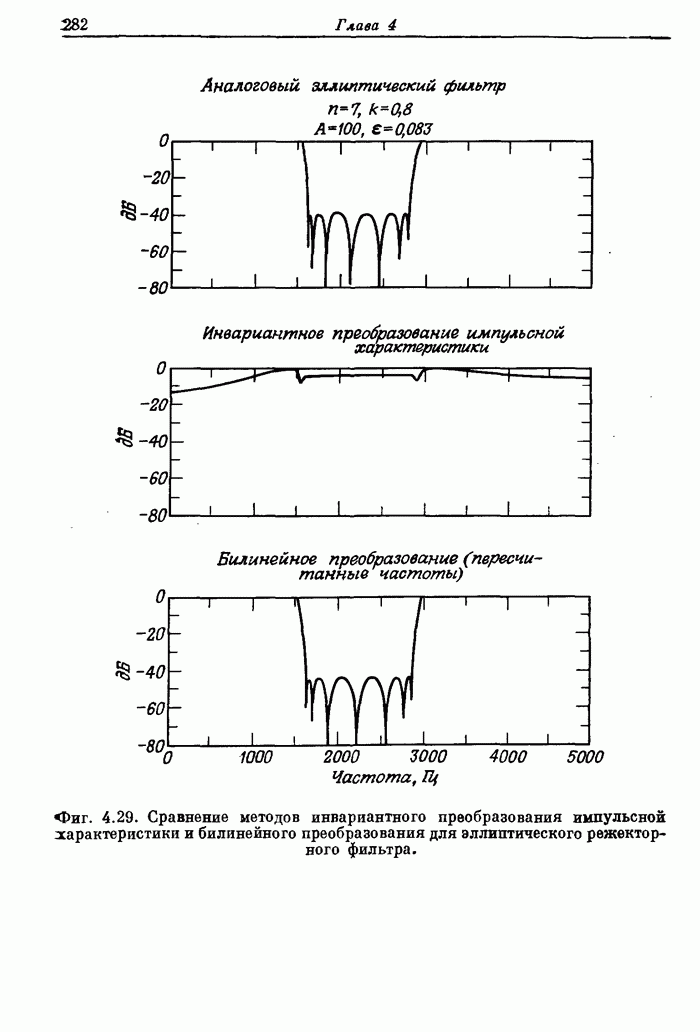
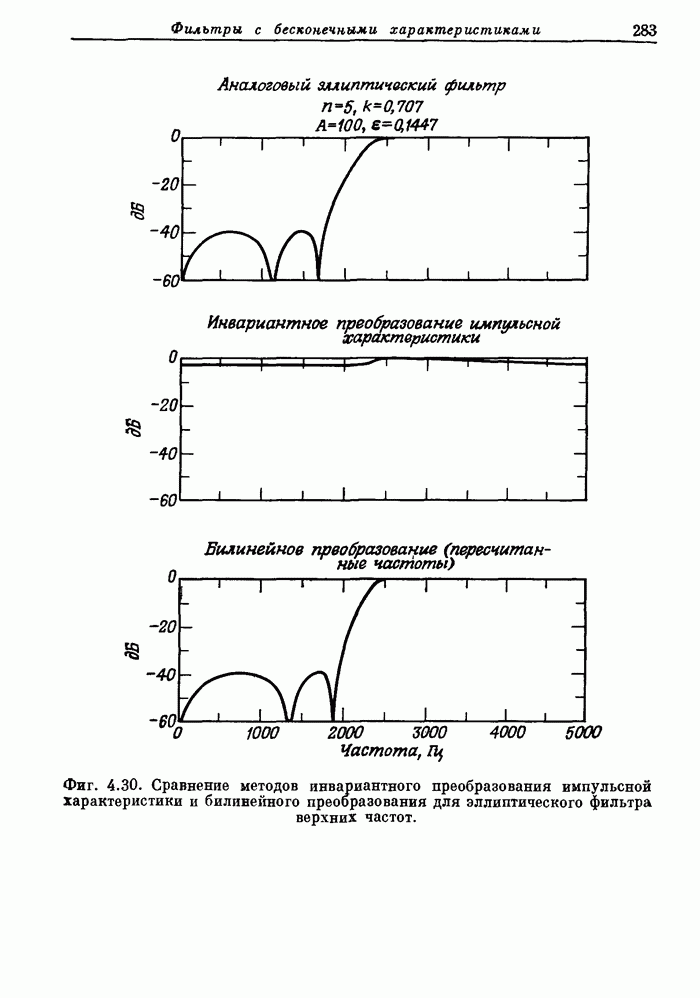
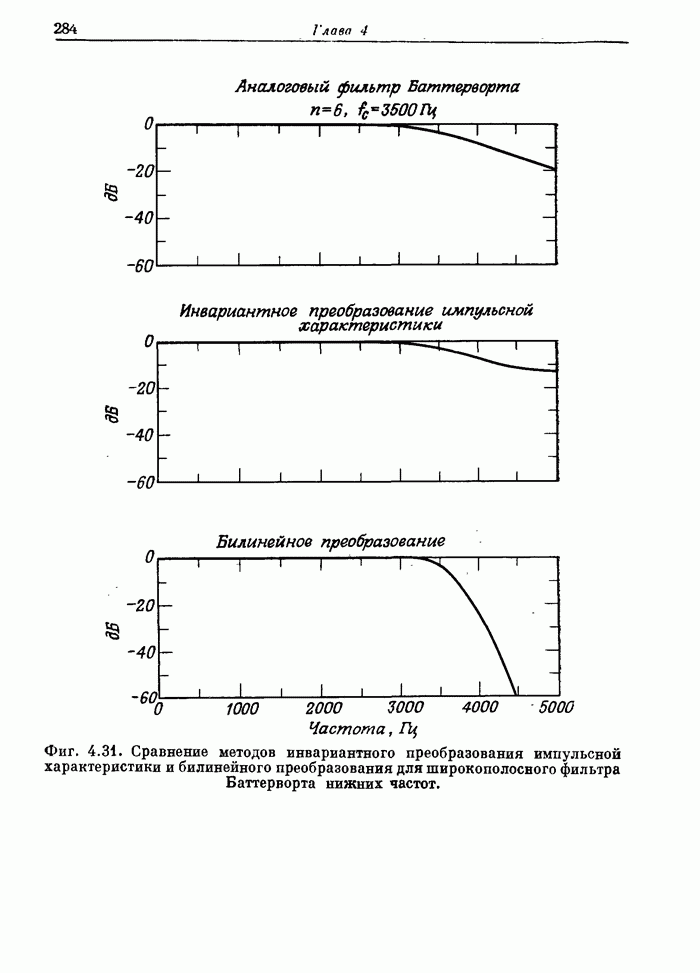
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
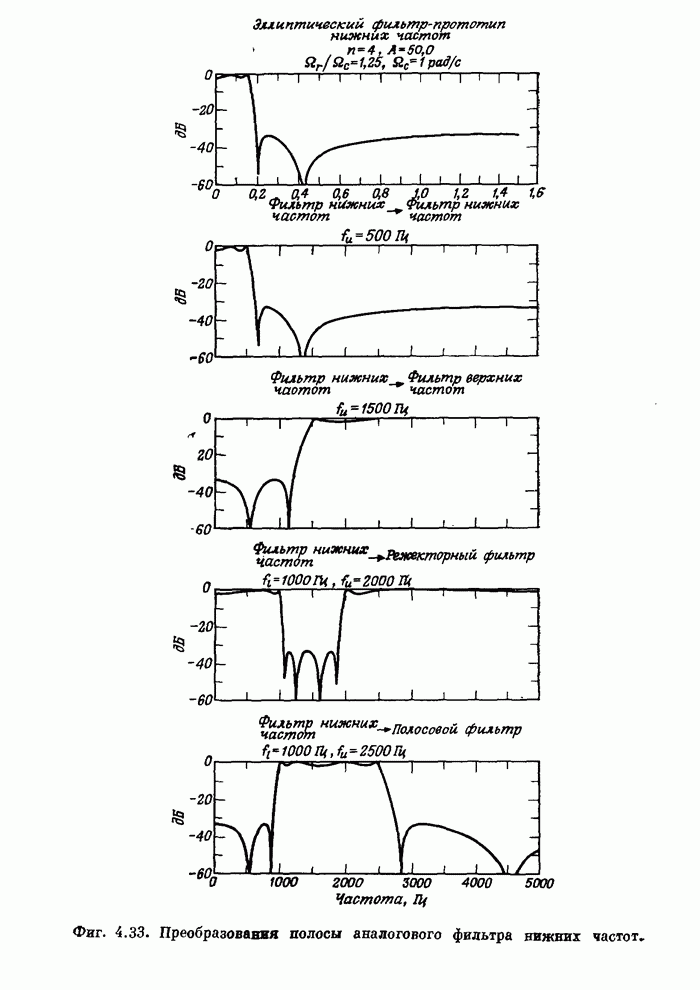
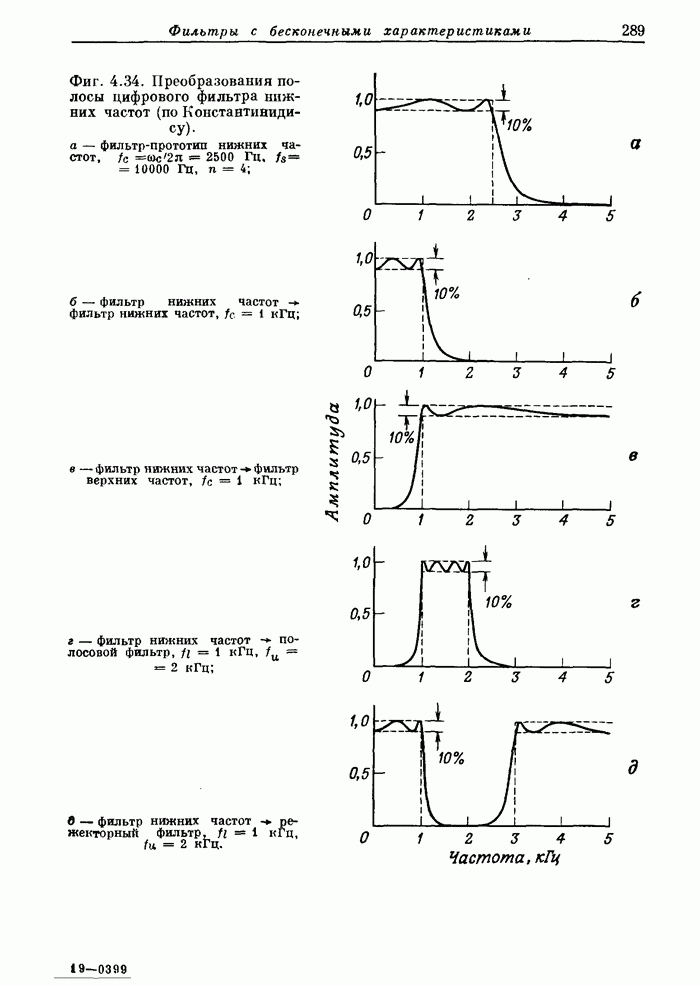
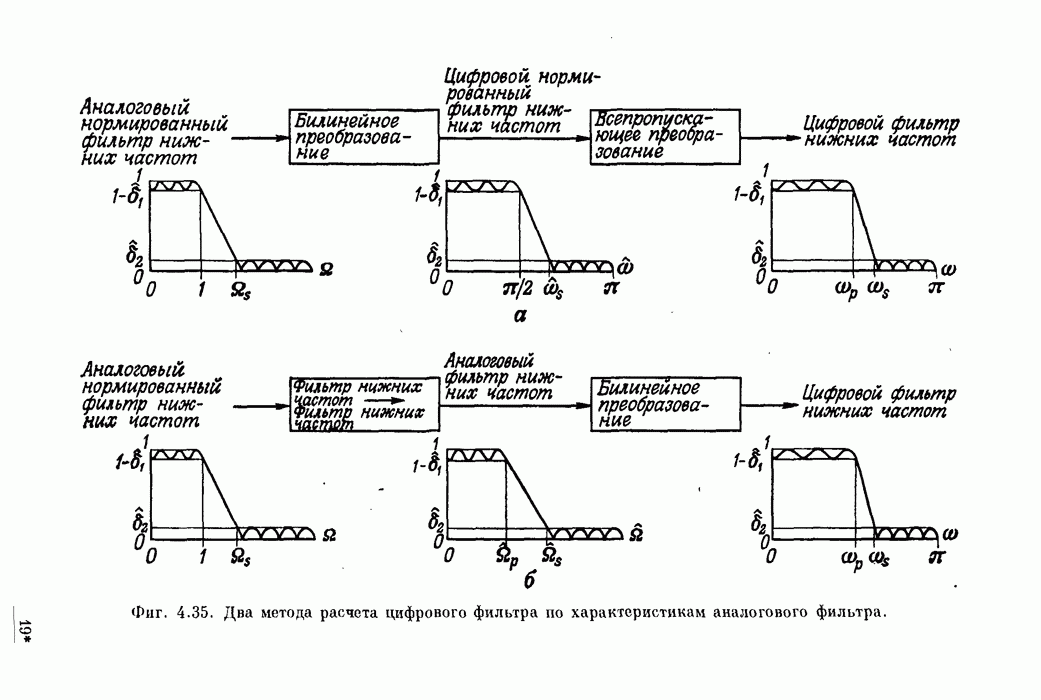
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
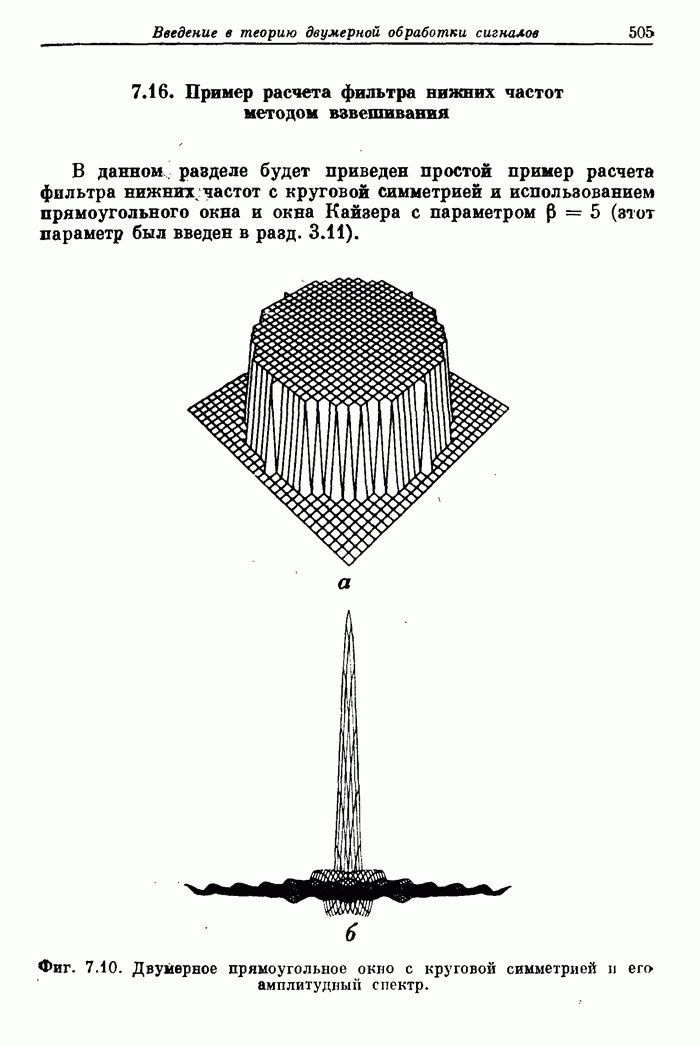
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
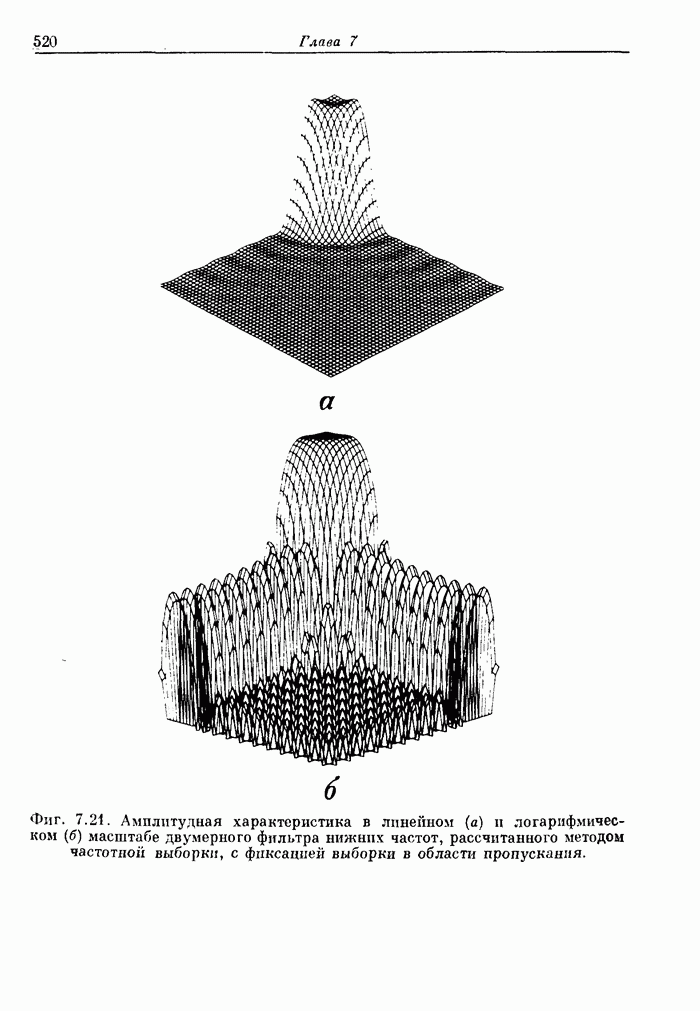
- 7.17. Фильтры с частотной выборкой
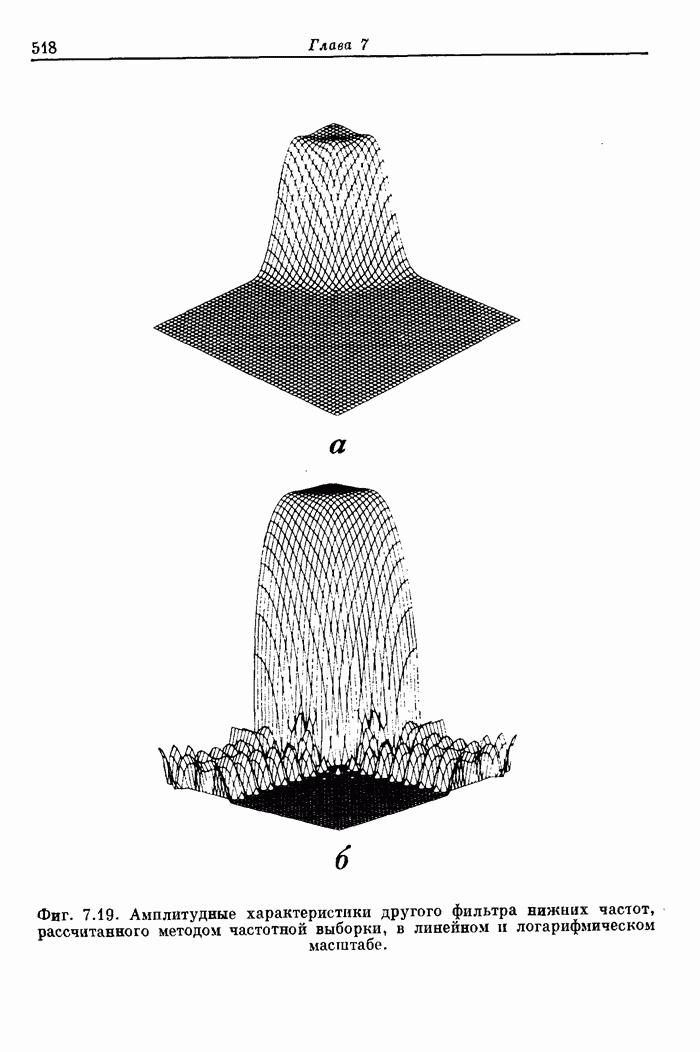
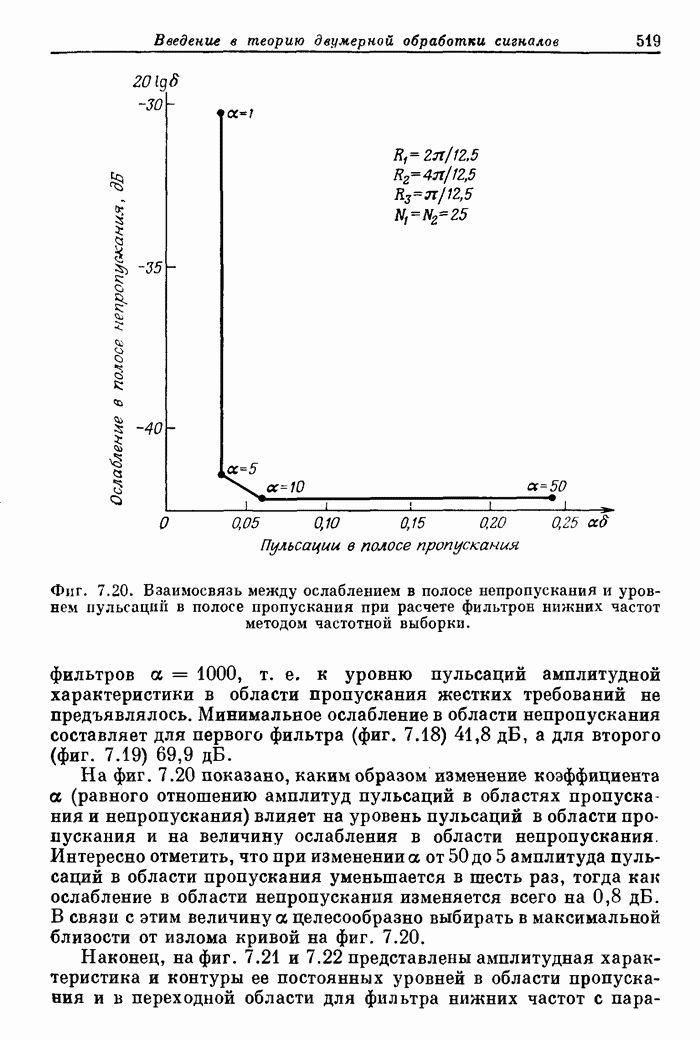
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
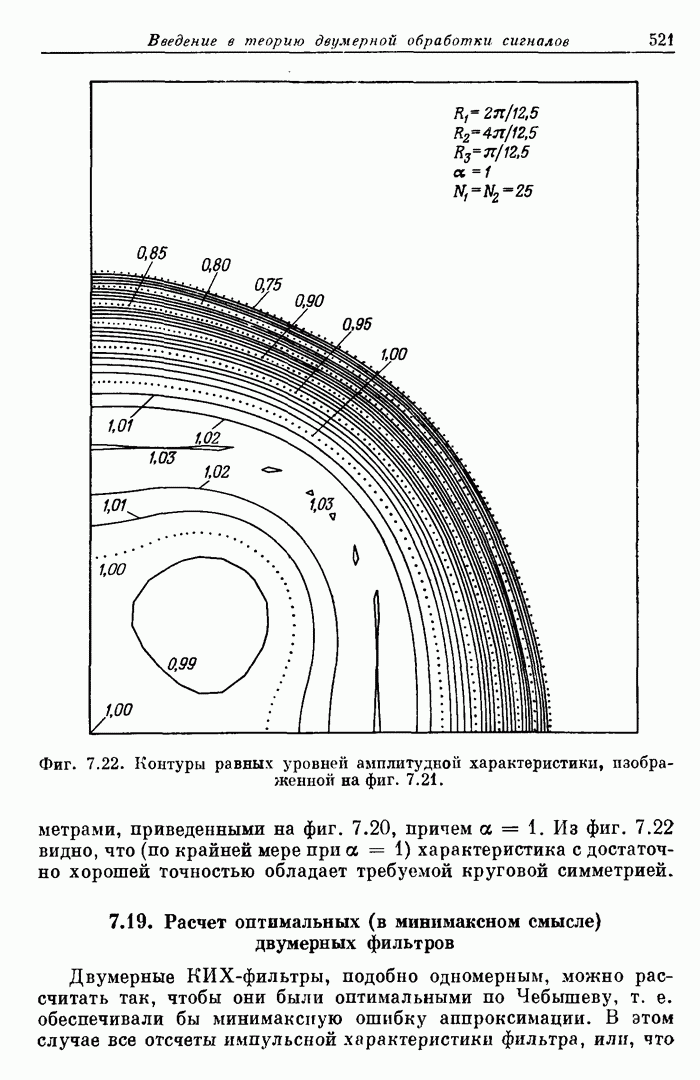
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
- 9.12. Специализированный цифровой синтезатор частот
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
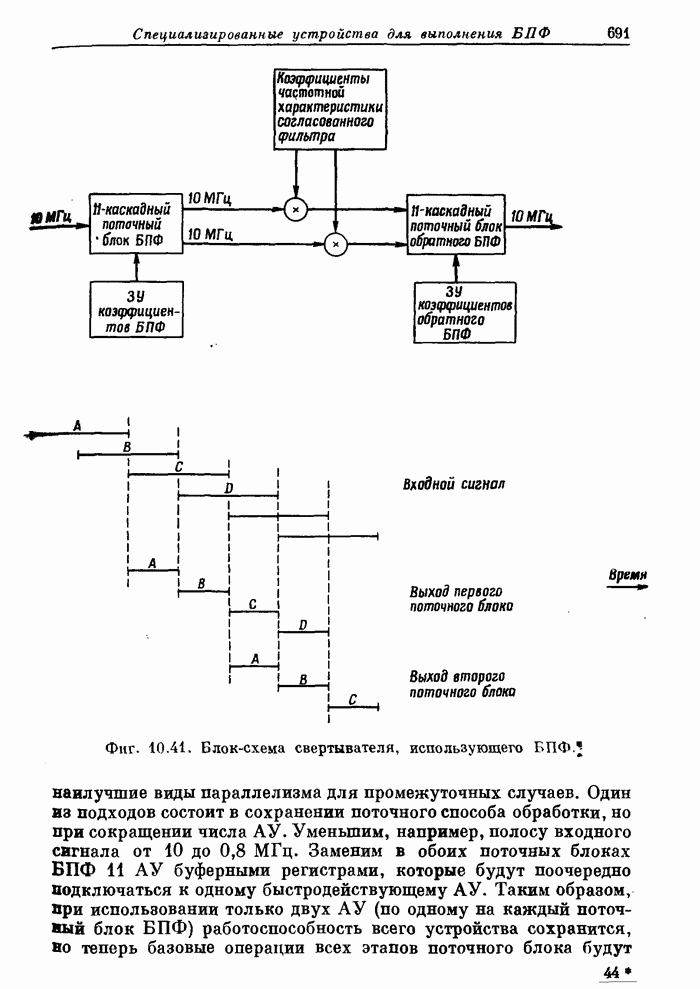
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
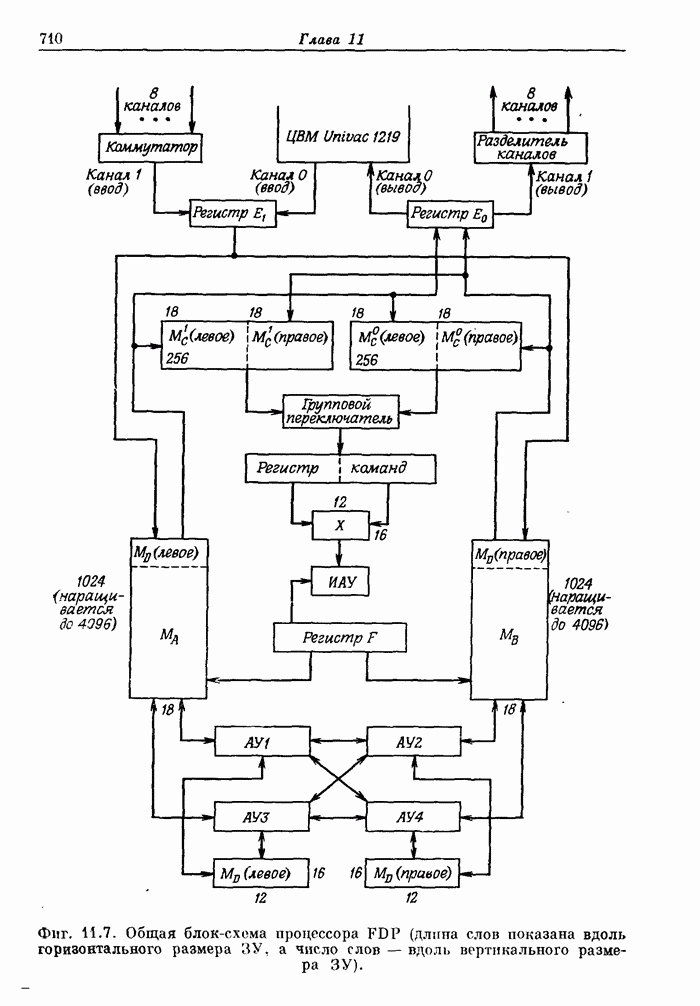
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
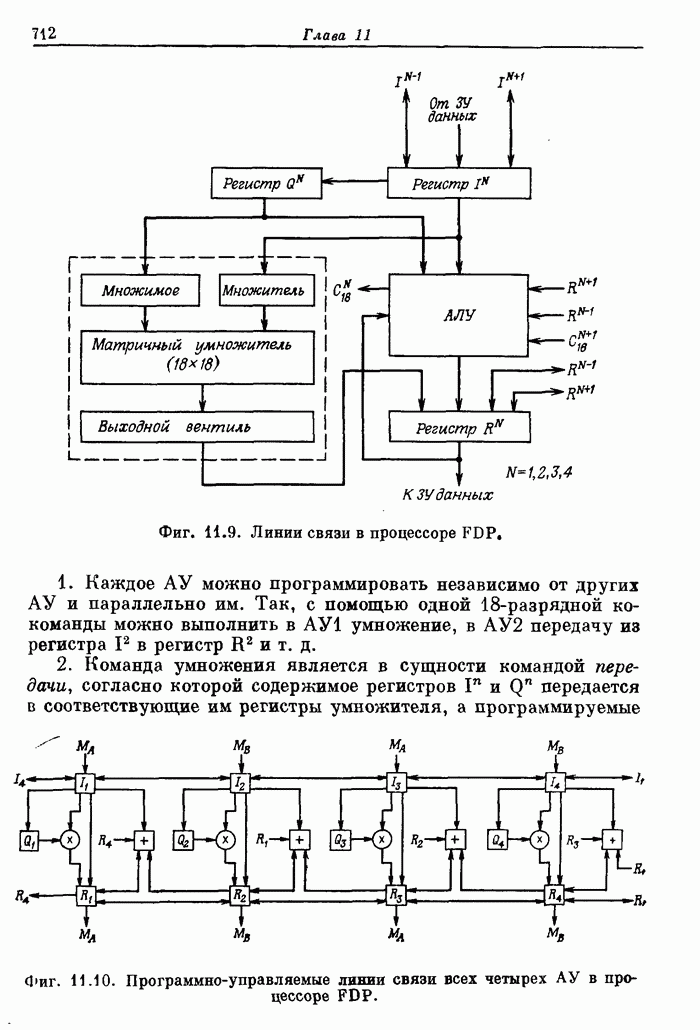
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
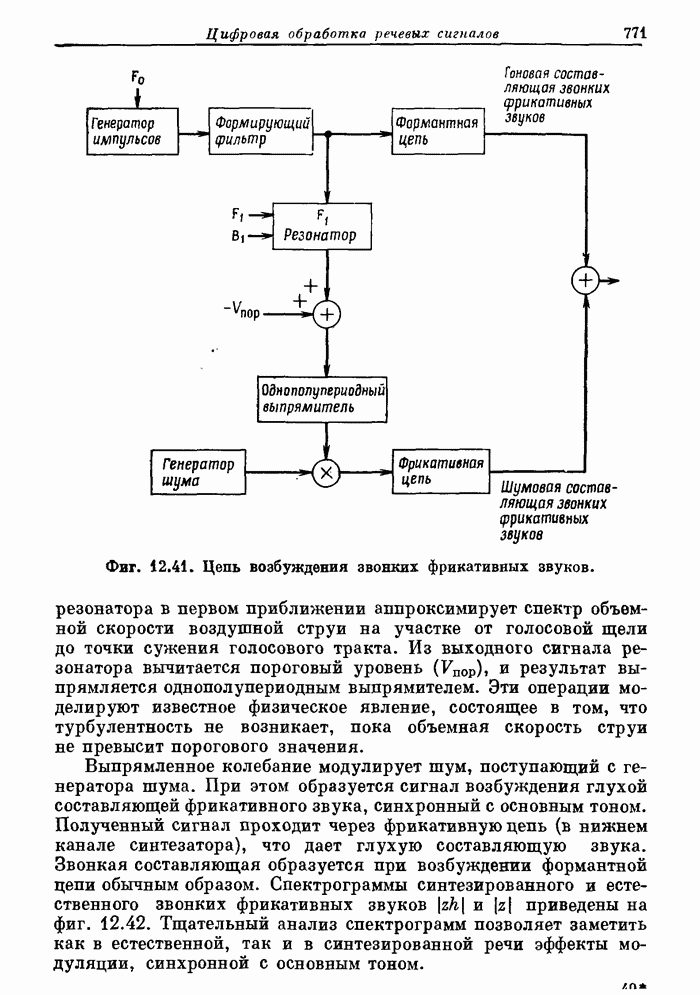
- 12.16. Цепь возбуждения звонких фрикативных звуков
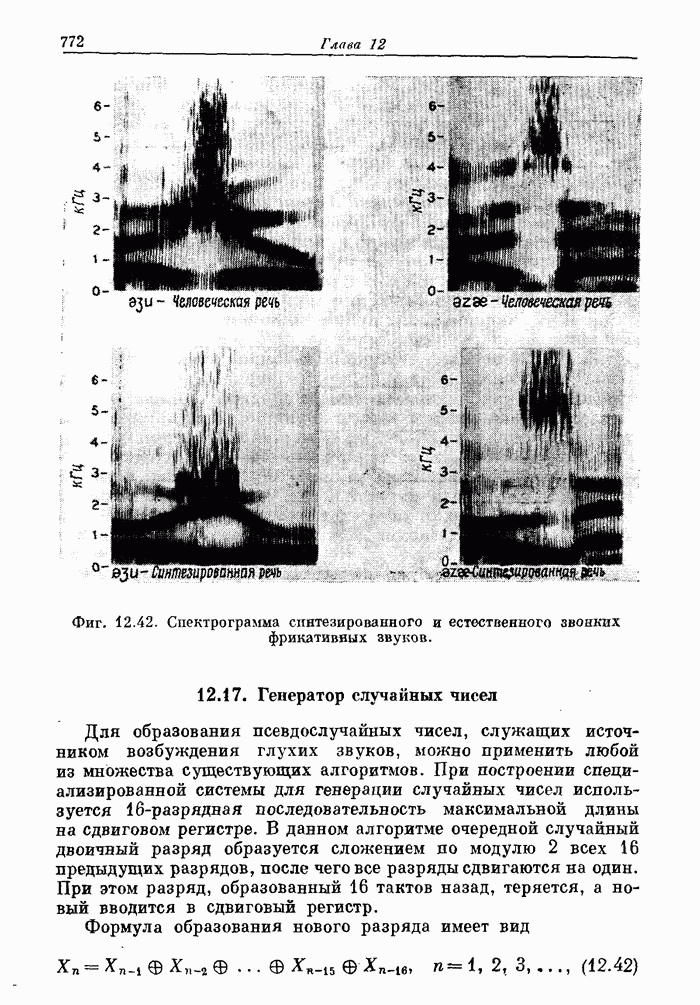
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
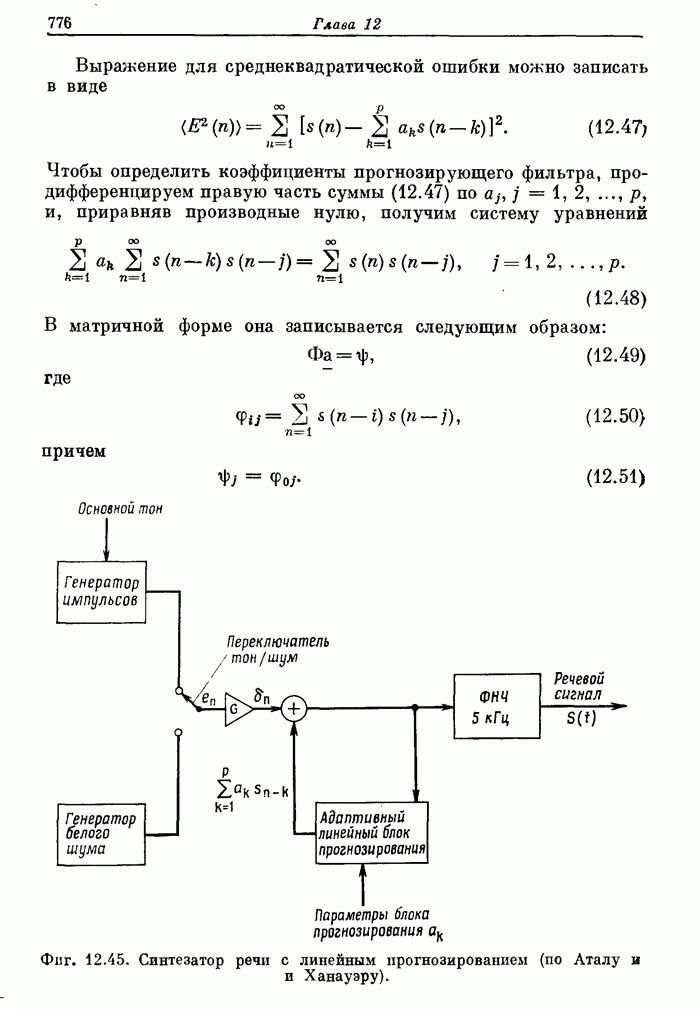
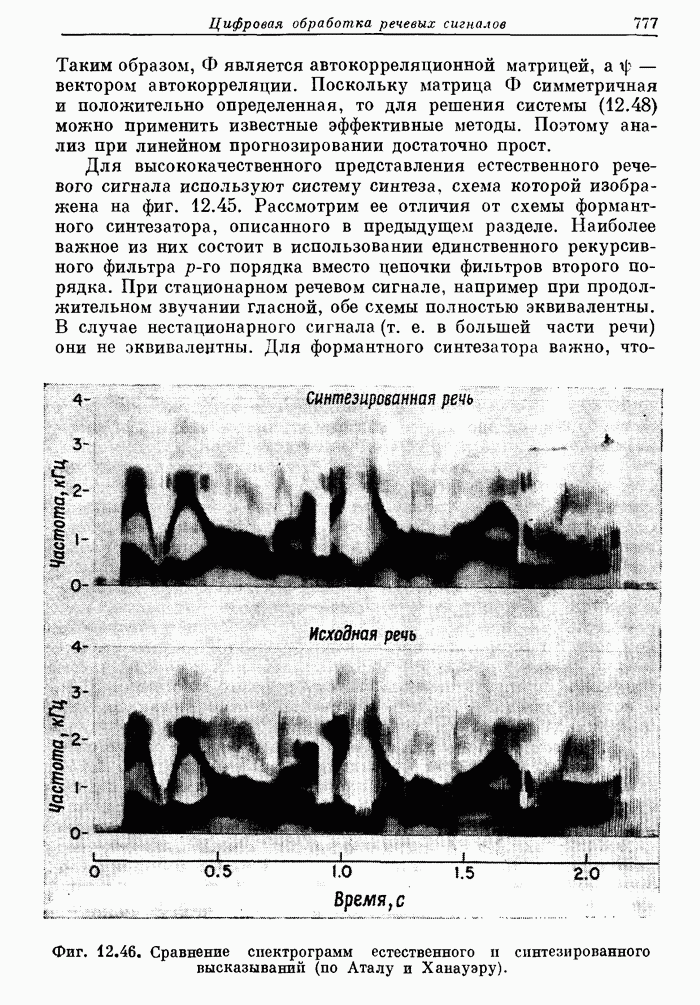
- 12.19. Линейное прогнозирование речи
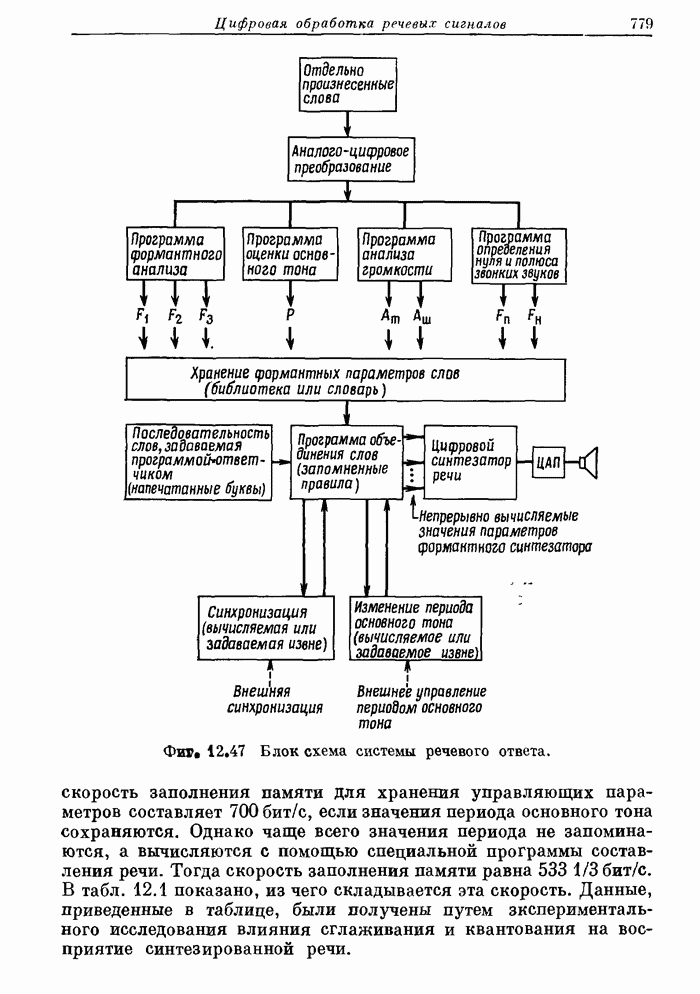
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
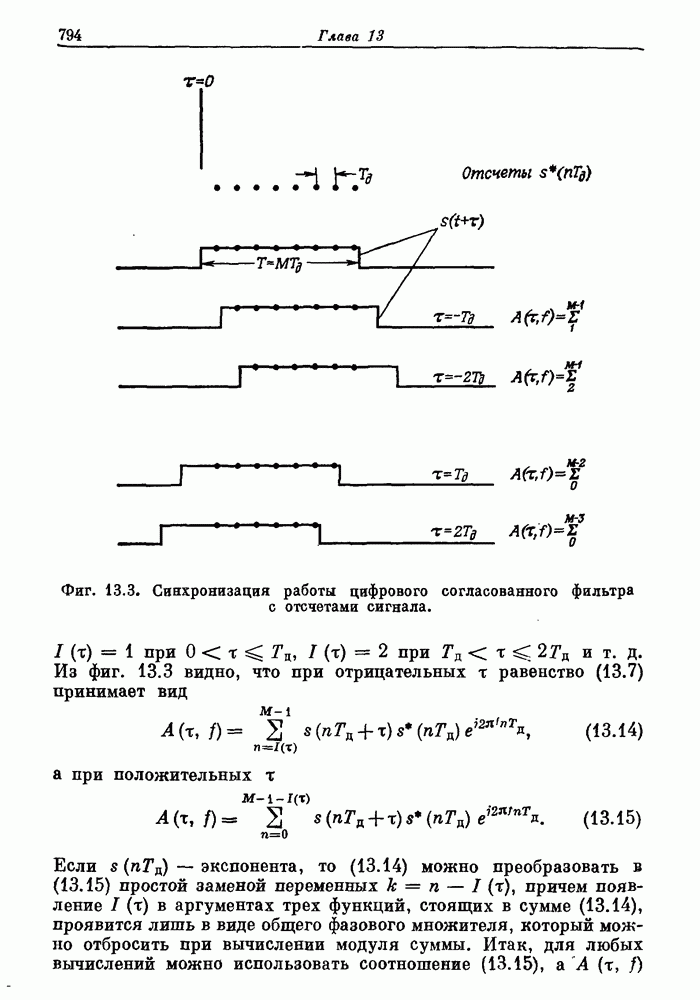
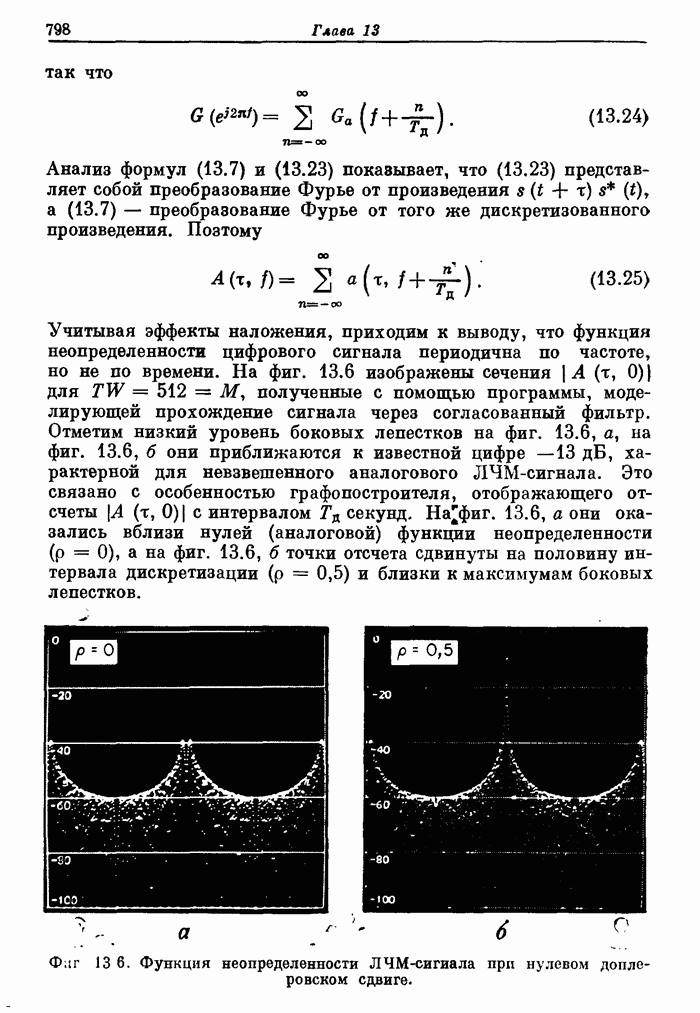
- 13.3. Выбор сигналов и функция неопределенности
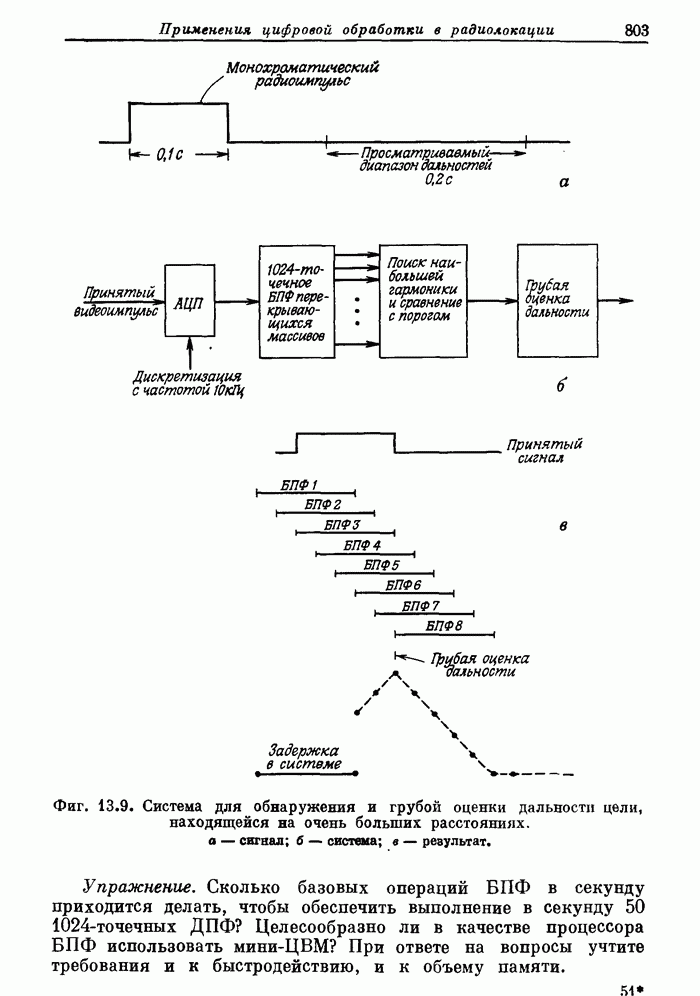
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
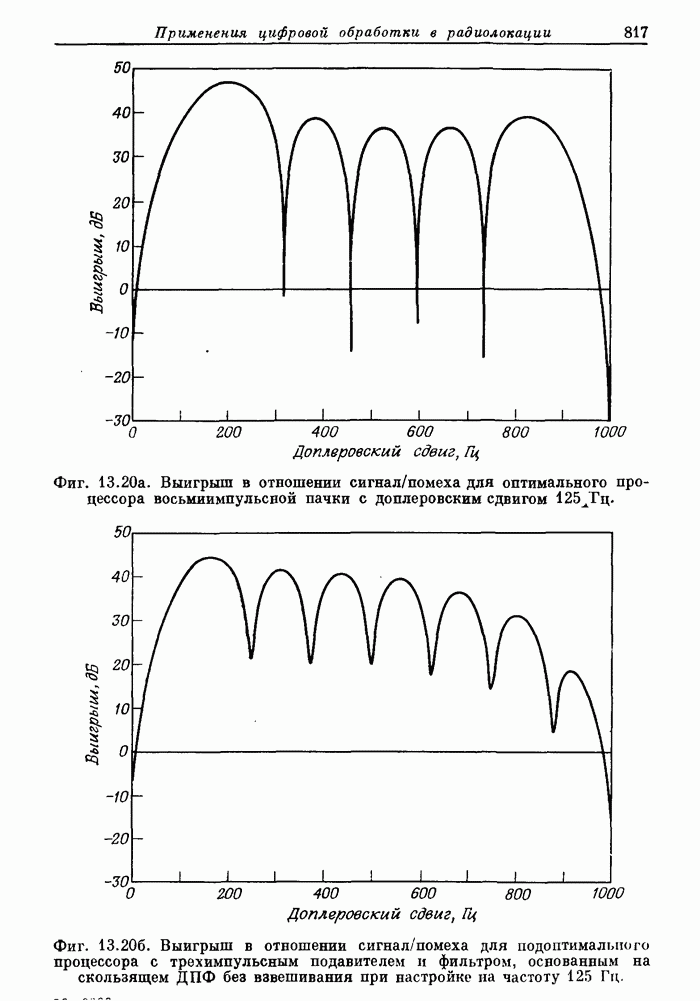
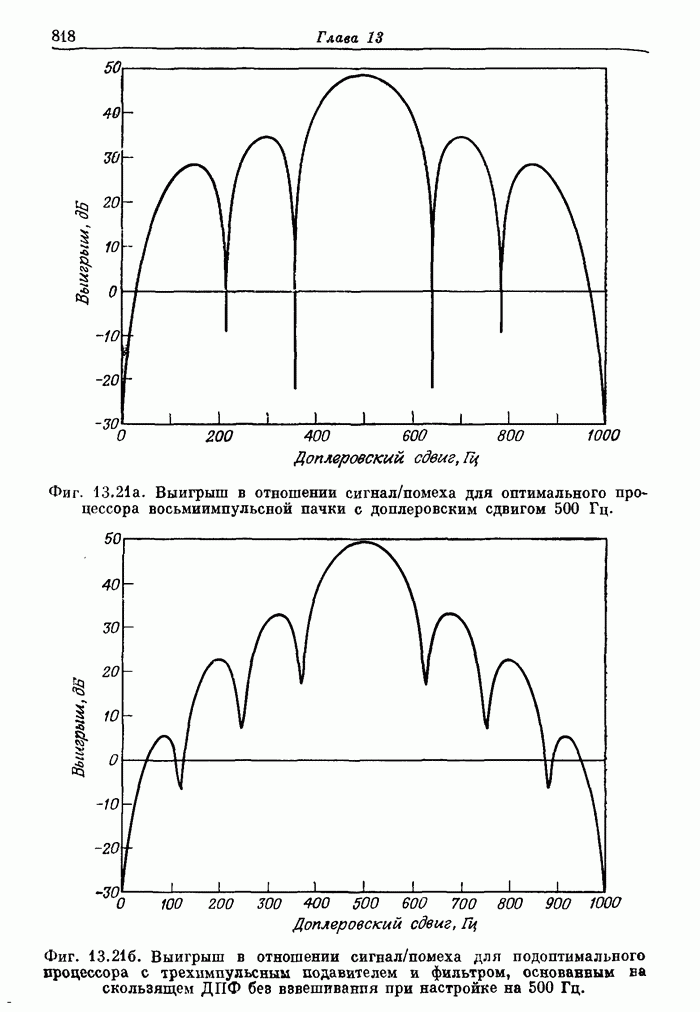
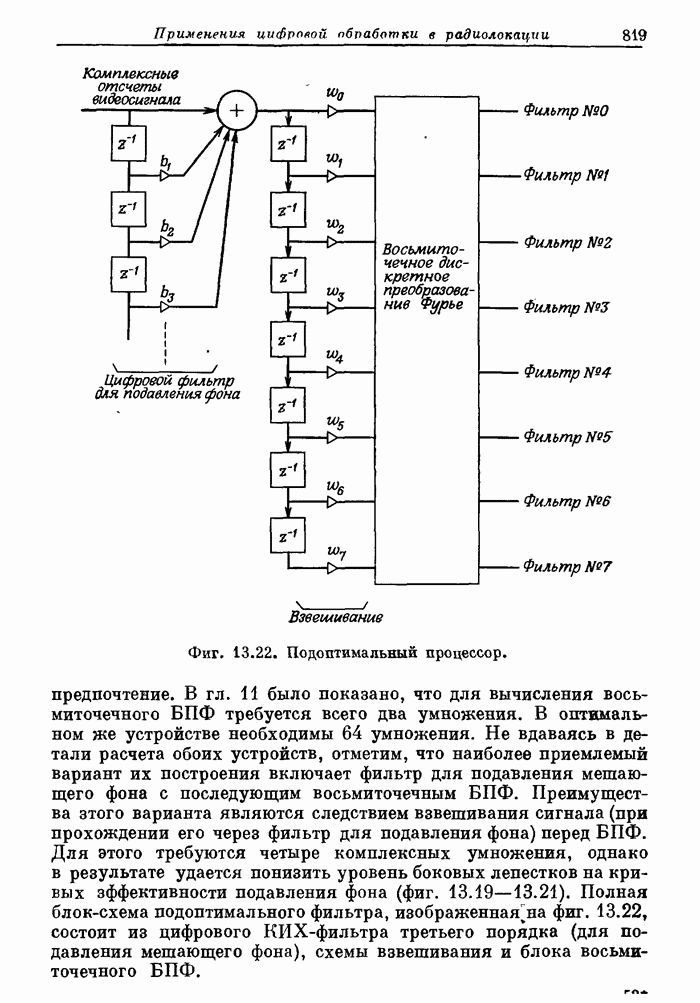
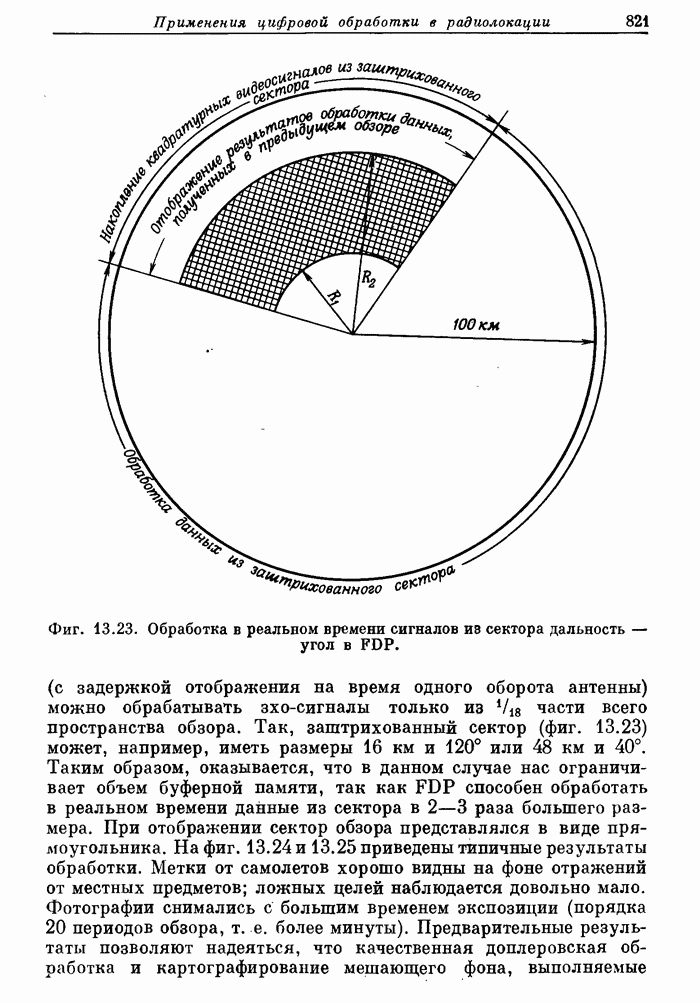
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение