| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.6. Умножители
Настоящий раздел посвящен умножителям, играющим особенно важную роль в устройствах цифровой обработки сигналов. С точки зрения принципа действия умножители можно разделить на многотактные и матричные. В обоих случаях произведение является результатом последовательных сложений с той лишь разницей, что достаточный параллелизм матричных умножителей позволяет обойтись без запоминания промежуточных результатов. Сначала кратко рассмотрим применяемые в умножителях системы числения, а затем опишем различные алгоритмы многотактного и матричного умножения. Более полный анализ систем счисления содержится в пятой главе.

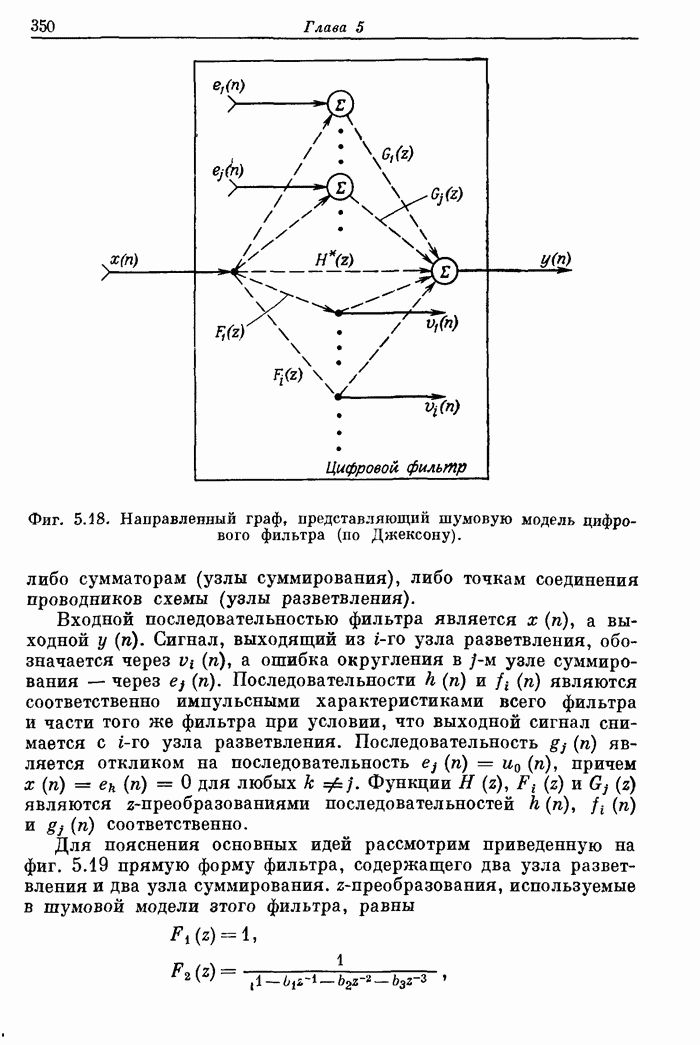
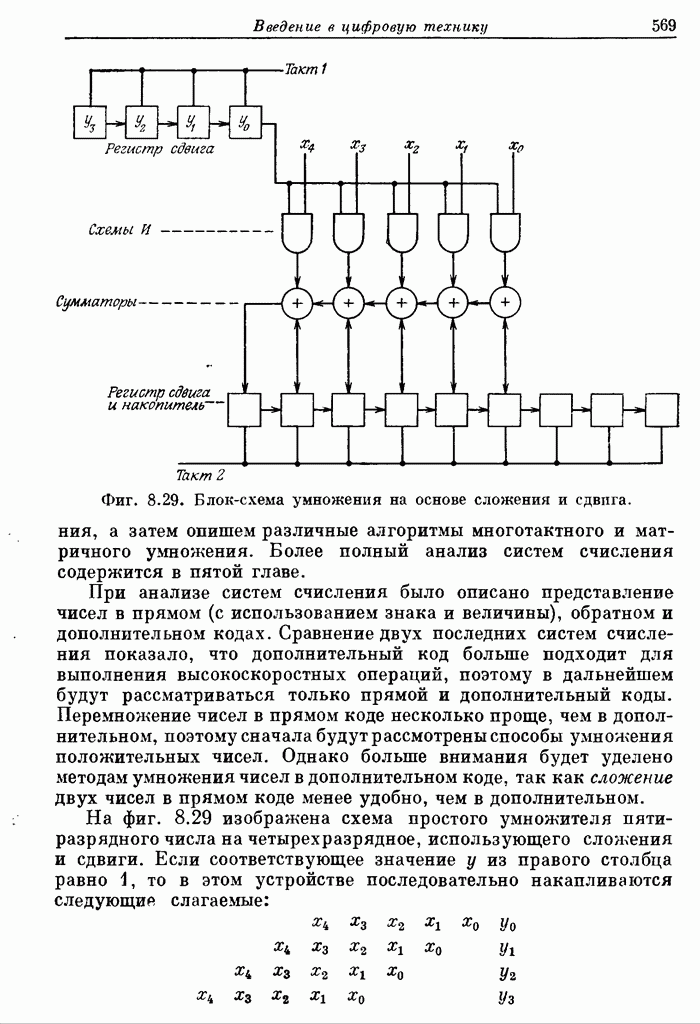
Фиг. 8.29. Блок-схема умножения на основе сложения и сдвига.
При анализе систем счисления было описано представление чисел в прямом (с использованием знака и величины), обратном и дополнительном кодах. Сравнение двух последних систем счисления показало, что дополнительный код больше подходит для выполнения высокоскоростных операций, поэтому в дальнейшем будут рассматриваться только прямой и дополнительный коды. Перемножение чисел в прямом коде несколько проще, чем в дополнительном, поэтому сначала будут рассмотрены способы умножения положительных чисел. Однако больше внимания будет уделено методам умножения чисел в дополнительном коде, так как сложение двух чисел в прямом коде менее удобно, чем в дополнительном.
На фиг. 8.29 изображена схема простого умножителя пятиразрядного числа на четырехразрядное, использующего сложения и сдвиги. Если соответствующее значение у из правого столбца равно 1, то в этом устройстве последовательно накапливаются следующие слагаемые:
![]()
![]()
![]()
![]()
При
![]() на
сумматор с выхода вентилей поступают нули. После логического умножения и
накопления очередной строки сумма сдвигается на один разряд вправо, чтобы
обеспечить в соответствии с требованием алгоритма добавление следующей строки
в более старшие разряды. По команде тактового импульса 1 (см. наверху) разряды
на
сумматор с выхода вентилей поступают нули. После логического умножения и
накопления очередной строки сумма сдвигается на один разряд вправо, чтобы
обеспечить в соответствии с требованием алгоритма добавление следующей строки
в более старшие разряды. По команде тактового импульса 1 (см. наверху) разряды
![]() последовательно
поступают на вентили И и обеспечивают подачу на вход сумматора либо числа
последовательно
поступают на вентили И и обеспечивают подачу на вход сумматора либо числа ![]() либо нуля. После
окончания цикла сложения по команде тактового импульса 2 результат суммирования
заносится в триггерный регистр накопителя и затем после завершения процесса
установления сдвигается на один разряд вправо. Этот умножитель достаточно простой,
но и медленный. Поскольку в сумматоре отсутствует схема ускорения переноса,
операция накопления завершается лишь после того, как сигнал переноса пройдет
через весь сумматор. Наибольшее значение времени установления для
либо нуля. После
окончания цикла сложения по команде тактового импульса 2 результат суммирования
заносится в триггерный регистр накопителя и затем после завершения процесса
установления сдвигается на один разряд вправо. Этот умножитель достаточно простой,
но и медленный. Поскольку в сумматоре отсутствует схема ускорения переноса,
операция накопления завершается лишь после того, как сигнал переноса пройдет
через весь сумматор. Наибольшее значение времени установления для ![]() -разрядного
сумматора примерно равно
-разрядного
сумматора примерно равно![]() , где
, где ![]() — соответственно время
распространения переноса и время образования суммы в одноразрядном сумматоре,
— соответственно время
распространения переноса и время образования суммы в одноразрядном сумматоре, ![]() — время установления
регистра сдвига
— время установления
регистра сдвига ![]() . Если
. Если ![]() -разрядное число умножается
на
-разрядное число умножается
на ![]() -разрядное,
то общее время умножения будет приблизительно равно
-разрядное,
то общее время умножения будет приблизительно равно ![]() .
.
Приведенная
на фиг. 8.29 схема отражает тот важный с аппаратурной точки зрения факт, что в
умножителях, основанных на сложении и сдвиге, разряды ![]() хранятся в
последовательном сдвиговом регистре. В гл. 9 будет показано, что представление
данных в виде последовательного потока положительно влияет на структуру
цифрового фильтра и приводит к снижению стоимости его памяти.
хранятся в
последовательном сдвиговом регистре. В гл. 9 будет показано, что представление
данных в виде последовательного потока положительно влияет на структуру
цифрового фильтра и приводит к снижению стоимости его памяти.
Рассмотрим
теперь, каким образом следует модифицировать этот умножитель для работы с
числами разного знака, заданными в дополнительном коде. Напомним сначала
формулы для представления и перемножения чисел в дополнительном коде. Значение
числа ![]() ,
представленного в дополнительном коде, равно
,
представленного в дополнительном коде, равно
![]() , (8.9)
, (8.9)
где ![]() — разряды
дополнительного кода, а
— разряды
дополнительного кода, а ![]() — знаковый разряд, причем сумма
понимается в арифметическом, а не логическом смысле. В качестве упражнения
предлагаем читателю, используя уравнение (8.9), составить алгоритм перевода
числа в дополнительном коде из положительного в отрицательное.
— знаковый разряд, причем сумма
понимается в арифметическом, а не логическом смысле. В качестве упражнения
предлагаем читателю, используя уравнение (8.9), составить алгоритм перевода
числа в дополнительном коде из положительного в отрицательное.
Из формулы (8.9)
можно получить арифметическое выражение для произведения ![]() двух чисел в
дополнительном коде, когда
двух чисел в
дополнительном коде, когда ![]() и
и ![]() соответственно
соответственно ![]() - и
- и ![]() -разрядные
числа:
-разрядные
числа:
 (8.10)
(8.10)
Первый и
четвертый члены в правой части (8.10) — положительные числа, второй и третий —
отрицательные. Четвертый член равен окончательному результату в случае
перемножения положительных чисел, который получается при последовательных
сложениях в схеме на фиг. 8.29. Из равенства (8.10) видно, что если ![]() или
или ![]() равны единице, то
суммы должны как складываться, так и вычитаться. Модификация логической
структуры умножителя, основанного на сложении и сдвиге, учитывающая знаковые
разряды, известна под названием алгоритма Бута. Чтобы понять этот алгоритм,
представим число
равны единице, то
суммы должны как складываться, так и вычитаться. Модификация логической
структуры умножителя, основанного на сложении и сдвиге, учитывающая знаковые
разряды, известна под названием алгоритма Бута. Чтобы понять этот алгоритм,
представим число ![]() в
следующем виде:
в
следующем виде:
 (8.11)
(8.11)
Итак, при
последовательном умножении множимого (![]() ) на разряды множителя (
) на разряды множителя (![]() ) операции будут
производиться над последовательными строками, составленными из разрядов
) операции будут
производиться над последовательными строками, составленными из разрядов ![]() , по следующим
правилам:
, по следующим
правилам:
1. Если ![]() , то накапливается
не множимое, а нулевая строка.
, то накапливается
не множимое, а нулевая строка.
2. Если ![]() , а
, а ![]() , то множимое добавляется в накопитель.
, то множимое добавляется в накопитель.
3. Если ![]() , а
, а ![]() , то множимое
вычитается из накопителя.
, то множимое
вычитается из накопителя.
В
качестве примера читателю предлагается, используя алгоритм Бута, умножить ![]() на
на ![]() и, кроме того,
модифицировать схему на фиг. 8.29 для реализации этого алгоритма.
и, кроме того,
модифицировать схему на фиг. 8.29 для реализации этого алгоритма.
Скорость выполнения алгоритма Бута можно увеличить в два раза, сдвигая множитель сразу на два разряда и анализируя одновременно три соседних разряда, чтобы определить характер накопления множимого; этот вариант также рекомендуется для самостоятельной проработки.
Самые
быстрые умножители состоят из двумерной матрицы одноразрядных сумматоров и
называются матричными умножителями. В отличие от многотактного умножителя
(фиг. 8.29) матричный умножитель представляет собой законченную логическую
схему без элементов памяти, поэтому результат умножения образуется после
подачи сомножителей за время, равное времени установления схемы. Существует
много различных вариантов построения матрицы, причем они могут быть достаточно
хорошо классифицированы
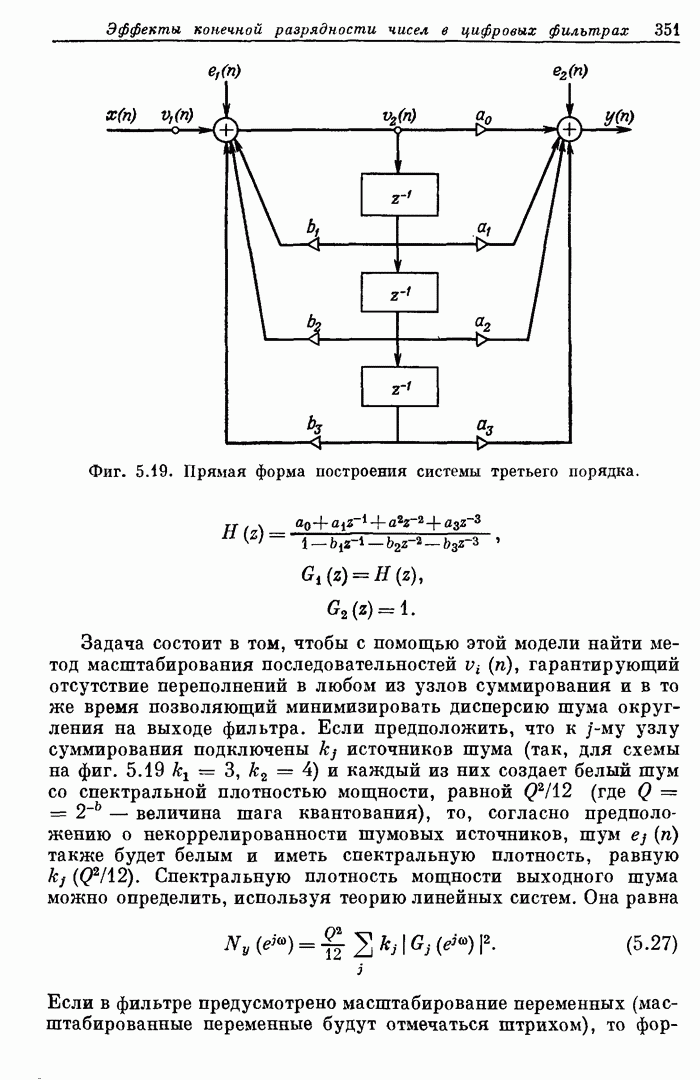
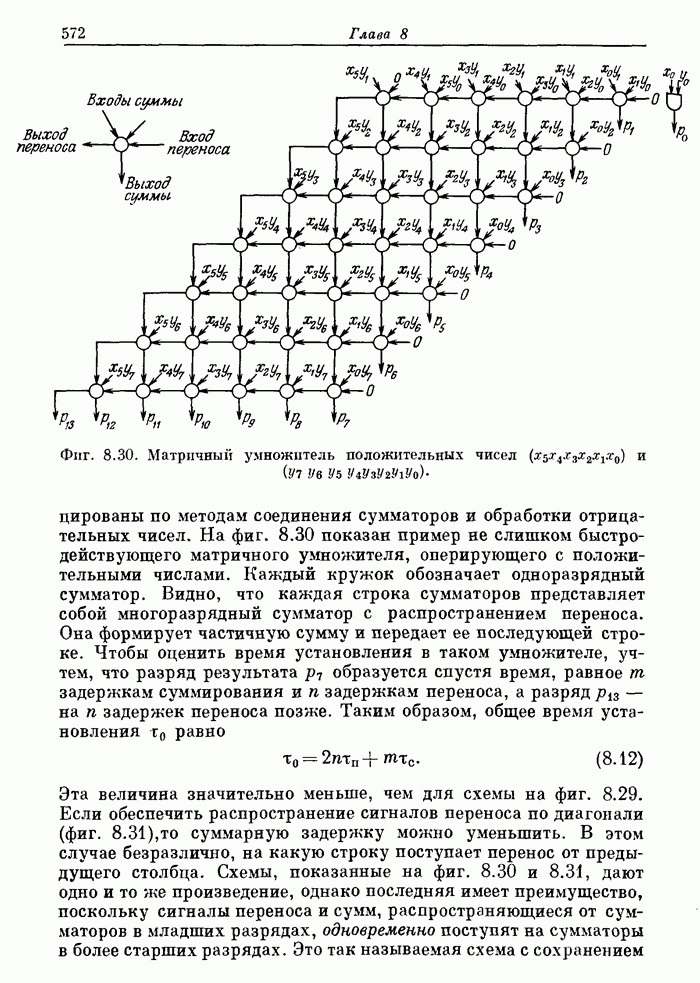
по методам соединения сумматоров и обработки отрицательных чисел. На фиг. 8.30
показан пример
не слишком быстродействующего матричного умножителя, оперирующего с положительными
числами. Каждый кружок обозначает одноразрядный сумматор. Видно, что каждая
строка сумматоров представляет собой многоразрядный сумматор с распространением
переноса. Она формирует частичную сумму и передает ее последующей строке.
Чтобы оценить время установления в таком умножителе, учтем, что разряд
результата ![]() образуется
спустя время, равное
образуется
спустя время, равное ![]() задержкам суммирования и
задержкам суммирования и ![]() задержкам
переноса, а разряд
задержкам
переноса, а разряд ![]() — на
— на ![]() задержек переноса
позже. Таким образом, общее время установления
задержек переноса
позже. Таким образом, общее время установления ![]() равно
равно
![]() (8.12)
(8.12)

Фиг.
8.30. Матричный умножитель положительных чисел ![]() и
и ![]()
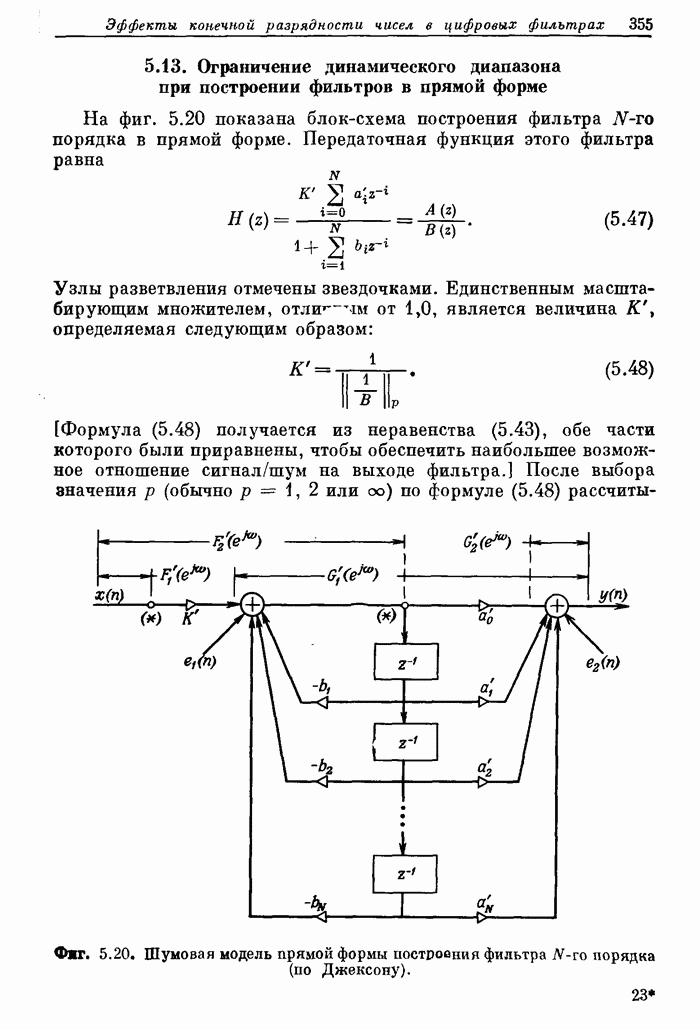
Эта величина значительно меньше, чем для схемы на фиг. 8.29. Если обеспечить распространение сигналов переноса по диагонали (фиг. 8.31),то суммарную задержку можно уменьшить. В этом случае безразлично, на какую строку поступает перенос от предыдущего столбца. Схемы, показанные на фиг. 8.30 и 8.31, дают одно и то же произведение, однако последняя имеет преимущество, поскольку сигналы переноса и сумм, распространяющиеся от сумматоров в младших разрядах, одновременно поступят на сумматоры в более старших разрядах. Это так называемая схема с сохранением переноса, которая применяется не только для матричных умножителей.

Фиг 8.31 Структура матричного умножителя, более быстродействующего по сравнению со схемой, изображенной на фиг. 8.30.
Например,
сигнал на выходе ![]() в
столбце 8 появится спустя время, равное пяти задержкам суммирования или восьми
задержкам переноса, в зависимости от того, какой отрезок времени длиннее.
Если они равны, то временем суммирования можно пренебречь. Поэтому для
последней строки сумматоров нужно учитывать суммарное время переноса. Таким
образом, если
в
столбце 8 появится спустя время, равное пяти задержкам суммирования или восьми
задержкам переноса, в зависимости от того, какой отрезок времени длиннее.
Если они равны, то временем суммирования можно пренебречь. Поэтому для
последней строки сумматоров нужно учитывать суммарное время переноса. Таким
образом, если![]() ,
то в наихудших условиях находится выход
,
то в наихудших условиях находится выход ![]() , задержка образования которого равна
, задержка образования которого равна
![]() . В
противном случае время умножения будет равно
. В
противном случае время умножения будет равно ![]() . Итак,
. Итак,
 | (8.13)
| (8.13)
При
использовании одноразрядных сумматоров, у которых ![]() значительно больше, чем
значительно больше, чем ![]() , нужна схема
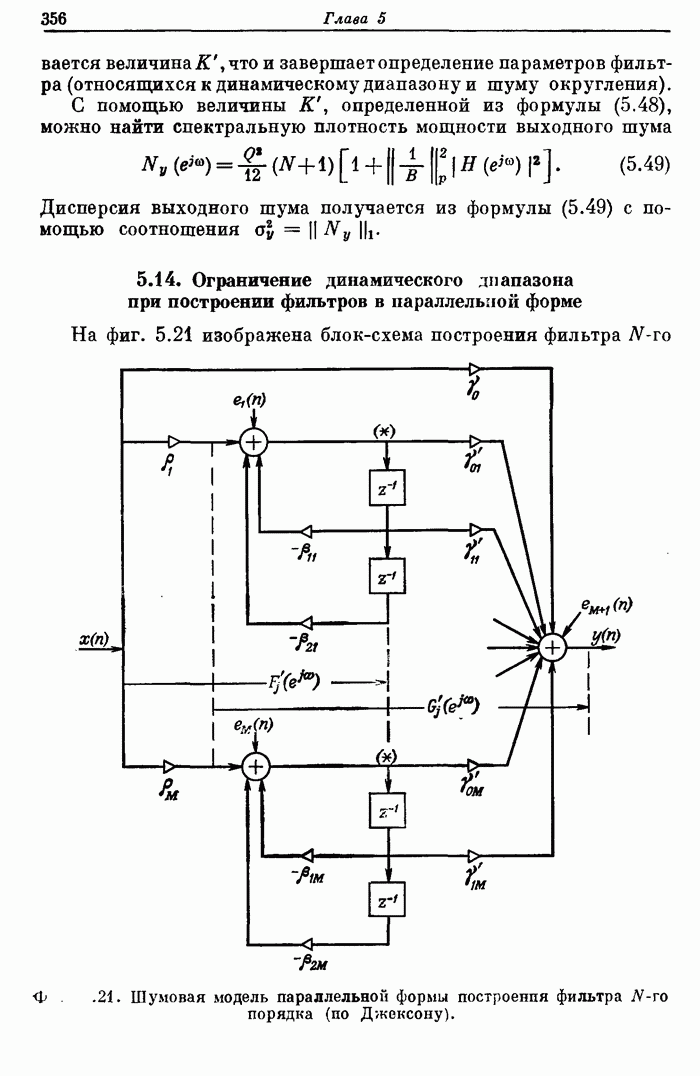
умножителя с минимальным числом последовательно выполняемых сложений. Идея
построения такого умножителя с матрицей сумматоров, организованной в виде
«дерева», иллюстрируется на фиг. 8.32. Он предназначен для умножения
, нужна схема
умножителя с минимальным числом последовательно выполняемых сложений. Идея
построения такого умножителя с матрицей сумматоров, организованной в виде
«дерева», иллюстрируется на фиг. 8.32. Он предназначен для умножения ![]() -разрядного
множимого на 16-разрядный множитель. Каждый из кружков обозначает
-разрядного
множимого на 16-разрядный множитель. Каждый из кружков обозначает ![]() -разрядный
сумматор. При такой организации время суммирования будет лишь учетверяться.
Общее количество сумматоров остается прежним, но больше строк сумматоров
работает теперь параллельно. Блок-схема умножителя такого типа с разрядностью,
равной, как и раньше, (6х8), в котором сигналы переноса распространяются вдоль
строк, показана на фиг. 8.33. Суммирование в каждой строке сумматоров
происходит за время формирования переноса, равное
-разрядный
сумматор. При такой организации время суммирования будет лишь учетверяться.
Общее количество сумматоров остается прежним, но больше строк сумматоров
работает теперь параллельно. Блок-схема умножителя такого типа с разрядностью,
равной, как и раньше, (6х8), в котором сигналы переноса распространяются вдоль
строк, показана на фиг. 8.33. Суммирование в каждой строке сумматоров
происходит за время формирования переноса, равное ![]() . Поскольку таких
уровней суммирования четыре, общее время умножения равно
. Поскольку таких
уровней суммирования четыре, общее время умножения равно ![]() . Таким образом,
если
. Таким образом,
если ![]() не
очень велико, эффективность данной схемы ниже, чем приведенной на фиг. 8.31.
не
очень велико, эффективность данной схемы ниже, чем приведенной на фиг. 8.31.

Фиг. 8.32. Древовидная структура матричного умножителя.
Возможно, что наибольшего быстродействия
можно достичь, сочетая идеи древовидного соединения и диагонального распространения
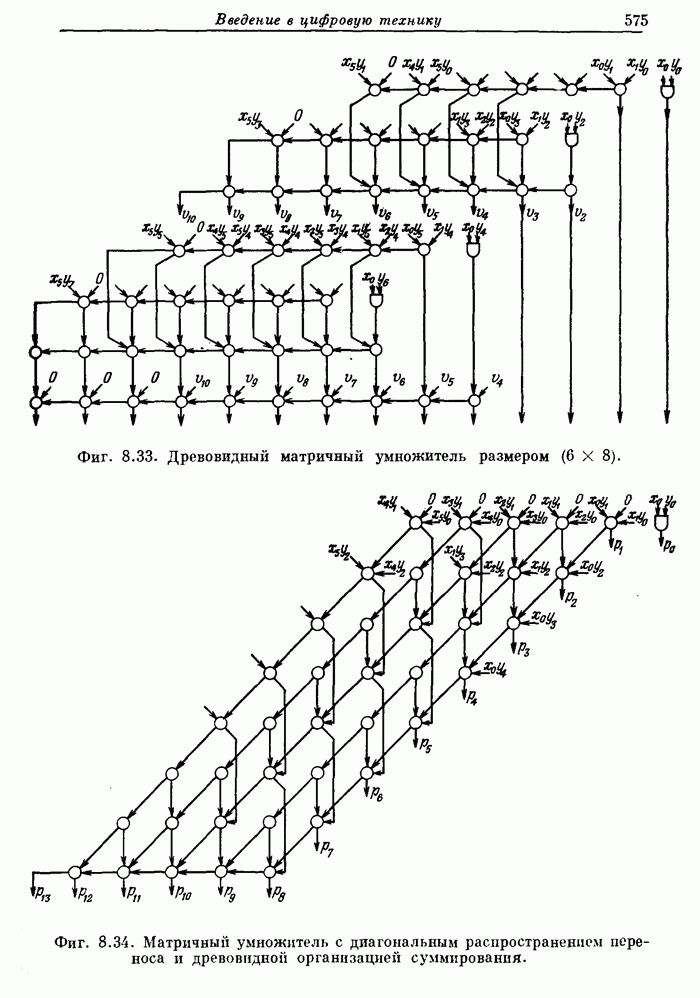
переносов. Соответствующая структурная схема приведена на фиг. 8.34. Так как
эта структура обладает, по-видимому, наибольшим быстродействием из
рассмотренных выше матричных схем, возникает вопрос о целесообразности
рассмотрения других матричных структур. Ответ на этот вопрос может быть получен
только в процессе проектирования системы на основе конкретных интегральных
схем. Обычно ИС разрабатываются и выпускаются в расчете на самые разнообразные
применения. Поэтому при создании матричного умножителя разработчик должен
выбрать наиболее подходящие ИС из числа имеющихся. В качестве примера рассмотрим
выпущенную в 1971 г. интересную ИС МС10181, которая представляет собой
четырехразрядный сумматор с ускоренным переносом. На ее основе можно построить
диагональную (как на фиг. 8.31) или горизонтальную (как на фиг. 8.30 и 8.33)
структуры. Хотя схема, приведенная на фиг. 8.31, и оказывается более быстродействующей,
для формирования частичных произведений ![]() требуются
дополнительные корпусы. В схеме с горизонтальным распространением переносов эти
корпусы не нужны, поскольку каждый управляющий разряд можно логически умножить
сразу на четыре входных разряда. Итак, выбор «наилучшей» схемы определяется
характеристиками используемых микросхем и компромиссом между быстродействием и
стоимостью умножителя.
требуются
дополнительные корпусы. В схеме с горизонтальным распространением переносов эти
корпусы не нужны, поскольку каждый управляющий разряд можно логически умножить
сразу на четыре входных разряда. Итак, выбор «наилучшей» схемы определяется
характеристиками используемых микросхем и компромиссом между быстродействием и
стоимостью умножителя.

Фиг. 8.33. Древовидный матричный умножитель размером (6x8)

Фиг. 8.34. Матричный умножитель с диагональным распространением переноса и древовидной организацией суммирования.
Рассмотрим умножение чисел, представленных в дополнительном коде, пользуясь основной формулой (8.9). Сущность этой формулы состоит в следующем: каждый разряд, за исключением знакового, принимает арифметические значения 0 или 1, а знаковый — значения 0 или -1. При таком подходе, выполняя суммирование согласно формуле (8.9), всегда будем получать правильный результат.
Одноразрядный сумматор может быть описан
подобно тому, как это делалось ранее, с помощью логических уравнений или
таблицы истинности. Если каждый из трех входных разрядов принимает (арифметические)
значения 0 или 1, то двухразрядный выход может иметь значения 0, 1, 2 или 3.
При реализации этой функции значения 0 или 2 приписываются разряду переноса, а
значения 0 или 1 — разряду суммы; оба эти разряда описывают выход сумматора.
Таблица истинности (Т.И.4) дает состояния выходных разрядов сумматора — суммы ![]() (младший
разряд) и переноса
(младший
разряд) и переноса ![]() — в зависимости от состояния
входов
— в зависимости от состояния
входов ![]() ,
,
![]() и
и
![]() . Ясно,
что совершенно необязательно обозначать два возможных состояния выходных
разрядов либо нулем, либо единицей; для этого можно использовать + или —, 0 или
2, 0 или 100 и т. д. Система обозначений, интуитивно принятая в таблице
истинности (Т.И.4), фактически соответствует двоичному представлению выхода
сумматора:
. Ясно,
что совершенно необязательно обозначать два возможных состояния выходных
разрядов либо нулем, либо единицей; для этого можно использовать + или —, 0 или
2, 0 или 100 и т. д. Система обозначений, интуитивно принятая в таблице
истинности (Т.И.4), фактически соответствует двоичному представлению выхода
сумматора:
 (Т.И.4)
(Т.И.4)
![]() ,
, ![]() ,
, ![]() — входы;
— входы; ![]() — сумма
(булева);
— сумма
(булева); ![]() —
перенос (арифметическая сумма минус булева сумма). Эту систему обозначении можно
обобщить на случай арифметического суммирования и положительных и
отрицательных чисел. Рассмотрим, например, трехвходовую схему, у которой один из
входных сигналов принимает значения — 1 или 0, а два других — значения 0 или 1.
В этом случае сумма по-прежнему принимает четыре возможных значения -1, 0, +1,
+2 и может быть представлена двухразрядным числом с младшим разрядом, равным 0
или -1, и старшим, равным 0 или 2.
—
перенос (арифметическая сумма минус булева сумма). Эту систему обозначении можно
обобщить на случай арифметического суммирования и положительных и
отрицательных чисел. Рассмотрим, например, трехвходовую схему, у которой один из
входных сигналов принимает значения — 1 или 0, а два других — значения 0 или 1.
В этом случае сумма по-прежнему принимает четыре возможных значения -1, 0, +1,
+2 и может быть представлена двухразрядным числом с младшим разрядом, равным 0
или -1, и старшим, равным 0 или 2.
Снова из таблицы истинности такой логической схемы (Т.И.5) следует, что результат сложения в сумматоре, рассматриваемый как арифметическая сумма двух выходов, соответствует также арифметической сумме всех трех входов. Аналогично можно рассмотреть еще два случая с таблицами истинности (Т.И.6) и (Т.И.7).
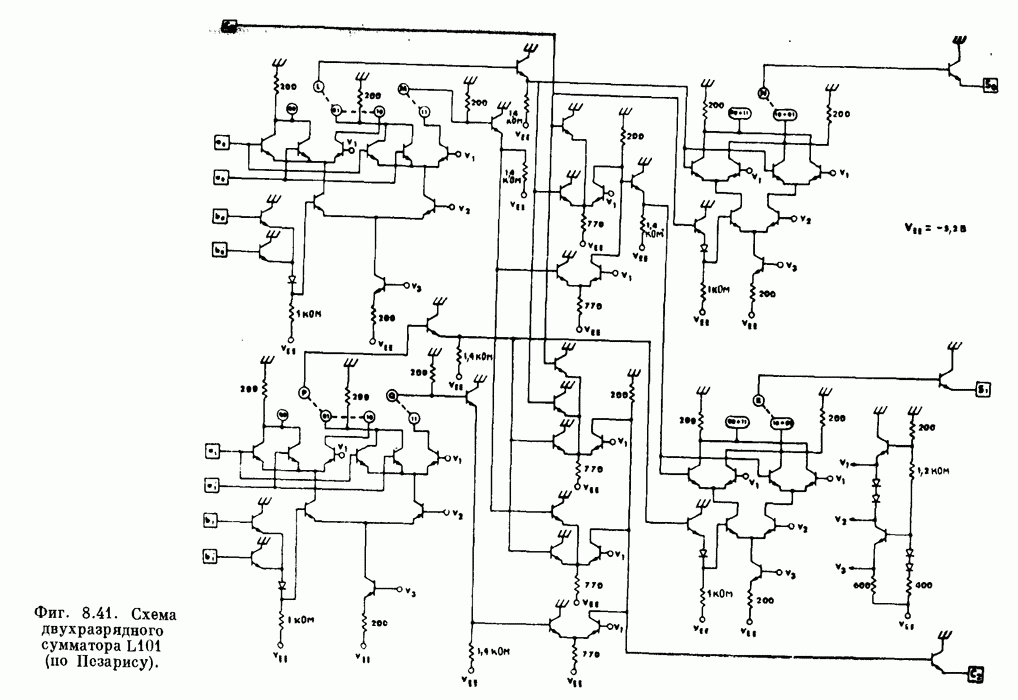
Воспользовавшись введенной системой обозначений и располагая интегральными схемами, способными суммировать отрицательные числа, можно построить матричный умножитель чисел в дополнительном коде, основанный на последовательных сложениях. Пример такого умножителя, в котором использованы три типа интегральных схем, — обычные сумматоры, описываемые таблицей истинности (Т.И.4), а также сумматоры, соответствующие (Т.И.6) и (Т.И.7), — показан на фиг. 8.35.

Фиг. 8.35. Матричный умножитель чисел в дополнительном коде размером (6х5).
 (Т.И.5)
(Т.И.5)
 (Т.И.6)
(Т.И.6)
Таблица 8.2. Сравнение различных умножителей
|
|
|
|
|
Тип основной |
|
|
|
Структура |
|
|
интегральной схемы |
|
||
|
Быстрая трапецеидальная (фиг. 8.35) |
Специальный двухразрядный сумматор |
|
||||
|
Древовидная |
|
|
|
Серийный четырехразрядный сумматор |
|
|
|
» |
|
|
|
То же |
|
|
|
» |
|
|
|
Серийная матрица (2х4) |
|
|
|
Многотактная с одновременным сдвигом на два разряда |
Специальный двухразрядный сумматор |
|
||||
|
То же |
|
|
|
Серийный двухразрядный сумматор |
|
|
|
» » |
|
|
|
То же |
|
|
Продолжение таблицы 8.2.
|
Тип |
Время умножения, нc |
Количество корпусов |
||||
|
логики |
16x12 |
16x8 |
9x9 |
16х12 |
16x8 |
9x9 |
|
ЭСЛ |
32 |
28 |
22 |
112 |
82 |
45 |
|
|
ЭСЛ |
62 |
48 |
40 |
160 |
120 |
85 |
|
|
ТТЛ |
155 |
100 |
85 |
160 |
120 |
85 |
|
|
ТТЛ |
261 |
195 |
135 |
80 |
58 |
30 |
|
|
ЭСЛ |
130 |
120 |
100 |
40 |
36 |
25 |
|
|
ЭСЛ |
210 |
140 |
116 |
40 |
36 |
25 |
|
|
ТТЛ |
450 |
300 |
250 |
40 |
36 |
25 |
 (Т.И.7)
(Т.И.7)
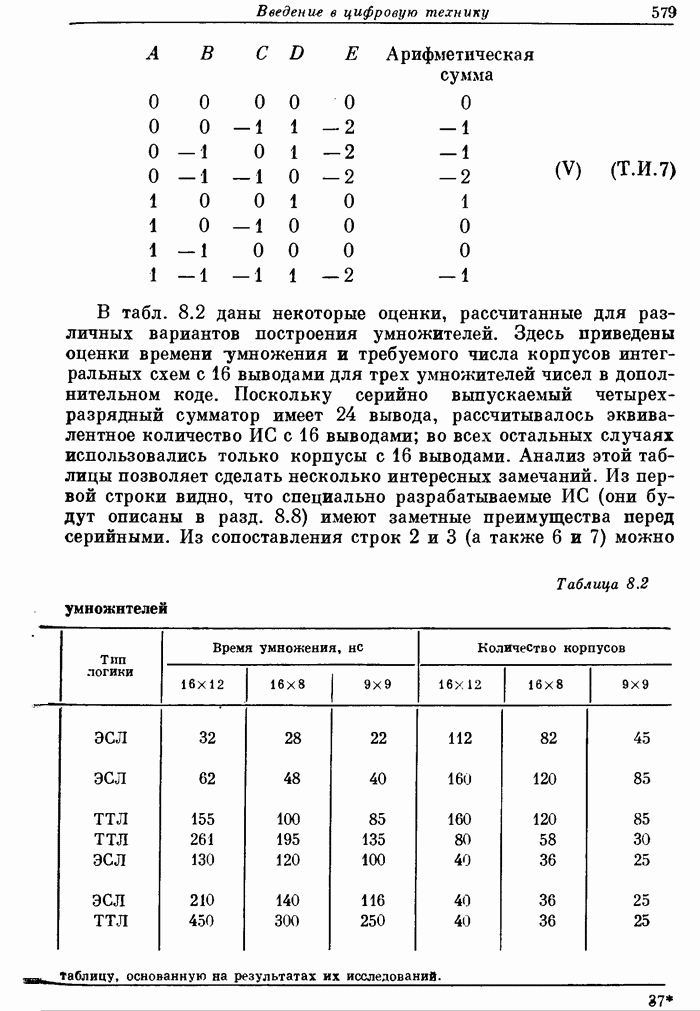
В табл. 8.2 даны некоторые оценки, рассчитанные для различных вариантов построения умножителей. Здесь приведены оценки времени умножения и требуемого числа корпусов интегральных схем с 16 выводами для трех умножителей чисел в дополнительном коде. Поскольку серийно выпускаемый четырехразрядный сумматор имеет 24 вывода, рассчитывалось эквивалентное количество ИС с 16 выводами; во всех остальных случаях использовались только корпусы с 16 выводами. Анализ этой таблицы позволяет сделать несколько интересных замечаний. Из первой строки видно, что специально разрабатываемые ИС (они будут описаны в разд. 8.8) имеют заметные преимущества перед серийными. Из сопоставления строк 2 и 3 (а также 6 и 7) можно оценить увеличение быстродействия умножителя при замене ИС ТТЛ на более быстродействующие ИС ЭЛС; оно возросло более чем в два раза. Влияние структуры умножителя как на его быстродействие, так и на количество корпусов можно проследить, обратившись к строкам 1 и 5; несколько неожиданно, что наилучший компромисс между быстродействием и числом корпусов достигается при построении матричных умножителей. Одной из причин является чрезвычайно простое управление матричным умножителем по сравнению с многотактным (строки 5, б, 7). Интересно также отметить, что с точки зрения общего количества корпусов двухразрядный сумматор с 16 выводами (строка 1) оказывается выгоднее использовать, чем четырехразрядный сумматор с 24 выводами (строка 2 или 3). Таким образом, в некоторых структурах, когда кристалл размещается в корпусе больших размеров, увеличение уровня интеграции может оказаться даже вредным.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
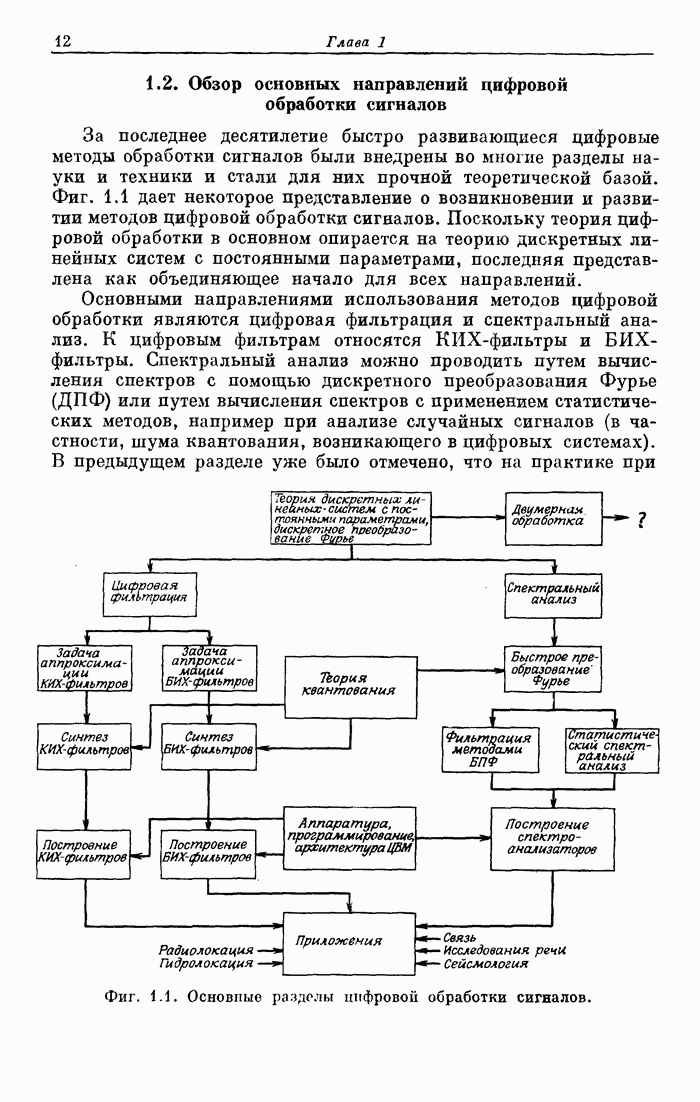
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
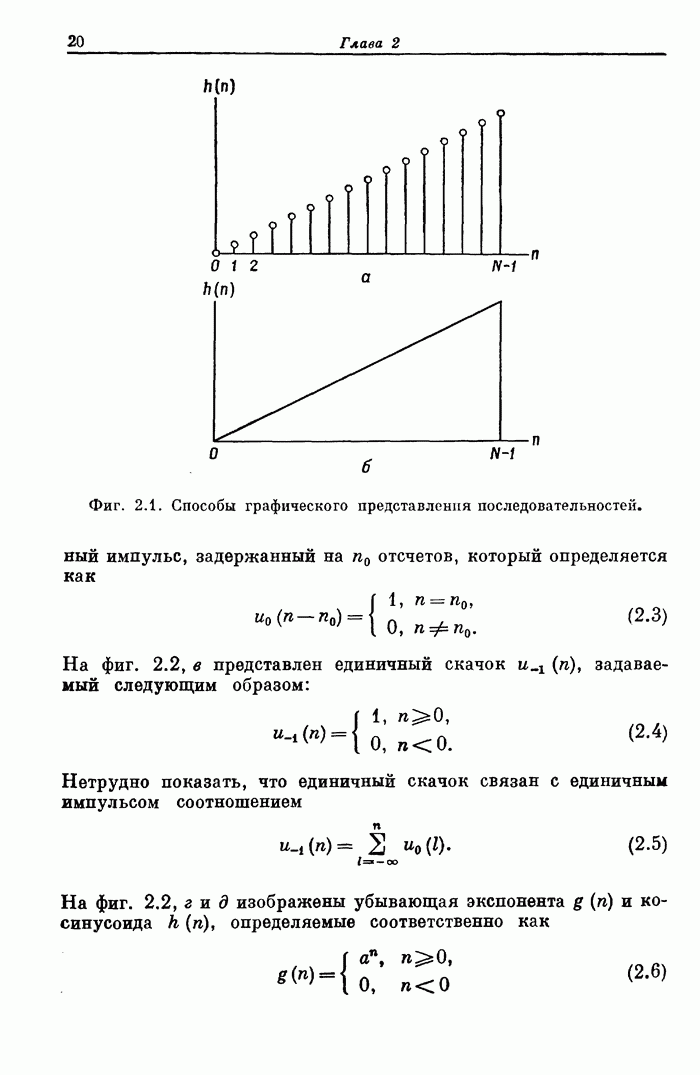
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
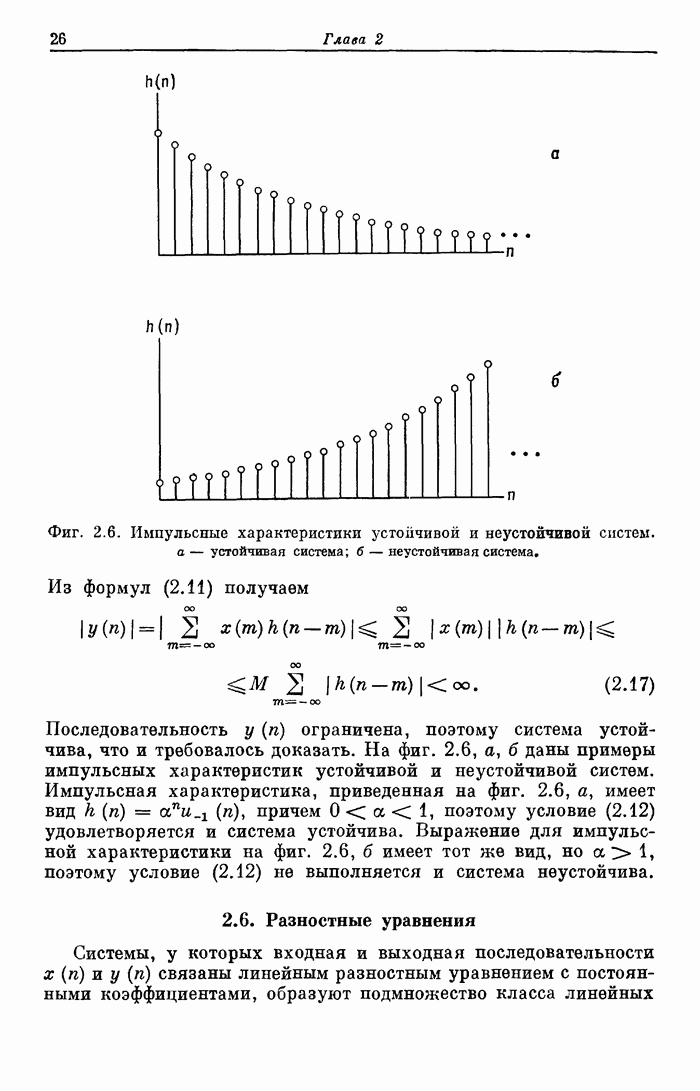
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
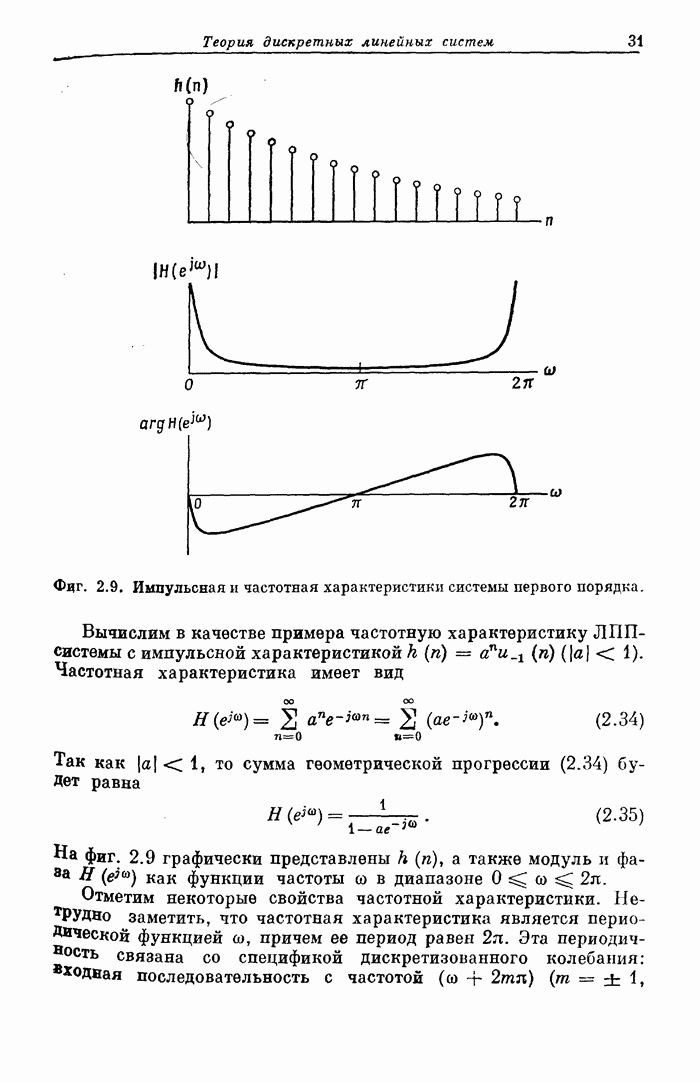
- 2.7. Частотная характеристика
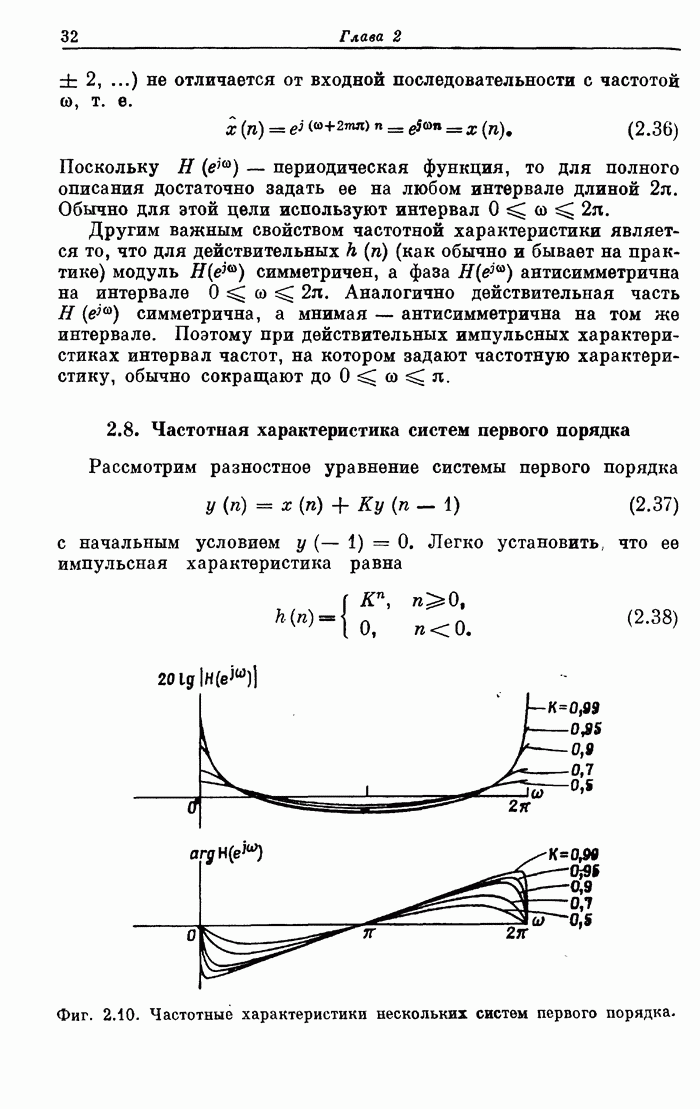
- 2.8. Частотная характеристика систем первого порядка
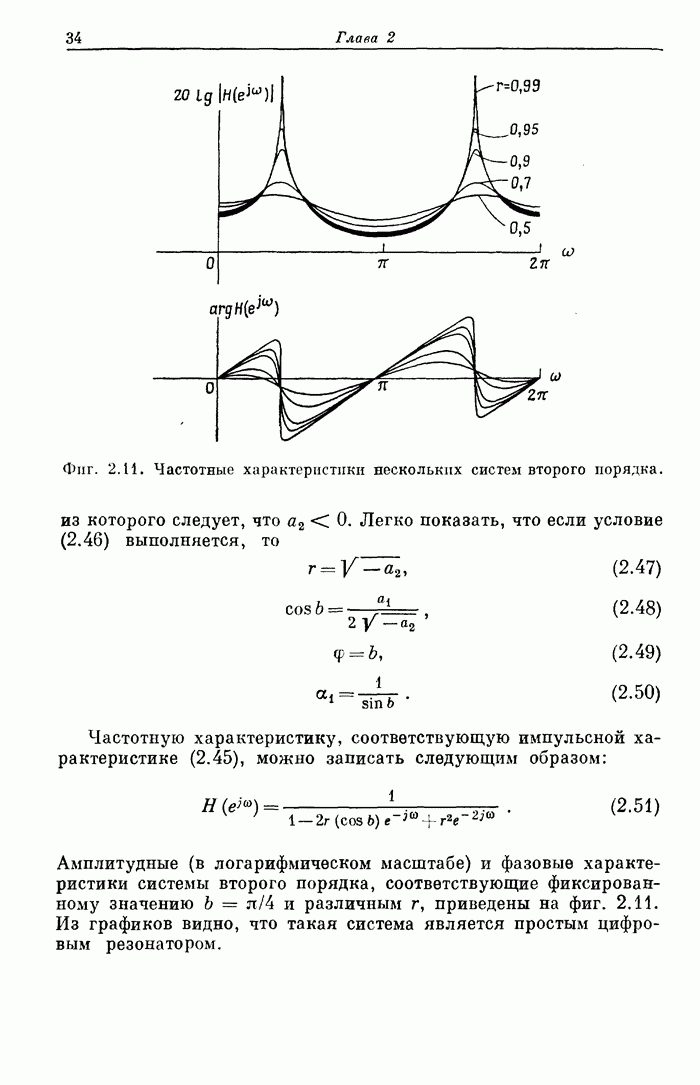
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
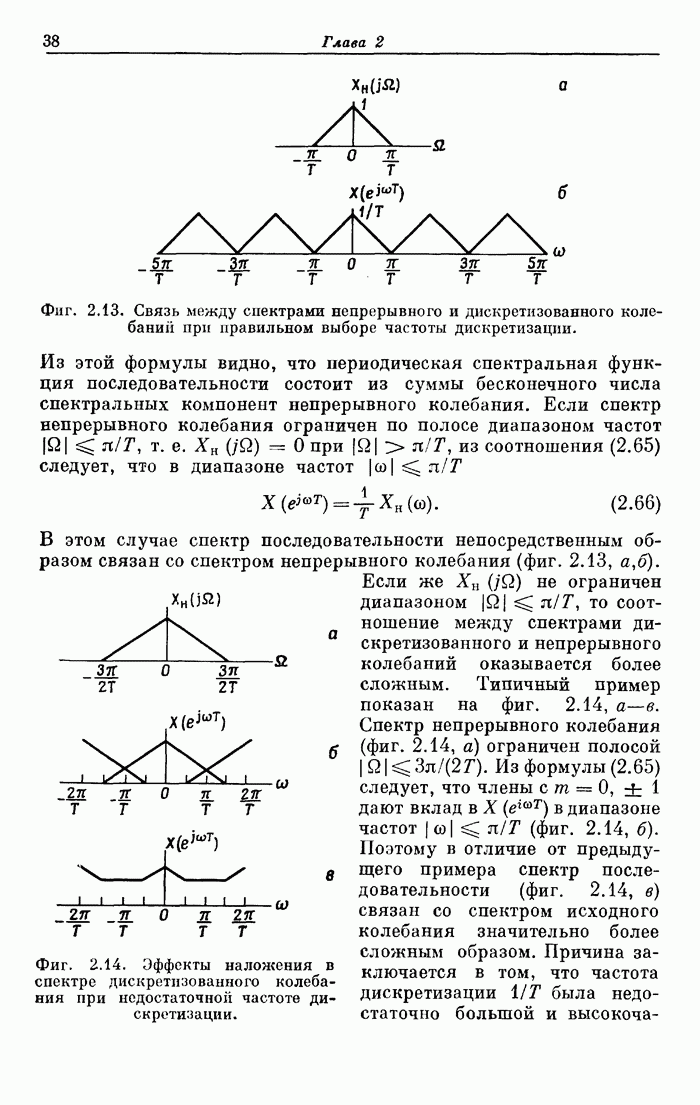
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
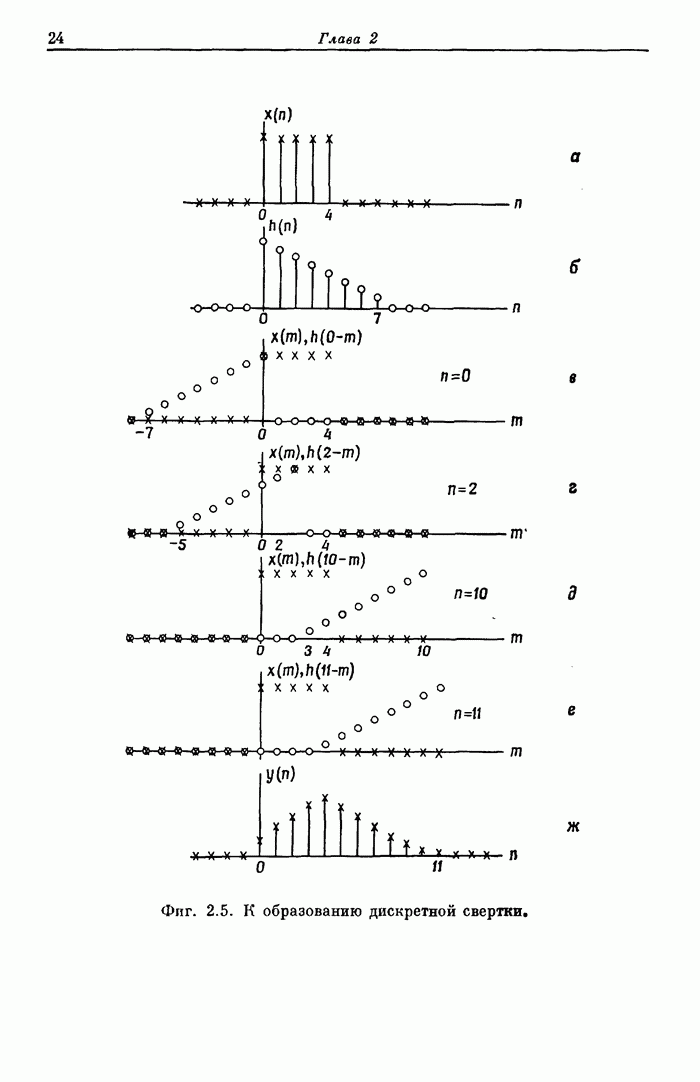
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
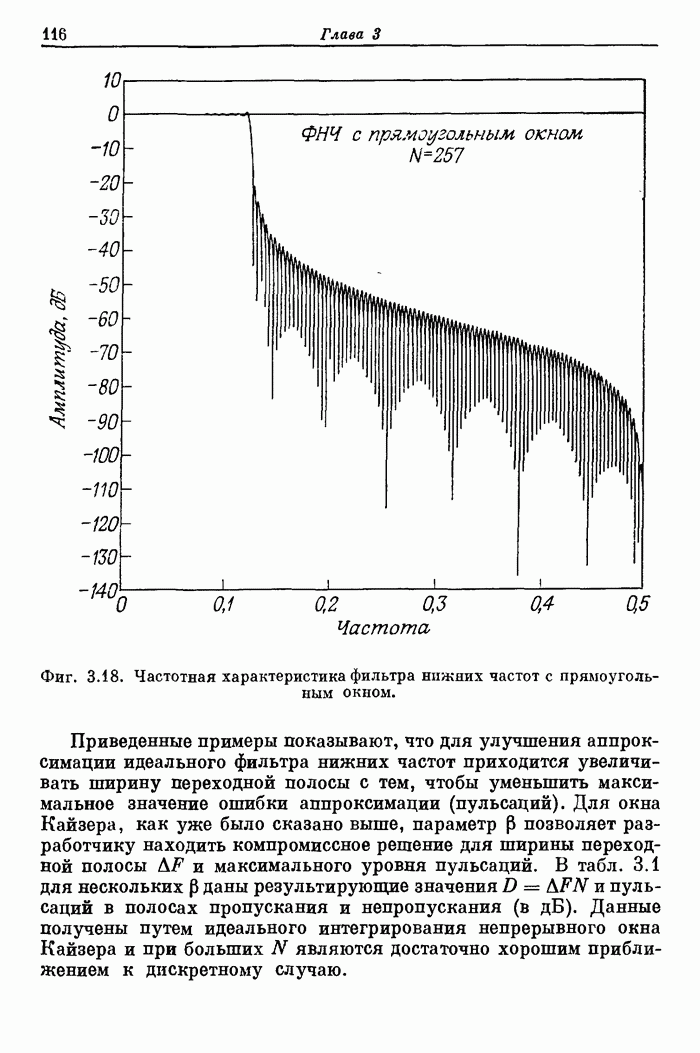
- 3.12. Примеры фильтров нижних частот с различными окнами
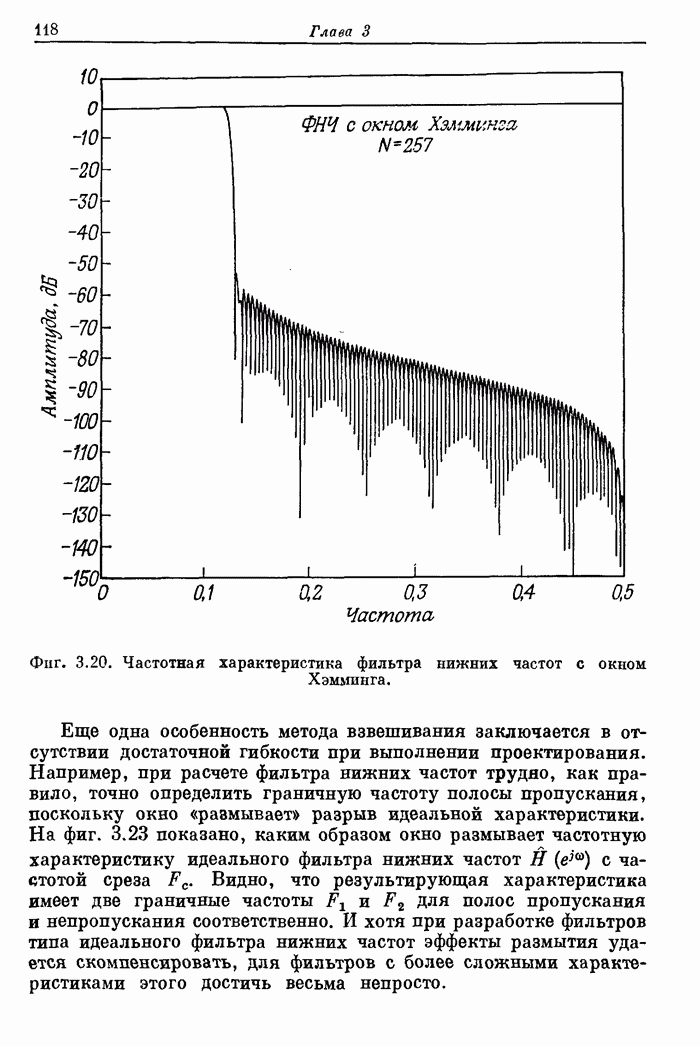
- 3.13. Особенности использования метода взвешивания
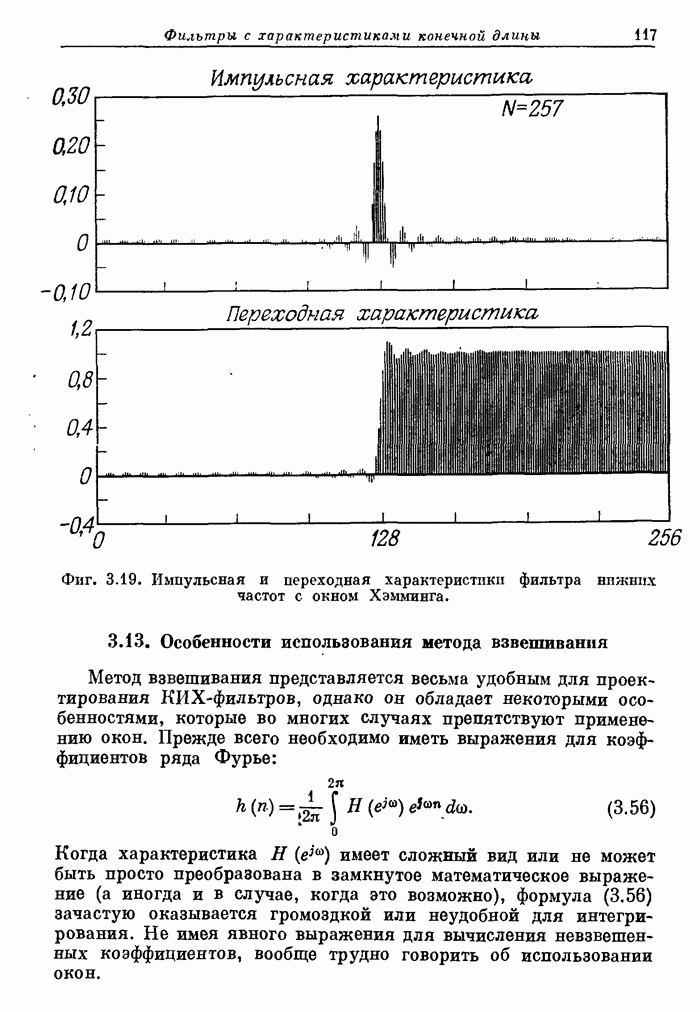
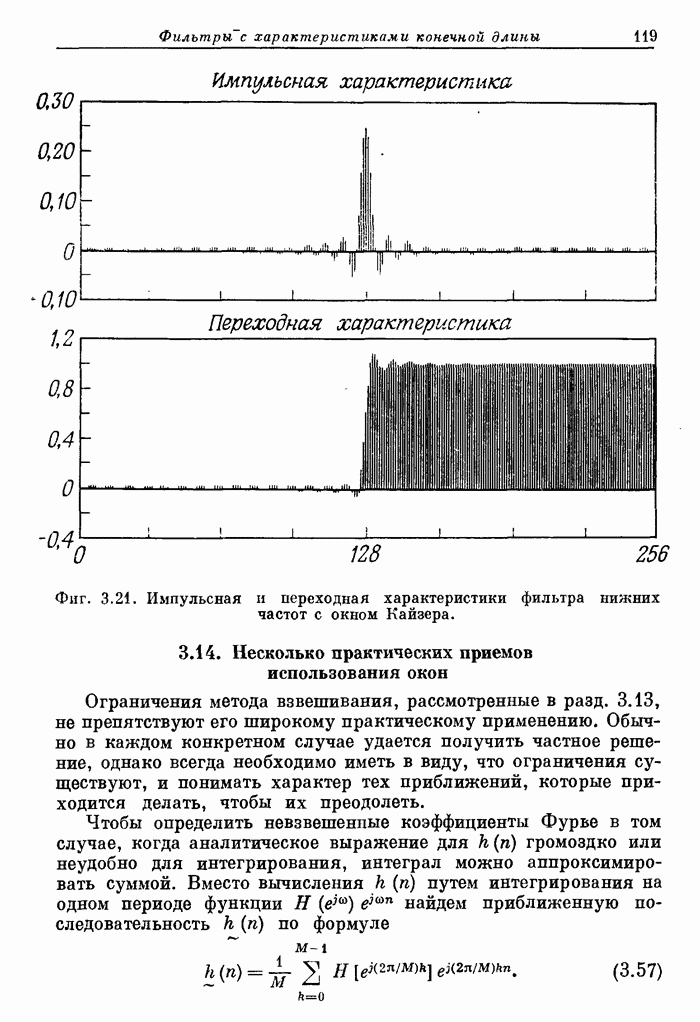
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
- 3.38. Многополосные оптимальные КИХ-фильтры
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
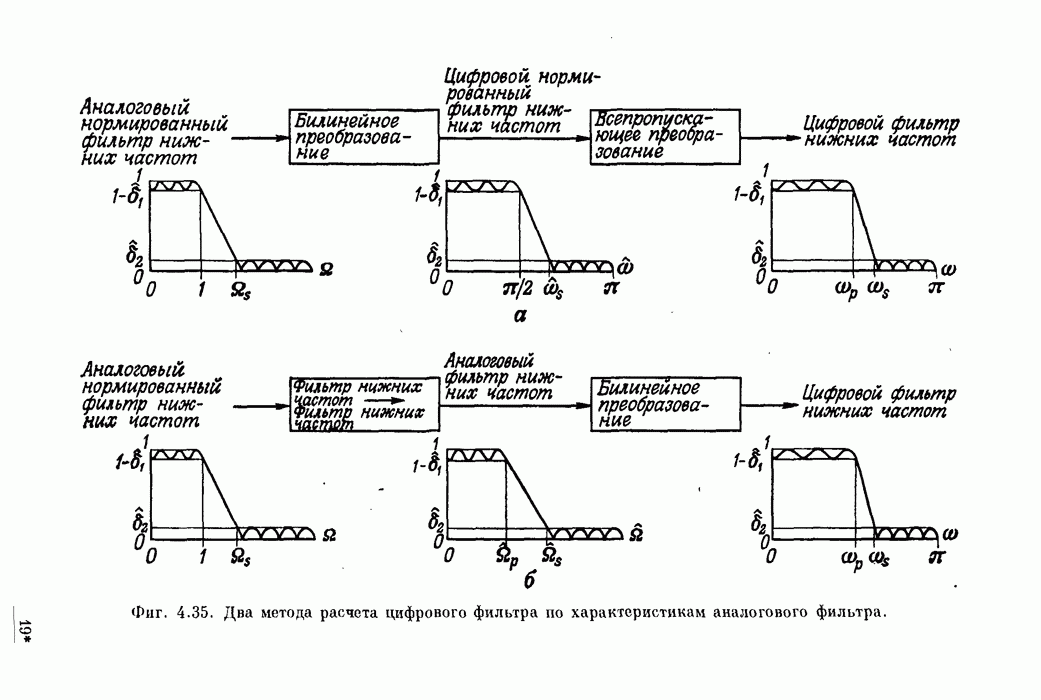
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
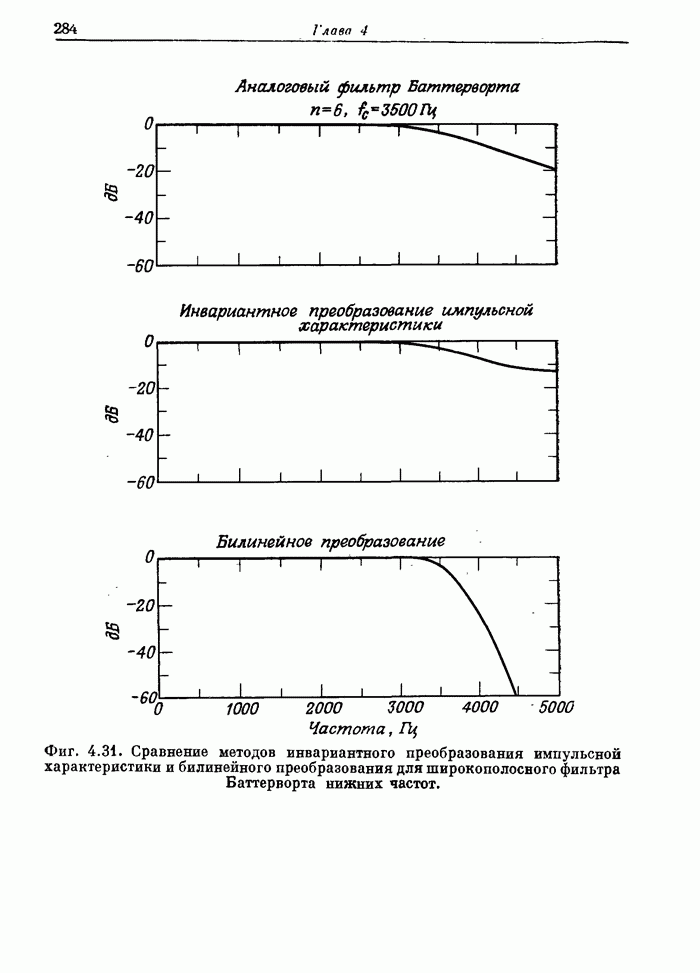
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
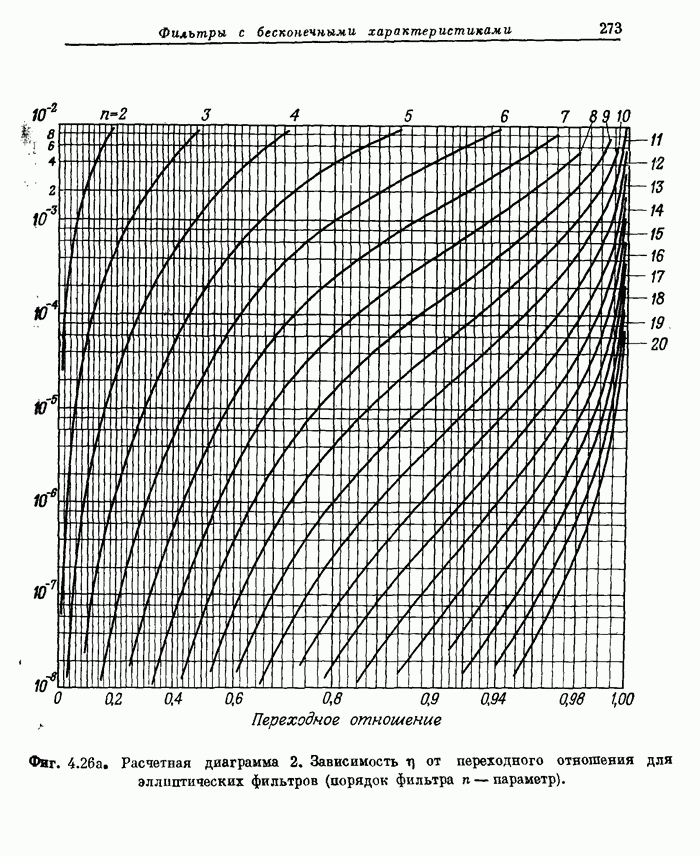
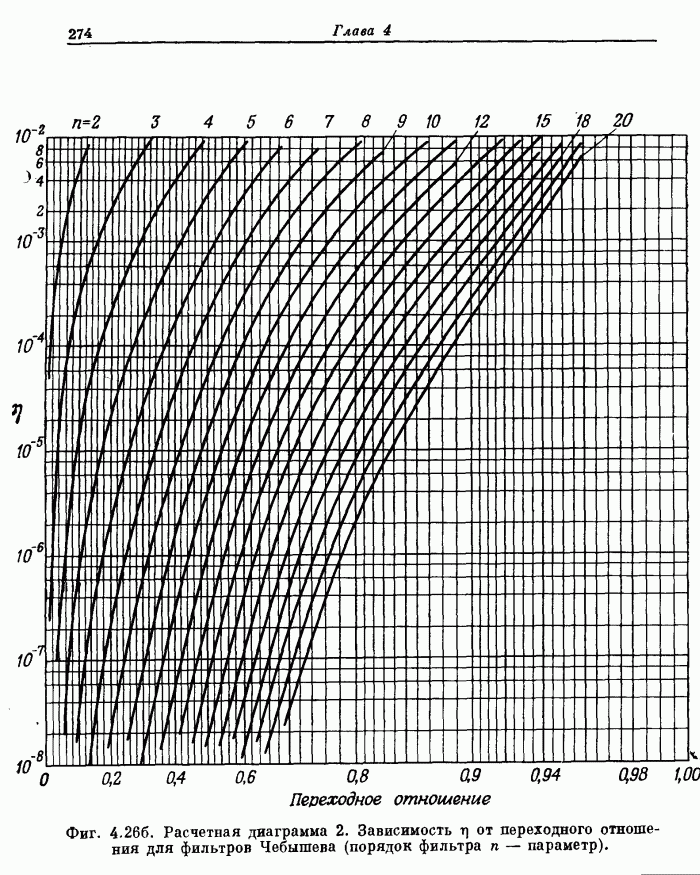
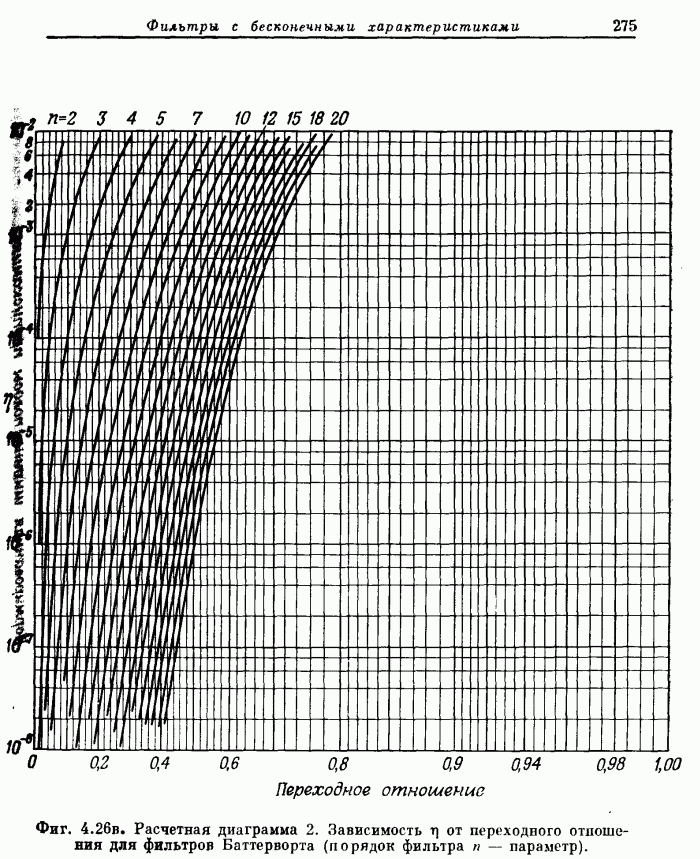
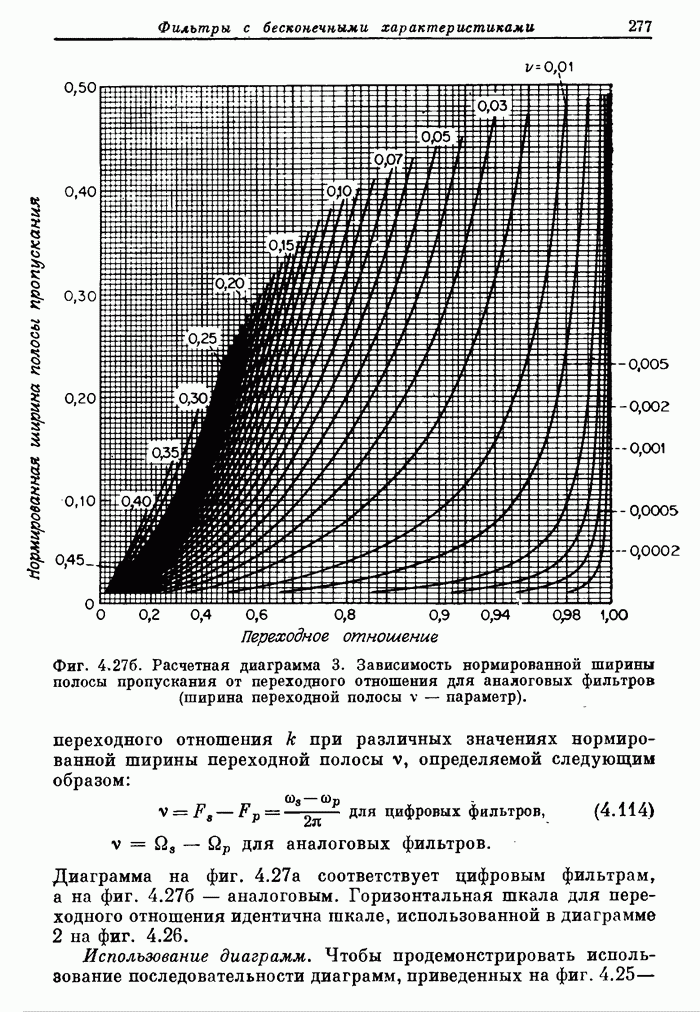
- 4.10. Расчетные диаграммы фильтров нижних частот
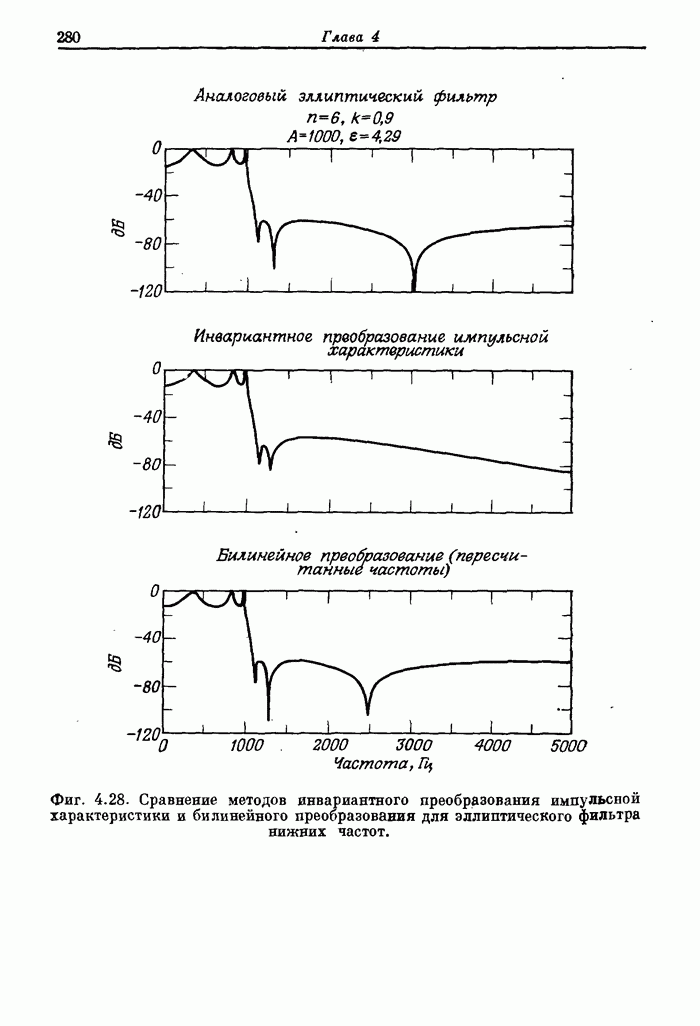
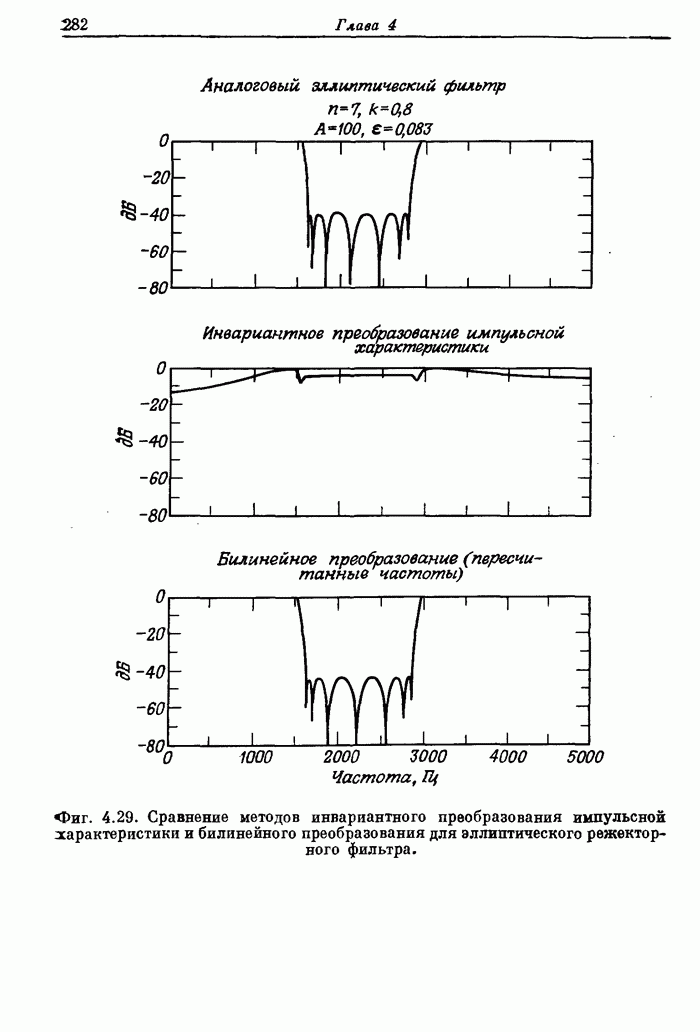
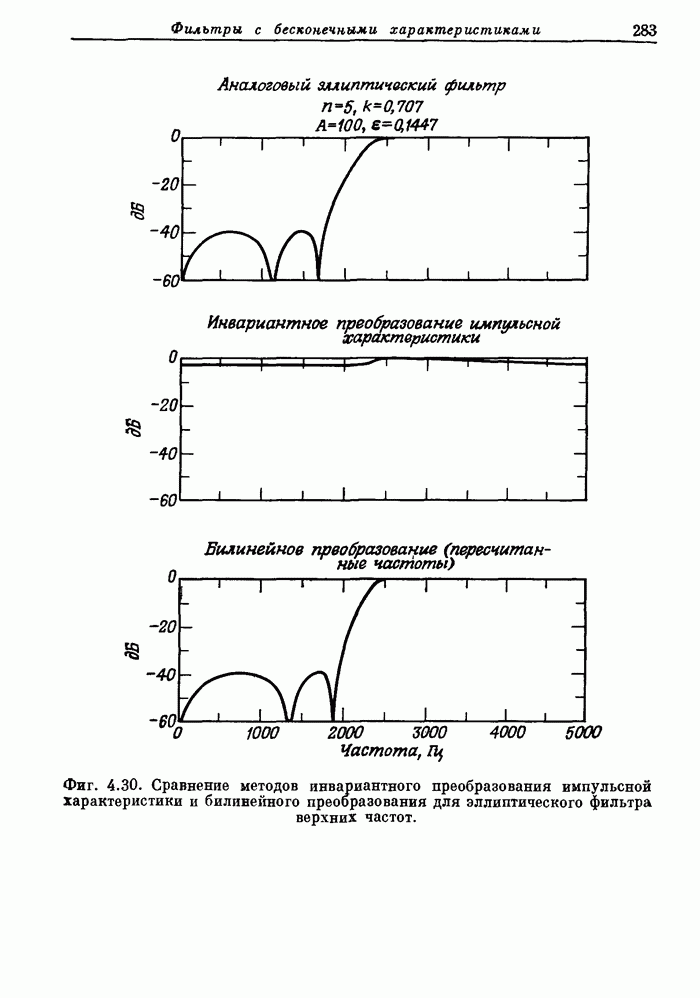
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
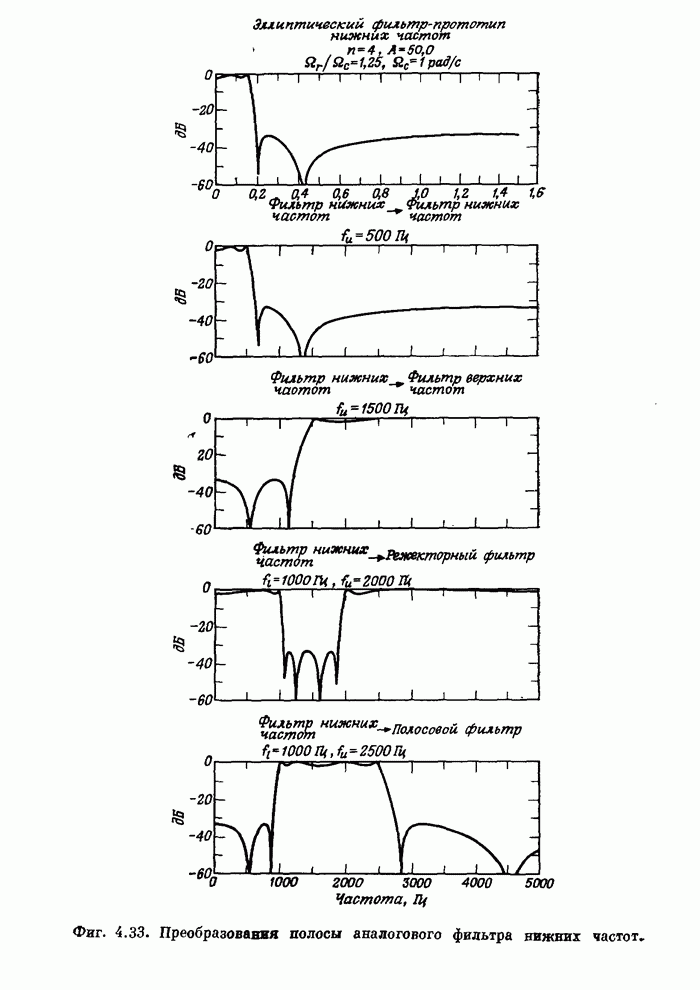
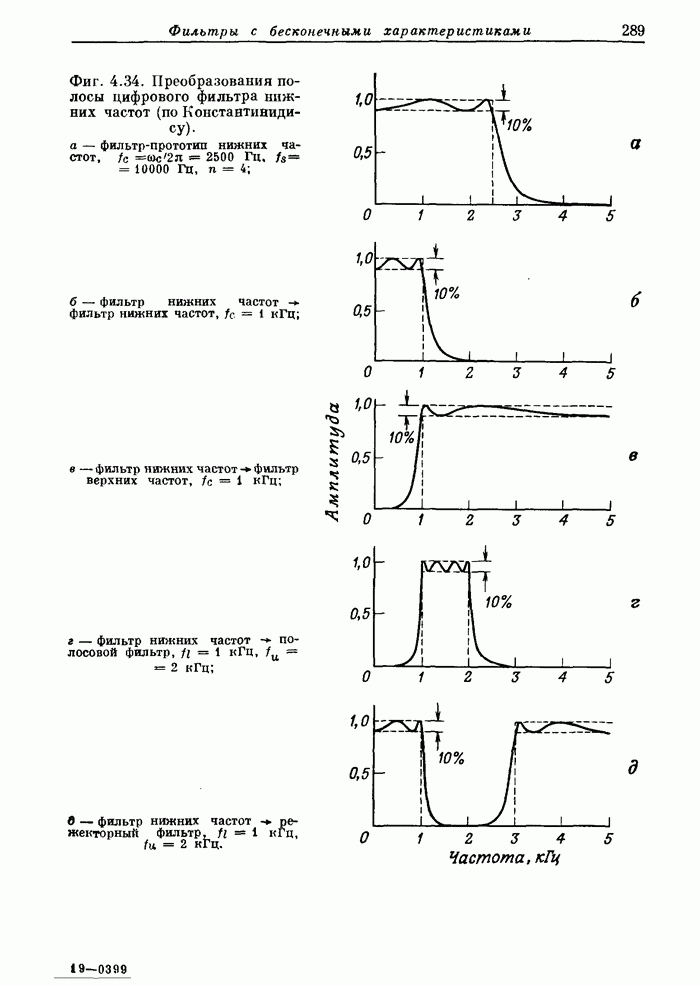
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
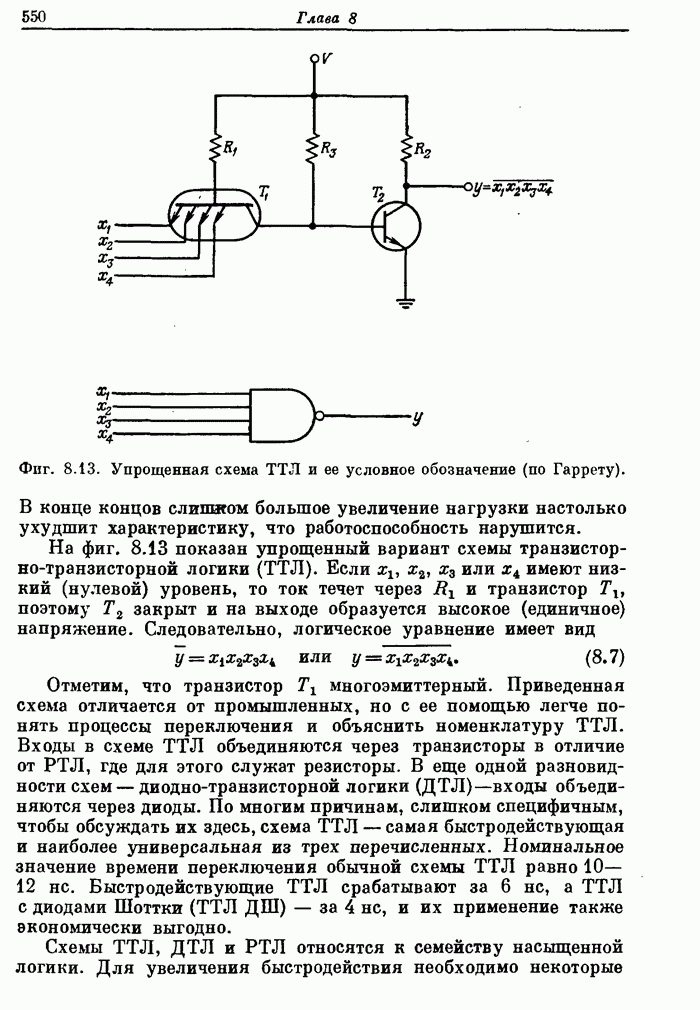
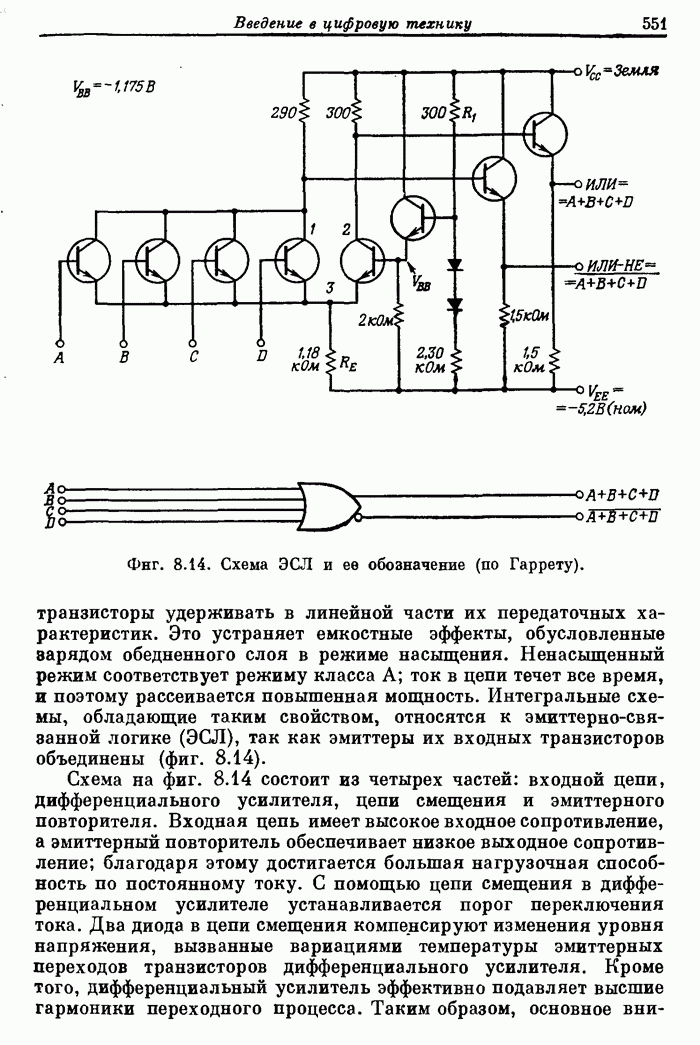
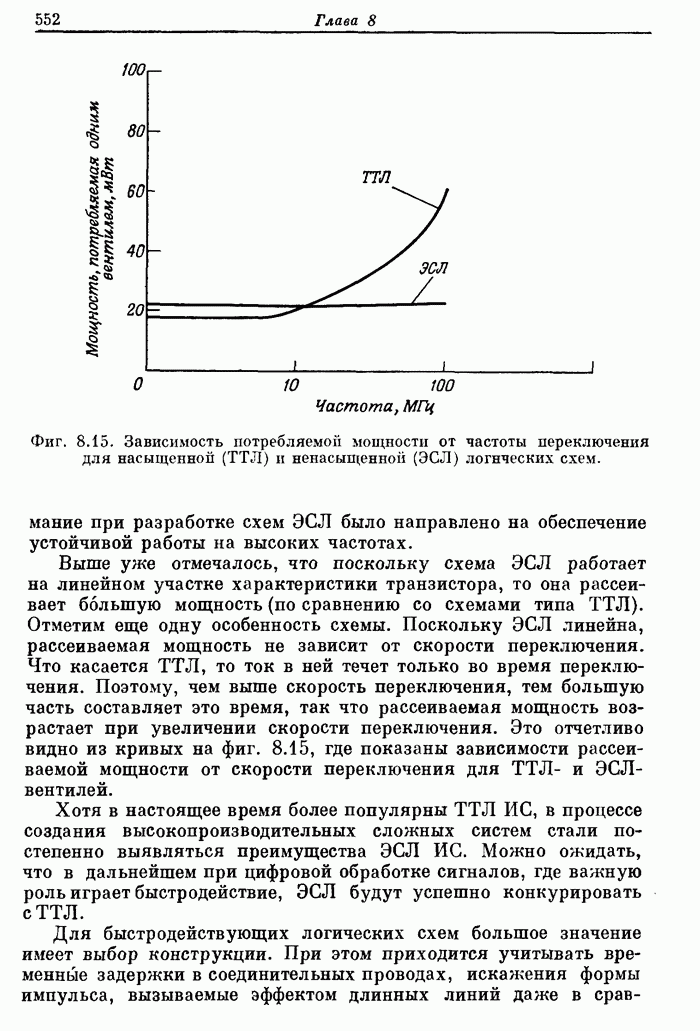
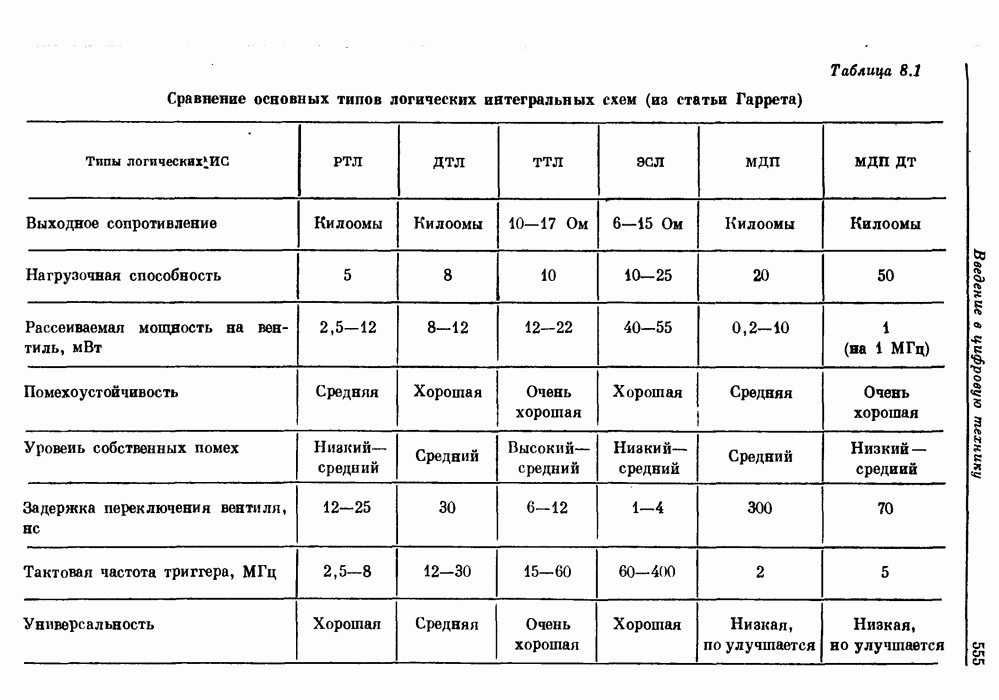
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
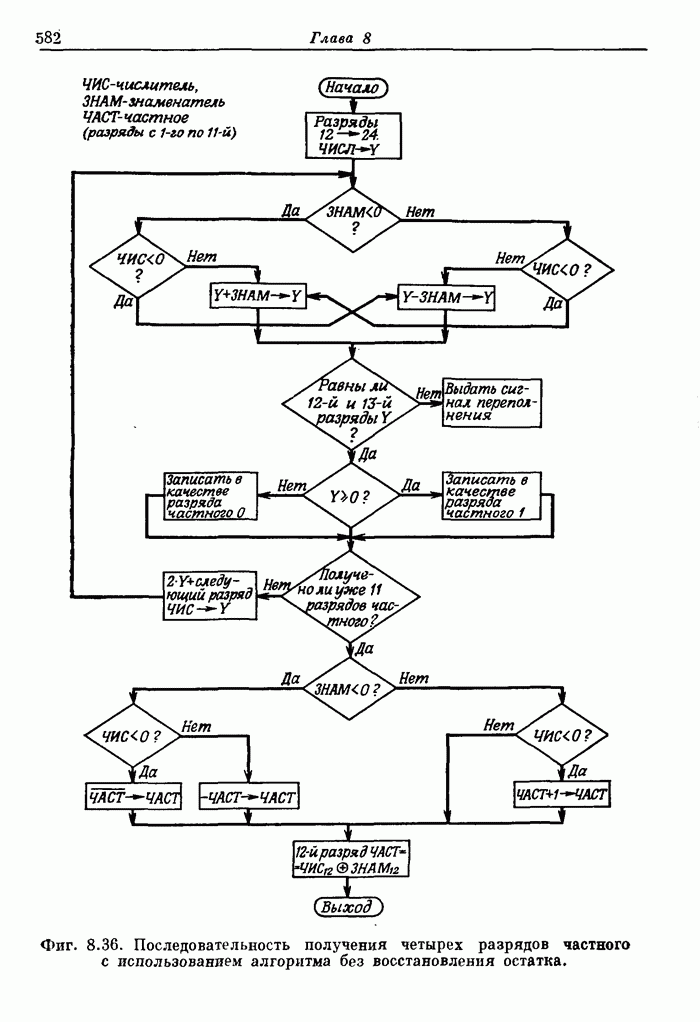
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
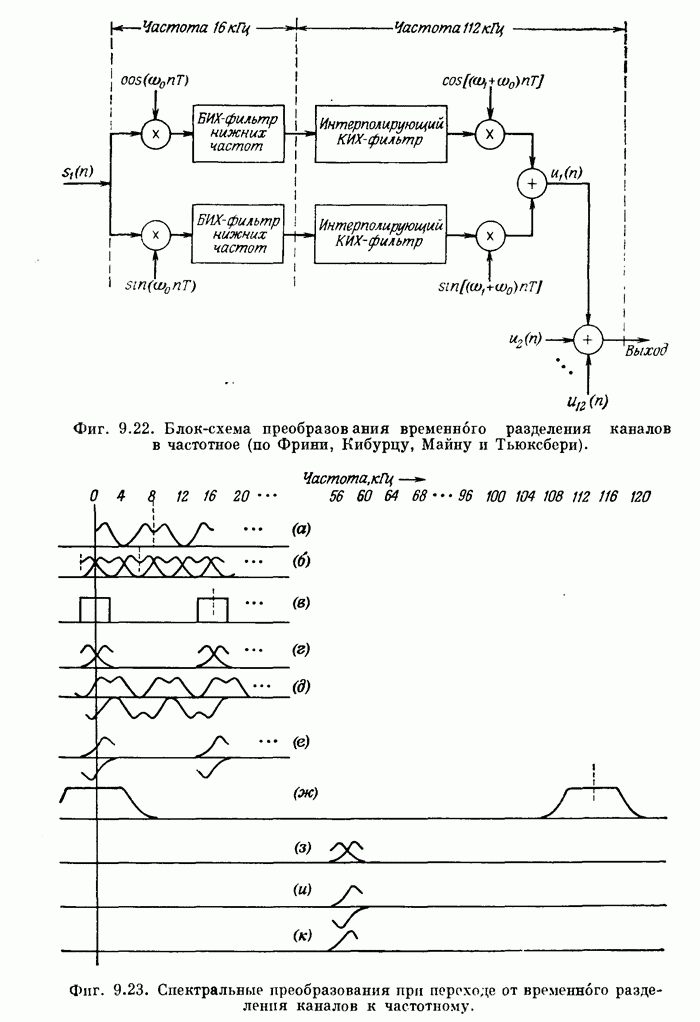
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
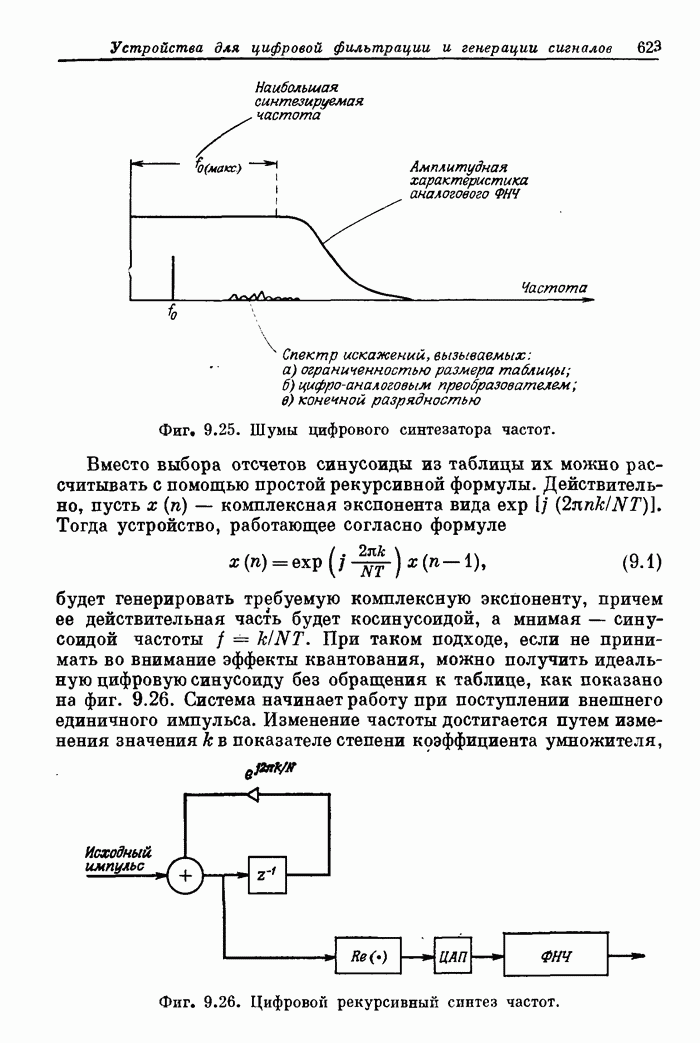
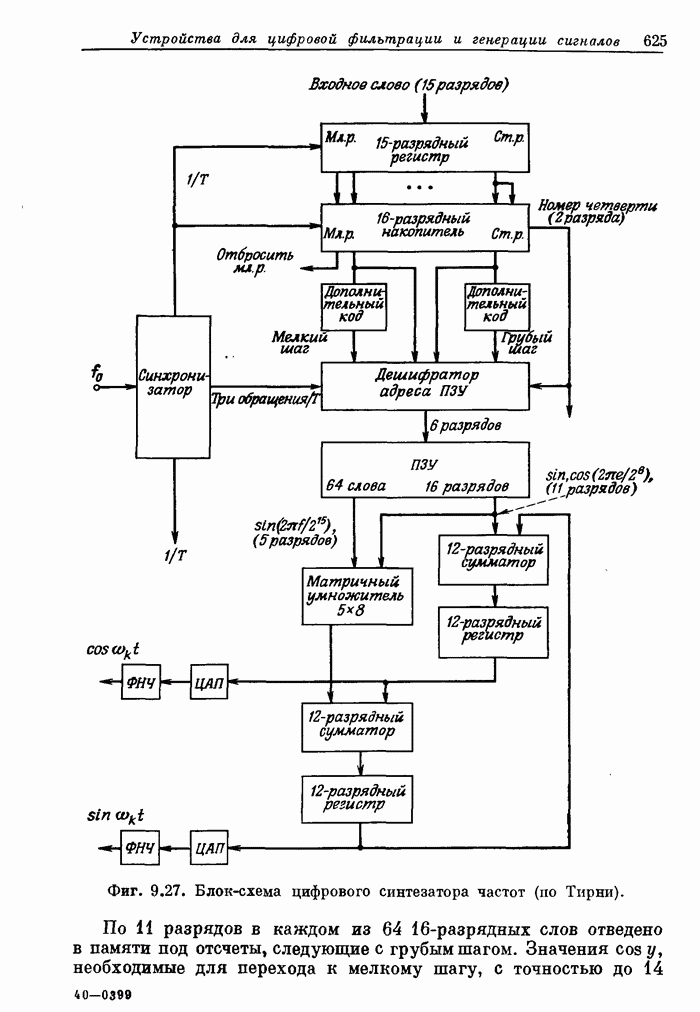
- 9.12. Специализированный цифровой синтезатор частот
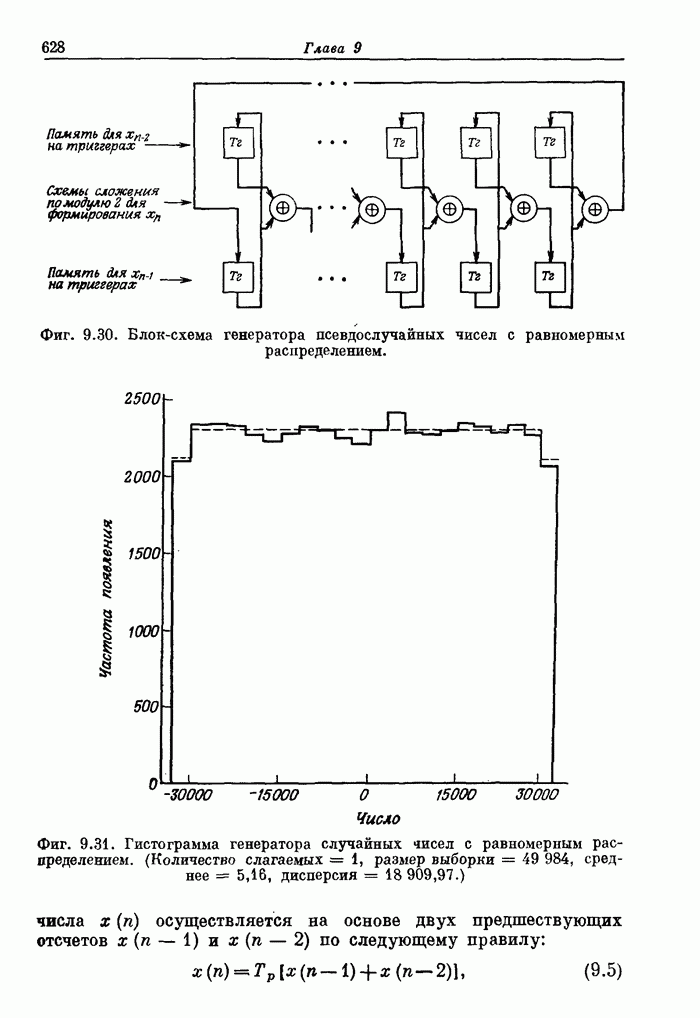
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
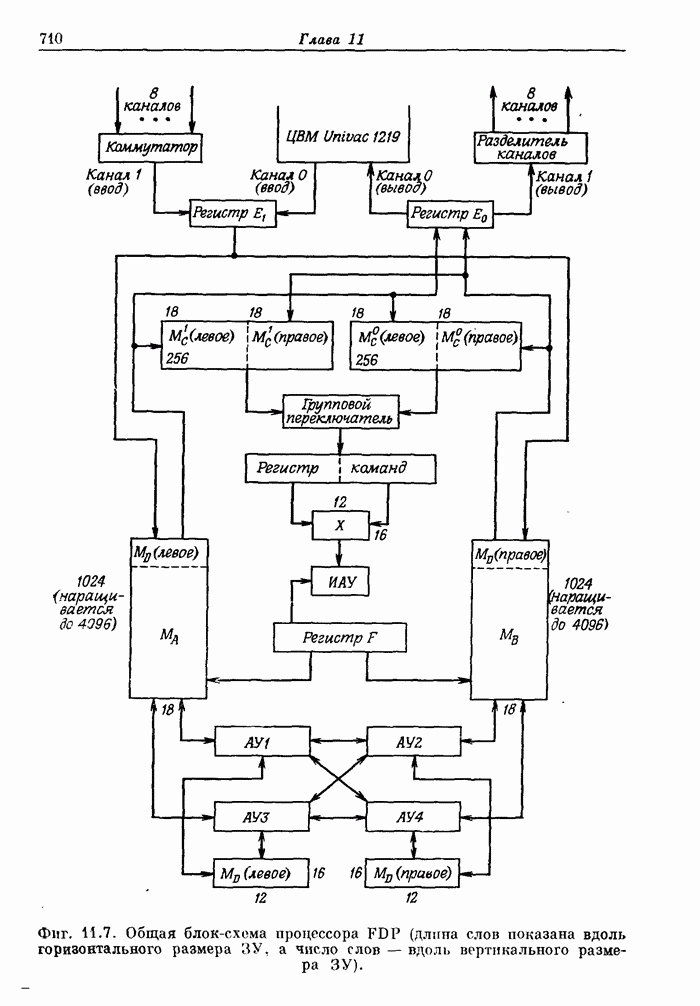
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
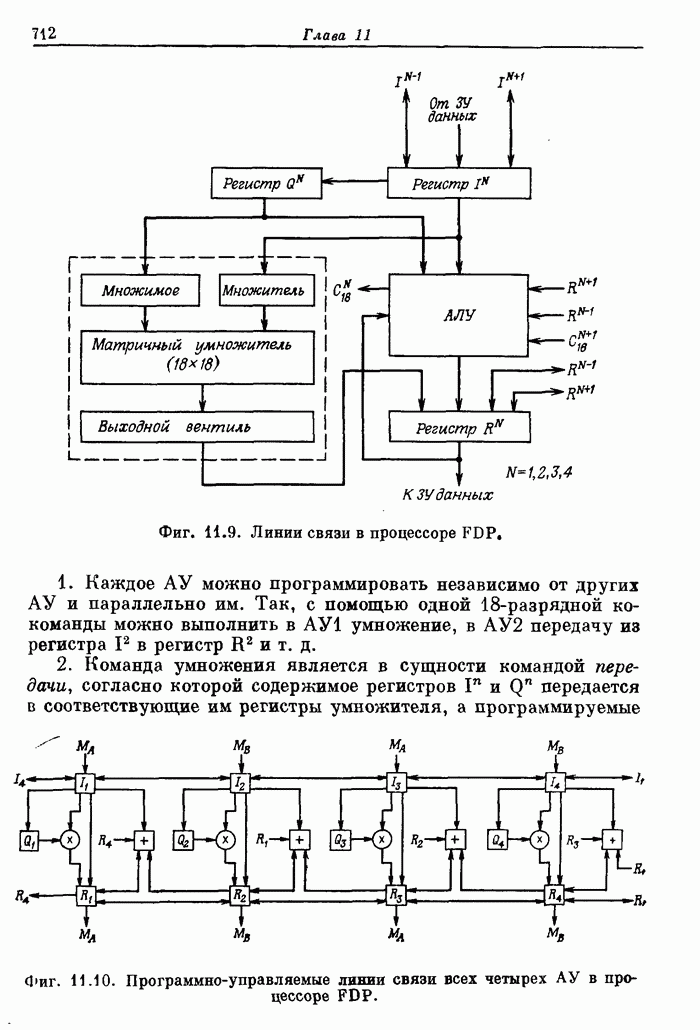
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
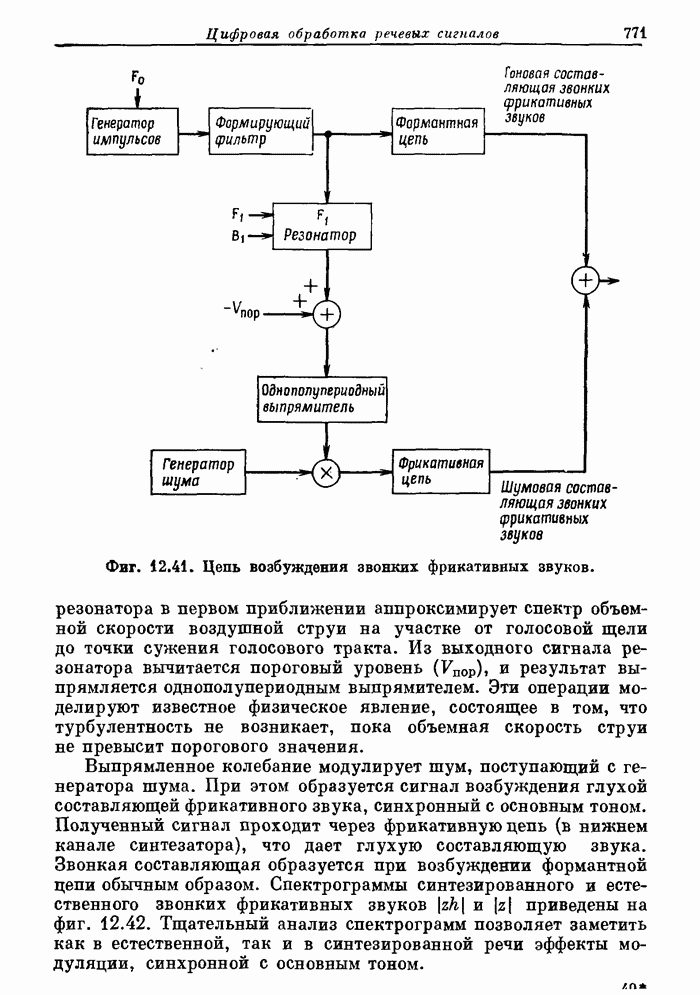
- 12.16. Цепь возбуждения звонких фрикативных звуков
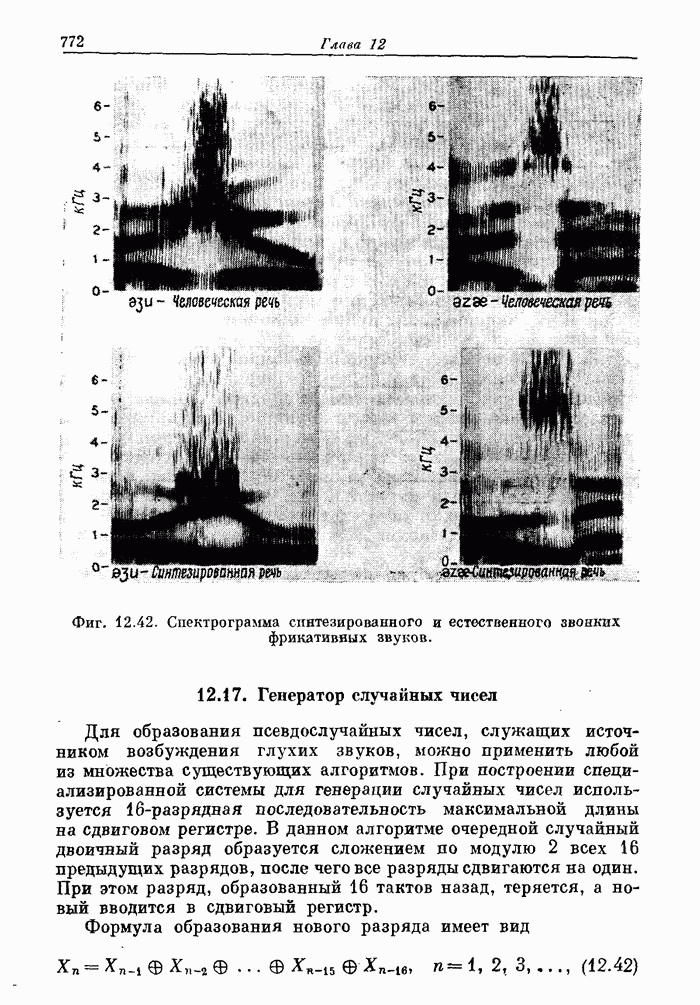
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
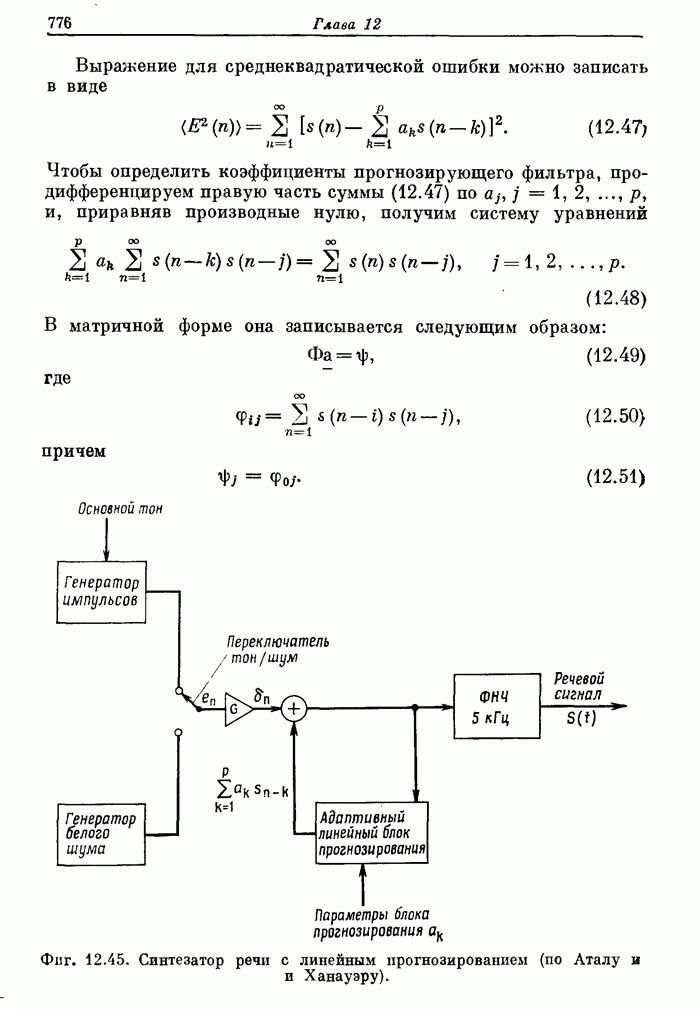
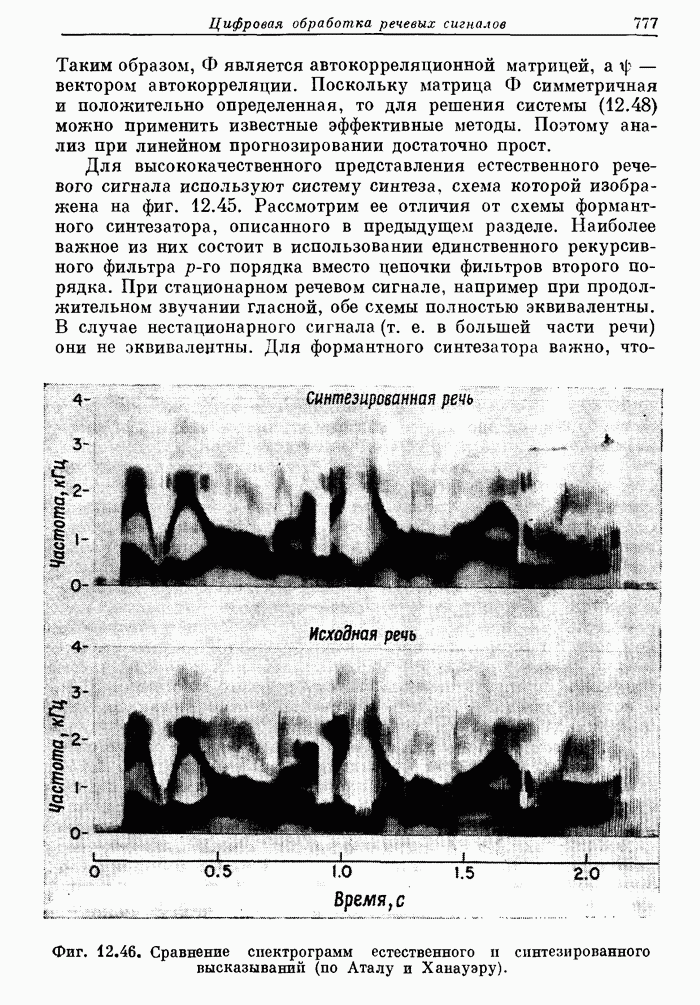
- 12.19. Линейное прогнозирование речи
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
- 13.3. Выбор сигналов и функция неопределенности
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
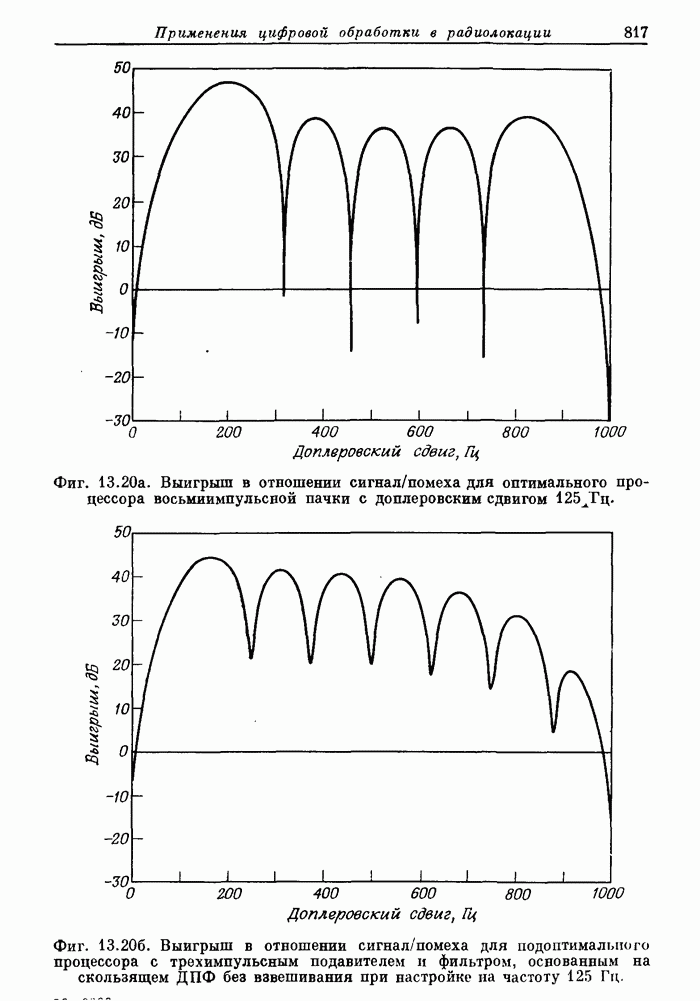
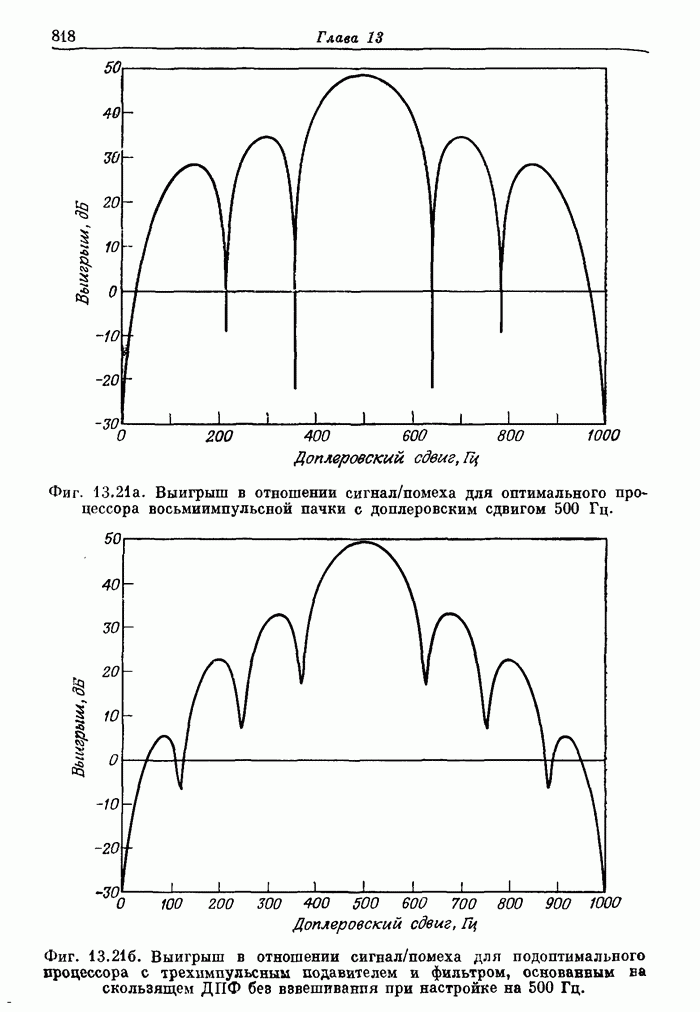
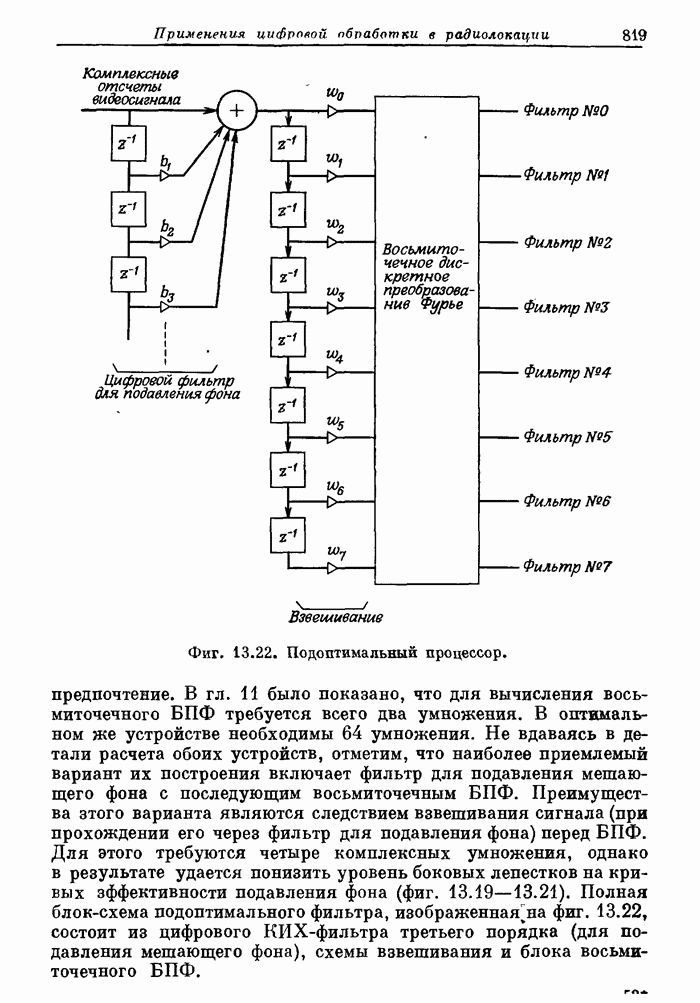
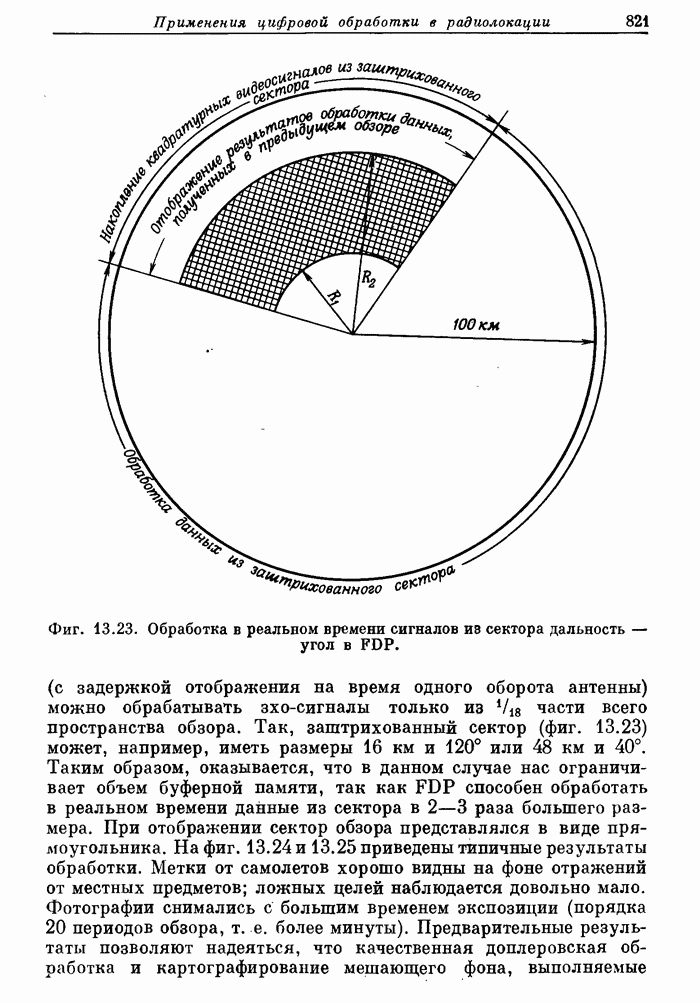
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение