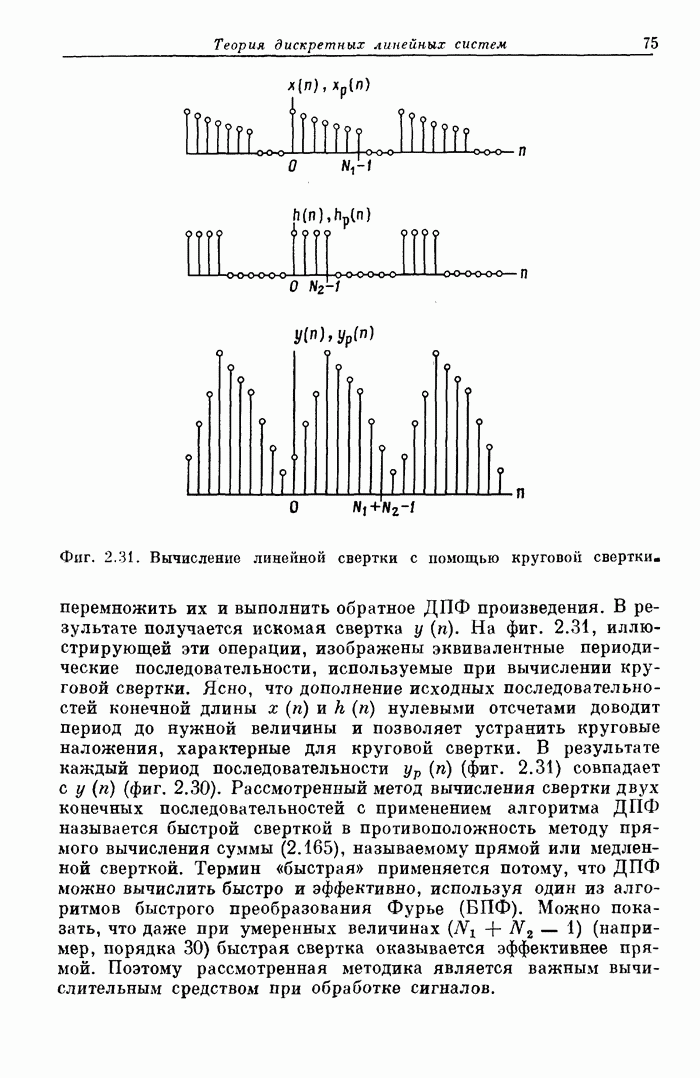
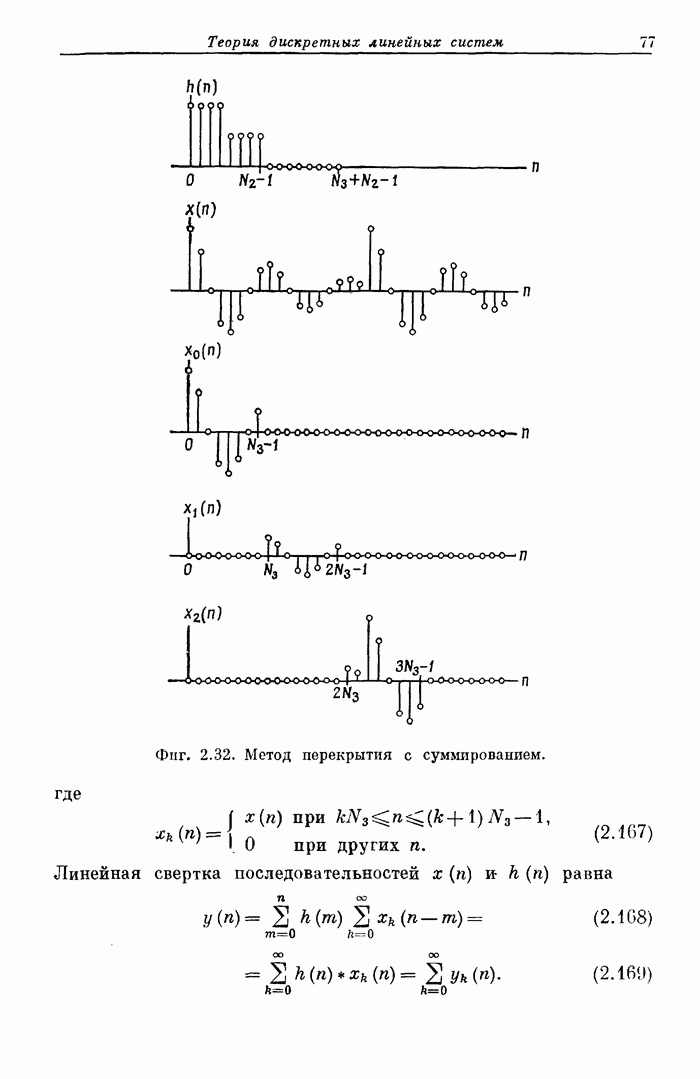
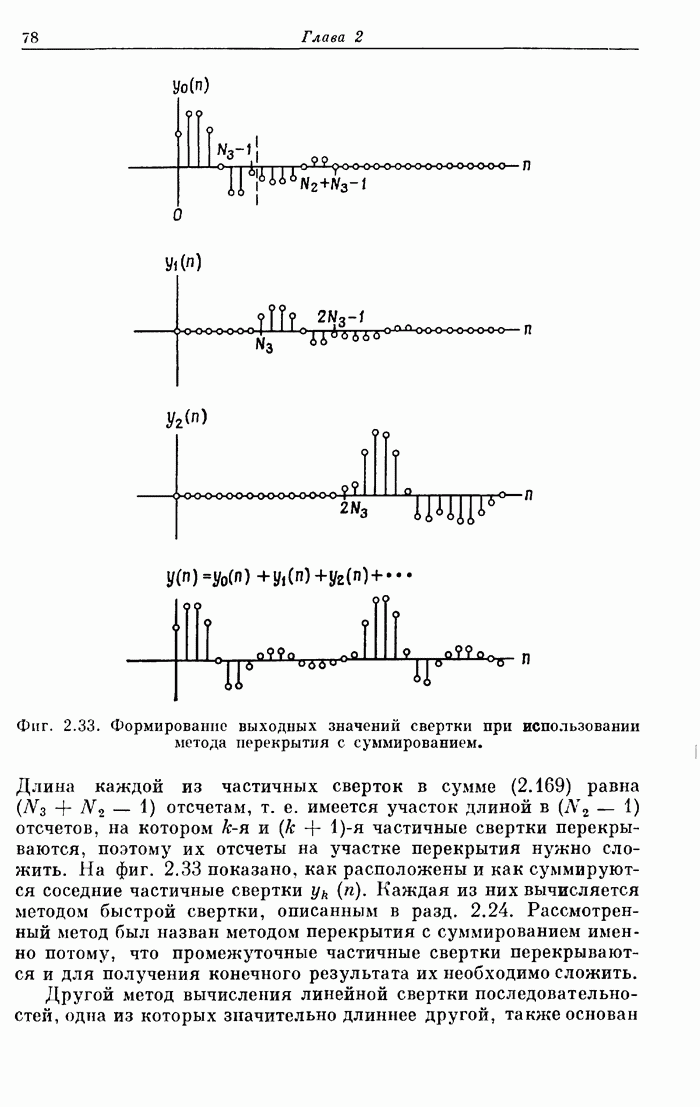
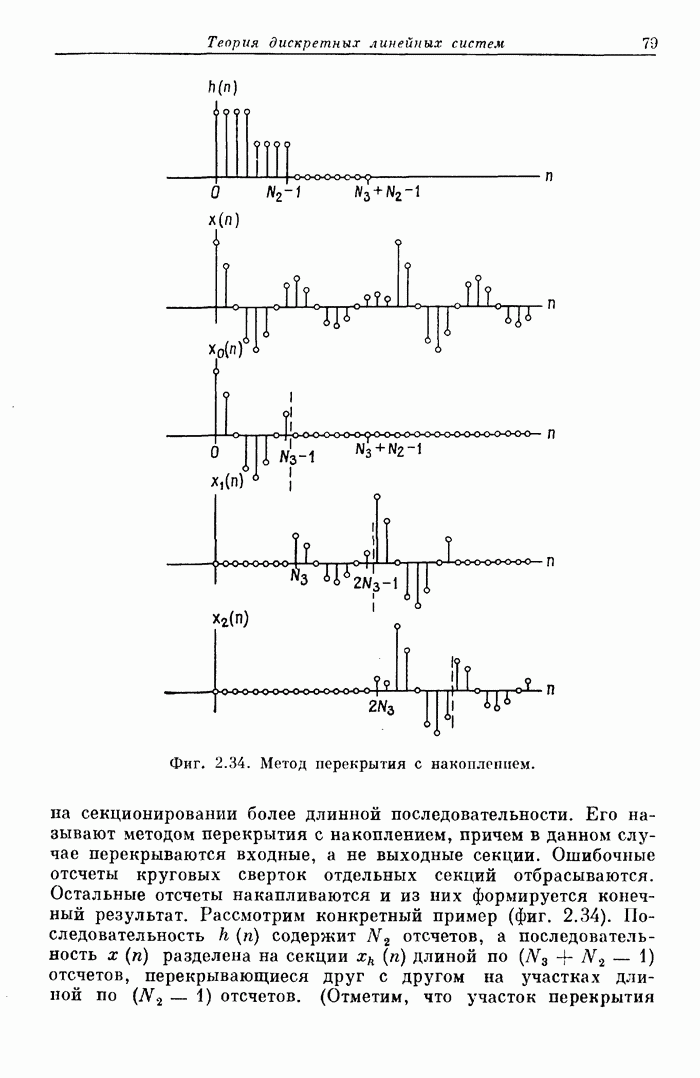
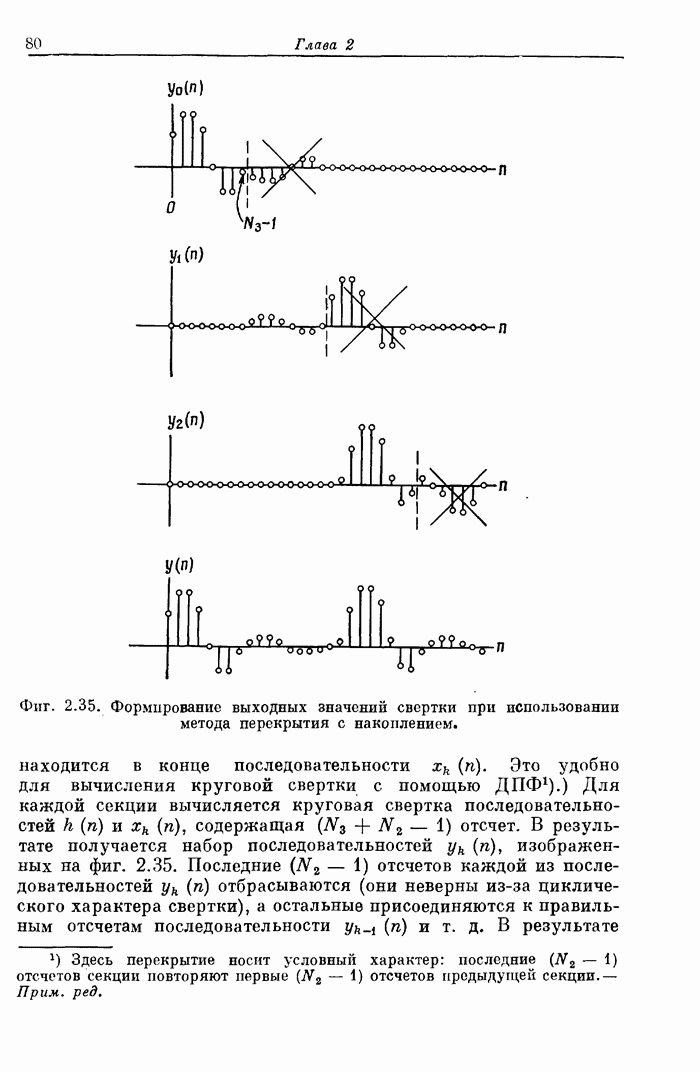
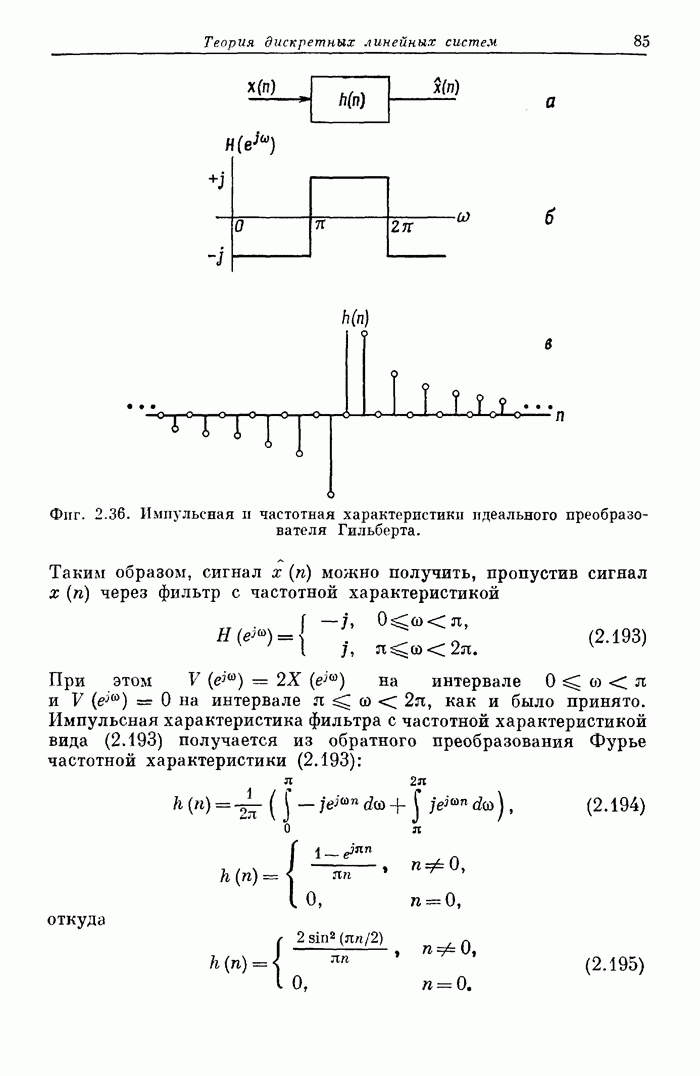
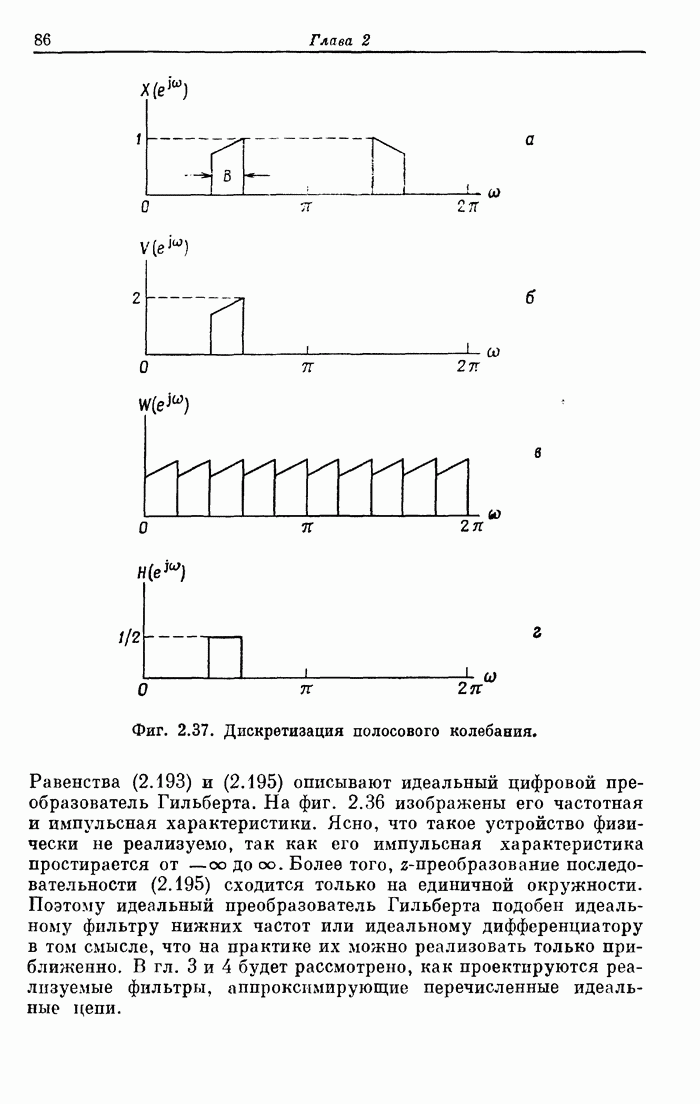
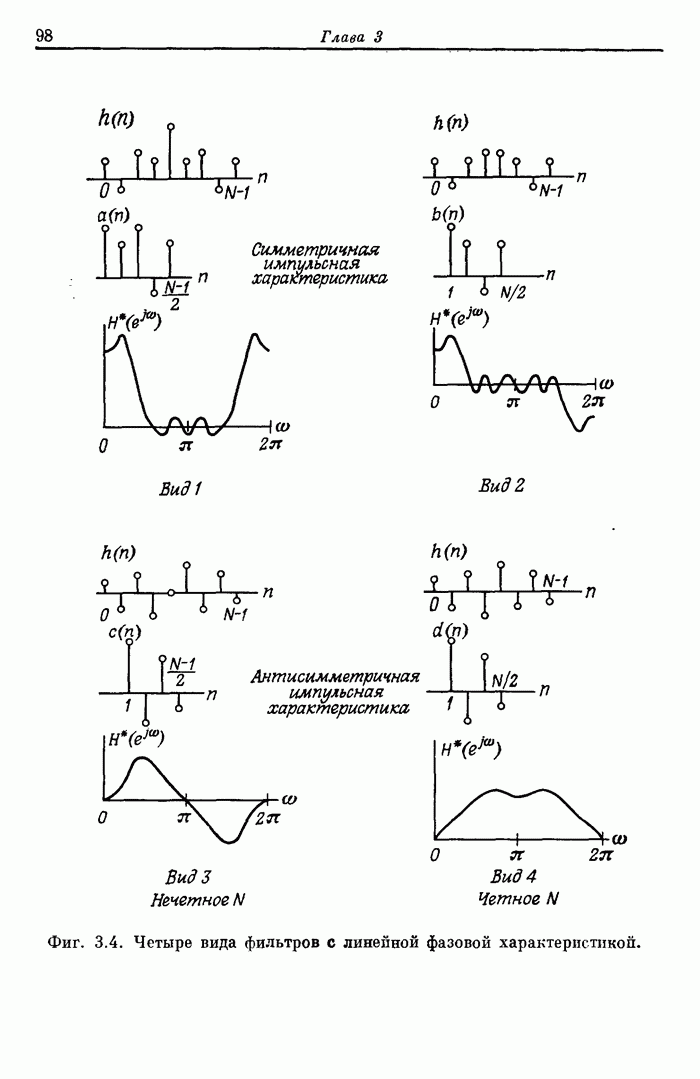
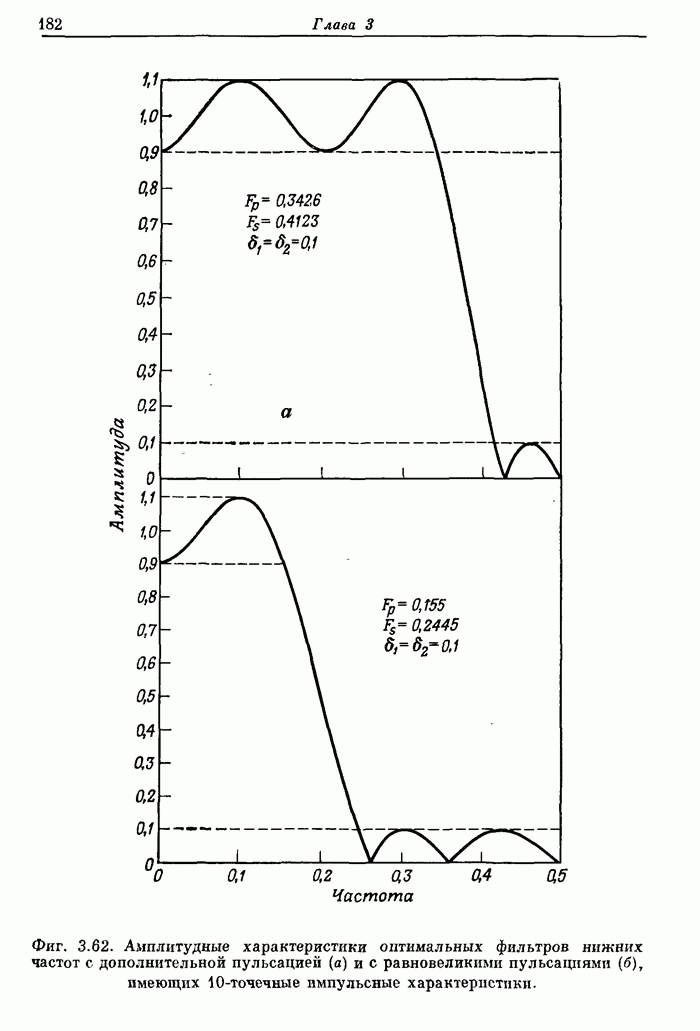
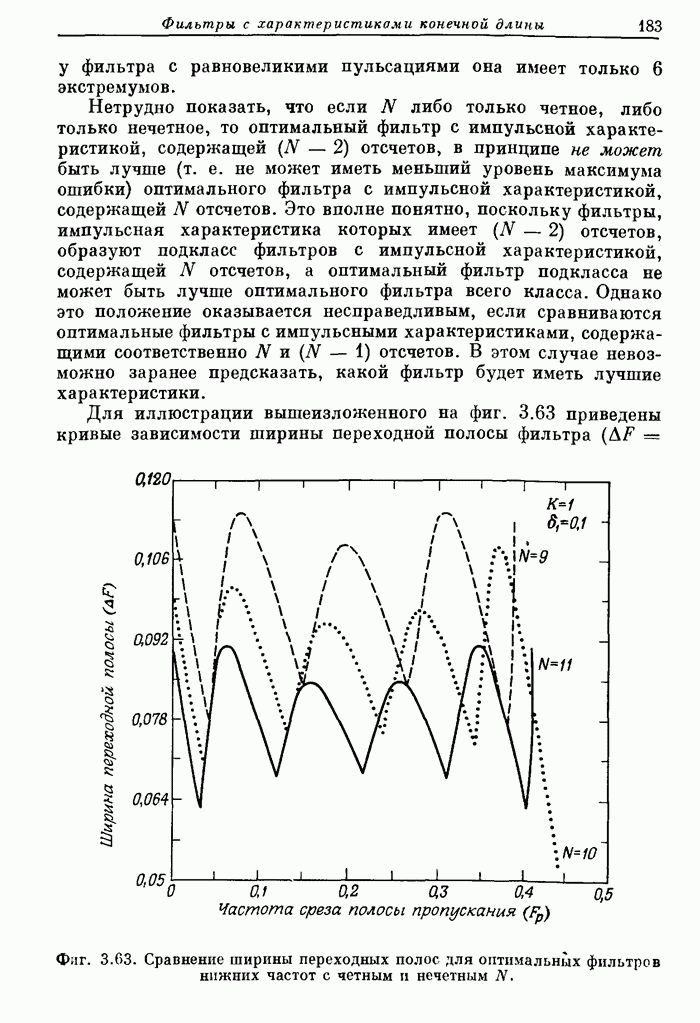
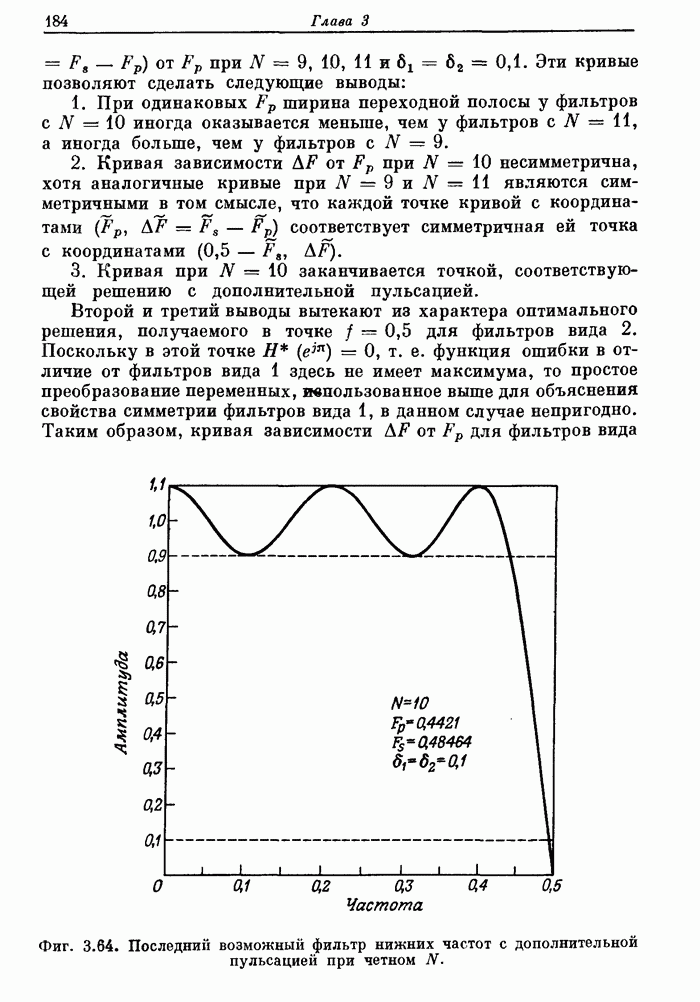
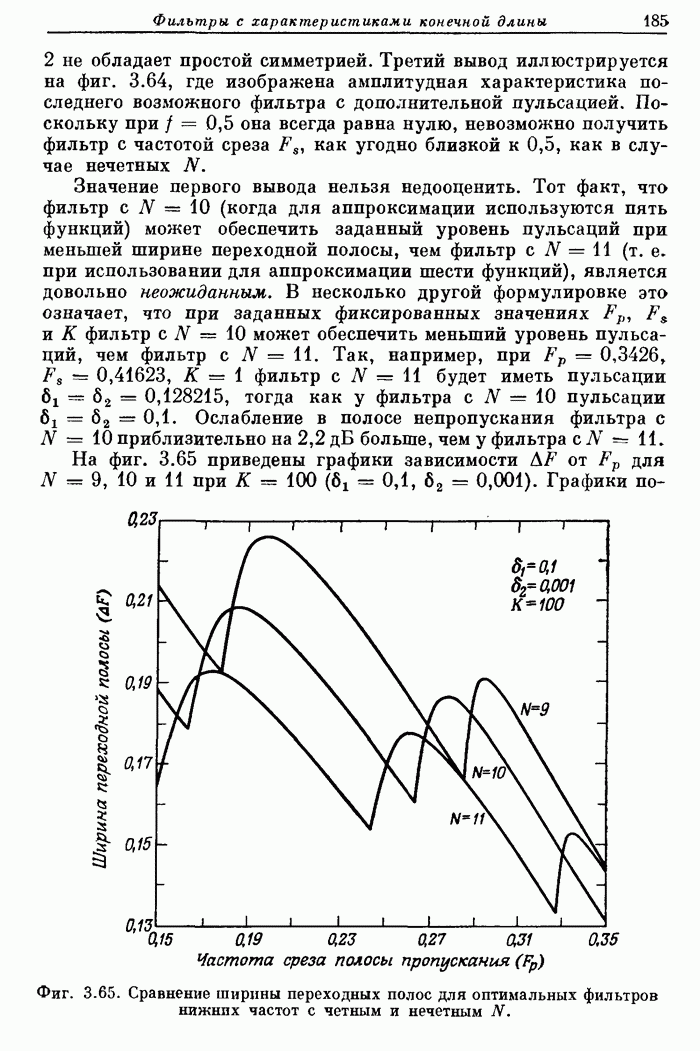
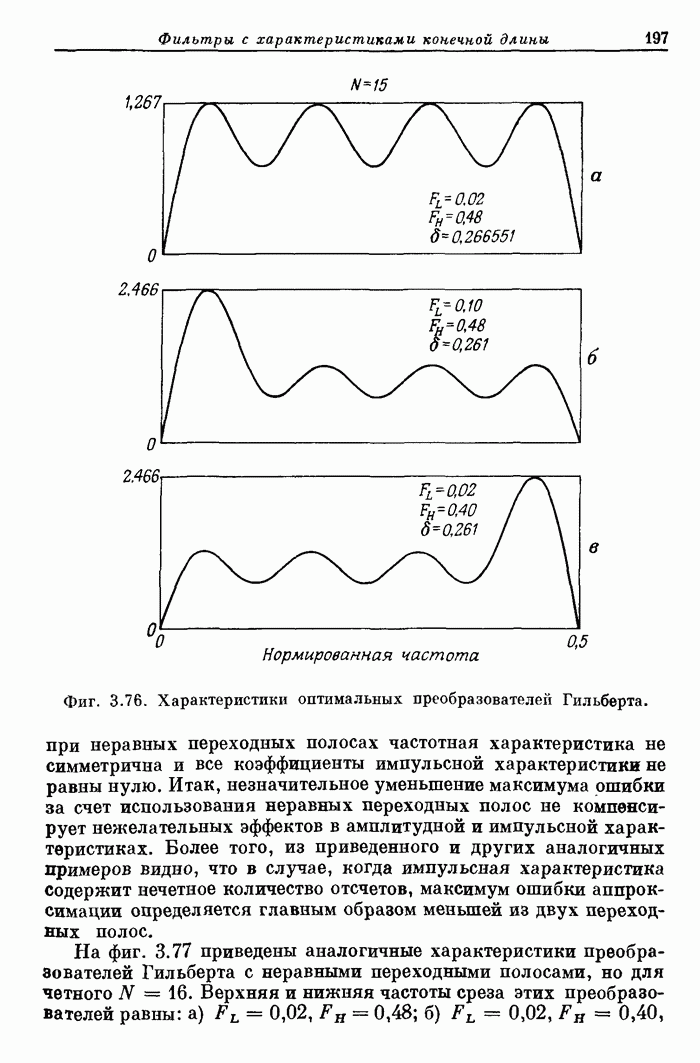
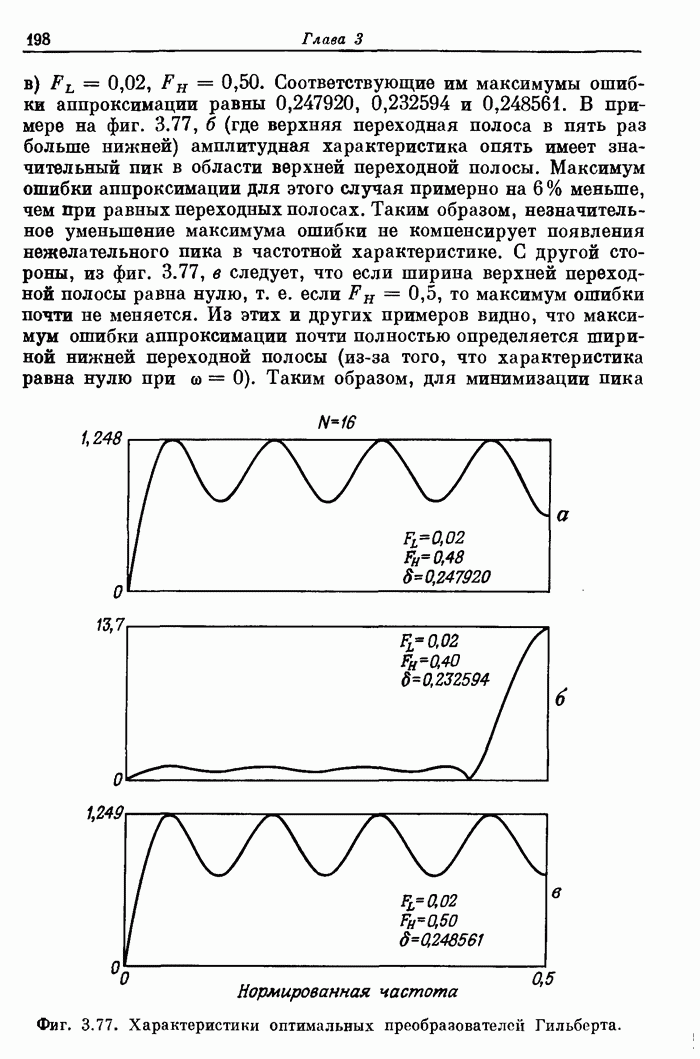
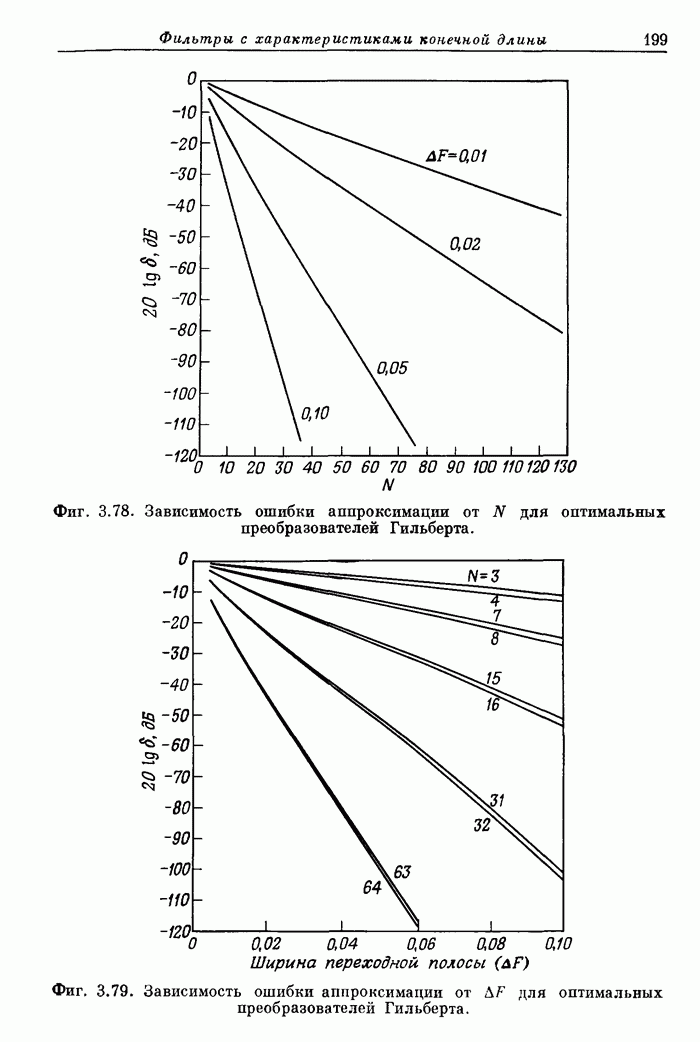
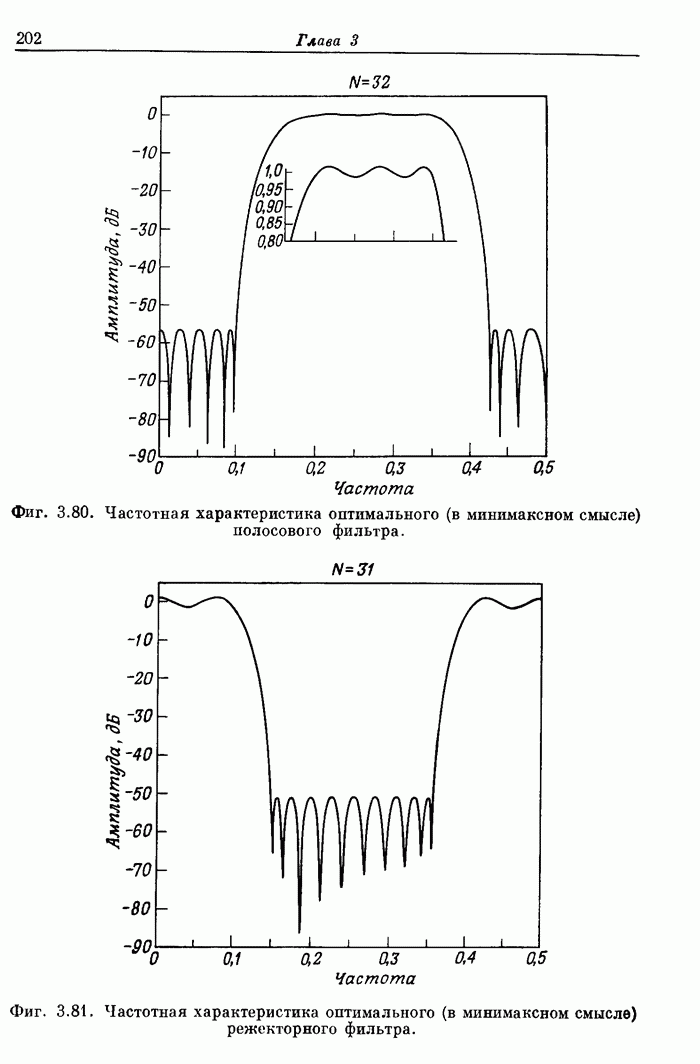
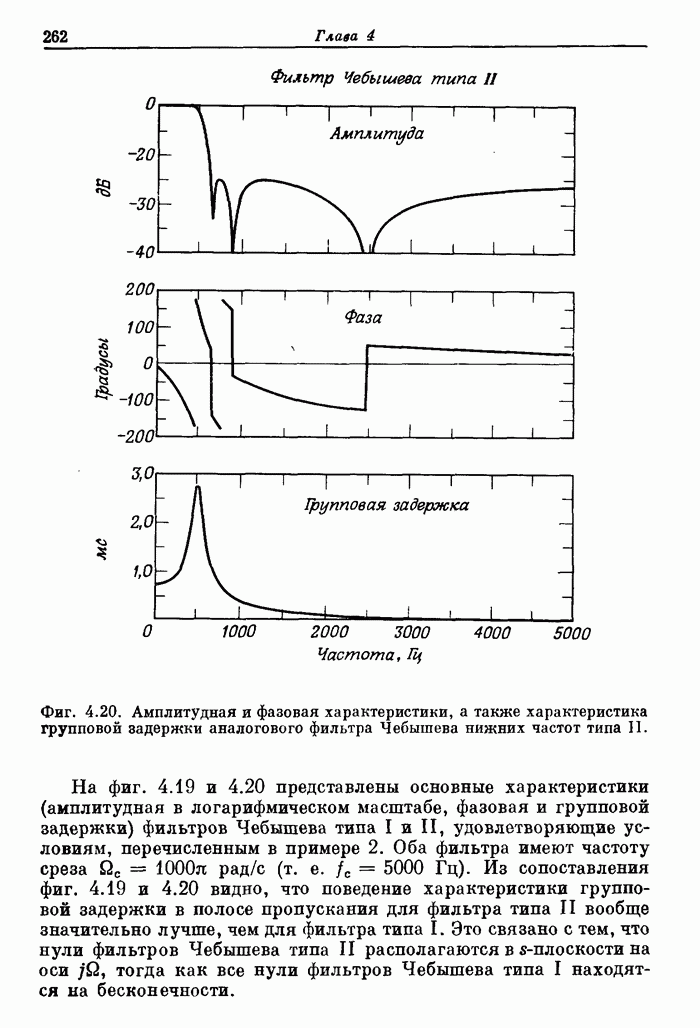
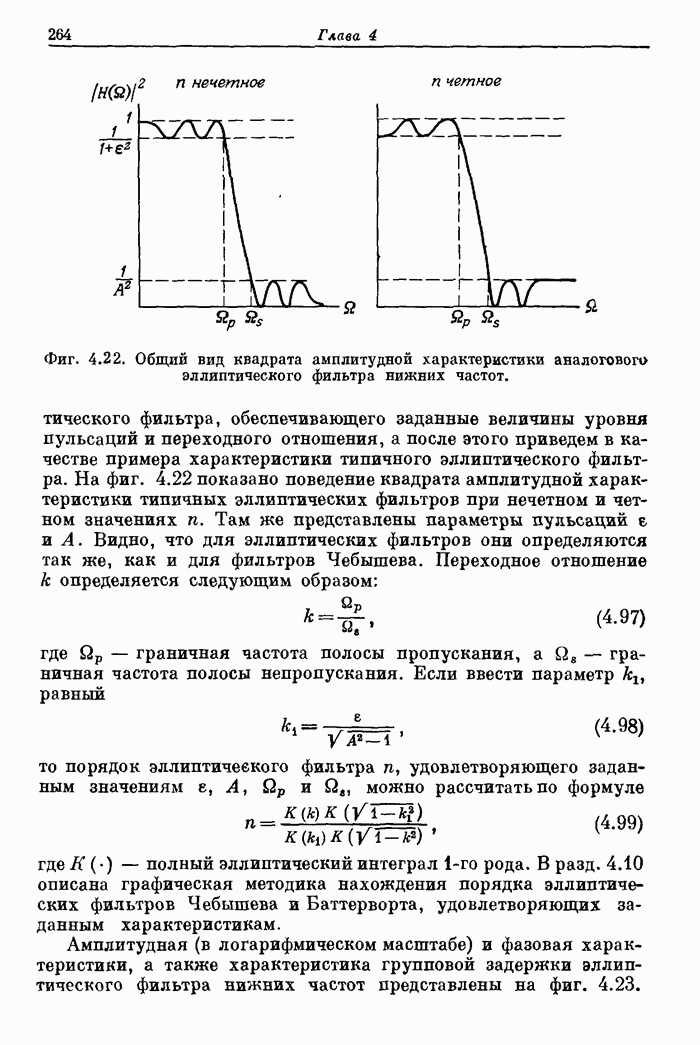
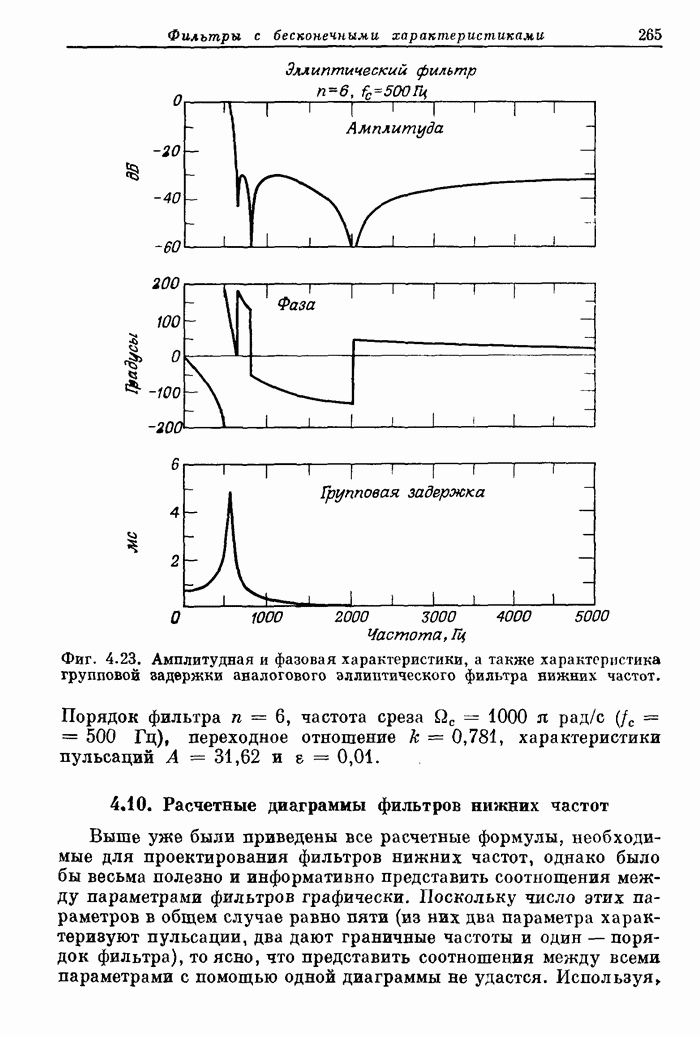
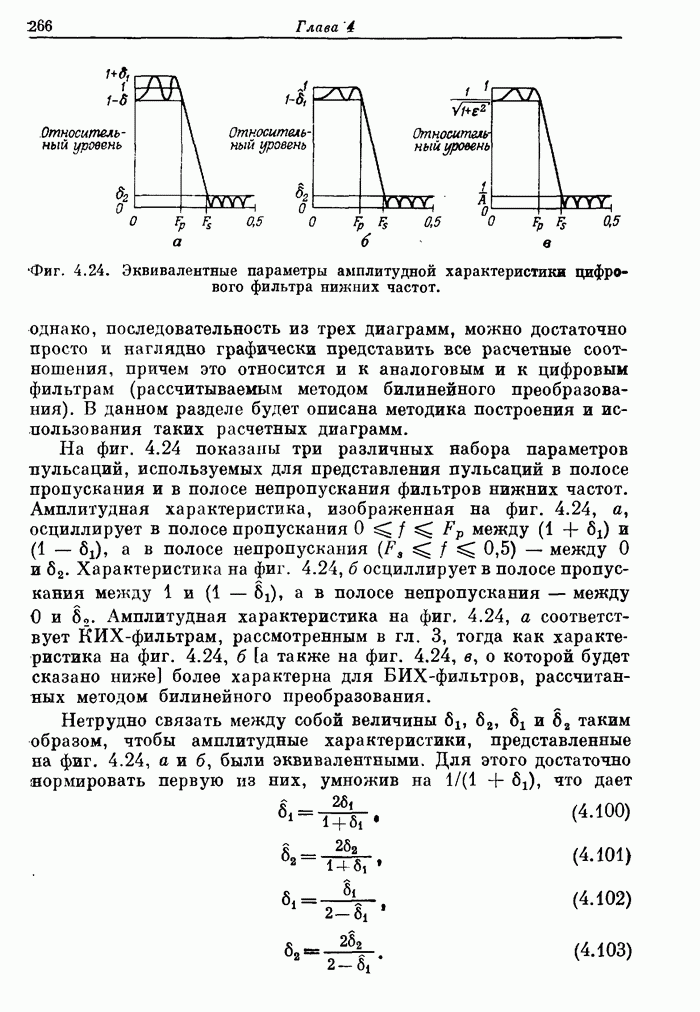
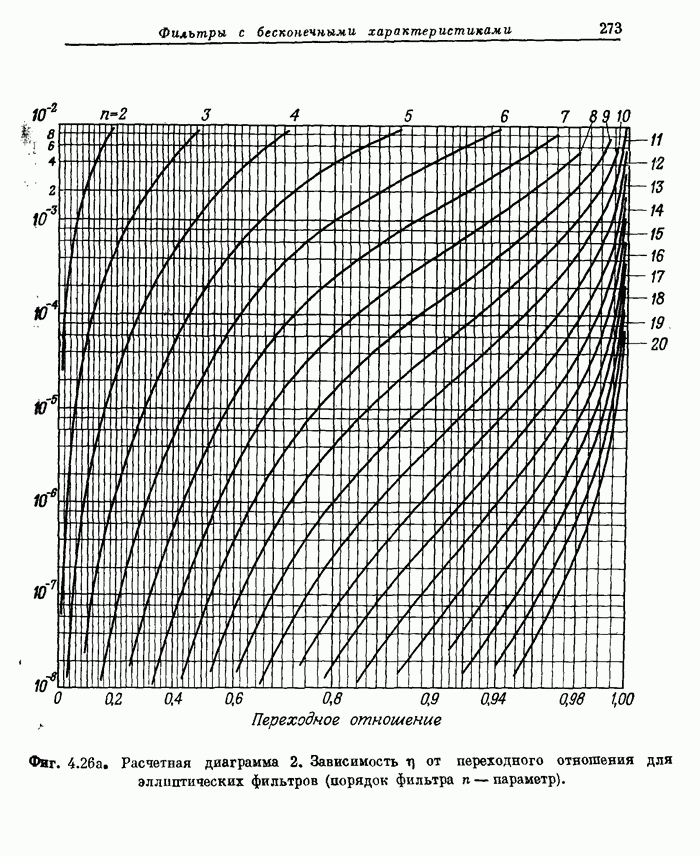
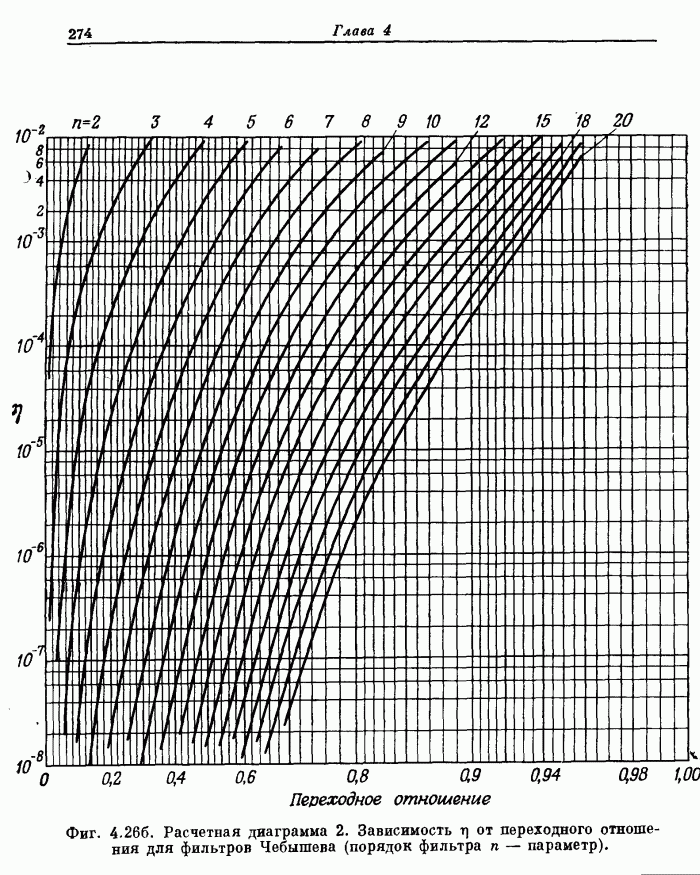
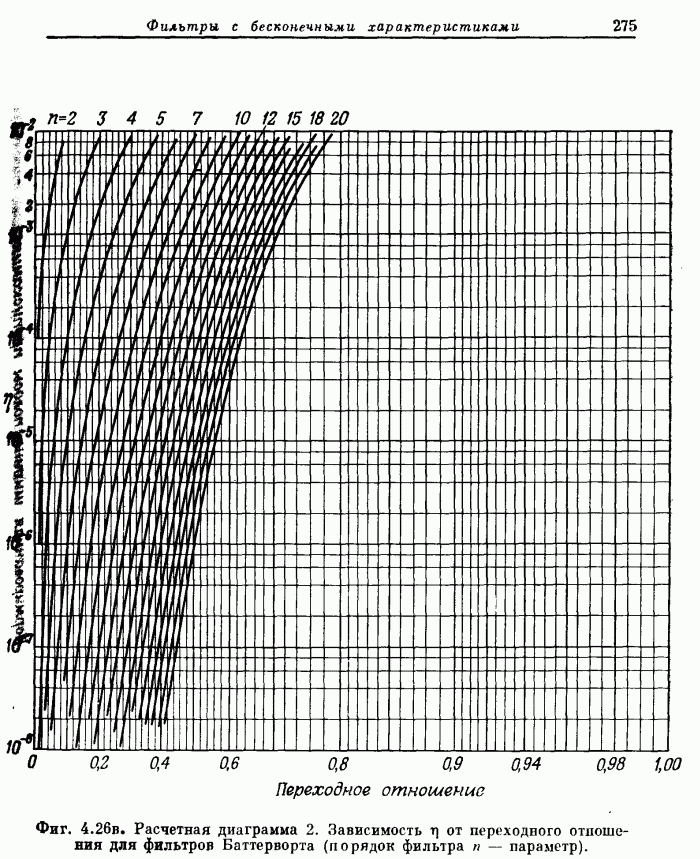
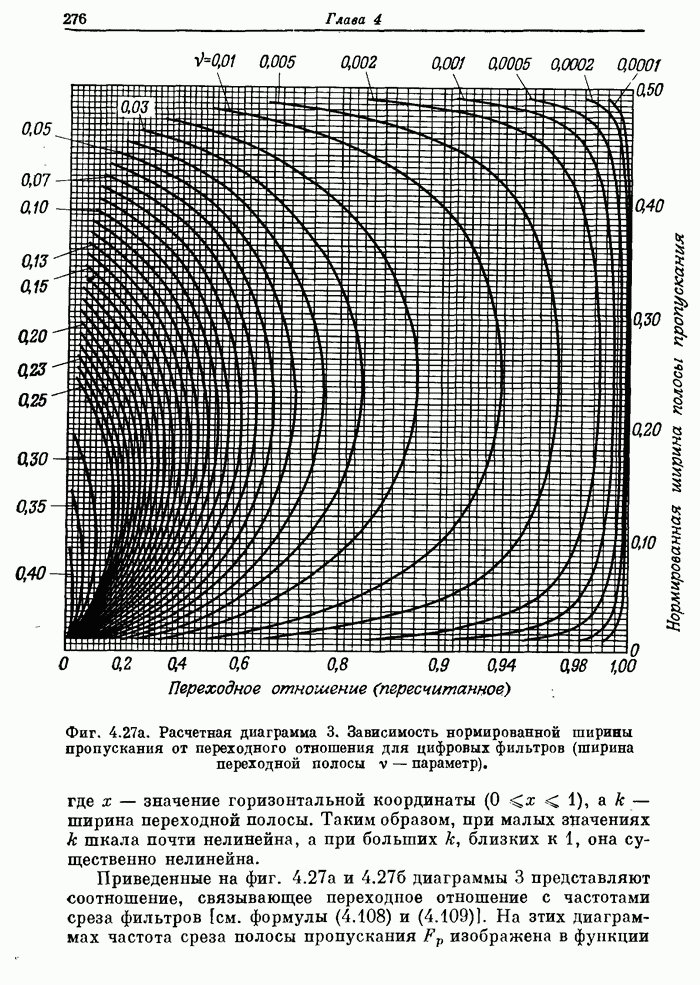
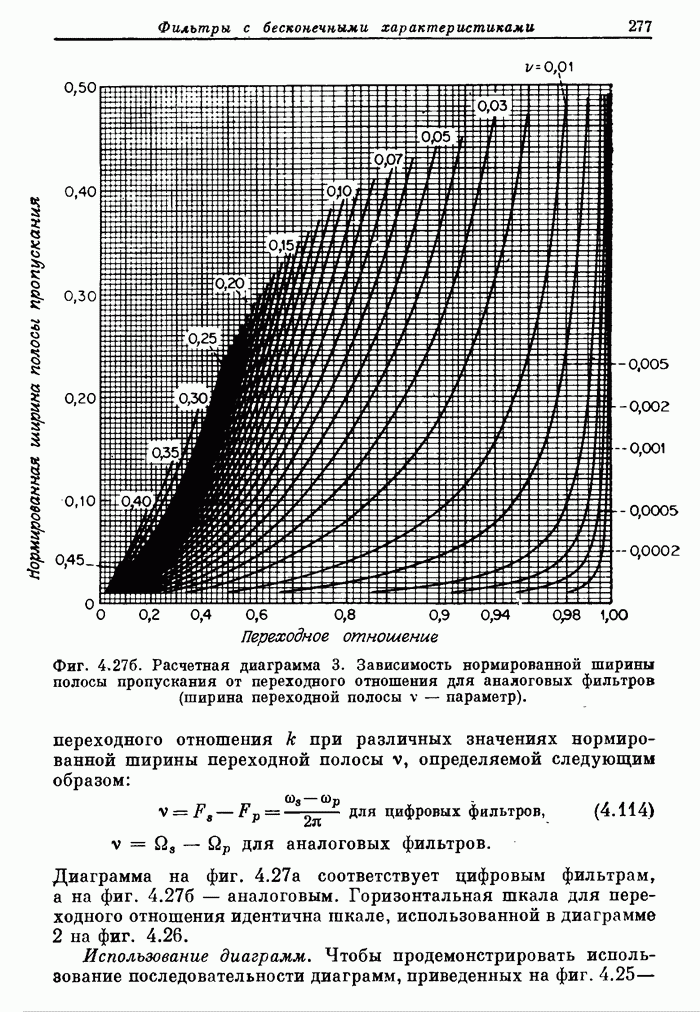
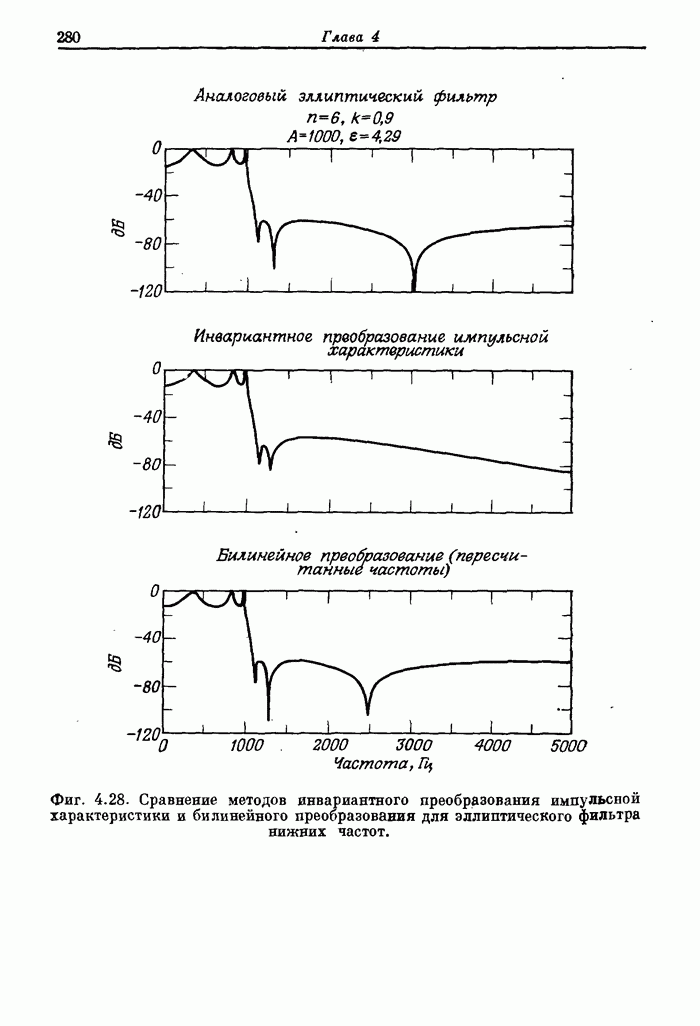
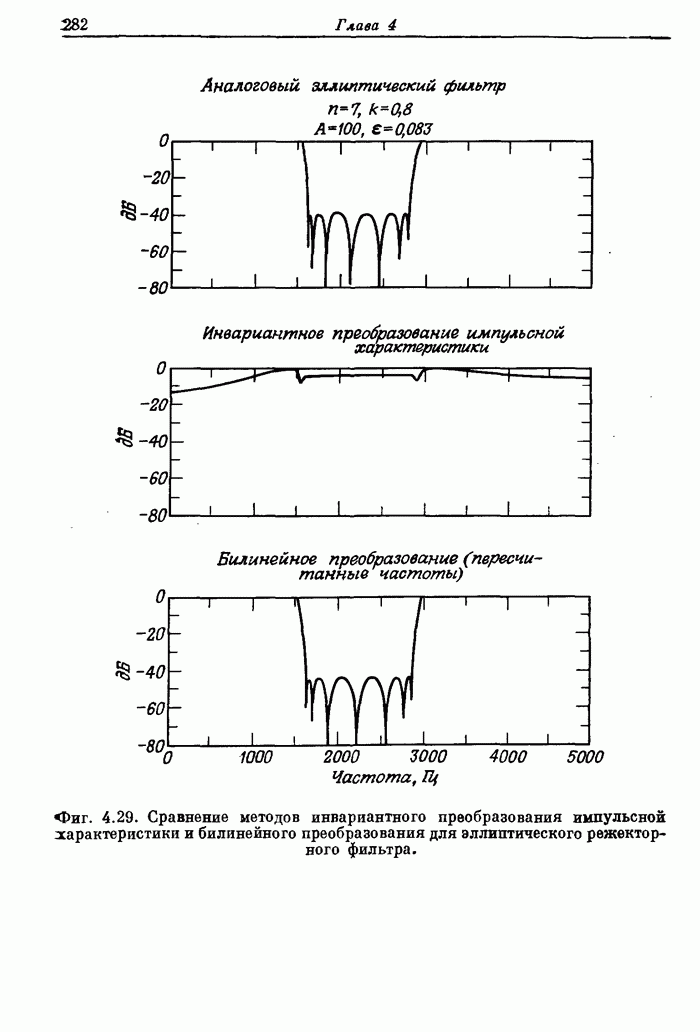
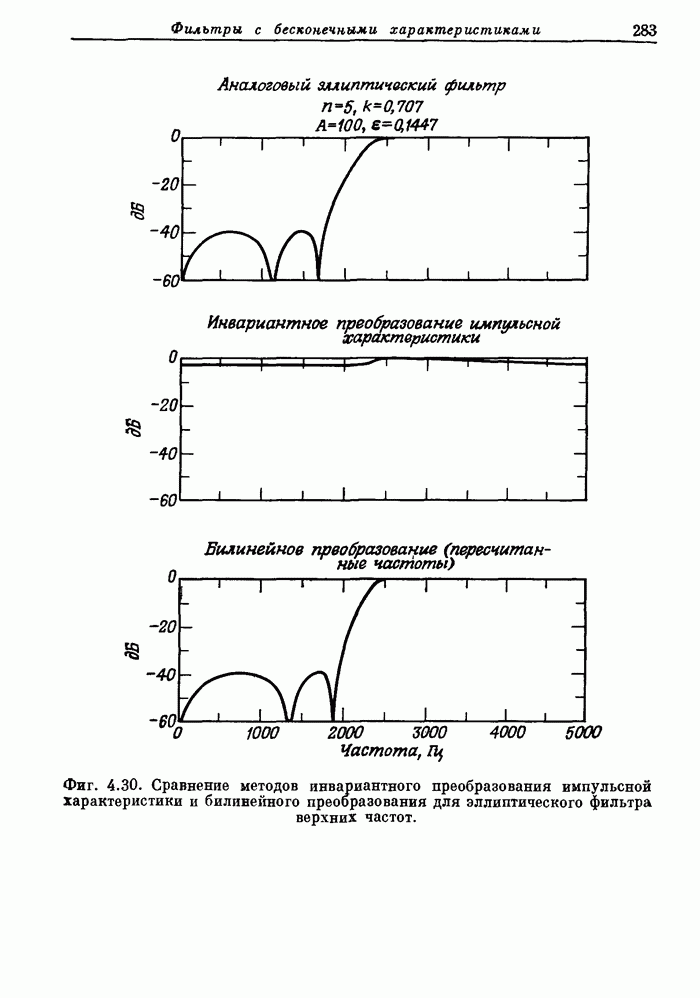
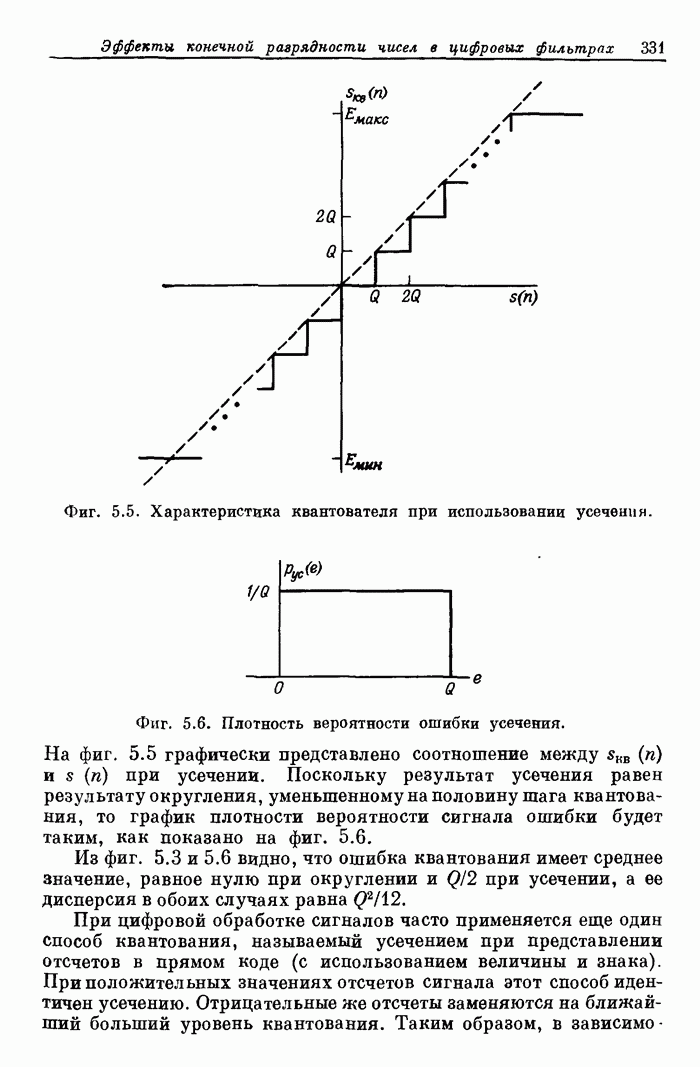
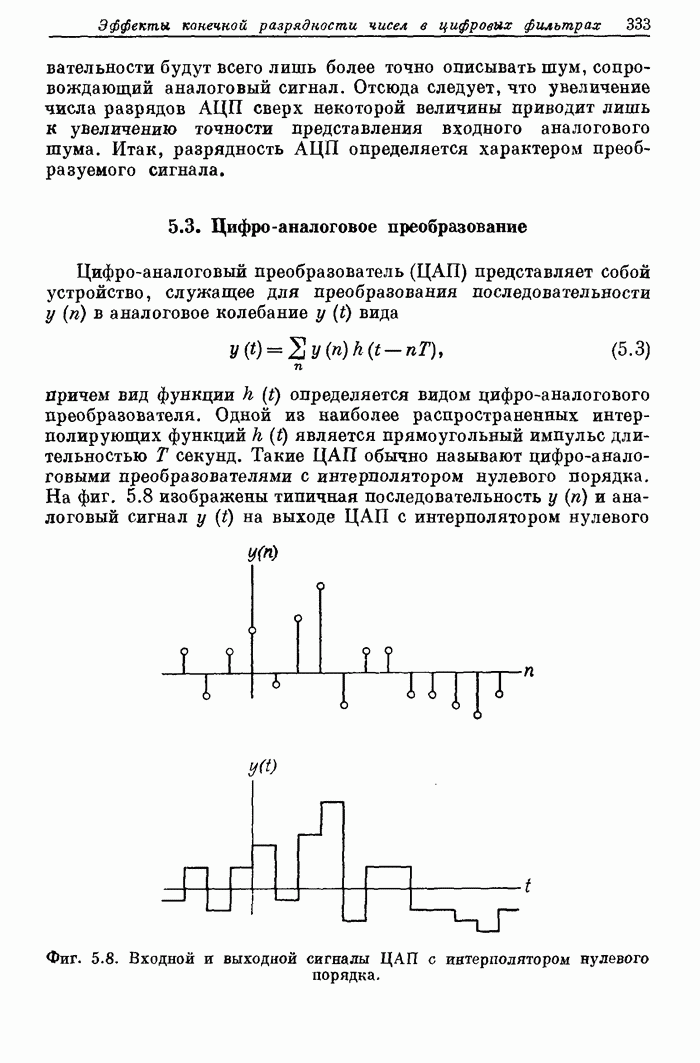
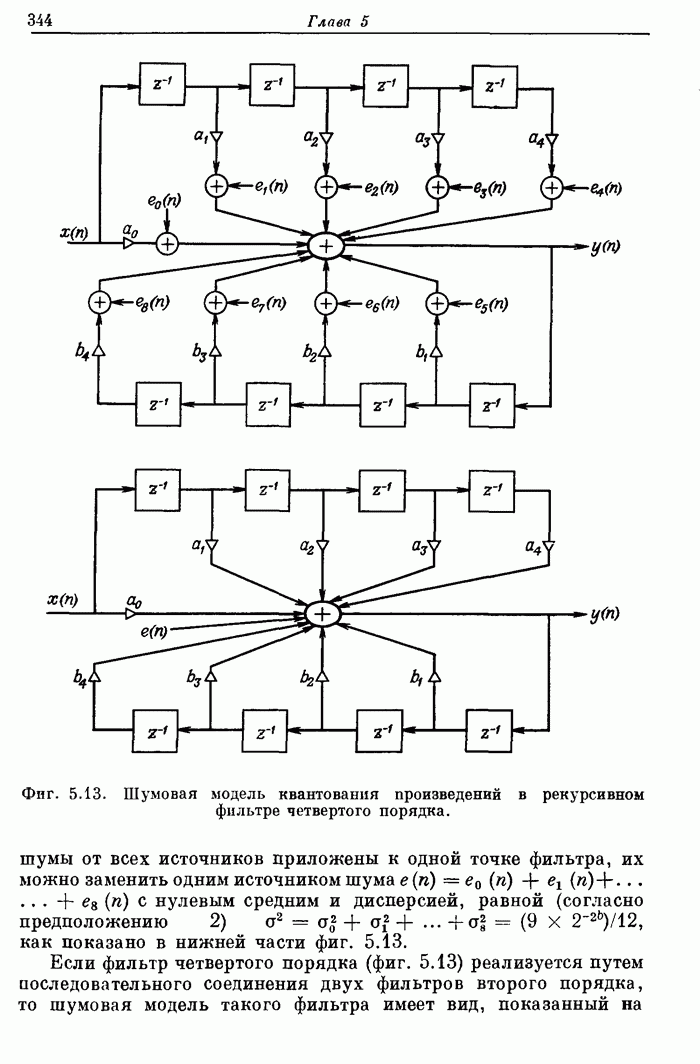
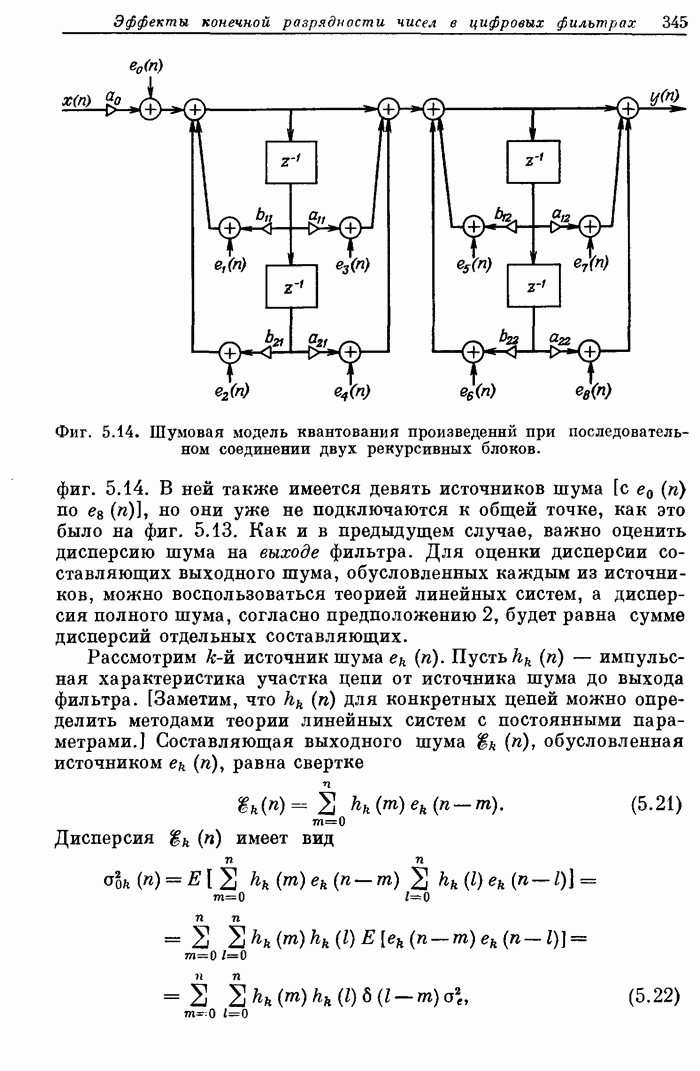
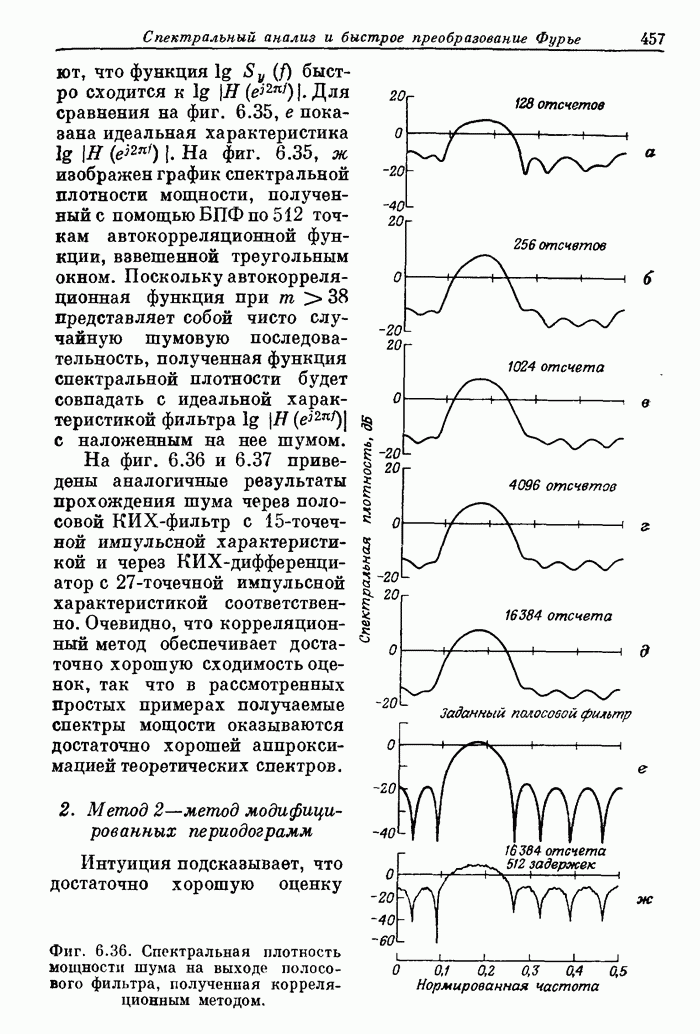
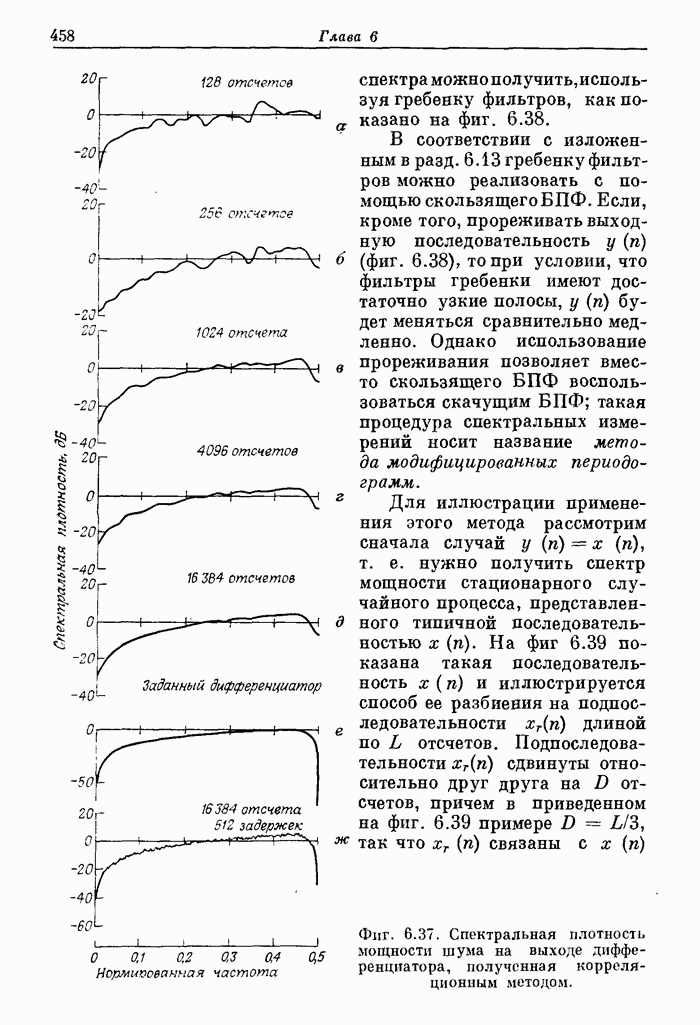
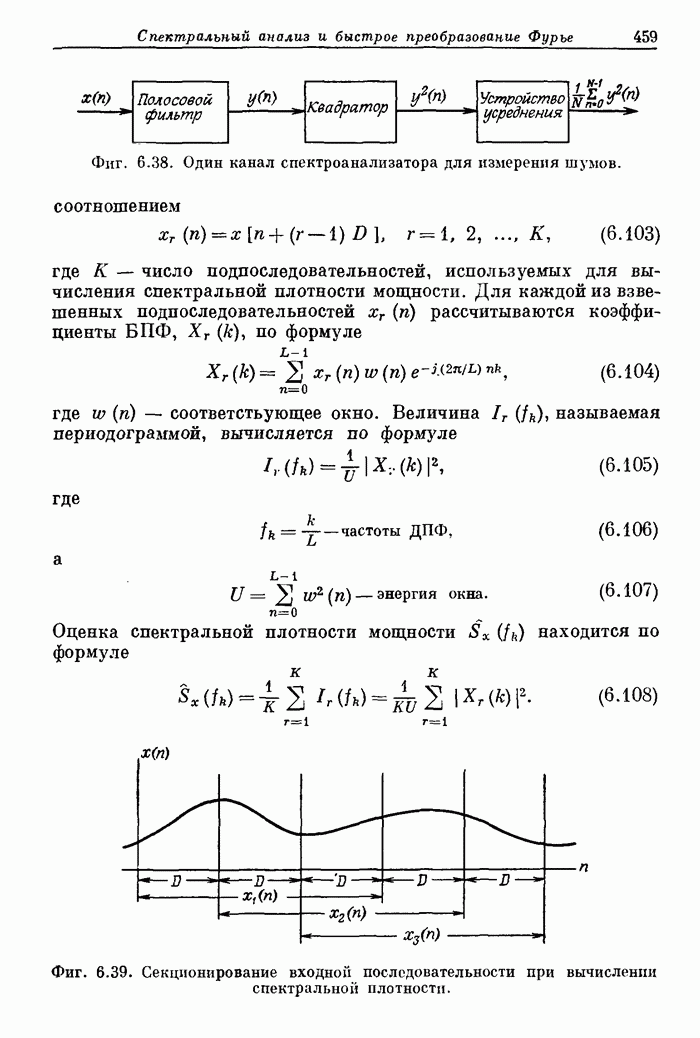
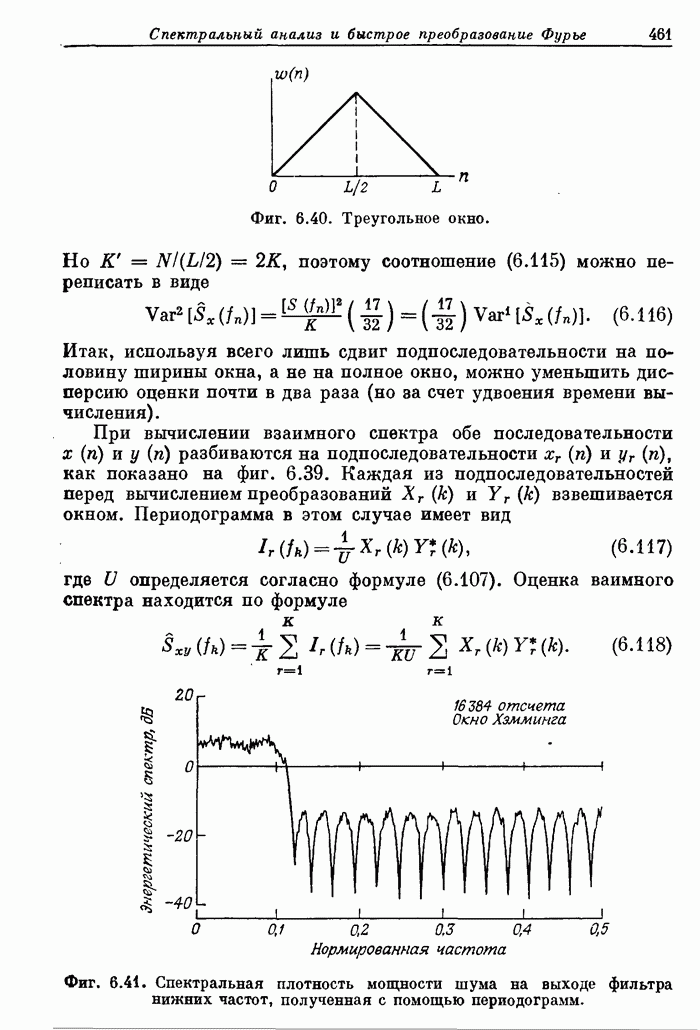
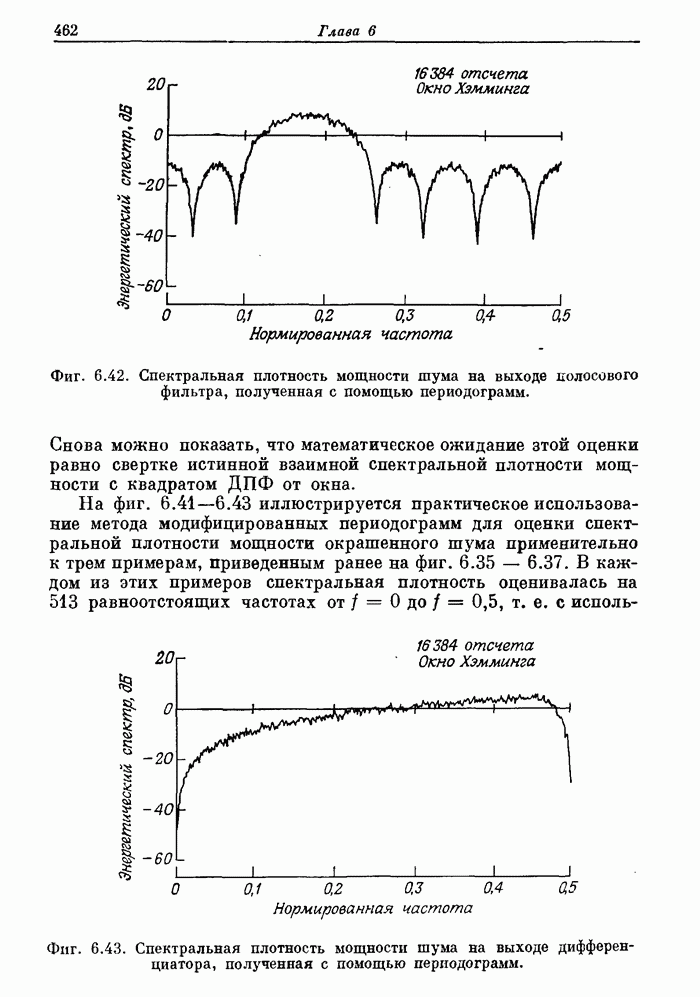
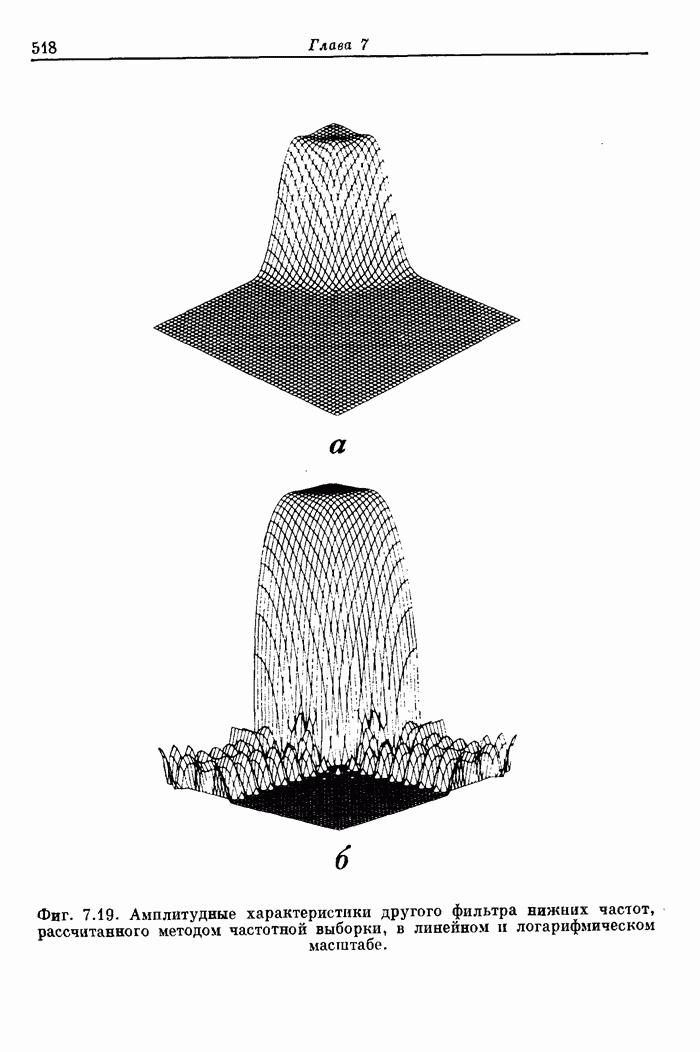
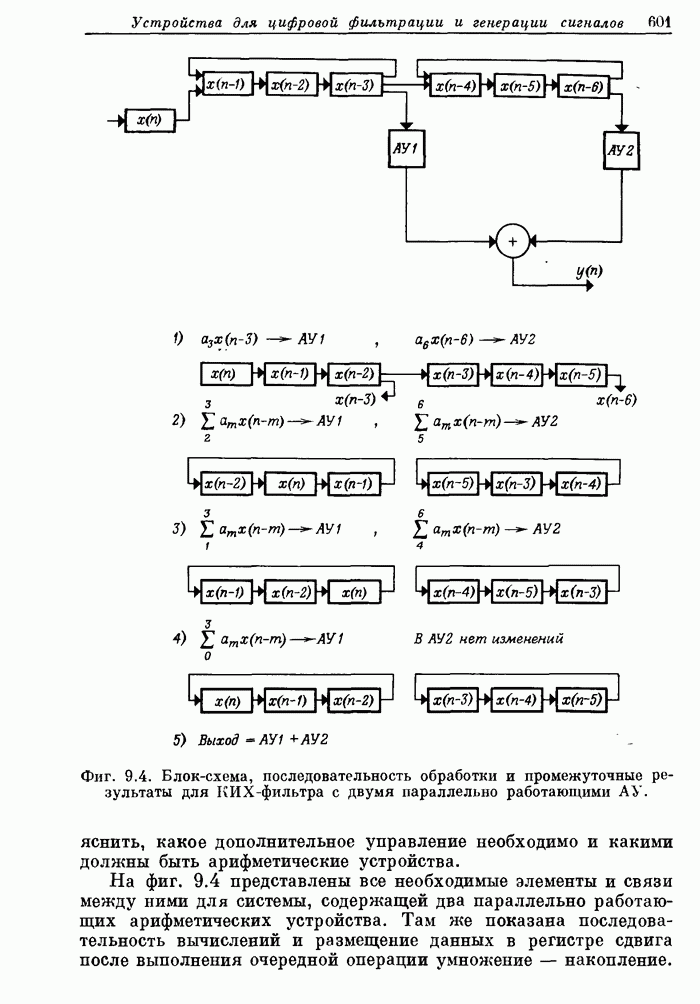
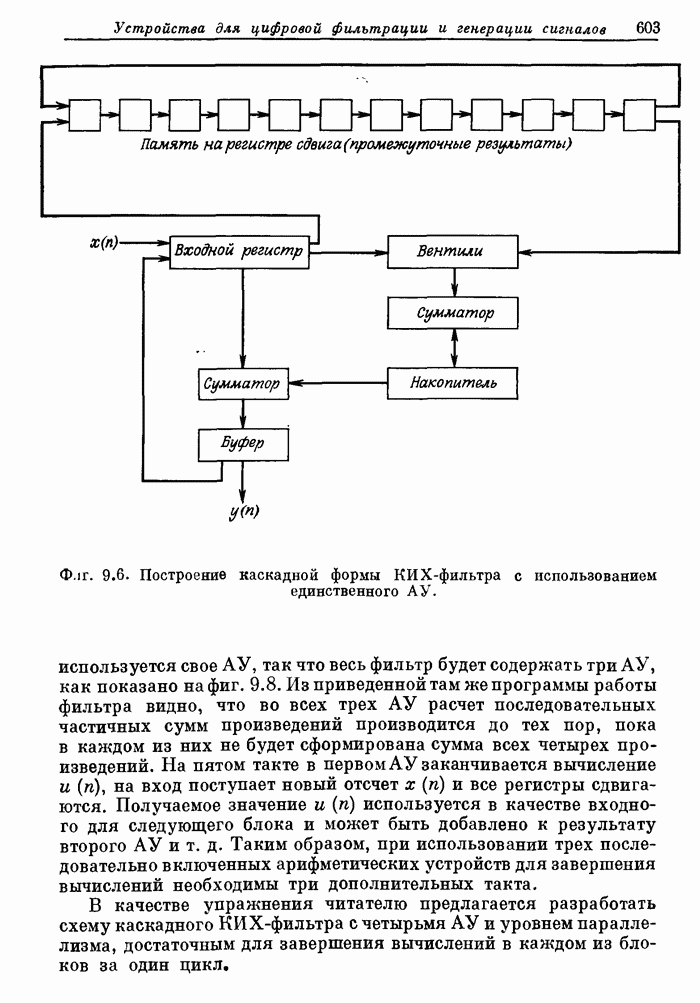
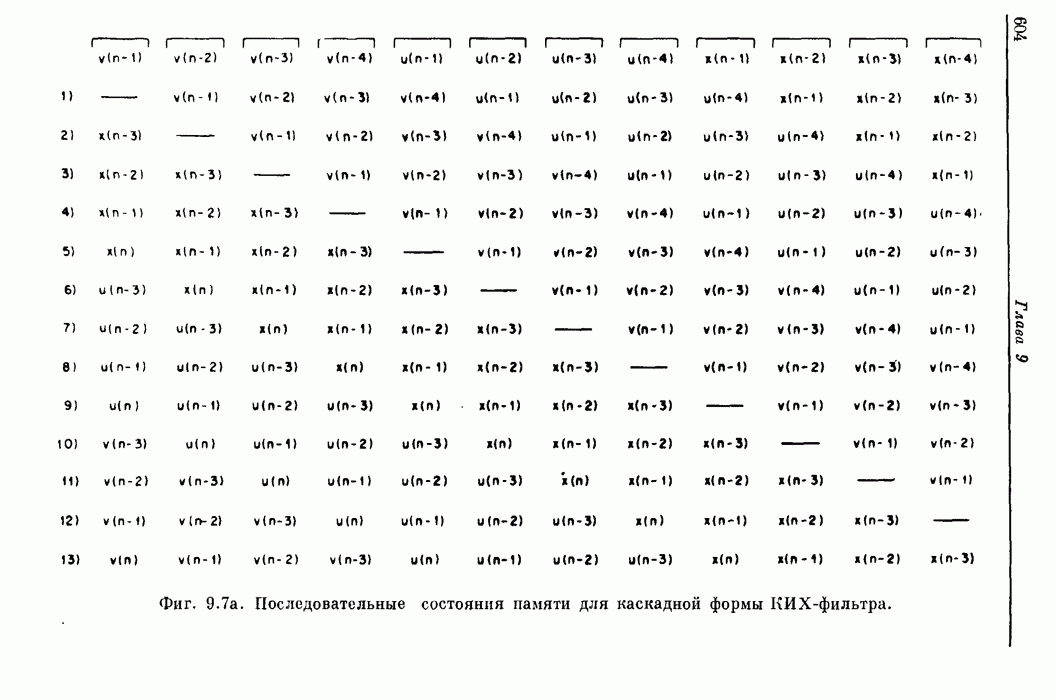
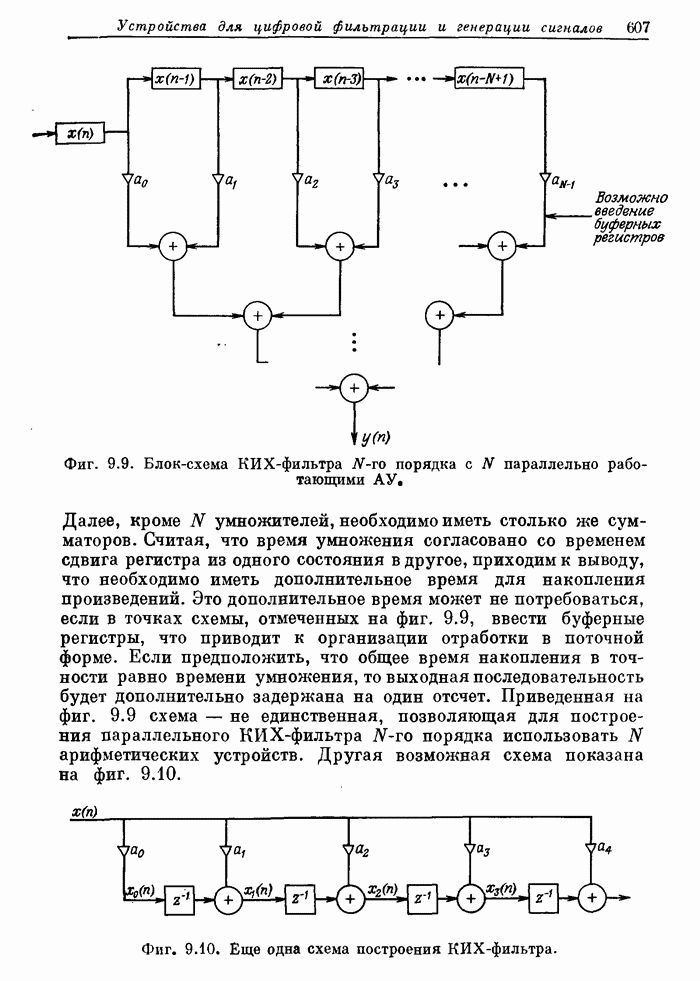
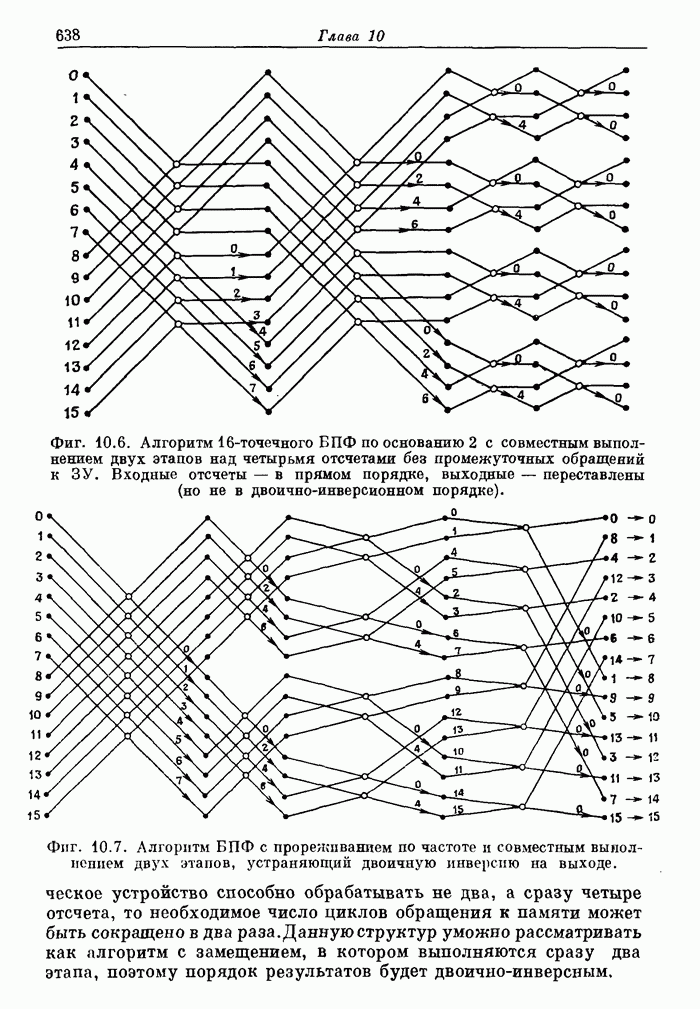
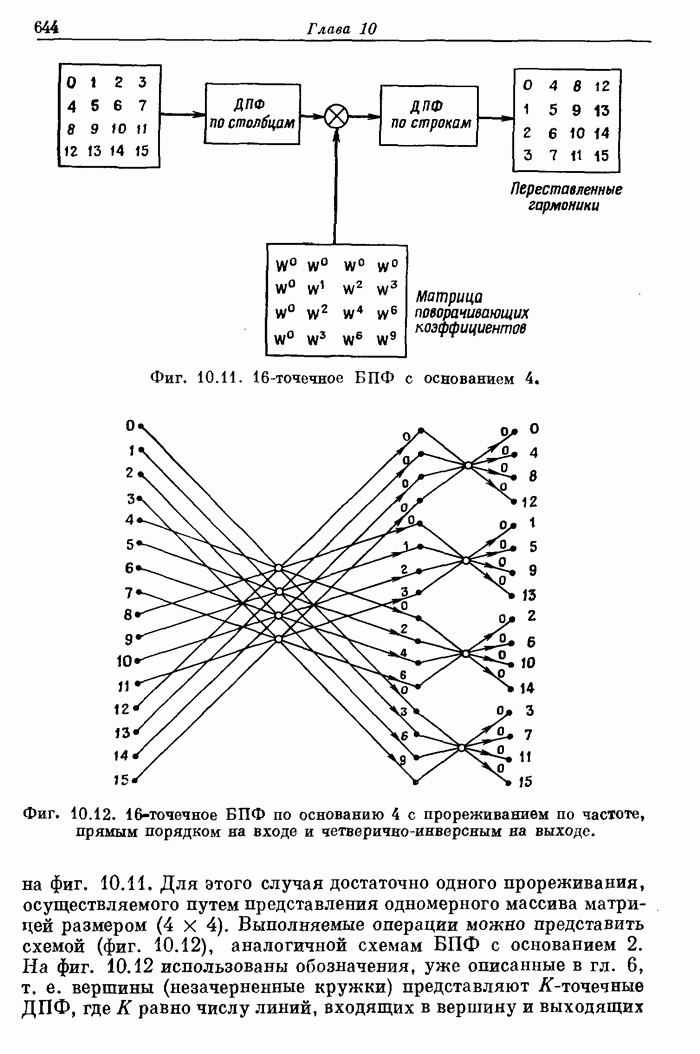
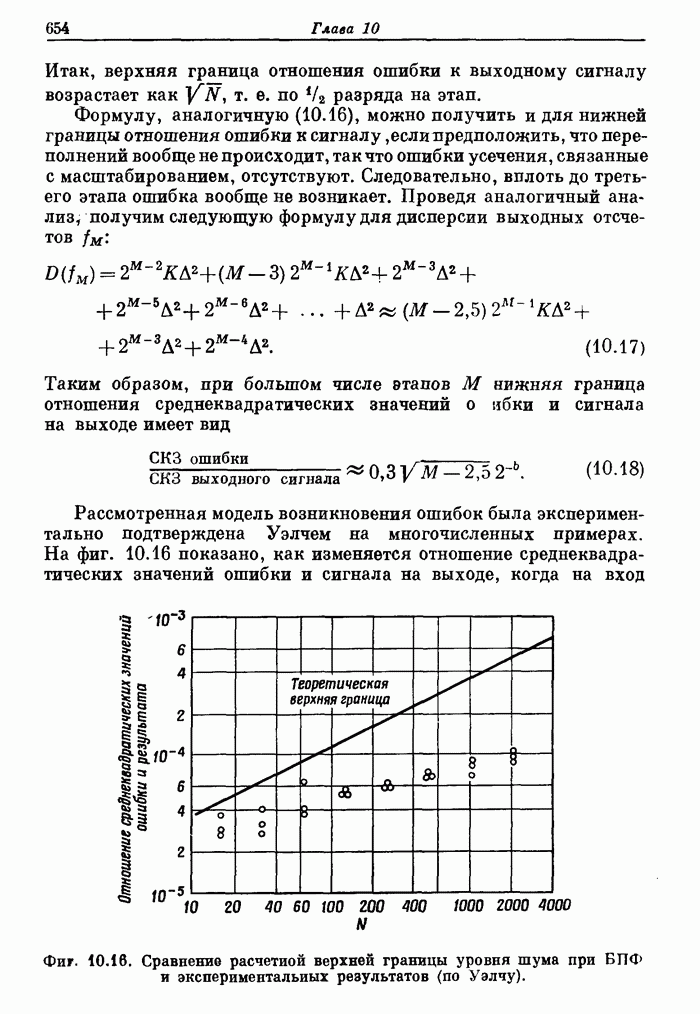
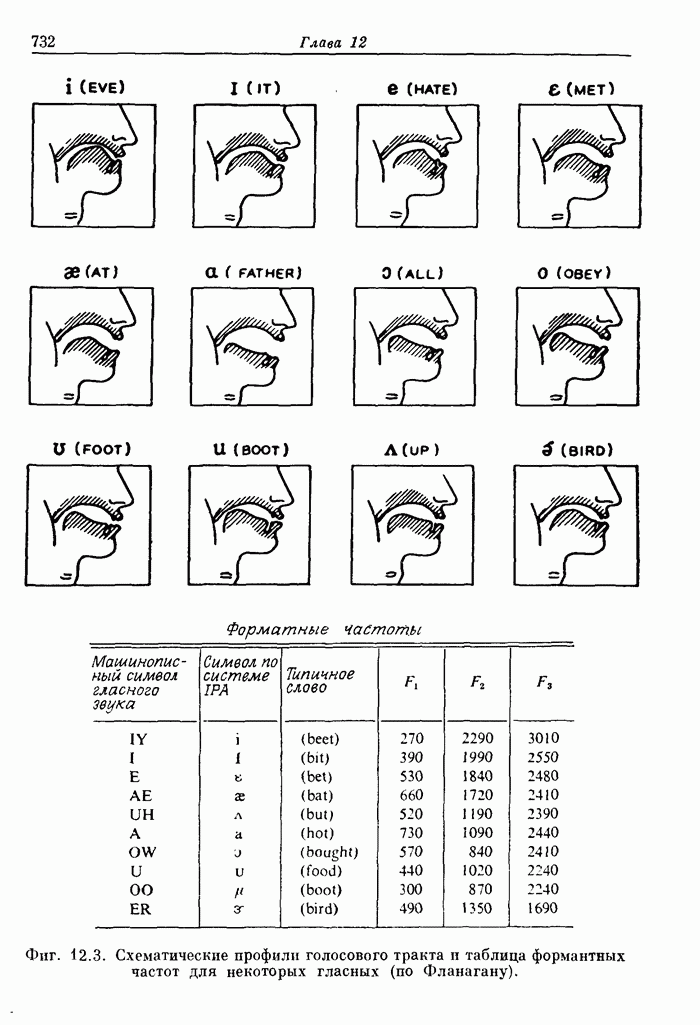
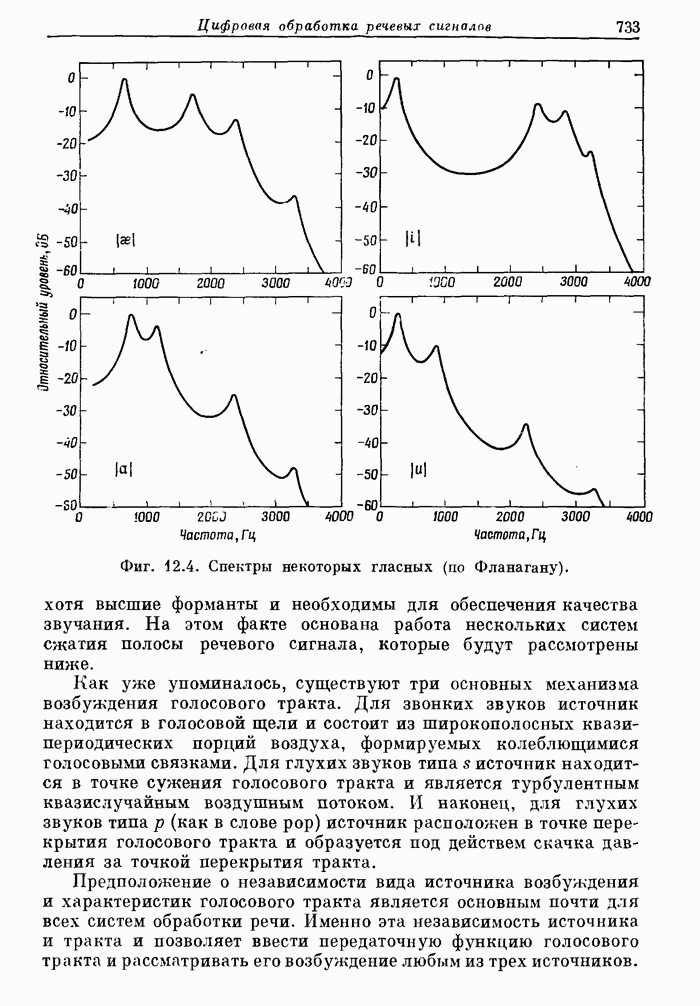
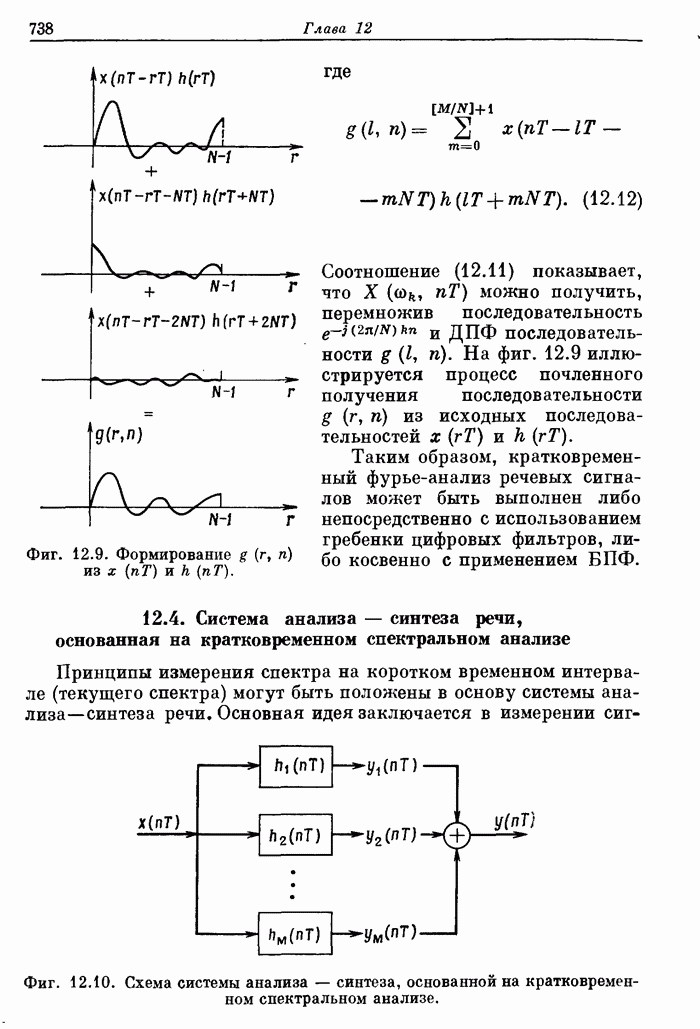
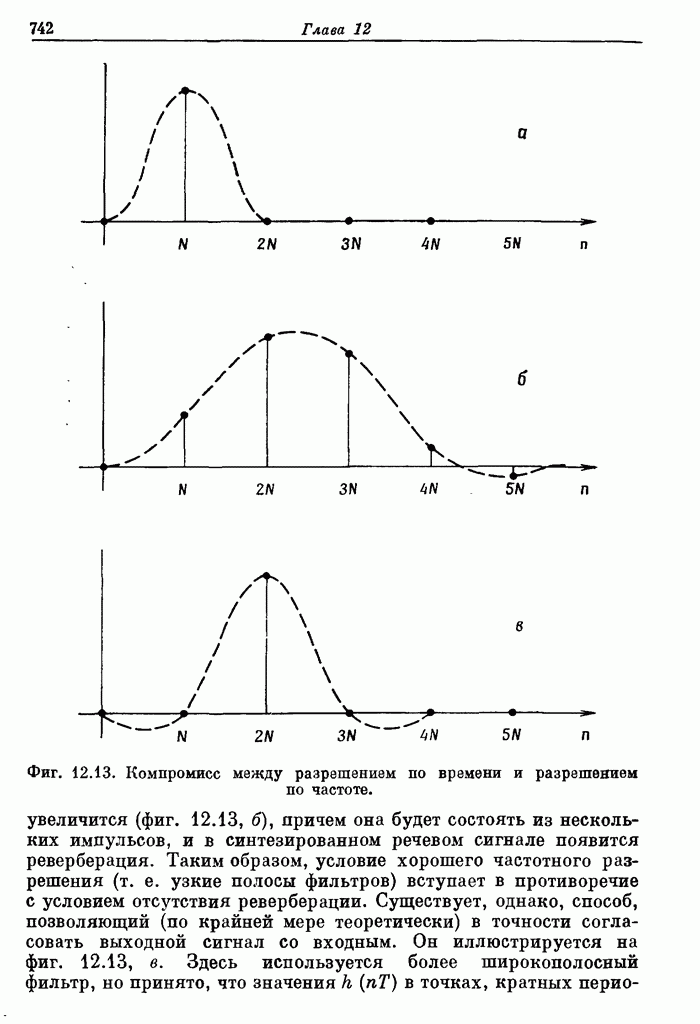
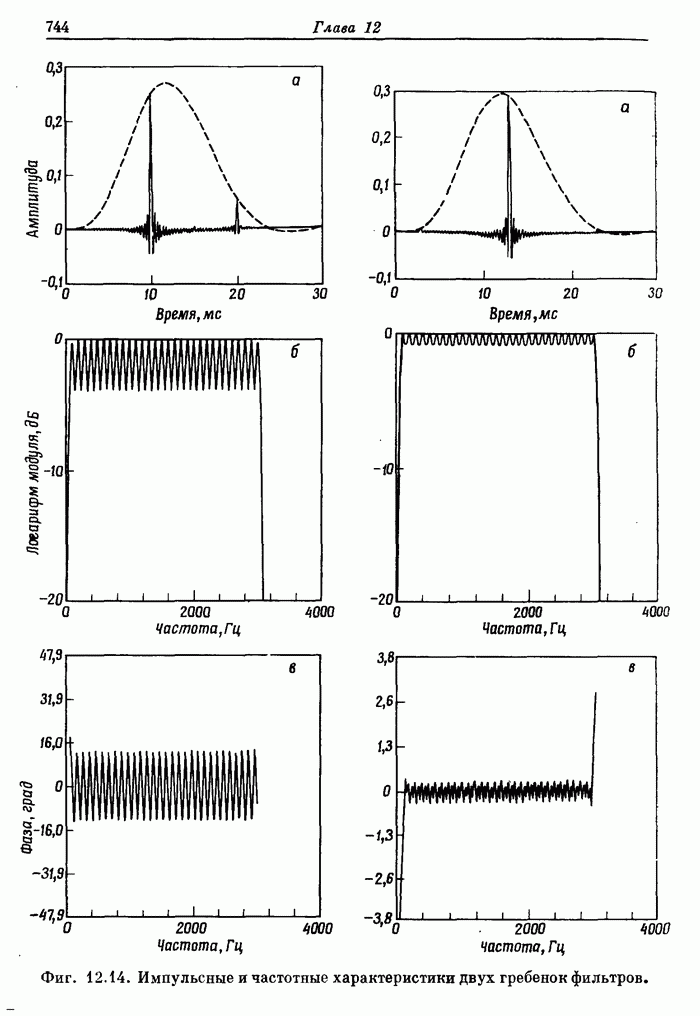
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
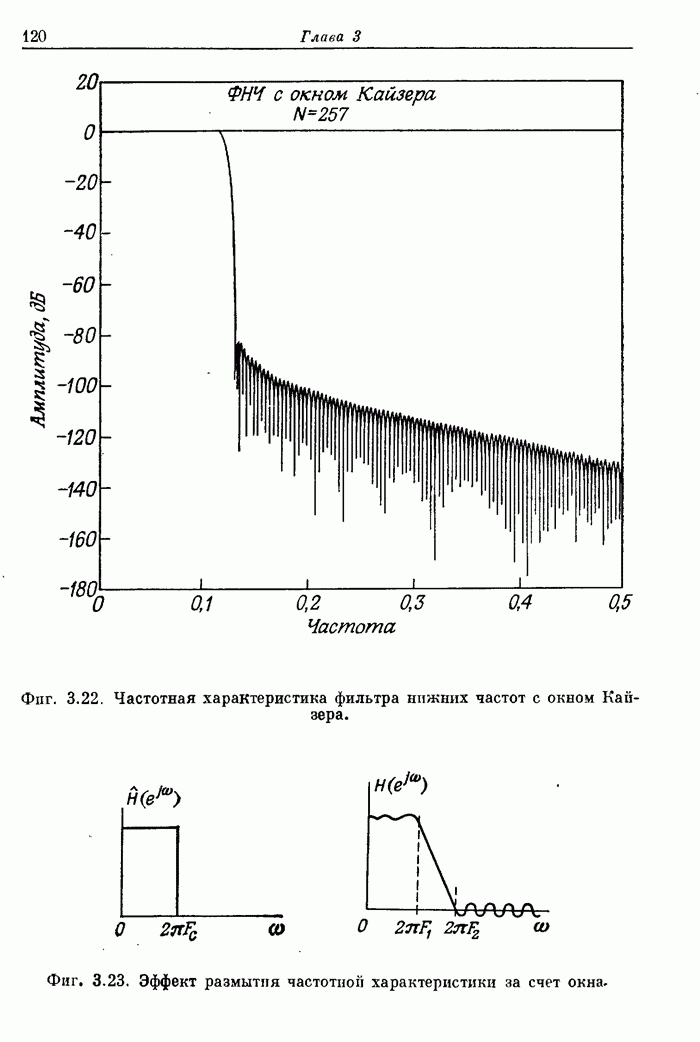
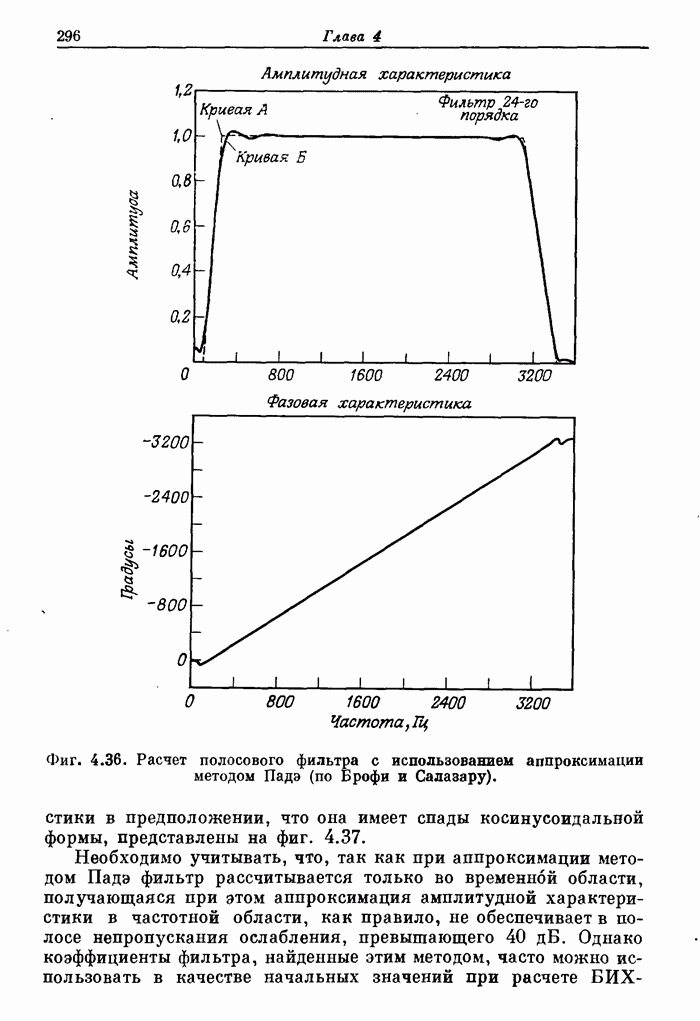
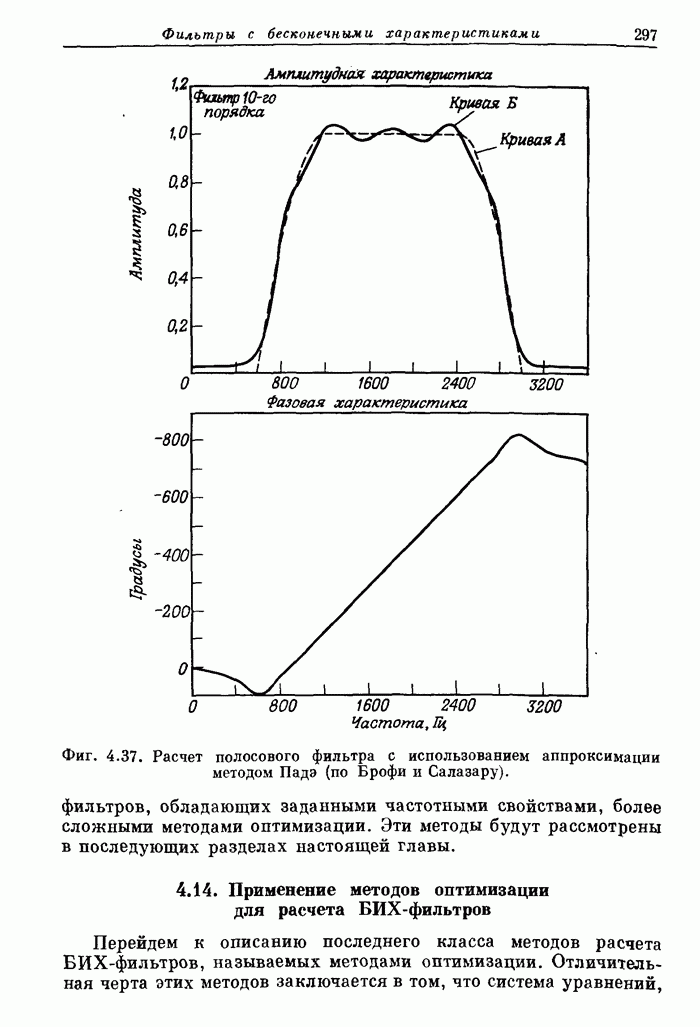
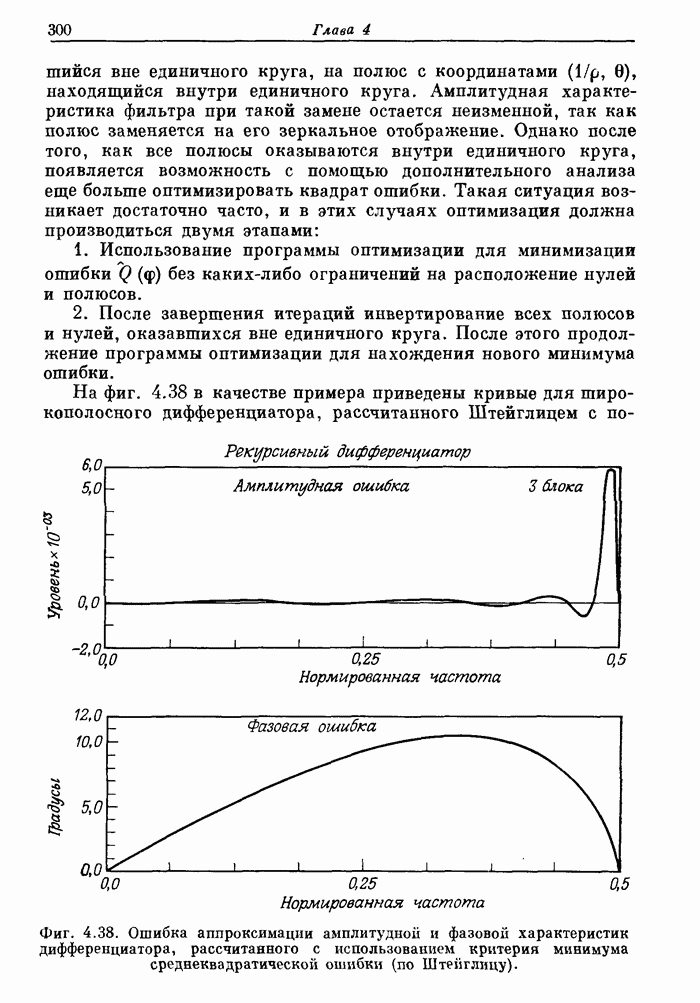
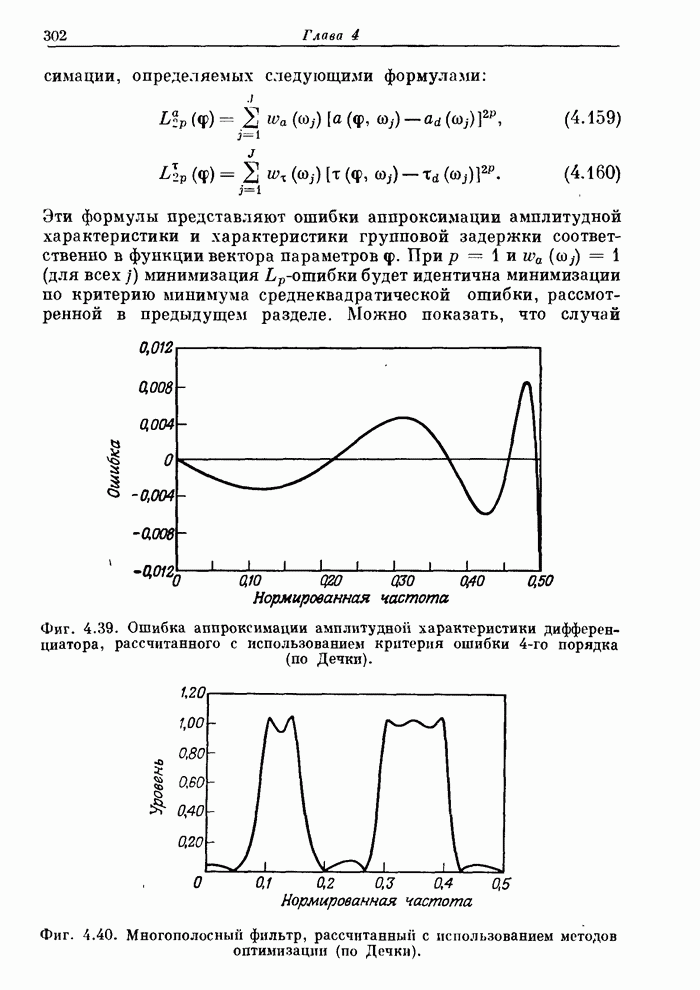
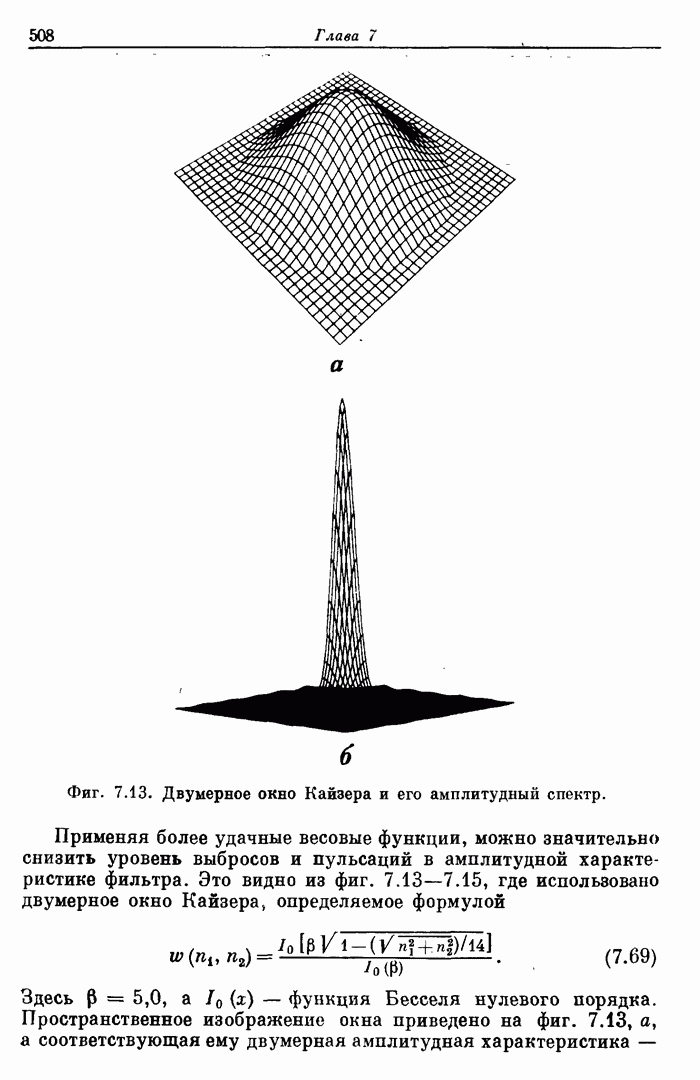
7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
Двумерные КИХ-фильтры, подобно одномерным, можно рассчитать так, чтобы они были оптимальными по Чебышеву, т. е. обеспечивали бы минимаксную ошибку аппроксимации. В этом случае все отсчеты импульсной характеристики фильтра, или, что то же самое, все коэффициенты ее ДПФ, считаются неизвестными и рассчитываются с использованием методики оптимизации.

Фиг. 7.23. Амплитудная характеристика в линейном (а) и логарифмическом (б) масштабе оптимального (в минимаксном смысле) двумерного фильтра нижних частот.
Для вычисления коэффициентов фильтра можно использовать методы линейного программирования. Другие методы, также обеспечивавшие чебышевскую аппроксимацию при расчете одномерных фильтров, здесь непригодны, так как обобщенную теорему Чебышева (см. разд. 3.26) непосредственно использовать для двумерного случая нельзя. (В разд. 7.20 будет рассмотрена методика преобразования оптимальных одномерных фильтров в двумерные, которые часто также оказываются оптимальными.)

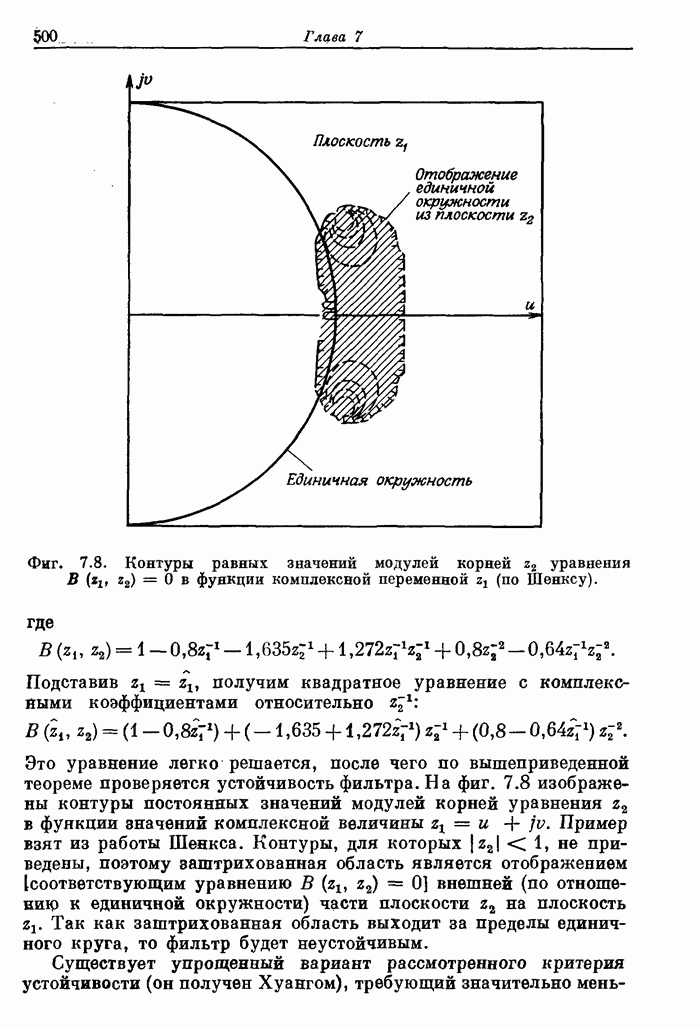
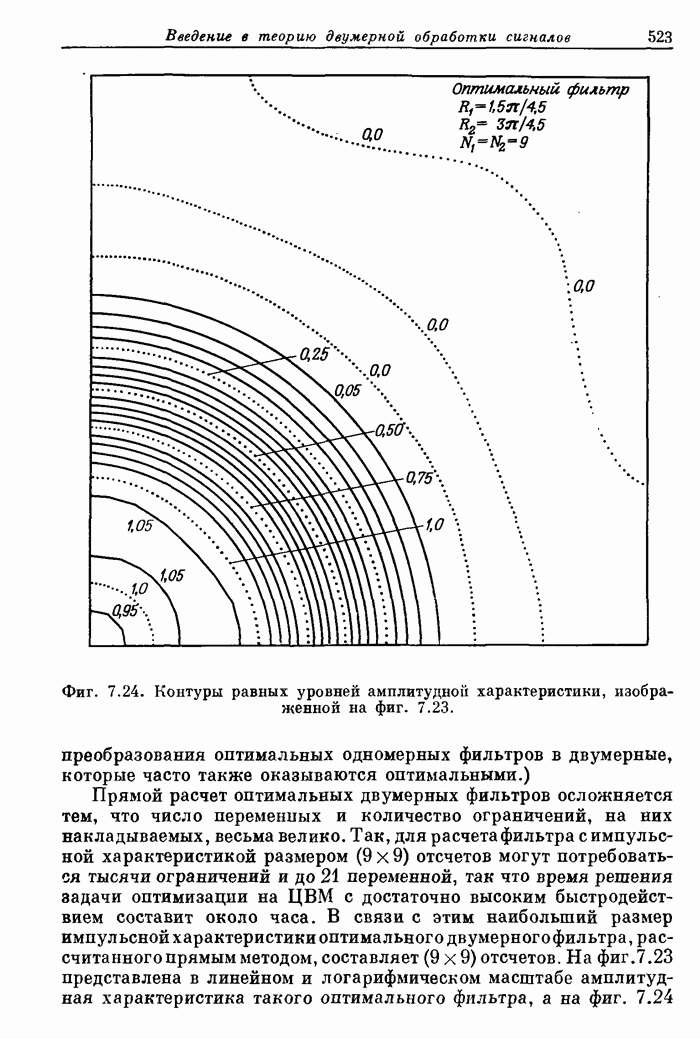
Фиг. 7.24. Контуры равных уровней амплитудной характеристики, изображенной на фиг. 7.23.
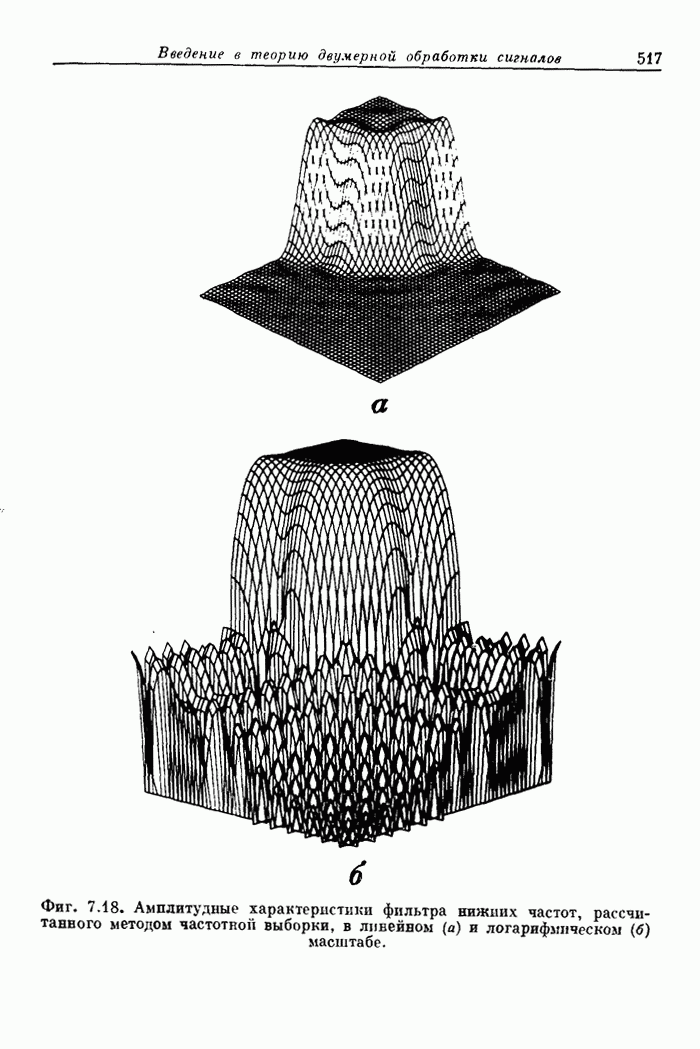
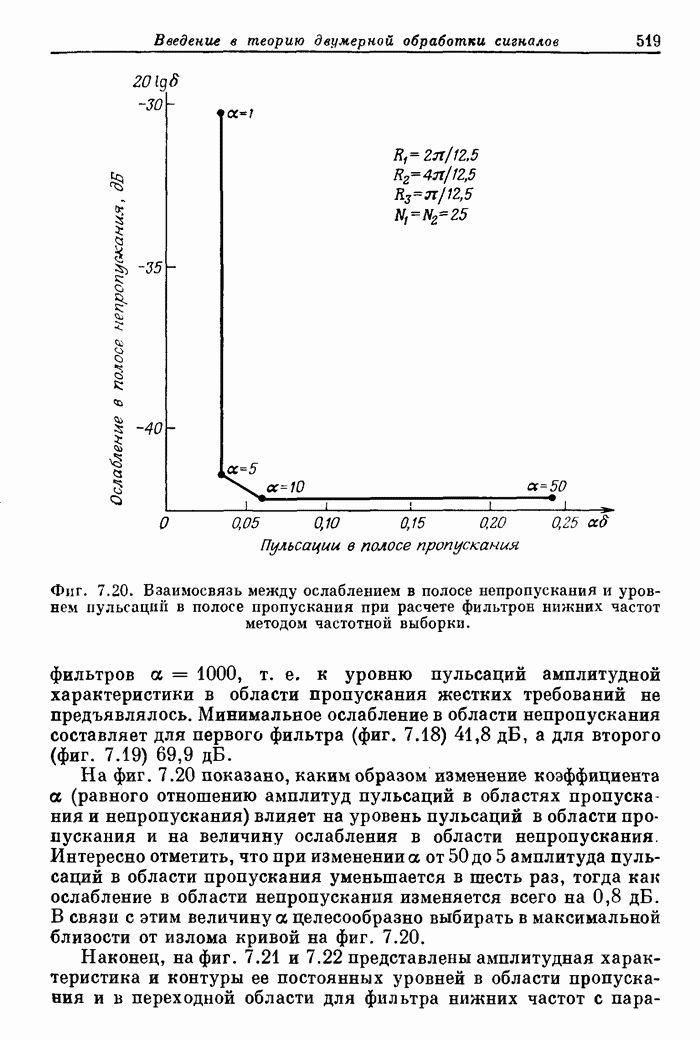
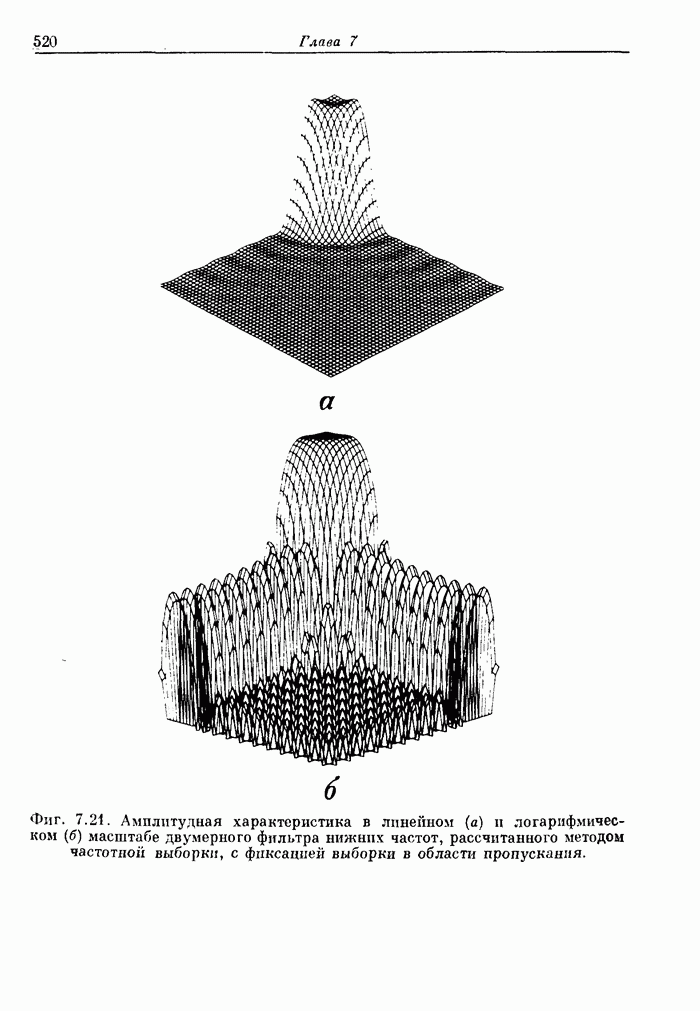
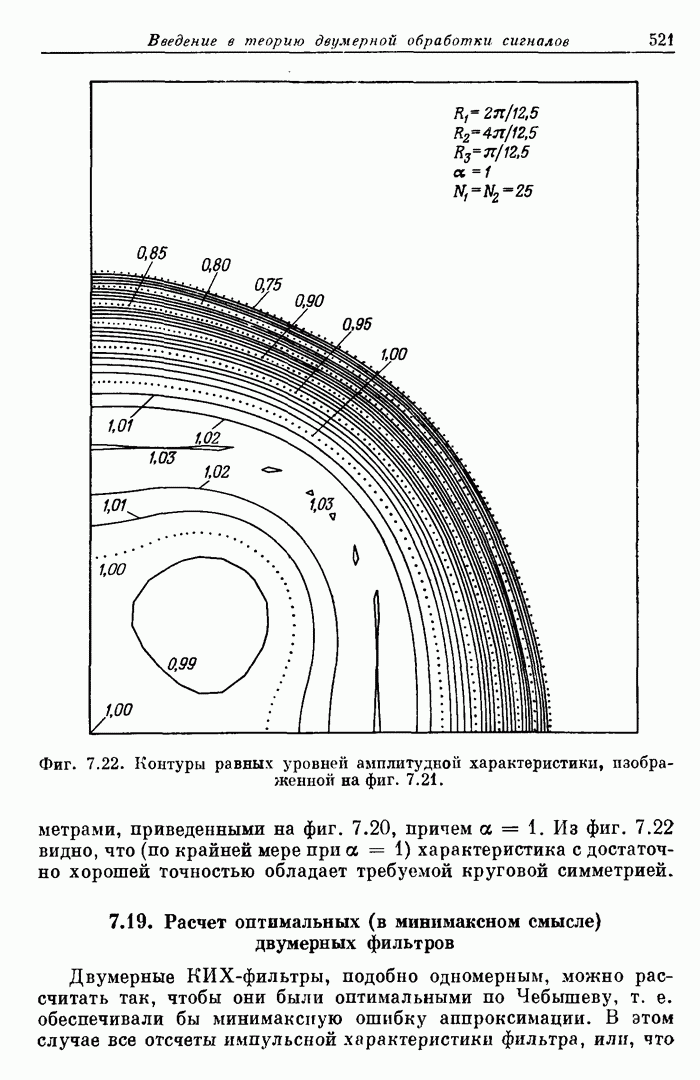
Прямой расчет оптимальных двумерных фильтров осложняется тем, что число переменпых и количество ограничений, на них накладываемых, весьма велико. Так, для расчета фильтра с импульсной характеристикой размером (9 x 9) отсчетов могут потребоваться тысячи ограничений и до 21 переменной, так что время решения задачи оптимизации на ЦВМ с достаточно высоким быстродействием составит около часа. В связи с этим наибольший размер импульсной характеристики оптимального двумерногофильтра, рассчитанного прямым методом, составляет (9 х 9) отсчетов. На фиг. 7.23 представлена в линейном и логарифмическом масштабе амплитудная характеристика такого оптимального фильтра, а на фиг. 7.24 изображены контуры равных уровней этой характеристики.
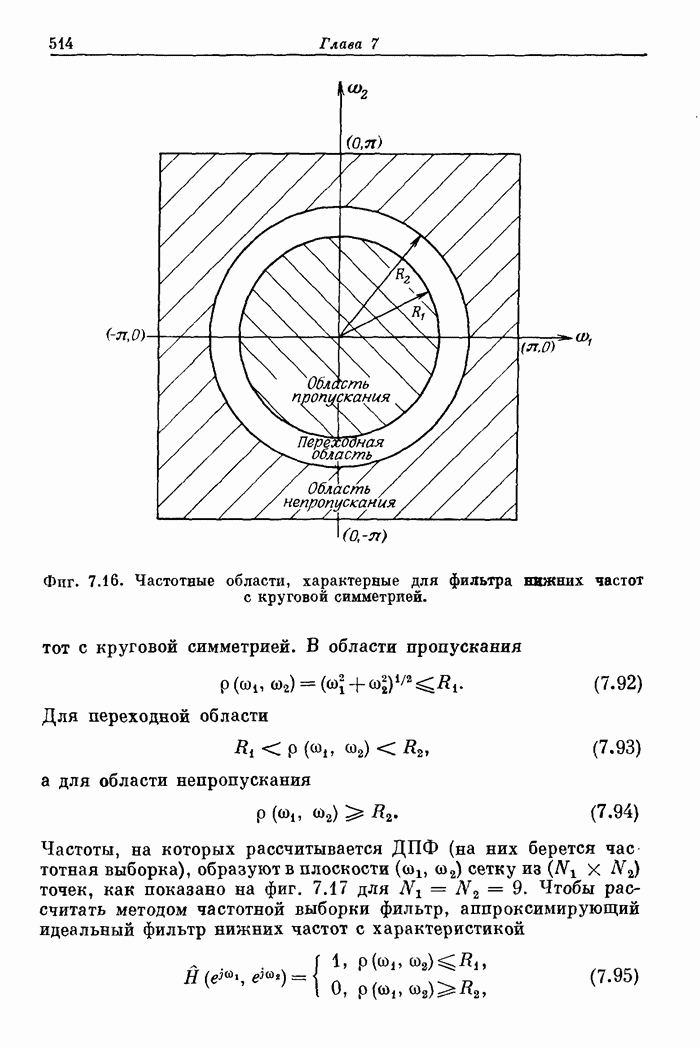
Из приведенных кривых видно, что пульсации ошибки апроксимации амплитудной характеристики, как и для одномерных фильтров, являются равновеликими. В то же время из фиг. 7.24 видно, что в области пропускания и в переходной области характеристика, как это и требуется, имеет приблизительно круговую симметрию. В области непропускания линии постоянного уровня уже не являются окружностями. Это объясняется тем, что отсчеты импульсной характеристики образуют прямоугольную сетку.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
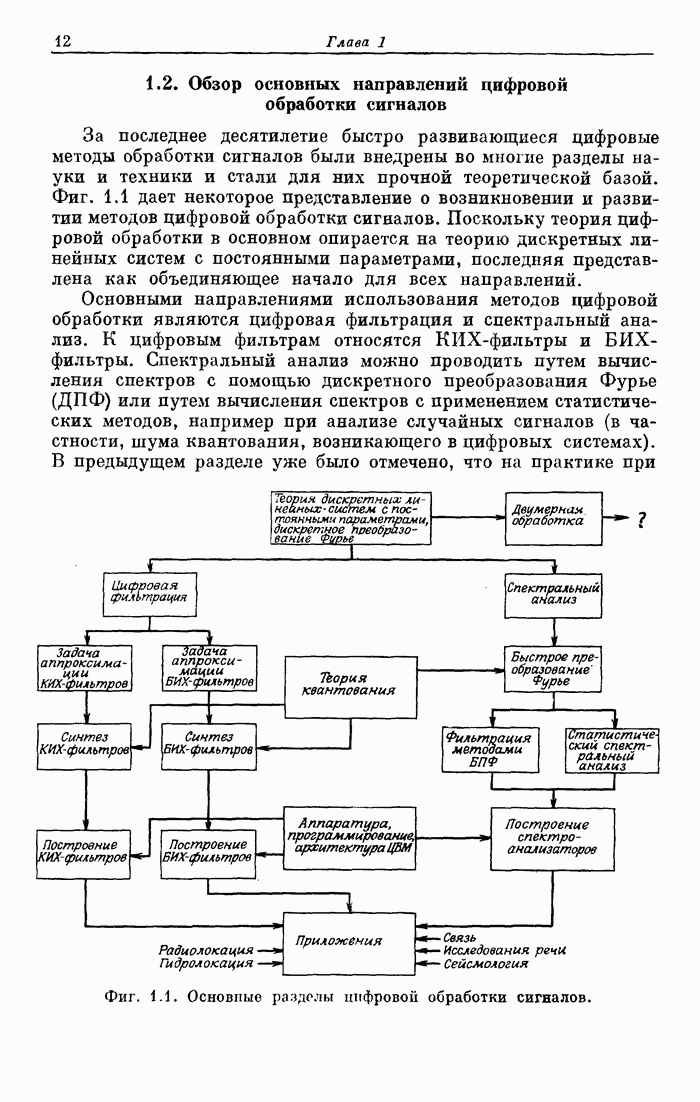
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
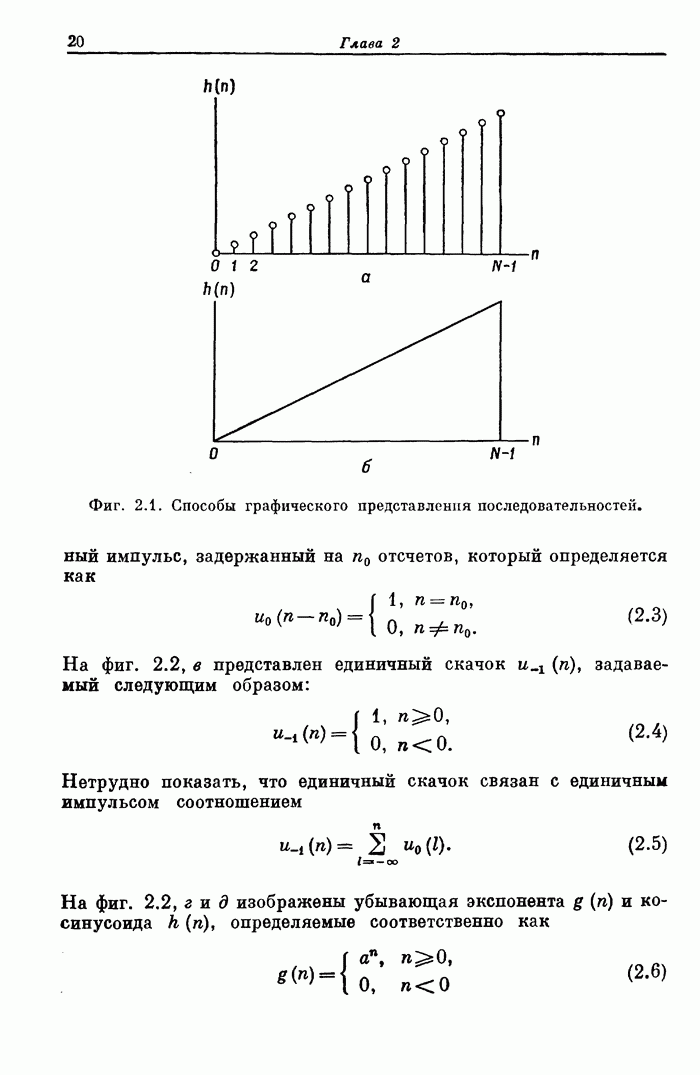
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
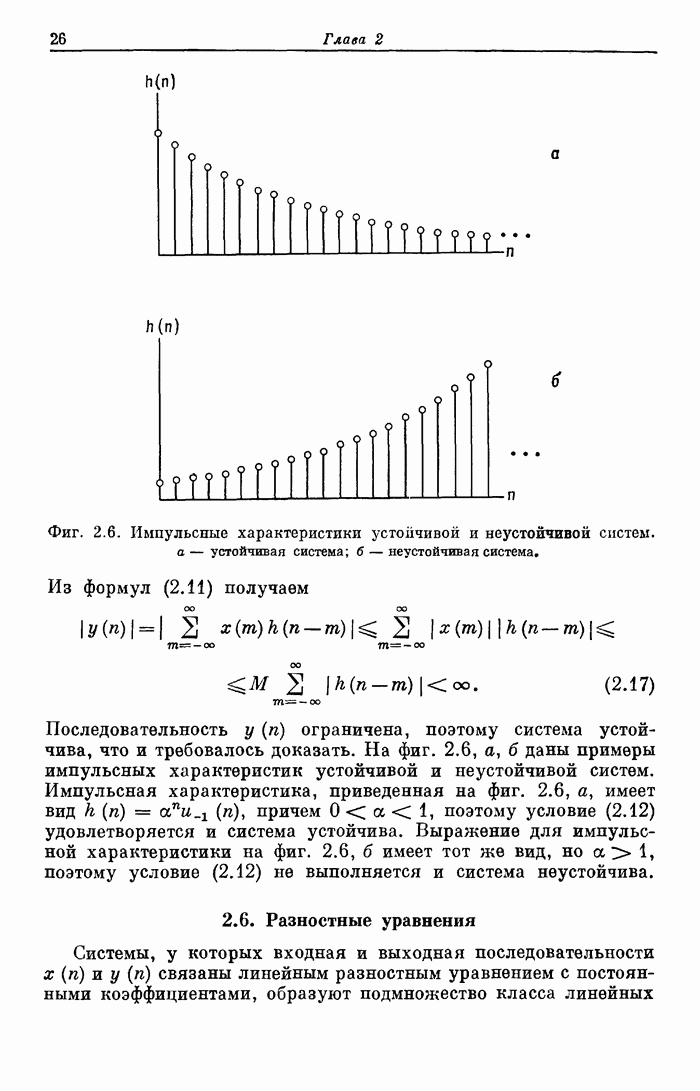
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
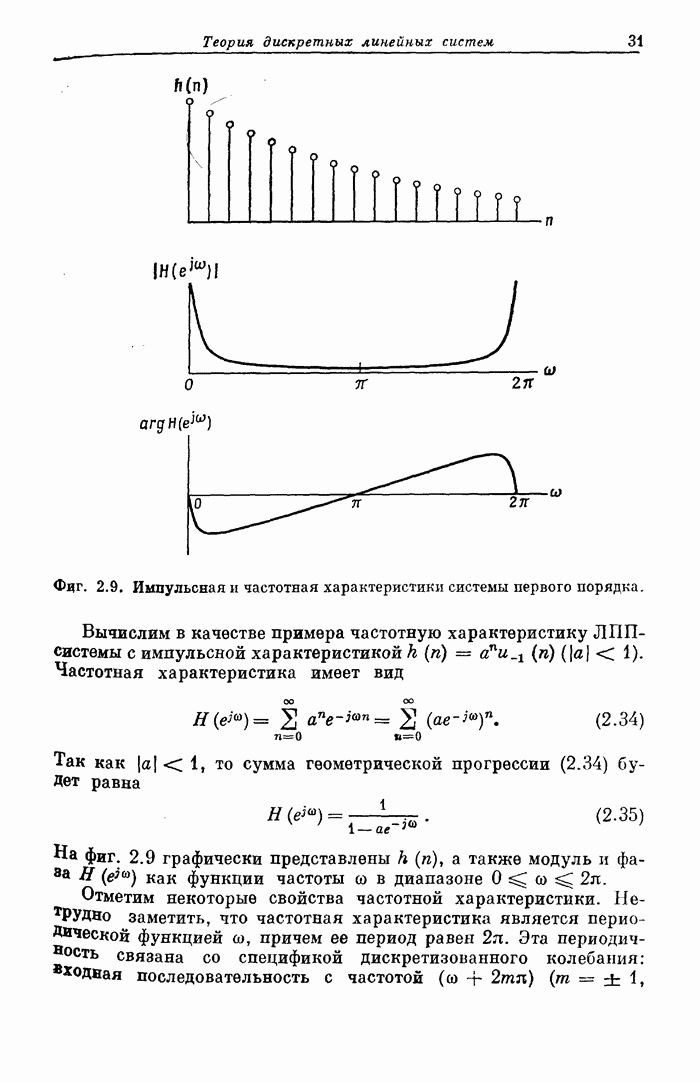
- 2.7. Частотная характеристика
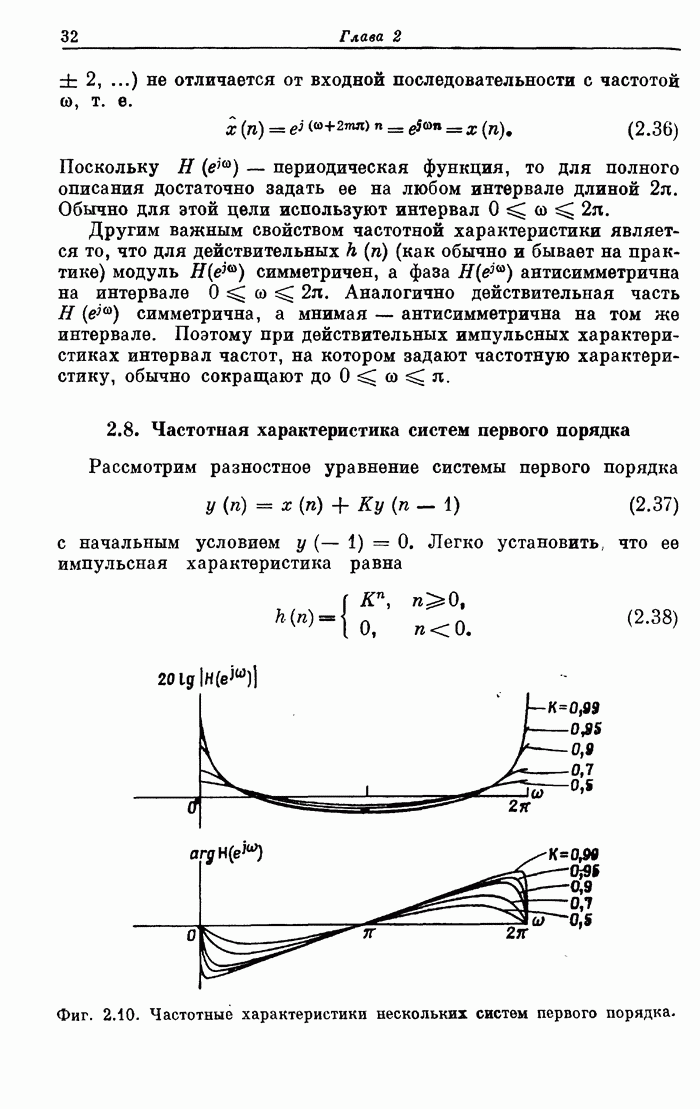
- 2.8. Частотная характеристика систем первого порядка
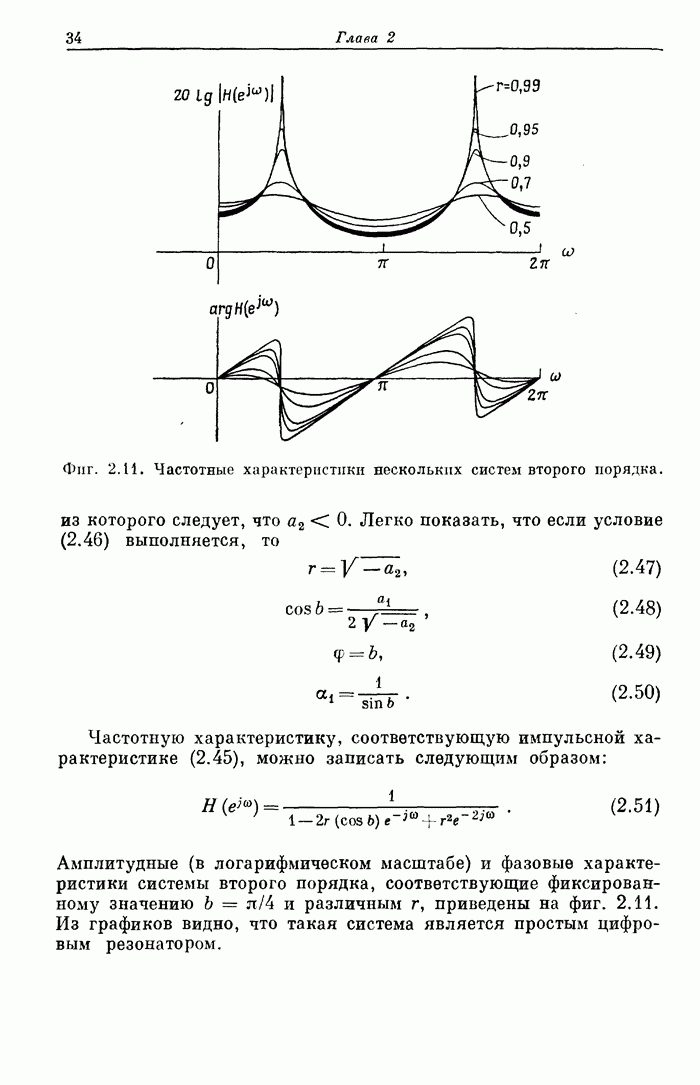
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
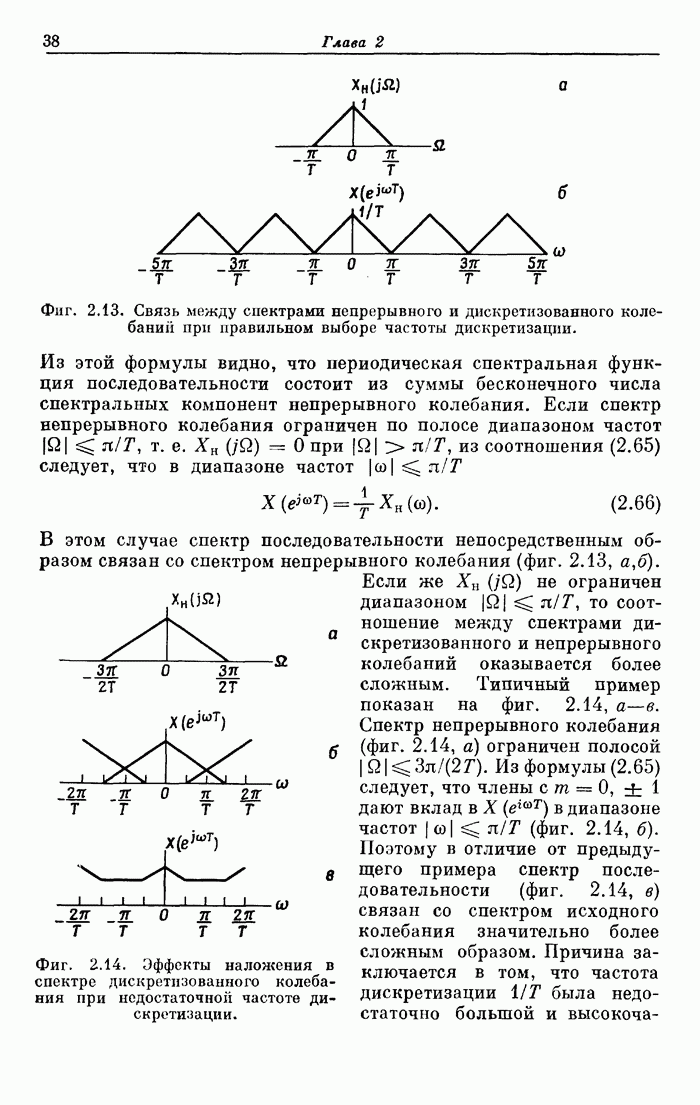
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
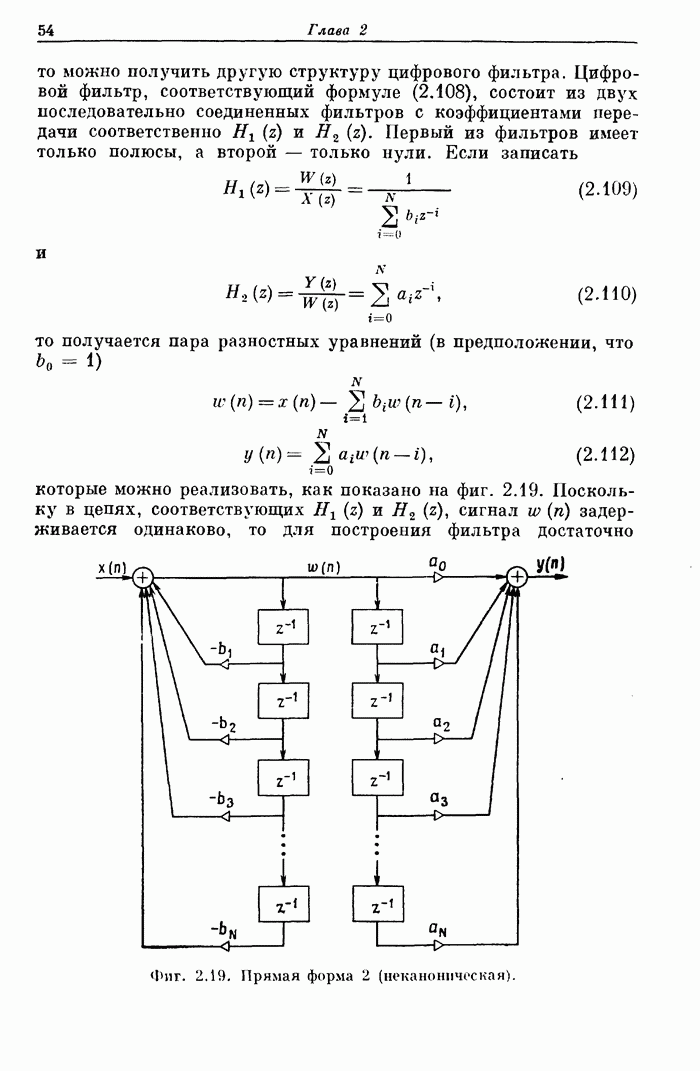
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
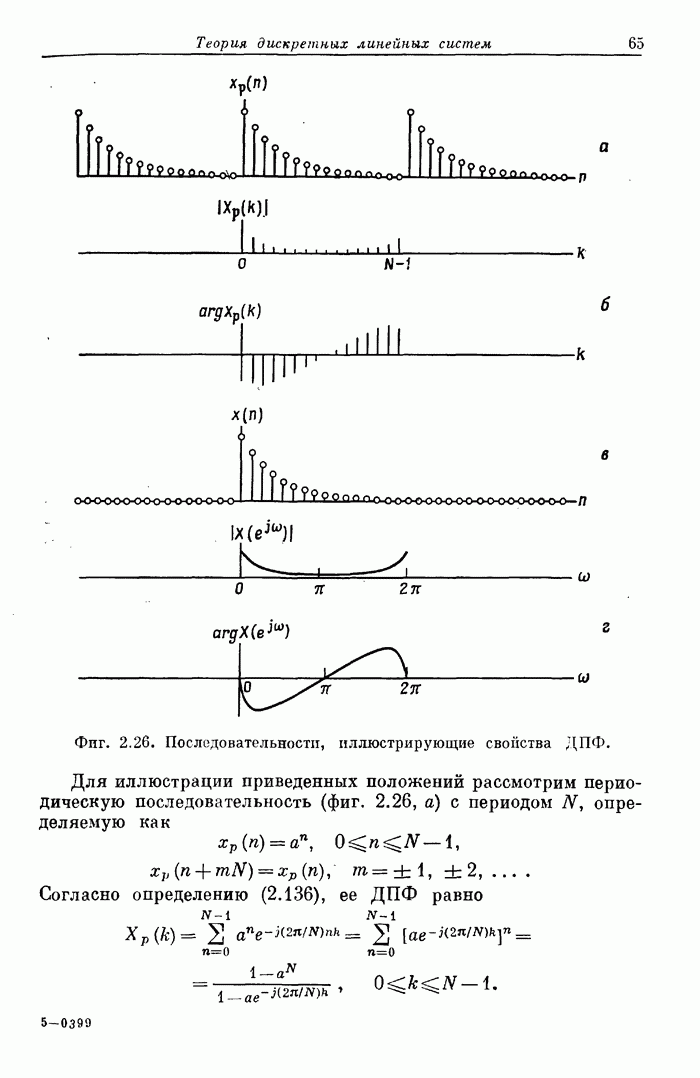
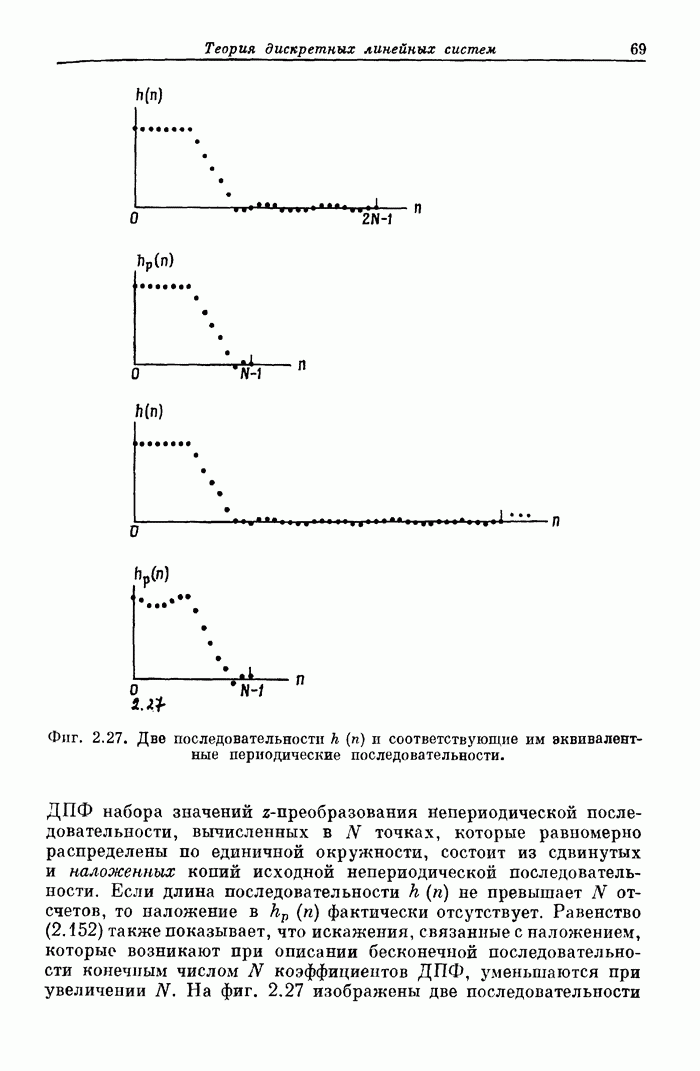
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
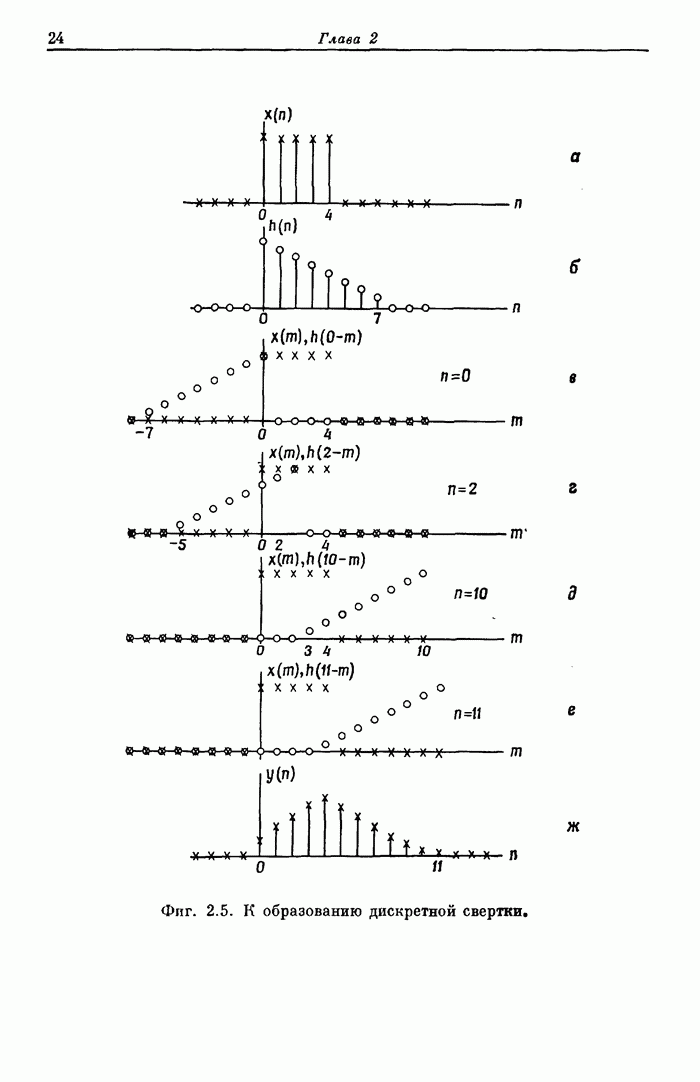
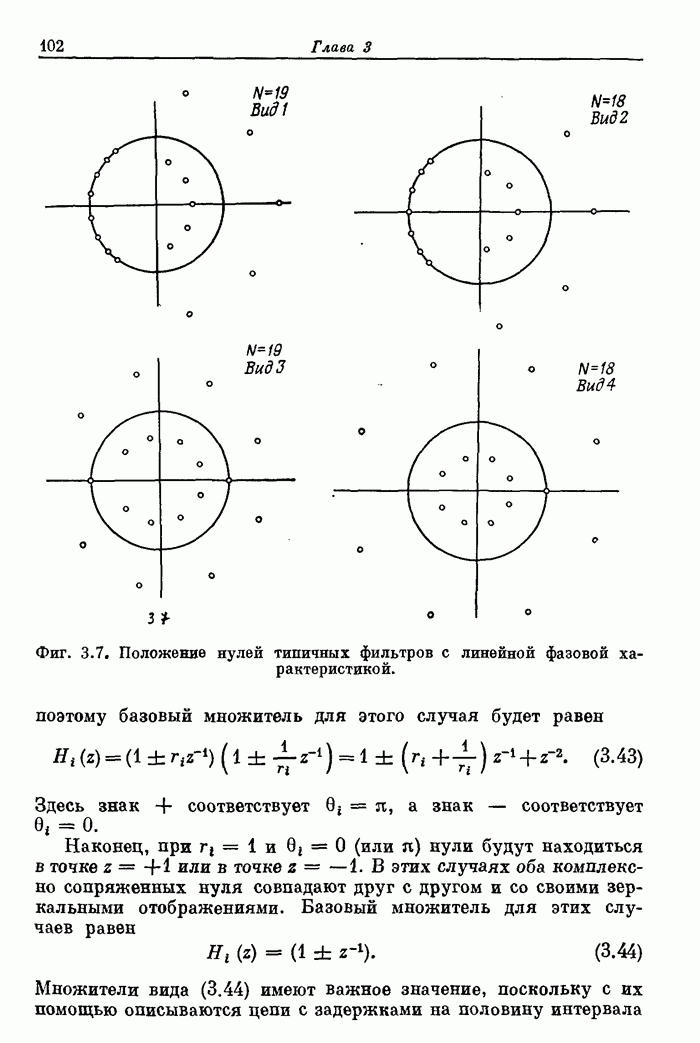
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
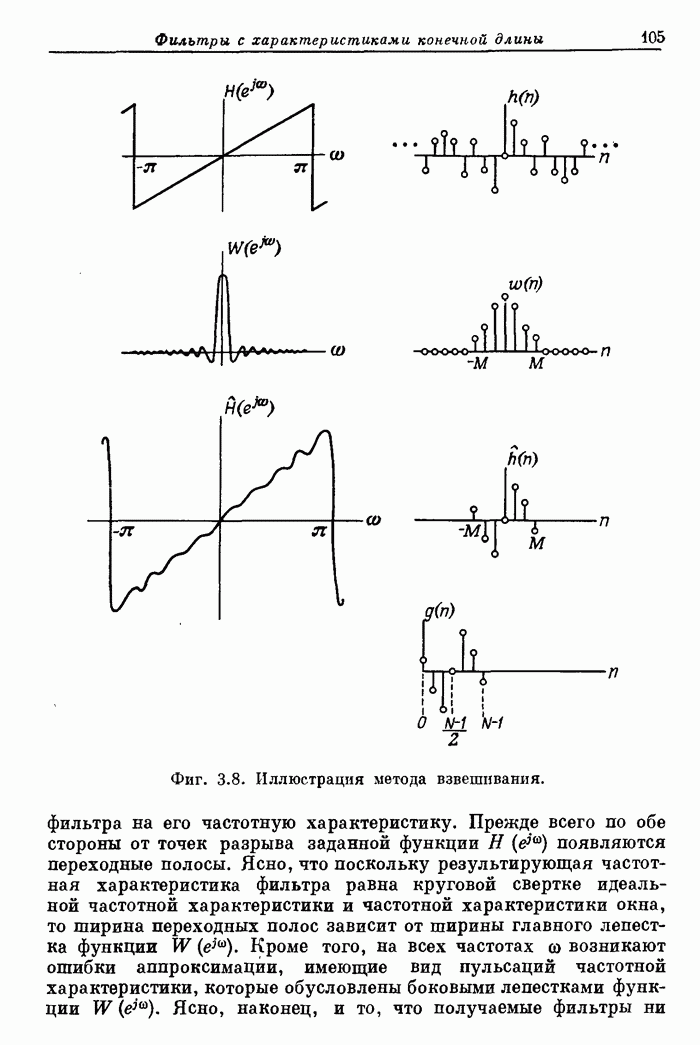
- 3.8. Первый метод расчета — метод взвешивания
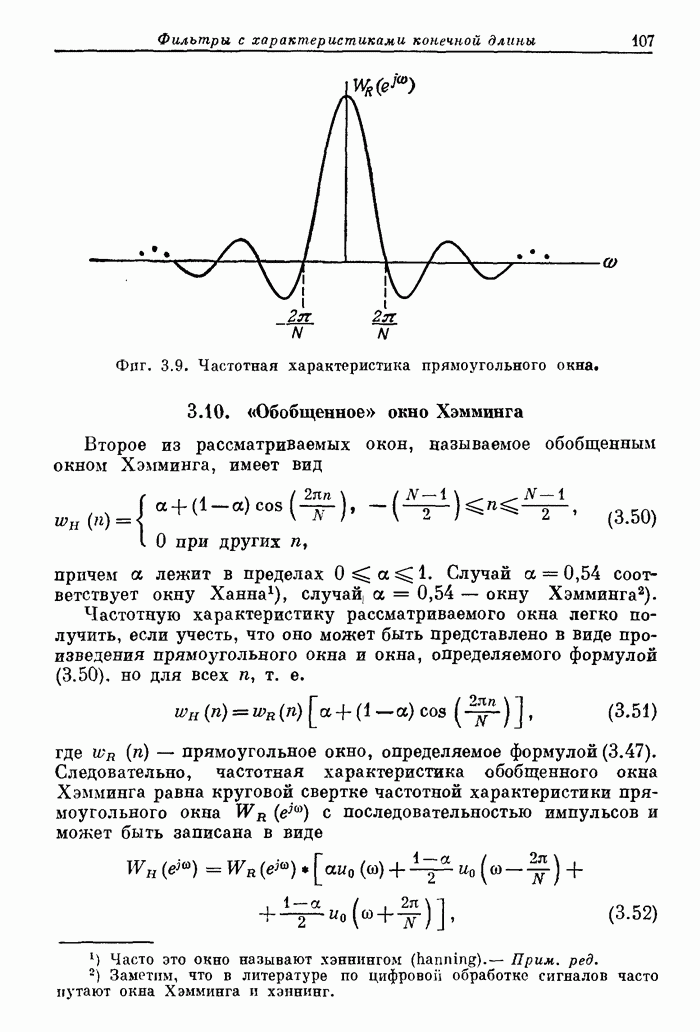
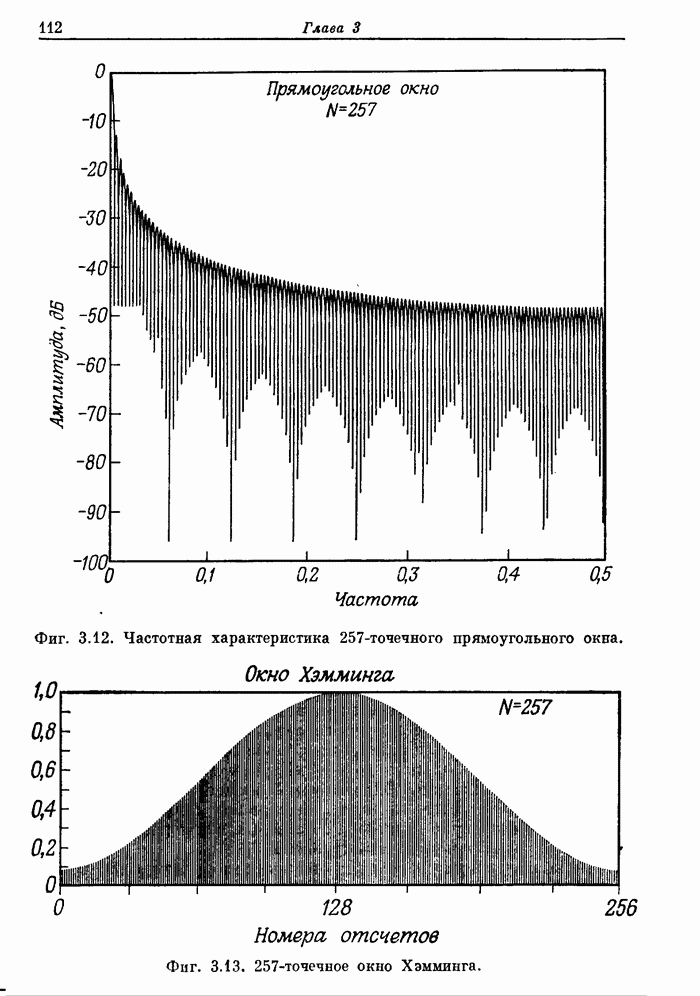
- 3.9. Прямоугольное окно
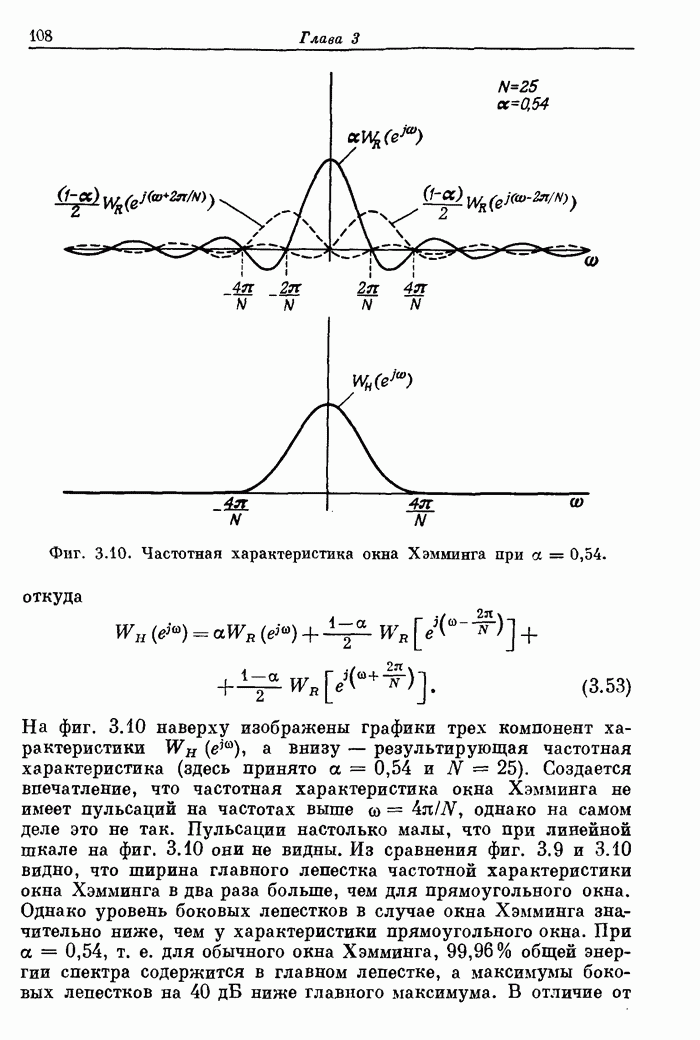
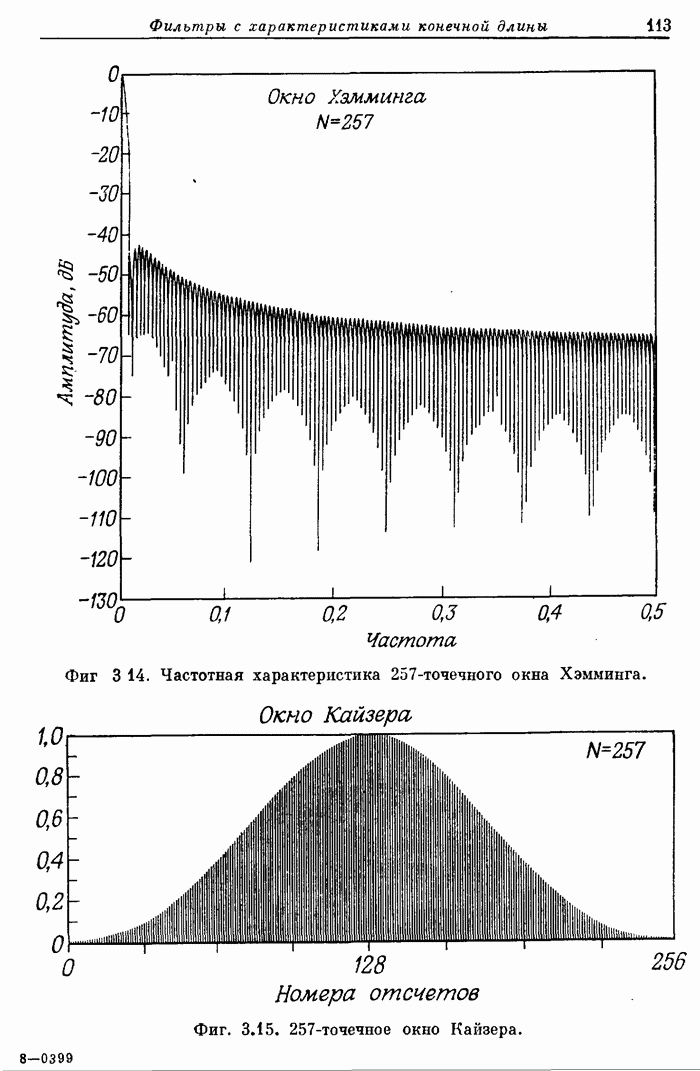
- 3.10. «Обобщенное» окно Хэмминга
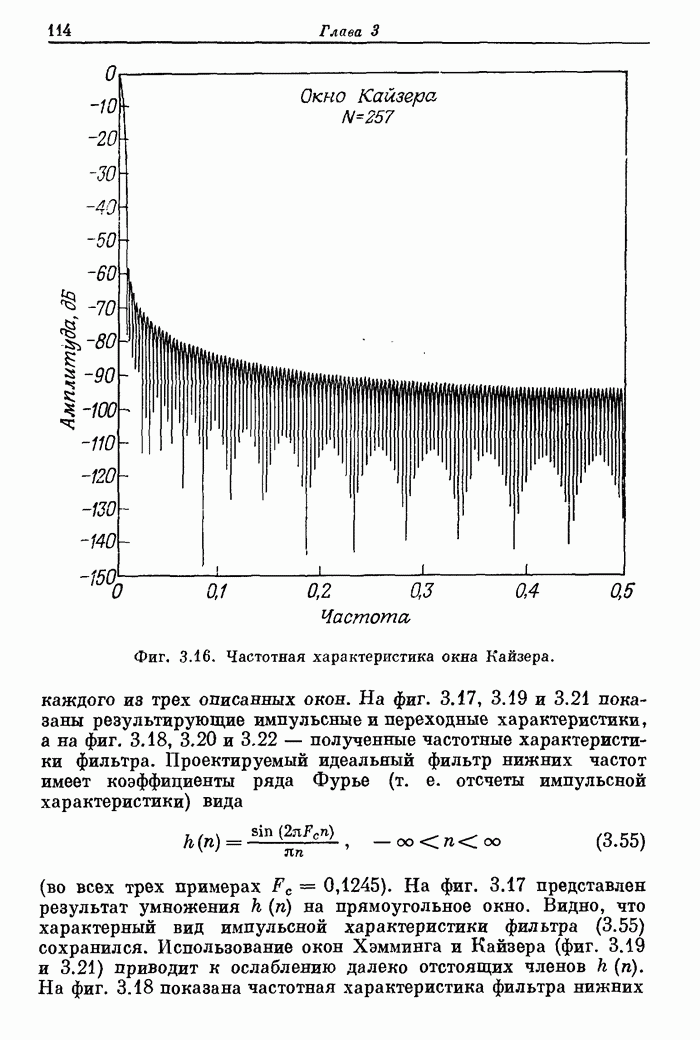
- 3.11. Окно Кайзера
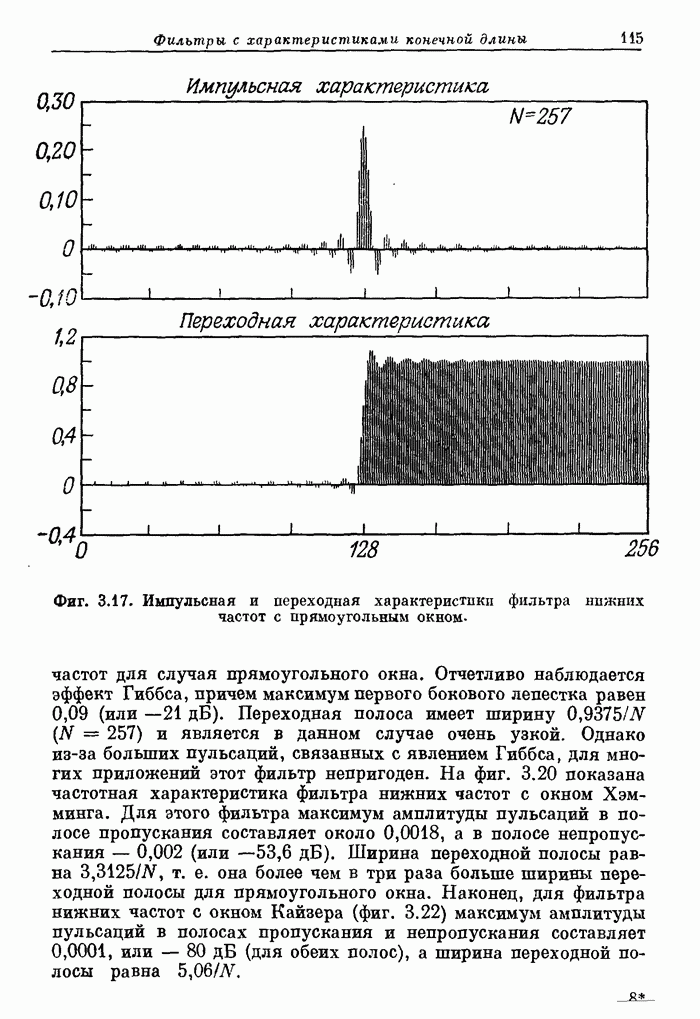
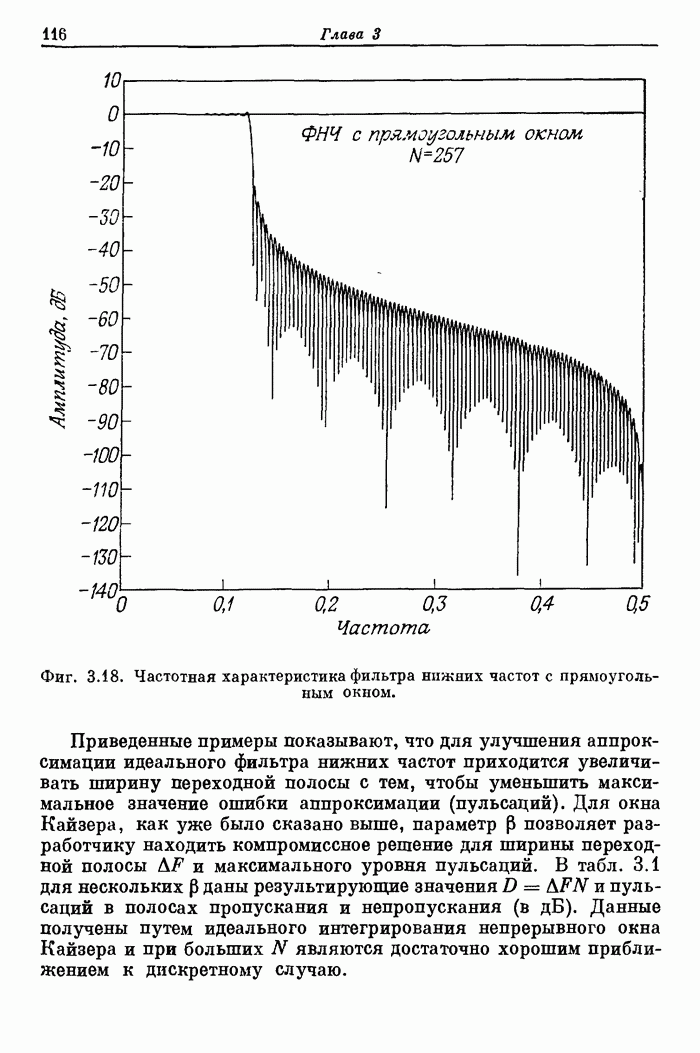
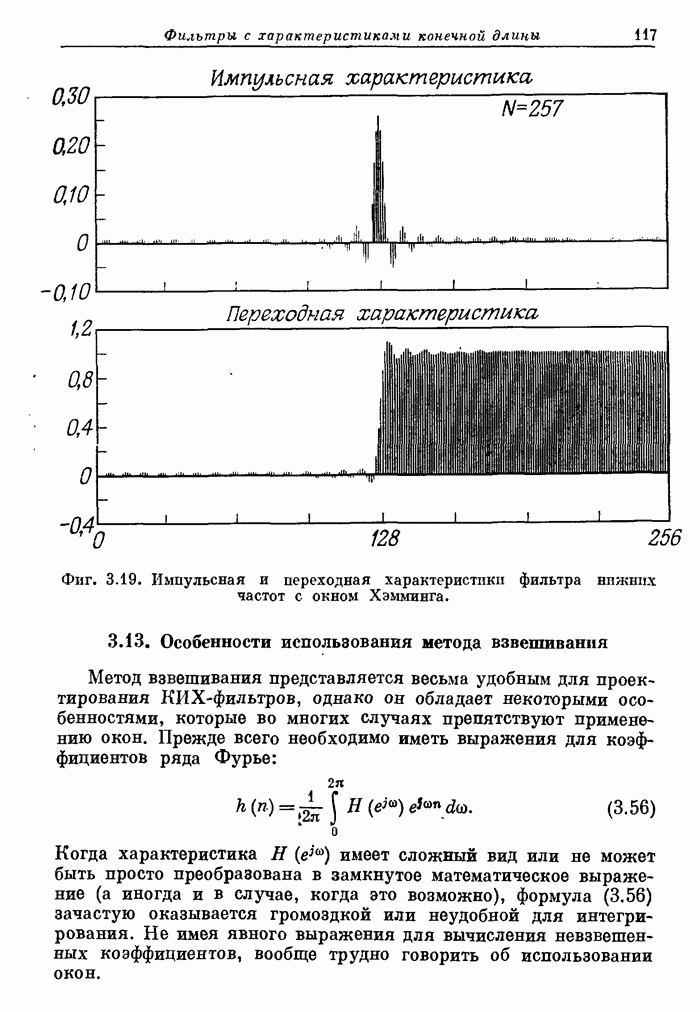
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
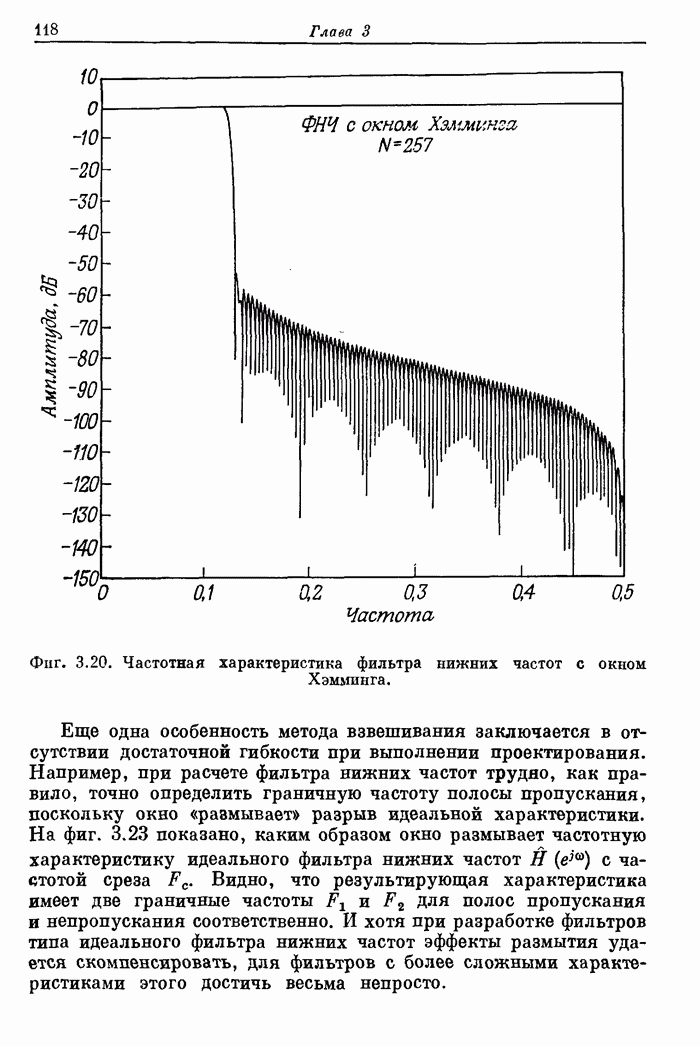
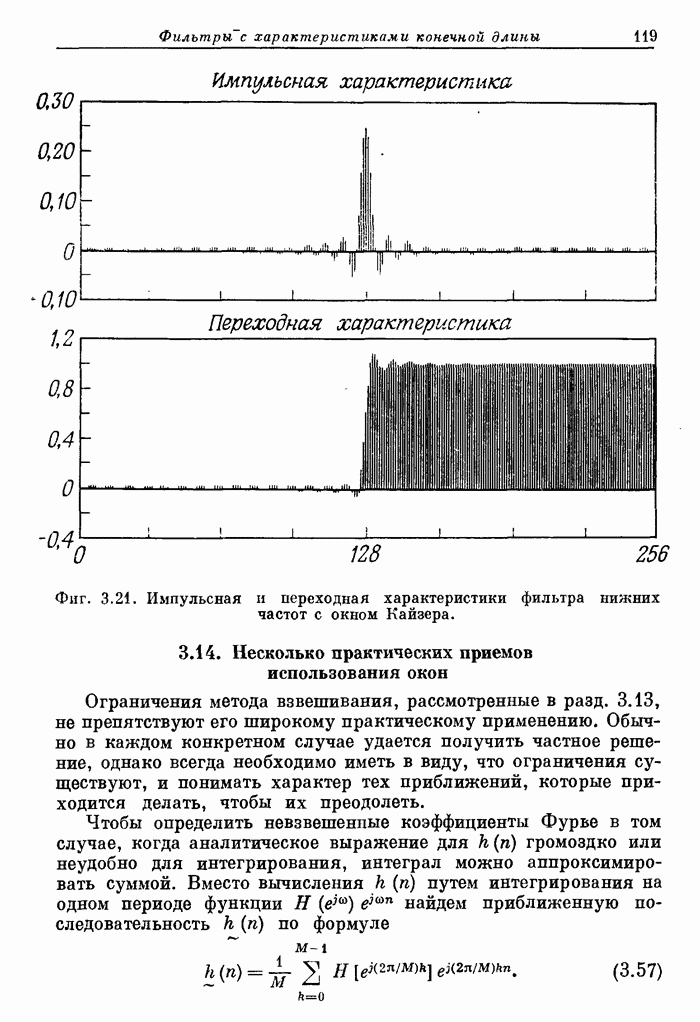
- 3.14. Несколько практических приемов использования окон
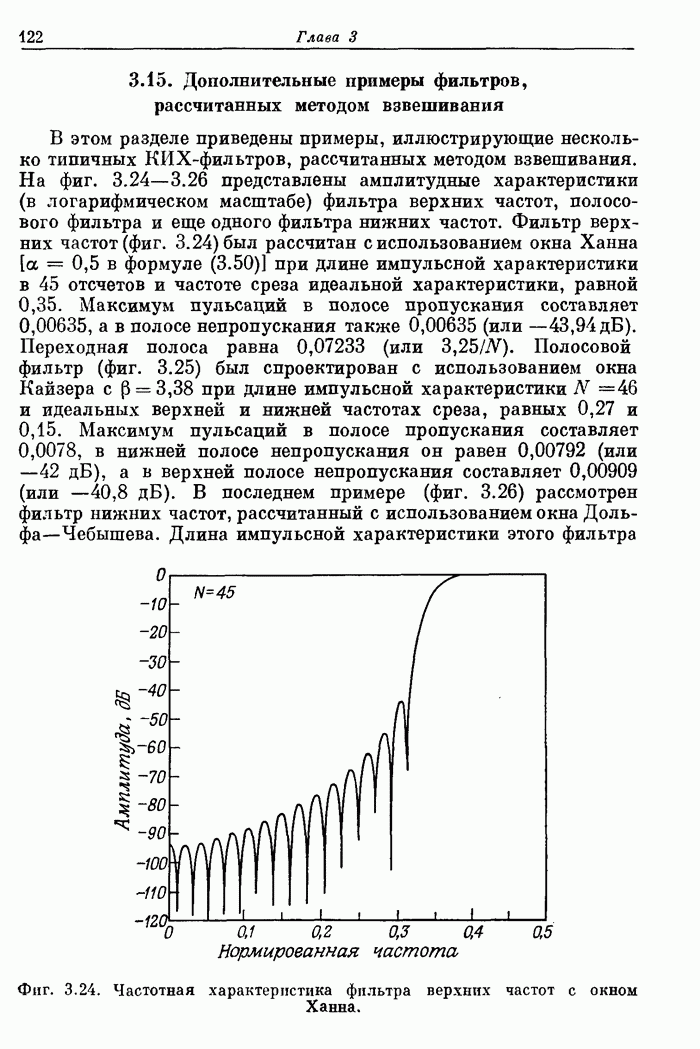
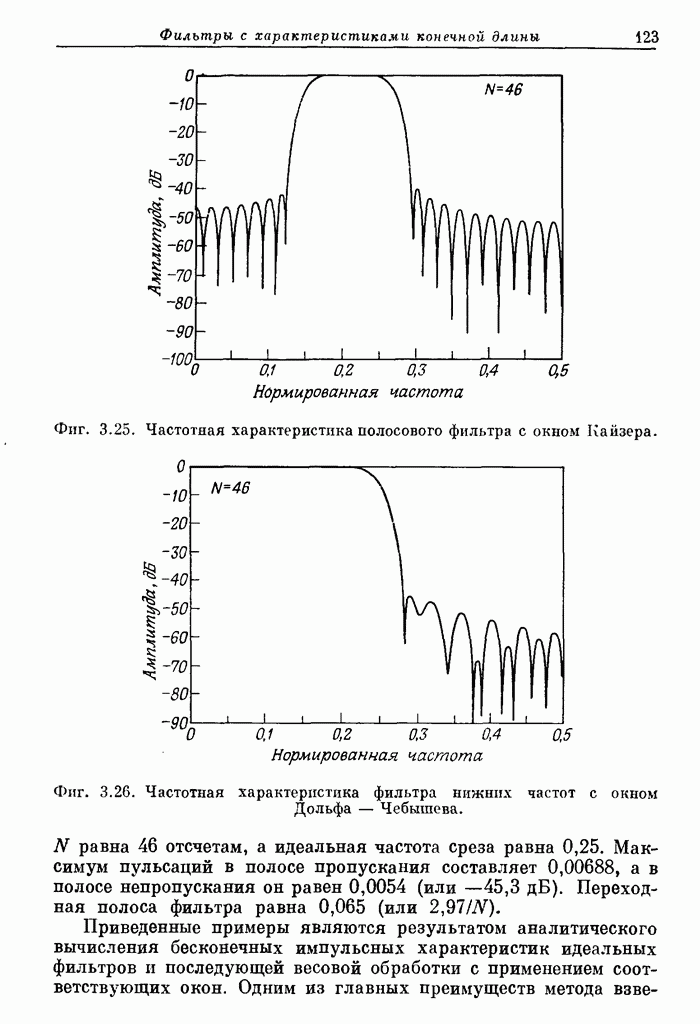
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
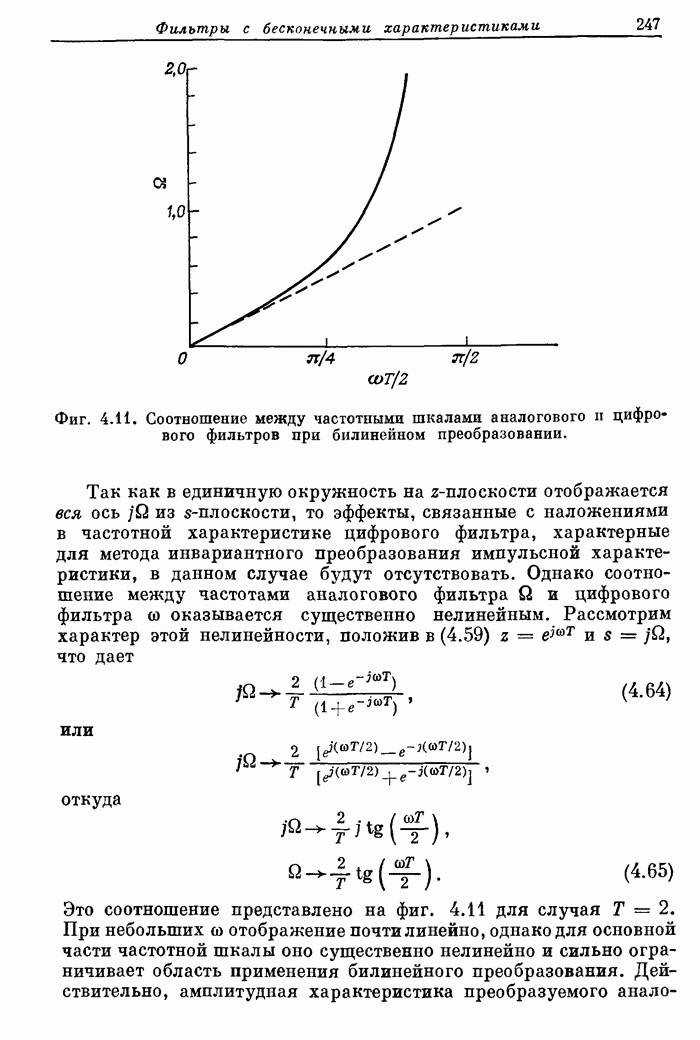
- 3.18. Решение задачи оптимизации
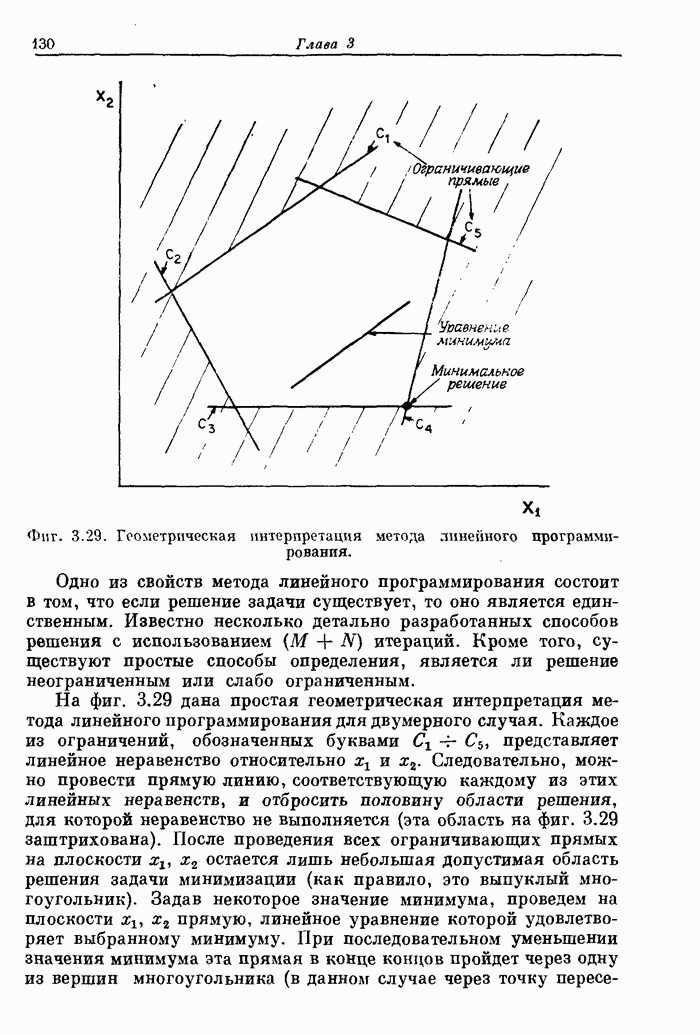
- 3.19. Линейное программирование
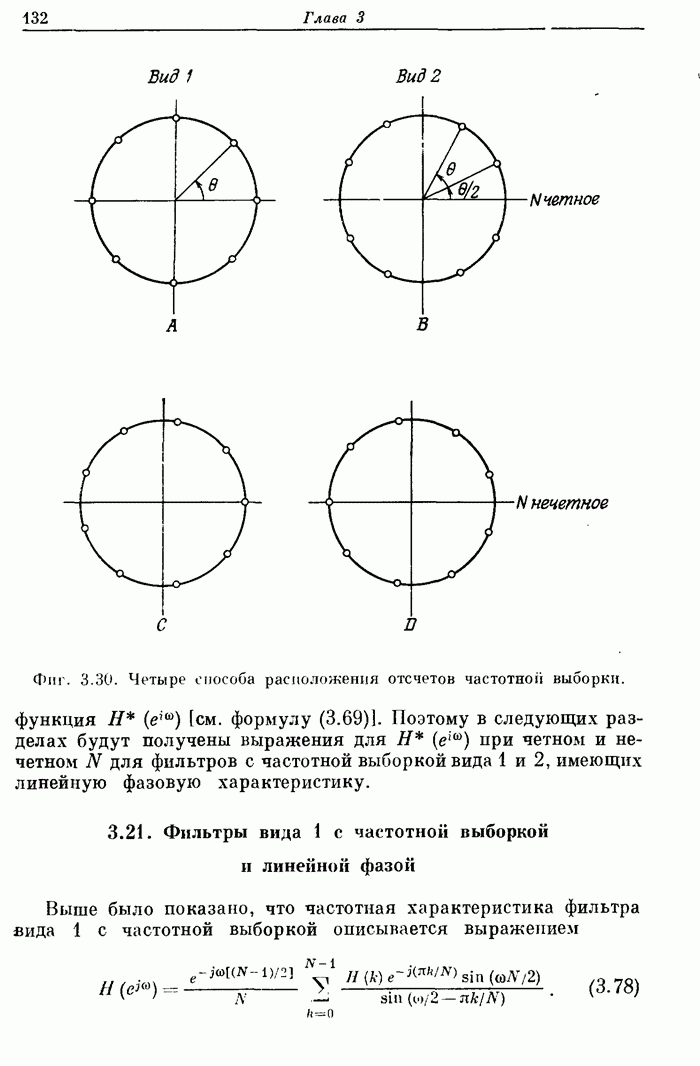
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
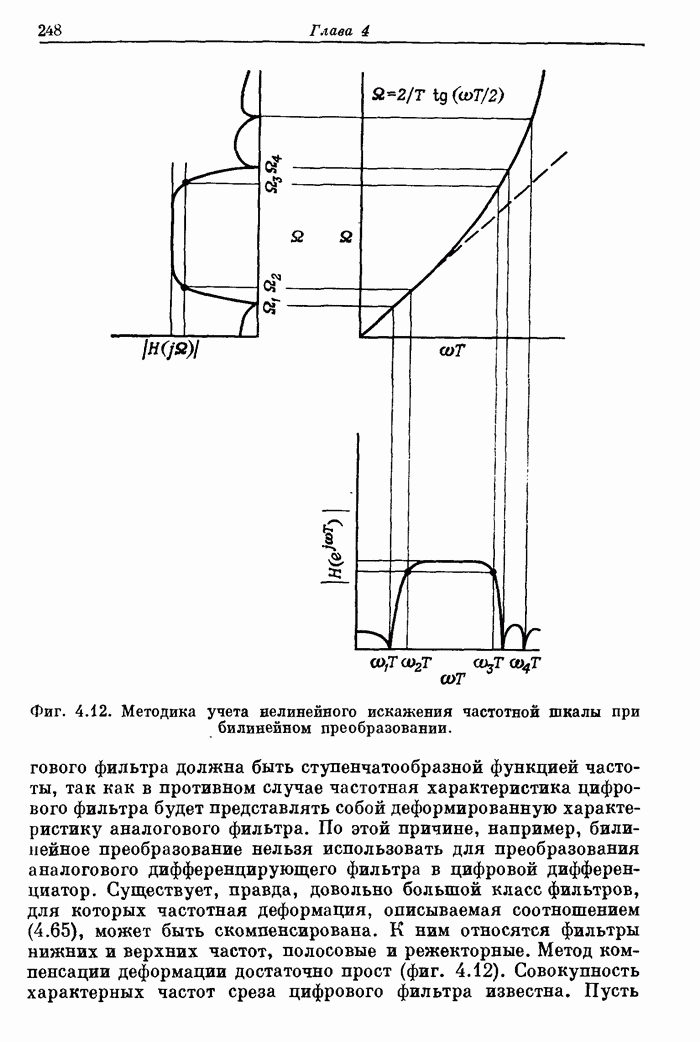
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
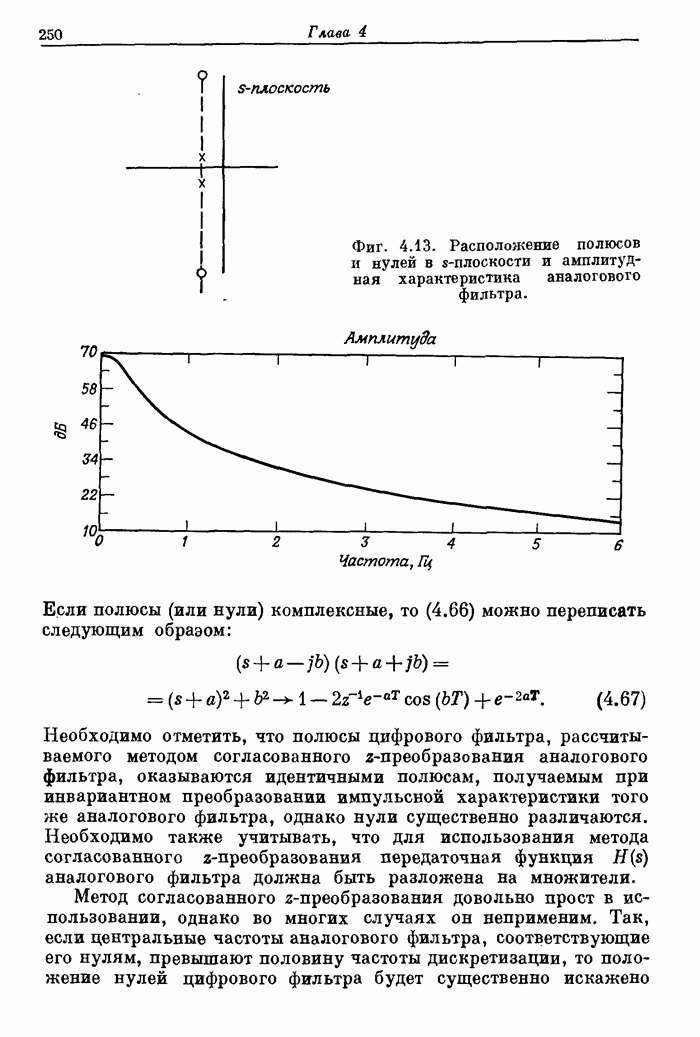
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
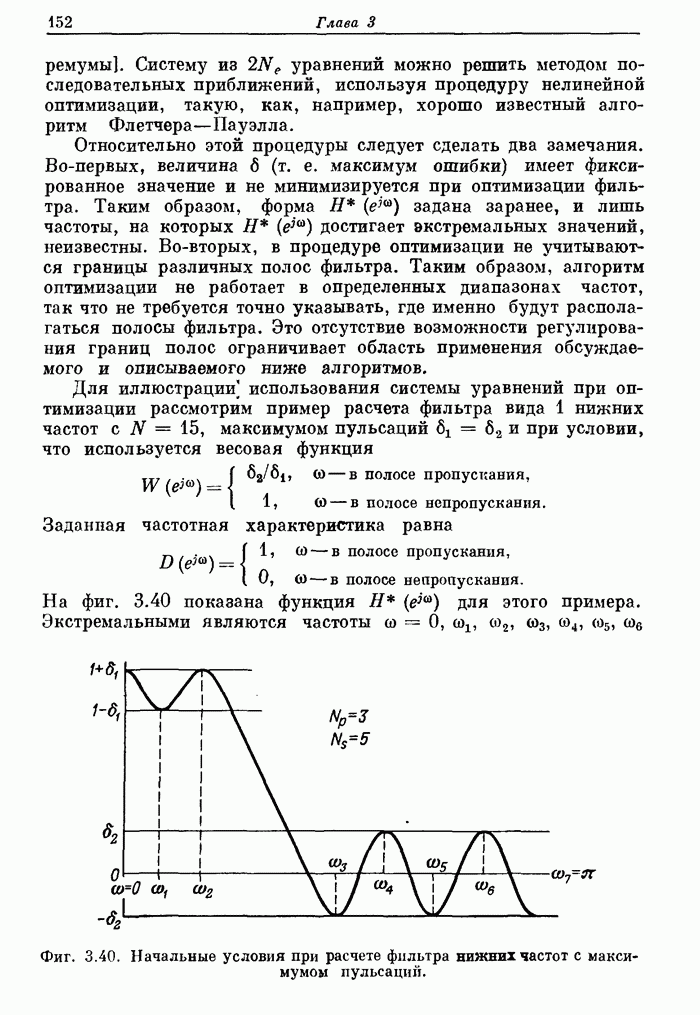
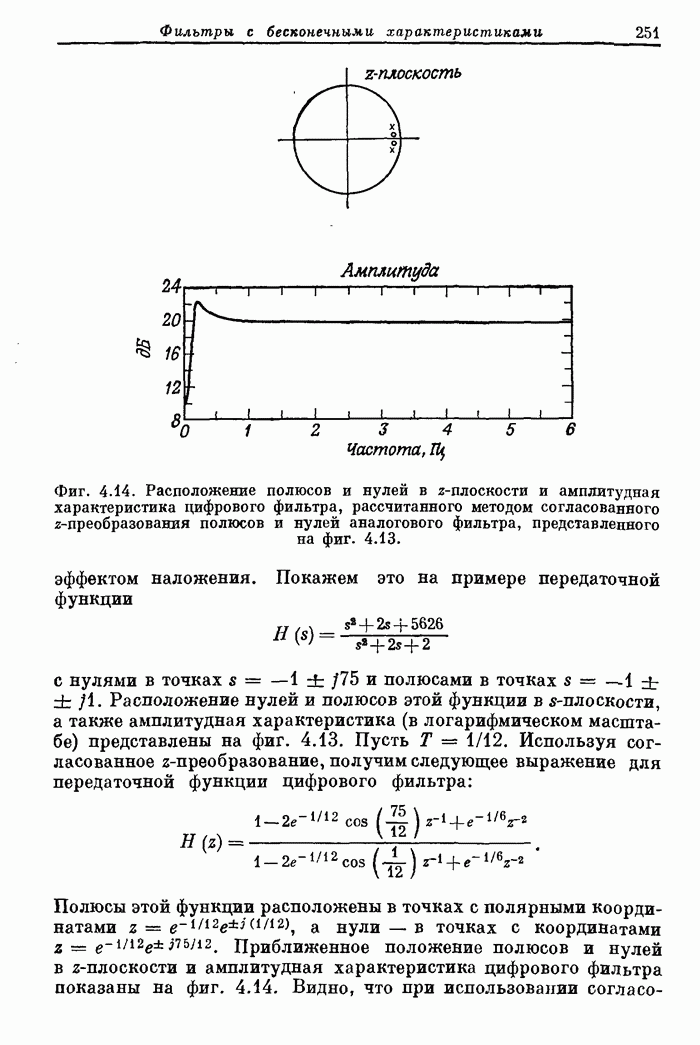
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
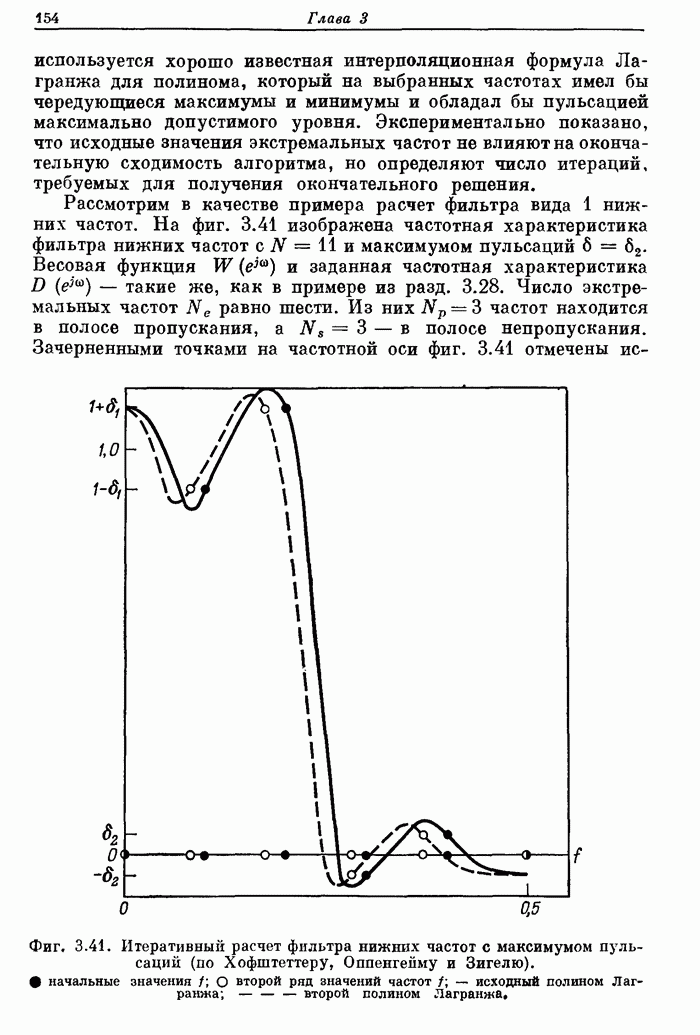
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
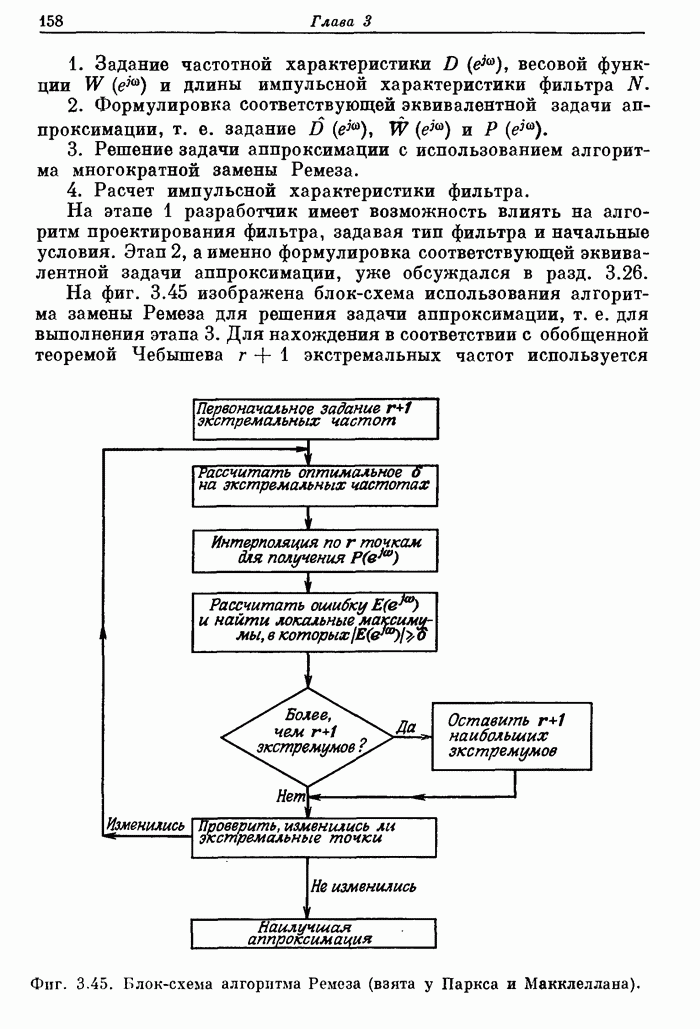
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
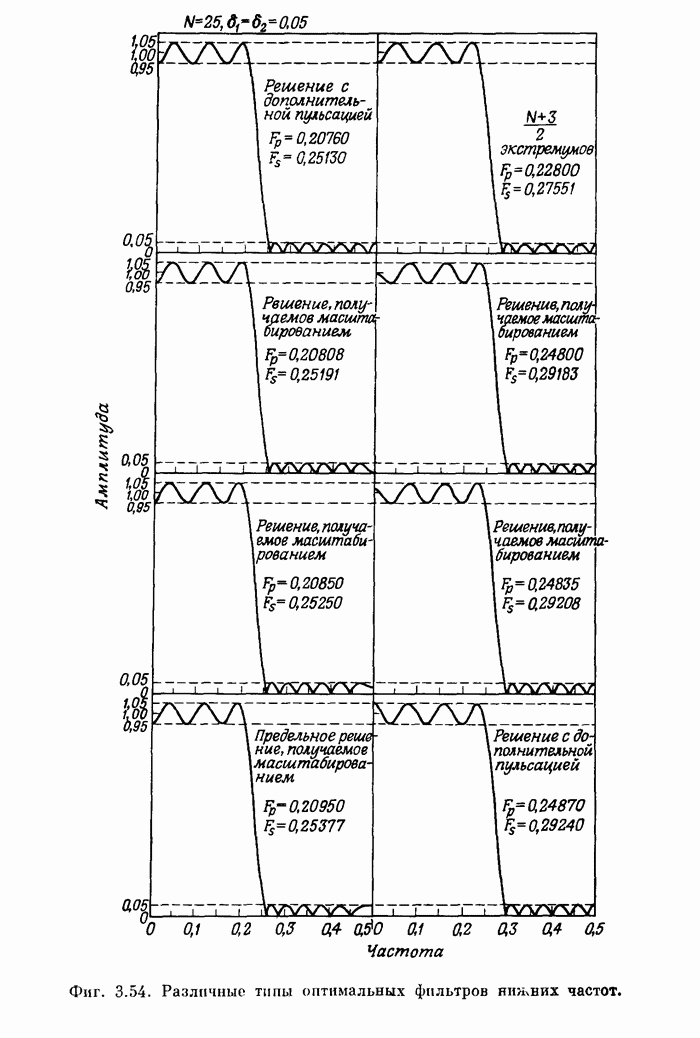
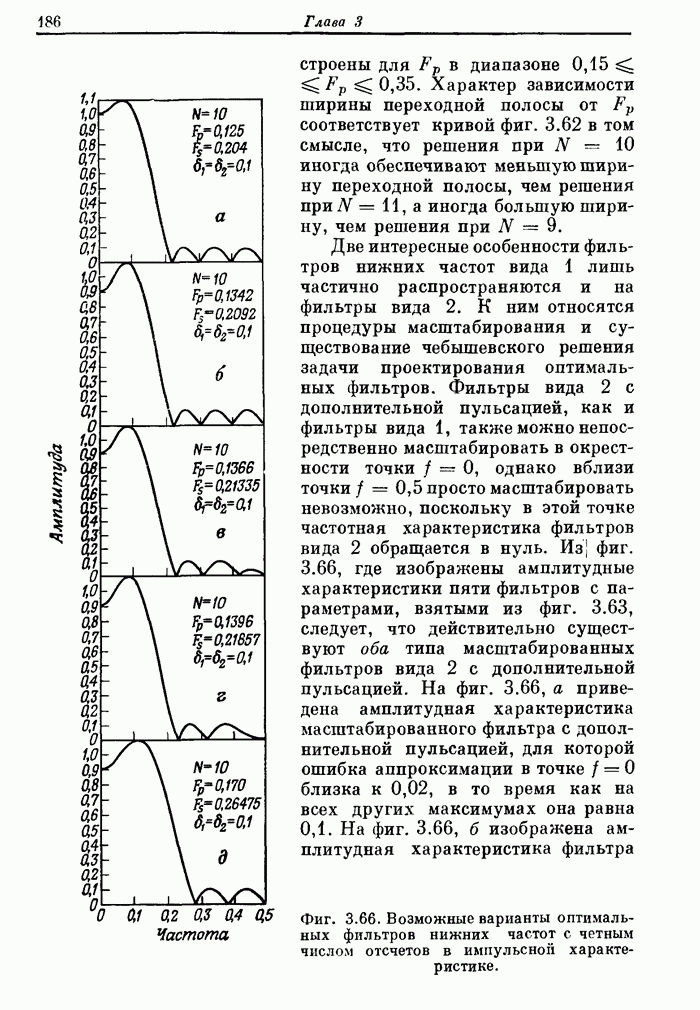
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
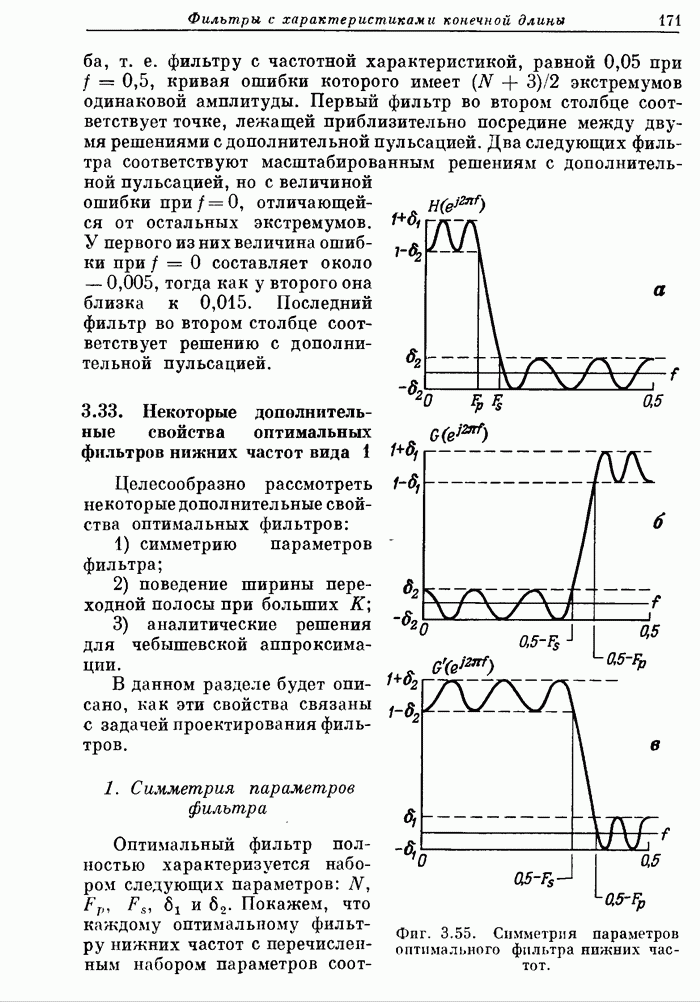
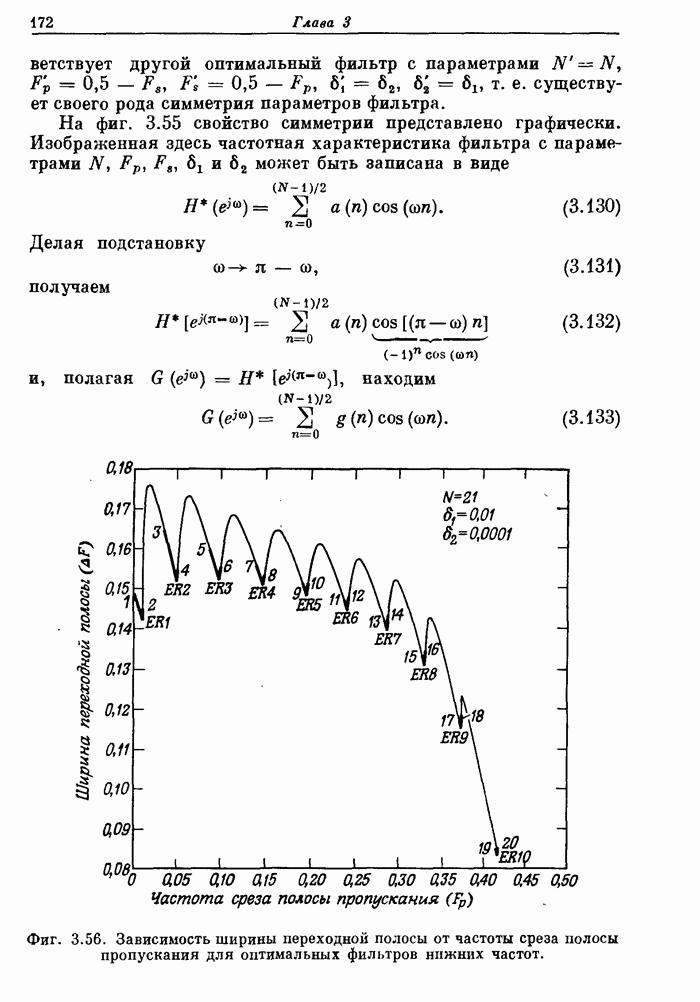
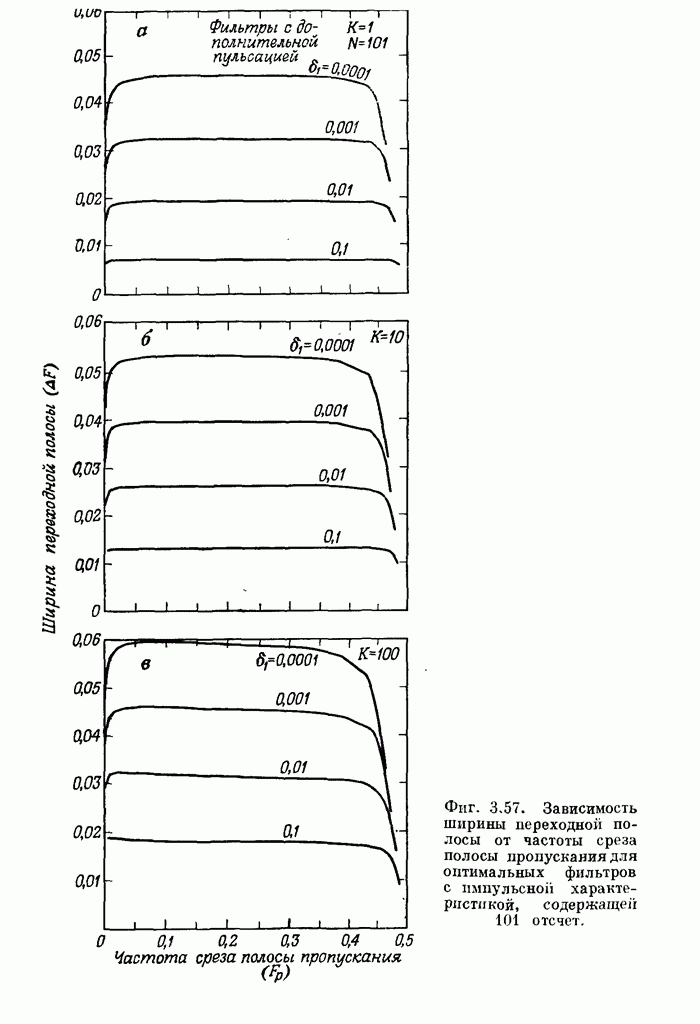
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
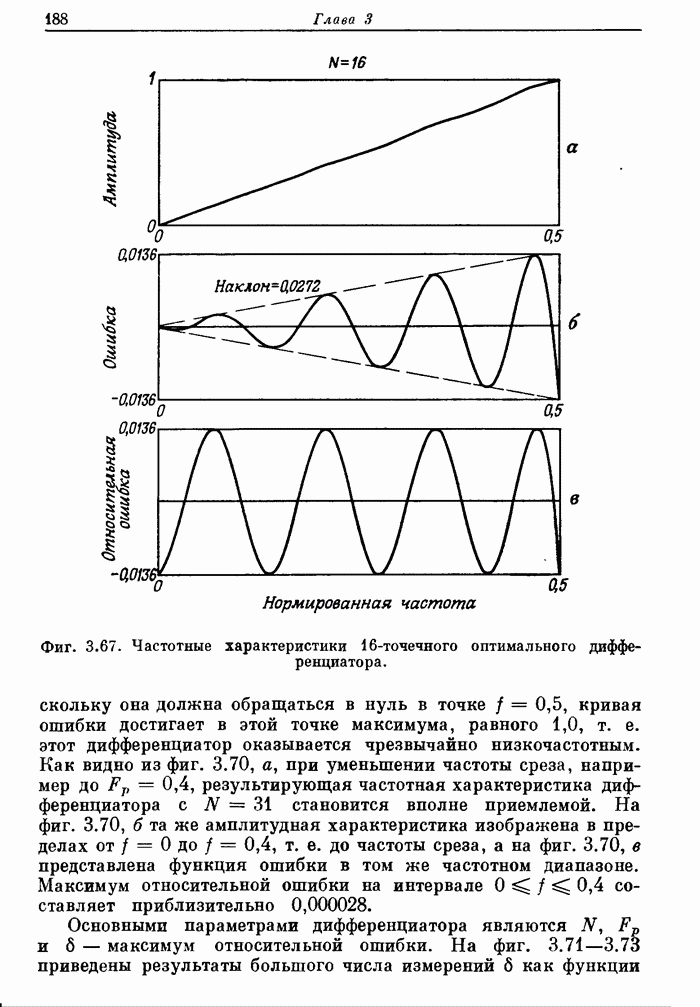
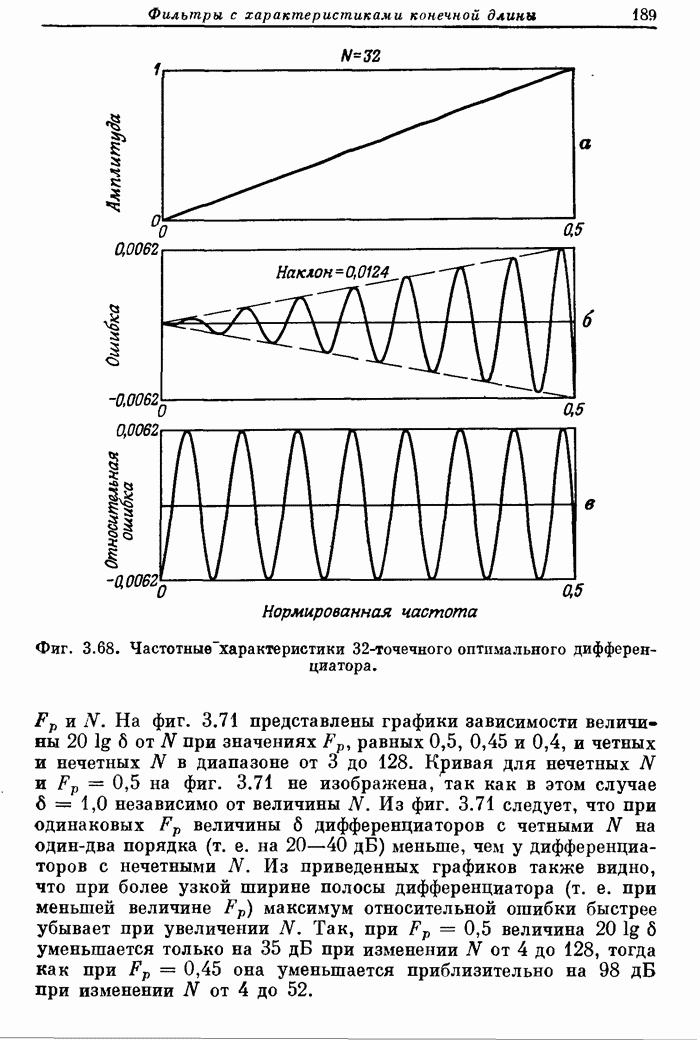
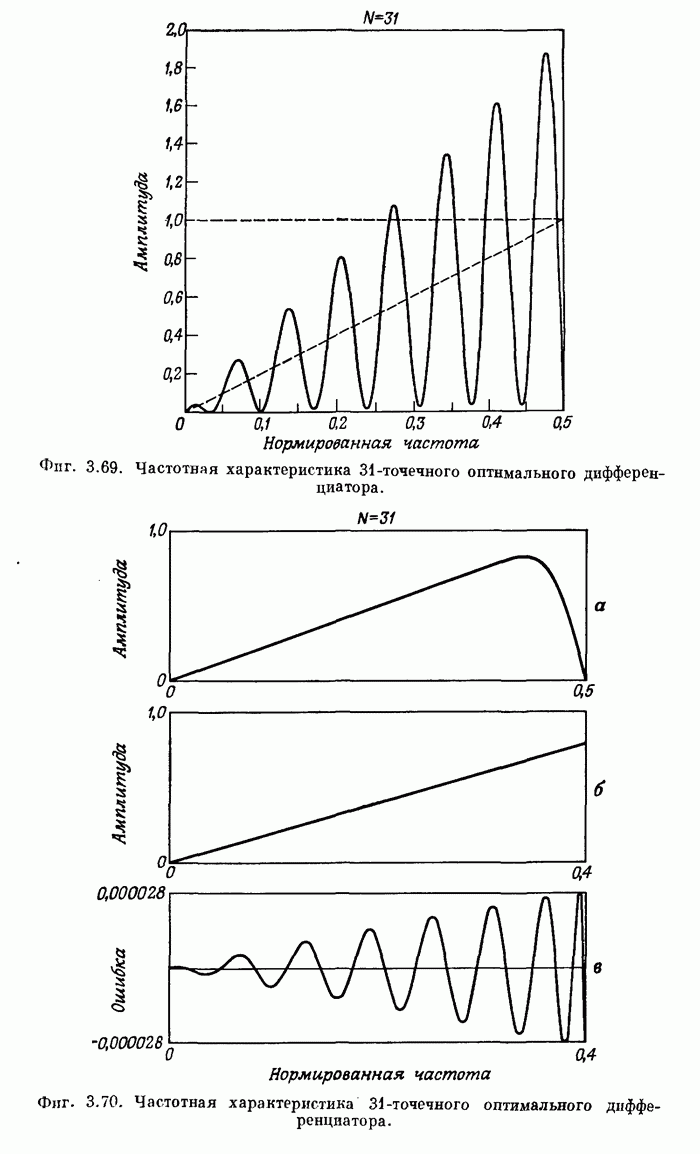
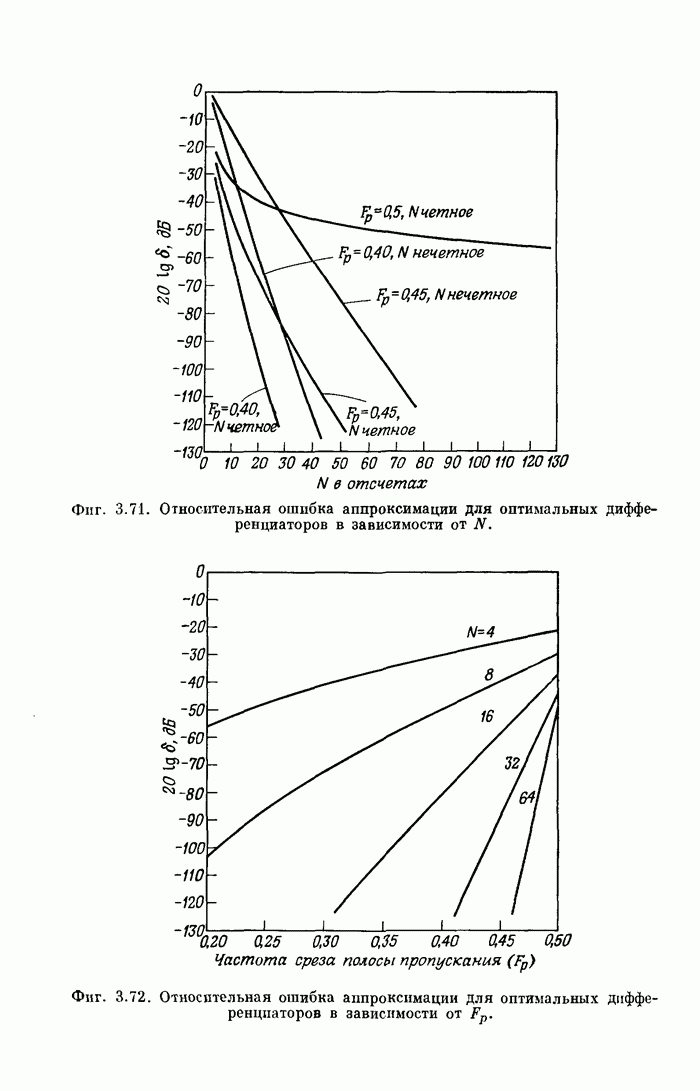
- 3.36. Характеристики оптимальных дифференциаторов
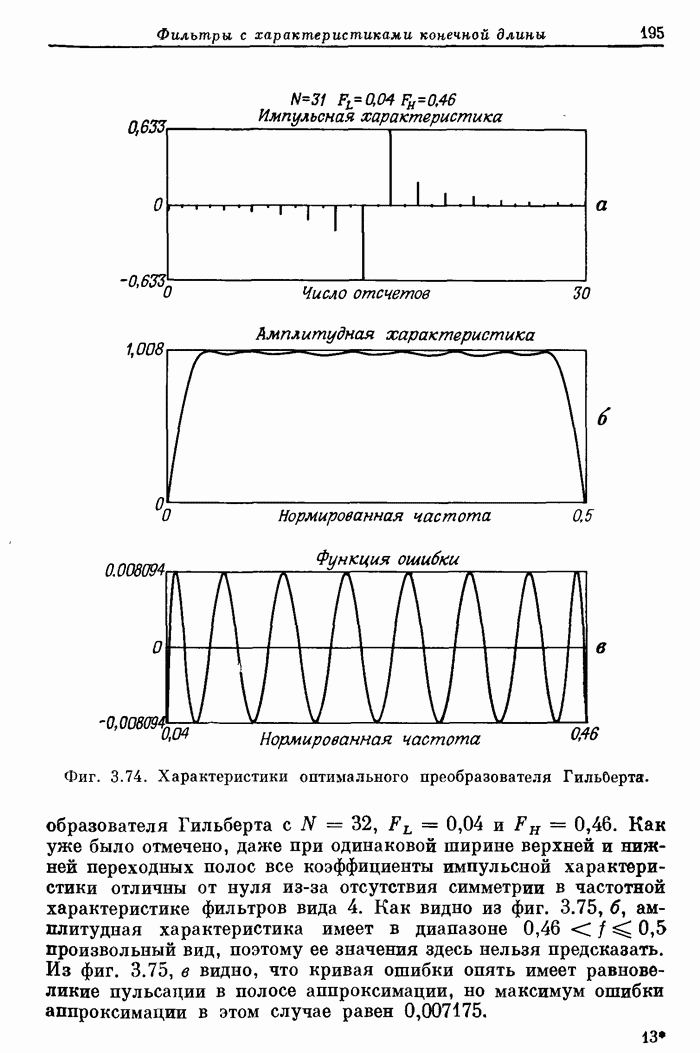
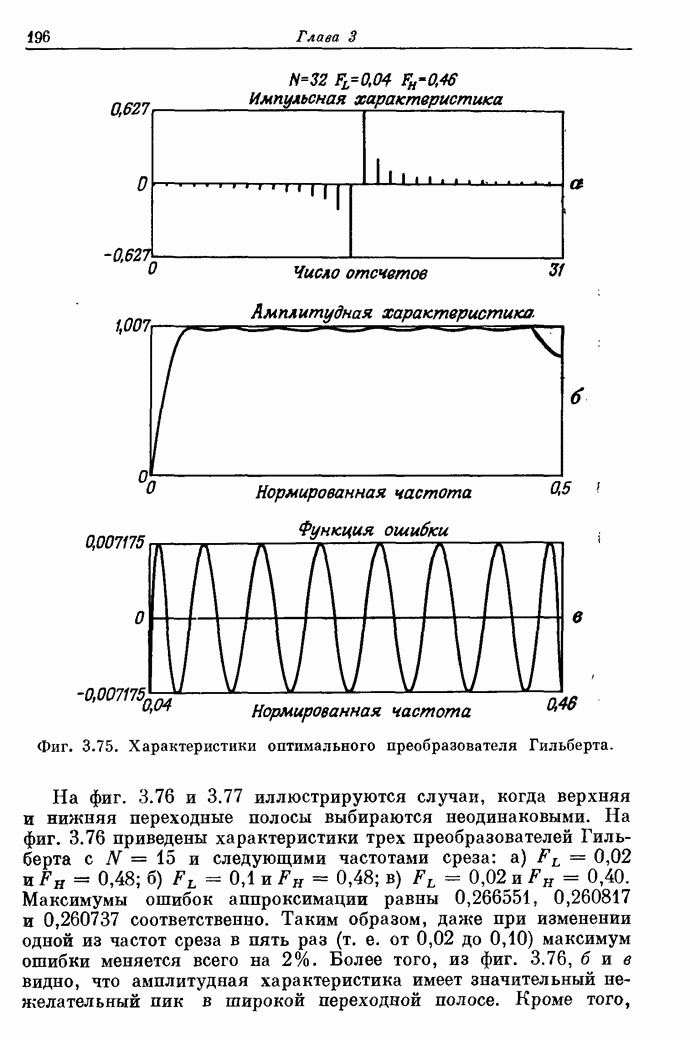
- 3.37. Характеристики оптимальных преобразователей Гильберта
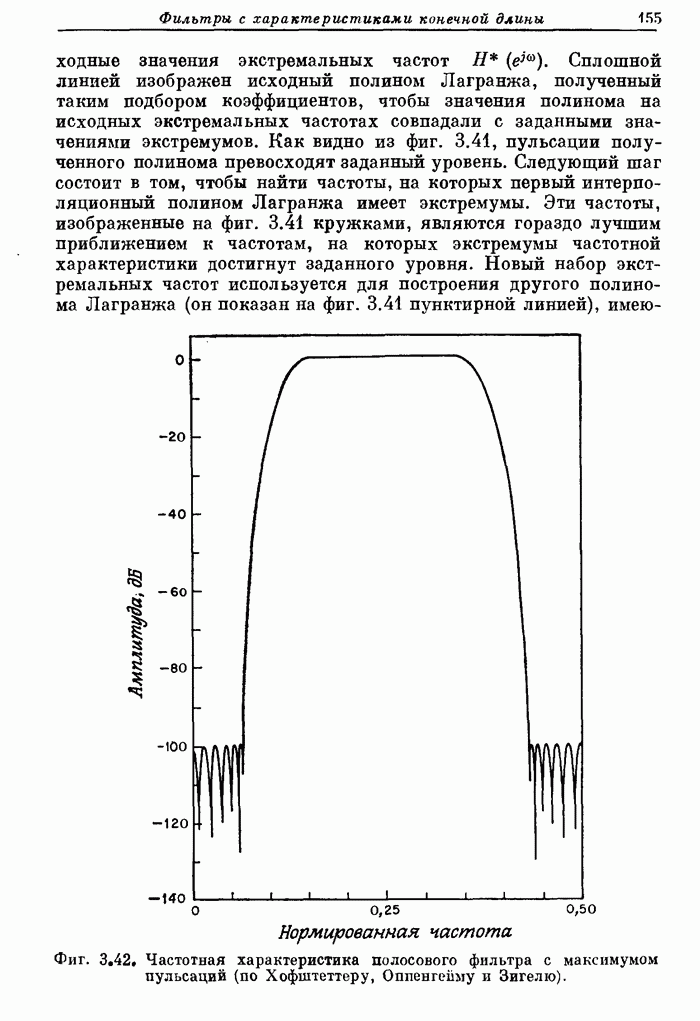
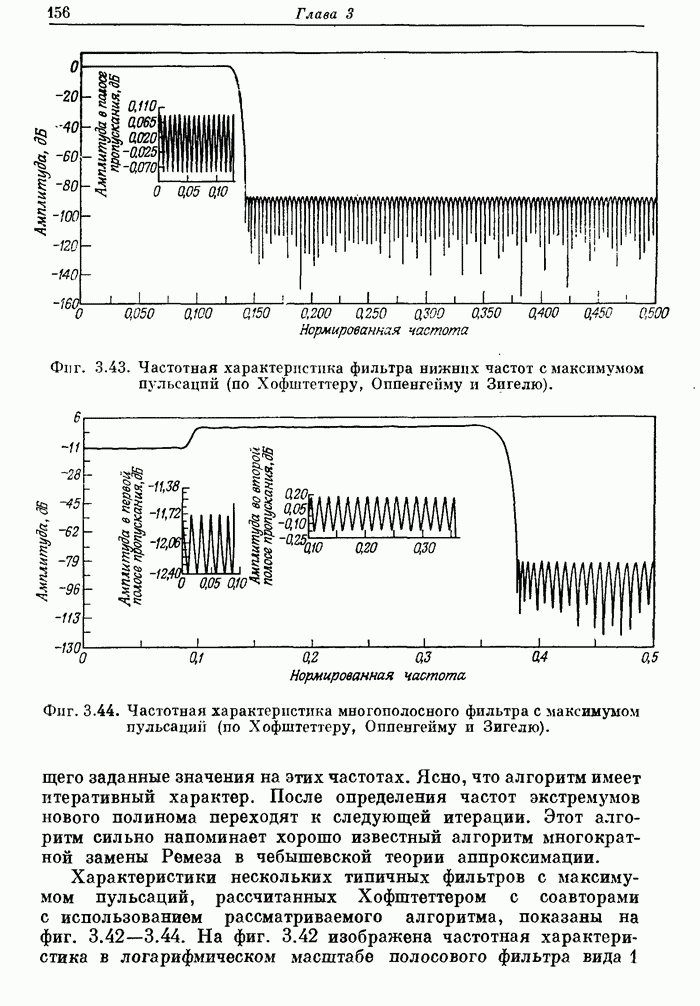
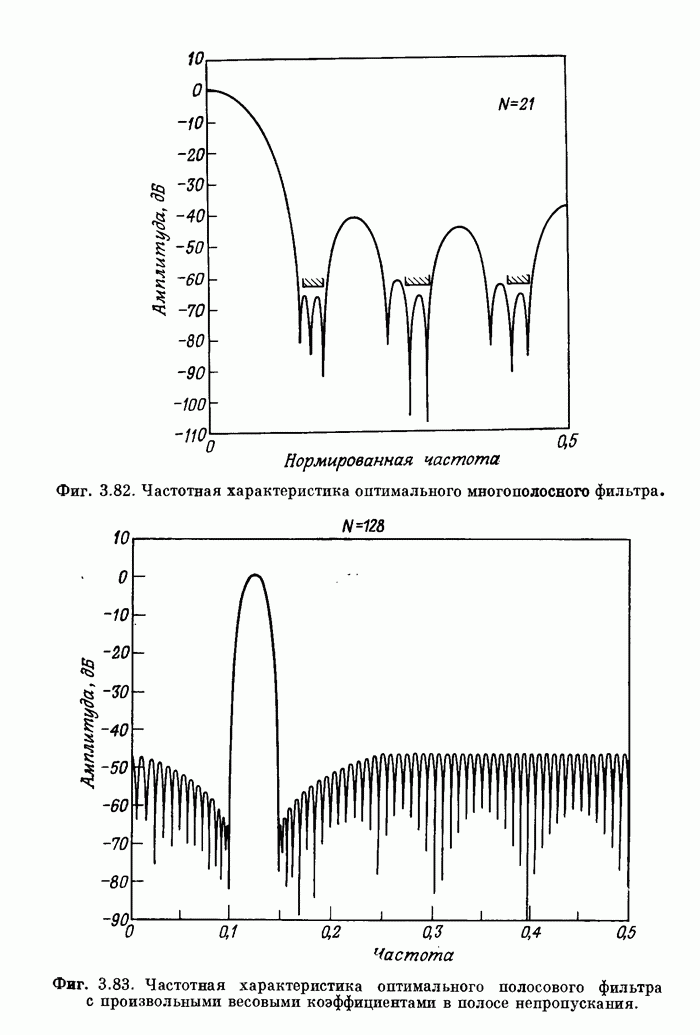
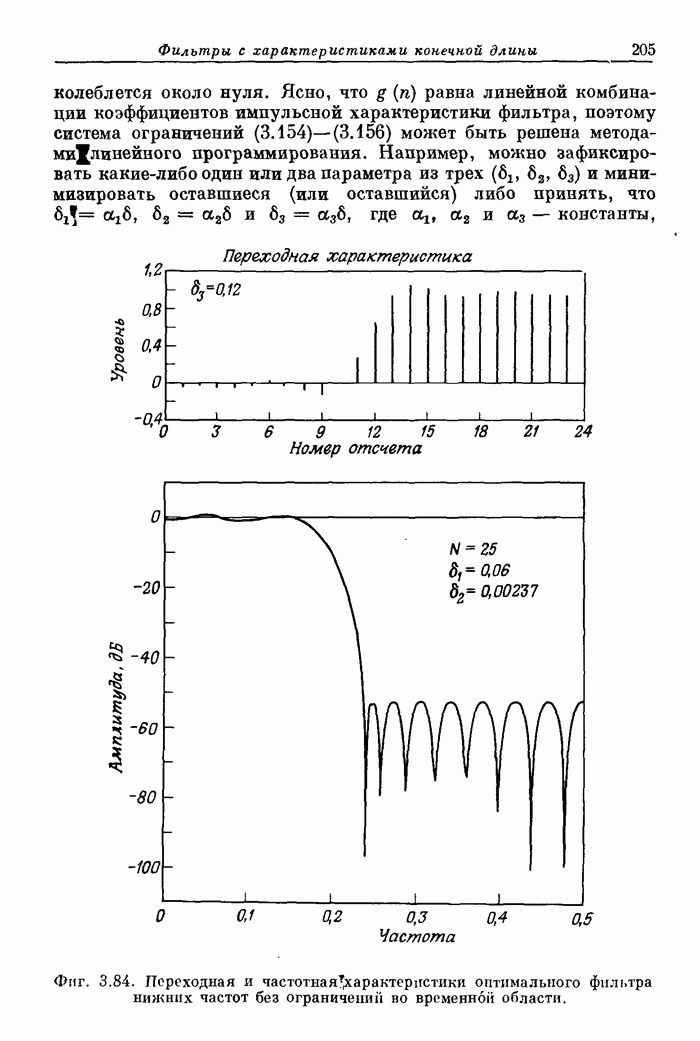
- 3.38. Многополосные оптимальные КИХ-фильтры
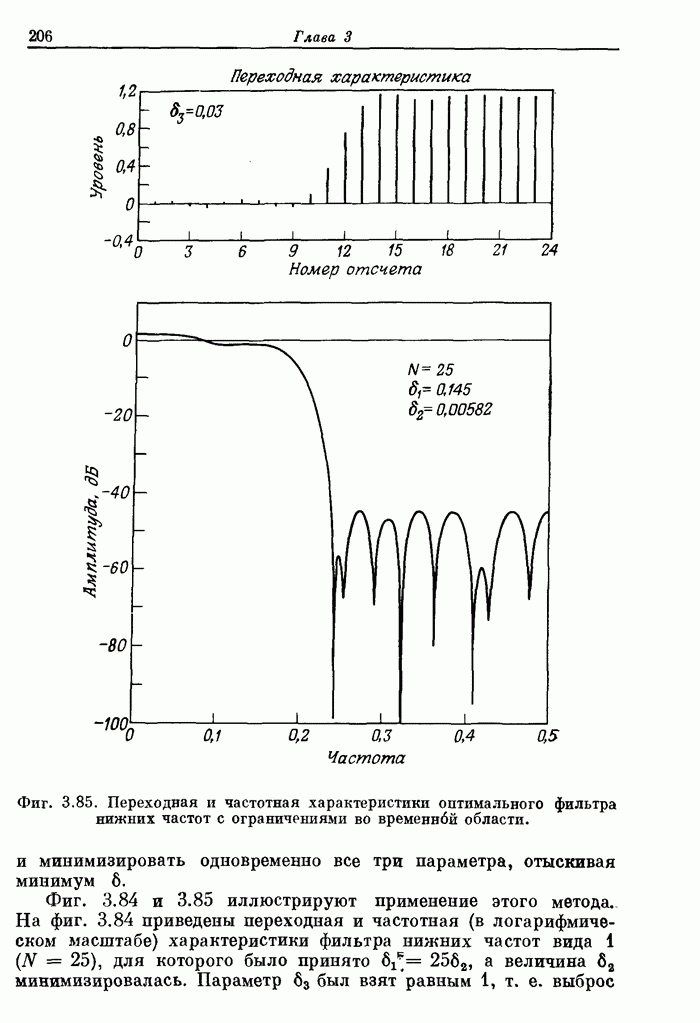
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
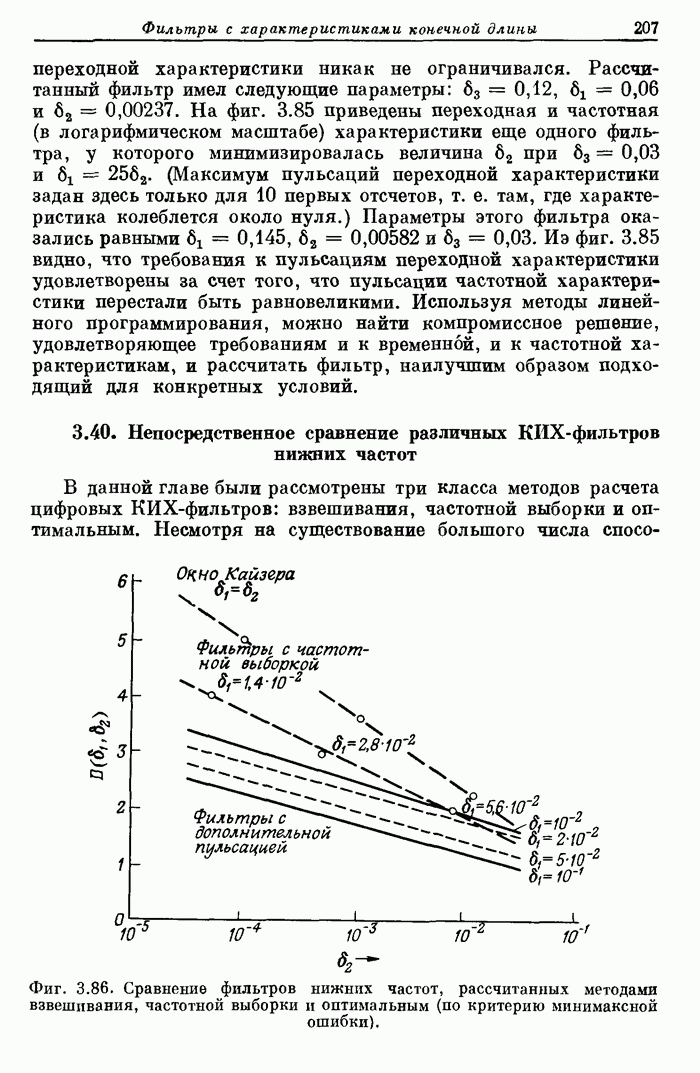
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
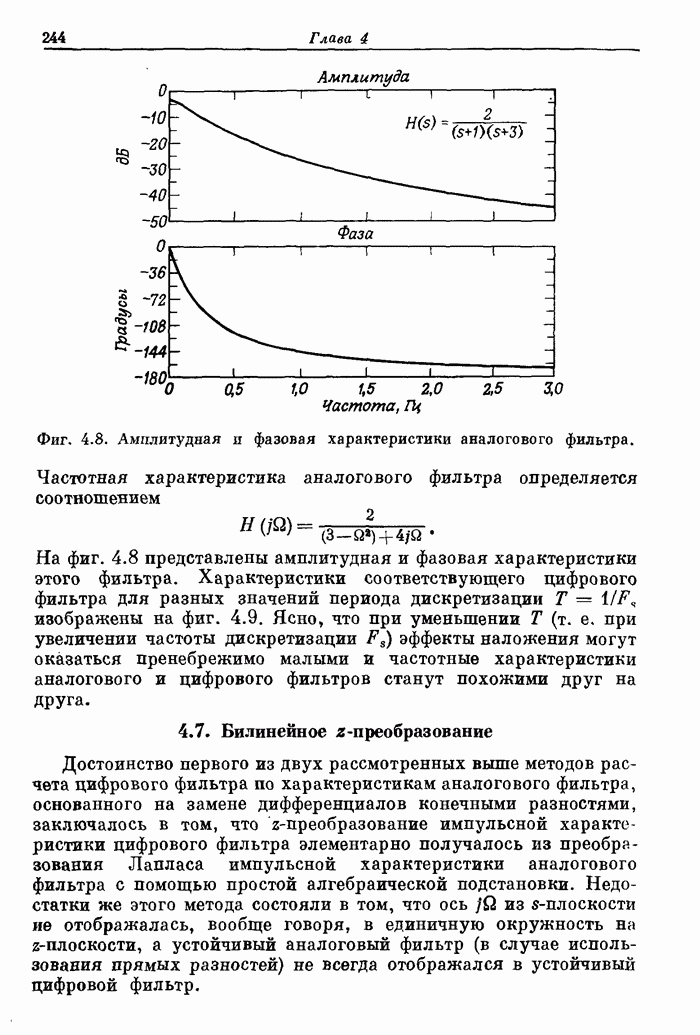
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
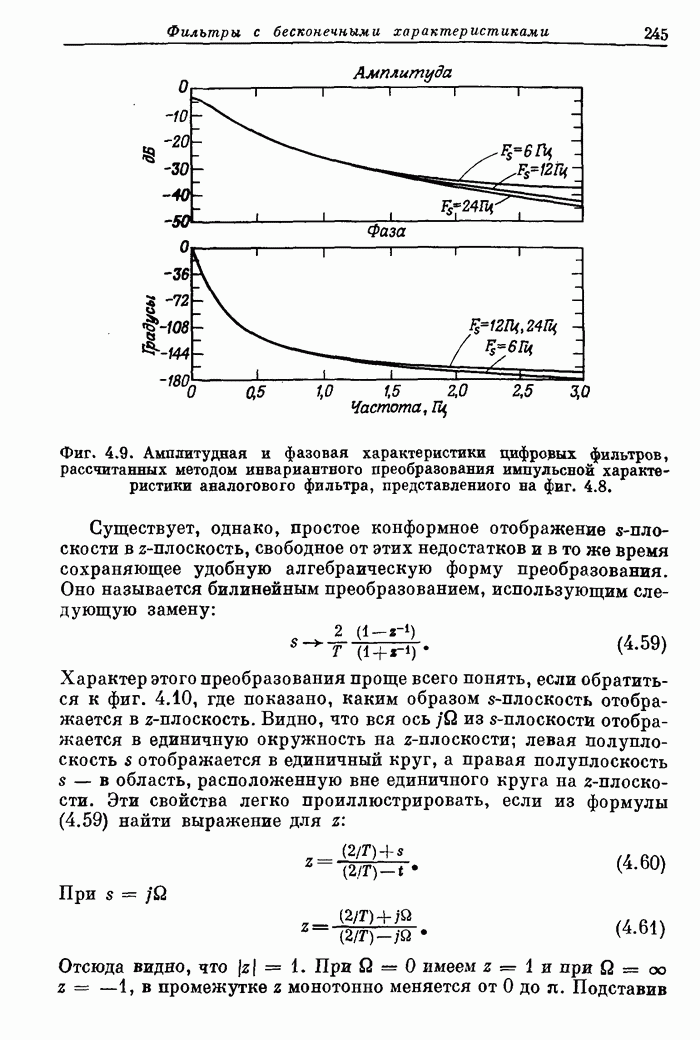
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
- 4.10. Расчетные диаграммы фильтров нижних частот
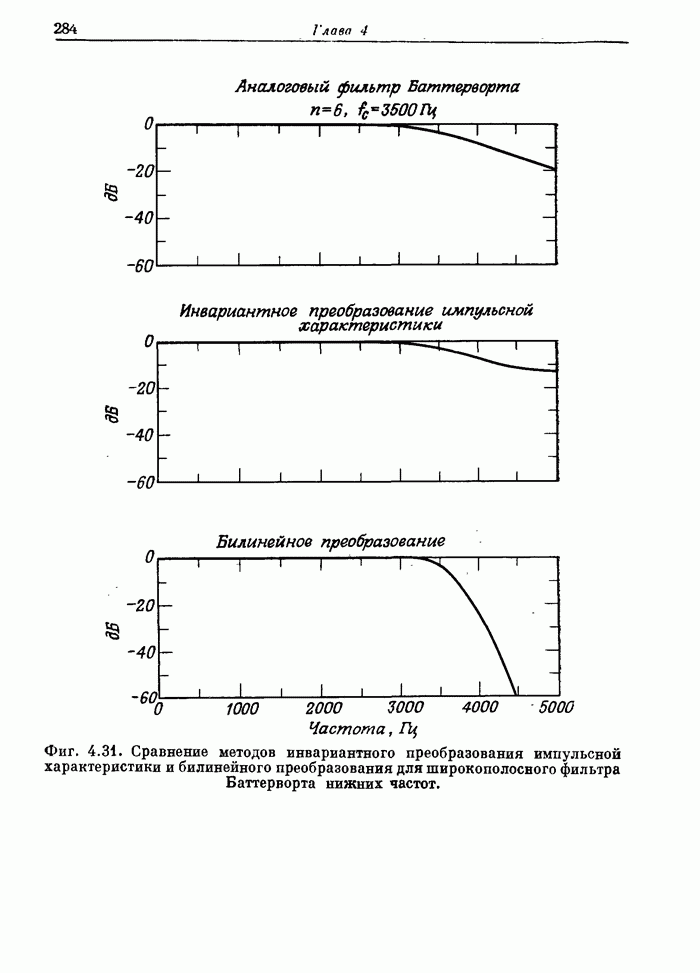
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
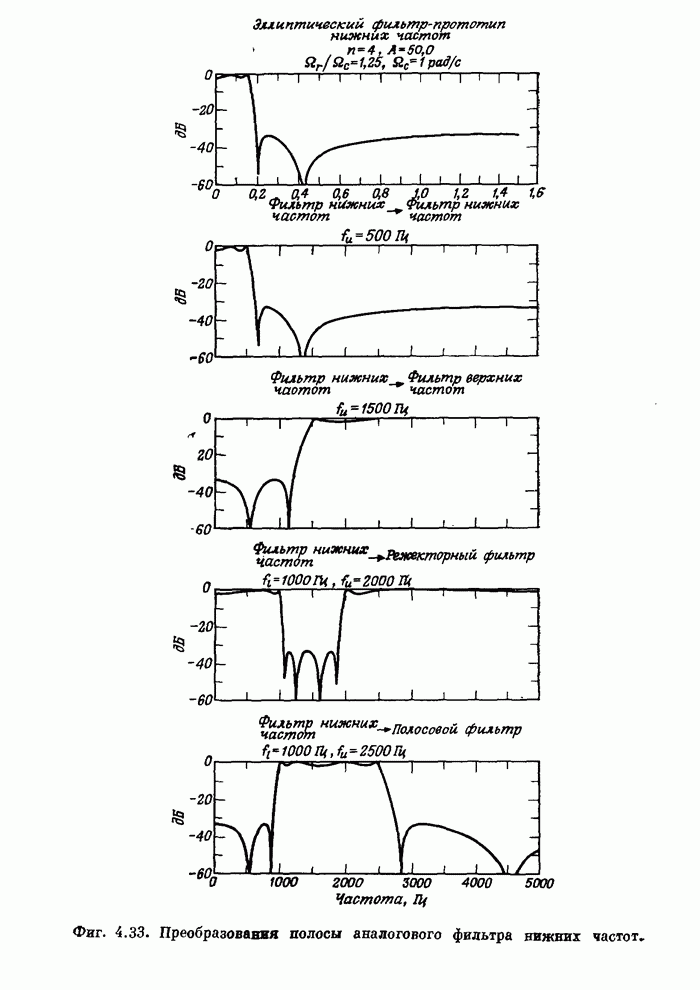
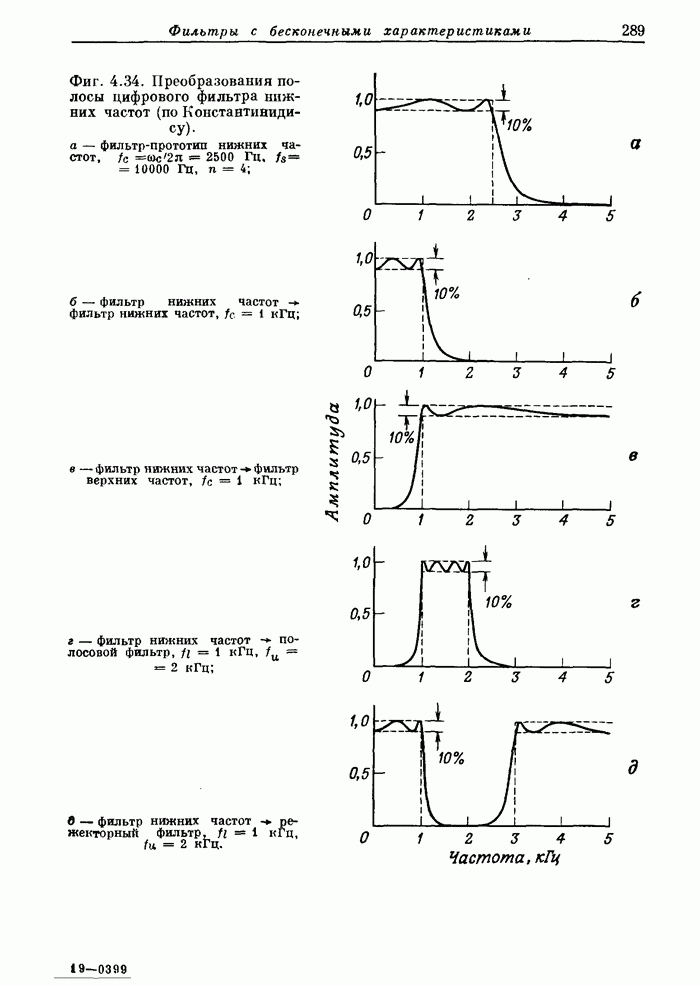
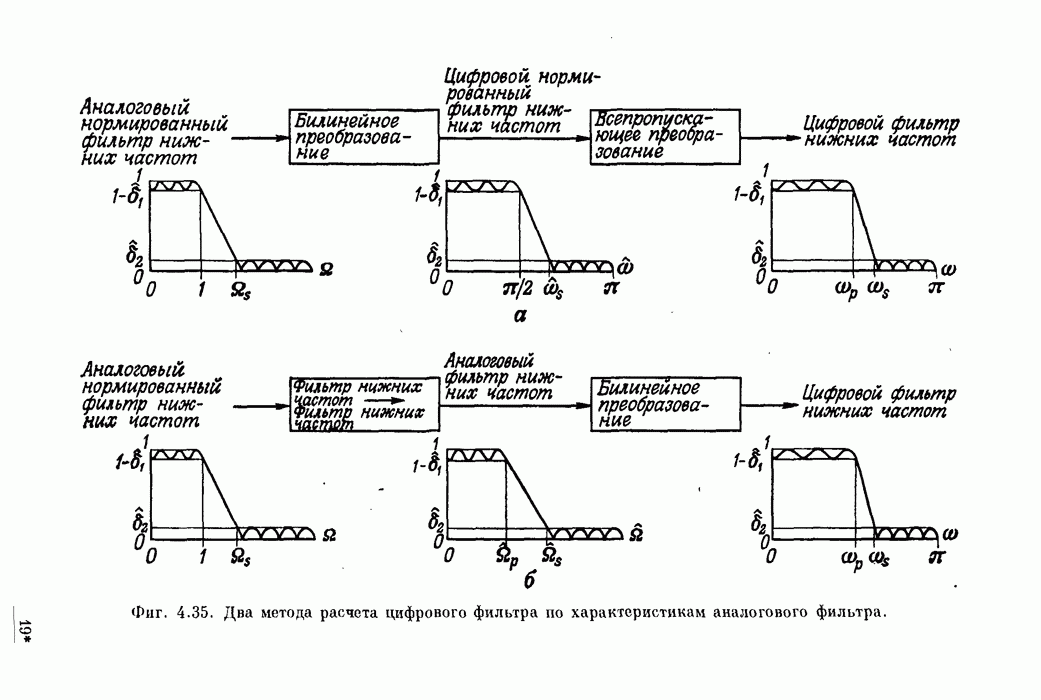
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
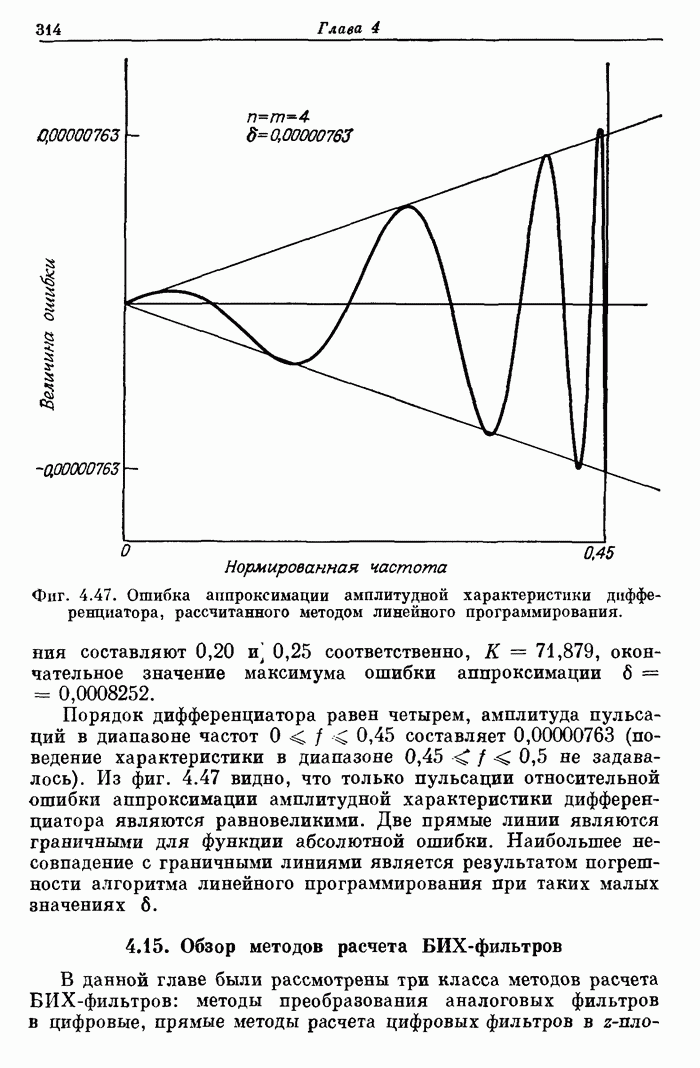
- 4.15. Обзор методов расчета БИХ-фильтров
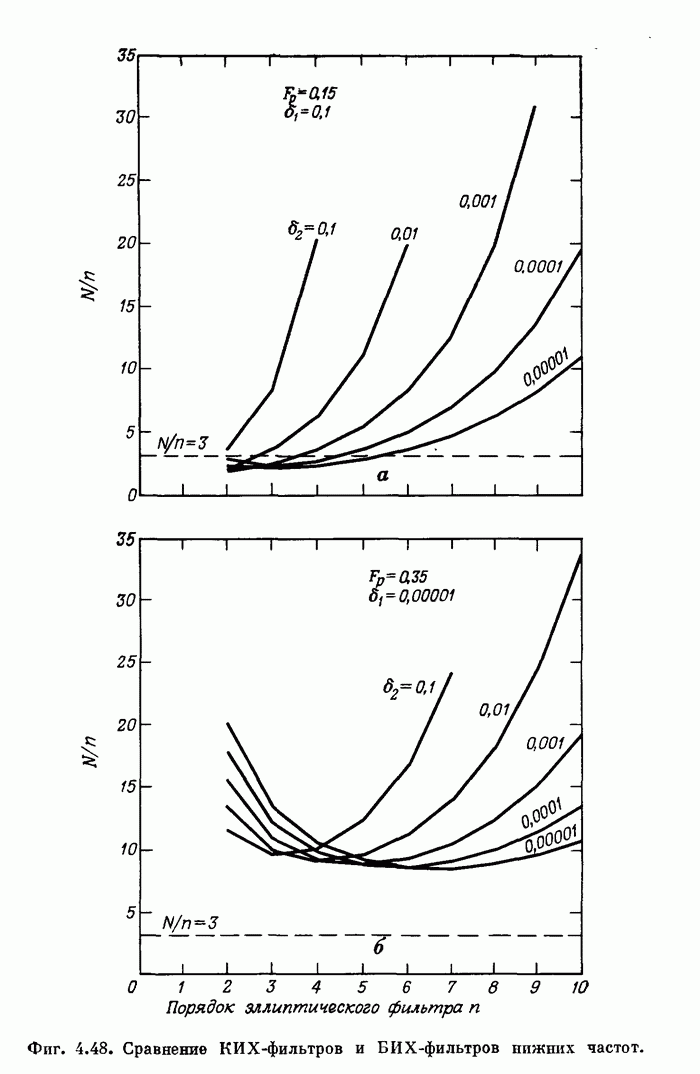
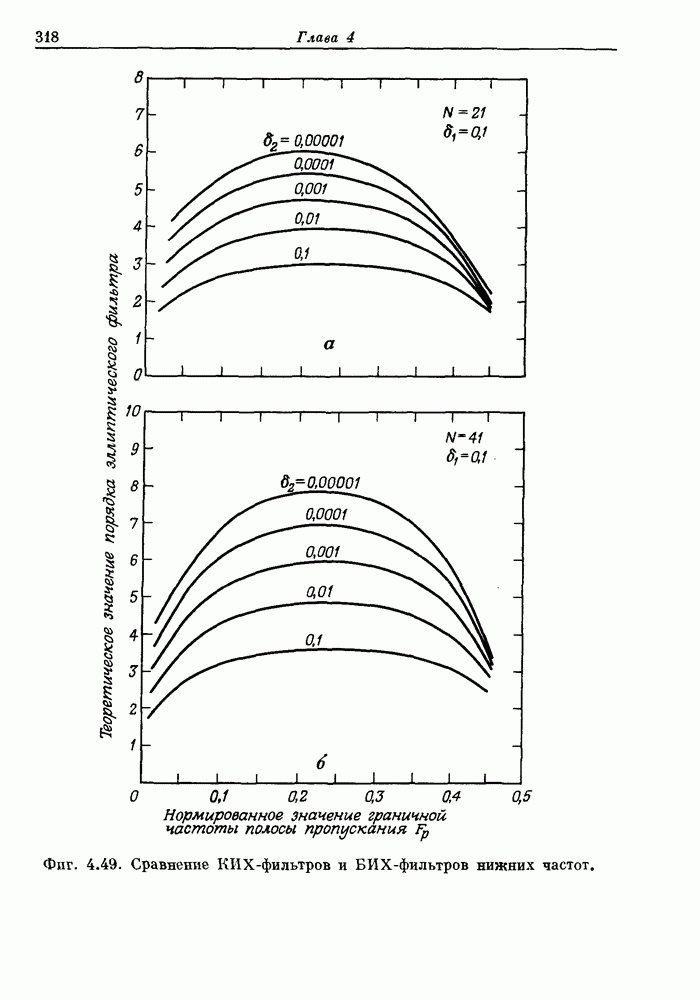
- 4.16. Сравнение КИХ- и БИХ-фильтров
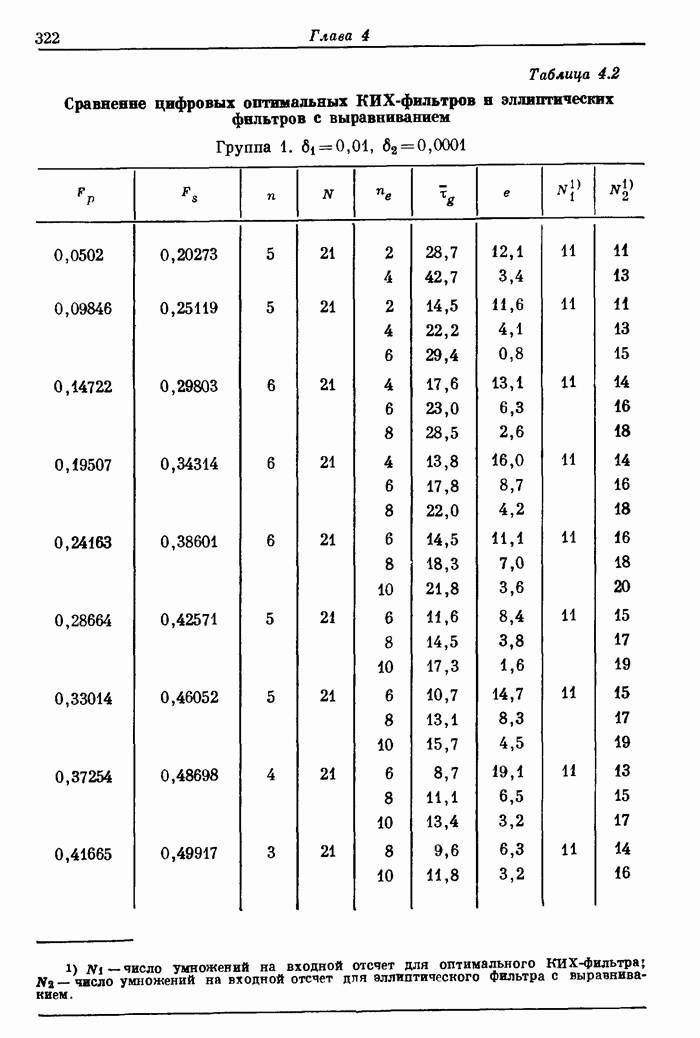
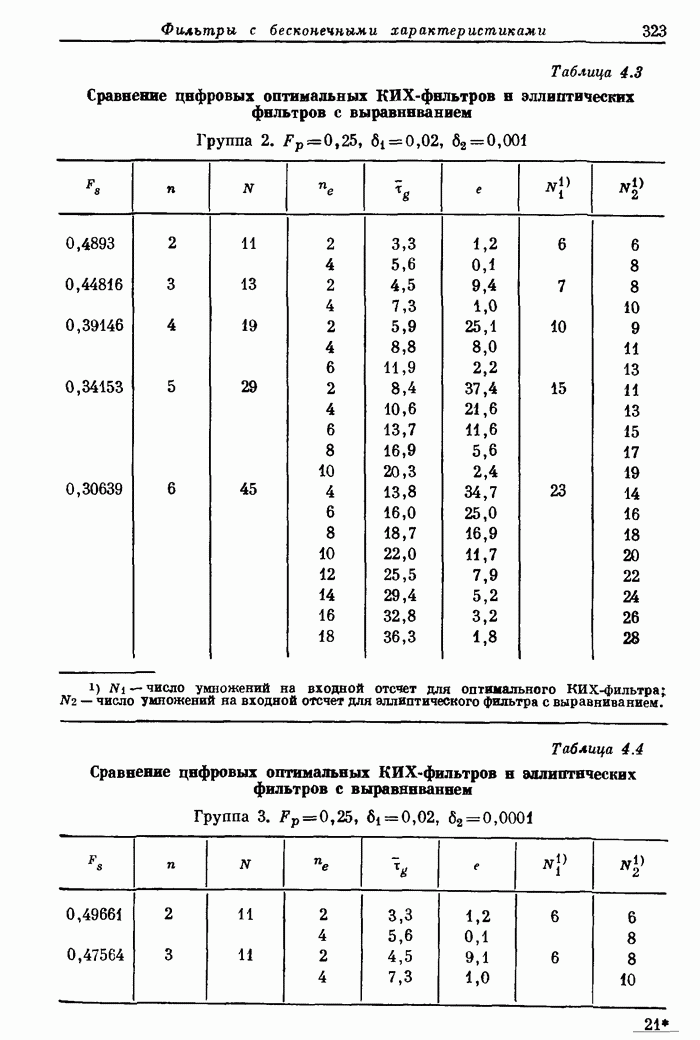
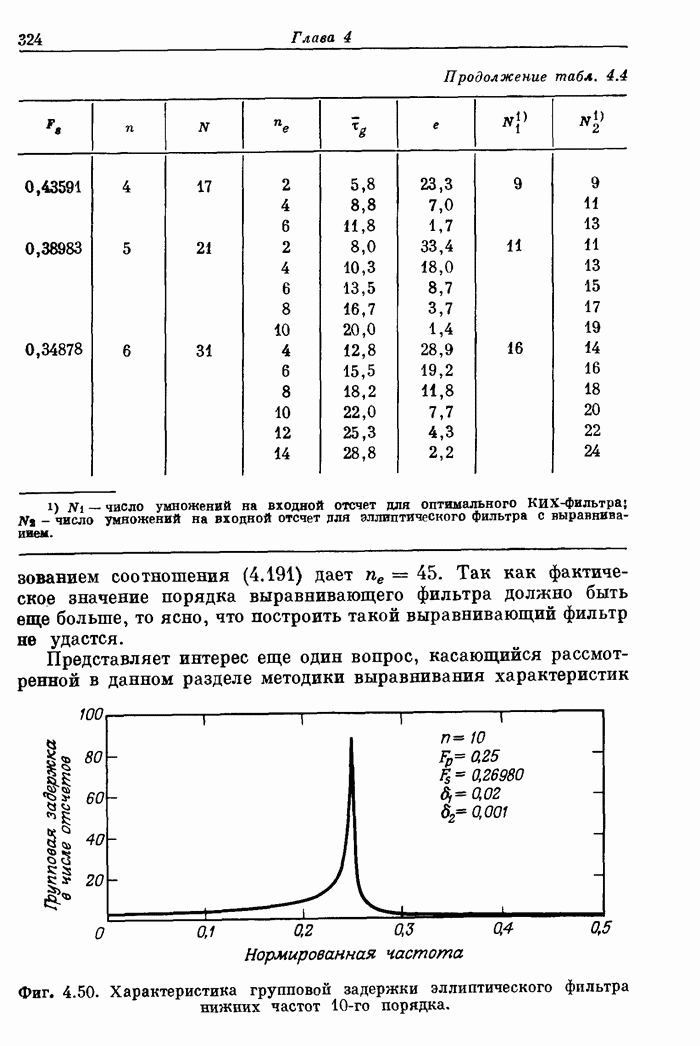
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
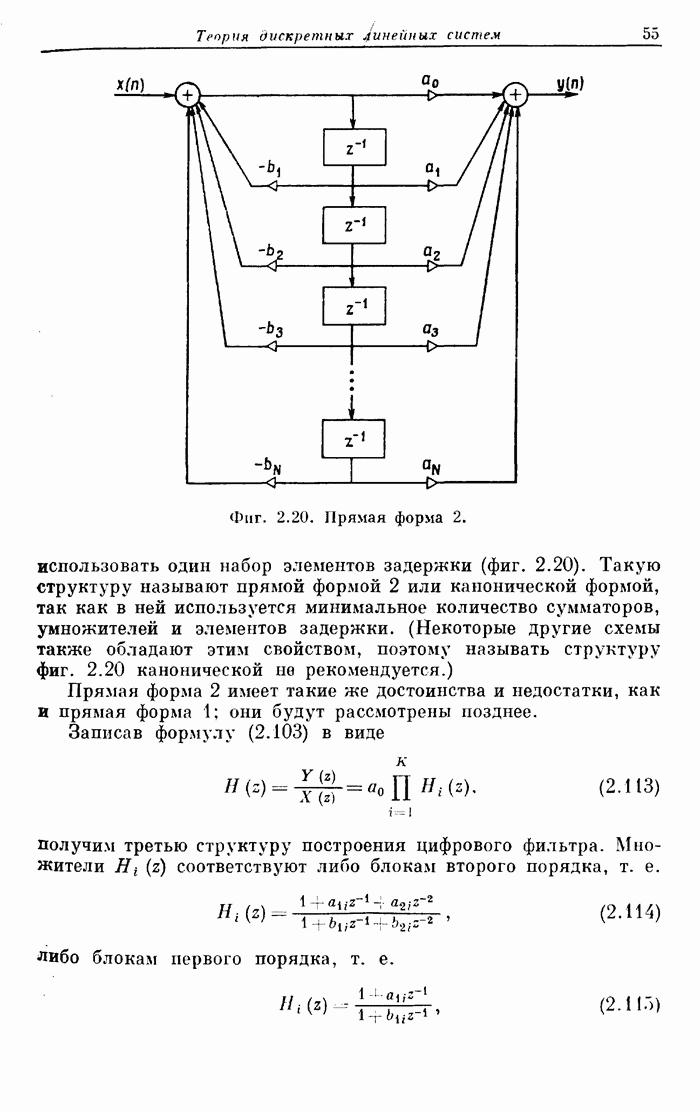
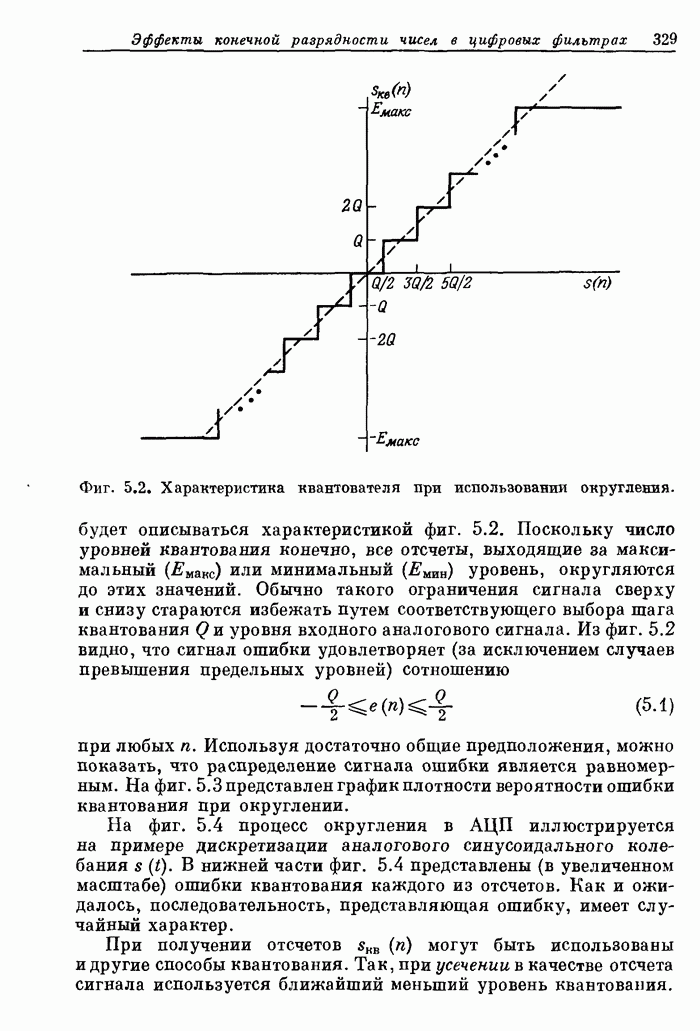
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
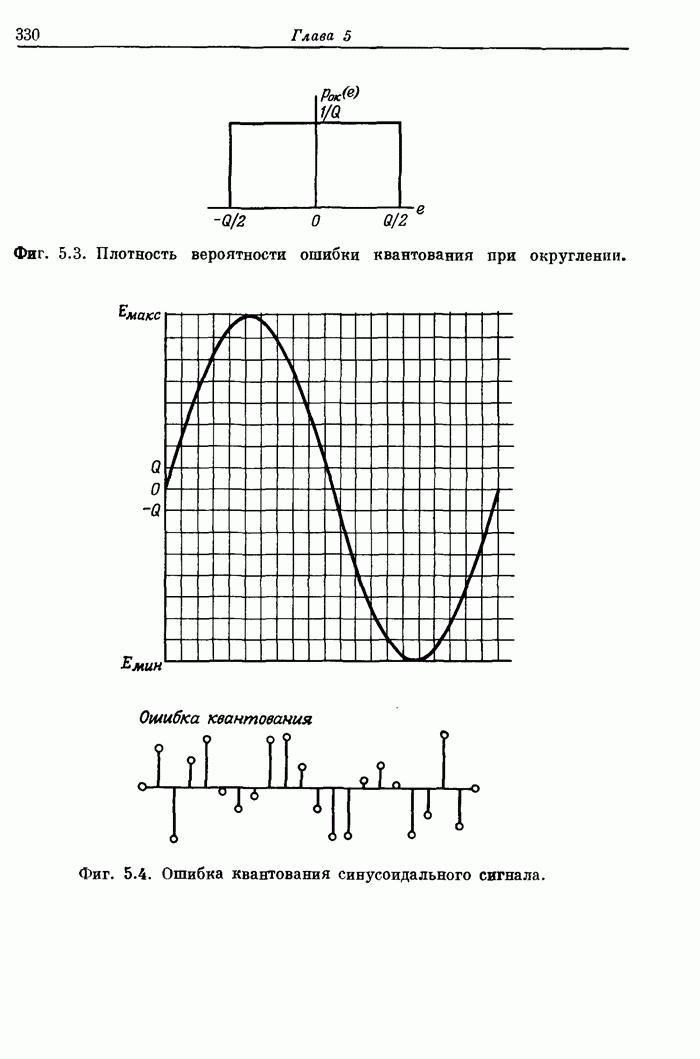
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
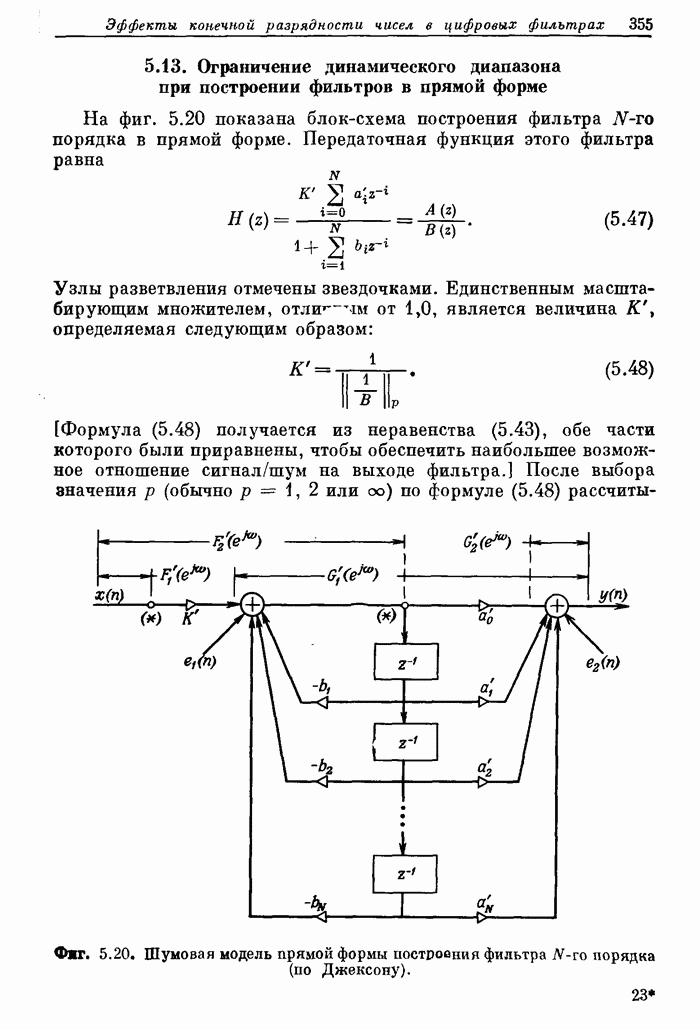
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
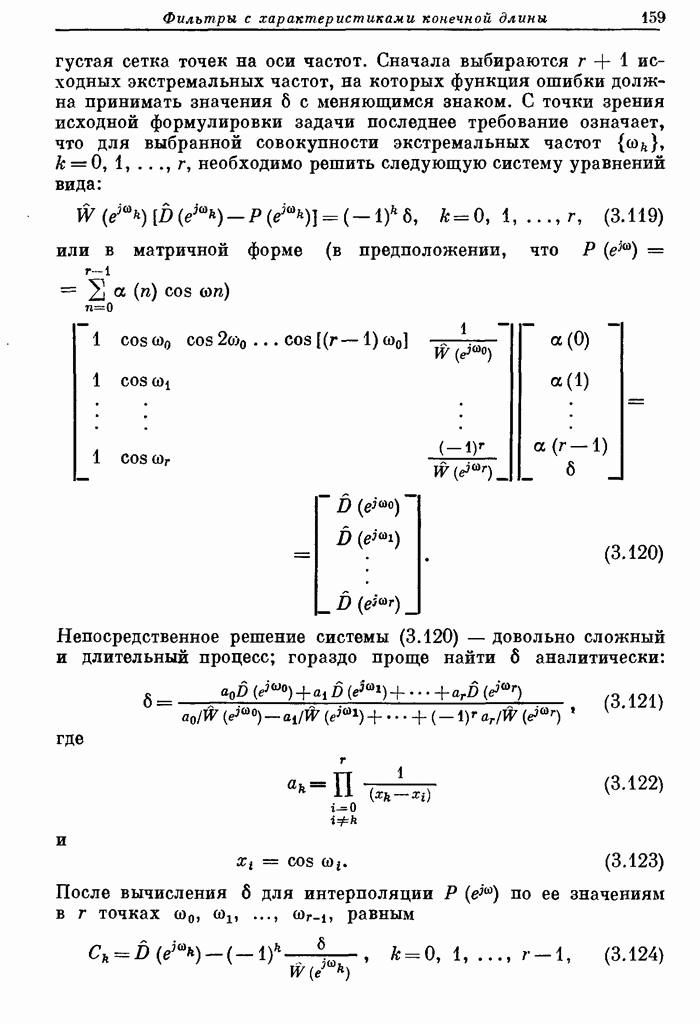
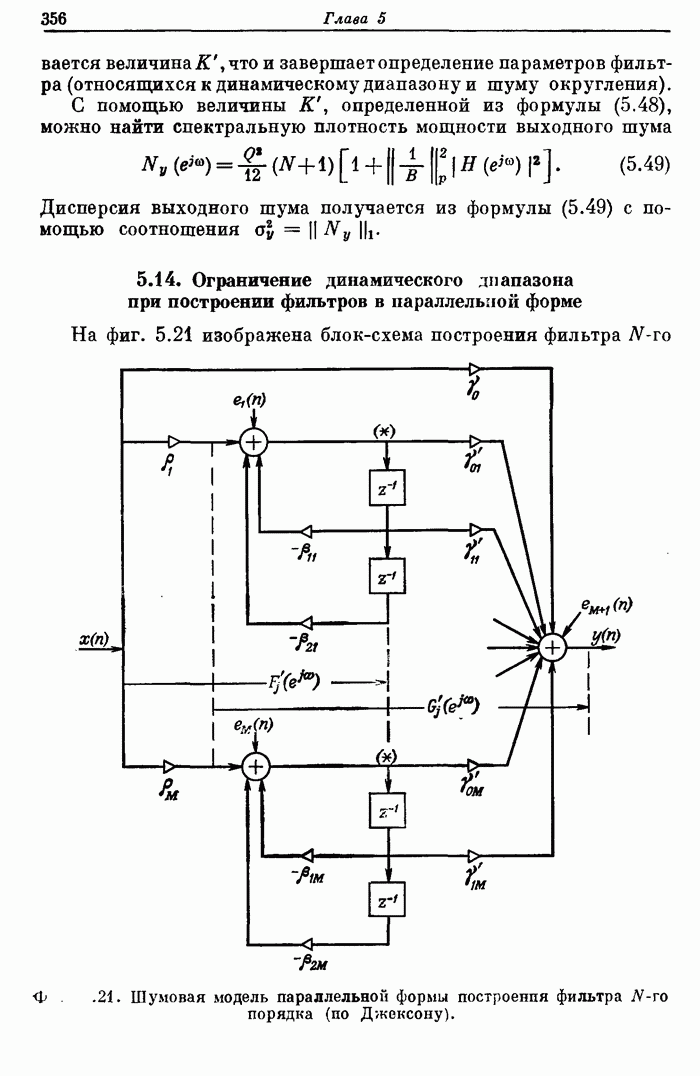
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
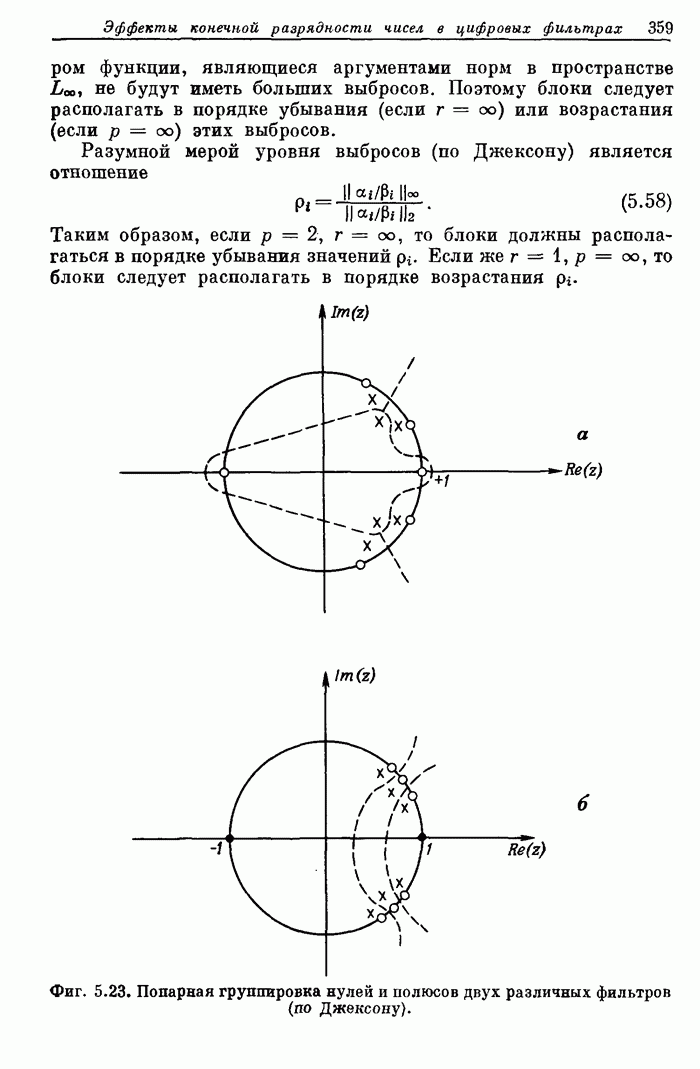
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
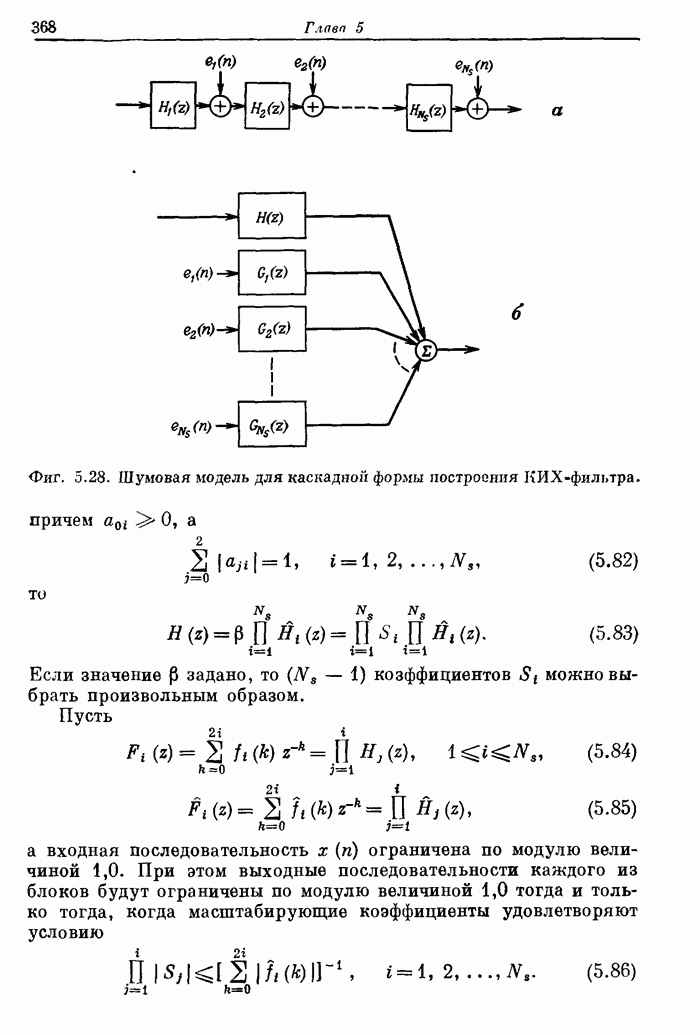
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
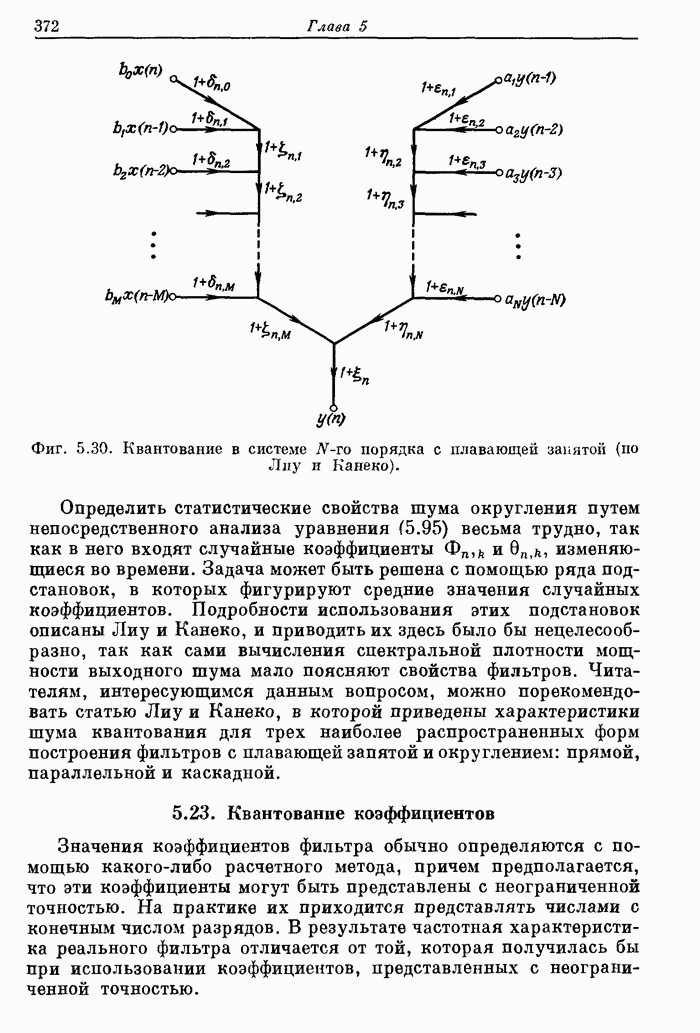
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
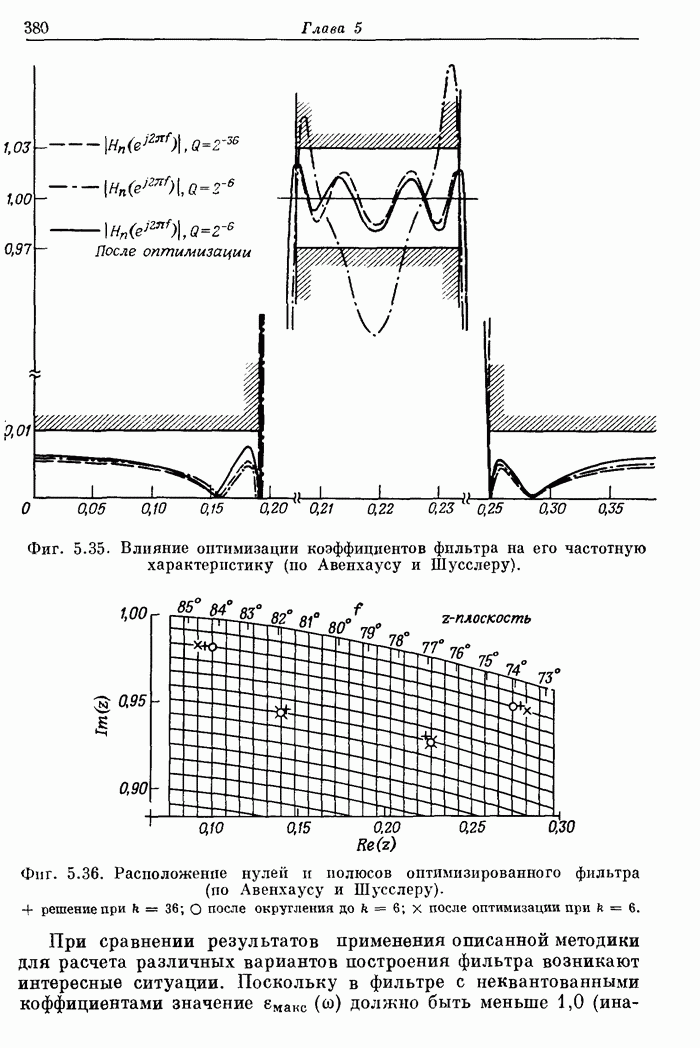
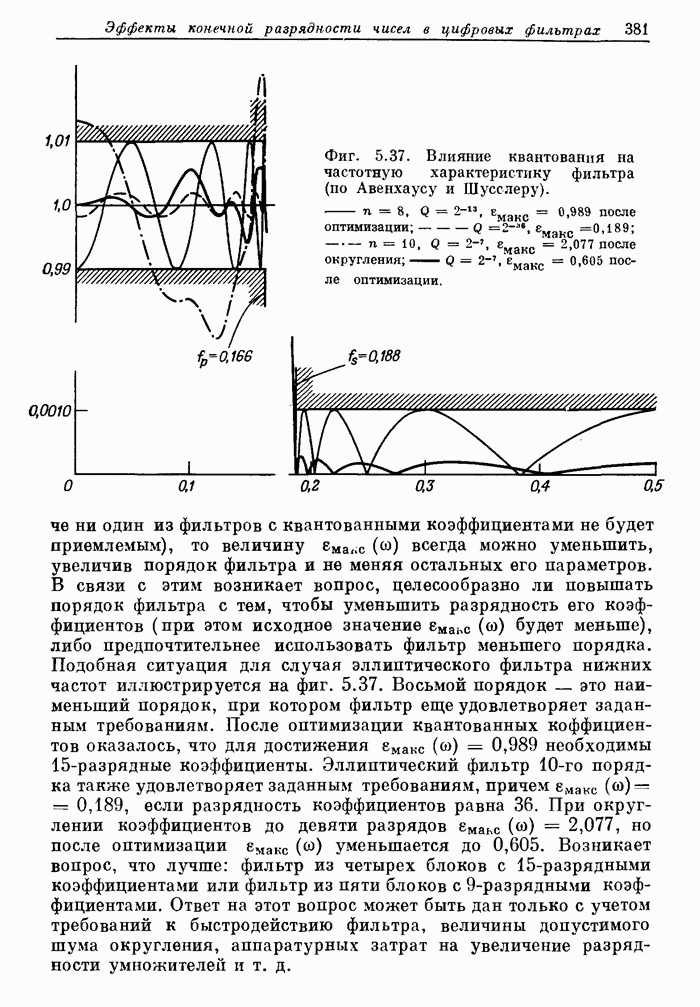
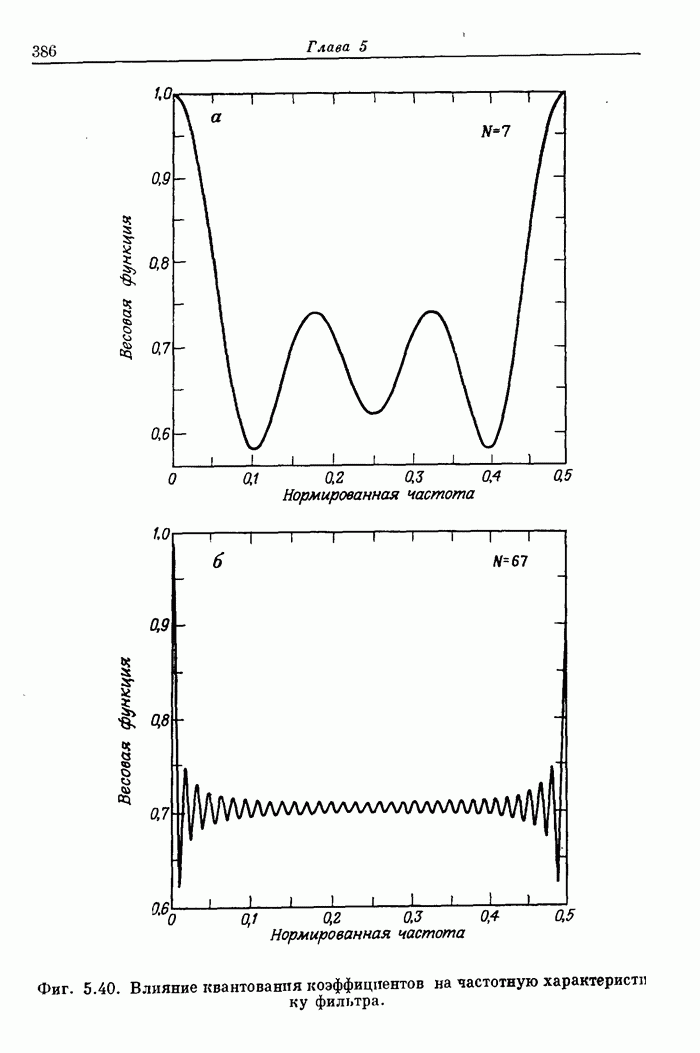
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
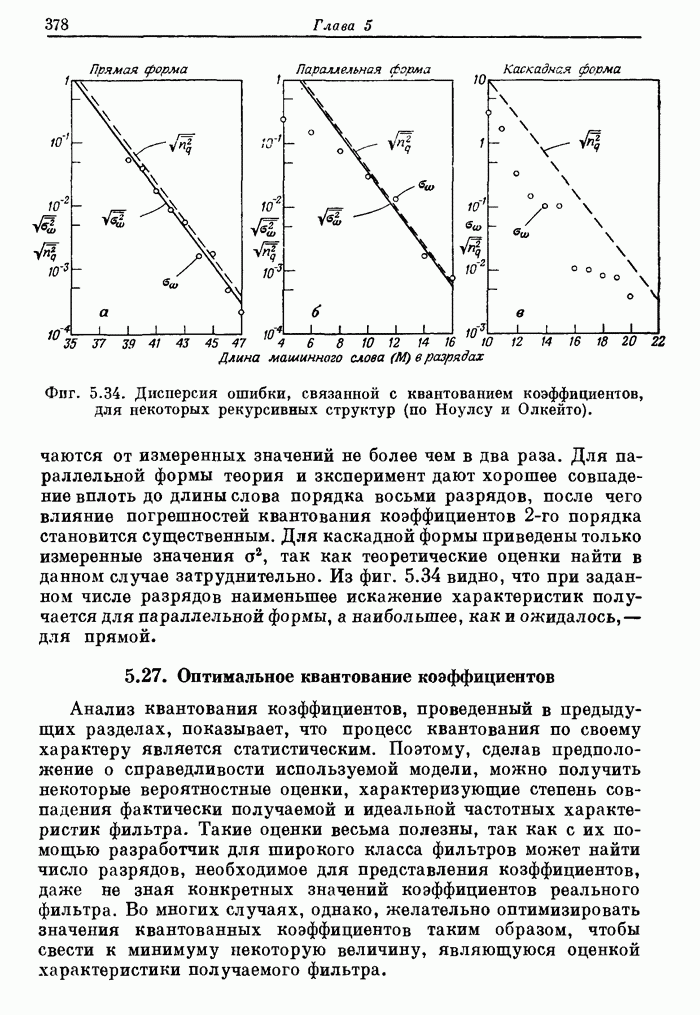
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
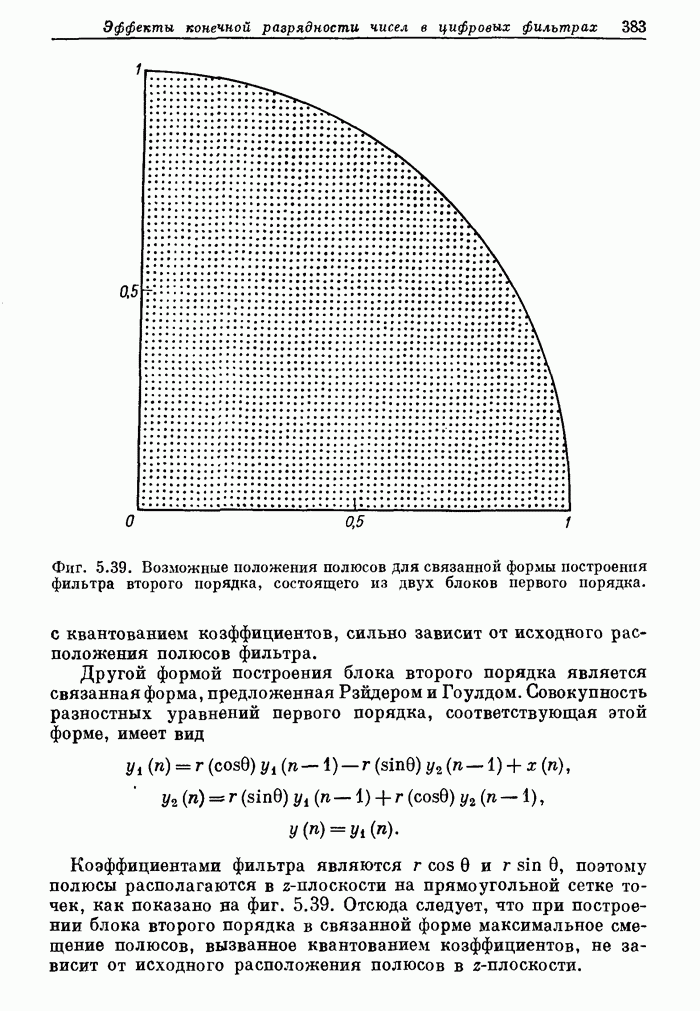
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
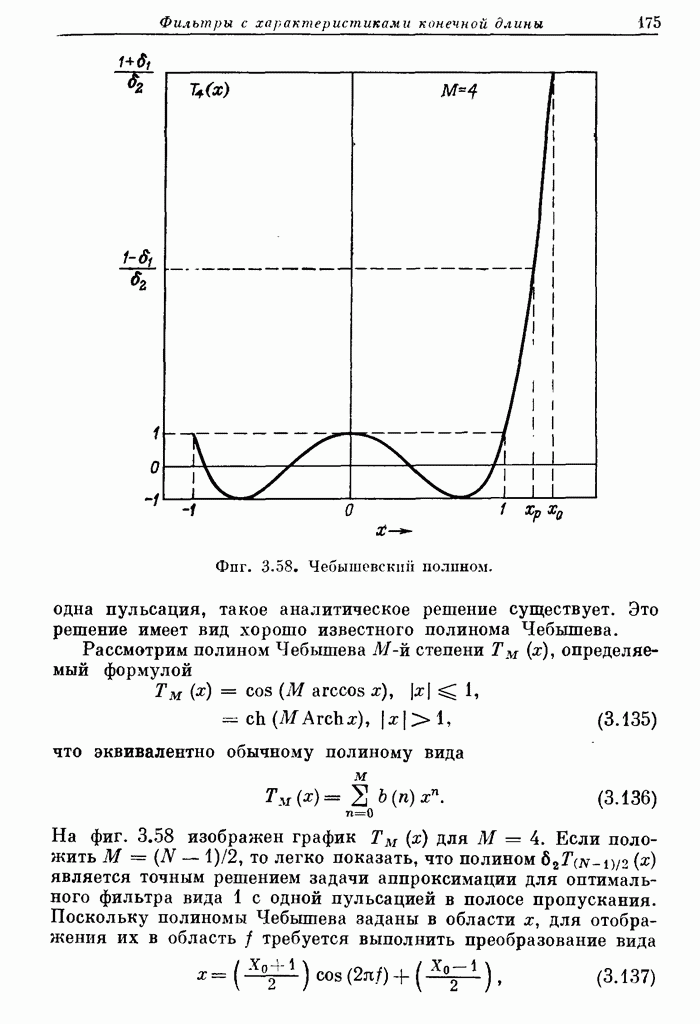
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
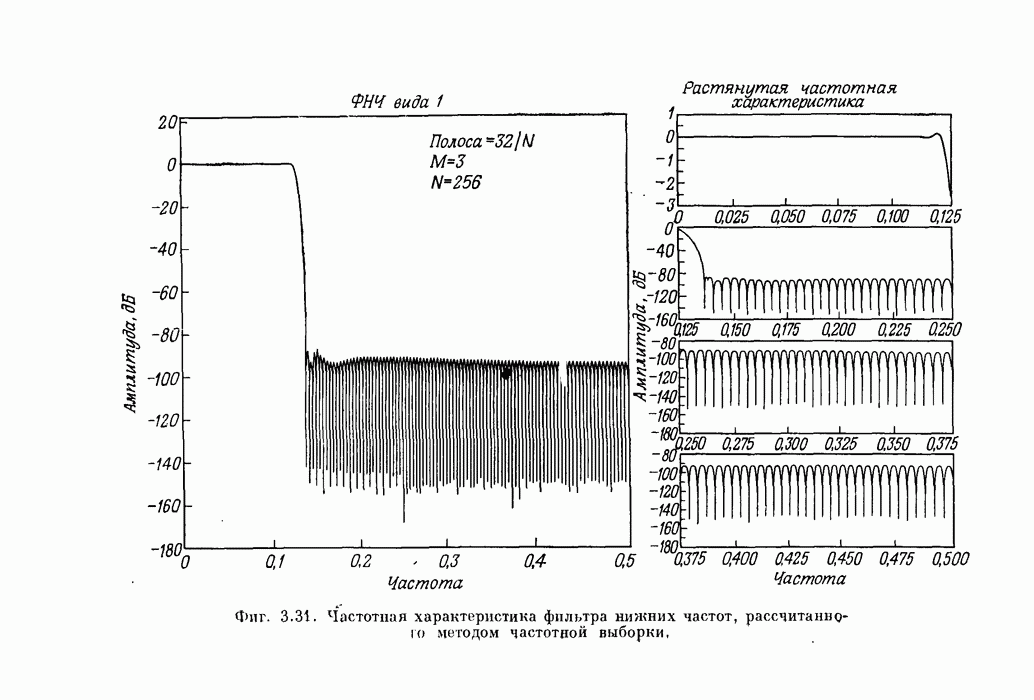
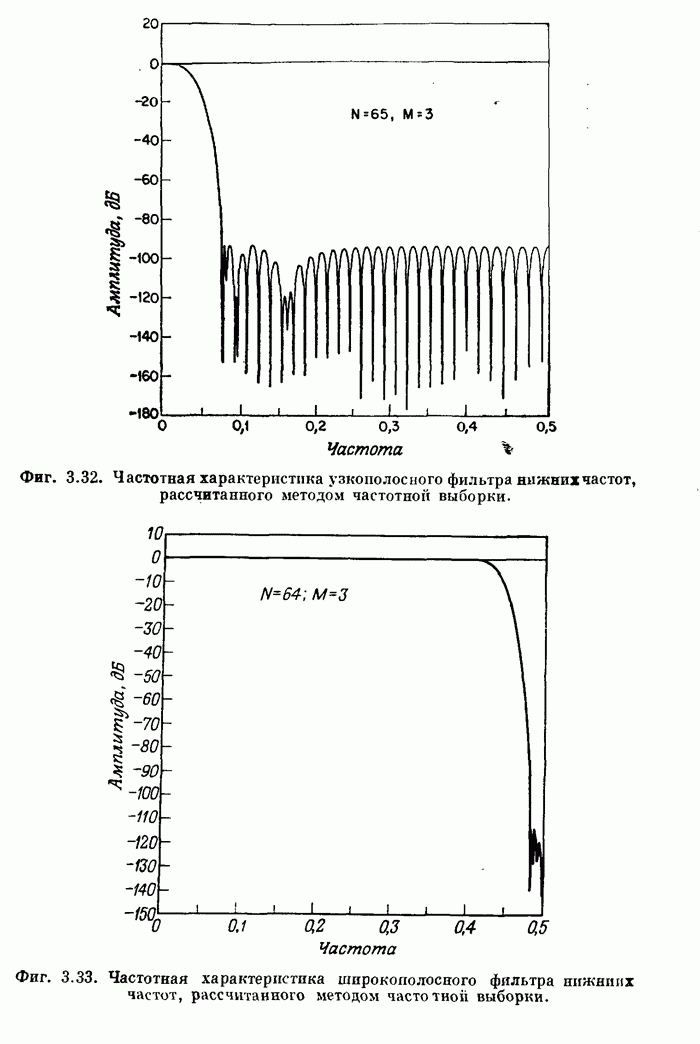
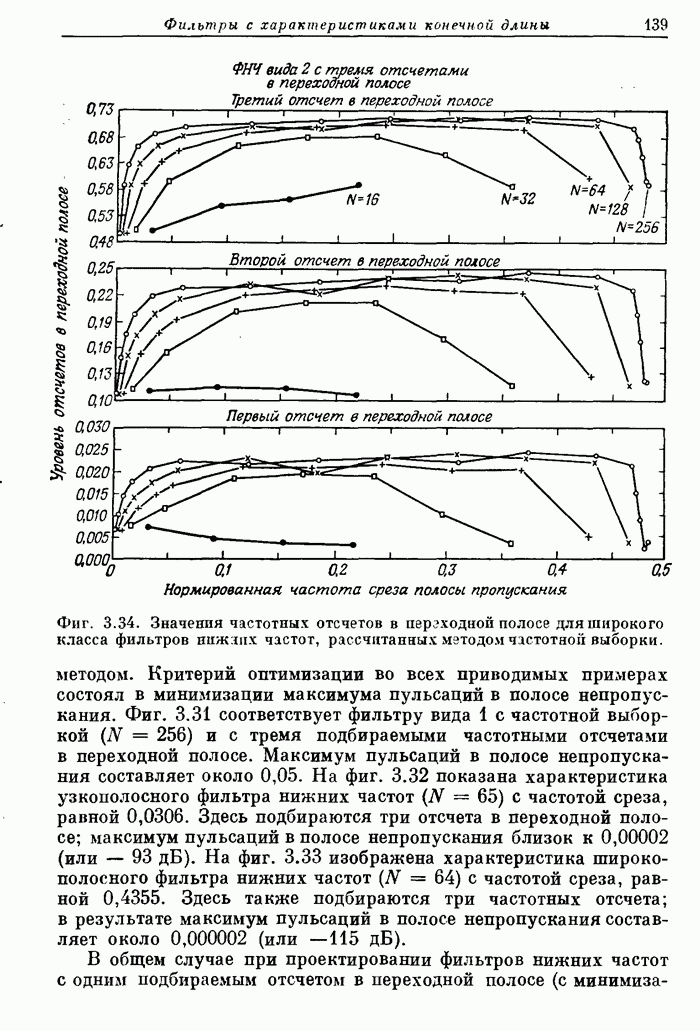
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
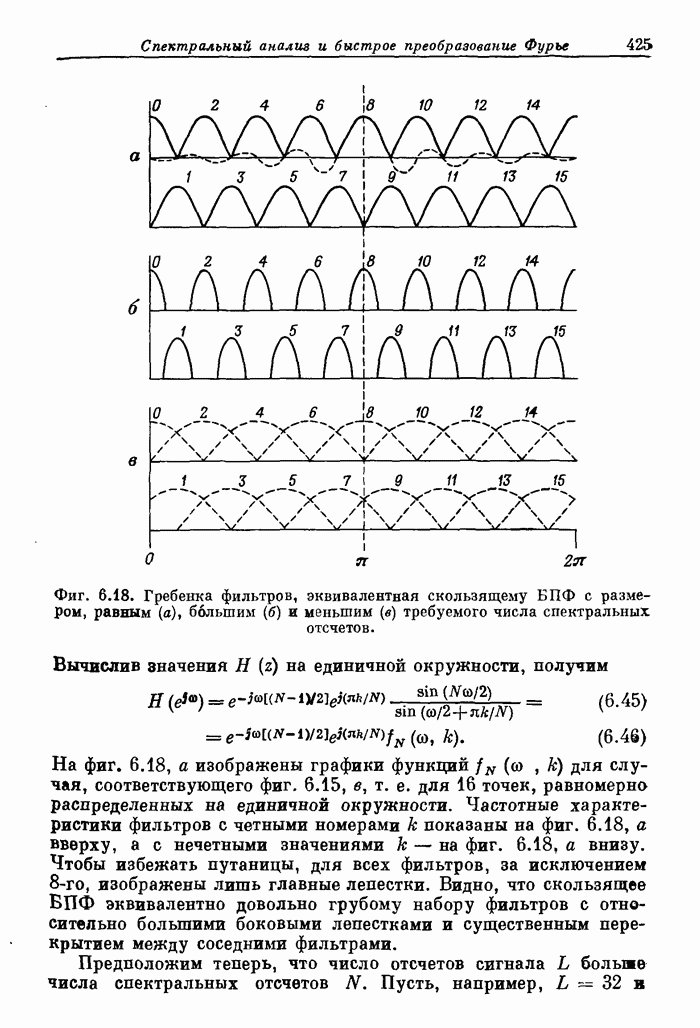
- 6.12. Некоторые характеристики спектрального анализа
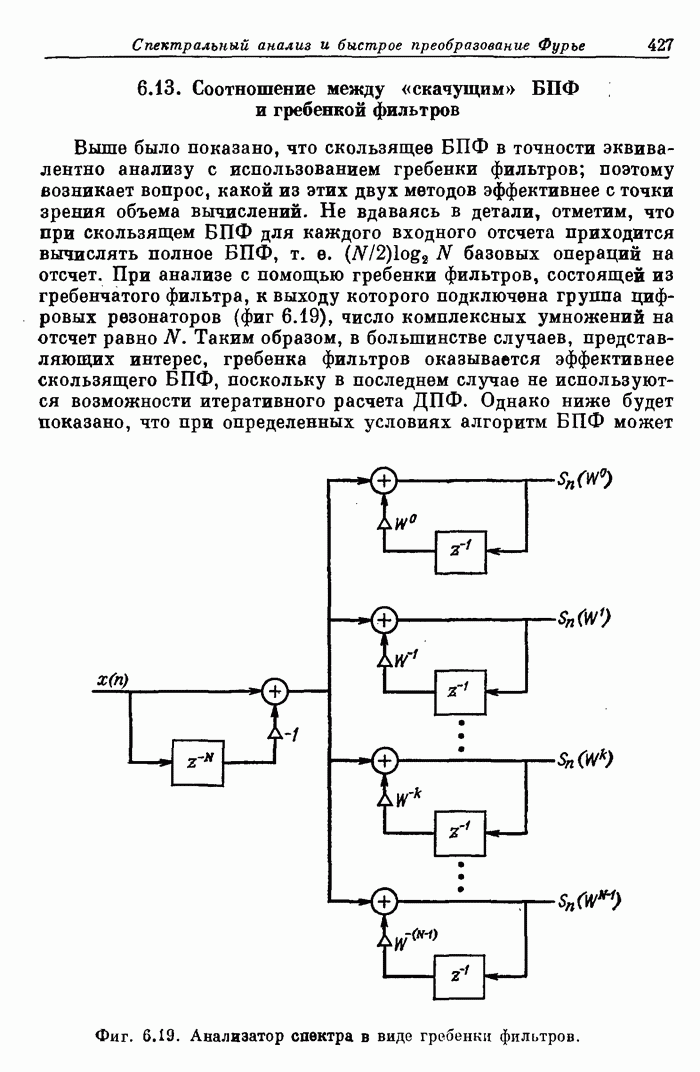
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
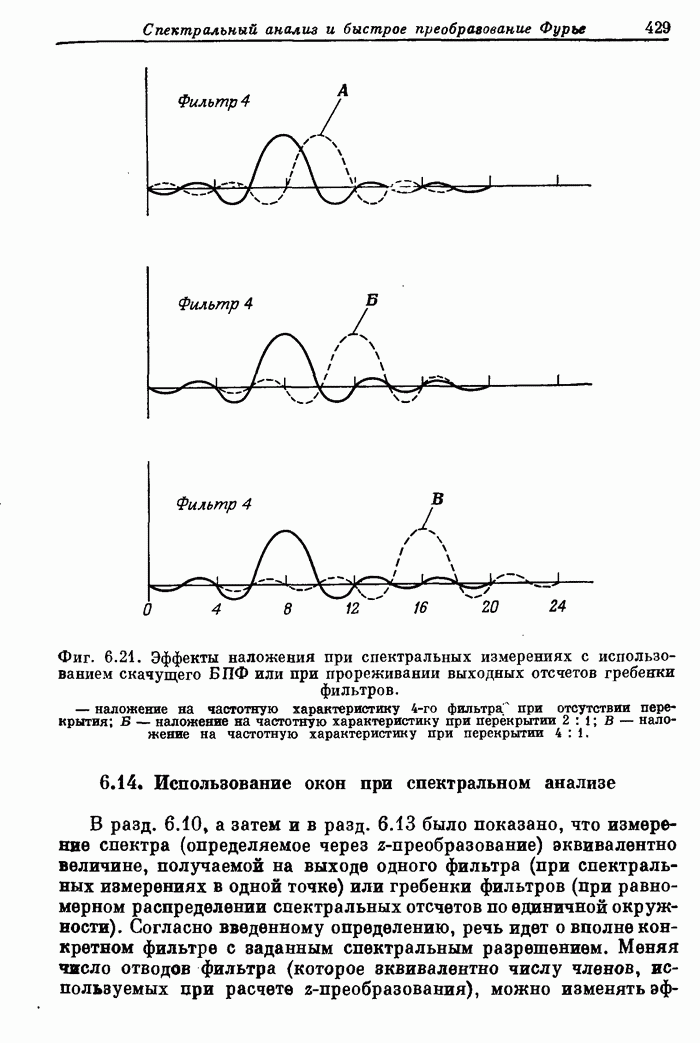
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
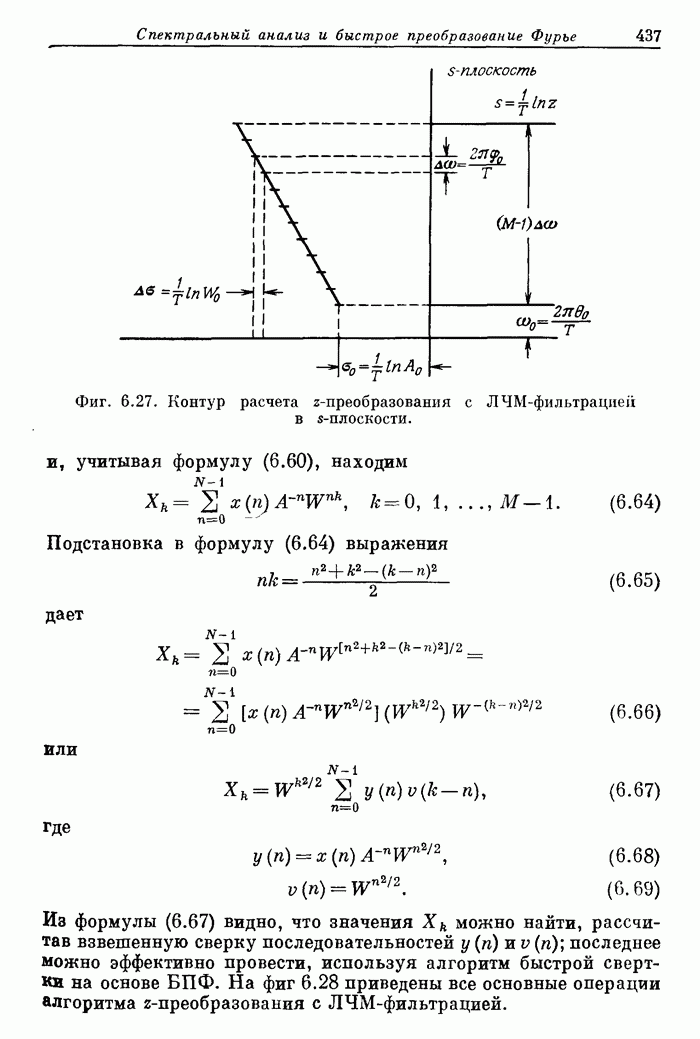
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
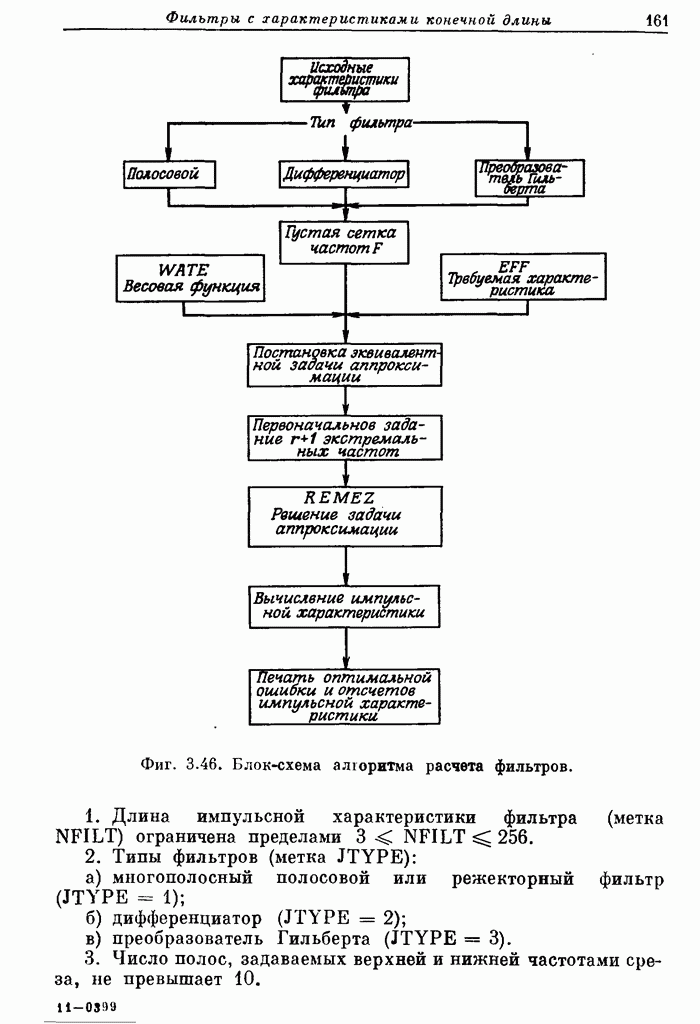
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
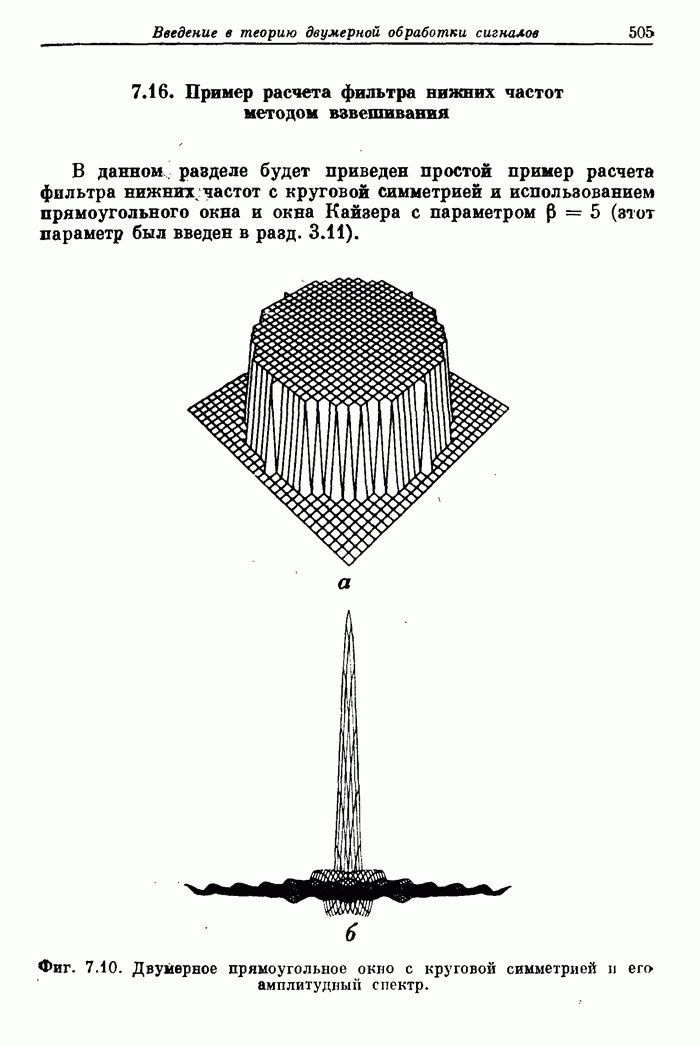
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
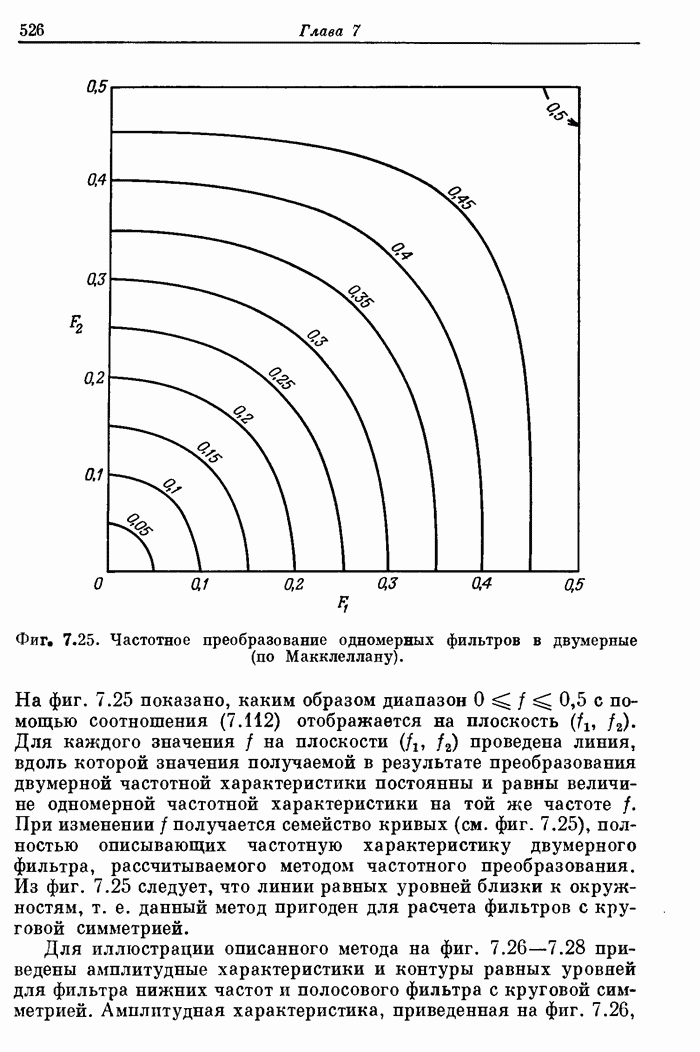
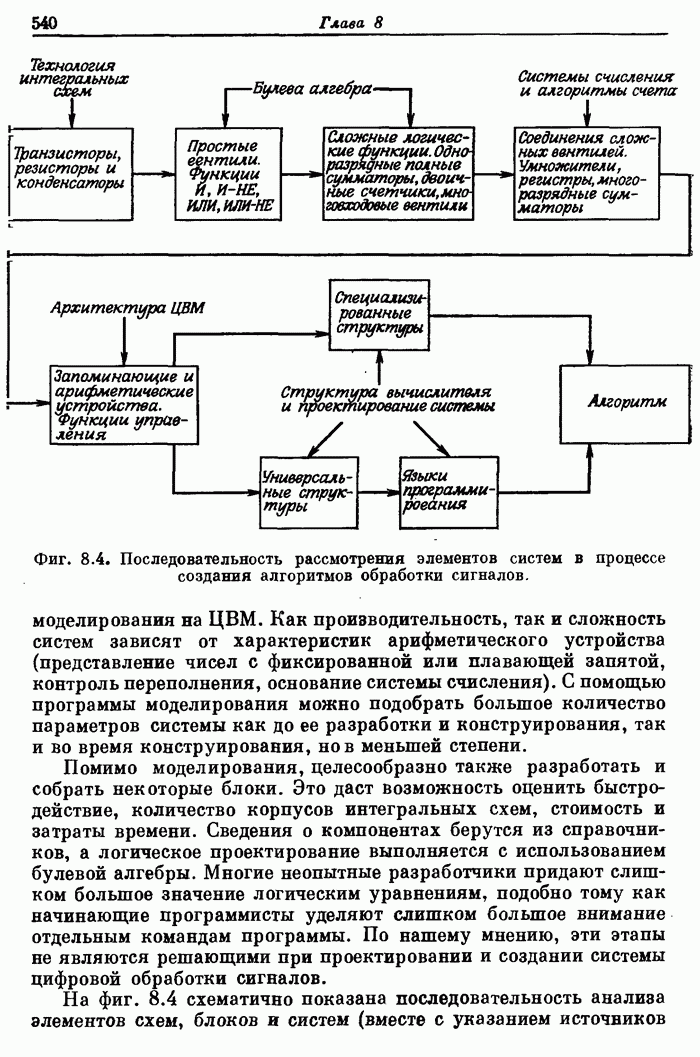
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
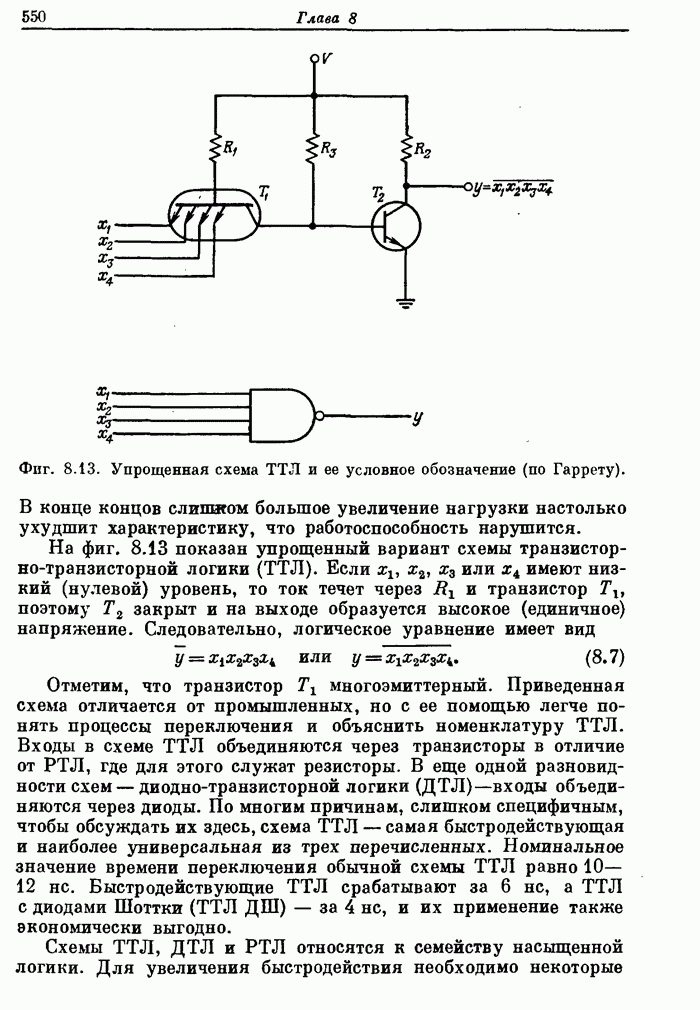
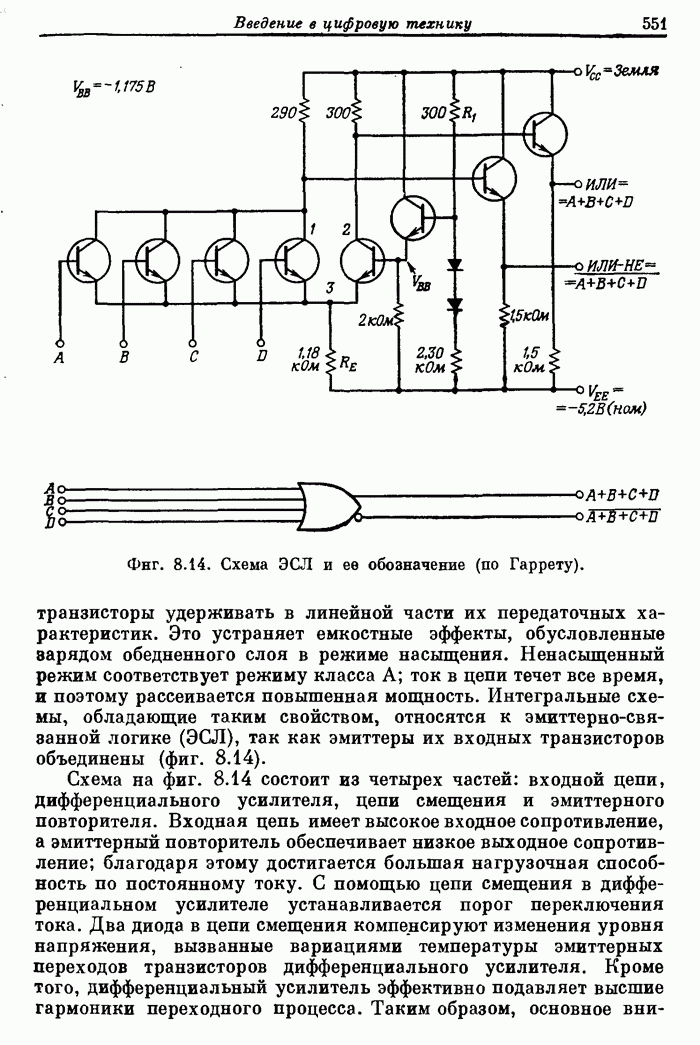
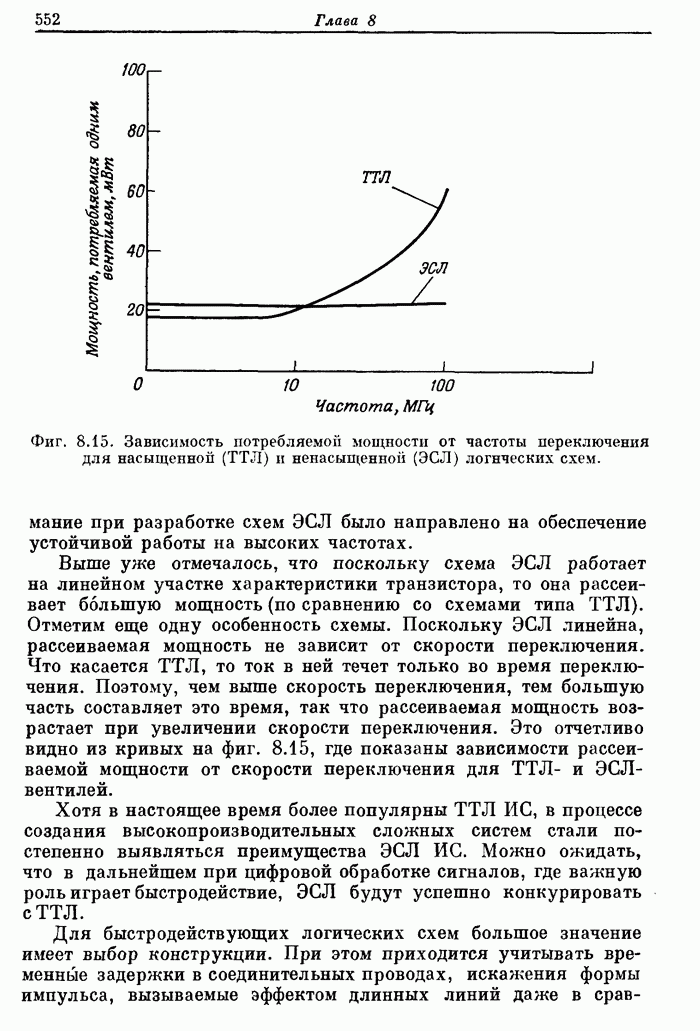
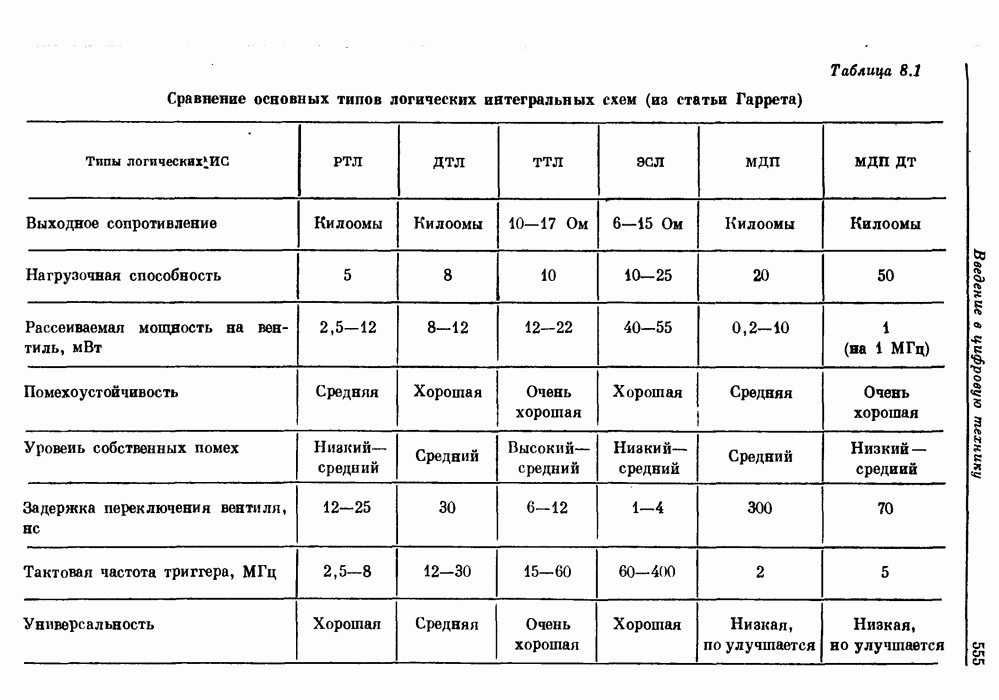
- 8.4. Основные типы интегральных логических схем
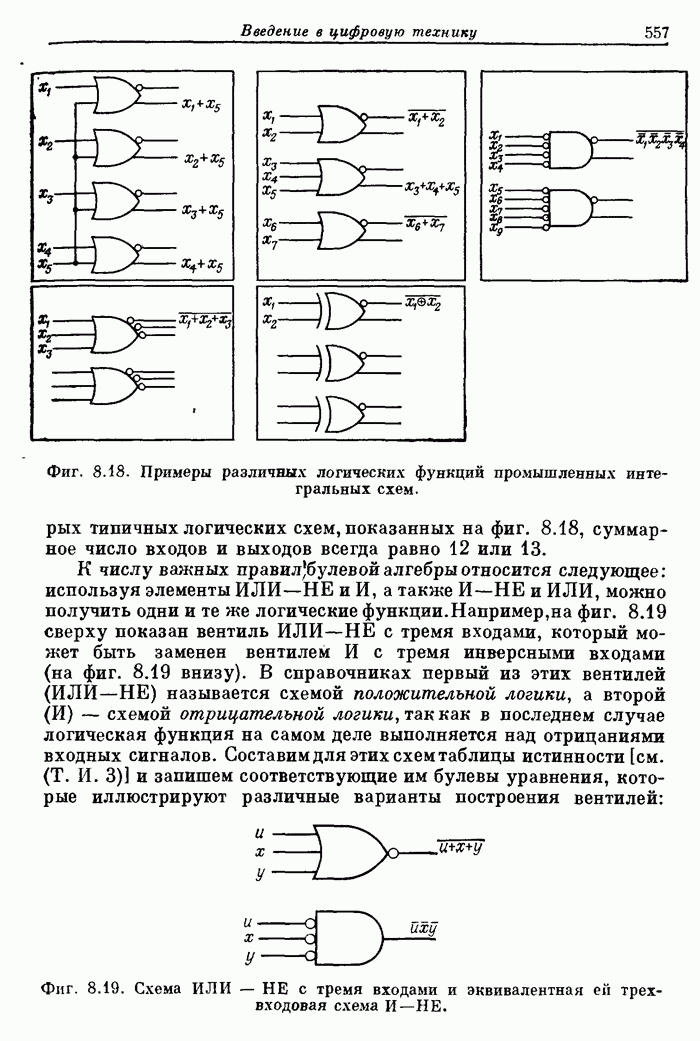
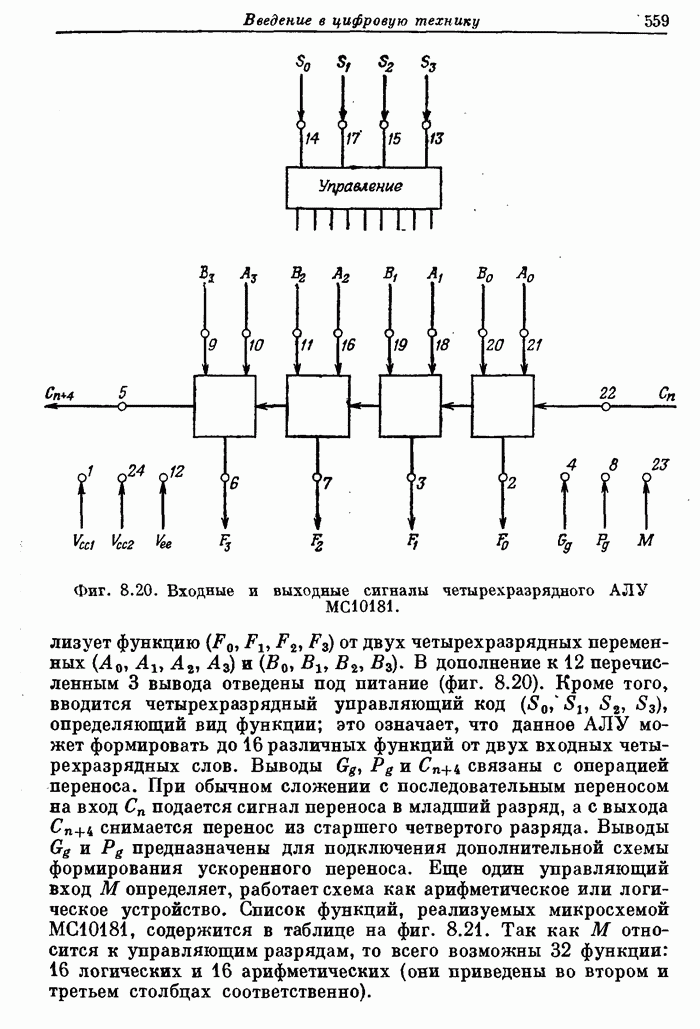
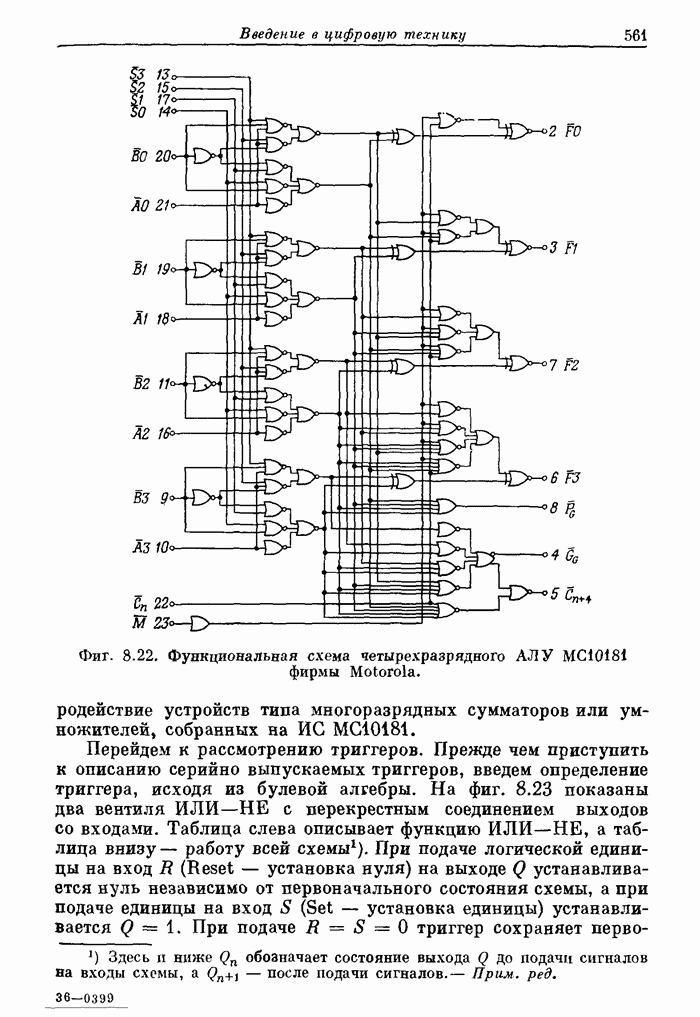
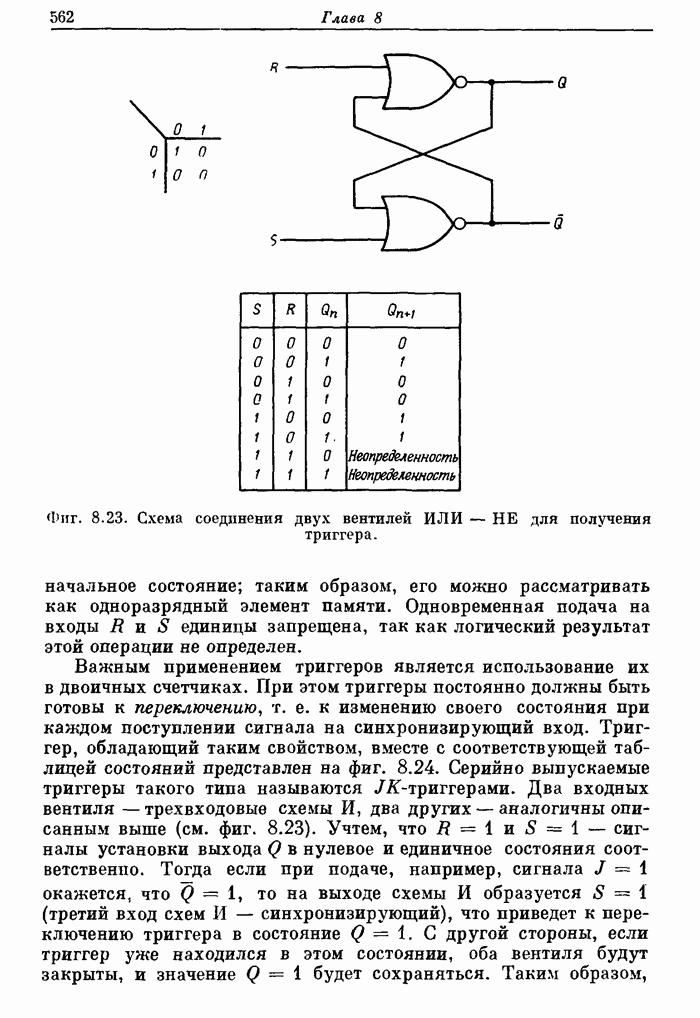
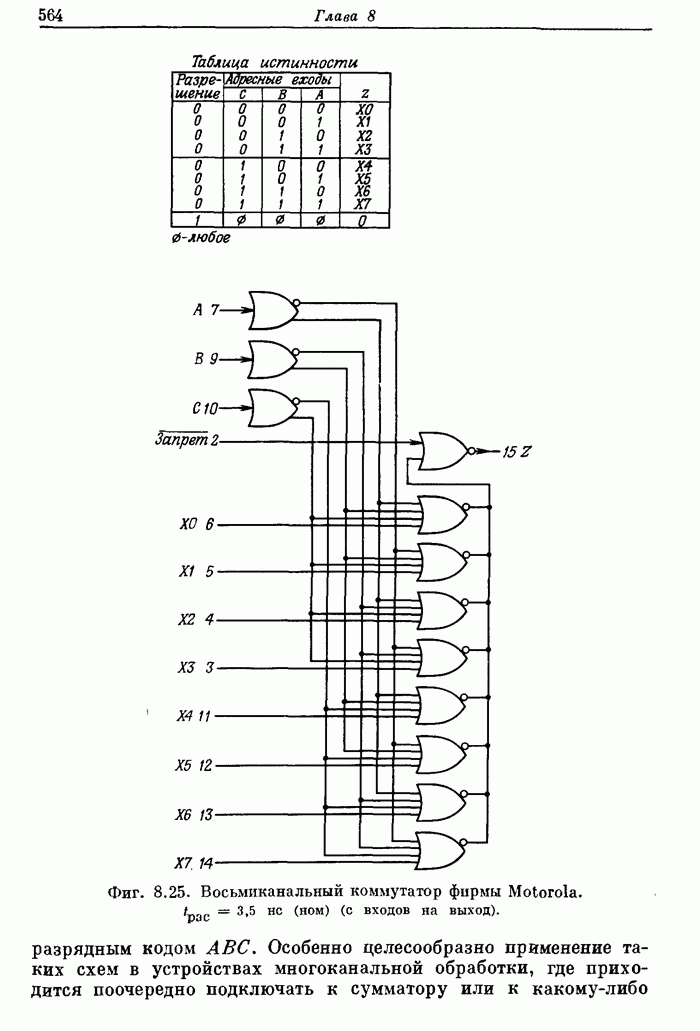
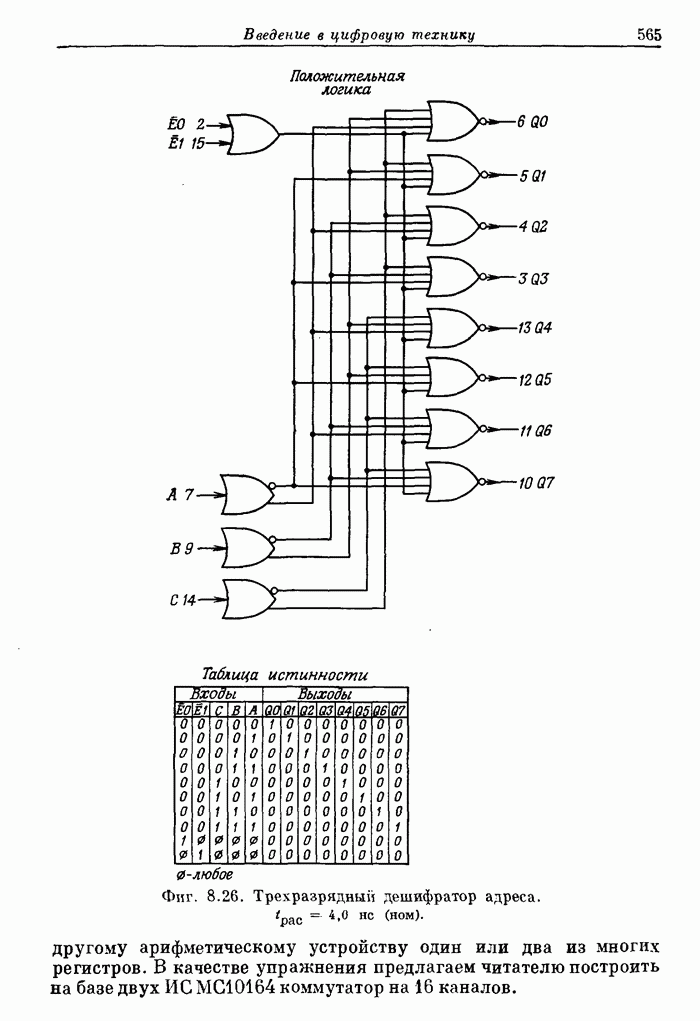
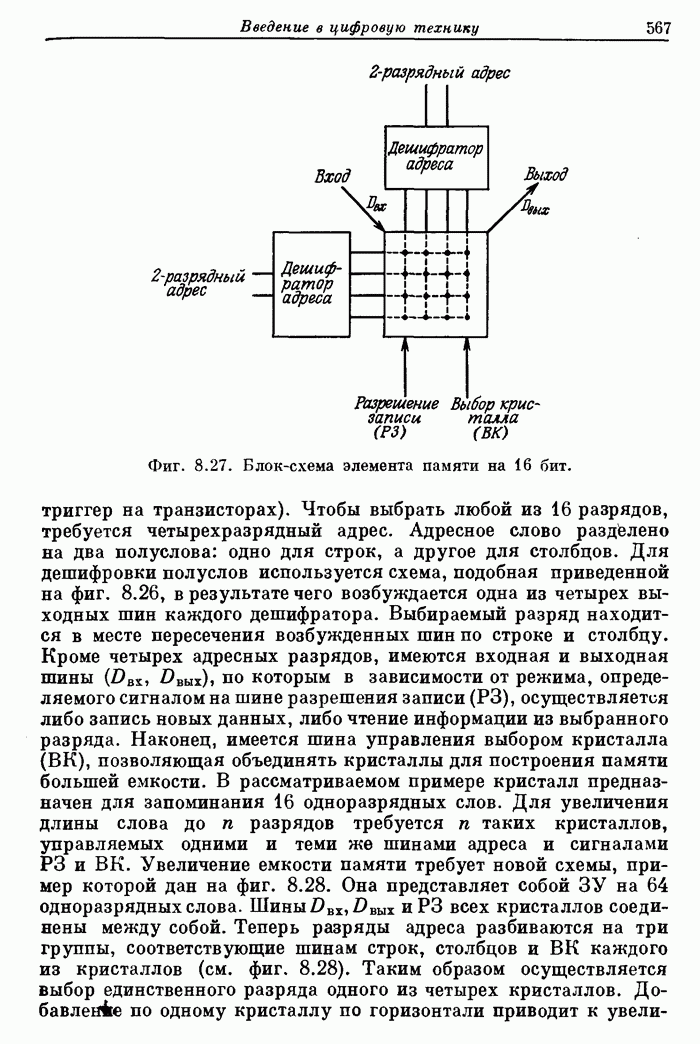
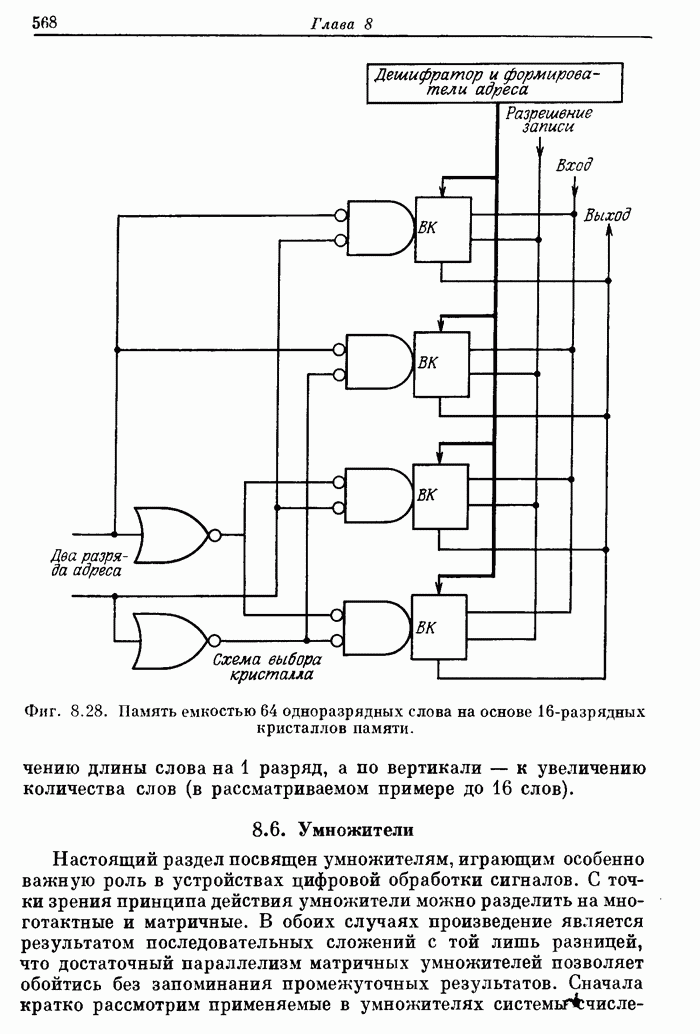
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
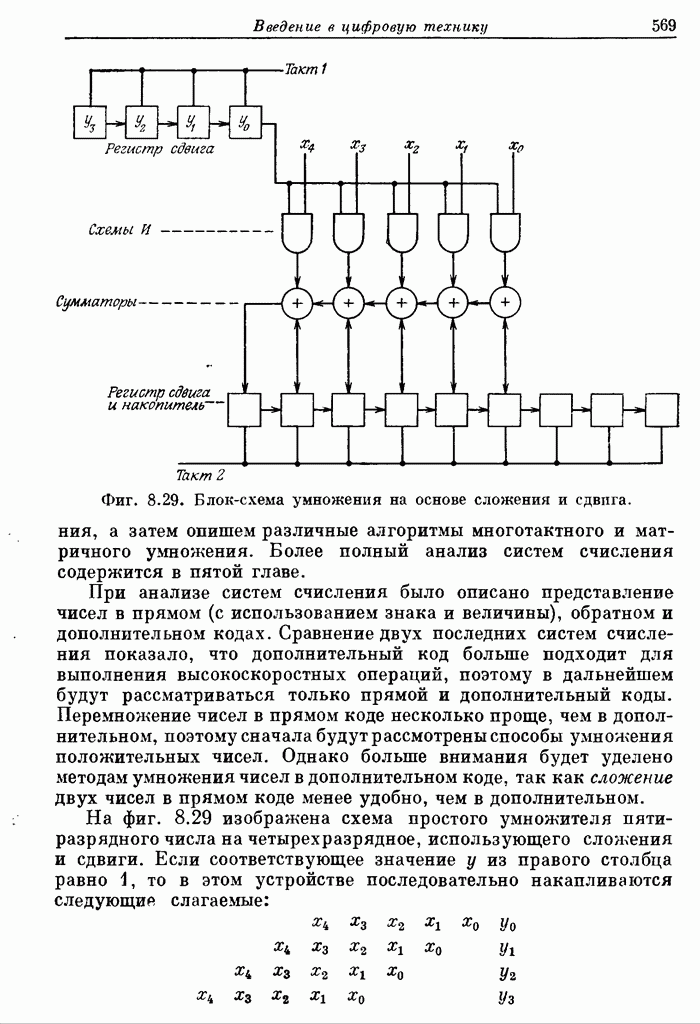
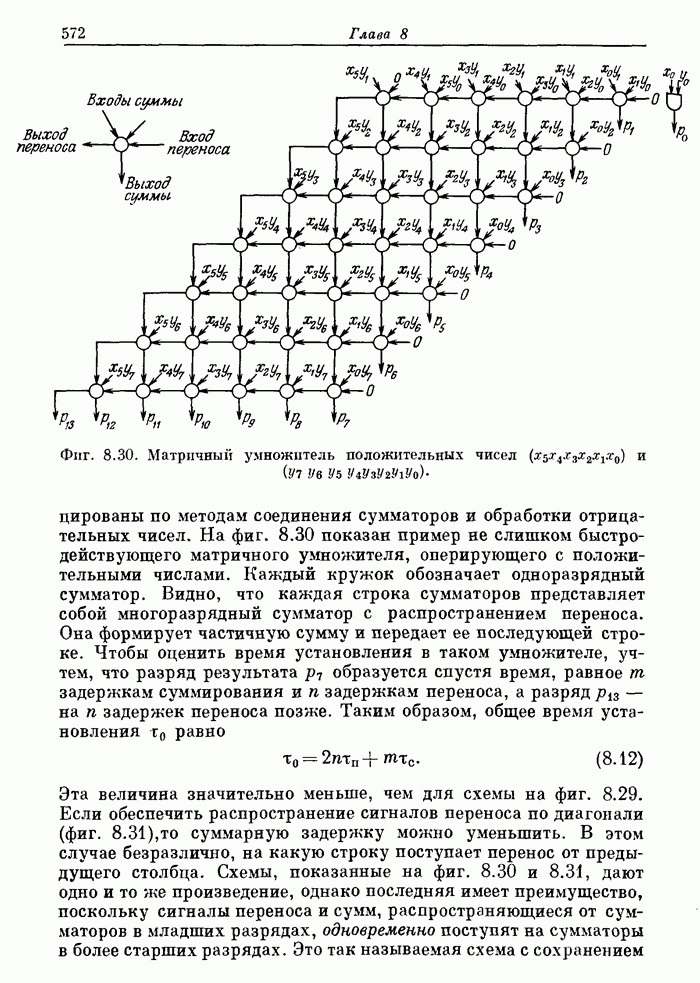
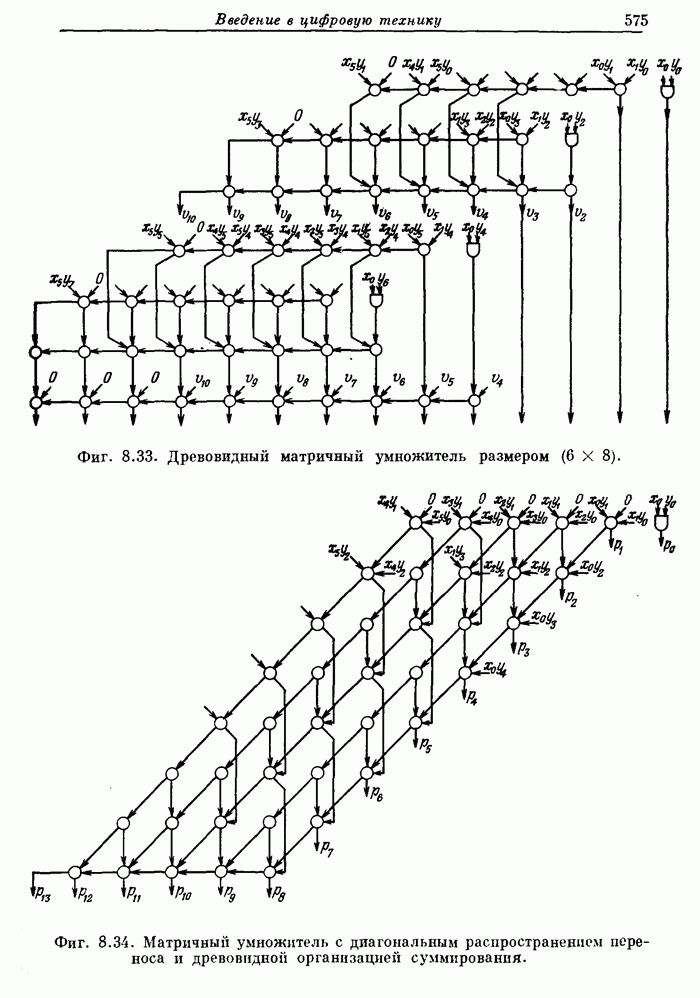
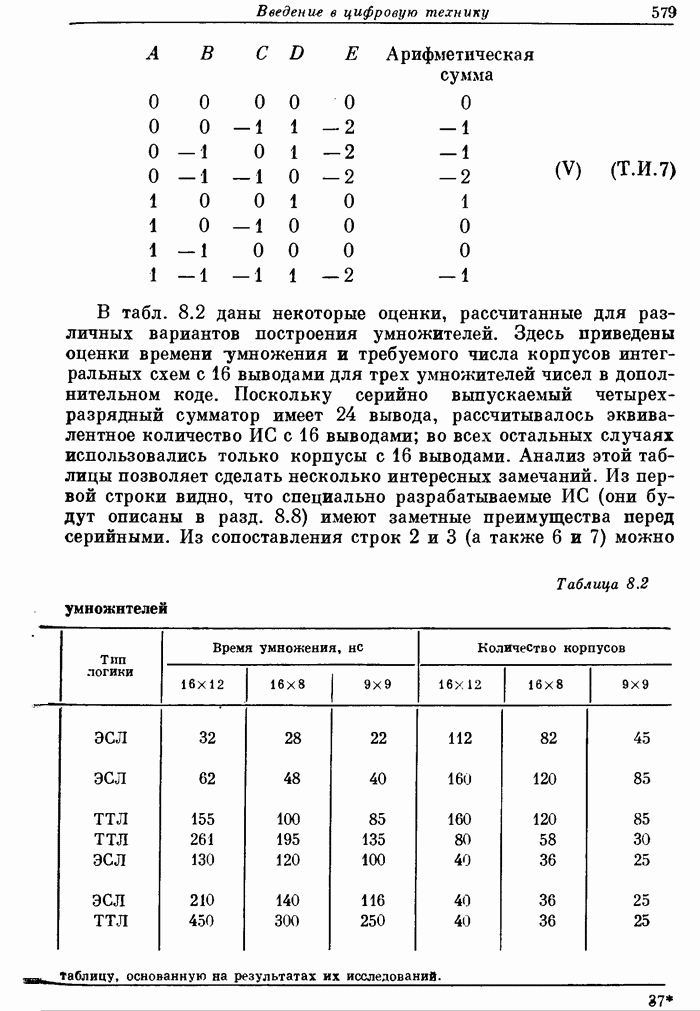
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
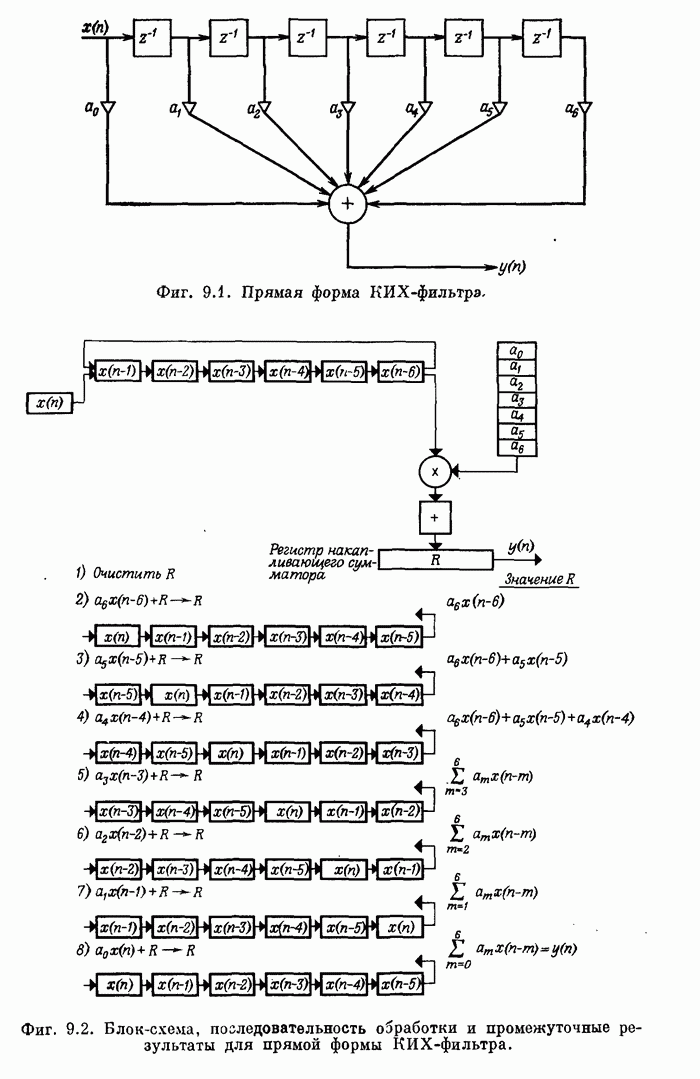
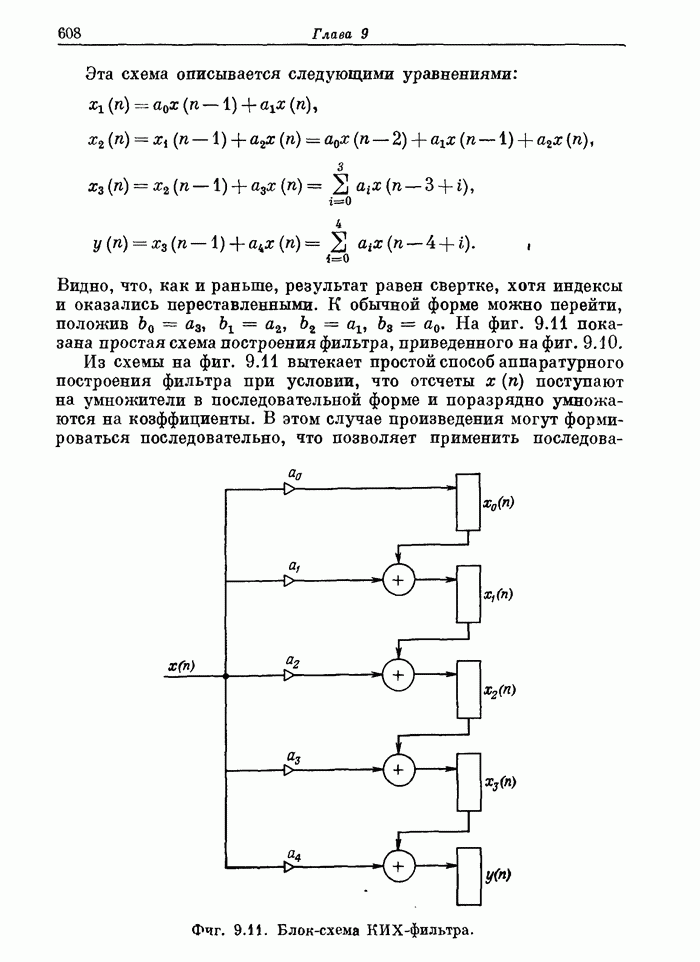
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
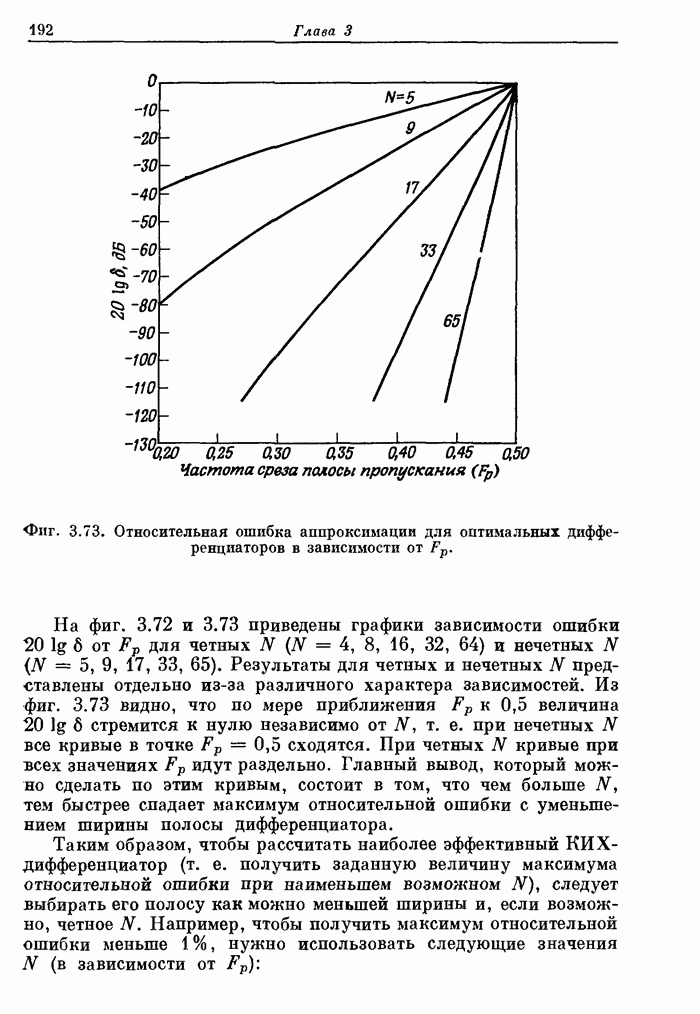
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
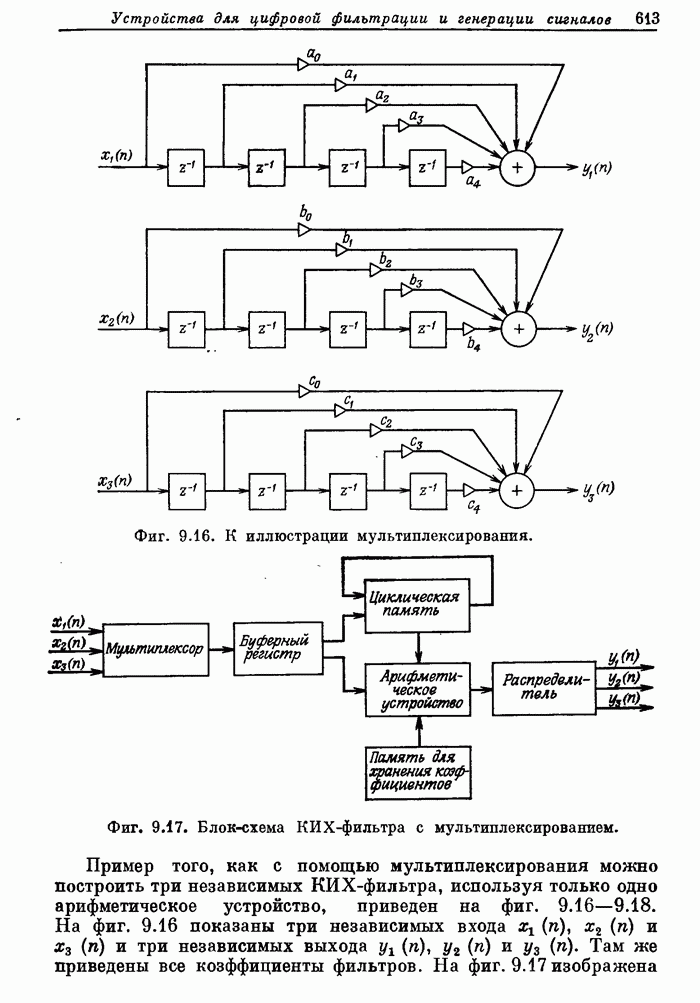
- 9.8. Мультиплексирование
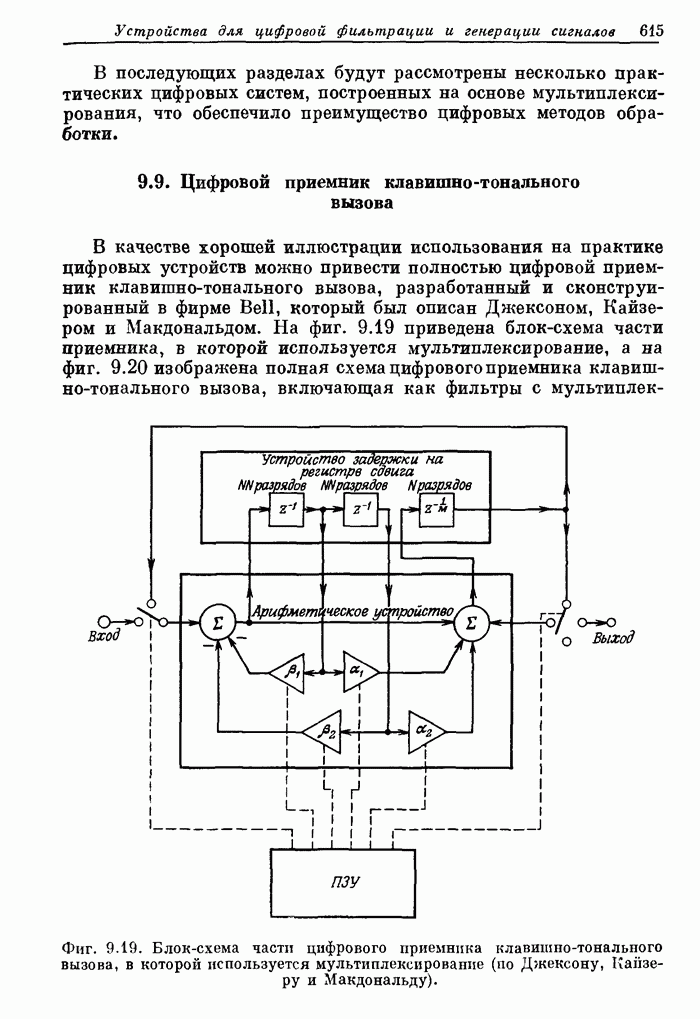
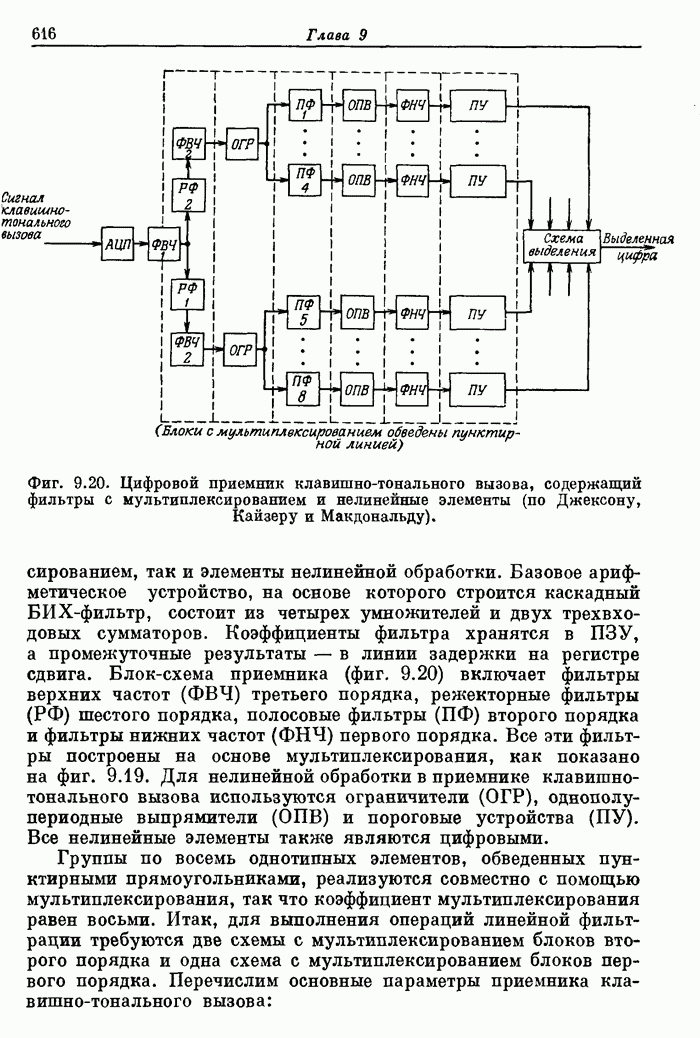
- 9.9. Цифровой приемник клавишно-тонального вызова
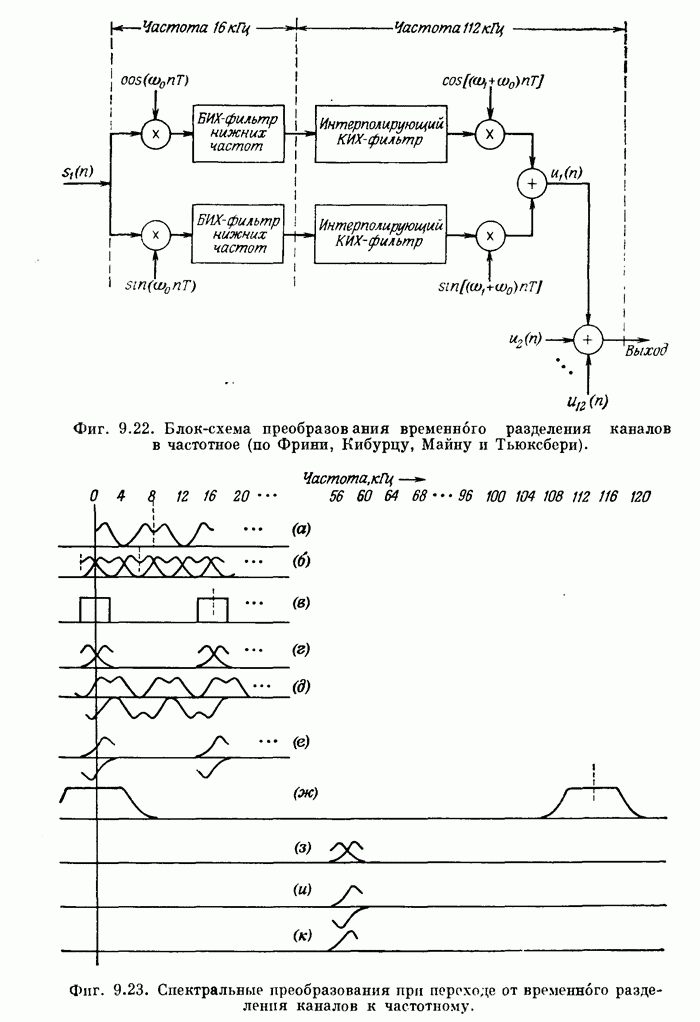
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
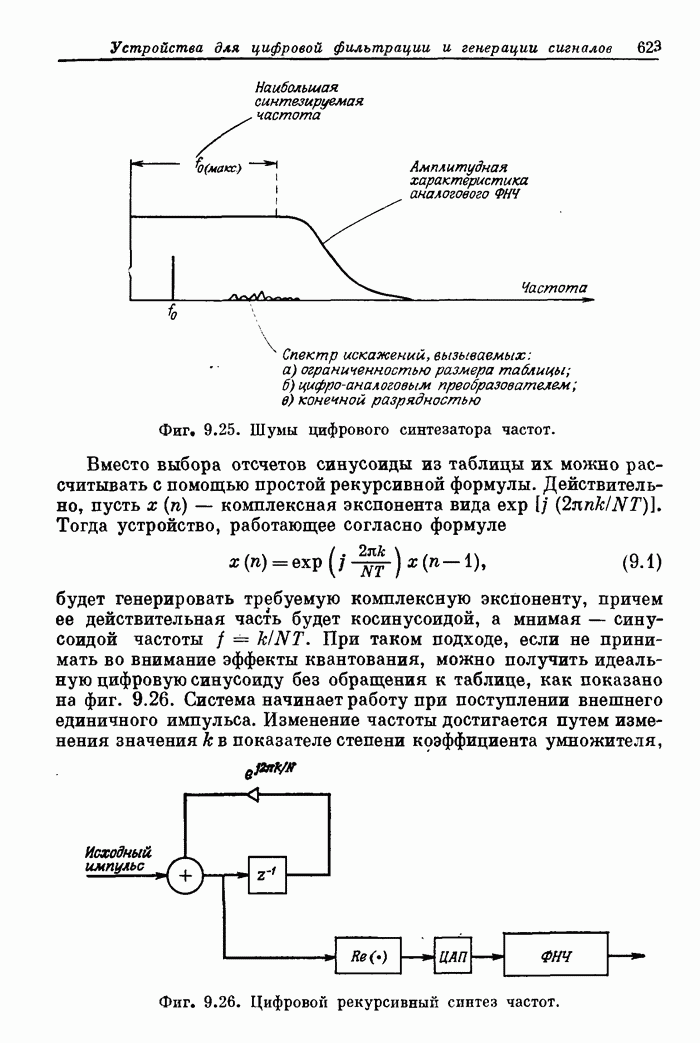
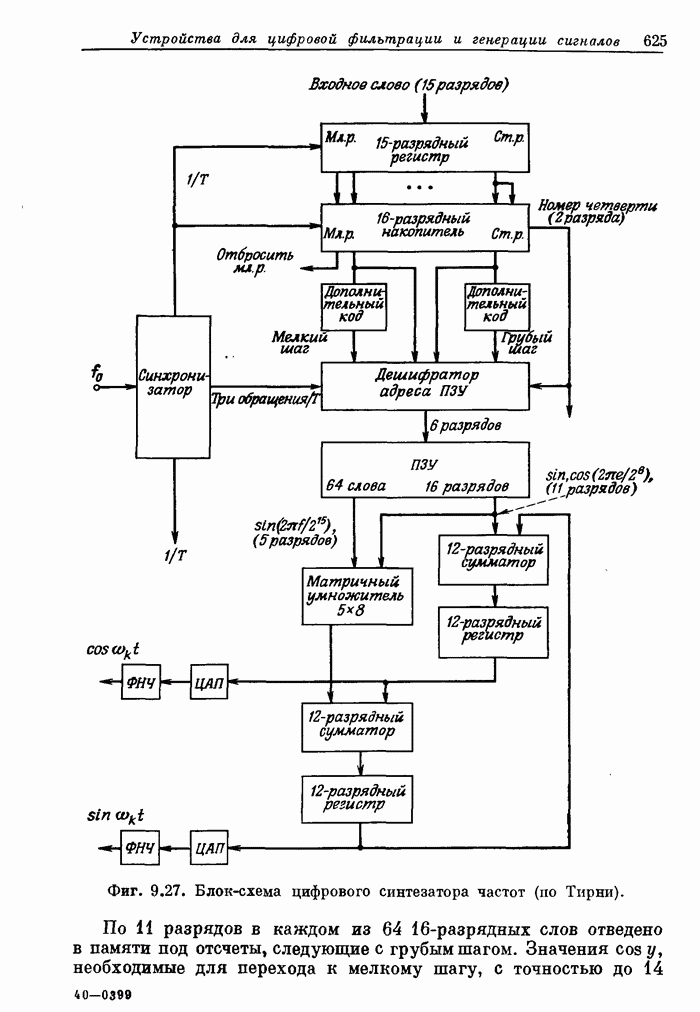
- 9.12. Специализированный цифровой синтезатор частот
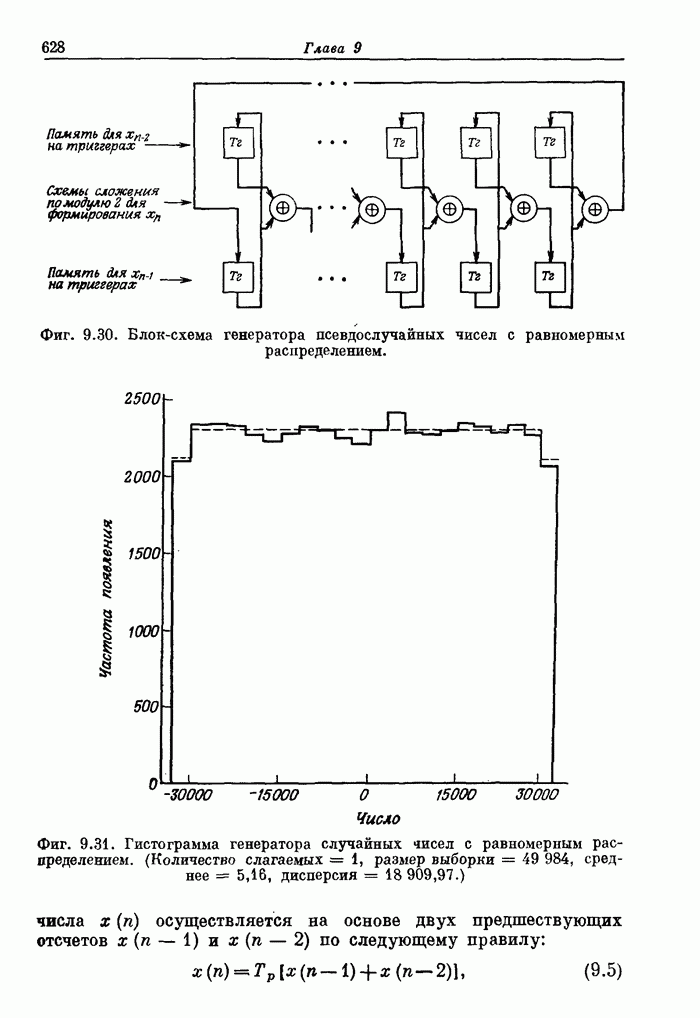
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
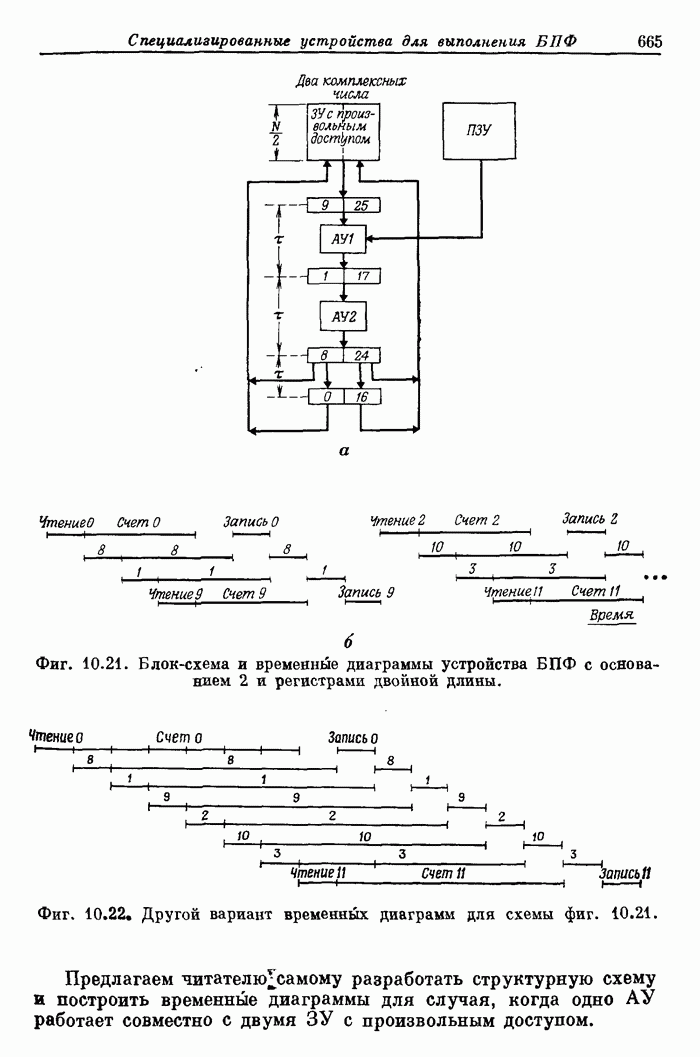
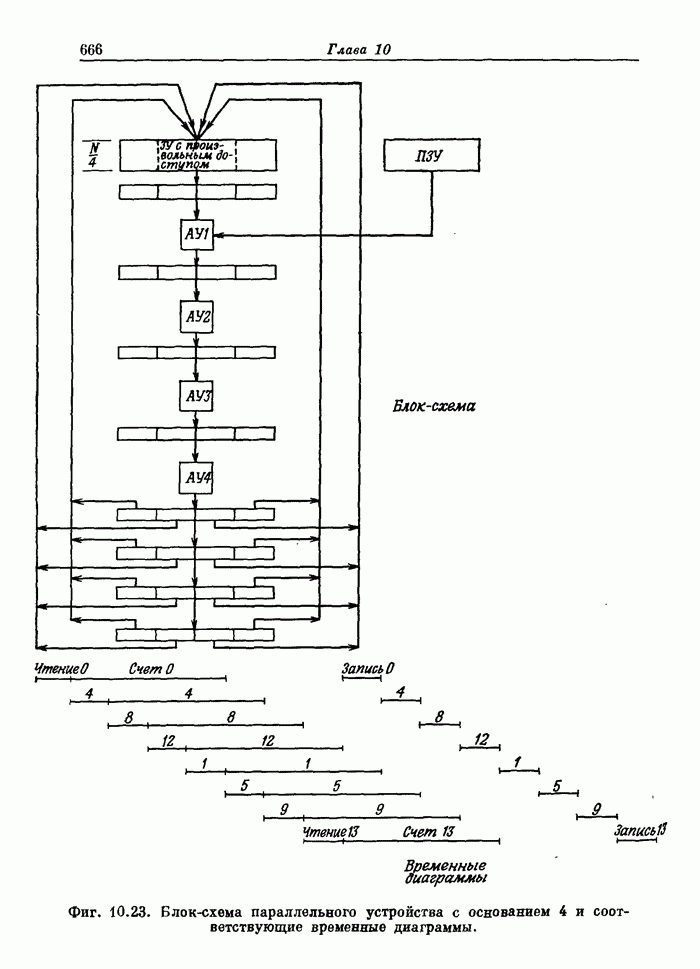
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
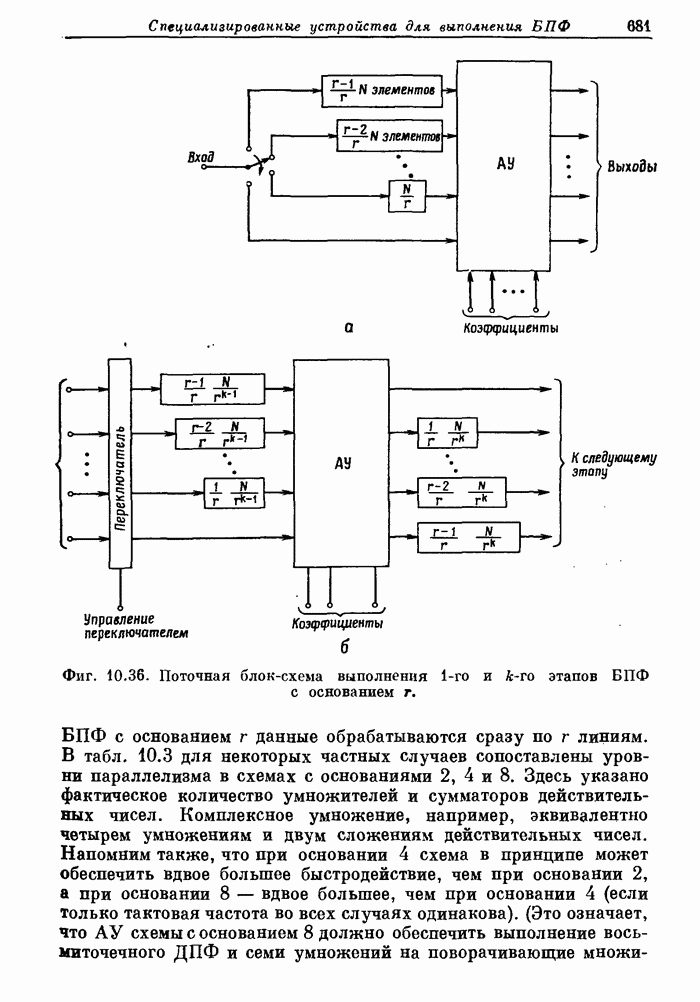
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
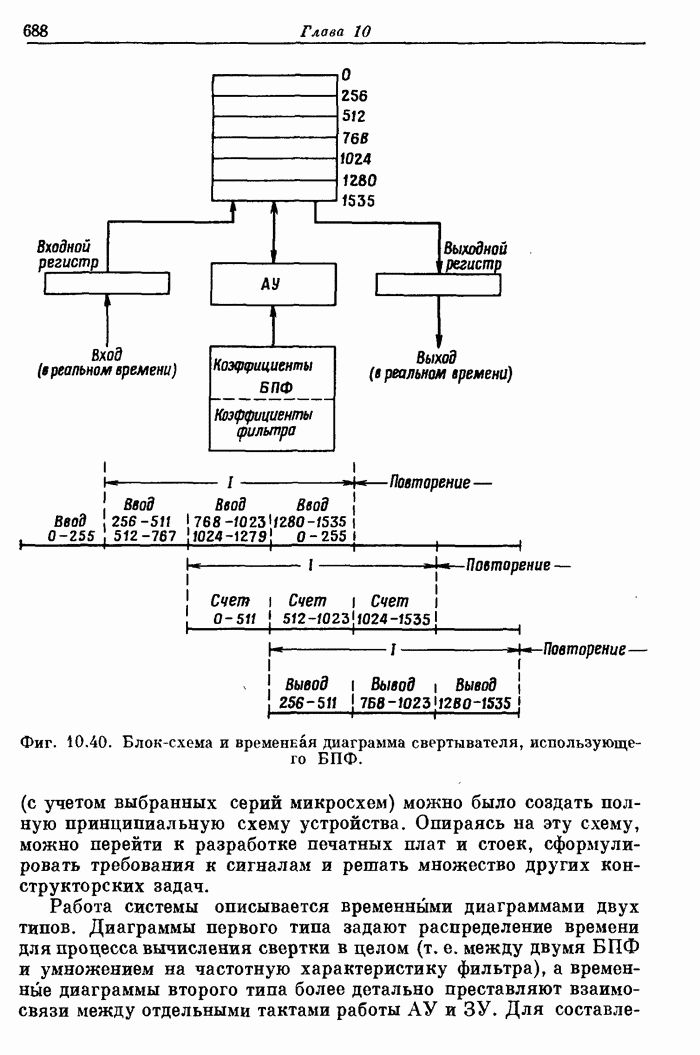
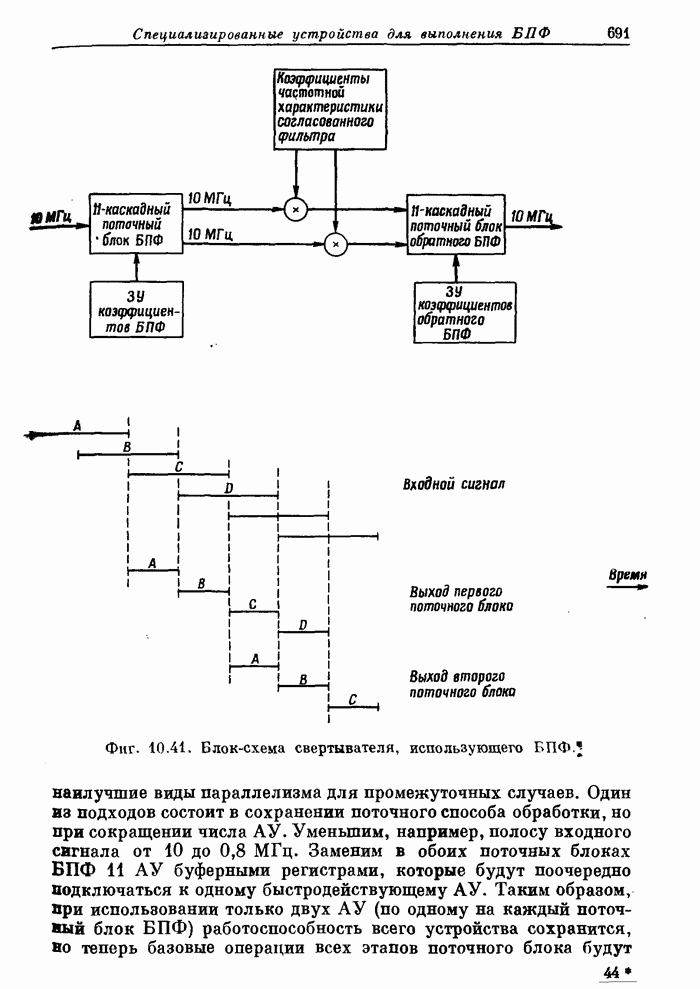
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
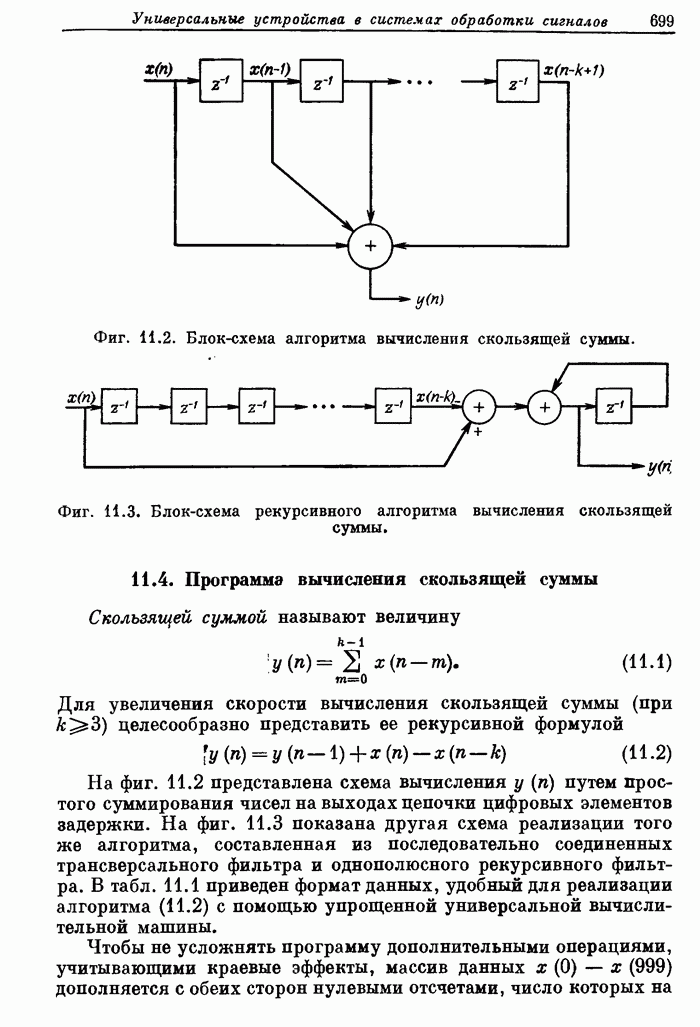
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
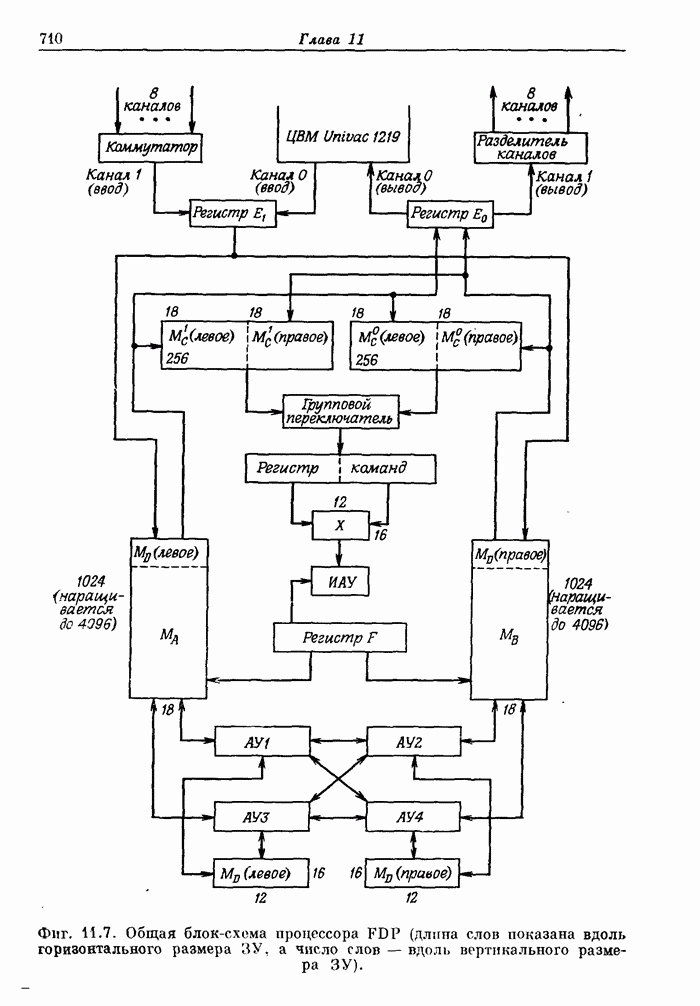
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
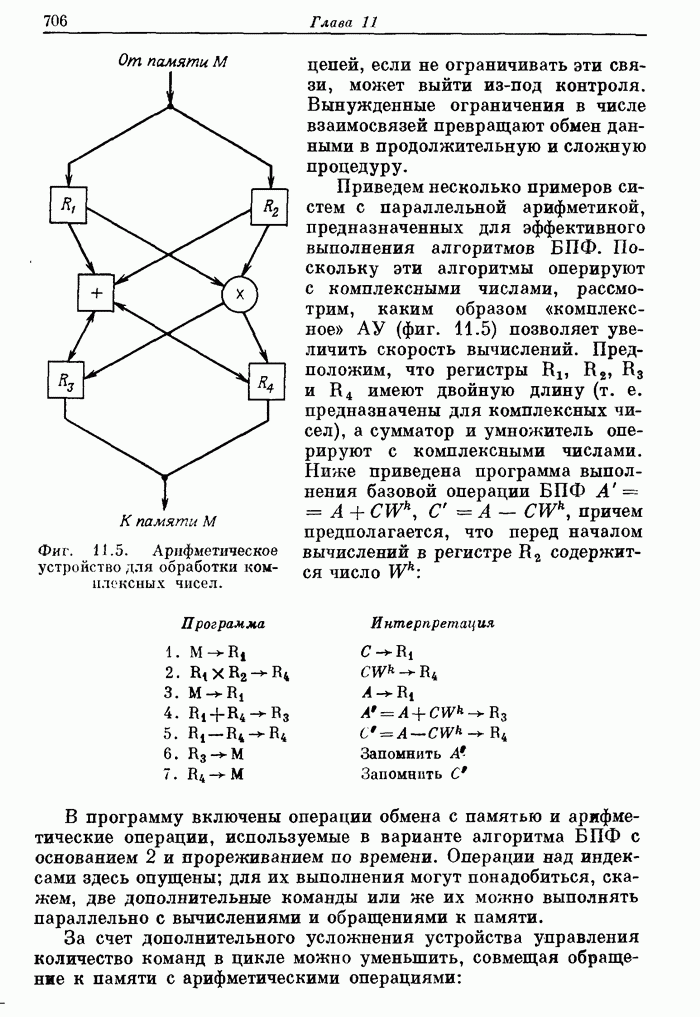
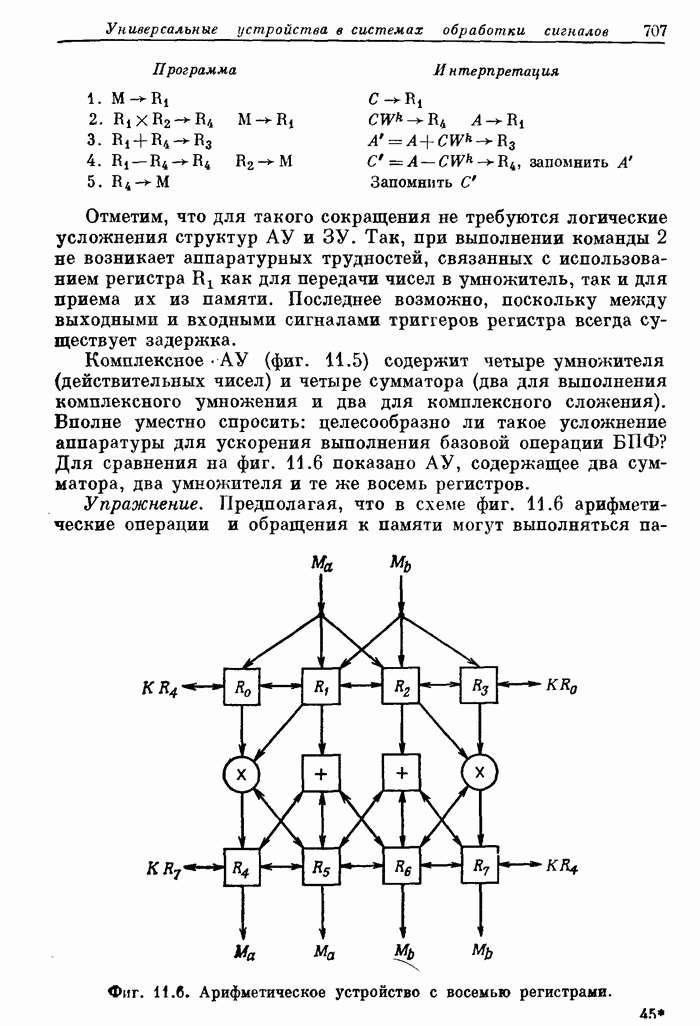
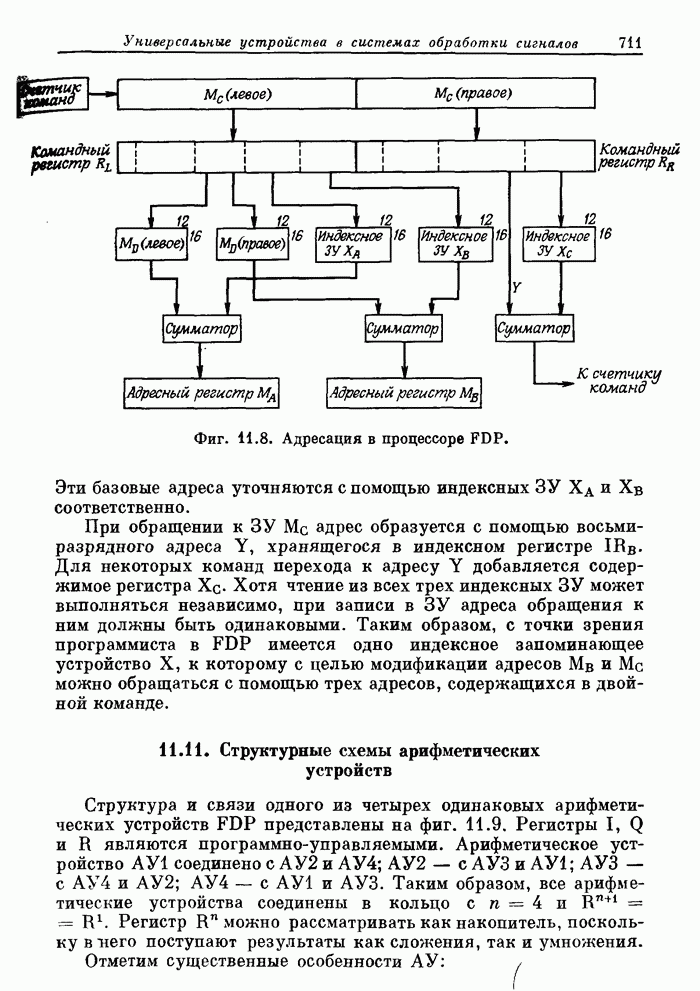
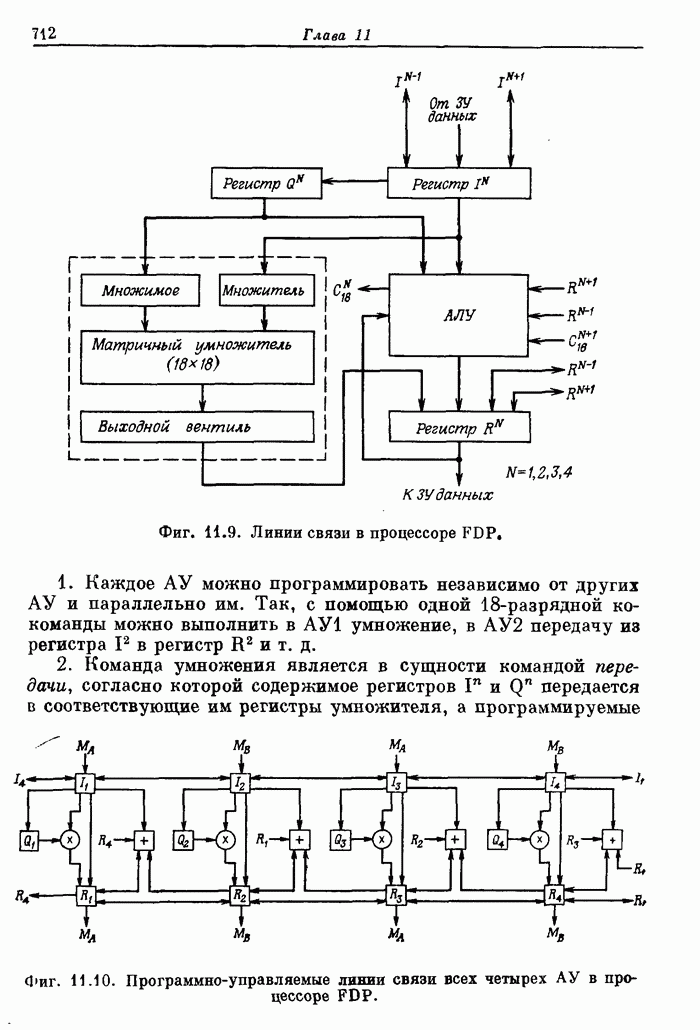
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
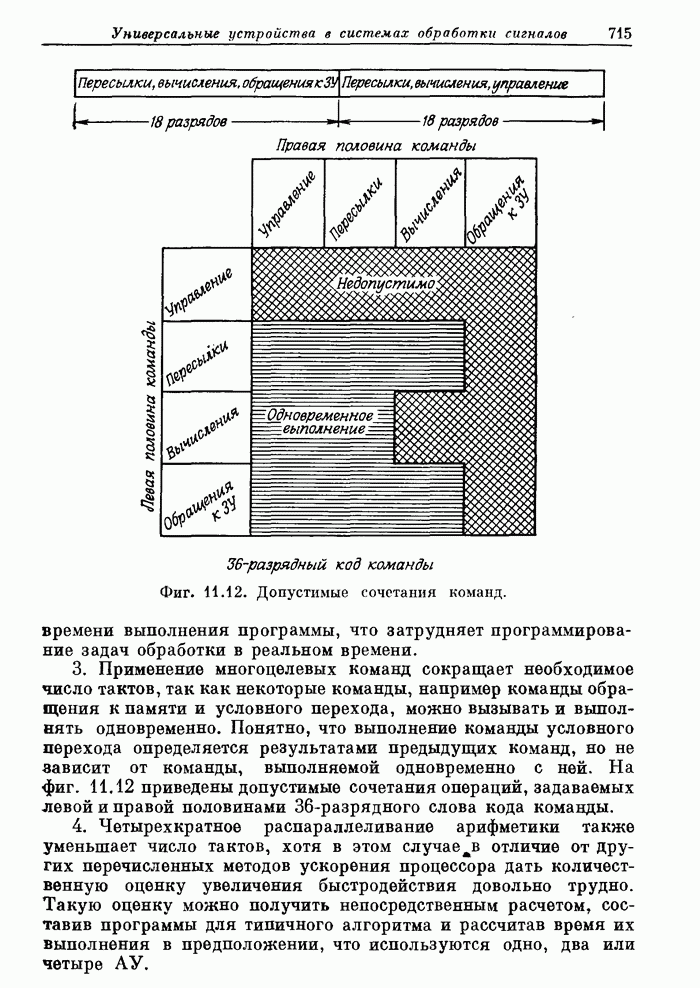
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
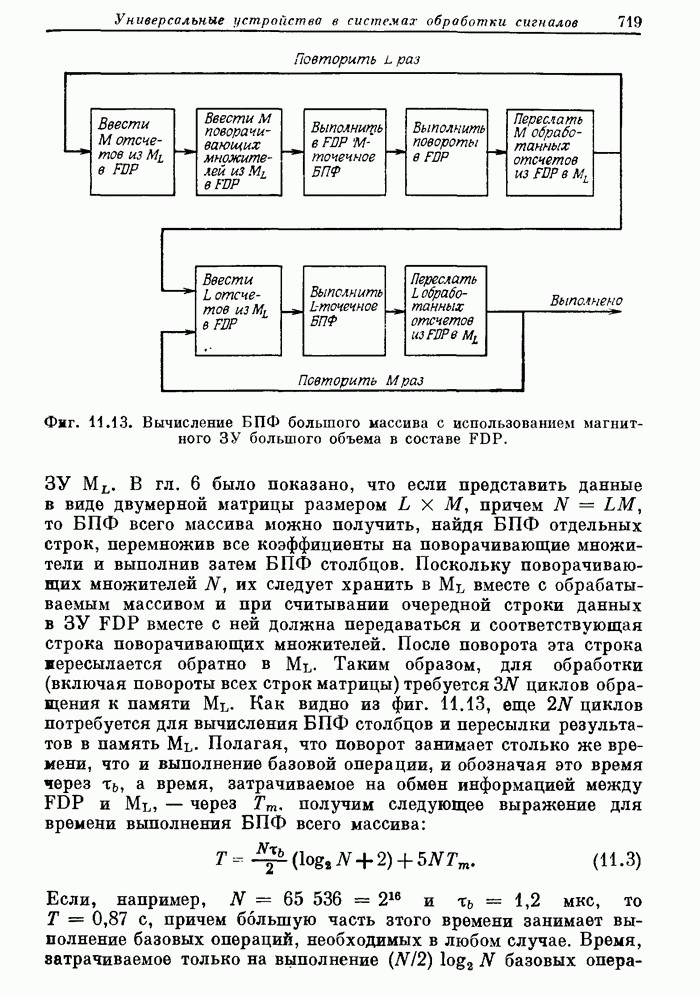
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
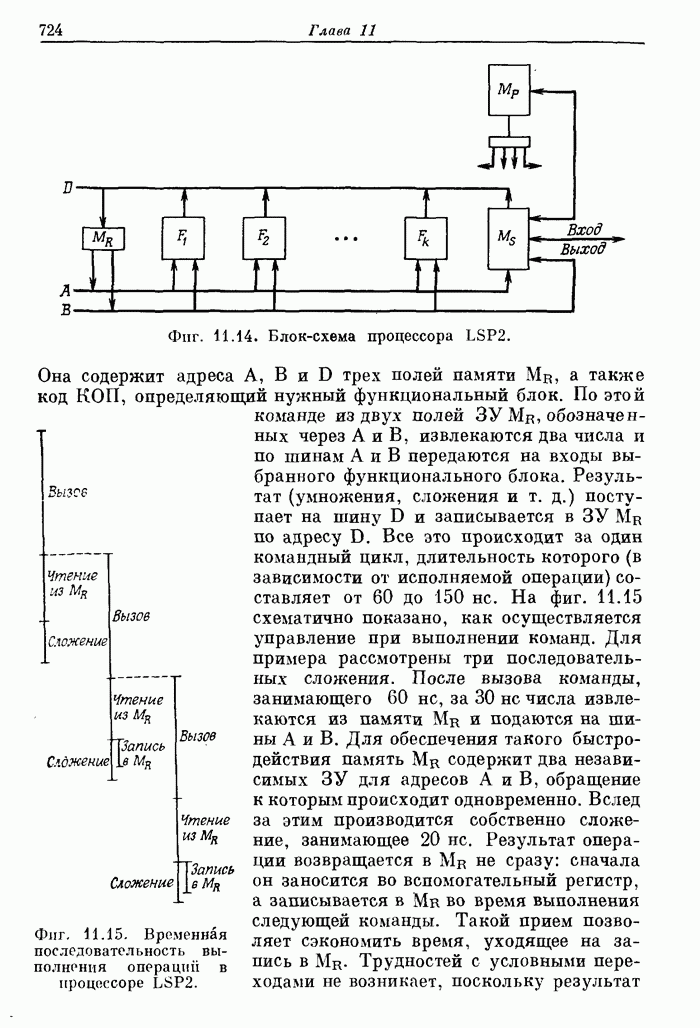
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
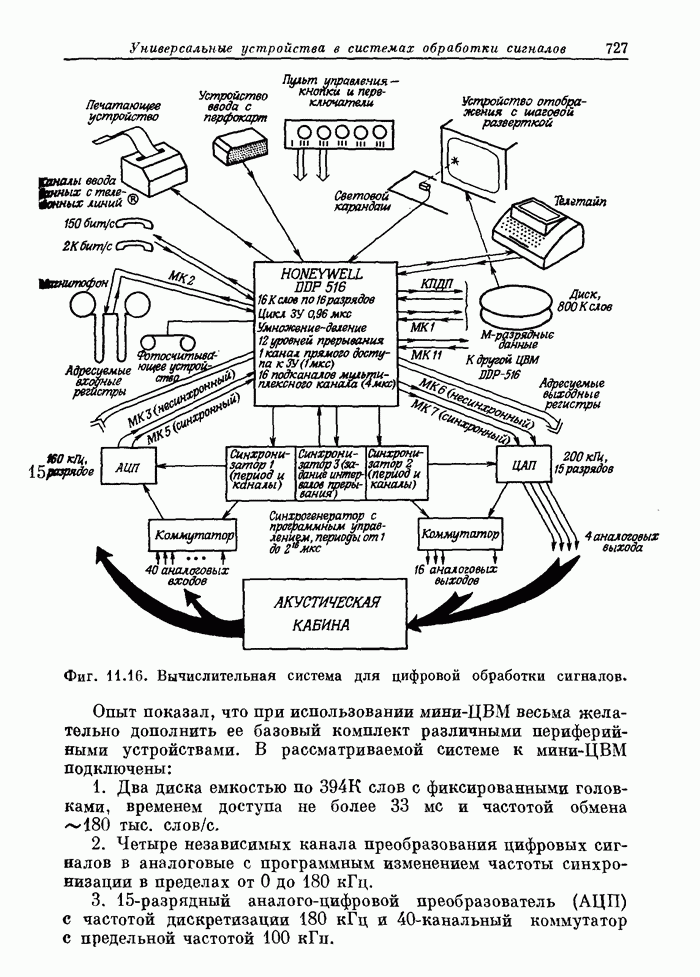
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
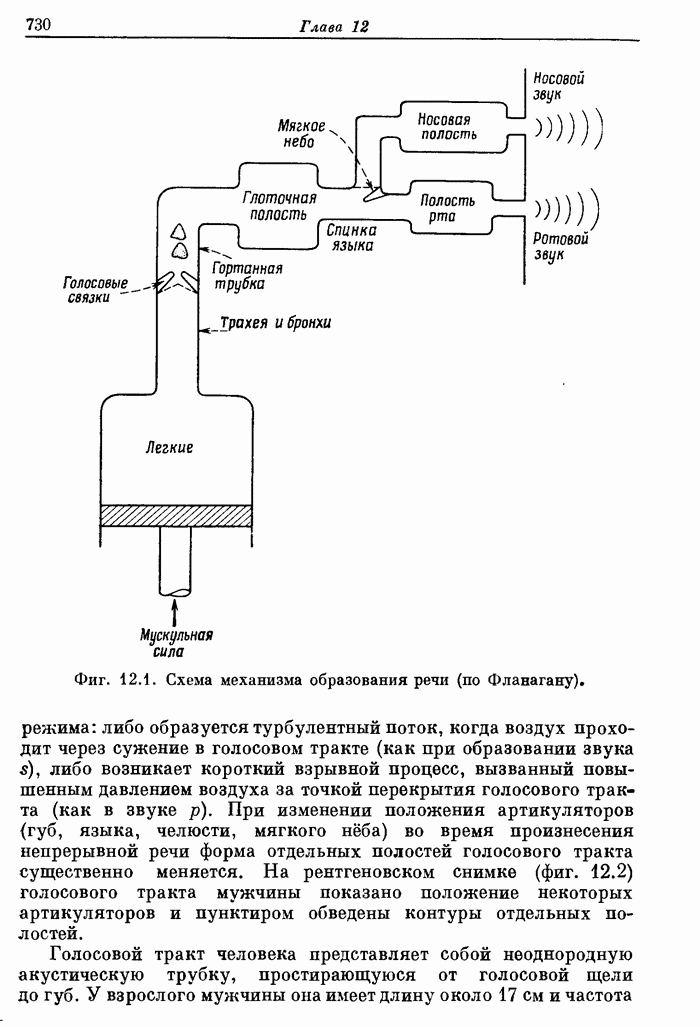
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
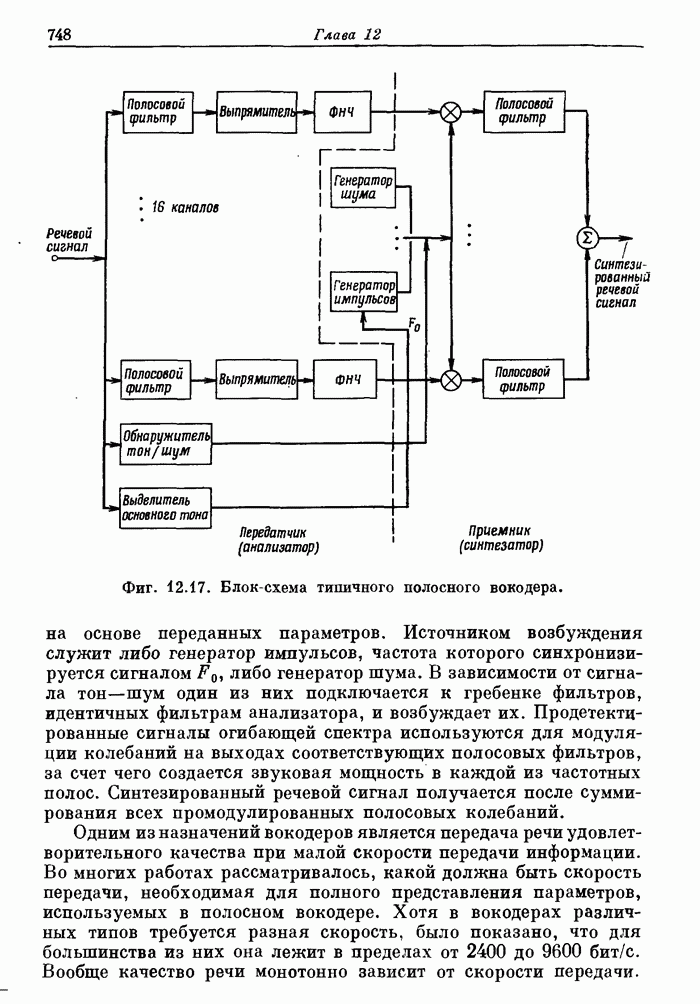
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
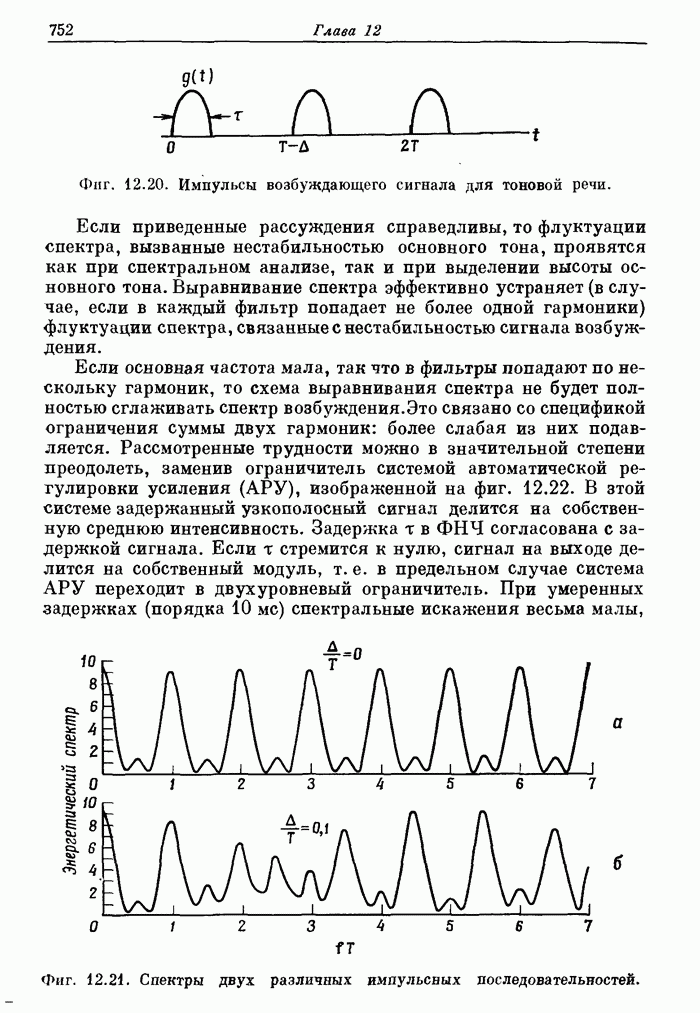
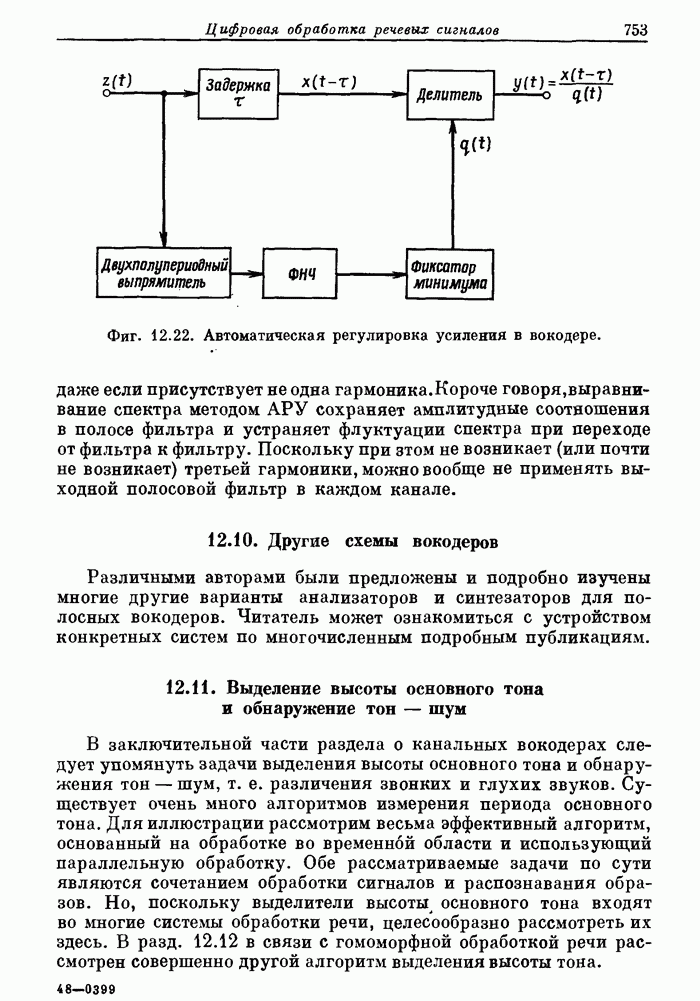
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
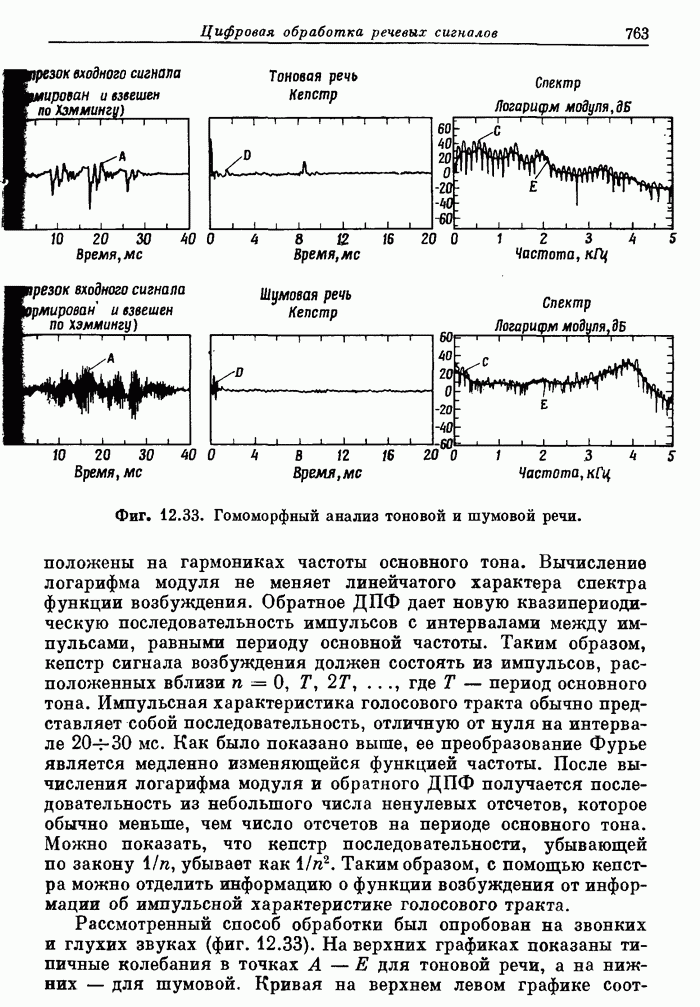
- 12.13. Гомоморфная обработка речи
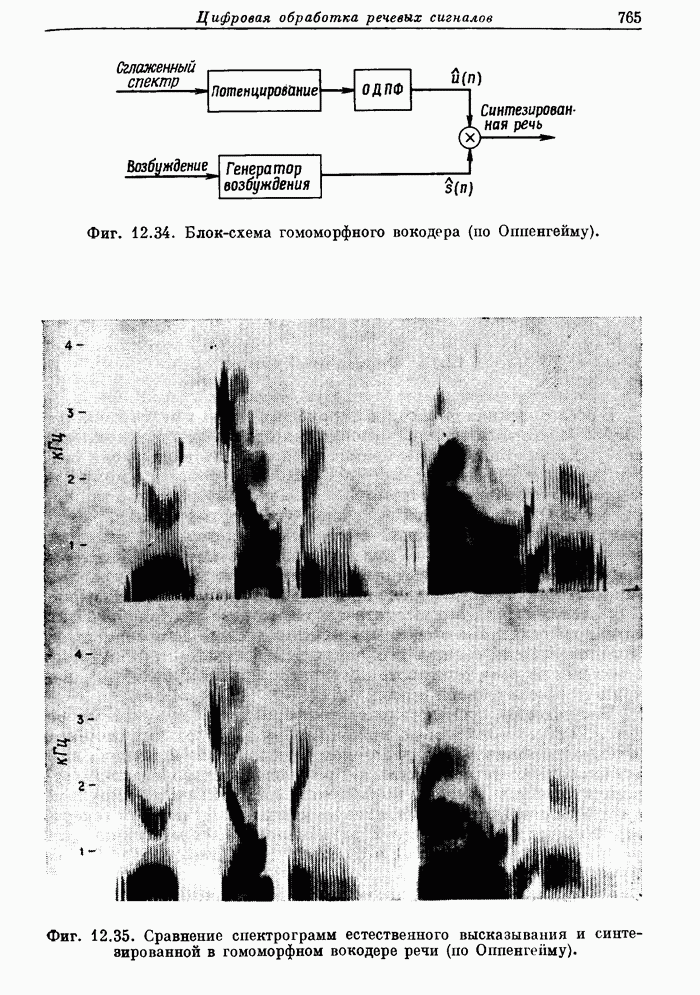
- 12.14. Гомоморфный вокодер
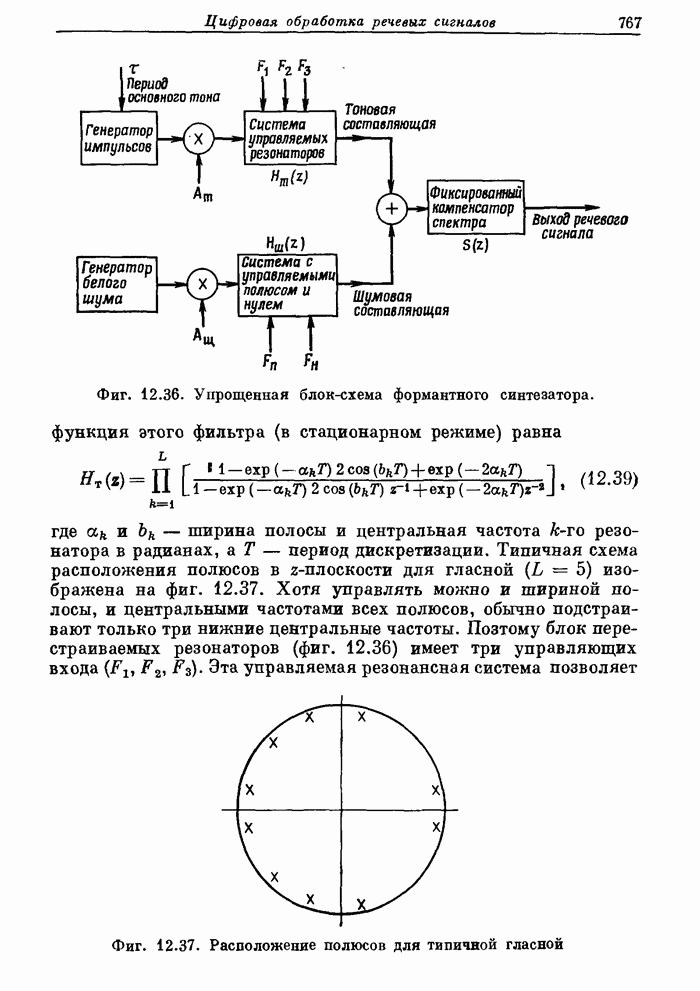
- 12.15. Формантный синтез
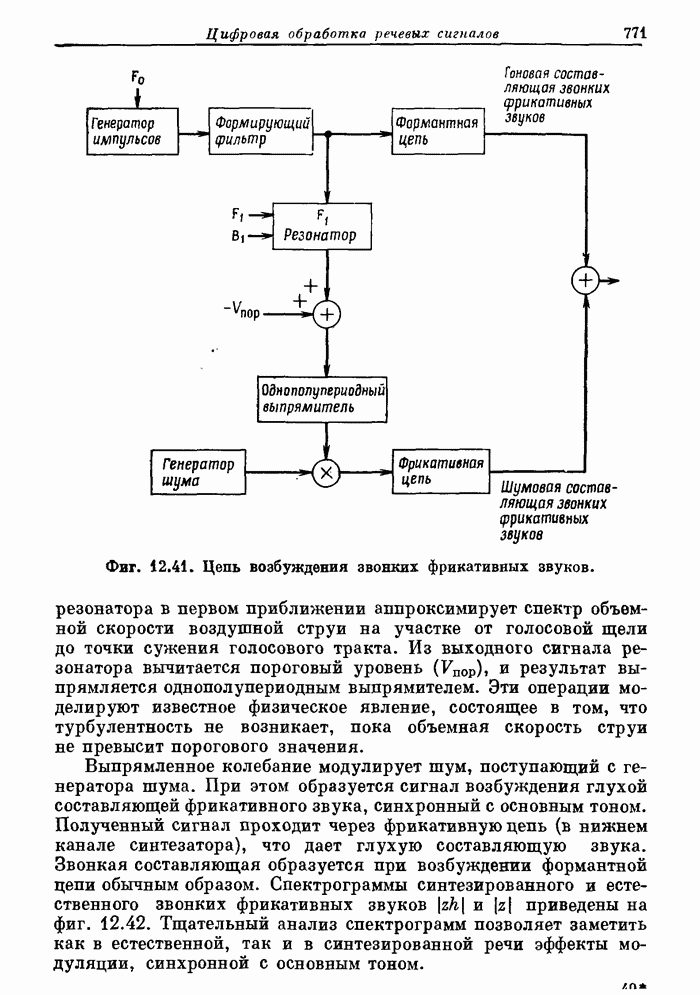
- 12.16. Цепь возбуждения звонких фрикативных звуков
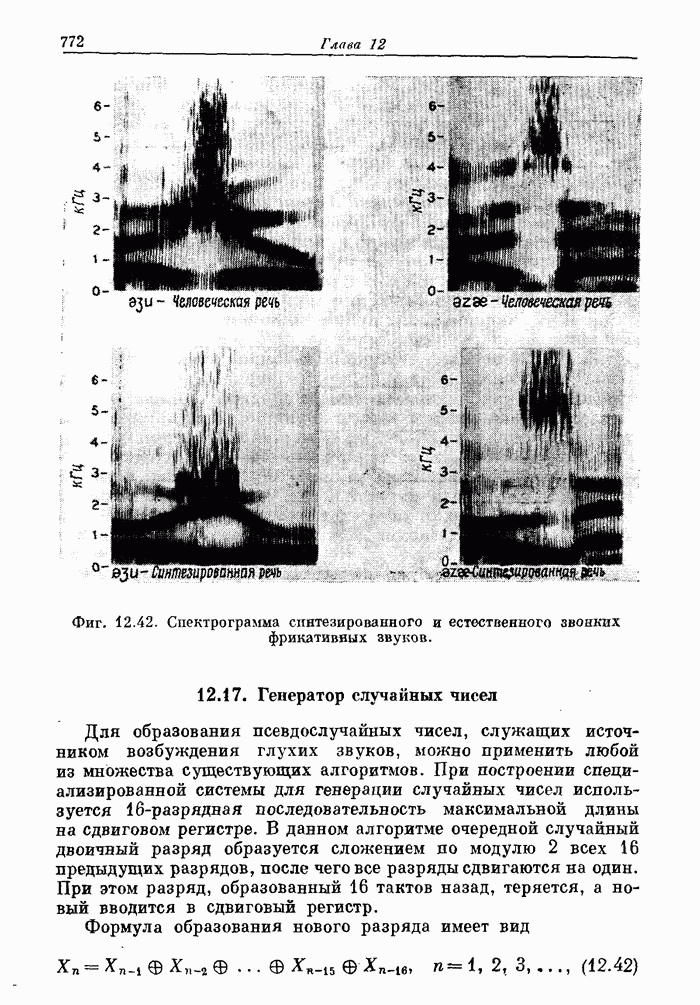
- 12.17. Генератор случайных чисел
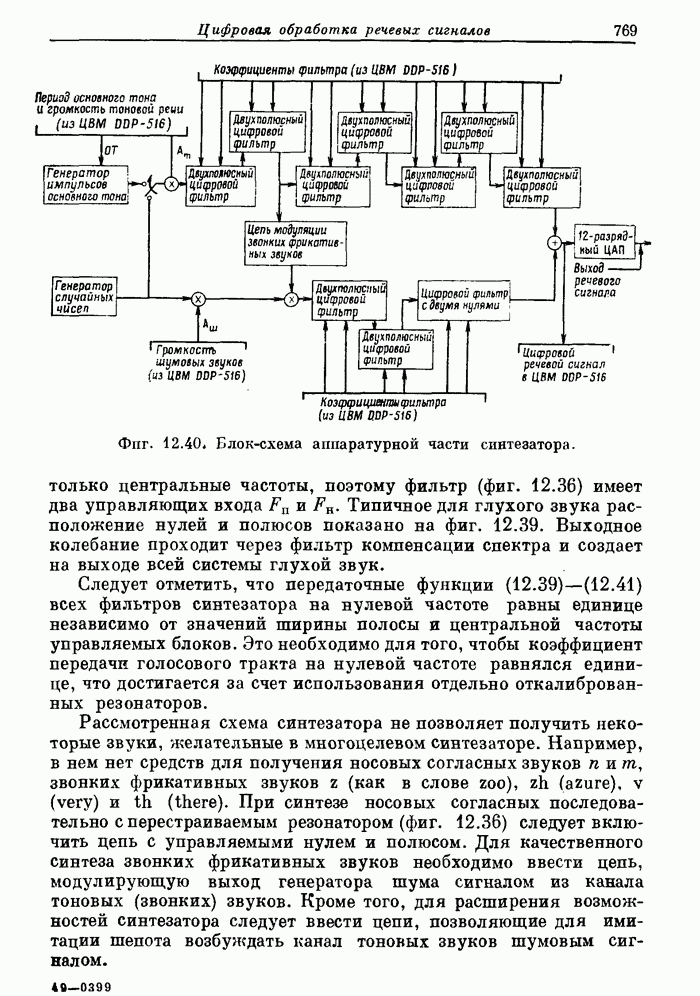
- 12.18. Цифровая обработка в формантном синтезаторе
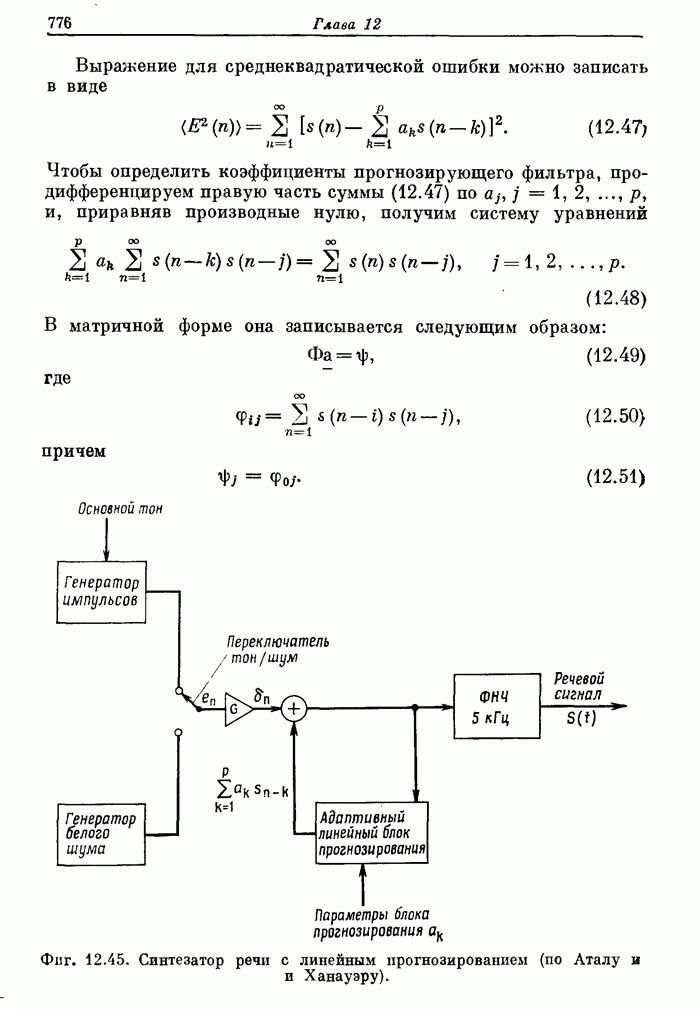
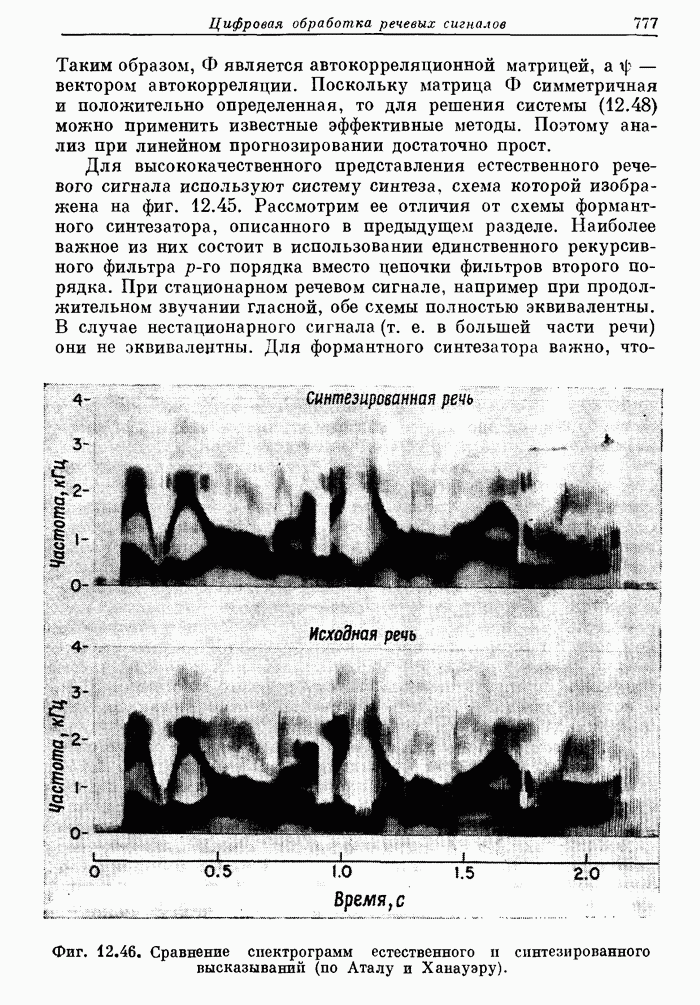
- 12.19. Линейное прогнозирование речи
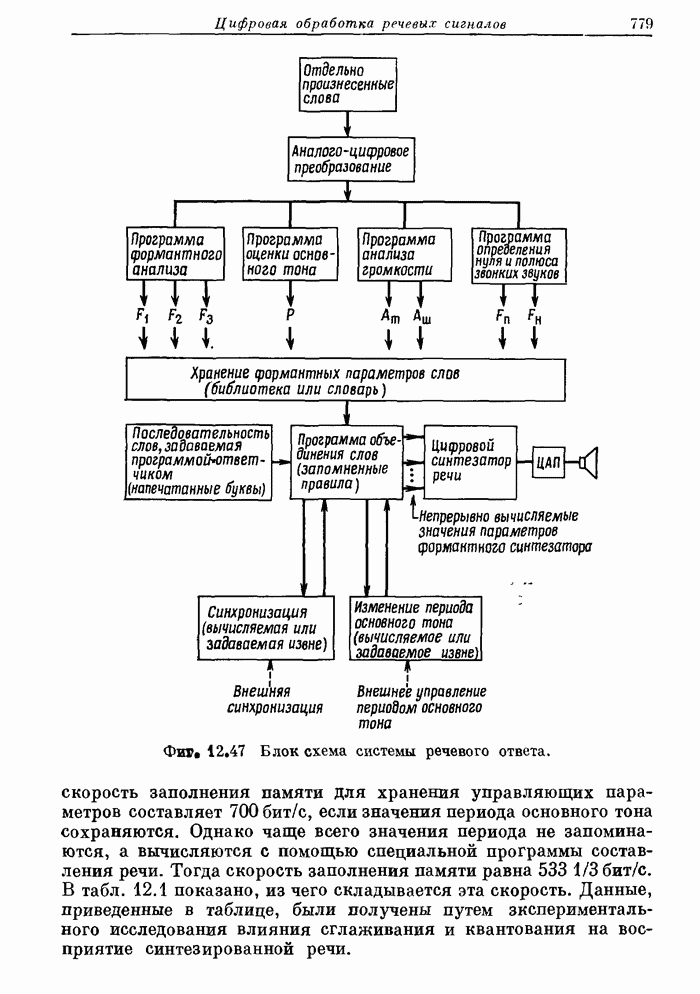
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
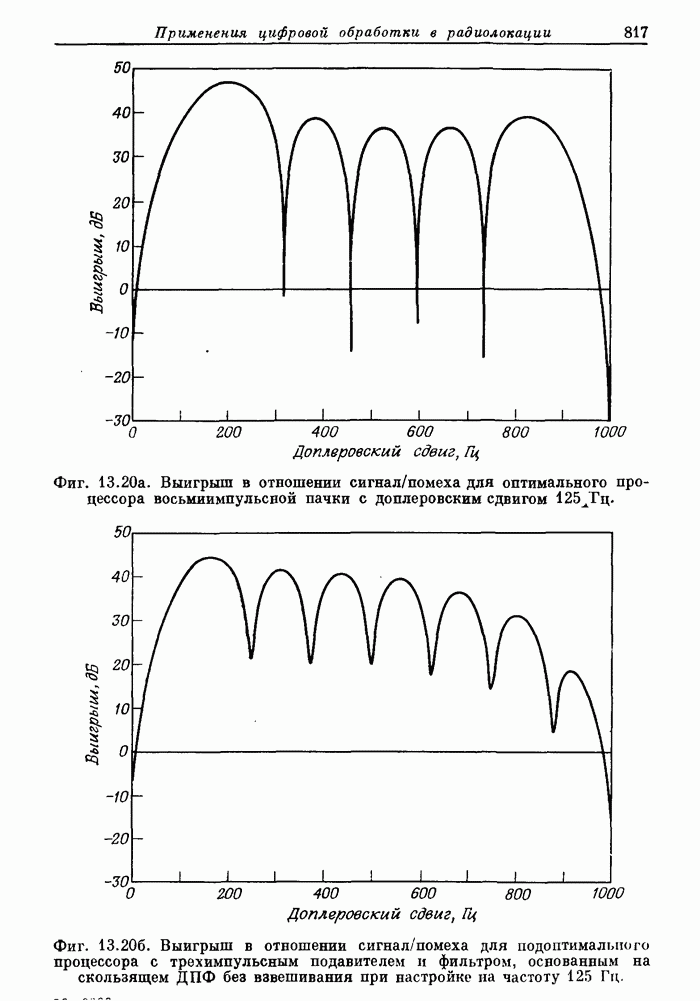
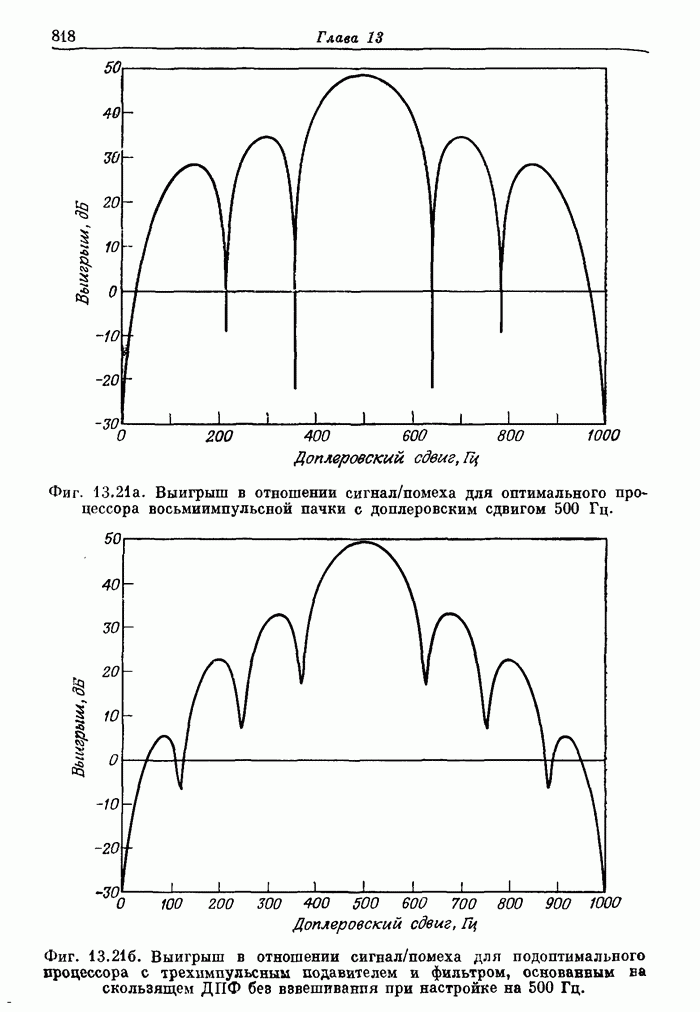
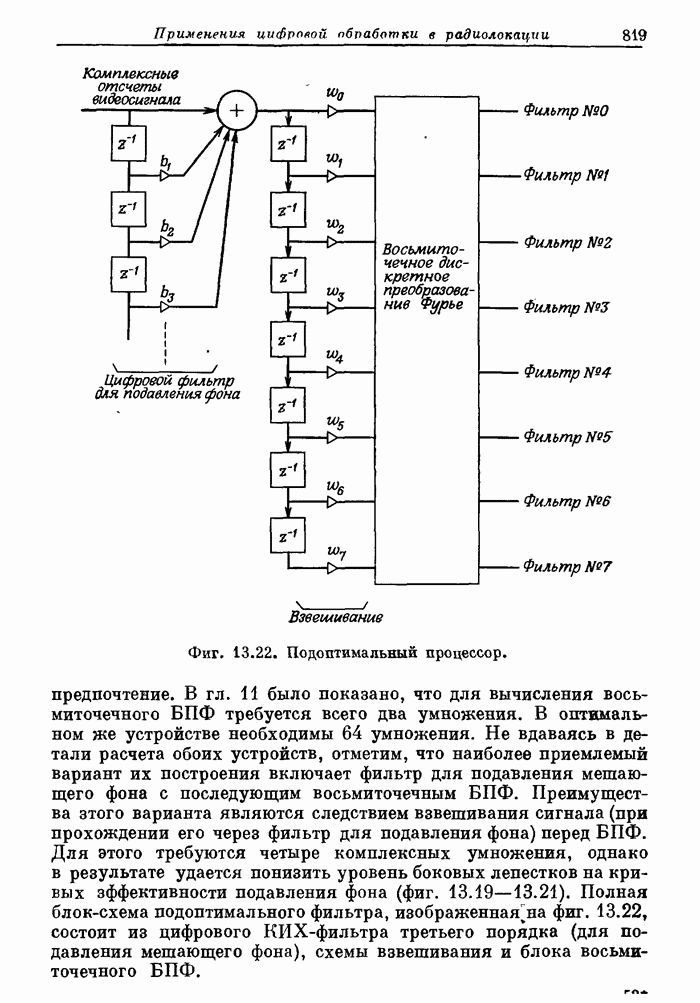
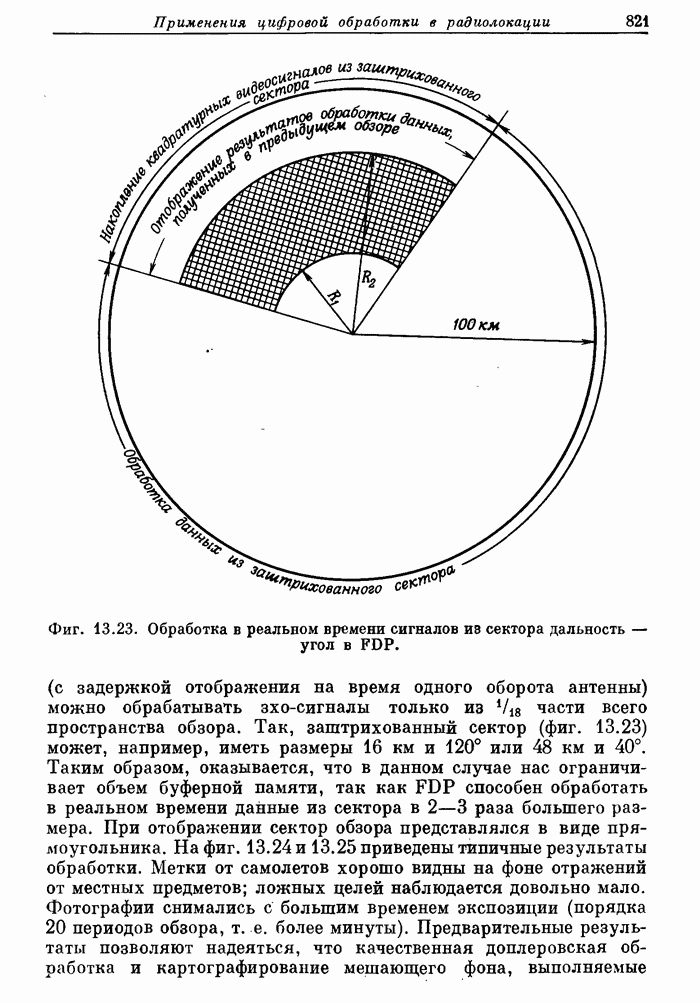
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
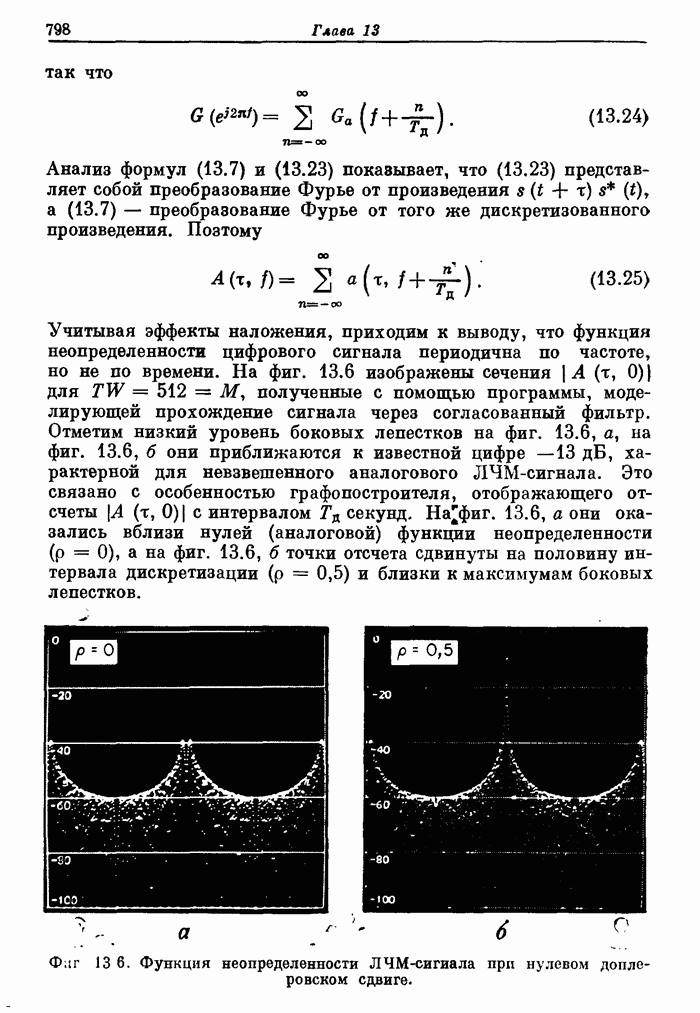
- 13.3. Выбор сигналов и функция неопределенности
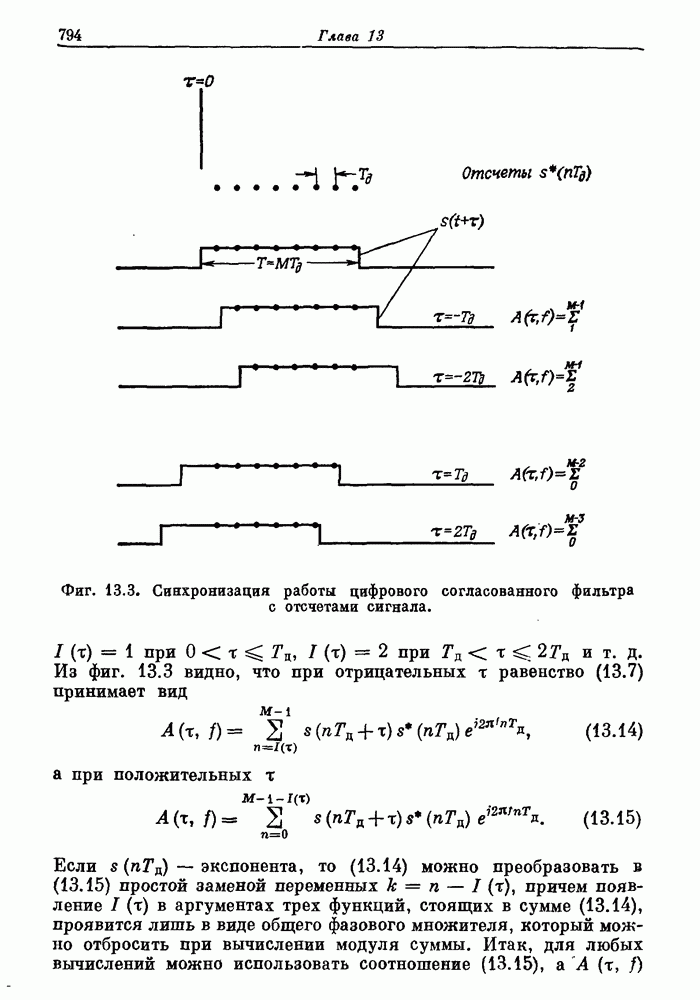
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
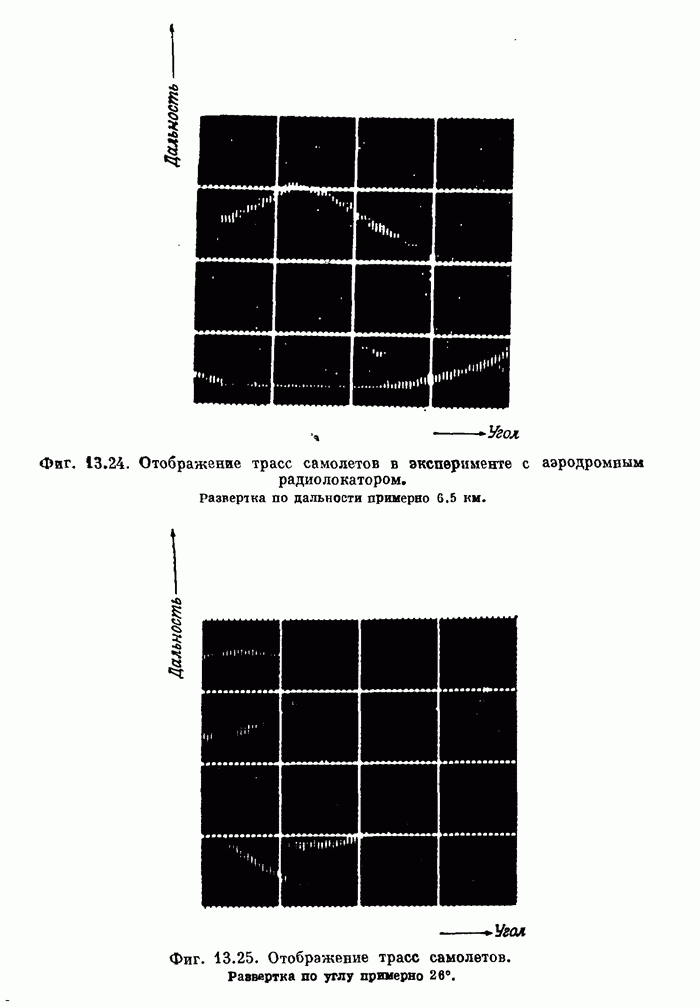
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
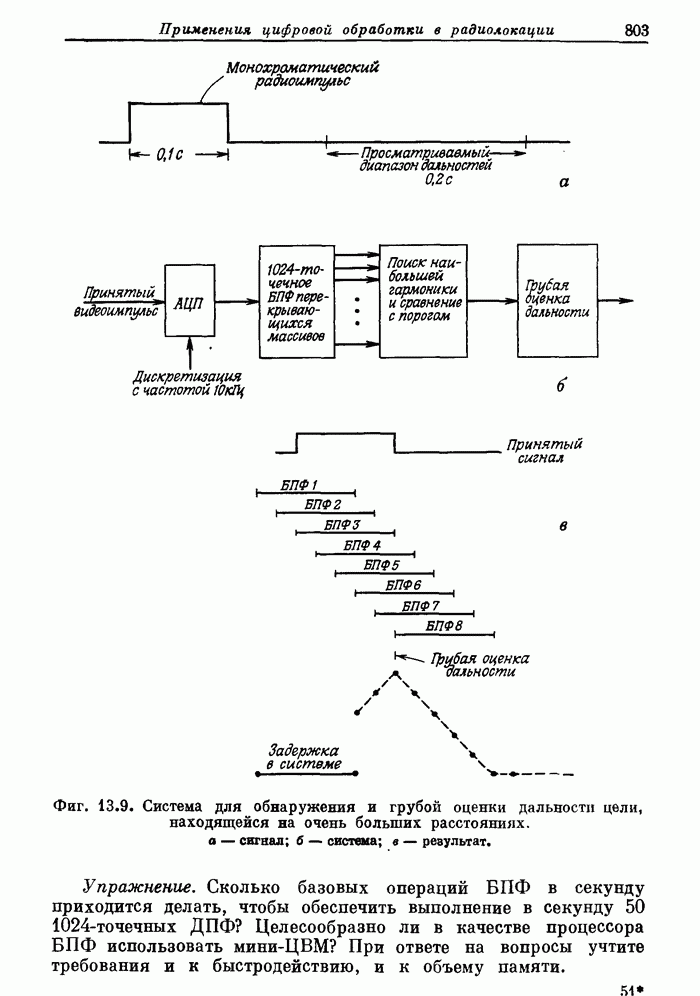
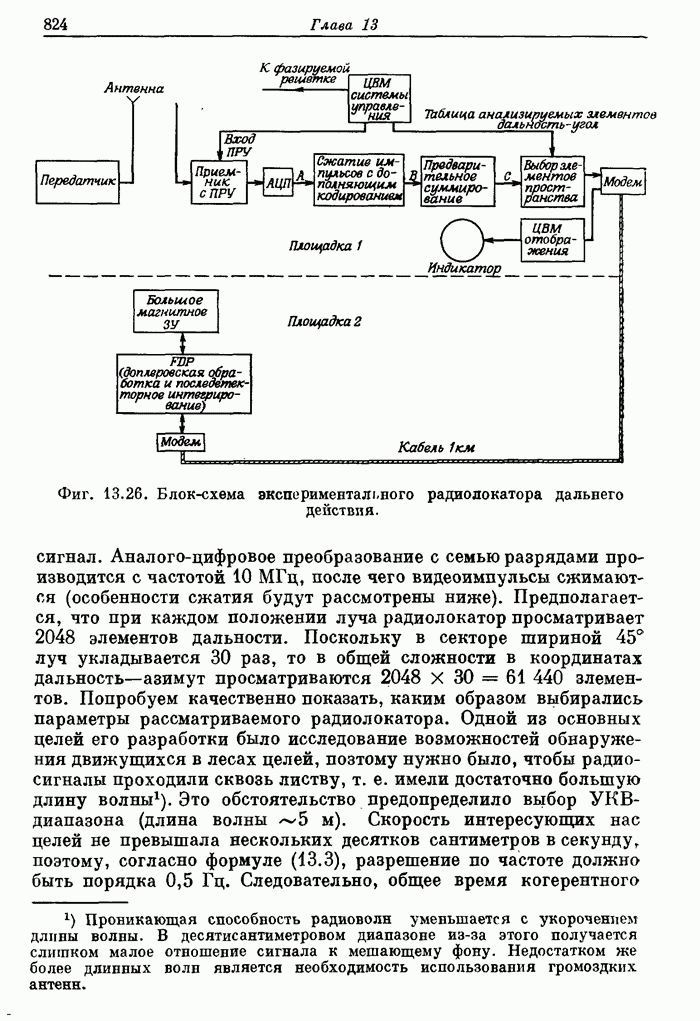
- 13.6. Экспериментальный радиолокатор дальнего действия
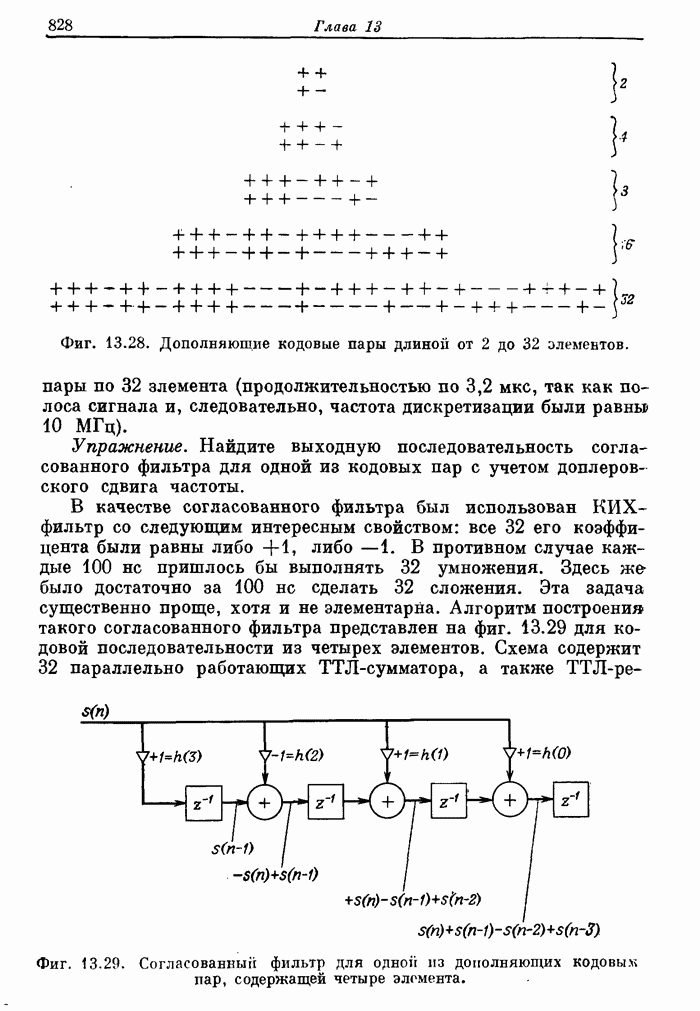
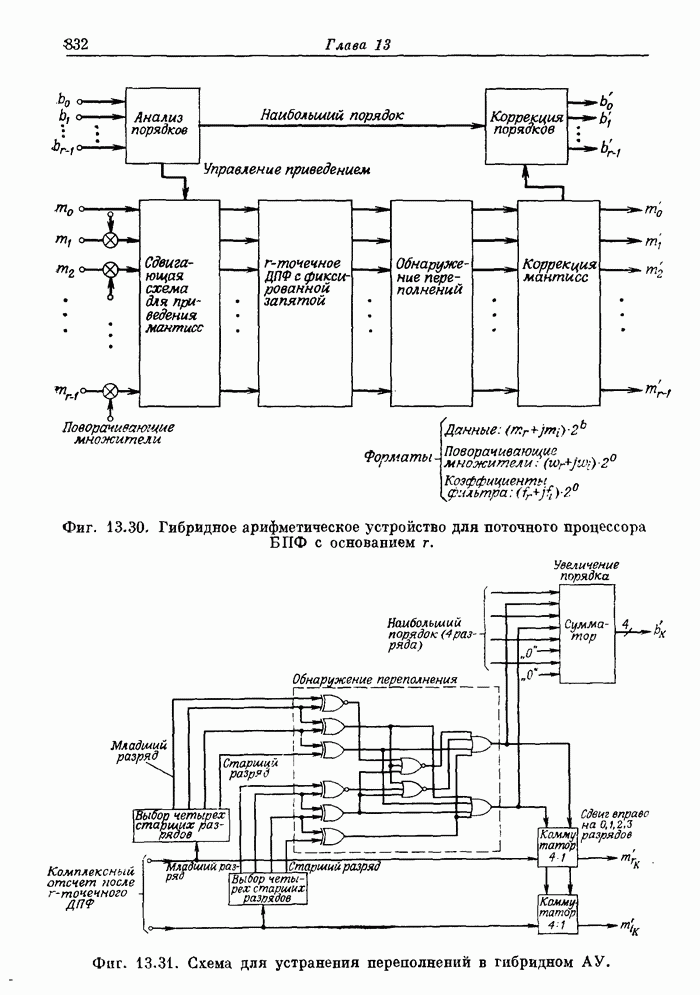
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение