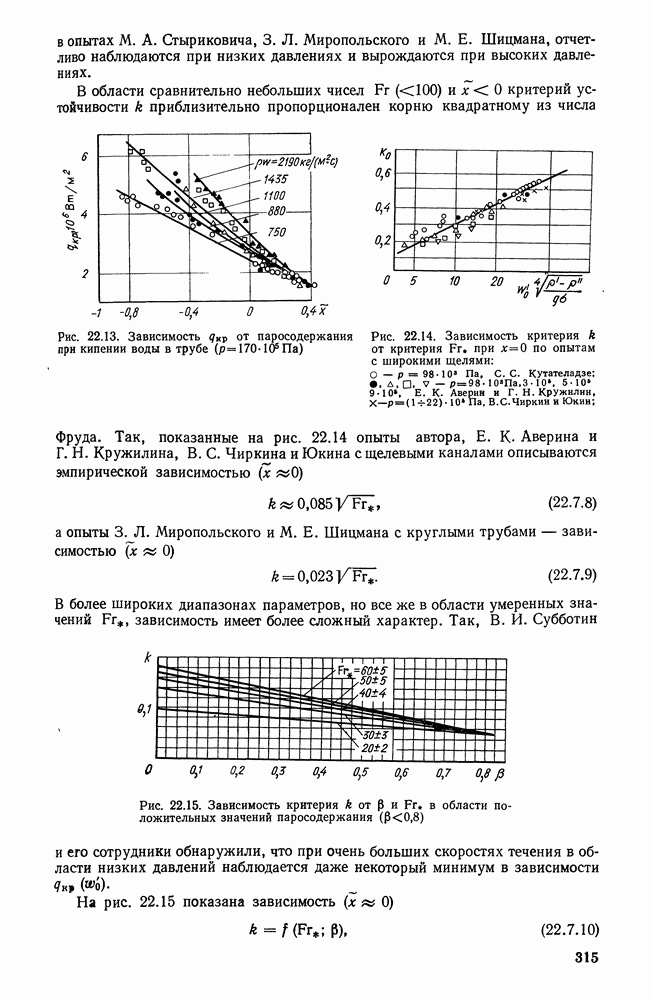
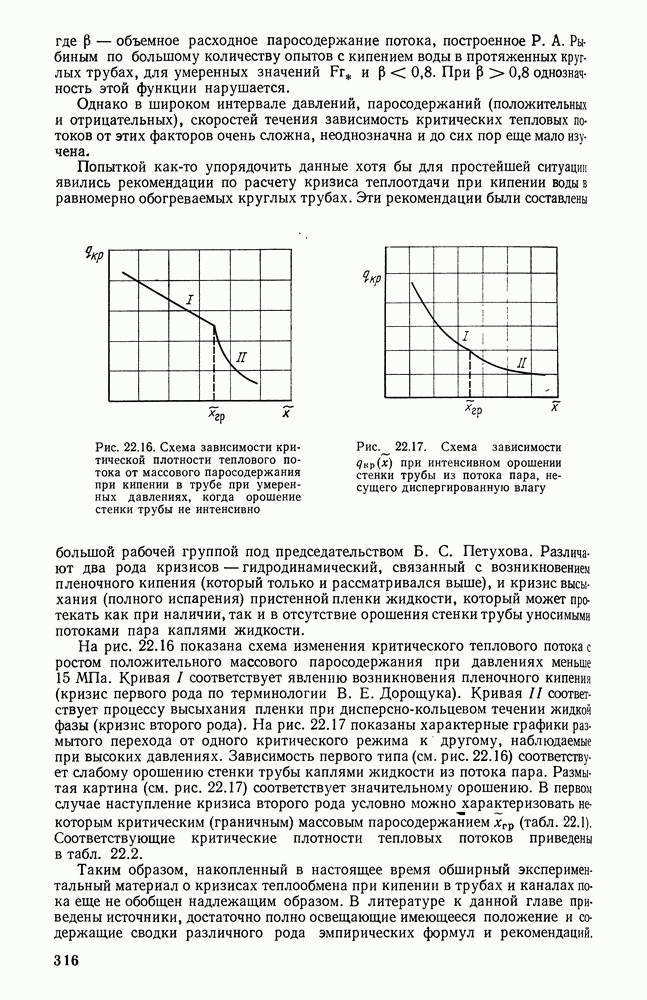
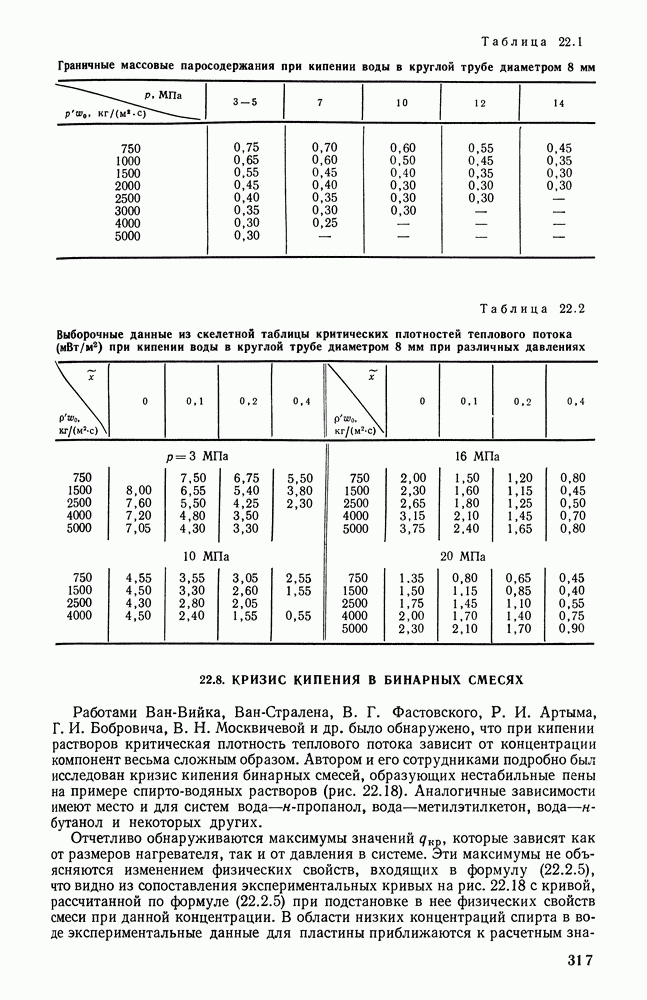
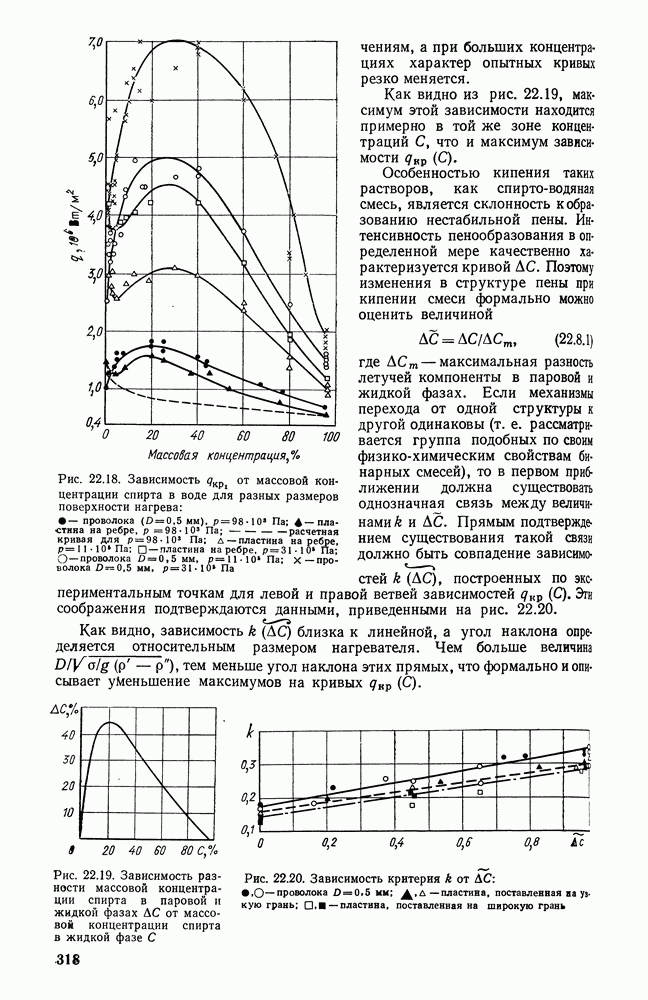
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
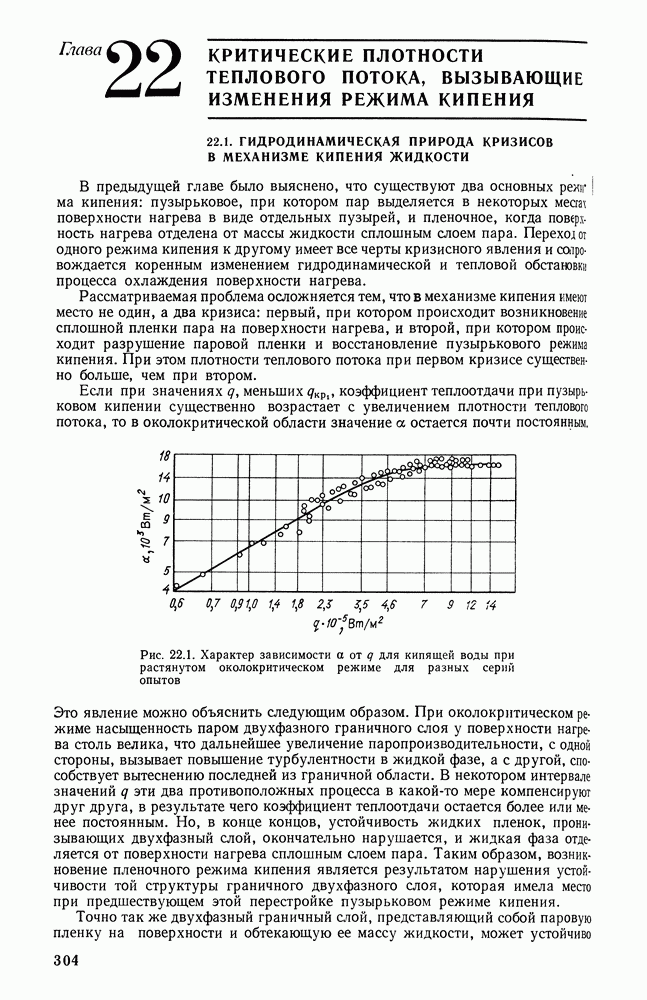
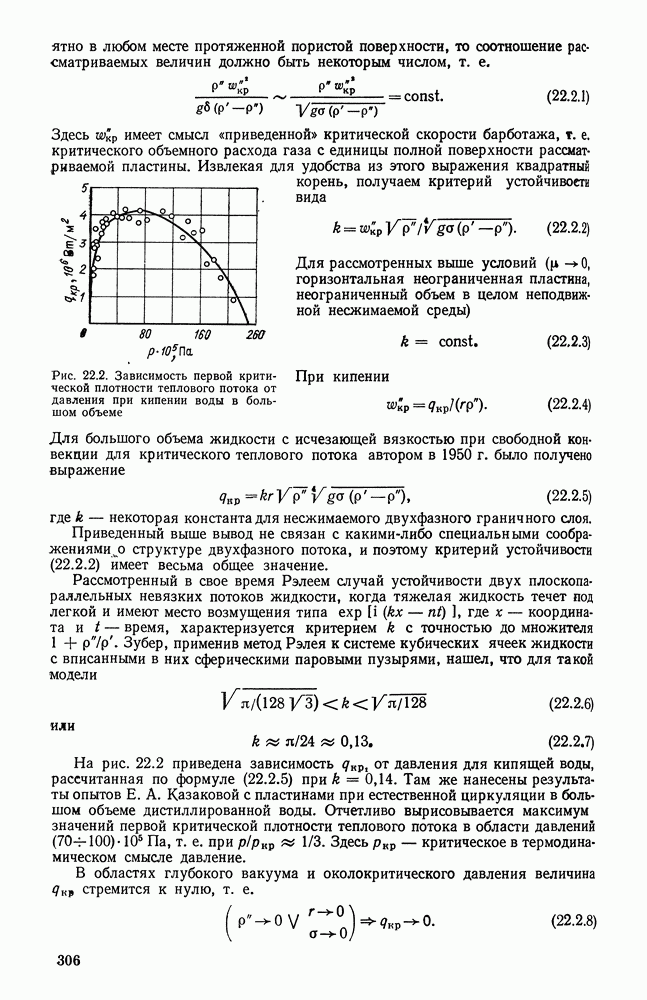
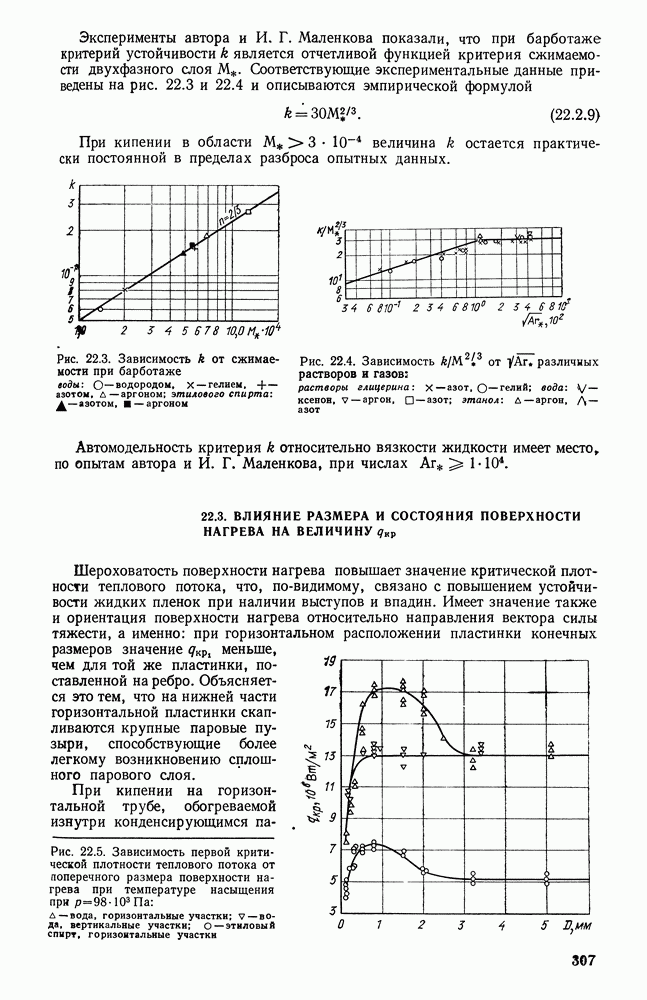
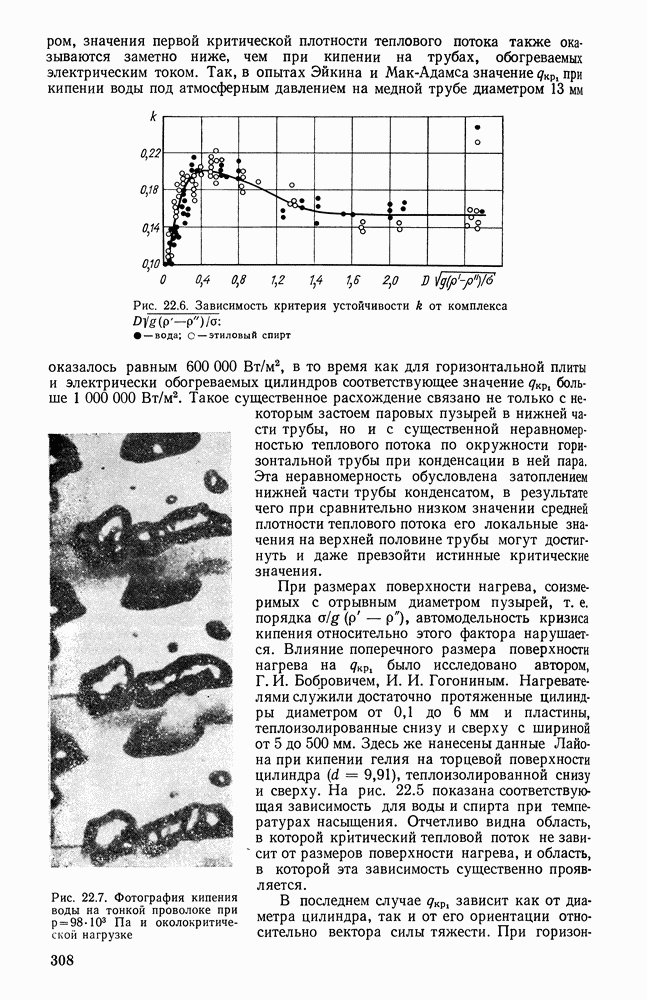
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 17. ТЕПЛООТДАЧА ПРИ СВОБОДНОЙ КОНВЕКЦИИ
17.1. СВОБОДНАЯ ТЕПЛОВАЯ КОНВЕКЦИЯ ОКОЛО ТВЕРДОЙ ПОВЕРХНОСТИ
Свободной конвекцией называется движение, возникающее вследствие различия плотностей неодинаково нагретых частей жидкой среды. Это определение следует уточнить в том смысле, что при свободной конвекции возникают специфические циркуляционные токи между поверхностью нагрева (или охлаждения) и ядром жидкой среды. Таким образом, в такое ограниченное понятие свободной конвекции не входят течения, хотя и обусловленные разностью плотностей в различных точках среды, но имеющие вполне определенное одностороннее направление, например движение газа при естественной тяге в дымовой трубе. В таких случаях хотя разность плотностей и является побудителем движения, но сам механизм процесса в значительной мере тождествен обычному вынужденному течению.
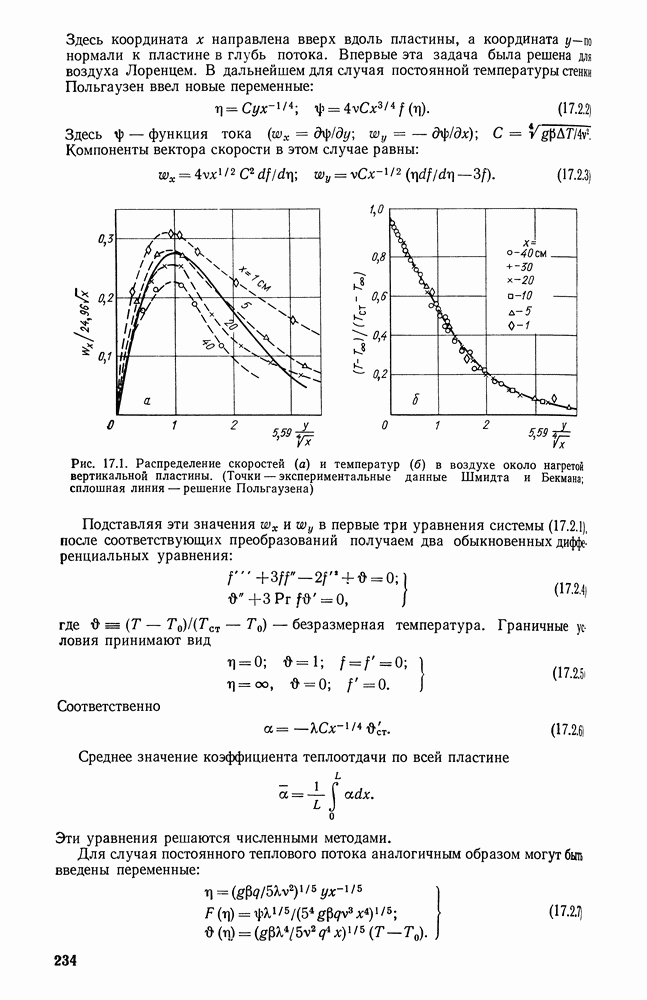
Фундаментальный вклад в исследования теплообмена при свободной тепловой конвекции был внесен Л. Лоренцем, В. Бекманом, В. С. Жуковским, М. А. Михеевым, Л. С. Эйгенсоном, Е. Шмидтом.
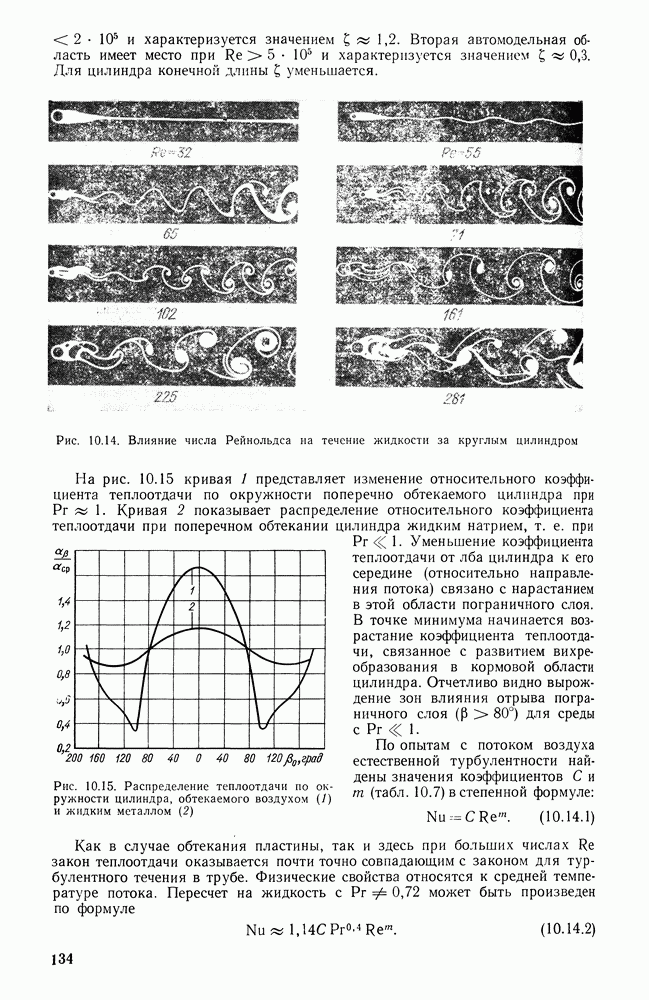
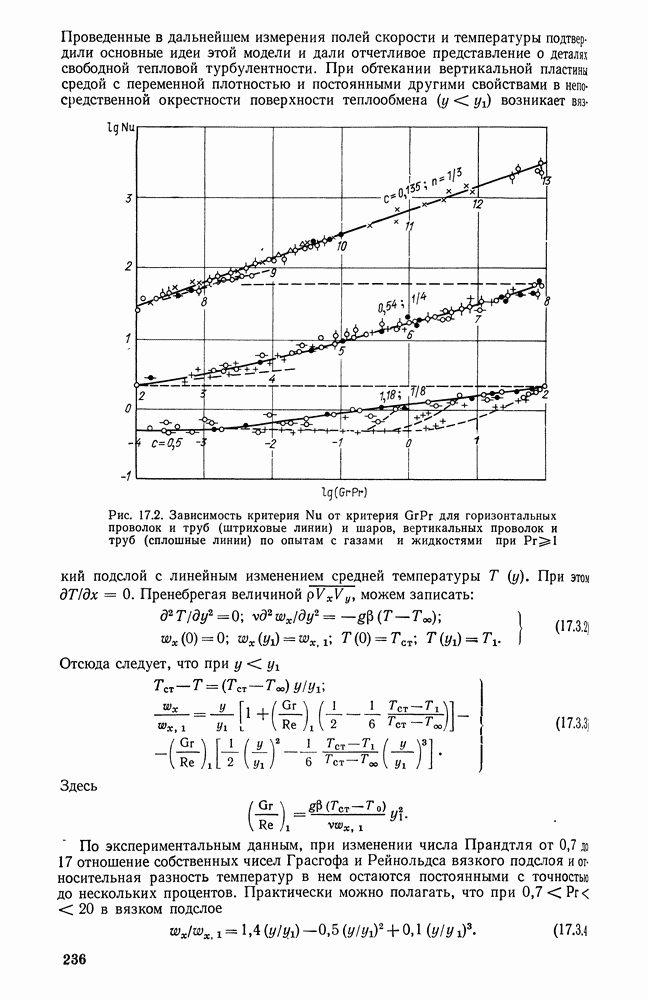
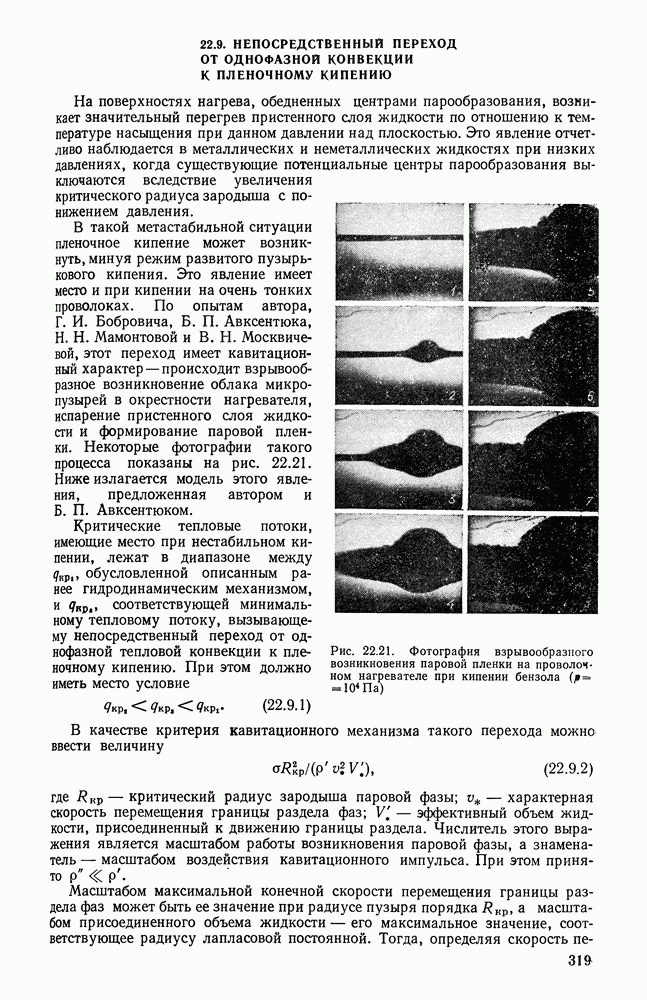
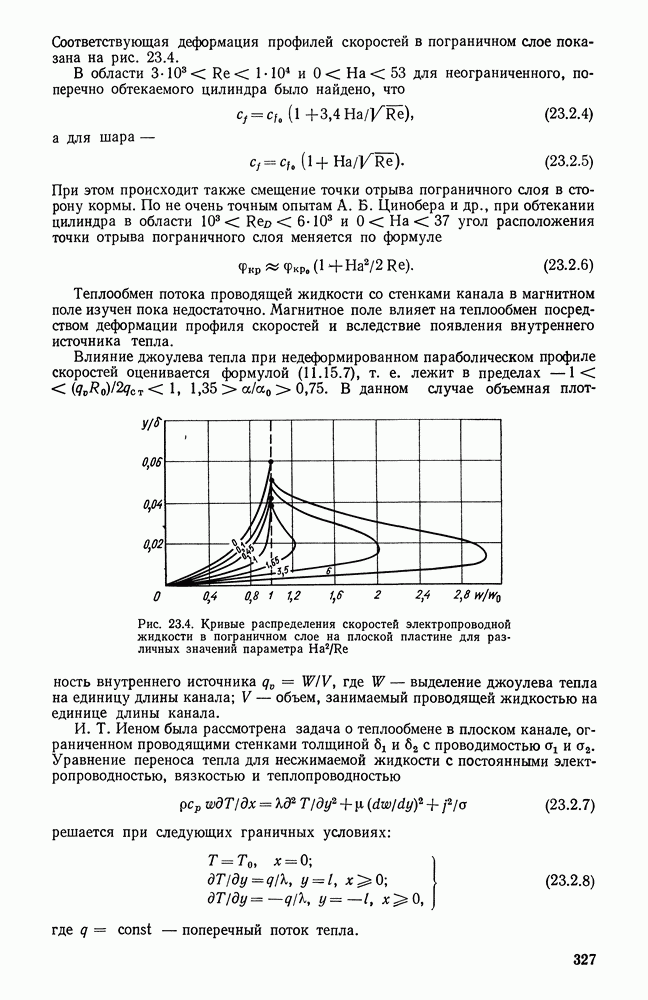
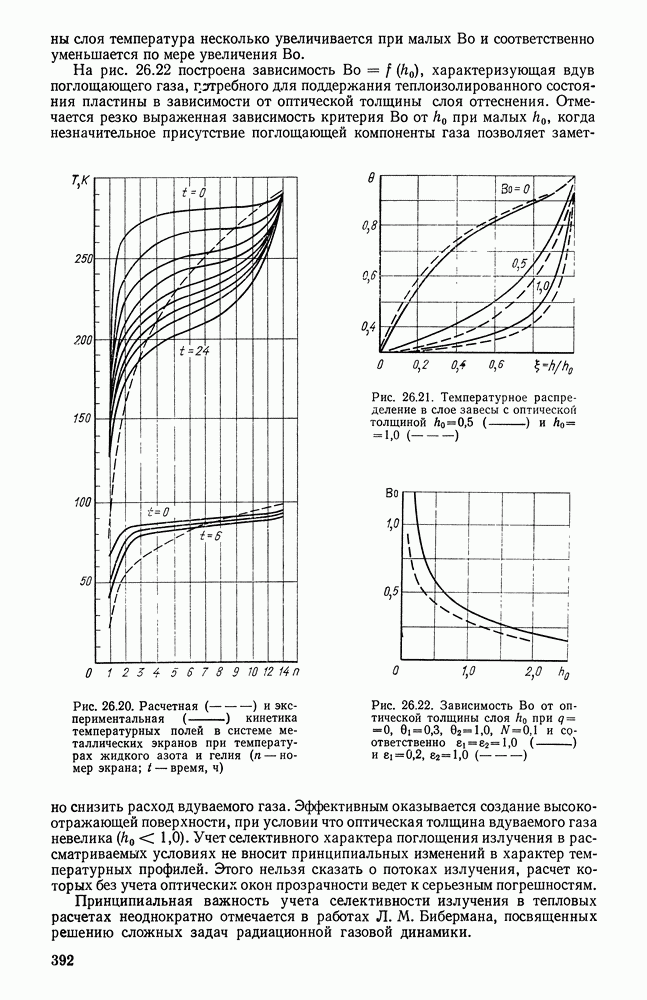
Фотографии движения воздуха около нагретой высокой плиты показывают, что на ее нижней части образуется утолщающийся ламинарный пограничный слой. На некотором расстоянии от нижнего среза плиты ламинарное течение нарушается и возникает специфическая тепловая турбулентность.
В области ламинарного пограничного слоя интенсивность теплоотдачи уменьшается с увеличением размера  как возрастает толщина этого слоя. В области тепловой турбулентности условия теплообмена определяются беспорядочным движением, характер которого статистически одинаков для различных частей поверхности нагрева, достаточно протяженных по сравнению с размерами отдельных вихрей. В этой области коэффициент теплоотдачи не зависит от размера тела.
как возрастает толщина этого слоя. В области тепловой турбулентности условия теплообмена определяются беспорядочным движением, характер которого статистически одинаков для различных частей поверхности нагрева, достаточно протяженных по сравнению с размерами отдельных вихрей. В этой области коэффициент теплоотдачи не зависит от размера тела.
Если твердое тело, введенное в жидкую среду, холоднее последней, то картина движения получается обратной, т. е. более холодные частицы жидкости будут двигаться около поверхности охлаждения сверху вниз.
Рассмотрим свободную конвекцию в условиях, когда размеры тела, нарушающего тепловое равновесие, малы по сравнению с объемом окружающей его жидкости. В этом случае область теплового и гидродинамического возмущения локализуется около рассматриваемого тела. Вне этого пограничного слоя жидкость можно считать неподвижной. Градиент давления в неподвижной жидкости равен  , где
, где  — плотность невозмущенной среды. Соответственно в уравнении движения можно произвести подстановку:
— плотность невозмущенной среды. Соответственно в уравнении движения можно произвести подстановку:
 (17.1.1)
(17.1.1)
где  — динамическая составляющая давления, обусловленная свободной конвекцией жидкости в тепловом пограничном слое;
— динамическая составляющая давления, обусловленная свободной конвекцией жидкости в тепловом пограничном слое;  — гидростатическое давление вне пограничного слоя. При не очень больших разностях температур, т. е. когда
— гидростатическое давление вне пограничного слоя. При не очень больших разностях температур, т. е. когда  влиянием переменности плотности на уравнение сплошности и на вязкостные члены уравнения движения можно пренебречь. Система основных уравнений принимает вид:
влиянием переменности плотности на уравнение сплошности и на вязкостные члены уравнения движения можно пренебречь. Система основных уравнений принимает вид:
 (17.1.2)
(17.1.2)
В более общем случае эти уравнения следует писать с учетом переменности  .
.
Условия однозначности рассматриваемой задачи включают в себя форму и размеры возмущающего тела, распределение температуры на его поверхности и ее абсолютный уровень, температуру невозмущенной жидкости, ее физические параметры ( ) и значение ускорения g. Скорость течения среды
) и значение ускорения g. Скорость течения среды  является в данном случае функцией процесса, т. е. не входит в условия однозначности, а полностью определяется заданием перечисленных выше независимых переменных.
является в данном случае функцией процесса, т. е. не входит в условия однозначности, а полностью определяется заданием перечисленных выше независимых переменных.
При этих условиях однозначности система уравнений (17.1.2) для стабилизированного течения дает два определяющих критерия:  . Таким образом, при свободной конвекции в неограниченном объеме при
. Таким образом, при свободной конвекции в неограниченном объеме при  в общем случае
в общем случае
 (17.1.3)
(17.1.3)
Если предположить, что решающее значение для теплообмена при свободной конвекции имеет термическое сопротивление ламинарного слоя около возмущающего тела, то в уравнении движения можно отбросить инерционный член, т. е. положить  . При таком упрощении исходная система уравнений дает только один определяющий критерий — число Рэлея:
. При таком упрощении исходная система уравнений дает только один определяющий критерий — число Рэлея:
 (17.1.4)
(17.1.4)
представляющее собою произведение критериев Грасгсфа и Прандтля, т. е. в этом случае
 (17.1.5)
(17.1.5)
При свободной конвекции, когда собственное движение жидкости полностью определяется процессом теплообмена, нельзя раздельно рассматривать тепловой и гидродинамический пограничные слои. Однако общие соображения об относительной глубине распространения влияния молекулярного трения и молекулярной теплопроводности, характеризуемой отношением  остаютей справедливыми и в данном случае.
остаютей справедливыми и в данном случае.
Следовательно, при  область существенного проявления молекулярной теплопроводности равна или меньше области существенного проявления молекулярной вязкости. Именно для этих условий физически обосновано указанное выше упрощение уравнения движения в результате отбрасывания инерционного члена.
область существенного проявления молекулярной теплопроводности равна или меньше области существенного проявления молекулярной вязкости. Именно для этих условий физически обосновано указанное выше упрощение уравнения движения в результате отбрасывания инерционного члена.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ТЕПЛООБМЕНА
- 1.1. ПРЕДМЕТ ТЕОРИИ ТЕПЛООБМЕНА
- 1.2. ПОЛЕ ТЕМПЕРАТУР И ПОЛЕ ТЕПЛОВЫХ ПОТОКОВ
- 1.3. КОЭФФИЦИЕНТЫ ТЕПЛООТДАЧИ И ТЕПЛОПЕРЕДАЧИ
- 1.4. ТЕРМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
- 1.5. БАЛАНСНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕННОГО АППАРАТА
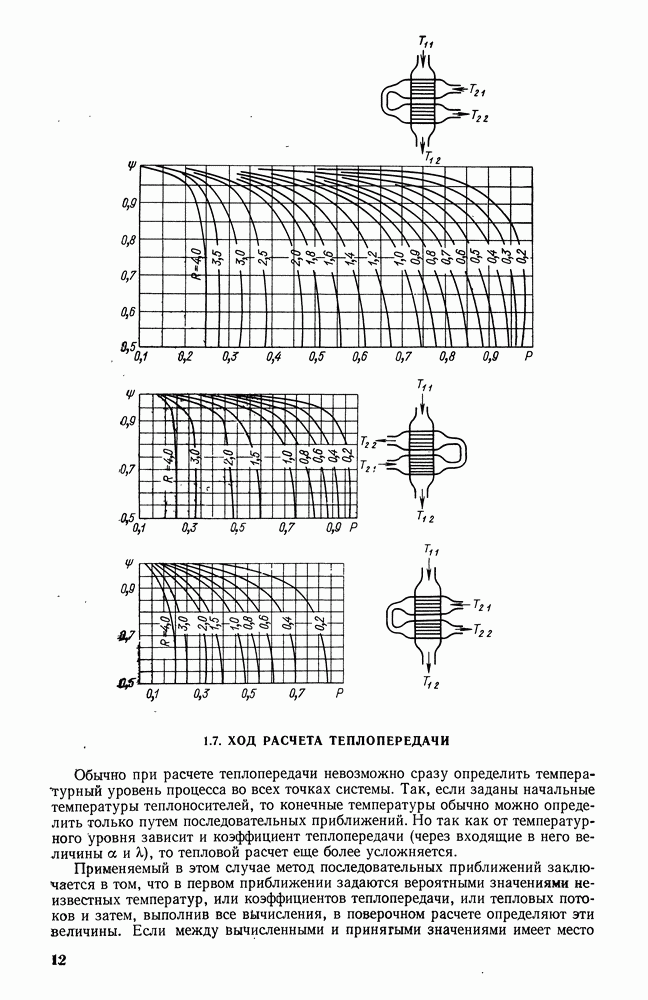
- 1.6. СРЕДНИЙ ТЕМПЕРАТУРНЫЙ НАПОР
- 1.7. ХОД РАСЧЕТА ТЕПЛОПЕРЕДАЧИ
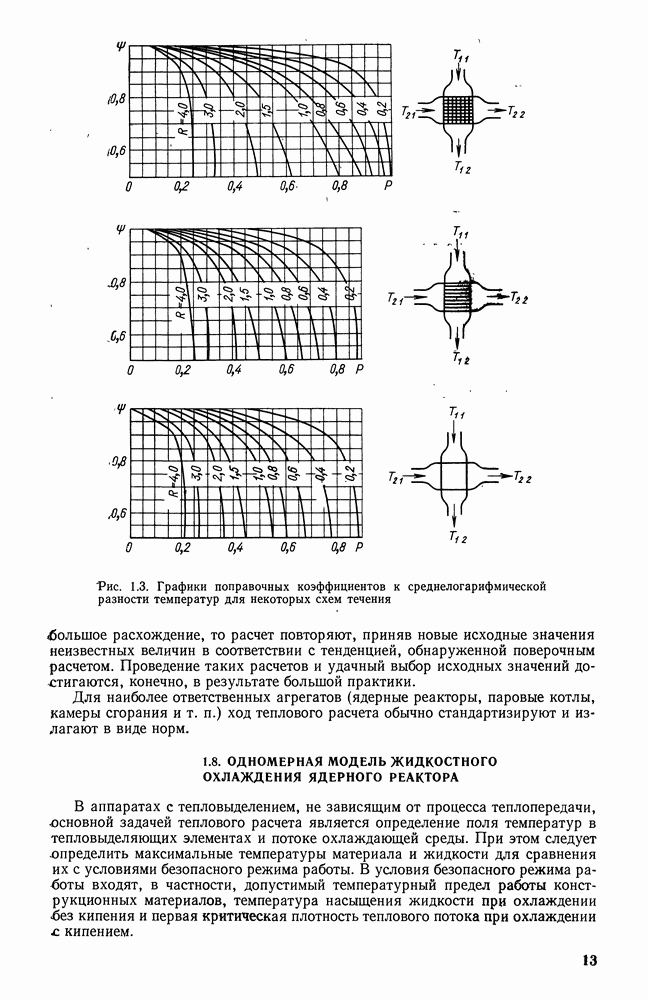
- 1.8. ОДНОМЕРНАЯ МОДЕЛЬ ЖИДКОСТНОГО ОХЛАЖДЕНИЯ ЯДЕРНОГО РЕАКТОРА
- Глава 2. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В ВЕЩЕСТВЕННОЙ СРЕДЕ
- 2.1. ГИПОТЕЗА О ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ ВЕКТОРА ТЕПЛОВОГО ПОТОКА ГРАДИЕНТУ ТЕМПЕРАТУР
- 2.2. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В ВЕЩЕСТВЕННОЙ СРЕДЕ
- 2.3. ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2.4. ТЕМПЕРАТУРА ТОРМОЖЕНИЯ
- 2.5. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ С КОНЕЧНОЙ СКОРОСТЬЮ РАСПРОСТРАНЕНИЯ ВОЗМУЩЕНИЯ
- Глава 3. УРАВНЕНИЯ ГИДРОДИНАМИКИ
- 3.1. СВЯЗЬ МЕЖДУ ПОЛЕМ ТЕМПЕРАТУР И ПОЛЕМ СКОРОСТЕЙ В ДВИЖУЩЕЙСЯ СРЕДЕ
- 3.2. УРАВНЕНИЕ СПЛОШНОСТИ ПОТОКА ЖИДКОСТИ
- 3.3. УРАВНЕНИЕ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- 3.4. ПОДЪЕМНАЯ СИЛА, ОБУСЛОВЛЕННАЯ НЕОДНОРОДНОСТЬЮ ТЕМПЕРАТУРНОГО ПОЛЯ
- Глава 4. УРАВНЕНИЯ ОСРЕДНЕННОГО ТУРБУЛЕНТНОГО ПОТОКА
- 4.1. ТУРБУЛЕНТНОСТЬ
- 4.2. УРАВНЕНИЯ ОСРЕДНЕННОГО ТУРБУЛЕНТНОГО ТЕЧЕНИЯ ЖИДКОСТИ
- 4.3. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА
- 4.4. ТУРБУЛЕНТНОЕ ТРЕНИЕ И ТУРБУЛЕНТНАЯ ТЕПЛОПРОВОДНОСТЬ В ПЛОСКОМ ПОТОКЕ ЖИДКОСТИ
- Глава 5. КРАЕВЫЕ УСЛОВИЯ
- 5.1. ВРЕМЕННЫЕ И ПРОСТРАНСТВЕННЫЕ КРАЕВЫЕ УСЛОВИЯ
- 5.2. КРАЕВЫЕ УСЛОВИЯ К УРАВНЕНИЯМ ГИДРОДИНАМИКИ
- 5.3. КРАЕВЫЕ УСЛОВИЯ К УРАВНЕНИЯМ ТЕПЛОПРОВОДНОСТИ
- 5.4. УСЛОВИЯ МЕХАНИЧЕСКОГО И ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ НА ГРАНИЦАХ ФАЗ В МНОГОФАЗНОЙ СИСТЕМЕ
- 5.5. РЕАКТИВНАЯ СИЛА ПРИ ФАЗОВОМ ПРЕВРАЩЕНИИ
- Глава 6. УСЛОВИЯ ПОДОБИЯ ПРОЦЕССОВ ТЕПЛООБМЕНА
- 6.1. ПОНЯТИЕ О ПОДОБИИ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- 6.2. КРИТЕРИИ ПОДОБИЯ
- 6.3. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ ПЕРЕМЕННЫЕ. УСЛОВИЯ ОДНОЗНАЧНОСТИ
- 6.4. КОМБИНИРОВАНИЕ КРИТЕРИЕВ. СОБСТВЕННО КРИТЕРИИ ПОДОБИЯ
- 6.5. КРИТЕРИИ ПОДОБИЯ КАК ОБОБЩЕННЫЕ БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ
- 6.6. ФИЗИЧЕСКИЙ СМЫСЛ НЕКОТОРЫХ КРИТЕРИЕВ ПОДОБИЯ
- 6.7. КРИТЕРИЙ ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ ПРИ ФИЗИКО-ХИМИЧЕСКОМ ПРЕВРАЩЕНИИ ВЕЩЕСТВА
- 6.8. БЕЗРАЗМЕРНЫЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
- Глава 7. УСТАНОВИВШИЙСЯ ТЕПЛОВОЙ ПОТОК В ТВЕРДЫХ ТЕЛАХ
- 7.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
- 7.2. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ
- 7.3. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ СТЕНКУ
- 7.4. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ШАРОВУЮ СТЕНКУ
- 7.5. ТЕПЛОПРОВОДНОСТЬ ВДОЛЬ СТЕРЖНЯ ПОСТОЯННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
- 7.6. ПРЯМОЕ РЕБРО ПОСТОЯННОГО ТЕПЛОВОГО НАПРЯЖЕНИЯ
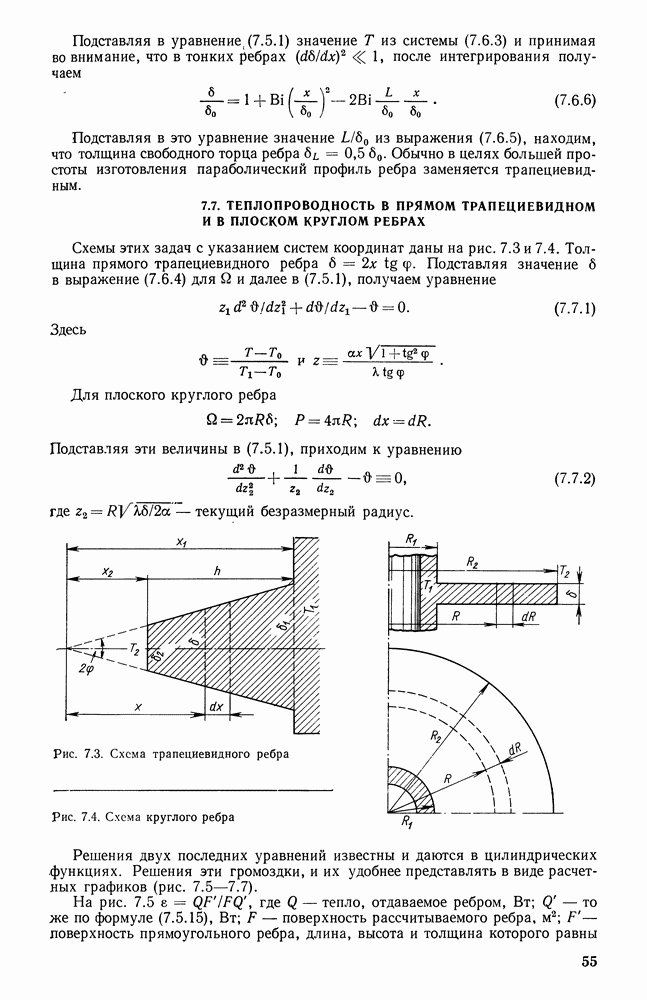
- 7.7. ТЕПЛОПРОВОДНОСТЬ В ПРЯМОМ ТРАПЕЦИЕВИДНОМ И В ПЛОСКОМ КРУГЛОМ РЕБРАХ
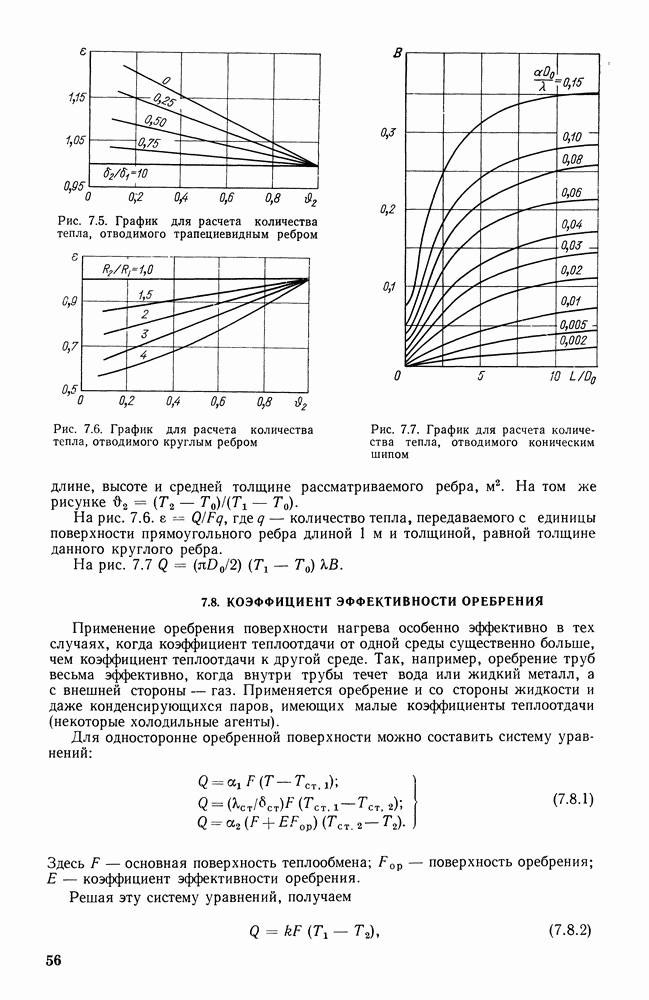
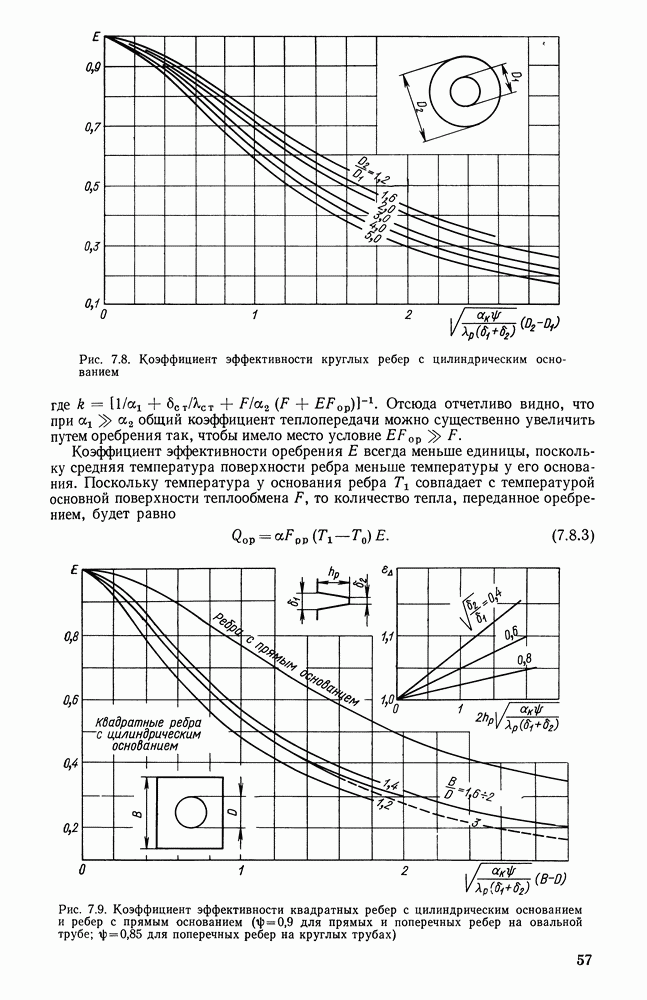
- 7.8. КОЭФФИЦИЕНТ ЭФФЕКТИВНОСТИ ОРЕБРЕНИЯ
- 7.9. ТЕПЛОПРОВОДНОСТЬ В СТЕРЖНЕ И ШАРЕ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛА
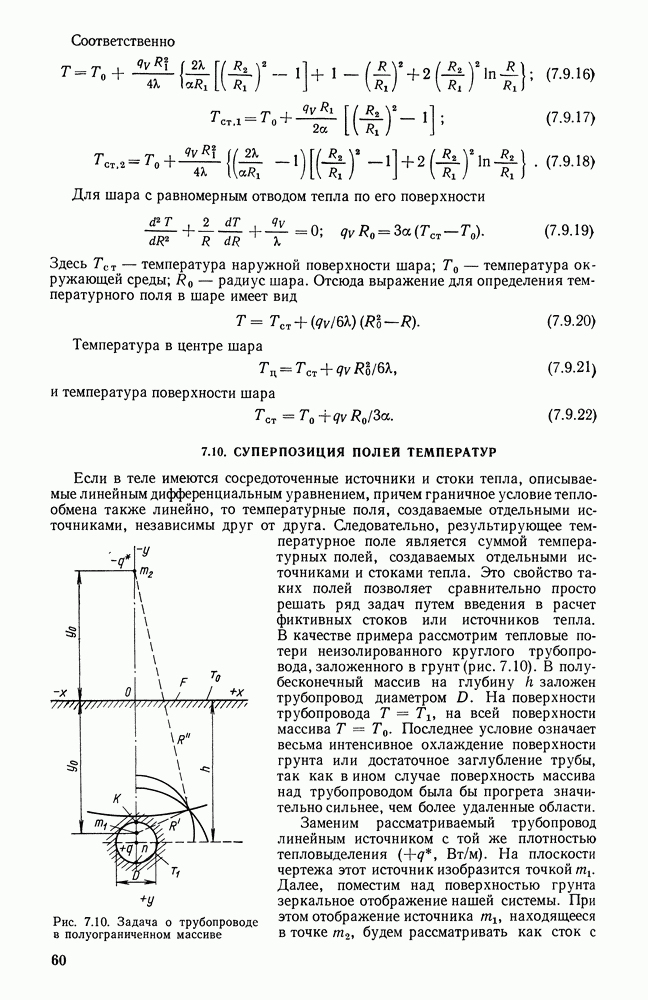
- 7.10. СУПЕРПОЗИЦИЯ ПОЛЕЙ ТЕМПЕРАТУР
- 7.11. УЧЕТ ВНЕШНЕГО ТЕРМИЧЕСКОГО СОПРОТИВЛЕНИЯ МЕТОДОМ ДОПОЛНИТЕЛЬНОЙ СТЕНКИ
- Глава 8. НЕУСТАНОВИВШИЙСЯ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ БЕЗ ВНУТРЕННИХ ИСТОЧНИКОВ
- 8.1. УРАВНЕНИЕ НЕСТАЦИОНАРНОГО ТЕМПЕРАТУРНОГО ПОЛЯ
- 8.2. РЕШЕНИЕ В ВИДЕ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ
- 8.3. ТЕМПЕРАТУРА — ФУНКЦИЯ ОДНОЙ КООРДИНАТЫ И ВРЕМЕНИ
- 8.4. МОНОТОННЫЙ ПЕРЕХОД К ТЕПЛОВОМУ РАВНОВЕСИЮ
- 8.5. ТЕМПЕРАТУРНОЕ ПОЛЕ В ТЕЛЕ ПРИ ТЕМПЕРАТУРЕ ВНЕШНЕЙ СРЕДЫ, ЛИНЕЙНО МЕНЯЮЩЕЙСЯ ВО ВРЕМЕНИ
- 8.6. РЕГУЛЯРНЫЙ РЕЖИМ ОХЛАЖДЕНИЯ
- 8.7. ОХЛАЖДЕНИЕ ВЫСОКОТЕПЛОПРОВОДНОГО ТЕЛА
- 8.8. ТЕПЛОВЫЕ ВОЛНЫ
- Глава 9. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
- 9.1. УРАВНЕНИЕ ТЕПЛОПЕРЕНОСА
- 9.2. СВЯЗЬ МЕЖДУ ТЕПЛООТДАЧЕЙ И ТРЕНИЕМ
- 9.3. ПОГРАНИЧНЫЙ СЛОЙ
- 9.4. СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕПЛООБМЕНА В ПОТОКЕ СЖИМАЕМОГО ГАЗА
- 9.5. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ПЛОСКОГО СТАЦИОНАРНОГО ПОГРАНИЧНОГО СЛОЯ НА НЕПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 9.6. РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И СКОРОСТЕЙ В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ
- 9.7. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТЕПЛОВОГО ПОТОКА И ТЕМПЕРАТУРЫ В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ
- 9.8. ПОЛУЭМПИРИЧЕСКИЕ ВЫРАЖЕНИЯ ТУРБУЛЕНТНОГО ОБМЕНА В ПЛОСКОМ НЕСЖИМАЕМОМ ПОТОКЕ ВБЛИЗИ ТВЕРДОЙ СТЕНКИ
- 9.9. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ТУРБУЛЕНТНОЙ ТЕПЛОПРОВОДНОСТИ И ВЯЗКОСТИ
- 9.10. ТУРБУЛЕНТНЫЙ ПЕРЕНОС В ВЯЗКОМ ПОДСЛОЕ
- 9.11. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ПЛОСКОМ НЕСЖИМАЕМОМ ПОТОКЕ ВБЛИЗИ СТЕНКИ
- 9.12. РАСПРОСТРАНЕНИЕ ПОЛУЭМПИРИЧЕСКИХ ВЫРАЖЕНИЙ ДЛЯ ТУРБУЛЕНТНЫХ ПЕРЕНОСОВ В НЕСЖИМАЕМОЙ ЖИДКОСТИ НА ПЛОСКИЙ ПОТОК ГАЗА
- 9.13. ПОРЯДОК ВЕЛИЧИНЫ вязкого подслоя НА НЕПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 9.14. ПРЕДЕЛЬНЫЕ ОТНОСИТЕЛЬНЫЕ ЗАКОНЫ ТРЕНИЯ И ТЕПЛООБМЕНА
- Глава 10. ТЕПЛООТДАЧА ПРИ ВНЕШНЕМ ОБТЕКАНИИ ТЕЛ НЕСЖИМАЕМОЙ ЖИДКОСТЬЮ
- 10.1. ХАРАКТЕР ВНЕШНЕГО ОБТЕКАНИЯ
- 10.2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ (ТОЧНОЕ РЕШЕНИЕ)
- 10.3. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПЛАСТИНЫ, ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.4. ТЕПЛООТДАЧА ПЛАСТИНЫ, ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ ПРИ Рr>=1 (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.5. ТЕПЛООТДАЧА ПЛАСТИНЫ. ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ ПРИ Рr<<1 (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.6. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПЛАСТИНЫ, ОБТЕКАЕМОЙ ТУРБУЛЕНТНЫМ ПОГРАНИЧНЫМ СЛОЕМ
- 10.7. ТЕПЛООТДАЧА ПЛАСТИНЫ. ОБТЕКАЕМОЙ ТУРБУЛЕНТНЫМ ПОГРАНИЧНЫМ СЛОЕМ С ПОСТОЯННЫМИ ФИЗИЧЕСКИМИ СВОЙСТВАМИ
- 10.8. НЕИЗОТЕРМИЧЕСКИЙ ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПЛАСТИНЕ
- 10.9. НЕИЗОТЕРМИЧЕСКИЙ ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПЛАСТИНЕ
- 10.10. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТИ
- 10.11. КОНСЕРВАТИВНОСТЬ ЗАКОНА ТЕПЛООБМЕНА ОТНОСИТЕЛЬНО ГРАДИЕНТА ДАВЛЕНИЯ
- 10.12. ИНТЕГРАЛ УРАВНЕНИЯ ЭНЕРГИИ
- 10.13. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ ШАРА
- 10.14. ТЕПЛООТДАЧА ПРИ ПОПЕРЕЧНОМ ОБТЕКАНИИ ОДИНОЧНОГО ЦИЛИНДРА
- Глава 11. ТЕПЛООТДАЧА ПРИ ТЕЧЕНИИ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
- 11.1. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ ИЗОТЕРМИЧЕСКОМ ТЕЧЕНИИ
- 11.2. ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ
- 11.3. УРАВНЕНИЕ ТЕПЛОПЕРЕНОСА В ТУРБУЛЕНТНОМ ПОТОКЕ
- 11.4. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ТЕПЛООТДАЧИ И ТРЕНИЯ
- 11.5. РЕШЕНИЕ ПРИ ЛИНЕЙНОМ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ СТЕНКИ
- 11.6. ТЕПЛООТДАЧА К ТУРБУЛЕНТНОМУ ПОТОКУ ПРИ Рr>1
- 11.7. ТЕПЛООТДАЧА К ТУРБУЛЕНТНОМУ ПОТОКУ ПРИ Рr«1
- 11.8. ТЕМПЕРАТУРНЫЙ ФАКТОР
- 11.9. ВЛИЯНИЕ ТЕМПЕРАТУРНОГО ФАКТОРА НА ТРЕНИЕ И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ ГАЗА
- 11.10. ВЛИЯНИЕ ТЕПЛОВОГО ПОТОКА НА ТЕПЛООТДАЧУ ПРИ ТЕЧЕНИИ КАПЕЛЬНЫХ ЖИДКОСТЕЙ
- 11.11. ТЕПЛООБМЕН И ТРЕНИЕ ВО ВХОДНОМ УЧАСТКЕ ТРУБЫ
- 11.12. ТЕПЛООБМЕН ПРИ ПРОДОЛЬНОМ ТЕЧЕНИИ В КАНАЛАХ НЕЦИЛИНДРИЧЕСКОЙ ФОРМЫ
- 11.13. ТЕПЛООБМЕН ПРИ ТЕЧЕНИИ ХИМИЧЕСКИ РЕАГИРУЮЩИХ ГАЗОВЫХ ТЕПЛОНОСИТЕЛЕЙ
- 11.14. ВЛИЯНИЕ ШЕРОХОВАТОСТИ СТЕНКИ ТРУБЫ НА ТЕПЛООТДАЧУ
- 11.15. ВЛИЯНИЕ ВНУТРЕННЕГО ИСТОЧНИКА ТЕПЛА
- Глава 12. ТЕПЛООБМЕН ПРИ БОЛЬШИХ СКОРОСТЯХ ТЕЧЕНИЯ ГАЗА
- 12.1. СВЯЗЬ МЕЖДУ ТЕМПЕРАТУРОЙ ТОРМОЖЕНИЯ И СКОРОСТЬЮ РАСПРОСТРАНЕНИЯ ЗВУКА В ГАЗЕ
- 12.2. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ТЕМПЕРАТУРЫ И ОБОБЩЕННЫЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
- 12.3. ТЕПЛООТДАЧА К ПЛАСТИНЕ
- 12.4. КОЭФФИЦИЕНТ ТРЕНИЯ ПЛАСТИНЫ ПРИ ЛАМИНАРНОМ ПОГРАНИЧНОМ СЛОЕ
- 12.5. ПРОФИЛЬ СКОРОСТЕЙ В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ НА НЕПРОНИЦАЕМОЙ ПЛАСТИНЕ
- 12.6. КОЭФФИЦИЕНТ ТРЕНИЯ И ТЕПЛООТДАЧИ ПЛАСТИНЫ ПРИ ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ
- 12.7. ТРЕНИЕ И ТЕПЛООБМЕН В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ ДИССОЦИИРОВАННОГО ГАЗА
- Глава 13. ТЕПЛООБМЕН И ТРЕНИЕ ПРИ ПЕРЕНОСЕ ВЕЩЕСТВА
- 13.1. МАССООБМЕН И ТЕПЛОПЕРЕДАЧА
- 13.2. УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ
- 13.3. ТРОЙНАЯ АНАЛОГИЯ
- 13.4. РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ТЕПЛОВОГО ПОТОКА В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ НА ПОЛУПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 13.5. ПРЕДЕЛЬНЫЙ ЗАКОН ТРЕНИЯ В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ
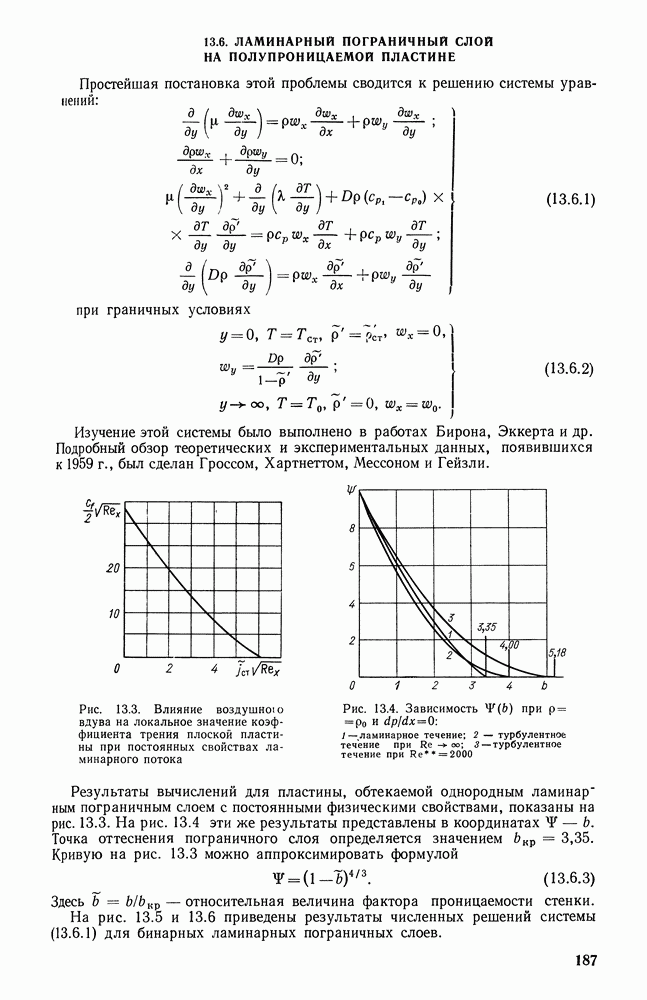
- 13.6. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ
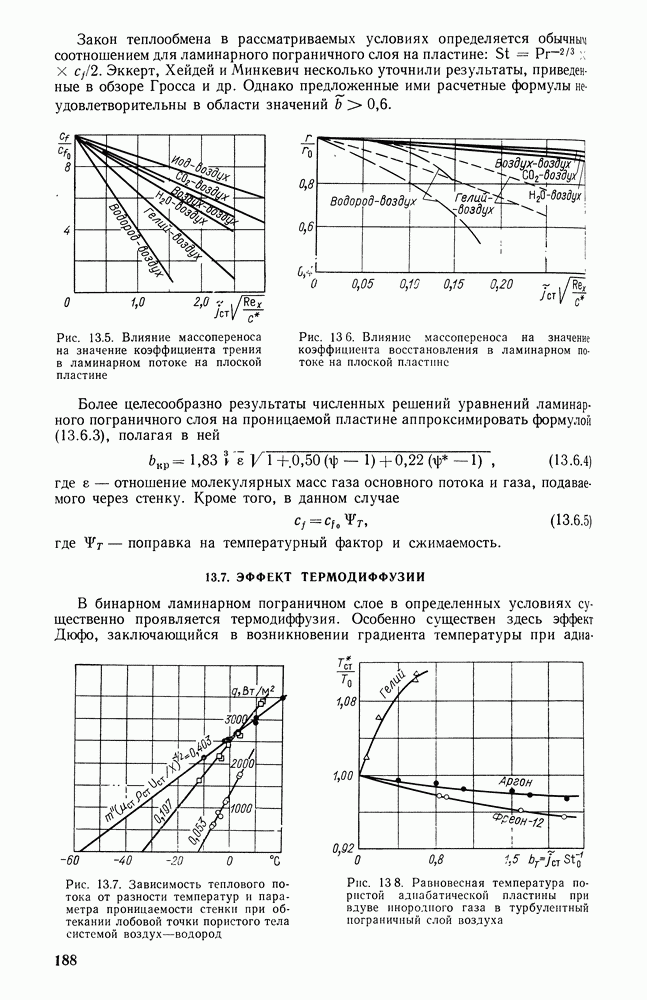
- 13.7. ЭФФЕКТ ТЕРМОДИФФУЗИИ
- 13.8. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ ПРИ
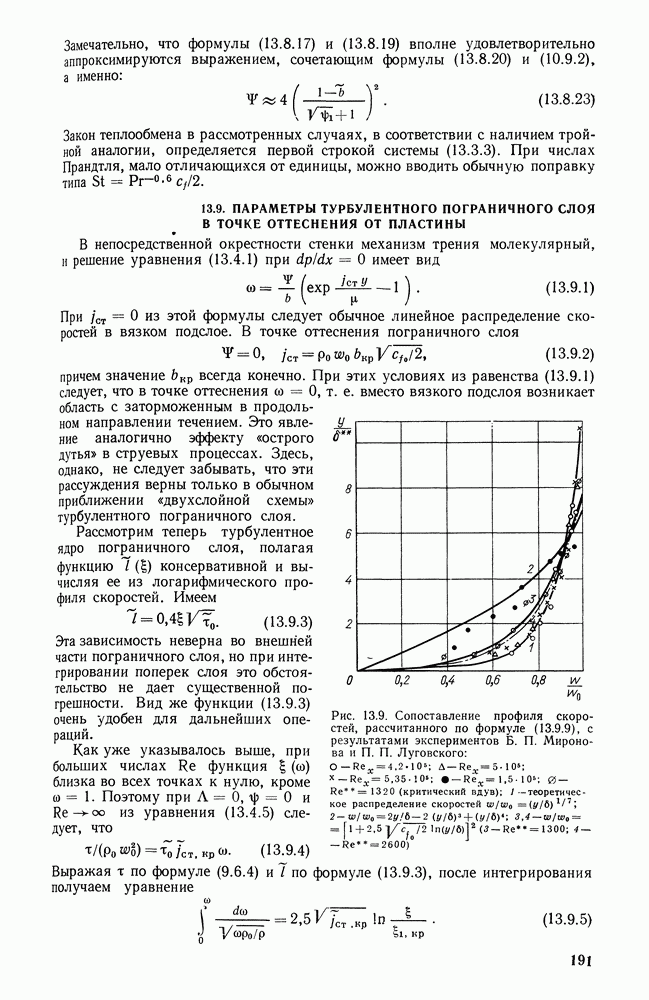
- 13.9. ПАРАМЕТРЫ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ В ТОЧКЕ ОТТЕСНЕНИЯ ОТ ПЛАСТИНЫ
- 13.10. ДВА ВАЖНЫХ ЧАСТНЫХ РЕШЕНИЯ УРАВНЕНИЯ ИМПУЛЬСОВ ДЛЯ ПОГРАНИЧНОГО СЛОЯ НА ПЛАСТИНЕ
- 13.11. ЗАКОНЫ ТРЕНИЯ И ТЕПЛООБМЕНА В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ ГАЗА ПРИ КОНЕЧНЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- Глава 14. ТЕПЛОВЫЕ ЗАВЕСЫ
- 14.1. ТИПЫ ЗАВЕС
- 14.2. ПОГРАНИЧНЫЙ СЛОЙ В ТЕПЛОВОЙ ЗАВЕСЕ НА АДИАБАТИЧЕСКОЙ ПОВЕРХНОСТИ
- 14.3. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ПРЕДВКЛЮЧЕННЫМ УЧАСТКОМ ТЕПЛООБМЕНА
- 14.4. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ПРЕДВКЛЮЧЕННЫМ ПОРИСТЫМ УЧАСТКОМ
- 14.5. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ГАЗОВОЙ ЗАВЕСОЙ
- 14.6. НЕАДИАБАТИЧЕСКАЯ ПЛАСТИНА С ГАЗОВОЙ ЗАВЕСОЙ
- 14.7. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ИМПУЛЬСОВ ПРИ ВЗАИМОДЕЙСТВИИ ЗАТОПЛЕННОЙ СТРУИ С ПЛОСКОЙ ПЛАСТИНОЙ
- 14.8. ТРЕНИЕ И ТЕПЛООБМЕН ПРИ ВЗАИМОДЕЙСТВИИ ЗАТОПЛЕННОЙ СТРУИ С ТВЕРДОЙ СТЕНКОЙ
- Глава 15. ТЕПЛООБМЕН В ПАКЕТАХ И ЗАСЫПКАХ
- 15.1. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ПАКЕТОВ ЦИЛИНДРОВ
- 15.2. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ПАКЕТОВ ЦИЛИНДРОВ
- 15.3. ПАКЕТЫ ШАРОВ
- 15.4. КИПЯЩИЙ СЛОЙ
- 15.5. НЕОДНОРОДНОСТИ И НЕУСТОЙЧИВОСТИ В СЛОЕ ЧАСТИЦ
- Глава 16. ГИДРОДИНАМИКА И ТЕПЛООБМЕН В СРЕДАХ С НЕЛИНЕЙНЫМ ЗАКОНОМ МОЛЕКУЛЯРНОГО ТРЕНИЯ
- 16.1. ЖИДКОСТИ С НЕЛИНЕЙНОЙ КРИВОЙ ТЕЧЕНИЯ
- 16.2. СВЯЗЬ МЕЖДУ ТЕКУЧЕСТЬЮ И КАСАТЕЛЬНЫМИ НАПРЯЖЕНИЯМИ В ПОТОКЕ ЖИДКОСТИ СО СТРУКТУРНОЙ ВЯЗКОСТЬЮ
- 16.3. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ СТАБИЛИЗИРОВАННОМ ИЗОТЕРМИЧЕСКОМ ТЕЧЕНИИ ЖИДКОСТИ С ЛИНЕЙНЫМ ЗАКОНОМ ТЕКУЧЕСТИ
- 16.4. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ ПРОДОЛЬНОМ ИЗОТЕРМИЧЕСКОМ ОБТЕКАНИИ ПЛАСТИНЫ
- 16.5. СВЯЗЬ МЕЖДУ ИСТИННОЙ И КАЖУЩЕЙСЯ ТЕКУЧЕСТЬЮ
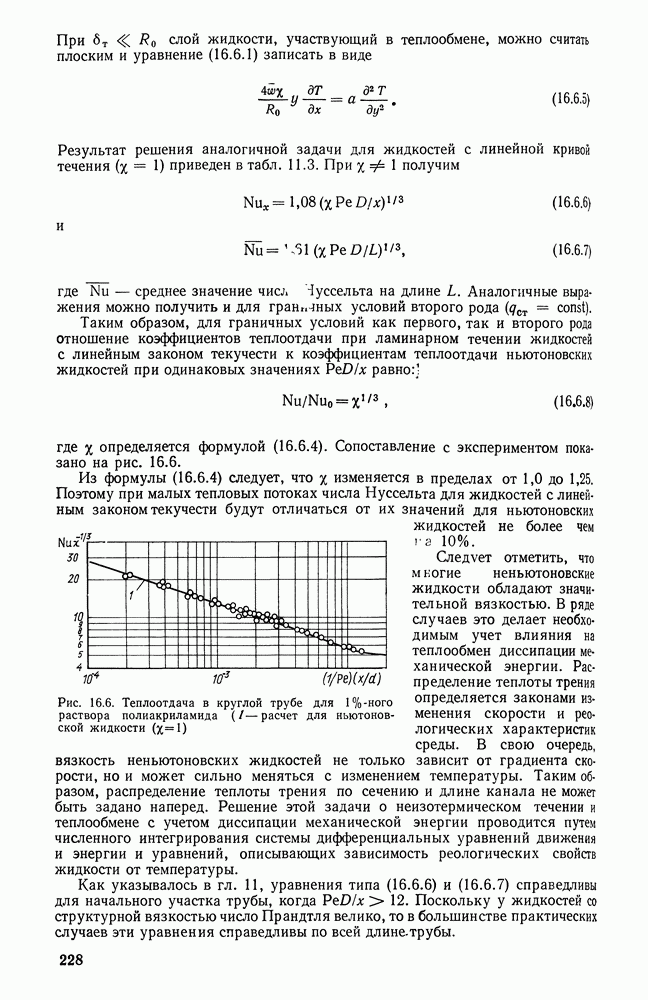
- 16.6. ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ ЖИДКОСТЕЙ С ЛИНЕЙНЫМ ЗАКОНОМ ТЕКУЧЕСТИ
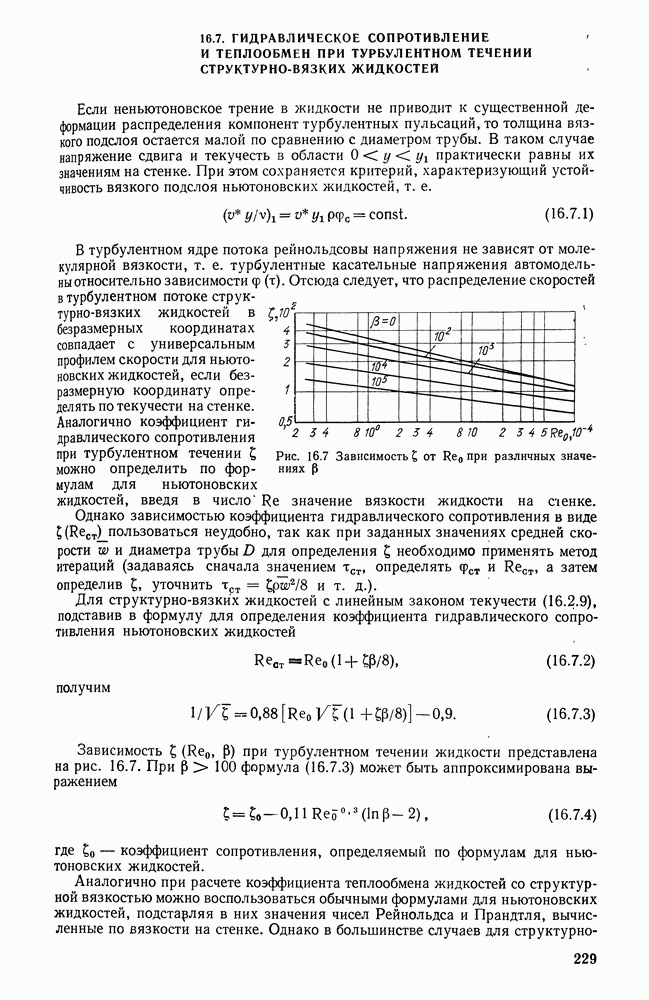
- 16.7. ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ СТРУКТУРНО-ВЯЗКИХ ЖИДКОСТЕЙ
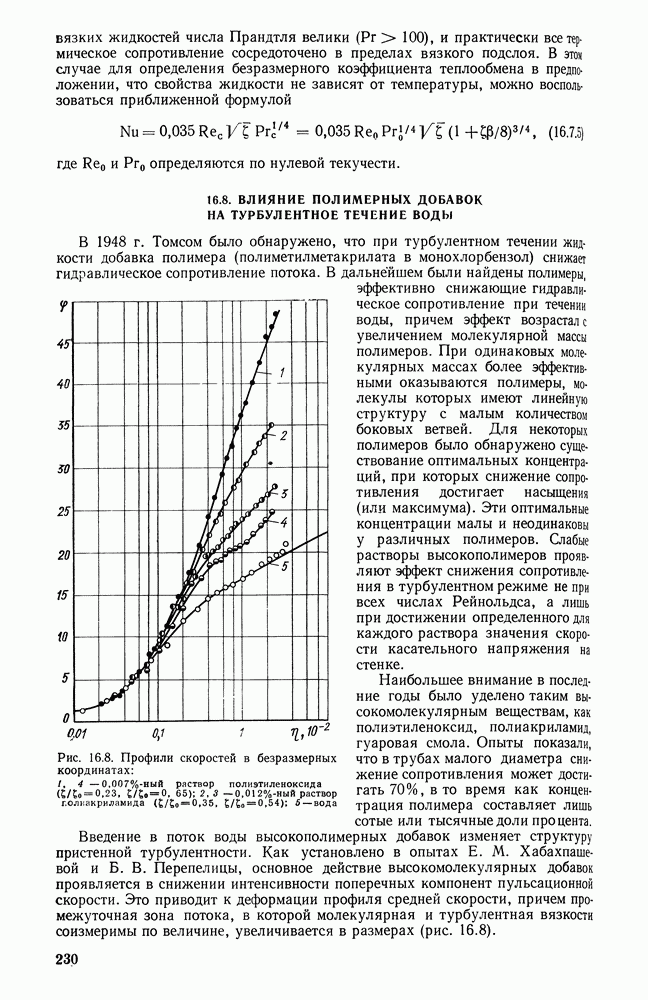
- 16.8. ВЛИЯНИЕ ПОЛИМЕРНЫХ ДОБАВОК НА ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ВОДЫ
- Глава 17. ТЕПЛООТДАЧА ПРИ СВОБОДНОЙ КОНВЕКЦИИ
- 17.1. СВОБОДНАЯ ТЕПЛОВАЯ КОНВЕКЦИЯ ОКОЛО ТВЕРДОЙ ПОВЕРХНОСТИ
- 17.2. ТЕПЛООТДАЧА В ОБЛАСТИ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ ПРИ Pr>=1
- 17.3. ГИДРОДИНАМИКА И ТЕПЛООБМЕН В ОБЛАСТИ РАЗВИТОЙ ТЕПЛОВОЙ ТУРБУЛЕНТНОСТИ ПРИ Рr>=1
- 17.4. ТЕПЛООТДАЧА ПРИ Рr<<1
- 17.5. ТЕПЛООТДАЧА В ЖИДКИХ И ГАЗОВЫХ СЛОЯХ
- 17.6. СОВМЕСТНОЕ ВЛИЯНИЕ СВОБОДНОЙ И ВЫНУЖДЕННОЙ КОНВЕКЦИИ
- Глава 18. ТЕПЛООБМЕН В РАЗРЕЖЕННЫХ ГАЗАХ
- 18.1. ОСОБЕННОСТИ ПРОЦЕССОВ ПЕРЕНОСА В РАЗРЕЖЕННОМ ГАЗЕ
- 18.2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ С ПОВЕРХНОСТЬЮ. СВОБОДНО-МОЛЕКУЛЯРНЫЙ ПЕРЕНОС ТЕПЛА
- 18.3. ТЕЧЕНИЕ СО СКОЛЬЖЕНИЕМ И ТЕМПЕРАТУРНЫМ СКАЧКОМ
- 18.4. ОСОБЕННОСТИ ТЕПЛООБМЕНА ПРИ ГИПЕРЗВУКОВЫХ СКОРОСТЯХ
- 18.5. РЕЛАКСАЦИОННЫЕ ЭФФЕКТЫ ПРИ ОБТЕКАНИИ ТЕЛ РАЗРЕЖЕННЫМ ГАЗОМ
- 18.6. СВОБОДНАЯ КОНВЕКЦИЯ В РАЗРЕЖЕННОМ ГАЗЕ
- 18.7. ВАКУУМНАЯ ИЗОЛЯЦИЯ
- Глава 19. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ПАРА НА ТВЕРДЫХ ПОВЕРХНОСТЯХ
- 19.1. ПЛЕНОЧНАЯ И КАПЕЛЬНАЯ КОНДЕНСАЦИЯ
- 19.2. ОСНОВНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА ПРИ ПЛЕНОЧНОЙ КОНДЕНСАЦИИ ЧИСТОГО НАСЫЩЕННОГО ПАРА
- 19.3. ЛАМИНАРНОЕ ТЕЧЕНИЕ ПЛЕНКИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ ПРИ МЕДЛЕННОМ ДВИЖЕНИИ ПАРА
- 19.4. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ПЛЕНКИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ ПРИ МЕДЛЕННОМ ДВИЖЕНИИ ПАРА
- 19.5. СРЕДНИЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ ПРИ СМЕШАННОМ ТЕЧЕНИИ ПЛЕНКИ КОНДЕНСАТА НА ВЕРТИКАЛЬНОЙ СТЕНКЕ
- 19.6. ВЛИЯНИЕ СКОРОСТИ ТЕЧЕНИЯ ЧИСТОГО ПАРА НА ТЕПЛООТДАЧУ ПРИ КОНДЕНСАЦИИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ
- 19.7. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ПАРА ВНУТРИ ТРУБЫ
- 19.8. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ЧИСТОГО ПАРА НА ВНЕШНЕЙ ПОВЕРХНОСТИ ГОРИЗОНТАЛЬНЫХ ТРУБ
- 19.9. ПЛЕНОЧНАЯ КОНДЕНСАЦИЯ НА НИЖНЕЙ ПОВЕРХНОСТИ ГОРИЗОНТАЛЬНОЙ ПЛИТЫ
- 9.10. ВЛИЯНИЕ ВЛАЖНОСТИ И ПЕРЕГРЕВА ПАРА
- 19.11. КАПЕЛЬНАЯ КОНДЕНСАЦИЯ
- Глава 20. КОНДЕНСАЦИЯ НА СВОБОДНОЙ ПОВЕРХНОСТИ ЖИДКОСТИ
- 20.1. ТЕПЛООБМЕН В СВОБОДНО ПАДАЮЩЕЙ СТРУЕ
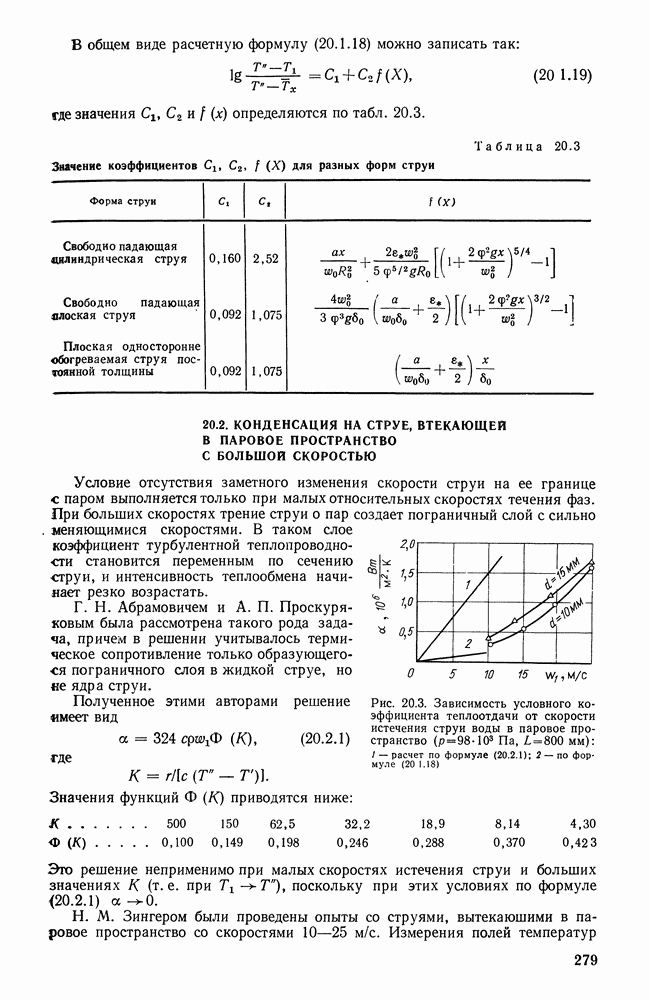
- 20.2. КОНДЕНСАЦИЯ НА СТРУЕ, ВТЕКАЮЩЕЙ В ПАРОВОЕ ПРОСТРАНСТВО С БОЛЬШОЙ СКОРОСТЬЮ
- Глава 21. ТЕПЛООТДАЧА ПРИ КИПЕНИИ ОДНОРОДНЫХ ЖИДКОСТЕЙ
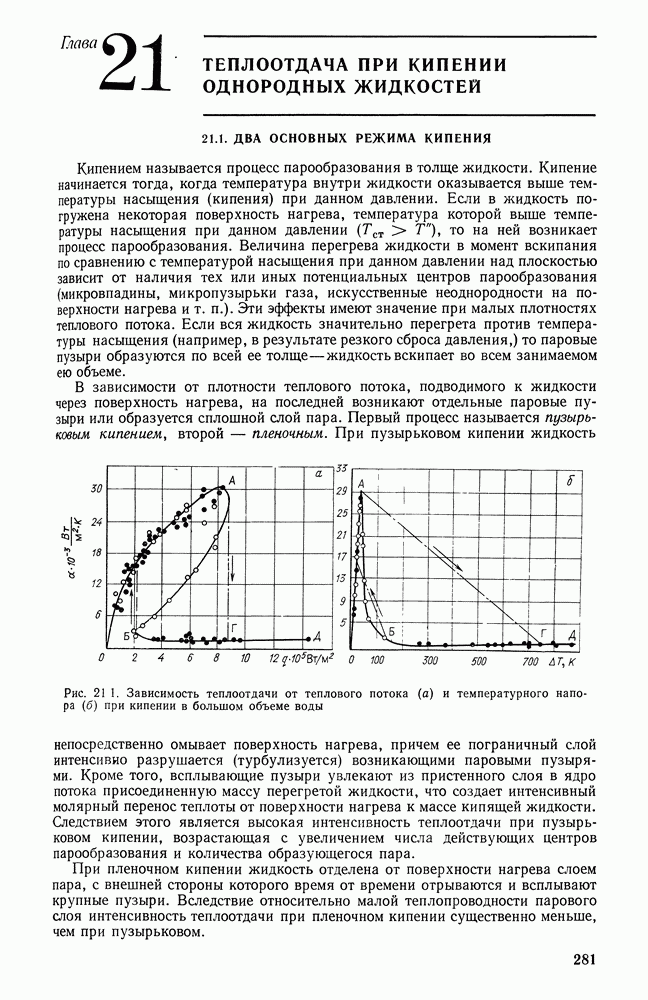
- 21.1. ДВА ОСНОВНЫХ РЕЖИМА КИПЕНИЯ
- 21.2. ТЕМПЕРАТУРНОЕ ПОЛЕ
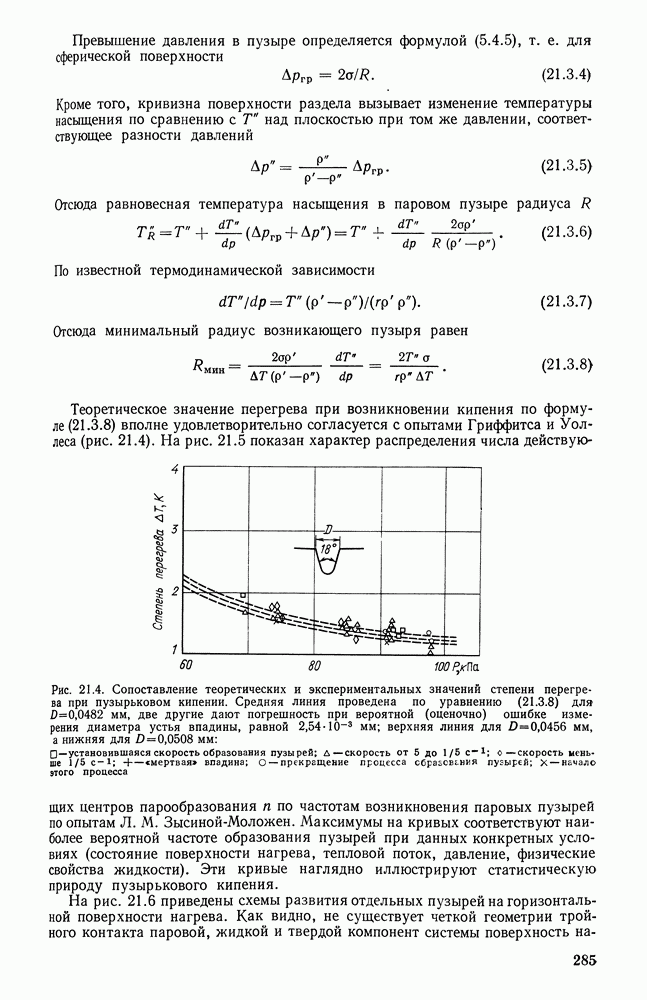
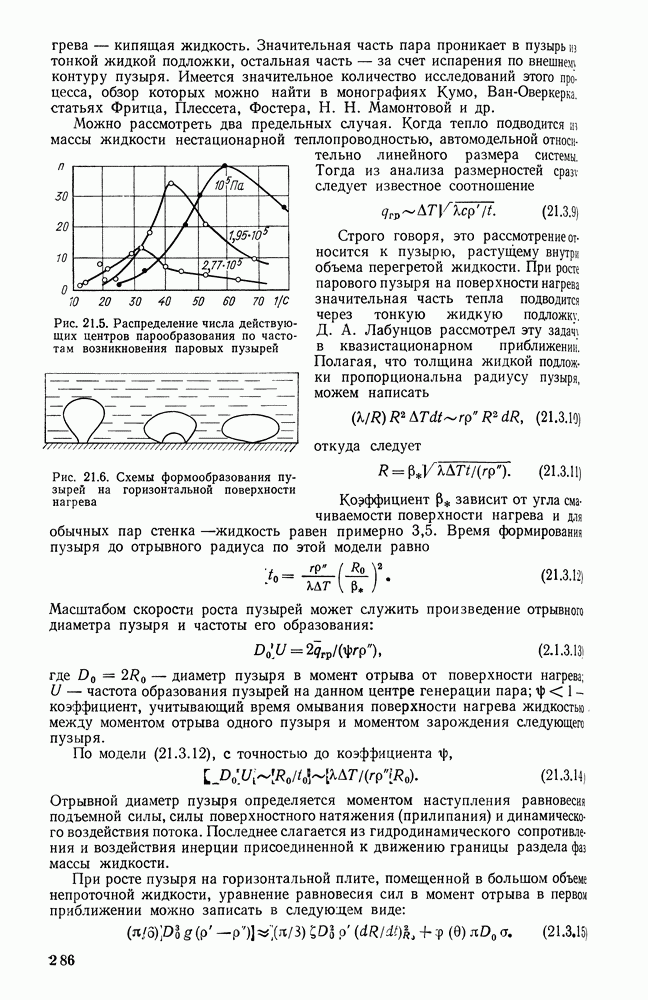
- 21.3. ПУЗЫРЬКОВОЕ КИПЕНИЕ, ЧАСТОТА И СКОРОСТЬ РОСТА ПАРОВЫХ ПУЗЫРЕЙ
- 21.4. ХАРАКТЕР ДВИЖЕНИЯ ПАРОЖИДКОСТНОЙ СМЕСИ В ТРУБАХ
- 21.5. ТЕПЛООТДАЧА ПРИ ПУЗЫРЬКОВОМ КИПЕНИИ
- 21.6. ПУЗЫРЬКОВОЕ КИПЕНИЕ ПРИ ВЫНУЖДЕННОЙ КОНВЕКЦИИ ЖИДКОСТИ
- 21.7. ТЕПЛООТДАЧА ПРИ ПЛЕНОЧНОМ КИПЕНИИ
- 21.8. ТЕПЛООТДАЧА ПРИ СВОБОДНОМ РАСТЕКАНИИ ЖИДКОСТИ ПО ПОВЕРХНОСТИ НАГРЕВА
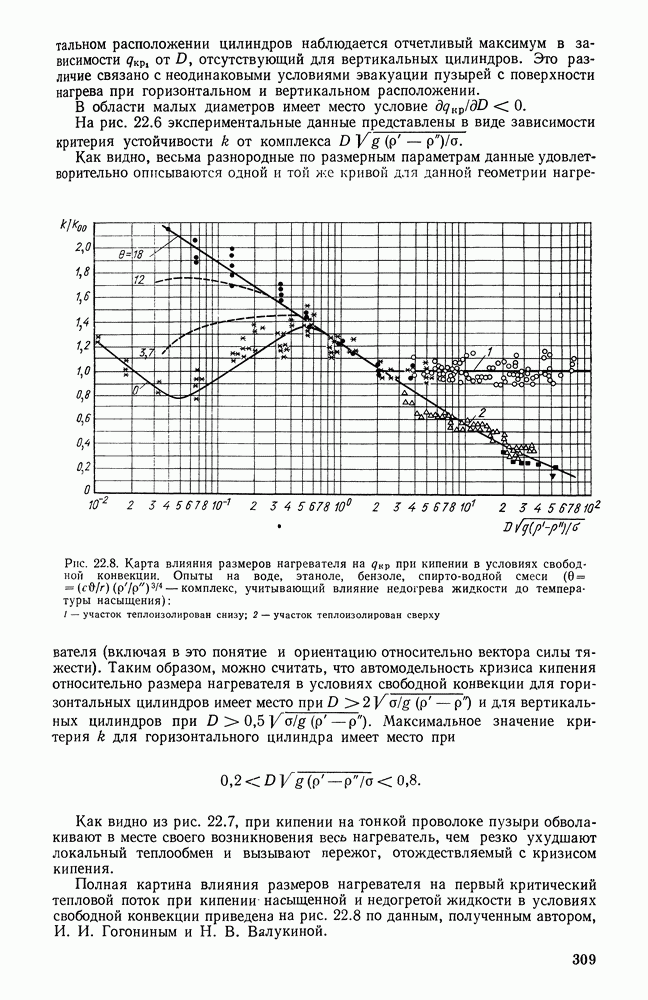
- Глава 22. КРИТИЧЕСКИЕ ПЛОТНОСТИ ТЕПЛОВОГО ПОТОКА, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЯ РЕЖИМА КИПЕНИЯ
- 22.1. ГИДРОДИНАМИЧЕСКАЯ ПРИРОДА КРИЗИСОВ В МЕХАНИЗМЕ КИПЕНИЯ ЖИДКОСТИ
- 22.2. КРИТЕРИЙ УСТОЙЧИВОСТИ ДВУХФАЗНОГО ГРАНИЧНОГО СЛОЯ ПРИ СВОБОДНОЙ КОНВЕКЦИИ В БОЛЬШОМ ОБЪЕМЕ КИПЯЩЕЙ ЖИДКОСТИ (ПЕРВЫЙ КРИЗИС РЕЖИМА КИПЕНИЯ)
- 22.3. ВЛИЯНИЕ РАЗМЕРА И СОСТОЯНИЯ ПОВЕРХНОСТИ НАГРЕВА НА ВЕЛИЧИНУ
- 22.4. ПЕРЕХОД ОТ ПЛЕНОЧНОГО РЕЖИМА КИПЕНИЯ К ПУЗЫРЬКОВОМУ РЕЖИМУ (ВТОРОЙ КРИЗИС РЕЖИМА КИПЕНИЯ)
- 22.5. КРИТЕРИЙ УСТОЙЧИВОСТИ ДВУХФАЗНОГО ГРАНИЧНОГО СЛОЯ ПРИ БОЛЬШИХ СКОРОСТЯХ ТЕЧЕНИЯ ЖИДКОСТИ
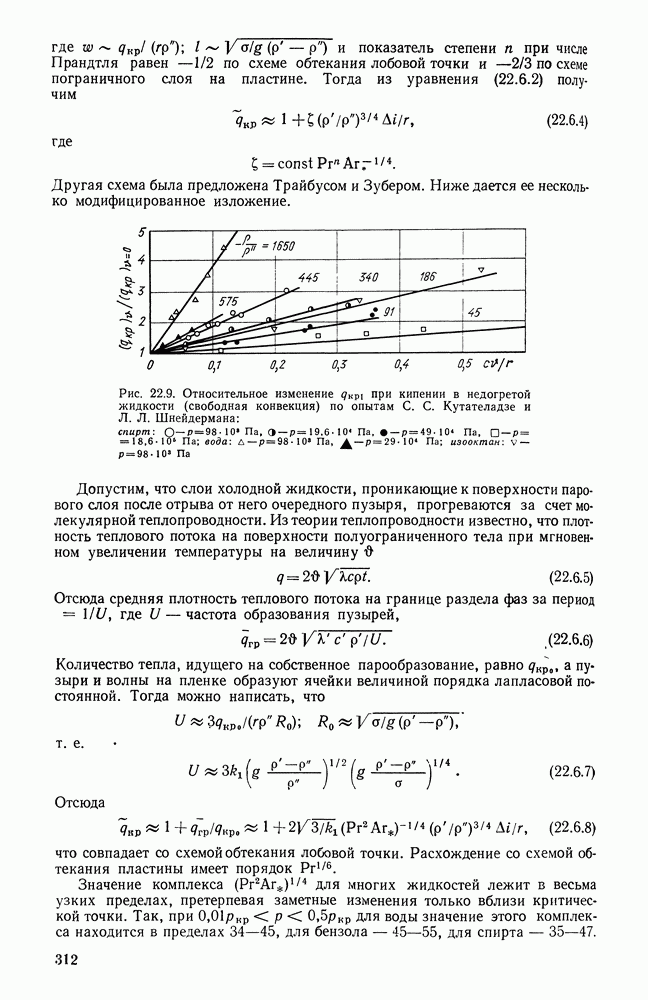
- 22.6. ВЛИЯНИЕ НЕДОГРЕВА ЖИДКОСТИ ДО ТЕМПЕРАТУРЫ НАСЫЩЕНИЯ НА КРИТИЧЕСКУЮ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА
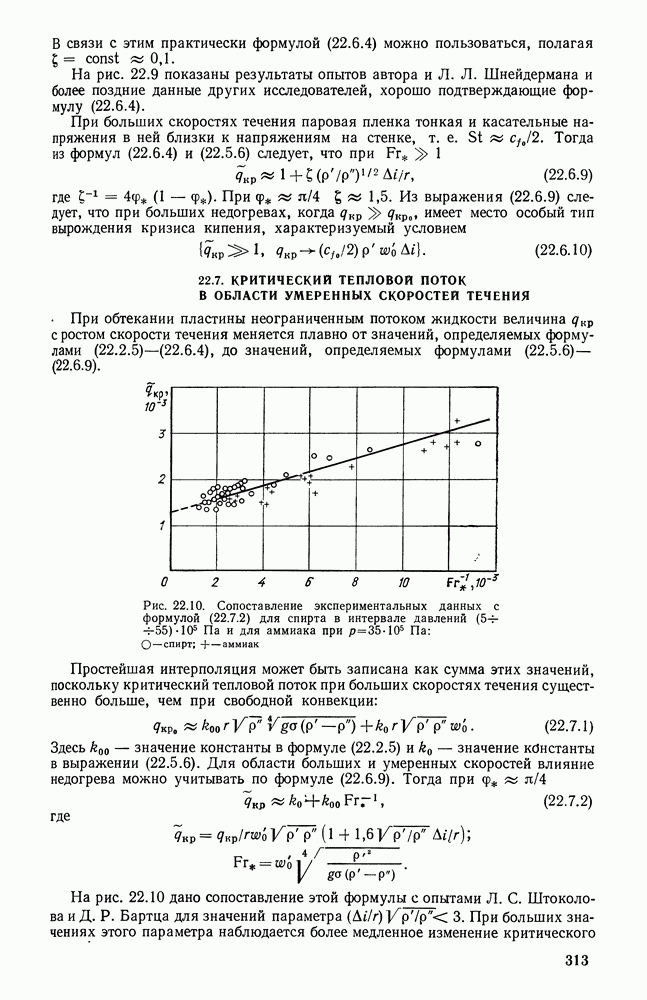
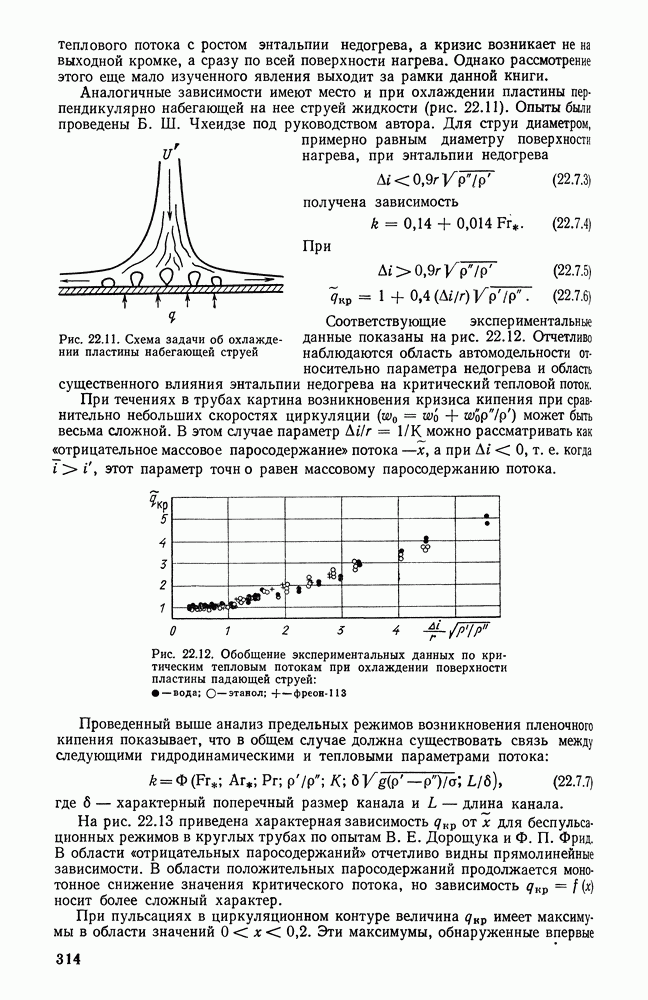
- 22.7. КРИТИЧЕСКИЙ ТЕПЛОВОЙ ПОТОК В ОБЛАСТИ УМЕРЕННЫХ СКОРОСТЕЙ ТЕЧЕНИЯ
- 22.8. КРИЗИС КИПЕНИЯ В БИНАРНЫХ СМЕСЯХ
- 22.9. НЕПОСРЕДСТВЕННЫЙ ПЕРЕХОД ОТ ОДНОФАЗНОЙ КОНВЕКЦИИ К ПЛЕНОЧНОМУ КИПЕНИЮ
- 22.10. ВЛИЯНИЕ МЕТАСТАБИЛЬНОСТИ ПРИСТЕННОГО СЛОЯ ЖИДКОСТИ НА ПЕРВУЮ КРИТИЧЕСКУЮ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА
- Глава 23. С ЭЛЕМЕНТЫ МАГНИТНОЙ ТЕРМОГИДРОДИНАМИКИ
- 23.1. ОСНОВНЫЕ УРАВНЕНИЯ
- 23.2. ВЛИЯНИЕ ПЕРПЕНДИКУЛЯРНОГО К ТЕЧЕНИЮ МАГНИТНОГО ПОЛЯ НА ГИДРОДИНАМИКУ И ТЕПЛООБМЕН В ЛАМИНАРНОМ ПОТОКЕ
- 23.3. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ НА ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОГО МЕТАЛЛА В КАНАЛАХ
- 23.4. ЭЛЕМЕНТЫ ТЕРМОГАЗОДИНАМИКИ НИЗКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ
- 23.5. ОБОБЩЕННЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРОДУГОВЫХ ПЛАЗМОТРОНОВ
- Глава 24. НЕУСТАНОВИВШИЙСЯ КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
- 24.1. КРИТЕРИИ ПОДОБИЯ, ХАРАКТЕРИЗУЮЩИЕ КОНВЕКТИВНУЮ НЕСТАЦИОНАРНОСТЬ
- 24.2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ С ПЕРЕМЕННОЙ ТЕМПЕРАТУРОЙ
- 24.3. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ СФЕРИЧЕСКИХ ЧАСТИЦ
- 24.4. НЕСТАЦИОНАРНЫЙ ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ТРУБЕ
- 24.5. ВЛИЯНИЕ ОСЦИЛЛЯЦИЙ
- 24.6. ВЛИЯНИЕ ОСЦИЛЛЯЦИЙ
- Глава 25. ОСНОВНЫЕ ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 25.1. ПРИРОДА ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 25.2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 25.3. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- 25.4. ИЗЛУЧЕНИЕ РЕАЛЬНЫХ ТЕЛ
- 25.5. КЛАССИФИКАЦИЯ ВИДОВ ПОЛУСФЕРИЧЕСКОГО И ОБЪЕМНОГО ИЗЛУЧЕНИЙ
- 25.6. ГЕОМЕТРИЯ ИЗЛУЧЕНИЯ. ГЕОМЕТРИЧЕСКИЕ ИНВАРИАНТЫ ИЗЛУЧЕНИЯ
- 25.7. ОБЩИЕ СВОЙСТВА ПОТОКОВ ИЗЛУЧЕНИЯ
- 25.8. АЛГЕБРАИЧЕСКИЙ МЕТОД РАСЧЕТА ИНТЕГРАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ИНВАРИАНТОВ ИЗЛУЧЕНИЯ
- Глава 26. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ПРОЗРАЧНЫХ И ПОГЛОЩАЮЩИХ СРЕДАХ
- 26.1. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ СИСТЕМЫ ТЕЛ, РАЗДЕЛЕННЫХ ПРОЗРАЧНОЙ СРЕДОЙ
- 26.2. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ ДИСКРЕТНОЙ СИСТЕМЫ ТЕЛ В ПРОЗРАЧНОЙ СРЕДЕ (ЗОНАЛЬНЫЙ МЕТОД)
- 26.3. ПРИЛОЖЕНИЕ ЗОНАЛЬНОГО МЕТОДА К РАСЧЕТУ ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ МЕЖДУ НЕСКОЛЬКИМИ СЕРЫМИ ТЕЛАМИ
- 26.4. ДЕЙСТВИЕ ЭКРАНОВ
- 26.5. УРАВНЕНИЕ ПЕРЕНОСА ЭНЕРГИИ ИЗЛУЧЕНИЯ В ПОГЛОЩАЮЩЕЙ СРЕДЕ
- 26.6. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ИЗЛУЧЕНИЯ В ПОГЛОЩАЮЩЕЙ СРЕДЕ
- 26.7. ОПТИЧЕСКИЕ СВОЙСТВА ПОГЛОЩАЮЩИХ СРЕД
- 26.8. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ ДИСКРЕТНОИ СИСТЕМЫ ТЕЛ В ПОГЛОЩАЮЩЕЙ СРЕДЕ (ЗОНАЛЬНЫЙ МЕТОД)
- 26.9. ПЕРЕНОС ИЗЛУЧЕНИЯ В ПЛОСКОМ СЛОЕ ПОГЛОЩАЮЩЕЙ СРЕДЫ
- 26.10. КОМБИНИРОВАННЫЙ РАДИАЦИОННЫЙ ТЕПЛООБМЕН
- 26.11. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ТОПОЧНЫХ УСТРОЙСТВАХ