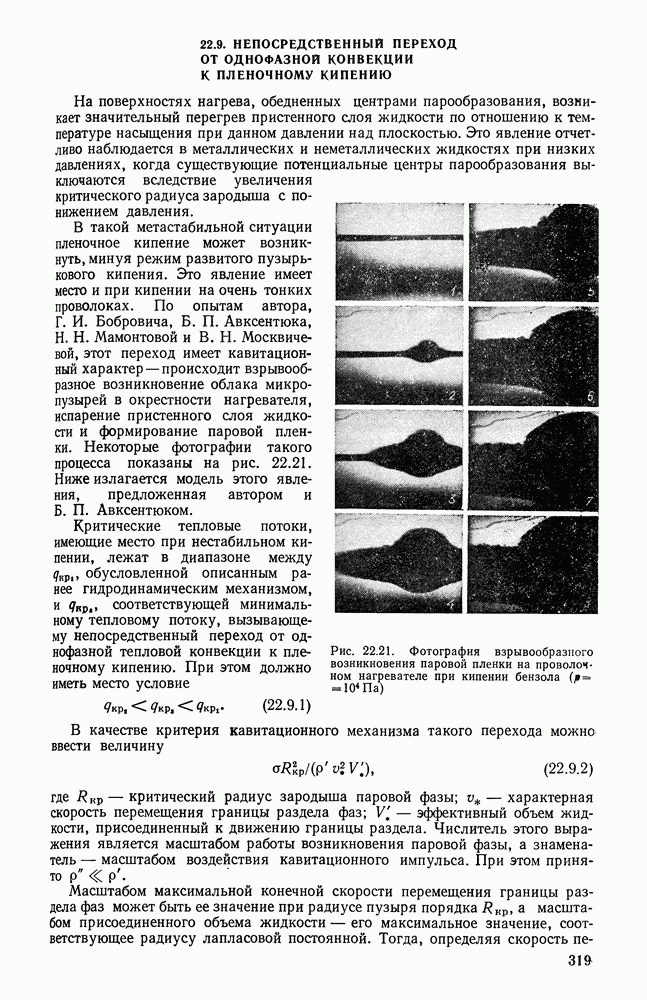
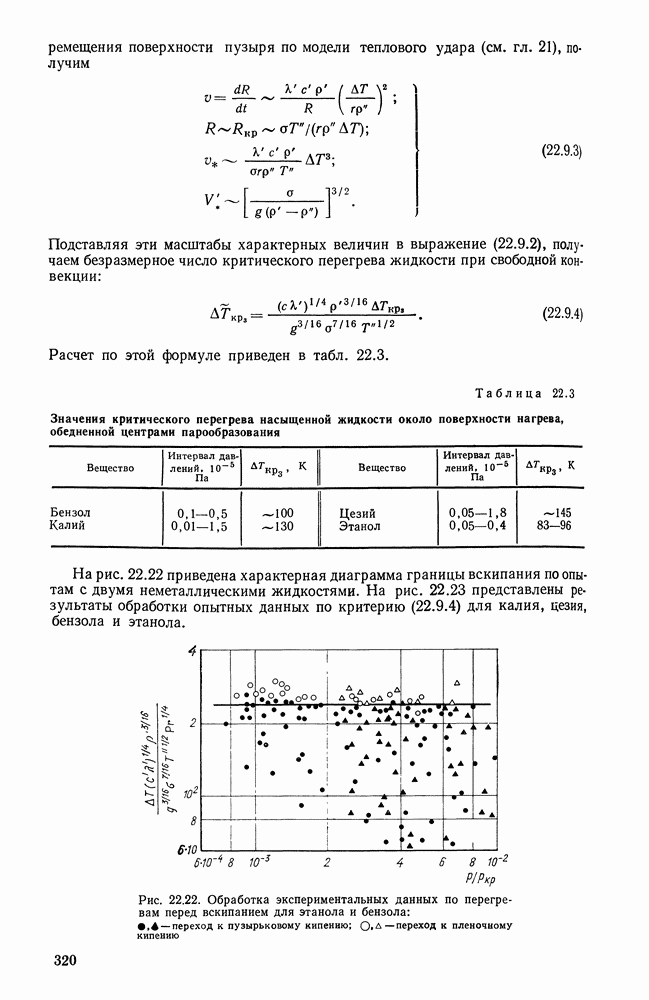
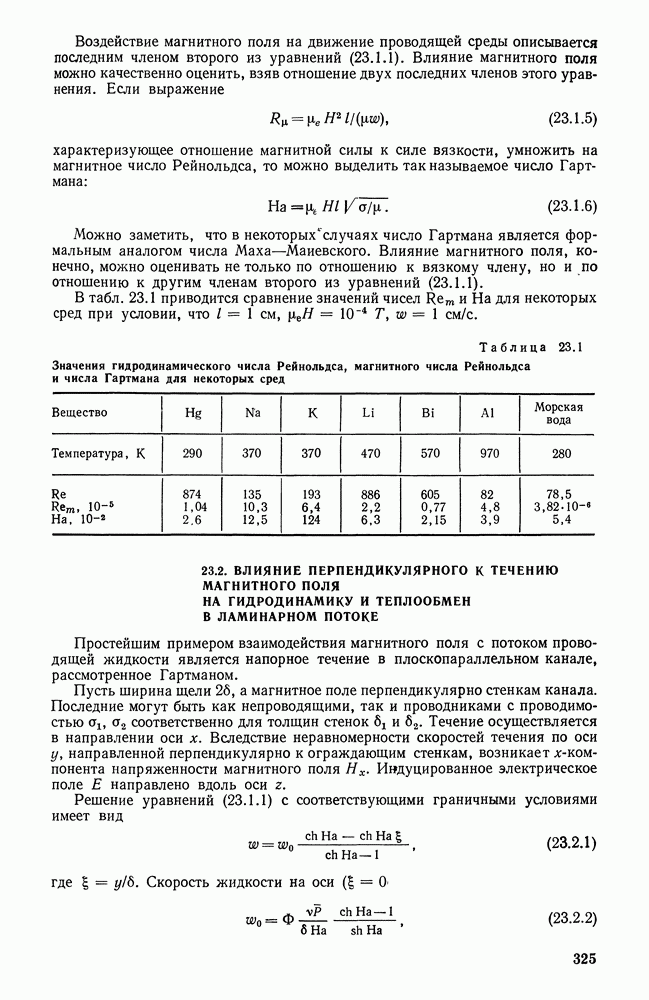
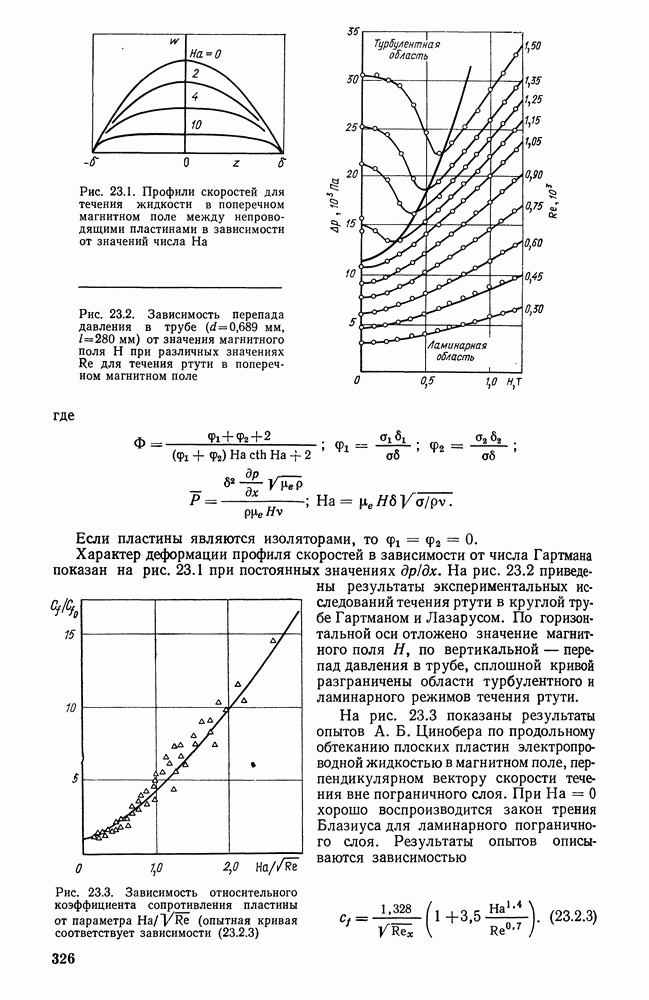
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8.3. ТЕМПЕРАТУРА — ФУНКЦИЯ ОДНОЙ КООРДИНАТЫ И ВРЕМЕНИ
Важнейшими частными случаями рассматриваемой проблемы являются процессы, в которых температура — функция только одной координаты. Уравнение (8.2.6) можно переписать в обыкновенных дифференциалах, и тогда оно примет вид:
для протяженной плоской стенки
 (8.3.1)
(8.3.1)
для протяженного цилиндра
 (8.3.2)
(8.3.2)
для шара
 (8.3.3)
(8.3.3)
При этом в уравнении (8.3.1) безразмерная координата  , где
, где  — в данном случае полутолщина стенки, а в уравнениях (8.3.2) и (8.3.3)
— в данном случае полутолщина стенки, а в уравнениях (8.3.2) и (8.3.3)  : здесь
: здесь  — характерный радиус тела.
— характерный радиус тела.
Уравнению (8.3.1) удовлетворяют тригонометрические функции

Решения уравнения (8.3.2) имеют вид

где  — функции Бесселя первого и второго рода нулевого порядка. Решениями уравнения (8.3.3) являются функции
— функции Бесселя первого и второго рода нулевого порядка. Решениями уравнения (8.3.3) являются функции
 (8.3.6)
(8.3.6)
Эти функции, являющиеся частными интегралами рассмотренных дифференциальных уравнений, распадаются на две группы — четные и нечетные. Суммируя и  , получаем: для протяженной плоской стенки
, получаем: для протяженной плоской стенки
 (8.3.7)
(8.3.7)
для протяженного цилиндра
 (8.3.8)
(8.3.8)
для шара
 (8.3.9)
(8.3.9)
Существуют процессы теплопроводности, которые нельзя описать рассмотренными выше решениями, представляющими температуру в виде произведена двух частных функций, каждая из которых зависит только от одной переменной. Тогда применяются функции иного типа, в которых рассмотренное выше разделение невозможно.
Дифференцированием и подстановкой можно показать, что, например, функции
 (8.3.10)
(8.3.10)
также являются интегралами дифференциального уравнения

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ТЕПЛООБМЕНА
- 1.1. ПРЕДМЕТ ТЕОРИИ ТЕПЛООБМЕНА
- 1.2. ПОЛЕ ТЕМПЕРАТУР И ПОЛЕ ТЕПЛОВЫХ ПОТОКОВ
- 1.3. КОЭФФИЦИЕНТЫ ТЕПЛООТДАЧИ И ТЕПЛОПЕРЕДАЧИ
- 1.4. ТЕРМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
- 1.5. БАЛАНСНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕННОГО АППАРАТА
- 1.6. СРЕДНИЙ ТЕМПЕРАТУРНЫЙ НАПОР
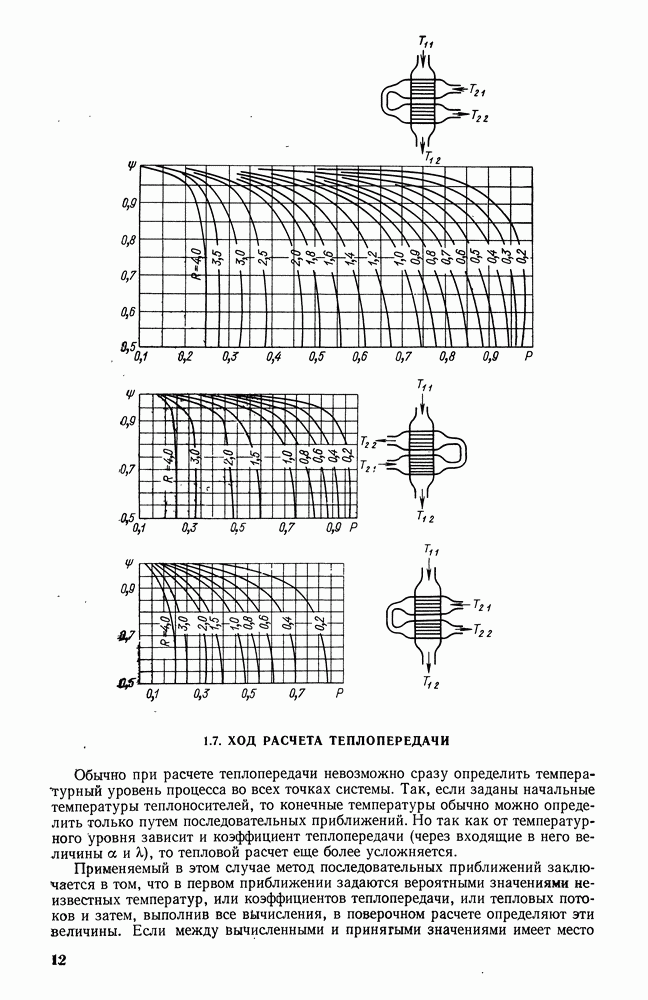
- 1.7. ХОД РАСЧЕТА ТЕПЛОПЕРЕДАЧИ
- 1.8. ОДНОМЕРНАЯ МОДЕЛЬ ЖИДКОСТНОГО ОХЛАЖДЕНИЯ ЯДЕРНОГО РЕАКТОРА
- Глава 2. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В ВЕЩЕСТВЕННОЙ СРЕДЕ
- 2.1. ГИПОТЕЗА О ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ ВЕКТОРА ТЕПЛОВОГО ПОТОКА ГРАДИЕНТУ ТЕМПЕРАТУР
- 2.2. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В ВЕЩЕСТВЕННОЙ СРЕДЕ
- 2.3. ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2.4. ТЕМПЕРАТУРА ТОРМОЖЕНИЯ
- 2.5. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ С КОНЕЧНОЙ СКОРОСТЬЮ РАСПРОСТРАНЕНИЯ ВОЗМУЩЕНИЯ
- Глава 3. УРАВНЕНИЯ ГИДРОДИНАМИКИ
- 3.1. СВЯЗЬ МЕЖДУ ПОЛЕМ ТЕМПЕРАТУР И ПОЛЕМ СКОРОСТЕЙ В ДВИЖУЩЕЙСЯ СРЕДЕ
- 3.2. УРАВНЕНИЕ СПЛОШНОСТИ ПОТОКА ЖИДКОСТИ
- 3.3. УРАВНЕНИЕ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- 3.4. ПОДЪЕМНАЯ СИЛА, ОБУСЛОВЛЕННАЯ НЕОДНОРОДНОСТЬЮ ТЕМПЕРАТУРНОГО ПОЛЯ
- Глава 4. УРАВНЕНИЯ ОСРЕДНЕННОГО ТУРБУЛЕНТНОГО ПОТОКА
- 4.1. ТУРБУЛЕНТНОСТЬ
- 4.2. УРАВНЕНИЯ ОСРЕДНЕННОГО ТУРБУЛЕНТНОГО ТЕЧЕНИЯ ЖИДКОСТИ
- 4.3. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА
- 4.4. ТУРБУЛЕНТНОЕ ТРЕНИЕ И ТУРБУЛЕНТНАЯ ТЕПЛОПРОВОДНОСТЬ В ПЛОСКОМ ПОТОКЕ ЖИДКОСТИ
- Глава 5. КРАЕВЫЕ УСЛОВИЯ
- 5.1. ВРЕМЕННЫЕ И ПРОСТРАНСТВЕННЫЕ КРАЕВЫЕ УСЛОВИЯ
- 5.2. КРАЕВЫЕ УСЛОВИЯ К УРАВНЕНИЯМ ГИДРОДИНАМИКИ
- 5.3. КРАЕВЫЕ УСЛОВИЯ К УРАВНЕНИЯМ ТЕПЛОПРОВОДНОСТИ
- 5.4. УСЛОВИЯ МЕХАНИЧЕСКОГО И ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ НА ГРАНИЦАХ ФАЗ В МНОГОФАЗНОЙ СИСТЕМЕ
- 5.5. РЕАКТИВНАЯ СИЛА ПРИ ФАЗОВОМ ПРЕВРАЩЕНИИ
- Глава 6. УСЛОВИЯ ПОДОБИЯ ПРОЦЕССОВ ТЕПЛООБМЕНА
- 6.1. ПОНЯТИЕ О ПОДОБИИ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- 6.2. КРИТЕРИИ ПОДОБИЯ
- 6.3. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ ПЕРЕМЕННЫЕ. УСЛОВИЯ ОДНОЗНАЧНОСТИ
- 6.4. КОМБИНИРОВАНИЕ КРИТЕРИЕВ. СОБСТВЕННО КРИТЕРИИ ПОДОБИЯ
- 6.5. КРИТЕРИИ ПОДОБИЯ КАК ОБОБЩЕННЫЕ БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ
- 6.6. ФИЗИЧЕСКИЙ СМЫСЛ НЕКОТОРЫХ КРИТЕРИЕВ ПОДОБИЯ
- 6.7. КРИТЕРИЙ ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ ПРИ ФИЗИКО-ХИМИЧЕСКОМ ПРЕВРАЩЕНИИ ВЕЩЕСТВА
- 6.8. БЕЗРАЗМЕРНЫЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
- Глава 7. УСТАНОВИВШИЙСЯ ТЕПЛОВОЙ ПОТОК В ТВЕРДЫХ ТЕЛАХ
- 7.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
- 7.2. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ
- 7.3. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ СТЕНКУ
- 7.4. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ШАРОВУЮ СТЕНКУ
- 7.5. ТЕПЛОПРОВОДНОСТЬ ВДОЛЬ СТЕРЖНЯ ПОСТОЯННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
- 7.6. ПРЯМОЕ РЕБРО ПОСТОЯННОГО ТЕПЛОВОГО НАПРЯЖЕНИЯ
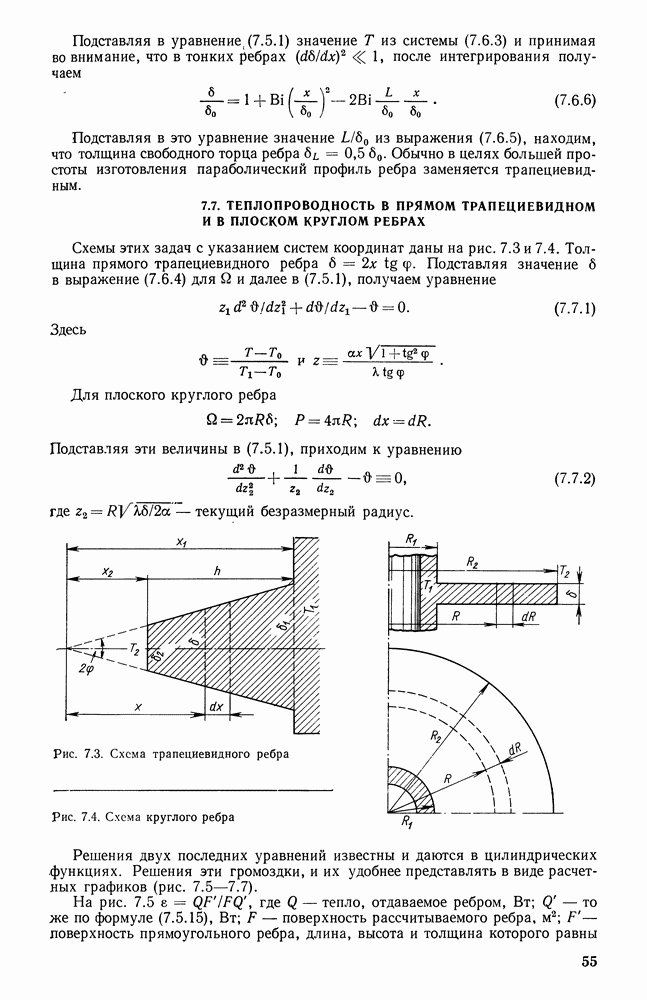
- 7.7. ТЕПЛОПРОВОДНОСТЬ В ПРЯМОМ ТРАПЕЦИЕВИДНОМ И В ПЛОСКОМ КРУГЛОМ РЕБРАХ
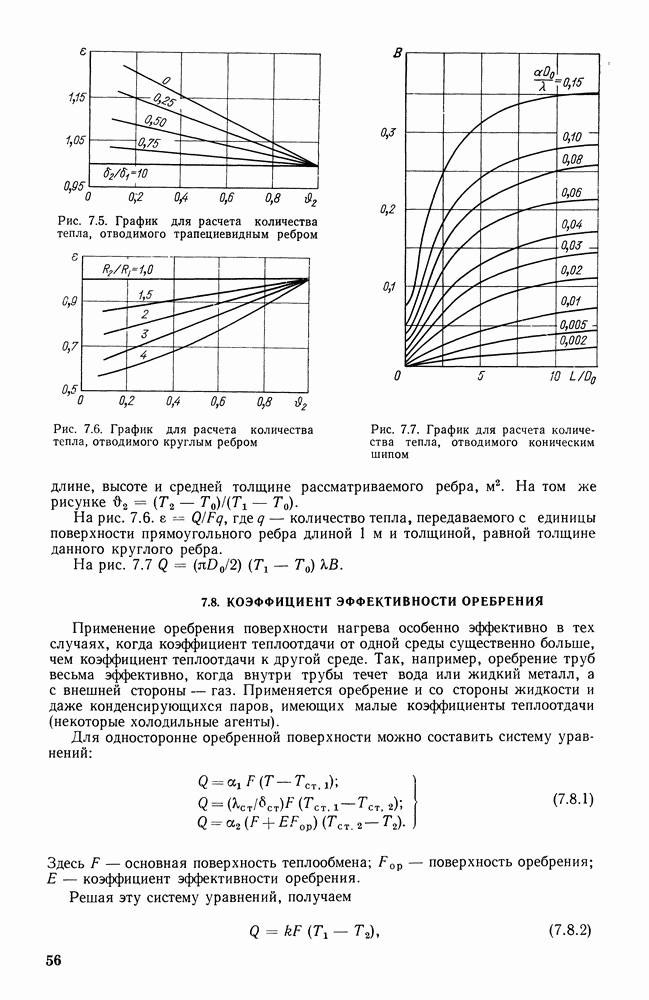
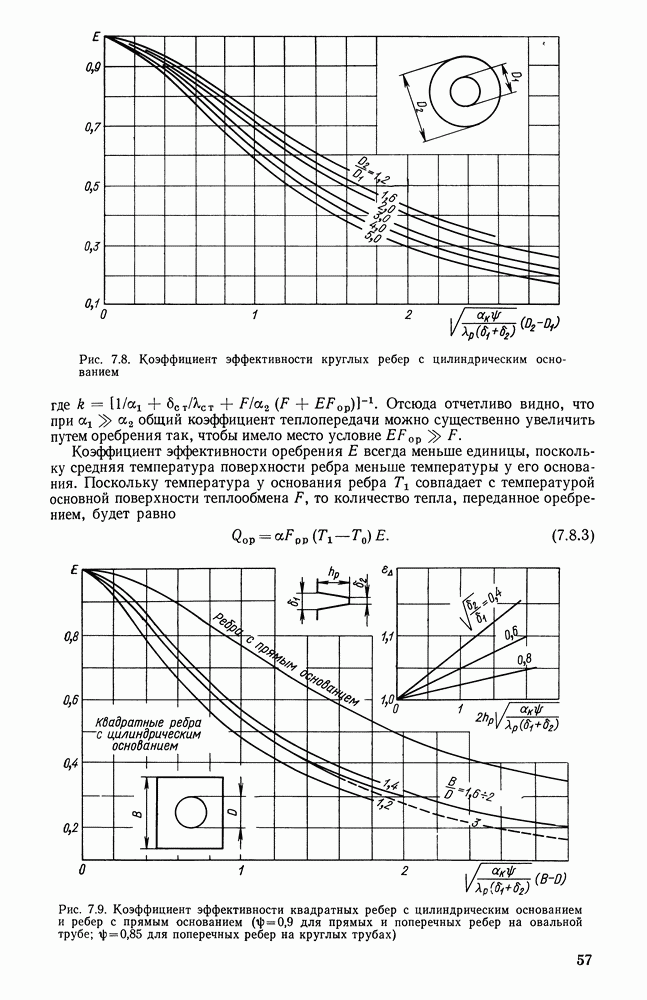
- 7.8. КОЭФФИЦИЕНТ ЭФФЕКТИВНОСТИ ОРЕБРЕНИЯ
- 7.9. ТЕПЛОПРОВОДНОСТЬ В СТЕРЖНЕ И ШАРЕ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛА
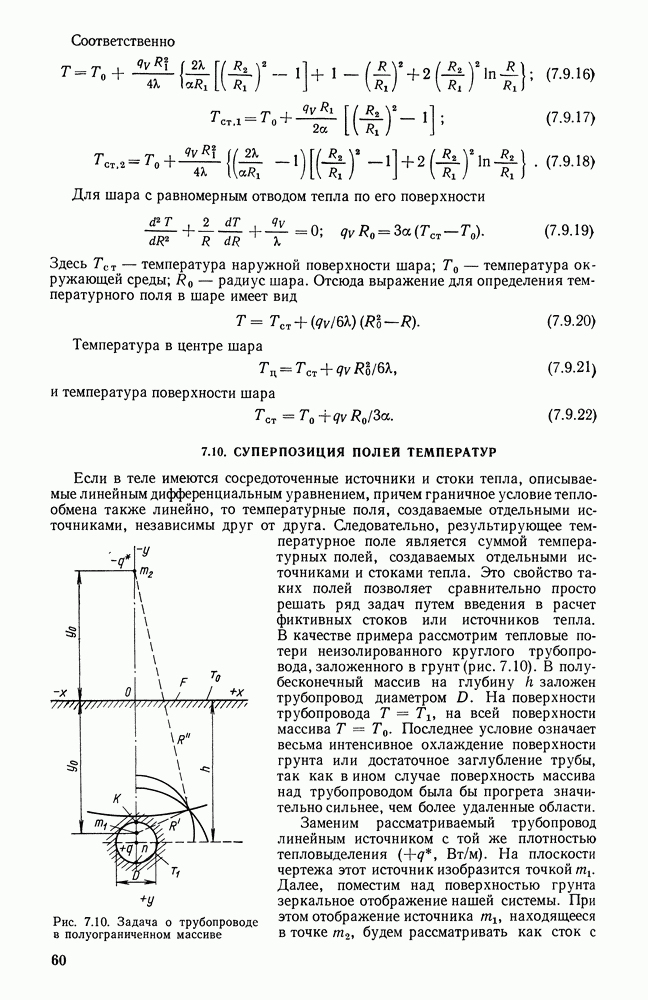
- 7.10. СУПЕРПОЗИЦИЯ ПОЛЕЙ ТЕМПЕРАТУР
- 7.11. УЧЕТ ВНЕШНЕГО ТЕРМИЧЕСКОГО СОПРОТИВЛЕНИЯ МЕТОДОМ ДОПОЛНИТЕЛЬНОЙ СТЕНКИ
- Глава 8. НЕУСТАНОВИВШИЙСЯ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ БЕЗ ВНУТРЕННИХ ИСТОЧНИКОВ
- 8.1. УРАВНЕНИЕ НЕСТАЦИОНАРНОГО ТЕМПЕРАТУРНОГО ПОЛЯ
- 8.2. РЕШЕНИЕ В ВИДЕ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ
- 8.3. ТЕМПЕРАТУРА — ФУНКЦИЯ ОДНОЙ КООРДИНАТЫ И ВРЕМЕНИ
- 8.4. МОНОТОННЫЙ ПЕРЕХОД К ТЕПЛОВОМУ РАВНОВЕСИЮ
- 8.5. ТЕМПЕРАТУРНОЕ ПОЛЕ В ТЕЛЕ ПРИ ТЕМПЕРАТУРЕ ВНЕШНЕЙ СРЕДЫ, ЛИНЕЙНО МЕНЯЮЩЕЙСЯ ВО ВРЕМЕНИ
- 8.6. РЕГУЛЯРНЫЙ РЕЖИМ ОХЛАЖДЕНИЯ
- 8.7. ОХЛАЖДЕНИЕ ВЫСОКОТЕПЛОПРОВОДНОГО ТЕЛА
- 8.8. ТЕПЛОВЫЕ ВОЛНЫ
- Глава 9. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
- 9.1. УРАВНЕНИЕ ТЕПЛОПЕРЕНОСА
- 9.2. СВЯЗЬ МЕЖДУ ТЕПЛООТДАЧЕЙ И ТРЕНИЕМ
- 9.3. ПОГРАНИЧНЫЙ СЛОЙ
- 9.4. СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕПЛООБМЕНА В ПОТОКЕ СЖИМАЕМОГО ГАЗА
- 9.5. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ПЛОСКОГО СТАЦИОНАРНОГО ПОГРАНИЧНОГО СЛОЯ НА НЕПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 9.6. РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И СКОРОСТЕЙ В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ
- 9.7. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТЕПЛОВОГО ПОТОКА И ТЕМПЕРАТУРЫ В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ
- 9.8. ПОЛУЭМПИРИЧЕСКИЕ ВЫРАЖЕНИЯ ТУРБУЛЕНТНОГО ОБМЕНА В ПЛОСКОМ НЕСЖИМАЕМОМ ПОТОКЕ ВБЛИЗИ ТВЕРДОЙ СТЕНКИ
- 9.9. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ТУРБУЛЕНТНОЙ ТЕПЛОПРОВОДНОСТИ И ВЯЗКОСТИ
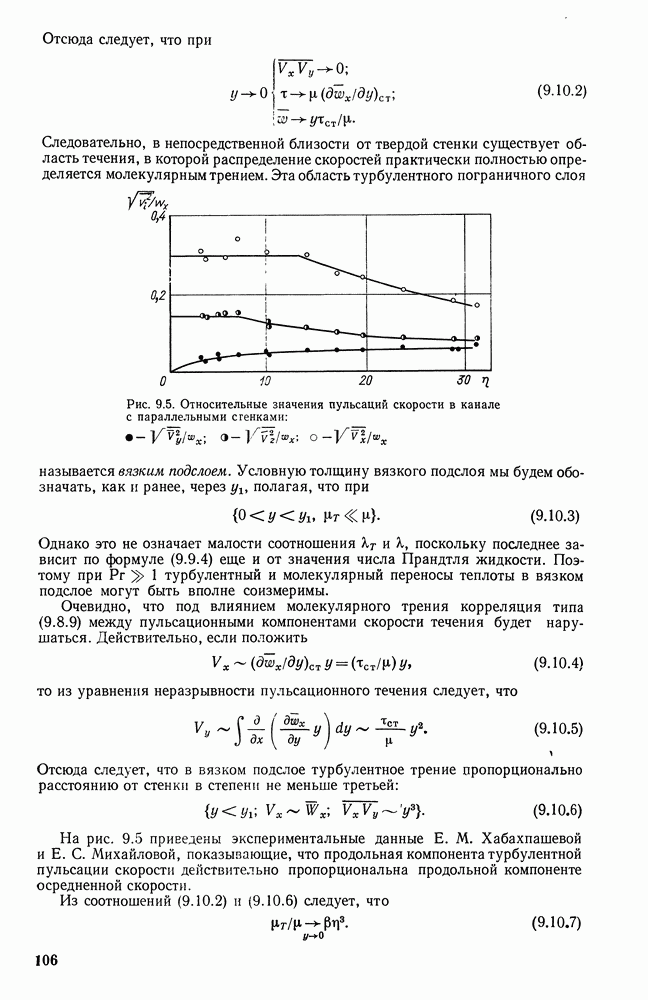
- 9.10. ТУРБУЛЕНТНЫЙ ПЕРЕНОС В ВЯЗКОМ ПОДСЛОЕ
- 9.11. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ПЛОСКОМ НЕСЖИМАЕМОМ ПОТОКЕ ВБЛИЗИ СТЕНКИ
- 9.12. РАСПРОСТРАНЕНИЕ ПОЛУЭМПИРИЧЕСКИХ ВЫРАЖЕНИЙ ДЛЯ ТУРБУЛЕНТНЫХ ПЕРЕНОСОВ В НЕСЖИМАЕМОЙ ЖИДКОСТИ НА ПЛОСКИЙ ПОТОК ГАЗА
- 9.13. ПОРЯДОК ВЕЛИЧИНЫ вязкого подслоя НА НЕПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 9.14. ПРЕДЕЛЬНЫЕ ОТНОСИТЕЛЬНЫЕ ЗАКОНЫ ТРЕНИЯ И ТЕПЛООБМЕНА
- Глава 10. ТЕПЛООТДАЧА ПРИ ВНЕШНЕМ ОБТЕКАНИИ ТЕЛ НЕСЖИМАЕМОЙ ЖИДКОСТЬЮ
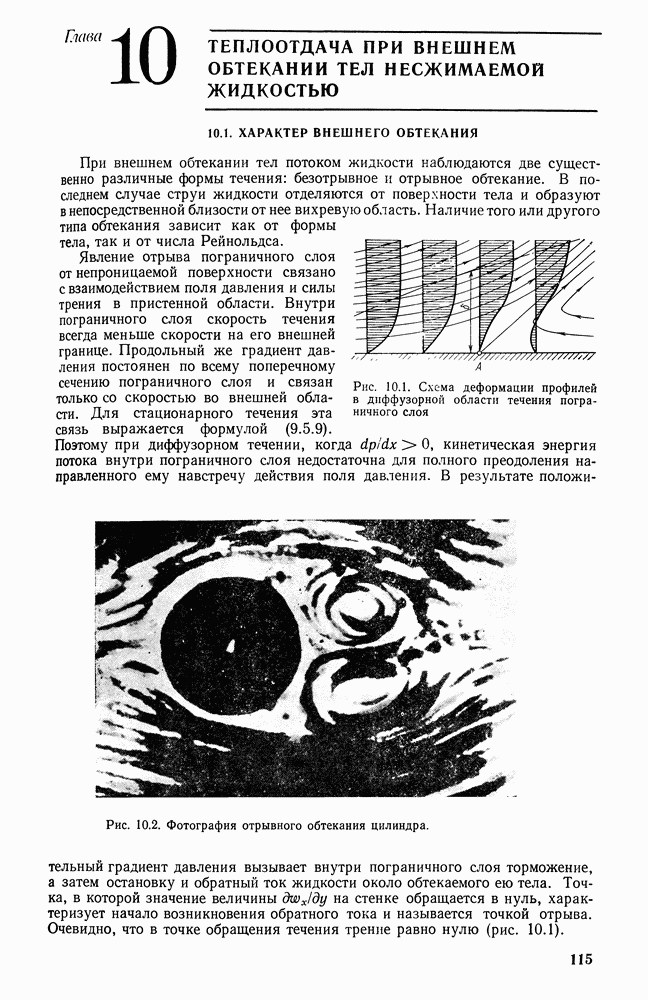
- 10.1. ХАРАКТЕР ВНЕШНЕГО ОБТЕКАНИЯ
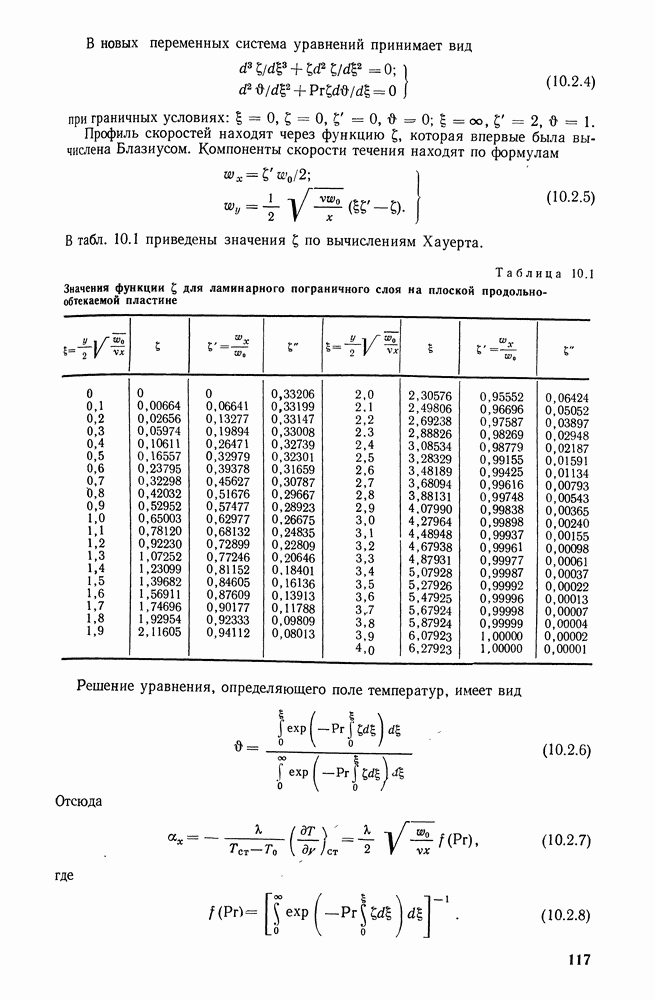
- 10.2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ (ТОЧНОЕ РЕШЕНИЕ)
- 10.3. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПЛАСТИНЫ, ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.4. ТЕПЛООТДАЧА ПЛАСТИНЫ, ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ ПРИ Рr>=1 (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.5. ТЕПЛООТДАЧА ПЛАСТИНЫ. ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ ПРИ Рr<<1 (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.6. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПЛАСТИНЫ, ОБТЕКАЕМОЙ ТУРБУЛЕНТНЫМ ПОГРАНИЧНЫМ СЛОЕМ
- 10.7. ТЕПЛООТДАЧА ПЛАСТИНЫ. ОБТЕКАЕМОЙ ТУРБУЛЕНТНЫМ ПОГРАНИЧНЫМ СЛОЕМ С ПОСТОЯННЫМИ ФИЗИЧЕСКИМИ СВОЙСТВАМИ
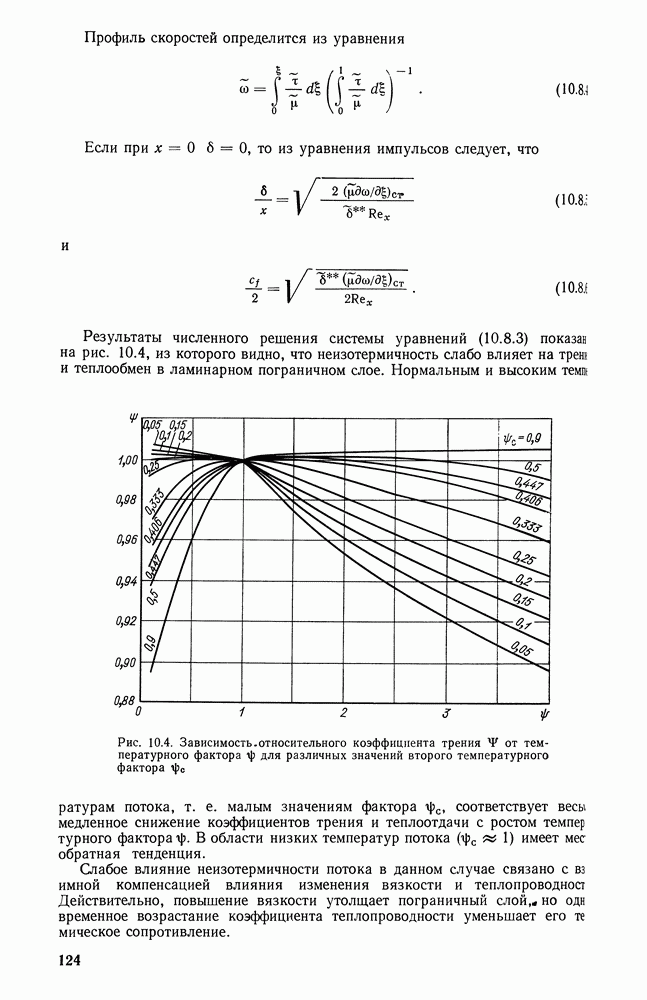
- 10.8. НЕИЗОТЕРМИЧЕСКИЙ ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПЛАСТИНЕ
- 10.9. НЕИЗОТЕРМИЧЕСКИЙ ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПЛАСТИНЕ
- 10.10. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТИ
- 10.11. КОНСЕРВАТИВНОСТЬ ЗАКОНА ТЕПЛООБМЕНА ОТНОСИТЕЛЬНО ГРАДИЕНТА ДАВЛЕНИЯ
- 10.12. ИНТЕГРАЛ УРАВНЕНИЯ ЭНЕРГИИ
- 10.13. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ ШАРА
- 10.14. ТЕПЛООТДАЧА ПРИ ПОПЕРЕЧНОМ ОБТЕКАНИИ ОДИНОЧНОГО ЦИЛИНДРА
- Глава 11. ТЕПЛООТДАЧА ПРИ ТЕЧЕНИИ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
- 11.1. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ ИЗОТЕРМИЧЕСКОМ ТЕЧЕНИИ
- 11.2. ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ
- 11.3. УРАВНЕНИЕ ТЕПЛОПЕРЕНОСА В ТУРБУЛЕНТНОМ ПОТОКЕ
- 11.4. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ТЕПЛООТДАЧИ И ТРЕНИЯ
- 11.5. РЕШЕНИЕ ПРИ ЛИНЕЙНОМ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ СТЕНКИ
- 11.6. ТЕПЛООТДАЧА К ТУРБУЛЕНТНОМУ ПОТОКУ ПРИ Рr>1
- 11.7. ТЕПЛООТДАЧА К ТУРБУЛЕНТНОМУ ПОТОКУ ПРИ Рr«1
- 11.8. ТЕМПЕРАТУРНЫЙ ФАКТОР
- 11.9. ВЛИЯНИЕ ТЕМПЕРАТУРНОГО ФАКТОРА НА ТРЕНИЕ И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ ГАЗА
- 11.10. ВЛИЯНИЕ ТЕПЛОВОГО ПОТОКА НА ТЕПЛООТДАЧУ ПРИ ТЕЧЕНИИ КАПЕЛЬНЫХ ЖИДКОСТЕЙ
- 11.11. ТЕПЛООБМЕН И ТРЕНИЕ ВО ВХОДНОМ УЧАСТКЕ ТРУБЫ
- 11.12. ТЕПЛООБМЕН ПРИ ПРОДОЛЬНОМ ТЕЧЕНИИ В КАНАЛАХ НЕЦИЛИНДРИЧЕСКОЙ ФОРМЫ
- 11.13. ТЕПЛООБМЕН ПРИ ТЕЧЕНИИ ХИМИЧЕСКИ РЕАГИРУЮЩИХ ГАЗОВЫХ ТЕПЛОНОСИТЕЛЕЙ
- 11.14. ВЛИЯНИЕ ШЕРОХОВАТОСТИ СТЕНКИ ТРУБЫ НА ТЕПЛООТДАЧУ
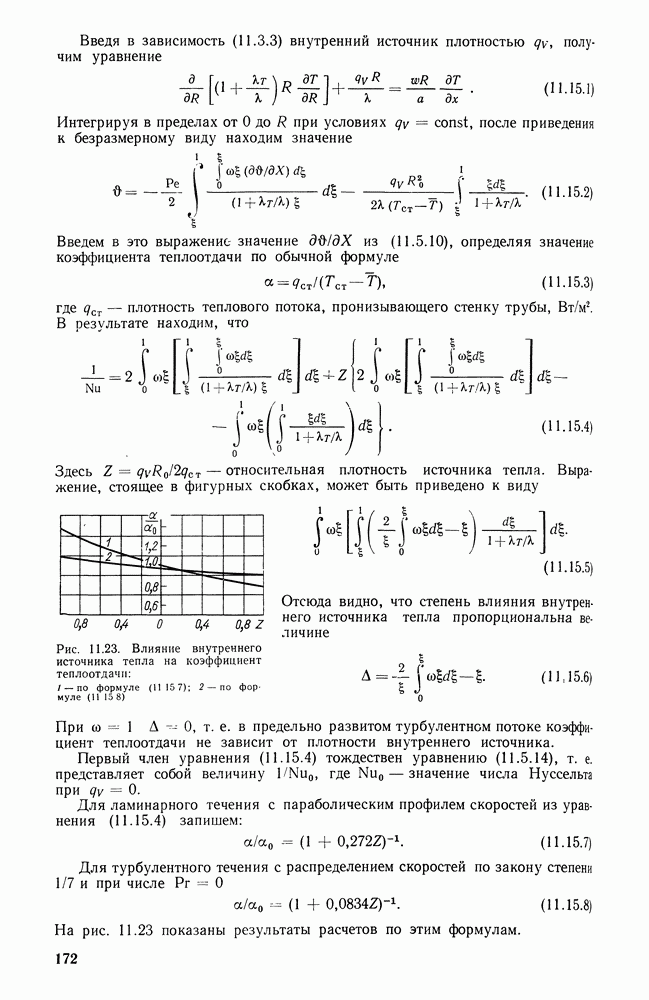
- 11.15. ВЛИЯНИЕ ВНУТРЕННЕГО ИСТОЧНИКА ТЕПЛА
- Глава 12. ТЕПЛООБМЕН ПРИ БОЛЬШИХ СКОРОСТЯХ ТЕЧЕНИЯ ГАЗА
- 12.1. СВЯЗЬ МЕЖДУ ТЕМПЕРАТУРОЙ ТОРМОЖЕНИЯ И СКОРОСТЬЮ РАСПРОСТРАНЕНИЯ ЗВУКА В ГАЗЕ
- 12.2. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ТЕМПЕРАТУРЫ И ОБОБЩЕННЫЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
- 12.3. ТЕПЛООТДАЧА К ПЛАСТИНЕ
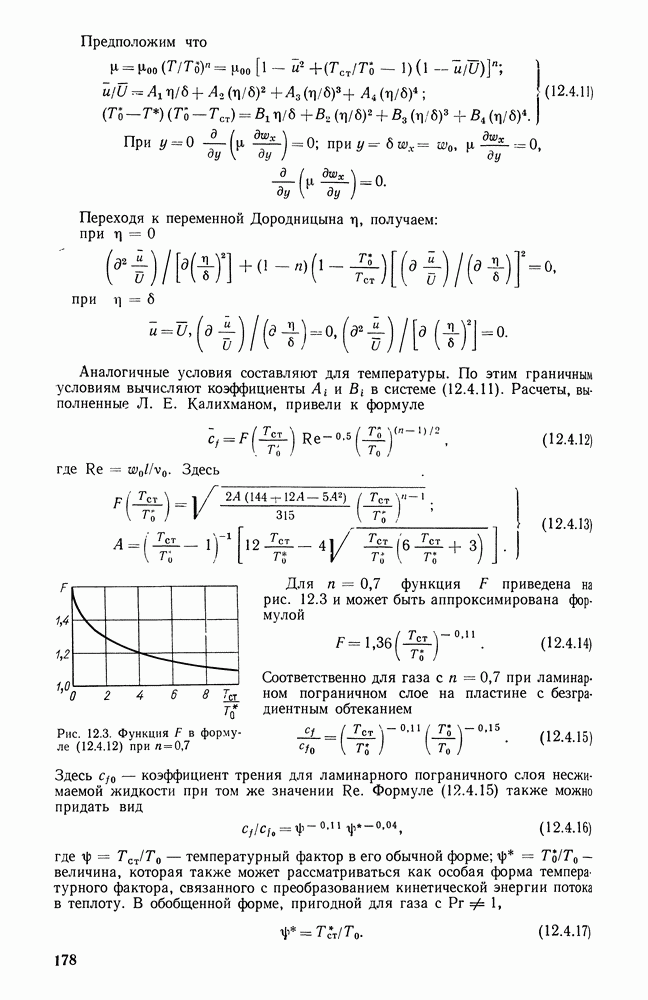
- 12.4. КОЭФФИЦИЕНТ ТРЕНИЯ ПЛАСТИНЫ ПРИ ЛАМИНАРНОМ ПОГРАНИЧНОМ СЛОЕ
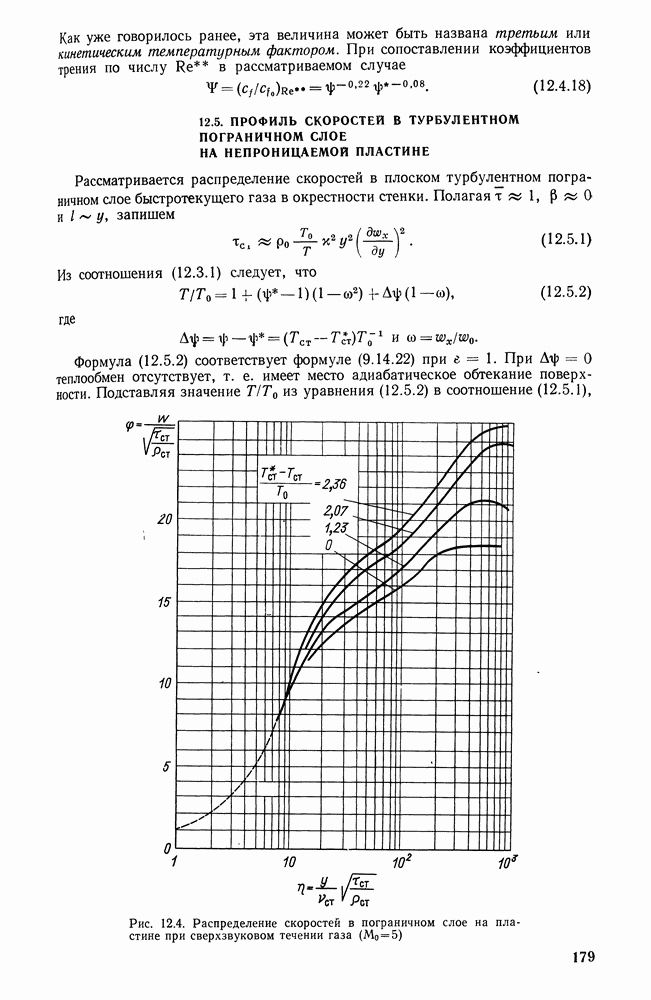
- 12.5. ПРОФИЛЬ СКОРОСТЕЙ В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ НА НЕПРОНИЦАЕМОЙ ПЛАСТИНЕ
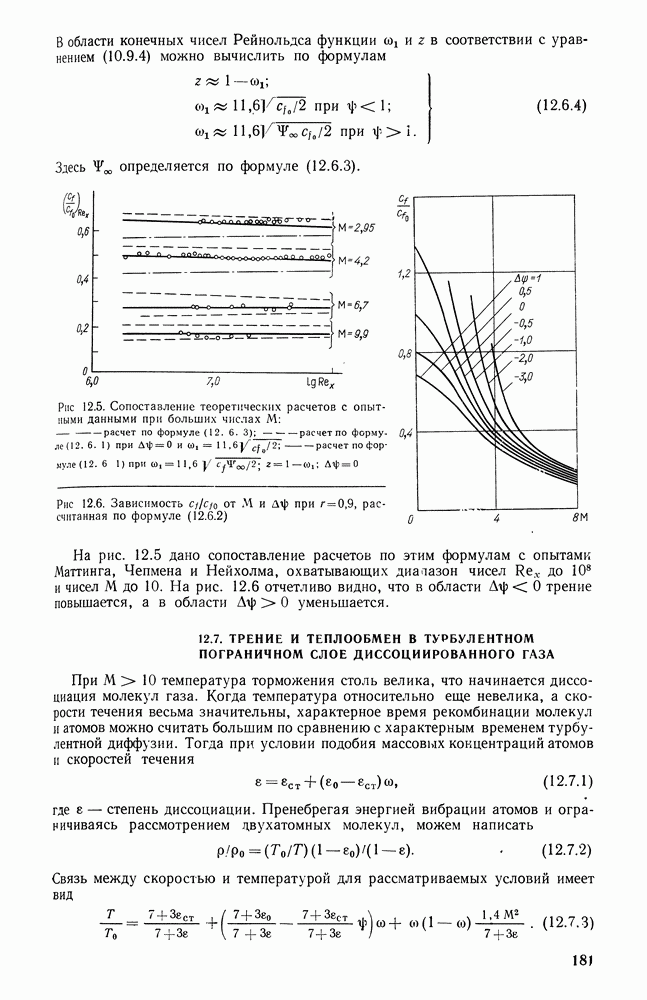
- 12.6. КОЭФФИЦИЕНТ ТРЕНИЯ И ТЕПЛООТДАЧИ ПЛАСТИНЫ ПРИ ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ
- 12.7. ТРЕНИЕ И ТЕПЛООБМЕН В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ ДИССОЦИИРОВАННОГО ГАЗА
- Глава 13. ТЕПЛООБМЕН И ТРЕНИЕ ПРИ ПЕРЕНОСЕ ВЕЩЕСТВА
- 13.1. МАССООБМЕН И ТЕПЛОПЕРЕДАЧА
- 13.2. УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ
- 13.3. ТРОЙНАЯ АНАЛОГИЯ
- 13.4. РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ТЕПЛОВОГО ПОТОКА В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ НА ПОЛУПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 13.5. ПРЕДЕЛЬНЫЙ ЗАКОН ТРЕНИЯ В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ
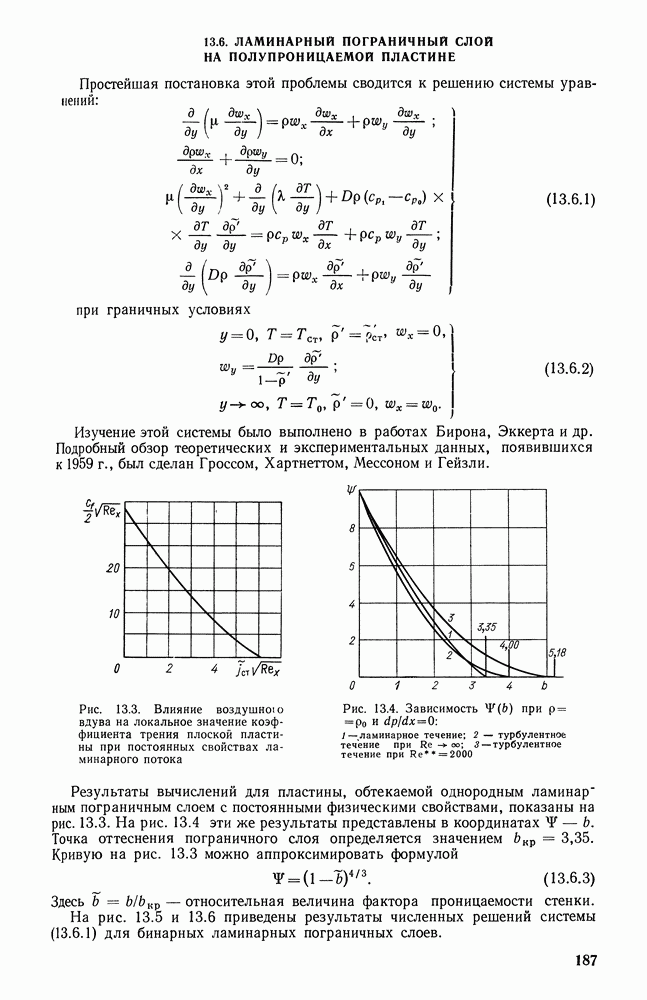
- 13.6. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ
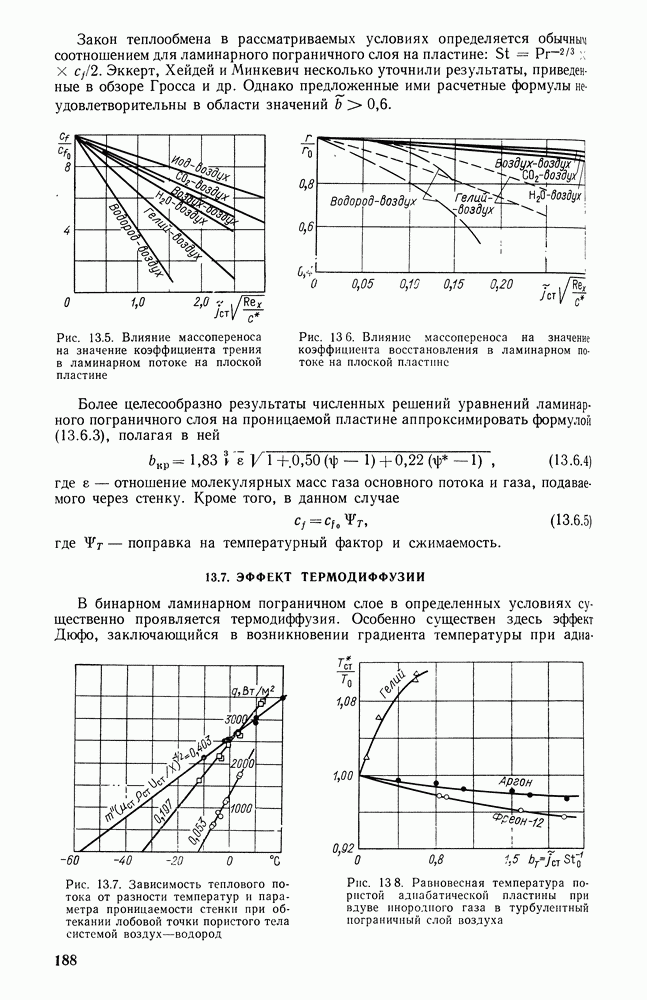
- 13.7. ЭФФЕКТ ТЕРМОДИФФУЗИИ
- 13.8. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ ПРИ
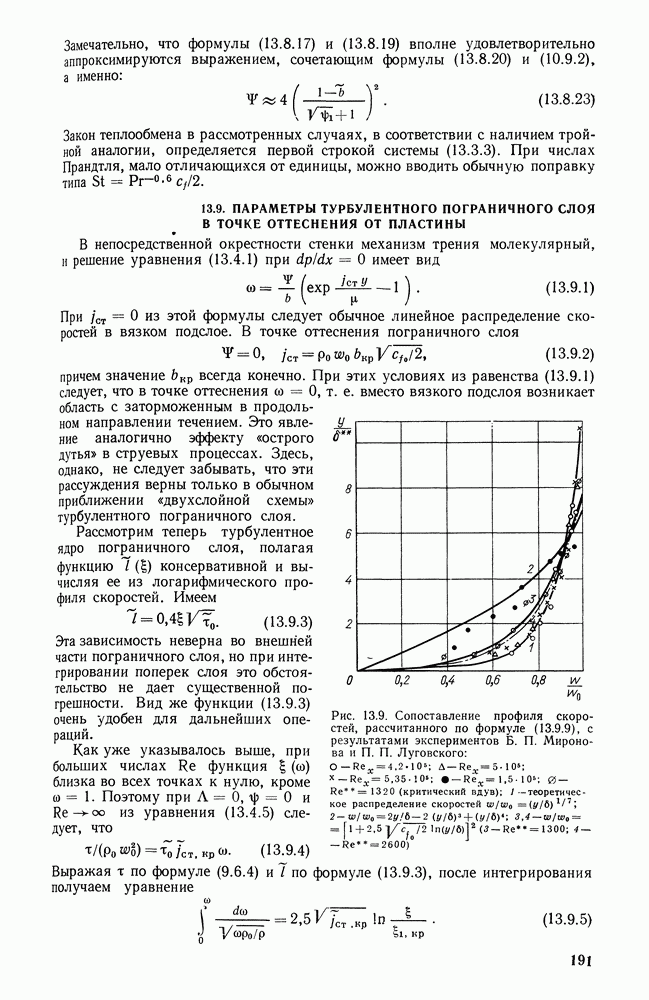
- 13.9. ПАРАМЕТРЫ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ В ТОЧКЕ ОТТЕСНЕНИЯ ОТ ПЛАСТИНЫ
- 13.10. ДВА ВАЖНЫХ ЧАСТНЫХ РЕШЕНИЯ УРАВНЕНИЯ ИМПУЛЬСОВ ДЛЯ ПОГРАНИЧНОГО СЛОЯ НА ПЛАСТИНЕ
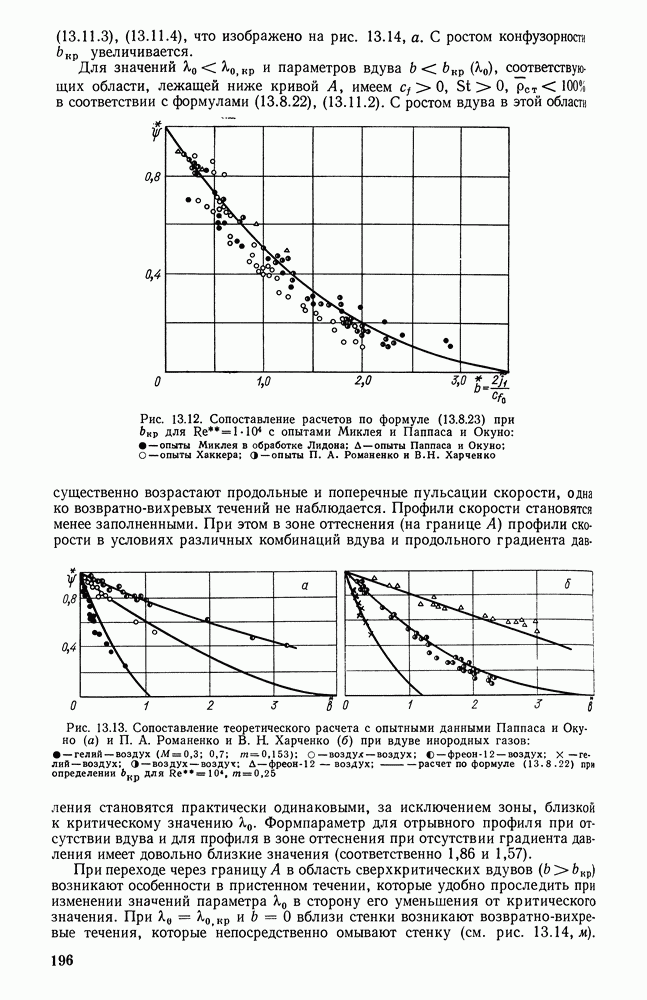
- 13.11. ЗАКОНЫ ТРЕНИЯ И ТЕПЛООБМЕНА В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ ГАЗА ПРИ КОНЕЧНЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- Глава 14. ТЕПЛОВЫЕ ЗАВЕСЫ
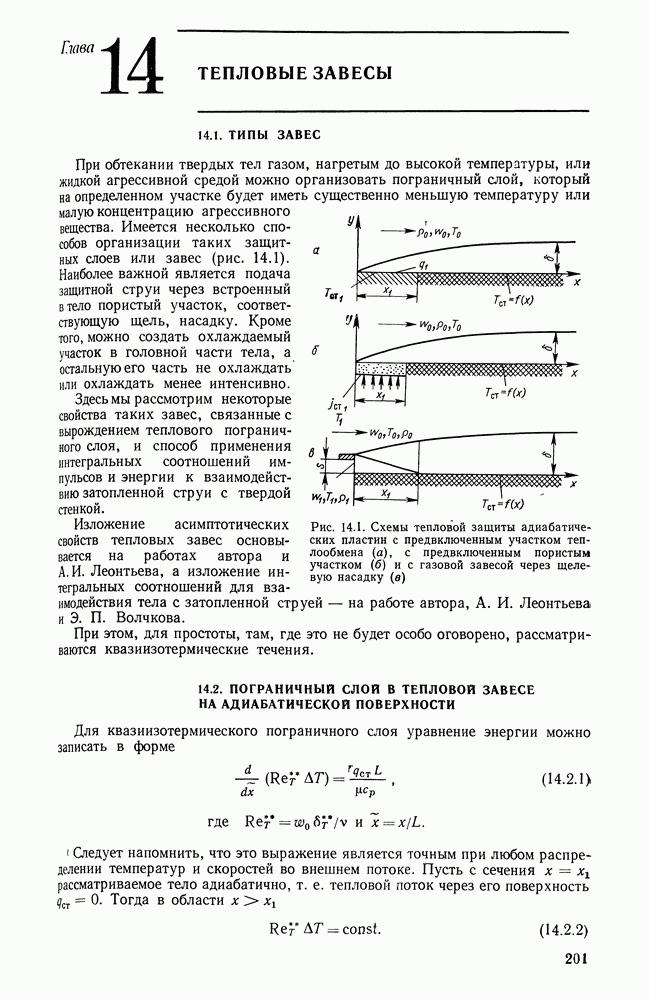
- 14.1. ТИПЫ ЗАВЕС
- 14.2. ПОГРАНИЧНЫЙ СЛОЙ В ТЕПЛОВОЙ ЗАВЕСЕ НА АДИАБАТИЧЕСКОЙ ПОВЕРХНОСТИ
- 14.3. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ПРЕДВКЛЮЧЕННЫМ УЧАСТКОМ ТЕПЛООБМЕНА
- 14.4. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ПРЕДВКЛЮЧЕННЫМ ПОРИСТЫМ УЧАСТКОМ
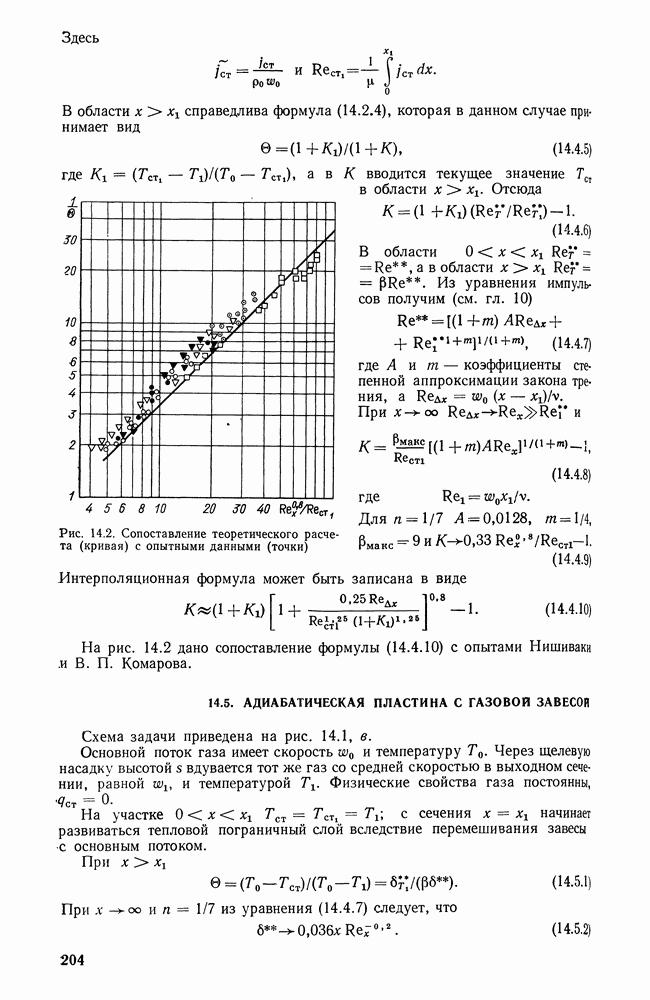
- 14.5. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ГАЗОВОЙ ЗАВЕСОЙ
- 14.6. НЕАДИАБАТИЧЕСКАЯ ПЛАСТИНА С ГАЗОВОЙ ЗАВЕСОЙ
- 14.7. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ИМПУЛЬСОВ ПРИ ВЗАИМОДЕЙСТВИИ ЗАТОПЛЕННОЙ СТРУИ С ПЛОСКОЙ ПЛАСТИНОЙ
- 14.8. ТРЕНИЕ И ТЕПЛООБМЕН ПРИ ВЗАИМОДЕЙСТВИИ ЗАТОПЛЕННОЙ СТРУИ С ТВЕРДОЙ СТЕНКОЙ
- Глава 15. ТЕПЛООБМЕН В ПАКЕТАХ И ЗАСЫПКАХ
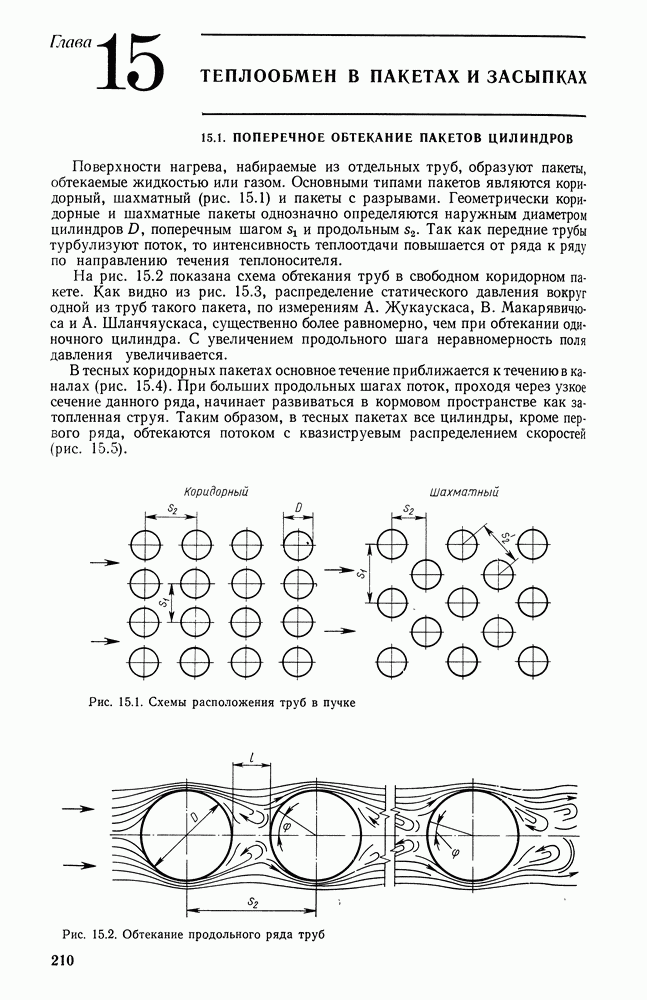
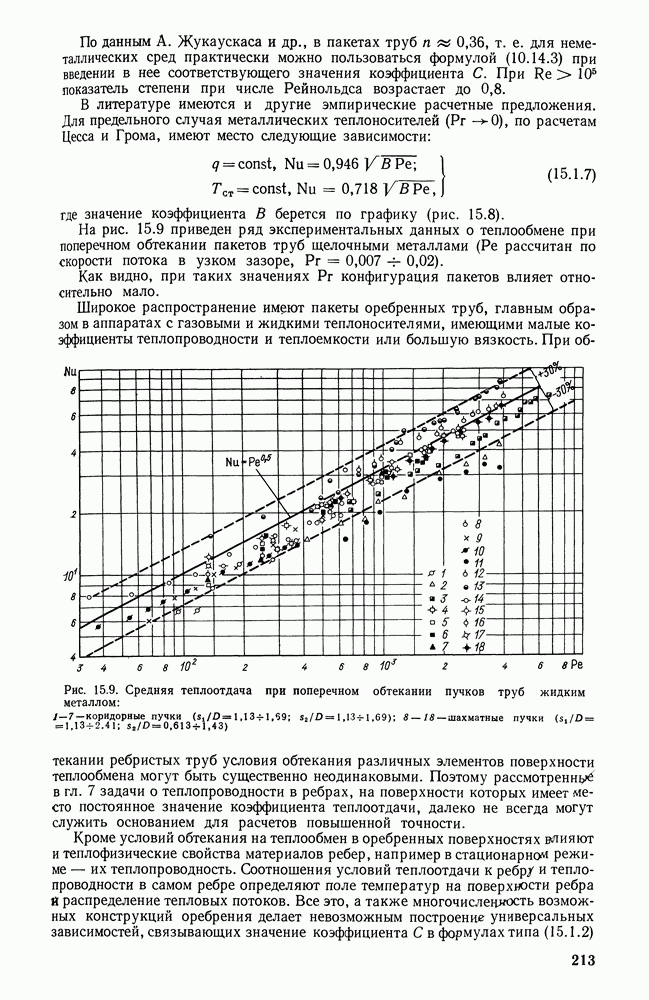
- 15.1. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ПАКЕТОВ ЦИЛИНДРОВ
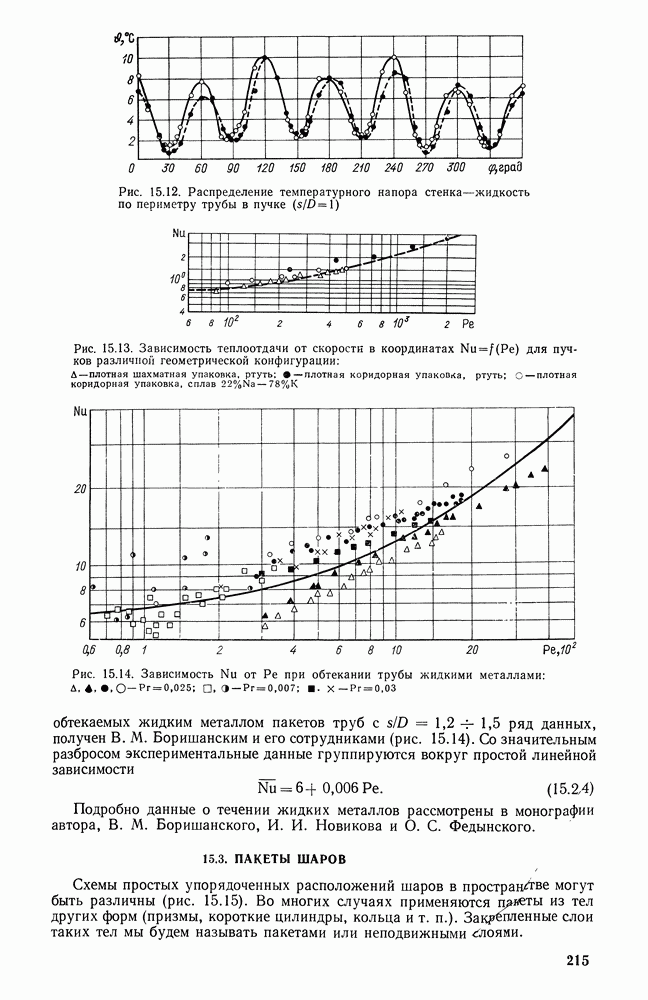
- 15.2. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ПАКЕТОВ ЦИЛИНДРОВ
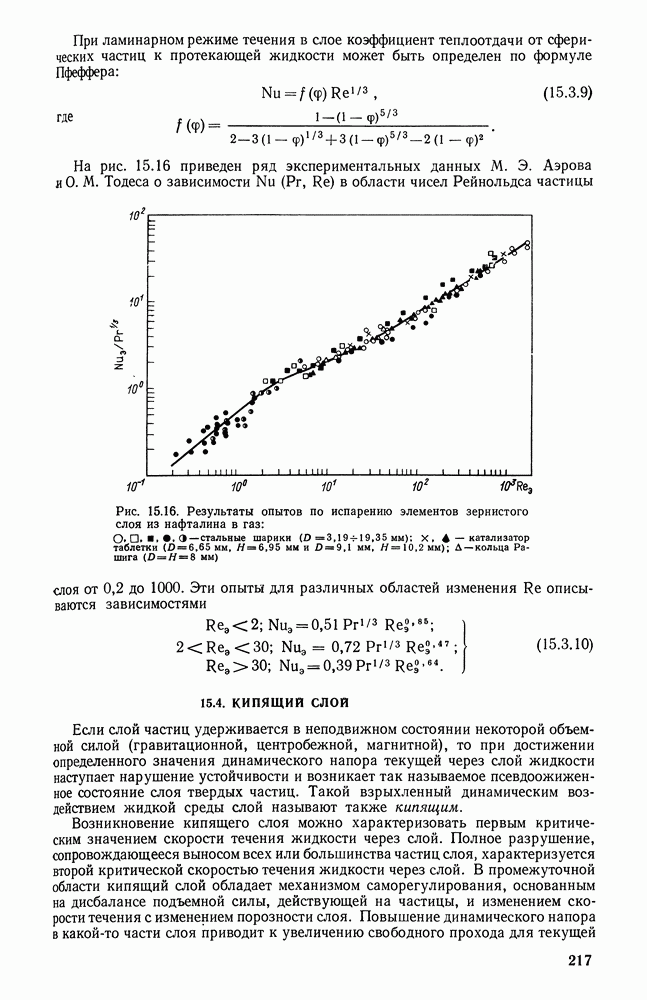
- 15.3. ПАКЕТЫ ШАРОВ
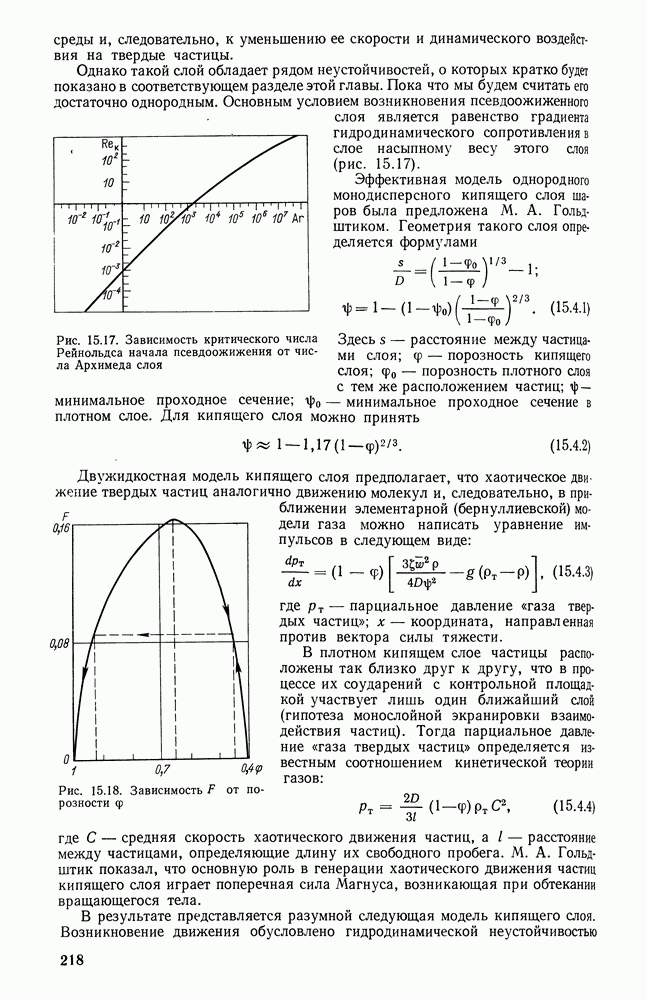
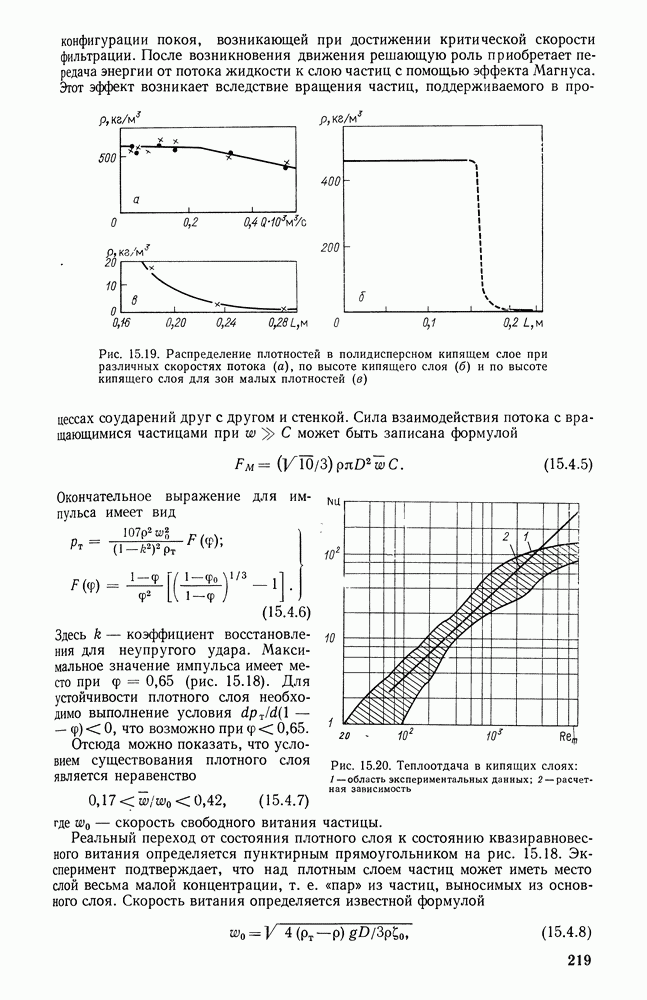
- 15.4. КИПЯЩИЙ СЛОЙ
- 15.5. НЕОДНОРОДНОСТИ И НЕУСТОЙЧИВОСТИ В СЛОЕ ЧАСТИЦ
- Глава 16. ГИДРОДИНАМИКА И ТЕПЛООБМЕН В СРЕДАХ С НЕЛИНЕЙНЫМ ЗАКОНОМ МОЛЕКУЛЯРНОГО ТРЕНИЯ
- 16.1. ЖИДКОСТИ С НЕЛИНЕЙНОЙ КРИВОЙ ТЕЧЕНИЯ
- 16.2. СВЯЗЬ МЕЖДУ ТЕКУЧЕСТЬЮ И КАСАТЕЛЬНЫМИ НАПРЯЖЕНИЯМИ В ПОТОКЕ ЖИДКОСТИ СО СТРУКТУРНОЙ ВЯЗКОСТЬЮ
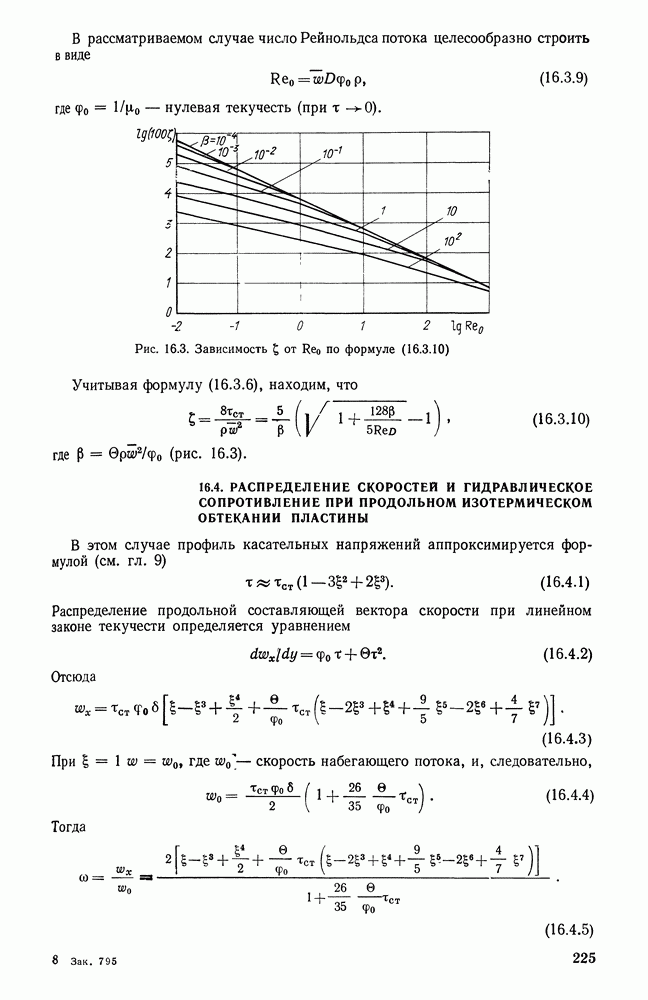
- 16.3. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ СТАБИЛИЗИРОВАННОМ ИЗОТЕРМИЧЕСКОМ ТЕЧЕНИИ ЖИДКОСТИ С ЛИНЕЙНЫМ ЗАКОНОМ ТЕКУЧЕСТИ
- 16.4. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ ПРОДОЛЬНОМ ИЗОТЕРМИЧЕСКОМ ОБТЕКАНИИ ПЛАСТИНЫ
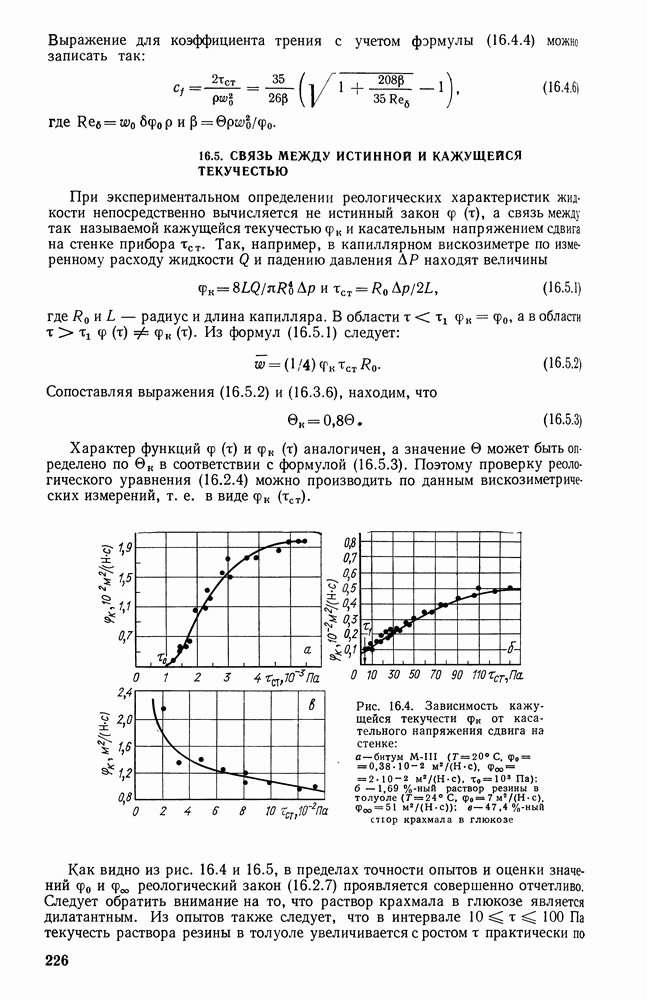
- 16.5. СВЯЗЬ МЕЖДУ ИСТИННОЙ И КАЖУЩЕЙСЯ ТЕКУЧЕСТЬЮ
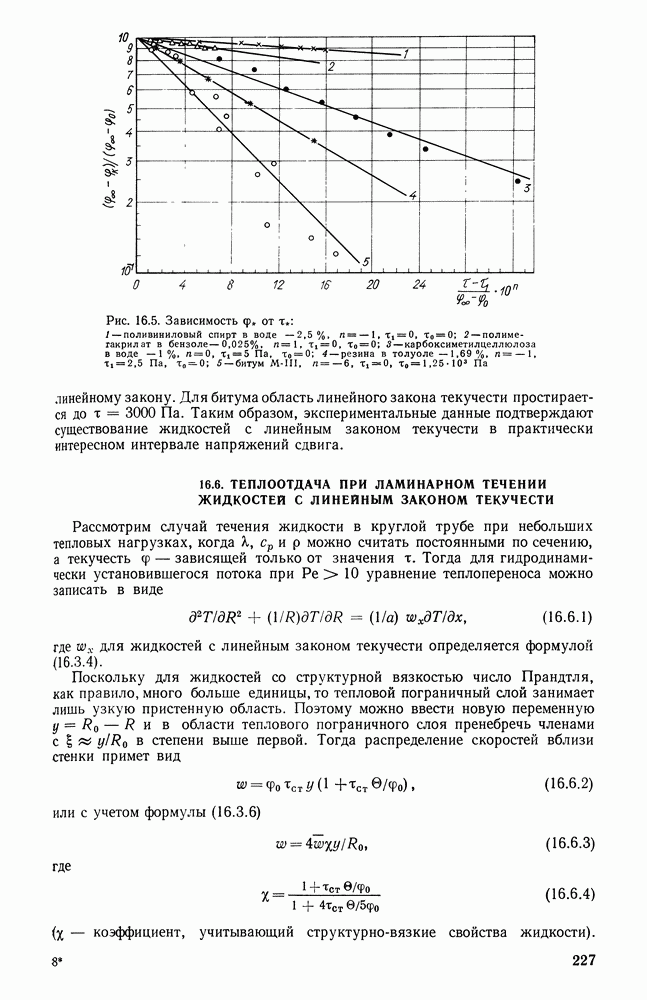
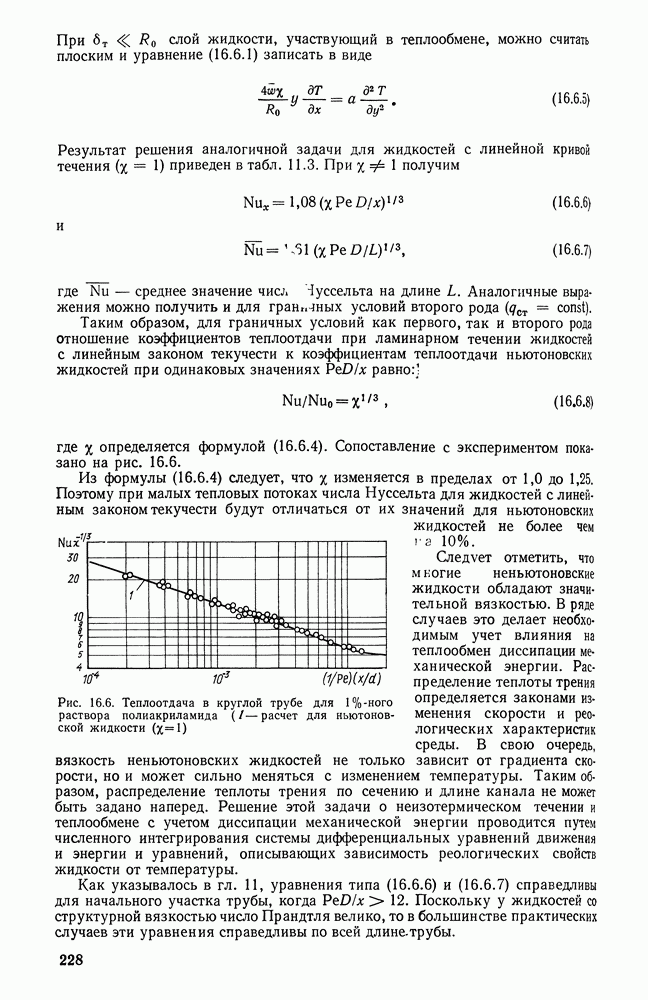
- 16.6. ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ ЖИДКОСТЕЙ С ЛИНЕЙНЫМ ЗАКОНОМ ТЕКУЧЕСТИ
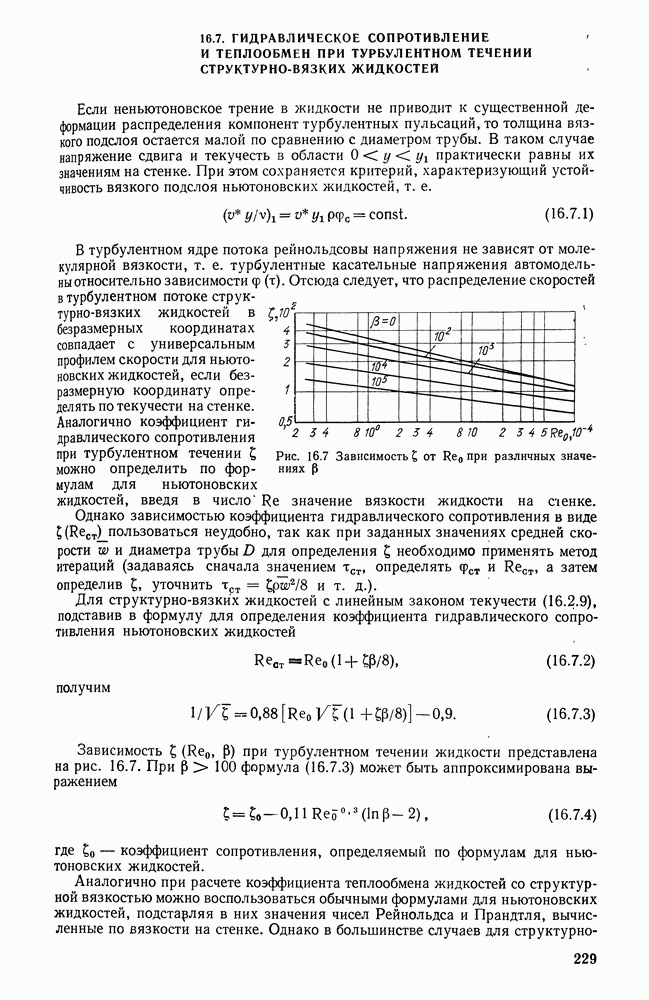
- 16.7. ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ СТРУКТУРНО-ВЯЗКИХ ЖИДКОСТЕЙ
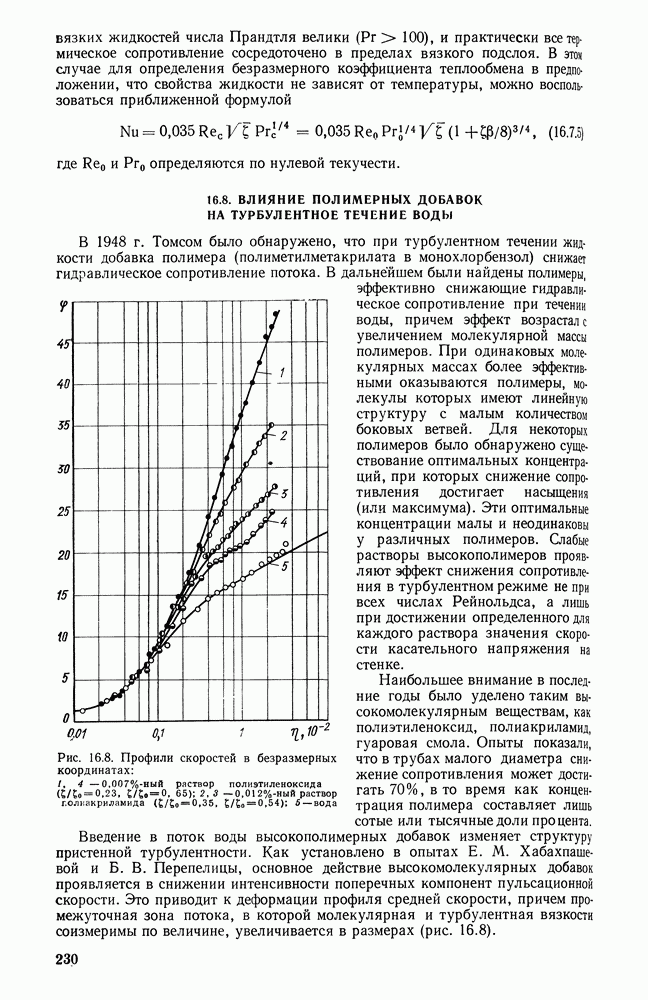
- 16.8. ВЛИЯНИЕ ПОЛИМЕРНЫХ ДОБАВОК НА ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ВОДЫ
- Глава 17. ТЕПЛООТДАЧА ПРИ СВОБОДНОЙ КОНВЕКЦИИ
- 17.1. СВОБОДНАЯ ТЕПЛОВАЯ КОНВЕКЦИЯ ОКОЛО ТВЕРДОЙ ПОВЕРХНОСТИ
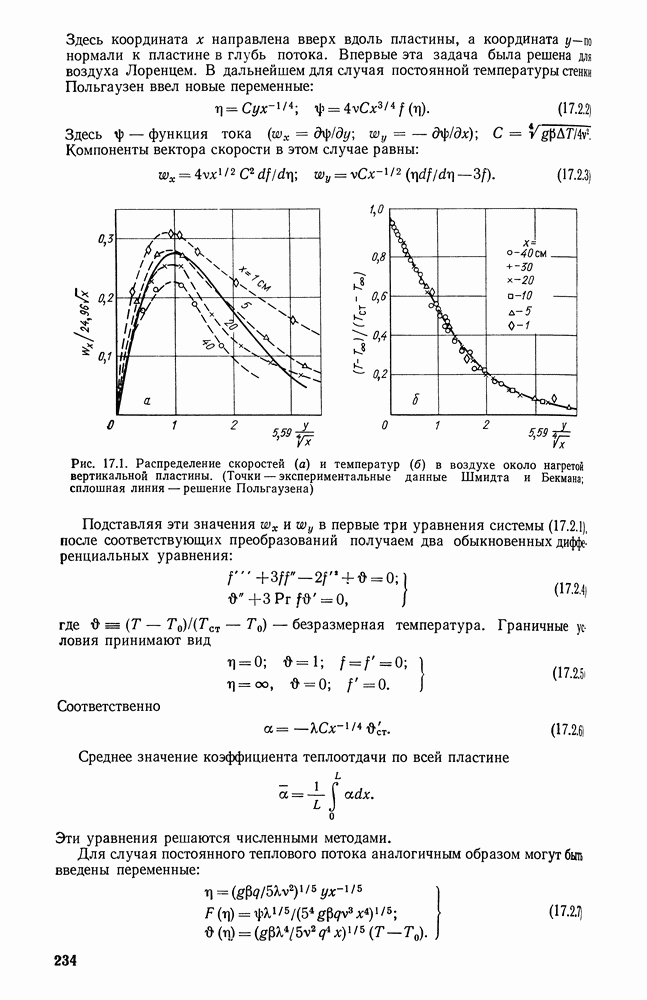
- 17.2. ТЕПЛООТДАЧА В ОБЛАСТИ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ ПРИ Pr>=1
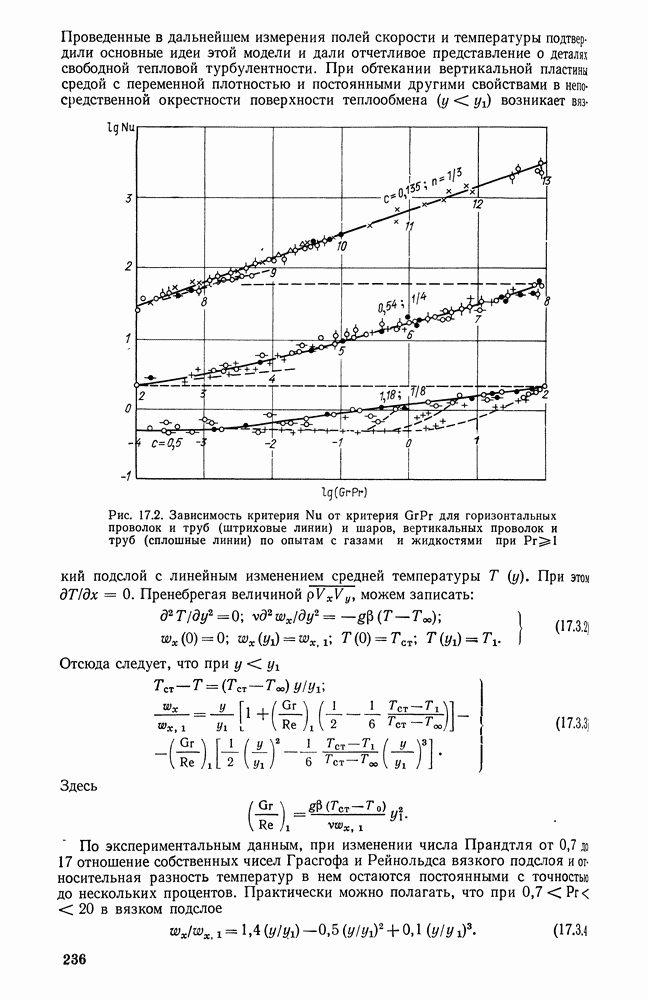
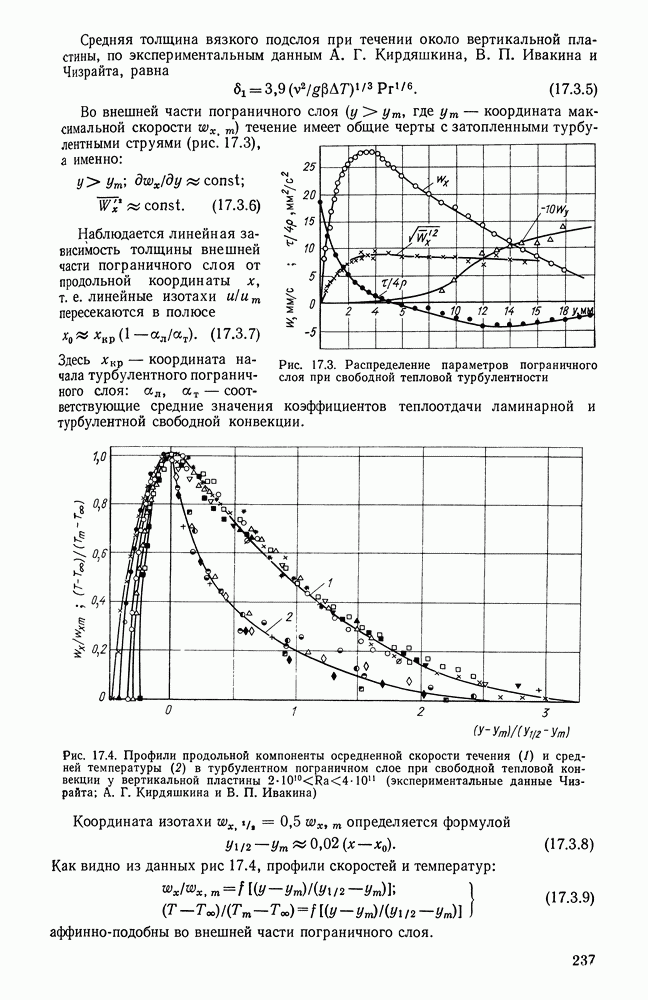
- 17.3. ГИДРОДИНАМИКА И ТЕПЛООБМЕН В ОБЛАСТИ РАЗВИТОЙ ТЕПЛОВОЙ ТУРБУЛЕНТНОСТИ ПРИ Рr>=1
- 17.4. ТЕПЛООТДАЧА ПРИ Рr<<1
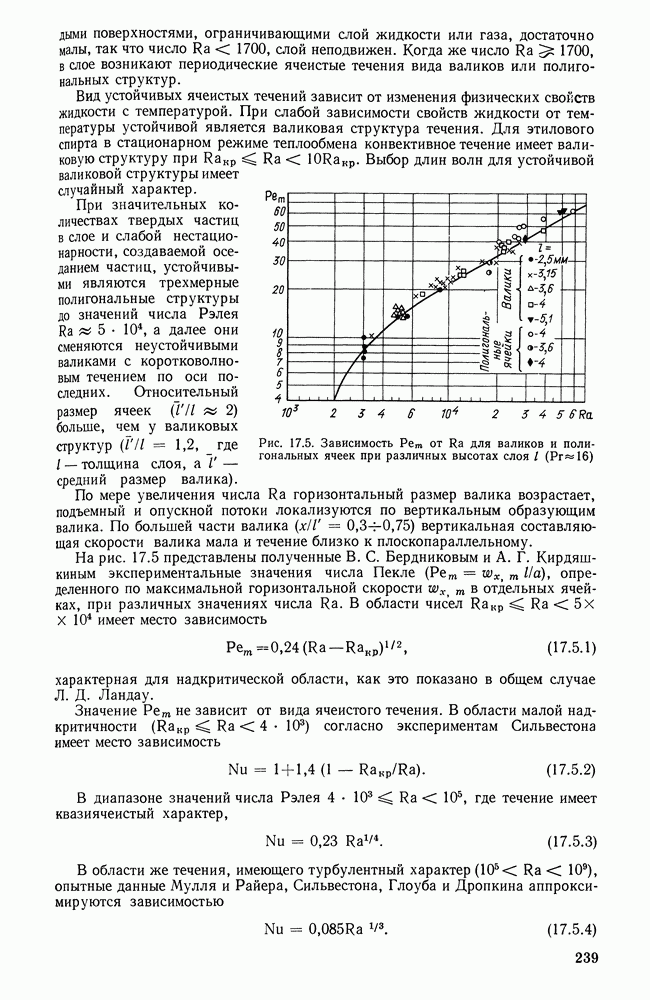
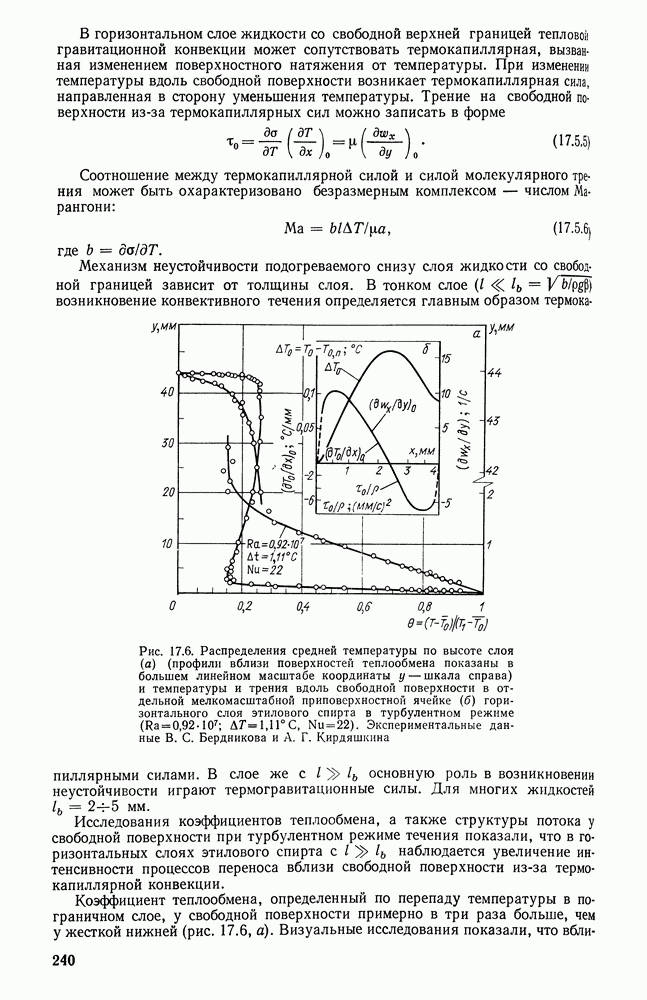
- 17.5. ТЕПЛООТДАЧА В ЖИДКИХ И ГАЗОВЫХ СЛОЯХ
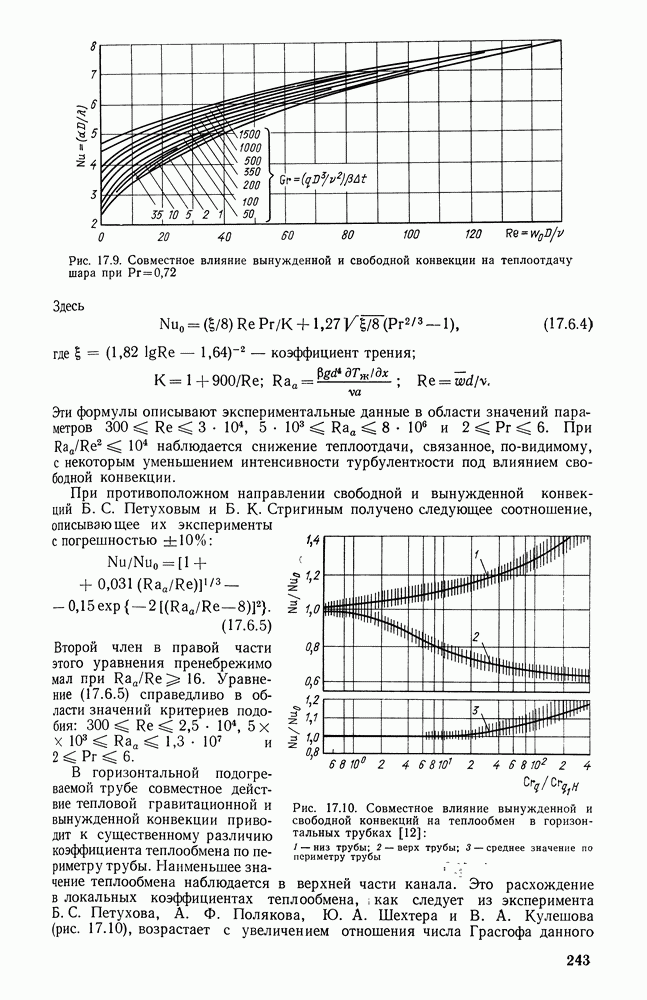
- 17.6. СОВМЕСТНОЕ ВЛИЯНИЕ СВОБОДНОЙ И ВЫНУЖДЕННОЙ КОНВЕКЦИИ
- Глава 18. ТЕПЛООБМЕН В РАЗРЕЖЕННЫХ ГАЗАХ
- 18.1. ОСОБЕННОСТИ ПРОЦЕССОВ ПЕРЕНОСА В РАЗРЕЖЕННОМ ГАЗЕ
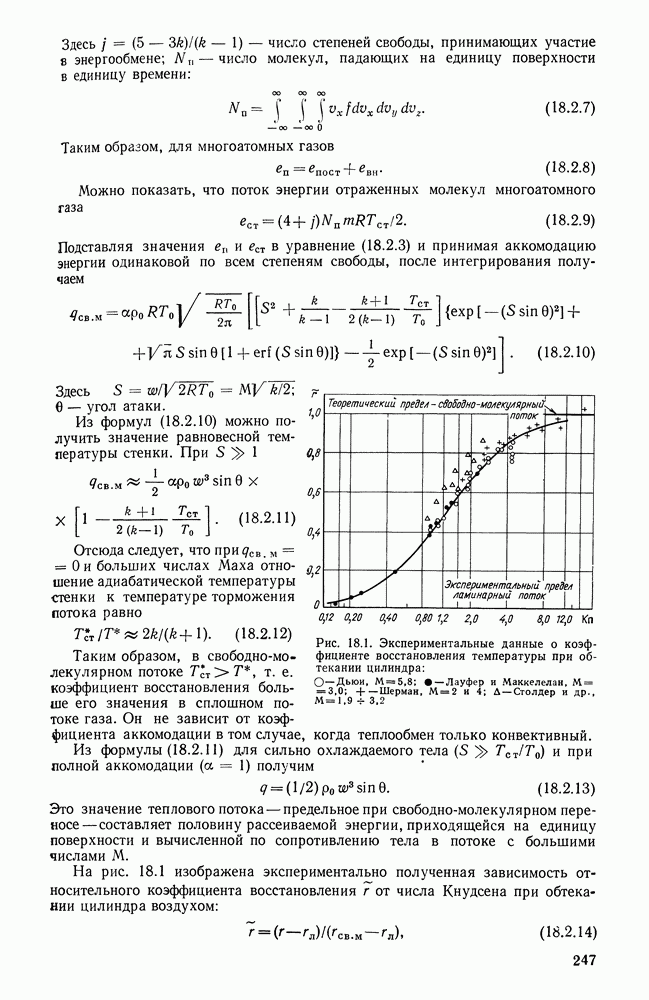
- 18.2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ С ПОВЕРХНОСТЬЮ. СВОБОДНО-МОЛЕКУЛЯРНЫЙ ПЕРЕНОС ТЕПЛА
- 18.3. ТЕЧЕНИЕ СО СКОЛЬЖЕНИЕМ И ТЕМПЕРАТУРНЫМ СКАЧКОМ
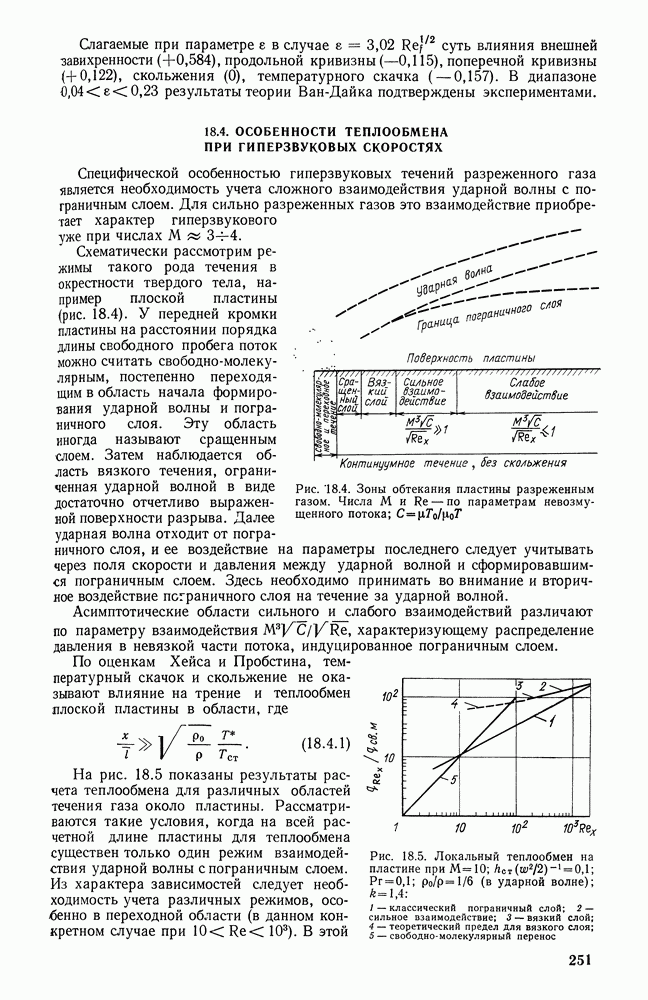
- 18.4. ОСОБЕННОСТИ ТЕПЛООБМЕНА ПРИ ГИПЕРЗВУКОВЫХ СКОРОСТЯХ
- 18.5. РЕЛАКСАЦИОННЫЕ ЭФФЕКТЫ ПРИ ОБТЕКАНИИ ТЕЛ РАЗРЕЖЕННЫМ ГАЗОМ
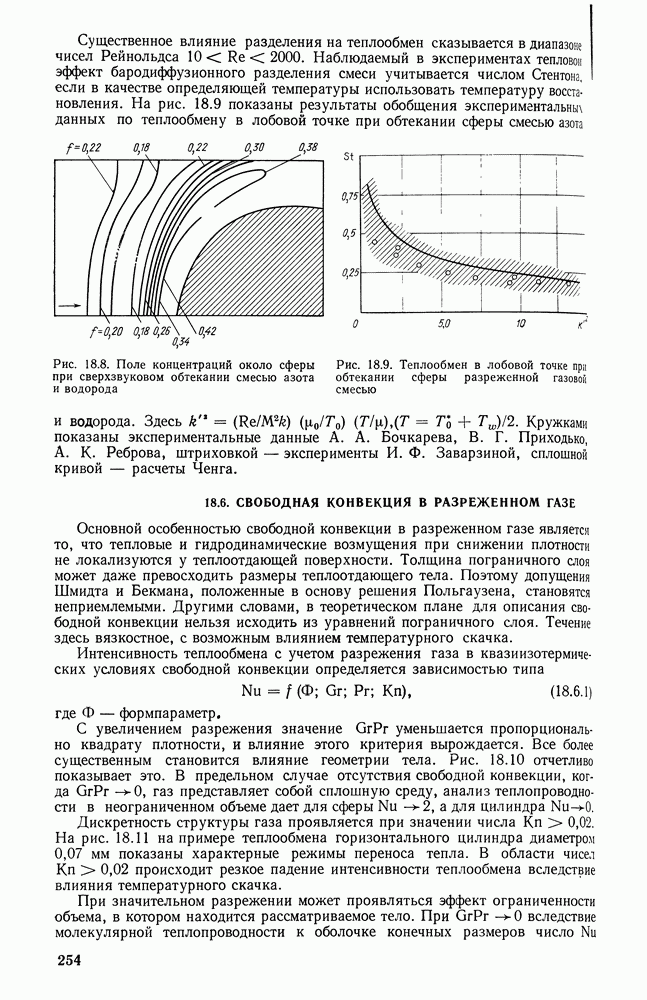
- 18.6. СВОБОДНАЯ КОНВЕКЦИЯ В РАЗРЕЖЕННОМ ГАЗЕ
- 18.7. ВАКУУМНАЯ ИЗОЛЯЦИЯ
- Глава 19. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ПАРА НА ТВЕРДЫХ ПОВЕРХНОСТЯХ
- 19.1. ПЛЕНОЧНАЯ И КАПЕЛЬНАЯ КОНДЕНСАЦИЯ
- 19.2. ОСНОВНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА ПРИ ПЛЕНОЧНОЙ КОНДЕНСАЦИИ ЧИСТОГО НАСЫЩЕННОГО ПАРА
- 19.3. ЛАМИНАРНОЕ ТЕЧЕНИЕ ПЛЕНКИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ ПРИ МЕДЛЕННОМ ДВИЖЕНИИ ПАРА
- 19.4. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ПЛЕНКИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ ПРИ МЕДЛЕННОМ ДВИЖЕНИИ ПАРА
- 19.5. СРЕДНИЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ ПРИ СМЕШАННОМ ТЕЧЕНИИ ПЛЕНКИ КОНДЕНСАТА НА ВЕРТИКАЛЬНОЙ СТЕНКЕ
- 19.6. ВЛИЯНИЕ СКОРОСТИ ТЕЧЕНИЯ ЧИСТОГО ПАРА НА ТЕПЛООТДАЧУ ПРИ КОНДЕНСАЦИИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ
- 19.7. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ПАРА ВНУТРИ ТРУБЫ
- 19.8. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ЧИСТОГО ПАРА НА ВНЕШНЕЙ ПОВЕРХНОСТИ ГОРИЗОНТАЛЬНЫХ ТРУБ
- 19.9. ПЛЕНОЧНАЯ КОНДЕНСАЦИЯ НА НИЖНЕЙ ПОВЕРХНОСТИ ГОРИЗОНТАЛЬНОЙ ПЛИТЫ
- 9.10. ВЛИЯНИЕ ВЛАЖНОСТИ И ПЕРЕГРЕВА ПАРА
- 19.11. КАПЕЛЬНАЯ КОНДЕНСАЦИЯ
- Глава 20. КОНДЕНСАЦИЯ НА СВОБОДНОЙ ПОВЕРХНОСТИ ЖИДКОСТИ
- 20.1. ТЕПЛООБМЕН В СВОБОДНО ПАДАЮЩЕЙ СТРУЕ
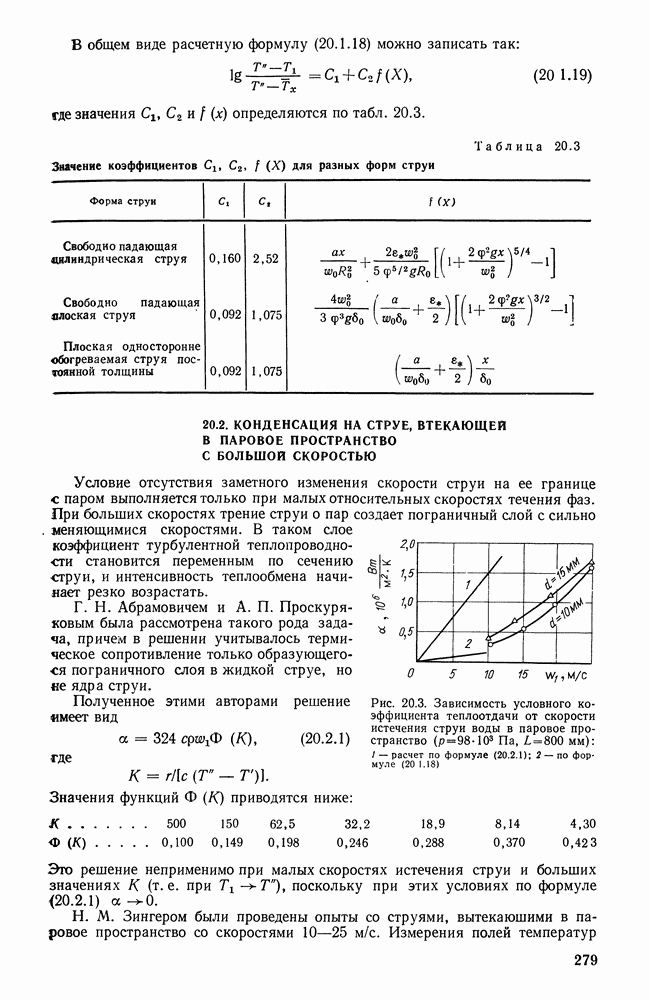
- 20.2. КОНДЕНСАЦИЯ НА СТРУЕ, ВТЕКАЮЩЕЙ В ПАРОВОЕ ПРОСТРАНСТВО С БОЛЬШОЙ СКОРОСТЬЮ
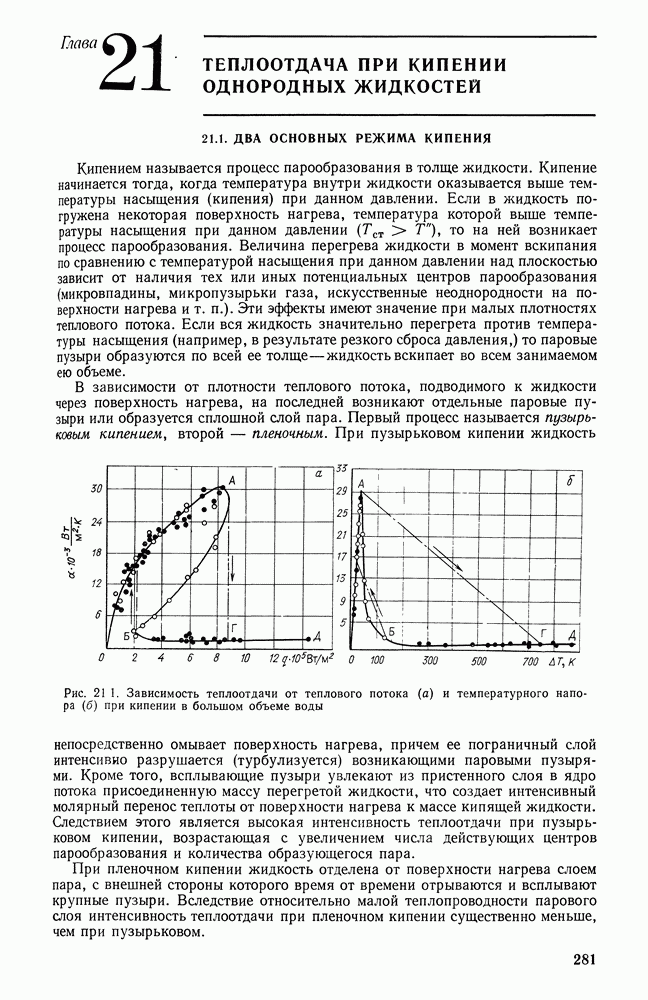
- Глава 21. ТЕПЛООТДАЧА ПРИ КИПЕНИИ ОДНОРОДНЫХ ЖИДКОСТЕЙ
- 21.1. ДВА ОСНОВНЫХ РЕЖИМА КИПЕНИЯ
- 21.2. ТЕМПЕРАТУРНОЕ ПОЛЕ
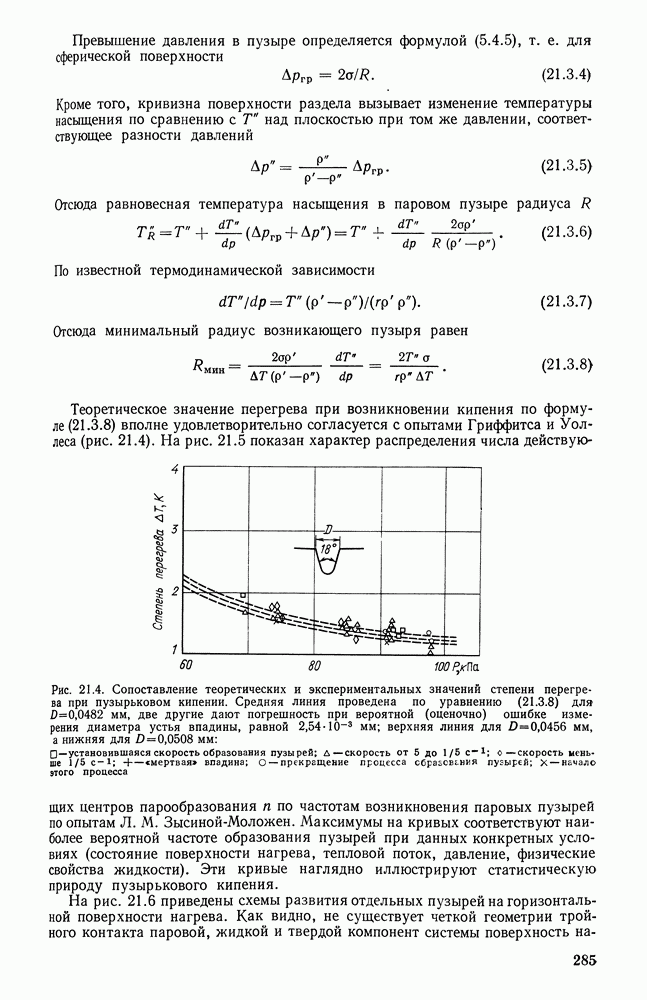
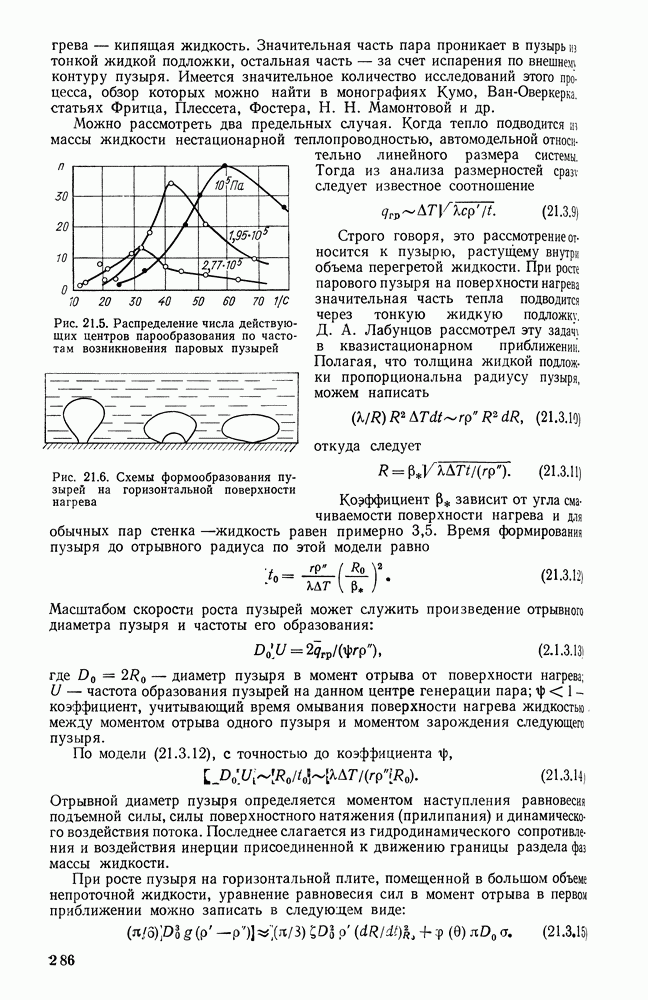
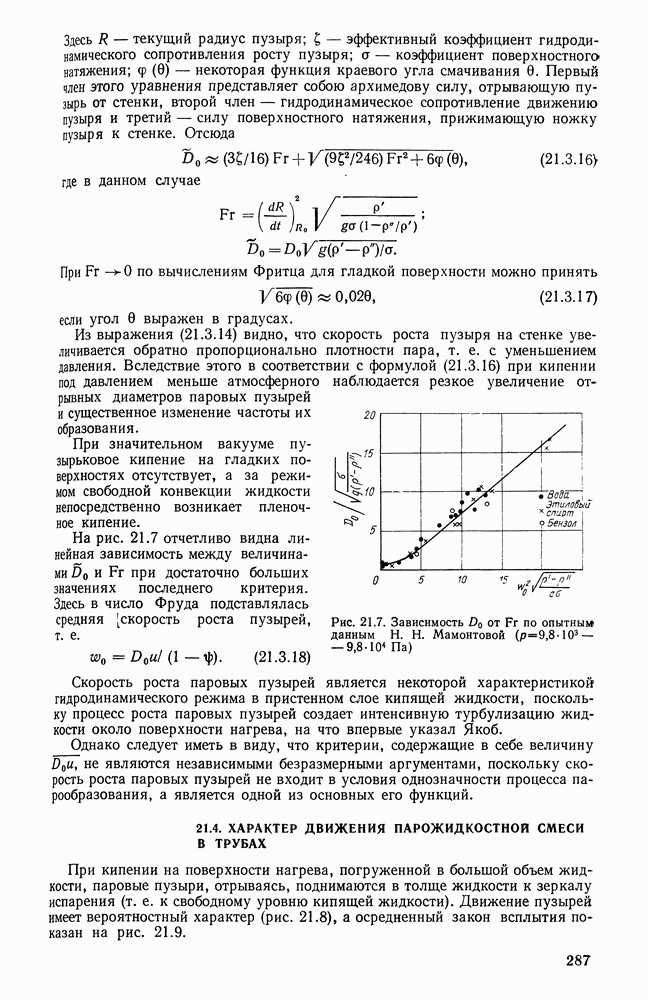
- 21.3. ПУЗЫРЬКОВОЕ КИПЕНИЕ, ЧАСТОТА И СКОРОСТЬ РОСТА ПАРОВЫХ ПУЗЫРЕЙ
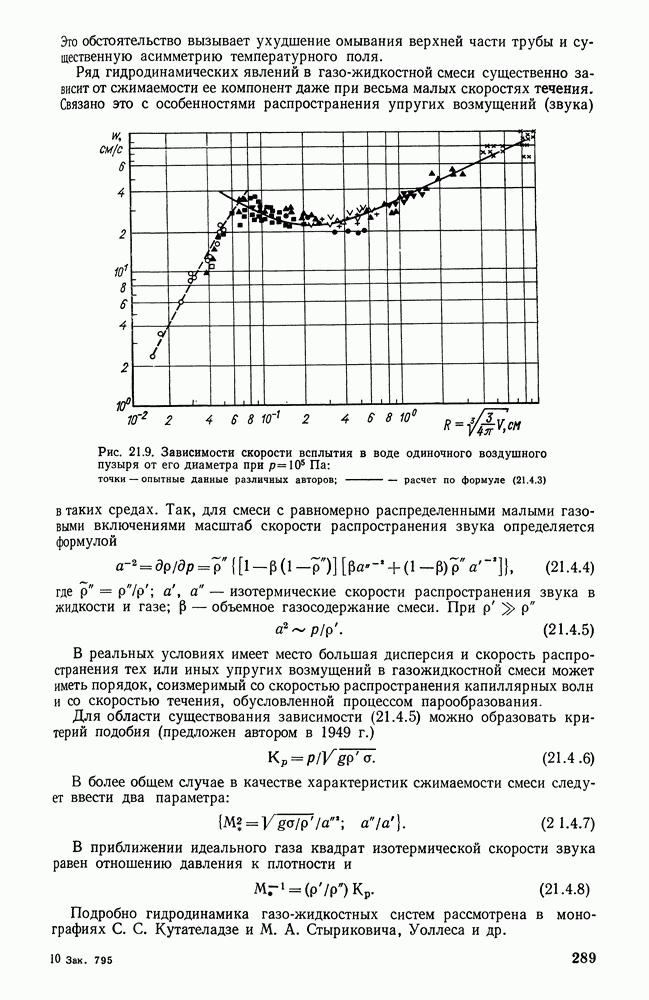
- 21.4. ХАРАКТЕР ДВИЖЕНИЯ ПАРОЖИДКОСТНОЙ СМЕСИ В ТРУБАХ
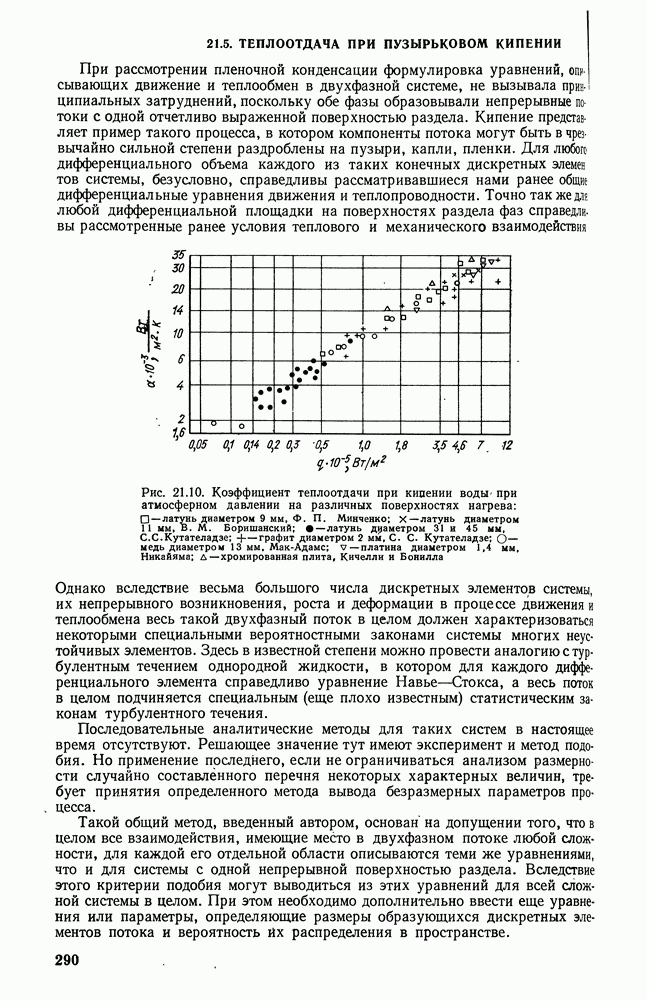
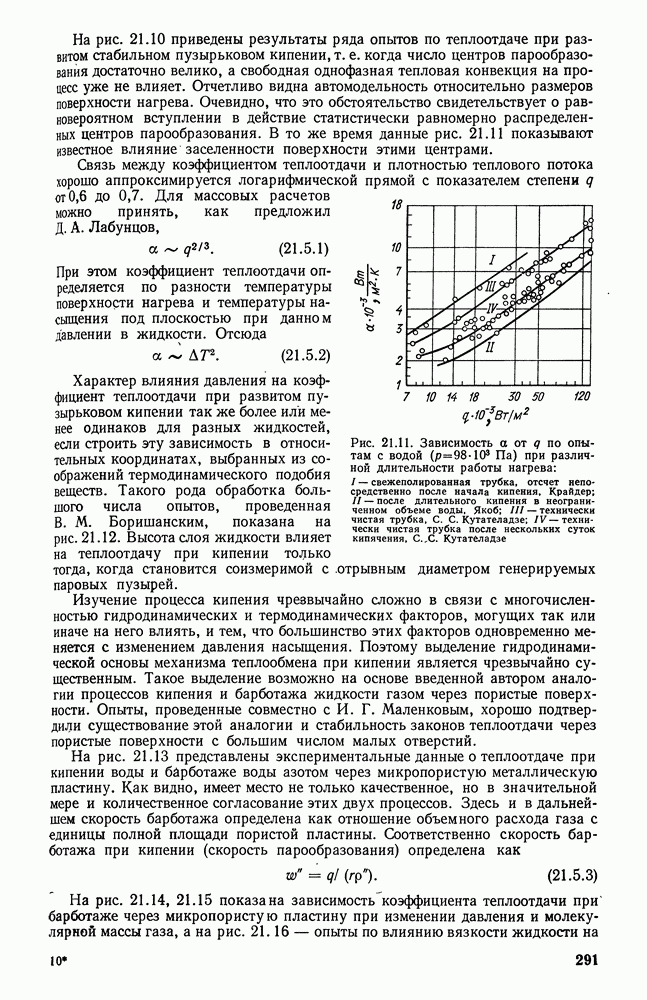
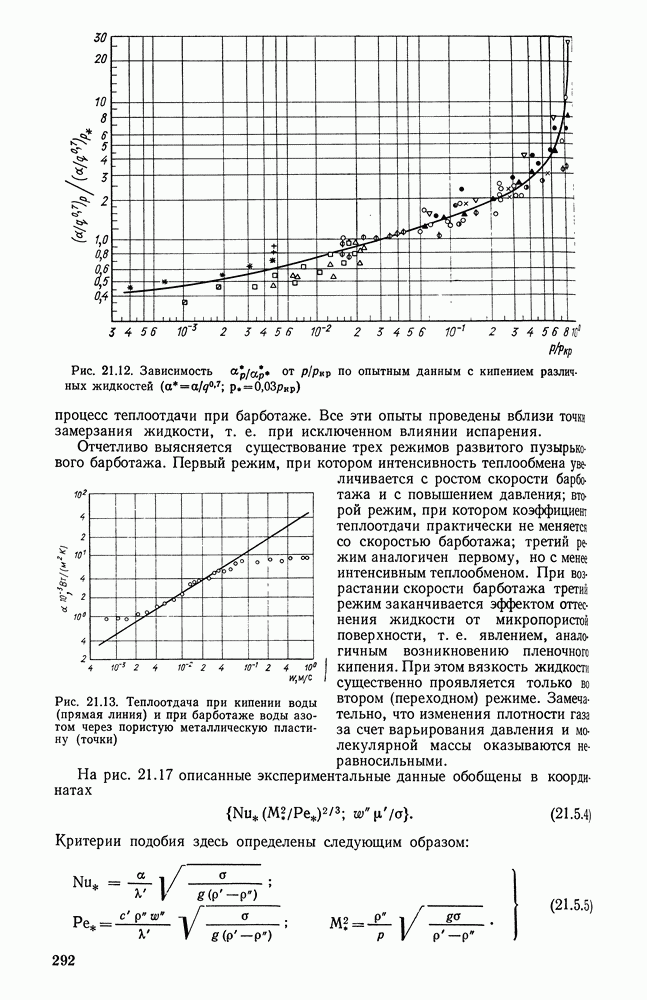
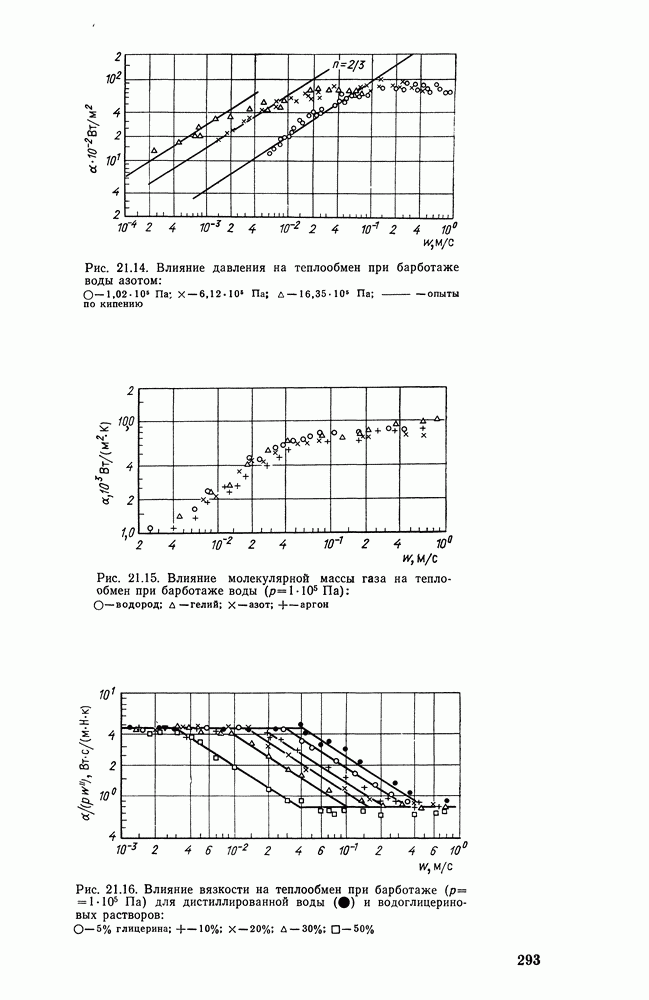
- 21.5. ТЕПЛООТДАЧА ПРИ ПУЗЫРЬКОВОМ КИПЕНИИ
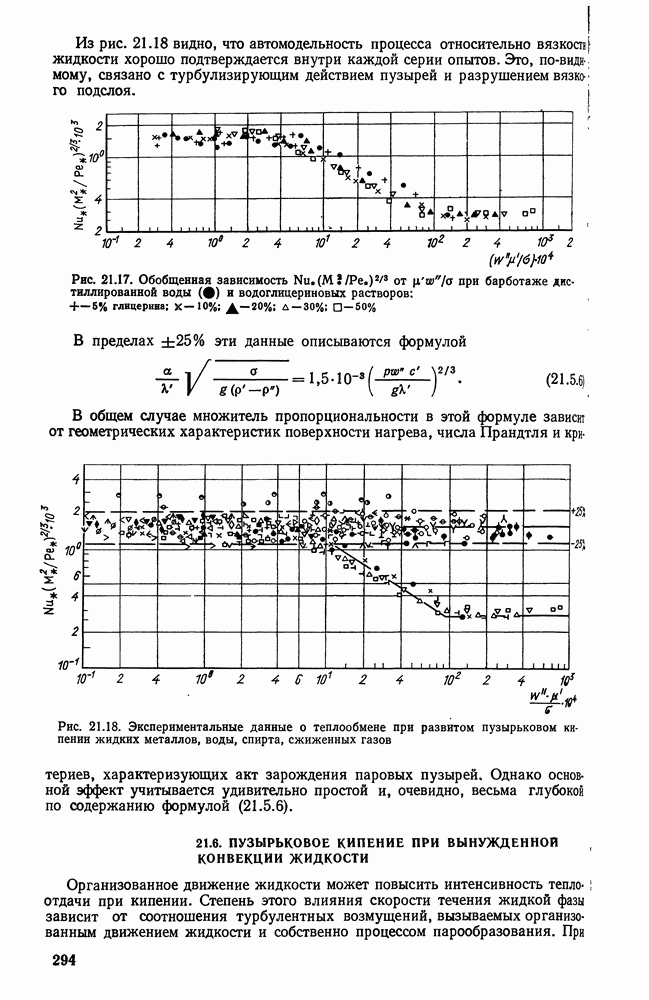
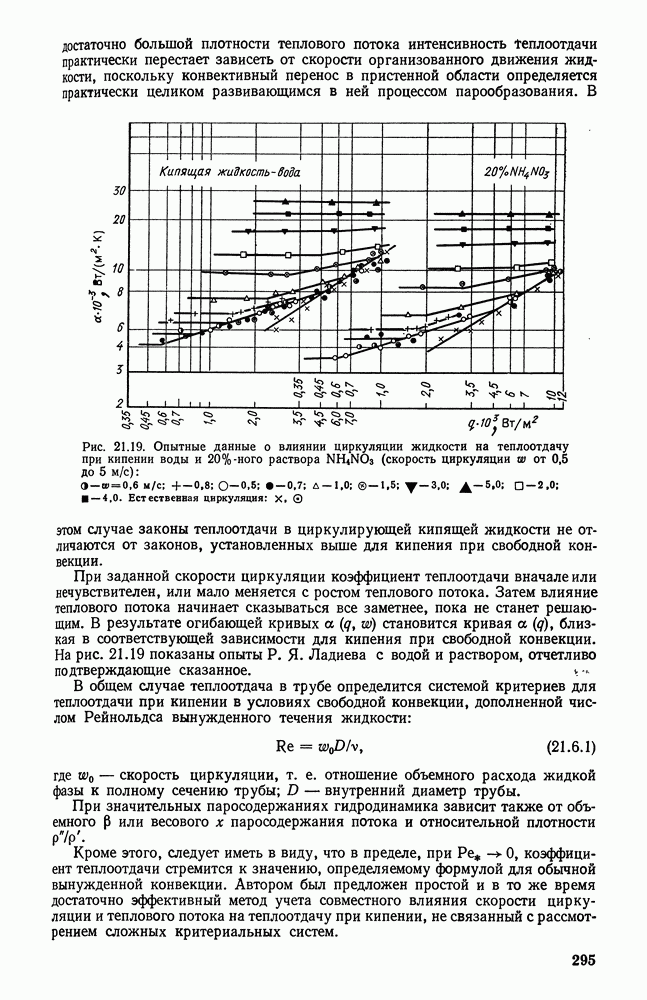
- 21.6. ПУЗЫРЬКОВОЕ КИПЕНИЕ ПРИ ВЫНУЖДЕННОЙ КОНВЕКЦИИ ЖИДКОСТИ
- 21.7. ТЕПЛООТДАЧА ПРИ ПЛЕНОЧНОМ КИПЕНИИ
- 21.8. ТЕПЛООТДАЧА ПРИ СВОБОДНОМ РАСТЕКАНИИ ЖИДКОСТИ ПО ПОВЕРХНОСТИ НАГРЕВА
- Глава 22. КРИТИЧЕСКИЕ ПЛОТНОСТИ ТЕПЛОВОГО ПОТОКА, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЯ РЕЖИМА КИПЕНИЯ
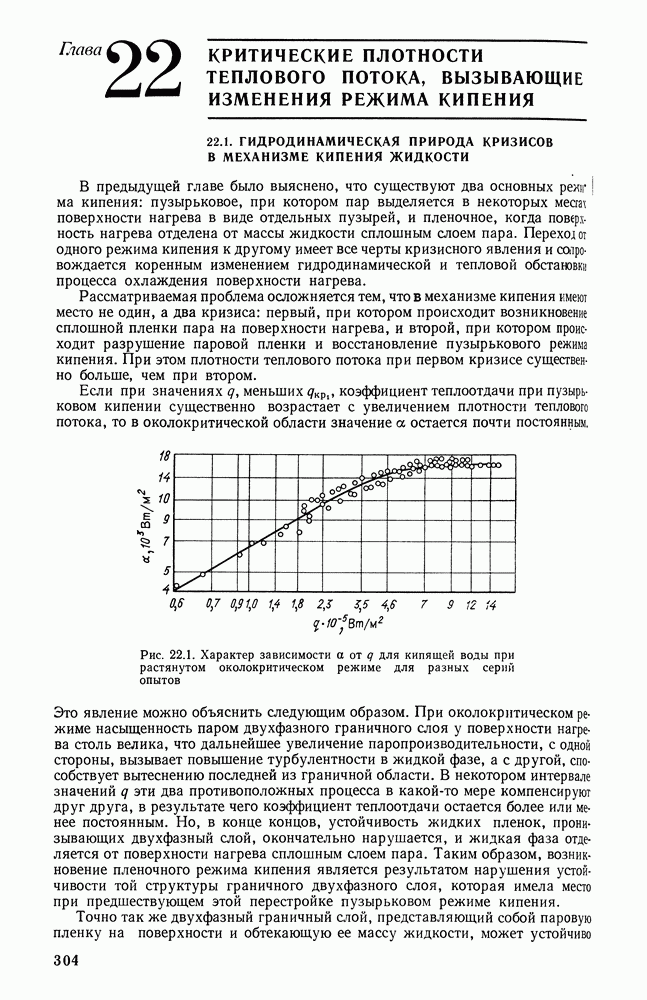
- 22.1. ГИДРОДИНАМИЧЕСКАЯ ПРИРОДА КРИЗИСОВ В МЕХАНИЗМЕ КИПЕНИЯ ЖИДКОСТИ
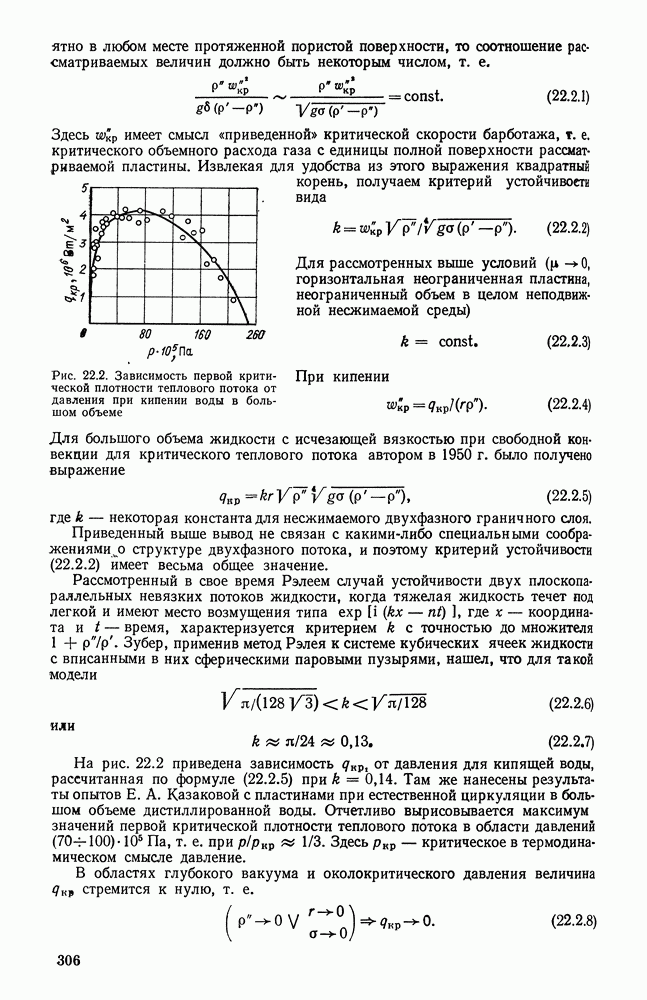
- 22.2. КРИТЕРИЙ УСТОЙЧИВОСТИ ДВУХФАЗНОГО ГРАНИЧНОГО СЛОЯ ПРИ СВОБОДНОЙ КОНВЕКЦИИ В БОЛЬШОМ ОБЪЕМЕ КИПЯЩЕЙ ЖИДКОСТИ (ПЕРВЫЙ КРИЗИС РЕЖИМА КИПЕНИЯ)
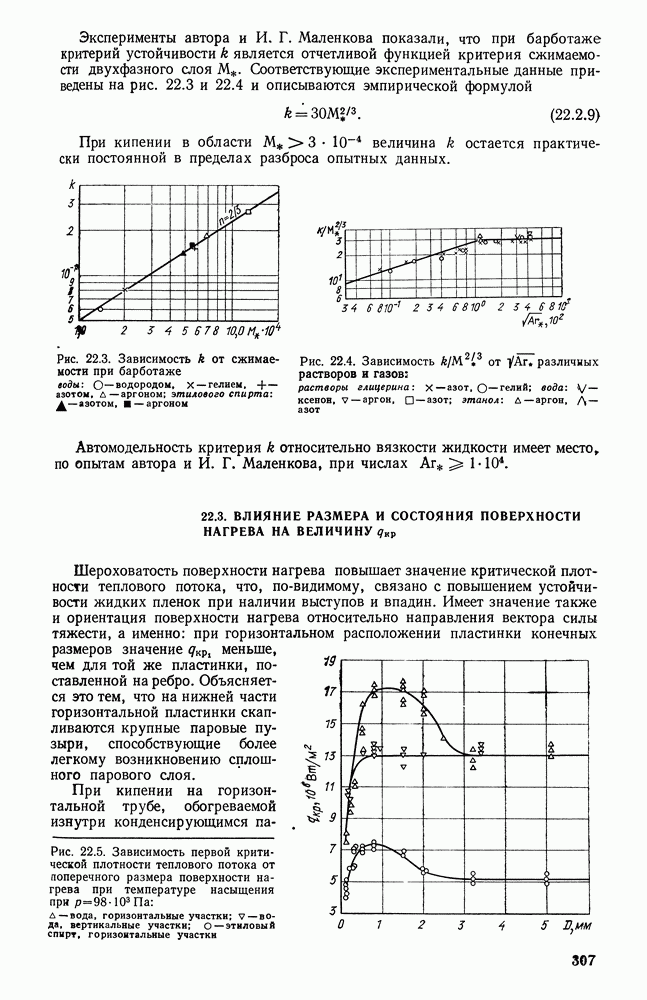
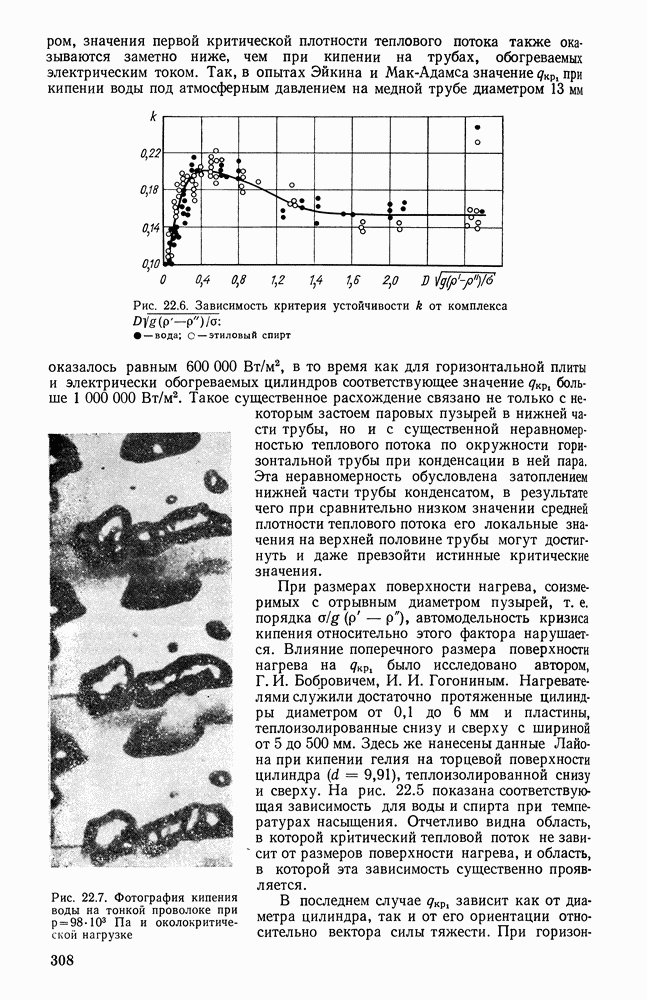
- 22.3. ВЛИЯНИЕ РАЗМЕРА И СОСТОЯНИЯ ПОВЕРХНОСТИ НАГРЕВА НА ВЕЛИЧИНУ
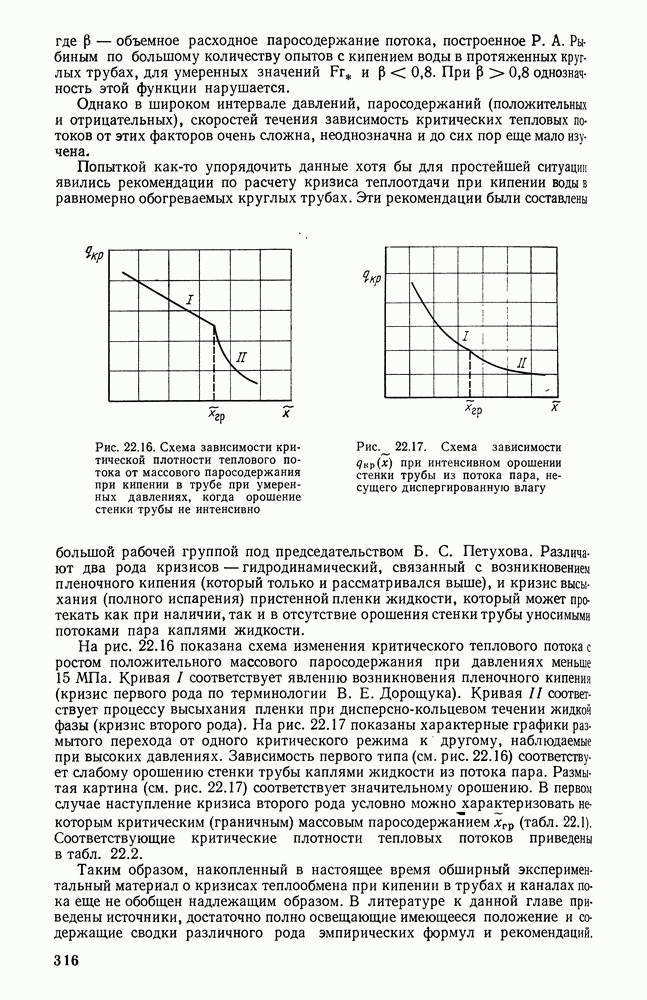
- 22.4. ПЕРЕХОД ОТ ПЛЕНОЧНОГО РЕЖИМА КИПЕНИЯ К ПУЗЫРЬКОВОМУ РЕЖИМУ (ВТОРОЙ КРИЗИС РЕЖИМА КИПЕНИЯ)
- 22.5. КРИТЕРИЙ УСТОЙЧИВОСТИ ДВУХФАЗНОГО ГРАНИЧНОГО СЛОЯ ПРИ БОЛЬШИХ СКОРОСТЯХ ТЕЧЕНИЯ ЖИДКОСТИ
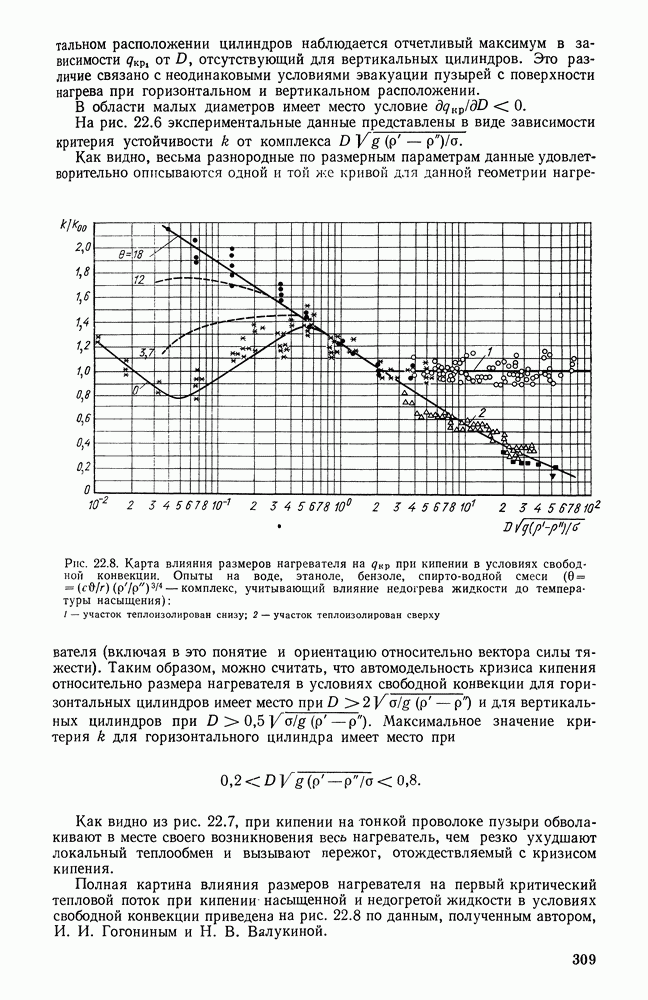
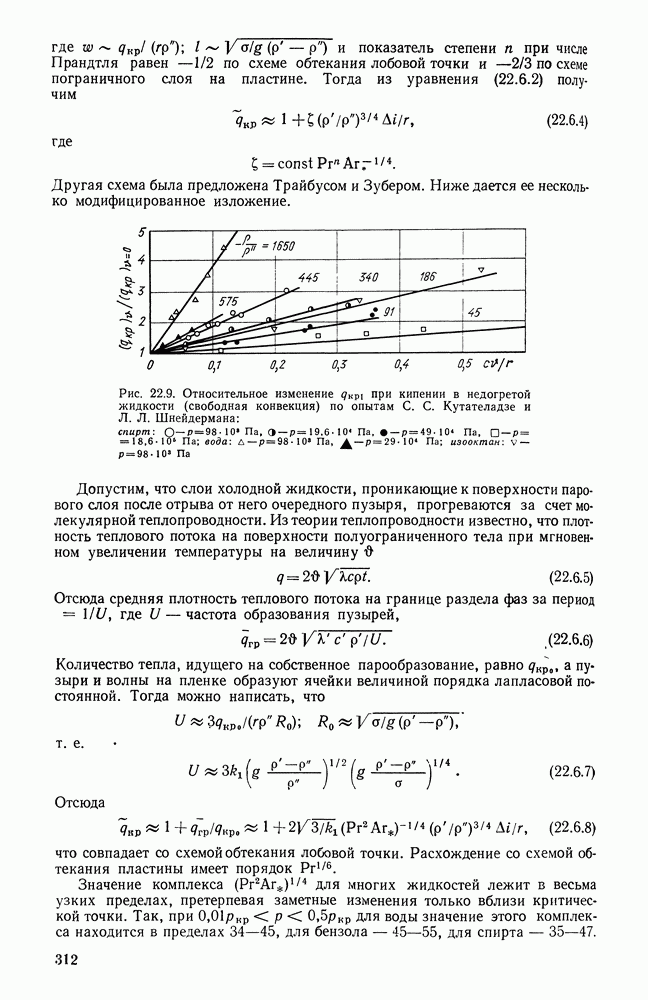
- 22.6. ВЛИЯНИЕ НЕДОГРЕВА ЖИДКОСТИ ДО ТЕМПЕРАТУРЫ НАСЫЩЕНИЯ НА КРИТИЧЕСКУЮ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА
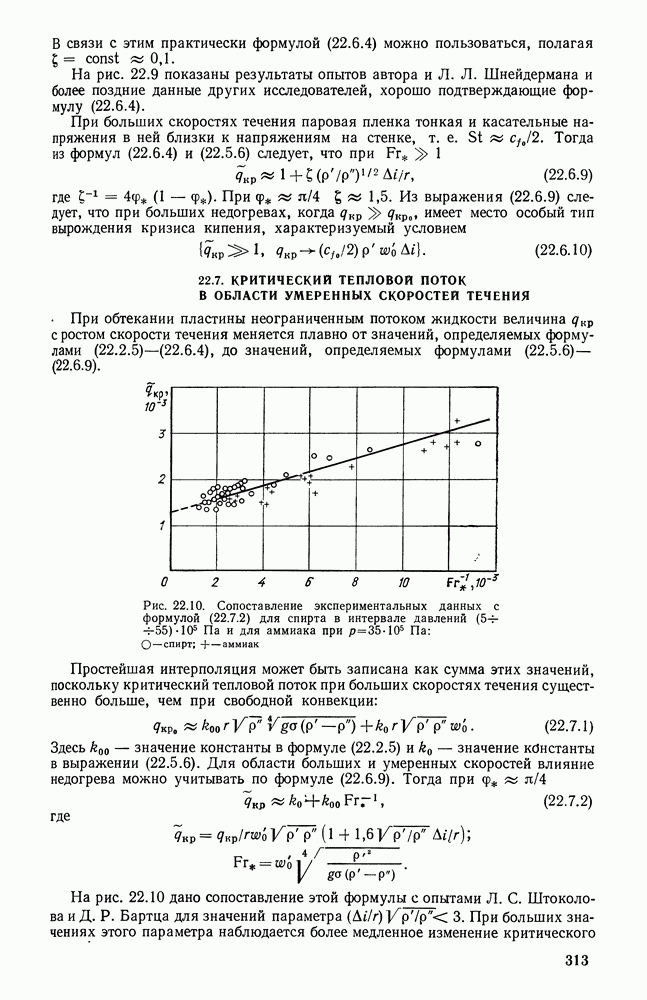
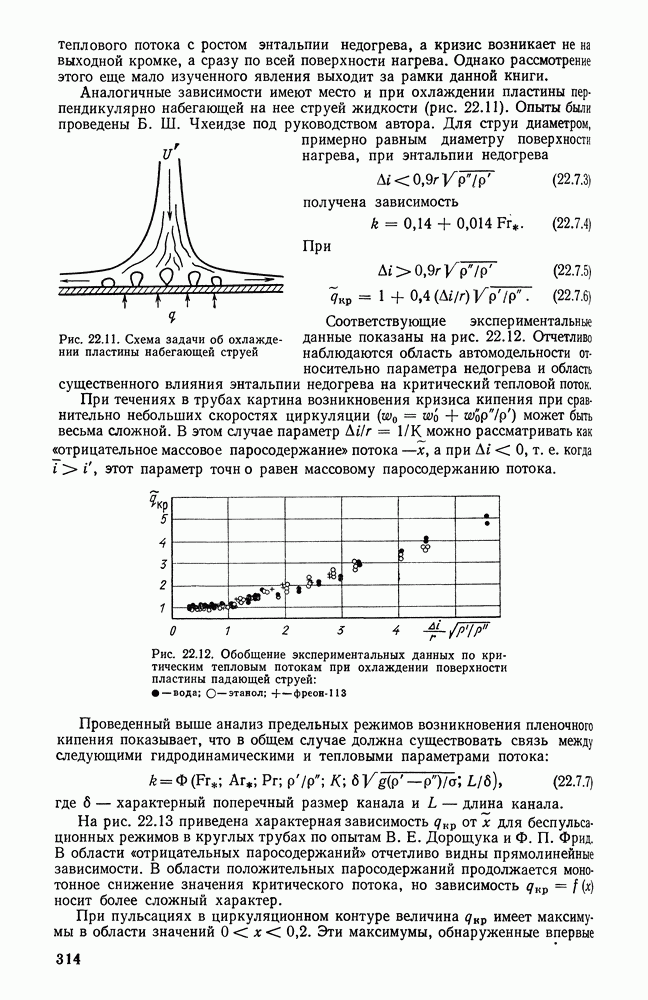
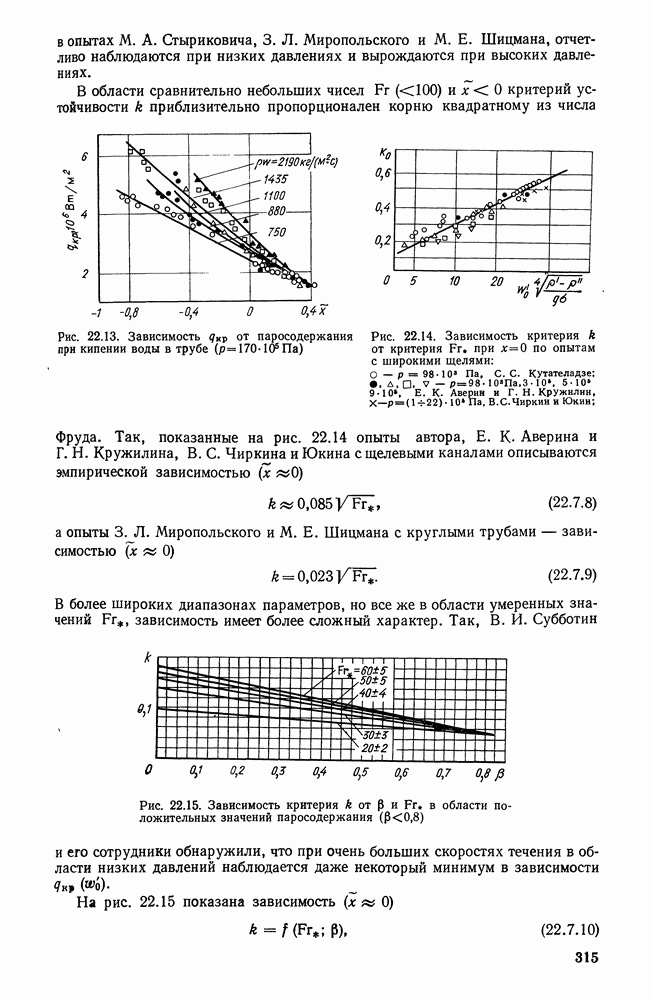
- 22.7. КРИТИЧЕСКИЙ ТЕПЛОВОЙ ПОТОК В ОБЛАСТИ УМЕРЕННЫХ СКОРОСТЕЙ ТЕЧЕНИЯ
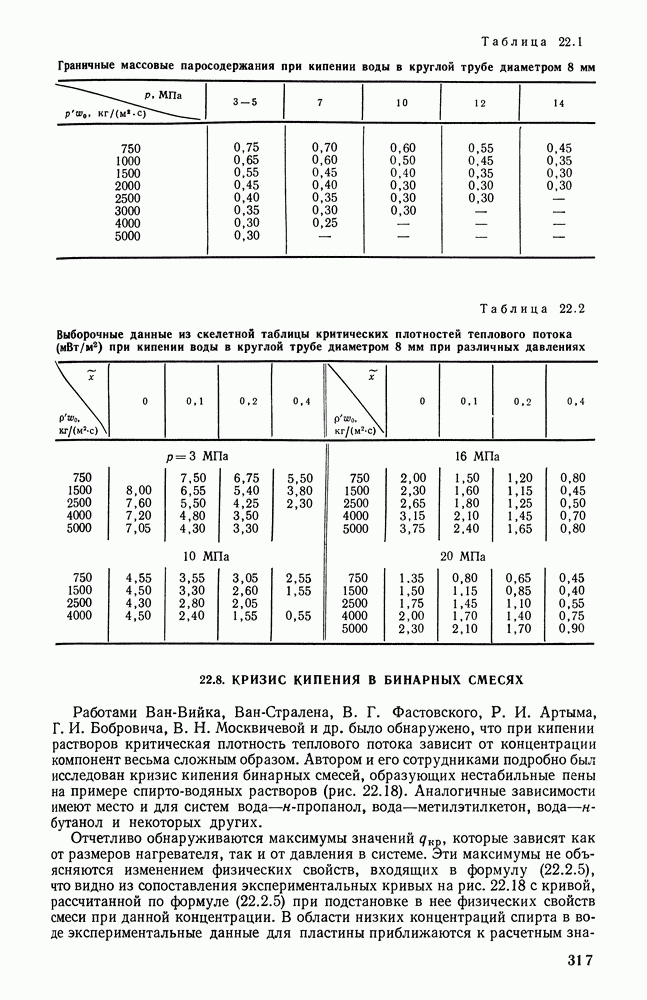
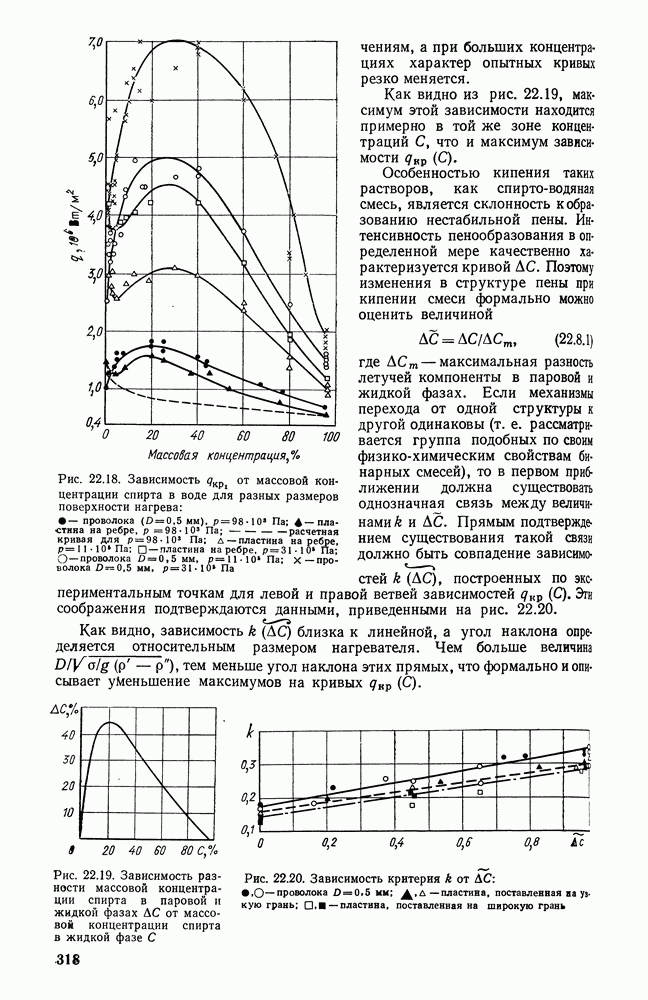
- 22.8. КРИЗИС КИПЕНИЯ В БИНАРНЫХ СМЕСЯХ
- 22.9. НЕПОСРЕДСТВЕННЫЙ ПЕРЕХОД ОТ ОДНОФАЗНОЙ КОНВЕКЦИИ К ПЛЕНОЧНОМУ КИПЕНИЮ
- 22.10. ВЛИЯНИЕ МЕТАСТАБИЛЬНОСТИ ПРИСТЕННОГО СЛОЯ ЖИДКОСТИ НА ПЕРВУЮ КРИТИЧЕСКУЮ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА
- Глава 23. С ЭЛЕМЕНТЫ МАГНИТНОЙ ТЕРМОГИДРОДИНАМИКИ
- 23.1. ОСНОВНЫЕ УРАВНЕНИЯ
- 23.2. ВЛИЯНИЕ ПЕРПЕНДИКУЛЯРНОГО К ТЕЧЕНИЮ МАГНИТНОГО ПОЛЯ НА ГИДРОДИНАМИКУ И ТЕПЛООБМЕН В ЛАМИНАРНОМ ПОТОКЕ
- 23.3. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ НА ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОГО МЕТАЛЛА В КАНАЛАХ
- 23.4. ЭЛЕМЕНТЫ ТЕРМОГАЗОДИНАМИКИ НИЗКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ
- 23.5. ОБОБЩЕННЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРОДУГОВЫХ ПЛАЗМОТРОНОВ
- Глава 24. НЕУСТАНОВИВШИЙСЯ КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
- 24.1. КРИТЕРИИ ПОДОБИЯ, ХАРАКТЕРИЗУЮЩИЕ КОНВЕКТИВНУЮ НЕСТАЦИОНАРНОСТЬ
- 24.2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ С ПЕРЕМЕННОЙ ТЕМПЕРАТУРОЙ
- 24.3. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ СФЕРИЧЕСКИХ ЧАСТИЦ
- 24.4. НЕСТАЦИОНАРНЫЙ ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ТРУБЕ
- 24.5. ВЛИЯНИЕ ОСЦИЛЛЯЦИЙ
- 24.6. ВЛИЯНИЕ ОСЦИЛЛЯЦИЙ
- Глава 25. ОСНОВНЫЕ ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 25.1. ПРИРОДА ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 25.2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
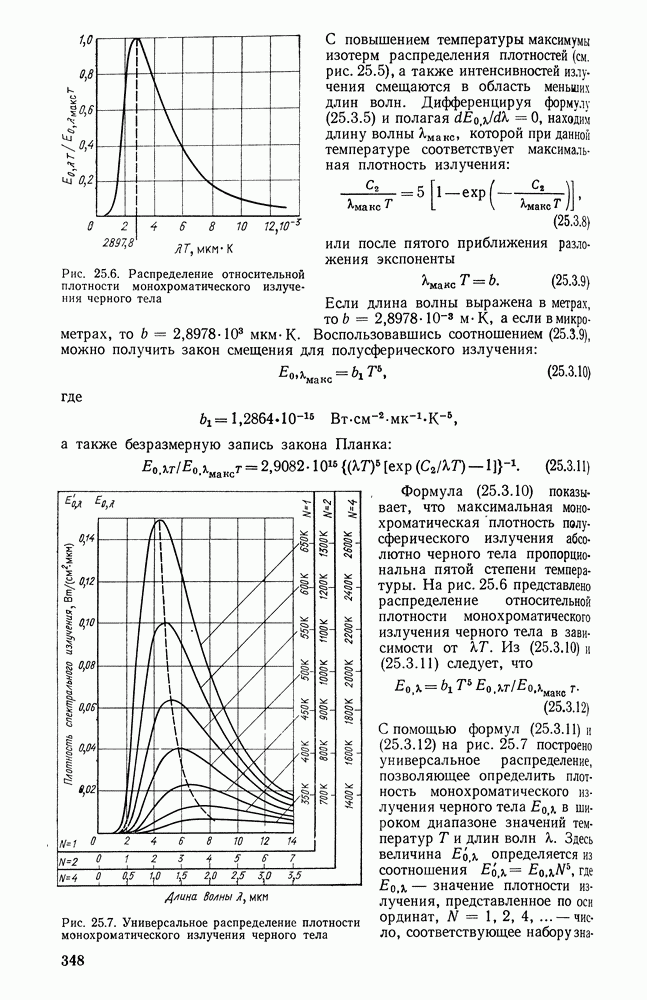
- 25.3. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
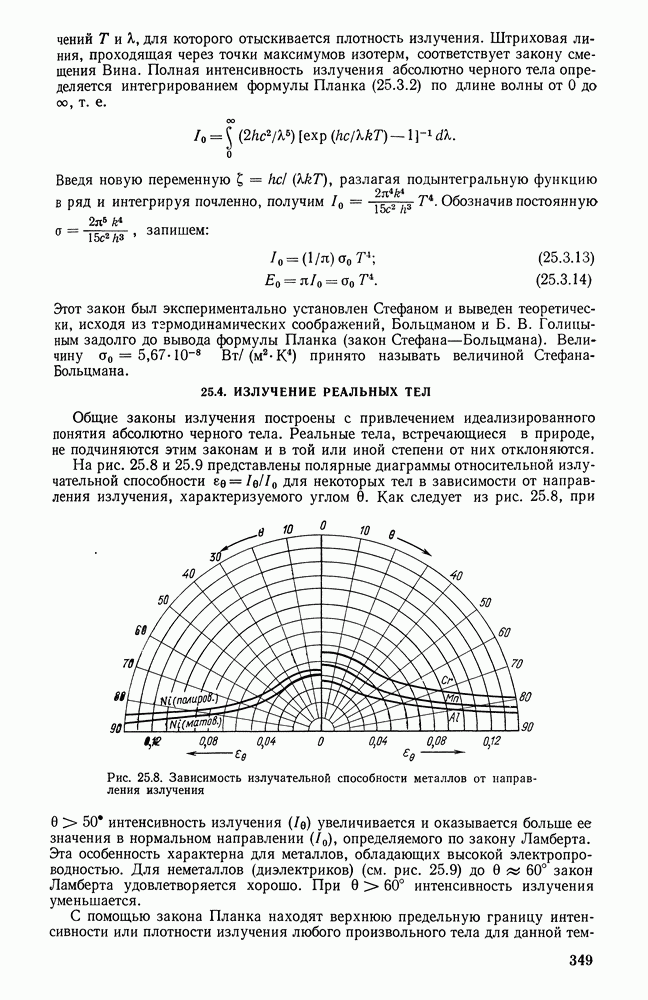
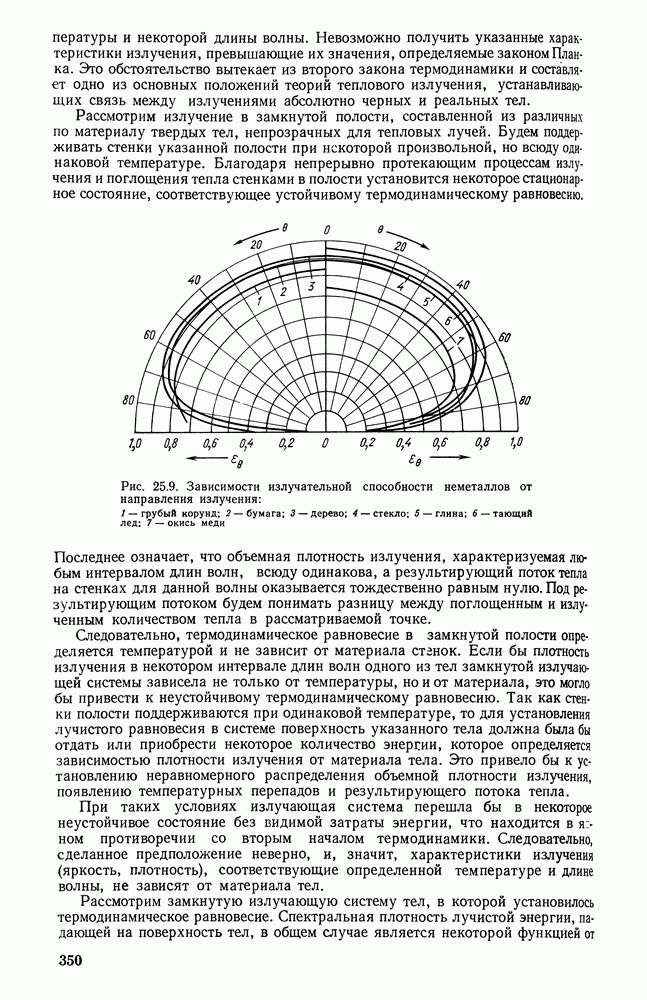
- 25.4. ИЗЛУЧЕНИЕ РЕАЛЬНЫХ ТЕЛ
- 25.5. КЛАССИФИКАЦИЯ ВИДОВ ПОЛУСФЕРИЧЕСКОГО И ОБЪЕМНОГО ИЗЛУЧЕНИЙ
- 25.6. ГЕОМЕТРИЯ ИЗЛУЧЕНИЯ. ГЕОМЕТРИЧЕСКИЕ ИНВАРИАНТЫ ИЗЛУЧЕНИЯ
- 25.7. ОБЩИЕ СВОЙСТВА ПОТОКОВ ИЗЛУЧЕНИЯ
- 25.8. АЛГЕБРАИЧЕСКИЙ МЕТОД РАСЧЕТА ИНТЕГРАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ИНВАРИАНТОВ ИЗЛУЧЕНИЯ
- Глава 26. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ПРОЗРАЧНЫХ И ПОГЛОЩАЮЩИХ СРЕДАХ
- 26.1. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ СИСТЕМЫ ТЕЛ, РАЗДЕЛЕННЫХ ПРОЗРАЧНОЙ СРЕДОЙ
- 26.2. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ ДИСКРЕТНОЙ СИСТЕМЫ ТЕЛ В ПРОЗРАЧНОЙ СРЕДЕ (ЗОНАЛЬНЫЙ МЕТОД)
- 26.3. ПРИЛОЖЕНИЕ ЗОНАЛЬНОГО МЕТОДА К РАСЧЕТУ ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ МЕЖДУ НЕСКОЛЬКИМИ СЕРЫМИ ТЕЛАМИ
- 26.4. ДЕЙСТВИЕ ЭКРАНОВ
- 26.5. УРАВНЕНИЕ ПЕРЕНОСА ЭНЕРГИИ ИЗЛУЧЕНИЯ В ПОГЛОЩАЮЩЕЙ СРЕДЕ
- 26.6. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ИЗЛУЧЕНИЯ В ПОГЛОЩАЮЩЕЙ СРЕДЕ
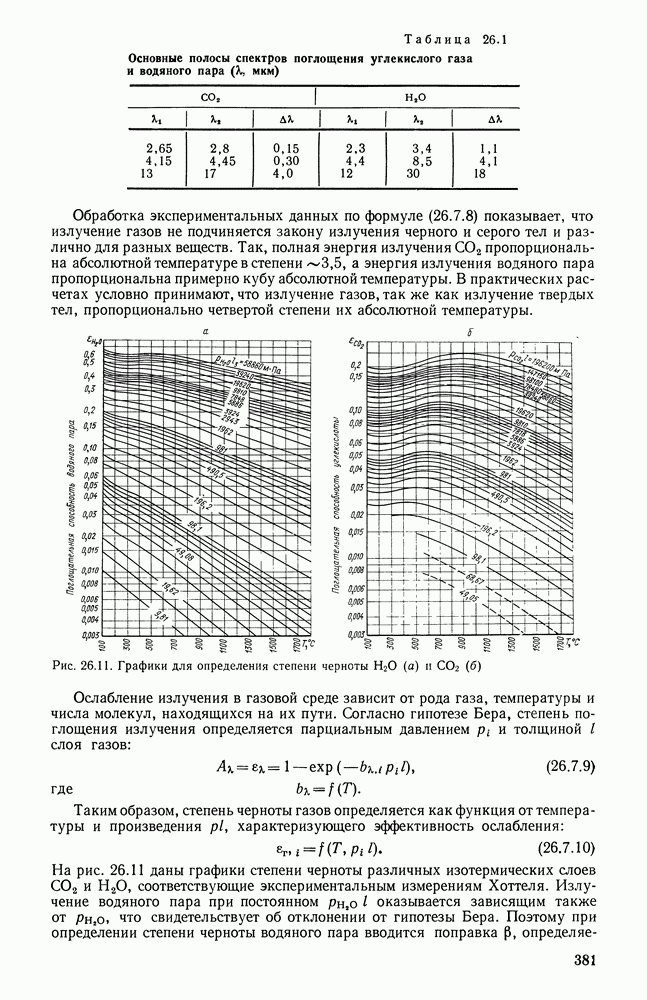
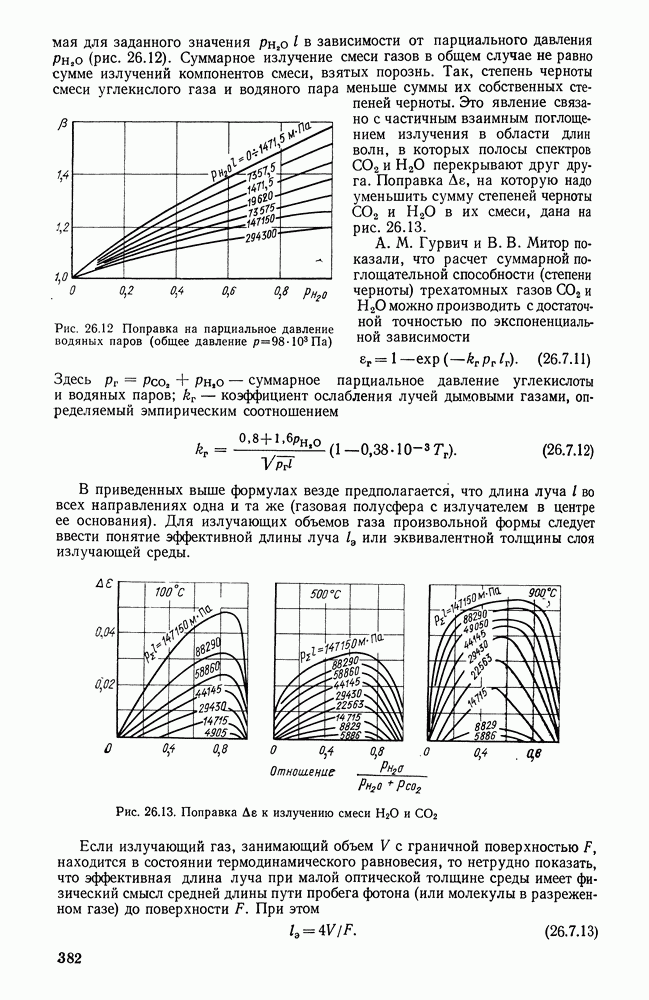
- 26.7. ОПТИЧЕСКИЕ СВОЙСТВА ПОГЛОЩАЮЩИХ СРЕД
- 26.8. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ ДИСКРЕТНОИ СИСТЕМЫ ТЕЛ В ПОГЛОЩАЮЩЕЙ СРЕДЕ (ЗОНАЛЬНЫЙ МЕТОД)
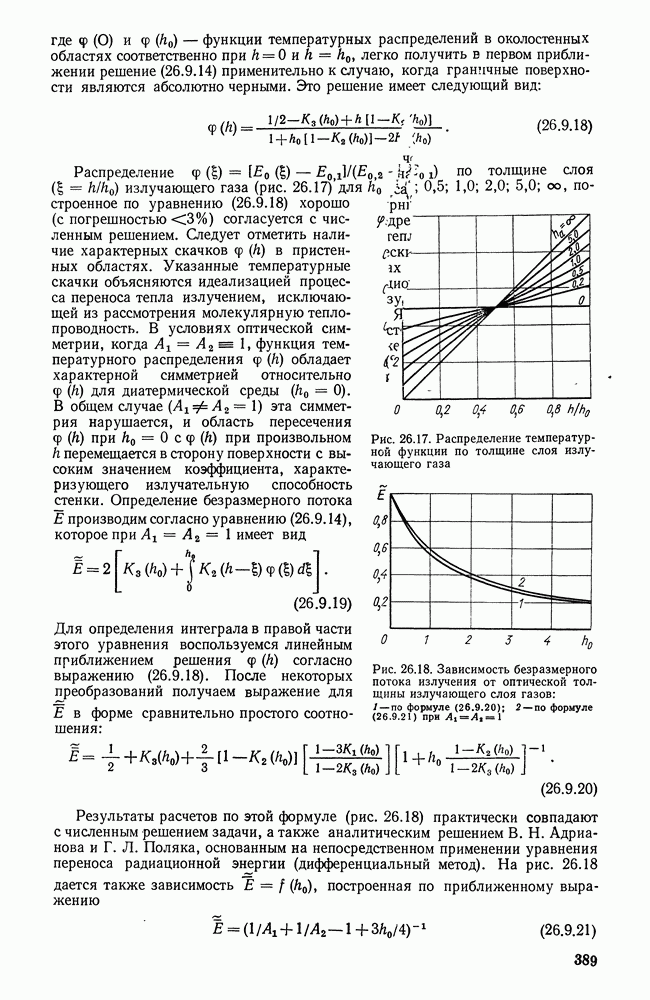
- 26.9. ПЕРЕНОС ИЗЛУЧЕНИЯ В ПЛОСКОМ СЛОЕ ПОГЛОЩАЮЩЕЙ СРЕДЫ
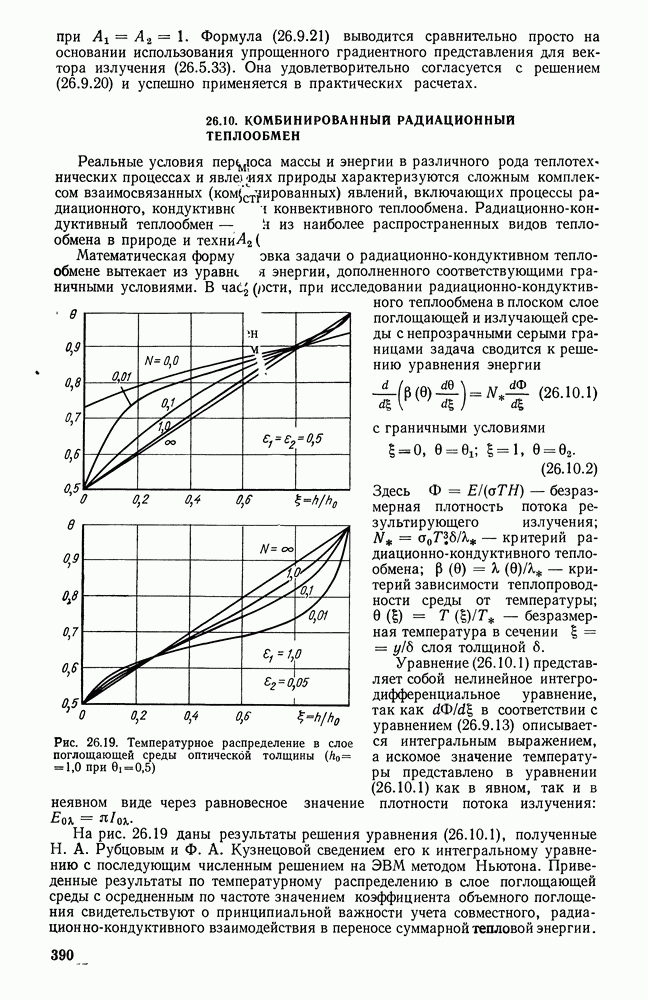
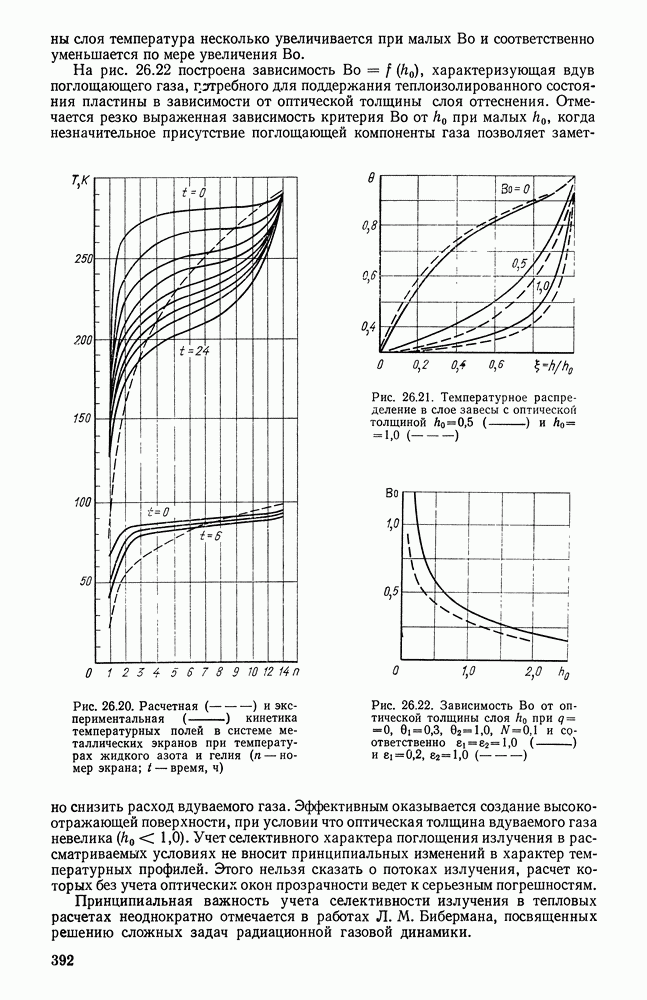
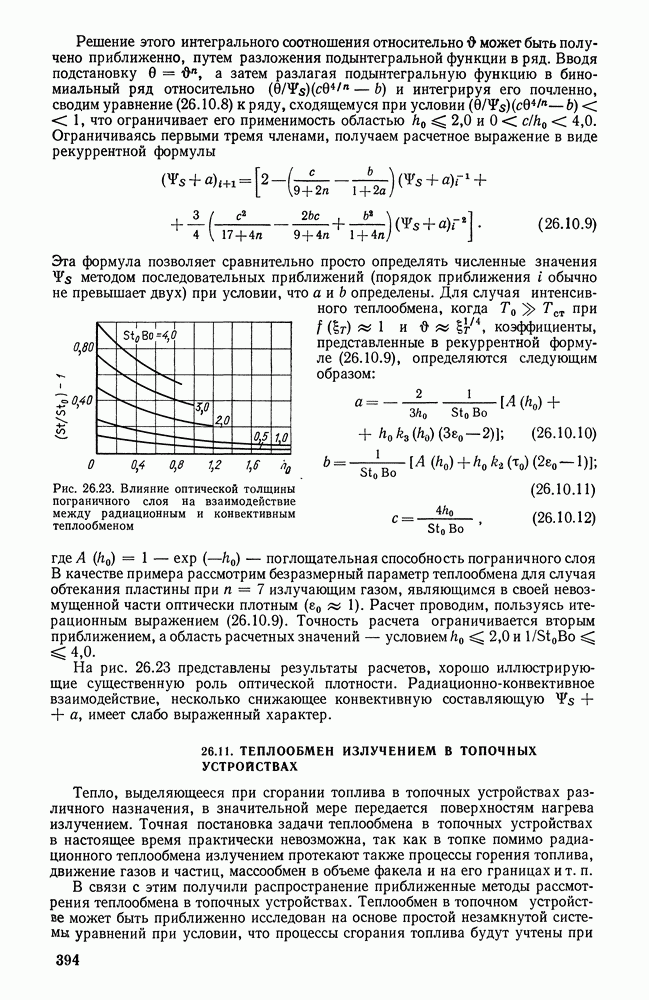
- 26.10. КОМБИНИРОВАННЫЙ РАДИАЦИОННЫЙ ТЕПЛООБМЕН
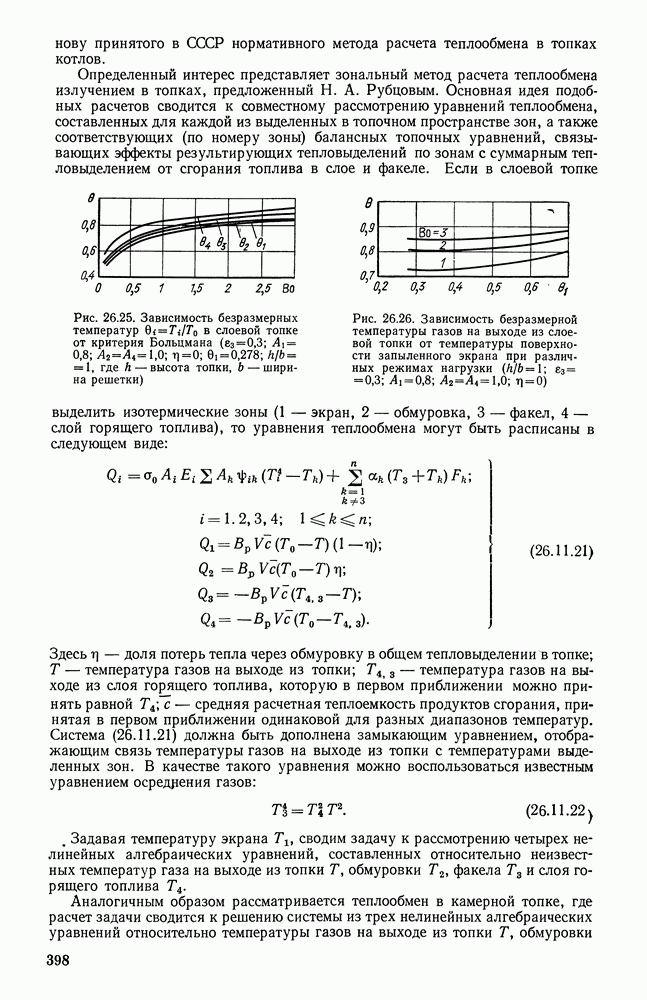
- 26.11. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ТОПОЧНЫХ УСТРОЙСТВАХ