| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
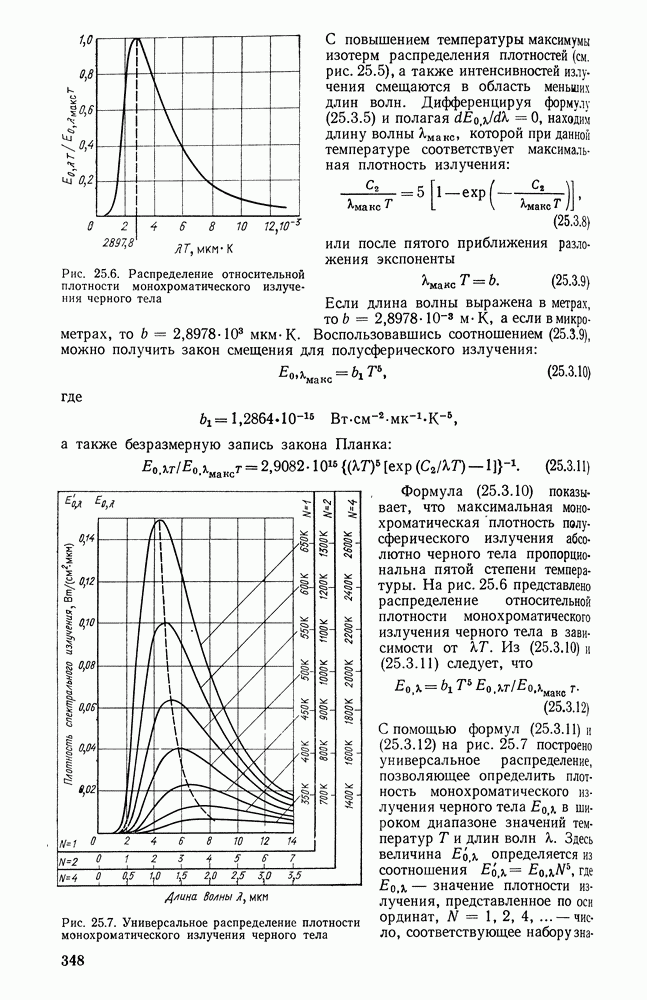
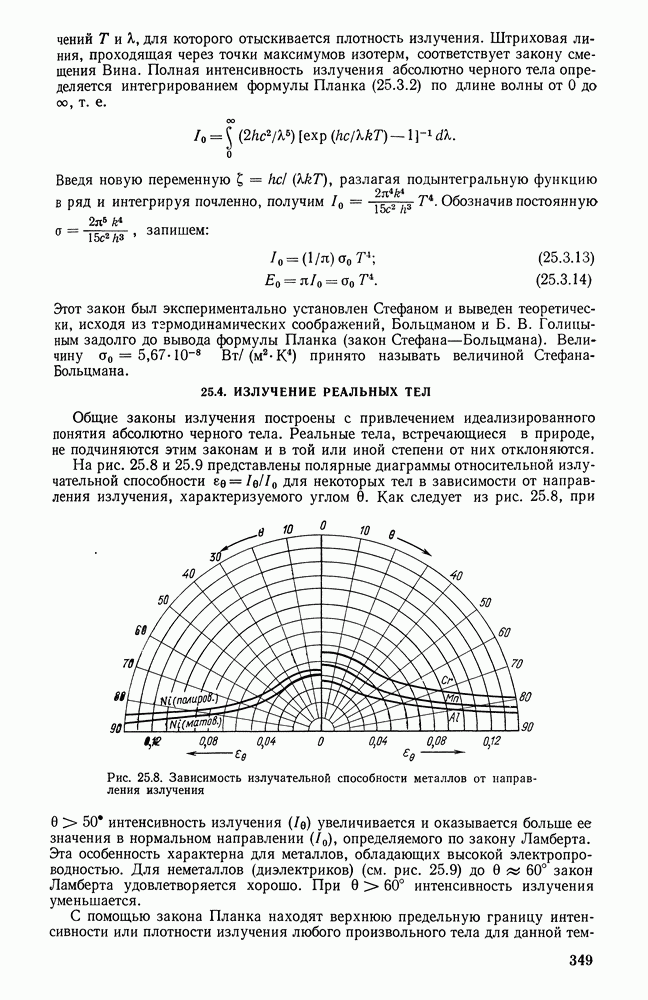
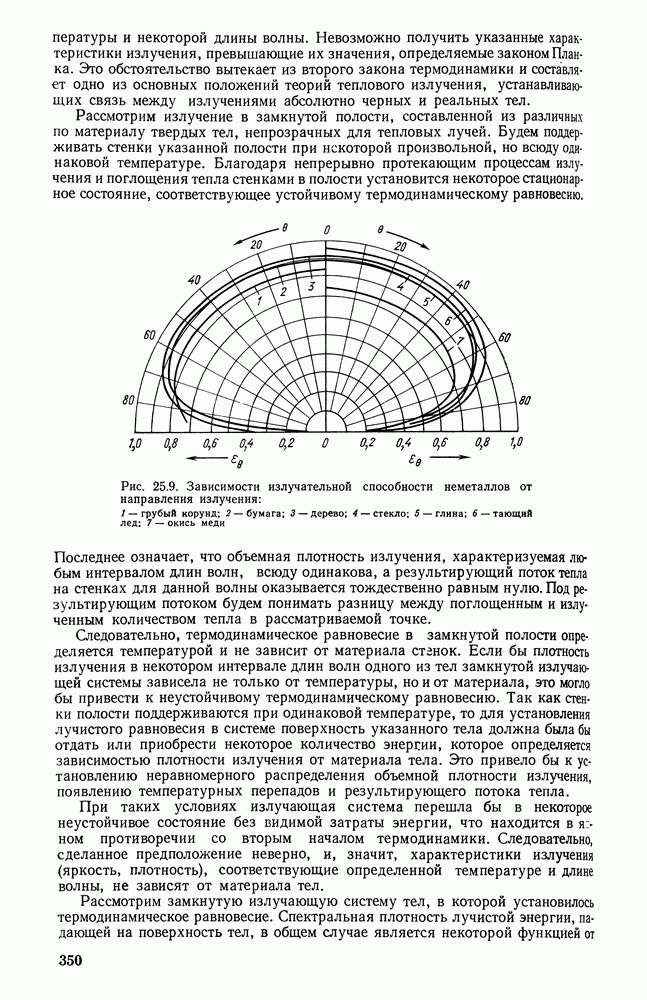
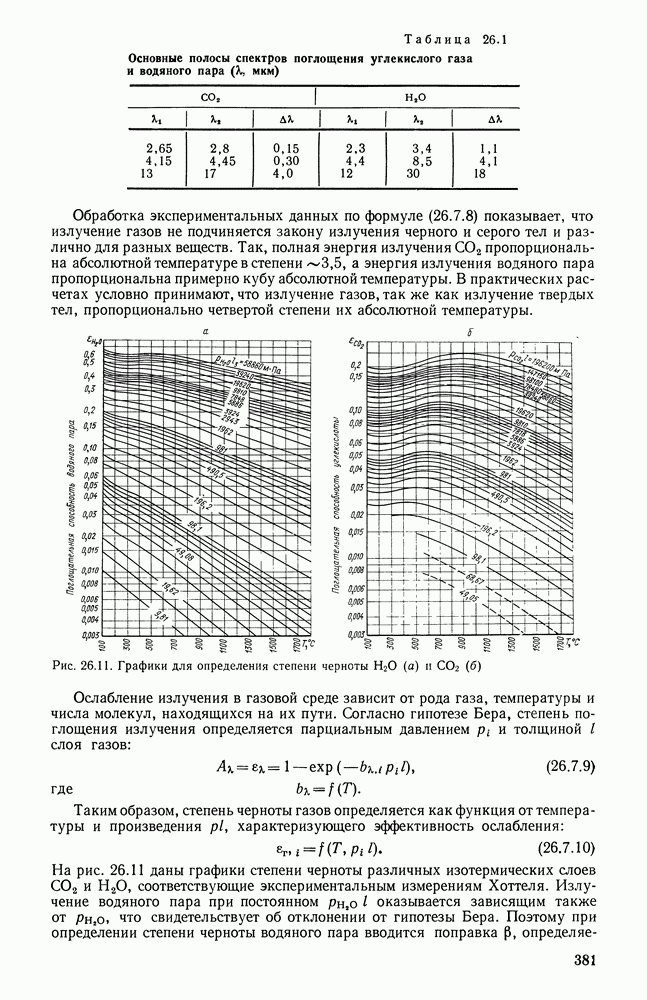
26.11. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ТОПОЧНЫХ УСТРОЙСТВАХ
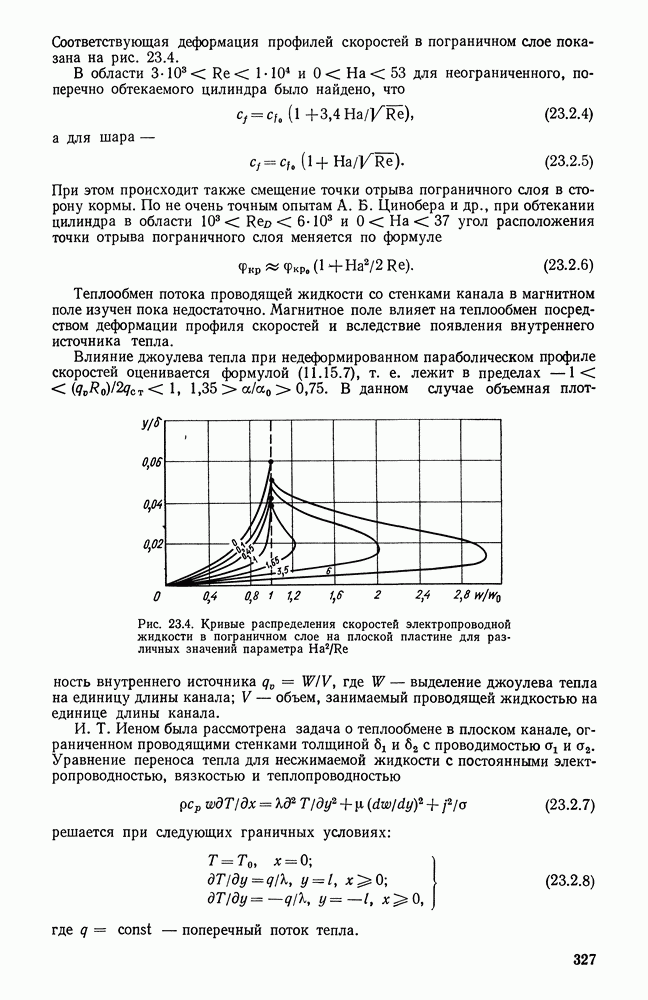
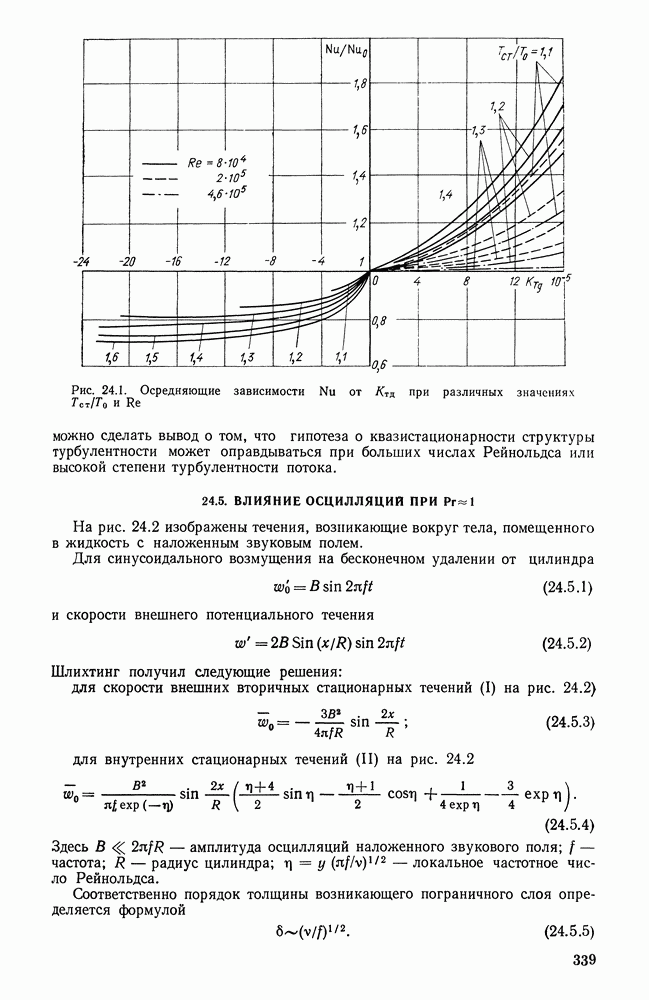
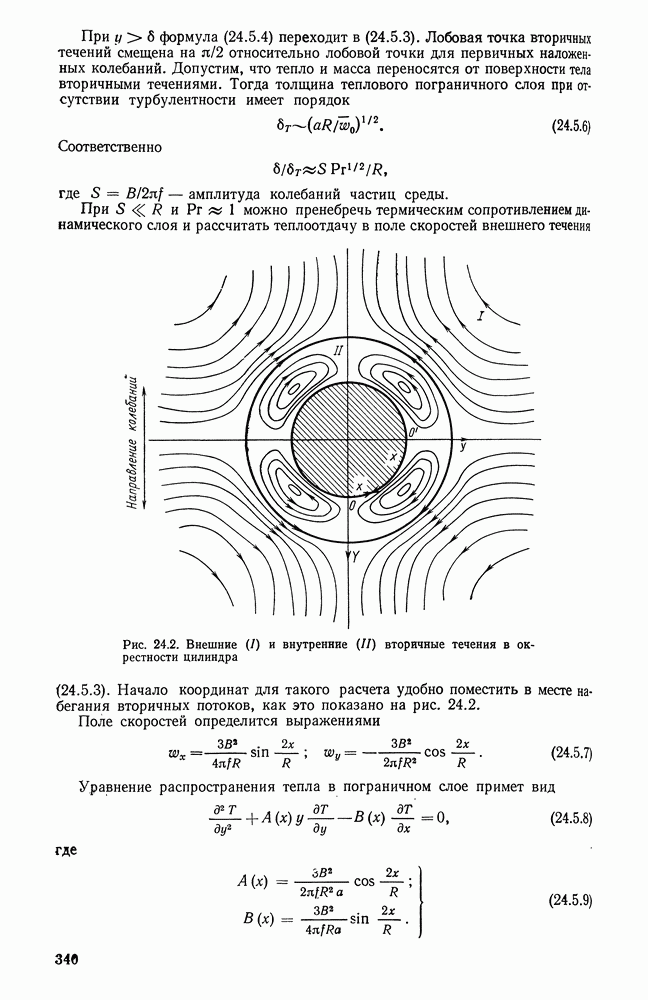
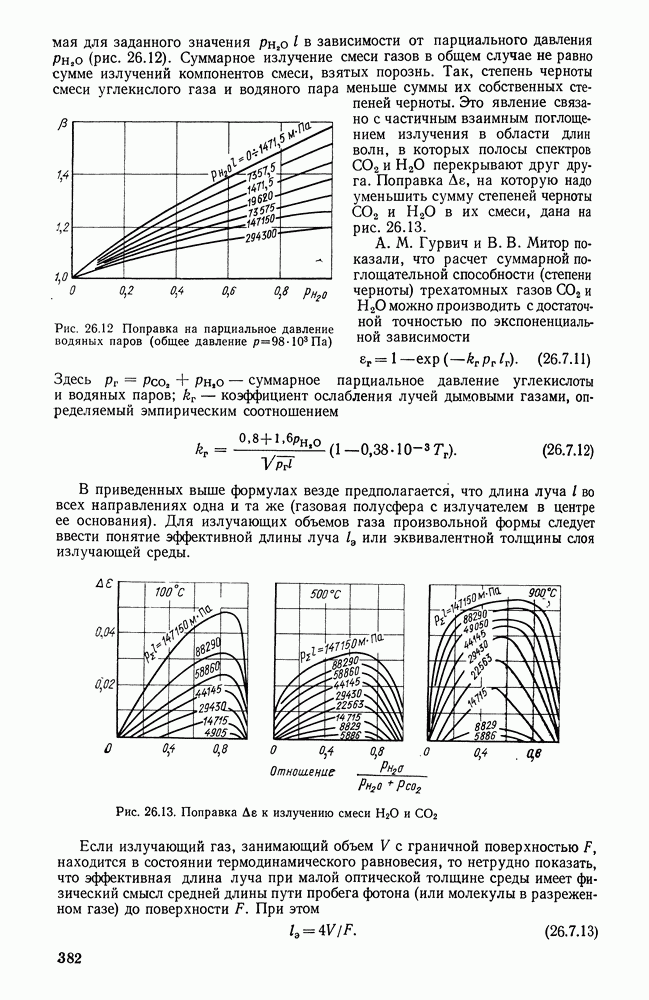
Тепло, выделяющееся при сгорании топлива в топочных устройствах различного назначения, в значительной мере передается поверхностям нагрева излучением. Точная постановка задачи теплообмена в топочных устройствах в настоящее время практически невозможна, так как в топке помимо радиационного теплообмена излучением протекают также процессы горения топлива, движение газов и частиц, массообмен в объеме факела и на его границах и т. п.
В связи с этим получили распространение приближенные методы рассмотрения теплообмена в топочных устройствах. Теплообмен в топочном устройстве может быть приближенно исследован на основе простой незамкнутой системы уравнений при условии, что процессы сгорания топлива будут учтены при определении равновесного излучения топочной среды и соответственно ее температуры.
Уравнения баланса энергии и теплопередачи, записанные в интегральной форме для любого текущего сечения потока среды в топке, имеют вид
 (26.11.1)
(26.11.1)
Здесь  и
и  — теплоотдача излучением и конвекцией, отнесенная к текущему сечению потока газов;
— теплоотдача излучением и конвекцией, отнесенная к текущему сечению потока газов;  — расход топлива; V — объем продуктов сгорания;
— расход топлива; V — объем продуктов сгорания;  — средняя расчетная теплоемкость продуктов сгорания;
— средняя расчетная теплоемкость продуктов сгорания;  — средняя теплоемкость продуктов сгорания в интервале от 0 до
— средняя теплоемкость продуктов сгорания в интервале от 0 до  — соответственно температура газов в рассматриваемом сечении и теоретическая температура сгорания;
— соответственно температура газов в рассматриваемом сечении и теоретическая температура сгорания;  — лучистая и конвективная поверхности нагрева в топке;
— лучистая и конвективная поверхности нагрева в топке;  — степень черноты топки в рассматриваемой области; Т — средняя эффективная температура пламени; Т — температура стенок.
— степень черноты топки в рассматриваемой области; Т — средняя эффективная температура пламени; Т — температура стенок.
Совмещая уравнения (26.11.1), получаем
 . Приведем уравнение (26.11.2) к безразмерному виду:
. Приведем уравнение (26.11.2) к безразмерному виду:
 (26.11.3)
(26.11.3)

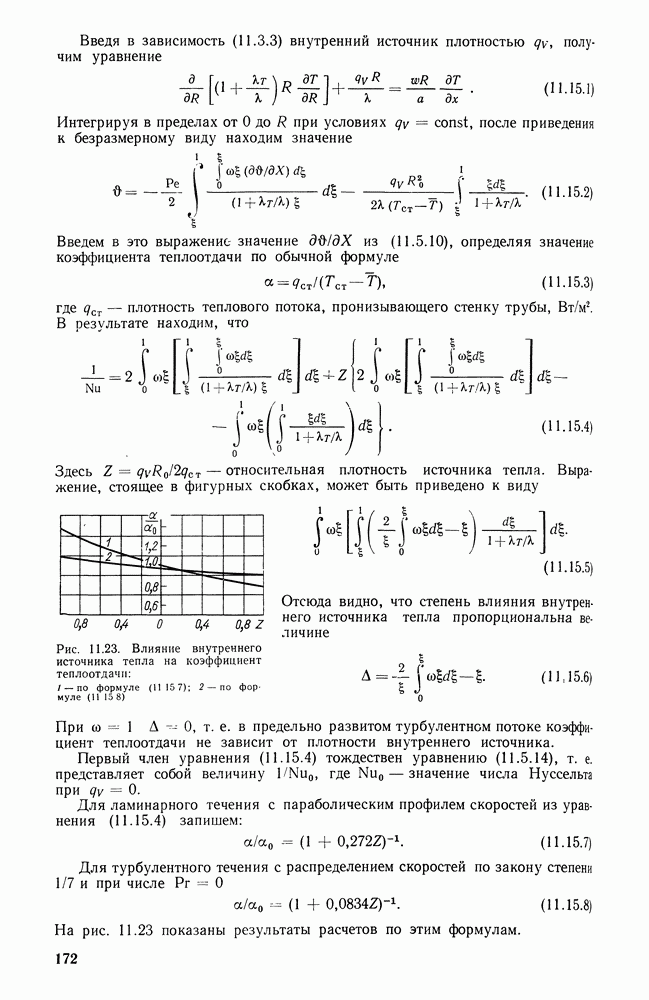
Здесь  — безразмерная температура. Комплекс, стоящий в первом члене этого уравнения, характеризует долю излучаемого тепла от общего тепловыделения в топке. Комплекс, стоящий во втором члене этого уравнения, характеризует долю конвективной теплоотдачи.
— безразмерная температура. Комплекс, стоящий в первом члене этого уравнения, характеризует долю излучаемого тепла от общего тепловыделения в топке. Комплекс, стоящий во втором члене этого уравнения, характеризует долю конвективной теплоотдачи.
Легко заметить, что так как скорость газов в топке пропорциональна  , то второй комплекс является специфической модификацией критерия, известного из теории конвективного теплообмена:
, то второй комплекс является специфической модификацией критерия, известного из теории конвективного теплообмена:
 (26.11.4)
(26.11.4)
Для больших топок, когда конвективный теплообмен мал по сравнению с радиационным, из выражения (26.11.4) запишем
 (26.11.5)
(26.11.5)
или, вводя обозначение режимного критерия Больцмана  , получаем
, получаем
 (26.11.6)
(26.11.6)
В качестве первого приближения Г. Л. Поляк и С. Н. Шорин предложили связать среднюю эффективную температуру с истинными температурами в данном сечении степенной зависимостью

Здесь постоянные  определяются условиями сгорания и охлаждения в топке. Уравнение (26.11.6) в таком случае принимает вид
определяются условиями сгорания и охлаждения в топке. Уравнение (26.11.6) в таком случае принимает вид
 (26.11.8)
(26.11.8)
В топках паровых котлов  , и уравнение (26.11.8) еще более упрощается:
, и уравнение (26.11.8) еще более упрощается:

Это уравнение впервые было получено Г. Л. Поляком. Приняв за рассматриваемое сечение выходное сечение топки, можно решить его относительно 0, которая в этом случае является безразмерной температурой продуктов сгорания на выходе из топочной камеры. Решение уравнения (26.11.9) может быть представлено в виде функциональной зависимости
 (26.11.10)
(26.11.10)
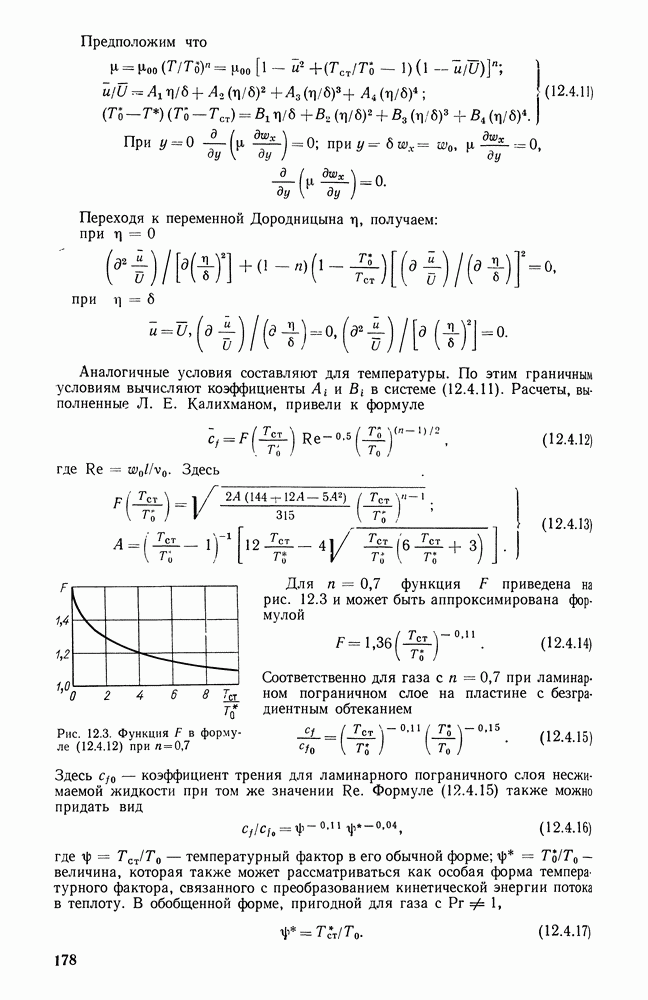
А. М. Гурвич и А. Г. Блох показали, что коэффициент С мало зависит от режима работы топки, рода топлива и способа сжигания и поэтому может быть принят постоянным. Показатель температурного режима  , зависящий от форсировки топочной камеры, определяемой величиной критерия Во, меняется в весьма широких пределах.
, зависящий от форсировки топочной камеры, определяемой величиной критерия Во, меняется в весьма широких пределах.
Анализ экспериментального материала по теплообмену дает возможность установить зависимость  от места расположения температурного максимума
от места расположения температурного максимума  по длине факела. Это в свою очередь позволяет записать выражение (26.11.10), учитывая постоянство С, в следующем виде:
по длине факела. Это в свою очередь позволяет записать выражение (26.11.10), учитывая постоянство С, в следующем виде:
 (26.11.11)
(26.11.11)
Вид функции (26.11.10) или (26.11.11) может быть установлен на основании опытных данных по теплообмену в топках. Эти данные приводят к формуле вида
 (26.11.12)
(26.11.12)
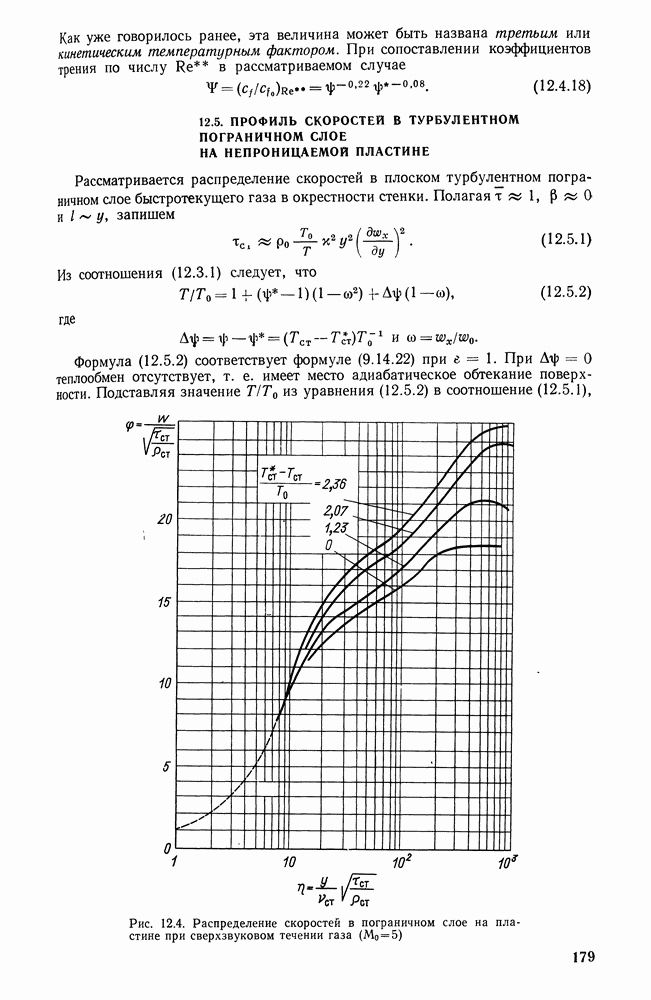
в которой для большинства топок коэффициенты М и С являются практически постоянными величинами. По предложению А. М. Гурвича связь безразмерной температуры с основными критериями, определяющими топочный процесс для  или
или  , выражается формулой
, выражается формулой

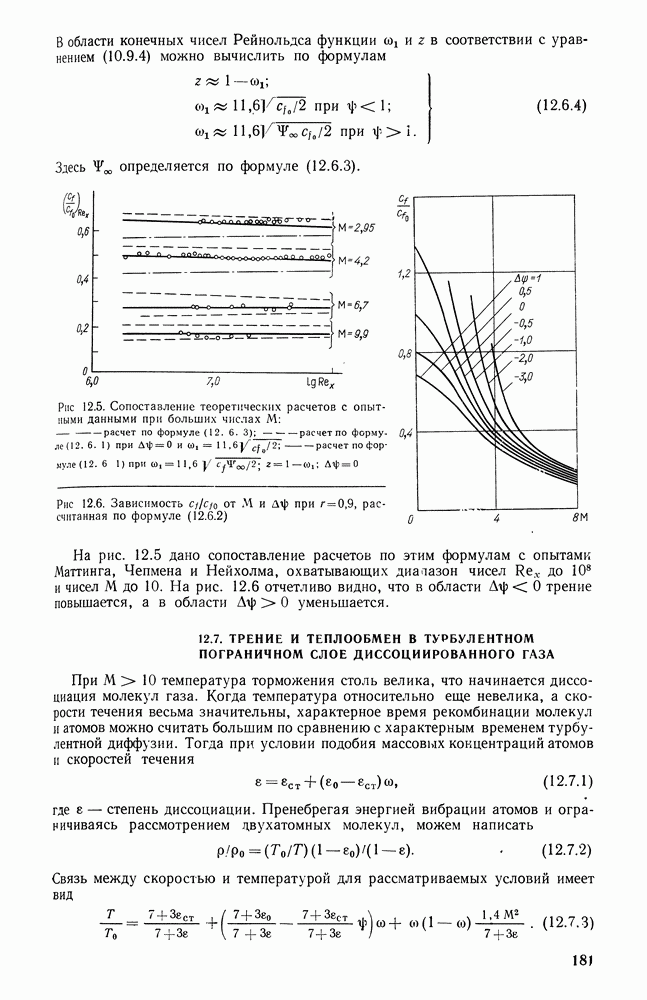
Степень черноты топки определяется оптической плотностью среды, заполняющей топку, оптическими свойствами поверхностей топки, а также геометрическими характеристиками, учитывающими степень экранирования топки и размеры площадки зеркала горения (в случае слоевой топки):
 (26.11.14)
(26.11.14)
При равномерном распределении поверхности нагрева экранов на стенах топочной камеры степень черноты топок приближенно определяется по следующим формулам:
для слоевой топки
 (26.11.15)
(26.11.15)
и для камерной топки
 (26.11.16)
(26.11.16)
Здесь  — степень черноты факела;
— степень черноты факела;  степень экранирования, указывающая на долю внутренней поверхности топочной камеры, закрытой экранами;
степень экранирования, указывающая на долю внутренней поверхности топочной камеры, закрытой экранами;  — геометрическая характеристика слоевой топки, дающая представление о доле площади зеркала горения, приходящейся на единицу поверхности экранов,
— геометрическая характеристика слоевой топки, дающая представление о доле площади зеркала горения, приходящейся на единицу поверхности экранов,  — условный коэффициент загрязнения поверхности экранов.
— условный коэффициент загрязнения поверхности экранов.
Степень черноты факела подсчитывается по формуле
 (26.11.17)
(26.11.17)
где степень черноты среды  определяется как
определяется как
 (26.11.18)
(26.11.18)
Здесь коэффициент ослабления k находится в зависимости от вида пламени, а толщина  — в соответствии с формулой (26.7.14).
— в соответствии с формулой (26.7.14).
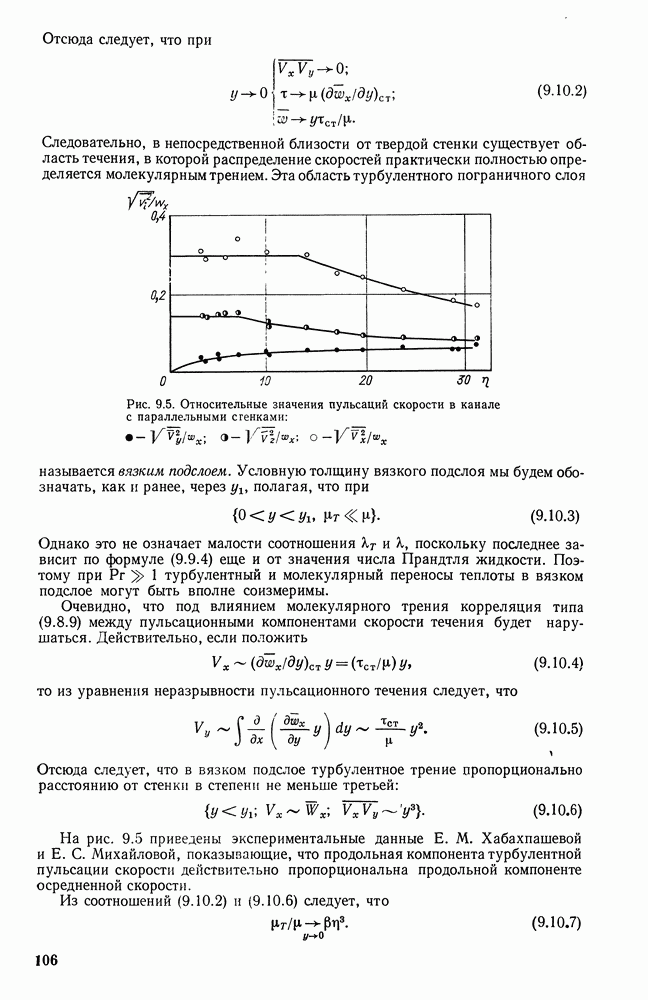
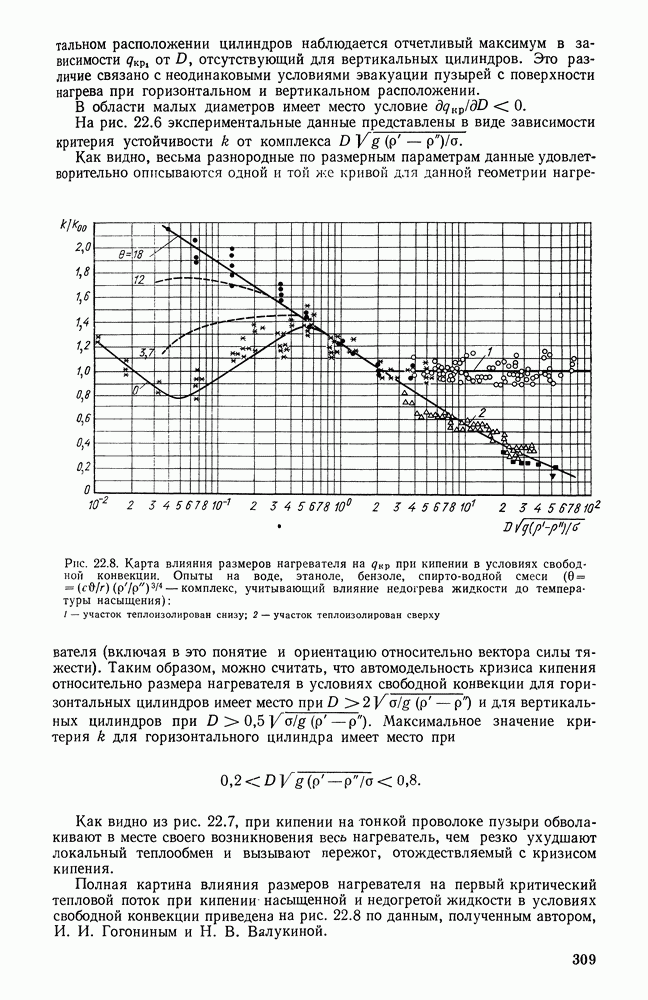
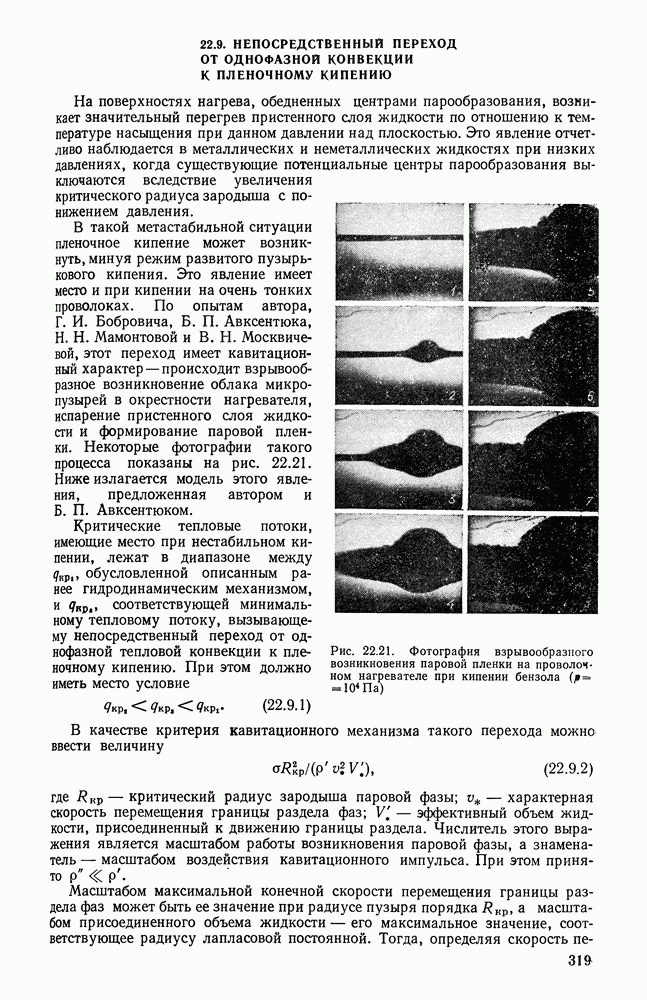
Поправочный коэффициент  в формуле (26.11.9) связан с характером заполнения объема топочной камеры пламенем и с теми особенностями, которые определяются горением и теплообменом. На рис. 26.24 приведены результаты исследования температурных полей и полей потоков излучения в мазутной топке. Как видно, неоднородность температурного поля, а также имеющая место неоднородность поля концентраций излучающих твердых частиц приводят к большой неоднородности излучения по сечению камеры. Эта сложность поля излучения сказывается и на характере распределения степени черноты в объеме топки. Таким образом, оптические характеристики сред, заполняющих топочную камеру, связаны с условиями сгорания топлива и с условиями теплообмена.
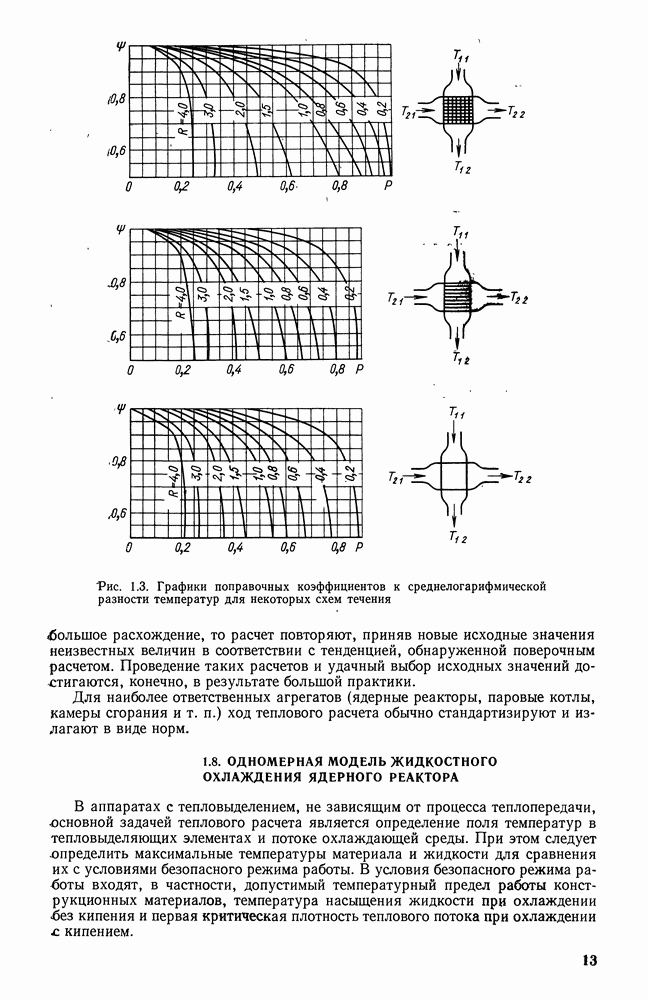
в формуле (26.11.9) связан с характером заполнения объема топочной камеры пламенем и с теми особенностями, которые определяются горением и теплообменом. На рис. 26.24 приведены результаты исследования температурных полей и полей потоков излучения в мазутной топке. Как видно, неоднородность температурного поля, а также имеющая место неоднородность поля концентраций излучающих твердых частиц приводят к большой неоднородности излучения по сечению камеры. Эта сложность поля излучения сказывается и на характере распределения степени черноты в объеме топки. Таким образом, оптические характеристики сред, заполняющих топочную камеру, связаны с условиями сгорания топлива и с условиями теплообмена.

Рис. 26.24. Характер полей температур (а), потоков излучения (б) и распределения степени черноты (в) в топочной камере
Существенное влияние на теплообмен в топке оказывает состояние поверхностей нагрева, расположенных в топке. Обычно такие поверхности бывают покрыты слоем пыли, обладающей низкой теплопроводностью. Это значительно снижает тепловую эффективность поверхностей нагрева. Оценка роли подобного рода загрязнений производится путем введения коэффициента загрязнения в формулу для определения степени черноты топок
 (26.11.19)
(26.11.19)
где  — коэффициент тепловой эффективности чистой поверхности нагрева при температуре насыщения; — коэффициент тепловой эффективности загрязненной поверхности. Последний определяется экспериментальным путем на основании следующего соотношения:
— коэффициент тепловой эффективности чистой поверхности нагрева при температуре насыщения; — коэффициент тепловой эффективности загрязненной поверхности. Последний определяется экспериментальным путем на основании следующего соотношения:
 (26.11.20)
(26.11.20)
где  — соответственно плотности тепловых потоков, падающих на станку топочной камеры, и эффективных потоков, посылаемых стенкой в топочное пространство.
— соответственно плотности тепловых потоков, падающих на станку топочной камеры, и эффективных потоков, посылаемых стенкой в топочное пространство.
А. М. Гурвич и В. В. Митор установили, что коэффициент загрязнения  зависит от вида топлива и геометрии поверхности нагрева. Изложенные выше соображения, а также результаты обработки большого экспериментального материала, выполненной А. М. Гурвичем и его сотрудниками, положены в основу принятого в СССР нормативного метода расчета теплообмена в топках котлов.
зависит от вида топлива и геометрии поверхности нагрева. Изложенные выше соображения, а также результаты обработки большого экспериментального материала, выполненной А. М. Гурвичем и его сотрудниками, положены в основу принятого в СССР нормативного метода расчета теплообмена в топках котлов.
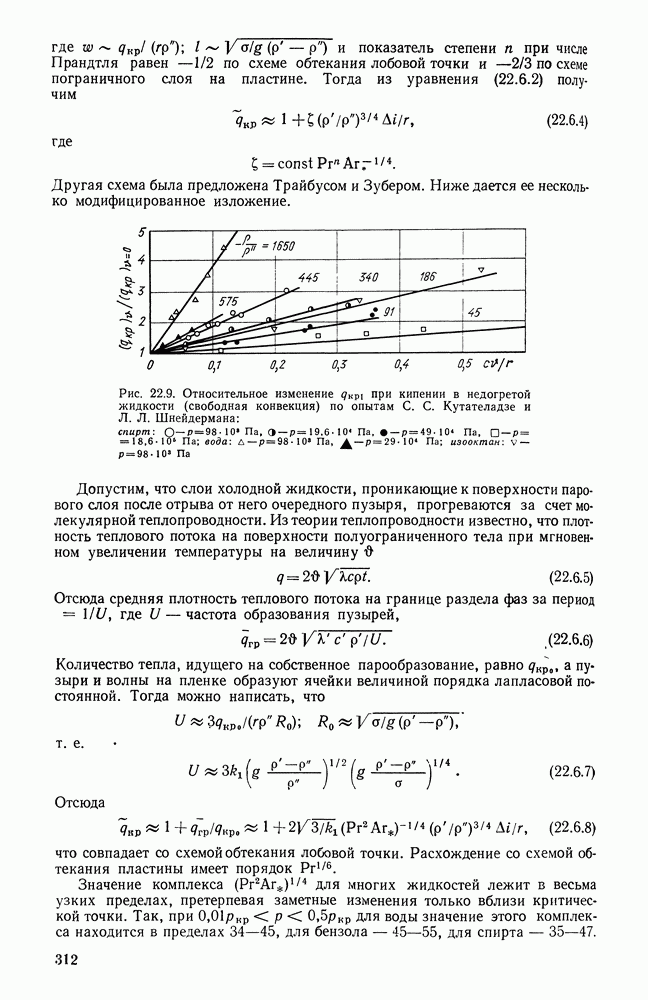
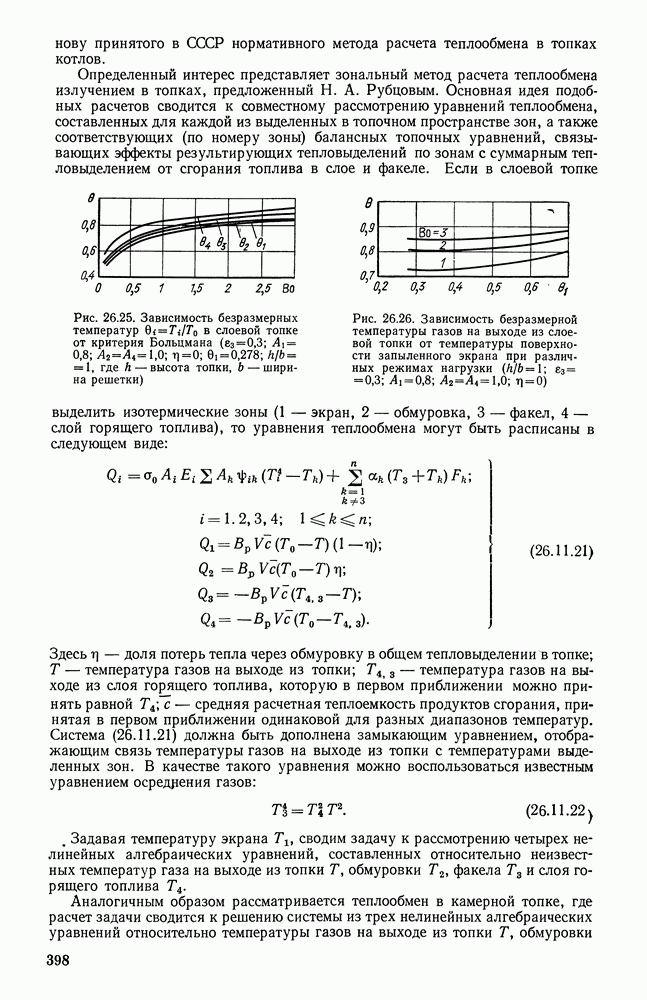
Определенный интерес представляет зональный метод расчета теплообмена излучением в топках, предложенный Н. А. Рубцовым. Основная идея подобных расчетов сводится к совместному рассмотрению уравнений теплообмена, составленных для каждой из выделенных в топочном пространстве зон, а также соответствующих (по номеру зоны) балансных топочных уравнений, связывающих эффекты результирующих тепловыделений по зонам с суммарным тепловыделением от сгорания топлива в слое и факеле. Если в слоевой топке выделить изотермические зоны (1 — экран, 2 — обмуровка, 3 — факел, 4 — слой горящего топлива), то уравнения теплообмена могут быть расписаны в следующем виде:
 (26.11.21)
(26.11.21)

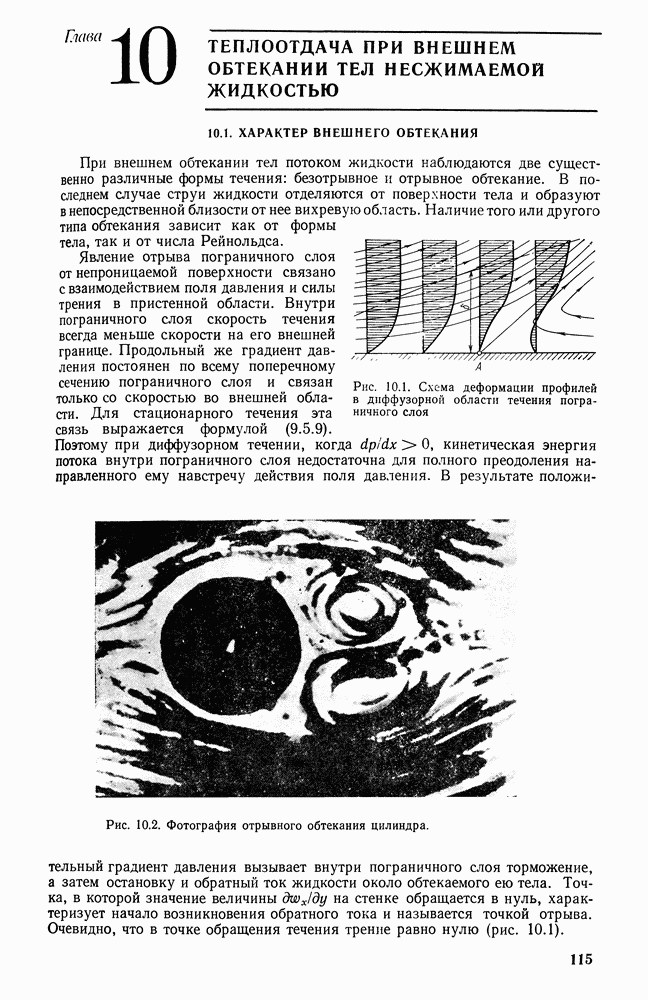
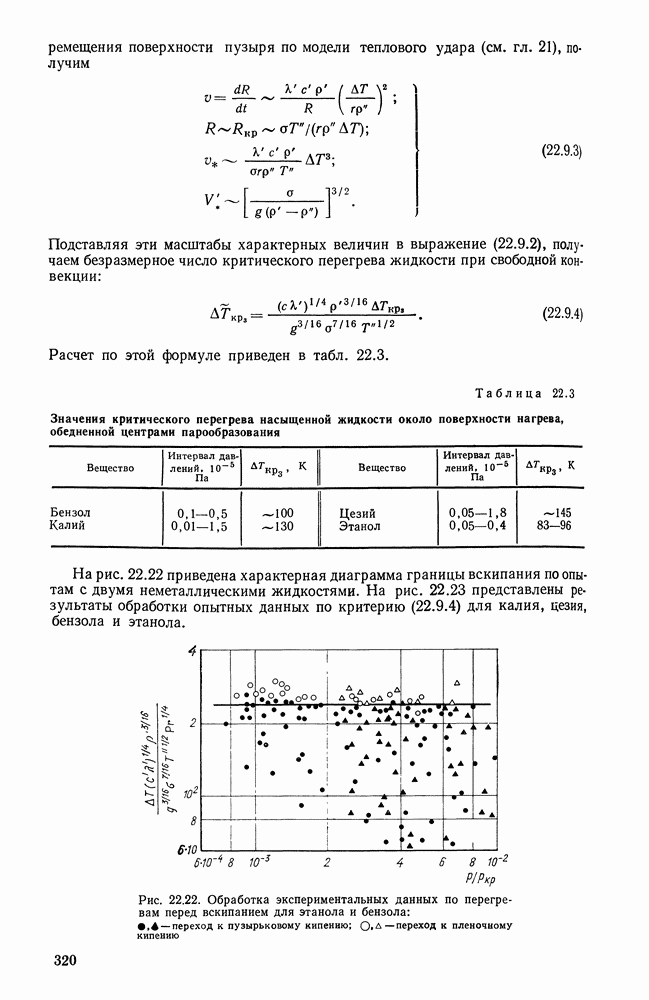
Рис. 26.25. Зависимость безразмерных температур  в слоевой топке от критерия Больцмана
в слоевой топке от критерия Больцмана

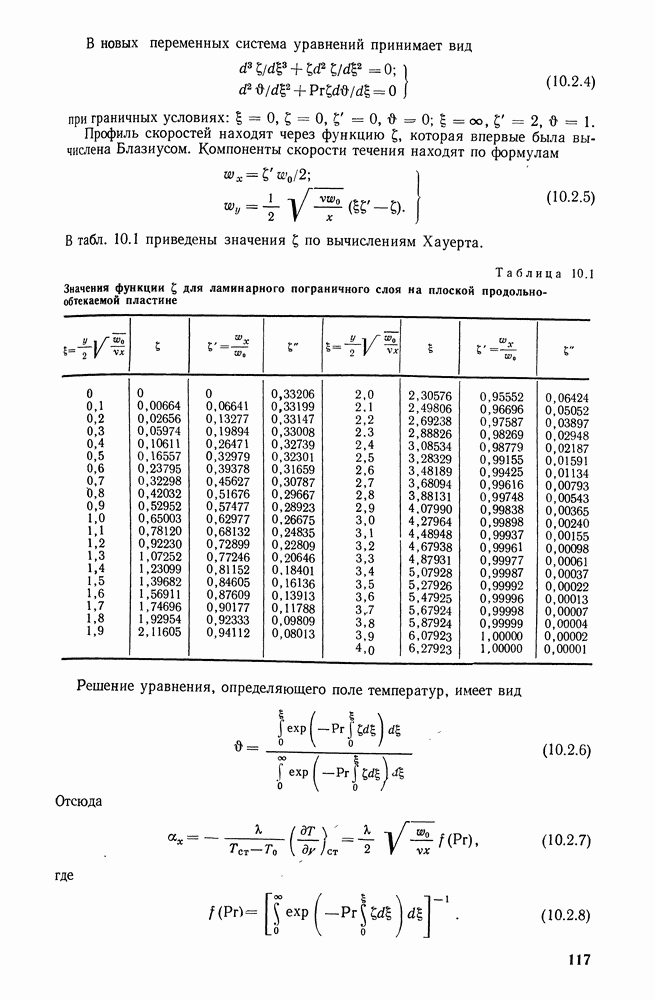
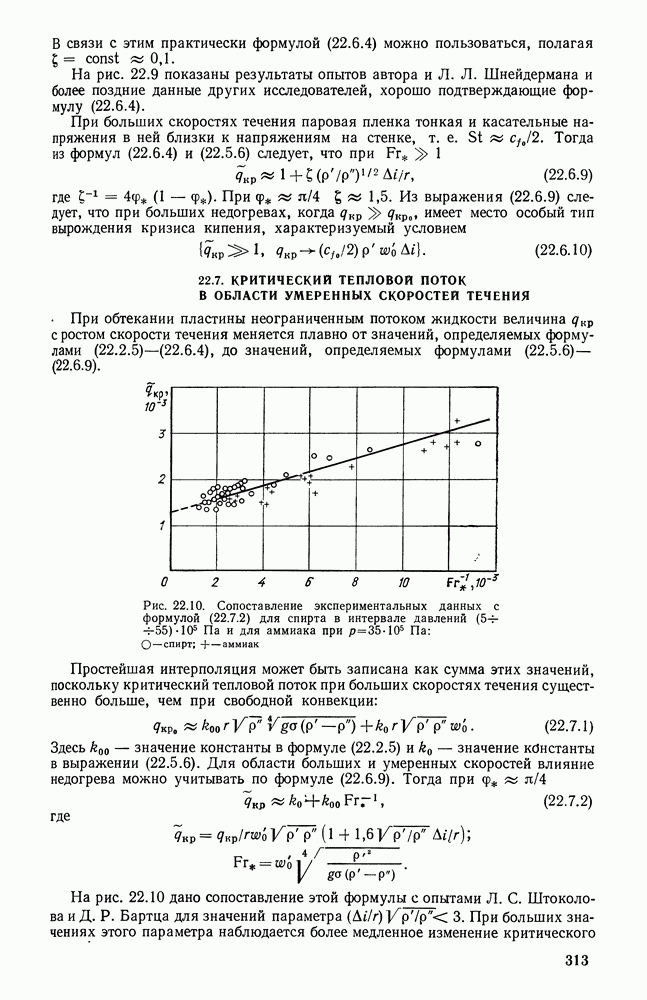
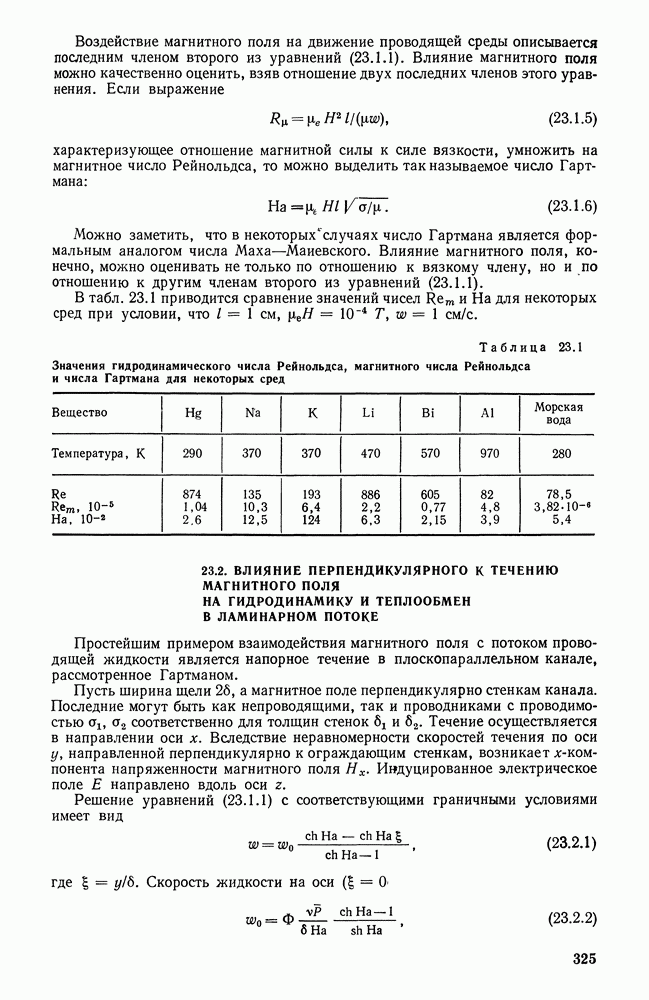
Рис. 26.26. Зависимость безразмерной температуры газов на выходе из слоевой топки от температуры поверхности запыленного экрана при различных режимах нагрузки
Здесь  — доля потерь тепла через обмуровку в общем тепловыделении в топке; Т — температура газов на выходе из топки;
— доля потерь тепла через обмуровку в общем тепловыделении в топке; Т — температура газов на выходе из топки;  — температура газов на выходе из слоя горящего топлива, которую в первом приближении можно принять равной
— температура газов на выходе из слоя горящего топлива, которую в первом приближении можно принять равной  — средняя расчетная теплоемкость продуктов сгорания, принятая в первом приближении одинаковой для разных диапазонов температур. Система (26.11.21) должна быть дополнена замыкающим уравнением, отображающим связь температуры газов на выходе из топки с температурами выделенных зон. В качестве такого уравнения можно воспользоваться известным уравнением осреднения газов:
— средняя расчетная теплоемкость продуктов сгорания, принятая в первом приближении одинаковой для разных диапазонов температур. Система (26.11.21) должна быть дополнена замыкающим уравнением, отображающим связь температуры газов на выходе из топки с температурами выделенных зон. В качестве такого уравнения можно воспользоваться известным уравнением осреднения газов:
 (26.11.22)
(26.11.22)
Задавая температуру экрана  сводим задачу к рассмотрению четырех нелинейных алгебраических уравнений, составленных относительно неизвестных температур газа на выходе из топки 7, обмуровки
сводим задачу к рассмотрению четырех нелинейных алгебраических уравнений, составленных относительно неизвестных температур газа на выходе из топки 7, обмуровки  факела
факела  и слоя горящего топлива
и слоя горящего топлива  .
.
Аналогичным образом рассматривается теплообмен в камерной топке, где расчет задачи сводится к решению системы из трех нелинейных алгебраических уравнений относительно температуры газов на выходе из топки  обмуровки
обмуровки  и факела
и факела  .
.
В качестве уравнения связи можно воспользоваться соотношением
 (26.11.23)
(26.11.23)
где поправочный коэффициент а, определяемый экспериментально, принимается близким к единице. Результаты подобных расчетов в части определения температуры газов на выходе из топки удовлетворительно согласуются с экспериментальным материалом, а также с формулами А. М. Гурвича. Точность расчета температур зон, выделенных в топке, очевидно, определяется теми соображениями, которые используются при составлении балансных топочных уравнений энергии, а также замыкающих уравнений связи.
Такой расчетный прием не только дает более полную информацию о тепловом состоянии топки в целом (см. рис. 26.24), но также позволяет проводить сравнительно простые приближенные анализы как оптико-геометрического (конструктивного), так и режимного характера (рис. 26.25). Действительно, из анализа расчетных уравнений легко установить влияние на температуру газов на выходе из топки оптической толщины факела, геометрии топки, температуры поверхности запыленного экрана (рис. 26.26) и т. п.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Адрианов В. Н., Поляк Г. Л. Дифференциальные методы исследования теплообмена излучением.— «Инж.-физ. журн.», 1964, № 4, с. 5.
1а. Биберман Л. М. Радиационный теплообмен при высоких температурах. — «Изв. АН СССР. Энергетика и транспорт, 1970, № 3, с. 105.
16. Биберман Л. М., Бронин С. Я. К теории нагрева при гиперзвуковом обтекании. — «Докл. АН СССР», 1968, т. 182, № 3, с. 522.
2. Блох А. Г. Основы теплообмена излучением. М.. Госэнергоиздат, 1962.
3. Гурвич А. М. Теплообмен в топках паровых котлов. Теория и расчет. М.— Л., Госэнергоиздат, 1950.
4. Гурвич А. М., Блох А. Г., Носовицкий А. И. Лучистый теплообмен в запыленной газовой среде.— «Теплоэнергетика», 1955, М 2, с. 3.
5. Гурвич А. М., Блох А. Г. О температуре топочного пространства.— «Энергомашиностроение», 1956, № 6, с. 11.
6. Гурвич А. М., Митор В. В. Тепловая эффективность радиационных поверхностей нагрева.— «Энергомашиностроение», 1957, № 2, с. 5.
7. Кондратьев К. Я. Лучистый теплообмен в атмосфере. ГИМИЗ, 1956.
8. Кутателадзе С. С., Боришанский В. М. Справочник по теплопередаче. М., Госэнергоиздат, 1959.
9. Кутателадзе С. С., Рубцов Н. А. Лучисто-конвективный теплообмен в плоском слое поглощающей завесы.— «Журн. прикл. механ. и техн. физ.», 1968, № 6, с. 57.
10. Невский А. С. Теплообмен излучением в металлургических печах и топках котлов. Свердловск, Металлургиздат, 1958.
11. Поляк Г. Л. Алгебра однородных потоков.— «Изв. ЭНИН АН СССР», 1935, т. 3, вып. 1-2, с. 53.
12. Поляк Г. Л. Лучистый теплообмен тел с произвольными индикатрисами отражения поверхностей.— В сб.: Конвективный и лучистый теплообмен. М., Изд-во АН СССР, 1960, с. 118 (ЭНИН АН СССР).
13. Поляк Г. Л., Шорин С. Н. О теории теплообмена в топках. — «Изв. АН СССР, ОТН», 1949, № 12, с. 1832.
14. Рубцов Н. А. К расчетам теплообмена в сложных системах лучеобменивающихся серых тел.— «Инж.-физ. журн.», 1960, № 8, с. 96.
15. Рубцов Н. А. К расчетам теплообмена излучением в промышленных печах и топках. Канд. дне. Новосибирск, 1961 (Ин-т теплофизики СО АН СССР).
16. Рубцов Н. А. К переносу теплового излучения в плоском слое поглощающей среды.— «Журн. прикл. механ. и техн. физ.», 1965, №5, с. 58.
17. Рубцов Н. А., Кузнецова Ф. А. Лучисто-кондуктивный теплообмен в плоском слое серой теплопроводной среды.— «Изв. СО АН СССР. Сер. техн. наук», 1968, вып. 3, № 13, с. 33.
18. Световое моделирование лучистого теплообмена.— В сб.: Теплопередача и тепловое моделирование. М., Изд-во АН СССР, 1959, с. 365. Авт.: С. Н. Шорин, Г. Л. Поляк, И. П. Колченогова и др.
19. Соболев В. В. Перенос лучистой энергии в атмосферах звезд и планет. М., Гос техиздат, 1956.
20. Суринов Ю. А. Об основных методах современной теории лучистого теплообмена.— В сб.: Проблемы энергетики. М., Изд-во АН СССР, 1959, с. 423.
21. Суринов Ю. А. О методах расчета интегральных и локальных коэффициентов излучения.— В сб.: Теплопередача и тепловое моделирование. М., Изд-во АН СССР, 1959, с. 319.
22. Теоретическая астрофизика. М.. Гостехиздат, 1952. Авт.: В. А. Амбарцумян,
Э. Р. Мустель, А. Б. Северный, В. В. Соболев.
23. Тепловой расчет котельных агрегатов (нормативный метод). М.— Л., Госэнергоиздат, 1957.
24. Чандрасекар С. Перенос лучистой энергии. Пер. с англ. М., Гостехиздат, 1953.
25. Шорин С. Н. Теплопередача. М., «Высшая школа», 1964.
26. Шорин С. Н. Лучистый теплообмен в поглощающей среде.— «Изв. АН СССР, ОТН», 1951, №3, с. 389.
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ТЕПЛООБМЕНА
- 1.1. ПРЕДМЕТ ТЕОРИИ ТЕПЛООБМЕНА
- 1.2. ПОЛЕ ТЕМПЕРАТУР И ПОЛЕ ТЕПЛОВЫХ ПОТОКОВ
- 1.3. КОЭФФИЦИЕНТЫ ТЕПЛООТДАЧИ И ТЕПЛОПЕРЕДАЧИ
- 1.4. ТЕРМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
- 1.5. БАЛАНСНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕННОГО АППАРАТА
- 1.6. СРЕДНИЙ ТЕМПЕРАТУРНЫЙ НАПОР
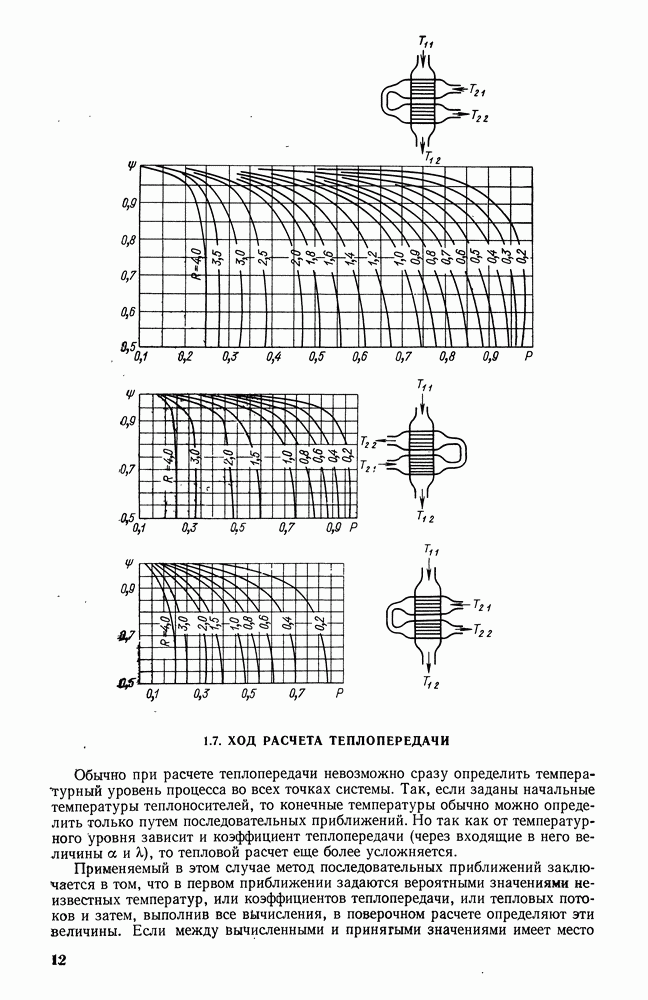
- 1.7. ХОД РАСЧЕТА ТЕПЛОПЕРЕДАЧИ
- 1.8. ОДНОМЕРНАЯ МОДЕЛЬ ЖИДКОСТНОГО ОХЛАЖДЕНИЯ ЯДЕРНОГО РЕАКТОРА
- Глава 2. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В ВЕЩЕСТВЕННОЙ СРЕДЕ
- 2.1. ГИПОТЕЗА О ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ ВЕКТОРА ТЕПЛОВОГО ПОТОКА ГРАДИЕНТУ ТЕМПЕРАТУР
- 2.2. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В ВЕЩЕСТВЕННОЙ СРЕДЕ
- 2.3. ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2.4. ТЕМПЕРАТУРА ТОРМОЖЕНИЯ
- 2.5. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ С КОНЕЧНОЙ СКОРОСТЬЮ РАСПРОСТРАНЕНИЯ ВОЗМУЩЕНИЯ
- Глава 3. УРАВНЕНИЯ ГИДРОДИНАМИКИ
- 3.1. СВЯЗЬ МЕЖДУ ПОЛЕМ ТЕМПЕРАТУР И ПОЛЕМ СКОРОСТЕЙ В ДВИЖУЩЕЙСЯ СРЕДЕ
- 3.2. УРАВНЕНИЕ СПЛОШНОСТИ ПОТОКА ЖИДКОСТИ
- 3.3. УРАВНЕНИЕ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- 3.4. ПОДЪЕМНАЯ СИЛА, ОБУСЛОВЛЕННАЯ НЕОДНОРОДНОСТЬЮ ТЕМПЕРАТУРНОГО ПОЛЯ
- Глава 4. УРАВНЕНИЯ ОСРЕДНЕННОГО ТУРБУЛЕНТНОГО ПОТОКА
- 4.1. ТУРБУЛЕНТНОСТЬ
- 4.2. УРАВНЕНИЯ ОСРЕДНЕННОГО ТУРБУЛЕНТНОГО ТЕЧЕНИЯ ЖИДКОСТИ
- 4.3. УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА
- 4.4. ТУРБУЛЕНТНОЕ ТРЕНИЕ И ТУРБУЛЕНТНАЯ ТЕПЛОПРОВОДНОСТЬ В ПЛОСКОМ ПОТОКЕ ЖИДКОСТИ
- Глава 5. КРАЕВЫЕ УСЛОВИЯ
- 5.1. ВРЕМЕННЫЕ И ПРОСТРАНСТВЕННЫЕ КРАЕВЫЕ УСЛОВИЯ
- 5.2. КРАЕВЫЕ УСЛОВИЯ К УРАВНЕНИЯМ ГИДРОДИНАМИКИ
- 5.3. КРАЕВЫЕ УСЛОВИЯ К УРАВНЕНИЯМ ТЕПЛОПРОВОДНОСТИ
- 5.4. УСЛОВИЯ МЕХАНИЧЕСКОГО И ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ НА ГРАНИЦАХ ФАЗ В МНОГОФАЗНОЙ СИСТЕМЕ
- 5.5. РЕАКТИВНАЯ СИЛА ПРИ ФАЗОВОМ ПРЕВРАЩЕНИИ
- Глава 6. УСЛОВИЯ ПОДОБИЯ ПРОЦЕССОВ ТЕПЛООБМЕНА
- 6.1. ПОНЯТИЕ О ПОДОБИИ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- 6.2. КРИТЕРИИ ПОДОБИЯ
- 6.3. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ ПЕРЕМЕННЫЕ. УСЛОВИЯ ОДНОЗНАЧНОСТИ
- 6.4. КОМБИНИРОВАНИЕ КРИТЕРИЕВ. СОБСТВЕННО КРИТЕРИИ ПОДОБИЯ
- 6.5. КРИТЕРИИ ПОДОБИЯ КАК ОБОБЩЕННЫЕ БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ
- 6.6. ФИЗИЧЕСКИЙ СМЫСЛ НЕКОТОРЫХ КРИТЕРИЕВ ПОДОБИЯ
- 6.7. КРИТЕРИЙ ТЕПЛОВОГО ВЗАИМОДЕЙСТВИЯ ПРИ ФИЗИКО-ХИМИЧЕСКОМ ПРЕВРАЩЕНИИ ВЕЩЕСТВА
- 6.8. БЕЗРАЗМЕРНЫЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
- Глава 7. УСТАНОВИВШИЙСЯ ТЕПЛОВОЙ ПОТОК В ТВЕРДЫХ ТЕЛАХ
- 7.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
- 7.2. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ
- 7.3. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ СТЕНКУ
- 7.4. ТЕПЛОПРОВОДНОСТЬ ЧЕРЕЗ ШАРОВУЮ СТЕНКУ
- 7.5. ТЕПЛОПРОВОДНОСТЬ ВДОЛЬ СТЕРЖНЯ ПОСТОЯННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
- 7.6. ПРЯМОЕ РЕБРО ПОСТОЯННОГО ТЕПЛОВОГО НАПРЯЖЕНИЯ
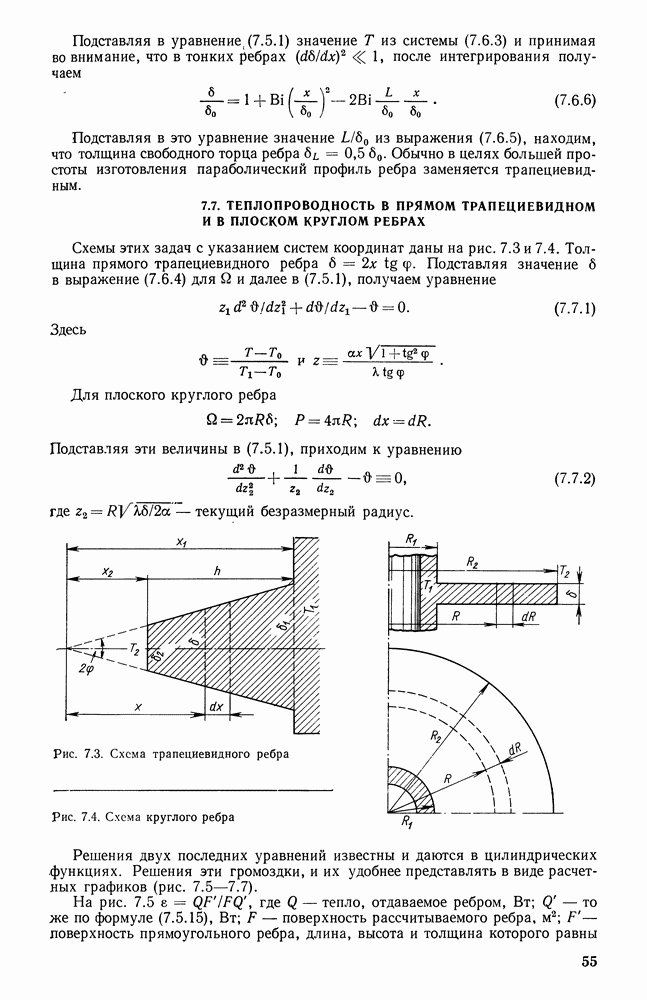
- 7.7. ТЕПЛОПРОВОДНОСТЬ В ПРЯМОМ ТРАПЕЦИЕВИДНОМ И В ПЛОСКОМ КРУГЛОМ РЕБРАХ
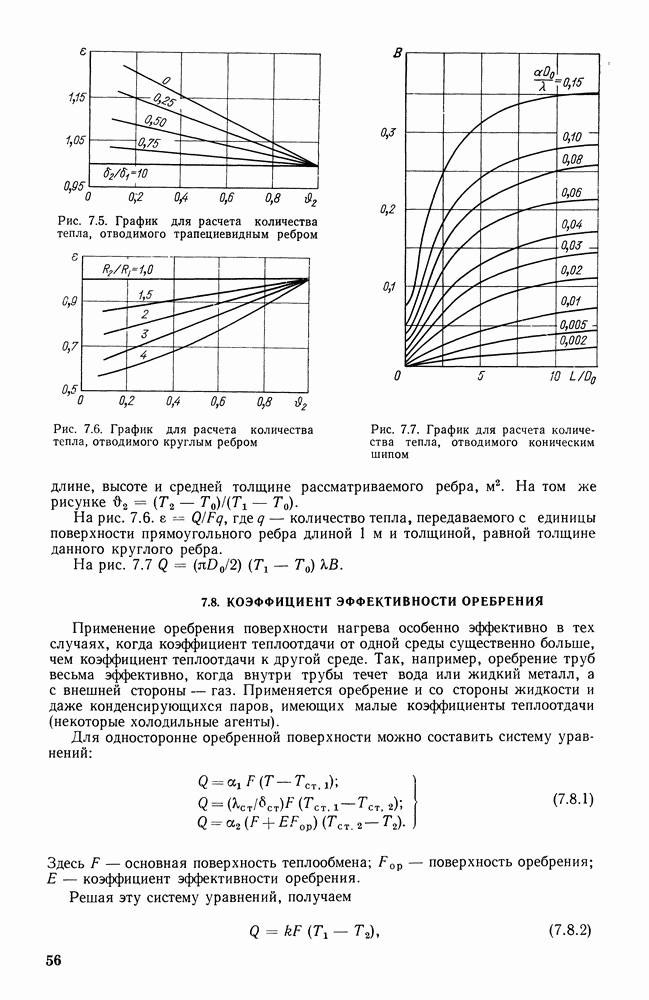
- 7.8. КОЭФФИЦИЕНТ ЭФФЕКТИВНОСТИ ОРЕБРЕНИЯ
- 7.9. ТЕПЛОПРОВОДНОСТЬ В СТЕРЖНЕ И ШАРЕ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛА
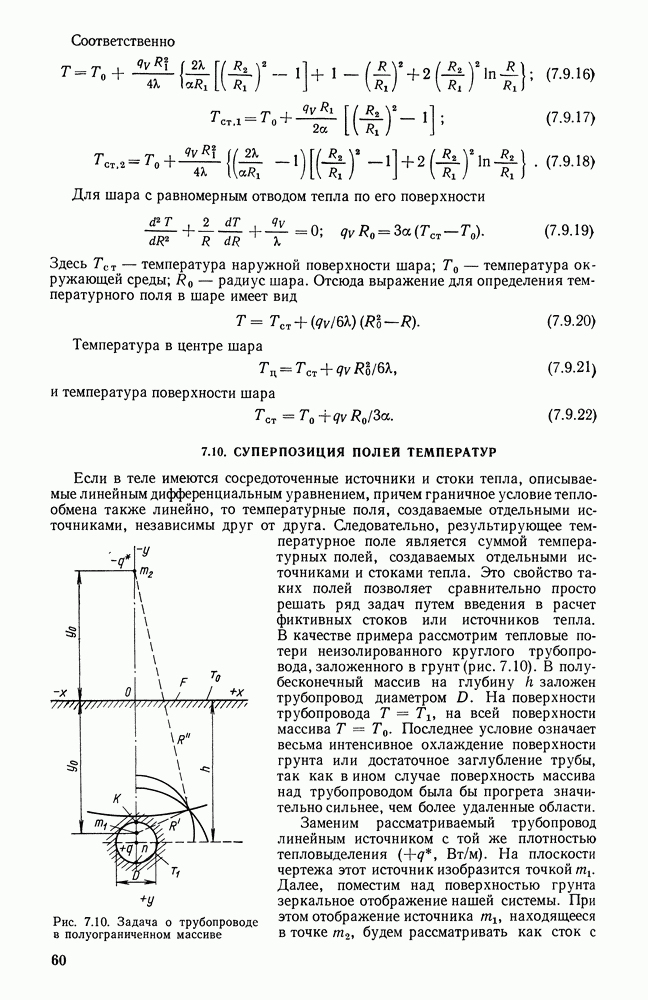
- 7.10. СУПЕРПОЗИЦИЯ ПОЛЕЙ ТЕМПЕРАТУР
- 7.11. УЧЕТ ВНЕШНЕГО ТЕРМИЧЕСКОГО СОПРОТИВЛЕНИЯ МЕТОДОМ ДОПОЛНИТЕЛЬНОЙ СТЕНКИ
- Глава 8. НЕУСТАНОВИВШИЙСЯ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ БЕЗ ВНУТРЕННИХ ИСТОЧНИКОВ
- 8.1. УРАВНЕНИЕ НЕСТАЦИОНАРНОГО ТЕМПЕРАТУРНОГО ПОЛЯ
- 8.2. РЕШЕНИЕ В ВИДЕ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ
- 8.3. ТЕМПЕРАТУРА — ФУНКЦИЯ ОДНОЙ КООРДИНАТЫ И ВРЕМЕНИ
- 8.4. МОНОТОННЫЙ ПЕРЕХОД К ТЕПЛОВОМУ РАВНОВЕСИЮ
- 8.5. ТЕМПЕРАТУРНОЕ ПОЛЕ В ТЕЛЕ ПРИ ТЕМПЕРАТУРЕ ВНЕШНЕЙ СРЕДЫ, ЛИНЕЙНО МЕНЯЮЩЕЙСЯ ВО ВРЕМЕНИ
- 8.6. РЕГУЛЯРНЫЙ РЕЖИМ ОХЛАЖДЕНИЯ
- 8.7. ОХЛАЖДЕНИЕ ВЫСОКОТЕПЛОПРОВОДНОГО ТЕЛА
- 8.8. ТЕПЛОВЫЕ ВОЛНЫ
- Глава 9. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
- 9.1. УРАВНЕНИЕ ТЕПЛОПЕРЕНОСА
- 9.2. СВЯЗЬ МЕЖДУ ТЕПЛООТДАЧЕЙ И ТРЕНИЕМ
- 9.3. ПОГРАНИЧНЫЙ СЛОЙ
- 9.4. СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕПЛООБМЕНА В ПОТОКЕ СЖИМАЕМОГО ГАЗА
- 9.5. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ПЛОСКОГО СТАЦИОНАРНОГО ПОГРАНИЧНОГО СЛОЯ НА НЕПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 9.6. РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И СКОРОСТЕЙ В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ
- 9.7. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТЕПЛОВОГО ПОТОКА И ТЕМПЕРАТУРЫ В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ
- 9.8. ПОЛУЭМПИРИЧЕСКИЕ ВЫРАЖЕНИЯ ТУРБУЛЕНТНОГО ОБМЕНА В ПЛОСКОМ НЕСЖИМАЕМОМ ПОТОКЕ ВБЛИЗИ ТВЕРДОЙ СТЕНКИ
- 9.9. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ТУРБУЛЕНТНОЙ ТЕПЛОПРОВОДНОСТИ И ВЯЗКОСТИ
- 9.10. ТУРБУЛЕНТНЫЙ ПЕРЕНОС В ВЯЗКОМ ПОДСЛОЕ
- 9.11. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ПЛОСКОМ НЕСЖИМАЕМОМ ПОТОКЕ ВБЛИЗИ СТЕНКИ
- 9.12. РАСПРОСТРАНЕНИЕ ПОЛУЭМПИРИЧЕСКИХ ВЫРАЖЕНИЙ ДЛЯ ТУРБУЛЕНТНЫХ ПЕРЕНОСОВ В НЕСЖИМАЕМОЙ ЖИДКОСТИ НА ПЛОСКИЙ ПОТОК ГАЗА
- 9.13. ПОРЯДОК ВЕЛИЧИНЫ вязкого подслоя НА НЕПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 9.14. ПРЕДЕЛЬНЫЕ ОТНОСИТЕЛЬНЫЕ ЗАКОНЫ ТРЕНИЯ И ТЕПЛООБМЕНА
- Глава 10. ТЕПЛООТДАЧА ПРИ ВНЕШНЕМ ОБТЕКАНИИ ТЕЛ НЕСЖИМАЕМОЙ ЖИДКОСТЬЮ
- 10.1. ХАРАКТЕР ВНЕШНЕГО ОБТЕКАНИЯ
- 10.2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ (ТОЧНОЕ РЕШЕНИЕ)
- 10.3. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПЛАСТИНЫ, ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
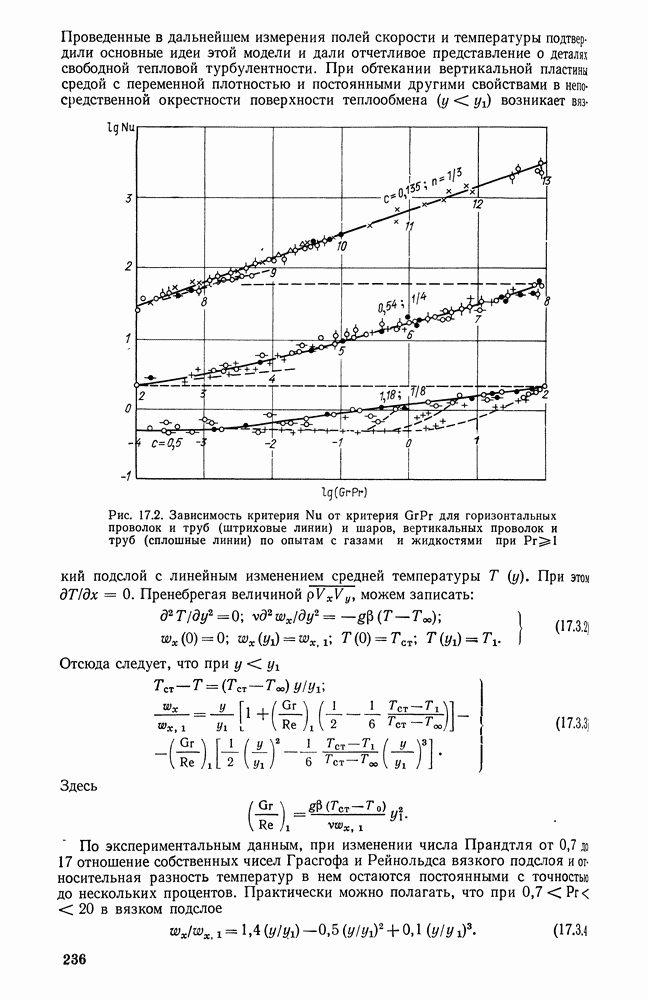
- 10.4. ТЕПЛООТДАЧА ПЛАСТИНЫ, ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ ПРИ Рr>=1 (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.5. ТЕПЛООТДАЧА ПЛАСТИНЫ. ОБТЕКАЕМОЙ ЛАМИНАРНЫМ ПОГРАНИЧНЫМ СЛОЕМ ПРИ Рr<<1 (ПРИБЛИЖЕННОЕ РЕШЕНИЕ)
- 10.6. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПЛАСТИНЫ, ОБТЕКАЕМОЙ ТУРБУЛЕНТНЫМ ПОГРАНИЧНЫМ СЛОЕМ
- 10.7. ТЕПЛООТДАЧА ПЛАСТИНЫ. ОБТЕКАЕМОЙ ТУРБУЛЕНТНЫМ ПОГРАНИЧНЫМ СЛОЕМ С ПОСТОЯННЫМИ ФИЗИЧЕСКИМИ СВОЙСТВАМИ
- 10.8. НЕИЗОТЕРМИЧЕСКИЙ ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПЛАСТИНЕ
- 10.9. НЕИЗОТЕРМИЧЕСКИЙ ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПЛАСТИНЕ
- 10.10. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТИ
- 10.11. КОНСЕРВАТИВНОСТЬ ЗАКОНА ТЕПЛООБМЕНА ОТНОСИТЕЛЬНО ГРАДИЕНТА ДАВЛЕНИЯ
- 10.12. ИНТЕГРАЛ УРАВНЕНИЯ ЭНЕРГИИ
- 10.13. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ ШАРА
- 10.14. ТЕПЛООТДАЧА ПРИ ПОПЕРЕЧНОМ ОБТЕКАНИИ ОДИНОЧНОГО ЦИЛИНДРА
- Глава 11. ТЕПЛООТДАЧА ПРИ ТЕЧЕНИИ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
- 11.1. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ ИЗОТЕРМИЧЕСКОМ ТЕЧЕНИИ
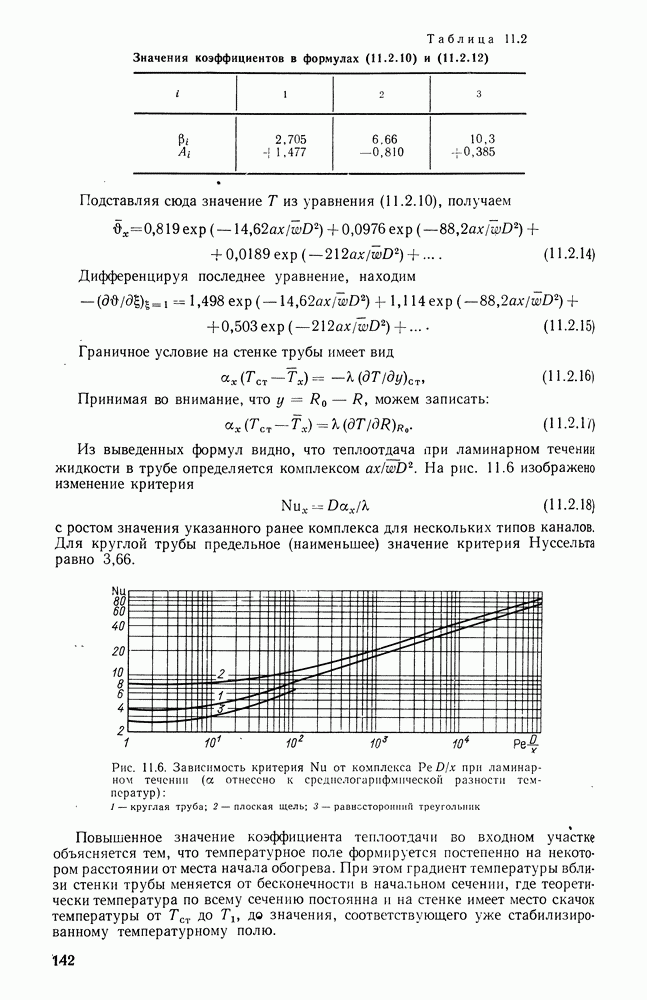
- 11.2. ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ
- 11.3. УРАВНЕНИЕ ТЕПЛОПЕРЕНОСА В ТУРБУЛЕНТНОМ ПОТОКЕ
- 11.4. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ТЕПЛООТДАЧИ И ТРЕНИЯ
- 11.5. РЕШЕНИЕ ПРИ ЛИНЕЙНОМ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ СТЕНКИ
- 11.6. ТЕПЛООТДАЧА К ТУРБУЛЕНТНОМУ ПОТОКУ ПРИ Рr>1
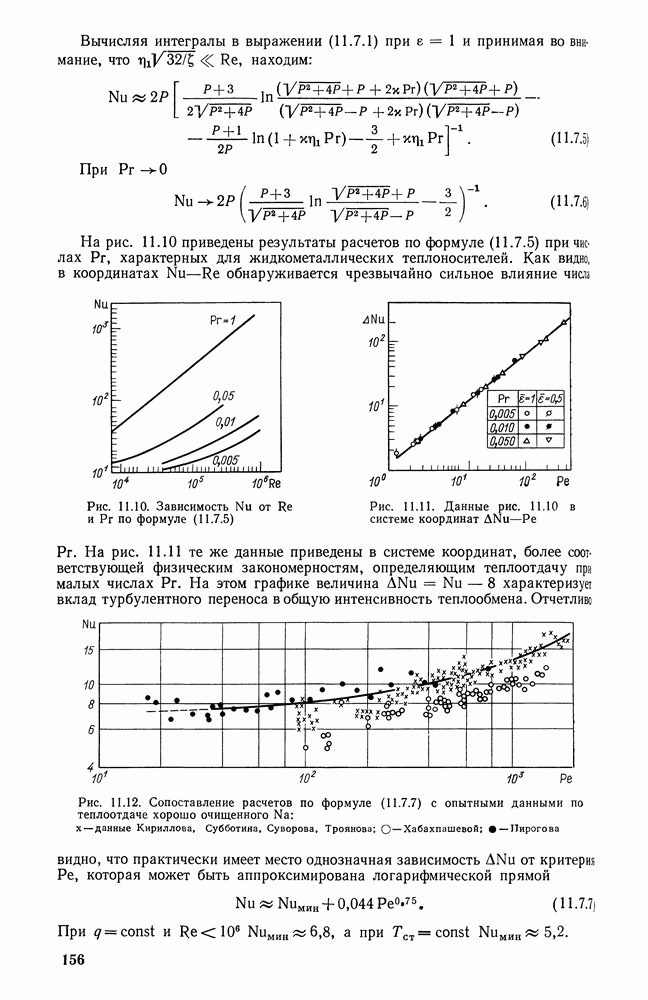
- 11.7. ТЕПЛООТДАЧА К ТУРБУЛЕНТНОМУ ПОТОКУ ПРИ Рr«1
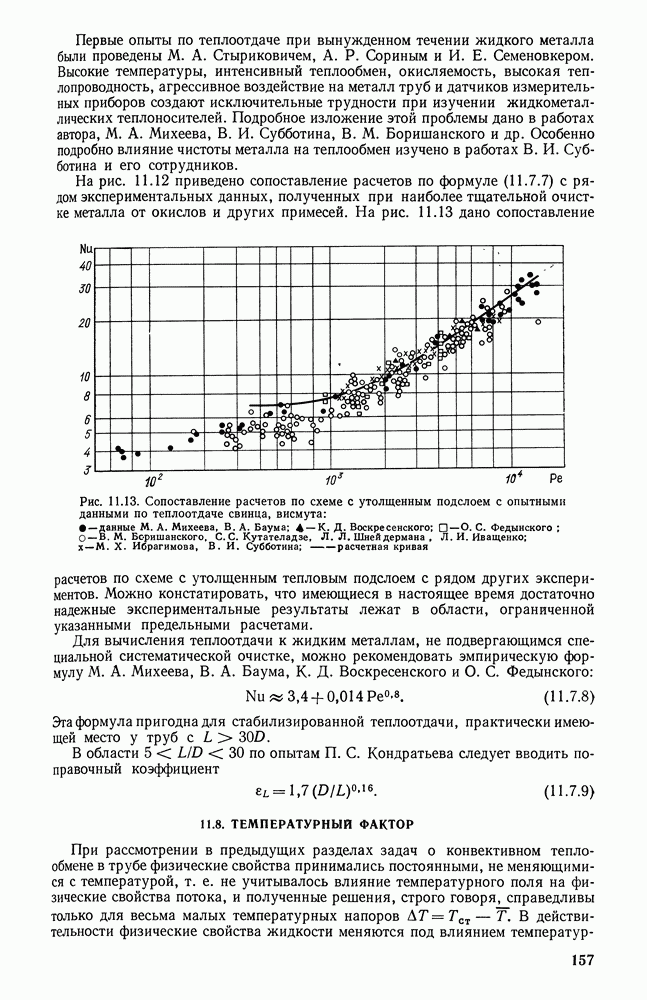
- 11.8. ТЕМПЕРАТУРНЫЙ ФАКТОР
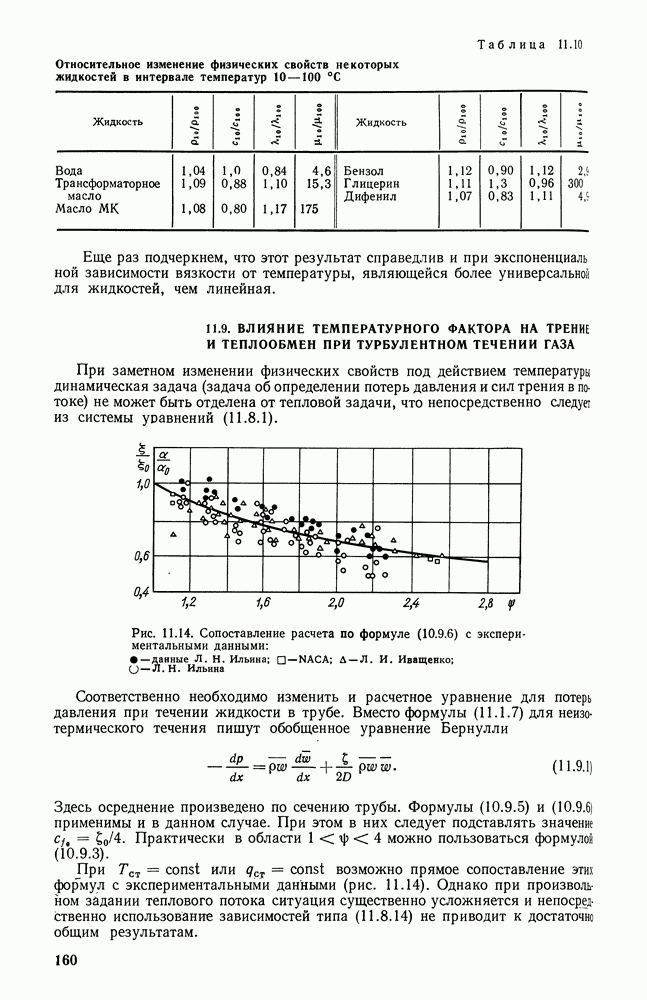
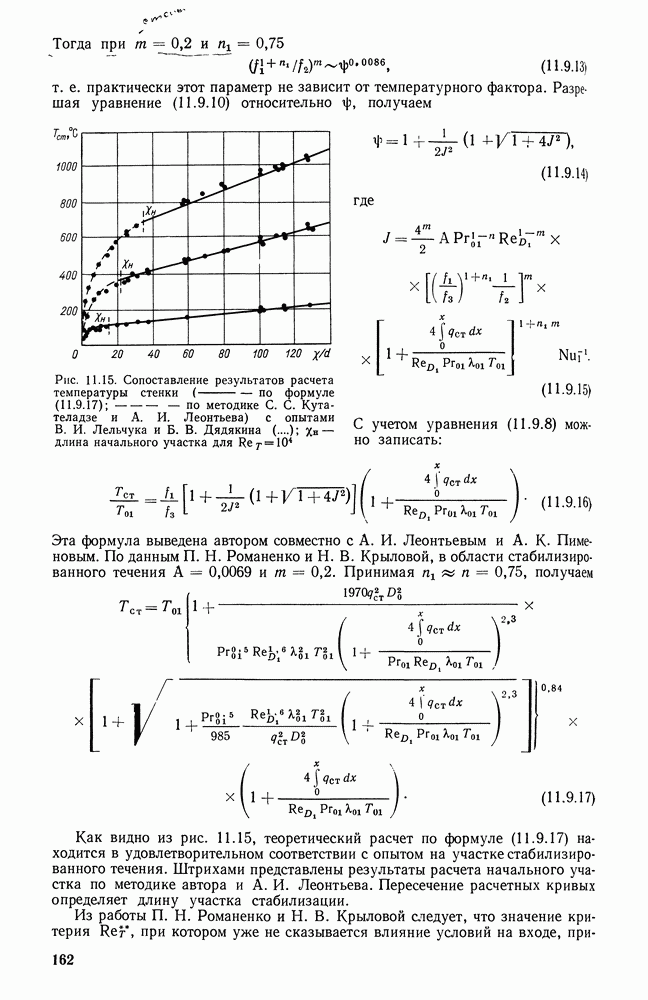
- 11.9. ВЛИЯНИЕ ТЕМПЕРАТУРНОГО ФАКТОРА НА ТРЕНИЕ И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ ГАЗА
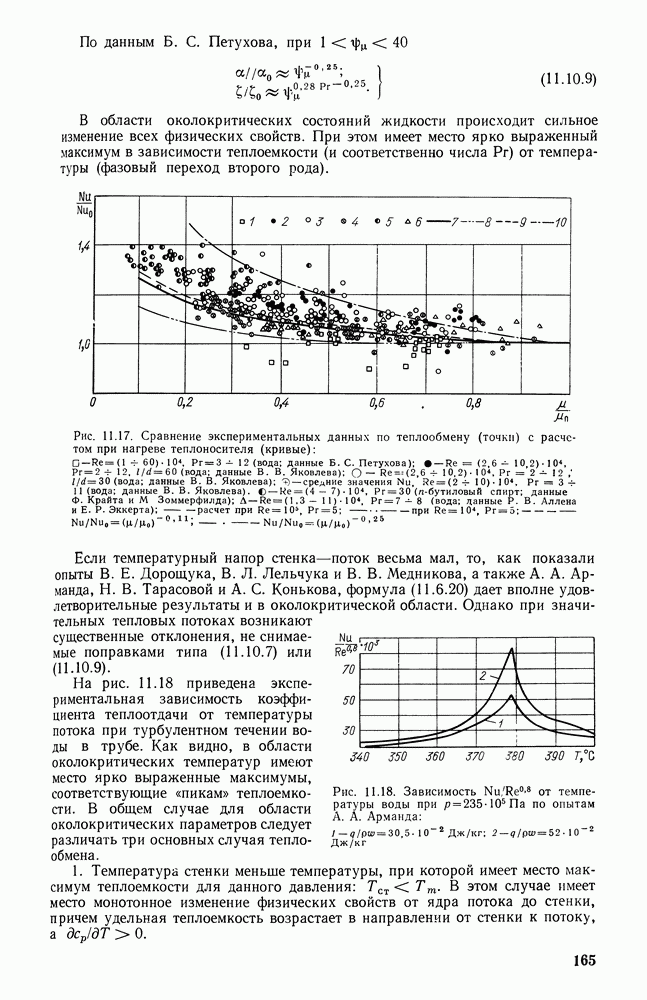
- 11.10. ВЛИЯНИЕ ТЕПЛОВОГО ПОТОКА НА ТЕПЛООТДАЧУ ПРИ ТЕЧЕНИИ КАПЕЛЬНЫХ ЖИДКОСТЕЙ
- 11.11. ТЕПЛООБМЕН И ТРЕНИЕ ВО ВХОДНОМ УЧАСТКЕ ТРУБЫ
- 11.12. ТЕПЛООБМЕН ПРИ ПРОДОЛЬНОМ ТЕЧЕНИИ В КАНАЛАХ НЕЦИЛИНДРИЧЕСКОЙ ФОРМЫ
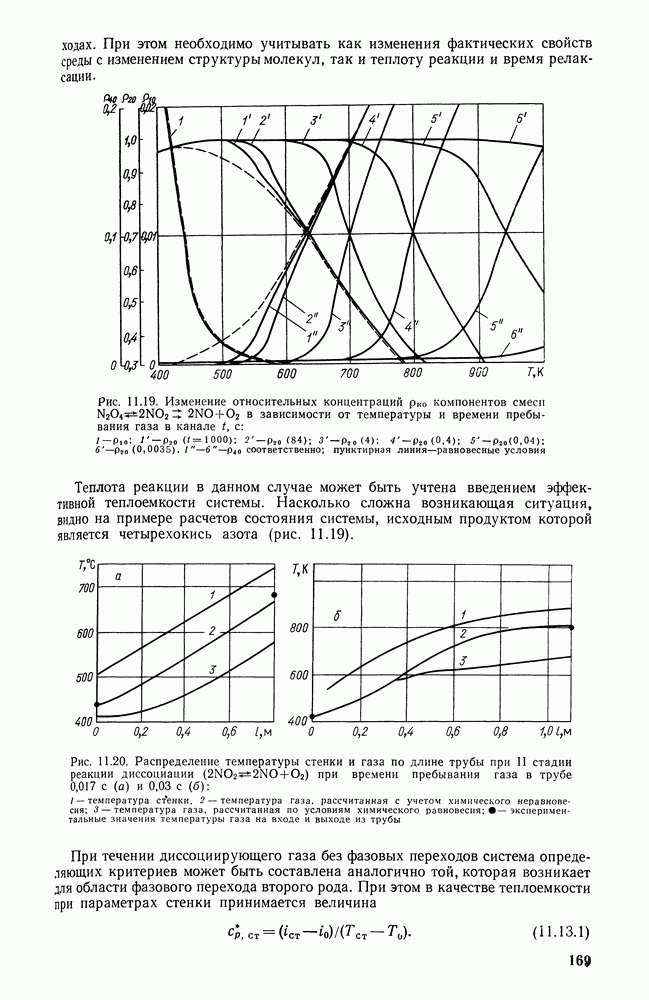
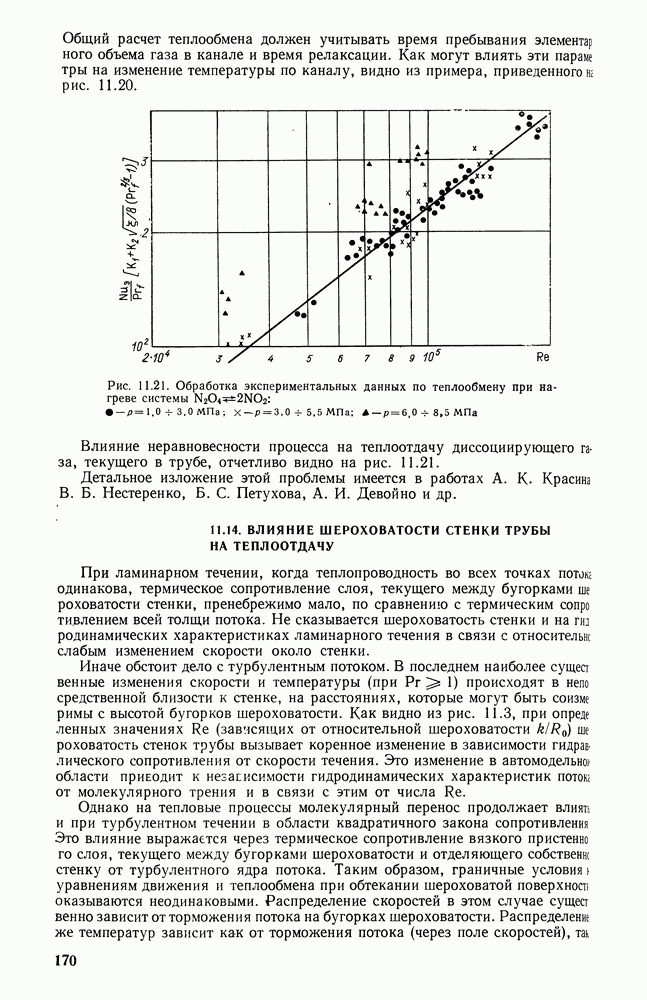
- 11.13. ТЕПЛООБМЕН ПРИ ТЕЧЕНИИ ХИМИЧЕСКИ РЕАГИРУЮЩИХ ГАЗОВЫХ ТЕПЛОНОСИТЕЛЕЙ
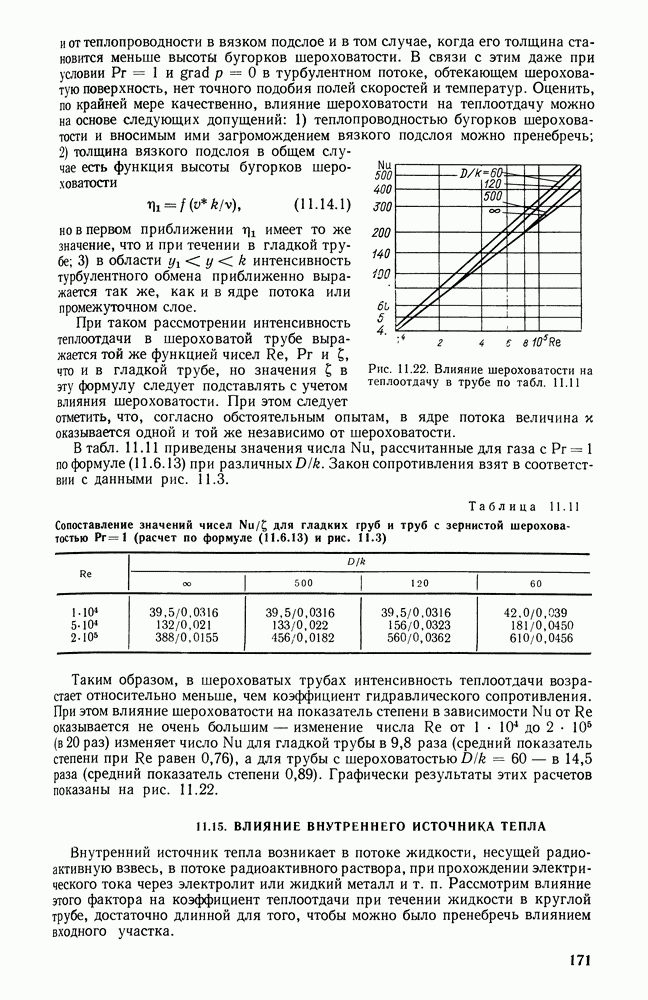
- 11.14. ВЛИЯНИЕ ШЕРОХОВАТОСТИ СТЕНКИ ТРУБЫ НА ТЕПЛООТДАЧУ
- 11.15. ВЛИЯНИЕ ВНУТРЕННЕГО ИСТОЧНИКА ТЕПЛА
- Глава 12. ТЕПЛООБМЕН ПРИ БОЛЬШИХ СКОРОСТЯХ ТЕЧЕНИЯ ГАЗА
- 12.1. СВЯЗЬ МЕЖДУ ТЕМПЕРАТУРОЙ ТОРМОЖЕНИЯ И СКОРОСТЬЮ РАСПРОСТРАНЕНИЯ ЗВУКА В ГАЗЕ
- 12.2. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ТЕМПЕРАТУРЫ И ОБОБЩЕННЫЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
- 12.3. ТЕПЛООТДАЧА К ПЛАСТИНЕ
- 12.4. КОЭФФИЦИЕНТ ТРЕНИЯ ПЛАСТИНЫ ПРИ ЛАМИНАРНОМ ПОГРАНИЧНОМ СЛОЕ
- 12.5. ПРОФИЛЬ СКОРОСТЕЙ В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ НА НЕПРОНИЦАЕМОЙ ПЛАСТИНЕ
- 12.6. КОЭФФИЦИЕНТ ТРЕНИЯ И ТЕПЛООТДАЧИ ПЛАСТИНЫ ПРИ ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ
- 12.7. ТРЕНИЕ И ТЕПЛООБМЕН В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ ДИССОЦИИРОВАННОГО ГАЗА
- Глава 13. ТЕПЛООБМЕН И ТРЕНИЕ ПРИ ПЕРЕНОСЕ ВЕЩЕСТВА
- 13.1. МАССООБМЕН И ТЕПЛОПЕРЕДАЧА
- 13.2. УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ
- 13.3. ТРОЙНАЯ АНАЛОГИЯ
- 13.4. РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ТЕПЛОВОГО ПОТОКА В ПЛОСКОМ ПОГРАНИЧНОМ СЛОЕ НА ПОЛУПРОНИЦАЕМОЙ ПОВЕРХНОСТИ
- 13.5. ПРЕДЕЛЬНЫЙ ЗАКОН ТРЕНИЯ В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ
- 13.6. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ
- 13.7. ЭФФЕКТ ТЕРМОДИФФУЗИИ
- 13.8. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ ГАЗА НА ПОЛУПРОНИЦАЕМОЙ ПЛАСТИНЕ ПРИ
- 13.9. ПАРАМЕТРЫ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ В ТОЧКЕ ОТТЕСНЕНИЯ ОТ ПЛАСТИНЫ
- 13.10. ДВА ВАЖНЫХ ЧАСТНЫХ РЕШЕНИЯ УРАВНЕНИЯ ИМПУЛЬСОВ ДЛЯ ПОГРАНИЧНОГО СЛОЯ НА ПЛАСТИНЕ
- 13.11. ЗАКОНЫ ТРЕНИЯ И ТЕПЛООБМЕНА В ТУРБУЛЕНТНОМ ПОГРАНИЧНОМ СЛОЕ ГАЗА ПРИ КОНЕЧНЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- Глава 14. ТЕПЛОВЫЕ ЗАВЕСЫ
- 14.1. ТИПЫ ЗАВЕС
- 14.2. ПОГРАНИЧНЫЙ СЛОЙ В ТЕПЛОВОЙ ЗАВЕСЕ НА АДИАБАТИЧЕСКОЙ ПОВЕРХНОСТИ
- 14.3. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ПРЕДВКЛЮЧЕННЫМ УЧАСТКОМ ТЕПЛООБМЕНА
- 14.4. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ПРЕДВКЛЮЧЕННЫМ ПОРИСТЫМ УЧАСТКОМ
- 14.5. АДИАБАТИЧЕСКАЯ ПЛАСТИНА С ГАЗОВОЙ ЗАВЕСОЙ
- 14.6. НЕАДИАБАТИЧЕСКАЯ ПЛАСТИНА С ГАЗОВОЙ ЗАВЕСОЙ
- 14.7. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ИМПУЛЬСОВ ПРИ ВЗАИМОДЕЙСТВИИ ЗАТОПЛЕННОЙ СТРУИ С ПЛОСКОЙ ПЛАСТИНОЙ
- 14.8. ТРЕНИЕ И ТЕПЛООБМЕН ПРИ ВЗАИМОДЕЙСТВИИ ЗАТОПЛЕННОЙ СТРУИ С ТВЕРДОЙ СТЕНКОЙ
- Глава 15. ТЕПЛООБМЕН В ПАКЕТАХ И ЗАСЫПКАХ
- 15.1. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ПАКЕТОВ ЦИЛИНДРОВ
- 15.2. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ПАКЕТОВ ЦИЛИНДРОВ
- 15.3. ПАКЕТЫ ШАРОВ
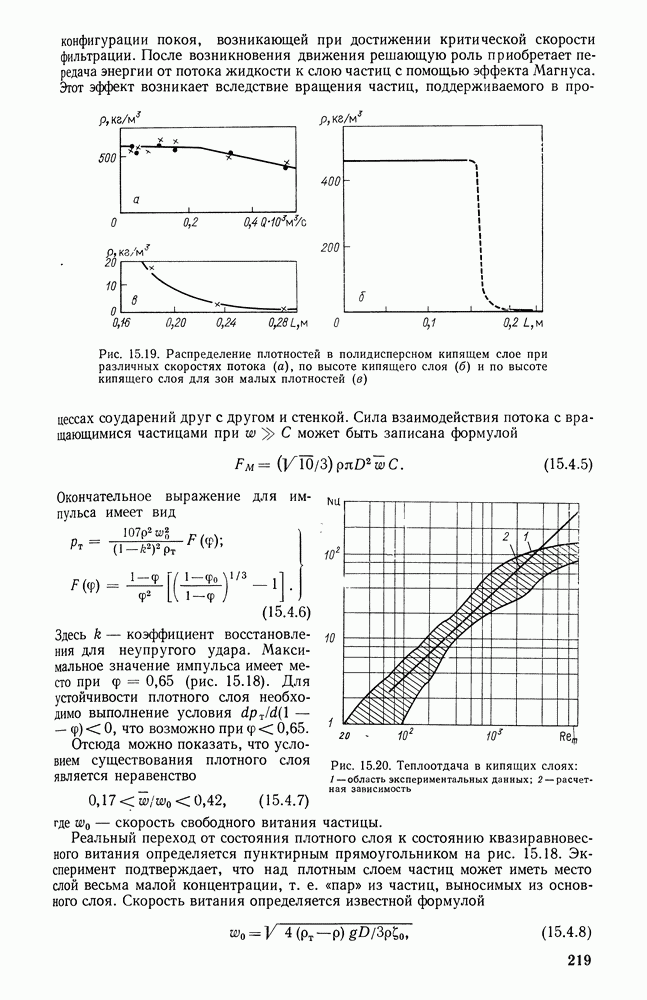
- 15.4. КИПЯЩИЙ СЛОЙ
- 15.5. НЕОДНОРОДНОСТИ И НЕУСТОЙЧИВОСТИ В СЛОЕ ЧАСТИЦ
- Глава 16. ГИДРОДИНАМИКА И ТЕПЛООБМЕН В СРЕДАХ С НЕЛИНЕЙНЫМ ЗАКОНОМ МОЛЕКУЛЯРНОГО ТРЕНИЯ
- 16.1. ЖИДКОСТИ С НЕЛИНЕЙНОЙ КРИВОЙ ТЕЧЕНИЯ
- 16.2. СВЯЗЬ МЕЖДУ ТЕКУЧЕСТЬЮ И КАСАТЕЛЬНЫМИ НАПРЯЖЕНИЯМИ В ПОТОКЕ ЖИДКОСТИ СО СТРУКТУРНОЙ ВЯЗКОСТЬЮ
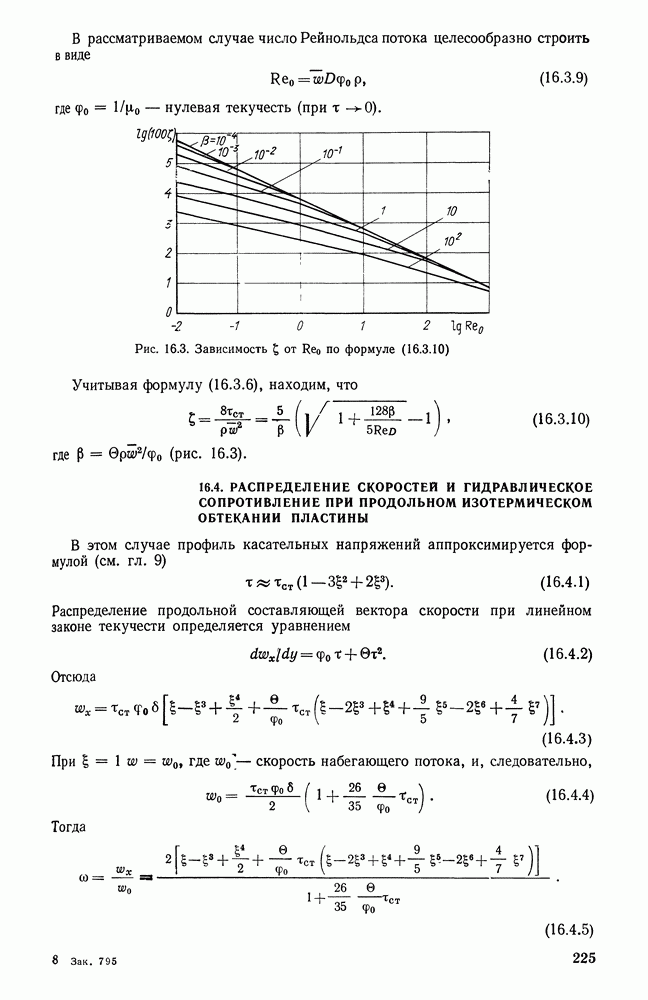
- 16.3. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ СТАБИЛИЗИРОВАННОМ ИЗОТЕРМИЧЕСКОМ ТЕЧЕНИИ ЖИДКОСТИ С ЛИНЕЙНЫМ ЗАКОНОМ ТЕКУЧЕСТИ
- 16.4. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ПРИ ПРОДОЛЬНОМ ИЗОТЕРМИЧЕСКОМ ОБТЕКАНИИ ПЛАСТИНЫ
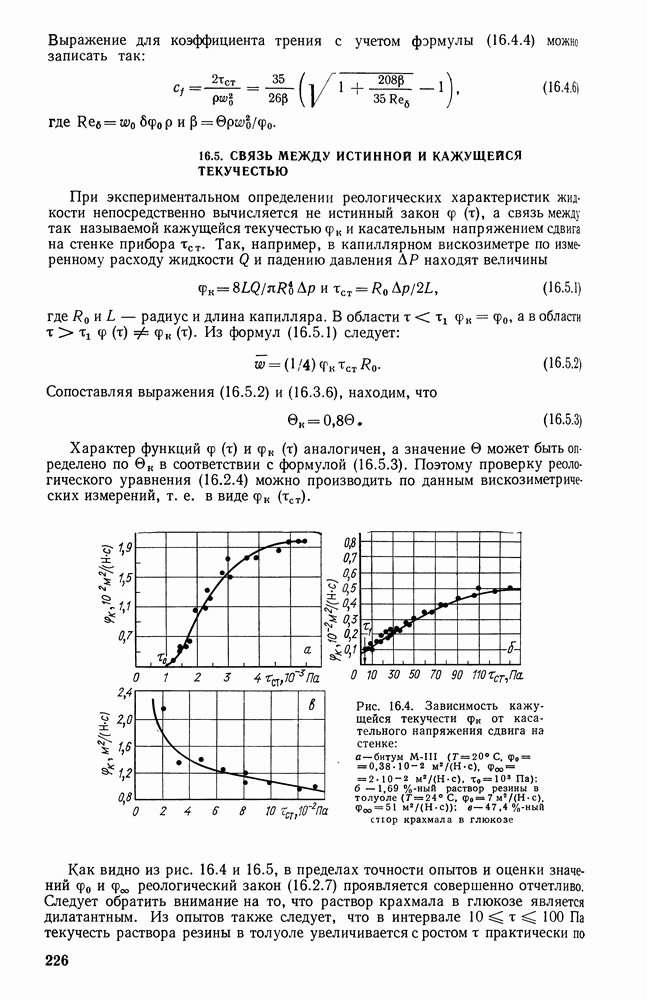
- 16.5. СВЯЗЬ МЕЖДУ ИСТИННОЙ И КАЖУЩЕЙСЯ ТЕКУЧЕСТЬЮ
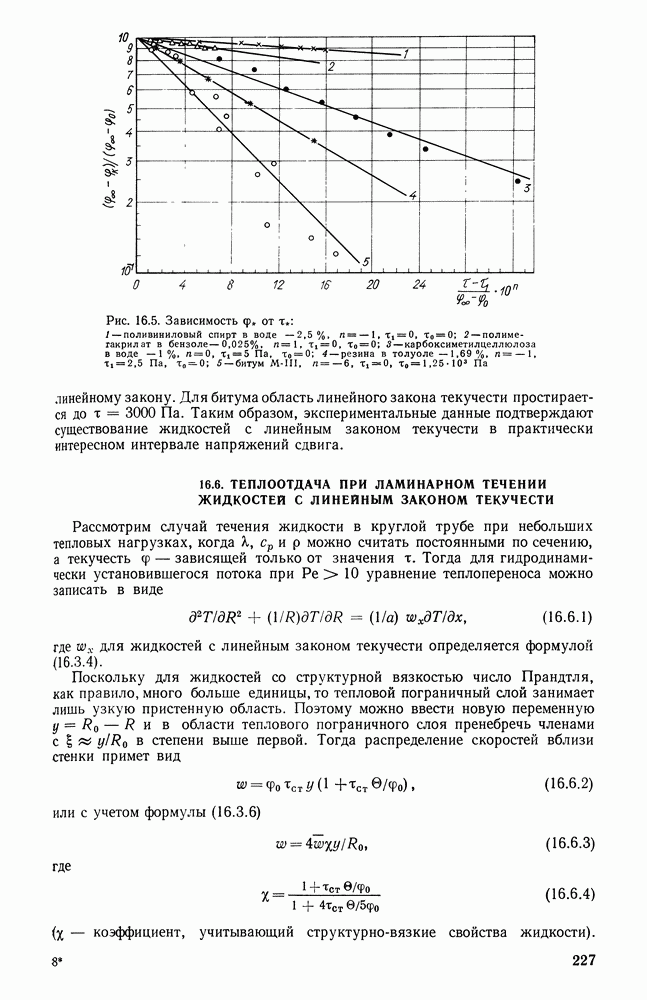
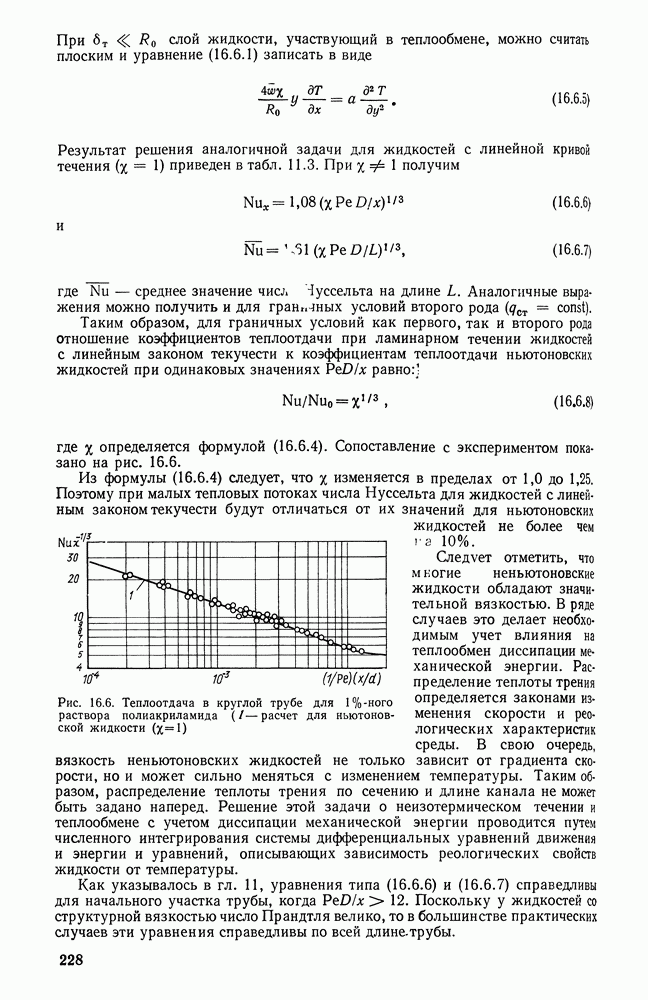
- 16.6. ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ ЖИДКОСТЕЙ С ЛИНЕЙНЫМ ЗАКОНОМ ТЕКУЧЕСТИ
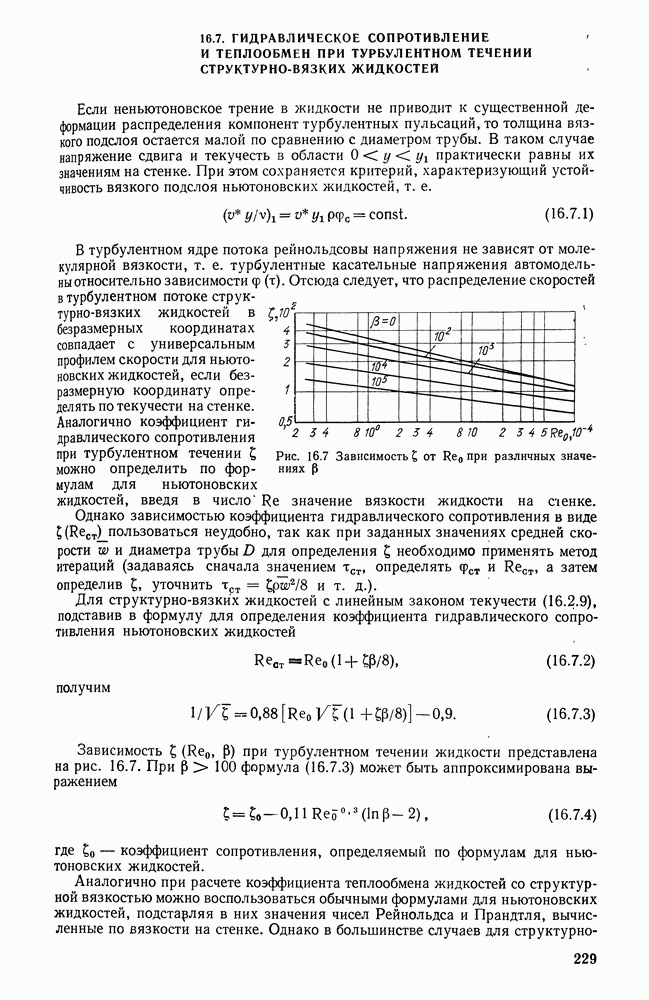
- 16.7. ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ СТРУКТУРНО-ВЯЗКИХ ЖИДКОСТЕЙ
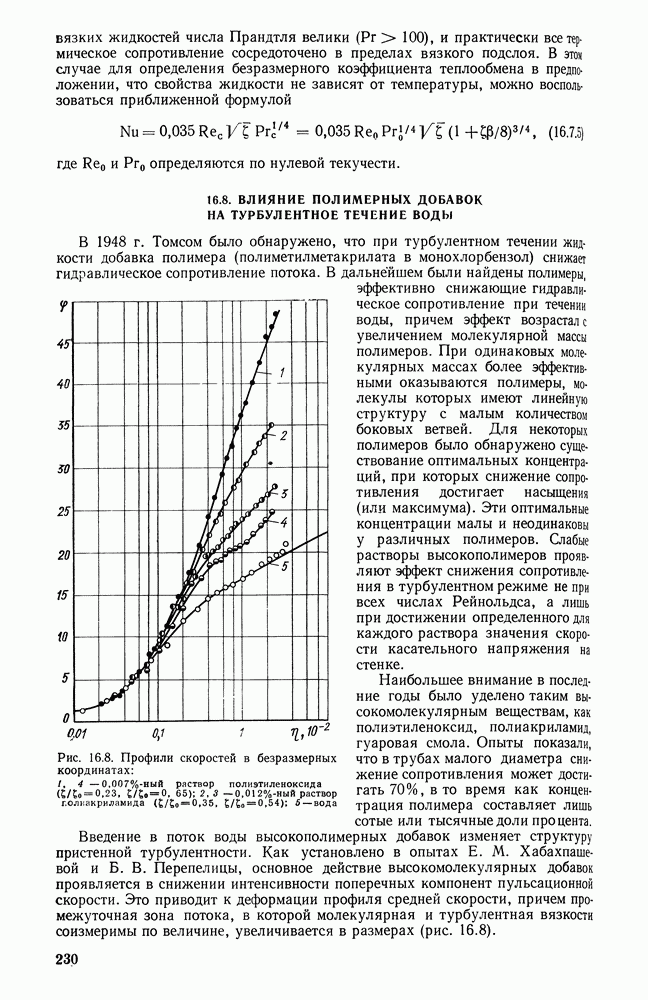
- 16.8. ВЛИЯНИЕ ПОЛИМЕРНЫХ ДОБАВОК НА ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ВОДЫ
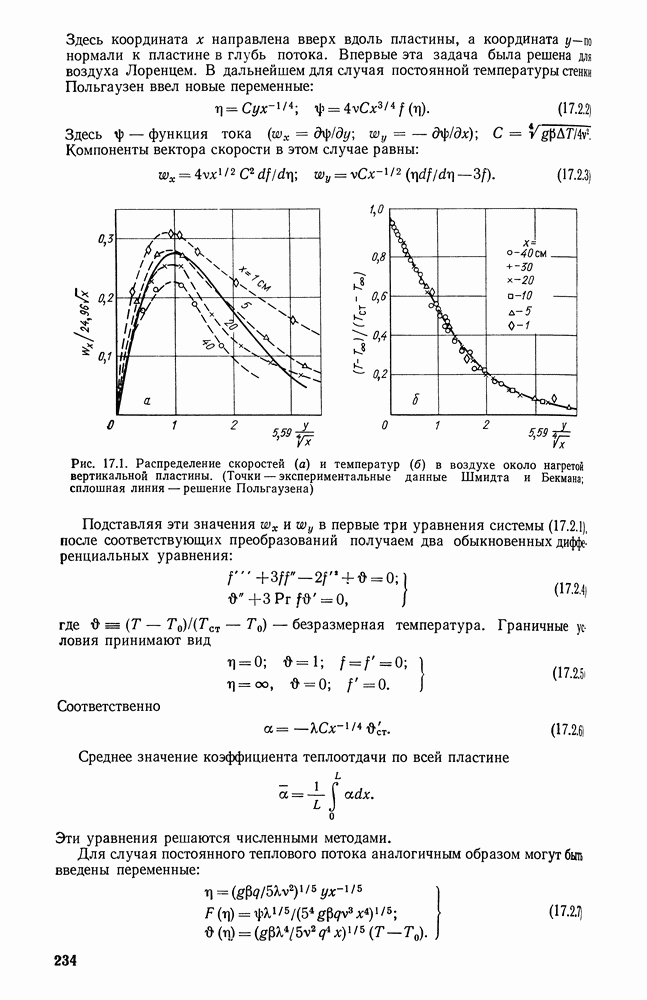
- Глава 17. ТЕПЛООТДАЧА ПРИ СВОБОДНОЙ КОНВЕКЦИИ
- 17.1. СВОБОДНАЯ ТЕПЛОВАЯ КОНВЕКЦИЯ ОКОЛО ТВЕРДОЙ ПОВЕРХНОСТИ
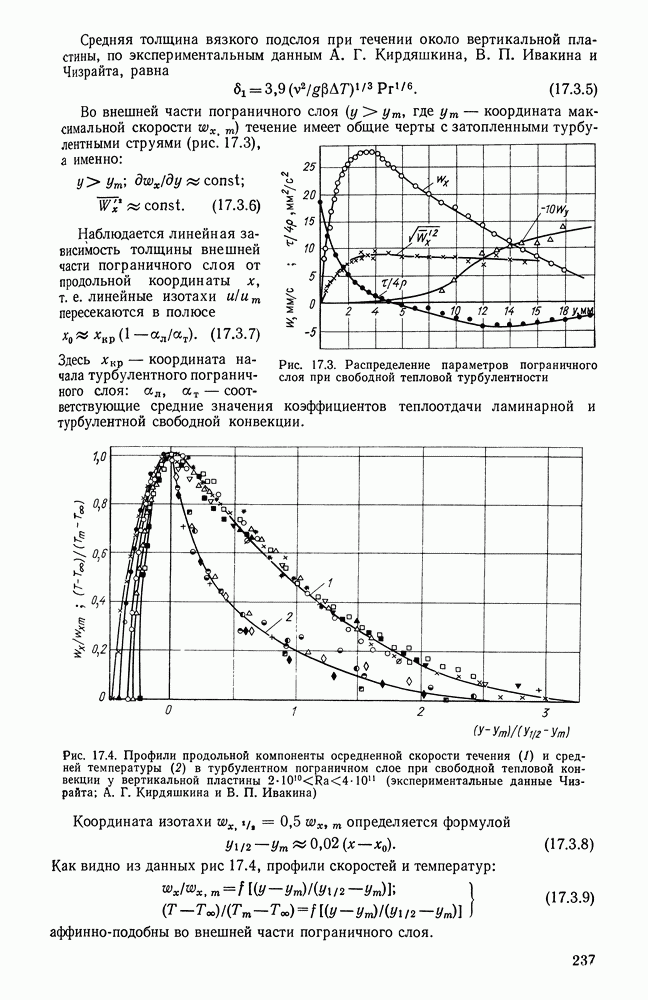
- 17.2. ТЕПЛООТДАЧА В ОБЛАСТИ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ ПРИ Pr>=1
- 17.3. ГИДРОДИНАМИКА И ТЕПЛООБМЕН В ОБЛАСТИ РАЗВИТОЙ ТЕПЛОВОЙ ТУРБУЛЕНТНОСТИ ПРИ Рr>=1
- 17.4. ТЕПЛООТДАЧА ПРИ Рr<<1
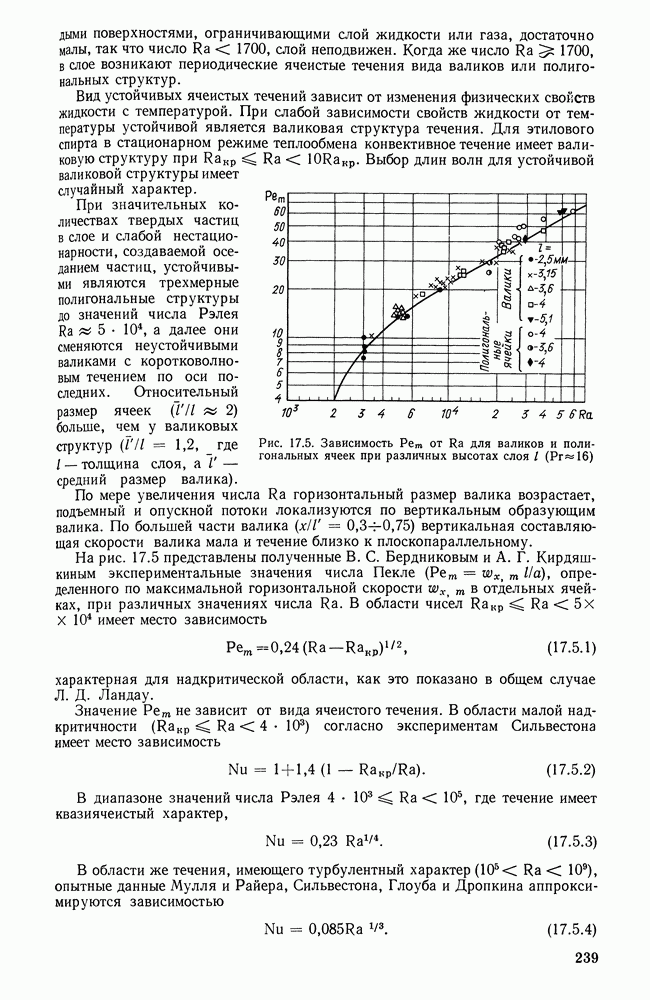
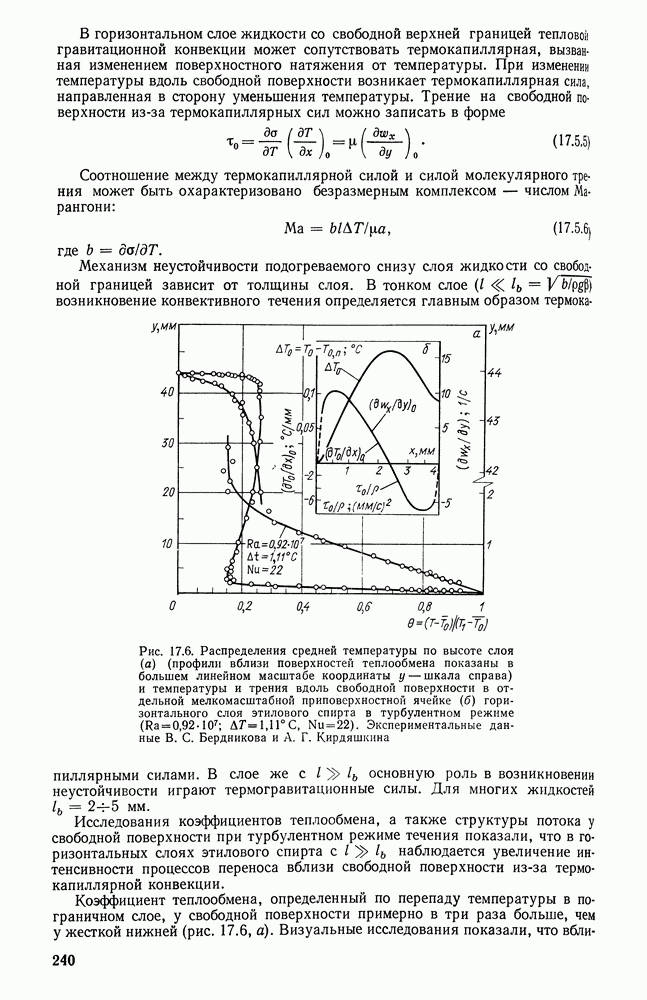
- 17.5. ТЕПЛООТДАЧА В ЖИДКИХ И ГАЗОВЫХ СЛОЯХ
- 17.6. СОВМЕСТНОЕ ВЛИЯНИЕ СВОБОДНОЙ И ВЫНУЖДЕННОЙ КОНВЕКЦИИ
- Глава 18. ТЕПЛООБМЕН В РАЗРЕЖЕННЫХ ГАЗАХ
- 18.1. ОСОБЕННОСТИ ПРОЦЕССОВ ПЕРЕНОСА В РАЗРЕЖЕННОМ ГАЗЕ
- 18.2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ С ПОВЕРХНОСТЬЮ. СВОБОДНО-МОЛЕКУЛЯРНЫЙ ПЕРЕНОС ТЕПЛА
- 18.3. ТЕЧЕНИЕ СО СКОЛЬЖЕНИЕМ И ТЕМПЕРАТУРНЫМ СКАЧКОМ
- 18.4. ОСОБЕННОСТИ ТЕПЛООБМЕНА ПРИ ГИПЕРЗВУКОВЫХ СКОРОСТЯХ
- 18.5. РЕЛАКСАЦИОННЫЕ ЭФФЕКТЫ ПРИ ОБТЕКАНИИ ТЕЛ РАЗРЕЖЕННЫМ ГАЗОМ
- 18.6. СВОБОДНАЯ КОНВЕКЦИЯ В РАЗРЕЖЕННОМ ГАЗЕ
- 18.7. ВАКУУМНАЯ ИЗОЛЯЦИЯ
- Глава 19. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ПАРА НА ТВЕРДЫХ ПОВЕРХНОСТЯХ
- 19.1. ПЛЕНОЧНАЯ И КАПЕЛЬНАЯ КОНДЕНСАЦИЯ
- 19.2. ОСНОВНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА ПРИ ПЛЕНОЧНОЙ КОНДЕНСАЦИИ ЧИСТОГО НАСЫЩЕННОГО ПАРА
- 19.3. ЛАМИНАРНОЕ ТЕЧЕНИЕ ПЛЕНКИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ ПРИ МЕДЛЕННОМ ДВИЖЕНИИ ПАРА
- 19.4. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ПЛЕНКИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ ПРИ МЕДЛЕННОМ ДВИЖЕНИИ ПАРА
- 19.5. СРЕДНИЙ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ ПРИ СМЕШАННОМ ТЕЧЕНИИ ПЛЕНКИ КОНДЕНСАТА НА ВЕРТИКАЛЬНОЙ СТЕНКЕ
- 19.6. ВЛИЯНИЕ СКОРОСТИ ТЕЧЕНИЯ ЧИСТОГО ПАРА НА ТЕПЛООТДАЧУ ПРИ КОНДЕНСАЦИИ НА ВЕРТИКАЛЬНОЙ ПОВЕРХНОСТИ
- 19.7. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ПАРА ВНУТРИ ТРУБЫ
- 19.8. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ ЧИСТОГО ПАРА НА ВНЕШНЕЙ ПОВЕРХНОСТИ ГОРИЗОНТАЛЬНЫХ ТРУБ
- 19.9. ПЛЕНОЧНАЯ КОНДЕНСАЦИЯ НА НИЖНЕЙ ПОВЕРХНОСТИ ГОРИЗОНТАЛЬНОЙ ПЛИТЫ
- 9.10. ВЛИЯНИЕ ВЛАЖНОСТИ И ПЕРЕГРЕВА ПАРА
- 19.11. КАПЕЛЬНАЯ КОНДЕНСАЦИЯ
- Глава 20. КОНДЕНСАЦИЯ НА СВОБОДНОЙ ПОВЕРХНОСТИ ЖИДКОСТИ
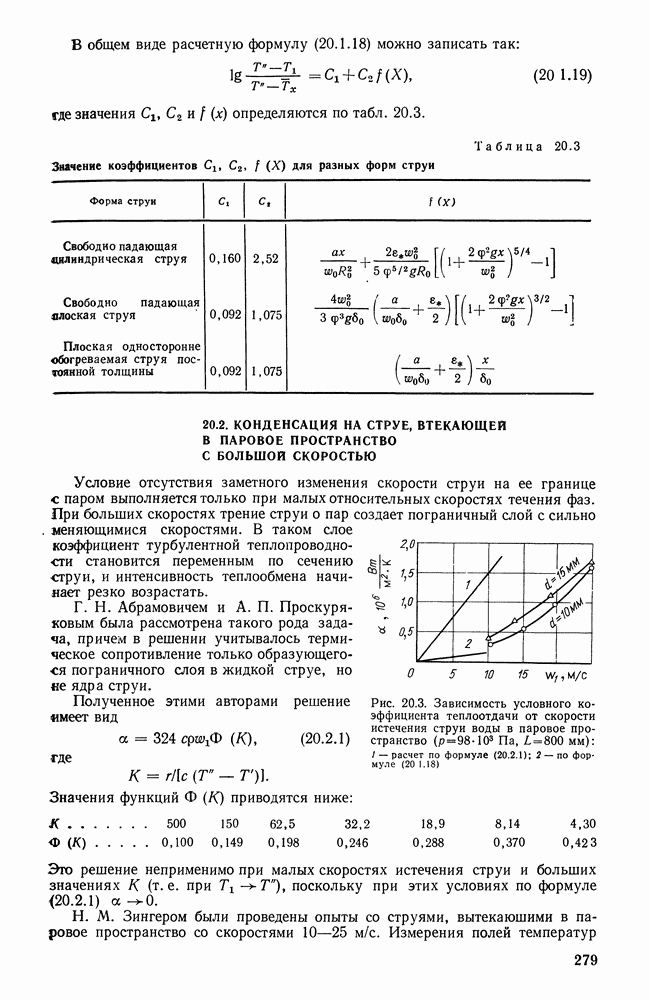
- 20.1. ТЕПЛООБМЕН В СВОБОДНО ПАДАЮЩЕЙ СТРУЕ
- 20.2. КОНДЕНСАЦИЯ НА СТРУЕ, ВТЕКАЮЩЕЙ В ПАРОВОЕ ПРОСТРАНСТВО С БОЛЬШОЙ СКОРОСТЬЮ
- Глава 21. ТЕПЛООТДАЧА ПРИ КИПЕНИИ ОДНОРОДНЫХ ЖИДКОСТЕЙ
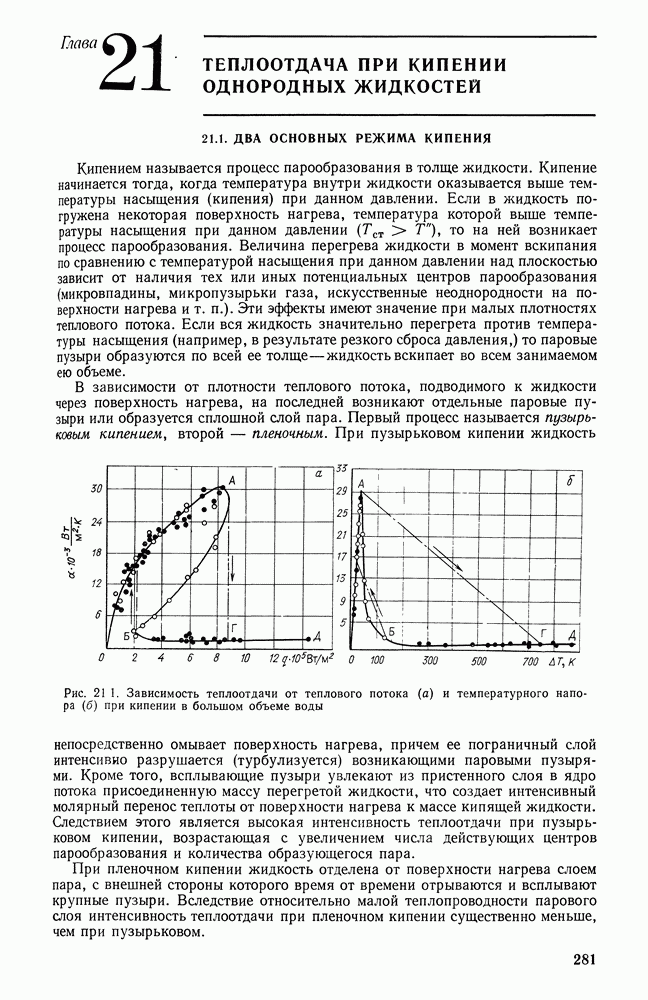
- 21.1. ДВА ОСНОВНЫХ РЕЖИМА КИПЕНИЯ
- 21.2. ТЕМПЕРАТУРНОЕ ПОЛЕ
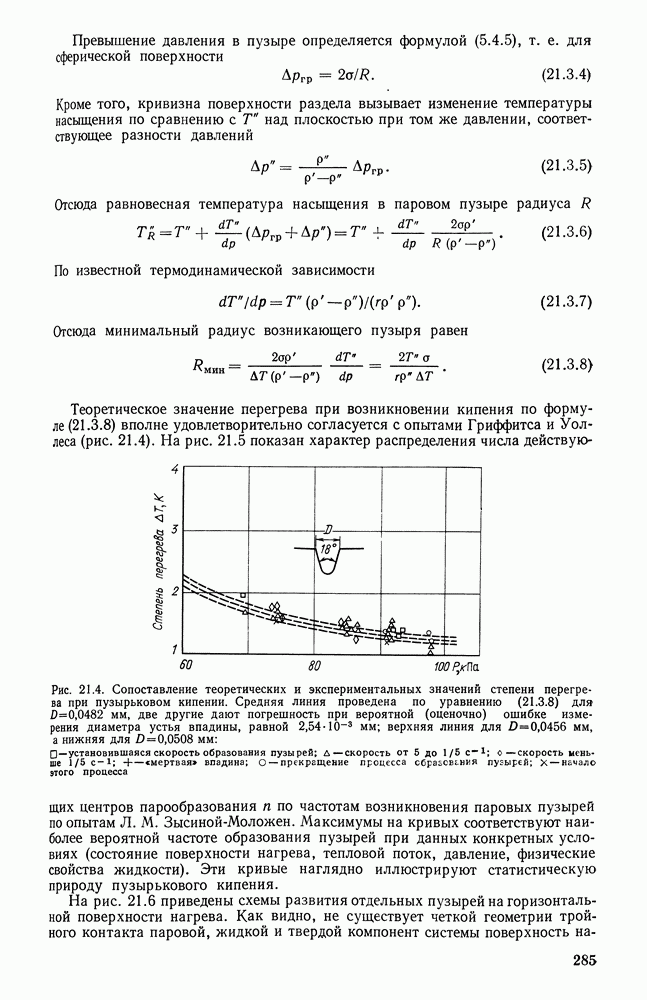
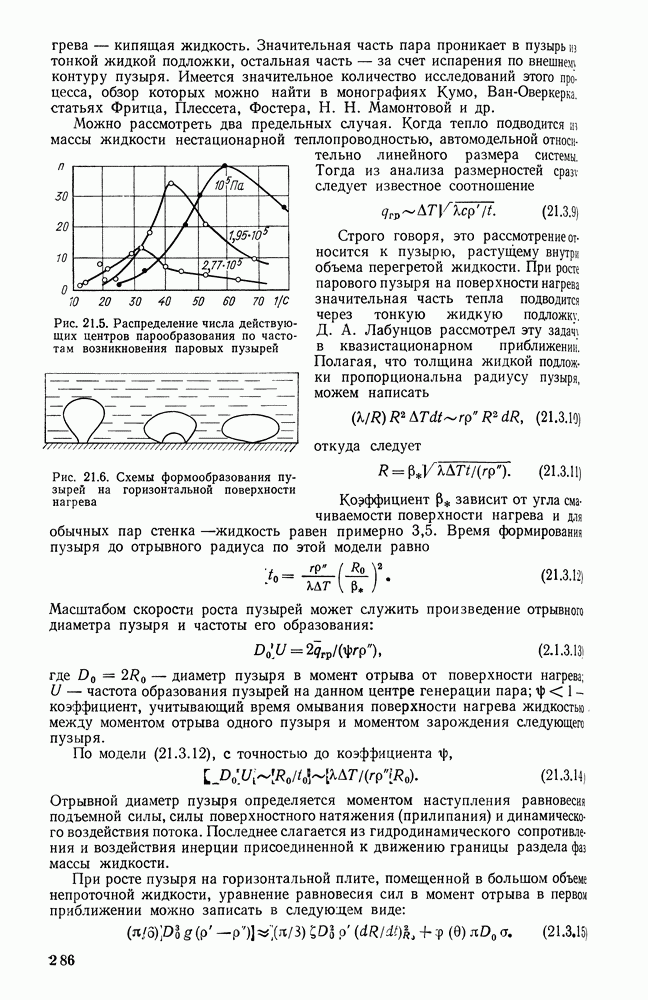
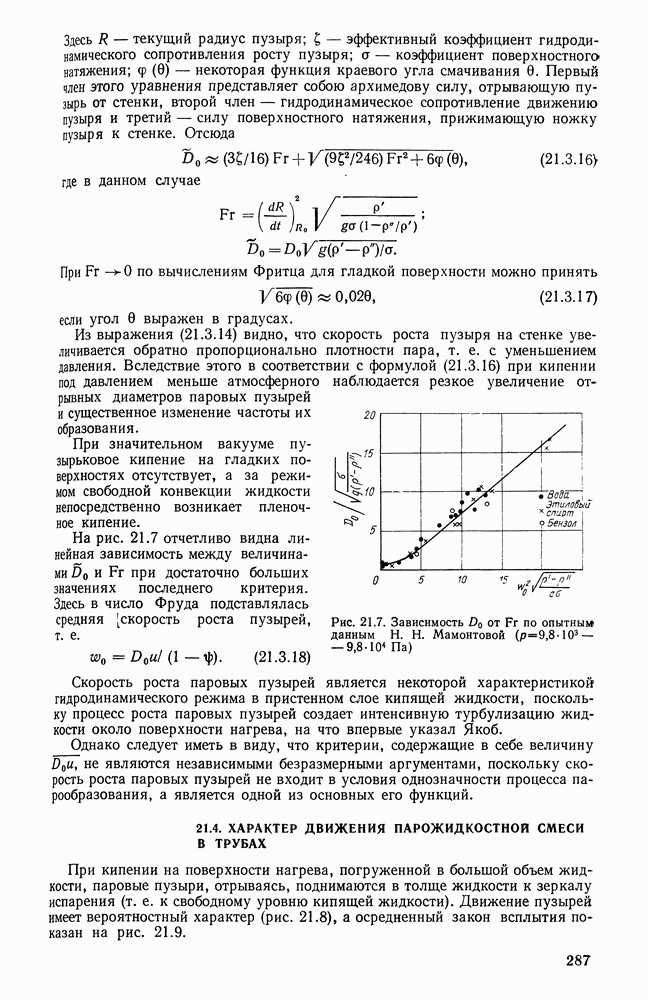
- 21.3. ПУЗЫРЬКОВОЕ КИПЕНИЕ, ЧАСТОТА И СКОРОСТЬ РОСТА ПАРОВЫХ ПУЗЫРЕЙ
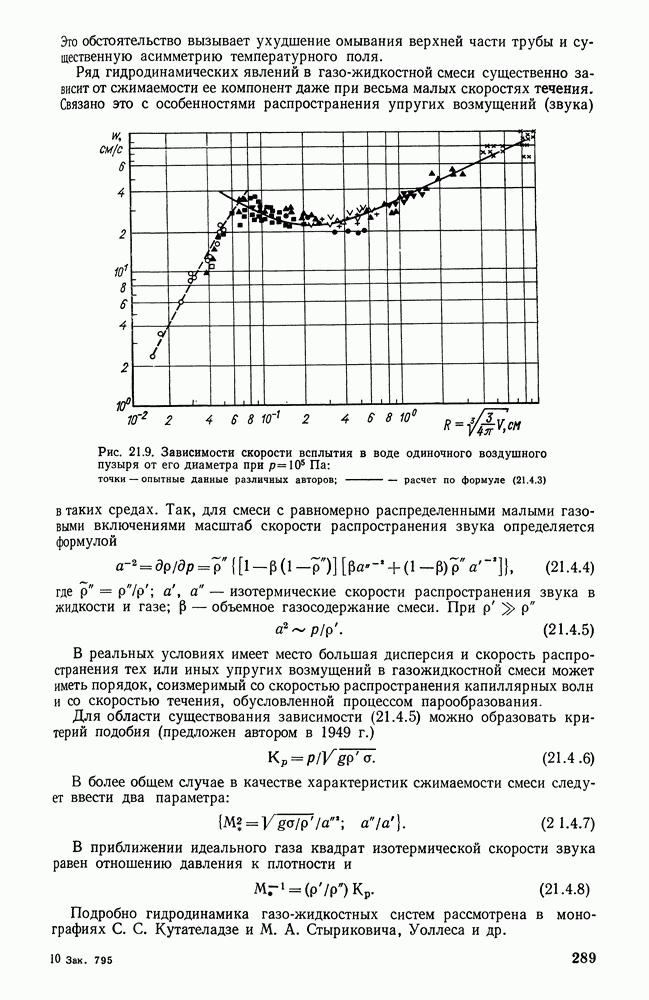
- 21.4. ХАРАКТЕР ДВИЖЕНИЯ ПАРОЖИДКОСТНОЙ СМЕСИ В ТРУБАХ
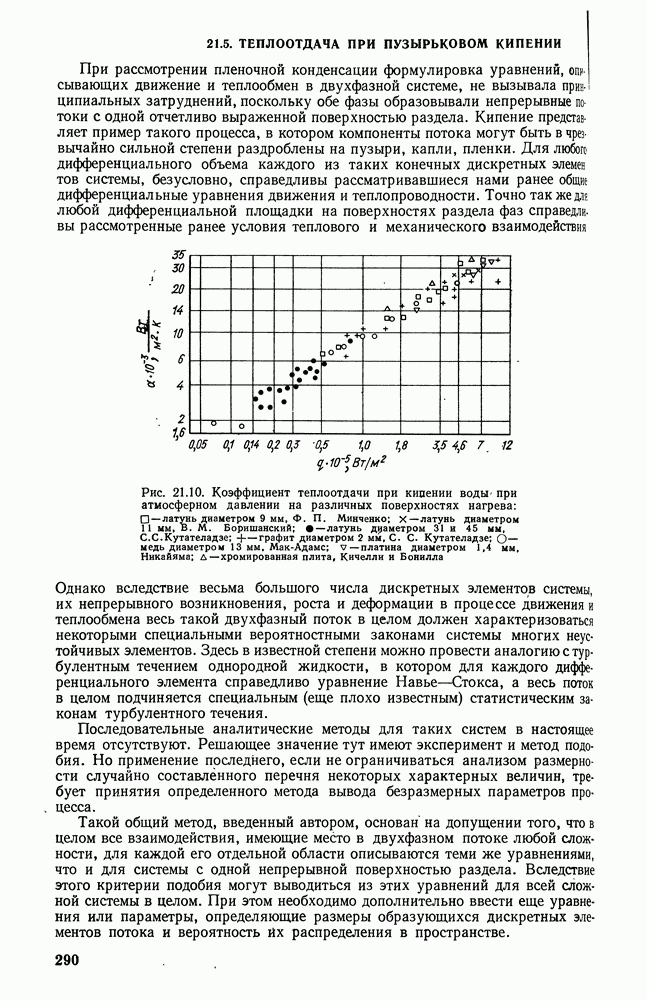
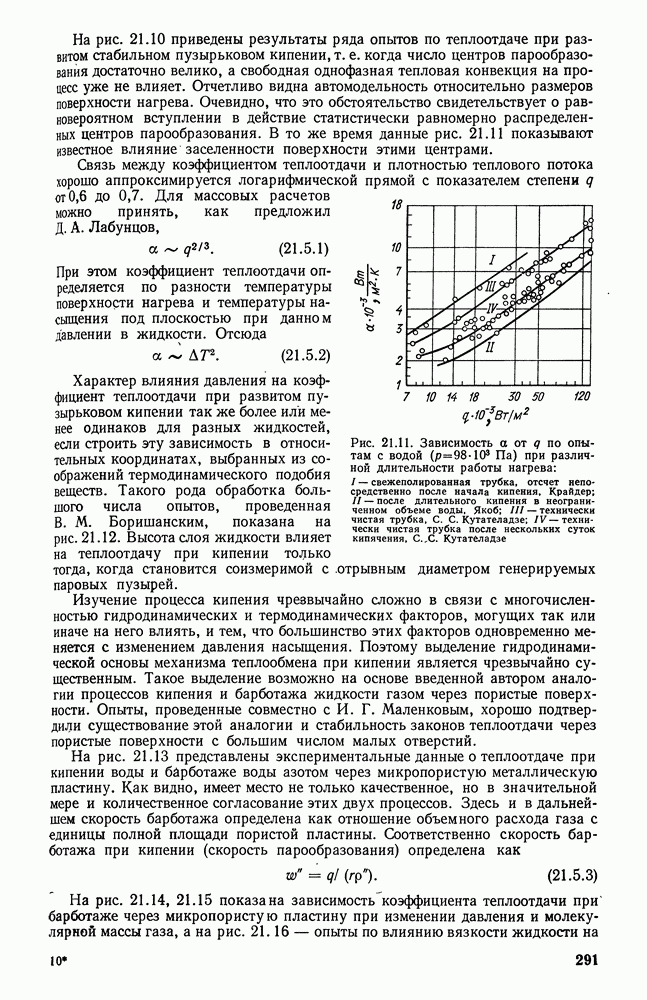
- 21.5. ТЕПЛООТДАЧА ПРИ ПУЗЫРЬКОВОМ КИПЕНИИ
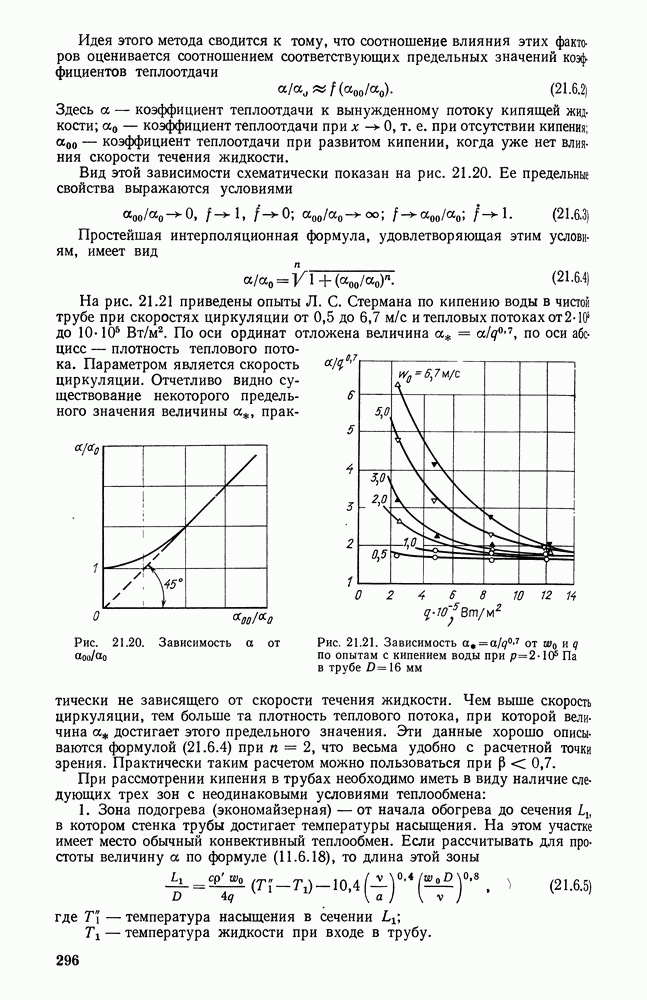
- 21.6. ПУЗЫРЬКОВОЕ КИПЕНИЕ ПРИ ВЫНУЖДЕННОЙ КОНВЕКЦИИ ЖИДКОСТИ
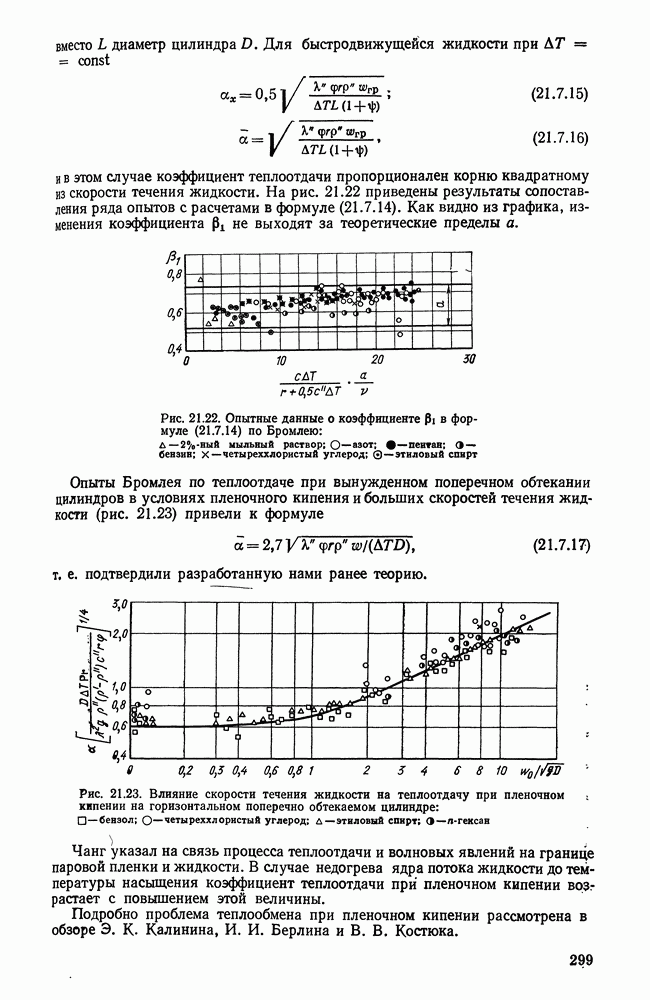
- 21.7. ТЕПЛООТДАЧА ПРИ ПЛЕНОЧНОМ КИПЕНИИ
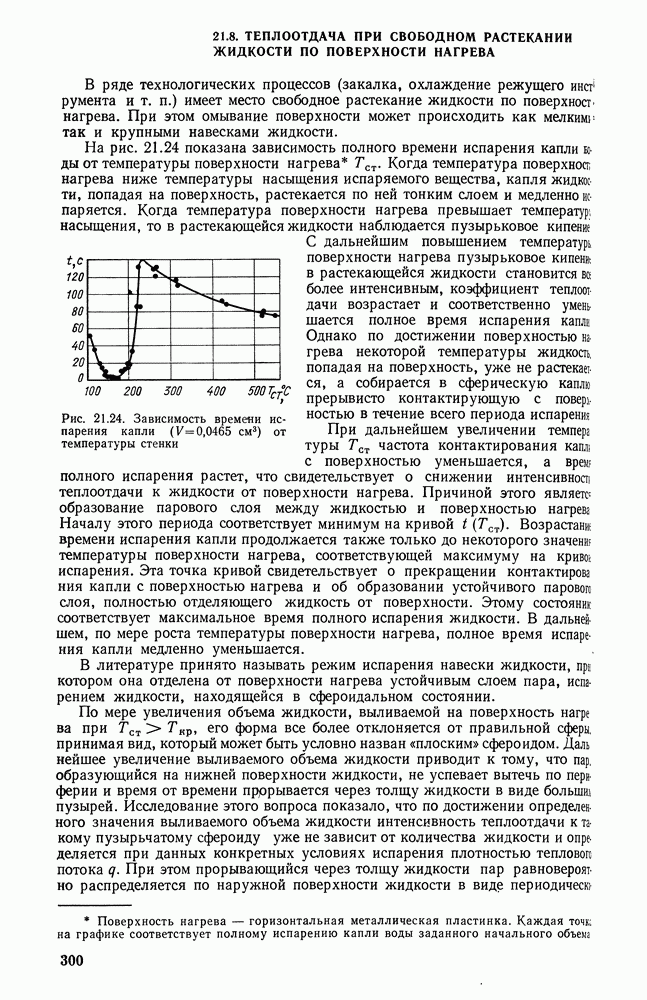
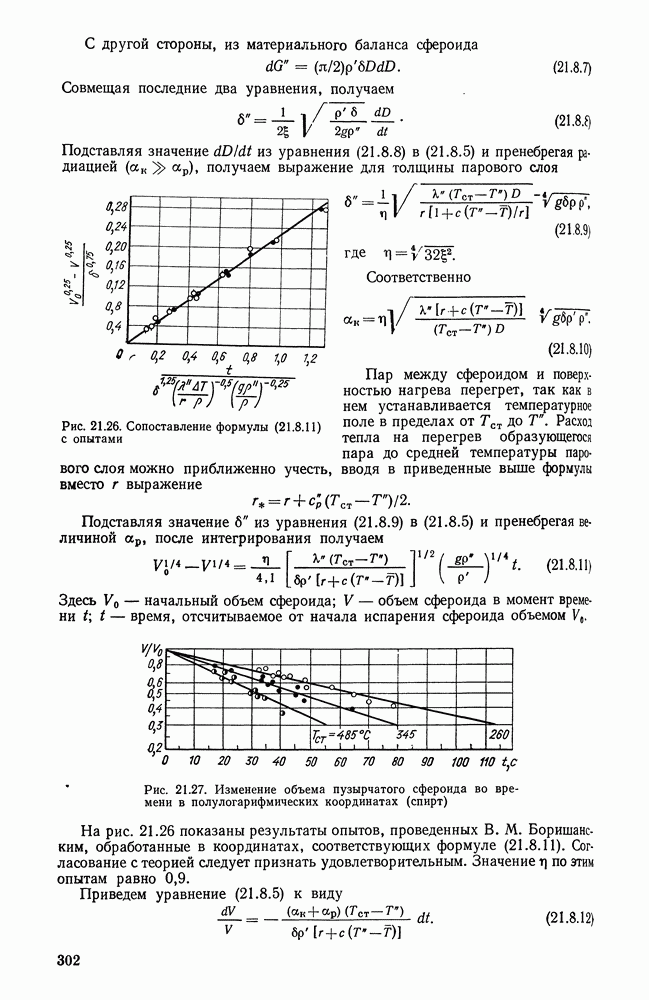
- 21.8. ТЕПЛООТДАЧА ПРИ СВОБОДНОМ РАСТЕКАНИИ ЖИДКОСТИ ПО ПОВЕРХНОСТИ НАГРЕВА
- Глава 22. КРИТИЧЕСКИЕ ПЛОТНОСТИ ТЕПЛОВОГО ПОТОКА, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЯ РЕЖИМА КИПЕНИЯ
- 22.1. ГИДРОДИНАМИЧЕСКАЯ ПРИРОДА КРИЗИСОВ В МЕХАНИЗМЕ КИПЕНИЯ ЖИДКОСТИ
- 22.2. КРИТЕРИЙ УСТОЙЧИВОСТИ ДВУХФАЗНОГО ГРАНИЧНОГО СЛОЯ ПРИ СВОБОДНОЙ КОНВЕКЦИИ В БОЛЬШОМ ОБЪЕМЕ КИПЯЩЕЙ ЖИДКОСТИ (ПЕРВЫЙ КРИЗИС РЕЖИМА КИПЕНИЯ)
- 22.3. ВЛИЯНИЕ РАЗМЕРА И СОСТОЯНИЯ ПОВЕРХНОСТИ НАГРЕВА НА ВЕЛИЧИНУ
- 22.4. ПЕРЕХОД ОТ ПЛЕНОЧНОГО РЕЖИМА КИПЕНИЯ К ПУЗЫРЬКОВОМУ РЕЖИМУ (ВТОРОЙ КРИЗИС РЕЖИМА КИПЕНИЯ)
- 22.5. КРИТЕРИЙ УСТОЙЧИВОСТИ ДВУХФАЗНОГО ГРАНИЧНОГО СЛОЯ ПРИ БОЛЬШИХ СКОРОСТЯХ ТЕЧЕНИЯ ЖИДКОСТИ
- 22.6. ВЛИЯНИЕ НЕДОГРЕВА ЖИДКОСТИ ДО ТЕМПЕРАТУРЫ НАСЫЩЕНИЯ НА КРИТИЧЕСКУЮ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА
- 22.7. КРИТИЧЕСКИЙ ТЕПЛОВОЙ ПОТОК В ОБЛАСТИ УМЕРЕННЫХ СКОРОСТЕЙ ТЕЧЕНИЯ
- 22.8. КРИЗИС КИПЕНИЯ В БИНАРНЫХ СМЕСЯХ
- 22.9. НЕПОСРЕДСТВЕННЫЙ ПЕРЕХОД ОТ ОДНОФАЗНОЙ КОНВЕКЦИИ К ПЛЕНОЧНОМУ КИПЕНИЮ
- 22.10. ВЛИЯНИЕ МЕТАСТАБИЛЬНОСТИ ПРИСТЕННОГО СЛОЯ ЖИДКОСТИ НА ПЕРВУЮ КРИТИЧЕСКУЮ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА
- Глава 23. С ЭЛЕМЕНТЫ МАГНИТНОЙ ТЕРМОГИДРОДИНАМИКИ
- 23.1. ОСНОВНЫЕ УРАВНЕНИЯ
- 23.2. ВЛИЯНИЕ ПЕРПЕНДИКУЛЯРНОГО К ТЕЧЕНИЮ МАГНИТНОГО ПОЛЯ НА ГИДРОДИНАМИКУ И ТЕПЛООБМЕН В ЛАМИНАРНОМ ПОТОКЕ
- 23.3. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ НА ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОГО МЕТАЛЛА В КАНАЛАХ
- 23.4. ЭЛЕМЕНТЫ ТЕРМОГАЗОДИНАМИКИ НИЗКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ
- 23.5. ОБОБЩЕННЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРОДУГОВЫХ ПЛАЗМОТРОНОВ
- Глава 24. НЕУСТАНОВИВШИЙСЯ КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
- 24.1. КРИТЕРИИ ПОДОБИЯ, ХАРАКТЕРИЗУЮЩИЕ КОНВЕКТИВНУЮ НЕСТАЦИОНАРНОСТЬ
- 24.2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ С ПЕРЕМЕННОЙ ТЕМПЕРАТУРОЙ
- 24.3. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ СФЕРИЧЕСКИХ ЧАСТИЦ
- 24.4. НЕСТАЦИОНАРНЫЙ ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ТРУБЕ
- 24.5. ВЛИЯНИЕ ОСЦИЛЛЯЦИЙ
- 24.6. ВЛИЯНИЕ ОСЦИЛЛЯЦИЙ
- Глава 25. ОСНОВНЫЕ ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 25.1. ПРИРОДА ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 25.2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 25.3. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- 25.4. ИЗЛУЧЕНИЕ РЕАЛЬНЫХ ТЕЛ
- 25.5. КЛАССИФИКАЦИЯ ВИДОВ ПОЛУСФЕРИЧЕСКОГО И ОБЪЕМНОГО ИЗЛУЧЕНИЙ
- 25.6. ГЕОМЕТРИЯ ИЗЛУЧЕНИЯ. ГЕОМЕТРИЧЕСКИЕ ИНВАРИАНТЫ ИЗЛУЧЕНИЯ
- 25.7. ОБЩИЕ СВОЙСТВА ПОТОКОВ ИЗЛУЧЕНИЯ
- 25.8. АЛГЕБРАИЧЕСКИЙ МЕТОД РАСЧЕТА ИНТЕГРАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ИНВАРИАНТОВ ИЗЛУЧЕНИЯ
- Глава 26. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ПРОЗРАЧНЫХ И ПОГЛОЩАЮЩИХ СРЕДАХ
- 26.1. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ СИСТЕМЫ ТЕЛ, РАЗДЕЛЕННЫХ ПРОЗРАЧНОЙ СРЕДОЙ
- 26.2. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ ДИСКРЕТНОЙ СИСТЕМЫ ТЕЛ В ПРОЗРАЧНОЙ СРЕДЕ (ЗОНАЛЬНЫЙ МЕТОД)
- 26.3. ПРИЛОЖЕНИЕ ЗОНАЛЬНОГО МЕТОДА К РАСЧЕТУ ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ МЕЖДУ НЕСКОЛЬКИМИ СЕРЫМИ ТЕЛАМИ
- 26.4. ДЕЙСТВИЕ ЭКРАНОВ
- 26.5. УРАВНЕНИЕ ПЕРЕНОСА ЭНЕРГИИ ИЗЛУЧЕНИЯ В ПОГЛОЩАЮЩЕЙ СРЕДЕ
- 26.6. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ИЗЛУЧЕНИЯ В ПОГЛОЩАЮЩЕЙ СРЕДЕ
- 26.7. ОПТИЧЕСКИЕ СВОЙСТВА ПОГЛОЩАЮЩИХ СРЕД
- 26.8. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ ДИСКРЕТНОИ СИСТЕМЫ ТЕЛ В ПОГЛОЩАЮЩЕЙ СРЕДЕ (ЗОНАЛЬНЫЙ МЕТОД)
- 26.9. ПЕРЕНОС ИЗЛУЧЕНИЯ В ПЛОСКОМ СЛОЕ ПОГЛОЩАЮЩЕЙ СРЕДЫ
- 26.10. КОМБИНИРОВАННЫЙ РАДИАЦИОННЫЙ ТЕПЛООБМЕН
- 26.11. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ В ТОПОЧНЫХ УСТРОЙСТВАХ