| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Простота кососимметричных тензоров
В заключении данного параграфа укажем один полезный результат для антисимметричных тензоров в произвольном  -мерном векторном пространстве
-мерном векторном пространстве  который устанавливает свойства, аналогичные свойствам симметричных объектов.
который устанавливает свойства, аналогичные свойствам симметричных объектов.
Предложение

(Тензор  представимый в виде такого кососимметричного произведения векторов, называется простым.) Необходимость этого условия показывается непосредственно: достаточно выразить второй множитель
представимый в виде такого кососимметричного произведения векторов, называется простым.) Необходимость этого условия показывается непосредственно: достаточно выразить второй множитель  через
через  а затем учесть, что каждое слагаемое в сумме должно обращаться в нуль вследствие равенства
а затем учесть, что каждое слагаемое в сумме должно обращаться в нуль вследствие равенства  Чтобы установить достаточность, заметим, во-первых, что указанное условие можно переписать в виде
Чтобы установить достаточность, заметим, во-первых, что указанное условие можно переписать в виде

В справедливости этого соотношения легко убедиться, выполнив антисимметризацию в первоначальном выражении явно и отделив слагаемые, в которых индекс в содержится в первом сомножителе  Свертка обеих частей равенства (3.5.31) с
Свертка обеих частей равенства (3.5.31) с  приводит к обращению в нуль левой его части, откуда следует, что
приводит к обращению в нуль левой его части, откуда следует, что  -индексный тензор
-индексный тензор

удовлетворяет тому же условию, что и сам тензор  Теперь предположим, что достаточность условия (3.5.30) для
Теперь предположим, что достаточность условия (3.5.30) для  -индексных тензоров уже доказана (в случае
-индексных тензоров уже доказана (в случае  доказательство тривиально); тогда мы заключаем, что это справедливо и для
доказательство тривиально); тогда мы заключаем, что это справедливо и для  -индексных тензоров. Таким образом, по предположению, при
-индексных тензоров. Таким образом, по предположению, при  имеем
имеем

для некоторых  Теперь выберем и
Теперь выберем и  так, чтобы выполнялось условие
так, чтобы выполнялось условие

и свернем обе части равенства (3.5.31) с  Это дает требуемое соотношение
Это дает требуемое соотношение

где

Таким образом, мы получаем доказательство по индукции.
Легко видеть, что условие, сформулированное в предложении (3.5.30), эквивалентно равенству

где тензор  (который имеет
(который имеет  индексов, если тензор
индексов, если тензор  имел
имел  индексов) определяется так же, как в (3.4.30) и (3.4.21), соотношением
индексов) определяется так же, как в (3.4.30) и (3.4.21), соотношением

[В  -мерном пространстве «альтернируюший> тензор
-мерном пространстве «альтернируюший> тензор  имеет
имеет  индексов, отличен от нуля и кососимметричен, см. формулу (2.3.4).] Поскольку равенство (3.5.32) симметрично относительно
индексов, отличен от нуля и кососимметричен, см. формулу (2.3.4).] Поскольку равенство (3.5.32) симметрично относительно  и
и  (с точностью до несущественного расположения индексов), мы имеем следующее предложение:
(с точностью до несущественного расположения индексов), мы имеем следующее предложение:
Предложение
Тензор  является простым при том и только при том условии, что простым является дуальный ему тензор
является простым при том и только при том условии, что простым является дуальный ему тензор 
Соотношения (3.5.30) — (3.5.34) справедливы в пространстве  измерений для кососимметричиых тензоров с произвольным числом индексов
измерений для кососимметричиых тензоров с произвольным числом индексов  Но для нас особенно важным будет случай бивектора
Но для нас особенно важным будет случай бивектора  в четырехмерном пространстве. В этом случае можно сформулировать дополнительные критерии простоты.
в четырехмерном пространстве. В этом случае можно сформулировать дополнительные критерии простоты.
Предложение
В четырехмерном пространстве бивектор  будет простым тогда и только тогда, когда выполняется одно из следующих условий:
будет простым тогда и только тогда, когда выполняется одно из следующих условий:

Доказательство. Легко видеть, что

для некоторого скаляра  и антисимметричного единичного тензора
и антисимметричного единичного тензора  Первое из этих тождеств совместно с предложением (3.5.30) позволяет доказать утверждение I. Сворачивая второе тождество в (3.5.36) с
Первое из этих тождеств совместно с предложением (3.5.30) позволяет доказать утверждение I. Сворачивая второе тождество в (3.5.36) с  при
при  , мы получаем условие II. Его можно проверить и непосредственно, переходя к специальной системе координат. Последнее условие III получается с помощью хорошо известной теоремы, утверждающей, что определитель кососимметричной матрицы есть полный квадрат. Действительно, в нашем случае
, мы получаем условие II. Его можно проверить и непосредственно, переходя к специальной системе координат. Последнее условие III получается с помощью хорошо известной теоремы, утверждающей, что определитель кососимметричной матрицы есть полный квадрат. Действительно, в нашем случае

Следовательно, условие III эквивалентно условию II, чем и завершается доказательство нашего предложения.
Отметим, что предложение (3.5.30) справедливо только для тензоров в фиксированной точке пространства и нарушается в случае тензорных полей. Замечательно простым примером может служить бивектор в евклидовом пространстве, который в декартовой системе координат  имеет компоненты.
имеет компоненты.

Он дуален радиус-вектору  и является простым в каждой точке в силу предложения (3.5.34), поскольку объект
и является простым в каждой точке в силу предложения (3.5.34), поскольку объект  очевидно, прост. Но из равенства (3.5.32) следует, что
очевидно, прост. Но из равенства (3.5.32) следует, что  . Тогда из
. Тогда из  следовало бы, что
следовало бы, что  т. е. векторы
т. е. векторы  должны быть ортогональны вектору
должны быть ортогональны вектору  Это означает, что на сфере постоянного радиуса
Это означает, что на сфере постоянного радиуса  задают нигде не обращающиеся в нуль касательные векторные поля. Но из топологии (теорема о «неподвижной точке») мы знаем, что такие поля не существуют. Отсюда явствует, что теорема нарушается даже в произвольно малой окрестности начала координат.
задают нигде не обращающиеся в нуль касательные векторные поля. Но из топологии (теорема о «неподвижной точке») мы знаем, что такие поля не существуют. Отсюда явствует, что теорема нарушается даже в произвольно малой окрестности начала координат.
Следует помнить, что и все другие результаты, перечисленные в данном параграфе, могут нарушаться при переходе от тензоров в точке к тензорным полям.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие переводчиков
- Введение
- 1. Геометрия мировых векторов и спин-векторов
- § 1. Векторное пространство Минковского
- § 2. Изотропные направления и спиновые преобразования
- Преобразования Лоренца и спиновые преобразования
- Связь с кватернионами
- § 3. Некоторые свойства преобразований Лоренца
- Частные случаи преобразования Лоренца, выделенные по характеру его действия на S+
- Двойные отношения изотропных направлений
- § 4. Изотропные флаги и спин-векторы
- Спин-вектор
- § 5. Спинорные объекты и спиновая структура
- Универсальные накрывающие пространства
- Определение спин-вектора
- Спинорная структура
- Спинорная структура для некомпактных моделей пространства-времени
- § 6. Геометрическая интерпретация спинорных операций
- Геометрический смысл внутреннего произведения
- Геометрическая интерпретация сложения
- 2. Метод абстрактных индексов и спинорная алгебра
- Классическая тензорная алгебра
- Бескоординатная тензорная алгебра
- § 2. Формализм абстрактных индексов и тензорная алгебра
- Аксиоматический подход
- Тензоры
- Тензорные операции
- Некоторые полезные свойства вполне рефлексивных модулей
- Включение одной тензорной системы в другую
- § 3. Базисы
- Компоненты в базисе
- § 4. Свойство модуля … быть вполне рефлексивным на многообразии
- § 5. Спинорная алгебра
- e-спиноры
- Комплексное сопряжение
- Спинорные базисы
- 3. Спиноры и мировые тензоры
- § 1. Мировые тензоры как спиноры
- Спиновые системы отсчета и связанные с ними тетрады
- Символы Инфельда — ван дер Вердена
- § 2. Изотропные флаги и комплексные изотропные векторы
- Свойства комплексных изотропных векторов
- Эрмитово-изотропные векторы
- § 3. Операции симметризации и антисимметризации
- Конкретные результаты для спиноров и мировых тензоров
- Разложение на симметричные спиноры
- Неприводимость
- § 4. Тензорное представление спинорных операций
- Дуальное преобразование
- Общий метод перехода к тензорам
- § 5. Простые свойства тензоров и спиноров в точке
- Главные изотропные направления
- Простота кососимметричных тензоров
- § 6. Преобразования Лоренца
- Несобственные преобразования
- Собственные преобразования
- Инфинитезимальные преобразования
- 4. Дифференцирование и кривизна
- Векторные поля
- Действительные и комплексные тензоры
- Градиент скаляра
- § 2. Ковариантная производная
- Кручение и кривизна
- Вариация оператора производной
- Производная по координатам
- § 3. Производные, не зависящие от связности
- Скобки Ли и производные Ли
- Риманова геометрия
- § 4. Дифференцирование спиноров
- Единственность
- Конструкции, основанные на производной Кристоффеля
- Тензорная запись спинорных дифференциальных уравнений
- § 5. Дифференцирование спинорных компонент
- Выражения для спиновых коэффициентов
- Связь между символами Инфельоа — ван дер Вердена и символами Кристоффеля
- § 6. Спиноры кривизны
- Уравнения Эйнштейна
- § 7. Спинорная формулировка теории Эйнштейна — Картана—Шьямы—Киббла
- § 8. Тензор Вейля и тензор Беля — Робинсона
- § 9. Спинорное представление коммутаторов
- § 10. Спинорная форма тождеств Бианки
- § 11. Спиноры кривизны и спиновые коэффициенты
- § 12. Модифицированный формализм спиновых коэффициентов
- Взвешенные скаляры
- Взвешенные дифференциальные операторы.
- Модифицированные уравнения
- § 13. Метод Картана
- Связь со спиновыми коэффициентами
- § 14. Приложение к двумерным поверхностям
- Голоморфные координаты
- Внешние величины
- Связь с внешним исчислением
- Об изотропной гиперповерхности
- § 15. Сферические гармоники со спиновым весом
- Конформные движения поверхности
- Вращения поверхности
- Уравнения, линейные по «дальта»
- Конформные свойства гармоник
- Ортогональность гармоник
- Ортонормированный базис для спиновых функций
- Явные координатные представления
- 5. Поля в пространстве-времени
- § 1. Электромагнитное поле и обобщенный оператор производной
- Заряженные поля
- Электромагнитный потенциал
- Максвелловский тензор поля
- Спинор электромагнитного поля
- Связь с 3-векторами электрического и магнитного полей
- § 2. Уравнения Эйнштейна — Максвелла в спинорной форме
- Свойства положительной определенности максвелловского тензора энергии-импульса
- § 3. Условия Райнича
- Дифференциальное условие Райнича
- § 4. Векторные расслоения
- Определение векторных расслоений
- Явное построение расслоений
- Связности в расслоенных пространствах
- § 5. Поля Янга — Миллса
- Потенциал Янга — Миллса и метрика
- Тензор поля Янга — Миллса
- Спинорная трактовка
- § 6. Конформные изменения масштаба
- Конформные плотности
- Поведение спиновых коэффициентов при конформном изменении масштаба
- Конформно-инвариантные операторы
- § 7. Безмассовые поля
- Конформная инвариантность
- § 8. Условия совместности
- Тензор энергии-импульса
- Совместные системы полей с высшими спинами
- § 9. Конформная инвариантность различных полевых величин
- § 10. Точные системы полей
- Свободные безмассовые поля
- Электромагнитные источники
- Гравитация
- Поля Эйнштейна — Максвелла
- Другие примеры
- § 11. Начальные данные на световом конусе
- «Ряд Тейлора» на световом конусе
- Подсчет степеней свободы
- Регулярность в точке О
- Геометрия светового конуса
- § 12. Явные полевые интегралы
- Доказательство основной формулы
- Конформно-плоское пространство-время
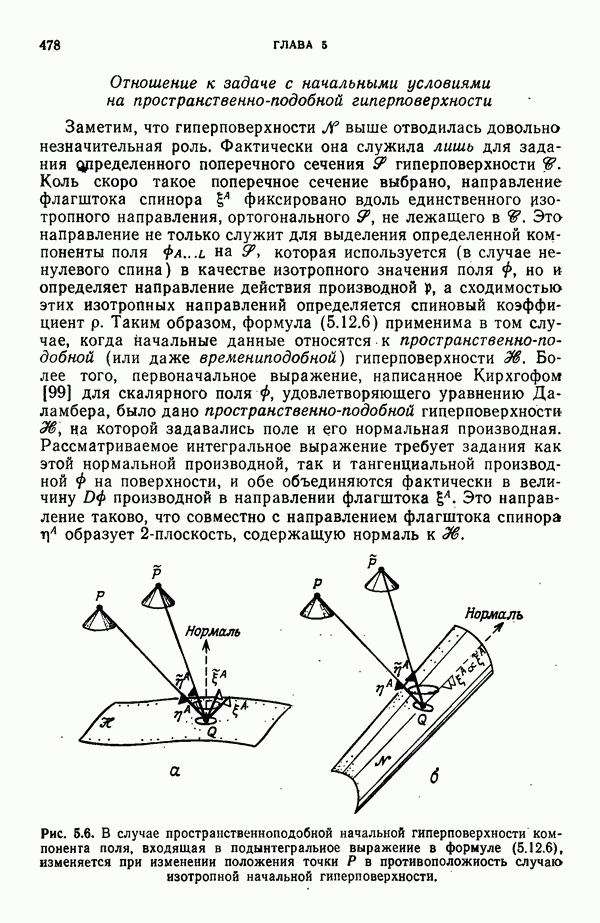
- Отношение к задаче с начальными условиями на пространственно-подобной гиперповерхности
- Фоновые поля
- Поля, соответствующие произвольным изотропным данным
- Поля в смысле обобщенных функций
- Поле Дирака
- Уравнения Максвелла — Дирака
- Приложение. Диаграммная система записи
- Литература