| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Дифференцирование спиноров
Теперь мы применим результаты, полученные в § 1—3, в том случае, когда  есть четырехмерное пространство-время, а также расширим определение ковариантной производной так, чтобы этот оператор действовал на спинорные поля. Мы обнаружим, что производная Кристоффеля, введенная в § 3, канонически продолжается на спинорные поля. Это и неудивительно, поскольку спиноры допускают естественную геометрическую трактовку на основе тензорных объектов (с точностью до знака, но эта неоднозначность не приводит к каким-либо трудностям при изучении дифференциальных свойств). Однако мы стремимся рассматривать спиноры как величины, более фундаментальные, чем мировые тензоры. В гл. 3, § 1 мы показали, каким образом мировые тензоры можно рассматривать как специальные случаи спиноров. При таком подходе нам потребуется также отождествить мировые векторы с касательными векторами к пространству-времени
есть четырехмерное пространство-время, а также расширим определение ковариантной производной так, чтобы этот оператор действовал на спинорные поля. Мы обнаружим, что производная Кристоффеля, введенная в § 3, канонически продолжается на спинорные поля. Это и неудивительно, поскольку спиноры допускают естественную геометрическую трактовку на основе тензорных объектов (с точностью до знака, но эта неоднозначность не приводит к каким-либо трудностям при изучении дифференциальных свойств). Однако мы стремимся рассматривать спиноры как величины, более фундаментальные, чем мировые тензоры. В гл. 3, § 1 мы показали, каким образом мировые тензоры можно рассматривать как специальные случаи спиноров. При таком подходе нам потребуется также отождествить мировые векторы с касательными векторами к пространству-времени  Следовательно, поля мировых векторов нужно отождествить с дифференцированиями на алгебре
Следовательно, поля мировых векторов нужно отождествить с дифференцированиями на алгебре  гладких
гладких  -действительных скалярных полей на
-действительных скалярных полей на  Здесь мы рискуем впасть в логический круг, поскольку поля мировых
Здесь мы рискуем впасть в логический круг, поскольку поля мировых  векторов строятся двумя разными способами. Но мы избежим
векторов строятся двумя разными способами. Но мы избежим
логических противоречий, положив, что пространство  полей мировых векторов
полей мировых векторов  есть пространство дифференцирований на алгебре
есть пространство дифференцирований на алгебре  , тогда как всякое пространство
, тогда как всякое пространство  содержащее элементы
содержащее элементы  или
или  должно отождествляться с
должно отождествляться с  в соответствии со сказанным в гл. 3, § 1.
в соответствии со сказанным в гл. 3, § 1.
В гл. 3, § 1 отмечалось, что существует два логически различающихся подхода к спинорной алгебре на  конструктивный и аксиоматический. Мы следовали конструктивному подходу в гл. 1. Четырехмерное пространство-время
конструктивный и аксиоматический. Мы следовали конструктивному подходу в гл. 1. Четырехмерное пространство-время  считалось заданным. На нем фиксирована сигнатура
считалось заданным. На нем фиксирована сигнатура  гладкая метрика, и предполагается, что многообразие в целом обладает следующими тремя свойствами: ориентируемостью во времени (1.5.1), ориентируемостью (1.5.2) и наличием спиновой структуры (1.5.3). Тогда спин-векторы можно определить геометрически (с точностью до несущественного общего знака пространства
гладкая метрика, и предполагается, что многообразие в целом обладает следующими тремя свойствами: ориентируемостью во времени (1.5.1), ориентируемостью (1.5.2) и наличием спиновой структуры (1.5.3). Тогда спин-векторы можно определить геометрически (с точностью до несущественного общего знака пространства  если
если  односвязно; если же оно многосвязно, то определение спин-векторов может содержать глобальные неоднозначности, зависящие от ряда дискретных параметров, см. гл. 1, § 5). Чтобы охарактеризовать элементы базисного модуля
односвязно; если же оно многосвязно, то определение спин-векторов может содержать глобальные неоднозначности, зависящие от ряда дискретных параметров, см. гл. 1, § 5). Чтобы охарактеризовать элементы базисного модуля  нам потребуется понятие
нам потребуется понятие  -гладкости для спин-векторного поля. Существует несколько эквивалентных способов дать такую локальную характеристику. Например, в односвязной окрестности всякой данной точки многообразия
-гладкости для спин-векторного поля. Существует несколько эквивалентных способов дать такую локальную характеристику. Например, в односвязной окрестности всякой данной точки многообразия  можно выбрать
можно выбрать  -систему ограниченных ортонормированных тетрад касательных векторов. В этом базисе спин-вектор
-систему ограниченных ортонормированных тетрад касательных векторов. В этом базисе спин-вектор  характеризуется своими компонентами
характеризуется своими компонентами  (см. гл. 1). Затем мы потребуем, чтобы
(см. гл. 1). Затем мы потребуем, чтобы  были гладкими функциями класса
были гладкими функциями класса  во всякой такой окрестности, т. е. чтобы они были локальными комплексными скалярными полями. В то же время во всякой такой окрестности можно использовать спинорный базис
во всякой такой окрестности, т. е. чтобы они были локальными комплексными скалярными полями. В то же время во всякой такой окрестности можно использовать спинорный базис  , определенный с помощью поля тетрад (знаки фиксируются по непрерывности), и постулировать, что они принадлежат классу С, так что
, определенный с помощью поля тетрад (знаки фиксируются по непрерывности), и постулировать, что они принадлежат классу С, так что  принадлежит классу
принадлежит классу  в той же окрестности, если только
в той же окрестности, если только  принадлежат этому классу. Понятие
принадлежат этому классу. Понятие  -гладкости, очевидно, не зависит от специального выбора ортонормированной тетрады; следовательно, оно характеризует геометрические величины, образующие
-гладкости, очевидно, не зависит от специального выбора ортонормированной тетрады; следовательно, оно характеризует геометрические величины, образующие  Определив таким образом базисный модуль
Определив таким образом базисный модуль  который, очевидно, будет модулем над кольцом
который, очевидно, будет модулем над кольцом  -комплексных скалярных полей
-комплексных скалярных полей  вполне рефлексивным в силу сказанного в гл. 2, § 4, мы строим
вполне рефлексивным в силу сказанного в гл. 2, § 4, мы строим  как в гл. 2, § 5. Элементы множества
как в гл. 2, § 5. Элементы множества  по определению есть действительные элементы множества
по определению есть действительные элементы множества  очевидно, что они находятся во взаимнооднозначном соответствии с касательными векторами
очевидно, что они находятся во взаимнооднозначном соответствии с касательными векторами  поскольку установлено локальное соответствие между тетрадой касательных векторов и спинорным базисом.
поскольку установлено локальное соответствие между тетрадой касательных векторов и спинорным базисом.
Можно также встать на аксиоматическую точку зрения. Тогда мы просто постулируем алгебраические требования к спинорной системе. Пространственно-временная структура, т. е. метрика, сигнатура, топологические требования, должна выводиться из этого набора постулатов. Конструктивный подход можно рассматривать как оправдание аксиом, выбранных для спинорной системы, поскольку они должны выполняться в любом пространстве-времени, в котором допустим конструктивный подход. В то же время существование спинорной алгебры можно рассматривать как более «глубокую» причину возникающей пространственно-временной структуры. Именно этому подходу мы будем в основном следовать. Таким образом, мы постулируем существование спинорной алгебры, следуя изложенному в гл. 2, § 5, а затем требуем, чтобы структуры  были изоморфны соответственно скалярным полям
были изоморфны соответственно скалярным полям  и их дифференцированиям на М, определенным в соответствии с аксиомами § 1.
и их дифференцированиям на М, определенным в соответствии с аксиомами § 1.
Требуемый изоморфизм между  сопоставляет каждому дифференцированию
сопоставляет каждому дифференцированию  единственный элемент
единственный элемент  и наоборот. (С учетом такого канонического изоморфизма не будет ошибкой называть
и наоборот. (С учетом такого канонического изоморфизма не будет ошибкой называть  также полями мировых векторов на
также полями мировых векторов на  .) Мы используем символ
.) Мы используем символ  (или, что эквивалентно,
(или, что эквивалентно,  для обозначения этого изоморфизма, т. е. отображение
для обозначения этого изоморфизма, т. е. отображение  будет зайисываться в виде
будет зайисываться в виде

Эти операторы действуют на действительные скаляры; следовательно,  есть отображение из в
есть отображение из в  . Можно расширить область определения этого оператора, включив в нее комплексные скаляры
. Можно расширить область определения этого оператора, включив в нее комплексные скаляры  что приводит к отображению из
что приводит к отображению из 

Далее можно определить

Следовательно, для любого данного  мы имеем отображение из
мы имеем отображение из  определенное как
определенное как  Очевидно, что оно
Очевидно, что оно  -линейно; стало быть, для
-линейно; стало быть, для  мы имеем элемент
мы имеем элемент

Из (4.4.2) и (4.4.3) следует, что  откуда
откуда

В частности, если  то
то  . Используя свойства дифференцирования, можно показать, что
. Используя свойства дифференцирования, можно показать, что

где 
Далее, мы желаем расширить определение оператора  задавая его действие на произвольный спинор. Мы будем следовать изложенному в § 2. Оператор спинорной ковариантной производной мы определяем как отображение
задавая его действие на произвольный спинор. Мы будем следовать изложенному в § 2. Оператор спинорной ковариантной производной мы определяем как отображение

удовлетворяющее требованиям

для всех  определение оператора
определение оператора  дано выше. Разумеется, мы можем написать
дано выше. Разумеется, мы можем написать  вместо
вместо  и использовать подстановку индексов, например
и использовать подстановку индексов, например 
Такую возможность мы будем всегда подразумевать. [Однако следует помнить, что  есть не подстановка индексов в
есть не подстановка индексов в  а
а  -свертка, а именно см. замечания после формулы (3.1.37).]
-свертка, а именно см. замечания после формулы (3.1.37).]
Мы расширим  до отображения из
до отображения из  потребовав, чтобы производная свертки
потребовав, чтобы производная свертки  удовлетворяла правилу Лейбница
удовлетворяла правилу Лейбница

Левая часть этого равенства определяет  как отображение из
как отображение из  в силу формул (4.4.6), (4.4.8) и (4.4.9); очевидно, что оно
в силу формул (4.4.6), (4.4.8) и (4.4.9); очевидно, что оно  -линейно. С учетом (4.4.6) нетрудно убедиться, что соотношения
-линейно. С учетом (4.4.6) нетрудно убедиться, что соотношения

имеют место для всех  Определим действие
Определим действие  на
на  и на
и на  с помощью отображений из
с помощью отображений из  а также из
а также из  соответственно, как комплексное сопряжение:
соответственно, как комплексное сопряжение:

Из выражения, комплексно-сопряженного выражению (4.4.10), и формулц  непосредственно следует, что правило
непосредственно следует, что правило
Лейбница также применимо к свертке  Более того, очевидно, что в силу формул (4.4.8), (4.4.9), (4.4.11) — (4.4.13) для
Более того, очевидно, что в силу формул (4.4.8), (4.4.9), (4.4.11) — (4.4.13) для  имеют место линейность и правило Лейбница.
имеют место линейность и правило Лейбница.
Теперь мы в состоянии определить действие  на спинор общего вида
на спинор общего вида  Как и в соотношении (4.2.8), мы просто требуем, чтобы правило Лейбница имело место для сверток вида
Как и в соотношении (4.2.8), мы просто требуем, чтобы правило Лейбница имело место для сверток вида  тогда соотношением
тогда соотношением

 определяется как
определяется как  -мультилинейное отображение из
-мультилинейное отображение из  в Таким образом, для всякого множества спиноров
в Таким образом, для всякого множества спиноров  оператор
оператор  определяет отображение
определяет отображение

Аналогично соотношениям (4.2.10) — (4.2.13) выполняются равенства

Оператор  обладает также свойством
обладает также свойством
(см. скан)
Далее,  коммутирует со сверткой (не содержащей А или А)
коммутирует со сверткой (не содержащей А или А)

Из (4.4.13) следует, что  коммутирует с операцией комплексного сопряжения:
коммутирует с операцией комплексного сопряжения: 

Формально это означает, что  — действительный оператор:
— действительный оператор: 
В частном случае действительных мировых векторов  оператором
оператором  определяется тензор ковариантной производной
определяется тензор ковариантной производной  удовлетворяющий условию
удовлетворяющий условию  в согласии с формулами (4.2.2) и (4.2.3). Обобщение такого
в согласии с формулами (4.2.2) и (4.2.3). Обобщение такого  на случай
на случай 
ствительных мировых тензоров, очевидно, согласуется с определением, данным выше, поскольку требования (4.2.10) — (4.2.13), которыми оно определяется однозначно, удовлетворяются в силу свойств (4.4.16) — (4.4.20).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчиков
- Введение
- 1. Геометрия мировых векторов и спин-векторов
- § 1. Векторное пространство Минковского
- § 2. Изотропные направления и спиновые преобразования
- Преобразования Лоренца и спиновые преобразования
- Связь с кватернионами
- § 3. Некоторые свойства преобразований Лоренца
- Частные случаи преобразования Лоренца, выделенные по характеру его действия на S+
- Двойные отношения изотропных направлений
- § 4. Изотропные флаги и спин-векторы
- Спин-вектор
- § 5. Спинорные объекты и спиновая структура
- Универсальные накрывающие пространства
- Определение спин-вектора
- Спинорная структура
- Спинорная структура для некомпактных моделей пространства-времени
- § 6. Геометрическая интерпретация спинорных операций
- Геометрический смысл внутреннего произведения
- Геометрическая интерпретация сложения
- 2. Метод абстрактных индексов и спинорная алгебра
- Классическая тензорная алгебра
- Бескоординатная тензорная алгебра
- § 2. Формализм абстрактных индексов и тензорная алгебра
- Аксиоматический подход
- Тензоры
- Тензорные операции
- Некоторые полезные свойства вполне рефлексивных модулей
- Включение одной тензорной системы в другую
- § 3. Базисы
- Компоненты в базисе
- § 4. Свойство модуля … быть вполне рефлексивным на многообразии
- § 5. Спинорная алгебра
- e-спиноры
- Комплексное сопряжение
- Спинорные базисы
- 3. Спиноры и мировые тензоры
- § 1. Мировые тензоры как спиноры
- Спиновые системы отсчета и связанные с ними тетрады
- Символы Инфельда — ван дер Вердена
- § 2. Изотропные флаги и комплексные изотропные векторы
- Свойства комплексных изотропных векторов
- Эрмитово-изотропные векторы
- § 3. Операции симметризации и антисимметризации
- Конкретные результаты для спиноров и мировых тензоров
- Разложение на симметричные спиноры
- Неприводимость
- § 4. Тензорное представление спинорных операций
- Дуальное преобразование
- Общий метод перехода к тензорам
- § 5. Простые свойства тензоров и спиноров в точке
- Главные изотропные направления
- Простота кососимметричных тензоров
- § 6. Преобразования Лоренца
- Несобственные преобразования
- Собственные преобразования
- Инфинитезимальные преобразования
- 4. Дифференцирование и кривизна
- Векторные поля
- Действительные и комплексные тензоры
- Градиент скаляра
- § 2. Ковариантная производная
- Кручение и кривизна
- Вариация оператора производной
- Производная по координатам
- § 3. Производные, не зависящие от связности
- Скобки Ли и производные Ли
- Риманова геометрия
- § 4. Дифференцирование спиноров
- Единственность
- Конструкции, основанные на производной Кристоффеля
- Тензорная запись спинорных дифференциальных уравнений
- § 5. Дифференцирование спинорных компонент
- Выражения для спиновых коэффициентов
- Связь между символами Инфельоа — ван дер Вердена и символами Кристоффеля
- § 6. Спиноры кривизны
- Уравнения Эйнштейна
- § 7. Спинорная формулировка теории Эйнштейна — Картана—Шьямы—Киббла
- § 8. Тензор Вейля и тензор Беля — Робинсона
- § 9. Спинорное представление коммутаторов
- § 10. Спинорная форма тождеств Бианки
- § 11. Спиноры кривизны и спиновые коэффициенты
- § 12. Модифицированный формализм спиновых коэффициентов
- Взвешенные скаляры
- Взвешенные дифференциальные операторы.
- Модифицированные уравнения
- § 13. Метод Картана
- Связь со спиновыми коэффициентами
- § 14. Приложение к двумерным поверхностям
- Голоморфные координаты
- Внешние величины
- Связь с внешним исчислением
- Об изотропной гиперповерхности
- § 15. Сферические гармоники со спиновым весом
- Конформные движения поверхности
- Вращения поверхности
- Уравнения, линейные по «дальта»
- Конформные свойства гармоник
- Ортогональность гармоник
- Ортонормированный базис для спиновых функций
- Явные координатные представления
- 5. Поля в пространстве-времени
- § 1. Электромагнитное поле и обобщенный оператор производной
- Заряженные поля
- Электромагнитный потенциал
- Максвелловский тензор поля
- Спинор электромагнитного поля
- Связь с 3-векторами электрического и магнитного полей
- § 2. Уравнения Эйнштейна — Максвелла в спинорной форме
- Свойства положительной определенности максвелловского тензора энергии-импульса
- § 3. Условия Райнича
- Дифференциальное условие Райнича
- § 4. Векторные расслоения
- Определение векторных расслоений
- Явное построение расслоений
- Связности в расслоенных пространствах
- § 5. Поля Янга — Миллса
- Потенциал Янга — Миллса и метрика
- Тензор поля Янга — Миллса
- Спинорная трактовка
- § 6. Конформные изменения масштаба
- Конформные плотности
- Поведение спиновых коэффициентов при конформном изменении масштаба
- Конформно-инвариантные операторы
- § 7. Безмассовые поля
- Конформная инвариантность
- § 8. Условия совместности
- Тензор энергии-импульса
- Совместные системы полей с высшими спинами
- § 9. Конформная инвариантность различных полевых величин
- § 10. Точные системы полей
- Свободные безмассовые поля
- Электромагнитные источники
- Гравитация
- Поля Эйнштейна — Максвелла
- Другие примеры
- § 11. Начальные данные на световом конусе
- «Ряд Тейлора» на световом конусе
- Подсчет степеней свободы
- Регулярность в точке О
- Геометрия светового конуса
- § 12. Явные полевые интегралы
- Доказательство основной формулы
- Конформно-плоское пространство-время
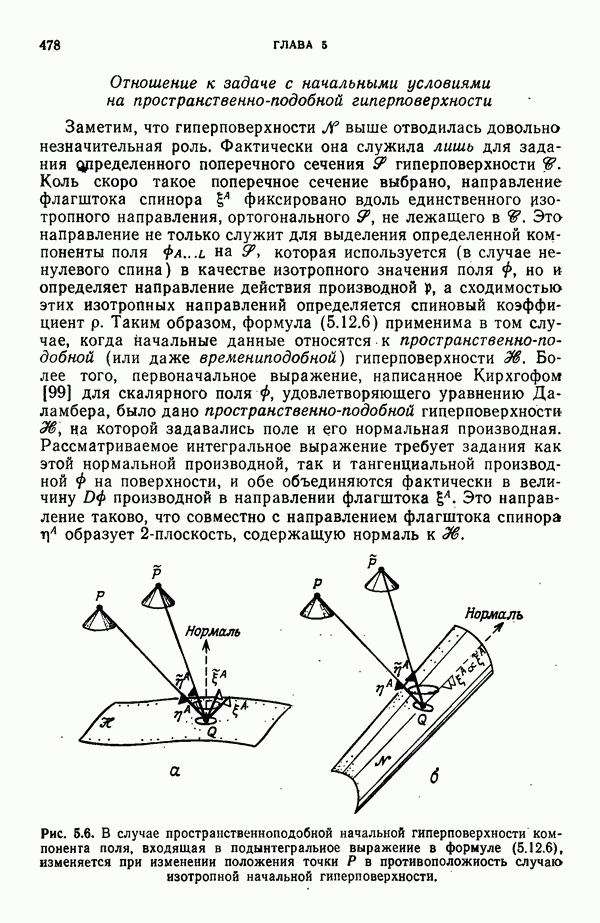
- Отношение к задаче с начальными условиями на пространственно-подобной гиперповерхности
- Фоновые поля
- Поля, соответствующие произвольным изотропным данным
- Поля в смысле обобщенных функций
- Поле Дирака
- Уравнения Максвелла — Дирака
- Приложение. Диаграммная система записи
- Литература