| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. Ковариантная производная
Мы видели в (4.1.32), что можно дать определение градиента скаляра, имеющее инвариантный смысл и зависящее лишь от дифференциальной структуры многообразия  (и даже только от алгебраической структуры множества
(и даже только от алгебраической структуры множества  ). В то же время не существует такого же однозначного инвариантного определения понятия градиента вектора
). В то же время не существует такого же однозначного инвариантного определения понятия градиента вектора  а также тензора любой валентности, кроме
а также тензора любой валентности, кроме  Однако на
Однако на  можно ввести дополнительную структуру, которая является операцией градиента на векторах и может быть однозначно продолжена на все тензорные поля на
можно ввести дополнительную структуру, которая является операцией градиента на векторах и может быть однозначно продолжена на все тензорные поля на  Эта структура называется связностью, а операция, которая ее определяет, — ковариантным дифференцированием. Как упоминалось в § 1, существуют определенные операторы, включающие дифференцирование (производная Ли, внешняя производная и др.), которые не требуют наличия связности на
Эта структура называется связностью, а операция, которая ее определяет, — ковариантным дифференцированием. Как упоминалось в § 1, существуют определенные операторы, включающие дифференцирование (производная Ли, внешняя производная и др.), которые не требуют наличия связности на  Тем не менее будет полезно обсудить и эти операции в связи с ковариантными производными, вместо того чтобы рассматривать их независимо.
Тем не менее будет полезно обсудить и эти операции в связи с ковариантными производными, вместо того чтобы рассматривать их независимо.
Оператор ковариантной производной может быть определен как отображение

удовлетворяющее двум требованиям:


для всех  где
где  есть обычный градиент
есть обычный градиент  определенный в § 1 [формулы (4.1.32), (4.1.40)]. Элементы
определенный в § 1 [формулы (4.1.32), (4.1.40)]. Элементы  и т. д. определяются на
и т. д. определяются на  подстановкой
подстановкой
индексов. В нашем формализме такая подстановка возможна в любой формуле.
Определение оператора  таково, что он однозначно продолжается на ковариантные векторы как отображение
таково, что он однозначно продолжается на ковариантные векторы как отображение

где  есть
есть  -линейное отображение из в
-линейное отображение из в  [формула (2.2.37)], определенное следующим образом:
[формула (2.2.37)], определенное следующим образом:

Доказательство его  -линейности следует из (4.1.43) и (4.2.2), а также из (4.1.44) и (4.2.3). Отметим, что такое определение отображения
-линейности следует из (4.1.43) и (4.2.2), а также из (4.1.44) и (4.2.3). Отметим, что такое определение отображения  прямо следует из требования, чтобы производная от
прямо следует из требования, чтобы производная от  удовлетворяла правилу Лейбница.
удовлетворяла правилу Лейбница.
Мы имеем

в силу формул (4.2.5), (4.1.43), (4.1.44).
Далее, рассмотрим общий тензор  Если потребовать, чтобы правило Лейбница удовлетворялось для производной от
Если потребовать, чтобы правило Лейбница удовлетворялось для производной от  то мы приходим к следующему соотношению:
то мы приходим к следующему соотношению:

Им определяется  как отображение (нетрудно убедиться, что оно будет линейным) из
как отображение (нетрудно убедиться, что оно будет линейным) из  [формула (2.2.38)]. Таким образом, любой оператор
[формула (2.2.38)]. Таким образом, любой оператор  удовлетворяющий условиям (4.2.1) — (4.2.3), однозначно продолжается до
удовлетворяющий условиям (4.2.1) — (4.2.3), однозначно продолжается до

наложением единственного требования, чтобы его действие на свертки типа  удовлетворяло правилу Лейбница. (Легко также установить, что в случае
удовлетворяло правилу Лейбница. (Легко также установить, что в случае  мы возвращаемся к первоначальному определению.)
мы возвращаемся к первоначальному определению.)
Преобразуя обе части каждого из двух следующих равенств по правилу (4.2.8), непосредственно убеждаемся в том, что

Ясно также, что
Операция  коммутирует с подстановкой любого индекса, кроме
коммутирует с подстановкой любого индекса, кроме 
Чтобы доказать коммутативность операции  с операцией свертки (исключая свертку по
с операцией свертки (исключая свертку по  мы можем, во-первых, представить
мы можем, во-первых, представить  как сумму прямых произведений векторов [формула (2.2.14)], а затем, используя линейность соотношения (4.2.10), применить правило Лейбница (4.2.11) к каждому из выражений
как сумму прямых произведений векторов [формула (2.2.14)], а затем, используя линейность соотношения (4.2.10), применить правило Лейбница (4.2.11) к каждому из выражений  используя формулы (4.2.11) и (4.2.5), получаем разложение Лейбница для
используя формулы (4.2.11) и (4.2.5), получаем разложение Лейбница для  и для
и для 
Непосредственно проверяется, что  -свертка первого выражения равна второму. Таким образом,
-свертка первого выражения равна второму. Таким образом,  -свертка выражения
-свертка выражения  равна
равна  что и требовалось доказать:
что и требовалось доказать:

Свойства (4.1.10), (4.2.1), (4.2.11) и (4.2.13) часто используются для аксиоматического введения ковариантной производной.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие переводчиков
- Введение
- 1. Геометрия мировых векторов и спин-векторов
- § 1. Векторное пространство Минковского
- § 2. Изотропные направления и спиновые преобразования
- Преобразования Лоренца и спиновые преобразования
- Связь с кватернионами
- § 3. Некоторые свойства преобразований Лоренца
- Частные случаи преобразования Лоренца, выделенные по характеру его действия на S+
- Двойные отношения изотропных направлений
- § 4. Изотропные флаги и спин-векторы
- Спин-вектор
- § 5. Спинорные объекты и спиновая структура
- Универсальные накрывающие пространства
- Определение спин-вектора
- Спинорная структура
- Спинорная структура для некомпактных моделей пространства-времени
- § 6. Геометрическая интерпретация спинорных операций
- Геометрический смысл внутреннего произведения
- Геометрическая интерпретация сложения
- 2. Метод абстрактных индексов и спинорная алгебра
- Классическая тензорная алгебра
- Бескоординатная тензорная алгебра
- § 2. Формализм абстрактных индексов и тензорная алгебра
- Аксиоматический подход
- Тензоры
- Тензорные операции
- Некоторые полезные свойства вполне рефлексивных модулей
- Включение одной тензорной системы в другую
- § 3. Базисы
- Компоненты в базисе
- § 4. Свойство модуля … быть вполне рефлексивным на многообразии
- § 5. Спинорная алгебра
- e-спиноры
- Комплексное сопряжение
- Спинорные базисы
- 3. Спиноры и мировые тензоры
- § 1. Мировые тензоры как спиноры
- Спиновые системы отсчета и связанные с ними тетрады
- Символы Инфельда — ван дер Вердена
- § 2. Изотропные флаги и комплексные изотропные векторы
- Свойства комплексных изотропных векторов
- Эрмитово-изотропные векторы
- § 3. Операции симметризации и антисимметризации
- Конкретные результаты для спиноров и мировых тензоров
- Разложение на симметричные спиноры
- Неприводимость
- § 4. Тензорное представление спинорных операций
- Дуальное преобразование
- Общий метод перехода к тензорам
- § 5. Простые свойства тензоров и спиноров в точке
- Главные изотропные направления
- Простота кососимметричных тензоров
- § 6. Преобразования Лоренца
- Несобственные преобразования
- Собственные преобразования
- Инфинитезимальные преобразования
- 4. Дифференцирование и кривизна
- Векторные поля
- Действительные и комплексные тензоры
- Градиент скаляра
- § 2. Ковариантная производная
- Кручение и кривизна
- Вариация оператора производной
- Производная по координатам
- § 3. Производные, не зависящие от связности
- Скобки Ли и производные Ли
- Риманова геометрия
- § 4. Дифференцирование спиноров
- Единственность
- Конструкции, основанные на производной Кристоффеля
- Тензорная запись спинорных дифференциальных уравнений
- § 5. Дифференцирование спинорных компонент
- Выражения для спиновых коэффициентов
- Связь между символами Инфельоа — ван дер Вердена и символами Кристоффеля
- § 6. Спиноры кривизны
- Уравнения Эйнштейна
- § 7. Спинорная формулировка теории Эйнштейна — Картана—Шьямы—Киббла
- § 8. Тензор Вейля и тензор Беля — Робинсона
- § 9. Спинорное представление коммутаторов
- § 10. Спинорная форма тождеств Бианки
- § 11. Спиноры кривизны и спиновые коэффициенты
- § 12. Модифицированный формализм спиновых коэффициентов
- Взвешенные скаляры
- Взвешенные дифференциальные операторы.
- Модифицированные уравнения
- § 13. Метод Картана
- Связь со спиновыми коэффициентами
- § 14. Приложение к двумерным поверхностям
- Голоморфные координаты
- Внешние величины
- Связь с внешним исчислением
- Об изотропной гиперповерхности
- § 15. Сферические гармоники со спиновым весом
- Конформные движения поверхности
- Вращения поверхности
- Уравнения, линейные по «дальта»
- Конформные свойства гармоник
- Ортогональность гармоник
- Ортонормированный базис для спиновых функций
- Явные координатные представления
- 5. Поля в пространстве-времени
- § 1. Электромагнитное поле и обобщенный оператор производной
- Заряженные поля
- Электромагнитный потенциал
- Максвелловский тензор поля
- Спинор электромагнитного поля
- Связь с 3-векторами электрического и магнитного полей
- § 2. Уравнения Эйнштейна — Максвелла в спинорной форме
- Свойства положительной определенности максвелловского тензора энергии-импульса
- § 3. Условия Райнича
- Дифференциальное условие Райнича
- § 4. Векторные расслоения
- Определение векторных расслоений
- Явное построение расслоений
- Связности в расслоенных пространствах
- § 5. Поля Янга — Миллса
- Потенциал Янга — Миллса и метрика
- Тензор поля Янга — Миллса
- Спинорная трактовка
- § 6. Конформные изменения масштаба
- Конформные плотности
- Поведение спиновых коэффициентов при конформном изменении масштаба
- Конформно-инвариантные операторы
- § 7. Безмассовые поля
- Конформная инвариантность
- § 8. Условия совместности
- Тензор энергии-импульса
- Совместные системы полей с высшими спинами
- § 9. Конформная инвариантность различных полевых величин
- § 10. Точные системы полей
- Свободные безмассовые поля
- Электромагнитные источники
- Гравитация
- Поля Эйнштейна — Максвелла
- Другие примеры
- § 11. Начальные данные на световом конусе
- «Ряд Тейлора» на световом конусе
- Подсчет степеней свободы
- Регулярность в точке О
- Геометрия светового конуса
- § 12. Явные полевые интегралы
- Доказательство основной формулы
- Конформно-плоское пространство-время
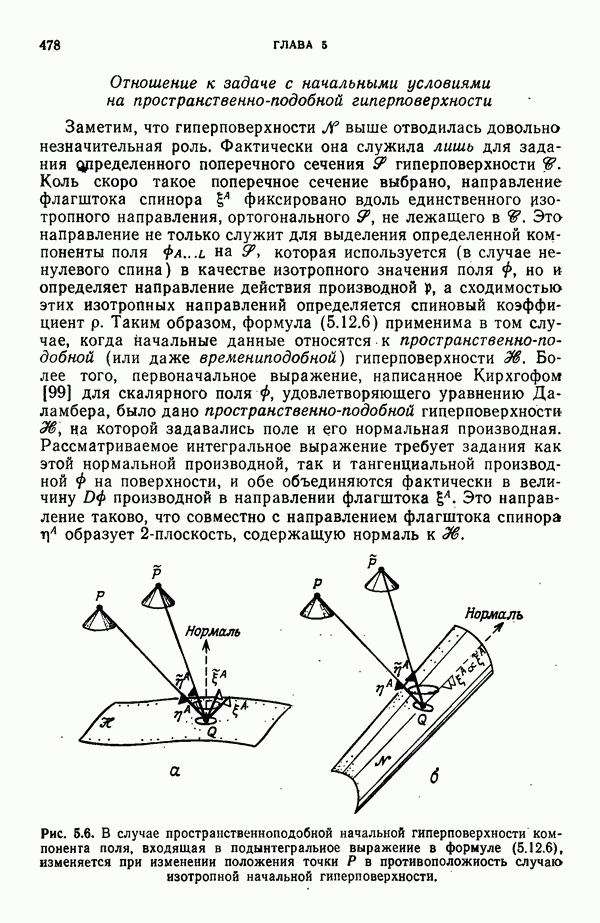
- Отношение к задаче с начальными условиями на пространственно-подобной гиперповерхности
- Фоновые поля
- Поля, соответствующие произвольным изотропным данным
- Поля в смысле обобщенных функций
- Поле Дирака
- Уравнения Максвелла — Дирака
- Приложение. Диаграммная система записи
- Литература