| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Риманова геометрия
Рассмотрим следствия введения метрики на М. Метрика есть симметричный тензор валентности  обозначаемый через
обозначаемый через  который по определению не сингулярен, т. е. существует обратный тензор
который по определению не сингулярен, т. е. существует обратный тензор  такой, что
такой, что

Мы имеем

Пусть  — произвольный контравариантный вектор, а
— произвольный контравариантный вектор, а  — симметричный оператор. Тогда производная Ли
— симметричный оператор. Тогда производная Ли  вдоль
вдоль  равна
равна

Повторная внешняя производная от  равна
равна

Оба эти выражения не зависят от связности. Складывая их, получаем

свертка этого выражения с  дает
дает

что также не должно зависеть от связности. Предположим, что симметричный оператор  удовлетворяет требованию
удовлетворяет требованию

Этим условием однозначно определяется оператор  Действительно, выражение (4.3.45) не зависит от связности, следовательно, в нем можно заменить
Действительно, выражение (4.3.45) не зависит от связности, следовательно, в нем можно заменить  на
на 

где др — произвольный симметричный оператор; в частности, это может быть оператор «производной по координатам», ассоциированный с локальными координатами  Если перейти к компонентам, то выражение (4.3.47) имеет привычный классический вид ковариантной производной, записанной через символы Кристоффеля.
Если перейти к компонентам, то выражение (4.3.47) имеет привычный классический вид ковариантной производной, записанной через символы Кристоффеля.
И наоборот, можно доказать, что существует симметричная связность  удовлетворяющая требованию (4.3.46). Мы определяем
удовлетворяющая требованию (4.3.46). Мы определяем  (локально) выражением (4.3.47). Тогда мы имеем равенство вида (4.2.46), где
(локально) выражением (4.3.47). Тогда мы имеем равенство вида (4.2.46), где  и
и

Таким образом, в силу формул (4.2.48), (4.3.40) и (4.3.41) имеем

Симметричный оператор  однозначно определяемый тензором
однозначно определяемый тензором  будем называть ковариантной производной Кристоффеля. (Мы доказали, что она существует локально, но локальное существование вместе с единственностью означает глобальное существование.)
будем называть ковариантной производной Кристоффеля. (Мы доказали, что она существует локально, но локальное существование вместе с единственностью означает глобальное существование.)
С помощью метрики индексы можно поднимать и опускать стандартным образом (гл. 3, § 1) (т. е.  устанавливает канонический изоморфизм между
устанавливает канонический изоморфизм между  Поскольку
Поскольку  «ковариантно постоянна»,
«ковариантно постоянна»,  операция поднятия и опускания индексов коммутирует с
операция поднятия и опускания индексов коммутирует с  То есть
То есть

Наконец, вычислим кривизну, определяемую ковариантной производной Кристоффеля. Если опустить последний индекс в 
то получим тензор Римана(-Кристоффеля)

(При принятом нами расположении индексов наше определение тензора Римана отличается знаком от определения, принятого в литературе. Его обычно используют в связи со спинорными разложениями.)
Действуя коммутатором производных на  мы получаем в силу формул (4.3.46) и (4.2.33) и с учетом равенства нулю кручения
мы получаем в силу формул (4.3.46) и (4.2.33) и с учетом равенства нулю кручения

т. е. тензор  антисимметричен по
антисимметричен по  и
и  Из (4.2.34) следует, что он также антисимметричен по а и Р; таким образом,
Из (4.2.34) следует, что он также антисимметричен по а и Р; таким образом,

Используя (4.2.38), получаем

Из этих соотношений следует, что

Стало быть, тензор  обладает также симметрией относительно перестановки пар индексов:
обладает также симметрией относительно перестановки пар индексов:

[Заметим, что для вывода равенства (4.3.56) достаточно использовать тождество  вместо (4.3.53).] Ввиду симметрий (4.3.53) и (4.3.54) [а следовательно, и (4.3.56)] полное число независимых компонент тензора
вместо (4.3.53).] Ввиду симметрий (4.3.53) и (4.3.54) [а следовательно, и (4.3.56)] полное число независимых компонент тензора  в каждой точке оказывается равным
в каждой точке оказывается равным  (см. стр. 187).
(см. стр. 187).
Тензор

называется тензором Риччи. В силу равенства (4.3.56) (и симметричности метрики) имеем

Тензор Риччи имеет  независимых компонент в каждой точке. Скалярная кривизна дается выражением
независимых компонент в каждой точке. Скалярная кривизна дается выражением

Переписав тождества Бианки (4.2.42) в виде

и свернув их с  мы получаем важное соотношение
мы получаем важное соотношение

В четырехмерном пространстве-времени это соотношение служит основой полевых уравнений Эйнштейна.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие переводчиков
- Введение
- 1. Геометрия мировых векторов и спин-векторов
- § 1. Векторное пространство Минковского
- § 2. Изотропные направления и спиновые преобразования
- Преобразования Лоренца и спиновые преобразования
- Связь с кватернионами
- § 3. Некоторые свойства преобразований Лоренца
- Частные случаи преобразования Лоренца, выделенные по характеру его действия на S+
- Двойные отношения изотропных направлений
- § 4. Изотропные флаги и спин-векторы
- Спин-вектор
- § 5. Спинорные объекты и спиновая структура
- Универсальные накрывающие пространства
- Определение спин-вектора
- Спинорная структура
- Спинорная структура для некомпактных моделей пространства-времени
- § 6. Геометрическая интерпретация спинорных операций
- Геометрический смысл внутреннего произведения
- Геометрическая интерпретация сложения
- 2. Метод абстрактных индексов и спинорная алгебра
- Классическая тензорная алгебра
- Бескоординатная тензорная алгебра
- § 2. Формализм абстрактных индексов и тензорная алгебра
- Аксиоматический подход
- Тензоры
- Тензорные операции
- Некоторые полезные свойства вполне рефлексивных модулей
- Включение одной тензорной системы в другую
- § 3. Базисы
- Компоненты в базисе
- § 4. Свойство модуля … быть вполне рефлексивным на многообразии
- § 5. Спинорная алгебра
- e-спиноры
- Комплексное сопряжение
- Спинорные базисы
- 3. Спиноры и мировые тензоры
- § 1. Мировые тензоры как спиноры
- Спиновые системы отсчета и связанные с ними тетрады
- Символы Инфельда — ван дер Вердена
- § 2. Изотропные флаги и комплексные изотропные векторы
- Свойства комплексных изотропных векторов
- Эрмитово-изотропные векторы
- § 3. Операции симметризации и антисимметризации
- Конкретные результаты для спиноров и мировых тензоров
- Разложение на симметричные спиноры
- Неприводимость
- § 4. Тензорное представление спинорных операций
- Дуальное преобразование
- Общий метод перехода к тензорам
- § 5. Простые свойства тензоров и спиноров в точке
- Главные изотропные направления
- Простота кососимметричных тензоров
- § 6. Преобразования Лоренца
- Несобственные преобразования
- Собственные преобразования
- Инфинитезимальные преобразования
- 4. Дифференцирование и кривизна
- Векторные поля
- Действительные и комплексные тензоры
- Градиент скаляра
- § 2. Ковариантная производная
- Кручение и кривизна
- Вариация оператора производной
- Производная по координатам
- § 3. Производные, не зависящие от связности
- Скобки Ли и производные Ли
- Риманова геометрия
- § 4. Дифференцирование спиноров
- Единственность
- Конструкции, основанные на производной Кристоффеля
- Тензорная запись спинорных дифференциальных уравнений
- § 5. Дифференцирование спинорных компонент
- Выражения для спиновых коэффициентов
- Связь между символами Инфельоа — ван дер Вердена и символами Кристоффеля
- § 6. Спиноры кривизны
- Уравнения Эйнштейна
- § 7. Спинорная формулировка теории Эйнштейна — Картана—Шьямы—Киббла
- § 8. Тензор Вейля и тензор Беля — Робинсона
- § 9. Спинорное представление коммутаторов
- § 10. Спинорная форма тождеств Бианки
- § 11. Спиноры кривизны и спиновые коэффициенты
- § 12. Модифицированный формализм спиновых коэффициентов
- Взвешенные скаляры
- Взвешенные дифференциальные операторы.
- Модифицированные уравнения
- § 13. Метод Картана
- Связь со спиновыми коэффициентами
- § 14. Приложение к двумерным поверхностям
- Голоморфные координаты
- Внешние величины
- Связь с внешним исчислением
- Об изотропной гиперповерхности
- § 15. Сферические гармоники со спиновым весом
- Конформные движения поверхности
- Вращения поверхности
- Уравнения, линейные по «дальта»
- Конформные свойства гармоник
- Ортогональность гармоник
- Ортонормированный базис для спиновых функций
- Явные координатные представления
- 5. Поля в пространстве-времени
- § 1. Электромагнитное поле и обобщенный оператор производной
- Заряженные поля
- Электромагнитный потенциал
- Максвелловский тензор поля
- Спинор электромагнитного поля
- Связь с 3-векторами электрического и магнитного полей
- § 2. Уравнения Эйнштейна — Максвелла в спинорной форме
- Свойства положительной определенности максвелловского тензора энергии-импульса
- § 3. Условия Райнича
- Дифференциальное условие Райнича
- § 4. Векторные расслоения
- Определение векторных расслоений
- Явное построение расслоений
- Связности в расслоенных пространствах
- § 5. Поля Янга — Миллса
- Потенциал Янга — Миллса и метрика
- Тензор поля Янга — Миллса
- Спинорная трактовка
- § 6. Конформные изменения масштаба
- Конформные плотности
- Поведение спиновых коэффициентов при конформном изменении масштаба
- Конформно-инвариантные операторы
- § 7. Безмассовые поля
- Конформная инвариантность
- § 8. Условия совместности
- Тензор энергии-импульса
- Совместные системы полей с высшими спинами
- § 9. Конформная инвариантность различных полевых величин
- § 10. Точные системы полей
- Свободные безмассовые поля
- Электромагнитные источники
- Гравитация
- Поля Эйнштейна — Максвелла
- Другие примеры
- § 11. Начальные данные на световом конусе
- «Ряд Тейлора» на световом конусе
- Подсчет степеней свободы
- Регулярность в точке О
- Геометрия светового конуса
- § 12. Явные полевые интегралы
- Доказательство основной формулы
- Конформно-плоское пространство-время
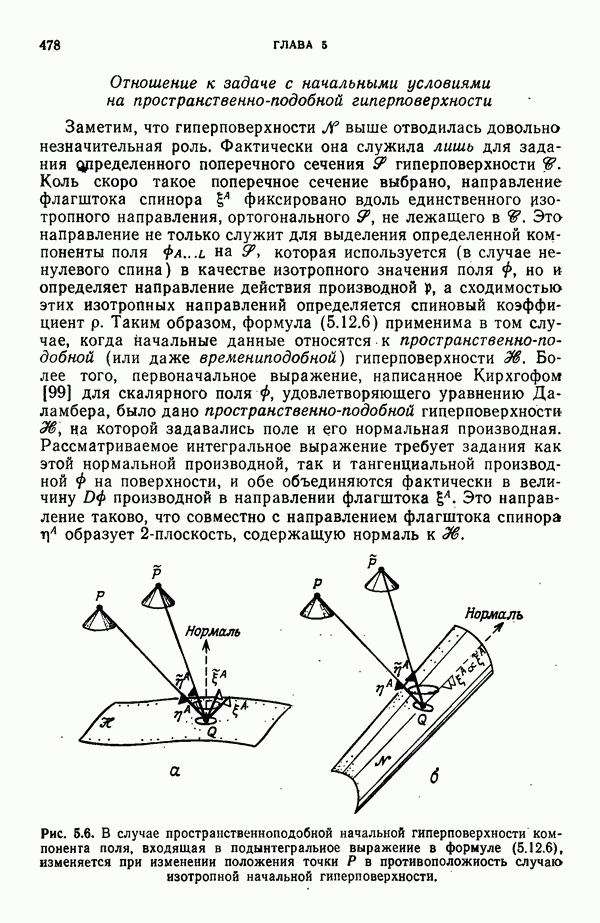
- Отношение к задаче с начальными условиями на пространственно-подобной гиперповерхности
- Фоновые поля
- Поля, соответствующие произвольным изотропным данным
- Поля в смысле обобщенных функций
- Поле Дирака
- Уравнения Максвелла — Дирака
- Приложение. Диаграммная система записи
- Литература