| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
Мы научились изображать любые числа, как рациональные, так и иррациональные, в виде цепных дробей. Выясним теперь, в чем заключаются преимущества и недостатки такого изображения.
Основное преимущество записи чисел в виде цепных дробей по сравнению с их записью в виде систематических (например, десятичных) дробей состоит в том, что эта запись не зависит от выбора системы счисления. Ведь неполные знаменатели получались путем выделения целой части из неправильных дробей, а эта операция при любой системе счисления приводит к одному и тому же результату (конечно, с точностью до записи в разных системах счисления самих неполных знаменателей). Поэтому запись числа в виде цепной дроби отражает его «существенные» арифметические свойства, а не свойства, связанные с выбором той или иной системы счисления.
Например, при записи рационального числа в виде систематической дроби может получиться либо конечная дробь, либо бесконечная периодическая или смешанная) дробь. При записи же рационального числа в виде цепной дроби всегда получается конечная дробь, причем это характерно только для рациональных чисел. Можно доказать, что квадратичные иррациональности, и. только они, представляются в виде периодических цепных дробей. Выразить же условие того, что данное число является квадратичной иррациональностью, в терминах систематических дробей невозможно.
Но самое важное преимущество цепных дробей по сравнению с систематическими заключается в том, что они дают наилучшие приближения данного числа с помощью дробей, имеющих не слишком большие знаменатели. Уточним это утверждение.
Пусть даны число а и несократимая дробь  Естественной мерой отклонения — от а является
Естественной мерой отклонения — от а является  Однако в теоретических гопросах оказалось удобнее
Однако в теоретических гопросах оказалось удобнее  осматривать в качестве меры отклонения число
осматривать в качестве меры отклонения число  . Ясно, что если
. Ясно, что если  мало, то тем более мало число
мало, то тем более мало число  Обратное верно не всегда, так как знаменатель
Обратное верно не всегда, так как знаменатель  может оказаться большим числом.
может оказаться большим числом.
Пусть число а разложено в цепную дробь. Легко оценить отклонение подходящей дроби от а. Так как а лежит между  , то имеем:
, то имеем:

Оказывается, для любой дроби, знаменатель которой не превосходит  отклонение больше, чем
отклонение больше, чем  . Иными словами, справедлива следующая
. Иными словами, справедлива следующая
Теорема 4. Если  подходящая дробь для разложения числа
подходящая дробь для разложения числа  в цепную дробь, то для любой дроби
в цепную дробь, то для любой дроби  такой, что
такой, что  выполняется неравенство
выполняется неравенство

Единственным исключением является подходящая дробь  для числа
для числа 
Доказательство этой теоремы мы опускаем.
Теорема 4 показывает, что подходящие дроби являются наилучшими приближениями для числа а по сравнению со всеми дробями, знаменатель которых не превосходит знаменателя подходящей дроби. Именно это свойство послужило причиной введения цепных дробей в математику и детального изучения их теории. В конце XVII века голландский математик и физик Гюйгенс хотел построить модель Солнечной системы с помощью зубчатых колес. При этом возникла задача определить число зубцов так, чтобы отношение этих чисел для двух связанных между собой колес было по возможности близко к отношению времен а обращения соответствующих планет, причем число зубцов не должно быть слишком большим. Таким образом, встал вопрос об отыскании рациональной дроби, числитель и знаменатель которой были бы не слишком большими числами и которая наилучшим образом приближала число а. С помощью теории цепных дробей задача была решена.
Отметим, что цепные дроби как аппарат для изображения действительных чисел имеют и недостатки: дело в том, что над действительными числами, изображенными в виде цепных дробей, практически трудно выполнять арифметические операции — сложение, вычитание, умножение и деление. (Попробуйте, например, сложить или перемножить дроби

не переводя их в обыкновенные.)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ
- ВВЕДЕНИЕ
- 2. Числовые множества.
- 3. Пустое множество.
- 4. Подмножество.
- 5. Пересечение множеств.
- 6. Сложение множеств.
- 7. Разбиение множеств.
- 8. Вычитание множеств.
- 9. Отображение множеств.
- 10. Краткие исторические сведения.
- Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
- § 1. Тождественные преобразования многочленов
- 2. Целые рациональные выражения и функции.
- 3. Степень с натуральным показателем и ее свойства.
- 4. Многочлены.
- 5. Умножение многочленов.
- 6. Числовые кольца и поля.
- 7. Кольцо многочленов над данным числовым полем.
- 8. Бином Ньютона.
- § 2. Деление многочленов. Корни многочленов
- 2. Теорема Безу. Схема Горнера.
- 3. Корни многочлена.
- 4. Интерполяционные формулы.
- 5. Кратные корни.
- 6. Многочлены второй степени.
- 7. Многочлены с целыми коэффициентами.
- 8. Краткие исторические сведения.
- Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1. Общая теория уравнений
- 2. Область допустимых значений.
- 3. Уравнения.
- 4. Совокупности уравнений.
- 5. Преобразования уравнений.
- 6. Теоремы о равносильности уравнений.
- § 2. Уравнения с одним неизвестным
- 2. Метод разложения на множители.
- 3. Метод введения нового неизвестного.
- 4. Биквадратные уравнения.
- 5. Возвратные уравнения 3-й и 4-й степеней.
- § 3. Функциональные неравенства
- 2. Равносильные неравенства.
- 3. Доказательство неравенств.
- 4. Линейные неравенства.
- 5. Решение неравенств второй степени.
- 6. Решение алгебраических неравенств высших степеней.
- 7. Краткие исторические сведения.
- Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
- § 1. Степени с целым показателем
- 2. Степень с нулевым показателем.
- 3. Степень с целым отрицательным показателем.
- § 2. Корни. Степени с рациональными показателями
- 2. Степени с рациональными показателями.
- 3. Свойства степеней с рациональными показателями.
- § 3. Иррациональные алгебраические выражения
- 2. Одночленные иррациональные выражения.
- 3. Сокращение показателей и приведение корней к общему показателю.
- 4. Извлечение корня из произведения и степени.
- 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.
- 6. Возведение корня в степень.
- 7. Извлечение корня из корня.
- 8. Подобные корни.
- 9. Сложение и вычитание корней.
- 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
- 11. Преобразование выражений вида …
- 12. Смешанные задачи на преобразование иррациональных выражений.
- § 4. Иррациональные уравнения и неравенства
- 2. Сведение иррациональных уравнений к рациональным.
- 3. Уединение радикала.
- 4. Введение нового неизвестного.
- 5. Особые случаи решения иррациональных уравнений.
- 6. Иррациональные неравенства.
- 7. Краткие историчесие сведения.
- Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 1. Системы алгебраических уравнений
- 2. Системы уравнений.
- 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
- 4. Совокупность уравнений.
- 5. Равносильные системы уравнений.
- 6. Метод подстановки.
- 7. Метод алгебраического сложения уравнений.
- 8. Метод введения новых неизвестных.
- 9. Системы однородных уравнений.
- 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
- § 2. Системы линейных уравнений
- 2. Теоремы о равносильности систем линейных уравнений.
- 3. Пример решения системы линейных уравнений методом Гаусса.
- 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
- 5. Решение обобщенно-треугольной системы линейных уравнений.
- 6. Системы однородных линейных уравнений.
- § 3. Симметрические многочлены и их приложения к решению систем уравнений
- 2. Выражение степенных сумм
- 3. Основная теорема о симметрических многочленах от двух переменных.
- 4. Системы симметрических алгебраических уравнений.
- 5. Применение симметрических многочленов к решению иррациональных уравнений.
- § 4. Неравенства с многими переменными
- 2. Среднее арифметическое и среднее геометрическое трех чисел.
- 3. Неравенство Коши (двумерный вариант).
- 4. Задачи на наибольшие и наименьшие значения.
- § 5. Решение неравенств
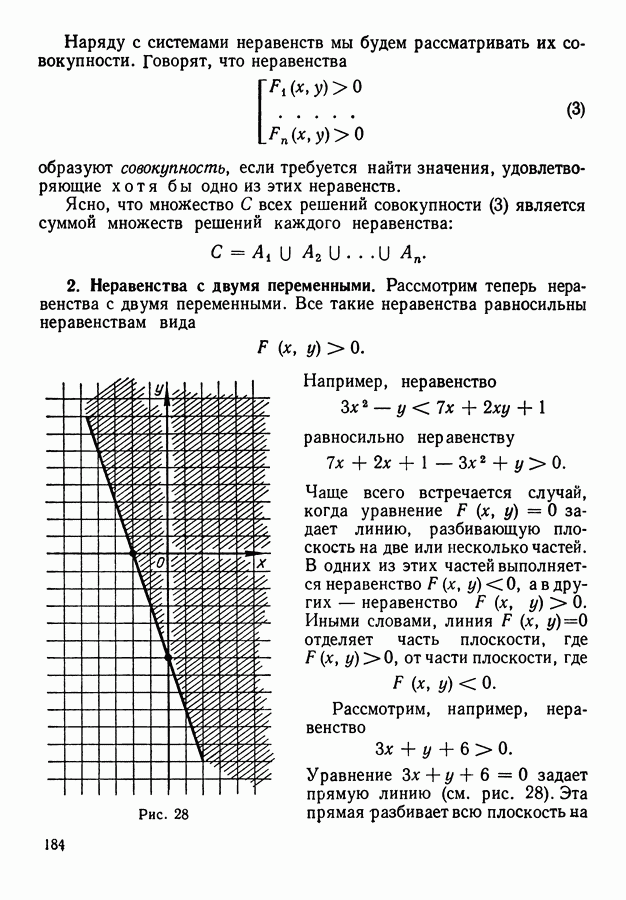
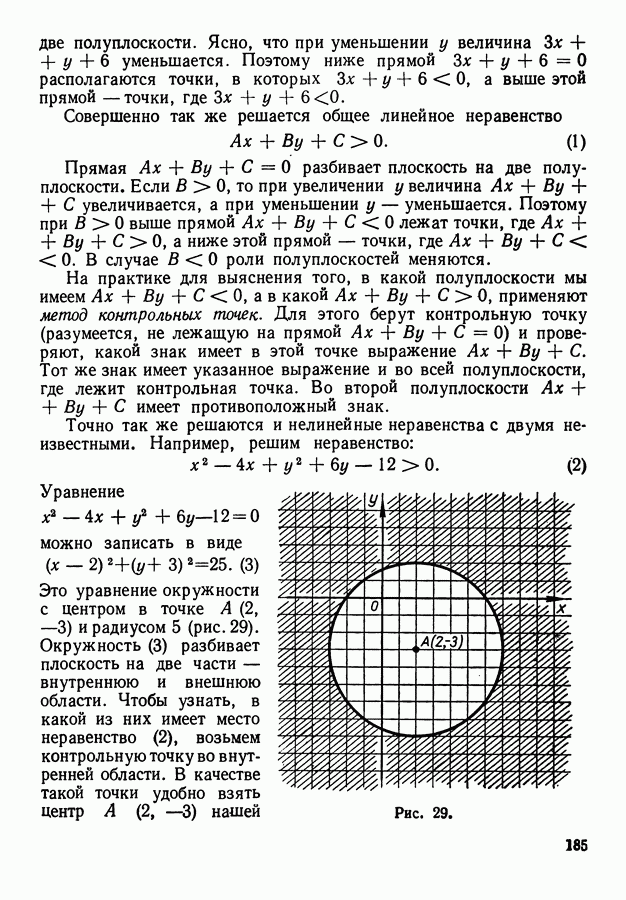
- 2. Неравенства с двумя переменными.
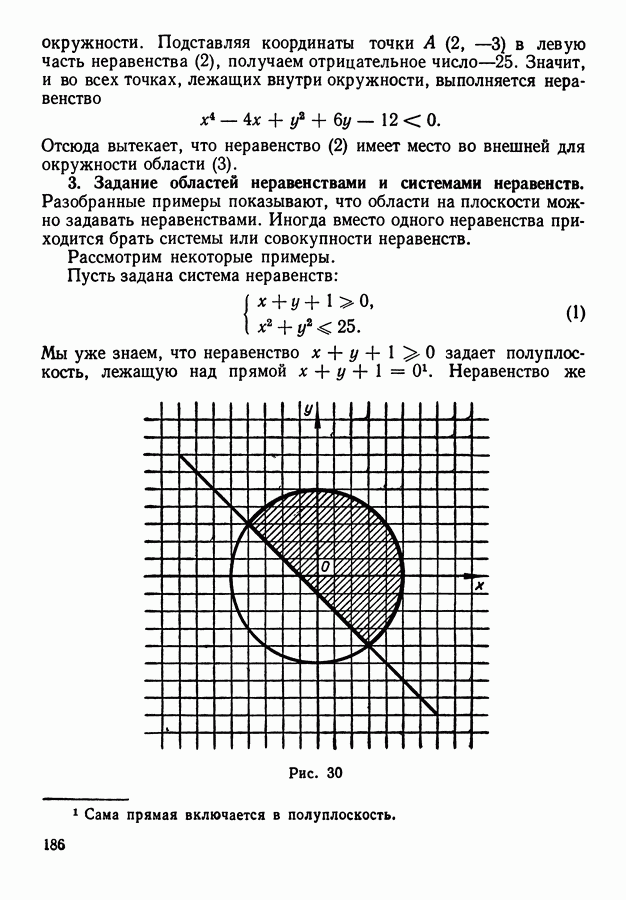
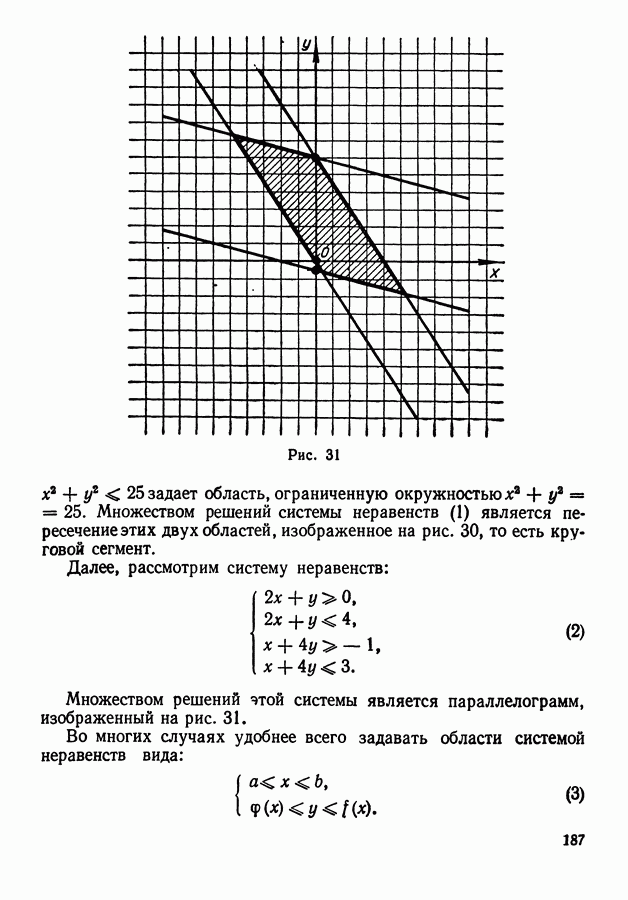
- 3. Задание областей неравенствами и системами неравенств.
- 4. Понятие о линейном программировании.
- 5. Краткие исторические сведения.
- Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
- § 1. Комплексные числа в алгебраической форме
- 2. Комплексные числа.
- 3. Сложение комплексных чисел; умножение на действительные числа.
- 4. Умножение комплексных чисел.
- 5. Квадратные уравнения с действительными коэффициентами.
- 6. Деление комплексных чисел.
- 7. Сопряженные комплексные числа.
- 8. Извлечение квадратных корней из комплексных чисел.
- § 2. Тригонометрическая форма комплексных чисел
- 2. Полярная система координат.
- 3. Тригонометрическая форма комплексного числа.
- 4. Умножение и деление комплексных чисел в тригонометрической форме.
- 5. Возведение комплексных чисел в степень. Формула Муавра.
- 6. Извлечение корня из комплексного числа.
- 7. Функции комплексного переменного и преобразования комплексной плоскости.
- § 3. Некоторые виды алгебраических уравнений
- 2. Двучленные уравнения.
- 3. Корни из единицы и построение правильных многоугольников.
- 4. Трехчленные уравнения.
- § 4. Основная теорема алгебры многочленов и ее следствия
- 2. Многочлены с действительными коэффициентами.
- 3. Разложение на множители многочленов с действительными коэффициентами.
- 4. Краткие исторические сведения.
- Глава VI. ЦЕПНЫЕ ДРОБИ
- § 1. Конечные цепные дроби
- 2. Пример цепной дроби.
- 3. Определение цепной дроби.
- 4. Представление рациональных чисел в виде конечной цепной дроби.
- 5. Подходящие дроби.
- 6. Свойства подходящих дробей.
- 8. Подходящие дроби и календарь.
- 9. Приближение цепной дроби подходящими дробями.
- § 2. Бесконечные цепные дроби
- 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
- 3. Цепные дроби как вычислительный инструмент.
- 4. Краткие исторические сведения.
- Глава VII. КОМБИНАТОРИКА
- § 1. Комбинаторные задачи
- § 2. Комбинаторные задачи. Продолжение
- § 3. Определения и формулы
- § 4. Соединения с повторениями
- § 5. Комбинаторные задачи. Окончание
- § 6. Бином Ньютона и его обобщения
- § 7. Краткие исторические сведения
- Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
- § 3. Примеры вычисления вероятностей
- § 4. Полная вероятность. Формула Байеса
- § 5. Повторение испытаний
- § 6. Примеры вычисления вероятностей. Окончание
- § 7. Краткие исторические сведения