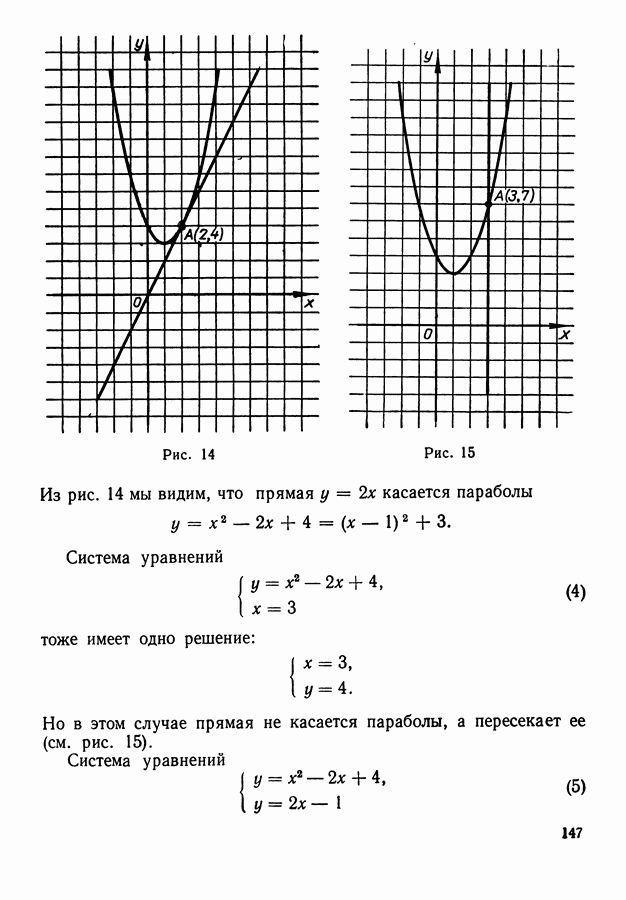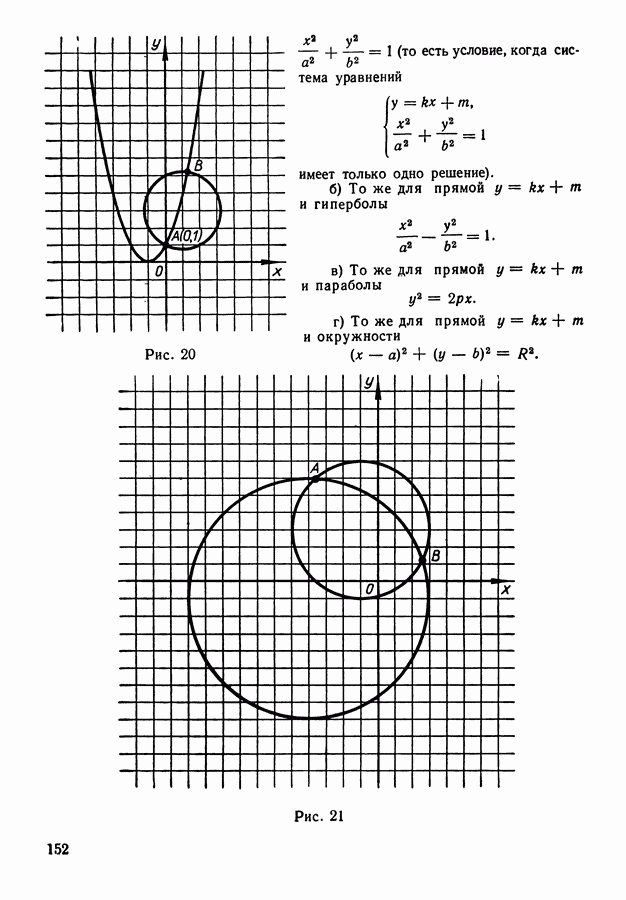| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8. Краткие исторические сведения.
Некоторые задачи, решаемые по сути дела алгебраическими методами, встречаются еще в вавилонских клинописных текстах (примерно 1700 г. до н. э.). В этих текстах изложены правила суммирования прогрессии, нахождения суммы квадратов, решения квадратного уравнения и т. д. Однако все эти правила лишь пояснялись на числовых примерах, но не формулировались в общем виде — не было буквенной символики.
В древней Греции начинается развитие алгебры как теоретической науки. Поскольку у греческих математиков не было общего понятия действительного числа, они развивали геометрическую алгебру. Например, вместо формулы (а  говорили, что площадь квадрата, построенного на отрезке, равном сумме двух отрезков, равна сумме площадей квадратов, построенных на слагаемых отрезках и удвоенной площади прямоугольника,
говорили, что площадь квадрата, построенного на отрезке, равном сумме двух отрезков, равна сумме площадей квадратов, построенных на слагаемых отрезках и удвоенной площади прямоугольника,
сторонами которого являются эти Отрезки. Выражения вида  трактовались как объемы геометрических тел. Лишь к III веку н. э. у Диофанта Александрийского появляются зачатки буквенной символики.
трактовались как объемы геометрических тел. Лишь к III веку н. э. у Диофанта Александрийского появляются зачатки буквенной символики.
После крушения античной цивилизации центр математической мысли перемещается в арабские государства. Крупнейшим достижением арабов было создание алгебры как самостоятельной ветви математики (само название «алгебра» — арабского происхождения: от аль-джебр — восстановление; так назывался один из методов решения уравнений). Арабские математики установили формулы для разложения  для суммы
для суммы  исследовали кубические уравнения и т. д.
исследовали кубические уравнения и т. д.
В странах, где в это время господствовала христианская церковь, математика почти не развивалась. В некоторых странах математические исследования были запрещены, они рассматривались как попытка возрождения язычества. Указ византийского императора Юстиниана запрещал заниматься математикой под страхом смертной казни. Лишь в отдельных трактатах по богословию и схоластической философии рассматривались некоторые математические вопросы.
Однако потребности практики, развитие промышленности, торговли и мореплавания привели к необходимости возродить науки, и в частности математику. Первоначально европейские ученые ограничивались изучением древнегреческой науки, но потом познакомились с достижениями арабских математиков, и в частности с алгеброй (многие европейские ученые получили образование в арабских университетах).
Как у арабов, так и у первых европейских алгебраистов, не было буквенной символики. Формулы излагались словесно, что затрудняло их чтение, преобразование и использование. Алгебраическая символика начинает развиваться с конца XV века. В это время у немецких алгебраистов появляются знаки  Однако итальянские математики еще долгое время продолжали пользоваться знаками
Однако итальянские математики еще долгое время продолжали пользоваться знаками  и
и  — сокращениями латинских слов
— сокращениями латинских слов  и
и  . Систематическое применение буквенных обозначений в алгебре начинается с работ французского алгебраиста Ф. Виета (1540—1603). В его работах буквы используются лишь для обозначения положительных чисел, причем показатели степеней обозначаются словами. Вместо скобок Виета писал черту.
. Систематическое применение буквенных обозначений в алгебре начинается с работ французского алгебраиста Ф. Виета (1540—1603). В его работах буквы используются лишь для обозначения положительных чисел, причем показатели степеней обозначаются словами. Вместо скобок Виета писал черту.
Особые обозначения для степеней неизвестных впервые появляются у голландского ученого С. Стевина (1548—1620) и его ученика француза Жирара (1595—1633). Они вместо  писали 3, а если в выражении содержались еще другие буквы, то писали
писали 3, а если в выражении содержались еще другие буквы, то писали  (от латинских слов secundus — второй, tertius — третий). Жирар впервые ввел скобки.
(от латинских слов secundus — второй, tertius — третий). Жирар впервые ввел скобки.
Символика Виета была усовершенствована английским математиком Т. Гэрриотом, который, однако, еще не применял обозначений для показателей степени, а выписывал все сомножители, входящие в одночлены. Современный вид алгебраических обозначений в основном принадлежит великому французскому математику и философу Р. Декарту (1596—1650).
Приведем некоторые примеры обозначений, применявшихся разными учеными:

Основные свойства арифметических действий, лежащие в основе алгебраических преобразований, были установлены еще в древней Греции (в геометрической форме). Однако полная и последовательная система основ арифметики была построена лишь в XIX веке немецкими математиками Г. Грассманом и Р. Дедекиндом (общепринятая в настоящее время аксиоматика исходит от итальянского математика Дж. Пеано). Такое построение оказалось необходимым после того, как были открыты величины (векторы, матрицы, кватернионы), правила действий над которыми отличались от правил действий над числами. Например, при изменении порядка сомножителей векторное произведение меняет знак. Для каждого типа величин надо было строить свою алгебру (векторная алгебра, матричная алгебра и т. д.). Это усилило интерес к изучению общих свойств алгебраических действий. Были построены теории колец и полей, структур и других алгебраических образований. Благодаря общности полученных в этих теориях результатов, они оказались приложимыми к величинам самых разных видов. В настоящее время изучение общих свойств алгебраических операций занимает важное место в алгебраической науке. Большой вклад в общую алгебру внесли советские математики О. Ю. Шмидт, А. Г. Курош, А. И. Мальцев и другие.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ
- ВВЕДЕНИЕ
- 2. Числовые множества.
- 3. Пустое множество.
- 4. Подмножество.
- 5. Пересечение множеств.
- 6. Сложение множеств.
- 7. Разбиение множеств.
- 8. Вычитание множеств.
- 9. Отображение множеств.
- 10. Краткие исторические сведения.
- Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
- § 1. Тождественные преобразования многочленов
- 2. Целые рациональные выражения и функции.
- 3. Степень с натуральным показателем и ее свойства.
- 4. Многочлены.
- 5. Умножение многочленов.
- 6. Числовые кольца и поля.
- 7. Кольцо многочленов над данным числовым полем.
- 8. Бином Ньютона.
- § 2. Деление многочленов. Корни многочленов
- 2. Теорема Безу. Схема Горнера.
- 3. Корни многочлена.
- 4. Интерполяционные формулы.
- 5. Кратные корни.
- 6. Многочлены второй степени.
- 7. Многочлены с целыми коэффициентами.
- 8. Краткие исторические сведения.
- Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1. Общая теория уравнений
- 2. Область допустимых значений.
- 3. Уравнения.
- 4. Совокупности уравнений.
- 5. Преобразования уравнений.
- 6. Теоремы о равносильности уравнений.
- § 2. Уравнения с одним неизвестным
- 2. Метод разложения на множители.
- 3. Метод введения нового неизвестного.
- 4. Биквадратные уравнения.
- 5. Возвратные уравнения 3-й и 4-й степеней.
- § 3. Функциональные неравенства
- 2. Равносильные неравенства.
- 3. Доказательство неравенств.
- 4. Линейные неравенства.
- 5. Решение неравенств второй степени.
- 6. Решение алгебраических неравенств высших степеней.
- 7. Краткие исторические сведения.
- Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
- § 1. Степени с целым показателем
- 2. Степень с нулевым показателем.
- 3. Степень с целым отрицательным показателем.
- § 2. Корни. Степени с рациональными показателями
- 2. Степени с рациональными показателями.
- 3. Свойства степеней с рациональными показателями.
- § 3. Иррациональные алгебраические выражения
- 2. Одночленные иррациональные выражения.
- 3. Сокращение показателей и приведение корней к общему показателю.
- 4. Извлечение корня из произведения и степени.
- 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.
- 6. Возведение корня в степень.
- 7. Извлечение корня из корня.
- 8. Подобные корни.
- 9. Сложение и вычитание корней.
- 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
- 11. Преобразование выражений вида …
- 12. Смешанные задачи на преобразование иррациональных выражений.
- § 4. Иррациональные уравнения и неравенства
- 2. Сведение иррациональных уравнений к рациональным.
- 3. Уединение радикала.
- 4. Введение нового неизвестного.
- 5. Особые случаи решения иррациональных уравнений.
- 6. Иррациональные неравенства.
- 7. Краткие историчесие сведения.
- Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 1. Системы алгебраических уравнений
- 2. Системы уравнений.
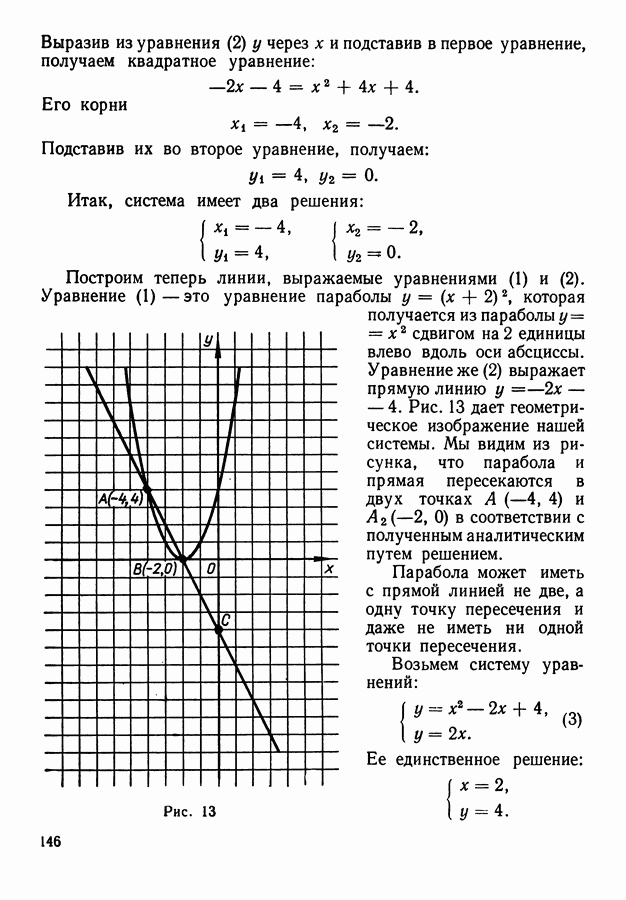
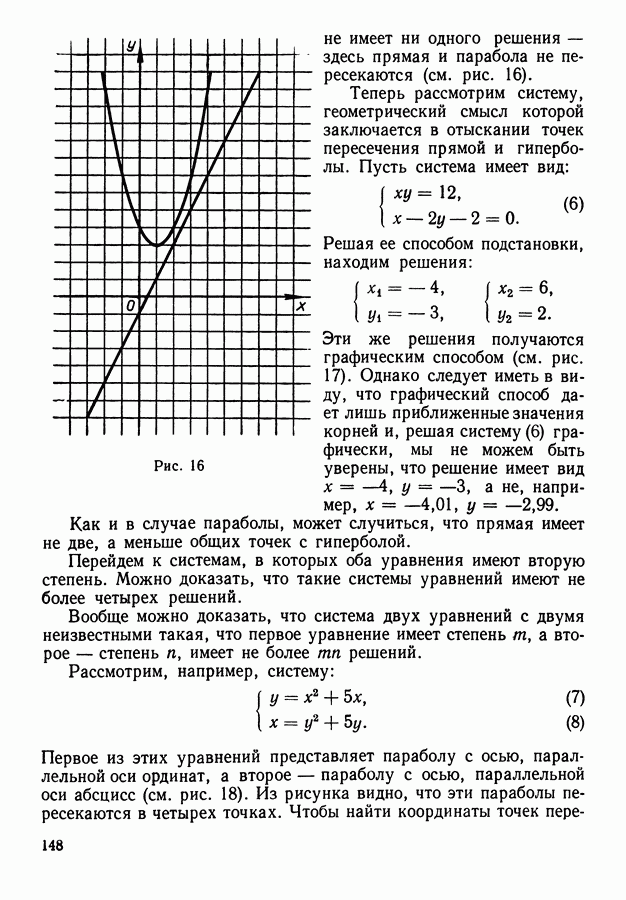
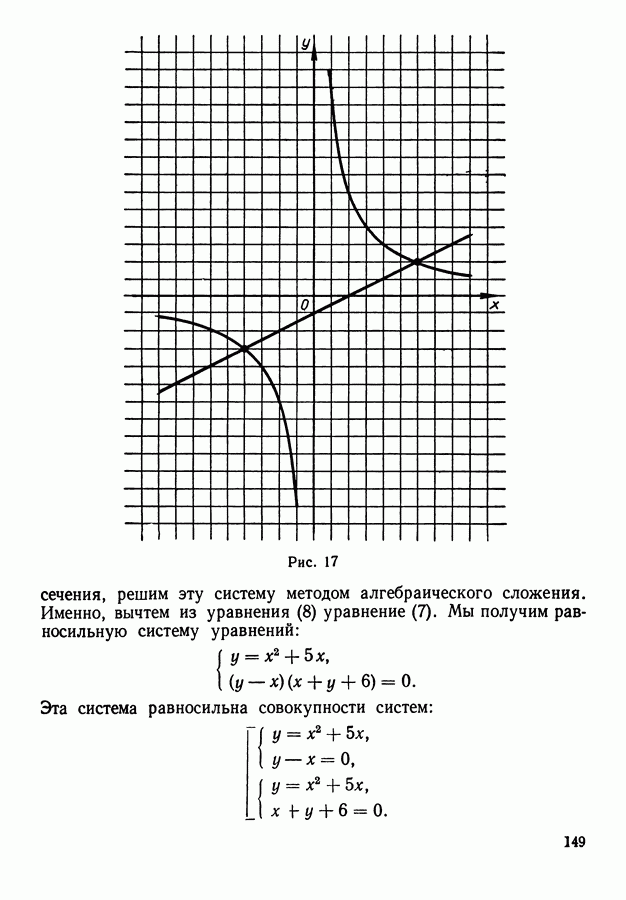
- 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
- 4. Совокупность уравнений.
- 5. Равносильные системы уравнений.
- 6. Метод подстановки.
- 7. Метод алгебраического сложения уравнений.
- 8. Метод введения новых неизвестных.
- 9. Системы однородных уравнений.
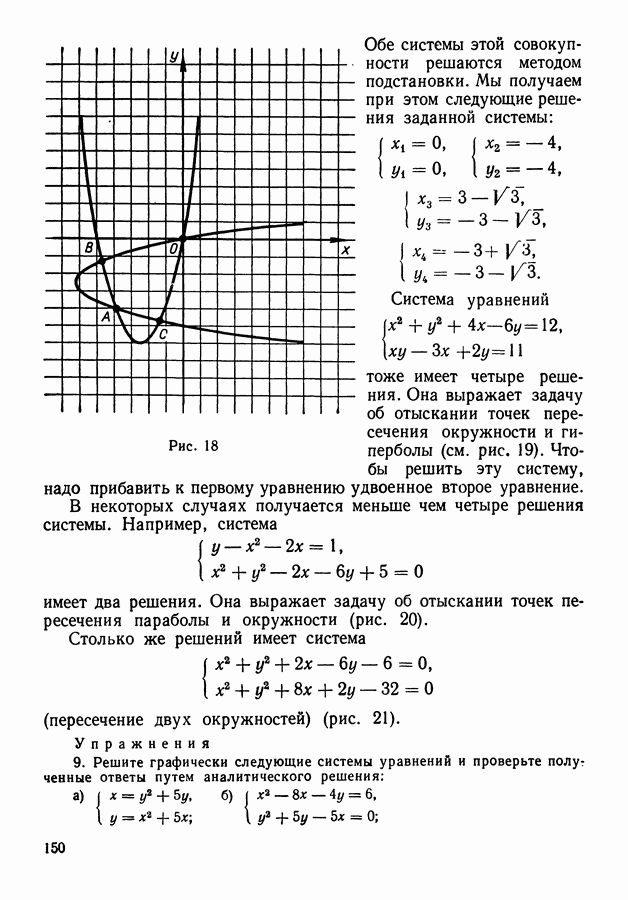
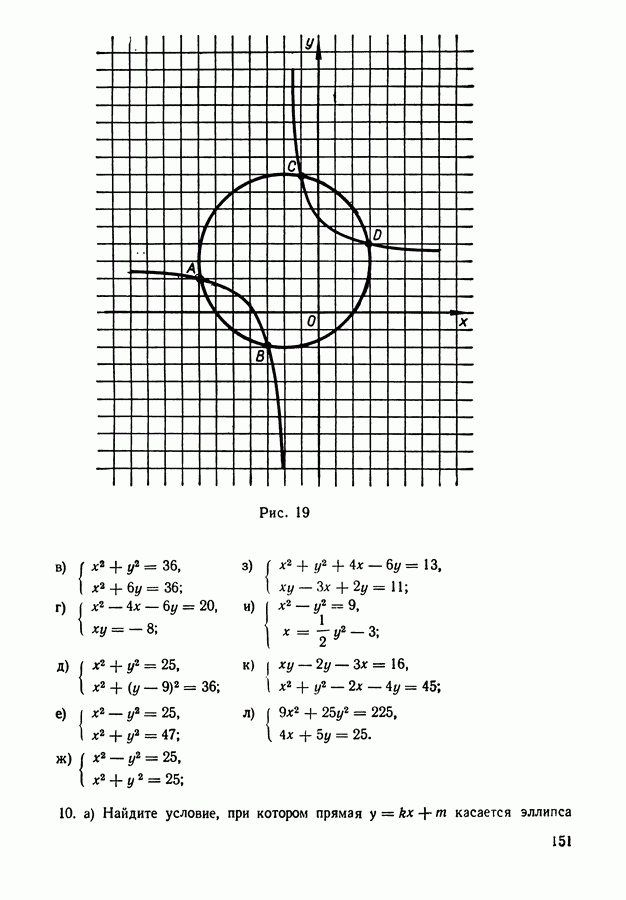
- 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
- § 2. Системы линейных уравнений
- 2. Теоремы о равносильности систем линейных уравнений.
- 3. Пример решения системы линейных уравнений методом Гаусса.
- 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
- 5. Решение обобщенно-треугольной системы линейных уравнений.
- 6. Системы однородных линейных уравнений.
- § 3. Симметрические многочлены и их приложения к решению систем уравнений
- 2. Выражение степенных сумм
- 3. Основная теорема о симметрических многочленах от двух переменных.
- 4. Системы симметрических алгебраических уравнений.
- 5. Применение симметрических многочленов к решению иррациональных уравнений.
- § 4. Неравенства с многими переменными
- 2. Среднее арифметическое и среднее геометрическое трех чисел.
- 3. Неравенство Коши (двумерный вариант).
- 4. Задачи на наибольшие и наименьшие значения.
- § 5. Решение неравенств
- 2. Неравенства с двумя переменными.
- 3. Задание областей неравенствами и системами неравенств.
- 4. Понятие о линейном программировании.
- 5. Краткие исторические сведения.
- Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
- § 1. Комплексные числа в алгебраической форме
- 2. Комплексные числа.
- 3. Сложение комплексных чисел; умножение на действительные числа.
- 4. Умножение комплексных чисел.
- 5. Квадратные уравнения с действительными коэффициентами.
- 6. Деление комплексных чисел.
- 7. Сопряженные комплексные числа.
- 8. Извлечение квадратных корней из комплексных чисел.
- § 2. Тригонометрическая форма комплексных чисел
- 2. Полярная система координат.
- 3. Тригонометрическая форма комплексного числа.
- 4. Умножение и деление комплексных чисел в тригонометрической форме.
- 5. Возведение комплексных чисел в степень. Формула Муавра.
- 6. Извлечение корня из комплексного числа.
- 7. Функции комплексного переменного и преобразования комплексной плоскости.
- § 3. Некоторые виды алгебраических уравнений
- 2. Двучленные уравнения.
- 3. Корни из единицы и построение правильных многоугольников.
- 4. Трехчленные уравнения.
- § 4. Основная теорема алгебры многочленов и ее следствия
- 2. Многочлены с действительными коэффициентами.
- 3. Разложение на множители многочленов с действительными коэффициентами.
- 4. Краткие исторические сведения.
- Глава VI. ЦЕПНЫЕ ДРОБИ
- § 1. Конечные цепные дроби
- 2. Пример цепной дроби.
- 3. Определение цепной дроби.
- 4. Представление рациональных чисел в виде конечной цепной дроби.
- 5. Подходящие дроби.
- 6. Свойства подходящих дробей.
- 8. Подходящие дроби и календарь.
- 9. Приближение цепной дроби подходящими дробями.
- § 2. Бесконечные цепные дроби
- 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
- 3. Цепные дроби как вычислительный инструмент.
- 4. Краткие исторические сведения.
- Глава VII. КОМБИНАТОРИКА
- § 1. Комбинаторные задачи
- § 2. Комбинаторные задачи. Продолжение
- § 3. Определения и формулы
- § 4. Соединения с повторениями
- § 5. Комбинаторные задачи. Окончание
- § 6. Бином Ньютона и его обобщения
- § 7. Краткие исторические сведения
- Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
- § 3. Примеры вычисления вероятностей
- § 4. Полная вероятность. Формула Байеса
- § 5. Повторение испытаний
- § 6. Примеры вычисления вероятностей. Окончание
- § 7. Краткие исторические сведения