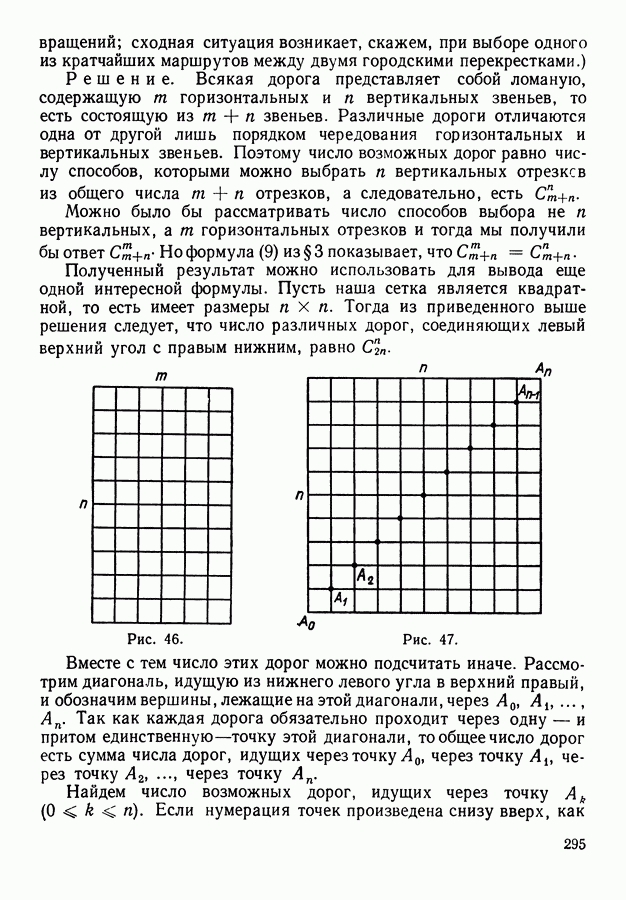
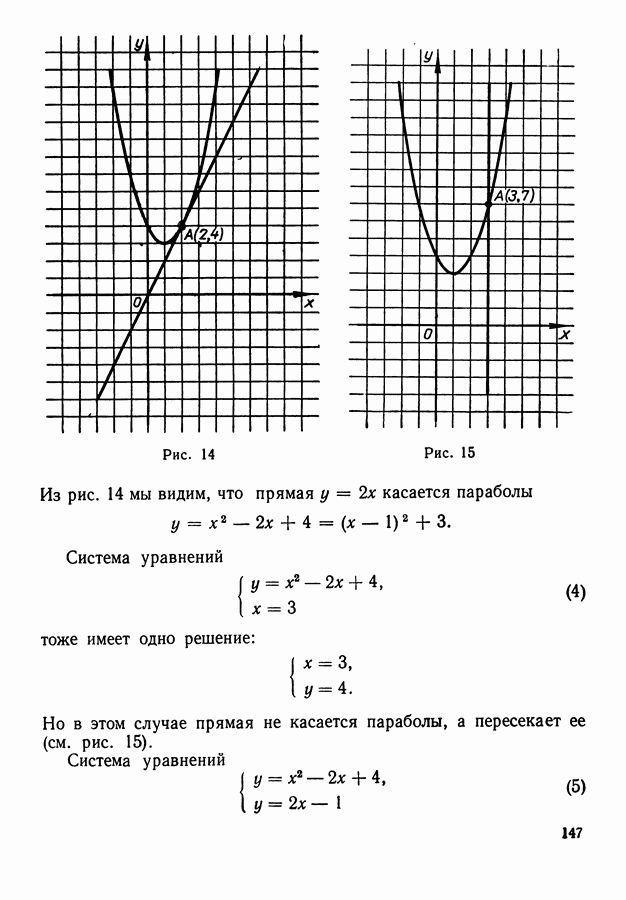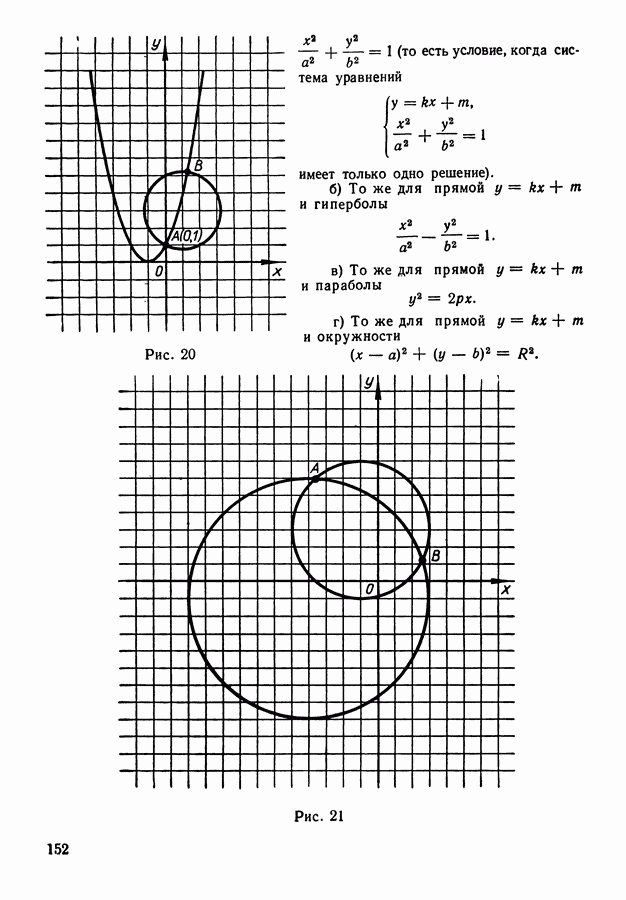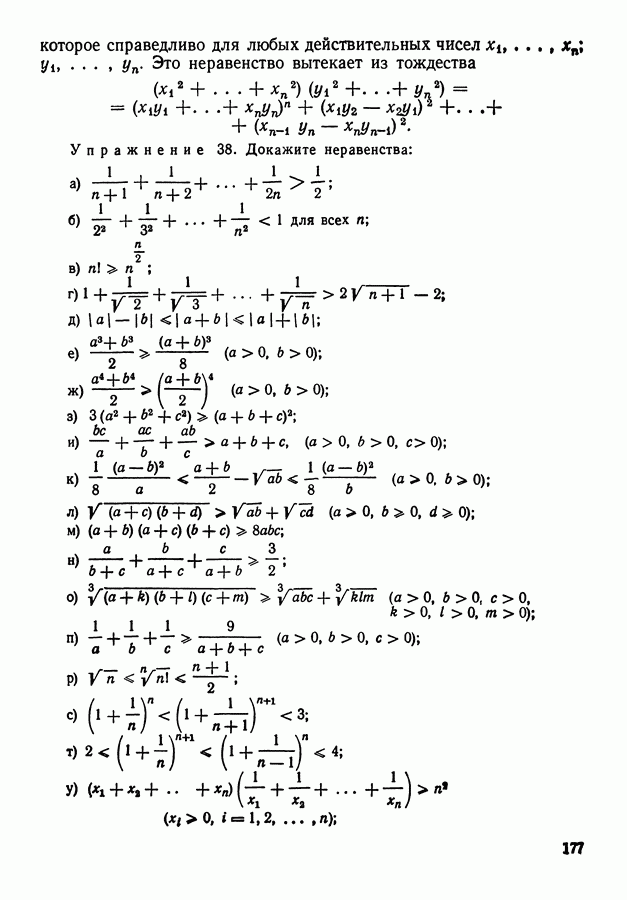| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Полная вероятность. Формула Байеса
При вычислении вероятностей сложных событий часто приходится одновременно применять теоремы сложения и умножения. Рассмотрим следующий пример.
Пример 1. Имеется три одинаковых на вид урны с различным составом белых и черных шаров. Пусть в первой урне находится  белых и
белых и  черных шаров, во второй урне соответственно
черных шаров, во второй урне соответственно  белых и
белых и  черных и, наконец, в третьей —
черных и, наконец, в третьей —  белых и
белых и  черных шара. Выбирается наугад одна из урн, и из нее вынимается один шар. Требуется определить вероятность того, что вынутый шар окажется белым.
черных шара. Выбирается наугад одна из урн, и из нее вынимается один шар. Требуется определить вероятность того, что вынутый шар окажется белым.
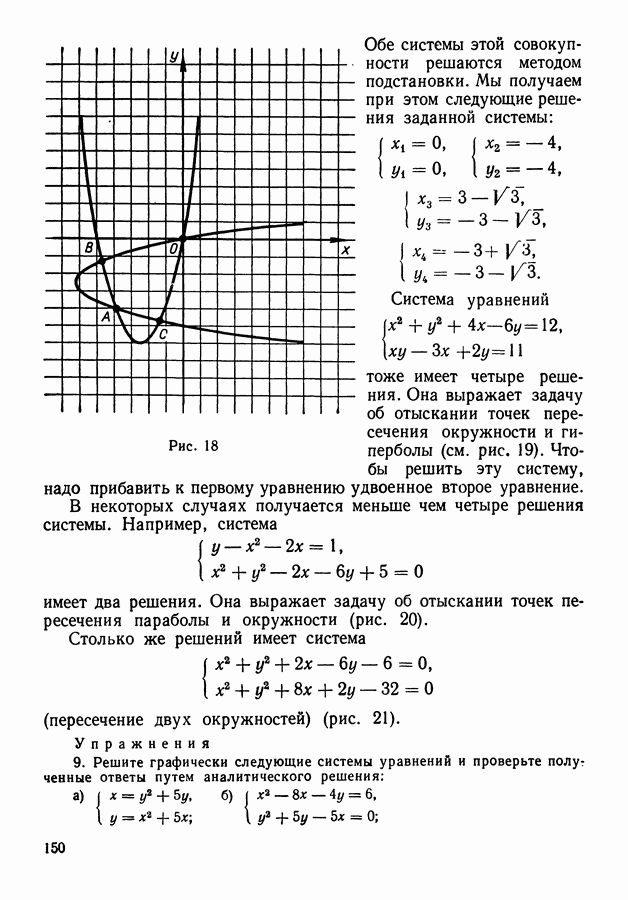
Решение. Сделаем сначала предположение, что шар вынут из первой урны. Можно сказать, что это предположение означает наступление события  или осуществление гипотезы Так как выбор любой урны равновероятен, то вероятность этой гипотезы равна
или осуществление гипотезы Так как выбор любой урны равновероятен, то вероятность этой гипотезы равна  Из предположения о составе шаров следует, что вероятность вынуть белый шар из первой урны (событие
Из предположения о составе шаров следует, что вероятность вынуть белый шар из первой урны (событие  ) равна
) равна

Рассмотрим сложное событие, состоящее в том, что выбрана первая урна и вынутый из нее шар оказался белым. Тогда вероятность такого события в силу теоремы умножения будет равна:

(см. формулу (4) предыдущего параграфа). Точно так же вероятность вынуть белый шар из второй урны есть вероятность сложного
события, состоящего в совмещении события Н2 (выбрана вторая урна) и события А2 (из второй урны вынут белый шар), в результате чего эта вероятность равна

а для третьей урны

Пусть теперь событие А означает извлечение белого шара независимо от того, из какой именно урны он был вынут. Тогда, учитывая, что события  являются несовместными, ибо выбирается лишь одна урна, мы можем воспользоваться для нахождения вероятности события теоремой сложения, которая дает
являются несовместными, ибо выбирается лишь одна урна, мы можем воспользоваться для нахождения вероятности события теоремой сложения, которая дает

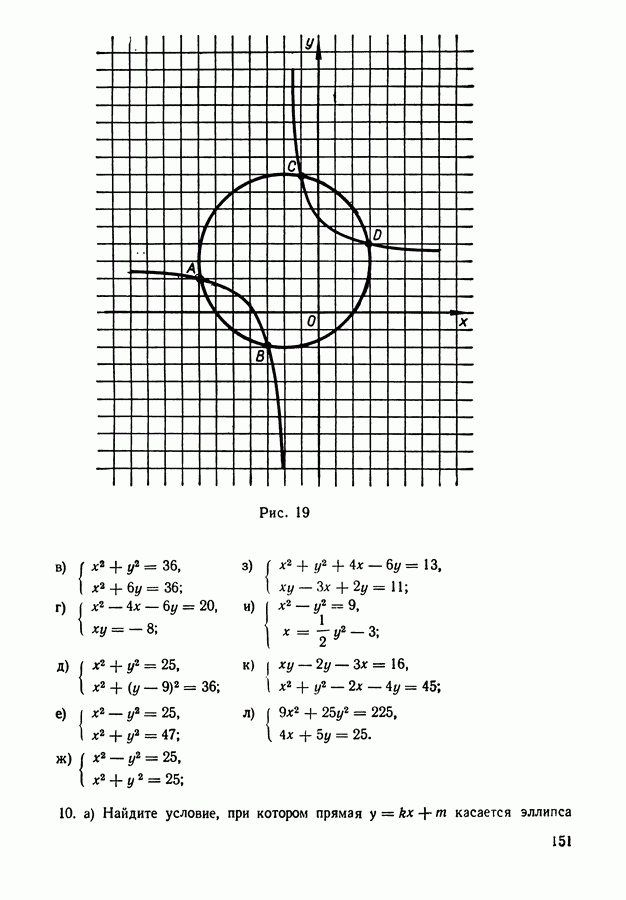
Сформулируем теперь общую задачу. Пусть события Ни  образуют полную группу событий и при наступлении каждого из них, например
образуют полную группу событий и при наступлении каждого из них, например  событие А может наступить с некоторой условной вероятностью
событие А может наступить с некоторой условной вероятностью  Какова вероятность наступления события А?
Какова вероятность наступления события А?
Воспользовавшись, как и в примере, с которого мы начали, теоремой умножения, найдем, что вероятность наступления А при условии наступления  равна
равна

Аналогично

Теперь для нахождения вероятности события А можно воспользоваться теоремой сложения, так как события  несовместны. Складывая все равенства (1) и (2), приходим к формуле:
несовместны. Складывая все равенства (1) и (2), приходим к формуле:

или, короче,

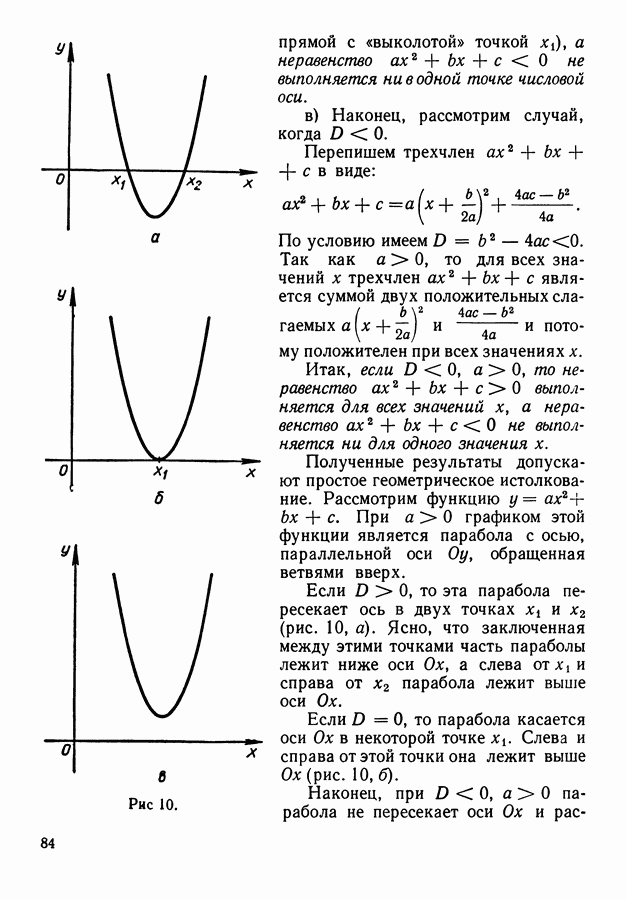
Формула (3) называется формулой полной вероятности.
События  обычно называют в таких случаях гипотезами 1. В рассмотренном выше примере 1 имелось три гипотезы
обычно называют в таких случаях гипотезами 1. В рассмотренном выше примере 1 имелось три гипотезы  которые были равновероятны между собой:
которые были равновероятны между собой:

Пример 2. При разрыве снаряда образуются крупные, средние и мелкие осколки, причем число крупных осколков составляет 0,1 их общего числа, а число средних и мелких — соответственно 0,3 и 0,6 общего числа осколков. При попадании в танк крупный осколок пробивает броню с вероятностью 0,9, средний — с вероятностью 0,3 и мелкий — с вероятностью 0,1. Какова вероятность того, что попавший в броню осколок пробьет ее?
Решение. В нашем примере имеется три гипотезы, вероятности которых  Пользуясь формулой полной вероятности (3), находим:
Пользуясь формулой полной вероятности (3), находим:

Используя формулу полной вероятности, можно получить еще одну важную формулу, которая называется формулой Бейеса или формулой вероятностей гипотез.
Пусть мы имеем некоторую полную группу событий — гипотез  вероятность каждой из которых
вероятность каждой из которых  до производства опыта имеет определенное значение. Предположим, что в результате опыта наступило некоторое событие А. Появление этого нового сведения — наступление события А — может повлечь за собой изменение первоначальных вероятностей гипотез.
до производства опыта имеет определенное значение. Предположим, что в результате опыта наступило некоторое событие А. Появление этого нового сведения — наступление события А — может повлечь за собой изменение первоначальных вероятностей гипотез.
Поясним сказанное примером. Пусть урна содержит три шара белого и черного цвета, однако распределение числа шаров по цветам неизвестно. До производства опыта о содержимом урны можно сделать четыре гипотезы:
1) 3 белых и 0 черных 
2) 2 белых и 1 черный 
3) 1 белый и 2 черных 
4) 0 белых и 3 черных 
которые мы будем считать равновероятными:  Допустим, что в результате опыта был
Допустим, что в результате опыта был
вынут белый шар (событие А). В таком случае вероятность гипотезы  делается равной нулю. Вероятности остальных трех гипотез также изменятся, причем их уже нельзя будет считать равновероятными; вероятность гипотезы
делается равной нулю. Вероятности остальных трех гипотез также изменятся, причем их уже нельзя будет считать равновероятными; вероятность гипотезы  например, больше, чем вероятность гипотезы
например, больше, чем вероятность гипотезы 
Поставим вопрос в общем виде: выяснить, каковы будут вероятности гипотез  после опыта в предположении, что в результате опыта наступило событие А.
после опыта в предположении, что в результате опыта наступило событие А.
Обозначим вероятности гипотез  до производства опыта соответственно через
до производства опыта соответственно через 

Вероятности тех же гипотез после опыта, в результате которого наступило событие А, обозначим через 

причем снова

так как события  по-прежнему несовместны и единственно возможны. Обозначим условную вероятность
по-прежнему несовместны и единственно возможны. Обозначим условную вероятность  через
через  и полную вероятность события А через
и полную вероятность события А через 
Пользуясь равенством (6) предыдущего параграфа, которое следует из теоремы умножения, напишем:

или с введенными обозначениями

Отсюда

Подставляя сюда выражение для полной вероятности Р из формулы (3), получим:

Нетрудно проверить, что сумма всех вероятностей  действительно равна единице.
действительно равна единице.
Формула (4), дающая выражение вероятности гипотезы  после опыта, и есть нужная нам формула Бейеса.
после опыта, и есть нужная нам формула Бейеса.
Вернемся снова к нашему примеру. В соответствии с принятыми обозначениями имеем:
Далее находим:

Окончательно получим:

Аналогично:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ
- ВВЕДЕНИЕ
- 2. Числовые множества.
- 3. Пустое множество.
- 4. Подмножество.
- 5. Пересечение множеств.
- 6. Сложение множеств.
- 7. Разбиение множеств.
- 8. Вычитание множеств.
- 9. Отображение множеств.
- 10. Краткие исторические сведения.
- Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
- § 1. Тождественные преобразования многочленов
- 2. Целые рациональные выражения и функции.
- 3. Степень с натуральным показателем и ее свойства.
- 4. Многочлены.
- 5. Умножение многочленов.
- 6. Числовые кольца и поля.
- 7. Кольцо многочленов над данным числовым полем.
- 8. Бином Ньютона.
- § 2. Деление многочленов. Корни многочленов
- 2. Теорема Безу. Схема Горнера.
- 3. Корни многочлена.
- 4. Интерполяционные формулы.
- 5. Кратные корни.
- 6. Многочлены второй степени.
- 7. Многочлены с целыми коэффициентами.
- 8. Краткие исторические сведения.
- Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1. Общая теория уравнений
- 2. Область допустимых значений.
- 3. Уравнения.
- 4. Совокупности уравнений.
- 5. Преобразования уравнений.
- 6. Теоремы о равносильности уравнений.
- § 2. Уравнения с одним неизвестным
- 2. Метод разложения на множители.
- 3. Метод введения нового неизвестного.
- 4. Биквадратные уравнения.
- 5. Возвратные уравнения 3-й и 4-й степеней.
- § 3. Функциональные неравенства
- 2. Равносильные неравенства.
- 3. Доказательство неравенств.
- 4. Линейные неравенства.
- 5. Решение неравенств второй степени.
- 6. Решение алгебраических неравенств высших степеней.
- 7. Краткие исторические сведения.
- Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
- § 1. Степени с целым показателем
- 2. Степень с нулевым показателем.
- 3. Степень с целым отрицательным показателем.
- § 2. Корни. Степени с рациональными показателями
- 2. Степени с рациональными показателями.
- 3. Свойства степеней с рациональными показателями.
- § 3. Иррациональные алгебраические выражения
- 2. Одночленные иррациональные выражения.
- 3. Сокращение показателей и приведение корней к общему показателю.
- 4. Извлечение корня из произведения и степени.
- 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.
- 6. Возведение корня в степень.
- 7. Извлечение корня из корня.
- 8. Подобные корни.
- 9. Сложение и вычитание корней.
- 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
- 11. Преобразование выражений вида …
- 12. Смешанные задачи на преобразование иррациональных выражений.
- § 4. Иррациональные уравнения и неравенства
- 2. Сведение иррациональных уравнений к рациональным.
- 3. Уединение радикала.
- 4. Введение нового неизвестного.
- 5. Особые случаи решения иррациональных уравнений.
- 6. Иррациональные неравенства.
- 7. Краткие историчесие сведения.
- Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 1. Системы алгебраических уравнений
- 2. Системы уравнений.
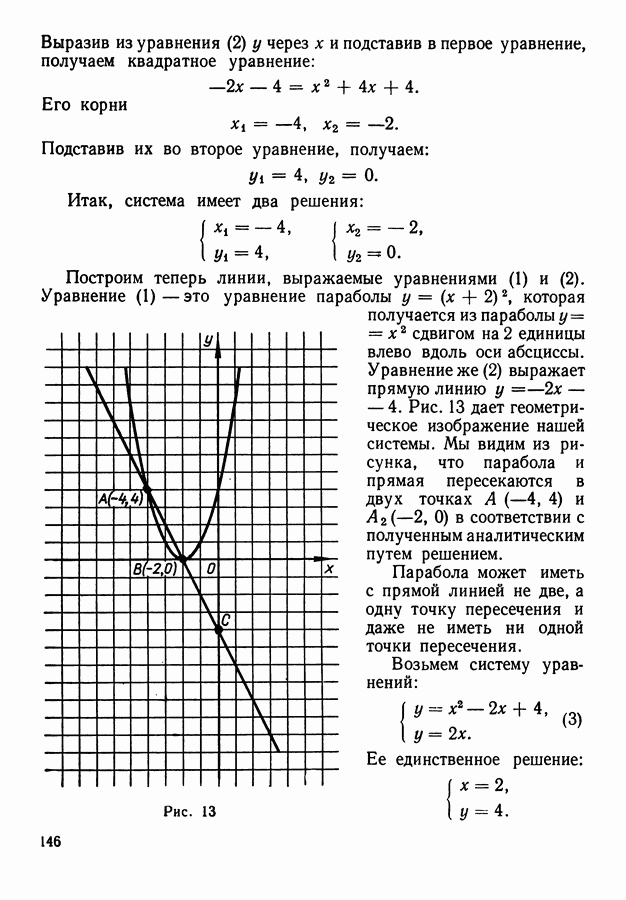
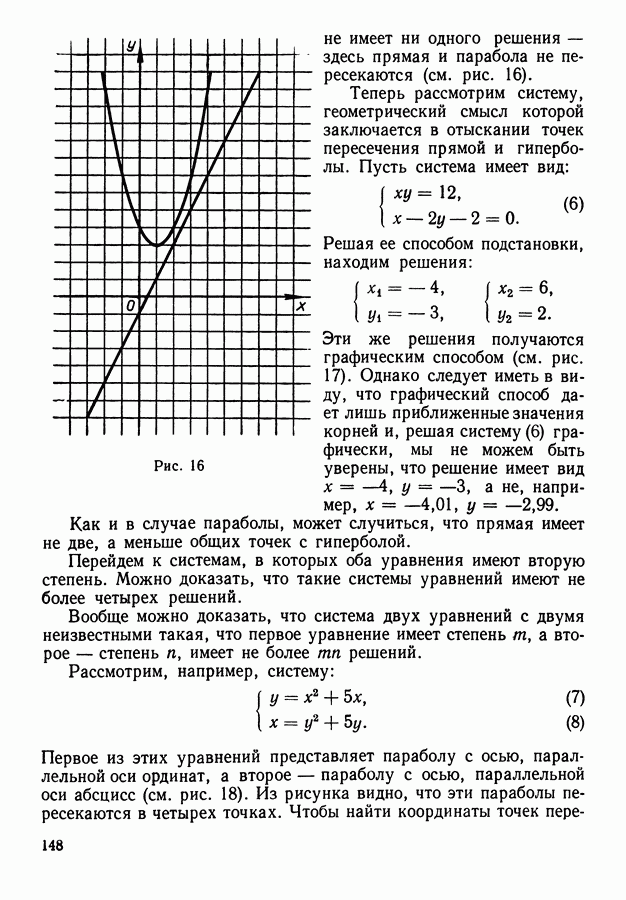
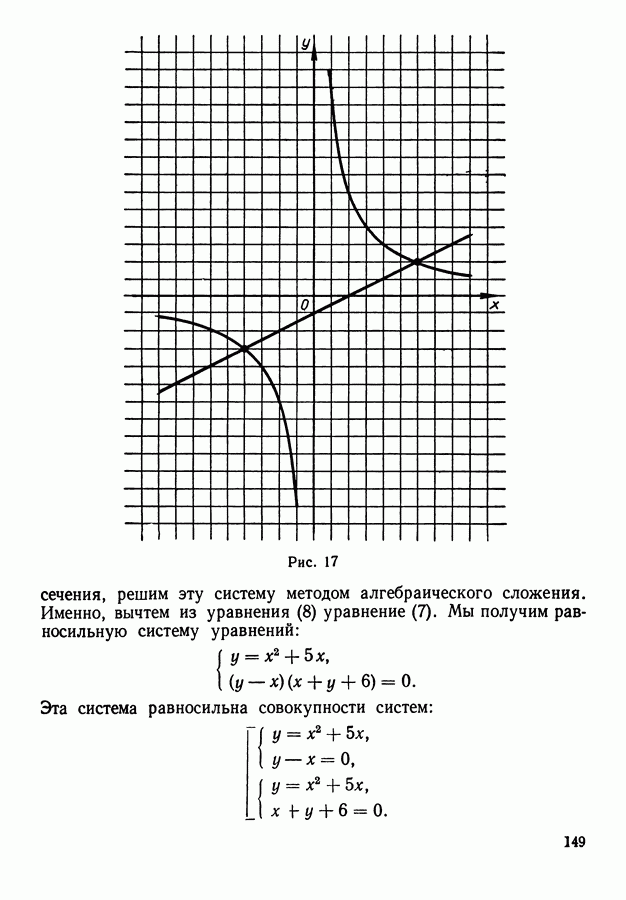
- 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
- 4. Совокупность уравнений.
- 5. Равносильные системы уравнений.
- 6. Метод подстановки.
- 7. Метод алгебраического сложения уравнений.
- 8. Метод введения новых неизвестных.
- 9. Системы однородных уравнений.
- 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
- § 2. Системы линейных уравнений
- 2. Теоремы о равносильности систем линейных уравнений.
- 3. Пример решения системы линейных уравнений методом Гаусса.
- 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
- 5. Решение обобщенно-треугольной системы линейных уравнений.
- 6. Системы однородных линейных уравнений.
- § 3. Симметрические многочлены и их приложения к решению систем уравнений
- 2. Выражение степенных сумм
- 3. Основная теорема о симметрических многочленах от двух переменных.
- 4. Системы симметрических алгебраических уравнений.
- 5. Применение симметрических многочленов к решению иррациональных уравнений.
- § 4. Неравенства с многими переменными
- 2. Среднее арифметическое и среднее геометрическое трех чисел.
- 3. Неравенство Коши (двумерный вариант).
- 4. Задачи на наибольшие и наименьшие значения.
- § 5. Решение неравенств
- 2. Неравенства с двумя переменными.
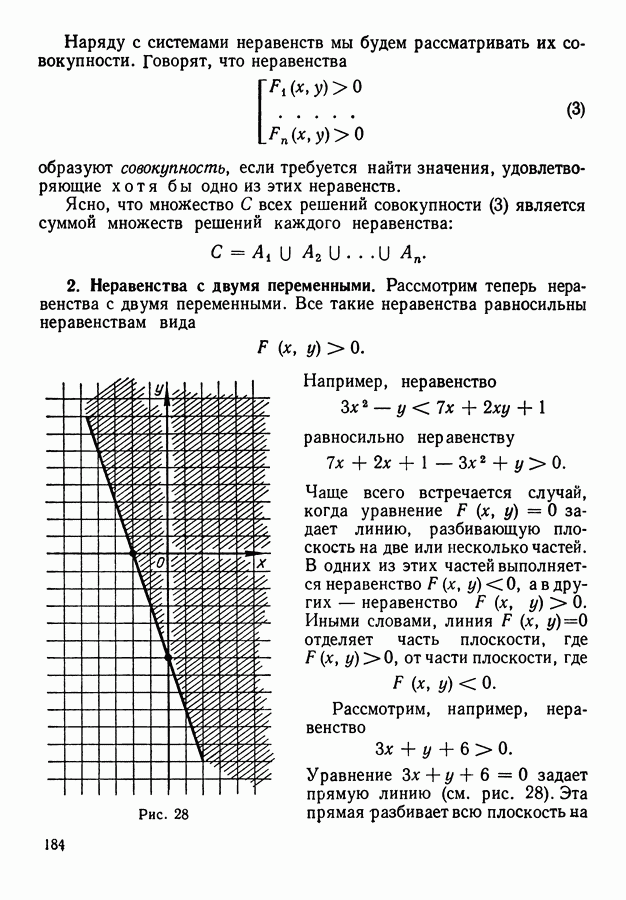
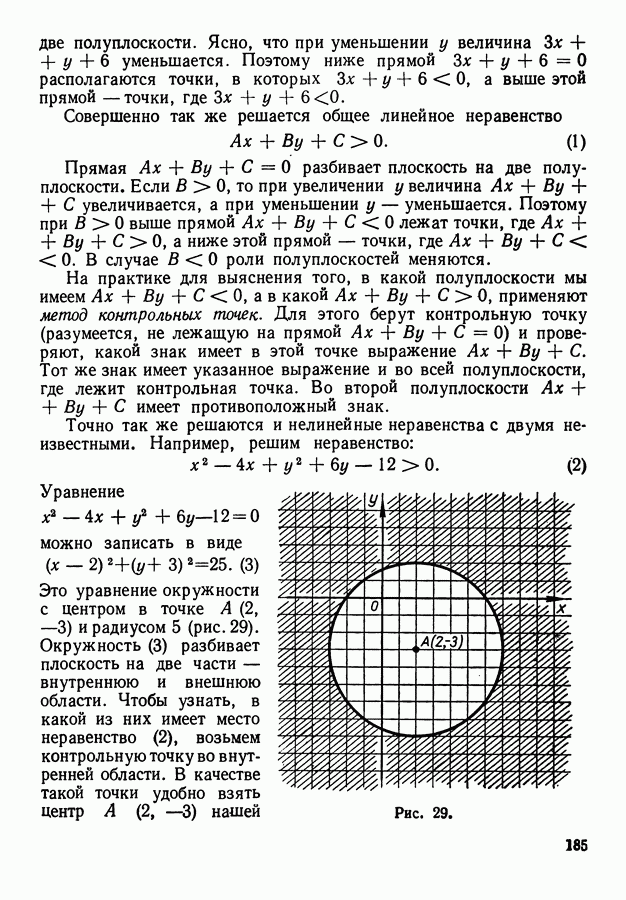
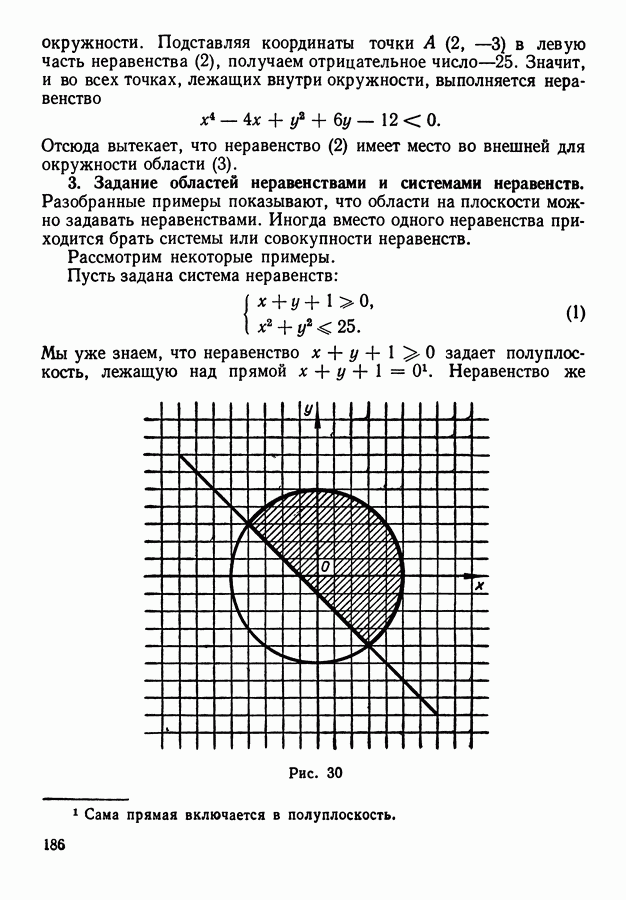
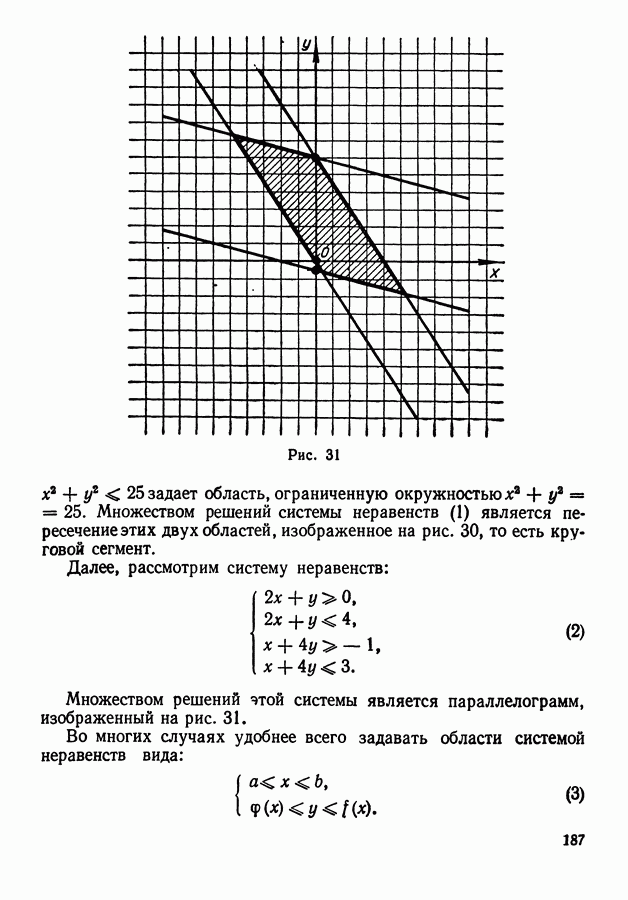
- 3. Задание областей неравенствами и системами неравенств.
- 4. Понятие о линейном программировании.
- 5. Краткие исторические сведения.
- Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
- § 1. Комплексные числа в алгебраической форме
- 2. Комплексные числа.
- 3. Сложение комплексных чисел; умножение на действительные числа.
- 4. Умножение комплексных чисел.
- 5. Квадратные уравнения с действительными коэффициентами.
- 6. Деление комплексных чисел.
- 7. Сопряженные комплексные числа.
- 8. Извлечение квадратных корней из комплексных чисел.
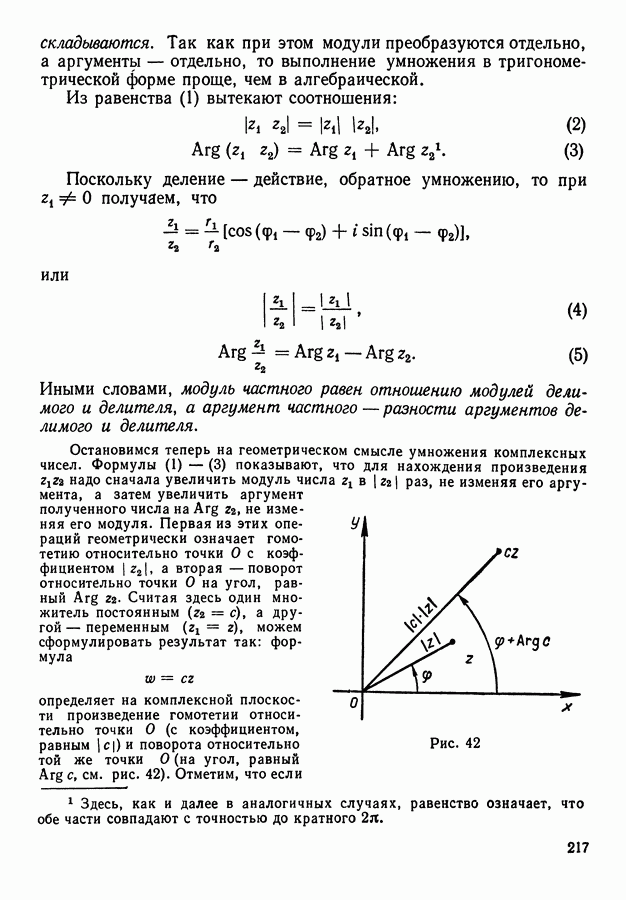
- § 2. Тригонометрическая форма комплексных чисел
- 2. Полярная система координат.
- 3. Тригонометрическая форма комплексного числа.
- 4. Умножение и деление комплексных чисел в тригонометрической форме.
- 5. Возведение комплексных чисел в степень. Формула Муавра.
- 6. Извлечение корня из комплексного числа.
- 7. Функции комплексного переменного и преобразования комплексной плоскости.
- § 3. Некоторые виды алгебраических уравнений
- 2. Двучленные уравнения.
- 3. Корни из единицы и построение правильных многоугольников.
- 4. Трехчленные уравнения.
- § 4. Основная теорема алгебры многочленов и ее следствия
- 2. Многочлены с действительными коэффициентами.
- 3. Разложение на множители многочленов с действительными коэффициентами.
- 4. Краткие исторические сведения.
- Глава VI. ЦЕПНЫЕ ДРОБИ
- § 1. Конечные цепные дроби
- 2. Пример цепной дроби.
- 3. Определение цепной дроби.
- 4. Представление рациональных чисел в виде конечной цепной дроби.
- 5. Подходящие дроби.
- 6. Свойства подходящих дробей.
- 8. Подходящие дроби и календарь.
- 9. Приближение цепной дроби подходящими дробями.
- § 2. Бесконечные цепные дроби
- 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
- 3. Цепные дроби как вычислительный инструмент.
- 4. Краткие исторические сведения.
- Глава VII. КОМБИНАТОРИКА
- § 1. Комбинаторные задачи
- § 2. Комбинаторные задачи. Продолжение
- § 3. Определения и формулы
- § 4. Соединения с повторениями
- § 5. Комбинаторные задачи. Окончание
- § 6. Бином Ньютона и его обобщения
- § 7. Краткие исторические сведения
- Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
- § 3. Примеры вычисления вероятностей
- § 4. Полная вероятность. Формула Байеса
- § 5. Повторение испытаний
- § 6. Примеры вычисления вероятностей. Окончание
- § 7. Краткие исторические сведения