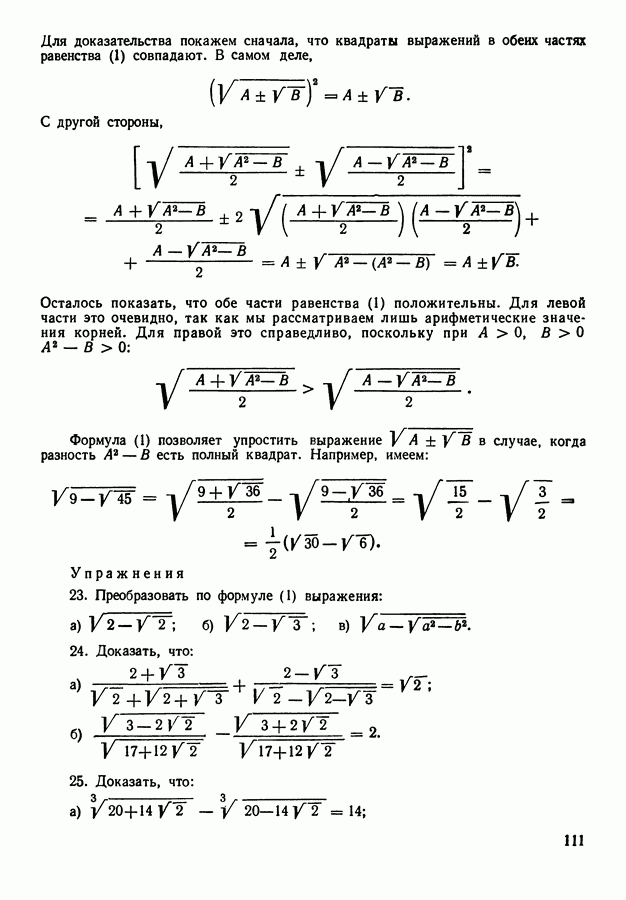| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. Подмножество.
Пусть даны два множества Л и Б, причем каждый элемент первого множества является элементом второго множества. Тогда множество А называют подмножеством (или частью) множества В. В этом случае пишут: А а В.
Примеры подмножеств:
а) числовой отрезок [1,3] есть подмножество числового отрезка [0, 4];

Рис. 5
б) множество всех квадратов есть подмножество множества всех прямоугольников;
в) множество всех целых чисел есть подмножество множества всех рациональных чисел.
Отметим, что пустое множество 0 является подмножеством любого множества А. Каждое множество А является одним из своих подмножеств. Эти два подмножества (0 и все множество) называют несобственными. Все остальные подмножества называют собственными.
Множества часто изображают наглядно как множество точек геометрической фигуры. Тогда подмножество — это множество точек части фигуры (рис. 5).
Упражнения
1. Даны множества:
а) множество А всех трапеций, б) множество В всех прямоугольников,
в) множество С всех четырехугольников, г) множество  всех квадратов, д) множество Е всех параллелограммов. Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
всех квадратов, д) множество Е всех параллелограммов. Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
2. Даны множества:
а) множество А всех рациональных чисел, б) множество В всех целых чисел, в) множество С всех действительных чисел, г) множество  всех четных натуральных чисел, д) множество Е всех натуральных чисел. Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
всех четных натуральных чисел, д) множество Е всех натуральных чисел. Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
3. Даны множества:
а) множество А учеников IX класса данной средней школы, б) множество В всех учеников данной средней школы, в) множество С мальчиков, обучающихся в IX классе данной средней школы, г) множество D всех учащихся средних школ в СССР, д) множество Е всех учащихся средних школ в городе, где находится школа. Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ
- ВВЕДЕНИЕ
- 2. Числовые множества.
- 3. Пустое множество.
- 4. Подмножество.
- 5. Пересечение множеств.
- 6. Сложение множеств.
- 7. Разбиение множеств.
- 8. Вычитание множеств.
- 9. Отображение множеств.
- 10. Краткие исторические сведения.
- Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
- § 1. Тождественные преобразования многочленов
- 2. Целые рациональные выражения и функции.
- 3. Степень с натуральным показателем и ее свойства.
- 4. Многочлены.
- 5. Умножение многочленов.
- 6. Числовые кольца и поля.
- 7. Кольцо многочленов над данным числовым полем.
- 8. Бином Ньютона.
- § 2. Деление многочленов. Корни многочленов
- 2. Теорема Безу. Схема Горнера.
- 3. Корни многочлена.
- 4. Интерполяционные формулы.
- 5. Кратные корни.
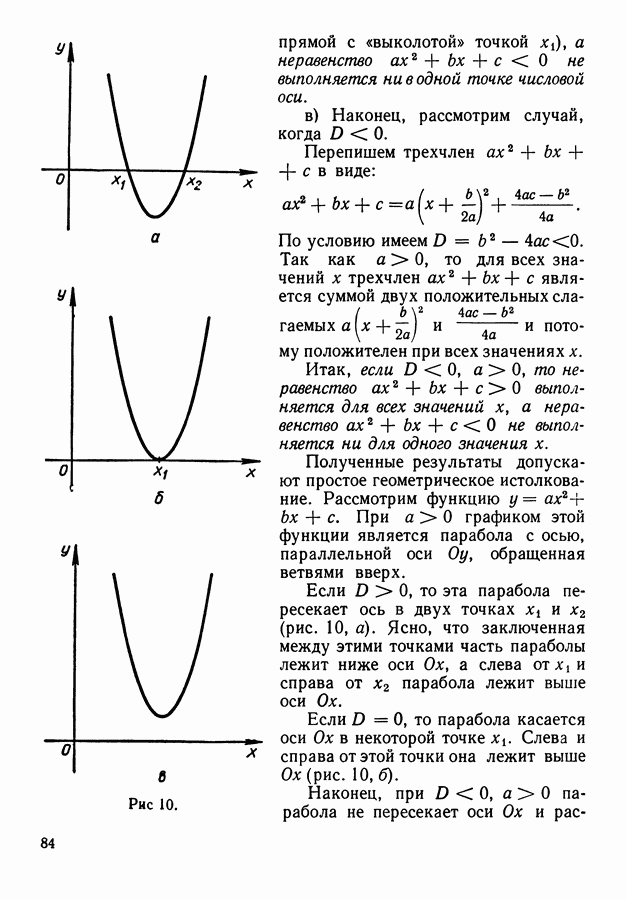
- 6. Многочлены второй степени.
- 7. Многочлены с целыми коэффициентами.
- 8. Краткие исторические сведения.
- Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1. Общая теория уравнений
- 2. Область допустимых значений.
- 3. Уравнения.
- 4. Совокупности уравнений.
- 5. Преобразования уравнений.
- 6. Теоремы о равносильности уравнений.
- § 2. Уравнения с одним неизвестным
- 2. Метод разложения на множители.
- 3. Метод введения нового неизвестного.
- 4. Биквадратные уравнения.
- 5. Возвратные уравнения 3-й и 4-й степеней.
- § 3. Функциональные неравенства
- 2. Равносильные неравенства.
- 3. Доказательство неравенств.
- 4. Линейные неравенства.
- 5. Решение неравенств второй степени.
- 6. Решение алгебраических неравенств высших степеней.
- 7. Краткие исторические сведения.
- Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
- § 1. Степени с целым показателем
- 2. Степень с нулевым показателем.
- 3. Степень с целым отрицательным показателем.
- § 2. Корни. Степени с рациональными показателями
- 2. Степени с рациональными показателями.
- 3. Свойства степеней с рациональными показателями.
- § 3. Иррациональные алгебраические выражения
- 2. Одночленные иррациональные выражения.
- 3. Сокращение показателей и приведение корней к общему показателю.
- 4. Извлечение корня из произведения и степени.
- 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.
- 6. Возведение корня в степень.
- 7. Извлечение корня из корня.
- 8. Подобные корни.
- 9. Сложение и вычитание корней.
- 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
- 11. Преобразование выражений вида …
- 12. Смешанные задачи на преобразование иррациональных выражений.
- § 4. Иррациональные уравнения и неравенства
- 2. Сведение иррациональных уравнений к рациональным.
- 3. Уединение радикала.
- 4. Введение нового неизвестного.
- 5. Особые случаи решения иррациональных уравнений.
- 6. Иррациональные неравенства.
- 7. Краткие историчесие сведения.
- Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 1. Системы алгебраических уравнений
- 2. Системы уравнений.
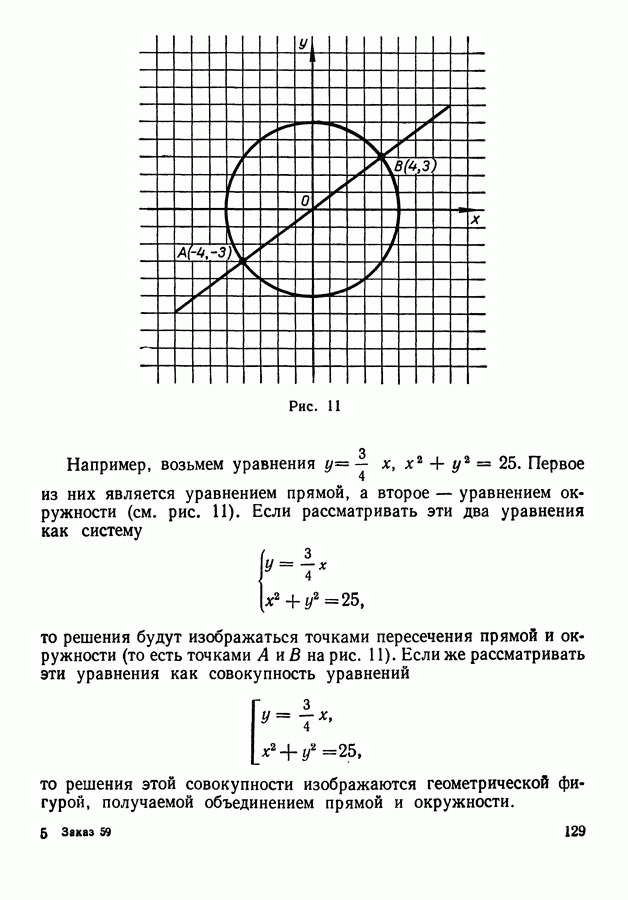
- 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
- 4. Совокупность уравнений.
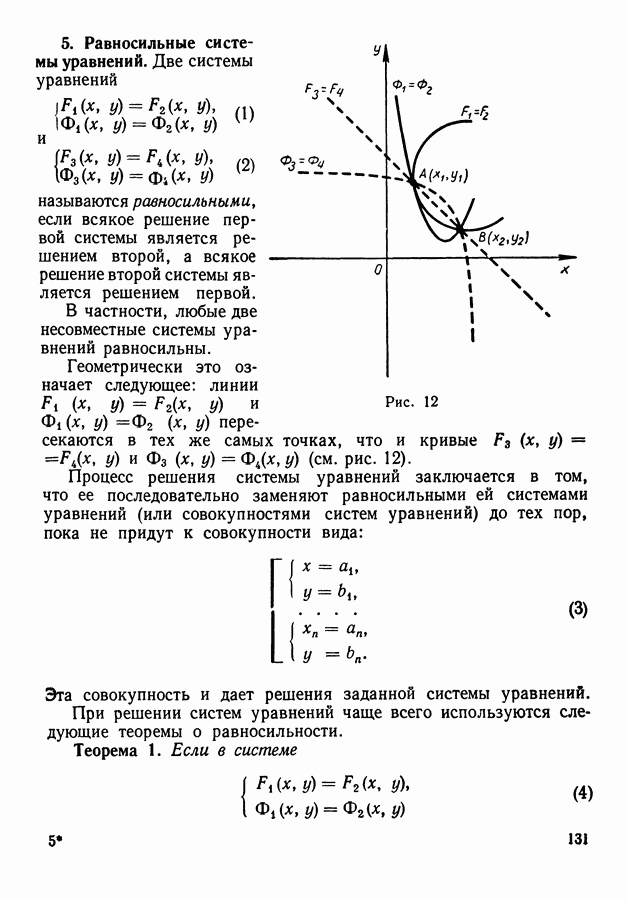
- 5. Равносильные системы уравнений.
- 6. Метод подстановки.
- 7. Метод алгебраического сложения уравнений.
- 8. Метод введения новых неизвестных.
- 9. Системы однородных уравнений.
- 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
- § 2. Системы линейных уравнений
- 2. Теоремы о равносильности систем линейных уравнений.
- 3. Пример решения системы линейных уравнений методом Гаусса.
- 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
- 5. Решение обобщенно-треугольной системы линейных уравнений.
- 6. Системы однородных линейных уравнений.
- § 3. Симметрические многочлены и их приложения к решению систем уравнений
- 2. Выражение степенных сумм
- 3. Основная теорема о симметрических многочленах от двух переменных.
- 4. Системы симметрических алгебраических уравнений.
- 5. Применение симметрических многочленов к решению иррациональных уравнений.
- § 4. Неравенства с многими переменными
- 2. Среднее арифметическое и среднее геометрическое трех чисел.
- 3. Неравенство Коши (двумерный вариант).
- 4. Задачи на наибольшие и наименьшие значения.
- § 5. Решение неравенств
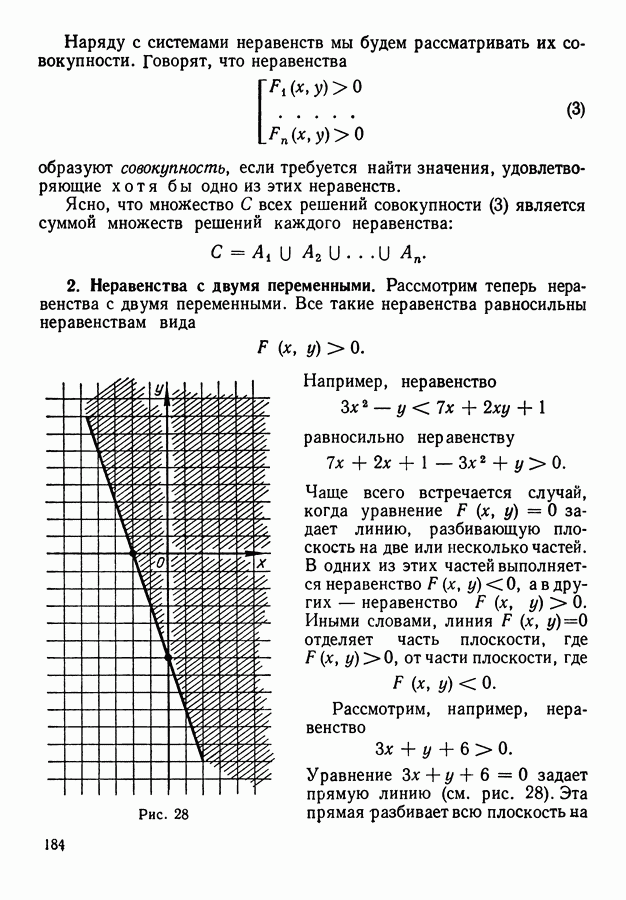
- 2. Неравенства с двумя переменными.
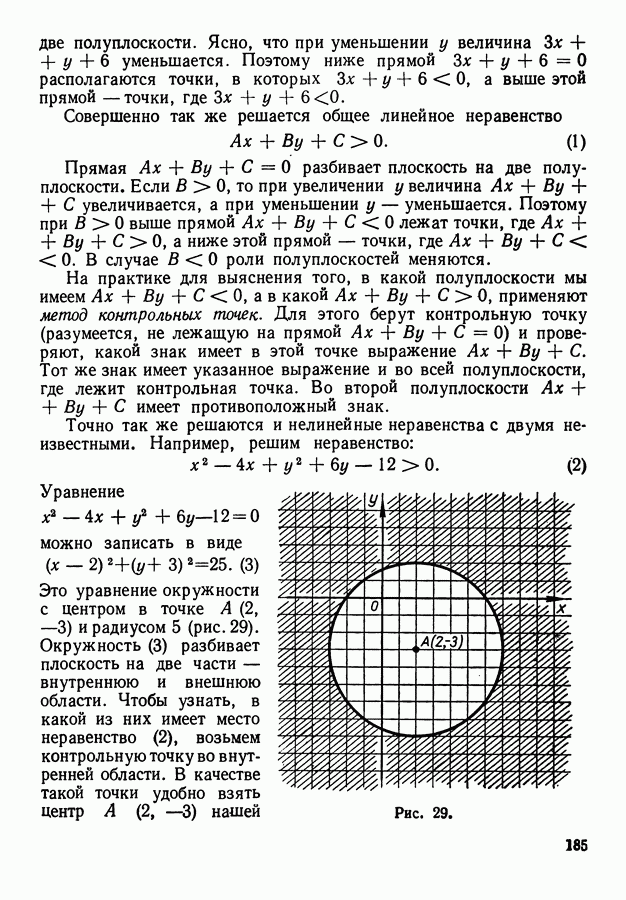
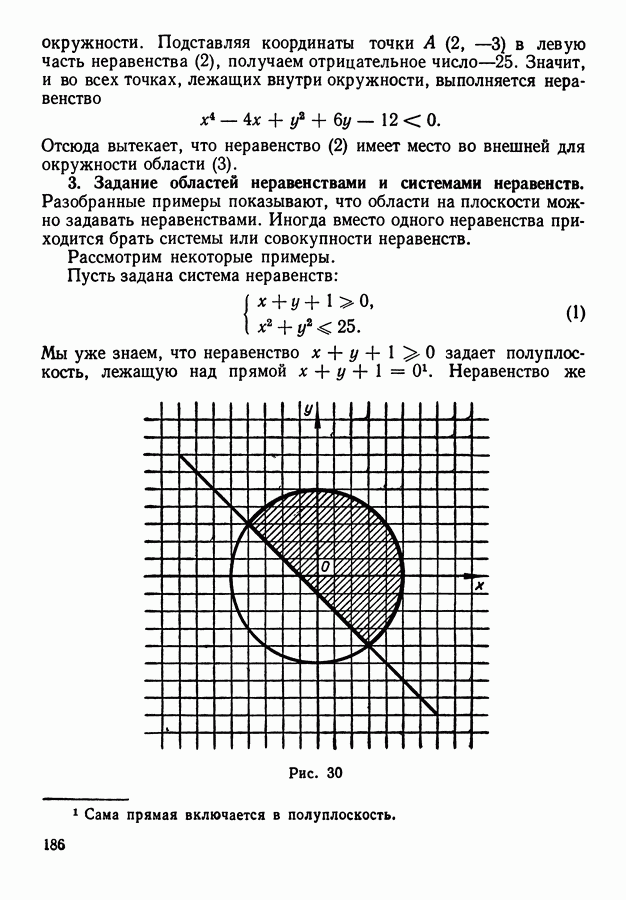
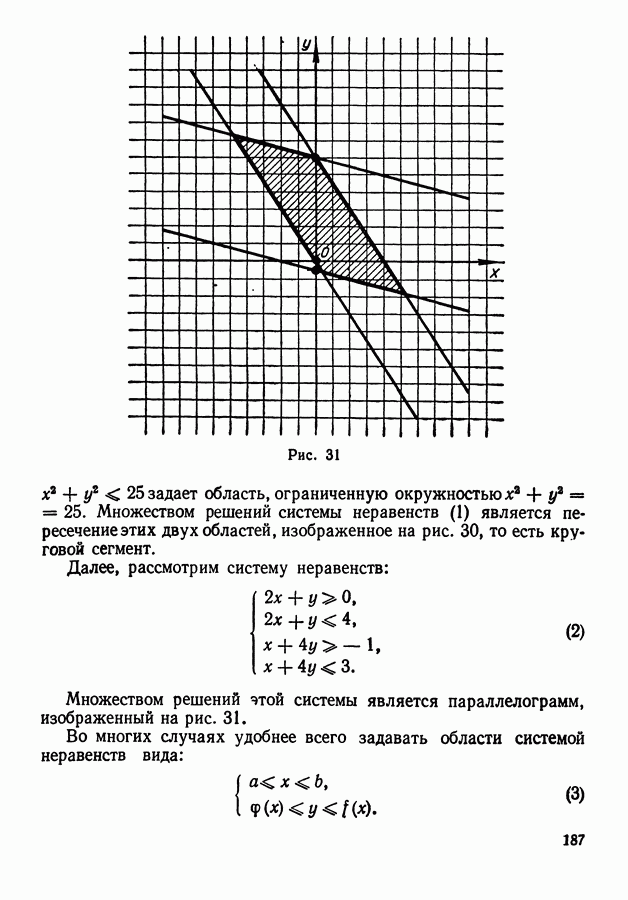
- 3. Задание областей неравенствами и системами неравенств.
- 4. Понятие о линейном программировании.
- 5. Краткие исторические сведения.
- Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
- § 1. Комплексные числа в алгебраической форме
- 2. Комплексные числа.
- 3. Сложение комплексных чисел; умножение на действительные числа.
- 4. Умножение комплексных чисел.
- 5. Квадратные уравнения с действительными коэффициентами.
- 6. Деление комплексных чисел.
- 7. Сопряженные комплексные числа.
- 8. Извлечение квадратных корней из комплексных чисел.
- § 2. Тригонометрическая форма комплексных чисел
- 2. Полярная система координат.
- 3. Тригонометрическая форма комплексного числа.
- 4. Умножение и деление комплексных чисел в тригонометрической форме.
- 5. Возведение комплексных чисел в степень. Формула Муавра.
- 6. Извлечение корня из комплексного числа.
- 7. Функции комплексного переменного и преобразования комплексной плоскости.
- § 3. Некоторые виды алгебраических уравнений
- 2. Двучленные уравнения.
- 3. Корни из единицы и построение правильных многоугольников.
- 4. Трехчленные уравнения.
- § 4. Основная теорема алгебры многочленов и ее следствия
- 2. Многочлены с действительными коэффициентами.
- 3. Разложение на множители многочленов с действительными коэффициентами.
- 4. Краткие исторические сведения.
- Глава VI. ЦЕПНЫЕ ДРОБИ
- § 1. Конечные цепные дроби
- 2. Пример цепной дроби.
- 3. Определение цепной дроби.
- 4. Представление рациональных чисел в виде конечной цепной дроби.
- 5. Подходящие дроби.
- 6. Свойства подходящих дробей.
- 8. Подходящие дроби и календарь.
- 9. Приближение цепной дроби подходящими дробями.
- § 2. Бесконечные цепные дроби
- 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
- 3. Цепные дроби как вычислительный инструмент.
- 4. Краткие исторические сведения.
- Глава VII. КОМБИНАТОРИКА
- § 1. Комбинаторные задачи
- § 2. Комбинаторные задачи. Продолжение
- § 3. Определения и формулы
- § 4. Соединения с повторениями
- § 5. Комбинаторные задачи. Окончание
- § 6. Бином Ньютона и его обобщения
- § 7. Краткие исторические сведения
- Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
- § 3. Примеры вычисления вероятностей
- § 4. Полная вероятность. Формула Байеса
- § 5. Повторение испытаний
- § 6. Примеры вычисления вероятностей. Окончание
- § 7. Краткие исторические сведения