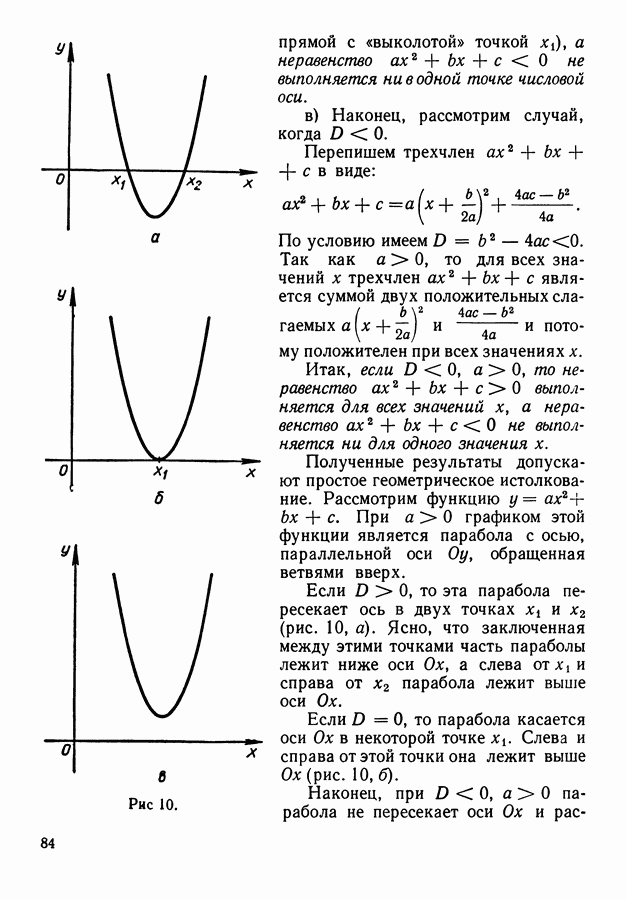
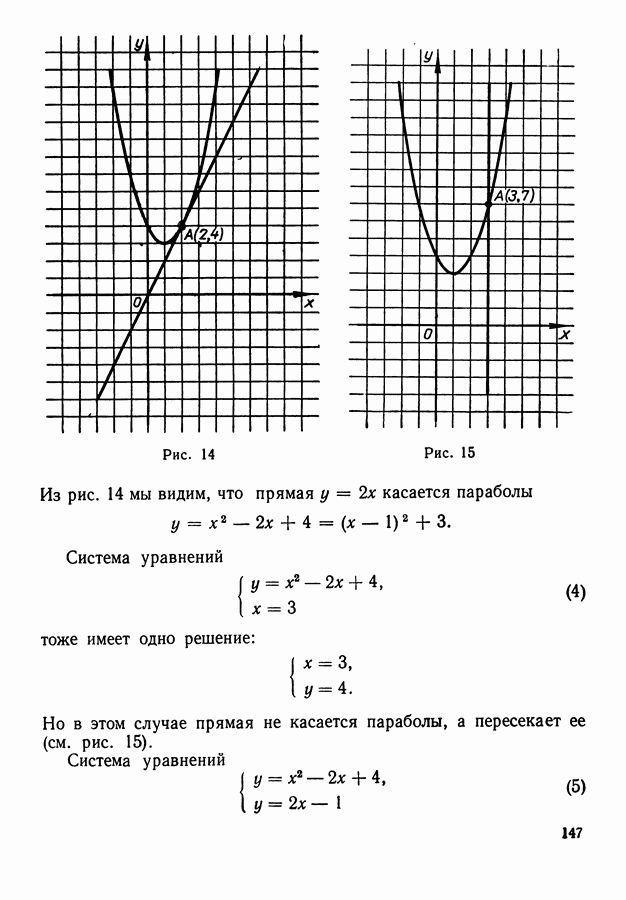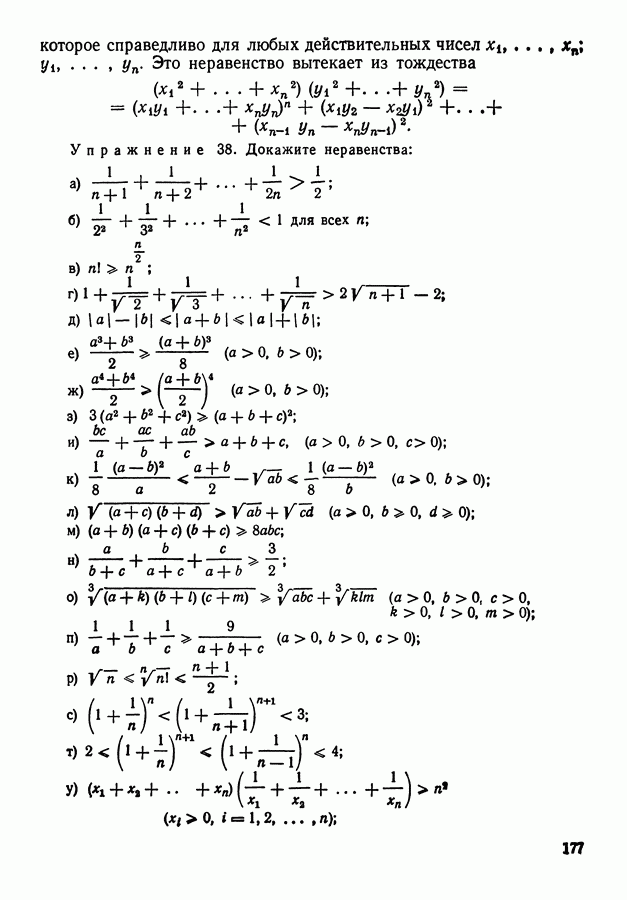| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Определения и формулы
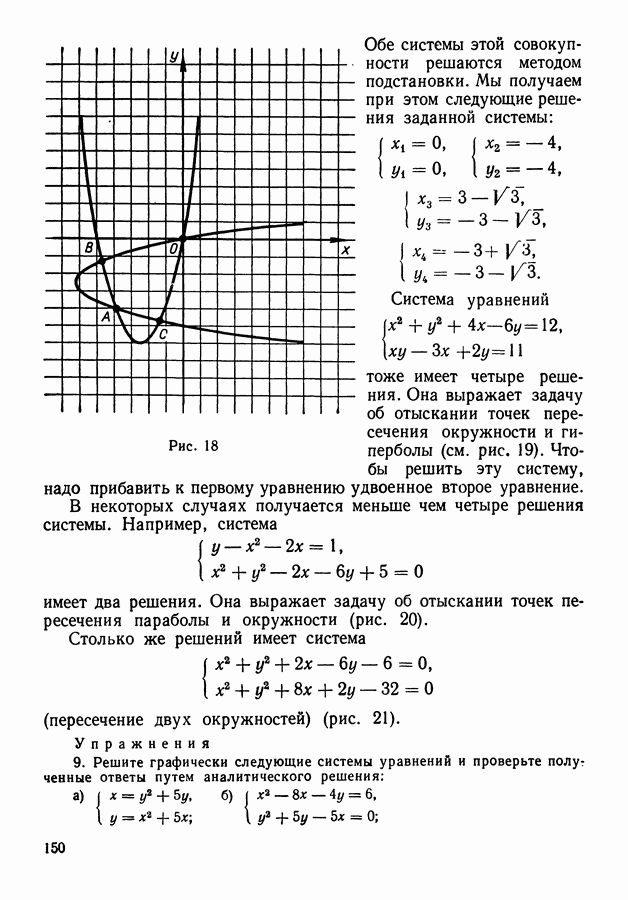
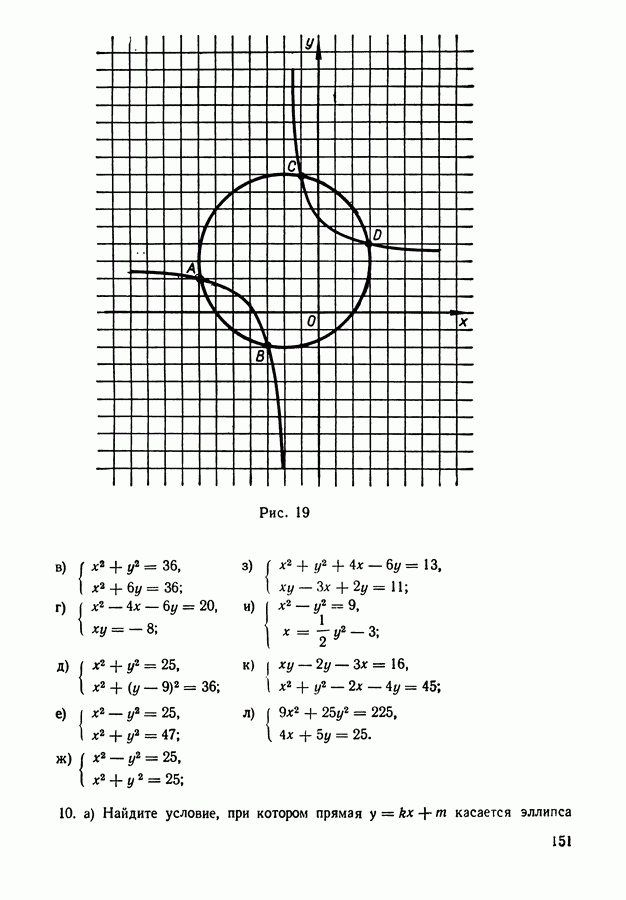
Примеров, рассмотренных в двух предыдущих параграфах, вполне достаточно, чтобы заметить некоторые общие закономерности и поставить общие задачи. Заметим прежде всего, что во всех рассмотренных примерах нам приходилось иметь дело с некоторыми конечными множествами и различными их подмножествами.
Нас интересовало или число всех возможных подмножеств (пример 5 из § 2), или число подмножеств, обладающих определенным количеством элементов (примеры 4, 7 из § 1, примеры 1, 2, 3, 6
из § 2). В других случаях нужно было рассматривать упорядоченные подмножества, в которых элементы были расположены определенным образом (примеры 3, 6 из § 1, пример 4 из § 2). Здесь нам нужно было знать число различных упорядоченных подмножеств, считая различным образом упорядоченные подмножества различными. Наконец, встречалась и задача, в которой нужно было определить количество различных способов упорядочить данное конечное множество, то есть расположить его элементы в определенном порядке (пример 2, § 1). Все эти задачи можно теперь рассмотреть в общем виде.
Рассмотрим прежде всего точное определение упоминавшегося выше термина упорядоченное множество.
Конечное множество, состоящее из  элементов, называется упорядоченным, если его элементы каким-либо образом занумерованы, числами
элементов, называется упорядоченным, если его элементы каким-либо образом занумерованы, числами 
«Номера», которые при этом приписываются элементам множества, позволяют мыслить элементы этого множества «расположенными» в каком-то «порядке»: первый элемент «предшествует» второму (а второй «следует» за первым), второй предшествует третьему и т. д.
Одно и то же конечное множество можно, разумеется, упорядочить разными способами. Например, множество учеников данного класса можно упорядочить по росту (опять-таки двумя противоположными способами), по весу, по возрасту, по алфавиту фамилий и т. д. и т. п.
Не следует, однако, думать, что каждый такой «порядок» связан непременно с каким-либо «естественным правилом» упорядочения. Скажем, множество шахматных фигур (каждого цвета по отдельности или все 32) можно, конечно, упорядочить слева направо в порядке их расстановки на доске или по силе (а фигуры одинаковой силы — слева направо или еще как угодно), но можно считать «упорядочением» и «беспорядочную» последовательность, в которой мы случайно поставили их на доску для данной партии. А можно было бы их просто расставить в ряд в произвольном «порядке». Аналогично множество учеников данного класса можно считать упорядоченным в соответствии с тем (в достаточной мере случайным!) порядком, в котором они сегодня пришли в школу.
Короче говоря, «нумерация», о которой говорится в определении упорядоченного множества, не предполагает, вообще говоря, никакого заранее известного «закона» — упорядочивая конечное множество, мы просто приписываем каким-либо образом номера его элементам. И если в приведенных примерах легко было все же указать некоторые «естественные» способы упорядочения, то для упорядочения, например, множества муравьев в муравейнике или рыб в озере трудно указать более «естественный» способ, чем переловить их всех по очереди и перенумеровать в порядке попадания их в банку или на удочку...
Таким образом, речь, как правило, идет лишь о теоретическом, мысленном упорядочении, которое для конечного множества всегда возможно.
В отличие от соглашений, принятых нами выше (Введение, п. 1 и п. 6) для множеств неупорядоченных, упорядоченные множества мы будем считать совпадающими (или равными) лишь тогда, когда они не только состоят из одних и тех же элементов, но и упорядочены (расположены, занумерованы и т.  одинаковым образом.
одинаковым образом.
Говоря о различных упорядоченных множествах, состоящих из одних и тех же элементов, мы уже несколько раз называли их различными упорядочениями какого-либо множества. Этим термином нам будет удобно пользоваться и в дальнейшем.
Поскольку в этой главе нам придется иметь дело только с конечны  и множествами и их подмножествами, мы не будем много говорить о распространении понятия упорядоченности на общий случай бесконечных множеств, ограничившись определением и парой примеров.
и множествами и их подмножествами, мы не будем много говорить о распространении понятия упорядоченности на общий случай бесконечных множеств, ограничившись определением и парой примеров.
Множество (безразлично — конечное или бесконечное) называется упорядоченным, если между его элементами установлено некоторое отношение, называемое отношением предшествования, обладающее следующими свойствами.
1) Для любых двух различных элементов а и  данного множества либо а предшествует
данного множества либо а предшествует  либо
либо  предшествует а.
предшествует а.
2) Для любых элементов  и с данного множества из того, что а предшествует
и с данного множества из того, что а предшествует  , а
, а  предшествует с, следует, что а предшествует с.
предшествует с, следует, что а предшествует с.
Примером упорядоченного множества может служить множество  натуральных чисел, «естественным» образом упорядоченное по величине: мы считаем, что
натуральных чисел, «естественным» образом упорядоченное по величине: мы считаем, что  предшествует
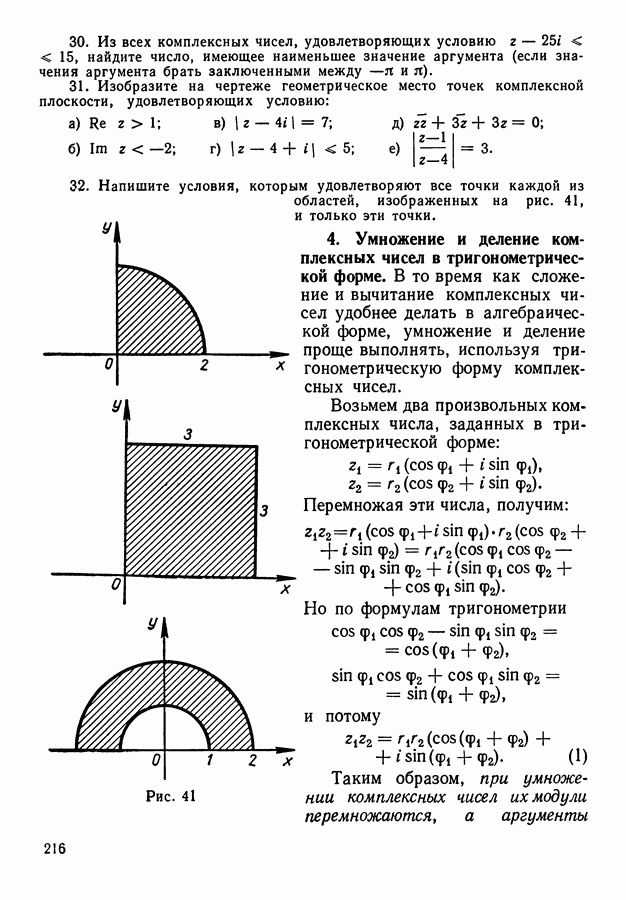
предшествует  если
если  (можно, конечно, было бы выбрать и упорядочение, обратное «естественному», то есть считать, что
(можно, конечно, было бы выбрать и упорядочение, обратное «естественному», то есть считать, что  предшествует
предшествует  когда
когда  Точно так же упорядочивается множество
Точно так же упорядочивается множество  всех действительных чисел. Множество К комплексных чисел, не обладающее никаким «естественным» порядком, можно, например, упорядочить, положив, что
всех действительных чисел. Множество К комплексных чисел, не обладающее никаким «естественным» порядком, можно, например, упорядочить, положив, что  предшествует
предшествует  если
если  а при
а при  если
если  Все эти множества можно, разумеется, упорядочить и иными способами.
Все эти множества можно, разумеется, упорядочить и иными способами.
Введем теперь следующее
Определение 1. Пусть дано конечное множество М, состоящее из  элементов. Размещением из
элементов. Размещением из  элементов по
элементов по  элементов называют всякое упорядоченное подмножество множества М, состоящее из
элементов называют всякое упорядоченное подмножество множества М, состоящее из  элементов.
элементов.
Из этого определения следует, что  и что различные размещения отличаются друг от друга составом входящих в них элементов или порядком их расположения. Как видно из предыдущих параграфов, в комбинаторных задачах требуется знать число различных размещений из
и что различные размещения отличаются друг от друга составом входящих в них элементов или порядком их расположения. Как видно из предыдущих параграфов, в комбинаторных задачах требуется знать число различных размещений из  элементов по
элементов по  элементов. Это число принято обозначать символом
элементов. Это число принято обозначать символом  (А — первая буква французского слова arrangement, что означает размещение, приведение в порядок).
(А — первая буква французского слова arrangement, что означает размещение, приведение в порядок).
Теорема 1. Число различных размещений из  элементов по
элементов по  элементов равно произведению
элементов равно произведению  последовательных натуральных чисел, начиная от
последовательных натуральных чисел, начиная от  и до
и до  включительно:
включительно:

Доказательство. Формула (1) была уже получена нами при разборе примера 4 в § 2. Здесь мы дадим вывод этой формулы, основанный на методе полной математической индукции. Индукцию будем вести по индексу 
Пусть дано множество М, состоящее из  элементов. Очевидно, что число различных подмножеств этого множества, содержащих по одному элементу, равно числу
элементов. Очевидно, что число различных подмножеств этого множества, содержащих по одному элементу, равно числу  элементов М, то есть
элементов М, то есть  (подмножества из одного элемента автоматически упорядочены, так как содержат только первый элемент).
(подмножества из одного элемента автоматически упорядочены, так как содержат только первый элемент).
Далее, из каждого размещения по одному элементу можно получить различные размещения по два элемента, присоединяя к выбранному первому элементу второй. Так как для выбора второго элемента мы имеем уже  возможностей (один из элементов уже использован!), то
возможностей (один из элементов уже использован!), то

Предположим теперь, что для некоторого значения  справедлива формула
справедлива формула

и докажем, что такая же формула имеет место и для  . Пусть образованы все размещения из
. Пусть образованы все размещения из  элементов по
элементов по  элементов. Размещения по
элементов. Размещения по  элементу могут быть получены присоединением к каждому из полученных еще одного элемента на
элементу могут быть получены присоединением к каждому из полученных еще одного элемента на  место.
место.
Из одного размещения по  элементов получится столько размещений по
элементов получится столько размещений по  элементу, сколько различных элементов можно присоединить, то есть
элементу, сколько различных элементов можно присоединить, то есть  Все получающиеся размещения будут различными, так как они отличаются последним элементом. Размещения по
Все получающиеся размещения будут различными, так как они отличаются последним элементом. Размещения по  элементу, получающиеся из различных размещений по
элементу, получающиеся из различных размещений по  элементов, также не могут совпасть, поскольку их первые
элементов, также не могут совпасть, поскольку их первые  элементов не совпадают. Остается добавить, что таким способом будут получены все размещения по
элементов не совпадают. Остается добавить, что таким способом будут получены все размещения по  элементу. Отсюда следует, что число размещений по
элементу. Отсюда следует, что число размещений по  элементу удовлетворяет равенству
элементу удовлетворяет равенству

Воспользовавшись предположенной по индукции формулой для  найдем:
найдем:

что и утверждалось. Справедливость этой формулы для  была уже установлена выше; из принципа математической индукции следует, что формула (1) верна для всех
была уже установлена выше; из принципа математической индукции следует, что формула (1) верна для всех 
Определение 2. Перестановками из  элементов называют различные упорядочения данного конечного множества, состоящего из
элементов называют различные упорядочения данного конечного множества, состоящего из  элементов.
элементов.
Таким образом, различные перестановки отличаются друг от друга лишь порядком элементов. Число возможных различных перестановок из  элементов обозначается символом
элементов обозначается символом  (от французского слова permutation — перестановка, перемещение).
(от французского слова permutation — перестановка, перемещение).
Теорема 2. Число различных перестановок из  элементов равно произведению всех последовательных целых чисел, начиная от
элементов равно произведению всех последовательных целых чисел, начиная от  и до
и до
1 включительно:

Доказательство этой теоремы окажется излишним, если мы заметим, что перестановки являются частным случаем размещений, а именно, при  Значит, согласно формуле (1),
Значит, согласно формуле (1),

Впрочем, нетрудно доказать эту теорему и независимо от понятия размещения. Рассмотрим всевозможные перестановки из  элементов и подсчитаем, сколько из них начинаются одним и тем же определенным элементом. Если поставить выделенный элемент перед каждой из перестановок из остальных элементов, то мы получим все возможные перестановки, начинающиеся данным элементом. Следовательно, число всех перестановок из
элементов и подсчитаем, сколько из них начинаются одним и тем же определенным элементом. Если поставить выделенный элемент перед каждой из перестановок из остальных элементов, то мы получим все возможные перестановки, начинающиеся данным элементом. Следовательно, число всех перестановок из  элементов, начинающихся одним определенным элементом, равно
элементов, начинающихся одним определенным элементом, равно  Но тогда для числа всех возможных перестановок из
Но тогда для числа всех возможных перестановок из  элементов находим:
элементов находим:

так как любой из  элементов может оказаться выделенным.
элементов может оказаться выделенным.
Формулу (3) можно использовать для доказательства нашей теоремы, пользуясь индукцией по числу элементов множества. Очевидно, что  так как один элемент может находиться только на первом месте. Допустим, что формула (2) верна для множества, содержащего
так как один элемент может находиться только на первом месте. Допустим, что формула (2) верна для множества, содержащего  элемент, то есть что
элемент, то есть что

На основании формулы (3) найдем, что

Таким образом, формула (2) верна для любого 
Упражнения
(см. скан)
Как было указано выше, число перестановок можно получить из числа размещений. Можно сделать и обратное, выразив число размещений через число перестановок.
Теорема 3. Число различных размещений из  элементов по
элементов по  элементов равно числу перестановок из
элементов равно числу перестановок из  элементов, деленному на число перестановок из
элементов, деленному на число перестановок из  элементов:
элементов:

Доказательство. Формулу (4) легко получить из формул (1) и (2). Действительно,

Это доказательство, несмотря на простоту и очевидность, часто вызывает чувство неудовлетворенности, так как сводится к формальным выкладкам и не показывает существа дела. Поэтому мы приведем еще одно доказательство, опирающееся только на определения размещений и перестановок.
Пусть дано некоторое множество из  элементов и все размещения его элементов по
элементов и все размещения его элементов по  Из каждого такого размещения можно получить перестановку элементов множества, присоединив к нему в произвольном порядке остальные
Из каждого такого размещения можно получить перестановку элементов множества, присоединив к нему в произвольном порядке остальные  элементов. В результате мы получим все перестановки из
элементов. В результате мы получим все перестановки из  элементов множества.
элементов множества.
Следовательно, каждое размещение из  элементов по
элементов по  элементов порождает столько перестановок по
элементов порождает столько перестановок по  элементов, сколькими различными способами к нему можно присоединить
элементов, сколькими различными способами к нему можно присоединить  оставшихся элементов. Так как это можно сделать
оставшихся элементов. Так как это можно сделать  различными способами, то общее число перестановок из
различными способами, то общее число перестановок из  элементов равно
элементов равно

откуда и следует равенство (4).
Упражнения
(см. скан)
Определение 3. Пусть дано конечное множество  состоящее из
состоящее из  элементов. Сочетанием из
элементов. Сочетанием из  элементов по
элементов по  элементов называется любое подмножество
элементов называется любое подмножество  содержащее
содержащее  элементов.
элементов.
Таким образом, сочетания являются неупорядоченными подмножествами, и различные сочетания различаются между собой только составом элементов. Число всех возможных сочетаний из  элементов по
элементов по  обозначают через
обозначают через  (от французского combinaison — сочетание, комбинация), а также через
(от французского combinaison — сочетание, комбинация), а также через  или
или 
Теорема 4. Число всех возможных сочетаний из  элементов по
элементов по  элементов
элементов  равно произведению
равно произведению  последовательных натуральных чисел от
последовательных натуральных чисел от  до
до  деленному на произведение
деленному на произведение  последовательных натуральных чисел от
последовательных натуральных чисел от  до 1:
до 1:

Доказательство этой теоремы сводится к доказательству следующего утверждения: число сочетаний из  элементов по
элементов по  элементов равно числу размещений из
элементов равно числу размещений из  элементов по
элементов по  элементов, деленному на число перестановок из
элементов, деленному на число перестановок из  элементов. В самом деле, из этого утверждения, пользуясь формулами (1) и (2), легко получаем формулу (5).
элементов. В самом деле, из этого утверждения, пользуясь формулами (1) и (2), легко получаем формулу (5).
Чтобы доказать теперь это утверждение, заметим, что каждое размещение из  элементов по
элементов по  элементов может быть получено из такого же сочетания путем различных перестановок его элементов. Следовательно, каждое сочетание порождает столько размещений
элементов может быть получено из такого же сочетания путем различных перестановок его элементов. Следовательно, каждое сочетание порождает столько размещений
сколько возможно различных перестановок его элементов. Отсюда следует, что  или
или

что и требовалось доказать.
Формулу (5) обычно приводят к более удобному для записи симметричному виду, умножая числитель и знаменатель на произведение всех натуральных чисел от  до 1 включительно. Тогда мы приходим к формуле:
до 1 включительно. Тогда мы приходим к формуле:

Формула (7) означает, что

Рекомендуем читателю самостоятельно разобраться в комбинаторном смысле этого равенства, доказавши его непосредственно, исходя лишь из определения перестановок и сочетаний.
Упражнения
(см. скан)
Как было указано в формулировке теоремы 4, символ имеет смысл при  и означает количество подмножеств множества М, содержащих ровно по
и означает количество подмножеств множества М, содержащих ровно по  элементов. Ясно, что
элементов. Ясно, что  это следует и из формулы (5), но формулу (7) в этом случае применить нельзя, так как она будет содержать бессмысленный символ
это следует и из формулы (5), но формулу (7) в этом случае применить нельзя, так как она будет содержать бессмысленный символ  Для общности принято полагать
Для общности принято полагать  . В этом случае формула (7) дает для
. В этом случае формула (7) дает для  то же значение 1.
то же значение 1.
Удобно также ввести в рассмотрение символ  что означает число пустых подмножеств множества М, то есть
что означает число пустых подмножеств множества М, то есть  . То же самое получится и из формулы (7), если воспользоваться принятым условием
. То же самое получится и из формулы (7), если воспользоваться принятым условием 
Принимаемое условие  имеет на самом деле более глубокий смысл, чем просто возможность вычислять
имеет на самом деле более глубокий смысл, чем просто возможность вычислять  или
или  по формуле (7).
по формуле (7).
Более существенное основание для того, чтобы считать выражение 0! равным единице, состоит в следующем. Выражение  можно рассматривать
можно рассматривать
бать как функцию, определенную лишь Для натурального аргумента  . В своей области определения она удовлетворяет функциональному уравнению
. В своей области определения она удовлетворяет функциональному уравнению  справедливость которого легко проверяется для всех натуральных
справедливость которого легко проверяется для всех натуральных  Действительно,
Действительно,  Если же в этом равенстве положить
Если же в этом равенстве положить  то мы получим
то мы получим 
Однако все эти соображения являются не слишком убедительными, так как нельзя быть уверенным в том, что нам не встретится другая формула, в которой будет удобно полагать 0! равным какому-нибудь другому числу. Окончательное решение можно получить, идя вот каким путем. Естественно поставить вопрос: можно ли построить непрерывную функцию, определенную для всех значений х, и такую, которая для целых значений аргумента совпа дает с  то есть доопределить функцию
то есть доопределить функцию  расширив ее область определения? Напомним, что в математическом анализе такое расширение производится, например, для показательной функции
расширив ее область определения? Напомним, что в математическом анализе такое расширение производится, например, для показательной функции  которая вначале была определена лишь для натурального показателя степени.
которая вначале была определена лишь для натурального показателя степени.
Поставленный вопрос был решен Эйлером и Гауссом. С помощью различных формул (Эйлер — через интеграл, а Гаусс — через бесконечное произведение) они определили функцию, обладающую нужным свойством, и доказали единственность такой функции при некоторых естественных предположениях. Эта функция называется гамма-функцией и обозначается  Она определена для всех
Она определена для всех  и удовлетворяет функциональному уравнению
и удовлетворяет функциональному уравнению  для натуральных
для натуральных  принимает значения
принимает значения 
Обе формулы, определяющие функцию  имеют смысл при
имеют смысл при  и определяют значение
и определяют значение  Но в силу равенства
Но в силу равенства  под выражением
под выражением  следует понимать именно значение
следует понимать именно значение 
Все выведенные нами в настоящем параграфе формулы для числа размещений, перестановок и сочетаний фактически уже неоднократно выводились нами ранее для различных частных конкретных случаев при рассмотрении примеров в § 1, 2. Рассмотрим еще некоторые свойства сочетаний, которые потребуются в дальнейшем.
Теорема 5. Число сочетаний из  элементов по
элементов по  элементов равно числу сочетаний из
элементов равно числу сочетаний из  элементов по
элементов по  элементов:
элементов:

Доказательство. Формально равенство (9) легко получить из формулы для числа сочетаний, записанной в виде (7). Действительно,

Комбинаторный смысл этого равенства также достаточно ясен. Каждому подмножеству из  элементов соответствует единственное определенное подмножество из
элементов соответствует единственное определенное подмножество из  элементов — именно, тех, которые не вошли в первоначальное. Поэтому количество тех и других возможных подмножеств одинаково. При рассмотрении примеров (см. примеры 3 и 6 из § 2) мы фактически уже пользовались этим соображением.
элементов — именно, тех, которые не вошли в первоначальное. Поэтому количество тех и других возможных подмножеств одинаково. При рассмотрении примеров (см. примеры 3 и 6 из § 2) мы фактически уже пользовались этим соображением.
Равенство (9) позволяет сокращать вычисления в тех случаях, когда 
Теорема 6. Число сочетаний из  элементов по
элементов по  элементов равно сумме числа сочетаний из
элементов равно сумме числа сочетаний из  элементов по
элементов по  элементов и по
элементов и по  элементов:
элементов:

Доказательство, как и в предыдущем случае, проведем двумя различными способами. Прежде всего, пользуясь формулой (7) для числа сочетаний, находим:

Второе доказательство состоит в следующем. Выделим некоторый фиксированный элемент а множества М и рассмотрим сочетания из  элементов по
элементов по  элементов, содержащие или не содержащие этот элемент. Число сочетаний по
элементов, содержащие или не содержащие этот элемент. Число сочетаний по  элементов, не содержащих элемента а, равно, очевидно, так как здесь рассматриваются подмножества по
элементов, не содержащих элемента а, равно, очевидно, так как здесь рассматриваются подмножества по  элементов, образованные из элементов множества, содержащего
элементов, образованные из элементов множества, содержащего  элемент (множество М без элемента а). Сочетания, содержащие а, можно получить так: образовать всевозможные сочетания по
элемент (множество М без элемента а). Сочетания, содержащие а, можно получить так: образовать всевозможные сочетания по  элементу из того же множества М без элемента а и к каждому из них присоединить а. Отсюда ясно, что число таких сочетаний равно
элементу из того же множества М без элемента а и к каждому из них присоединить а. Отсюда ясно, что число таких сочетаний равно  . Так как каждое сочетание по
. Так как каждое сочетание по  элементов либо содержит данный элемент а, либо не содержит его, то оно принадлежит либо одной, либо другой группе. Поэтому
элементов либо содержит данный элемент а, либо не содержит его, то оно принадлежит либо одной, либо другой группе. Поэтому

что и утверждалось
Размещения, перестановки и сочетания вместе часто называют одним словом — соединения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ
- ВВЕДЕНИЕ
- 2. Числовые множества.
- 3. Пустое множество.
- 4. Подмножество.
- 5. Пересечение множеств.
- 6. Сложение множеств.
- 7. Разбиение множеств.
- 8. Вычитание множеств.
- 9. Отображение множеств.
- 10. Краткие исторические сведения.
- Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
- § 1. Тождественные преобразования многочленов
- 2. Целые рациональные выражения и функции.
- 3. Степень с натуральным показателем и ее свойства.
- 4. Многочлены.
- 5. Умножение многочленов.
- 6. Числовые кольца и поля.
- 7. Кольцо многочленов над данным числовым полем.
- 8. Бином Ньютона.
- § 2. Деление многочленов. Корни многочленов
- 2. Теорема Безу. Схема Горнера.
- 3. Корни многочлена.
- 4. Интерполяционные формулы.
- 5. Кратные корни.
- 6. Многочлены второй степени.
- 7. Многочлены с целыми коэффициентами.
- 8. Краткие исторические сведения.
- Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1. Общая теория уравнений
- 2. Область допустимых значений.
- 3. Уравнения.
- 4. Совокупности уравнений.
- 5. Преобразования уравнений.
- 6. Теоремы о равносильности уравнений.
- § 2. Уравнения с одним неизвестным
- 2. Метод разложения на множители.
- 3. Метод введения нового неизвестного.
- 4. Биквадратные уравнения.
- 5. Возвратные уравнения 3-й и 4-й степеней.
- § 3. Функциональные неравенства
- 2. Равносильные неравенства.
- 3. Доказательство неравенств.
- 4. Линейные неравенства.
- 5. Решение неравенств второй степени.
- 6. Решение алгебраических неравенств высших степеней.
- 7. Краткие исторические сведения.
- Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
- § 1. Степени с целым показателем
- 2. Степень с нулевым показателем.
- 3. Степень с целым отрицательным показателем.
- § 2. Корни. Степени с рациональными показателями
- 2. Степени с рациональными показателями.
- 3. Свойства степеней с рациональными показателями.
- § 3. Иррациональные алгебраические выражения
- 2. Одночленные иррациональные выражения.
- 3. Сокращение показателей и приведение корней к общему показателю.
- 4. Извлечение корня из произведения и степени.
- 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.
- 6. Возведение корня в степень.
- 7. Извлечение корня из корня.
- 8. Подобные корни.
- 9. Сложение и вычитание корней.
- 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
- 11. Преобразование выражений вида …
- 12. Смешанные задачи на преобразование иррациональных выражений.
- § 4. Иррациональные уравнения и неравенства
- 2. Сведение иррациональных уравнений к рациональным.
- 3. Уединение радикала.
- 4. Введение нового неизвестного.
- 5. Особые случаи решения иррациональных уравнений.
- 6. Иррациональные неравенства.
- 7. Краткие историчесие сведения.
- Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 1. Системы алгебраических уравнений
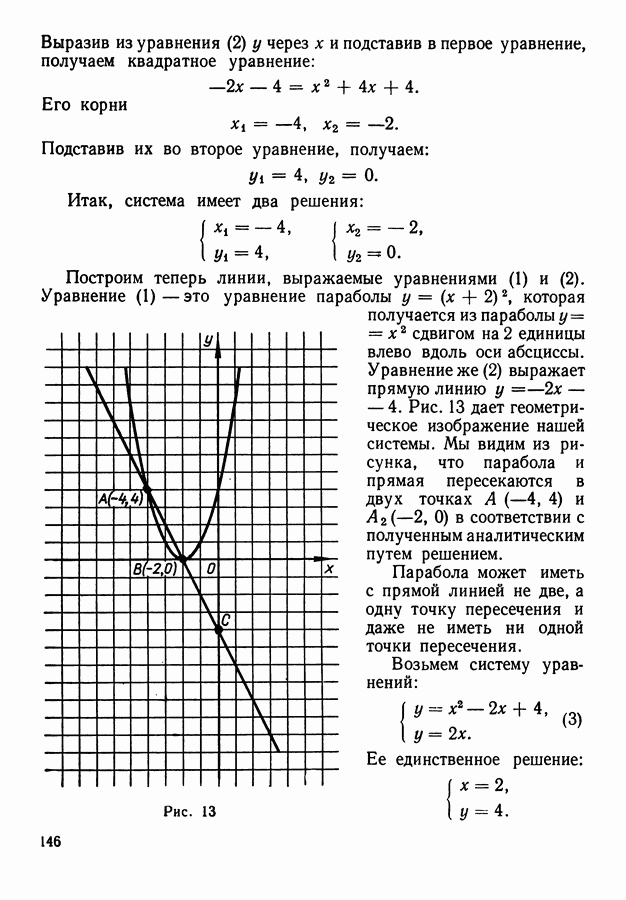
- 2. Системы уравнений.
- 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
- 4. Совокупность уравнений.
- 5. Равносильные системы уравнений.
- 6. Метод подстановки.
- 7. Метод алгебраического сложения уравнений.
- 8. Метод введения новых неизвестных.
- 9. Системы однородных уравнений.
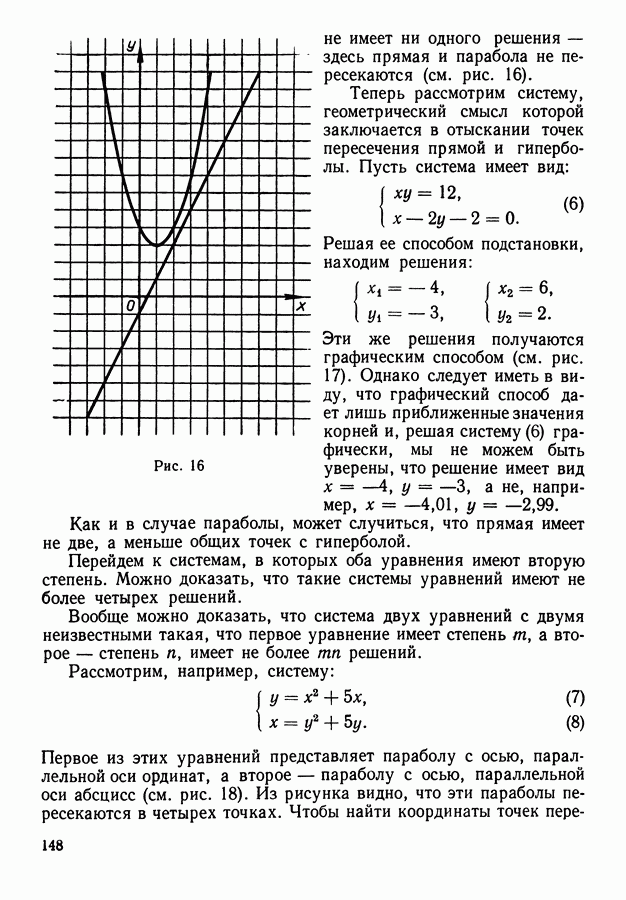
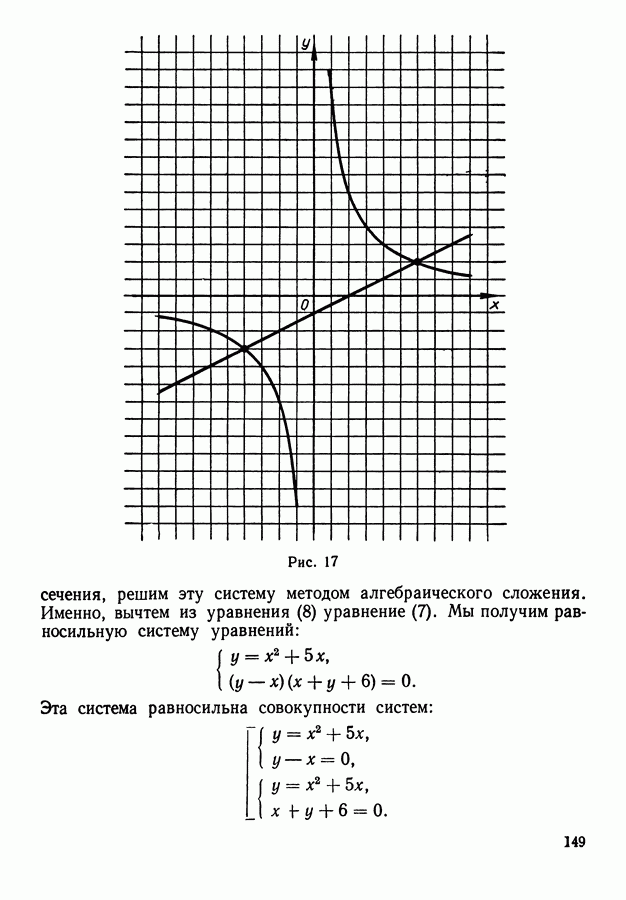
- 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
- § 2. Системы линейных уравнений
- 2. Теоремы о равносильности систем линейных уравнений.
- 3. Пример решения системы линейных уравнений методом Гаусса.
- 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
- 5. Решение обобщенно-треугольной системы линейных уравнений.
- 6. Системы однородных линейных уравнений.
- § 3. Симметрические многочлены и их приложения к решению систем уравнений
- 2. Выражение степенных сумм
- 3. Основная теорема о симметрических многочленах от двух переменных.
- 4. Системы симметрических алгебраических уравнений.
- 5. Применение симметрических многочленов к решению иррациональных уравнений.
- § 4. Неравенства с многими переменными
- 2. Среднее арифметическое и среднее геометрическое трех чисел.
- 3. Неравенство Коши (двумерный вариант).
- 4. Задачи на наибольшие и наименьшие значения.
- § 5. Решение неравенств
- 2. Неравенства с двумя переменными.
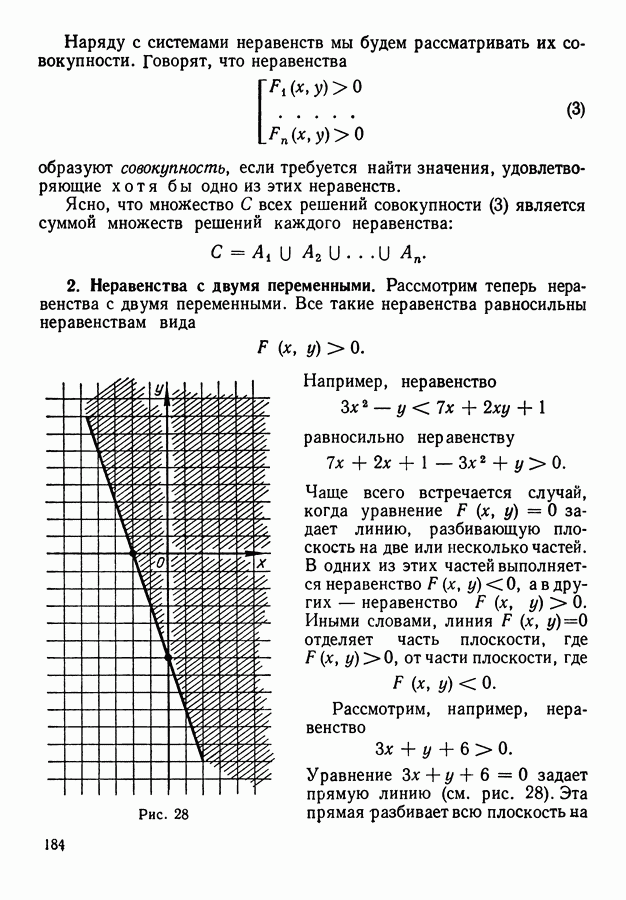
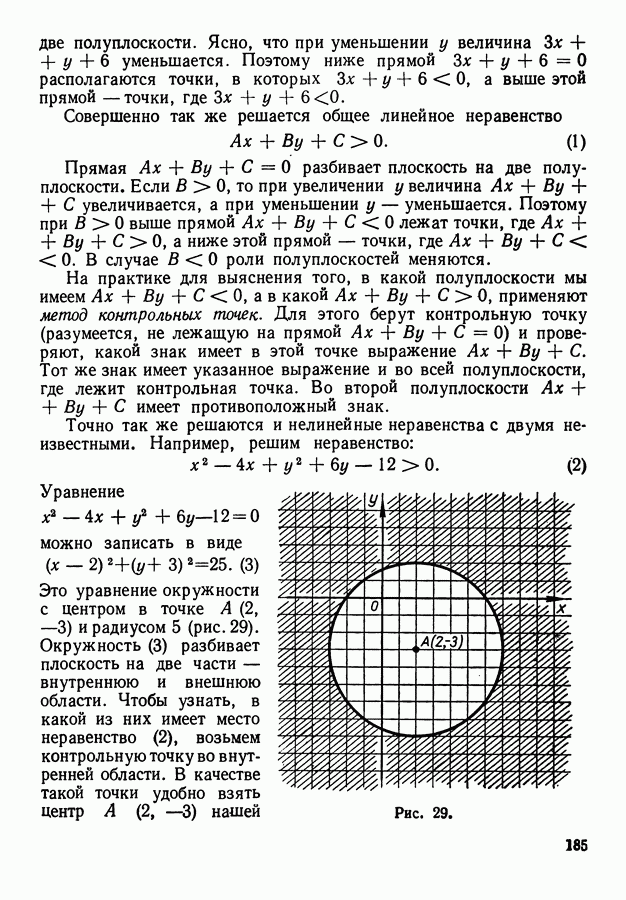
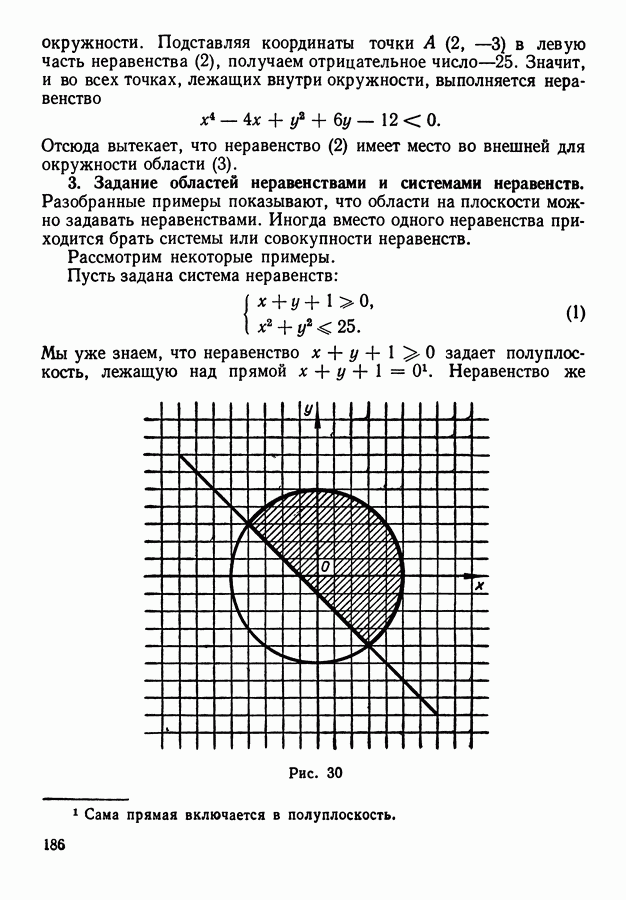
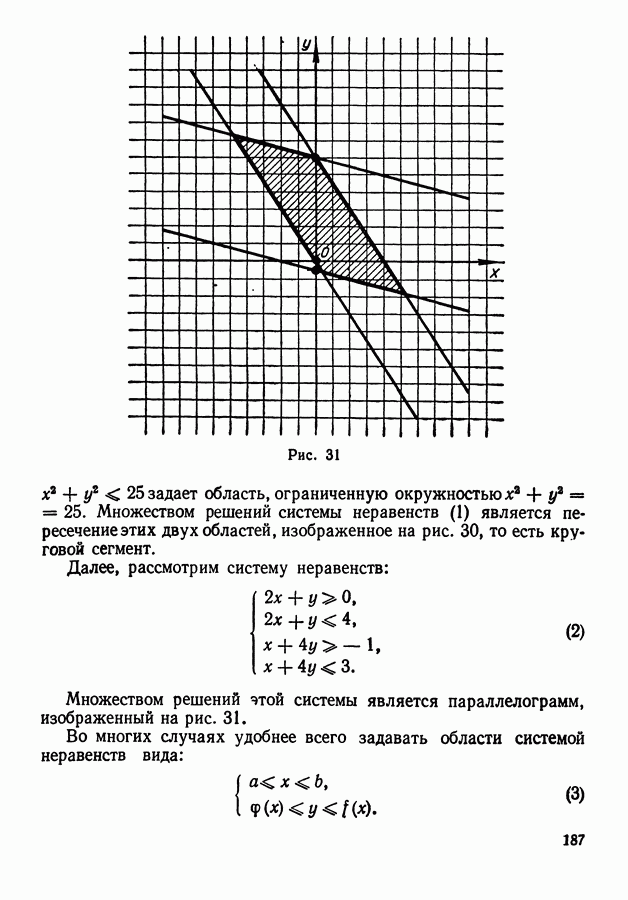
- 3. Задание областей неравенствами и системами неравенств.
- 4. Понятие о линейном программировании.
- 5. Краткие исторические сведения.
- Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
- § 1. Комплексные числа в алгебраической форме
- 2. Комплексные числа.
- 3. Сложение комплексных чисел; умножение на действительные числа.
- 4. Умножение комплексных чисел.
- 5. Квадратные уравнения с действительными коэффициентами.
- 6. Деление комплексных чисел.
- 7. Сопряженные комплексные числа.
- 8. Извлечение квадратных корней из комплексных чисел.
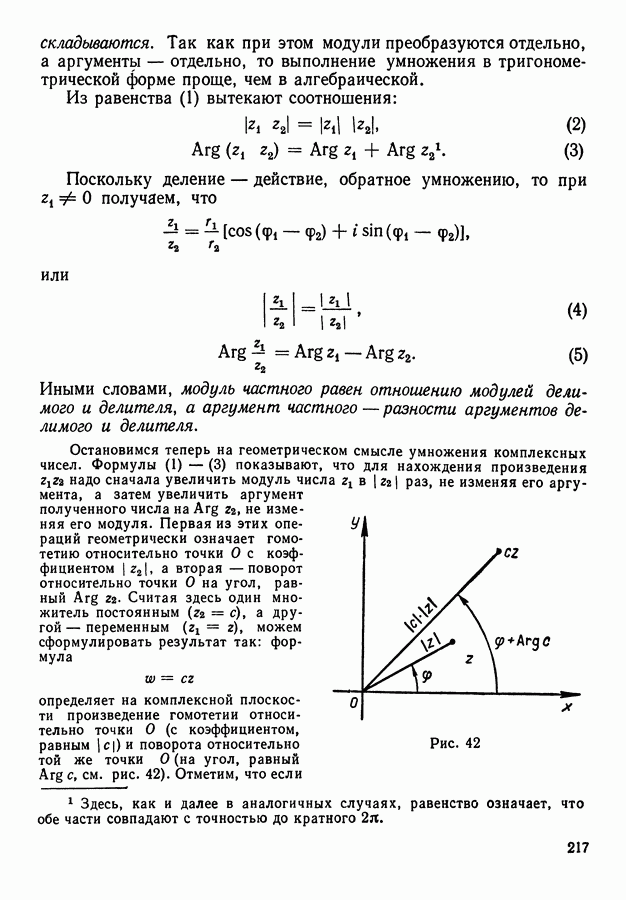
- § 2. Тригонометрическая форма комплексных чисел
- 2. Полярная система координат.
- 3. Тригонометрическая форма комплексного числа.
- 4. Умножение и деление комплексных чисел в тригонометрической форме.
- 5. Возведение комплексных чисел в степень. Формула Муавра.
- 6. Извлечение корня из комплексного числа.
- 7. Функции комплексного переменного и преобразования комплексной плоскости.
- § 3. Некоторые виды алгебраических уравнений
- 2. Двучленные уравнения.
- 3. Корни из единицы и построение правильных многоугольников.
- 4. Трехчленные уравнения.
- § 4. Основная теорема алгебры многочленов и ее следствия
- 2. Многочлены с действительными коэффициентами.
- 3. Разложение на множители многочленов с действительными коэффициентами.
- 4. Краткие исторические сведения.
- Глава VI. ЦЕПНЫЕ ДРОБИ
- § 1. Конечные цепные дроби
- 2. Пример цепной дроби.
- 3. Определение цепной дроби.
- 4. Представление рациональных чисел в виде конечной цепной дроби.
- 5. Подходящие дроби.
- 6. Свойства подходящих дробей.
- 8. Подходящие дроби и календарь.
- 9. Приближение цепной дроби подходящими дробями.
- § 2. Бесконечные цепные дроби
- 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
- 3. Цепные дроби как вычислительный инструмент.
- 4. Краткие исторические сведения.
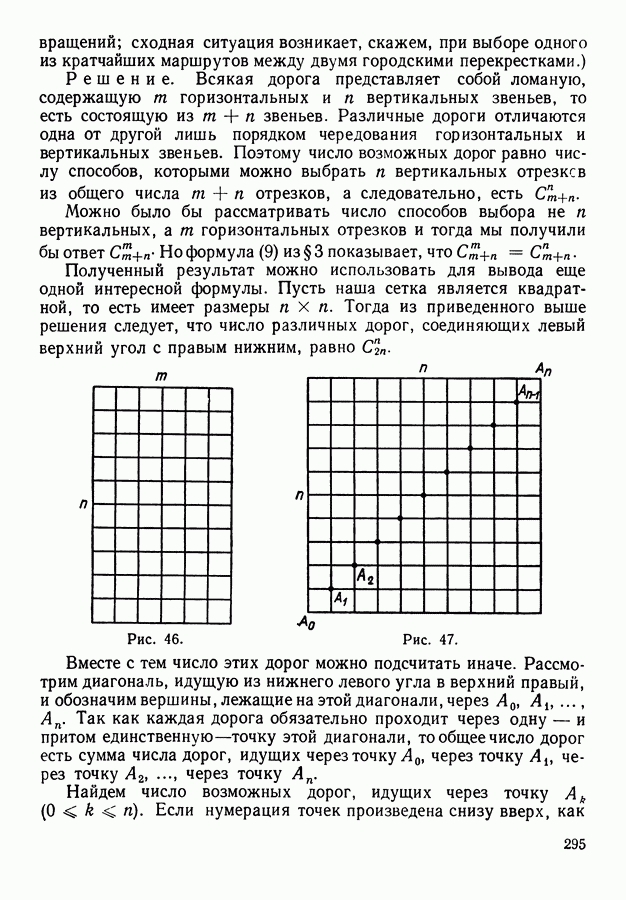
- Глава VII. КОМБИНАТОРИКА
- § 1. Комбинаторные задачи
- § 2. Комбинаторные задачи. Продолжение
- § 3. Определения и формулы
- § 4. Соединения с повторениями
- § 5. Комбинаторные задачи. Окончание
- § 6. Бином Ньютона и его обобщения
- § 7. Краткие исторические сведения
- Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
- § 3. Примеры вычисления вероятностей
- § 4. Полная вероятность. Формула Байеса
- § 5. Повторение испытаний
- § 6. Примеры вычисления вероятностей. Окончание
- § 7. Краткие исторические сведения