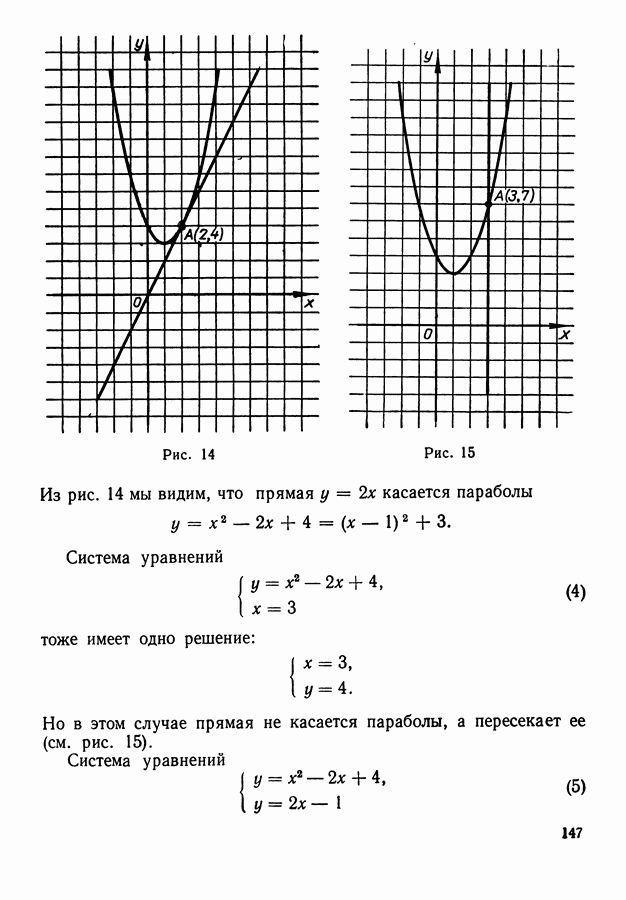| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Комбинаторные задачи. Окончание
В этом параграфе мы рассмотрим еще несколько комбинаторных задач, при решении которых будем пользоваться установленными выше формулами и правилами.
Пример 1. В некотором государстве каждые два человека отличаются набором зубов. Каково максимально возможное число жителей этого государства, если наибольшее число зубов у человека равно 32?
Решение. Эту задачу можно решить двумя способами. Первый способ заключается в том, что мы сначала ищем, сколько людей может иметь  зубов, а потом просуммируем полученные результаты от
зубов, а потом просуммируем полученные результаты от  до
до  . Ясно, что
. Ясно, что  мест из 32 можно выбрать
мест из 32 можно выбрать  способами. Поэтому ровно k зубов имеют не более чем
способами. Поэтому ровно k зубов имеют не более чем  жителей. А тогда общее число жителей не превосходит
жителей. А тогда общее число жителей не превосходит

Полученный этим способом ответ оказался очень громоздким. Выгоднее избрать другой путь, которым мы уже пользовались при решении примера 5 в § 2, — применить метод индукции.
Если речь идет об одном зубе, то возможны только два человека — один с зубом и второй без него. При двух зубах число возможных наборов зубов становится равным четырем: нет ни одного зуба, есть первый, есть второй и есть оба.
Увеличив число зубов до трех, мы удвоим число возможностей и получим восемь различных наборов. Действительно, каждый из рассмотренных наборов двух зубов может встретиться дважды — когда нет третьего зуба и когда он есть.
Обозначим число возможных наборов  зубов через
зубов через  . Предыдущими рассуждениями мы доказали, что
. Предыдущими рассуждениями мы доказали, что  Допустим, что для некоторого
Допустим, что для некоторого  справедливо равенство
справедливо равенство  и докажем, что аналогичное равенство справедливо и для случая
и докажем, что аналогичное равенство справедливо и для случая  зубов. Среди всех различных наборов, входящих в
зубов. Среди всех различных наборов, входящих в  имеется ровно
имеется ровно  наборов, в которых отсутствует (к
наборов, в которых отсутствует (к  зуб, и столько же наборов, в которых
зуб, и столько же наборов, в которых  зуб имеется. Поэтому
зуб имеется. Поэтому

Таким образом, при возможных  зубах число всех людей, отличающихся набором зубов, равно
зубах число всех людей, отличающихся набором зубов, равно  . В нашем случае
. В нашем случае  поэтому мы получаем
поэтому мы получаем  Как известно,
Как известно,  . Поэтому
. Поэтому  , так что возможное население этого государства больше нынешнего населения всего земного шара.
, так что возможное население этого государства больше нынешнего населения всего земного шара.
Заметим, что полученный нами результат на самом деле дает больше, чем только оценку возможного населения забавного государства. Сравнивая полученное значение  с написанным выше выражением
с написанным выше выражением  как суммы сочетаний, мы приходим к формуле:
как суммы сочетаний, мы приходим к формуле:

Более того, из приведенного выше доказательства по индукции вытекает, что аналогичное равенство справедливо при любом  то есть что имеет место формула
то есть что имеет место формула

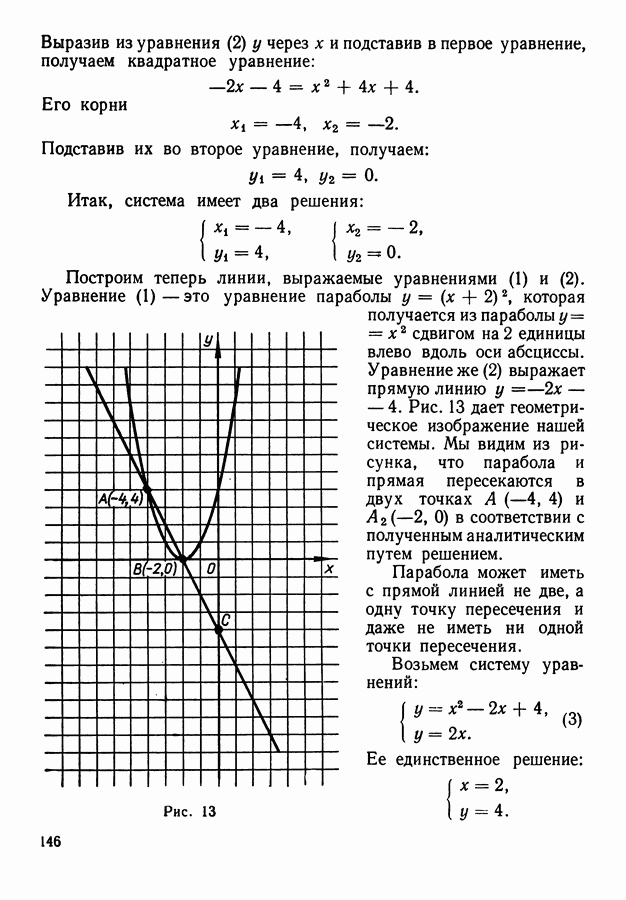
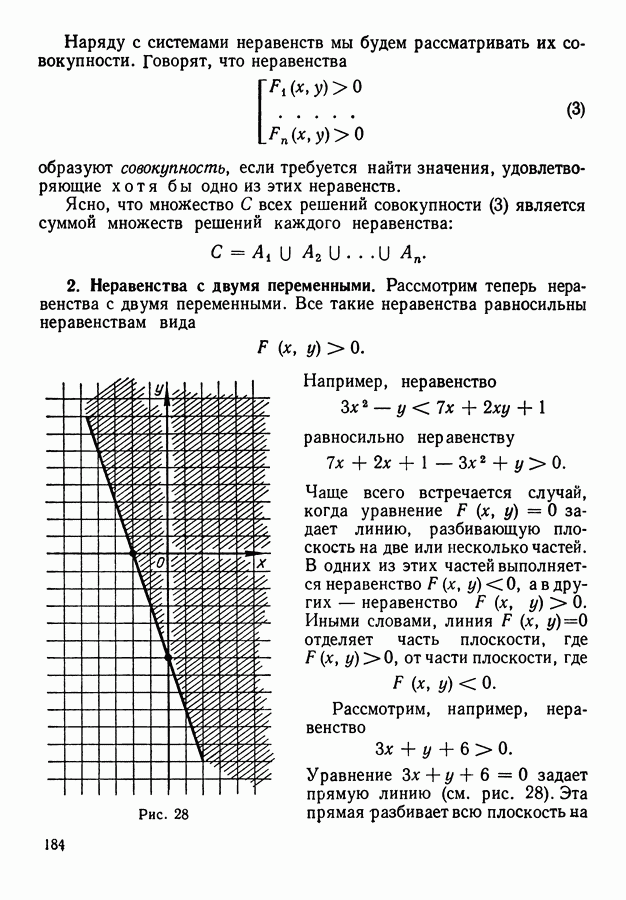
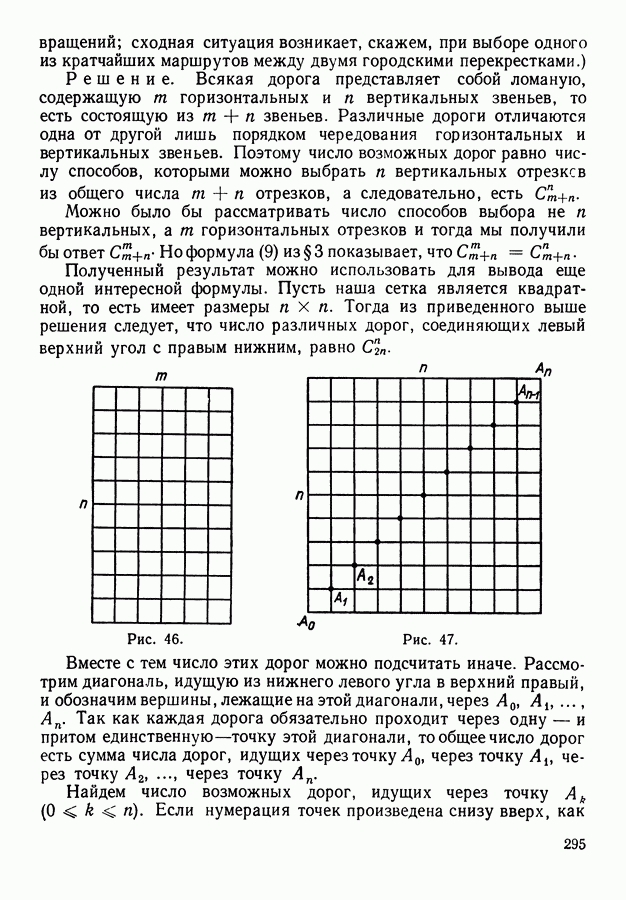
Пример 2. Дана прямоугольная сетка квадратов размером  . Каково число различных дорог на этой сетке, ведущих из левого верхнего угла в правый нижний (рис. 46)? (Все звенья дороги предполагаются идущими или вправо, или вниз — без возвращений;
. Каково число различных дорог на этой сетке, ведущих из левого верхнего угла в правый нижний (рис. 46)? (Все звенья дороги предполагаются идущими или вправо, или вниз — без возвращений;
сходная ситуация возникает, скажем, при выборе одного из кратчайших маршрутов между двумя городскими перекрестками.)
Решение. Всякая дорога представляет собой ломаную, содержащую  горизонтальных и
горизонтальных и  вертикальных звеньев, то есть состоящую из
вертикальных звеньев, то есть состоящую из  звеньев. Различные дороги отличаются одна от другой лишь порядком чередования горизонтальных и вертикальных звеньев. Поэтому число возможных дорог равно числу способов, которыми можно выбрать
звеньев. Различные дороги отличаются одна от другой лишь порядком чередования горизонтальных и вертикальных звеньев. Поэтому число возможных дорог равно числу способов, которыми можно выбрать  вертикальных отрезксв из общего числа
вертикальных отрезксв из общего числа  отрезков, а следовательно, есть
отрезков, а следовательно, есть 
Можно было бы рассматривать число способов выбора не  вертикальных, а
вертикальных, а  горизонтальных отрезков и тогда мы получили бы ответ
горизонтальных отрезков и тогда мы получили бы ответ  Но формула (9) из § 3 показывает, что
Но формула (9) из § 3 показывает, что 
Полученный результат можно использовать для вывода еще одной интересной формулы. Пусть наша сетка является квадратной, то есть имеет размеры  Тогда из приведенного выше решения следует, что число различных дорог, соединяющих левый верхний угол с правым нижним, равно
Тогда из приведенного выше решения следует, что число различных дорог, соединяющих левый верхний угол с правым нижним, равно  .
.

Рис. 46.

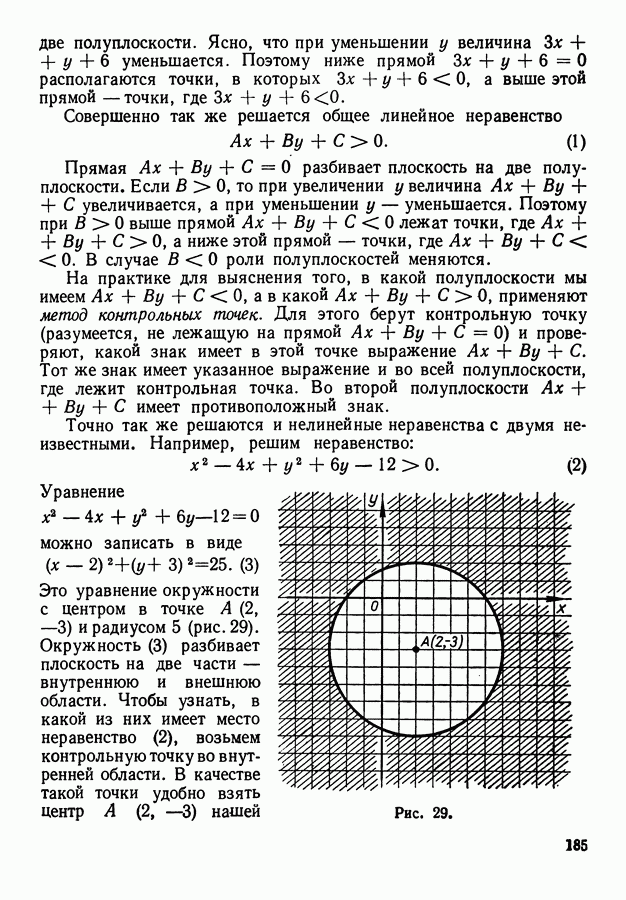
Рис. 47.
Вместе с тем число этих дорог можно подсчитать иначе. Рассмотрим диагональ, идущую из нижнего левого угла в верхний правый, и обозначим вершины, лежащие на этой диагонали, через  . Так как каждая дорога обязательно проходит через одну — и притом единственную точку этой диагонали, то общее число дорог есть сумма числа дорог, идущих через точку
. Так как каждая дорога обязательно проходит через одну — и притом единственную точку этой диагонали, то общее число дорог есть сумма числа дорог, идущих через точку  через точку
через точку  через точку
через точку  через точку
через точку  .
.
Найдем число возможных дорог, идущих через точку  Если нумерация точек произведена снизу вверх, как
Если нумерация точек произведена снизу вверх, как
это показано на рис. 47, то точка  отстоит от нижней горизонтали на расстоянии
отстоит от нижней горизонтали на расстоянии  считая за единицу измерения длину стороны квадрата сетки. От правой вертикали ее отделяют тогда
считая за единицу измерения длину стороны квадрата сетки. От правой вертикали ее отделяют тогда  горизонтальных отрезка.
горизонтальных отрезка.
Дорог, соединяющих верхний левый угол с точкой  будет тогда
будет тогда  а дорог, соединяющих точку
а дорог, соединяющих точку  с нижним правым углом, будет
с нижним правым углом, будет  (это видно из рассмотрения равных прямоугольников, противоположными вершинами которых служат верхний левый угол исходного квадрата и точка
(это видно из рассмотрения равных прямоугольников, противоположными вершинами которых служат верхний левый угол исходного квадрата и точка  и соответственно точка
и соответственно точка  и нижний правый угол квадрата). Поэтому общее число дорог, соединяющих верхний левый угол с нижним правым и проходящих через
и нижний правый угол квадрата). Поэтому общее число дорог, соединяющих верхний левый угол с нижним правым и проходящих через  равно
равно  Но тогда общее число всех дорог равно сумме
Но тогда общее число всех дорог равно сумме

Сравнивая полученную сумму с найденным выше выражением для числа дорог, мы придем к формуле:

Пример 3. Шесть пассажиров садятся на остановке в трамвайный поезд, состоящий из трех трамвайных вагонов. Каким числом различных способов могут они распределиться в вагонах?
Решение. Прежде всего необходимо указать, что задача сформулирована недостаточно точно и допускает два различных толкования. Нас может интересовать или только число пассажиров в каждом вагоне или же кто именно в каком вагоне находится. Рассмотрим обе возможные формулировки.
Сначала рассмотрим случай, когда учитывается, кто в каком вагоне находится, то есть когда случаи «пассажир А в первом вагоне, а пассажир В — во втором» и «пассажир В в первом вагоне, а пассажир А — во втором» считаются различными.
Здесь мы имеем размещения с повторениями из трех элементов по шесть элементов: для каждого из шести пассажиров имеются три возможности. Пользуясь формулой (1) из § 4, получаем, что число различных способов, которыми шесть пассажиров могут распределиться в трех вагонах, равно:

Иной результат получится в том случае, если нас интересует лишь число пассажиров в каждом вагоне, так что случай «один пассажир в первом вагоне и один во втором» является единственным, независимо от того, кто из пассажиров где находится. Здесь нужно
Но подсчитывать уже не размещения, а Сочетания с повторениями. По формуле (4) из §4 находим, что число различных способов распределения пассажиров в этом случае равно

Пример 4. Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей?
Решение. Первый игрок может выбрать 7 костей  способами. После этого второй игрок должен выбрать 7 костей из оставшихся 21 кости. Это можно сделать
способами. После этого второй игрок должен выбрать 7 костей из оставшихся 21 кости. Это можно сделать  способами. Третий игрок может выбрать кости Си способами, а четвертый —
способами. Третий игрок может выбрать кости Си способами, а четвертый —  способом. Всего получаем
способом. Всего получаем

способов раздела костей.
Эту задачу можно решить иначе. Упорядочим все кости и отдадим первые 7 костей первому игроку, вторые 7 костей — второму игроку и т. д. Так как 28 костей можно упорядочить 28! способами, то получаем 28! способов раздела. Но некоторые из этих способов приводят к одинаковым результатам — игрокам неважно, в каком порядке приходят к ним кости, а важно лишь, какие именно кости они получат. Поэтому результат не изменится, если мы как угодно переставим друг с другом первые 7 костей, потом вторые 7 костей и т. д. Первые 7 костей можно переставить 7! способами, вторые 7 костей — тоже 7! способами и т. д. Всего получим  перестановок, дающих то же распределение костей, что и данная. Поэтому число способов раздела костей равно
перестановок, дающих то же распределение костей, что и данная. Поэтому число способов раздела костей равно

Пример 5. Сколькими способами можно разделить 40 яблок между 4 мальчиками (все яблоки считаются одинаковыми)?
Решение. Возьмем три одинаковые перегородки и рассмотрим всевозможные перестановки 43 предметов: 40 яблок и 3 перегородок. Каждой такой перестановке соответствует свой способ раздела: первый мальчик получает все яблоки от начала до первой перегородки, второй — все яблоки между первой и второй перегородками, третий — все яблоки между второй и третьей перегородками, а четвертый — все остальные яблоки. (Если, например, первая и вторая перегородки оказались рядом, то второй мальчик ничего не получает.) Значит, число способов раздела равно числу
перестановок 40 яблок и 3 перегородок. По формуле числа перестановок с повторениями получаем, что это число равно

Пример 6. Сколькими способами можно разделить 40 яблок между 4 мальчиками так, чтобы каждый получил по крайней мере 3 яблока (все яблоки по-прежнему считаются одинаковыми)?
Решение. Сначала дадим каждому мальчику по 3 яблока. А потом разделим оставшиеся 28 яблок так, как было сделано в предыдущей задаче. Всего получаем

способов раздела.
Пример 7. Имеется  различных сигнальных флагов и
различных сигнальных флагов и  мачт, на которых их вывешивают. Значение сигнала зависит от того, в каком порядке развешаны флаги. Сколько сигналов можно передать этими флагами, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
мачт, на которых их вывешивают. Значение сигнала зависит от того, в каком порядке развешаны флаги. Сколько сигналов можно передать этими флагами, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
Решение. Добавим к  флагам
флагам  перегородку и рассмотрим всевозможные перестановки из
перегородку и рассмотрим всевозможные перестановки из  различных флагов и
различных флагов и  -одинаковых перегородок. Как и в примере 5, каждой перестановке соответствует свой сигнал (на первую мачту вывешиваются по порядку все флаги от начала до первой перегородки и т. д.). Поэтому число сигналов равно числу таких перестановок, то есть равно
-одинаковых перегородок. Как и в примере 5, каждой перестановке соответствует свой сигнал (на первую мачту вывешиваются по порядку все флаги от начала до первой перегородки и т. д.). Поэтому число сигналов равно числу таких перестановок, то есть равно

Если бы мы не потребовали, чтобы все флаги были использованы, то число сигналов оказалось бы больше. В этом случае задача решалась бы в два этапа. Сначала выберем, какие флаги будут участвовать в сигнале. Если число выбираемых флагов равно  то выбор можно сделать
то выбор можно сделать  способами. Как мы уже знаем, с помощью данных
способами. Как мы уже знаем, с помощью данных  флагов можно передать
флагов можно передать  сигналов. Поэтому всего имеем
сигналов. Поэтому всего имеем  сигналов, передаваемых
сигналов, передаваемых  флагами. А общее число сигналов равно
флагами. А общее число сигналов равно

Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ
- ВВЕДЕНИЕ
- 2. Числовые множества.
- 3. Пустое множество.
- 4. Подмножество.
- 5. Пересечение множеств.
- 6. Сложение множеств.
- 7. Разбиение множеств.
- 8. Вычитание множеств.
- 9. Отображение множеств.
- 10. Краткие исторические сведения.
- Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
- § 1. Тождественные преобразования многочленов
- 2. Целые рациональные выражения и функции.
- 3. Степень с натуральным показателем и ее свойства.
- 4. Многочлены.
- 5. Умножение многочленов.
- 6. Числовые кольца и поля.
- 7. Кольцо многочленов над данным числовым полем.
- 8. Бином Ньютона.
- § 2. Деление многочленов. Корни многочленов
- 2. Теорема Безу. Схема Горнера.
- 3. Корни многочлена.
- 4. Интерполяционные формулы.
- 5. Кратные корни.
- 6. Многочлены второй степени.
- 7. Многочлены с целыми коэффициентами.
- 8. Краткие исторические сведения.
- Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1. Общая теория уравнений
- 2. Область допустимых значений.
- 3. Уравнения.
- 4. Совокупности уравнений.
- 5. Преобразования уравнений.
- 6. Теоремы о равносильности уравнений.
- § 2. Уравнения с одним неизвестным
- 2. Метод разложения на множители.
- 3. Метод введения нового неизвестного.
- 4. Биквадратные уравнения.
- 5. Возвратные уравнения 3-й и 4-й степеней.
- § 3. Функциональные неравенства
- 2. Равносильные неравенства.
- 3. Доказательство неравенств.
- 4. Линейные неравенства.
- 5. Решение неравенств второй степени.
- 6. Решение алгебраических неравенств высших степеней.
- 7. Краткие исторические сведения.
- Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
- § 1. Степени с целым показателем
- 2. Степень с нулевым показателем.
- 3. Степень с целым отрицательным показателем.
- § 2. Корни. Степени с рациональными показателями
- 2. Степени с рациональными показателями.
- 3. Свойства степеней с рациональными показателями.
- § 3. Иррациональные алгебраические выражения
- 2. Одночленные иррациональные выражения.
- 3. Сокращение показателей и приведение корней к общему показателю.
- 4. Извлечение корня из произведения и степени.
- 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.
- 6. Возведение корня в степень.
- 7. Извлечение корня из корня.
- 8. Подобные корни.
- 9. Сложение и вычитание корней.
- 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
- 11. Преобразование выражений вида …
- 12. Смешанные задачи на преобразование иррациональных выражений.
- § 4. Иррациональные уравнения и неравенства
- 2. Сведение иррациональных уравнений к рациональным.
- 3. Уединение радикала.
- 4. Введение нового неизвестного.
- 5. Особые случаи решения иррациональных уравнений.
- 6. Иррациональные неравенства.
- 7. Краткие историчесие сведения.
- Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
- § 1. Системы алгебраических уравнений
- 2. Системы уравнений.
- 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
- 4. Совокупность уравнений.
- 5. Равносильные системы уравнений.
- 6. Метод подстановки.
- 7. Метод алгебраического сложения уравнений.
- 8. Метод введения новых неизвестных.
- 9. Системы однородных уравнений.
- 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
- § 2. Системы линейных уравнений
- 2. Теоремы о равносильности систем линейных уравнений.
- 3. Пример решения системы линейных уравнений методом Гаусса.
- 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
- 5. Решение обобщенно-треугольной системы линейных уравнений.
- 6. Системы однородных линейных уравнений.
- § 3. Симметрические многочлены и их приложения к решению систем уравнений
- 2. Выражение степенных сумм
- 3. Основная теорема о симметрических многочленах от двух переменных.
- 4. Системы симметрических алгебраических уравнений.
- 5. Применение симметрических многочленов к решению иррациональных уравнений.
- § 4. Неравенства с многими переменными
- 2. Среднее арифметическое и среднее геометрическое трех чисел.
- 3. Неравенство Коши (двумерный вариант).
- 4. Задачи на наибольшие и наименьшие значения.
- § 5. Решение неравенств
- 2. Неравенства с двумя переменными.
- 3. Задание областей неравенствами и системами неравенств.
- 4. Понятие о линейном программировании.
- 5. Краткие исторические сведения.
- Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
- § 1. Комплексные числа в алгебраической форме
- 2. Комплексные числа.
- 3. Сложение комплексных чисел; умножение на действительные числа.
- 4. Умножение комплексных чисел.
- 5. Квадратные уравнения с действительными коэффициентами.
- 6. Деление комплексных чисел.
- 7. Сопряженные комплексные числа.
- 8. Извлечение квадратных корней из комплексных чисел.
- § 2. Тригонометрическая форма комплексных чисел
- 2. Полярная система координат.
- 3. Тригонометрическая форма комплексного числа.
- 4. Умножение и деление комплексных чисел в тригонометрической форме.
- 5. Возведение комплексных чисел в степень. Формула Муавра.
- 6. Извлечение корня из комплексного числа.
- 7. Функции комплексного переменного и преобразования комплексной плоскости.
- § 3. Некоторые виды алгебраических уравнений
- 2. Двучленные уравнения.
- 3. Корни из единицы и построение правильных многоугольников.
- 4. Трехчленные уравнения.
- § 4. Основная теорема алгебры многочленов и ее следствия
- 2. Многочлены с действительными коэффициентами.
- 3. Разложение на множители многочленов с действительными коэффициентами.
- 4. Краткие исторические сведения.
- Глава VI. ЦЕПНЫЕ ДРОБИ
- § 1. Конечные цепные дроби
- 2. Пример цепной дроби.
- 3. Определение цепной дроби.
- 4. Представление рациональных чисел в виде конечной цепной дроби.
- 5. Подходящие дроби.
- 6. Свойства подходящих дробей.
- 8. Подходящие дроби и календарь.
- 9. Приближение цепной дроби подходящими дробями.
- § 2. Бесконечные цепные дроби
- 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
- 3. Цепные дроби как вычислительный инструмент.
- 4. Краткие исторические сведения.
- Глава VII. КОМБИНАТОРИКА
- § 1. Комбинаторные задачи
- § 2. Комбинаторные задачи. Продолжение
- § 3. Определения и формулы
- § 4. Соединения с повторениями
- § 5. Комбинаторные задачи. Окончание
- § 6. Бином Ньютона и его обобщения
- § 7. Краткие исторические сведения
- Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
- § 3. Примеры вычисления вероятностей
- § 4. Полная вероятность. Формула Байеса
- § 5. Повторение испытаний
- § 6. Примеры вычисления вероятностей. Окончание
- § 7. Краткие исторические сведения