| << Предыдущий параграф |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Задача 128. Парамагнитная и диамагнитная восприимчивости без учета спина
Вычислить парамагнитную и диамагнитную восприимчивости на один связанный электрон, находящийся в центральном поле. Спин электрона не учитывать.
Решение. Пусть на рассматриваемый атомный электрон, движение которого описывается гамильтонианом  дополнительно действует магнитное поле
дополнительно действует магнитное поле  Выбирая калибровку, при которой дивергенция вектор-потенциала обращается в нуль, получаем
Выбирая калибровку, при которой дивергенция вектор-потенциала обращается в нуль, получаем

Чтобы удовлетворить условию калибровки, положим

тогда

или

Магнитная энергия в состоянии  (посредством
(посредством  обозначена вся совокупность квантовых чисел, характеризующих одноэлектронное состояние) с точностью до членов второго порядка равна
обозначена вся совокупность квантовых чисел, характеризующих одноэлектронное состояние) с точностью до членов второго порядка равна

Пусть далее все атомы вещества находятся в основном состоянии (такое предположение действительно разумно, так как
энергия возбуждения, как правило, составляет несколько электрон-вольт, что значительно больше тепловой энергии). Допустим, что в этом основном состоянии рассматриваемый электрон обладает орбитальным моментом  следовательно, может иметь различные значения проекции момента
следовательно, может иметь различные значения проекции момента  на направление магнитного поля. В этом случае первый член формулы (128.4) даст в магнитную энергию (отнесенную к одному электрону) вклад вида
на направление магнитного поля. В этом случае первый член формулы (128.4) даст в магнитную энергию (отнесенную к одному электрону) вклад вида

В состоянии теплового равновесия число электронов с проекцией момента  пропорционально, согласно Больцману,
пропорционально, согласно Больцману,  поэтому средняя магнитная энергия, приходящаяся на один электрон, будет равна
поэтому средняя магнитная энергия, приходящаяся на один электрон, будет равна

где

Безразмерная величина а для всех разумных значений напряженности поля  значительно меньше единицы, и фигурирующие выше экспоненты можно разложить в ряд. Таким образом, имеем
значительно меньше единицы, и фигурирующие выше экспоненты можно разложить в ряд. Таким образом, имеем

Все эти суммы симметричны относительно  поэтому суммы, содержащие нечетные степени
поэтому суммы, содержащие нечетные степени  обращаются в нуль, и мы можем написать
обращаются в нуль, и мы можем написать

причем здесь мы опустили члены порядка  и выше. Отсюда для плотности магнитной энергии получаем
и выше. Отсюда для плотности магнитной энергии получаем

где  число электронов с моментом
число электронов с моментом  Следует заметить, что плотность энергии пропорциональна квадрату
Следует заметить, что плотность энергии пропорциональна квадрату
напряженности поля, хотя исходная энергия  зависела от поля линейно.
зависела от поля линейно.
Второй член формулы (128.4)

оказывается (см. ниже) значительно меньше, чем  поэтому он не играет большой роли в тех случаях, когда первый член отличен от нуля. Эти же соображения относятся и к третьему члену формулы (128.4). Таким образом, для всех
поэтому он не играет большой роли в тех случаях, когда первый член отличен от нуля. Эти же соображения относятся и к третьему члену формулы (128.4). Таким образом, для всех  магнитные свойства вещества определяются первым членом, в случае же
магнитные свойства вещества определяются первым членом, в случае же  эти свойства определяются энергией
эти свойства определяются энергией  Так как
Так как

то мы можем написать

где  означает волновую функцию, соответствующую основному
означает волновую функцию, соответствующую основному  -состоянию, а
-состоянию, а  -среднее значение
-среднее значение  в этом состоянии. В данном случае необходимость в температурном усреднении отпадает. Первый и третий члены формулы (128.4) в случае
в этом состоянии. В данном случае необходимость в температурном усреднении отпадает. Первый и третий члены формулы (128.4) в случае  -состояния обращаются в нуль, так как
-состояния обращаются в нуль, так как  поэтому теперь их можно не рассматривать.
поэтому теперь их можно не рассматривать.
Согласно электродинамике Максвелла, изменение поля  на
на  приводит к изменению плотности магнитной энергии:
приводит к изменению плотности магнитной энергии:

где  - так называемая намагниченность, т. е. магнитный дипольный момент
- так называемая намагниченность, т. е. магнитный дипольный момент  вещества, индуцированный полем
вещества, индуцированный полем  Предполагается, что она пропорциональна полю
Предполагается, что она пропорциональна полю 

Коэффициент пропорциональности х называется магнитной восприимчивостью. Комбинируя соотношения (128.10) и (128.11), получаем

и, следовательно, плотность магнитной энергии будет равна

Если  положительная величина, то мы говорим о парамагнетизме, если
положительная величина, то мы говорим о парамагнетизме, если  отрицательная величина, то — о диамагнетизме.
отрицательная величина, то — о диамагнетизме.
Макроскопическое выражение (128.12) для плотности магнитной энергии мы должны отождествить либо с выражением (128.7), если  либо с умноженным на
либо с умноженным на  выражением (128.9), если
выражением (128.9), если
 В первом случае мы имеем дело с парамагнетизмом, причем
В первом случае мы имеем дело с парамагнетизмом, причем

во втором же случае

и, следовательно, мы имеем дело с диамагнетизмом.
Как и следовало ожидать, формула (128.13) совпадает с классической формулой Ланжевена, полученной усреднением по ориентациям постоянного дипольного момента

Диамагнитная восприимчивость значительно меньше парамагнитной восприимчивости, поэтому ее можно не учитывать при рассмотрении парамагнитных веществ. В этом можно убедиться, оценив отношение

Фактически это есть отношение вращательной и тепловой энергий электрона. Первая из них составляет несколько электрон-вольт, вторая по порядку величины равна  при комнатной температуре.
при комнатной температуре.
| << Предыдущий параграф |
Оглавление
- Предисловие редактора перевода
- I. Общие принципы
- Задача 1. Закон сохранения вероятности
- Задача 2. Вариационный принцип Шредингера
- Задача 3. Классическая механика для пространственных средних
- Задача 4. Классические законы для момента количества движения
- Задача 5. Закон сохранения энергии
- Задача 6. Эрмитово сопряжение
- Задача 7. Построение эрмитова оператора
- Задача 8. Дифференцирование оператора
- Задача 9. Изменение средних значений со временем
- Задача 10. Картина Шредингера и картина Гейзенберга
- Задача 11. Гамильтониан, зависящий от времени
- Задача 12. Повторное измерение
- Задача 13. Криволинейные координаты
- Задача 14. Волновые функции в импульсном представлении
- Задача 15. Пространство импульсов. Периодические и непериодические волновые функции
- II. Одночастичные задачи без учета спина
- Задача 16. Фундаментальные решения в случае свободного движения
- Задача 17. Волновой пакет в случае свободного движения
- Задача 18. Стоячие волны
- Задача 19. Полупроницаемая перегородка
- Задача 20. Полупроницаемая перегородка в виде «дельта»-образного потенциального барьера
- Задача 21. Рассеяние на «дельта»-образном потенциальном барьере
- Задача 22. Рассеяние на симметричном потенциальном барьере
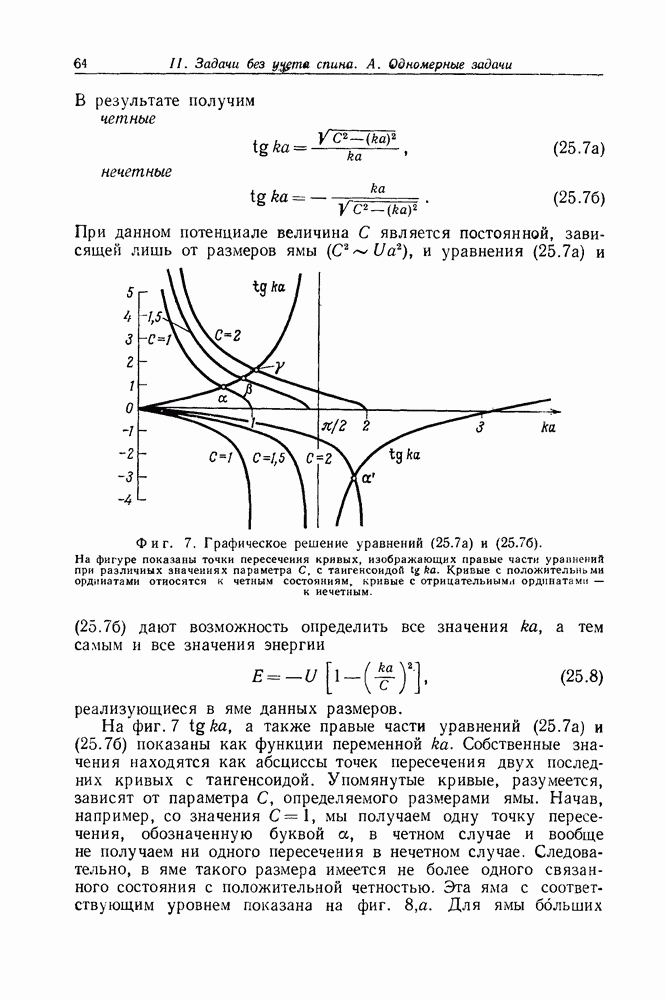
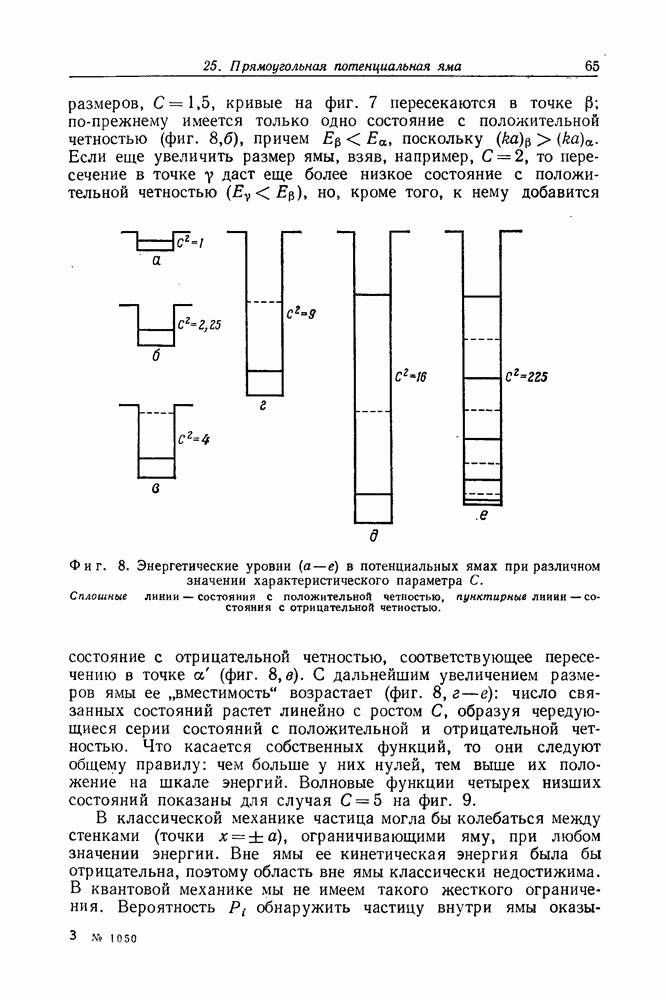
- Задача 23. Отражение от прямоугольного барьера
- Задача 24. Инверсия отражения
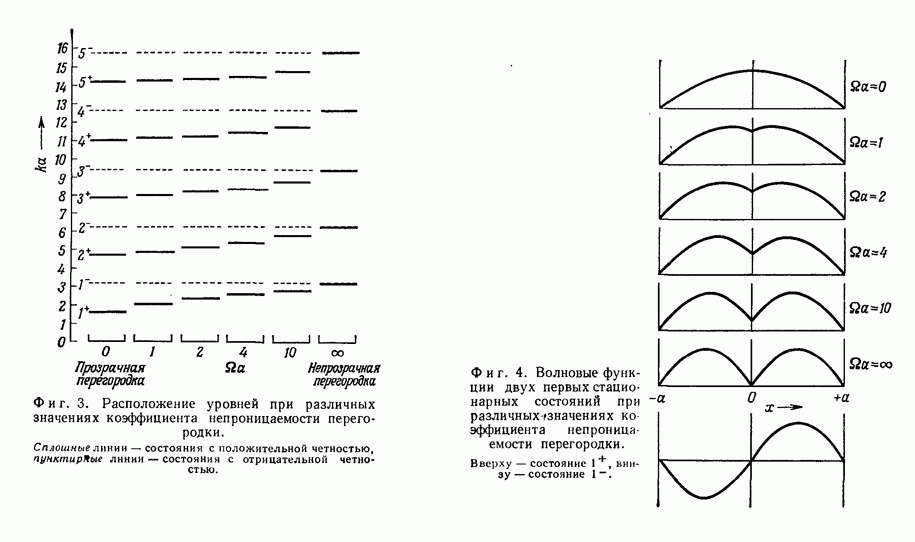
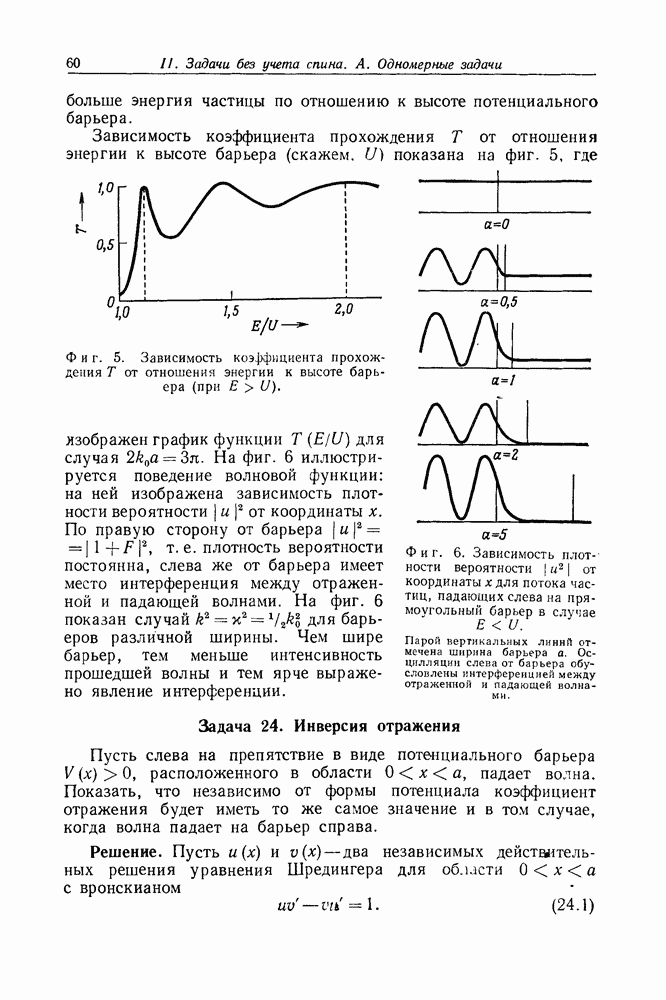
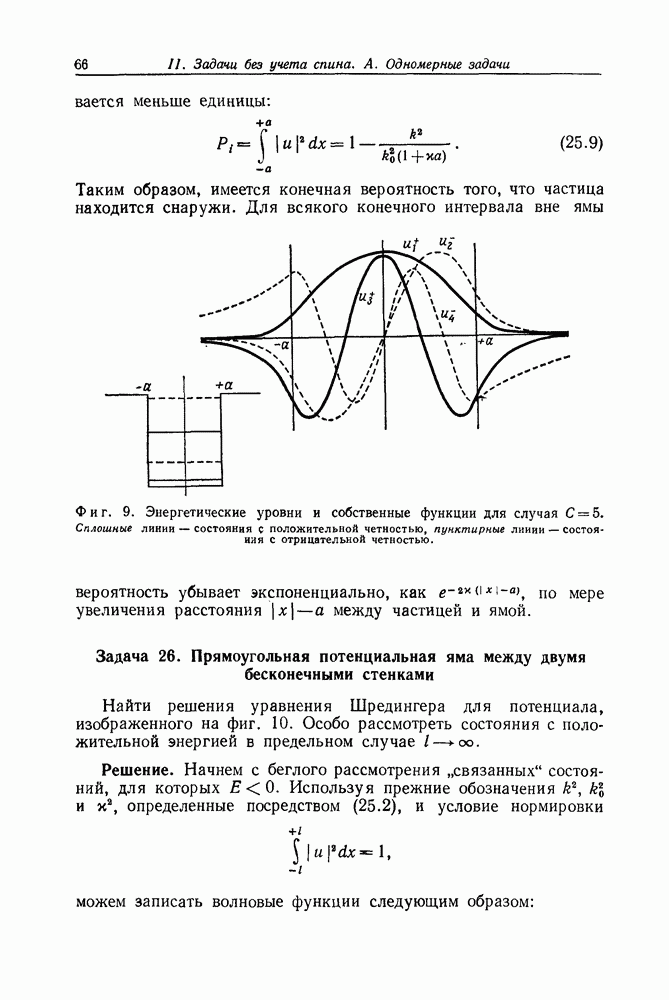
- Задача 25. Прямоугольная потенциальная яма
- Задача 26. Прямоугольная потенциальная яма между двумя бесконечными стенками
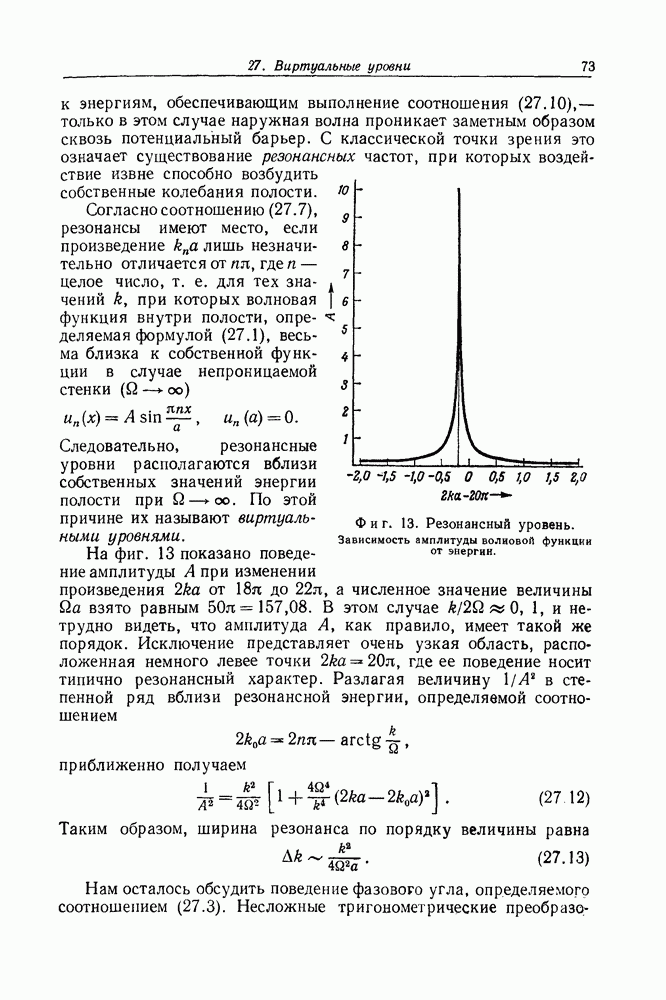
- Задача 27. Виртуальные уровни
- Задача 28. Периодический потенциал
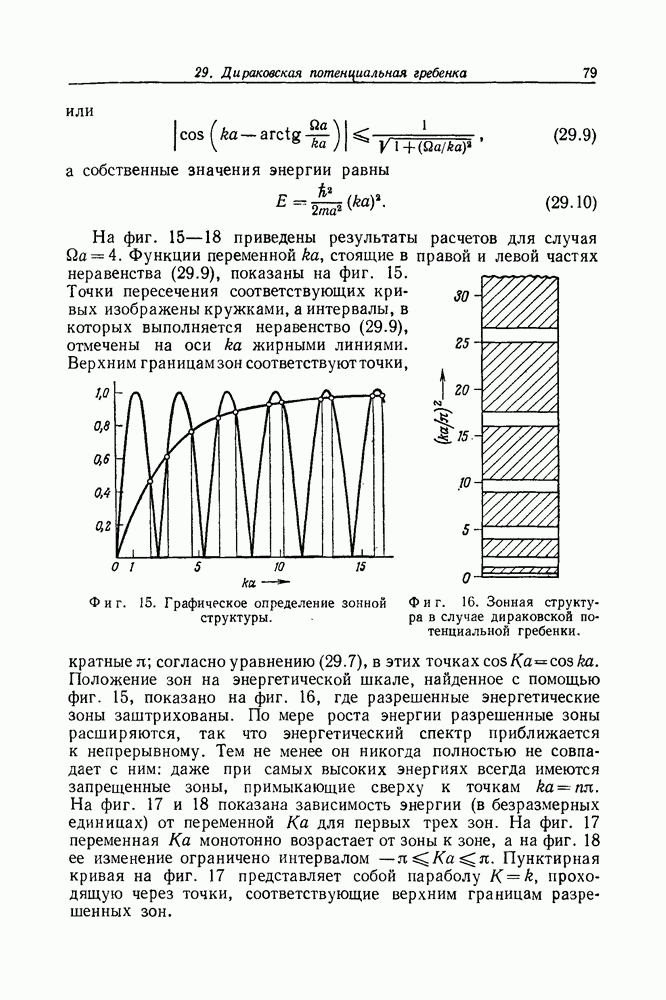
- Задача 29. Дираковская потенциальная гребенка
- Задача 30. Гармонический осциллятор
- Задача 31. Осциллятор в абстрактном гильбертовом пространстве (осциллятор в представлении Фока)
- Задача 32. Использование лестничных операторов для нахождения собственных функций осциллятора
- Задача 33. Гармонический осциллятор в матричном представлении
- Задача 34. Волновые функции осциллятора в пространстве импульсов
- Задача 35. Ангармонический осциллятор
- Задача 36. Приближенные волновые функции
- Задача 37. Потенциальная ступенька
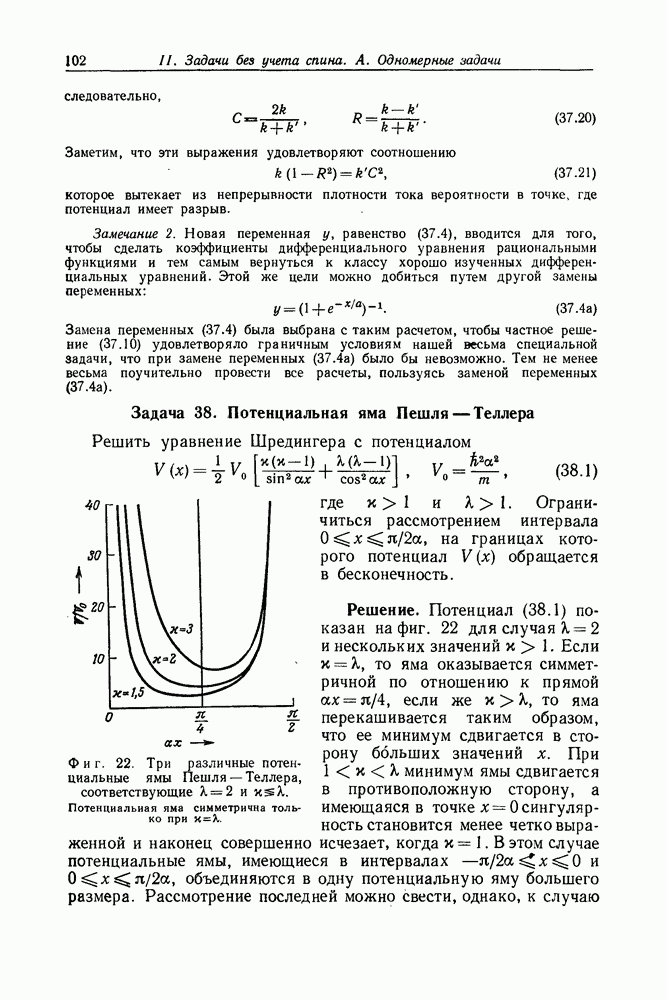
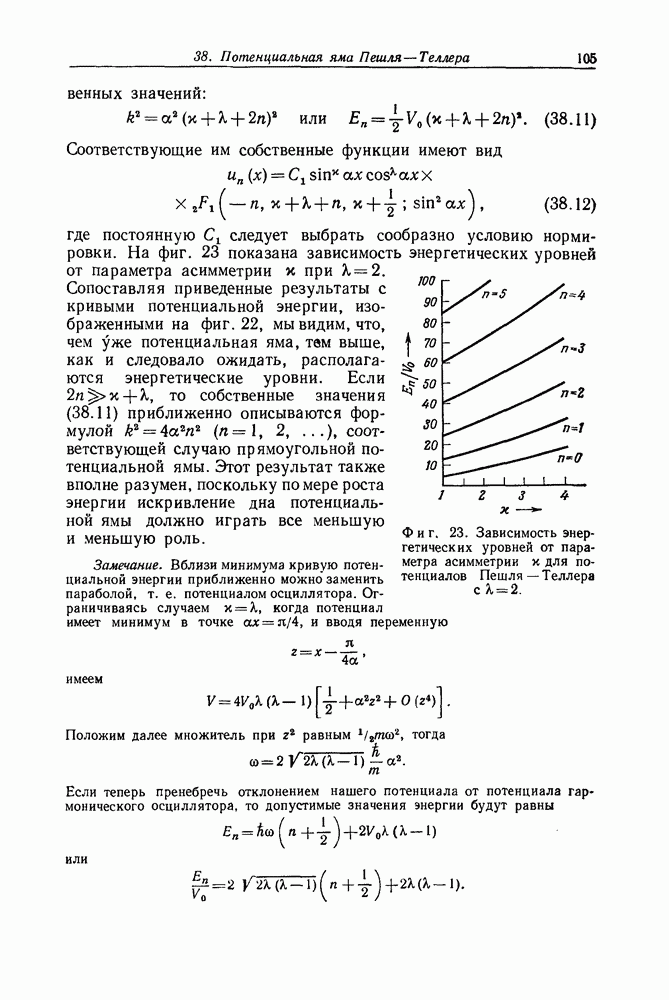
- Задача 38. Потенциальная яма Пешля — Теллера
- Задача 39. Модифицированная потенциальная яма Пешля—Теллера
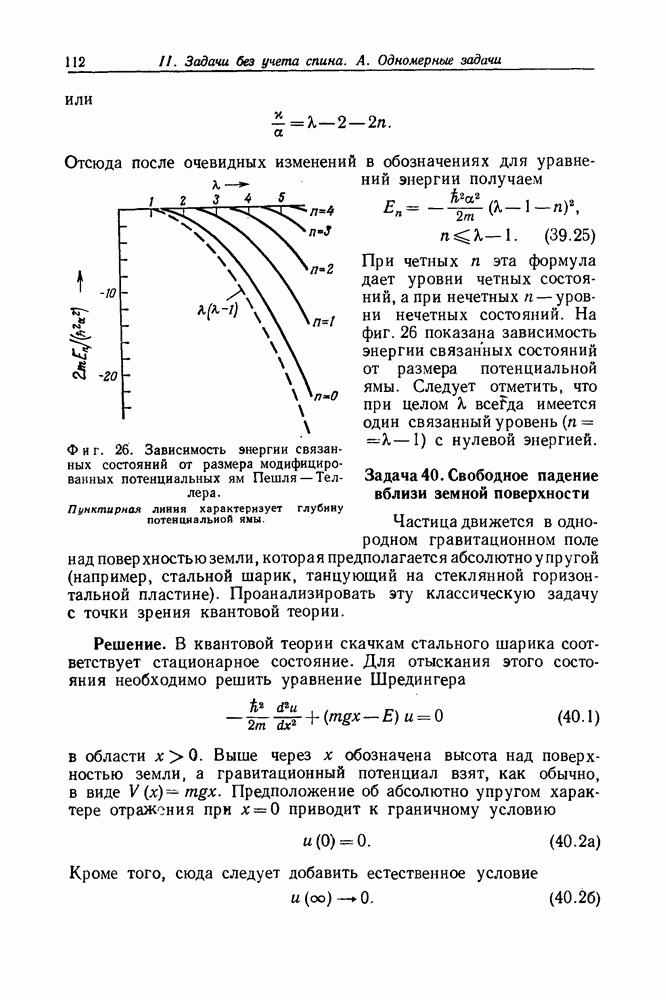
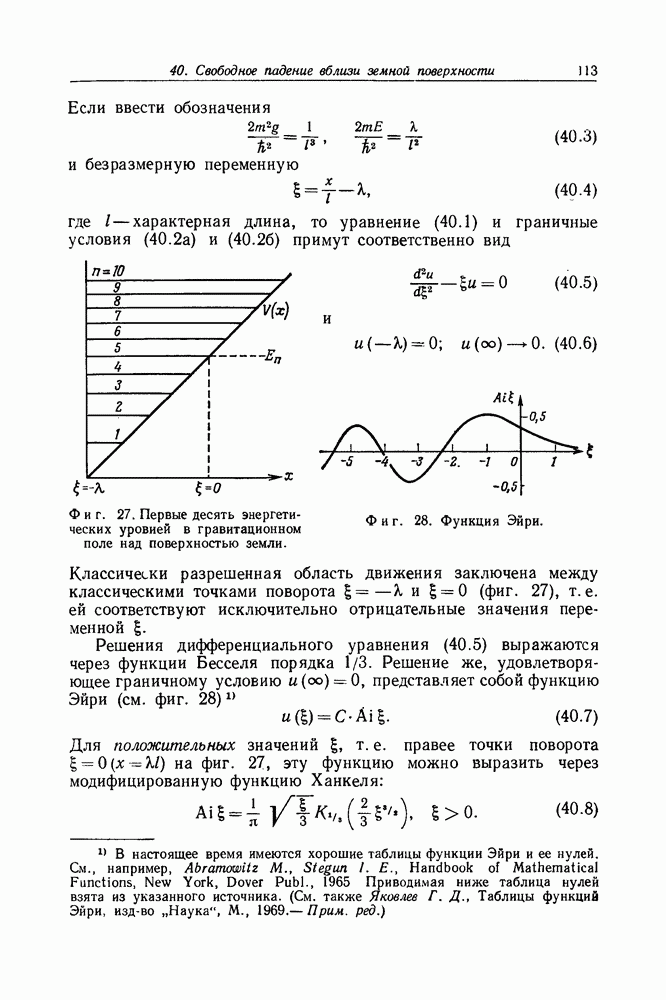
- Задача 40. Свободное падение вблизи земной поверхности
- Задача 41. Ускоряющее электрическое поле
- Б. Задачи с двумя или тремя степенями свободы без сферической симметрии
- Задача 42. Круговой осциллятор
- Задача 43. Эффект Штарка для двумерного ротатора
- Задача 44. Ион молекулы водорода
- Задача 45. Наклонное падение плоской волны
- Задача 46. Симметричный волчок
- В. Момент количества движения
- Задача 47. Бесконечно малые вращения
- Задача 48. Момент количества движения в сферических координатах
- Задача 49. Момент количества движения и оператор Лапласа
- Задача 50. Преобразования в гильбертовом пространстве
- Задача 51. Коммутаторы в координатном представлении
- Задача 52. Частица со спином 1
- Задача 53. Перестановочные соотношения компонент тензора
- Задача 54. Тензор квадрупольного момента. Сферические гармоники
- Задача 55. Преобразование сферических гармоник
- Задача 56. Построение собственных векторов оператора Lx в абстрактном гильбертовом пространстве
- Задача 57. Ортогональность сферических гармоник
- Г. Сферически симметричные потенциалы
- Задача 58. Средние значения компонент момента количества движения
- Задача 59. Радиальная компонента оператора импульса
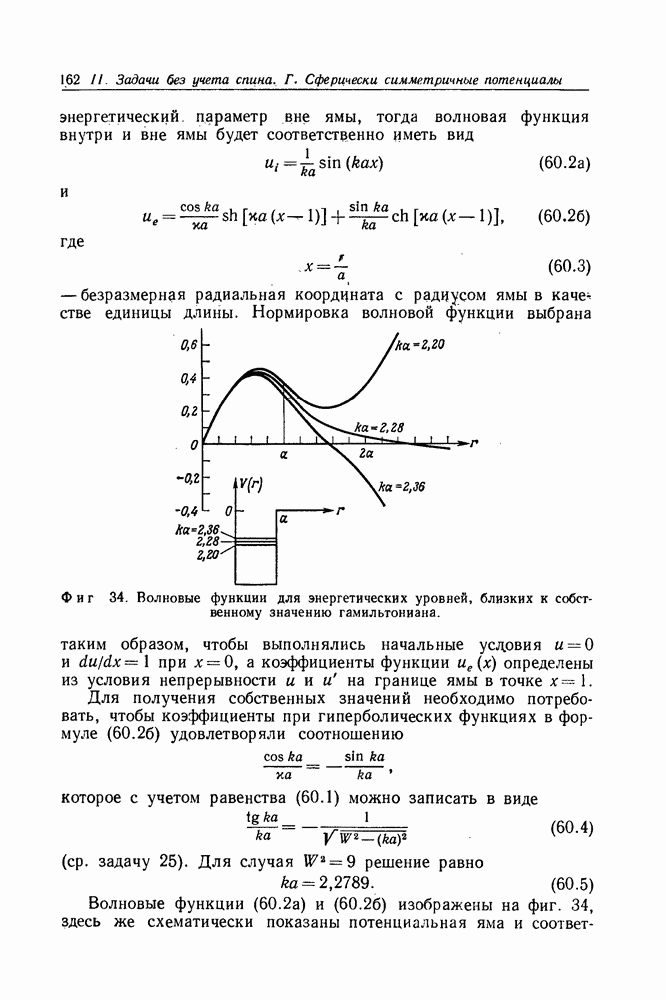
- Задача 60. Решения, близкие к собственным функциям
- Задача 61. Квадрупольный момент
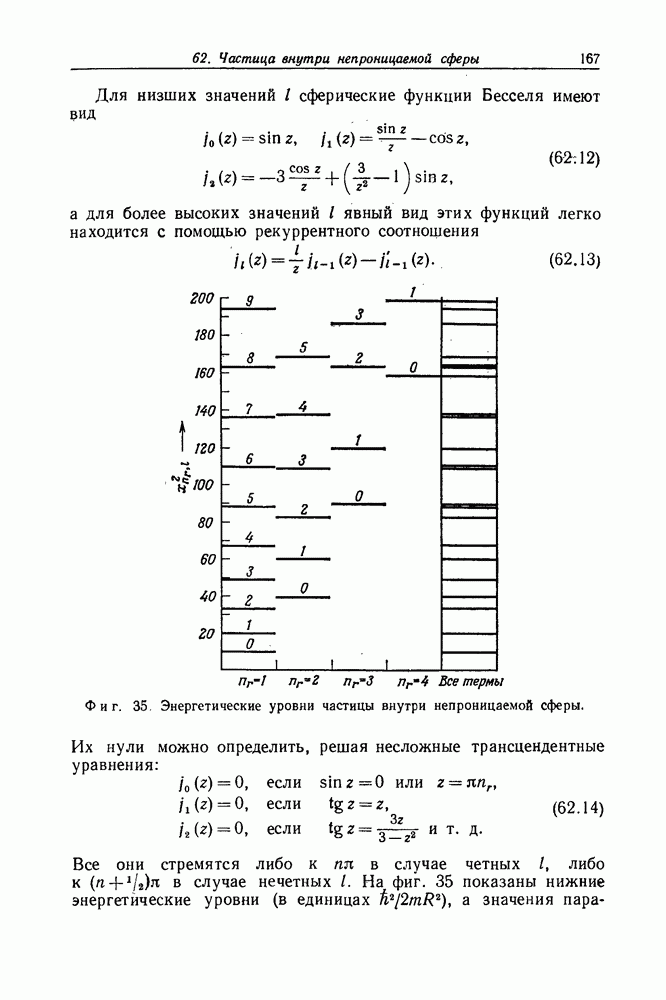
- Задача 62. Частица внутри непроницаемой сферы
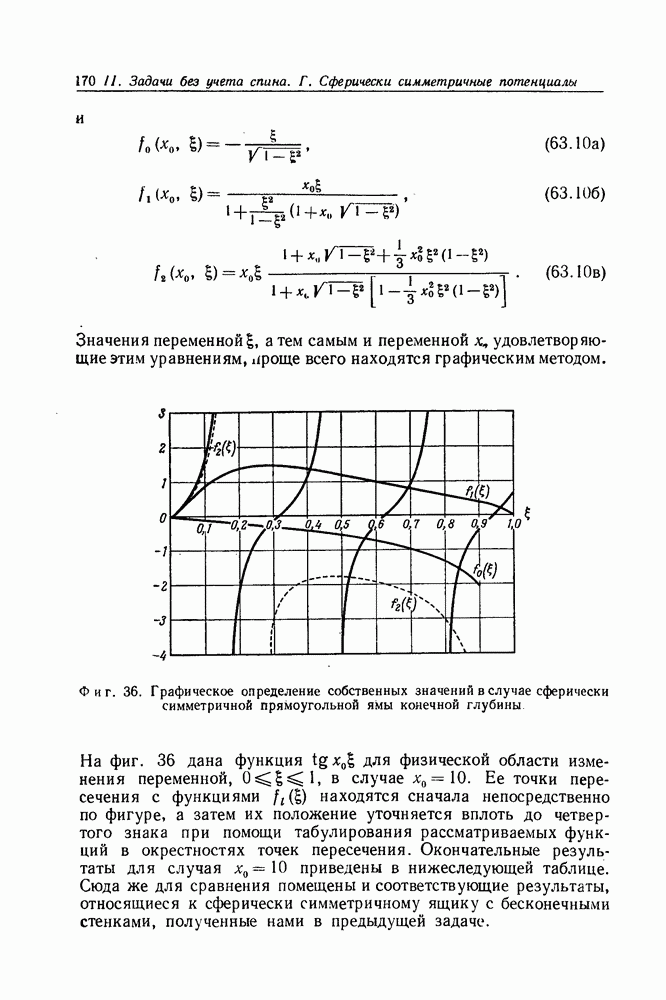
- Задача 63. Сферически симметричная прямоугольная яма конечной глубины
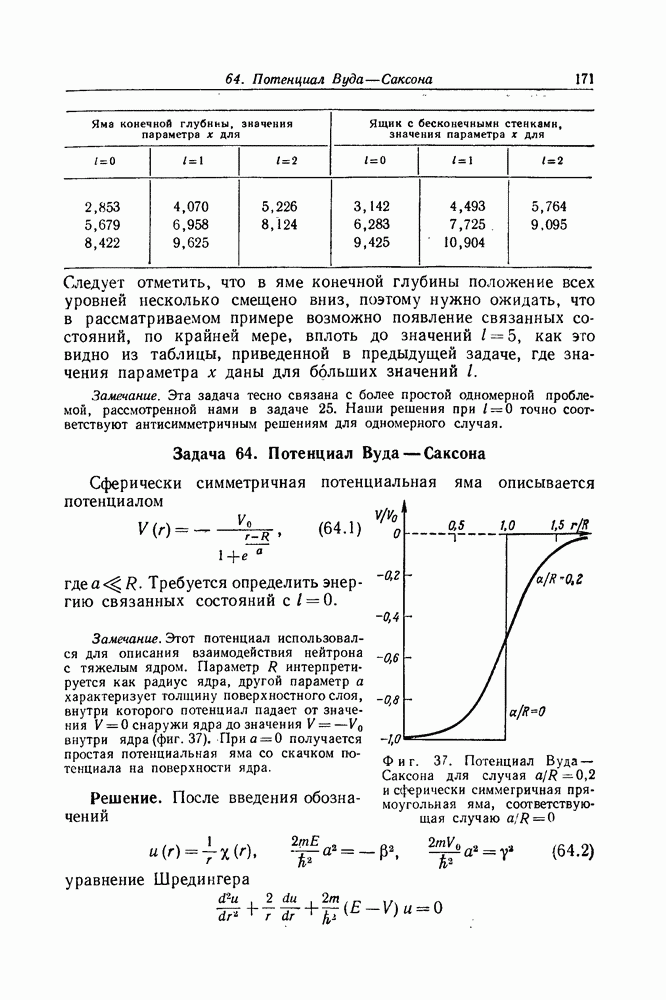
- Задача 64. Потенциал Вуда — Саксона
- Задача 65. Изотропный осциллятор
- Задача 66. Вырожденные состояния изотропного осциллятора
- Задача 67. Проблема Кеплера
- Задача 68. Потенциал Хюльтена
- Задача 69. Молекулярный потенциал Кратцера
- Задача 70. Потенциал Морса
- Задача 71. Ротационные поправки к формуле Морса
- Задача 72. Потенциал Юкавы
- Задача 73. Изотопический сдвиг границы рентгеновского излучения
- Задача 74. Основное состояние мезоатома
- Задача 75. Модель дейтрона с центральным взаимодействием
- Задача 76. Импульсное представление для волновых функций в поле центральных сил
- Задача 77. Уравнение Шредингера в импульсном представлении в поле центральных сил
- Задача 78. Водородные волновые функции в импульсном пространстве
- Задача 79. Штарк-эффект у пространственного ротатора
- Задача 80. Интерференция падающей и рассеянной волн
- Задача 81. Разложение плоской волны по парциальным волнам
- Задача 82. Разложение амплитуды рассеяния по парциальным волнам
- Задача 83. Рассеяние при низких энергиях
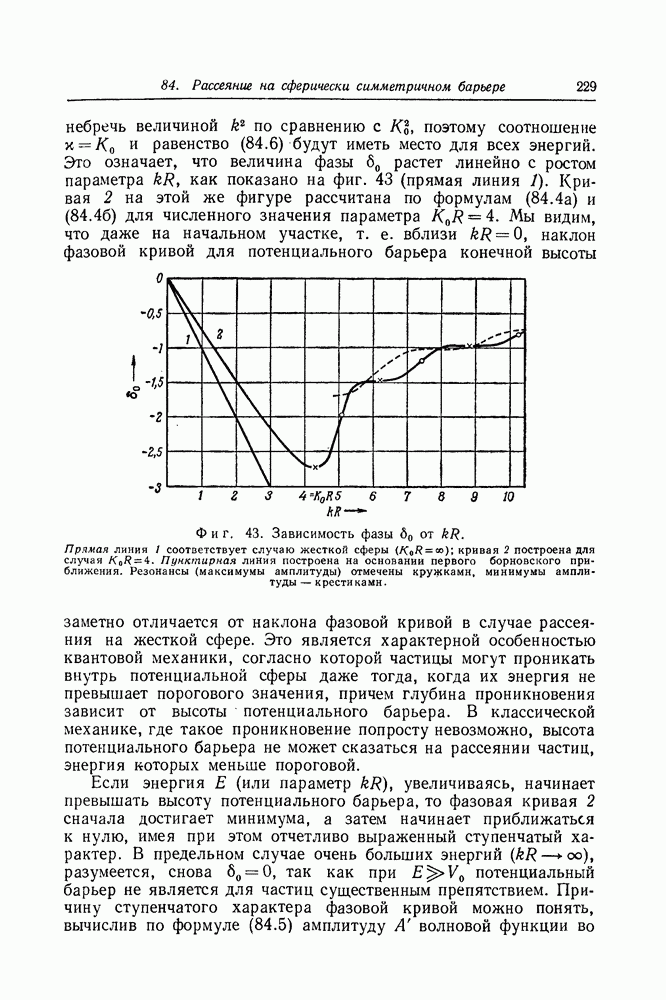
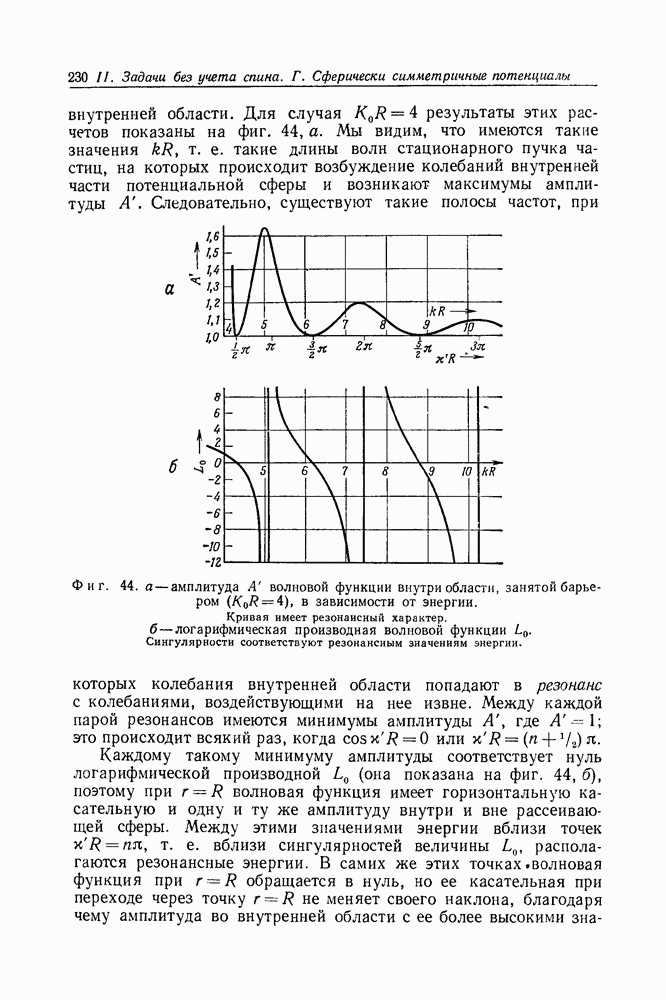
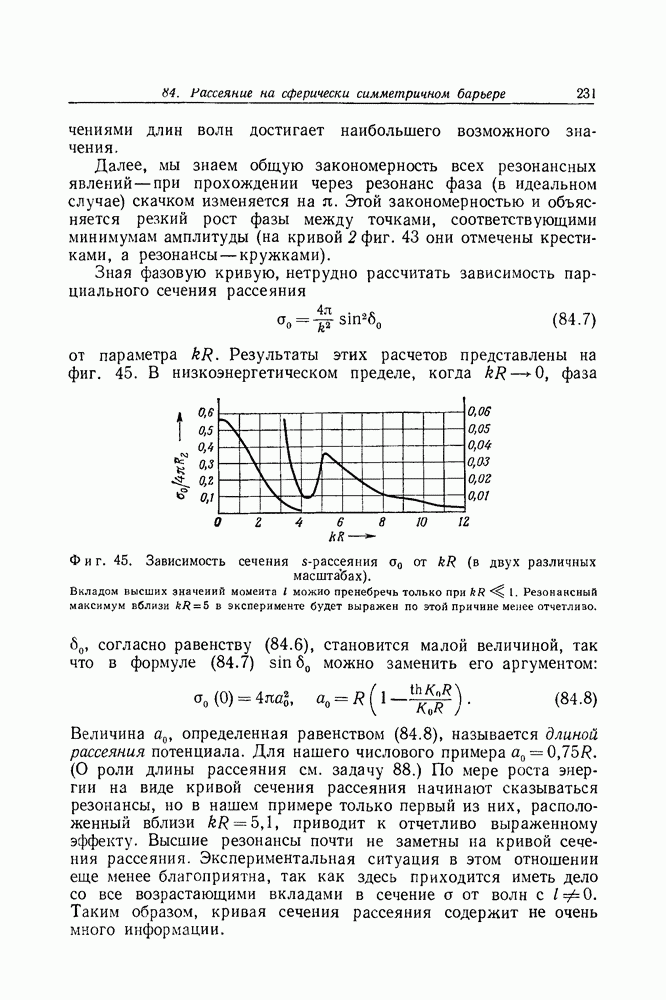
- Задача 84. Рассеяние на сферически симметричном прямоугольном потенциальном барьере
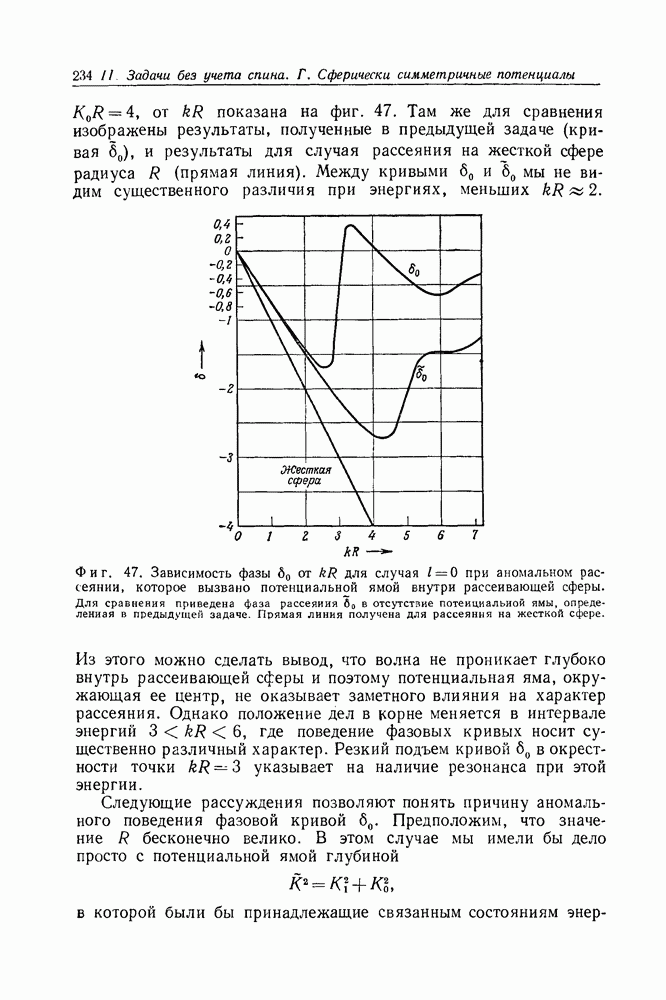
- Задача 85. Аномальное рассеяние
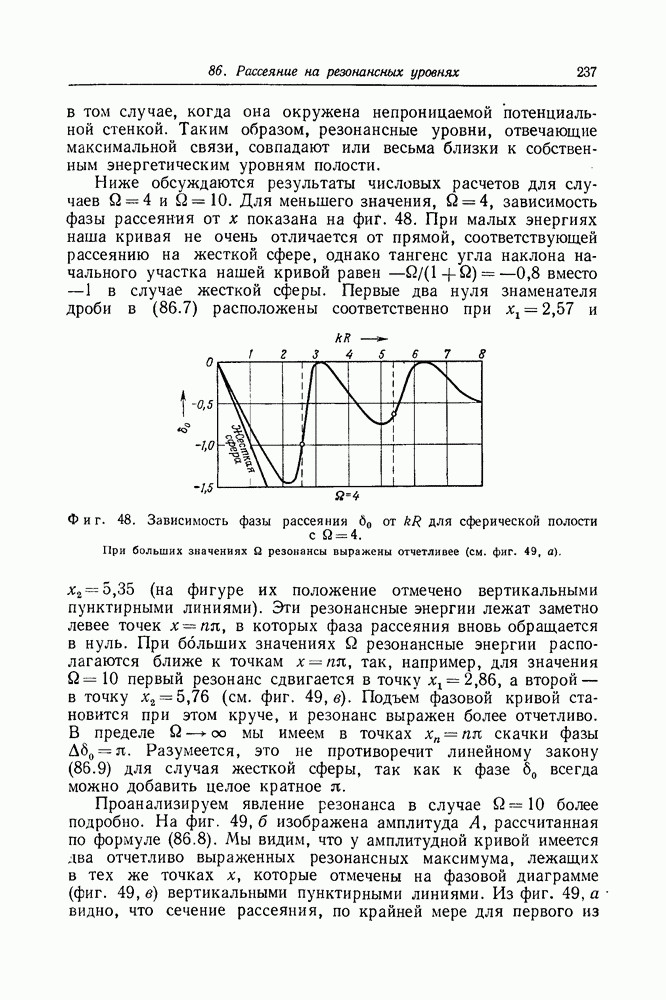
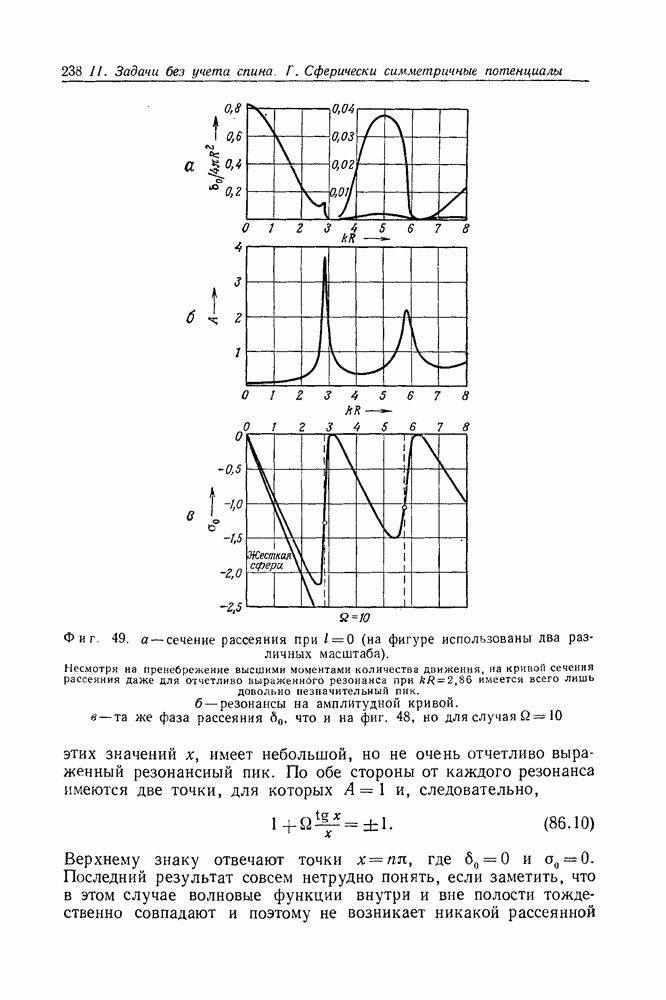
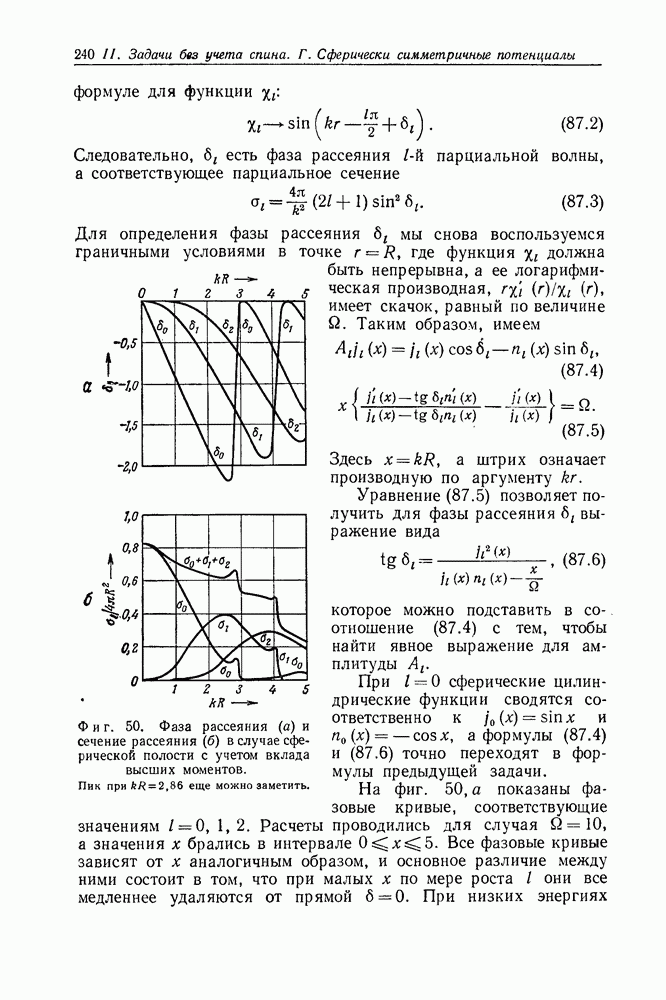
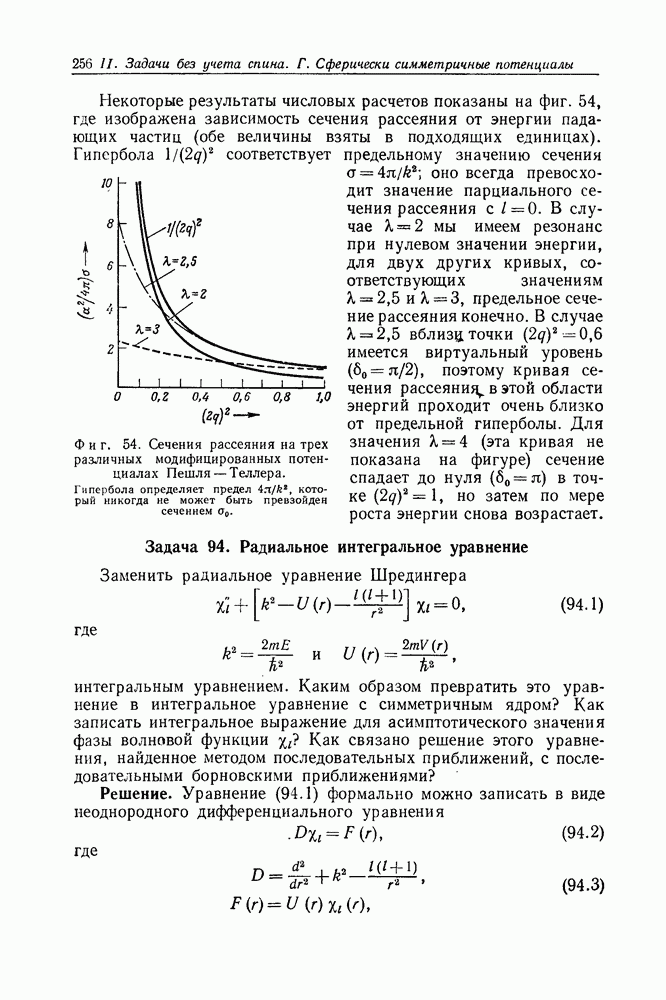
- Задача 86. Рассеяние на резонансных уровнях
- Задача 87. Вклад состояний с высшими значениями момента количества движения
- Задача 88. Приближение, не зависящее от формы потенциала
- Задача 89. Низкоэнергетическое рассеяние на сферически симметричной прямоугольной яме
- Задача 90. Низкоэнергетическое рассеяние и связанные состояния
- Задача 91. Дейтронный потенциал с жесткой сердцевиной и без нее
- Задача 92. Низкоэнергетическое рассеяние при наличии жесткой сердцевины и без нее
- Задача 93. Низкоэнергетическое рассеяние на модифицированном потенциале Пешля — Теллера
- Задача 94. Радиальное интегральное уравнение
- Задача 95. Вариационный принцип Швингера
- Задача 96. Последовательные приближения для фазы рассеяния
- Задача 97. Уравнение Калоджеро
- Задача 98. Линеаризация уравнения Калоджеро
- Задача 99. Длина рассеяния потенциала, имеющего вид степенной функции
- Задача 100. Второе приближение к уравнению Калоджеро
- Задача 101. Длина рассеяния для сферически симметричной прямоугольной потенциальной ямы
- Задача 102. Длина рассеяния потенциала Юкавы
- Задача 103. Улучшение сходимости рядов сферических гармоник
- Задача 104. Интеграл по прицельному расстоянию
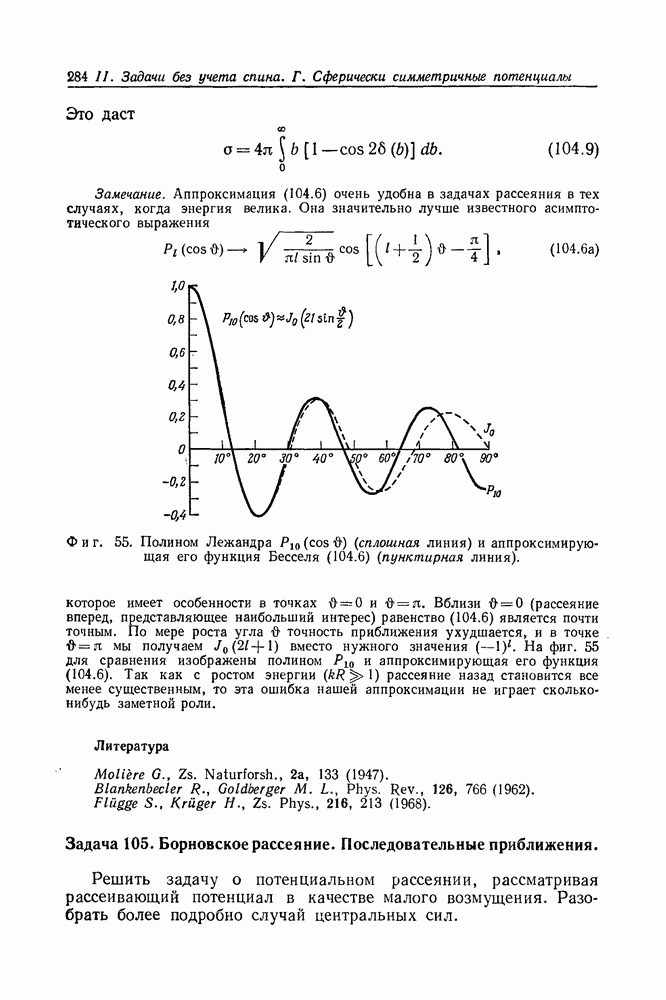
- Задача 105. Борновскоерассеяние. Последовательные приближения.
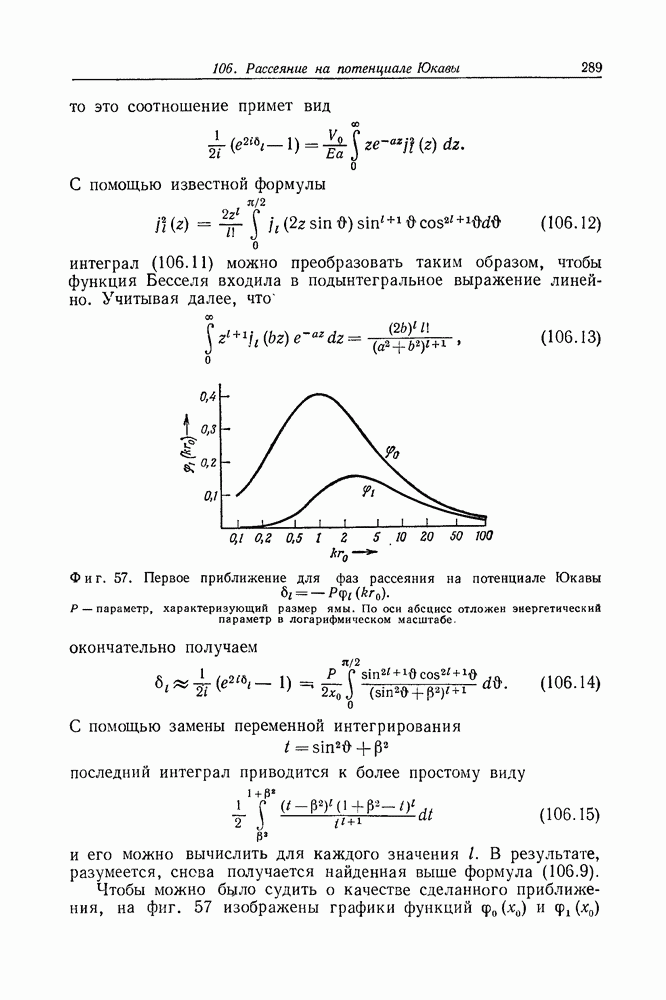
- Задача 106. Рассеяние на потенциале Юкавы
- Задача 107. Рассеяние на экспоненциальном потенциале
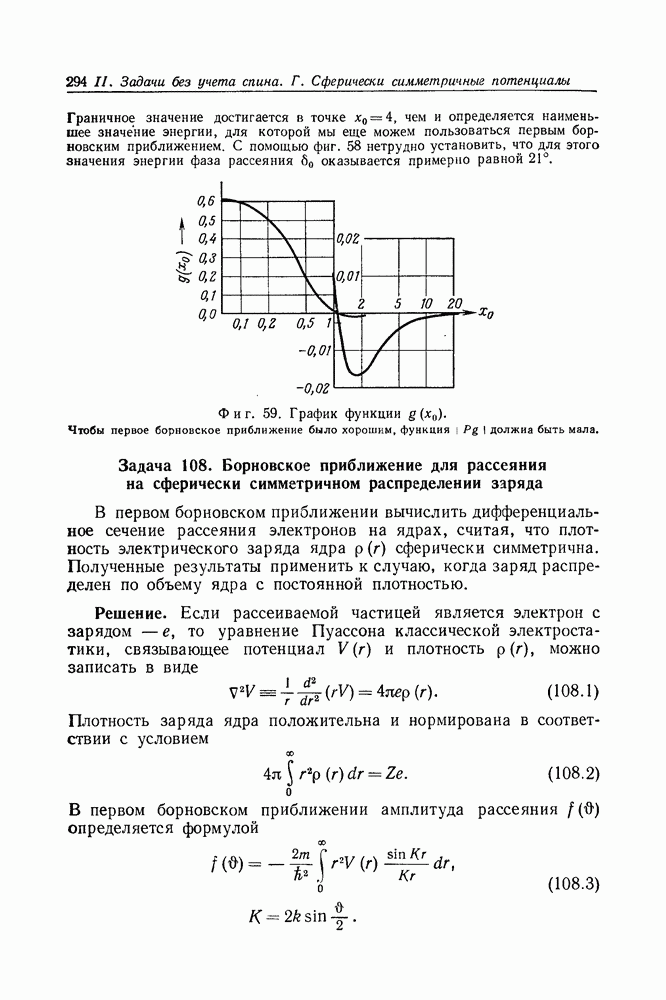
- Задача 108. Борновское приближение для рассеяния на сферически симметричном распределении заряда
- Задача 109. Высокоэнергетическое рассеяние на жесткой сфере
- Задача 110. Формула Резерфорда
- Задача 111. Разложение кулоновской функции по парциальным волнам
- Задача 112. Аномальное рассеяние
- Задача 113. Преобразование Зоммерфельда — Ватсона
- Задача 114. Полюс Редже
- Д. Приближение Вентцеля — Крамерса — Бриллюэна (ВКБ)
- Задача 115. Разложение эйконала
- Задача 116. Применение метода ВКБ к радиальному уравнению
- Задача 117. Граничное ВКБ-условие Лангера
- Задача 118. Гармонический осциллятор в приближении ВКБ
- Задача 120. Проблема Кеплера в приближении ВКБ
- Задача 121. Фазы ВКБ для свободного движения
- Задача 122. Вычисление фаз ВКБ
- Задача 123. Расчет кулоновских фаз методом ВКБ
- Задача 124. Квазипотенциал
- Е. Магнитное поле
- Задача 125. Введение магнитного поля
- Задача 126. Плотность тока в присутствии магнитного поля
- Задача 127. Нормальный эффект Зеемана
- Задача 128. Парамагнитная и диамагнитная восприимчивости без учета спина