| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 84. Рассеяние на сферически симметричном прямоугольном потенциальном барьере
Дан потенциал  при
при  при
при  Для случая
Для случая  найти зависимость фазы рассеяния
найти зависимость фазы рассеяния  и парциального сечения
и парциального сечения  от энергии падающих частиц.
от энергии падающих частиц.
Решение. Вводя обозначения

можно записать радиальную волновую функцию  следующим образом:
следующим образом:
если энергия  меньше порогового значения
меньше порогового значения  то
то

если же энергия  выше порогового значения
выше порогового значения  то
то

в последнем случае величина к оказывается чисто мнимой:  . У волновой функции вне сферы нормировка во всех случаях одинакова, поэтому амплитуды
. У волновой функции вне сферы нормировка во всех случаях одинакова, поэтому амплитуды  характеризуют степень возбуждения области, заключенной внутри сферы. Заметим, что приведенные выше выражения уже написаны с учетом граничного условия.
характеризуют степень возбуждения области, заключенной внутри сферы. Заметим, что приведенные выше выражения уже написаны с учетом граничного условия.
Непрерывность функций  в точке
в точке  предполагает непрерывность логарифмической производной, значение которой при
предполагает непрерывность логарифмической производной, значение которой при  т. е.
т. е.

можно получить двумя способами, беря для волновой функции выражения, соответственно справедливые либо в области  либо в области
либо в области  Таким образом, имеем
Таким образом, имеем

и

Только в случае  решение во внутренней области оказывается периодическим и выражение для амплитуды А представляет интерес:
решение во внутренней области оказывается периодическим и выражение для амплитуды А представляет интерес:

Прежде всего обсудим полученные формулы для предельно низких энергий. Когда  величину к следует заменить величиной
величину к следует заменить величиной  Кроме того, чтобы величина
Кроме того, чтобы величина  была конечной, аргумент котангенса в правой части равенства (84.4а) должен стремиться к нулю как
была конечной, аргумент котангенса в правой части равенства (84.4а) должен стремиться к нулю как  Таким образом, в этом предельном случае равенство (84.4а) принимает вид
Таким образом, в этом предельном случае равенство (84.4а) принимает вид

и, следовательно,

Если высота потенциального барьера  очень велика (т. е.
очень велика (т. е.  жесткая сфера), то при всех энергиях мы можем
жесткая сфера), то при всех энергиях мы можем
пренебречь величиной  по сравнению с
по сравнению с  поэтому соотношение
поэтому соотношение  и равенство (84.6) будут иметь место для всех энергий. Это означает, что величина фазы
и равенство (84.6) будут иметь место для всех энергий. Это означает, что величина фазы  растет линейно с ростом параметра
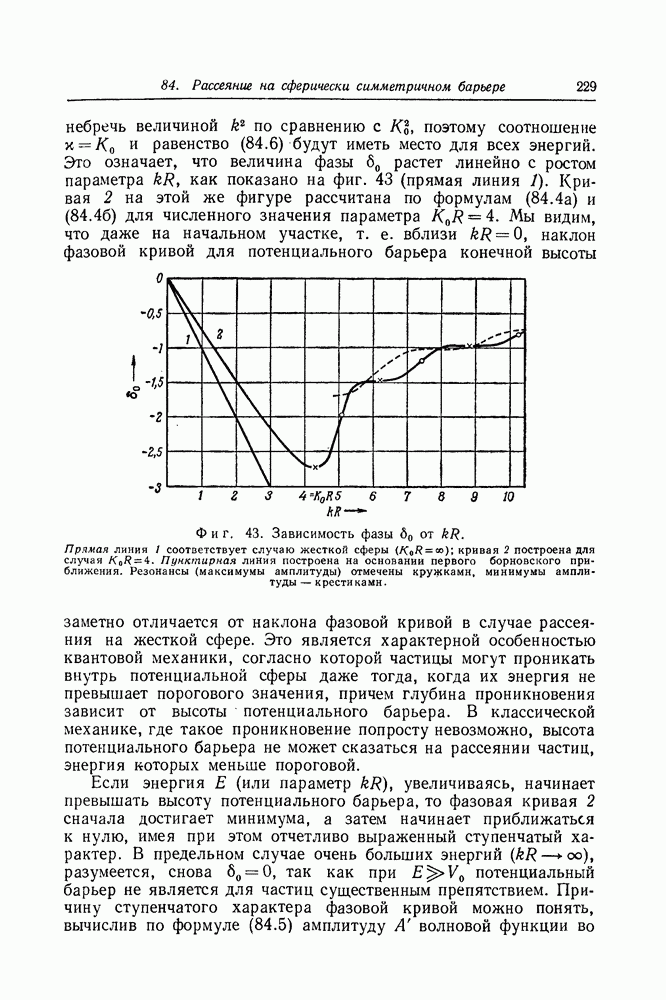
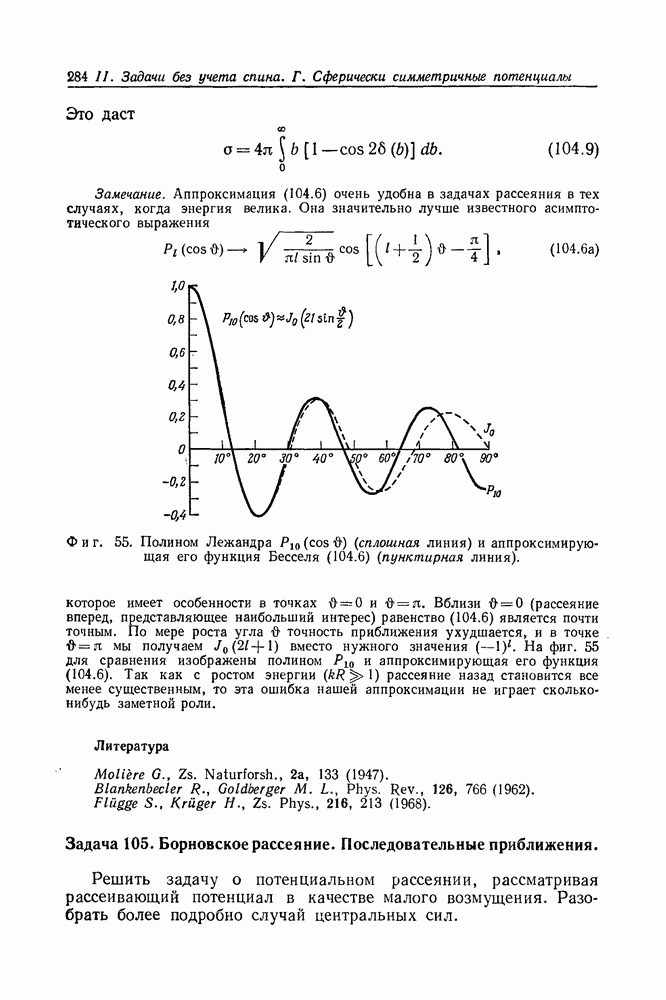
растет линейно с ростом параметра  как показано на фиг. 43 (прямая линия
как показано на фиг. 43 (прямая линия  Кривая 2 на этой же фигуре рассчитана по формулам (84.4а) и (84.46) для численного значения параметра
Кривая 2 на этой же фигуре рассчитана по формулам (84.4а) и (84.46) для численного значения параметра  Мы видим, что даже на начальном участке, т. е. вблизи
Мы видим, что даже на начальном участке, т. е. вблизи  наклон фазовой кривой для потенциального барьера конечной высоты заметно отличается от наклона фазовой кривой в случае рассеяния на жесткой сфере.
наклон фазовой кривой для потенциального барьера конечной высоты заметно отличается от наклона фазовой кривой в случае рассеяния на жесткой сфере.

Фиг. 43. Зависимость фазы 60 от  Прямая линия 1 соответствует случаю жесткой сферы
Прямая линия 1 соответствует случаю жесткой сферы  кривая 2 построена для случая
кривая 2 построена для случая  Пунктирная линия построена на основании первого борновского приближения. Резонансы (максимумы амплитуды) отмечены кружками, минимумы амплитуды — крестиками.
Пунктирная линия построена на основании первого борновского приближения. Резонансы (максимумы амплитуды) отмечены кружками, минимумы амплитуды — крестиками.
Это является характерной особенностью квантовой механики, согласно которой частицы могут проникать внутрь потенциальной сферы даже тогда, когда их энергия не превышает порогового значения, причем глубина проникновения зависит от высоты потенциального барьера. В классической механике, где такое проникновение попросту невозможно, высота потенциального барьера не может сказаться на рассеянии частиц, энергия которых меньше пороговой.
Если энергия  (или параметр
(или параметр  увеличиваясь, начинает превышать высоту потенциального барьера, то фазовая кривая 2 сначала достигает минимума, а затем начинает приближаться к нулю, имея при этом отчетливо выраженный ступенчатый характер. В предельном случае очень больших энергий
увеличиваясь, начинает превышать высоту потенциального барьера, то фазовая кривая 2 сначала достигает минимума, а затем начинает приближаться к нулю, имея при этом отчетливо выраженный ступенчатый характер. В предельном случае очень больших энергий  разумеется, снова
разумеется, снова  так как при
так как при  потенциальный барьер не является для частиц существенным препятствием. Причину ступенчатого характера фазовой кривой можно понять, вычислив по формуле (84.5) амплитуду А волновой функции во
потенциальный барьер не является для частиц существенным препятствием. Причину ступенчатого характера фазовой кривой можно понять, вычислив по формуле (84.5) амплитуду А волновой функции во
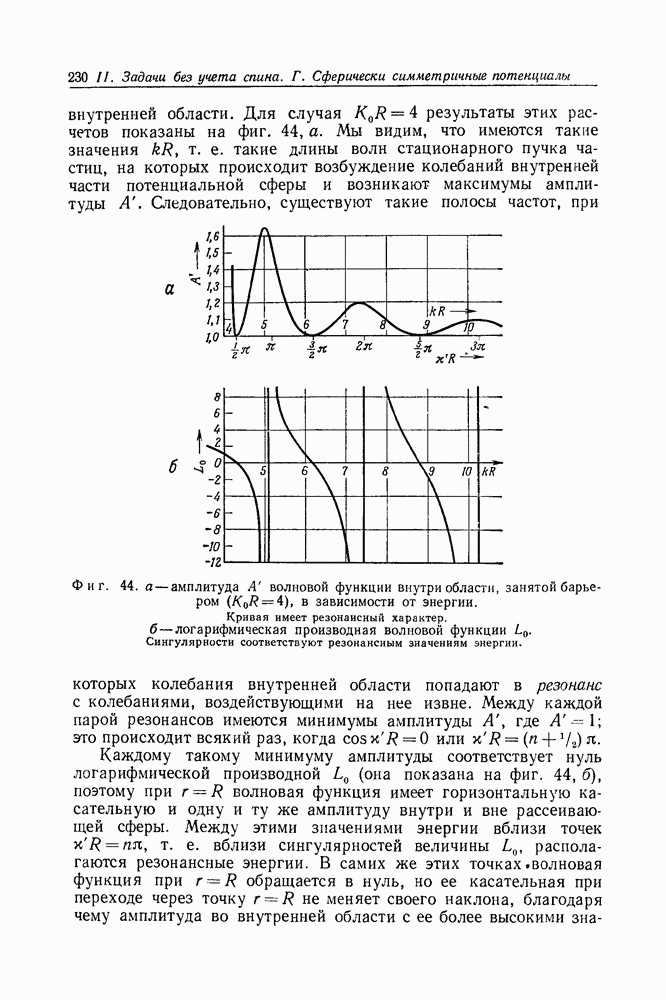
внутренней области. Для случая  результаты этих расчетов показаны на фиг. 44, а. Мы видим, что имеются такие значения
результаты этих расчетов показаны на фиг. 44, а. Мы видим, что имеются такие значения  такие длины волн стационарного пучка частиц, на которых происходит возбуждение колебаний внутренней части потенциальной сферы и возникают максимумы амплитуды А. Следовательно, существуют такие полосы частот, при которых колебания внутренней области попадают в резонанс с колебаниями, воздействующими на нее извне.
такие длины волн стационарного пучка частиц, на которых происходит возбуждение колебаний внутренней части потенциальной сферы и возникают максимумы амплитуды А. Следовательно, существуют такие полосы частот, при которых колебания внутренней области попадают в резонанс с колебаниями, воздействующими на нее извне.

Фиг. 44. а — амплитуда А волновой функции внутри области, занятой барьером  в зависимости от энергии. Кривая имеет резонансный характер. б - логарифмическая производная волновой функции
в зависимости от энергии. Кривая имеет резонансный характер. б - логарифмическая производная волновой функции  Сингулярности соответствуют резонансным значениям энергии.
Сингулярности соответствуют резонансным значениям энергии.
Между каждой парой резонансов имеются минимумы амплитуды А, где 1; это происходит всякий раз, когда  или
или  Каждому такому минимуму амплитуды соответствует нуль логарифмической производной
Каждому такому минимуму амплитуды соответствует нуль логарифмической производной  (она показана на фиг. 44, б), поэтому при
(она показана на фиг. 44, б), поэтому при  волновая функция имеет горизонтальную касательную и одну и ту же амплитуду внутри и вне рассеивающей сферы. Между этими значениями энергии вблизи точек
волновая функция имеет горизонтальную касательную и одну и ту же амплитуду внутри и вне рассеивающей сферы. Между этими значениями энергии вблизи точек  т. е. вблизи сингулярностей величины
т. е. вблизи сингулярностей величины  располагаются резонансные энергии. В самих же этих точках волновая функция при
располагаются резонансные энергии. В самих же этих точках волновая функция при  обращается в нуль, но ее касательная при переходе через точку
обращается в нуль, но ее касательная при переходе через точку  не меняет своего наклона, благодаря чему амплитуда во внутренней области с ее более высокими
не меняет своего наклона, благодаря чему амплитуда во внутренней области с ее более высокими
значениями длин волн достигает наибольшего возможного значения.
Далее, мы знаем общую закономерность всех резонансных явлений — при прохождении через резонанс фаза (в идеальном случае) скачком изменяется на я. Этой закономерностью и объясняется резкий рост фазы между точками, соответствующими минимумам амплитуды (на кривой 2 фиг. 43 они отмечены крестиками, а резонансы — кружками).
Зная фазовую кривую, нетрудно рассчитать зависимость парциального сечения рассеяния

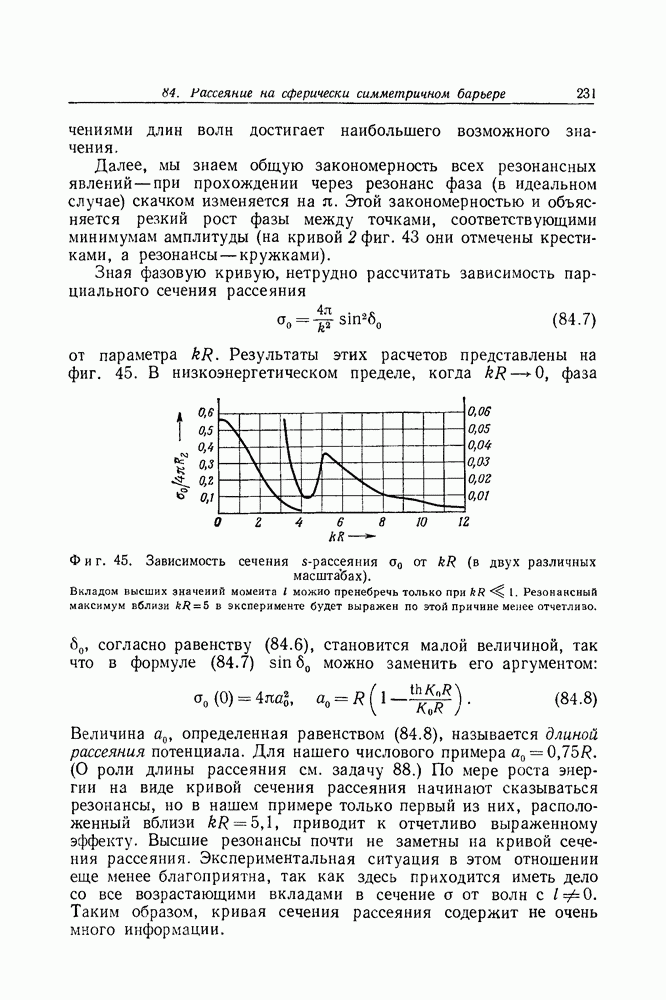
от параметра  Результаты этих расчетов представлены на фиг. 45.
Результаты этих расчетов представлены на фиг. 45.

Фиг. 45. Зависимость сечения  -рассеяния
-рассеяния  от
от  (в двух различных масштабах). Вкладом высших значений момента I можно пренебречь только при
(в двух различных масштабах). Вкладом высших значений момента I можно пренебречь только при  Резонансный максимум вблизи
Резонансный максимум вблизи  в эксперименте будет выражен по этой причине менее отчетливо.
в эксперименте будет выражен по этой причине менее отчетливо.
В низкоэнергетическом пределе, когда  фаза
фаза  , согласно равенству (84.6), становится малой величиной, так что в формуле
, согласно равенству (84.6), становится малой величиной, так что в формуле  можно заменить его аргументом:
можно заменить его аргументом:

Величина  определенная равенством (84.8), называется длиной рассеяния потенциала. Для нашего числового примера
определенная равенством (84.8), называется длиной рассеяния потенциала. Для нашего числового примера  (О роли длины рассеяния см. задачу 88.) По мере роста энергии на виде кривой сечения рассеяния начинают сказываться резонансы, но в нашем примере только первый из них, расположенный вблизи
(О роли длины рассеяния см. задачу 88.) По мере роста энергии на виде кривой сечения рассеяния начинают сказываться резонансы, но в нашем примере только первый из них, расположенный вблизи  приводит к отчетливо выраженному эффекту. Высшие резонансы почти не заметны на кривой сечения рассеяния. Экспериментальная ситуация в этом отношении еще менее благоприятна, так как здесь приходится иметь дело со все возрастающими вкладами в сечение о от волн с
приводит к отчетливо выраженному эффекту. Высшие резонансы почти не заметны на кривой сечения рассеяния. Экспериментальная ситуация в этом отношении еще менее благоприятна, так как здесь приходится иметь дело со все возрастающими вкладами в сечение о от волн с  Таким образом, кривая сечения рассеяния содержит не очень много информации.
Таким образом, кривая сечения рассеяния содержит не очень много информации.
Замечание. Каким образом фаза рассеяния  стремится к нулю при очень больших энергиях, можно выяснить, воспользовавшись первым борновским приближением (см. задачу 105). При
стремится к нулю при очень больших энергиях, можно выяснить, воспользовавшись первым борновским приближением (см. задачу 105). При  имеем
имеем

откуда для частного вида потенциала, рассматривавшегося выше, получаем 

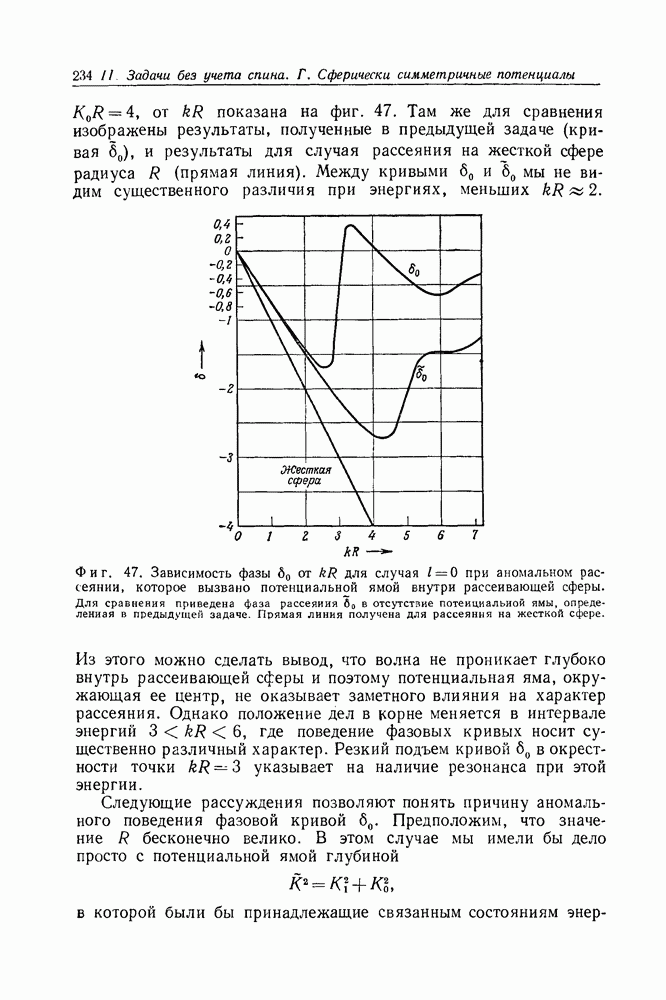
Рассчитанная по этой формуле фаза рассеяния показана на фиг. 43 пунктирной линией. Для представленной там энергетической области значения фазы рассеяния еще довольно велики, поэтому от борновского приближения не следует ожидать результатов, удовлетворительных в количественном отношении. Замечательно уже то, что даже для этих энергий борновская формула, если отвлечься от смещения резонансов, правильно передает ход фазовой кривой, включая ее ступенеобразный характер; последнее, конечно, объясняется наличием члена с синусом в формуле (84.9).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- I. Общие принципы
- Задача 1. Закон сохранения вероятности
- Задача 2. Вариационный принцип Шредингера
- Задача 3. Классическая механика для пространственных средних
- Задача 4. Классические законы для момента количества движения
- Задача 5. Закон сохранения энергии
- Задача 6. Эрмитово сопряжение
- Задача 7. Построение эрмитова оператора
- Задача 8. Дифференцирование оператора
- Задача 9. Изменение средних значений со временем
- Задача 10. Картина Шредингера и картина Гейзенберга
- Задача 11. Гамильтониан, зависящий от времени
- Задача 12. Повторное измерение
- Задача 13. Криволинейные координаты
- Задача 14. Волновые функции в импульсном представлении
- Задача 15. Пространство импульсов. Периодические и непериодические волновые функции
- II. Одночастичные задачи без учета спина
- Задача 16. Фундаментальные решения в случае свободного движения
- Задача 17. Волновой пакет в случае свободного движения
- Задача 18. Стоячие волны
- Задача 19. Полупроницаемая перегородка
- Задача 20. Полупроницаемая перегородка в виде «дельта»-образного потенциального барьера
- Задача 21. Рассеяние на «дельта»-образном потенциальном барьере
- Задача 22. Рассеяние на симметричном потенциальном барьере
- Задача 23. Отражение от прямоугольного барьера
- Задача 24. Инверсия отражения
- Задача 25. Прямоугольная потенциальная яма
- Задача 26. Прямоугольная потенциальная яма между двумя бесконечными стенками
- Задача 27. Виртуальные уровни
- Задача 28. Периодический потенциал
- Задача 29. Дираковская потенциальная гребенка
- Задача 30. Гармонический осциллятор
- Задача 31. Осциллятор в абстрактном гильбертовом пространстве (осциллятор в представлении Фока)
- Задача 32. Использование лестничных операторов для нахождения собственных функций осциллятора
- Задача 33. Гармонический осциллятор в матричном представлении
- Задача 34. Волновые функции осциллятора в пространстве импульсов
- Задача 35. Ангармонический осциллятор
- Задача 36. Приближенные волновые функции
- Задача 37. Потенциальная ступенька
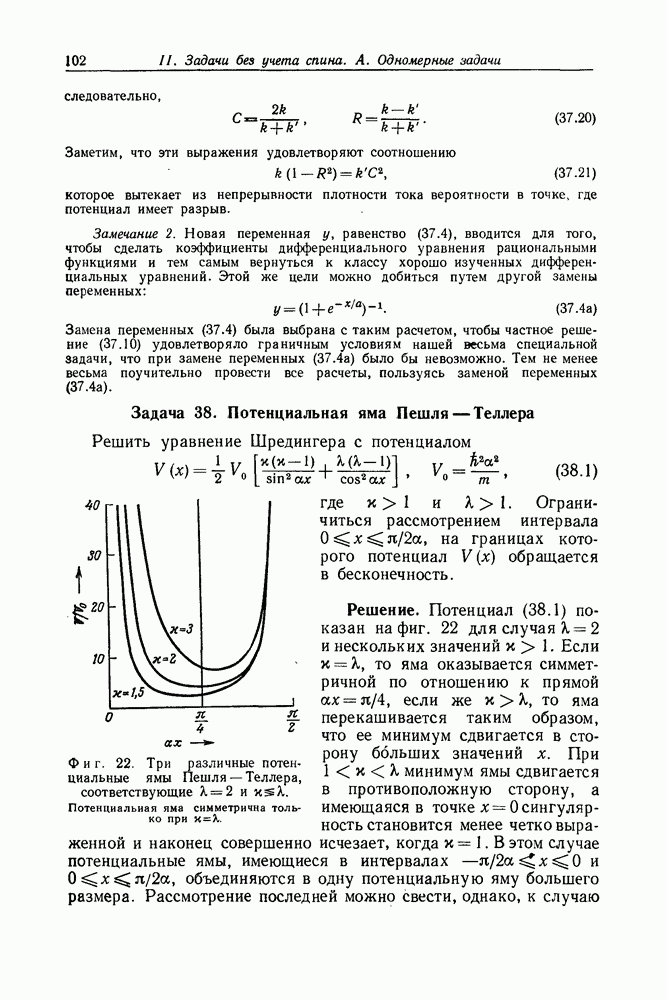
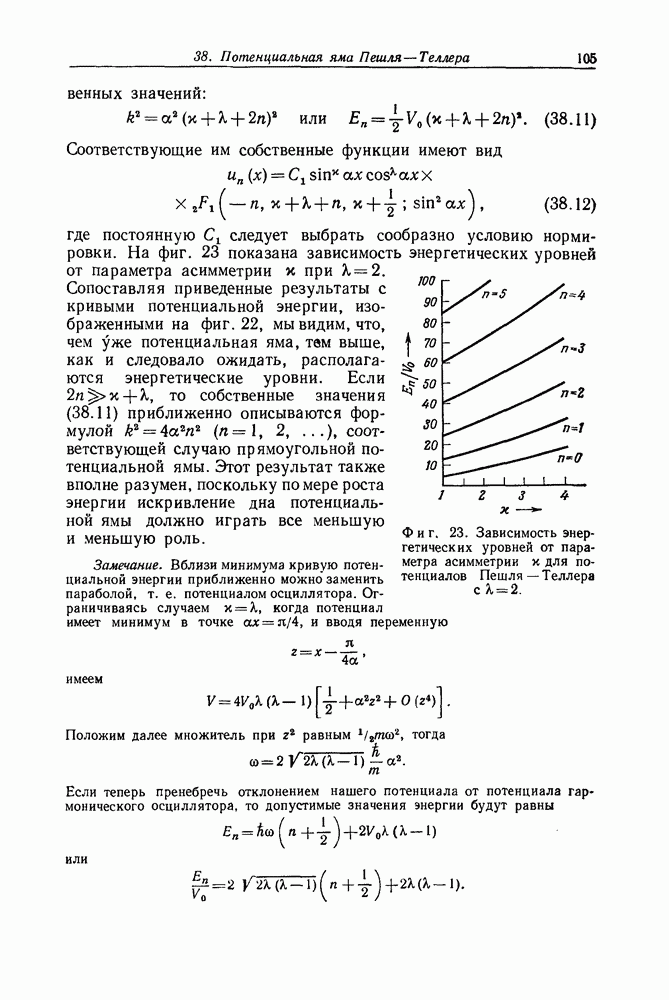
- Задача 38. Потенциальная яма Пешля — Теллера
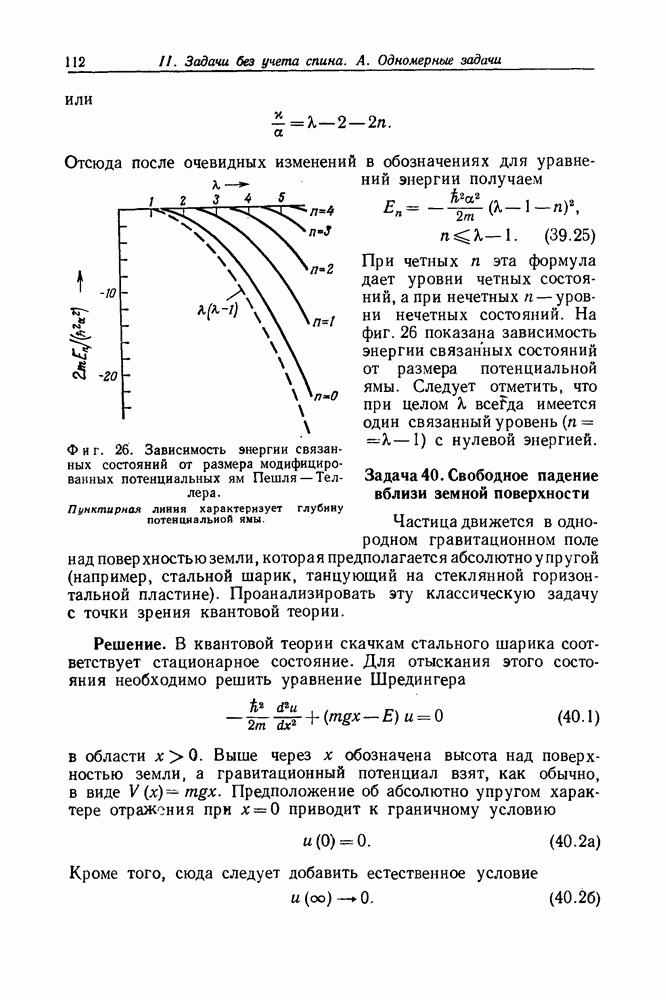
- Задача 39. Модифицированная потенциальная яма Пешля—Теллера
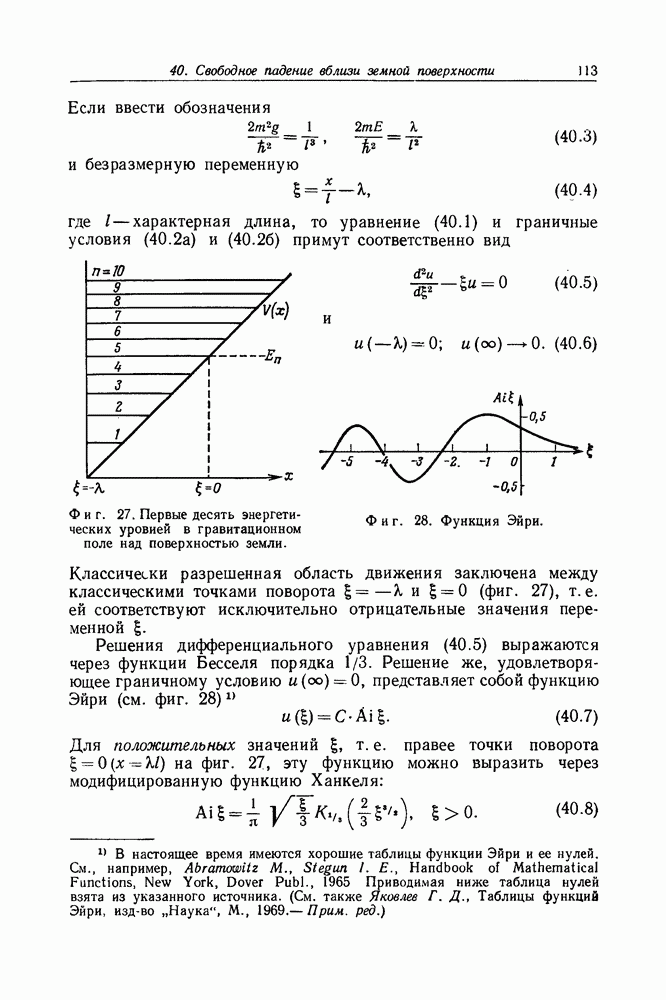
- Задача 40. Свободное падение вблизи земной поверхности
- Задача 41. Ускоряющее электрическое поле
- Б. Задачи с двумя или тремя степенями свободы без сферической симметрии
- Задача 42. Круговой осциллятор
- Задача 43. Эффект Штарка для двумерного ротатора
- Задача 44. Ион молекулы водорода
- Задача 45. Наклонное падение плоской волны
- Задача 46. Симметричный волчок
- В. Момент количества движения
- Задача 47. Бесконечно малые вращения
- Задача 48. Момент количества движения в сферических координатах
- Задача 49. Момент количества движения и оператор Лапласа
- Задача 50. Преобразования в гильбертовом пространстве
- Задача 51. Коммутаторы в координатном представлении
- Задача 52. Частица со спином 1
- Задача 53. Перестановочные соотношения компонент тензора
- Задача 54. Тензор квадрупольного момента. Сферические гармоники
- Задача 55. Преобразование сферических гармоник
- Задача 56. Построение собственных векторов оператора Lx в абстрактном гильбертовом пространстве
- Задача 57. Ортогональность сферических гармоник
- Г. Сферически симметричные потенциалы
- Задача 58. Средние значения компонент момента количества движения
- Задача 59. Радиальная компонента оператора импульса
- Задача 60. Решения, близкие к собственным функциям
- Задача 61. Квадрупольный момент
- Задача 62. Частица внутри непроницаемой сферы
- Задача 63. Сферически симметричная прямоугольная яма конечной глубины
- Задача 64. Потенциал Вуда — Саксона
- Задача 65. Изотропный осциллятор
- Задача 66. Вырожденные состояния изотропного осциллятора
- Задача 67. Проблема Кеплера
- Задача 68. Потенциал Хюльтена
- Задача 69. Молекулярный потенциал Кратцера
- Задача 70. Потенциал Морса
- Задача 71. Ротационные поправки к формуле Морса
- Задача 72. Потенциал Юкавы
- Задача 73. Изотопический сдвиг границы рентгеновского излучения
- Задача 74. Основное состояние мезоатома
- Задача 75. Модель дейтрона с центральным взаимодействием
- Задача 76. Импульсное представление для волновых функций в поле центральных сил
- Задача 77. Уравнение Шредингера в импульсном представлении в поле центральных сил
- Задача 78. Водородные волновые функции в импульсном пространстве
- Задача 79. Штарк-эффект у пространственного ротатора
- Задача 80. Интерференция падающей и рассеянной волн
- Задача 81. Разложение плоской волны по парциальным волнам
- Задача 82. Разложение амплитуды рассеяния по парциальным волнам
- Задача 83. Рассеяние при низких энергиях
- Задача 84. Рассеяние на сферически симметричном прямоугольном потенциальном барьере
- Задача 85. Аномальное рассеяние
- Задача 86. Рассеяние на резонансных уровнях
- Задача 87. Вклад состояний с высшими значениями момента количества движения
- Задача 88. Приближение, не зависящее от формы потенциала
- Задача 89. Низкоэнергетическое рассеяние на сферически симметричной прямоугольной яме
- Задача 90. Низкоэнергетическое рассеяние и связанные состояния
- Задача 91. Дейтронный потенциал с жесткой сердцевиной и без нее
- Задача 92. Низкоэнергетическое рассеяние при наличии жесткой сердцевины и без нее
- Задача 93. Низкоэнергетическое рассеяние на модифицированном потенциале Пешля — Теллера
- Задача 94. Радиальное интегральное уравнение
- Задача 95. Вариационный принцип Швингера
- Задача 96. Последовательные приближения для фазы рассеяния
- Задача 97. Уравнение Калоджеро
- Задача 98. Линеаризация уравнения Калоджеро
- Задача 99. Длина рассеяния потенциала, имеющего вид степенной функции
- Задача 100. Второе приближение к уравнению Калоджеро
- Задача 101. Длина рассеяния для сферически симметричной прямоугольной потенциальной ямы
- Задача 102. Длина рассеяния потенциала Юкавы
- Задача 103. Улучшение сходимости рядов сферических гармоник
- Задача 104. Интеграл по прицельному расстоянию
- Задача 105. Борновскоерассеяние. Последовательные приближения.
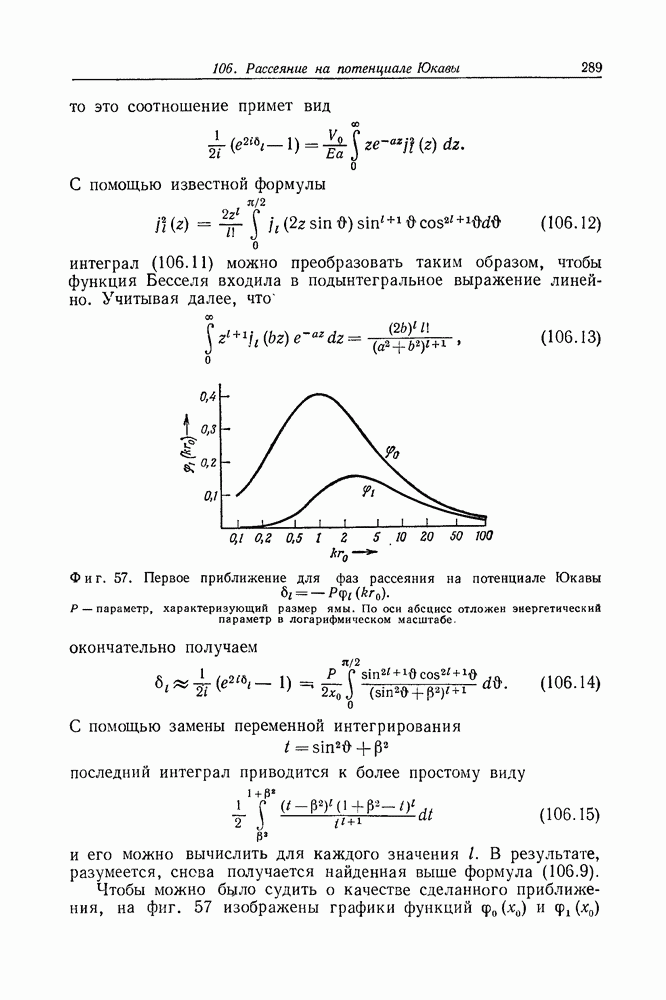
- Задача 106. Рассеяние на потенциале Юкавы
- Задача 107. Рассеяние на экспоненциальном потенциале
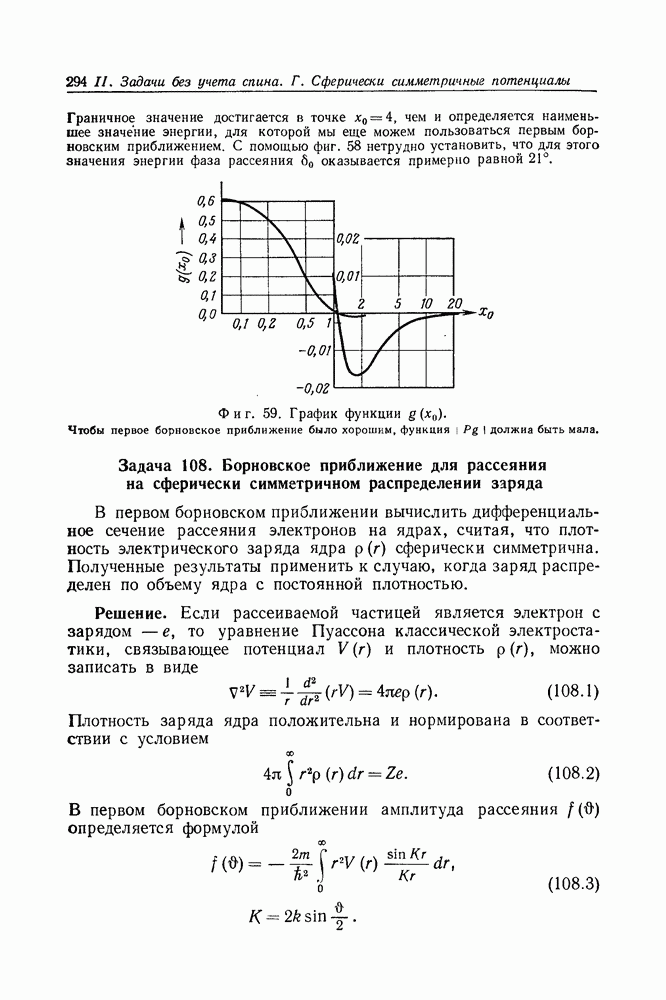
- Задача 108. Борновское приближение для рассеяния на сферически симметричном распределении заряда
- Задача 109. Высокоэнергетическое рассеяние на жесткой сфере
- Задача 110. Формула Резерфорда
- Задача 111. Разложение кулоновской функции по парциальным волнам
- Задача 112. Аномальное рассеяние
- Задача 113. Преобразование Зоммерфельда — Ватсона
- Задача 114. Полюс Редже
- Д. Приближение Вентцеля — Крамерса — Бриллюэна (ВКБ)
- Задача 115. Разложение эйконала
- Задача 116. Применение метода ВКБ к радиальному уравнению
- Задача 117. Граничное ВКБ-условие Лангера
- Задача 118. Гармонический осциллятор в приближении ВКБ
- Задача 120. Проблема Кеплера в приближении ВКБ
- Задача 121. Фазы ВКБ для свободного движения
- Задача 122. Вычисление фаз ВКБ
- Задача 123. Расчет кулоновских фаз методом ВКБ
- Задача 124. Квазипотенциал
- Е. Магнитное поле
- Задача 125. Введение магнитного поля
- Задача 126. Плотность тока в присутствии магнитного поля
- Задача 127. Нормальный эффект Зеемана
- Задача 128. Парамагнитная и диамагнитная восприимчивости без учета спина