| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
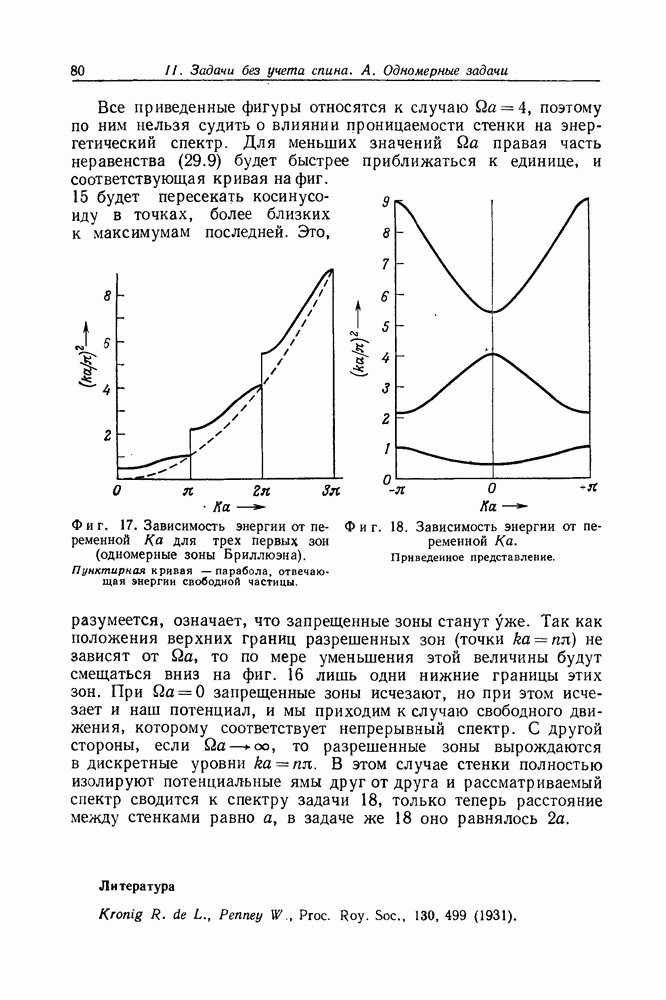
Задача 73. Изотопический сдвиг границы рентгеновского излучения
В тяжелых атомах средний радиус орбиты  -электрона примерно в 100 раз превышает радиус ядра
-электрона примерно в 100 раз превышает радиус ядра  Следовательно, благодаря конечному размеру ядра энергетический уровень К-электрона должен претерпеть небольшое смещение. Рассчитать указанное смещение, считая электрический заряд равномерно распределенным по объему ядра. Кроме того, определить изотопическое смещение границы рентгеновского К-излучения таллия
Следовательно, благодаря конечному размеру ядра энергетический уровень К-электрона должен претерпеть небольшое смещение. Рассчитать указанное смещение, считая электрический заряд равномерно распределенным по объему ядра. Кроме того, определить изотопическое смещение границы рентгеновского К-излучения таллия 
для двух изотопов с атомными весами  пользуясь для радиуса ядра формулой
пользуясь для радиуса ядра формулой

Эффектом экранировки  -электрона пренебречь.
-электрона пренебречь.
Решение. Энергия взаимодействия электрона с ядром имеет

Начнем с невозмущенной задачи о движении электрона в поле точечного ядра  . В этом случае
. В этом случае

Здесь  и
и  -соответственно волновая функция и энергия основного состояния кеплеровской проблемы (см. задачу 67). Энергия возмущения равна разности
-соответственно волновая функция и энергия основного состояния кеплеровской проблемы (см. задачу 67). Энергия возмущения равна разности

Отсюда для сдвига энергетического уровня получаем

В области интегрирования показатель  всегда меньше
всегда меньше  поэтому в подынтегральном выражении (73.5) мы можем положить
поэтому в подынтегральном выражении (73.5) мы можем положить

Используя далее величину  в качестве переменной интегрирования, после элементарных вычислений получаем
в качестве переменной интегрирования, после элементарных вычислений получаем

где  означает боровский радиус. В случае
означает боровский радиус. В случае  формула (73.3) дает
формула (73.3) дает

Полный сдвиг уровня  для изотопа с атомным весом
для изотопа с атомным весом 
согласно формулам (73.1) и (73.6), оказывается равным

Изотопический сдвиг, т. е. разность между значениями  в случае
в случае  и в случае
и в случае  получается отсюда дифференцированием:
получается отсюда дифференцированием:

Для рассматриваемого примера это приводит к значению

В то время как абсолютное значение энергии  -оболочки, согласно формуле (73.8), сдвигается вверх на вполне заметную величину
-оболочки, согласно формуле (73.8), сдвигается вверх на вполне заметную величину  разностный эффект для соседних изотопов
разностный эффект для соседних изотопов  (который можно было бы обнаружить по расщеплению
(который можно было бы обнаружить по расщеплению  -линии рентгеновского излучения, будь он достаточно велик) составляет, согласно (73.9), менее одной миллионной.
-линии рентгеновского излучения, будь он достаточно велик) составляет, согласно (73.9), менее одной миллионной.
Замечание. Эффект экранировки, конечно, значительно больше рассмотренных сдвигов, однако он совершенно одинаков для обоих изотопов. Эксперимент для границы  -линии таллия дает значение 6310 ридберг, или
-линии таллия дает значение 6310 ридберг, или  вместо нашего неэкранированного значения (73.7). Что касается изотопического расщепления, то оно почти не зависит от этой поправки.
вместо нашего неэкранированного значения (73.7). Что касается изотопического расщепления, то оно почти не зависит от этой поправки.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- I. Общие принципы
- Задача 1. Закон сохранения вероятности
- Задача 2. Вариационный принцип Шредингера
- Задача 3. Классическая механика для пространственных средних
- Задача 4. Классические законы для момента количества движения
- Задача 5. Закон сохранения энергии
- Задача 6. Эрмитово сопряжение
- Задача 7. Построение эрмитова оператора
- Задача 8. Дифференцирование оператора
- Задача 9. Изменение средних значений со временем
- Задача 10. Картина Шредингера и картина Гейзенберга
- Задача 11. Гамильтониан, зависящий от времени
- Задача 12. Повторное измерение
- Задача 13. Криволинейные координаты
- Задача 14. Волновые функции в импульсном представлении
- Задача 15. Пространство импульсов. Периодические и непериодические волновые функции
- II. Одночастичные задачи без учета спина
- Задача 16. Фундаментальные решения в случае свободного движения
- Задача 17. Волновой пакет в случае свободного движения
- Задача 18. Стоячие волны
- Задача 19. Полупроницаемая перегородка
- Задача 20. Полупроницаемая перегородка в виде «дельта»-образного потенциального барьера
- Задача 21. Рассеяние на «дельта»-образном потенциальном барьере
- Задача 22. Рассеяние на симметричном потенциальном барьере
- Задача 23. Отражение от прямоугольного барьера
- Задача 24. Инверсия отражения
- Задача 25. Прямоугольная потенциальная яма
- Задача 26. Прямоугольная потенциальная яма между двумя бесконечными стенками
- Задача 27. Виртуальные уровни
- Задача 28. Периодический потенциал
- Задача 29. Дираковская потенциальная гребенка
- Задача 30. Гармонический осциллятор
- Задача 31. Осциллятор в абстрактном гильбертовом пространстве (осциллятор в представлении Фока)
- Задача 32. Использование лестничных операторов для нахождения собственных функций осциллятора
- Задача 33. Гармонический осциллятор в матричном представлении
- Задача 34. Волновые функции осциллятора в пространстве импульсов
- Задача 35. Ангармонический осциллятор
- Задача 36. Приближенные волновые функции
- Задача 37. Потенциальная ступенька
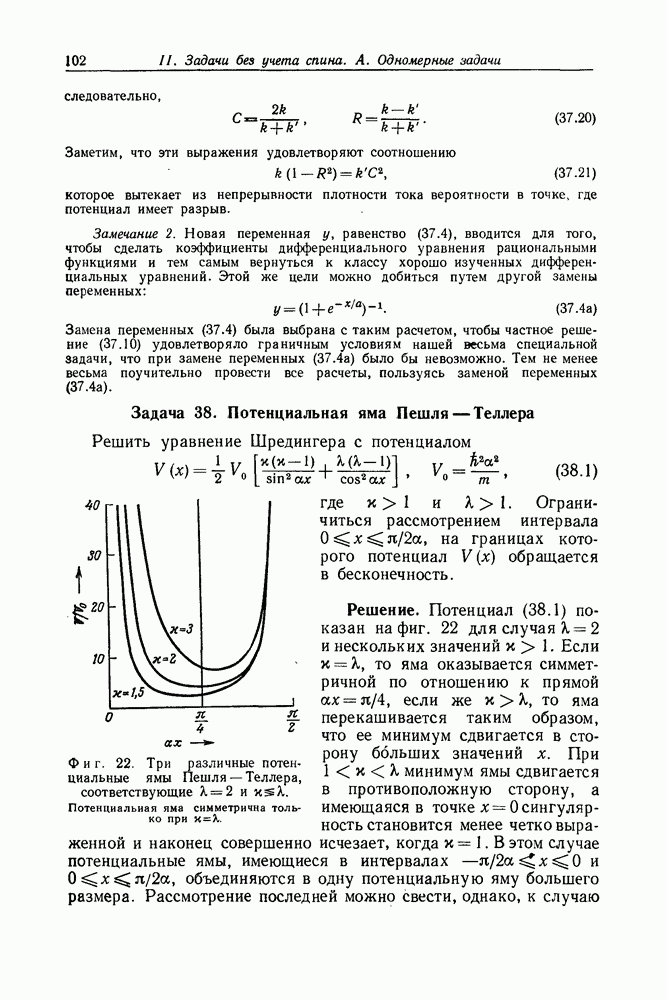
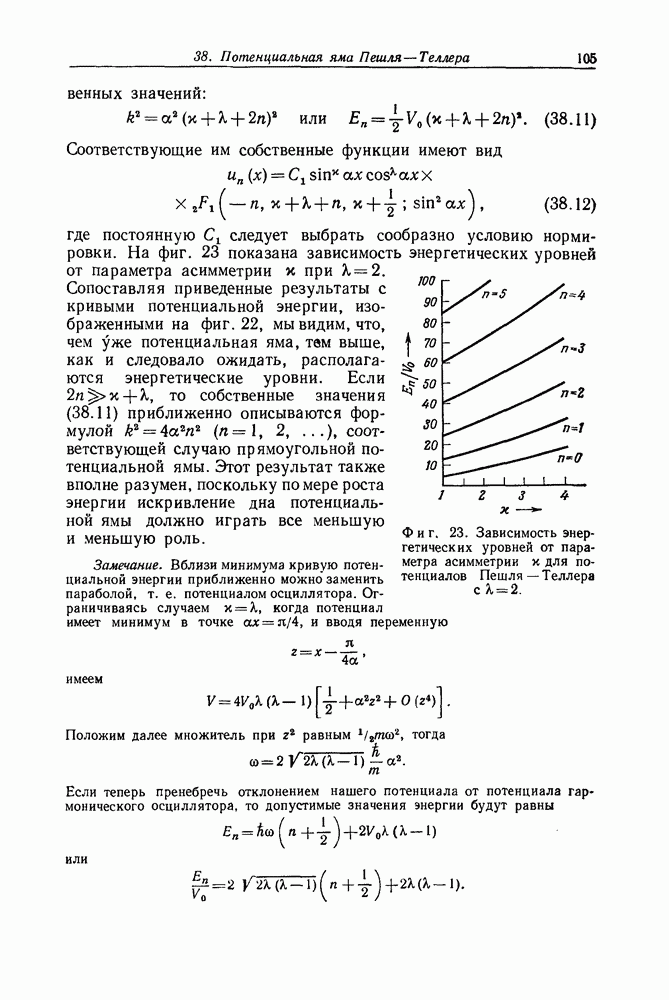
- Задача 38. Потенциальная яма Пешля — Теллера
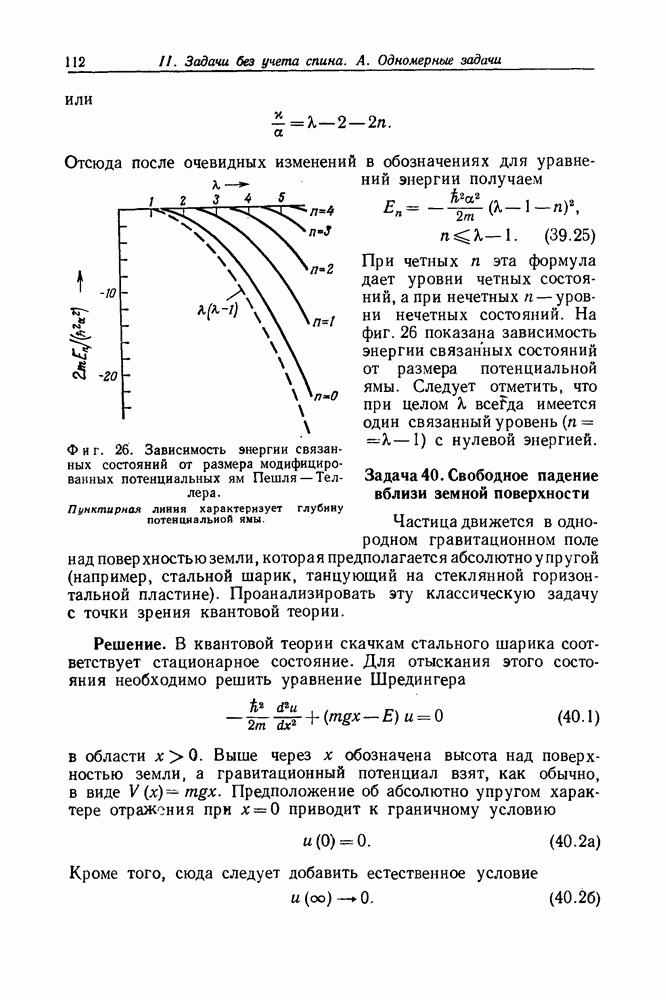
- Задача 39. Модифицированная потенциальная яма Пешля—Теллера
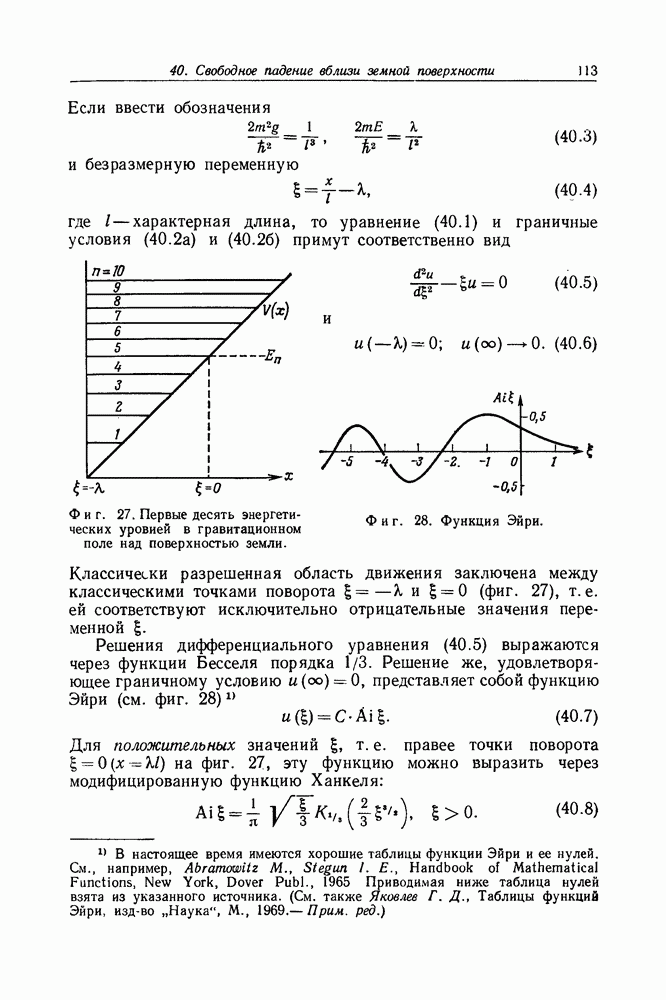
- Задача 40. Свободное падение вблизи земной поверхности
- Задача 41. Ускоряющее электрическое поле
- Б. Задачи с двумя или тремя степенями свободы без сферической симметрии
- Задача 42. Круговой осциллятор
- Задача 43. Эффект Штарка для двумерного ротатора
- Задача 44. Ион молекулы водорода
- Задача 45. Наклонное падение плоской волны
- Задача 46. Симметричный волчок
- В. Момент количества движения
- Задача 47. Бесконечно малые вращения
- Задача 48. Момент количества движения в сферических координатах
- Задача 49. Момент количества движения и оператор Лапласа
- Задача 50. Преобразования в гильбертовом пространстве
- Задача 51. Коммутаторы в координатном представлении
- Задача 52. Частица со спином 1
- Задача 53. Перестановочные соотношения компонент тензора
- Задача 54. Тензор квадрупольного момента. Сферические гармоники
- Задача 55. Преобразование сферических гармоник
- Задача 56. Построение собственных векторов оператора Lx в абстрактном гильбертовом пространстве
- Задача 57. Ортогональность сферических гармоник
- Г. Сферически симметричные потенциалы
- Задача 58. Средние значения компонент момента количества движения
- Задача 59. Радиальная компонента оператора импульса
- Задача 60. Решения, близкие к собственным функциям
- Задача 61. Квадрупольный момент
- Задача 62. Частица внутри непроницаемой сферы
- Задача 63. Сферически симметричная прямоугольная яма конечной глубины
- Задача 64. Потенциал Вуда — Саксона
- Задача 65. Изотропный осциллятор
- Задача 66. Вырожденные состояния изотропного осциллятора
- Задача 67. Проблема Кеплера
- Задача 68. Потенциал Хюльтена
- Задача 69. Молекулярный потенциал Кратцера
- Задача 70. Потенциал Морса
- Задача 71. Ротационные поправки к формуле Морса
- Задача 72. Потенциал Юкавы
- Задача 73. Изотопический сдвиг границы рентгеновского излучения
- Задача 74. Основное состояние мезоатома
- Задача 75. Модель дейтрона с центральным взаимодействием
- Задача 76. Импульсное представление для волновых функций в поле центральных сил
- Задача 77. Уравнение Шредингера в импульсном представлении в поле центральных сил
- Задача 78. Водородные волновые функции в импульсном пространстве
- Задача 79. Штарк-эффект у пространственного ротатора
- Задача 80. Интерференция падающей и рассеянной волн
- Задача 81. Разложение плоской волны по парциальным волнам
- Задача 82. Разложение амплитуды рассеяния по парциальным волнам
- Задача 83. Рассеяние при низких энергиях
- Задача 84. Рассеяние на сферически симметричном прямоугольном потенциальном барьере
- Задача 85. Аномальное рассеяние
- Задача 86. Рассеяние на резонансных уровнях
- Задача 87. Вклад состояний с высшими значениями момента количества движения
- Задача 88. Приближение, не зависящее от формы потенциала
- Задача 89. Низкоэнергетическое рассеяние на сферически симметричной прямоугольной яме
- Задача 90. Низкоэнергетическое рассеяние и связанные состояния
- Задача 91. Дейтронный потенциал с жесткой сердцевиной и без нее
- Задача 92. Низкоэнергетическое рассеяние при наличии жесткой сердцевины и без нее
- Задача 93. Низкоэнергетическое рассеяние на модифицированном потенциале Пешля — Теллера
- Задача 94. Радиальное интегральное уравнение
- Задача 95. Вариационный принцип Швингера
- Задача 96. Последовательные приближения для фазы рассеяния
- Задача 97. Уравнение Калоджеро
- Задача 98. Линеаризация уравнения Калоджеро
- Задача 99. Длина рассеяния потенциала, имеющего вид степенной функции
- Задача 100. Второе приближение к уравнению Калоджеро
- Задача 101. Длина рассеяния для сферически симметричной прямоугольной потенциальной ямы
- Задача 102. Длина рассеяния потенциала Юкавы
- Задача 103. Улучшение сходимости рядов сферических гармоник
- Задача 104. Интеграл по прицельному расстоянию
- Задача 105. Борновскоерассеяние. Последовательные приближения.
- Задача 106. Рассеяние на потенциале Юкавы
- Задача 107. Рассеяние на экспоненциальном потенциале
- Задача 108. Борновское приближение для рассеяния на сферически симметричном распределении заряда
- Задача 109. Высокоэнергетическое рассеяние на жесткой сфере
- Задача 110. Формула Резерфорда
- Задача 111. Разложение кулоновской функции по парциальным волнам
- Задача 112. Аномальное рассеяние
- Задача 113. Преобразование Зоммерфельда — Ватсона
- Задача 114. Полюс Редже
- Д. Приближение Вентцеля — Крамерса — Бриллюэна (ВКБ)
- Задача 115. Разложение эйконала
- Задача 116. Применение метода ВКБ к радиальному уравнению
- Задача 117. Граничное ВКБ-условие Лангера
- Задача 118. Гармонический осциллятор в приближении ВКБ
- Задача 120. Проблема Кеплера в приближении ВКБ
- Задача 121. Фазы ВКБ для свободного движения
- Задача 122. Вычисление фаз ВКБ
- Задача 123. Расчет кулоновских фаз методом ВКБ
- Задача 124. Квазипотенциал
- Е. Магнитное поле
- Задача 125. Введение магнитного поля
- Задача 126. Плотность тока в присутствии магнитного поля
- Задача 127. Нормальный эффект Зеемана
- Задача 128. Парамагнитная и диамагнитная восприимчивости без учета спина