| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Задача 53. Перестановочные соотношения компонент тензора
Рассмотрев бесконечно малые вращения системы координат, получить перестановочные соотношения компонент симметричного тензора с компонентами оператора момента количества движения.
Решение. Как было показано в задаче 50, всякий квантово-механический оператор при бесконечно малых вращениях
преобразуется по закону

Если преобразование координат задается формулой  то тензор определяется трансформационными свойствами своих компонент:
то тензор определяется трансформационными свойствами своих компонент:

Так как при бесконечно малых вращениях  то отсюда
то отсюда

сравнив с соотношением (53.1), находим

Формула (53.4) является основой для решения нашей задачи. Ниже мы ограничимся вращением вокруг оси х, когда

В этом случае

поэтому для симметричного тензора разность

также оказывается симметричной. Левая часть этого равенства, согласно (53.4), должна равняться  следовательно,
следовательно,

Перестановочные соотношения с компонентами  можно найти, рассмотрев вращения вокруг осей у и z или, что еще проще, с помощью циклических перестановок символов в формулах (53.6):
можно найти, рассмотрев вращения вокруг осей у и z или, что еще проще, с помощью циклических перестановок символов в формулах (53.6):

Следует отметить, что все три компоненты  коммутируют со следом тензора:
коммутируют со следом тензора:

Последнее обстоятельство становится понятным, если записать симметричный тензор в виде

где  Следовательно, след тензора
Следовательно, след тензора  представляет собой скаляр (тензорный инвариант), но, как было показано в конце задачи 50, скаляр всегда коммутирует с компонентами
представляет собой скаляр (тензорный инвариант), но, как было показано в конце задачи 50, скаляр всегда коммутирует с компонентами 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- I. Общие принципы
- Задача 1. Закон сохранения вероятности
- Задача 2. Вариационный принцип Шредингера
- Задача 3. Классическая механика для пространственных средних
- Задача 4. Классические законы для момента количества движения
- Задача 5. Закон сохранения энергии
- Задача 6. Эрмитово сопряжение
- Задача 7. Построение эрмитова оператора
- Задача 8. Дифференцирование оператора
- Задача 9. Изменение средних значений со временем
- Задача 10. Картина Шредингера и картина Гейзенберга
- Задача 11. Гамильтониан, зависящий от времени
- Задача 12. Повторное измерение
- Задача 13. Криволинейные координаты
- Задача 14. Волновые функции в импульсном представлении
- Задача 15. Пространство импульсов. Периодические и непериодические волновые функции
- II. Одночастичные задачи без учета спина
- Задача 16. Фундаментальные решения в случае свободного движения
- Задача 17. Волновой пакет в случае свободного движения
- Задача 18. Стоячие волны
- Задача 19. Полупроницаемая перегородка
- Задача 20. Полупроницаемая перегородка в виде «дельта»-образного потенциального барьера
- Задача 21. Рассеяние на «дельта»-образном потенциальном барьере
- Задача 22. Рассеяние на симметричном потенциальном барьере
- Задача 23. Отражение от прямоугольного барьера
- Задача 24. Инверсия отражения
- Задача 25. Прямоугольная потенциальная яма
- Задача 26. Прямоугольная потенциальная яма между двумя бесконечными стенками
- Задача 27. Виртуальные уровни
- Задача 28. Периодический потенциал
- Задача 29. Дираковская потенциальная гребенка
- Задача 30. Гармонический осциллятор
- Задача 31. Осциллятор в абстрактном гильбертовом пространстве (осциллятор в представлении Фока)
- Задача 32. Использование лестничных операторов для нахождения собственных функций осциллятора
- Задача 33. Гармонический осциллятор в матричном представлении
- Задача 34. Волновые функции осциллятора в пространстве импульсов
- Задача 35. Ангармонический осциллятор
- Задача 36. Приближенные волновые функции
- Задача 37. Потенциальная ступенька
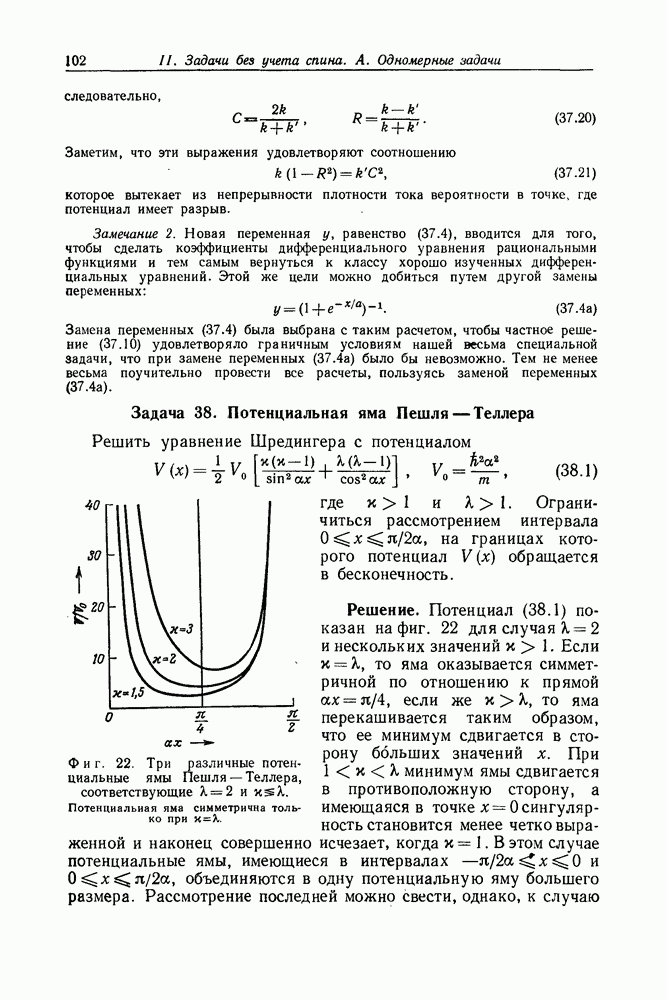
- Задача 38. Потенциальная яма Пешля — Теллера
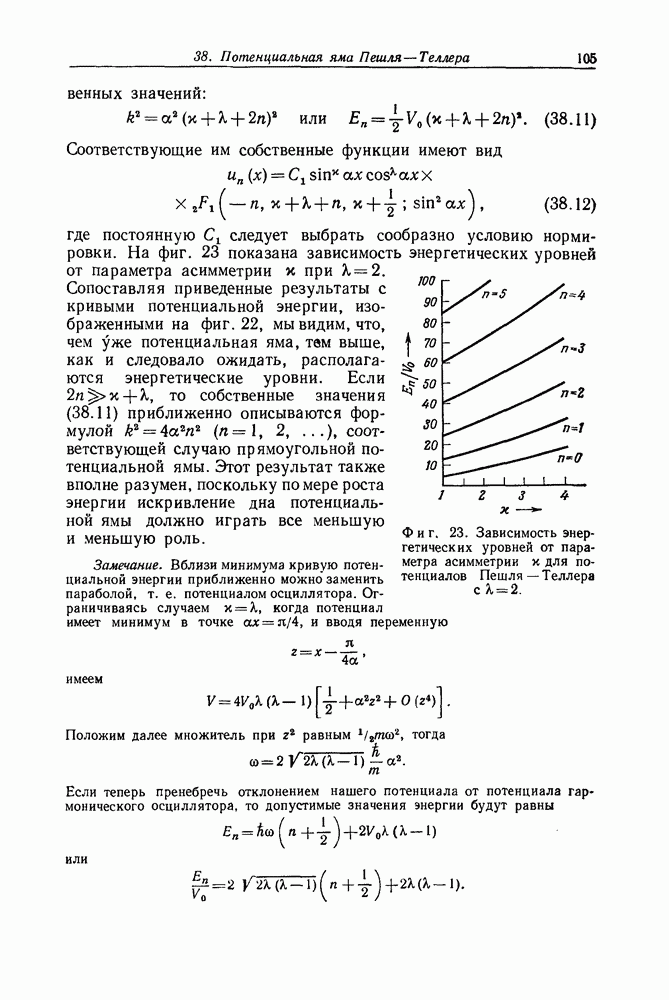
- Задача 39. Модифицированная потенциальная яма Пешля—Теллера
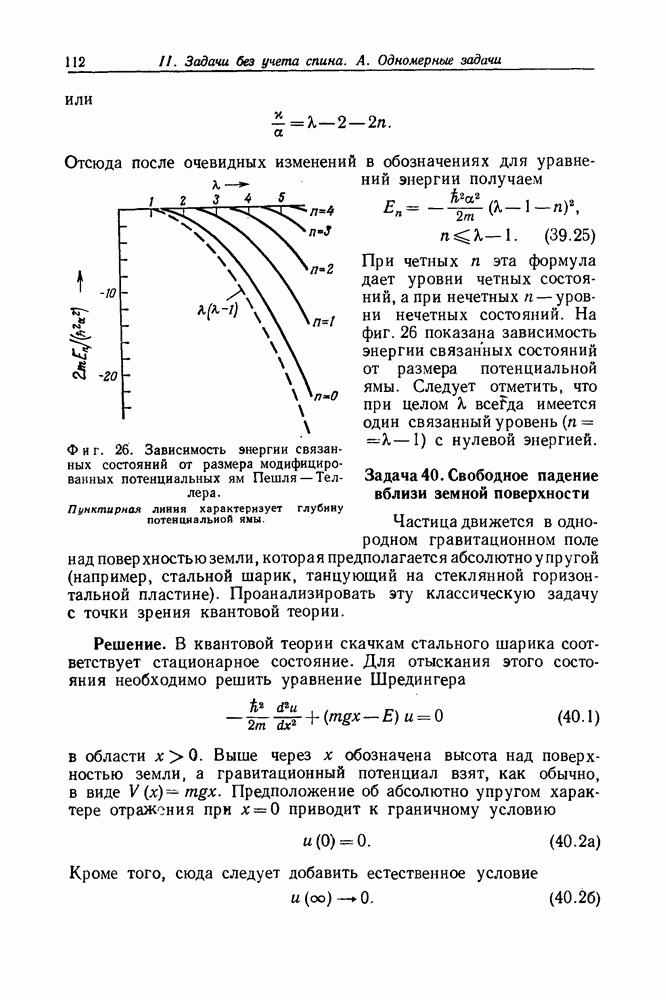
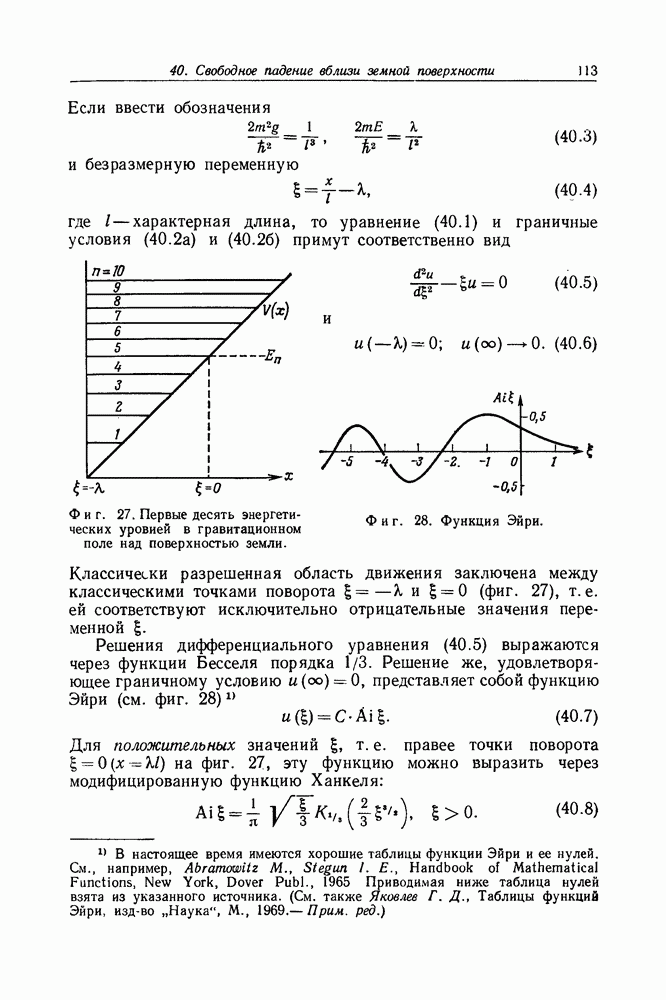
- Задача 40. Свободное падение вблизи земной поверхности
- Задача 41. Ускоряющее электрическое поле
- Б. Задачи с двумя или тремя степенями свободы без сферической симметрии
- Задача 42. Круговой осциллятор
- Задача 43. Эффект Штарка для двумерного ротатора
- Задача 44. Ион молекулы водорода
- Задача 45. Наклонное падение плоской волны
- Задача 46. Симметричный волчок
- В. Момент количества движения
- Задача 47. Бесконечно малые вращения
- Задача 48. Момент количества движения в сферических координатах
- Задача 49. Момент количества движения и оператор Лапласа
- Задача 50. Преобразования в гильбертовом пространстве
- Задача 51. Коммутаторы в координатном представлении
- Задача 52. Частица со спином 1
- Задача 53. Перестановочные соотношения компонент тензора
- Задача 54. Тензор квадрупольного момента. Сферические гармоники
- Задача 55. Преобразование сферических гармоник
- Задача 56. Построение собственных векторов оператора Lx в абстрактном гильбертовом пространстве
- Задача 57. Ортогональность сферических гармоник
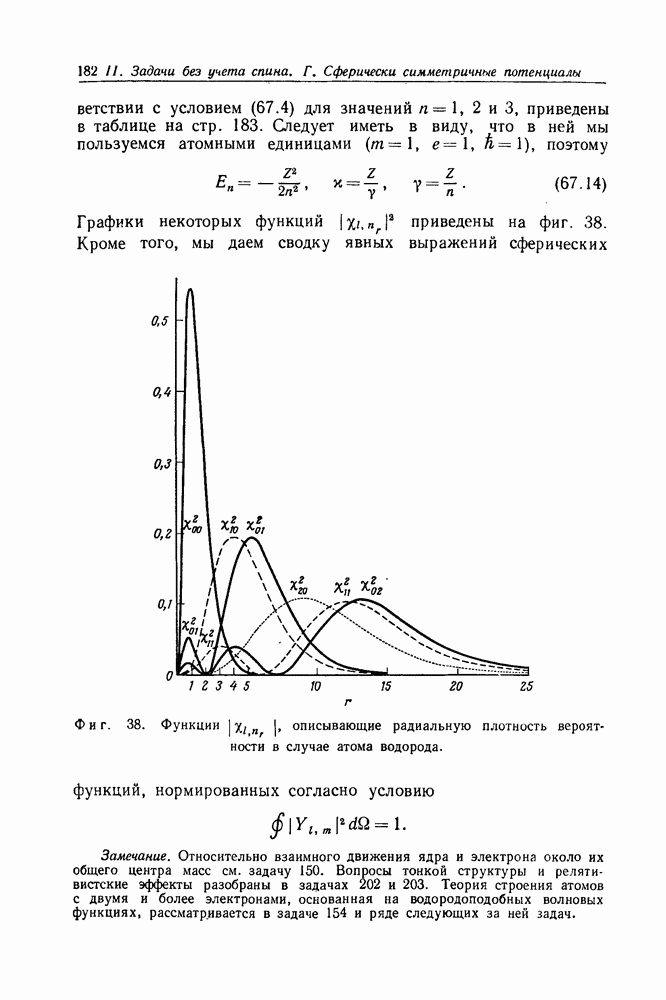
- Г. Сферически симметричные потенциалы
- Задача 58. Средние значения компонент момента количества движения
- Задача 59. Радиальная компонента оператора импульса
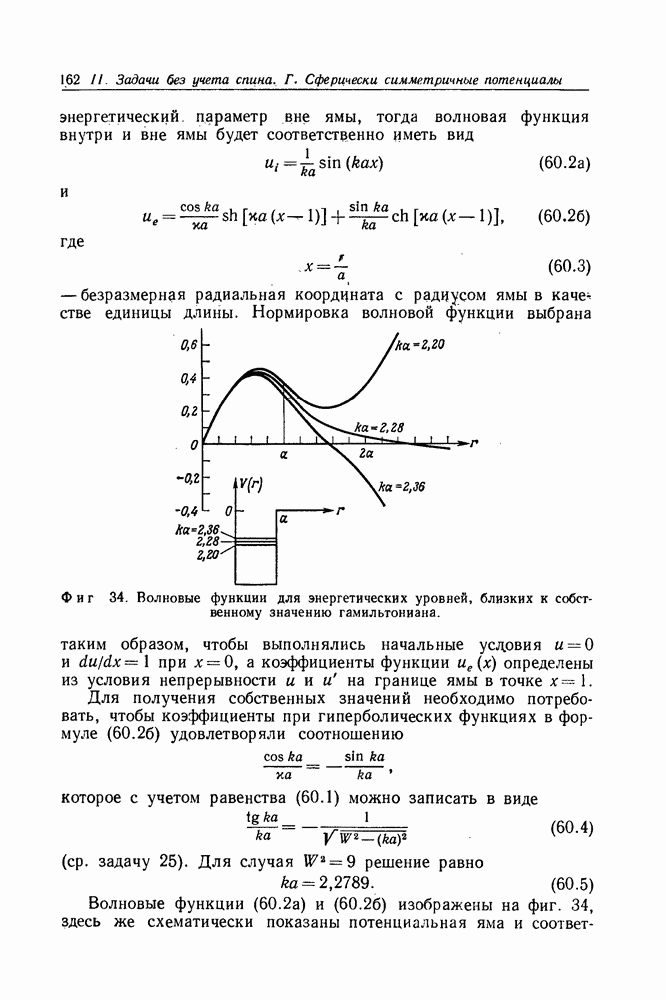
- Задача 60. Решения, близкие к собственным функциям
- Задача 61. Квадрупольный момент
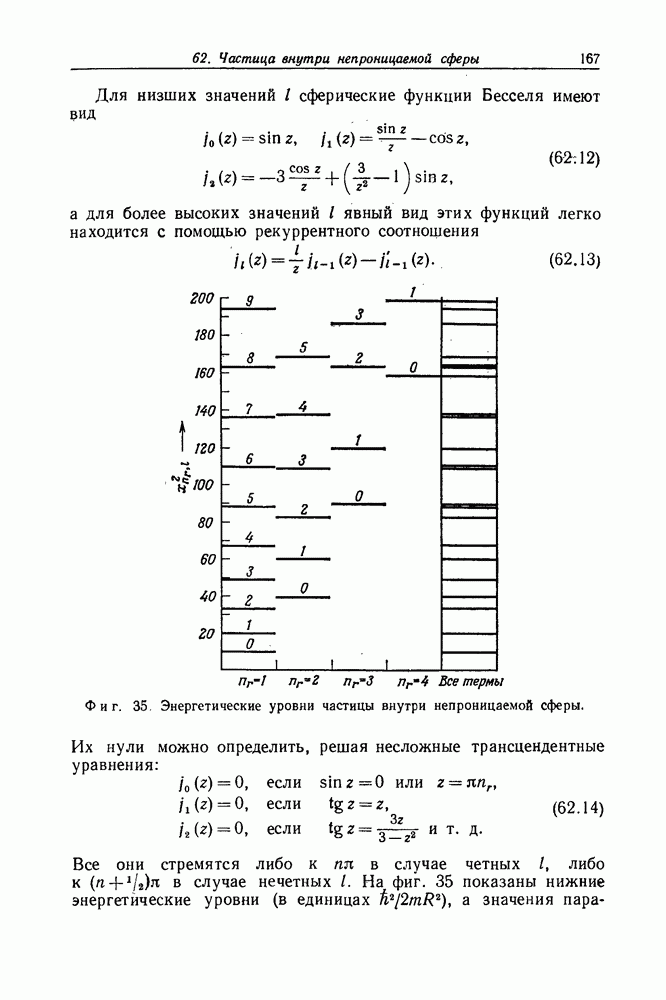
- Задача 62. Частица внутри непроницаемой сферы
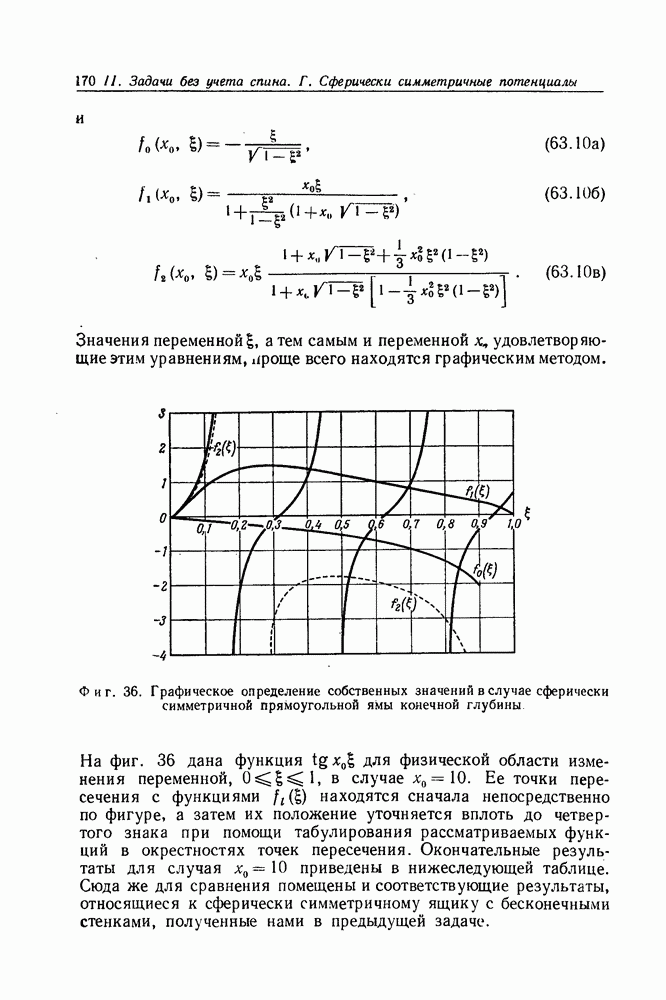
- Задача 63. Сферически симметричная прямоугольная яма конечной глубины
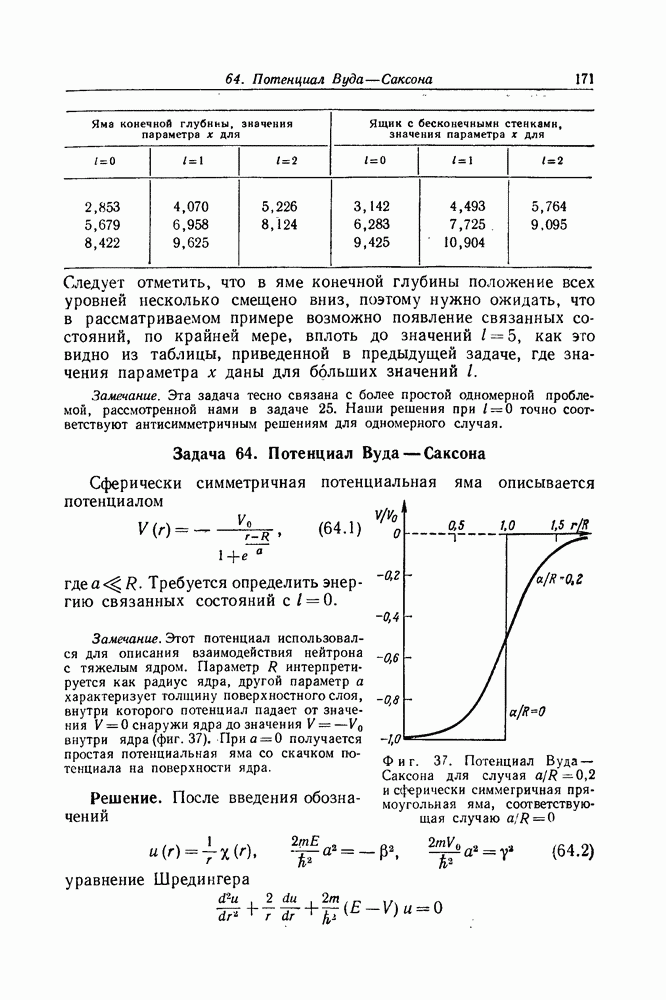
- Задача 64. Потенциал Вуда — Саксона
- Задача 65. Изотропный осциллятор
- Задача 66. Вырожденные состояния изотропного осциллятора
- Задача 67. Проблема Кеплера
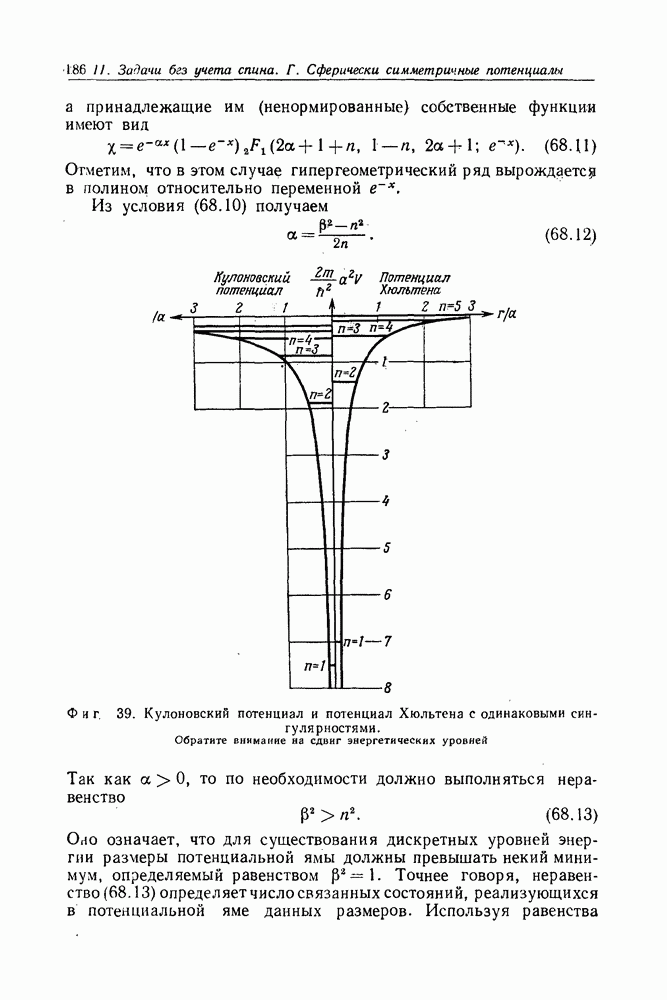
- Задача 68. Потенциал Хюльтена
- Задача 69. Молекулярный потенциал Кратцера
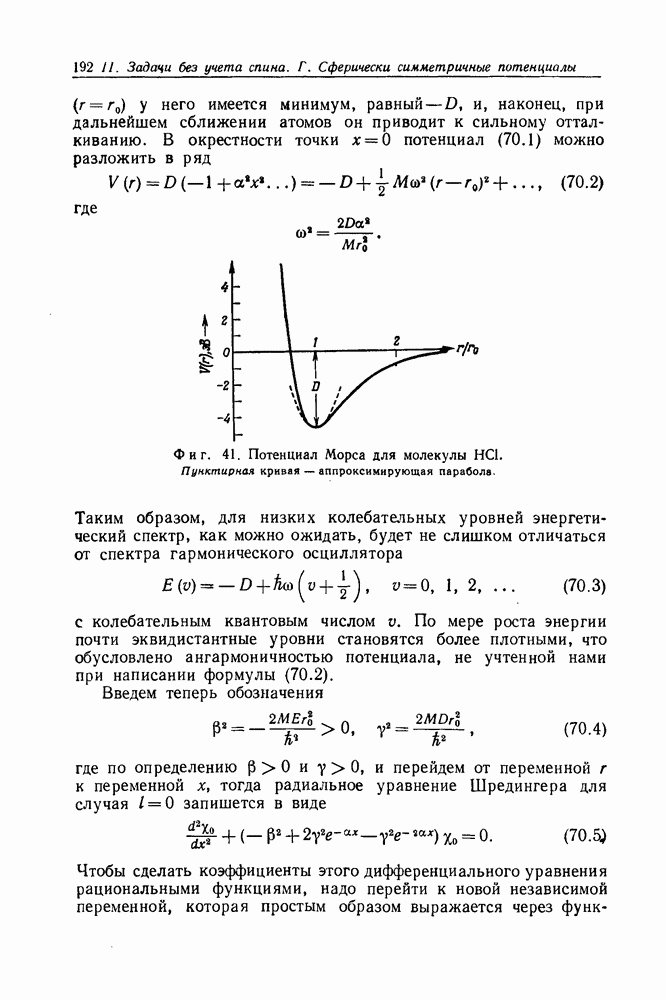
- Задача 70. Потенциал Морса
- Задача 71. Ротационные поправки к формуле Морса
- Задача 72. Потенциал Юкавы
- Задача 73. Изотопический сдвиг границы рентгеновского излучения
- Задача 74. Основное состояние мезоатома
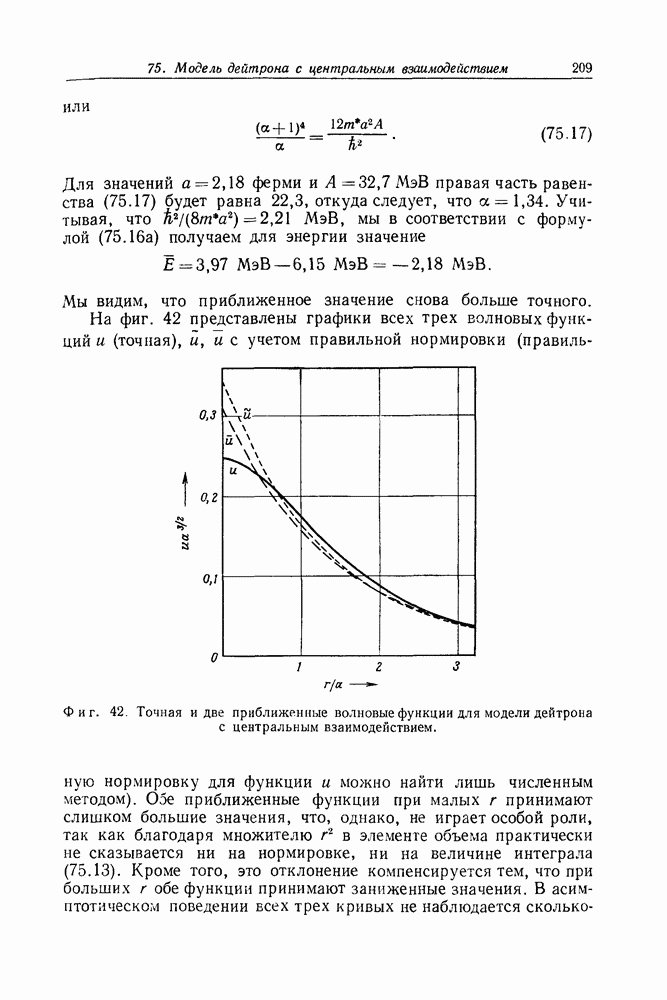
- Задача 75. Модель дейтрона с центральным взаимодействием
- Задача 76. Импульсное представление для волновых функций в поле центральных сил
- Задача 77. Уравнение Шредингера в импульсном представлении в поле центральных сил
- Задача 78. Водородные волновые функции в импульсном пространстве
- Задача 79. Штарк-эффект у пространственного ротатора
- Задача 80. Интерференция падающей и рассеянной волн
- Задача 81. Разложение плоской волны по парциальным волнам
- Задача 82. Разложение амплитуды рассеяния по парциальным волнам
- Задача 83. Рассеяние при низких энергиях
- Задача 84. Рассеяние на сферически симметричном прямоугольном потенциальном барьере
- Задача 85. Аномальное рассеяние
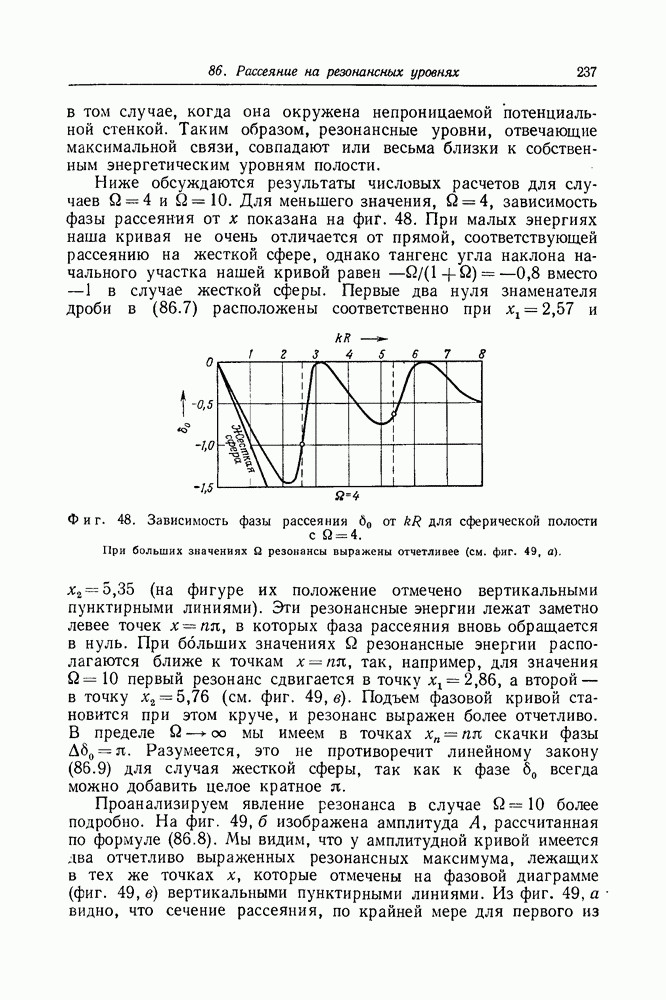
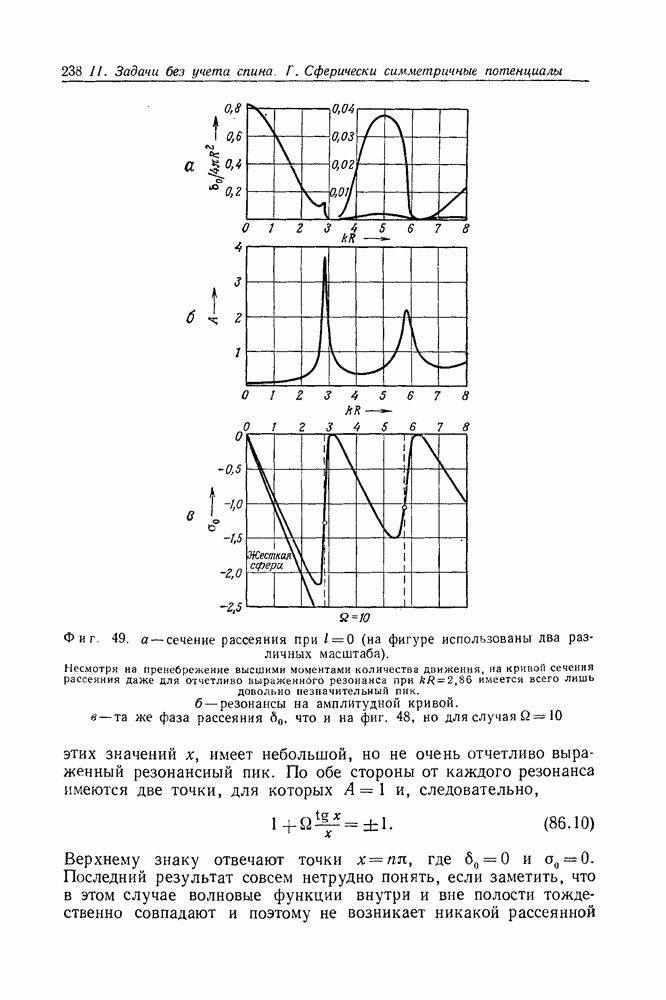
- Задача 86. Рассеяние на резонансных уровнях
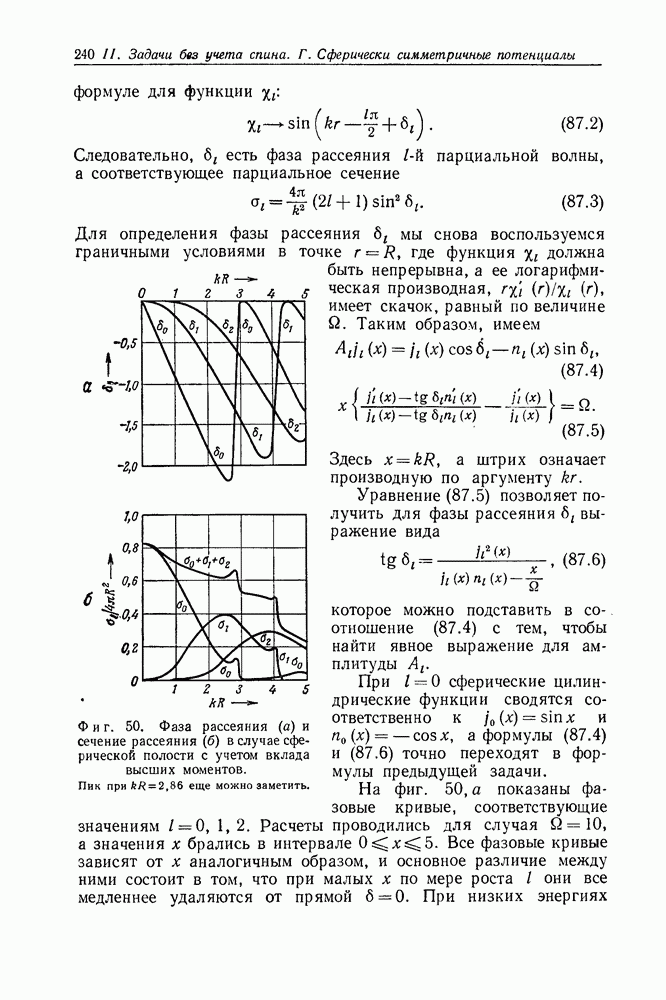
- Задача 87. Вклад состояний с высшими значениями момента количества движения
- Задача 88. Приближение, не зависящее от формы потенциала
- Задача 89. Низкоэнергетическое рассеяние на сферически симметричной прямоугольной яме
- Задача 90. Низкоэнергетическое рассеяние и связанные состояния
- Задача 91. Дейтронный потенциал с жесткой сердцевиной и без нее
- Задача 92. Низкоэнергетическое рассеяние при наличии жесткой сердцевины и без нее
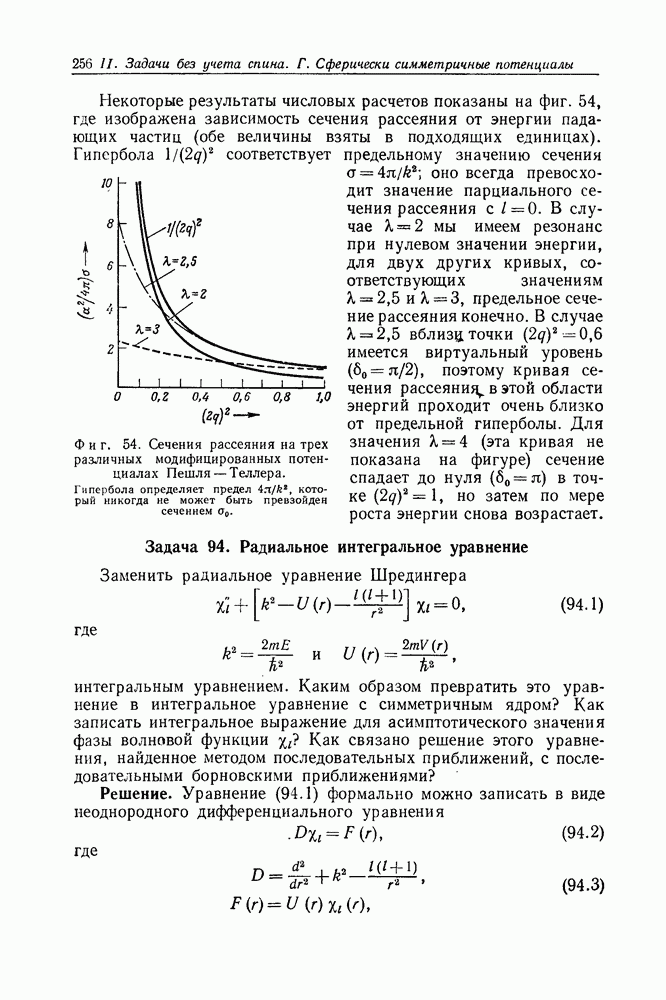
- Задача 93. Низкоэнергетическое рассеяние на модифицированном потенциале Пешля — Теллера
- Задача 94. Радиальное интегральное уравнение
- Задача 95. Вариационный принцип Швингера
- Задача 96. Последовательные приближения для фазы рассеяния
- Задача 97. Уравнение Калоджеро
- Задача 98. Линеаризация уравнения Калоджеро
- Задача 99. Длина рассеяния потенциала, имеющего вид степенной функции
- Задача 100. Второе приближение к уравнению Калоджеро
- Задача 101. Длина рассеяния для сферически симметричной прямоугольной потенциальной ямы
- Задача 102. Длина рассеяния потенциала Юкавы
- Задача 103. Улучшение сходимости рядов сферических гармоник
- Задача 104. Интеграл по прицельному расстоянию
- Задача 105. Борновскоерассеяние. Последовательные приближения.
- Задача 106. Рассеяние на потенциале Юкавы
- Задача 107. Рассеяние на экспоненциальном потенциале
- Задача 108. Борновское приближение для рассеяния на сферически симметричном распределении заряда
- Задача 109. Высокоэнергетическое рассеяние на жесткой сфере
- Задача 110. Формула Резерфорда
- Задача 111. Разложение кулоновской функции по парциальным волнам
- Задача 112. Аномальное рассеяние
- Задача 113. Преобразование Зоммерфельда — Ватсона
- Задача 114. Полюс Редже
- Д. Приближение Вентцеля — Крамерса — Бриллюэна (ВКБ)
- Задача 115. Разложение эйконала
- Задача 116. Применение метода ВКБ к радиальному уравнению
- Задача 117. Граничное ВКБ-условие Лангера
- Задача 118. Гармонический осциллятор в приближении ВКБ
- Задача 120. Проблема Кеплера в приближении ВКБ
- Задача 121. Фазы ВКБ для свободного движения
- Задача 122. Вычисление фаз ВКБ
- Задача 123. Расчет кулоновских фаз методом ВКБ
- Задача 124. Квазипотенциал
- Е. Магнитное поле
- Задача 125. Введение магнитного поля
- Задача 126. Плотность тока в присутствии магнитного поля
- Задача 127. Нормальный эффект Зеемана
- Задача 128. Парамагнитная и диамагнитная восприимчивости без учета спина