| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 86. Рассеяние на резонансных уровнях
Сферическая полость радиуса  окружена тонкой потенциальной стенкой, непроницаемость которой характеризуется безразмерным коэффициентом
окружена тонкой потенциальной стенкой, непроницаемость которой характеризуется безразмерным коэффициентом  так что потенциал имеет вид
так что потенциал имеет вид

Исследовать рассеяние парциальной волны с 
Замечание. Эта задача тесно связана с одномерным случаем, рассмотренным нами в задаче 27. Однако определение коэффициента непроницаемости здесь отличается от определения, данного в задаче 20 и использованного в задаче 27, наличием множителя  в знаменателе формулы (86.1). Дело в том, что в одномерном случае в нашем распоряжении не было характерного параметра, имеющего размерность длины, который был бы подобен радиусу сферической полости настоящей задачи. Заметьте, кстати, что одномерная
в знаменателе формулы (86.1). Дело в том, что в одномерном случае в нашем распоряжении не было характерного параметра, имеющего размерность длины, который был бы подобен радиусу сферической полости настоящей задачи. Заметьте, кстати, что одномерная  -функция имеет размерность обратной длины.
-функция имеет размерность обратной длины.
Решение. Уравнение Шредингера для радиальной волновой функции  в случае потенциала (86.1) имеет вид
в случае потенциала (86.1) имеет вид

Сама функция  должна быть непрерывной в точке, где у потенциала имеется сингулярность, ее же производная
должна быть непрерывной в точке, где у потенциала имеется сингулярность, ее же производная  в этой точке претерпевает разрыв, что можно установить, проинтегрировав уравнение (86.2) вблизи поверхности потенциальной стенки. Это интегрирование дает
в этой точке претерпевает разрыв, что можно установить, проинтегрировав уравнение (86.2) вблизи поверхности потенциальной стенки. Это интегрирование дает 

так что для логарифмической производной

в результате получаются граничные условия

С помощью соотношения (86.4) теперь можно связать выражения для волновой функции внутри сферической полости:

и вне ее

В результате имеем

Последнее уравнение можно переписать в виде, более удобном для определения фазы:

Амплитуда А, фигурирующая в выражении (86.5а), легко находится с помощью условия непрерывности функции 

Исключая отсюда с помощью уравнения (86.7) фазу 60, получаем

Как нетрудно убедиться, для непроницаемой потенциальной стенки  из уравнения (86.7) следует результат, соответствующий предельному случаю рассеяния на жесткой сфере:
из уравнения (86.7) следует результат, соответствующий предельному случаю рассеяния на жесткой сфере:

В этом случае амплитуда А, согласно формуле (86.8), обращается в нуль.
При конечных, но достаточно больших значениях  вблизи нулей знаменателя дроби, стоящей справа в уравнении (86.7), имеются такие узкие полосы значений энергии, для которых в характере рассеяния наблюдаются существенные отличия от рассеяния на жесткой сфере. Это те же самые узкие энергетические полосы, для которых, как показывает формула (86.8), амплитуда А внутри полости становится большой. Таким образом, налицо типичное явление резонанса, когда для узких энергетических полос имеется сильная связь между колебаниями внутри и вне полости, а для всех прочих энергий такая связь почти полностью отсутствует. Чем более проницаема потенциальная стенка, тем менее отчетливо выражено явление резонанса.
вблизи нулей знаменателя дроби, стоящей справа в уравнении (86.7), имеются такие узкие полосы значений энергии, для которых в характере рассеяния наблюдаются существенные отличия от рассеяния на жесткой сфере. Это те же самые узкие энергетические полосы, для которых, как показывает формула (86.8), амплитуда А внутри полости становится большой. Таким образом, налицо типичное явление резонанса, когда для узких энергетических полос имеется сильная связь между колебаниями внутри и вне полости, а для всех прочих энергий такая связь почти полностью отсутствует. Чем более проницаема потенциальная стенка, тем менее отчетливо выражено явление резонанса.
Если то резонансы имеют место вблизи точек 
Но это соответствует как раз тем энергиям, для которых  другими словами, это собственные уровни полости
другими словами, это собственные уровни полости
в том случае, когда она окружена непроницаемой потенциальной стенкой. Таким образом, резонансные уровни, отвечающие максимальной связи, совпадают или весьма близки к собственным энергетическим уровням полости.
Ниже обсуждаются результаты числовых расчетов для случаев  Для меньшего значения,
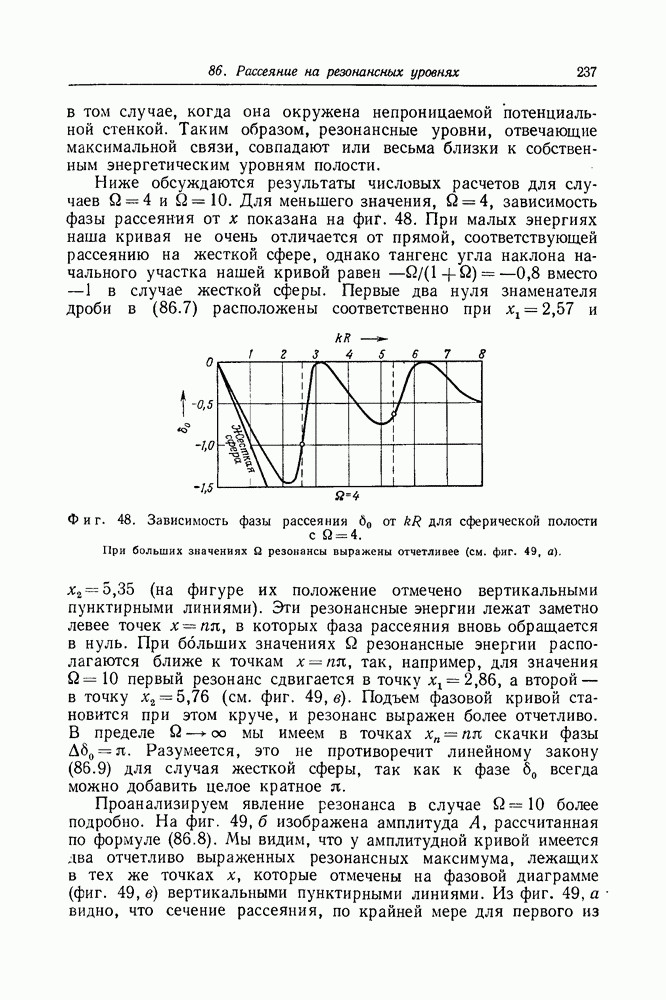
Для меньшего значения,  зависимость фазы рассеяния от х показана на фиг. 48. При малых энергиях наша кривая не очень отличается от прямой, соответствующей рассеянию на жесткой сфере, однако тангенс угла наклона начального участка нашей кривой равен
зависимость фазы рассеяния от х показана на фиг. 48. При малых энергиях наша кривая не очень отличается от прямой, соответствующей рассеянию на жесткой сфере, однако тангенс угла наклона начального участка нашей кривой равен  вместо —1 в случае жесткой сферы. Первые два нуля знаменателя дроби в (86.7) расположены соответственно при
вместо —1 в случае жесткой сферы. Первые два нуля знаменателя дроби в (86.7) расположены соответственно при  и
и  (на фигуре их положение отмечено вертикальными пунктирными линиями).
(на фигуре их положение отмечено вертикальными пунктирными линиями).

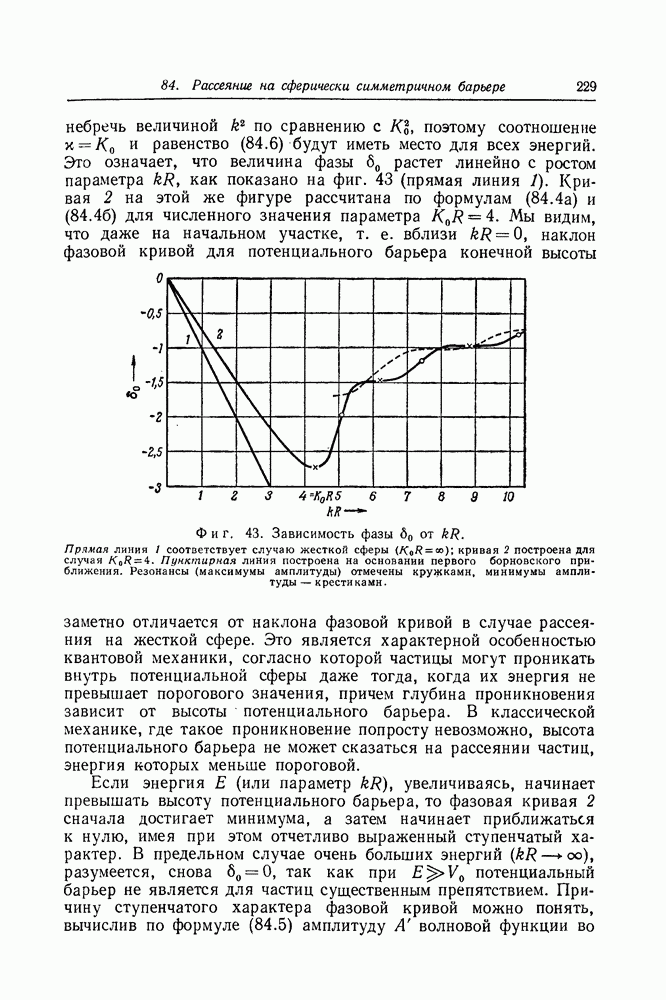
Фиг. 48. Зависимость фазы рассеяния 60 от  для сферической полости с
для сферической полости с  При больших значениях
При больших значениях  резонансы выражены отчетливее (см. фиг. 49, а).
резонансы выражены отчетливее (см. фиг. 49, а).
Эти резонансные энергии лежат заметно левее точек  в которых фаза рассеяния вновь обращается в нуль. При больших значениях
в которых фаза рассеяния вновь обращается в нуль. При больших значениях  резонансные энергии располагаются ближе к точкам
резонансные энергии располагаются ближе к точкам  так, например, для значения
так, например, для значения  первый резонанс сдвигается в точку
первый резонанс сдвигается в точку  а второй — в точку
а второй — в точку  (см. фиг. 49, б). Подъем фазовой кривой становится при этом круче, и резонанс выражен более отчетливо. В пределе
(см. фиг. 49, б). Подъем фазовой кривой становится при этом круче, и резонанс выражен более отчетливо. В пределе  мы имеем в точках
мы имеем в точках  скачки фазы
скачки фазы  Разумеется, это не противоречит линейному закону (86.9) для случая жесткой сферы, так как к фазе
Разумеется, это не противоречит линейному закону (86.9) для случая жесткой сферы, так как к фазе  всегда можно добавить целое кратное я.
всегда можно добавить целое кратное я.
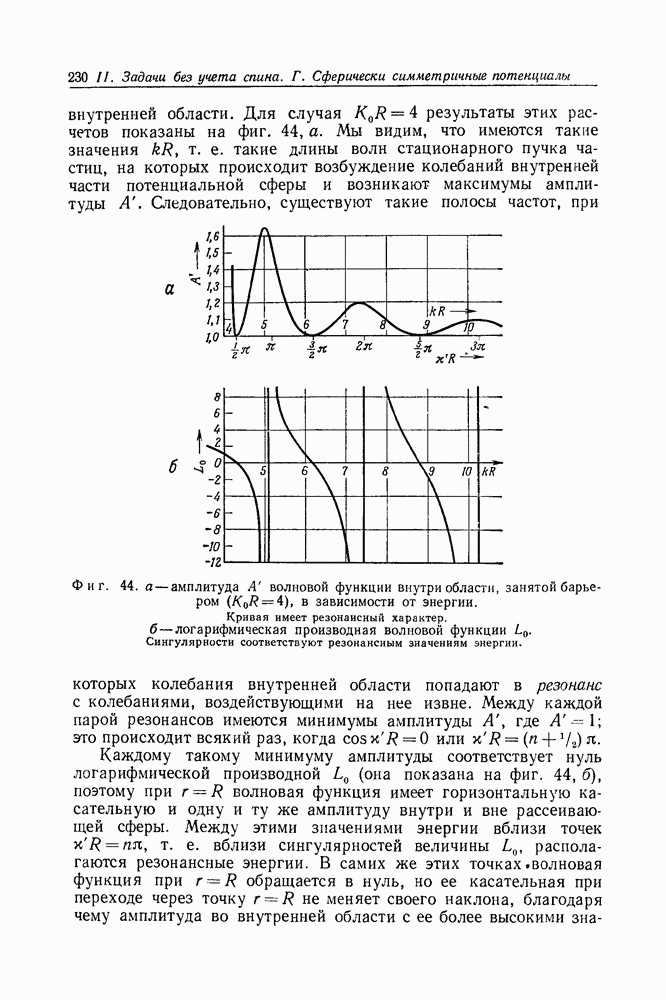
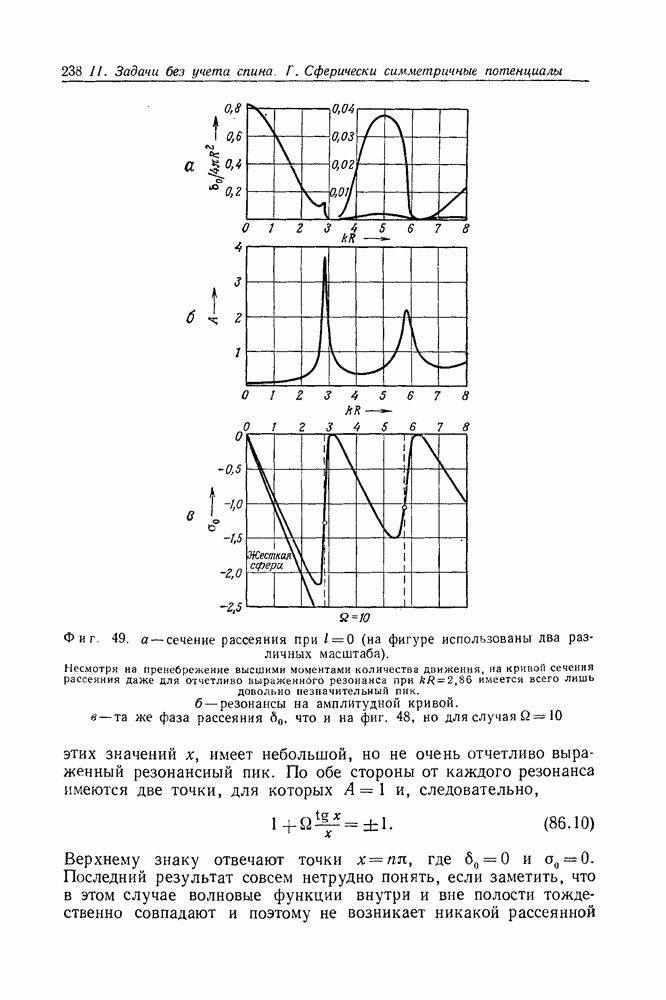
Проанализируем явление резонанса в случае  более подробно. На фиг. 49, б изображена амплитуда А, рассчитанная по формуле (86.8). Мы видим, что у амплитудной кривой имеется два отчетливо выраженных резонансных максимума, лежащих в тех же точках х, которые отмечены на фазовой диаграмме (фиг. 49, б) вертикальными пунктирными линиями. Из фиг. 49, а
более подробно. На фиг. 49, б изображена амплитуда А, рассчитанная по формуле (86.8). Мы видим, что у амплитудной кривой имеется два отчетливо выраженных резонансных максимума, лежащих в тех же точках х, которые отмечены на фазовой диаграмме (фиг. 49, б) вертикальными пунктирными линиями. Из фиг. 49, а  видно, что сечение рассеяния, по крайней мере для первого из
видно, что сечение рассеяния, по крайней мере для первого из

Фиг. 49. а — сечение рассеяния при  (на фигуре использованы два различных масштаба). Несмотря на пренебрежение высшими моментами количества движения, на кривой сечения рассеяния даже для отчетливо выраженного резонанса при
(на фигуре использованы два различных масштаба). Несмотря на пренебрежение высшими моментами количества движения, на кривой сечения рассеяния даже для отчетливо выраженного резонанса при  имеется всего лишь довольно незначительный пик. б - резонансы на амплитудной кривой. в — та же фаза рассеяния
имеется всего лишь довольно незначительный пик. б - резонансы на амплитудной кривой. в — та же фаза рассеяния  что и на фиг. 48, но для случая
что и на фиг. 48, но для случая 
этих значений х, имеет небольшой, но не очень отчетливо выраженный резонансный пик. По обе стороны от каждого резонанса имеются две точки, для которых  следовательно,
следовательно,

Верхнему знаку отвечают точки  где
где  Последний результат совсем нетрудно понять, если заметить, что в этом случае волновые функции внутри и вне полости тождественно совпадают и поэтому не возникает никакой рассеянной
Последний результат совсем нетрудно понять, если заметить, что в этом случае волновые функции внутри и вне полости тождественно совпадают и поэтому не возникает никакой рассеянной
волны вообще. Нижнему знаку в формуле (86.10) отвечают точки, расположенные вблизи минимумов фазы рассеяния. Из соотношения

легче получить, что фаза рассеяния стационарна в точках

Для случая  мы находим
мы находим  и 5,406, в то время как формула (86.10) при выборе нижнего знака дает
и 5,406, в то время как формула (86.10) при выборе нижнего знака дает

что при том же значении  приводит к значениям
приводит к значениям  располагающимся очень близко к точкам минимумов фазовой кривой.
располагающимся очень близко к точкам минимумов фазовой кривой.
Кривая сечения рассеяния содержит довольно скудную информацию (см. фиг. 49,а). Первый резонанс приводит лишь к небольшому пику. На кривой не заметно никаких следов второго резонанса, если не считать двух нулей, расположенных много правее и много левее от него. Наличие этих нулей говорит лишь о том, что где-то между ними имеется резонанс неизвестной высоты и ширины. Еще меньше сведений мы можем получить из экспериментальной кривой сечения рассеяния, так как возрастающий с ростом х вклад состояний с высшими значениями момента может замаскировать наличие нулей на кривой сечения 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- I. Общие принципы
- Задача 1. Закон сохранения вероятности
- Задача 2. Вариационный принцип Шредингера
- Задача 3. Классическая механика для пространственных средних
- Задача 4. Классические законы для момента количества движения
- Задача 5. Закон сохранения энергии
- Задача 6. Эрмитово сопряжение
- Задача 7. Построение эрмитова оператора
- Задача 8. Дифференцирование оператора
- Задача 9. Изменение средних значений со временем
- Задача 10. Картина Шредингера и картина Гейзенберга
- Задача 11. Гамильтониан, зависящий от времени
- Задача 12. Повторное измерение
- Задача 13. Криволинейные координаты
- Задача 14. Волновые функции в импульсном представлении
- Задача 15. Пространство импульсов. Периодические и непериодические волновые функции
- II. Одночастичные задачи без учета спина
- Задача 16. Фундаментальные решения в случае свободного движения
- Задача 17. Волновой пакет в случае свободного движения
- Задача 18. Стоячие волны
- Задача 19. Полупроницаемая перегородка
- Задача 20. Полупроницаемая перегородка в виде «дельта»-образного потенциального барьера
- Задача 21. Рассеяние на «дельта»-образном потенциальном барьере
- Задача 22. Рассеяние на симметричном потенциальном барьере
- Задача 23. Отражение от прямоугольного барьера
- Задача 24. Инверсия отражения
- Задача 25. Прямоугольная потенциальная яма
- Задача 26. Прямоугольная потенциальная яма между двумя бесконечными стенками
- Задача 27. Виртуальные уровни
- Задача 28. Периодический потенциал
- Задача 29. Дираковская потенциальная гребенка
- Задача 30. Гармонический осциллятор
- Задача 31. Осциллятор в абстрактном гильбертовом пространстве (осциллятор в представлении Фока)
- Задача 32. Использование лестничных операторов для нахождения собственных функций осциллятора
- Задача 33. Гармонический осциллятор в матричном представлении
- Задача 34. Волновые функции осциллятора в пространстве импульсов
- Задача 35. Ангармонический осциллятор
- Задача 36. Приближенные волновые функции
- Задача 37. Потенциальная ступенька
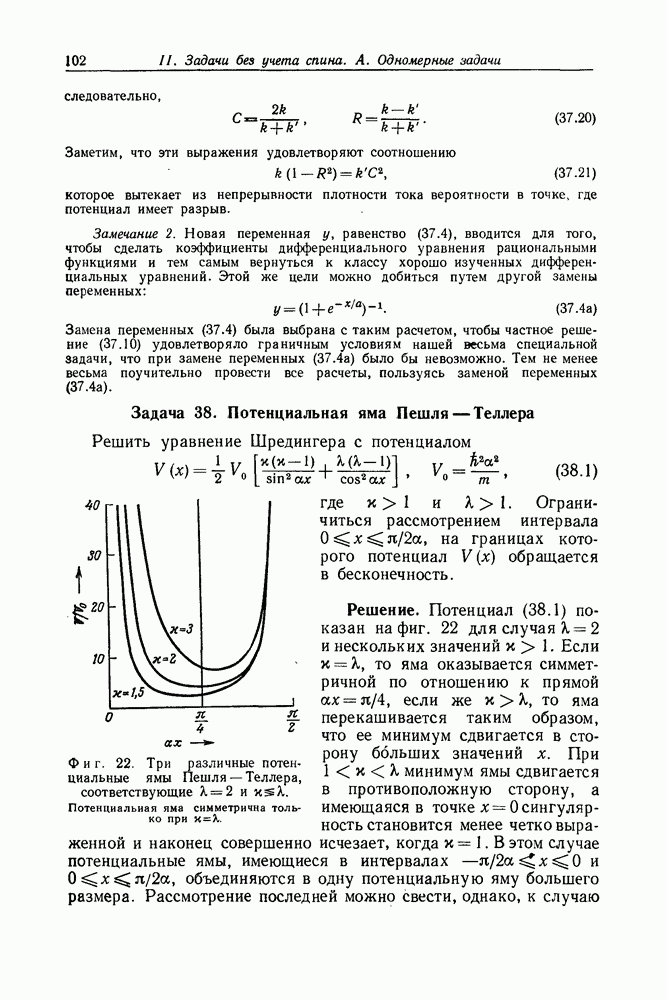
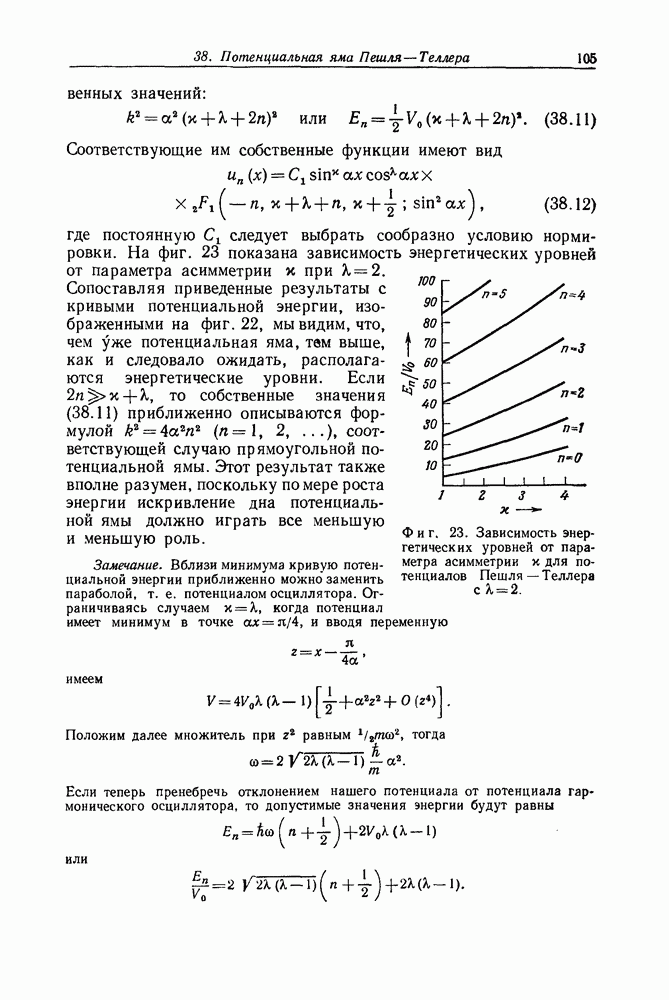
- Задача 38. Потенциальная яма Пешля — Теллера
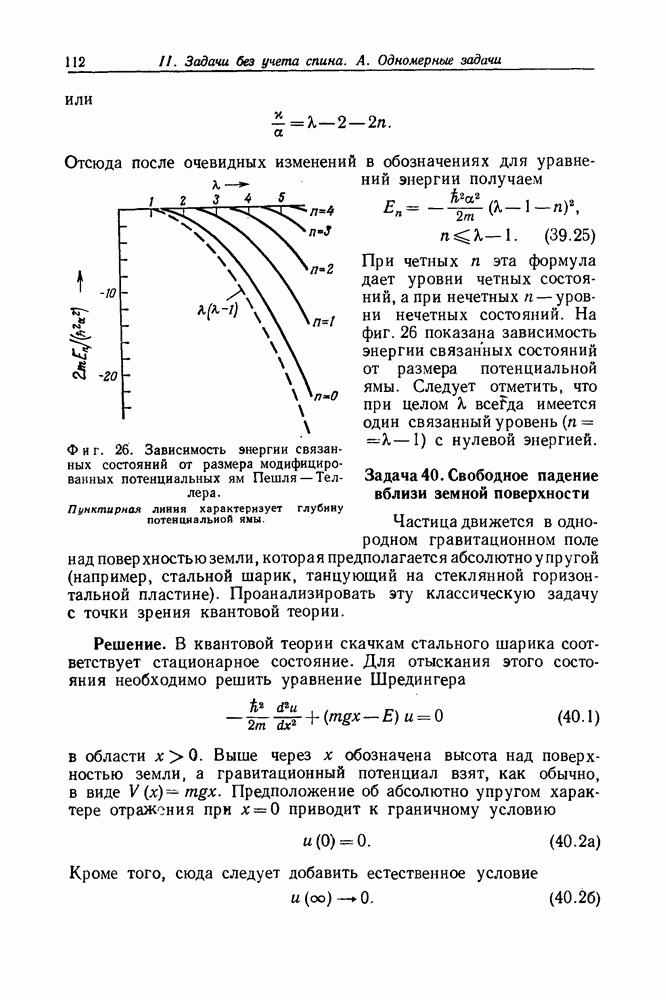
- Задача 39. Модифицированная потенциальная яма Пешля—Теллера
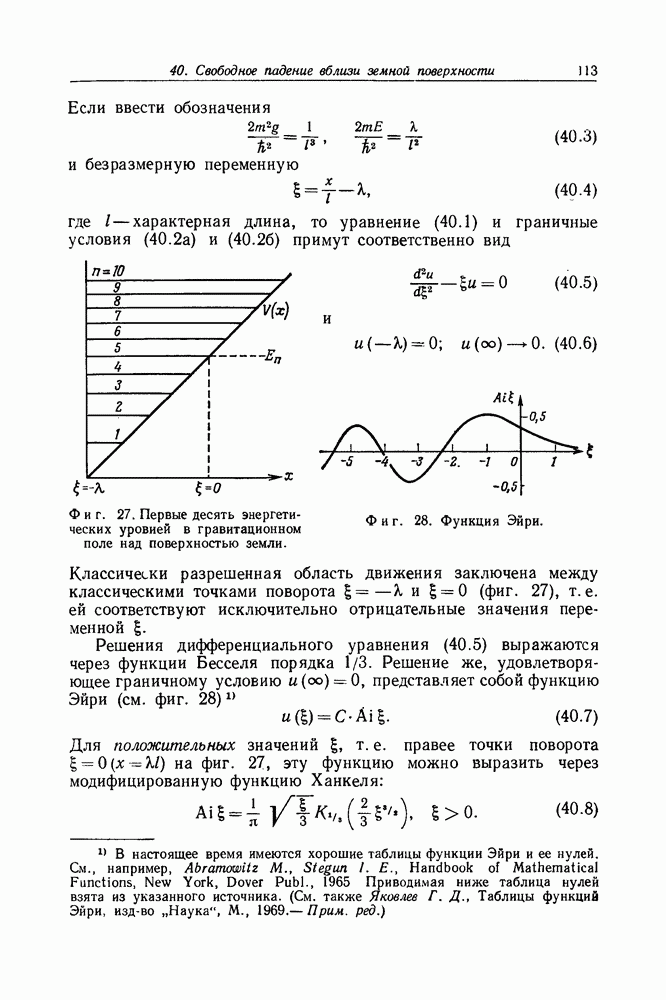
- Задача 40. Свободное падение вблизи земной поверхности
- Задача 41. Ускоряющее электрическое поле
- Б. Задачи с двумя или тремя степенями свободы без сферической симметрии
- Задача 42. Круговой осциллятор
- Задача 43. Эффект Штарка для двумерного ротатора
- Задача 44. Ион молекулы водорода
- Задача 45. Наклонное падение плоской волны
- Задача 46. Симметричный волчок
- В. Момент количества движения
- Задача 47. Бесконечно малые вращения
- Задача 48. Момент количества движения в сферических координатах
- Задача 49. Момент количества движения и оператор Лапласа
- Задача 50. Преобразования в гильбертовом пространстве
- Задача 51. Коммутаторы в координатном представлении
- Задача 52. Частица со спином 1
- Задача 53. Перестановочные соотношения компонент тензора
- Задача 54. Тензор квадрупольного момента. Сферические гармоники
- Задача 55. Преобразование сферических гармоник
- Задача 56. Построение собственных векторов оператора Lx в абстрактном гильбертовом пространстве
- Задача 57. Ортогональность сферических гармоник
- Г. Сферически симметричные потенциалы
- Задача 58. Средние значения компонент момента количества движения
- Задача 59. Радиальная компонента оператора импульса
- Задача 60. Решения, близкие к собственным функциям
- Задача 61. Квадрупольный момент
- Задача 62. Частица внутри непроницаемой сферы
- Задача 63. Сферически симметричная прямоугольная яма конечной глубины
- Задача 64. Потенциал Вуда — Саксона
- Задача 65. Изотропный осциллятор
- Задача 66. Вырожденные состояния изотропного осциллятора
- Задача 67. Проблема Кеплера
- Задача 68. Потенциал Хюльтена
- Задача 69. Молекулярный потенциал Кратцера
- Задача 70. Потенциал Морса
- Задача 71. Ротационные поправки к формуле Морса
- Задача 72. Потенциал Юкавы
- Задача 73. Изотопический сдвиг границы рентгеновского излучения
- Задача 74. Основное состояние мезоатома
- Задача 75. Модель дейтрона с центральным взаимодействием
- Задача 76. Импульсное представление для волновых функций в поле центральных сил
- Задача 77. Уравнение Шредингера в импульсном представлении в поле центральных сил
- Задача 78. Водородные волновые функции в импульсном пространстве
- Задача 79. Штарк-эффект у пространственного ротатора
- Задача 80. Интерференция падающей и рассеянной волн
- Задача 81. Разложение плоской волны по парциальным волнам
- Задача 82. Разложение амплитуды рассеяния по парциальным волнам
- Задача 83. Рассеяние при низких энергиях
- Задача 84. Рассеяние на сферически симметричном прямоугольном потенциальном барьере
- Задача 85. Аномальное рассеяние
- Задача 86. Рассеяние на резонансных уровнях
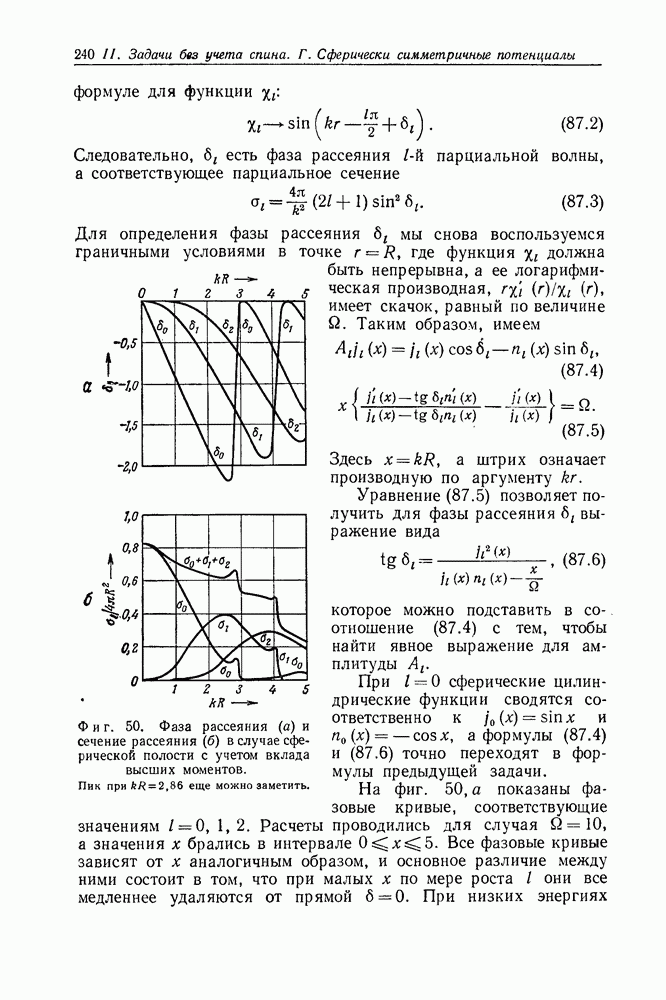
- Задача 87. Вклад состояний с высшими значениями момента количества движения
- Задача 88. Приближение, не зависящее от формы потенциала
- Задача 89. Низкоэнергетическое рассеяние на сферически симметричной прямоугольной яме
- Задача 90. Низкоэнергетическое рассеяние и связанные состояния
- Задача 91. Дейтронный потенциал с жесткой сердцевиной и без нее
- Задача 92. Низкоэнергетическое рассеяние при наличии жесткой сердцевины и без нее
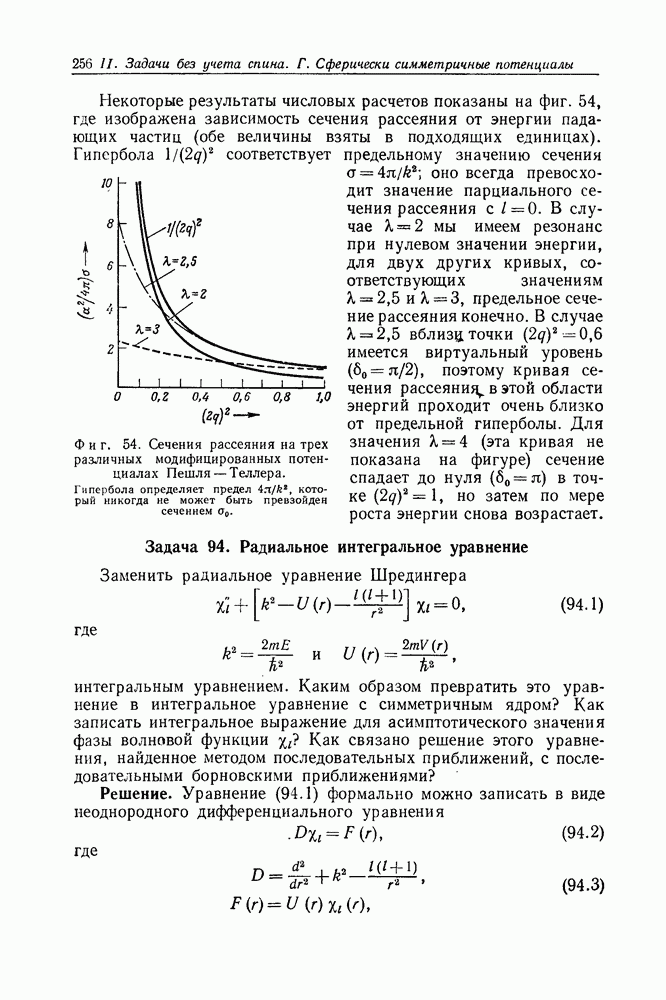
- Задача 93. Низкоэнергетическое рассеяние на модифицированном потенциале Пешля — Теллера
- Задача 94. Радиальное интегральное уравнение
- Задача 95. Вариационный принцип Швингера
- Задача 96. Последовательные приближения для фазы рассеяния
- Задача 97. Уравнение Калоджеро
- Задача 98. Линеаризация уравнения Калоджеро
- Задача 99. Длина рассеяния потенциала, имеющего вид степенной функции
- Задача 100. Второе приближение к уравнению Калоджеро
- Задача 101. Длина рассеяния для сферически симметричной прямоугольной потенциальной ямы
- Задача 102. Длина рассеяния потенциала Юкавы
- Задача 103. Улучшение сходимости рядов сферических гармоник
- Задача 104. Интеграл по прицельному расстоянию
- Задача 105. Борновскоерассеяние. Последовательные приближения.
- Задача 106. Рассеяние на потенциале Юкавы
- Задача 107. Рассеяние на экспоненциальном потенциале
- Задача 108. Борновское приближение для рассеяния на сферически симметричном распределении заряда
- Задача 109. Высокоэнергетическое рассеяние на жесткой сфере
- Задача 110. Формула Резерфорда
- Задача 111. Разложение кулоновской функции по парциальным волнам
- Задача 112. Аномальное рассеяние
- Задача 113. Преобразование Зоммерфельда — Ватсона
- Задача 114. Полюс Редже
- Д. Приближение Вентцеля — Крамерса — Бриллюэна (ВКБ)
- Задача 115. Разложение эйконала
- Задача 116. Применение метода ВКБ к радиальному уравнению
- Задача 117. Граничное ВКБ-условие Лангера
- Задача 118. Гармонический осциллятор в приближении ВКБ
- Задача 120. Проблема Кеплера в приближении ВКБ
- Задача 121. Фазы ВКБ для свободного движения
- Задача 122. Вычисление фаз ВКБ
- Задача 123. Расчет кулоновских фаз методом ВКБ
- Задача 124. Квазипотенциал
- Е. Магнитное поле
- Задача 125. Введение магнитного поля
- Задача 126. Плотность тока в присутствии магнитного поля
- Задача 127. Нормальный эффект Зеемана
- Задача 128. Парамагнитная и диамагнитная восприимчивости без учета спина