| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.11. О МЕХАНИКЕ ХРУПКОГО РАЗРУШЕНИЯ
Известно, что реальная прочность конструкционных материалов в десятки, а иногда и сотни раз меньше теоретической прочности, т. е. прочности на отрыв двух слоев атомов (или прочности на разрыв одиночной цепочки атомов), равной примерно одной десятой величины модуля упругости  Только на тонких нитях (стеклянных, кварцевых и т. д. и на тонких нитевидных кристаллах,
Только на тонких нитях (стеклянных, кварцевых и т. д. и на тонких нитевидных кристаллах,

Рис. 11.18
так называемых усах) удалось достигнуть прочности, приближающейся к теоретической. Однако с увеличением толщины нитей и усов их прочность на разрыв быстро уменьшается. Характер изменения величины разрушающего напряжения от диаметра нитей и усов имеет вид, представленный на рис. 11.18.
Столь значительная разница в теоретической и реальной прочности конструкционных материалов объясняется различного рода дефектами, неизбежно присутствующими в каждом материале. Такими дефектами являются прежде всего дефекты кристаллической решетки (дислокации, вакансии, внедрения и т. п.), наличие различного рода микропор и включений и т. д.
К дефектам, возникающим при изготовлении материала в металлургическом производстве, добавляются дефекты, появляющиеся в процессе изготовления детали при механической обработке, сварке, закалке и т. д., а также дефекты, появляющиеся в процессе эксплуатации конструкций или машин как результат взаимодействия их деталей друг с другом и с окружающей, часто агрессивной средой.
Именно малым количеством и малыми размерами дефектов в тонких нитях и усах можно объяснить их высокую прочность.
О существенном влиянии состояния поверхностного слоя на прочность детали свидетельствует опыт, проведенный академиком А. Ф. Иоффе (1920 г.). В этом опыте определялась прочность кристалла каменной соли при испытании на воздухе и в воде. Оказалось, что в результате растворения в воде всегда имеющего повреждения поверхностного слоя разрушающее напряжение для кристалла возросло с 45 до  и почти достигло теоретического значения, равного приблизительно
и почти достигло теоретического значения, равного приблизительно 
Установление закономерностей начального этапа разрушения требует исследования дефектов кристаллов на атомном уровне и представляет предмет интенсивных исследований методами химии, физики твердого тела и материаловедения.
Когда же трещина (или система трещин) по какой-либо причине возникла и захватила достаточное количество зерен, чтобы материалу можно было приписать свойство сплошности и однородности, дальнейшее развитие трещин может быть исследовано методами механики сплошной среды. Раздел механики деформируемого тела, в котором исследуется проблема распространения трещин, называют механикой хрупкого разрушения.
В основе механики хрупкого разрушения лежит представление о том, что материал всегда имеет какие-либо дефекты, которые отождествляются с некоторой системой начальных трещин. Эти трещины вызывают значительную концентрацию напряжений на их фронте, которая при некоторых условиях приводит к быстрому росту трещин.
Каждая из трещин, как показал Гриффитс (1920 г.), начинает расти только после того, как средние напряжения в теле достигнут некоторого критического именно для данной трещины значения,
зависящего от ее размеров, ориентировки по отношению к направлению действующей нагрузки и физико-механических свойств материала.
В своей теории распространения трещин, которая положена в основу современной механики хрупкого разрушения, Гриффитс исходил из следующих соображений.
Для расширения трещины требуется затратить некоторую энергию, равную в случае идеально хрупкого материала работе сил поверхностного натяжения (поверхностной энергии) на вновь образовавшихся свободных поверхностях трещины, которые до начала ее развития не существовали.
Источником необходимой для этого энергии является потенциальная энергия деформации, накопленная в теле, как в аккумуляторе энергии. Часть упругой энергии освобождается при увеличении размеров трещины вследствие роста объема охватывающих почти всю поверхность трещины областей пониженных напряжений (см. заштрихованные области на рис. 11.15).
Освободившаяся в результате уменьшения напряжений и деформаций в части материала тела упругая энергия как бы стекает к краям трещины — местам концентрации напряжений, где и происходит преобразование упругой энергии в поверхностную. Этот процесс реализуется при напряжениях, близких к теоретической прочности хрупкого материала. При определенном значении нагрузки  такие напряжения возникают на контуре трещины вследствие высокой концентрации напряжений в этом месте. Таким образом, причиной хрупкого разрушения является концентрация напряжений, возникающая на фронте трещины.
такие напряжения возникают на контуре трещины вследствие высокой концентрации напряжений в этом месте. Таким образом, причиной хрупкого разрушения является концентрация напряжений, возникающая на фронте трещины.
Рассмотрим теперь возможные соотношения между приращениями упругой и поверхностной энергии тела с трещиной.
Если количество  освободившейся упругой энергии будет меньше энергии
освободившейся упругой энергии будет меньше энергии  необходимой для соответствующего увеличения свободных поверхностей трещины, т. е. в случае
необходимой для соответствующего увеличения свободных поверхностей трещины, т. е. в случае  то трещина расти не будет. Если же освобождающаяся энергия превзойдет энергию, требующуюся для разрыва материала на фронте трещины, т. е.
то трещина расти не будет. Если же освобождающаяся энергия превзойдет энергию, требующуюся для разрыва материала на фронте трещины, т. е.  то начнется лавинообразное распространение трещины.
то начнется лавинообразное распространение трещины.
Критерием начала развития трещины является равенство.

Из этого равенства следует, что хрупкое разрушение может развиваться без какой-либо дополнительной работы внешних сил только за счет соответствующего уменьшения потенциальной энергии деформации тела. Поскольку естественным состоянием тела является состояние, соответствующее минимуму потенциальной энергии, то трещина всегда имеет тенденцию к неограниченному росту.
Если в тонкой, подвергнутой одноосному растяжению пластинке (рис. 11.19) образовалась малая по сравнению с размерами пластинки поперечная трещина, то потенциальная энергия деформации

Рис. 11.19

Рис. 11.20
пластинки уменьшится, как показал Гриффитс на величину

где  — номинальные напряжения в пластинке;
— номинальные напряжения в пластинке;  — длина трещины. Толщина пластинки для простоты принята равной единице.
— длина трещины. Толщина пластинки для простоты принята равной единице.
При увеличении размера трещины на  упругая энергия пластинки уменьшится на
упругая энергия пластинки уменьшится на  а энергия поверхностного натяжения
а энергия поверхностного натяжения  увеличится на
увеличится на  где у — необратимая работа, затраченная на создание единицы площади свободной поверхности трещины.
где у — необратимая работа, затраченная на создание единицы площади свободной поверхности трещины.
Согласно критерию (11.24) трещина начинает самопроизвольно расти при

Равенство (11.26) устанавливает связь между минимальной длиной (называемой критической) начальной трещины, величиной напряжения, при котором эта трещина начинает расти, и физико-механическими свойствами материала. График зависимости критической длины трещины  от величины действующего напряжения
от величины действующего напряжения  в пластинке
в пластинке

представлен на рис. 11.20. Аналогичные закономерности развития трещин имеют место и в телах более сложной формы.
Итак, для каждой величины напряжения о в каждом конкретном материале существует своя критическая длина  трещины и, пока напряжения в материале не достигли критического для данной трещины значения
трещины и, пока напряжения в материале не достигли критического для данной трещины значения  эта трещина расти не будет. Именно поэтому реальные материалы обладают свойством прочности, несмотря на наличие в них трещин и иных дефектов.
эта трещина расти не будет. Именно поэтому реальные материалы обладают свойством прочности, несмотря на наличие в них трещин и иных дефектов.
Критическая длина трещины быстро уменьшается с ростом уровня напряжений (см. рис. 11.20) и при больших эксплуатационных напряжениях может быть очень малой  порядка нескольких микрон. Этим частично объясняется повышенная чувствительность высокопрочных материалов к различного рода дефектам их структуры.
порядка нескольких микрон. Этим частично объясняется повышенная чувствительность высокопрочных материалов к различного рода дефектам их структуры.
Дальнейшие теоретические и экспериментальные исследования показали, что заключения о росте трещины, когда ее размеры
достигают некоторой критической величины, справедливы не только для очень хрупких материалов типа стекла, керамики и т. п., но и для конструкционных материалов, разрушение которых сопровождается пластической деформацией.
На контуре трещины в упруго пластическом материале образуются сначала значительные по величине пластические деформации порядка десятков процентов и лишь затем, когда исчерпывается способность материала пластически деформироваться, происходит отрыв берегов трещины друг от друга, причем затраты энергии  на создание пластических деформаций при образовании единицы свободной поверхности трещины могут во много раз превышать интенсивность поверхностной энергии у. Для металлов, например,
на создание пластических деформаций при образовании единицы свободной поверхности трещины могут во много раз превышать интенсивность поверхностной энергии у. Для металлов, например, 
Оказалось также, что все соотношения, полученные для идеально хрупких материалов, справедливы и для упруго пластических тел, если пластические деформации образуются только в узком слое, примыкающем непосредственно к поверхности трещины. Такой случай разрушения называют квазихрупким. Надо только в этих соотношениях заменить  на сумму
на сумму 
Так, например, для тонкой пластинки из упруго пластического материала с малой поперечной трещиной критическая длина  трещины связана с растягивающими пластинку напряжениями соотношением
трещины связана с растягивающими пластинку напряжениями соотношением

Величину  называют удельной энергией диссипации, энергией разрушения или эффективной поверхностной энергией.
называют удельной энергией диссипации, энергией разрушения или эффективной поверхностной энергией.
Из (11.28) следует, что параметр

можно рассматривать как величину постоянную для каждого материала. Чем больше этот параметр, тем больше критическая длина трещины, т. е. тем больше сопротивление материала развитию трещины.
Способность материала сопротивляться развитию трещин называется вязкостью или трещиностойкостью.
Вязкость зависит, в первую очередь, от способности материала пластически деформироваться, т. е. способности поглощать энергию на необратимые процессы перед разрушением. Именно поэтому пластичные металлы с относительно невысокими пределами прочности обладают высокой трещиностойкостью, что является лучшей гарантией от внезапных разрушений.
В то же время в высокопрочных жестких материалах затраты энергии на образование необратимых пластических деформаций малы и в них при нагружении тела аккумулируется много потенциальной энергии. Эта энергия выделяется в больших количествах при росте трещин, что приводит при определенных условиях к лавинному их распространению и полному разрушению тела.
Однако вязкость определяется не только пластическими свойствами, но и структурой материала — наличием в нем блокирующих развитие трещин поверхностей раздела, подобных границам между компонентами армированных материалов. Именно благодаря наличию поверхностей раздела многие композиционные материалы, например стеклопластики, обладают вязкостью, несмотря на то, что составляющие их компоненты являются хрупкими материалами.
В более широком смысле вязкость — это способность структуры материала блокировать развитие трещин.
Вязкость присуща сложному, неоднородному материалу, тогда как однородные материалы всегда проявляют свойство хрупкости.
Следует иметь в виду, что далеко не всякие границы раздела в материале вызывают торможение трещин. Объяснить это можно особенностями распределения напряжений вблизи фронта трещины и величинами сил сцепления материала на поверхности раздела.
В кончике трещины в растянутом теле возникает высокая концентрация напряжений  быстро убывающая по мере удаления от трещины вдоль оси х (см. рис. 11.15). Но на некотором расстоянии от этого кончика возникает вытянутая вдоль оси х (в направлении трещины) область растягивающих напряжений
быстро убывающая по мере удаления от трещины вдоль оси х (см. рис. 11.15). Но на некотором расстоянии от этого кончика возникает вытянутая вдоль оси х (в направлении трещины) область растягивающих напряжений  параллельных трещине и нормальных к линии действия нагрузки.
параллельных трещине и нормальных к линии действия нагрузки.
По некоторым оценкам наибольшая величина этих растягивающих напряжений  лишь примерно в пять раз меньше максимального значения напряжений
лишь примерно в пять раз меньше максимального значения напряжений  на кончике трещины.
на кончике трещины.
Область растягивающих напряжений движется всегда впереди трещины и первой подходит к поверхности раздела. Если силы сцепления на этой поверхности будут достаточно велики, то поверхность раздела не разрушится, трещина пересечет ее и распространится дальше. Если же поверхность раздела недостаточно прочна, то эта граница разрушится на некотором участке, прежде чем к нему подойдет основная трещина. Образуется новая трещина, перпендикулярная основной и палаллельная линии действия нагрузки, а такие трещины обычно не развиваются. Встреча основной трещины с разрушившейся поверхностью раздела приводит к резкому увеличению радиуса на фронте этой трещины, а следовательно, и к резкому уменьшению концентрации напряжений на кончике трещины. В результате рост основной трещины прекращается.
Таким образом, трещина в процессе роста, по-видимому, сама создает возможность затормозить ее развитие при оптимальном сочетании прочности основного материала и сил сцепления на границах раздела.
Энергетический подход Гриффитса оказался весьма трудоемким для исследования хрупкого и квазихрупкого разрушения тел сложной формы при сложных схемах нагружения. Однако то обстоятельство, что вершина трещины, где сосредоточен механизм разрушения, играет роль стока освобождающейся потенциальной энергии, которая здесь же расходуется на разрушение материала, позволило сформулировать условие разрушения материала на кончике трещины исходя из рассмотрения полей напряжений и деформаций непосредственно

Рис. 11.21
вблизи вершины трещины. Такой «силовой» подход был предложен Ирвином в 1957 г. Им же был сформулирован критерий локального разрушения в вершине трещины, полностью эквивалентный энергетическому критерию Гриффитса, но более удобный для практических приложений, так как позволяет оценивать опасность разрушения по интенсивности напряженного состояния в локализованной области на фронте трещины.
Определение теоретическим путем напряжений и деформаций в окрестности кончика трещины, где напряженное состояние существенно трехмерное, а материал не подчиняется закону Гука, предствляет сложную и до сих пор не разрешенную задачу. Поэтому для определения полей напряжений и деформаций на фронте трещины пользуются решениями, полученными методами линейной теории упругости, чем и объясняется наименование такого подхода — линейная механика трещин.
Согласно решениям теории упругости, распределение напряжений в окрестности кончика прямолинейной трещины описывается формулами

Здесь  — полярные координаты рассматриваемой точки с полюсом в вершине трещины; К — коэффициент пропорциональности, называемый коэффициентом интенсивности напряжений. Его размерность, как следует из (11.30),
— полярные координаты рассматриваемой точки с полюсом в вершине трещины; К — коэффициент пропорциональности, называемый коэффициентом интенсивности напряжений. Его размерность, как следует из (11.30), 
Коэффициент интенсивности напряжений зависит от ряда факторов, в том числе и от типа раскрытия трещины при ее распространении.
В случае, когда берега трещины расходятся друг от друга вследствие отрыва частиц на ее фронте (рис. 11.21, а), этому коэффициенту приписывают индекс I и обозначают  . В случае, когда берега трещины сдвигаются друг относительно друга в направлении самой трещины (рис. 11.21,б), этот коэффициент обозначают К и, а в случае сдвига берегов перпендикулярно направлению трещины (рис. 11.20, в), коэффициент интенсивности напряжений обозначают
. В случае, когда берега трещины сдвигаются друг относительно друга в направлении самой трещины (рис. 11.21,б), этот коэффициент обозначают К и, а в случае сдвига берегов перпендикулярно направлению трещины (рис. 11.20, в), коэффициент интенсивности напряжений обозначают 
Из формул (11.30) следует, что напряжения  по мере приближения к трещине
по мере приближения к трещине  что является естественным следствием применения линейной теории упругости. Однако в линейной механике этой физически невозможной ситуации
что является естественным следствием применения линейной теории упругости. Однако в линейной механике этой физически невозможной ситуации
приписывается определенный смысл, для чего рассматриваются не напряжения на самом фронте трещины, а интенсивность поля напряжений в некотором объеме материала, окружающем кончик трещины. Эта интенсивность как раз и определяется коэффициентом интенсивности напряжений.
Коэффициенты интенсивности напряжений К имеют исключительно важное фундаментальное значение в механике хрупкого разрушения. Задачам их определения посвящено большое количество теоретических исследований.
Аналитическое определение коэффициентов интенсивности напряжений в телах сложной формы и при сложных схемах нагружения представляет собой значительные математические трудности, и поэтому для решения этой задачи широко используются численные методы с реализацией их на ЭВМ.
Сравнительно просто находятся коэффициенты интенсивности напряжения в пластинках с трещинами несложной формы. Так, при растяжении пластины неограниченных размеров со сквозной центральной трещиной размером  , перпендикулярной линии действия нагрузки (см. рис. 11.19), коэффициент интенсивности напряжений
, перпендикулярной линии действия нагрузки (см. рис. 11.19), коэффициент интенсивности напряжений

Для трещин, развивающихся в таких пластинах от сдвига,

Для пластин ограниченных размеров, при ином расположении и ориентации трещины в выражения (11.32) вводятся поправочные функции  и коэффициенты интенсивности напряжений записывают в виде
и коэффициенты интенсивности напряжений записывают в виде

Так, например, коэффициент интенсивности напряжений в растягиваемой полосе для сквозной поперечной трещины длиной  и выходящей на свободную поверхность
и выходящей на свободную поверхность  тогда как для центральной поперечной трещины той же длины согласно
тогда как для центральной поперечной трещины той же длины согласно 
Таким образом, трещина в поверхностном слое, выходящая на поверхность, опаснее внутренней трещины
Сравнивая формулы (11.29) и (11.31), приходим к заключению, что коэффициент интенсивности напряжений можно трактовать как величину, характеризующую приток энергии к вершине трещины при ее развитии, что подтверждает эквивалентность энергетического, и силового критерия разрушения.
Коэффициент интенсивности напряжения растет с ростом средних напряжений о в детали и при некотором значении  когда трещина начнет развиваться (начнется разрушение), коэффициент интенсивности напряжений достигнет предельного значения
когда трещина начнет развиваться (начнется разрушение), коэффициент интенсивности напряжений достигнет предельного значения

Согласно критерию (11.33), трещина начнет расти, как только коэффициент интенсивности напряжений достигнет критического значения, характерного для данного материала.
Для трещины в поле растягивающих напряжений условие (11.33) записывается как

Величина  является численной характеристикой трещиностойкости, или иначе, вязкости разрушения в случае развития трещины разрывного типа и является фундаментальной характеристикой материала.
является численной характеристикой трещиностойкости, или иначе, вязкости разрушения в случае развития трещины разрывного типа и является фундаментальной характеристикой материала.
Критическое значение коэффициента интенсивности напряжений  определяется экспериментально путем испытания образцов определенной формы и размеров с искусственно созданными начальными трещинами.
определяется экспериментально путем испытания образцов определенной формы и размеров с искусственно созданными начальными трещинами.
В процессе испытания регистрируется зависимость между нагрузкой на образец Р и величиной расхождения  берегов начальной трещины и устанавливается критическое значение
берегов начальной трещины и устанавливается критическое значение  нагрузки. По критической нагрузке
нагрузки. По критической нагрузке  вычисляются критические напряжения в образце
вычисляются критические напряжения в образце  а по ним — значение коэффициента
а по ним — значение коэффициента  Например, при испытаниях на растяжение плоского образца со сквозной поперечной трещиной длиной
Например, при испытаниях на растяжение плоского образца со сквозной поперечной трещиной длиной  величина
величина  вычисляется по формуле (11.31), которая в этом случае будет иметь вид:
вычисляется по формуле (11.31), которая в этом случае будет иметь вид:

Найденная экспериментальным путем величина  принимается в качестве механической характеристики материала, определяющей его трещипостойкость (вязкость).
принимается в качестве механической характеристики материала, определяющей его трещипостойкость (вязкость).
Однако для того, чтобы экспериментально найденную величину  действительно можно было принять в качестве механической характеристики, подобной пределу текучести
действительно можно было принять в качестве механической характеристики, подобной пределу текучести  и пределу прочности
и пределу прочности  необходимо выполнение определенных условий, относящихся к формам и размерам образцов, размерам начальной трещины и условиям нагружения образцов в процессе испытания. Эти условия обосновываются теоретически и регламентируются стандартами.
необходимо выполнение определенных условий, относящихся к формам и размерам образцов, размерам начальной трещины и условиям нагружения образцов в процессе испытания. Эти условия обосновываются теоретически и регламентируются стандартами.
Критерий (11.33) начала распространения трещины позволяет записать условие прочности тел с трещинами в виде

и определить тем самым допустимый размер трещины  в случае заданных нагрузок или допустимое значение напряжений а, если известен размер трещины.
в случае заданных нагрузок или допустимое значение напряжений а, если известен размер трещины.
Например, при расчете детали в форме пластины, имеющей сквозную трещину размера  , по известному значению
, по известному значению  можно найти разрушающее напряжение
можно найти разрушающее напряжение  из соотношения (11.35)
из соотношения (11.35)

Для обеспечения прочности при наличии дефектов напряжения в детали не должны превышать величины  т. е.
т. е.

Запас, прочности  при этом выбирается несколько меньше, чем при обычном расчете на прочность, поскольку
при этом выбирается несколько меньше, чем при обычном расчете на прочность, поскольку 
Из соотношения (11.38) можно найти допускаемые напряжения  в детали при данных размерах дефектов, либо установить допускаемые размеры
в детали при данных размерах дефектов, либо установить допускаемые размеры  дефектов, соответствующих действующим в детали напряжениям о. Запас прочности детали с трещинами определяется из соотношения
дефектов, соответствующих действующим в детали напряжениям о. Запас прочности детали с трещинами определяется из соотношения

Для предупреждения внезапных разрушений существенно, к какому типу принадлежит трещина при достижении предельного условия  Если в предельном состоянии трещина равновесна, т. е. ее длина увеличивается только при условии роста нагрузки, что можно объяснить сравнительно малым запасом потенциальной энергии в детали, то опасности немедленного полного разрушения нет. Признаком равновесия трещины является неравенство
Если в предельном состоянии трещина равновесна, т. е. ее длина увеличивается только при условии роста нагрузки, что можно объяснить сравнительно малым запасом потенциальной энергии в детали, то опасности немедленного полного разрушения нет. Признаком равновесия трещины является неравенство

где Р — нагрузка на деталь.
Если трещина неравновесна, то при предельном состоянии  начинается лавинное распространение трещины.
начинается лавинное распространение трещины.
Лавинному распространению трещины часто предшествует ее медленный рост, связанный с постепенным развитием деформаций в вершине трещины и накоплением рассеянных повреждений. Чем больше трещиностойкость материала, тем медленнее происходит этот процесс. Условием неустойчивости трещины является неравенство

В заключение отметим, что механика хрупкого разрушения уже на настоящей стадии ее развития позволяет объяснить многие эффекты хрупкого разрушения, прогнозировать с той или иной степенью достоверности разрушение отдельных элементов сложной формы и правильно ставить прочностные эксперименты и интерпретировать их результаты.
| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ
- 1.3. КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ
- 1.4, ФОРМЫ ТЕЛ, РАССМАТРИВАЕМЫХ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
- 1.5. ОПОРНЫЕ УСТРОЙСТВА. ОПОРНЫЕ РЕАКЦИИ
- 1.6. ОСНОВНЫЕ ГИПОТЕЗЫ О СВОЙСТВАХ МАТЕРИАЛА
- 1.7. ПОНЯТИЕ О РАСЧЕТНОЙ СХЕМЕ
- 1.8. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ
- 1.9. НАПРЯЖЕНИЕ. ПОНЯТИЕ О НАПРЯЖЕННОМ СОСТОЯНИИ
- 1.10. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
- 1.11. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ В БРУСЕ
- 1.12. ВИДЫ ДЕФОРМАЦИЙ БРУСА
- ГЛАВА 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОГО БРУСА
- 2.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ БРУСА
- 2.3. КОЭФФИЦИЕНТ ПОПЕРЕЧНОЙ ДЕФОРМАЦИИ (КОЭФФИЦИЕНТ ПУАССОНА)
- 2.4. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ
- 2.5. НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ
- 2.6. ЗАКОН ГУКА ПРИ ОДНООСНОМ РАСТЯЖЕНИИ. ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ
- 2.7. УДЛИНЕНИЯ И ПЕРЕМЕЩЕНИЯ
- 2.8. ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА ПРИ РАСТЯЖЕНИИ
- 2.9. ДИАГРАММЫ УСЛОВНЫХ И ИСТИННЫХ НАПРЯЖЕНИЙ
- 2.10. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛА
- 2.11. ЗАКОН РАЗГРУЗКИ И ПОВТОРНОГО НАГРУЖЕНИЯ
- 2.12. ПЛАСТИЧНЫЕ И ХРУПКИЕ МАТЕРИАЛЫ
- 2.13. МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ СЖАТИИ
- 2.14. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 2.15. ПОЛЗУЧЕСТЬ. ПОСЛЕДЕЙСТВИЕ И РЕЛАКСАЦИЯ
- 2.16. ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- 2.17. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
- 2.18. О РАСЧЕТЕ НА ПРОЧНОСТЬ
- 2.19. ДВА ТИПА РАСЧЕТОВ НА ПРОЧНОСТЬ
- 2.20. ЭПЮРЫ НОРМАЛЬНЫХ СИЛ, НОРМАЛЬНЫХ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ
- 2.21. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
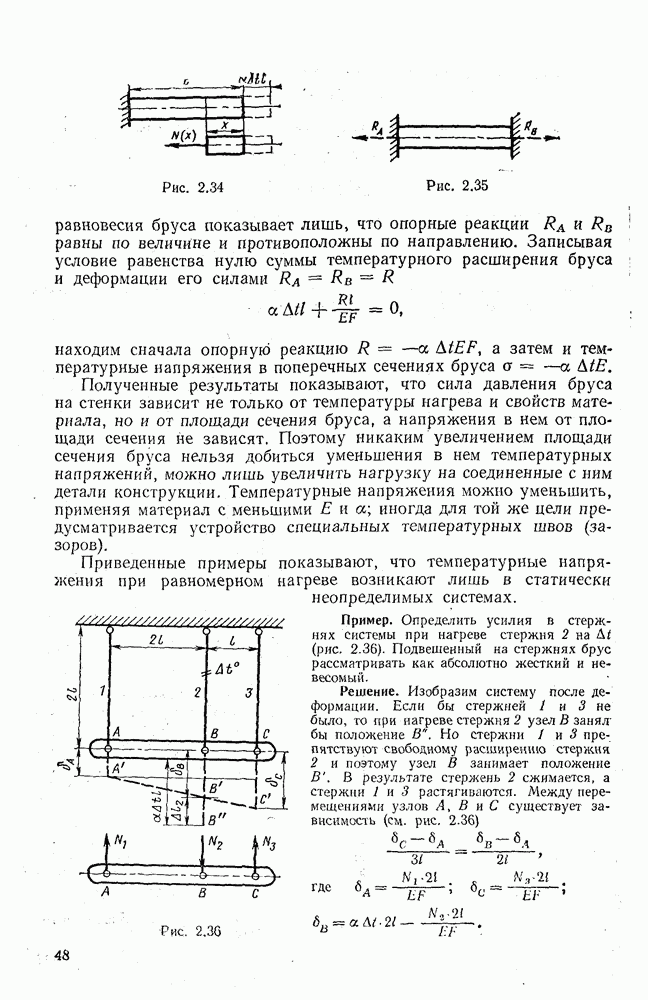
- 2.22. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- 2.23. МОНТАЖНЫЕ УСИЛИЯ
- 2.24. НАПРЯЖЕНИЯ ПРИ ДВУХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ
- 2.25. ЗАКОН ГУКА ПРИ ДВУХОСНОМ И ТРЕХОСНОМ РАСТЯЖЕНИИ
- 2.26. ИЗМЕНЕНИЕ ОБЪЕМА ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ
- 2.27. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ
- 2.28. ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- ГЛАВА 3. СДВИГ
- 3.2. ЧИСТЫЙ СДВИГ
- 3.3. СВЯЗЬ МЕЖДУ УПРУГИМИ ПОСТОЯННЫМИ Е, G И «МЮ» ДЛЯ ИЗОТРОПНОГО ТЕЛА
- 3.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ СДВИГЕ
- ГЛАВА 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
- 4.2. ЦЕНТР ТЯЖЕСТИ СЕЧЕНИЯ
- 4.3. ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- 4.4. МОМЕНТЫ ИНЕРЦИИ ПРОСТЕЙШИХ ФИГУР
- 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ ФИГУР
- 4.6. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ КООРДИНАТ
- 4.7. ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
- 4.8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ
- ГЛАВА 5. КРУЧЕНИЕ
- 5.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ЦИЛИНДРИЧЕСКОГО БРУСА КРУГЛОГО СЕЧЕНИЯ
- 5.3. НАПРЯЖЕНИЯ В РАЗЛИЧНО ОРИЕНТИРОВАННЫХ СЕЧЕНИЯХ И ХАРАКТЕР РАЗРУШЕНИЯ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО СЕЧЕНИЯ
- 5.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ
- 5.5. О НАПРАВЛЕНИИ ВЕКТОРА КАСАТЕЛЬНОГО НАПРЯЖЕНИЯ В КОНТУРНЫХ ТОЧКАХ СЕЧЕНИЯ ЦИЛИНДРИЧЕСКОГО БРУСА
- 5.6. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ЗАМКНУТОГО ПРОФИЛЯ
- 5.7. КРУЧЕНИЕ БРУСА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
- 5.8. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ОТКРЫТОГО ПРОФИЛЯ
- 5.9. ОБОБЩЕНИЕ РАСЧЕТНЫХ УРАВНЕНИЙ ДЛЯ БРУСЬЕВ РАЗЛИЧНЫХ СЕЧЕНИЙ
- 5.10. ЭПЮРЫ КРУТЯЩИХ МОМЕНТОВ, НАПРЯЖЕНИЙ И УГЛОВ ЗАКРУЧИВАНИЯ
- 5.11. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ
- 5.12. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ МАЛОГО ШАГА
- 5.13. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ
- ГЛАВА 6. ИЗГИБ
- 6.2. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ИЗГИБЕ БРУСА
- 6.3. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
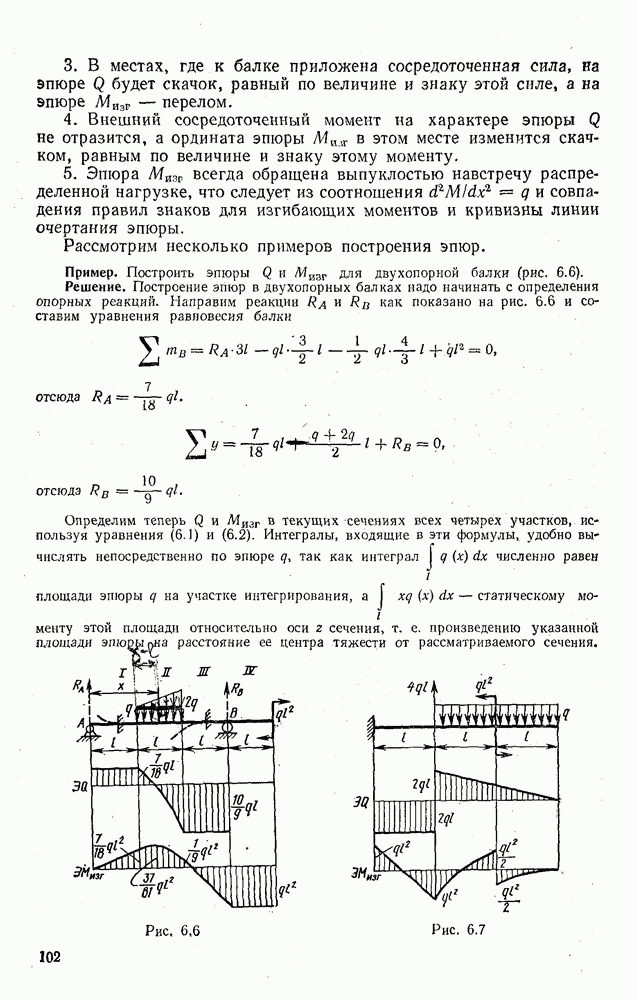
- 6.4. ЭПЮРЫ ПЕРЕРЕЗЫВАЮЩИХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
- 6.5. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ЧИСТОМ ИЗГИБЕ
- 6.6. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ. ФОРМУЛА ЖУРАВСКОГО
- 6.7. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ ТОНКОСТЕННЫХ БАЛОК
- 6.8. ЦЕНТР ИЗГИБА
- 6.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
- 6.10. РАЦИОНАЛЬНЫЕ ФОРМЫ ПОПЕРЕЧНЫХ СЕЧЕНИЙ
- 6.11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- 6.12. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ УПРУГОЙ ЛИНИИ И ЕГО ИНТЕГРИРОВАНИЕ
- 6.13. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ БАЛОК. ИНТЕГРАЛ МОРА
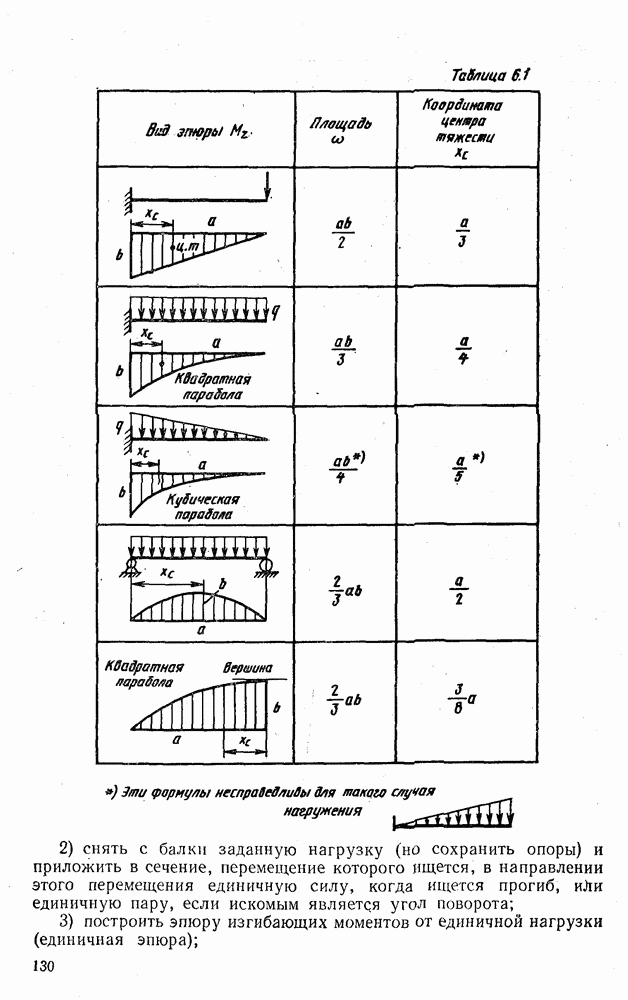
- 6.14. СПОСОБ ВЕРЕЩАГИНА
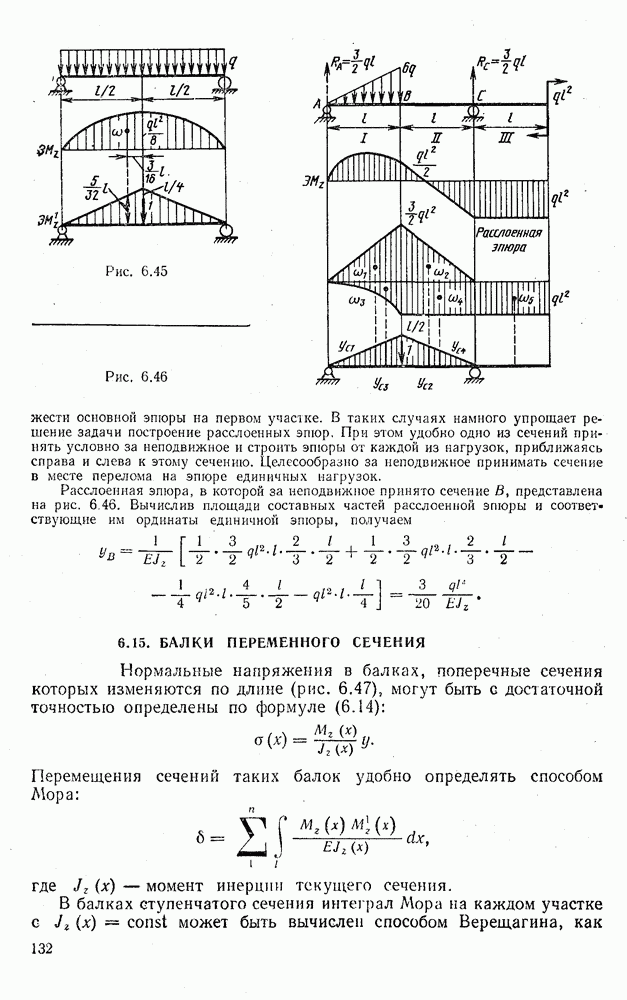
- 6.15. БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
- ГЛАВА 7. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
- 7.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ПРОСТРАНСТВЕННОМ БРУСЕ МАЛОЙ КРИВИЗНЫ. ИНТЕГРАЛ МОРА
- 7.3. ПЛОСКИЕ РАМЫ
- 7.4. ПРОСТРАНСТВЕННЫЕ РАМЫ
- 7.5. ПЛОСКОПРОСТРАНСТВЕННЫЕ РАМЫ
- 7.6. ФЕРМЫ
- 7.7. СМЕШАННЫЕ СИСТЕМЫ
- 7.8. ОТНОСИТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ СЕЧЕНИЙ СТЕРЖНЕВОЙ СИСТЕМЫ
- ГЛАВА 8. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
- 8.2. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ
- 8.3. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ЗАДАЧ
- 8.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
- 8.5. О РАЦИОНАЛЬНОМ ВЫБОРЕ ОСНОВНОЙ СИСТЕМЫ. ИСПОЛЬЗОВАНИЕ ПРЯМОЙ И ОБРАТНОЙ СИММЕТРИИ
- ГЛАВА 9. КОСОЙ ИЗГИБ. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
- 9.2. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
- ГЛАВА 10. ОСНОВЫ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
- 10.3. НАПРЯЖЕНИЯ НА ПРОИЗВОЛЬНО НАКЛОНЕННОЙ К ОСЯМ КООРДИНАТ ПЛОЩАДКЕ
- 10.4. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ НА НАКЛОННОЙ ПЛОЩАДКЕ
- 10.5. ГЛАВНЫЕ ПЛОЩАДКИ И ГЛАВНЫЕ НАПРЯЖЕНИЯ. ИНВАРИАНТЫ НАПРЯЖЕННОГО СОСТОЯНИЯ
- 10.6. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ПЛОЩАДОК
- 10.7. ЭЛЛИПСОИД НАПРЯЖЕНИЙ
- 10.8. ЭКСТРЕМАЛЬНЫЕ ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ПЛОЩАДКИ ИХ ДЕЙСТВИЯ
- 10.9. КРУГОВАЯ ДИАГРАММА НАПРЯЖЕНИЙ (КРУГИ МОРА)
- 10.10. НАПРЯЖЕНИЯ НА ПЛОЩАДКАХ, РАВНОНАКЛОННЫХ К ГЛАВНЫМ (ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ)
- 10.11. ПОНЯТИЕ О ШАРОВОМ ТЕНЗОРЕ И ДЕВИАТОРЕ НАПРЯЖЕНИЙ
- 10.12. КЛАССИФИКАЦИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
- 10.13. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
- 10.14. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ГЛАВНЫЕ ПЛОЩАДКИ В БРУСЕ
- 10.15. ДЕФОРМИРОВАННОЕ СССТОЯНИЕ В ТОЧКЕ ТЕЛА. АНАЛОГИЯ МЕЖДУ ЗАВИСИМОСТЯМИ ТЕОРИИ НАПРЯЖЕНИЙ И ТЕОРИИ ДЕФОРМАЦИЙ
- 10.16. ОБОБЩЕННЫЙ ЗАКОН ГУКА ДЛЯ ИЗОТРОПНОГО ТЕЛА
- 10.17. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ И ЕЕ ДЕЛЕНИЕ НА УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ОБЪЕМА И УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ФОРМЫ
- 10.18. ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ И ГЛАВНЫХ ДЕФОРМАЦИЙ ПО РЕЗУЛЬТАТАМ ЭКСПЕРИМЕНТА
- ГЛАВА 11. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
- 11.2. НАЗНАЧЕНИЕ ТЕОРИЙ ПРЕДЕЛЬНОГО СОСТОЯНИЯ
- 11.3. ТЕОРИЯ НАИБОЛЬШИХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
- 11.4. ТЕОРИЯ НАИБОЛЬШИХ ОТНОСИТЕЛЬНЫХ УДЛИНЕНИЙ
- 11.5. ТЕОРИЯ НАИБОЛЬШИХ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- 11.6. ТЕОРИЯ УДЕЛЬНОЙ ЭНЕРГИИ ИЗМЕНЕНИЯ ФОРМЫ
- 11.7. ТЕОРИЯ МОРА
- 11.8. СООТНОШЕНИЯ МЕЖДУ ПРЕДЕЛАМИ ТЕКУЧЕСТИ ПРИ ПРОСТОМ РАСТЯЖЕНИИ И ЧИСТОМ СДВИГЕ ПО РАЗЛИЧНЫМ ТЕОРИЯМ
- 11.9. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ВЫБОРЕ ТЕОРИИ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ ПРИ РАСЧЕТАХ
- 11.10. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ЕЕ ВЛИЯНИЕ НА ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ ВО ВРЕМЕНИ НАПРЯЖЕНИЯХ
- 11.11. О МЕХАНИКЕ ХРУПКОГО РАЗРУШЕНИЯ
- ГЛАВА 12. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ПЕРЕМЕННЫХ ВО ВРЕМЕНИ
- 12.2. МЕХАНИЗМ УСТАЛОСТНОГО РАЗРУШЕНИЯ
- 12.3. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 12.4. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПРЕДЕЛА ВЫНОСЛИВОСТИ. ПРЕДЕЛ ОГРАНИЧЕННОЙ ВЫНОСЛИВОСТИ
- 12.5. ЗАВИСИМОСТЬ ПРЕДЕЛА ВЫНОСЛИВОСТИ ОТ СТЕПЕНИ АСИММЕТРИИ ЦИКЛА. ДИАГРАММА ПРЕДЕЛЬНЫХ АМПЛИТУД
- 12.6. ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ЯВЛЕНИЯ УСТАЛОСТИ
- 12.7. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
- 12.8. ФАКТОРЫ, ВЛИЯЮЩИЕ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- 12.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ОДНООСНОМ НАПРЯЖЕННОМ СОСТОЯНИИ И ЧИСТОМ СДВИГЕ (ИЗГИБЕ, РАСТЯЖЕНИИ И КРУЧЕНИИ)
- 12.10. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОЕ НАПРЯЖЕННОМ СОСТОЯНИИ
- 12.11. СОПРОТИВЛЕНИЕ УСТАЛОСТИ ПРИ НЕСТАЦИОНАРНЫХ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- ГЛАВА 13. РАСЧЕТЫ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
- 13.2. СХЕМАТИЗАЦИЯ ДИАГРАММ РАСТЯЖЕНИЯ
- 13.3. РАСЧЕТ ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ
- 13.4. РАСЧЕТ БАЛОК ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ
- 13.5. НЕСУЩАЯ СПОСОБНОСТЬ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ
- 13.6. ЧИСТЫЙ УПРУГОПЛАСТИЧЕСКИЙ ИЗГИБ ПРЯМОГО БРУСА
- 13.7. РАЗГРУЗКА И ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ
- ГЛАВА 14. РАСЧЕТ ПРОСТЕЙШИХ ОСЕСИММЕТРИЧНО НАГРУЖЕННЫХ ТОНКОСТЕННЫХ ОБОЛОЧЕК ВРАЩЕНИЯ
- 14.2. УРАВНЕНИЯ РАВНОВЕСИЯ ЭЛЕМЕНТА СИММЕТРИЧНОЙ БЕЗМОМЕНТНОЙ ОБОЛОЧКИ
- 14.3. ТЕОРЕМА О ДАВЛЕНИИ НА КРИВОЛИНЕЙНУЮ СТЕНКУ
- 14.4. РАСЧЕТ СФЕРИЧЕСКИХ И ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК НА НОРМАЛЬНОЕ ДАВЛЕНИЕ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ
- ГЛАВА 15. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, ДВИЖУЩИХСЯ С УСКОРЕНИЕМ
- 15.2. РАСЧЕТ ПОСТУПАТЕЛЬНО ДВИЖУЩИХСЯ СИСТЕМ
- 15.3. НАПРЯЖЕНИЯ В ТОНКОСТЕННОМ ВРАЩАЮЩЕМСЯ КОЛЬЦЕ
- 15.4. РАСЧЕТ РАВНОМЕРНО ВРАЩАЮЩЕГОСЯ ПРЯМОГО БРУСА
- 15.5. ВРАЩАЮЩИЕСЯ РАМЫ
- ГЛАВА 16. УДАР
- 16.2. УДАР ПАДАЮЩЕГО ГРУЗА ПО УПРУГОЙ СИСТЕМЕ, МАССА КОТОРОЙ МАЛА ПО СРАВНЕНИЮ С МАССОЙ ГРУЗА
- 16.3. ПРИВЕДЕННАЯ МАССА. КОЭФФИЦИЕНТ ПРИВЕДЕНИЯ
- 16.4. УДАР ПО СИСТЕМЕ, МАССА КОТОРОЙ СОИЗМЕРИМА С МАССОЙ УДАРЯЮЩЕГО ГРУЗА
- ГЛАВА 17. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. ПРОДОЛЬНЫЙ ИЗГИБ
- 17.2. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ МЕТОДОМ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ УПРУГОЙ ЛИНИИ СТЕРЖНЯ. ФОРМУЛА ЭЙЛЕРА
- 17.3. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА
- 17.4. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ ПРОПОРЦИОНАЛЬНОСТИ. ГРАФИК КРИТИЧЕСКИХ НАПРЯЖЕНИЙ
- 17.5. ПРАКТИЧЕСКИЕ СПОСОБЫ РАСЧЕТА НА ПРОДОЛЬНЫЙ ИЗГИБ
- 17.6. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ
- 17.7. ДИНАМИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ
- ГЛАВА 18. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
- 18.3. ПРИБЛИЖЕННАЯ ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ ПРОГИБА БАЛКИ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ
- 18.4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ ИЗГИБАЮЩИХ МОМЕНТОВ
- 18.5. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ