6.10. РАЦИОНАЛЬНЫЕ ФОРМЫ ПОПЕРЕЧНЫХ СЕЧЕНИЙ

Для балок из пластичных материалов, одинаково работающих на растяжение и сжатие (ат.Р целесообразно выбирать сечения, симметричные относительно их нейтральных осей; при этом условии обеспечивается одинаковый запас прочности сечения по растянутым и сжатым волокнам.

Если кроме условия прочности исходить еще и из требования минимальной массы балки, то наиболее рациональным будет сечение, которое при заданном моменте сопротивления имеет наименьшую площадь сечения а при заданной площади — наибольший момент сопротивления

Рис. 6.32

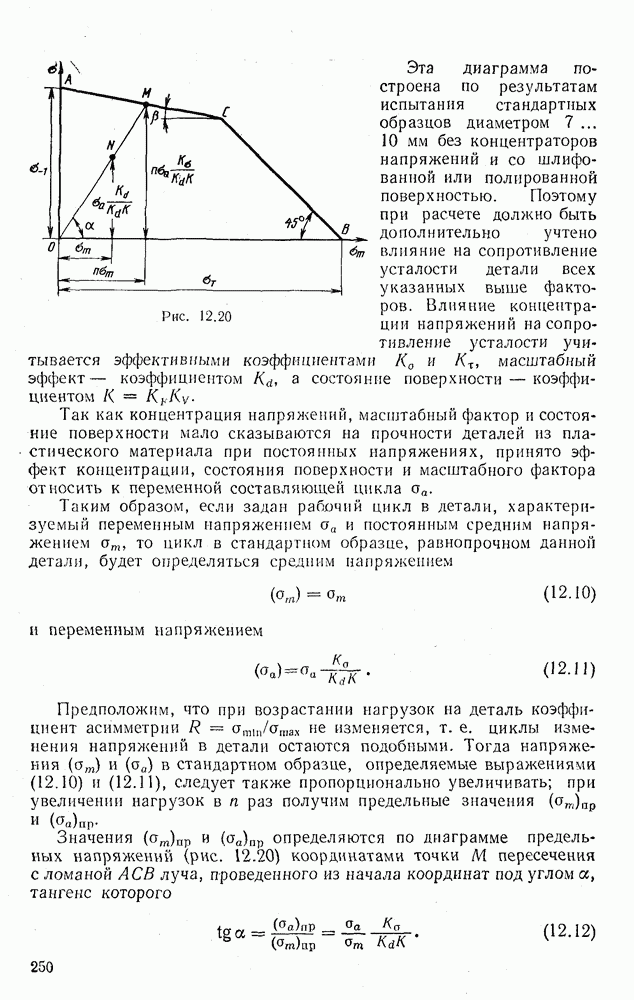
Сравнивая с этих позиций, например, прямоугольное сечение с двутавровым (рис. 6.32), нетрудно убедиться в преимуществе последнего.

Действительно, у балки прямоугольного сечения материал вблизи нейтральной оси полностью не используется, так как находится в наименее напряженной зоне сечения; у двутавровой балки большая часть материала расположена в наиболее напряженной зоне. Поэтому при одинаковой прочности двутавровая прокатная балка оказывается в раза легче прямоугольной.

Для материалов хрупких, обладающих различной прочностью при растяжении и сжатии, рациональным будет сечение, несимметричное относительно нейтральной оси, например тавровое, несимметричное двутавровое и т.

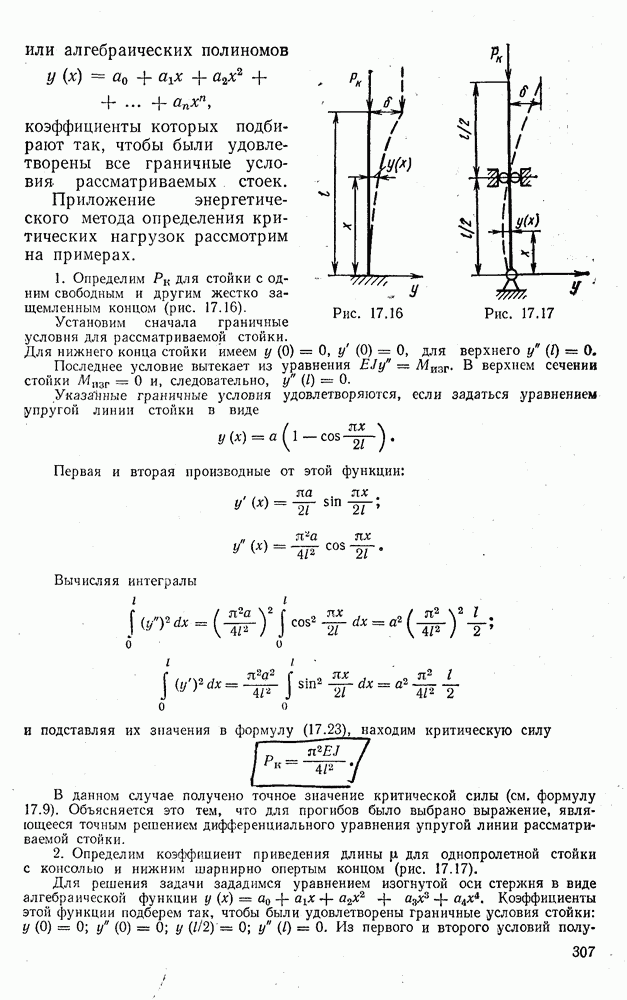
Пример. Стальная балка (рис. 6.33) выполнена из бруса прямоугольного сечения и из прокатного двутавра. Интенсивность нагрузки Н/см, Определить размеры прямоугольного сечения и подобрать по сортаменту прокатный двутавр, приняв Сравнить массы этих балок и вычислить максимальные касательные напряжения.

Решение. Строим эпюры и Мизг (см. рис. 6.33) и вычисляем максимальный изгибающий момент

Момент сопротивления прямоугольного сечения , а допускаемое напряжение

Согласно условию прочности

Отсюда находим размеры прямоугольного сечения, обеспечивающие заданную прочность балки. Округляя результаты, получаем .

Из условия прочности двутавровой балки находим потребную величину а затем по сортаменту подбираем двутавр с ближайшим большим моментом сопротивления. Им оказывается двутавр .

При найденных размерах сечений максимальные нормальные напряжения в обеих балках ашах

Массы балок относятся как площади их сечений: т. е. при одинаковой прочности на изгиб балка прямоугольного сечения в 2,5 раза тяжелее двутавровой.

Рис. 6.33

Максимальные касательные напряжения возникают в сечении, где .

В прямоугольном сечении (см. разд. 6.6).

Для вычисления ттах при изгибе двутавра в сортаменте приводятся значения статических моментов половины сечения. В рассматриваемом случае Следовательно, в двутавровой балке согласно формуле (6.18)

Полученные результаты подтверждают, что при изгибе тгаах существенно меньше