17.6. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ

Определение критической нагрузки методом интегрирования дифференциального уравнения упругой линии стержня во многих практически важных случаях представляет значительные трудности, так как требует численного решения громоздких трансцендентных уравнений. Поэтому широкое распространение получил энергетический метод, позволяющий определять критические нагрузки непосредственно, не прибегая к составлению и интегрированию дифференциальных уравнений.

Энергетический метод основан на исследовании изменения потенциальной энергии при переходе стержня из прямолинейной криволинейную форму равновесия.

Предположим, что прямой стержень, сжатый силой Р, был выведен какой-либо поперечной силой из прямолинейного состояния и искривился. При этом на деформацию стержня была затрачена энергия, равная сумме работы А, произведенной поперечной силой,

Рис. 17,14

и работы, совершенной силой Р на смещение верхнего конца стержня (рие. 17.14). Работа силы Р, равная всегда положительна, и произведение не делится пополам потому, что величина этой силы Р в процессе перемещения не изменяется.

Энергия, затраченная на искривление стержня, накапливается в нем в виде потенциальной энергии изгиба

отсюда

При малой величине силы Р стержень будет сохранять свою прямолинейную форму, и для его искривления надо затратить некоторую энергию. Следовательно, в этом случае а потенциальная энергия т. е. запас потенциальной энергии в искривленном стержне превышает работу, совершенную силой Р на смещении К. Поэтому при удалении поперечной силы стержень вернется в первоначальное состояние, так как обладает большей потенциальной энергией, чем необходимо для преодоления сопротивления силы Р.

В процессе постепенного возрастания сила Р достигает такого значения, при котором

В этом случае и при любом малом искривлении стержень не будет возвращаться в первоначальное прямолинейное состояние, так как кроме прямолинейной возможна и криволинейная форма равновесия.

Если величина силы Р такова, что то и стержень будет изгибаться только от действия силы Р без помощи поперечной силы.

Условием перехода от устойчивой формы равновесия к неустойчивой, из которого и находится критическое значение силы будет равенство

Определим и К. Потенциальная энергия изгиба вычисляется, как было показано в теории поперечного изгиба, по формуле

Замечая, что выражение для потенциальной энергии можем записать

Для определения К выделим элемент стержня длиной Длина этого элемента при искривлении стержня остается неизменной, но элемент повернется и составит с осью х угол а, причем

Рис. 17.15

Опускание верхнего конца оси элемента, вызванное наклоном элемента (рис, 17.15),

Вследствие малости угла а можно принять

Отсюда

Суммируя по длине стержня, находим смещение его верхнего конца: 1

Подставляя выражения (17.22) и (17.21) в равенство (17.20), получаем следующую формулу для определения критической силы:

Для определения критической силы по формуле (17.23) необходимо заранее знать уравнение изогнутой оси стержня, так как в эту формулу входят первая и вторая производные от прогибов. Если уравнение этой оси заранее неизвестно, то можно использовать уравнения (17.23) для приближенного определения критической силы. Для этого надо подобрать подходящее уравнение для изогнутой оси стержня. Эта выбранная кривая должна удовлетворять всем граничным условиям рассматриваемого стержня.

Энергетический метод дает очень небольшую погрешность, если принятая кривая прогибов надлежащим образом подобрана, причем всегда значение критической силы получается несколько выше действительного. Объясняется это тем, что стержень всегда искривляется по кривой наименьшего сопротивления, соответствующей наименьшему возможному значению коэффициента (см. разд. 17.2). Приближенно выбранная кривая, как правило, отличается от кривой наименьшего сопротивления, требует для своей реализации большей затраты энергии и поэтому формула (17.23) дает значения больше действительных.

Приближенно кривые прогибов стоек представляют в виде тригонометрических

Рис. 17.16

Рис. 17.17

или алгебраических полиномов

коэффициенты которых подбирают так, чтобы были удовлетворены все граничные условия. рассматриваемых стоек.

Приложение энергетического метода определения критических нагрузок рассмотрим на примерах.

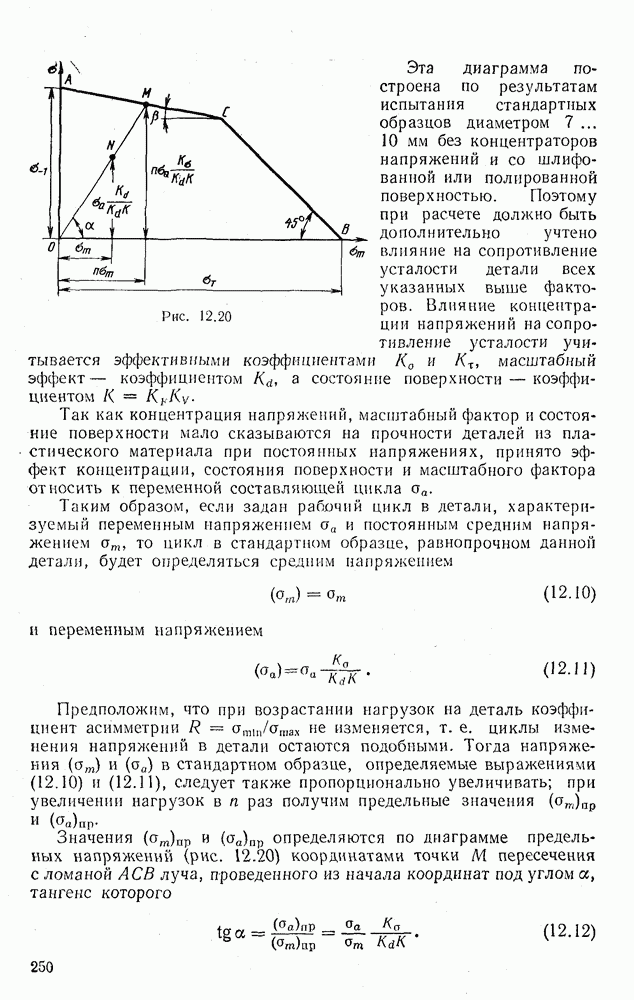
1. Определим для стойки с одним свободным и другим жестко защемленным концом (рис. 17.16).

Установим сначала граничные условия для рассматриваемой стойки.

Для нижнего конца стойки имеем для верхнего .

Последнее условие вытекает из уравнения . В верхнем сечении стойки , следовательно,

Указанные граничные условия удовлетворяются, если задаться уравнением упругой линии стойки в виде

Первая и вторая производные от этой функции:

Вычисляя интегралы

и подставляя их значения в формулу (17.23), находим критическую силу

В данном случае получено точное значение критической силы (см. формулу 17.9). Объясняется это тем, что для прогибов было выбрано выражение, являющееся точным решением дифференциального уравнения упругой линии рассматриваемой стойки.

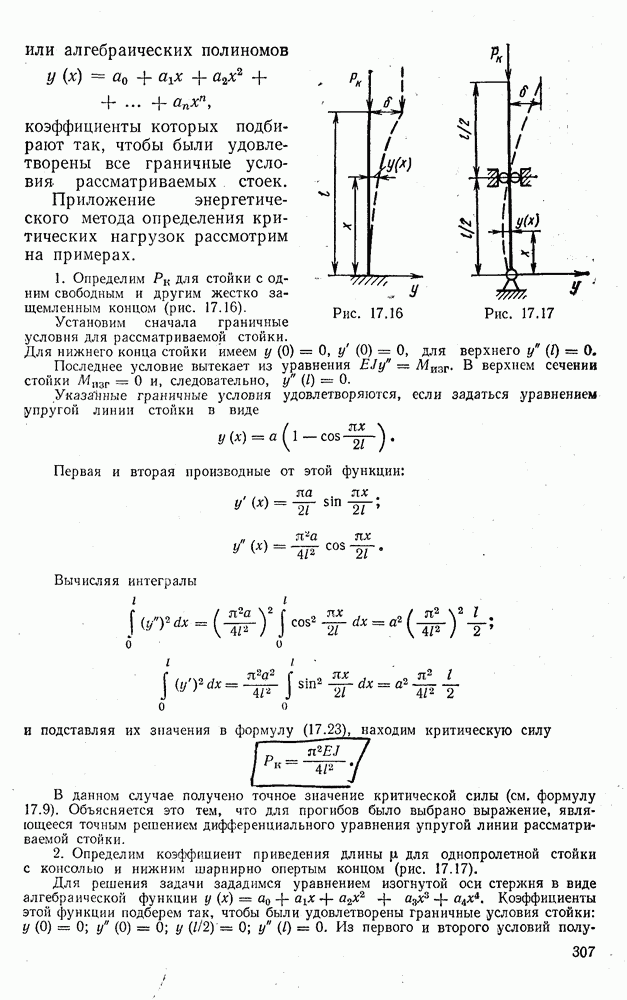
2. Определим коэффициент приведения длины для однопролетной стойки с консолыо и нижним шарнирно опертым концом (рис. 17.17).

Для решения задачи зададимся уравнением изогнутой оси стержня в виде алгебраической функции Коэффициенты этой функции подберем так, чтобы были удовлетворены граничные условия стойки: Из первого и второго условий

получаем Третье условие дает Из четвертого условия лолучаем

Итак, для определения коэффициентов имеем систему уравнений:

Решая эту систему, получаем Следовательно, уравнение упругой линии стержня получает вид

Далее находим

Интегралы

Подставляя найденные значения интегралов в формулу (17.23), получаем

Преобразуем это выражение к виду (17.14):

Следовательно,

и искомый коэффициент приведения длины

Значение для данной стойки, полученное интегрированием дифференциального уравнения ее упругой линии, приведено на рис. 17.11 и равно 1,35. Таким образом, погрешность приближенного решения составляет