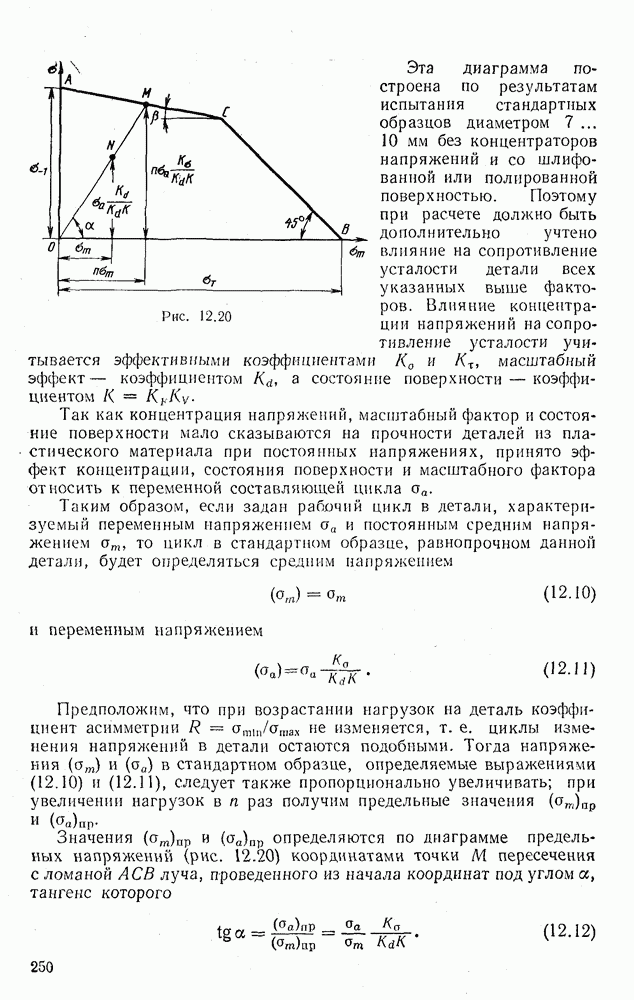
17.4. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ ПРОПОРЦИОНАЛЬНОСТИ. ГРАФИК КРИТИЧЕСКИХ НАПРЯЖЕНИЙ
Тщательно поставленные опыты показали справедливость формулы Эйлера для стержней большой гибкости 
. В то же время эти опыты подтвердили неприменимость формулы Эйлера для стержней, гибкость которых 
Для таких стержней формула Эйлера дает значения критических нагрузок, превышающие их действительные значения. Попытки использовать формулу Эйлера для стержней средней и малой гибкости 
стпц) приводили иногда к серьезным катастрофам.
Теория устойчивости стержней за пределом пропорциональности была развита Т. Карманом 
Для критической нагрузки им было получено уравнение, аналогичное по структуре формуле Эйлера:
и
где Т — приведенный модуль, или модуль Кармана.
Модуль Т является величиной переменной, зависящей как от величины напряжений 
так и от формы сечения. Зависимость модуля Т от напряжений 
устанавливается на основании диаграммы сжатия материала стойки в осях о, е. При напряжениях 
приведенный модуль Т принимает значение модуля упругости Е. Однако, оказалось, что определяемые формулой (17.15) критические напряжения несколько выше экспериментальных.
Рис. 17.12
Лучшее согласование с экспериментальными данными дает формула Энгессера—Шенли
где 
— касательный модуль упругости, численно равный тангенсу угла наклона касательной к диаграмме сжатия 
материала при 
Использование формул (17.14), (17.15) и (17.16) требует построения диаграммы сжатия для материала стержня, что осложняет их применение. Поэтому в практических, расчетах на устойчивость при 
часто пользуются либо непосредственно экспериментальными данными, либо эмпирическими формулами.
Наибольшее распространение имеет линейная формула, предложенная Ф. С. Ясинским (1895 г.):
В этой формуле X — гибкость стержня, а 
— коэффициенты, зависящие от свойств материала. Например, для стали 3 при 
и 
формула (17.17) имеет вид
По формуле (17.17) проводится расчет на устойчивость стержней средней гибкости, разрушение которых при сжатии сопровождается значительным боковым выпучиванием.
Для стержней малой гибкости 
понятие потери устойчивости неприменимо в том смысле, в каком применяется для стержней большой гибкости. Стержни, у которых длина невелика по отношению к размерам поперечного сечения, выходят из строя главным образом из-за того, что напряжения сжатия в них достигают предела текучести 
(при пластичном материале) или предела прочности 
(при хрупком материале). Поэтому для стержней малой гибкости в качестве критического напряжения принимается предел текучести 
или предел прочности 
Четкой границы между стержнями малой и средней гибкости провести нельзя. В расчетах принимают 
Выбрав 
можно найти коэффициенты а и 
в формуле (17.17), составляя уравнение прямой, проходящей через две точки с координатами 
Зависимость критических напряжений 
от гибкости X изображается графически в виде диаграммы критических напряжений. Такая диаграмма для сталипредставлена на рис. 17.12.
Для стержней малой гибкости зависимость 
от X выражена горизонтальной прямой, для стержней средней гибкости — наклонной прямой (17.17), а для стержней большой гибкости — гиперболой Эйлера.
Если известна гибкость рассчитываемого стержня, то критическое напряжение может быть найдено непосредственно по диаграмме критических напряжений.
