2.21. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ

Конструкции, усилия в элементах которых не могут быть найдены из одних лишь уравнений равновесия, называются статически неопределимыми, а задачи определения усилий в таких системах называются статически неопределимыми задачами.

Степенью статической неопределимости называется разность между числом искомых неизвестных усилий и числом всех независимых уравнений равновесия, которые для этой системы можно составить.

Рис. 2.28

Рис. 2.29

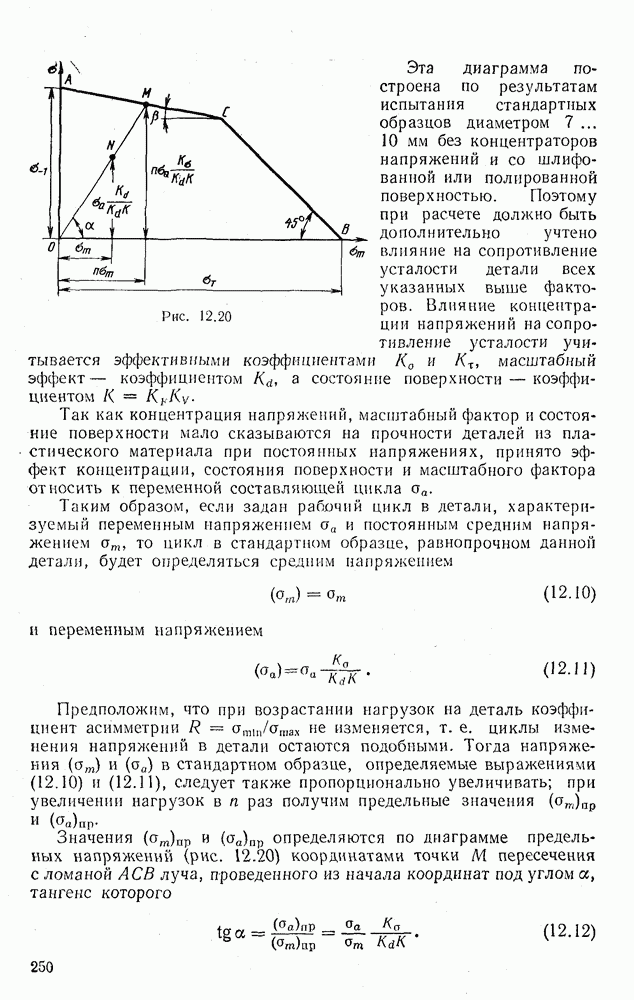
Например, трехстержневая система (рис. 2.28) один раз статически неопределима, так как для вычисления усилий в трех ее стержнях можно составить всего лишь два независимых уравнения равновесия узла А:

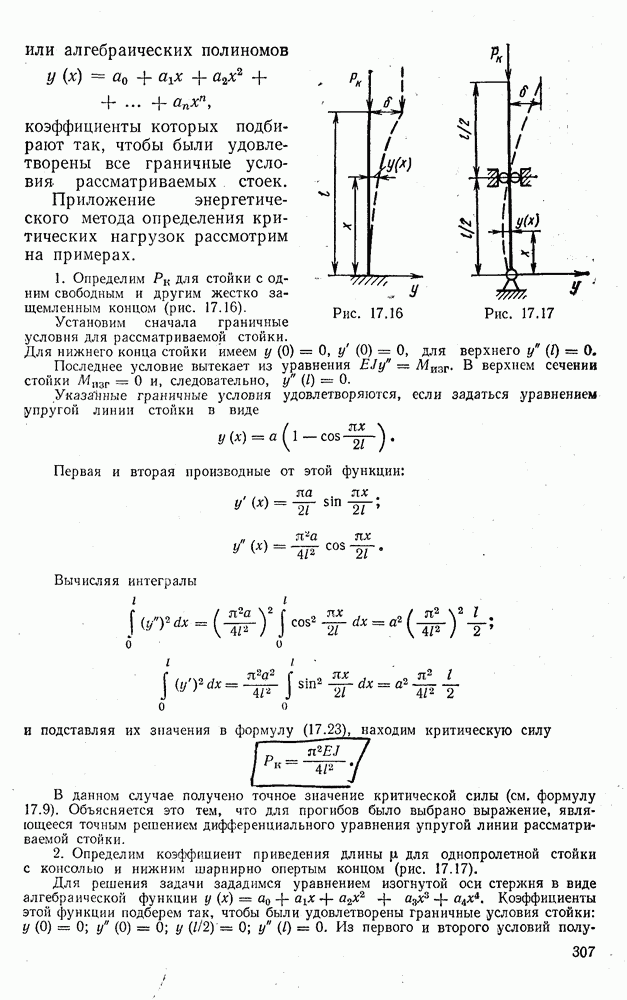
Двухстержневая ферма (рис. 2.29) является, очевидно, статически определимой, так как усилия в ее стержнях полностью определяются из одних лишь уравнений равновесия

Заметим, что при записи уравнений равновесия мы не учитываем изменение углов между направлением сил вызванные деформацией фермы. Объясняется это тем, что при малых деформациях (а именно такие деформации, как правило, и рассматриваются в сопротивлении материалов) углы между стержнями фермы изменяются весьма незначительно и тем более незначительно изменяются тригонометрические функции этих углов. В этом проявляется принцип, называемый в сопротивлении материалов принципом сохранения начальных размеров. Согласно этому принципу в случае малых деформаций при составлении уравнений равновесия конструкцию можно рассматривать как жесткую, имеющую первоначальные размеры и форму. Этот принцип, естественно, не справедлив при больших деформациях.

Неопределенность рассматриваемых задач объясняется наличием в статически неопределимых системах избыточных или, иначе, лишних связей, не являющихся безусловно необходимыми для восприятия нагрузки. Так, в трехстержневой ферме можно удалить один из стержней, но она будет способна воспринимать нагрузку, оставаясь геометрически неизменяемой. Однако удалить одновременно два стержня нельзя, так как ферма станет геометрически изменяемой, подвижной системой. Следовательно, эта ферма имеет одну

избыточную связь. Отмеченное свойство является общим для любых статически неопределимых систем — степень статической неопределимости всегда равна числу лишних связей.

Статически неопределимые задачи не имеют решения, если считать материал абсолютно твердым, и имеют вполне определенное решение, если учитывать упругие свойства материала. Записывая условия неразрывности деформированной системы, всегда можно составить необходимое число дополнительных уравнений, разрешающих статическую неопределимость задачи. Эти дополнительные уравнения должны описать единственно возможные соотношения между перемещениями точек деформированной системы при заданных нагрузках. Поэтому они называются уравнениями совместимости перемещений, или уравнениями совместимости деформаций.

Для составления уравнений совместимости перемещений полезно изобразить систему после деформации, а затем по чертежу установить соотношения между перемещениями одних ее сечений или узлов относительно других. Для наглядности эти перемещения, как и удлинения стержней, изображаются на чертеже в весьма увеличенном виде. В действительности удлинения стержней, изменение углов между ними и перемещения узлов системы обычно весьма малы. Например, удлинение стального стержня длиной 100 см и площадью сечения при растяжении силой в 104 Н будет составлять всего

т. е. удлинение в 2000 раз меньше длины этого стержня. Поэтому изображать эти удлинения приходится в утрированно увеличенном виде.

Представив вид системы после деформации, нетрудно составить уравнения совместности перемещений. Запишем, например, уравнение совместности деформаций для рассмотренной выше трехстержневой системы. Удлинение среднего стержня согласно рис. 2.28 равно перемещению узла А. Удлинение крайнего стержня можно найти графически, проведя дугу радиуса с центром в точке В. Вследствие малости деформаций дугу этой окружности можно заменить перпендикуляром, опущенным из точки А на новое положение стержня. Рассматривая прямоугольный треугольник (на рис. 2.28 заштрихован), находим связь между удлинениями стержней 1 и

Изменением угла а пренебрегаем, так как оно незначительно. Переходя по закону Гука от удлинений стержней к искомым усилиям в них, получаем

Решая совместно уравнения равновесия и уравнение совместности перемещений, находим усилия в стержнях фермы.

Рис. 2.30

Рис. 2.31

При составлении уравнений совместности перемещений и записи уравнений равновесия необходимо обращать внимание на соответствие направлений искомых усилий представленному на чертеже характеру деформации (растяжение или сжатие) каждого стержня системы.

Отличительной особенностью любых статически неопределимых систем является зависимость распределения усилий по элементам системы от соотношения жесткостей этих элементов. Например, при сжатии медного цилиндра и стальной трубы между плитами пресса (рис. 2.30) доля сжимающего усилия Р, приходящаяся на цилиндр и трубу, зависит от соотношения их жесткостей

Для доказательства определим сжимающие усилия в трубе и цилиндре Рассекая цилиндр и трубу плоскостью, нормальной их оси, и рассматривая равновесие отсеченной части (см. рис. 2.30), получаем

Уравнением совместимости деформаций является равенство укорочений трубы и цилиндра

Решая систему уравнений равновесия и совместности деформаций, находим нормальные силы в сечениях трубы и цилиндра

Из этих формул видно, что с увеличением жесткости трубы при одновременном уменьшении жесткости цилиндра нормальные силы в ее сечениях возрастают, а в сечениях цилиндра уменьшаются, и, наоборот, при увеличении жесткости цилиндра возрастает доля воспринимаемой им нагрузки.

Таким образом, изменяя соотношение жесткостей элементов статически неопределимой системы, конструктор может по своему усмотрению уменьшать нагрузку на одни элементы за счет увеличения ее на других элементах.

Пример. Найти усилия в стержнях симметричной фермы, нагруженной силой Р (рис. 2.31), если материал и площади сечений всех стержней одинаковы. Определить необходимую площадь сечения стержней и перемещение узла А при и коэффициенте запаса прочности по пределу текучести Стержни выполнены из конструкционной малоуглеродистой стали 3.

Решение. При нагружении фермы стержни растягиваются, узел А смещается вниз и давит на стержень 3, вызывая растяжение стержней 4 и 5 и перемещение узла В. Очевидно, перемещение 6 узла А больше, чем смещение узла В, и их разность равна абсолютной величине сжатия стержня 3:

Это и есть уравнение совместности деформаций для данной фермы. Выражая перемещения узлов через удлинения стержней (см. заштрихованные треугольники на рис. 2.31), получаем

Переходя далее по закону Гука от удлинений к искомым усилиям в стержнях и учитывая, что записываем уравнение совместности так:

Направляя усилия в стержнях соответственно характеру деформации каждого стержня (см. рис. 2.31), составляем уравнения равновесия узлов А и В:

Решая систему уравнений равновесия и совместности деформаций, находим искомые усилия в стержнях:

усилия оказались с положительными знаками. Это означает, что стержни 1, 2, 4 и 5 действительно растянуты, а стержень 3 сжат. В соответствии с принятым правилом знаков для нормальных сил усилию в третьем стержне Должен быть приписан минус. Подставляя численное значение нагрузки Р, имеем

Необходимую площадь сечения стержней найдем по величине наибольшего усилия . Согласно условию прочности,

Предел текучести стали Следовательно, искомая площадь Принимаем

Перемещение узла А при см:

Пример. Определить усилия в стержнях и перемещение точки приложения силы Р (рис. 2.32). Диск рассматривать как абсолютно жесткий.

Решение. Данная система один раз статически неопределима, так как для определения усилий и в стержнях имеем одно только уравнение равновесия в которое не входили бы не интересующие нас по условию задачи опорные реакции

Рис. 2.32

Представим характер деформации системы. При приложении силы Р диск повернется вокруг неподвижной точки С, а шарниры А и В переместятся по дугам и окружностей с радиусами Вследствие малости деформаций эти дуги можно заменить их хордами и (см. рис. 2.32).

При вращении диска перемещение его точек пропорционально их расстояниям от центра вращения. Поэтому

где

Следовательно,

Это соотношение является уравнением совместности перемещений для данной системы.

Найдем связь между удлинениями стержней и перемещениями Для этого опустим из точек А и В перпендикуляры на исходные положения стержней. Из прямоугольных треугольников (см. рис. 2.32) получаем

Здесь

Подставив эти соотношения в уравнение совместности перемещений, выразим его через искомые усилия

Направляя усилия в стержнях в соответствии с характером их деформации, составляем уравнение равновесия диска:

Решая совместно уравнение совместности перемещений и уравнение равновесия, находим

Усилия надо приписать знак минус, так как решение подтверждает, что стержень 2 сжат. Окончательно

Рис. 2.33

Точка приложения силы Р смещается в направлении нормали к линии а величина смещения в два раза меньше

Пример, Построить эпюры а и 5 для стального бруса, нагруженного равномерно распределенной нагрузкой интен сивности и сосредоточенной силой (рис. 2.33). Определить запас прочности бруса, если см и а предел текучести материала

Решение. Данный брус представляет собой один раз статически неопределимую систему, так как для определения его двух опорных реакций и (показаны на рис. 2.33 пунктиром) можно записать всего одно независимое уравнение равновесия:

К составлению уравнения совместности перемещений можно подойти различными путями. Поступим так: отбросим одну из опор, например правую, и заменим ее действие неизвестной пока силой

Полученная система (см. рис. 2.33) . будет эквивалентна данной, если перемещение сечения В относительно А в этой системе, как и в данной, будет равно нулю: Из этогоусловия определяется искомая опорная реакция -Перемещение равно сумме удлинений всех трех участков бруса. Следовательно,

Определяя далее методом сечений нормальные силы в текущих сечениях каждого участка и вычисляя удлинения этих участков по формулам (2.13) и (2.14), получаем

и

Отсюда

Изложенный здесь прием раскрытия статической неопределимости называется методом сил. Итак, нормальные силы в сечениях бруса

а нормальные напряжения в тех же текучих сечениях

Перемещения сечений бруса будем отсчитывать от правого неподвижною сечения. Тогда

При отсчете от левого неподвижного сечения эпюра будет такой, как показано на рис. 2.33. Из эпюры о видно, что наибольшего значения напряжения достигают в конечном сечении первого участка и в сечениях третьего участка, но они различны по знаку. Сталь 45 одинаково работает на растяжение и сжатие. Поэтому все эти сечения равноопасны (для хрупкого материала опасными были бы сечения третьего участка, где действуют растягивающие напряжения). Подсчитывая максимальное напряжение и зная предельное напряжение для материала находим запас прочности бруса

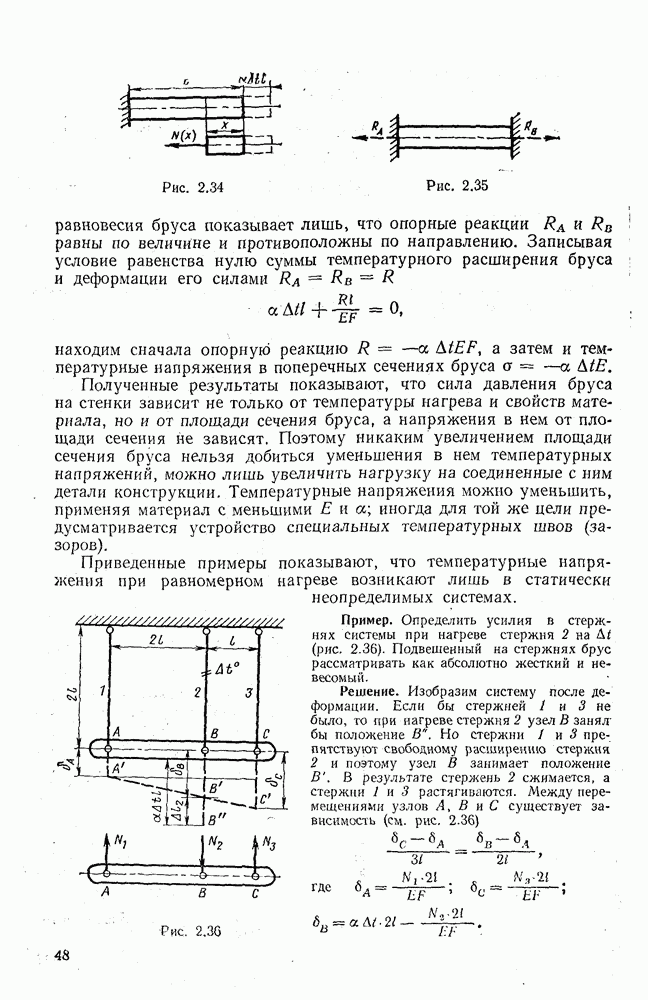
Усилия в элементах статически неопределимых систем могут возникать не только от внешних сил, но и от температурного воздействия, а при сборке — и от неточности изготовления деталей конструкций. При совместном воздействии указанных факторов удобно воспользоваться принципом независимости действия сил и находить усилия в элементах конструкции суммированием усилий от каждого воздействия в отдельности.