| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАКРУЧЕННЫЕ ЛОПАТКИ
Для обеспечения высоких КПД рабочие лопатки компрессоров и турбин при  обычно выполняют закрученными (с переменным углом установки а). Полный угол закрученности
обычно выполняют закрученными (с переменным углом установки а). Полный угол закрученности  достигает 45—60°.
достигает 45—60°.
Слабо закрученные лопатки. Для слабо закрученных лопаток с относительной толщиной сечений  а также для лопаток, у которых параметр закрученности
а также для лопаток, у которых параметр закрученности

влияние закрученности проявляется только в изменении положения оси наименьшей жесткости  по длине лопатки. Жесткости на изгиб
по длине лопатки. Жесткости на изгиб  и на растяжение
и на растяжение  остаются без изменения. Упругая крутизна оси при изгибе в плоскости наименьшей жесткости
остаются без изменения. Упругая крутизна оси при изгибе в плоскости наименьшей жесткости

связана с кривизнами оси лопатки в неподвижной системе координат х, у,  (см. рис. 7) соотношениями
(см. рис. 7) соотношениями

где  — прогибы в направлении осей у.
— прогибы в направлении осей у.
Таким образом,

Соотношения (77) позволяют рассчитать статические прогибы и провести расчет на колебания слабо закрученных лопаток. Изгибающий момент  вызывает в этом случае прогиб не только в направлении оси у, но и в перпендикулярном направлении вдоль оси
вызывает в этом случае прогиб не только в направлении оси у, но и в перпендикулярном направлении вдоль оси  т. е. лопатка испытывает «косой» изгиб.
т. е. лопатка испытывает «косой» изгиб.
Для более сильно закрученных лопаток, особенно с тонкими профилями, закрученность вызывает изменение жесткостей на изгиб и растяжение и приводит к появлению связи между деформациями изгиба, растяжения и кручения.

Рис. 26. Удлинение наклонного волокна закрученной лопатки при повороте сечений
В этом случае лопатку рассчитывают как закрученный стержень.
Основные соотношения теории закрученных стержней. В закрученных лопатках продольные волокна представляют собой винтовые линии. На рис. 26 показано одно из таких волокон, находящееся на расстоянии  от оси и соединяющее две соответственные точки в сеченнях
от оси и соединяющее две соответственные точки в сеченнях  (принято
(принято  ). Угол наклона волокна
). Угол наклона волокна

где  — угол начальной закрученности.
— угол начальной закрученности.
При деформациях лопатки закрученность меняется

и угол наклона волокна становится равным

при этом длина наклонного волокна  увеличивается на отрезок
увеличивается на отрезок

В лопатках углы  как правило, не превышают нескольких градусов, что позволяет считать
как правило, не превышают нескольких градусов, что позволяет считать

и аналогично для 
Тогда при 

и дополнительная относительная деформация, связанная с поворотом наклониого волокна, при  будет
будет

Суммируя величину Де с относительным удлинением стержня при плоском изгибе (см. с. 336), для закрученной лопатки получим

где  — удлинение волокна, совпадающего с осью лопатки;
— удлинение волокна, совпадающего с осью лопатки;  — угол поворота сечения относительно осн наименьшей жесткости
— угол поворота сечения относительно осн наименьшей жесткости  . Поворотом сечений относительно осн
. Поворотом сечений относительно осн  можно пренебречь
можно пренебречь
Напряжение в наклонном волокне, практически равное напряжению в поперечном сечении,

Из условий равновесия

(где  — растягивающая сила; — изгибающий момент в сечении лопатки) следует:
— растягивающая сила; — изгибающий момент в сечении лопатки) следует:

Здесь учтено, что оси  проходят через центр тяжести сечения
проходят через центр тяжести сечения  и обозначено
и обозначено

В закрученных лопатках крутящий момент в сечеиии  уравновешивается не только моментом касательных напряжений
уравновешивается не только моментом касательных напряжений  (см. гл. 18), но и моментом проекций нормальных напряжений в наклонных волокнах на плоскость поперечного сечения
(см. гл. 18), но и моментом проекций нормальных напряжений в наклонных волокнах на плоскость поперечного сечения  (рис. 26), так что
(рис. 26), так что

или с учетом формулы (80)

где

Подставив в равенство (85) выражения для и  из уравнения (82), найдем
из уравнения (82), найдем

где  — коэффициенты податливости;
— коэффициенты податливости;

Подставив выражение (87) в равенство (82), получим

где

Для незакрученнон лопатки  соотношения (87) и (89) принимают обычный вид:
соотношения (87) и (89) принимают обычный вид:

Выражениями  можно пользоваться также при расчете слабо закрученных лопаток и лопаток с относительно толстыми сечениями.
можно пользоваться также при расчете слабо закрученных лопаток и лопаток с относительно толстыми сечениями.
Для сечеиий, симметричных относительно хорды профиля, величины  т. е. основное соотношение теории изгиба неза крученных стержней
т. е. основное соотношение теории изгиба неза крученных стержней

остается в этом случае справедливым и для стержней закрученных. Выражениями (91) можно приближенно пользоваться при расчете на изгиб лопаток со слабо изогнутыми сечениями (примерно до  см. рис. 13).
см. рис. 13).
В закрученной лопатке жесткости на изгиб и растяжение убывают, жесткость на кручение возрастает, а все виды деформаций оказываются взаимозаменяемыми.
Геометрические и жесткостные характеристики закрученных лопаток. Определение основных геометрических и жесткостных характеристик, необходимых для расчета закрученных лопаток, может быть выполнено по следующим приближенным формулам.
(см. скан)
где 
Коэффициенты  находят по данным рис. 11 в зависимости от значения коэффициента
находят по данным рис. 11 в зависимости от значения коэффициента  определяемого по фактической площади сечения. Ориентировочно можно считать
определяемого по фактической площади сечения. Ориентировочно можно считать  Момент инерции
Момент инерции  определяют по формуле (32).
определяют по формуле (32).
Раскрутка от центробежных сил. Центробежные силы, действующие на лопатку с прямой осью, приводят к
появлению в поперечных сечениях лопатки растягивающей силы

[см. формулу (2)] и крутящего момента (рис. 27)

Введя формулы (93) и (94) в выражение (87) при  и проинтегрировав его по всей длине лопатки, найдем, что конец лопатки повернется на угол
и проинтегрировав его по всей длине лопатки, найдем, что конец лопатки повернется на угол

Для равномерно закрученной лопатки постоянного сечения при 

где  — угол полной закрученности;
— угол полной закрученности;  определяется формулой (5).
определяется формулой (5).
Из выражения (96) следует, что центробежные силы уменьшают начальную закрученность лопаткн.
С увеличением начальной закрученности угол  вначале возрастает, а затем, достигнув максимума, начинает убывать (из-за увеличения крутильной жесткости лопатки).
вначале возрастает, а затем, достигнув максимума, начинает убывать (из-за увеличения крутильной жесткости лопатки).
Рис. 27. (см. скан) Возникновение крутящего момента от центробежных сил
Угол  может составлять несколько градусов, что необходимо учитывать при газодинамическом расчете. Так как для разных материалов
может составлять несколько градусов, что необходимо учитывать при газодинамическом расчете. Так как для разных материалов  то угол
то угол  практически не зависит от материала лопатки.
практически не зависит от материала лопатки.
Упругое удлинение лопатки. Подставив формулы (93) и (94) в первое выражение (89) при  и проинтегрировав его по всей длине лопатки, найдем, что лопатка удлинится на величину
и проинтегрировав его по всей длине лопатки, найдем, что лопатка удлинится на величину

Для равномерно закрученной лопатки постоянного сечения при 

где  — определяется формулой (11).
— определяется формулой (11).
С увеличением начальной закрученности удлинение  возрастает.
возрастает.
Напряжения от центробежных сил. Пренебрегая влиянием крутящего момента, можно считать

а распределение напряжений согласно формуле (80) будет определяться выражением

где среднее напряжение по сечению  определяется формулой (2).
определяется формулой (2).
В закрученной лопатке напряжения от растяжения распределяются по поперечному сечению неравномерно.
В центральной части сечения напряжения выше средних, у кромок — ниже. У оси лопатки 

где

Зависимость коэффициента  от параметра Закрученности
от параметра Закрученности  и относительной изогнутости профиля
и относительной изогнутости профиля  приведена на рис. 28. Графиком можно пользоваться для приближенной оценки максимальных напряжений от центробежных сил в закрученной лопатке.
приведена на рис. 28. Графиком можно пользоваться для приближенной оценки максимальных напряжений от центробежных сил в закрученной лопатке.
При растяжении тонких, сильно закрученных лопаток на кромках появляются сжимающие напряжения, что может привести к короблению кромок.

Рис. 28. Зависимость коэффициента увеличения напряжений в закрученной лопатке от параметров 
Колебания лопаток. При колебаниях закрученной лопатки по основной форме  и
и

Для такой же незакручениой лопатки

где

Из сравнения выражений (101) и (102) следует, что основную частоту колебаний закрученной лопатки можно приближенно определить теми же методами, что и основную частоту соответствующей незакрученной лопатки (см. с. 285), но с заменой момента инерции сечения  эффективной геометрической жесткостью на изгиб
эффективной геометрической жесткостью на изгиб  где
где

Для равномерно закрученной лопатки постоянного сечения при 

где  — частота колебаний соответствующей иезакручеиьой лопатки.
— частота колебаний соответствующей иезакручеиьой лопатки.
Основная частота колебаний убывает с увеличением параметров закрученности  и относительной изогнутости профиля
и относительной изогнутости профиля 
Из формул (101) следует, что изгибные колебания закрученной лопатки сопровождаются поворотом сечений. Относительный угол поворота периферийного сечения лопатки

где  — перемещение конца лопатки, перпендикулярное хорде.
— перемещение конца лопатки, перпендикулярное хорде.
Для равномерно закрученной лопатки постоянного сечеиия при 

Таблицы для расчета основной собственной частоты колебаний закрученных лопаток. Первую собственную частоту колебаний консольных закрученных лопаток, Гц, рассчитывают по формуле

где  — длина лопатки, см;
— длина лопатки, см;  — максимальная толщина корневого сечеиия, см.
— максимальная толщина корневого сечеиия, см.
Значения коэффициента А. приведены в табл. 5, где  параметр закрученности
параметр закрученности  — хорда лопатки, см; принята постоянной по ее длине;
— хорда лопатки, см; принята постоянной по ее длине;  — полный угол закрученности, градусы);
— полный угол закрученности, градусы);  - относительная изогнутость корневого сечения;
- относительная изогнутость корневого сечения;  — максимальная толщина,
— максимальная толщина,  — стрела изогнутости периферийного сечения).
— стрела изогнутости периферийного сечения).
Таблица рассчитана для  при определении X ее можно использовать и при других значениях отношения
при определении X ее можно использовать и при других значениях отношения  так как его основное влияние отражено в параметре у.
так как его основное влияние отражено в параметре у.
Пример. Найти первую собственную частоту колебаний для лопатки, данные которой были приведены в примере на с. 288 при угле закрученности Да  .
.
Определяем

По табл. 5 путем линейной интерполяции находим  и
и

Учет закрученности привел к заметному снижению основной частоты коле.бяиий.
В уточненных расчетах лопатки турбоматии рассматриваются как оболочки переменного сечения с закручечно-изогнутой срединной поверхностью Их статические и динамические численные расчеты проводят на ЭВМ. Используются в основном различные вариационные методы Рчтца, конечных элементов.

(кликните для просмотра скана)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
- НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
- РАСТЯЖЕНИЕ И СЖАТИЕ
- ИЗГИБ
- СРЕЗ И СМЯТИЕ
- КРУЧЕНИЕ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- НАПРЯЖЕННО-ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ
- Глава 2. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ
- СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- СВОЙСТВА ПРИ ВЫСОКИХ И НИЗКИХ ТЕМПЕРАТУРАХ
- СВОЙСТВА ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- МАЛОЦИКЛОВАЯ И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ
- ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН
- РАЗРУШЕНИЯ И ИЗЛОМЫ
- ОЦЕНКА ПРОЧНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ПРОЧНОСТИ ПО НЕСУЩЕЙ СПОСОБНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- РАСЧЕТЫ НА ПРОЧНОСТЬ
- МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ
- УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- РАСЧЕТ НАПРЯЖЕНИЙ КРУЧЕНИЯ
- ВЫБОР ПРЕДВАРИТЕЛЬНОЙ ЗАТЯЖКИ
- РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СОЕДИНЕНИЯХ
- ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 4. ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
- ТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ
- НАПРЯЖЕННОЕ СОСТОЯНИЕ ФЛАНЦА И ТРУБЫ
- Глава 5. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- РАСЧЕТ ШЛИЦЕВЫХ СОЕДИНЕНИЙ НА ПРОЧНОСТЬ
- ИЗНАШИВАНИЕ СОЕДИНЕНИЙ
- Глава 6. СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ НАТЯГОМ
- РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 7. СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ
- КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ
- РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ВЛИЯНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- ПАЯНЫЕ СОЕДИНЕНИЯ
- Глава 8. ВАЛЫ
- КОНСТРУКТИВНЫЕ ФОРМЫ И МАТЕРИАЛЫ ВАЛОВ
- ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
- НАГРУЗКИ НА ВАЛЫ И РАСЧЕТНЫЕ СХЕМЫ
- РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА КОЛЕБАНИЯ
- КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- Глава 9. ПОДШИПНИКИ КАЧЕНИЯ
- ОСНОВНЫЕ КОНСТРУКЦИИ И ХАРАКТЕРИСТИКИ
- ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ В ПОДШИПНИКАХ КАЧЕНИЯ
- ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ ПОДШИПНИКОВ
- ЭКВИВАЛЕНТНАЯ НАГРУЗКА И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
- СМАЗЫВАНИЕ ПОДШИПНИКОВ
- НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ
- Глава 10. ПРУЖИНЫ
- ВИТЫЕ ПРУЖИНЫ
- РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
- РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
- ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- ПРОРЕЗНЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ ПРУЖИНЫ
- РЕЗИНОВЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- Глава 11. ЗУБЧАТЫЕ ПЕРЕДАЧИ
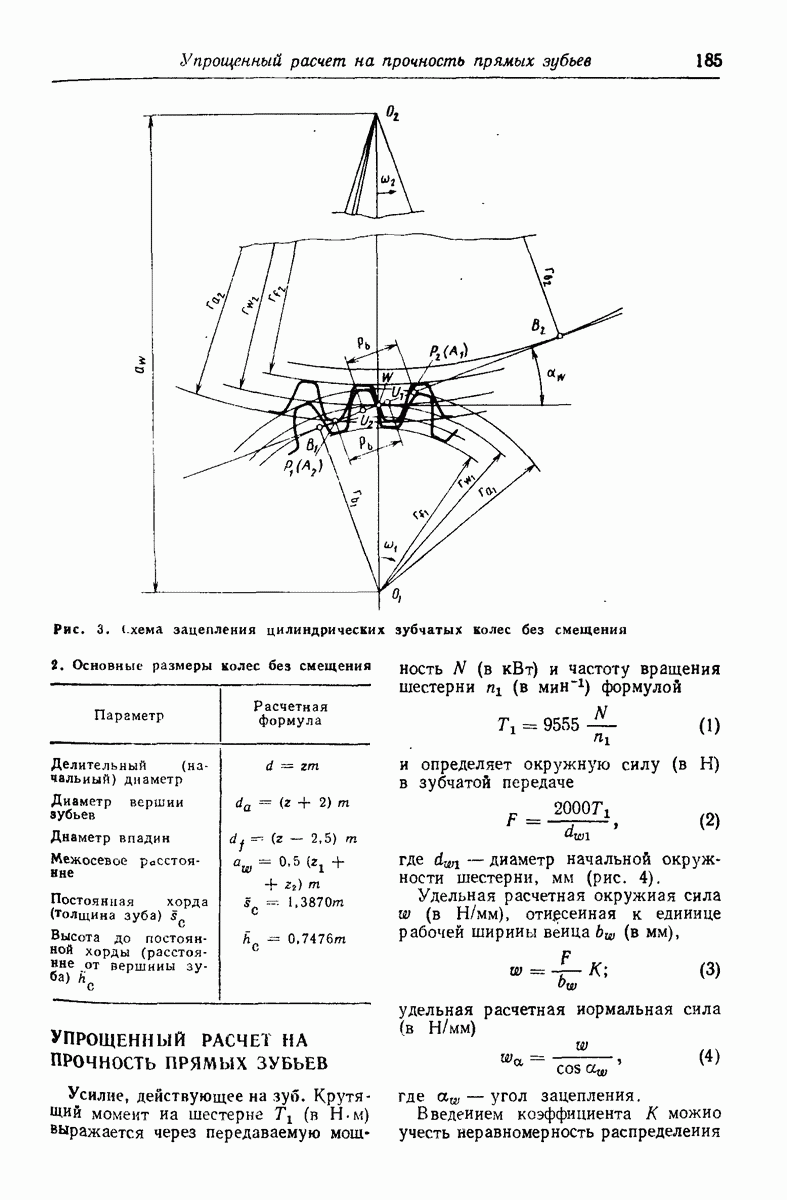
- УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ
- СТРУКТУРА РАСЧЕТНЫХ ФОРМУЛ ПО ГОСТ 21354—87
- НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ
- РАСЧЕТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
- РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ
- РАБОТА ПЕРЕДАЧ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ
- ОСОБЕННОСТИ РАСЧЕТА ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ М. Л. НОВИКОВА
- Глава 12. ШАРИКОВИНТОВЫЕ ПЕРЕДАЧИ
- КОНСТРУКЦИИ ПЕРЕДАЧ И МАТЕРИАЛЫ
- РАСЧЕТ ПЕРЕДАЧ
- Глава 13. РЕМЕННЫЕ ПЕРЕДАЧИ
- МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ
- РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
- ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ
- ПОРЯДОК РАСЧЕТА И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ
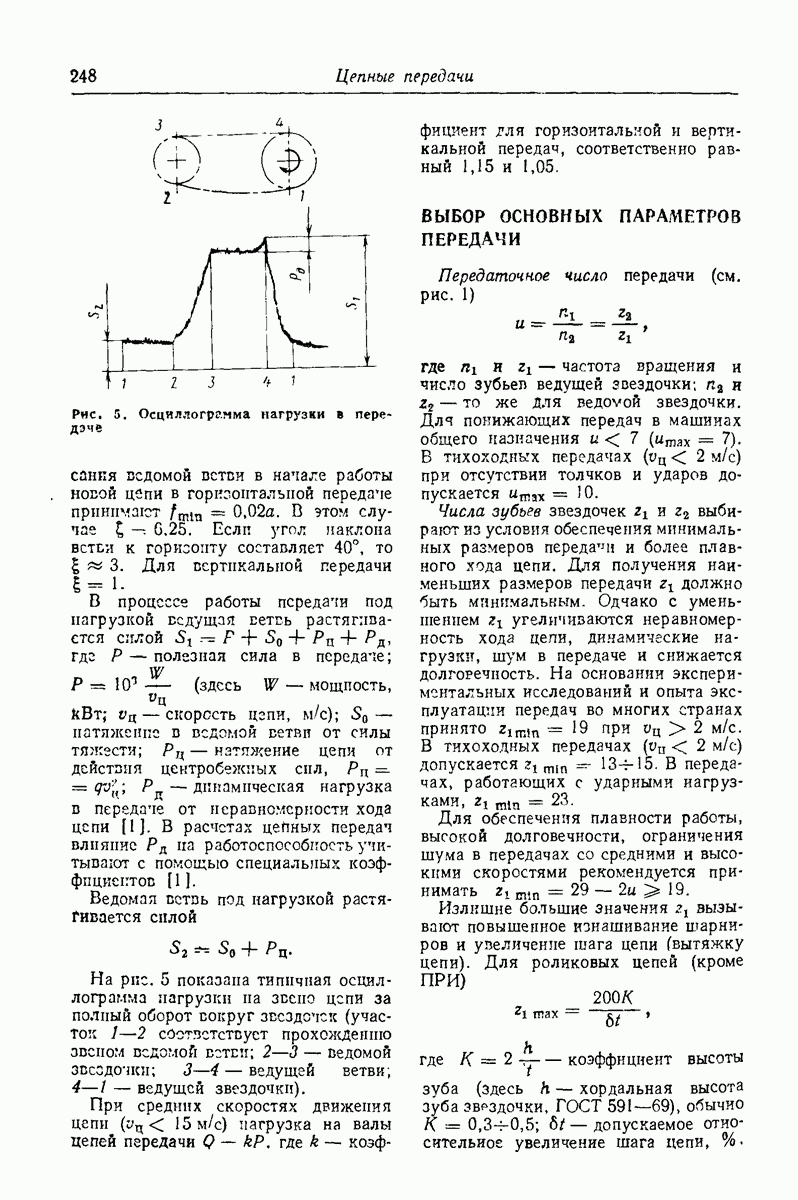
- Глава 14. ЦЕПНЫЕ ПЕРЕДАЧИ
- СИЛЫ В ПЕРЕДАЧЕ
- ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ
- НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ
- ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ
- ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ
- Глава 15. РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
- РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ
- РАСЧЕТ ШАТУНОВ
- РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА
- РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ
- РАСЧЕТ ДНИЩА ПОРШНЯ
- ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОРПУСА
- РАСЧЕТ КЛАПАННЫХ ПРУЖИН
- Глава 16. РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН
- РАСЧЕТ ЛОПАТОК НА ИЗГИБ
- ЗАПАС ПРОЧНОСТИ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ
- РАВНОПРОЧНЫЕ ЛОПАТКИ
- ОХЛАЖДАЕМЫЕ ЛОПАТКИ
- ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК
- ЗАКРУЧЕННЫЕ ЛОПАТКИ
- ШАРНИРНЫЕ ЛОПАТКИ
- БАНДАЖИРОВАННЫЕ ЛОПАТКИ
- РАСЧЕТ ЗАМКОВ ЛОПАТОК
- ВИБРАЦИЯ ЛОПАТОК
- РАСЧЕТ ДИСКОВ. НАПРЯЖЕНИЯ НА КОНТУРЕ
- ЗАПАСЫ ПРОЧНОСТИ ДИСКА
- ПРОФИЛИРОВАНИЕ РАВНОПРОЧНЫХ ДИСКОВ
- ОСНОВНЫЕ УРАВНЕНИЯ ПРИ РАСЧЕТЕ ДИСКОВ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ ТОЛЩИНЫ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ ТОЛЩИНЫ
- ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- УПРУГАЯ ЛИНИЯ СТЕРЖНЯ
- ОПРЕДЕЛЕНИЕ ПРОГИБОВ С ПОМОЩЬЮ ИНТЕГРАЛА МОРА
- ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- Глава 18. КРУЧЕНИЕ СТЕРЖНЕЙ
- СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
- СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
- РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- ТРУБЧАТЫЕ СТЕРЖНИ
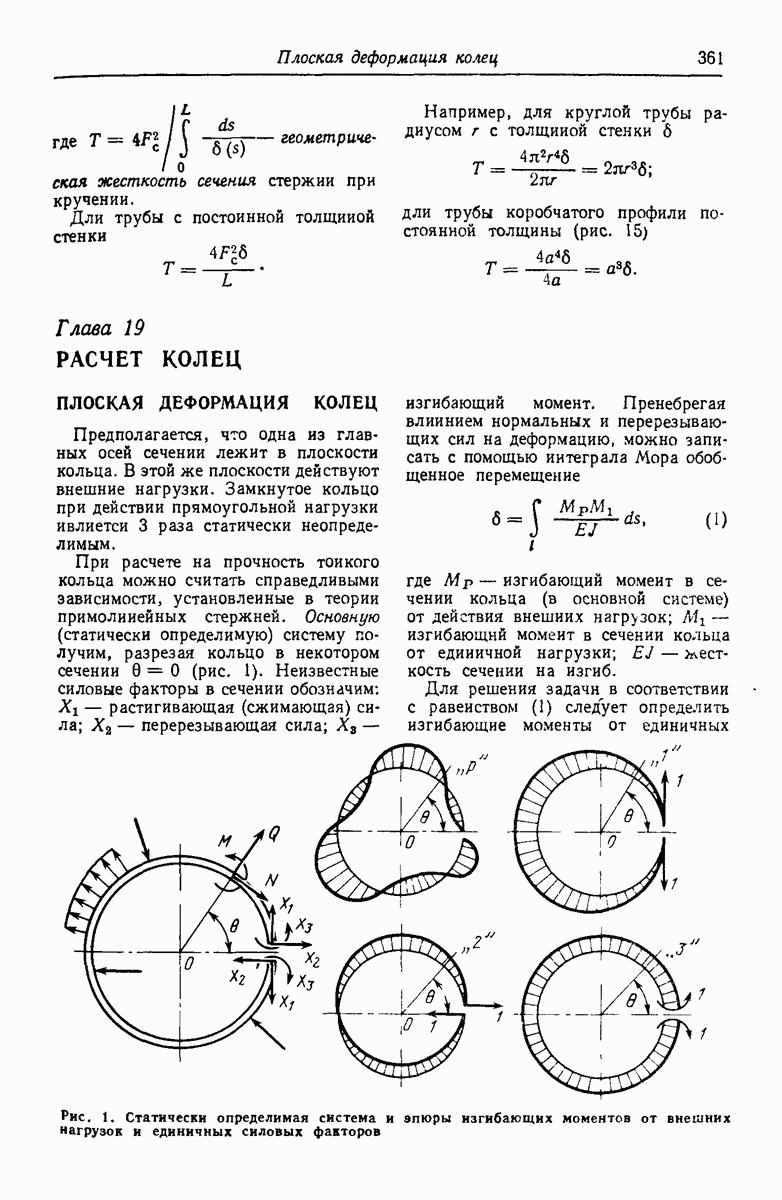
- Глаза 19. РАСЧЕТ КОЛЕЦ
- ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- Глава 20. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
- ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
- ВЛИЯНИЕ НАЧАЛЬНОГО ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ НА ВЫПУЧИВАНИЕ СТЕРЖНЯ
- РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ. ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАГРЕВЕ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ СКРУЧИВАНИИ
- Глава 21. КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
- МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- КРУТИЛЬНЫЕ КОЛЕБАНИЯ
- ИЗГИБНЫЕ КОЛЕБАНИЯ
- ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ
- Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ
- ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ
- Глава 23. РАСЧЕТ ПЛАСТИНОК
- ПРОРЫВНЫЕ МЕМБРАНЫ
- ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ
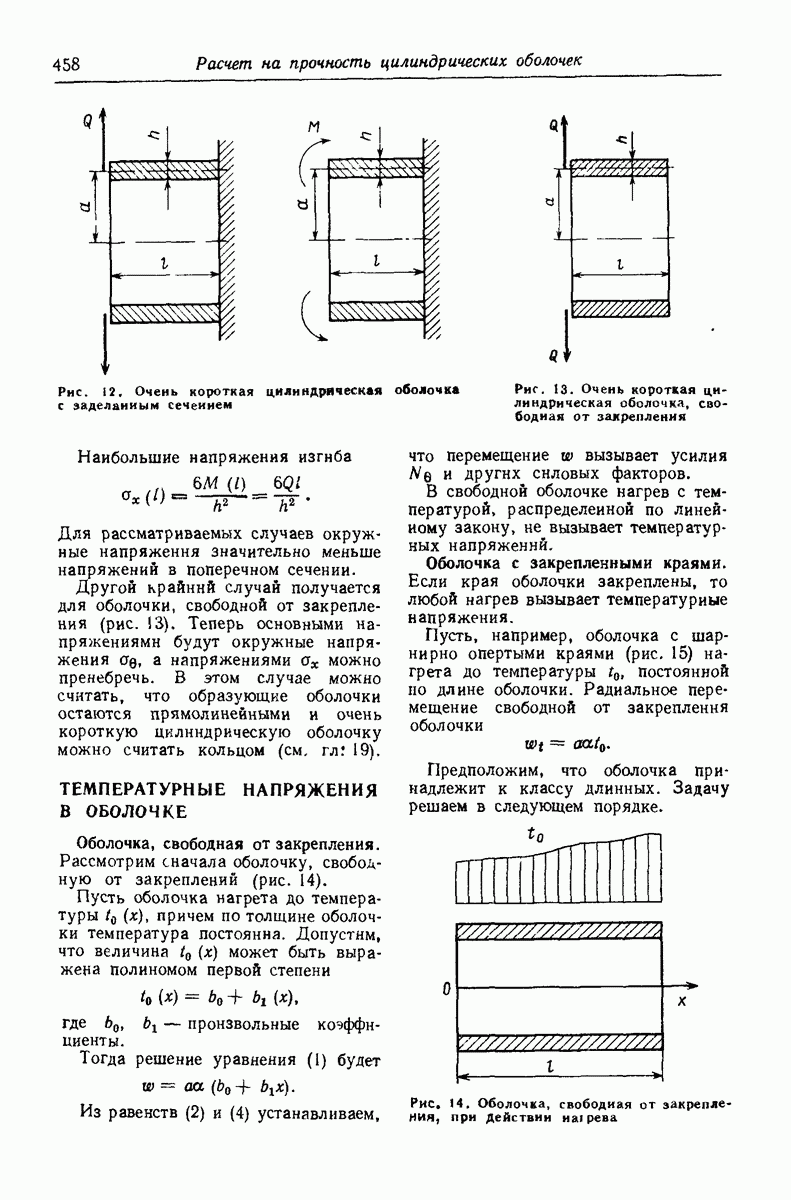
- Глава 24. РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК
- РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
- Глава 25. УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК
- УСТОЙЧИВОСТЬ КОЛЕЦ
- УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ КОНИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ
- УСТОЙЧИВОСТЬ АНИЗОТРОПНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК
- Глава 26. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
- ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД
- МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- ДИНАМИЧЕСКИЕ РАСЧЕТЫ
- Глава 27. РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- УРАВНЕНИЯ ПЛАСТИЧНОСТИ
- УРАВНЕНИЯ ПОЛЗУЧЕСТИ
- РАСЧЕТ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ)
- РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ НАГРУЖЕНИИ
- Глава 28. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЙ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ И ПОЛЗУЧЕСТИ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- Глава 29. КОНТАКТНЫЕ ЗАДАЧИ
- КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ ФОРМЫ
- КОНСТРУКЦИОННЫЕ КОНТАКТНЫЕ ЗАДАЧИ
- ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ
- ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ
- Глава 30. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
- КРИТЕРИИ ДЛИТЕЛЬНОЙ И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ
- Глава 31. РАСЧЕТ НА УСТАЛОСТЬ
- ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ
- УСЛОВИЯ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ
- СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ
- Глава 32. ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ
- СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ
- Глава 33. ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ
- ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ
- ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ
- ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ
- ПРОГНОЗИРУЕМАЯ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ
- ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- НАДЕЖНОСТЬ СИСТЕМЫ ПОСЛЕДОВАТЕЛЬНЫХ ЭЛЕМЕНТОВ
- НАДЕЖНОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ
- АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ
- РАСЧЕТ ЧИСЛА ИЗДЕЛИЙ, НАХОДЯЩИХСЯ В ЭКСПЛУАТАЦИИ
- КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
- Глава 34. ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН
- УПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ
- ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ ОБРАБОТКА
- ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ
- Глава 35. ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ
- МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОД РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ
- ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- Глава 36. ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ
- СПИСОК ЛИТЕРАТУРЫ