| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
При центральном приложении силы в любом поперечном сечении витка пружины возникают результирующая внутренняя сича Р, параллельная оси пружины, к момент  — плоскость которого совпадает с плоскостью пары сил Р (рис. 6). Нормальное поперечное сечение витка наклонено к плоскости момента под углом а. В этом сечении будут действовать силы и моменты (см. рис. 6)
— плоскость которого совпадает с плоскостью пары сил Р (рис. 6). Нормальное поперечное сечение витка наклонено к плоскости момента под углом а. В этом сечении будут действовать силы и моменты (см. рис. 6)

Ввиду малссти угла подъема витков (обычно  ) можно считать, что сечение пружины работает на кручении.
) можно считать, что сечение пружины работает на кручении.
Максимальное касательное напряжение в сечении пружины

где  момент сопротивления сечения вала кручению
момент сопротивления сечения вала кручению  учетом кривизны витков и равенства (1) соотношение (2) примет вид
учетом кривизны витков и равенства (1) соотношение (2) примет вид

где  — коэффициент, учитывающий кривизну витков и форму сечеиия (поправка к формуле для кручения прямого бруса); Р — внешняя нагрузка (растягивающая или сжимающая);
— коэффициент, учитывающий кривизну витков и форму сечеиия (поправка к формуле для кручения прямого бруса); Р — внешняя нагрузка (растягивающая или сжимающая);

Рис. 5. Диаграмма сдвига

Рис. 6. Силовые факторы в сечении нагруженной пружины
 — средний диаметр пружины;
— средний диаметр пружины;  — допускаемое касательное напряжение при кручении (табл. 2).
— допускаемое касательное напряжение при кручении (табл. 2).
Значение коэффициента  для пружин из круглой проволоки при индексе с
для пружин из круглой проволоки при индексе с  можно вычислить по формуле
можно вычислить по формуле

а для пружин прямоугольного сечення  рис. 7.
рис. 7.
Для пружин прямоугольного поперечного сечения

2. Допускаемые напряжения для цилиндрических витых пружии растяжения-сжатия
(см. скан)
Рис. 7. (см. скан) К определению коэффициента к для пружин растяжения-сжатия  тугольного сечения
тугольного сечения
где  — высота,
— высота,  ширина прямоугольника; а — коэффициент, зависящий от отношения сторои
ширина прямоугольника; а — коэффициент, зависящий от отношения сторои  (табл. 3).
(табл. 3).
Если пружина иавита из круглой проволоки, то  совпадает с полярным моментом сопротивления и тогда
совпадает с полярным моментом сопротивления и тогда

Осевое перемещение торцов пружины с углом подъема 

Податливость пружины наиболее просто определить из энергетических соотношений.
Потенциальная энергия пружины

где  - крутящий момент в сечении пружины от силы
- крутящий момент в сечении пружины от силы  ;
;  — жесткость сечения витка на кручение;
— жесткость сечения витка на кручение;  — полная длина рабочей части витков;
— полная длина рабочей части витков;  — число
— число
3. Значения коэффициентов 
(см. скан)

Рис. 8. Характеристика пружииы сжатия
витков пружины;  — геометрическая жесткость на кручение.
— геометрическая жесткость на кручение.
Из соотношения (8) следует:

где  — осевая податливость одного витка (осадка в мм при действии
— осевая податливость одного витка (осадка в мм при действии  ),
),

Для пружины из круглой проволоки полярный момент инерции сечения

и тогда формула  примет вид
примет вид

где  — модуль сдвига,
— модуль сдвига,  модуль упругости материала пружины. Для пружин с прямоугольным поперечным сечеиием
модуль упругости материала пружины. Для пружин с прямоугольным поперечным сечеиием

где а — наименьшая сторона сечеиия (коэффициент  по табл. 3).
по табл. 3).
Геометрическая жесткость на кручение для прямоугольного сечения

коэффициент  — по табл. 3.
— по табл. 3.
На рис. 8 показана зависимость между нагрузкой и осадкой пружины сжатия. Если пружина установлена с предварительной затяжкой (осадкой) с усилием  то ее установочная длина
то ее установочная длина

Длииа пружины при действии наибольшей внешней нагрузки 

При действии нагрузки  соответствующей
соответствующей  длина пружины будет наименьшей:
длина пружины будет наименьшей:

В соотношениях  — длииа пружины в свободном (ненагруженном) состоянии.
— длииа пружины в свободном (ненагруженном) состоянии.
Угол наклона прямой  (см. рис. 8) к оси абсцисс
(см. рис. 8) к оси абсцисс

В зависимости от назначения пружины усилие предварительной затяжки 
Наибольшая допускаемая внешняя нагрузка для пружии растяжения и сжатия

Конечный участок диаграммы пружины от силы  до усилия
до усилия  сжимающего пружину до соприкосновения витков, может оказаться нелинейным из-за неравномерности шага.
сжимающего пружину до соприкосновения витков, может оказаться нелинейным из-за неравномерности шага.
Рабочий ход (осадка) пружины

Если ход пружины задан, то необходимое число рабочих витков для обеспечения этого перемещения

Число витков округляют до полувитка  и до одного витка при
и до одного витка при 
Полное число витков

Дополнительные  витка идут на поджатие для создания опорных поверхностей у пружины.
витка идут на поджатие для создания опорных поверхностей у пружины.
Полная длина ненагруженной пружины

где  -длина пружины, сжатой до соприкосновения соседних рабочих витков
-длина пружины, сжатой до соприкосновения соседних рабочих витков 

 — шаг пружины, находящийся в зависимости от наибольшей осадки пружины,
— шаг пружины, находящийся в зависимости от наибольшей осадки пружины,

где наибольшая осадка пружины

В табл. 4 приведены значения наибольших допускаемых внешних нагрузок  и податливостей витка пружины X в зависимости от индекса с и диаметр а проволоки
и податливостей витка пружины X в зависимости от индекса с и диаметр а проволоки 
Длина проволоки, необходимая для изготовления пружины,

где а — угол подъема витков ненагруженной пружины,  6-7-9°.
6-7-9°.
Для предотвращения выпучивания пружины от потери устойчивости ее гибкость  должна быть менее 2,5.
должна быть менее 2,5.
Если по конструктивным соображениям это ограничение не выполняется, то пружину, как указано выше, следует ставить на оправках или монтировать в Гильзах.
Длина пружины растяжения в ненагруженном состоянии

где  — высота одного зацепа,
— высота одного зацепа, 
Длина пружины при максимальной внешней нагрузке 

где ?! — усилие первоначального сжатия витков при навивке.
Для изготовления пружины из проволоки

здесь 13 — длина проволоки для одного зацепа.
Расчет пружин обычно начинают с определения диаметра проволоки (или размера сечения для некруглой проволоки), задаваясь значением  и индексом пружины с.
и индексом пружины с.
Диаметр проволоки находят из условия прочности (7)

Если пружина имеет прямоугольное сечение, то ширина прямоугольника

Далее по формулам (13), (21)-(27) определяют размеры пружины.
Расчет цилиндрических пружин растяжения — сжатия из проволоки круглого сечения при  мм; с
мм; с  можно проводить, используя табл. 4.
можно проводить, используя табл. 4.
Пример 1. Заданы: ход пружины  усилие предварительной затяжки
усилие предварительной затяжки  и наибольшая внешняя нагрузка
и наибольшая внешняя нагрузка 
Из соотношения (19) находим  и далее по табл. 4 подбираем
и далее по табл. 4 подбираем  и X. Потребное число витков пружины находим из соотношения (21), а размеры пружины — по формулам
и X. Потребное число витков пружины находим из соотношения (21), а размеры пружины — по формулам 
Пример 2. Заданы: наибольшая нагрузка  установочная длина
установочная длина  и ход пружины
и ход пружины 
По табл. 4 для заданного значения  после вычисления
после вычисления  находим
находим  и X. Потребное число витков пружины и ее размеры находим, задаваясь значением
и X. Потребное число витков пружины и ее размеры находим, задаваясь значением  или
или 

(кликните для просмотра скана)

(кликните для просмотра скана)

Рис. 9. Фасонные пружины
Решение задачи такого типа не однозначно, на выбор того или иного варианта могут влиять дополнительные конструктивные соображения, связанные, например, с выбором Р. и  Выбор пружин из проволоки диаметром от 0,2 до 50 мм для сталей, приведенных в табл 2 проводят по ГОСТ 13764-86 - ГОСТ 13776-86. Эти стандарты распространяются на вянтовые цилиндрические пружины растяжения и сжатия для нагрузок от 1 до
Выбор пружин из проволоки диаметром от 0,2 до 50 мм для сталей, приведенных в табл 2 проводят по ГОСТ 13764-86 - ГОСТ 13776-86. Эти стандарты распространяются на вянтовые цилиндрические пружины растяжения и сжатия для нагрузок от 1 до  с индексами
с индексами  и наружными диаметрами 1—700 мм. В зависимости от долговечности стандартные пружинь! делятся на классы (см. табл. 2).
и наружными диаметрами 1—700 мм. В зависимости от долговечности стандартные пружинь! делятся на классы (см. табл. 2).
При больших нагрузках и ограниченных габаритах используют составные пружины сжатия (см. рис. 3) — набор из нескольких (чаще двух) концентрически расположенных пружин, одновременно воспринимающих внешнюю нагрузку. Для предотвращения сильного закручиваиня торцовых опор и перекосов навивку соседних пружин выполняют в противоположных направлениях (левом и правом). Опоры выполняют так, чтобы обеспечивалась взаимная центровка пружин (см. рис. 3, 4).
Обычно составные пружины имеют одинаковые осадки. При их проектировании стремятся к тому, чтобы длины пружин, сжатых  соприкосновения витков, были приблизительно одинаковы, а наибольшие касательные напряжения у всех пружин были равны допускаемому.
соприкосновения витков, были приблизительно одинаковы, а наибольшие касательные напряжения у всех пружин были равны допускаемому.
Первые Два условия для пружин, навитых из круглой проволоки, эквивалентны равенству их индексов.
При расчете двух концентрических клапанных пружин автотракторных двигателей часто средние диаметры пружин выбирают по конструктивным соображениям (в зависимости от диаметра горловины клапана) Радиальный зазор в таких пружинах составляет 2 мм.
Далее, принимая, что наружная пружина воспринимает 50—70% внешней нагрузки, находят диаметр проволоки ( — номер пружины)
— номер пружины)

и определяют длину пружины.
В последние годы получили распространение многожильные пружины, при изготовлении которых вместо одной проволоки используется трос, свитый издвх — шести проволок малого диаметра  . По конструктивному решению такие пружины эквивалентны концентрическим пружинам. Благодаря высокой демпфирующей способности (за счет трения между жилами) и податливости многожильные пружины хорошо работают в амортизаторах и других подобных устройствах. При действии переменных нагрузок многожильные пружины довольно быстро выходят из строя от изнашивания жил.
. По конструктивному решению такие пружины эквивалентны концентрическим пружинам. Благодаря высокой демпфирующей способности (за счет трения между жилами) и податливости многожильные пружины хорошо работают в амортизаторах и других подобных устройствах. При действии переменных нагрузок многожильные пружины довольно быстро выходят из строя от изнашивания жил.
В конструкциях, работающих в условиях вибраций нагрузок, иногда применяют фасонные пружины (рис. 9) с нелинейной зависимостью между внешней силой и упругим перемещением пружины
Расчет фасонных и многожильных пружин дан в работе 16], гл. 27.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
- НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
- РАСТЯЖЕНИЕ И СЖАТИЕ
- ИЗГИБ
- СРЕЗ И СМЯТИЕ
- КРУЧЕНИЕ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- НАПРЯЖЕННО-ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ
- Глава 2. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ
- СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- СВОЙСТВА ПРИ ВЫСОКИХ И НИЗКИХ ТЕМПЕРАТУРАХ
- СВОЙСТВА ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- МАЛОЦИКЛОВАЯ И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ
- ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН
- РАЗРУШЕНИЯ И ИЗЛОМЫ
- ОЦЕНКА ПРОЧНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ПРОЧНОСТИ ПО НЕСУЩЕЙ СПОСОБНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- РАСЧЕТЫ НА ПРОЧНОСТЬ
- МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ
- УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- РАСЧЕТ НАПРЯЖЕНИЙ КРУЧЕНИЯ
- ВЫБОР ПРЕДВАРИТЕЛЬНОЙ ЗАТЯЖКИ
- РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СОЕДИНЕНИЯХ
- ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 4. ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
- ТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ
- НАПРЯЖЕННОЕ СОСТОЯНИЕ ФЛАНЦА И ТРУБЫ
- Глава 5. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- РАСЧЕТ ШЛИЦЕВЫХ СОЕДИНЕНИЙ НА ПРОЧНОСТЬ
- ИЗНАШИВАНИЕ СОЕДИНЕНИЙ
- Глава 6. СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ НАТЯГОМ
- РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 7. СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ
- КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ
- РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ВЛИЯНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- ПАЯНЫЕ СОЕДИНЕНИЯ
- Глава 8. ВАЛЫ
- КОНСТРУКТИВНЫЕ ФОРМЫ И МАТЕРИАЛЫ ВАЛОВ
- ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
- НАГРУЗКИ НА ВАЛЫ И РАСЧЕТНЫЕ СХЕМЫ
- РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА КОЛЕБАНИЯ
- КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- Глава 9. ПОДШИПНИКИ КАЧЕНИЯ
- ОСНОВНЫЕ КОНСТРУКЦИИ И ХАРАКТЕРИСТИКИ
- ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ В ПОДШИПНИКАХ КАЧЕНИЯ
- ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ ПОДШИПНИКОВ
- ЭКВИВАЛЕНТНАЯ НАГРУЗКА И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
- СМАЗЫВАНИЕ ПОДШИПНИКОВ
- НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ
- Глава 10. ПРУЖИНЫ
- ВИТЫЕ ПРУЖИНЫ
- РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
- РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
- ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- ПРОРЕЗНЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ ПРУЖИНЫ
- РЕЗИНОВЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- Глава 11. ЗУБЧАТЫЕ ПЕРЕДАЧИ
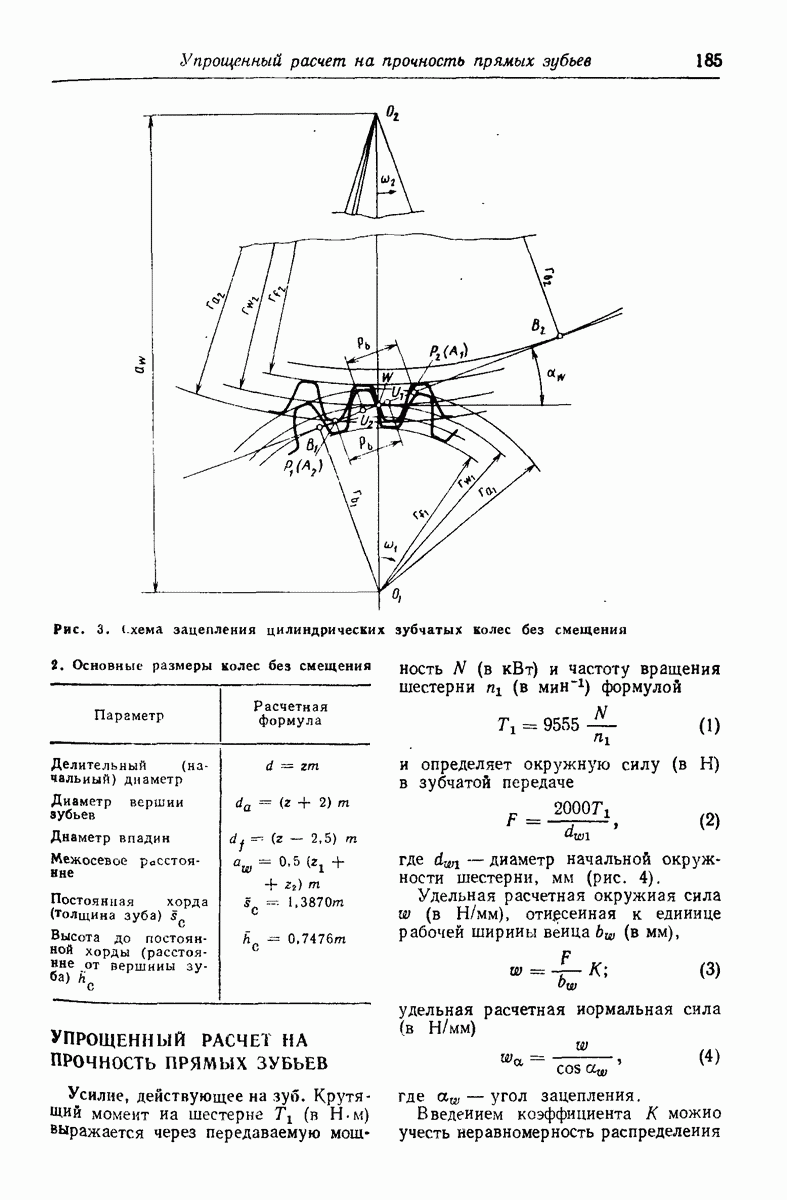
- УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ
- СТРУКТУРА РАСЧЕТНЫХ ФОРМУЛ ПО ГОСТ 21354—87
- НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ
- РАСЧЕТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
- РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ
- РАБОТА ПЕРЕДАЧ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ
- ОСОБЕННОСТИ РАСЧЕТА ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ М. Л. НОВИКОВА
- Глава 12. ШАРИКОВИНТОВЫЕ ПЕРЕДАЧИ
- КОНСТРУКЦИИ ПЕРЕДАЧ И МАТЕРИАЛЫ
- РАСЧЕТ ПЕРЕДАЧ
- Глава 13. РЕМЕННЫЕ ПЕРЕДАЧИ
- МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ
- РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
- ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ
- ПОРЯДОК РАСЧЕТА И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ
- Глава 14. ЦЕПНЫЕ ПЕРЕДАЧИ
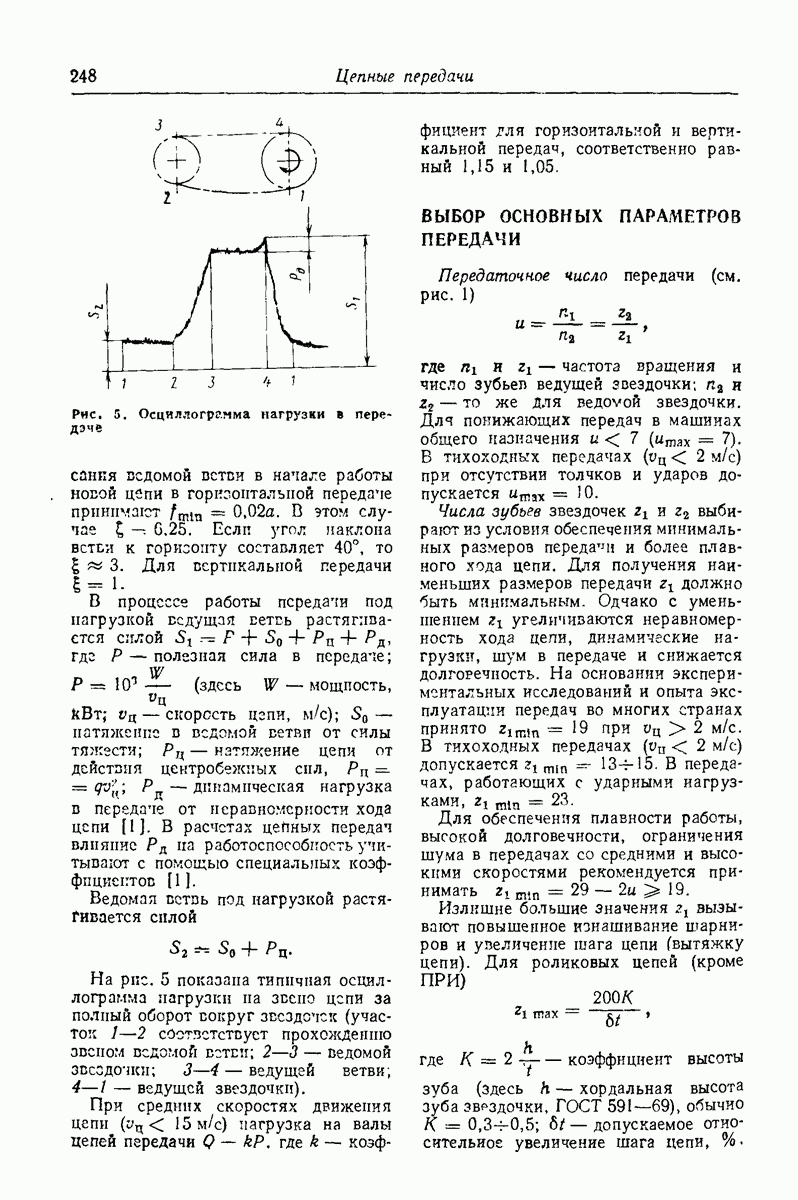
- СИЛЫ В ПЕРЕДАЧЕ
- ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ
- НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ
- ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ
- ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ
- Глава 15. РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
- РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ
- РАСЧЕТ ШАТУНОВ
- РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА
- РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ
- РАСЧЕТ ДНИЩА ПОРШНЯ
- ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОРПУСА
- РАСЧЕТ КЛАПАННЫХ ПРУЖИН
- Глава 16. РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН
- РАСЧЕТ ЛОПАТОК НА ИЗГИБ
- ЗАПАС ПРОЧНОСТИ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ
- РАВНОПРОЧНЫЕ ЛОПАТКИ
- ОХЛАЖДАЕМЫЕ ЛОПАТКИ
- ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК
- ЗАКРУЧЕННЫЕ ЛОПАТКИ
- ШАРНИРНЫЕ ЛОПАТКИ
- БАНДАЖИРОВАННЫЕ ЛОПАТКИ
- РАСЧЕТ ЗАМКОВ ЛОПАТОК
- ВИБРАЦИЯ ЛОПАТОК
- РАСЧЕТ ДИСКОВ. НАПРЯЖЕНИЯ НА КОНТУРЕ
- ЗАПАСЫ ПРОЧНОСТИ ДИСКА
- ПРОФИЛИРОВАНИЕ РАВНОПРОЧНЫХ ДИСКОВ
- ОСНОВНЫЕ УРАВНЕНИЯ ПРИ РАСЧЕТЕ ДИСКОВ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ ТОЛЩИНЫ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ ТОЛЩИНЫ
- ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- УПРУГАЯ ЛИНИЯ СТЕРЖНЯ
- ОПРЕДЕЛЕНИЕ ПРОГИБОВ С ПОМОЩЬЮ ИНТЕГРАЛА МОРА
- ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- Глава 18. КРУЧЕНИЕ СТЕРЖНЕЙ
- СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
- СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
- РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- ТРУБЧАТЫЕ СТЕРЖНИ
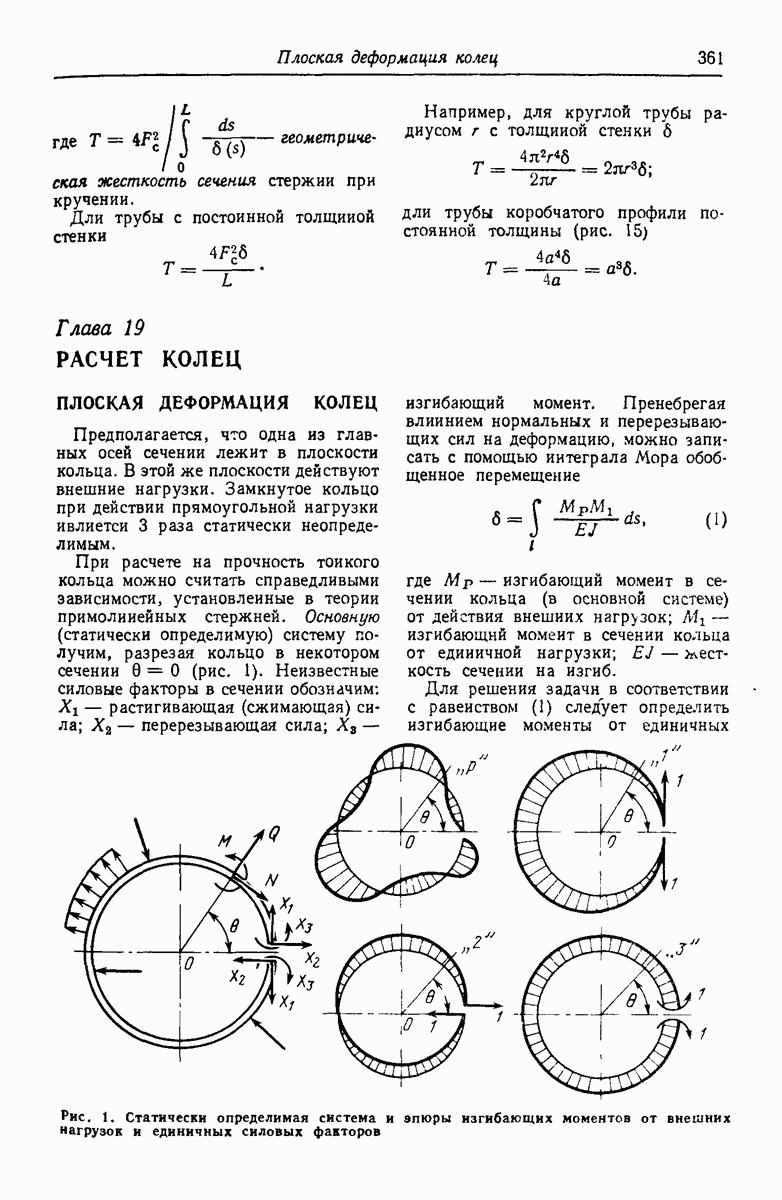
- Глаза 19. РАСЧЕТ КОЛЕЦ
- ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- Глава 20. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
- ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
- ВЛИЯНИЕ НАЧАЛЬНОГО ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ НА ВЫПУЧИВАНИЕ СТЕРЖНЯ
- РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ. ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАГРЕВЕ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ СКРУЧИВАНИИ
- Глава 21. КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
- МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- КРУТИЛЬНЫЕ КОЛЕБАНИЯ
- ИЗГИБНЫЕ КОЛЕБАНИЯ
- ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ
- Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ
- ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ
- Глава 23. РАСЧЕТ ПЛАСТИНОК
- ПРОРЫВНЫЕ МЕМБРАНЫ
- ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ
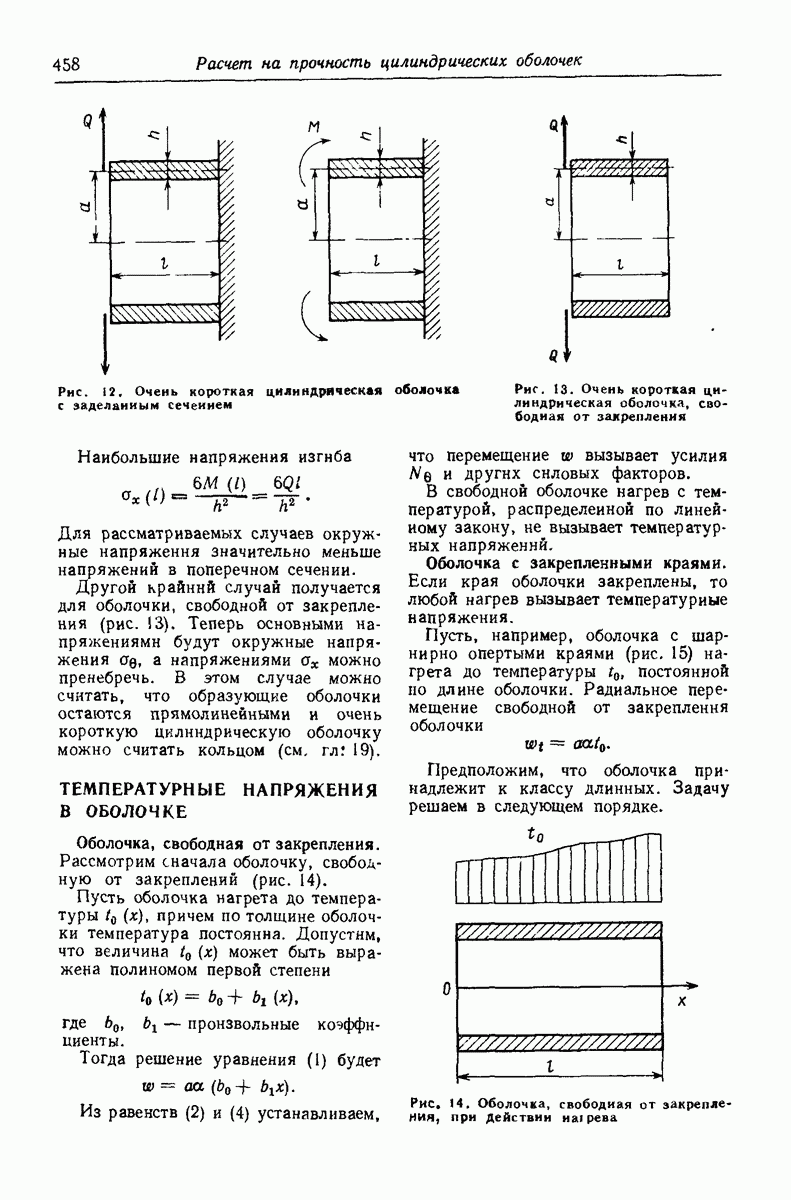
- Глава 24. РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК
- РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
- Глава 25. УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК
- УСТОЙЧИВОСТЬ КОЛЕЦ
- УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ КОНИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ
- УСТОЙЧИВОСТЬ АНИЗОТРОПНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК
- Глава 26. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
- ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД
- МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- ДИНАМИЧЕСКИЕ РАСЧЕТЫ
- Глава 27. РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- УРАВНЕНИЯ ПЛАСТИЧНОСТИ
- УРАВНЕНИЯ ПОЛЗУЧЕСТИ
- РАСЧЕТ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ)
- РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ НАГРУЖЕНИИ
- Глава 28. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЙ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ И ПОЛЗУЧЕСТИ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- Глава 29. КОНТАКТНЫЕ ЗАДАЧИ
- КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ ФОРМЫ
- КОНСТРУКЦИОННЫЕ КОНТАКТНЫЕ ЗАДАЧИ
- ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ
- ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ
- Глава 30. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
- КРИТЕРИИ ДЛИТЕЛЬНОЙ И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ
- Глава 31. РАСЧЕТ НА УСТАЛОСТЬ
- ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ
- УСЛОВИЯ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ
- СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ
- Глава 32. ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ
- СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ
- Глава 33. ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ
- ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ
- ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ
- ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ
- ПРОГНОЗИРУЕМАЯ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ
- ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- НАДЕЖНОСТЬ СИСТЕМЫ ПОСЛЕДОВАТЕЛЬНЫХ ЭЛЕМЕНТОВ
- НАДЕЖНОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ
- АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ
- РАСЧЕТ ЧИСЛА ИЗДЕЛИЙ, НАХОДЯЩИХСЯ В ЭКСПЛУАТАЦИИ
- КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
- Глава 34. ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН
- УПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ
- ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ ОБРАБОТКА
- ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ
- Глава 35. ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ
- МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОД РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ
- ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- Глава 36. ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ
- СПИСОК ЛИТЕРАТУРЫ