| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
ВАЛ С ОДНИМ ДИСКОМ
Понятие критической частоты вращения. Рассмотрим вал на двух опорах с диском посредине (рис. 1), вращающийся с угловой скоростью со.
Для того чтобы выяснить, является ли вращение вала с прямолинейной осью устойчивым, предположим, что вал получил некоторое отклонение и центр тяжести диска стал двигаться по Окружности радиусом у. Тогда на диск действуют центробежная сила и вила упругости:

Цгде  — масса диска, а — прогиб среднего сечения вала от действия единичной силы для вала постоянного сечения,
— масса диска, а — прогиб среднего сечения вала от действия единичной силы для вала постоянного сечения,

Если  то после отклонения вал снова вернется в первоначальное положение, т.
то после отклонения вал снова вернется в первоначальное положение, т.  прямолинейное положение оси является устойчивы
прямолинейное положение оси является устойчивы
В момент равновесия, т. е. в момент начала потери устойчивости, когда  прогибы могут безгранично возрастать. В этом случае центробежные силы в отклоненном положении равны силам упругости, стремящимся вернусь вал в исходное состояние. Частоты вращения, при которых наступает равенство центробежных сил и сил упругости, называют критическими.
прогибы могут безгранично возрастать. В этом случае центробежные силы в отклоненном положении равны силам упругости, стремящимся вернусь вал в исходное состояние. Частоты вращения, при которых наступает равенство центробежных сил и сил упругости, называют критическими.

Рис. 1. Вал на двух опорах с диском посредине
При критическом значении со величина  отсюда
отсюда

или

Критическая частота вращения, 

Равенство центробежных сил и сил упругости имеет место при любом прогибе, так как в пределах применимости линейной теории обе указанные силы пропорциональны прогибам.
Можно представить, что при критической частоте вращения вал совершенно теряет жесткость на изгиб; даже малая сила может вызвать значительные прогибы.
Из равенства (1) следует, что критическая угловая скорость совпадает с круговой частотой поперечных (изгибных) колебаний вала. Этот вывод справедлив и в общем случае, если детали, закрепленные на валу, рассматривают как точечные массы.
Учет начального эксцентриситета центра тяжести диска. В практических задачах центр тяжести лиска имеет некоторое смещение относительно своей геометрической оси и, следовательно, оси вала.
Для уменьшения этого эксцентриситета быстровращающиеся валы подвергаются балансировке, которая, однако, имеет ограниченную точность. Например, детали массой 100—300 кг балансируют обычно с точностью порядка  Кроме того, следует учесть, что в рабочих условиях вследствие нагрева, остаточных деформаций и других причин дисбаланс возрастает.
Кроме того, следует учесть, что в рабочих условиях вследствие нагрева, остаточных деформаций и других причин дисбаланс возрастает.
При наличии эксцентриситета вал получает прогибы даже при малой угловой скорости, так как к нему приложена неуравновешенная сила.

Рис. 2. Начальный эжсцентригитет диска

Рис. 3. Зависимость прогиба валя от угловой скооости
Обозначим абсолютную величину эксцентриситета диска  (величине
(величине  соответствует дисбаланс
соответствует дисбаланс  где
где  — сила тяжести диска).
— сила тяжести диска).
На диск действует сила инерции С и сила упругости  (рис. 21.
(рис. 21.
Предполагая величины у и  положительными, получим
положительными, получим

Из условия равновесия следует  Подставляя в это равенство зависимости (2), нахоцим
Подставляя в это равенство зависимости (2), нахоцим

Если угловая скорость вращения  меньше критической угловой скороси
меньше критической угловой скороси  то решение соответствует положительной величине у (направления прогиба и эксцентриситета совпадают, см. рис. 2).
то решение соответствует положительной величине у (направления прогиба и эксцентриситета совпадают, см. рис. 2).
При  (закрнтнческий режим) величина
(закрнтнческий режим) величина  (направления эксцентриситета и прогиба противоположны). В закритической области центр тяжести диска расположен ближе коси вращения, чем точка крепления диска к валу.
(направления эксцентриситета и прогиба противоположны). В закритической области центр тяжести диска расположен ближе коси вращения, чем точка крепления диска к валу.
Из уравнения (3) следует, что при очень больших угловых скоростях  т. е. центр тяжести диска оказывается на оси вращения.
т. е. центр тяжести диска оказывается на оси вращения.
Такое явление называют самоцстановлением вала в закритической области.
Рассмотрим теперь критический режим, когда 
Из уравнения (3) следует, что при совпадении угловой скорости с критической угловой скоростью прогибы вала неограниченно возрастают.
Зависимость прогиба вала от  показана на рис 3 Подобным образом возрастает и реакция на опоры.
показана на рис 3 Подобным образом возрастает и реакция на опоры.
В действительности прогибы при  остаются конечными, так как всегда существуют ограничения (защемление в подшипниках, трение и т. п.) и, кроме того, при больших дрформяциях нарушается линейная зависимость между силой и перемещением.
остаются конечными, так как всегда существуют ограничения (защемление в подшипниках, трение и т. п.) и, кроме того, при больших дрформяциях нарушается линейная зависимость между силой и перемещением.
Однако приближение угловой скорости к критической может оказаться опасным, и поэтому зону частот вращения от  до
до  не рекомендуется использовать для рабочих режимов.
не рекомендуется использовать для рабочих режимов.
Во всех случаях желательно работать с жесткими роторами (валами), для которых 
Работа вала с одним диском при со  сок возможна, но при этом часто требуются специальные демпфирующие опоры для прохождения через критические частоты и для успокоения вибрации в закритической области.
сок возможна, но при этом часто требуются специальные демпфирующие опоры для прохождения через критические частоты и для успокоения вибрации в закритической области.
Если вал имеет несколько дисков и соответственно несколько критических угловых скоростей  то критическое состояние наступает при совпадении угловой скорости с любой из критических скоростей.
то критическое состояние наступает при совпадении угловой скорости с любой из критических скоростей.
Для устойчивой работы вала диапазон частот вращения

рекомендуется исключить из рабочих режимов.
Для вала с несколькими дисками условия для устойчивой работы в закритической области  более благоприятны, чем для вала с одним диском.
более благоприятны, чем для вала с одним диском.

Рис. 4. Вал на пругнх опорах
Учет упругости опор. В действительных условиях опоры вовлекаются в колебания. Если пренебречь массой опоры, то в простейшем случае ее можно схематизировать в виде пружины (рис. 4).
Предположим для простоты, что опоры обладают одинаковой жесткостью. Для определения критических частот вращения следует рассмотреть равновесие системы при изогнутой оси вала. Центр тяжести диска будет перемещаться по окружности радиусом у, центры опор — по окружности радиусом 
Если  — коэффициент податливости опоры в
— коэффициент податливости опоры в  то
то

Далее следует учесть равенства 

где а — коэффициент податливости вала.
Так как  то из уравнения (5) следует:
то из уравнения (5) следует:

Приравнивая соотношения (4) и (6), находим

где

является критической угловой скоростью вала на жестких опорах.
Из формулы (7) следует, что поправка, связанная с учетом податливости опор, зависит от податливости вала.
Одни и те же опоры можно рассматривать как жесткие или как податливые в зависимости от жесткости вала. В практических конструкциях податливость опор составляет обычно  причем податливость подшипников качения для вала диаметром 60— 80 мм приблизительно равна
причем податливость подшипников качения для вала диаметром 60— 80 мм приблизительно равна 
При критических частотах вращения в вале возникают постоянные по времени напряжения, тогда как в опорах напряжения будут изменяться по времени, что способствует увеличению сил демпфирования.
В технике применяют конструкции, в которых относительно жесткий ротор закреплен на податливых опорах. В силу этого критическая частота может лежать в рабочем диапазоне  но, как показала практика, это не нарушает нормальной работы.
но, как показала практика, это не нарушает нормальной работы.
Прогибы ротора при критических частотах вращения всей системы оказываются малыми, если критическая частота вращения ротора на жестких опорах превышает максимальную 
Учет гироскопического эффекта дисков. Рассмотрим центробежные силы, действующие на диск (рис. 5). Ось х является осью вращении, ось  направлена по оси диска. Пусть элемент массы
направлена по оси диска. Пусть элемент массы  находится в точке А. К нему приложена центробежная сила
находится в точке А. К нему приложена центробежная сила  действующая в плоскости вращения, причем
действующая в плоскости вращения, причем

где  длина отрезка ОА.
длина отрезка ОА.
Центробежная сила  может быть разложена на две составляющие
может быть разложена на две составляющие  но усилия
но усилия  вследствие симметрии образуют взаимную уравновешенную систему сил и для дальнейшего не существенны.
вследствие симметрии образуют взаимную уравновешенную систему сил и для дальнейшего не существенны.
Рис. 5. (см. скан) Гироскопический вффект диска
Усилие

так как отрезок  представляет собой проекцию отрезка ОА на плоскость
представляет собой проекцию отрезка ОА на плоскость 
Приведем все нагрузки, действующие  диск, к силе С и паре сил М, приложенным в центре тяжести диска. Сила
диск, к силе С и паре сил М, приложенным в центре тяжести диска. Сила

интеграл распространяется на весь объем диска.
Величины у (смещение центра тяжести) и  (угол поворота плоскости диска) одинаковы для всех точек диска и могут быть вынесены из-под знака интеграла.
(угол поворота плоскости диска) одинаковы для всех точек диска и могут быть вынесены из-под знака интеграла.
Тогда

Учитывая, что

как статический момент относительно прямой, проходящей через центр тяжести, получим

где  — масса всего диска.
— масса всего диска.
Но центробежные силы создают еще и момент, который для рассматриваемого вида движения (диск неподвижен относительно плоскости, содержащей изогнутую ось вала) может быть легко определен.
Этот момент называют гироскопическим.

или с учетом соотношения (9)

Последний интеграл разбивается на два:

из которых первый равен нучю. Таким образом,

где  — осевой момент инерции,
— осевой момент инерции,  .
.
Для тонких дисков 

Рис. 6. Влияние гироскопического эффекта на критическую частоту вращения вала
Так как рассматриваются малые Отклонения вала от прямолинейной формы, то 
Момент, создаваемый диском,

При малых углах поворота

Существенно, что этот момент препятствует прогибу. Следовательно, с учетом гироскопического момента дисков критические числа оборотов повышаются.
Перейдем к определению критических частот вращения вала с одним диском с учетом гироскопического момента (рис. 6).
Под действием силы С и момента М вал в месте крепления диска прогибается на величину у и поворачивается на угол

где  — прогиб и угол поворота
— прогиб и угол поворота  действия единичной силы,
действия единичной силы,  — прогиб и угол поворота от действия единичного момента.
— прогиб и угол поворота от действия единичного момента.
Направление единичных силовых факторов показано на рис. 6 По условию взаимности упругих систем величины у и 5 численно равны.
Подставляя равенства (10; и (11) в уравнение (12), получим

или

Приравнивая отношение у к  из равенств (13) и (14), находим
из равенств (13) и (14), находим

или

Из последнего уравнения получаем величину критической угловой скорости

Если  то получим известный результат
то получим известный результат

Влияние гироскопического момента особенно существенно для дисков, расположенных вблизи опор.
Если вал имеет концевые опоры и несет несколько дисков, то повышение критических частот вращения вследствие влияния гироскопического эффекта дисков невелико.
Учет массы вала. В приближенных расчетах массу вала учитывают
увеличением массы диска. Обычнс к массе диска добавляют половину массы вала. Приближенный расчет допустим, если масса вала составляет не более 30% массы диска.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
- НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
- РАСТЯЖЕНИЕ И СЖАТИЕ
- ИЗГИБ
- СРЕЗ И СМЯТИЕ
- КРУЧЕНИЕ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- НАПРЯЖЕННО-ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ
- Глава 2. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ
- СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- СВОЙСТВА ПРИ ВЫСОКИХ И НИЗКИХ ТЕМПЕРАТУРАХ
- СВОЙСТВА ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- МАЛОЦИКЛОВАЯ И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ
- ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН
- РАЗРУШЕНИЯ И ИЗЛОМЫ
- ОЦЕНКА ПРОЧНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ПРОЧНОСТИ ПО НЕСУЩЕЙ СПОСОБНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- РАСЧЕТЫ НА ПРОЧНОСТЬ
- МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ
- УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- РАСЧЕТ НАПРЯЖЕНИЙ КРУЧЕНИЯ
- ВЫБОР ПРЕДВАРИТЕЛЬНОЙ ЗАТЯЖКИ
- РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СОЕДИНЕНИЯХ
- ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 4. ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
- ТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ
- НАПРЯЖЕННОЕ СОСТОЯНИЕ ФЛАНЦА И ТРУБЫ
- Глава 5. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- РАСЧЕТ ШЛИЦЕВЫХ СОЕДИНЕНИЙ НА ПРОЧНОСТЬ
- ИЗНАШИВАНИЕ СОЕДИНЕНИЙ
- Глава 6. СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ НАТЯГОМ
- РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 7. СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ
- КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ
- РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ВЛИЯНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- ПАЯНЫЕ СОЕДИНЕНИЯ
- Глава 8. ВАЛЫ
- КОНСТРУКТИВНЫЕ ФОРМЫ И МАТЕРИАЛЫ ВАЛОВ
- ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
- НАГРУЗКИ НА ВАЛЫ И РАСЧЕТНЫЕ СХЕМЫ
- РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА КОЛЕБАНИЯ
- КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- Глава 9. ПОДШИПНИКИ КАЧЕНИЯ
- ОСНОВНЫЕ КОНСТРУКЦИИ И ХАРАКТЕРИСТИКИ
- ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ В ПОДШИПНИКАХ КАЧЕНИЯ
- ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ ПОДШИПНИКОВ
- ЭКВИВАЛЕНТНАЯ НАГРУЗКА И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
- СМАЗЫВАНИЕ ПОДШИПНИКОВ
- НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ
- Глава 10. ПРУЖИНЫ
- ВИТЫЕ ПРУЖИНЫ
- РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
- РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
- ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- ПРОРЕЗНЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ ПРУЖИНЫ
- РЕЗИНОВЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- Глава 11. ЗУБЧАТЫЕ ПЕРЕДАЧИ
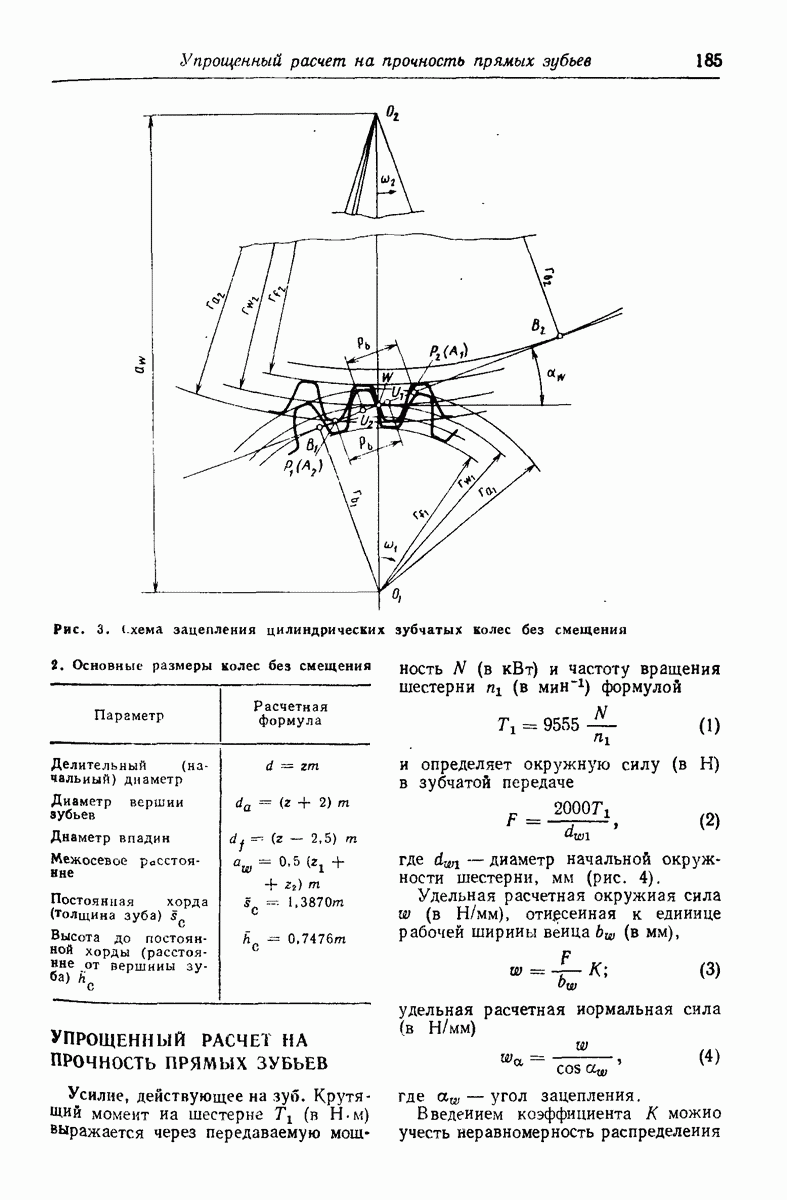
- УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ
- СТРУКТУРА РАСЧЕТНЫХ ФОРМУЛ ПО ГОСТ 21354—87
- НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ
- РАСЧЕТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
- РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ
- РАБОТА ПЕРЕДАЧ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ
- ОСОБЕННОСТИ РАСЧЕТА ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ М. Л. НОВИКОВА
- Глава 12. ШАРИКОВИНТОВЫЕ ПЕРЕДАЧИ
- КОНСТРУКЦИИ ПЕРЕДАЧ И МАТЕРИАЛЫ
- РАСЧЕТ ПЕРЕДАЧ
- Глава 13. РЕМЕННЫЕ ПЕРЕДАЧИ
- МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ
- РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
- ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ
- ПОРЯДОК РАСЧЕТА И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ
- Глава 14. ЦЕПНЫЕ ПЕРЕДАЧИ
- СИЛЫ В ПЕРЕДАЧЕ
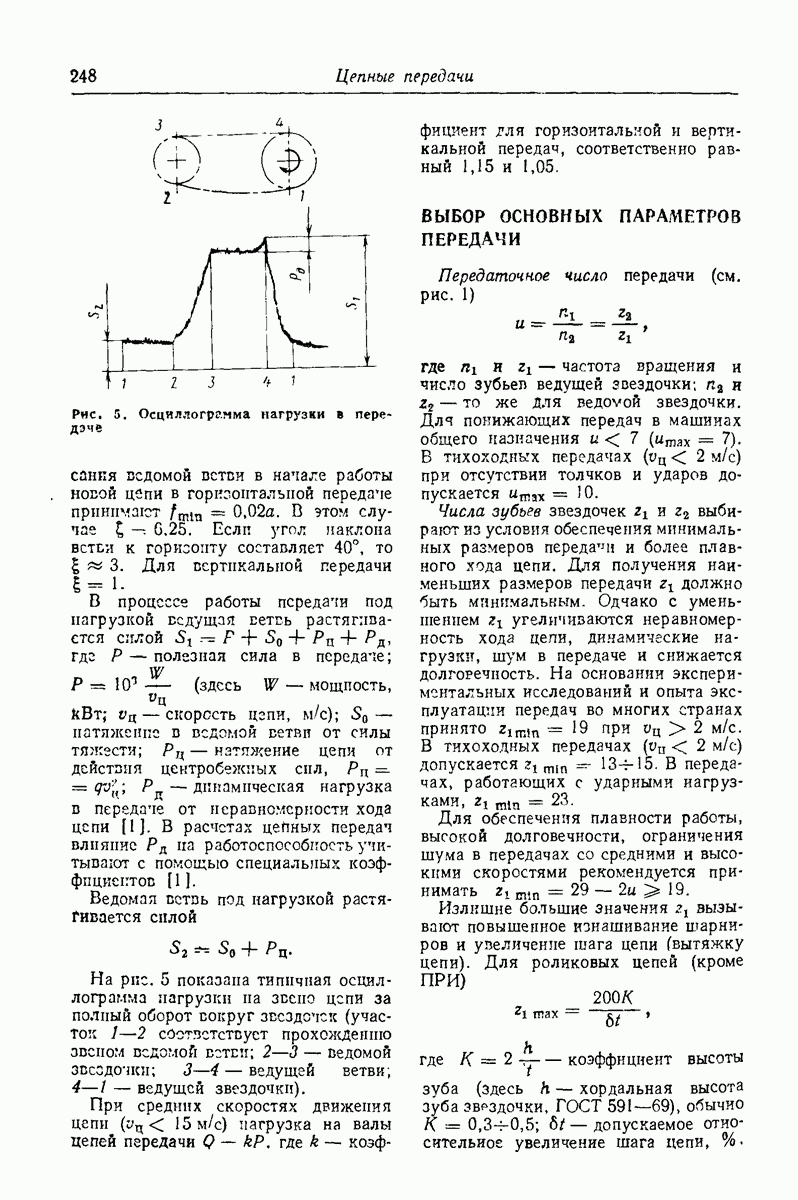
- ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ
- НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ
- ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ
- ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ
- Глава 15. РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
- РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ
- РАСЧЕТ ШАТУНОВ
- РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА
- РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ
- РАСЧЕТ ДНИЩА ПОРШНЯ
- ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОРПУСА
- РАСЧЕТ КЛАПАННЫХ ПРУЖИН
- Глава 16. РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН
- РАСЧЕТ ЛОПАТОК НА ИЗГИБ
- ЗАПАС ПРОЧНОСТИ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ
- РАВНОПРОЧНЫЕ ЛОПАТКИ
- ОХЛАЖДАЕМЫЕ ЛОПАТКИ
- ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК
- ЗАКРУЧЕННЫЕ ЛОПАТКИ
- ШАРНИРНЫЕ ЛОПАТКИ
- БАНДАЖИРОВАННЫЕ ЛОПАТКИ
- РАСЧЕТ ЗАМКОВ ЛОПАТОК
- ВИБРАЦИЯ ЛОПАТОК
- РАСЧЕТ ДИСКОВ. НАПРЯЖЕНИЯ НА КОНТУРЕ
- ЗАПАСЫ ПРОЧНОСТИ ДИСКА
- ПРОФИЛИРОВАНИЕ РАВНОПРОЧНЫХ ДИСКОВ
- ОСНОВНЫЕ УРАВНЕНИЯ ПРИ РАСЧЕТЕ ДИСКОВ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ ТОЛЩИНЫ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ ТОЛЩИНЫ
- ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- УПРУГАЯ ЛИНИЯ СТЕРЖНЯ
- ОПРЕДЕЛЕНИЕ ПРОГИБОВ С ПОМОЩЬЮ ИНТЕГРАЛА МОРА
- ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- Глава 18. КРУЧЕНИЕ СТЕРЖНЕЙ
- СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
- СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
- РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- ТРУБЧАТЫЕ СТЕРЖНИ
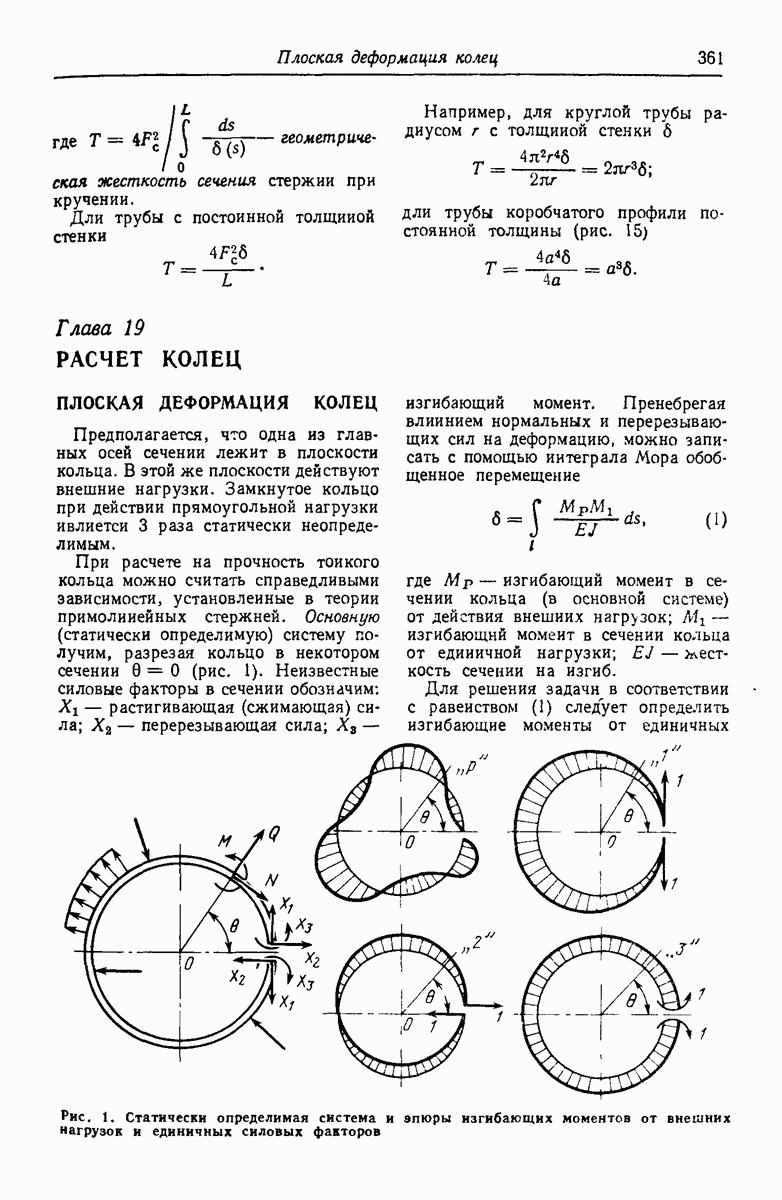
- Глаза 19. РАСЧЕТ КОЛЕЦ
- ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- Глава 20. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
- ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
- ВЛИЯНИЕ НАЧАЛЬНОГО ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ НА ВЫПУЧИВАНИЕ СТЕРЖНЯ
- РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ. ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАГРЕВЕ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ СКРУЧИВАНИИ
- Глава 21. КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
- МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- КРУТИЛЬНЫЕ КОЛЕБАНИЯ
- ИЗГИБНЫЕ КОЛЕБАНИЯ
- ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ
- Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ
- ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ
- Глава 23. РАСЧЕТ ПЛАСТИНОК
- ПРОРЫВНЫЕ МЕМБРАНЫ
- ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ
- Глава 24. РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК
- РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК
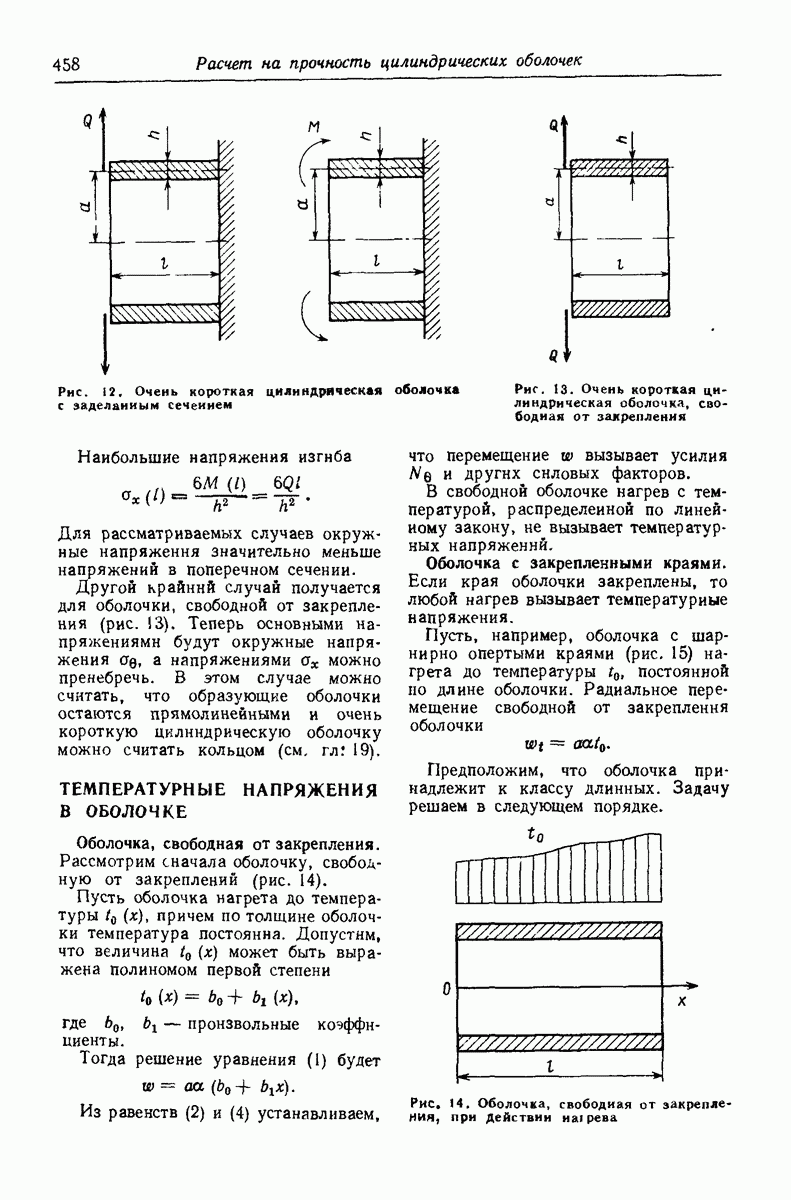
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
- Глава 25. УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК
- УСТОЙЧИВОСТЬ КОЛЕЦ
- УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ КОНИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ
- УСТОЙЧИВОСТЬ АНИЗОТРОПНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК
- Глава 26. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
- ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД
- МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- ДИНАМИЧЕСКИЕ РАСЧЕТЫ
- Глава 27. РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- УРАВНЕНИЯ ПЛАСТИЧНОСТИ
- УРАВНЕНИЯ ПОЛЗУЧЕСТИ
- РАСЧЕТ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ)
- РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ НАГРУЖЕНИИ
- Глава 28. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЙ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ И ПОЛЗУЧЕСТИ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- Глава 29. КОНТАКТНЫЕ ЗАДАЧИ
- КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ ФОРМЫ
- КОНСТРУКЦИОННЫЕ КОНТАКТНЫЕ ЗАДАЧИ
- ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ
- ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ
- Глава 30. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
- КРИТЕРИИ ДЛИТЕЛЬНОЙ И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ
- Глава 31. РАСЧЕТ НА УСТАЛОСТЬ
- ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ
- УСЛОВИЯ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ
- СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ
- Глава 32. ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ
- СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ
- Глава 33. ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ
- ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ
- ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ
- ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ
- ПРОГНОЗИРУЕМАЯ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ
- ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- НАДЕЖНОСТЬ СИСТЕМЫ ПОСЛЕДОВАТЕЛЬНЫХ ЭЛЕМЕНТОВ
- НАДЕЖНОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ
- АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ
- РАСЧЕТ ЧИСЛА ИЗДЕЛИЙ, НАХОДЯЩИХСЯ В ЭКСПЛУАТАЦИИ
- КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
- Глава 34. ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН
- УПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ
- ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ ОБРАБОТКА
- ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ
- Глава 35. ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ
- МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОД РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ
- ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- Глава 36. ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ
- СПИСОК ЛИТЕРАТУРЫ