| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
Максимальное касательное напряжение действует на середине большей стороны  как показано на рис. 6:
как показано на рис. 6:


Рис. 6. Касательные напряжения при кручении стержня прямоугольного сечения
Коэффициент с достаточной точностью может быть найден по приближенной формуле

Угол поворота на единицу длины стержня

Для сечения в виде вытянутого прямоугольника

Таким образом,

Для тонкостенных стержней (открытого профиля)

где  — толщина стенки;
— толщина стенки;  — элемент дуги средней линии, длина которой
— элемент дуги средней линии, длина которой 
Наибольшее напряжение

При стесненном кручении стержня с сечением в виде вытянутого прямоугольника наибольшее нормальное напряжение в заделке может достигать 
Эти напряжения быстро затухают, т. е. носят местный характер. У тонкостенных стержней (типа швеллера, двутавра) искажение напряженного состояния в районе заделки затухает медленно и при расчете следует учитывать стесненное кручение. Это составляет предмет исследований теории тонкостенных стержней. Если для сечения стержня параметр

где  — минимальный момент инерции сечения, то можно применять обычную теорию изгиба и кручения стержней.
— минимальный момент инерции сечения, то можно применять обычную теорию изгиба и кручения стержней.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
- НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
- РАСТЯЖЕНИЕ И СЖАТИЕ
- ИЗГИБ
- СРЕЗ И СМЯТИЕ
- КРУЧЕНИЕ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- НАПРЯЖЕННО-ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ
- Глава 2. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ
- СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- СВОЙСТВА ПРИ ВЫСОКИХ И НИЗКИХ ТЕМПЕРАТУРАХ
- СВОЙСТВА ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- МАЛОЦИКЛОВАЯ И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ
- ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН
- РАЗРУШЕНИЯ И ИЗЛОМЫ
- ОЦЕНКА ПРОЧНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ПРОЧНОСТИ ПО НЕСУЩЕЙ СПОСОБНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- РАСЧЕТЫ НА ПРОЧНОСТЬ
- МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ
- УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- РАСЧЕТ НАПРЯЖЕНИЙ КРУЧЕНИЯ
- ВЫБОР ПРЕДВАРИТЕЛЬНОЙ ЗАТЯЖКИ
- РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СОЕДИНЕНИЯХ
- ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 4. ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
- ТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ
- НАПРЯЖЕННОЕ СОСТОЯНИЕ ФЛАНЦА И ТРУБЫ
- Глава 5. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- РАСЧЕТ ШЛИЦЕВЫХ СОЕДИНЕНИЙ НА ПРОЧНОСТЬ
- ИЗНАШИВАНИЕ СОЕДИНЕНИЙ
- Глава 6. СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ НАТЯГОМ
- РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 7. СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ
- КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ
- РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ВЛИЯНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- ПАЯНЫЕ СОЕДИНЕНИЯ
- Глава 8. ВАЛЫ
- КОНСТРУКТИВНЫЕ ФОРМЫ И МАТЕРИАЛЫ ВАЛОВ
- ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
- НАГРУЗКИ НА ВАЛЫ И РАСЧЕТНЫЕ СХЕМЫ
- РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА КОЛЕБАНИЯ
- КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- Глава 9. ПОДШИПНИКИ КАЧЕНИЯ
- ОСНОВНЫЕ КОНСТРУКЦИИ И ХАРАКТЕРИСТИКИ
- ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ В ПОДШИПНИКАХ КАЧЕНИЯ
- ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ ПОДШИПНИКОВ
- ЭКВИВАЛЕНТНАЯ НАГРУЗКА И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
- СМАЗЫВАНИЕ ПОДШИПНИКОВ
- НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ
- Глава 10. ПРУЖИНЫ
- ВИТЫЕ ПРУЖИНЫ
- РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
- РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
- ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- ПРОРЕЗНЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ ПРУЖИНЫ
- РЕЗИНОВЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- Глава 11. ЗУБЧАТЫЕ ПЕРЕДАЧИ
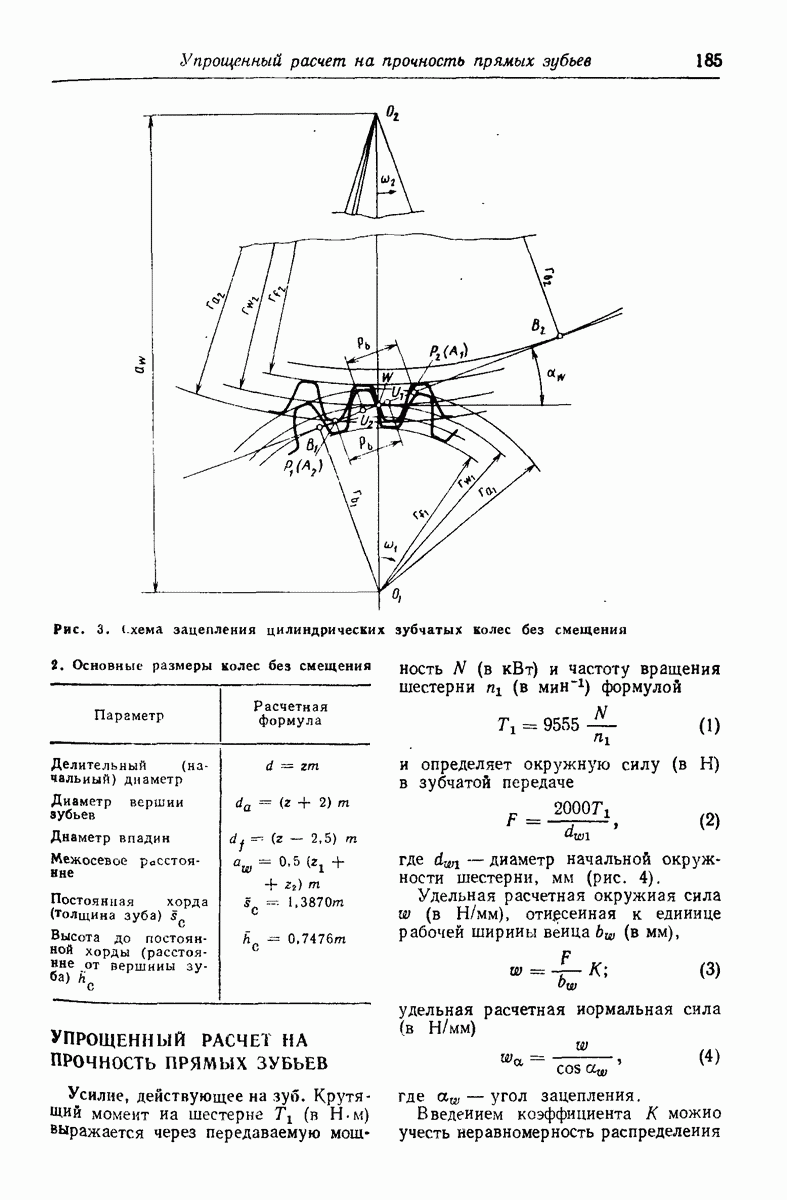
- УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ
- СТРУКТУРА РАСЧЕТНЫХ ФОРМУЛ ПО ГОСТ 21354—87
- НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ
- РАСЧЕТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
- РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ
- РАБОТА ПЕРЕДАЧ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ
- ОСОБЕННОСТИ РАСЧЕТА ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ М. Л. НОВИКОВА
- Глава 12. ШАРИКОВИНТОВЫЕ ПЕРЕДАЧИ
- КОНСТРУКЦИИ ПЕРЕДАЧ И МАТЕРИАЛЫ
- РАСЧЕТ ПЕРЕДАЧ
- Глава 13. РЕМЕННЫЕ ПЕРЕДАЧИ
- МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ
- РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
- ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ
- ПОРЯДОК РАСЧЕТА И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ
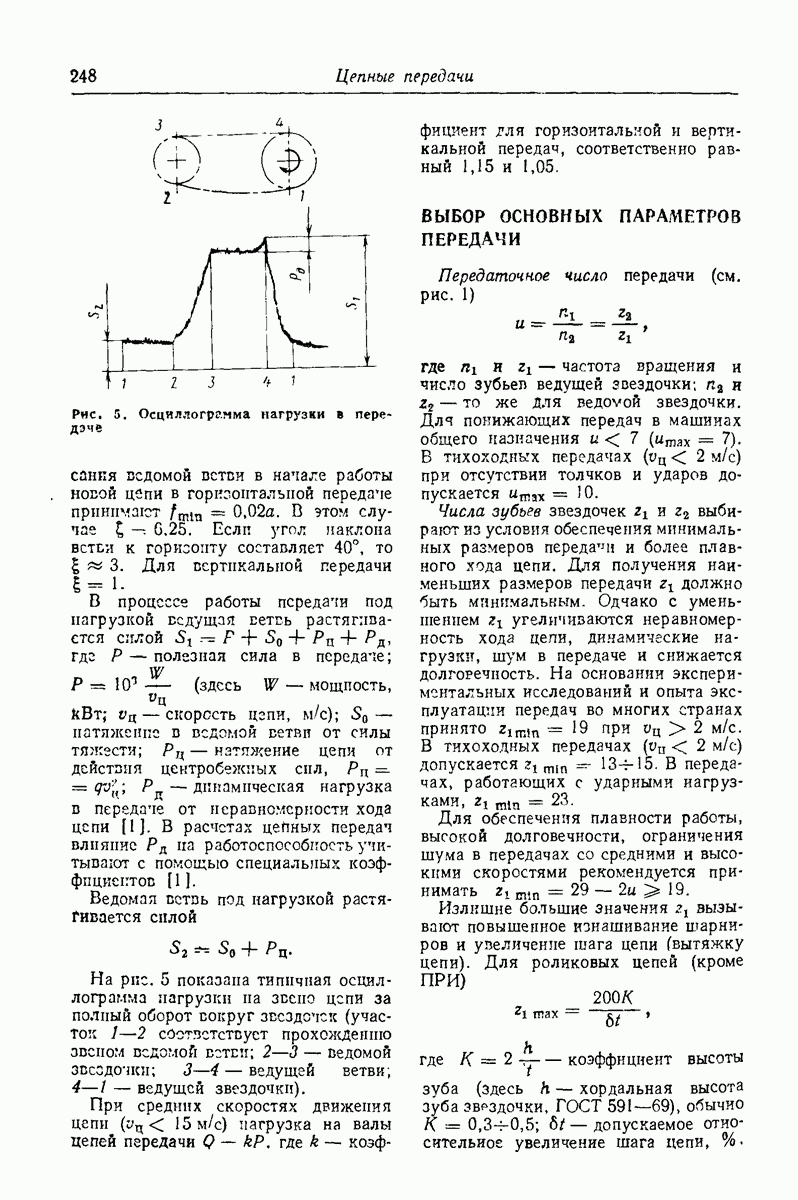
- Глава 14. ЦЕПНЫЕ ПЕРЕДАЧИ
- СИЛЫ В ПЕРЕДАЧЕ
- ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ
- НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ
- ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ
- ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ
- Глава 15. РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
- РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ
- РАСЧЕТ ШАТУНОВ
- РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА
- РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ
- РАСЧЕТ ДНИЩА ПОРШНЯ
- ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОРПУСА
- РАСЧЕТ КЛАПАННЫХ ПРУЖИН
- Глава 16. РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН
- РАСЧЕТ ЛОПАТОК НА ИЗГИБ
- ЗАПАС ПРОЧНОСТИ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ
- РАВНОПРОЧНЫЕ ЛОПАТКИ
- ОХЛАЖДАЕМЫЕ ЛОПАТКИ
- ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК
- ЗАКРУЧЕННЫЕ ЛОПАТКИ
- ШАРНИРНЫЕ ЛОПАТКИ
- БАНДАЖИРОВАННЫЕ ЛОПАТКИ
- РАСЧЕТ ЗАМКОВ ЛОПАТОК
- ВИБРАЦИЯ ЛОПАТОК
- РАСЧЕТ ДИСКОВ. НАПРЯЖЕНИЯ НА КОНТУРЕ
- ЗАПАСЫ ПРОЧНОСТИ ДИСКА
- ПРОФИЛИРОВАНИЕ РАВНОПРОЧНЫХ ДИСКОВ
- ОСНОВНЫЕ УРАВНЕНИЯ ПРИ РАСЧЕТЕ ДИСКОВ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ ТОЛЩИНЫ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ ТОЛЩИНЫ
- ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- УПРУГАЯ ЛИНИЯ СТЕРЖНЯ
- ОПРЕДЕЛЕНИЕ ПРОГИБОВ С ПОМОЩЬЮ ИНТЕГРАЛА МОРА
- ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- Глава 18. КРУЧЕНИЕ СТЕРЖНЕЙ
- СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
- СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
- РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- ТРУБЧАТЫЕ СТЕРЖНИ
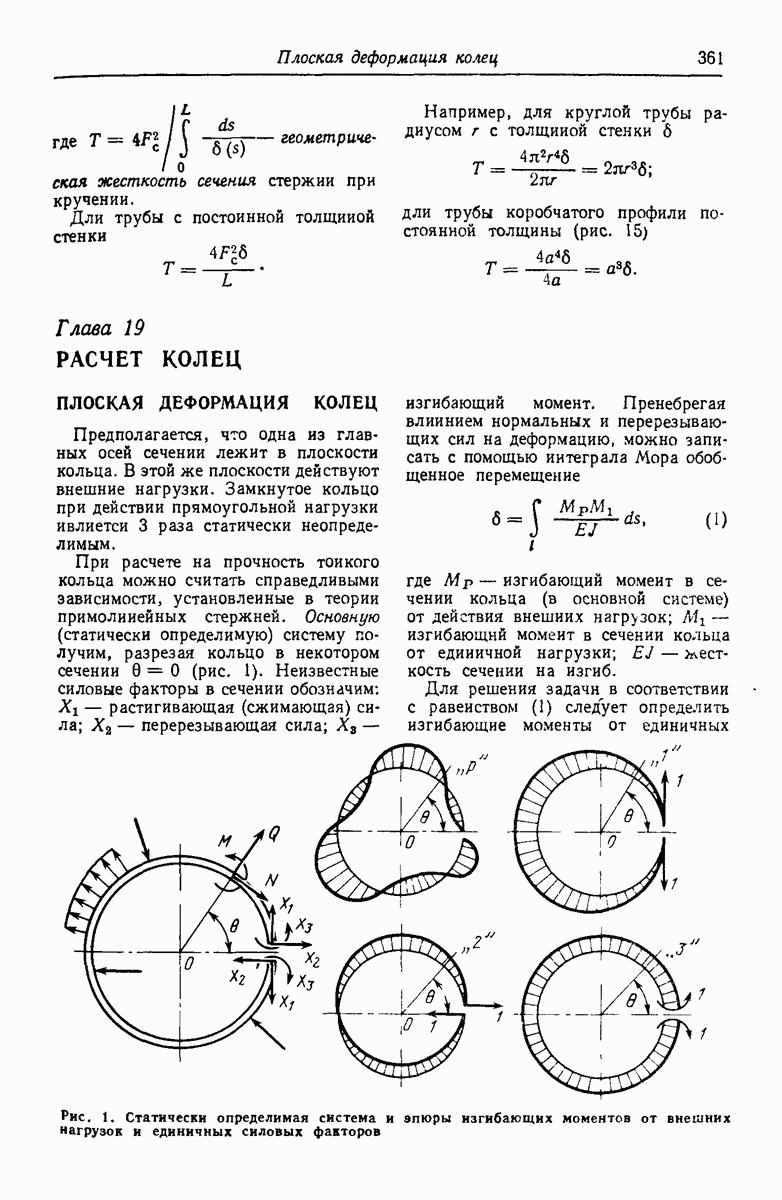
- Глаза 19. РАСЧЕТ КОЛЕЦ
- ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- Глава 20. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
- ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
- ВЛИЯНИЕ НАЧАЛЬНОГО ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ НА ВЫПУЧИВАНИЕ СТЕРЖНЯ
- РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ. ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАГРЕВЕ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ СКРУЧИВАНИИ
- Глава 21. КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
- МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- КРУТИЛЬНЫЕ КОЛЕБАНИЯ
- ИЗГИБНЫЕ КОЛЕБАНИЯ
- ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ
- Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ
- ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ
- Глава 23. РАСЧЕТ ПЛАСТИНОК
- ПРОРЫВНЫЕ МЕМБРАНЫ
- ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ
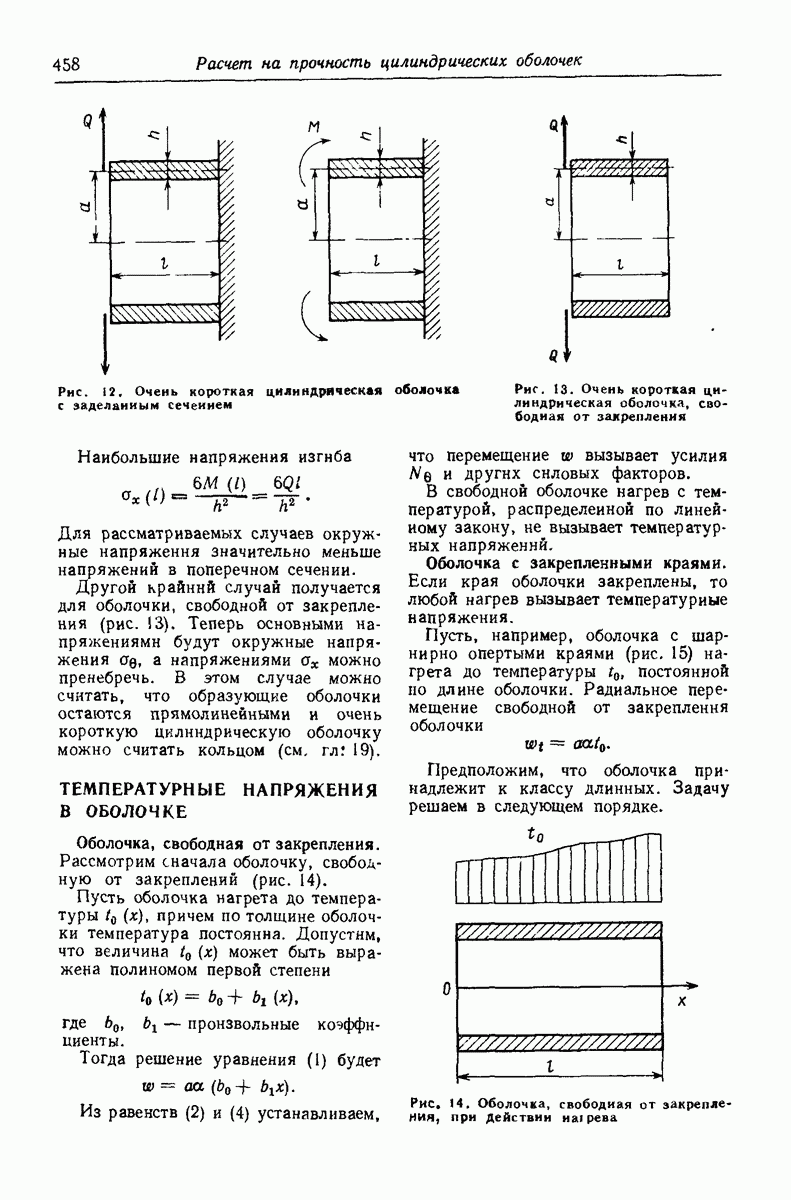
- Глава 24. РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК
- РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
- Глава 25. УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК
- УСТОЙЧИВОСТЬ КОЛЕЦ
- УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ КОНИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ
- УСТОЙЧИВОСТЬ АНИЗОТРОПНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК
- Глава 26. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
- ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД
- МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- ДИНАМИЧЕСКИЕ РАСЧЕТЫ
- Глава 27. РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- УРАВНЕНИЯ ПЛАСТИЧНОСТИ
- УРАВНЕНИЯ ПОЛЗУЧЕСТИ
- РАСЧЕТ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ)
- РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ НАГРУЖЕНИИ
- Глава 28. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЙ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ И ПОЛЗУЧЕСТИ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- Глава 29. КОНТАКТНЫЕ ЗАДАЧИ
- КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ ФОРМЫ
- КОНСТРУКЦИОННЫЕ КОНТАКТНЫЕ ЗАДАЧИ
- ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ
- ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ
- Глава 30. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
- КРИТЕРИИ ДЛИТЕЛЬНОЙ И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ
- Глава 31. РАСЧЕТ НА УСТАЛОСТЬ
- ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ
- УСЛОВИЯ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ
- СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ
- Глава 32. ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ
- СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ
- Глава 33. ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ
- ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ
- ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ
- ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ
- ПРОГНОЗИРУЕМАЯ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ
- ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- НАДЕЖНОСТЬ СИСТЕМЫ ПОСЛЕДОВАТЕЛЬНЫХ ЭЛЕМЕНТОВ
- НАДЕЖНОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ
- АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ
- РАСЧЕТ ЧИСЛА ИЗДЕЛИЙ, НАХОДЯЩИХСЯ В ЭКСПЛУАТАЦИИ
- КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
- Глава 34. ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН
- УПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ
- ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ ОБРАБОТКА
- ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ
- Глава 35. ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ
- МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОД РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ
- ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- Глава 36. ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ
- СПИСОК ЛИТЕРАТУРЫ