ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД

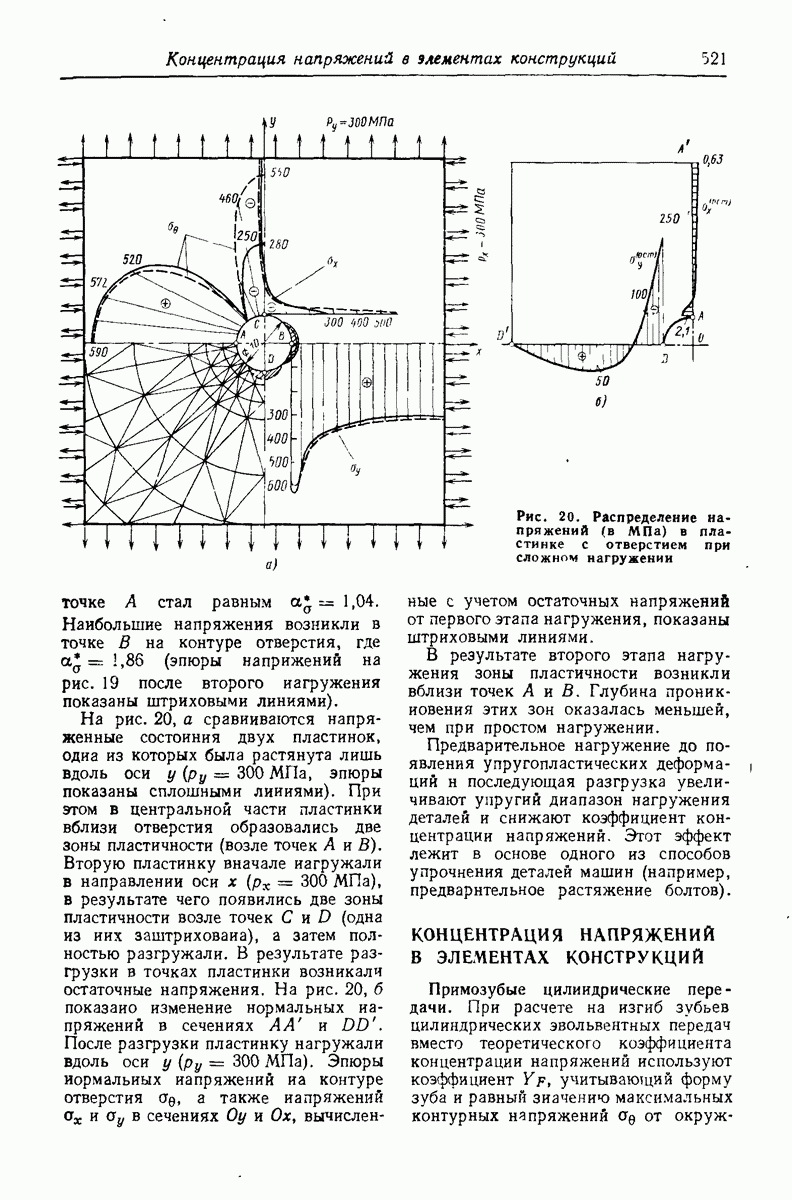
Сущность метода поисиим на примере плоской задачи теории упругости при отсутствии температурных и дополнительных деформаций.

Учитывая уравнение (6) и связь между деформациями и перемещениями (соответственно в направлении осей можно записать

где для плоского напряженного состояния коэффициенты

а для плоской деформации

В равенстве тела (единичной толщины) в плоскости

Вариационное уравнение (1) при отсутствии массовых сил

где — проекции на оси x и у компонентов внешней нагрузки на границе области с контуром

Для получения приближенного решения уравнения (18) удобно контур области аппроксимировать конечным числом прямолинейных отрезков. Исследуемая область покрывается нерегулярной (или регулярной) сеткой, состоящей линий Точки пересечения прямоугольной сетки должны совпадать на границах области с точками на отрезках, аппроксимирующих контур (рис. 1, а).

Кроме того, на область наносят дополнительную сетку, линии которой проходят посередине линий основной сетки. Точки пересечения линий

Рис. 1. Сеточная разметка пластинки

основной сетки называют узлами. Подобласти, границы которых образованы контурными отрезками (линиями основной сетки) и линиями дополнительной сетки, называют ячейками. При этом каждая ячейка (заштрихована на рис. 1, б) содержит одну узловую точку и может быть прямоугольником либо треугольником.

В качестве основных неизвестных принимаем смещения в узловых точках где — номер узла.

Потенциальную энергию деформации каждой ячейки можно найти в предположении, что смещения точек между узлами изменяются линейно и их производные остаются постоянными в каждой ячейке.

Используем конечно-разностные соотношения для первых производных в точке (см. рис. 1):

где — соответственно номера горизонтали и вертикали; и — шаги сетки (знаки указывают, что соответствующие шаги приняты в направлении увеличения или уменьшения координаты).

С учетом равенства (16) получим приближенное выражение для потенциальной энергии элементарной ячейки

1 с центральным узлом , см. рис. 1, б:

(см. скан)

где «вес» ячейки — для ячейки, целиком лежащей внутри области; то же для ячейки, примыкающей к косой границе (треугольной ячейки); то же для ячейки вне области — номер центрального узла.

Влияние температуры учитывается введением в выражение (19) дополнительного слагаемого:

Так как аппроксимации для каждой ячейки имеют вид (19), то, суммируя потенциальную энергию деформации (19) по всем ячейкам сеточной области, получим соотношение для полной потенциальной энергии деформации

где число узлов на области.

Вариация потенциальной энергии деформации

Потенциальная функция внешних сил

где компоненты внешних сил, относящиеся к внешнему граничному узлу номер граничного узла; — длина элемента границы возле узла

Вариация потенциальной функции внешних сил

Так как вариации произвольны, то из условия (18) следует:

Величины входят в соотношения (19) лишь для двенадцати (из шестнадцати) ячеек, окружающих узел .

Поэтому, записав соотношения типа (19) для каждой из 12 ячеек, прилежащих к узлу продифференцировав их отдельно по и просуммировав полученные выражения согласно равенствам (21), с учетом равенств (22) и (23) получим два разрешающих уравнения, связывающих смещения в узле с неизвестными смещениями в восьми соседних узлах (см. рис. 1, б) и действующими в них компонентами внешней нагрузки.

Записывая разрешающие уравнения для всех узлов сеточной области, получим линейных алгебраических уравнений; здесь — число неизвестных смещений соответственно которые можно представить в матричной форме

где — симметричная, положительно определенная матрица коэффициентов; - вектор-столбец с компонентами смещений — известный вектор-столбец, характеризующий внешние нагрузки.

Система линейных алгебраических уравнений относительно смещений решается достаточно просто одним из известных методов. Для получения единственного решения система дополняется граиичиыми условиями в перемещениях.

В результате расчета при заданных нагрузках на контуре находят смещения во всех узлах сеточной области. Далее можно найти деформации и напряжения в каждом узле.

Примеры расчета напряженного состояния в элементах конструкции вариационно-разностным методом приведены в гл. 28 и 29.

Вывод разрешающих уравнений для пространственной задачи аналогичен приведенному.