| << Предыдущий параграф | Следующий параграф >> |
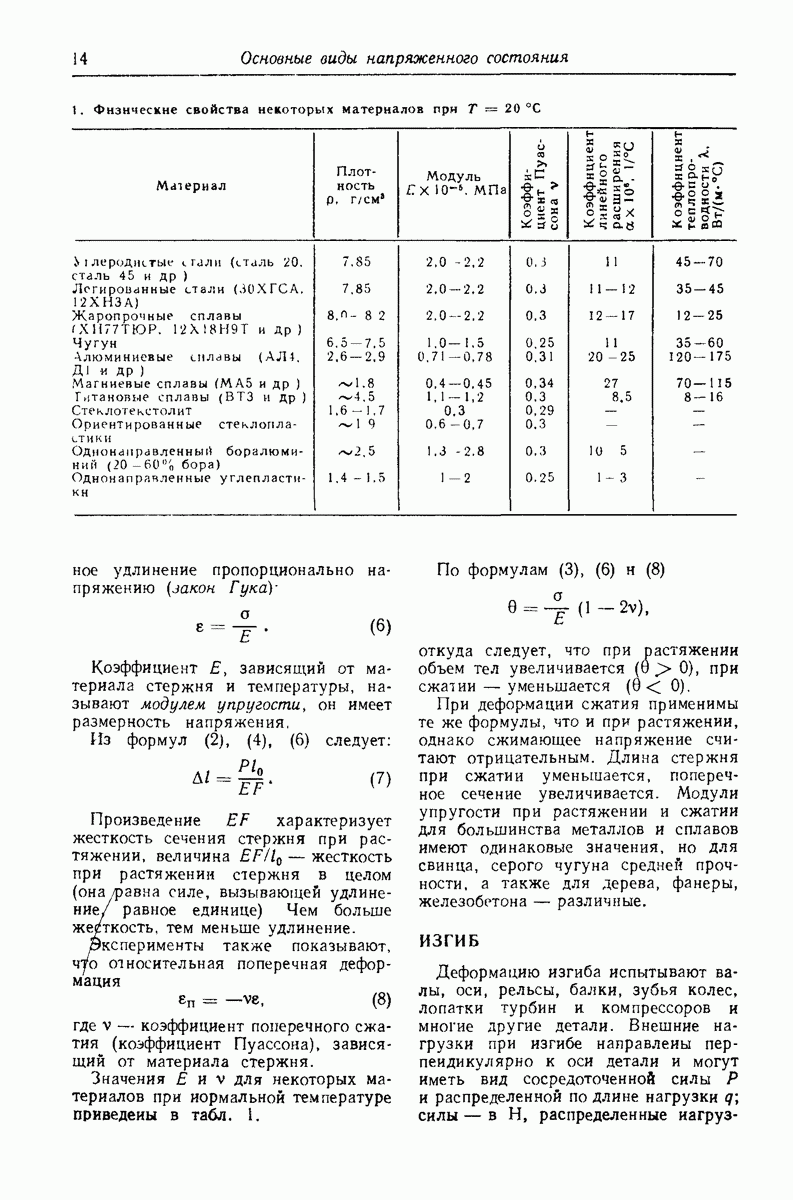
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ДИНАМИЧЕСКИЕ РАСЧЕТЫ
Численные методы широко используются при расчетах собственных частот и форм колебаний элементов конструкций, напряжений при установившихся вынужденных колебаниях, при исследованиях границ динамической устойчивости и при решении ряда других сложных проблем динамики. Многие из таких методов, относящихся главным образом к стационарным динамическим процессам, широко освещены в технической литературе [2 и др.].
Рис. 4. (см. скан) Разбиение стержня на элементы (а) и напряженно-инерционное состояние элементов в моменты времени t (б) и  (в)
(в)
Более сложными и менее разработанными являются методы расчета нестационарных задач для деформируемых конструкций, в особенности при меняющихся граничных условиях (ударное и виброударное нагружения, переходы через резонансные состояния, динамика систем с зазорами и переменными точками контакта, воздействие движущихся нагрузок и пр.). К наиболее математически простым, а вместе с тем физически корректным методам численного анализа нестационарных явлений в континуальных одномерных системах относится разработанный в последние годы метод прямого математического моделирования  на ЭВМ процессов распространения волн механических возмущений (напряжений, деформаций, скоростей и т.п.)
на ЭВМ процессов распространения волн механических возмущений (напряжений, деформаций, скоростей и т.п.) 
Его сущность изложим на примере расчета продольных волновых процессов в упругом стержне длиной  постоянного поперечного сечения площадью
постоянного поперечного сечения площадью  боковая поверхность которого свободна от нагрузок.
боковая поверхность которого свободна от нагрузок.
Разобьем стержень на  равных элементов длиной
равных элементов длиной  номера элементов
номера элементов  номера сечений
номера сечений  (рис. 4, а). Пусть в момент времени
(рис. 4, а). Пусть в момент времени  каждый элемент имеет постоянные в его пределах продольную скорость
каждый элемент имеет постоянные в его пределах продольную скорость  напряжение
напряжение  и деформацию
и деформацию  причем
причем  , где Е — модуль упругости материала (рис. 4, б). На границах смежных элементов эти параметры могут отличаться на произвольную величину (иметь «сильные» разрывы), которые, однако, в тот же момент времени
, где Е — модуль упругости материала (рис. 4, б). На границах смежных элементов эти параметры могут отличаться на произвольную величину (иметь «сильные» разрывы), которые, однако, в тот же момент времени  должны распасться, в результате чего напряжение на правой границе
должны распасться, в результате чего напряжение на правой границе  элемента
элемента  станет равным напряжению на левой границе
станет равным напряжению на левой границе  элемента то же относится к границе
элемента то же относится к границе  элементов и к скоростям:
элементов и к скоростям:

Зоны «возмущения» с параметрами (58) будут распространяться в глубь соответствующих элементов в соответствии с законами механики упругого тела со скоростью с, так что
глубина их проникновения за время  будет
будет  . Так, для правой границы
. Так, для правой границы  элемента получим следующие соотношения.
элемента получим следующие соотношения.
Закон сохранения импульса. Изменение количества движения  массы
массы  должно быть равно импульсу постоянных сил
должно быть равно импульсу постоянных сил  действующих на границах этой массы в течение времени
действующих на границах этой массы в течение времени  откуда
откуда

Условие сплошности тела. Разность перемещений  границ зоны возмущения за время
границ зоны возмущения за время  должна быть равна ее абсолютному удлинению
должна быть равна ее абсолютному удлинению  откуда
откуда

Закон упругости. Изменение напряжений  — связано с изменением деформаций
— связано с изменением деформаций  соотношением
соотношением

Выражения (59)-(61) удовлетворяются совместно только при

что соответствует известной формуле распространения упругих волн в стержне.
Аналогично для левой границы  элемента
элемента

Решив уравнения  совместно при учете первых двух условий (58), найдем значения напряжений и скоростей, распространяющихся в глубь
совместно при учете первых двух условий (58), найдем значения напряжений и скоростей, распространяющихся в глубь  элемента от его границы с
элемента от его границы с  элементом:
элементом:

т. е. напряжение и скорость изменятся на 
Аналогично для левой границы  элемента
элемента

Изменение параметров составит 
По принципу суперпозиции линейных деформаций волны (64) и (65) распространяются независимо, поэтому эти соотношения будут справедливы в течение времени  до встречи с противоположными границами элемента. В момент времени
до встречи с противоположными границами элемента. В момент времени  во всем
во всем  элементе установятся новые напряжения
элементе установятся новые напряжения

и скорости

Формулы (64)-(67) образуют систему рекуррентных (повторяющихся) соотношений, позволяющих по известным в момент  значениям напряжений и скоростей в
значениям напряжений и скоростей в  и в двух соседних
и в двух соседних  элементах найти новые значения напряжений и скоростей в
элементах найти новые значения напряжений и скоростей в  элементе для момента времени
элементе для момента времени  Добавляя условия на внешних границах стержня (заданные напряжения, скорости, перемещения) и последовательно решая эти системы для всех элементов с шагом по времени
Добавляя условия на внешних границах стержня (заданные напряжения, скорости, перемещения) и последовательно решая эти системы для всех элементов с шагом по времени  получим точную и исчерпывающую картину динамического процесса в стержне при самых произвольных условиях нагружения.
получим точную и исчерпывающую картину динамического процесса в стержне при самых произвольных условиях нагружения.
В более общих постановках задачи произвольно меняющиеся по времени нагрузки аппроксимируются ступенчатыми функциями с постоянными в пределах  значениями. Распределенные по длине стержня нагрузки
значениями. Распределенные по длине стержня нагрузки
считаются приложенными на границах элементов в сечениях  . В число внешних сил могут включаться силы трения, неизвестные силы реакции и прочие. Стержни переменного сечения представляются ступенчатыми с постоянными в пределах элементов площадями
. В число внешних сил могут включаться силы трения, неизвестные силы реакции и прочие. Стержни переменного сечения представляются ступенчатыми с постоянными в пределах элементов площадями  . Если Е и
. Если Е и  меняются по длине стержня, он разбивается на элементы разной длины так, чтобы их длины
меняются по длине стержня, он разбивается на элементы разной длины так, чтобы их длины  удовлетворяли условию
удовлетворяли условию  , где
, где  при
при  одинаковом для всего стержня. При этом в пределах
одинаковом для всего стержня. При этом в пределах  элемента принимается
элемента принимается  . При уменьшении отрезков времени
. При уменьшении отрезков времени  , а следовательно, и
, а следовательно, и  принятые условия позволяют воспроизводить переменные характеристики с необходимой точностью.
принятые условия позволяют воспроизводить переменные характеристики с необходимой точностью.
Так как при принятых допущениях соотношения  являются точными, то процесс расчета абсолютно устойчив при любом числе элементов и временных этапов.
являются точными, то процесс расчета абсолютно устойчив при любом числе элементов и временных этапов.
Для общего случая зависимости типа (64), (65) можно объединить, записав их для упругого стержня в виде

где 
Напряжения определяются затем по формулам (59) или  Условия равновесия на границах элементов
Условия равновесия на границах элементов

Если  — перемещение границы
— перемещение границы  элемента в начале этапа, то в конце его
элемента в начале этапа, то в конце его

Пример. Упругий стержень длиной 21 и площадью поперечного сечения  ударяет со скоростью
ударяет со скоростью  но упругому стержню длиной
но упругому стержню длиной  и площадью
и площадью  из того же материала, имеющему такую же встречную скорость
из того же материала, имеющему такую же встречную скорость  (рис. 5, а). Определим скорость отскока огск
(рис. 5, а). Определим скорость отскока огск  упругом ударе и изучим динамическую картину соударения.
упругом ударе и изучим динамическую картину соударения.
Рис. 5. (см. скан) К расчету соударения  стержней
стержней
Так как массы и скорости стержней равны, то по элементарной теории соударения упругих тел они разлетятся с той же скоростью  Однако действительная картина удара из-за разной конфигурации стержней будет иной.
Однако действительная картина удара из-за разной конфигурации стержней будет иной.
Представим 1-й стержень в виде двух элементов, 2-й — в виде одного элемента длиной  Начальные условия (в момент начала контакта).
Начальные условия (в момент начала контакта). 
Граничные условия:  При контакте стержней
При контакте стержней  после отскока
после отскока  Первый шаг по времени
Первый шаг по времени 
Первый элемент
левая граница, формула (63):

правая граница, вторая формула

овые значения

Второй элемент
левая граница, 
правая граница, формула (68) при 

 есть контакт
есть контакт
Новые значения

Третий элемент,
левая граница

правая граница

Новые значения

Затем проводится аналогичный расчет для момента времени  и далее в том же порядке На рис 5, 6 приведены результаты расчета в виде зависимостей
и далее в том же порядке На рис 5, 6 приведены результаты расчета в виде зависимостей  номера шага
номера шага  . В момент
. В момент  когда упругая волна, отраженная от левой свободной границы первого элемента, возвращается к плоскости контакта, происходит отскок стержней В этот момент второй стержень не напряжен к имеет скорость
когда упругая волна, отраженная от левой свободной границы первого элемента, возвращается к плоскости контакта, происходит отскок стержней В этот момент второй стержень не напряжен к имеет скорость  которую он и сохраняет в дальнейшем Элементы первого стержня при этом имеют такую же скорость
которую он и сохраняет в дальнейшем Элементы первого стержня при этом имеют такую же скорость  но они испытывают напряжение растяжения
но они испытывают напряжение растяжения  всех точках, кроме внешних границ, что является источником последующих колебаний) В дальнейшем первый стержень будет двигаться с той же средней скоростью
всех точках, кроме внешних границ, что является источником последующих колебаний) В дальнейшем первый стержень будет двигаться с той же средней скоростью  но в нем будут происходить незатухающие (в отсутствии сил внутреннего трения) колебательные процессы в виде волн напряжений и скоростей, как показано на рис
но в нем будут происходить незатухающие (в отсутствии сил внутреннего трения) колебательные процессы в виде волн напряжений и скоростей, как показано на рис  Полная энергия системы стержней после отскока сохраняется постоянной и равной (например, при определении ее в моменты
Полная энергия системы стержней после отскока сохраняется постоянной и равной (например, при определении ее в моменты 

что в точности равно начальной кинетической энергии стержней и подтверждает упругий характер удара.
Потеря скорости из-за упругих колебаний стержней в данном случае составляет 
Из приведенного примера следует, что расчет чрезвычайно легко алгоритмизируется.
Методом прямого математического моделирования решены задачи кручения и изгиба стержней, деформации струн, плоских и сферических волн, деформации упруговязких и упругопластичных материалов. Им успешно решаются многие технические задачи, связанные с проблемами анализа нестационарных процессов в деформируемых элементах машин и конструкций, с динамикой поездов и пр. [4, 5, 6]
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
- НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
- РАСТЯЖЕНИЕ И СЖАТИЕ
- ИЗГИБ
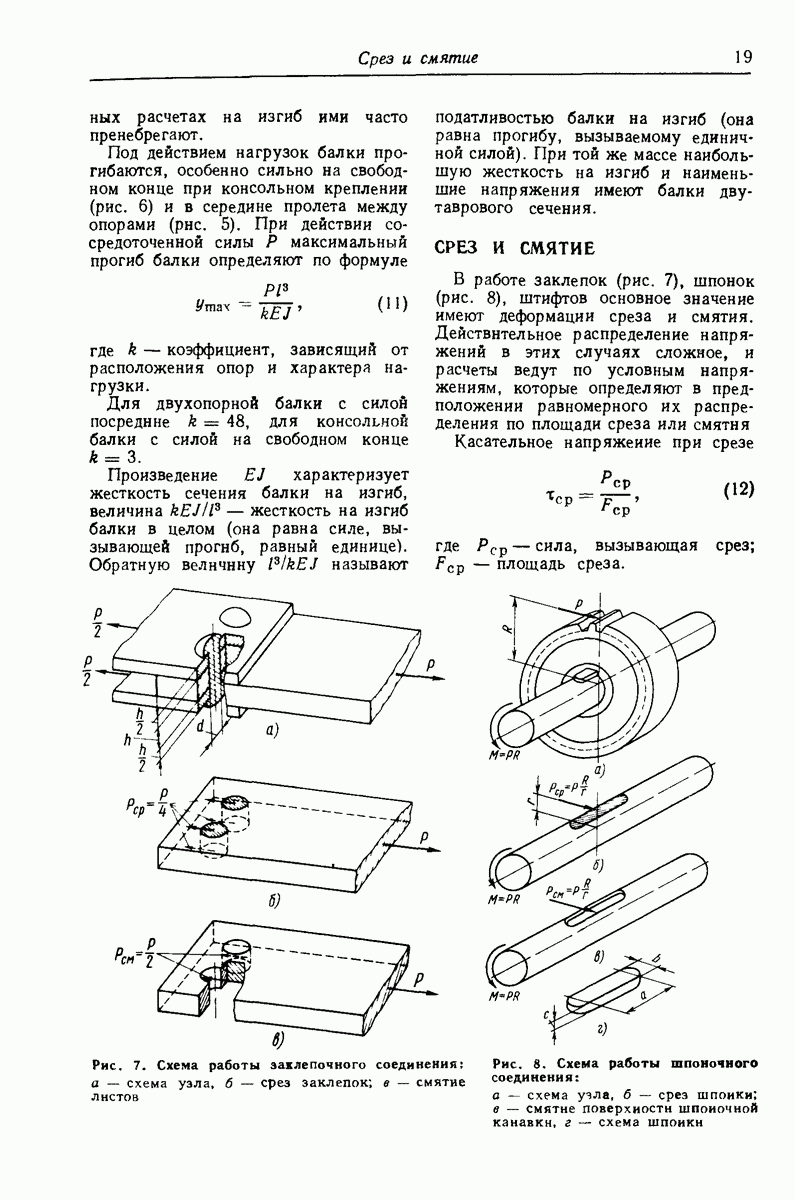
- СРЕЗ И СМЯТИЕ
- КРУЧЕНИЕ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- НАПРЯЖЕННО-ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ
- Глава 2. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ
- СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- СВОЙСТВА ПРИ ВЫСОКИХ И НИЗКИХ ТЕМПЕРАТУРАХ
- СВОЙСТВА ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- МАЛОЦИКЛОВАЯ И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ
- ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН
- РАЗРУШЕНИЯ И ИЗЛОМЫ
- ОЦЕНКА ПРОЧНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ПРОЧНОСТИ ПО НЕСУЩЕЙ СПОСОБНОСТИ
- ЗАПАСЫ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
- ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
- РАСЧЕТЫ НА ПРОЧНОСТЬ
- МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ
- УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
- РАСЧЕТ НАПРЯЖЕНИЙ КРУЧЕНИЯ
- ВЫБОР ПРЕДВАРИТЕЛЬНОЙ ЗАТЯЖКИ
- РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СОЕДИНЕНИЯХ
- ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 4. ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
- ТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ
- УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ
- НАПРЯЖЕННОЕ СОСТОЯНИЕ ФЛАНЦА И ТРУБЫ
- Глава 5. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
- РАСЧЕТ ШЛИЦЕВЫХ СОЕДИНЕНИЙ НА ПРОЧНОСТЬ
- ИЗНАШИВАНИЕ СОЕДИНЕНИЙ
- Глава 6. СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ НАТЯГОМ
- РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ
- ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- Глава 7. СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ
- КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ
- РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
- ВЛИЯНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
- ПАЯНЫЕ СОЕДИНЕНИЯ
- Глава 8. ВАЛЫ
- КОНСТРУКТИВНЫЕ ФОРМЫ И МАТЕРИАЛЫ ВАЛОВ
- ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
- НАГРУЗКИ НА ВАЛЫ И РАСЧЕТНЫЕ СХЕМЫ
- РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА КОЛЕБАНИЯ
- КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- Глава 9. ПОДШИПНИКИ КАЧЕНИЯ
- ОСНОВНЫЕ КОНСТРУКЦИИ И ХАРАКТЕРИСТИКИ
- ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ В ПОДШИПНИКАХ КАЧЕНИЯ
- ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ ПОДШИПНИКОВ
- ЭКВИВАЛЕНТНАЯ НАГРУЗКА И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
- СМАЗЫВАНИЕ ПОДШИПНИКОВ
- НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ
- Глава 10. ПРУЖИНЫ
- ВИТЫЕ ПРУЖИНЫ
- РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
- РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
- РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
- РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
- ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- ПРОРЕЗНЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ПРУЖИНЫ
- КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ ПРУЖИНЫ
- РЕЗИНОВЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- Глава 11. ЗУБЧАТЫЕ ПЕРЕДАЧИ
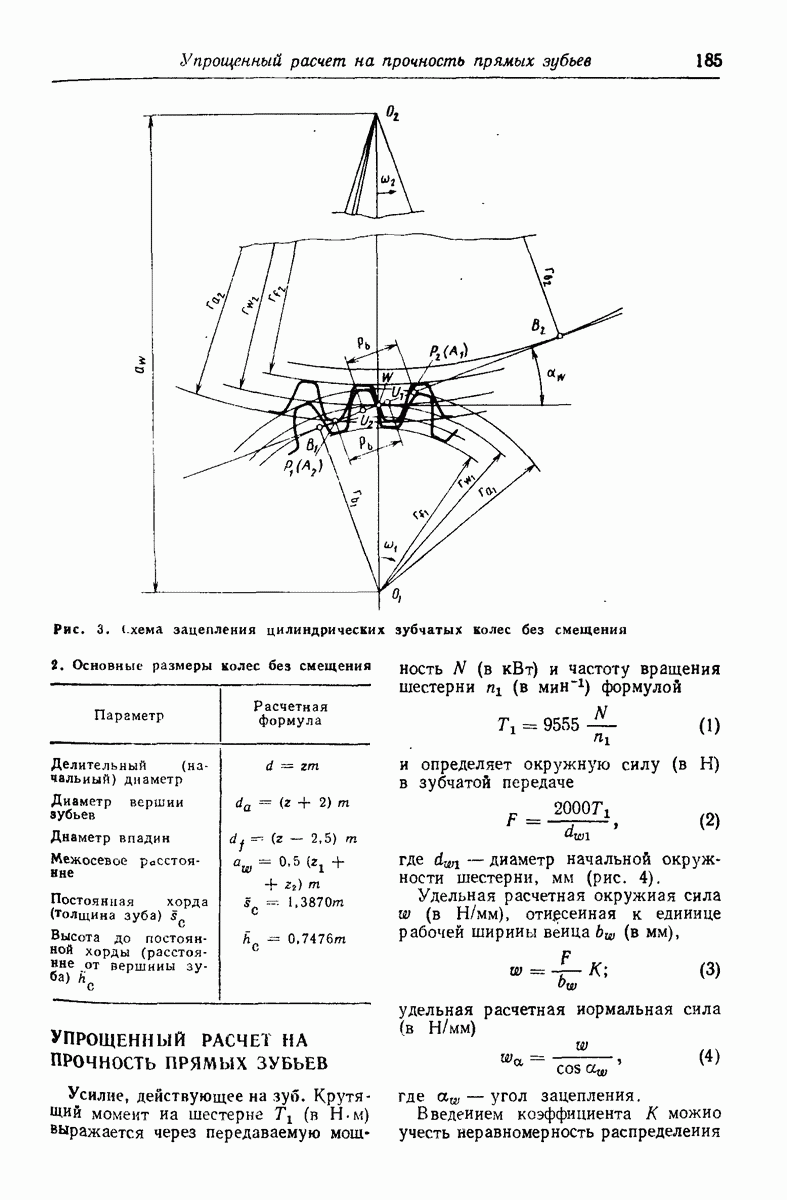
- УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ
- СТРУКТУРА РАСЧЕТНЫХ ФОРМУЛ ПО ГОСТ 21354—87
- НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ
- РАСЧЕТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
- РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ
- РАБОТА ПЕРЕДАЧ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ
- ОСОБЕННОСТИ РАСЧЕТА ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ М. Л. НОВИКОВА
- Глава 12. ШАРИКОВИНТОВЫЕ ПЕРЕДАЧИ
- КОНСТРУКЦИИ ПЕРЕДАЧ И МАТЕРИАЛЫ
- РАСЧЕТ ПЕРЕДАЧ
- Глава 13. РЕМЕННЫЕ ПЕРЕДАЧИ
- МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ
- РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
- ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ
- ПОРЯДОК РАСЧЕТА И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ
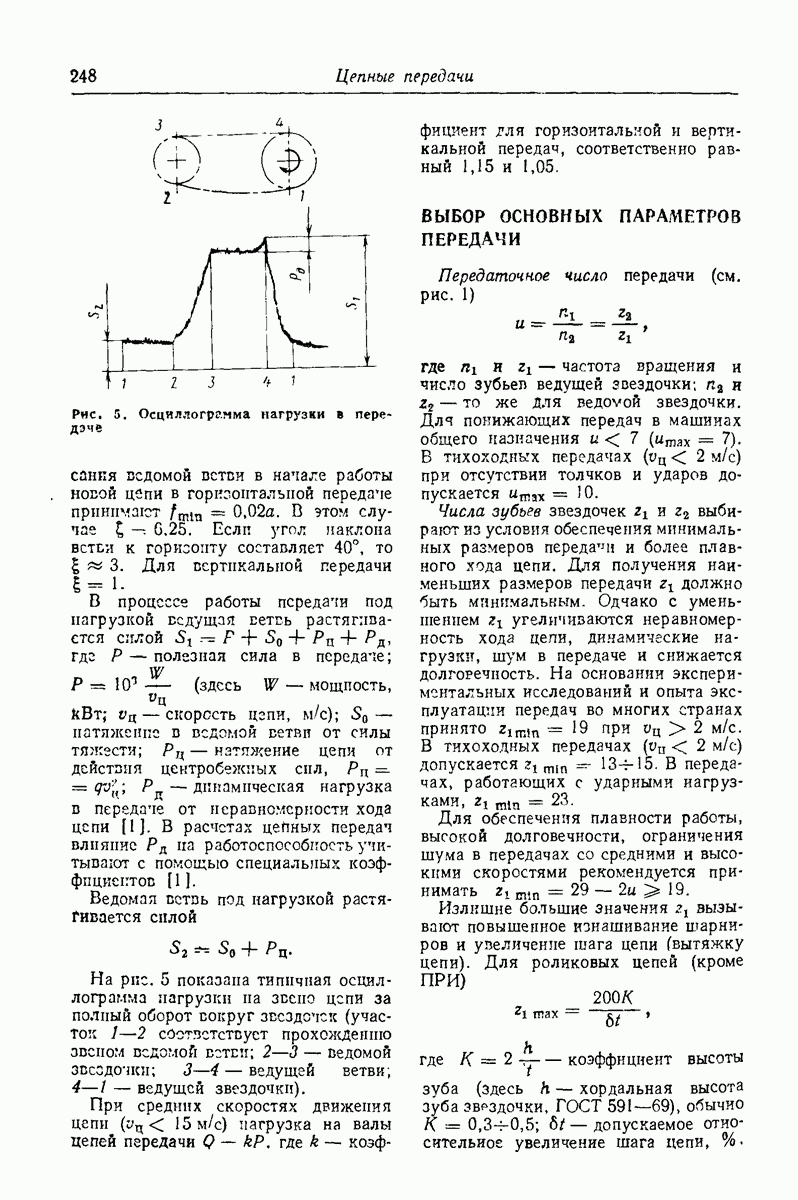
- Глава 14. ЦЕПНЫЕ ПЕРЕДАЧИ
- СИЛЫ В ПЕРЕДАЧЕ
- ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ
- НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ
- ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ
- ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ
- Глава 15. РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
- РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ
- РАСЧЕТ ШАТУНОВ
- РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА
- РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ
- РАСЧЕТ ДНИЩА ПОРШНЯ
- ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОРПУСА
- РАСЧЕТ КЛАПАННЫХ ПРУЖИН
- Глава 16. РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН
- РАСЧЕТ ЛОПАТОК НА ИЗГИБ
- ЗАПАС ПРОЧНОСТИ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ
- РАВНОПРОЧНЫЕ ЛОПАТКИ
- ОХЛАЖДАЕМЫЕ ЛОПАТКИ
- ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК
- ЗАКРУЧЕННЫЕ ЛОПАТКИ
- ШАРНИРНЫЕ ЛОПАТКИ
- БАНДАЖИРОВАННЫЕ ЛОПАТКИ
- РАСЧЕТ ЗАМКОВ ЛОПАТОК
- ВИБРАЦИЯ ЛОПАТОК
- РАСЧЕТ ДИСКОВ. НАПРЯЖЕНИЯ НА КОНТУРЕ
- ЗАПАСЫ ПРОЧНОСТИ ДИСКА
- ПРОФИЛИРОВАНИЕ РАВНОПРОЧНЫХ ДИСКОВ
- ОСНОВНЫЕ УРАВНЕНИЯ ПРИ РАСЧЕТЕ ДИСКОВ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ ТОЛЩИНЫ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ ТОЛЩИНЫ
- ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
- НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- УПРУГАЯ ЛИНИЯ СТЕРЖНЯ
- ОПРЕДЕЛЕНИЕ ПРОГИБОВ С ПОМОЩЬЮ ИНТЕГРАЛА МОРА
- ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- Глава 18. КРУЧЕНИЕ СТЕРЖНЕЙ
- СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
- СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
- РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
- УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
- ТРУБЧАТЫЕ СТЕРЖНИ
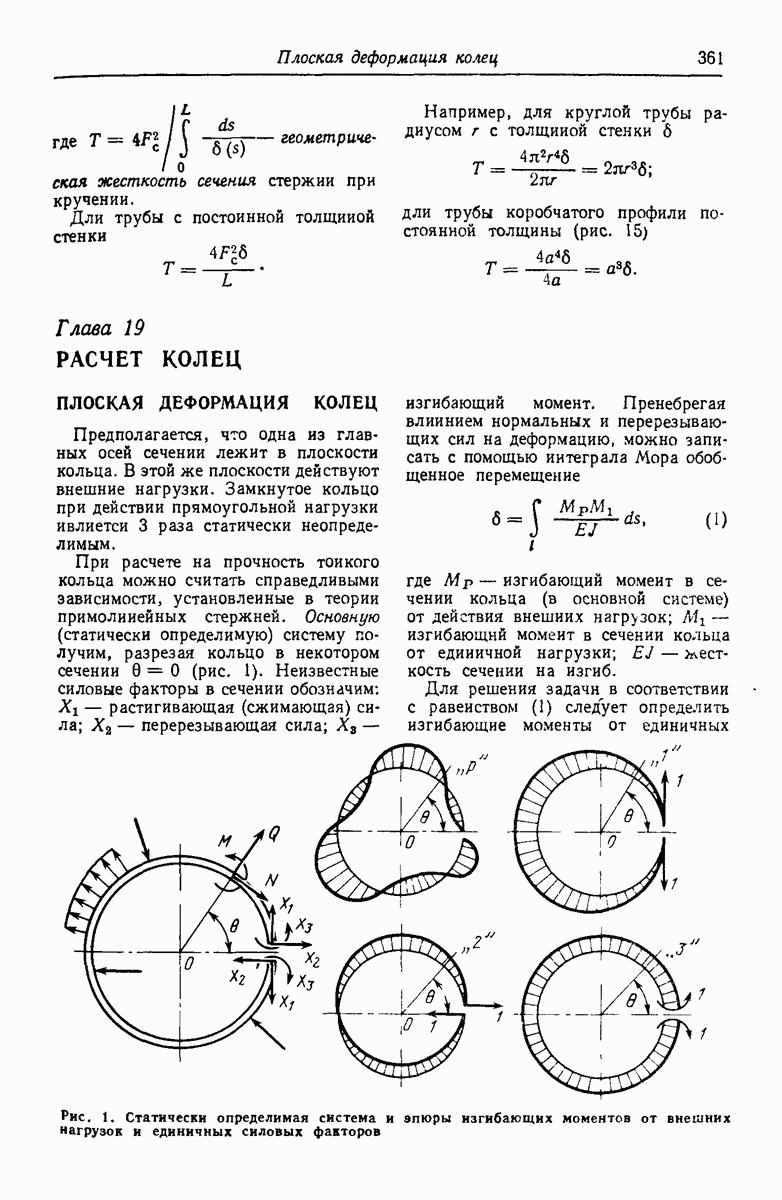
- Глаза 19. РАСЧЕТ КОЛЕЦ
- ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ
- Глава 20. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
- ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
- ВЛИЯНИЕ НАЧАЛЬНОГО ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ НА ВЫПУЧИВАНИЕ СТЕРЖНЯ
- РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
- ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ. ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАГРЕВЕ
- ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА
- ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ СКРУЧИВАНИИ
- Глава 21. КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
- МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
- КРУТИЛЬНЫЕ КОЛЕБАНИЯ
- ИЗГИБНЫЕ КОЛЕБАНИЯ
- ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ
- Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ
- ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ
- ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ
- Глава 23. РАСЧЕТ ПЛАСТИНОК
- ПРОРЫВНЫЕ МЕМБРАНЫ
- ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ
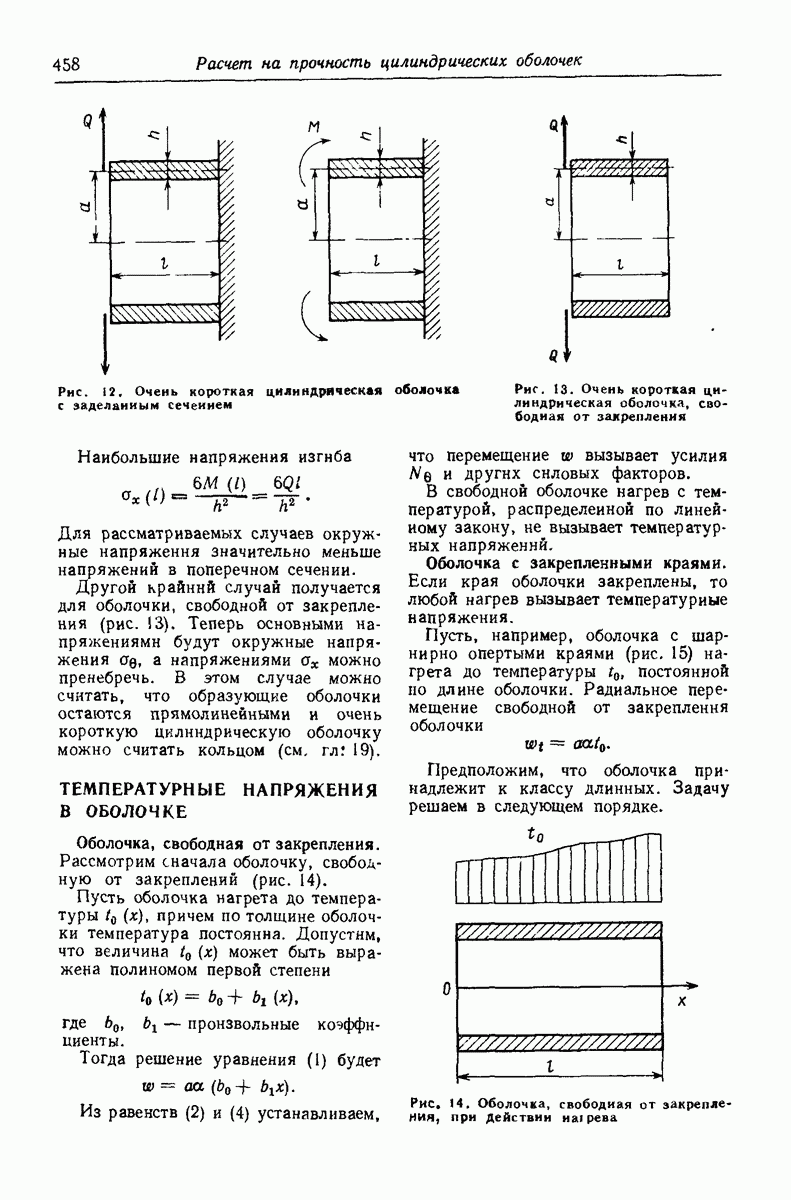
- Глава 24. РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК
- РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК
- ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
- Глава 25. УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК
- УСТОЙЧИВОСТЬ КОЛЕЦ
- УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ КОНИЧЕСКИХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ
- УСТОЙЧИВОСТЬ АНИЗОТРОПНЫХ ОБОЛОЧЕК
- УСТОЙЧИВОСТЬ ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК
- Глава 26. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
- ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД
- МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- ДИНАМИЧЕСКИЕ РАСЧЕТЫ
- Глава 27. РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- УРАВНЕНИЯ ПЛАСТИЧНОСТИ
- УРАВНЕНИЯ ПОЛЗУЧЕСТИ
- РАСЧЕТ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ)
- РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ НАГРУЖЕНИИ
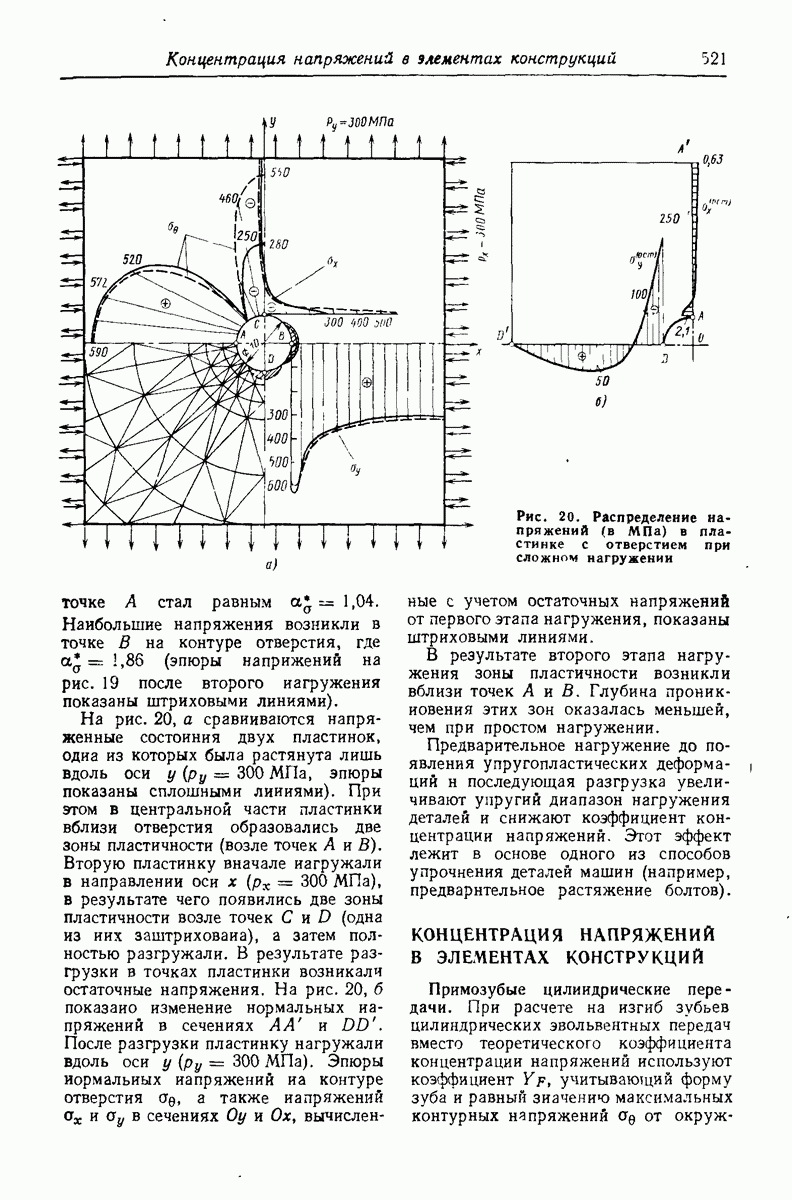
- Глава 28. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЙ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ И ПОЛЗУЧЕСТИ
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
- Глава 29. КОНТАКТНЫЕ ЗАДАЧИ
- КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ ФОРМЫ
- КОНСТРУКЦИОННЫЕ КОНТАКТНЫЕ ЗАДАЧИ
- ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ
- ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ
- Глава 30. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
- КРИТЕРИИ ДЛИТЕЛЬНОЙ И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ
- Глава 31. РАСЧЕТ НА УСТАЛОСТЬ
- ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ
- УСЛОВИЯ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
- ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ
- СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ
- Глава 32. ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
- ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ
- СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ
- Глава 33. ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ
- ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ
- ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ
- ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ
- ПРОГНОЗИРУЕМАЯ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ
- ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
- НАДЕЖНОСТЬ СИСТЕМЫ ПОСЛЕДОВАТЕЛЬНЫХ ЭЛЕМЕНТОВ
- НАДЕЖНОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ
- АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ
- РАСЧЕТ ЧИСЛА ИЗДЕЛИЙ, НАХОДЯЩИХСЯ В ЭКСПЛУАТАЦИИ
- КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
- Глава 34. ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН
- УПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ
- ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ ОБРАБОТКА
- ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ
- Глава 35. ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ
- МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- МЕТОД РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ
- ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- Глава 36. ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ
- СПИСОК ЛИТЕРАТУРЫ