| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
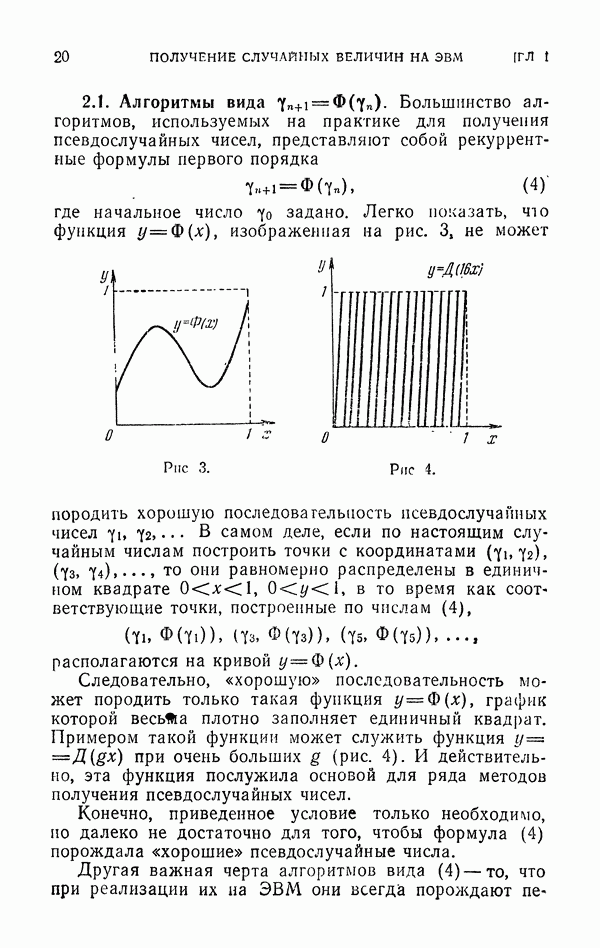
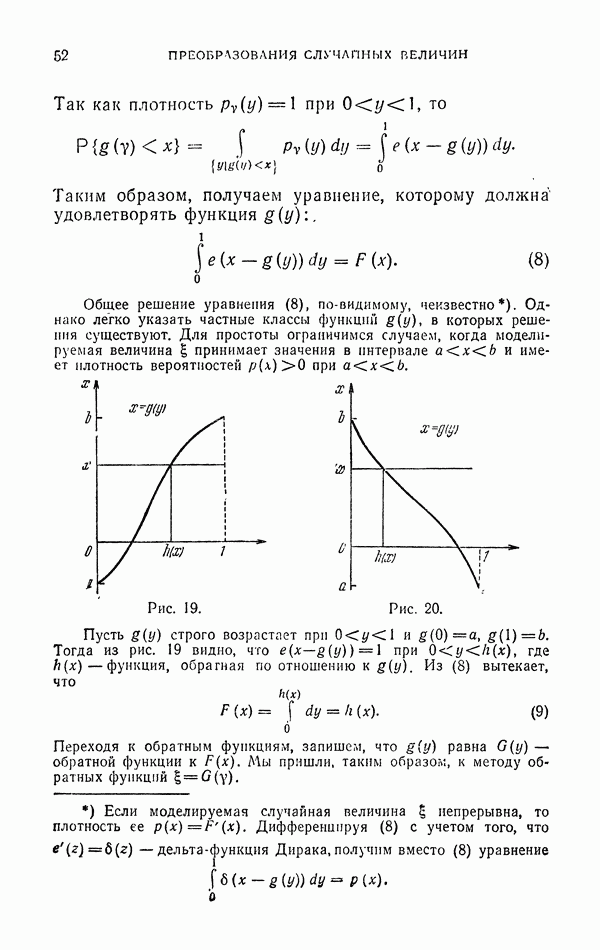
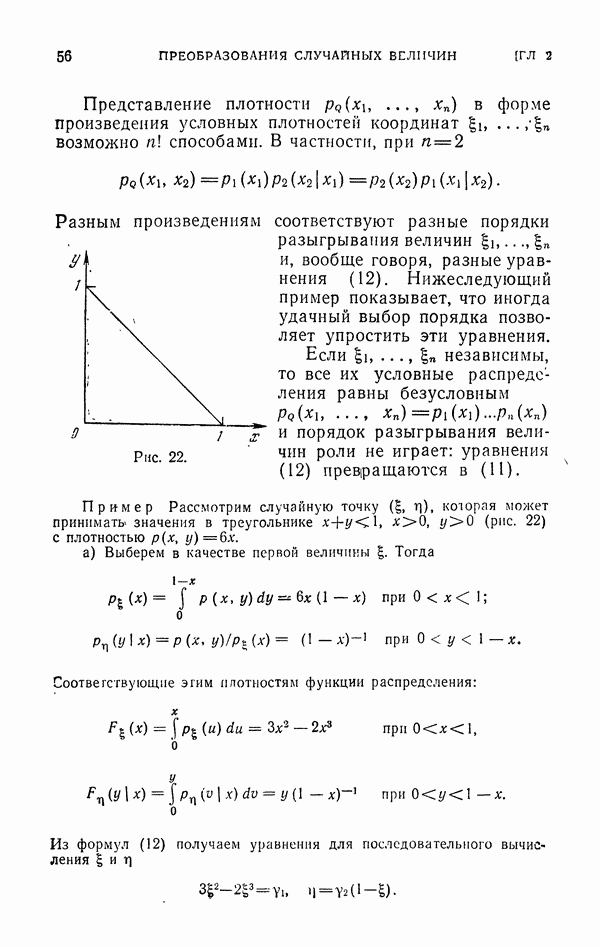
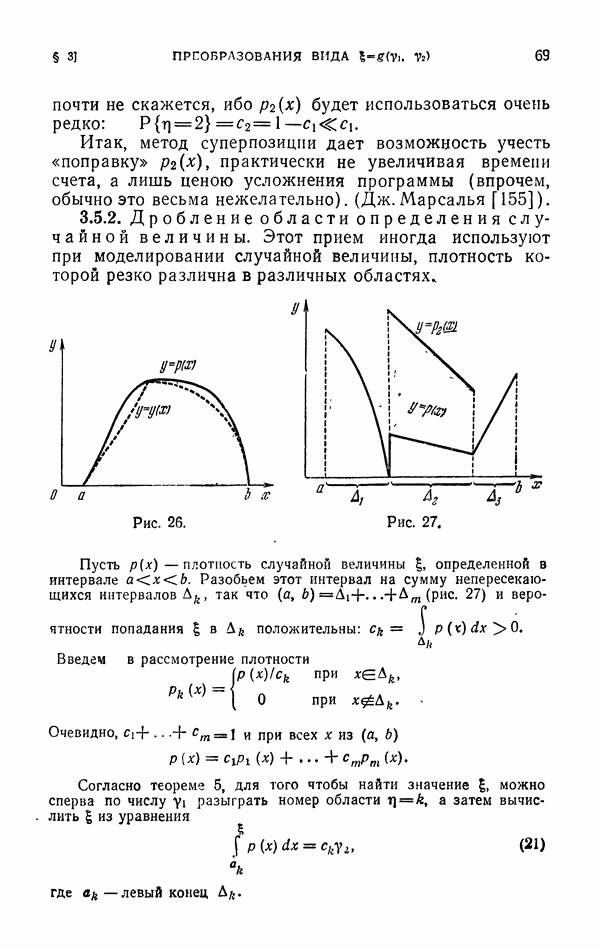
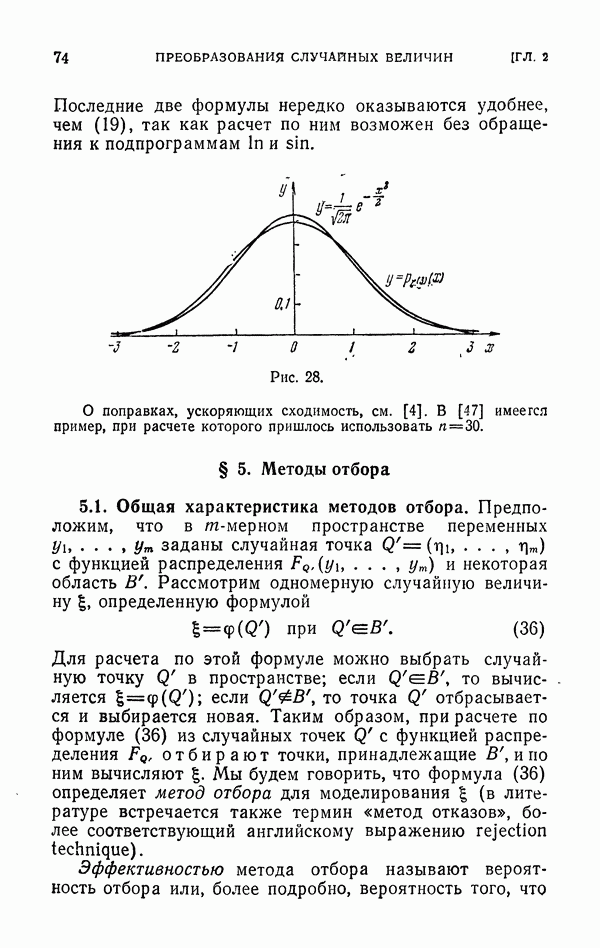
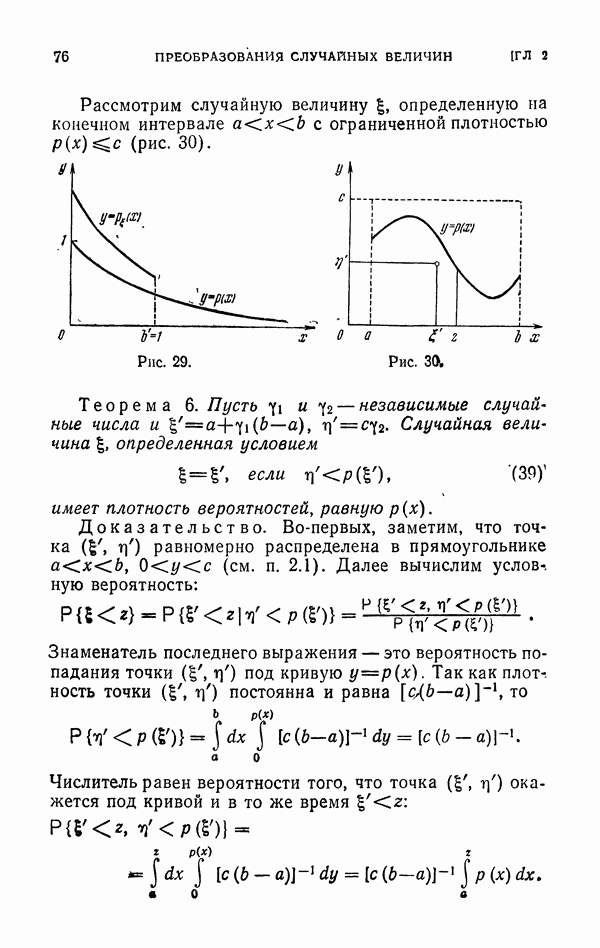
5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
В ограниченной связной области G плоскости  с простой границей
с простой границей  рассмотрим
рассмотрим
дифференциальное уравнение с частными производными

где  - искомая функция. Уравнение (72) при
- искомая функция. Уравнение (72) при  называется уравнением Лапласа, а при
называется уравнением Лапласа, а при  — уравнением Пуассона.
— уравнением Пуассона.
Предположим, что на границе  задана некоторая функция
задана некоторая функция  (часто пишут
(часто пишут  , где
, где  — длина дуги границы, отсчитываемая от какой-нибудь фиксированной точки). Требуется найти такое решение
— длина дуги границы, отсчитываемая от какой-нибудь фиксированной точки). Требуется найти такое решение  уравнения (72), которое на границе совпадает с
уравнения (72), которое на границе совпадает с 

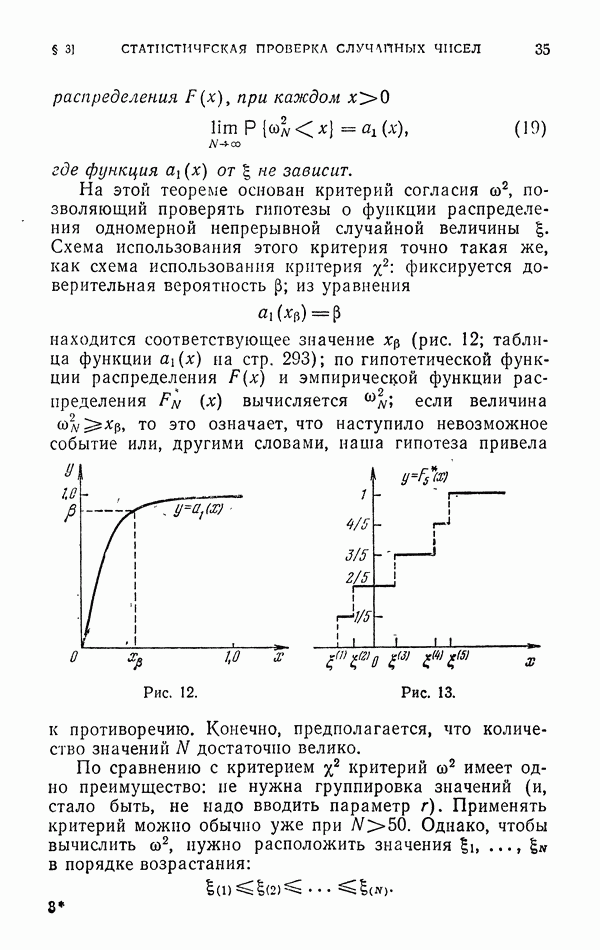
Задачу об отыскании решения уравнения (72), удовлетворяющего граничному условию (73), называют задачей Дирихле.

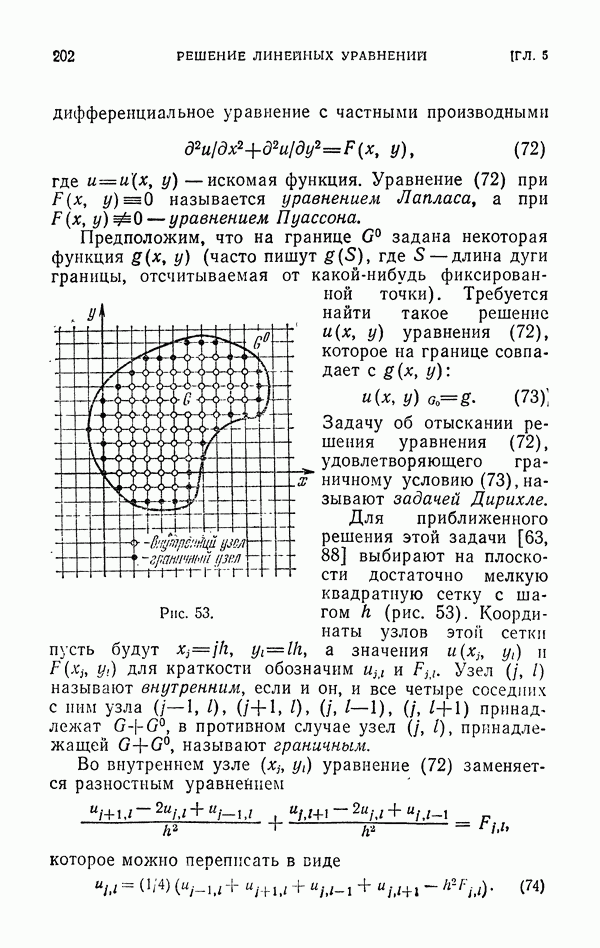
Рис. 53.
Для приближенного решения этой задачи [63, 88] выбирают на плоскости достаточно мелкую квадратную сетку с шагом h (рис. 53). Координаты узлов этой сетки пусть будут  а значения
а значения  для краткости обозначим
для краткости обозначим  Узел
Узел  называют внутренним, если и он, и все четыре соседних с ним узла
называют внутренним, если и он, и все четыре соседних с ним узла  принадлежат
принадлежат  в противном случае узел
в противном случае узел  принадлежащей
принадлежащей  называют граничным.
называют граничным.
Во внутреннем узле  уравнение (72) заменяется разностным уравнением
уравнение (72) заменяется разностным уравнением

которое можно переписать в виде

В граничных узлах полагают

(Значения  «сносят» с ближайших точек границы
«сносят» с ближайших точек границы  ) Решение алгебраической системы (74) — (75) при
) Решение алгебраической системы (74) — (75) при  приближается к решению задачи Дирихле для уравнения (72).
приближается к решению задачи Дирихле для уравнения (72).
Если перенумеровать все узлы, принадлежащие  произвольном порядке), и переписать в том же порядке уравнения (74) и (75), то получим систему вида (55)
произвольном порядке), и переписать в том же порядке уравнения (74) и (75), то получим систему вида (55)

( - количество узлов), с весьма своеобразной матрицей А: внутреннему узлу с номером а отвечает строка
- количество узлов), с весьма своеобразной матрицей А: внутреннему узлу с номером а отвечает строка  , в которой 4 элемента равны 1/4, а остальные — нули; граничному узлу с номером а отвечает строка
, в которой 4 элемента равны 1/4, а остальные — нули; граничному узлу с номером а отвечает строка  все диагональные элементы
все диагональные элементы  . (Можно доказать, что все собственные значения такой матрицы по абсолютной величине меньше единицы.) Свободные члены этой системы равны
. (Можно доказать, что все собственные значения такой матрицы по абсолютной величине меньше единицы.) Свободные члены этой системы равны  если узел номер а внутренний, и
если узел номер а внутренний, и  если узел номер а граничный.
если узел номер а граничный.
Воспользуемся методом п. 5.3. и построим метод Монте-Карло для расчета  значения решения в одном заранее заданном) узле. Выберем матрицу переходов
значения решения в одном заранее заданном) узле. Выберем матрицу переходов

( - символ Кронекера:
- символ Кронекера:  при
при 
Процесс построения цепи по такому закону оказывается очень наглядным: 1) начинаем с  если узел
если узел  внутренний, то с одинаковой вероятностью
внутренний, то с одинаковой вероятностью  выбираем в качестве
выбираем в качестве  номер одного из соседних с ним узлов; 3) если узел
номер одного из соседних с ним узлов; 3) если узел  граничный, то цепь останавливается:
граничный, то цепь останавливается: 
Расчет весов вдоль такой цепи также чрезвычайно прост: пока цепь не попала на границу  далее
далее 
Поэтому случайная величина (67) оказывается равной

где  — номер первого выхода цепи на границу. В (76) все
— номер первого выхода цепи на границу. В (76) все  вычисляются по формуле
вычисляются по формуле  и лишь последнее
и лишь последнее  равно значению
равно значению  . Замечание. Если вместо граничных условий
. Замечание. Если вместо граничных условий  заданы более сложные условия, например:
заданы более сложные условия, например:

та уравнения (75) наряду с  будут содержать также значения
будут содержать также значения  в некоторых соседних узлах. И случайная цепь, попав на границу, останавливаться не будет.
в некоторых соседних узлах. И случайная цепь, попав на границу, останавливаться не будет.
Пример. Пусть  - решение уравнения Лапласа
- решение уравнения Лапласа  в единичном квадрате
в единичном квадрате  удовлетворяющее граничным условиям
удовлетворяющее граничным условиям  Вычислить значение
Вычислить значение 

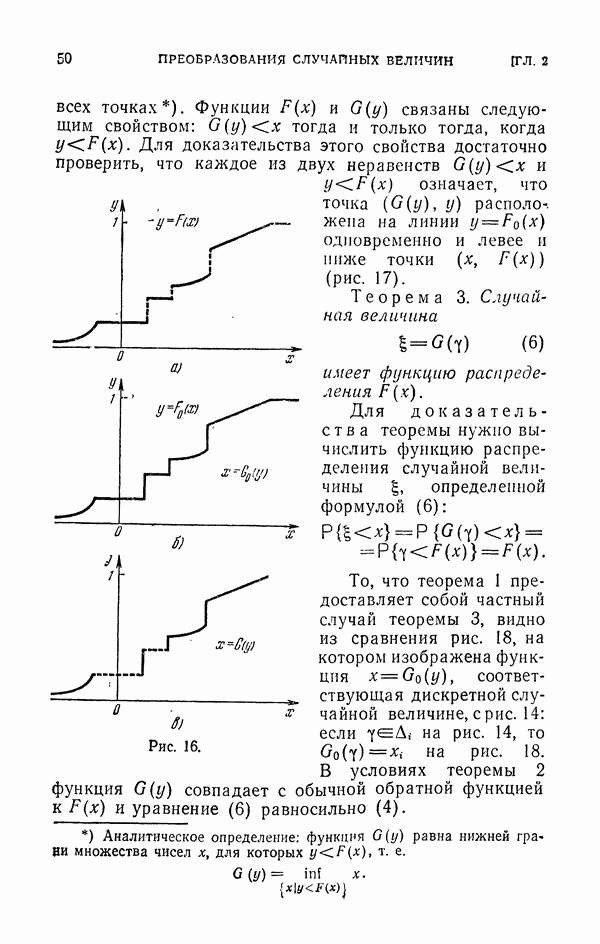
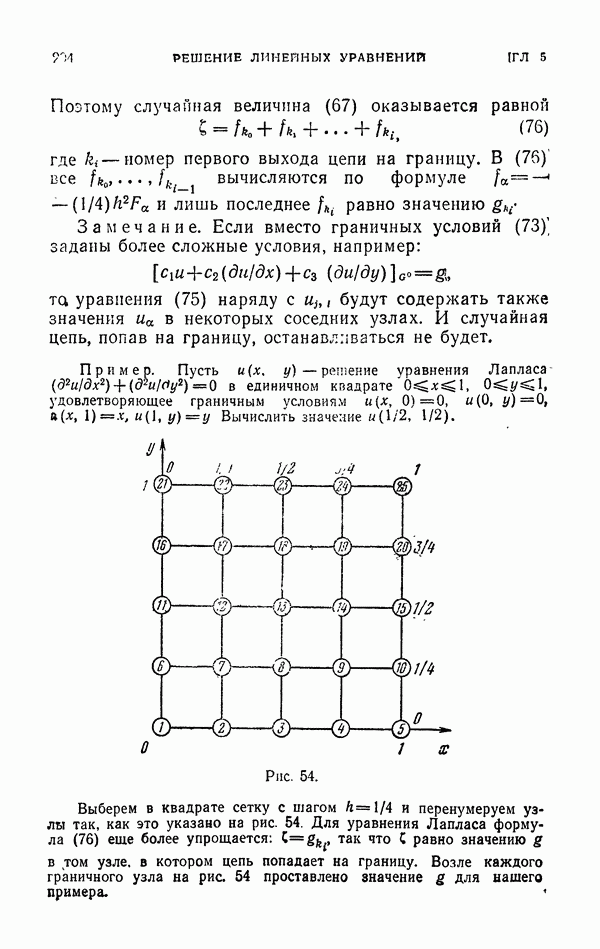
Рис. 54.
Выберем в квадрате сетку с шагом  и перенумеруем узлы так, как это указано на рис. 54. Для уравнения Лапласа формула (76) еще более упрощается: С так что С равно значению
и перенумеруем узлы так, как это указано на рис. 54. Для уравнения Лапласа формула (76) еще более упрощается: С так что С равно значению  в том узле, в котором цепь попадает на границу. Возле каждого граничного узла на рис. 54 проставлено значение g для нашего примера. 1
в том узле, в котором цепь попадает на границу. Возле каждого граничного узла на рис. 54 проставлено значение g для нашего примера. 1
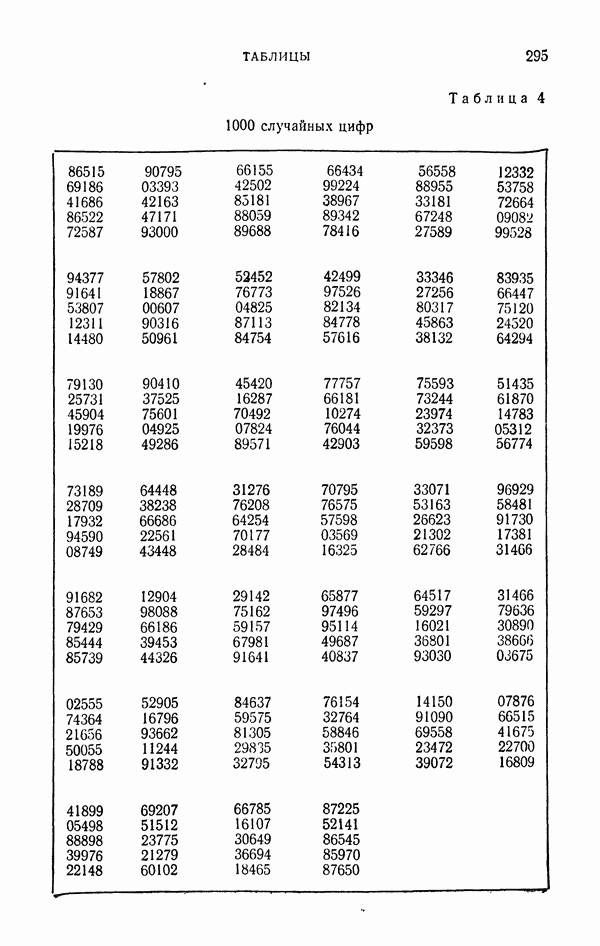
Для построения цепей воспользуемся таблицей случайных цифр, приведенной на стр. 295. Если случайная цифра  окажется 0 или 4, то будем перемещаться в соседний узел справа; если в равно 1 или 5, то будем перемещаться влево; если
окажется 0 или 4, то будем перемещаться в соседний узел справа; если в равно 1 или 5, то будем перемещаться влево; если  равно 2 или 6, то перемещаемся вверх; если
равно 2 или 6, то перемещаемся вверх; если  равно 3 или 7, то перемещаемся вниз; значения
равно 3 или 7, то перемещаемся вниз; значения  , равные 8 или 9, опускаем.
, равные 8 или 9, опускаем.
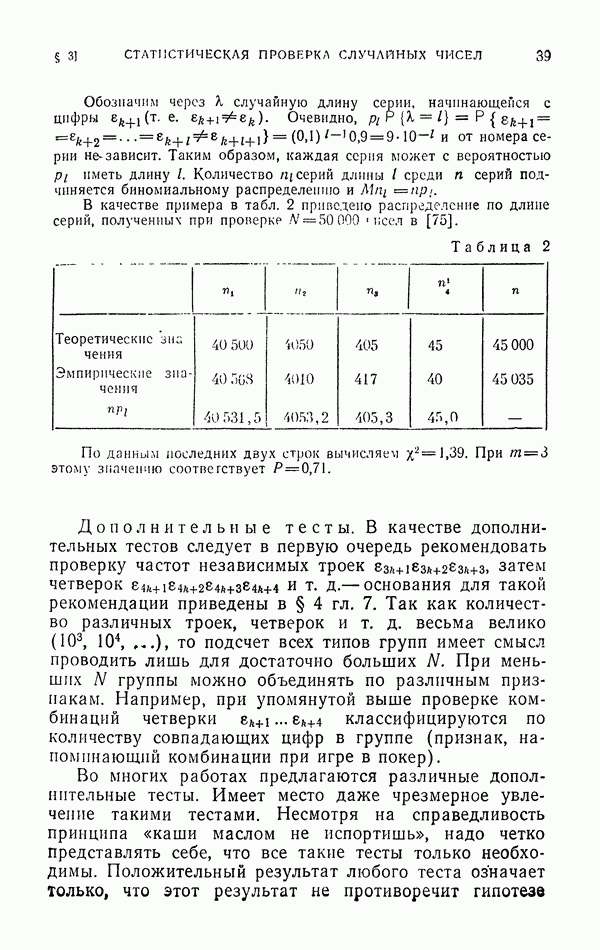
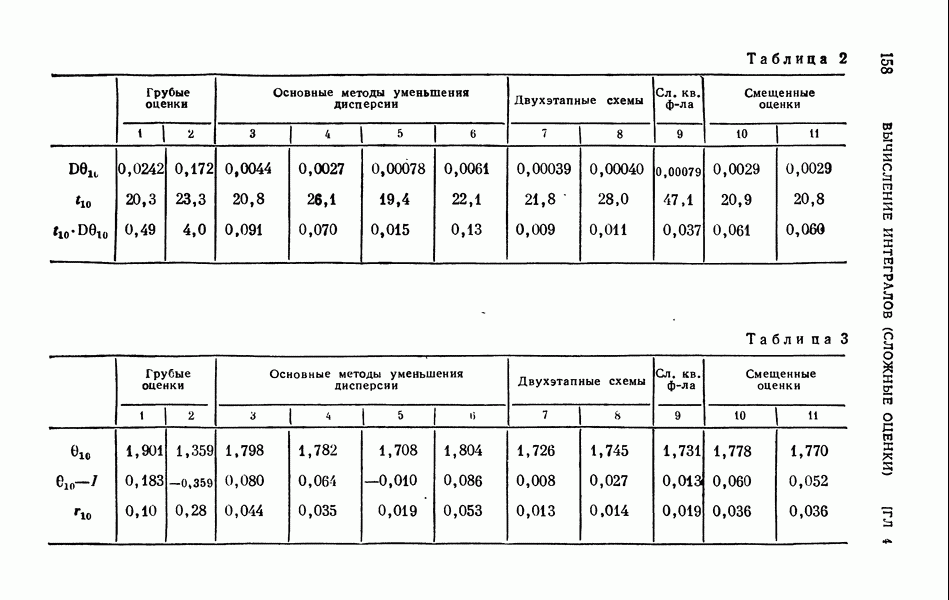
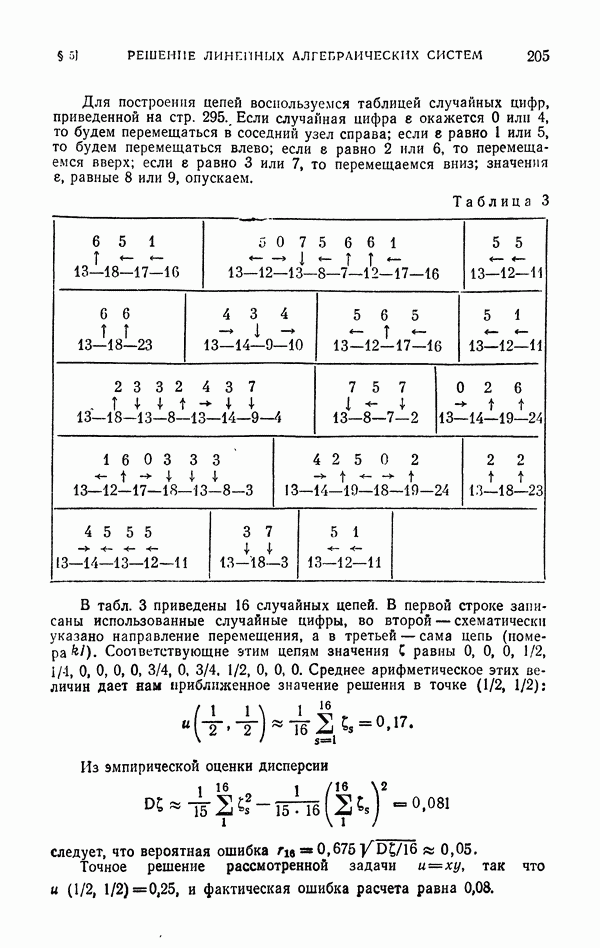
Таблица 3

В табл. 3 приведены 16 случайных цепей. В первой строке записаны использованные случайные цифры, во второй — схематически указано направление перемещения, а в третьей — сама цепь (номера  ). Соответствующие этим цепям значения С равны
). Соответствующие этим цепям значения С равны  Среднее арифметическое этих величин дает нам приближенное значение решения в точке (1/2, 1/2):
Среднее арифметическое этих величин дает нам приближенное значение решения в точке (1/2, 1/2):

Из эмпирической оценки дисперсии

следует, что вероятная ошибка  .
.
Точное решение рассмотренной задачи  так что и
так что и  и фактическая ошибка расчета равна 0,08.
и фактическая ошибка расчета равна 0,08.
Метод настоящего пункта позволяет вычислять решения разностных уравнений, аппроксимирующих дифференциальные уравнения. Связь таких задач с блужданиями по сетке была впервые установлена в [113]. В § 3 гл. 8 указан метод Монте-Карло для решения задачи Дирихле, не связанный с разностными уравнениями.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
- § 1. Моделирование путем имитации
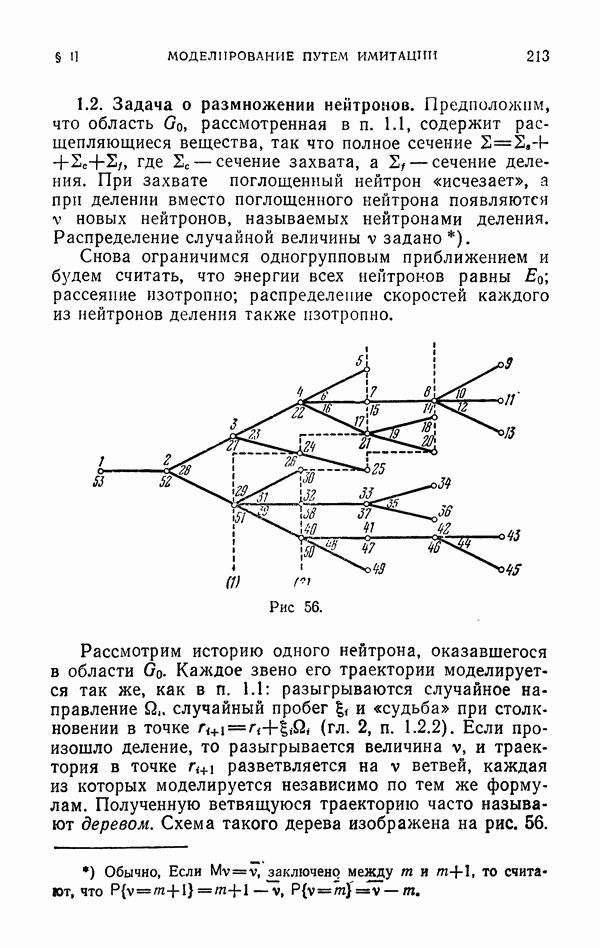
- 1.2. Задача о размножении нейтронов.
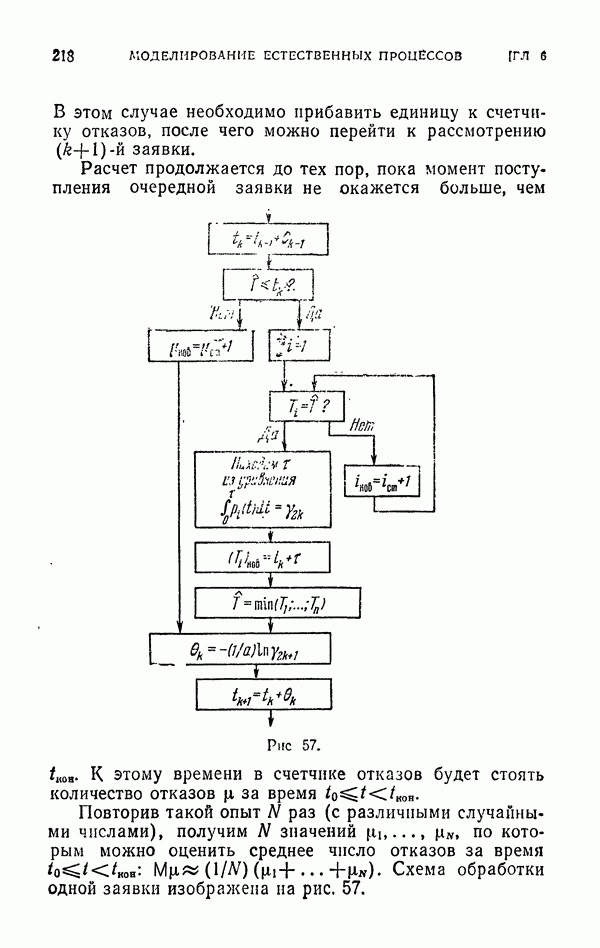
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
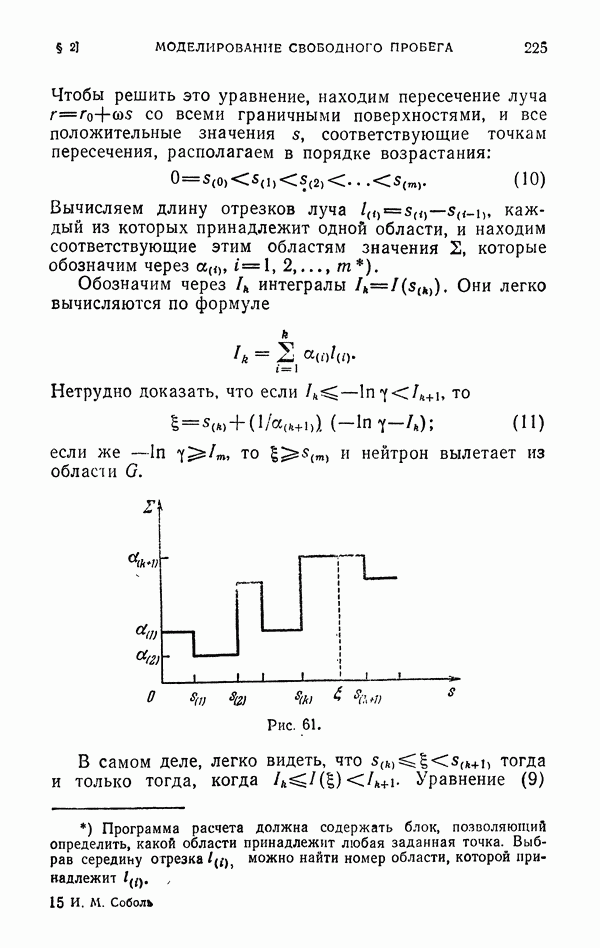
- § 2. Моделирование свободного пробега
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА