| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
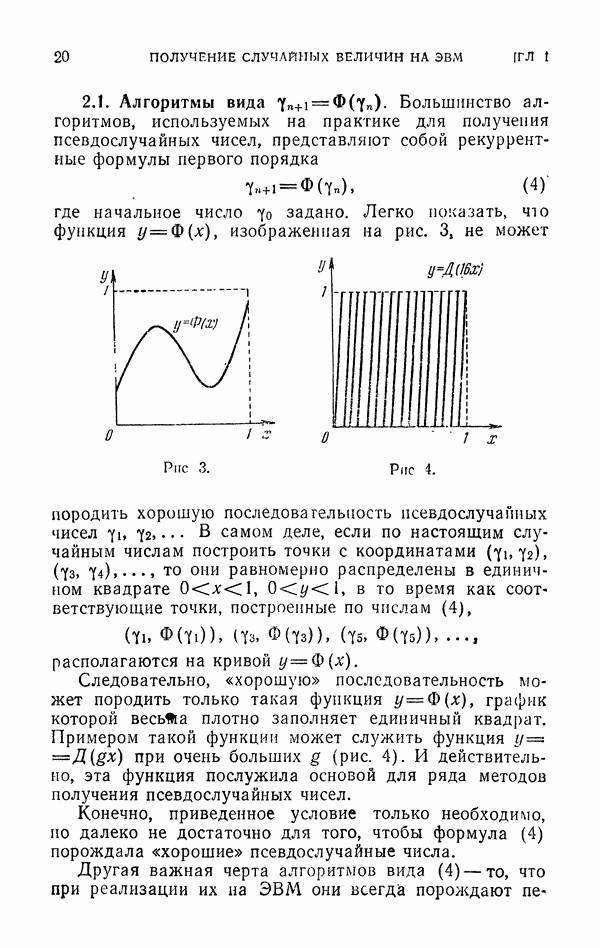
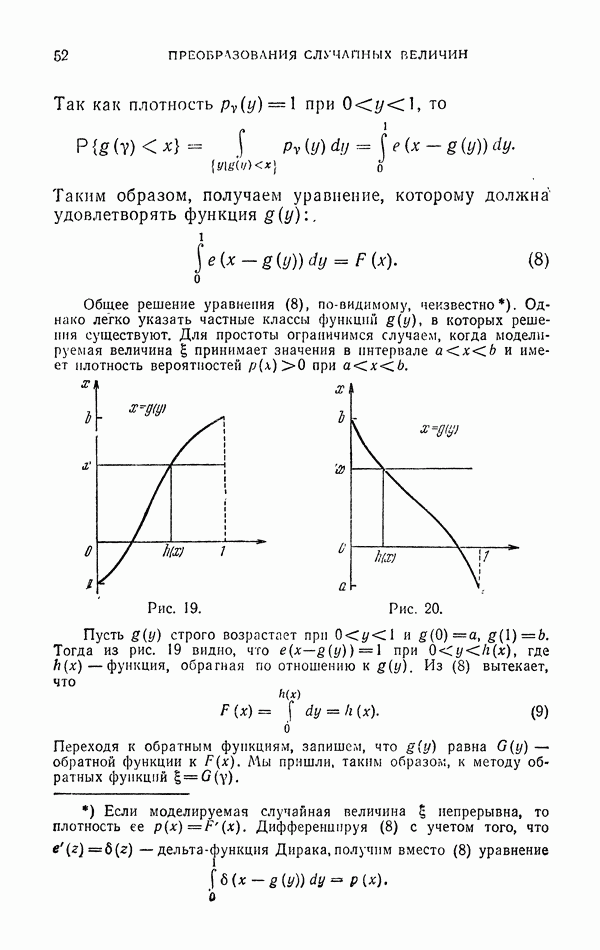
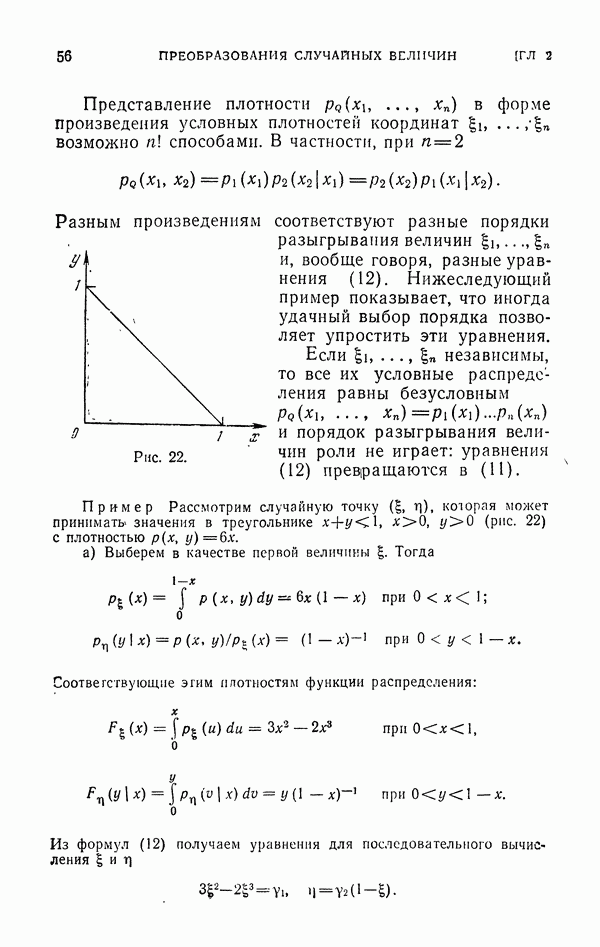
2.3. Случайные интерполяционные квадратурные формулы.
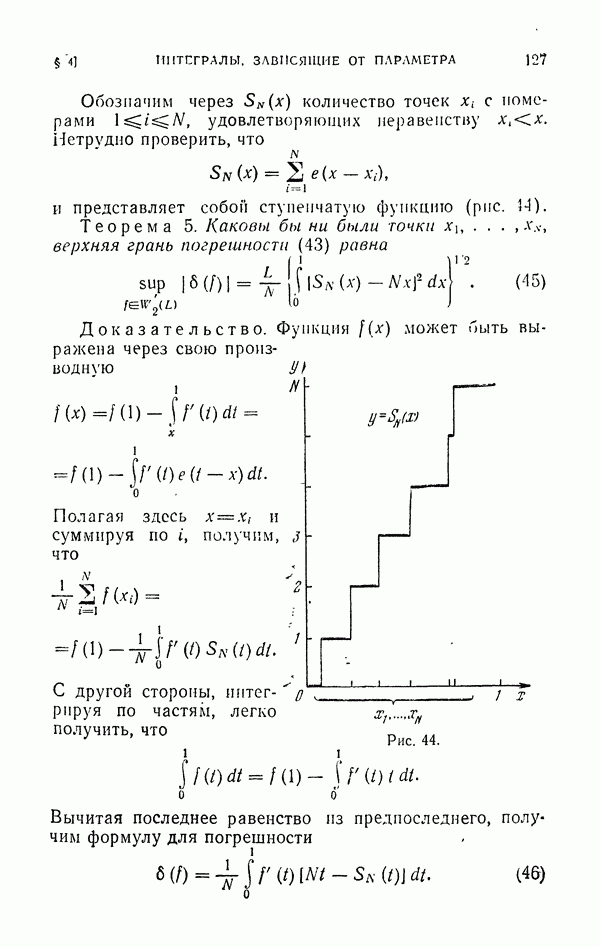
Обозначим для краткости  -мерную область, точки которой
-мерную область, точки которой  через
через  и пусть
и пусть  . Пусть далее
. Пусть далее  — множество точек Т, в которых
— множество точек Т, в которых 
Определим случайные точки  в G и в качестве оценки интеграла (21) рассмотрим случайную величину
в G и в качестве оценки интеграла (21) рассмотрим случайную величину

Теорема 4. Если совместная плотность распределения случайных точек  в В равна
в В равна

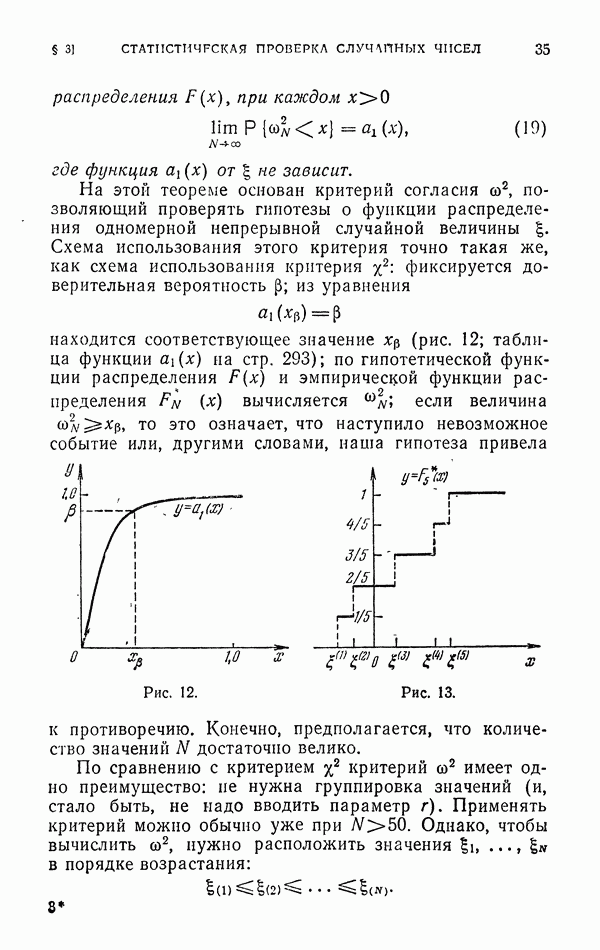
то для любой функции  из
из 

Доказательство. Выберем произвольную конечную функцию  из
из  и обозначим через
и обозначим через  коэффициенты Фурье
коэффициенты Фурье  . Пусть
. Пусть

Если  то, введя функцию
то, введя функцию  получим представление
получим представление

Легко проверить, что  ортогональна ко всем
ортогональна ко всем  и нормирована:
и нормирована:

Если  , то представление (31) также справедливо: в качестве
, то представление (31) также справедливо: в качестве  можно выбрать любую нормированную функцию, ортогональную ко всем
можно выбрать любую нормированную функцию, ортогональную ко всем  . Подставив (31) в (24), получим, что
. Подставив (31) в (24), получим, что

С помощью последней формулы нетрудно вычислить математическое ожидание оценки (27):

Из последних двух интегралов первый равен  по лемме 1, а второй равен нулю по лемме 2. Таким образом,
по лемме 1, а второй равен нулю по лемме 2. Таким образом,  что равносильно (29).
что равносильно (29).
Перейдем к вычислению дисперсии:

Так как здесь  по той же лемме 1, то
по той же лемме 1, то  откуда вытекает
откуда вытекает
неравенство, равносильное (30):

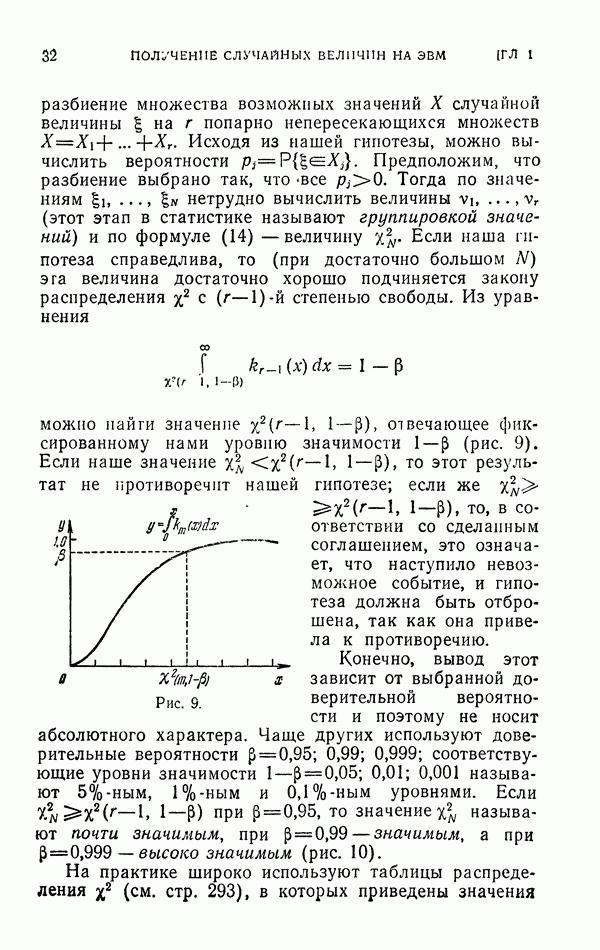
Впервые эта теорема была доказана в [34], а уточнение к ней — в [32]. Из доказательства видно, что знак равенства в (30) реализуется тогда и только тогда, когда

Это условие будет выполнено для любых функций  если объем
если объем  (
( -мерный) равен нулю. Иными словами, если
-мерный) равен нулю. Иными словами, если  только на многообразных меньшего числа измерений, чем
только на многообразных меньшего числа измерений, чем  как, например,
как, например,  и т. п.
и т. п.
Равенство (32) не будет выполнено для некоторых функций  если функции
если функции  линейно зависимы в какой-то области
линейно зависимы в какой-то области  с положительным
с положительным  -мерным объемом: в этом случае
-мерным объемом: в этом случае  в области
в области  с положительным
с положительным  объемом, и объем
объемом, и объем  положителен.
положителен.
Легко показать, что оба эти случая возможны. В самом деле, пусть G — интервал  так что В — квадрат
так что В — квадрат  Если выбрать
Если выбрать  , то
, то

и множество  состоит из точек, расположенных на диагонали
состоит из точек, расположенных на диагонали  квадрата В. Если выбрать
квадрата В. Если выбрать  то легко вычислить, что
то легко вычислить, что

 в двух четвертях
в двух четвертях  квадрата В.
квадрата В.
Верхняя граница (30) для дисперсии  имеет простой геометрический смысл: она равна квадрату расстояния (в метрике пространства
имеет простой геометрический смысл: она равна квадрату расстояния (в метрике пространства  ) от функции
) от функции  до линейного подпространства, определяемого функциями
до линейного подпространства, определяемого функциями 
Пример. Рассмотрим интеграл  . Пусть
. Пусть  и заданы две ортонормированные функции:
и заданы две ортонормированные функции:  .
.
Обозначим через  две случайные точки (вместо
две случайные точки (вместо  ) и вычислим определители, входящие в (27):
) и вычислим определители, входящие в (27):

Из (27) и (29) вытекает оценка интеграла 

где  имеют совместную плотность распределения
имеют совместную плотность распределения

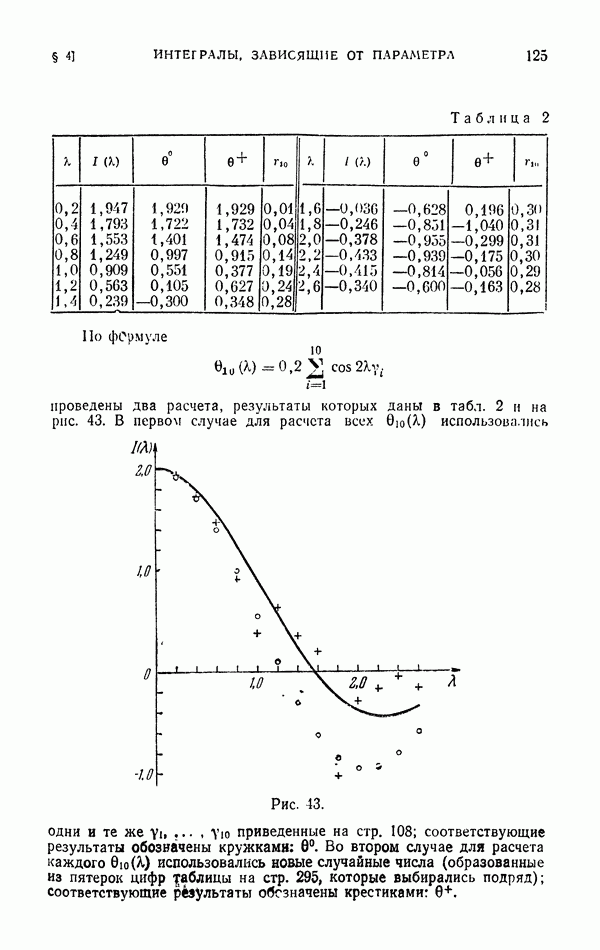
Для расчета интеграла  по десяти значениям подынтегральной функции запишем оценку
по десяти значениям подынтегральной функции запишем оценку

Дисперсия этой оценки, согласно (30), где имеет место знак равенства, есть

Уменьшение дисперсии по сравнению с простейшим методом весьма значительное.
Так как  то удобно находить значения
то удобно находить значения  методом Неймана (п. 5.3 гл. 2): выбираем три случайных числа
методом Неймана (п. 5.3 гл. 2): выбираем три случайных числа  и проверяем условие
и проверяем условие  Если оно выполнено, то
Если оно выполнено, то  Эффективность отбора
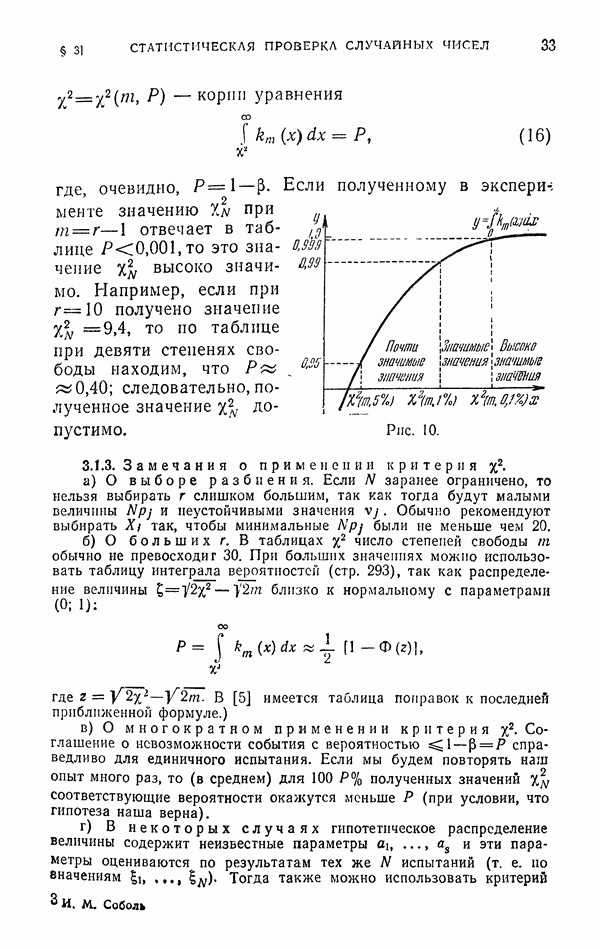
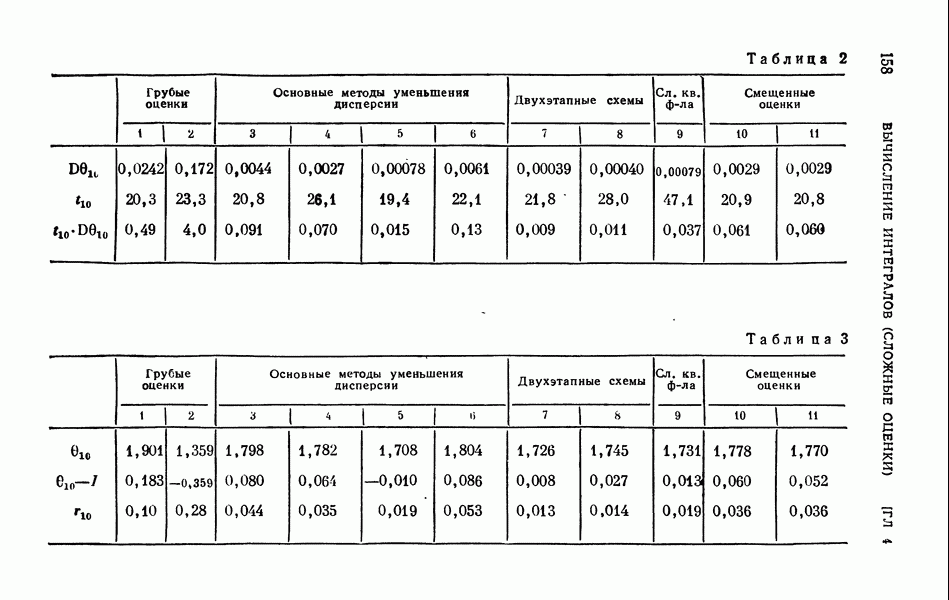
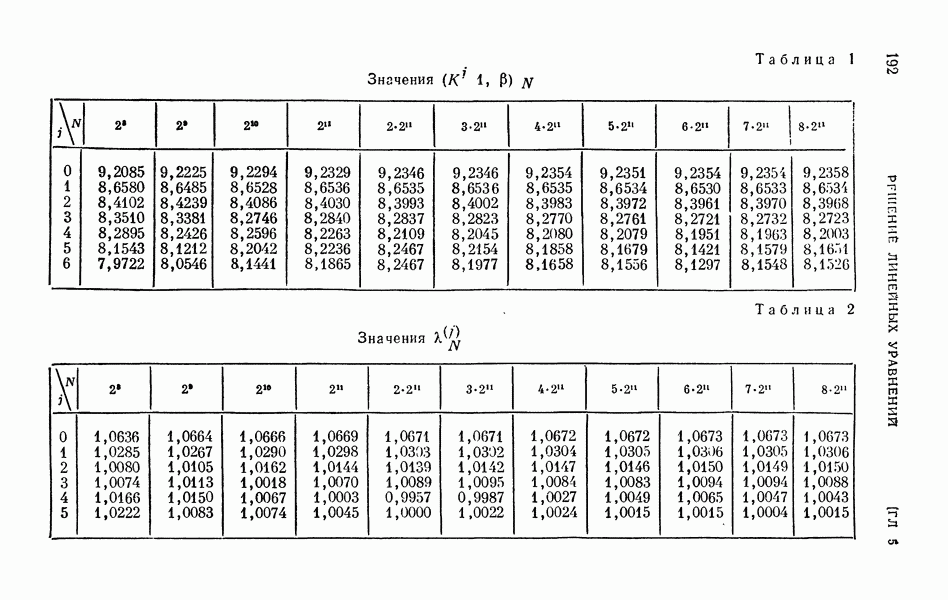
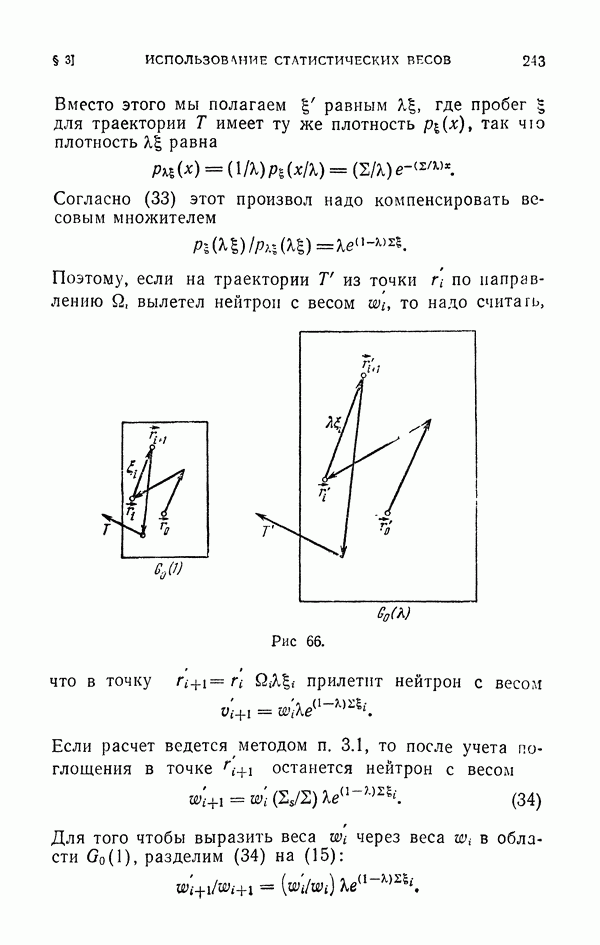
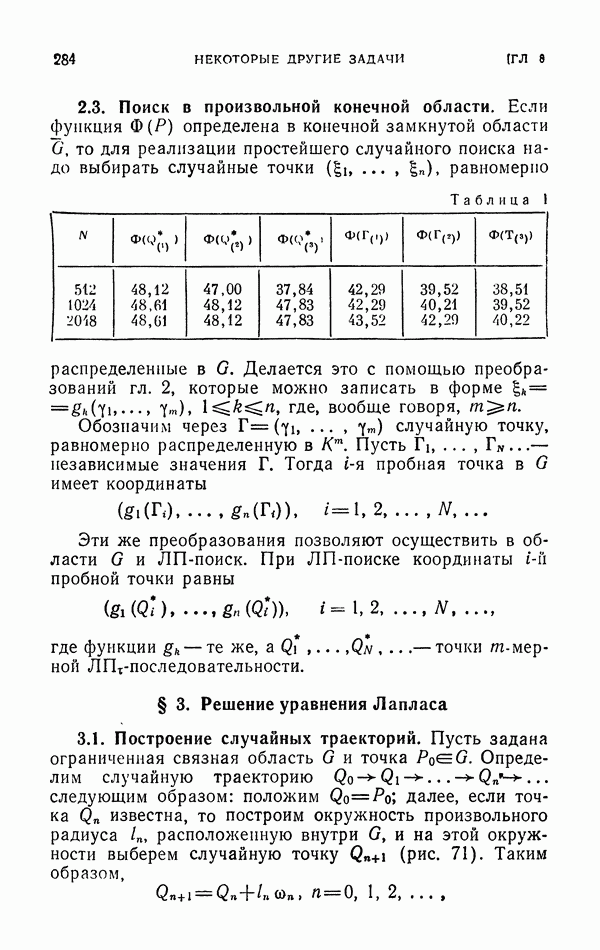
Эффективность отбора  Пример расчета по формуле (34) приведен в табл. 1. Результат этого расчета
Пример расчета по формуле (34) приведен в табл. 1. Результат этого расчета 
Замечания. Методу п. 2.3 посвящено несколько работ [20, 31, 137]. Исследователей привлекает большая общность метода и значительное уменьшение дисперсии. Однако он имеет и свои недостатки. Во-первых, пока нет удобных и достаточно общих приемов для разыгрывания точек  с плотностыо (28). Во-вторых,
с плотностыо (28). Во-вторых,
Таблица 1

в формуле (27), вообще говоря, присутствуют отрицательные случайные веса (ср. пример п. 2.3); а формула со знакопеременными весами практически плоха, если число слагаемых велико. Чтобы устранить эти недостатки, надо использовать другие плотности  отличные от (28) (см. [33]). Наиболее подробно изучен случай, когда все точки
отличные от (28) (см. [33]). Наиболее подробно изучен случай, когда все точки  представляют собой функции от одной случайной точки
представляют собой функции от одной случайной точки  (Б. Л. Грановский [20, 21]).
(Б. Л. Грановский [20, 21]).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
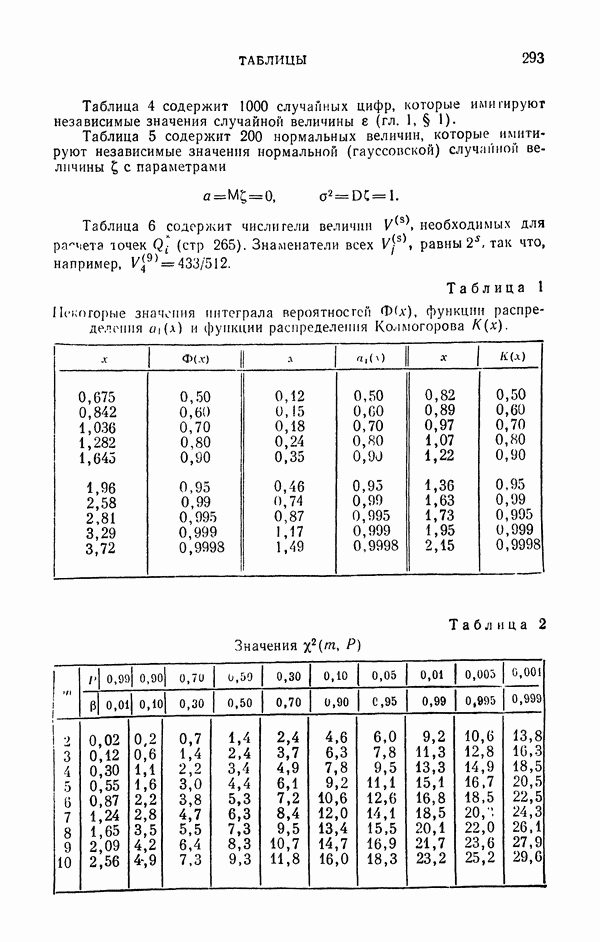
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
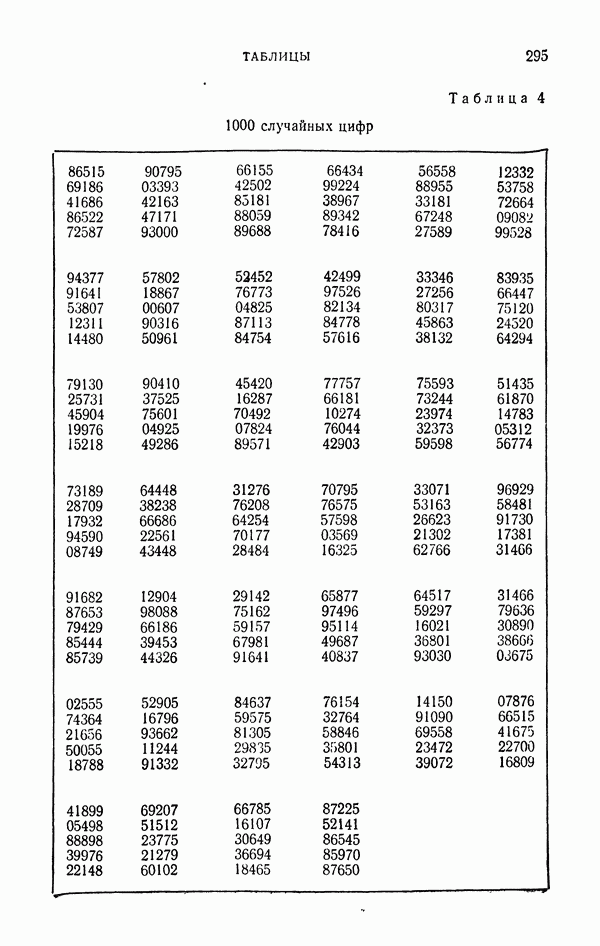
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
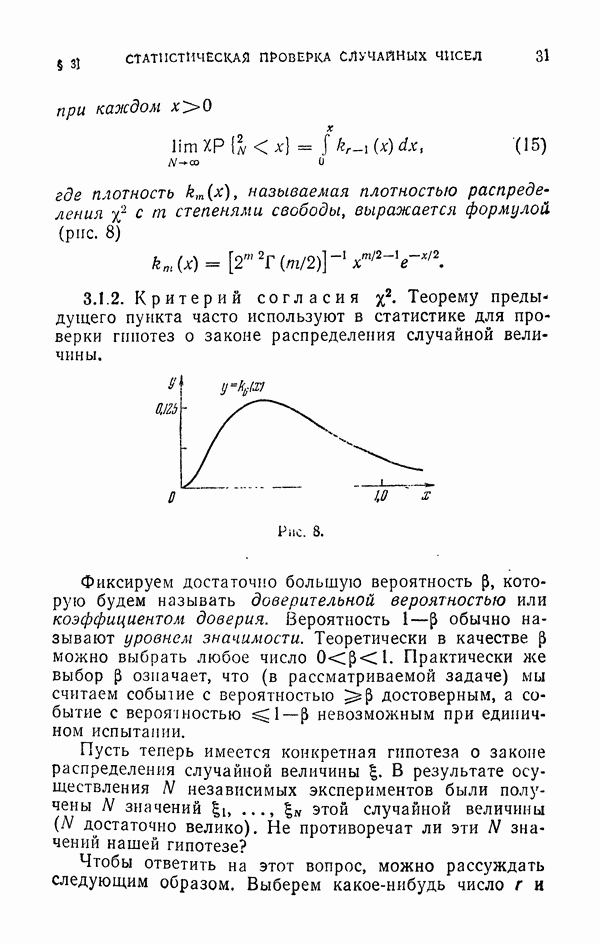
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
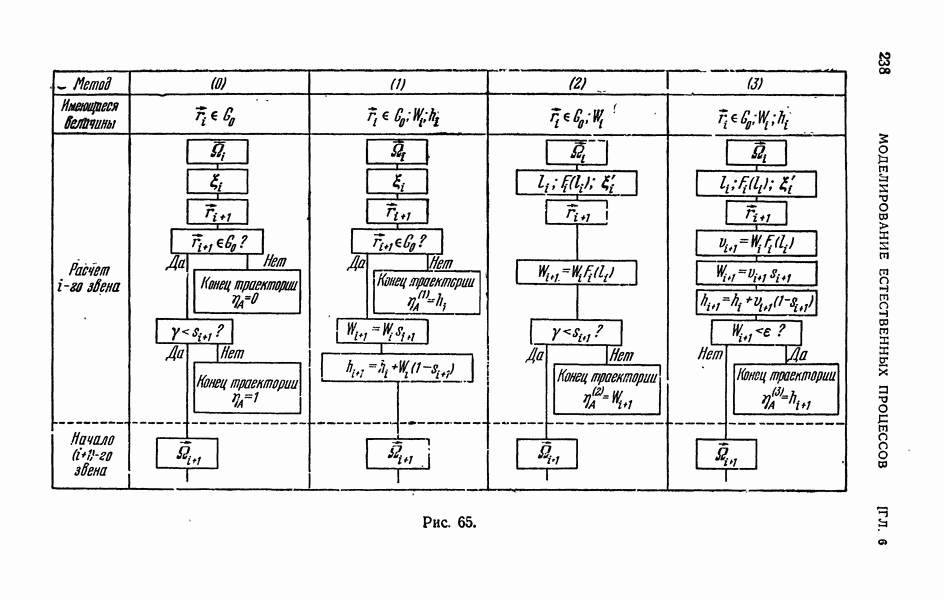
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
- § 1. Моделирование путем имитации
- 1.2. Задача о размножении нейтронов.
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
- § 2. Моделирование свободного пробега
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА