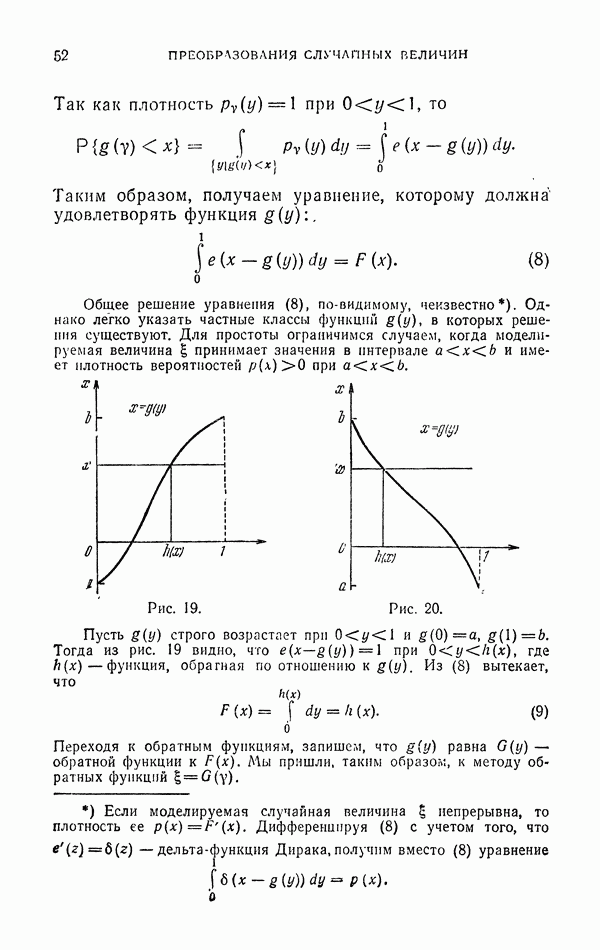
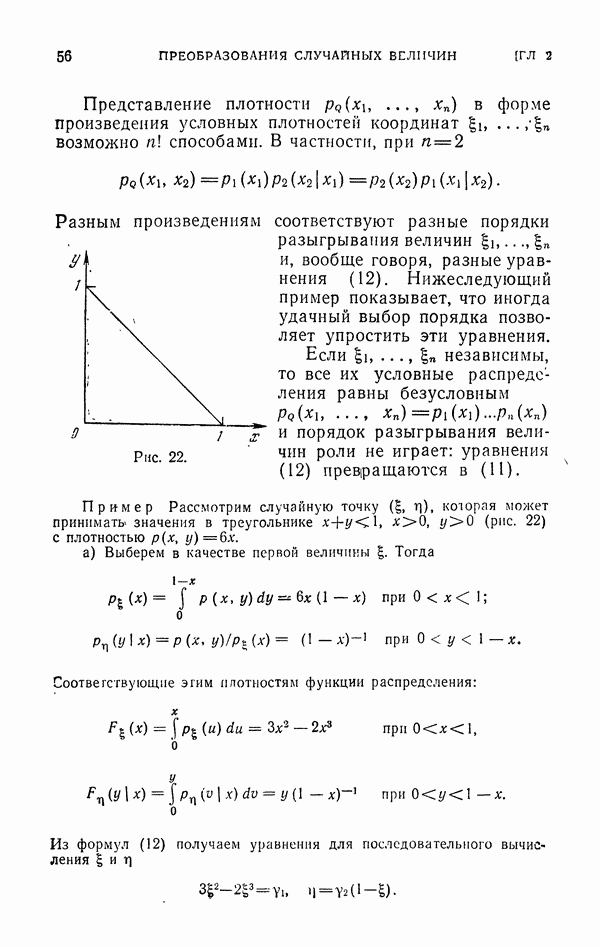
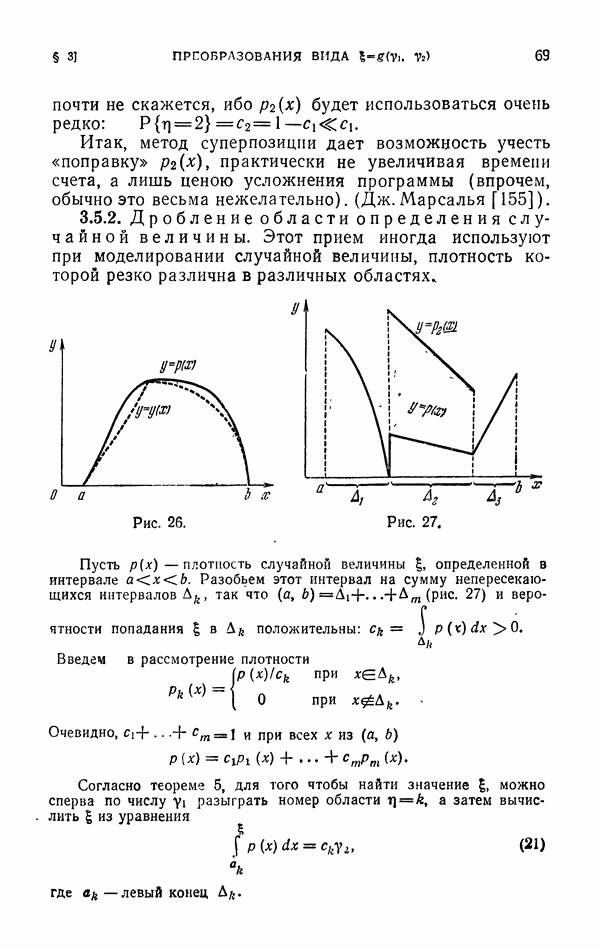
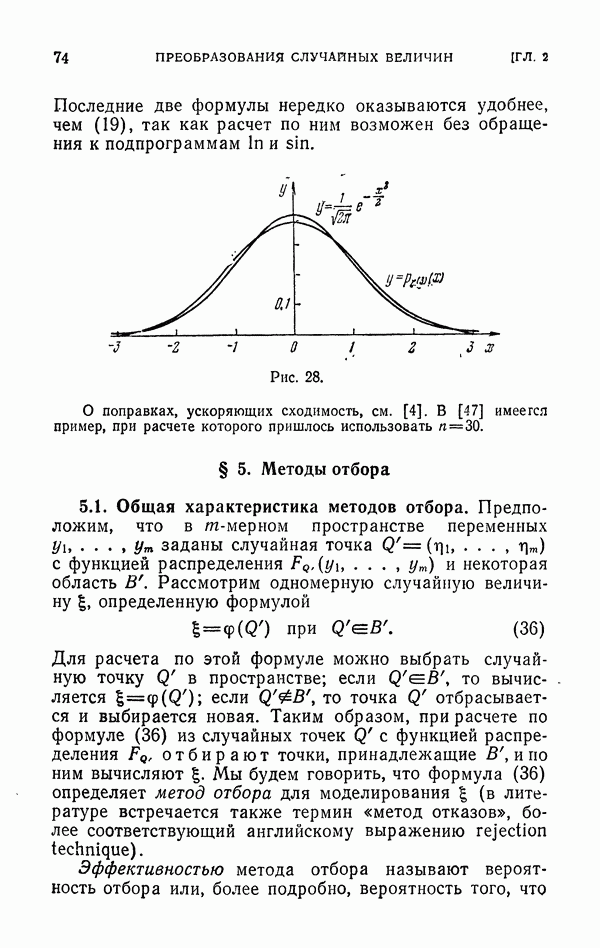
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
§ 1. Методы Монте-Карло с повышенной скоростью сходимости
1.1. Выборка по группам.
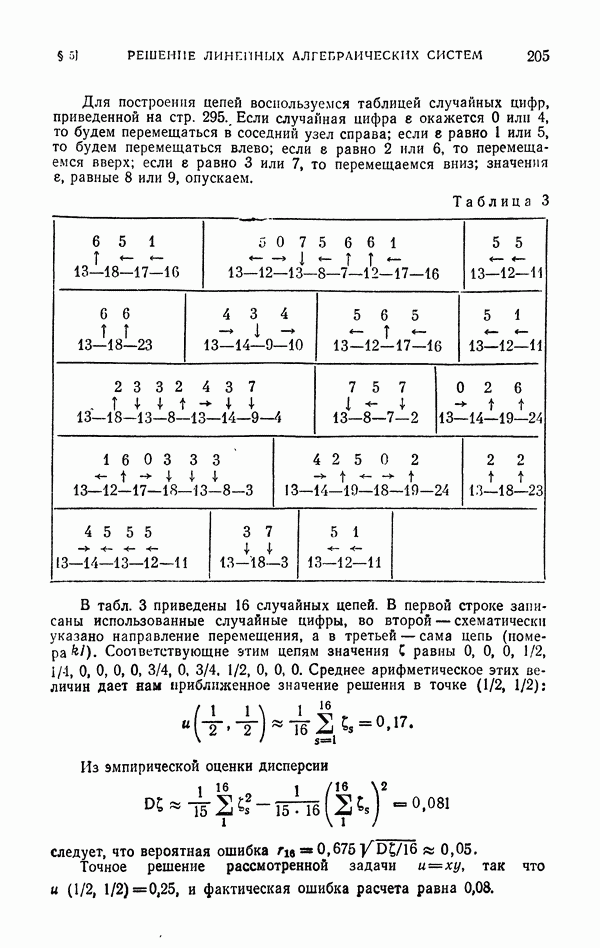
Этот хорошо известный в статистике прием ([24], стр. 218) может быть с успехом использован для уменьшения дисперсии. По идее он весьма близок к методу существенной выборки: здесь также предлагается выбирать больше точек в более «существенных» областях, однако выбор регулируется не специальной плотностью, а указанием количества точек в различных областях.
Итак, пусть требуется вычислить интеграл

Разобьем область интегрирования G на  частей
частей

и введем обозначения

Очевидно,

В области  рассмотрим случайную точку
рассмотрим случайную точку  с плотностью
с плотностью  и для оценки
и для оценки  воспользуемся
воспользуемся
простейшим методом Монте-Карло: так как

то, выбрав N, независимых реализаций  точки
точки  можем записать оценку для
можем записать оценку для

Складывая такие оценки для всех 14, получим новую несмещенную оценку

Общее количество случайных точек в формуле (2) обозначим по-прежнему через N:

Заметим сразу, что оценку (2) можно считать квадратурной суммой со случайными узлами. В самом деле, обычная квадратурная формула записывается в форме

где точки  принадлежащие G, называются узлами, а числа
принадлежащие G, называются узлами, а числа  весами. Если квадратурная формула точна для функций
весами. Если квадратурная формула точна для функций  , то
, то  .
.
Оценка (2) дает нам такую же приближенную формулу

причем и здесь

Предположим, что  . Тогда точность простейшего метода Монте-Карло для расчета I характеризуется дисперсией оценки (14) гл. 3, которая равна
. Тогда точность простейшего метода Монте-Карло для расчета I характеризуется дисперсией оценки (14) гл. 3, которая равна

где

Найдем теперь дисперсию оценки (2). Очевидно,

и так как здесь точки  при
при  независимы, то
независимы, то

Легко вычислить, что

Теорема 1. Если разбиение  число N фиксированы, то минимум выражения (4) при
число N фиксированы, то минимум выражения (4) при  дополнительном условии (3) равен
дополнительном условии (3) равен

и реализуется при

Доказательство. Согласно (6) величина  равна
равна

Используя неравенство Коши—Буняковского, получим

где справа стоит (4). Остается проверить, что при подстановке (7) в (4) получается (6).
В реальных задачах дисперсии  как правило, заранее неизвестны. Известны лишь вероятности
как правило, заранее неизвестны. Известны лишь вероятности  Оказывается, этого уже достаточно, чтобы выбрать
Оказывается, этого уже достаточно, чтобы выбрать  обеспечивающие уменьшение дисперсии (т. е. неравенство
обеспечивающие уменьшение дисперсии (т. е. неравенство  ).
).
Теорема 2. Если разбиение  фиксировано, то при
фиксировано, то при

величина (4) не превосходит 
Доказательство. Умножив (5) на  и просуммировав по
и просуммировав по  от 1 до
от 1 до  получим
получим

Далее

Следовательно,

Подставив (8) в (4), получим выражение

которое в силу предыдущего неравенства не превосходит  . Таким образом теорема доказана.
. Таким образом теорема доказана.
Теоремы 1 и 2 доказаны в [24] для случая выборки из конечного множества. Если выполнено условие (8), то выборка называется типической.
В действительности выбирать  , по формуле (7) или (8) нельзя, так как
, по формуле (7) или (8) нельзя, так как  обязаны быть целыми. Обычно выбирают любые из ближайших к (7) или (8) целых чисел, лишь бы удовлетворялось условие (3).
обязаны быть целыми. Обычно выбирают любые из ближайших к (7) или (8) целых чисел, лишь бы удовлетворялось условие (3).
Пример. Чтобы вычислить интеграл 

с помощью N = 10 точек, разобьем (0, 1) на две равные части и выберем в  всего 4 равномерно распределенные точки а в
всего 4 равномерно распределенные точки а в  равномерно распределенных точек
равномерно распределенных точек  Тогда
Тогда 

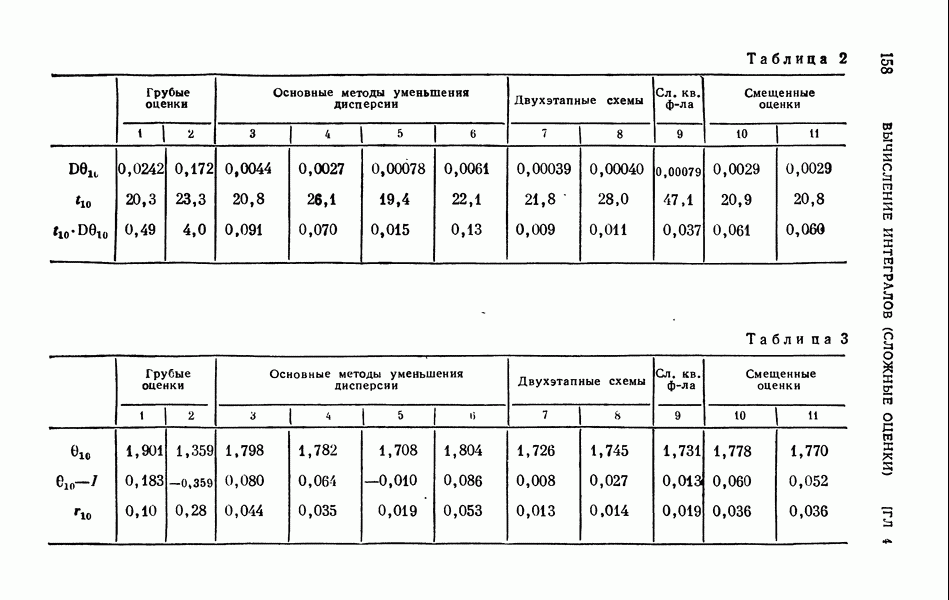
Дисперсия этой оценки  , где
, где

Следовательно,  в то время как дисперсия простейшего метода
в то время как дисперсия простейшего метода  Значения и
Значения и  легко вычисляются по формулам и
легко вычисляются по формулам и 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
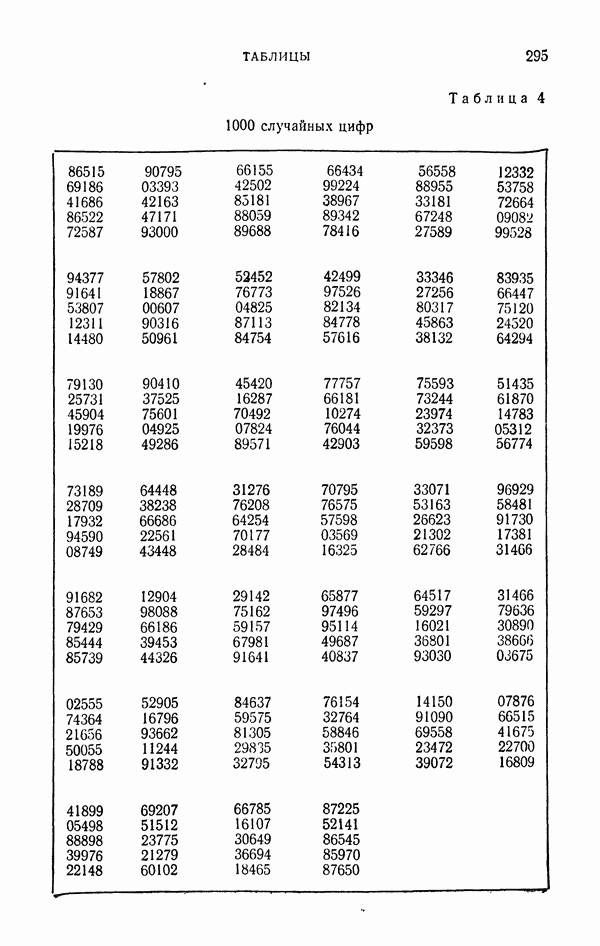
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
- § 1. Моделирование путем имитации
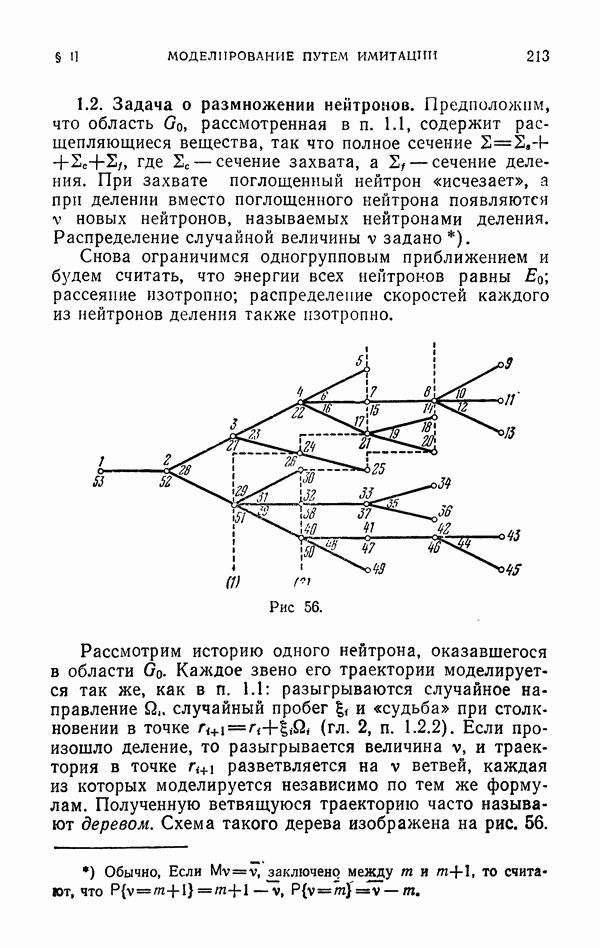
- 1.2. Задача о размножении нейтронов.
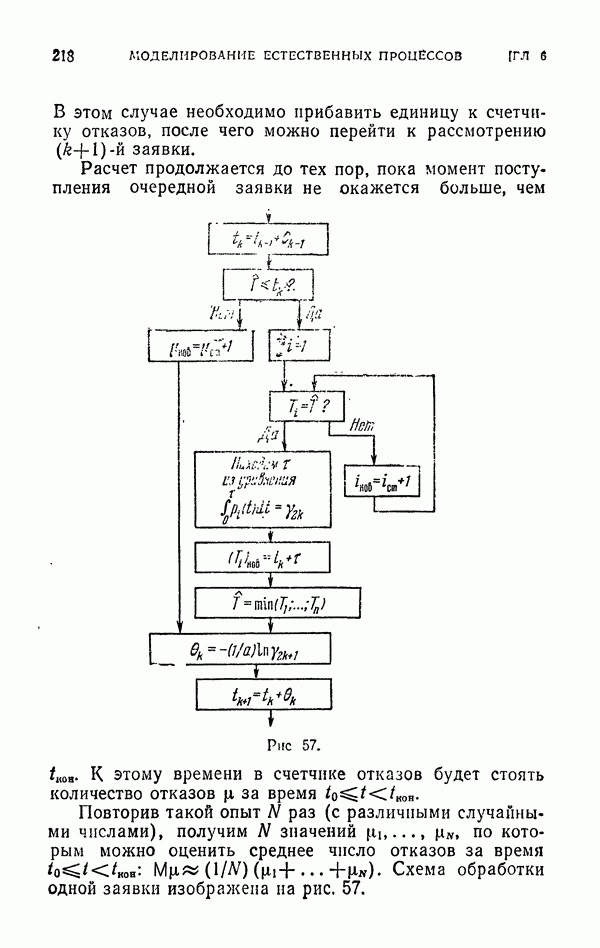
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
- § 2. Моделирование свободного пробега
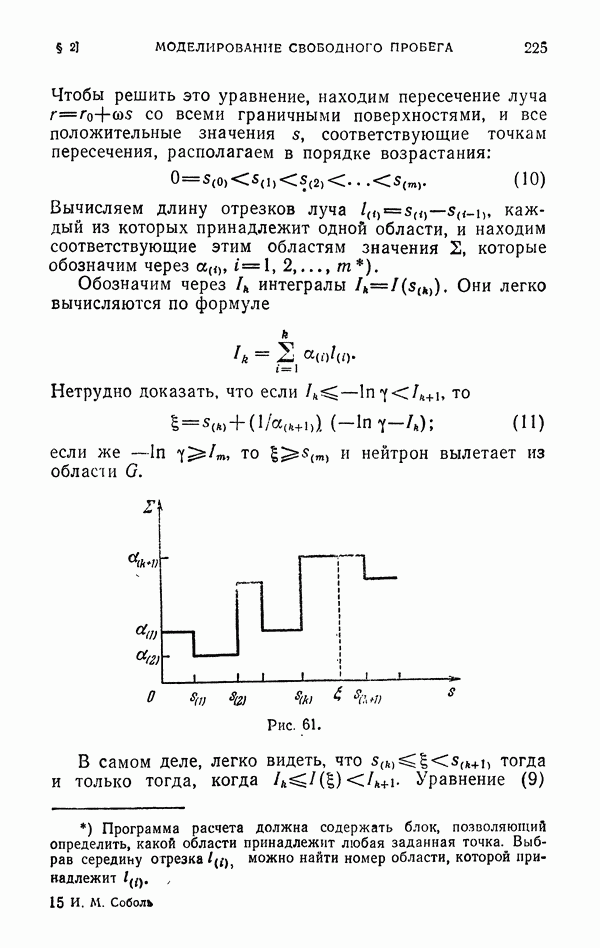
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
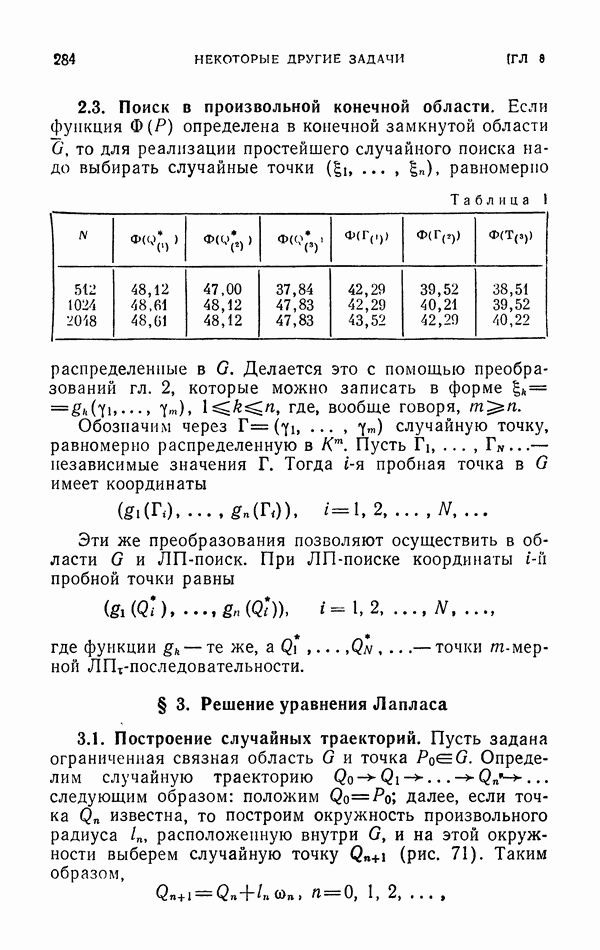
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА