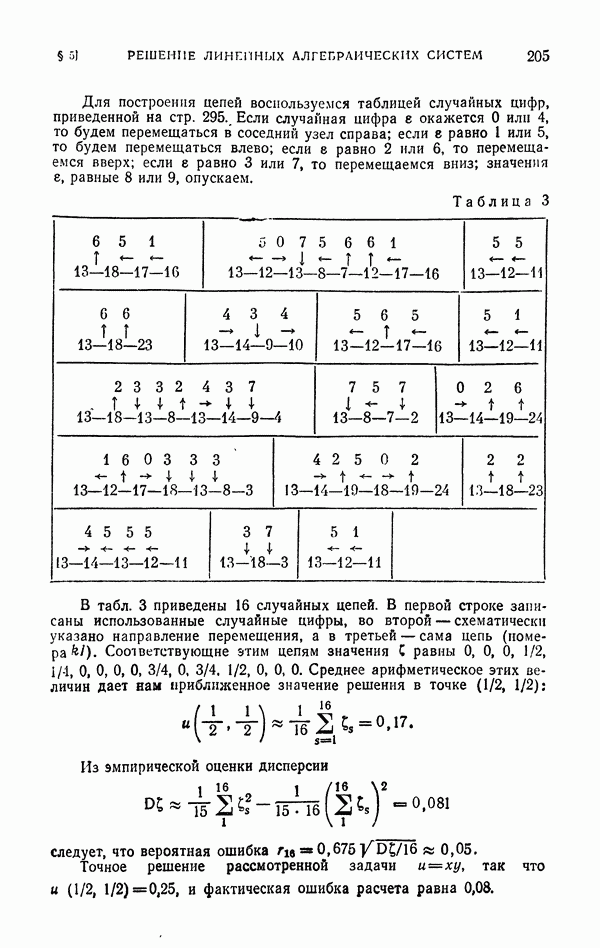
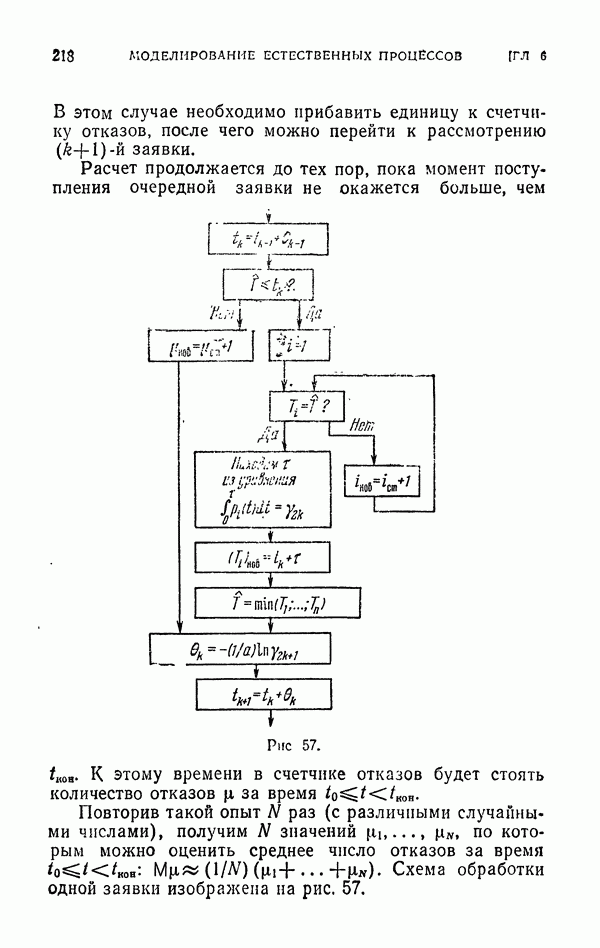
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Метод существенной выборки.
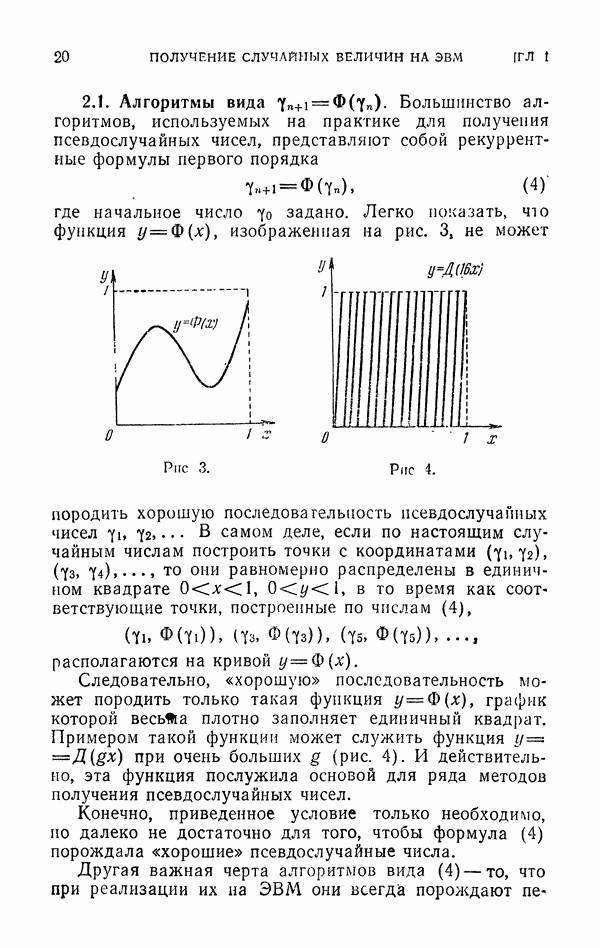
До сих пор мы рассматривали интегралы вида (12) и использовали при вычислении их случайные точки с плотностью  Предположим теперь, что требуется вычислить абсолютно сходящийся интеграл
Предположим теперь, что требуется вычислить абсолютно сходящийся интеграл

где область G может быть как ограниченной, так и неограниченной, и квадрат функции  не обязательно интегрируем. Предполагается только, что
не обязательно интегрируем. Предполагается только, что 
3.2.1. Плотность  определенную в G, назовем допустимой по отношению к
определенную в G, назовем допустимой по отношению к  если
если  в тех точках, в которых
в тех точках, в которых 
Если  всюду в G, то эта плотность допустима по отношению к любым
всюду в G, то эта плотность допустима по отношению к любым  . Вообще же допустимая плотность может обращаться в пуль, но только там, где
. Вообще же допустимая плотность может обращаться в пуль, но только там, где  Множество точек, в которых
Множество точек, в которых  назовем
назовем  и пусть
и пусть 
Выберем произвольную допустимую плотность  и рассмотрим функцию
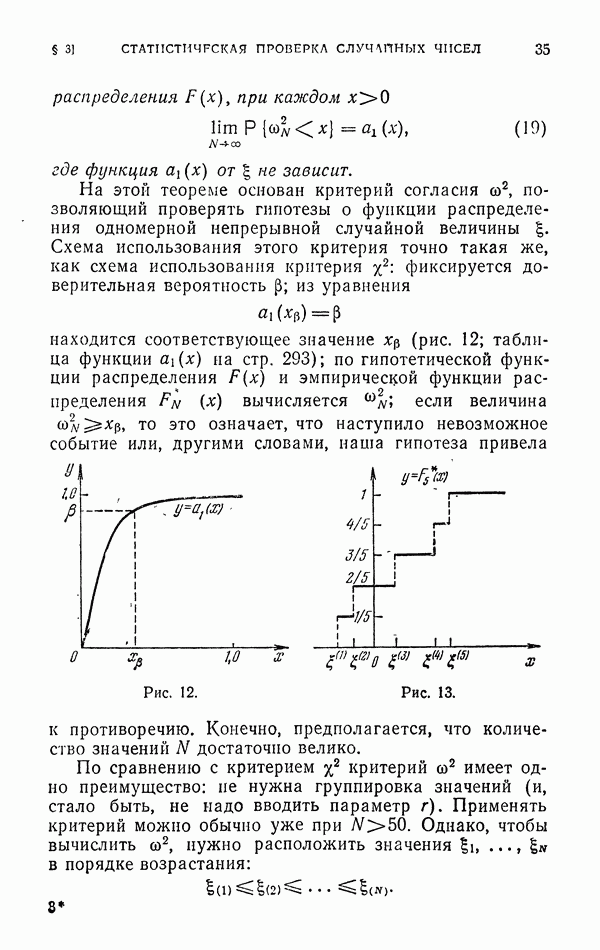
и рассмотрим функцию

Если Q — случайная точка, определенная в G с плотностью  , то
, то

ибо вне множества  функция
функция  .
.
Согласно п. 2.1 для приближенного расчета  можно использовать независимые реализации
можно использовать независимые реализации  случайной точки Q и оценку
случайной точки Q и оценку

Вероятная ошибка этой оценки зависит от дисперсии  которую нетрудно вычислить: так как
которую нетрудно вычислить: так как

то

Величина эта зависит от выбора плотности  и даже не обязательно конечна. Естественно поставить вопрос о выборе
и даже не обязательно конечна. Естественно поставить вопрос о выборе  так, чтобы минимизировать
так, чтобы минимизировать 
Теорема 3. Минимальная дисперсия  реализуется в случае, когда плотность
реализуется в случае, когда плотность  пропорциональна
пропорциональна  и равна
и равна

Доказательство. Если плотность  пропорциональна
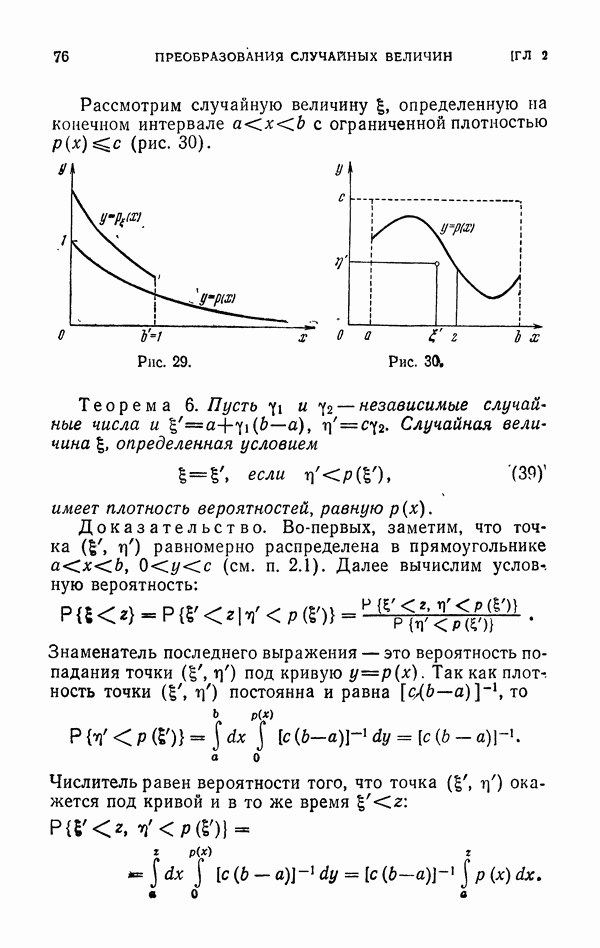
пропорциональна  она равна
она равна

Подставив (31) в (29), получим, что 
Осталось доказать, что, какова бы ни была допустимая плотность  дисперсия
дисперсия  . А это легко доказывается с помощью неравенства (1), стр. 292:
. А это легко доказывается с помощью неравенства (1), стр. 292:

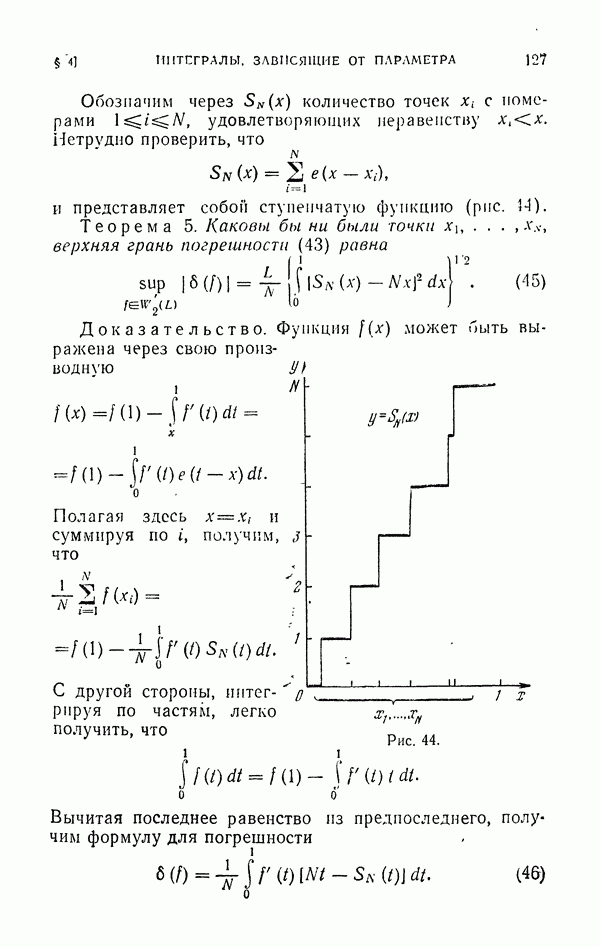
Следствие. Если подынтегральная функция  не меняет знака в
не меняет знака в  , то,
, то,  .
.
Отметим, что плотность  тождественно равна нулю в области
тождественно равна нулю в области  в которой
в которой  Этот результат согласуется с выводом из теоремы 1, что область, в которой
Этот результат согласуется с выводом из теоремы 1, что область, в которой  выгодно при интегрировании исключить.
выгодно при интегрировании исключить.
В действительности использовать плотность (31) для расчета интеграла (28) нельзя, ибо в (31) входит значение  вычисление которого представляет собой задачу, эквивалентную по трудности исходной задаче (в случае знакопостоянной функции
вычисление которого представляет собой задачу, эквивалентную по трудности исходной задаче (в случае знакопостоянной функции  — в точности эквивалентную). Однако из теоремы 3 можно сделать вывод, что желательно выбирать плотность
— в точности эквивалентную). Однако из теоремы 3 можно сделать вывод, что желательно выбирать плотность  по возможности пропорциональной
по возможности пропорциональной  . Такой метод выбора
. Такой метод выбора  часто приводит к величинам
часто приводит к величинам  с небольшими дисперсиями. Он был предложен Г. Капом [142] и называется методом существенной выборки (importance sampling), ибо если
с небольшими дисперсиями. Он был предложен Г. Капом [142] и называется методом существенной выборки (importance sampling), ибо если  пропорциональна
пропорциональна  то в тех частях области G, в которых
то в тех частях области G, в которых  больше и вклад которых в
больше и вклад которых в  более существен, будет выбираться больше случайных точек.
более существен, будет выбираться больше случайных точек.
Возможна и другая интерпретация целесообразности выбора  пропорционально
пропорционально  случае знакопостоянной
случае знакопостоянной  : чем ближе
: чем ближе  к постоянной, тем меньше дисперсия
к постоянной, тем меньше дисперсия 
Очень сложные плотности  использовать не рекомендуется, так как тогда процесс реализации случайных точек Q с плотностью
использовать не рекомендуется, так как тогда процесс реализации случайных точек Q с плотностью  станет очень трудоемким. Заметим, что для вычисления интеграла
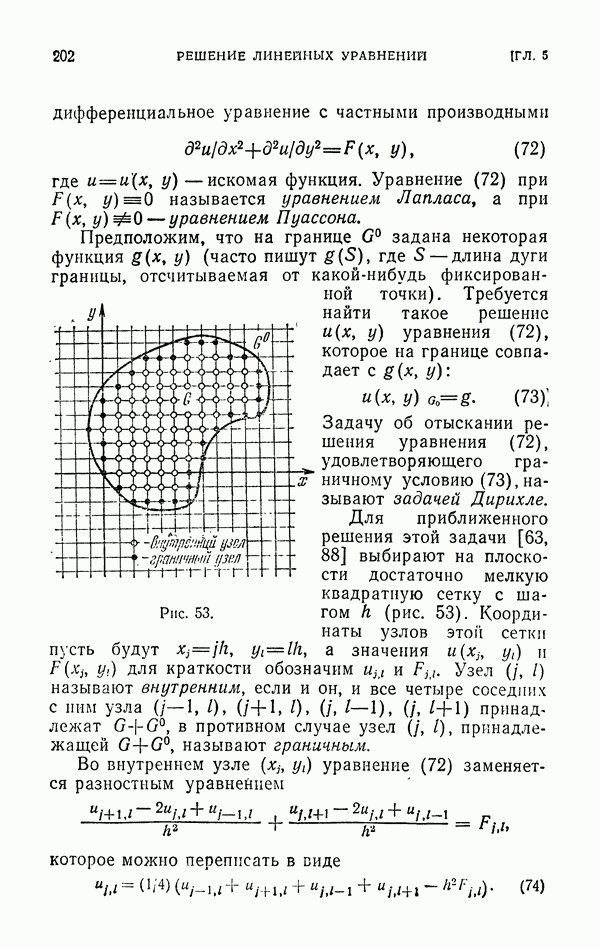
станет очень трудоемким. Заметим, что для вычисления интеграла

не обязательно использовать оценку  можно применить какой-нибудь из методов п. 3.1.
можно применить какой-нибудь из методов п. 3.1.
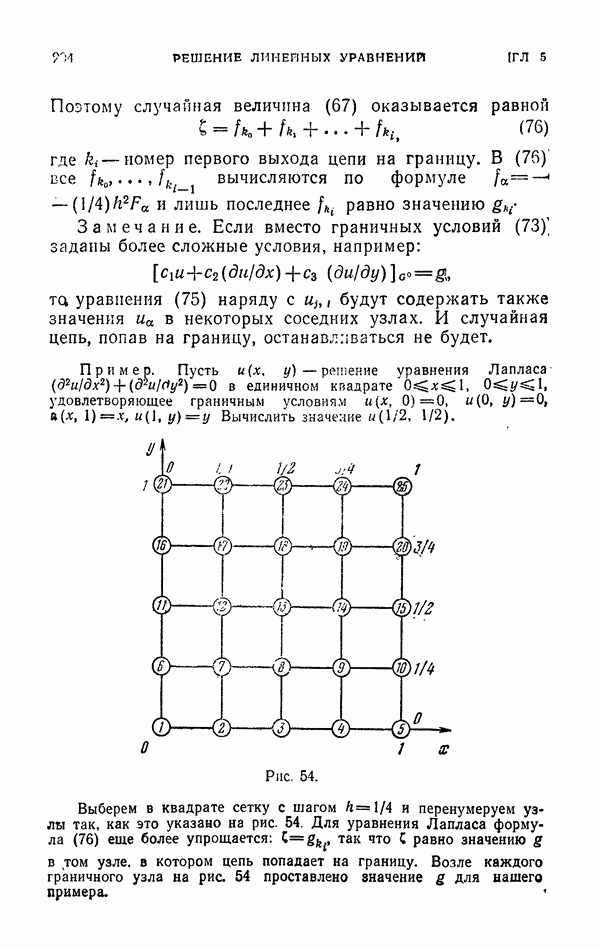
Пример. Интеграл

рассмотренный в пп. 2 3 и 3.1.1, можно представить в виде

где  . Значения случайной величины
. Значения случайной величины  с плотностью
с плотностью  вычисляются по формуле
вычисляются по формуле  (метод обратных функций), а оценка равна
(метод обратных функций), а оценка равна

В этом примере дисперсия осредняемой величины  равна
равна

Это гораздо меньше, чем в п. 2.3, и меньше, чем в п. 3.1.1.
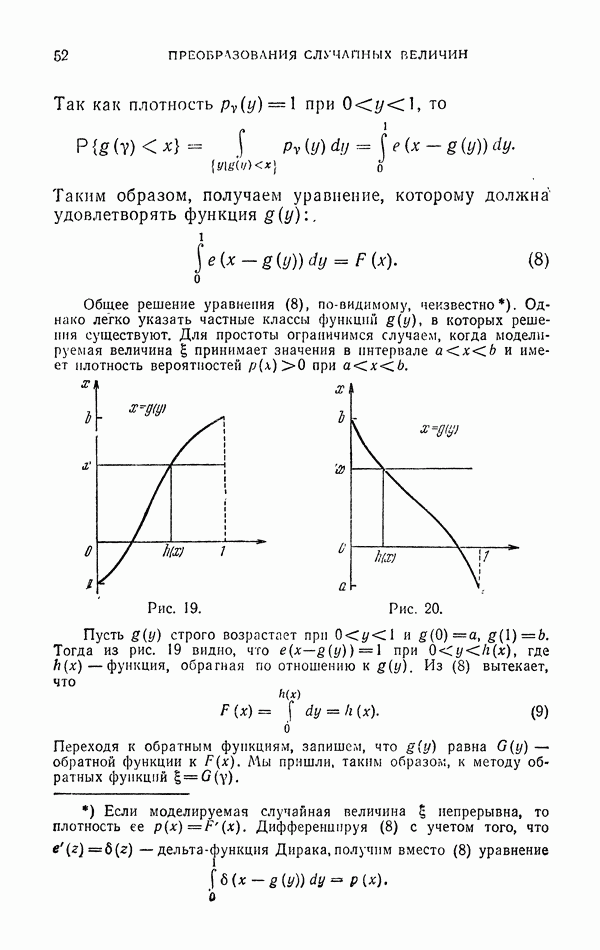
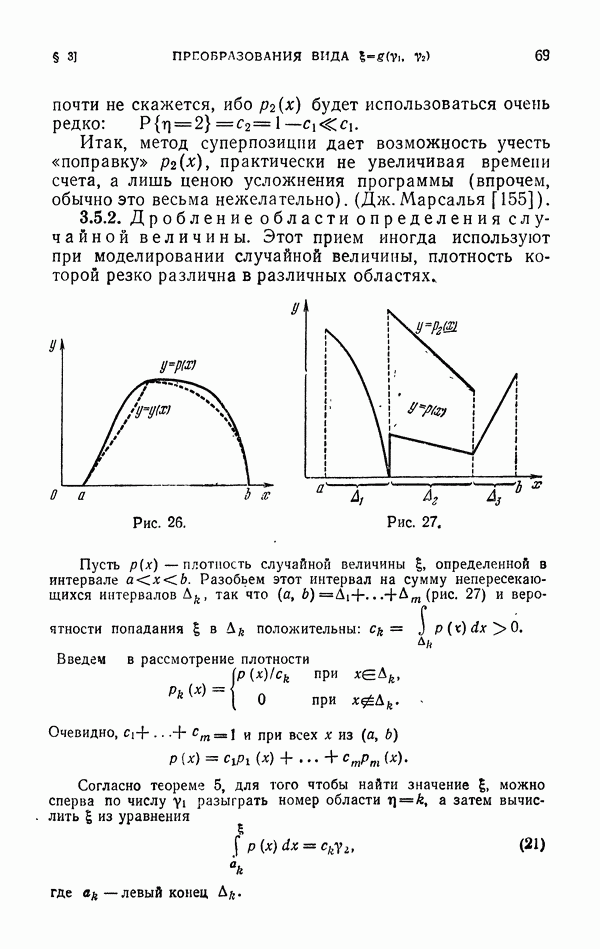
3.2.2. Метод существенной выборки позволяет строить хор яиие оценки для несобственных интегралов (28). Предположим, что область G ограничена, но

В этом случае простейший метод Монте-Карло позволяет записать оценку интеграла (28)

где точки  равномерно распределены в G, a
равномерно распределены в G, a  — объем G. Однако оценка эта плохая, ибо
— объем G. Однако оценка эта плохая, ибо  . В то же время оценка, полученная методом существенной выборки будет иметь конечную дисперсию, если выбрать допустимую плотность
. В то же время оценка, полученная методом существенной выборки будет иметь конечную дисперсию, если выбрать допустимую плотность  так, чтобы интеграл, фигурирующий в выражении (29), сходился. Такие плотности всегда существуют. В частности, этому требованию удовлетворяет плотность (31).
так, чтобы интеграл, фигурирующий в выражении (29), сходился. Такие плотности всегда существуют. В частности, этому требованию удовлетворяет плотность (31).
На практике, если подынтегральная функция  имеет особенность, то стараются выбрать плотность
имеет особенность, то стараются выбрать плотность  с той же особенностью, так, чтобы отношение
с той же особенностью, так, чтобы отношение  было ограниченным. Прием этот часто называют включением особенности в плотность.
было ограниченным. Прием этот часто называют включением особенности в плотность.
Предположим теперь, что функция  в (28) особенностей не имеет, но область интегрирования G неограничепа. Чтобы оценить такой интеграл, можно
в (28) особенностей не имеет, но область интегрирования G неограничепа. Чтобы оценить такой интеграл, можно
выбрать ограниченную область  так, что
так, что

и строить оценку для интеграла по области  Вместо этого можно попытаться заменой переменных преобразовать G в конечную область. Однако наиболее естественным, по-видимому, надо считать использование метода существенной выборки. И в этом случае также рекомендуется включать особенность в плотность, т. е. выбирать
Вместо этого можно попытаться заменой переменных преобразовать G в конечную область. Однако наиболее естественным, по-видимому, надо считать использование метода существенной выборки. И в этом случае также рекомендуется включать особенность в плотность, т. е. выбирать  так, чтобы отношение
так, чтобы отношение  стремилось к постоянной при
стремилось к постоянной при 
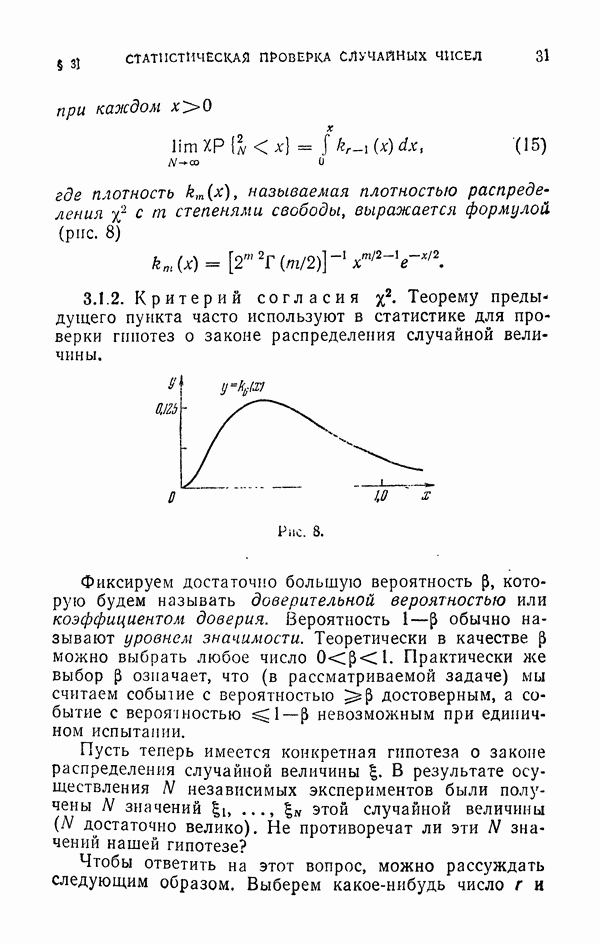
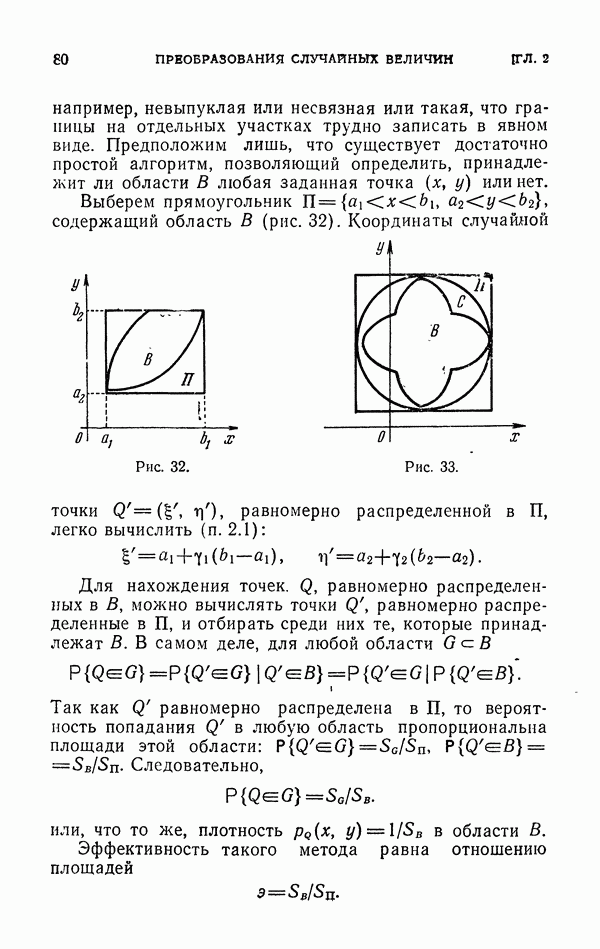
3.2.3. Один тип интегралов с особенностью. Обозначим через G шар  Во многих разделах физики и механики встречаются интегралы вида
Во многих разделах физики и механики встречаются интегралы вида

где обе точки  принадлежат
принадлежат  расстояние между этими точками:
расстояние между этими точками: 
Рассмотрим интеграл такого типа с особенностью

где функция  ограничена и
ограничена и  Интеграл (33) абсолютно сходится при
Интеграл (33) абсолютно сходится при 
А. Для того чтобы вычислить интеграл (33) простейшим методом Монте-Карло, выберем две независимые случайные точки  равномерно распределенные в G. Так как плотности их
равномерно распределенные в G. Так как плотности их  то положим
то положим  Тогда
Тогда  а дисперсия Z равна
а дисперсия Z равна

При  последний интеграл расходится и
последний интеграл расходится и 
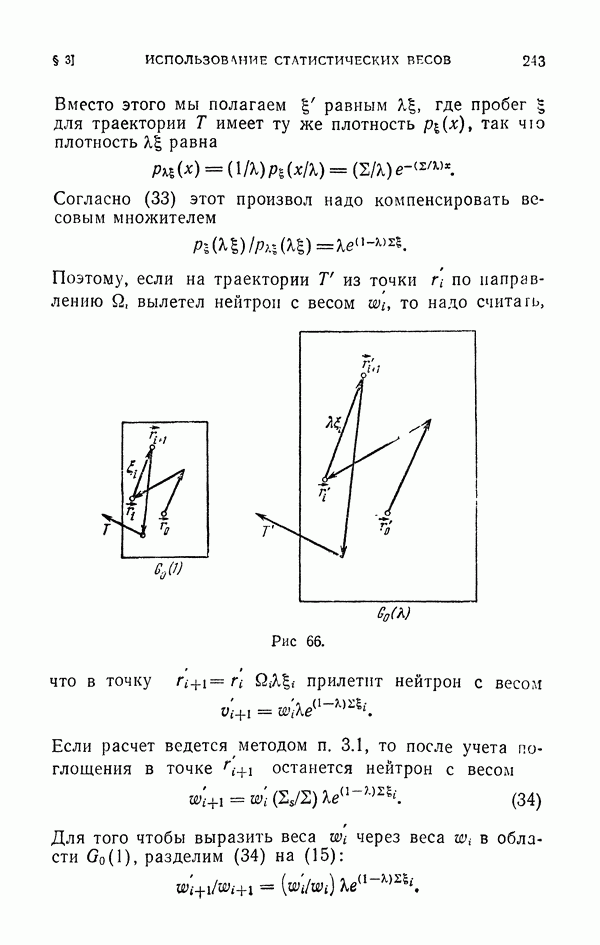
Б. Воспользуемся методом существенной выборки и выберем совместную плотность  случайных точек
случайных точек  так, чтобы она содержала такую же особенность, как подынтегральная функция. Так как
так, чтобы она содержала такую же особенность, как подынтегральная функция. Так как  то точку Q будем по-прежнему считать равномерно распределенной в
то точку Q будем по-прежнему считать равномерно распределенной в 
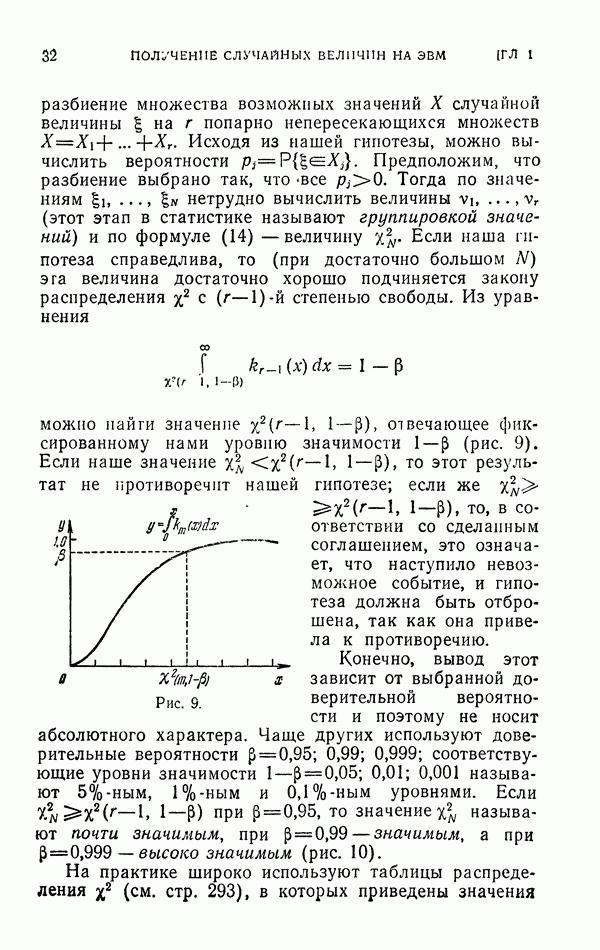
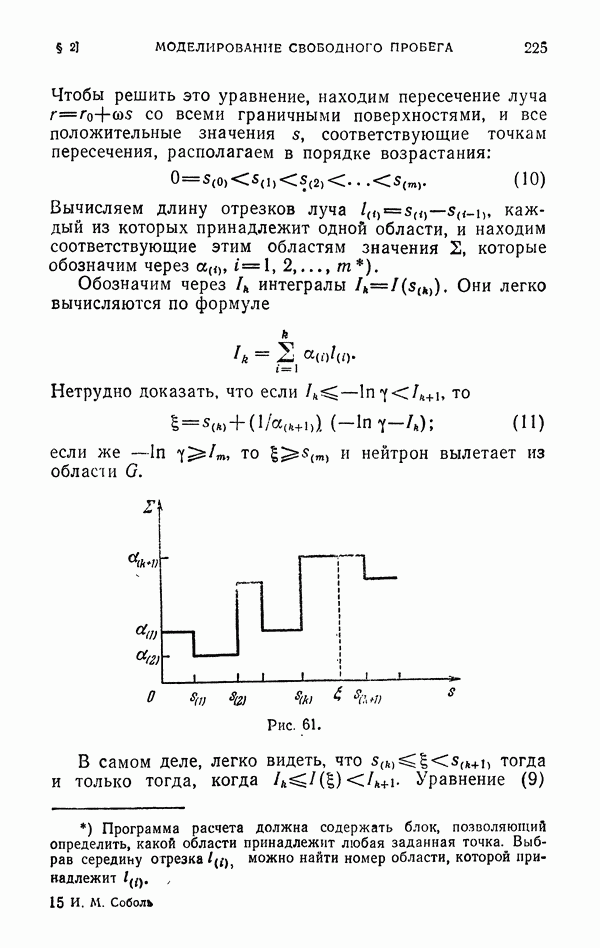
Для определения  перенесем начало координат в точку Р и выберем сферические координаты
перенесем начало координат в точку Р и выберем сферические координаты  с центром в Р (рис. 38). Направление (из точки Р) условимся задавать единичным вектором
с центром в Р (рис. 38). Направление (из точки Р) условимся задавать единичным вектором  , а расстояние по этому направлению от точки Р до границы шара G назовем
, а расстояние по этому направлению от точки Р до границы шара G назовем  Пусть
Пусть

где 
Нетрудно проверить, что формула (34) действительно определяет условную плотность вероятностей: при любой фиксированной точке Р

Рассмотрим скалярную случайную величину

где  . Нетрудно вычислить, что
. Нетрудно вычислить, что

a дисперсия этой величины равна

Так как функция  ограничена,
ограничена,  не превосходит диаметра шара G, то последний интеграл сходится, и дисперсия DZ конечна при всех
не превосходит диаметра шара G, то последний интеграл сходится, и дисперсия DZ конечна при всех 
В. Из-за симметрии задачи интеграл (33) может быть сведен к трехкратному. В расчетной схеме методов Монте-Карло этот факт учитывается «автоматически», если при реализации случайных точек принимать во внимание симметрию. Чтобы показать это выведем расчетные формулы для обоих способов расчета  .
.

Рис. 38.
Сферические координаты точки Q в обоих случаях можно вычислять по формулам (14) гл. 2. Однако из соображений симметрии ясно, что точку Q можно выбрать на оси 
Поэтому положим 
В способе А точка Q также равномерно распределена в G. Из соображений симметрии ясно, что можно ее выбирать в плоскости  и считать, что
и считать, что

где 
Получаем следующий алгоритм для расчета  методом А:
методом А:
1) Формулы для  испытания
испытания

2) Если  — значение
— значение  , полученное в
, полученное в  испытании, то
испытании, то

В способе Б случайную точку Q с плотностью (34) можно строить следующим образом: сперва из точки Q надо выбрать случайное направление  (п. 2.4.2 гл. 2); затем на луче
(п. 2.4.2 гл. 2); затем на луче  выбрать случайное расстояние
выбрать случайное расстояние  с функцией распределения
с функцией распределения  (где
(где  ); тогда
); тогда 
В самом деле, условная плотность точки Q (при условии  в сферических координатах
в сферических координатах  о центром в Р равна
о центром в Р равна 


Рис. 39.
Первый сомножитель равен плотности случайного направления  (в сферических координатах), а второй — это условная плотность случайного расстояния на луче
(в сферических координатах), а второй — это условная плотность случайного расстояния на луче  при условии, что со уже выбрано.
при условии, что со уже выбрано.
Те же соображения симметрии, что в случае А, позволяют выбирать направление  в плоскости
в плоскости  Оно определяется одним параметром
Оно определяется одним параметром  . Вычислив расстояние
. Вычислив расстояние  получим следующий алгоритм для расчета I методом Б:
получим следующий алгоритм для расчета I методом Б:
1) Формулы для  испытания
испытания

2) Если  значения
значения  , полученные в
, полученные в  испытании. то
испытании. то

В обоих алгоритмах — (35) и (36) — на каждое испытание затрачивается всего три случайных числа, так что фактически вычисляется
трехкратный интеграл. В общем случае, когда функция  зависит не только от расстояния
зависит не только от расстояния  а от самих точек Р и Р, пришлось бы моделировать все шесть координат точек
а от самих точек Р и Р, пришлось бы моделировать все шесть координат точек 
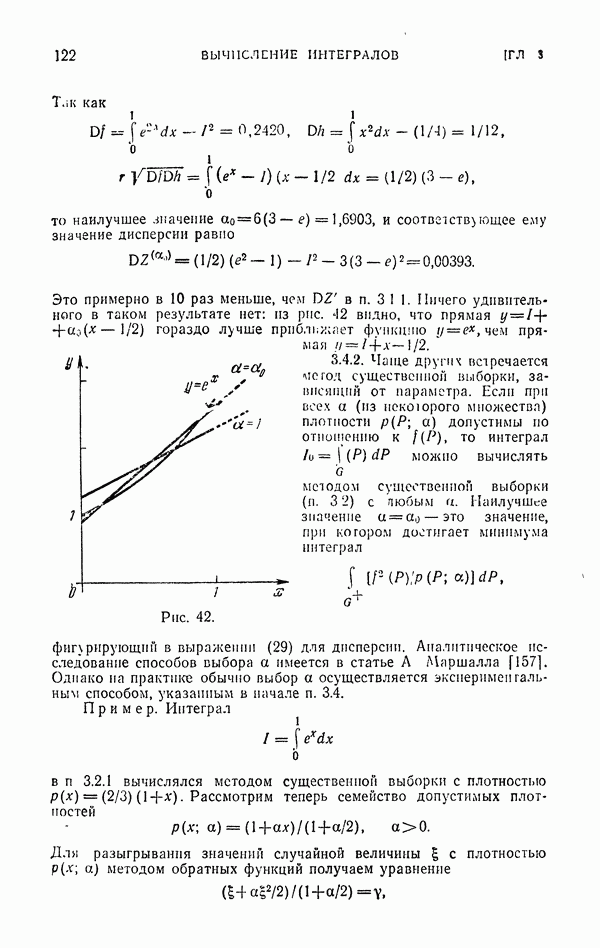
Г. Рассмотрим численный пример: интеграл (33) в случае 

где  единичный шар
единичный шар  Некоторые значения этого интеграла:
Некоторые значения этого интеграла: 
Запишем оценки (35) и (36) для 

Нетрудно заметить, что в этом случае оценка  зависит лишь от двух случайных чисел.
зависит лишь от двух случайных чисел.
Вычислим дисперсии соответствующих этим методам величин  приведены в пунктах А и Б):
приведены в пунктах А и Б):

откуда следует, что  . Для оценок типа Б
. Для оценок типа Б 

Пусть  , так что
, так что  . Тогда
. Тогда

откуда следует, что  . Интересно отмстить, что
. Интересно отмстить, что  Этот пример показывает, что неудачное использование существенной выборки приводит к увеличению дисперсии.
Этот пример показывает, что неудачное использование существенной выборки приводит к увеличению дисперсии.
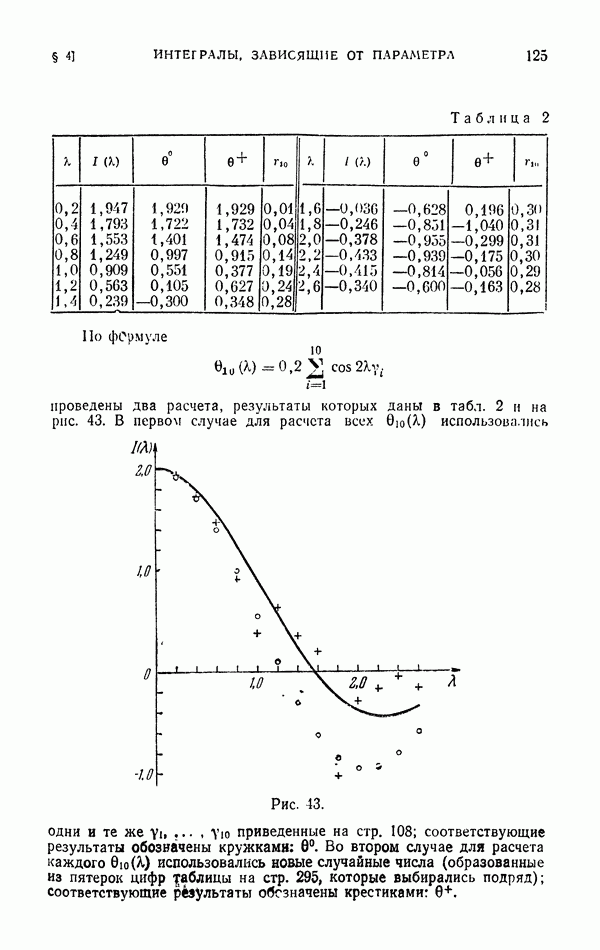
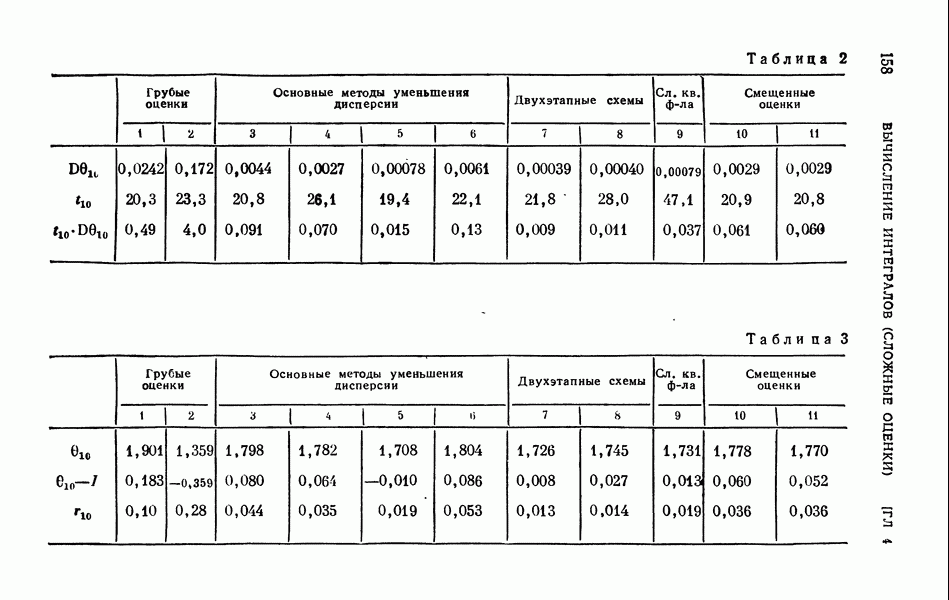
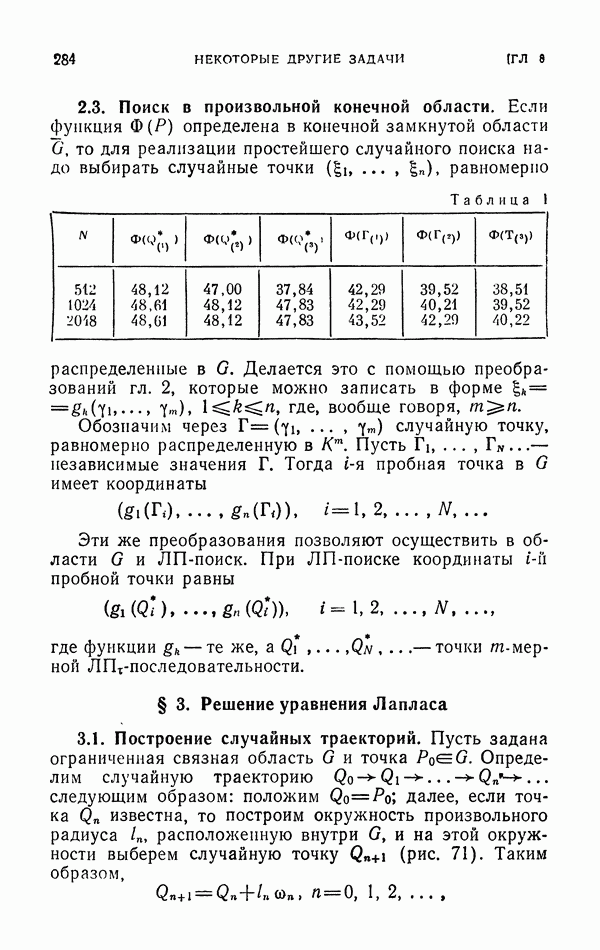
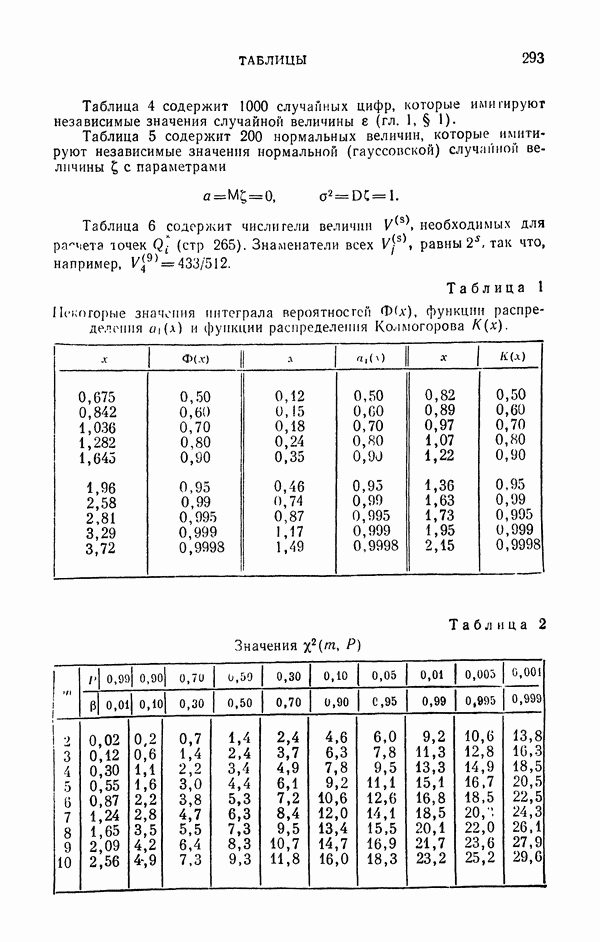
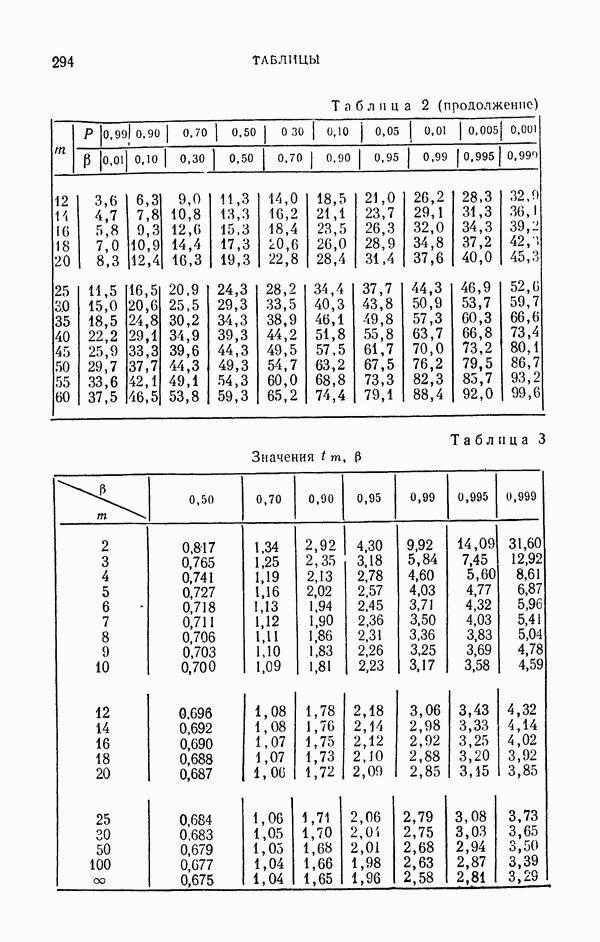
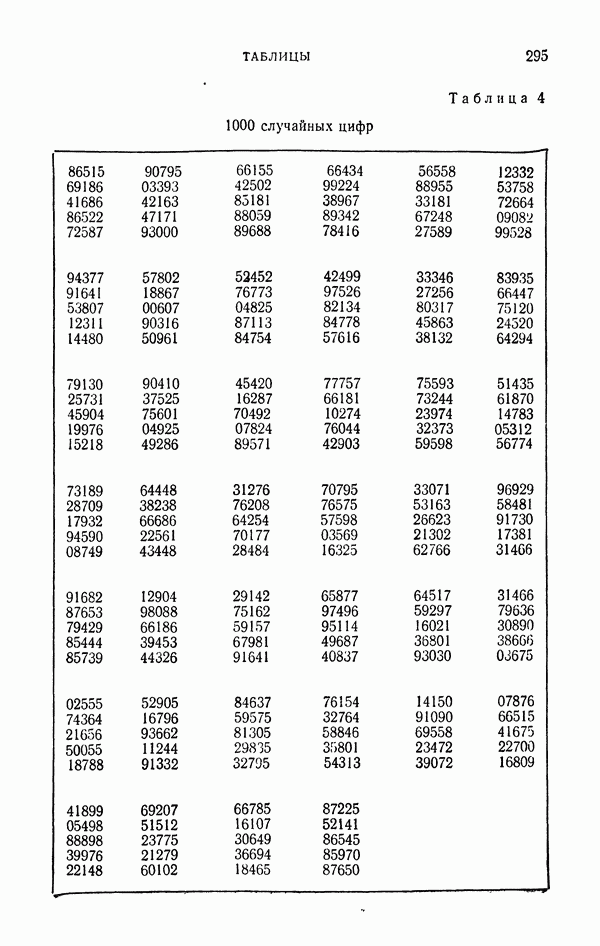
Таблица 1

В табл. 1 приведены результаты расчета всех четырех оценок при  с использованием случайных чисел, указанных на стр. 108. Здесь же указаны ошибки расчета и вероятные ошибки
с использованием случайных чисел, указанных на стр. 108. Здесь же указаны ошибки расчета и вероятные ошибки 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
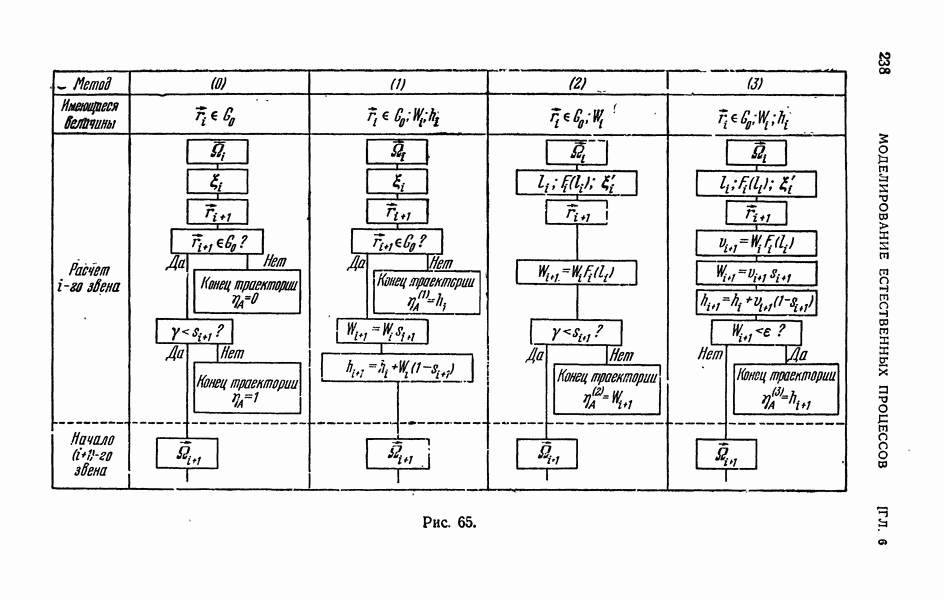
- § 1. Моделирование путем имитации
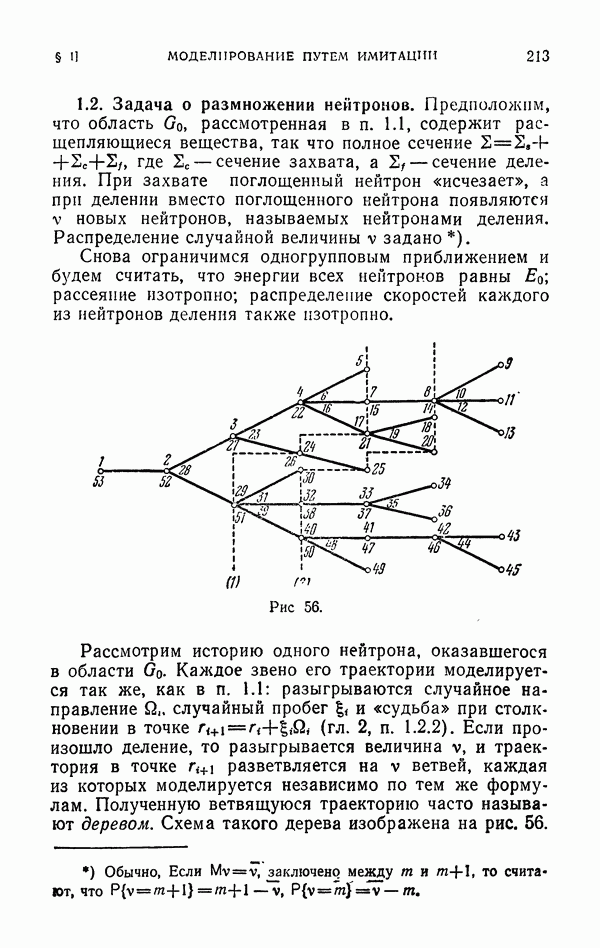
- 1.2. Задача о размножении нейтронов.
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
- § 2. Моделирование свободного пробега
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
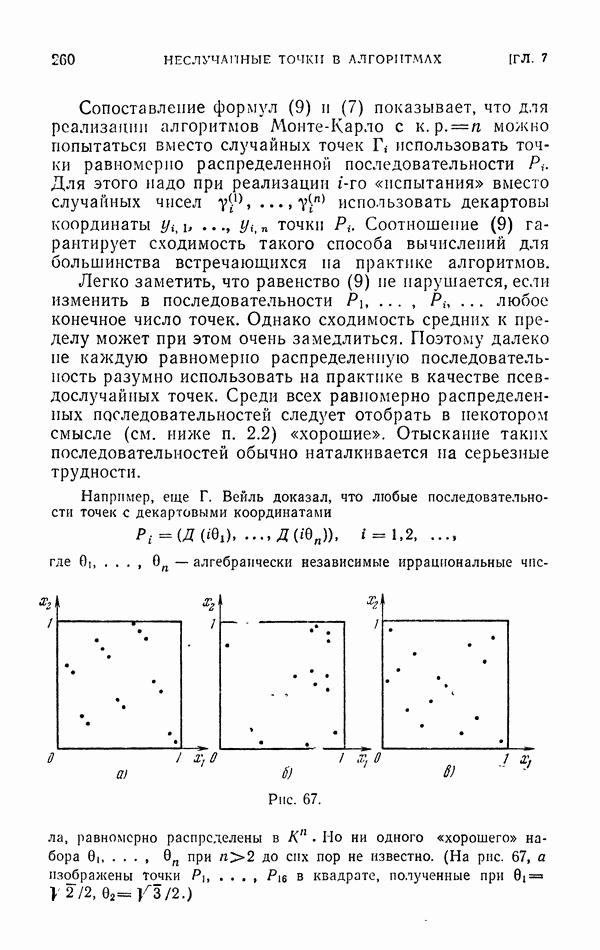
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА