| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
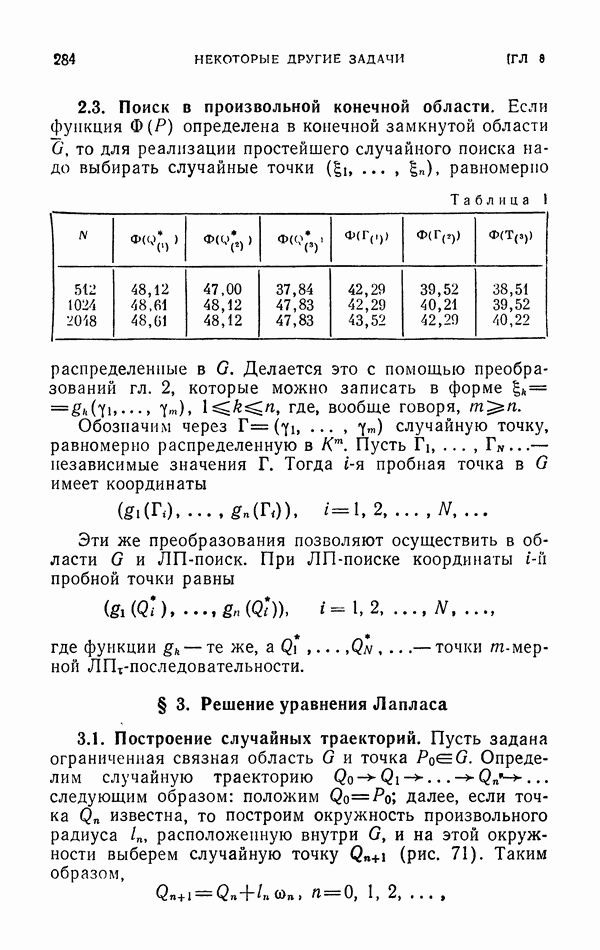
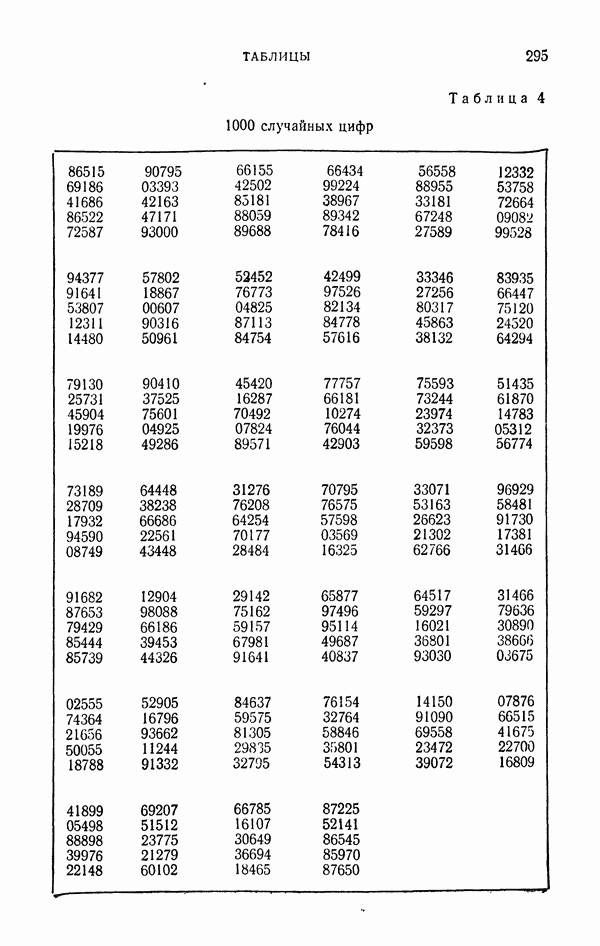
1.3. Таблицы случайных цифр.
Предположим, что мы осуществили N независимых опытов, в результате которых получили  случайных цифр
случайных цифр  Записав эти цифры (в порядке появления) в таблицу, получим то, что называется таблицей случайных цифр (см. стр. 295, где цифры объединены в группы только ради удобства чтения).
Записав эти цифры (в порядке появления) в таблицу, получим то, что называется таблицей случайных цифр (см. стр. 295, где цифры объединены в группы только ради удобства чтения).
Способ употребления такой таблицы весьма прост. Если в ходе расчета некоторой задачи нам потребуется случайная цифра  , то мы можем взять любую цифру
, то мы можем взять любую цифру  из этой таблицы. Если нам понадобится случайное число
из этой таблицы. Если нам понадобится случайное число  , то мы можем взять из таблицы
, то мы можем взять из таблицы  очередных цифр и считать, что
очередных цифр и считать, что  Выбирать цифры из такой таблицы в случайном порядке не обязательно. Их можно выбирать подряд. Но, конечно, можно начинать с любого места, читать в любом направлении, использовать любой заранее заданный алгоритм
Выбирать цифры из такой таблицы в случайном порядке не обязательно. Их можно выбирать подряд. Но, конечно, можно начинать с любого места, читать в любом направлении, использовать любой заранее заданный алгоритм
выбора, не зависящий от конкретных значений цифр таблицы.
Все сказанное выше относится к «идеальной» таблице случайных цифр и не вызывает никаких сомнений. Мы не будем подробно останавливаться на трудностях, возникающих при переходе к «реальным» таблицам, но отметим некоторые из них.
Во-первых, изготовление хорошей таблицы — весьма сложное дело, ибо в любом реальном опыте всегда возможны ошибки. Например, для изготовления таблицы [166], содержащей миллион случайных цифр, была построена и тщательно отлажена специальная «рулетка» (с использованием электроники). Тем не менее после некоторого периода хорошей работы она стала выдавать, как показала проверка, не равновероятные цифры. Таким образом, проверка «качества» таблицы абсолютно необходима. Никакие априорные соображения о тщательности постановки опыта не гарантируют нас от ошибок.
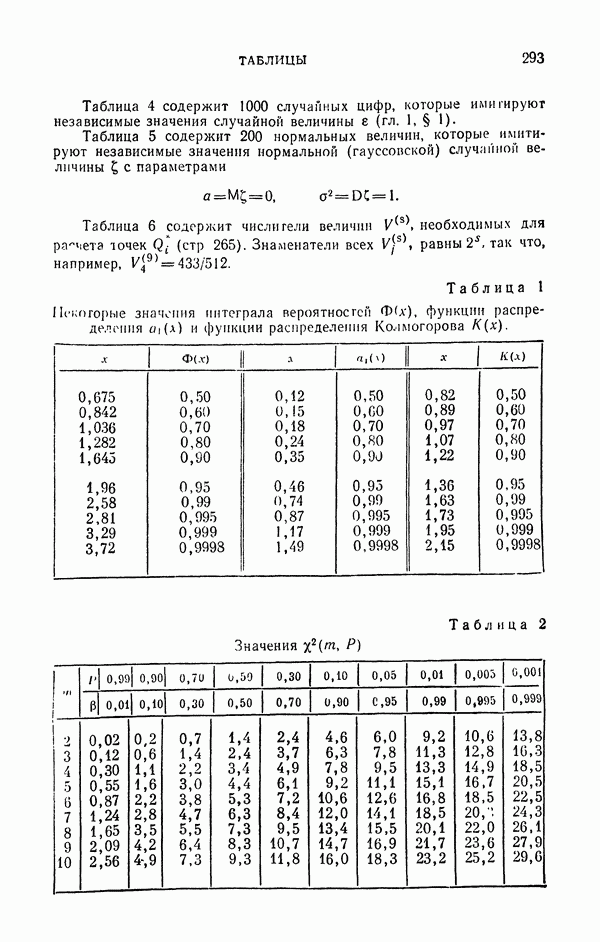
Тесты для проверки таблиц случайных цифр рассмотрены ниже в § 3. Здесь только поясним, что проверяется частота каждой из десяти цифр, частота различных соседних пар и т. п.
Вторая трудность связана с «незаконностью» многократного использования одной и той же таблицы. Вычислителей этот вопрос не очень беспокоит, так как интуитивно ясно, что таблицу можно повторно использовать при решении независимых задач (впрочем, что такое «независимые» задачи — не очень ясно). Возможность использования одних и тех же случайных величин для решения целых классов задач доказана ниже в гл. 3, § 4.
Наконец, отметим еще известный парадокс: в большой таблице найдутся плохие участки. (Например, в таблице, содержащей  цифр, вполне вероятно найти
цифр, вполне вероятно найти
100 пулей подряд.) Очевидно, самостоятельное использование таких участков недопустимо.
В настоящее время таблицы случайных цифр (или более разнообразные таблицы случайных величин) используют главным образом при расчетах вручную; для расчетов на ЭВМ ими практически не пользуются. Основная причина этого — чисто техническая: внутренний накопитель всех современных ЭВМ сравнительно мал и большая таблица туда не помещается; а обращение к внешним запоминающим устройствам сильно замедляет счет. Вторая причина — ограниченность объема существующих таблиц, — по-видимому, играет второстепенную роль: можно заготовить таблицу любого объема, если это потребуется.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
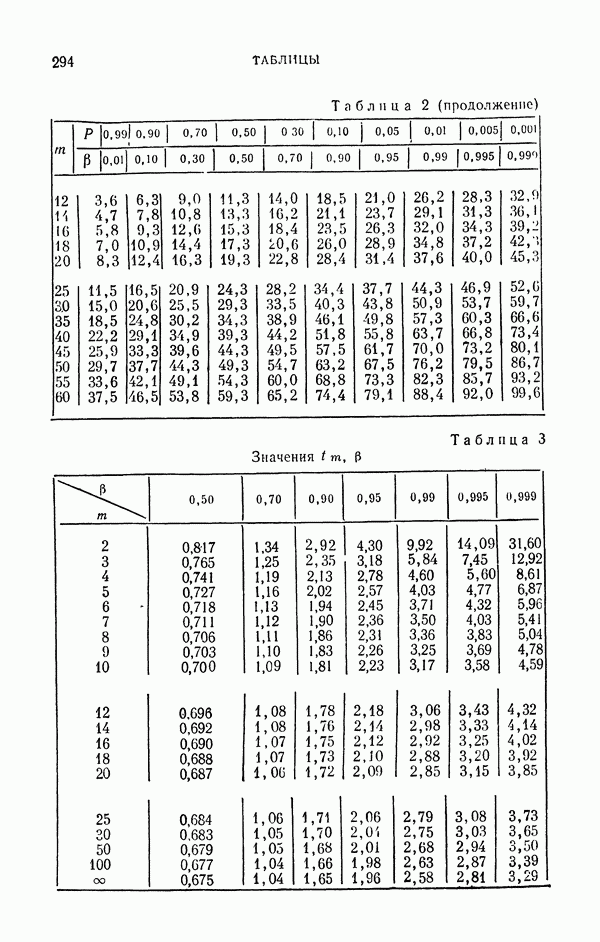
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
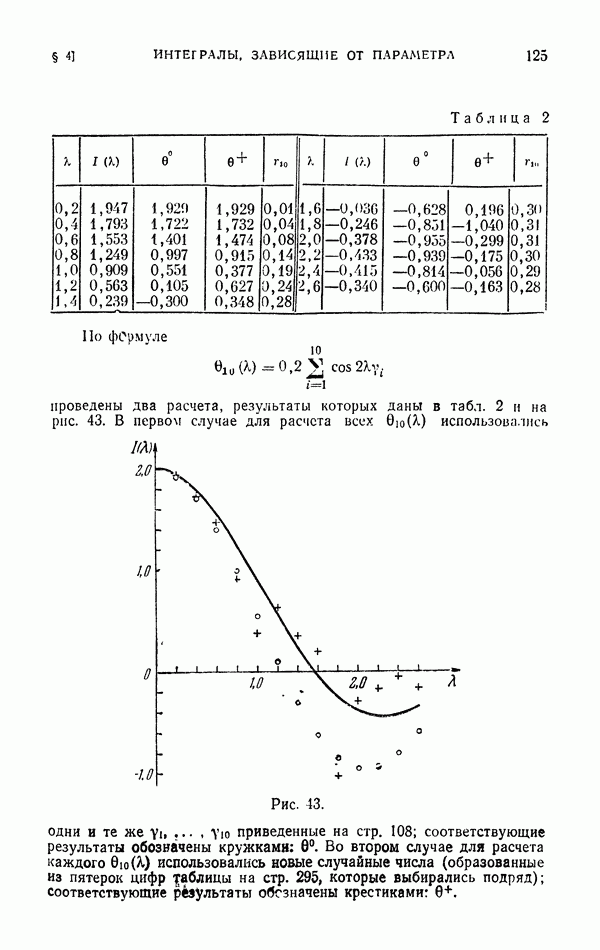
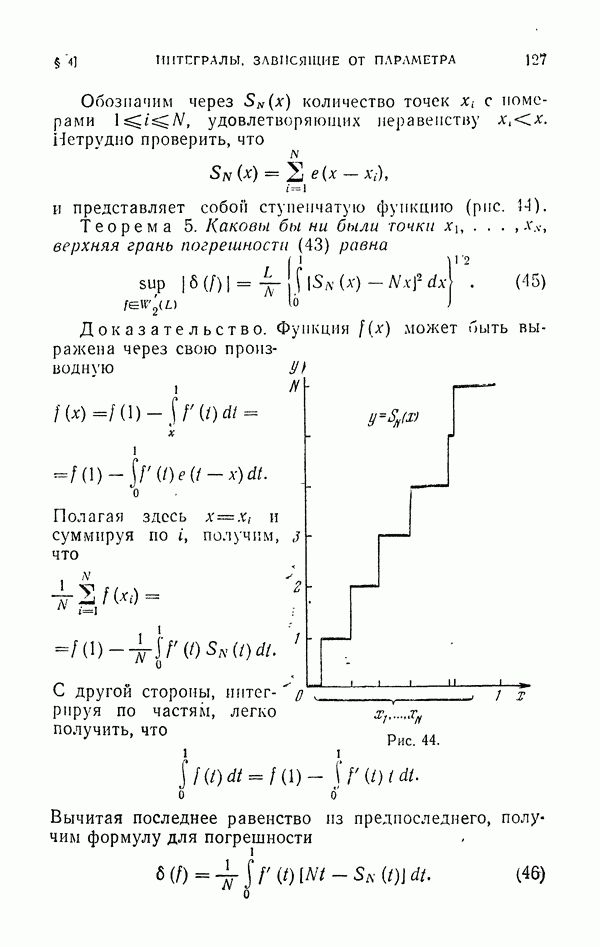
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
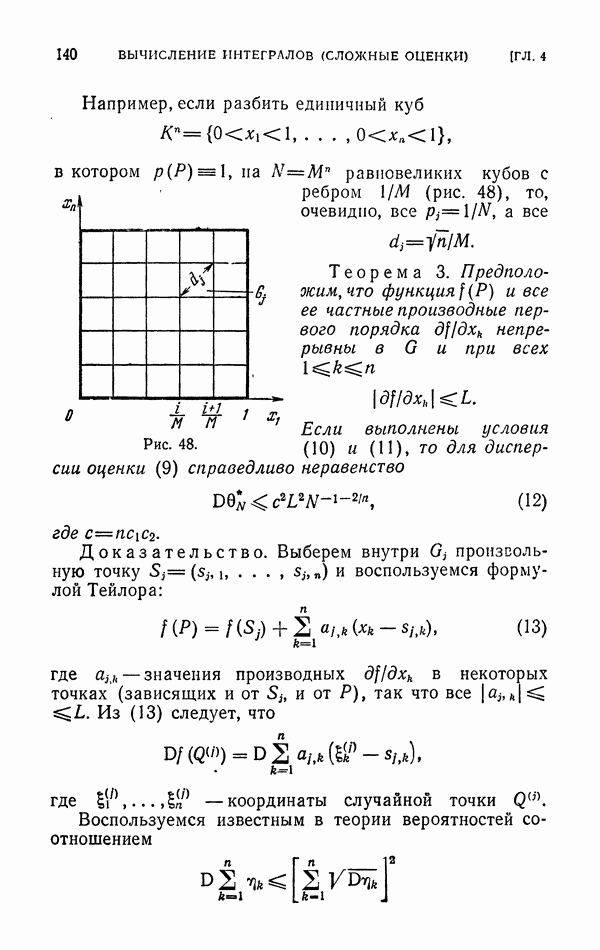
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
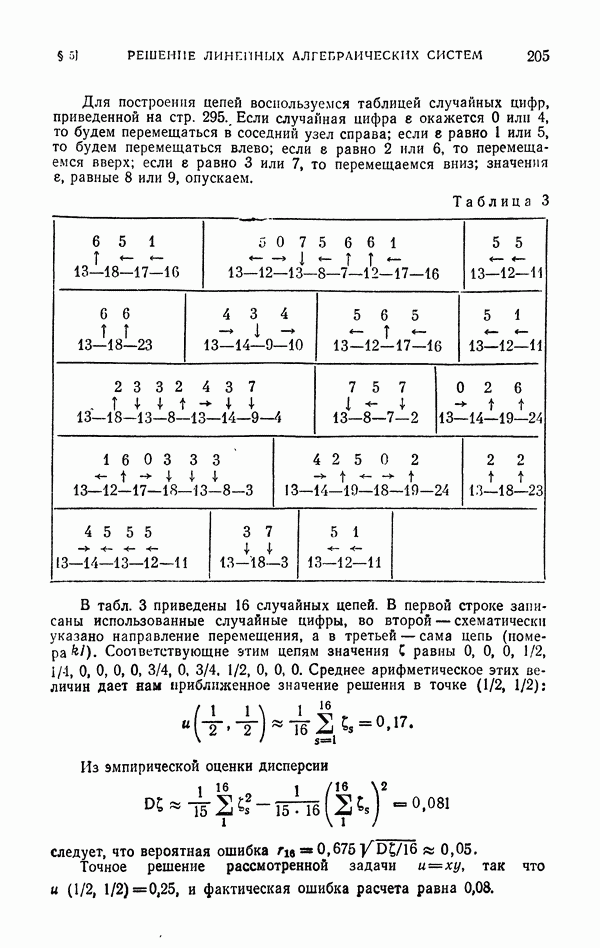
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
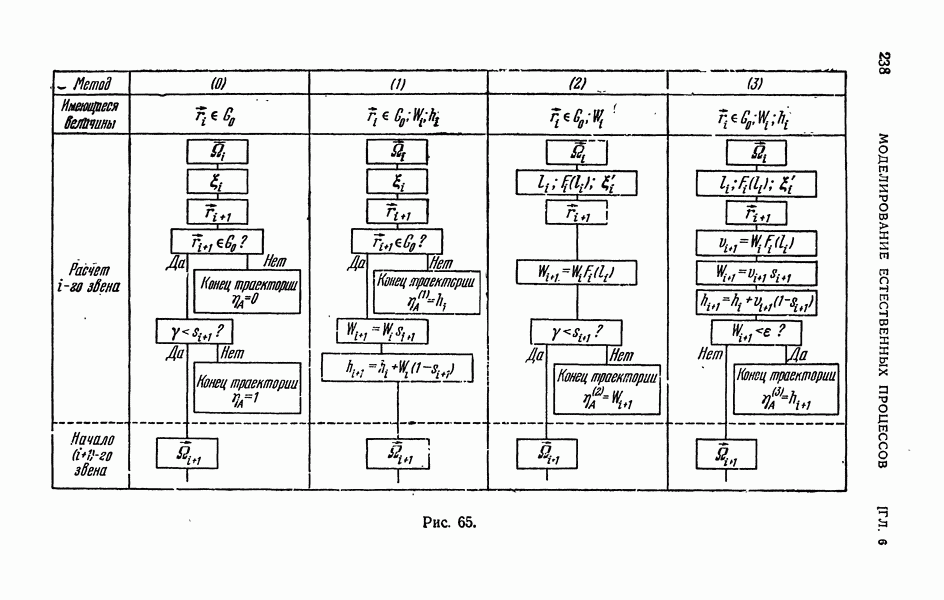
- § 1. Моделирование путем имитации
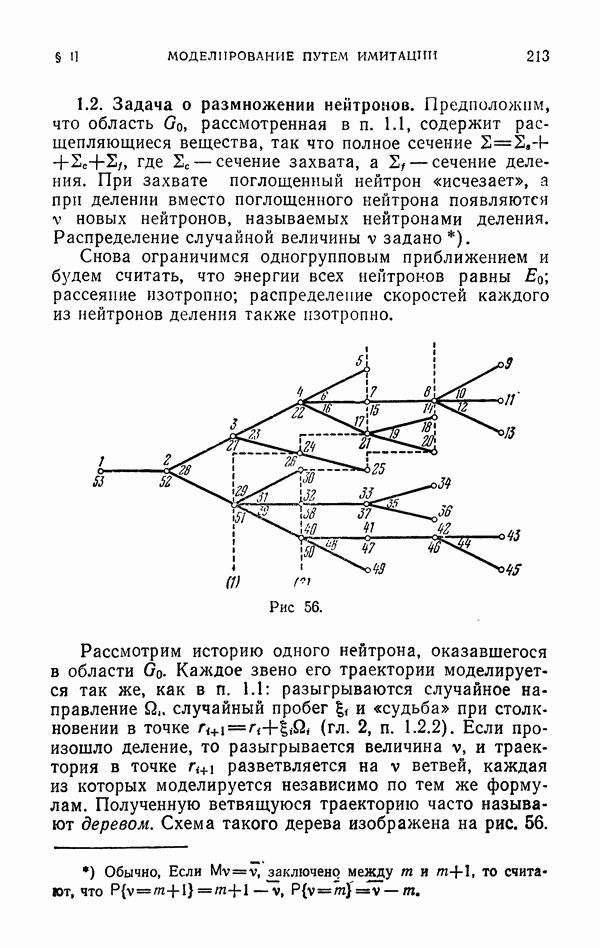
- 1.2. Задача о размножении нейтронов.
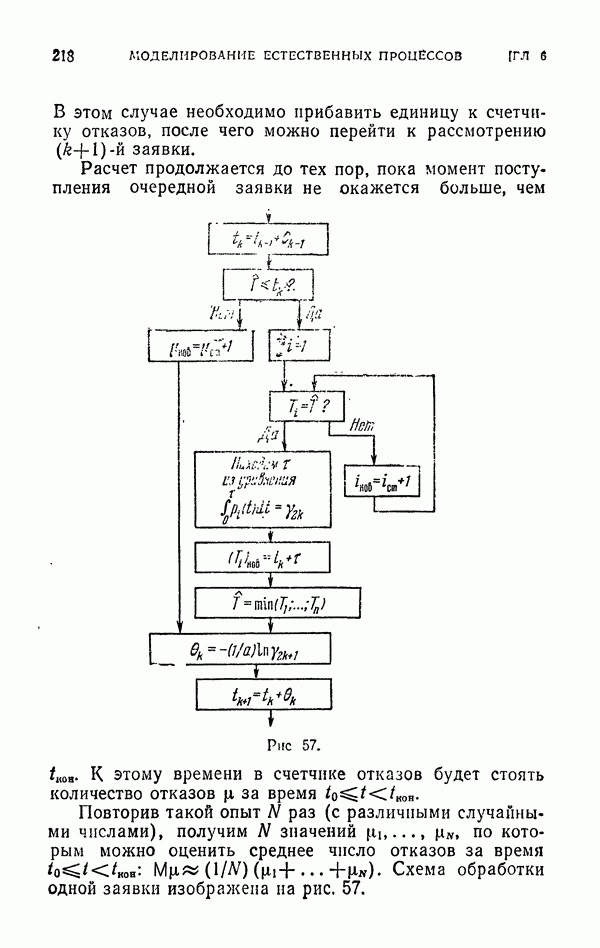
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
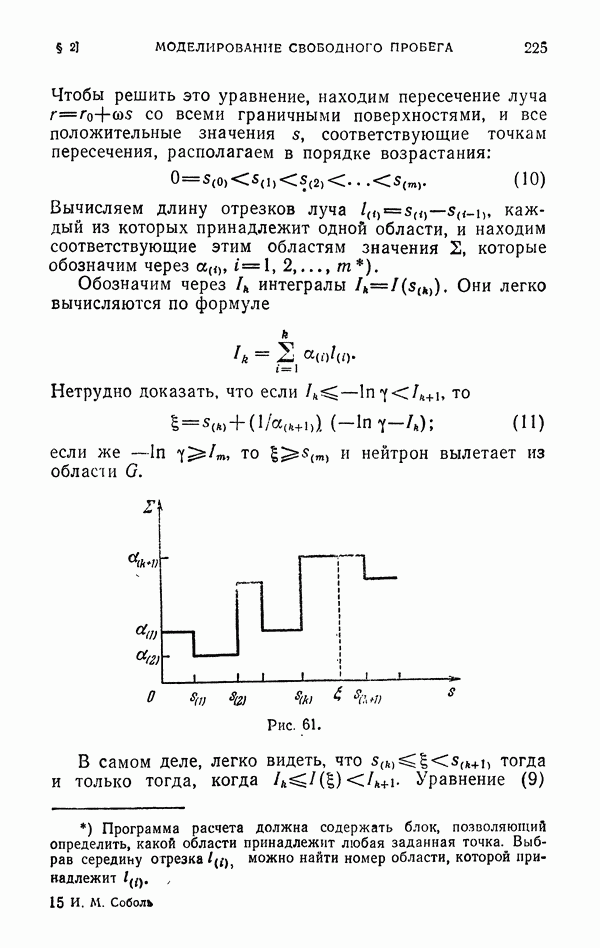
- § 2. Моделирование свободного пробега
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
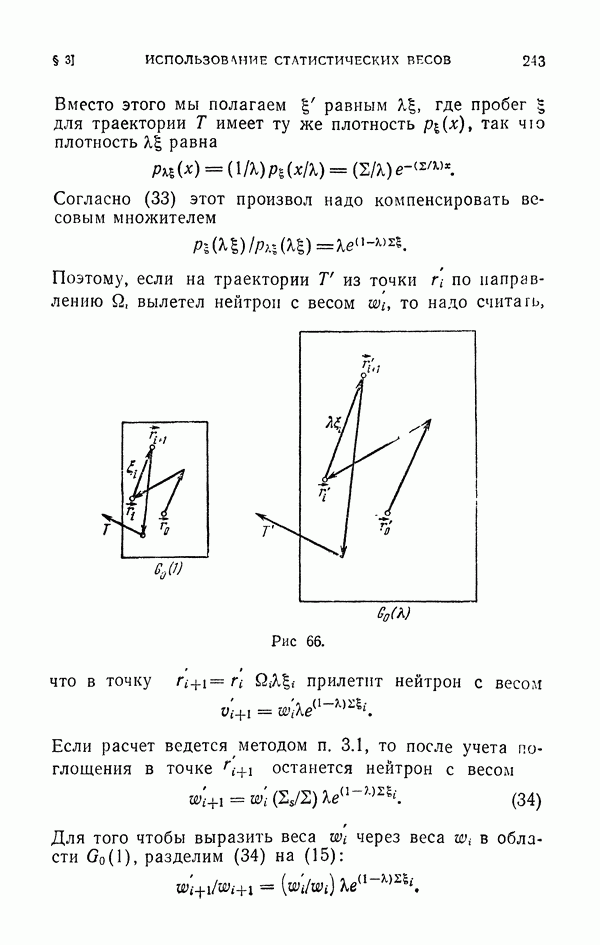
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
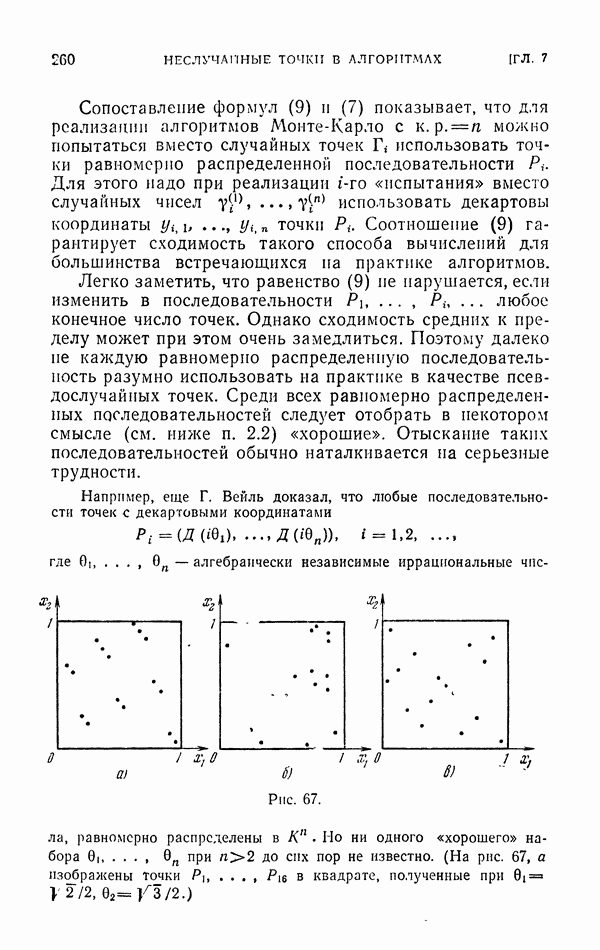
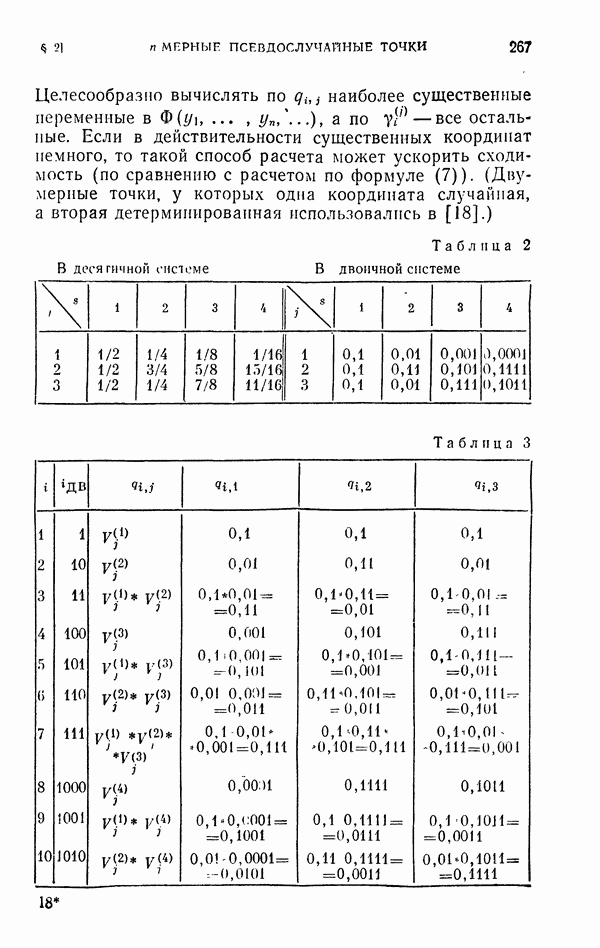
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА