| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
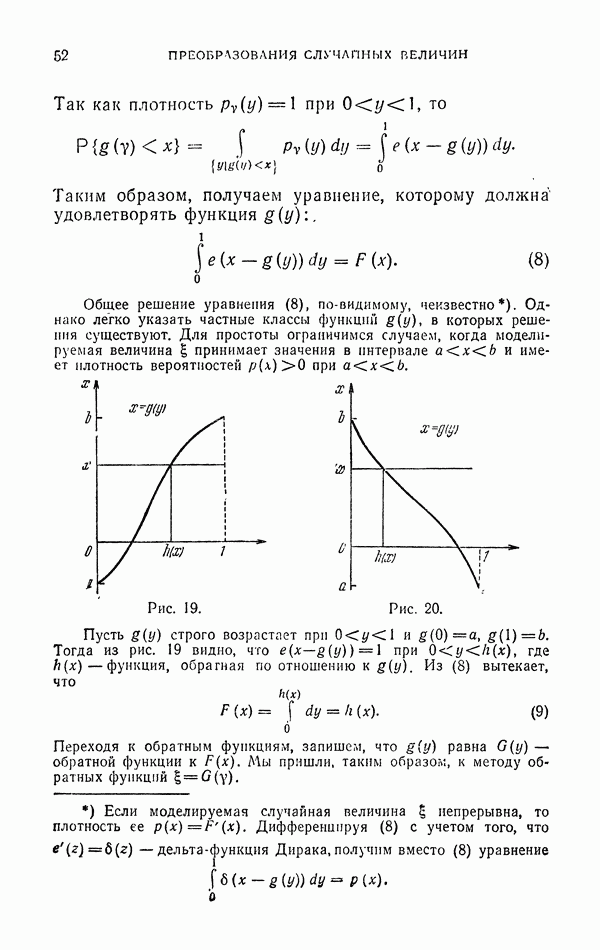
2.4. Использование замены переменных.
Во многих случаях удается упростить формулы моделирования многомерной случайной величины путем удачного выбора координат.
Правило преобразования плотности при преобразовании координат П усть  взаимно однозначное дифференцируемое отображение области В в пространстве
взаимно однозначное дифференцируемое отображение области В в пространстве  на область В в пространстве
на область В в пространстве  Если плотность случайной точки Q — в В равна
Если плотность случайной точки Q — в В равна  то плотность случайной точки
то плотность случайной точки  в В, где
в В, где  равна
равна

в правой части  должны быть выражены через
должны быть выражены через 
Доказательство. Пусть D — произвольная область внутри  ее прообраз при рассматриваемом отображении. Очевидно,
ее прообраз при рассматриваемом отображении. Очевидно,  По правилу замены переменных в интеграле
По правилу замены переменных в интеграле

а по определению плошосги 

Приравнивая эти вероятности и принимая во внимание произвольность D, получим требуемый результат.
2.4.1. Пример. Случайнаяточка Q равномерно распределена в шаре 
Обозначим через  декартовы координаты точки Q. Их совместная плотность распределения в шаре постоянна:
декартовы координаты точки Q. Их совместная плотность распределения в шаре постоянна:  Однако плотности распределения каждой из координат достаточно громоздки (см. ниже п. 3.2.1). Поэтому перейдем к сферическим координатам (рис. 23):
Однако плотности распределения каждой из координат достаточно громоздки (см. ниже п. 3.2.1). Поэтому перейдем к сферическим координатам (рис. 23):

В новых координатах шар превращается в параллелепипед  Так как якобиан преобразования
Так как якобиан преобразования

то в новых координатах плотность

Легко видеть, что эта плотность представляет собой произведение трех плотностей

и, следовательно, сферические координаты  точки Q независимы. Уравнения (11) для их нахождения можно записать так:
точки Q независимы. Уравнения (11) для их нахождения можно записать так:

Отсюда получаем широко распространенные формулы

По этим значениям нетрудно вычислить и декартовы координаты точки 

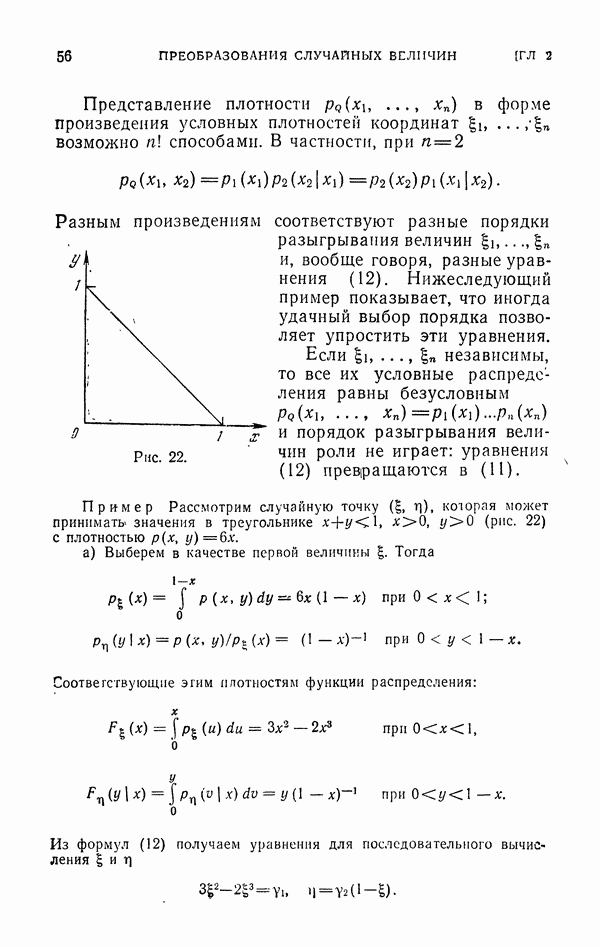
2.4.2. Пример. Выбор случайного направления в пространстве.
Обычно, говоря о «случайном» направлении, подразумевают выбор случайного направления в условиях, когда все направления равновероятны (в противном случае должно быть задано распределение вероятностей различных направлений).

Рис. 23

Рис. 24.
Направление условимся характеризовать единичным вектором

где  . Нас интересует такой случайный вектор
. Нас интересует такой случайный вектор  , что для любого телесного угла
, что для любого телесного угла 

Легко видеть, что если Q — случайная точка, равномерно распределенная в шаре  то направление ее радиуса-вектора обладает нужным нам свойством. Действительно, если
то направление ее радиуса-вектора обладает нужным нам свойством. Действительно, если  и
и  - два равных телесных угла, то объемы соответствующих им шаровых секторов равны (рис. 24), и вероятность того, что точка Q попадет в каждый из них, одинакова. Поэтому из (14) получаем формулы для выбора «случайного» направления.
- два равных телесных угла, то объемы соответствующих им шаровых секторов равны (рис. 24), и вероятность того, что точка Q попадет в каждый из них, одинакова. Поэтому из (14) получаем формулы для выбора «случайного» направления.

Декартовы координаты вектора со вычисляются по обычным формулам:

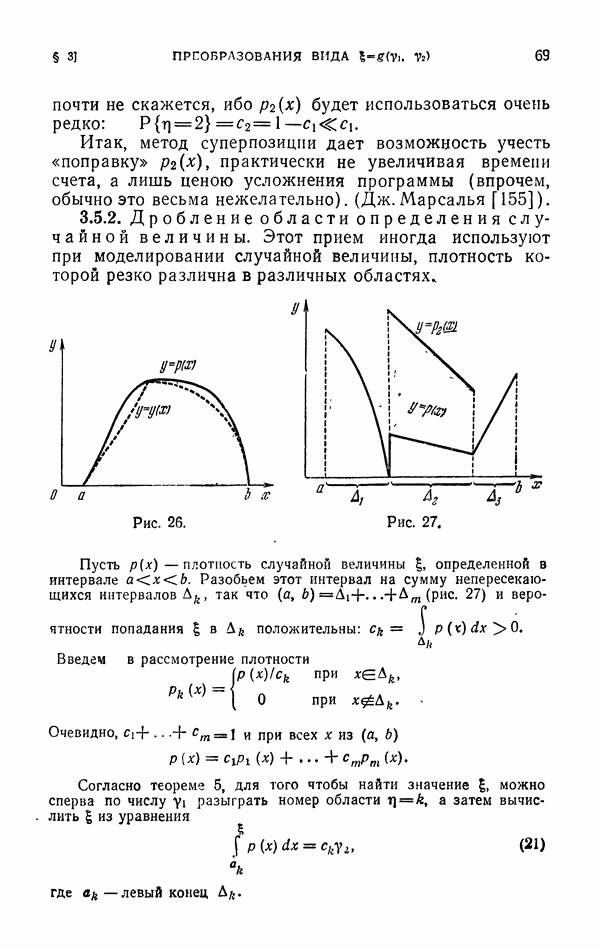
2.4.3. Пример [8]. Случайная точка  подчиняется
подчиняется  -мерному нормальному (гауссовскому) распределению с математическими ожиданиями
-мерному нормальному (гауссовскому) распределению с математическими ожиданиями  и вторыми моментами
и вторыми моментами  Определитель матрицы
Определитель матрицы  положителен:
положителен: 
Плотность такой случайной точки выражается формулой

где  — матрица обратная, по отношению к В, а
— матрица обратная, по отношению к В, а  — ее определитель.
— ее определитель.
Как известно, линейным преобразованием координат можно привести положительно определенную квадратичную форму, стоящую в показателе, к сумме квадратов. Удобно при этом использовать векторные обозначения: если и  векторы, то их скалярное произведение
векторы, то их скалярное произведение

если  квадратная матрица
квадратная матрица  , то
, то  - это вектор с компонентами
- это вектор с компонентами  квадратичная форма выражается через скалярное произведение
квадратичная форма выражается через скалярное произведение

Выберем новые координаты  и пусть
и пусть  . Тогда
. Тогда

где Т — транспонированная матрица Т. Последнее выражение обратится и  если
если  единичная матрица. Отсюда
единичная матрица. Отсюда
 . Таким образом, матрица преобразования Т должна удовлетворять уравнению
. Таким образом, матрица преобразования Т должна удовлетворять уравнению

Якобиан преобразования  равен определителю матрицы:
равен определителю матрицы:  . Из (16) следует,
. Из (16) следует,  , а так как
, а так как  . Значит,
. Значит,

Теперь можно записать плотность точки Q в новых координатах

откуда видно, что новые координаты точки Q независимы и нормальны с параметрами 

Рис. 25.
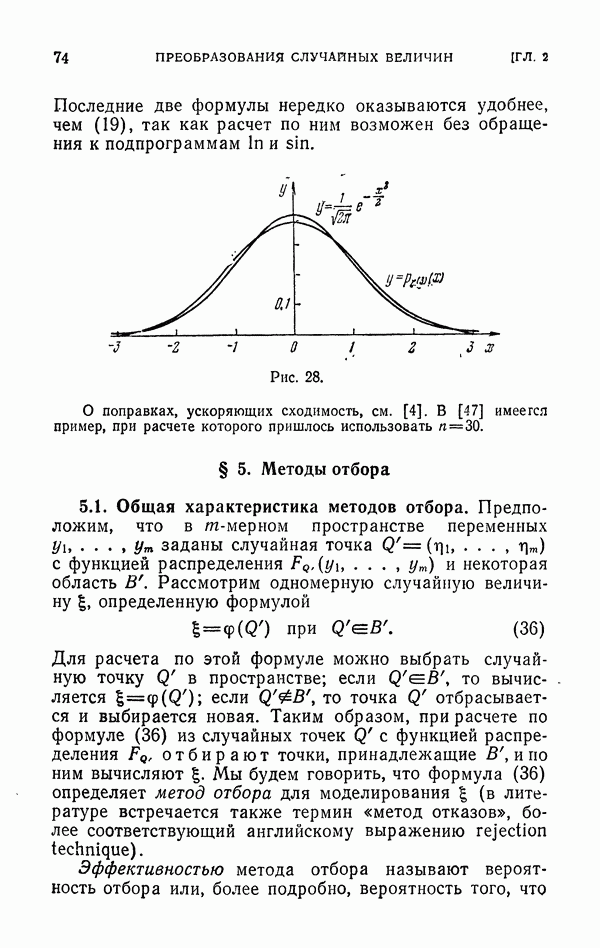
Итак, для того чтобы вычислить значения надо найти  независимых значений
независимых значений  нормальной величины с параметрами
нормальной величины с параметрами  — как это сделать, см. п. 3.2.2. или п. 4.4, и тогда
— как это сделать, см. п. 3.2.2. или п. 4.4, и тогда

При практической реализации этого метода единственное сложное место — расчет матрицы Т. Из теории матриц следует [64], что существует треугольная матрица  удовлетворяющая (16). Если при
удовлетворяющая (16). Если при  все
все  то (16) превращается в систему, состоящую из
то (16) превращается в систему, состоящую из  уравнений
уравнений

и все  могут быть последовательно вычислены в порядке, схематически указанном в рис. 25. Матрицу С вычислять не надо.
могут быть последовательно вычислены в порядке, схематически указанном в рис. 25. Матрицу С вычислять не надо.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
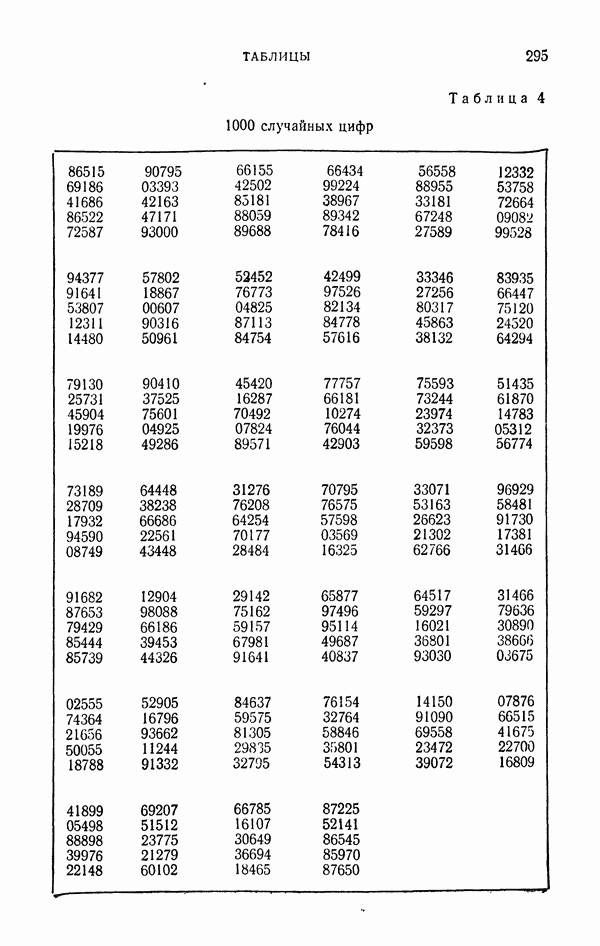
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
- § 1. Моделирование путем имитации
- 1.2. Задача о размножении нейтронов.
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
- § 2. Моделирование свободного пробега
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
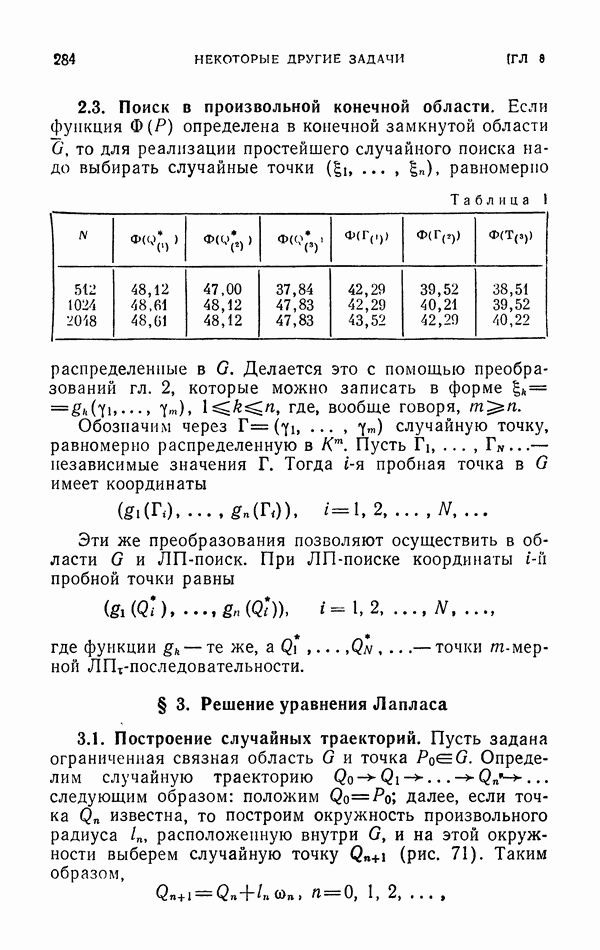
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА