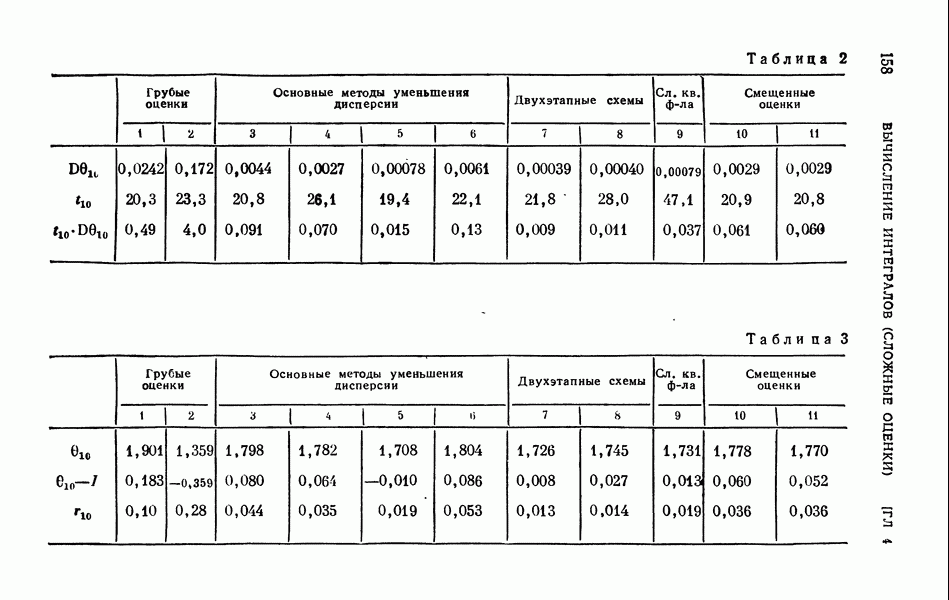
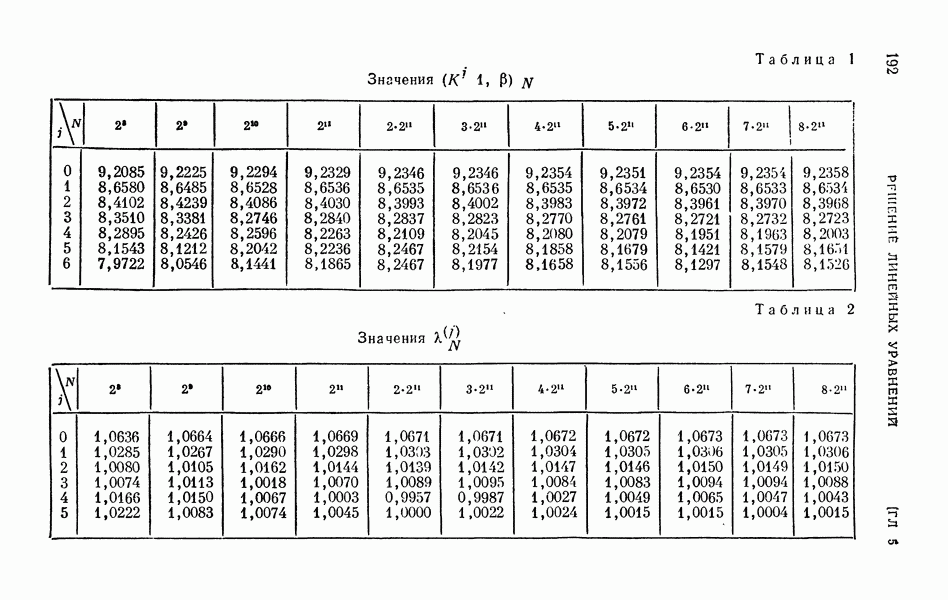
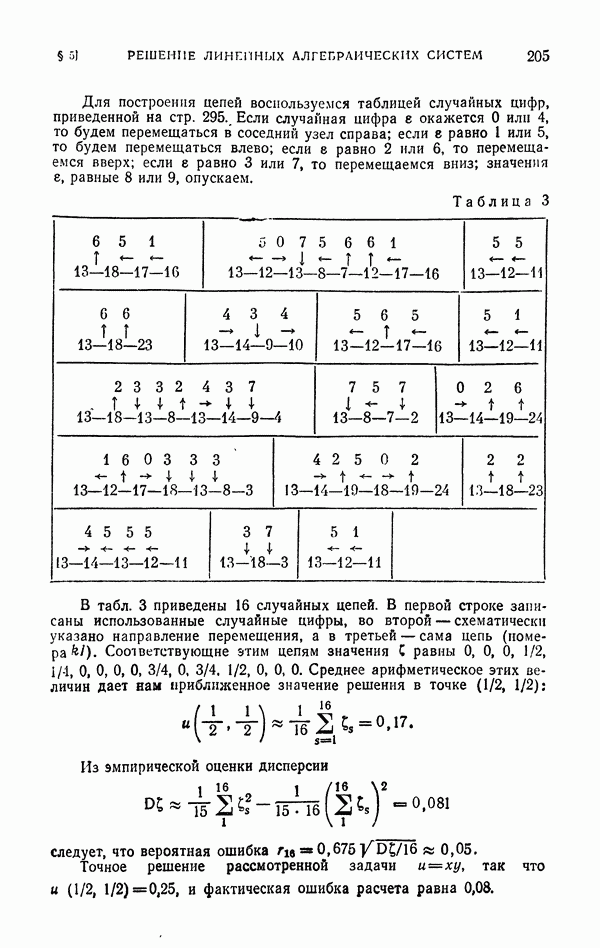
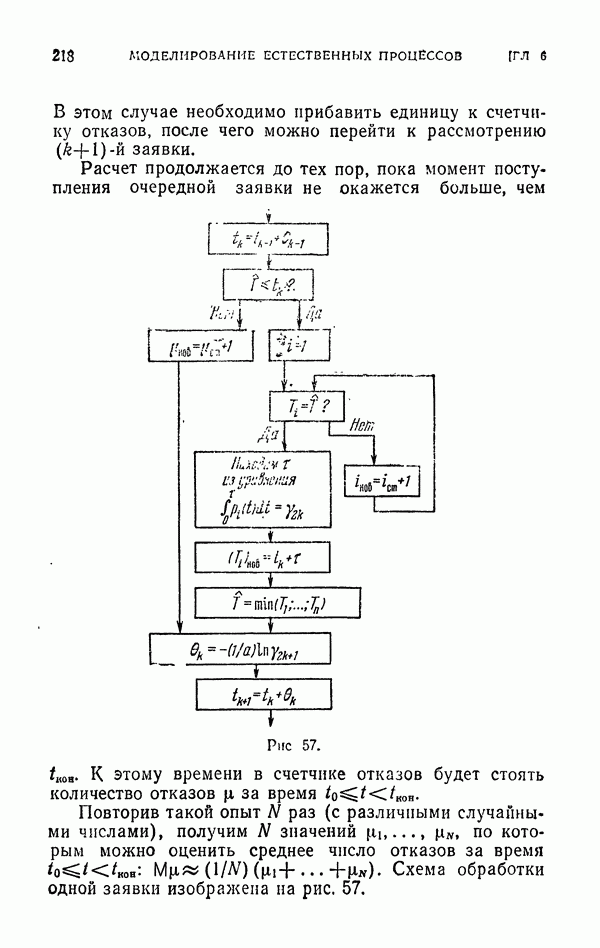
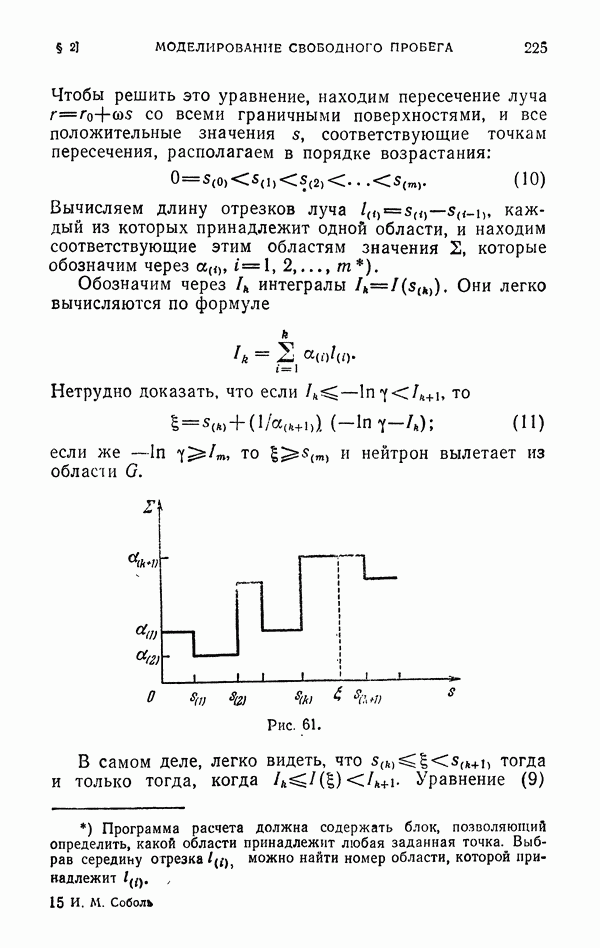
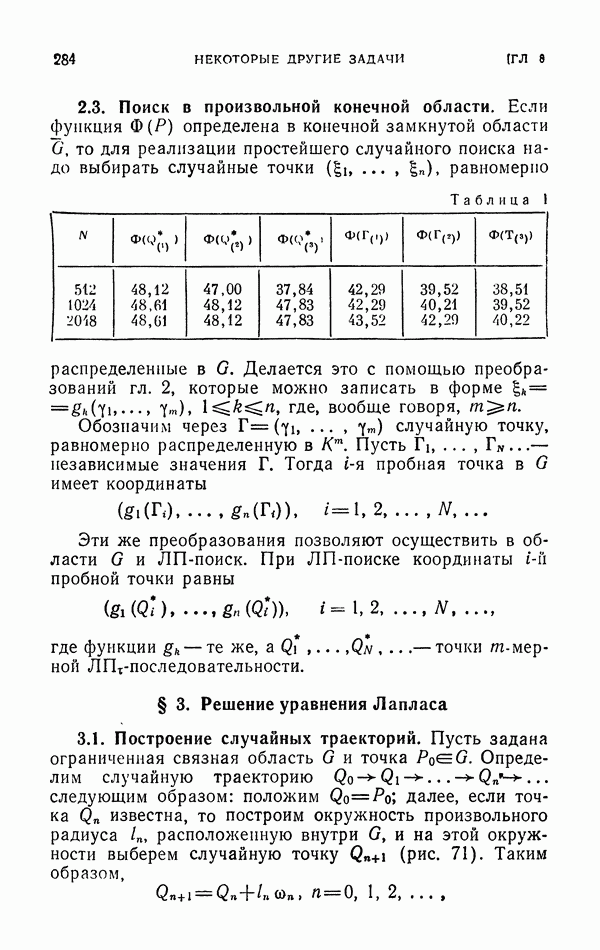
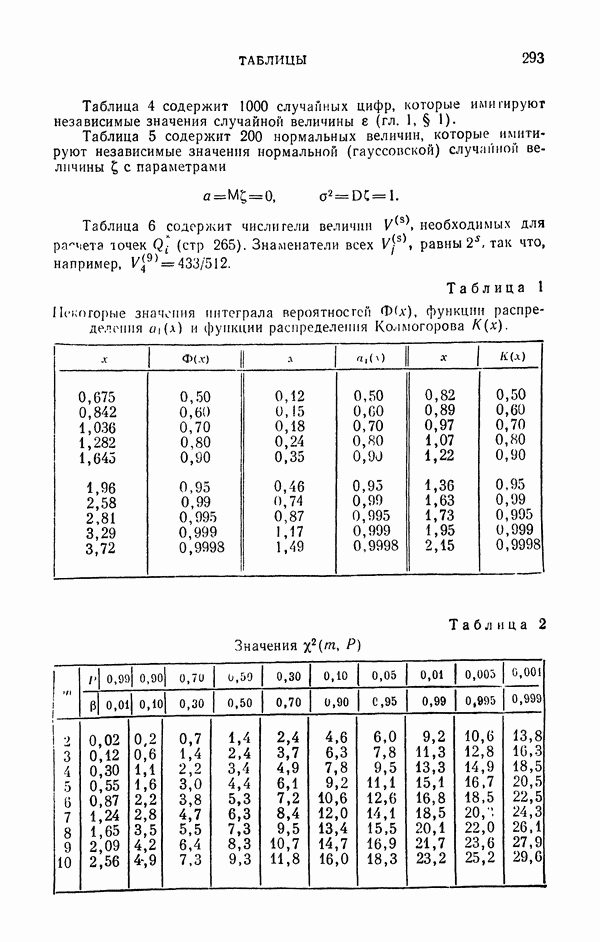
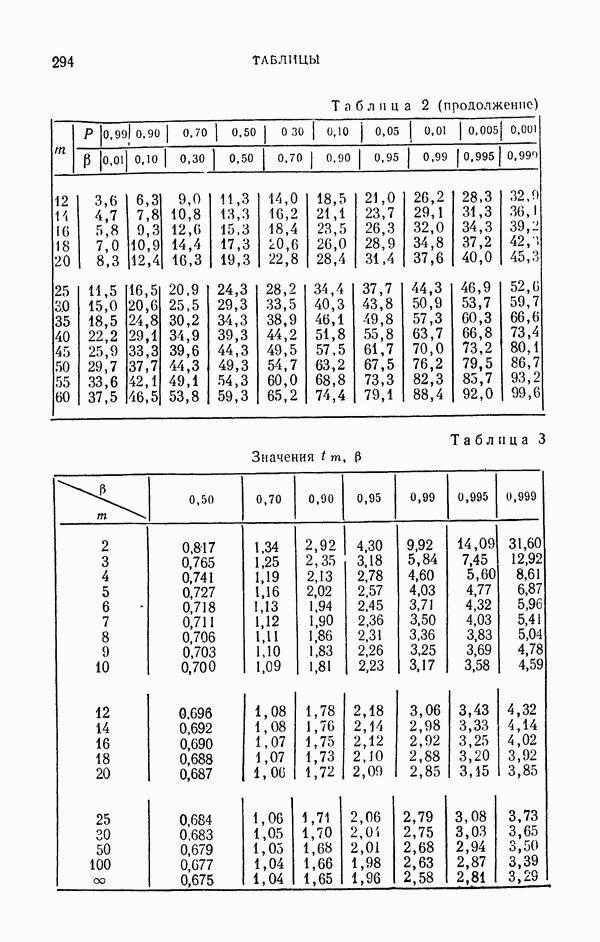
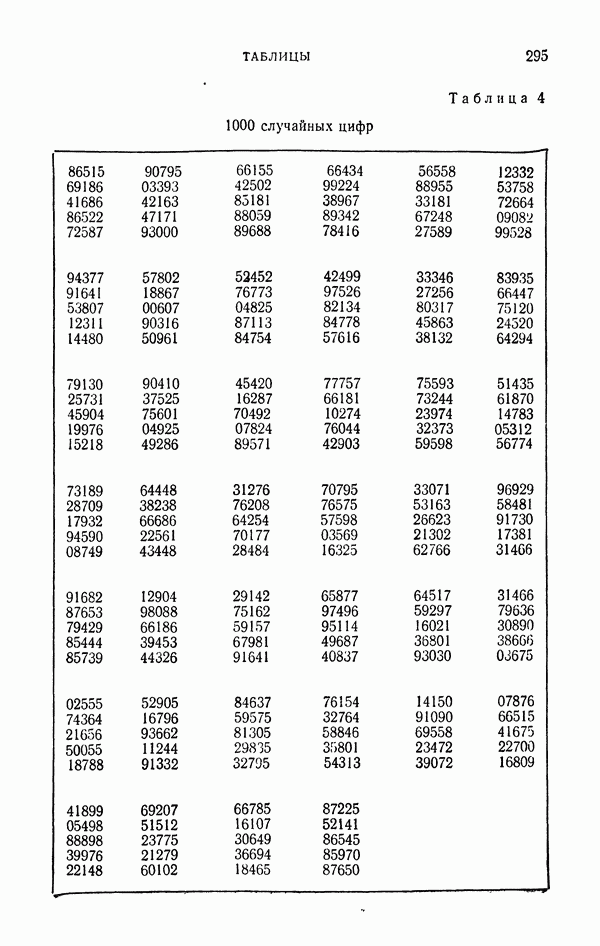
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
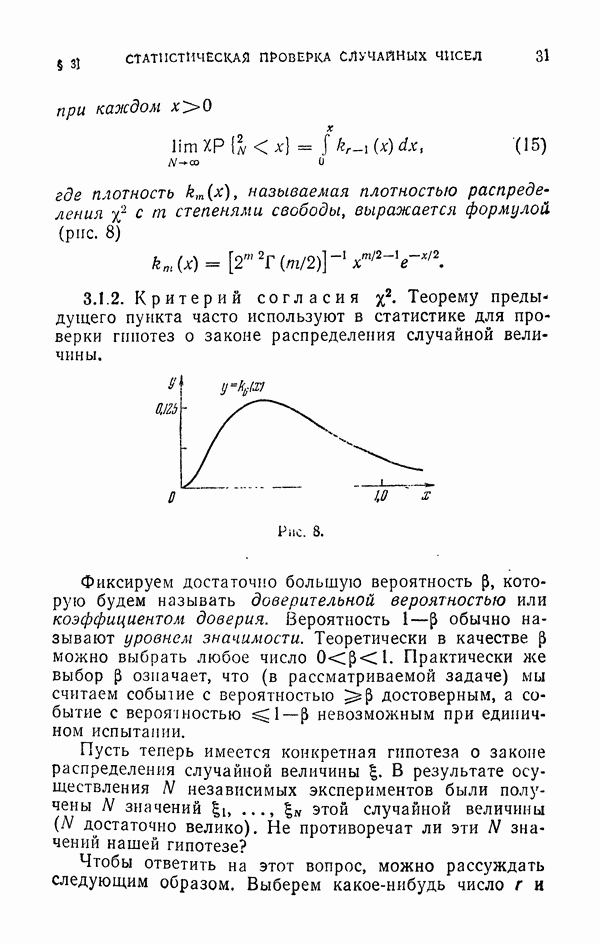
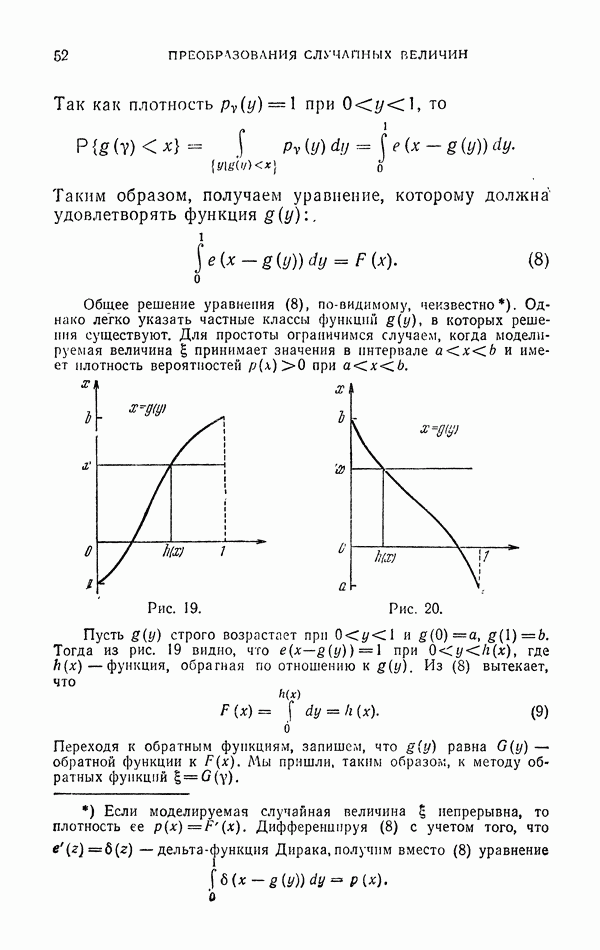
3.1.2. Интегрирование по части области.
Допустим, что мы умеем (аналитически) вычислить интегралы по некоторой части В области G:

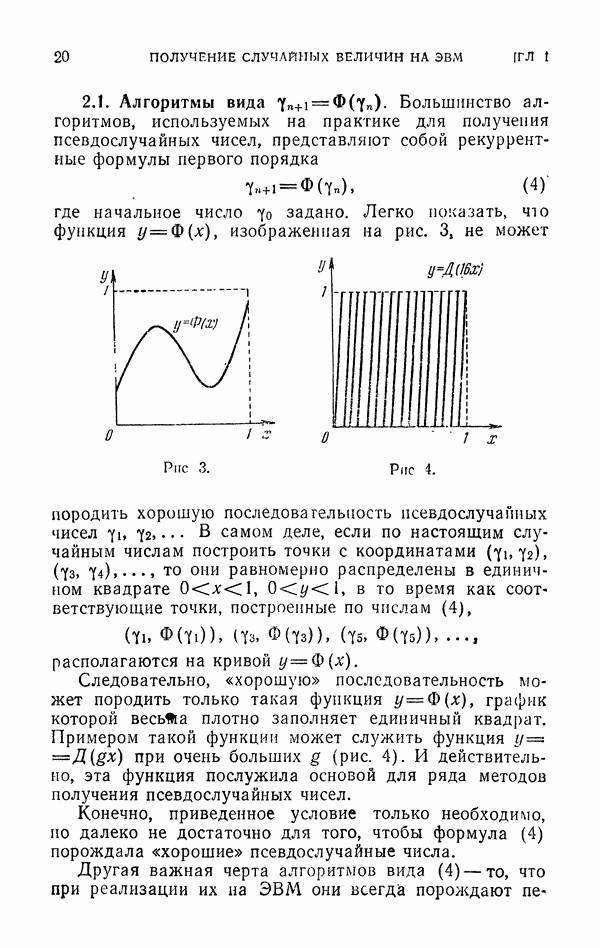
где  . Докажем, что, как правило, всегда выгодно представить интеграл (12) в виде суммы
. Докажем, что, как правило, всегда выгодно представить интеграл (12) в виде суммы

и вычислять простейшим методом только интеграл по области  . (Если С близко к
. (Если С близко к  то можно считать, что мы выделяем главную часть; по данный прием выгоден и тогда, когда область В заметно меньше, чем G (рис. 35); правда, и понижение дисперсии в этом случае будет заметно меньше.)
то можно считать, что мы выделяем главную часть; по данный прием выгоден и тогда, когда область В заметно меньше, чем G (рис. 35); правда, и понижение дисперсии в этом случае будет заметно меньше.)

Рис. 35.
В области  определим плотность
определим плотность  и рассмотрим случайную величину
и рассмотрим случайную величину

где Q — случайная точка с плотностью  . Легко видеть, что
. Легко видеть, что  Поэтому для расчета
Поэтому для расчета  можно использовать оценку
можно использовать оценку

где  - независимые реализации точки Q. Чтобы сравнить эту оценку с оценкой (14), сравним дисперсии
- независимые реализации точки Q. Чтобы сравнить эту оценку с оценкой (14), сравним дисперсии  , где
, где 
Теорема 1. Если существует дисперсия  , то
, то

Доказательство. Согласно определению дисперсии

Умножив  на
на  и вычтя
и вычтя  , получим, что
, получим, что

Оставшийся интеграл по области В выразим через неотрицательную величину

Тогда окажется, что

что и требовалось доказать.
Предположим, что задан какой-либо алгоритм расчета точек Q в G. Тогда трудоемкость алгоритма (14) равна  где
где  время расчета одной точки Q, а
время расчета одной точки Q, а  время расчета одного значения
время расчета одного значения  .
.
Рассмотрим оценку (25). Если никакого более удобного способа моделирования точек Q в  пет, то можно отбирать точки Q среди точек Q (п. 5.2 гл. 2). Эффективность такого отбора
пет, то можно отбирать точки Q среди точек Q (п. 5.2 гл. 2). Эффективность такого отбора  . Поэтому время расчета одной точки Q в среднем равно
. Поэтому время расчета одной точки Q в среднем равно  , где
, где  - время, затрачиваемое на отбор (т. е. на проверку условия
- время, затрачиваемое на отбор (т. е. на проверку условия  ). Трудоемкость алгоритма (25) в этих условиях равна
). Трудоемкость алгоритма (25) в этих условиях равна 
Легко доказать, что если

то трудоемкость алгоритма  не больше, чем трудоемкость алгоритма (14). В самом деле,
не больше, чем трудоемкость алгоритма (14). В самом деле,

Условие (27) легко проверяется на практике. Если область В «простая», а функция  «сложная», то, очевидно,
«сложная», то, очевидно,

Рис. 36.
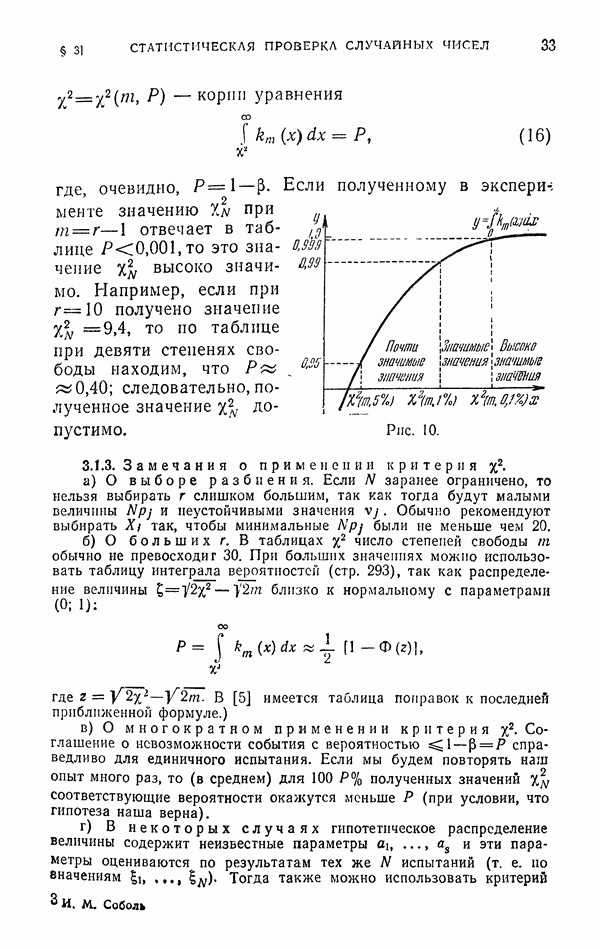
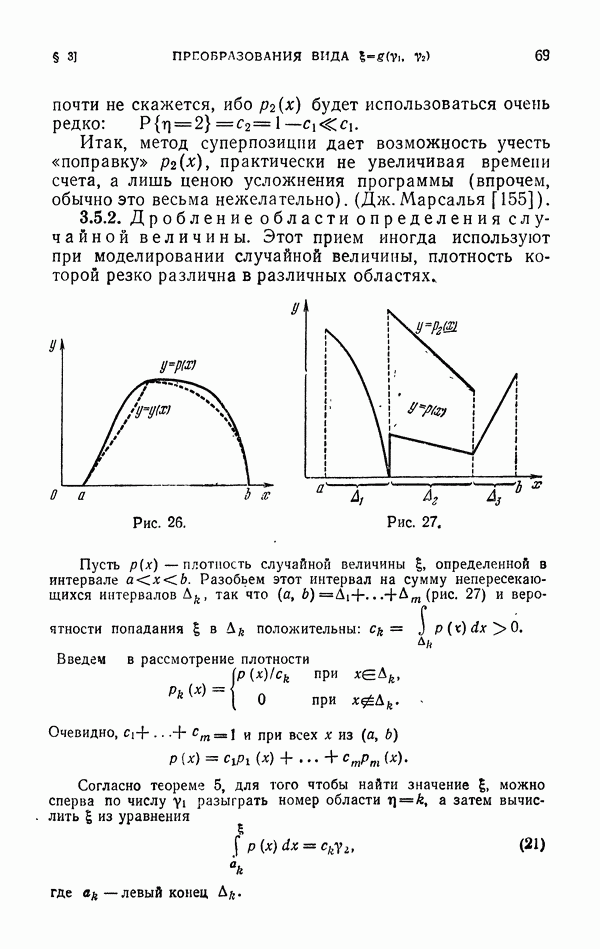
Пример. Требуется вычислить объем фигуры V, ограниченной поверхностью (в сферических координатах)

где 
Обозначим через  вписанный в V и описанный около V шары, радиусы которых равны
вписанный в V и описанный около V шары, радиусы которых равны  Объемы
Объемы  будем обозначать темп же буквами. Воспользуемся геометрическим методом: выберем случайные точки равномерно распределенные в
будем обозначать темп же буквами. Воспользуемся геометрическим методом: выберем случайные точки равномерно распределенные в  и если v из этих точек попадут внутрь V, то будем считать, что объем V приближенно равен
и если v из этих точек попадут внутрь V, то будем считать, что объем V приближенно равен

Выделим теперь объем шара  . Для этого достаточно выбрать случайные точки
. Для этого достаточно выбрать случайные точки  равномерно распределенные в шаровом слое
равномерно распределенные в шаровом слое  ; если v из этих точек принадлежат V, то объем V приближенно равен
; если v из этих точек принадлежат V, то объем V приближенно равен

Вместо сравнения дисперсий осредняемых величин сравним в этом примере дисперсии самих оценок. Так как  подчиняются биномиальным распределениям с параметрами
подчиняются биномиальным распределениям с параметрами  и соответственно
и соответственно  , то
, то  . Поэтому
. Поэтому  Очевидно, всегда
Очевидно, всегда 
Если отношение  то в оценке
то в оценке  мы фактически выделяем главную часть задачи, и уменьшение дисперсии
мы фактически выделяем главную часть задачи, и уменьшение дисперсии  по сравнению с
по сравнению с  должно быть особенно заметным. Действительно, так как
должно быть особенно заметным. Действительно, так как  то можно записать, что
то можно записать, что  , где
, где  . Тогда нетрудно сосчитать, что величина
. Тогда нетрудно сосчитать, что величина

пропорциональна  , а величина
, а величина

 второго порядка малости.
второго порядка малости.
Наконец, покажем, что если моделировать точки  в сферических координатах (п. 2.4.1 гл. 2), то алгоритмы, соответствующие обоим рассмотренным методам, примерно одинаково сложны:
в сферических координатах (п. 2.4.1 гл. 2), то алгоритмы, соответствующие обоим рассмотренным методам, примерно одинаково сложны:
В самом деле, в обоих случаях для  испытания нужны три случайных числа
испытания нужны три случайных числа  Координаты точек и вычисляются соответственно по формулам
Координаты точек и вычисляются соответственно по формулам

или

где  . Условие принадлежности точки
. Условие принадлежности точки  объему V проверяется одинаково:
объему V проверяется одинаково:  это условие выполнено, то к счетчику v (соответственно v) добавляется единица.
это условие выполнено, то к счетчику v (соответственно v) добавляется единица.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОЛУЧЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН НА ЭВМ
- 1.2. О приближенных случайных числах.
- 1.3. Таблицы случайных цифр.
- 1.4. Датчики случайных чисел.
- 1.5. Метод псевдослучайных чисел.
- 1.6. Сравнение трех способов с практической точки зрения.
- § 2. Псевдослучайные числа
- 2.2. Некоторые конкретные алгоритмы.
- 2.3. Оценка L для алгоритмов вида …
- 2.4. О более сложных алгоритмах.
- § 3. Статистическая проверка случайных чисел
- 3.1.2. Критерий согласия «хи-квадрат».
- 3.1.3. Замечания о применении критерия «хи-квадрат»
- 3.1.4. Критерий «омега-квадрат»
- 3.2. Проверка таблиц случайных цифр.
- 3.3. Проверка псевдослучайных чисел.
- 3.4. О проверке датчиков случайных чисел.
- 3.5. О проверке больших массивов случайных чисел.
- Упражнения к главе 1
- ГЛАВА 2. ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
- 1.2. Моделирование случайных событий.
- 1.3. Моделирование непрерывных случайных величин.
- 1.4. Метод обратных функций.
- 1.5. Преобразования вида …
- § 2. Моделирование многомерных случайных величин
- 2.2. Моделирование n-мерной непрерывной случайной точки (с произвольными координатами).
- 2.3. Возможные обобщения теоремы 4.
- 2.4. Использование замены переменных.
- § 3. Преобразования вида …
- 3.2. Применение полярных координат.
- 3.3. Метод суперпозиции.
- 3.4. Метод интегральной суперпозиции.
- 3.5. Некоторые приложения метода суперпозиции.
- § 4. Преобразования вида …
- 4.1. Извлечение корней из случайных чисел.
- 4.2. Моделирование гамма-распределения.
- 4.3. Моделирование семейства биномиальных распределений.
- 4.4. Приближенное моделирование нормального (гауссовского) распределения.
- § 5. Методы отбора
- 5.1. Общая характеристика методов отбора.
- 5.2. Моделирование усеченных распределений.
- 5.3. Метод Неймана [163].
- 5.4. О некоторых обобщениях метода Неймана.
- 5.5. Выбор равномерно распределенных точек в сложных областях.
- 5.6. Алгоритмы, соответствующие методам отбора.
- 5.7. Заключительные замечания.
- Упражнения к главе 2
- ГЛАВА 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
- § 1. Общий метод оценки математических ожиданий
- 1.2. Погрешность метода.
- 1.3. Вероятная ошибка метода.
- 1.4. Эмпирическая оценка дисперсии.
- 1.5. Оценка ошибки без расчета дисперсии.
- 1.6. Случай …
- 1.7. Замечание. О некоторых терминах, употребляемых в математической статистике [24, 44].
- § 2. Простейший метод Монте-Карло для вычисления интеграла
- 2.2. Геометрический метод Монте-Карло.
- 2.3. Сравнение точности методов Монте-Карло.
- 2.4. Сравнение трудоемкости алгоритмов Монте-Карло.
- § 3. Важнейшие способы построения хороших оценок (способы уменьшения дисперсии)
- 3.1.2. Интегрирование по части области.
- 3.1.3. Интегрирование по части переменных (понижение порядка интеграла).
- 3.2. Метод существенной выборки.
- 3.3. Симметризация подынтегральной функции.
- 3.3.2. О сложной симметризации.
- 3.4. Двухэтапные схемы расчета.
- § 4. Интегралы, зависящие от параметра
- 4.2. Вспомогательная теорема о погрешности простейшей квадратурной формулы.
- 4.3. Оценка погрешности метода Монте-Карло с помощью распределения w2.
- 4.4. Численное дифференцирование оценки (51).
- 4.5. О таблицах случайных чисел.
- Упражнения к главе 3
- ГЛАВА 4. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (СЛОЖНЫЕ ОЦЕНКИ)
- § 1. Методы Монте-Карло с повышенной скоростью сходимости
- 1.2. Оценки с повышенной скоростью сходимости.
- 1.3. Сравнение с квадратурными формулами.
- § 2. Случайные квадратурные формулы
- 2.2. Некоторые свойства интерполяционных квадратурных формул.
- 2.3. Случайные интерполяционные квадратурные формулы.
- § 3. Использование смещенных оценок
- 3.2. Простейший метод Монте-Карло с поправочным множителем.
- 3.3. Численный пример.
- Упражнения к главе 4
- ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.2. Вычисление линейных функционалов от итерированных функций.
- 1.3. Вычисление значений итерированных функций.
- 1.4. Случайные траектории с поглощением.
- 1.5. Сравнение точности оценок (8) и (20).
- § 2. Неоднородные интегральные уравнения
- 2.2. Оценка линейных функционалов от
- 2.3. Метод существенной выборки для траекторий
- 2.4. Оценка линейных функционалов от z.
- 2.5. Сравнение точности оценок (38) и (11).
- 2.6. Использование сопряженного уравнения.
- 2.7. Усложненные оценки линейных функционалов от z.
- § 3. Пример: рассеяние частиц
- 3.2. Использование истинных траекторий.
- 3.3. Использование искусственных траекторий.
- 3.4. Существенная выборка.
- 3.5. Рассеяние в области G.
- § 4. Однородные интегральные уравнения
- 4.2. Метод существенной выборки для траекторий
- 4.3. О других методах расчета
- 4.4. Пример: интегральное уравнение Пайерлса.
- § 5. Решение линейных алгебраических систем
- 5.2. Случайная цепь для решения алгебраической системы.
- 5.3. Вычисление одной компоненты решения.
- 5.4. Обращение матрицы.
- 5.5. Решение дифференциальных уравнений Лапласа и Пуассона.
- 5.6. Случай очень большого числа переменных.
- Упражнения к главе 5
- ГЛАВА 6. МОДЕЛИРОВАНИЕ ЕСТЕСТВЕННЫХ ПРОЦЕССОВ
- § 1. Моделирование путем имитации
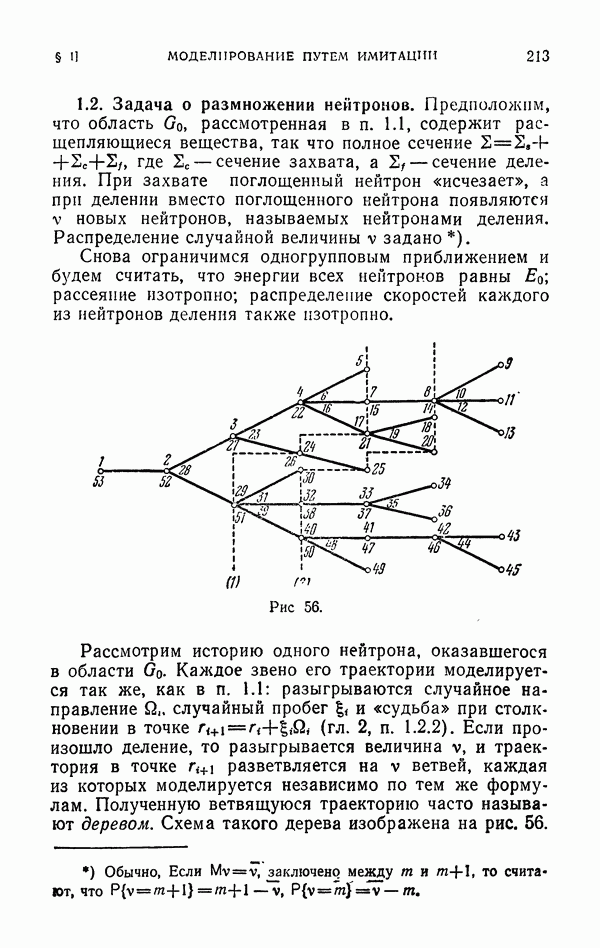
- 1.2. Задача о размножении нейтронов.
- 1.3. Системы массового обслуживания.
- 1.4. Расчет вероятностных характеристик сложной случайной величины.
- § 2. Моделирование свободного пробега
- 2.2. Моделирование свободного пробега нейтрона.
- 2.3. Моделирование свободного пробега заряженной частицы.
- § 3. Использование статистических весов
- 3.2. Веса, учитывающие вылет из области G0.
- 3.3. Веса, заменяющие розыгрыш поглощения и учитывающие вылет из области G0.
- 3.4. Различные статистические веса.
- 3.5. Статистические веса и существенная выборка.
- 3.6. Метод подобных траекторий.
- 3.7. Векторные веса.
- § 4. Статистические веса и интегральные уравнения
- 4.2. Плотность первых столкновений.
- 4.5. Веса, учитывающие вылет, как метод решения интегрального уравнения.
- 4.6. Веса, заменяющие розыгрыш поглощения и учитывающие вылет, как метод решения интегрального уравнения.
- 4.7. Веса п. 3.3 при решении уравнения Пайерлса.
- Упражнения к главе 6
- ГЛАВА 7. НЕСЛУЧАЙНЫЕ ТОЧКИ В АЛГОРИТМАХ МОНТЕ-КАРЛО
- § 1. Конструктивная размерность алгоритмов Монте-Карло
- 1.1. Алгоритмы с конечной конструктивной размерностью.
- 1.2. Алгоритм с бесконечной конструктивной размерностью.
- § 2. n-мерные псевдослучайные точки
- 2.2. Геометрическая характеристика равномерно распределенных последовательностей.
- 2.3. Ускорение сходимости.
- 2.4. «Хорошие» псевдослучайные точки.
- 2.5. Замечание о роли дисперсии.
- § 3. Поиски «универсальных» псевдослучайных чисел
- 3.2. Вполне равномерно распределенные последовательности чисел.
- 3.3. Асимптотически вполне равномерно распределенные последовательности чисел.
- § 4. Проверка псевдослучайных чисел с детерминистической точки зрения
- 4.2. Многомерные критерии.
- 4.3. О системах тестов.
- Упражнения к главе 7
- ГЛАВА 8. НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
- § 1. Интерполирование функций от большого числа переменных
- 1.2. Метод Монте-Карло.
- § 2. Простейший случайный поиск
- 2.2. ЛП-поиск.
- 2.3. Поиск в произвольной конечной области.
- § 3. Решение уравнения Лапласа
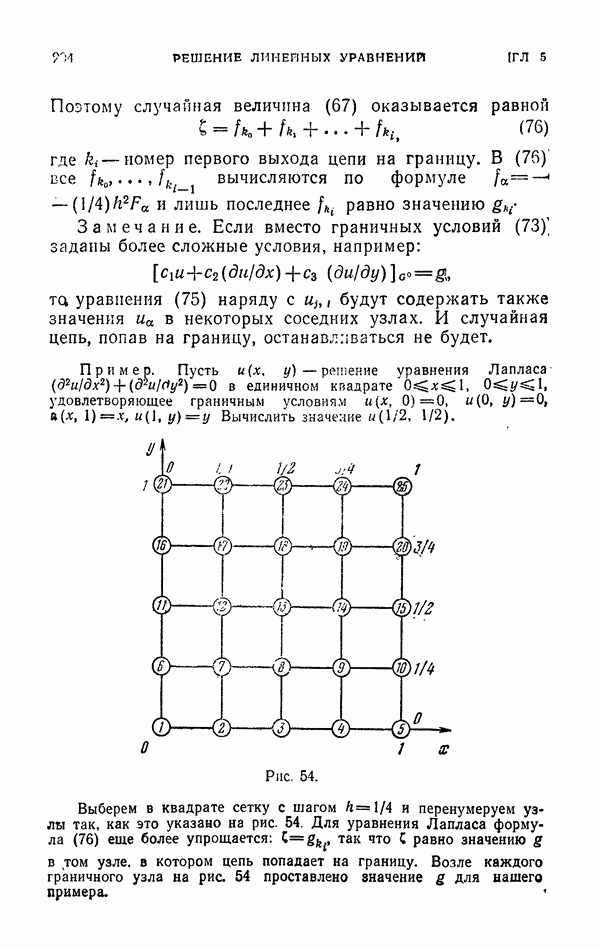
- 3.2. Решение задачи Дирихле для уравнения Лапласа.
- § 4. Вычисление винеровских интегралов
- 4.2. Приближенное построение броуновских траекторий.
- 4.3. Замена континуального интеграла многомерным.
- ПРИЛОЖЕНИЯ
- ЛИТЕРАТУРА