| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 8. РЯДЫ ФУРЬЕ
Изучаемая в настоящей главе проблема разложения функции в ряд Фурье является обобщением и развитием идеи разложения вектора по базису.
Из линейной алгебры известно, что если в линейном пространстве конечной размерности выбрать некоторый базис, то любой вектор этого пространства может быть разложен по базису, т. е. представлен в виде линейной комбинации базисных векторов. Гораздо более сложными являются вопросы о выборе базиса и о разложении по базису для случая бесконечномерного пространства. В настоящей главе эти вопросы изучаются для случая евклидовых бесконечномерных пространств и для базисов специального типа (ортонормированных базисов).
Особенно подробно изучается базис, образованный в пространстве всех кусочно непрерывных на некотором сегменте функций так называемой тригонометрической системой.
§ 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
1. Ортонормированные системы.
Будем рассматривать произвольное евклидово пространство бесконечной размерности. Напомним, что линейное пространство  называется евклидовым, если выполнены два условия:
называется евклидовым, если выполнены два условия:
1) известно правило, посредством которого любым двум элементам  пространства
пространства  ставится в соответствие число, называемое скалярным произведением этих элементов и обозначаемое символом
ставится в соответствие число, называемое скалярным произведением этих элементов и обозначаемое символом 
2) указанное правило удовлетворяет следующим четырем аксиомам:
 (переместительное свойство);
(переместительное свойство);
 (распределительное свойство);
(распределительное свойство);
 для любого вещественного I;
для любого вещественного I;
 если
если  — ненулевой элемент;
— ненулевой элемент;
 если
если  — нулевой элемент.
— нулевой элемент.
Напомним, далее, что линейное (и, в частности, евклидово) яространство называется бесконечномерным, если в этом пространстве найдется любое наперед взятое число линейно независимых элементов.
Приведем классический пример евклидова пространства бесконечной размерности.
Напомним, что функция  называется кусочно непрерывной на сегменте
называется кусочно непрерывной на сегменте  если она непрерывна всюду на этом сегменте, за исключением конечного числа точек, в каждой из которых она имеет разрыв первого рода
если она непрерывна всюду на этом сегменте, за исключением конечного числа точек, в каждой из которых она имеет разрыв первого рода 
Для линейного пространства всех кусочно непрерывных на сегменте  функций естественно ввести скалярное произведение любых двух функций
функций естественно ввести скалярное произведение любых двух функций  определив его равенством
определив его равенством

Легко проверяется, что при таком определении справедливы первые три аксиомы скалярного произведения. Однако для тогог чтобы оказалась справедливой и четвертая аксиома, приходится принять дополнительную договоренность о том, чтобы значение кусочно непрерывной функции  в каждой ее точке разрыва х,-равнялось полусумме правого и левого ее пределов в этой точке:
в каждой ее точке разрыва х,-равнялось полусумме правого и левого ее пределов в этой точке:

В самом деле, во-первых, всегда  Далее, заметим, что так как
Далее, заметим, что так как  кусочно непрерывна на
кусочно непрерывна на  та весь сегмент
та весь сегмент  распадается на конечное число сегментов
распадается на конечное число сегментов  на каждом из которых функция
на каждом из которых функция  непрерывна при условии, что в качестве значений
непрерывна при условии, что в качестве значений  на концах соответствующего сегмента
на концах соответствующего сегмента  берутся
берутся  Из равенства
Из равенства  вытекает, что для каждого сегмента
вытекает, что для каждого сегмента  справедливо равенство
справедливо равенство 
Из этого равенства и из непрерывности  на сегменте
на сегменте  вытекает, что на этом сегменте
вытекает, что на этом сегменте  . В частности,
. В частности,  равны нулю. Так как эти рассуждения справедливы для любого сегмента
равны нулю. Так как эти рассуждения справедливы для любого сегмента  т. е. для всех
т. е. для всех  то правый и левый пределы в любой точке
то правый и левый пределы в любой точке  равны нулю, а отсюда в силу соотношения (8.2) и само значение
равны нулю, а отсюда в силу соотношения (8.2) и само значение  в любой точке
в любой точке  равно. Итак, функция
равно. Итак, функция  равна нулю во всех точках сегмента
равна нулю во всех точках сегмента  , т. е. является нулевым элементом линейного пространства всех кусочно непрерывных на сегменте
, т. е. является нулевым элементом линейного пространства всех кусочно непрерывных на сегменте  функций.
функций.
Тем самым мы доказали, что пространство всех кусочно непрерывных на сегменте  функций с условием (8.2) в каждой точке разрыва и со скалярным произведением, определяемым соотношением (8.1), является евклидовым пространством.
функций с условием (8.2) в каждой точке разрыва и со скалярным произведением, определяемым соотношением (8.1), является евклидовым пространством.
Это евклидово пространство мы в дальнейшем будем обозначать символом 
Напомним теперь два общих свойства любого евклидова пространства, которыми, естественно, будет обладать и пространство 
1) во всяком евклидовом пространстве для любых двух элементов  справедливо неравенство
справедливо неравенство

называемое неравенством Коши — Буняковского;
2) во всяком евклидовом пространстве для любого элемента  этого пространства можно ввести понятие нормы этого элемента, определив ее как число, обозначаемое символом
этого пространства можно ввести понятие нормы этого элемента, определив ее как число, обозначаемое символом  и определяемое равенством
и определяемое равенством

так что будут справедливы следующие три свойства:
 причем
причем  лишь тогда, когда
лишь тогда, когда  — нулевой элемент,
— нулевой элемент,
 для любого элемента
для любого элемента  и любого вещественного X;
и любого вещественного X;

для любых двух элементов  (это неравенство называется неравенством треугольника).
(это неравенство называется неравенством треугольника).
В самом деле, справедливость свойства Г сразу же вытекает из (8.4) и из аксиомы 4° скалярного произведения.
Для обоснования свойства 2° заметим, что в силу (8.4) и аксиом скалярного произведения

Наконец, справедливость свойства 3° вытекает из (8.4), из аксиом скалярного произведения и из неравенства Коши—Буняковского (8.3). Действительно,

В частности, во введенном выше евклидовом пространстве  всех кусочно непрерывных на сегменте
всех кусочно непрерывных на сегменте  функций норма (8.4) любого элемента
функций норма (8.4) любого элемента  определяется равенством
определяется равенством

а неравенства Коши—Буняковского (8.3) и треугольника (8.5) принимают вид

Введем теперь в произвольном бесконечномерном евклидовом пространстве  понятия ортогональных элементов и ортонормированной системы элементов.
понятия ортогональных элементов и ортонормированной системы элементов.
Определение 1. Два элемента  евклидова пространства называются ортогональными, если скалярное произведение
евклидова пространства называются ортогональными, если скалярное произведение  этих элементов равно нулю.
этих элементов равно нулю.
Рассмотрим в произвольном бесконечномерном евклидовом пространстве  некоторую последовательность элементов.
некоторую последовательность элементов.

Определение 2. Последовательность (8.9) называется ортонормированной системой, если входящие в эту последовательность элементы попарно ортогональны и имеют норму, равную единице.
Классическим примером ортонормированной системы в пространстве  всех кусочно непрерывных на сегменте
всех кусочно непрерывных на сегменте  функций является так называемая тригонометрическая система
функций является так называемая тригонометрическая система

Читатель легко проверит, что все функции (8.10) попарно ортогональны (в смысле скалярного произведения (8.1), взятого
при  и что норма каждой из этих функций (определяемая равенством (8.6) при
и что норма каждой из этих функций (определяемая равенством (8.6) при  равна единице.
равна единице.
В математике и ее приложениях часто встречаются различные ортонормированные (на соответствующих множествах) системы функций. Приведем некоторые примеры таких систем.
Примеры. 1°. Многочлены, определяемые равенством

принято называть полиномами Лежандра.
Нетрудно убедиться, что образованные с помощью многочленов (8.11) функции

образуют ортонормированную (на сегменте  систему функций.
систему функций.
2°. Многочлены, определяемые равенствами  при
при  называются полиномами Чебышева. Среди всех многочленов
называются полиномами Чебышева. Среди всех многочленов  степени с коэффициентом при
степени с коэффициентом при  равным единице, полином Чебышева
равным единице, полином Чебышева  имеет наименьший на сегменте
имеет наименьший на сегменте  максимум модуля. Можно доказать, что полученные с помощью полиномов Чебышева функции
максимум модуля. Можно доказать, что полученные с помощью полиномов Чебышева функции

образуют ортонормированную на сегменте  систему.
систему.
3°. В теории вероятностей часто применяется система Радемахера

где 
Легко проверяется, что эта система ортонормирована на сегменте 
4°. В ряде исследований по теории функций находит применение система Хаара, являющаяся ортонормированной на сегменте  Элементы этой системы определяются для всех
Элементы этой системы определяются для всех  и для всех
и для всех  принимающих значения
принимающих значения  Они имеют вид
Они имеют вид

Каждая функция Хаара представляет собой ступеньку такого же вида, как функция  сегменте
сегменте  Для каждого фиксированного номера
Для каждого фиксированного номера  при увеличении значения
при увеличении значения  эта ступенька сдвигается вправо. Всюду вне соответствующей ступеньки каждая функция Хаара тождественно равна нулю.
эта ступенька сдвигается вправо. Всюду вне соответствующей ступеньки каждая функция Хаара тождественно равна нулю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
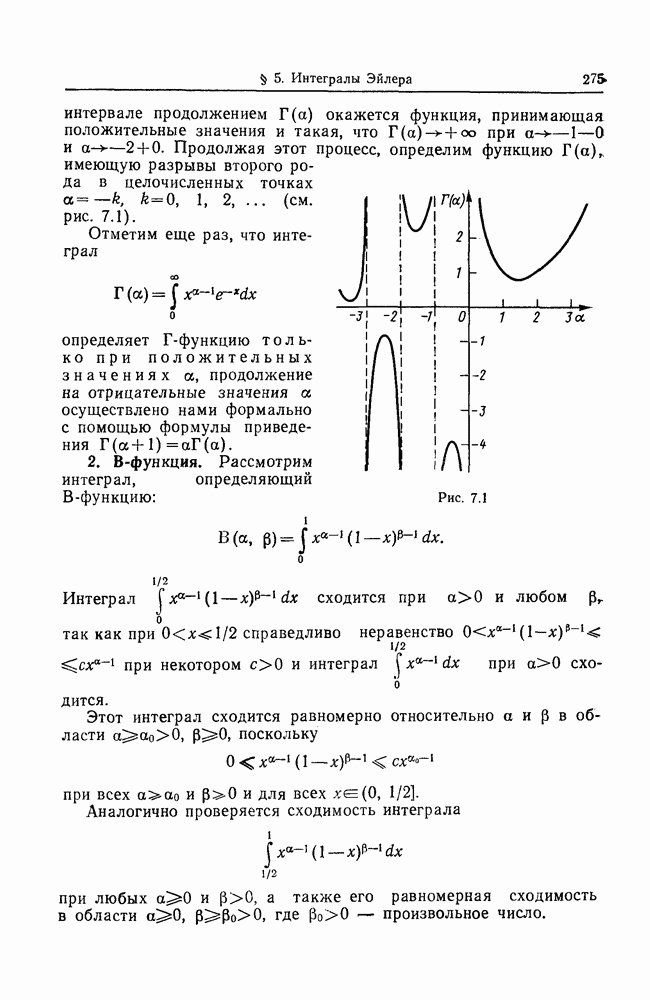
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ