| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. Критерий Коши равномерной сходимости последовательности (ряда).
Справедливы следующие фундаментальные теоремы.
Теорема 2.1. Для того чтобы функциональная последовательность  равномерно на множестве
равномерно на множестве  сходилась к некоторой предельной функции, необходимо и достаточно, чтобы для произвольного
сходилась к некоторой предельной функции, необходимо и достаточно, чтобы для произвольного  нашелся номер
нашелся номер  гарантирующий справедливость неравенства
гарантирующий справедливость неравенства

для всех номеров  удовлетворяющих условию
удовлетворяющих условию  всех натуральных
всех натуральных  и всех точек х из множества
и всех точек х из множества 
Теорема 2.2. Для того чтобы функциональный ряд

равномерно на множестве  сходился к некоторой сумме, необходимо и достаточно, чтобы для произвольного
сходился к некоторой сумме, необходимо и достаточно, чтобы для произвольного  нашелся номер
нашелся номер  гарантирующий справедливость неравенства
гарантирующий справедливость неравенства

для всех номеров  удовлетворяющих условию всех натуральных
удовлетворяющих условию всех натуральных  и всех точек х множества
и всех точек х множества 
Достаточно провести доказательство только теоремы 2.1, так как теорема 2.2 является следствием теоремы 2.1 (заметим, что в левой части (2.9) под знаком модуля стоит разность  частичных сумм с номерами
частичных сумм с номерами  функционального ряда
функционального ряда 
Доказательство теоремы 2.1. Необходимость. Предположим, что последовательность  сходится равномерно на множестве
сходится равномерно на множестве  к предельной функции
к предельной функции  Тогда, фиксировав произвольное
Тогда, фиксировав произвольное  мы найдем для него номер
мы найдем для него номер  такой, что неравенство
такой, что неравенство

будет справедливо для всех номеров  удовлетворяющих условию
удовлетворяющих условию  и для всех точек х множества
и для всех точек х множества 
Если  — любое натуральное число, то при
— любое натуральное число, то при  номер
номер  тем более будет удовлетворять условию
тем более будет удовлетворять условию  а поэтому для всех номеров
а поэтому для всех номеров  удовлетворяющих условию
удовлетворяющих условию  всех натуральных
всех натуральных  и всех точек х множества
и всех точек х множества  тем более будет справедливо неравенство
тем более будет справедливо неравенство

Так как модуль суммы двух величин не превосходит суммы их модулей, то в силу (2.10) и (2.11) получим, что

(для всех номеров  удовлетворяющих условию
удовлетворяющих условию  всех натуральных
всех натуральных  и всех х из множества
и всех х из множества  Необходимость доказана.
Необходимость доказана.
Достаточность. Предположим, что для произвольного  существует номер
существует номер  такой, что неравенство (2.7) справедливо для всех номеров
такой, что неравенство (2.7) справедливо для всех номеров  удовлетворяющих условию
удовлетворяющих условию  всех натуральных
всех натуральных  и всех точек х множества
и всех точек х множества 
Из неравенства (2.7) и из критерия Коши сходимости числовой последовательности (см. п. 3 § 3 гл. 3 ч. 1) вытекает сходимость последовательности  в каждой точке х множества
в каждой точке х множества  и существование определенной в каждой точке х множества
и существование определенной в каждой точке х множества  предельной функции
предельной функции 
Фиксировав произвольный номер  удовлетворяющий условию
удовлетворяющий условию  и произвольную точку х множества
и произвольную точку х множества  перейдем в неравенстве (2.7) к пределу при
перейдем в неравенстве (2.7) к пределу при  Используя теорему 3.13 п. 4 § 1 гл. 3 ч. 1, мы получим, что для произвольного номера
Используя теорему 3.13 п. 4 § 1 гл. 3 ч. 1, мы получим, что для произвольного номера  [удовлетворяющего условию
[удовлетворяющего условию  и произвольной точки х множества
и произвольной точки х множества  справедливо неравенство
справедливо неравенство

Это и доказывает, что последовательность  сходится к предельной функции
сходится к предельной функции  равномерно на множестве
равномерно на множестве  Достаточность доказана.
Достаточность доказана.
Наличие критерия Коши не снимает вопроса об установлении удобных для приложений достаточных признаков равномерной сходимости функциональных последовательностей и рядов, к которому мы сейчас и переходим.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
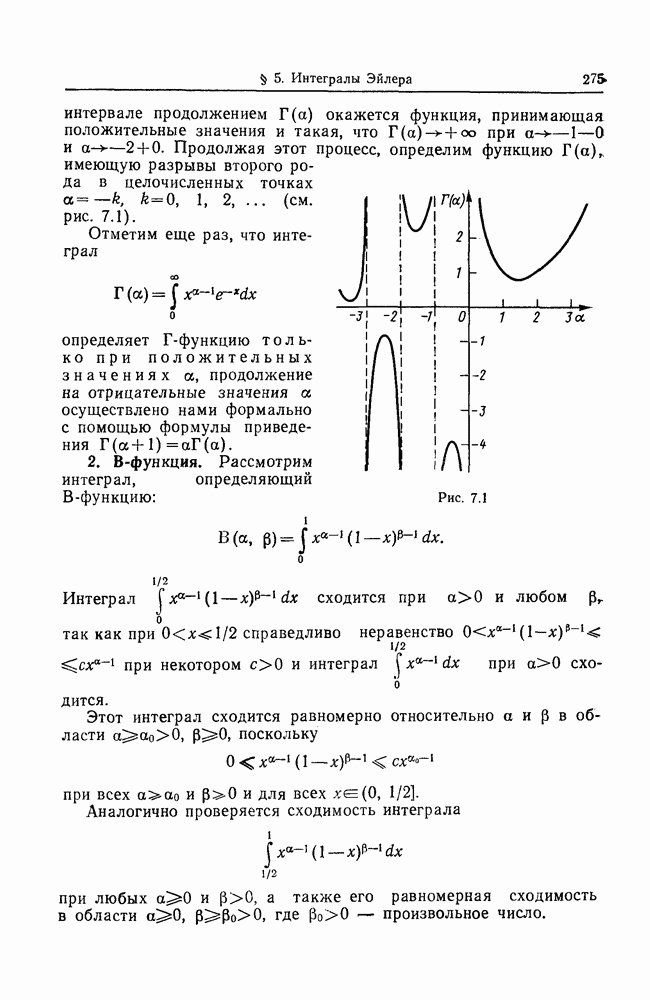
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
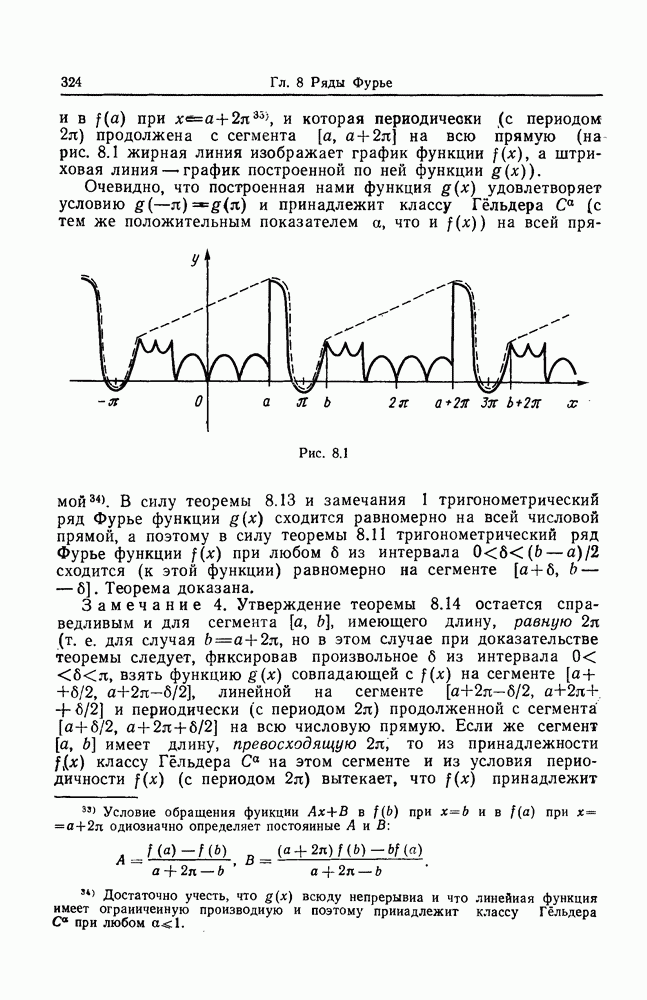
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ