| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
В этой главе будет рассмотрен вопрос об интегрировании функций, заданных на поверхностях в трехмерном евклидовом пространстве  а также исследуется вопрос о понятии поверхности и понятии площади поверхности.
а также исследуется вопрос о понятии поверхности и понятии площади поверхности.
§ 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
1. Понятие поверхности.
Определение 1. Отображение  области
области  на плоскости на множество
на плоскости на множество  трехмерного пространства называется гомеомор
трехмерного пространства называется гомеомор  если это отображение осуществляет взаимно однозначное соответствие между точками
если это отображение осуществляет взаимно однозначное соответствие между точками  при котором каждая фундаментальная последовательность точек
при котором каждая фундаментальная последовательность точек  переходит в фундаментальную последовательность точек
переходит в фундаментальную последовательность точек  и, наоборот, каждая фундаментальная последовательность точек
и, наоборот, каждая фундаментальная последовательность точек  является образом фундаментальной последовательности точек
является образом фундаментальной последовательности точек 
Определение 2. Отображение  области
области  на
на  называется локально гомеоморфным, если у каждой точки
называется локально гомеоморфным, если у каждой точки  есть окрестность, которая гомеоморфно отображается на свой образ.
есть окрестность, которая гомеоморфно отображается на свой образ.
Определение 3. Область  на плоскости Т называется элементарной, если эта область является образом открытого круга D при гомеоморфном отображении этого круга на плоскость Т.
на плоскости Т называется элементарной, если эта область является образом открытого круга D при гомеоморфном отображении этого круга на плоскость Т.
Определение 4. Связная область  на плоскости Т называется простой, если любая точка
на плоскости Т называется простой, если любая точка  имеет окрестность, являющуюся элементарной областью.
имеет окрестность, являющуюся элементарной областью.
Определение 5. Множество точек Ф пространства называется поверхностью, если это множество является образом простой плоской области  при локально гомеоморфном отображении
при локально гомеоморфном отображении  области
области  в пространство
в пространство 
В дальнейшем мы договоримся называть окрестностью точки М поверхности Ф подмножество точек Ф, принадлежащее окрестности точки М в 
Пример. Пусть  — простая область на плоскости
— простая область на плоскости  (например, круг),
(например, круг),  — координаты точек
— координаты точек  — непрерывная в
— непрерывная в  функция,
функция,  — график этой функции. Очевидно, отображение
— график этой функции. Очевидно, отображение  области
области  на
на  задаваемое соотношениями
задаваемое соотношениями

является гомеоморфным отображением этой области на множество  а
а  является поверхностью.
является поверхностью.
Пусть на плоскости  задана простая область
задана простая область  и для всех точек этой области определены три функции:
и для всех точек этой области определены три функции:

или, что то же самое, одна векторная функция

где  — вектор с компонентами
— вектор с компонентами  .
.
Будем считать выполненными следующие два требования А:
1) функции (5.1) имеют в области  непрерывные частные производные первого порядка по переменным и и и;
непрерывные частные производные первого порядка по переменным и и и;
2) всюду в области  матрица
матрица

имеет ранг, равный двум.
Утверждение. При выполнении этих двух требований А множество Ф точек, определяемых уравнениями (5.1), представляет собой поверхность, т. е. является образом плоской области  при локально гомеоморфном отображении
при локально гомеоморфном отображении  в
в 
Пусть  — любая точка
— любая точка  Ясно, что малая окрестность этой точки отображается в малую окрестность точки
Ясно, что малая окрестность этой точки отображается в малую окрестность точки  где
где  (для этого достаточно, чтобы функции (5.1) являлись непрерывными в
(для этого достаточно, чтобы функции (5.1) являлись непрерывными в  что в нашем случае заведомо выполняется).
что в нашем случае заведомо выполняется).
Ясно также, что если  — фундаментальная последовательность точек в малой окрестности точки
— фундаментальная последовательность точек в малой окрестности точки  то последовательность образов этих точек
то последовательность образов этих точек  где
где  также является фундаментальной в Ф. Это сразу вытекает из непрерывности функций (5.1); например, разность
также является фундаментальной в Ф. Это сразу вытекает из непрерывности функций (5.1); например, разность  может быть сделана меньше произвольного числа
может быть сделана меньше произвольного числа  при
при 
Остается доказать, что при отображении, определяемом уравнениями (5.1), каждой точке множества Ф из достаточно малой окрестности точки  отвечает определенная точка области
отвечает определенная точка области  из малой окрестности точки
из малой окрестности точки  причем любой фундаментальной последовательности точек
причем любой фундаментальной последовательности точек  из указанной окрестности точки
из указанной окрестности точки  отвечает фундаментальная последовательность
отвечает фундаментальная последовательность  точек
точек 
Так как в каждой точке  ранг матрицы (5.2) равен двум, то в этой точке
ранг матрицы (5.2) равен двум, то в этой точке  отличен от нуля хотя бы один
отличен от нуля хотя бы один  второго порядка матрицы (5.2).
второго порядка матрицы (5.2).
Пусть это будет минор

Объединяя это условие с первым из двух требований А, придем к выводу, что для системы

в окрестности точки  выполнены все условия теоремы Юнга — Ковалевского (см. § 2 гл. 13 ч. 1). Поэтому система (5.3) имеет в окрестности точки
выполнены все условия теоремы Юнга — Ковалевского (см. § 2 гл. 13 ч. 1). Поэтому система (5.3) имеет в окрестности точки  единственное непрерывное и дифференцируемое решение
единственное непрерывное и дифференцируемое решение

Это означает, что существует гомеоморфное отображение малой окрестности точки  на малую окрестность точки
на малую окрестность точки  плоскости
плоскости  (В одну сторону это отображение задается непрерывными функциями (5.4), а в другую сторону — первыми двумя соотношениями (5.1), в которых функции
(В одну сторону это отображение задается непрерывными функциями (5.4), а в другую сторону — первыми двумя соотношениями (5.1), в которых функции  также непрерывны; непрерывность и тех и других функций обеспечивает перевод фундаментальной последовательности в окрестности одной из точек
также непрерывны; непрерывность и тех и других функций обеспечивает перевод фундаментальной последовательности в окрестности одной из точек  или
или  в фундаментальную последовательность в окрестности другой из этих точек.)
в фундаментальную последовательность в окрестности другой из этих точек.)
Подставляя функции (5.4) в третью функцию (5.1), получим; непрерывную в окрестности точки  функцию
функцию

Эта функция осуществляет гомеоморфное отображение малой окрестности точки  плоскости
плоскости  на малую окрестность точки
на малую окрестность точки  Можно сказать, что (5.5) проектирует Ф в малой окрестности точки
Можно сказать, что (5.5) проектирует Ф в малой окрестности точки  на плоскость
на плоскость 
Так как суперпозиция гомеоморфных отображений представляет собой снова гомеоморфное отображение, то гомеоморфно и отображение малой окрестности точки  на малую окрестность точки
на малую окрестность точки 
Таким образом, множество Ф точек, определяемых уравнения  при выполнении этих требований А представляет собой поверхность.
при выполнении этих требований А представляет собой поверхность.
Замечание 1. Поверхность Ф, определяемую уравнениями (5.1), при выполнении первого из двух требований А принято называть гладкой, а при выполнении второго из требований А — не имеющей особых точек.
Итак, можно сказать, что поверхность Ф, определяемая уравнениями (5.1), при выполнении этих требований А, является гладкой и не имеет особых точек.
Замечание 2. Попутно мы установили, что гладкая без особых точек поверхность в достаточно малой окрестности каждой из своих точек однозначно проектируется хотя бы на одну из трех координатных плоскостей.
Рассмотрим поверхность Ф, определяемую уравнениями (5.1), для которых выполнены два требования А.
Записав уравнения (5.1) в векторном виде (5.1), выясним геометрический смысл векторной функции  Если фиксировать некоторое значение
Если фиксировать некоторое значение  из области
из области  то уравнение
то уравнение  будет определять кривую на поверхности Ф, называемую координатной линией, а вектор -(и,
будет определять кривую на поверхности Ф, называемую координатной линией, а вектор -(и,  будет являться касательным к этой линии. Аналогично при
будет являться касательным к этой линии. Аналогично при  уравнение
уравнение  будет определять другую координатную линию, а вектор
будет определять другую координатную линию, а вектор  будет касательным к этой линии. Через точку
будет касательным к этой линии. Через точку  где
где  будут проходить обе указанные линии.
будут проходить обе указанные линии.
Второе условие требований А, говорящее о том, что ранг матрицы (5.2) равен двум, т. е. условие отсутствия особых точек, означает, что векторы  компоненты которых составляют строки матрицы (5.2), являются линейно независимыми, т. е. неколлинеарными. Это означает, что эти два вектора определяют плоскость, которая является касательной плоскостью к поверхности Ф в точке
компоненты которых составляют строки матрицы (5.2), являются линейно независимыми, т. е. неколлинеарными. Это означает, что эти два вектора определяют плоскость, которая является касательной плоскостью к поверхности Ф в точке  Нормальный вектор этой касательной плоскости называется вектором нормали (или нормалью) к поверхности Ф в точке
Нормальный вектор этой касательной плоскости называется вектором нормали (или нормалью) к поверхности Ф в точке  Этот вектор -
Этот вектор -  может быть определен как векторное произведение векторов -
может быть определен как векторное произведение векторов -  Таким образом, вектор
Таким образом, вектор

представляет собой вектор единичной нормали к поверхности Ф. В силу требований, наложенных на функции (5.1), этот вектор непрерывен по и и  в некоторой окрестности произвольной
в некоторой окрестности произвольной
точки поверхности. В этом случае говорят, что в окрестности любой точки гладкой поверхности без особых точек существует непрерывное векторное поле нормалей.
В целом на всей поверхности такого непрерывного поля нормалей может и не существовать.
Пример. Лист Мёбиуса. Если склеить прямоугольник  . А так, чтобы А совпала с В, а В совпала с А, получится поверхность, называемая листом Мёбиуса. При обходе по листу Мёбиуса нормаль меняет направление на противоположное (см. рис. 5.1).
. А так, чтобы А совпала с В, а В совпала с А, получится поверхность, называемая листом Мёбиуса. При обходе по листу Мёбиуса нормаль меняет направление на противоположное (см. рис. 5.1).
В дальнейшем будем рассматривать только такие поверхности Ф, на которых в целом существует непрерывное поле нормалей. Такие поверхности принято называть двусторонними.
Поверхность Ф называется полной, если любая фундаментальная последовательность точек этой поверхности сходится к точке этой поверхности.

Рис. 5.1
Поверхность Ф называется ограниченной, если существует трехмерный шар, содержащий все точки этой поверхности.
Плоскость, сфера, эллипсоид, однополостный гиперболоид — примеры полных поверхностей. При этом сфера и эллипсоид — ограниченные поверхности. Круг без границы, любое открытое связное множество» на сфере — неполные поверхности.
В дальнейшем мы будем рассматривать поверхность Ф, определяемую уравнениями (5.1) и удовлетворяющую пяти требованиям: она должна быть 1) гладкой, 2) без особых точек, 3) двусторонней, 4) полной и 5) ограниченной.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
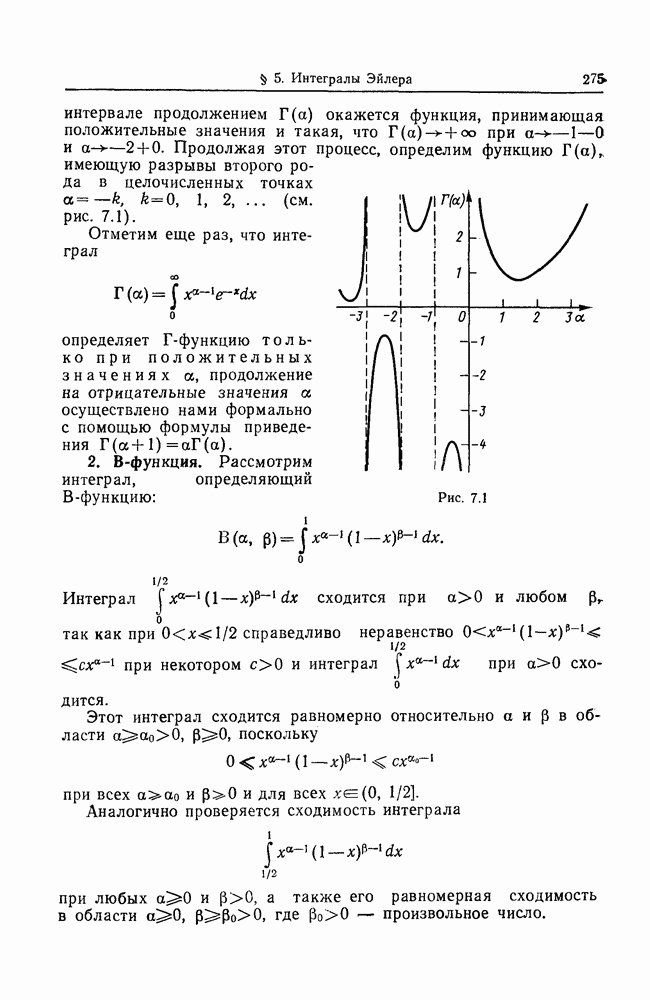
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
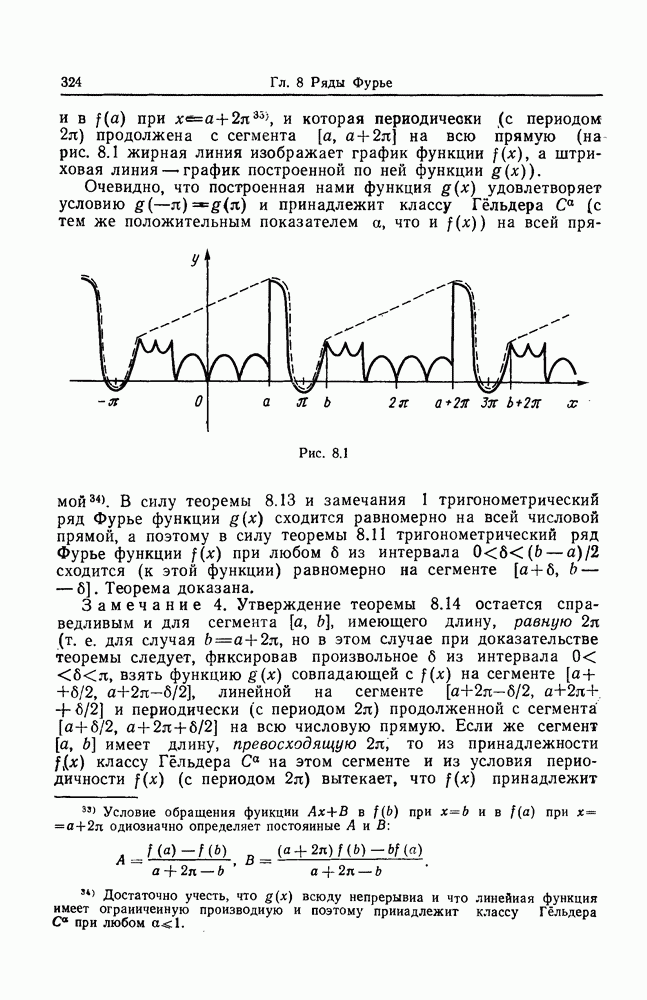
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ