| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
Рассмотрим произвольную точку х пространства  и произвольное множество
и произвольное множество  пространства
пространства  для которого эта точка
для которого эта точка
является предельной. При этом точка х может сама не принадлежать множеству 
Теорема 2.7. Если функциональный ряд

сходится равномерно на множестве  к сумме
к сумме  и у всех членов этого ряда существует в точке х предел
и у всех членов этого ряда существует в точке х предел

то и сумма ряда  имеет в точке х предел, причем
имеет в точке х предел, причем

т. e. символ  предела и символ
предела и символ  суммирования можно переставлять местами (или, как говорят, к пределу можно переходить почленно).
суммирования можно переставлять местами (или, как говорят, к пределу можно переходить почленно).
Доказательство. Сначала докажем сходимость числового ряда  . В силу критерия Коши, примененного к функциональному ряду (2.31), для любого
. В силу критерия Коши, примененного к функциональному ряду (2.31), для любого  найдется номер
найдется номер  такой, что
такой, что

для всех номеров  удовлетворяющих условию
удовлетворяющих условию  всех натуральных
всех натуральных  и всех точек х множества
и всех точек х множества  Считая в неравенстве (2.33) фиксированными номера пира переходя в этом неравенстве к пределу при
Считая в неравенстве (2.33) фиксированными номера пира переходя в этом неравенстве к пределу при  (такой предельный переход можно осуществить по любой последовательности точек множества
(такой предельный переход можно осуществить по любой последовательности точек множества  сходящейся к точке
сходящейся к точке  получим
получим

(для каждого  и каждого натурального
и каждого натурального  ). В силу критерия Коши ряд
). В силу критерия Коши ряд  сходится.
сходится.
Оценим теперь разность

для всех точек х множества  из достаточно малой окрестности точки х. Так как
из достаточно малой окрестности точки х. Так как

для всех точек х множества  то для любого номера
то для любого номера  справедливо тождество
справедливо тождество

из которого получаем неравенство

справедливое для всех точек х множества 
Фиксируем произвольное  Так как ряд
Так как ряд  сходится, а ряд
сходится, а ряд  сходится равномерно на множестве
сходится равномерно на множестве  то для фиксированного
то для фиксированного  найдется номер
найдется номер  такой, что для всех точек х множества
такой, что для всех точек х множества 

Так как предел конечной суммы равен сумме пределов слагаемых, то для фиксированного нами  и выбранного номера
и выбранного номера  можно указать
можно указать  такое, что
такое, что

для всех точек х множества  удовлетворяющих условию
удовлетворяющих условию  Из (2.34) — (2.36) следует, что для всех таких
Из (2.34) — (2.36) следует, что для всех таких 

Это доказывает существование предела  в точке х, а следовательно, и справедливость равенства (2.32). Теорема доказана.
в точке х, а следовательно, и справедливость равенства (2.32). Теорема доказана.
В терминах функциональных последовательностей теорема 2.7 звучит так:
Теорема 2.7. Если функциональная последовательность  сходится равномерно на множестве
сходится равномерно на множестве  к предельной функции
к предельной функции  и все элементы этой последовательности имеют предел в точке х, то и предельная функция
и все элементы этой последовательности имеют предел в точке х, то и предельная функция  имеет предел
имеет предел  точке х, причем
точке х, причем

т. e. символ  предела последовательности и символ
предела последовательности и символ  предела функции можно переставлять местами (или, как говорят, к пределу при
предела функции можно переставлять местами (или, как говорят, к пределу при  можно переходить почленно).
можно переходить почленно).
Следствие 1 из теоремы 2.7. Если в условиях теоремы 2.7 дополнительно потребовать, чтобы точка х принадлежала множеству  и чтобы все члены
и чтобы все члены  функционального ряда (2.31) были непрерывны в точке х, то и сумма
функционального ряда (2.31) были непрерывны в точке х, то и сумма  этого ряда будет непрерывна в точке х.
этого ряда будет непрерывна в точке х.
В самом деле, в этом случае  и равенство (2.32) принимает вид
и равенство (2.32) принимает вид

а это и означает непрерывность суммы  в точке х.
в точке х.
Следствие 2 из теоремы 2.7. Если все члены функционального ряда (функциональной последовательности) непрерывны на плотном в себе множестве  и если этот функциональный ряд (эта функциональная последовательность) сходится равномерно на множестве
и если этот функциональный ряд (эта функциональная последовательность) сходится равномерно на множестве  то и сумма указанного ряда (предельная функция указанной последовательности) непрерывна на множестве
то и сумма указанного ряда (предельная функция указанной последовательности) непрерывна на множестве 
Для доказательства достаточно применить предыдущее следствие к каждой точке х множества 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
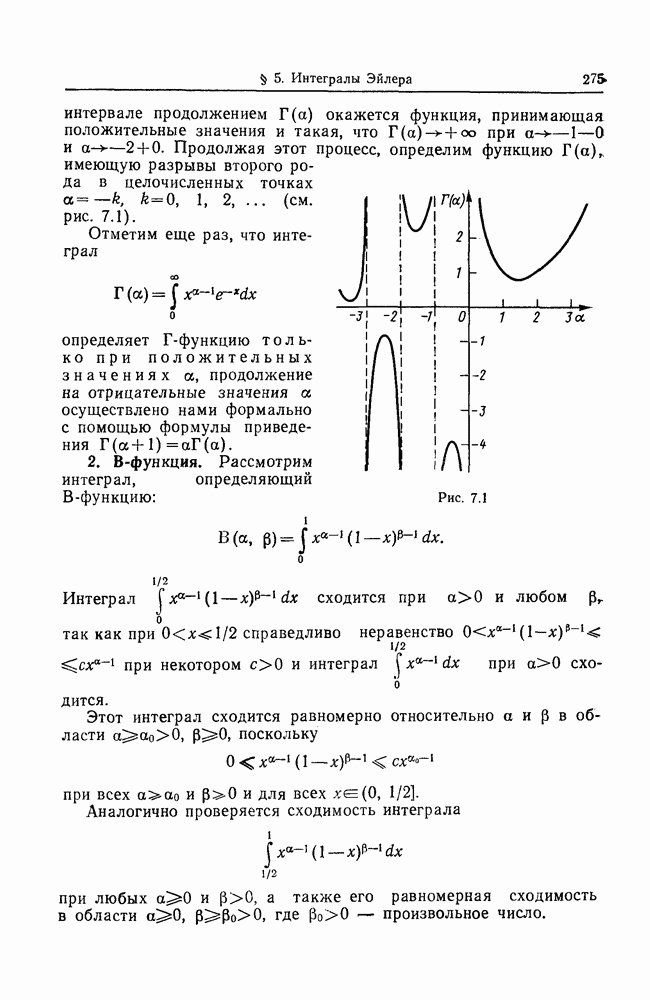
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
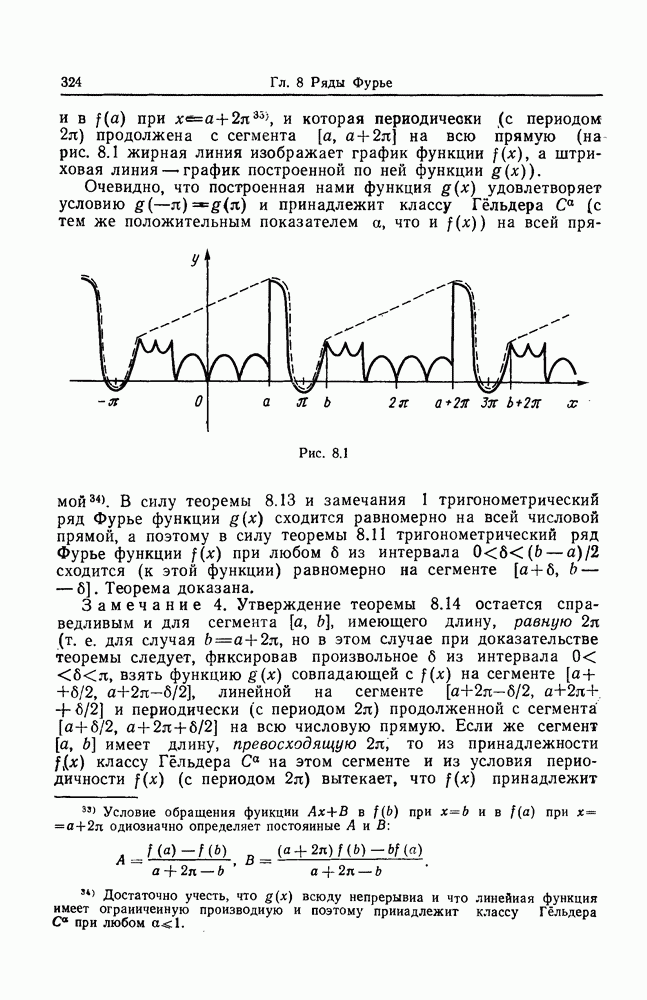
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ